Chương 7: Lý Thuyết Trò Chơi và Kinh Tế Học Hợp Tác môn Kinh tế vi mô 1 | Học viện Tài chính

Chương 7 LÝ THUYẾT TRÒ CHƠI
VÀ KINH TẾ HỌC CỦA SỰ HỢP TÁC
MỤC ĐÍCH VÀ YÊU CẦU HỌC TẬP
Trong chương này, chúng tôi sẽ giới thiệu các thành tố cơ bản của một mô hình lý
thuyết trò chơi, bao gồm các đối thủ, chiến lược, lợi ích, thứ tự các bước đi, và thông tin.
Với những thành tố này, một trò chơi có thể được trình bày dưới dạng ma trận lợi ích hay
dưới dạng sơ đồ hình cây. Các cách giải trò chơi cơ bản như loại bỏ các chiến lược bị lấn
át, sử dụng khái niệm cân bằng Nash, chiến lược hỗn hợp hay suy luận ngược cũng đã
được giới thiệu thông qua các ví dụ cụ thể.
Thông qua một số ví dụ minh họa cho lý thuyết trò chơi, giúp cho sinh viên hiểu
được tại sao những người tham gia trò chơi không thích hợp tác với nhau cho dù hợp tác
là có lợi cho cả hai bên.
Mặc dù các cách giải một trò chơi là rất lô-gíc và hữu ích trong việc giải thích, dự
đoán các hiện tượng kinh tế - xã hội, nhưng đó không phải là những lời giải hoàn hảo cho
các tình huống trên thực tế. Giữa lý thuyết và thực tế luôn tồn tại một khoảng cách, bởi lý
thuyết luôn đơn giản hóa thực tế. Sinh viên cần nhớ rằng, các lý thuyết luôn dựa trên
những giả định không phải lúc nào cũng đúng trên thực tế.
1. NỘI DUNG CƠ BẢN CỦA LÝ THUYẾT TRÒ CHƠI
Giả định khi nghiên cứu lý thuyết trò chơi:
Đối với lý thuyết trò chơi, việc coi các đối thủ là những người duy lý là giả định
cốt lõi, nhưng lại gây tranh cãi nhiều nhất. Con người không phải là cái máy, và do vậy,
không phải lúc nào cũng tìm được sự lựa chọn tối ưu trong các quyết định của mình, đặc
biệt là trong những tình huống phức tạp.
Tuy nhiên, cho đến nay, phần lớn các nhà kinh tế học, trong đó có các chuyên gia
về lý thuyết trò chơi, vẫn sử dụng giả định này, bởi tính hữu ích của nó. Có một số lý do:
Thứ nhất, nếu các đối thủ trong trò chơi không phải là những người duy lý, sẽ rất
khó để mô hình hóa, giải thích và dự đoán các hiện tượng kinh tế xã hội (các kết cục của
trò chơi) trên thực tế, đặc biệt là việc giải thích, dự báo về sự tiến hóa của xã hội. Làm thế 1
nào chúng ta có thể giải thích được sự tiến bộ của xã hội loài người, trong khi các chủ thể
kinh tế đều hành động không duy lý ? Ngược lại, với giả định về tính duy lý của các đối
thủ trong trò chơi, lý thuyết trò chơi vẫn có thể giải thích, dự báo được các trạng thái kinh
tế xã hội mang tính trì trệ (các kết cục tồi – cân bằng tồi), chẳng hạn như trong trò chơi
Nghịch cảnh của Người tù.
Thứ hai, mặc dù trên thực tế không phải lúc nào con người cũng đưa ra được
những quyết định hợp lý, nhưng về mặt lý thuyết, các quyết định không hợp lý này có thể
gán cho việc thiếu thông tin cần thiết, chứ không nhất thiết phải là do các chủ thể không duy lý.
Thứ ba, trong dài hạn, khi các thông tin là đầy đủ và con người có thể sửa sai đối
với các quyết định của mình, giả định về tính duy lý lại trở nên phù hợp.
Ngày nay, một số chuyên gia về lý thuyết trò chơi đã từ bỏ giả định về tính duy lý
và xây dựng một lý thuyết trò chơi mới dựa trên những giả định khác về hành vi của các
đối thủ và được gọi là lý thuyết trò chơi hành vi (behavioral game theory). Tuy nhiên,
tính hữu ích của cách tiếp cận này còn chờ thực tế kiểm định.
1.1. Sự ra đời của lý thuyết trò chơi
Điểm khác biệt giữa các mô hình độc quyền tập đoàn với mô hình độc quyền
thuần túy hay cạnh tranh hoàn hảo nằm ở chỗ, trong mô hình độc quyền tập đoàn các
doanh nghiệp độc quyền, khi đưa ra quyết định của mình, phải tính tới hành vi của các
doanh nghiệp độc quyền khác.
Tình huống mà trong đó quyết định tối ưu của một đối thủ phụ thuộc vào hành vi
của các đối thủ khác được gọi là tình huống chiến lược (strategic situation). Lý thuyết trò
chơi nghiên cứu những tình huống như vậy.
Mặc dù các tình huống chiến lược đã được phân tích lần đầu tiên trong nghiên cứu
của Cournot (1838) - nhà triết học và toán học người Pháp sống ở thế kỷ XIX, nhưng chỉ
từ thế kỷ XX, sau khi lý thuyết trò chơi ra đời, người ta mới tìm được những lời giải có
tính tổng quát cao cho các tình huống loại này. Nói cách khác, sự ra đời của lý thuyết trò
chơi đã đem đến những hiểu biết sâu sắc và mang tính hệ thống về các tương tác chiến lược.
Năm 1944 “Lý thuyết trò chơi và hành vi kinh tế” được hai nhà kinh tế học là Von
Neuman và Morgéntem hợp tác biên soạn, nghiên cứu quyết sách khi hành vi của các chủ 2
thể ra quyết định phát sinh tác dụng tương hỗ trực tiếp cùng với vấn đề công bằng của
loại quyết sách này. Lý đầu lý thuyết này được vận dụng việc định ra sách lược và lựa
chọn khi chơi cờ, chơi bài và chiến tranh, còn hai Ông lại vận dụng lý thuyết này với tính
chất mở đầu cho lĩnh vực kinh tế. Sau đó người đầu tiên thử nghiệm đưa lý thuyết trò
chơi vào phân tích chính sách kinh tế vĩ mô và vào lý thuyết điều hòa kinh tế quốc tế là
Scitovssky và Harry Johnson. Những bài viết về thuế thương mại và sự trả đũa mà các
Ông viết vào những năm 40, 50 của thế kỷ XX chính là một loạt phân tích mang tính chất
thăm dò từ góc độ lý thuyết trò chơi tương đối sớm tiến hành trong xung đột thương mại
quốc tế. Đến nay đã có ba nhà kinh tế gành được giải thưởng Nobel do đã mở rộng và đi
sâu vận dụng lý thuyết trò chời trong phân tích hành vi kinh tế, đó là: John Harsanyi (ĐH
Cochow Mỹ); John Nash (ĐH Princeton Mỹ) và R. Selten (ĐH Born Đức).
Với sự ra đời của lý thuyết trò chơi, kinh tế học đã nhận được một công cụ phân
tích đa năng. Ngày nay, nhờ tính tổng quát của mình, lý thuyết trò chơi không chỉ được
áp dụng trong phân tích về cấu trúc thị trường, mà còn trong nhiều lĩnh vực khác không
có thị trường. Lý thuyết trò chơi được áp dụng rộng rãi trong những lĩnh vực như chính
trị, quân sự, luật, kiểm toán, hoạch định chính sách kinh tế … Có thể nói, lý thuyết trò
chơi ngày nay được áp dụng trong bất kỳ lĩnh vực nào có sự hiện diện của các tương tác chiến lược.
1.2. Phân loại lý thuyết trò chơi
Xét từ góc độ lợi ích thu được trong trò chơi, vấn đề trò chơi được chia ra thành
trò chơi có tổng bằng 0 (Zero- sum Game) và trò chơi tổng khác 0 (Non - zero- sum Game).
Trò chơi tổng bằng 0 biểu thị tổng lợi ích của tất cả các bên chơi bằng 0 hoặc bằng
một hằng số. Có nghĩa là, một bên được thì bên kia nhất định phải mất. Trong trò chơi
tổng bằng 0, các bên chơi không được hợp tác với nhau.
Trò chơi tổng khác 0 biểu thị tổng lợi ích thu được của các bên chơi dưới các tổ
hợp sách lược khác nhau là biến lượng không xác định, cho nên còn được gọi là trò chơi
tổng biến đổi. Nếu một sự lựa chọn chiến lược nào đó có thể khiến cho tổng lợi ích của
các bên biến đổi lớn, đồng thời lại làm gia tăng tổng lợi ích của các bên, thì có thể xuất
hiện cục diện hợp tác với nhau. Vậy, trong trò chơi tổng khác 0, các bên chơi tồn tại khả
năng hợp tác. Có thể nói, có nhiều vấn đề trong kinh tế đều thuộc về trò chơi có tổng 3
khác 0, điều này có nghĩa là lợi thế của các bên trong quan hệ kinh tế không nhất thiết
phải xung đột với nhau.
Căn cứ vào số lần lặp lại, trò chơi chia thành trò chơi một lần và trò chơi lặp lại.
Trò chơi lựa chọn một lần, xảy ra khi một số người chỉ có cơ hội một lần trong đời
để thú tội hoặc không nhận tội trong tình thế lượng nan của người tù.
Trò chơi lặp lại, là trò chơi được các đối thủ cạnh tranh lặp đi lặp lai và mỗi lần
như vậy các đối thủ có thể nâng cao uy tín và hành vi của mình đồng thời nghiên cứu
hành vi của đối thủ cạnh tranh.
Một chiến lược thường được sử dụng trong trò chơi lặp lại là chiến lược “ăn
miếng trả miếng”, trong đó một người chơi theo cách hợp tác chừng nào mà đối thủ cũng
làm như thế, có thể là tối ưu cho tình thế lưỡng nan của người tù lặp lại.
Căn cứ vào thời điểm đưa ra quyết định, trò chơi có thể chia thành trò chơi
bước đi đồng thời và trò chơi tuần tự.
Trò chơi bước đi đồng thời là trò chơi mà các đổi thủ cạnh tranh đưa ra quyết định
của mình cùng một lúc. Ví dụ mô hình lưỡng quyền Cournot, cả hai hãng chọn mức sản lượng cùng một lúc.
Trò chơi tuần tự là trò chơi mà người chơi sẽ tiến hành tuần từ những bước đi. Mô
hình Stackelberg là một ví dụ về trò chơi tuần tự: một hãng đặt trước sản lượng trước
hãng kia. Trò chơi tuần tự thường dễ phân tích hơn các trò chơi trong đó các người chơi
cùng đi lúc. Trong trò chơi tuần tự, điểm then chốt là phải nghĩ đến hết các hành động có
thể có và các phản ứng hợp lý của mỗi người chơi.
Dựa vào tiêu chí thông tin, các trò chơi được phân loại thành: trò chơi với đầy
đủ thông tin (games with complet information) và trò chơi với thông tin không đầy đủ
(games with incomplete information).
Trong loại trò chơi thứ nhất, các đối thủ biết được hàm lợi ích của nhau, còn trong
loại trò chơi thứ hai, hàm lợi của một hoặc nhiều đối thủ là ẩn số đối với những đối thủ còn lại.
Căn cứ vào hành vi của trò chơi, lý thuyết trò chơi chia thành là trò chơi hợp
tác và trò chơi phi hợp tác. 4
Trò chơi hợp tác (cooperative game), giả định rằng, một nhóm người chơi sẽ tìm
được kết cục tốt nhất cho cả nhóm, khi đó hành vi chơi của các bên tác động lẫn nhau và
tiến đến một hiệp định (thỏa thuận) mang tính ràng buộc.
Trò chơi phi hợp tác (non-cooperative game), dựa trên giả định rằng, mỗi người
chơi chỉ quan tâm đến lợi ích của bản thân mình (mạnh ai người nấy chạy). Giả định này
sẽ dẫn đến hệ quả là không phải lúc nào kết cục mang lại lợi ích tốt nhất cho cả nhóm
(miếng bánh to nhất) cũng đạt được; hành vi chơi của các bên tác động lẫn nhau nhưng
không tiến đến một thỏa thuận mang tính ràng buộc.
Trong trò chơi hợp tác, điều nhấn mạnh ở đây là tính tập thể, sự lựa chọn chiến
lược của các bên chơi sẽ làm cho kết quả của vấn đề trò chơi phát triển theo hướng tiến
đến cân bằng hiệu quả Pareto. Trong trò chơi phi hợp tác, điều nhấn mạnh ở đây là tính
cá nhân, lựa chọn chiến lược của các bên chơi sẽ khiến kết quả của vấn đề trò chơi tiến
đến cân bằng Nash. Có nghĩa là chuẩn tắc hành vi của các bên chơi là lựa chọn chiến
lược tốt nhất cho mình khi đã định chiến lược của các bên khác; còn kết quả trò chơi, đối
với tổng các bên mặc dù không phải là xấu nhất, nhưng xét tổng thể lợi ích thu được của
các bên tham gia chơi lại là tối thiểu.
Ngày nay, phần lớn các nghiên cứu đều xoay quanh lý thuyết trò chơi phi hợp tác.
Bởi vậy, trong chương này, chúng tôi cũng chỉ giới thiệu nhánh lý thuyết trò chơi này.
1.3. Thành tố của trò chơi
Lý thuyết trò chơi khởi nguồn từ cuộc sống. Tuy nhiên, không phải trò chơi nào
cũng là đối tượng nghiên cứu của lý thuyết trò chơi. Những trò chơi như bốc thăm trúng
thưởng không phải là đối tượng nghiên cứu của lý thuyết trò chơi. Lý thuyết trò chơi chỉ
quan tâm đến những tình huống chiến lược, trong đó có sự tương tác giữa các chủ thể trong trò chơi.
Chẳng hạn, trong thể thao, những trò chơi mang tính đối kháng như tennis, bóng
bàn là đối tượng nghiên cứu của lý thuyết trò chơi. Trong lĩnh vực quân sự, lý thuyết trò
chơi quan tâm đến những tình huống chiến lược như chạy đua vũ trang hay giải trừ quân
bị. Trong chính trị, các chuyên gia lý thuyết trò chơi quan tâm đến các cuộc vận động
tranh cử giữa các ứng viên tổng thống hay giữa các đảng phái khác nhau. Trong lĩnh vực
kinh tế, sự cạnh tranh giữa các công ty cũng được coi là một trò chơi và là đối tượng
nghiên cứu của các nhà kinh tế học. 5
Các thành tố cơ bản của một trò chơi
Để mô phỏng các trò chơi thường gặp trong cuộc sống, trước tiên, người ta phải
xác định những thành tố cơ bản của một trò chơi. Thông thường, một mô hình lý thuyết
trò chơi bao gồm các thành tố sau:
Thứ nhất là các đối thủ (players). Các đối thủ là những người đưa ra các quyết
định trong trò chơi. Họ có thể là một cá nhân, một tổ chức hay một quốc gia. Chẳng hạn,
trong thi đấu tennis, bóng bàn hay tranh cử chức vụ tổng thống, đối thủ là những cá nhân.
Trong cạnh tranh kinh tế, các đối thủ có thể là những công ty trên thị trường. Trong chiến
tranh hay chạy đưa vũ trang, các quốc gia là những đối thủ trong trò chơi.
Trong lý thuyết trò chơi tổng quát, số lượng các đối thủ tham gia có thể rất lớn.
Tuy nhiên, trong khuôn khổ của phần này, với mục đích chính là trình bày các nội dung
cơ bản của lý thuyết trò chơi, chúng tôi chỉ giới thiệu các trò chơi có 2 đối thủ. Điều này
sẽ giúp cho người đọc dễ nắm bắt hơn được các ý tưởng cốt lõi của lý thuyết. Hơn nữa,
mặc dù có tính tổng quát cao, nhưng lý thuyết trò chơi thường mang lại hiệu quả trong
những tình huống mà số lượng các đối thủ không lớn. Ngoài ra, việc mở rộng từ trò chơi
có 2 đối thủ sang trò chơi có nhiều đối thủ cũng không quá phức tạp.
Thành tố cơ bản thứ hai của trò chơi là các chiến lược (strategies). Trong lý
thuyết trò chơi thuật ngữ chiến lược được sử dụng để chỉ các lựa chọn của các đối thủ.
Chiến lược có thể là một hành động (action) hay một kế hoạch hành động theo một quy
tắc nào đó. Chẳng hạn, trong tennis hay bóng bàn, chiến lược có thể là đánh về phía trái
tay hay thuận tay của đối thủ. Trong cạnh tranh kinh tế, chiến lược của một công ty có thể
là tăng giá hay giảm giá. Trong lĩnh vực chính trị, chiến lược có thể là các cương lĩnh tranh cử khác nhau.
Mỗi đối thủ trong trò chơi có thể có nhiều chiến lược. Số lượng các chiến lược có
thể là vô số, ví dụ như các công ty có thể lựa chọn vô số các mức giá khác nhau trong
một khoảng nào đó khi tham gia cạnh tranh.
Khi mỗi đối thủ lựa chọn một chiến lược, thì tập hợp các chiến lược này được gọi
là một lát cắt chiến lược (strategic profile). Chẳng hạn, nếu trong trò chơi có 2 đối thủ là
A và B, và mỗi đối thủ có 2 chiến lược được ký hiệu là a1, b2 và b1, b2, thì sẽ có tất cả 4
lát cắt chiến lược, bao gồm: (a1, b1), (a1, b2), (a2, b1), (a2, b2). 6
Thành tố thứ ba của một trò chơi là lợi ích (pay-off). Với mỗi một lát cắt chiến
lược, mỗi đối thủ sẽ nhận được một phần thưởng/phạt và được gọi là lợi ích. Những lợi
ích này có thể là tiền hoặc phi tiền tệ. Các lợi ích có thể được biểu diễn thông qua các con
số hay các hàm lợi ích.
Ngoài 3 thành tố cơ bản nêu trên, các trò chơi còn có các thành tố khác.
Thứ tự các bước đi hay thứ tự hành động của các đối thủ (order of moves). Nếu
các đối thủ hành động cùng một lúc, ta có trò chơi với những bước đi đồng thời (strategic
games hay static games). Ví dụ, sự cạnh tranh giữa các công ty công nghệ trong việc đưa
ra một mẫu điện thoại di động mới vào một thời điểm nào đó (chẳng hạn như tại một
triển lãm công nghệ) là một trò chơi với những bước đi đồng thời. Ngược lại, các trò chơi
như cờ vua, cờ tướng, tú-lơ-khơ được gọi là những trò chơi với những bước đi tuần tự
(sequential games hay dynamic games), trong đó một người đi trước, sau đó đến lượt
người kia đi và cứ tuần tự như vậy.
Một thành tố nữa của trò chơi là thông tin (information). Trong lý thuyết trò chơi
thông tin được hiểu là những điều mà các đối thủ biết khi đưa ra lựa chọn chiến lược của mình.
Trong phần này, chúng tôi sẽ không giới thiệu các trò chơi với thông tin không
đầy đủ, tức là chỉ giới thiệu 2 loại trò chơi với thông tin đầy đủ: trò chơi với các bước đi
đồng thời và trò chơi với các bước đi tuần tự. 1.4. Trình bày trò chơi
Có 2 cách thức thường được sử dụng để trình bày một trò chơi.
Cách thức thứ nhất là trình bày trò chơi dưới dạng ma trận. Hình thức trình bày
này còn được gọi là hình thức trình bày thông thường (normal form) hay hình thức trình
bày dưới dạng chiến lược (strategic form).
Theo cách thức thứ hai, trò chơi có thể được trình bày dưới dạng sơ đồ hình cây (extensive form).
Để hiểu rõ các hình thức trình bày một trò chơi, chúng ta cùng xem xét một ví dụ
về trò chơi, trong đó có 2 đối thủ A và B và mỗi đối thủ có 2 chiến lược, tương ứng là (a1, a2) và (b1, b2). 7
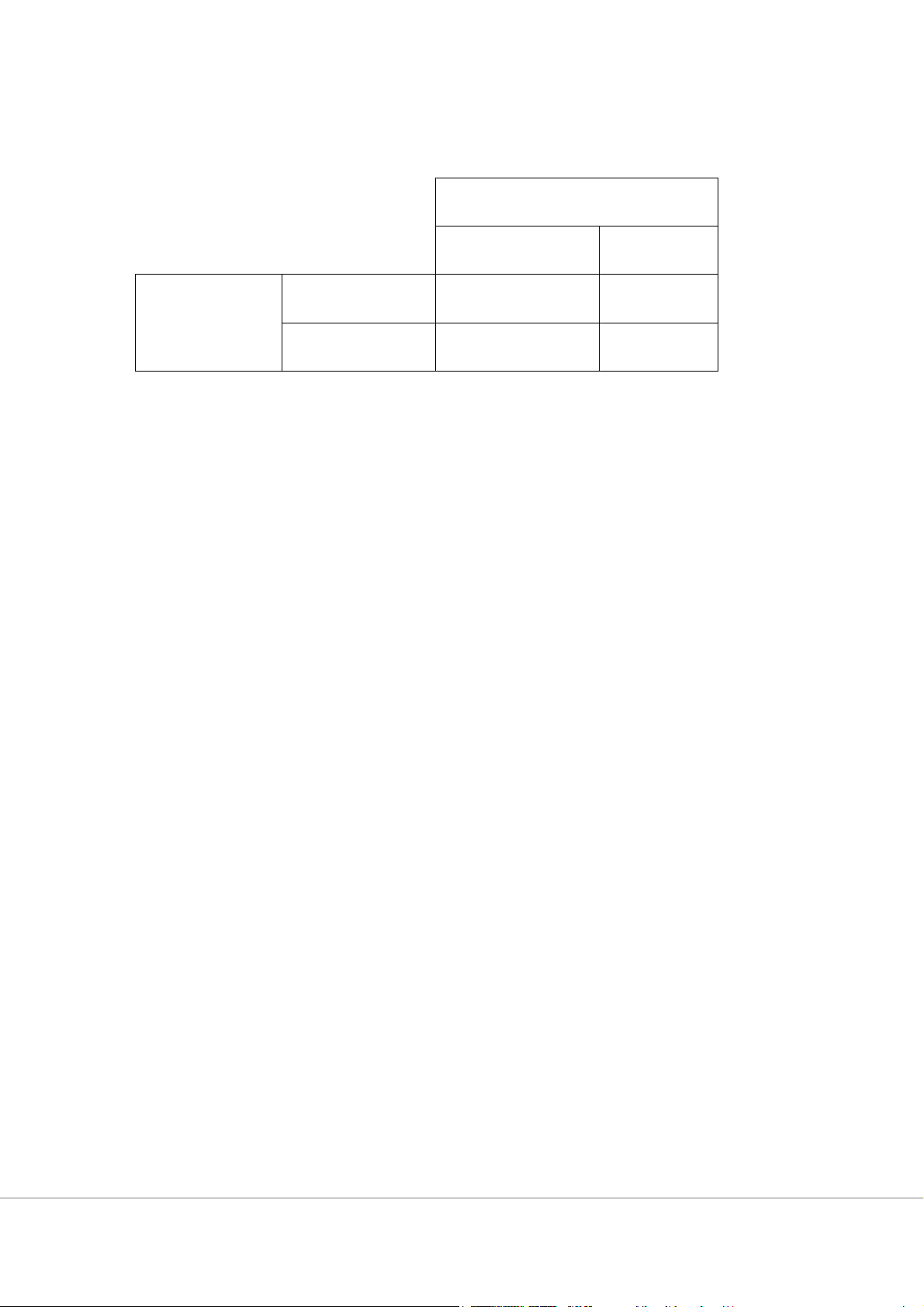
Theo cách thức trình bày thông thường, trò chơi được biểu diễn dưới dạng ma trận như trong bảng 7.1. ĐỐI THỦ B Chiến lược b1 Chiến lược b2 Chiến lược a1 (1; 3) (7; 4) ĐỐI THỦ A Chiến lược a2 (7; 7) (6; 8)
Hình 7.1: Cách thức trình bày trò chơi dưới dạng thông thường
Trong bảng 7.1, đối thủ A được xếp theo hàng ngang và đối thủ B được xếp theo
hàng dọc. Đối thủ A có 2 chiến lược là a1 và a2, còn đối thủ B có 2 chiến lược là b1 và
b2. Các cặp số ở trong các ngoặc đơn của ma trận kép biểu thị lợi ích mà mỗi đối thủ
nhận được tương ứng với mỗi lát cắt chiến lược. Thông thường, số thứ nhất trong ngoặc
đơn biểu thị lợi ích của đối thủ được xếp theo hàng ngang và số thứ hai trong ngoặc đơn
biểu thị lợi ích của đối thủ được xếp theo hàng dọc.
Cụ thể, với lát cắt chiến lược (a1, b1), đối thủ A sẽ nhận được lợi ích là 1 và đối
thủ B sẽ nhận được lợi ích là 3. Tương tự, với lát cắt chiến lược (a2, b2), đối thủ A sẽ
nhận được lợi ích là 6, còn lợi ích đối thủ B nhận được sẽ là 8….
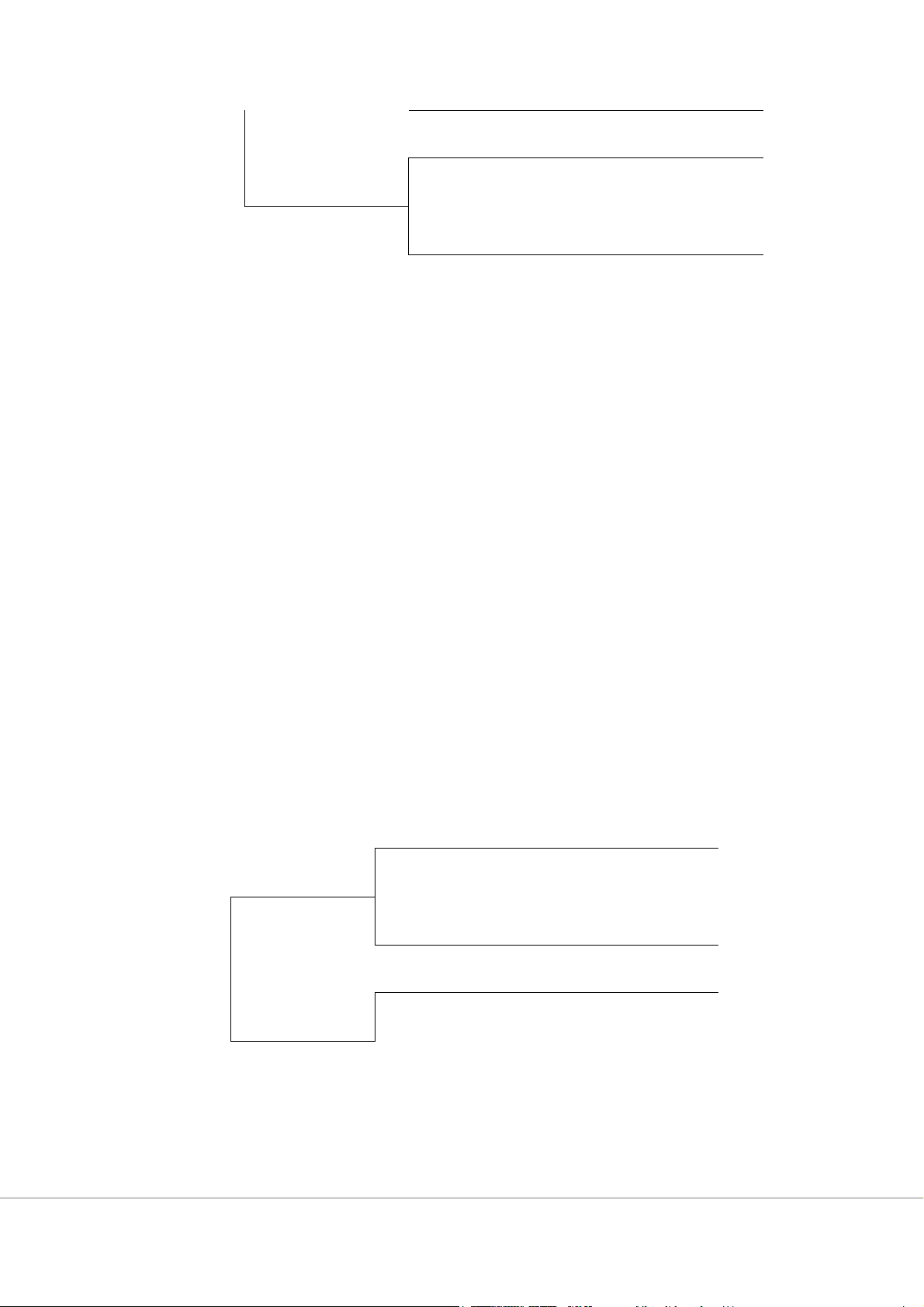
Trò chơi nói trên cũng có thể được trình bày dưới dạng sơ đồ hình cây như trong Hình 7.1: Chiến lược a1 ĐỐI THỦ B Chiến lược b1 (1; 3) Chiến lược b2 (7; 4) ĐỐI THỦ A Chiến lược b1 (7; 7) Chiến lược a2 ĐỐI THỦ B Chiến lược b2 (6; 8)
Hình 7.1: Cách trình bày trò chơi dưới dạng hình cây 8
Như vậy, với mỗi lát cắt chiến lược, sẽ có một kết cục kèm theo với những lợi ích
nhất định cho mỗi người chơi.
Câu hỏi trung tâm của lý thuyết trò chơi là các đối thủ sẽ chọn chiến lược nào?
Hay nói cách khác, đâu sẽ là kết cục của trò chơi?
2. PHƯƠNG PHÁP GIẢI TRÒ CHƠI
Để đưa ra lời giải cho các trò chơi, các chuyên gia lý thuyết trò chơi phi hợp tác
cũng dựa trên 2 giả định thường gặp trong kinh tế học: đó là các đối thủ trong trò chơi là
những người duy lý (rational) và chỉ quan tâm đến lợi ích của bản thân mình (selfish).
Đây là 2 yếu tố quyết định sự lựa chọn của các đối thủ.
Tuy nhiên, những giả định này không phải lúc nào cũng đủ để dự đoán kết cục của
trò chơi. Chính vì vậy, các nhà kinh tế học còn dựa vào một khái niệm khác rất thông
dụng trong kinh tế học, đó là khái niệm cân bằng (equilibrium).
2.1. Loại bỏ các chiến lược bị lấn án (elimination of dominated strategies)
Trong một số trò chơi, các đối thủ có thể nhận thấy rằng một hoặc một vài chiến
lược của mình luôn luôn đem lại các kết cục kém hơn các chiến lược khác. Các chiến
lược kém hơn này được gọi là các chiến lược bị lấn át, còn các chiến lược tốt hơn kia
được gọi là chiến lược lấn át.
Trong các tình huống như vậy, lợi ích của người chơi sẽ không bị tổn hại nếu
người đó loại bỏ các chiến lược bị lấn át. Cách giải một trò chơi trên cơ sở loại bỏ các
chiến lược bị lấn át có thể thấy rõ trong một trò chơi nổi tiếng có tên là Nghịch cảnh của
Người tù (Prisoner`s Dilemma), lần đầu tiên được nhà kinh tế học A. Tucker mô phỏng vào những năm 1940.
Trò chơi tình thế lưỡng nan của Người tù mô phỏng một tình huống sau: có 2
người cùng nhau phạm tội và bị công an bắt. Tuy nhiên, do không có đầy đủ các chứng
cứ, tòa án chỉ có thể buộc tội mỗi người 1 năm tù giam. Mặc dù vậy, phía công an cho
rằng, mức độ phạm tội của họ nghiêm trọng hơn nhiều. Để khai thác các đối tượng phạm
tội nói trên, công an tách 2 nghi can sang 2 phòng riêng biệt để hỏi cung. Điều kiện đặt ra
là: nếu 2 người cùng không khai nhận, mỗi người sẽ bị kết án 1 năm tù. Nếu 2 người
cùng khai nhận, mỗi người sẽ bị kết án 3 năm tù. Tuy nhiên, nếu chỉ một người khai
nhận, người đó sẽ được tha bổng, còn người kia sẽ bị kết án 5 năm tù. 9
Tình huống trên (còn được gọi là thế lưỡng nan của người tù) có thể được mô
phỏng dưới dạng ma trận như sau: NGHI CAN 2 Khai Không khai Khai (-3; -3) (0; -5) NGHI CAN 1 Không khai (-5; 0) (-1; -1)
Bảng 7.2: Trò chơi Nghịch cảnh của Người tù
Trong tình huống trên, do cả 2 nghi can đều là những người duy lý và chỉ quan
tâm đến lợi ích của bản thân mình, nên họ sẽ suy luận như sau: nếu người kia chọn
phương án “khai”, thì tốt nhất là mình cũng nên chọn phương án “khai” và bị kết án 3
năm tù (-3), bởi nếu chọn phương án “không khai”, mình sẽ bị kết án 5 năm tù (-5). Nếu
người kia chọn phương án “không khai”, thì tốt nhất mình cũng nên chọn phương án
“khai”, bởi như thế mình sẽ được tha bổng (0), trong khi việc chọn phương án “không
khai” sẽ dẫn đến hậu quả là bị kết án 3 năm tù (-3).
Như vậy, với cả 2 nghi can ở trên, chiến lược “khai” luôn luôn tốt hơn chiến lược
“không khai” hay nói cách khác là chiến lược “không khai” luôn bị chiến lược “khai” lấn
át, vì nó luôn đem lại lợi ích nhỏ hơn, bất chấp người kia chọn chiến lược nào đi chăng
nữa. Kết quả là sẽ không ai chọn chiến lược “bị lấn át”.
Kết cục của trò chơi là cả 2 nghi can đều chọn chiến lược “khai” và bị kết án 3
năm tù. Kết cục này, rõ ràng là tồi hơn so với kết cục cả 2 người đều không khai nhận tội
lỗi của mình cũng như của đồng phạm.
Trò chơi tình thế lưỡng nan của người tù cho thấy, việc mọi người theo đuổi lợi
ích của mình không phải lúc nào cũng đem lại kết cục tốt cho bản thân, cũng như cho cả
cộng đồng (ở đây cộng đồng chỉ giới hạn trong 2 người phạm tội). Nó cũng cho thấy
rằng, các lợi ích tập thể, nếu không hài hòa với lợi ích cá nhân, sẽ không có được sự bền vững. 10
Loại bỏ các chiến lược bị lấn át là một trong những cách giải trò chơi rất đơn giản
và lô-gíc. Tuy nhiên, trên thực tế, không phải lúc nào trong trò chơi cũng có những chiến
lược bị lấn át như vậy (điều này phụ thuộc vào cấu trúc ma trận lợi ích của trò chơi). 2.2. Cân bằng Nash
Để đưa ra lời giải cho những trò chơi không có chiến lược lấn át hay bị lấn át, các
nhà kinh tế dựa vào một khái niệm được gọi là cân bằng Nash, mang tên nhà toán học
người Mỹ được giải thưởng Nobel Kinh tế năm 1994, John Nash – người đầu tiên đưa ra
khái niệm cân bằng này và đồng thời cũng là người khai sinh ra lý thuyết trò chơi phi hợp tác.
2.2.1. Nội dung cân bằng Nash (Nash Equilibrium)
Cân bằng Nash là một lát cắt chiến lược, trong đó không có đối thủ nào muốn đơn
phương thay đổi chiến lược của mình, một khi đã biết được chiến lược mà các đối thủ khác sử dụng.
Để hiểu rõ hơn khái niệm cân bằng Nash, chúng ta cùng xem xét ví dụ ở bảng 7.3.
Trong ma trận lợi ích được trình bày tại bảng 7.3, các đối thủ A và B đều không có
các chiến lược nào lấn át hay bị lấn bởi chiến lược khác. Nếu đối thủ A chọn chiến lược
a1, thì chiến lược tốt nhất cho đối thủ B là chiến lược b2 (mang lại lợi ích là 4 và lớn hơn
lợi ích là 3 khi sử dụng chiến lược b1). Ngược lại, nếu đối thủ A chọn chiến lược a2, thì
chiến lược tốt nhất của B là b1 (vì 8>7). Đối với đối thủ A cũng vậy. Nếu B chọn chiến
lược b1, thì a2 là chiến lược tốt nhất đối với A. Nhưng nếu B chọn b2, thì a1 mới là chiến lược tốt nhất. ĐỐI THỦ B
Chiến lược b1 Chiến lược b2 Chiến lược a1 (1; 3) (7; 4) ĐỐI THỦ A Chiến lược a2 (7; 8) (6; 7) Bảng 7.3: Cân bằng Nash
Câu hỏi đặt ra là các đối thủ A và B sẽ chọn chiến lược nào, khi không biết được
chiến lược của người kia ? Hay nói cách khác, đâu là kết cục của trò chơi. 11
Khái niệm cân bằng Nash chỉ ra rằng, lát cắt chiến lược (a2; b1) chính là kết cục
của trò chơi. Tại điểm cân bằng này, không đối thủ nào muốn đơn phương thay đổi chiến
lược một khi đã biết được chiến lược của người kia.
Tại lát cắt chiến lược (a2, b1), đối thủ A nhận được lợi ích là 7 và đối thủ B nhận
được lợi ích là 8. Nếu A chuyển sang áp dụng chiến lược a1, trong khi B vẫn giữ nguyên
chiến lược b1, lợi ích của A sẽ chỉ còn 1 (nhỏ hơn 7). Tương tự, nếu A vẫn giữ chiến lược
a2 mà B chuyển sang chiến lược b2, lợi ích của B sẽ bị giảm từ 8 xuống còn 7.
Như vậy là tại điểm cân bằng Nash (cặp chiến lược a2, b1), tốt nhất là cả 2 đối thủ
đều nên giữ nguyên lựa chọn chiến lược của mình. Nói cách khác, cân bằng Nash, một
khi đã đạt được, thì sẽ có được sự ổn định.
Thuộc tính ổn định của cân bằng Nash cũng là thuộc tính của các điểm cân bằng
trong kinh tế học mà chúng ta thường gặp. Nhờ thuộc tính này, khái niệm cân bằng Nash
có thể giúp giải thích được nhiều hiện tượng kinh tế - xã hội tồn tại trên thực tế, chẳng
hạn như tại sao các cải cải cách kinh tế, chính trị lại khó thực hiện. Khi một trạng thái
kinh tế xã hội nào đó đã đạt được cân bằng Nash, thì sẽ không dễ bị thay đổi.
Tóm lại, cân bằng Nash là một tập hợp các chiến lược hoặc hành động mà một
người chơi có thể làm điều tốt nhất cho mình, khi cho trước hành động của các đối thủ.
Cân bằng chiến lược ưu thế là một trường hợp đặc biệt của cân bằng Nash.
Tôi đang làm điều tốt nhất có thể được cho tôi, bất kể bạn
Các chiến lược ưu thế
có làm gì đi nữa. Bạn đang làm điều tốt nhất có thể được
cho bạn, bất kể tôi làm gi đi nữa.
Tôi đang làm điều tốt nhất có thể được, cho trước cái bạn Cân bằng Nash
đang làm. Bạn đang làm điều tiốt nhất có thể được, cho
trước cái tôi đang làm.
2.2.2. Một số nhân xét về cân bằn Nash
Mặc dù cân bằng Nash là một khái niệm rất hữu ích trong việc giải thích các hiện
tượng kinh tế - xã hội, về mặt lý thuyết, có một số vấn đề liên quan đến cân bằng Nash.
Thứ nhất, mặc dù cân bằng Nash là kết cục mà tại đó mỗi đối thủ đều chọn được
chiến lược tốt nhất (không muốn đơn phương thay đổi) để đối phó với những chiến lược 12
cho trước của các đối thủ khác, nhưng lý thuyết trò chơi không cho biết: bằng cách nào
các đối thủ đạt được cân bằng Nash?
Thứ hai, trong một trò chơi có thể tồn tại nhiều cân bằng Nash. Trong ví dụ trên,
chúng ta thấy rằng, lát cắt chiến lược (a1, b2) cũng là một cân bằng Nash. Tại đây, nếu
đối thủ A giữ nguyên chiến lược a1, thì đối thủ B cũng không có động cơ chuyển sang
chiến lược b1, vì khi đó lợi ích của B sẽ bị giảm từ 4 xuống còn 3. Ngược lại, nếu đối thủ
B giữ nguyên chiến lược b2, đối thủ A cũng không có động cơ chuyển sang chiến lược
a2, bởi lợi ích của A sẽ bị giảm từ 7 xuống còn 6. Như vậy, với một trò chơi có nhiều cân
bằng Nash, việc dự đoán kết cục của trò chơi vẫn là một vấn đề còn bỏ ngỏ.
Thứ ba, người ta có thể đặt câu hỏi: liệu có phải trò chơi nào cũng tồn tại cân bằng
Nash hay có những trò chơi không có cân bằng Nash nào cả? Về câu hỏi này, John Nash
đã chứng minh rằng, bất cứ trò chơi nào cũng có ít nhất một cân bằng Nash, nếu tính cả
các chiến lược hỗn hợp. Tuy nhiên, nếu không tính các chiến lược hỗn hợp, có những trò
chơi không có cân bằng Nash.
2.3. Chiến lược hỗn hợp (mix strategies) với bước đi đồng thời
Như đã nói ở trên, trong một số trò chơi, nếu các đối thủ không sử dụng chiến lược
hỗn hợp, thì trò chơi sẽ không có cân bằng Nash. Điều này có thể thấy rõ khi xem xét trò
chơi Oản Tù Tì quen thuộc với tất cả mọi người.
Trong trò chơi này, mỗi đối thủ A và B có 3 chiến lược, được gọi là Đấm, Lá và
Kéo. Quy tắc của trò chơi là Đấm thắng Kéo, Kéo thắng Lá và Lá thắng Đấm. Nếu một
người thắng người kia, thì người thắng sẽ nhận lợi ích là +1 và người thua nhận lợi ích là
-1. Nếu 2 người sử dụng cùng một chiến lược, kết quả là 2 bên hòa nhau và mỗi người
nhận được lợi ích là 0. Trò chơi Oản Tù Tì có thể được trình bày dưới dạng ma trận lợi ích như sau (bảng 7.4): ĐỐI THỦ B Đấm Lá Kéo ĐỐI Đấm (0; 0) (-1; +1) (+1; -1) THỦ A Lá (+1; -1) (0; 0) (-1; +1) 13 Kéo (-1; +1) (+1; -1) (0; 0)
Bảng 7.4: Trò chơi Oản Tù Tì
Theo bảng ma trận lợi ích nói trên, chúng ta có thể dễ dàng nhận thấy rằng trò chơi
sẽ không có cân bằng Nash nếu các đối thủ chỉ sử dụng các chiến lược thuần (pure
strategies). Trong trò chơi Oản Tù Tì, thì Đấm, Lá và Kéo là các chiến lược thuần). Mỗi
khi một đối thủ sử dụng một chiến lược thuần nào đó, đối thủ kia có thể đơn phương chọn
một chiến lược khác để mang lại lợi ích lớn hơn cho bản thân mình.
Chẳng hạn, nếu lát cắt chiến lược được chọn là (Đấm; Lá), thì đối thủ A nhận
được lợi ích là -1 và đối thủ B nhận được lợi ích là +1. Tuy nhiên, đối thủ A có thể
chuyển sang sử dụng chiến lược Kéo để dành lợi ích +1 và lúc đó đối thủ B chỉ nhận
được lợi ích là -1. Đến lượt mình, đối thủ B, để dành phần thắng trong trường hợp đối thủ
A sử dụng chiến lược Kéo, sẽ phải chuyển sang chiến lược Đấm…Như vậy, việc đơn
phương thay đổi chiến lược sẽ luôn diễn ra và không có điểm dừng, tức là không có điểm cân bằng Nash nào cả.
Mặc dù vậy, trò chơi này vẫn có điểm cân bằng Nash nếu như các đối thủ áp dụng
chiến lược hỗn hợp (mix strategies), tức là lựa chọn các chiến lược thuần một cách ngẫu
nhiên (Đấm, Lá, Kéo) theo một tỷ lệ xác suất nào đó.
Về mặt trực giác, chúng ta có thể đoán rằng, mục đích của việc lựa chọn các chiến
lược thuần theo cách thức không thể dự đoán là để không bị đối thủ “bắt bài”. Tuy nhiên,
sự tối ưu của chiến lược hỗn hợp sẽ phụ thuộc vào tỷ lệ xác suất đối với mỗi chiến lược
thuần mà các đối thủ áp dụng.
Trong trò chơi Oản Tù Tì nói trên, do tính đối xứng của trò chơi, chúng ta không
khó để đoán rằng, mỗi đối thủ sẽ chọn xác suất 1/3 cho mỗi chiến lược thuần. Chiến lược
hỗn hợp với tỷ lệ xác suất 1/3 cho mỗi chiến lược thuần (Đấm, Lá, Kéo) của mỗi đối thủ
sẽ tạo nên một cân bằng Nash, bởi nếu đối thủ nào chọn một tỷ lệ xác suất khác, kết quả sẽ không tốt hơn.
Để kiểm tra lời khẳng định trên, chúng ta hãy giả định là đối thủ B sẽ áp dụng tỷ lệ
xác suất 1/3 cho mỗi chiến lược thuần. Nếu A cũng áp dụng chiến lược hỗn hợp (1/3, 13,
1/3), lợi ích kỳ vọng của A đối với mỗi lát cắt chiến lược sẽ được biểu diễn trong Hình
7.6. Và lợi ích kỳ vọng tổng thể của A sẽ là 0. 14 Cặp chiến lược Xác suất xảy ra Lợi ích đối thủ A thu Lợi ích kỳ vọng A-B (1)
được từ một lần chơi của A (2) (1) x (2) Đấm – Đấm 1/3*1/3 0 0 Đấm – Lá 1/3*1/3 -1 -1/9 Đấm – Kéo 1/3*1/3 1 1/9 Lá – Đấm 1/3*1/3 1 1/9 Lá – Lá 1/3*1/3 0 0 Lá - Kéo 1/3*1/3 -1 -1/9 Kéo – Đấm 1/3*1/3 -1 -1/9 Kéo – Lá 1/3*1/3 1 1/9 Kéo – Kéo 1/3*1/3 0 0 Tổng 0
Bảng 7.5: Lợi ích của đối thủ A khi áp dụng chiến lược hỗn hợp (1/3, 1/3, 1/3) trong
điều kiện đối thủ B áp dụng chiến lược hỗn hợp (1/3, 1/3, 1/3)
Điều gì sẽ xảy ra nếu A sử dụng chiến lược hỗn hợp khác, chẳng hạn như (1/5,
1/5, 3/5) cho các chiến lược thuần Đấm, Lá, Kéo? Kết quả cho thấy, lợi ích kỳ vọng tổng
thể của A vẫn là 0 và như vậy, A không có động cơ để đơn phương thay đổi chiến lược.
Điều tương tự cũng đúng với B nếu A chơi chiến lược hỗn hợp (1/3, 1/3, 1/3). Lợi ích đối thủ Xác suất xảy Lợi ích kỳ vọng Cặp chiến lược A thu được từ ra của A A-B một lần chơi (1) (1) x (2) (2) 15 Đấm – Đấm 1/5*1/3 0 0 Đấm – Lá 1/5*1/3 -1 -1/15 Đấm – Kéo 1/5*1/3 1 1/15 Lá – Đấm 1/5*1/3 1 1/15 Lá – Lá 1/5*1/3 0 0 Lá - Kéo 1/5*1/3 -1 -1/15 Kéo – Đấm 3/5*1/3 -1 -3/15 Kéo – Lá 3/5*1/3 1 3/15 Kéo – Kéo 3/5*1/3 0 0 Tổng 0
Bảng 7.6: Lợi ích của đối thủ A khi áp dụng chiến lược hỗn hợp (1/5, 1/5, 3/5) trong
điều kiện đối thủ B áp dụng chiến lược hỗn hợp (1/3, 1/3, 1/3)
Tuy nhiên, nếu A chơi chiến lược hỗn hợp khác với chiến lược (1/3, 1/3, 1/3),
chẳng hạn như chiến lược (1/5, 1/5, 3/5), B sẽ có động cơ thay đổi chiến lược để cải thiện
kết quả của mình. Chẳng hạn, B có thể chơi chiến lược hỗn hợp (3/5, 1/5, 1/5) và sẽ nhận
lợi ích kỳ vọng tổng thể là 4/25 (bảng 7.7). Lợi ích đối thủ B Xác suất xảy Lợi ích kỳ vọng Cặp chiến lược thu được từ một ra của B A-B lần chơi (1) (1) x (2) (2) Đấm – Đấm 1/5*3/5 0 0 Đấm – Lá 1/5*1/5 1 1/25 Đấm – Kéo 1/5*1/5 -1 -1/25 16 Lá – Đấm 1/5*3/5 -1 -3/25 Lá – Lá 1/5*1/5 0 0 Lá - Kéo 1/5*1/5 1 1/25 Kéo – Đấm 3/5*3/5 1 9/25 Kéo – Lá 3/5*1/5 -1 -3/25 Kéo – Kéo 3/5*1/5 0 0 Tổng 4/25
Bảng 7.7: Lợi ích của đối thủ B khi áp dụng chiến lược hỗn hợp (3/5, 1/5, 1/5) trong
điều kiện đối thủ A áp dụng chiến lược hỗn hợp (1/5, 1/5, 3/5)
Như vậy, cặp chiến lược hỗn hợp (1/5, 1/5, 3/5) của A và (1/3, 1/3, 1/3) của B
cũng không phải là cân bằng Nash, vì B có động cơ đơn phương thay đổi chiến lược hỗn
hợp của mình, chẳng hạn như chuyển sang chơi chiến lược (3/5, 1/5, 1/5).
Chỉ có cặp chiến lược hỗn hợp (1/3, 1/3, 1/3) của A và (1/3, 1/3, 1/3) của B là cân bằng Nash.
2.4. Suy luận ngược (Backward Induction) với bước đi tuần tự
Trong những phần trên chúng ta chủ yếu đề cập đến các trò chơi với các bước đi
đồng thời. Tuy nhiên, phần lớn các trò chơi thường gặp trong cuộc sống lại là các trò chơi
với những bước đi tuần tự, trong đó một đối thủ đi trước và đối thủ còn lại, tùy thuộc vào
sự lựa chọn của đối thủ kia, sẽ chọn bước đi của mình.
Để tìm lời giải cho những trò chơi với các bước đi tuần tự, người ta có thể áp dụng
phương pháp suy luận ngược. Phương pháp suy luận ngược sẽ được làm rõ trong ví dụ sau: Chiến lược a1 ĐỐI THỦ B Chiến lược b1 (1; 3) Chiến lược b2 (7; 4) 17 ĐỐI THỦ A Chiến lược b1 (7; 7) Chiến lược a2 ĐỐI THỦ B Chiến lược b2 (6; 8)
Hình 7.2: Phương pháp suy luận ngược (1)
Trong trò chơi được trình bày ở hình 7.2, đối thủ A là người lựa chọn chiến lược
trước. Đối thủ B, tùy thuộc vào lựa chọn của đối thủ A, sẽ chọn bước đi của mình. Câu
hỏi đặt ra là đối thủ A sẽ chọn bước đi nào? Để xác định bước đi của mình, đối thủ A sẽ suy luận ngược như sau:
Nếu A chọn chiến lược a1, B sẽ chọn chiến lược b2, vì chiến lược này sẽ đem lại
cho B lợi ích là 4, trong khi việc chọn chiến lược b1 chỉ đem lại lợi ích là 3. Nếu B chọn
chiến lược b2 và A chọn chiến lược a1, lợi ích của A sẽ là 7.
Nếu A chọn chiến lược a2, B sẽ chọn chiến lược b2, vì chiến lược này sẽ đem lại
cho B lợi ích là 8, trong khi việc chọn chiến lược b1 chỉ đem lại lợi ích là 7 (7<8). Nếu B
chọn chiến lược b2 và A chọn chiến lược a1, lợi ích của A sẽ là 6.
Như vậy, bằng cách suy luận ngược (suy luận từ sự lựa chọn của B), A thấy rằng,
mình nên chọn chiến lược a1 để đạt lợi ích là 7 và B sẽ chọn chiến lược b2 để đạt lợi ích
là 4. Lát cắt chiến lược (a1, b2) sẽ là kết cục của trò chơi.
Trong trò chơi với các bước đi tuần tự, thứ tự thực hiện các bước đi sẽ ảnh hưởng
đến kết cục của trò chơi. Để thấy được tầm quan trọng của các quy định về thứ tự thực
hiện các bước đi, chúng ta có thể đặt câu hỏi: điều gì sẽ xảy ra nếu đối thủ B được thực
hiện bước đi trước tiên? Chiến lược b1 ĐỐI THỦ A Chiến lược a1 (3; 1) Chiến lược a2 (7; 7) ĐỐI THỦ B Chiến lược a1 (4; 7) 18 Chiến lược b2 ĐỐI THỦ A Chiến lược a2 (8; 6)
Hình 7.3: Phương pháp suy luận ngược (2)
Với việc được thực hiện bước đi trước tiên, đối thủ B sẽ suy luận như sau:
Nếu B chọn chiến lược b1, A sẽ chọn chiến lược a2 để đạt lợi ích là 7, thay vì
chọn chiến lược a1 và nhận lợi ích là 1. Lúc đó, lợi ích của B sẽ là 7.
Nếu B chọn chiến lược b2, A sẽ chọn chiến lược a1 để nhận lợi ích là 7, thay vì
chọn chiến lược a1 và nhận lợi ích là 6. Lúc đó, lợi ích của B sẽ là 4.
Như vậy, dựa trên việc suy luận ngược, đối thủ B sẽ chọn chiến lược b1, để A sẽ chọn chiến lược a2.
So sánh 2 kết quả của 2 trò chơi có cùng đối thủ, chiến lược, cũng như ma trận lợi
ích ở trên, chúng ta thấy rằng, kết cục của 2 trò chơi này sẽ khác nhau, nếu thứ tự thực
hiện các bước đi được thay đổi. Trong trò chơi A được đi trước, kết cục của trò chơi là lát
cắt chiến lược (a1, b2) và A sẽ nhận được lợi ích là 7, còn B sẽ nhận được lợi ích là 4.
Nhưng nếu B được đi trước, kết cục của trò chơi sẽ là lát cắt chiến lược (b1, a2) và lợi ích
A nhận được là 7, còn lợi ích B nhận được là 7.
3. MỘT SỐ VÍ DỤ MINH HỌA VỀ LÝ THUYẾT TRÒ CHƠI
3.1. Trò chơi lợi thế người đi trước
Giả định có hai hãng sản xuất thức ăn sang bằng ngũ cốc trong cùng một thị trường, trong
đó hai loại lương thực chế biến mới có thể được tung ra thành công- nếu mỗi loại chỉ do
một hãng tung ra. Có một thị trường “đồ ăn giòn” mới và một htị trường khác “đồ ăn
ngọt” mới, nhưng mỗi hãng chỉ đủ nguồn lực để sản xuất ra một loại sản phẩm mới mà
thôi. Ma trận lợi ích được tổng hợp trong bảng 7.8 sau đây: Hãng 2 Đồ ăn giòn Đồ ăn ngọt Đồ ăn giòn (-5; -5) (10; 10) Hãng 1 Đồ ăn ngọt (10; 10) (-5; -5) 19
Bảng 7.8: vấn đề lựa chọn sản phẩm
Trong trò chời này, có một lợi thế của người đi trước, bằng cách tung ra đồ ăn ngọt, hãng
1 tạo ra một sự đã rồi, để cho hãng 2 ít lựa chọn hơn, đó là chỉ còn cách tung ra thị trường
đồ ăn giòn. Điều này giống với lợi thế của người đi đầu trong mô hình Stackelberg.
Trong mô hình này hãng đi trước có thể chọn mức sản lượng cao, do đó tạo cho đối thủ
cạnh tranh ít lựa chọn, chỉ còn lựa chọn mức sản lượng thấp mà thôi.
Để làm rõ bản chất lợi thế của người đi trước, việc xem lại mô h ình Stackelberg và so
sánh nó với mô hình Cournot; trong đó cả hai cùng chọn mức sản lượng một lúc sẽ giúp
ta rất nhiều. Giả định hai hang lưỡng quyền đứng trước một đường cầu thị trường: P = 30 – Q
Trong đó: Q là tổng sản lượng của thị trường, được xác định Q = q1 + q2; q1 là sản lượng
của hãng 1 và q2 là sản lượng của hãng 2. Giả định MC = 0.
Cân bằng Cournot là khi q1 = q2 = 10, do đó P = 10 và mỗi hãng thu được lợi nhuận là
100. Nếu hai hãng câu kết với nhau thì mức sản lượng là q1 = q2= 7,5 , do đó P =15, mỗi
hãng thu được lợi nhuận bằng 112,5.
Nếu theo mô hình Stackelberg, trong đó hãng 1 đi trước thì kết quả là q1 = 15 và q2 = 7,5
và do đó P= 7,5, lợi nhuận tương ứng của các hãng là 112,5 và 56,25. Hãng 2 7,5 10 15 7,5 112,5; 112,5 93,75; 125 56,25; 112,5 Hãng 1 10 125; 93,75 100; 100 50; 75 15 112,5; 56,25 75; 50 0; 0
Bảng 7.9: tổng hợp lợi ích thu được khi quyết định sản lượng
Nếu cả hai hãng cùng chời một lúc thì giải pháp duy nhất cho trò chơi này là cả hai hãng
cùng sản xuất 10 sản phẩm và thu được lợi nhuận là 100. Ở cân bằng Cournot, mỗi hãng 20