Chương 7: Quang Học Lượng Tử và Hiện Tượng Phát Xạ Năng Lượng | Môn Vật lý đại cương - Đại học Xây Dựng Hà Nội

7.
QUANG HỌC LƯỢNG TỬ
(Bản chất hạt của các bức xạ) Hiện tượng giao thoa,
nhiễu xạ và phân cực ánh sáng là những hiện tượng chứng tỏ ánh sáng có bản chất sóng. Nhưng
vào cuối thế kỉ 19 và đầu thế kỉ 20, người ta đã phát hiện những hiện tượng quang học mới như
hiện tượng phát xạ nhiệt, hiệu ứng quang điện… không thể giải thích được nếu chỉ dựa vào quang
học sóng. Để giải thích những hiện tượng đó, phải dựa vào thuyết lượng tử của Planck và thuyết photon của Einstein. 7.1 BỨC XẠ NHIỆT
7.1.1 Những khái niệm mở đầu
Bằng một cách nào đó kích thích các phân tử, nguyên tử làm cho chúng từ trạng thái cơ bản
chuyển sang trạng thái kích thích, thì khi chúng từ các trạng thái kích thích này trở về trạng thái
cơ bản, năng lượng thu được sẽ trả lại môi trường, thường là dưới dạng năng lượng sóng điện từ
(bức xạ điện từ). Có nhiều cách cung cấp năng lượng để kích thích các phân tử, nguyên tử. Nếu
năng lượng cung cấp ở dạng nhiệt thì bức xạ điện từ phát ra gọi là bức xạ nhiệt và hiện tượng đó
gọi là phát xạ (vì) nhiệt.
Bức xạ nhiệt có một đặc tính là trong một số điều kiện đặc biệt nó có thể tồn tại cân bằng
với vật. Như thế có nghĩa là khi đó năng lượng bức xạ do vật phát ra đúng bằng năng lượng dưới
dạng nhiệt mà vật thu vào bằng hấp thụ bức xạ. Khi đó vật ở trạng thái cân bằng (động) ứng với
một nhiệt độ xác định.
7.1.2 Các đại lượng đặc trưng
a) Năng suất phát xạ đơn sắc
Ta xét một phần tử diện tích dS ở mặt ngoài một vật phát xạ (cân
bằng). Khi đó vật có nhiệt độ xác định T. Trong quá trình phát xạ, vật phát d S
ra mọi bức xạ điện từ có tần số từ nhỏ đến lớn. Năng lượng bức xạ phát ra
từ dS trong một đơn vị thời gian (năng thông bức xạ phát ra từ dS) mang
đi bởi các bức xạ điện từ có tần số trong khoảng
, + d được kí hiệu
là dWP( , T). Rõ ràng là đại lượng này tỉ lệ với dS và với d Hình 7.1 Sự phát xạ
dWP( , T) = r( , T)dSd năng lượng
Đại lượng r( , T) được gọi là năng suất phát xạ đơn sắc ứng với tần số của vật. Đại lượng
R(T) = r ( , T)d (7-1) 0
được gọi là năng suất phát xạ toàn phần hay độ trưng của vật phát xạ.
b) Hệ số hấp thụ đơn sắc
Giả sử năng thông ứng với khoảng tần số ( , + d ) gửi tới dS là dW( , T), trong số đó
dS hấp thụ năng thông dWt ( T, ), theo định nghĩa, tỉ số dW(t (7-2) a (T, ) = dW(
được gọi là hệ số hấp thụ đơn sắc ứng với tần số của vật. Rõ ràng a (T, ) 1.
Nói chung trong thực tế: a (T, ) 1
Những vật mà a (T, ) = 1 với mọi T, được gọi là vật đen tuyệt đối.
Trong thực tế không có vật đen tuyệt đối, chỉ có những vật có tính chất gần với tính chất vật đen tuyệt đối.
Thí dụ : Một bình kín rỗng cách nhiệt có khoét một lỗ nhỏ, mặt trong được phủ một lớp chất
xốp đen (mồ hóng) có thể coi là vật đen tuyệt đối. Trong trường hợp này khi một tia bức xạ lọt
qua lỗ vào bình, nó sẽ bị phản xạ liên tiếp trên thành và thực tế có thể coi là bị hấp thụ hoàn toàn.
Đại lượng A(T)= a( ν,T)dν gọi là hệ số hấp thụ toàn phần của vật. 0
7.1.3 Định luật Kirchhoff
Giả sử đặt trong một bình kín cách nhiệt một số vật A1. A2, A3
… khác nhau. Các vật này sẽ đồng thời phát xạ và hấp thụ bức xạ A A 1 2
nhiệt. Khi trạng thái cân bằng được thiết lập thì hiển nhiên vật nào
hấp thụ bức xạ mạnh cũng sẽ phát xạ mạnh. Nếu không như vậy thì
sẽ xảy ra hiện tượng trạng thái cân bằng của vật đó tự phá huỷ A
không cần tác động của bên ngoài (trái với nguyên lí quán tính của 3 vật lý).
Từ nhận xét đó Kirchhoff đi đến kết luận rằng khả năng phát
xạ và khả năng hấp thụ của một vật tỉ lệ thuận với Hình 7.2 Sự hấp thụ và bức xạ nhau, nghĩa là
giữa hai đại lượng r( , T) và a( , T) của các trong bình cách nhiệt vật 1, 2, 3 … có quan hệ tỉ lệ: r (1 r (2 ... f( (7-3) a (1 a (2
Phát biểu định luật Kirchhoff: Tỉ số giữa năng suất phát xạ đơn sắc và hệ số hấp thụ đơn
sắc của cùng một vật ở nhiệt độ nhất định là một hàm phụ thuộc vào tần số bức xạ và nhiệt độ
T mà không phụ thuộc vào bản chất của vật đó.
Hàm f( , T) thường được gọi là hàm phổ biến. r( f( (7-4) a(
Ý nghĩa của hàm phổ biến f( , T):
Theo công thức trên nếu áp dụng cho vật đen tuyệt đối a( , T) = 1, ta được r( , T) = f( , T) (7-5)
Vậy f( , T) chính là năng suất phát xạ đơn sắc của vật đen tuyệt dối ứng với các bức xạ tần
số ở nhiệt độ T.
Từ đây ta có hai hệ quả quan trọng:
a) Từ công thức (7-4) ta có r( , T) = a( , T)f( , T), với một vật bất kì a( , T) 1 do đó
r( , T) f( , T). Vậy năng suất phát xạ đơn sắc của một vật bất kì luôn nhỏ hơn của
vật đen tuyệt đối ứng với các bức xạ tần số ở nhiệt độ T.
b) Từ công thức (7-5) ta có thể phát biểu: Điều kiện cần và đủ để một vật phát xạ được bức
xạ có tần số ở nhiệt độ T là ở cùng điều kiện đó vật đen tuyệt đối cũng phát ra được bức xạ đó.
7.1.4 Các định luật thực nghiệm về bức xạ của vật đen tuyệt đối
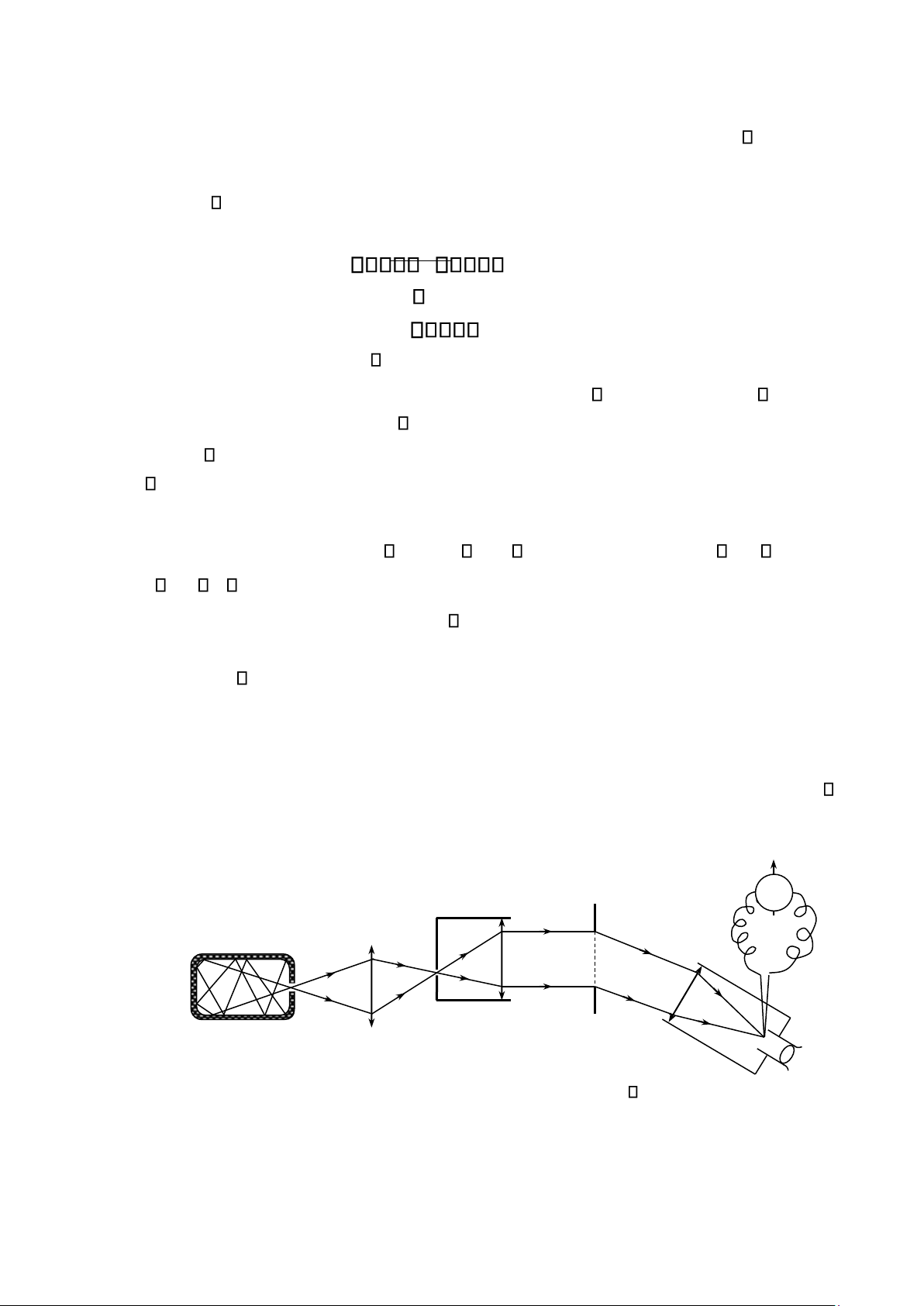
Làm thí nghiệm trên các mô hình của vật đen tuyệt đối người ta có thể xác định được f( , T) bằng thực nghiệm. T C A O
Hình 7.3a Thí nghiệm xác định hàm f( ,T)
Sơ đồ thí nghiệm được mô tả trên hình Hình 7-3a.
Kính ngắm T quay sau cách tử C cho phép đặt cặp nhiệt điện O vào những cực đại của các
ánh sáng đơn sắc có bước sóng khác nhau, do đó cho
phép xác định được r( , T) của vật đen lí tưởng A ở nhiệt f(,T)
độ T, tức là xác định được f( ,T). T T
1 < T 2 < T 3 3
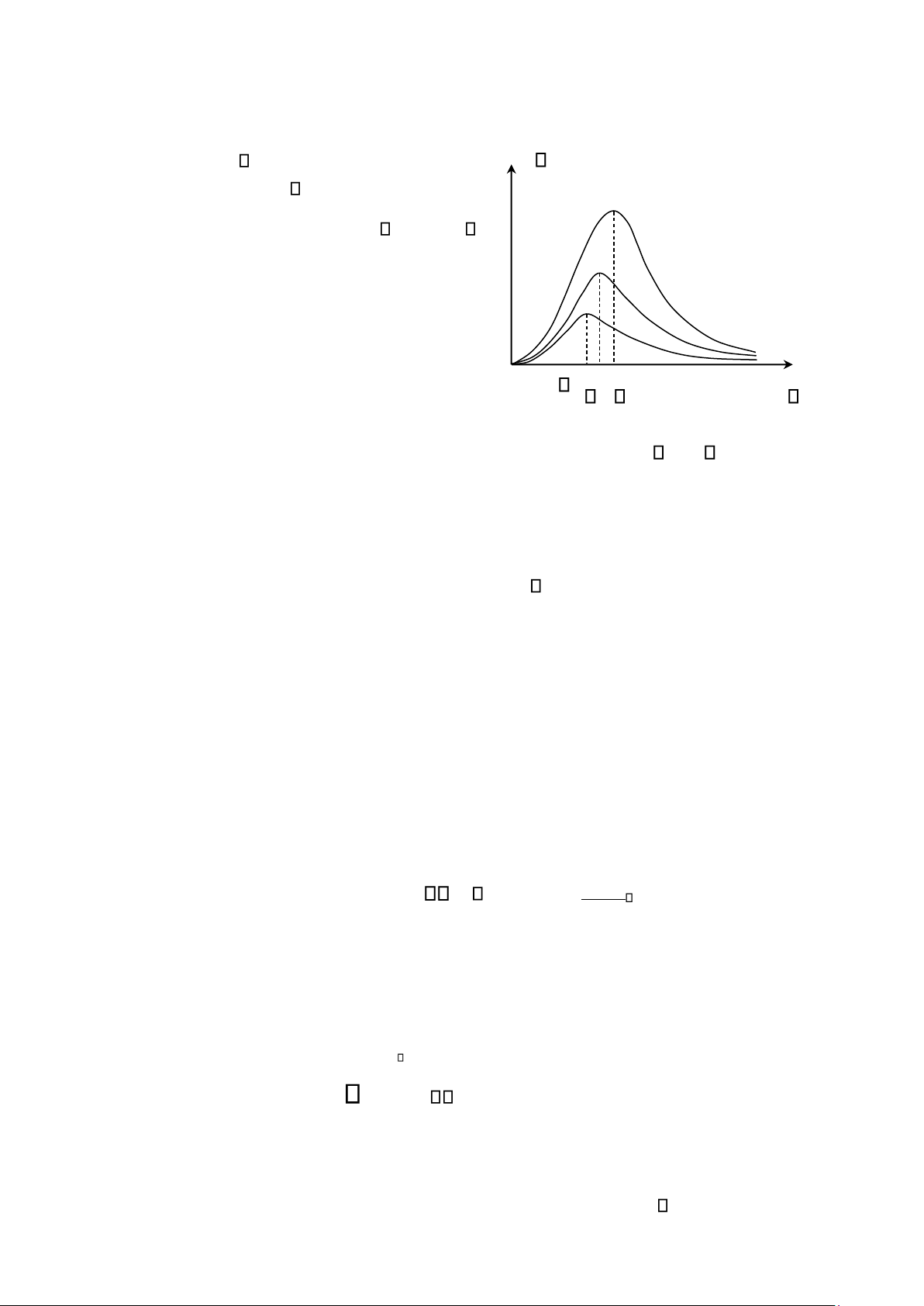
Kết quả thu được các đồ thị của f( , T) theo ở
các nhiệt độ T khác nhau trên hình Hình 7.3b.
Các kết quả thực nghiệm của vật đen tuyệt đối được T 2 phát biểu như sau: T 1 m1 m2 m3
Hình 7.3b Đồ thị của f( ,T) theo ở các nhiệt độ T khác nhau
Định luật Stefan – Boltzmann: Năng suất phát xạ toàn phần của một vật đen tuyệt đối tỉ lệ
với luỹ thừa bốn của nhiệt độ tuyệt đối của vật ấy.
Định luật Wien: Đối với vật đen tuyệt đối, bước sóng m của chùm bức xạ đơn sắc mang
nhiều năng lượng nhất tỉ lệ nghịch với nhiệt độ tuyệt đối của vật.
7.2 THUYẾT LƯỢNG TỬ PLANCK
7.2.1 Sự thất bại của thuyết sóng ánh sáng trong việc giải thích hiện tượng bức xạ nhiệt
Xuất phát từ quan niệm của vật lí kinh điển coi các nguyên tử, phân tử phát xạ hoặc hấp thụ
một cách liên tục, trên cơ sở lí thuyết bức xạ điện từ cổ điển, Rêlây và Jeans đã tìm được biểu
thức sau đây của hàm phổ biến: 2 2 f( , T) = k TB , (7-6) c
trong đó kB là hằng số Boltzmann, có giá trị bằng: kB = 1,38.10-23 J/K (7-7)
Từ biểu thức đó có thể tính được năng suất phát xạ toàn phần của một vật đen tuyệt đối:
R(T) = f( , T) d = ∞ ! 0
Kết quả dẫn tới một đại lượng lớn vô cùng: đó là bế tắc của quan niệm vật lí cổ điển về phát
xạ và hấp thụ năng lượng điện từ. Bế tắc này tồn tại trong một khoảng thời gian dài cuối thế kỉ
19 được gọi là: "sự khủng hoảng ở vùng tử ngoại" (khi tần số bức xạ lớn thì f( , T) càng lớn dẫn
tới tích phân vô cùng lớn).
7.2.2 Thuyết lượng tử của Planck
Năm 1900 Planck đã nêu lên một thuyết mới thay thế cho quan niệm cổ điển. Đó là thuyết
lượng tử năng lượng của Planck.
a) Các nguyên tử, phân tử phát xạ hay hấp thụ năng lượng của bức xạ điện từ một cách gián
đoạn: phần năng lượng phát xạ hay hấp thụ luôn là bội số nguyên của một lượng năng lượng nhỏ
xác định gọi là lượng tử năng lượng hay quantum năng lượng.
b) Đối với một bức xạ điện từ đơn sắc tần số , bước sóng lượng tử năng lượng tương ứng bằng: c ε = h = h (7-8)
trong đó h là một hằng số gọi là hằng số Planck và có giá trị h
= 6,625 . 10-34 J.s (7-9) c) Công thức Planck
Xuất phát từ thuyết lượng tử năng lượng nói trên, Planck đã tìm ra được biểu thức của làm
phổ biến f( , T) tức là năng suất phát xạ đơn sắc của vật đen tuyệt đối: 2 2 h c
f( , T) = 2 ek ThB -1 (7-10)
Công thức (7-10) gọi là công thức Planck.
Chú ý: Khi h k ThB -1 ≈ h 1 thì e k TBk TB 2 2
và (7-10) thành: f( , T) = c2 k TB : ta lại thu được biểu thức của Rêlây - Jeans.
7.2.3 Từ thuyết lượng tử Planck ta thu được các định luật bức xạ của vật đen
tuyệt đối phù hợp với thực nghiệm
Nếu ta khảo sát sự biến thiên của hàm f( , T) cho bởi công thức Planck theo ở những nhiệt
độ khác nhau thì ta được những đường cong hoàn toàn phù hợp với thực nghiệm.
Ngoài ra từ công thức Planck có thể suy ra những hệ quả quan trọng diễn tả các quy luật phát
xạ của vật đen tuyệt đối. 2 2 h
R(T) = f( , T) d = d 0 B 2 h c e -1 kT h
Thực hiện phép đổi biến số: x = k TB ta được: R(T) = 2 c hk T 2 3B4 4 x dxe -13x x dx3 π4
Phép tích phân cho ta kết quả: e -1x 15
Vậy có thể viết: R(T) = T4 (7-
11) trong đó là một hằng số gọi là hằng số Stefan - Boltzmann.
= 5,67.10-8 W/m2K4 (7-12) Công thức (7-11)
diễn tả định luật Stefan - Boltzmann:
Năng suất phát xạ toàn phần của một vật đen tuyệt đối tỉ lệ với luỹ thừa bốn của nhiệt độ
tuyệt đối của vật ấy.
Đối với một vật bất kì (không phải vật đen tuyệt đối), định luật Stefan – Boltzmann có dạng:
R’(T) = α T4, trong đó α là một hệ số thoả mãn 0 α 1
Nếu ta tính đạo hàm của f( , T) theo thì thấy đạo hàm này triệt tiêu tại một giá trị đặc biệt
m của tần số nghĩa là một giá trị đặc biệt m của bước sóng của bức xạ điện từ sao cho: m T = b, (7-13)
b là một hằng số gọi là hằng số Wien b = 2,898.10-3 m.K (7-14)
Ứng với bước sóng m hàm f( , T) có một giá trị cực đại nghĩa là với bức xạ m vật đen
tuyệt đối phát xạ mạnh nhất. Đó là nội dung định luật Wien.
Đối với vật đen tuyệt đối, bước sóng m của chùm bức xạ đơn sắc mang nhiều năng lượng
nhất tỉ lệ nghịch với nhiệt độ tuyệt đối của vật.
7.3 THUYẾT PHOTON CỦA EINSTEIN
Thuyết lượng tử của Planck đã nêu lên quan điểm hiện đại về năng lượng: năng lượng điện
từ phát xạ hay hấp thụ có những giá trị gián đoạn; chúng luôn luôn là bội số nguyên của lượng
tử năng lượng ε; ta nói rằng năng lượng điện từ phát xạ hay hấp thụ bị lượng tử hoá. Nhưng
thuyết lượng tử của Planck chưa nêu lên bản chất gián đoạn của bức xạ điện từ. Đến năm 1905,
Einstein dựa trên thuyết lượng tử về năng lượng của Planck đã nêu lên thuyết lượng tử ánh sáng (photon).
7.3.1 Thuyết photon của Einstein
a) Bức xạ điện từ cấu tạo bởi vô số các hạt gọi là lượng tử ánh sáng hay photon.
b) Với mỗi bức xạ điện từ đơn sắc nhất định, các photon đều giống nhau và mang một năng lượng xác định bằng c hh (7-15)
c) Trong mọi môi trường (và cả trong chân không) các photon truyền đi với cùng vận tốc c = 3.108 m/s
d) Khi một vật phát xạ hay hấp thụ bức xạ điện từ thì có nghĩa là vật đó phát hay hấp thụ các photon.
e) Cường độ của chùm bức xạ tỉ lệ với số photon phát xạ từ nguồn trong một đơn vị thời gian.
Dựa vào thuyết photon của Einstein người ta đã giải thích được nhiều hiện tượng, trong đó
đặc biệt có hiện tượng (hiệu ứng) quang điện, hiện tượng Compton.
7.3.2 Động lực học photon
Photon ứng với bức xạ điện từ đơn sắc tần số mang năng lượng ε = h Theo
thuyết tương đối Einstein, photon có khối lượng cho bởi: ε = mc2 m c h 2 hc2 c λ (7-16)
Mặt khác khối lượng phụ thuộc vận tốc theo hệ thức: m 0 m 2 v 1 2 c 2 v m m 1 2
m0 là khối lượng nghỉ: c 0
Đối với photon = c. Suy ra m0 = 0.
Vậy photon có khối lượng nghỉ bằng 0.
Photon luôn chuyển động với vận tốc c do đó nó có động lượng bằng h p = mc = (7-17) c h hay p = (7- 18) λ
Như vậy động lượng của photon tỉ lệ thuận với tần số hoặc tỉ lệ nghịch với bước sóng của bức
xạ điện từ tương ứng.
7.3.3 Hiệu ứng Compton
Hiện tượng Compton là một trong những hiện tượng thể hiện rõ nét bản chất hạt của các bức
xạ điện từ, nói riêng nó chứng minh sự tồn tại động lượng của các hạt photon.
Năm 1892 Compton đã làm thí nghiệm cho một
chùm tia X bước sóng dọi vào các chất như paraphin, p
graphit… Compton nhận thấy khi đi qua các chất này
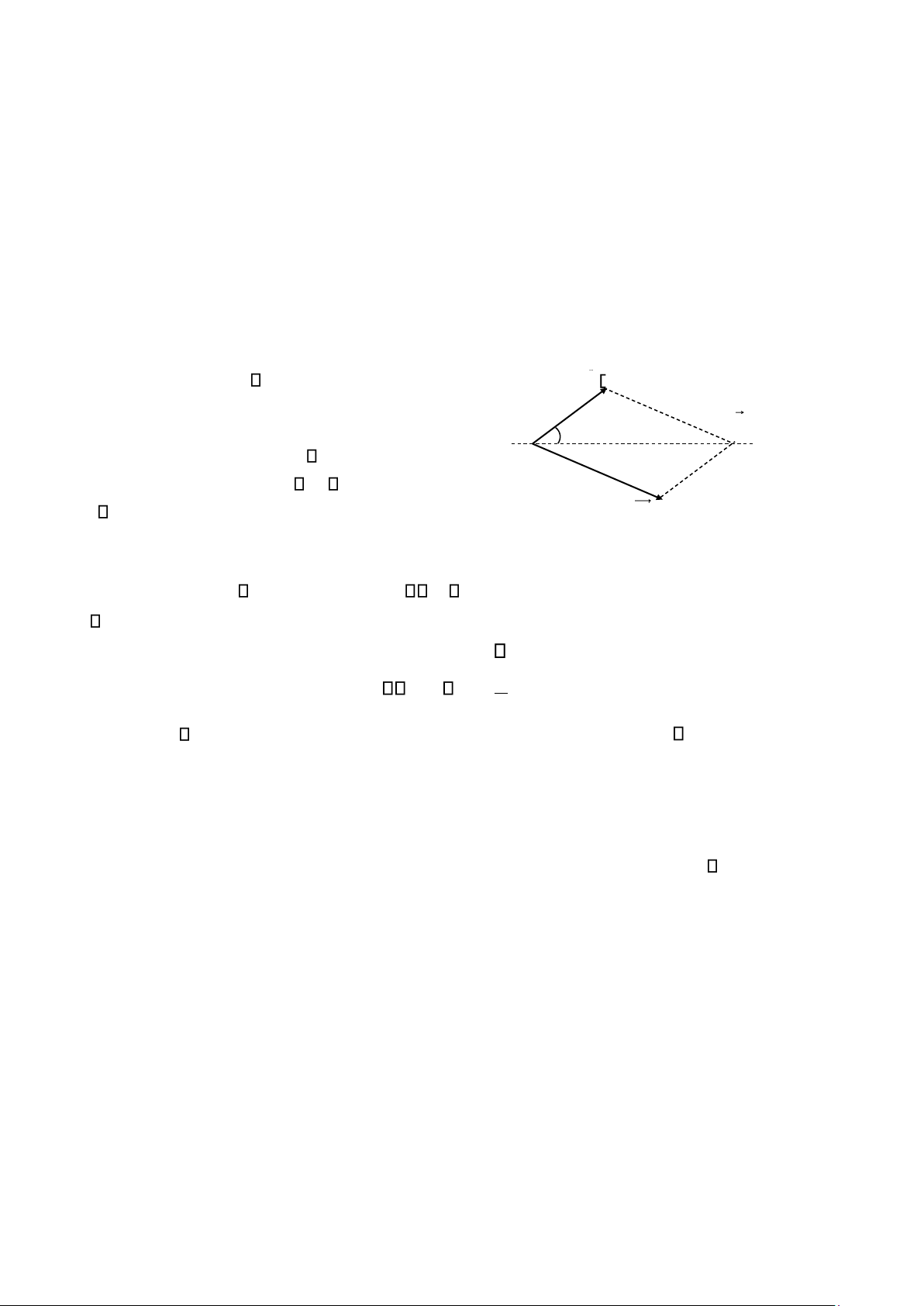
chùm tia X bị tán xạ. Trong phổ tia X tán xạ ngoài vạch p θ
có bước sóng bằng bước sóng của chùm tia X tới, còn
xuất hiện vạch có bước sóng ' > . Thực nghiệm chứng
tỏ ' không phụ thuộc cấu tạo các chất được dọi tia X mà p e chỉ phụ
Hình 7.4 Tán xạ của tia X trên electron
thuộc vào góc tán xạ . Độ tăng bước sóng = '
- được tính theo công thức = 2 c sin2 2 (7-19)
trong đó c là một hằng số chung cho mọi chất gọi là bước sóng Compton. c = 2,426.10-12m
Ta hãy tính toán hiện tượng Compton dựa vào thuyết photon của Einstein.
Hiệu ứng Compton là kết quả của quá trình tán xạ đàn hồi của chùm tia X lên các electron
trong các chất. Trong phổ các vạch tán xạ, vạch có bước sóng đúng bằng bước sóng của chùm
tia X dọi tới tương ứng với sự tán xạ của chùm tia X với các electron ở sâu trong nguyên tử, liên
kết mạnh với hạt nhân, vạch có bước sóng ' < tương ứng với sự tán xạ của chùm tia X với các
electron liên kết yếu với hạt nhân: các electron này có thể coi như electron tự do (vì năng lượng liên
kết của các electrron ấy rất nhỏ so với năng lượng chùm tia X dọi tới). Bây giờ ta hãy tính độ tăng bước sóng
= ' - dựa vào thuyết photon. Theo thuyết này ta xét sự va chạm của một photon X với một electron tự do.
Giả sử trước khi va chạm với chùm photon X, các electron đứng yên. Ta hãy tính lần lượt năng
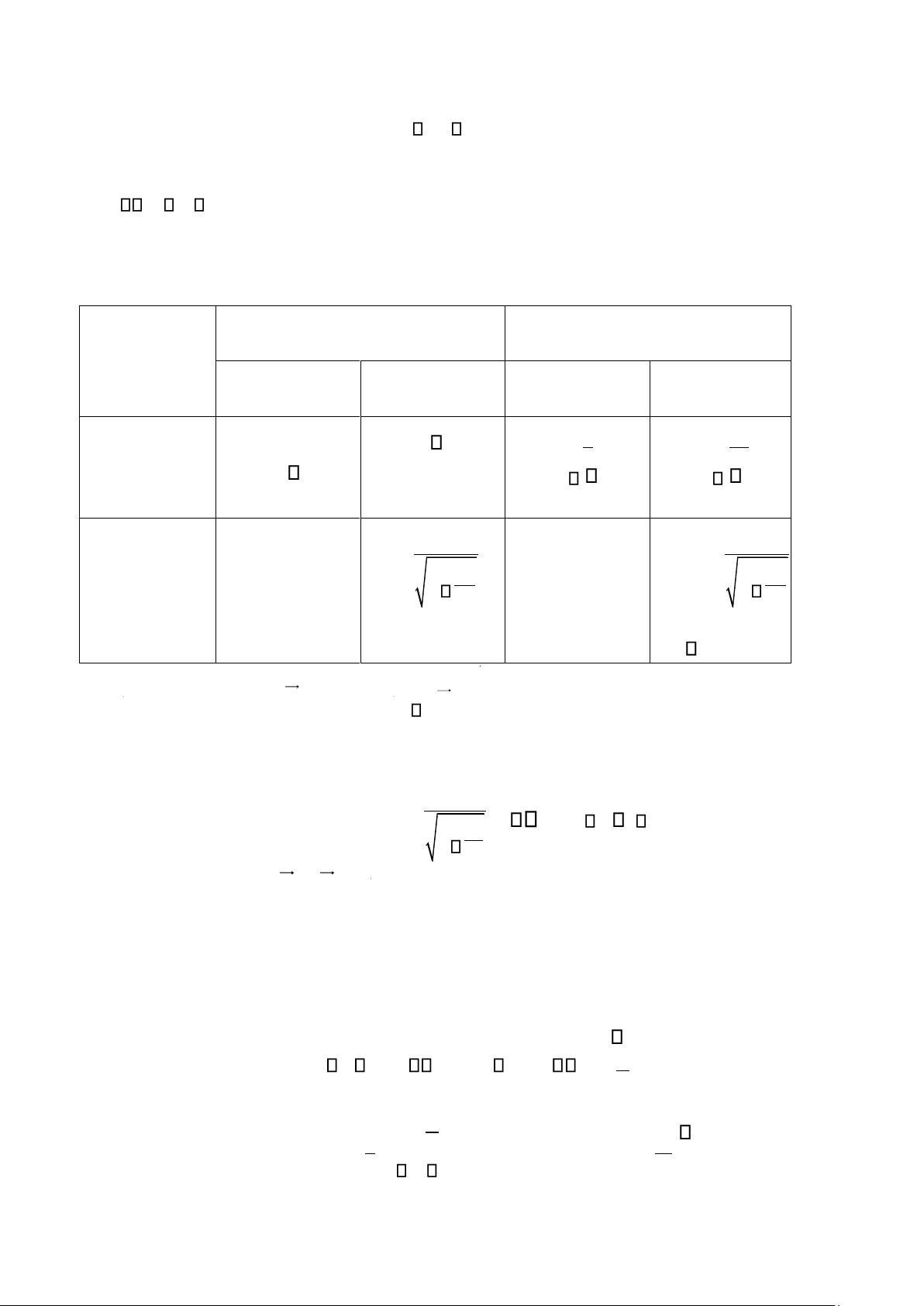
lượng và động lượng của photon X cũng như của electron trước và sau va chạm. Năng lượng Động lượng Hạt Trước va chạm Sau va chạm Trước va chạm Sau va chạm h ' h h ' Photon h P P c c m c m v 2 v 2 1 v 1 Electron m ec2 2 0 c 2 c 2 2 e Pe e
Trước va chạm động lượng của hạt photon X là P , sau va chạm động lượng của hạt photon X là
P' và của electron là Pe: góc giữa P' và P là .
Theo định luật bảo toàn năng lượng và động lượng ta có: e 2 h
m c2 h ' m ce 2 v 1 2 (7-20) c
P = P' + Pe (7-21)
(me : khối lượng nghỉ của electron)
Bình phương 2 vế của các phương trình này rồi lấy phương trình thứ nhất trừ đi phương trình thứ hai ta tìm được: mec2 ( - ') = h ' (1- cos ) = 2h ' sin2 2 h 2 (7-22) hay: ' - = 2 sin m ce 2 Hệ số của sin2 chính là hai lần bước sóng Compton 2 h c (7-23) mce
Như vậy nhờ lý thuyết photon của Einstein ta đã giải thích và tìm được những kết quả phù hợp
thực nghiệm đối với hiện tượng tán xạ Compton.
Một ứng dụng trực tiếp của hiện tượng này ta có thể đo c bằng thực nghiệm, từ đó tính được giá
trị của hằng số Planck h.
Chú ý: Trong hiệu ứng Compton, quá trình tán xạ của photon lên các electron là tán xạ đàn hồi
vì trong đó có bảo toàn động năng của hệ photon và electron. Quả vậy, động năng của hệ trước tán
xạ bằng h , sau tán xạ bằng 1 ' 2 h mc ( 1 ) 0 2 v 1 2 c 1 Ta có 2 h h' mc ( 1 ) 0
, từ đó su y ra (7 - 20 ). 2 v 1 2 c
Ví dụ 1: Một lò luyện kim, có cửa sổ quan sát rộng 4cm x 6cm, phát xạ mỗi giây một năng lượng
bằng 33,12 calo. Coi lò như một vật đen tuyệt đối.
a) Hãy xác định nhiệt độ T của lò.
b) Hãy xác định bước sóng ứng với năng suất phát xạ cực đại của lò. Bước sóng ấy thuộc vùng nào của quang phổ? Giải: a)
Năng suất phát xạ toàn phần của vật đen tuyệt đối được xác định theo định luật: R(T) = T4
Vì R là năng lượng do một đơn vị diện tích của cửa sổ phát ra trong một đơn vị thời gian nên
R liên hệ với năng lượng W do diện tích S của lò phát xạ trong thời gian t bằng biểu thức sau: W = RSt = T4St Theo đầu bài
W = 33,12 calo = 138,44J, S = 24.10-4m1, t = 1s. 1 hc mc 2 e E h mce W 138,44 Suy ra: T 4
St 4 5,67.10 24.10 8 4 1000K b)
Bước sóng ứng với năng suất phát xạ cực đại của lò được xác định theo định luật Wien
m = b/T = 2,898.10-6 m.
Ví dụ 2: Xác định độ tăng bước sóng ∆λ và góc tán xạ θ trong hiện tượng tán xạ compton, cho biết
bước sóng ban đầu λ = 0,03A và vận tốc của electron bắn ra là v = 0,6c. Giải:
Năng lượng của hệ photon – electron trước tán xạ ' ' mce 2
Năng lượng của hệ sau tán xạ E h 2 v 1 2 c 2 hc mc 2 ’ hay e e hc mc ' 2 Vì hệ kín, do đó E = E v 1 2 c 1 Từ đó rút ra: ' 1 m ce 2 1 h v 1 2 c 1 Thay số ta được: ' = 0,0434A Suy ra
∆λ = ' - = 0,0434 – 0,03 = 0,0134A h 2 Ta có ∆λ = ' - = 2 sin m ce 2 Rút ra sin
.m ce suy ra = 63023’. 2 2h 7.4 BÀI TẬP
7.4.1 Một dây tóc bóng đèn làm bằng vonfram có diện tích bề mặt phát xạ là 5 mm2, nhiệt độ của dây
tóc là 2515K. Coi bức xạ của dây tóc như bức xạ của vật đen tuyệt đối.
a) Tính công suất bức xạ của dây tóc
b) Tính bước sóng của ánh sáng đơn sắc ứng với năng suất phát xạ cực đại của nó. Đáp số: a) P = 11,34W
b) m = 1,15μm.
7.4.2 Photon có năng lượng 0,8 MeV, bay đến va chạm với một electron đứng yên và bị tán xạ.
a) Xác định năng lượng của photon tán xạ theo góc 1200
b) Tính động năng cực đại của electron giật lùi. Đáp số: a) W’ = 0,24MeV b) Wđmax = 0,61MeV