









Preview text:
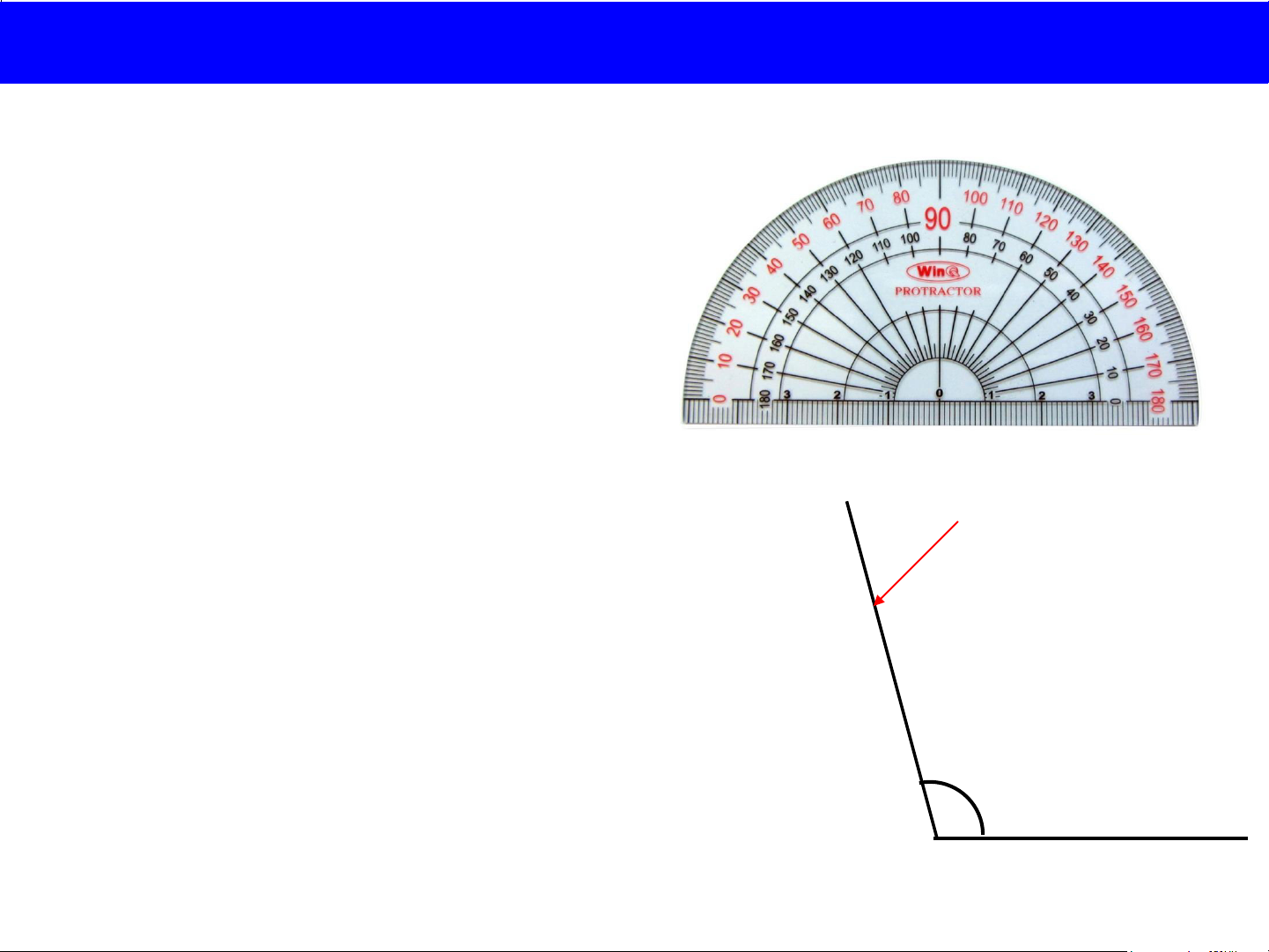
Qúy thầy cô về dự giờ thăm lớp Gv: Tớ nghĩ góc xAy x Tớ nghĩ góc này nhỏ hơn 90o. bằng 90o. A y
Theo em, bạn nào nói đúng?
BÀI 7: SỐ ĐO GÓC. CÁC GÓC ĐẶC BIỆT 1. Thước đo góc
Cấu tạo thước đo góc: - Là một nửa hình tròn
được chia thành 180 phần
bằng nhau được ghi từ 0 đến 180.
- Các số từ 0 đến 180 được ghi theo hai vòng ngược
chiều nhau để thuận tiện cho việc đo.
- Tâm của nửa hình tròn là tâm của thước
- Độ là đơn vị đo góc: Ví dụ 20 độ kí hiệu là 200
BÀI 7: SỐ ĐO GÓC. CÁC GÓC ĐẶC BIỆT
2. Cách đo góc. Số đo góc
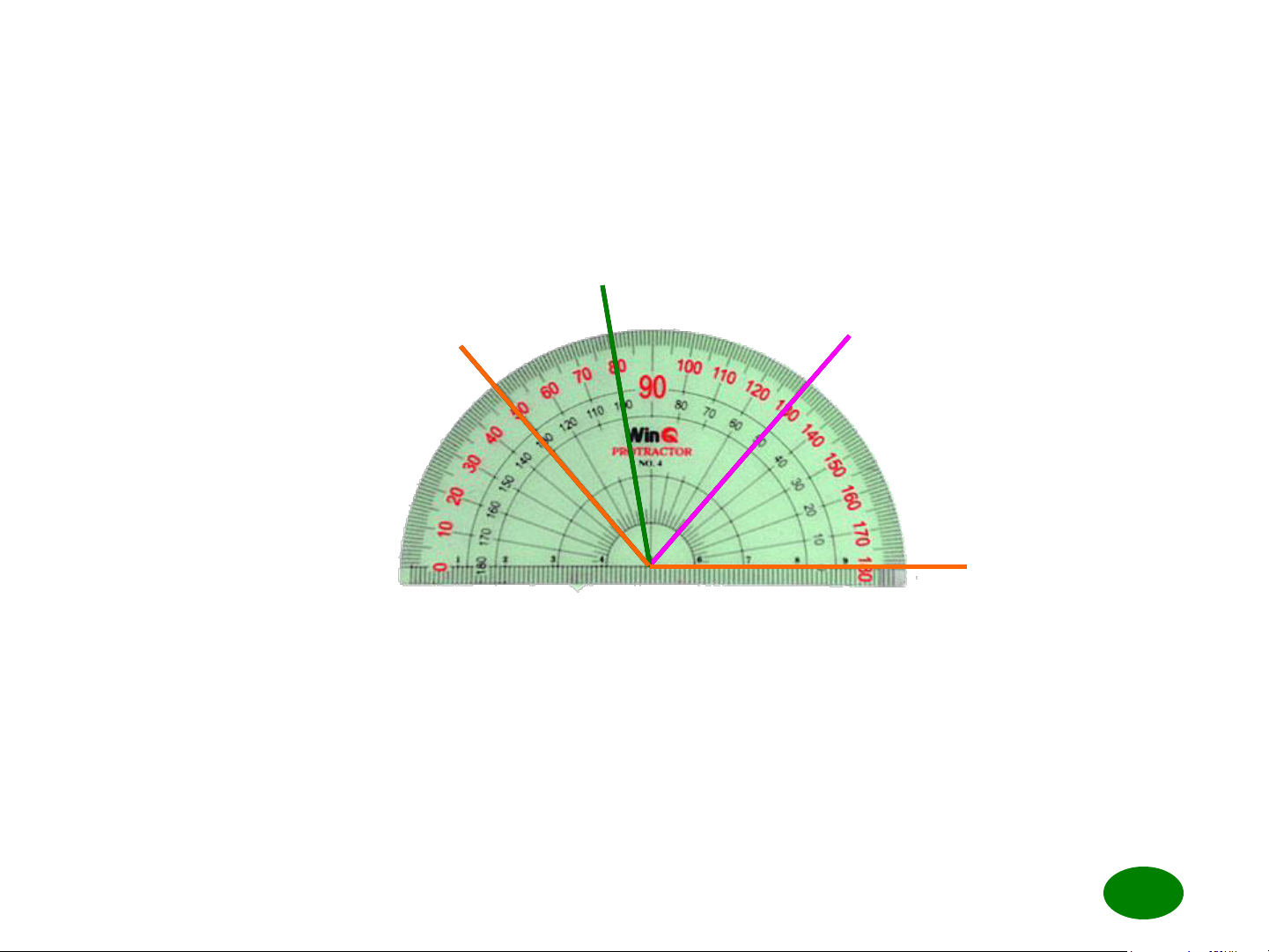
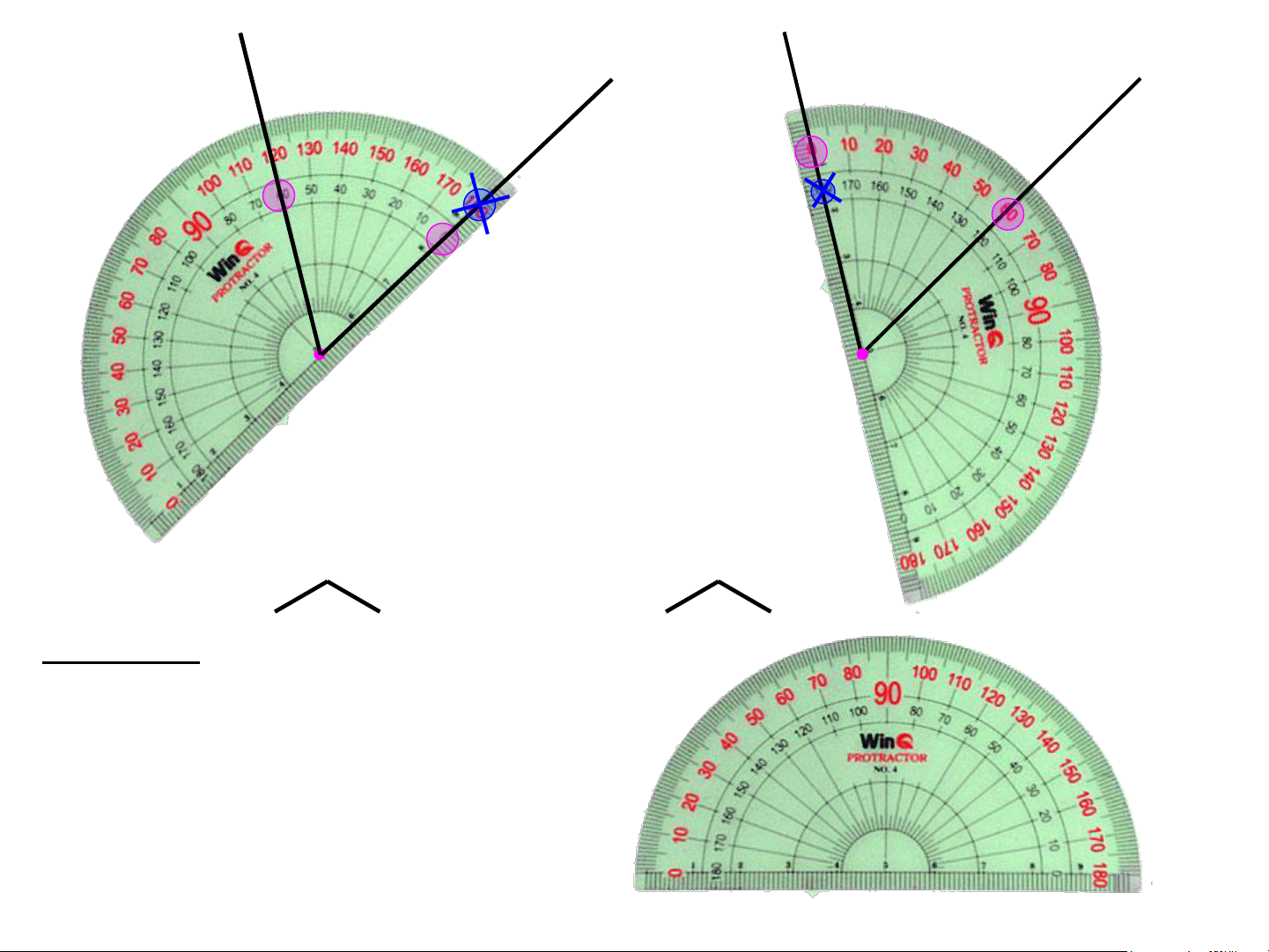
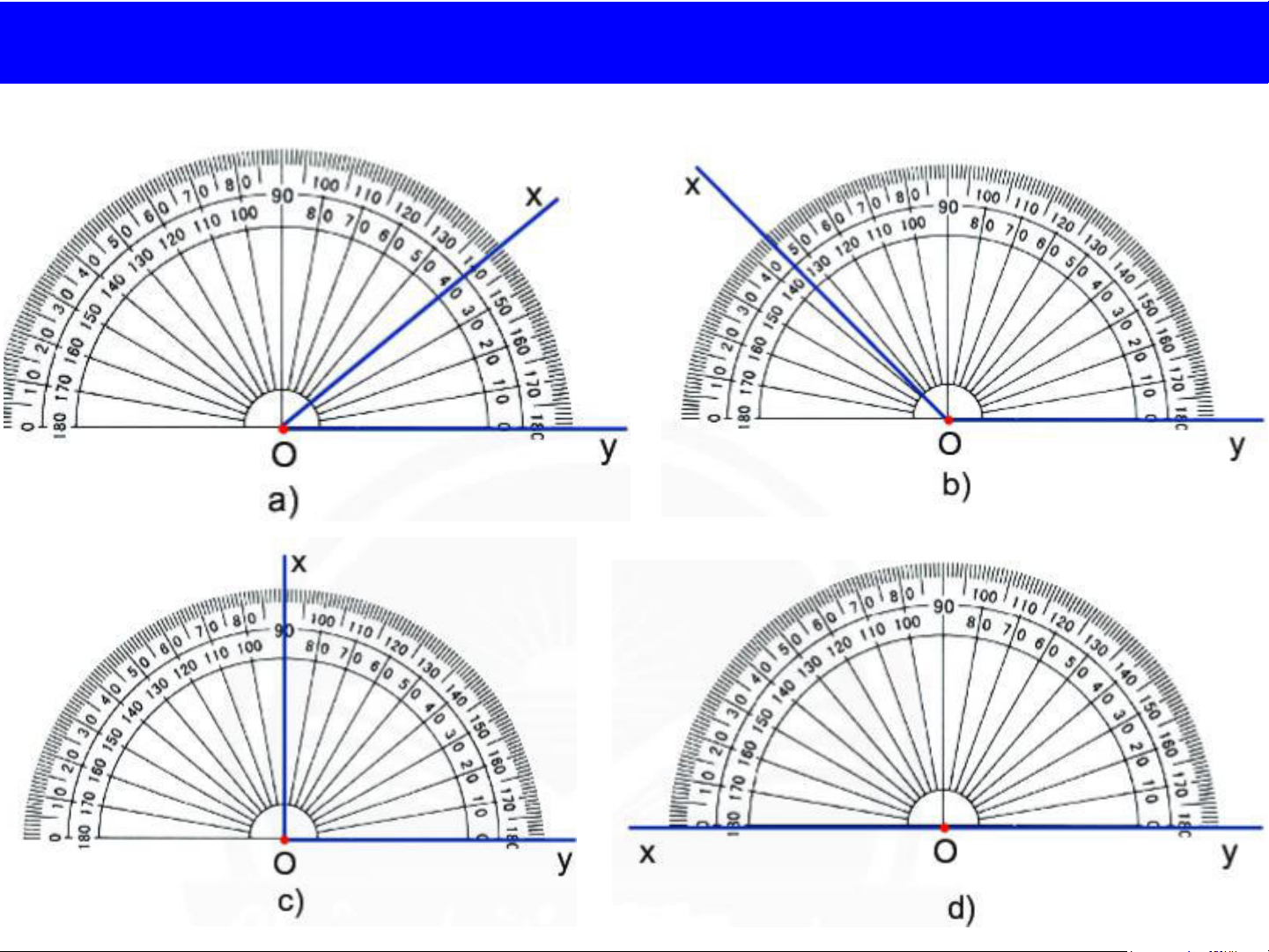
• Đặt thước sao cho tâm của
thước trùng với đỉnh của góc.
• Một cạnh của góc đi qua vạch số 0 của thước.
• Cạnh còn lại của góc đi qua
vạch nào thì đó là số đo của góc x Vạch số 105 cần đo. 1050 y O 0 0
xOy = 105 hay yOx = 105 y x O Đỉnh của góc Tâm của thước y y x x O O
Ký hiệu: xOy = 600 hay yOx = 600
Hãy đọc số đo các góc sau? Cho biết mỗi góc có mấy số
đo? Số đo của góc bẹt bằng bao nhiêu độ? v s 700 1450 u I O t Nhận xét :
+ Mỗi góc có 1 số đo.
+ Số đo của góc bẹt là 1800
+ Số đo của mỗi góc không vượt 1800 quá 1800 p A q
BÀI 7: SỐ ĐO GÓC. CÁC GÓC ĐẶC BIỆT
2. Cách đo góc. Số đo góc
Nhìn hình, đọc số đo của các góc:xOy; xOz; xOt z y t 0 xOy = 50 0 xOz = 100 x O 0 xOt = 130
BÀI 7: SỐ ĐO GÓC. CÁC GÓC ĐẶC BIỆT
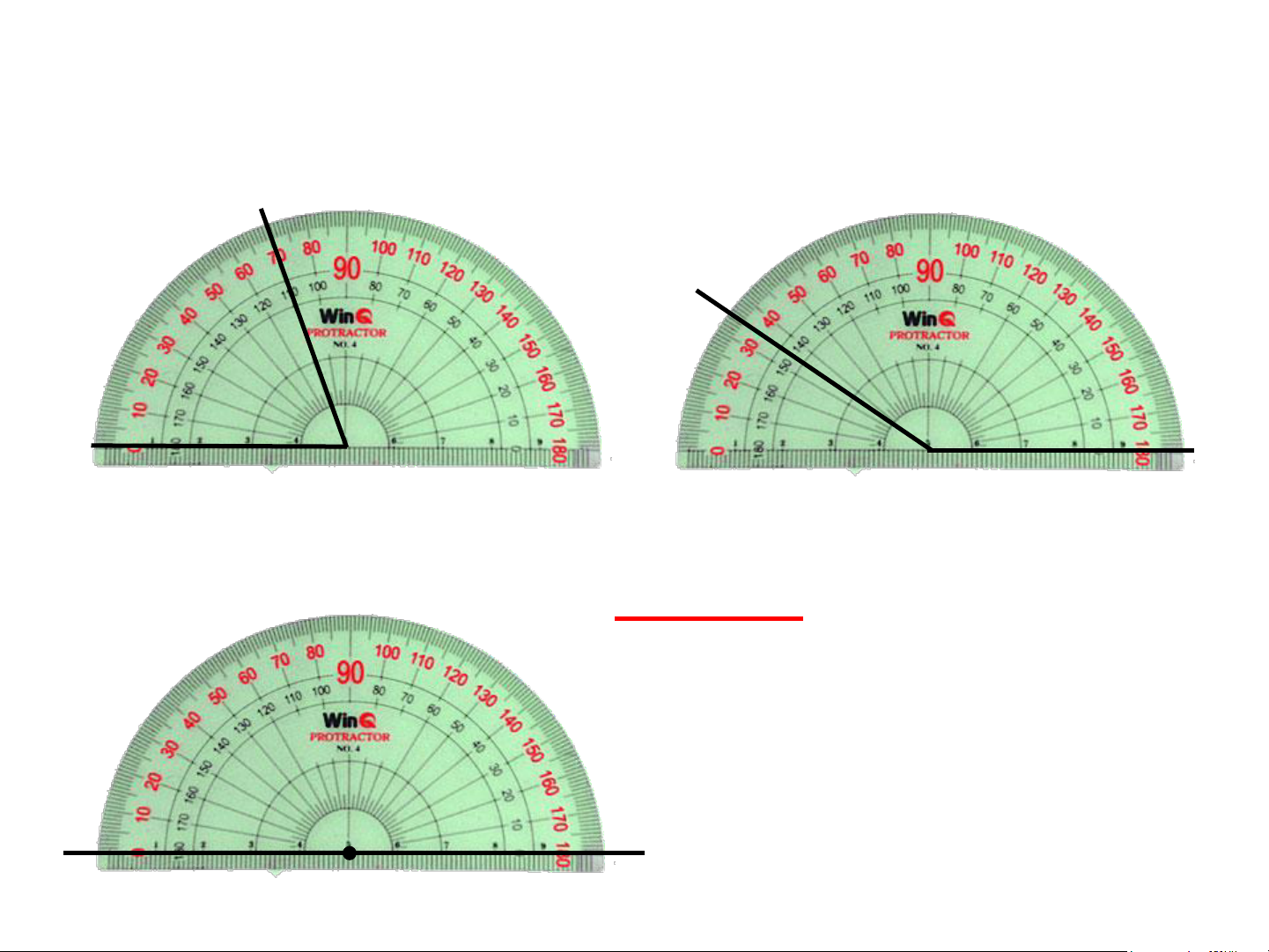
2. Cách đo góc. Số đo góc Hãy đọc số đo các góc có trong hình. 0 xOy = 135 0 xOy = 40 0 0 xOy = 180 xOy = 90
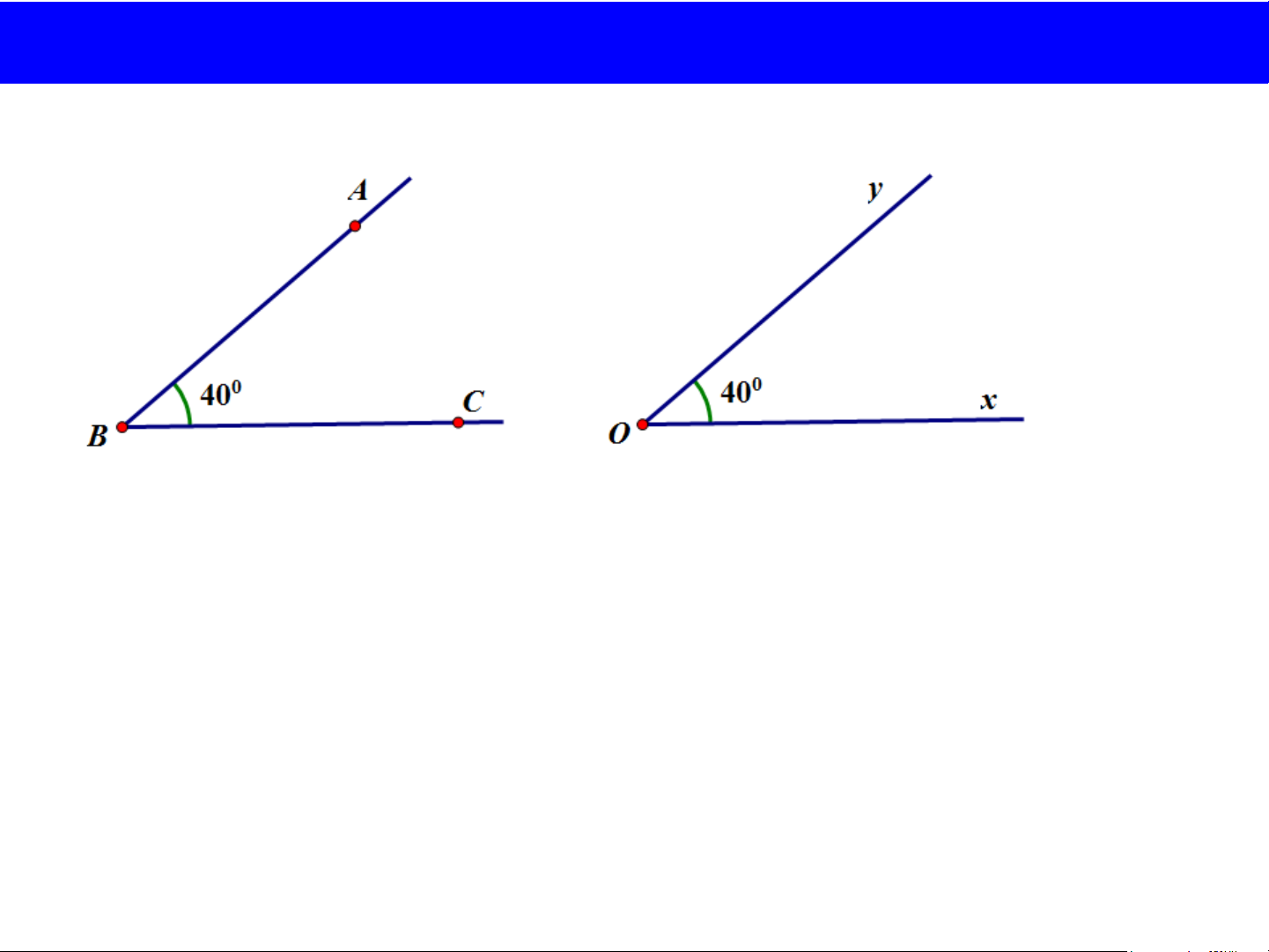
BÀI 7: SỐ ĐO GÓC. CÁC GÓC ĐẶC BIỆT 3. So sánh hai góc 0 ABC 40 0 xOy 40 ABC xOy
Hai góc bằng nhau nếu số đo của chúng bằng nhau
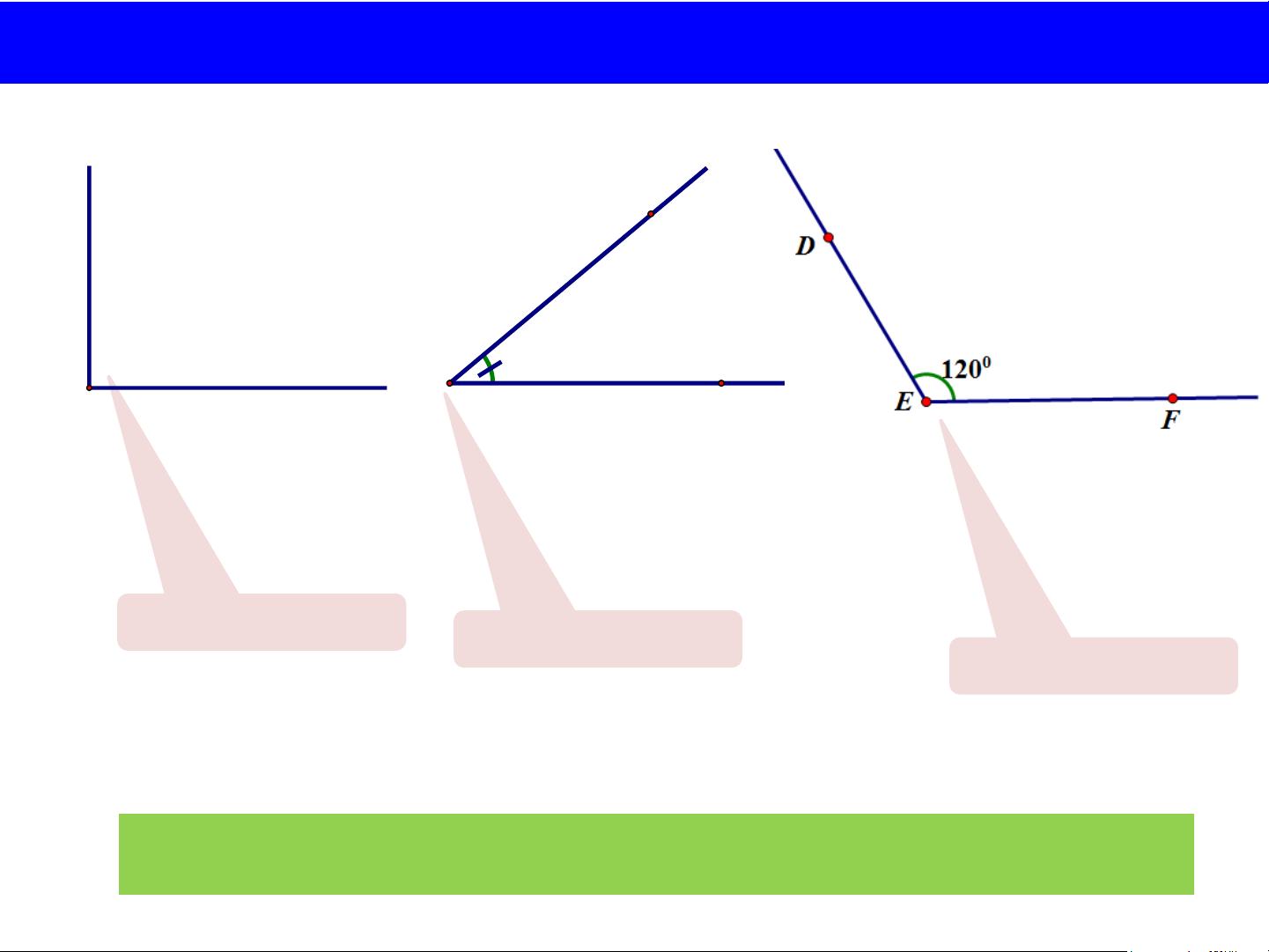
BÀI 7: SỐ ĐO GÓC. CÁC GÓC ĐẶC BIỆT 3. So sánh hai góc A 40 B C 0 0 DEF 120 ABC 40
- Góc ABC nhỏ hơn góc DEF: ABC DEF
- Góc DEF lớn hơn góc ABC: DEF ABC
BÀI 7: SỐ ĐO GÓC. CÁC GÓC ĐẶC BIỆT
4. Các góc đặc biệt v A 40 90 t O B C 0 0 0 tOv 90 ; ABC 40 DEF 120 Góc vuông Góc nhọn Góc tù
Hãy so sánh số đo các góc trên đây với 900
BÀI 7: SỐ ĐO GÓC. CÁC GÓC ĐẶC BIỆT
4. Các góc đặc biệt
- Góc có số đo bằng 900 là góc vuông.
- Góc có số đo nhỏ hơn 900 là góc nhọn.
- Góc có số đo lớn hơn 900 và nhỏ hơn 1800 là góc tù.
LUYỆN TẬP – VẬN DỤNG
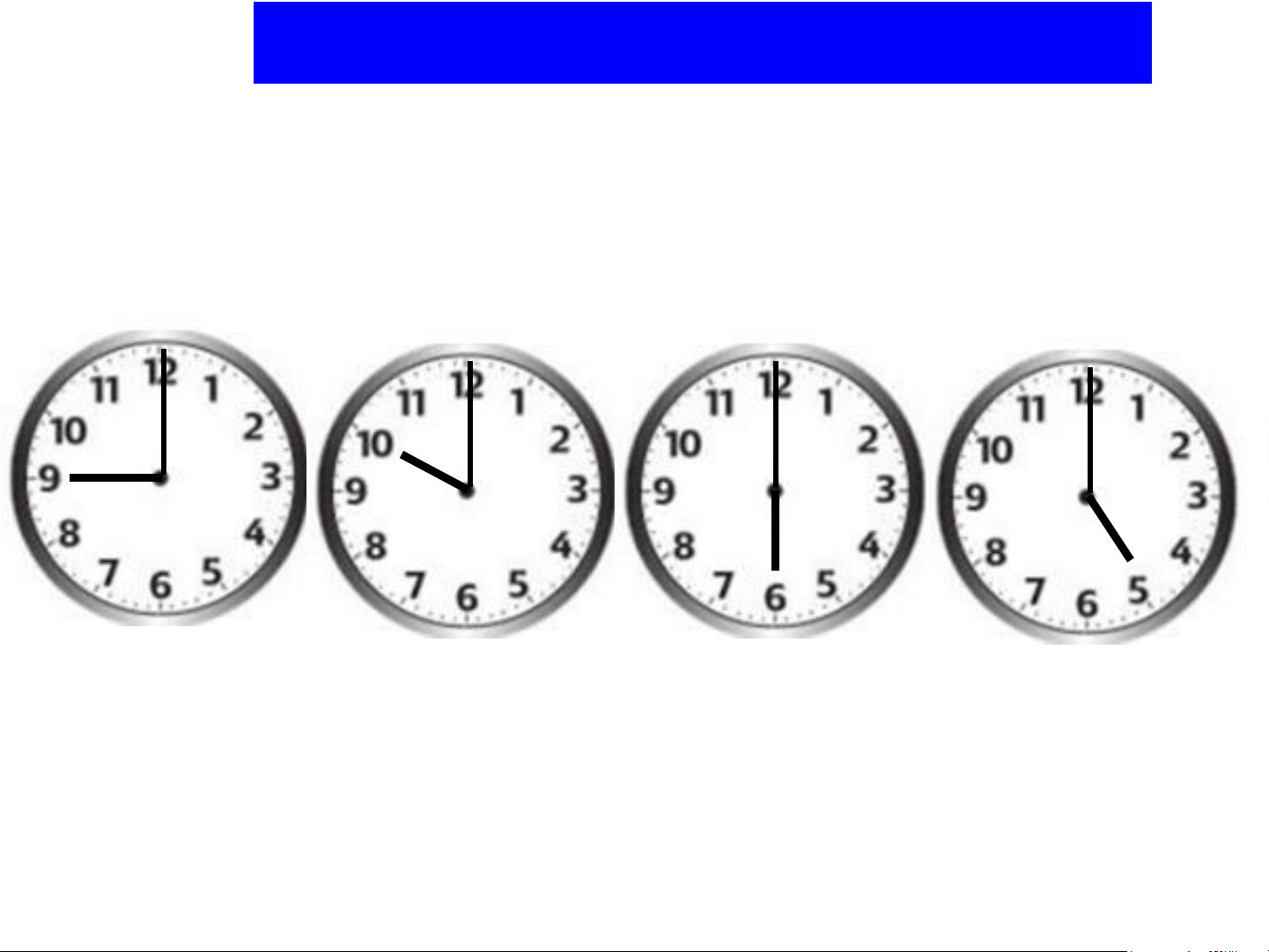
Bài 1: Thảo luận và cho biết góc tạo bởi kim phút và kim
giờ tại thườ điểm 9 giờ, 10 giờ, 6 giờ, 5 giờ lần lượt là bao nhiêu độ. 900 600 1800 1500
LUYỆN TẬP – VẬN DỤNG
Bài 2: Hãy kể tên các đồ vật trong thực tiễn có hình ảnh góc
nhọn, góc vuông, góc tù, góc bẹt. 750 - 800 750 - 800 Hình 1 Hình 2 1 2 3 4 1 2 3 4
Câu 1. Góc tạo bởi kim phút và kim giờ lúc 2 giờ 30 phút là A.1200. B.1050. C.900. D.1000. Đáp án: B.1050.
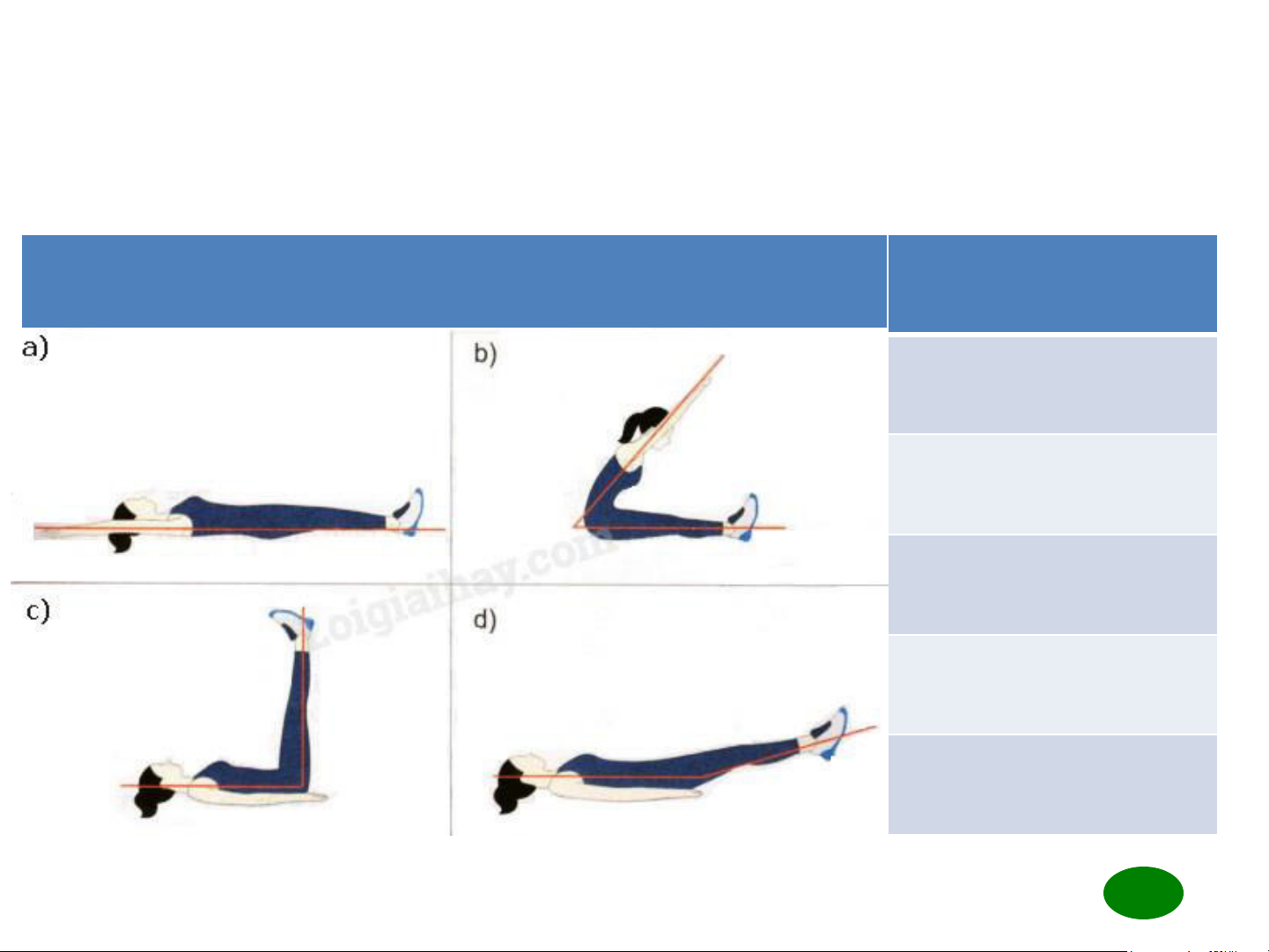
Câu 2. Cho hình ảnh sau. Các tia màu đỏ minh họa các góc ở
các tư thế của một vận động viên tập luyện. Hãy nối cột A với
cột B để có khẳng định đúng Cột A Cột B 1. Góc vuông 2. Góc nhọn 3. Góc tù 4. Góc bẹt a. 4 b. 2 c. 1 d. 3
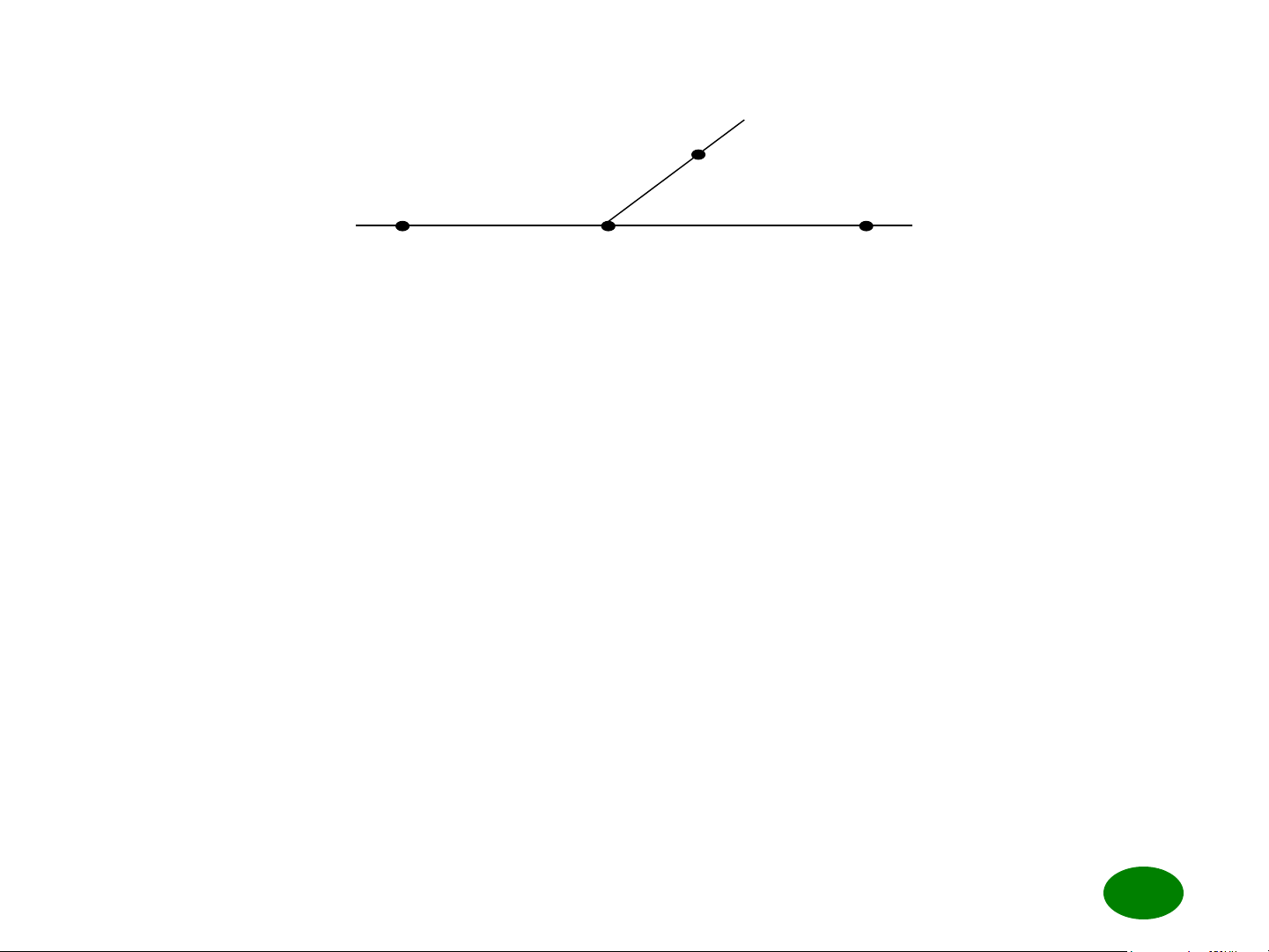
Câu 3. Cho hình vẽ sau C B A D Trên hình vẽ có
Có tất cả bao nhiêu góc? ba góc
Đọc tên các góc Góc BAC, góc CAD, góc BAD
Kí hiệu tương ứng là BAC,CAD, BAD
Câu 4. Điền vào chỗ (…) để có khẳng định đúng z t y x O xOy ... 0 0 50 xOz ... 0 100 xOt .. 1 .30