Chương I: Điện Trường Tĩnh - Định Luật Coulomb và Nguyên Lý Chồng Chất môn Vật lý đại cương 2 | Trường Đại học Bách Khoa Hà Nội

TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI HANOI UNIVERSITY OF SCIENCE AND TECC HN H OLOƯ GY Ơ (HU N
ST) G I Viện Vật lý Kỹ thuật
School of Engineering Physics (SEP) TRƯỜNG TĨNH ĐIỆN 1. Mở đầu 2. Định luật Coulomb 3. Điện trường
4. Định lý Ôxtrôgratxki -Gaox (Ô -G) 5. Điện thế
6. Cường độ điện trường và điện thế 1 1 1. Mở đầu Điện tích
FThuộc tính tự nhiên của những hạt cơ bản có kích thước rất
nhỏ (không thể nhìn thấy bằng mắt thường) tạo nên liên kết về
điện trong nguyên tử. Nguyên tử F Proton (p):
Phần tử cơ sở cấu tạo vật chất: điện tích (+)
tTrạng thái bình thường:trung hòa
điện Þsố evà pbằng nhau, Neutron:
tpgắn cố định trong hạt nhân Không điện tích
nguyên tử, ecó thể dễ dàng di chuyển Electron (e) -điện tử:
Þdễ tạo ra sự mất cân bằng điện tích điện tích (-)
giữa 2vật trung hòa điện khi được cho
tiếp xúc với nhau Þtạo ra i-ôn Điện tích điểm
FĐiện tích có kích thước không đáng kể so với khoảng cách giữa điện
tích và 1điểm trong không gian nằm trong vùng ảnh hưởng của nó. 2 2 1.Mởđầu Điệntíchnguyêntố
FĐiện tích của một electron (hoặc một proton) có giá trị là là e
= 1,6.10-19 C,được qui ước làm giá trị một đơn vi điện tích. Hạt cơ bản Khối lượng Điện tích
Electron 9,11.10-31 kg -1,60.10-19 C (-e)
Proton 1,672.10-27 kg +1,60.10-19 C (+p) Neutron 1,674.10-27 kg 0
Điệntíchcủavậtthểtíchđiện
FĐại lượng vô hướng được xác định bằng một số nguyên (kết
quả sự chênh lệch số các proton và electron) lần điện tích
nguyên tố trong vật thể, tức là Q=e.(Np-Ne) = n.e 3 3 1.Mởđầu Phânloại FĐiện tích dương: FĐiện tích âm: Truyềnđiệntĩnh ++
Cùng dấu:đẩy nhau Khác dấu:hút nhau Ma sát (tiếp xúc) Cảm ứng Dẫn điện Bảotoànđiệntích (điện hưởng)
FĐiệntíchkhôngtựsinhrahaymấtđimàchỉdịchchuyểnbên
trongmộtvậthoặctừvậtnàysangvậtkhác 4 4 2.ĐịnhluậtCoulomb
(Định luật về tương tác tĩnh điện) Dây xoắn ® Charles-Augustin de Coulomb (1736 -1806)
Cân xoắn Coulomb Nguyên lý xác định tương tác tĩnh
điện bằng cân xoắn Coulomb 5 5 2.ĐịnhluậtCoulomb 1.Nộidung:
tLựctươngtáctĩnhđiệngiữa2điệntíchq1,q2đặttrong
chânkhông,cóphươngnằmtrênđườngthẳngnối2điệntích,
cóchiềuphụthuộcvàodấu2điệntích,cóđộlớntỉlệthuận
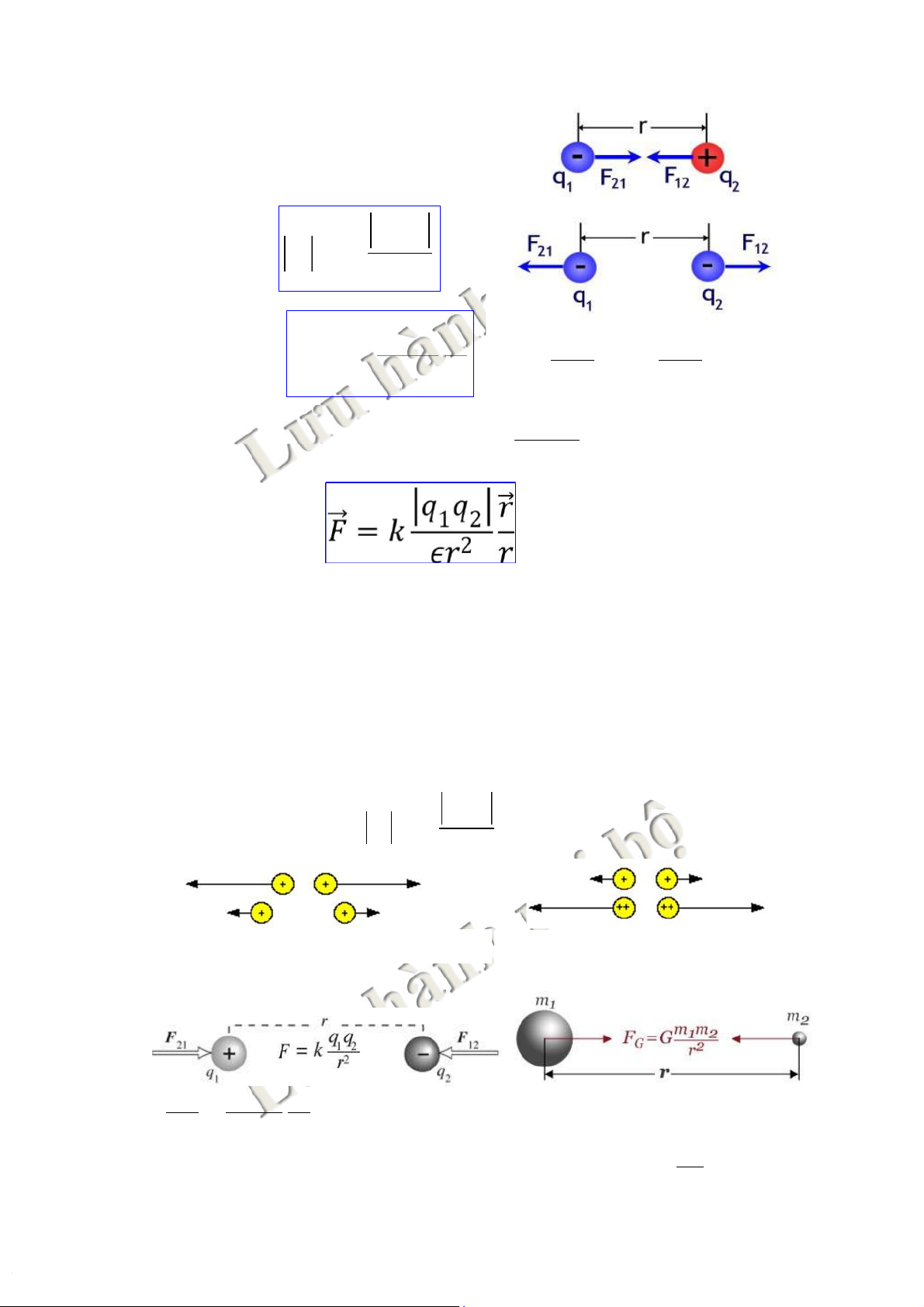
tíchsốq1,q2vàtỉlệnghịchvớibìnhphươngkhoảngcách giữachúng. 6 6 2.ĐịnhluậtCoulomb 1.Nộidung: tTrong chân không và KK: q q 1 2 F= k 2 r ! ! q q r 2 F = k 1 2 1 Nm 9 Tổng quát: k = = 1 . 9 0 r 2 r 2 4pe C 0 2 C 12 Với: e gọi là 8h 8 ,- = ằ 5. ng 1s0 ố điện 2 N0m . tTrong môi trường:
εgọi là hằng số điện môi 7 7 2.ĐịnhluậtCoulomb
2.Đặcđiểm:lực Coulomb phụ thuộc: tkhoảng cách; q q 1 2
tđộ lớn các điện tích. F= k 2 r
Gấp đôi khoảng cách, lực giảm 4 lần Gấp đôi điện tích, lực tăng 4 lần
FLực Coulomb và lực hấp dẫn F q q k e 1 2 = F m m G G 1 2 F
tĐ/v electron:|q|= 1,6.10 e
-19 C, m= 9,31.10-31 kg Þ 42 = 1 , 4 7 1 . 0 FG 8 8 2.ĐịnhluậtCoulomb
3.Nguyênlýchồngchất ! ! !
FĐiện tích q0chịu tác dụng của các lực bở 1 i F h ,2 ệ F đ ,. /.t.,íc Fh n q ! 1,q2,...,qn ! q0 q1 F F 2 1
tTương tác tổng cộng của hệ ! điện tích lên q0: 3 F n ! ! ! ! ! F F = F 1 + ... 2 + F + n = F å i i =1 q2q3 9 9 2.ĐịnhluậtCoulomb
3.Nguyênlýchồngchất
FVật bất kỳ (vòng tròn) mang đ/tích
qtác dụng lên đ/tích điểm q0Þchia
nhỏ qthành các điện tích vô cùng nhỏ
dq,sao cho, dqđược coi là đ/tích
điểm Þxác định lực tổng hợp của
các đ/tích dqlên q0. q dq F = 0 ò 2 4pee Q1 Q2 0 () r V S Fi
F2quả cầu đồng chất phân bố đ/tíchq0
đều (Q1và Q2)Û2đ/tích điểm có vị r r
trí tại tâm 2quả cầu và rlà khoảng
cách tính từ tâm của chúng. dq 10 10 2.ĐịnhluậtCoulomb
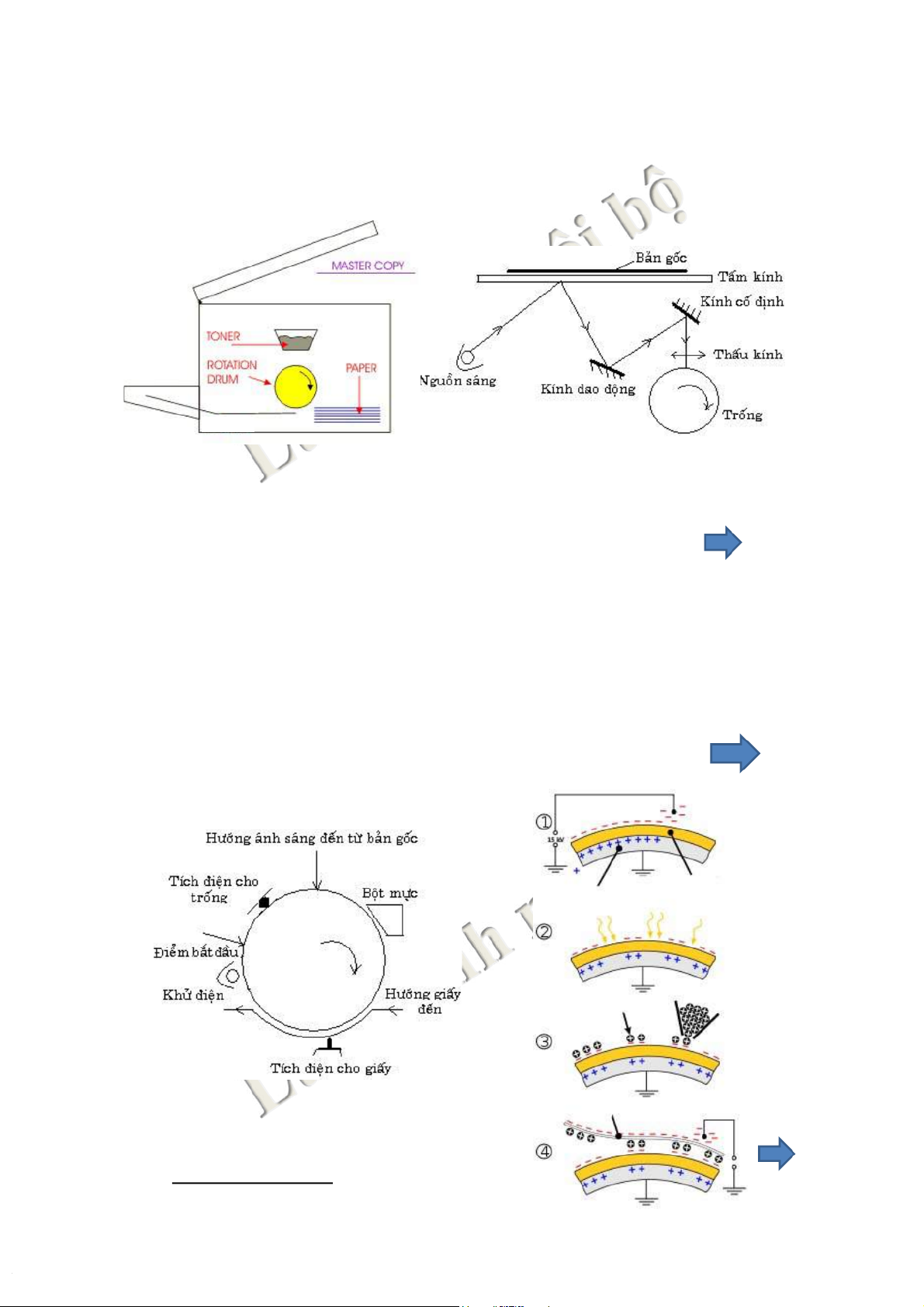
Ứng dụng tương tác tĩnh điện trong kỹ thuật: Máy photocopy
Sơ đồ cấu trúc nguyên lý của máy photocopy 11 11 2.ĐịnhluậtCoulomb
Ứng dụng tương tác tĩnh điện trong kỹ thuật: Máy photocopy Lớp vật liệu quang dẫn Trống tĩnh điện
Ánh sáng từ gương phản xạ
Hạt mực tích điện cảm ứng
Nguyên lý hoạt động của
Giấy được tích điện hút hạt mực trống máy photocopy
Vật liệu quang dẫn:
Polymer polyvinylcarbazole hoặc Selenium 12 12 3.Điệntrường “Trường”
FKhông gian mà một đại lượng vật lý được xác định tại mỗi điểm trong đó.
tĐại lượng vector Þtrường vector;
tĐại lượng vô hướng Þtrường vô hướng.
1.Kháiniệmđiệntrường F Thuyếttácdụngxa:
tTươngtácgiữacácđiệntíchđiểmđượctruyềnđitứcthời(v~ ¥)
tTươngtácđượcthựchiệnkhôngcósựthamgiacủavậtchất trunggian
tKhichỉcó1điệntích
Þ tínhchấtvậtlýcủakhoảngkhônggian
baoquanhkhôngbịbiếnđổi.
Tồn tại vận động phi vật chất Þtrái với triết học duy vật
biện chứng ÞKhông phù hợp! 13 13 3.Điệntrường
1.Kháiniệmđiệntrường(tiếp)
FThuyếttácdụnggần:
tTươngtácgiữacácđiệntíchđiểmđượctruyềnđikhôngtức thời(vhữuhạn)
tTươngtácđượcthựchiệnthôngquasựthamgiacủavật chấttrunggian
tKhichỉcó1điệntích
Þ tạorađiệntrườngxungquanh Þ
giữvaitròtruyềntươngtác.
Phù hợp với triết học duy vật biện chứng Þđược khoa học công nhận!
tĐiện trường:khoảngkhônggianbaoquanhcácđiệntích,
thôngquađótươngtác(lực)tĩnhđiệnđượcxácđịnh.
tĐiện trường là trường vector. 14 14 3.Điệntrường
Q Điện tích thử
2.Vectorcườngđộđiệntrường
FXét điện tích q0= 1C(đ/tích thử) r
đặt trong điện trường của Q. tLực Coulomb ! ! ! Qq r æ Q r ö F. = k 0= = q ç ÷ 2 0 k q 2 0 E r r è r r ø ! ! ! F Q r FKhái niệm: E = = k q r2 r 0
tCườngđộđiệntrườngtại1điểmnàođólàđạilượngvậtlýcó
độlớnbằngđộlớncủalựcđiệntrườngtácdụnglên1đơnvịđiện
tích+1Cđặttạiđiểmđó. 15 15 3.Điệntrường
2.Vectorcườngđộđiệntrường tĐộ lớn: 9 1 . 9 10 Q Q Q E = k = = 2 2 2 4 r pee r e r 0
tÝnghĩa:Đặctrưngchokhả
năngtácdụnglực(mạnh,yếu)của
điệntrườngtạicácvịtríkhông giankhácnhautrongđó.
tĐơn vị:N/Choặc V/m. 16 16 3.Điệntrường
3.Nguyênlýchồngchậpđiệntrường ! ! ! ! FXét q F 1,q2tác dụng lực 1 F ,Flê 2 n q0(đặt tại P): ! E ! ! ! tcó: F ! F F= 1 F+ 2 2 ! ! ! ! P ! F1 E E F 1 2 1 F 2 F ! ! q0 Þ = + r r 1 2 0 q q 0 q 0
tĐiện trường gây bởi q1và q2: q q2 1 = ! + ! = ! ! ! 1 æ+ ö q r q r E E E çç 1 1 2 2 2 2 ÷÷ 1 4 2 pee0 è 1r 1r 2 r r2 ø 17 17 3.Điệntrường
3.Nguyênlýchồngchậpđiệntrường(tiếp)
FĐiện trường gây bởi nđiện tích điểm tại vị trí bất kỳ: ! ! ! ! ! n ! n 1 q r E =E +E +... +E 1 4 2 å = E = å i i n r i 2 pee i=1 0 i= i 1 ri P
tVec t orcườngđộđiệntrường
gâybởimộthệđiệntíchtạibất
kỳđiểmnàotrongtrườnglàtổng + -
cácvectorcườngđộđiệntrường
gâybởitừngđiệntíchtạiđiểm + đó. - + - + 18 18 3.Điệntrường
3.Nguyênlýchồngchậpđiệntrường(tiếp)
FĐiện trường gây bởi vật mang điện có điện tích phân bố liên tục:
tChia vật thành vô số các phần tử vô cùng nhỏ
mang điện tích dqÛđiện tích điểm. dEi S EP
tĐiện trường gây bởi dqtại 1điểm cách dq P P đoạn r: 9 ! ! 1 . 9 0 dq r rr E d P = e r2 r dq
tĐiện trường tổng hợp gây bởi toàn bộ vật dq
mang điện tại 1điểm trong không gian của điện trường: ! ! ! 9 9.10 dq r E = ò = E d ò Pr e r 2 toàn bô vât toàn bô vât 19 19 3.Điệntrường
3.Nguyênlýchồngchậpđiệntrường(tiếp)
FĐiện trường gây bởi vật mang điện có điện tích phân bố liên tục (tiếp) t !
Dây tích điện có độ dài l 9 ! Þ E = . 9 10 òl dl r
Đ/tích của vi phân độ dài:dq= ldl e 2 r (lr)
(l:mật độ điện dài =điện tích/đơn vị độ dài)
tMặt tích điện có diện tích S ! 9 ! . 9 10 s dS r
Đ/tích của vi phân diện tích:dq= sdS Þ E = ò 2 e Sr r
(s:mật độ điện mặt =điện tích/đơn vị diện tích) ( )
tKhối tích điện có thể tích V ! 9 ! 1 . 9 0 r dV r
Đ/tích của vi phân thể tích:dq= rdV Þ E = ò 2 e Vr r ( )
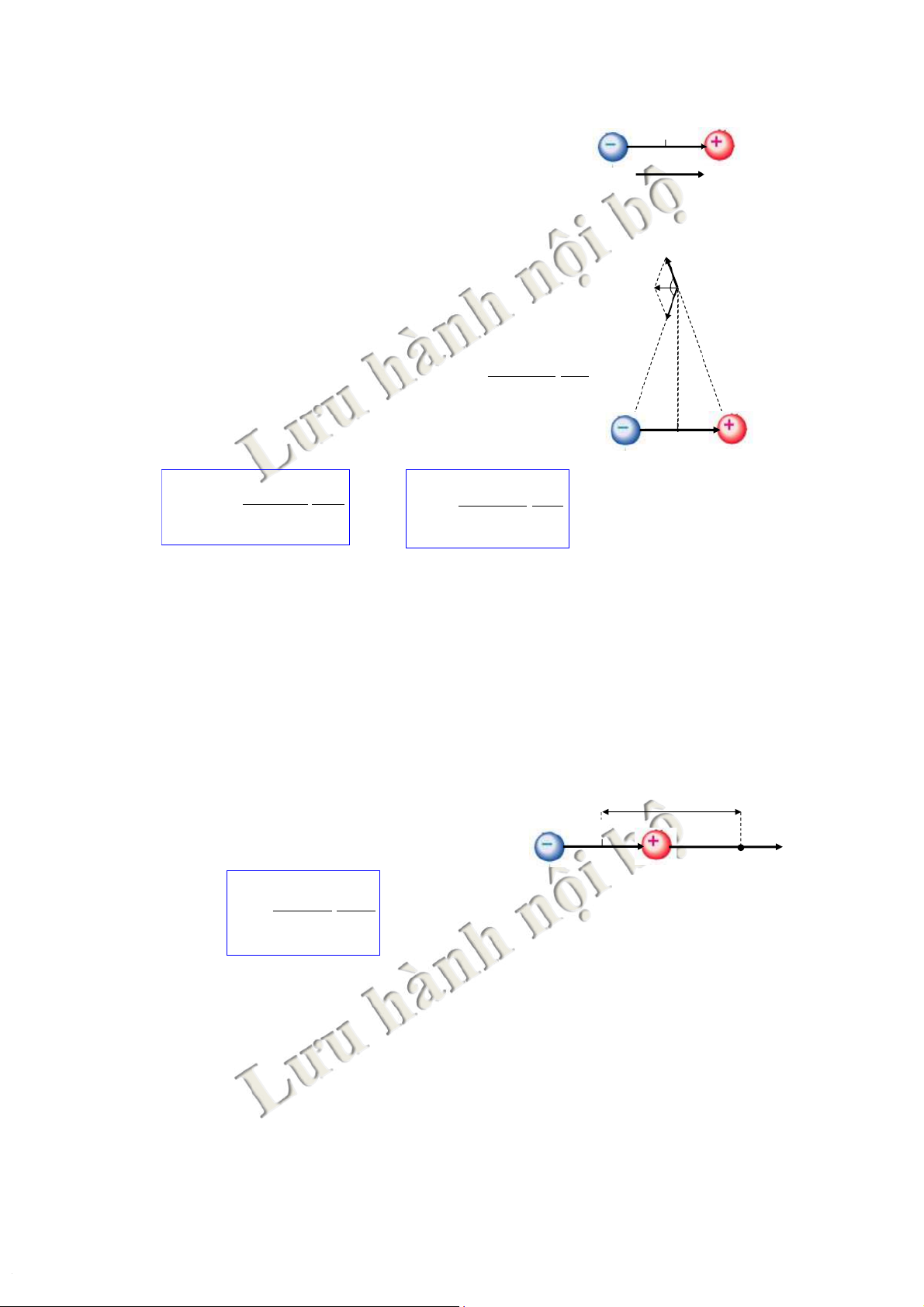
(r :mật độ điện khối =đ/tích/đơn vị thể tích) 20 20 3.Điệntrường 4.Vídụ *Lưỡngcựcđiện 0!
FKhái niệm:hệ2điệntíchđiểmtráidấu -q d +q !
cóđộlớnbằngnhaucáchnhaumộtkhoảng p
d(rấtnhỏ),đặctrưngbởiđạilượ!ng != ! momentlưỡngcực: pe d q E2 ! F a
Điện trường gây bởi lưỡng cực điện: E a M !
tTại điểm nằm trên đường trung trực E1
(r1=r2 » r>> d) ! ! ! 1 q r1 r r2 có : E E E = + với: E = E = 1 2 2 14 2 pee r 0 Hay:E=E1.cos a +E2.cos a ! 0
=2E1.cos a ;(cos a =d/2r1) -q+q d ! 1 qd ! 1 p Þ E = E - e= 3 4pee r 3 hay: 4pee 0 r 0 21 21 3.Điệntrường 4.Vídụ *Lưỡngcựcđiện r
tTại điểm nằm trên trục lưỡng cực 0 ! E (r>> d) ! ! -q+q d N ! 1 2 p Có: Ee= 3 4pee r 0 22 22 3.Điệntrường
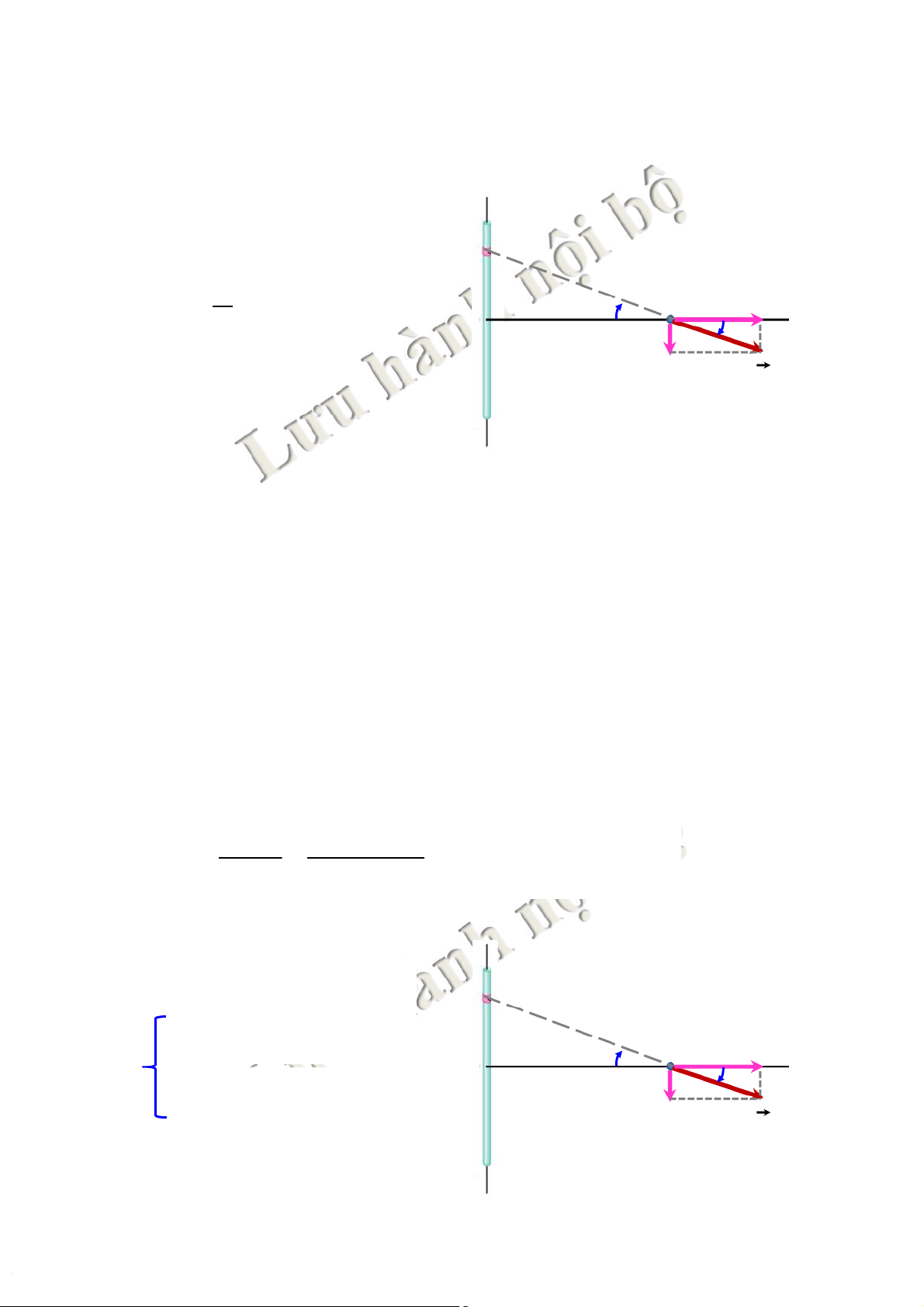
*Điệntrườnggâybởidâydẫnthẳngdàivôhạn
FDây: độ dài l,điện tích Q,mật độ điện tích dài l. y +l/2
tChia dây thành các phần tử độ
dài dlvô cùng nhỏ, có điện tích:dQdl r Q dQ = dl d l = l aa P dEx l O x x
tĐiện trường tại Pgây bởi dQ: Q dEy ! ! ! dE E d E d = xE d + y -l/2
với dEx=dE.cos a + / 2 l + / 2 l + / 2 l + / 2 l + / 2 l l E ò x dl = dE ò = dE dE dE a x ò + = y ò cos = ò 3 / 2 2 2 x pee -+/2 4 ly - / 2 l - / 2 l - / 2 0 l - / 2 l () ! " # 23 = 0 23 3.Điệntrường
*Điệntrườnggâybởidâydẫnthẳngdàivôhạn / 2 2 x l l dl ll = 3 / 2 =ò 2 2 4pee pee 020 (x + y ) 1/ 2 2 2 x x + l 0 () y +l/2 dQ l dl x<< lÞ E = r 2pee x aa P dE 0 x O Q x x x>> lÞ Epee = 2 dE 4x y 0 dE -l/2 24 24 3.Điệntrường
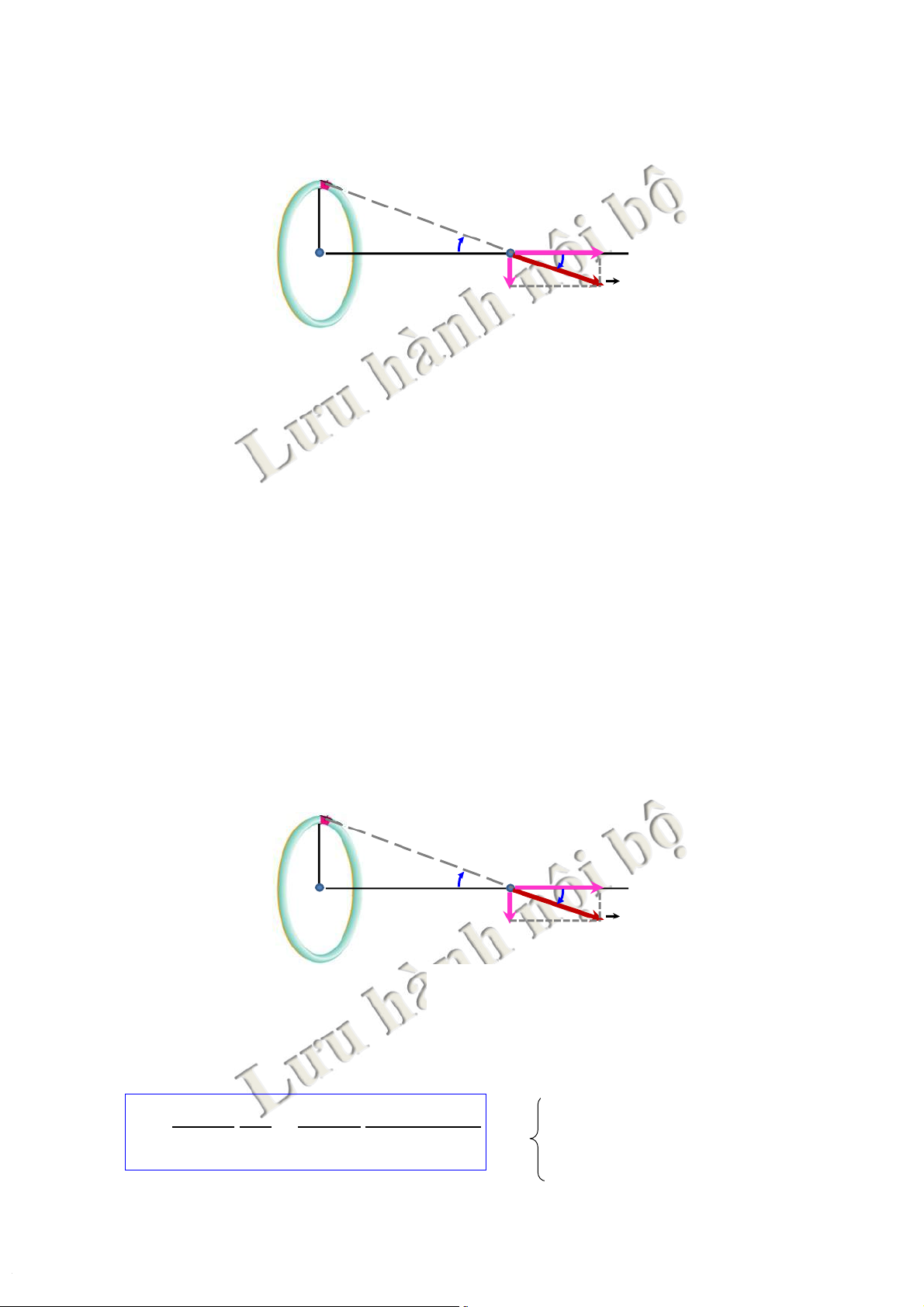
*Điệntrườnggâybởivòngdâytròntíchđiệnđều
FDây tròn: bán kính R,mật độ điện tích dài l,điện tích Q.
dQ = ldl r R Q dEx O a P O a x x dEy dE
tChia dây thành các phần tử độ dài dlvô cùng nhỏ, có điện tích dQ= ldl
tĐiện trường tại Pgây bởi dQ: ! ! ! dE dE= x dE+ y
với dEx=dE.cos a 25 25 3.Điệntrường
*Điệntrườnggâybởivòngdâytròntíchđiệnđều
dQ = ldl r R Q dE a P x O a x x dEy dE 2 R p 1 dQ l x E = ò cosa = dE = òdE + dE dl x ò y ò 2 3 ò p 4 ee04r pee0 r vòng tròn vòng tròn vòng tròn vòng tròn 0 ! ! " # $ =0 1 Q 1 Qx 1 Qx
x<< R: E = E 3 = = 4pee R 0 3 4pee Þ 04r pee0 () 3 / 2 2 2 x + R x>> R: 1 Q E = 2 4pee r 0 26 26 3.Điệntrường
*Điệntrườnggâybởimặtđĩatíchđiệnđều
FĐĩa: bán kính R,điện tích Q,mật độ điện tích s:
tXét hình vành khăn có diện tích ds,độ rộng dR ’ mang điện tích dQ: = s = dQ s p ds 2 R d ' R ' dR’
tĐiện trường gây bởi dQ: r R R’ R’ dQ ps dEx 2x R' dR' = E = E dE dEcosa x =x = O ò = ò ò 3/ 2 x 2 '2 4pee0 0 (x )+R æ ö RQ ç ÷ s ç 1 ÷ = ç1 - 2 ÷ e 2 e R 0 çç 1 + 2 ÷÷ è x ø s
tNếu R®¥(mặt phẳng vô hạn) Þ E =2ee 27 0 27 3.Điệntrường
5.Đườngsứcđiệntrường
FĐườngconghìnhhọcmôtảđiện
trườngmàtiếptuyếntạimỗiđiểmcủa
nótrùngvớiphươngcủavectorcường
độđiệntrườngtạiđiểmđó.
FChiều đường sức điện trường là
chiều vector cường độ điện trường.
FĐiệnphổ:tập hợp các
đường sức điện trường 28 28 3.Điệntrường
Điệntíchtrongđiệntrườngngoài
FCho trước 1điện tích Þtạo ra điện trường xung quanh nó!
FCho trước 1điện trường Þảnh hưởng của đ/trường lên điện tích đặt trong đó? ! !
tĐiện trường tác dụng lên điện tích 1lực điện: F = q E .
tChiều của Fkhông phụ thuộc chiều Emà phụ thuộc dấu điện tích !º !
Điện tích qchuyển động cùng chiều điện trường đều E v E ! ! = = !.
FPhương trình động lực học: ma F q E q = a y=a E +q m q = Þ= v y.v E t v m 1 E t q 2 y= . (ph/trình CĐ) 2 m 29 29 3.Điệntrường
Điệntíchtrongđiệntrườngngoài ! !^
Điện tích -q đi vào vùng điện trường đều Evới vận tốc ban đầu,v E 0 v0 qE Các đặc trưng ax= 0 ; ay= m ÞPhương trình quĩ đạo: động học theo 2 v q æ E ö x=v phương Ox và Oy: 0 ; vy÷= ç t è æ ö m ø 1x qE 2 = æ ö y÷ ÷ çç 2 x=v 1t qE 2 2 èmv ø 0.t; y÷= ç 0 30 2 è m ø 30
4.ĐịnhlýÔxtrôgratxki-Gaox(Ô-G)
1.Vectorđiệncảm–điệndịch Johann Carl-Friederich Gauss (1777-1855)
Vec to r cường độ điện trường:
Vec to r cảm ứng điện (điện cảm) ! ! ! ! 1 q r 1 D q Þ Ïe EÎ e = ee E E = 0 Þ D = 2 4pee r 2 r 4p r 0
ÞPhổ đường sức của vector
ÞPhổ đường sức của vector
điện trường gián đoạn khi qua
điện cảm là liên tục khi qua mặt
mặt phân cách 2môi trường phân cách 2môi trường 33 33
4.ĐịnhlýÔxtrôgratxki-Gaox(Ô-G) 2.Điệnthông
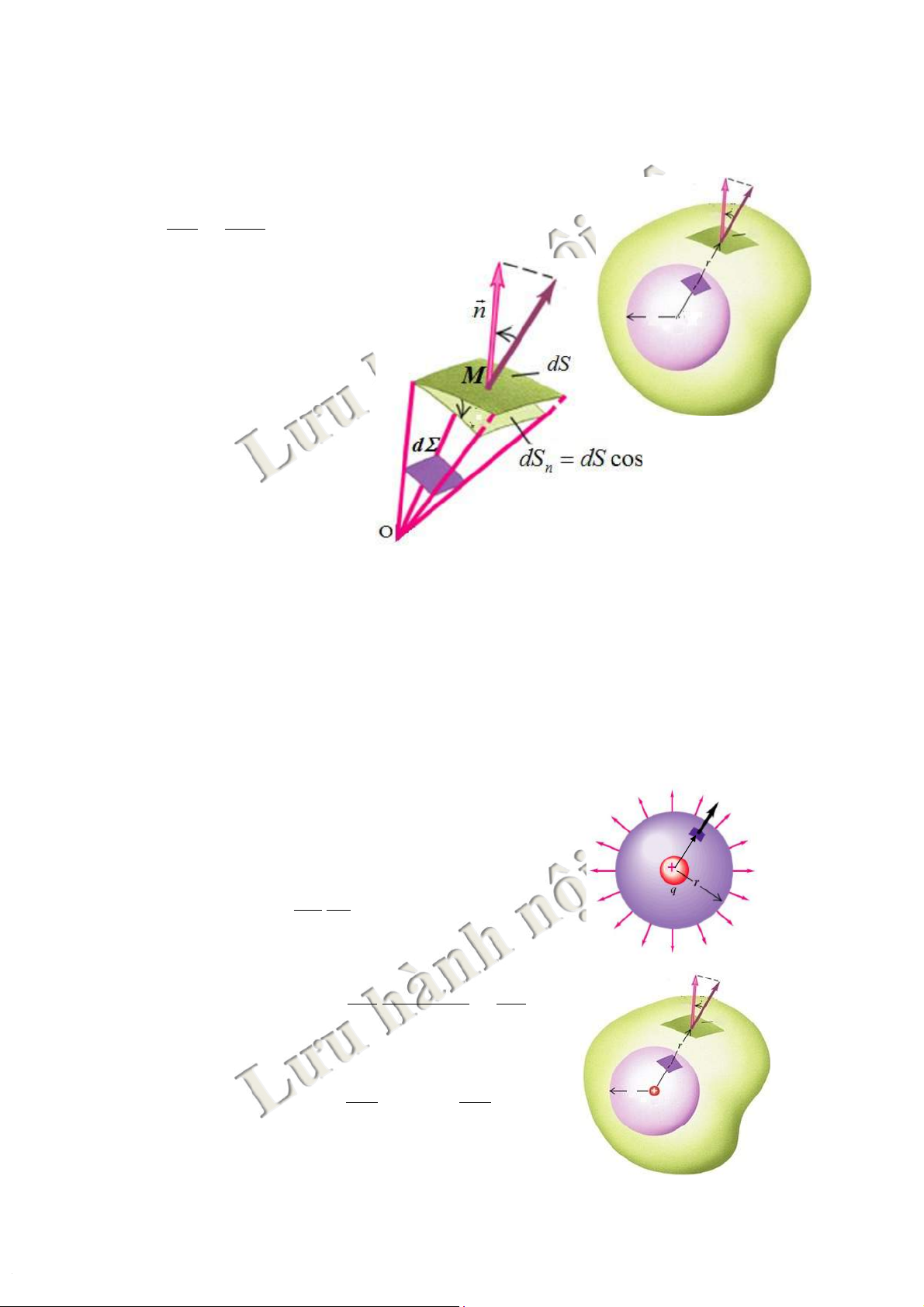
FKhái niệm:Thônglượngvectorđiệncảm
gửiquamộtthiếtdiệncótrịsốtỉlệvớisố !D
đườngsứccắtvuônggócthiếtdiệnđó. Fe= D.S0 S0
FTiết diện (S)bất kỳ, tạo với S0góc a ÞS0=S.cos a! n! a = !, t
là vector pháp tuyến của mặt S, cũng có: (n)D
Fe=D.S0=D.S.cos a =DnS ! ! ! n t a !
Dnlà hình chiếu của D lên phương pháp tuyếnn a D p (S0)(S) ae < Þ F > 0 2 p ae > Þ F < 0 2 p Þae F= 2= 0 34 34
4.ĐịnhlýÔxtrôgratxki-Gaox(Ô-G) 2.Điệnthông(tiếp)
FĐiện trường bất kỳ:xét phần tử diện tích dS ! ! ! a ! n
dFe = D.S0=D.dS.cos a Þ deF D. dS = D dS tĐiện thông toàn phần: ! ! (S) D F S d = D edS ò= . ò n S S
tĐơn vị: N-m2/C 35 35
4.ĐịnhlýÔxtrôgratxki-Gaox(Ô-G) 3.Góckhối da dS cos FGóc khối vi phân: W = a 2 r a nhọn ÞdW> 0 atù ÞdW< 0 a (!r) OM = a dS Hay: dnW = 2 r 36 36
4.ĐịnhlýÔxtrôgratxki-Gaox(Ô-G)
FXét mặt kín bất kỳ Þxây dựng mặt cầu S,tâm O, bán kính đơn
vị (tức là, R= 1), sao cho dS nằm trong hình nón tạo góc khối dW. ! n a dnS dS Có: dS = Þçd W ç=dS 2 2 1r M ! t n hướng ra ngoài: dS Þd W =+d S a R O S ! t n hướng vào trong: Þd W =-d S a
F W =±4 p(1)2=±4 p a 37 37
4.ĐịnhlýÔxtrôgratxki-Gaox(Ô-G)
4.Điệnthôngxuấtpháttừđiệntíchđiểmq ! n !
Trong mặt cầu kín Shoặc mặt kín bất kỳ D d OM
FVec to r điện cảm (điện trường) ºphương OM S r 1 q Có: Dp= 2 4 r
tĐiện thông qua diện tích vi phân dS: ! n cos a q dS q F cos a
de4d = DdS 2 = = W a !D dS 4p p r
tĐiện thông qua mặt kín S: M dS q q O p W Rq e ò = d d = q 4 Fò = Fe = S 4p 4p S S
tMặt kín bao quanh điện tích điểm hay vật
mang điện:mặt Gauss 38 38
4.ĐịnhlýÔxtrôgratxki-Gaox(Ô-G)
4.Điệnthôngxuấtpháttừđiệntíchđiểmq(tiếp)
Ngoài mặt kín Sbất kỳ
FĐường sức vector điện cảm là đường !
hở Þhoặc không cắt hoặc cắt số chẵn lần n
(một đi vào mặt S1,một ra khỏi mặt S2). S1 a ! q ! D tCó: Φ S2 e = dΩ ò q !n a π 4 S n a W t = Với: + W ò d W òd òd ! S S 1 S 2 a ! ! ! n D
tS1tương ứng hn ướng ngược chiều D ! !
tS2tương ứng n hướng cùng chiều D t òd + Wò dW= ( - DS ) + (+DS =)0 1 S 2 S tVì vậy: Fe=0 39 39
4.ĐịnhlýÔxtrôgratxki-Gaox(Ô-G) Nội dung
tThônglượngđiệncảmgửiquamộtmặtkínbấtkỳbằngtổngđại
sốcácđiệntíchnằmtrongmặtkínđó. n Φ D dS e = q ò n. = å i (S ) i=1 40 40
4.ĐịnhlýÔxtrôgratxki-Gaox(Ô-G)
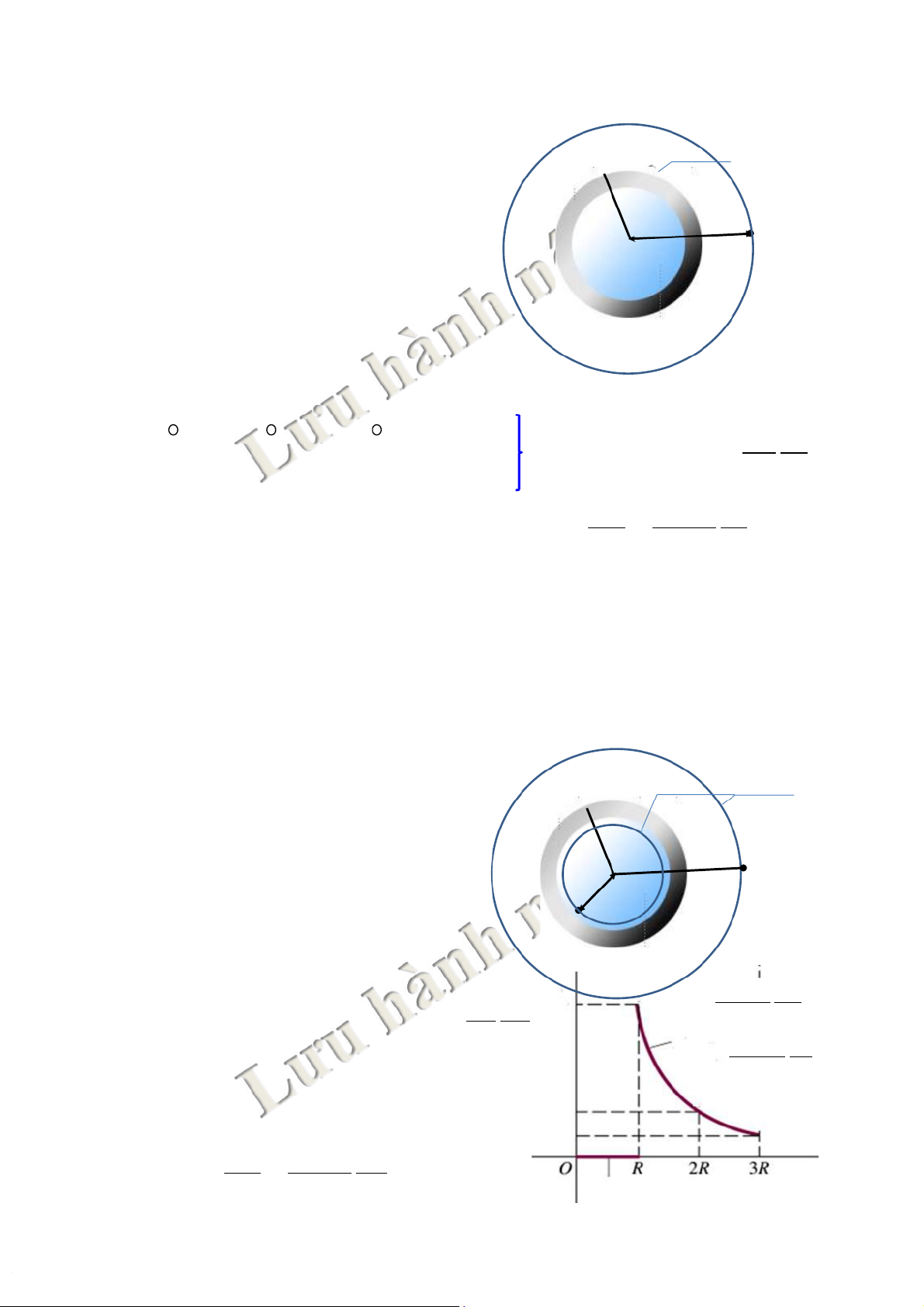
5.Xácđịnhcườngđộđiệntrường ứngdụngđịnhlýGauss Mặt Gauss Q ËËË Ë
Quả cầu rỗng (bán kính R) tích Ë R r
điện đều (Q > 0) trên bề mặt Ë Ë O Ë P
FĐiểm Pbên ngoài, cách Okhoảng r. ËË Ë t Ë Ë
Dựng mặt Gauss bao quanh, bán kính r>R.
tThông lượng điện cảm qua mặt Gauss, bk r: 2 D dS D.4 p er . n = = ò= ò ò 1 Q 2 D Þ = . p 4= r . Q D tĐịnh lý Gauss: Φ 2 p e= Q 4 r D 1 Q
tCường độ điện trường bên ngoài quả cầu: E = = 2 ee 04 pe 0 e r 41 41
4.ĐịnhlýÔxtrôgratxki-Gaox(Ô-G) Mặt Gauss
5.Xácđịnhcườngđộđiệntrường
ứngdụngđịnhlýGauss(tiếp) ËË Ë
Quả cầu rỗng (bán kính R) tích Ë Ë
điện đều (Q > 0) trên bề mặt (tiếp) R Ë rP Ë r’ O
FĐiểm P ’ bên trong, cách O Ë Ë khoảng r’. P’ Ë Ë Ë Ë
tDựng mặt Gauss sát mặt cầu,
bán kính r’ <R. 1 Q 1 Q E E(R pe ) e = tTương tự có: 2 D Þ = . p 4= r . ' Q D 2 4 2 0 p 4 r' 1 Q
tBên trong q/cầu ko có điện tích: E(r p ) ee= 2 4 0 Q= 0 ÞE= 0
tTrên bề mặt:r=R,có: E= 0 D 1 Q Epee = = r 2 ee 04 0 42 R 42