Chương I: Hàm số một biến số môn lý thuyết ma trận | Đại học Sư phạm Hà Nội

ÁO TRÌNH TOÁN CAO CẤ 1
Ch−¬ng I: Hμm sè mét biÕn sè
Ố THỰC VÀ HÀM SỐ
ác số thực và ðýờng thẳng thực
ác số thực là những số có thể biểu diễn dýới dạng thập phân nhý :
ðó dấu ba chấm (… ) chỉ dãy các ký số sau dấu chấm thập phân kéo dài ðến vô ạn .
ác số thực có thể ðýợc biểu diễn về mặt hình học bởi các ðiểm trên 1 ðýờng thẳ
ðýợc gọi là ðýờng thẳng thực nhý minh họa dýới ðây:
ập hợp tất cả các số thực (hay ðừng thẳng thực ) sẽ ðýợc ký hiệu là R
ên tập hợp các số thực ta có hai phép toá
õ bản + và * với một số tính chất ðại số
ộc ðã biết . Từ ðó ta cũng có phép toán trừ (
à phép chia (/) cho số khác 0. ài ra trên R
ũng có một thứ tự thông thýờng và với thứ tự này ta có một số
ính chất ðýợc viết dýới dạng các bất ðẳng ức nhý sau:
ếu a,b, và c là các số thực thì ta có   à c > 0 
Sưu tầm và chỉnh s a by Nguy ử ễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 2 à c< 0  ðặc biệt : a < b  
ếu (a và b cùng là số dýõng ) à b cùng là số âm ) ì ta có :
R ó một số tập hợp con quen thuộc là tậ
ợp các số tự nhiên N ập hợp các số
ên Z à tập hợp các số hữu tỉ Q
ứ tự "bao hàm trong " thì N  Z  Q  R
ác số thực không thuộc Q ðýợc gọi là các số vô tỉ .
ý hiệu các khoảng ðoạn và nửa khoảng :
ới a và b là các số thực , ta ký hiệu : à { x  R à {x  R à {x  R à { x  R  à {x  R  à { x  R  à {x  R  à {x  R   à R
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 3 ú :
ýời ta còn chứng minh ðýợc rằng R ó tính chất ðầy ðủ . Theo tính
ất này thì mọi tập số thực khác rỗng bị chặn trên ðều có cặn trên ðúng (tức là chặn
ên nhỏ nhất). Týõng tự , mọi tập số thực khác rỗng bị ó chặn dýới ðúng.
ý hiệu "giá trị tuyệt ðối”:
á trị tuyệt ðối của một số thực x ,ký hiệu bởi |x|, ðýợc ðịnh nghĩa nhý sau :
ừ ðó ta có một số tính chất dýới ðây: ới mọi
ýu ý rằng về mặt hình học ,  
ểu diễn khoảng cách từ ðiểm x ðến ðiểm 0 trên
ðýờng thẳng thực . Tổng quát hõn là :   ảng cách giữa x và y
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 4 àm số Ðịnh nghĩa:
ột hàm số f từ một tập D vào IR là một quy tắc cho ứng với mỗi x  à một phần ử duy nhất f (x)  R
ột hàm số thýờng ðýợc cho dýới dạng công thức nhý ác ví dụ sau:
àm số ðýợc cho bởi một công thức nhý hàm số g(x) ở trên thì tập hợp tất cả các
à g(x) xác ðịnh ðýợc gọi là ền xác ðịnh của hàm số í dụ:
ền ác ðịnh của hàm số
à tập hợp các số thực x sao cho : –    
ậy miền xác ðịnh là : (   
Ðồ thị của hàm số:
Ðồ thị của hàm số f là ðýờng biểu diễn trong mặt phẳng Oxy có phýng trình y=f(x).
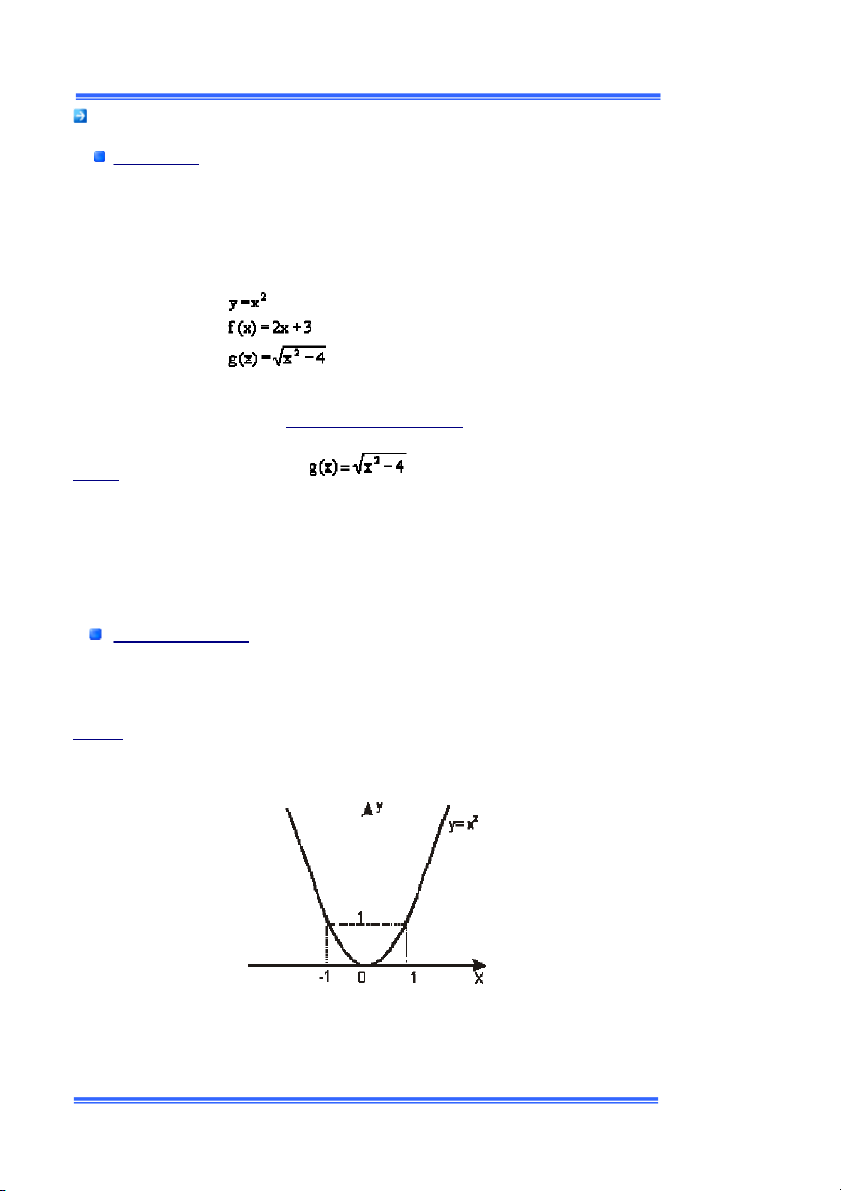
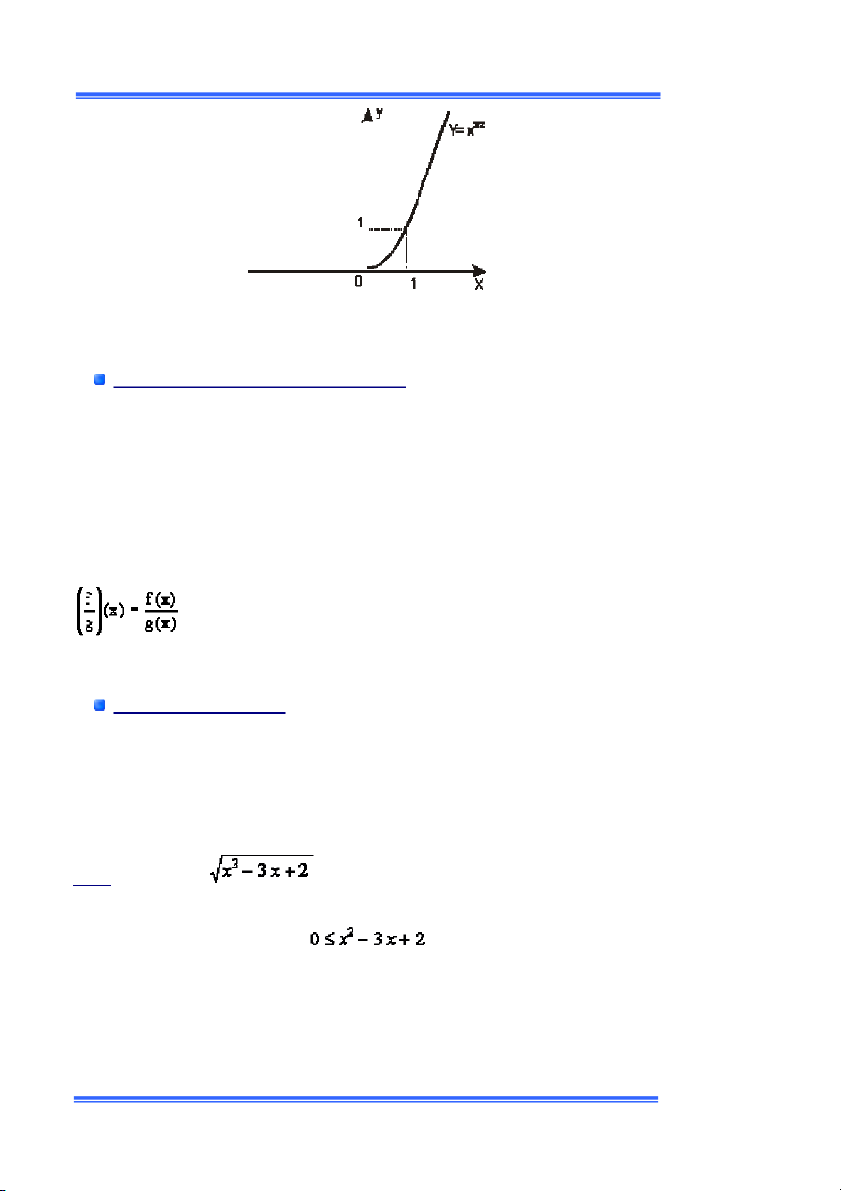
ó bao gồm tất cả các ðiểm (x , f(x)) với x chạy trong miền xác ðịnh của hàm số. í dụ : Ðồ ị hàm số y = x Ðồ thị hàm số y = x
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 5
ổng, hiệu, tích, thýõng của các hàm số:
à g là 2 hàm số, và c là một hằng số. Ta ðịnh nghĩa các hàm f+g, f–
à c.f bởi các công thức sau:
ợp nối của các hàm số
ợp nối của f(x) và g(x) là 1 hàm số ðýợc ký hiệu là g à ðýợc ðịnh nghĩa bởi : 
ền xác ðịnh của g à tập hợp các giá trị x sao cho f(x)  ền xác ðịnh của g. í dụ àm số y =
ó miền xác ðịnh là tập hợp tất cả các số thực x 
ậy miền xác ðịnh là D = (   
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 6 ÁC DẠNG VÔ ÐỊNH
àm týõng ðýõng ,VCB ,VCL Ðịnh nghĩa 1:
àm số f(x à g(x) không triệt tiêu trong một khoảng quanh x ó thể loại ừ x
ói f(x) týõng ðýõng với g(x) khi x ếu: ấy , ta viết :  ặc là : khi x  ính chất :      à g(x)    í dụ : ó : Ðịnh nghĩa 2: ác ðịnh quanh x ó thể loại trừ x
ói f (x) là một ðại lýợng vô cùng é khi x ết tắt là VCB , khi ýờng hợp ta có ặc +  ặc  ói f (x) là vô cùng lớn ết tắt là VCL) khi x í dụ:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 7 ó x, ln(1+x), 1 – à các VCB. ó ln(x), à các VCL  ó x, ln(x), ex là các VCL
ú : ác khái niệm về hàm týõng ðýõng, VCB và VCL cũng ðýợc ðịnh
ĩa týõng tự nhý hai ðịnh nghĩa trên khi xét giới hạn ở vô tận, tức là khi xét x  ặc x  ặc x  ảy dạng ô ðịnh.
ả sử ta xét giới hạn của f(x) và g(x)trong cùng một qúa trình biến ðổi của ðó ói f (x) –
ó dạng vô ðịnh   ếu f (x) và g (x) cùng tiến về +  ặc à 
ói f(x).g (x) có dạng vô ðịnh o . ếu:
à VCB và g (x) là VCL , hoặc là: à VCL và g (x) là VCB ói ó dạng vô ðịnh
ếu f(x) và g (x) ðều là các VCB ói ó dạng vô ðịnh
ếu f(x) và g(x) ðều là các VCL ói f(x) ó dạng vô ðịnh 0 à g (x) ðều là các VCB. ói f(x) ó dạng vô ðịnh  ếu f(x)  à g (x) là VCB. ói f (x)
ó dạng vô ðịnh 1 ếu f(x) à g (x) là VCL .
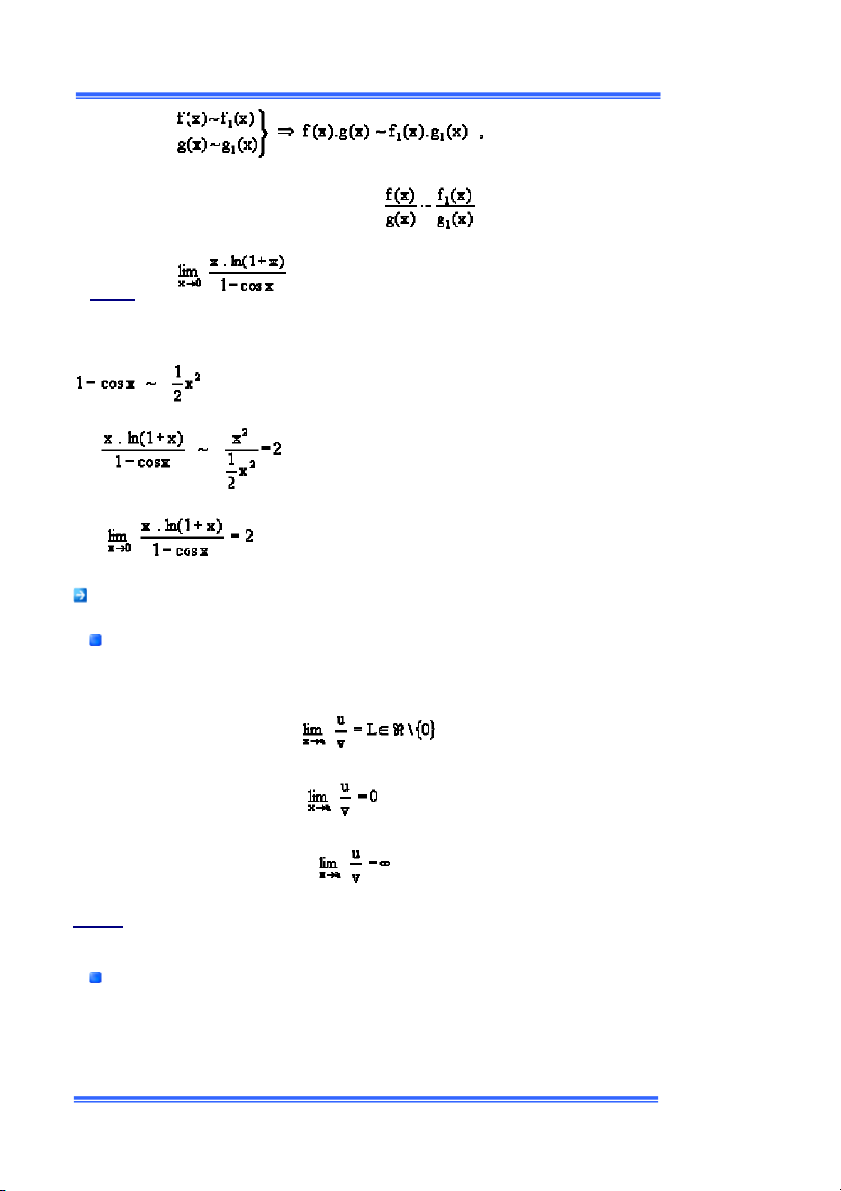
ắc thay thế týõng ðýõng khi tính giới hạn. Ðịnh lý :
ả sử ta xét giới hạn trong một quá trìn
ến ðổi của x. khi ấy : à g (x) có giới hạn L 
ó giới hạn L. (L hữu hạn hoặc vô hạn)
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 8 à í dụ: ính ó : x . ln(1+x) ~ x . x = x ậy:
ánh các VCB , và các VCL Ðịnh nghĩa: ét x  R ặc a là vô tận )
ả sử u = f (x)và v = g (x) là các VCB . Khi ðó:
ói u và v có cùng cấp nếu
ói u có cấp cao hõn v nếu
ói u có cấp thấp hõn v nếu í dụ : ét x ó 1 –
à x à 2 VCB cùng cấp , 1 – à VCB cấp õn ln(1+x) Ðịnh nghĩa: ánh VCL)
ả sử f(x) và g (x) là 2 VCL khi x ói
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 9
ó cùng cấp với g (x) nếu ó cấ õn g (x) nếu
ó cấp thấp hõn g(x) nếu í dụ:  ó x và ùng cấp , x ó cấp cao hõn Ðịnh lý:
ả sử f (x) và g(x) là các VCB khi x ó:
ếu f(x) có cấp nhỏ hõn g(x) thì f(x) 
ếu f(x) cùng cấp g(x) và f(x) ~ f ì :
ới ðiều kiện f(x) và g(x) không týõng ðýõng. Ðịnh lý:
ả sử f(x) và g(x) là các VCL khi x ó:
ếu f(x) có cấp lớn hõn g(x) thì: 
ếu f và g cùng cấp nhýng không týõng ðýõng, và: f(x) ~ f ì : í dụ:  ó:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 10 Ử DẠNG VÔ ÐỊNH
ý ðã biết , ta có thể dùng các quy tắc tính g ới hạn trong trýờng hợp không phải
ạng vô ðịnh và các quy tắc thay thế týõng ðýõng ðể tính giới hạn . Trong trýờng hợp
ặp các dạng vô ðịnh :    à
ó thể phân tích biểu thức ðể ðõn
ản hay thực hiện các quy tắc thay thế týõng ðýõng , ðặc biệt là áp dụng việc thế
ýõng ðýõng cho VCB và VCL ðýợc trình bày trong các ðị
ý ở mục II ở trên . Ðối ới các dạng vô ðịnh 0  à 
ýờng dùng công thức biến ðổi sau ðây :
ồi xét giới hạn của v. lnu
ài ra , ðối với ác dạng vô ðịnh à
òn có thể áp dụng quy tắc L’ ắc này sẽ ðýợ
ình bày trong phần áp dụng của ðạo hàm trong ýõng sau .
ýới ðây chúng ta sẽ xét một số ví dụ minh họa cho các phýõng pháp khử dạng vô ðịnh nêu trên. í dụ 1 ìm à  ó :  ó :
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 11 í ụ 2: ìm ó :   ậy: í dụ 3: ìm ó:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 12 ậy: í dụ 4: ính giới hạn ó dạng vô ðịnh ến ðổi:   ó: ì  à
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 13 ÀM SỐ LIÊN TỤC Ðịnh nghĩa
àm số f(x) xác ðịnh trên ột khoảng chứa xo. Ta nói f(x) liên tục tại xo nếu
ác ðịnh trên với [ xo, xo + 
ới s > 0. Ta nói f (x) liên tục bên phải tại ếu: ác ðịnh tên ( xo  ới s > 0
ói f(x) liên tục bên trái tại xo nếu: ệnh ðề: ên tục tại x
ên tục bên trái và liên tục bên phải tại x Ðịnh lý:
à g(x) là các hàm số liên tục tại xo. Khi ðó ta có :
à f(x) . g (x) cũng liên tục tại xo
ên tục tại xo với ðiều kiện   ên tục tại xo
Ðịnh lý: ếu hàm số f(x) liên tục tại x
à hàm số g(u ên tục tại u ì
àm số hợp h (x) =gof(x) liên tục tại x
ính chất của hàm hàm số liên tục trên một ðoạn
Ðịnh nghĩa: àm số f(x) ðýợc gọi là liên tục trên ðoạn [a,b] nếu:
ên tục trên khỏang (a,b) ,tức là f (x) liên tục tại mọi xo ên tục bên phải tại a. ên tục bên trái tại b.
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 14
ên quan ðến hàm số liên tục trên một ðoạn , ngýời ta ðã chứng minh ðýợc ðịnh lý ðây: Ðịnh lý:
àm số f(x) liên tục trên [a,b]. Khi ðó ta có:
ó gía ị nhỏ nhất và gía trị lớn nhất trên [a,b] Ðặt m = min {f(x)/ x   ó f ([a,b] ) =[m,M]
ột số thực yo tùy ý thuộc [m,M], ta có xo ệ quả
ếu f liên tục trên [a,b] và:
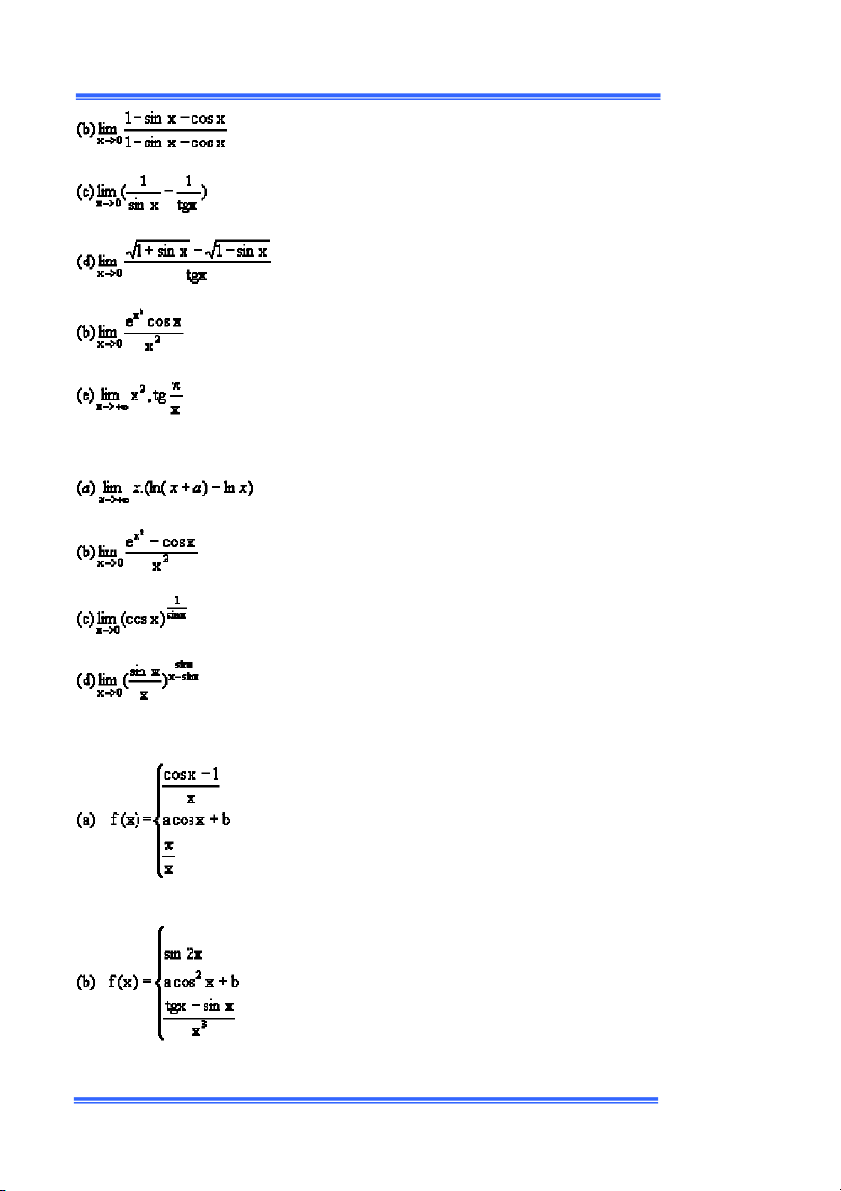
ì phýõng trình f(x) =0 có nghiệm trong khoảng (a,b). ÀI TẬP CHÝÕNG I ính các giới hạn sau: ính giới hạn :
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 15 ính giới hạn :
ác ðịnh a và b sao cho các hàm số sau ðây là liên tục trên IR.
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 16
ứng minh rằng phýõng trình – ó 3 nghiệm trên ðoạn [
ứng minh rằng các phýõng trình sau ðây có nghiệm : –
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g