Chương I: Ứng dụng đạo hàm để khảo sát hàm số môn Toán 12

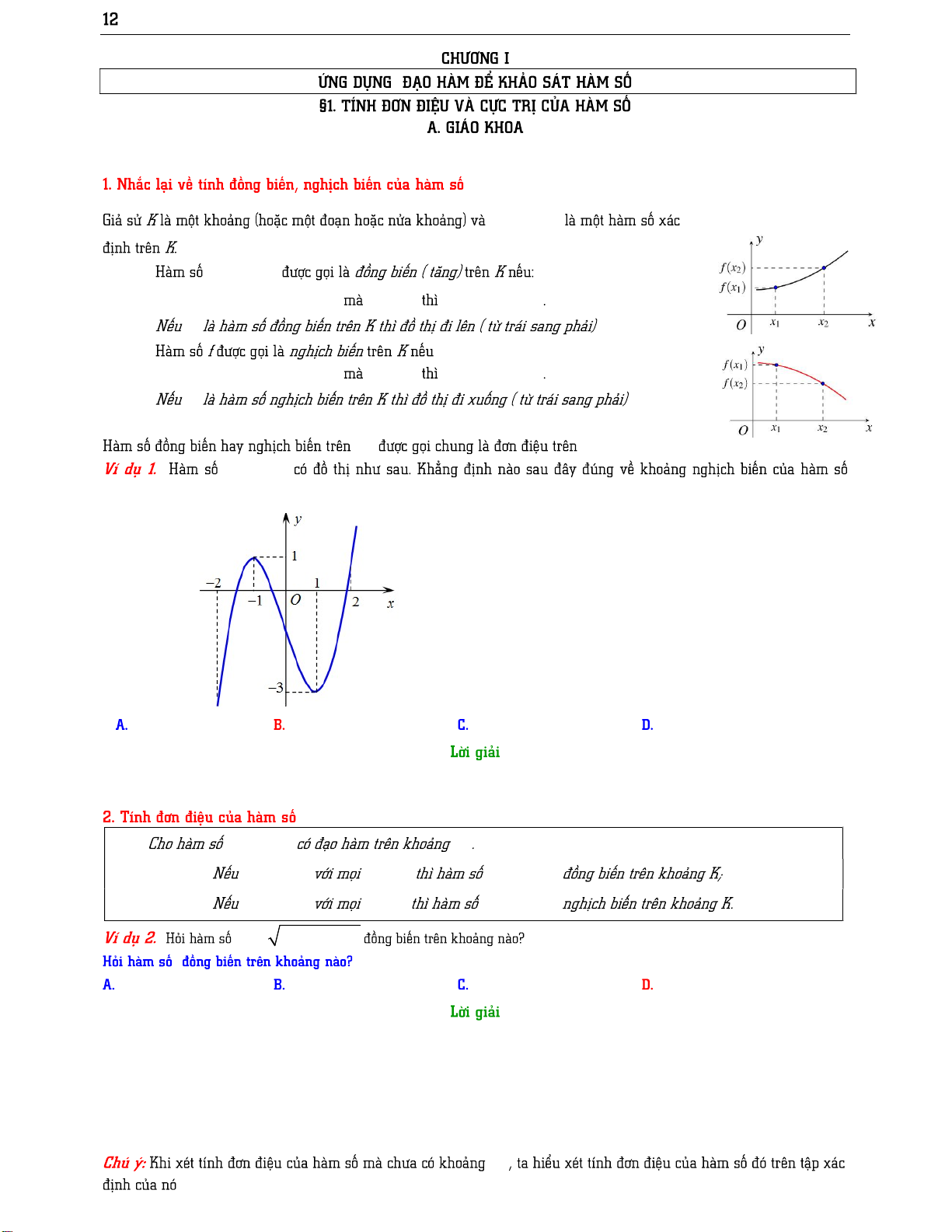
_KSHS y  f  x  y  f  x x  , x  K x  x f (x )  f (x ) 1 2 1 2 1 2 f  x  , x  K x  x f (x )  f (x ) 1 2 1 2 1 2 f K K y  f  x y  f  x  3  ;  1 1;  1 ; 1 1; y  f  x K f (x)  0 x  K y  f x f (x)  0 x  K y  f x 2 y  x  4 x  3 2; ;3  ;   1 3; K 1 _KSHS f  x K D f ' x x D f ' x 0 f ' x y  f x K f 'x 0 x  K f 'x 0 K y  f x K f 'x 0 x  K f 'x 0 K f 'x 0 x  K K x  3 y  x  3 
;3 3;
;3 3; R
;3 3;  ;  3    3;   4 2 x y  x  x  1 1 y  2 y  x 1 3 y  x  x x  3 2 y  x  4 x  3 2;  ;  3  ;   1 3; 2 _KSHS y  f  x  ;ab y O a x1 x2 x3 b x
y  f  x  0, ; a b f  x  0 1  f  x  0 x ;x 2 3  2  y  f x f  x f  x 2;0 f  x 0;  f  x  ;  3 f  x 3; 2 y  f 'x. y  f  x 0;  1 2; 1;2 2; 0;  1 3 _KSHS y  f  x
f  x  x x  2 x  3 1 1  x  2 y  f  x  ;    1 0;  1 1;  1  ;0 3 2
y  x  mx  4m  9 x  5  4 _KSHS mx  5 y  x1 m  5  m  5  m  5 m  5 3 2 y  x  3x  3mx 1 0; m  1 m  1 m  ;  1  1; m  1 5 _KSHS x  2  2m y  1;2 x  m 2 2 m  m1 2   m  2  m 1 3 3 3 m  1;2 m  1;2 1;2 1;2 6 _KSHS y  f ' x. f  x  y  f  x  1 x , x2    f  1 x   f  x2  1 x  x2    f  1 x   f  x2  1 x , x2    f  1 x   f  x2  1 x  x2    f  1 x   f  x2  0; 1 2; 1;2 2; 0;  1 y  f  x a;b y  f  x a;b
f   x  0, x  a;b.
f  x  0,x  a;b y  f  x a;b y  f  x a;b
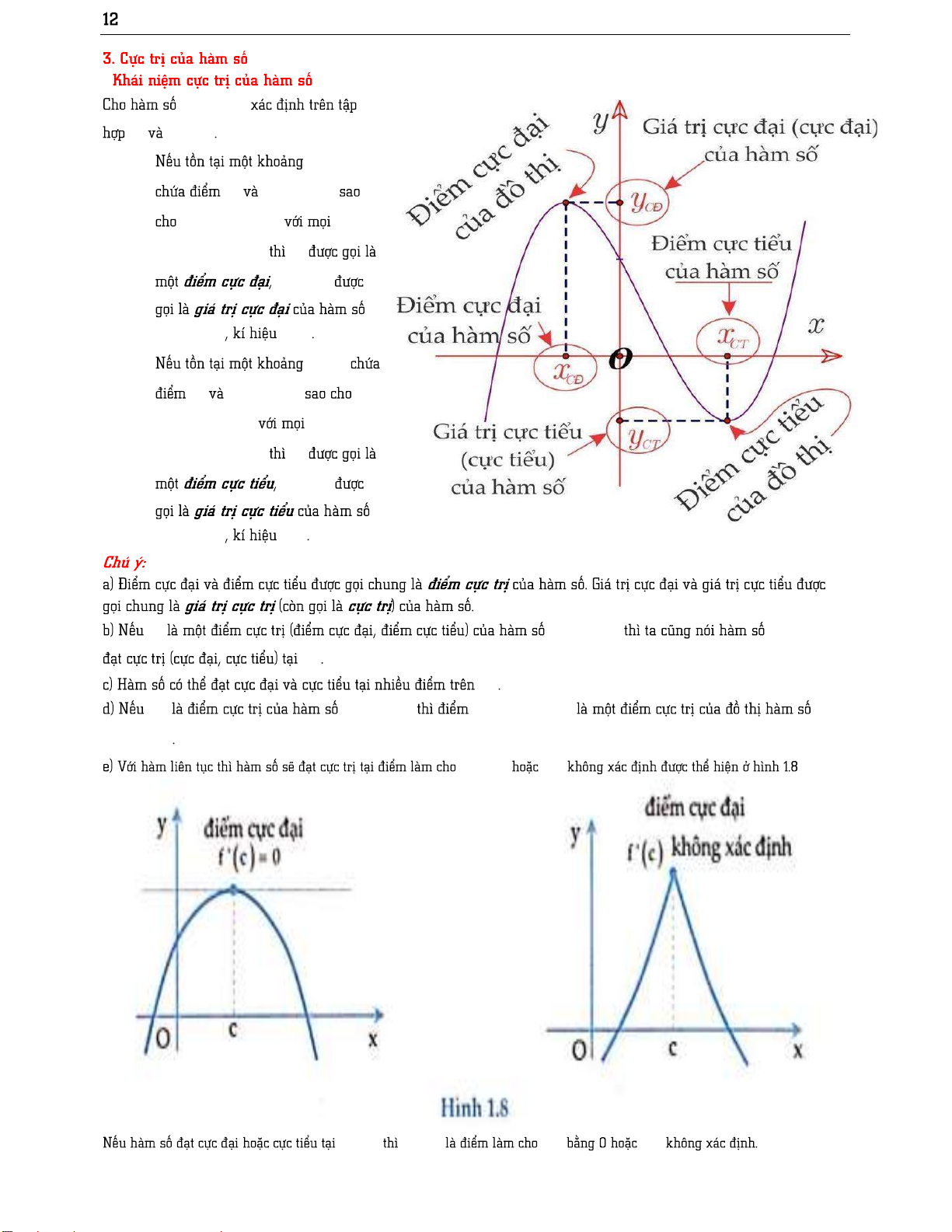
f  x  0,x  a;b y  f  x a;b 3 2 y  x 3x  4 3 0 2 1  2  ;0  ;  2   0;  y  f (x) f '(x)  0, x   x 1 f ( )  f (1) x 2 x y     x 1 ; 0  0;1 ;1
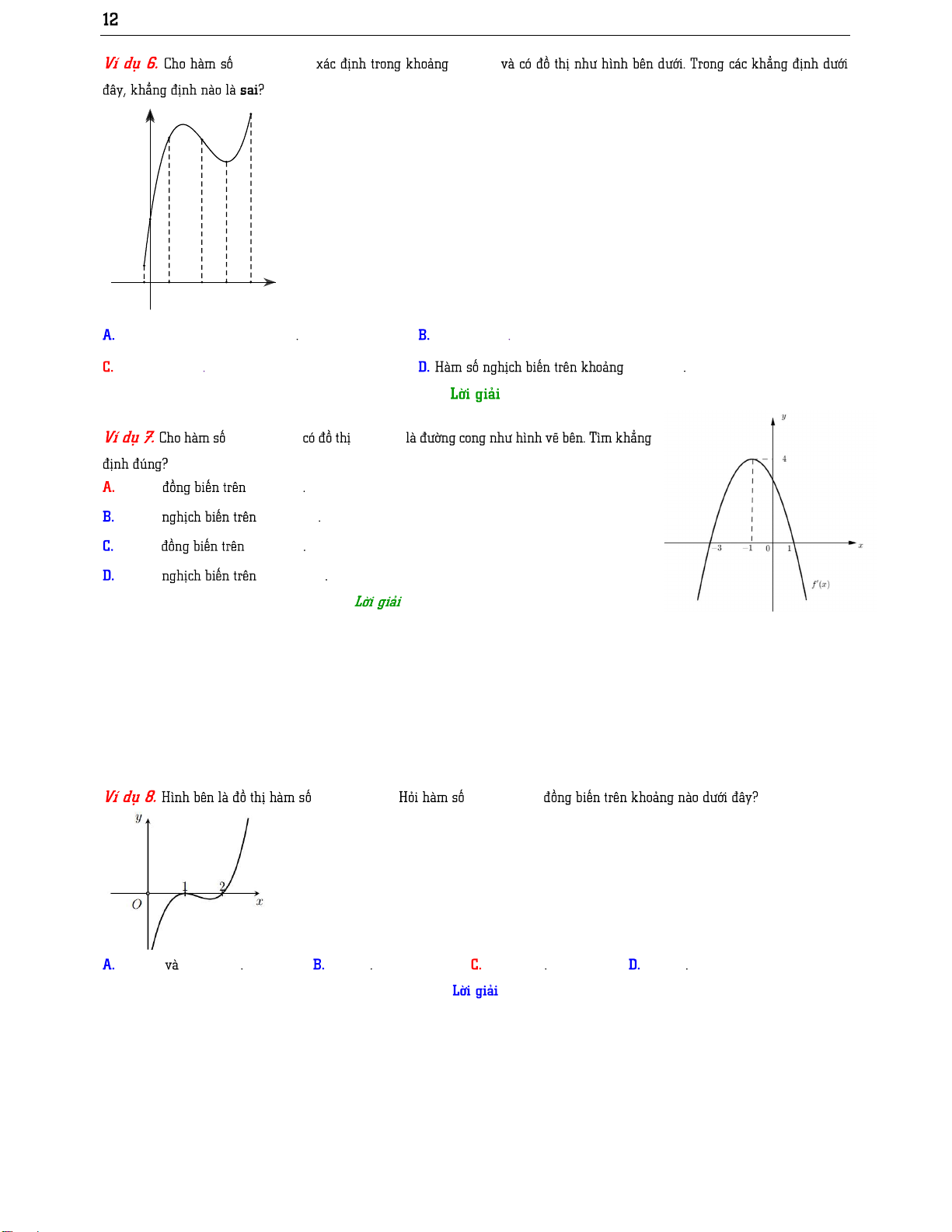
;01; 0;  1 ;1 1; ;  1 1;  x  1 6 _KSHS 4 2 y  x  2x 1 y  sin x  cos x  3x  ;    1  ;  0 0;1 1;2 0;  ;    1  ;   0;1  1  ;0 2x  3 y  2 x 1   3   3  ;  1 1;   ;    2   2   3  1;   ;  1  2  x 1 3 y  x  x 1 y  x1 3 y  x  2x 3 4 2 y  x  2x  3 y  f  x f  x f  x  2  ;0 f x 0; f x  ;  3 2 y  2 x  x f x  3  ; 2  ;  2 0;1 1;2 1; 7 _KSHS y  f  x f  x  f  x 2 '  x 1 x   y  f ' x 1;  1  ;  1 f  x  ;  0 1;2  ;   f  x 0;2 f  x 2;  1 f  x  1  ;  1
y   x   x  2 2 1 y  x   x  2 2 1  ;    1 .  1  ;2. y  f  x
f  x  x x  2 x  3 1 1  x  2 y  f  x  ;  2  .  ;    1 0; 1 1;  1  ;0  2  ;0. 2 y  2 x  1 0;  1  ;  1  ;    ;  0 8 _KSHS y  f x  y  f  x  f  x
f 2  f 2  0 y  f 'x
y  gx  f 1 x 1 y  g  x  ;    2 y  g  x 1;   y  g  x  2  ;      2 y f x y  g  x  2  ;  1  2  ;  1  3  1;    2   1  ;  1 1;2 f  x y  f  x ' y  f x g  x  f  3x y  f   x 2 2 1  x 1 x 4;7 2; 3 ;  1  ;  2 2;0  ;    1  1  ;2  3  ; 2   9 _KSHS f  x  y  f  x h x  f  x   2 2 3 1  9x  6x  4 y  f (x) y  f  2 2  x   1  ;0 1; h x   2  ;  1 0; 1.  1  h x 1  ;    3   1  h x 1  ;    3  h x  10 _KSHS y  f  x D x  D o   ;ab x  ;ab  D o f  x  f  xo  x  ; a b \x x o o f  xo  y  f  x yCÑ   ;ab x  ;ab  D o f  x  f  xo  x  ; a b \x x o o f  xo  y  f  x yCT x y  f  x y  f  x o xo D x y  f  x M x ; f x o  o o y  f  x y '  0 y ' x  c x  c y ' y ' 1 4 _KSHS y  f  x x  4 x 1; x  4; x  6 7 y  f  x y  f  x y  1 0; 2    1  ;  1 y  f  x  ;ab x  ;ax x ;b o  o  o  f ' x  0 x  ; a x f ' x  0 x  x ;b y  f  x o  o  xo  f ' x  0 x  ; a x f ' x  0 x  x ;b y  f  x o  o  xo 4 2 y  x  4x  2 4 1 2 3 15 _KSHS y  f  x D f ' x x D f ' x 2 x  3x y  x 1 2 10  3 3 2 y  x  x  x 1. x  a x  b 2 2 2a  b 2 11 2 11 2 2 2a  b  2 2 2a  b  2 2 2a  b  2 2 2a  b  3 3 9 9 m 3 2 2
y  mx  x  (m  6)x 1 x  1 4 2 1 3 1 6 _KSHS 3 2 y  mx 3mx m  1 x 4 m  1   1   1   1  0;   0; 0;  0;    4   4   4     4  3 2 y  x  2x  3x 1 26x  9 y  15  0 25x  9 y  15  0 26x  9 y  15  0 25x  9 y  15  0 17 _KSHS 3 2
y  x  3x  31 m x 1 3m
 : 2mx  y  2m  2  0
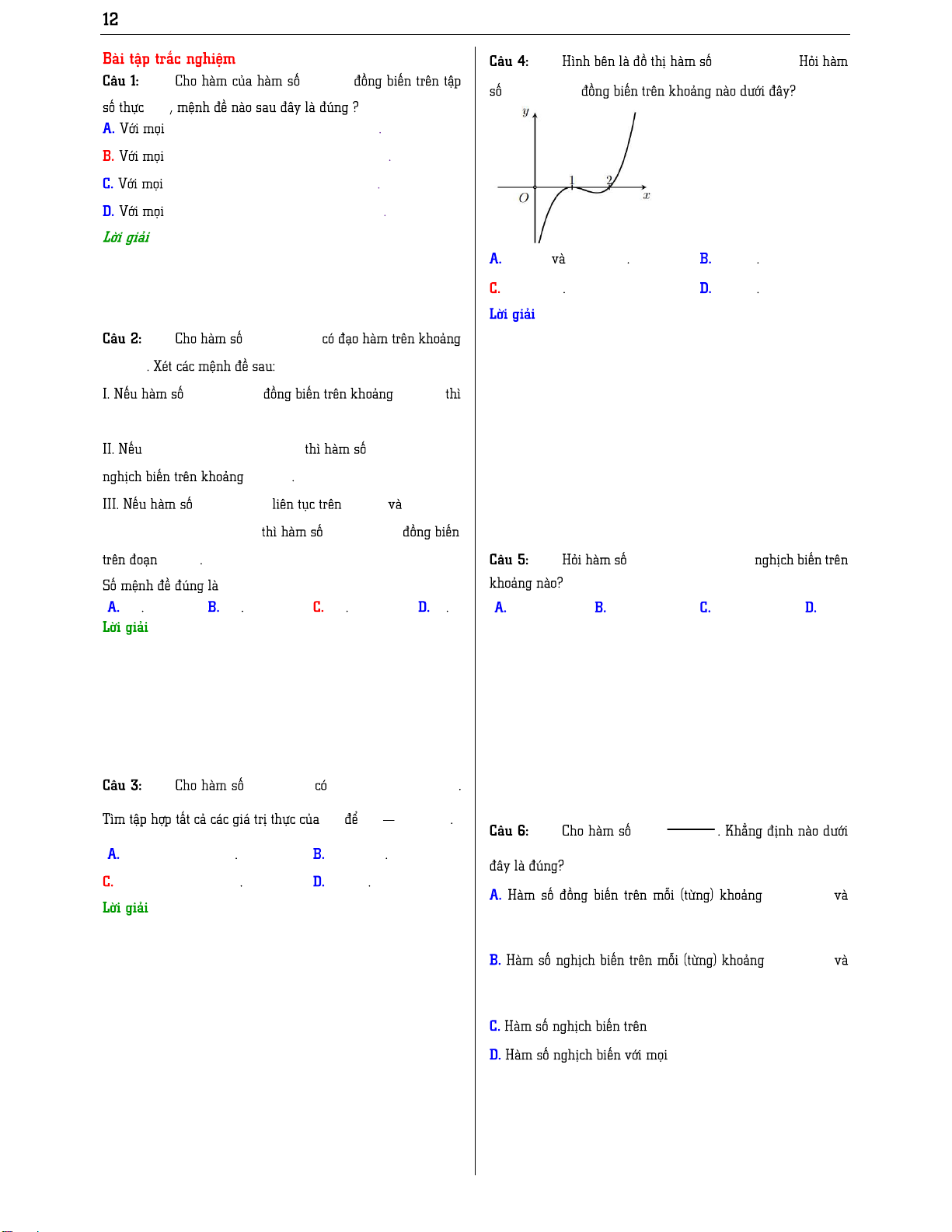
 : 2mx  y  2m  2  0  : y  202  200x  : y  202  200x 1 8 _KSHS y  f x f  x  1 x , 2 x    f  1 x   f  2 x  1 x  2 x    f  1 x   f  x2  1 x , 2 x    f  1 x   f  2 x  1 x  2 x    f  1 x   f  2 x  0;3 0;4 2;3 2;0 y  f (x) f '(x)  0, x   1 x f ( )  f (1) x  ;00;  1  ;   1   ax b f x  cxd  ;  01; 0;  1 y 1 O 1 x f  x 
f x  0 x 0; f   1  f 2 f 3  f   1 f   1  f   1 ;  1 1;  4   5  f  f     ;  1  3   4  1; 2 1 0 3 f  x y  f x
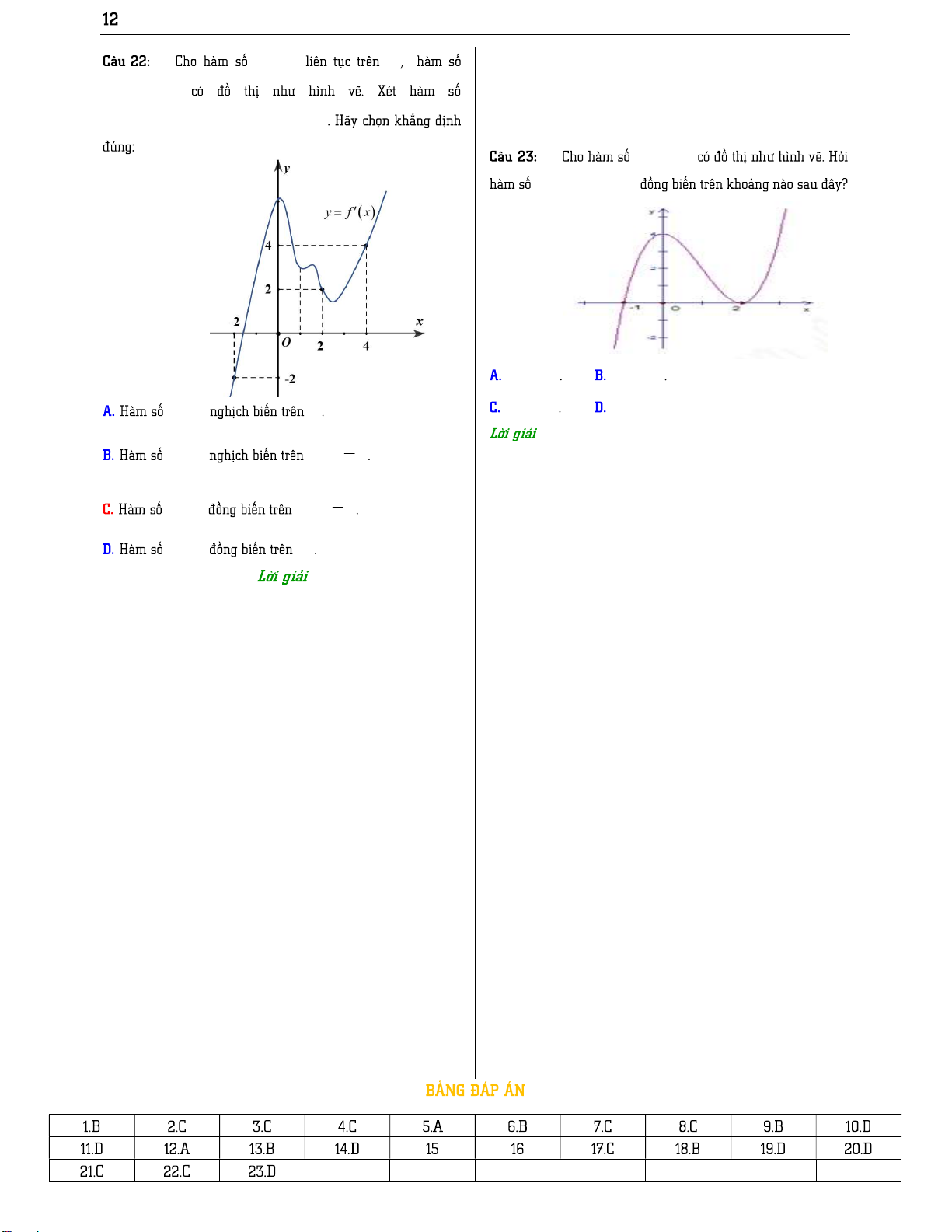
f  x  0,x   f 2  1 x – -1 0 + f 0  f 3 f 4  f 3  2 y' – 0 + 0 – 0 + f   1  1 1  f 4 + 2 + y -2 -2 y  f  x  2  ;  ;  2    1  ;0  2  ;2 19 _KSHS y  f  x  \  0 y  f x 2 y '  x x  2  ;  0 2; 2; 0;2  0;  1  1;  1  1;0  1  ; y  f  x  y  f  x y y  f  x y  f  x  ;ab  ;    2 y  f  x 1;5 O a x1 x2 x3 b x y  f  x 1;1 y  f  x 1;  1
y  f  x  0,a;b f x  0 1  f  x  0 2  x ;x 2 3  2 0 _KSHS y  f ' x. 3 2 y  x  3x 1 y  f  x 0; 0;2 ;2 ;0 2; 0;  1 2; 1;2 2; 0;  1 4 3 y  x  4x  3  2;0, 2;  ; 2,0; 2 3; 0;3 2x 1 y  x 1  \   1 1 y  x . 4 2 y  2x 4x 2019.  x ;  1 2 x  3 2 1;   y  . y  x 4x 1  1 .x x 3
;1 1; ;1 1;  4 2 y  x  2x  3 3 2 y  x  3x  2x 1 y  tan x 3 y  x  3x  4  y  f  x 2  x1   21 _KSHS 2 y  x  4x  5
y   x   x  2 2 1 5; 2;  ;    1 y  x   x  2 2 1  ;  2  ;    1 . 1;2. ;2. 2;0. 2 y  x  sin x  1;2  ;2 y  f (x)  f (x)
f (x)  1  xx  2.gx  2018 g  x    0, x  y  f 1 (  x)  2018x  2019  ;1   3 ; 0     ; 3  3 ;  y  f  x x  2 x  2 y  y  x 1 x 1 x  2 x  3 y  y  x 1 x 1 5 2 0 1 2 2