ÁO TRÌNH TOÁN CAO CẤ 46
Ch−¬ng III: tÝch ph©n bÊt ®Þnh
ÐỊNH NGHĨA & TÍNH CHẤT Ðịnh nghĩa
ọi một nguyên hàm của hàm số f(x) trên (a,b) là một hàm F(x) mà F’(x)= f(x) ,  í dụ:
à một nguyên hàm của f(x) = x trên R
à một nguyên hàm của hàm f(x) = 1 + tg
ên các khoảng xác ðịnh của Ðịnh lý
ếu F(x) là một nguyên hàm của f(x) trên
ảng (a,b) thì mọi nguyên hàm của f(x)
ên khoảng (a,b) ðều có dạng F(x) + C với C là một hằng số. Ðịnh nghĩa:
ếu F(x ) là một nguyên hàm f(x) thì biểu thức F(x) +
ðó C là hằng số có thể
ấy giá trị tùy ý, ðýợc gọi là tích phân bất ðịnh của hàm số f ý hiệu là ậy: ấu
ðýợc gọi là dấu tích phân, f(x) là hàm dýới dấu tích phân, f(x)dx là biểu thức
ýới dấu tích phân và x là biến tích phân. ác tính chất
ảng các tích phân cõ bản
Sưu tầm và chỉnh s a by Nguy ử ễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 47    à hằng số tùy ý) í dụ 1: ính:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 48 í dụ 2: ính:
ÝÕNG PHÁP TÍNH TÍCH PHÂN
ýõng pháp phân tích ích phân 
ó thể ðýợc tính bằng cách phân tích hàm số f(x) thành tổng của
ác hàm ðõn giản hõn hay dễ tính tích phân hõn : … +fn à áp dụng công thức : í dụ: ính
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 49 ới n 
ờ hệ thức này ta có thể tính I ới n tùy ý.
ýõng pháp ðổi biến
ýõng pháp ðổi biến trong tích phân bất ðịnh có 2 dạng sau ðây : ạng 1:
ả sử biểu thức dýới dấu tích phân có dạng: ’(x)dx
ðó u(x) là một hàm số khả vi. Khi ấy ta có thể ðổi biến bằng cách ðặt u=u(x),và ó: ạng 2: Ðặt x =  ðó 
à một hàm khả vi, ðõn ðiệu ðối với biến t, ó : í dụ:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 50 ính: Ðặt: u = x ới u = sinx ính: Ðặt u = x ính Ðặt u = e ó : du = e à:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 51 ính Ðặt u = cos ó: ính Ðặt: x = sint ;    ó: dx = cost dt
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 52 à à t = arcsin x ên:
ýõng pháp tích phân từng phần
ả sử u = u(x) và v = v(x) là các hàm số có ðạo hàm liên tục u’= u’(x) và v’= v’(x) : ết: ’= u’v+u.v’ ’= (uv)’ ’ ừ ðó suy ra công thức:
ông thức này ðýợc gọi là công thức tích phân từng phần , và còn ðýợc viết dýới ạng :
ông thức tích phân từng phần thýờng ðýợc áp dụng trong trýờng hợp hàm dýới dấu
ích phân có dạng f(x) = u.v’ mà hàm g = v.u’ có tích phân dễ tính hõn.
ột số bài toán, sau khi áp dụng công thức tích phân từng phần ở vế phải lại
ất hiện tích phân ðã cho ban ðầu với hệ số khác, tức là : ðó ta tính ðýợc : í dụ: ính
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 53 Ðặt ’= x
Áp dụng công thức tích phân từng phần, ta có : ính Ðặt u = arctg x ’= x ,  ó : ính Ðặt ’ = cos x
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 54 ’= e  Ðể tính: ðặt: ’ ’ ậy: ính Ðặt ’ = 1 ó:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 55 ðó: ậy ính Ðặt ’=1 v = x ó:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 56
ìm công thức truy hồi ðể tính tích phân ó: ới n  ðặt: ’ = 1 v = x ó: ậy: ÀI TẬP CHÝÕNG 3 ính các tích phân:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
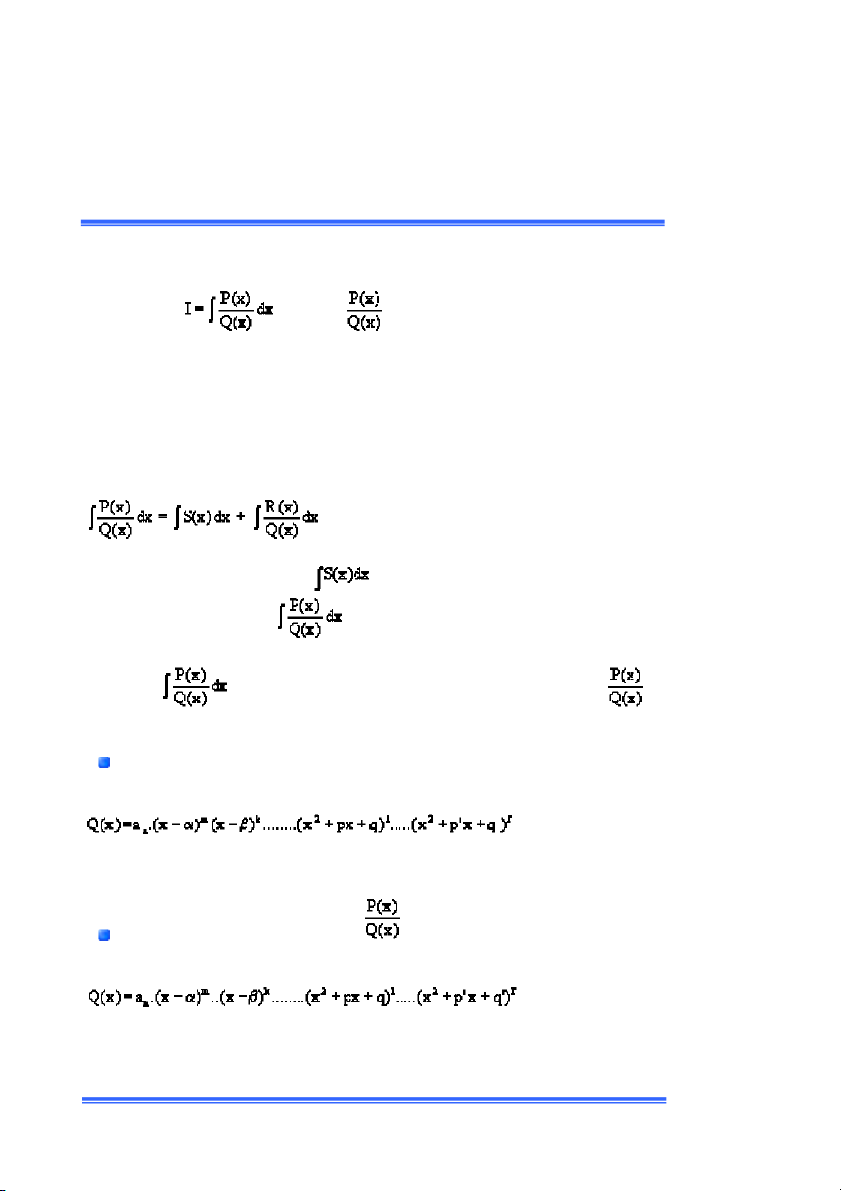
ÁO TRÌNH TOÁN CAO CẤ 59 ÍC ÂN HÀM HỮU TỈ ích phân ðó
à một phân thức hữu tỉ tối giản theo x. ế
ậc của P(x)  ậc của Q(x) thì bằng cách chia ða thức P(x) cho Q(x) ta viết ðýợc:
ới bậc R(x) < bậc Q(x) ðó:
ì S(x) là một ða thức th ên
ó thể tính ðýợc một cách dễ dàng. Nhý
ậy ta chỉ cần tìm cách tính
ới bậc ủa R(x) < bậc của Q(x). ích phân
ó thể ðýợc tính bằng cách phân tích phân thức hữu tỉ
ành tổng của các phân thức hữu tỉ ðõn giản hõn dựa vào 2 mệnh ðề sau ðây. ệnh ðề 1:
ọi ða thức Q(x) với hệ số thực ðều có thể phân tích thành tích của
ác nhị thức bậc nhất và các tam thức bậc 2 không có nghiệm thực : ðó các tam thức x … ., x
’x + q’ không có nghiệm thực ệnh ðề 2:
ả sử phân thức hữu tỉ ó bậc của P(x)ó dạng ðó các tam thức (x … .,(x
’x + q’) không có nghiệm thực. Khi ấy
ân thức hữu tỉ có thể phân tích thành tổng của các phân thức ðõn giản hõn nhý sau:
Sưu tầm và chỉnh s a by Nguy ử ễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 60 ðó các hệ số A … , Am, B … ., Bk, M … ., Ml, Nl,… … , R
… ..,Rl’ ’ à các hằng số, và ta có thể tính ðýợc các hằng số này bằng phýõng pháp
ệ số bất ðịnh, phýõng pháp trị riêng hay phýõng phá
ân tích từng býớc. (Các
ýõng pháp này sẽ ðýợc minh họa qua các ví dụ bên dýới).
ý vậy việc tính tích phân
ðýợc ðýa về việc tính 2 loại tích phân sau : à: ới p ức là x ông có nghiệm thực). Ðể tính I ỉ cần ðặt u = – Ðể tính I ó thể phân tích I ýới dạng: ích phân
ðýợc tính dễ dàng bằn ách ðặt: u = x Ðối với ến ðổi x à ðặt u = x – ðể ðýa về dạng:
à ta ðã biết cách tính trong ví dụ 6 ), Mục II.3. í dụ :
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 61 ính – – ðó: ân 2 vế cho x – ðýợc:
ồi x = 1 vào ta ðýợc :1 = à 1 = 3c 
Ðồng nhất các hệ số của x
ở 2 vế của ðẳng thức trên (ðúng với mọi x) ta ðýợc à C=
ào, rồi giải hệ này sẽ ðýợc: ậy: ó:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 62 ính ân tích phân thức ðýợc: ó :
ông thức truy hồi trong ví dụ 6) mục II,3, ta có
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 63  ậy ính
ýớc hết ta ðổi biến ðể ðõn giản hóa tính phân trên bằng cách ðặt u = x2 ,du = 
ÍCH PHÂN HÀM LÝỢNG GIÁC ét tích phân I = 
ðó R(u, v) là hàm hữu tỉ ðối với u và v.
Ðể tính tích phân này ta có thể dùng cá
ýõng pháp ðổi biến sau : ýõng pháp chung Ðặt
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 64 ó: ích
ân này có dạng tích phân của phân thức hữu tỉ ðã xét trong mục III. í dụ: ính: Ðặt:  ính: Ðặt: 
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 65 ân tích phân ức hữu tỉ ta ðýợc: 
ột số trýờng hợp ðặc biệt ếu R( ì ðặt u=tgxhoặc u=cotgx ếu R(sinx, ì ðặ ếu R( ì ðặt u = cosx ích phân dạng 
ới m và n là các số chẵn dýõng.Ta có thể ðổi
ến bằng cách dùng công thức : í dụ :
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 66 ính: Ðặt ính: Ðặt u = sinx  ính: Ðặt u = cosx 
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 67 ính: ó: ú ý:
Ðối với các tích phân dạng
ùng các công thức biến ðổi tích thành tổng:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 68 Í
ÂNHÀM HỮU TỈ ÐỐI VỚI À ét tích phân
ðó R(u,v) là hàm hữu tỉ ðối với u à v và a
à một tam thức bậc 2 không có nghiệm kép.
ýõng pháp tổng quát
ùy theo dấu của hệ số a ta ðýa tam thức a
ề dạng tổng hay ệu hai bình
ýõng . Khi ðó tích phân I có một trong ba dạng sau: Ðặt: ới  Ðặt:  Ðặt:  í dụ : ến ðổi : x
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 69 ét trýờng hợp x+1  Ðặt ó: ðó: à:  ýờng hợp x + 1 <
ông thức (*) ở trên vẫn ðúng vì ðạo hàm của hàm số ở vế ải (*) luôn bằng: Ðặt ó dx = ( 1 + tg
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 70 Ðặt u = sin x  ðó: à à tgt cùng dấu với  ích phân dạng
Ðể tính tích phân dạng này ta có thể ðặt : ích phân dạng
Ðể tính các tích phân dạng ta biến ðổi tam thức ax
ành tổng hoặc hiệu của
ình phýõng rồi ðổi biến ðể ðýa về các dạng tích phân ðã biết sau ðây:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 71
í dụ : ính các tích phân: ến ðổi: x Ðặt u = x –  ó : ến ðổi: 3 – – – Ðặt u = 2x + 1  ó:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 74
ỘT SỐ DẠNG TÍCH PHÂN KHÁC ích phân dạng
ðó R là một hàm hữu tỉ và m,… ,k là các số nguyên dýõng; a, b, c, d là cá ằng ố
Ðể tính tích phân này ta gọi x là một bội số chung nhỏ nhất của m,… ,k và ðặt:
ừ ðó, tích phân sẽ ðýợc chuyển về dạng:
ðó R à một hàm hữu tỉ ðối với u í dụ: ính Ðặt ó: 
Sưu tầm và chỉnh s a by Nguy ử ễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 75
ích phân hàm hữu tỉ ðối với e
ðó R là một hàm hữu tỉ ðối và a 
Ðể tính phân tích này ta ðặt : u = eax  ðó d à:
ó dạng tích phân hàm hữu tỉ. í dụ: Ðặt: u = e 
ác tích phân có dạng:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 76
ðó p(x) là một ða thức theo biến x.
Ðể tính các tích phân này ta dùng phýõng pháp tích phân toàn phần bằng cách ðặt : í dụ: Ðặt: 
ác tích phân có dạng :
Ðể tính các tích phân này ta dùng phýõng pháp tích phân toàn phần bằng cách ðặt: í dụ: ính  Ðặt u = ó
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 77 ậy:
ỘT SỐ TÍCH PHÂN KHÔNG BIỂU DIỄN ÐÝỢC
ÝỚI DẠNG HÀM SÕ CẤP
ếu hàm số f(x) liên tục trên (a,b) thì f (x) luôn luôn có nguyên hàm trên khoảng ðó , ức là tíc ân 
ồn tại . Tuy nhiên có một số tích phân không thể biểu diễn
ýới dạng hàm sõ cấp , chẳng hạn các tích phân nhý sau ðây:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g ÁO TRÌNH TOÁN CAO CẤ 72 ÀI TẬP CHÝÕNG 3 ính các tích phân: ính các tích phân:
ính tích phân bằng phýõng pháp tích phân toàn phần:
ính tích phân hàm hữu tỉ.
ính tích phân hàm lýợng giác.
ính tích phân hàm vô tỉ.
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g ÁO TRÌNH TOÁN CAO CẤ 73 ính các tích phân sau: ính tích phân:
ập công thức truy hồi và tính tích phân: à tính I à tính I ính tích phân:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g