






Preview text:
CHƯƠNG VIII PHƯƠNG TRÌNH SAI PHÂN
Các ví dụ
Ví dụ 1: Giải phương trình sai phân:
yn+2 + 3yn+1 + 2yn = 0, n N (1)
Giải
Phương trình sai phân tuyến tính cấp 2 thuần nhất (1) có phương trình đặc
trưng là t2 + 3t + 2 = 0t11
t22
- Phương trình sai phân thuần nhất (1) đã cho có nghiệm tổng quát là
yn = C1(–1)n + C2(– 2)n với n N và C1, C2 là các hằng số thực tùy ý.
Ví dụ 2: Giải phương trình sai phân:
yn+2 – 4yn+1 + 4yn = 0, n N (2)
Giải
Phương trình sai phân tuyến tính cấp 2 thuần nhất (2) có phương trình đặc
trưng là t2 – 4t + 4 = 0 t1 t2 2
- Phương trình sai phân thuần nhất (2) đã cho có nghiệm tổng quát là yn = (C1 + C2 n)2n với n N và C1, C2 là các hằng số thực tùy ý.
Ví dụ 3: Giải phương trình sai phân:
yn+2 – yn+1 + yn = 0, n N (3)
Giải
Phương trình sai phân tuyến tính cấp 2 thuần nhất (3) có phương trình đặc
| 1 | | | ||||||||||||||||||
| 3 i | cos | i sin | ||||||||||||||||||
t1 | |||||||||||||||||||||
2 | 3 | 3 | |||||||||||||||||||
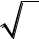
trưng là t2 – t + 1 = 0 | | ||||||||||||||||||||
| | 1 | 3 i | cos | | i sin | | với r =1, = π/3. | |||||||||||||
t2 | |||||||||||||||||||||
2 | 3 | 3 | |||||||||||||||||||
| |||||||||||||||||||||
- Phương trình sai phân thuần nhất (3) đã cho có nghiệm tổng quát là
yn C1cos n3C2sin n3 với n N và C1, C2 là các hằng số thực tùy ý.
1
Ví dụ 4: Giải phương trình sai phân:
yn+2 + 8yn+1 – 9yn = (11n + 35)2n, n N (4)
Giải
Phương trình sai phân tuyến tính cấp 2 thuần nhất tương ứng của (4) là :
yn+2 + 8yn+1 – 9yn = 0
Phương trình này có phương trình đặc trưng là t2 | t19 | |
+ 8t – 9 = 0t 1 | ||
2 |
- Phương trình thuần nhất tương ứng của (4) có nghiệm tổng quát :
= C | ( – 9)n + C | với n N và C , C | là các hằng số thực tùy ý. | ||||
y | n | 2 | |||||
1 | 2 | 1 |
Ta có VP(4) = (11n + 35)2n có dạng r(n) = Pk (n).αn với Pk(n) = 11n + 35 là đa thức bậc k = 1và αn = 2n với α = 2 không phải là nghiệm của phương
trình đặc trưng nên phương trình (4) có nghiệm riêng có dạng:
y* | = (an + b)2n | |||||||
n | ||||||||
| y* | = [a(n + 1) + b].2n + 1 | = (2an + 2a +2b)2n; | |||||
n1 | ||||||||
yn*2 = [a(n +2) + b].2n + 2 | = (4an + 8a + 4b)2n . | |||||||
Thay | y* | , | y* | , | y* vào phương trình (4) ta được : | |||
n2 | n1 | n | ||||||
( 4an + 8a | + 4b | |||||||
- 16an + 16a + 16b
– 9an– 9b )2n = (11n + 35)2n 11an + 24a +11b =11n + 35
Đồng nhất hai vế của phương trình này theo n, ta được :
| 11 | | a 1 | |||
11a | yn* = ( n + 1)2n. | |||||
| | | ||||
24a 11b 35 | b 1 | |||||
Vậy nghiệm tổng quát của phương trình (4) đã cho:
= | y* | (– 9)n + C | + ( n + 1)2n | ||||||||
y | n | y | n | + | = C | 2 | |||||
n | 1 |
với n N và C1, C2 là các hằng số thực tùy ý.

2
Ví dụ 5: Giải phương trình sai phân:
yn+2 9yn+1 + 14yn = (4n + 5)3n, n N (5)
Giải
Phương trình sai phân tuyến tính cấp 2 thuần nhất tương ứng của (5) là:
yn+2 9yn+1 + 14yn = 0
t1 2
Phương trình này có phương trình đặc trưng là t2 9t + 14 = 0t2 7
- Phương trình thuần nhất tương ứng của (5) có nghiệm tổng quát là
= C | 2n + C 7n | với n N và C | , C | là các hằng số thực tùy ý. | ||||
y | n | 2 | ||||||
1 | 2 | 1 |
Ta có VP(5) = (4n + 5)3n có dạng r(n) = Pk (n).αn với Pk(n) = 4n + 5 là đa thức bậc k = 1và αn = 3n với α = 3 không phải là nghiệm của phương trình
đặc trưng nên phương trình (5) có nghiệm riêng có dạng:
y* | = (an + b)3n | |||||||
n | ||||||||
| y* | = [a(n + 1)+b].3n + 1 = (3an+3a +3b)3n; | ||||||
n1 | ||||||||
yn*2 | = [a(n +2)+b].3n + 2 | = (9an +18a + 9b)3n . | ||||||
Thay | y* | , | y* | , y* | vào phương trình (5) ta được : | |||
n2 | n1 | n | ||||||
( 9an + 18a + 9b
– 27an – 27a – 27b
+14an + 14b) 3n = (4n + 5)3n – 4an –9a – 4b = 4n + 5.
Đồng nhất hai vế của phương trình này theo n, ta được :
| 4a | | 4 | | a1 | y* | = (– n +1)3n. | |
5 | | |||||||
9a 4b | b1 | n | ||||||
| | |||||||
Vậy nghiệm tổng quát của phương trình (5) đã cho:
= | y* | 2n + C 7 n + (– n+1)3n | |||||||
y | n | y | n | + | = C | ||||
n | 1 | 2 |
với n N và C1, C2 là các hằng số thực tùy ý.

3
Ví dụ 6: Giải phương trình sai phân:
yn+2 + 4yn+1 5yn = 12n + 8, n N (6)
Giải
Phương trình sai phân tuyến tính cấp 2 thuần nhất tương ứng của (6):
yn+2 + 4yn+1 5yn = 0
Phương trình này có phương trình đặc trưng: t2 | t11 | ||
+ 4t 5 = 0 | 5 | ||
t2 | |||
- Nghiệm tổng quát của phương trình thuần nhất tương ứng của (6):
yn = C1 + C2(–5)n với n N và C1, C2 là các hằng số thực tùy ý.
Ta có VP(6) =12n + 8 có dạng Pk(n). n với Pk(n) = 12n + 8 là đa thức bậc
k = 1 và α =1= t1 là nghiệm đơn của phương trình đặc trưng nên nghiệm
riêng yn* của phương trình (6) có dạng
yn* = n(an + b) = an2 + bn
y* = a(n + 1)2 + b(n + 1) = an2 + (2a + b)n + a + b
n1
và y* = a(n + 2)2 +b(n + 2) = an2 + (4a + b)n + 4a + 2b.
n2
Thay y* , y* , y* vào phương trình (6) ta được:
n 2 n 1 n
an2 + (4a + b)n + 4a + 2b
- 4an2 + (8a + 4b)n + 4a + 4 b
– 5an2 – 5bn = 12n + 8.
12an + 8a + 6b = 12n + 8.
Đồng nhất hai vế của phương trình này theo n, ta được :
12a | 12 | a1 | * | |||
| | = n2 . | ||||
| | yn | ||||
8a 6b 8 | b 0 | |||||
Vậy nghiệm tổng quát của phương trình (6) đã cho là :
yn = yn + yn* = C1 + C2(5)n + n2
với n N và C1, C2 là các hằng số thực tùy ý.
4
Ví dụ 7:Giải phương trình sai phân: | |
yn+2 – 5yn+1 + 6yn = (2n + 14)2n, n N | (7) |
Giải
Phương trình sai phân tuyến tính cấp 2 thuần nhất tương ứng của (7):
yn+2 – 5yn+1 + 6yn = 0
Phương trình này có phương trình đặc trưng: t2 5t + 6 = 0 t1 2, t2 3
- Nghiệm tổng quát của phương trình thuần nhất tương ứng của (7):
yn = C1 2n + C23n với n N và C1, C2 là các hằng số thực tùy ý.
Ta có VP(7) = (2n + 14)2n có dạng Pk(n). n với Pk(n) = 2n + 14 là đa
thức bậc k = 1và α =2= t1 là nghiệm đơn của phương trình đặc trưng nên
nghiệm riêng y* của phương trình (6) có dạng | |||||||||||||||||
n | |||||||||||||||||
y* = n(an + b)2n = (an2 + bn) 2n | |||||||||||||||||
n | |||||||||||||||||
y* | = [a(n + 1)2 | + b(n + 1)]2n + 1 = [2an2 | + (4a + 2b)n + 2a + 2b]2n | ||||||||||||||
n1 | |||||||||||||||||
và y* | = [a(n + 2)2 | +b(n + 2)]2n+ 2 | = [4an2 | + (16a +4 b)n + 16a + 8b]2n. | |||||||||||||
n2 | |||||||||||||||||
Thay yn*2 , yn*1 , yn* vào phương trình (7) ta được: | |||||||||||||||||
[4an2 + (16a + 4b)n | + 16a + 8b | ||||||||||||||||
–10an2 + ( – 20a – 10b)n – 10a – 10b | |||||||||||||||||
+ 6an2 | + 6bn] 2n | = (2n + 14)2n. | |||||||||||||||
| – 4an | + 6a – 2b | = | 2n + 14. | |||||||||||||
Đồng nhất hai vế của phương trình này theo n, ta được : | |||||||||||||||||
4a 2 | a 1 | 1 | 17 | ||||||||||||||
| | 2 | y* | ( | n 2 | | n) 2n . | ||||||||||
2 | 2 | ||||||||||||||||
6a 2b14 | b17 | ||||||||||||||||
| 2 | ||||||||||||||||
| |||||||||||||||||
Vậy nghiệm tổng quát của phương trình (7) đã cho là :
y* | 2n + C 3n + ( | 1 | n 2 | | 17 | n) 2n | |||||||||
y | n | = | y | n | + | = C | |||||||||
n | 1 | 2 | 2 | 2 | |||||||||||
với | n N và C1, C2 là các hằng số thực tùy ý. | ||||||||||||||
5 | |||||||||||||||
Ví dụ 8: Giải phương trình : yn+2 + 6yn+1 + 9yn = (n2 + 1)3n, n N (8)
Giải
Phương trình sai phân tuyến tính cấp 2 thuần nhất tương ứng của (8):
yn+2 + 6yn+1 + 9yn = 0
Phương trình này có phương trình đặc trưng: t2 + 6t + 9 = 0 t1 t23
- Nghiệm tổng quát của phương trình thuần nhất tương ứng của (8):
yn = (C1 + C2n)(–3)n với n N và C1, C2 là các hằng số thực tùy ý.
Ta có VP(8) = (n2 + 1)3n có dạng Pk(n). n với Pk(n) = n2 + 1 là đa thức
bậc k = 2 và α =3 không phải là nghiệm của phương trình đặc trưng nên
nghiệm riêng | y* của phương trình (8) có dạng y* = (an2 + bn + c) 3n | ||
n | n | ||
y* | = [a(n +1)2 + b(n + 1)+ c]3n + 1 | = [3an2 + (6a + 3b)n + 3a + 3b+ 3c ]3n | |
n1 | |||
y* | = [a(n +2)2+ b(n +2) + c]3n+ 2 | = [9an2 + (36a +9b)n +36a +18b+9c]3n. | |
n2 | |||
Thay yn*2 , | yn*1 , yn* vào phương trình (8) ta được: | ||
[9an2 + (36a + 9b)n + 36a + 18b + 9c
- 18an2 + (36a + 18b)n + 18a + 18b +18c
+ 9an2 | + 9bn | + 9c ] 3n | = (n2 + 1)3n. | |||||||||||||
36an2 + (72a + 36b)n + 54a + 36b +36c = | n2 + 1. | |||||||||||||||
Đồng nhất hai vế của phương trình này theo n, ta được : | ||||||||||||||||
36a | 1 | a 136 | ||||||||||||||
| | |||||||||||||||
72a 36b | 0 | b1 | * | 1 | 2 | 1 | 1 n | |||||||||
| | 18 | y ( | 36 | n | | 18 | n | 24 | )3 . | ||||||
54a 36b 36c1 | | |||||||||||||||
| c 1 | 24 | ||||||||||||||
| ||||||||||||||||
Vậy nghiệm tổng quát của phương trình (8) đã cho là :
y* | n)(–3)n + ( | 1 | n2 | 1 | n | 1 | )3n | ||||||||||||
y | n | = | y | n | + | = (C | + C | ||||||||||||
n | 1 | 2 | 36 | 18 | 24 | ||||||||||||||
với | n N và C1, C2 là các hằng số thực tùy ý. | ||||||||||||||||||
6
Ví dụ 9: Giải phương trình sai phân:
yn+2 – 7yn+1 + 12yn = 2n+ 1 + 6n – 5, n N (9)
Giải
Phương trình sai phân tuyến tính cấp 2 thuần nhất tương ứng của (9):
yn+2 – 7yn+1 + 12yn = 0
Phương trình này có phương trình đặc trưng: t2 7t + 12 = 0 t1 = 3, t2 = 4
- Nghiệm tổng quát của phương trình thuần nhất tương ứng của (9):
y | n | = C | 1 | 3n + C 4n với | n N và C | , C là các hằng số thực tùy ý. | ||||
2 | 1 | 2 | ||||||||
Ta có VP(9) = 2n+ 1 + 6n – 5 có dạng Pk(n).(1) n + Pl(n).(2) n | ||||||||||
Gọi ( y1)*n | là nghiệm riêng của phương trình | yn+2 | – 7yn+1 + 12yn = 2n+ 1 (a) | |||||||
và ( y2 )*n là nghiệm riêng của phương trình | yn+2 | – 7yn+1 + 12yn = 6n – 5 (b) | ||||||||
Khi đó nghiệm riêng của phương trình (9) đã cho là yn* = ( y1)*n + ( y2 )*n
Ta có * VP(a) = 2n+1= 2.2n = Pk(n).(1) n với Pk(n) = 2 là đa thức bậc k = 0 và α1 = 2 không phải là nghiệm của phương trình đặc trưng nên nghiệm riêng ( y1)*n của phương trình (a) có dạng ( y1)*n = a2n
( y )* = a2n+1= 2a2n và ( y )* = a2n+2= 4a2n thay ( y )* , ( y )* , ( y )*
1 n 1 1 n 2 1 n 2 1 n 1 1 n
vào (a), ta được (4a – 14a + 12a)2n = 2.2n 2a = 2 a = 1 ( y1)*n = 2n
- VP(b) = 6n – 5 = Pl(n).(2) n với Pl(n) = 6n – 5 là đa thức bậc l = 1 và α2 = 1 không phải là nghiệm của phương trình đặc trưng nên nghiệm
riêng ( y2 )*n của phương trình (b) có dạng ( y2 )*n = an + b
( y2 )*n1= an + a + b và ( y2 )*n2 = an + 2a + b thay ( y2 )*n2 , ( y2 )*n1, ( y2 )*n | ||
vào (b), ta được 6an – 5a + 12b = 6n – 5 a = 1, b = 0 ( y )* n | ||
2 n | ||
nghiệm riêng của phương trình (9) là y* = ( y )* | + ( y )* = 2n + n | |
n | 1 n | 2 n |
Vậy nghiệm tổng quát của phương trình (9) đã cho là :
y = y + y* = C 3n+ C 4n + 2n + n
n n n 1 2
7



