ÁO TRÌNH TOÁN CAO CẤ 104
Ch−¬ng V: Lý thuyÕt chuçi ÁI NIỆM CHUỖI SỐ Ðịnh nghĩa ãy số thực 
 ới n = 1, 2, 3, … . Biểu thức tổng vô hạn ðýợc gọi là một
ỗi số à un ðýợc gọi là số hạng tổng quát (thứ n) của chuỗi số. ổng số
ðýợc gọi là ổng riêng
ứ n của chuỗi số. Nếu dãy các tổng riêng   ó giới hạn là ột số thự
  ì chuỗi số ðýợc gọi là ội tụ à S ðýợc gọi là tổng của
ỗi; trong trýờng hợp này ta viết ýợc lại, nếu dãy  
ông hội tụ thì chuỗi số ðýợc gọi là ân kỳ
í dụ: ét chuỗi hình học có dạng ðó a là số khác 0. ó:  ếu |q| < 1 thì
Sưu tầm và chỉnh s a by Nguy ử ễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 105
ó chuỗi hội tụ và có tổng là ếu |q| > 1 thì ó chuỗi phân kỳ.
ýờng hợp |q| = 1, ta dễ thấy rằng chuỗi phân ỳ. ết luận:
ỗi hình học hội tụ khi và chỉ khi |q| < 1. Khi ðó
ác tính chấ ủa chuỗi số
ục này sẽ phát biểu một số tính chất của chuỗi số. Các tính chất này có thể
ểm chứng dễ dàng từ ðịnh nghĩa của chuỗi số. Ðịnh lý: ính hội tụ
ân kỳ của một chuỗi số sẽ không ðổi khi ta bỏ ði một số hữu hạn số
ạng ðầu của chuỗi số. ệ quả:
ính hội tụ hay phân kỳ của một chuỗi số sẽ không ðổi nếu ta bỏ ði hay thêm vào một
ố hữu hạn số hạng ở những vị trí bất kỳ. Ðịnh lý ếu chuỗi số
ội tụ và có tổng bằng S thì vớc ta có chuỗi ũng hội ụ và Ðịnh lý: ếu à
à các chuỗi số hội tụ thì các chuỗi tổng và chuỗi hiệu sau ðây
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 106 à
ũng là các ch ỗi hội tụ. Hõn nữa: à
êu chuẩn hội tụ Cauchy:
Ðịnh lý: Ðiều kiện cần và ðủ ðể chuỗi số ội tụ là với mọi 
ất kỳ, tồn tại số N (phụ thuộc  ới mọi n tùy ý lớn
õn N ðiều kiện sau ðâu ðýợc thỏa mãn:  ới mọi p = 0, 1, 2, …
ừ ðịnh lý trên ta suy ra ðịnh lý về ðiều kiện cần cho sự hội tụ của một chuỗi số sau ðây. Ðịnh lý: ếu chuỗi ội tụ thì ậy chuỗi số ân kỳ nếu  
ông tiến về 0 khi n  í dụ: ỗi ân kỳ vì ác 0.
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 107 ỗi ân kỳ vì ông tồn tại. ỖI SỐ DÝÕNG ỗi số
ðýợc gọi là ch ỗi số dýõng nếu tất cả các số hạng của chuỗi số
ðều là số dýõng. Trýờng hợp tất cả các số hạng ðều là số không âm thì chuỗi số ðýợc
ọi là chuỗi số không âm. Lýu ý rằng khi xét tính hội tụ hay phân kỳ cũng nhý tính
ổng của chuỗi số không âm ta có thể loạ ỏ ra các số hạng bằng 0, nên chuỗi số
ông âm cũng thýờng ðýợc gọi là chuỗi số dýõng.
ận xét rằng dãy các tổng riêng 
 ủa chuỗi số dýõng là dãy tãng nên chuỗi
ố hội tụ khi và chỉ khi dãy   ị chặn trên.
ác tiêu chuẩn so sánh Ðịnh lý:
ả sử hai chuỗi số dýõng à ỏa ðiều kiện un  ới n khá lớn
ĩa là ứng với mọi n lớn hõn một số n ào ðó). Khi ðó ếu ội tụ thì ội tụ. ếu ân kỳ thì ân kỳ. ận xét: ỗi số dýõng à
ội tụ khi và chỉ khi chuỗi ội ụ. í dụ:
ảo sát sự hội tụ của chuỗi số
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 108
ới mọi n = 1, 2, 3, … ta có:
ì chuỗi hình học có số hạng tổng quát
ội tụ nên theo tiêu chuẩn so sánh ðýợc
át biểu trong ðịnh lý trên chuỗi số ội tụ. ệ quả: ếu tồn tại giới hạn
ới L là một số thực dýõn ì các chuỗi số ýõng à
ùng hội tụ hoặc cùng phân kỳ. ếu
ì từ sự hội tụ của chuỗi
ẽ kéo theo sự hội tụ của ỗi
à từ sự phân kỳ của chuỗi
ẽ kéo theo sự phân kỳ của chuỗi ếu
ì từ sự hội tụ của chuỗi
ẽ kéo theo sự hội tụ của ỗi
à từ sự phân kỳ của chuỗi
ẽ kéo theo sự phân kỳ của chuỗi ú:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 109 ýờng hợp
ói un týõng ðýõng với vn (khi n   à viết
à un ~ vn . Vậy: nếu un ~ vn ì các chuỗi số dýõng à ùng hội tụ ặc cùng phân kỳ.
Ðể áp dụng các tiêu chuẩn so ánh ta phải ghi nhớ tính chất hội tụ hay phân kỳ của
ột số chuỗi thýờng gặp, chẳng hạn chuỗi hình học. Ở ðây ta công nhận kết quả sau
ðây về sự hội tụ của chuỗi  à t ố): ỗi ội tụ  
ết quả này có thể ðýợc chứng minh bằng cách áp dụng tiêu chuẩn tích phân Cauchy
ẽ ðýợc trình bày sau. Ứng với trýờng hợp  ó chuỗi ân kỳ. í dụ:
ảo sát sự hội tụ của chuỗi số ó: à chuỗi
ân kỳ và  à một hằng số khác 0 nên ỗi ũng phân kỳ.
ảo sát sự hội tụ của chuỗi số   ó 
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 110 
ì chuỗi hình học có số hạng tổng quát
ội tụ nên theo tiêu chuẩn so sánh ta có ỗi ũng hội tụ.
ảo sát sự hội tụ của chuỗi số   ó   ì chuỗi ân kỳ nên chuỗi ũng phân kỳ. êu chuẩ ’Alembert. Ðịnh lý:
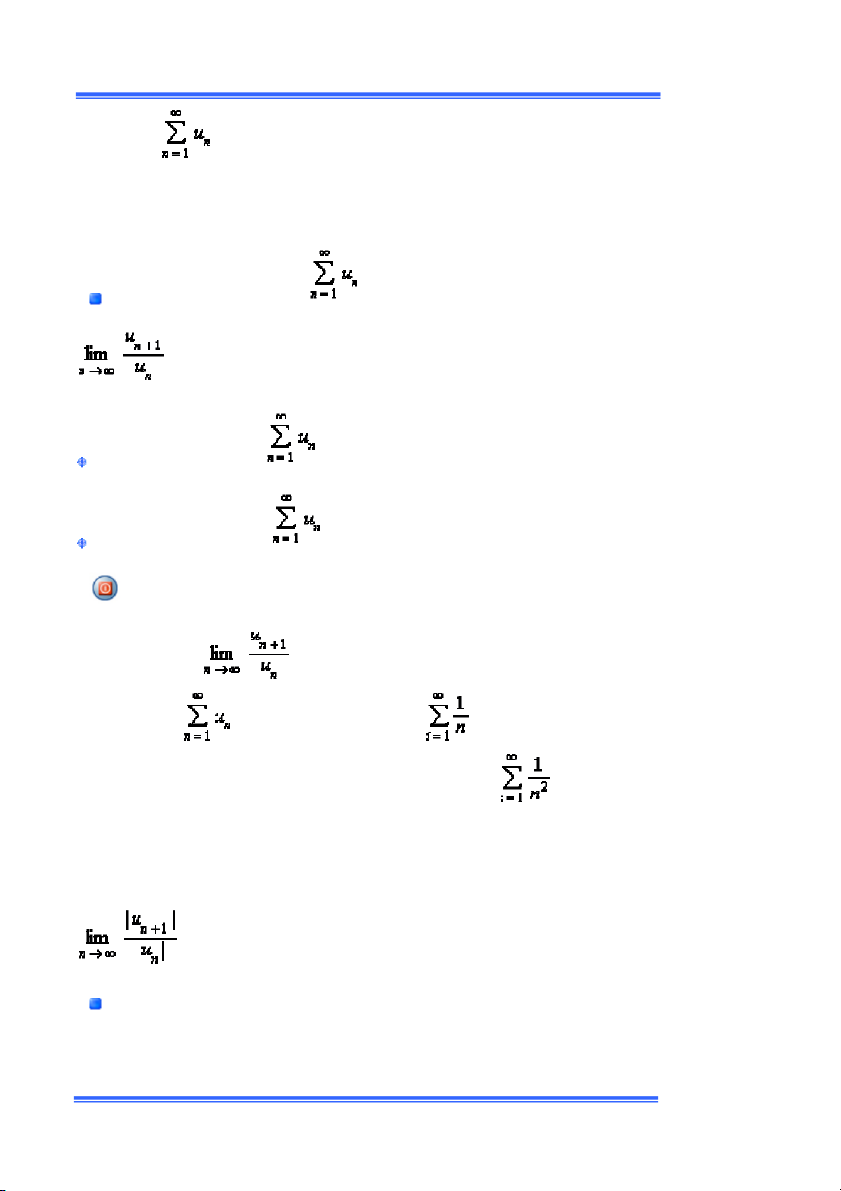
êu chuẩn d’Alembert) Xét chuỗi số dýõng Ðặt ó:
ếu có một số q < 1 và có một số tự nhiên n   ì chuỗi số ội tụ.
ếu có một số tự nhiên n  
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 111 ì chuỗi số ân kỳ.
ừ ðịnh lý trên ta rút ra hệ quả sau ðây, cũng ðýợc gọi là tiêu chuẩn hội tụ ’Alembert: ệ quả: ỗi số dýõng ả sử  ếu  ì chuỗi số ội tụ. ếu  ì chuỗi số ân kỳ. ýu ý: ýờng hợp
ì ta chýa kết luận ðýợc một cách chính xác ỗi số dýõng
ội tụ hay phân kỳ. Chuỗi
à một ví dụ cho trýờng
ợp chuỗi số dýõng phân kỳ thỏa mãn ðiều kiện (*), và chuỗi à một í dụ
ýờng hợp chuỗi số dýõng hội tụ thỏa mãn ðiều kiện (*).
ác khẳng ðịnh (i) và (ii) trong hệ quả trên cũng ðúng cho chuỗi bất kỳ với giả thiết ằng  í dụ:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 112 ét chuỗi số
ới x là một số thực cho trýớc. Khảo sát sự hội tụ của ỗi ố.
ố hạng thứ n của chuỗi số là
ận xét rằng với x = 0 thì các số hạng ðều
ằng 0 nên chuỗi hội tụ. Xét trýờng hợp x  ó: ậy chuỗi ội tụ với mọi
ảo sát sự hội tụ của chuỗi số
ố hạng thứ n của chuỗi số là ó: à ỗi ân kỳ.
êu chuẩn cãn thức Cauchy.
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 113 Ðịnh lý:
êu chuẩn cãn thức Cauchy) Xét chuỗi số dýõng Ðặt Cn =
ếu có một số q < 1 và có một số tự nhiên n   ì chuỗi số ội tụ.
ếu có một số tự nhiên n   ì chuỗi số ân kỳ.
ừ ðịnh lý trên ta rút ra hệ quả sau ðây, cũng ðýợc gọi là tiêu chuẩn cãn thức ệ quả: ỗi số dýõng ả sử  ếu  ì chuỗi số ội tụ. ếu  ì chuỗi số ân kỳ. ýu ý: ýờng hợp
ì ta chýa kết luận ðýợc một cách chính xác ỗi ố dýõng
ội tụ hay phân kỳ. Chuỗi
à một ví dụ cho trýờng
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 114
ợp chuỗi số dýõng phân kỳ ỏa mãn ðiều kiện (*), và chuỗi à một ví dụ
ýờng hợp chuỗi số dýõng hội tụ thỏa mãn ðiều kiện (*).
ác khẳng ðịnh (i) và (ii) trong hệ quả trên cũng ðúng cho chuỗ ất kỳ với giả thiết ằng  í dụ: ét chuỗi số
ới x là một số thực cho trýớc. Khảo sát sự hội tụ của chuỗi số.
ố hạng thứ n của chuỗi số là ó:   
ừ tiêu chuẩn Cauchy ta suy ra chuỗi ội tụ với mọi x.
ét sự hội tụ của chuỗi số
ố hạng thứ n của chuỗi số là ó:    ỗi số
ân kỳ theo tiêu chuẩn Cauchy.
êu chuẩn tích phân Cauchy. Ðịnh lý:
êu chuẩn tích phân Cauchy)
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 115 ếu chuỗi số ó dạng ĩa là
ới mọi n; trong ðó f là ột hàm số liên tục
ông âm và giảm trên [1, + ì ta có: ội tụ  ội tụ í dụ:
ét sự hội tụ của chuỗi ðiều hòa mở rộng
ýớc hết ta thấy rằng nếu   ì 
ông hội tụ về 0 nên chuỗi phân ỳ. Xét trýờng hợp 
ễ thấy rằng các tiêu chuẩn d’Alembert và tiêu chuẩn cãn
ức Cauchy ðều không cho ta kết luận ðýợc về tính hội tụ hay ân kỳ của chuỗi số. àm số f(x) =
ỏa các ðiều kiện giả thiết trong tiêu chuẩn tích phân Cauchy. Do ích phân suy rộng
ội tụ khi và chỉ khi  ên chuỗi ội tụ khi à chỉ khi  óm lại ta có: ội tụ  
ét sự hội tụ của chuỗi
ố hạng thứ n của chuỗi số là ó: ới
àm số f(x) thỏa các ðiệu kiện của tiêu chuẩ
ích phân Cauchy. Xét tích phân
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 116
Ðổi biến: u = ln(x), thì ðýợc  ậy chuỗi ân kỳ.
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 130 ỖI TỖNG QUÁT ỗ ðan dấu ãy 
 ác số dýõng, chuỗi số có số hạng tổng quát u
ðýợc gọi là chuỗi ðan dấu. Liên quan ðến chuỗi ðan dấu ta có tiêu chuẩn hội tụ ý sau:
Ðịnh lý: êu chuẩn Leibnits) ếu chuỗi ðan dấu ỏa mãn 2 ðiều kiện: ãy 
 à dãy dýõng giảm, và
ì chuỗi hội tụ. Hõn nữa tổng S của chuỗi thỏa 0 < S  ú thích:
ỗi thỏa ðiều kiện của tiêu chuẩn Leibn
ðịnh lý trên ðýợc gọi là chuỗi ếu dùng tổng
ðể xấp xĩ tổng của chuỗi Leibnitz thì phần dý thứ n của chuỗi là Rn thỏa:  í dụ
ảo sát sự hội tụ của chuỗi
Sưu tầm và chỉnh s a by Nguy ử ễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 131
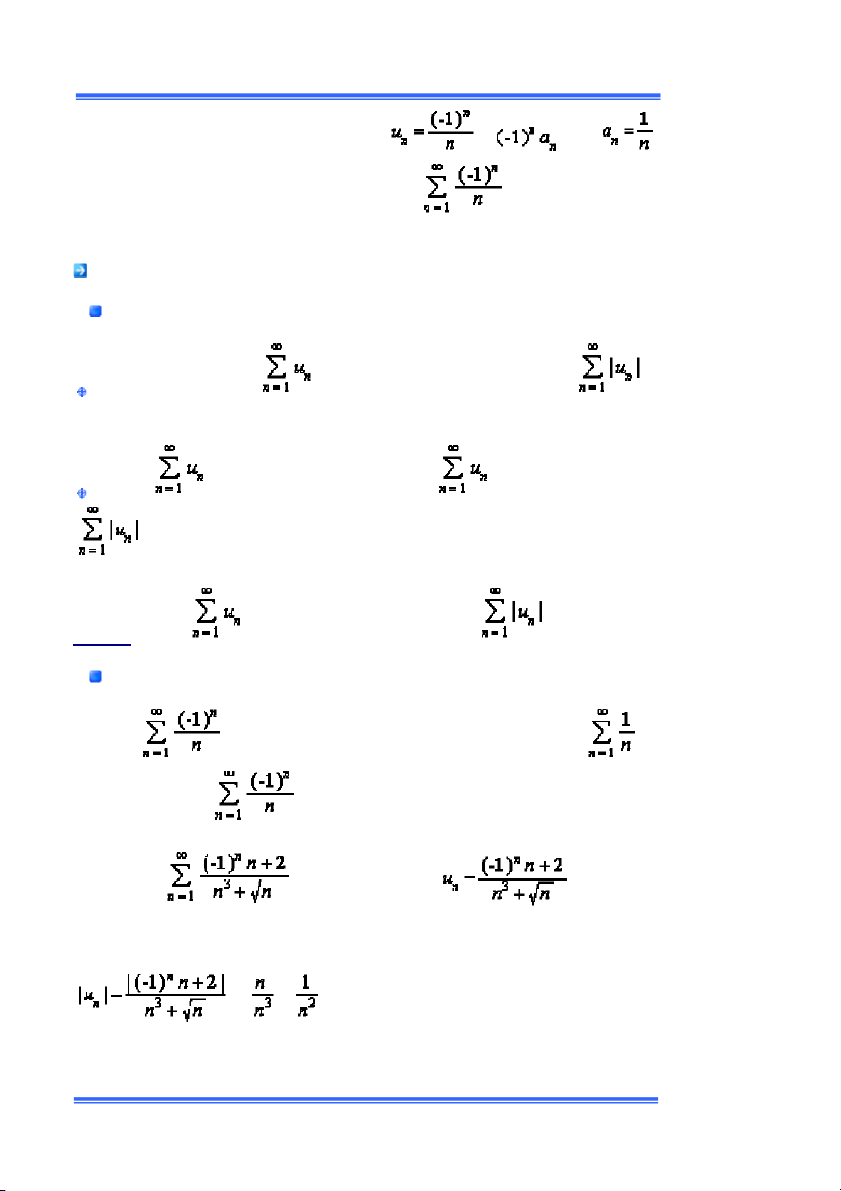
ỗi số là chuỗi ðan dấu có số hạng thứ n là ới
à dãy số dýõng giảm và hội tụ về 0. Vậy chuỗi số à chuỗi Leibnitz nên ỗi hội tụ.
ội tụ tuyệt ðối Ðịnh nghĩa:
ỗi số (có dấu bất kỳ)
ðýợc gọi là ội tụ tuyệt ðối ếu chuỗi ội tụ. ỗi số
ðýợc gọi là án hội tụ ếu chuỗi ội tụ nhýng ỗi ân kỳ. ú ỗi
ông dẫn tới sự hội tụ của chuỗi í dụ: ỗi
ội tụ theo tiêu chuẩn Leibnitz nhýng chuỗi ðiều hòa ân kỳ. Vậy chuỗi à bán hội tụ. ét chuỗi ó số hạng tổng quát ó:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 132
à chuỗi ðiều hòa mở rộng ội tụ. Suy ra chuỗi ội tụ theo tiêu ẩn so sánh. Vậy chuỗi ội tụ tuyệt ðối. Ðịnh lý: ếu chuỗi ội tụ thì chuỗi ội tụ và
ýới ðây là một số tính chất ðã ðýợc chứng minh ên quan ðến các chuỗi hội tụ ệt ðối. Ðịnh lý: ả sử chuỗi
án hội ụ. Khi ðó với mọi số S hữu hạn hoặc là S =   ồn tại
ột cách thay ðổi vị trí của các số hạng của chuỗi ðể ðýợc một chuỗi mới có tổng là Ðịnh lý: ếu chuỗi
ội tụ tuyệt ðối thì khi thay ðổi vị trí các số hạng của chuỗi một
ách tùy ý ta vẫn ðýợc một chuỗi mới hội tụ tuyệt ðối và có cúng tổng với chuỗi ban ðầu. Ðịnh lý: ếu các chuỗi à
ội tụ tuyệt ðối và có tổng lần lýợt là S và T thì ỗi gồm mọi số hạng
… , n; j = 1, 2, … , n) theo một thứ tự bất kỳ
ôn hội tụ tuyệt ðối à có tổng bằng ST.
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 133 ỖI HÀM Ðịnh nghĩa ãy hàm số
ới n = 1, 2, … ùng xác ðịnh trên một tập E các số thực. Khi ðó với mỗi x  ó chuỗi số
ét x biến thiên trong E, ta gọi chuỗi à một ỗi hàm Ðiểm x  à chuỗi
ội tụ ðýợc gọi là ðiểm hội tụ
ũng nói chuỗi hàm hội tụ tại
ập tất cả các ðiểm hội ụ ðýợc gọi là ền hội tụ ủa chuỗi hàm. Gọi D là miền
ội tụ của chuỗi lũy thừa, ta có:
à các hàm số của x xác ðịnh trên D. Sn(x) ðýợc gọi là tổng riêng thứ n của chuỗi
àm, S(x) là tổng của chuỗi hàm và Rn(x) là phần dý thứ n của chuỗi hàm. Tổng
ó thể biểu diễn dýới dạng ới mọi x  ó ên ĩa là phần dý
ủa chuỗi hàm hội tụ ðến 0 khi n   í dụ:
ìm miền hội tụ của chuỗi hàm
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 134
Ðã biết rằng chuỗi số
ội tụ khi và chỉ khi  ðó chuỗi
ội tụ khi và chỉ khi ln(x) > 1, hay x > e. Suy ra miền hội tụ của chuỗi hàm là D = (e, 
ìm miền hội tụ của chuỗi hàm ới mỗi x, chuỗi số ó số hạng tổng quát ới 
êu chuẩn hội tụ d’Alembert ta có:   ỗi (*) hội tụ.   ỗi (*) phân kỳ.   ỗi (*) có dạng à chuỗi phân kỳ.
ậy miền hội tụ của chuỗi hàm à D = ( 
ìm miền hội tụ của chuỗi hàm
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 135 ới mỗi x, chuỗi số
ó có số hạng tổng quát ới  
êu chuẩn cãn Cauchy ta có chuỗi phân kỳ (với mọi x). Vậy miền hội tụ của
ỗi hàm à tập hợp rỗng. ội tụ ðều Ðịnh nghĩa:
ét x biến thiên trong một tập X nào ðó nằm trong miền hội tụ của chuỗi hàm
ọi S(x) là tổng của chuỗi hàm và Sn(x) là tổng riêng thứ n của chuỗi àm. Nếu với mọi  ồn tại n       – 
ì ta nói chuỗi hàm ội tụ ðều ới hàm S(x) trên tập X, hoặc dãy hàm Sn(x) hội tụ ðều
ới hàm S(x) trên tập X. Ðiều này cũng có nghĩa là dãy các phần dý Rn(x) = S(x)
ội tụ ðều tới 0 trên X.
Ðịnh lý sau ðây cho ta một tiêu chuẩn về sự hội tụ cũng nhý hội tụ ðều của chuỗi àm. Ðịnh lý: êu chuẩn Weierstrass) ếu
ứng với mọi n lớn hõn một n ào ðó và với mọi x  à chuỗi số ýõng ội tụ, thì chuỗi hàm
ội tụ ðều và hội tụ tuyệt ðối trên X. í dụ:
ảo sát sự hội tụ của chuỗi hàm
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 136 ó: ứng với mọi x  à do chuỗi ội tụ , nên chuỗi àm ội tụ
ðều và hội tụ tuyệt ðối trên toàn trục số theo tiêu chuẩn Weierstrass.
ảo sát sự hội tụ của chuỗi hàm ên tồn tại n ới mọi n  ì ới mọi n 
à với mọi số thực x ta có: 
à chuỗi số ðiều hòa (mở rộng)
ội tụ. Vậy theo tiêu chuẩn Weierstrass ỗi hàm
ội tụ ðều và hội tụ tuyệt ðối trê àn trục số.
ính chất của chuỗi hàm hội tụ ðều
ục nầy sẽ phát biểu một số ðịnh lý về tính chất của các chuỗi hàm hội tụ ðều. Ðịnh lý:
ính liên tục của hàm tổng)
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 137 ếu mọi hàm
ên tục trên X và chuỗi hàm
ội tụ ðều ðến hàm S(x)
ên X, thì S(x) cũng liên tục trên X.
Ðịnh lý: ích phân từng số hạng) ếu mọi hàm
ên tục trên [a, b] và chuỗi hàm ội tụ ðều ðến hàm ên [a, b], thì 
Ðịnh lý: ðạo hàm từng số hạng)
ả sử ta có các ðiều kiện sau ðây: ác hàm
ó ðạo àm liên tục trong khoảng (a, b); ỗi hàm
ội tụ ðến S(x) trong (a, b); ỗi các ðạo hàm ội tụ ðều trong (a, b).
ðó S(x) có ðạo hàm trong khoảng (a, b) và ’(x) 
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 138 ỖI LŨY THỪA Ðịnh nghĩa ọi chuỗi hàm có dạng à ỗi lũy thừa ác hằng số
ðýợc gọi là các ệ số ủa chuỗi lũy ừa, hệ số
ðýợc gọi là hệ số tổng quát của chuỗi. Ta gọi à
ố hạng tổng quát của chuỗi lũy thừa.
ếu thực hiện phép ðổi biến
ì chuỗi lũy thừa trên trở thành chuỗi có ạng
ðó trong các mục tiếp theo dýới ðây ta chỉ chuỗi lũy thừa có ạng í dụ: ỗi lũy thừa ó hệ số tổng quát là ỗi lũy thừa
Sưu tầm và chỉnh s a by Nguy ử ễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 139 ó hệ số tổng quát là
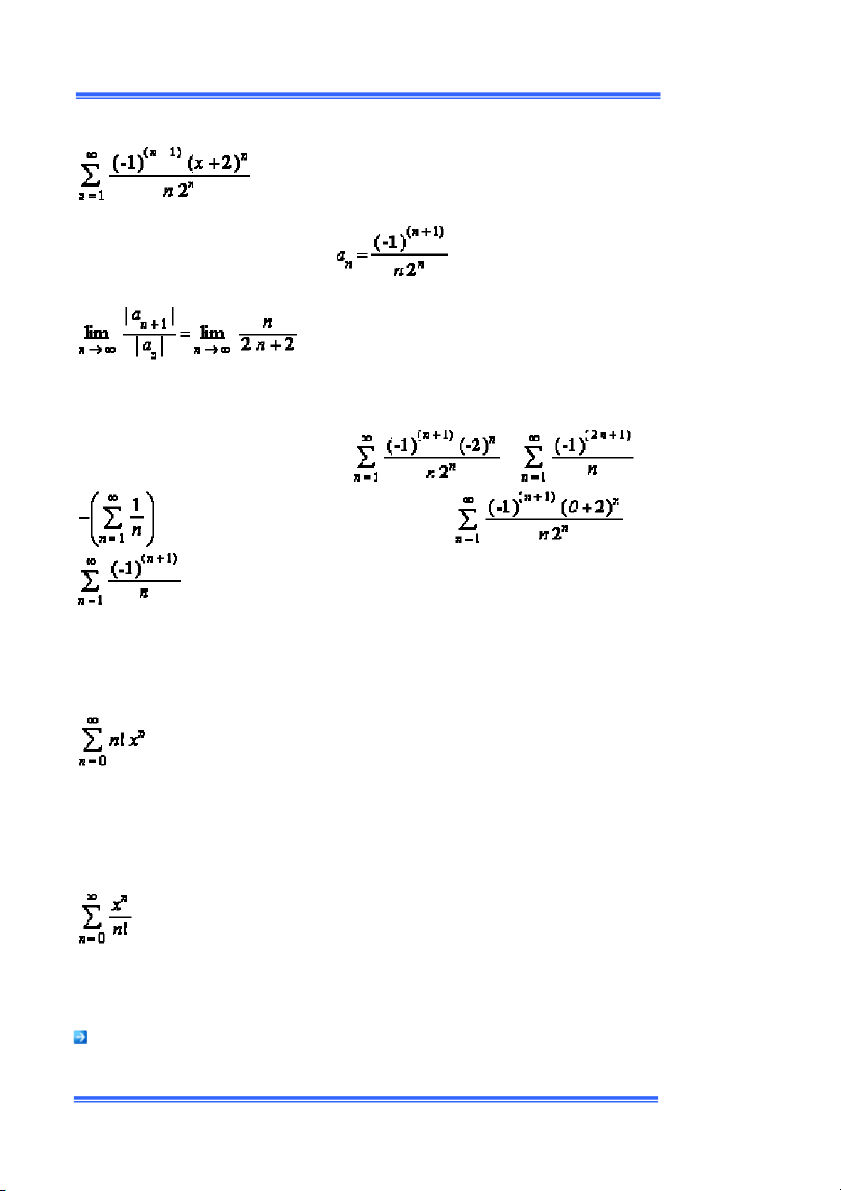
ằng cách ðổi biến X = x+2, chuỗi lũy thừa ðýợc chuyển về dạng
án kính hội tụ và miền hội tụ
ột trong những vấn ðề ðýợc xem xét ðối với chuỗi lũy thừa là tìm miền hội tụ. Cho ỗi lũy thừa
ýớc hết có thể thấy rằng chuỗi (*) hội tụ tại x = 0. Ðịnh lý sau ðây là một trong
ững kết quả quan trọng liên quan ðến vấn ðề tìm miền hội tụ của chuỗi lũy thừa. Ðịnh lý: ếu chuỗi lũy thừa ội tụ tại
ì chuỗi cũng hội tụ tuyệt ðối tại ọi x  ếu chuỗi lũy thừa ân kỳ tại
ì chuỗi cũng phân kỳ tại mọi x  ứng minh: ả sử chuỗ ũy thừa ội tụ tại ĩa là chuỗi số ội ụ. Khi ðó  ó số dýõng M sao cho  ới mọi số tự nhiên n.
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 140 ột số thực x  ó:  ới 0  ỗi hình học
ội tụ do q < 1, nên chuỗi ội tụ tuyệt ðối.
óm lại ta có chuỗi lũy thừa ội ụ tuyệt ðối trên ần (i)
ủa ðịnh lý ðýợc chứng minh.
ây giờ giả sử chuỗi lũy thừa ân kỳ tại ĩa là chuỗi số
ân kỳ. Nếu có số thực x  à chuỗi ội tụ
ì theo phần chứng minh ở trên ta có chuỗi
ội tụ (mâu thuẩn). Vậy
ỗi phân kỳ tại mọi x 
ần (ii) của ðịnh lý ðýợc chứng minh.
ừ ðịnh lý Abel ta có một số nhận ét về dạng của miền hội tụ của chuỗi lũy thừa
ý sau. Trýớc hết chuỗi hội tụ tại x = 0 với tổng bp sau ðây:
ýờng hợp 1: Chuỗi chỉ hội tụ tại x = 0.
ýờng hợp 2: Chuỗi hội tụ trên toàn trục số. ýờng hợp 3: Chuỗi ó ðiểm hội tụ à có ðiể ân kỳ ất ên là
ðịnh lý Abel. Vậy miền hội tụ D của chuỗi lũy thừa phả ỏa D 
ên bị chặn. Do tính ðầy ðủ của tập số thực D có cận trên
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 141
ðúng R. Có thể thấy rằng nếu
ì chuỗi phân kỳ tại x, và nếu x  ì ỗi hội tụ tại x. Ðịnh nghĩa: án kính hội tụ) ỗi lũy thừa
ếu tồn tại số dýõng R sao cho chuỗi lũy thừa hội tụ ại mọi x mà
à chuỗi phân kỳ tại mọi x mà ì R ðýợc gọi là bán
ính ội tụ của chuỗi lũy thừa. Trýờng hợp chuỗi chỉ hội tụ tại x = 0 ta nói bán kính hội
ụ của chuỗi lũy thừa là R = 0; nếu chuỗi hội tụ trên toàn trục số t ì ta nói bán kính ội tụ là R = +
ðịnh nghĩa trên ta có các trýờng hợp về miền hội tụ của chuỗi lũy thừa nhý
ếu bán kính hội tụ R là một số thực dýõ
ì miền hội tụ D của chuỗi lũy thừa là
ột trong 4 trýờng hợp sau:
ỗi không hội tụ tại  ỗi hội tụ tại  ỗi hội tụ tại
ýng không hội tụ tại R.
ỗi hội tụ ại R nhýng không hội tụ tại
ếu R = 0 thì miền hội tụ của chuỗi lũy thừa là D =   ếu R = +
ì miền hội tụ của chuỗi lũy thừa là D =
ậy việc tìm bán kính hội tụ của chuỗi lũy thừa là býớc rất quan trọng cho việc tìm
ền hội tụ của chuỗi lũy thừa. Ta có thể tính bán kính hội tụ của chuỗi lũy thừa dựa ðịnh lý ýới ðây. Ðịnh lý: ìm bán kính hội tụ) ỗi lũy thừa ả sử
ðó bán kính hội tụ R của chuỗi lũy thừa là ếu à số thực dýõng; ếu   ếu í dụ:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 142
ìm miền hội tụ của chuỗi lũy thừa
ệ số tổng quát của chuỗi lũy thừa là ó 
Ðể xác ðịnh miền hội tụ
ần xét sự hội tụ của chuỗi tại các ðiểm à +1. Xét tại x ấy chuỗi số
ân kỳ. Tại x = 1, ta có chuỗi ố
ũng phân kỳ(do số hạng tổng quát của chuỗi số không dần về
ậy miền hội tụ của chuỗi lũy thừa là D = (
ìm miền hội tụ của chuỗi lũy thừa
ệ số tổng quát của chuỗi lũy thừa là ó
 án kính hội tụ R = 1. ét tại x = ðýợc chuỗi
à chuỗi Leibnitz nên hội tụ. Tại x = 1 ta có ỗi ðiều hòa ên là chuỗi phân kỳ.
ậy miền hội tụ của chuỗi lũy thừa là D = [
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 143
ìm miền hội tụ của chuỗi lũy thừa
ệ số tổng quát của chuỗi lũy ừa là ới x ó
 án kính hội tụ R = 2. ét tại x = x – ðýợc chuỗi số ân kỳ. Tại x = x ðýợc chuỗi ội tụ theo tiê ẩn Leibnitz.
ậy miền hội tụ của chuỗi lũy thừa là D = (
ìm miền hội tụ của chuỗi lũy thừa
ó thể tính ðýợc bán kính hội tụ của chuỗi lũy thừa là R = ỗi chỉ hội tụ
ại x = 0, tức là miền hội tụ D =  
ìm miền hội tụ của chuỗi lũy thừa
ó thể tính ðýợc bán kính hội tụ của chuỗi lũy thừa là R =  ỗi hội tụ tại
ọi x, tức là miền hội tụ D =
ác tính chất của chuỗi lũy thừa
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 144
ục này sẽ nêu lên một số tính chất của chuỗi lũy thừa liên quan ðến sự hội tụ
ðều, tính liên tục, tính ðạo hàm và tích phân. ính chất 1:
ỗi lũy thừa hội tụ ðều trên mọi ðoạn [a, b] nằm trong khoảng hội tụ của nó. ính chất 2:
ổng của chuỗi lũy thừa là một hàm liên tục trong khoảng hội tụ của nó. ính chất 3:
ó thể lấy tích phân từng số hạng của chuỗi lũy thừa trên ðoạn [a, b] nằm trong
ảng hội tụ của nó. Nói cách khác ta có
ài ra, nếu gọi S(x) là hàm tổng của chuỗi lũy thừa và R là bán kính hội tụ thì với
ọi x thuộc khoảng hội tụ ( ó: ính chất 4:
ó thể lấy ðạo hàm từng số hạng của chuỗi lũy thừa trong khoảng hội tụ của nó và
ỗi mới nhận ðýợc cũng có cùng bán kính hội tụ với chuỗi ðầu. í dụ: ính tổng
ó thể tính ðýợc dễ dàng là bán kính hội tụ của
ỗi lũy thừa là R = 1, vậy khoảng ội tụ là (
ảng hội tụ này, ta lấy ðạo hàm từng số hạng của chuỗi thì ðýợc
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g
ÁO TRÌNH TOÁN CAO CẤ 145
ấy tích phân của S’(x) trên ðoạn [0, x] sẽ ðýợc ính tổng ó:
ấy ðạo hàm từng số hạng trong khoảng ( ì ðýợc
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g ÁO TRÌNH TOÁN CAO CẤ 117 ÀI TẬP CHÝÕNG 5
ùng ðịnh nghĩa ðể khảo sát sự hội tụ và tính tổng (nếu có) của chuỗi số:
ảo sát dự hội tụ của các chuỗi số.
ử dụng tiêu chuẩn cãn thức Cauchy khảo sát sự hội tụ của các chuỗi số sau:
ử dụng tiêu chuẩn d’Alembert khảo sát sự hội tụ của các chuỗi số sau:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g ÁO TRÌNH TOÁN CAO CẤ 118
ử dụng tiêu chuẩn tích phân Cauchy khảo sát sự hội tụ của các chuỗi số sau:
ác chuỗi sau ðây hội tụ hay phân kỳ:
ứng minh rằng nếu các chuỗi à ội tụ thì chuỗi số ội tụ tuyệt ðối.
ác chuỗi số sau ðây hội tụ tuyệt ðối, bán hội tụ hay phân kỳ?
ìm miền hội tụ của chuỗi hàm.
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g ÁO TRÌNH TOÁN CAO CẤ 119
ìm miền hội tụ của các chuỗi sau ðây: àm số y = f(x) =
ìm miền xác ðịnh của f(x).
ứng minh rằng hàm số y = f(x) nghiệm ðúng phýõng trình ’ = 1 + x – ển Maclaurin các hàm sau:
Sưu tầm và chỉnh sửa by Nguyễn Hải Đăng y g y g