Chương Trình - Chuẩn hóa Văn Phạm Chomsky (Thctd). Môn Chương trình dịch (Phenika) | Đại học Trường Đại học Phenika.

lOMoAR cPSD| 59285474 Chuẩn hóa Chomsky:
Bước 1: Loại bỏ epsilon (ε) Các quy tắc có ε: • S → ε • A → ε
Khi thay thế S và A vào các quy tắc khác, ta có:
S → A (S) B | A ( ) B | (S) B | ( ) B | B A → S | SB | x B → SB | y
Bước 2: Tạo biến mới cho ký hiệu đầu cuối
Vì trong dạng Chomsky, mỗi quy tắc phải có dạng A → BC hoặc A → a, ta phải thay các ký hiệu đầu cuối
riêng biệt bằng biến mới. Đặt: X -> x Y -> y
S → A (S) B | A ( ) B | (S) B | ( ) B | B A → S | SB | X B → SB | Y X -> x Y -> y lOMoAR cPSD| 59285474
Bước 1: Xóa các quy tắc có hơn 2 ký hiệu ở vế phải
Các quy tắc như Expr → Expr AddOp Term có 3 ký hiệu, nên cần thay thế: •
Đặt E' cho AddOp Term •
Đặt T' cho MulOp Factor •
Đặt F' cho Factor ^ Primary
Expr → Term | Expr E' | E’ E' → AddOp Term Term → Factor | Term T' T' → MulOp Factor
Factor → Primary | Factor F' F' → K’ Primary K’ -> ^
Primary → number | variable | ( Expr ) AddOp → + | - MulOp → * | / lOMoAR cPSD| 59285474
Bước 1: Tạo biến mới cho ký hiệu đầu cuối Đặt: • X_a= a • X_b= b S → X_a B | X_b A A
A → X_a B A A | X_a S B | X_b | X_a B B B → X_b S X_a → a X_b → b S → aA | bB | ε A → bSB A → bA
Chuẩn hóa về dạng Chomsky (CNF):
Bước 1: Loại bỏ ε (rỗng) • Quy tắc có ε: S→ ε •
Thay thế S vào các nơi sử dụng nó: lOMoAR cPSD| 59285474 • A → bSB | bB
Sau khi thay thế, cập nhật lại tập quy tắc: S → aA | bB A → bS B | b B B → b A
Bước 2: Tạo biến mới cho ký hiệu đầu cuối Đặt: • X_a= a • X_b= b
Thay thế vào các quy tắc: S → X_a A | X_b B A → X_b S B | X_b B B → X_b A X_a → a X_b → b
Bước 1: Loại bỏ epsilon (ε)
B → b | ε có chứa epsilon, nên thay B vào các vế phải khác: lOMoAR cPSD| 59285474
o A → B | S → A → b | S o S
→ aB → S → aB | a Cập nhật lại tập luật: S → A S A | a B | a A → b | S B → b
Bước 2: Tạo biến mới cho ký hiệu đầu cuối
Dạng Chomsky không cho phép nhiều hơn hai ký hiệu trong vế phải, cũng như ký hiệu đầu cuối
(terminal) đứng lẫn với non-terminal. Đặt: o X_a = a o X_b = b Thay thế: S → A S A | X_a B | X_a A → X_b | S B → X_b X_a → a X_b → b Tính First,Follow lOMoAR cPSD| 59285474 S → Ac | BBc (1) C → b | bCd (2) D → bd | bDd (3) A → BC (4) B → dBb | dDb | ε (5)
Từ (4) FIRST(A) = FIRST(B) mà ε thuôc FIRST(B) và ε không thuộc First(C)=> FIRST(A)=FIRST(B)\ ε
+FIRST(C)={d,b} Từ (5) FIRST(B)={d, ε} Từ (2) FIRST(C) ={b} Từ (3) => FIRST(D) ={b}
Từ (1) => FIRST(S) = FIRST(A) và FIRST(s) = FIRST(B) mà ε thuôc FIRST(B) => FIRST(S) = FIRST(A) +
FIRST(B)\ ε +c ={d,b,c} Vậy ta có: FIRST(S) ={d,b,c} FIRST(A)={ d,b} FIRST(B)={d, ε} FIRST(C) =FIRST (D) ={b} FOLLOW: lOMoAR cPSD| 59285474 -
Áp dụng luật 1 Fo(S) = {$} Luật 2: o Từ (1) Fo(A)={c}, Fo(B) = Fi(B)\ {ε} + {c} ={b,c,d} LU
o Từ (2) Fo( C )={d} o Từ (3) Fo(D) ={d} o
Từ (4) Fo(B)=Fi(C)={b} o Từ (5) Fo(B) = {b} ,
Fo(D)={b} - Luật 3: o Từ (4) F,o(A)=Fo(C)={c} Vậy:
Fo(S) = {$}, Fo(A)={c}, Fo( C )={c,d} ,Fo(D) ={d}, Fo(B)={b,c,d} S → AD | abc (1) B → dBc | CC (2) C → DCb | CDb | ε (3) A → Bc (4) D → Dd | ε (5) FIRST: Từ (5) Fi(D) ={d, ε}
Từ (3) Fi (C) = Fi(D) mà ε thuôc Fi(D) => Fi(C)= {b,d,ε}
Từ (2) Fi(B)={d} và Fi{B}=Fi(C)={b,d, ε}
Từ (4) => Fi(A)= Fi(B) \{ ε }+{c}={b,c,d}
Từ (1) => Fi(S) = Fi(A) +{a} ={a,b,c,d} FOLLOW: Luật 1: - Fo(S)={$} Luật 2: -
Từ (1) Fo(A)=Fi(B)\{ ε }={b,d} -
Từ (2) Fo(B)= {c} , Fo(C) = Fi(C)\{ ε} = {b,d} -
Từ (3) Fo(D) = Fi(C)\{ε} + {b} = {b,d}, Fo(C) = Fi(D)\{ ε} + {b} = {b,d} - Từ (4) Fo(B)={c} - Từ (5) Fo(D)={d} Luật 3: - Từ (1) Fo(D) = Fo(S) = {$} - Từ (2) Fo (C) = Fo(B) = {c} Vậy:
Fo(S) = {$}, Fo(A)={b,d}, Fo( C )={b,c,d} ,Fo(D) ={$,b,d}, Fo(B)={c} lOMoAR cPSD| 59285474 1 . Tính tập FIRST
Dựa vào định nghĩa FIRST: • FIRST(F) = {a} •
FIRST(S) = FIRST(F) ∪ FIRST((S + F)) = {a, (} → Tóm tắt FIRST FIRST(S) = {a, (} FIRST(F) = {a}
2 . Tính tập FOLLOW FOLLOW(S): o $ vì S là start symbol. o S
→ (S + F), nên FOLLOW(S) chứa + và ). o
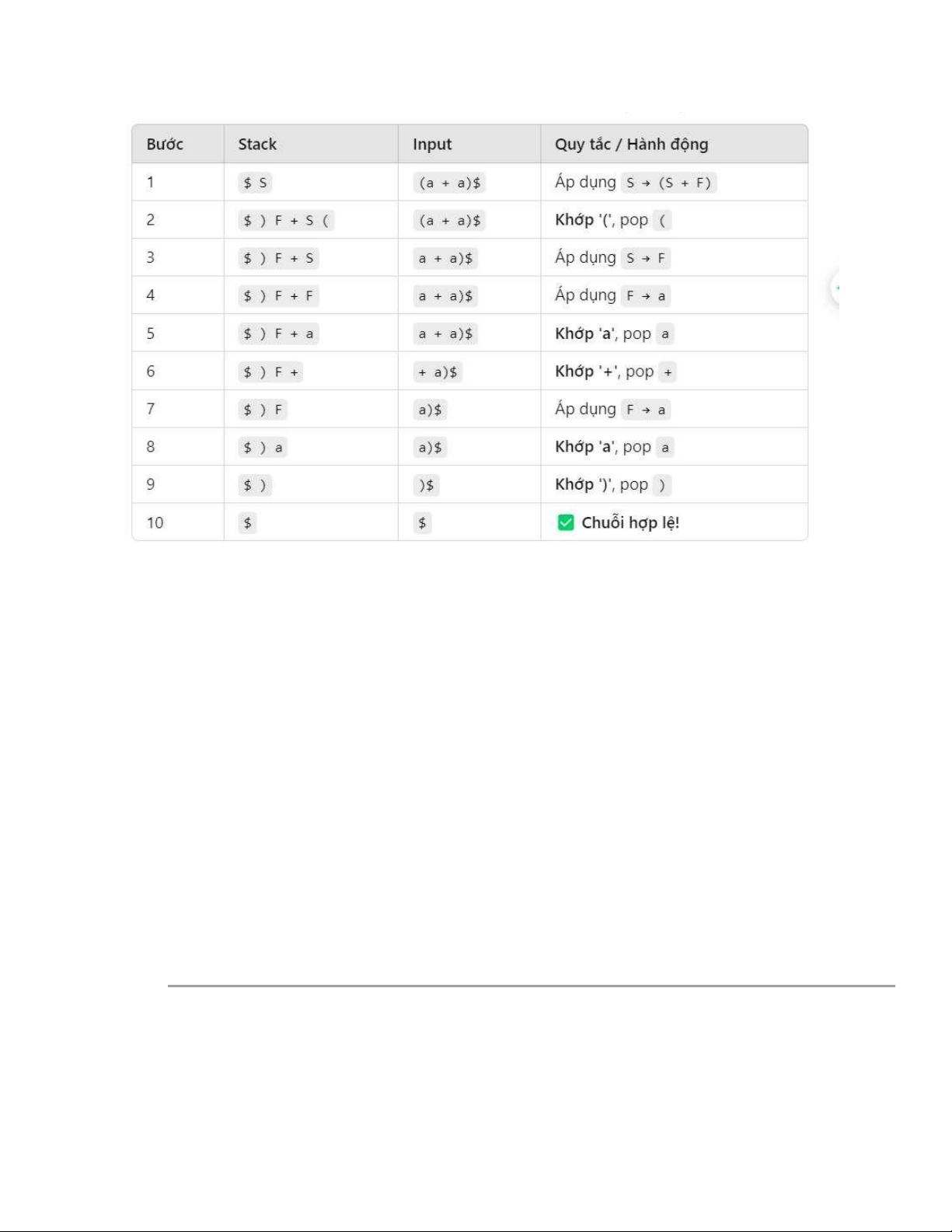
FOLLOW(S) = {$, +, )} FOLLOW(F): o S → (S + F), nên FOLLOW(F) chứa + và ). o FOLLOW(F) = {+, )} → Tóm tắt FOLLOW FOLLOW(S) = {$, +, )} FOLLOW(F) = {+, )} Bảng phân tích lOMoAR cPSD| 59285474 Bài 4 Văn phạm: S → A A → T | A + T T → b | (A) 1 . Tính tập FIRST • FIRST(T) = {b, (} •
FIRST(A) = FIRST(T) ∪ FIRST(A + T) = {b, (} • FIRST(S) = FIRST(A) = {b, (} → Tóm tắt FIRST FIRST(S) = {b, (} FIRST(A) = {b, (} FIRST(T) = {b, (} 2 . Tính tập FOLLOW • FOLLOW(S) = {$} • FOLLOW(A) = {+, )} • FOLLOW(T) = {+, )} → Tóm tắt FOLLOW lOMoAR cPSD| 59285474 FOLLOW(S) = {$} FOLLOW(A) = {+, )} FOLLOW(T) = {+, )} Bài 5 Văn phạm: E → E or T | T T → T and F | F F → not F | (E) | x 1 . Tính tập FIRST • FIRST(F) = {not, (, x} •
FIRST(T) = FIRST(F) = {not, (, x} •
FIRST(E) = FIRST(T) = {not, (, x} → Tóm tắt FIRST
FIRST(E) = {not, (, x} FIRST(T) = {not, (, x} FIRST(F) = {not, (, x} 2 . Tính tập FOLLOW • FOLLOW(E) = {$, )} • FOLLOW(T) = {or, ), $} •
FOLLOW(F) = {and, or, ), $} → Tóm tắt FOLLOW FOLLOW(E) = {$, )} FOLLOW(T) = {or, ), $} FOLLOW(F) = {and, or, ), $} Bài 6 Văn phạm: lOMoAR cPSD| 59285474 S → aBDh B → cC C → bC | ε D → EF E → g | ε F → f | ε 1 . Tính tập FIRST • FIRST(F) = {f, ε} • FIRST(E) = {g, ε} •
FIRST(D) = FIRST(E) FIRST(F) = {g, f, ε} • FIRST(C) = {b, ε} • FIRST(B) = {c} •
FIRST(S) = {a} → Tóm tắt FIRST FIRST(S) = {a} FIRST(B) = {c} FIRST(C) = {b, ε} FIRST(D) = {g, f, ε} FIRST(E) = {g, ε} FIRST(F) = {f, ε} 2 . Tính tập FOLLOW • FOLLOW(S) = {$} • FOLLOW(B) = {b, h} • FOLLOW(C) = {h} • FOLLOW(D) = {h} • FOLLOW(E) = {f, h} • FOLLOW(F) = {h} → Tóm tắt FOLLOW FOLLOW(S) = {$} FOLLOW(B) = {b, h} lOMoAR cPSD| 59285474 FOLLOW(C) = {h} FOLLOW(D) = {h} FOLLOW(E) = {f, h} FOLLOW(F) = {h}