Chuyên đề 2 Mô hình hồi quy hai biến: Ước lượng & Kiểm định giả thuyết môn Kinh tế vi mô 1 | Học viện Tài chính

CHUYÊN ĐỀ 2
MÔ HÌNH HỒI QUY HAI BIẾN, ƯỚC LƯỢNG
VÀ KIỂM ĐỊNH GIẢ THIẾT MỞ ĐẦU
Trong bài này sẽ trình bày vấn đề ước lượng hàm hồi qui tổng thể (PRF)
trên cơ sở số liệu của một mẫu. Thực chất là xác định các tham số trong hàm hồi
qui mẫu, trên cơ sở các giả thiết tiến hành ước lượng và kiểm định các giả thiết,
từ đó xây dựng hàm hồi qui tổng thể. Có nhiều phương pháp ước lượng hàm hồi
hồi qui tổng thể. Trong thực tế thường sử dụng phương pháp bình phương nhỏ
nhất hoặc phương pháp OLS (Ordinarry Least Square). Các nội dung chính của bài:
- Cách ước lượng các tham số của hàm hồi qui bằng phương pháp OLS.
- Các giả thiết của phương pháp OLS.
- Cách tính phương sai và sai số chuẩn của các ước lượng.
- Cách xác định hệ số tương quan và hệ số xác định, tính chất và ý nghĩa của các hệ số đó.
- Cách xác định khỏng tin cậy của các tham số trong hàm hồi qui tổng thể và phương sai của nó.
- Phương pháp kiểm định giả thiết về các hệ số hồi qui.
- Phương pháp kiểm định sự phù hợp của hàm hồi qui. Phân tích hồi qui và phân tích phương sai.
- Ứng dụng phân tích hồi qui, trình bày kết qủa và đánh giá kết quả của phân tích hồi qui.
Yêu cầu người học cần có các kiến thức về xác suất thống kê toán, toán
cao cấp, lý thuyết kinh tế học.
I. Giới thiệu mô hình hồi quy hai biến
1. Hàm hồi quy tổng thể và hàm hồi quy mẫu a) Hàm hồi quy tổng thể
Một cách tổng quát hàm hồi quy tổng thể E(Y/X i) là một hàm của Xi E(Y/Xi) = f(Xi) (1.1)
trong đó f(Xi) là một hàm nào đó của biến giải thích Xi, với ví dụ trên f(Xi) là hàm tuyến tính.
Phương trình (1.1) gọi là hàm hồi quy tổng thể (PRF) hoặc hồi quy tổng
thể (PR). Nếu như hàm hồi quy tổng thổ có một biến độc lập gọi là hàm hồi quy
đơn, có hơn một biến độc lập gọi là hàm hồi quy bội. Hàm hồi quy tổng thể cho
chúng ta biết giá trị trung bình của biến Y sẽ thay đổi như thế nào theo X Hàm
f(X i) có dạng như thế nào - tuyến tính hay phi tuyến - chúng ta chưa biết được
bởi lẽ trong thực tế chúng ta chưa có sẵn tổng thể để kiểm tra. Xác định dạng
hàm hồi quy là vấn đề thực nghiệm (chúng ta sẽ đề cập đến vấn đề này các chương sau...).
Giả sử rằng PRF E(Y/Xi) là hàm tuyến tính: E(Y/Xj) = ß1 + ß2Xi
trong đó ß1, ß2 là các tham số chưa biết nhưng cố định, và đuợc gọi là các hộ số hồi quy.
ß1là hộ số tự do (hộ số chặn), ß2 là hộ số góc.
Phương trình (1.2) gọi là phương trình hồi quy tuyến tính đơn.
b) Sai số ngẫu nhiên và bản chất của nó
Giả sử chúng ta đã có hàm hồi quy tổng thể E(Y/Xi); vì E(Y/Xi) là giá trị
trụng bình của biến Y với giá tri Xi đã biết, cho nên các giá trị cá biệt Yi không
phải bao giờ cũng trùng với E(Y/Xi), mà chúng xoay quanh E(Y/Xi).
Ký hiệu Ui, là chênh lệch giữa giá trị cá biệt Yi và E(Y/Xj): Ui = Yi -
E(Y/Xi) hay: Yi = E(Y/Xi) + Ui, (1.3)
Ui là biến ngẫu nhiên, người ta gọi Ui là yếu tố ngẫu nhiên (hoặc nhiễu)
và (1.3) được gọi PRF ngẫu nhiên. Nếu như E(Y/Xi) là tuyến tính đối với Xi thì Yi= β1+ β2 Xi+ Ui
yếu tố Ui, vẫn tồn tại vì một sô' lý do sau đây:
- Chứng ta có thể biết một cách chính xác biến giải thích X và biến phụ
thuộc Y, nhung chúng ta không biết hoặc biết không rõ về các biến khác ảnh
hưởng đến Y. Vì vậy, Ư, được sừ dụng như yếu tố đại diện cho tất cả các biến không có trong mô hình.
- Ngay cả khi biết các biến bị loại khỏi mô hình là các biến nào, khi đó
chúng ta có thể xây dựng mô hình hồi quy bội, nhưng có thể không có các số liệu cho các biến này.
- Ngoài các biến giải thích đã có trong mô hình còn có một số biến khác
nhưng ảnh hưởng của chúng đến Y rất nhỏ. Trong trường hợp này, chúng ta
cũng sử dụng yếu tô' ngẫu nhiên Ui đại diện cho chúng. Trong thí dụ đã trình
bày ở phần trên: số con trong gia đình, giới tính, tôn giáo..., cũng ảnh hưởng đến
chi tiêu trong gia đình, Ư, đại diện cho chúng.
- Vê mặt kỹ thuật và kinh tế, chúng ta muốn có một mô hình đơn giản
nhất có thể được. Nếu như chúng ta có thể giải thích được hành vi của biến Y
bàng một số nhỏ nhất các biến giải thích và nếu như ta không biết tường minh
những biến khác là những biến nào có thể bị loại ra khỏi mô hình thì ta dùng yếu
tô' n để thay cho tất cả các biến này. Trên đây là một vài lý do về sự.tồn tại của
Ư,. u, giữ vai trò đặc biệt trong phân tích hồi quy, chúng phải thỏa mãn những
điều kiện nhất định thì việc phân tích trên mô hình hồi quy mới có ý nghĩa. Sẽ là
sai lầm nghiêm trọng nếu như sử (lụng một công cụ mà không biết những điều
kiện để sử dụng nó có được thỏa mãn hay không. Trong phạm vi của cuốn sách
này chúng tôi đặc biệt quan tâm đến những điều kiện để vận dụng mô hình. Tuy
nhiên, trong thực tiễn những điều kiện này không phải bao giờ cũng được thỏa
mãn và bạn đọc có thể tìm thấy cách phát hiện và cách khắc phục nếu như có
một sô' giả thiết của mô hình không được thỏa mãn. Những vấn đề này sẽ được
trình bày dần dần trong các chương sau.
2- PHƯƠNG PHÁP BÌNH PHƯƠNG NHỎ NHẤT (OLS- Ordinary least Square) a- Nội dung phương pháp
Để tìm hàm Y = ß1 + ß2 X ta dùng phương pháp OLS do nhà toán học
Đức là Carl Friedrich Gauss đưa ra. Nội dung của phương pháp như sau:
Giả sử E(Yi/Xi) = β1+ β2 Xi là PRF
Khi đó giá trị quan sát Yi= β1+ β2 Xi+ Ui ˆ i Y ˆ ˆ l à S RF 1 2 Xi ˆ ˆ V à Y i 1 2 Xi e i ˆ ˆ ˆ Vấn đề là phải tìm: i Y 1 2 Xi
Giả sử ta có n cặp quan sát của Y và X, ta phải tìm i Yˆ sao cho nó càng
gần giá trị thực của Y, hay phần dư càng nhỏ càng tốt: e Yi i Y Yi ˆ Xi ˆ ˆ ( 1 2 ) min i
Do ei có thể âm, có thể dương vậy cần tìm i Y
ˆ sao cho tổng bình phương
của các phần dư đạt cực tiểu, tức là: n n 2 ˆ i e ( iY Y ) 2 i i 1 i 1 n ˆ ˆ ( i Y ) 2 1 2 i X Min i 1 ˆ ˆ
;1 2 là nghiệm của hệ phương trình: ˆ ˆ n f ( , ) 1 2 2( Y ˆ ˆ )( ) 1 0 1 2 X i i ˆ i 1 1 n n H : a nyˆ ˆ X 1 2 i Yi i 1 1 i ˆ ˆ n f( , ) à : V 1 2 2( Y ˆ ˆ )( ) 0 1 2 X X i i i ˆ2 i 1 n n n : H ˆ ay ˆ X 1 i X 2 2 X Y i i i i 1 i 1 1 i
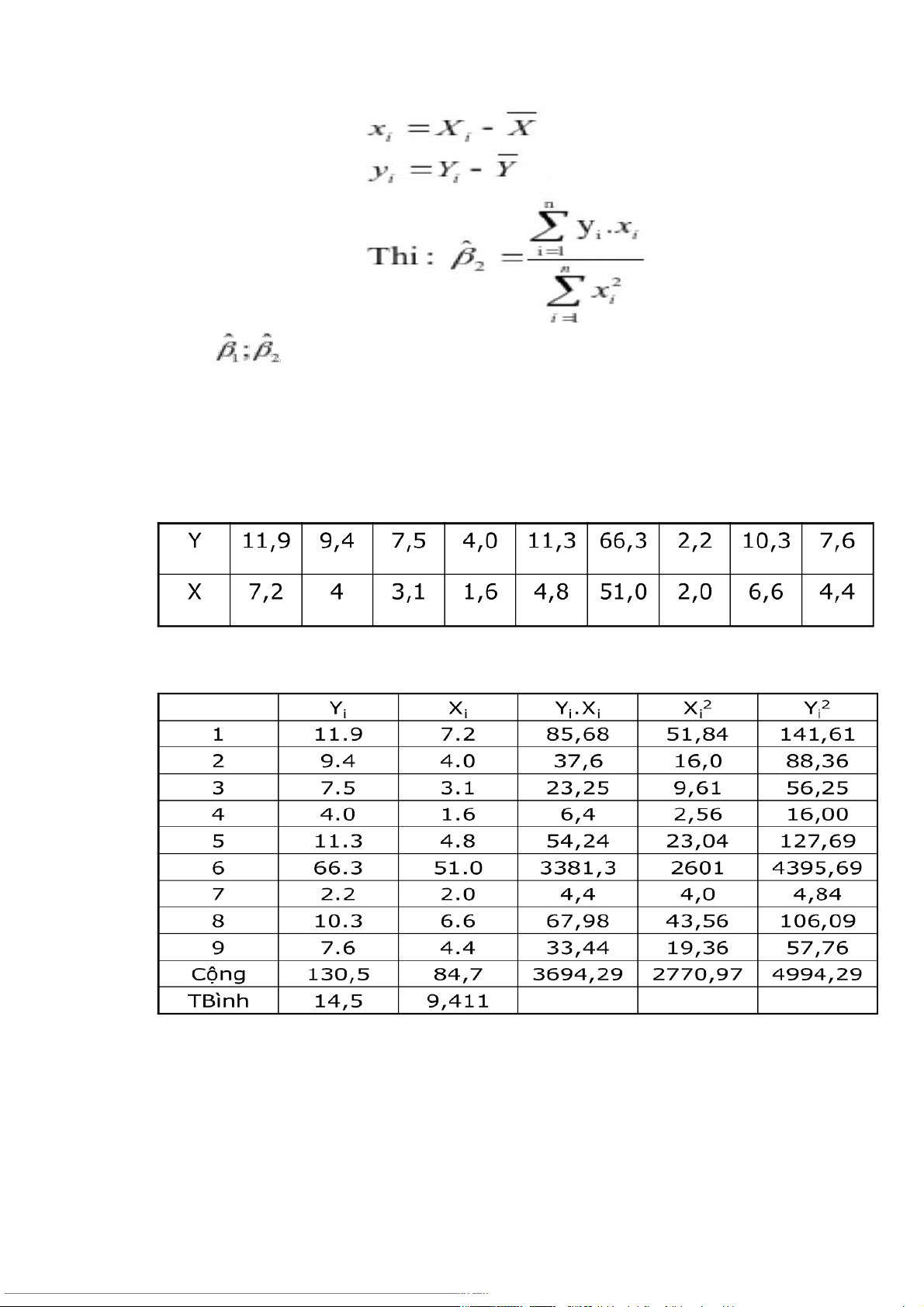
Từ đó ta có hệ phương trình chuẩn: n n ˆ ˆ 1 n2 X Y i i i 1 i 1 n n n ˆ ˆ 1 X 2 2 X Y X i i i i i 1 i 1 1 i n n n n Y X X Y i i i Hay ˆ i 1 i 1 i 1 : 2 n n n 2 X ( X 2 ) i i i 1 i 1 ˆ ˆ 1 Y 2 X Nếu đặt: x X X i i y Y Y i i n y . i x i ˆ i 1 Thi : 2 n x 2i i 1 ˆ ˆ
;1 2 là các ước lượng của β1, β2 được tính bằng phương pháp bình
phương nhỏ nhất - gọi là các ước lượng bình phương nhỏ nhất.
Ví dụ: có số liệu về lãi suất (Y) và tỷ lệ lạm phát (X) trong năm N của 9
quốc gia. Giả sử sự phụ thuộc E(Y/X) có dạng tuyến tính. Hãy ước lượng hàm
hồi quy và tính các đặc trưng của nó. Ta có bảng tính toán sau:
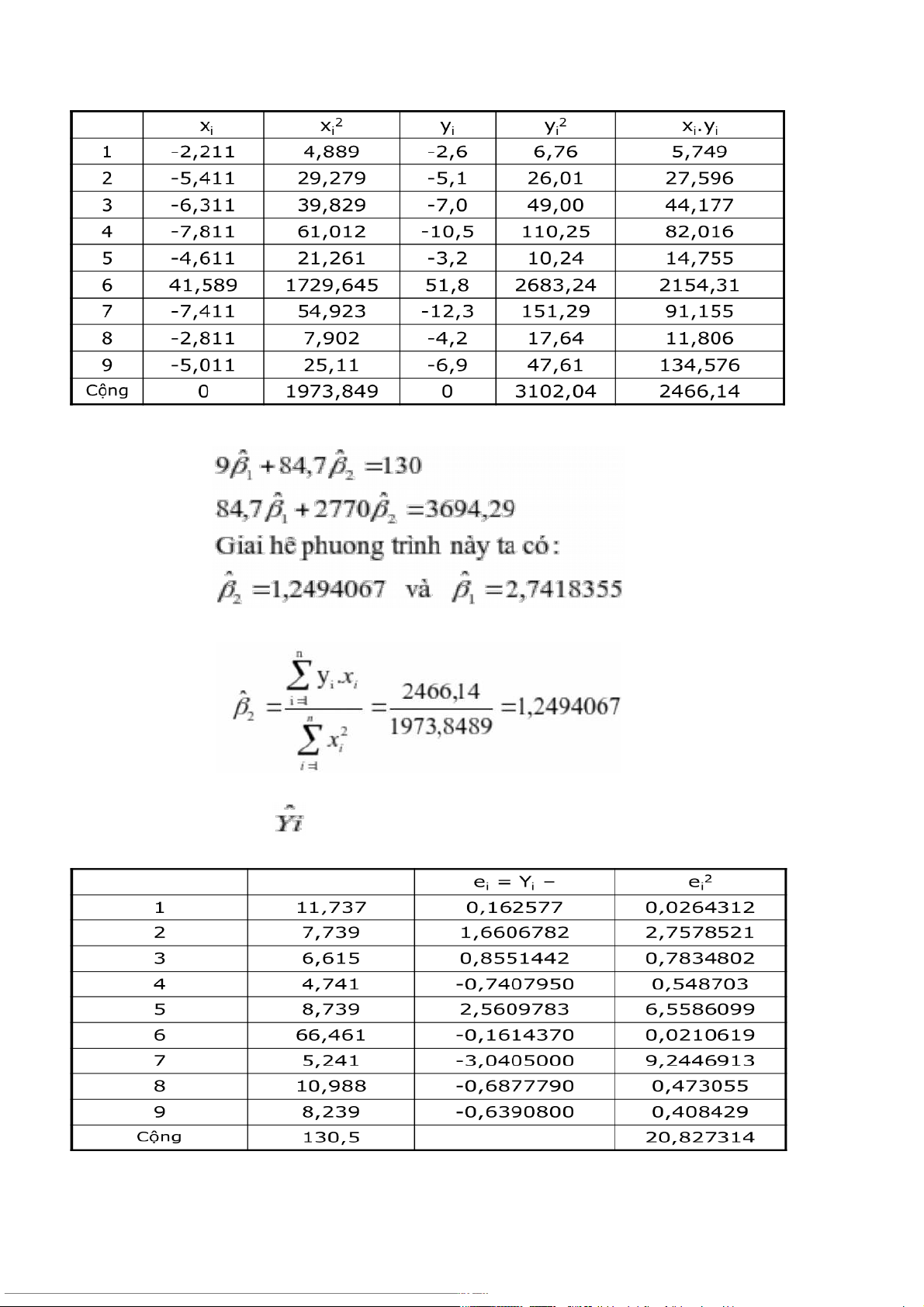
Hoặc bảng ước lượng chi tiết: Ta có hệ phương trình: ˆ ˆ 9 84 7 , 130 1 2 ˆ ˆ 84 7 , 1 2770 2 369 , 4 29 Giai h ê p huon g trình này ta c ó : ˆ ˆ , 1 249406 7 v à 7 , 2 418355 2 1 Hoặc: n yi.xi i 1 2466 1 , 4 ˆ 2 , 1 2494067 n 2 1973 8 , 489 xi 1 i Vậy SRF là: i Y ˆ = 2,7418355 + 1,2494067Xi Từ đó ta có:
b- Các tính chất của các ước lượng bình phương nhỏ nhất ˆ ˆ
;1 2 được xác định một cách duy nhất ứng với cặp quan sát Xi,Yi ˆ ˆ 1;
2 là các ước lượng điểm của β1,β2 và là các đại lượng ngẫu nhiên,
với mẫu khác nhau chúng có giá trị khác nhau. ˆ i Y ˆ ˆ X 1 2 hay SRF có tính chất: ˆ ˆ
SRF đi qua trung bình mẫu: Y 1 2 X Giá trị của i
Yˆ bằng giá trị trung bình của các quan sát: ˆY Y
Tổng giá trị của các phần dư bằng không: e 0 i
Các phần dư ei không tương quan với và Xi: . 0 v a ˆ Y e e X 0 i i i
c- Các giả thiết cơ bản của phương pháp bình phương nhỏ nhất
Các giả thiết này làm cho các ước lượng là tuyến tính, không chệch, có phương sai nhỏ nhất:
- Các biến giải thích là phi ngẫu nhiên, tức là giá trị của chúng đã được xác định.
- Kỳ vọng của yếu tố ngẫu nhiên Ui bằng không:
E(Ui/Xi) = 0 Giả thiết này kéo theo: E(Yi/Xi)= β1+ β2 Xi
- Phương sai bằng nhau (phương sai thuần nhất) của các Ui (Homoscedasticity of Ui)
Var(Ui/Xi) = Var(Uj/Xj) = với mọi i ≠ j
- Không có sự tương quan giữa các Ui
- Ui và Xi không tương quan với nhau
d- Độ chính xác của các ước lượng bình phương nhỏ nhất ˆ ˆ
;1 2 là các ước lượng của SRF, với mẫu khác nhau có ước lượng khác
nhau. Vì phương sai hay độ lệch chuẩn đặc trưng cho độ phân tán của đại lượng
ngẫu nhiên, nên ta dùng chúng để đo chất lượng của các ước lượng. Để đo chất
lượng của các ước lượng ta dùng phương sai hay độ lệch chuẩn: 2 2 ˆ ˆ r va ( ) se ( ) 2 n 2 n 2 2 x x i i i 1 i 1
e- Hệ số r2 đo độ phù hợp của hàm hồi quy mẫu srf
Hệ số xác định R2 cho biết số phần trăm sự thay đổi của Y được giải thích
bằng mô hình (hay biến độc lập).
TSS (Total Sum of Squares) là tổng bình phương các chênh lệch giữa các
giá trị quan sát Yi với giá trị bình quân của nó.
ESS (Explain Sum of Squares) là tổng bình phương của tất cả các sai lệch
giữa các giá trị quan sát Yi với giá trị bình quân của nó nhận được từ mẫu.
RSS (Residual Sum of Squares) là tổng bình phương các chênh lệch giữa
các giá trị quan sát Yi với giá trị nhận được từ hàm hồi quy. TSS = ESS + RSS
Nếu hàm hồi qui mẫu phù hợp tốt với các số liệu quan sát thì ESS sẽ càng
lớn hơn RSS. Nếu tất cả các giá trị quan sát của Y đều nằm trên SRF thì ESS sẽ
bằng TSS và do đó RSS = 0. Ngược lại, nếu hàm hồi qui mẫu kém phù hợp với
các giá trị quan sát thì RSS sẽ càng lớn hơn ESS. 2 2 TSS y (Yi Y ) i 2 2 ˆ ESS ˆ y ( i Y Y ) i 2 2 ˆ RSS e ( Yi i Y ) i T đó ù : 2 2 ESS RSS e R 1 1 i 2 TSS TSS yi Hoac : 2 x 2 2 ˆ R . i 2 2 yi
0tất cả các sai lệch của Y (so với giá trị trung bình) đều giải thích được bởi mô
hình hồi qui. Khi R2 = 0 chứng tỏ X và Y không có quan hệ.
Đại lượng R2 gọi là hệ số xác định (coefficient of determination) và được
sử dụng để đo mức độ phù hợp của hàm hồi qui mẫu. Theo ví dụ trên, ta có:
R2 = 1- 20,827314/3102,04 = 0,9932
Kết quả này có nghĩa là trong hàm hồi qui mẫu, biến X (Tỷ lệ lạm phát)
giải thích 99,32% sự thay đổi của biến Y (Lãi suất). Do vậy có thể nói rằng
trong trường hợp này mức độ phù hợp của SRF khá cao.
Sử dụng hệ số tương quan mẫu R:Thông thường, để xét mức độ chặt chẽ
của quan hệ tuyến tính giữa X và Y, người ta sử dụng hệ số tương quan mẫu. n x. y i i 2 S X i 1 ˆ R R 2 2 2 S Y ( x )( y ) i i 2 . X Y X.Y e 2 i i i i R R 1 i 2 S . X S y Y i Trong đó: 2 2 Sx X (X) 2 2 Sy Y ( ) Y
Các tính chất của hệ số tương quan R:
- R có thể âm, dương (phụ thuộc vào dấu của hệ số góc). - Kết quả: -1 ≤ R ≤ 1
- R có tính chất đối xứng: R(X,Y)=R(Y,X)
- Nếu X’ = aX + c; Y’ = bX + d; a,b c,d là hằng số a,b>0 thì: R(X’,Y’) = R(X,Y)
- Nếu X,Y độc lập với nhau thì R(X,Y) = 0; điều ngược lại không đúng.
- R đo sự phụ thuộc tuyến tính. Nhưng không có ý nghĩa trong việc định
rõ tính chất các quan hệ phi tuyến tính.
- R đo độ phụ thuộc tuyến tính giữa X và Y, vậy không đòi hỏi X,Y có mối quan hệ nhân quả. Bài tập thực hành
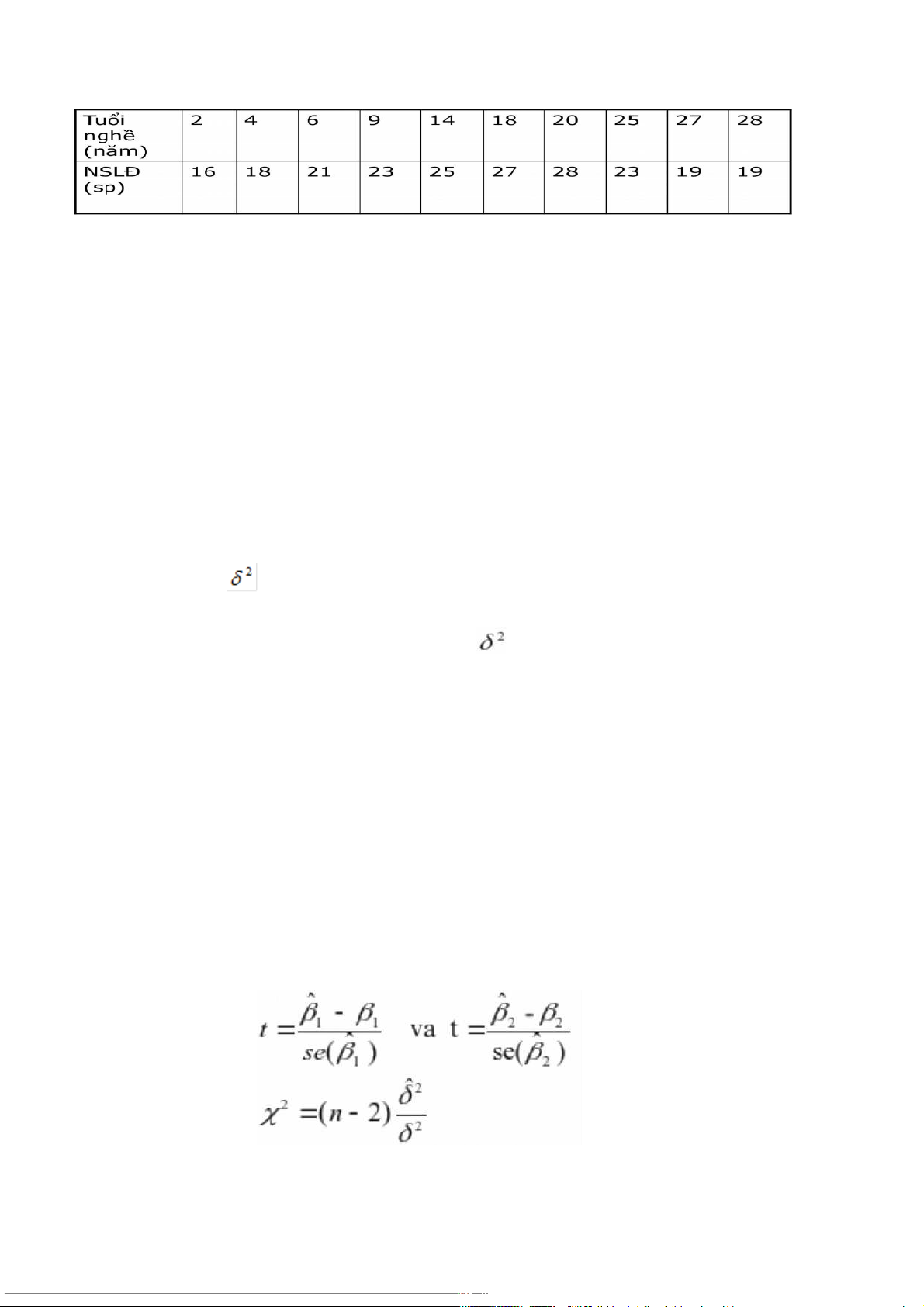
Có tài liệu về mối quan hệ giữa tuổi nghề và năng suất lao động của 10 công nhân như sau:
Yêu cầu: ước lượng hàm hồi quy tổng thể từ mẫu trên. Nêu ý nghĩa các
tham số và hệ số tương quan.
II- ƯỚC LƯỢNG VÀ KIỂM ĐỊNH GIẢ THIẾT
1- Phân bố xác suất của Ui
Mục đích của phân tích hồi qui không phải là chỉ suy đoán về P 1, P 2 hay
PRF mà còn phải kiểm tra bản chất của sự phụ thuộc, còn phải thực hiện các dự
đoán khác. Nếu tiến hành lấy mẫu nhiều lần, ta sẽ nhận được tập hợp nhiều giá
trị khác nhau của Ui , Ui tạo thành một đại lượng ngẫu nhiên. Ta cần phải tìm
hiểu và nghiên cứu luật phân phối xác suất của hai loại tham số này. Các phân
phối này phụ thuộc vào phân phối của Ui. E(Ui) = 0 Var(Ui) = Cov(Ui, Uj) = 0 2
Ta có thêm giả thiết: Ui có phân bố N(0, )
Từ đó các ước lượng OLS sẽ là tuyến tính, không chệch, phương sai cực
tiểu, số quan sát đủ lớn thì các ước lượng này xấp xỉ giá trị thực của phân bố.
2- Khoảng tin cậy và kiểm định giả thiết về các hệ số hồi quy
Như chúng ta đã biết, một ước lượng đơn có nhiều khả năng khác với giá
trị đúng. Trong thống kê, độ tin cậy của một ước lượng điểm được đo bằng sai
số chuẩn của nó. Do vậy, thay vì chỉ dựa vào ước lượng điểm, ta có thể xây
dựng một khoảng xung quanh giá trị ước lượng điểm, để xác suất mà giá trị
đúng của tham số cần ước lượng nằm trong khoảng này là 1- a, tức là:
P( ¡3 -e < p 1 < ¡3 + e ) = 1- a. Hoặc P( ¡3 - e < p2 - ¡3 + e) =1- a.
Đối với các tham số β1,β2 sử dụng thống kê T(n-2) (Student), đối với
phương sai sử dụng thống kê khi bình phương bậc tự do (n-2). ˆ ˆ - 1 1 2 2 t va t ˆ ˆ se( ) se( ) 1 2 2 ˆ 2 (n 2) 2
* Khoảng tin cậy của β1:
Với hệ số tin cậy 1- (hay với mức ý nghĩa ) ta có khoảng tin cậy của tham số β1 là: ˆ ˆ ˆ ˆ ( 2). (t n ) Se t (n ) 2 .Se ( ) 1 1 1 1 1 2 2
* Kiểm định giả thiết đối với β1 : thường nhỏ hơn 0,1.
Kiểm định giả thiết thống kê được phát biểu đơn giản như sau: Kết quả
tìm được dựa trên số liệu thu thập từ thực tế có phù hợp với một giả thiết nêu ra
hay không? Từ “phù hợp” được dùng ở đây được hiểu
là “đủ” sát với giá trị
giả thiết nêu ra để ta không bác bỏ giả thiết đã nêu.
Như vậy, nếu căn cứ vào một lý thuyết hay kinh nghiệm từ trước là ta tin
rằng hệ số góc (p2) trong ví dụ 1 bằng 0,8 thì giá trị quan sát (J§ ) là 0,5091
được tính từ mẫu có phù hợp với giả thiết phát
Nếu phù hợp ta không bác bỏ giả thiết; nếu không phù hợp thì ta bác bỏ giả thiết nêu trên.
Trong thống kê toán, giả thiết phát biểu (giả thiết cần kiểm định) được gọi
là giả thiết không và kí hiệu là H0. Một mệnh đề đối lập với H0 được gọi là giả
thiết đối và được kí hiệu là H1. Chẳng hạn, giả thiết không là: Ho: p 2 = 0,8; khi
đó giả thiết đối có thể là H1: p 2 #0,8, hoặc H1: p 2 > 0,8, hoặc H1: p 2 < 0,8.
Lý thuyết kiểm định xây dựng các qui tắc hay thủ tục để quyết định bác
bỏ hay không bác bỏ giả thiết không. Có hai cách tiếp cận bổ sung lẫn nhau để
xây dựng qui tắc đó, gọi là khoảng tin cậy và kiểm định ý nghĩa. Cả hai phương
pháp này đều dựa trên cơ sở: Đã xác định được qui luật phân phối xác suất của
đại lượng ngẫu nhiên được dùng là tiêu chuẩn kiểm định (thống kê kiểm định).
Phần lớn các giả thiết mà ta tiến hành kiểm định là đưa ra các phát biểu hay
khẳng định liên quan đến (các) giá trị hay (các) tham số đặc trưng của thống kê kiểm định. Quy tắc quyết định:
* Khoảng tin cậy của β2 : ˆ t ˆ n Se ˆ t n Se ˆ ( 2) ( ) ( 2) ( ) 2 / 2 2 2 2 / 2 2
* Kiểm định giả thiết đối với β2: nếu β2=β2*=0 có nghĩa là biến độc lập
X không ảnh hưởng đến biến phụ thuộc Y.
Ví dụ: Kiểm định giả thiết: Ho: β2 = β2* = 0 H1: β2 ≠ 0
Với mức ý nghĩa 5% (0,05) ta có: t0,05/2(9-2)=2,365 (tra bảng phân phối t) ˆ , 1 2494067 0 2 2 t 3 , 2 2 ˆ se ( ) 0 , 0 388 2 Vây :t t (7 ) 2,365 b ác b o H o 0,025
* Kiểm định sự phù hợp của hàm hồi quy: Ho: β2 = β2* = 0 hay R2 = 0 H1: β2 ≠ 0 hay R2 > 0 Sử dụng tiêu chuẩn F: 2 R n k F F (k , 1 n k) 1 2 R k 1 Bá c H bo o
* Khoảng tin cậy đối với phương sai: ˆ 2 ˆ (n 2) (n 2) 2 2 2 (n 2) 2 (n 2) / 2 1 / 2
* Kiểm định giả thiết đối với phương sai: III- DỰ BÁO
1- Dự báo giá trị trung bình có điều kiện của Y với một giá trị X0 ˆ ˆ ˆ ˆ ( 2 Y ) t ( n )Se ( Y /E ) Yi X Y t ( n 2) ( SeY ) 0 0 0 0 0 2 2 Trong đó: 2 1 (X X ) 2 0 S ( ˆ eY ) 0 2 n xi
Theo ví dụ trên với Xo = 5%: 2 1 (X X 0 ) 2 S ( ˆ eY ) 0 2 n xi 1 (5 , 9 41 ) 1 2 9 , 2 7 5 , 0 8 9 1973 8 , 5 ˆ Y 7 , 2 418335 2 , 1 494067x 5 9 , 8 88867 0 8 , 7 89767 E ( Y /Xo ) 10 0 , 87967
2- Dự báo giá trị riêng biệt có điều kiện của Y với một giá trị X0 ˆ ˆ Y t n SeY Y Y t n SeY 0 ( 2) ( ) 0 0 0 ( 2) ( 0 ) 2 2 Trong đó: 2 2 1 ( 0 X X ) Se 0( Y ) 1 2 n i x KẾT LUẬN
Mô hình hồi qui hai biến là mô hình đơn giản nhất trong lớp mô hình hồi
qui tuyến tính, trong mô hình chỉ có một biến phụ thuộc và một biến độc lập, giá
trị của biến độc lập cho trước. Để xác định giá trị trung bình của biến phụ thuộc;
Trước hết ta căn cứ vào một mẫu có sẵn, sử dụng phương pháp OLS để ước
lượng các tham số của mẫu; Xác định hàm hồi qui mẫu, kiểm tra tính hợp lý của
các tham số (các hệ số trong hàm SRF). Nếu phù hợp ta tiến hành xác định
phương sai và sai số chuẩn đối với các ước lượng trên, từ đó xác định hệ số
tương quan và hệ số xác định để kiểm tra mức độ chặt chễ của quan hệ giữa hai
biến và mức độ phù hợp của hàm SRF.
Trên cơ sở hàm hồi qui mẫu, các giả thiết của phương pháp OLS và giả
thiết về phân phối xác suất của các ước lượng, tiến hành xác định khoảng tin cậy
của các tham số trong hàm PRF; Kiểm định giả thiết về các hệ số hồi qui; Kiểm
định sự phù hợp của hàm hồi qui. Phân tích hồi qui và phân tích phương sai. Sau
khi đã có kết luận về mức độ tin cậy của hàm hồi qui, ta tiến hành dự báo giá trị
của biến phụ thuộc khi biết giá trị của biến độc lập trong tương lai (kế hoạch).
Cuối cùng ta trình bày kết quả và đánh giá các kết quả của phân tích hồi qui. HƯỚNG DẪN NGHIÊN CỨU
1. Nghiên cứu những vấn đề cơ bản về nội dung phương pháp OLS?
2. Nghiên cứu những vấn đề cơ bản về các chỉ tiêu phân tích của mô hình hồi quy?
Hà Nội, ngày 29 tháng 11 năm 2021 NGƯnI BIÊN SOoN GIẢNG VIÊN
Đại úy, ThS Nguyễn Tân Dương