CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG
BÀI 3: CÁC GÓC TẠO BỞI MỘT ĐƯỜNG THẲNG CẮT HAI ĐƯỜNG THẲNG Mục tiêu  Kiến thức
+ Phân biệt được các góc so le trong và góc đồng vị tạo thành bởi một đường thẳng cắt hai đường thẳng.
+ Nắm vững tính chất về góc so le trong và góc đồng vị.  Kĩ năng
+ Chỉ ra được các cặp góc so le trong, đồng vị.
+ Vận dụng được các tính chất về góc. Trang 1 I. LÍ THUYẾT TRỌNG TÂM
Góc so le trong. Góc đồng vị
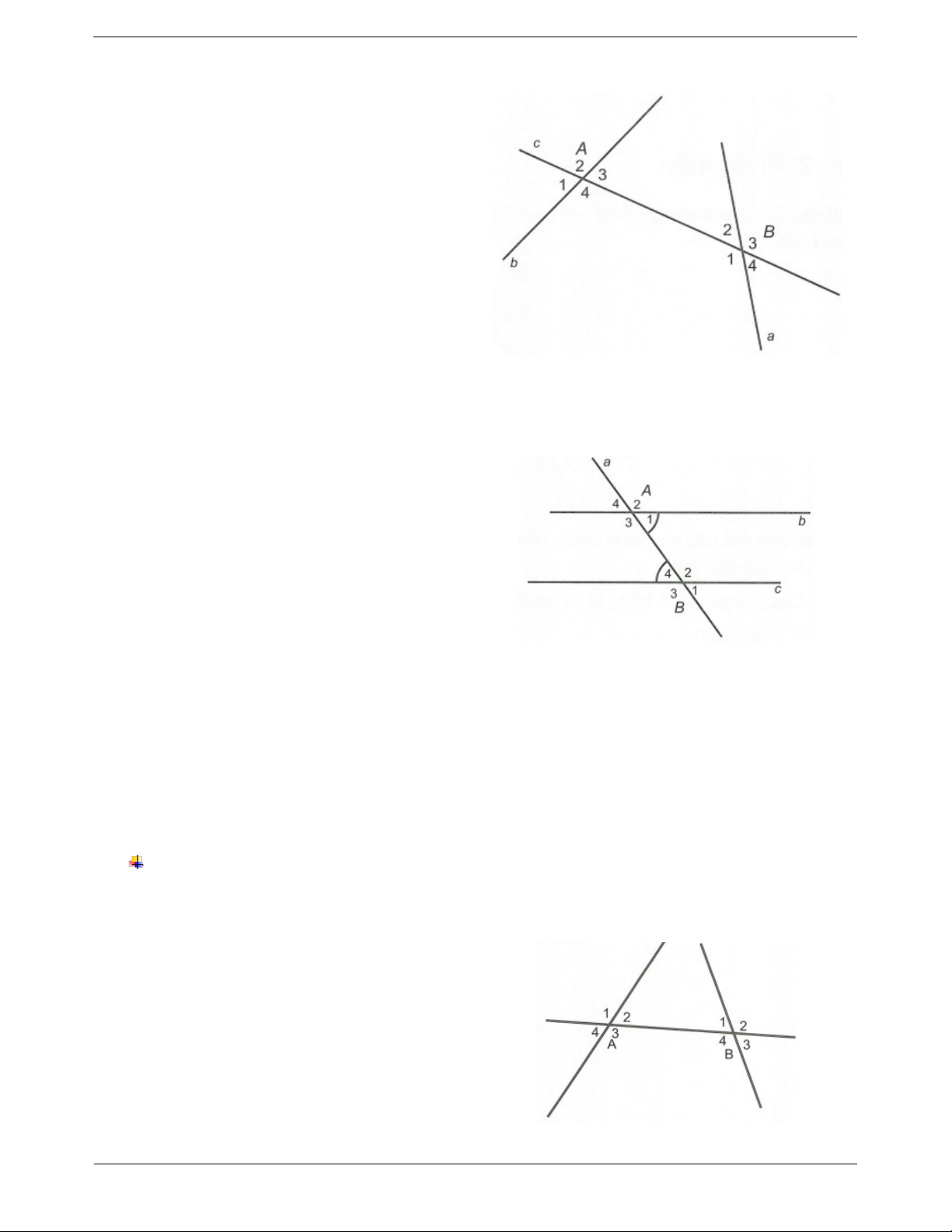
Cho đường thẳng c cắt hai đường thẳng a và b lần
lượt tại A và B như hình vẽ. Khi đó: a) Hai cặp góc  A và  B ,  A và  B được gọi là 3 1 4 2 cặp góc so le trong. b) Bốn cặp góc  A và  B ,  A và  B ,  A và  B , 1 1 2 2 3 3  A và 
B , được gọi là các cặp góc đồng vị. 4 4 c) Hai cặp góc  A và  B ,  A và  B được gọi là 3 2 4 1 các góc trong cùng phía. d) Hai cặp góc  A và  B ,  A và  B được gọi là 2 3 1 4 các góc ngoài cùng phía. Tính chất
Nếu đường thẳng a cắt hai đường thẳng b, c và
trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
a) Hai góc so le trong còn lại bằng nhau.
b) Hai góc đồng vị bằng nhau.
c) Hai góc trong cùng phía bù nhau.  A   B 3 2    A   B   A   B 1 4 1 1 A  B 180  1 2  II. CÁC DẠNG BÀI TẬP
Dạng 1: Xác định các cặp góc so le trong, cặp góc trong cùng phía, cặp góc đồng vị Phương pháp giải
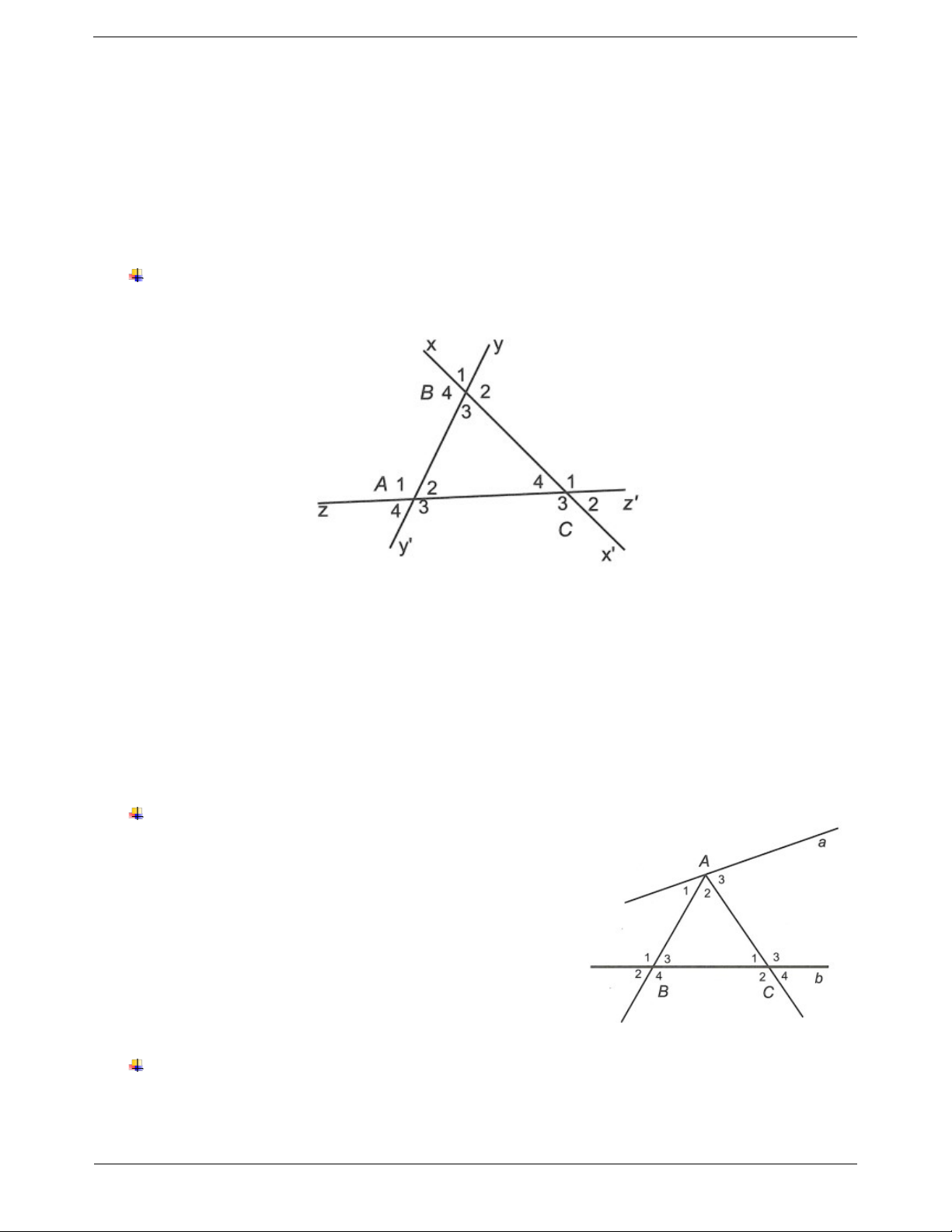
Căn cứ vào vị trí của hai góc so với hai đường Ví dụ: Cho đường thẳng cắt hai đường thẳng khác
thẳng và đường thẳng thứ ba cắt chúng. như hình vẽ Trang 2
Xác định các cặp góc so le trong, đồng vị. Hướng dẫn giải
Các cặp góc so le trong là  A và  B ,  A và  B . 3 1 2 4
Các cặp góc đồng vị là  A và  B ,  A và  B ,  A và  B ,  A và  B . 1 1 2 2 3 3 4 4 Ví dụ mẫu
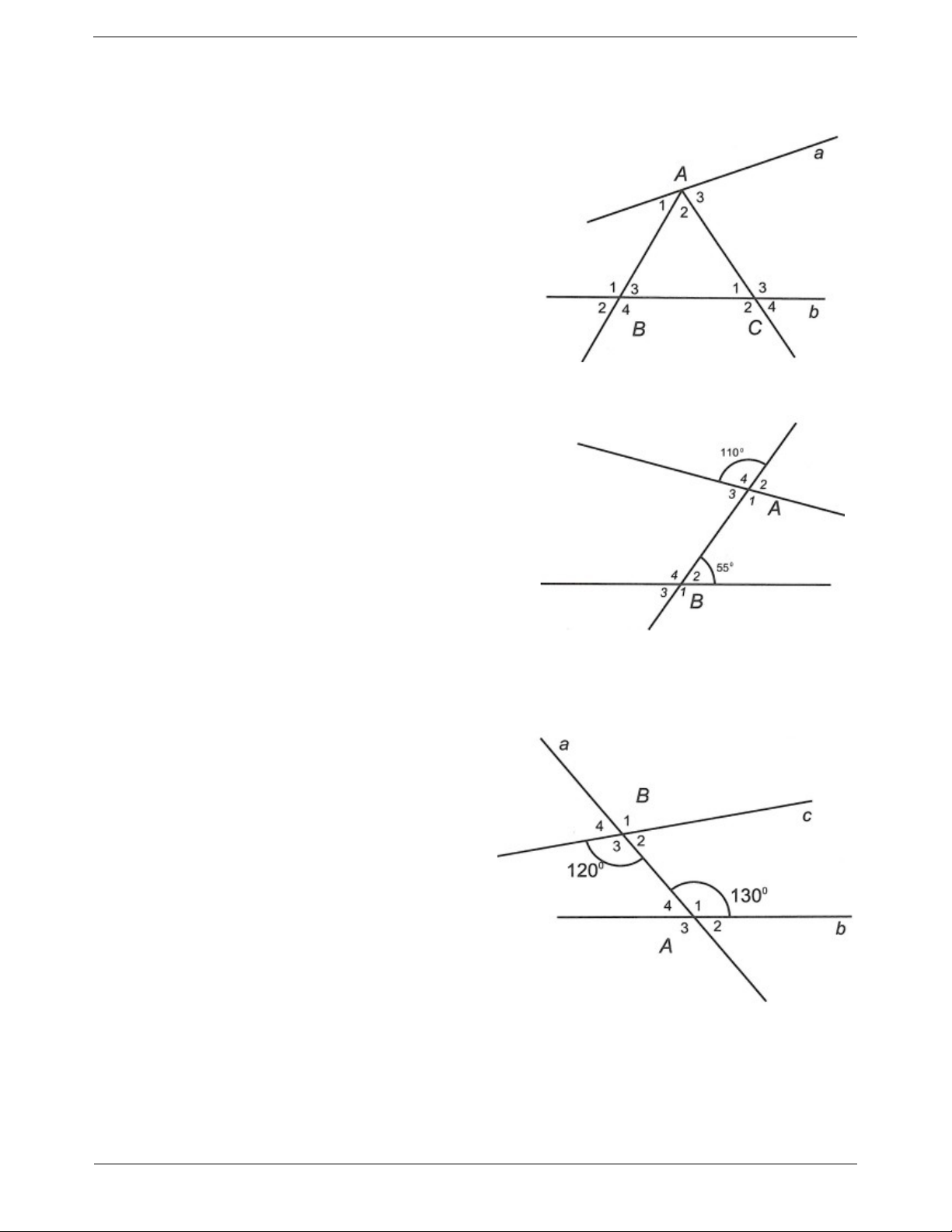
Ví dụ. Cho ba đường thẳng xx , yy và zz đôi một cắt nhau tại A, B và C như hình vẽ:
Xác định các cặp góc so le trong, đồng vị. Hướng dẫn giải
Các cặp góc so le trong là  A và  B ,  A và  B ,  A và  C ,  A và  C ,  B và 1 3 2 4 2 3 3 4 2  C ,  B và  C . 4 3 1
Các cặp góc đồng vị là  A và  B ,  A và  B ,  A và  B ,  A và  B ,  A và  C ,  A và  C ,  A và  C , 1 1 2 2 4 4 3 3 1 4 2 1 3 2  A và  C ,  B và  C ,  B và  C ,  B và  C ,  B và  C . 4 3 1 1 2 2 3 3 4 4
Bài tập tự luyện dạng 1 Cho hình vẽ:
a) Góc nào đồng vị với  A . 3
b) Góc nào so le trong, trong cùng phía, đồng vị với góc  A . 2 Dạng 2: Tính góc Phương pháp giải
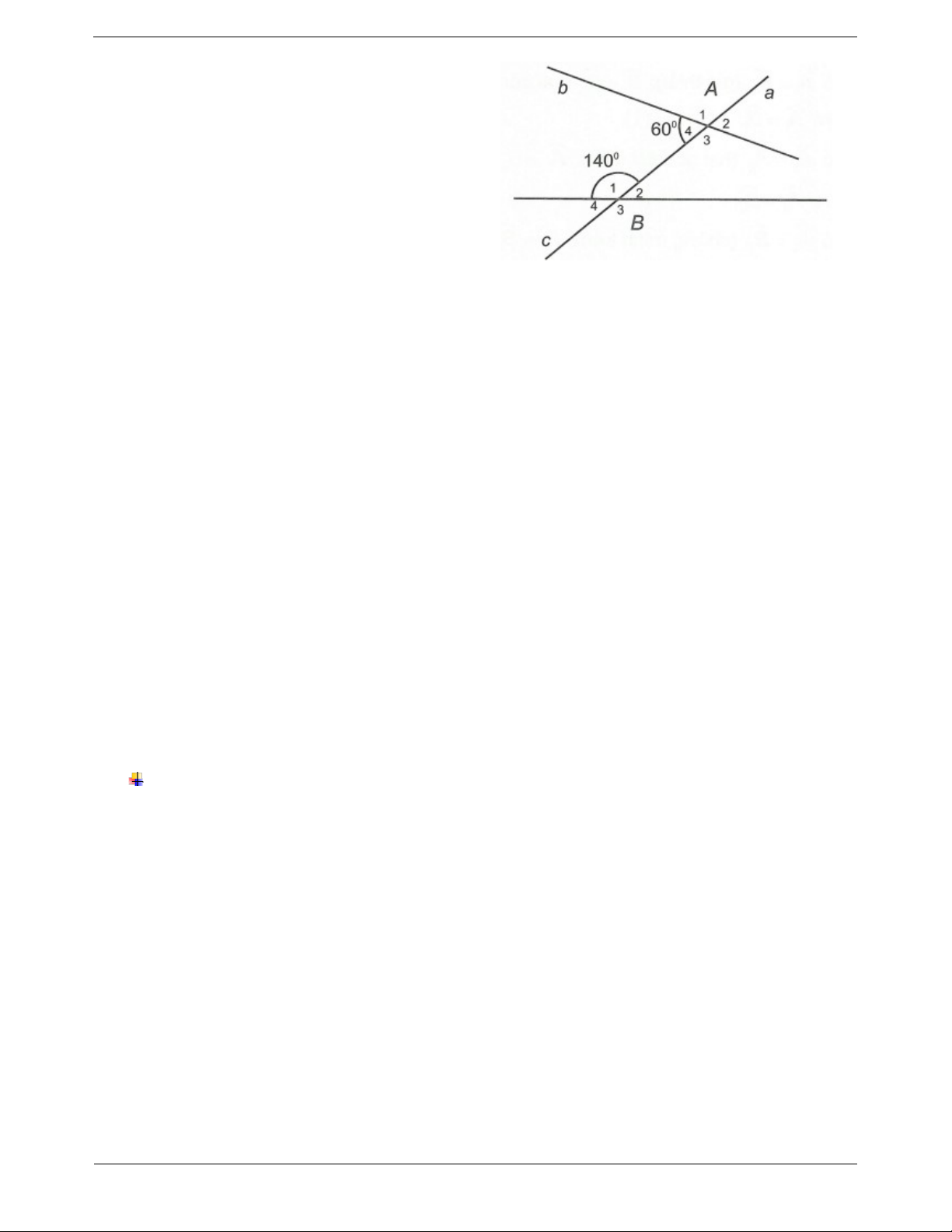
Áp dụng tính chất của hai góc đối đỉnh, hai góc kề Ví dụ: Cho hình vẽ:
bù, hai góc so le trong, hai góc đồng vị để tính góc. Trang 3
Xác định số đo của các góc còn lại. Hướng dẫn giải Ta có  A  
A  180 (hai góc kề bù). 1 4 Mà  A  60 nên 4  A  180  
A  180  60  120 . 1 4 Vậy  A  
A  120 (hai góc đối đỉnh); 1 3  A  
A  60 (hai góc đối đỉnh). 2 4 Lại có  B  
B  180 (hai góc kề bù). 1 2 Mà  B  140 nên 1  B  180  
B  180 140  40 . 2 1 Vậy  B  
B  140 (hai góc đối đỉnh); 1 3  B  
B  40 (hai góc đối đỉnh). 2 4 Ví dụ mẫu
Ví dụ 1. Vẽ một đường thẳng cắt hai đường thẳng. Trong các góc tạo thành có một cặp góc so le trong
bằng nhau. Đặt tên cho các góc đó. Chứng minh:
a) Cặp góc so le trong còn lại và các góc đồng vị bằng nhau.
b) Các cặp góc trong cùng phía bù nhau.
c) Các cặp góc ngoài cùng phía bù nhau. Hướng dẫn giải
Hình vẽ: Đường thẳng a cắt hai đường thẳng b và c lần lượt tại A, B. Hai góc so le trong  A và  B 1 4 bằng nhau. Trang 4
a) +) Chứng minh các góc so le trong còn lại bằng nhau. Ta có  A  
A  180 (hai góc kề bù);  B  
B  180 (hai góc kề bù). 1 3 2 4 Mà  A   B (giả thiết) nên  A   B . 1 4 3 2
Vậy cặp góc so le trong còn lại bằng nhau.
+) Chứng minh các góc đồng vị bằng nhau. Ta có  A   B (giả thiết);  B   B (hai góc đối đỉnh). 1 4 1 4 Suy ra  A   B .   1 1 1 Ta có  A  
A (hai góc đối đỉnh);  A   B (chứng minh trên). 3 2 3 2 Suy ra  A   B . 2 2 2 Ta có  A   B (chứng minh trên);  B   B (hai góc đối đỉnh). 3 2 3 2 Suy ra  A   B . 3 3 3 Ta có  A   B (giả thiết);  A   A (hai góc đối đỉnh). 1 4 1 4 Suy ra  A   B . 4 4 4 Từ  
1 , 2 , 3 và 4 ta có các góc đồng vị bằng nhau.
b) Chứng minh các cặp góc trong cùng phía bù nhau. Ta có  A   B (giả thiết);  A  
A  180 (hai góc kề bù). Suy ra  B  
A  180 (hai góc trong cùng 1 4 1 3 4 3 phía bù nhau). Ta có  A   B (giả thiết);  B  
B  180 (hai góc kề bù). Suy ra  B  
A  180 (hai góc trong cùng 1 4 4 2 2 1 phía bù nhau).
c) Chứng minh các cặp góc ngoài cùng phía bù nhau. Ta có  A   B (chứng minh trên);  B  
B  180 (hai góc kề bù). 2 2 2 1 Suy ra  A  
B  180 (hai góc ngoài cùng phía bù nhau). 2 1 Ta có  A  
B (hai góc đồng vị bằng nhau);  B  
B  180 (hai góc kề bù). 4 4 3 4 Suy ra  A  
B  180 (hai góc ngoài cùng phía bù nhau). 4 3 Trang 5 Ví dụ 2.
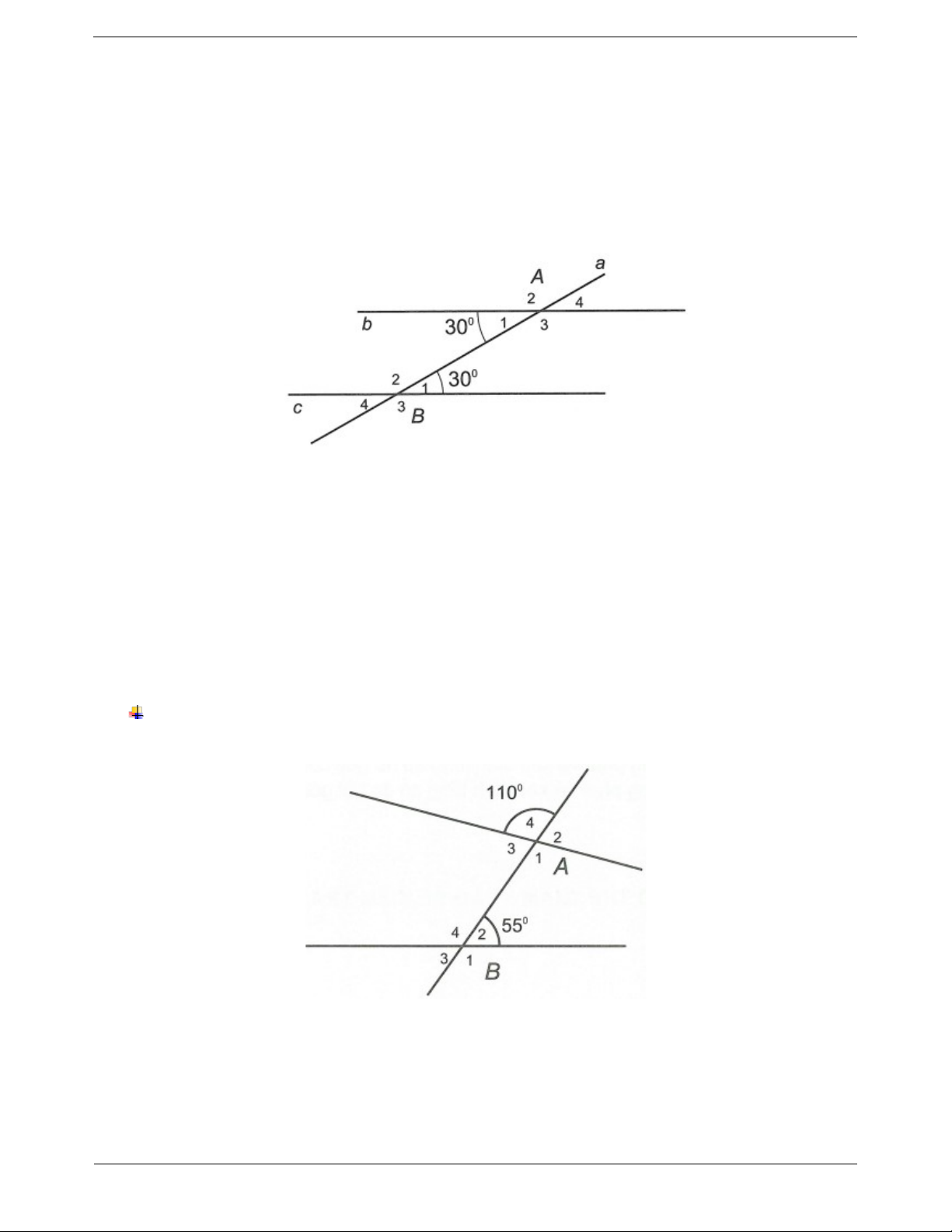
a) Vẽ một đường thẳng cắt hai đường thẳng để trong các góc tạo thành có một cặp góc so le trong bằng
nhau với số đo là 30°. Đặt tên cho các góc tạo thành.
b) Hãy viết tên các cặp góc đồng vị có số đo là 150°.
c) Viết tên các cặp góc so le trong có số đo là 150°. Hướng dẫn giải a) Hình vẽ Ta có  A  
A  180 (hai góc kề bù) mà 
A  30 (như hình vẽ) nên  A  180  
A  180  30  50 . 1 2 1 2 1 Vậy  A  
A  30 (hai góc đối đỉnh);  A  
A  150 (hai góc đối đỉnh). 1 4 2 3 Tương tự ta có  B  
B  30 (hai góc đối đỉnh),  B  
B  150 (hai góc đối đỉnh). 1 4 2 3
b) Vì đường thẳng a cắt hai đường thẳng b, c tạo một cặp góc so le trong bằng nhau nên  A  
B  150 (hai góc đồng vị bằng nhau);  A  
B  150 (hai góc đồng vị bằng nhau). 2 2 3 3
c) Vì đường thẳng a cắt hai đường thẳng b, c tạo một cặp góc so le trong bằng nhau nên  A  
B  150 (hai góc so le trong còn lại bằng nhau). 3 2
Bài tập tự luyện dạng 2
Câu 1: Cho hình vẽ sau. Xác định số đo của các góc còn lại.
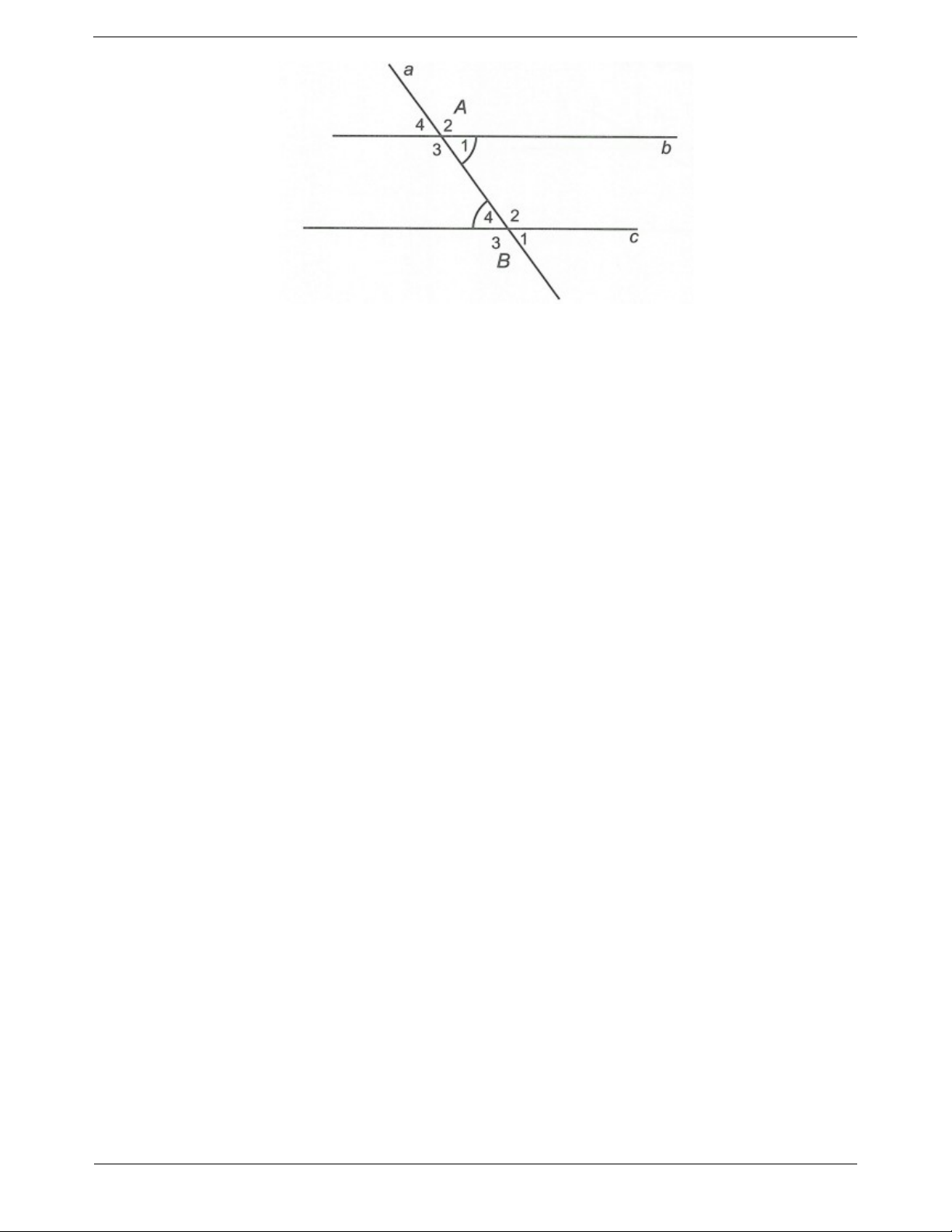
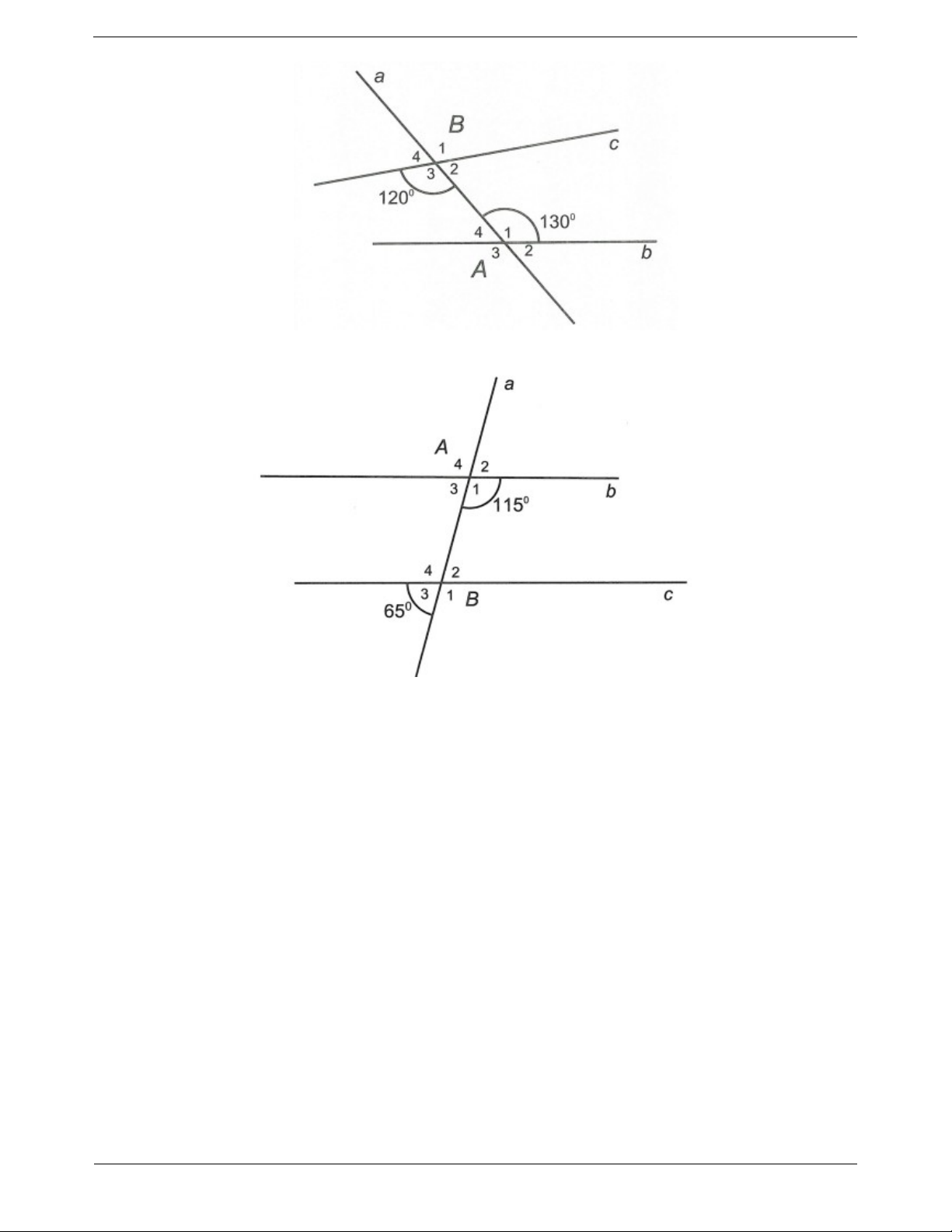
Câu 2: Cho đường thẳng a cắt hai đường thẳng b, c như hình vẽ.
a) Nêu tên những cặp góc so le trong, những cặp góc đồng vị. b) Biết  A  130 và 
B  120 , hãy tính các góc còn lại. 1 3 Trang 6
Câu 3: Cho hình vẽ với  A  115 ,  B  65 . 1 3
a) Xác định số đo của các góc còn lại.
b) Viết tên các cặp góc đồng vị và ghi rõ số đo góc của chúng.
c) Viết tên một cặp góc so le trong và nói rõ số đo của chúng.
d) Viết tên một cặp góc trong cùng phía và xác định tổng số đo góc của chúng.
e) Viết tên một cặp góc ngoài cùng phía và xác định tổng số đo hai góc đó. Trang 7 ĐÁP ÁN
Dạng 1. Xác định các cặp góc so le trong, cặp góc trong cùng phía, cặp góc đồng vị
a) Xét đường thẳng đi qua A, C cắt đường thẳng a và b thì  A đồng vị  C . 3 4
b) Xét đường thẳng đi qua A, C cắt đường thẳng AB và b thì  A so le trong với  C ,  A trong cùng phía với  C , 2 3 2 1  A đồng vị với  C . 2 2
Xét đường thẳng đi qua A, B cắt đường thẳng AC và b thì  A so le trong với  B ,  A trong cùng phía với  B ,  A 2 1 2 3 2 đồng vị với  B . 4 Dạng 2. Tính góc Câu 1. Ta có  A  
A  180 (hai góc kề bù). 2 4 Mà  A  110 nên  A  180  
A  180 110  70 . 4 2 4 Vậy  A  
A  110 (hai góc đối đỉnh),  A   A  70 1 4 3 2 (hai góc đối đỉnh). Mặt khác  B  
B  180 (hai góc kề bù). 2 4 Mà  B  55 nên  B  180  
B  180  55  125 . 2 4 2 Vậy  B  
B  55 (hai góc đối đỉnh),  B  
B  125 (hai góc đối đỉnh). 2 3 1 4 Câu 2.
a) Các cặp góc so le trong:  A và  B ,  A và  B . 1 3 4 2
Các cặp góc đồng vị:  A và  B ,  A và  B ,  A và 1 1 2 2 3  B ,  A và  B 3 4 4 b) Ta có  B  
B  180 (hai góc kề bù). 2 3 Mà 
B  120 (giả thiết) nên 3  B  180  
B  180 120  60 . 2 3 Vậy  B  
B  120 (hai góc đối đỉnh); 1 3  B  
B  60 (hai góc đối đỉnh). 2 4 Ta có  A  
A  180 (hai góc kề bù). 1 4 Mà 
A  130 (giả thiết) nên  A  180  
A  180 130  50 1 4 1 Vậy  A  
A  130 (hai góc đối đỉnh);  A  
A  50 (hai góc đối đỉnh). 1 3 2 4 Câu 3. Trang 8 a) Ta có  A  
A  180 (hai góc kề bù). 1 2 Mà 
A  115 (hình vẽ) nên 1  A  180  
A  180 115  65 . 2 1 Vậy  A  
A  115 (hai góc đối đỉnh), 1 4  A  
A  65 (hai góc đối đỉnh). 3 2 Lại có  B  
B  180 (hai góc kề bù). 1 3 Mà 
B  65 (hình vẽ) nên  B  180  
B  180  65  115 . 3 1 3 Vậy  B  
B  115 (hai góc đối đỉnh),  B  
B  65 (hai góc đối đỉnh). 1 4 2 3
b) Các cặp góc đồng vị là  A và  B  A  
 B 115 , A và B A    B 65 ; 2 2  1 1  1 1 2 2  A và  B  A  
 B 65 , A và B A    B 115 . 4 4  3 3  3 3 4 4
c) Các cặp góc so le trong là  A và  B  A  
 B 65 , A và B A    B 115 . 1 4  3 2  3 2 1 4
d) Các cặp góc trong cùng phía và xác định tổng số đo hai góc đó.  A và  B có  A  
B  65 115  180 ;  A và  B có  A  
B  65 115  180 . 1 2 1 2 3 4 3 4
e) Các cặp góc ngoài cùng phía và xác định tổng số đo hai góc đó.  A và  B có  A  
B  65 115  180 ; 2 1 2 1  A và  B có  A  
B  115  65  180 . 4 3 4 3 Trang 9