Chuyên đề giới hạn, hàm số liên tục Toán 11

Tài liệu gồm 67 trang, được biên soạn bởi tác giả Toán Từ Tâm, bao gồm lý thuyết, các dạng bài tập và bài tập luyện tập chuyên đề giới hạn, hàm số liên tục môn Toán 11. Mời bạn đọc đón xem!

41 21 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

TOÁN TỪ TÂM

ttt

GIỚI HẠN

HÀM SỐ LIÊN TỤC

TÁC GIẢ

TOÁN TỪ TÂM

Trang 1

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

MỤC LỤC

Bài 1. GIỚI HẠN DÃY SỐ

A. Lý thuyết

1. Giới hạn hữu hạn của dãy số .................................................................................................................. 3

2. Định lí về giới hạn hữu hạn ..................................................................................................................... 3

3. Tổng của cấp số nhân lùi vô hạn ........................................................................................................ 4

4. Giới hạn vô cực ......................................................................................................................................... 4

5. Quy tắc tìm giới hạn vô cực .................................................................................................................. 4

B. Các dạng bài tập

 Dạng 1. Dùng định nghĩa chứng minh giới hạn ................................................................................... 6

 Dạng 2. Giới hạn dãy số: dạng phân thức .............................................................................................. 9

 Dạng 3. Giới hạn dãy số: dạng lũy thừa ............................................................................................... 12

 Dạng 4. Giới hạn dãy số: dạng căn thức ............................................................................................... 14

C. Luyện tập

A. Câu hỏi – Trả lời trắc nghiệm ................................................................................................................. 16

B. Câu hỏi – Trả lời đúng/sai ....................................................................................................................... 21

C. Câu hỏi – Trả lời ngắn ............................................................................................................................. 23

Bài 2. GIỚI HẠN HÀM SỐ

A. Lý thuyết

1. Giới hạn hữu hạn của hàm số tại một điểm .................................................................................... 26

2. Giới hạn một bên .................................................................................................................................... 26

3. Giới hạn hữu hạn của hàm số tại vô cực .......................................................................................... 27

4. Giới hạn vô cực của hàm số ................................................................................................................ 27

5. Quy tắc tìm giới hạn vô cực của hàm số ......................................................................................... 28

B. Các dạng bài tập

 Dạng 1. Giới hạn của hàm số tại 1 điểm ............................................................................................... 29

 Dạng 2. Giới hạn của hàm số tại vô cực ............................................................................................... 33

 Dạng 3. Giới hạn một bên của hàm số .................................................................................................. 37

C. Luyện tập

A. Câu hỏi – Trả lời trắc nghiệm ................................................................................................................. 40

B. Câu hỏi – Trả lời đúng/sai ....................................................................................................................... 43

C. Câu hỏi – Trả lời ngắn ............................................................................................................................. 44

Bài 3. HÀM SỐ LIÊN TỤC

A. Lý thuyết

1. Hàm số liên tục tại một điểm .............................................................................................................. 47

2. Hàm số liên tục trên một khoảng ..................................................................................................... 47

Trang 2

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

3. Một số định lí .......................................................................................................................................... 48

B. Các dạng bài tập

 Dạng 1. Xét tính liên tục của hàm số tại 1 điểm .................................................................................. 49

 Dạng 2. Tìm tham số để hàm số liên tục – gián đoạn tại 1 điểm ...................................................... 51

 Dạng 3. Chứng minh phương trình có nghiệm ................................................................................... 55

C. Luyện tập

A. Câu hỏi – Trả lời trắc nghiệm ................................................................................................................. 58

B. Câu hỏi – Trả lời đúng/sai ....................................................................................................................... 62

C. Câu hỏi – Trả lời ngắn ............................................................................................................................. 65

Trang 3

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

1. Giới hạn hữu hạn của dãy số

2. Định lí về giới hạn hữu hạn

GIỚI HẠN DÃY SỐ

Bài 1.

Chương 03

Lý thuyết

Định nghĩa: Giới hạn dãy số = 0

 Ta nói dãy số có giới hạn là khi nếu có thể nhỏ hơn một số

dương bé tùy ý, kể từ một số hạng nào đó trở đi.

» Kí hiệu: hay khi .

Định nghĩa: Giới hạn dãy số = số thực khác 0

 Ta nói dãy số có giới hạn là khi nếu

» Kí hiệu: hay khi .

Từ nay về sau, thay cho , ta viết tắt là .

Lưu ý

⑴ ; ( với là số nguyên dương).

⑵ (nếu ).

⑶ Nếu (với là hằng số) thì .

Tính chất

Định lý

 Nếu và thì

• ;

• ; (nếu ).

 Nếu thì và .



Nếu với mọi và thì và .

Trang 4

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

3. Tổng của cấp số nhân lùi vô hạn

4. Giới hạn vô cực

5. Quy tắc tìm giới hạn vô cực

Định nghĩa



CSN vô hạn có công bội được gọi là cấp số nhân lùi vô hạn.

Định lý

 Cho cấp số nhân lùi vô hạn có công bội (với ).

Gọi là tổng vô hạn của . Khi đó

Định nghĩa

 Ta nói dãy số có giới hạn khi nếu có thể lớn hơn số dương

tùy ý, kể từ một số hạng nào đó trở đi.

» Kí hiệu: hoặc hoặc .



Ta nói dãy số có giới hạn khi nếu có thể nhỏ hơn số âm tùy ý,

kể từ một số hạng nào đó trở đi.

» Kí hiệu: hoặc hoặc .

⁂ Nhận xét. .

⑴ (với là số nguyên dương).

⑵ (nếu ).

Tính chất

Định lý 1

 Nếu và thì .

Định lý 2

 Nếu và thì được cho bằng:

Trang 5

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

Định lý 3

 Nếu và thì được cho bằng:

Dấu của

Định lý 4

 Nếu , và hoặc thì được cho bằng:

Dấu của

Trang 6

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

 Dạng 1. Dùng định nghĩa chứng minh giới hạn

 Lời giải

........................................................................................................................................................

Các dạng bài tập

⑴ Để chứng minh ta chứng minh

nhỏ tùy ý luôn tồn tại một số sao cho

⑵ Để chứng minh ta chứng minh

⑶ Để chứng minh ta chứng minh

lớn tùy ý luôn tồn tại một số sao cho

⑷ Để chứng minh ta chứng minh

⑸ Một dãy số nếu có giới hạn thì giới hạn đó là duy nhất.

Phương pháp

Ví dụ 1.1.

Chứng minh rằng:

⑴ . ⑵

Trang 7

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

 Lời giải

........................................................................................................................................................

Ví dụ 1.2.

Chứng minh rằng:

⑴ ⑵

⑶

⑷

Trang 8

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

 Lời giải

........................................................................................................................................................

Ví dụ 1.3.

Chứng minh rằng:

⑴ . ⑵

Trang 9

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

 Dạng 2. Giới hạn dãy số: dạng phân thức

 Lời giải

........................................................................................................................................................

Tính giới hạn trong đó và là các đa thức bậc .

 Bước 1: Đặt với là số mũ cao nhất của đa thức và là số mũ cao nhất

của đa thức ra làm nhân tử chung.

 Bước 2: Áp dụng kết quả .

Phương pháp

Ví dụ 2.1.

Tính các giới hạn sau:

⑴ . ⑵ ⑶

Trang 10

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

 Lời giải

........................................................................................................................................................

Ví dụ 2.2.

Tìm giới hạn của các dãy số sau:

⑴ . ⑵ ⑶

Trang 11

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

 Lời giải

........................................................................................................................................................

Ví dụ 2.3.

Tính các giới hạn sau:

⑴ ⑵

⑶ ⑷

Trang 12

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

 Dạng 3. Giới hạn dãy số: dạng lũy thừa

 Lời giải

........................................................................................................................................................

 Lời giải

........................................................................................................................................................

Tính giới hạn trong đó và là các lũy thừa dạng

 Bước 1: Đưa biểu thức về cùng số mũ .

 Bước 2: Chia tử và mẫu số cho trong đó là số có trị tuyệt đối lớn nhất.

 Bước 3: Áp dụng kết quả “ Nếu thì ”.

Phương pháp

Ví dụ 3.1.

Tính các giới hạn sau:

⑴ . ⑵

Ví dụ 3.2.

Tính các giới hạn sau:

⑴ ⑵

⑶ ⑷

Trang 13

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

 Lời giải

........................................................................................................................................................

 Lời giải

........................................................................................................................................................

Ví dụ 3.3.

Tính các giới hạn sau:

⑴ ⑵

Ví dụ 3.4.

Cho dãy số , xác định bởi

⑴ . . Tính giới hạn

⑵ . Tính giới hạn

Trang 14

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

 Dạng 4. Giới hạn dãy số: dạng căn thức

 Lời giải

........................................................................................................................................................

Tính giới hạn trong đó và chứa căn thức

Ở dạng này ta thường gặp 2 trường hợp:

» Trường hợp 1: Đơn giản – Chỉ rút nhân tử chung ( như dạng 2)

Lưu ý: , ở đây ta chỉ có nên

» Trường hợp 2: Nhân lượng liên hợp, khi giới hạn ở dạng vô định:

▪ ▪

Bên cạnh đó áp dụng các tính chất để tính được kết quả của giới hạn:

⑴ ; ( với là số nguyên dương).

⑵ (nếu ).

⑶ Nếu (với là hằng số) thì .

Phương pháp

Ví dụ 4.1.

Tính các giới hạn sau:

⑴ . ⑵

Trang 15

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

 Lời giải

........................................................................................................................................................

 Lời giải

........................................................................................................................................................

Ví dụ 4.2.

Tính các giới hạn sau:

⑴ . ⑵

Ví dụ 4.3.

Tính các giới hạn sau:

⑴ . ⑵

Trang 16

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

A. Câu hỏi – Trả lời trắc nghiệm

» Câu 1. Trong các mệnh đề dưới đây, mệnh đề nào sai?

A. Nếu

 lim

và

0limv

thì

 

 lim

B. Nếu

0lim

và

 limv

thì









lim

C. Nếu

0lim

và

0limv

thì



 





lim

D. Nếu

0lim

và

0limv

và

0

với mọi

thì



 





lim

» Câu 2. Trong các khẳng định dưới đây có bao nhiêu khẳng định đúng?

(I)

 lim

với

nguyên dương.

(II)

 lim

nếu

1q

(III)

 lim

nếu

1q

. B.

. C.

. D.

» Câu 3. Phát biểu nào sau đây là sai?

lim

(



là hằng số). B.

0lim

 

1q

0lim

. D.

0lim

 

1k

» Câu 4.

53

lim

bằng

. B.

. C.



. D.

» Câu 5.

25

lim

bằng

. B.

. C.



. D.

» Câu 6. Tìm

7 2 1

3 2 1







lim .

. B.



. C.

. D.

» Câu 7.





lim

bằng:

. B.

. C.



. D.

3

» Câu 8. Tính giới hạn







lim

 L

. B.

2L

. C.

1L

. D.

0L

» Câu 9. Dãy số nào sau đây có giới hạn bằng

Luyện tập

Trang 17

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03







. B.







. C.







. D.







» Câu 10. Giá trị của





lim

bằng

. B.

. C.

1

. D.

» Câu 11.

1 19

18 19



lim

bằng

. B.

. C.



. D.

» Câu 12. Dãy số nào sau đây có giới hạn khác

. B.

. C.

1n

. D.

sin n

» Câu 13. Tìm

8 2 1

4 2 1





lim

. B.

. C.

. D.

» Câu 14.

2 2 2

4 2 5





lim

bằng

. B.

. C.



. D.

» Câu 15. Giới hạn của dãy số

 

với







là:

2

. B.

. C.

. D.



» Câu 16. Tính

8 3 1

4 5 2





lim

. B.



. C.

. D.



» Câu 17. Cho hai dãy số

 

và

 

có





;





. Tính

lim

. B.

. C.

. D.



» Câu 18.



lim

bằng.

. B.



. C.



. D.

» Câu 19. Dãy số nào sau đây có giới hạn bằng

 

0 999,

. B.

 

1

. C.

 

1 0001 ,

. D.

 

1 2345,

» Câu 20.

100 3 99

10 2 98





lim

là



. B.

100

. C.

100

. D.

» Câu 21.

 

3 4lim

là



. B.



. C.

. D.

Trang 18

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

» Câu 22. Tính giới hạn

3 2 2 3







lim

. B.

. C.

. D.

6

» Câu 23. Tính giới hạn





16 4 16 3



   lim

n n n n

0T

. B.

T

. C.

T

. D.

T

» Câu 24. Cho dãy số

 

thỏa

2 

với mọi

 *n

. Khi đó

lim

không tồn tại. B.

1lim

0lim

. D.

2lim

» Câu 25. Gọi S là tập hợp các tham số nguyên

thỏa mãn





  







lim

. Tổng các phần

tử của

bằng

. B.

. C.

. D.

» Câu 26. Dãy số

 

với

  

 

3 1 3







có giới hạn bằng phân số tối giản

. Tính

.ab

192

128

» Câu 27. Biết

2 4 1







lim

với

là tham số. Khi đó

aa

bằng

12

. B.

2

. C.

. D.

6

» Câu 28. Giới hạn

2 2 2 2 2

1 2 3 4

    



...

lim

có giá trị bằng?

. B.

. C.

. D.

» Câu 29. Tìm

2 2 2



  





lim ...

n n n



. B.

. C.

. D.

» Câu 30.

   

2 3 1lim nn

là:





» Câu 31. Giới hạn

 

1 5 4 3

   



...

lim

bằng

. B.



. C.

. D.

» Câu 32. Tìm

lim

biết

 

1 3 5 2 1

    





...

. B.



. C.

. D.



» Câu 33.





31  lim n n n

bằng

Trang 19

» TOÁN TỪ TÂM – 0901.837.432

GIỚI HẠN – HÀM SỐ LIÊN TỤC

Chương 03

3

. B.



. C.

. D.



» Câu 34. Trong các giới hạn sau đây, giới hạn nào có giá trị bằng



lim

. B.





lim





21  lim n n n

. D.



lim .

» Câu 35. Tính giới hạn





9 2 1 4 1    limL n n n



. B.

. C.



. D.

» Câu 36. Tính giới hạn





3 2 2 3

8 3 2 5 8     lim L n n n n



. B.

7

. C.

. D.

» Câu 37. Tính giới hạn





8 3 4 2 6    lim L n n n



. B.

. C.

. D.

» Câu 38. Tính giới hạn





2   lim L n n n



. B.

. C.

. D.

» Câu 39. Tính giới hạn





4 2 6

1   limL n n n



. B.

. C.

. D.



» Câu 40. Tính giới hạn





2 3 2

1    limL n n n n



. B.

. C.

. D.

» Câu 41. Dãy số nào sau đây có giới hạn bằng







. B.







. C.







. D.









» Câu 42. Tính tổng

của cấp số nhân lùi vô hạn có số hạng đầu

1u

và công bội

q

2S

. B.

S

. C.

1S

. D.

S

» Câu 43. Tổng vô hạn sau đây

2 2 2

     ... ...

có giá trị bằng

. B.

. C.

. D.

» Câu 44. Số thập phân vô hạn tuần hoàn

 

3 15555 3 1 5, ... ,

viết dưới dạng hữu tỉ là

. B.

142

. C.

. D.

Bấm Tải xuống để xem toàn bộ.

| 1/67

| | Tải xuống

Preview text:

ttt TOÁN TỪ TÂM GIỚI HẠN HÀ H M À M SỐ S Ố LI L Ê I N Ê N TỤ T C Ụ TÁC GIẢ TOÁN TỪ TÂM
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC MỤC LỤC
Bài 1. GIỚI HẠN DÃY SỐ A. Lý thuyết
1. Giới hạn hữu hạn của dãy số .................................................................................................................. 3
2. Định lí về giới hạn hữu hạn ..................................................................................................................... 3
3. Tổng của cấp số nhân lùi vô hạn ........................................................................................................ 4
4. Giới hạn vô cực ......................................................................................................................................... 4
5. Quy tắc tìm giới hạn vô cực .................................................................................................................. 4
B. Các dạng bài tập
 Dạng 1. Dùng định nghĩa chứng minh giới hạn ................................................................................... 6
 Dạng 2. Giới hạn dãy số: dạng phân thức .............................................................................................. 9
 Dạng 3. Giới hạn dãy số: dạng lũy thừa ............................................................................................... 12
 Dạng 4. Giới hạn dãy số: dạng căn thức ............................................................................................... 14 C. Luyện tập
A. Câu hỏi – Trả lời trắc nghiệm ................................................................................................................. 16
B. Câu hỏi – Trả lời đúng/sai ....................................................................................................................... 21
C. Câu hỏi – Trả lời ngắn ............................................................................................................................. 23
Bài 2. GIỚI HẠN HÀM SỐ A. Lý thuyết
1. Giới hạn hữu hạn của hàm số tại một điểm .................................................................................... 26
2. Giới hạn một bên .................................................................................................................................... 26
3. Giới hạn hữu hạn của hàm số tại vô cực .......................................................................................... 27
4. Giới hạn vô cực của hàm số ................................................................................................................ 27
5. Quy tắc tìm giới hạn vô cực của hàm số ......................................................................................... 28
B. Các dạng bài tập
 Dạng 1. Giới hạn của hàm số tại 1 điểm ............................................................................................... 29
 Dạng 2. Giới hạn của hàm số tại vô cực ............................................................................................... 33
 Dạng 3. Giới hạn một bên của hàm số .................................................................................................. 37 C. Luyện tập
A. Câu hỏi – Trả lời trắc nghiệm ................................................................................................................. 40
B. Câu hỏi – Trả lời đúng/sai ....................................................................................................................... 43
C. Câu hỏi – Trả lời ngắn ............................................................................................................................. 44
Bài 3. HÀM SỐ LIÊN TỤC A. Lý thuyết
1. Hàm số liên tục tại một điểm .............................................................................................................. 47
2. Hàm số liên tục trên một khoảng ..................................................................................................... 47
» TOÁN TỪ T ÂM – 0901.837.432 Trang 1
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC
3. Một số định lí .......................................................................................................................................... 48
B. Các dạng bài tập
 Dạng 1. Xét tính liên tục của hàm số tại 1 điểm .................................................................................. 49
 Dạng 2. Tìm tham số để hàm số liên tục – gián đoạn tại 1 điểm ...................................................... 51
 Dạng 3. Chứng minh phương trình có nghiệm ................................................................................... 55 C. Luyện tập
A. Câu hỏi – Trả lời trắc nghiệm ................................................................................................................. 58
B. Câu hỏi – Trả lời đúng/sai ....................................................................................................................... 62
C. Câu hỏi – Trả lời ngắn ............................................................................................................................. 65
» TOÁN TỪ T ÂM – 0901.837.432 Trang 2
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC Chương 03 Bài 1. GIỚI HẠN DÃY SỐ Lý thuyết
1. Giới hạn hữu hạn của dãy số
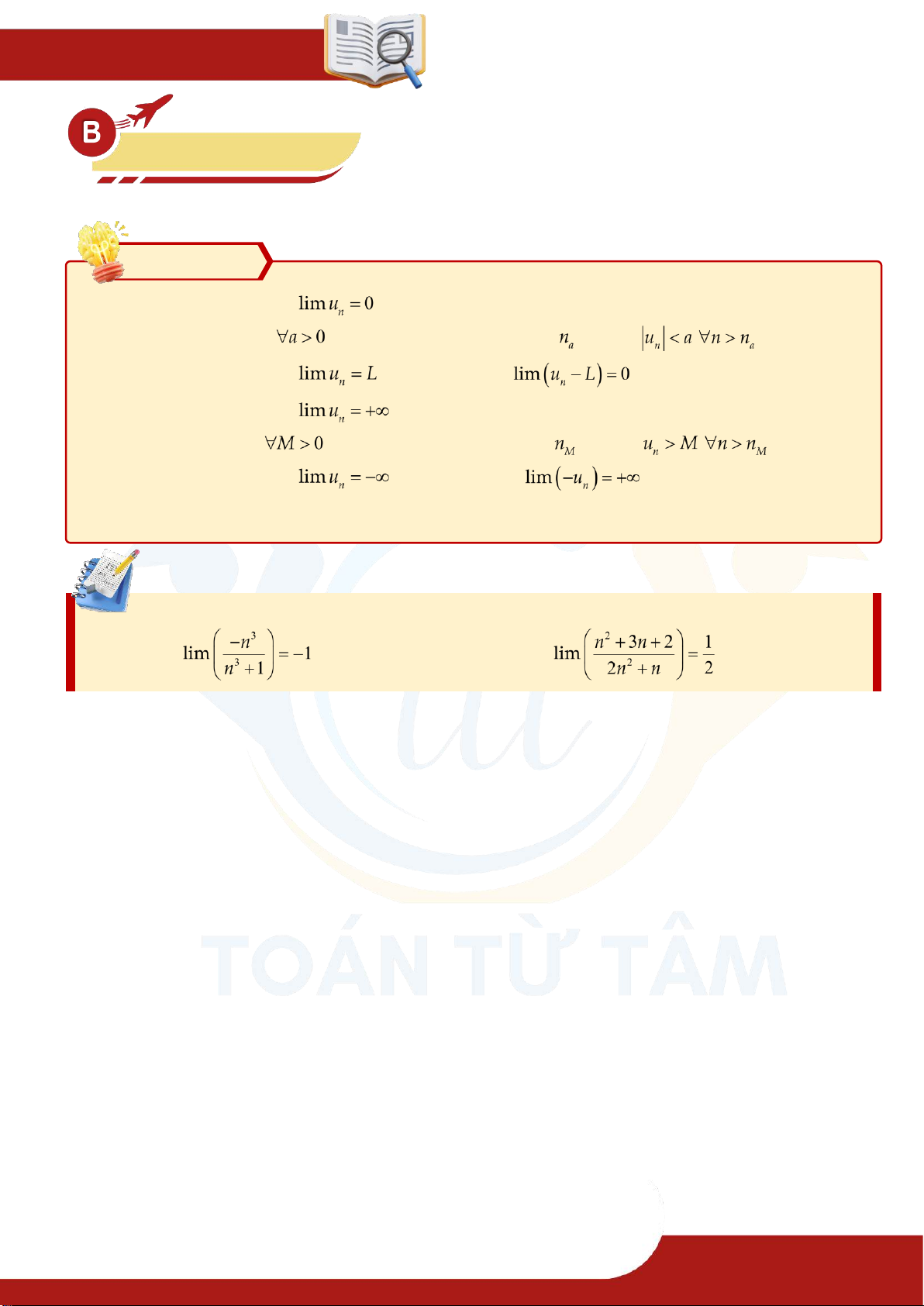
Định nghĩa: Giới hạn dãy số = 0  Ta nói dãy số
có giới hạn là khi nếu
có thể nhỏ hơn một số
dương bé tùy ý, kể từ một số hạng nào đó trở đi. » Kí hiệu: hay khi .
Định nghĩa: Giới hạn dãy số = số thực khác 0  Ta nói dãy số
có giới hạn là khi nếu » Kí hiệu: hay khi . Lưu ý Từ nay về sau, thay cho , ta viết tắt là . Tính chất ⑴ ;
( với là số nguyên dương). ⑵ (nếu ). ⑶ Nếu (với là hằng số) thì .
2. Định lí về giới hạn hữu hạn Định lý  Nếu và thì • ; • ; (nếu ).  Nếu thì và .  Nếu với mọi và thì và .
» TOÁN TỪ T ÂM – 0901.837.432 Trang 3
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC
3. Tổng của cấp số nhân lùi vô hạn Định nghĩa  CSN vô hạn có công bội
được gọi là cấp số nhân lùi vô hạn. Định lý
 Cho cấp số nhân lùi vô hạn có công bội (với ). Gọi là tổng vô hạn của . Khi đó 4. Giới hạn vô cực Định nghĩa  Ta nói dãy số có giới hạn khi nếu
có thể lớn hơn số dương
tùy ý, kể từ một số hạng nào đó trở đi. » Kí hiệu: hoặc hoặc .  Ta nói dãy số có giới hạn khi nếu
có thể nhỏ hơn số âm tùy ý,
kể từ một số hạng nào đó trở đi. » Kí hiệu: hoặc hoặc .
⁂ Nhận xét. . Tính chất ⑴
(với là số nguyên dương). ⑵ (nếu ).
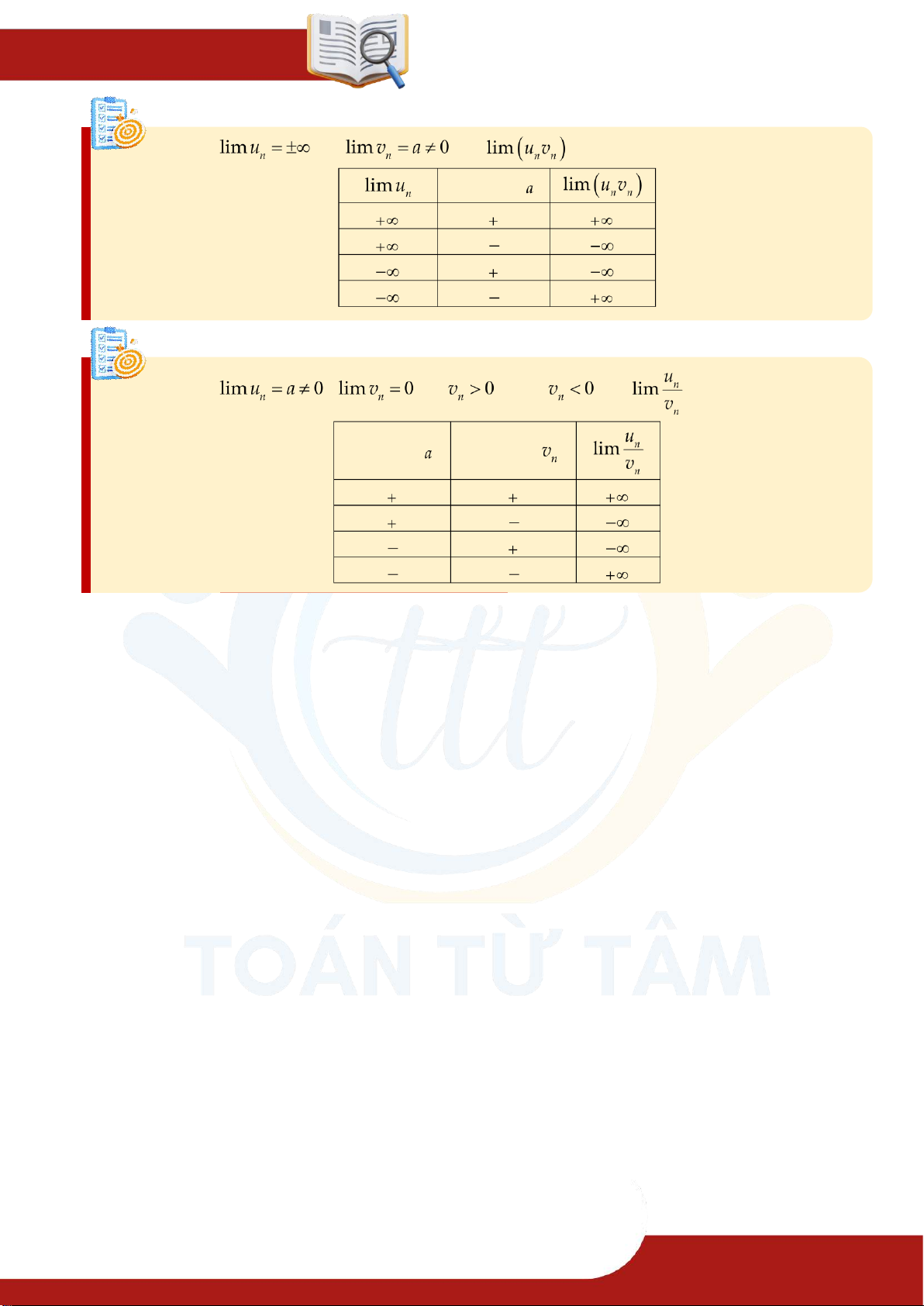
5. Quy tắc tìm giới hạn vô cực Định lý 1  Nếu và thì . Định lý 2  Nếu và thì được cho bằng:
» TOÁN TỪ T ÂM – 0901.837.432 Trang 4
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC Định lý 3  Nếu và thì được cho bằng: Dấu của Định lý 4  Nếu , và hoặc thì được cho bằng: Dấu của Dấu của
» TOÁN TỪ T ÂM – 0901.837.432 Trang 5
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC Các dạng bài tập
 Dạng 1. Dùng định nghĩa chứng minh giới hạn Phương pháp ⑴ Để chứng minh ta chứng minh
nhỏ tùy ý luôn tồn tại một số sao cho ⑵ Để chứng minh ta chứng minh ⑶ Để chứng minh ta chứng minh
lớn tùy ý luôn tồn tại một số sao cho ⑷ Để chứng minh ta chứng minh
⑸ Một dãy số nếu có giới hạn thì giới hạn đó là duy nhất. Ví dụ 1.1. Chứng minh rằng: ⑴ . ⑵
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 6
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC Ví dụ 1.2. Chứng minh rằng: ⑴ ⑵ ⑶ ⑷
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 7
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC Ví dụ 1.3. Chứng minh rằng: ⑴ . ⑵
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 8
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC
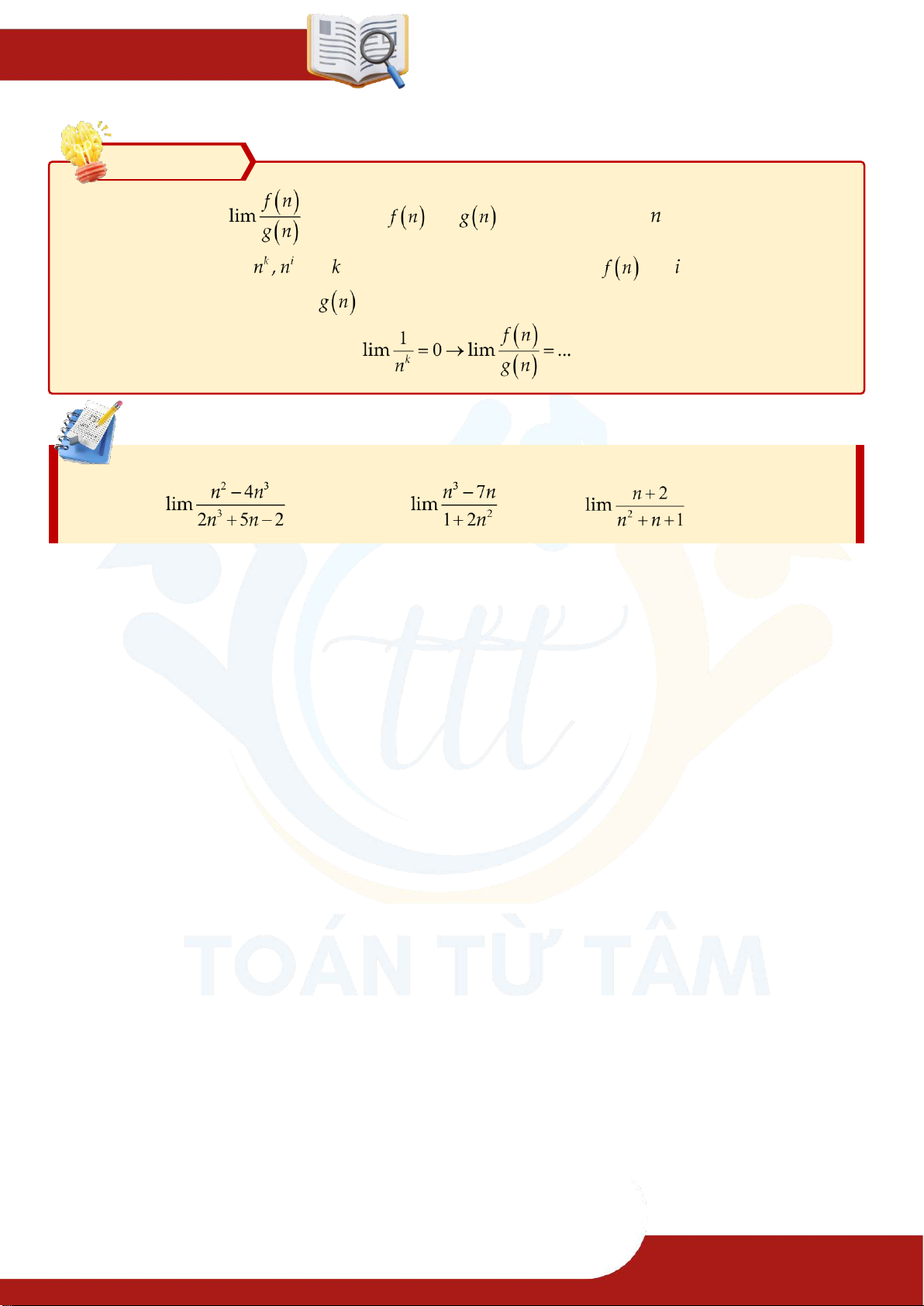
 Dạng 2. Giới hạn dãy số: dạng phân thức Phương pháp Tính giới hạn trong đó và
là các đa thức bậc .  Bước 1: Đặt
với là số mũ cao nhất của đa thức và là số mũ cao nhất của đa thức ra làm nhân tử chung.
 Bước 2: Áp dụng kết quả . Ví dụ 2.1. Tính các giới hạn sau: ⑴ . ⑵ ⑶
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 9
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC Ví dụ 2.2.
Tìm giới hạn của các dãy số sau: ⑴ . ⑵ ⑶
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 10
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC Ví dụ 2.3. Tính các giới hạn sau: ⑴ ⑵ ⑶ ⑷
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 11
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC
 Dạng 3. Giới hạn dãy số: dạng lũy thừa Phương pháp Tính giới hạn trong đó và là các lũy thừa dạng
 Bước 1: Đưa biểu thức về cùng số mũ .
 Bước 2: Chia tử và mẫu số cho trong đó là số có trị tuyệt đối lớn nhất.
 Bước 3: Áp dụng kết quả “ Nếu thì ”. Ví dụ 3.1. Tính các giới hạn sau: ⑴ . ⑵
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................ Ví dụ 3.2. Tính các giới hạn sau: ⑴ ⑵ ⑶ ⑷
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 12
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC Ví dụ 3.3. Tính các giới hạn sau: ⑴ ⑵
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................ Ví dụ 3.4. Cho dãy số , xác định bởi ⑴ . . Tính giới hạn ⑵ . Tính giới hạn
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 13
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC
 Dạng 4. Giới hạn dãy số: dạng căn thức Phương pháp Tính giới hạn trong đó và chứa căn thức
Ở dạng này ta thường gặp 2 trường hợp:
» Trường hợp 1: Đơn giản – Chỉ rút nhân tử chung ( như dạng 2) Lưu ý: , ở đây ta chỉ có nên
» Trường hợp 2: Nhân lượng liên hợp, khi giới hạn ở dạng vô định: ▪ ▪ ▪ ▪
Bên cạnh đó áp dụng các tính chất để tính được kết quả của giới hạn: ⑴ ;
( với là số nguyên dương). ⑵ (nếu ). ⑶ Nếu (với là hằng số) thì . Ví dụ 4.1. Tính các giới hạn sau: ⑴ . ⑵
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 14
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC Ví dụ 4.2. Tính các giới hạn sau: ⑴ . ⑵
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................ Ví dụ 4.3. Tính các giới hạn sau: ⑴ . ⑵
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 15
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC Luyện tập
A. Câu hỏi – Trả lời trắc nghiệm
» Câu 1. Trong các mệnh đề dưới đây, mệnh đề nào sai?
A. Nếu limu   và limv  a  0 thì limu v . n n    n n  u 
B. Nếu lim u  a  0 và limv   thì lim  n   0 . n n  vn   u 
C. Nếu lim u  a  0 và limv  0 thì lim  n    . n n  vn   u 
D. Nếu limu  a  0 và limv  0 và v  0 với mọi n thì lim  n    . n n n  vn 
» Câu 2. Trong các khẳng định dưới đây có bao nhiêu khẳng định đúng? (I) lim k
n   với k nguyên dương. (II) lim n
q   nếu q  1. (III) lim n
q   nếu q 1 A. 0 . B. 1. C. 3 . D. 2 .
» Câu 3. Phát biểu nào sau đây là sai?
A. limu  c ( u  c là hằng số). B. lim n
q  0  q   1 . n n 1 1 C. lim  0. D. lim  0 k   1 . n k n 1 » Câu 4. lim bằng 5n  3 1 1 A. 0 . B. . C.  . D. . 3 5 1 » Câu 5. lim bằng 2n  5 1 1 A. . B. 0 . C.  . D. . 2 5 2 3 7n  2n 1
» Câu 6. Tìm I  lim . 3 2 3n  2n 1 7 2 A. . B.  . C. 0 . D. 1. 3 3 2 2n  3 » Câu 7. lim bằng: 6 5 n  5n 3  A. 2 . B. 0 . C. . D. 3  . 5 2n 1
» Câu 8. Tính giới hạn L  lim ? 2 2  n  n
A. L   . B. L  2  .
C. L  1 . D. L  0 .
» Câu 9. Dãy số nào sau đây có giới hạn bằng 0 ?
» TOÁN TỪ T ÂM – 0901.837.432 Trang 16
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC 2 n  2 2 n  2n 1 2n 2 1 2n A. u  . B. u  . C. u  . D. u  . n 2 5n  3n n 2 5n  3n n 2 5n  3n n 2 5n  3n 2  n
» Câu 10. Giá trị của lim bằng n 1 A. 1. B. 2 . C. 1. D. 0 . 119n » Câu 11. lim bằng 18n 19 19 1 1 A. . B. . C.  . D. . 18 18 19
» Câu 12. Dãy số nào sau đây có giới hạn khác 0 ? 1 1 n 1 sin n A. . B. . C. . D. . n n n n 5 3 8n  2n 1 » Câu 13. Tìm lim . 5 2 4n  2n 1 A. 2 . B. 8 . C. 1. D. 4 . 4 2n  2n  2 » Câu 14. lim bằng 4 4n  2n  5 2 1 A. . B. . C.  . D. 0 . 11 2 2n 1
» Câu 15. Giới hạn của dãy số u với u  n * , là: n  n 3  n 2 1 A. 2  . B. . C. 1. D.  . 3 3 2 8n  3n 1 » Câu 16. Tính lim . 2 4  5n  2n 1 1 A. 2 . B.  . C. 4 . D.  . 2 4 1 3 u
» Câu 17. Cho hai dãy số u và v có u  ; v  . Tính lim n . n  n  n n 1 n n  3 vn 1 A. 0 . B. 3 . C. . D.  . 3
» Câu 18. lim 2n bằng. n A. 2 . B.  . C.  . D. 0 .
» Câu 19. Dãy số nào sau đây có giới hạn bằng 0 ? n n n n
A. 0,999 . B.   1 . C.  1  ,000  1 . D. 1,2345 . n 1 100   3 9 . 9n » Câu 20. lim là 2n n 1 10  2 9 . 8  1 A.  . B. 100. C. . D. 0 . 100
» Câu 21. lim 3n  4n  là 4 A.  . B.  . C. . D. 1. 3
» TOÁN TỪ T ÂM – 0901.837.432 Trang 17
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC n 1  n 1 3 2 . 2 3   .
» Câu 22. Tính giới hạn lim . 4  3n 3 6 A. . B. 0 . C. . D. 6  . 2 5
» Câu 23. Tính giới hạn lim  n 1  n n 1 16 4 16      3n T . 1 1 1
A. T  0.
B. T  .
C. T  . D. T  . 4 8 16 1
» Câu 24. Cho dãy số u thỏa u  2 
với mọi n * . Khi đó n  n 3 n
A. lim u không tồn tại.
B. lim u  1. n n
C. lim u  0 .
D. lim u  2 . n n  3n  2 
» Câu 25. Gọi S là tập hợp các tham số nguyên a thỏa mãn 2 lim
 a  4a  0   . Tổng các phần  n  2 
tử của S bằng A. 4 . B. 3 . C. 5 . D. 2 .
3n 13n2 a
» Câu 26. Dãy số u với u 
có giới hạn bằng phân số tối giản . Tính . a b n  n 4n53 b A. 192 B. 68 C. 32 D. 128 3 2 2n  n  4 1 » Câu 27. Biết lim
 với a là tham số. Khi đó 2
a  a bằng 3 an  2 2 A. 12 . B. 2  . C. 0 . D. 6  . 2 2 2 2 2
1  2  3  4  ...  n
» Câu 28. Giới hạn lim
có giá trị bằng? 3 n  2n  7 2 1 1 A. . B. . C. 0 . D. . 3 6 3  1 2 n  » Câu 29. Tìm lim   ...   . 2 2 2  n n n  1 1 A.  . B. . C. . D. 0 . 2 n 4 3
» Câu 30. lim 2  3n n   1 là: A.  B.  C. 81 D. 2
1 5  ...  4n  3
» Câu 31. Giới hạn lim bằng 2n 1 2 A. 1. B.  . C. . D. 0 . 2
n 1 3  5  ...  2n   1
» Câu 32. Tìm lim u biết u  n n 2 2n 1 1 A. . B.  . C. 1. D.  . 2 » Câu 33. lim  2
n  3n 1  n bằng
» TOÁN TỪ T ÂM – 0901.837.432 Trang 18
Chương 03
GIỚI HẠN – HÀM SỐ LIÊN TỤC 3 A. 3  . B.  . C. 0 . D.  . 2
» Câu 34. Trong các giới hạn sau đây, giới hạn nào có giá trị bằng 1? n 1 3   2n 2 3n  n A. lim . B. lim . 5  3n 2 4n  5 3 2n  3 C. lim  2 2
n  2n  n 1 . D. lim . 2 1 2n
» Câu 35. Tính giới hạn L  lim  2 2
9n  2n 1  4n 1 . 9 A.  . B. 1. C.  . D. . 4
» Câu 36. Tính giới hạn L  lim  3 3 2 3 2 3
8n  3n  2  5n 8 n . 53 2 A.  . B. 7  . C. . D. . 2 3
» Câu 37. Tính giới hạn L  lim  3 3 2
8n  3n  4  2n  6 . 25 53 1 A.  . B. . C. . D. . 4 2 2
» Câu 38. Tính giới hạn L  lim  3 3
n  n  n  2. 1 A.  . B. 2 . C. 1. D. . 2
» Câu 39. Tính giới hạn L  lim  4 2 3 6
n  n  n 1 . 5 1 5 A.  . B. . C. . D.  . 4 2 3
» Câu 40. Tính giới hạn L  lim  2 3 3 2
n  n 1  n  n . 5 53 1 A.  . B. . C. . D. . 4 2 6
» Câu 41. Dãy số nào sau đây có giới hạn bằng 0 ?  n n n n 4   1   5   5  A.   . B.   . C.   . D.   .  e   3   3   3  1
» Câu 42. Tính tổng S của cấp số nhân lùi vô hạn có số hạng đầu u  1 và công bội q   . 1 2 3 2
A. S  2 . B. S  .
C. S 1. D. S  . 2 3 2 2 2
» Câu 43. Tổng vô hạn sau đây S  2    ...
 ... có giá trị bằng 2 3 3 3n 8 A. . B. 3 . C. 4 . D. 2 . 3
» Câu 44. Số thập phân vô hạn tuần hoàn 3 1 , 5555...  3, 
1 5 viết dưới dạng hữu tỉ là 63 142 1 7 A. . B. . C. . D. . 20 45 18 2
» TOÁN TỪ T ÂM – 0901.837.432 Trang 19

Chuyên đề giới hạn, hàm số liên tục Toán 11

Thông tin :

Tài liệu liên quan:

Chuyên đề toán thực tế thống kê môn Toán 11

Đơn vị của cường độ điện trường là gì? Công thức tính cường độ điện trường? | Toán 11

Đề thi học sinh giỏi Toán 11 năm 2024 – 2025 trường THPT Bình Chiểu – TP HCM

Ôn tập giữa kì 1 Toán 11 năm 2024 – 2025 trường THPT Trần Phú – Hà Nội

Đề cương học kỳ 1 Toán 11 năm 2024 – 2025 trường THPT Yên Hòa – Hà Nội