
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 1
Sưu tầm và biên soạn
BÀI 1: PHÉP TÍNH LŨY THỪA
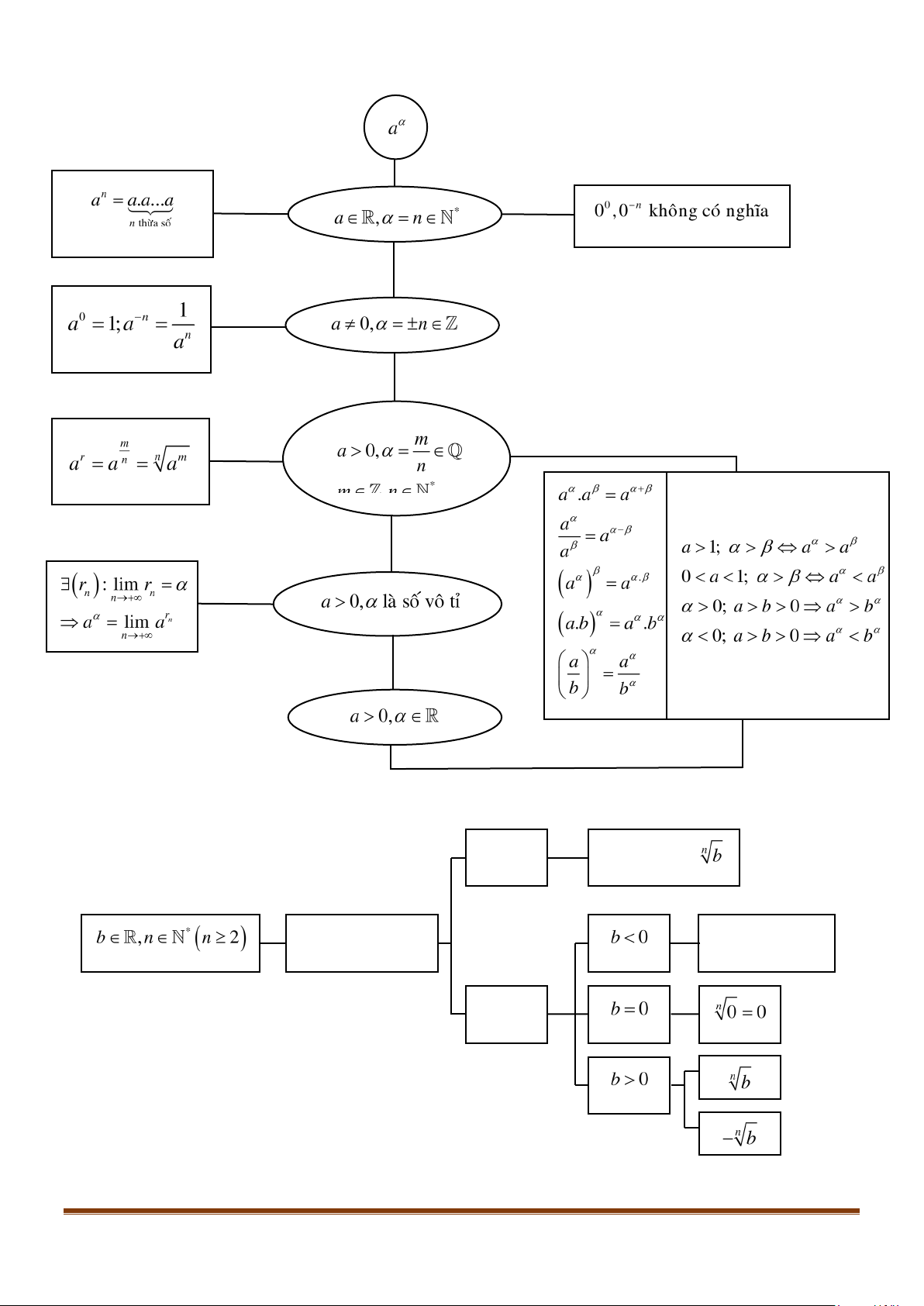
1. Lũy thừa với số mũ nguyên
Cho
n
là một số nguyên dương. Ta định nghĩa:
Với
a
là số thực tùy ý:
. ...
n
a aa a=
(
n
thừa số
a
).
Với
a
là số thực khác
0
:
0
1
1;
n
n
aa
a
−
= =
.
Trong biểu thức
m
a
,
a
gọi là cơ số,
m
gọi là số mũ.
Chú ý:
1)
0
0
và
0
n−
không có nghĩa.
2) Nếu
1a >
thì
mn
aa>
khi và chỉ khi
mn>
.
3) Nếu
01a<<
thì
mn
aa>
khi và chỉ khi
mn<
.
2. Căn bậc
n
a) Định nghĩa: Cho số thực
a
và số nguyên dương
2n ≥
. Số
b
được gọi là căn bậc
n
của số
a
nếu
n
ba=
.
Chú ý:
- Với
n
chẵn, ta xét ba trường hợp sau:
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
LÝ THUYẾT.
I

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 2
Sưu tầm và biên soạn
- Với
n
lẻ,
a
∈
: Có duy nhất một căn bậc
n
của
a
, ký hiệu là
n
a
.
3. Lũy thừa với số mũ hữu tỉ
Cho số thực
0a >
và số hữu tỉ
m
r
n
=
, trong đó
, ,0mn n∈>
. Lũy thừa của
a
với số mũ
r
,
kí hiệu là
r
a
, được xác định bởi
m
n
rm
n
aa a= =
.
4. Lũy thừa với số mũ thực:
Giới hạn của dãy số
( )
n
r
a
gọi là lũy thừa của số thực dương
a
với số mũ
α
. Kí hiệu là:
lim
n
r
aa
α
=
với
lim
n
n
r
α
→+∞
=
5. Tính chất của phép tính lũy thừa
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 3
Sưu tầm và biên soạn
SƠ ĐỒ HỆ THỐNG HÓA LŨY THỪA
Căn bậc n của b
n lẻ
n chẵn
Có duy nhất
Không tồn tại
Định nghĩa
Tính chất

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 4
Sưu tầm và biên soạn
Dạng 1: Tính giá trị của biểu thức
Câu 1: Tính giá trị của biểu thức
5
5
4. 8P = −
Câu 2: Tính giá trị của
1
3
27
bằng
Câu 3: Cho
1
256
a =
và
1
27
b =
. Tính
4
3
3
4
Aa b
−
−
= +
Câu 4: Giá trị của
2
1,25
3
11
27 16
A
−−
= +
bằng:
Câu 5: Giá trị của
42 54
43 5 4
3 .3 2 .2
2 .2 2.3 .3
A
−−
−
+
=
−
bằng:
Câu 6: Giá trị của
( )
34
3
52
01
32
11
3. 2
34
31
5 .25
2 25
A
−
−
−
−
+
=
+
bằng:
Câu 7: Cho
44 7
xx−
+=
. Biểu thức
52 2
8 4.2 4.2
xx
xx
P
−
−
++
=
−−
có giá trị bằng
Câu 8: Cho
a
là một số thực dương. Giá trị của biểu thức
(
)
4
2
a
a
P =
bằng
Câu 9: Cho
9 9 23
xx−
+=
. Khi đó biểu thức
53 3
13 3
xx
xx
a
A
b
−
−
++
= =
−−
với
a
b
là phân số tối giản và
,ab∈
.
Tích
.ab
bằng
Câu 10: Biết
4 4 14
xx−
+=
, tính giá trị của biểu thức
22
xx
P
−
= +
.
Câu 11: Cho
44 7
xx−
+=
. Khi đó biểu thức
11
52 2
32 2
xx
xx
a
P
b
−
+−
−−
= =
++
với
a
b
tối giản và
,ab
+
∈∈
. Tính
tổng
ab+
có giá trị bằng
DẠNG 2: BIẾN ĐỔI, RÚT GỌN, BIỂU DIỄN CÁC BIỂU THỨC
Câu 12: Rút gọn biểu thức với .
Câu 13: Đơn giản biểu thức
21
2
1
.Pa
a
−
=
với
0a >
, được kết quả là
Câu 14: Rút gọn biểu thức
7
3
3
:Qa a=
với
0a >
Câu 15: Rút gọn biểu thức
1
6
3
4
xx
P
x
, với
0x
.
Câu 16: Rút gọn biểu thức
1
6
3
., 0A x xx= >
ta được
Câu 17: Cho
a
là một số thực dương tùy ý. Viết
2
3
.aa
dưới dạng lũy thừa của
a
với số mũ hữu tỉ.
2
6
5
.Px x=
0x >
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 5
Sưu tầm và biên soạn
Câu 18: Cho
a
là một số thực dương. Viết biểu thức
3
3
2
5
.Pa a=
dưới dạng lũy thừa với số mũ hữu tỉ.
Câu 19: Viết biểu thức
3
4
.P xx=
(
0x >
) dưới dạng luỹ thừa với số mũ hữu tỷ.
Câu 20: Rút gọn biểu thức
3
P aaa
=
,
( )
0a >
ta được kết quả là
Câu 21: Rút gọn biểu thức
1
6
3
5
3
.
Px x=
với
0x
>
.
Câu 22: Cho
44 7
xx
−
+=
. Biểu thức
52 2
8 4.2 4.2
xx
xx
P
−
−
++
=
−−
có giá trị bằng
DẠNG 3: BÀI TOÁN LÃI SUẤT KÉP – DÂN SỐ
Câu 23: Một người gửi 100 triệu đồng vào ngân hàng với lãi suất 0,4% / tháng. Biết rằng nếu không rút
tiền ta khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được lập vào vốn ban đầu để tính lãi
cho tháng tiếp theo. Hỏi sau 6 tháng, người đó được lĩnh số tiền bao nhiêu, nếu trong khoảng thời
gian này người đó không rút tiền ra và lãi xuất không thay đổi?
Câu 24: Một người gửi số tiền
300
triệu đồng vào một ngân hàng với lãi suất kép
6%
một năm. Biết rằng
nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi suất sẽ được nhập vào vốn
ban đầu. Hỏi sau 3 năm không rút tiền gốc và lãi, số tiền trong ngân hàng của người đó là bao
nhiêu?
Câu 25: Một học sinh A khi đủ 18 tuổi được cha mẹ cho
200000000
VNĐ. Số tiền này được bảo quản
trong ngân hàng MSB với kì hạn thanh toán 1 năm và học sinh A chỉ nhận được số tiền này khi
học xong 4 năm đại học. Biết rằng khi đủ 22 tuổi, số tiền mà học sinh A được nhận sẽ là
243 101 250
VNĐ. Vậy lãi suất kì hạn một năm của ngân hàng MSB là bao nhiêu?
Câu 26: Một người gửi
50
triệu đồng vào ngân hàng theo thể thức lãi kép với lãi suất
5,5% /
năm, kì hạn
1
năm. Hỏi sau
4
năm, người đó rút cả vốn lẫn lãi được số tiền bao nhiêu?
Câu 27: Ông A gửi 200 triệu vào một ngân hàng theo hình thức lãi kép, với lãi suất là 6,5% một năm và
lãi suất không đổi trong suốt thời gian gửi. Sau 6 năm, số tiền lãi của ông bằng bao nhiêu?
Câu 28: Một học sinh A khi đủ 18 tuổi được cha mẹ cho
200000000
VNĐ. Số tiền này được bảo quản
trong ngân hàng MSB với kì hạn thanh toán 1 năm và học sinh A chỉ nhận được số tiền này khi
học xong 4 năm đại học. Biết rằng khi đủ 22 tuổi, số tiền mà học sinh A được nhận sẽ là
243 101 250
VNĐ. Vậy lãi suất kì hạn một năm của ngân hàng MSB là bao nhiêu?
Câu 29: Một người gửi
200
vào ngân hàng với lãi suất
0, 2% /
tháng. Biết rằng nếu không rút tiền khỏi
ngân hàng thì cứ sau mỗi tháng số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho tháng
tiếp theo. Hỏi sau đúng
10
tháng người đó được lĩnh số tiền bao nhiêu?
Câu 30: Ông Đại mới xin được việc làm nên gửi tiết kiệm vào ngân hàng với hình thức cứ mỗi đầu tháng
đóng vào 5 triệu đồng với lãi suất 0,33%/ tháng. Tính số tiền mà ông Đại thu được từ ngân hàng
sau 5 năm.
Câu 31: Ông Bình vay vốn ngân hàng với số tiền
100000000
đồng. Ông dự định sau đúng
5
năm thì trả
hết nợ theo hình thức: sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ, hai lần hoàn nợ
liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là như nhau. Hỏi theo cách đó, số
tiền
a
mà ông sẽ phải trả cho ngân hàng trong mỗi lần hoàn nợ là bao nhiêu? Biết lãi suất hàng
tháng là
1, 2%
và không thay đổi trong thời gian ông hoàn nợ.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 6
Sưu tầm và biên soạn
Câu 32: Lãi suất cho vay tại PVcomBank trong tháng 5/2022 rất ưu đãi, ở mức 5%/năm, được áp dụng
trong 6 tháng đầu, từ tháng thứ 7 trở đi ấn định mức lãi 12%/năm. Tại ngân hàng này, thời hạn
cho vay mua nhà tối đa là 20 năm, mức vay tối đa 85% giá trị tài sản đảm bảo. Một người có khả
năng trả cố định hằng tháng là 15 triệu. Giả sử người đó có thể mượn người thân
15%
giá trị
căn nhà, nếu được sử dụng gói vay ở trên với thời hạn tối đa và mức vay tối đa thì có thể mua
được căn nhà có giá trị tối đa khoảng
Câu 33: Số người trong cộng đồng sinh viên đã nghe một tin đồn nào đó là
(
)
0,15
1e
d
NP
−
= −
trong đó
P
là tổng số sinh viên của cộng đồng và
d
là số ngày trôi qua kể từ khi tin đồn bắt đầu. Trong một
cộng đồng 1000 sinh viên, cần bao nhiêu ngày để 450 sinh viên nghe được tin đồn?

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 1
Sưu tầm và biên soạn
BÀI 1: PHÉP TÍNH LŨY THỪA
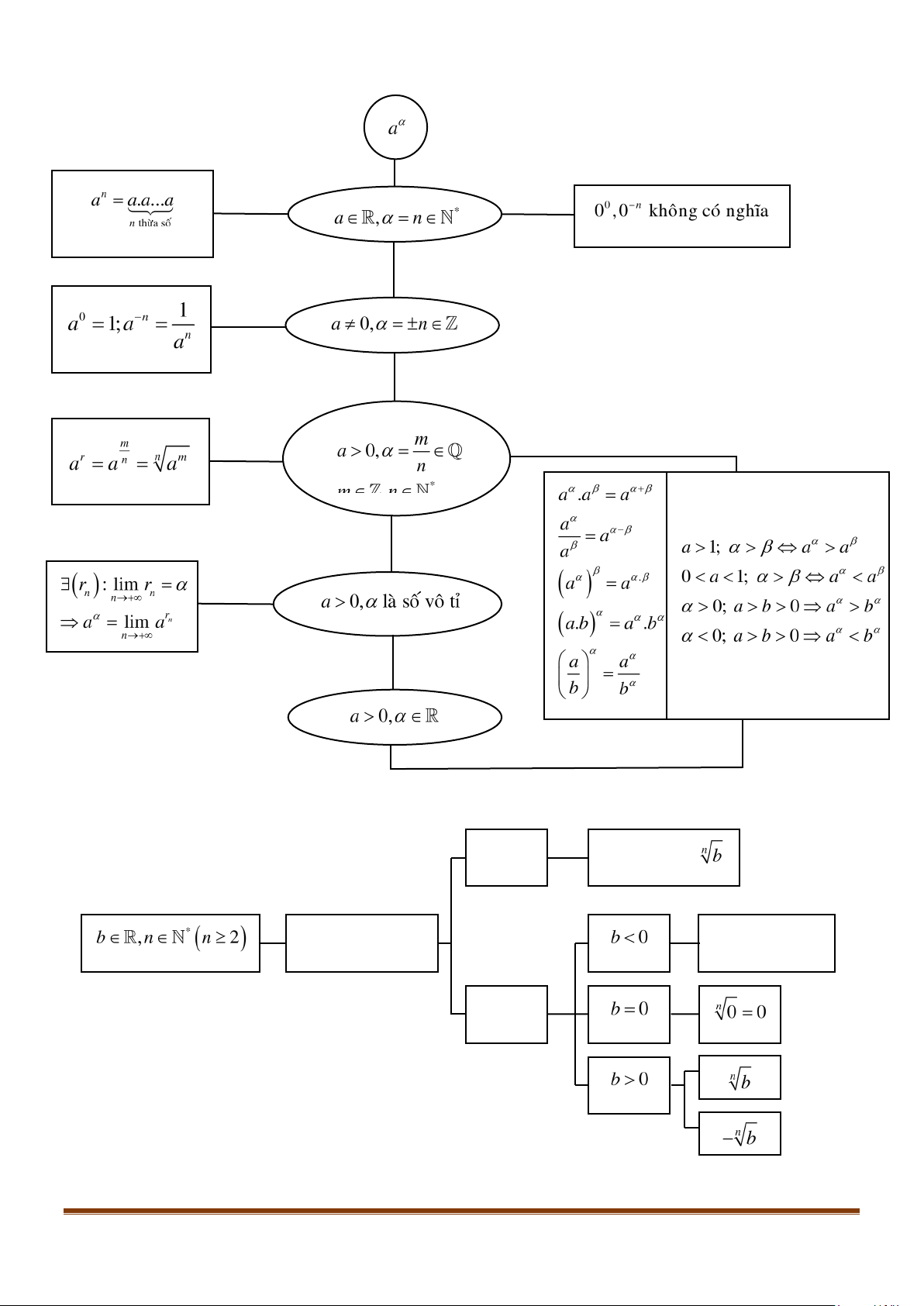
1. Lũy thừa với số mũ nguyên
Cho
n
là một số nguyên dương. Ta định nghĩa:
Với
a
là số thực tùy ý:
. ...
n
a aa a=
(
n
thừa số
a
).
Với
a
là số thực khác
0
:
0
1
1;
n
n
aa
a
−
= =
.
Trong biểu thức
m
a
,
a
gọi là cơ số,
m
gọi là số mũ.
Chú ý:
1)
0
0
và
0
n−
không có nghĩa.
2) Nếu
1a >
thì
mn
aa>
khi và chỉ khi
mn>
.
3) Nếu
01a<<
thì
mn
aa>
khi và chỉ khi
mn<
.
2. Căn bậc
n
a) Định nghĩa: Cho số thực
a
và số nguyên dương
2n ≥
. Số
b
được gọi là căn bậc
n
của số
a
nếu
n
ba=
.
Chú ý:
- Với
n
chẵn, ta xét ba trường hợp sau:
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
LÝ THUYẾT.
I

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 2
Sưu tầm và biên soạn
- Với
n
lẻ,
a
∈
: Có duy nhất một căn bậc
n
của
a
, ký hiệu là
n
a
.
3. Lũy thừa với số mũ hữu tỉ
Cho số thực
0a >
và số hữu tỉ
m
r
n
=
, trong đó
, ,0mn n∈>
. Lũy thừa của
a
với số mũ
r
,
kí hiệu là
r
a
, được xác định bởi
m
n
rm
n
aa a= =
.
4. Lũy thừa với số mũ thực:
Giới hạn của dãy số
( )
n
r
a
gọi là lũy thừa của số thực dương
a
với số mũ
α
. Kí hiệu là:
lim
n
r
aa
α
=
với
lim
n
n
r
α
→+∞
=
5. Tính chất của phép tính lũy thừa
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 3
Sưu tầm và biên soạn
SƠ ĐỒ HỆ THỐNG HÓA LŨY THỪA
Căn bậc n của b
n lẻ
n chẵn
Có duy nhất
Không tồn tại
Định nghĩa
Tính chất

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 4
Sưu tầm và biên soạn
Dạng 1: Tính giá trị của biểu thức
Câu 1: Tính giá trị của biểu thức
5
5
4. 8
P = −
Lời giải
Ta có
( )
5
5
5
4. 8 32 2P
=− =−=−
.
Câu 2: Tính giá trị của
1
3
27
bằng
Lời giải
Ta có
3
3
1
27 3
27 = =
.
Câu 3: Cho
1
256
a =
và
1
27
b =
. Tính
4
3
3
4
Aa b
−
−
= +
Lời giải
Thay
1
256
a
=
,
1
27
b =
vào
4
3
3
4
Aa b
−
−
= +
ta được
( ) ( )
34
4
3
34
43
4 3 34
3
4
43
11
4 3 4 3 145
256 27
Aa b
−−
−
−
−−
−−
= + = + = + =+=
.
Câu 4: Giá trị của
2
1,25
3
11
27 16
A
−−
= +
bằng:
Lời giải
2
1,25
2
5
3
3 34
2 5 6 20 2 5
4
3
4
11
27 16 27 16 3 2 3 2 41
27 16
A
−−
= + = + = + = + =+=
Câu 5: Giá trị của
42 54
43 5 4
3 .3 2 .2
2 .2 2.3 .3
A
−−
−
+
=
−
bằng:
Lời giải
42 54 2
43 5 4 7
3 .3 2 .2 3 2 11
2 .2 2.3 .3 2 2.3 122
A
−−
−
++
= = =
−−
Câu 6: Giá trị của
( )
34
3
52
01
32
11
3. 2
34
31
5 .25
2 25
A
−
−
−
−
+
=
+
bằng:
Lời giải
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 5
Sưu tầm và biên soạn
( )
34
3
52
22
01
2
32
11
3. 2
3 2 13
34
5 5 30
31
5 .25
2 25
A
−
−
−
−
+
+
= = =
+
+
Câu 7: Cho
44 7
xx−
+=
. Biểu thức
52 2
8 4.2 4.2
xx
xx
P
−
−
++
=
−−
có giá trị bằng
Lời giải
(
)
2
44 7 22 9 22 3.
xx xx xx
−− −
+=⇔+ =⇔+=
Suy ra
52 2 53
2.
8 4.2 4.2 8 12
xx
xx
P
−
−
++ +
= = = −
−− −
.
Câu 8: Cho
a
là một số thực dương. Giá trị của biểu thức
(
)
4
2
a
a
P
=
bằng
Lời giải
Ta có
(
)
4
.
2
4
4
2
2
2 2 2 24
a
a
a
a
a
a
P
= = = = =
.
Câu 9: Cho
9 9 23
xx−
+=
. Khi đó biểu thức
53 3
13 3
xx
xx
a
A
b
−
−
++
= =
−−
với
a
b
là phân số tối giản và
,ab∈
.
Tích
.ab
bằng
Lời giải
Ta có:
( )
2
9 9 23 3 3 25
xx xx−−
+=⇔+ =
33 5
xx−
⇔+ =
vì
3 3 0,
xx
x
−
+ > ∀∈
⇒
53 3 55 5
13 3 15 2
xx
xx
A
−
−
++ + −
= = =
−− −
.
Vậy
. 10ab= −
.
Câu 10: Biết
4 4 14
xx−
+=
, tính giá trị của biểu thức
22
xx
P
−
= +
.
Lời giải
Ta có
4 4 14
xx−
+=
( ) ( )
22
2 2 2 16
xx−
⇔ + +=
( )
2
2 2 16
xx−
⇔+ =
22 4
22 4
xx
xx
−
−
+=
⇔
+=−
22 4
xx−
⇔+ =
.
Vậy
4P =
.
Câu 11: Cho
44 7
xx−
+=
. Khi đó biểu thức
11
52 2
32 2
xx
xx
a
P
b
−
+−
−−
= =
++
với
a
b
tối giản và
,ab
+
∈∈
. Tính
tổng
ab+
có giá trị bằng
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 6
Sưu tầm và biên soạn
Ta có:
( )
2
2 2 4 4 2.2 .2
xx xx xx− −−
+ =++
72= +
9=
. Suy ra:
22 3
xx−
+=
.
( )
( )
11
522
52 2
32 2
3 22 2
xx
xx
xx
xx
P
−
−
+−
−
−+
−−
= =
++
++
53
3 2.3
−
=
+
2
9
=
Suy ra:
2a =
,
9 11b ab=⇒+=
.
DẠNG 2: Biến đổi, rút gọn, biểu diễn các biểu thức
Câu 12: Rút gọn biểu thức với .
Lời giải
.
Câu 13: Đơn giản biểu thức
21
2
1
.Pa
a
−
=
với
0a >
, được kết quả là
Lời giải
Ta có:
( )
21
21
2 2 1 2 21
2 21 1
1
.. .Pa a a aa a a a
a
−
−
− −+ −
+
= = = = =
=
.
Câu 14: Rút gọn biểu thức
7
3
3
:Qa a=
với
0a >
Lời giải
Ta có:
7 7 1 71
2
3
3 3 3 33
::Qa aaa a a
−
= = = =
.
Câu 15: Rút gọn biểu thức
1
6
3
4
xx
P
x
, với
0x
.
Lời giải
Ta có
1 11
111 1
6
3 36
4
364 4
1
4
4
.x x xx
P x xx
x
x
.
Câu 16: Rút gọn biểu thức
1
6
3
., 0A x xx= >
ta được
Lời giải
Ta có:
1
1
6
3
2
.Ax x x x= = =
.
Câu 17: Cho
a
là một số thực dương tùy ý. Viết
2
3
.aa
dưới dạng lũy thừa của
a
với số mũ hữu tỉ.
Lời giải
Ta có:
2 2 21 7
1
3 3 32 6
2
..a a aa a a
+
= = =
.
Câu 18: Cho
a
là một số thực dương. Viết biểu thức
3
3
2
5
.Pa a=
dưới dạng lũy thừa với số mũ hữu tỉ.
2
6
5
.Px x=
0x >
2 2 1 2 1 17
6
5 5 6 5
6 30
..P x x xx x x
+
= = = =

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 7
Sưu tầm và biên soạn
Lời giải
Ta có
3 3 2 3 2 19
3
2
5 5 3 5 3 15
..
P a a aa a a
+
= = = =
.
Câu 19: Viết biểu thức
3
4
.
P xx=
(
0x >
) dưới dạng luỹ thừa với số mũ hữu tỷ.
Lời giải
1
15 5
3
3
3
4
4 4 12
..P x x xx x x
= = = =
.
Câu 20: Rút gọn biểu thức
3
P aaa=
,
( )
0a >
ta được kết quả là
Lời giải
Ta có
3
P aaa=
1 11 5
1
1
6 26 3
2
..aa a a a
++
= = =
.
Câu 21: Rút gọn biểu thức
1
6
3
5
3
.Px x=
với
0x >
.
Lời giải
Ta có
1 5 1 5 11
3 18 3 18 18
.
P xx x x
.
Câu 22: Cho
44 7
xx−
+=
. Biểu thức
52 2
8 4.2 4.2
xx
xx
P
−
−
++
=
−−
có giá trị bằng
Lời giải
Có
( ) ( )
2
44 7 22 22.2 7
xx xx xx− −−
+=⇔+ − =
( )
2
2 2 27
xx−
⇔ + −=
( )
2
22 9
xx−
⇔+ =
22 3
xx
−
⇔+ =
.
Khi đó:
( )
( )
522
52 2 53
2
8 4.2 4.2 8 4.3
8 4. 2 2
xx
xx
xx
xx
P
−
−
−
−
++
++ +
= = = = −
−− −
−+
.
DẠNG 3: BÀI TOÁN LÃI SUẤT KÉP – DÂN SỐ
Câu 23: Một người gửi 100 triệu đồng vào ngân hàng với lãi suất 0,4% / tháng. Biết rằng nếu không rút
tiền ta khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được lập vào vốn ban đầu để tính lãi
cho tháng tiếp theo. Hỏi sau 6 tháng, người đó được lĩnh số tiền bao nhiêu, nếu trong khoảng thời
gian này người đó không rút tiền ra và lãi xuất không thay đổi?
Lời giải
Áp dụng công thức lãi kép ta có sau đúng 6 tháng, người đó lĩnh được số tiền:
Ta có:
6
0
0, 4
(1 ) 100.000.000 1 102.424.128
100
n
n
AA r
= += + =
Câu 24: Một người gửi số tiền
300
triệu đồng vào một ngân hàng với lãi suất kép
6%
một năm. Biết rằng
nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi suất sẽ được nhập vào vốn
ban đầu. Hỏi sau 3 năm không rút tiền gốc và lãi, số tiền trong ngân hàng của người đó là bao

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 8
Sưu tầm và biên soạn
nhiêu?
Lời giải
Áp dụng công thức tính lãi suất theo hình thức lãi kép:
(
)
1
n
PA r
= +
.
Trong đó:
P
là số tiền gồm vốn lẫn lãi tại thời điểm
n
tính từ thời điểm gửi;
A
là số tiền gửi vào
ban đầu và
(
)
%
r
là lãi suất.
Với
300.000.000
3
6%
A
n
r
=
=
=
, suy ra
( )
3
300.000.000 1 6% 357.304.800 357.305.000P = += ≈
.
Câu 25: Một học sinh A khi đủ 18 tuổi được cha mẹ cho
200000000
VNĐ. Số tiền này được bảo quản
trong ngân hàng MSB với kì hạn thanh toán 1 năm và học sinh A chỉ nhận được số tiền này khi
học xong 4 năm đại học. Biết rằng khi đủ 22 tuổi, số tiền mà học sinh A được nhận sẽ là
243 101 250
VNĐ. Vậy lãi suất kì hạn một năm của ngân hàng MSB là bao nhiêu?
Lời giải
Gọi lãi suất kỳ hạn một năm của ngân hàng MSB là r. Áp dụng công thức lãi suất kép
(
)
1
n
Pa r
= +
trong đó ta có :
(
) (
)
44
0
2
0
43101250 200
2
0000
43101250
1
200 0
01
0
0
00
r
r⇔== +
+
44
243101250 243101250
1 1 0,05
200000000 200000000
rr r⇔+= ⇔= −⇔=
.
Câu 26: Một người gửi
50
triệu đồng vào ngân hàng theo thể thức lãi kép với lãi suất
5,5% /
năm, kì hạn
1
năm. Hỏi sau
4
năm, người đó rút cả vốn lẫn lãi được số tiền bao nhiêu?
Lời giải
Gọi số tiền ban đầu
A
. Lãi suất tính theo năm là
r
.
Số tiền cả vốn lẫn lãi sau
n
năm được tính theo công thức:
( )
1
n
n
AA r
= +
.
Thay số với
50; 5,5%, 4Ar n= = =
ta được số tiền là:
4
4
5,5
50. 1 61,94
100
A
=+=
Câu 27: Ông A gửi 200 triệu vào một ngân hàng theo hình thức lãi kép, với lãi suất là 6,5% một năm và
lãi suất không đổi trong suốt thời gian gửi. Sau 6 năm, số tiền lãi của ông bằng bao nhiêu?
Lời giải
Ta có
( ) ( )
6
1 200. 1 6,5% 292
n
TA r
= += +
triệu.
Vậy số tiền lãi là
292 200 92−=
triệu.
Câu 28: Một học sinh A khi đủ 18 tuổi được cha mẹ cho
200000000
VNĐ. Số tiền này được bảo quản
trong ngân hàng MSB với kì hạn thanh toán 1 năm và học sinh A chỉ nhận được số tiền này khi
học xong 4 năm đại học. Biết rằng khi đủ 22 tuổi, số tiền mà học sinh A được nhận sẽ là
243 101 250
VNĐ. Vậy lãi suất kì hạn một năm của ngân hàng MSB là bao nhiêu?

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 9
Sưu tầm và biên soạn
Lời giải
Gọi lãi suất kỳ hạn một năm của ngân hàng MSB là r. Áp dụng công thức lãi suất kép
(
)
1
n
Pa r
= +
trong đó ta có :
( )
( )
44
0
2
0
43101250 200
2
0000
43101250
1
200 0
01
0
0
00
r r⇔== + +
44
243101250 243101250
1 1 0,05
200000000 200000000
rr r
⇔+= ⇔= −⇔=
.
Câu 29: Một người gửi
200
vào ngân hàng với lãi suất
0, 2% /
tháng. Biết rằng nếu không rút tiền khỏi
ngân hàng thì cứ sau mỗi tháng số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho tháng
tiếp theo. Hỏi sau đúng
10
tháng người đó được lĩnh số tiền bao nhiêu?
Lời giải
Theo công thức lãi kép ta có số tiền cả lãi và vốn sau 10 tháng là:
( ) ( )
10
1 200 1 0.2% 204,036
n
TX r= += + ≈
triệu đồng.
Câu 30: Ông Đại mới xin được việc làm nên gửi tiết kiệm vào ngân hàng với hình thức cứ mỗi đầu tháng
đóng vào 5 triệu đồng với lãi suất 0,33%/ tháng. Tính số tiền mà ông Đại thu được từ ngân hàng
sau 5 năm.
Lời giải
Với
a
là số tiền ông Đại đóng vào hằng tháng,
%r
lãi suất ông Đại gửi tiết kiệm hằng tháng.
Gọi
n
P
là số tiền mà ông Đại thu được sau
n
tháng
( )
1≥n
.
Suy ra
( )
1
.1 %= +Pa r
.
(
)( )
( ) ( )
2
21
1% .1% .1%
=+ + =+ ++PPa r ar ar
( )( ) (
) (
) ( )
32
32
1% .1% .1% .1%=+ + =+ ++ ++PPa r ar ar ar
……………………………………………………………………….
…………………………………………………………………………
…………………………………………………………………………
( )( )
( ) ( ) ( )
1
1
1% .1% .1% ....1%
−
−
= + + =+ ++ +++
nn
nn
PPa r ar ar ar
Xét cấp số nhân có số hạng đầu là
( )
1
.1 %= +ua r
và công bội
1%= +qr
thì
12 1
1
...
1
−
= + ++ =
−
n
nn
q
Puu u u
q
.
Vậy số tiền ông Đại nhận được từ ngân hàng sau 5 năm là

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 10
Sưu tầm và biên soạn
( )
( )
60
60
60 1
1 1,0033
1
5. 1,0033 . 332
1 0,0033
−
−
= = ≈
−
q
Pu
q
triệu đồng.
Câu 31: Ông Bình vay vốn ngân hàng với số tiền
100000000
đồng. Ông dự định sau đúng
5
năm thì trả
hết nợ theo hình thức: sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ, hai lần hoàn nợ
liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là như nhau. Hỏi theo cách đó, số
tiền
a
mà ông sẽ phải trả cho ngân hàng trong mỗi lần hoàn nợ là bao nhiêu? Biết lãi suất hàng
tháng là
1, 2%
và không thay đổi trong thời gian ông hoàn nợ.
Lời giải
Gọi
, , ,
n
mrT a
lần lượt là số tiền vay ngân hàng, lãi suất hàng tháng, tổng số tiền vay còn lại
sau
n
tháng, số tiền trả đều đặn mỗi tháng.
● Sau khi hết tháng thứ nhất
( )
1n =
thì còn lại:
( )
1
1.T mr a= +−
● Sau khi hết tháng thứ hai
( )
2n =
thì còn lại:
( ) ( )
2
11Tmrara= +− +−
( )
( ) ( ) ( ) ( ) ( )
2 2 22
1 1 1 2 1 1 1.
a
mr ar a mr ar mr r
r
= +− +−= +− += +− +−
● Sau khi hết tháng thứ ba
( )
3n =
thì còn:
( ) (
) ( )
22
3
1 11 1
a
T mr r r a
r
= +− +− +−
( )
( )
33
1 1 1.
a
mr r
r
= +− +−
● Sau khi hết tháng thứ
n
thì còn lại:
( ) ( )
1 11
nn
n
a
T mr r
r
= +− +−
Áp dụng công thức trên, ta có
( )
( )
60
5
60
1, 2
12.10 1
1
100
0
11
1, 2
11
100
n
n
n
mr r
Ta
r
+
+
=⇔= =
+−
+−
.
Câu 32: Lãi suất cho vay tại PVcomBank trong tháng 5/2022 rất ưu đãi, ở mức 5%/năm, được áp dụng
trong 6 tháng đầu, từ tháng thứ 7 trở đi ấn định mức lãi 12%/năm. Tại ngân hàng này, thời hạn
cho vay mua nhà tối đa là 20 năm, mức vay tối đa 85% giá trị tài sản đảm bảo. Một người có khả
năng trả cố định hằng tháng là 15 triệu. Giả sử người đó có thể mượn người thân
15%
giá trị
căn nhà, nếu được sử dụng gói vay ở trên với thời hạn tối đa và mức vay tối đa thì có thể mua
được căn nhà có giá trị tối đa khoảng
Lời giải
Gọi
A
là số tiền tối đa người này có thể vay,
i
A
là số tiền nợ sau tháng thứ
i
.
1
5%
12
r =
là lãi suất/1 tháng, trong
6
tháng đầu

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 11
Sưu tầm và biên soạn
2
12%
1%
12
r
= =
là lãi suất/1 tháng, từ tháng thứ 7 trở đi.
Sau 1 tháng, số tiền gốc và lãi là
( )
1Ar+
, người đó trả
15
triệu nên còn nợ:
( )
1
1 15AA r= +−
Sau tháng thứ 2:
(
)
(
)
(
)
( )
(
)
2
2
21 1 1 1 1 1
1
15
1 15 1 15 1 15 1 (1 ) 1
AA r Ar r Ar r
r
= +−= +− +−= + − + −
Sau tháng thứ 3:
( )
3
3
31 1
1
15
1 (1 ) 1
AA r r
r
= +− +−
…….
Sau tháng thứ 6:
( )
6
6
61 1
1
15
1 (1 ) 1AA r r
r
= +− +−
.
Sau tháng thứ 7:
( )
76 2
1 15AA r= +−
Sau tháng thứ 8:
( )
2
2
86 2 2
2
15
1 (1 ) 1AA r r
r
= +− +−
………
Sau tháng thứ
240
:
( )
234
234
240 6 2 2
2
15
1 (1 ) 1AAr r
r
=+− +−
Vì phải trả hết nợ sau
20
năm nên
(
)
234
2
240 6
234
22
15 (1 ) 1
0 1353,819328
1
r
AA
rr
+−
=⇔= ≈
+
(
)
6
61
1
6
1
15
(1 ) 1
1409,163992
1
Ar
r
A
r
+ +−
⇒= ≈
+
.
Vậy người này có thể mua được căn nhà có giá trị tối đa là
1657,83999
85%
A
≈
triệu đồng
1,65784≈
tỷ đồng.dd
Câu 33: Số người trong cộng đồng sinh viên đã nghe một tin đồn nào đó là
( )
0,15
1e
d
NP
−
= −
trong đó
P
là tổng số sinh viên của cộng đồng và
d
là số ngày trôi qua kể từ khi tin đồn bắt đầu. Trong một
cộng đồng 1000 sinh viên, cần bao nhiêu ngày để 450 sinh viên nghe được tin đồn?
Lời giải
Ta có:

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 12
Sưu tầm và biên soạn
( ) (
)
0,15 0,15
0,15
1 e 450 1000. 1
11
ln 3, 98
20
dd
d
NP e
ed
−−
−
=− ⇔= −
⇔=⇔
Vậy cần 4 ngày để 450 sinh viên nghe được tin đồn.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 7
Sưu tầm và biên soạn
BÀI 1: PHÉP TÍNH LŨY THỪA
DẠNG 1. RÚT GỌN BIỂU THỨC LŨY THỪA
Câu 1: Cho
0, ,
a mn
>∈
. Khẳng định nào sau đây đúng?
A.
.
m n mn
aaa
+
+=
B.
..
m n mn
aa a
−
=
C.
( ) ( ).
mn nm
aa=
D.
.
m
nm
n
a
a
a
−
=
Câu 2: Với
a
là số thực dương tùy ý,
1
4
2
.
aa
bằng
A.
8
a
. B.
2
a
. C.
7
2
a
. D.
9
2
a
.
Câu 3: Cho số thực dương
a
và số nguyên dương
n
tùy ý. Mệnh đề nào dưới đây đúng?
A.
2+
=
nn
aa
. B.
2
=
nn
aa
. C.
2
=
n
n
aa
. D.
2
=
n
n
aa
.
Câu 4: Cho
a
là số thực dương. Biểu thức
3
32
.aa
được viết dưới dạng lũy thừa với số mũ hữu tỉ là
A.
11
3
a
B.
2
a
C.
5
3
a
D.
8
3
a
Câu 5: Viết biểu thức
( )
3
4
., 0P xx x= >
dưới dạng lũy thừa với số mũ hữu tỷ
A.
5
4
Px=
. B.
1
12
Px=
. C.
1
7
Px=
. D.
5
12
Px=
.
Câu 6: Cho
a
là một số thực dương. Giá trị của biểu thức
(
)
4
2
a
a
P =
bằng
A.
4
. B.
2
. C.
8
. D.
1
.
Câu 7: Với
a
là số thực dương, biểu thức
1
3
.Pa a
=
bằng
A.
1
6
a
. B.
2
5
a
. C.
5
6
a
. D.
4
3
a
.
Câu 8: Cho
1a ≠
là số thực dương. Viết và rút gọn biểu thức
3
2022
2022
aa⋅
dưới dạng lũy thừa với số mũ
hữu tỉ. Tìm số mũ của biểu thức rút gọn đó.
A.
1
1011
. B.
2
3
2022
. C.
2
1011
. D.
3
1011
.
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 8
Sưu tầm và biên soạn
Câu 9: Rút gọn biểu thức với .
A. . B. . C. . D. .
Câu 10: Đơn giản biểu thức
21
2
1
.Pa
a
−
=
với
0a >
, được kết quả là
A.
2
a
.
B.
221
a
−
.
C.
12
a
−
. D.
a
.
Câu 11: Rút gọn biểu thức
7
3
3
:Qa a=
với
0a >
A.
4
3
Qa
−
=
. B.
2
Qa=
. C.
8
3
Qa=
. D.
4
Qa=
.
Câu 12: Với
a
là số thực dương tùy ý,
5
3
a
bằng
A.
5
3
a
. B.
3
5
a
. C.
8
a
. D.
2
a
.
Câu 13: Với
a
là số thực dương tùy ý khi đó
2
5
.aa
bằng
A.
11
10
a
. B.
1
10
a
. C.
22
5
a
. D.
10
11
a
.
Câu 14: Với
a
là số thực dương tuỳ ý,
3
a
bằng
A.
1
6
a
. B.
2
3
a
. C.
6
a
. D.
3
2
a
.
Câu 15: Rút gọn biểu thức
1
6
3
4
xx
P
x
, với
0x
.
A.
4
Px
. B.
1
6
Px
. C.
Px
. D.
1
6
Px
.
Câu 16: Rút gọn biểu thức
1
6
3
., 0A x xx= >
ta được
A.
Ax=
. B.
2
9
Ax=
. C.
2
Ax=
. D.
81
Ax=
.
Câu 17: Với
0x
thì
2
xxx
bằng
A.
x
. B.
2
x
. C.
x
. D.
4
x
.
Câu 18: Với
a
là số thực dương tùy ý,
3
1
a
bằng?
A.
3
a
−
. B.
3
2
a
. C.
1
6
a
. D.
3
2
a
−
.
Câu 19: Cho
0a >
, khi đó
4
a
bằng
A.
4
1
a
. B.
4
a
. C.
4
1
a
. D.
4
a
−
.
Câu 20: Với
a
là số thực dương tuỳ ý,
3
4
aa
bằng
A.
17
6
a
. B.
13
8
a
. C.
13
6
a
. D.
17
4
a
.
2
6
5
.Px x=
0x >
1
15
Px=
17
15
Px=
17
30
Px=
Px=

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 9
Sưu tầm và biên soạn
Câu 21: Cho số thực
a
dương tùy ý. Đặt
5
3
4
p
a aa a⋅=
. Khẳng định đúng là:
A.
19
12
p =
. B.
23
12
p =
. C.
13
12
p =
. D.
23
24
p
=
.
Câu 22: Cho
x
là số thực dương. Biết
3
3
.
b
a
x xxx x
=
với
a
,
b
là các số tự nhiên và
a
b
là phân số
tối giản. Tính
ab
+
.
A.
16
. B.
15
. C.
14
. D.
17
.
Câu 23: Cho
x
là số thực dương. Biểu thức
2
4
3
xx
được viết dưới dạng lũy thừa với số mũ hữu tỉ là
A.
12
7
x
. B.
5
6
x
. C.
7
12
x
. D.
6
5
x
.
Câu 24: Cho hai số thực dương
,ab
. Rút gọn biểu thức
11
33
44
12 12
a bb a
A
ab
+
=
+
ta thu được
.
mn
A ab=
. Tích
của
.mn
là
A.
1
9
. B.
1
16
. C.
1
18
. D.
1
8
.
Câu 25: Biết biểu thức
( )
6
32
3
0
P xxxx= >
được viết dưới dạng lũy thừa với số mũ hữu tỷ là
x
α
.
Khi đó, giá trị của
α
bằng
A.
37
15
. B.
23
36
. C.
23
30
. D.
53
30
.
Câu 26: Cho hàm số
( )
(
)
(
)
2
3
2
3
3
1
88
31
8
aa a
fa
aa a
−
−
−
=
−
với
0, 1aa>≠
. Giá trị của
( )
2022
2021Mf=
là
A.
1011
2021
B.
1011
2021 1+
C.
1011
2021 1−+
D.
1011
2021 1−−
Câu 27: Cho
a
là số thực dương. Rút gọn biểu thức
3
A aa aa=
về dạng
m
n
a
trong đó
m
n
là phân
số tối giản và
,mn
∗
∈
. Tính giá trị của biểu thức
22
Tm n
= +
.
A.
2425
. B.
539
. C.
593
. D.
1369
.
Câu 28: Rút gọn biểu thức
7
3
5
3
7
42
.
.
aa
A
aa
−
=
với
0a >
ta được kết quả
m
n
Aa=
, trong đó
*
,mn∈
và
m
n
là
phân số tối giản. Khẳng định nào sau đây đúng?
A.
2
3 22mn−=
. B.
22
43mn+=
. C.
2
2 15mn+=
. D.
22
25mn+=
.
Câu 29: Biết biểu thức
(
)
6
3
32
0P xxxx= >
được viết dưới dạng lũy thừa với số mũ hữu tỉ là
x
α
. Khi
đó, giá trị của
α
bằng
A.
37
15
. B.
23
36
. C.
23
30
. D.
53
30
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 10
Sưu tầm và biên soạn
Câu 30: Với
α
là số thực bất kì, mệnh đề nào sau đây sai?
A.
( )
10 10
α
α
=
. B.
2
10 10
α
α
=
. C.
( )
(
)
2
10 100
α
α
=
. D.
( )
( )
2
2
10 10
α
α
=
.
Câu 31: Rút gọn biểu thức
=
5
3
3
:Qb b
với
> 0
b
.
A.
−
=
4
3
Qb
B.
=
4
3
Qb
C.
=
5
9
Qb
D.
=
2
Qb
Câu 32: Rút gọn biểu thức
1
6
3
.Px x=
với
0
x >
.
A.
Px=
B.
1
8
Px
=
C.
2
9
Px=
D.
2
Px=
Câu 33: Cho biểu thức
4
3
23
..P xx x=
, với
0x >
. Mệnh đề nào dưới đây đúng?
A.
2
3
Px=
B.
1
2
Px=
C.
13
24
Px=
D.
1
4
Px=
Câu 34: Cho biểu thức
1
1
6
3
2
. .xP xx
=
với
0x >
. Mệnh đề nào dưới đây đúng?
A.
Px=
B.
11
6
Px=
C.
7
6
Px=
D.
5
6
Px=
Câu 35: Rút gọn biểu thức
1
3
6
Px x= ⋅
với
0x >
.
A.
1
8
Px=
B.
Px=
C.
2
9
Px=
D.
2
Px=
Câu 36: Viết biểu thức
3
4
.P xx=
(
0x >
) dưới dạng luỹ thừa với số mũ hữu tỷ.
A.
5
4
Px=
. B.
5
12
Px=
. C.
1
7
Px=
. D.
1
12
Px=
.
Câu 37: Cho biểu thức
6
4
5 3
.. ,P xx x=
với
0x >
. Mệnh đề nào dưới đây đúng?
A.
15
16
Px=
. B.
7
16
Px=
. C.
5
42
Px=
. D.
47
48
Px=
.
Câu 38: Cho biểu thức
4
3
23
..P xx x=
, với
0
x
>
. Mệnh đề nào dưới đây đúng?
A.
2
3
Px=
. B.
1
4
Px=
. C.
13
24
Px=
. D.
1
2
Px=
.
Câu 39: Giả sử
a
là số thực dương, khác
1
. Biểu thức
3
aa
được viết dưới dạng
a
α
. Khi đó
A.
2
3
α
=
. B.
5
3
α
=
. C.
1
6
α
=
. D.
11
6
α
=
.
Câu 40: Biểu thức
3
22K
=
viết dưới dạng lũy thừa với số mũ hữu tỉ là
A.
4
3
2
. B.
5
3
2
. C.
1
3
2
. D.
2
3
2
.
Câu 41: Biểu thức
6
5
3
. . ( 0)xxxx>
viết dưới dạng luỹ thừa với số mũ hữu tỷ là
A.
2
3
x
. B.
5
2
x
. C.
7
3
x
. D.
5
3
x
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 11
Sưu tầm và biên soạn
Câu 42: Cho biểu thức
(
)
71 2 7
22
22
.
aa
P
a
+−
+
−
=
với
0a >
. Rút gọn biểu thức
P
được kết quả là
A.
5
Pa=
. B.
3
Pa=
. C.
Pa=
. D.
4
Pa=
.
Câu 43: Cho a là số thực dương. Viết và rút gọn biểu thức
3
2018
2018
.aa
dưới dạng lũy thừa với số mũ hữu
tỉ. Tìm số mũ của biểu thức rút gọn đó.
A.
2
1009
. B.
1
1009
. C.
3
1009
. D.
2
3
2018
.
Câu 44: Rút gọn biểu thức
31 2 3
22
22
.
aa
P
a
với
0a
.
A.
Pa
. B.
3
Pa
. C.
4
Pa
. D.
5
Pa
.
Câu 45: Biểu thức
3
2
5
P xx x x
α
= =
, giá trị của
α
là
A.
1
2
. B.
5
2
. C.
9
2
. D.
3
2
.
Câu 46: Cho
a
là số thực dương khác
1
. Khi đó
2
4
3
a
bằng
A.
3
2
a
. B.
8
3
a
. C.
3
8
a
. D.
6
a
.
Câu 47: Rút gọn biểu thức
31 2 3
22
22
.aa
P
a
với
0a
A.
Pa=
B.
3
Pa=
C.
4
Pa
=
D.
5
Pa=
Câu 48: Cho biểu thức
3
5
4
.Px x
−
=
,
0x
>
. Khẳng định nào sau đây là đúng?
A.
2
Px
−
=
B.
1
2
Px
−
=
C.
1
2
Px=
D.
2
Px=
Câu 49:
Cho biểu thức
3
3
4
.P xx x=
, với
0.x
>
Mệnh đề nào dưới đây đúng?
A.
1
2
.Px=
B.
7
12
.Px=
C.
5
8
.
Px=
D.
7
24
.Px=
Câu 50: Cho hai số thực dương
,ab
. Rút gọn biểu thức
11
33
66
a bb a
A
ab
+
=
+
ta thu được
.
mn
A ab=
. Tích
của
.
mn
là
A.
1
8
B.
1
21
C.
1
9
D.
1
18
Câu 51: Rút gọn biểu thức
11
3
7
3
7
45
.
.
aa
A
aa
−
=
với
0
a >
ta được kết quả
m
n
Aa=
trong đó
,mn
*
N∈
và
m
n
là
phân số tối giản. Khẳng định nào sau đây đúng?
A.
22
312mn−=
. B.
22
543mn+=
. C.
22
312mn−=−
. D.
22
409.mn+=

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 12
Sưu tầm và biên soạn
Câu 52: Cho
a
là số thực dương. Đơn giản biểu thức
41 2
33 3
13 1
44 4
aa a
P
aa a
.
A.
( )
1P aa= +
. B.
1Pa= −
. C.
Pa=
. D.
1
Pa= +
.
Câu 53: Cho
,
ab
là các số thực dương. Rút gọn
44
33
33
a b ab
P
ab
ta được
A.
P ab
. B.
P ab
. C.
44
P a b ab
. D.
P ab a b
.
Câu 54: Cho biểu thức
5
3
822 2
m
n
=
, trong đó
m
n
là phân số tối giản. Gọi
22
Pm n
= +
. Khẳng định nào
sau đây đúng?
A.
( )
330;340P∈
. B.
( )
350;360P
∈
. C.
( )
260;370P∈
. D.
( )
340;350P∈
.
Câu 55: Cho
0>a
,
0>b
, giá trị của biểu thức
( ) ( )
1
2
2
1
1
2
1
2 . .1
4
−
=+ +−
ab
T a b ab
ba
bằng
A.
1
. B.
1
2
. C.
2
3
. D.
1
3
.
DẠNG 2. TÍNH GIÁ TRỊ BIỂU THỨC
Câu 56: Biểu thức
5
5
4. 8P
= −
có giá trị bằng
A.
42
. B.
2−
. C. 2. D.
42−
.
Câu 57: Giá trị
35
2021. 2021
viết dưới dạng lũy thữa với số mũ hữu tỷ là
A.
2
5
2021
. B.
1
15
2021
. C.
8
15
2021
. D.
1
10
2021
Câu 58: Giá trị của
1
3
27
bằng
A. 6. B. 81. C. 9. D. 3.
Câu 59: Cho
1
256
a =
và
1
27
b =
. Tính
4
3
3
4
Aa b
−
−
= +
A.
23
. B.
89
. C.
145
. D.
26
.
Câu 60: Cho
44 7
xx−
+=
. Biểu thức
52 2
8 4.2 4.2
xx
xx
P
−
−
++
=
−−
có giá trị bằng
A.
3
2
P =
. B.
5
2
P = −
. C.
2P =
. D.
2P = −
.
Câu 61: Cho
9 9 23
xx−
+=
. Khi đó biểu thức
53 3
13 3
xx
xx
a
A
b
−
−
++
= =
−−
với
a
b
là phân số tối giản và
,ab∈
.
Tích
.ab
bằng
A.
10−
. B.
10
. C.
8−
. D.
8
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 13
Sưu tầm và biên soạn
Câu 62: Cho biểu thức
1
2
2
1
1
3. 2 4
2
x
x
x
T
−
−−
=+−
. Khi
23
x
=
thì giá trị của biểu thức
T
là
A.
93
2
. B.
53
2
. C.
33
2
. D.
73
2
.
Câu 63: Biết
4 4 14
xx−
+=
, tính giá trị của biểu thức
22
xx
P
−
= +
.
A.
4
. B.
16
. C.
17
. D.
4
±
.
Câu 64: Cho
44 7
xx
−
+=
. Khi đó biểu thức
11
52 2
32 2
xx
xx
a
P
b
−
+−
−−
= =
++
với
a
b
tối giản và
,ab
+
∈∈
. Tính
tổng
ab+
có giá trị bằng
A.
8
. B.
11
. C.
17
. D.
4
.
Câu 65: Tính giá trị của biểu thức
( ) ( )
2017 2016
7 43 43 7P
=+−
A.
( )
2016
7 43P
= +
B.
1
P
=
C.
7 43P = −
D.
7 43P = +
Câu 66: Cho biểu thức
3
3
222
333
P =
. Mệnh đề nào trong các mệnh đề sau là đúng?
A.
1
8
2
3
P
=
. B.
18
2
3
P
=
. C.
1
18
2
3
P
=
. D.
1
2
2
3
P
=
.
Câu 67: Cho hàm số
( )
(
)
(
)
1
3
4
3
3
1
88
31
8
a aa
fa
aa a
−
−
−
=
−
với
0, 1
aa>≠
. Tính giá trị
( )
2016
2017Mf=
A.
1008
2017 1M
= −
B.
1008
2017 1
M =−−
C.
2016
2017 1M = −
D.
2016
1 2017M
= −
Câu 68: Giá trị của biểu thức
( )
3 1 34
0
32
2 .2 5 .5
10 :10 0,1
P
−−
−−
+
=
−
là
A.
9−
. B.
10−
. C.
10
. D.
9
.
Câu 69: Cho hàm số
( )
(
)
(
)
2
3
2
3
3
1
88
31
8
aa a
fa
aa a
−
−
−
=
−
với
0, 1aa>≠
. Tính giá trị
( )
2018
2017Mf=
.
A.
2018
2017 1.+
B.
1009
2017 1.−−
C.
1009
2017 .
D.
1009
2017 1.+
DẠNG 3. SO SÁNH CÁC BIỂU THỨC CHỨA LŨY THỪA
Câu 70: Nếu
11
3 6
aa>
và
35
bb>
thì
A.
1; 0 1ab< <<
. B.
1; 1ab><
. C.
0 1; 1ab<< <
D.
1; 0 1ab> <<
.
Câu 71: Cho
1a >
. Mệnh đề nào dưới đây đúng?
A.
2016 2017
11
aa
<
. B.
1
3
aa>
. C.
3
5
1
a
a
−
>
. D.
3
2
1
a
a
>
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 14
Sưu tầm và biên soạn
Câu 72: Trong các mệnh đề sau, mệnh đề nào SAI?
A.
( ) ( )
2018 2017
31 31− >−
. B.
+
>
3
21
22
.
C.
( )
( )
2017 2018
21 21− >−
. D.
2019 2018
22
11
22
− <−
.
Câu 73: Khẳng định nào sau đây đúng?
A.
2017 2018
( 5 2) ( 5 2)
−−
+ <+
. B.
2018 2019
( 5 2) ( 5 2)+ >+
.
C.
2018 2019
( 5 2) ( 5 2)− >−
. D.
2018 2019
( 5 2) ( 5 2)− <−
.
Câu 74: Khẳng định nào dưới đây là đúng?
A.
33
35
.
78
>
B.
11
23
ππ
−−
<
. C.
2
2
1
3
5
−
<
. D.
( )
50
100
1
2
4
−
<
.
Câu 75: Trong các khẳng định sau, khẳng định nào sai?
A.
2018 2017
22
11
22
− <−
. B.
( ) ( )
2017 2018
21 21− >−
.
C.
( ) ( )
2018 2017
31 31− >−
. D.
21 3
22
+
>
.
Câu 76: Tìm tập tất cả các giá trị của
a
để
7
52
21
aa>
?
A.
0a >
.
B.
01a
<<
.
C.
1a >
. D.
52
21 7
a<<
.
DẠNG 4. BÀI TOÁN LÃI SUẤT – DÂN SỐ
Câu 77: Anh An gửi số tiền 58 triệu đồng vào một ngân hàng theo hình thức lãi kép và ổn định trong 9
tháng thì lĩnh về được 61758000đ. Hỏi lãi suất ngân hàng hàng tháng là bao nhiêu? Biết rằng lãi
suất không thay đổi trong thời gian gửi.
A.
0,8 %
B.
0,6 %
C.
0,7 %
D.
0,5 %
Câu 78: Ông An gửi tiết kiệm
50
triệu đồng vào ngân hàng với kỳ hạn
3
tháng, lãi suất
8, 4%
một năm
theo hình thức lãi kép. Ông gửi được đúng
3
kỳ hạn thì ngân hàng thay đổi lãi suất, ông gửi tiếp
12
tháng nữa với kỳ hạn như cũ và lãi suất trong thời gian này là
12%
một năm thì ông rút tiền
về. Số tiền ông An nhận được cả gốc lẫn lãi là:
A.
62255910
đồng. B.
59895767
đồng. C.
59993756
đồng. C.
63545193
đồng.
Câu 79: Một học sinh
A
khi
15
tuổi được hưởng tài sản thừa kế
200 000 000
VNĐ. Số tiền này được
bảo quản trong ngân hàng
B
với kì hạn thanh toán
1
năm và học sinh
A
chỉ nhận được số tiền
này khi
18
tuổi. Biết rằng khi
18
tuổi, số tiền mà học sinh
A
được nhận sẽ là
231 525 000
VNĐ. Vậy lãi suất kì hạn một năm của ngân hàng
B
là bao nhiêu?
A.
8% /
năm. B.
7% /
năm. C.
6% /
năm. D.
5% /
năm.
Câu 80: Ông Anh gửi vào ngân hàng
60
triệu đồng theo hình thức lãi kép. Lãi suất ngân hàng là
8%
trên
năm. Sau
5
năm ông An tiếp tục gửi thêm
60
triệu đồng nữa. Hỏi sau
10
năm kể từ lần gửi đầu
tiên ông An đến rút toàn bộ tiền gốc và tiền lãi được là bao nhiêu?.
A.
231,815
. B.
197,201
. C.
217,695
. D.
190,271
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 15
Sưu tầm và biên soạn
Câu 81: Anh Nam gửi 100 triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn là một quý với lãi suất
3% một quý. Sau đúng 6 tháng anh Nam gửi thêm 100 triệu đồng với kì hạn và lãi suất như trước
đó.Hỏi sau 1 năm số tiền anh Nam nhận được là bao nhiêu?.
A.
218,64
triệu đồng. B.
208, 25
triệu đồng. C.
210,45
triệu đồng. D.
209,25
triệu đồng.
Câu 82: Ông tuấn gửi 100 triệu vào ngân hàng với hình thức lãi kép, kỳ hạn 1 năm với lãi suất
8%
. Sau
5 năm ông rút toàn bộ tiền và dùng một nữa để sửa nhà, số tiền còn lại ông tiếp tục gửi ngân hàng
với lãi suất như lần trước. Số tiền lãi ông tuấn nhận được sau 10 năm gửi gần nhất với giá trị nào
dưới đây?
A.
46,933
triệu. B.
34,480
triệu. C.
81,413
triệu. D.
107,946
triệu.
Câu 83: Dân số thế giới được ước tính theo công thức
.
ni
S Ae=
, trong đó
A
là dân số của năm lấy làm
mốc,
S
là dân số sau
n
năm,
i
là tỉ lệ tăng dân số hằng năm. Dân số Việt Nam năm 2019 là
95,5
triệu người, tỉ lệ tăng dân số hằng năm từ 2009 đến nay là
1,14%
. Hỏi dân số Việt Nam
năm 2009 gần với số nào nhất trong các số sau?
A.
94, 4
triệu người. B.
85, 2
triệu người. C.
86, 2
triệu người. D.
83, 9
triệu người.
Câu 84: Để dự báo dân số của một quốc gia, người ta sử dụng công thức
;
nr
S Ae=
trong đó
A
là dân số
của năm lấy làm mốc tính,
S
là dân số sau
n
năm,
r
là tỉ lệ tăng dân số hàng năm. Năm 2017,
dân số Việt nam là
93.671.600
người. Giả sử tỉ lệ tăng dân số hàng năm không đổi là
0,81%,
dự báo dân số Việt nam năm 2035 là bao nhiêu người?
A.
109.256.100
. B.
108.374.700
. C.
107.500.500
. D.
108.311.100
.
Câu 85: COVID19 là một loại bệnh viêm đường hô hấp cấp do chủng mới của virus corona bắt nguồn từ
Trung Quốc gây ra với tốc độ truyền bệnh rất nhanh. Giả sử ban đầu có 1 người bị nhiễm bệnh
và cứ sau 1 ngày sẽ lây sang 4 người khác. Tất cả những người nhiễm bệnh lại tiếp tục lây sang
những người khác với tốc độ như trên. Hỏi sau 7 ngày sẽ có tổng cộng bao nhiêu người nhiễm
bệnh?.
A. người. B. người. C. người. D. người.
Câu 86: Ông An gửi 100 triệu đồng vào một ngân hàng với lãi suất 0,8%/ tháng. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi tháng số tiền lãi sẽ được nhập vào gốc để tính lãi cho tháng
tiếp theo và từ tháng thứ hai trở đi, mỗi tháng ông gửi them vào tài khoản với số tiền 2 triệu đồng.
Hỏi sau đúng 2 năm số tiền ông An nhận được cả gốc lẫn lãi là bao nhiêu? Biết rằng trong suốt
thời gian gửi lãi suất không thay đổi và ông An không rút tiền ra.
A.
169.871.000
đồng. B.
171.761.000
đồng. C.
173.807.000
đồng. D.
169.675.000
đồng.
Câu 87: Ông Chính gửi 200 triệu đồng vào một ngân hàng với lãi suất
7%
năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm
tiếp theo và từ năm thứ 2 trở đi, mỗi năm ông gửi thêm vào tài khoản với số tiền 20 triệu đồng.
Hỏi sau 18 năm số tiền ông Chính nhận được cả gốc lẫn lãi là bao nhiêu? Giả định trong suốt
thời gian gửi lãi suất không thay đổi và ông Chính không rút tiền ra.
A.
1.686.898.000
VNĐ. B.
743.585.000
VNĐ.
C.
739.163.000
VNĐ. D.
1.335.967.000
VNĐ.
Câu 88: Một người gửi tiết kiệm số tiền
80000000
đồng với lãi suất
6,9%
/ năm. Biết rằng tiền lãi hàng
năm được nhập vào tiền gốc, hỏi sau đúng 5 năm người đó rút được cả tiền gốc lẫn tiền lãi gần
với con số nào sau đây?
A.
105370000
đồng B.
111680000
đồng C.
107667000
đồng D.
116570000
đồng
77760
16384
62500
78125

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 16
Sưu tầm và biên soạn
Câu 89: Ngày 01 tháng 01năm 2017, ông An đem 800 triệu đồng gửi vào một ngân hàng với lãi suất 0,5%
một tháng. Từ đó, cứ tròn mỗi tháng, ông đến ngân hàng rút 6 triệu để chi tiêu cho gia đình. Hỏi
đến ngày 01tháng 01 năm 2018, sau khi rút tiền, số tiền tiết kiệm của ông An còn lại là bao nhiêu?
Biết rằng lãi suất trong suốt thời gian ông An gửi không thay đổi
A.
11
800.(1,005) 72−
B.
12
1200 400.(1,005)
−
C.
12
800.(1,005) 72−
D.
11
1200 400.(1,005)−
Câu 90: Vào ngày
15
hàng tháng ông An đều đến gửi tiết kiệm tại ngân hàng
SHB
số tiền
5
triệu đồng
theo hình thức lãi kép với kì hạn một tháng, lãi suất tiết kiệm không đổi trong suốt quá trình gửi
là
7, 2% /
năm. Hỏi sau đúng
3
năm kể từ ngày bắt đầu gửi ông An thu được số tiền cả gốc và lãi
là bao nhiêu?.
A.
195251000
B.
201453000
C.
195252000
D.
201452000

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 1
Sưu tầm và biên soạn
BÀI 1: PHÉP TÍNH LŨY THỪA
DẠNG 1. RÚT GỌN BIỂU THỨC LŨY THỪA
Câu 1: Cho
0, ,
a mn
>∈
. Khẳng định nào sau đây đúng?
A.
.
m n mn
aaa
+
+=
B.
..
m n mn
aa a
−
=
C.
( ) ( ).
mn nm
aa=
D.
.
m
nm
n
a
a
a
−
=
Lời giải
Tính chất lũy thừa
Câu 2: Với
a
là số thực dương tùy ý,
1
4
2
.
aa
bằng
A.
8
a
. B.
2
a
. C.
7
2
a
. D.
9
2
a
.
Lời giải
Ta có
1 19
4
4
2 22
.aa a a
+
= =
.
Câu 3: Cho số thực dương
a
và số nguyên dương
n
tùy ý. Mệnh đề nào dưới đây đúng?
A.
2+
=
nn
aa
. B.
2
=
nn
aa
. C.
2
=
n
n
aa
. D.
2
=
n
n
aa
.
Lời giải
Ta có:
2
=
n
n
aa
.
Câu 4: Cho
a
là số thực dương. Biểu thức
3
32
.aa
được viết dưới dạng lũy thừa với số mũ hữu tỉ là
A.
11
3
a
B.
2
a
C.
5
3
a
D.
8
3
a
Lời giải
2 2 11
3
3
32 3
3 33
.. .a a aa a a
+
= = =
Câu 5: Viết biểu thức
( )
3
4
., 0P xx x= >
dưới dạng lũy thừa với số mũ hữu tỷ
A.
5
4
Px=
. B.
1
12
Px=
. C.
1
7
Px=
. D.
5
12
Px=
.
Lời giải
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 2
Sưu tầm và biên soạn
Ta có
1 55
33
3
4
4 4 12
..P x x xx x x= = = =
.
Câu 6: Cho
a
là một số thực dương. Giá trị của biểu thức
(
)
4
2
a
a
P =
bằng
A.
4
. B.
2
. C.
8
. D.
1
.
Lời giải
Ta có
(
)
4
.
2
4
4
2
2
2 2 2 24
a
a
a
a
a
a
P
= = = = =
.
Câu 7: Với
a
là số thực dương, biểu thức
1
3
.Pa a=
bằng
A.
1
6
a
. B.
2
5
a
. C.
5
6
a
. D.
4
3
a
.
Lời giải
1 15
1
3 36
2
..P a a aa a= = =
.
Câu 8: Cho
1a ≠
là số thực dương. Viết và rút gọn biểu thức
3
2022
2022
aa⋅
dưới dạng lũy thừa với số mũ
hữu tỉ. Tìm số mũ của biểu thức rút gọn đó.
A.
1
1011
. B.
2
3
2022
. C.
2
1011
. D.
3
1011
.
Lời giải
Ta có:
3 3 1 31 2
2022
2022 2022 2022 2022 2022 1011
a aa a a a
+
⋅=⋅= =
.
Câu 9: Rút gọn biểu thức với .
A. . B. . C. . D. .
Lời giải
.
Câu 10: Đơn giản biểu thức
21
2
1
.Pa
a
−
=
với
0a >
, được kết quả là
A.
2
a
.
B.
221
a
−
.
C.
12
a
−
. D.
a
.
Lời giải
Ta có:
( )
21
21
2 2 1 2 21 2 21 1
1
.. .Pa a a aa a a a
a
−
−
− −+ −+
= = = = = =
.
Vậy
.Pa=
Câu 11: Rút gọn biểu thức
7
3
3
:Qa a=
với
0a >
2
6
5
.Px x=
0x >
1
15
Px=
17
15
Px=
17
30
Px=
Px=
2 2 1 2 1 17
6
5 5 6 5 6 30
..P x x xx x x
+
= = = =

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 3
Sưu tầm và biên soạn
A.
4
3
Qa
−
=
. B.
2
Qa=
. C.
8
3
Qa=
. D.
4
Qa
=
.
Lời giải
Ta có:
7 7 1 71
2
3
3 3 3 33
::Qa aaa a a
−
= = = =
.
Câu 12: Với
a
là số thực dương tùy ý,
5
3
a
bằng
A.
5
3
a
. B.
3
5
a
. C.
8
a
. D.
2
a
.
Lời giải
Với
0a >
ta có:
5
3
5
3
aa=
.
Câu 13: Với
a
là số thực dương tùy ý khi đó
2
5
.aa
bằng
A.
11
10
a
. B.
1
10
a
. C.
22
5
a
. D.
10
11
a
.
Lời giải
Với
0a >
ta có
1 11 11
22
5
5 5 10
..a a aa a a= = =
.
Câu 14: Với
a
là số thực dương tuỳ ý,
3
a
bằng
A.
1
6
a
. B.
2
3
a
. C.
6
a
. D.
3
2
a
.
Lời giải
Ta có
3
3
2
aa=
.
Câu 15: Rút gọn biểu thức
1
6
3
4
xx
P
x
, với
0x
.
A.
4
Px
. B.
1
6
Px
. C.
Px
. D.
1
6
Px
.
Lời giải
Ta có
1 11
111 1
6
3 36
4
364 4
1
4
4
.x x xx
P x xx
x
x
.
Câu 16: Rút gọn biểu thức
1
6
3
., 0A x xx= >
ta được
A.
Ax=
. B.
2
9
Ax=
. C.
2
Ax=
. D.
81
Ax=
.
Lời giải
Ta có:
1
1
6
3
2
.Ax x x x= = =
.
Câu 17: Với
0x
thì
2
xxx
bằng
A.
x
. B.
2
x
. C.
x
. D.
4
x
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 4
Sưu tầm và biên soạn
Ta có
2
..xxx xxx xx x
Câu 18: Với
a
là số thực dương tùy ý,
3
1
a
bằng?
A.
3
a
−
. B.
3
2
a
. C.
1
6
a
. D.
3
2
a
−
.
Lời giải
Ta có:
( )
1
3
1
2
3
2
2
33
11
aa
aa
−
−
= = =
.
Câu 19: Cho
0a >
, khi đó
4
a
bằng
A.
4
1
a
. B.
4
a
. C.
4
1
a
. D.
4
a
−
.
Lời giải
Ta có
1
4
4
aa=
.
Câu 20: Với
a
là số thực dương tuỳ ý,
3
4
aa
bằng
A.
17
6
a
. B.
13
8
a
. C.
13
6
a
. D.
17
4
a
.
Lời giải
Ta có
13
1 13
33
4
8
44
.a a aa a a
= = =
.
Câu 21: Cho số thực
a
dương tùy ý. Đặt
5
3
4
p
a aa a⋅=
. Khẳng định đúng là:
A.
19
12
p =
. B.
23
12
p =
. C.
13
12
p =
. D.
23
24
p =
.
Lời giải
Ta có
3
55
3
44
1
1
2.
2
..a aa aaa⋅=
2
511
1
426
23
a a
++
= =
.
Suy ra
23
12
p =
.
Câu 22: Cho
x
là số thực dương. Biết
3
3
.
b
a
x xxx x=
với
a
,
b
là các số tự nhiên và
a
b
là phân số
tối giản. Tính
ab+
.
A.
16
. B.
15
. C.
14
. D.
17
.
Lời giải
Ta có
1 2 57
3
3
3
3
3 3 99
. . ..x xxx xxxx xxx xx x= = = =
.
Khi đó
7
a =
;
7b =
nên
16ab+=
.
Câu 23: Cho
x
là số thực dương. Biểu thức
2
4
3
xx
được viết dưới dạng lũy thừa với số mũ hữu tỉ là

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 5
Sưu tầm và biên soạn
A.
12
7
x
. B.
5
6
x
. C.
7
12
x
. D.
6
5
x
.
Lời giải
Ta có:
17
7
44
22
4
3
33
12
.
x x xx x x= = =
với
0
x >
.
Câu 24: Cho hai số thực dương
,
ab
. Rút gọn biểu thức
11
33
44
12 12
a bb a
A
ab
+
=
+
ta thu được
.
mn
A ab
=
. Tích
của
.mn
là
A.
1
9
. B.
1
16
. C.
1
18
. D.
1
8
.
Lời giải
Ta có
11 1 1
4 4 12 12
11
11
33
44
44
11
12 12
12 12
ab b a
a bb a
A ab
ab
ab
+
+
= = =
+
+
Suy ra
11 1
..
4 4 16
mn
= =
Câu 25: Biết biểu thức
( )
6
32
3
0
P xxxx= >
được viết dưới dạng lũy thừa với số mũ hữu tỷ là
x
α
.
Khi đó, giá trị của
α
bằng
A.
37
15
. B.
23
36
. C.
23
30
. D.
53
30
.
Lời giải
Ta có
5 23
1
6
6
3
6
32 32 3
3
6 36
2
..P xxx xxx xx x= = = =
.
Câu 26: Cho hàm số
( )
(
)
(
)
2
3
2
3
3
1
88
31
8
aa a
fa
aa a
−
−
−
=
−
với
0, 1aa>≠
. Giá trị của
( )
2022
2021Mf=
là
A.
1011
2021
B.
1011
2021 1+
C.
1011
2021 1−+
D.
1011
2021 1−−
Lời giải
Ta có:
( )
(
)
(
)
2 21
11
2
33 3
22
3
2
3
3
1
2
1 11
13 1
88
31
8 22
88 8
11
1
1
11
aa a
aa
aa a
a
fa a
aa
aa a
aa a
−
−
−
−
−− +
−
−
= = = = =−−
−−
−
−
Khi đó
( ) ( )
1
2022 2022 1011
2
2021 2021 1 2021 1Mf= =− −=− −
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 6
Sưu tầm và biên soạn
Câu 27: Cho
a
là số thực dương. Rút gọn biểu thức
3
A aa aa=
về dạng
m
n
a
trong đó
m
n
là phân
số tối giản và
,
mn
∗
∈
. Tính giá trị của biểu thức
22
Tm n= +
.
A.
2425
. B.
539
. C.
593
. D.
1369
.
Lời giải
Ta có
1 3 1 1 23
31
1
3
8 248 8
24
...A aa aa aaaa a a
+++
= = = =
23; 8mn
⇒= =
22 22
23 8 593Tm n⇒= + = + =
.
Câu 28: Rút gọn biểu thức
7
3
5
3
7
42
.
.
aa
A
aa
−
=
với
0a >
ta được kết quả
m
n
Aa=
, trong đó
*
,mn∈
và
m
n
là
phân số tối giản. Khẳng định nào sau đây đúng?
A.
2
3 22mn−=
. B.
22
43mn
+=
. C.
2
2 15
mn+=
. D.
22
25mn
+=
.
Lời giải
Ta có:
7 5 7 57
26 2
54
3
3 3 3 33
4
77
2 2 26
42
7
4
4
7 77
..
.
.
aa aa a a
A aa
aa
aa a a
+
−
−
−
−
= = = = = =
2
2; 7 2 15m n mn⇒ = =⇒ +=
.
Câu 29: Biết biểu thức
(
)
6
3
32
0P xxxx= >
được viết dưới dạng lũy thừa với số mũ hữu tỉ là
x
α
. Khi
đó, giá trị của
α
bằng
A.
37
15
. B.
23
36
. C.
23
30
. D.
53
30
.
Lời giải
3 2 1 23
6
3
32
6 18 36 36
P xxx x x
++
= = =
.
Câu 30: Với
α
là số thực bất kì, mệnh đề nào sau đây sai?
A.
( )
10 10
α
α
=
. B.
2
10 10
α
α
=
.
C.
( )
( )
2
10 100
α
α
=
. D.
( )
( )
2
2
10 10
α
α
=
.
Lời giải
Theo định nghĩa và các tính chất của lũy thừa, ta thấy A, B, C là các mệnh đề đúng.
Xét mệnh đề D: với
1
α
=
, ta có:
( )
( )
2
2
1
1
10 100 10 10=≠=
nên mệnh đề D sai.
Câu 31: Rút gọn biểu thức
=
5
3
3
:Qb b
với
> 0b
.
A.
−
=
4
3
Qb
B.
=
4
3
Qb
C.
=
5
9
Qb
D.
=
2
Qb

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 7
Sưu tầm và biên soạn
Lời giải
= = =
5 51 4
3
3 33 3
::Qb bbb b
Câu 32: Rút gọn biểu thức
1
6
3
.Px x
=
với
0x
>
.
A.
Px=
B.
1
8
Px
=
C.
2
9
Px=
D.
2
Px=
Lời giải
Ta có:
1 1 1 11
1
6
3 3 6 36
2
..P x x xx x x x
+
= = = = =
Câu 33: Cho biểu thức
4
3
23
..P xx x=
, với
0
x
>
. Mệnh đề nào dưới đây đúng?
A.
2
3
Px=
B.
1
2
Px=
C.
13
24
Px=
D.
1
4
Px=
Lời giải
Ta có, với
0:
>x
7 13
3 7 13
44
33
44
4
3
23 2
66
2 2 24
.. .. . .= = = = = =P xx x xxx xx xx x x
.
Câu 34: Cho biểu thức
1
1
6
3
2
. .x
P xx=
với
0x
>
. Mệnh đề nào dưới đây đúng?
A.
Px=
B.
11
6
Px=
C.
7
6
Px=
D.
5
6
Px=
Lời giải
1 111
1
6
3 236
2
. .xP xx x x
++
= = =
Câu 35: Rút gọn biểu thức
1
3
6
Px x= ⋅
với
0x
>
.
A.
1
8
Px=
B.
Px=
C.
2
9
Px=
D.
2
Px=
Lời giải
Với
1 1 11
1
6 3 63
2
0; .x P xx x x x
+
>= = ==
Câu 36: Viết biểu thức
3
4
.P xx=
(
0x >
) dưới dạng luỹ thừa với số mũ hữu tỷ.
A.
5
4
Px=
. B.
5
12
Px=
. C.
1
7
Px=
. D.
1
12
Px=
.
Lời giải
Ta có
11
1 55
33
4 4 12
.P xx x x
= = =
.
Câu 37: Cho biểu thức
6
4
5 3
.. ,P xx x=
với
0x >
. Mệnh đề nào dưới đây đúng?
A.
15
16
Px=
. B.
7
16
Px=
. C.
5
42
Px=
. D.
47
48
Px=
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 8
Sưu tầm và biên soạn
3 11
7
51
6
4
2 46
5
16
3
..
P xx x x x
++
= = =
.
Câu 38: Cho biểu thức
4
3
23
..
P xx x=
, với
0
x >
. Mệnh đề nào dưới đây đúng?
A.
2
3
Px=
. B.
1
4
Px=
. C.
13
24
Px=
. D.
1
2
Px=
.
Lời giải
Chọn C
Ta có
7 13
3 7 13
44
33
44
4
3
23 2
66
2 2 24
.. .. . .P xx x xxx xx xx x x= = = = = =
.
Câu 39: Giả sử
a
là số thực dương, khác
1
. Biểu thức
3
aa
được viết dưới dạng
a
α
. Khi đó
A.
2
3
α
=
. B.
5
3
α
=
. C.
1
6
α
=
. D.
11
6
α
=
.
Lời giải
12
1
3
33
2
3
aa a a a
α
α
+
= = = ⇒=
.
Câu 40: Biểu thức
3
22
K =
viết dưới dạng lũy thừa với số mũ hữu tỉ là
A.
4
3
2
. B.
5
3
2
. C.
1
3
2
. D.
2
3
2
.
Lời giải
1
1 44 2
2
3
3 33 3
2 2 2.2 2 2 2K
= = = = =
.
Câu 41: Biểu thức
6
5
3
. . ( 0)xxxx>
viết dưới dạng luỹ thừa với số mũ hữu tỷ là
A.
2
3
x
. B.
5
2
x
. C.
7
3
x
. D.
5
3
x
.
Lời giải
1 5 10 5
1
6
5
3
36 6 3
2
. . ..xxx xxx x x= = =
.
Câu 42: Cho biểu thức
( )
71 2 7
22
22
.aa
P
a
+−
+
−
=
với
0a >
. Rút gọn biểu thức
P
được kết quả là
A.
5
Pa=
. B.
3
Pa=
. C.
Pa=
. D.
4
Pa=
.
Lời giải
( )
71 2 7 3
5
2
22
22
.aa a
Pa
a
a
+−
−
+
−
= = =
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 9
Sưu tầm và biên soạn
Câu 43: Cho a là số thực dương. Viết và rút gọn biểu thức
3
2018
2018
.aa
dưới dạng lũy thừa với số mũ hữu
tỉ. Tìm số mũ của biểu thức rút gọn đó.
A.
2
1009
. B.
1
1009
. C.
3
1009
. D.
2
3
2018
.
Lời giải
3 31 4 2
2018
2018 2018 2018 2018 1009
..= = =
a aaaaa
. Vậy số mũ của biểu thức rút gọn bằng
2
1009
.
Câu 44: Rút gọn biểu thức
31 2 3
22
22
.aa
P
a
với
0
a
.
A.
Pa
. B.
3
Pa
. C.
4
Pa
. D.
5
Pa
.
Lời giải
31 2 3 312 3 3
5
2
22
22 22
22
.aa a a
Pa
a
a
a
.
Câu 45: Biểu thức
3
2
5
P xx x x
α
= =
, giá trị của
α
là
A.
1
2
. B.
5
2
. C.
9
2
. D.
3
2
.
Lời giải
11
1 5 31
53
3
5
3
22
5
2 2 22
3
1
.. .
2
P xx x xxx xx x x
α
= = = = = ⇒=
Câu 46: Cho
a
là số thực dương khác
1
. Khi đó
2
4
3
a
bằng
A.
3
2
a
. B.
8
3
a
. C.
3
8
a
. D.
6
a
.
Lời giải
Ta có:
1
2 2 21 1
4
.
4
6
3 3 34 6
aa aa a
= = = =
Câu 47: Rút gọn biểu thức
31 2 3
22
22
.aa
P
a
với
0a
A.
Pa=
B.
3
Pa=
C.
4
Pa
=
D.
5
Pa=
Lời giải
Ta có
31 2 3 3
5
24
22
22
.aa a
Pa
a
a
Câu 48: Cho biểu thức
3
5
4
.Px x
−
=
,
0x >
. Khẳng định nào sau đây là đúng?

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 10
Sưu tầm và biên soạn
A.
2
Px
−
=
B.
1
2
Px
−
=
C.
1
2
Px=
D.
2
Px=
Lời giải
Ta có
3
5
4
.
Px x
−
=
3 5 35 1
4 4 44 2
.
xx x x
− −+
= = =
.
Câu 49:
Cho biểu thức
3
3
4
.P xx x=
, với
0.x
>
Mệnh đề nào dưới đây đúng?
A.
1
2
.Px=
B.
7
12
.Px=
C.
5
8
.Px=
D.
7
24
.Px=
Lời giải
Ta có:
5
3
3
4
8
.P xx x x= =
Câu 50: Cho hai số thực dương
,ab
. Rút gọn biểu thức
11
33
66
a bb a
A
ab
+
=
+
ta thu được
.
mn
A ab=
. Tích
của
.mn
là
A.
1
8
B.
1
21
C.
1
9
D.
1
18
Lời giải
11 1 1
33 6 6
1 1 11
11
11
3 3 33
22
33
11 11
66
66 66
.
..
.
ab b a
a b b a ab ba
A ab
ab
ab ab
+
++
= = = =
+
++
1
3
m⇒=
,
1
3
n =
1
.
9
mn⇒=
.
Câu 51: Rút gọn biểu thức
11
3
7
3
7
45
.
.
aa
A
aa
−
=
với
0a >
ta được kết quả
m
n
Aa=
trong đó
,mn
*
N∈
và
m
n
là
phân số tối giản. Khẳng định nào sau đây đúng?
A.
22
312mn−=
. B.
22
543mn+=
. C.
22
312mn−=−
. D.
22
409.mn+=
Lời giải
Ta có:
11 7 11
19
3
76
3 33
7
5 23
7
45
4
77
..
.
.
aa aa a
Aa
aa
aa a
−
−
= = = =
Mà
m
n
Aa=
,
,mn
*
N∈
và
m
n
là phân số tối giản
22
19, 7
312
mn
mn
⇒= =
⇒ −=
Câu 52: Cho
a
là số thực dương. Đơn giản biểu thức
41 2
33 3
13 1
44 4
aa a
P
aa a
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 11
Sưu tầm và biên soạn
A.
( )
1P aa
= +
. B.
1
Pa= −
. C.
Pa
=
. D.
1Pa= +
.
Lời giải
41 2
33 3
4 1 42
2
3 3 33
13 1 1
13 1
44 4 4
44 4
1
11
.
..
aa a
aa
a a aa a a
Pa
aa
aa aa
aa a
.
Câu 53: Cho
,
ab
là các số thực dương. Rút gọn
44
33
33
a b ab
P
ab
ta được
A.
P ab
. B.
P ab
. C.
44
P a b ab
. D.
P ab a b
.
Lời giải
11
33
441 1
333 3
11 11
33
33 33
..
.
ab a b
a b ab a a b ab b
P ab
ab
ab ab
Câu 54: Cho biểu thức
5
3
822 2
m
n
=
, trong đó
m
n
là phân số tối giản. Gọi
22
Pm n
= +
. Khẳng định nào
sau đây đúng?
A.
( )
330;340P ∈
. B.
( )
350;360P
∈
. C.
( )
260;370P∈
. D.
( )
340;350P ∈
.
Lời giải
Chọn D
Ta có
3 1 1 3 1 1 11
55
3
33
5 10 30 5 10 30 15
8 2 2 2 2 2 2 .2 .2 2 2
++
= = = =
22 2 2
11
11
11 15 346
15
15
m
m
Pm n
n
n
=
⇒ = ⇒ ⇒= + = + =
=
.
Câu 55: Cho
0>a
,
0>b
, giá trị của biểu thức
( ) ( )
1
2
2
1
1
2
1
2 . .1
4
−
=+ +−
ab
T a b ab
ba
bằng
A.
1
. B.
1
2
. C.
2
3
. D.
1
3
.
Lời giải
Cách 2:
Ta có
( ) ( )
1
2
2
1
1
2
1
2 . .1
4
−
=+ +−
ab
T a b ab
ba

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 12
Sưu tầm và biên soạn
(
) (
)
1
2
2
1
1
2
1
2 . .1
4
−
−
=++
ab
a b ab
ab
( ) ( )
( )
1
2
2
1
1
2
2 . .1
4
−
−
=++
ab
a b ab
ab
( ) ( )
( )
1
2
2
1
1
2
2 ..
4
−
+
= +
ab
a b ab
ab
(
)
( )
( )
1
2
1
2
1
2. . 1
2
+
= =
+
ab
ab
ab
ab
.
DẠNG 2. TÍNH GIÁ TRỊ BIỂU THỨC
Câu 56: Biểu thức
5
5
4. 8P = −
có giá trị bằng
A.
42
. B.
2−
. C. 2. D.
42−
.
Lời giải
Ta có
( )
5
5
5
4. 8 32 2P =− =−=−
.
Câu 57: Giá trị
35
2021. 2021
viết dưới dạng lũy thữa với số mũ hữu tỷ là
A.
2
5
2021
. B.
1
15
2021
. C.
8
15
2021
. D.
1
10
2021
Lời giải
1 1 11 8
35
3 5 3 5 15
2021. 2021 2021 .2021 2021 2021 .
+
= = =
Câu 58: Giá trị của
1
3
27
bằng
A. 6. B. 81. C. 9. D. 3.
Lời giải
Ta có
3
3
1
27 327
= =
.
Câu 59: Cho
1
256
a =
và
1
27
b =
. Tính
4
3
3
4
Aa b
−
−
= +
A.
23
. B.
89
. C.
145
. D.
26
.
Lời giải
Thay
1
256
a =
,
1
27
b
=
vào
4
3
3
4
Aa b
−
−
= +
ta được
(
) ( )
34
4
3
34
43
4 3 34
3
4
43
11
4 3 4 3 145
256 27
Aa b
−−
−
−
−−
−−
= + = + = + =+=
.
Câu 60: Cho
44 7
xx−
+=
. Biểu thức
52 2
8 4.2 4.2
xx
xx
P
−
−
++
=
−−
có giá trị bằng
A.
3
2
P =
. B.
5
2
P = −
. C.
2P =
. D.
2P = −
.
Lời giải
( )
2
44 7 22 9 22 3.
xx xx xx−− −
+=⇔+ =⇔+=

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 13
Sưu tầm và biên soạn
Suy ra
52 2 53
2.
8 4.2 4.2 8 12
xx
xx
P
−
−
++ +
= = = −
−− −
.
Câu 61: Cho
9 9 23
xx
−
+=
. Khi đó biểu thức
53 3
13 3
xx
xx
a
A
b
−
−
++
= =
−−
với
a
b
là phân số tối giản và
,ab
∈
.
Tích
.ab
bằng
A.
10−
. B.
10
. C.
8−
. D.
8
.
Lời giải
Ta có:
(
)
2
9 9 23 3 3 25
xx xx
−−
+=⇔+ =
33 5
xx−
⇔+ =
vì
3 3 0,
xx
x
−
+ > ∀∈
⇒
53 3 55 5
13 3 15 2
xx
xx
A
−
−
++ + −
= = =
−− −
.
Vậy
. 10ab= −
.
Câu 62: Cho biểu thức
1
2
2
1
1
3. 2 4
2
x
x
x
T
−
−−
=+−
. Khi
23
x
=
thì giá trị của biểu thức
T
là
A.
93
2
. B.
53
2
. C.
33
2
. D.
73
2
.
Lời giải
Ta có:
(
)
1
11
22
1
22
1
1 1 9 93
3. 2 4 2 3. 2 4 2.2 3.2 .2 .2
2 22 2
x
x
x
x
x xx x x
x
T
−
−
+
−−
= + −=+ − =+− = =
.
Câu 63: Biết
4 4 14
xx−
+=
, tính giá trị của biểu thức
22
xx
P
−
= +
.
A.
4
. B.
16
. C.
17
. D.
4±
.
Lời giải
Ta có
4 4 14
xx−
+=
( ) ( )
22
2 2 2 16
xx−
⇔ + +=
( )
2
2 2 16
xx−
⇔+ =
22 4
22 4
xx
xx
−
−
+=
⇔
+=−
22 4
xx−
⇔+ =
.
Vậy
4P =
.
Câu 64: Cho
44 7
xx−
+=
. Khi đó biểu thức
11
52 2
32 2
xx
xx
a
P
b
−
+−
−−
= =
++
với
a
b
tối giản và
,ab
+
∈∈
. Tính
tổng
ab+
có giá trị bằng
A.
8
. B.
11
. C.
17
. D.
4
.
Lời giải
Ta có:
( )
2
2 2 4 4 2.2 .2
xx xx xx− −−
+ =++
72= +
9=
. Suy ra:
22 3
xx−
+=
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 14
Sưu tầm và biên soạn
( )
( )
11
522
52 2
32 2
3 22 2
xx
xx
xx
xx
P
−
−
+−
−
−+
−−
= =
++
++
53
3 2.3
−
=
+
2
9
=
Suy ra:
2a =
,
9 11b ab
=⇒+=
.
Câu 65: Tính giá trị của biểu thức
( ) ( )
2017 2016
7 43 43 7P
=+−
A.
(
)
2016
7 43P = +
B.
1
P
=
C.
7 43P = −
D.
7 43P = +
Lời giải
( )
( ) ( ) ( )( )
( )
( )
2016
2017 2016
2016
7 43 43 7 7 43. 7 43 43 7
7 43 1 7 43.
P
=+ −=+ + −
=+ −=+
Câu 66: Cho biểu thức
3
3
222
333
P =
. Mệnh đề nào trong các mệnh đề sau là đúng?
A.
1
8
2
3
P
=
. B.
18
2
3
P
=
. C.
1
18
2
3
P
=
. D.
1
2
2
3
P
=
.
Lời giải
Cách 1:
Ta có:
3
3
222
333
P =
3
2
3
3
22
33
=
31 3 1
.1
23 2 2
33
2 22
3 33
+
= = =
.
Câu 67: Cho hàm số
(
)
(
)
(
)
1
3
4
3
3
1
88
31
8
a aa
fa
aa a
−
−
−
=
−
với
0, 1aa>≠
. Tính giá trị
( )
2016
2017Mf=
A.
1008
2017 1M = −
B.
1008
2017 1M
=−−
C.
2016
2017 1M = −
D.
2016
1 2017M = −
Lời giải
( )
(
)
(
)
1
3
4
3
3
1
88
31
8
1
1
1
a aa
a
fa a
a
aa a
−
−
−
−
= = =−−
−
−
nên
(
)
2016 2016 1008
2017 1 2017 1 2017Mf
= =−− =−−
Câu 68: Giá trị của biểu thức
( )
3 1 34
0
32
2 .2 5 .5
10 :10 0,1
P
−−
−−
+
=
−
là
A.
9−
. B.
10−
. C.
10
. D.
9
.
Lời giải
Ta có
( )
3134 3134
0
32 1
32
2 .2 5 .5 2 5 4 5 9
10.
1
10 1 10 1
10 :10 0,1
1
10
P
− − − −+
−+ −
−−
+ ++
= = = = = −
−−
−
−
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 15
Sưu tầm và biên soạn
Câu 69: Cho hàm số
( )
(
)
(
)
2
3
2
3
3
1
88
31
8
aa a
fa
aa a
−
−
−
=
−
với
0, 1aa>≠
. Tính giá trị
( )
2018
2017
Mf=
.
A.
2018
2017 1.
+
B.
1009
2017 1.
−−
C.
1009
2017 .
D.
1009
2017 1.+
Lời giải
Ta có
( )
2 21
3 33
1
2
1
13 1
2
88 8
1
1
1
aa a
a
fa a
a
aa a
−
−
−
−
= = =−−
−
−
.
Do đó
( )
( )
1
2018 2018 1009
2
2017 1 2017 1 2017Mf= =−− =−−
.
DẠNG 3. SO SÁNH CÁC BIỂU THỨC CHỨA LŨY THỪA
Câu 70: Nếu
11
3 6
aa>
và
35
bb>
thì
A.
1; 0 1ab< <<
. B.
1; 1
ab><
. C.
0 1; 1ab<< <
D.
1; 0 1ab> <<
.
Lời giải
Ta có:
11
36
>
, lại có
11
3
6
aa>
1a⇒>
.
Ta có:
35<
, lại có
35
bb>
01b⇒<<
.
Câu 71: Cho
1a
>
. Mệnh đề nào dưới đây đúng?
A.
2016 2017
11
aa
<
. B.
1
3
aa>
. C.
3
5
1
a
a
−
>
. D.
3
2
1
a
a
>
.
Lời giải
Vì
1
a >
nên
35
35
11
aa
aa
<⇒ > ⇒
3
5
1
a
a
−
>
.
Câu 72: Trong các mệnh đề sau, mệnh đề nào SAI?
A.
( ) ( )
2018 2017
31 31− >−
. B.
+
>
3
21
22
.
C.
(
)
(
)
2017 2018
21 21− >−
. D.
2019 2018
22
11
22
− <−
.
Lời giải
A.
( )
( )
2018 2017
31 31
− >−
. Cùng cơ số,
0 311< −<
, hàm nghịch biến, số mũ lớn hơn nên bé
hơn. Sai
B.
+
>
3
21
22
. Cùng cơ số,
21>
, hàm đồng biến, số mũ
( ) ( )
22
21 322 3 3+=+ > =
nên lớn
hơn. Đúng

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 16
Sưu tầm và biên soạn
C.
( )
( )
2017 2018
21 21− >−
. Cùng cơ số,
0 211< −<
, hàm nghịch biến, số mũ bé hơn nên lớn
hơn. Đúng.
D.
2019 2018
22
11
22
− <−
. Cùng cơ số,
2
01 1
2
<− <
, hàm nghịch biến, số mũ lớn hơn nên
bé hơn. Đúng
Câu 73: Khẳng định nào sau đây đúng?
A.
2017 2018
( 5 2) ( 5 2)
−−
+ <+
. B.
2018 2019
( 5 2) ( 5 2)+ >+
.
C.
2018 2019
( 5 2) ( 5 2)− >−
. D.
2018 2019
( 5 2) ( 5 2)− <−
.
Lời giải
2018 2019
0 521
( 5 2) ( 5 2)
2018 2019
C
< −<
⇒− >− ⇒
<
đúng.
2017 2018
521
( 5 2) ( 5 2)
2017 2018
A
−−
+>
⇒+ >+ ⇒
− >−
sai
2018 2019
521
( 5 2) ( 5 2)
2018 2019
B
+>
⇒+ <+ ⇒
<
sai
2018 2019
0 521
( 5 2) ( 5 2)
2018 2019
D
< −<
⇒− >− ⇒
<
sai.
Câu 74: Khẳng định nào dưới đây là đúng?
A.
33
35
.
78
>
B.
11
23
ππ
−−
<
. C.
2
2
1
3
5
−
<
. D.
( )
50
100
1
2
4
−
<
.
Lời giải
Ta có:
33
35 3 5
78 7 8
<⇒ <
. Phương án A Sai.
11 1 1
23 2 3
ππ
−−
>⇒ <
. Phương án B Đúng.
2
22 2
1
35 3 5 3
5
−− −
<⇒>⇒>
. Phương án C Sai.
( )
( )
( )
50
100
50
100
2 100 100
1
2 2 2 22
4
−
−
−
< ⇒ < ⇒<
. Phương án D Sai.
Câu 75: Trong các khẳng định sau, khẳng định nào sai?

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 17
Sưu tầm và biên soạn
A.
2018 2017
22
11
22
− <−
. B.
( ) ( )
2017 2018
21 21− >−
.
C.
( ) ( )
2018 2017
31 31− >−
. D.
21 3
22
+
>
.
Lời giải
+)
0 211
2017 2018
< −<
<
( )
( )
2017 2018
21 21⇒− >−
nên A đúng.
+)
0 311
2018 2017
< −<
>
( ) ( )
2018 2017
31 31⇒− <−
nên B sai.
+)
21
21 3
>
+>
21 3
22
+
⇒>
nên C đúng.
+)
2
01 1
2
2018 2017
<− <
>
2018 2017
22
11
22
⇒− <−
nên D đúng.
Câu 76: Tìm tập tất cả các giá trị của
a
để
7
52
21
aa>
?
A.
0a >
.
B.
01
a
<<
.
C.
1a >
. D.
52
21 7
a<<
.
Lời giải
7
26
21
aa=
.
Ta có
7
52 5 6
21 21 21
aa aa>⇔>
mà
56<
vậy
01a<<
.
DẠNG 4. BÀI TOÁN LÃI SUẤT – DÂN SỐ
Câu 77: Anh An gửi số tiền 58 triệu đồng vào một ngân hàng theo hình thức lãi kép và ổn định trong 9
tháng thì lĩnh về được 61758000đ. Hỏi lãi suất ngân hàng hàng tháng là bao nhiêu? Biết rằng lãi
suất không thay đổi trong thời gian gửi.
A.
0,8 %
B.
0,6 %
C.
0,7 %
D.
0,5 %
Lời giải
Áp dụng công thức
( )
0
1= +
n
n
AA r
với
n
là số kỳ hạn,
0
A
là số tiền ban đầu,
n
A
là số tiền có
được sau
n
kỳ hạn,
r
là lãi suất.
Suy ra
( )
9
9
9
90
0
1 1 0,7%= + ⇒ = −=
A
AA r r
A
.
Câu 78: Ông An gửi tiết kiệm
50
triệu đồng vào ngân hàng với kỳ hạn
3
tháng, lãi suất
8, 4%
một năm
theo hình thức lãi kép. Ông gửi được đúng
3
kỳ hạn thì ngân hàng thay đổi lãi suất, ông gửi tiếp
12
tháng nữa với kỳ hạn như cũ và lãi suất trong thời gian này là
12%
một năm thì ông rút tiền
về. Số tiền ông An nhận được cả gốc lẫn lãi là:
A.
62255910
đồng. B.
59895767
đồng. C.
59993756
đồng. C.
63545193
đồng.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 18
Sưu tầm và biên soạn
Đợt I, ông An gửi số tiền
0
50P =
triệu, lãi suất
8, 4%
một năm tức là
2,1%
mỗi kỳ hạn. Số
tiền cả gốc và lãi ông thu được sau
3
kỳ hạn là:
( )
3
3
50000000. 1.021P =
.
Đợt II, do ông không rút ra nên số tiền
3
P
được xem là số tiền gửi ban đầu của đợt II, lãi suất
đợt II là
3%
mỗi kỳ hạn. Ông gửi tiếp
12
tháng bằng
4
kỳ hạn nên số tiền thu được cuối cùng
là:
(
) ( ) ( )
4 34
3
1.03 50000000. 1.021 . 1.03 59895767PP= = ≈
đồng.
Câu 79: Một học sinh
A
khi
15
tuổi được hưởng tài sản thừa kế
200 000 000
VNĐ. Số tiền này được
bảo quản trong ngân hàng
B
với kì hạn thanh toán
1
năm và học sinh
A
chỉ nhận được số tiền
này khi
18
tuổi. Biết rằng khi
18
tuổi, số tiền mà học sinh
A
được nhận sẽ là
231 525 000
VNĐ. Vậy lãi suất kì hạn một năm của ngân hàng
B
là bao nhiêu?
A.
8% /
năm. B.
7% /
năm. C.
6% /
năm. D.
5% /
năm.
Lời giải
Ta có: số tiền nhận được của gốc và lãi là:
( )
3
200 000 000 1 231 525 000r+=
5%
r⇔=
/năm
Câu 80: Ông Anh gửi vào ngân hàng
60
triệu đồng theo hình thức lãi kép. Lãi suất ngân hàng là
8%
trên
năm. Sau
5
năm ông An tiếp tục gửi thêm
60
triệu đồng nữa. Hỏi sau
10
năm kể từ lần gửi đầu
tiên ông An đến rút toàn bộ tiền gốc và tiền lãi được là bao nhiêu?.
A.
231,815
. B.
197,201
.
C.
217,695
. D.
190,271
.
Lời giải
Số tiền ông An nhận được sau
5
năm đầu là:
( )
5
60 1 8% 88,160+=
Số tiền ông An nhận được sau
10
năm là:
(
)( )
5
88,16 60 1 8% 217,695
++=
.
Câu 81: Anh Nam gửi 100 triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn là một quý với lãi suất
3% một quý. Sau đúng 6 tháng anh Nam gửi thêm 100 triệu đồng với kì hạn và lãi suất như trước
đó.Hỏi sau 1 năm số tiền anh Nam nhận được là bao nhiêu?.
A.
218,64
triệu đồng. B.
208, 25
triệu đồng.
C.
210,45
triệu đồng. D.
209,25
triệu đồng.
Lời giải
• Số tiền anh Nam nhận được sau 6 tháng là:
(
)
2
0
10
100 1 3 / 106,09T =+=
triệu đồng.
• Số tiền anh Nam nhận được sau một năm là:
( )
( )
2
0
20
106,09 100 1 3 / 218,64T = ++≈
triệu đồng.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 19
Sưu tầm và biên soạn
Câu 82: Ông tuấn gửi 100 triệu vào ngân hàng với hình thức lãi kép, kỳ hạn 1 năm với lãi suất
8%
. Sau
5 năm ông rút toàn bộ tiền và dùng một nữa để sửa nhà, số tiền còn lại ông tiếp tục gửi ngân hàng
với lãi suất như lần trước. Số tiền lãi ông tuấn nhận được sau 10 năm gửi gần nhất với giá trị nào
dưới đây?
A.
46,933
triệu. B.
34,480
triệu. C.
81, 413
triệu. D.
107,946
triệu.
Lời giải
Năm năm đầu ông Tuấn có số tiền cả gốc và lãi là
( )
5
1
100. 1 0.08 146,933T =+=
Sau khi sửa nhà số tiền còn lại gửi vào ngân hàng trong 5 năm thì số tiền cả gốc và lãi là
( )
5
2
146,932
1 0.08 107,946.
2
T = +=
Số tiền lãi trong 10 năm là
( ) ( )
146,933 100 107,946 73, 466 81,413.L = −+ − =
Câu 83: Dân số thế giới được ước tính theo công thức
.
ni
S Ae=
, trong đó
A
là dân số của năm lấy làm
mốc,
S
là dân số sau
n
năm,
i
là tỉ lệ tăng dân số hằng năm. Dân số Việt Nam năm 2019 là
95,5
triệu người, tỉ lệ tăng dân số hằng năm từ 2009 đến nay là
1,14%
. Hỏi dân số Việt Nam
năm 2009 gần với số nào nhất trong các số sau?
A.
94, 4
triệu người. B.
85, 2
triệu người. C.
86, 2
triệu người. D.
83, 9
triệu người.
Lời giải
Áp dụng công thức
.
ni
S Ae=
trong đó:
95,5S =
triệu người,
10n =
năm,
1,14%i =
Ta có số dân Việt Nam năm 2009 là:
10.1,14%
95,5
85, 2
ni
S
A
ee
= = ≈
triệu người
Câu 84: Để dự báo dân số của một quốc gia, người ta sử dụng công thức
;
nr
S Ae=
trong đó
A
là dân số
của năm lấy làm mốc tính,
S
là dân số sau
n
năm,
r
là tỉ lệ tăng dân số hàng năm. Năm 2017,
dân số Việt nam là
93.671.600
người. Giả sử tỉ lệ tăng dân số hàng năm không đổi là
0,81%,
dự báo dân số Việt nam năm 2035 là bao nhiêu người?
A.
109.256.100
. B.
108.374.700
. C.
107.500.500
. D.
108.311.100
.
Lời giải
Lấy năm 2017 làm mốc, ta có
93.671.600; 2035 2017 18An= =−=
⇒
Dân số Việt Nam vào năm 2035 là
.
0,
1
81
100
8
93.671.600. 108.374.700Se= ≈
Câu 85: COVID19 là một loại bệnh viêm đường hô hấp cấp do chủng mới của virus corona bắt nguồn từ
Trung Quốc gây ra với tốc độ truyền bệnh rất nhanh. Giả sử ban đầu có 1 người bị nhiễm bệnh
và cứ sau 1 ngày sẽ lây sang 4 người khác. Tất cả những người nhiễm bệnh lại tiếp tục lây sang
những người khác với tốc độ như trên. Hỏi sau 7 ngày sẽ có tổng cộng bao nhiêu người nhiễm
bệnh?.
A. người. B. người. C. người. D. người.
Lời giải
Sau 1 ngày, tổng số người nhiễm bệnh là người.
Sau 2 ngày, tổng số người nhiễm bệnh là người.
77760
16384
62500
78125
14 5+=
( ) ( ) ( )
2
14 14.4 14+ ++ =+

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 20
Sưu tầm và biên soạn
Sau 3 ngày, tổng số người nhiễm bệnh là người.
Sau 7 ngày, tổng số người nhiễm bệnh là người.
Ngoài ra chúng ta có thể áp dụng công thức lãi kép để tính nhanh:
, với , , .
Câu 86: Ông An gửi 100 triệu đồng vào một ngân hàng với lãi suất 0,8%/ tháng. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi tháng số tiền lãi sẽ được nhập vào gốc để tính lãi cho tháng
tiếp theo và từ tháng thứ hai trở đi, mỗi tháng ông gửi them vào tài khoản với số tiền 2 triệu đồng.
Hỏi sau đúng 2 năm số tiền ông An nhận được cả gốc lẫn lãi là bao nhiêu? Biết rằng trong suốt
thời gian gửi lãi suất không thay đổi và ông An không rút tiền ra.
A.
169.871.000
đồng. B.
171.761.000
đồng. C.
173.807.000
đồng. D.
169.675.000
đồng.
Lời giải
Với 100 triệu ban đầu số tiền cả lãi và gốc thu được sau hai năm là
( )
24
6
1
100. 1 0,8% .10 121074524T =+=
Mỗi tháng tiếp theo gửi 2 triệu thì tổng số tiền cả lãi và gốc là
( ) ( )
23
6
2
2
. 1 0,008 1 . 1 0,008 10 50686310
0,008
T
= + −+ =
Vậy tổng số tiền là
12
171.761.000TTT=+=
Câu 87: Ông Chính gửi 200 triệu đồng vào một ngân hàng với lãi suất
7%
năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm
tiếp theo và từ năm thứ 2 trở đi, mỗi năm ông gửi thêm vào tài khoản với số tiền 20 triệu đồng.
Hỏi sau 18 năm số tiền ông Chính nhận được cả gốc lẫn lãi là bao nhiêu? Giả định trong suốt
thời gian gửi lãi suất không thay đổi và ông Chính không rút tiền ra.
A.
1.686.898.000
VNĐ. B.
743.585.000
VNĐ.
C.
739.163.000
VNĐ. D.
1.335.967.000
VNĐ.
Lời giải
Gọi
200a =
triệu;
20b =
triệu;
7%
α
=
.
Số tiền sau 1 năm:
( )
1a
α
+
.
Số tiền sau 2 năm:
( ) ( )
2
11ab
αα
+ ++
.
Số tiền sau 3 năm:
( ) ( ) ( )
32
111abb
ααα
+++ ++
.
……………………
Số tiền sau 18 năm:
( ) ( ) ( ) ( )
18 17 16
1 1 1 ... 1ab
α αα α
+ + + ++ +++
( ) ( )
( )
17
18
11
1 1.ab
α
αα
α
+−
=+++
Vậy số tiền ông Chính nhận sau 18 năm là:
1.335.967.000
VNĐ.
Câu 88: Một người gửi tiết kiệm số tiền
80000000
đồng với lãi suất
6,9%
/ năm. Biết rằng tiền lãi hàng
năm được nhập vào tiền gốc, hỏi sau đúng 5 năm người đó rút được cả tiền gốc lẫn tiền lãi gần
với con số nào sau đây?
( ) ( ) ( )
22 3
14 14.4 14+ ++ =+
⇒
( )
7
1 4 78125+=
( ) ( )
7
1 1. 1 4 78125
n
n
SA r= +=+=
1A =
4r =
7n =

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 21
Sưu tầm và biên soạn
A.
105370000
đồng B.
111680000
đồng C.
107667000
đồng D.
116570000
đồng
Lời giải
Gọi
0
P
là số tiền gửi ban đầu,
r
là lãi suất / năm.
Số tiền gốc và lãi sau năm thứ nhất:
( )
100 0
.1P P Pr P r=+= +
.
Số tiền gốc và lãi sau năm thứ hai:
( )
2
2 11 0
.1P P Pr P r
=+= +
.
….
Số tiền gốc và lãi người đó rút ra được sau 5 năm là
( ) ( )
55
50
. 1 80000000. 1 6,9% 111680799PP r= += + ≈
.
Câu 89: Ngày 01 tháng 01năm 2017, ông An đem 800 triệu đồng gửi vào một ngân hàng với lãi suất 0,5%
một tháng. Từ đó, cứ tròn mỗi tháng, ông đến ngân hàng rút 6 triệu để chi tiêu cho gia đình. Hỏi
đến ngày 01tháng 01 năm 2018, sau khi rút tiền, số tiền tiết kiệm của ông An còn lại là bao nhiêu?
Biết rằng lãi suất trong suốt thời gian ông An gửi không thay đổi
A.
11
800.(1,005) 72−
B.
12
1200 400.(1,005)−
C.
12
800.(1,005) 72
−
D.
11
1200 400.(1,005)−
Lời giải
Gửi ngân hàng số tiền là A đồng với lãi suất
%r
./tháng. Mỗi tháng vào ngày ngân hàng tính
lãi, rút ra số tiền là X đồng. Sô tiền còn lại sau n tháng đươc tính theo công thức:
( )
( )
( )
( )
12
1
12
2
1 1 1,005 1
1 800 1,005 6. 775.3288753
0
1200 400.(1,0
%
5
,5
0)
n
n
n
r
SA r X
r
+− −
−= +− = − = =
Câu 90: Vào ngày
15
hàng tháng ông An đều đến gửi tiết kiệm tại ngân hàng
SHB
số tiền
5
triệu đồng
theo hình thức lãi kép với kì hạn một tháng, lãi suất tiết kiệm không đổi trong suốt quá trình gửi
là
7, 2% /
năm. Hỏi sau đúng
3
năm kể từ ngày bắt đầu gửi ông An thu được số tiền cả gốc và lãi
là bao nhiêu?.
A.
195251000
B.
201453000
C.
195252000
D.
201452000
Lời giải
Gọi
n
T
là số tiền cả gốc lẫn lãi sau
n
tháng,
a
là số tiền gốc,
r
là lãi xuất, ta có:
Cuối tháng thứ
1
ông An có số tiền là:
( )
1
1= +Ta r
Đầu tháng thứ
2
ông An có số tiền là:
( )
2
1= ++Ta ra
Cuối tháng thứ
2
ông An có số tiền là:
(
) ( )
(
)
( ) (
)
2
2
1 1 11= +++ ++ = ++ +Taraarararar
……………………………………………………………
Cuối tháng thứ
n
ông An có số tiền là::
( )
( ) ( )
2
1 1 ... 1=++++++
n
n
Tarar ar
( ) ( ) ( )
( )
( ) (
)
( )
( ) ( )
( )
( )
2
11 111 1
1 1 ... 1 . 1
11
+ +− + +−
= + ++ +++ = =
+−
nn
n
rr arr
ar r r a
rr
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 22
Sưu tầm và biên soạn
Với kì hạn một tháng, suy ra 3 năm có 36 kỳ. Lãi xuất của một năm là
7, 2%
, suy ra lãi xuất
của 1 tháng là:
7, 2
% 0.6%
12
=
. Áp dụng
( )
1
ta có:
5000000; 0.6% 0.072; 36= = = =ar n
( ) ( )
( )
36
36
5000000 1 0.6% 1 0.6% 1
201453000
0.6%
+ +−
=>= ≈T

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 17
Sưu tầm và biên soạn
BÀI 2: PHÉP TÍNH LOGARIT
1. KHÁI NIỆM LOGARIT
Cho hai số thực dương
,ab
với
1a ≠
. Số thực
α
để
ab
α
=
được gọi là logarit cơ số
a
của
b
và kí hiệu là
log
a
b
, nghĩa là
log .
a
bab
α
α
= ⇔=
Chú ý:
Không có logarit của số
0
và số âm vì
0, a
α
α
>∀
.
log
a
b
xác định
0
1
0
a
a
b
>
⇔≠
>
Theo định nghĩa của logarit, ta có:
1) log 1 0
2) log 1
a
a
a
=
=
.
3) log
a
b
ab=
.
log
4)
a
b
ab=
.
2. TÍNH LOGARIT BẰNG MÁY TÍNH CẦM TAY
3. TÍNH CHẤT CỦA PHÉP TÍNH LOGARIT
Với
;, ;
a MN
α
<≠ > ∈ 01 0
, khi đó:
( )
)log . log log
)log log log
)log .log
a aa
a aa
aa
MN M N
M
MN
N
MM
α
α
= +
= −
=
1
2
3
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
LÝ THUYẾT.
I

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 18
Sưu tầm và biên soạn
4. CÔNG THỨC ĐỔI CƠ SỐ
Câu 1: Tính
( )
2
log 243
5
8
Câu 2: Cho số thực
01a<≠
. Tính giá trị của biểu thức
( )
2
3
log
a
aa
.
Câu 3: Cho
0
a >
,
1
a ≠
. Tính giá trị của biểu thức
3
3
1
log
a
P
a
=
.
Câu 4: Xét các số thực dương
,ab
thỏa mãn
5
log 5
a =
và
3
2
log
3
b =
. Tính giá trị biểu thức
( )
3
65 1
9
2log log 5 logI ab= +
.
Câu 5: Cho số thực dương
a
khác
1
. Tính giá trị của biểu thức
( )
2
log 4a
Câu 6: Tính giá trị của biểu thức
3
36
log log
a
a
Pb b= +
trong đó
,ab
là các số thực dương tùy ý và
1a ≠
.
Câu 7: Tính giá trị của biểu thức
2
3
log 8 log 9P = +
Câu 8: Cho
log 3, log 4.
aa
bc= = −
Khi đó, tính giá trị của biểu thức
3
2
log
a
ac
P
b
=
?
Câu 9: Cho các số thực
,ab
thỏa mãn
1ab>>
và
11
2022.
log log
ba
ab
+=
Tính giá trị của biểu thức
11
.
log log
ab ab
P
ba
= −
Câu 10: Cho các số thực dương
1, 1xy≠≠
thỏa mãn
2
log log 16
y
x =
và tích
64xy =
. Tính giá trị của
biểu thức
2
2
log
y
x
Câu 11: Gọi
,ab
là các số thực lớn hơn 1 sao cho biểu thức
( )
3
3
log log
b
a
T ba= +
đạt giá trị nhỏ nhất.
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 19
Sưu tầm và biên soạn
Tính giá trị của biểu thức
4
log
a
P ab=
bằng
Câu 12: Cho
, ab
là hai số thực dương thỏa mãn
2
2
log ( . )
3
43
ab
a=
. Giá trị của
2
ab
bằng
Câu 13: Với mọi số thực
a
dương thoả mãn
3
log 5a =
. Khi đó
( )
3
log 3a
bằng
Câu 14: Cho
2
log 3 a=
. Hãy tính
9
log 2
theo
a
.
Câu 15: Biết
2
log 3a =
,
3
log 5b =
. Tính
2
log 5
theo
a
và
b
Câu 16: Cho
,xy
là hai số thực dương,
1x ≠
thỏa mãn
25
25
log ,log .
52
x
y
yx
y
= =
Tính giá trị của
22
2.Py x= −
Câu 17: Cho , Khi đó bằng:
Câu 18: Tính
81
log 25
theo
5
log 3 b=
:
Câu 19: Với mọi số
,ab
thỏa mãn:
log 3
a
b =
. Tính giá trị của biểu thức
( )
32
log
a
ab
Câu 20: Cho
35
log 5 ;log 7ab= =
, khi đó
45
log 175
bằng.
Câu 21: Cho hai số dương
,, 1aba≠
, thỏa mãn
2
2
log log 2
a
a
bb+=
. Tính
log
a
b
.
Câu 22: Cho
2
log 3 a=
. Giá trị của biểu thức
6
log 12P =
bằng
Câu 23: Cho
73
log 5, log 5ab= =
. Biểu thức
21
log 5M =
bằng
Câu 24: Cho số thực dương
,ab
thỏa mãn
16 20 25
2
log log log
3
ab
ab
−
= =
. Tỉ số
a
b
thuộc khoảng nào sau
đây?
Câu 25: Cho biết
2
log 5a =
và
5
log 7.b =
Tính
3
5
49
log
8
theo
a
và
.b
Câu 26: Đặt
2
log 3a =
, khi đó
6
log 72
bằng
Câu 27: Biết
x
và
y
là hai số thực thỏa mãn
( )
496
log log log 2x y xy= = −
. Giá trị của
x
y
bằng
Câu 28: Cho
942
log 5 ,log 7 , log 3abc= = =
. Biết
24
log 175
mb nac
pc q
+
=
+
với
,, ,mn pq∈
và
q
là số
nguyên tố. Tính
A mnpq=
.
Câu 29: Cho ba số thực dương
,,abc
đều khác
1
thoả mãn
log 2log 4log= =
abc
bca
và
2 3 48++=abc
. Khi đó
=P abc
bằng bao nhiêu?
Câu 30: Cho
a
và
b
là hai số thực dương thỏa mãn
2
9ab =
. Giá trị của biểu thức
33
log 2logab+
bằng
Câu 31: Cho
,ab
là các số thực dương và
a
khác
1
, thỏa mãn
2
3
5
3
log 3
a
a
b
=
. Giá trị của biểu thức
log
a
b
bằng
Câu 32: Cho
log 2, log 3
ab
xx= =
với
,ab
là các số thực lớn hơn 1. Tính
2
log
a
b
Px=
?
Câu 33: Cho
,,0,1abc a>≠
và
log 2022
a
b =
. Tính
6
7
6
4
log . .
a
ab
2
log 3 a=
2
log 5 .b=
15
log 8

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 20
Sưu tầm và biên soạn
Câu 34: Cho
25
log 7a =
;
2
log 5b =
. Tính
5
49
log
8
theo
a
,
b
.
Câu 35: Cho
, ab
là các số thực dương khác
1
thỏa mãn
log 3.=
a
b
Giá trị của
3
log
b
a
b
a
là
Câu 36: Cho
a,b
là các số thực dương lớn hơn
1
thỏa mãn
log 3
a
b =
. Tính gái trị biểu thức
22
3
4
log 3log 2.log
ab a
a
Pa
b
= −
.
Câu 37: Cho
a
và
b
là hai số thực dương thỏa mãn
32
32ab =
. Giá trị của
22
3log 2logab+
bằng
Câu 38: Tính giá trị biểu thức:
2 3 2021
11 1
...
log 2021! log 2021! log 2021!
P = + ++
Câu 39: Cho các số dương
,ab
khác
1
sao cho
2
39
16
log log log 2
b
a
ab= =
. Tính giá trị của biểu thức
3
b
a
:
Câu 40: Cho
,xy
là hai số thực dương,
1x ≠
thỏa mãn
25
25
log ,log .
52
x
y
yx
y
= =
Tính giá trị của
22
2.Py x= −
Câu 41: Cho các số thực dương
1, 1xy≠≠
thỏa mãn
2
log log 16
y
x =
và tích
64xy =
. Tính giá trị của
biểu thức
2
2
log
y
x
Câu 42: Cho các số thực
,ab
thỏa mãn
1ab>>
và
11
2022.
log log
ba
ab
+=
Tính giá trị của biểu thức
11
.
log log
ab ab
P
ba
= −
Câu 43: Cho ba số thực dương theo thứ tự lập thành một cấp số nhân và . Tính giá
trị của biểu thức
Câu 44: Cho là ba số thực dương khác và . Biết . Khi
đó giá trị của bằng bao nhiêu?
,,abc
64abc++=
( ) ( )
22
3log logP ab bc ca abc= ++ −
,,ab c
1
1abc ≠
10
log 5 3,log 5 4,log 5
17
a b abc
= = =
log 5
c

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 1
Sưu tầm và biên soạn
BÀI 2: PHÉP TÍNH LOGARIT
1. KHÁI NIỆM LOGARIT
Cho hai số thực dương
,ab
với
1a ≠
. Số thực
α
để
ab
α
=
được gọi là logarit cơ số
a
của
b
và kí hiệu là
log
a
b
, nghĩa là
log .
a
bab
α
α
= ⇔=
Chú ý:
Không có logarit của số
0
và số âm vì
0, a
α
α
>∀
.
log
a
b
xác định
0
1
0
a
a
b
>
⇔≠
>
Theo định nghĩa của logarit, ta có:
1) log 1 0
2) log 1
a
a
a
=
=
.
3) log
a
b
ab=
.
log
4)
a
b
ab=
.
2. TÍNH LOGARIT BẰNG MÁY TÍNH CẦM TAY
3. TÍNH CHẤT CỦA PHÉP TÍNH LOGARIT
Với
;, ;
a MN
α
<≠ > ∈ 01 0
, khi đó:
( )
)log . log log
)log log log
)log .log
a aa
a aa
aa
MN M N
M
MN
N
MM
α
α
= +
= −
=
1
2
3
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
LÝ THUYẾT.
I

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 2
Sưu tầm và biên soạn
4. CÔNG THỨC ĐỔI CƠ SỐ
Câu 1: Tính
( )
2
log 243
5
8
Lời giải
Ta có:
( )
( )
5
2
2
22
1
log 243
.log 3
3
log 3 log 3
3
5
5
8 8 8 2 3 27= = = = =
Câu 2: Cho số thực
01a<≠
. Tính giá trị của biểu thức
( )
2
3
log
a
aa
.
Lời giải
( )
11
22
17
22
3
33
7
14
3
log lo
g .
log
1
3
2
a
aa
a a aa a
= = = =
.
Câu 3: Cho
0a >
,
1a ≠
. Tính giá trị của biểu thức
3
3
1
log
a
P
a
=
.
Lời giải
Tự luận :
1
3
3
3
3
1
log log 9log 9
a
a
a
P aa
a
−
= = =−=−
.
Trắc nghiệm : Sử dụng máy tính, thay rồi nhập biểu thức vào máy
bấm = ta được kết quả .
Câu 4: Xét các số thực dương
,ab
thỏa mãn
5
log 5a =
và
3
2
log
3
b =
. Tính giá trị biểu thức
( )
3
65 1
9
2log log 5 logI ab= +
.
Lời giải
2a =
3
3
1
log
a
a
9P = −
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 3
Sưu tầm và biên soạn
Ta có:
( ) ( )
3
65 1 6 5 3
9
3
2log log 5 log 2log 1 log log
2
I ab a b= + = +−
6
32
2log 6 . 2 1 1
23
= − = −=
.
Câu 5: Cho số thực dương
a
khác
1
. Tính giá trị của biểu thức
( )
2
log 4a
Lời giải
Ta có
( )
2 22 2
log 4 log 4 log 2 loga aa=+=+
.
Câu 6: Tính giá trị của biểu thức
3
36
log log
a
a
Pb b= +
trong đó
,ab
là các số thực dương tùy ý và
1a ≠
.
Lời giải
Ta có:
3
36
1
log log 3log 6. log 5.log
3
a a aa
a
Pb b b b b=+=+ =
.
Câu 7: Tính giá trị của biểu thức
2
3
log 8 log 9P = +
Lời giải
Ta có
1
2
32
2 2 23
3
3
log 8 log 9 log 2 log 3 3log 2 4log 3 3 4 7P
= + = + = + =+=
.
Câu 8: Cho
log 3, log 4.
a
a
bc
= = −
Khi đó, tính giá trị của biểu thức
3
2
log
a
ac
P
b
=
?
Lời giải
1
3
3 23 2
2
2
log log log log log log log 2log
1
3
2
a a a aaa a a
ac
P ac b a c b c b
b
==− −−
+
= = +
( )
4 2.3 5
1
3
2
−−+ = −=
.
Câu 9: Cho các số thực
,ab
thỏa mãn
1ab>>
và
11
2022.
log log
ba
ab
+=
Tính giá trị của biểu thức
11
.
log log
ab ab
P
ba
= −
Lời giải
11
2022 log log 2022 (*).
log log
ab
ba
ba
ab
+ = ⇔+=
11
log ( ) log ( ) log log .
log log
b a ba
ab ab
P ab ab a b
ba
=−= − =−
Đặt
log
a
tb=
thì
(*)
trở thành:

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 4
Sưu tầm và biên soạn
2
2022 2018 1
2018
1
2
2022 2022 1 0 .
2022 2018 1
2018
2
t Pt
t
t tt
t
t Pt
t
+
= ⇒ = −=−
+ = ⇔ − += ⇔
−
= ⇒ = −=
1 0 log 1
a
ab b> >⇔ < <
nên
11
0 1 1 0 2018.t Pt P
tt
<<⇒ >⇒ =−> ⇒ =
Câu 10: Cho các số thực dương
1, 1xy≠≠
thỏa mãn
2
log log 16
y
x =
và tích
64xy =
. Tính giá trị của
biểu thức
2
2
log
y
x
Lời giải
Đặt
2
log log 16
y
xt
= =
. Suy ra
4
2
2
2
2
2
4
4log 2
log
log 2
2
4
t
t
t
t
t
y
y
x
x
x
x
t
t
y
y
t
=
=
=
=
⇔⇔⇔
=
=
=
=
.
Ta có
4
6
4
64 2 .2 2 6
t
t
xy t
t
= ⇔ = ⇔+ =
.
Ta có
( )
2 22
2
22
2 22
2
4 16 4
log log log 8 16 6 16 20
y
y x t tt
x tt t
= − = − = −+=+ −=−=
.
Câu 11: Gọi
,ab
là các số thực lớn hơn 1 sao cho biểu thức
(
)
3
3
log log
b
a
T ba
= +
đạt giá trị nhỏ nhất.
Tính giá trị của biểu thức
4
log
a
P ab=
bằng
Lời giải
Do
,ab
lớn hơn 1 nên
log 0
a
b >
. Khi đó:
( )
3
3
3
111
log log 27 log
3log 3log 3log
ba
a
aaa
T ba b
bbb
= += +++
Do đó
3
4
111
4 27 log . . . 4
3log 3log 3log
a
aaa
Tb
bbb
≥=
.
Dấu bằng xảy ra khi
3
1
log
3
a
b ab=⇔=
Khi đó
3
4
2
log log
3
a
b
P ab b= = =
.
Câu 12: Cho
,
ab
là hai số thực dương thỏa mãn
2
2
log ( . )
3
43
ab
a=
. Giá trị của
2
ab
bằng
Lời giải
Ta có
( )
2
2
2
log ( . )
32 3 2
4 3 .3 3
ab
a a b a ab=⇔ =⇔=
.
Câu 13: Với mọi số thực
a
dương thoả mãn
3
log 5a =
. Khi đó
( )
3
log 3a
bằng
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 5
Sưu tầm và biên soạn
( )
3 33 3
log 3 log 3 log 1 log 6a aa=+=+=
.
Câu 14: Cho
2
log 3 a=
. Hãy tính
9
log 2
theo
a
.
Lời giải
Ta có:
2
93
3
2
1 11
log 2 log log 2
2 2log 3 2
a
a
= = = =
.
Câu 15: Biết
2
log 3a =
,
3
log 5b =
. Tính
2
log 5
theo
a
và
b
Lời giải
Ta có
2 23
log 5 log 3.log 5 ab= =
.
Câu 16: Cho
,xy
là hai số thực dương,
1x ≠
thỏa mãn
25
25
log ,log .
52
x
y
yx
y
= =
Tính giá trị của
22
2.Py x= −
Lời giải
Ta có:
2
2
25
25
25
2
2
log
25
5
log
5
5
5
5
1
5
log
25
log
log
log 25
2
2
2
5
x
x
x
y
y
y
y
y
y
y
x
yx
x
x
y
y
=
=
=
=
=
⇔ ⇔ ⇔⇔
=
=
=
=
=
Vậy
22
2 25.Py x=−=−
Câu 17: Cho , Khi đó bằng:
Lời giải
Ta có: .
Vậy .
Câu 18: Tính
81
log 25
theo
5
log 3 b=
:
Lời giải
Ta có
2
55
81
4
55
log 25 log 5
log 25
log 81 log 3
= =
.
5
21
4log 3 2b
= =
.
Câu 19: Với mọi số
,ab
thỏa mãn:
log 3
a
b =
. Tính giá trị của biểu thức
( )
32
log
a
ab
Lời giải
2
log 3 a=
2
log 5 .b=
15
log 8
( )
( )
3
15
8 22
2
22
11 1 3 3
log 8
1
log 15 log 3.5 log 3 log 5
log 3 log 5
3
ab
= = = = =
++
+
15
3
log 8
ab
=
+

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 6
Sưu tầm và biên soạn
Từ giả thiết:
log 3
a
b =
1
log 3
2
a
b
⇔=
log 6
a
b⇔=
.
Khi đó:
( )
32 3 2
log log log 3 2log 15
a aa a
ab a b b=+=+ =
.
Câu 20: Cho
35
log 5 ;log 7ab= =
, khi đó
45
log 175
bằng.
Lời giải
Ta có
2
5
45
2
55
log 5 .7
2 2 (2 )
log 175 .
2
log 3 .5 1 2log 3 2
1
b ba b
a
a
+ ++
= = = =
++
+
Câu 21: Cho hai số dương
,, 1aba≠
, thỏa mãn
2
2
log log 2
a
a
bb+=
. Tính
log
a
b
.
Lời giải
Ta có:
2
2
14
log log 2 log 2log 2 log
25
a aa a
a
bb b b b+ =⇔ + =⇔=
Câu 22: Cho
2
log 3
a=
. Giá trị của biểu thức
6
log 12P =
bằng
Lời giải
Ta có
( )
66 6
22
1 1 12
log 12 log 6.2 1 log 2 1 1 1
log 6 1 log 3 1 1
a
P
aa
+
= = =+ =+ =+ =+=
+ ++
.
Câu 23: Cho
73
log 5, log 5ab= =
. Biểu thức
21
log 5M =
bằng
Lời giải
Ta có
21
log 5M
=
5
1
log 21
=
55
1
log 3 log 7
=
+
37
1
11
log 5 log 5
=
+
73
73
1
log 5 log 5
log 5.log 5.
=
+
73
73
log 5.log 5
log 5 log 5.
=
+
ab
ab
=
+
.
Câu 24: Cho số thực dương
,ab
thỏa mãn
16 20 25
2
log log log
3
ab
ab
−
= =
. Tỉ số
a
b
thuộc khoảng nào sau
đây?
Lời giải
Đặt
16 20 25
16
2
log log log 20
3
2 3.25
x
x
x
a
ab
a b xb
ab
=
−
= = =⇔=
−=
Suy ra
16 25
2.16 20 3.25 2. 3. 1 0
20 20
xx
xx x
− = ⇔ − −=
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 7
Sưu tầm và biên soạn
2
4
1( )
5
4 5 44
2. 3. 1 0 2. 3 0
5 4 55
43
52
x
x x xx
x
PTVN
= −
⇔ − −= ⇔ − − = ⇔
=
Vậy
( )
16 4 3
1; 2
20 5 2
x
x
x
a
b
= = = ∈
Câu 25: Cho biết
2
log 5a =
và
5
log 7.b =
Tính
3
5
49
log
8
theo
a
và
.b
Lời giải
Ta có
3
5 55
5
49 49 9 3
log 3log 6log 7 9log 2 6 3 2 .
88
bb
aa
= = − = −= −
Câu 26: Đặt
2
log 3a =
, khi đó
6
log 72
bằng
Lời giải
Ta có
( )
(
)
32
2
2 22
6
2 2 22
log 2 .3
log 72 3log 2 2log 3
23
log 72
log 6 log 2.3 log 2 log 3 1
a
a
+
+
= = = =
++
.
Vậy
6
23
log 72
1
+
=
+
a
a
.
Câu 27: Biết
x
và
y
là hai số thực thỏa mãn
( )
496
log log log 2x y xy= = −
. Giá trị của
x
y
bằng
Lời giải
Đặt
( )
2
496
4
2
log log log 2 9
3
26
t
t
t
t
x
x
x y x yt y
y
xy
=
= = − =⇒ = ⇒=
−=
Khi đó:
( )
2
2
1
3
22
4 2.9 6 2 0
33
2
2
3
t
tt
t tt
t
loai
= −
− = ⇔ − −=⇔
=
.
Suy ra
2
2
2
2 4.
3
t
x
y
= = =
Câu 28: Cho
942
log 5 ,log 7 , log 3abc= = =
. Biết
24
log 175
mb nac
pc q
+
=
+
với
,, ,mn pq∈
và
q
là số
nguyên tố. Tính
A mnpq=
.
Lời giải
Ta có
3 33
22
24
2 .3 2 .3 2 .3
log 175 log 5 .7 log 5 log 7= = +

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 8
Sưu tầm và biên soạn
33
5 7 55 77
21 2 1
log 2 .3 log 2 .3 3.log 2 log 3 3log 2 log 3
=+= +
++
Theo giả thiết ta có:
7
93
42 5
2
5
log 3
2
log 5 log 5 2
1
log 7 log 7 2 log 3
2
log 3
1
log 2
2
c
b
aa
bb
a
c
ac
=
=⇒=
=⇒=⇒ =
=
=
.
Suy ra:
24
2 1 2 1 4 2 42
log 175
313 3 3
33 3
2 2 22 2 2
ac b ac b
c cc
c cc
ac a b b ac b
+
= + = + =+=
++
++ +
++
.
Vậy ta có:
2
4
24
1
3
m
n
mnpq
p
q
=
=
⇒=
=
=
.
Câu 29: Cho ba số thực dương
,,abc
đều khác
1
thoả mãn
log 2log 4log= =
abc
bca
và
2 3 48++=abc
. Khi đó
=P abc
bằng bao nhiêu?
Lời giải
Do
,,abc
đều khác
1
nên
log , log , log
abc
bca
đều khác
0
.
Ta có:
2
log 2log log .log 2log log 2log
a bac ba b
bccbccc
= ⇔ = ⇔=
.
2
log 4log log .log 4 log log 4log
= ⇔ = ⇔=
acacccc
bacbaba
.
Nên
22
log .log 8log .log
ac bc
cb ca=
2
log 8log
ab
ba⇔=
3
log 8
a
b⇔=
2
log 2
a
b ba⇔ =⇔=
.
Mà
2
log 2log log 2log
= ⇔ = ⇔=
a ba
a
b c b c bc
.
Ta lại có
2 3 48abc++=
22
2 3 48aa a⇔++=
2
5 48 0aa⇔ +− =
16
5
3
a
a
= −
⇔
=
.
Do
,,abc
đều là số thực dương nên
39a bc=⇒==
.
Vậy
243P abc= =
.
Câu 30: Cho
a
và
b
là hai số thực dương thỏa mãn
2
9ab =
. Giá trị của biểu thức
33
log 2 logab+
bằng
Lời giải
Ta có
( )
22
3 33 2
9 log log 9 log 2log 2ab ab a b=⇒ =⇒+ =
.
Câu 31: Cho
,ab
là các số thực dương và
a
khác
1
, thỏa mãn
2
3
5
3
log 3
a
a
b
=
. Giá trị của biểu thức
log
a
b
bằng
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 9
Sưu tầm và biên soạn
Ta có
2
3
5
3
log 3
a
a
b
=
3
3
5
13
log log 3 3 log 6
25
aa a
ab b
⇔ − =⇔− =
log 5
a
b⇔=−
.
Câu 32: Cho
log 2, log 3
ab
xx= =
với
,ab
là các số thực lớn hơn 1. Tính
2
log
a
b
Px=
?
Lời giải
Với
,ab
là các số thực lớn hơn 1 và
0, 1xx>≠
, ta có:
2
2
11
log
log 2log
log
a
xx
b
x
Px
a
ab
b
= = =
−
11
6.
1 2 12
log log 2 3
ab
P
xx
⇔= = =−
−−
Câu 33: Cho
,,0,1abc a>≠
và
log 2022
a
b =
. Tính
6
7
6
4
log . .
a
ab
Lời giải
Ta có:
6 66
77
66
44
7 21
log . log log 6. 2022 2022.
42
a aa
ab a b
= + =+=+
Câu 34: Cho
25
log 7a =
;
2
log 5b =
. Tính
5
49
log
8
theo
a
,
b
.
Lời giải
Ta có:
2
25 5 5
5
1
log 7 log 7 log 7 log 7 2
2
aa= = = ⇒=
và
25
1
log 5 log 2b
b
=⇒=
23
5 5 55 5 5 5
49 1 4 3
log log 49 log 8 log 7 log 2 2log 7 3log 2 2.2 3.
8
ab
a
bb
−
= − = − = − = −=
Câu 35: Cho
, ab
là các số thực dương khác
1
thỏa mãn
log 3.=
a
b
Giá trị của
3
log
b
a
b
a
là
Lời giải
Ta có:
3
log 3= ⇔= ⇒
a
b ba
3
2
3
3
3
1
2
31
1
32
log log .
33
1
2
−
= = = −
−
b
a
a
a
ba
a
a
Câu 36: Cho
a,b
là các số thực dương lớn hơn
1
thỏa mãn
log 3
a
b =
. Tính gái trị biểu thức
22
3
4
log 3log 2.log
ab a
a
Pa
b
= −
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 10
Sưu tầm và biên soạn
Lời giải
Ta có:
3
log 3
a
b ba=⇔=
2 2 52
33
44
3
log 3log 2.log log 3log 2.log
ab a a a
aa
Pa a
ba
=−=−
2
2
2
31 1
3. .log 2.log
52
a
a
= −
.
2
22
3 1 1 33 33 21
3. .log 2. .log .log 2.log
5 2 2 52 5210
aa
aa
−
=− =+ =+=
.
Câu 37: Cho
a
và
b
là hai số thực dương thỏa mãn
32
32ab =
. Giá trị của
22
3log 2 logab+
bằng
Lời giải
32 32 3 2
2 2 22 2 2
32 log ( ) log 32 log log 5 3log 2log 5.ab ab a b a b=⇔ =⇔+=⇔ + =
Câu 38: Tính giá trị biểu thức:
2 3 2021
11 1
...
log 2021! log 2021! log 2021!
P
= + ++
Lời giải
Ta có:
2 3 2021
11 1
...
log 2021! log 2021! log 2021!
P
= + ++
2021! 2021! 2021!
log 2 log 3 ...log 2021P⇔= + +
2021! 2021!
log 2.3...2021 log 2021! 1P⇔= = =
Câu 39: Cho các số dương
,ab
khác
1
sao cho
2
39
16
log log log 2
b
a
ab
= =
. Tính giá trị của biểu thức
3
b
a
:
Lời giải
Đặt
2
39
16
log log log 2
b
a
ab t= = =
2
3
3
3
18 54
54
16
16
16
2
2 16
t
t
tt
t
t
a
a
ba b
b
=
=
⇔= ⇔=
=
=
( )
*
.
Từ
( )
*
suy ra
3
216 3
1
2 2 216 1
6
t
tt= ⇔ =⇔=
. Suy ra
3
3
4, 4 1
b
ab
a
= =⇒=
.
Câu 40: Cho
,xy
là hai số thực dương,
1x ≠
thỏa mãn
25
25
log ,log .
52
x
y
yx
y
= =
Tính giá trị của
22
2.Py x
= −
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 11
Sưu tầm và biên soạn
Ta có:
2
2
25
25
25
2
2
log
25
5
log
5
5
5
5
1
5
log
25
log
log
log 25
2
2
2
5
x
x
x
y
y
y
y
y
y
y
x
yx
x
x
y
y
=
=
=
=
=
⇔ ⇔ ⇔⇔
=
=
=
=
=
Vậy
22
2 25.Py x=−=−
Câu 41: Cho các số thực dương
1, 1xy≠≠
thỏa mãn
2
log log 16
y
x =
và tích
64xy =
. Tính giá trị của
biểu thức
2
2
log
y
x
Lời giải
Đặt
2
log log 16
y
xt= =
. Suy ra
4
2
2
2
2
2
4
4log 2
log
log 2
2
4
t
t
t
t
t
y
y
x
x
x
x
t
t
y
y
t
=
=
=
=
⇔⇔⇔
=
=
=
=
.
Ta có
4
6
4
64 2 .2 2 6
t
t
xy t
t
= ⇔ = ⇔+ =
.
Ta có
( )
2 22
2
22
2 22
2
4 16 4
log log log 8 16 6 16 20
y
y x t tt
x tt t
= − = − = −+=+ −=−=
.
Câu 42: Cho các số thực
,ab
thỏa mãn
1ab>>
và
11
2022.
log log
ba
ab
+=
Tính giá trị của biểu thức
11
.
log log
ab ab
P
ba
= −
Lời giải
11
2022 log log 2022 (*).
log log
ab
ba
ba
ab
+ = ⇔+=
11
log ( ) log ( ) log log .
log log
b a ba
ab ab
P ab ab a b
ba
=−= − =−
Đặt
log
a
tb=
thì
(*)
trở thành:
2
2022 2018 1
2018
1
2
2022 2022 1 0 .
2022 2018 1
2018
2
t Pt
t
t tt
t
t Pt
t
+
= ⇒
= −=
−
+ = ⇔ − += ⇔
−
= ⇒
= −=
1 0 log 1
a
ab b> >⇔ < <
nên
11
0 1 1 0 2018.t
Pt P
tt
<<⇒ >⇒ =−> ⇒ =
Câu 43: Cho ba số thực dương theo thứ tự lập thành một cấp số nhân và . Tính giá
trị của biểu thức
,,abc
64abc++=
( ) ( )
22
3log logP ab bc ca abc= ++ −

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 12
Sưu tầm và biên soạn
Lời giải
Ta có: theo thứ tự lập thành một cấp số nhân .
.
Câu 44: Cho là ba số thực dương khác và . Biết . Khi
đó giá trị của bằng bao nhiêu?
Lời giải
Ta có
Khi đó:
Vậy: .
,,abc
2
ac b⇒=
( ) ( )
22
3log logP ab bc ca abc= ++ −
( ) ( )
22
22
3log log .ab bc b b b= ++ −
( )
( )
3
22
3log logbabc b= ++ −
( )
3
22
3log 64 logbb= −
( )
( )
3
3
22
log 64 logbb= −
( )
3
6
2
3
2.
log
b
b
=
18 3
2
3
2.
log
b
b
=
18
2
log 2 18= =
,,ab c
1
1abc ≠
10
log 5 3,log 5 4,log 5
17
a b abc
= = =
log 5
c
5
1
log 5 3 log .
3
a
a=⇒=
5
1
log 5 4 log .
4
b
b=⇒=
5
10 17
log 5 log .
17 10
abc
abc=⇒=
5 555 5 5 55
17 1 1 67
log log log log log log log log
10 3 4 60
abc a b c c abc a b=++⇒= −−=−−=
60
log 5
67
c
=
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 21
Sưu tầm và biên soạn
BÀI 2: LOGARIT
Câu 1: Cho
,,abc
là các số thực dương và
,1ab≠
. Khẳng định nào sau đây là sai?
A.
log .log 1
ab
ba=
. B.
log log
ac
ca= −
. C.
log
log
log
b
a
b
c
c
a
=
. D.
log log .log
a ab
c bc=
.
Câu 2: Cho
0 1, 0
<≠ >ax
. Mệnh đề nào sau đây là sai?
A.
log 1=
a
a
. B.
log =
x
a
ax
. C.
log 1 0=
a
. D.
log
=
a
x
xx
.
Câu 3: Cho ba số thực dương
,,abc
và
1a ≠
. Khẳng định nào sau đây là sai?
A.
(
)
log log log
a aa
bc b c= +
. B.
log
a
b
ab=
.
C.
log log
aa
bb
α
α
=
. D.
ln
log
ln
a
a
b
b
=
.
Câu 4: Cho
a
,
b
là các số thực dương tùy ý. Khẳng định nào sau đây là đúng?
A.
( )
ln ln lnab a b= +
. B.
( )
ln ln lnab a b+= +
.
C.
( )
ln ln .lnab a b
=
. D.
( )
ln ln .lnab a b+=
.
Câu 5: Cho
a
là số thực dương khác 1. Mệnh đề nào sau đây đúng với mọi số thực dương
,?xy
A.
log log log
a aa
x
xy
y
= +
. B.
( )
log log
aa
x
xy
y
= −
.
C.
log log log
a aa
x
xy
y
= −
. D.
log
log
log
a
a
a
x
x
yy
=
.
Câu 6: Có bao nhiêu số thực dương
1n ≠
để
log 265
n
là một số nguyên?
A.
2
. B.
4
. C.
6
. D.
8
.
Câu 7: Cho ba số thực dương
,,abc
đều khác
1
thoả mãn
log 2log 4 log= =
abc
bca
và
2 3 48++=abc
. Khi đó
=P abc
bằng bao nhiêu?
A.
243
. B.
521
. C.
512
. D.
324
.
Câu 8: Giá trị của biểu thức
log 3
2
4
bằng
A.
3
. B.
3
. C.
3
2
. D.
23
.
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 22
Sưu tầm và biên soạn
Câu 9: Giá trị của
2
1
log
16
bằng
A.
4.
B.
1
.
4
C.
1
.
8
D.
4.
Câu 10: Với mọi
,
ab
dương thỏa mãn
22
log log 3
ab
−=
, khẳng định nào dưới đây đúng?
A.
2
64ab=
. B.
2
64ab =
. C.
8ab
−=
. D.
3
a
b
=
.
Câu 11: Cho
0
>a
và
1
≠a
, khi đó
5
log
a
a
bằng
A.
1
5
. B.
5−
. C. 5. D.
1
5
−
.
Câu 12: Cho
0a >
và
1a ≠
, khi đó
2021
2022
log
a
a
bằng
A.
2021
. B.
2022
2021
. C.
2021
2022
. D.
2022
.
Câu 13: Cho
0
a
>
và
1a ≠
, khi đó
3
log
a
a
bằng
A.
1
3
−
. B.
3
. C.
3−
. D.
1
3
.
Câu 14: Với
a
là số dương tùy ý khác 1,
log
a
a
bằng
A.
1
2
. B.
2a
. C.
2
. D.
1
2
a
.
Câu 15: Với mọi số thực
a
dương khác 1,
3
log
a
a
bằng
A.
1
3
. B.
3
. C.
3−
. D.
0
.
Câu 16: Với mọi số thực
a
dương,
4
4
log
a
bằng
A.
4
. B.
4
4log a
. C.
4
1
log
4
a
. D.
1
4
.
Câu 17: Cho
a
là số thực dương khác
2
. Tính
2
2
log
4
a
a
I
=
.
A.
1
2
I =
. B.
1
2
I = −
. C.
2I =
. D.
2I = −
.
Câu 18: Cho
a
là số thực dương khác
5
. Tính
3
5
log
125
a
a
I
=
.
A.
1
3
I
. B.
3I
. C.
1
3
I
. D.
3I
.
Câu 19: Với
a
là số thực dương tùy ý,
( )
4
log 4a
bằng
A.
4
1 log a−
. B.
4
1 log a+
. C.
4
4 log a−
. D.
4
4 log a+
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 23
Sưu tầm và biên soạn
Câu 20: Với
,
ab
là hai số dương tùy ý thì
( )
32
log ab
có giá trị bằng biểu thức nào sau đây?
A.
1
3log log
2
ab
+
. B.
2log 3logab+
. C.
3log 2logab+
. D.
1
3 log log
2
ab
+
.
Câu 21: Tính giá trị của biểu thức
( )
2
log
2 log
a
b
a
Pa= +
( )
0, 1aa>≠
.
A.
2
a
Pb
= +
. B.
P ab= −
. C.
2P ab= +
. D.
P ab
= +
.
Câu 22: Cho
0, 1aa>≠
, biểu thức
3
log
a
Da=
có giá trị bằng bao nhiêu?
A.
1
3
. B.
3
. C.
1
3
−
. D.
3−
.
Câu 23: Cho hàm số
2
( ) log
fx x
=
. Với
0x >
, giá trị của biểu thức
68
3
x
Pf f
x
= +
bằng
A.
2P =
. B.
1
P =
. C.
4P =
. D.
3P =
.
Câu 24: Giá trị của
3
1
log
a
a
với
0
a
>
và
1a ≠
bằng
A.
3
2
−
. B.
3
2
. C.
2
3
−
. D.
2
3
.
Câu 25: Với
a
là số thực dương bất kỳ, mệnh đề nào dưới đây đúng?
A.
4
ln 4lnaa=
. B.
(
)
ln 4 4lnaa
=
. C.
( )
1
ln 4 ln
4
aa=
. D.
3
1
ln ln
3
aa=
.
Câu 26: Cho
,ab
là các số thực dương và
a
khác
1
, thỏa mãn
2
3
5
3
log 3
a
a
b
=
. Giá trị của biểu thức
log
a
b
bằng
A.
5.
−
B.
5.
C.
1
.
5
D.
1
.
5
−
Câu 27: Cho
25
log 5 ;log 3ab= =
. Tinh
5
log 24
theo
a
và
b
.
A.
5
3
log 24
ab
b
+
=
. B.
5
3
log 24
ab
a
+
=
. C.
5
3
log 24
ab
a
+
=
. D.
5
log 24
3
ab
ab
+
=
.
Câu 28: Cho
log 3,log 4
ab
xx
= =
với
,ab
là các số thực lớn hơn
1
. Tính
log
ab
Px=
.
A.
12
P =
. B.
7
12
P =
. C.
1
12
P =
. D.
12
7
.
Câu 29: Với các số thực dương
a
,
b
bất kì. Mệnh đề nào dưới đây đúng
A.
3
2 22
2
log 1 3log log
=+−
a
ab
b
. B.
3
2 22
21
log 1 log log
3
=+−
a
ab
b
.
C.
3
2 22
2
log 1 3log log
=++
a
ab
b
. C.
3
2 22
21
log 1 log log
3
=++
a
ab
b
.
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 24
Sưu tầm và biên soạn
Câu 30: Cho
2
log 5x =
. Giá trị của biểu thức
2
log
x
Px=
bằng
A.
15P = +
. B.
5
51
P
=
+
. C.
1
5
. D.
5
15+
.
Câu 31: Cho các số thực dương
a
và
b
thỏa mãn
2
16 0ab−=
. Tính giá trị của biểu thức
2
2
log logP ab= −
.
A.
2P =
. B.
4P =
. C.
16
P =
. D.
2P
=
.
Câu 32: Cho
0a
và
1a
. Khi đó
2
log
a
a
bằng
A.
1
. B.
1
4
. C. 4. D.
2
.
Câu 33: Cho
a
và
b
là hai số thực dương thỏa mãn
25
64ab =
. Giá trị của
22
2log 5logP ab= +
là
A.
7
P =
. B.
64P =
. C.
6P =
. D.
2P =
.
Câu 34: Cho
,
xy
là các số thực lớn hơn
1
thỏa mãn
22
96x y xy+=
. Tính
(
)
12 12
12
1 log log
2log 3
xy
M
xy
++
=
+
.
A.
1
4
M =
. B.
1
2
M =
. C.
1
3
M =
. D.
1M =
.
Câu 35: Cho
0a >
và
1a ≠
, khi đó
( )
log 2
3
a
a
bằng
A.
64
. B.
8
. C.
12
. D.
23
.
Câu 36: Cho
,ab
là các số thực dương
( , 1)≠ab
và
log 16
a
b =
. Tính giá trị của biểu thức
log
a
P b=
.
A.
256
. B.
4
. C.
23
. D.
8
.
Câu 37: Cho
,,0,1abc a>≠
và
log 2022
a
b =
. Tính
6
7
6
4
log . .
a
ab
A.
2022
42
6
+
. B.
7
6 2022
4
+
. C.
21
2022
2
+
. D.
2
2022
21
+
.
Câu 38: Cho
25
log 7a =
;
2
log 5b =
. Tính
5
49
log
8
theo
a
,
b
.
A.
43a
b
−
. B.
43ab
b
+
. C.
53ab
b
−
. D.
43ab
b
−
.
Câu 39: Cho
,
ab
là các số thực dương khác
1
thỏa mãn
log 3.=
a
b
Giá trị của
3
log
b
a
b
a
là
A.
3.−
B.
2 3.−
C.
3.
D.
1
.
3
−
Câu 40: Cho
a
,
b
là các số thực dương thỏa mãn
log 2
a
b =
. Tính giá trị của biểu thức
( )
3
log .
a
b
P ab=
.
A.
2
15
P =
. B.
2
9
P = −
. C.
10
9
P = −
. D.
2
3
P =
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 25
Sưu tầm và biên soạn
Câu 41: Cho
log 2;log 3
aa
bc
= =
. Tính
( )
3
log
a
Q bc=
.
A.
4Q
=
. B.
9Q =
. C.
10Q =
. D.
12Q
=
.
Câu 42: Cho
log 2
=
a
x
,
log 3
=
b
x
với
a
,
b
là các số thực lớn hơn
1
. Tính
2
log=
a
b
Px
.
A.
6
. B.
6−
. C.
1
6
. D.
1
6
−
.
Câu 43: Cho các số thực dương
a
,
b
thỏa mãn
3log 2 log 1ab+=
. Mệnh đề nào sau đây đúng?
A.
32
1
ab+=
. B.
3 2 10ab
+=
. C.
32
10ab =
. D.
32
10ab+=
.
Câu 44: Cho
,,abc
là các số thực dương, trong đó
,1ab
>
và thỏa mãn
log 3,
a
c =
log 4
b
c =
. Tính giá
trị biểu thức
log ?
ab
Pc=
A.
12
.
7
P =
B.
7
.
12
P =
C.
1
.
12
P =
D.
12.P =
Câu 45: Cho
,ab
là các số thực dương lớn hơn
1
thỏa mãn
log 3
a
b =
.Tính giá trị biểu thức
22
3
4
log 3log 2.log
ab a
a
Pa
b
= −
.
A.
21
10
P =
. B.
7
5
P =
. C.
18
25
P =
. D.
15
8
P =
.
Câu 46: Cho
log 2
a
b =
với
a
,
b
là các số thực dương và
a
khác
1
. Giá trị biểu thức
2
6
log log
a
a
Tb b= +
bằng
A.
8
. B.
7
. C.
5
. D.
6
.
Câu 47: Cho
a,b
là các số thực dương lớn hơn
1
thỏa mãn
log 3
a
b
=
. Tính gái trị biểu thức
22
3
4
log 3log 2.log
ab a
a
Pa
b
= −
.
A.
15
8
P =
. B.
18
25
P =
. C.
21
10
P =
. D.
7
5
P =
.
Câu 48: Cho
,ab
là các số thực dương và
1a ≠
thoả mãn
( )
2
1
log
2
a
ab =
. Giá trị của
2
log
a
b
bằng
A.
3
4
−
. B.
3
2
−
. C.
3−
. D.
3
4
.
Câu 49: Với mọi
,ab
thỏa mãn
( )
23
33
log 3 log 4ab
+=
, khẳng định nào dưới đây đúng?
A.
23
81ab =
. B.
33
1 81ab+ +=
. C.
23
27ab
=
. D.
23
27ab+=
.
Câu 50: Cho số thực
0a >
;
1
1,
27
aa≠≠
và số thực
x
thỏa mãn
log 3
a
x=
. Tính
27
log 9
a
theo
x
.
A.
2
3
x
x +
. B.
2
31
x
x +
. C.
( )
23 1x +
. D.
2
31x +
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 26
Sưu tầm và biên soạn
Câu 51: Cho
a
,
b
là các số thực dương khác
1
thoả mãn
2
log 2a
=
và
4
log 3b
=
. Giá trị biểu thức
(
)
2
log
a
P ab=
bằng
A.
10
P
=
. B.
5P =
. C.
2P =
. D.
1P =
.
Câu 52: Cho
,ab
là các số thực dương và
a
khác
1
, thỏa mãn
3
4
5
log 2
a
a
b
=
. Giá trị của biểu thức
log
a
b
bằng
A.
4
. B.
1
4
. C.
1
4
−
. D.
4−
.
Câu 53: Cho
a
,
b
là các số thực dương thỏa mãn
log 2
a
b =
. Tính giá trị của biểu thức
( )
3
log .
a
b
P ab=
.
A.
2
15
P
=
. B.
2
9
P
= −
. C.
10
9
P = −
. D.
2
3
P
=
.
Câu 54: Cho các số dương
,
ab
khác
1
sao cho
2
39
16
log log log 2
b
a
ab= =
. Giá trị của
3
b
a
bằng:
A.
1
. B.
2
. C.
4
. D.
8
.
Câu 55: Giá trị của biểu thức
log 3
2
4
bằng
A.
3
. B.
3
. C.
3
2
. D.
23
.
Câu 56: Cho
10
5
2
3 27 243P =
. Tính
3
log P
.
A.
45
28
. B.
21
100
. C.
45
56
. D.
13
100
Câu 57: Cho
,xy
là hai số thực dương,
1x ≠
thỏa mãn
25
25
log , log .
52
x
y
yx
y
= =
Tính giá trị của
22
2.Py x= −
A.
1P =
. B.
0P =
. C.
25P = −
. D.
25
P =
.
Câu 58: Cho
,xy
là hai số thực dương,
1
x
≠
thỏa mãn
3
2
3 32
log ,log .
8
x
y
yx
y
= =
Tính giá trị của
22
Px y= −
.
A.
120
P =
. B.
132P =
. C.
240P
=
. D.
340P =
.
Câu 59: Có bao nhiêu số thực dương
1n ≠
để
log 265
n
là một số nguyên?
A.
2
. B.
4
. C.
6
. D.
8
.
Câu 60: Cho các số thực
,ab
thỏa mãn
1ab>>
và
11
2022.
log log
ba
ab
+=
Giá trị của biểu thức
11
.
log log
ab ab
P
ba
= −
A.
2018.
B.
2020.
C.
2016.
D.
2022.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 27
Sưu tầm và biên soạn
Câu 61: Với
,ab
là các số thực dương tùy ý và
1a ≠
. Ta có
( )
3
log
a
ab
bằng
A.
3.log
a
b
. B.
1
.log
3
a
b
. C.
1
log
3
a
b+
. D.
3 log
a
b+
.
Câu 62: Với
a
,
b
là hai số dương tùy ý,
(
)
23
log
ab
bằng:
A.
11
log log
23
ab+
. B.
2log log
ab+
. C.
2log 3logab+
. D.
log 3logab
+
.
Câu 63: Cho
0a >
,
1a ≠
, khi đó
( )
3
log .
a
aa
bằng
A.
4
. B.
4
3
. C.
4
3
−
. D.
1
3
.
Câu 64: Cho
0a
>
và
1a ≠
, khi đó
2
3
4
log
a
a
bằng
A.
3
8
−
. B.
3
4
. C.
3
8
. D.
3
2
.
Câu 65: Cho
a
là số thực dương,
1a
≠
, khi đó
log 5
a
a
bằng
A.
5
log a
. B.
log 5
a
. C.
5
a
. D.
5
.
Câu 66: Với
,ab
là hai số thực dương tùy ý, khi đó
( )
32
ln ea b
bằng:
A.
2ln 3lnab
+
. B.
3ln 2lnab+
. C.
1 3ln 2lnab++
. D.
1 6 ln .lnab+
.
Câu 67: Với
a
,
b
là các số thực dương bất kỳ,
2
4
log
a
b
bằng
A.
( )
22
log log 4ab−
. B.
2
1
log
4
a
b
. C.
2
2log
a
b
. D.
22
log 4logab−
.
Câu 68: Cho
a
là số thực dương. Khi đó
3
4
log 8a
bằng
A.
2
3
log
2
a
+
. B.
2
33
log
22
a+
. C.
2
2 3log a+
. D.
2
6 6log a+
.
Câu 69: Với mọi số thực
a
dương,
( )
5
log 5a
bằng
A.
5
1 log a
+
. B.
5
log
a
. C.
5
5log a
. D.
5
1 log a
−
.
Câu 70: Với
a
là số thực dương tùy ý,
( )
3
4
log a
bằng
A.
3
3log a
. B.
2
2
log
3
a
. C.
2
3
log
2
a
. D.
4
3 log a
+
.
Câu 71: Với mọi số thực
a
dương,
2
2
log
4
a
bằng
A.
( )
2
2 log 1a −
. B.
2
log 2a −
. C.
2
log 1a −
. D.
2
2log 1a −
.
Câu 72: Cho
0a >
và
1a ≠
, khi đó
3
log
a
a
bằng
A.
1
3
. B.
3
. C.
1
3
−
. D.
3−
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 28
Sưu tầm và biên soạn
Câu 73: Với mọi số thực
a
dương,
22
2
log a
bằng
A.
2
2
2log a
. B.
2
2
4log
a
. C.
2
2
2log a
. D.
2
4log
a
.
Câu 74: Với
,
ab
là các số thực dương tùy ý và
1≠a
,
3
log
a
b
A.
3 log+
a
b
. B.
3
log
a
b
. C.
1
3
log+
a
b
. D.
1
3
log
a
b
.
Câu 75: Với
a
là số thực dương tùy ý,
3
3
log
a
bằng
A.
3
1 log
−
a
. B.
3
3 log− a
. C.
3
1
log a
. D.
3
1 log
+
a
.
Câu 76: Với
a
là số thực dương tùy ý,
( )
5
log 5a
bằng
A.
5
5 log+ a
. B.
5
5 log− a
. C.
5
1 log+ a
. D.
5
1 log− a
.
Câu 77: Giả sử
,ab
là các số thực dương tùy ý thỏa mãn
23 4
4ab =
. Mệnh đề nào sau đây đúng?
A.
22
2log 3log 8ab+=
. B.
22
2log 3log 8ab−=
.
C.
22
2log 3log 4ab−=
. D.
22
2log 3log 4ab+=
.
Câu 78: Với
,ab
là hai số thực dương tùy ý,
(
)
3
3
log
ab
bằng
A.
33
1
log log
3
ab+
. B.
( )
33
3 log logab+
. C.
33
log 3logab+
. D.
33
3log logab+
.
Câu 79: Với
a
là số thực dương tùy ý,
2
log 2
a
bằng
A.
2
1 log a+
. B.
2
1 log a−
. C.
2
2 log a−
. D.
2
2 log a+
.
Câu 80: Với mọi số thực
a
dương,
2
3
log
9
a
bằng
A.
( )
3
2 log 1
a −
B.
3
1
log
2
a
C.
3
log 1a −
D.
3
log 2a +
Câu 81: Với
a
là số thực dương tùy ý,
( )
2
3
log 3a
bằng
A.
3
3 2log a+
. B.
3
1
1 log
2
a+
. C.
3
1 2log a+
. D.
3
1 2log a−
.
Câu 82: Với
a
là số thực dương tùy ý,
( )
3
log 100a
bằng
A.
6log a
. B.
2 3log a+
. C.
11
log
23
a+
. D.
3 3log a+
.
Câu 83: Với mọi số thực
a
dương và
1a ≠
,
( )
3
log 3
a
a
bằng
A.
log 3 1
a
−
. B.
1
. C.
( )
3 log 3 1
a
+
. D.
( )
1
log 3 1
3
a
+
.
Câu 84: Với
a
là số thực dương tùy ý,
5
2
log a
bằng
A.
2
5 log a+
B.
2
1
log
5
a+
C.
2
1
log
5
a
D.
2
5log a

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 29
Sưu tầm và biên soạn
Câu 85: Với
a
là số thực dương tùy ý,
5
25
log
a
bằng
A.
5
2 log a−
. B.
5
5
log a
. C.
5
5 log a−
. D.
5
2
log a
.
Câu 86: Với mọi
,ab
thỏa mãn
2
33
log log 5
ab+=
, khẳng định nào sau đây đúng?
A.
2
9
ab=
. B.
2
243ab=
. C.
2
243
ab
+=
. D.
3
15ab+=
.
Câu 87: Với
a
là số thực dương tùy ý,
( )
1
2
log 8a
bằng
A.
2
1
log .
2
a+
B.
2
3 log .a
−+
C.
( )
3
2
log .a−
D.
2
3 log a−−
.
Câu 88: Cho các số thực dương
,ab
thỏa mãn
log 2log 1ab+=
. Mệnh đề nào sau đây đúng?
A.
2
1ab+=
. B.
2 10ab+=
. C.
2
10ab =
. D.
2
10
ab
+=
.
Câu 89: Giả sử
a
,
b
là các số thực dương tùy ý thỏa mãn
23 4
4ab =
. Mệnh đề nào sau đây là đúng?
A.
22
2log 3log 4ab+=
. B.
22
2log 3log 8ab+=
.
C.
22
2log 3log 32ab+=
. D.
22
2log 3log 16ab+=
.
Câu 90: Với mọi
,ab
thỏa mãn
2
33
log log 5ab+=
, khẳng định nào sau đây đúng?
A.
2
9ab=
. B.
2
243ab=
. C.
2
243ab+=
. D.
3
15ab+=
.
Câu 91: Với mọi
a
,
b
thỏa mãn
23
33
log 3 log 4
ab+=
, khẳng định nào dưới đây đúng?
A.
23
1 81ab+ +=
. B.
23
27ab =
. C.
23
27ab+=
. D.
23
81ab
=
.
Câu 92: Với mọi số thực dương
a
,
b
thoả mãn
5
33
1
log log 2
a
b
−=
. Khẳng định nào dưới đây đúng?
A.
5
3ab
=
. B.
5
3ab=
. C.
5
1
3a
b
−=
. D.
5
1
9a
b
−=
.
Câu 93: Cho
x
,
y
là các số thực dương thỏa mãn điều kiện
22
9ln 4ln 12ln .lnx y xy+=
. Đẳng thức nào
sau đây đúng?
A.
32
xy=
. B.
xy=
. C.
32xy
=
. D.
33
xy=
.
Câu 94: Với
,ab
là các số thực dương tùy ý thỏa mãn
39
log 2log 2ab−=
, mệnh đề nào dưới đây đúng?
A.
2
9ab
=
. B.
9ab=
. C.
6ab=
. D.
9ba=
.
Câu 95: Với mọi
,ab
thỏa mãn
3
22
log log 5ab
+=
. Khẳng định nào sau đây đúng?
A.
3
32
ab+=
. B.
3
25ab+=
. C.
3
32ab=
. D.
3
25ab=
.
Câu 96: Cho các số thực âm
a
,
b
thỏa mãn
2
3
3
log log 2ba −=
. Khẳng định nào sau đây đúng?
A.
2
9
a
b
= −
. B.
3
a
b
=
. C.
2
3
a
b
= −
. D.
3
a
b
= −
.
Câu 97: Với mọi
,
ab
thỏa mãn
( )
( )
9
8
2
log 2 log 3+=ab
. Khẳng định nào dưới đây đúng?
A.
9
8+=ab
. B.
23
2=ab
. C.
3
4=
ab
. D.
9
8=ab
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 30
Sưu tầm và biên soạn
Câu 98: Cho
,ab
là các số dương thỏa mãn
33
4log 7log 2ab
+=
. Khẳng định nào sau đây là đúng?
A.
472ab+=
. B.
47
2ab
=
. C.
47
9ab =
. D.
479ab+=
.
Câu 99: Với mọi số thực dương
a
,
b
,
c
thỏa mãn
2
log log log 0a bc+−=
, khẳng định nào sau đây
đúng?
A.
2
0a bc+−=
. B.
2
0
bc
a
−=
. C.
2
1a bc+−=
. D.
2
1ab c−=
.
Câu 100: Với
,ab
là các số thực dương tùy ý thỏa mãn
4
22
log 2 log 5ab+=
, khẳng định nào sau đây đúng?
A.
4
32ab=
. B.
4
32ab+=
. C.
4
16ab+=
. D.
4
16ab=
.
Câu 101: Cho
,ab
là hai số thực dương thỏa mãn
25
39
log log 4ab− =
, khẳng định nào dưới đây đúng?
A.
5
27ab−=
. B.
5
27
a
b
=
. C.
52
81ab−=
. D.
5
81
a
b
=
.
Câu 102: Biết
2 42 1
2
log 6 log 4log log
x a bc=−−
. Tìm kết luận đúng.
A.
3
2
ac
x
b
=
. B.
32
xa b c=−+
. C.
3
2
ac
x
b
=
. D.
3
2
a
x
bc
=
.
Câu 103: Đặt
2
log 3a =
và
5
log 3b =
. Hãy biểu diễn
6
log 45
theo
a
và
b
.
A.
6
2
log 45
a ab
ab b
+
=
+
. B.
2
6
22
log 45
a ab
ab
−
=
.
C.
6
2
log 45
a ab
ab
+
=
. D.
2
6
22
log 45
a ab
ab b
−
=
+
.
Câu 104: Cho các số thực dương
,ab
thỏa mãn
32
3
2log 2.log 3log 4
ab−=
, mệnh đề nào dưới đây đúng?
A.
3
9
a
b
=
. B.
4ab
=
. C.
4
ab =
. D.
3
9
ab=
.
Câu 105: Với mọi
a
,
b
thỏa mãn
32
2
log .log 3
log 1
1 log 5
a
b+=
+
. Khẳng định nào dưới đây đúng?
A.
1ab+=
. B.
2
1 log 5ab= −
. C.
10ab =
. D.
2
log 5 1ab+=
.
Câu 106: Nếu
222
log 5log 4logxab= +
(
,0
ab>
) thì
x
bằng
A.
45
ab
. B.
54ab+
. C.
45ab
+
. D.
54
ab
.
Câu 107: Cho hai số thực dương
,ab
bất kì thỏa mãn
22
4ln 9ln 12 ln .lna b ab+=
. Khẳng định nào dưới
đây đúng?
A.
32ab=
. B.
23
ab=
. C.
23ab=
. D.
32
ab=
.
Câu 108: Với mọi
a
,
b
,
x
là các số thực dương thỏa mãn
3 33
log 2log 3logx ab= +
, mệnh đề nào dưới
đây đúng?
A.
23x ab= +
. B.
32xab= +
. C.
23
x ab=
. D.
23
xa b= +
.
Câu 109: Với mọi
,ab
thoả mãn
32
2
log
log 1
.log 3
51 log
b
a
+=
+
. Khẳng định nào sau đây đúng?
A.
2
1 log 5ab= −
. B.
10ab =
. C.
2
log 5 1ab+=
. D.
1ab+=
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 31
Sưu tầm và biên soạn
Câu 110: Xét tất cả các số dương
a
và
b
thỏa mãn
(
)
339
log log log
a b ab
+=
. Tính giá trị của
ab
.
A.
1
ab
=
. B.
2ab
=
. C.
1
2
ab =
. D.
0ab =
.
Câu 111: Cho
25
log 5 ; log 3 .ab= =
Tính
5
log 24
theo
a
và
b
.
A.
5
3
log 24 .
ab
a
+
=
B.
5
3
log 24 .
ab
a
+
=
C.
5
log 24 .
3
ab
ab
+
=
D.
5
3
log 24 .
ab
b
+
=
Câu 112: Cho
,ab
là các số thực dương và
1a ≠
thỏa mãn
( )
22
log 1
a
ab =
. Giá trị của
3
log
a
b
bằng
A.
1
6
−
. B.
1
3
. C.
1
6
. D.
1
.
Câu 113: Cho
73
log 5, log 5ab= =
. Biểu thức
21
log 5
M =
bằng
A.
ab
ab+
. B.
ab
. C.
1
ab
. D.
ab
ab
+
.
Câu 114: Cho
2
log 3 a=
. Giá trị của biểu thức
6
log 12P =
tính theo
a
bằng
A.
2
a
a+
. B.
1
2
a
a
+
+
. C.
1
a
a+
. D.
2
1
a
a
+
+
.
Câu 115: Cho hai số tự nhiên
,xy
thỏa mãn
28 28
log 2 log 7 2xy+=
. Giá trị của
xy+
bằng
A.
5
. B.
6
. C.
4
. D.
8
.
Câu 116: Cho
15
1 log 3
log 30
log 3 log 5
a
bc
+
=
+
, với
,,abc
là các số nguyên. Giá trị của
.ab c+
bằng
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 117: Biết
x
và
y
là hai số thực thỏa mãn
( )
496
log log log 2 .x y xy= = −
Giá trị của
x
y
bằng
A.
2
2
3
log 2
. B.
1
. C.
4
. D.
2
.
Câu 118: Với hai số thực dương
,ab
tùy ý và
35
6
3
log 5log
log 2
1 log 2
a
b−=
+
. Khẳng định nào dưới đây là khẳng
định đúng?
A.
6
log 2ab=
. B.
36ab=
. C.
230ab+=
. D.
6
log 3ab=
.
Câu 119: Ba số
248
log 3; log 3; log 3aaa+++
theo thứ tự lập thành cấp số nhân. Công bội của cấp số
nhân này bằng
A.
1
4
. B.
1
. C.
1
3
. D.
1
2
.
Câu 120: Đặt
25
log 3 , log 3ab= =
. Nếu biểu diễn
( )
6
log 45
()
a m nb
ba p
+
=
+
thì
mn p++
bằng:
A.
3−
. B.
3
. C.
6
. D.
4
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 1
Sưu tầm và biên soạn
BÀI 2: LOGARIT
Câu 1: Cho
,,abc
là các số thực dương và
,1ab≠
. Khẳng định nào sau đây là sai?
A.
log .log 1
ab
ba=
. B.
log log
ac
ca= −
. C.
log
log
log
b
a
b
c
c
a
=
. D.
log log .log
a ab
c bc=
.
Lời giải
Ta có
1
log log
log
ac
c
ca
a
= ≠−
. Suy ra đáp án B sai.
Câu 2: Cho
0 1, 0<≠ >ax
. Mệnh đề nào sau đây là sai?
A.
log 1=
a
a
. B.
log
=
x
a
ax
. C.
log 1 0
=
a
. D.
log
=
a
x
xx
.
Lời giải
Với
0 1, 0<≠ >
ax
ta có:
log 1
=
a
a
⇒
Phương án
A
đúng.
log =
x
a
ax
⇒
Phương án
B
đúng.
log 1 0=
a
⇒
Phương án
C
đúng.
log
=
a
x
ax
⇒
log
=
a
x
xx
sai
⇒
Phương án
D
sai.
Câu 3: Cho ba số thực dương
,,abc
và
1a ≠
. Khẳng định nào sau đây là sai?
A.
(
)
log log log
a aa
bc b c= +
. B.
log
a
b
ab=
.
C.
log log
aa
bb
α
α
=
. D.
ln
log
ln
a
a
b
b
=
.
Lời giải
Ta có
ln
log
ln
a
b
b
a
=
, nên đáp án D sai.
Câu 4: Cho
a
,
b
là các số thực dương tùy ý. Khẳng định nào sau đây là đúng?
A.
( )
ln ln lnab a b= +
. B.
( )
ln ln lnab a b+= +
.
C.
( )
ln ln .lnab a b=
. D.
( )
ln ln .lnab a b+=
.
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 2
Sưu tầm và biên soạn
Lời giải
Theo quy tắc logarit ta có:
(
)
ln ln ln
ab a b
= +
.
Câu 5: Cho
a
là số thực dương khác 1. Mệnh đề nào sau đây đúng với mọi số thực dương
,?xy
A.
log log log
a aa
x
xy
y
= +
. B.
( )
log log
aa
x
xy
y
= −
.
C.
log log log
a aa
x
xy
y
= −
. D.
log
log
log
a
a
a
x
x
yy
=
.
Lời giải
Theo quy tắc tính logarit của một thương ta có
log log log , 0, 0
a aa
x
x yx y
y
= − ∀> >
.
Câu 6: Có bao nhiêu số thực dương
1n
≠
để
log 265
n
là một số nguyên?
A.
2
. B.
4
. C.
6
. D.
8
.
Lời giải
Ta có:
8
2
8
log 256 log 2 8log 2
log
nnn
n
= = =
.
Để
log 265
n
là một số nguyên thì
2
log { 1; 2; 4; 8}n ∈±±±±
11 1 1
; 2; ; 4; ;16; ; 256
2 4 16 256
n
⇔∈
Vậy có tất cả 8 số thực dương
1n ≠
thỏa mãn điều kiện bài toán.
Câu 7: Cho ba số thực dương
,,
abc
đều khác
1
thoả mãn
log 2log 4 log= =
abc
bca
và
2 3 48
++=abc
. Khi đó
=P abc
bằng bao nhiêu?
A.
243
. B.
521
. C.
512
. D.
324
.
Lời giải
Do
,,abc
đều khác
1
nên
log , log , log
abc
bca
đều khác
0
ta có:
2
log 2log log .log 2log log 2log= ⇔ = ⇔=
a bac ba b
bccbccc
.
2
log 4log log .log 4log log 4log= ⇔ = ⇔=
acacccc
bacbaba
.
Nên
22 2 3 2
log .log 8log .log log 8log log 8 log 2= ⇔= ⇔=⇔=⇔=
ac bc a b a a
cb cabab bba
.
Mà
2
log 2log log 2log= ⇔ = ⇔=
a ba
a
b c b c bc
.
Ta lại có
22 2
16
2 3 48 2 3 48 5 48 0
5
3
= −
++=⇔++=⇔+−=⇔
=
a
abc aa a aa
a
Do
,,abc
đều là số thực dương
3 9, 9 243⇒=⇒= =⇒ = =a b c P abc
.
Câu 8: Giá trị của biểu thức
log 3
2
4
bằng
A.
3
. B.
3
. C.
3
2
. D.
23
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 3
Sưu tầm và biên soạn
(
)
( )
2
log 3
2
2
2 log 3
2
2 2 33
log 3
2
4
= = = =
.
Câu 9: Giá trị của
2
1
log
16
bằng
A.
4.
B.
1
.
4
C.
1
.
8
D.
4.
Lời giải
4
22
1
log log 2 4.
16
−
= = −
Câu 10: Với mọi
,
ab
dương thỏa mãn
22
log log 3
ab−=
, khẳng định nào dưới đây đúng?
A.
2
64ab
=
. B.
2
64ab
=
. C.
8ab−=
. D.
3
a
b
=
.
Lời giải
Ta có
22 2
log log 3 log 3
a
ab
b
−=⇔ =
32
2 64
a
ab
b
⇔ = ⇔=
.
Câu 11: Cho
0>a
và
1≠a
, khi đó
5
log
a
a
bằng
A.
1
5
. B.
5−
. C. 5. D.
1
5
−
.
Lời giải
Ta có:
5
log
a
a
=
( )
1
5
log
a
a
=
1
5
Câu 12: Cho
0
a >
và
1a ≠
, khi đó
2021
2022
log
a
a
bằng
A.
2021
. B.
2022
2021
. C.
2021
2022
. D.
2022
.
Lời giải
Với
0
a >
và
1a ≠
ta có:
2022
2021
2022
2021
2022 2022
log log log
2021 2021
aa a
aa a= = =
.
Câu 13: Cho
0a >
và
1a ≠
, khi đó
3
log
a
a
bằng
A.
1
3
−
. B.
3
. C.
3−
. D.
1
3
.
Lời giải
Ta có:
31
3
log log 3log 3
a
a
a
aaa= = =
Câu 14: Với
a
là số dương tùy ý khác 1,
log
a
a
bằng
A.
1
2
. B.
2a
. C.
2
. D.
1
2
a
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 4
Sưu tầm và biên soạn
Ta có
1
2
1
log log
2
aa
aa
= =
.
Câu 15: Với mọi số thực
a
dương khác 1,
3
log
a
a
bằng
A.
1
3
. B.
3
. C.
3
−
. D.
0
.
Lời giải
Ta có
1
3
3
11
log log log
33
aa a
aa a= = =
.
Câu 16: Với mọi số thực
a
dương,
4
4
log a
bằng
A.
4
. B.
4
4log a
. C.
4
1
log
4
a
. D.
1
4
.
Lời giải
4
4 44
log 4log 4loga aa
= =
.
Câu 17: Cho
a
là số thực dương khác
2
. Tính
2
2
log
4
a
a
I
=
.
A.
1
2
I =
. B.
1
2
I = −
. C.
2I =
. D.
2I = −
.
Lời giải
2
2
22 2
log log 2log 2
42 2
aa a
aa a
I
= = = =
.
Câu 18: Cho
a
là số thực dương khác
5
. Tính
3
5
log
125
a
a
I
=
.
A.
1
3
I
. B.
3I
. C.
1
3
I
. D.
3I
.
Lời giải
Ta có:
3
3
55
log log 3
125 5
aa
aa
I
.
Câu 19: Với
a
là số thực dương tùy ý,
( )
4
log 4a
bằng
A.
4
1 log
a−
. B.
4
1 log a+
. C.
4
4 log a−
. D.
4
4 log a+
.
Lời giải
Với
0a >
ta có:
( )
4
log 4a
44
log 4 log a
= +
4
1 log a= +
.
Câu 20: Với
,ab
là hai số dương tùy ý thì
( )
32
log ab
có giá trị bằng biểu thức nào sau đây?
A.
1
3log log
2
ab+
. B.
2log 3logab+
. C.
3log 2logab+
. D.
1
3 log log
2
ab
+
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 5
Sưu tầm và biên soạn
Lời giải
Do
,
ab
là hai số dương nên ta có :
(
)
32 3 2
log log log 3log 2logab a b a b=+=+
.
Câu 21: Tính giá trị của biểu thức
(
)
2
log
2 log
a
b
a
Pa= +
( )
0, 1aa>≠
.
A.
2
a
Pb= +
. B.
P ab= −
. C.
2P ab= +
. D.
P ab= +
.
Lời giải
Ta có
( )
2
log
2 log
a
b
a
P a ab=+=+
.
Câu 22: Cho
0, 1
aa>≠
, biểu thức
3
log
a
Da=
có giá trị bằng bao nhiêu?
A.
1
3
. B.
3
. C.
1
3
−
. D.
3
−
.
Lời giải
3
11
log log
33
a
a
Da a
= = =
Câu 23: Cho hàm số
2
( ) logfx x=
. Với
0x
>
, giá trị của biểu thức
68
3
x
Pf f
x
= +
bằng
A.
2P
=
. B.
1
P =
. C.
4P =
. D.
3P =
.
Lời giải
6 8 68
. (16) 4
33
xx
Pf f f f
xx
=+= ==
.
Câu 24: Giá trị của
3
1
log
a
a
với
0a >
và
1a ≠
bằng
A.
3
2
−
. B.
3
2
. C.
2
3
−
. D.
2
3
.
Lời giải
Ta có:
3
2
3
13
log log
2
aa
a
a
−
= = −
.
Câu 25: Với
a
là số thực dương bất kỳ, mệnh đề nào dưới đây đúng?
A.
4
ln 4ln
aa=
. B.
( )
ln 4 4lnaa=
. C.
( )
1
ln 4 ln
4
aa=
. D.
3
1
ln ln
3
aa=
.
Lời giải
Mệnh đề đúng là
4
ln 4ln
aa=
.
Câu 26: Cho
,ab
là các số thực dương và
a
khác
1
, thỏa mãn
2
3
5
3
log 3
a
a
b
=
. Giá trị của biểu thức
log
a
b
bằng
A.
5.−
B.
5.
C.
1
.
5
D.
1
.
5
−

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 6
Sưu tầm và biên soạn
Lời giải
Ta có
2
3
5
3
log 3
a
a
b
=
3
3
5
13
log log 3 3 log 6
25
aa a
ab b
⇔ − =⇔− =
log 5
a
b
⇔=−
.
Câu 27: Cho
25
log 5 ;log 3ab= =
. Tinh
5
log 24
theo
a
và
b
.
A.
5
3
log 24
ab
b
+
=
. B.
5
3
log 24
ab
a
+
=
. C.
5
3
log 24
ab
a
+
=
. D.
5
log 24
3
ab
ab
+
=
.
Lời giải
5 555
log 24 log 8.3 log 8 log 3= = +
55 5
2
3 33
3.log 2 log 3 log 3
log 5
ab
b
aa
+
= += +=+=
Câu 28: Cho
log 3,log 4
ab
xx= =
với
,ab
là các số thực lớn hơn
1
. Tính
log
ab
Px=
.
A.
12P =
. B.
7
12
P =
. C.
1
12
P =
. D.
12
7
.
Lời giải
Ta có :
log .log
1 1 1 12
log
11
log log log log log 7
log log
ab
ab
x xx ab
ab
xx
Px
ab a b x x
xx
= = = = = =
++
+
Vậy :
12
7
P =
.
Câu 29: Với các số thực dương
a
,
b
bất kì. Mệnh đề nào dưới đây đúng
A.
3
2 22
2
log 1 3log log
=+−
a
ab
b
. B.
3
2 22
21
log 1 log log
3
=+−
a
ab
b
.
C.
3
2 22
2
log 1 3log log
=++
a
ab
b
. C.
3
2 22
21
log 1 log log
3
=++
a
ab
b
.
Lời giải
( )
3
33
2 2 2 22 2 22
2
log log 2 log log 2 log log 1 3log log
= −=+ −=+ −
a
a b a b ab
b
.
Câu 30: Cho
2
log 5x =
. Giá trị của biểu thức
2
log
x
Px=
bằng
A.
15P = +
. B.
5
51
P =
+
. C.
1
5
. D.
5
15+
.
Lời giải
Ta có:
5
2
log 5 2 1xx= ⇔= >
nên
log 2
x
,
log
x
x
,
log 2
x
x
đều xác định và
log 02
x
x ≠
Cách 1.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 7
Sưu tầm và biên soạn
2
2
1
11
2 2l
1 1 1 15
log
1
o
og
1
l g log
5
log
5
x
x
xx
Px
xx
x
⇒
+
+
=
+
= = = = =
+
.
Cách 2.
22
2
2 22
log log
5
log
log 2 log 2 log
15
x
xx
Px
xx
= = = =
+
+
.
Câu 31: Cho các số thực dương
a
và
b
thỏa mãn
2
16 0
ab
−=
. Tính giá trị của biểu thức
2
2
log logP ab= −
.
A.
2P =
. B.
4
P
=
. C.
16
P =
. D.
2P =
.
Lời giải
2
2 2 22 2
2
log log 2log 2log log 16 log 16 4
16
a
Pa aa=− = − +==
.
Câu 32: Cho
0a
và
1a
. Khi đó
2
log
a
a
bằng
A.
1
. B.
1
4
. C. 4. D.
2
.
Lời giải
Với
0a
và
1a
, ta có:
4
2
log log log 4.14. 4
aa a
aa a
.
Câu 33: Cho
a
và
b
là hai số thực dương thỏa mãn
25
64ab =
. Giá trị của
22
2log 5log
P ab= +
là
A.
7P =
. B.
64P =
. C.
6P
=
. D.
2P =
.
Lời giải
Theo bài ra:
,0ab>
;
( )
25 25
2 2 22
64 log log 64 2log 5log 6ab ab a b=⇔ =⇔+=
.
Vậy
6P =
.
Câu 34: Cho
,xy
là các số thực lớn hơn
1
thỏa mãn
22
96
x y xy
+=
. Tính
( )
12 12
12
1 log log
2log 3
xy
M
xy
++
=
+
.
A.
1
4
M =
. B.
1
2
M
=
. C.
1
3
M =
. D.
1M =
.
Lời giải
Ta có
( )
2
22
96 3 0 3x y xy x y x y+ = ⇔ − =⇔=
.
Suy ra
( )
2
12 12 12
2
12 12
1 log 3 log log 36
1
2log 6 log 36
yy y
M
yy
++
= = =
.
Câu 35: Cho
0a >
và
1a ≠
, khi đó
(
)
log 2
3
a
a
bằng
A.
64
. B.
8
. C.
12
. D.
23
.
Lời giải
Ta có
( ) ( )
( )
6
log 2 2log 2
6log 2 log 2
33 6
2 64
a
a
aa
a a aa= = = = =
.
Câu 36: Cho
,ab
là các số thực dương
( , 1)≠ab
và
log 16
a
b =
. Tính giá trị của biểu thức
log
a
P b=
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 8
Sưu tầm và biên soạn
A.
256
. B.
4
. C.
23
. D.
8
.
Lời giải
Theo tính chất của logarit ta có
(
)
1
2
11
.16 8
log log log
22
aa a
P bb b
= =
= = =
.
Câu 37: Cho
,,0,1abc a
>≠
và
log 2022
a
b =
. Tính
6
7
6
4
log . .
a
ab
A.
2022
42
6
+
. B.
7
6 2022
4
+
. C.
21
2022
2
+
. D.
2
2022
21
+
.
Lời giải
Ta có:
6 66
77
66
44
7 21
log . log log 6. 2022 2022.
42
a aa
ab a b
= + =+=+
Câu 38: Cho
25
log 7a =
;
2
log 5
b =
. Tính
5
49
log
8
theo
a
,
b
.
A.
43
a
b
−
. B.
43
ab
b
+
. C.
53
ab
b
−
. D.
43
ab
b
−
.
Lời giải
Ta có:
2
25 5 5
5
1
log 7 log 7 log 7 log 7 2
2
aa= = = ⇒=
và
25
1
log 5 log 2b
b
=⇒=
23
5 5 55 5 5 5
49 1 4 3
log log 49 log 8 log 7 log 2 2log 7 3log 2 2.2 3.
8
ab
a
bb
−
= − = − = − = −=
Câu 39: Cho
, ab
là các số thực dương khác
1
thỏa mãn
log 3.=
a
b
Giá trị của
3
log
b
a
b
a
là
A.
3.−
B.
2 3.
−
C.
3.
D.
1
.
3
−
Lời giải
Ta có:
3
log 3= ⇔= ⇒
a
b ba
3
2
3
3
3
1
2
31
1
32
log log .
33
1
2
−
= = = −
−
b
a
a
a
ba
a
a
Câu 40: Cho
a
,
b
là các số thực dương thỏa mãn
log 2
a
b =
. Tính giá trị của biểu thức
( )
3
log .
a
b
P ab=
.
A.
2
15
P =
. B.
2
9
P = −
. C.
10
9
P = −
. D.
2
3
P =
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 9
Sưu tầm và biên soạn
Ta có
( )
( )
1
3
3
3
1
2
11
1 log 1 .2
log .
log log
10
33
log .
11
9
log 2
log log
log
22
a
a
aa
a
b
a
aa
a
b
ab
ab
P ab
a
b
ab
b
++
+
= = = = = = −
−−
−
.
Câu 41: Cho
log 2;log 3
aa
bc= =
. Tính
( )
3
log
a
Q bc=
.
A.
4Q =
. B.
9
Q =
. C.
10Q =
. D.
12Q =
.
Lời giải
Ta có
( )
3
log 3log log 3.2 3 9.
a aa
Q bc b c= = + = +=
Câu 42: Cho
log 2=
a
x
,
log 3=
b
x
với
a
,
b
là các số thực lớn hơn
1
. Tính
2
log=
a
b
Px
.
A.
6
. B.
6−
. C.
1
6
. D.
1
6
−
.
Lời giải
Vì
a
,
b
là các số thực lớn hơn
1
nên ta có:
2
3
23 3
2
3
log 2
log 3
=
=
⇔ ⇔ = ⇔= ⇔=
=
=
a
b
x
xa
a b a b ab
x
xb
.
31
22
2
2
log log log 2log 6
−
=== =−=−
ab
bb
b
b
Pxx x x
.
Câu 43: Cho các số thực dương
a
,
b
thỏa mãn
3log 2 log 1
ab+=
. Mệnh đề nào sau đây đúng?
A.
32
1ab+=
. B.
3 2 10
ab+=
. C.
32
10ab
=
. D.
32
10ab+=
.
Lời giải
Ta có:
3log 2log 1ab
+=
32
log log 1ab⇔+=
( )
32
log 1ab⇔=
32
10
ab
⇔=
.
Câu 44: Cho
,,
abc
là các số thực dương, trong đó
,1ab>
và thỏa mãn
log 3,
a
c =
log 4
b
c =
. Tính giá
trị biểu thức
log ?
ab
Pc=
A.
12
.
7
P =
B.
7
.
12
P =
C.
1
.
12
P =
D.
12.P =
Lời giải
Từ giả thiết ta suy ra
1
c ≠
và
11 11
log ; log
log 3 log 4
cc
ab
ab
cc
= = = =
.
Khi đó,
( )
1 1 1 12
log .
11
log log log 7
34
ab
c cc
Pc
ab a b
= = = = =
+
+
Câu 45: Cho
,ab
là các số thực dương lớn hơn
1
thỏa mãn
log 3
a
b =
.Tính giá trị biểu thức
22
3
4
log 3log 2.log
ab a
a
Pa
b
= −
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 10
Sưu tầm và biên soạn
A.
21
10
P
=
. B.
7
5
P
=
. C.
18
25
P
=
. D.
15
8
P =
.
Lời giải
Từ
log 3
a
b =
suy ra
3
ba=
( )
1, 1ab>>
.
Thay vào biểu thức cần tính ta được:
( )
52
32
4
log 3log 2.log
aa
Pa a
−
= −
2
33
.log .log 2
52
a
a= +
3 3 21
5 2 10
=+=
.
Câu 46: Cho
log 2
a
b =
với
a
,
b
là các số thực dương và
a
khác
1
. Giá trị biểu thức
2
6
log log
a
a
Tb b= +
bằng
A.
8
. B.
7
. C.
5
. D.
6
.
Lời giải
2
6
log log
a
a
Tb b= +
1
3log log
2
aa
bb= +
7
log
2
a
b=
7=
.
Câu 47: Cho
a,b
là các số thực dương lớn hơn
1
thỏa mãn
log 3
a
b =
. Tính gái trị biểu thức
22
3
4
log 3log 2.log
ab a
a
Pa
b
= −
.
A.
15
8
P =
. B.
18
25
P =
. C.
21
10
P =
. D.
7
5
P =
.
Lời giải
Ta có:
3
log 3
a
b ba=⇔=
2 2 52
33
44
3
log 3log 2.log log 3log 2.log
ab a a a
aa
Pa a
ba
=−=−
2
2
2
31 1
3. .log 2.log
52
a
a
= −
.
2
22
3 1 1 33 33 21
3. .log 2. .log .log 2.log
5 2 2 52 5210
aa
aa
−
=− =+ =+=
.
Câu 48: Cho
,ab
là các số thực dương và
1a ≠
thoả mãn
( )
2
1
log
2
a
ab =
. Giá trị của
2
log
a
b
bằng
A.
3
4
−
. B.
3
2
−
. C.
3−
. D.
3
4
.
Lời giải
Từ giả thiết ta có
( )
22
1 1 13
log log log log 2
2 2 22
a aa a
ab a b b
= ⇔ + = ⇔ = −=−
.
Vậy giá trị của
2
1 13 3
log log .
2 22 4
a
a
bb
= = −=−
.
Câu 49: Với mọi
,ab
thỏa mãn
( )
23
33
log 3 log 4ab+=
, khẳng định nào dưới đây đúng?
A.
23
81ab =
. B.
33
1 81ab+ +=
. C.
23
27ab =
. D.
23
27
ab+=
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 11
Sưu tầm và biên soạn
Lời giải
( )
2 3 2 3 23 23
33 3
log 3 log 4 log 3 . 4 3 81 27
a b a b ab ab+ =⇔ =⇔ =⇔=
.
Câu 50: Cho số thực
0a
>
;
1
1,
27
aa≠≠
và số thực
x
thỏa mãn
log 3
a
x=
. Tính
27
log 9
a
theo
x
.
A.
2
3
x
x
+
. B.
2
31
x
x
+
. C.
( )
23 1x +
. D.
2
31x +
.
Lời giải
Ta có:
3
27
3 33 3
log 9
2 2 2 22
log 9
11
log 27 log 27 log 3 log 3 1
33
log 3
a
a
x
a aa x
x
= = = = = =
++ +
++
.
Câu 51: Cho
a
,
b
là các số thực dương khác
1
thoả mãn
2
log 2a =
và
4
log 3b =
. Giá trị biểu thức
( )
2
log
a
P ab=
bằng
A.
10P =
. B.
5P =
. C.
2
P =
. D.
1P =
.
Lời giải
Với
a
,
b
là các số thực dương khác
1
ta có:
2
2
log 2 2 4aa=⇔= =
.
3
4
log 3 4bb=⇔=
Vậy
( ) ( )
2 23
4
log log 4 .4 5
a
P ab= = =
.
Câu 52: Cho
,ab
là các số thực dương và
a
khác
1
, thỏa mãn
3
4
5
log 2
a
a
b
=
. Giá trị của biểu thức
log
a
b
bằng
A.
4
. B.
1
4
. C.
1
4
−
. D.
4−
.
Lời giải
Ta có:
3
5
1
4
5
4
1
2 log log
3
a
a
aa
b
b
= =
1
5
4
1
log log
3
aa
ab
= −
11
5 log
34
a
b
= −
6
1
5 log
4
a
b− =⇒
4log
a
b = −⇒
.
Câu 53: Cho
a
,
b
là các số thực dương thỏa mãn
log 2
a
b =
. Tính giá trị của biểu thức
( )
3
log .
a
b
P ab=
.
A.
2
15
P =
. B.
2
9
P = −
. C.
10
9
P = −
. D.
2
3
P =
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 12
Sưu tầm và biên soạn
Ta có
( )
( )
1
3
3
3
1
2
11
1 log 1 .2
log .
log log
10
33
log .
11
9
log 2
log log
log
22
a
a
aa
a
b
a
aa
a
b
ab
ab
P ab
a
b
ab
b
++
+
= = = = = = −
−−
−
.
Câu 54: Cho các số dương
,ab
khác
1
sao cho
2
39
16
log log log 2
b
a
ab= =
. Giá trị của
3
b
a
bằng:
A.
1
. B.
2
. C.
4
. D.
8
.
Lời giải
Đặt
2
39
16
log log log 2
b
a
ab t= = =
2
3
3
3
18 54
54
16
16
16
2
2 16
t
t
tt
t
t
a
a
ba b
b
=
=
⇔= ⇔=
=
=
( )
*
.
Từ
( )
*
suy ra
3
216 3
1
2 2 216 1
6
t
tt= ⇔ =⇔=
. Suy ra
3
3
4, 4 1
b
ab
a
= =⇒=
.
Câu 55: Giá trị của biểu thức
log 3
2
4
bằng
A.
3
. B.
3
. C.
3
2
. D.
23
.
Lời giải
(
)
( )
2
log 3
2
2
2 log 3
2
2 2 33
log 3
2
4
= = = =
.
Câu 56: Cho
10
5
2
3 27 243P =
. Tính
3
log
P
.
A.
45
28
. B.
21
100
. C.
45
56
. D.
13
100
Lời giải
Ta có:
10
5
2
3 27 243P =
1 11 111 21
. ..
10 10 5 10 5 2 100
3 .27 .243 3P⇒= =
21
100
33
21
log log 3
100
P⇒= =
.
Câu 57: Cho
,
xy
là hai số thực dương,
1x ≠
thỏa mãn
25
25
log , log .
52
x
y
yx
y
= =
Tính giá trị của
22
2.Py x= −
A.
1P =
. B.
0P =
. C.
25P = −
. D.
25P =
.
Lời giải
Ta có:
2
2
25
25
25
2
2
log
25
5
log
5
5
5
5
1
5
log
25
log
log
log 25
2
2
2
5
x
x
x
y
y
y
y
y
y
y
x
yx
x
x
y
y
=
=
=
=
=
⇔ ⇔ ⇔⇔
=
=
=
=
=
Vậy
22
2 25.
Py x=−=−

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 13
Sưu tầm và biên soạn
Câu 58: Cho
,xy
là hai số thực dương,
1x
≠
thỏa mãn
3
2
3 32
log ,log .
8
x
y
yx
y
= =
Tính giá trị của
22
Px y= −
.
A.
120
P
=
. B.
132P =
. C.
240
P =
. D.
340
P =
.
Lời giải
Ta có:
2
2
2
32 32 16
log 2log 16log 2 (*).
log
x
x xy
y yx
= ⇔ = ⇔= =
( )
3
33
log 3log log log 16log 2 2log 2
8 88
x x xx x
x
y yy
y yy=⇔ =⇔=⇔ =
( )
2
log 16log 2 log 2
xx x
⇔=
2
1
16log 2 4 log 2 log 4 16.
4
xx
xx⇔ =⇔ =⇔ =⇔=
Từ
(*)
suy ra
4y =
.
Vậy
22 22
16 4 240.Px y=−= −=
Câu 59: Có bao nhiêu số thực dương
1n ≠
để
log 265
n
là một số nguyên?
A.
2
. B.
4
. C.
6
. D.
8
.
Lời giải
Ta có:
8
2
8
log 256 log 2 8log 2
log
nnn
n
= = =
.
Để
log 265
n
là một số nguyên thì
2
log { 1; 2; 4; 8}n ∈±±±±
11 1 1
; 2; ;4; ;16; ; 256
2 4 16 256
n
⇔∈
Vậy có tất cả 8 số thực dương
1n ≠
thỏa mãn điều kiện bài toán.
Câu 60: Cho các số thực
,ab
thỏa mãn
1ab>>
và
11
2022.
log log
ba
ab
+=
Giá trị của biểu thức
11
.
log log
ab ab
P
ba
= −
A.
2018.
B.
2020.
C.
2016.
D.
2022.
Lời giải
11
2022 log log 2022 (*).
log log
ab
ba
ba
ab
+ = ⇔+=
11
log ( ) log ( ) log log .
log log
b a ba
ab ab
P ab ab a b
ba
=−= − =−
Đặt
log
a
tb
=
thì
(*)
trở thành:

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 14
Sưu tầm và biên soạn
2
2022 2018 1
2018
1
2
2022 2022 1 0 .
2022 2018 1
2018
2
t Pt
t
t tt
t
t Pt
t
+
= ⇒ = −=−
+ = ⇔ − += ⇔
−
= ⇒ = −=
1 0 log 1
a
ab b> >⇔ < <
nên
11
0 1 1 0 2018.t Pt P
tt
<<⇒ >⇒ =−> ⇒ =
Câu 61: Với
,
ab
là các số thực dương tùy ý và
1
a ≠
. Ta có
( )
3
log
a
ab
bằng
A.
3.log
a
b
. B.
1
.log
3
a
b
. C.
1
log
3
a
b+
. D.
3 log
a
b+
.
Lời giải
Ta có:
(
)
(
)
33
log log log 3 log , 0; 1
a aa a
ab a b b ab a= + =+ >≠
.
Câu 62: Với
a
,
b
là hai số dương tùy ý,
( )
23
log ab
bằng:
A.
11
log log
23
ab
+
. B.
2log logab+
. C.
2log 3logab
+
. D.
log 3log
ab+
.
Lời giải
Ta có
( )
23 2 3
log log log 2log 3log 2 log 3logab a b a b a b=+= + = +
.
Câu 63: Cho
0a >
,
1a ≠
, khi đó
( )
3
log .
a
aa
bằng
A.
4
. B.
4
3
. C.
4
3
−
. D.
1
3
.
Lời giải
Với
0a
>
,
1a ≠
nên ta có
(
)
33
14
log . log log 1 .
33
a aa
aa a a= + =+=
Vậy
( )
3
4
log .
3
a
aa=
.
Câu 64: Cho
0a >
và
1a ≠
, khi đó
2
3
4
log
a
a
bằng
A.
3
8
−
. B.
3
4
. C.
3
8
. D.
3
2
.
Lời giải
Ta có
2
3
3
4
4
1 13 3
log .log . .log
2 24 8
aa
a
aa a= = =
.
Câu 65: Cho
a
là số thực dương,
1a ≠
, khi đó
log 5
a
a
bằng
A.
5
log a
. B.
log 5
a
. C.
5
a
. D.
5
.
Lời giải
Áp dụng công thức
log
a
b
ab=
ta có
log 5
5
a
a =
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 15
Sưu tầm và biên soạn
Câu 66: Với
,ab
là hai số thực dương tùy ý, khi đó
(
)
32
ln ea b
bằng:
A.
2ln 3lnab+
. B.
3ln 2lnab+
. C.
1 3ln 2lnab++
. D.
1 6 ln .lnab
+
.
Lời giải
Ta có:
(
)
( )
( )
( )
32 3 2
ln ln ln ln 1 3ln 2ln
ea b e a b a b
= + + =++
.
Câu 67: Với
a
,
b
là các số thực dương bất kỳ,
2
4
log
a
b
bằng
A.
( )
22
log log 4ab−
. B.
2
1
log
4
a
b
. C.
2
2log
a
b
. D.
22
log 4logab−
.
Lời giải
4
2 22 2 2
4
log log log log 4log
a
ab a b
b
=−=−
.
Câu 68: Cho
a
là số thực dương. Khi đó
3
4
log 8
a
bằng
A.
2
3
log
2
a+
. B.
2
33
log
22
a+
. C.
2
2 3log a+
. D.
2
6 6log a+
.
Lời giải
Ta có
22
3 33
4 44 2
22
33
log 8 log 8 log log 2 3log log
22
a a aa
=+= + =+
.
Câu 69: Với mọi số thực
a
dương,
( )
5
log 5a
bằng
A.
5
1 log
a+
. B.
5
log a
. C.
5
5log a
. D.
5
1 log
a−
.
Lời giải
Suy ra
( )
5 55 5
log 5 log 5 log 1 loga aa
=+=+
.
Câu 70: Với
a
là số thực dương tùy ý,
(
)
3
4
log a
bằng
A.
3
3log a
. B.
2
2
log
3
a
. C.
2
3
log
2
a
. D.
4
3 log a
+
.
Lời giải
Có
( ) ( )
2
33
42
2
3
log log log .
2
aa a= =
Câu 71: Với mọi số thực
a
dương,
2
2
log
4
a
bằng
A.
( )
2
2 log 1a −
. B.
2
log 2a −
. C.
2
log 1a −
. D.
2
2log 1a −
.
Lời giải
Ta có
( )
2
2
2 22 2 2
log log log 4 2log 2 2 log 1
4
a
a aa= − = −= −
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 16
Sưu tầm và biên soạn
Câu 72: Cho
0a >
và
1a ≠
, khi đó
3
log
a
a
bằng
A.
1
3
. B.
3
. C.
1
3
−
. D.
3−
.
Lời giải
Với
0
a
>
và
1
a
≠
ta có:
1
3
3
log log 3log 3= = =
a
a
a
aa a
.
Câu 73: Với mọi số thực
a
dương,
22
2
log a
bằng
A.
2
2
2log
a
. B.
2
2
4log
a
. C.
2
2
2log
a
. D.
2
4log a
.
Lời giải
(
)
2
22 2
222
log 2log 4 logaaa
= =
Câu 74: Với
,ab
là các số thực dương tùy ý và
1≠
a
,
3
log
a
b
A.
3 log+
a
b
. B.
3log
a
b
. C.
1
3
log+
a
b
. D.
1
3
log
a
b
.
Lời giải
Ta có:
3
1
log log .
3
=
a
a
bb
Câu 75: Với
a
là số thực dương tùy ý,
3
3
log
a
bằng
A.
3
1 log− a
. B.
3
3 log−
a
. C.
3
1
log a
. D.
3
1 log+ a
.
Lời giải
Ta có
3 33
3
log log 3 log
= −
a
a
3
1 log= − a
.
Câu 76: Với
a
là số thực dương tùy ý,
( )
5
log 5
a
bằng
A.
5
5 log+ a
. B.
5
5 log− a
. C.
5
1 log+ a
. D.
5
1 log− a
.
Lời giải
Ta có
( )
5 55 5
log 5 log 5 log 1 log=+=+a aa
.
Câu 77: Giả sử
,ab
là các số thực dương tùy ý thỏa mãn
23 4
4ab =
. Mệnh đề nào sau đây đúng?
A.
22
2log 3log 8ab+=
. B.
22
2log 3log 8ab−=
.
C.
22
2log 3log 4ab−=
. D.
22
2log 3log 4ab+=
.
Lời giải
Ta có
23 4
2 2 22
log log 4 2log 3log 8ab a b=⇔ +=
.
Câu 78: Với
,ab
là hai số thực dương tùy ý,
( )
3
3
log ab
bằng

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 17
Sưu tầm và biên soạn
A.
33
1
log log
3
ab+
. B.
( )
33
3 log logab+
. C.
33
log 3log
ab+
. D.
33
3log logab+
.
Lời giải
Ta có:
( )
33
3 33 3 3
log log log log 3log
ab a b a b
=+=+
.
Câu 79: Với
a
là số thực dương tùy ý,
2
log 2a
bằng
A.
2
1 log a+
. B.
2
1 log a−
. C.
2
2 log a−
. D.
2
2 log a+
.
Lời giải
2 22 2
log 2 log 2 log 1 log
a aa=+=+
.
Câu 80: Với mọi số thực
a
dương,
2
3
log
9
a
bằng
A.
( )
3
2 log 1a −
B.
3
1
log
2
a
C.
3
log 1a −
D.
3
log 2a
+
Lời giải
Câu 81: Với
a
là số thực dương tùy ý,
( )
2
3
log 3a
bằng
A.
3
3 2log a+
. B.
3
1
1 log
2
a+
. C.
3
1 2log a+
. D.
3
1 2log a−
.
Lời giải
Ta có:
(
)
22
3 33
log 3 log 3 logaa= +
3
1 2log
a= +
.
Câu 82: Với
a
là số thực dương tùy ý,
( )
3
log 100
a
bằng
A.
6log
a
. B.
2 3log a+
. C.
11
log
23
a+
. D.
3 3log a+
.
Lời giải
Ta có
( )
3 3 23
log 100 log100 log log10 log 2 3loga a aa= += +=+
.
Câu 83: Với mọi số thực
a
dương và
1a ≠
,
( )
3
log 3
a
a
bằng
A.
log 3 1
a
−
. B.
1
. C.
( )
3 log 3 1
a
+
. D.
( )
1
log 3 1
3
a
+
.
Lời giải
( ) ( ) ( ) ( )
3
11 1
log 3 log 3 log 3 log log 3 1
33 3
a aa a
a
aa a= = += +
Câu 84: Với
a
là số thực dương tùy ý,
5
2
log a
bằng
A.
2
5 log a+
B.
2
1
log
5
a+
C.
2
1
log
5
a
D.
2
5log a
Lời giải
Ta có:
5
22
log 5logaa=

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 18
Sưu tầm và biên soạn
Câu 85: Với
a
là số thực dương tùy ý,
5
25
log
a
bằng
A.
5
2 log a−
. B.
5
5
log a
. C.
5
5 log a−
. D.
5
2
log a
.
Lời giải
Ta có
2
5 5 55 5 5
25
log log 25 log log 5 log 2 log
a aa
a
= −= −=−
.
Câu 86: Với mọi
,ab
thỏa mãn
2
33
log log 5ab+=
, khẳng định nào sau đây đúng?
A.
2
9
ab=
. B.
2
243
ab
=
. C.
2
243ab+=
. D.
3
15ab
+=
.
Lời giải
Ta có:
2 2 252
33 3
log log 5 log ( . ) 5 . 3 . 243
a b ab ab ab+ =⇔ =⇔=⇔=
.
Câu 87: Với
a
là số thực dương tùy ý,
( )
1
2
log 8
a
bằng
A.
2
1
log .
2
a+
B.
2
3 log .a−+
C.
( )
3
2
log .
a
−
D.
2
3 log a−−
.
Lời giải
Ta có:
(
) ( )
( )
3
1 22 2 2 2
2
log 8 log 8 log log 2 log 3 loga a aa
=− + =− + =−−
.
Câu 88: Cho các số thực dương
,ab
thỏa mãn
log 2log 1ab
+=
. Mệnh đề nào sau đây đúng?
A.
2
1ab+=
. B.
2 10ab+=
. C.
2
10ab =
. D.
2
10ab+=
.
Lời giải
2 22
log 2log 1 log log 1 log 1 10
a b a b ab ab+ =⇔ + =⇔ =⇔=
.
Câu 89: Giả sử
a
,
b
là các số thực dương tùy ý thỏa mãn
23 4
4ab =
. Mệnh đề nào sau đây là đúng?
A.
22
2log 3log 4
ab+=
. B.
22
2log 3log 8ab+=
.
C.
22
2log 3log 32ab+=
. D.
22
2log 3log 16ab+=
.
Lời giải
Ta có
( )
23 4 23 4 2 3 8
2 2 222 2 2
4 log log 4 log log log 2 2log 3log 8ab ab a b a b=⇔ =⇔+=⇔ + =
Câu 90: Với mọi
,ab
thỏa mãn
2
33
log log 5ab+=
, khẳng định nào sau đây đúng?
A.
2
9ab=
. B.
2
243ab=
. C.
2
243ab+=
. D.
3
15ab
+=
.
Lời giải
Ta có:
2 2 252
33 3
log log 5 log ( . ) 5 . 3 . 243a b ab ab ab+ =⇔ =⇔=⇔=
.
Câu 91: Với mọi
a
,
b
thỏa mãn
23
33
log 3 log 4ab+=
, khẳng định nào dưới đây đúng?
A.
23
1 81ab+ +=
. B.
23
27
ab =
. C.
23
27ab+=
. D.
23
81ab =
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 19
Sưu tầm và biên soạn
Ta có
23
33
log 3 log 4ab
+=
23
33
1 log log 4
ab
⇔+ + =
23
33
log log 3ab⇔+=
23
3
log 3
ab
⇔=
23
27.ab⇔=
Câu 92: Với mọi số thực dương
a
,
b
thoả mãn
5
33
1
log log 2
a
b
−=
. Khẳng định nào dưới đây đúng?
A.
5
3
ab=
. B.
5
3ab=
. C.
5
1
3
a
b
−=
. D.
5
1
9a
b
−=
.
Lời giải
Ta có
( )
( )
2
5 5 55
33 33 3
1
log log 2 log log 2 log 2 3 3.
a a b ab ab
b
− =⇔ + =⇔ =⇔= =
Câu 93: Cho
x
,
y
là các số thực dương thỏa mãn điều kiện
22
9ln 4ln 12ln .lnx y xy+=
. Đẳng thức nào
sau đây đúng?
A.
32
xy
=
. B.
xy=
. C.
32xy=
. D.
33
xy
=
.
Lời giải
Ta có
(
)
2
22
9ln 4ln 12ln .ln 3ln 2 ln 0x y xy x y
+ = ⇔− =
32
3ln 2 lnx yxy⇔ = ⇔=
.
Câu 94: Với
,ab
là các số thực dương tùy ý thỏa mãn
39
log 2log 2ab
−=
, mệnh đề nào dưới đây đúng?
A.
2
9
ab
=
. B.
9ab=
. C.
6ab=
. D.
9ba=
.
Lời giải
Ta có:
39
log 2log 2ab−=
33
log log 2ab⇔−=
3
log 2
a
b
⇔=
9ab⇔=
.
Câu 95: Với mọi
,ab
thỏa mãn
3
22
log log 5ab+=
. Khẳng định nào sau đây đúng?
A.
3
32ab+=
. B.
3
25ab+=
. C.
3
32ab=
. D.
3
25ab=
.
Lời giải
Ta có:
(
)
3 33
22 2
log log 5 log 5 32a b ab ab
+ =⇔ =⇔=
.
Câu 96: Cho các số thực âm
a
,
b
thỏa mãn
2
3
3
log log 2ba −=
. Khẳng định nào sau đây đúng?
A.
2
9
a
b
= −
. B.
3
a
b
=
. C.
2
3
a
b
= −
. D.
3
a
b
= −
.
Lời giải
Ta có
2
2 22
3 33
3
log log 2 log log 2 9
a
b ab
b
a
−=⇔−=⇔=
.
Theo giả thiết
a
,
b
là các số thực âm nên
0
a
b
>
. Khi đó
2
93
aa
bb
=⇔=
.
Câu 97: Với mọi
,ab
thỏa mãn
( )
(
)
9
8
2
log 2 log 3+=ab
. Khẳng định nào dưới đây đúng?
A.
9
8+=ab
. B.
23
2=ab
. C.
3
4=ab
. D.
9
8=ab
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 20
Sưu tầm và biên soạn
Ta có:
( ) (
)
2
9 3 23 23
8 22
2
log 2 log 3 log 2 log 3 4 8 2+ =⇒ + =⇒ =⇔=a b a b ab ab
.
Câu 98: Cho
,ab
là các số dương thỏa mãn
33
4log 7log 2ab+=
. Khẳng định nào sau đây là đúng?
A.
472ab+=
. B.
47
2
ab
=
. C.
47
9ab =
. D.
479ab
+=
.
Lời giải
Ta có:
4 7 47 47
3 3 33 3
4log 7log 2 log log 2 log 2 9a b a b ab ab+ =⇔ + =⇔ =⇔=
.
Câu 99: Với mọi số thực dương
a
,
b
,
c
thỏa mãn
2
log log log 0a bc+−=
, khẳng định nào sau đây
đúng?
A.
2
0
a bc+−=
. B.
2
0bc
a
−=
. C.
2
1a bc+−=
. D.
2
1ab c
−=
.
Lời giải
Ta có:
( )
2 2 22
log log log 0 log log 0a b c ab c ab c ab c+ − =⇔ = ⇔ =⇔ −=
Câu 100: Với
,
ab
là các số thực dương tùy ý thỏa mãn
4
22
log 2 log 5ab
+=
, khẳng định nào sau đây đúng?
A.
4
32ab
=
. B.
4
32ab+=
. C.
4
16
ab
+=
. D.
4
16ab=
.
Lời giải
( )
4 4 5 44
22
log 2 log 5 2 2 2 16a b ab ab
+ =⇔ =⇔==
Câu 101: Cho
,ab
là hai số thực dương thỏa mãn
25
39
log log 4ab− =
, khẳng định nào dưới đây đúng?
A.
5
27ab−=
. B.
5
27
a
b
=
. C.
52
81ab−=
. D.
5
81
a
b
=
.
Lời giải
Ta có:
2
55
55 5
39 3 3 3
3
2
3
2
log log 4 log log 4 log log 4 log 4 81
aa
ababab
bb
=⇔=⇔ =⇔−− =⇔=−
.
Câu 102: Biết
2 42 1
2
log 6log 4log logx a bc
=−−
. Tìm kết luận đúng.
A.
3
2
ac
x
b
=
. B.
32
xa b c=−+
. C.
3
2
ac
x
b
=
. D.
3
2
a
x
bc
=
.
Lời giải
2 42 1
2
log 6 log 4log logx a bc
=−−
32
22 2 2
log log log logxa b c⇔= − +
3
22
2
log log
ac
x
b
⇔=
3
2
ac
x
b
⇔=
.
Câu 103: Đặt
2
log 3a =
và
5
log 3b =
. Hãy biểu diễn
6
log 45
theo
a
và
b
.
A.
6
2
log 45
a ab
ab b
+
=
+
. B.
2
6
22
log 45
a ab
ab
−
=
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 21
Sưu tầm và biên soạn
C.
6
2
log 45
a ab
ab
+
=
. D.
2
6
22
log 45
a ab
ab b
−
=
+
.
Lời giải
(
)
(
)
2
3
6
3
log 5.3
log 45
log 2.3
=
3
3
log 5 2
log 2 1
+
=
+
1
2
1
1
b
a
+
=
+
2a ab
ab b
+
=
+
.
Câu 104: Cho các số thực dương
,ab
thỏa mãn
32
3
2log 2.log 3log 4
ab
−=
, mệnh đề nào dưới đây đúng?
A.
3
9
a
b
=
. B.
4ab=
. C.
4ab =
. D.
3
9ab=
.
Lời giải
Ta có
32
3
2log 2.log 3log 4ab−=
1
2
3 33
3
2log 3log 4 log 3log 2a b ab⇔ − =⇔− =
3 23
33 3
33
log log 2 log 2 3 9
aa
a b ab
bb
⇔ − =⇔ =⇔ = ⇔=
Câu 105: Với mọi
a
,
b
thỏa mãn
32
2
log .log 3
log 1
1 log 5
a
b+=
+
. Khẳng định nào dưới đây đúng?
A.
1ab
+=
. B.
2
1 log 5ab= −
. C.
10ab =
. D.
2
log 5 1ab+=
.
Lời giải
Ta có
32
2
log .log 3
log 1
1 log 5
a
b+=
+
2
2
log
log 1
log 10
a
b⇔ +=
log log 1
ab⇔+=
log 1ab
⇔=
10
ab⇔=
.
Câu 106: Nếu
222
log 5log 4logxab= +
(
,0ab>
) thì
x
bằng
A.
45
ab
. B.
54
ab
+
. C.
45ab+
. D.
54
ab
.
Lời giải
Ta có
54 54
2 2 2 22
log 5log 4log log logx a b x ab x ab= + ⇔ = ⇔=
.
Câu 107: Cho hai số thực dương
,
ab
bất kì thỏa mãn
22
4ln 9 ln 12ln .lna b ab
+=
. Khẳng định nào dưới
đây đúng?
A.
32ab=
. B.
23
ab=
. C.
23ab=
. D.
32
ab
=
.
Lời giải
Ta có:
22
4ln 9ln 12 ln .ln
a b ab+=
( )
2
2ln 3ln 0ab⇔− =
2ln 3lnab⇔=
23
ab⇔=
.
Câu 108: Với mọi
a
,
b
,
x
là các số thực dương thỏa mãn
3 33
log 2log 3logx ab= +
, mệnh đề nào dưới
đây đúng?
A.
23x ab= +
. B.
32xab= +
. C.
23
x ab=
. D.
23
xa b= +
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 22
Sưu tầm và biên soạn
Lời giải
Từ giả thiết ta có
( )
2 3 23 23
3 3 3 33 3 33
log 2 log 3log log log log log logx a b x a b x ab x ab= + ⇔ = + = ⇔=⇔
Câu 109: Với mọi
,ab
thoả mãn
32
2
log
log 1
.log 3
51 log
b
a
+=
+
. Khẳng định nào sau đây đúng?
A.
2
1 log 5ab= −
. B.
10ab =
. C.
2
log 5 1ab+=
. D.
1
ab+=
.
Lời giải
Ta có:
32
22
2
log
log
log 1 log 1
o
1l
.l g 3
g 51
lo
0og
b
a
b
a
+=⇔ +=
+
log 1log
ab+=
⇔
( )
log 1 10ab ab⇔ =⇔=
.
Câu 110: Xét tất cả các số dương
a
và
b
thỏa mãn
( )
339
log log loga b ab+=
. Tính giá trị của
ab
.
A.
1ab =
. B.
2ab =
. C.
1
2
ab =
. D.
0
ab =
.
Lời giải
Ta có:
( )
( ) ( )
( ) (
)
2
339 3 3 3
3
1
log log log log log log log
2
a b ab ab ab ab ab+=⇔= ⇔=
( )
3
1
log 0 1.
2
ab ab⇔ =⇔=
Câu 111: Cho
25
log 5 ; log 3 .ab= =
Tính
5
log 24
theo
a
và
b
.
A.
5
3
log 24 .
ab
a
+
=
B.
5
3
log 24 .
ab
a
+
=
C.
5
log 24 .
3
ab
ab
+
=
D.
5
3
log 24 .
ab
b
+
=
Lời giải
Ta có
(
)
3
5 5 55
log 24 log 3.2 log 3 3log 2= = +
5
2
3 33
log 3
log 5
ab
b
aa
+
= + =+=
.
Câu 112: Cho
,ab
là các số thực dương và
1
a ≠
thỏa mãn
(
)
22
log 1
a
ab =
. Giá trị của
3
log
a
b
bằng
A.
1
6
−
. B.
1
3
. C.
1
6
. D.
1
.
Lời giải
Ta có:
( )
22 2 2
1
log 1 log log 1 2 2log 1 log
2
a aa a a
ab a b b b=⇔ + =⇔+ =⇔ =−
Vậy:
3
11
log log
36
a
a
bb= = −
.
Câu 113: Cho
73
log 5, log 5ab= =
. Biểu thức
21
log 5M =
bằng
A.
ab
ab+
. B.
ab
. C.
1
ab
. D.
ab
ab
+
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 23
Sưu tầm và biên soạn
Ta có:
(
)
21
5 5 55
73
11 1 1 1
log 5
1 1 11
log 21 log 7.3 log 7 log 3
log 5 log 5
ab
M
ab
ab
= = = = = = =
++
++
.
Câu 114: Cho
2
log 3 a=
. Giá trị của biểu thức
6
log 12P =
tính theo
a
bằng
A.
2
a
a+
. B.
1
2
a
a
+
+
. C.
1
a
a+
. D.
2
1
a
a
+
+
.
Lời giải
Ta có
( )
22 2
6
22 2
log 12 log (4.3) 2 log 3
log 12
log 6 log 2.3 1 log 3
P
+
= = = =
+
2
1
a
a
+
=
+
.
Câu 115: Cho hai số tự nhiên
,xy
thỏa mãn
28 28
log 2 log 7 2xy+=
. Giá trị của
xy+
bằng
A.
5
. B.
6
. C.
4
. D.
8
.
Lời giải
Ta có:
( )
2
28 28 28
log 2 log 7 2 log 2 7 2 2 7 28
xy xy
xy+ =⇔ =⇔=
( )
2
2 42
27 27 27 27
xy xy
⇔= ⇔=
Vì
,
xy
là số tự nhiên nên
4, 2 6.x y xy= =⇒+=
Câu 116: Cho
15
1 log 3
log 30
log 3 log 5
a
bc
+
=
+
, với
,,abc
là các số nguyên. Giá trị của
.ab c+
bằng
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
Ta có:
15
log30 log10 log3 1 log3
log 30
log15 log3 log5 log3 log5
++
= = =
++
.
Suy ra:
1, 1, 1 . 2abc abc= = =⇒ +=
Câu 117: Biết
x
và
y
là hai số thực thỏa mãn
( )
496
log log log 2 .x y xy= = −
Giá trị của
x
y
bằng
A.
2
2
3
log 2
. B.
1
. C.
4
. D.
2
.
Lời giải
Đk
0
0
2
x
y
xy
>
>
>
Đặt
( )
496
log log log 2x y x yt= = −=

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 24
Sưu tầm và biên soạn
( )
2
4
1
3
42
9 4 2.9 6 2
0
93
2
26
2
3
t
t
tt
t t tt
t
t
x
loai
y
xy
=
= −
⇒ = ⇒ − = ⇔ − −=⇔
−=
=
Khi đó .
Câu 118: Với hai số thực dương
,ab
tùy ý và
35
6
3
log 5log
log 2
1 log 2
a
b−=
+
. Khẳng định nào dưới đây là khẳng
định đúng?
A.
6
log 2ab=
. B.
36ab=
. C.
230ab+=
. D.
6
log 3ab=
.
Lời giải
Ta có
35
6
3
log 5log
log 2
1 log 2
a
b−=
+
3
6
3
log
log 2
log 6
a
b⇔ −=
66
log log 2ab⇔−=
6
log 2 36 36
aa
ab
bb
⇔ =⇔ = ⇔=
.
Câu 119: Ba số
248
log 3; log 3; log 3aaa+++
theo thứ tự lập thành cấp số nhân. Công bội của cấp số
nhân này bằng
A.
1
4
. B.
1
. C.
1
3
. D.
1
2
.
Lời giải
Theo giả thiết, ta có:
( ) ( )( )
( )
( )
2
22
4 2 8 2 2 22
2
22
1 41
log 3 log 3 log 3 log 3 log 3 log 3 log 3
2 33
11
log 3 log 3
3 12
a aa a a
a
+ =+ +⇔ + = +
⇔=−
2
1
log 3
4
a⇔=−
Vậy:
22
4
2
22
11
log 3 log 3
log 3
1
42
1
log 3 3
log 3 log 3
4
a
q
a
−+
+
= = =
+
−+
Câu 120: Đặt
25
log 3 , log 3ab= =
. Nếu biểu diễn
( )
6
log 45
()
a m nb
ba p
+
=
+
thì
mn p++
bằng:
A.
3−
. B.
3
. C.
6
. D.
4
.
Lời giải
Ta có:
2
42
4
93
tt
x
y
= = =

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 25
Sưu tầm và biên soạn
3 33
6
3 33
log 45 log 9 log 5
log 45
log 6 log 2 log 3
+
= =
+
2
3
5
3
2
1
1
log 3
2
log 3
(1 2 )
11
( 1)
log 3 1
log 3
ab
b
ba
a
+
+
+
= = =
+
++
.
Theo bài ra:
( )
6
log 45
()
a m nb
ba p
+
=
+
.
Từ và ta có:
1, 2, 1mn p= = =
.
Vậy
4mn p++ =
.
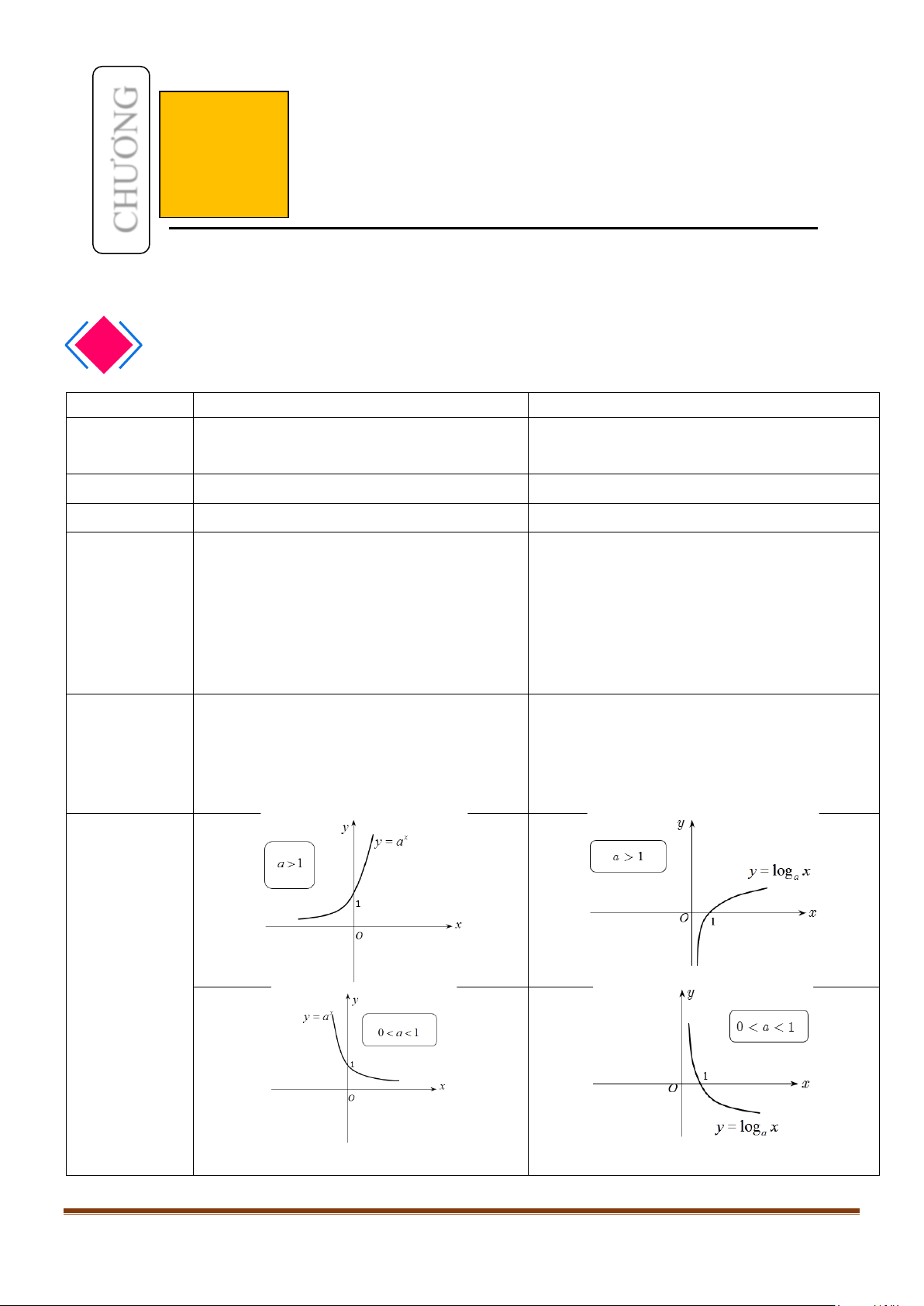
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 32
Sưu tầm và biên soạn
BÀI 3: HÀM SỐ MŨ – HÀM SỐ LOGARIT
Hàm số mũ
Hàm số logarit
Định nghĩa
Hàm số được gọi là
hàm số mũ cơ số a.
Hàm số được gọi là
hàm số lôgarit cơ số a.
Tập xác định
Tập giá trị
Tính đơn
điệu
Khi : Hàm số đồng biến trên
;
lim 0; lim
xx
xx
aa
→−∞ →+∞
= = +∞
Khi : Hàm số nghịch biến
trên ;
lim ; lim 0
xx
xx
aa
→−∞ →+∞
= +∞ =
Khi : Hàm số đồng biến trên
;
0
lim log ; lim log
aa
x
x
xx
+
→+∞
→
= −∞ = +∞
Khi : Hàm số nghịch
biến trên ;
0
lim log ; lim log
aa
x
x
xx
+
→+∞
→
= +∞ = −∞
Đồ thị:
- Đi qua điểm và
(
)
;
a1
.
- Liên tục trên
.
- Nằm ở phía trên trục hoành.
Đồ thị:
- Đi qua điểm và
( )
;a 1
.
- Liên tục trên
( )
;+∞0
.
- Nằm ở bên phải trục tung.
Đồ thị
, ( 0, 1)
x
ya a a= >≠
log , ( 0, 1)
a
y xa a= >≠
D =
(0, ).D = +∞
(0; )T
= +∞
= T
1a >
x
ya=
01a<<
x
ya=
1a >
log
a
yx=
D
01a<<
log
a
yx=
D
(
)
0;1
(
)
1; 0
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
LÝ THUYẾT.
I

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 33
Sưu tầm và biên soạn
DẠNG 1: TÌM TẬP XÁC ĐỊNH CỦA HÀM SỐ MŨ – LOGARIT
Câu 1: Tìm tập xác định của hàm số
( )
2
2
log 9= −yx
Câu 2: Tìm tập xác định của hàm
( )
2021
log 3yx= −
Câu 3: Tìm tập xác định của hàm
( )
2
log 2 3yx= −
Câu 4: Tìm tập xác định của hàm
3
7
x
y
−
=
Câu 5: Tìm tập xác định của hàm
3
log (2 )
yx= −
Câu 6: Tìm tập xác định của hàm
(
)
2022
y log 3 1x
= +
Câu 7: Tìm tập xác định của hàm số
( )
2
ln 3yx
= −+
là
Câu 8: Tìm tập xác định
D
của hàm số
5
3
log
2
x
y
x
−
=
+
.
Câu 9: Tìm tập xác định của hàm số
1
ln 1
2
yx
x
là
Câu 10: Tìm tập xác định của hàm số
( )
2
5
log 4= −y xx
Câu 11: Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
1
1x mx
ye
++
=
có tập xác định là
.
Câu 12: Tìm tập xác định của hàm số
2
1
log 1
y
x
=
−
Câu 13: Tìm tập xác định của hàm số
( )
2
2022
log 3= −y xx
.
Câu 14: Tìm tập xác định của hàm số
(
)
2
3
log 4 3y xx
= −+
là:
Câu 15: Tìm tập xác định của hàm số
2021
3
log
2
x
y
x
+
=
−
là:
Câu 16: Tất cả các giá trị thực của tham số
m
để hàm số
( )
2
log 2 1
y x xm= − −+
có tập xác định là
.
Câu 17: Có bao nhiêu giá trị nguyên của
m
thuộc đoạn
[ ]
2021;2021−
để hàm số
( )
2
log 2 2y x xm
= − −+
có tập xác định
.
DẠNG 2: BÀI TOÁN LÃI SUẤT KÉP
Câu 18: Lãi suất gửi tiền tiết kiệm của các ngân hàng trong thời gian qua liên tục thay đổi. Bác Mạnh gửi
vào một ngân hàng số tiền 5 triệu đồng với lãi suất 0,7%/tháng. Sau sáu tháng gửi tiền, lãi suất
tăng lên 0,9%/tháng. Đến tháng thứ 10 sau khi gửi tiền, lãi suất giảm xuống 0,6%/tháng và giữ
ổn định. Biết rằng nếu bác Mạnh không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền
lãi sẽ được nhập vào vốn ban đầu. Sau một năm gửi tiền, bác Mạnh rút được số tiền là bao nhiêu?
Câu 19: Ông
A
gửi tiền tiết kiệm với lãi suất
8,1%
/ năm và lãi suất hằng năm được nhập vào vốn. Hỏi
sau bao nhiêu năm Ông
A
được số tiền gấp đôi số tiền ban đầu?
Câu 20: Một người gửi
100
triệu đồng vào một ngân hàng với lãi suất
6%
/ năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm
tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn
300
triệu đồng
bao gồm cả gốc lẫn lãi?.
H
Ệ
TH
Ố
NG BÀI T
Ậ
P.
II

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 34
Sưu tầm và biên soạn
Câu 21: Một người gửi số tiền
300
triệu đồng vào một ngân hàng với lãi suất kép
6%
một năm. Biết rằng
nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi suất sẽ được nhập vào vốn
ban đầu. Hỏi sau 3 năm không rút tiền gốc và lãi, số tiền trong ngân hàng của người đó gần nhất
với số nào sau đây?
Câu 22: Tại thời điểm ban đầu nếu đầu tư
P
đô la với tỷ lệ lãi suất được tính gộp liên tục hàng năm
không đổi là
r
thì giá trị tương lai của khoản đầu tư này sau
t
năm là
( )
.
rt
B t Pe
=
đô la. Giả sử
tỷ lệ lãi suất tính gộp hàng năm là
8%
. Hỏi sau bao nhiêu năm thì số tiền đầu tư ban đầu tăng
thêm ít nhất
50%
.
Câu 23: Một người gởi 60 triệu đồng vào ngân hàng với lãi suất
6%
một năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ nhập vào gốc để tính lãi cho năm tiếp
theo. Hỏi sau ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 100 triệu đồng gồm
cả gốc lẫn lãi?
Câu 24: Một người gửi 100 triệu đồng vào ngân hàng với lãi suất 0,4% / tháng. Biết rằng nếu không rút
tiền ta khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được lập vào vốn ban đầu để tính lãi
cho tháng tiếp theo. Hỏi sau 6 tháng, người đó được lĩnh số tiền gần nhất với số tiền nào dưới
đây, nếu trong khoảng thời gian này người đó không rút tiền ra và lãi xuất không thay đổi?
Câu 25: Một người gửi
50
triệu đồng vào ngân hàng theo thể thức lãi kép với lãi suất
5,5% /
năm, kì hạn
1
năm. Hỏi sau
4
năm, người đó rút cả vốn lẫn lãi được số tiền gần với số nào nhất trong các số
tiền sau?
Câu 26: Một người gửi
200
vào ngân hàng với lãi suất
0, 2% /
tháng. Biết rằng nếu không rút tiền khỏi
ngân hàng thì cứ sau mỗi tháng số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho tháng
tiếp theo. Hỏi sau đúng
10
tháng người đó được lĩnh số tiền gần nhất với số tiền nào dưới đây?
Câu 27: Một người gửi
100
triệu đồng vào một ngân hàng với lãi suất
0,7%/ thaùng
. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu để tính
lãi cho tháng tiếp theo. Hỏi sau đúng
5
tháng, người đó được lĩnh số tiền gần nhất với số tiền
nào dưới đây, nếu trong khoảng thời gian này người đó không rút tiền ra và lãi suất không thay
đổi?
Câu 28: Ông A gửi 200 triệu vào một ngân hàng theo hình thức lãi kép, với lãi suất là 6,5% một năm và
lãi suất không đổi trong suốt thời gian gửi. Sau 6 năm, số tiền lãi của ông bằng bao nhiêu?
Câu 29: Ông A vay ngân hàng
100
triệu đồng với lãi suất
1%
một tháng. Cứ sau mỗi tháng kể từ ngày
vay ông trả góp số tiền
5
triệu đồng. Hỏi sau ít nhất bao nhiêu tháng thì ông A trả hết nợ, biết
tháng cuối cùng ông có thể trả số tiền ít hơn 5 triệu đồng?
Câu 30: Ông Bình vay vốn ngân hàng với số tiền
100000000
đồng. Ông dự định sau đúng
5
năm thì trả
hết nợ theo hình thức: sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ, hai lần hoàn nợ
liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là như nhau. Hỏi theo cách đó, số
tiền
a
mà ông sẽ phải trả cho ngân hàng trong mỗi lần hoàn nợ là bao nhiêu? Biết lãi suất hàng
tháng là
1, 2%
và không thay đổi trong thời gian ông hoàn nợ.
Câu 31: Anh Nam vay tiền ngân hàng
1
tỷ đồng theo phương thức trả góp với lãi suất
0
0
0,5
/ tháng. Nếu
cuối mỗi tháng bắt đầu từ tháng thứ nhất anh Nam trả
30
triệu đồng. Hỏi sau bao nhiêu tháng
anh Nam trả hết nợ?
Câu 32: Một nhóm bạn thực hiện dự án khởi nghiệp làm tinh dầu tự nhiên từ cây xả. Trong bản kế hoạch
nhóm đề ra vay ngân hàng
300
triệu đồng theo phương thức trả góp với lãi suất
0
0
0,5
/ tháng.
Nếu cuối mỗi tháng bắt đầu từ tháng thứ chín nhóm bắt đầu trả trả
10
triệu đồng. Hỏi sau bao
nhiêu tháng kể từ ngày vay nhóm trả hết nợ?

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 35
Sưu tầm và biên soạn
Câu 33: Anh A vay ngân hàng
600.000.000
đồng để mua xe ô tô với lãi suât
7, 8%
một năm. Anh A bắt
đầu trả nợ cho ngân hàng theo cách: sau đúng 1 năm kể từ ngày vay anh bắt đầu trả nợ và hai lần
trả nợ liên tiếp cách nhau đúng 1 năm. Số tiền trả nợ là như nhau ở mỗi lần và sau đúng 8 năm
thì anh A trả hết nợ. Biết rằng lãi suất ngân hàng không thay đổi trong suốt thời gian anh A trả
nợ. Số tiền anh A trả nợ ngân hàng trong mỗi lần là:
Câu 34: Hai anh em An và Bình cùng vay tiền ở ngân hàng với lãi suất
0,7%
một tháng với tổng số tiền
vay là
200
triệu đồng. Sau đúng
1
tháng kể từ khi vay, mỗi người bắt đầu trả nợ cho ngân hàng
khoản vay của mình. Mỗi tháng hai người trả số tiền bằng nhau cho ngân hàng để trừ vào tiền
gốc và lãi. Để trả hết gốc và lãi cho ngân hàng thì An cần
10
tháng, Bình cần
15
tháng. Hỏi số
tiền mà mỗi người trả cho ngân hàng mỗi tháng là bao nhiêu?

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 1
Sưu tầm và biên soạn
BÀI 3: HÀM SỐ MŨ – HÀM SỐ LOGARIT
Hàm số mũ
Hàm số logarit
Định nghĩa
Hàm số được gọi là
hàm số mũ cơ số a.
Hàm số được gọi là
hàm số lôgarit cơ số a.
Tập xác định
Tập giá trị
Tính đơn
điệu
Khi : Hàm số đồng biến trên
;
lim 0; lim
xx
xx
aa
→−∞ →+∞
= = +∞
Khi : Hàm số nghịch biến
trên ;
lim ; lim 0
xx
xx
aa
→−∞ →+∞
= +∞ =
Khi : Hàm số đồng biến trên
;
0
lim log ; lim log
aa
x
x
xx
+
→+∞
→
= −∞ = +∞
Khi : Hàm số nghịch
biến trên ;
0
lim log ; lim log
aa
x
x
xx
+
→+∞
→
= +∞ = −∞
Đồ thị:
- Đi qua điểm và
(
)
;
a1
.
- Liên tục trên
.
- Nằm ở phía trên trục hoành.
Đồ thị:
- Đi qua điểm và
( )
;a 1
.
- Liên tục trên
( )
;+∞0
.
- Nằm ở bên phải trục tung.
Đồ thị
, ( 0, 1)
x
ya a a= >≠
log , ( 0, 1)
a
y xa a= >≠
D =
(0, ).D = +∞
(0; )T
= +∞
= T
1a >
x
ya=
01a<<
x
ya=
1a >
log
a
yx=
D
01a<<
log
a
yx=
D
(
)
0;1
(
)
1; 0
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
LÝ THUYẾT.
I

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 2
Sưu tầm và biên soạn
DẠNG 1: TÌM TẬP XÁC ĐỊNH CỦA HÀM SỐ MŨ – LOGARIT
Câu 1: Tìm tập xác định của hàm số
( )
2
2
log 9= −yx
Lời giải
Điều kiện
2
3
90
3
>
−>⇔
<−
x
x
x
.
Câu 2: Tìm tập xác định của hàm
(
)
2021
log 3yx= −
Lời giải
Điều kiện xác định là:
30 3
xx
−>↔<
.
Vậy hàm số có TXĐ:
(
)
;3D
= −∞
.
Câu 3: Tìm tập xác định của hàm
( )
2
log 2 3yx= −
Lời giải
Hàm số
( )
2
log 2 3yx= −
xác định
3
2 30
2
xx⇔ −>⇔ >
.
Vậy tập xác định của hàm số là:
3
;
2
D
= +∞
.
Câu 4: Tìm tập xác định của hàm
3
7
x
y
−
=
Lời giải
Điều kiện:
30x −≥
3x⇔≥
.
Vậy tập xác định là
[
)
3;D = +∞
.
Câu 5: Tìm tập xác định của hàm
3
log (2 )yx= −
Lời giải
Điều kiện:
2 0 2.xx−>⇔<
Vậy tập xác định
( ;2).D
= −∞
Câu 6: Tìm tập xác định của hàm
( )
2022
y log 3 1x= +
Lời giải
Điều kiện:
1
3 10
3
xx
−
+> ⇔ >
.
Câu 7: Tìm tập xác định của hàm số
( )
2
ln 3yx= −+
là
Lời giải
Điều kiện xác định:
2
30 3 3
xx− + > ⇔− < <
.
H
Ệ
TH
Ố
NG BÀI T
Ậ
P.
II

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 3
Sưu tầm và biên soạn
Câu 8: Tìm tập xác định
D
của hàm số
5
3
log
2
x
y
x
−
=
+
.
Lời giải
Điều kiện
3
3
0
2
2
x
x
x
x
>
−
>⇔
<−
+
Vậy tập xác định
( ; 2) (3; )D
= −∞ − ∪ +∞
Câu 9: Tìm tập xác định của hàm số
1
ln 1
2
yx
x
là
Lời giải
Hàm số xác định khi
20 2
12
10 1
xx
x
xx
.
Vậy
1; 2D
.
Câu 10: Tìm tập xác định của hàm số
( )
2
5
log 4= −y xx
Lời giải
Điều kiện xác định của hàm số trên là
2
4 00 4
− >⇔<<xx x
.
Câu 11: Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
1
1x mx
ye
++
=
có tập xác định là
.
Lời giải
Hàm số có tập xác định là
khi và chỉ khi
+ + > ∀∈
2
1 0,x mx x
⇔∆<0
2
40m⇔ −<
22m
⇔− < <
.
Câu 12: Tìm tập xác định của hàm số
2
1
log 1
y
x
=
−
Lời giải
Hàm số xác định khi
22
00
0
log 1 0 log 1
2
xx
x
xx
x
>>
>
⇔⇔
−≠ ≠
≠
Vậy tập xác định
( ) { }
0; \ 2D = +∞
.
Câu 13: Tìm tập xác định của hàm số
( )
2
2022
log 3= −y xx
.
Lời giải
Hàm số xác định khi:
( )
2
3 0 0; 3xx x− >⇔∈
Vậy
( )
0; 3D =
Câu 14: Tìm tập xác định của hàm số
( )
2
3
log 4 3y xx= −+
là:
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 4
Sưu tầm và biên soạn
Điều kiện
2
1
4 30
3
x
xx
x
<
− +>⇔
>
. Vậy tập xác định của hàm số:
( ) ( )
;1 3;−∞ ∪ +∞
.
Câu 15: Tìm tập xác định của hàm số
2021
3
log
2
x
y
x
+
=
−
là:
Lời giải
Hàm số
2021
3
log
2
x
y
x
+
=
−
xác định khi
3
0
2
x
x
+
>
−
32x
⇔− < <
.
Suy ra tập xác định của hàm số:
( )
3; 2
D
= −
.
Câu 16: Tất cả các giá trị thực của tham số
m
để hàm số
( )
2
log 2 1y x xm= − −+
có tập xác định là
.
Lời giải
Điều kiện:
2
2 10x xm− − +>
.
Để hàm số có tập xác định là
2
2 10x xm x⇔ − − + > ∀∈
( )
( )
2
1 10 0mm⇔− −− + < ⇔ <
.
Câu 17: Có bao nhiêu giá trị nguyên của
m
thuộc đoạn
[
]
2021;2021−
để hàm số
( )
2
log 2 2y x xm
= − −+
có tập xác định
.
Lời giải
Điều kiện:
2
2 20x xm− − +>
.
Hàm số
( )
2
ln 2 2y x xm= − −+
có tập xác định
2
2 2 0,x xm x⇔ − − + > ∀∈
.
'1 20 1mm⇔∆ = + − < ⇔ <
.
Do
m
nguyên thuộc đoạn
[ ]
2021;2021−
nên có 2022 giá trị
m
thỏa yêu cầu bài toán.
DẠNG 2: BÀI TOÁN LÃI SUẤT KÉP
Câu 18: Lãi suất gửi tiền tiết kiệm của các ngân hàng trong thời gian qua liên tục thay đổi. Bác Mạnh gửi
vào một ngân hàng số tiền 5 triệu đồng với lãi suất 0,7%/tháng. Sau sáu tháng gửi tiền, lãi suất
tăng lên 0,9%/tháng. Đến tháng thứ 10 sau khi gửi tiền, lãi suất giảm xuống 0,6%/tháng và giữ
ổn định. Biết rằng nếu bác Mạnh không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền
lãi sẽ được nhập vào vốn ban đầu. Sau một năm gửi tiền, bác Mạnh rút được số tiền là bao nhiêu?
Lời giải
Số tiền bác Mạnh thu được:
( ) (
) ( )
633
5 1 0,007 1 0,009 1 0,006 5,452733453+ + +=
triệu
đồng.
Câu 19: Ông
A
gửi tiền tiết kiệm với lãi suất
8,1%
/ năm và lãi suất hằng năm được nhập vào vốn. Hỏi
sau bao nhiêu năm Ông
A
được số tiền gấp đôi số tiền ban đầu?
Lời giải
Gọi số tiền ban đầu ông
A
gửi tiết kiệm là
B
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 5
Sưu tầm và biên soạn
Theo công thức lãi kép ta có số tiền sau
n
năm là:
(
)
1 0,081
n
B
+
.
Để số tiền tăng gấp đôi thì
n
phải thỏa mãn phương trình:
(
)
1 0,081 2
n
BB+=
( )
1,081
1,081 2 log 2 8,899
n
nn⇔ =⇔= ⇔=
.
Như vậy sau 9 năm Ông
A
sẽ thu được số tiền gấp đôi số tiền ban đầu.
Câu 20: Một người gửi
100
triệu đồng vào một ngân hàng với lãi suất
6%
/ năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm
tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn
300
triệu đồng
bao gồm cả gốc lẫn lãi?.
Lời giải
Theo công thức tính lãi suất kép, ta có vốn tích luỹ sau
n
năm là
( )
1
n
n
P =P r+
với
P
là vốn
ban đầu,
r
là lãi suất.
1 06
6
300 100 1 log 3 19
100
n
,
n=
⇒= + ⇔ ≈
.
Câu 21: Một người gửi số tiền
300
triệu đồng vào một ngân hàng với lãi suất kép
6%
một năm. Biết rằng
nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi suất sẽ được nhập vào vốn
ban đầu. Hỏi sau 3 năm không rút tiền gốc và lãi, số tiền trong ngân hàng của người đó gần nhất
với số nào sau đây?
Lời giải
Áp dụng công thức tính lãi suất theo hình thức lãi kép:
( )
1
n
PA r
= +
.
Trong đó:
P
là số tiền gồm vốn lẫn lãi tại thời điểm
n
tính từ thời điểm gửi;
A
là số tiền gửi vào
ban đầu và
( )
%r
là lãi suất.
Với
300.000.000
3
6%
A
n
r
=
=
=
, suy ra
( )
3
300.000.000 1 6% 357.304.800 357.305.000P = += ≈
.
Câu 22: Tại thời điểm ban đầu nếu đầu tư
P
đô la với tỷ lệ lãi suất được tính gộp liên tục hàng năm
không đổi là
r
thì giá trị tương lai của khoản đầu tư này sau
t
năm là
( )
.
rt
B t Pe=
đô la. Giả sử
tỷ lệ lãi suất tính gộp hàng năm là
8%
. Hỏi sau bao nhiêu năm thì số tiền đầu tư ban đầu tăng
thêm ít nhất
50%
.
Lời giải
Theo đề ra ta có:
0,08.
. 1, 5
t
Pe P>
0,08
ln 1, 5
1, 5 0, 08 ln 1, 5 5, 06
0,08
t
e tt⇔ > ⇒ > ⇒>
.
Câu 23: Một người gởi 60 triệu đồng vào ngân hàng với lãi suất
6%
một năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ nhập vào gốc để tính lãi cho năm tiếp
theo. Hỏi sau ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 100 triệu đồng gồm
cả gốc lẫn lãi?
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 6
Sưu tầm và biên soạn
Ta có:
( )
.1
n
SA r= +
. Để số tiền cả gốc lẫn lãi lớn hơn 100 triệu
1 1 6%
100
log log 8,766
60
r
S
n
A
++
⇒> = ≈
.
Câu 24: Một người gửi 100 triệu đồng vào ngân hàng với lãi suất 0,4% / tháng. Biết rằng nếu không rút
tiền ta khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được lập vào vốn ban đầu để tính lãi
cho tháng tiếp theo. Hỏi sau 6 tháng, người đó được lĩnh số tiền gần nhất với số tiền nào dưới
đây, nếu trong khoảng thời gian này người đó không rút tiền ra và lãi xuất không thay đổi?
Lời giải
Áp dụng công thức lãi kép ta có sau đúng 6 tháng, người đó lĩnh được số tiền:
Ta có:
6
0
0, 4
(1 ) 100.000.000 1 102.424.128
100
n
n
AA r
= += + =
Câu 25: Một người gửi
50
triệu đồng vào ngân hàng theo thể thức lãi kép với lãi suất
5,5% /
năm, kì hạn
1
năm. Hỏi sau
4
năm, người đó rút cả vốn lẫn lãi được số tiền gần với số nào nhất trong các số
tiền sau?
Lời giải
Gọi số tiền ban đầu
A
. Lãi suất tính theo năm là
r
.
Số tiền cả vốn lẫn lãi sau
n
năm được tính theo công thức:
( )
1
n
n
AA r= +
.
Thay số với
50; 5,5%, 4Ar n= = =
ta được số tiền là:
4
4
5,5
50. 1 61,94
100
A
=+=
Câu 26: Một người gửi
200
vào ngân hàng với lãi suất
0, 2% /
tháng. Biết rằng nếu không rút tiền khỏi
ngân hàng thì cứ sau mỗi tháng số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho tháng
tiếp theo. Hỏi sau đúng
10
tháng người đó được lĩnh số tiền gần nhất với số tiền nào dưới đây?
Lời giải
Theo công thức lãi kép ta có số tiền cả lãi và vốn sau 10 tháng là:
( ) ( )
10
1 200 1 0.2% 204,036
n
TX r= += + ≈
triệu đồng.
Câu 27: Một người gửi
100
triệu đồng vào một ngân hàng với lãi suất
0,7%/ thaùng
. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu để tính
lãi cho tháng tiếp theo. Hỏi sau đúng
5
tháng, người đó được lĩnh số tiền gần nhất với số tiền
nào dưới đây, nếu trong khoảng thời gian này người đó không rút tiền ra và lãi suất không thay
đổi?
Lời giải
Sau
5
tháng, người đó được lĩnh số tiền là
( )
5
6
100.10 . 1 0,7% 103.549.000S = +=
đồng.
Câu 28: Ông A gửi 200 triệu vào một ngân hàng theo hình thức lãi kép, với lãi suất là 6,5% một năm và
lãi suất không đổi trong suốt thời gian gửi. Sau 6 năm, số tiền lãi của ông bằng bao nhiêu?
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 7
Sưu tầm và biên soạn
Ta có
(
)
(
)
6
1 200. 1 6,5% 292
n
TA r= += +
triệu.
Vậy số tiền lãi là
292 200 92−=
triệu.
Câu 29: Ông A vay ngân hàng
100
triệu đồng với lãi suất
1%
một tháng. Cứ sau mỗi tháng kể từ ngày
vay ông trả góp số tiền
5
triệu đồng. Hỏi sau ít nhất bao nhiêu tháng thì ông A trả hết nợ, biết
tháng cuối cùng ông có thể trả số tiền ít hơn 5 triệu đồng?
Lời giải
Sau
n
tháng, ông A còn vay số tiền là:
(
) (
) ( ) ( )
( )
12
11
100 1 5 1 1 ... 1 100 1 5 .
n
n nn n
r
r rr r
r
−−
+−
+− + ++ ++= +−
với
r
là lãi suất/1 tháng.
Để tháng thứ n ông trả hết nợ thì:
(
)
( )
(
)
1, 01 1
5
100 1,01 5 0 1,01 23
0,01 4
n
nn
n
−
− =⇔ =⇔≈
tháng.
Câu 30: Ông Bình vay vốn ngân hàng với số tiền
100000000
đồng. Ông dự định sau đúng
5
năm thì trả
hết nợ theo hình thức: sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ, hai lần hoàn nợ
liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là như nhau. Hỏi theo cách đó, số
tiền
a
mà ông sẽ phải trả cho ngân hàng trong mỗi lần hoàn nợ là bao nhiêu? Biết lãi suất hàng
tháng là
1, 2%
và không thay đổi trong thời gian ông hoàn nợ.
Lời giải
Gọi
, , ,
n
mrT a
lần lượt là số tiền vay ngân hàng, lãi suất hàng tháng, tổng số tiền vay còn lại
sau
n
tháng, số tiền trả đều đặn mỗi tháng.
● Sau khi hết tháng thứ nhất
(
)
1
n
=
thì còn lại:
( )
1
1.T mr a= +−
● Sau khi hết tháng thứ hai
( )
2n =
thì còn lại:
( ) ( )
2
11Tmrara= +− +−
( ) ( )
( ) ( ) ( )
( )
2 2 22
1 1 1 2 1 1 1.
a
mr ar a mr ar mr r
r
= +− +−= +− += +− +−
● Sau khi hết tháng thứ ba
(
)
3n =
thì còn:
( )
( ) ( )
22
3
1 11 1
a
T mr r r a
r
= +− +− +−
( ) ( )
33
1 1 1.
a
mr r
r
= +− +−
● Sau khi hết tháng thứ
n
thì còn lại:
( ) ( )
1 11
nn
n
a
T mr r
r
= +− +−

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 8
Sưu tầm và biên soạn
Áp dụng công thức trên, ta có
( )
( )
60
5
60
1, 2
12.10 1
1
100
0
11
1, 2
11
100
n
n
n
mr r
Ta
r
+
+
=⇔= =
+−
+−
.
Câu 31: Anh Nam vay tiền ngân hàng
1
tỷ đồng theo phương thức trả góp với lãi suất
0
0
0,5
/ tháng. Nếu
cuối mỗi tháng bắt đầu từ tháng thứ nhất anh Nam trả
30
triệu đồng. Hỏi sau bao nhiêu tháng
anh Nam trả hết nợ?
Gọi
a
là số tiền vay,
r
là lãi suất,
m
là số tiền hàng tháng trả.
Số tiền nợ sau tháng thứ nhất là:
( )
1
1Na rm= +−
.
Số tiền nợ sau tháng thứ hai là:
(
) (
)
2
11
N a rm a rmrm
= +− + −− −
(
)
( )
2
1 11arm r= + − ++
….
Số tiền nợ sau
n
tháng là:
(
) ( ) ( ) ( )
( )
12
11
1 1 1 ... 1 1
n
n nn n
n
r
Narm r r arm
r
−−
+−
=+− + ++ ++=+−
.
Sau
n
tháng anh Nam trả hết nợ:
( )
( )
11
10
n
n
n
r
Na r m
r
+−
=+− =
( )
(
)
1 0,005 1
1000 1 0,005 30 0
0,005
36,55
n
n
n
+−
⇔+ − =
⇔=
Vậy
37
tháng thì anh Nam trả hết nợ.
Câu 32: Một nhóm bạn thực hiện dự án khởi nghiệp làm tinh dầu tự nhiên từ cây xả. Trong bản kế hoạch
nhóm đề ra vay ngân hàng
300
triệu đồng theo phương thức trả góp với lãi suất
0
0
0,5
/ tháng.
Nếu cuối mỗi tháng bắt đầu từ tháng thứ chín nhóm bắt đầu trả trả
10
triệu đồng. Hỏi sau bao
nhiêu tháng kể từ ngày vay nhóm trả hết nợ?
Lời giải
Gọi
a
là tổng số tiền vay số tiền vay ngân hàng sau
8
tháng,
r
là lãi,
m
là số tiền hàng
tháng trả.
Ta có:
( )
8
300 1 0,5%
a = +
Số tiền nợ sau tháng thứ chín là:
( )
1
1
= +−Na rm
.
Số tiền nợ sau tháng thứ mười là:
(
) ( )
( ) ( )
2
2
11
1 11
= +− + −− −
= + − ++
N a rm a rmrm
arm r
….
Số tiền nợ sau tháng thứ
9
n +
là:
( )
( )
11
1
+−
=+−
n
n
n
r
Na r m
r
.
Sau
9n +
tháng trả hết nợ:
( )
( )
11
10
+−
=+− =
n
n
n
r
Na r m
r
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 9
Sưu tầm và biên soạn
( ) (
)
( )
8
1 0,5% 1
300. 1 0,5% 1 0,5% 10. 0 23
0,5%
n
n
n
+−
⇔ + + − =⇒≈
.
Vậy
31
tháng thì nhóm bạn trả hết nợ.
Câu 33: Anh A vay ngân hàng
600.000.000
đồng để mua xe ô tô với lãi suât
7, 8%
một năm. Anh A bắt
đầu trả nợ cho ngân hàng theo cách: sau đúng 1 năm kể từ ngày vay anh bắt đầu trả nợ và hai lần
trả nợ liên tiếp cách nhau đúng 1 năm. Số tiền trả nợ là như nhau ở mỗi lần và sau đúng 8 năm
thì anh A trả hết nợ. Biết rằng lãi suất ngân hàng không thay đổi trong suốt thời gian anh A trả
nợ. Số tiền anh A trả nợ ngân hàng trong mỗi lần là:
Lời giải
Đặt
7, 8%r
Gọi
M
là số tiền anh A trả hàng năm.
Sau năm thứ 1, số tiền còn lại:
( )
1
600 1V rM= +−
.
Sau năm thứ 2, số tiền còn lại:
( )
21
1VV rM= +−
( ) ( )
2
600 1 1r M rM
= + − +−
.
………
Sau năm thứ
n
, số tiền còn lại:
(
) ( )
( )
1
600 1 1 ... 1
nn
n
V rMr MrM
−
= +−+−−+−
.
Vậy sau 8 năm anh A trả hết nợ, ta có:
( )
( )
8
8
11
600 1 0
r
rM
r
+−
+− =
( )
( )
8
8
600 1 .
11
rr
M
r
+
⇔=
+−
( )
( )
8
8
600 1 7,8% .7,8%
1 7,8% 1
M
+
⇔=
+−
103,618≈
triệu đồng.
Câu 34: Hai anh em An và Bình cùng vay tiền ở ngân hàng với lãi suất
0,7%
một tháng với tổng số tiền
vay là
200
triệu đồng. Sau đúng
1
tháng kể từ khi vay, mỗi người bắt đầu trả nợ cho ngân hàng
khoản vay của mình. Mỗi tháng hai người trả số tiền bằng nhau cho ngân hàng để trừ vào tiền
gốc và lãi. Để trả hết gốc và lãi cho ngân hàng thì An cần
10
tháng, Bình cần
15
tháng. Hỏi số
tiền mà mỗi người trả cho ngân hàng mỗi tháng là bao nhiêu?
Lời giải
Gọi số tiền vay ban đầu là
0
u
, tiền trả hàng tháng là
x
, lãi suất hàng tháng là
0,7%
.
Số tiền còn lại sau
1
tháng:
10
1,007uu x
= −
.
Số tiền còn lại sau
2
tháng:
( )
22
21 0 0
1,007 1,007 1,007 1,007 1 1,007u u xu xxu x= −= − −= − +
.
Số tiền còn lại sau
n
tháng:

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 10
Sưu tầm và biên soạn
(
)
21
0
1,007 1 1,007 1,007 ... 1,007
nn
n
uu x
−
= − + + ++
0
1,007 1
1,007
0,007
n
n
ux
−
= −
.
Sau
n
tháng thì hết nợ
( )
0
1,007 1
0
0,007.1,007
n
n
n
x
uu
−
⇒=⇔=
.
Để trả hết nợ thì An cần
10
tháng và Bình cần
15
tháng, ta được:
( ) (
)
10 15
8
10 15
1,007 1 1,007 1
2.10 8397068,067
0,007.1,007 0,007.1,007
xx
x
−−
+ = ⇔=
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 36
Sưu tầm và biên soạn
BÀI 3: HÀM SỐ MŨ – HÀM SỐ LOGARIT
BÀI TẬP TRẮC NGHIỆM TRÍCH TỪ ĐỀ THAM KHẢO VÀ ĐỀ CHÍNH THỨC
CỦA BỘ GIÁO DỤC TỪ NĂM 2017 ĐẾN NAY
Câu 1: (MĐ 103-2022) Cho
5
3a =
,
2
3
b
=
và
6
3c =
. Mệnh đề nào dưới đây đúng?
A.
a cb<<
. B.
abc<<
. C.
bac<<
. D.
cab<<
.
Câu 2: (MĐ 104-2022) Cho
5
3a =
,
2
3
b =
và
6
3c =
. Mệnh đề nào dưới đây đúng?
A.
abc
<<
. B.
acb
<<
. C.
cab
<<
. D.
bac
<<
.
Câu 3: (MĐ 101-2022) Tập xác định của hàm số
( )
3
log 4x −
là
A.
( )
5; +∞
. B.
( )
;−∞ +∞
. C.
( )
4; +∞
. D.
( )
;4−∞ −
.
Câu 4: (MĐ 103-2022) Tập xác định của hàm số
( )
2
log 1yx= −
là
A.
( )
2; +∞
. B.
( )
;−∞ +∞
. C.
( )
1; +∞
. D.
( )
;1−∞
.
Câu 5: (MĐ 101-2022) Có bao nhiêu số nguyên thuộc tập xác định của hàm số
( )( )
log 6 2
y xx= −+
?
A.
7
. B.
8
. C.
9
. D. Vô số.
Câu 6: (MĐ 101-2022) Với mọi số thực
a
dương tuỳ ý
4log a
bằng
A.
2log a−
. B.
2log a
. C.
4log a−
. D.
8log a
.
Câu 7: (MĐ 103-2022) Với
a
là số thực dương tùy ý,
(
)
log 100
a
bằng
A.
1 log a−
. B.
2 log a+
. C.
2 log a−
. D.
1 log a+
.
Câu 8: (MĐ 103-2022) Với
,ab
là các số thực dương tùy ý và
1a ≠
,
1
3
1
log
a
b
bằng
A.
3log
a
b
. B.
log
a
b
. C.
3log
a
b−
. D.
1
log
3
a
b
.
Câu 9: (MĐ 104-2022) Với
,ab
là các số thực dương tuỳ ý và
1
3
1
1, log
a
a
b
≠
bằng
A.
log
a
b
. B.
3log
a
b−
. C.
1
log
3
a
b
. D.
3log
a
b
.
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 37
Sưu tầm và biên soạn
Câu 10: (TK 2020-2021) Với
a
là số thực dương tùy ý,
3
a
bằng
A.
6
.a
B.
3
2
.a
C.
2
3
.
a
D.
1
6
.
a
Câu 11: (TK 2020-2021) Với
a
là số thực dương tùy ý,
( )
3
log 9a
bằng
A.
3
1
log .
2
a+
B.
3
2log a
C.
(
)
2
3
log .a
D.
3
2 log .a
+
Câu 12: Cho
0a >
và
1a ≠
, khi đó
4
log
a
a
bằng
A.
4
. B.
1
4
. C.
1
4
−
. D.
4
.
Câu 13: (MĐ 102 2020-2021 – ĐỢT 1) Cho
0
a >
và
1a ≠
, khi đó
3
log
a
a
bằng
A.
3−
. B.
1
3
. C.
1
3
−
. D.
3
.
Câu 14: (MĐ 103 2020-2021 – ĐỢT 1) Cho
0a >
và
1
a ≠
, khi đó
log
a
a
bằng
A.
2
. B.
2−
. C.
1
2
−
. D.
1
2
.
Câu 15: (MĐ 104 2020-2021 – ĐỢT 1) Cho
0
a
>
và
a1≠
, khi đó
5
log
a
a
bằng
A.
1
5
. B.
1
5
−
. C.
5
. D.
5−
Câu 16: Với mọi
,
ab
thỏa mãn
3
22
log log 6ab+=
, khẳng định nào sau đây đúng?
A.
3
64
ab=
. B.
3
36
ab=
. C.
3
64ab+=
. D.
3
36ab+=
.
Câu 17: (MĐ 102 2020-2021 – ĐỢT 1) Với mọi
,ab
thỏa mãn
3
22
log log 8ab+=
. Khẳng định nào dưới
đây đúng?
A.
3
64ab+=
. B.
3
256ab=
. C.
3
64ab
=
. D.
3
256ab+=
.
Câu 18: (MĐ 103 2020-2021 – ĐỢT 1) Với mọi
a
,
b
thỏa mãn
3
22
log log 7ab+=
. Khẳng định nào
dưới đây đúng?
A.
3
49
ab+=
. B.
3
128
ab=
. C.
3
128ab
+=
. D.
3
49ab=
.
Câu 19: (MĐ 104 2020-2021 – ĐỢT 1) Với mọi
,ab
thỏa mãn
3
22
log log 5ab+=
, khẳng định nào dưới
đây là đúng?
A.
3
32ab=
. B.
3
25ab
=
. C.
3
25ab+=
. D.
3
32ab+=
.
Câu 20: Với
0
a >
đặt
( )
2
log 2ab=
, khi đó
( )
4
2
log 8a
bằng
A.
47b +
. B.
43b +
. C.
4b
. D.
41b −
.
Câu 21: Với
0a >
, đặt
( )
2
log 2ab=
, khi đó
( )
3
2
log 4
a
bằng
A.
35b +
. B.
3b
. C.
32b +
. D.
31b −
.
Câu 22: (MĐ 103 2020-2021 – ĐỢT 2) Với
0a >
, đặt
( )
3
log 3
ab=
, khi đó
( )
3
3
log 9a
bằng
A.
3b
. B.
31b −
. C.
32b +
. D.
35b +
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 38
Sưu tầm và biên soạn
Câu 23: (MĐ 104 2020-2021 – ĐỢT 2) Với
0a >
, đặt
( )
3
log 3ab=
khi đó
( )
4
3
log 27a
bằng
A.
43b +
. B.
4b
. C.
41b −
. D.
47b +
.
Câu 24: (Mã 105 2017) Rút gọn biểu thức
5
3
3
:Qb b=
với
0b >
.
A.
4
3
Qb
−
=
B.
4
3
Qb=
C.
5
9
Qb=
D.
2
Qb=
Câu 25: (Mã 110 2017) Rút gọn biểu thức
1
6
3
.Px x=
với
0x >
.
A.
Px=
B.
1
8
Px=
C.
2
9
Px=
D.
2
Px=
Câu 26: (Mã 102 2017) Cho biểu thức
4
3
23
..P xx x=
, với
0x >
. Mệnh đề nào dưới đây đúng?
A.
2
3
Px=
B.
1
2
Px=
C.
13
24
Px=
D.
1
4
Px=
Câu 27: (Đề Tham Khảo 2017) Tính giá trị của biểu thức
( ) ( )
2017 2016
7 43 43 7P =+−
A.
( )
2016
7 43P = +
B.
1P =
C.
7 43P = −
D.
7 43P = +
Câu 28: (Mã 101 - 2020 Lần 1) Với
,ab
là các số thực dương tùy ý và
1a ≠
,
5
log
a
b
bằng:
A.
5log
a
b
. B.
1
log
5
a
b+
. C.
5 log
a
b+
. D.
1
log
5
a
b
.
Câu 29: (Mã 102 - 2020 Lần 1) Với , là các số thực dương tùy ý và , bằng
A. . B. . C. . D. .
Câu 30: (Mã 103 - 2020 Lần 1) Với a,b là các số thực dương tùy ý và
1a ≠
,
3
log
a
b
bằng
A.
3 log
a
b+
B.
3log
a
b
C.
1
3
log
a
b+
D.
1
3
log
a
b
Câu 31: (Mã 103 2018) Với
a
là số thực dương tùy ý,
( ) ( )
ln 7 ln 3aa−
bằng
A.
ln 7
ln 3
B.
7
ln
3
C.
( )
ln 4a
D.
( )
( )
ln 7
ln 3
a
a
Câu 32: (Mã 101 2018) Với
a
là số thực dương tùy ý,
( ) ( )
ln 5 ln 3aa−
bằng:
A.
5
ln
3
B.
ln 5
ln 3
C.
( )
( )
ln 5
ln 3
a
a
D.
( )
ln 2a
Câu 33: (Mã 110 2017) Cho
log 2
a
b =
và
log 3
a
c =
. Tính
( )
23
log
a
P bc=
.
A.
13P =
B.
31P =
C.
30P =
D.
108P =
Câu 34: (Mã 102 2019) Cho
a
và
b
là hai số thực dương thỏa mãn
32
32ab =
. Giá trị của
22
3log 2logab+
bằng
A.
4
. B.
5
. C.
2
. D.
32
.
a
b
1a ≠
2
log
a
b
1
log
2
a
b+
1
log
2
a
b
2 log
a
b+
2log
a
b

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 39
Sưu tầm và biên soạn
Câu 35: (Đề Tham Khảo 2017) Cho
,ab
là các số thực dương thỏa mãn
1a ≠
,
ab≠
và
log 3
a
b =
.
Tính
P log
b
a
b
a
=
.
A.
5 33P =−+
B.
13P =−+
C.
13P =−−
D.
5 33P =−−
Câu 36: (Mã 103 2019) Cho
a
và
b
là hai số thực dương thỏa mãn
23
16ab =
. Giá trị của
22
2log 3logab+
bằng
A.
2
. B.
8
. C.
16
. D.
4
.
Câu 37: (Mã 101 2019) Cho
a
và
b
là hai số thực dương thỏa mãn
4
16ab=
.
Giá trị của
22
4log logab+
bằng
A.
4
. B.
2
. C.
16
. D.
8
.
Câu 38: (Mã 123 2017) Với
a
,
b
là các số thực dương tùy ý và
a
khác
1
, đặt
2
36
log log
a
a
Pb b= +
.
Mệnh đề nào dưới đây đúng?
A.
6log
a
Pb=
B.
27log
a
Pb=
C.
15log
a
Pb=
D.
9log
a
Pb=
Câu 39: (Mã 105 2017) Cho
3
log 2a =
và
2
1
log
2
b =
. Tính
( )
2
33 1
4
2log log 3 logI ab
= +
.
A.
5
4
I =
B.
0I =
C.
4I =
D.
3
2
I =
Câu 40: (Mã 104 2017) Với mọi
a
,
b
,
x
là các số thực dương thoả mãn
2 22
gl lo 5lo gg 3oabx +=
.
Mệnh đề nào dưới đây đúng?
A.
53x ab= +
B.
53
xa b= +
C.
53
x ab=
D.
35x ab= +
Câu 41: (Mã 104 2019) Cho
a
và
b
là hai số thực dương thỏa mãn
3
8ab =
. Giá trị của
22
log 3logab+
bằng
A.
6
. B.
2
. C.
3
. D.
8
.
Câu 42: (Mã 123 2017) Cho
log 3, log 4
ab
xx= =
với $a,b$ là các số thực lớn hơn 1. Tính
log .
ab
Px=
A.
12P =
B.
12
7
P =
C.
7
12
P =
D.
1
12
P =
Câu 43: (Mã 110 2017) Cho
, xy
là các số thực lớn hơn
1
thoả mãn
22
96x y xy+=
. Tính
( )
12 12
12
1 log log
2log 3
xy
M
xy
++
=
+
.
A.
1
2
M =
. B.
1
3
M =
. C.
1
4
M =
. D.
1M =
Câu 44: (Đề Tham Khảo 2020 Lần 2) Xét số thực
a
và
b
thỏa mãn
( )
39
log 3 .9 log 3
ab
=
. Mệnh đề nào
dưới đây đúng
A.
22ab+=
. B.
421ab+=
. C.
41ab =
. D.
241ab+=
.
Câu 45: (Mã 102 - 2020 Lần 1) Cho
a
và
b
là hai số thực dương thỏa mãn
2
log ( )
43
ab
a=
. Giá trị của
2
ab
bằng
A. . B. . C. . D. .
3
6
2
12

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 40
Sưu tầm và biên soạn
Câu 46: (Mã 102 - 2020 Lần 2) Với
,
ab
là các số thực dương tùy ý thỏa mãn
39
log 2log 2ab
−=
, mệnh
đề nào dưới đây đúng?
A.
2
9ab=
. B.
9ab=
. C.
6ab=
. D.
2
9ab=
.
Câu 47: (Mã 103 - 2020 Lần 2) Với
,ab
là các số thực dương tùy ý thỏa mãn
39
log 2log 3ab−=
, mệnh
đề nào dưới đây đúng?
A.
27ab=
. B.
9ab=
. C.
4
27
ab
=
. D.
2
27
ab
=
.
Câu 48: (Mã 104 - 2020 Lần 2) Với
,
ab
là các số thực dương tùy ý thỏa mãn
24
log 2log 4ab−=
, mệnh
đề nào dưới đây đúng?
A.
2
16ab
=
. B.
8ab=
. C.
16ab=
. D.
4
16ab=
.
Câu 49: (Đề Tham Khảo 2019) Đặt
3
log 2 a=
khi đó
16
log 27
bằng
A.
3
4
a
B.
3
4a
C.
4
3a
D.
4
3
a
Câu 50: (Đề Minh Họa 2017) Đặt
25
log 3, log 3.ab= =
Hãy biểu diễn
6
log 45
theo
a
và
b
.
A.
2
6
22
log 45
a ab
ab
−
=
B.
6
2
log 45
a ab
ab b
+
=
+
C.
2
6
22
log 45
a ab
ab b
−
=
+
D.
6
2
log 45
a ab
ab
+
=
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 1
Sưu tầm và biên soạn
BÀI 3: HÀM SỐ MŨ – HÀM SỐ LOGARIT
BÀI TẬP TRẮC NGHIỆM TRÍCH TỪ ĐỀ THAM KHẢO VÀ ĐỀ CHÍNH THỨC
CỦA BỘ GIÁO DỤC TỪ NĂM 2017 ĐẾN NAY
Câu 1: (MĐ 103-2022) Cho
5
3a =
,
2
3
b
=
và
6
3c =
. Mệnh đề nào dưới đây đúng?
A.
a cb<<
. B.
abc<<
. C.
bac<<
. D.
cab<<
.
Lời giải
Chọn C
Vì
256
<<
nên
256
33 3<<
hay
bac<<
.
Câu 2: (MĐ 104-2022) Cho
5
3a =
,
2
3
b =
và
6
3c =
. Mệnh đề nào dưới đây đúng?
A.
abc
<<
. B.
acb<<
. C.
cab<<
. D.
bac<<
.
Lời giải
Chọn D
Ta có
24
33b
= =
. Vì
456<<
và
31>
nên
456
333<<
. Vậy
bac<<
.
Câu 3: (MĐ 101-2022) Tập xác định của hàm số
( )
3
log 4x −
là
A.
( )
5; +∞
. B.
( )
;−∞ +∞
. C.
(
)
4; +∞
. D.
( )
;4−∞ −
.
Lời giải
Chọn C
Hàm số đã cho xác định
40 4xx⇔−>⇔>
Vậy tập xác định của hàm số là
( )
4; .D = +∞
Câu 4: (MĐ 103-2022) Tập xác định của hàm số
( )
2
log 1yx= −
là
A.
( )
2; +∞
. B.
( )
;−∞ +∞
. C.
( )
1; +∞
. D.
( )
;1−∞
.
Lời giải
Chọn C
Điều kiện xác định:
10 1xx−> ⇔ >
.
Vậy tập xác định của hàm số
( )
2
log 1yx= −
là
( )
1; +∞
.
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 2
Sưu tầm và biên soạn
Câu 5: (MĐ 101-2022) Có bao nhiêu số nguyên thuộc tập xác định của hàm số
( )
( )
log 6 2y xx= −+
?
A.
7
. B.
8
. C.
9
. D. Vô số.
Lời giải
Chọn A
Điều kiện:
( )( )
6 20 2 6xx x− + > ⇔− < <
( ) { }
,
: 2;6 1; 0;1; 2;3; 4;5
x Dx
TXÐ D x
∈∈
⇒ = − → ∈ − ⇒
có 7 giá trị của
x
thỏa mãn bài toán.
Câu 6: (MĐ 101-2022) Với mọi số thực
a
dương tuỳ ý
4log a
bằng
A.
2log
a−
. B.
2log
a
. C.
4log
a−
. D.
8log
a
.
Lời giải
Chọn B
Ta có
1
2
1
4log 4log 4. log 2log .
2
aa aa
= = =
.
Câu 7: (MĐ 103-2022) Với
a
là số thực dương tùy ý,
( )
log 100a
bằng
A.
1 log
a
−
. B.
2 log a
+
. C.
2 log a−
. D.
1 log a+
.
Lời giải
Chọn B
Ta có
(
)
log 100 log100 log 2 loga aa
= +=+
.
Câu 8: (MĐ 103-2022) Với
,ab
là các số thực dương tùy ý và
1a ≠
,
1
3
1
log
a
b
bằng
A.
3log
a
b
. B.
log
a
b
. C.
3log
a
b−
. D.
1
log
3
a
b
.
Lời giải
Chọn A
Ta có
1
3
1
3
1
log log 3log
a
a
a
bb
b
−
−
= =
.
Câu 9: (MĐ 104-2022) Với
,ab
là các số thực dương tuỳ ý và
1
3
1
1, log
a
a
b
≠
bằng
A.
log
a
b
. B.
3log
a
b−
. C.
1
log
3
a
b
. D.
3log
a
b
.
Lời giải
Chọn D
- Ta có
1
3
1
3
1
log log 1.( 3)log 3log
aa
a
a
b bb
b
−
−
= =−− =
Câu 10: (TK 2020-2021) Với
a
là số thực dương tùy ý,
3
a
bằng
A.
6
.a
B.
3
2
.a
C.
2
3
.a
D.
1
6
.a
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 3
Sưu tầm và biên soạn
Ta có
n
n
m
m
aa
với mọi
0a
và
3
3
2
,.mn a a
Câu 11: (TK 2020-2021) Với
a
là số thực dương tùy ý,
( )
3
log 9a
bằng
A.
3
1
log .
2
a+
B.
3
2log
a
C.
( )
2
3
log .a
D.
3
2 log .a+
Lời giải
Ta có
3 33 3
log (9 ) log 9 log 2 log .a aa
Câu 12: Cho
0a
>
và
1a ≠
, khi đó
4
log
a
a
bằng
A.
4
. B.
1
4
. C.
1
4
−
. D.
4
.
Lời giải
Với
0a >
và
1
a
≠
ta có:
1
4
4
11
log log log
44
aa a
aa a= = =
.
Câu 13: (MĐ 102 2020-2021 – ĐỢT 1) Cho
0a >
và
1a ≠
, khi đó
3
log
a
a
bằng
A.
3−
. B.
1
3
. C.
1
3
−
. D.
3
.
Lời giải
Với
0a
>
và
1a
≠
, ta có
1
3
3
11
log log log
33
aa a
aa a= = =
.
Câu 14: (MĐ 103 2020-2021 – ĐỢT 1) Cho
0a >
và
1
a
≠
, khi đó
log
a
a
bằng
A.
2
. B.
2−
. C.
1
2
−
. D.
1
2
.
Lời giải
Với
0
a >
và
1a ≠
, ta có:
1
2
11
log log log
22
aa a
aa a= = =
.
Câu 15: (MĐ 104 2020-2021 – ĐỢT 1) Cho
0
a >
và
a1≠
, khi đó
5
log
a
a
bằng
A.
1
5
. B.
1
5
−
. C.
5
. D.
5−
Lời giải
Ta có
1
5
5
1
log log
5
aa
aa= =
.
Câu 16: Với mọi
,ab
thỏa mãn
3
22
log log 6ab+=
, khẳng định nào sau đây đúng?
A.
3
64ab=
. B.
3
36ab=
. C.
3
64ab+=
. D.
3
36ab+=
.
Lời giải
Ta có:
( )
3 3 36
22 2
log log 6 log 6 2 64a b ab ab+ =⇔ =⇔==
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 4
Sưu tầm và biên soạn
Câu 17: (MĐ 102 2020-2021 – ĐỢT 1) Với mọi
,ab
thỏa mãn
3
22
log log 8ab
+=
. Khẳng định nào
dưới đây đúng?
A.
3
64ab+=
. B.
3
256ab=
. C.
3
64ab
=
. D.
3
256ab+=
.
Lời giải
(
)
3 3 38 3
22 2
log log 8 log 8 2 256
a b ab ab ab
+ =⇔ =⇔=⇔=
Câu 18: (MĐ 103 2020-2021 – ĐỢT 1) Với mọi
a
,
b
thỏa mãn
3
22
log log 7ab+=
. Khẳng định nào
dưới đây đúng?
A.
3
49ab+=
. B.
3
128ab=
. C.
3
128ab+=
. D.
3
49ab=
.
Lời giải
Điều kiện:
0, 0
ab
>>
. Ta có:
( )
3 3 37 3
22 2
log log 7 log 7 2 128a b ab ab ab+ =⇔ =⇔=⇔=
.
Câu 19: (MĐ 104 2020-2021 – ĐỢT 1) Với mọi
,ab
thỏa mãn
3
22
log log 5ab+=
, khẳng định nào dưới
đây là đúng?
A.
3
32
ab
=
. B.
3
25ab=
. C.
3
25ab
+=
. D.
3
32
ab
+=
.
Lời giải
Ta có:
( )
3 33
22 2
log log 5 log 5 32a b ab ab
+ =⇔ =⇔=
.
Câu 20: Với
0a >
đặt
(
)
2
log 2ab=
, khi đó
( )
4
2
log 8
a
bằng
A.
47
b +
. B.
43b +
. C.
4
b
. D.
41b −
.
Lời giải
Ta có
( )
2 22
log 2 1 log log 1a b ab ab
= ⇔+ = ⇔ = −
.
Khi đó
( )
( )
44
2 22
log 8 3 log 3 4log 3 4 1 4 1a a a bb=+ =+ =+ −= −
.
Vậy
( )
4
2
log 8 4 1ab
= −
.
Câu 21: Với
0
a >
, đặt
( )
2
log 2ab=
, khi đó
( )
3
2
log 4a
bằng
A.
35b +
. B.
3b
. C.
32b +
. D.
31b −
.
Lời giải
Ta có:
( )
2 22 2
log 2 log 2 log 1 loga aa=+=+
2
log 1
ab⇒=−
( )
( ) ( )
22
3
22 22
log 4 log 2 . log 2 log 2 1 3 1a a a a a bb b
= = + = +−= −
.
Câu 22: (MĐ 103 2020-2021 – ĐỢT 2) Với
0a >
, đặt
( )
3
log 3ab=
, khi đó
( )
3
3
log 9a
bằng
A.
3b
. B.
31b −
. C.
32b +
. D.
35b +
.
Lời giải
Ta có
( )
3 33
log 3 1 log log 1a b ab ab= ⇒+ = ⇒ = −

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 5
Sưu tầm và biên soạn
Suy ra
( )
(
)
2
33
log 9 2 3log 2 3 1 3 1
a a bb
=+ =+ −= −
.
Câu 23: (MĐ 104 2020-2021 – ĐỢT 2) Với
0a >
, đặt
( )
3
log 3ab=
khi đó
( )
4
3
log 27a
bằng
A.
43b +
. B.
4
b
. C.
41b −
. D.
47
b +
.
Lời giải
Ta có
( )
33
log 3 1 log
a b ab= ⇔+ =
3
log 1ab⇒=−
( )
44
3 33 3
log 27 log 27 log 3 4log 3 4( 1) 4 1a a a bb
= + =+ =+ −= −
Câu 24: (Mã 105 2017) Rút gọn biểu thức
5
3
3
:Qb b=
với
0b >
.
A.
4
3
Qb
−
=
B.
4
3
Qb
=
C.
5
9
Qb=
D.
2
Qb=
Lời giải
Chọn B
5 51 4
3
3 33 3
::Qb bbb b= = =
Câu 25: (Mã 110 2017) Rút gọn biểu thức
1
6
3
.Px x=
với
0
x >
.
A.
Px=
B.
1
8
Px=
C.
2
9
Px=
D.
2
Px
=
Lời giải
Chọn A
Ta có:
1 1 1 11
1
6
3 3 6 36
2
..P x x xx x x x
+
= = = = =
Câu 26: (Mã 102 2017) Cho biểu thức
4
3
23
..P xx x=
, với
0x
>
. Mệnh đề nào dưới đây đúng?
A.
2
3
Px=
B.
1
2
Px=
C.
13
24
Px
=
D.
1
4
Px=
Lời giải
Chọn C
Ta có, với
0:x
>
7 13
3 7 13
44
33
44
4
3
23 2
66
2 2 24
.. .. . .P xx x xxx xx xx x x= = = = = =
.
Câu 27: (Đề Tham Khảo 2017) Tính giá trị của biểu thức
( ) ( )
2017 2016
7 43 43 7P =+−
A.
( )
2016
7 43P = +
B.
1P =
C.
7 43
P = −
D.
7 43P = +
Lời giải
Chọn D

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 6
Sưu tầm và biên soạn
( )
( )
( )
( )
( )
( )
( )
2016
2017 2016
2016
7 43 43 7 7 43. 7 43 43 7
7 43 1 7 43.
P
=+ −=+ + −
=+ −=+
Câu 28: (Mã 101 - 2020 Lần 1) Với
,ab
là các số thực dương tùy ý và
1a ≠
,
5
log
a
b
bằng:
A.
5log
a
b
. B.
1
log
5
a
b+
. C.
5 log
a
b+
. D.
1
log
5
a
b
.
Lời giải
Chọn D
Câu 29: (Mã 102 - 2020 Lần 1) Với , là các số thực dương tùy ý và , bằng
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có .
Câu 30: (Mã 103 - 2020 Lần 1) Với a,b là các số thực dương tùy ý và
1a ≠
,
3
log
a
b
bằng
A.
3 log
a
b+
B.
3log
a
b
C.
1
3
log
a
b+
D.
1
3
log
a
b
Lời giải
Chọn D
Ta có:
3
1
log log .
3
a
a
bb=
Câu 31: (Mã 103 2018) Với
a
là số thực dương tùy ý,
( ) ( )
ln 7 ln 3aa−
bằng
A.
ln 7
ln 3
B.
7
ln
3
C.
( )
ln 4a
D.
( )
( )
ln 7
ln 3
a
a
Lời giải
Chọn B
( ) ( )
ln 7 ln 3aa−
7
ln
3
a
a
=
7
ln
3
=
.
Câu 32: (Mã 101 2018) Với
a
là số thực dương tùy ý,
( ) ( )
ln 5 ln 3aa−
bằng:
A.
5
ln
3
B.
ln 5
ln 3
C.
( )
( )
ln 5
ln 3
a
a
D.
( )
ln 2a
Lời giải
Chọn A
( ) ( )
ln 5 ln 3aa−
5
ln
3
=
.
Câu 33: (Mã 110 2017) Cho
log 2
a
b =
và
log 3
a
c =
. Tính
( )
23
log
a
P bc=
.
a
b
1a ≠
2
log
a
b
1
log
2
a
b+
1
log
2
a
b
2 log
a
b+
2log
a
b
2
1
log log
2
a
a
bb=

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 7
Sưu tầm và biên soạn
A.
13
P =
B.
31P =
C.
30P =
D.
108
P
=
Lời giải
Chọn A
Ta có:
(
)
23
log 2log 3log 2.2 3.3 13
a aa
bc b c
= + =+=
.
Câu 34: (Mã 102 2019) Cho
a
và
b
là hai số thực dương thỏa mãn
32
32ab
=
. Giá trị của
22
3log 2logab+
bằng
A.
4
. B.
5
. C.
2
. D.
32
.
Lời giải
Chọn B
Ta có:
32
2 2 22
log log 32 3log 2log 5ab a b
=⇔+=
Câu 35: (Đề Tham Khảo 2017) Cho
,ab
là các số thực dương thỏa mãn
1a ≠
,
ab≠
và
log 3
a
b =
. Tính
P log
b
a
b
a
=
.
A.
5 33P =−+
B.
13P
=−+
C.
13P =−−
D.
5 33P =−−
Lời giải
Chọn C
Cách 1: Phương pháp tự luận.
( )
( )
11
log
log 1 3 1
31
22
1
log 1 3 2
log 1
log
2
a
a
a
a
a
b
b
a
P
bb
b
a
−−
−
= = = =
−−
−
13=−−
.
Cách 2: Phương pháp trắc nghiệm.
Chọn
2a =
,
3
2b =
. Bấm máy tính ta được
13P =−−
.
Câu 36: (Mã 103 2019) Cho
a
và
b
là hai số thực dương thỏa mãn
23
16ab
=
. Giá trị của
22
2log 3logab+
bằng
A.
2
. B.
8
. C.
16
. D.
4
.
Lời giải
Chọn D
Ta có
( )
23
2 22 2
2log 3log log log 16 4a b ab
+= ==
Câu 37: (Mã 101 2019) Cho
a
và
b
là hai số thực dương thỏa mãn
4
16ab=
.
Giá trị của
22
4log logab+
bằng
A.
4
. B.
2
. C.
16
. D.
8
.
Lời giải
Chọn A
(
)
44 4
222 22 2 2
4log log log log log log 16 log 2 4a b a b ab+= += = = =
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 8
Sưu tầm và biên soạn
Câu 38: (Mã 123 2017) Với
a
,
b
là các số thực dương tùy ý và
a
khác
1
, đặt
2
36
log log
a
a
Pb b= +
.
Mệnh đề nào dưới đây đúng?
A.
6log
a
Pb=
B.
27log
a
Pb=
C.
15log
a
Pb=
D.
9log
a
Pb=
Lời giải
Chọn A
2
36
6
log log 3log log 6log
2
a aaa
a
Pb b b b b=+=+=
.
Câu 39: (Mã 105 2017) Cho
3
log 2a =
và
2
1
log
2
b =
. Tính
( )
2
33 1
4
2log log 3 logI ab
= +
.
A.
5
4
I
=
B.
0
I =
C.
4I =
D.
3
2
I
=
Lời giải
Chọn D
( ) (
)
2
2
33 1 33 3
2
4
2log log 3 log 2log log 3 log 2logI ab a b
−
== + ++
13
2
22
=−=
.
Câu 40: (Mã 104 2017) Với mọi
a
,
b
,
x
là các số thực dương thoả mãn
2 22
gl
lo 5lo gg 3oabx +=
.
Mệnh đề nào dưới đây đúng?
A.
53x ab= +
B.
53
xa b= +
C.
53
x ab=
D.
35
x ab= +
Lời giải
Chọn C
Có
5 3 53 53
2 2 22 2 2
log 5log 3log log log logx a b a b ab x ab= + = + = ⇔=
.
Câu 41: (Mã 104 2019) Cho
a
và
b
là hai số thực dương thỏa mãn
3
8ab =
. Giá trị của
22
log 3log
ab+
bằng
A.
6
. B.
2
. C.
3
. D.
8
.
Lời giải
Chọn C
Ta có
( )
33
2 222 2 2
log 3log log log log log 8 3a b a b ab+ =+= ==
.
Câu 42: (Mã 123 2017) Cho
log 3, log 4
ab
xx= =
với $a,b$ là các số thực lớn hơn 1. Tính
log .
ab
Px=
A.
12P =
B.
12
7
P =
C.
7
12
P =
D.
1
12
P
=
Lời giải
Chọn B
1 1 1 12
log
11
log log log 7
34
ab
x xx
Px
ab a b
= = = = =
+
+

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 9
Sưu tầm và biên soạn
Câu 43: (Mã 110 2017) Cho
, xy
là các số thực lớn hơn
1
thoả mãn
22
96x y xy+=
. Tính
( )
12 12
12
1 log log
2log 3
xy
M
xy
++
=
+
.
A.
1
2
M =
. B.
1
3
M =
. C.
1
4
M =
. D.
1M =
Lời giải
Chọn D
Ta có
( )
2
22
96 3 0 3x y xy x y x y+ = ⇔ − =⇔=
.
Khi đó
( )
( )
( )
( )
( )
2
12
12
12 12
2
2
12
12
12
log 36
log 12
1 log log
1
2log 3
log 36
log 3
y
xy
xy
M
xy
y
xy
++
= = = =
+
+
.
Câu 44: (Đề Tham Khảo 2020 Lần 2) Xét số thực
a
và
b
thỏa mãn
( )
39
log 3 .9 log 3
ab
=
. Mệnh đề nào
dưới đây đúng
A.
22ab+=
. B.
421ab+=
. C.
41ab =
. D.
241ab+=
.
Lời giải
Chọn D
Ta có:
( ) ( )
2
2
3 93
3
1
2
2
33
log 3 .9 log 3 log 3 .3 log 3
1
log 3 log 3 2 2 4 1.
2
ab a b
ab
ab ab
+
=⇔=
⇔ = ⇔+=⇔+=
Câu 45: (Mã 102 - 2020 Lần 1) Cho
a
và
b
là hai số thực dương thỏa mãn
2
log ( )
43
ab
a=
. Giá trị của
2
ab
bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Từ giả thiết ta có :
Câu 46: (Mã 102 - 2020 Lần 2) Với
,ab
là các số thực dương tùy ý thỏa mãn
39
log 2log 2ab−=
, mệnh
đề nào dưới đây đúng?
A.
2
9ab=
. B.
9ab=
. C.
6ab=
. D.
2
9ab=
.
3
6
2
12
2
log ( )
43
ab
a=
2 22
log ( ).log 4 log (3 )ab a⇔=
22 22
2(log log ) log log 3ab a⇔ +=+
2 22
log 2log log 3ab⇔+ =
2
22
log ( ) log 3ab⇔=
2
3ab⇔=

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 10
Sưu tầm và biên soạn
Lời giải
Chọn B
Ta có:
39
log 2log 2ab−=
33
log log 2ab⇔−=
3
log 2
a
b
⇔=
9ab⇔=
.
Câu 47: (Mã 103 - 2020 Lần 2) Với
,ab
là các số thực dương tùy ý thỏa mãn
39
log 2log 3ab−=
, mệnh
đề nào dưới đây đúng?
A.
27ab=
. B.
9ab=
. C.
4
27ab=
. D.
2
27ab=
.
Lời giải
Chọn A
Ta có:
3 9 33 3
log 2log 3 log log 3 log 3 27 27
aa
a b a b ab
bb
− =⇔ − =⇔ =⇔ = ⇔=
.
Câu 48: (Mã 104 - 2020 Lần 2) Với
,ab
là các số thực dương tùy ý thỏa mãn
24
log 2log 4
ab
−=
, mệnh
đề nào dưới đây đúng?
A.
2
16ab=
. B.
8ab=
. C.
16ab=
. D.
4
16ab=
.
Lời giải
Chọn C
Ta có
24
log 2log 4ab−=
2
2
2
22
22
2
4
log 2log 4
1
log 2. log 4
2
log log 4
log 4
2
16
ab
ab
ab
a
b
a
b
ab
⇔− =
⇔− =
⇔−=
⇔=
⇔=
⇔=
Câu 49: (Đề Tham Khảo 2019) Đặt
3
log 2
a=
khi đó
16
log 27
bằng
A.
3
4
a
B.
3
4a
C.
4
3a
D.
4
3
a
Lời giải
Chọn B
Ta có
16 2
3
3 33
log 27 log 3
4 4.log 2 4a
= = =
Câu 50: (Đề Minh Họa 2017) Đặt
25
log 3, log 3.ab= =
Hãy biểu diễn
6
log 45
theo
a
và
b
.
A.
2
6
22
log 45
a ab
ab
−
=
B.
6
2
log 45
a ab
ab b
+
=
+
C.
2
6
22
log 45
a ab
ab b
−
=
+
D.
6
2
log 45
a ab
ab
+
=

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 11
Sưu tầm và biên soạn
Lời giải
Chọn B
( )
( )
2
2
2
23 5
22
6
22
log 3
2
2
log 3 .5
2 log 3.log 5 log 3
2log 3 log 5
2
log 45
log 2.3 1 log 3 1 1 1
a
a
a
a
a ab
b
a a a ab b
+
+
+
+
+
= = = = = =
+ + + ++
CASIO: Sto\Gán
25
log 3, log 3AB
= =
bằng cách: Nhập
2
log 3
\shift\Sto\
A
tương tự
B
Thử từng đáp án A:
6
2
log 45 1,34
A AB
AB
+
−≈
( Loại)
Thử đáp án C:
6
2
log 45 0
A AB
AB
+
−=
( chọn ).
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 41
Sưu tầm và biên soạn
BÀI 3: HÀM SỐ MŨ – HÀM SỐ LOGARIT
DẠNG 1: TẬP XÁC ĐỊNH
Câu 1: Tập xác định của hàm số
3
log 2yx
=
là
A.
( )
;0−∞
. B.
( )
0; +∞
. C.
. D.
( )
1; +∞
.
Câu 2: Tập xác định của hàm số
8=
x
y
là
A.
. B.
[
)
0;+∞
. C.
(
)
0;
+∞
. D.
{ }
\0
.
Câu 3: Tập xác định của hàm số
( )
3
x
y =
là
A.
. B.
[
)
0;+∞
. C.
\ {0}
. D.
( )
0;
+∞
.
Câu 4: Tập xác định của hàm số
( )
0,5
log 1yx= +
là:
A.
( )
1;D = − +∞
. B.
{
}
\1
D = −
. C.
( )
0;D = +∞
. D.
(
)
;1D = −∞ −
.
Câu 5: Tập xác định của hàm số
lnyx=
là
A.
( )
0; +∞
. B.
. C.
[
)
0;+∞
. D.
{ }
\0
.
Câu 6: Tập xác định của hàm số
log( 1)
yx= −
là
A.
[ 1; )− +∞
. B.
(1; )+∞
. C.
[1; )+∞
. D.
( 1; )− +∞
.
Câu 7: Tập xác định
D
của hàm số
(
)
ln 1
yx= −
là
A.
\ {1}D =
. B.
D =
. C.
( ;1)D = −∞
. D.
(1; )D = +∞
.
Câu 8: Tập xác định của hàm số
( )
2
log 2
yx= −
là:
A.
( )
2; +∞
. B.
)
2;
+∞
. C.
( )
;2
−∞
. D.
.
Câu 9: Tìm tập xác định của hàm số
( )
3
log 3yx= +
.
A.
( )
3;D = − +∞
. B.
[
)
3;D = − +∞
. C.
( )
0;D = +∞
. D.
{ }
\3D = −
.
Câu 10: Tập xác định
D
của hàm số
4
log=yx
là
A.
( )
0;= +∞D
. B.
( )
;0= −∞D
. C.
= D
. D.
{ }
\0= D
.
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 42
Sưu tầm và biên soạn
Câu 11: Tập xác định của hàm số
( )
2
2
log 1yx= −
là
A.
(
)
1;− +∞
. B.
{ }
\1
. C.
. D.
( )
1;+∞
.
Câu 12: Có bao nhiêu số nguyên thuộc tập xác định của hàm số
( )
2
ln 15yx= −
?
A.
7
. B.
6
. C.
5
. D.
8
.
Câu 13: Tập xác định của hàm số
( )
2
log 3yx= −
là
A.
( )
;−∞ +∞
. B.
( )
3; +∞
. C.
(
]
;3−∞
. D.
( )
;3−∞
.
Câu 14: Tập xác định của hàm số
( )
ln 2 9yx x= −+ −
là
A.
[
)
9; +∞
. B.
[ ]
2;9
. C.
( )
2;9
. D.
(
]
2;9
.
Câu 15: Tập xác định của hàm số
( )
2
ln 1x −
là:
A.
{ }
\1D =
. B.
( )
1;D = +∞
. C.
. D.
[
)
1;D = +∞
Câu 16: Tìm tất cả các giá trị thực của tham số
m
để hàm số
( )
2
3
log 4 1y x xm= − −+
xác định với mọi
x ∈
.
A.
3m
<−
. B.
3m >
. C.
3m >−
. D.
3m <
.
Câu 17: Tập xác định của hàm số
2
1
log 1
y
x
=
−
là
A.
{ }
\2R
. B.
( )
0; +∞
. C.
(
) { }
0; \ 2+∞
. D.
( ) { }
0; \ 1+∞
.
Câu 18: Có tất cả bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
( )
2
2
log 2 2022
y xx m= −+ −
có tập xác định là
?
A.
2022
. B.
2021
. C.
2020
. D.
2019
.
DẠNG 2: SỰ BIẾN THIÊN
Câu 19: Trong bốn hàm số sau, hàm số nào nghịch biến trên
?
A.
2022
x
y =
. B.
2022
2021
x
y
=
. C.
2022
logyx=
. D.
2021
2022
x
y
=
.
Câu 20: Hàm số nào sau đây đồng biến trên
?
A.
2
5
x
y
=
. B.
1
3
x
y
=
. C.
2005
x
y =
. D.
2022y =
.
Câu 21: Hàm số nào sau đây luôn đồng biến trên tập xác định.
A.
0.3=
x
y
. B.
1
3
log=yx
. C.
3
2
y log x=
. D.
2
3
=
x
y
.
Câu 22: Hàm số nào sau đây đồng biến trên
?
A.
( )
2 2.
x
y = −
B.
( )
31
x
y = −
. C.
3
x
y
π
=
. D.
4
x
e
.
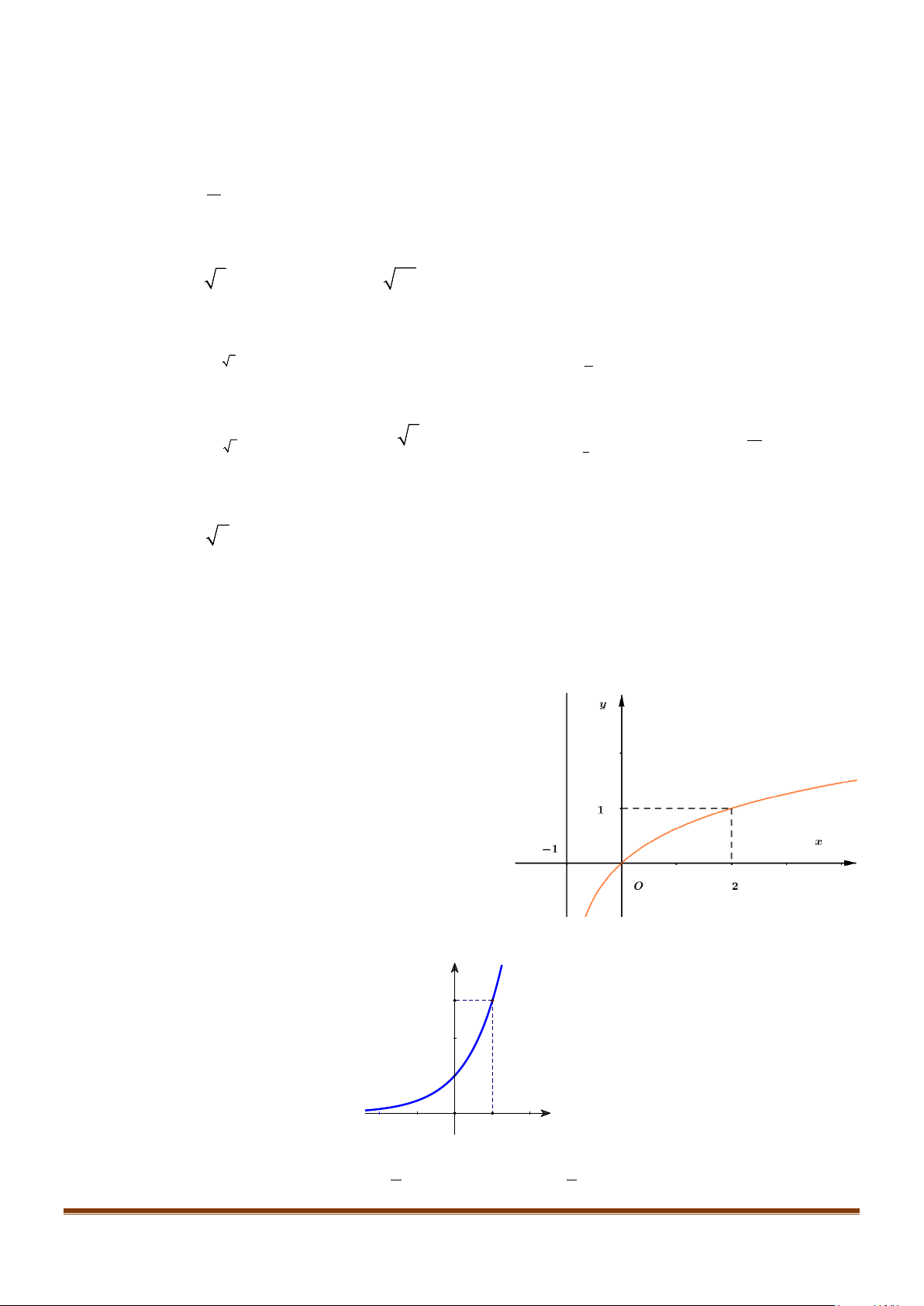
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 43
Sưu tầm và biên soạn
Câu 23: Hàm số nào trong các hàm số sau đây nghịch biến trên
?
A.
5
logyx=
. B.
5
x
y
=
. C.
(
)
0,5
x
y
=
. D.
0,5
logyx=
.
Câu 24: Hàm số nào sau đây nghịch biến trên
?
A.
4
π
=
x
y
. B.
=
x
ye
. C.
2022=
x
y
. D.
2=
x
y
.
Câu 25: Trong các hàm số dưới đây, hàm số nào nghịch biến trên
?
A.
( )
52
x
y = −
. B.
x
y
π
=
. C.
2021
x
y =
. D.
x
e
.
Câu 26: Hàm số nào sau đây nghịch biến trên tập xác định của nó.
A.
3
log .=yx
B.
2
log .=yx
C.
log .
e
yx=
π
D.
log .
π
=yx
Câu 27: Hàm số nào đồng biến trên toàn tập xác định của nó?
A.
2
logyx=
. B.
( )
22
x
y
−
=
. C.
1
2
logyx=
. D.
x
e
y
π
=
.
Câu 28: Hàm số nào trong các hàm số sau đây đồng biến trên
( )
0; +∞
A.
( )
21
x
y = −
. B.
9
logyx=
. C.
( )
0,6
x
y
=
. D.
0.7
log x
.
Câu 29: Cho hàm số mũ
( )
6
x
ya= −
với a là tham số. Có bao nhiêu số tự nhiên a để hàm số đã cho đồng
biến trên
?
A.
3
. B.
6
. C.
5
. D.
4
.
DẠNG 3: ĐỒ THỊ
Câu 30: Đồ thị sau là đồ thị của hàm số nào?
A.
2
log 1yx
= +
. B.
2
log ( 1)yx= +
.
C.
3
logyx=
. D.
3
log ( 1)x +
.
Câu 31: Đồ thị hình bên dưới là đồ thị của hàm số nào?
A.
2
x
y =
. B.
1
2
x
y
=
. C.
1
3
x
y
=
. D.
3
x
y =
.
x
y
3
O
1
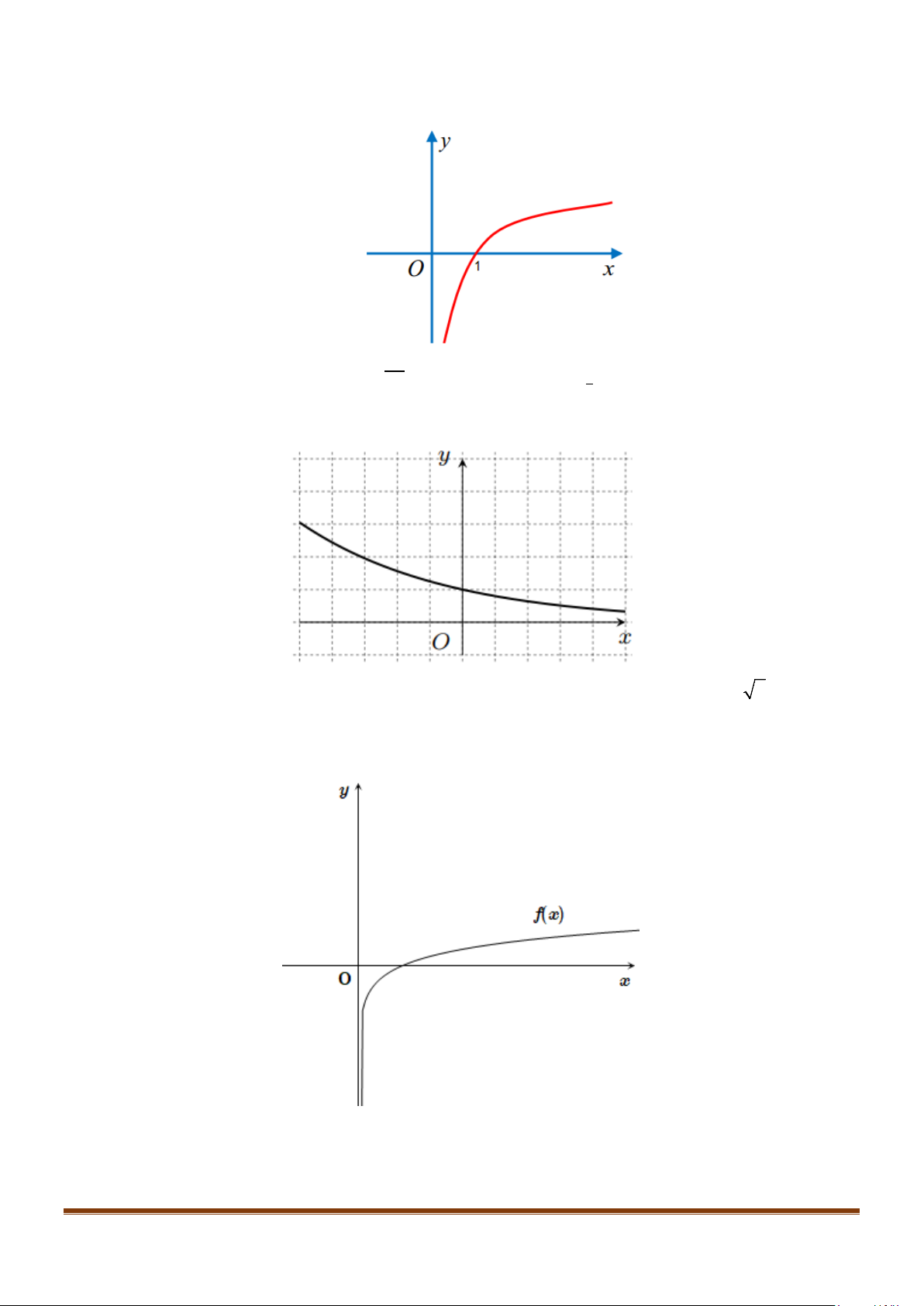
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 44
Sưu tầm và biên soạn
Câu 32: Đồ thị sau đây là đồ thị của một trong bốn hàm số cho ở các phương án A, B, C, D. Hỏi đó là
hàm số nào?
A.
2
logyx=
. B.
1
2
x
y =
. C.
1
2
logyx=
. D.
2
x
y =
.
Câu 33: Đường cong trong hình bên là của đồ thị hàm số nào sau đây?
A.
2
logyx=
. B.
( )
0,8
x
y =
. C.
0,4
logyx=
. D.
( )
2
x
y
=
.
Câu 34: Cho đồ thị hàm số
( )
y fx=
như hình vẽ bên. Hàm số
( )
y fx=
có thể là hàm số nào dưới đây?
A.
x
ye
−
=
. B.
logyx=
. C.
lnyx= −
. D.
x
ye=
.
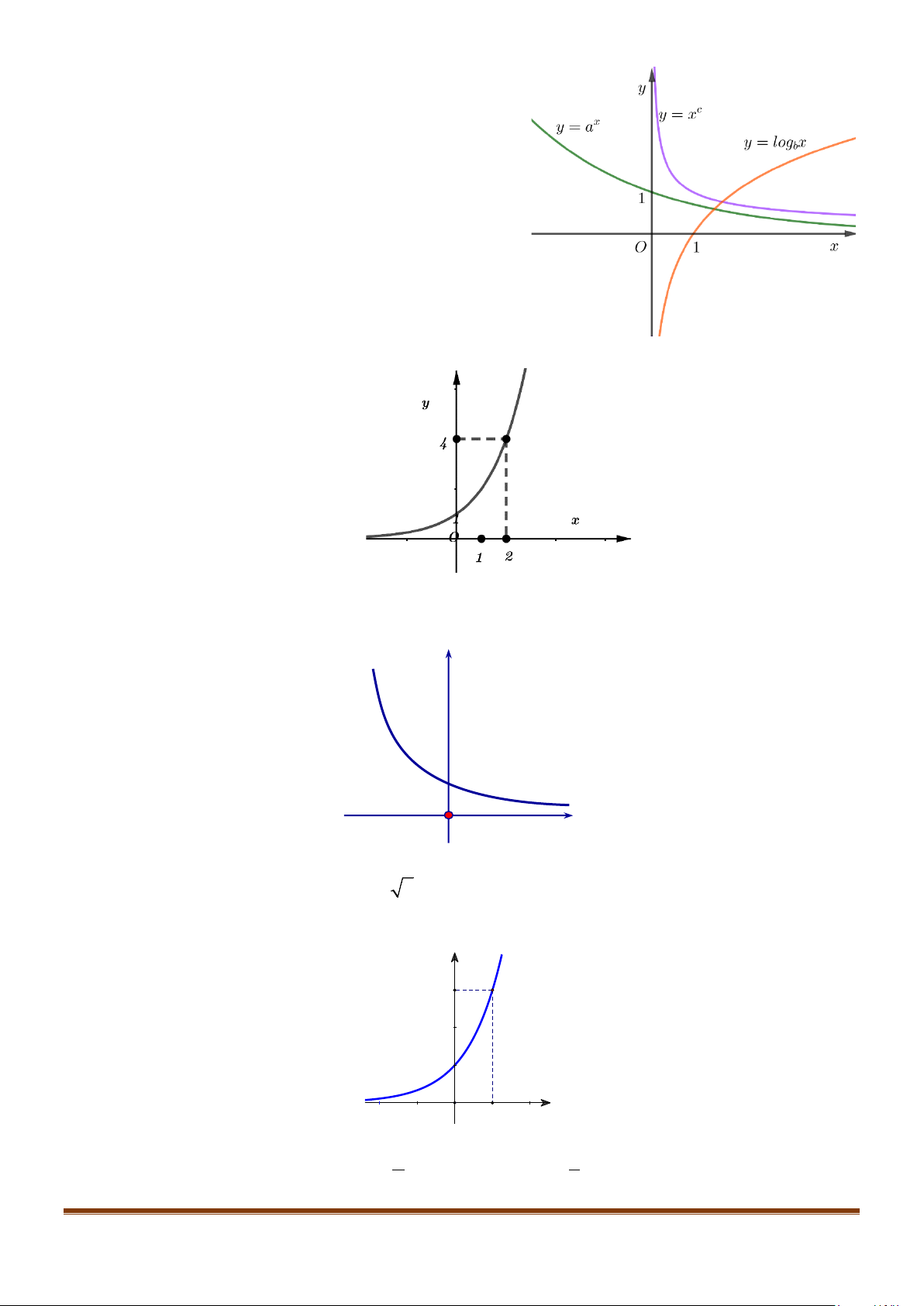
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 45
Sưu tầm và biên soạn
Câu 35: Cho các đồ thị hàm số
, log ,
xc
b
y a y xy x
ở hình vẽ sau đây.
Khẳng định nào sau đây đúng?
A.
01 .c ab
B.
0 1.
cab
C.
0 1.c ab
D.
0 1.cab
Câu 36: Đồ thị của hàm số sau là đồ thị của hàm số nào?
A.
2
yx=
. B.
3
x
y =
. C.
3
logyx=
. D.
2
x
y =
.
Câu 37: Hình bên là đồ thị của hàm số nào trong các hàm số sau đây?
A.
(
)
0, 4
x
. B.
( )
2
x
y
=
. C.
2
logyx=
. D.
0,4
logyx=
.
Câu 38: Đồ thị hình bên dưới là đồ thị của hàm số nào?
A.
2
x
y =
. B.
1
2
x
y
=
. C.
1
3
x
y
=
. D.
3
x
y =
.
x
y
3
O
1
O
x
y
1
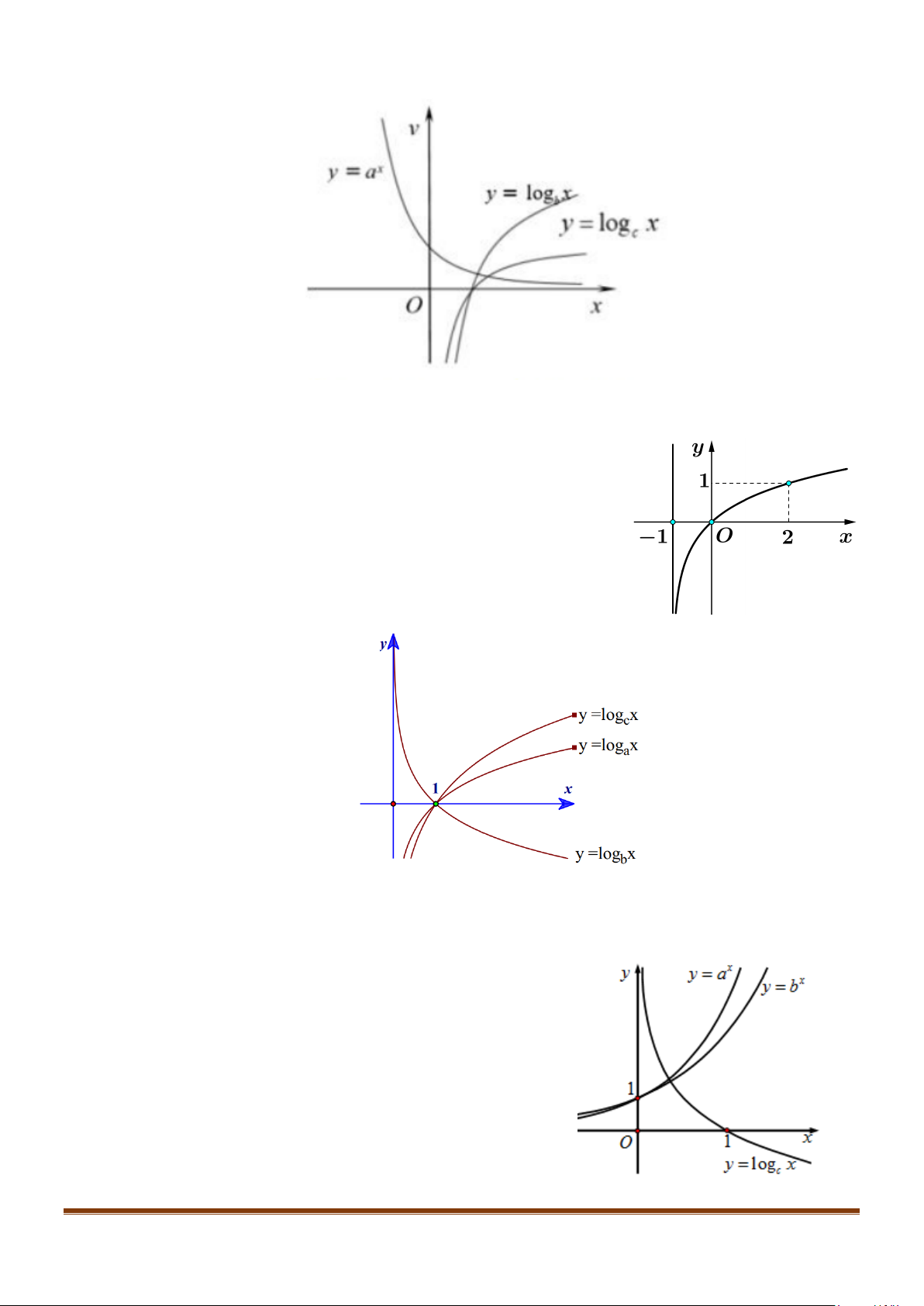
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 46
Sưu tầm và biên soạn
Câu 39: Cho các hàm số
,=
x
ya
log ,=
b
yx
log=
c
yx
có đồ thị như hình vẽ bên. Chọn khẳng định đúng?
A.
>>bca
. B.
>>bac
. C.
>>
abc
D.
>>
cba
.
Câu 40: Đồ thị sau là đồ thị của hàm số nào?
A.
2
log 1.yx= +
B.
( )
2
log 1 .yx= +
C.
3
log .yx=
D.
( )
3
log 1 .yx= +
Câu 41: Cho các hàm số
log
a
yx=
,
log
b
yx=
,
log
c
yx=
có đồ thị như
hình vẽ dưới đây. Chọn mệnh đề đúng.
A.
acb
>>
. B.
abc>>
. C.
cab
>>
. D.
bca
>>
.
Câu 42: Cho đồ thị hàm số
x
ya=
;
x
yb
=
;
log
c
yx=
như hình vẽ. Tìm mối liên hệ của
,,abc
.
A.
cba<<
. B.
bac<<
.
C.
abc<<
. D.
cab<<
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 47
Sưu tầm và biên soạn
Câu 43: Đường cong trong hình dưới đây là đồ thị của hàm số nào trong bốn hàm số sau?
A.
2
logyx=
. B.
2
2
logyx=
. C.
2
log 2yx=
. D.
1
2
logyx=
.
Câu 44: Cho
a
,
b
,
c
là ba số thực dương khác
1
. Đồ thị hàm số
x
ya=
,
x
yb=
,
x
yc
=
được cho ở hình
vẽ dưới đây. Mệnh nào nào sau đây đúng?
A.
abc
<<
. B.
bca<<
. C.
cab<<
. D.
acb<<
.
Câu 45: Trong hình vẽ dưới đây có đồ thị của các hàm số
, , log
xx
c
y ay by x= = =
.
Mệnh đề nào sau đây đúng?
A.
abc<<
.
B.
abc<=
.
C.
bca<<
.
D.
a cb<<
.
x
y
1
-1
1
2
O
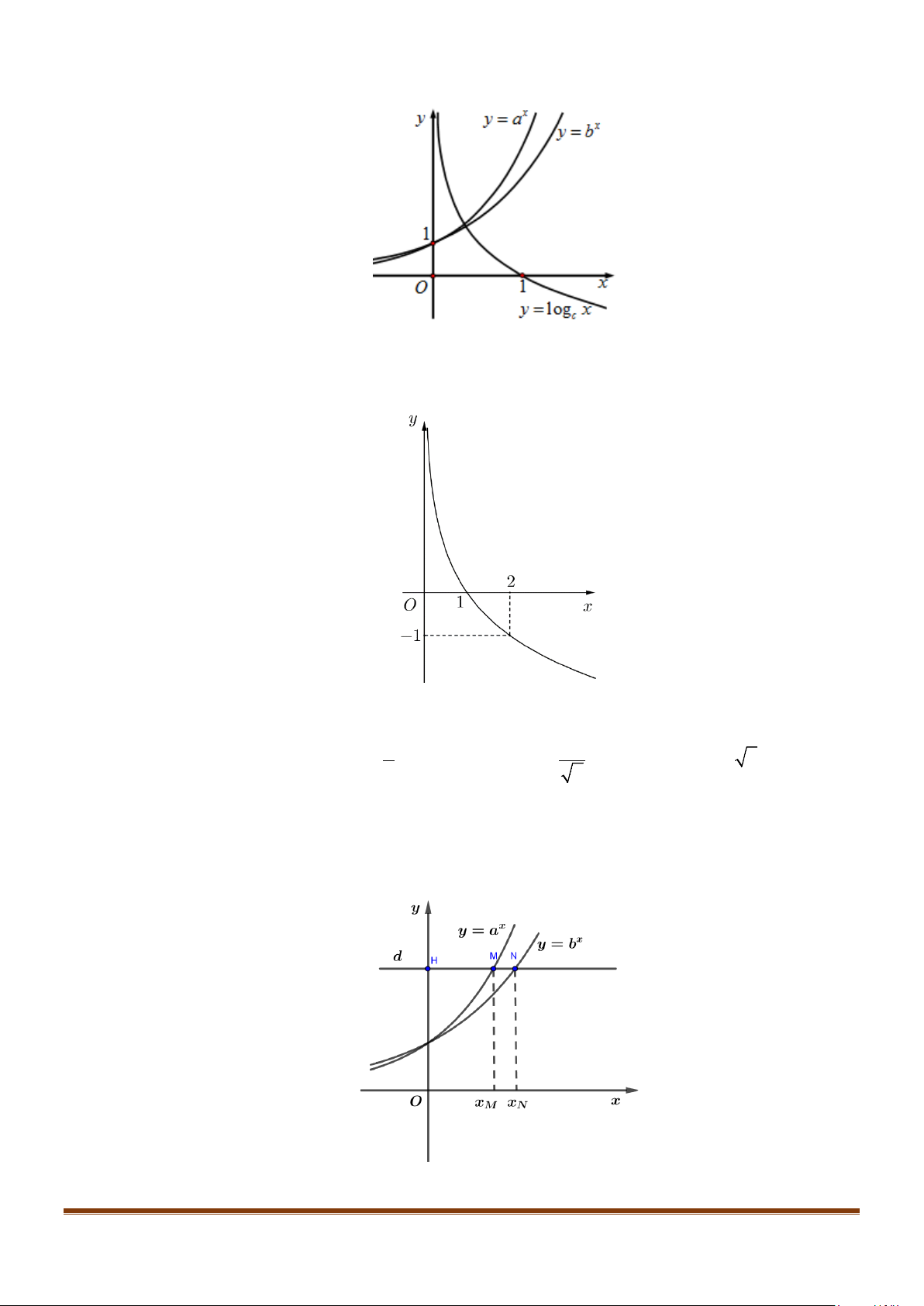
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 48
Sưu tầm và biên soạn
Câu 46: Cho đồ thị hàm số
x
ya=
;
x
yb=
;
log
c
yx=
như hình vẽ. Tìm mối liên hệ của
,a
,b
c
.
A.
cba<<
. B.
bac<<
. C.
abc<<
. D.
cab<<
.
Câu 47: Cho hàm số
log
a
yx=
(
)
0, 1
aa
>≠
có đồ thị như hình vẽ.
Giá trị của
a
bằng
A.
2a =
. B.
1
2
a =
. C.
1
2
a =
. D.
2a =
.
Câu 48: Cho
,ab
là các số thực dương khác
1
, đường thẳng
d
song song trục hoành cắt trục tung, đồ thị
hàm số
x
ya
=
, đồ thị hàm số
x
yb
=
lần lượt tại
H
,
M
,
N
. Biết
3HM MN=
. Mệnh đề nào
sau đây đúng?
A.
43ab=
. B.
43
ba=
. C.
34
ba=
. D.
34ab=
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 49
Sưu tầm và biên soạn
Câu 49: Cho số thực dương
a
khác
1
. Biết rằng bất kì đường thẳng nào song song với trục
Ox
mà cắt
các đồ thị
4,
xx
y ya
= =
, trục tung lần lượt tại
,
MN
và
A
thì
2AN AM=
. Giá trị của
a
bằng
A.
1
3
. B.
2
2
. C.
1
4
. D.
1
2
.
Câu 50: Biết đồ thị hàm số
( )
y fx=
đối xứng với đồ thị hàm số
(
)
0, 1
x
ya a a
= >≠
qua điểm
( )
1;1I
.
Giá trị của biểu thức
1
2 log
2022
a
f
+
bằng
A.
2022−
. B.
2021
. C.
2022
. D.
2020−
.
Câu 51: Cho các hàm số
x
ya=
và
x
yb=
với
,
ab
là những số thực dương khác 1, có đồ thị như hình
vẽ. Đường thẳng
3y =
cắt trục tung, đồ thị hàm số
x
ya=
và
x
yb=
lần lượt tại
,,HMN
. Biết
rằng
23HM MN=
, khẳng định nào sau đây đúng?
A.
53
ab=
B.
35
ab=
C.
23
ab=
D.
35
ab=

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 50
Sưu tầm và biên soạn
DẠNG 4: BÀI TOÁN LÃI SUẤT
Câu 52: Một người gửi 100 triệu đồng vào một ngân hàng với lãi suất
6%
/ năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm
tiếp theo. Hỏi ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 300 triệu bao gồm cả
gốc lẫn lãi?.
A.
20
năm. B.
18
năm. C.
21
năm. D.
19
năm.
Câu 53: Ông
A
gửi
100
triệu vào ngân hàng theo hình thức lãi kép trong một thời gian khá lâu với lãi
suất ổn định trong suốt thời gian tiết kiệm là
10%
/1 năm. Tết năm nay do dịch bệnh nên ông rút
hết tiền trong ngân hàng ra để gia đình chi tiêu. Sau khi rút cả vốn lẫn lãi, ông trích ra 10 triệu để
sắm sửa đồ Tết thì ông còn 240 triệu. Hỏi ông đã gửi tiết kiệm trong bao nhiêu năm?
A.
9
năm. B.
20
năm. C.
12
năm. D.
10
năm.
Câu 54: Ông Nguyễn Văn B là thương binh hạng
4/4
, được hưởng trợ cấp hàng tháng là
2082000
đồng.
Do tình hình dịch bệnh Covid-19 diễn biến phức tạp nên từ tháng 4 năm 2021 ông không đi lĩnh
tiền mà nhờ thủ quỹ lập một sổ tiết kiệm ở ngân hàng để gởi số tiền hàng tháng vào đó với lãi
suất
0,5% /
tháng. Hỏi đến đầu tháng 4 năm 2022 ông đến ngân hàng nhận được số tiền là bao
nhiêu?
A.
25 811 054
đồng. B.
2 210 413
đồng. C.
25 682 641
đồng. D.
27 893 054
đồng.
Câu 55: Ông Nguyễn Văn B là thương binh hạng
4/4
, được hưởng trợ cấp hàng tháng là
2082000
đồng.
Do tình hình dịch bệnh Covid-19 diễn biến phức tạp nên từ tháng 4 năm 2021 ông không đi lĩnh
tiền mà nhờ thủ quỹ lập một sổ tiết kiệm ở ngân hàng để gởi số tiền hàng tháng vào đó với lãi
suất
0,5% /
tháng. Hỏi đến đầu tháng 4 năm 2022 ông đến ngân hàng nhận được số tiền là bao
nhiêu?
A.
25 811 054
đồng. B.
2 210 413
đồng. C.
25 682 641
đồng. D.
27 893 054
đồng.
Câu 56: Đầu mỗi tháng, anh Hiếu gửi tiết kiệm ngân hàng số tiền 10 triệu đồng với hình thức lãi kép, lãi
suất là 0,5%/ tháng. Hỏi sau đúng 5 năm thì anh Hiếu nhận được số tiền cả gốc và lãi gần nhất
với số tiền nào dưới đây, giả sử rằng trong suốt quá trình gửi, anh Hiếu không rút tiền ra và lãi
suất của ngân hàng không thay đổi.
A.
60
600 10.1,005+
. B.
60
1,005 1
10.1,005.
0,005
−
.
C.
60
10.1,005
. D.
60
1,005 1
10.
0,005
−
.
Câu 57: Gia đình nhà bác Long Thắm gửi số tiền 100 triệu đồng vào ngân hàng với lãi suất
7%
/năm.
Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào
vốn ban đầu. Sau 10 năm, nếu không rút lãi lần nào thì số tiền mà nhà bác Long Thắm nhận được
gồm cả gốc lẫn lãi tính theo công thức nào dưới đây?
A.
( )
9
8
10 . 1 0,07+
. B.
( )
10
8
10 1 0,7+
. C.
( )
10
8
10 . 1 0,07+
. D.
8 10
10 .0,07
.
Câu 58: Bác Minh gửi
60
triệu vào ngân hàng kì hạn 1 năm với lãi suất
5, 6%
/năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ nhập vào gốc để tính lãi cho năm tiếp
theo. Hỏi sau ít nhất bao nhiêu năm bác Minh nhận được số tiền nhiều hơn
120
triệu đồng bao
gồm cả gốc và lãi?
A.
11
năm. B.
12
năm. C.
13
năm. D.
14
năm.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 51
Sưu tầm và biên soạn
Câu 59: Một học sinh A khi đủ 18 tuổi được cha mẹ cho
200000000
VNĐ. Số tiền này được bảo quản
trong ngân hàng MSB với kì hạn thanh toán 1 năm và học sinh A chỉ nhận được số tiền này khi
học xong 4 năm đại học. Biết rằng khi đủ 22 tuổi, số tiền mà học sinh A được nhận sẽ là
243 101 250
VNĐ. Vậy lãi suất kì hạn một năm của ngân hàng MSB là bao nhiêu?
A.
8%
. B.
7%
. C.
6%
D.
5%
.
Câu 60: Một người gửi số tiền
3
triệu đồng vào một ngân hàng với lãi suất
0,55% /
tháng. Biết rằng nếu
người đó không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn
ban đầu. Số tiền người đó lãnh được sau hai năm, nếu trong khoảng thời gian này không rút tiền
ra và lãi suất không đổi là:
A.
( )
2
3. 1.0055
triệu đồng. B.
(
)
24
3. 1,0055
triệu đồng.
C.
( )
24
3. 1,055
triệu đồng. D.
( )
24
3,0055
triệu đồng.
Câu 61: Vào ngày
15
hàng tháng, ông An đều đến gửi tiết kiệm tại ngân hàng với số tiền
5
triệu đồng
theo hình thức lãi kép với lãi suất không đổi trong suốt quá trình gửi là
0,6% /
tháng. Hỏi sau
đúng ba năm, ông An thu được số tiền cả gốc lẫn lãi là bao nhiêu?
A.
195251000
. B.
195252000
. C.
201450000
. D.
201453000
.
Câu 62: Một người gửi số tiền
100
triệu đồng vào ngân hàng với lãi suất
0
0
7
/ năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho
năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó lĩnh được số tiền nhiều hơn
200
triệu
đồng, nếu trong khoảng thời gian này người đó không rút tiền ra và lãi suất không đổi?
A.
11
năm. B.
12
năm. C.
10
năm. D.
9
năm.
Câu 63: Vợ chồng nhà chị Thơm vay ngân hàng 400 triệu đồng để mua nhà với hình thức trả góp, chị
chọn gói lãi suất ưu đãi cố định
0,5%
tháng trong 12 tháng đầu và sang tháng thứ 13 trở đi thì
ngân hàng tính lãi suất thả nổi theo quy định. Gia đình chị hoàn nợ cho ngân hàng theo cách: sau
đúng một tháng kể từ ngày vay thì bắt
đầu
hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một
tháng, số tiền hoàn nợ ở mỗi tháng là 15 triệu đồng. Sau khi hết 12 tháng ưu đãi thì chị Thơm
phải trả lãi suất thả nổi là 1%tháng. Biết rằng mỗi tháng ngân hàng chỉ tính lãi trên số dư nợ thực
tế của tháng đó và lãi suất thả nổi của ngân hàng không thay đổi trong thời gian chị Thơm hoàn
nợ. Hỏi chị Thơm cần bao nhiêu tháng để trả hết nợ ngân hàng kể từ khi vay?
A.
17
tháng. B.
29
tháng. C.
30
tháng. D.
18
tháng.
Câu 64: Bạn Bình được gia đình gửi vào sổ tiết kiệm 200 triệu đồng với lãi suất 0,45% một tháng theo
hình thức lãi kép. Nếu mỗi tháng Bình rút ra một số tiền như nhau vào ngày ngân hàng trả lãi thì
hàng tháng Bình rút ra số tiền gần nhất với số nào sau đây để đúng 4 năm vừa hết số tiền trong
sổ tiết kiệm?
A.
4620000
. B.
4529000
. C.
4756000
. D.
4642000
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 1
Sưu tầm và biên soạn
BÀI 3: HÀM SỐ MŨ – HÀM SỐ LOGARIT
DẠNG 1: TẬP XÁC ĐỊNH
Câu 1: Tập xác định của hàm số
3
log 2yx
=
là
A.
( )
;0−∞
. B.
( )
0; +∞
. C.
. D.
( )
1; +∞
.
Lời giải
Hàm số
3
log 2
yx=
xác định khi
20 0xx>⇔>
.
Câu 2: Tập xác định của hàm số
8=
x
y
là
A.
. B.
[
)
0;+∞
. C.
(
)
0;+∞
. D.
{ }
\0
.
Lời giải
Hàm số
8=
x
y
có tập xác định là
Câu 3: Tập xác định của hàm số
( )
3
x
y =
là
A.
. B.
[
)
0;
+∞
. C.
\ {0}
. D.
( )
0;+∞
.
Lời giải
Tập xác định hàm số
( )
3
x
y =
là
.
Câu 4: Tập xác định của hàm số
( )
0,5
log 1yx= +
là:
A.
( )
1;D = − +∞
. B.
{ }
\1D = −
. C.
( )
0;D = +∞
. D.
( )
;1D = −∞ −
.
Lời giải
Hàm số
( )
0,5
log 1x +
xác định khi và chỉ khi
10 1xx+ > ⇔ >−
.
Vậy tập xác định của hàm số là:
( )
1;D = − +∞
.
Câu 5: Tập xác định của hàm số
lnyx=
là
A.
( )
0; +∞
. B.
. C.
[
)
0;+∞
. D.
{ }
\0
.
Lời giải
Hàm số
lnyx=
có tập xác định là
( )
0;D = +∞
.
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 2
Sưu tầm và biên soạn
Câu 6: Tập xác định của hàm số
log( 1)yx
= −
là
A.
[ 1; )
− +∞
. B.
(1; )+∞
. C.
[1; )+∞
. D.
( 1; )− +∞
.
Lời giải
Hàm số xác định
10 1xx⇔ −> ⇔ >
.
Câu 7: Tập xác định
D
của hàm số
( )
ln 1yx= −
là
A.
\ {1}D =
. B.
D
=
. C.
( ;1)D = −∞
. D.
(1; )D = +∞
.
Lời giải
Hàm số xác định
10 1
xx
⇔− > ⇔ <
.
Câu 8: Tập xác định của hàm số
( )
2
log 2yx
= −
là:
A.
( )
2; +∞
. B.
)
2;
+∞
. C.
( )
;2
−∞
. D.
.
Lời giải
Điều kiện:
20 2xx−>⇔>
Vậy tập xác định của hàm số
( )
2
log 2yx= −
là
( )
2; +∞
.
Câu 9: Tìm tập xác định của hàm số
(
)
3
log 3yx
= +
.
A.
( )
3;D = − +∞
. B.
[
)
3;D = − +∞
. C.
( )
0;D = +∞
. D.
{ }
\3D = −
.
Lời giải
Hàm số xác định khi và chỉ khi
3 0 3.xx+ > ⇔ >−
Vậy TXĐ của hàm số
(
)
3;D = − +∞
.
Câu 10: Tập xác định
D
của hàm số
4
log
=yx
là
A.
( )
0;= +∞
D
. B.
( )
;0= −∞D
. C.
= D
. D.
{ }
\0= D
.
Lời giải
Điều kiện xác định
4
00>⇔≠x
x
.
Vậy tập xác định của hàm số là
{ }
\0=
D
.
Câu 11: Tập xác định của hàm số
( )
2
2
log 1yx= −
là
A.
( )
1;− +∞
. B.
{ }
\1
. C.
. D.
(
)
1;+∞
.
Lời giải
Điều kiện xác định:
( )
2
10 1xx− >⇔≠
.
Vậy tập xác định của hàm số đã cho là
{ }
\1= D
.
Câu 12: Có bao nhiêu số nguyên thuộc tập xác định của hàm số
( )
2
ln 15yx= −
?
A.
7
. B.
6
. C.
5
. D.
8
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 3
Sưu tầm và biên soạn
ĐKXĐ:
2
15 0 15 15xx− > ⇔− < <
. Do
{ }
3;2;1;0xx∈ ⇒ =±±±
.
Câu 13: Tập xác định của hàm số
( )
2
log 3yx= −
là
A.
( )
;
−∞ +∞
. B.
( )
3; +∞
. C.
(
]
;3−∞
. D.
( )
;3−∞
.
Lời giải
A.
{ }
\2
. B.
( )
0; +∞
. C.
( ) { }
0; \ 2+∞
. D.
( ) { }
0; \ 1+∞
.
Câu 14: Tập xác định của hàm số
( )
ln 2 9yx x= −+ −
là
A.
[
)
9; +∞
. B.
[ ]
2;9
. C.
( )
2;9
. D.
(
]
2;9
.
Lời giải
Ta có điều kiện xác định của hàm số
(
]
20
2;9
90
x
x
x
−>
⇔∈
−≥
.
Câu 15: Tập xác định của hàm số
( )
2
ln 1x −
là:
A.
{ }
\1D =
. B.
( )
1;D = +∞
. C.
. D.
[
)
1;D = +∞
Lời giải
Điều kiện hàm số có nghĩa là
(
)
2
10 1
xx− >⇔≠
.
Vậy tập xác định của hàm số là:
{ }
\1D =
.
Câu 16: Tìm tất cả các giá trị thực của tham số
m
để hàm số
( )
2
3
log 4 1
y x xm= − −+
xác định với mọi
x ∈
.
A.
3m <−
. B.
3m >
. C.
3m >−
. D.
3
m <
.
Lời giải
Hàm số
( )
2
3
log 4 1y x xm= − −+
xác định với mọi
x
∈
2
4 1,x xm x− − + ∀∈
0 10
3
'0 4 10
a
m
m
Câu 17: Tập xác định của hàm số
2
1
log 1
y
x
=
−
là
A.
{
}
\2
R
. B.
( )
0; +∞
. C.
( ) { }
0; \ 2+∞
. D.
( ) { }
0; \ 1+∞
.
Lời giải
Tập xác định của hàm số
( ) { }
2
0
0
0; \ 1
log 0
1
x
x
x
x
x
>
>
⇔ ⇔ ∈ +∞
≠
≠
Câu 18: Có tất cả bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
( )
2
2
log 2 2022y xx m= −+ −
có tập xác định là
?
A.
2022
. B.
2021
. C.
2020
. D.
2019
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 4
Sưu tầm và biên soạn
Lời giải
Điều kiện xác định:
2
2 2022 0xx m− + −>
.
Hàm số
(
)
2
2
log 2 2022
y xx m= −+ −
có tập xác định là
khi và chỉ khi
2
2 2022 0,xx m x− + − > ∀∈
( )
'
1 2022 0m⇔∆ = − − <
2021.m⇔<
Vậy có
2020
giá trị của
m
thỏa mãn bài toán.
DẠNG 2: SỰ BIẾN THIÊN
Câu 19: Trong bốn hàm số sau, hàm số nào nghịch biến trên
?
A.
2022
x
y =
. B.
2022
2021
x
y
=
. C.
2022
logyx=
. D.
2021
2022
x
y
=
.
Lời giải
Hàm số
x
ya=
nghịch biến trên
khi
01a<<
.
Câu 20: Hàm số nào sau đây đồng biến trên
?
A.
2
5
x
y
=
. B.
1
3
x
y
=
. C.
2005
x
y =
. D.
2022y =
.
Lời giải
Ta có
2005
x
y =
có
2005 1>
nên hàm số đồng biến trên
.
Câu 21: Hàm số nào sau đây luôn đồng biến trên tập xác định.
A.
0.3=
x
y
. B.
1
3
log=yx
. C.
3
2
y log x=
. D.
2
3
=
x
y
.
Lời giải
Ta có
3
1
2
>
suy ra hàm số
3
2
y log .
x=
đồng biến trên tập xác định của nó.
Câu 22: Hàm số nào sau đây đồng biến trên
?
A.
( )
2 2.
x
y = −
B.
( )
31
x
y = −
. C.
3
x
y
π
=
. D.
4
x
e
.
Lời giải
Xét hàm số
3
x
y
π
=
với
1
3
a
π
= >
nên hàm số
3
x
y
π
=
đồng biến trên
.
Câu 23: Hàm số nào trong các hàm số sau đây nghịch biến trên
?
A.
5
logyx=
. B.
5
x
y =
. C.
( )
0,5
x
y =
. D.
0,5
logyx=
.
Lời giải
Hàm số
( )
0,5
x
y =
nghịch biến trên
vì
0 0,5 1<<
.
Câu 24: Hàm số nào sau đây nghịch biến trên
?

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 5
Sưu tầm và biên soạn
A.
4
π
=
x
y
. B.
=
x
ye
. C.
2022=
x
y
. D.
2=
x
y
.
Lời giải
Hàm số
=
x
ya
đồng biến trên
khi
1
>
a
, nghịch biến trên
khi
01
<<
a
.
Câu 25: Trong các hàm số dưới đây, hàm số nào nghịch biến trên
?
A.
( )
52
x
y = −
. B.
x
y
π
=
. C.
2021
x
y =
. D.
x
e
.
Lời giải
Ta có
0 521< −<
nên hàm số
( )
52
x
y = −
nghịch biến trên
.
Câu 26: Hàm số nào sau đây nghịch biến trên tập xác định của nó.
A.
3
log .
=
yx
B.
2
log .=yx
C.
log .
e
yx=
π
D.
log .
π
=yx
Lời giải
Hàm số logarit
log
e
yx=
π
với cơ số
,0 1
e
aa= <<
π
là hàm số nghịch biến trên tập xác định, các
hàm số logarit
3
log ,yx=
2
logyx=
và
logyx=
π
có cơ số lớn hơn 1 là các hàm số đồng biến
trên tập xác định của nó.
Câu 27: Hàm số nào đồng biến trên toàn tập xác định của nó?
A.
2
logyx=
. B.
(
)
22
x
y
−
=
. C.
1
2
logyx=
. D.
x
e
y
π
=
.
Lời giải
Hàm số
2
logyx=
có cơ số
21
a = >
nên đồng biến trên tập xác định của nó là
(
)
0; +∞
.
Hàm số
( )
1
22
22
x
x
y
−
= =
có cơ số
1
01
22
a<= <
nên nghịch biến trên tập xác định của
nó là
.
Hàm số
1
2
logyx=
có cơ số
1
01
2
a
<=<
nên nghịch biến trên tập xác định của nó là
( )
0; +∞
.
Hàm số
x
e
y
π
=
có cơ số
01
e
a
π
<= <
nên nghịch biến trên tập xác định của nó là
.
Câu 28: Hàm số nào trong các hàm số sau đây đồng biến trên
( )
0; +∞
A.
( )
21
x
y = −
. B.
9
logyx=
. C.
( )
0,6
x
y =
. D.
0.7
log x
.
Lời giải
Ta có
9
logyx=
đồng biến trên
(
)
0; +∞
, vì cơ số
91a = >
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 6
Sưu tầm và biên soạn
Câu 29: Cho hàm số mũ
( )
6
x
ya= −
với a là tham số. Có bao nhiêu số tự nhiên a để hàm số đã cho đồng
biến trên
?
A.
3
. B.
6
. C.
5
. D.
4
.
Lời giải
Hàm số
( )
6
x
ya
= −
đồng biến trên
61 5aa⇔− >⇔ <
Mà
{
}
0;1; 2;3; 4aa
∈ ⇒∈
Vậy có
5
giá trị của
a
thỏa mãn.
DẠNG 3: ĐỒ THỊ
Câu 30: Đồ thị sau là đồ thị của hàm số nào?
A.
2
log 1yx= +
. B.
2
log ( 1)yx= +
. C.
3
logyx=
. D.
3
log ( 1)x +
.
Lời giải
Đồ thị hàm số đi qua
(2;1)
, chọn hàm số
3
log ( 1)yx= +
.
Câu 31: Đồ thị hình bên dưới là đồ thị của hàm số nào?
A.
2
x
y =
. B.
1
2
x
y
=
. C.
1
3
x
y
=
. D.
3
x
y =
.
Lời giải
Đồ thị hàm số “đi lên” và qua điểm có tọa độ
( )
1;3
.
Câu 32: Đồ thị sau đây là đồ thị của một trong bốn hàm số cho ở các phương án A, B, C, D. Hỏi
đó là hàm số nào?
x
y
3
O
1

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 7
Sưu tầm và biên soạn
A.
2
logyx=
. B.
1
2
x
y =
. C.
1
2
logyx=
. D.
2
x
y =
.
Lời giải
Câu 33: Đường cong trong hình bên là của đồ thị hàm số nào sau đây?
A.
2
logyx=
. B.
( )
0,8
x
y =
. C.
0,4
logyx=
. D.
( )
2
x
y =
.
Lời giải
Dựa vào đồ thị, ta có hàm số có tập xác định
và hàm số nghịch biến suy ra
( )
0,8
x
y =
.
Câu 34: Cho đồ thị hàm số
( )
y fx=
như hình vẽ bên. Hàm số
( )
y fx=
có thể là hàm số nào dưới đây?
A.
x
ye
−
=
. B.
logyx=
. C.
lnyx= −
. D.
x
ye=
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 8
Sưu tầm và biên soạn
Lời giải
Nhận xét hàm số
(
)
y fx
=
có miền giá trị là
nên ta loại phương án
,AD
Mặt khác quan sát đò thị hàm số
( )
y fx= ⇒
( )
0fx
′
>
nên
logyx=
.
Câu 35: Cho các đồ thị hàm số
, log ,
xc
b
y a y xy x
ở hình vẽ sau đây.
Khẳng định nào sau đây đúng?
A.
01 .c ab
B.
0 1.cab
C.
0 1.
c ab
D.
0 1.
cab
Lời giải
Ta thấy đồ thị
c
yx
đi xuống nên
0
c
, đồ thị
x
ya
đi xuống nên
01a
, đồ thị
log
b
yx
đi lên nên
1.b
Câu 36: Đồ thị của hàm số sau là đồ thị của hàm số nào?
A.
2
yx=
. B.
3
x
y
=
. C.
3
logyx=
. D.
2
x
y =
.
Lời giải
Nhận thấy đồ thị hàm số đi qua hai điểm
( )
0;1
và
( )
2;4
, đối chiếu với các hàm số ta chọn hàm
số
2
x
y =
.
Câu 37: Hình bên là đồ thị của hàm số nào trong các hàm số sau đây?

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 9
Sưu tầm và biên soạn
A.
( )
0, 4
x
. B.
( )
2
x
y =
. C.
2
logyx=
. D.
0,4
log
yx
=
.
Lời giải
Hình bên là đồ thị của hàm mũ có cơ số
:0 1aa<<
.
Câu 38: Đồ thị hình bên dưới là đồ thị của hàm số nào?
A.
2
x
y =
. B.
1
2
x
y
=
. C.
1
3
x
y
=
. D.
3
x
y =
.
Lời giải
Đồ thị hàm số “đi lên” và qua điểm có tọa độ
( )
1;3
.
Câu 39: Cho các hàm số
,=
x
ya
log ,=
b
yx
log=
c
yx
có đồ thị như hình vẽ bên. Chọn khẳng định đúng?
A.
>>bca
. B.
>>bac
. C.
>>abc
D.
>>cba
.
Lời giải
Hàm
=
x
ya
nghịch biến nên
01<<a
.
x
y
3
O
1
O
x
y
1

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 10
Sưu tầm và biên soạn
Hàm
log ,=
b
yx
log=
c
yx
đồng biến nên
,1
>
bc
Đường thẳng
1y
=
cắt ĐTHS
log
c
yx=
,
log
b
yx=
tại các điểm có hoành độ lần lượt là
c
và
b
. Ta thấy
bc<
.
Câu 40: Đồ thị sau là đồ thị của hàm số nào?
A.
2
log 1.yx= +
B.
( )
2
log 1 .yx= +
C.
3
log .
yx=
D.
( )
3
log 1 .yx= +
Lời giải
Dựa vào đồ thị, ta thấy
Hàm số xác định trên khoảng
( )
1;− +∞ ⇒
loại A và C
Đồ thị hàm số đi qua điểm
( )
2;1 ⇒
Chọn D
Câu 41: Cho các hàm số
log
a
yx=
,
log
b
yx=
,
log
c
yx=
có đồ thị như hình vẽ dưới đây. Chọn mệnh
đề đúng.
A.
acb>>
. B.
abc>>
. C.
cab>>
. D.
bca>>
.
Lời giải
Dựa vào đồ thị ta có hàm số
log
b
yx=
là một hàm số nghịch biến trên tập xác định của nó nên
01b<<
; hàm số
log
a
yx=
,
log
c
yx=
là các hàm số đồng biến trên tập xác định của nó nên
,1ac>
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 11
Sưu tầm và biên soạn
Kẻ đường thẳng
1y
=
cắt đồ thị hàm số
log
c
yx=
,
log
a
yx=
lần lượt tại điểm
(
)
;1Ac
và
( )
;1Ba
.
Dựa vào đồ thị ta thấy
AB
x x ca< ⇔<
.
Vậy
acb>>
.
Câu 42: Cho đồ thị hàm số
x
ya=
;
x
yb=
;
log
c
yx=
như hình vẽ. Tìm mối liên hệ của
,a
,
b
c
.
A.
cba<<
. B.
bac<<
. C.
abc<<
. D.
cab
<<
.
Lời giải
Nhìn đồ thị ta thấy hàm số
x
ya=
là hàm số đồng biến nên
1
a >
;
x
yb=
là hàm số đồng biến
nên
1b >
;
log
c
yx=
là hàm số nghịch biến nên
01c<<
do vậy ta có
0
0
ca
cb
<<
<<
Khi thay
1x =
vào hai hàm số
;
xx
y ayb= =
ta thu được
ab>
vậy
.cb a<<
Câu 43: Đường cong trong hình dưới đây là đồ thị của hàm số nào trong bốn hàm số sau?

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 12
Sưu tầm và biên soạn
A.
2
logyx=
. B.
2
2
logyx=
. C.
2
log 2yx=
. D.
1
2
logyx=
.
Lời giải
Dựa vào hình dạng đồ thị, loại đáp án
D
.
Do đồ thị hàm số đi qua điểm
( )
1; 0
nên loại đáp án
C
.
Do đồ thị hàm số đi qua điểm
1
;1
2
−
nên loại đáp án
B
.
Câu 44: Cho
a
,
b
,
c
là ba số thực dương khác
1
. Đồ thị hàm số
x
ya=
,
x
yb=
,
x
yc
=
được cho ở hình
vẽ dưới đây. Mệnh nào nào sau đây đúng?
A.
abc<<
. B.
bca<<
. C.
cab<<
. D.
acb<<
.
Lời giải
Dựa vào đồ thị, dễ thấy
01
,1
a
bc
<<
>
.
Đường thẳng
1
x =
cắt hai đồ thị
x
yb=
,
x
yc=
lần lượt tại
b
,
c
và ta thấy
bc>
.
Vậy
acb<<
.
Câu 45: Trong hình vẽ dưới đây có đồ thị của các hàm số
, , log
xx
c
y ay by x= = =
.
x
y
1
-1
1
2
O
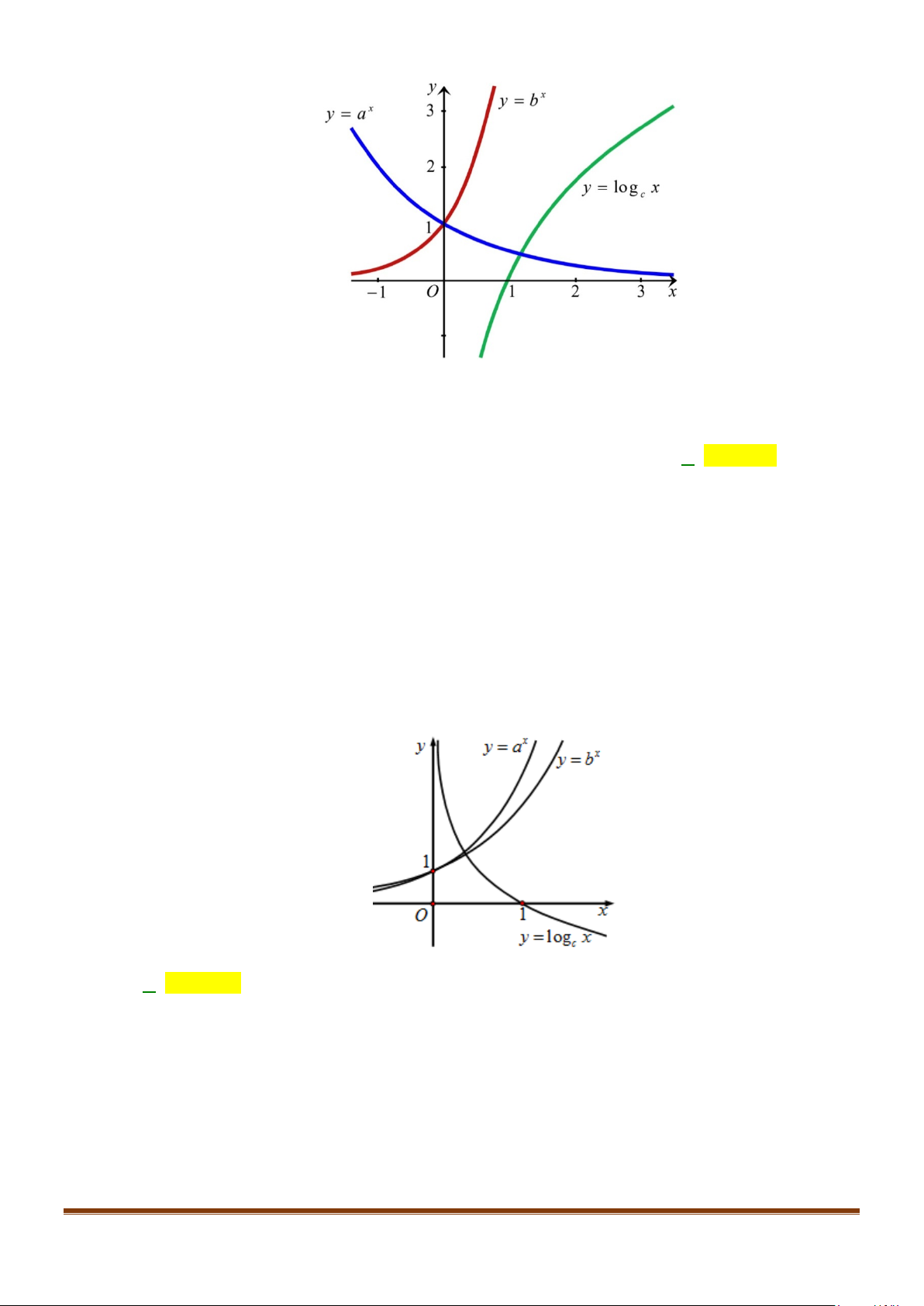
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 13
Sưu tầm và biên soạn
Mệnh đề nào sau đây đúng?
A.
abc<<
.
B.
abc<=
.
C.
bca<<
.
D.
a cb<<
.
Lời giải
- Hàm số
x
ya=
nghịch biến trên
nên
01
a<<
.
- Các hàm số
, log
x
c
yby x= =
đồng biến biến trên tập xác định của nó nên
,1bc>
.
Suy ra
0 ,1a bc<< <
- Xét đồ thị hàm số
log
c
yx=
, ta có
log 2 1 2
c
c>⇔<
.
- Xét đồ thị hàm số
x
yb=
, ta có
1
22bb>⇔>
.
Do đó:
0 acb<<<
.
Câu 46: Cho đồ thị hàm số
x
ya=
;
x
yb=
;
log
c
yx=
như hình vẽ. Tìm mối liên hệ của
,a
,b
c
.
A.
cba<<
. B.
bac<<
. C.
abc<<
. D.
cab<<
.
Lời giải
Nhìn đồ thị ta thấy hàm số
x
ya=
là hàm số đồng biến nên
1a >
;
x
yb=
là hàm số đồng biến
nên
1b >
;
log
c
yx=
là hàm số nghịch biến nên
01c<<
do vậy ta có
0
0
ca
cb
<<
<<
Khi thay
1x =
vào hai hàm số
;
xx
y ayb= =
ta thu được
ab>
vậy
.cba<<
Câu 47: Cho hàm số
log
a
yx=
( )
0, 1aa>≠
có đồ thị như hình vẽ.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 14
Sưu tầm và biên soạn
Giá trị của
a
bằng
A.
2
a =
. B.
1
2
a =
. C.
1
2
a
=
. D.
2a =
.
Lời giải
Đồ thị hàm số
log
a
yx=
đi qua điểm
(
)
2; 1
−
nên
log 2 1
a
= −
.
Khi đó
1
11
22
2
aa
a
−
=⇔ =⇔=
.
Câu 48: Cho
,ab
là các số thực dương khác
1
, đường thẳng
d
song song trục hoành cắt trục tung, đồ thị
hàm số
x
ya=
, đồ thị hàm số
x
yb
=
lần lượt tại
H
,
M
,
N
. Biết
3HM MN
=
. Mệnh đề nào
sau đây đúng?
A.
43ab=
. B.
43
ba=
. C.
34
ba=
. D.
34ab=
.
Lời giải
Đường thẳng
d
cắt đồ thị hàm số
x
ya=
tại điểm
( )
;
MM
Mx y
M
x
M
ya⇒=
.
Đường thẳng
d
cắt đồ thị hàm số
x
yb=
tại điểm
( )
;
NN
Nx y
N
x
N
yb⇒=
.
Mà
MN
yy=
N
M
x
x
ab
⇒=
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 15
Sưu tầm và biên soạn
Ta có:
3HM MN=
3
4
HM HN⇒=
3
4
MN
xx
⇒=
3
4
N
N
x
x
ab⇒=
3
4
ab⇔=
34
ab⇔=
.
Câu 49: Cho số thực dương
a
khác
1
. Biết rằng bất kì đường thẳng nào song song với trục
Ox
mà cắt
các đồ thị
4,
xx
y ya
= =
, trục tung lần lượt tại
,
MN
và
A
thì
2AN AM=
. Giá trị của
a
bằng
A.
1
3
. B.
2
2
. C.
1
4
. D.
1
2
.
Lời giải
Giả sử:
( ) ( ) ( )
4
0; , log ; , log ;
a
A t N tt M tt
. Thì:
4
log , log
a
AN t AM t
=−=
.
Theo giả thiết:
1
42
1
2 log 2log log log
2
a
a
AN AM t t t t a
−
= ⇒− = ⇔ = ⇔ =
Câu 50: Biết đồ thị hàm số
( )
y fx=
đối xứng với đồ thị hàm số
( )
0, 1
x
ya a a= >≠
qua điểm
( )
1;1I
.
Giá trị của biểu thức
1
2 log
2022
a
f
+
bằng
A.
2022−
. B.
2021
. C.
2022
. D.
2020−
.
Lời giải
Đồ thị đối xứng với đồ thị hàm số
( )
1
x
ya C=
là đồ thị hàm số
( )
2
log
a
y xC=
.
Gọi
( ) ( ) ( ) ( )
12
;;
AA BB
Axy C Bxy C∈⇒ ∈
là điểm đối xứng với điểm
A
qua điểm
( )
1;1I
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 16
Sưu tầm và biên soạn
Ta có
( )
( )
1
21
2
22
1
2
AB
AB
AB
AB
xx
xx
yy
yy
+
=
+=
⇔
+
+=
=
.
Với
1
2 log 2 log 1 log 2022 2 log 2022
2022
B a aa a
x
=+ =+− =−
.
Từ ta có
2 log 2022
AB A a
xx x+=⇔=
. Suy ra
log 2022
2022
a
A
ya= =
.
Từ ta có
2 2 2022 2020
AB B
yy y+=⇔=− =−
.
Vậy
( )
1
2 log 2020
2022
Ba B
y f fx
=+==−
.
Câu 51: Cho các hàm số
x
ya
=
và
x
yb=
với
,ab
là những số thực dương khác 1, có đồ thị như hình
vẽ. Đường thẳng
3
y =
cắt trục tung, đồ thị hàm số
x
ya=
và
x
yb=
lần lượt tại
,,
HMN
. Biết
rằng
23
HM MN=
, khẳng định nào sau đây đúng?
A.
53
ab=
B.
35ab
=
C.
23
ab=
D.
35
ab
=
Lời giải
3
23
5
HM MN HM HN= ⇒=
.
Gọi
( )
11
;3 log 3
x
a
Mx y a x∈= ⇒ =
.
(
)
12
;3 log 3
x
b
Nx y b x
∈= ⇒ =
.
Khi đó
5
35
3
33
33
3 3 13 5
log 3 log 3 log log
5 5 log 5log 3
ab
HM HN a b a b a b
ab
= ⇔ = ⇔ = ⇔ = ⇔= ⇔ =
.
DẠNG 4: BÀI TOÁN LÃI SUẤT
Câu 52: Một người gửi 100 triệu đồng vào một ngân hàng với lãi suất
6%
/ năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm
tiếp theo. Hỏi ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 300 triệu bao gồm cả
gốc lẫn lãi?.
A.
20
năm. B.
18
năm. C.
21
năm. D.
19
năm.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 17
Sưu tầm và biên soạn
Áp dụng công thức lãi kép thì sau
n
năm, số tiền người gửi nhận được là
8
10 .1,06
n
A =
.
Để nhận được số tiền hơn 300 triệu thì
88 8
1,06
3.10 10 .1,06 3.10 1,06 3 log 3 18,85
nn
An>⇔ >⇔>⇔> ≈
.
Vậy ít nhất sau 18 năm thì người đó nhận được số tiền nhiều hơn 300 triệu.
Câu 53: Ông
A
gửi
100
triệu vào ngân hàng theo hình thức lãi kép trong một thời gian khá lâu với lãi
suất ổn định trong suốt thời gian tiết kiệm là
10%
/1 năm. Tết năm nay do dịch bệnh nên ông rút
hết tiền trong ngân hàng ra để gia đình chi tiêu. Sau khi rút cả vốn lẫn lãi, ông trích ra 10 triệu để
sắm sửa đồ Tết thì ông còn 240 triệu. Hỏi ông đã gửi tiết kiệm trong bao nhiêu năm?
A.
9
năm. B.
20
năm. C.
12
năm. D.
10
năm.
Lời giải
Giả sử ông
A
đã gửi tiết kiệm trong
n
năm.
Số tiền ông đã nhận được là 250 triệu.
Theo công thức lãi suất kép, ta có
( )
66
1,1
250.10 100.10 1 0,1 log 2,5 9,61
n
nn= + ⇔= ⇔≈
Vậy, ông
A
đã gửi tiết kiệm trong 10 năm.
Câu 54: Ông Nguyễn Văn B là thương binh hạng
4/4
, được hưởng trợ cấp hàng tháng là
2082000
đồng.
Do tình hình dịch bệnh Covid-19 diễn biến phức tạp nên từ tháng 4 năm 2021 ông không đi lĩnh
tiền mà nhờ thủ quỹ lập một sổ tiết kiệm ở ngân hàng để gởi số tiền hàng tháng vào đó với lãi
suất
0,5% /
tháng. Hỏi đến đầu tháng 4 năm 2022 ông đến ngân hàng nhận được số tiền là bao
nhiêu?
A.
25 811 054
đồng. B.
2 210 413
đồng. C.
25 682 641
đồng. D.
27 893 054
đồng.
Lời giải
Ta có
( )
( )
( )
12
1 1 1 0,5% 1
(1 ). 2 082 000 1 0,5% . 25811054,06
0,5%
n
r
TA r
r
+− + −
= + −= + =
là số
tiền ông B sẽ nhận được.
Câu 55: Ông Nguyễn Văn B là thương binh hạng
4/4
, được hưởng trợ cấp hàng tháng là
2082000
đồng.
Do tình hình dịch bệnh Covid-19 diễn biến phức tạp nên từ tháng 4 năm 2021 ông không đi lĩnh
tiền mà nhờ thủ quỹ lập một sổ tiết kiệm ở ngân hàng để gởi số tiền hàng tháng vào đó với lãi
suất
0,5% /
tháng. Hỏi đến đầu tháng 4 năm 2022 ông đến ngân hàng nhận được số tiền là bao
nhiêu?
A.
25 811 054
đồng. B.
2 210 413
đồng. C.
25 682 641
đồng. D.
27 893 054
đồng.
Lời giải
Ta có
( )
( )
( )
12
1 1 1 0,5% 1
(1 ). 2 082 000 1 0,5% . 25811054,06
0,5%
n
r
TA r
r
+− + −
= + −= + =
là số
tiền ông B sẽ nhận được.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 18
Sưu tầm và biên soạn
Câu 56: Đầu mỗi tháng, anh Hiếu gửi tiết kiệm ngân hàng số tiền 10 triệu đồng với hình thức lãi kép, lãi
suất là 0,5%/ tháng. Hỏi sau đúng 5 năm thì anh Hiếu nhận được số tiền cả gốc và lãi gần nhất
với số tiền nào dưới đây, giả sử rằng trong suốt quá trình gửi, anh Hiếu không rút tiền ra và lãi
suất của ngân hàng không thay đổi.
A.
60
600 10.1,005+
. B.
60
1,005 1
10.1,005.
0,005
−
.
C.
60
10.1,005
. D.
60
1,005 1
10.
0,005
−
.
Lời giải
Sau đúng 5 năm thì anh Hiếu nhận được số tiền cả gốc và lãi là
( )
(
)
60
60
76
60
1 0,5% 1
1,005 1
10 . 1 0,5% 10.1,005. .10
0,5% 0,005
T
+−
−
=+=
60
1,005 1
10.1,005.
0,005
−
=
.
Câu 57: Gia đình nhà bác Long Thắm gửi số tiền 100 triệu đồng vào ngân hàng với lãi suất
7%
/năm.
Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào
vốn ban đầu. Sau 10 năm, nếu không rút lãi lần nào thì số tiền mà nhà bác Long Thắm nhận được
gồm cả gốc lẫn lãi tính theo công thức nào dưới đây?
A.
( )
9
8
10 . 1 0,07+
. B.
( )
10
8
10 1 0,7+
.
C.
( )
10
8
10 . 1 0,07+
. D.
8 10
10 .0,07
.
Lời giải
Áp dụng công thức lãi kép thì số tiền mà nhà bác Long Thắm nhận được gồm cả gốc lẫn lãi là
( ) (
)
10 10
88
10 . 1 7% 10 . 1 0,07+=+
.
Câu 58: Bác Minh gửi
60
triệu vào ngân hàng kì hạn 1 năm với lãi suất
5, 6%
/năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ nhập vào gốc để tính lãi cho năm tiếp
theo. Hỏi sau ít nhất bao nhiêu năm bác Minh nhận được số tiền nhiều hơn
120
triệu đồng bao
gồm cả gốc và lãi?
A.
11
năm. B.
12
năm. C.
13
năm. D.
14
năm.
Lời giải
Sau
n
năm số tiền bác Minh nhận được cả gốc và lãi là:
( )
60 1 5,6%
n
+
.
Vậy bác Minh nhận được số tiền nhiều hơn
120
triệu đồng bao gồm cả gốc và lãi khi:
( )
60 1 5,6% 120
n
+>
1,056
log 2 12,7n⇔> ≈
.
Vậy bác Minh cần gửi ít nhất 13 năm.
Câu 59: Một học sinh A khi đủ 18 tuổi được cha mẹ cho
200000000
VNĐ. Số tiền này được bảo quản
trong ngân hàng MSB với kì hạn thanh toán 1 năm và học sinh A chỉ nhận được số tiền này khi

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 19
Sưu tầm và biên soạn
học xong 4 năm đại học. Biết rằng khi đủ 22 tuổi, số tiền mà học sinh A được nhận sẽ là
243 101 250
VNĐ. Vậy lãi suất kì hạn một năm của ngân hàng MSB là bao nhiêu?
A.
8%
. B.
7%
. C.
6%
D.
5%
.
Lời giải
Gọi lãi suất kỳ hạn một năm của ngân hàng MSB là r. Áp dụng công thức lãi suất kép
( )
1
n
Pa r= +
trong đó ta có :
( ) ( )
44
0
2
0
43101250 200
2
0000
43101250
1
200 0
01
0
0
00
r r⇔== + +
44
243101250 243101250
1 1 0,05
200000000 200000000
rr r⇔+= ⇔= −⇔=
.
Câu 60: Một người gửi số tiền
3
triệu đồng vào một ngân hàng với lãi suất
0,55% /
tháng. Biết rằng nếu
người đó không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn
ban đầu. Số tiền người đó lãnh được sau hai năm, nếu trong khoảng thời gian này không rút tiền
ra và lãi suất không đổi là:
A.
( )
2
3. 1.0055
triệu đồng. B.
( )
24
3. 1,0055
triệu đồng.
C.
( )
24
3. 1,055
triệu đồng. D.
( )
24
3,0055
triệu đồng.
Lời giải
+) Áp dụng công thức lãi kép:
( )
0
1
n
n
TT r= +
trong đó:
0
T
là số tiền gửi ban đầu.
n
T
là số tiền cả gốc lẫn lãi sau
n
kì.
r
là lãi suất một kì.
+) Thời gian gửi là
2
năm với chu kì
1
tháng nên số chu kì là
24=n
.
Suy ra số tiền người đó lãnh được sau hai năm là:
( )
( )
24 24
3 0,55 1,00. 51 % 3. 5=+=
n
T
triệu
đồng.
Câu 61: Vào ngày
15
hàng tháng, ông An đều đến gửi tiết kiệm tại ngân hàng với số tiền
5
triệu đồng
theo hình thức lãi kép với lãi suất không đổi trong suốt quá trình gửi là
0,6% /
tháng. Hỏi sau
đúng ba năm, ông An thu được số tiền cả gốc lẫn lãi là bao nhiêu?
A.
195251000
. B.
195252000
.
C.
201450000
. D.
201453000
.
Lời giải
Đặt
5A =
triệu,
0,6%r =
.
Sau một tháng ông An có số tiền cả vốn và lãi là
( )
1Ar+
, tiếp tục gửi vào ngân hàng
A
đồng
nên số tiền trong ngân hàng lúc này là
( ) (
)
1
1 11T A r AA r= ++= ++
.
Sau hai tháng ông An có số tiền cả vốn và lãi là
( ) ( ) ( )
2
21
1 1 11T T r AA r r
= ++= + +++
.
….

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 20
Sưu tầm và biên soạn
Sau
36
tháng ông An có số tiền cả vốn và lãi là
( ) (
) (
)
( )
37
36 35
36
11
1 1 ... 1 1 . 201453000
r
T A r r r AA A
r
+−
= + ++ ++++−= −≈
đồng.
Câu 62: Một người gửi số tiền
100
triệu đồng vào ngân hàng với lãi suất
0
0
7
/ năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho
năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó lĩnh được số tiền nhiều hơn
200
triệu
đồng, nếu trong khoảng thời gian này người đó không rút tiền ra và lãi suất không đổi?
A.
11
năm. B.
12
năm. C.
10
năm. D.
9
năm.
Lời giải
Áp dụng công thức lãi kép gửi 1 lần:
( )
1= +
n
NA r
, với
6
100.10
A =
và
0
0
7r =
.
Theo đề bài ta tìm
n
bé nhất sao cho:
( )
86
10 1 7% 200.10
n
+>
( )
1 7% 2
n
⇔+ >
107
100
log 2 10,245n⇔> ≈
.
Câu 63: Vợ chồng nhà chị Thơm vay ngân hàng 400 triệu đồng để mua nhà với hình thức trả góp, chị
chọn gói lãi suất ưu đãi cố định
0,5%
tháng trong 12 tháng đầu và sang tháng thứ 13 trở đi thì
ngân hàng tính lãi suất thả nổi theo quy định. Gia đình chị hoàn nợ cho ngân hàng theo cách: sau
đúng một tháng kể từ ngày vay thì bắt
đầu
hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một
tháng, số tiền hoàn nợ ở mỗi tháng là 15 triệu đồng. Sau khi hết 12 tháng ưu đãi thì chị Thơm
phải trả lãi suất thả nổi là 1%tháng. Biết rằng mỗi tháng ngân hàng chỉ tính lãi trên số dư nợ thực
tế của tháng đó và lãi suất thả nổi của ngân hàng không thay đổi trong thời gian chị Thơm hoàn
nợ. Hỏi chị Thơm cần bao nhiêu tháng để trả hết nợ ngân hàng kể từ khi vay?
A.
17
tháng. B.
29
tháng. C.
30
tháng. D.
18
tháng.
Lời giải
Số tiền chị Thơm nợ sau một tháng là
400 400.0,5% 400(1 0,5%)+=+
.
Sau 1 tháng thì số tiền chị Thơm phải trả là
400(1 0,5%) 15+−
.
Sau 2 tháng thì số tiền chị Thơm phải trả là
400(1 0,5%) 15 [400(1 0,5%) 15] 0,5% 15+−++−⋅−
2
400(1 0,5%) 15[(1 0,5%) 1]= + −+ +
.
Sau 12 tháng thì số tiền chị Thơm phải trà là
12 11 10
400(1 0,5%) 15 (1 0,5%) (1 0,5%) (1 0,5%) 1A
= + − + ++ +…++ +
12
12 12 12
(1 0,5%) 1 15
400(1 0,5%) 15 400(1 0,5%) (1 0,5%) 1
(1 0,5%) 1 0,5%
+−
=+− =+− +−
+−
.
239,637=
.
Gọi
n
là số tháng tiếp theo mà chị Thơm cần đề trả hết nợ, tương tự như trên ta được

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 21
Sưu tầm và biên soạn
1 1%
15 (1 1%) 1
15
(1 1%) 0 log 17.49
1% .1% 15
n
n
An
A
+
+−
−
+ − =⇔= ≈
−
.
Tức là chị Thơm cần thêm 18 tháng để trả hết nợ.
Vậy chị Thơm cần
12 18 30+=
tháng để trà hết nợ ngân hàng kể từ khi vay.
Câu 64: Bạn Bình được gia đình gửi vào sổ tiết kiệm 200 triệu đồng với lãi suất 0,45% một tháng theo
hình thức lãi kép. Nếu mỗi tháng Bình rút ra một số tiền như nhau vào ngày ngân hàng trả lãi thì
hàng tháng Bình rút ra số tiền gần nhất với số nào sau đây để đúng 4 năm vừa hết số tiền trong
sổ tiết kiệm?
A.
4620000
. B.
4529000
. C.
4756000
. D.
4642000
.
Lời giải
Gọi số tiền bạn Bình rút ra hàng tháng là
x
x 0
, số tiền ban đầu là
P
,
P 0
, lãi suất
tiền gửi hàng tháng là
r
,
r 0
.
Lãi suất nhận được sau tháng thứ nhất là:
.Pr
.
Số tiền cuối tháng thứ nhất sau khi rút còn lại:
PP rx
1
1
.
Lãi suất nhận được sau tháng thứ nhất là:
.Pr
1
.
Số tiền cuối tháng thứ nhất sau khi rút còn lại:
PP rxP r x rx
2
21
1 11
.
Cứ như thế, số tiền còn lại sau
n
tháng là:
....
nn n
n
PPrxr xr xrx
12
11 1 1
.
n
n
n
r
PP r x
r
11
1
.
Sau 48 tháng, số vừa hết khi và chỉ khi
n
P
0
.
r
Pr x
r
48
48
11
10
,
,.
,
x
48
48
1 0045 1
200 1 0045 0
0 0045
,x4 642
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 52
Sưu tầm và biên soạn
BÀI 4: PHƯƠNG TRÌNH – BẤT PHƯƠNG TRÌNH – MŨ – LOGARIT
1. PHƯƠNG TRÌNH MŨ
Phương trình mũ cơ bản có dạng:
( )
0, 1
x
a ba a= >≠
.
● Phương trình có một nghiệm duy nhất khi và chỉ khi
0
b >
.
( )
log 0, 1, 0
x
a
a b x ba a b=⇔= > ≠ >
● Phương trình vô nghiệm khi và chỉ khi
0b ≤
.
Ví dụ:
Câu 1: Giải phương trình
1
39
x−
=
.
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
I
LÝ THUYẾT.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 53
Sưu tầm và biên soạn
Câu 2: Giải phương trình
1
1
5
25
x
x
−
=
.
Câu 3: Giải phương trình
42
3
3 81
xx
−
=
.
Câu 4: Giải phương trình
2
2 54
7 49
++
=
xx
.
Câu 5: Giải phương trình
2
5 23
32
23
xx x−− +
=
.
Câu 6: Giải phương trình
sin 2
91
x
=
.
Câu 7: Giải phương trình
2
24 4
24
xx x− + +−+
=
.
Câu 8: Tìm
m
để phương trình
2
22
2020 1
mx x m− +−
=
có hai nghiệm trái dấu.
Câu 9: Tính tổng các nghiệm của phương trình
2
22
28
xx x+−
=
.
Câu 10: Giải phương trình:
1 13
5 52 2
x xx x+ ++
−= +
Câu 11: Giải phương trình:
3
3
3
2 . 4 . 0.125 4 2
xx
x
=
.
Câu 12: Giải phương trình:
222
32 2 65 3 37
44 4 1
xx xx xx−+ ++ ++
+=+
.
Câu 13: Tìm
m
để phương trình
2
2 32
55
mx x m m x+ ++ +
=
có hai nghiệm trái dấu
Câu 14: Tìm
m
để phương trình
2
22
77
mx x mx m+−
=
có hai nghiệm
12
;xx
thỏa mãn
Câu 15: Tìm
m
để phương trình:
( )
22
5 6 1 65
.2 2 2.2 1
xx x x
mm
−+ − −
+= +
có 4 nghiệm phân biệt.
2. PHƯƠNG TRÌNH LÔGARIT
Phương trình cơ bản có dạng:
( )
log 0, 0, 1
a
x bx a a= >>≠
luôn có nghiệm duy nhất
b
xa
=
với mọi
b
22
12
22
21
2
xx
xx
+≤

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 54
Sưu tầm và biên soạn
Ví dụ:
Câu 16: Giải phương trình sau:
3
log 4
x =
.
Câu 17: Giải phương trình sau:
( )
2
log 2 2 3x
−=
.
Câu 18: Giải phương trình sau:
( )
2
4
log 5 10 2xx++ =
.
Câu 19: Giải phương trình sau:
(
)
2
log 1 2
x
−=
.
Câu 20: Giải phương trình sau:
2
5
log 3 1 1
xx
− +=
.
Câu 21: Giải phương trình sau:
(
)
( )
2
22
log 1 1 log 2xx x x−++ + = +
.
Câu 22: Giải phương trình sau:
( ) ( )
22
log 5 log 2 3xx−+ +=
.
Câu 23: Giải phương trình:
( )
2
25 5 3
log 4 5 log log 27xx++ =
.
Câu 24: Giải phương trình:
234 20
log log log logxxx x++=
Câu 25: Tìm tập nghiệm S của phương trình
33
log (2 1) log ( 1) 1xx+− −=
.
Câu 26: Gọi
12
,xx
là nghiệm của phương trình
16
log 2 log 0
x
x
−=
. Tính
12
.xx
.
Câu 27: Tổng tất cả các nghiệm thực của phương trình
22
log .log (32 ) 4 0xx+=
bằng
Câu 28: Cho phương trình
2
31
3
3
log 2log 2log 3 0x xx− − −=
có hai nghiệm phân biệt là
1
x
,
2
x
. Tính giá
trị của biểu thức
3 1 27 2
log log
P xx+=
biết
12
x x<
.
Câu 29: Tổng tất cả các nghiệm của phương trình:
( ) ( ) ( )
8
93
3
11
log 3 log 1 log 4
24
xxx++ − =
Câu 30: Giải phương trình:
( )
2
3
3
2
log 2 log 0
33
x
x
xx
−+ =
−+
.
Câu 31: Giải phương trình:
( )
( )
2
21
2
log 8 log 1 1 2 0x xx− + ++ − −=
.
3. BẤT PHƯƠNG TRÌNH MŨ

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 55
Sưu tầm và biên soạn
CHÚ Ý:
Nếu
1a >
,
0b >
thì
( ) ( )
() ()f x gx
a a f x gx
>⇔ >
( )
()
log
fx
a
a b fx b>⇔ >
Nếu
01a<<
,
0b >
thì
( ) ( )
() ()f x gx
a a f x gx>⇔ <
( )
()
log
fx
a
a b fx b>⇔ <
Lưu ý:
0b ≤
thì
(x)
f
ab>
đúng với mọi
x
thỏa mãn điều kiện xác định của
( )
fx
, còn
(x)f
ab
≤
vô nghiệm.
4. BẤT PHƯƠNG TRÌNH LOGARIT

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 56
Sưu tầm và biên soạn
CHÚ Ý:
Nếu
1a
>
thì
( ) ( )
( )
( ) ( )
0
log log
aa
gx
f x gx
f x gx
>
>⇔
>
Nếu
01a<<
thì
( ) ( )
( )
( ) ( )
0
log log
aa
fx
f x gx
f x gx
>
>⇔
<
Ví dụ:
Câu 32: Giải bất phương trình
2
4
4
3
1
x −
≥
.
Câu 33: Có bao nhiêu số nguyên
10x ≤
là nghiệm của bất phương trình
2
1
3
3
x
x
+
−
≥
?
Câu 34: Tìm số nghiệm nguyên của bất phương trình
( )
11
22
log 3 log 4−≥x
.
Câu 35: Giải bất phương trình:
( ) ( )
log 3 2 log 1xx−≥ +
.
Câu 36: Giải bất phương trình
( )
2
1
2
log 5 7 0xx−+>
.
Câu 37: Bất phương trình
( ) ( )
33
log 3 1 log 7xx+< +
có bao nhiêu nghiệm nguyên?
Câu 38: Tìm tập nghiệm
S
của bất phương trình
( )
0,5 0,5
log 1 log 2xx+>
Câu 39: Tìm tập nghiệm
S
của bất phương trình
3
log 3 log 3
xx
<
Câu 40: Có bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
( ) ( )
22
55
log 1 1 log 4x mx x m+ +≥ + +
nghiệm đúng với mọi
x ∈
?

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 1
Sưu tầm và biên soạn
BÀI 4: PHƯƠNG TRÌNH – BẤT PHƯƠNG TRÌNH – MŨ – LOGARIT
1. PHƯƠNG TRÌNH MŨ
Phương trình mũ cơ bản có dạng:
( )
0, 1
x
a ba a= >≠
.
● Phương trình có một nghiệm duy nhất khi và chỉ khi
0
b >
.
( )
log 0, 1, 0
x
a
a b x ba a b=⇔= > ≠ >
● Phương trình vô nghiệm khi và chỉ khi
0b ≤
.
Ví dụ:
Câu 1: Giải phương trình
1
39
x−
=
.
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
I
LÝ THUYẾT.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 2
Sưu tầm và biên soạn
Lời giải
1
39
x−
=
12
33
x
−
⇔=
3x⇔=
.
Câu 2: Giải phương trình
1
1
5
25
x
x
−
=
.
Lời giải
1 12
11
5 5 5 12
25 3
x
x xx
x xx
− −−
= ⇔ = ⇔ −=− ⇔ =
.
Câu 3: Giải phương trình
42
3
3 81
xx−
=
.
Lời giải
42
2
3 42 42 2
2
1
3 81 3 4 3 4 0 4 2
4
xx
x
xx xx x x
x
−
= −
=⇔− =⇔− −=⇔ ⇔=⇔=±
=
.
Câu 4: Giải phương trình
2
2 54
7 49
++
=
xx
.
Lời giải
2
2 54
7 49
++
=
xx
2
2 54 2
77
++
⇔=
xx
2
2 5 42⇔ + +=
xx
2
2 5 20⇔ + +=xx
2
1
2
= −
⇔
= −
x
x
.
Câu 5: Giải phương trình
2
5 23
32
23
xx x−− +
=
.
Lời giải
Ta có
2
5 23
32
23
xx x−− +
=
2
5 23
33
22
xx x−− − −
⇔=
2
5 23
xx x⇔ −−=− −
2
1
20
2
x
xx
x
=
⇔ +−=⇔
= −
.
Câu 6: Giải phương trình
sin 2
91
x
=
.
Lời giải
Ta có
( )
sin 2
9 1sin202 2 ,
x
x xk xk k
ππ
=⇔ =⇔ = ⇔= ∈
.
Câu 7: Giải phương trình
2
24 4
24
xx x− + +−+
=
.
Lời giải
Ta có
2
24 4 2 2
2 4 24 42 24 2
xx x
xx x xx x
− + +−+
=⇔− + +−+=⇔− + +=−
.
( )
2
2
20
24 2
x
xx x
−≥
⇔
− + += −
2
2
2 60
x
xx
≥
⇔
−=
2
3
0
3
x
x
x
x
≥
⇔ ⇔=
=
=
.
Vậy phương trình đã cho có nghiệm duy nhất là
3x =
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 3
Sưu tầm và biên soạn
Câu 8: Tìm
m
để phương trình
2
22
2020 1
mx x m
− +−
=
có hai nghiệm trái dấu.
Lời giải
2
22 2
2020 1 2 2 0
mx x m
mx x m
− +−
=⇔ − + −=
.
Phương trình đã cho có hai nghiêm trái dấu khi và chỉ khi
( )
20 0 2mm m− <⇔< <
.
Câu 9: Tính tổng các nghiệm của phương trình
2
22
28
xx x+−
=
.
Lời giải
(
)
22 2
2
2 2 2 3 2 63 2 2
1
2 8 2 2 2 2 2 63 5 6 0
6
x
xx x xx xx x
x
x x xx x
x
−
+− + +−
=
= ⇔ = ⇔ = ⇔+=−⇔+−=⇔
= −
Vậy tổng các nghiệm của phương trình
2
22
28
xx x+−
=
bằng
( )
16 5+− =−
Câu 10: Giải phương trình:
1 13
5 52 2
x xx x+ ++
−= +
Lời giải
1 13 3
5 5 2 2 5.5 5 2.2 2 .2
x x x x xx x x+ ++
−= + ⇔ −= +
5 10 5
4.5 10.2 1
2 42
x
xx
x
⇔ = ⇔ = =⇔=
Vậy phương trình cho có nghiệm
1.
x =
Câu 11: Giải phương trình:
3
3
3
2 . 4 . 0.125 4 2
xx
x
=
.
Lời giải
Điều kiện:
1
3
3
x
x
≥
∈
.
Phương trình đã cho tương đương với phương trình:
1
1 17
2.
3
2
3 3 32 3
2
1
2 .2 . 2 .2 2 .2 2 2
8
xx
x
x
x
x
−
=⇔=
17
2
232 3
1
17
2 2 5 14 3 0
5
232 3
3
xx
x
x
xx
xx
x
x
+−
= −
⇔ = ⇔ + − = ⇔ − −=⇔
=
.
Kết hợp với điều kiện ta có
3x
=
là nghiệm của phương trình.
Câu 12: Giải phương trình:
222
32 2 65 3 37
44 4 1
xx xx xx−+ ++ ++
+=+
.
Lời giải
Phương trình đã cho tương đương với phương trình:
2 2 22
32 2 65 322 65
4 4 4 .4 1
xx xx xx xx−+ ++ −+ ++
+= +
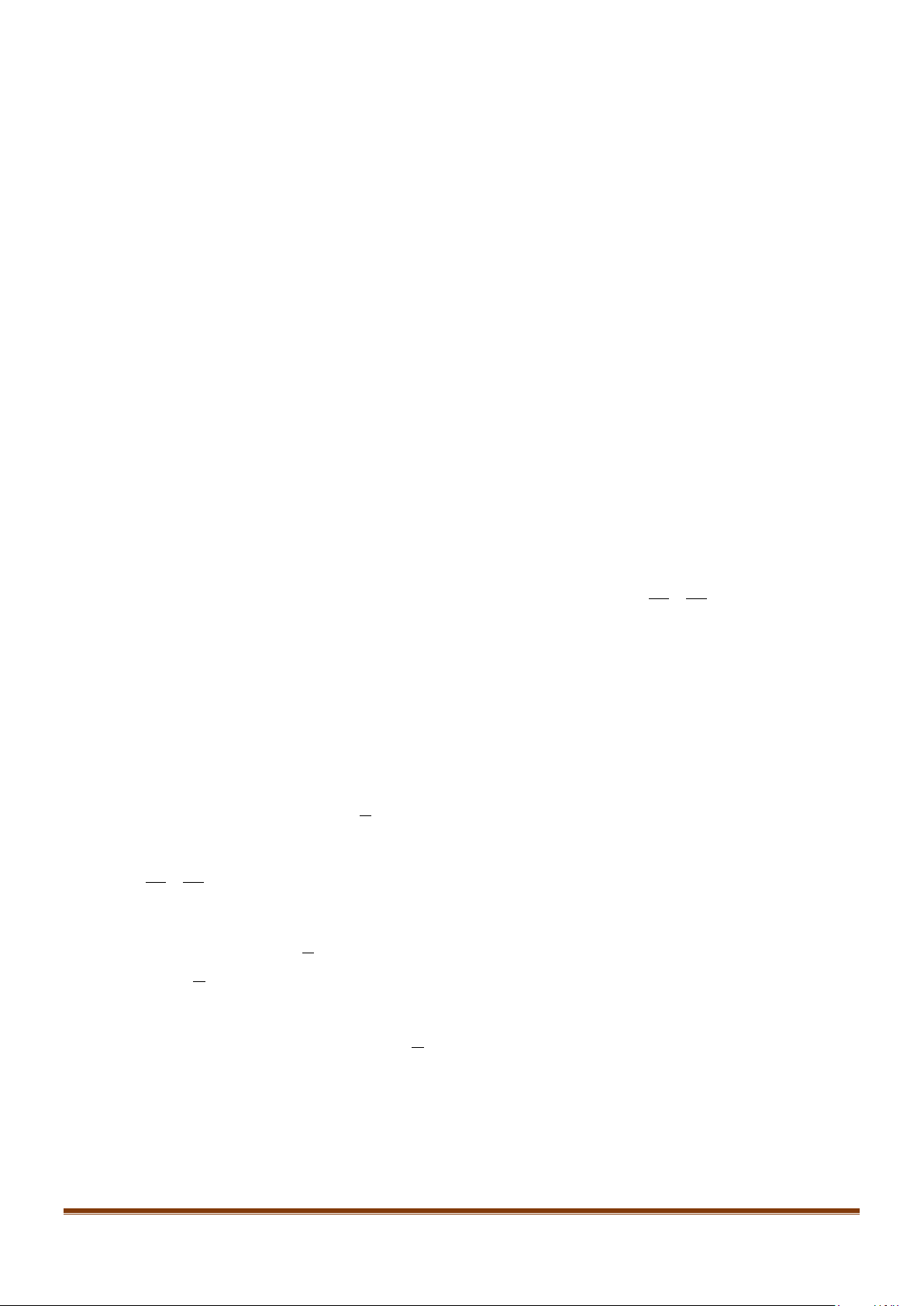
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 4
Sưu tầm và biên soạn
2 2 22
32 2 65 322 65
4 1 4 4 .4 0
xx xx xx xx−+ ++ −+ ++
⇔ −+ − =
( )( )
22
32 2 65
4 14 1 0
xx xx−+ ++
⇔ − −=
2
32 2
1
4 1 3 20
2
xx
x
xx
x
−+
=
=⇔ − +=⇔
=
.
2
2 65 2
4 1 2 6 50
xx
xx
++
=⇔ + +=
, phương trình này vô nghiệm.
Vậy phương trình đã cho có
2
nghiệm
1
2
x
x
=
=
.
Câu 13: Tìm
m
để phương trình
2
2 32
55
mx x m m x+ ++ +
=
có hai nghiệm trái dấu
Lời giải
( ) ( )
2
2 32 2 2
5 5 1 2 3 2 3 0 2
mx x m m x
mx x m m x mx x m
+ ++ +
= ⇔ + ++ = + ⇔ +++ =
Phương trình
( )
1
có
2
nghiệm trái dấu
⇔
phương trình
( )
2
có
2
nghiệm trái dấu
⇔
(
)
0 3 03 0
ac m m m<⇔ + <⇔−< <
Vậy
{ }
3;2;1
m =−−−
thỏa mãn yêu cầu bài toán.
Câu 14: Tìm
m
để phương trình
2
22
77
mx x mx m+−
=
có hai nghiệm
12
;xx
thỏa mãn
Lời giải
(
) (
) (
)
2
22 2 2
7 7 1 2 2 2 1 0 2
mx x mx m
mx x mx m mx m x m
+−
= ⇔+=−⇔−−+=
Phương trình
( )
1
có
2
nghiệm
12
;xx
phương trình
( )
2
có
2
nghiệm
12
;
xx
⇔
( )
0
0
*
1
'12 0
2
m
m
m
m
≠
≠
⇔
∆= − ≥
≤
( )
( )( )
22
2
44 22 22 22
12
12 12 12 12 1212
22
21
22 00 0
xx
xx xx xx xx xxxx
xx
+ ≤⇔+≤ ⇔ − ≤⇔−=⇔ − + =
⇔
'0
1
2
0
1
m
b
m
a
∆=
=
⇔
−=
=
Kết hợp điều kiện
( )
*
ta suy ra
1
2
m =
thỏa mãn yêu cầu bài toán
Câu 15: Tìm
m
để phương trình:
( )
22
5 6 1 65
.2 2 2.2 1
xx x x
mm
−+ − −
+= +
có 4 nghiệm phân biệt.
Lời giải
Viết lại phương trình
( )
1
dưới dạng:
22
12
22
21
2
xx
xx
+≤
⇔
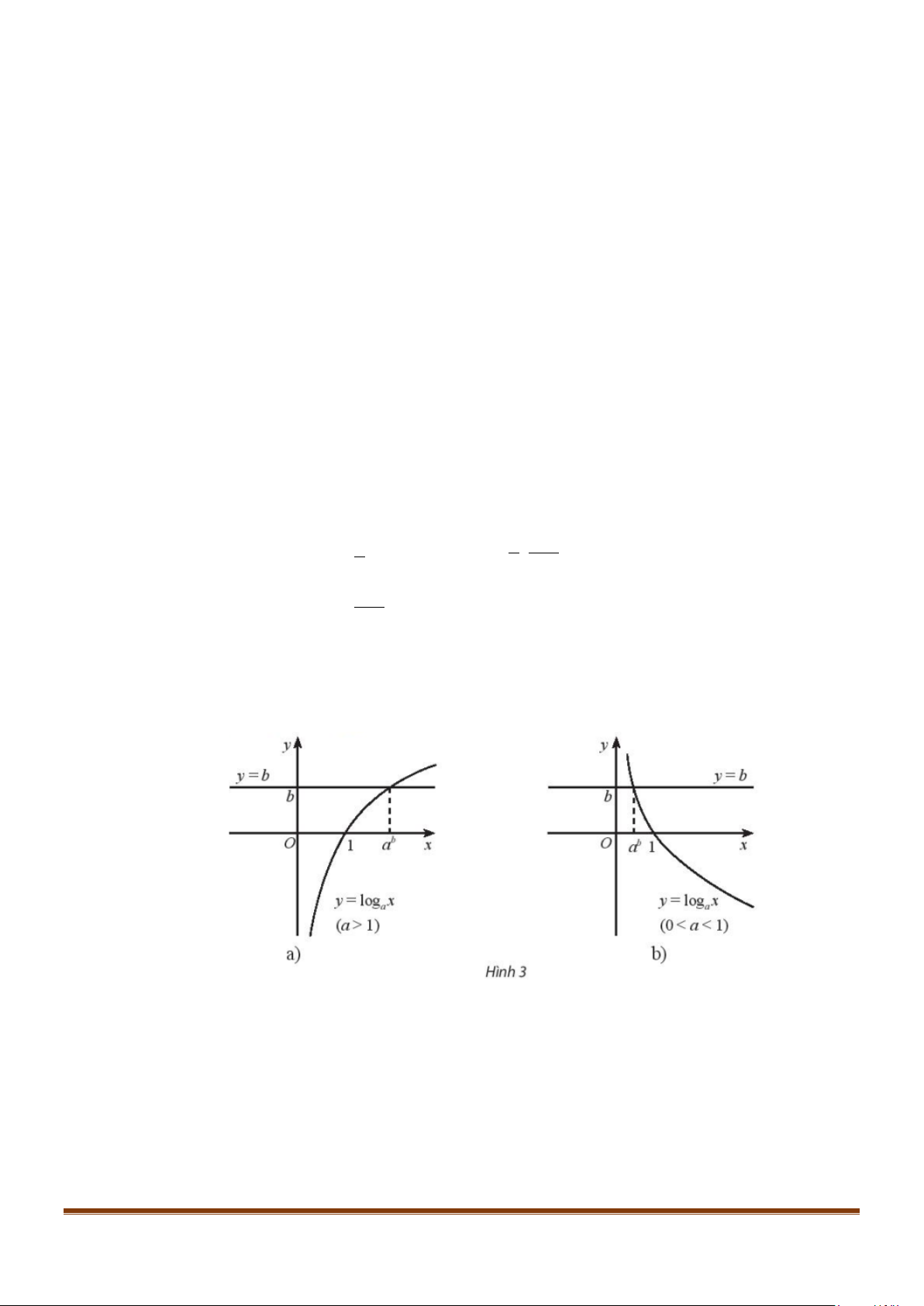
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 5
Sưu tầm và biên soạn
(
)
(
)
22
561
22 22
56 1 75 56 1
.2 2 2 .2 2 2
xx x
xx x x xx x
m mm m
− + +−
−+ − − −+ −
+=+⇔ += +
2 22 2
56 1 561
.2 2 2 .2
xx x xx x
mm
−+ − −+ −
⇔ += +
( )( )
22
56 1
2 12 0
xx x
m
−+ −
⇔ − −=
( )
2
56
2
1
2
1
3
21
2
2
2
xx
x
x
x
x
m
m
−+
−
−
=
=
⇔ ⇔=
=
= ∗
.
( )
22
22
00
1 log 1 log
mm
x mx m
>>
∗⇔ ⇔
−= =−
( )
1
có
4
nghiệmphânbiệt
(
)
⇔∗
có
2
nghiệmphânbiệtkhác
2
và
3
.
(
)
2
2
2
0
0
2
1 log 0
11
1
0; 2 \ ;
1 log 4
8 256
8
1
1 log 9
256
m
m
m
m
m
m
m
m
m
>
>
<
−>
⇔ ⇔ ⇔∈
≠
−≠
−≠
≠
.
2. PHƯƠNG TRÌNH LÔGARIT
Phương trình cơ bản có dạng:
( )
log 0, 0, 1
a
x bx a a= >>≠
luôn có nghiệm duy nhất
b
xa
=
với mọi
b

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 6
Sưu tầm và biên soạn
Ví dụ:
Câu 16: Giải phương trình sau:
3
log 4x =
.
Lời giải
Điều kiện:
0x >
Ta có:
4
3
log 4 3 81xx x
=⇔= ⇔=
.
Vậy nghiệm của phương trình là
81x =
.
Câu 17: Giải phương trình sau:
( )
2
log 2 2 3x −=
.
Lời giải
Điều kiện:
2 20 1xx
−>⇔>
Ta có:
( )
2
log 2 2 3 2 2 8 2 10 5x x xx− =⇔ −=⇔ = ⇔=
(nhận).
Vậy nghiệm của phương trình là
5x =
.
Câu 18: Giải phương trình sau:
( )
2
4
log 5 10 2xx++ =
.
Lời giải
Vì
2
2
5 15
5 10 0,
24
xx x x
+ + = + + > ∀∈
nên tập xác định
D
.
Ta có:
( )
222
4
1
log 5 10 2 5 10 16 5 6 0
6
x
xx xx xx
x
=
++ =⇔++=⇔+−=⇔
= −
.
Vậy nghiệm của phương trình là
1x =
hay
6x = −
.
Câu 19: Giải phương trình sau:
(
)
2
log 1 2x −=
.
Lời giải
Điều kiện:
( )
2
10 1xx
− >⇔≠
Ta có:
( ) ( )
22
1 10 11
log 1 2 1 100 1 10
1 10 9
xx
xx x
xx
−= =
−=⇔−= ⇔−=⇔ ⇔
−=− =−
(nhận).
Vậy nghiệm của phương trình là
11x =
hay
9x = −
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 7
Sưu tầm và biên soạn
Câu 20: Giải phương trình sau:
2
5
log 3 1 1xx− +=
.
Lời giải
Điều kiện:
2
35
2
3 10
35
2
x
xx
x
−
<
− +> ⇔
+
>
.
Pt
22 2
3 1 5 3 1 25 3 24 0
xx xx xx⇔ −+=⇔−+= ⇔−−=
3 105
2
3 105
2
x
x
−
=
⇔
+
=
(nhận)
Vậy nghiệm của phương trình là
3 105
2
x
−
=
hay
3 105
2
x
+
=
.
Câu 21: Giải phương trình sau:
(
)
( )
2
22
log 1 1 log 2xx x x
−++ + = +
.
Lời giải
Điều kiện:
2
2
10
10
1
1
2
1 10
20
xx
x
x
x
x
xx x
x
−+≥
+≥
≥−
⇔ ⇔ ≥−
>−
−++ +>
+>
( )
1
.
(
)
( )
2
22
log 1 1 log 2
xx x x
−++ + = +
2
1 12xx x x⇔ −++ += +
( )
(
)
2 22
1 12 1 1 4 4xx x xx x x x⇔ − ++ ++ − + + = + +
33
2 14 2 12 1xx xx⇔ += +⇔ += +
3 2 32
1
2
11
0
0
22
2 22
2 22
14 4 1 4 4 0
2 22
x
x
xx
x
x
x
x xx xxx
x
≥−
=
≥− ≥−
=
⇔ ⇔ ⇔⇔
= +
= +
+= + + − − =
= −
(thỏa
( )
1
).
Vậy nghiệm của phương trình là
0x =
hay
2 22x = +
.
Câu 22: Giải phương trình sau:
( ) ( )
22
log 5 log 2 3xx−+ +=
.
Lời giải
Điều kiện:
50 5
5
20 2
xx
x
xx
−> >
⇔ ⇔>
+ > >−

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 8
Sưu tầm và biên soạn
Ta có:
(
) ( ) ( )( ) ( )( )
22 2
log 5 log 2 3 log 5 2 3 5 2 8x x xx xx−+ +=⇔ − +=⇔− +=
2
3
3 18 0
6
x
xx
x
= −
⇔−−=⇔
=
.
Kết hợp với điều kiện, ta được nghiệm của phương trình là
6
x
=
.
Câu 23: Giải phương trình:
( )
2
25 5 3
log 4 5 log log 27xx++ =
.
Lời giải
Điều kiện:
0.x >
Phương trình đã cho trở thành:
(
)
55
log 4 5 log 3
xx++ =
2
5
4 5 125 0
25
4
x
xx
x
=
⇔ +− =⇔
= −
.
Câu 24: Giải phương trình:
234 20
log log log logxxx x++=
Lời giải
Điều kiện:
0.x >
Phương trình đã cho tương đương với phương trình:
22 2
2
22 2
log log log
log
log 3 log 4 log 20
xx x
x ++=
22
222
11 1
log 1 0 log 0 1
log 3 log 4 log 20
x xx
⇔ + + − =⇔ =⇔=
Vậy phương trình đã cho có nghiệm
1.x =
Câu 25: Tìm tập nghiệm S của phương trình
33
log (2 1) log ( 1) 1xx+− −=
.
Lời giải
+ Ta có: Điều kiện xác định
2 10
10
x
x
+>
−>
1x⇔>
.
+
33
log (2 1) log ( 1) 1xx+− −=
3
21
log 1
1
x
x
+
⇔=
−
33
21
log log 3
1
x
x
+
⇔=
−
21 21 4
3 3 0 0 4.
11 1
xx x
x
xx x
+ + −+
⇔ =⇔ −=⇔ =⇔ =
−− −
Thỏamãnđiềukiệnxácđịnh.
Câu 26: Gọi
12
,xx
là nghiệm của phương trình
16
log 2 log 0
x
x−=
. Tính
12
.
xx
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 9
Sưu tầm và biên soạn
Điều kiện:
01x<≠
.
16
log 2 log 0
x
x−=
4
2
2
2
11
log 2 log 0 lo
g 0
log 4
x
xx
x
⇔− =⇔ − =
1
2
2
2
2
2
4
4
log 2
(log ) 4
1
1
log 2
4
4
x
x
x
x
x
x
x
=
=
=
⇔ =⇔ ⇔⇒
= −
=
=
(nhận).
Vậy tích
12
1
. 4. 1
4
xx= =
.
Câu 27: Tổng tất cả các nghiệm thực của phương trình
22
log .log (32 ) 4 0xx+=
bằng
Lời giải
Điều kiện xác định:
0x >
.
Khi đó
22
log .log (32 ) 4 0xx+=
22
log .(log 5) 4 0xx⇔ + +=
2
22
log 5.log 4 0xx⇔ + +=
2
2
1
log 1
2
1
log 4
16
x
x
x
x
=
= −
⇔⇔
= −
=
.
Do đó tổng tất cả các nghiệm của phương trình đã cho bằng .
Câu 28: Cho phương trình
2
31
3
3
log 2log 2log 3 0x xx− − −=
có hai nghiệm phân biệt là
1
x
,
2
x
. Tính giá
trị của biểu thức
3 1 27 2
log logP xx+=
biết
12
x x<
.
Lời giải
Điều kiện
0x >
.
2
31
3
3
log 2log 2log 3 0x xx− − −=
2
333
log 4log 2log 3 0xxx⇔ − + −=
2
33
log 2log 3 0xx⇔ − −=
3
3
1
log 1
3
log 3
27
x
x
x
x
= −
=
⇔⇔
=
=
.
Do
12
xx<
nên
1
1
3
x =
và
2
27x =
.
Vậy
3 1 27 2 3 27
1
log log log log 27 0
3
xxP = =+ +=
.
Câu 29: Tổng tất cả các nghiệm của phương trình:
( ) ( ) ( )
8
93
3
11
log 3 log 1 log 4
24
xxx++ − =
Lời giải
9
16

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 10
Sưu tầm và biên soạn
Điều kiện:
1
0
x
x
≠
>
.
Ta có:
( )
(
)
(
)
8
93
3
11
log 3 log 1 log 4
24
xxx
++ − =
( )
( )
3 33
log 3 log 1 log 4xx x⇔ + + −=
( )
( )
33
log 3 . 1 log 4xx x⇔ + − =
(
)
3. 1 4
xx x
⇔ + −=
( )
1
.
+ Nếu
01x<<
thì phương trình
( )
1
trở thành
( ) ( )
( )
( )
2
3 23
3.1 4 6 3 0
3 23
x tm
x xx xx
xl
=−+
+ − = ⇔− − + = ⇔
=−−
.
+ Nếu
1x >
thì phương trình
( )
1
trở thành
( ) ( )
( )
( )
2
3
3. 1 4 2 3 0
1
x tm
x x xx x
xl
=
+ − = ⇔ − −=⇔
= −
.
Phương trình đã cho có tập nghiệm là
{
}
3 2 3;3S =−+
.
Vậy tổng tất cả các nghiệm của phương trình là
23
.
Câu 30: Giải phương trình:
( )
2
3
3
2
log 2 log 0
33
x
x
xx
−+ =
−+
.
Lời giải
Điều kiện:
0 2.x<≠
Phương trình cho tương đương với phương trình:
( )
2
2
33
2
log 2 log 0
33
x
x
xx
−+ =
−+
( )
2
2
3
2
log 2 . 0
33
x
x
xx
⇔− =
−+
( )
2
2
2
2. 1
33
x
x
xx
⇔− =
−+
32
1
2 11 18 9 0 3
3
2
x
xxx x
x
=
⇔ − + −=⇔ =
=
.
Câu 31: Giải phương trình:
( )
( )
2
21
2
log 8 log 1 1 2 0x xx− + ++ − −=
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 11
Sưu tầm và biên soạn
Điều kiện:
1 1.x
−≤ ≤
Phương trình đã cho tương đương với phương trình:
( )
(
)
2
22
log 8 2 log 1 1
x xx
− =+ ++ −
( )
2
8 41 1
x xx⇔− = ++ −
( )
∗
Đặt
11txx= ++ −
, phươngtrình
( )
∗
trởthành:
( )
( )
2
2
2 48 0 2t tt t− + + = ⇔=
.
1 12 0xx x++ −=⇔=
.
3. BẤT PHƯƠNG TRÌNH MŨ
CHÚ Ý:
Nếu
1a >
,
0b >
thì
( ) ( )
() ()f x gx
a a f x gx>⇔ >
( )
()
log
fx
a
a b fx b>⇔ >
Nếu
01a<<
,
0b >
thì
( ) ( )
() ()f x gx
a a f x gx>⇔ <
( )
()
log
fx
a
a b fx b>⇔ <

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 12
Sưu tầm và biên soạn
Lưu ý:
0b ≤
thì
(x)
f
ab
>
đúng với mọi
x
thỏa mãn điều kiện xác định của
( )
fx
, còn
(x)f
ab
≤
vô nghiệm.
4. BẤT PHƯƠNG TRÌNH LOGARIT
CHÚ Ý:
Nếu
1a
>
thì
( ) ( )
( )
( ) ( )
0
log log
aa
gx
f x gx
f x gx
>
>⇔
>
Nếu
01a<<
thì
( ) (
)
(
)
( ) ( )
0
log log
aa
fx
f x gx
f x gx
>
>⇔
<
Ví dụ:
Câu 32: Giải bất phương trình
2
4
4
3
1
x −
≥
.
Lời giải
Bất phương trình
2
4
2
2
14
4
.
3
0
2
x
x
x
x
−
≤−
≥⇔ −≥ ⇔
≥
Vậy tập nghiệm của bất phương trình đã cho là
(
] [
)
; 2 2;S = −∞ − ∪ +∞
.
Câu 33: Có bao nhiêu số nguyên
10x ≤
là nghiệm của bất phương trình
2
1
3
3
x
x
+
−
≥
?
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 13
Sưu tầm và biên soạn
22
2
00
1 11
3 2 20 2 2
3 33
2
2
1
x xx
x
xx
x xx x x
x
xx
x
++
−
≥≥
> ⇔ ≥ ⇔ +≤⇔ +≥ ⇔ ≥−⇔≥
≥
+≤
≤−
Theo giả thiết số nguyên
10x ≤
[
]
2;10x⇒∈
.
Vậy có
9
số nguyên
x
thỏa mãn yêu cầu bài toán.
Câu 34: Tìm số nghiệm nguyên của bất phương trình
( )
11
22
log 3 log 4−≥x
.
Lời giải
Bất phương trình
( )
11
22
log 3 log 4−≥x
34
30
−≤
⇔
−>
x
x
7
37
3
x
x
x
≤
⇔ ⇔<≤
>
.
Vì
37
∈
<≤
x
x
{ }
4;5;6;7
⇒∈x
.
Vậy bất phương trình đã cho có tất cả
4
nghiệm nguyên.
Câu 35: Giải bất phương trình:
( ) ( )
log 3 2 log 1xx−≥ +
.
Lời giải
( ) ( )
1
10
2
log 3 2 log 1 1
2
32 1
3
3
x
x
xx x
xx
x
>−
+>
− ≥ + ⇔ ⇔ ⇔− < ≤
− ≥+
≤
.
Vậy tập nghiệm của bất phương trình đã cho là
2
1;
3
S
= −
.
Câu 36: Giải bất phương trình
( )
2
1
2
log 5 7 0xx−+>
.
Lời giải
( )
22
1
2
log 5700 571xx xx−+>⇔<−+<
.
2
2
5 60
5 70
xx
xx
− +<
⇔
− +>
23x⇔<<
.
Vậy tập nghiệm của bất phương trình đã cho là
( )
2;3S =
.
Câu 37: Bất phương trình
( ) ( )
33
log 3 1 log 7xx+< +
có bao nhiêu nghiệm nguyên?
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 14
Sưu tầm và biên soạn
Ta có:
( ) ( )
33
31 7
log 3 1 log 7
3 10
xx
xx
x
+< +
+< + ⇔
+>
3
1
3
x
x
<
⇔
>−
1
3
3
x⇔− < <
.
Vì
x
là số nguyên nên
{ }
0;1; 2x ∈
. Vậy bất phương trình có 3 nghiệm nguyên.
Câu 38: Tìm tập nghiệm
S
của bất phương trình
( )
0,5 0,5
log 1 log 2xx+>
Lời giải
Điều kiện:
10
0
20
x
x
x
+>
⇔>
>
.
Ta có:
(
)
0,5 0,5
log 1 log 2 1 2 1x xx xx+ > ⇔ +< ⇔ >
, kết hợp điều kiện ta được
1x
>
.
Vậy tập nghiệm của bất phương trình là
( )
1;S = +∞
.
Câu 39: Tìm tập nghiệm
S
của bất phương trình
3
log 3 log 3
xx
<
Lời giải
Điều kiện:
0
1
3
x
x
x
>
≠
≠
.
Ta có:
3
log 3 log 3
xx
<
3
3
11
log
log
3
x
x
⇔<
33
11
0
log log 1xx
⇔− <
−
( )
33
1
0
log . log 1xx
−
⇔<
−
( )
3
3
3
33
3
3
3
log 0
log 1 0
log 0
log . log 1 0
log 1
log 0
log 1 0
x
x
x
xx
x
x
x
<
−<
<
⇔ − >⇔ ⇔
>
>
−>
1
3
x
x
<
⇔
>
,
kết hợp điều kiện ta được
01
x
<<
hoặc
3x >
.
Vậy tập nghiệm của bất phương trình là
( ) ( )
0; 1 3;S = ∪ +∞
.
Câu 40: Có bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
( ) ( )
22
55
log 1 1 log 4x mx x m+ +≥ + +
nghiệm đúng với mọi
x ∈
?
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 15
Sưu tầm và biên soạn
Bất phương trình nghiệm đúng với mọi
( )
2
22
40
,
51 4
mx x m
xx
x mx x m
+ +>
∈ ⇔ ∀∈
+≥ + +
(dễ thấy
m=0 không thỏa mãn hệ)
(
)
(
)
(
)
2
1
2
2
0
16 4 0
50
16 4 5 0
m
m
m
m
>
∆= − <
⇔
−>
∆= − − ≤
0
22
5
37
m
mm
m
mm
>
<− ∨ >
⇔
<
≤∨ ≥
23m⇔< ≤
.
Do
m ∈
nên
3m =
.
Vậy có 1 giá trị nguyên của
m
thoả mãn.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 56
Sưu tầm và biên soạn
BÀI 4: PHƯƠNG TRÌNH – BẤT PHƯƠNG TRÌNH – MŨ – LOGARIT
BÀI TẬP TRẮC NGHIỆM TRÍCH TỪ ĐỀ THAM KHẢO VÀ ĐỀ CHÍNH THỨC
CỦA BỘ GIÁO DỤC TỪ NĂM 2017 ĐẾN NAY
Câu 1: (MĐ 101-2022) Nghiệm của phương trình
21 2
33
xx+−
=
là
A.
1
3
x =
. B.
0
. C.
1x = −
. D.
1x =
.
Câu 2: (MĐ 102-2022) Nghiệm của phương trình
21 2
33
xx+−
=
là
A.
1
3
x =
. B.
0x =
. C.
1x = −
. D.
1x =
.
Câu 3: (MĐ 103-2022) Số nghiệm thực của phương trình
2
1
24
x +
=
là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 4: (MĐ 104-2022) Số nghiệm thực của phương trình
2
1
24
x +
=
là
A.
1
. B.
2
. C.
0
. D.
3
.
Câu 5: (MĐ 103-2022) Nghiệm của phương trình
( )
1
2
log 2 1 0x −=
là
A.
3
4
x =
. B.
1x =
. C.
1
2
x =
. D.
2
3
x =
Câu 6: (MĐ 104-2022) Nghiệm của phương trình
( )
1
2
log 2 1 0x −=
là
A.
1x =
. B.
3
4
x =
. C.
2
3
x =
. D.
1
2
x =
.
Câu 7: (TK 2020-2021) Nghiệm của phương trình
24
5 25
x−
=
là:
A.
3.x =
B.
2.x =
C.
1.x =
D.
1.x = −
Câu 8: (TK 2020-2021) Nghiệm của phương trình
( )
2
log 3 3x =
là:
A.
3.x =
B.
2.x =
C.
8
.
3
x =
D.
1
.
2
x =
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 57
Sưu tầm và biên soạn
Câu 9: (MĐ 102 2020-2021 – ĐỢT 1) Nghiệm của phương trình
( )
5
log 3 2x =
là
A.
25x =
. B.
32
3
x =
. C.
32x =
. D.
25
3
x =
.
Câu 10: (MĐ 103 2020-2021 – ĐỢT 1) Nghiệm của phương trình
( )
3
log 2 2x =
là
A.
9
2
x =
. B.
9x =
. C.
4x =
. D.
8x =
.
Câu 11: (MĐ 104 2020-2021 – ĐỢT 1) Nghiệm của phương trình
( )
2
log 5 3x =
là:
A.
8
5
x =
. B.
9
5
x =
. C.
8x =
. D.
9x =
.
Câu 12: Nghiệm của phương trình
53
x
=
là:
A.
3
5x =
. B.
3
5
x =
. C.
3
log 5x =
. D.
5
log 3x =
.
Câu 13: Nghiệm của phương trình
52=
x
là:
A.
2
log 5=x
. B.
5
log 2=x
. C.
2
5
=x
. D.
5
=
x
Câu 14: (MĐ 103 2020-2021 – ĐỢT 2) Nghiệm của phương trình
72
x
là
A.
2
log 7x
. B.
7
log 2x
. C.
2
7
x
. D.
7x
.
Câu 15: (MĐ 104 2020-2021 – ĐỢT 2) Nghiệm của phương trình
73
x
là
A.
3
7
x
. B.
3
7x
. C.
7
log 3x
. D.
3
log 7x
.
Câu 16: (Đề Minh Họa 2020 Lần 1) Nghiệm của phương trình
( )
3
log 2 1 2x −=
là:
A.
3x =
. B.
5x =
. C.
9
2
x =
. D.
7
2
x =
.
Câu 17: (Mã 101 - 2020 Lần 1) Nghiệm của phương trình
( )
3
log 1 2x −=
là
A.
8x =
. B.
9x =
. C.
7x =
. D.
10x =
.
Câu 18: (Mã 102 - 2020 Lần 1) Nghiệm của phương trình là
A. . B. . C. . D. .
Câu 19: (Mã 103 - 2020 Lần 1) Nghiệm của phương trình
( )
2
log 2 3x −=
là:
A.
6x =
. B.
8x =
. C.
11x =
. D.
10x =
.
Câu 20: (Mã 104 - 2020 Lần 1) Nghiệm của phương trình
( )
3
log 2 2x −=
là
A.
11x =
. B.
10x =
. C.
7x =
. D.
8
.
Câu 21: (Mã 102 - 2020 Lần 2) Nghiệm của phương trình
( )
2
log 9 5x +=
là
A.
41x =
. B.
23x =
. C.
1x =
. D.
16x =
.
Câu 22: (Mã 103 - 2020 Lần 2) Nghiệm của phương trình
( )
2
log 6 5x +=
là:
A.
4x =
. B.
19x =
. C.
38x =
. D.
26x =
.
( )
2
log 1 3x −=
10x =
8x =
9x =
7x =

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 58
Sưu tầm và biên soạn
Câu 23: (Mã 104 - 2020 Lần 2) Nghiệm của phương trình
( )
2
log 7 5x +=
là
A.
18x =
. B.
25x =
. C.
39x =
. D.
3x =
.
Câu 24: (Mã 101 - 2020 Lần 2) Nghiệm của phương trình
2
log ( 8) 5x +=
bằng
A.
17x =
. B.
24x
=
. C.
2x =
. D.
40
x
=
.
Câu 25: (Đề Tham Khảo 2019) Tập nghiệm của phương trình
( )
2
2
log 2 1xx
−+ =
là :
A.
{ }
0
B.
{
}
0;1
C.
{ }
1; 0−
D.
{ }
1
Câu 26: (Đề Minh Họa 2017) Giải phương trình
4
log ( 1) 3.
−=x
A.
65=x
B.
80=x
C.
82=x
D.
63=x
Câu 27: (Mã 110 2017) Tìm nghiệm của phương trình
(
)
2
log 1 2x−=
.
A.
5x =
. B.
3x = −
. C.
4x = −
. D.
3x =
.
Câu 28: (Mã 102 2018) Tập nghiệm của phương trình
( )
2
2
log 1 3x −=
là
A.
{
}
10; 10−
B.
{ }
3; 3−
C.
{ }
3−
D.
{ }
3
Câu 29: (Mã 104 2017) Tìm nghiệm của phương trình
( )
2
log 5 4x −=
.
A.
11x =
B.
13
x =
C.
21x =
D.
3x =
Câu 30: (Mã 103 2018) Tập nghiệm của phương trình
2
3
log ( 7) 2
x −=
là
A.
{ }
4
B.
{ }
4−
C.
{ 15; 15}−
D.
{ 4;4}−
Câu 31: (Mã 105 2017) Tìm nghiệm của phương trình
(
)
+=
25
1
log 1
2
x
.
A.
= 6x
B.
= 4x
C.
=
23
2
x
D.
= −6x
Câu 32: (Đề Tham Khảo 2017) Tìm tập nghiệm
S
của phương trình
( ) ( )
22
log 1 log 1 3xx−+ +=
.
A.
{ }
3S =
B.
{
}
10; 10S = −
C.
{
}
3; 3
S = −
D.
{ }
4S =
Câu 33: (Mã 103 - 2019) Nghiệm của phương trình
( ) ( )
22
log 1 1 log 3 1xx+ += −
là
A.
1x =
. B.
2x =
. C.
1x
= −
. D.
3
x =
.
Câu 34: (Mã 105 2017) Tìm tập nghiệm
S
của phương trình
( ) (
)
+− −=
33
log 2 1 log 1 1xx
.
A.
{ }
= 3S
B.
{
}
=
4S
C.
{ }
= 1S
D.
{ }
= −2S
Câu 35: (Mã 101 - 2019) Nghiệm của phương trình
(
) ( )
33
log 1 1 log 4 1xx
+ += +
A.
4x =
. B.
2x =
. C.
3
x =
. D.
3x = −
.
Câu 36: (Mã 104 - 2019) Nghiệm của phương trình
( ) ( )
33
log 2 1 1 log 1xx+=+ −
là
A.
4x =
. B.
2x = −
. C.
1x =
. D.
2x =
.
Câu 37: (Mã 102 -2019) Nghiệm của phương trình
( ) ( )
22
log 1 1 log 1xx+=+ −
là
A.
3x =
. B.
2x =
. C.
1x =
. D.
2x = −
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 59
Sưu tầm và biên soạn
Câu 38: (Mã 110 2017) Tìm tập nghiệm
S
của phương trình
( ) ( )
1
2
2
log 1 log 1 1.xx−+ +=
A.
{ }
3S =
B.
{ }
2 5;2 5
S =−+
C.
{ }
25
S = +
D.
3 13
2
S
+
=
Câu 39: (Đề Tham Khảo 2018) Tổng giá trị tất cả các nghiệm của phương trình
3 9 27 81
2
log .log .log .log
3
xx x x=
bằng
A.
0.
B.
80
.
9
C.
9.
D.
82
.
9
Câu 40: (Mã 110 2017) Tìm tập nghiệm
S
của phương trình
( ) (
)
1
2
2
log 1 log 1 1.xx−+ +=
A.
{
}
3S =
B.
{ }
2 5;2 5S =−+
C.
{ }
25S = +
D.
3 13
2
S
+
=
Câu 41: (Mã 104 2017) Xét các số nguyên dương
a
,
b
sao cho phương trình
2
ln ln 5 0a xb x+ +=
có
hai nghiệm phân biệt
1
x
,
2
x
và phương trình
2
5log log 0xb xa+ +=
có hai nghiệm phân biệt
3
x
,
4
x
thỏa mãn
12 34
xx xx
>
. Tính giá trị nhỏ nhất
min
S
của
23S ab= +
.
A.
min
17S =
B.
min
30
S
=
C.
min
25S =
D.
min
33S =
Câu 42: (Đề Minh Họa 2020 Lần 1) Cho phương trình
( ) ( )
2
22
log 2 2 log 2 0x m xm− + + −=
(
m
là tham
số thực). Tập hợp tất cả các giá trị của
m
để phương trình đã cho có hai nghiệm phân biệt thuộc
đoạn
[
]
1; 2
là
A.
( )
1; 2
. B.
[ ]
1; 2
. C.
[
)
1; 2
. D.
[
)
2; +∞
.
Câu 43: (Mã 102 2019) Cho phương trình
( )
2
93 3
log log 6 1 logxx m− −=−
(
m
là tham số thực). Có tất
cả bao nhiêu giá trị nguyên của
m
để phương trình đã cho có nghiệm?
A.
7
. B.
6
. C.
5
. D. Vô số.
Câu 44: (MĐ 101-2022) Tập nghiệm của bất phương trình
( )
5
log 1 2x +>
là:
A.
( )
9 ;+∞
. B.
( )
25 ; .+∞
C.
( )
31 ; +∞
. D.
( )
24 ;+∞
.
Câu 45: (MĐ 102-2022) Tập nghiệm của bất phương trình
( )
5
log 1 2x +>
là
A.
( )
24; +∞
. B.
( )
9; +∞
. C.
(
)
25; +∞
. D.
( )
31; +∞
.
Câu 46: (MĐ 101-2022) Có bao nhiêu số nguyên dương
a
sao cho ứng với mỗi
a
có đúng ba số nguyên
b
thỏa mãn
( )( )
3 3 .2 18 0
bb
a− −<
?
A.
72.
B.
73⋅
C.
71⋅
D.
74⋅

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 60
Sưu tầm và biên soạn
Câu 47: (MĐ 102-2022) Có bao nhiêu số nguyên dương
a
sao cho ứng với mỗi
a
có đúng hai số nguyên
b
thỏa mãn
( )( )
5 1 .2 5 0
bb
a− −<
A.
20
. B.
21
. C.
22
. D.
19
.
Câu 48: (MĐ 103-2022) Có bao nhiêu số nguyên dương
a
sao cho ứng với mỗi
a
có đúng hai số nguyên
b
thỏa mãn
( )( )
4 1 .3 10 0?
bb
a− −<
A.
182
. B.
179
. C.
180
. D.
181
.
Câu 49: (MĐ 104-2022) Có bao nhiêu số nguyên dương
a
sao cho ứng với mỗi
a
có đúng hai số nguyên
b
thoả mãn
( )( )
3 3 .2 16 0?
bb
a− −<
A.
34
. B.
32
. C.
31
. D.
33
.
Câu 50: (2020-2021 – ĐỢT 1) Tập nghiệm của bất phương trình
32
x
<
là
A.
( )
3
;log 2−∞
. B.
( )
3
log 2; +∞
. C.
( )
2
;log 3−∞
. D.
( )
2
log 3; +∞
.
Câu 51: (2020-2021 – ĐỢT 1) Tập nghiệm của bất phương trình
25
x
>
là
A.
2
( ; log 5)−∞
. B.
5
(log 2; )+∞
. C.
5
( ;log 2)−∞
. D.
2
(log 5; )+∞
Câu 52: (2020-2021 – ĐỢT 1) Tập nghiệm của bất phương trình
( )
2
log 3 5x >
là
A.
32
0;
3
. B.
32
;
3
+∞
. C.
25
0;
3
. D.
25
;
3
+∞
.
Câu 53: (2020-2021 – ĐỢT 2) Tập nghiệm của bất phương trình
( )
2
log 3 3x >
là
A.
( )
3; +∞
. B.
8
;
3
+∞
. C.
8
0;
3
. D.
( )
0;3
.
Câu 54: (2020-2021 – ĐỢT 2) Tập nghiệm của bất phương trình
( )
3
log 2 4x >
A.
( )
0;32
. B.
81
0;
2
. C.
( )
32; +∞
. D.
81
;
2
+∞
.
Câu 55: (Đề Minh Họa 2020 Lần 1) Tập nghiệm của bất phương trình
2
19
55
x xx− −−
≥
là
A.
[ ]
2; 4−
. B.
[ ]
4; 2−
.
C.
(
] [
)
; 2 4;−∞ − ∪ +∞
. D.
(
] [
)
; 4 2;−∞ − ∪ +∞
.
Câu 56: (Đề Tham Khảo 2020 Lần 2) Tập nghiệm của bất phương trình
9 2.3 3 0
xx
+ −>
là
A.
[
)
0;+∞
. B.
( )
0;+∞
. C.
( )
1;+∞
. D.
[
)
1;+∞
.
Vậy tập nghiệm của bất phương trình đã cho là
( )
0;+∞
.
Câu 57: (Mã 101 - 2020 Lần 1) Tập nghiệm của bất phương trình
2
13
3 27
x −
<
là
A.
( )
4;+∞
. B.
( )
4;4−
. C.
( )
;4−∞
. D.
( )
0;4
.
Câu 58: (Mã 102 - 2020 Lần 1) Tập nghiệm của bất phương trình
là
A. . B. . C. . D. .
2
23
39
x −
<
( )
5;5−
( )
;5−∞
( )
5; +∞
( )
0;5

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 61
Sưu tầm và biên soạn
Câu 59: (Mã 103 - 2020 Lần 1) Tập nghiệm của bất phương trình
2
7
24
x
−
<
là
A.
( 3; 3)−
. B.
(0;3)
. C.
( ;3)−∞
. D.
(3; )+∞
.
Câu 60: (Mã 104 - 2020 Lần 1) Tập nghiệm của bất phương trình
2
1
28
x
−
<
là
A.
( )
0; 2
. B.
( )
;2−∞
. C.
( )
2; 2−
. D.
( )
2; +∞
.
Câu 61: (Đề Tham Khảo 2018) Tập nghiệm của bất phương trình
26
22
xx
là:
A.
;6
B.
0; 64
C.
6;
D.
0;6
Câu 62: (Đề Tham Khảo 2019) Tập nghiệm của bất phương trình
2
2
3 27
xx−
<
là
A.
( )
3; +∞
B.
( )
1; 3−
C.
( ) ( )
; 1 3;−∞ − ∪ +∞
D.
( )
;1−∞ −
Câu 63: (Đề Tham Khảo 2017) Tìm tập nghiệm
S
của bất phương trình
1
1
50
5
x+
−>
.
A.
( )
;2S = −∞ −
. B.
( )
1;S = +∞
. C.
( )
1;S = − +∞
. D.
( )
2;S
= − +∞
.
Câu 64: (Đề Tham Khảo 2019) Tập nghiệm của bất phương trình
2
2
3 27
xx−
<
là
A.
( )
;1−∞ −
B.
( )
3; +∞
C.
(
)
1; 3−
D.
(
) ( )
; 1 3;
−∞ − ∪ +∞
Câu 65: (Đề Tham Khảo 2020 Lần 2) Tập nghiệm của bất phương trình
log 1
x
≥
là
A.
( )
10; +∞
. B.
( )
0; +∞
. C.
[
)
10; +∞
. D.
( )
;10−∞
.
Câu 66: (Mã 102 - 2020 Lần 2) Tập nghiệm của bất phương trình
( )
2
3
log 13 2x−≥
là
A.
(
]
[
)
; 2 2:
−∞ − ∪ +∞
. B.
(
]
;2−∞
.
C.
(
]
0; 2
. D.
[ ]
2; 2−
.
Câu 67: (Mã 103 - 2020 Lần 2) Tập nghiệm của bất phương trình
( )
2
3
log 36 3x−≥
là
A.
(
] [
)
; 3 3;−∞ − ∪ +∞
. B.
(
]
;3−∞
. C.
[ ]
3; 3−
. D.
(
]
0;3
.
Câu 68: (Mã 101 - 2020 Lần 2) Tập nghiệm của bất phương trình
( )
2
3
log 18 2x−≥
là
A.
(
]
;3−∞
. B.
(
]
0;3
.
C.
[ ]
3;3−
. D.
(
]
[
)
; 3 3;−∞ − ∪ + ∞
.
Câu 69: (Mã 104 - 2020 Lần 2) Tập nghiệm của bất phương trình
( )
2
3
log 31 3x−≥
là
A.
(
]
;2−∞
. B.
[ ]
2; 2−
. C.
(
] [
)
; 2 2;−∞ − ∪ +∞
. D.
(
]
0; 2
.
Câu 70: (Đề Minh Họa 2017) Giải bất phương trình
( )
2
log 3 1 3x −>
.
A.
3x >
B.
1
3
3
x<<
C.
3x <
D.
10
3
x >
Câu 71: (Mã 123 2017) Tìm tập nghiệm
S
của bất phương trình
− +≥
2
22
log 5log 4 0xx
.
A.
= −∞ ∪ +∞( ; 1] [4 ;) S
B.
= [2 ;16]S
C.
= ∪ +∞(0 ; 2] [16
;) S
D.
−∞ ∪ +∞
( ; 2] [ 6 1; )

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 62
Sưu tầm và biên soạn
Câu 72: Có bao nhiêu số nguyên
x
thỏa mãn
( )
( )
2
3
3 9 . log 25 3 0?
xx
x− + −≤
A.
24.
B. Vô số. C.
26.
D.
25.
Câu 73: (MĐ 102 2020-2021 – ĐỢT 1) Có bao nhiêu số nguyên
x
thỏa mãn
(
)
( )
2
2
3 9 log 30 5 0
xx
x− + −≤
A.
30
. B. Vô số. C.
31
. D.
29
.
Câu 74: (MĐ 103 2020-2021 – ĐỢT 1) Có bao nhiêu số nguyên
x
thoả mãn
( )
( )
2
2
2 4 log 14 4 0
xx
x− + −≤
?
A.
14
. B.
13
. C. Vô số. D.
15
.
Câu 75: (MĐ 104 2020-2021 – ĐỢT 1) Có bao nhiêu số nguyên
x
thỏa mãn
(
)
( )
2
3
2 4 log 25 3 0
xx
x− + −≤
?
A.
24
. B. Vô số. C.
25
. D.
26
.
Câu 76: Có bao nhiêu số nguyên
x
thỏa mãn
( )
( )
( )
21
22
log 1 log 31 32 2 0
x
xx
−
+− + − ≥
?
A. 27. B. Vô số. C. 26. D. 28.
Câu 77: Có bao nhiêu số nguyên
x
thoả mãn
( )
( )
( )
21
33
log 1 log 21 . 16 2 0?
x
xx
−
+− + − ≥
A.
17
. B.
18
. C.
16
. D. Vô số.
Câu 78: (MĐ 103 2020-2021 – ĐỢT 2) Có bao nhiêu số nguyên
x
thỏa mãn
21
22
log ( 1) log ( 21) (16 2 ) 0?
x
xx
−
+− + − ≥
A. Vô số. B.
17
. C.
16
. D.
18
.
Câu 79: (MĐ 104 2020-2021 – ĐỢT 2) Có bao nhiêu số nguyên
x
thỏa mãn
( ) ( )
21
33
log 1 log ( 31) 32 2 0?
x
xx
−
+− + − ≥
A.
27
. B.
26
. C. Vô số. D.
28
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 1
Sưu tầm và biên soạn
BÀI 4: PHƯƠNG TRÌNH – BẤT PHƯƠNG TRÌNH – MŨ – LOGARIT
BÀI TẬP TRẮC NGHIỆM TRÍCH TỪ ĐỀ THAM KHẢO VÀ ĐỀ CHÍNH THỨC
CỦA BỘ GIÁO DỤC TỪ NĂM 2017 ĐẾN NAY
Câu 1: (MĐ 101-2022) Nghiệm của phương trình
21 2
33
xx+−
=
là
A.
1
3
x =
. B.
0
. C.
1x = −
. D.
1x =
.
Lời giải
Chọn A
Ta có:
21 2
1
3 3 2 12 3 1
3
xx
x xx x
+−
= ⇔+=−⇔=⇔=
.
Câu 2: (MĐ 102-2022) Nghiệm của phương trình
21 2
33
xx+−
=
là
A.
1
3
x
=
. B.
0x =
. C.
1x
= −
. D.
1x =
.
Lời giải
Chọn A
Ta có:
21 2
1
3 3 2 12
3
xx
x xx
+−
= ⇔ += − ⇔ =
.
Câu 3: (MĐ 103-2022) Số nghiệm thực của phương trình
2
1
24
x +
=
là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn B
Ta có
2
12 2
1
2 4 12 1
1.
x
x
xx
x
+
=
= ⇔ += ⇔ =⇔
= −
Vậy số nghiệm thực của phương trình
2
1
24
x +
=
là
2
.
Câu 4: (MĐ 104-2022) Số nghiệm thực của phương trình
2
1
24
x +
=
là
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải
Chọn B
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 2
Sưu tầm và biên soạn
Ta có:
22
1 12 2
2422 12 1
xx
xx
++
= ⇔ = ⇔ += ⇔ =±
.
Câu 5: (MĐ 103-2022) Nghiệm của phương trình
( )
1
2
log 2 1 0x −=
là
A.
3
4
x =
. B.
1x =
. C.
1
2
x =
. D.
2
3
x =
Lời giải
Chọn B
Điều kiện:
( )
1
2 10 *
2
xx−> ⇔ >
.
Với điều kiện
( )
*
phương trình tương đương:
( )
1
2
log210 211 21 1x x xx− = ⇔ −=⇔ =⇔ =
(thỏa mãn).
Câu 6: (MĐ 104-2022) Nghiệm của phương trình
( )
1
2
log 2 1 0x −=
là
A.
1x =
. B.
3
4
x =
. C.
2
3
x =
. D.
1
2
x =
.
Lời giải
Chọn A
Ta có:
( )
1
2
log210 211 1x xx− = ⇔ −=⇔ =
.
Câu 7: (TK 2020-2021) Nghiệm của phương trình
24
5 25
x−
=
là:
A.
3.x =
B.
2.x =
C.
1.x =
D.
1.x = −
Lời giải
Ta có
24 24 2
5 25 5 5 2 4 2 3.
xx
xx
Câu 8: (TK 2020-2021) Nghiệm của phương trình
( )
2
log 3 3x =
là:
A.
3.x =
B.
2.x =
C.
8
.
3
x =
D.
1
.
2
x
=
Lời giải
Ta có
3
2
8
log (3 ) 3 3 2 .
3
x xx
Câu 9: (MĐ 102 2020-2021 – ĐỢT 1) Nghiệm của phương trình
( )
5
log 3 2x =
là
A.
25x =
. B.
32
3
x =
. C.
32x =
. D.
25
3
x =
.
Lời giải
Ta có
( )
5
2
30
25
log 3 2
3
35
x
xx
x
>
=⇔ ⇔=
=
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 3
Sưu tầm và biên soạn
Câu 10: (MĐ 103 2020-2021 – ĐỢT 1) Nghiệm của phương trình
( )
3
log 2 2
x =
là
A.
9
2
x =
. B.
9x =
. C.
4x =
. D.
8
x =
.
Lời giải
Điều kiện:
0
x >
. Với điều kiện phương trình đã cho tương đương
2
239
x = =
9
2
x
⇔=
.
Câu 11: (MĐ 104 2020-2021 – ĐỢT 1) Nghiệm của phương trình
( )
2
log 5 3x =
là:
A.
8
5
x =
. B.
9
5
x =
. C.
8x =
. D.
9x =
.
Lời giải
Điều kiện
0x >
( )
2
log 5 3x =
3
52x⇔=
58x⇔=
8
5
x
⇔=
(nhận).
Câu 12: Nghiệm của phương trình
53
x
=
là:
A.
3
5x
=
. B.
3
5
x =
. C.
3
log 5x =
. D.
5
log 3x =
.
Lời giải
Ta có
5
5 3 log 3
x
x=⇔=
.
Vậy nghiệm của phương trình
53
x
=
là
5
log 3x =
.
Câu 13: Nghiệm của phương trình
52=
x
là:
A.
2
log 5=x
. B.
5
log 2=
x
. C.
2
5
=x
. D.
5=
x
Lời giải
Ta có:
5
5 2 log 2=⇔=
x
x
. Chọn B
Câu 14: (MĐ 103 2020-2021 – ĐỢT 2) Nghiệm của phương trình
72
x
là
A.
2
log 7x
. B.
7
log 2x
. C.
2
7
x
. D.
7x
.
Lời giải
Ta có
7
7 2 log 2
x
x
.
Câu 15: (MĐ 104 2020-2021 – ĐỢT 2) Nghiệm của phương trình
73
x
là
A.
3
7
x
. B.
3
7x
. C.
7
log 3x
. D.
3
log 7x
.
Lời giải
Ta có
7
7 3 log 3
x
x
Câu 16: (Đề Minh Họa 2020 Lần 1) Nghiệm của phương trình
( )
3
log 2 1 2x −=
là:

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 4
Sưu tầm và biên soạn
A.
3x =
. B.
5x =
. C.
9
2
x =
. D.
7
2
x =
.
Lời giải
Chọn B
Điều kiện:
1
2 10
2
xx−> ⇔ >
Ta có
( )
3
2
1
log 2 1 2
2
2 13
x
x
x
>
−=⇔
−=
1
2
5
x
x
>
⇔
=
5x⇔=
.
Vậy phương trình có nghiệm
5x =
.
Câu 17: (Mã 101 - 2020 Lần 1) Nghiệm của phương trình
( )
3
log 1 2x −=
là
A.
8x =
. B.
9x =
. C.
7x =
. D.
10x =
.
Lời giải
Chọn D
TXĐ:
( )
1;D = +∞
( )
2
3
log 1 2 1 3 10xxx− = ⇔ −= ⇔ =
Câu 18: (Mã 102 - 2020 Lần 1) Nghiệm của phương trình là
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có .
Câu 19: (Mã 103 - 2020 Lần 1) Nghiệm của phương trình
( )
2
log 2 3x −=
là:
A.
6x =
. B.
8x =
. C.
11x =
. D.
10x =
.
Lời giải
Chọn D
Điều kiện:
20 2xx−>⇔>
.
( )
2
log 2 3 2 8 10x xx− =⇔−=⇔=
(thỏa).
Vậy phương trình có nghiệm
10x =
.
Câu 20: (Mã 104 - 2020 Lần 1) Nghiệm của phương trình
( )
3
log 2 2x −=
là
A.
11x =
. B.
10x =
. C.
7x =
. D.
8
.
Lời giải
Chọn A
Điều kiện:
2x >
Phương trình tương đương với
2
2 3 11xx−= ⇔=
Câu 21: (Mã 102 - 2020 Lần 2) Nghiệm của phương trình
( )
2
log 9 5x +=
là
( )
2
log 1 3x −=
10x =
8x =
9x =
7x =
( )
2
log 1 3x −=
⇔
3
10
12
x
x
−>
−=
⇔
1
9
x
x
>
=
⇔
9x =

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 5
Sưu tầm và biên soạn
A.
41
x
=
. B.
23x =
. C.
1x =
. D.
16x =
.
Lời giải
Chọn B
ĐK:
9x >−
Ta có:
( )
5
2
log 9 5 9 2xx
+ =⇔+=
23x⇔=
.
Câu 22: (Mã 103 - 2020 Lần 2) Nghiệm của phương trình
( )
2
log 6 5x +=
là:
A.
4x
=
. B.
19x =
. C.
38x =
. D.
26x =
.
Lời giải
Chọn D
Điều kiện
60 6xx+ > ⇔ >−
Ta có:
( )
2
log 6 5x +=
( )
5
22
log 6 log 2x⇔ +=
( )
6 32x⇔+=
32 6x⇔= −
( )
26xTM⇔=
Vậy nghiệm của phương trình:
26x =
Câu 23: (Mã 104 - 2020 Lần 2) Nghiệm của phương trình
( )
2
log 7 5x +=
là
A.
18x =
. B.
25x =
. C.
39x
=
. D.
3x
=
.
Lời giải
Chọn B
( )
5
2
log 7 5 7 2xx+ =⇔+=
25x⇔=
.
Câu 24: (Mã 101 - 2020 Lần 2) Nghiệm của phương trình
2
log ( 8) 5x +=
bằng
A.
17x =
. B.
24x =
. C.
2x =
. D.
40
x
=
.
Lời giải
Chọn B
Ta có
5
2
log ( 8) 5 8 2 24xxx+ =⇔+= ⇔ =
.
Câu 25: (Đề Tham Khảo 2019) Tập nghiệm của phương trình
( )
2
2
log 2 1xx−+ =
là :
A.
{ }
0
B.
{ }
0;1
C.
{ }
1; 0−
D.
{ }
1
Lời giải
Chọn B
( )
22
2
0
log 2 1 2 2
1
x
xx xx
x
=
−+ =⇔ −+=⇔
=
Câu 26: (Đề Minh Họa 2017) Giải phương trình
4
log ( 1) 3.−=x
A.
65=x
B.
80=x
C.
82=x
D.
63=x
Lời giải
Chọn A
ĐK:
10 1⇔ −> ⇔ >
xx

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 6
Sưu tầm và biên soạn
Phương trình
( )
4
log 1 3−=
x
3
1 4 65
⇔ −= ⇔ =xx
.
Câu 27: (Mã 110 2017) Tìm nghiệm của phương trình
( )
2
log 1 2x−=
.
A.
5x =
. B.
3
x = −
. C.
4x = −
. D.
3x =
.
Lời giải
Chọn B
Ta có
( )
2
log 1 2x
−=
14x⇔− =
3x
⇔=−
.
Câu 28: (Mã 102 2018) Tập nghiệm của phương trình
( )
2
2
log 1 3x −=
là
A.
{ }
10; 10−
B.
{ }
3; 3−
C.
{
}
3−
D.
{ }
3
Lời giải
Chọn B
( )
2
2
log 1 3x −=
2
18x⇔ −=
2
9x⇔=
3
x
⇔=±
.
Câu 29: (Mã 104 2017) Tìm nghiệm của phương trình
( )
2
log 5 4x
−=
.
A.
11x =
B.
13x =
C.
21x =
D.
3x =
Lời giải
Chọn C
ĐK:
50 5xx−>⇔ >
Khi đó
( )
2
log 5 4x −=
5 16 21xx⇔−= ⇔ =
.
Câu 30: (Mã 103 2018) Tập nghiệm của phương trình
2
3
log ( 7) 2x −=
là
A.
{ }
4
B.
{ }
4−
C.
{ 15; 15}−
D.
{ 4;4}
−
Lời giải
Chọn D
2
3
log ( 7) 2x −=
2
79x⇔ −=
4
4
x
x
=
⇔
= −
Câu 31: (Mã 105 2017) Tìm nghiệm của phương trình
( )
+=
25
1
log 1
2
x
.
A.
=
6x
B.
= 4
x
C.
=
23
2
x
D.
= −6x
Lời giải
Chọn B
Điều kiện:
>−1x
Xét phương trình
( ) ( )
+=⇔ +=
25 5
1
log 1 log 1 1
2
xx
⇔+=⇔ =15 4
xx
.
Câu 32: (Đề Tham Khảo 2017) Tìm tập nghiệm
S
của phương trình
(
) ( )
22
log 1 log 1 3xx−+ +=
.
A.
{ }
3S =
B.
{ }
10; 10S = −
C.
{ }
3; 3S = −
D.
{ }
4S =
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 7
Sưu tầm và biên soạn
Chọn A
Điều kiện
> 1x
. Phương trình đã cho trở thành
( )
−=
2
2
log 1 3x
⇔ −=
2
18x
⇔=±3x
Đối chiếu điều kiện, ta được nghiệm duy nhất của phương trình là
{ }
=⇒=33xS
Câu 33: (Mã 103 - 2019) Nghiệm của phương trình
( )
(
)
22
log 1 1 log 3 1xx
+ += −
là
A.
1x
=
. B.
2x =
. C.
1x = −
. D.
3x =
.
Lời giải
Chọn D
Điều kiện phương trình:
1
3
x >
.
( ) ( ) ( ) ( ) ( )
2 22 2
log 1 1 log 3 1 log 1 .2 log 3 1 2 1 3 1 3x x x x x xx++= −⇔ + = −⇔ += −⇔=
.
Ta có
3x =
( Thỏa mãn điều kiện phương trình)
Vậy nghiệm phương trình là
3x =
.
Câu 34: (Mã 105 2017) Tìm tập nghiệm
S
của phương trình
( ) ( )
+− −=
33
log 2 1 log 1 1xx
.
A.
{ }
= 3S
B.
{
}
= 4S
C.
{ }
= 1S
D.
{
}
= −2S
Lời giải
Chọn B
ĐK:
−
+>
>
⇔ ⇔>
−>
>
1
2 10
1.
2
10
1
x
x
x
x
x
Ta có
( ) ( )
+− −=
33
log 2 1 log 1 1xx
++
⇔ =⇔ =⇔=
−−
3
21 21
log 1 3 4
11
xx
x
xx
(thỏa)
Câu 35: (Mã 101 - 2019) Nghiệm của phương trình
( ) (
)
33
log 1 1 log 4 1xx+ += +
A.
4x
=
. B.
2
x =
. C.
3x
=
. D.
3
x = −
.
Lời giải
Chọn B
Điều kiện:
1
.
4
x >−
Ta có:
( ) ( )
( )
33
log 1 1 log 4 1
1
1
4
2.
4
3 141
2
xx
x
x
x
xx
x
+ += +
−
−
>
>
⇔ ⇔ ⇔=
+= +
=
Vậy: Nghiệm của phương trình là
2.x =
Câu 36: (Mã 104 - 2019) Nghiệm của phương trình
( ) ( )
33
log 2 1 1 log 1xx+=+ −
là
A.
4x =
. B.
2x
= −
. C.
1x =
. D.
2x =
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 8
Sưu tầm và biên soạn
Chọn A
Điều kiện:
2 10
1
10
x
x
x
+>
⇔>
−>
.
Ta có:
( ) ( )
33
log 2 1 1 log 1xx+=+ −
( )
( )
33
log 2 1 log 3 1
xx
⇔ += ⋅−
2 13 3
xx⇔ += −
4x⇔=
(nhận).
Câu 37: (Mã 102 -2019) Nghiệm của phương trình
(
) ( )
22
log 1 1 log 1xx+=+ −
là
A.
3x =
. B.
2x
=
. C.
1x =
. D.
2
x
= −
.
Lời giải
Chọn A
Điều kiện:
1
1
1
x
x
x
>−
⇔>
>
.
Phương trình đã cho tương đương với
( ) ( )
22
log 1 1 log 1xx+=+ −
.
( ) (
)
22
log 1 log 2. 1
xx⇔ += −
12 2 3xx x⇔ += − ⇔ =
(Thỏa mãn).
Câu 38: (Mã 110 2017) Tìm tập nghiệm
S
của phương trình
( )
( )
1
2
2
log 1 log 1 1.xx−+ +=
A.
{ }
3S =
B.
{ }
2 5;2 5S =−+
C.
{ }
25
S = +
D.
3 13
2
S
+
=
Lời giải
Chọn C
Điều kiện
10
1 (*)
10
x
x
x
−>
⇔>
+>
.
Phương trình
( ) ( )
22
2log 1 log 1 1xx⇔ −− +=
( ) ( )
2 22
2log 1 log 1 log 2xx⇔ −= ++
( ) ( )
2
22
log 1 log 2 1xx⇔ −= +
2
2 12 2xx x⇔ − += +
( )
2
25
4 10
25
xL
xx
x
= −
⇔ − −= ⇔
= +
. Vậy tập nghiệm phương trình
{ }
25S = +

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 9
Sưu tầm và biên soạn
Câu 39: (Đề Tham Khảo 2018) Tổng giá trị tất cả các nghiệm của phương trình
3 9 27 81
2
log .log .log .log
3
xx x x=
bằng
A.
0.
B.
80
.
9
C.
9.
D.
82
.
9
Lời giải
Chọn D
Điều kiện
0x
>
.
Phương trình đã cho tương đương với
3
4
33 3 3 3
3
9
log 2
1 11 2
log . .log . log . log (log ) 16
1
log 2
2 34 3
9
=
=
=⇔=⇔ ⇔
= −
=
x
x
xxx x
x
x
Câu 40: (Mã 110 2017) Tìm tập nghiệm
S
của phương trình
( ) ( )
1
2
2
log 1 log 1 1.xx−+ +=
A.
{ }
3S
=
B.
{ }
2 5;2 5S =−+
C.
{ }
25S = +
D.
3 13
2
S
+
=
Lời giải
Chọn C
Điều kiện
10
1 (*)
10
x
x
x
−>
⇔>
+>
.
Phương trình
( ) ( )
22
2log 1 log 1 1xx⇔ −− +=
(
) ( )
2 22
2log 1 log 1 log 2xx⇔ −= ++
( ) ( )
2
22
log 1 log 2 1xx⇔ −= +
2
2 12 2xx x⇔ − += +
(
)
2
25
4 10
25
xL
xx
x
= −
⇔ − −= ⇔
= +
. Vậy tập nghiệm phương trình
{ }
25S = +
Câu 41: (Mã 104 2017) Xét các số nguyên dương
a
,
b
sao cho phương trình
2
ln ln 5 0a xb x+ +=
có
hai nghiệm phân biệt
1
x
,
2
x
và phương trình
2
5log log 0xb xa+ +=
có hai nghiệm phân biệt
3
x
,
4
x
thỏa mãn
12 34
xx xx>
. Tính giá trị nhỏ nhất
min
S
của
23S ab= +
.
A.
min
17S =
B.
min
30S =
C.
min
25S =
D.
min
33S =
Lời giải
Chọn B

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 10
Sưu tầm và biên soạn
Điều kiện
0x >
, điều kiện mỗi phương trình có 2 nghiệm phân biệt là
2
20ba>
.
Đặt
ln , log
t xu x
= =
khi đó ta được
( )
2
5 01
at bt+ +=
,
( )
2
5 02t bt a+ +=
.
Ta thấy với mỗi một nghiệm
t
thì có một nghiệm
x
, một
u
thì có một
x
.
Ta có
1 2 12
12
..
b
t t tt
a
xx e e e e
−
+
= = =
,
12
5
34
. 10 10
b
uu
xx
−
+
= =
, lại có
5
12 34
10
bb
a
xx xx e
−−
> ⇔>
5
ln10 3
5 ln10
bb
aa
a
⇒− >− ⇔ > ⇔ ≥
( do
,ab
nguyên dương), suy ra
2
60 8bb
> ⇒≥
.
Vậy
2 3 2.3 3.8 30
S ab
=+≥+=
, suy ra
min
30S
=
đạt được
3, 8
ab= =
.
Câu 42: (Đề Minh Họa 2020 Lần 1) Cho phương trình
( ) ( )
2
22
log 2 2 log 2 0x m xm− + + −=
(
m
là tham
số thực). Tập hợp tất cả các giá trị của
m
để phương trình đã cho có hai nghiệm phân biệt thuộc
đoạn
[ ]
1; 2
là
A.
( )
1; 2
. B.
[ ]
1; 2
. C.
[
)
1; 2
. D.
[
)
2; +∞
.
Lời giải
Chọn C
( ) ( )
2
22
log 2 2 log 2 0x m xm− + + −=
( ) ( )
2
2
1 log 2 log 2 0x m xm⇔ + − + + −=
( )
*
Đặt
( )
2
logt x gx= =
01t
⇒ ≤≤
và mỗi giá trị của
x
sẽ cho một giá trị của
t
( )
*
trở thành
( ) (
)
2
1 2 20t m tm+ − + + −=
2
21 2 20t t mt t m⇔ + +− − + − =
( )
2
11t mt⇔ −= −
( )(
)
11 0ttm⇔ − +− =
(
)
( )
11
12
tm
t
= −
⇔
=
Với
1t =
thì phương trình có một nghiệm
2x
=
Vậy để phương trình ban đầu có hai nghiệm phân biệt thì phương trình
( )
1
phải có một nghiệm
1t ≠
0 11m
≤ −<
12m
⇔≤ <
Vậy
[
)
1; 2
m ∈
để thoả mãn yêu cầu bài toán.
Câu 43: (Mã 102 2019) Cho phương trình
(
)
2
93 3
log log 6 1 logxx m− −=−
(
m
là tham số thực). Có tất
cả bao nhiêu giá trị nguyên của
m
để phương trình đã cho có nghiệm?
A.
7
. B.
6
. C.
5
. D. Vô số.
Lời giải
Chọn C
Xét phương trình
( )
2
93 3
log log 6 1 logxx m− −=−
.
Điều kiện:
1
6
0
x
m
>
>
.
Khi đó

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 11
Sưu tầm và biên soạn
(
) ( )
( ) ( )
2
9 3 3 33 3
log log 6 1 log log log log 6 1
6 1 6 11
x x m xm x
mx x x m
− −=− ⇔ + = −
⇔ = −⇔ − =
+) Với
6m =
, phương trình (1) trở thành
01=
(vô lý).
+) Với
6m ≠
, phương trình (1) có nghiệm
1
6
x
m
=
−
11 11
0
6 66 6
mm
⇒ >⇔ −>
−−
00 6
6
m
m
m
⇔ >⇔< <
−
.
Vậy
06m
<<
. Mà
{
}
1;2;3;4;5mm∈⇒∈
. Vậy có 5 giá trị nguyên của
m
thỏa mãn.
Câu 44: (MĐ 101-2022) Tập nghiệm của bất phương trình
( )
5
log 1 2x +>
là:
A.
( )
9 ;+∞
. B.
( )
25 ; .+∞
C.
( )
31 ; +∞
. D.
(
)
24 ;+∞
.
Lời giải
Chọn D
Ta có:
( )
2
5
log 1 2 1 5 25 1 24xxxx+>⇔+> ⇔> −⇔>
.
Vậy tập nghiệm của bất phương trình là:
( )
24 ;S = +∞
.
Câu 45: (MĐ 102-2022) Tập nghiệm của bất phương trình
( )
5
log 1 2x
+>
là
A.
( )
24; +∞
. B.
( )
9; +∞
. C.
( )
25; +∞
. D.
(
)
31;
+∞
.
Lời giải
Chọn A
Ta có
( )
5
2
1
log 1 2 24
15
x
xx
x
>−
+ >⇔ ⇔>
+>
.
Câu 46: (MĐ 101-2022) Có bao nhiêu số nguyên dương
a
sao cho ứng với mỗi
a
có đúng ba số nguyên
b
thỏa mãn
( )( )
3 3 .2 18 0
bb
a− −<
?
A.
72.
B.
73⋅
C.
71⋅
D.
74⋅
Lời giải
Chọn B
Xét
( )( )
2
1
3 30
3 3 .2 18 0
18
log
.2 18 0
b
bb
b
b
a
b
a
a
=
−=
− −=⇔ ⇔
=
−=
.
TH1: Nếu
2
18
log 1 0 9.a
a
>⇔ < <
Khi đó ta có bảng xét dấu vế trái BPT như sau:
Để với mỗi
a
có đúng ba số nguyên
b
thì
{ }
2; 3; 4b ∈
nên
2
18 18 9 9
4 log 5 16 32
16 8
a
aa
< ≤⇔ < ≤ ⇔ ≤<
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 12
Sưu tầm và biên soạn
Vậy
1a =
.TH này có 1 giá trị
a
thỏa mãn.
TH2: Nếu
2
18
log 1 9.
a
a
<⇔ >
Khi đó ta có bảng xét dấu vế trái BPT như sau:
Để với mỗi
a
có đúng ba số nguyên
b
thì
{ }
2; 1; 0b ∈− −
nên
32
2
18 18
3 log 2 2 2 72 144
a
aa
−−
− ≤ <− ⇔ ≤ < ⇔ < ≤
.
Vậy
{
}
73;74;...;144a
∈
. TH này có 72 giá trị của
a
thỏa mãn.
Gom cả hai trường hợp ta có 73 giá trị của
a
thỏa.
Câu 47: (MĐ 102-2022) Có bao nhiêu số nguyên dương
a
sao cho ứng với mỗi
a
có đúng hai số nguyên
b
thỏa mãn
(
)( )
5 1 .2 5 0
bb
a
− −<
A.
20
. B.
21
. C.
22
. D.
19
.
Lời giải
Chọn B
( )
( )
5 1 .2 5 0
bb
a− −<
TH1:
2
2
0
5 10
5
0 log
5
log
.2 5 0
b
b
b
b
b
a
a
a
>
−>
⇔ ⇔<<
<
−<
Để có đúng hai số nguyên
b
thỏa mãn thì
2
5 55
2 log 3
84
a
a
< ≤⇔ ≤<
1a⇒=
(có 1 giá trị
a
).
TH2:
2
2
0
5 10
5
log 0
5
log
.2 5 0
b
b
b
b
b
a
a
a
<
−<
⇔ ⇔ <<
>
−>
Để có đúng hai số nguyên
b
thỏa mãn thì
2
5 151
3 log 2 20 40
84
a
aa
− ≤ <− ⇔ ≤ < ⇔ < ≤
{ }
21;22;...;40a⇒∈
(có 20 giá trị
a
).
Vậy có tất cả 21 giá trị a thỏa mãn yêu cầu bài toán.
Câu 48: (MĐ 103-2022) Có bao nhiêu số nguyên dương
a
sao cho ứng với mỗi
a
có đúng hai số nguyên
b
thỏa mãn
( )( )
4 1 .3 10 0?
bb
a− −<
A.
182
. B.
179
. C.
180
. D.
181
.
Lời giải
Chọn D
Ta có
1,ab≥∈
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 13
Sưu tầm và biên soạn
( )( )
3
0
4 1 .3 10 0
10
log
bb
b
a
b
a
=
− −=⇔
=
Trường hợp 1:
10
1 10a
a
>⇔ <
.
Tập nghiệm bất phương trình
3
10
0;logS
a
=
.
Yêu cầu bài toán
3
10
10
9
2 log 3 1
10
27
a
a
a
a
<
⇔< ≤⇔ ⇔=
≥
.
Trường hợp 2:
10
0 1 10a
a
< <⇔ >
Tập nghiệm bất phương trình
3
10
log ;0S
a
=
.
Yêu cầu bài toán
3
270
10
3 log 2 90 270
90
a
a
a
a
≤
⇔− ≤ <− ⇔ ⇔ < ≤
>
.
Cả 2 trường hợp có tất cả 181 giá trị nguyên của
a
thỏa yêu cầu bài toán.
Câu 49: (MĐ 104-2022) Có bao nhiêu số nguyên dương
a
sao cho ứng với mỗi
a
có đúng hai số nguyên
b
thoả mãn
( )(
)
3 3 .2 16 0?
bb
a
− −<
A.
34
. B.
32
. C.
31
. D.
33
.
Lời giải
Chọn D
Do
a
+
∈
nên ta có
( )( )
3 3 .2 16 0
bb
a− −<
( )
( )
1
3 30
16
2
.2 16 0
1
3 30
16
.2 16 0
2
b
b
b
b
b
b
b
I
a
a
b
II
a
a
<
−<
>
−>
⇔⇔
>
−>
−<
<

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 14
Sưu tầm và biên soạn
Trường hợp 1: Nếu
b
thoả mãn
16
2
b
a
>
. Khi đó hệ
( )
II
vô nghiệm.
Do đó để có đúng hai giá trị
b
thoả mãn yêu cầu bài toán khi và chỉ khi
{ }
0;1b =
thoả mãn
( )
I
{ }
2
1 16
32
2
33;34;.....;64
16 64
2
a
a
a
a
a
−
>
>
⇔ ⇔ ⇒=
≤
≤
Trường hợp 2: Nếu
b
thoả mãn
16
2
b
a
<
. Khi đó hệ
( )
I
vô nghiệm
Do đó để có đúng hai giá trị
b
thoả mãn yêu cầu bài toán khi và chỉ khi
{ }
2;3b =
thoả mãn
yêu cầu bài toán
16
8
2
1
16 1
16
a
a
a
a
a
>
<
⇔ ⇔ ⇒=
≥
≥
Vậy có
33
giá trị
a
thoả mãn yêu cầu bài toán
Câu 50: (2020-2021 – ĐỢT 1) Tập nghiệm của bất phương trình
32
x
<
là
A.
( )
3
;log 2−∞
. B.
( )
3
log 2; +∞
. C.
( )
2
;log 3−∞
. D.
(
)
2
log 3;
+∞
.
Lời giải
Ta có
3
3 2 log 2
x
x<⇔<
.
Vậy tập nghiệm của bất phương trình đã cho là
( )
3
;log 2S = −∞
.
Câu 51: (2020-2021 – ĐỢT 1) Tập nghiệm của bất phương trình
25
x
>
là
A.
2
( ; log 5)−∞
. B.
5
(log 2; )+∞
. C.
5
( ;log 2)−∞
. D.
2
(log 5; )+∞
Lời giải
Ta có:
2
2 5 log 5.
x
x>⇔>
Tập nghiệm của bất phương trình là:
2
(log 5; )+∞
Câu 52: (2020-2021 – ĐỢT 1) Tập nghiệm của bất phương trình
( )
2
log 3 5x >
là
A.
32
0;
3
. B.
32
;
3
+∞
. C.
25
0;
3
. D.
25
;
3
+∞
.
Lời giải
Ta có
( )
5
2
32
log 3 5 3 2
3
x xx>⇔ > ⇔>
.
Vậy tập nghiệm của bất phương trình đã cho là:
32
;
3
+∞
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 15
Sưu tầm và biên soạn
Câu 53: (2020-2021 – ĐỢT 2) Tập nghiệm của bất phương trình
( )
2
log 3 3x >
là
A.
( )
3; +∞
. B.
8
;
3
+∞
. C.
8
0;
3
. D.
( )
0;3
.
Lời giải
Ta có :
( )
3
2
8
log3 332 38
3
x x xx>⇔ > ⇔ >⇔>
Câu 54: (2020-2021 – ĐỢT 2) Tập nghiệm của bất phương trình
( )
3
log 2 4x >
A.
( )
0;32
. B.
81
0;
2
. C.
( )
32; +∞
. D.
81
;
2
+∞
.
Lời giải
Ta có:
( )
3
log 2 4x >
4
81
23
2
xx⇔ > ⇔>
Câu 55: (Đề Minh Họa 2020 Lần 1) Tập nghiệm của bất phương trình
2
19
55
x xx− −−
≥
là
A.
[ ]
2; 4−
. B.
[ ]
4; 2−
.
C.
(
] [
)
; 2 4;−∞ − ∪ +∞
. D.
(
] [
)
; 4 2;−∞ − ∪ +∞
.
Lời giải
Chọn A
2
19 2 2
5 5 1 9 2 80 2 4
x xx
x xx x x x
− −−
≥ ⇔ − ≥ − − ⇔ − − ≤ ⇔− ≤ ≤
.
Vậy Tập nghiệm của bất phương trình là
[ ]
2; 4−
.
Câu 56: (Đề Tham Khảo 2020 Lần 2) Tập nghiệm của bất phương trình
9 2.3 3 0
xx
+ −>
là
A.
[
)
0;+∞
. B.
( )
0;+∞
. C.
( )
1;+∞
. D.
[
)
1;+∞
.
Lời giải
Chọn B
( )( )
9 2.3 3 0 3 1 3 3 0 3 1
xx x x x
+ −>⇔ − + >⇔ >
(vì
3 0,
x
x> ∀∈
)
0x⇔>
.
Vậy tập nghiệm của bất phương trình đã cho là
( )
0;+∞
.
Câu 57: (Mã 101 - 2020 Lần 1) Tập nghiệm của bất phương trình
2
13
3 27
x −
<
là
A.
( )
4;+∞
. B.
( )
4;4−
. C.
( )
;4−∞
. D.
( )
0;4
.
Lời giải
Chọn B
Ta có:
22
13 13 3 2 2
3 27 3 3 13 3 16 4 4 4
xx
x xx x
−−
< ⇔ < ⇔ − <⇔ < ⇔ <⇔−<<
.
Vậy tập nghiệm của bất phương trình đã cho là
( )
4;4S = −
.
Câu 58: (Mã 102 - 2020 Lần 1) Tập nghiệm của bất phương trình
là
A. . B. . C. . D. .
2
23
39
x −
<
( )
5;5−
( )
;5−∞
( )
5; +∞
( )
0;5

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 16
Sưu tầm và biên soạn
Lời giải
Chọn A
Ta có .
Vậy nghiệm của bất phương trình là .
Câu 59: (Mã 103 - 2020 Lần 1) Tập nghiệm của bất phương trình
2
7
24
x −
<
là
A.
( 3; 3)−
. B.
(0;3)
. C.
( ;3)−∞
. D.
(3; )+∞
.
Lời giải
Chọn A
Ta có :
2
7
24
x
2
72
22
x
2
72 x
2
9x
3; 3 . x
Câu 60: (Mã 104 - 2020 Lần 1) Tập nghiệm của bất phương trình
2
1
28
x −
<
là
A.
( )
0; 2
. B.
( )
;2−∞
. C.
( )
2; 2−
. D.
( )
2; +∞
.
Lời giải
Chọn C
Từ phương trình ta có
2
13 2 2xx− < ⇔− < <
.
Câu 61: (Đề Tham Khảo 2018) Tập nghiệm của bất phương trình
26
22
xx
là:
A.
;6
B.
0; 64
C.
6;
D.
0;6
Lời giải:
Chọn A
Cách 1:
26
22 2 6 6
xx
xx x
Cách 2:
Đặt
2
x
t
,
0t
Bất phương trình trở thành:
2
64 0tt
0 64t
0 2 64 6
x
x
.
Câu 62: (Đề Tham Khảo 2019) Tập nghiệm của bất phương trình
2
2
3 27
xx−
<
là
A.
( )
3; +∞
B.
( )
1; 3−
C.
( ) ( )
; 1 3;−∞ − ∪ +∞
D.
( )
;1−∞ −
Lời giải
Chọn B
Ta có
2
22 2
3 27 2 3 2 3 0 1 3
xx
xx xx x
−
<⇔−<⇔−−<⇔−<<
.
Câu 63: (Đề Tham Khảo 2017) Tìm tập nghiệm
S
của bất phương trình
1
1
50
5
x+
−>
.
A.
( )
;2S = −∞ −
. B.
( )
1;S = +∞
. C.
( )
1;S = − +∞
. D.
( )
2;S = − +∞
.
Lời giải
2
23 2 2
3 9 23 2 25 5 5
x
xx x
−
<⇔ − <⇔ < ⇔−<<
2
23
39
x −
<
( )
5;5−

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 17
Sưu tầm và biên soạn
Bất phương trình tương đương
11
5 5 1 1 2.
x
xx
+−
> ⇔ + >− ⇔ >−
Câu 64: (Đề Tham Khảo 2019) Tập nghiệm của bất phương trình
2
2
3 27
xx−
<
là
A.
( )
;1−∞ −
B.
(
)
3;
+∞
C.
( )
1; 3−
D.
( ) ( )
; 1 3;−∞ − ∪ +∞
Lời giải
Chọn C
Ta có
2
22 2
3 27 2 3 2 3 0 1 3
xx
xx xx x
−
<⇔−<⇔−−<⇔−<<
.
Câu 65: (Đề Tham Khảo 2020 Lần 2) Tập nghiệm của bất phương trình
log 1x ≥
là
A.
( )
10; +∞
. B.
( )
0; +∞
. C.
[
)
10; +∞
. D.
( )
;10−∞
.
Lời giải
Chọn C
{
0
log 1 10.
10
x
xx
x
>
≥⇔ ⇔ ≥
≥
Vậy bất phương trình đã cho có tập nghiệm là
[
)
10; .+∞
Câu 66: (Mã 102 - 2020 Lần 2) Tập nghiệm của bất phương trình
( )
2
3
log 13 2x−≥
là
A.
(
]
[
)
; 2 2:
−∞ − ∪ +∞
. B.
(
]
;2−∞
.
C.
(
]
0; 2
. D.
[ ]
2; 2
−
.
Lời giải
Chọn D
Bất phương trình
( )
22
2
3
22
13 0 13
log 13 2
13 9 4
xx
x
xx
−> <
− ≥⇔ ⇔
−≥ ≤
13 13
22
22
x
x
x
− <<
⇔ ⇔− ≤ ≤
−≤ ≤
.
Vậy, tập nghiệm của bất phương trình
( )
2
3
log 13 2x−≥
là
[ ]
2; 2
−
.
Câu 67: (Mã 103 - 2020 Lần 2) Tập nghiệm của bất phương trình
( )
2
3
log 36 3x−≥
là
A.
(
] [
)
; 3 3;−∞ − ∪ +∞
. B.
(
]
;3
−∞
. C.
[ ]
3; 3−
. D.
(
]
0;3
.
Lời giải
Chọn C
Ta có:
( )
2 22
3
log 36 3 36 27 9 0 3 3x xx x− ≥⇔−≥ ⇔−≥⇔−≤≤
.
Câu 68: (Mã 101 - 2020 Lần 2) Tập nghiệm của bất phương trình
( )
2
3
log 18 2x−≥
là
A.
(
]
;3−∞
. B.
(
]
0;3
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 18
Sưu tầm và biên soạn
C.
[ ]
3;3−
. D.
(
] [
)
; 3 3;−∞ − ∪ + ∞
.
Lời giải
Chọn C
Điều kiện:
( )
2
18 0 32;32xx− > ⇔ ∈−
(*).
Khi đó ta có:
(
)
2
3
log 18 2x−≥
2
18 9x⇔−≥
33x⇔− ≤ ≤
.
Kết hợp với điều kiện (*) ta được tập ngiệm của bất phương trình đã cho là
[
]
3;3−
.
Câu 69: (Mã 104 - 2020 Lần 2) Tập nghiệm của bất phương trình
(
)
2
3
log 31 3
x−≥
là
A.
(
]
;2−∞
. B.
[ ]
2; 2−
. C.
(
] [
)
; 2 2;−∞ − ∪ +∞
. D.
(
]
0; 2
.
Lời giải
Chọn B
(
)
[ ]
2 22
3
log 31 3 31 27 4 0 2;2x xx x− ≥ ⇔ − ≥ ⇔ − ≤ ⇔ ∈−
.
Câu 70: (Đề Minh Họa 2017) Giải bất phương trình
( )
2
log 3 1 3x −>
.
A.
3x
>
B.
1
3
3
x
<<
C.
3x <
D.
10
3
x >
Lời giải
Chọn A
Đkxđ:
1
3 10
3
xx−> ⇔ >
Bất phương trình
3
3 12 3 9 3
x xx⇔ −> ⇔ > ⇔ >
(t/m đk).
Vậy bpt có nghiệm
3x
.
Câu 71: (Mã 123 2017) Tìm tập nghiệm
S
của bất phương trình
− +≥
2
22
log 5log 4 0xx
.
A.
= −∞ ∪ +∞( ; 1] [4 ;) S
B.
= [2 ;16]S
C.
= ∪ +∞
(0 ; 2] [16
;)
S
D.
−∞ ∪ +∞
( ; 2] [ 6 1; )
Lời giải
Chọn C
Điều kiện
> 0x
Bpt
≥
≥
⇔⇔
≤≤
2
2
log 4
16
log 1 2
x
x
xx
Kết hợp điều kiện ta có
( )
= ∪ +∞
0;2 16;S
.
Câu 72: Có bao nhiêu số nguyên
x
thỏa mãn
( )
( )
2
3
3 9 . log 25 3 0?
xx
x− + −≤

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 19
Sưu tầm và biên soạn
A.
24.
B. Vô số. C.
26.
D.
25.
Lời giải
Điều kiện:
(
)
25 * .x
>−
Trường hợp 1:
( ) ( )
22
2
2
33
0
0
390 3 3
2
.
2
2
25 27
log 25 3 0 log 25 3
2
xx x x
x
x
xx
x
x
x
xx
x
≤
≤
−≥ ≥
≥
⇔ ⇔ ⇔⇔
≥
=
+≤
+ −≤ + ≤
≤
Kết hợp với điều kiện
( )
*
ta được
(
]
{ }
25; 0 2 .x ∈− ∪
Mà
{ }
24; 23;...;1;0;2xx∈ ⇒ ∈− − ⇒
có 26 giá trị nguyên của
x
thỏa mãn.
Trường hợp 2:
( ) ( )
( )
22
2
2
33
02
390 3 3
2
2.
2
25 27
log 25 3 0 log 25 3
xx x x
x
xx
x tm
x
x
xx
≤≤
−≤ ≤
≤
⇔ ⇔ ⇔ ⇔=
≥
+≥
+ −≥ + ≥
Kết hợp các trường hợp, ta có tất cả 26 giá trị nguyên của của
x
thỏa mãn đề.
Câu 73: (MĐ 102 2020-2021 – ĐỢT 1) Có bao nhiêu số nguyên
x
thỏa mãn
( )
( )
2
2
3 9 log 30 5 0
xx
x− + −≤
A.
30
. B. Vô số. C.
31
. D.
29
.
Lời giải
Điều kiện:
30x >−
Trường hợp 1:
( ) ( )
22
2
2
22
0
0
390 3 3
2
2
2
30 32
log 30 5 0 log 30 5
2
xx x x
x
x
xx
x
x
x
xx
x
≤
≤
−≥ ≥
≥
⇔ ⇔ ⇔⇔
≥
=
+≤
+ −≤ + ≤
≤
Kết hợp điều kiện ta có:
30 0
2
x
x
− <≤
=
. Nên
{ }
29, 28,...0,2x ∈− −
nên có
31
số nguyên
Trường hợp 2:
( ) ( )
22
2
2
22
02
390 3 3
2
2
2
30 32
log 30 5 0 log 30 5
xx x x
x
xx
x
x
x
xx
≤≤
−≤ ≤
≤
⇔ ⇔ ⇔ ⇔=
≥
+≥
+ −≥ + ≥
Vậy tổng cộng có
31
số nguyên thỏa mãn yêu cầu bài toán.
Câu 74: (MĐ 103 2020-2021 – ĐỢT 1) Có bao nhiêu số nguyên
x
thoả mãn
( )
( )
2
2
2 4 log 14 4 0
xx
x− + −≤
?
A.
14
. B.
13
. C. Vô số. D.
15
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 20
Sưu tầm và biên soạn
Ta có:
( )
( )
2
2
2 4 log 14 4 0
xx
x− + −≤
( )
( )
2
2
2
2
2 40
log 14 4 0
2 40
log 14 4 0
xx
xx
x
x
−≥
+ −≤
⇔
−≤
+ −≥
( )
( )
2
2
2
2
2
2
22
log 14 4
22
log 14 4
xx
xx
x
x
≥
+≤
⇔
≤
+≥
2
2
2
0 14 16
2
14 16
xx
x
xx
x
≥
<+ ≤
⇔
≤
+≥
2
0
14 2
02
2
x
x
x
x
x
≥
≤
⇔
− <≤
≤≤
≥
2
14 0
2
x
x
x
=
⇔− < ≤
=
2
14 0
x
x
=
⇔
− <≤
.
Vì
x
nguyên nên
{
}
13; 12;...;0;2x ∈− −
. Vậy có
15
số nguyên
x
thỏa mãn yêu cầu bài toán.
Câu 75: (MĐ 104 2020-2021 – ĐỢT 1) Có bao nhiêu số nguyên
x
thỏa mãn
( )
(
)
2
3
2 4 log 25 3 0
xx
x− + −≤
?
A.
24
. B. Vô số. C.
25
. D.
26
.
Lời giải
ĐK:
25x >−
+) Ta có
( )
( )
2
2
3
0
2
2 4 log 25 3 0
2
25 27
xx
x
xx
x
x
x
=
=
− + −=⇔ ⇔
=
+=
Ta có bảng xét dấu
( )
( )
( )
2
3
2 4 log 25 3
xx
fx x= − +−
+) Suy ra:
( )
25 0
0
2
x
fx
x
− <≤
≤⇔
=
+) Vì
x ∈
nên ta có
{ }
24; 23;...; 1;0;2x ∈− − −
. Vậy có
26
giá trị
x
nguyên thỏa bài toán.
Câu 76: Có bao nhiêu số nguyên
x
thỏa mãn
( )
( )
( )
21
22
log 1 log 31 32 2 0
x
xx
−
+− + − ≥
?
A. 27. B. Vô số. C. 26. D. 28.
Lời giải
Ta có
( )
( )
( )
21
22
log 1 log 31 32 2 0
x
xx
−
+− + − ≥

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 21
Sưu tầm và biên soạn
( )
( )
( )
( )
[ ]
2
2
22
1
2
2
22
1
31
31
31
5
log 1 log 31
30 0
6
15
32 2
6
31
31
31
30 0
log 1 log 31
5; 6
15
32 2
6
x
x
x
x
x
x
xx
xx
x
x
x
x
x
x
xx
xx
x
x
x
−
−
>−
>−
>−
≤−
+≥ +
−− ≥
≥
−≤
≥
≤
⇔ ⇔⇔
>−
>−
>−
−− ≤
+≤ +
∈−
−≥
≤
≥
31 5
6
x
x
< ≤−
⇔
=
Do
x
nguyên nên
{ }
30; 29; 28;...; 5;6x ∈−−− −
.
Vậy có 27 giá trị nguyên của
x
thỏa mãn bất phương trình đã cho.
Câu 77: Có bao nhiêu số nguyên
x
thoả mãn
( )
( )
( )
21
33
log 1 log 21 . 16 2 0?
x
xx
−
+− + − ≥
A.
17
. B.
18
. C.
16
. D. Vô số.
Lời giải
Điều kiện:
21.x
>−
Khi đó
( )
(
)
( )
( )
(
)
( )
( )
21
33
2
33
1
2
33
1
log 1 log 21 . 16 2 0
log 1 log 21 0
()
16 2 0
log 1 log 21 0
()
16 2 0
x
x
x
xx
xx
I
xx
II
−
−
−
+− + − ≥
+− + ≥
−≥
⇔
+− + ≤
−≤
Giải
(
)
I
ta có
( )
( )
(
)
( )
22
33 3 3
1 14
log 1 log 21 0 log 1 log 21
16 2 0 2 2
xx
xx x x
−−
+− + ≥ +≥ +
⇔
−≥ ≤
22
4
4
1 21 20 0
.
5
5
14 5
5
x
x
x x xx
x
x
xx
x
≤−
≤−
+≥ + − − ≥
⇔ ⇔ ⇔⇔
≥
=
−≤ ≤
≤
Kết hợp điều kiện ta được
21 4
5
x
x
− < ≤−
=
( )
1
.
Giải
( )
II
ta có
( )
( )
( )
( )
22
33 3 3
1 14
log 1 log 21 0 log 1 log 21
16 2 0 2 2
xx
xx x x
−−
+− + ≤ +≤ +
⇔
−≤ ≥

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 22
Sưu tầm và biên soạn
( )
22
45
1 21 20 0
5 2.
5
14 5
x
x x xx
x
x
xx
−≤ ≤
+≤ + − − ≤
⇔ ⇔ ⇔ ⇔=
≥
−≥ ≥
Từ
( )
1
và
( )
2
ta có các giá trị của
x
thoả mãn bất phương trình đã cho là
21 4
5
x
x
− < ≤−
=
.
Vì
x ∈Ζ
nên suy ra
{ }
20; 19;...; 4;5
x ∈− − −
. Vậy có tất cả 18 số nguyên
x
thoả mãn đề bài.
Câu 78: (MĐ 103 2020-2021 – ĐỢT 2) Có bao nhiêu số nguyên
x
thỏa mãn
21
22
log ( 1) log ( 21) (16 2 ) 0?
x
xx
−
+− + − ≥
A. Vô số. B.
17
. C.
16
. D.
18
.
Lời giải
Điều kiện:
21 0 21
xx+ > ⇔ >−
Đặt
21
22
( ) log ( 1) log ( 21) (16 2 )
x
fx x x
−
= +− + −
Ta có:
22
22 2 2
log ( 1) log ( 21) 0 log ( 1) log ( 21)
xx x x
+− + =⇔ += +
22
21
21 21
5
5
4
1 21 20 0
4
x
xx
x
x
x
x x xx
x
>−
>− >−
=
⇔ ⇔ ⇔⇔
=
= −
+= + −− =
= −
1 1 14
16 2 0 2 16 2 2 1 4 5
xx x
xx
−− −
−=⇔=⇔=⇔−=⇔=
Bảng xét dấu:
Từ bảng xét dấu ta có:
( ) 0 21 4fx x≥ ⇔− < ≤−
Vì
{ }
20; 19; 18...; 4xx∈⇒∈−−− −
Vậy, có
17
số nguyên
x
thỏa mãn yêu cầu bài toán.
Câu 79: (MĐ 104 2020-2021 – ĐỢT 2) Có bao nhiêu số nguyên
x
thỏa mãn
( ) ( )
21
33
log 1 log ( 31) 32 2 0?
x
xx
−
+− + − ≥
A.
27
. B.
26
. C. Vô số. D.
28
.
Lời giải
Đặt
( )
( ) ( )
21
33
log 1 log ( 31) 32 2
x
hx x x
−
= +− + −
.
Điều kiện:
31x
>−
.
Ta có:
( )
( ) ( )
22
33 3 3
11
log 1 log ( 31) 0 log 1 log ( 31)
0
32 2 0 2 32
xx
xx xx
hx
−−
+− + = += +
=⇔⇔
−= =

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 23
Sưu tầm và biên soạn
22
5
1 31 30 0
6
66
x
x x xx
x
xx
= −
+= + −− =
⇔⇔ ⇔
=
= =
Bảng xét dấu
( )
hx
Từ bảng xét dấu của
( )
hx
ta suy ra
( ) ( )
21
33
log 1 log ( 31) 32 2 0 ( 31; 5] {6}
x
xx x
−
+ − + − ≥ ⇔ ∈− − ∪
Vậy có 27 số nguyên
x
thỏa mãn.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 63
Sưu tầm và biên soạn
BÀI 4: PHƯƠNG TRÌNH – BẤT PHƯƠNG TRÌNH – MŨ – LOGARIT
DẠNG 1: PHƯƠNG TRÌNH MŨ
Câu 1: Nghiệm của phương trình
35
2 16
x−
=
là
A.
3x =
. B.
2x
=
. C.
7x =
. D.
1
3
x =
.
Câu 2: Tập nghiệm của bất phương trình
2
23
21
xx−−
=
là
A.
{ }
1; 3S = −
. B.
{
}
2S =
. C.
{ }
1; 3S = −
. D.
{ }
0S =
.
Câu 3:
2x
=
là nghiệm của phương trình nào sau đây?
A.
38
x
=
. B.
4 16
x
=
. C.
3
9x =
. D.
16 4
x
=
.
Câu 4: Tìm tất cả các giá trị của tham số
m
để phương trình
1
1
3
x
m
= −
có nghiệm
A.
0
m
<
hoặc
1m =
. B.
1m
>
. C.
0
m ≥
. D.
01m<≤
.
Câu 5: Phương trình nào sau đây vô nghiệm?
A.
21=
x
. B.
23=
x
. C.
20=
x
. D.
23=
xx
.
Câu 6: Nghiệm của phương trình
31
x
=
là
A.
0x =
. B.
1x
=
. C.
2x =
. D.
1x = −
.
Câu 7: Phương trình
( )
36
31
x−
=
có nghiệm là:
A.
0x =
. B.
2x =
. C.
7
3
x =
. D.
6x =
.
Câu 8: Nghiệm của phương trình
2
35
x
=
là
A.
5
log 3
2
. B.
3
log 5
2
. C.
125
2
. D.
5
2log 3
.
Câu 9: Số nghiệm của phương trình
2
2
31
xx−
=
là
A.
0
. B.
2
. C.
3
. D. 4.
Câu 10: Nghiệm của phương trình
1
3 27
x−
=
là
A.
5x =
. B.
4x =
. C.
3x =
. D.
2x =
.
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 64
Sưu tầm và biên soạn
Câu 11: Nghiệm của phương trình
3
2 64
x
=
là
A.
2
. B.
4
. C.
3
. D.
5
.
Câu 12: Nghiệm của phương trình
23 7
22
xx++
=
là:
A.
10
3
x =
. B.
4
3
x
=
. C.
4x =
. D.
10x =
.
Câu 13: Nghiệm của phương trình
1
1
5
25
x
là
A.
3
. B.
1
. C.
1
. D.
3
.
Câu 14: Tổng bình phương các nghiệm của phương trình
2
45
39
xx−+
=
là
A.
12
⋅
B.
10
⋅
C.
11
⋅
D.
9
⋅
Câu 15: Nghiệm của phương trình
72
x
=
là
A.
7
log 2x =
. B.
2
log 7x =
. C.
2
7
x =
. D.
7x =
.
Câu 16: Nghiệm của phương trình
21
4 64
x+
=
là
A.
2x =
. B.
15
2
x =
. C.
15x =
. D.
1
x
=
.
Câu 17: Nghiệm của phương trình
5 10
x
=
là
A.
5
log 10x =
. B.
10
log 5
x =
. C.
2x =
. D.
1
2
x =
.
Câu 18: Tìm tất cả các giá trị thực của
m
để phương trình
3
x
m=
có nghiệm thực.
A.
0m
>
. B.
1m
≥
. C.
0m ≥
. D.
0m
≠
.
Câu 19: Nghiệm của phương trình
2
1
1
3
9
x
x
+
=
là:
A.
1x =
. B.
1x = −
. C.
1
5
x =
. D.
1
5
x = −
.
Câu 20: Tổng tất cả các nghiệm của phương trình
2
22
28
xx x+−
=
bằng
A.
5−
. B.
6
−
. C.
5
. D.
6
.
Câu 21: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
59
x
m= −
có nghiệm thực?
A.
6
. B.
5
. C.
4
. D.
7
.
Câu 22: Tập nghiệm của phương trình:
2
32
31
xx−+
=
là:
A.
3I =
. B.
{ }
1; 2S =
. C.
{ }
1S =
. D.
{
}
2S =
.
Câu 23: Tất cả các giá trị của tham số
m
để phương trình
2
1
31
x
m
+
= −
có nghiệm là
A.
4m ≥
. B.
4m >
. C.
1m >
. D.
1m ≥
.
Câu 24: Số nghiệm thực của phương trình
2
22
xx−
=
là:
A.
1
. B.
3
. C.
2
. D.
0
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 65
Sưu tầm và biên soạn
Câu 25: Phương trình
2
11
5 25
xx
−+
=
có tập nghiệm là
A.
{ }
1; 3−
. B.
{ }
1; 3
. C.
{ }
3;1−
. D.
{ }
3; 1−−
.
Câu 26: Tổng các nghiệm của phương trình
2
2
24
xx
là:
A.
0
. B.
4
. C.
1
. D.
2
.
Câu 27: Phương trình
2
3
3 81
xx−
=
có tổng các nghiệm là
A.
3−
. B.
3
. C.
4−
. D.
5−
.
Câu 28: Số nghiệm dương của phương trình
2
4
1
9
3
xx−
=
là
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 29: Giải phương trình
( )
1
57
2
2,5
5
x
x
+
−
=
.
A.
1x ≥
. B.
1x =
. C.
1x <
. D.
2x =
.
Câu 30: Nghiệm của phương trình
( )
9
31
5
2, 4
12
x
x
−
+
=
là
A.
2x
= −
B.
5x
= −
C.
5x
=
D.
2x =
Câu 31: Gọi
12
,
xx
là hai nghiệm của phương trình
2
23
1
1
7
7
xx
x
−−
+
=
. Khi đó
12
xx
+
bằng:
A.
2−
. B.
1−
. C.
2
. D.
1
.
Câu 32: Cho phương trình
2
8 13
2 40
xx x
−+ −
−=
có hai nghiệm
12
;xx
. Tính
12
Sxx= +
.
A.
2S =
. B.
1S = −
. C.
4S =
. D.
5.
S = −
Câu 33: Gọi S là tổng các nghiệm của phương trình
22 2
32 65 2 37
222 1
xx xx xx−+ ++ ++
+= +
. Khi đó S có giá trị
là:
A.
3
. B.
6−
. C.
3−
. D.
5
.
DẠNG 2: PHƯƠNG TRÌNH LOGARIT
Câu 34: Giải phương trình
( )
3
log 1 2x −=
.
A.
7x
=
. B.
9x =
. C.
8x =
. D.
10x =
.
Câu 35: Nghiệm của phương trình
( )
2
log 5 3x −=
là
A.
21.x =
B.
11.x =
C.
13.x =
D.
14.x =
Câu 36: Phương trình
( )
3
log 1 2x +=
có nghiệm là
A.
7.x =
B.
8.x =
C.
5.x =
D.
9.x =
Câu 37: Tập nghiệm
S
của phương trình
(
)
3
log 2 3 1x +=
là
A.
{ }
1.S = −
B.
{ }
3.S =
C.
{ }
0.S =
D.
{ }
1.S =
Câu 38: Nghiệm của phương trình
( )
2
log 3 4 1x −=−
là:
A.
2x =
. B.
3
2
x
=
. C.
7
6
x =
. D.
5
3
x =
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 66
Sưu tầm và biên soạn
Câu 39: Nghiệm của phương trình
2
log ( 1) 3x
+=
là
A.
5
x =
. B.
7x =
. C.
9x =
. D.
8
x =
.
Câu 40: Nghiệm của phương trình
(
)
ln 3 2x
=
là
A.
3
ex
=
. B.
3
e
2
x =
. C.
3
ex =
. D.
2
e
3
x =
.
Câu 41: Nghiệm của phương trình
( )
9
1
log 2
2
x =
là
A.
2x =
. B.
1
2
x =
. C.
1x
=
. D.
3
2
x =
.
Câu 42: Nghiệm của phương trình
(
)
3
log 2 1 2
x
+=
là:
A.
2x =
. B.
4x =
. C.
1
2
x = −
. D.
2x = −
.
Câu 43: Nghiệm của phương trình
2
log 1x = −
là
A.
2x =
. B.
1
2
x =
. C.
2x
= −
D.
1
2
x
= −
.
Câu 44: Nghiệm của phương trình
( )
2
log 1 3x −=
là
A.
9x =
. B.
5x =
. C.
1x
=
. D.
10x =
.
Câu 45: Tập nghiệm của phương trình
( )
2
ln 2 1 0
xx
−+ =
là
A.
{ }
0
. B.
1
0;
2
. C.
1
2
. D.
∅
.
Câu 46: Nghiệm của phương trình
( )
2
log 2 3x −=
là
A.
6x =
. B.
11x =
. C.
8x =
. D.
10
x =
.
Câu 47: Số nghiệm của phương trình
(
)
2
3
log 2 3
x
+=
là
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 48: Nghiệm của phương trình
22
log log 3 0x +=
là
A.
3x = −
. B.
1
8
x =
. C.
1
3
x =
. D.
3x =
.
Câu 49: Phương trình
( ) (
)
55
log 2 3 log 2xx+= +
A.
1x =
. B.
5x =
. C.
1x
= −
. D.
5x = −
.
Câu 50: Nghiệm của phương trình
( )
5
5
321log log
x =−
là
A.
62x =
. B.
12x =
. C.
1x =
. D.
2x =
.
Câu 51: Phương trình
2
5
log ( 2 1) 2xx
+ +=
có tập nghiệm là.
A.
{ }
4
. B.
{ }
6; 4−
. C.
{ }
4;6
. D.
{ }
2; 4−
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 67
Sưu tầm và biên soạn
Câu 52: Tập nghiệm
S
của phương trình
( ) ( )
22
log 1 log 2 1xx−= +
là
A.
{ }
0S =
. B.
{ }
2S =
. C.
{ }
2S = −
. D.
S = ∅
.
Câu 53: Số nghiệm của phương trình
( )
22
log log 1 1xx+ −=
là
A.
1
. B.
2
. C.
0
. D.
3
.
Câu 54: Tổng các nghiệm thực của phương trình
2
22
log (2 5) 2log ( 2)xx−= −
bằng
A.
1
. B.
7
3
. C.
3
. D.
16
3
.
Câu 55: Gọi
S
là tập nghiệm của phương trình
( ) ( )
2
22
2log 2 2 log 3 2xx−+ − =
trên
. Tổng các phần
tử của
S
bằng
A.
42+
. B.
8
. C.
82+
. D.
62+
.
Câu 56: Có tất cả bao nhiêu giá trị của tham số
m
để phương trình
22
33
log ( 2) log ( 1) 6 2
x x m xm m
+= − − + − +
có hai nghiệm trái dấu?
A.
4
. B.
3
. C. vô số. D.
5
.
Câu 57: Tìm tất cả các giá trị của tham số
m
để phương trình
( ) ( )
ln 2 lnx mx−=
có nghiệm
A.
01m<<
. B.
1m >
. C.
1
2
m <
. D.
1
0
2
m
<<
.
Câu 58:
Nghiệm của phương trình
22
log (2 3) log ( 1)xx−= +
là
A.
2x =
.
B.
2x = −
.
C.
4
x =
.
D.
4x = −
.
Câu 59: Số nghiệm thực của phương trình
( )
( )
3
31
3
3log 1 log 5 3xx−− − =
là
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 60: Số nghiệm của phương trình
2
22
log 2log (3 4)
xx= +
là
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 61: Nghiệm của phương trình
(
)
21
2
log log 2 1 0
xx+ −=
thuộc khoảng nào sau đây?
A.
( )
6; +∞
. B.
( )
4;6
. C.
( )
0; 2
. D.
( )
2; 4
.
Câu 62: Biết nghiệm lớn nhất của phương trình
( )
1
2
2
log log 2 1 1xx+ −=
là
2xab= +
(
, ab
là hai số
nguyên). Giá trị của
2ab+
bằng
A.
4
. B.
6
. C.
0
. D.
1
.
Câu 63: Tập nghiệm của phương trình
(
)
2
22
5
log 4 3 1 log
2
xx x
− + − −= −
là
A.
{ }
2; 4
. B.
{ }
4
. C.
{ }
2;3
. D.
{ }
2
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 68
Sưu tầm và biên soạn
Câu 64: Gọi
S
là tập nghiệm của phương trình
(
)
(
)
22
log 3 log 1 3
xx
−+ −=
. Tổng tất cả các phần tử của
S
bằng
A.
4
. B.
5
. C.
6
. D.
2
.
Câu 65: Số nghiệm của phương trình
( ) ( ) ( )
log 1 log 3 log 3xx x−+ − = +
là
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 66: Số nghiệm của phương trình
(
)
( )
2
ln 6x 7 ln 3−+= −xx
là:
A.
2
. B.
0
. C.
3
. D.
1
.
Câu 67: Tổng tất cả các nghiệm của phương trình
( )
2
22
log 1 2 logxx x++ =+
bằng
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 68: Biết nghiệm của phương trình
(
)
(
)
33
log 1 log 5 1
xx
−+ − =
có dạng
( )
,x a b ab
=+∈
. Tính
giá trị biểu thức
T ab= +
.
A.
5
T
=
. B.
4T
= −
. C.
10T =
. D.
2T = −
.
Câu 69: Số nghiệm của phương trình
(
)
( )
33
log 2 1 log 3 2
xx++ − =
là
A.
0
B.
1
. C.
2
. D.
3
.
Câu 70: Số nghiệm của phương trình
( )
( )
2
13
3
log 3 1 log 2 0xx x− −+ − =
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 71: Tổng các nghiệm của phương trình
8
42
2
11
log 3 log 1 log 4
42
x xx
là
A.
4 23
. B.
3 23
. C.
6
. D.
4
.
Câu 72: Phương trình
( ) ( )
2
3
3
log 2 log 4 0xx−+ − =
có hai nghiệm
12
,xx
. Khi đó
(
)
2
12
= −S xx
bằng
A. 1. B. 9. C. 7. D. 2.
DẠNG 3: BẤT PHƯƠNG TRÌNH MŨ
Câu 73: Tập nghiệm của bất phương trình
24
x
≤
là:
A.
(
]
;2−∞
B.
[ ]
0; 2
C.
( )
;2−∞
D.
( )
0; 2
Câu 74: Nghiệm của phương trình
35
x
<
là
A.
3
log 5x
>
. B.
3
log 3x >
. C.
3
log 5x <
. D.
3
log 3
x <
.
Câu 75: Tập nghiệm của phương trình:
1
2 .3 72
xx+
≤
là:
A.
( )
2; +∞
. B.
( )
;2−∞
. C.
(
]
;2−∞
. D.
[
)
2; +∞
.
Câu 76: Tập nghiệm của bất phương trình
24
22
xx+
<
là
A.
( )
;4−∞
. B.
( )
0; 4
. C.
( )
0;16
. D.
( )
4; +∞
.
Câu 77: Tập nghiệm của bất phương trình
39
x
>
là
A.
( )
2;+∞
. B.
( )
0;2
. C.
( )
0;+∞
. D.
( )
2;− +∞
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 69
Sưu tầm và biên soạn
Câu 78: Tập các nghiệm của bất phương trình
26
x
>
là
A.
( )
2
log 6; +∞
. B.
( )
;3−∞
. C.
( )
3; +∞
. D.
( )
2
;log 6−∞
.
Câu 79: Tập nghiệm của bất phương trình
23
1
5
25
x
+
>
là:
A.
5
;
2
− +∞
. B.
5
;
2
−∞ −
. C.
( )
0; +∞
. D.
1
;
2
− +∞
.
Câu 80: Tập nghiệm của bất phương trình
32
x
<
là
A.
( )
3
;log 2−∞
. B.
(
)
2
;log 3−∞
. C.
( )
3
log 2; +∞
. D.
( )
2
log 3; +∞
.
Câu 81: Tập nghiệm của bất phương trình
42
x
≥
là
A.
1
;.
4
+∞
B.
1
;.
4
+∞
C.
1
;.
2
+∞
D.
1
;.
2
+∞
Câu 82: Tập nghiệm của phương trình
2
1
5
5
−
≤
x
là
A.
[
)
1; +∞
. B.
(
)
;0−∞
. C.
[
)
2;
+∞
. D.
(
]
;1
−∞
.
Câu 83: Tập nghiệm của bất phương trình
1
1
2
16
x+
≥
là
A.
(
]
;5−∞ −
. B.
[
)
3; +∞
. C.
[
)
3;− +∞
. D.
[
)
5;
− +∞
.
Câu 84: Tập nghiệm của bất phương trình
( )
0,8 3
x
<
là
A.
( )
0,8
;log 3−∞
. B.
( )
3
log 2;+∞
. C.
( )
( )
3
;log 0,8−∞
. D.
( )
0,8
log 3; +∞
.
Câu 85: Tập nghiệm của bất phương trình
2
11
7 49
xx+
>
là
A.
(
)
;1−∞
. B.
( ) ( )
; 2 1;−∞ − ∪ +∞
. C.
( )
1;
+∞
. D.
( )
2;1−
.
Câu 86: Tập nghiệm của bất phương trình
2
1
9
3
x+
≥
là
A.
[
)
0;
+∞
. B.
[
)
4;
− +∞
. C.
(
]
;4−∞ −
. D.
(
]
;4−∞
.
Câu 87: Tập nghiệm của bất phương trình
1
2
3
<
x
là
A.
2
1
log ;
3
+∞
. B.
2
1
;log
3
−∞
. C.
1
3
;log 2
−∞
. D.
1
3
log 2;
+∞
.
Câu 88: Tập nghiệm của bất phương trình
0,6 3
x
>
là
A.
( )
0,6
;log 3−∞
. B.
( )
0,6
log 3; +∞
. C.
( )
3
;log 0, 6
−∞
. D.
( )
3
log 0, 6;+∞
.
Câu 89: Tập nghiệm của bất phương trình
1
5
2
x
≥
là
A.
(
]
2
; log 5−∞ −
. B.
[
)
2
log 5;− +∞
. C.
[
)
5
log 2;− +∞
. D.
(
]
5
; log 2−∞ −
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 70
Sưu tầm và biên soạn
Câu 90: Tập nghiệm của bất phương trình
1
9
3
x
>
là
A.
( )
2;+∞
. B.
( )
;2−∞ −
. C.
(
)
2;
− +∞
. D.
( )
;2−∞
Câu 91: Tập nghiệm của bất phương trình
1
2
2
x
≥
là
A.
(
]
;1−∞ −
. B.
[
)
1;− +∞
. C.
( )
;1
−∞ −
. D.
( )
1;− +∞
.
Câu 92: Tập nghiệm
S
của bất phương trình
1
8
2
x
<
là
A.
( )
;3S = −∞ −
. B.
( )
3;S = +∞
. C.
( )
3;S = − +∞
. D.
( )
1; 3S =
.
Câu 93: Tập nghiệm của bất phương trình
1
8
3
x
≤
là
A.
1
3
;log 8
−∞
. B.
(
]
;2−∞
. C.
[
)
2;+∞
. D.
1
3
log 8;
+∞
.
Câu 94: Tập nghiệm của bất phương trình
0.5 4
x
là
A.
;2
. B.
;2
. C.
2;
. D.
2;
.
Câu 95: Tìm số nghiệm nguyên của bất phương trình
2
16
3 81
x−
≥
.
A. 9. B. 4. C. 7. D. 5.
Câu 96: Tập nghiệm của bất phương trình
21
5 125
x
là
A.
3;
. B.
1
;
2
. C.
1
;
3
. D.
2;
.
Câu 97: Tập nghiệm của bất phương trình
2
2
4 64
xx−
<
là
A.
( )
1; 3−
. B.
( ) ( )
; 1 3;−∞ − ∪ +∞
.
C.
( )
;1−∞ −
. D.
( )
3; +∞
.
Câu 98: Tập nghiệm của bất phương trình
12
1
3. 1
2
x
−
<
là
A.
1
2
11 1
; log
22 3
−∞ +
. B.
1
2
11 1
log ;
22 3
− +∞
.
C.
1
2
11 1
; log
22 3
−∞ −
. D.
1
2
11
; log
23
−∞ −
.
Câu 99: Giải bất phương trình
2
4
3
1
4
x −
≥
ta được tập nghiệm
T
. Tìm
T
.
A.
[ ]
2; 2T = −
. B.
[
)
2;T = +∞
.
C.
(
]
;2T = −∞ −
. D.
(
] [
)
; 2 2;T = −∞ − ∪ +∞

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 71
Sưu tầm và biên soạn
Câu 100: Bất phương trình
23
xx
>
có tập nghiệm là
A.
( )
0;1S =
. B.
( )
;0S = −∞
. C.
( )
1;S = +∞
. D.
( )
1;1S = −
.
Câu 101: Tập nghiệm
S
của bất phương trình
1
8
2
x
>
là
A.
( )
3; .S = +∞
B.
( )
3; .S = − +∞
C.
( )
; 3.S = −∞ −
D.
( )
;3 .S = −∞
Câu 102: Tập nghiệm của bất phương trình
1
25
52
x−
<
là
A.
( )
0; +∞
. B.
(
)
;0−∞
. C.
( )
;2−∞
. D.
( )
2; +∞
.
Câu 103: Tập nghiệm của bất phương trình
11
28
x
<
là
A.
( )
3; +∞
. B.
( )
;3−∞
. C.
[
)
3; +∞
. D.
(
]
;3−∞
.
Câu 104: Tập nghiệm của bất phương trình
13
33
44
xx− −+
>
là
A.
( )
2; +∞
. B.
( )
;2−∞
. C.
[
)
2;
+∞
. D.
(
]
;2−∞
.
Câu 105: Tập nghiệm của bất phương trình
1
11
5 125
x−
≤
là
A.
( )
3; +∞
. B.
[
)
4; +∞
. C.
(
]
;4−∞
. D.
( )
;4−∞
.
Câu 106: Tìm tập nghiệm của bất phương trình
2
4
1
2
2
xx
x
−
−
>
bằng
A.
( )
2;− +∞
. B.
( ) (
)
; 2 2;−∞ − ∪ +∞
. C.
( )
2; +∞
. D.
( )
2; 2−
Câu 107: Số nghiệm nguyên của bất phương trình
2
3x
52
1
5
5
x
−
+
<
là
A.
3
. B.
1
. C.
2
. D.
4
.
Câu 108: Tập nghiệm của bất phương trình
2 27
39
xx++
<
là
A.
( )
;4−∞ −
. B.
( )
4;− +∞
. C.
( )
;5−∞ −
. D.
(
)
5:− +∞
.
Câu 109: Tập nghiệm của bất phương trình
2
1
1
e
e
xx−−
<
là
A.
( )
1; +∞
. B.
( )
1; 2
. C.
( )
0;1
. D.
( )
;0−∞
.
Câu 110: Tìm tập nghiệm
S
của bất phương trình
1 3x
2 25
54
−
≥
.
A.
(
]
,1S = −∞
. B.
1
,
3
S
= +∞
. C.
1
,
3
S
= −∞
. D.
[
)
1,S = +∞
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 72
Sưu tầm và biên soạn
Câu 111: Tập nghiệm
S
của bất phương trình
2
1
5
25
x
x
−
+
≥
là
A.
( )
1;S = +∞
. B.
(
]
;2S = −∞
. C.
[
)
2;
S = +∞
. D.
( )
;2S = −∞
.
Câu 112: Bất phương trình
3
31
29
34
−−
<
xx x
tương đương với bất phương trình nào sau đây?
A.
3
5 20
− −<
xx
. B.
3
5 20
− +<
xx
. C.
3
20− ++<xx
. D.
3
20− −−<xx
.
Câu 113: Tập nghiệm của phương trình
22
2
1
5
5
x
x
−
+
>
là:
A.
( )
;4 .−∞
B.
( )
0; .+∞
C.
( )
4; .+∞
D.
(
)
; 4.−∞ −
Câu 114: Tập nghiệm của bất phương trình
2021
1
2
2
x
>
là
A.
( )
;2021−∞ ⋅
B.
(
)
; 2021−∞ − ⋅
C.
( )
2021;− +∞ ⋅
D.
( )
2021;+∞ ⋅
Câu 115: Tập nghiệm của bất phương trình
1
4
1
11
22
x−
<
là
A.
( )
2;
S = +∞
. B.
5
1;
4
S
=
. C.
( )
0;1S =
. D.
( )
;0S = −∞
.
Câu 116: Tìm tập nghiệm
S
của bất phương trình
2
3
11
24
xx−+
<
.
A.
[ ]
1;2S =
. B.
( )
;1S = −∞
. C.
( )
1;2S =
. D.
( )
2;S = +∞
.
Câu 117: Bất phương trình
2
4
11
2 32
xx+
>
có tập nghiệm là
( )
;S ab=
, khi đó
ba
−
là?
A.
4
. B.
2
. C.
6
. D.
8
.
Câu 118: Tập hợp tất cả các giá trị thực của tham số
m
để bất phương trình
( ) ( )
( )
2
31 2 1
23 23
x x mx−− +
+ >−
đúng
x∀∈
có dạng
( )
,ab
. Tính
S ab= +
?
A.
2
. B.
5
2
. C.
2−
. D.
3
.
Câu 119: Tập nghiệm của bất phương trình
21
1
(3 9)(3 ) 3 1 0
27
xx x+
− − −≤
chứa bao nhiêu số nguyên ?
A. 2. B. 3. C. 4. D. 5.
DẠNG 4: BẤT PHƯƠNG TRÌNH LOGARIT
Câu 120: Nghiệm của bất phương trình
( )
2
log 1 3x −>
A.
9x >
. B.
19x<<
. C.
10x >
. D.
1 10x<<
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 73
Sưu tầm và biên soạn
Câu 121: Tập nghiệm của bất phương trình
2
log 3x ≤
là
A.
(
]
0;8
. B.
(
]
;8
−∞
. C.
(
]
0;9
. D.
( )
0;8
.
Câu 122: Tập nghiệm của bất phương trình
( )
2
log x 1 3+<
là
A.
( )
;8S = −∞
. B.
(
)
;7
S
= −∞
. C.
( )
1; 8S = −
. D.
( )
1; 7S = −
.
Câu 123: Bất phương trình
2
log 3x <
có tập nghiệm là
A.
(
)
8; +∞
. B.
( )
;8−∞
. C.
( )
0;8
. D.
( )
;6−∞
.
Câu 124: Tìm tập nghiệm của bất phương trình
( )
2
5
log 4 1 0x − +>
A.
13
4;
2
. B.
13
4;
2
. C.
13
;
2
−∞
. D.
13
;
2
+∞
.
Câu 125: Tập nghiệm của bất phương trình
3
log 1 1
x
là
A.
;4
. B.
;4
. C.
1; 4
. D.
0; 4
.
Câu 126: Tập nghiệm của bất phương trình
( )
2
log 3 1 3x −<
là
A.
( )
;3−∞
. B.
1
;3
3
. C.
1
;3
3
. D.
( )
3; +∞
.
Câu 127: Tập nghiệm của bất phương trình
3
log 2x ≤
là
A.
( )
;9
−∞
. B.
(
)
0;6
. C.
( )
;6−∞
. D.
(
]
0;9
.
Câu 128: Bất phương trình
( )
2021
log 1 0x −≤
có bao nhiêu nghiệm nguyên?
A.
1
. B.
2022
. C.
2
. D.
0
.
Câu 129: Giải bất phương trình
2
log ( 1) 5.x
−>
A.
33.x >
B.
33.x <
C.
11.x <
D.
11.x >
Câu 130: Tập nghiệm của bất phương trình
2
3
log 2x >
là
A.
4
0;
9
. B.
4
;
9
+∞
. C.
( )
3
4;+∞
. D.
4
;
9
−∞
.
Câu 131: Tập nghiệm của bất phương trình
1
2
log ( 2) 1x −>
là
A.
5
2;
2
. B.
5
;
2
+∞
. C.
5
2;
2
. D.
5
;
2
−∞
Câu 132: Tập nghiệm của bất phương trình
( )
1
3
log 3 2x − <−
.
A.
( )
;12−∞
. B.
( )
12;+∞
. C.
( )
3;12
. D.
7
;
3
−∞
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 74
Sưu tầm và biên soạn
Câu 133: Tìm tập nghiệm
S
của bất phương trình
( )
( )
11
33
log 1 log 2 3xx−> +
.
A.
2
;
3
S
= −∞ −
. B.
2
;
3
S
= − +∞
. C.
2
;1
3
S
= −
. D.
( )
1;S = +∞
.
Câu 134: Tập nghiệm của bất phương trình
( )
( )
11
22
log 3 2 log 4xx−> −
là
A.
2
;3
3
S
=
. B.
3
;
2
S
= −∞
. C.
23
;
32
S
=
. D.
3
;4
2
S
=
.
Câu 135: Tập nghiệm của bất phương trình
( )
2
1
2
log 5 7 0xx−+>
là
A.
( )
(
)
; 2 3;
−∞ ∪ + ∞
. B.
( )
3; +∞
. C.
( )
;2−∞
. D.
( )
2;3
.
Câu 136: Tập nghiệm của bất phương trình
(
) ( )
log 2 log 6xx
<+
là:
A.
( )
6; +∞
. B.
(0; 6)
. C.
[0; 6)
. D.
( )
;6−∞
.
Câu 137: Tập nghiệm của bất phương trình
( )
1
2
log 1 0x +≥
là
A.
[
)
0; +∞
. B.
(
]
;0−∞
. C.
1
1;
2
−
. D.
(
]
1; 0
−
.
Câu 138: Tập nghiệm
S
của bất phương trình
( ) ( )
11
55
log 1 log 2 1xx+< −
là
A.
1
;2
2
S
=
. B.
(
)
;2S = −∞
. C.
( )
2;S = +∞
. D.
( )
1; 2S
= −
.
Câu 139: Tập nghiệm
S
của bất phương trình
( )
22
log 2 1 logxx
−>
là
A.
1
;
2
S
= +∞
. B.
( )
0;1S =
. C.
( )
0;S = +∞
. D.
( )
1;S = +∞
.
Câu 140: Có bao nhiêu số nguyên dương thuộc tập nghiệm của bất phương trình
( )
2
3
log 31 3x−≥
?
A.
5
. B.
4
. C.
3
. D.
2
.
Câu 141: Tập nghiệm của bất phương trình
( )
2
1
2
log 3 2xx− ≤−
là
A.
(
] [
)
; 1 4;
−∞ − ∪ +∞
. B.
( ) ( )
; 0 3;−∞ ∪ +∞
. C.
[ ]
1; 4−
. D.
[
) (
]
1; 0 3; 4−∪
.
Câu 142: Bất phương trình
( ) (
)
11
22
log 2 3 log 5 2
xx−< −
có tập nghiệm là
( )
;ab
. Tính giá trị
S ab= +
.
A.
=
11
2
S
. B.
=
7
2
S
. C.
=
13
2
S
. D.
=
9
2
S
.
Câu 143: Tập nghiệm của bất phương trình
( )
( )
2
13
3
log 6 5 log 1 0xx x− ++ −≤
là
A.
(
]
5; 6S =
. B.
( )
1;S
= +∞
. C.
[ ]
1; 6
S =
. D.
[
)
6;S = +∞
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 75
Sưu tầm và biên soạn
Câu 144: Bất phương trình
( )
(
)
22
log 3 2 log 6 5
xx−> −
có tập nghiệm là
A.
1
;3 .
2
B.
(
)
3;1 .
−
C.
( )
0; .+∞
D.
6
1; .
5
Câu 145: Tập nghiệm của bất phương trình
( ) ( )
66
log 2 log 7 2
ππ
−> −xx
là
A.
( )
3; .+∞
B.
( )
2;3 .
C.
(
)
;3 .−∞
D.
7
3; .
2
Câu 146: Tập nghiệm của bất phương trình
( )
2
2
2
log 2 logxx x−≤
là
A.
1
;1
2
. B.
(0;1)
. C.
[ ]
0;1
. D.
1
;1
2
.
Câu 147: Tập nghiệm của bất phương trình
( ) ( )
12
2
log 1 log 5 2 0xx
++ − ≥
là:
A.
4
1;
3
−
. B.
4
;
3
−∞
C.
45
;
32
. D.
4
1;
3
−
.
Câu 148: Bất phương trình
2
22
1 log ( 2) log ( 3 2)x xx
+ −> −+
có tập nghiệm là
A.
( )
3; .
S = +∞
B.
(
)
2;3 .S =
C.
( )
2; .S = +∞
D.
( )
1; 3 .S =
Câu 149: Bất phương trình
( )
( )
2
42
log 4 log 8xx x−> −
có bao nhiêu nghiệm nguyên?
A. vô số. B.
2
. C.
3
. D.
1
.
Câu 150: Tập nghiệm
S
của bất phương trình
( ) ( )
28
log 11 5 3log 1 0xx
− − −≥
là
A.
5
1;
3
S
=
. B.
(
]
1; 2S =
. C.
11
2;
5
S
=
. D.
5 11
;
35
S
=
.
Câu 151: Tập nghiệm của bất phương trình
( ) ( )
13
3
log 1 log 11 2 0xx−+ − ≥
là
A.
(
]
1; 4S =
. B.
11
3;
2
S
=
. C.
(
]
;4S
= −∞
. D.
(
)
1; 4
S =
.
Câu 152: Tập nghiệm
S
của bất phương trình
( )
(
)
2
0,5 2
log 8 3 log 0x xx
− + −≤
là
A.
[ ]
4; 2−
. B.
[
)
8
4;1 2;
3
S
=−∪
. C.
( )
0;1
S =
. D.
[
) (
]
4; 0 1; 2S =−∪
.
Câu 153: Bất phương trình
21
3
37
log log 0
3
x
x
−
≥
+
có tập nghiệm là
(
]
;ab
. Tính giá trị
3P ab= −
.
A.
4P = ⋅
B.
5P = ⋅
C.
7P = ⋅
D.
10P = ⋅
Câu 154: Bất phương trình
( )
2
2
3
log 2 1 0xx−+ <
có tập nghiệm là
A.
3
0;
2
S
=
. B.
( )
1
;0 ; .
2
S
= −∞ ∪ +∞
C.
( )
3
;1 ;
2
S
= −∞ ∪ +∞
. D.
3
1;
2
S
= −
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 76
Sưu tầm và biên soạn
Câu 155: Số nghiệm nguyên của bất phương trình
21
5
log log 0x
−≤
là
A. Vô số. B.
4
. C.
3
. D.
2
.
Câu 156: Tìm tập nghiệm của bất phương trình
( )
2
2
log 4 6 1−+>xx
A.
∅
.
D.
{ }
2.
C.
.
D.
{ }
\2.
Câu 157: Có bao nhiêu số nguyên
x
không vượt quá
30
thoả mãn
( )
( )
2
1
5
9 3 log 23 2 0?
x xx
x
++
− + −≤
A.
30
. B.
15
. C.
32
. D.
16
.
Câu 158: Có bao nhiêu số nguyên
x
thỏa mãn
( )
( )
2
3
2 4 log 25 3 0
xx
x− + −≤
?
A.
24
. B.
26
. C.
25
. D. Vô số.
Câu 159: Số nghiệm nguyên của bất phương trình
( )
2
log log (4 6) 1
x
x
−≤
là
A. 1. B. 0. C. 4. D. Vô số.
Câu 160: Có bao nhiêu số nguyên dương
y
sao cho ứng với mỗi
y
đều có nhưng không quá
5
số nguyên
x
thỏa mãn
( )( )
10
2 2 2 11 0
xx
y yx− − −<
?
A.
992
. B.
961
. C.
481
. D.
1921
.
Câu 161: Có bao nhiêu số nguyên
x
thỏa mãn
(
)
( )
2
3
2 4 log 25 3 0
xx
x− + −≤
?
A.
24
. B. Vô số. C.
25
. D.
26
.
Câu 162: Bất phương trình
(
)
(
)
3
9 ln 5 0
xxx
− +≤
có bao nhiêu nghiệm nguyên dương?
A.
3
. B.
7
. C.
6
. D. Vô số.
Câu 163: Có bao nhiêu giá trị nguyên dương của
y
để tập nghiệm của bất phương trình
( )
( )
2
log 2 2 0
x
xy− −<
có ít nhất
1
số nguyên và không quá
6
số nguyên?
A.
2048
. B.
2016
. C.
1012
. D.
2023
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 1
Sưu tầm và biên soạn
BÀI 4: PHƯƠNG TRÌNH – BẤT PHƯƠNG TRÌNH – MŨ – LOGARIT
DẠNG 1: PHƯƠNG TRÌNH MŨ
Câu 1: Nghiệm của phương trình
35
2 16
x−
=
là
A.
3x =
. B.
2x
=
. C.
7x =
. D.
1
3
x =
.
Lời giải
Ta có
35 35 4
2 16 2 2 3 5 4 3
xx
xx
−−
= ⇔ = ⇔ −=⇔ =
.
Câu 2: Tập nghiệm của bất phương trình
2
23
21
xx−−
=
là
A.
{ }
1; 3S = −
. B.
{ }
2S =
. C.
{ }
1; 3S = −
. D.
{ }
0S =
.
Lời giải
Ta có
2
23 2
1
2 1 2 30
3
xx
x
xx
x
−−
= −
=⇔ − −=⇔
=
.
Tập nghiệm của bất phương trình
2
23
21
xx−−
=
là
{ }
1; 3S = −
.
Câu 3:
2x =
là nghiệm của phương trình nào sau đây?
A.
38
x
=
. B.
4 16
x
=
. C.
3
9x =
. D.
16 4
x
=
.
Lời giải
2
4 16 4 4 2.
xx
x= ⇔ = ⇔=
Câu 4: Tìm tất cả các giá trị của tham số
m
để phương trình
1
1
3
x
m
= −
có nghiệm
A.
0m <
hoặc
1m =
. B.
1m >
. C.
0m ≥
. D.
01m<≤
.
Lời giải
Phương trình có nghiệm
10 1mm⇔ −> ⇔ >
.
Câu 5: Phương trình nào sau đây vô nghiệm?
A.
21=
x
. B.
23=
x
. C.
20=
x
. D.
23=
xx
.
Lời giải
Ta có: hàm số mũ luôn dương
CHƯƠNG
VI
HÀM SỐ MŨ
VÀ HÀM SỐ LOGARIT
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 2
Sưu tầm và biên soạn
Vậy
20=
x
vô nghiệm.
Câu 6: Nghiệm của phương trình
31
x
=
là
A.
0x =
. B.
1x
=
. C.
2x =
. D.
1
x
= −
.
Lời giải
Ta có
0
3133 0
xx
x
=⇔ = ⇔=
.
Câu 7: Phương trình
(
)
36
31
x
−
=
có nghiệm là:
A.
0
x =
. B.
2
x
=
. C.
7
3
x =
. D.
6x =
.
Lời giải
Phương trình
( )
36
3 1 3 60 2
x
xx
−
=⇔ −=⇔=
.
Câu 8: Nghiệm của phương trình
2
35
x
=
là
A.
5
log 3
2
. B.
3
log 5
2
. C.
125
2
. D.
5
2log 3
.
Lời giải
Ta có
2
3
3
log 5
3 5 2 log 5
2
x
xx
=⇔ = ⇔=
.
Câu 9: Số nghiệm của phương trình
2
2
31
xx
−
=
là
A.
0
. B.
2
. C.
3
. D. 4.
Lời giải
Ta có:
2
2
31
xx−
=
2
20
33
xx
−
⇔=
2
20xx⇔−=
0
2
x
x
=
⇔
=
.
Câu 10: Nghiệm của phương trình
1
3 27
x−
=
là
A.
5x =
. B.
4
x =
. C.
3x =
. D.
2x =
.
Lời giải
Ta có
1
3 27 1 3 4.
x
xx
−
= ⇔ −= ⇔ =
Vậy
4x =
là nghiệm của phương trình.
Câu 11: Nghiệm của phương trình
3
2 64
x
=
là
A.
2
. B.
4
. C.
3
. D.
5
.
Lời giải
Ta có
3 36
2 64 2 2 3 6 2
xx
xx= ⇔ = ⇔ =⇔=
.
Câu 12: Nghiệm của phương trình
23 7
22
xx++
=
là:
A.
10
3
x =
. B.
4
3
x =
. C.
4x =
. D.
10x
=
.
Lời giải
Ta có
23 7
2 2 23 7 4
xx
xx x
++
= ⇔ +=+⇔=
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 3
Sưu tầm và biên soạn
Vậy phương trình có nghiệm duy nhất
4x =
.
Câu 13: Nghiệm của phương trình
1
1
5
25
x
là
A.
3
. B.
1
. C.
1
. D.
3
.
Lời giải
Ta có
1 12
1
5 5 5 12 1
25
xx
xx
.
Câu 14: Tổng bình phương các nghiệm của phương trình
2
45
39
xx−+
=
là
A.
12
⋅
B.
10⋅
C.
11⋅
D.
9
⋅
Lời giải
Ta có:
2
45
39
xx
−+
=
2
3
2
1
22
12
2
4 5 log 9
4 30
1
10.
3
xx
xx
x
xx
x
⇔ − +=
⇔ − +=
=
⇔ ⇒+=
=
Câu 15: Nghiệm của phương trình
72
x
=
là
A.
7
log 2x
=
. B.
2
log 7x =
. C.
2
7
x
=
. D.
7x =
.
Lời giải
7
7 2 log 2
x
x=⇔=
.
Câu 16: Nghiệm của phương trình
21
4 64
x+
=
là
A.
2x =
. B.
15
2
x =
. C.
15x =
. D.
1
x =
.
Lời giải
Ta có
21 21 3
4 64 4 4 2 1 3 1
xx
xx
++
= ⇔ = ⇔ += ⇔ =
.
Câu 17: Nghiệm của phương trình
5 10
x
=
là
A.
5
log 10
x =
. B.
10
log 5x =
. C.
2x =
. D.
1
2
x =
.
Lời giải
5 10
x
=
5
log 10.x
⇔=
Câu 18: Tìm tất cả các giá trị thực của
m
để phương trình
3
x
m=
có nghiệm thực.
A.
0m >
. B.
1m ≥
. C.
0m ≥
. D.
0m ≠
.
Lời giải
Để phương trình
3
x
m=
có nghiệm thực thì
0m >
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 4
Sưu tầm và biên soạn
Câu 19: Nghiệm của phương trình
2
1
1
3
9
x
x+
=
là:
A.
1
x
=
. B.
1x = −
. C.
1
5
x =
. D.
1
5
x = −
.
Lời giải
2
1
14
1
3
9
33
1
14
5
x
x
xx
x xx
+
+−
=
⇔=
−
⇔ +=− ⇔ =
Câu 20: Tổng tất cả các nghiệm của phương trình
2
22
28
xx x+−
=
bằng
A.
5−
. B.
6−
. C.
5
. D.
6
.
Lời giải
Ta có
2
22
28
xx x
+−
=
2
2 63
22
xx x+−
⇔=
2
2 63xx x⇔+=−
2
5 60xx⇔ + −=
1
6
x
x
=
⇔
= −
.
Tổng tất cả các nghiệm của phương trình là:
( )
16 5+− =−
.
Câu 21: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
59
x
m= −
có nghiệm thực?
A.
6
. B.
5
. C.
4
. D.
7
.
Lời giải
YCBT
2
9 03 3mm⇔ − > ⇔− < <
.
Do
m ∈
nên
{ 2; 1; 0;1; 2}m ∈− −
.
Câu 22: Tập nghiệm của phương trình:
2
32
31
xx−+
=
là:
A.
3
I =
. B.
{ }
1; 2
S =
. C.
{ }
1S =
. D.
{ }
2S =
.
Lời giải
Ta có:
2
32 2
1
3 1 3 20
2
xx
x
xx
x
+
=
=⇔ − +=⇔
=
.
Vậy tập nghiệm của phương trình là:
{ }
1; 2S =
Câu 23: Tất cả các giá trị của tham số
m
để phương trình
2
1
31
x
m
+
= −
có nghiệm là
A.
4m ≥
. B.
4m >
. C.
1m >
. D.
1m ≥
.
Lời giải
Ta có:
22
01
33 3 3
xx+
≥⇔ ≥
.
Phương trình
2
1
31
x
m
+
= −
có nghiệm khi và chỉ khi
13 4
mm−≥ ⇔ ≥
.
Câu 24: Số nghiệm thực của phương trình
2
22
xx−
=
là:
A.
1
. B.
3
. C.
2
. D.
0
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 5
Sưu tầm và biên soạn
Ta có :
2
22
xx−
=
0
2
x
xx
≥
⇔
= −
1x⇔=
.
Câu 25: Phương trình
2
11
5 25
xx−+
=
có tập nghiệm là
A.
{ }
1; 3
−
. B.
{
}
1; 3
. C.
{ }
3;1−
. D.
{ }
3; 1−−
.
Lời giải
Ta có
22
1 1 1 22 2
3
5 25 5 5 1 2 2
1
x xx x
x
xx
x
− + −+
=
= ⇔ = ⇔ −= + ⇔
= −
Vậy tập nghiệm của phương trình
{ }
3; 1S = −
.
Câu 26: Tổng các nghiệm của phương trình
2
2
24
xx
là:
A.
0
. B.
4
. C.
1
. D.
2
.
Lời giải
Ta có
22
2 42
0
24 22 40
4
xxxx
x
xx
x
.
Vậy tổng các nghiệm của phương trình là
404
.
Câu 27: Phương trình
2
3
3 81
xx−
=
có tổng các nghiệm là
A.
3
−
. B.
3
. C.
4−
. D.
5
−
.
Lời giải
Ta có:
2
3
3 81
xx−
=
2
1
34
4
x
xx
x
= −
⇔−=⇔
=
.
Vậy tổng các nghiệm của phương trình là
3
.
Câu 28: Số nghiệm dương của phương trình
2
4
1
9
3
xx−
=
là
A.
2
. B.
1
. C.
3
. D.
0
.
Lời giải
Ta có
2
4
22
1
94242022
3
xx
xx xx x
−
=⇔−=−⇔−+=⇔=±
.
Câu 29: Giải phương trình
( )
1
57
2
2,5
5
x
x
+
−
=
.
A.
1
x ≥
. B.
1x =
. C.
1x <
. D.
2x =
.
Lời giải
Ta có
( )
1 57 1
57
255
2,5 5 7 1 1
522
x xx
x
x xx
+ − −−
−
= ⇔ = ⇔ − =−−⇔ =
.
Câu 30: Nghiệm của phương trình
( )
9
31
5
2, 4
12
x
x
−
+
=
là

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 6
Sưu tầm và biên soạn
A.
2x = −
B.
5x = −
C.
5x =
D.
2x =
Lời giải
Ta có:
( )
9319 319
31
5 12 5 5 5
2, 4
12 5 12 12 12
x xx xx
x
− + − −− −
+
=⇔=⇔ =
31 9 4 8 2xx x x⇔− − = − ⇔ = ⇔ =
Vậy phương trình đã cho có nghiệm duy nhất một nghiệm
2x =
.
Câu 31: Gọi
12
,
xx
là hai nghiệm của phương trình
2
23
1
1
7
7
xx
x
−−
+
=
. Khi đó
12
xx+
bằng:
A.
2−
. B.
1−
. C.
2
. D.
1
.
Lời giải
( )
2
2
23
23
1
1 1 22
2
1
1
7 7 7 1 2 3 20 .
2
7
xx
xx
xx
x
x x x xx
x
−−
− −−
++
= −
= ⇔ = ⇔+=− + +⇔ −−=⇔
=
Vậy
12
1xx+=
.
Câu 32: Cho phương trình
2
8 13
2 40
xx x
−+ −
−=
có hai nghiệm
12
;xx
. Tính
12
Sxx= +
.
A.
2S =
. B.
1S = −
. C.
4S =
. D.
5.
S = −
Lời giải
Phương trình:
2
8 13
2 40
xx x−+ −
−=
22
8 13 8 2(13)
22
2422
826 5 60
xx x xx x
xx x x x
−+ − −+ −
⇔=⇔=
⇔ −+=− ⇔ + +=
Vậy
12
5Sxx=+=−
.
Câu 33: Gọi S là tổng các nghiệm của phương trình
22 2
32 65 2 37
222 1
xx xx xx−+ ++ ++
+= +
. Khi đó S có giá trị
là:
A.
3
. B.
6−
. C.
3−
. D.
5
.
Lời giải
Ta có
( ) ( )
22 2
2 37 32 65xx xx xx+ += − + + + +
. Khi đó
.
( ) ( )
( ) ( )
22 2
2
2 2 32 2
2 22
2
22
2
32 65 2 37
32 65 65
32 65 32
32
32 65
65
222 1
2 2 2 .2 1
212210
2 10
2 1.1 2 0
12 0
xx
xx xx xx
xx xx xx
xx xx xx
xx
xx xx
xx
−+
−+ ++ ++
−+ ++ ++
−+ ++ −+
−+
−+ ++
++
+= +
⇔+= +
⇔ −− −=
−=
⇔ −− =⇔
−=
2
2
32 2
2
65
1
2 1 3 20 2
1
6 50
21
5
xx
xx
x
xx x
x
xx
x
−+
++
=
= − += =
⇔⇔ ⇔
= −
+ +=
=
= −
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 7
Sưu tầm và biên soạn
Vậy
3
S = −
.
DẠNG 2: PHƯƠNG TRÌNH LOGARIT
Câu 34: Giải phương trình
( )
3
log 1 2
x −=
.
A.
7x
=
. B.
9
x
=
. C.
8x =
. D.
10x =
.
Lời giải
Điều kiện:
1.x
>
( )
2
3
log 1 2 1 3 10.
xxx− = ⇔ −= ⇔ =
Câu 35: Nghiệm của phương trình
( )
2
log 5 3x −=
là
A.
21.
x
=
B.
11.x =
C.
13.x =
D.
14.x =
Lời giải
Điều kiện xác định:
5x >
.
Phương trình
( )
2
log 5 3 5 8 13x xx− =⇔−=⇔ =
.
Vậy phương trình có nghiệm
13x =
.
Câu 36: Phương trình
( )
3
log 1 2x +=
có nghiệm là
A.
7.x
=
B.
8.x =
C.
5.x
=
D.
9.x =
Lời giải
( )
3
2
log 1 2
13
8.
x
x
x
+=
⇔ +=
⇔=
Câu 37: Tập nghiệm
S
của phương trình
(
)
3
log 2 3 1x
+=
là
A.
{ }
1.S = −
B.
{
}
3.
S =
C.
{
}
0.S
=
D.
{ }
1.S =
Lời giải
Điều kiện:
3
2 30 .
2
xx+ > ⇔ >−
Ta có:
( )
3
log231233 0
x xx+ =⇔ +=⇔=
Vậy Tập nghiệm của phương trình
( )
3
log 2 3 1
x +=
là
{ }
0.S =
Câu 38: Nghiệm của phương trình
( )
2
log 3 4 1x −=−
là:
A.
2x =
. B.
3
2
x =
. C.
7
6
x =
. D.
5
3
x =
.
Lời giải
( )
1
2
13
log34 1342
22
xx x
−
− =−⇔ − = = ⇔ =
.
Câu 39: Nghiệm của phương trình
2
log ( 1) 3x +=
là
A.
5x =
. B.
7x =
. C.
9x =
. D.
8x =
.
Lời giải
Điều kiện:
1x >−
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 8
Sưu tầm và biên soạn
Với điều kiện đó, ta có
3
2
log ( 1) 3 1 2 8 7 (tm)
xx x
+ = ⇔ += = ⇔ =
.
Câu 40: Nghiệm của phương trình
( )
ln 3 2x =
là
A.
3
e
x
=
. B.
3
e
2
x =
. C.
3
ex =
. D.
2
e
3
x =
.
Lời giải
( )
2
2
e
ln3 23e
3
x xx=⇔ = ⇔=
.
Câu 41: Nghiệm của phương trình
( )
9
1
log 2
2
x =
là
A.
2x =
. B.
1
2
x =
. C.
1
x
=
. D.
3
2
x =
.
Lời giải
Điều kiện:
0
x >
.
Ta có:
(
)
1
2
9
13
log 2 2 9
22
x xx=⇔ = ⇔=
.
Vậy phương trình có nghiệm là
3
2
x =
.
Câu 42: Nghiệm của phương trình
( )
3
log 2 1 2
x +=
là:
A.
2x =
. B.
4x =
. C.
1
2
x = −
. D.
2x = −
.
Lời giải
Điều kiện:
1
2
x >−
.
Ta có
( )
3
log212219 4x xx+ = ⇔ += ⇔ =
Vậy phương trình có nghiệm là:
4x =
.
Câu 43: Nghiệm của phương trình
2
log 1
x = −
là
A.
2x
=
. B.
1
2
x =
. C.
2x = −
D.
1
2
x = −
.
Lời giải
Ta có
1
2
1
log 1 2
2
xx
−
=−⇔ = =
Vậy nghiệm của phương trình đã cho là
1
2
x
=
Câu 44: Nghiệm của phương trình
( )
2
log 1 3x −=
là
A.
9x =
. B.
5x =
. C.
1x =
. D.
10x =
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 9
Sưu tầm và biên soạn
Điều kiện:
1
x >
Ta có:
(
)
( )
3
2
log 1 3 1 2 9 TMxxx− = ⇔ −= ⇔ =
.
Câu 45: Tập nghiệm của phương trình
( )
2
ln 2 1 0
xx−+ =
là
A.
{
}
0
. B.
1
0;
2
. C.
1
2
. D.
∅
.
Lời giải
Phương trình đã cho tương đương với
22
0
2 11 2 0
1
2
x
xx xx
x
=
−+=⇔ − = ⇒
=
.
Do đó tập nghiệm
1
0;
2
S
=
Câu 46: Nghiệm của phương trình
( )
2
log 2 3x −=
là
A.
6x =
. B.
11x =
. C.
8x =
. D.
10x =
.
Lời giải
Ta có
( )
3
2
log 2 3 2 2 2 8 10x x xx− =⇔−= ⇔−=⇔=
.
Câu 47: Số nghiệm của phương trình
( )
2
3
log 2 3
x +=
là
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Điều kiện xác định của phương trình :
x ∈
(
)
2 2 32
3
5
log 2 3 2 3 25 ( )
5
x
x x x tm
x
=
+ =⇔ += ⇔ = ⇔
= −
Vậy, phương trình trên có hai nghiệm.
Câu 48: Nghiệm của phương trình
22
log log 3 0
x +=
là
A.
3x = −
. B.
1
8
x =
. C.
1
3
x =
. D.
3x
=
.
Lời giải
Ta có:
22 2 2
log log 3 0 log log 3
xx+=⇔=−
22
11
log log
33
xx⇔ = ⇔=
.
Câu 49: Phương trình
( ) ( )
55
log 2 3 log 2
xx+= +
A.
1x =
. B.
5x =
. C.
1x = −
. D.
5x = −
.
Lời giải
Điều kiện:
3
2 30
3
2
20
2
2
x
x
x
x
x
+>
>−
⇔ ⇔ >−
+>
>−
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 10
Sưu tầm và biên soạn
Phương trình
( ) ( )
55
log 2 3 log 2xx+= +
⇔
23 2xx+=+
⇔
1x = −
.
Vậy nghiệm của phương trình là
1x = −
.
Câu 50: Nghiệm của phương trình
( )
5 5
321log logx =−
là
A.
62x =
. B.
12x
=
. C.
1x =
. D.
2x =
.
Lời giải
( )
55
log log 3 221 213
xx
x−−⇔⇔== =
.
Câu 51: Phương trình
2
5
log ( 2 1) 2
xx+ +=
có tập nghiệm là.
A.
{ }
4
. B.
{ }
6; 4
−
. C.
{ }
4;6
. D.
{ }
2; 4−
.
Lời giải
Điều kiện:
22
2 1 0 ( 1) 0 1xx x x+ +>⇔ + >⇔∀≠−
.
Ta có:
1
22 2
5
2
6
log ( 2 1) 2 2 1 25 2 24 0 ( )
4
x
xx xx xx tm
x
= −
++=⇔++=⇔+−=⇔
=
Vậy tập nghiệm của phương trình
{ }
6; 4 .S = −
Câu 52: Tập nghiệm
S
của phương trình
( ) ( )
22
log 1 log 2 1xx−= +
là
A.
{ }
0S =
. B.
{ }
2S =
. C.
{ }
2S = −
. D.
S = ∅
.
Lời giải
Ta có:
( ) ( )
22
log 1 log 2 1xx−= +
10
12 1
x
xx
−>
⇔
−= +
1
2
x
x
>
⇔
= −
Vậy phương trình vô nghiệm hay
S
= ∅
.
Câu 53: Số nghiệm của phương trình
( )
22
log log 1 1xx+ −=
là
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải
Điêì kiện:
1x >
.
( )
22
log log 1 1xx+ −=
( )
2
log 1 1xx⇔ −=
( )
12xx⇔ −=
2
20xx⇔ −−=
1
2
x
x
= −
⇔
=

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 11
Sưu tầm và biên soạn
Đối chiếu đk chỉ có
2x =
thỏa mãn
Vậy tập nghiệm của phương trình là
{ }
2S =
Câu 54: Tổng các nghiệm thực của phương trình
2
22
log (2 5) 2log ( 2)xx−= −
bằng
A.
1
. B.
7
3
. C.
3
. D.
16
3
.
Lời giải
Điều kiện xác định:
2
5
2
x
x
>
≠
.
2 22
2 22 2
2 22
log (2 5) 2log ( 2) log (2 5) log ( 2)
3
(2 5) ( 2) 3 16 21 0 .
7
3
x x xx
x
x x xx
x
−= −⇔ −= −
=
⇔ − =− ⇔ − +=⇔
=
So sánh điều kiện suy ra phương trình có các nghiệm
1 2 12
7 16
3; .
33
x x xx
= =⇒+=
Câu 55: Gọi
S
là tập nghiệm của phương trình
( ) ( )
2
22
2log 2 2 log 3 2
xx−+ − =
trên
. Tổng các phần
tử của
S
bằng
A.
42+
. B.
8
. C.
82+
. D.
62
+
.
Lời giải
Điều kiện:
( )
2
2 20
1
3
30
x
x
x
x
−>
>
⇔
≠
−>
.
Phương trình đã cho tương đương với:
( ) ( )
22
22
log 2 2 log 3 2xx−+ −=
( )
(
)
22
2
log 4 8 4 6 9 2
xx xx
⇔ −+ −+ =
432
4 32 88 96 32 0
xxxx⇔ − + − +=
22
2
22
x
x
x
= +
⇔=
= −
. So với điều kiện, nhận
2x =
và
22x = +
.
Do đó, tập nghiệm của phương trình đã cho là:
{ }
2;2 2S = +
.
Vậy tổng các phần tử của tập
S
là:
42+
.
Câu 56: Có tất cả bao nhiêu giá trị của tham số
m
để phương trình
22
33
log ( 2) log ( 1) 6 2x x m xm m
+= − − + − +
có hai nghiệm trái dấu?
A.
4
. B.
3
. C. vô số. D.
5
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 12
Sưu tầm và biên soạn
Phương trình đã cho tương đương:
22
2
( 1) 6 2 2
x
x m xm m x
>−
− − + − +=+
.
(
)
22
2
6 0*
x
x mx m m
>−
⇔
−+−=
Yêu cầu đề bài khi và chỉ khi phương trình
( )
*
có hai nghiệm
12
,xx
thỏa
12
20xx−< < <
.
( )( ) ( )
2
12 12
2
1 2 12 1 2
.0 .0
60 0 6
2 2 0 2 40
2
4 40
xx xx
mm m
x x xx x x
m
mm
<<
− < <<
⇔ ⇔ ⇔⇔
+ + > + + +>
≠
− +>
.
Vì
m ∈
nên
{ }
1;3;4;5m ∈
.
Suy ra có
4
giá trị của tham số
m
thoả mãn điều kiện bài toán.
Câu 57: Tìm tất cả các giá trị của tham số
m
để phương trình
( )
(
)
ln 2 lnx mx−=
có nghiệm
A.
01m<<
. B.
1m >
. C.
1
2
m <
. D.
1
0
2
m<<
.
Lời giải
(
)
( )
(
)
2
20
ln 2 ln
12
2
x
x
x mx
mx
x mx
>
−>
−= ⇔ ⇔
−=−
−=
.
Phương trình
( ) ( )
ln 2 lnx mx−=
có nghiệm
⇔
phương trình
( )
12mx−=−
có nghiệm
2x >
.
Xét phương trình
( )
12mx−=−
Nếu
1m =
, vô nghiệm.
Nếu
1m ≠
,
2
1
x
m
⇔=−
−
có nghiệm
2
x >
21
21 0 00 1
1 11
m
m
m mm
⇔− >⇔+ <⇔ <⇔< <
− −−
.
Vậy
01m<<
thỏa mãn yêu cầu bài toán.
Câu 58:
Nghiệm của phương trình
22
log (2 3) log ( 1)xx−= +
là
A.
2x =
.
B.
2x = −
.
C.
4x =
.
D.
4x = −
.
Lời giải
Điều kiện
3
2
x >
PT tương đương:
2 3 1 4( / )x x x tm−= +⇔ =
Vậy phương trình có nghiệm
4x =
.
Câu 59: Số nghiệm thực của phương trình
( ) ( )
3
31
3
3log 1 log 5 3xx−− − =
là
A.
3
. B.
1
. C.
2
. D.
0
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 13
Sưu tầm và biên soạn
Điều kiện:
5x >
.
( )
( )
3
31
3
3log 1 log 5 3xx−− − =
(
) (
)
33
3log 1 3log 5 3xx⇔ −+ − =
(
) ( )
33
log 1 log 5 1xx⇔ −+ − =
(
)(
)
3
log 1 5 1xx
⇔ − −=
( )( )
1 53xx
⇔− −=
2
6 20 3 7xx x⇔ − +=⇔=±
Đối chiếu điều kiện suy ra phương trình có
1
nghiệm
37x = +
Câu 60: Số nghiệm của phương trình
2
22
log 2log (3 4)xx= +
là
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Điều kiện:
2
0
0
4
3 40
3
x
x
x
x
≠
>
⇔
>−
+>
.
2
22
log 2log (3 4)
xx= +
( )
2
22
1
3 4 8 24 16 0
2
x
xx xx
x
= −
⇒= + ⇔ + +=⇔
= −
.
So điều kiện
1x⇒=−
.
Câu 61: Nghiệm của phương trình
( )
21
2
log log 2 1 0xx+ −=
thuộc khoảng nào sau đây?
A.
( )
6; +∞
. B.
( )
4;6
. C.
( )
0; 2
. D.
( )
2; 4
.
Lời giải
( ) ( )
21 2 2
2
0
log log 2 1 0 log log 2 1 1
21
x
xx xx x
xx
>
+ −=⇔ = −⇔ ⇔=
= −
.
Câu 62: Biết nghiệm lớn nhất của phương trình
( )
1
2
2
log log 2 1 1xx+ −=
là
2xab= +
(
, ab
là hai số
nguyên). Giá trị của
2ab+
bằng
A.
4
. B.
6
. C.
0
. D.
1
.
Lời giải
Điều kiện
1
2
x >
.
( ) ( )
2
2
1 22 2
2
2
log log 2 1 1 2log log 2 1 1 log 1 4 2 0
21
x
x x x x xx
x
+ −=⇔ − −=⇔ =⇔ − +=
−
.
Nghiệm lớn nhất của phương trình là
22 2,1 24x a b ab=+ ⇒= =⇒+ =
.
Câu 63: Tập nghiệm của phương trình
( )
2
22
5
log 4 3 1 log
2
xx x
− + − −= −
là
A.
{ }
2; 4
. B.
{ }
4
. C.
{ }
2;3
. D.
{ }
2
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 14
Sưu tầm và biên soạn
ĐKXĐ:
2
4 30
5
0
2
xx
x
− + −>
−>
13
5
2
x
x
<<
⇔
<
5
1
2
x⇔< <
.
Ta có:
(
)
2
22
5
log 4 3 1 log
2
xx x
− + − −= − ⇔
( )
2
2 22
5
log 4 3 log log 2
2
xx x
−+ −= − +
.
22
4352 680x x xx x⇔− + − = − ⇔ − + =
( )
( )
2
4
xn
xl
=
⇔
=
.
Nghiệm của phương trình là:
2x =
.
Câu 64: Gọi
S
là tập nghiệm của phương trình
( ) ( )
22
log 3 log 1 3
xx−+ −=
. Tổng tất cả các phần tử của
S
bằng
A.
4
. B.
5
. C.
6
. D.
2
.
Lời giải
Đkxđ:
3
x
>
.
Khi đó:
( ) (
) (
)
( )
22 2
log 3 log 1 3 log 1 3 3x x xx−+ −=⇔ − − =
( )
( )
22
1
4 38 4 50
5
x ktm
xx xx
x tm
= −
⇔ − +=⇔ − −=⇔
=
.
Vậy tập nghiệm của phương trình là
{ }
5S =
.
Câu 65: Số nghiệm của phương trình
( ) ( ) ( )
log 1 log 3 log 3xx x−+ − = +
là
A.
0
. B.
3
. C.
2
. D.
1
.
Lời giải
TXĐ:
( )
3;D = +∞
.
Khi đó:
( ) (
) (
)
log 1 log 3 log 3−+ − = +xx x
(
)( ) ( )
log 1 3 log 3⇔ − −= +
xx x
( )
( )
13 3⇔− −=+
xx x
2
50
⇔−=xx
0
5
=
⇔
=
x
x
Kết hợp với TXĐ, phương trình có nghiệm
5
x =
.
Câu 66: Số nghiệm của phương trình
( )
( )
2
ln 6x 7 ln 3−+= −xx
là:
A.
2
. B.
0
. C.
3
. D.
1
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 15
Sưu tầm và biên soạn
( )
( )
2
22
3
30 3
ln 6 7 ln 3 5
5
6 7 3 7 10 0
2
>
−> >
− + = − ⇔ ⇔ ⇔ ⇔=
=
− +=− − + =
=
x
xx
xx x x
x
xx x xx
x
Câu 67: Tổng tất cả các nghiệm của phương trình
( )
2
22
log 1 2 logxx x++ =+
bằng
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Đk:
0x >
.
( ) ( )
( )
( )
22
2 22 2
22
log 1 2 log log 1 log 4
35
2
14 3 10
35
2
xx x xx x
x tm
xx x x x
x tm
++ =+ ⇔ ++ =
+
=
⇔ + += ⇔ − += ⇔
−
=
.
Vậy tổng các nghiệm bằng
3
.
Câu 68: Biết nghiệm của phương trình
( )
( )
33
log 1 log 5 1
xx−+ − =
có dạng
( )
,
x a b ab=+∈
. Tính
giá trị biểu thức
T ab= +
.
A.
5T =
. B.
4T = −
. C.
10
T
=
. D.
2T = −
.
Lời giải
+ Điều kiện:
5x >
.
+ Phương trình đã cho tương đương với
( )( )
33
log 1 5 log 3xx− −=
.
( )
22
33
log 6 5 log 3 6 5 3xx xx⇔ −+= ⇔−+=
.
( )
( )
2
37
6 20
37
x KTM
xx
x TM
= −
⇔ − +=⇔
= +
.
Suy ra
3
10
7
a
T ab
b
=
⇒ =+=
=
.
Câu 69: Số nghiệm của phương trình
( ) ( )
33
log 2 1 log 3 2xx++ − =
là
A.
0
B.
1
. C.
2
. D.
3
.
Lời giải
Điều kiện xác định của phương trình là
3x >
.
Ta có:
( ) ( ) (
)( )
33 3
log 2 1 log 3 2 log 2 1 3 2x x xx++ − =⇔ + − =
(
)( )
2
21 33xx⇔ + −=
2
4( )
2 5 12 0
3
()
2
x TM
xx
xL
=
⇔ −−=⇔
= −

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 16
Sưu tầm và biên soạn
Vậy phương trình có một nghiệm duy nhất
4x =
.
Câu 70: Số nghiệm của phương trình
( )
( )
2
13
3
log 3 1 log 2 0xx x− −+ − =
A.
1
. B.
3
. C.
2
. D.
0
.
Lời giải
ĐK:
2
3 10
20
xx
x
− −>
−>
( )
( )
( )
( )
( )
( )
22
13 33
3
22
33
log 3 1 log 2 0 log 3 1 log 2 0
1
log 3 1 log 2 2 3 0
3
xx x xx x
x
xx x xx
x
− −+ − =⇔− − −+ − =
= −
⇔ − − = − ⇔ − −=⇔
=
Đối chiếu với đk thì
1x = −
là nghiệm của phương trình.
Câu 71: Tổng các nghiệm của phương trình
8
42
2
11
log 3 log 1 log 4
42
x xx
là
A.
4 23
. B.
3 23
. C.
6
. D.
4
.
Lời giải
Ta có
8
42
2
11
log 3 log 1 log 4
42
x xx
22 2
0, 3
log 3 log 1 log 4
xx
xx x
22
0, 3
4
log 3 log
1
xx
x
x
x
0, 3
4
30
1
xx
x
x
x
2
2
0, 3
0, 3
4
3
6 30
1
4
2 30
3
1
xx
xx
x
x
xx
x
x
xx
x
x
1
3 23
x
x
Vậy tổng các nghiệm của phương trình là:
4 23
Câu 72: Phương trình
( ) ( )
2
3
3
log 2 log 4 0xx
−+ − =
có hai nghiệm
12
,xx
. Khi đó
( )
2
12
= −
S xx
bằng
A. 1. B. 9. C. 7. D. 2.
Lời giải
Điều kiện:
24x<≠
.
Với điều kiện trên, phương trình đã cho trở thành
( ) ( )
( )
33 3
2log 2 2log 4 0 log 2 4 0 2 4 1x x xx xx
− + −=⇔ − −=⇔ − −=

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 17
Sưu tầm và biên soạn
( )( )
( )( )
2
2
4
4
2 41
6 70
32
4
4
3
2 41
6 90
≥
≥
− −=
− +=
= +
⇔ ⇔⇔
<
<
=
− −=−
− +=
x
x
xx
xx
x
x
x
x
xx
xx
Kết hợp điều kiện, PT có nghiệm
12
3 2; 3=+=xx
. Vậy
2=S
.
DẠNG 3: BẤT PHƯƠNG TRÌNH MŨ
Câu 73: Tập nghiệm của bất phương trình
24
x
≤
là:
A.
(
]
;2
−∞
B.
[
]
0; 2
C.
( )
;2
−∞
D.
(
)
0; 2
Lời giải
Ta có
24 2
x
x≤⇔≤⇒
Tập nghiệm của bất phương trình là
(
]
;2−∞
.
Câu 74: Nghiệm của phương trình
35
x
<
là
A.
3
log 5x >
. B.
3
log 3x >
. C.
3
log 5x <
. D.
3
log 3x <
.
Lời giải
Ta có
3
3 5 log 5
x
x<⇔<
.
Câu 75: Tập nghiệm của phương trình:
1
2 .3 72
xx+
≤
là:
A.
( )
2; +∞
. B.
( )
;2−∞
. C.
(
]
;2−∞
. D.
[
)
2; +∞
.
Lời giải
Ta có:
1
2 .3 72 2 .3 .2 72 6 36 2
x x xx x
x
+
≤⇔ ≤⇔≤⇔≤
.
Vậy tập nghiệm của bất phương trình là:
(
]
;2−∞
.
Câu 76: Tập nghiệm của bất phương trình
24
22
xx+
<
là
A.
( )
;4−∞
. B.
( )
0; 4
. C.
( )
0;16
. D.
( )
4; +∞
.
Lời giải
Ta có
24
22 2 4 4
xx
xx x
+
< ⇔ <+⇔<
.
Tập nghiệm của bất phương trình
( )
;4S = −∞
.
Câu 77: Tập nghiệm của bất phương trình
39
x
>
là
A.
( )
2;+∞
. B.
( )
0;2
. C.
( )
0;+∞
. D.
( )
2;− +∞
.
Lời giải
Ta có
( )
2
3933 2 2;
xx
xx> ⇔ > ⇔ > ⇔ ∈ +∞
.
Tập nghiệm của bất phương trình
39
x
>
là
( )
2;+∞
.
Câu 78: Tập các nghiệm của bất phương trình
26
x
>
là

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 18
Sưu tầm và biên soạn
A.
( )
2
log 6; +∞
. B.
( )
;3−∞
. C.
( )
3; +∞
. D.
( )
2
;log 6−∞
.
Lời giải
26
x
>
2
log 6x
⇔>
(
)
2
log 6;
x
⇔ ∈ +∞
.
Câu 79: Tập nghiệm của bất phương trình
23
1
5
25
x+
>
là:
A.
5
;
2
− +∞
. B.
5
;
2
−∞ −
. C.
( )
0;
+∞
. D.
1
;
2
− +∞
.
Lời giải
Ta có:
23 23 2
15
5 5 5 232
25 2
xx
xx
+ +−
> ⇔ > ⇔ + >− ⇔ >−
.
Vậy tập nghiệm của bất phương trình đã cho là:
5
;
2
S
= − +∞
.
Câu 80: Tập nghiệm của bất phương trình
32
x
<
là
A.
( )
3
;log 2−∞
. B.
( )
2
;log 3−∞
. C.
(
)
3
log 2;
+∞
. D.
( )
2
log 3; +∞
.
Lời giải
Ta có
3
3 2 log 2
x
x
<⇔<
. Do đó tập nghiệm
(
)
3
;log 2S = −∞
.
Câu 81: Tập nghiệm của bất phương trình
42
x
≥
là
A.
1
;.
4
+∞
B.
1
;.
4
+∞
C.
1
;.
2
+∞
D.
1
;.
2
+∞
Lời giải
Ta có:
21
1
422 2 21
2
xx
xx≥⇔ ≥ ⇔ ≥⇔≥
Vậy
1
;.
2
S
= +∞
Câu 82: Tập nghiệm của phương trình
2
1
5
5
−
≤
x
là
A.
[
)
1;
+∞
. B.
(
)
;0−∞
. C.
[
)
2; +∞
. D.
(
]
;1−∞
.
Lời giải
Chọn D
Ta có
2
1
5 21 1
5
−
≤ ⇔ − ≤− ⇔ ≤
x
xx
Tập nghiệm của phương trình là
(
]
;1−∞
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 19
Sưu tầm và biên soạn
Câu 83: Tập nghiệm của bất phương trình
1
1
2
16
x
+
≥
là
A.
(
]
;5−∞ −
. B.
[
)
3; +∞
. C.
[
)
3;− +∞
. D.
[
)
5;− +∞
.
Lời giải
Vậy tập nghiệm của bất phương trình là
[
)
5;
− +∞
.
Câu 84: Tập nghiệm của bất phương trình
( )
0,8 3
x
<
là
A.
( )
0,8
;log 3−∞
. B.
( )
3
log 2;+∞
. C.
( )
( )
3
;log 0,8−∞
. D.
( )
0,8
log 3; +∞
.
Lời giải
( )
( )
0,8 0,8
0,8 3 log 3 log 3;
x
xx<⇒> ⇒∈ +∞
.
Câu 85: Tập nghiệm của bất phương trình
2
11
7 49
xx
+
>
là
A.
(
)
;1
−∞
. B.
( ) ( )
; 2 1;−∞ − ∪ +∞
. C.
( )
1; +∞
. D.
( )
2;1−
.
Lời giải
Ta có:
2
22
11
2 20 2 1
7 49
xx
xx xx x
+
> ⇔ +<⇔ +−<⇔−<<
Câu 86: Tập nghiệm của bất phương trình
2
1
9
3
x+
≥
là
A.
[
)
0; +∞
. B.
[
)
4;
− +∞
. C.
(
]
;4−∞ −
. D.
(
]
;4−∞
.
Lời giải
2
22
1
9 3 3 2 2 4.
3
x
x
xx
+
−−
≥ ⇔ ≥ ⇔− − ≥ ⇔ ≤−
Vậy tập nghiệm của bất phương trình là
(
]
;4S = −∞ −
Câu 87: Tập nghiệm của bất phương trình
1
2
3
<
x
là
A.
2
1
log ;
3
+∞
. B.
2
1
;log
3
−∞
. C.
1
3
;log 2
−∞
. D.
1
3
log 2;
+∞
.
Lời giải
1
3
1
2 log 2
3
<⇔>
x
x
.
Vậy tập nghiệm
1
3
log 2;
= +∞
S
.
Câu 88: Tập nghiệm của bất phương trình
0,6 3
x
>
là

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 20
Sưu tầm và biên soạn
A.
( )
0,6
;log 3
−∞
. B.
( )
0,6
log 3; +∞
. C.
( )
3
;log 0, 6−∞
. D.
( )
3
log 0, 6;+∞
.
Lời giải
Ta có
0,6
0,6 3 log 3
x
x>⇔<
.
Vậy tập nghiệm của bất phương trình đã cho là
( )
0,6
;log 3S = −∞
.
Câu 89: Tập nghiệm của bất phương trình
1
5
2
x
≥
là
A.
(
]
2
; log 5
−∞ −
. B.
[
)
2
log 5;− +∞
. C.
[
)
5
log 2;− +∞
. D.
(
]
5
; log 2−∞ −
.
Lời giải
Ta có
12
2
1
5 log 5 log 5
2
x
xx
≥⇔≤ ⇔≤−
.
Vậy tập nghiệm của bất phương trình là
(
]
2
; log 5S = −∞ −
.
Câu 90: Tập nghiệm của bất phương trình
1
9
3
x
>
là
A.
( )
2;+∞
. B.
(
)
;2−∞ −
. C.
( )
2;− +∞
. D.
( )
;2−∞
Lời giải
Ta có
1
9
3
x
>
⇔
2
33
x−
>
⇔
22xx
− > ⇔ <−
Vậy tập nghiệm của bất phương trình là:
( )
;2−∞ −
Câu 91: Tập nghiệm của bất phương trình
1
2
2
x
≥
là
A.
(
]
;1−∞ −
. B.
[
)
1;− +∞
. C.
( )
;1−∞ −
. D.
( )
1;− +∞
.
Lời giải
Ta có :
1
2
2
x
≥
22
x−
⇔≥
1x⇔ ≤−
.
Câu 92: Tập nghiệm
S
của bất phương trình
1
8
2
x
<
là
A.
( )
;3S
= −∞ −
. B.
( )
3;S = +∞
. C.
( )
3;S = − +∞
. D.
(
)
1; 3
S =
.
Lời giải
Ta có
3
1 11
83
2 22
xx
x
−
< ⇔ < ⇔ >−
.
Vậy
( )
3;S = − +∞
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 21
Sưu tầm và biên soạn
Câu 93: Tập nghiệm của bất phương trình
1
8
3
x
≤
là
A.
1
3
;log 8
−∞
. B.
(
]
;2−∞
. C.
[
)
2;+∞
. D.
1
3
log 8;
+∞
.
Lời giải
Áp dụng tính chất:
( )
0 1, 0 log
x
a
ab a b x b≤ << > ⇔≥
.
Do đó
1
3
1
8 log 8
3
x
x
≤⇔≥
. Vì vậy tập nghiệm của bất phương trình là
1
3
log 8;
+∞
Câu 94: Tập nghiệm của bất phương trình
0.5 4
x
là
A.
;2
. B.
;2
. C.
2;
. D.
2;
.
Lời giải
Ta có
0.5
0.5 4 log 4 2
x
xx
. Vậy tập nghiệm của bất phương trình là
2;
.
Câu 95: Tìm số nghiệm nguyên của bất phương trình
2
16
3 81
x−
≥
.
A. 9. B. 4. C. 7. D. 5.
Lời giải
22
16 16 4 2
3 81 3 3 12 0 2 3 2 3
xx
xx
−−
≥⇔ ≥⇔−≥⇔− ≤≤
Các nghiệm nguyên thỏa mãn là
{ }
3; 2; 1; 0;1; 2;3
x ∈− − −
.
Câu 96: Tập nghiệm của bất phương trình
21
5 125
x
là
A.
3;
. B.
1
;
2
. C.
1
;
3
. D.
2;
.
Lời giải
Ta có
21 21 3
5 125 5 5 2 1 3 2
xx
xx
.
Vậy tập nghiệm của bất phương trình đã cho là
2;
.
Câu 97: Tập nghiệm của bất phương trình
2
2
4 64
xx−
<
là
A.
( )
1; 3−
. B.
( ) (
)
; 1 3;−∞ − ∪ +∞
.
C.
( )
;1−∞ −
. D.
(
)
3; +∞
.
Lời giải
Ta có:
22
2 23 2 2
4 64 4 4 2 3 2 3 0 1 3
xx xx
xx xx x
−−
<⇔ <⇔−<⇔−−<⇔−<<
.
Vậy tập nghiệm của bất phương trình là
( )
1; 3S = −
.
Câu 98: Tập nghiệm của bất phương trình
12
1
3. 1
2
x−
<
là

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 22
Sưu tầm và biên soạn
A.
1
2
11 1
; log
22 3
−∞ +
. B.
1
2
11 1
log ;
22 3
− +∞
.
C.
1
2
11 1
; log
22 3
−∞ −
. D.
1
2
11
; log
23
−∞ −
.
Lời giải
Ta có:
12 12
11
22
1 1 1 1 11 1
3. 1 1 2 log log
2 2 3 3 22 3
xx
xx
−−
<⇔ <⇔− > ⇔<−
.
Câu 99: Giải bất phương trình
2
4
3
1
4
x −
≥
ta được tập nghiệm
T
. Tìm
T
.
A.
[ ]
2; 2T = −
. B.
[
)
2;
T = +∞
.
C.
(
]
;2T = −∞ −
. D.
(
] [
)
; 2 2;T = −∞ − ∪ +∞
Lời giải
Bất phương trình
[ ]
2
4
2
3
1 4 0 2; 2
4
x
xx
−
≥ ⇔ − ≤ ⇔ ∈−
Vậy tập nghiệm
[ ]
2; 2= −T
.
Câu 100: Bất phương trình
23
xx
>
có tập nghiệm là
A.
( )
0;1S =
. B.
( )
;0S = −∞
. C.
( )
1;S
= +∞
. D.
( )
1;1S = −
.
Lời giải
Ta có
2
103
3
2
x
xx
x
⇔ >⇔ <
>
.
Câu 101: Tập nghiệm
S
của bất phương trình
1
8
2
x
>
là
A.
( )
3; .S = +∞
B.
( )
3; .S = − +∞
C.
(
)
; 3.S = −∞ −
D.
( )
;3 .S = −∞
Lời giải
Ta có
3
1
8 2 2 3 3.
2
x
x
xx
−
>⇔ > ⇔−>⇔<−
Vậy tập nghiệm của bất phương trình là
( )
; 3.S = −∞ −
Câu 102: Tập nghiệm của bất phương trình
1
25
52
x−
<
là
A.
( )
0; +∞
. B.
( )
;0−∞
. C.
( )
;2−∞
. D.
( )
2; +∞
.
Lời giải
1 11
2 52 2
11 0
5 25 5
xx
xx
− −−
< ⇔ < ⇔ − >− ⇔ >
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 23
Sưu tầm và biên soạn
Vậy tập nghiệm của bất phương trình đã cho là
( )
0; +∞
.
Câu 103: Tập nghiệm của bất phương trình
11
28
x
<
là
A.
( )
3; +∞
. B.
(
)
;3
−∞
. C.
[
)
3; +∞
. D.
(
]
;3−∞
.
Lời giải
Ta có
3
111 1
3
282 2
xx
x
<⇔ < ⇔>
.
Vậy tập nghiệm của bất phương trình là
( )
3;S = +∞
.
Câu 104: Tập nghiệm của bất phương trình
13
33
44
xx− −+
>
là
A.
( )
2; +∞
. B.
( )
;2−∞
. C.
[
)
2; +∞
. D.
(
]
;2−∞
.
Lời giải
Vì cơ số
3
1
4
<
nên
13
33
1 324 2
44
xx
xx x x
− −+
> ⇔ − <− + ⇔ < ⇔ <
.
Vậy tập nghiệm của bất phương trình đã cho là
( )
;2−∞
.
Câu 105: Tập nghiệm của bất phương trình
1
11
5 125
x−
≤
là
A.
(
)
3; +∞
. B.
[
)
4;
+∞
. C.
(
]
;4−∞
. D.
( )
;4
−∞
.
Lời giải
Ta có:
1 13
1 11 1
13 4
5 125 5 5
xx
xx
−−
≤ ⇔ ≤ ⇔ −≥ ⇔ ≥
.
Câu 106: Tìm tập nghiệm của bất phương trình
2
4
1
2
2
xx
x
−
−
>
bằng
A.
(
)
2;− +∞
. B.
( ) ( )
; 2 2;−∞ − ∪ +∞
. C.
( )
2; +∞
. D.
( )
2; 2−
Lời giải
2
2
44
1
22 2
2
xx
x xx x
−
− −+ −
>⇔ >
2
4
x xx⇔− + > −
2
40x⇔− + >
22x⇔− < <
Câu 107: Số nghiệm nguyên của bất phương trình
2
3x
52
1
5
5
x
−
+
<
là
A.
3
. B.
1
. C.
2
. D.
4
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 24
Sưu tầm và biên soạn
Bất phương trình
2
2
3
52 3 52 2
1
555352
5
x
x xx
xx
−
++
<⇔<⇔<+
2
1
3 5 20 2
3
xx x⇔ − −<⇔−<<
.
Vì
x
∈
nên
{
}
0;1x ∈
. Vậy bất phương trình có
2
nghiệm nguyên.
Câu 108: Tập nghiệm của bất phương trình
2 27
39
xx++
<
là
A.
( )
;4−∞ −
. B.
(
)
4;− +∞
. C.
( )
;5−∞ −
. D.
( )
5:− +∞
.
Lời giải
2 27
39
xx++
<
2 4 14
33
xx++
⇔<
2 4 14xx⇔+< +
3 12x⇔− <
4x⇔ >−
.
Câu 109: Tập nghiệm của bất phương trình
2
1
1
e
e
xx−−
<
là
A.
( )
1; +∞
. B.
( )
1; 2
. C.
( )
0;1
. D.
( )
;0−∞
.
Lời giải
Ta có
22
1 11 2 2
1
e e e 11 00 1
e
xx xx
xx xx x
−− −− −
<⇔ < ⇔−−<−⇔−<⇔<<
.
Vậy tập nghiệm của bất phương trình là
( )
0;1=S
.
Câu 110: Tìm tập nghiệm
S
của bất phương trình
1 3x
2 25
54
−
≥
.
A.
(
]
,1S = −∞
. B.
1
,
3
S
= +∞
. C.
1
,
3
S
= −∞
. D.
[
)
1,S = +∞
.
Lời giải
1 3x 1 3x 2
2 25 2 2
1 3x 2 1
5 45 5
x
− −−
≥ ⇔ ≥ ⇔ − ≤− ⇔ ≥
.
Vậy tập nghiệm của bất phương trình là
[
)
1,S = +∞
.
Câu 111: Tập nghiệm
S
của bất phương trình
2
1
5
25
x
x
−
+
≥
là
A.
( )
1;S = +∞
. B.
(
]
;2S = −∞
. C.
[
)
2;S = +∞
. D.
( )
;2S = −∞
.
Lời giải
Ta có
2 22
1
5 5 5 22 2
25
x
x xx
x xx
−
++
≥ ⇔ ≥ ⇔+≥ ⇔≤
.
Câu 112: Bất phương trình
3
31
29
34
−−
<
xx x
tương đương với bất phương trình nào sau đây?
A.
3
5 20− −<xx
. B.
3
5 20− +<
xx
. C.
3
20− ++<xx
. D.
3
20− −−<xx
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 25
Sưu tầm và biên soạn
Lời giải
Ta có
33
3 1 3 22
33
2 922
3 2 2 20
3 433
x x x xx x
x x x xx
− − − −+
< ⇔ < ⇔ − >− + ⇔− + + <
.
Câu 113: Tập nghiệm của phương trình
22
2
1
5
5
x
x
−
+
>
là:
A.
( )
;4 .−∞
B.
( )
0; .+∞
C.
( )
4; .+∞
D.
( )
; 4.−∞ −
Lời giải
22
2
1
5
5
x
x
−
+
>
( )
22
21
55
x
x
−
+−
⇔>
2 22
55
xx
+−
⇔>
22 2xx⇔+> −
4.x⇔<
Vậy tập nghiệm của bất phương trình là
( )
;4 .−∞
Câu 114: Tập nghiệm của bất phương trình
2021
1
2
2
x
>
là
A.
( )
;2021−∞ ⋅
B.
( )
; 2021
−∞ − ⋅
C.
( )
2021;− +∞ ⋅
D.
( )
2021;
+∞ ⋅
Lời giải
Ta có
( )
2021 2021
1
2 2 2 2021 hay ; 2021 .
2
x
x
xx
−
>⇔>⇔<− ∈−∞−
Câu 115: Tập nghiệm của bất phương trình
1
4
1
11
22
x
−
<
là
A.
( )
2;S
= +∞
. B.
5
1;
4
S
=
. C.
( )
0;1S =
. D.
(
)
;0S = −∞
.
Lời giải
Điều kiện:
1x ≠
.
1
4
1
1 1 1 54 5
4 01
22 1 1 4
x
x
x
xx
−
−
< ⇔ >⇔ >⇔<<
−−
.
Câu 116: Tìm tập nghiệm
S
của bất phương trình
2
3
11
24
xx−+
<
.
A.
[ ]
1;2S =
. B.
( )
;1S = −∞
. C.
( )
1;2S =
. D.
( )
2;
S = +∞
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 26
Sưu tầm và biên soạn
Ta có:
22
3 32
22
1 11 1
3 2 3 20 1 2
2 42 2
xx xx
xx xx x
−+ −+
< ⇔ < ⇔− + >⇔ − +<⇔<<
.
Vậy tập nghiệm của bất phương trình đã cho là
( )
1;2S =
.
Câu 117: Bất phương trình
2
4
11
2 32
xx+
>
có tập nghiệm là
( )
;S ab=
, khi đó
ba−
là?
A.
4
. B.
2
. C.
6
. D.
8
.
Lời giải
Bất phương trình tương đương
2
45
2
11
45 5 1
22
xx
xx x
+
> ⇔ + < ⇔− < <
.
Vậy
( )
5;1 6S ba=− ⇒−=
.
Câu 118: Tập hợp tất cả các giá trị thực của tham số
m
để bất phương trình
( ) ( )
( )
2
31 2 1
23 23
x x mx−− +
+ >−
đúng
x
∀∈
có dạng
( )
,ab
. Tính
S ab= +
?
A.
2
. B.
5
2
. C.
2−
. D.
3
.
Lời giải
Ta có:
( )
( )
( )
2
31 2 1
23 23
x x mx−− +
+ >−
(
) ( )
( )
2
31 2 1
23 23
x x mx−− − +
⇔+ >+ ⇔
2
31 2 2
x x mx− − >− −
( )
2
2 3 10x mx⇔ + − +>
.
Bất phương trình
( )
2
2 3 10x mx+ − +>
, x∀∈
2
10
0
0
4 12 5 0
a
mm
>
>
⇔⇔
∆<
− +<
15
22
m⇔<<
.
15
3
22
S ab⇒ =+= + =
.
Câu 119: Tập nghiệm của bất phương trình
21
1
(3 9)(3 ) 3 1 0
27
xx x+
− − −≤
chứa bao nhiêu số nguyên ?
A. 2. B. 3. C. 4. D. 5.
Lời giải
Điều kiện
11
3 10 3 1 1
xx
x
++
− ≥ ⇔ ≥ ⇔ ≥−
.
Ta có
1x = −
là một nghiệm của bất phương trình.
Với
1x >−
, bất phương trình tương đương với
2
1
(3 9)(3 ) 0
27
xx
− −≤
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 27
Sưu tầm và biên soạn
Đặt
30
x
t = >
, ta có
2
1
( 9)( ) 0
27
tt−−≤
1
( 3)( 3)( ) 0
27
ttt
⇔− + − ≤
3
1
3
27
t
t
≤−
⇔
≤≤
. Kết
hợp điều kiện
30
x
t = >
ta được nghiệm
1
3
27
t≤≤
1
33 3 1
27
x
x⇔ ≤ ≤ ⇔− ≤ ≤
. Kết hợp
điều kiện
1
x >−
ta được
11x
−< ≤
suy ra trường hợp này bất phương trình có 2 nghiệm
nguyên.
Vậy bất phương trình đã cho có tất cả 3 nghiệm nguyên.
DẠNG 4: BẤT PHƯƠNG TRÌNH LOGARIT
Câu 120: Nghiệm của bất phương trình
( )
2
log 1 3x −>
A.
9x >
. B.
19x<<
. C.
10
x >
. D.
1 10
x
<<
.
Lời giải
Điều kiện:
1x >
( )
2
log 1 3 1 8 9x xx− >⇔−>⇔>
.
Vậy tập nghiệm của bất phương trình là
9x >
.
Câu 121: Tập nghiệm của bất phương trình
2
log 3x
≤
là
A.
(
]
0;8
. B.
(
]
;8−∞
. C.
(
]
0;9
. D.
( )
0;8
.
Lời giải
Ta có:
3
2
log 3 0 2 0 8xx x≤⇔<≤ ⇔<≤
nên tập nghiệm của bpt là
(
]
0;8
.
Câu 122: Tập nghiệm của bất phương trình
( )
2
log x 1 3+<
là
A.
( )
;8S = −∞
. B.
( )
;7S = −∞
. C.
( )
1; 8S = −
. D.
( )
1; 7S = −
.
Lời giải
Ta có:
( )
2
13log x +<
3
0 12x⇔ < +<
17x
⇔− < <
Vậy tập nghiệm của bất phương trình
( )
2
13log x
+<
là
( )
1; 7S = −
Câu 123: Bất phương trình
2
log 3x <
có tập nghiệm là
A.
( )
8; +∞
. B.
( )
;8−∞
. C.
( )
0;8
. D.
( )
;6−∞
.
Lời giải
Ta có
3
2
log 3 0 2 0 8xx x<⇔<< ⇔<<
.
Tập nghiệm của bất phương trình là
( )
0;8
.
Câu 124: Tìm tập nghiệm của bất phương trình
(
)
2
5
log 4 1 0x − +>
A.
13
4;
2
. B.
13
4;
2
. C.
13
;
2
−∞
. D.
13
;
2
+∞
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 28
Sưu tầm và biên soạn
Lời giải
Điều kiện:
40x −>
4x⇔>
.
( )
2
5
log 4 1x − >−
5
4
2
x
⇔−<
13
2
x⇔<
.
Vậy
13
4;
2
S
=
.
Câu 125: Tập nghiệm của bất phương trình
3
log 1 1x
là
A.
;4
. B.
;4
. C.
1; 4
. D.
0; 4
.
Lời giải
Ta có
( )
3
log 1 1 0 1 3 1 4x xx− ≤⇔ < −≤ ⇔< ≤
.
Câu 126: Tập nghiệm của bất phương trình
( )
2
log 3 1 3x −<
là
A.
( )
;3−∞
. B.
1
;3
3
. C.
1
;3
3
. D.
( )
3; +∞
.
Lời giải
ĐK:
1
3
x >
( )
2
log313318 3
x xx− <⇔ −<⇔<
KHĐK:
1
3
x >
1
3
3
x⇒<<
Vậy tập nghiệm của bất phương trình là
1
;3
3
Câu 127: Tập nghiệm của bất phương trình
3
log 2x ≤
là
A.
( )
;9−∞
. B.
( )
0;6
. C.
(
)
;6−∞
. D.
(
]
0;9
.
Lời giải
Ta có
3
2
0
log 2 0 9
3
x
xx
x
>
≤⇔ ⇔<≤
≤
.
Tập nghiệm của bất phương trình
3
log 2x ≤
là
(
]
0;9S =
.
Câu 128: Bất phương trình
( )
2021
log 1 0x −≤
có bao nhiêu nghiệm nguyên?
A.
1
. B.
2022
. C.
2
. D.
0
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 29
Sưu tầm và biên soạn
( )
2021
0
10
1
log 1 0 1 2
2
1 2021
x
x
xx
x
x
−>
>
− ≤ ⇔ ⇔ ⇔< ≤
≤
−≤
.
Vì
x ∈
và
12x
<≤
nên
2x =
.
Câu 129: Giải bất phương trình
2
log ( 1) 5.x −>
A.
33.x >
B.
33.
x
<
C.
11.x
<
D.
11.x
>
Lời giải
Ta có:
2
2
10
1
log ( 1) 5 33
log ( 1) 5
1 32
x
x
xx
x
x
−>
>
−>⇔ ⇔ ⇔>
−>
−>
.
Câu 130: Tập nghiệm của bất phương trình
2
3
log 2x >
là
A.
4
0;
9
. B.
4
;
9
+∞
. C.
( )
3
4;+∞
. D.
4
;
9
−∞
.
Lời giải
Chọn A
Điều kiện:
0x >
Ta có
2
3
log 2x >
2
22
33
2
log log
3
x
⇔>
2
2
3
x
⇔<
4
9
x⇔<
Vậy tập nghiệm của bất phương trình là
4
0;
9
.
Câu 131: Tập nghiệm của bất phương trình
1
2
log ( 2) 1x −>
là
A.
5
2;
2
. B.
5
;
2
+∞
. C.
5
2;
2
. D.
5
;
2
−∞
Lời giải
Ta có:
1
2
log ( 2) 1
20
5
2
1
2
2
2
x
x
x
x
−>
−>
⇔ ⇔<<
−<
Câu 132: Tập nghiệm của bất phương trình
(
)
1
3
log 3 2x − <−
.
A.
( )
;12−∞
. B.
( )
12;+∞
. C.
( )
3;12
. D.
7
;
3
−∞
.
Lời giải
Điều kiện
30 3xx
−>⇔ >
( )
2
1
3
1
log 3 2 3 3 9 12
3
x x xx
−
− <−⇔−> ⇔−>⇔ >
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 30
Sưu tầm và biên soạn
Vậy tập nghiệm của bất phương trình đã cho là:
( )
12;S = +∞
Câu 133: Tìm tập nghiệm
S
của bất phương trình
(
)
(
)
11
33
log 1 log 2 3
xx−> +
.
A.
2
;
3
S
= −∞ −
. B.
2
;
3
S
= − +∞
. C.
2
;1
3
S
= −
. D.
( )
1;
S
= +∞
.
Lời giải
Bất phương trình tương đương với
10
1 23
x
xx
−>
−< +
1
2
3
x
x
<
⇔
>−
2
1
3
x⇔− < <
.
Vậy tập nghiệm của bất phương trình là:
2
;1
3
S
= −
.
Câu 134: Tập nghiệm của bất phương trình
( ) ( )
11
22
log 3 2 log 4xx−> −
là
A.
2
;3
3
S
=
. B.
3
;
2
S
= −∞
. C.
23
;
32
S
=
. D.
3
;4
2
S
=
.
Lời giải
Điều kiện:
2
3 20
2
4
3
40
3
4
x
x
x
x
x
−>
>
⇔ ⇔ <<
−>
<
.
Trong điều kiện trên, ta có
( ) ( )
11
22
3
log 3 2 log 4 3 2 4
2
x x x xx
− > − ⇔ −<− ⇔ <
.
So với điều kiện ta được
23
32
x<<
.
Vậy tập nghiệm của bất phương trình:
23
32
x<<
.
Câu 135: Tập nghiệm của bất phương trình
( )
2
1
2
log 5 7 0xx−+>
là
A.
( ) ( )
; 2 3;−∞ ∪ + ∞
. B.
( )
3; +∞
. C.
( )
;2−∞
. D.
( )
2;3
.
Lời giải
(
)
22
1
2
log 570 0 571
xx xx−+>⇔<−+<
2
2
5 60
5 70
xx
xx
− +<
⇔
− +>
23x⇔<<
.
Câu 136: Tập nghiệm của bất phương trình
(
) ( )
log 2 log 6xx<+
là:
A.
(
)
6; +∞
. B.
(0; 6)
. C.
[0; 6)
. D.
( )
;6−∞
.
Lời giải
Điều kiện xác định:
0.x >

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 31
Sưu tầm và biên soạn
Bất phương trình
266xx x
⇔ <+⇔<
. Vậy tập nghiệm của bất phương trình là:
( )
0;6
Câu 137: Tập nghiệm của bất phương trình
( )
1
2
log 1 0
x
+≥
là
A.
[
)
0; +∞
. B.
(
]
;0−∞
. C.
1
1;
2
−
. D.
(
]
1; 0
−
.
Lời giải
Điều kiện
10 1
xx+ > ⇔ >−
.
Ta có
(
)
1
2
log 1 0x
+≥
0
1
1 11 0
2
x xx
+≤ ⇔ +≤⇔ ≤
.
So điều kiện, tập nghiệm của bất phương trình là
(
]
1; 0S = −
.
Câu 138: Tập nghiệm
S
của bất phương trình
( ) ( )
11
55
log 1 log 2 1xx+< −
là
A.
1
;2
2
S
=
. B.
( )
;2S = −∞
. C.
( )
2;S = +∞
. D.
( )
1; 2
S
= −
.
Lời giải
ĐKXĐ:
1
2
x >
( )
(
)
11
55
log 1 log 2 1 1 2 1 2x x xxx
+< −⇔+> −⇔<
Kết hợp ĐKXĐ ta có
1
;2
2
S
=
Câu 139: Tập nghiệm
S
của bất phương trình
( )
22
log 2 1 logxx
−>
là
A.
1
;
2
S
= +∞
. B.
( )
0;1S
=
. C.
( )
0;S = +∞
. D.
( )
1;S = +∞
.
Lời giải
Điều kiện xác định:
1
2
x >
.
Ta có
( )
22
log 2 1 log 2 1 1x x x xx− > ⇔ −> ⇔ >
.
Kết hợp với điều kiện xác định, ta được tập nghiệm của bất phương trình là
( )
1;S = +∞
.
Câu 140: Có bao nhiêu số nguyên dương thuộc tập nghiệm của bất phương trình
( )
2
3
log 31 3x−≥
?
A.
5
. B.
4
. C.
3
. D.
2
.
Lời giải
Ta có
( )
2 22
3
log 31 3 31 27 4 0 2 2x xx x− ≥⇔−≥ ⇔−≥⇔−≤≤
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 32
Sưu tầm và biên soạn
Mà
x
nguyên dương nên
{
}
1; 2x ∈
.
Câu 141: Tập nghiệm của bất phương trình
( )
2
1
2
log 3 2xx− ≤−
là
A.
(
] [
)
; 1 4;−∞ − ∪ +∞
. B.
( ) ( )
; 0 3;
−∞ ∪ +∞
. C.
[
]
1; 4−
. D.
[
)
(
]
1; 0 3; 4−∪
.
Lời giải
ĐK:
2
3
30
0
x
xx
x
>
− >⇔
<
( )
2 22
1
2
4
log3234340
1
x
xx xx xx
x
≥
− ≤−⇔−≥⇔−−≥⇔
≤−
Vậy tập nghiệm của bất phương trình là
(
] [
)
; 1 4;S = −∞ − ∪ +∞
.
Câu 142: Bất phương trình
(
) (
)
11
22
log 2 3 log 5 2
xx−< −
có tập nghiệm là
( )
;ab
. Tính giá trị
S ab= +
.
A.
=
11
2
S
. B.
=
7
2
S
. C.
=
13
2
S
. D.
=
9
2
S
.
Lời giải
Ta có:
( )
( )
11
22
5
52 0
5
log 2 3 log 5 2 2
2
2 352
2
2
x
x
xx x
xx
x
−>
<
− < − ⇔ ⇔ ⇔<<
−>−
>
Suy ra tập nghiệm của bất phương trình là
5
2;
2
.
Khi đó:
5
2;
2
ab= =
. Vậy:
59
2
22
S
=+=
.
Câu 143: Tập nghiệm của bất phương trình
( )
( )
2
13
3
log 6 5 log 1 0xx x− ++ −≤
là
A.
(
]
5; 6S =
. B.
( )
1;S = +∞
. C.
[ ]
1; 6S =
. D.
[
)
6;S = +∞
.
Lời giải
Bất phương trình
( )
( )
2
33
log 6 5 log 1 0xx x⇔− − + + − ≤
( )
( )
2
33
log 6 5 log 1xx x⇔ −+≥ −
2
65 1
10
xx x
x
− +≥−
⇔
−>
2
1
7 60
6
6
1
1
x
xx
x
x
x
x
≤
− +≥
⇔ ⇔ ⇔≥
≥
>
>
.
Tập nghiệm của bất phương trình
[
)
6;S = +∞
.
Câu 144: Bất phương trình
( ) ( )
22
log 3 2 log 6 5xx−> −
có tập nghiệm là

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 33
Sưu tầm và biên soạn
A.
1
;3 .
2
B.
( )
3;1 .−
C.
( )
0; .+∞
D.
6
1; .
5
Lời giải
Ta có
( ) ( )
22
2
3
3 20
66
log 3 2 log 6 5 6 5 0 1
55
3 265
1
x
x
x xx x x
xx
x
>
−>
− > − ⇔ − > ⇔ < ⇔< <
−>−
>
Vậy tập nghiệm của bất phương trình là
6
1; .
5
S
=
Câu 145: Tập nghiệm của bất phương trình
( ) ( )
66
log 2 log 7 2
ππ
−> −xx
là
A.
( )
3; .+∞
B.
( )
2;3 .
C.
( )
;3 .−∞
D.
7
3; .
2
Lời giải
Ta có
( ) ( )
66
20 2
log 2 log 7 2 2 3
272 3 9
xx
xx x
x xx
ππ
−> >
− > − ⇔ ⇔ ⇔<<
−<− <
.
Câu 146: Tập nghiệm của bất phương trình
( )
2
2
2
log 2 logxx x−≤
là
A.
1
;1
2
. B.
(0;1)
. C.
[ ]
0;1
. D.
1
;1
2
.
Lời giải
ĐK:
2
20
1
2
0
xx
x
x
−>
⇔>
>
.
( )
2
2
2
log 2 logxx x−≤
( )
22
22
log 2 logxx x⇔ −≤
2 22
2 00 1xxx xx x⇔ −≤ ⇔ −≤⇔<≤
Vậy tập nghiệm là:
1
;1
2
Câu 147: Tập nghiệm của bất phương trình
( ) (
)
12
2
log 1 log 5 2 0xx++ − ≥
là:
A.
4
1;
3
−
. B.
4
;
3
−∞
C.
45
;
32
. D.
4
1;
3
−
.
Lời giải
Điều kiện:
5
1
2
x−< <
.
Với điều kiện trên bất phương trình
( ) ( )
12
2
log 1 log 5 2 0xx++ − ≥

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 34
Sưu tầm và biên soạn
( )
( )
22
log 5 2 log 1
52 1
4
3
xx
xx
x
⇔ −≥ +
⇔− ≥+
⇔≤
Kết hợp với điều kiện ta được
4
1
3
x−< ≤
.
Câu 148: Bất phương trình
2
22
1 log ( 2) log ( 3 2)
x xx
+ −> −+
có tập nghiệm là
A.
( )
3; .S = +∞
B.
( )
2;3 .S =
C.
( )
2; .S = +∞
D.
( )
1; 3 .S =
Lời giải
ĐK:
2
20
2
2
12
3 20
x
x
x
xx
xx
−>
>
⇔ ⇔>
<∨ >
− +>
.
2
22
1 log ( 2) log ( 3 2)x xx+ −> −+
( )
( )
2
22
log 2 2 log 3 2x xx⇔ −> −+
2
24 32x xx⇔ −> − +
2
5 60xx⇔ − +<
23x⇔<<
.
So điều kiện
( )
2;3 .x⇒∈
Câu 149: Bất phương trình
( )
( )
2
42
log 4 log 8xx x−> −
có bao nhiêu nghiệm nguyên?
A. vô số. B.
2
. C.
3
. D.
1
.
Lời giải
Điều kiện
2
48
40
0
80
x
xx
x
x
<<
−>
⇔
<
−>
.
Bất phương trình tương đương
22
4 16 64
x xx x−>− +
16
12 64
3
xx
⇔ > ⇔>
.
Đối chiếu điều kiện ta được
16
8
3
x
<<
suy ra có 2 nghiệm nguyên.
Câu 150: Tập nghiệm
S
của bất phương trình
( ) ( )
28
log 11 5 3log 1 0xx− − −≥
là
A.
5
1;
3
S
=
. B.
(
]
1; 2S =
. C.
11
2;
5
S
=
. D.
5 11
;
35
S
=
.
Lời giải

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 35
Sưu tầm và biên soạn
Đk:
(
)
11
11 5 0
11
1*
5
10
5
1
x
x
x
x
x
−>
<
⇔ ⇔< <
−>
>
Bất phương trình:
( ) (
) ( ) ( )
(
) ( )
( ) ( )
3
28 2
2
22
22
log 11 5 3log 1 0 log 11 5 3log 1 0
log 11 5 log 1 0
log 11 5 log 1
11 5 1
5 1 11
6 12
2
xx x x
xx
xx
xx
xx
x
x
− − −≥⇔ − − −≥
⇔ − − −≥
⇔ −≥ −
⇔ − ≥−
⇔− − ≥− −
⇔− ≥−
⇔≤
Kết hợp điều kiện
( )
*1 2x⇒< ≤
Vậy tập nghiệm
(
]
1; 2S
=
Câu 151: Tập nghiệm của bất phương trình
( ) ( )
13
3
log 1 log 11 2 0xx−+ − ≥
là
A.
(
]
1; 4S =
. B.
11
3;
2
S
=
. C.
(
]
;4S = −∞
. D.
( )
1; 4S =
.
Lời giải
Điều kiện xác định
11 2 0
10
x
x
−>
−>
Ta có:
( ) ( )
13
3
log 1 log 11 2 0xx−+ − ≥
( ) ( )
1
3
3
log 1 log 11 2 0xx
−
⇔ −+ − ≥
( )
( )
3
3
log 1 log 11 2 0
xx
⇔− − + − ≥
(
)
( )
3
3
log 11 2 log 1xx
⇔ −≥ −
11 2 1
10
xx
x
− ≥−
⇔
−>
3 12
10
x
x
− ≥−
⇔
−>
4
1
x
x
≤
⇔
>
1 4.x⇔< ≤
Câu 152: Tập nghiệm
S
của bất phương trình
( )
( )
2
0,5 2
log 8 3 log 0x xx− + −≤
là
A.
[ ]
4; 2−
. B.
[
)
8
4;1 2;
3
S
=−∪
.
C.
( )
0;1S =
. D.
[
) (
]
4; 0 1; 2S =−∪
.
Lời giải
ĐKXĐ:
2
8
8
83 0
3
1
3
1
0
0
0
x
x
x
x
xx
x
x
<
−>
<<
⇔⇔
>
−>
<
<
.
( )
1

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 36
Sưu tầm và biên soạn
Ta có:
(
)
( )
2
0,5 2
log 8 3 log 0x xx
− + −≤
( )
( )
2
11
22
log 8 3 log 0x xx⇔ − − −≤
( )
( )
2
11
22
log 8 3 logx xx⇔ −≤ −
2
83xx x⇔ −≤−
2
2 80
xx
⇔ + −≤
42x⇔− ≤ ≤
(
)
2
Từ
( )
1
và
(
)
2
ta có tập nghiệm của bất phương trình trên là
[
) (
]
4; 0 1; 2S =−∪
.
Câu 153: Bất phương trình
21
3
37
log log 0
3
x
x
−
≥
+
có tập nghiệm là
(
]
;ab
. Tính giá trị
3
P ab= −
.
A.
4P = ⋅
B.
5P = ⋅
C.
7P = ⋅
D.
10P = ⋅
Lời giải
Điều kiện:
37 7
01 5
33
x
x
x
−
< <⇔ < <
+
.
Khi đó ta có:
21 2 1 1
3 33
37 37 1 371
log log 0 log 1 log 1 log
3 3 3 33
3 7 1 8 24
0 03 3
33 3 9
x xx
x xx
xx
x
xx
− −−
≥ = ⇔ ≥= ⇔ ≤
+ ++
−−
⇔ −≤⇔ ≤⇔−<≤
++
Kết hợp với điều kiện ta có:
7
7
3 34
3
3
3
a
x P ab
b
=
<≤⇔ ⇒ = −=
=
Câu 154: Bất phương trình
( )
2
2
3
log 2 1 0xx−+ <
có tập nghiệm là
A.
3
0;
2
S
=
. B.
( )
1
;0 ; .
2
S
= −∞ ∪ +∞
C.
( )
3
;1 ;
2
S
= −∞ ∪ +∞
. D.
3
1;
2
S
= −
.
Lời giải
Ta có
( )
22
2
3
0
log210211
1
2
x
xx xx
x
<
−+ <⇔ −+>⇔
>
.
Câu 155: Số nghiệm nguyên của bất phương trình
21
5
log log 0x
−≤
là
A. Vô số. B.
4
. C.
3
. D.
2
.
Lời giải
Ta có
21 1 1
5 55
log log 0 0 log 1 1 log 0 5 1 1 5x x x xx
− ≤ ⇔ <− ≤⇔−≤ < ⇔ ≥ >⇔< ≤
.
Vậy có 4 nghiệm nguyên.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 37
Sưu tầm và biên soạn
Câu 156: Tìm tập nghiệm của bất phương trình
( )
2
2
log 4 6 1−+>xx
A.
∅.
D.
{
}
2.
C.
.
D.
{ }
\2.
Lời giải
( )
( )
2
2 2 12
2
log 461 462 440 2 0 2−+>⇔−+>⇔−+>⇔− >⇔≠xx xx xx x x
.
Vậy tập nghiệm
{ }
\2= S
.
Câu 157: Có bao nhiêu số nguyên
x
không vượt quá
30
thoả mãn
( )
( )
2
1
5
9 3 log 23 2 0?
x xx
x
++
− + −≤
A.
30
. B.
15
. C.
32
. D.
16
.
Lời giải
Điều kiện:
23
x >−
.
Trường hợp 1:
(
)
( )
2
2
2
1
22
5
1
20
9 3 0
33
21
2
2
log 23 2 0
23 25
2
x xx
x xx
x
xx
x
x
x
x
x
x
++
++
≤−
−−≥
−≤
≤
⇔ ⇔ ⇔ ⇔≥
≥
≥
+ −≥
+≥
≥
Trường hợp 2:
( )
( )
2
2
2
1
22
5
12
20
9 3 0
33
1 22
2
2
log 23 2 0
23 25
x xx
x xx
x
xx
x
x
x
x
x
++
++
−≤ ≤
−−≤
−≥
≥
⇔ ⇔ ⇔ ⇔− ≤ ≤
≤
≤
+ −≤
+≤
Từ
(
)
( )
1&2
và kết hợp điều kiện
23x >−
ta có
1x ≥−
.
Mà
, 30
xx∈≤
nên có
32
số nguyên
x
thỏa yêu cầu đề bài.
Câu 158: Có bao nhiêu số nguyên
x
thỏa mãn
( )
( )
2
3
2 4 log 25 3 0
xx
x− + −≤
?
A.
24
. B.
26
. C.
25
. D. Vô số.
Lời giải
Điều kiện:
25x >−
.
Đặt
( )
( )
( )
2
3
2 4 log 25 3
xx
fx x= − +−
.
◦
22
22
0
2 402 2 2
2
xx x x
x
xx
x
=
−=⇔ = ⇔= ⇔
=
.
◦
( ) ( )
3
33
log 25 3 0 log 25 3 25 3 2x xxx+ −=⇔ + =⇔+ = ⇔ =
.
Bảng xét dấu
Từ bảng xét dấu,
( )
25 0
0
2
x
fx
x
− <≤
≤⇔
=
.

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 38
Sưu tầm và biên soạn
Vậy có 26 số nguyên
x
thỏa yêu cầu.
Câu 159: Số nghiệm nguyên của bất phương trình
( )
2
log log (4 6) 1
x
x
−≤
là
A. 1. B. 0. C. 4. D. Vô số.
Lời giải
Điều kiện:
( )
4 44
4
2
0, 1 0, 1 0, 1
4 6 0 log 6 log 6 log 7
4 6 1 log 7
log 4 6 0
x
x
x
xx xx xx
x xx
x
>≠ >≠ >≠
−> ⇔> ⇔> ⇔>
−> >
−>
.
Ta có:
( )
22
2
log log (4 6) 1 log (4 6)
462 4260
2 3 log 3
xx
x
x x xx
x
x
x
− ≤⇔ − ≤
⇔ −≤ ⇔ − −≤
⇔ ≤⇔≤
Kết hợp với điều kiện ta có:
42
log 7 log 3x<≤
Vì
x ∈
nên bất phương trình không có nghiệm nguyên.
Câu 160: Có bao nhiêu số nguyên dương
y
sao cho ứng với mỗi
y
đều có nhưng không quá
5
số nguyên
x
thỏa mãn
( )( )
10
2 2 2 11 0
xx
y yx− − −<
?
A.
992
. B.
961
. C.
481
. D.
1921
.
Lời giải
Điều kiện xác định
11 0 11xx
−≥⇔≤
.
Theo giả thiết ta có
( )
(
)
10
2 2 2 11 0
xx
y yx− − −<
( )(
)
10
10
22
11 0
11
11
log 10 log
22
2 22 0
x
xx
x
x
x
yx y
yy
yy
−>
<
<
⇔ ⇔⇔
<< +
<<
− −<
.
Yêu cầu bài toán được thỏa mãn khi và chỉ khi
5 10
2
5 log 10 2 2≤ < ⇔ ≤<yy
.
Do
∗
∈ y
, nên số giá trị nguyên dương
y
thỏa mãn yêu cầu bài toán là
992
.
Câu 161: Có bao nhiêu số nguyên
x
thỏa mãn
( )
( )
2
3
2 4 log 25 3 0
xx
x− + −≤
?
A.
24
. B. Vô số. C.
25
. D.
26
.
Lời giải
Ta xét:
22
22
2402 2 20
xx x x
xx−=⇔ = ⇔−=
0
2
x
x
=
⇔
=
.
( ) ( )
33
25
log 25 3 0 log 25 3 2
25 27
x
xx x
x
>−
+ −=⇔ + =⇔ ⇔ =
+=
.
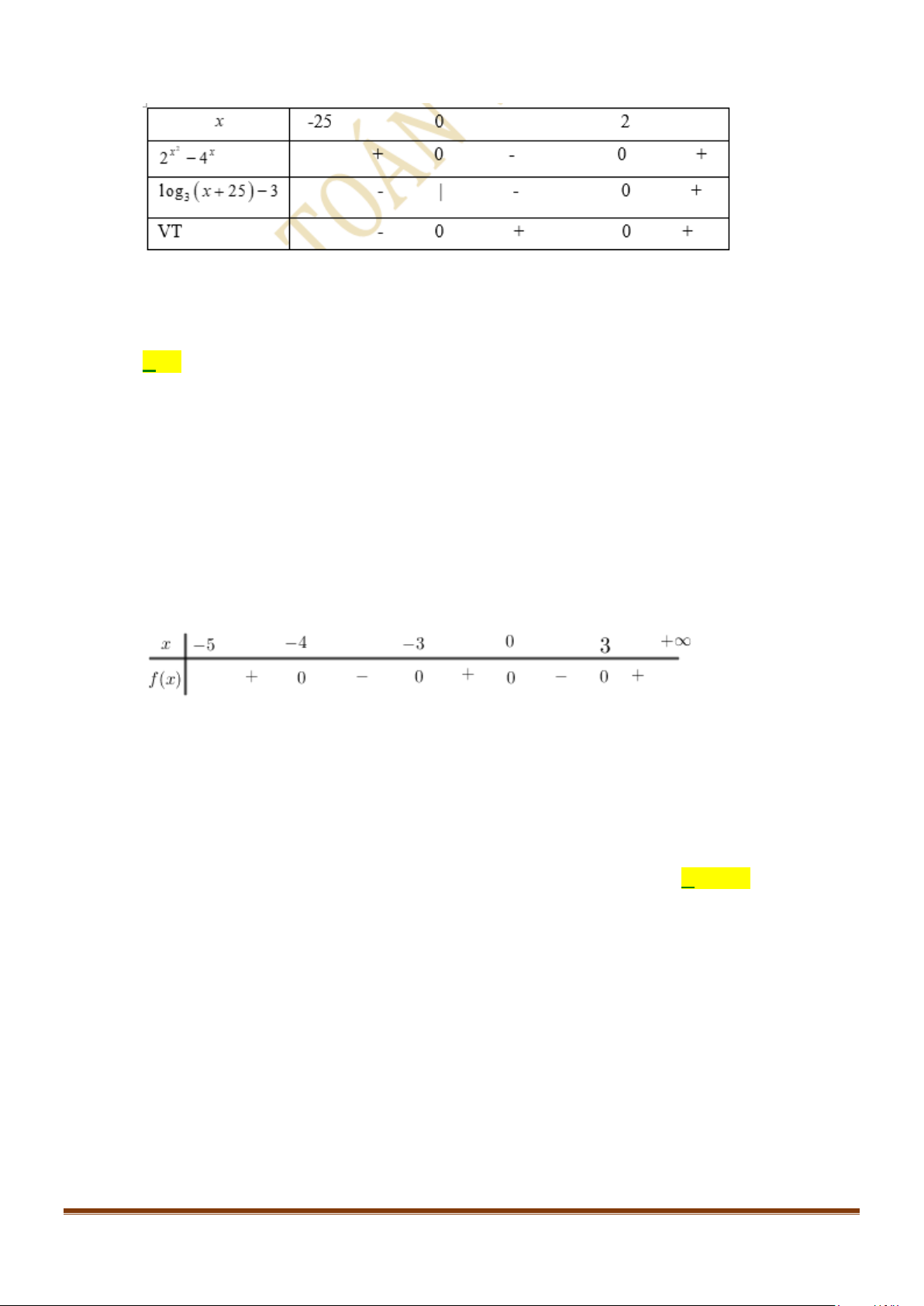
CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 39
Sưu tầm và biên soạn
Bảng xét dấu:
Suy ra
0
VT
≤
⇔
(
]
{ }
25; 0 2x ∈− ∪
. Vậy có 26 số thỏa yêu cầu bài toán.
Câu 162: Bất phương trình
( )
( )
3
9 ln 5 0xxx− +≤
có bao nhiêu nghiệm nguyên dương?
A.
3
. B.
7
. C.
6
. D. Vô số.
Lời giải
Điều kiện:
5
x >−
.
Đặt
(
)
( )
( )
3
9 ln 5fx x x x
=−+
.
( )
( )
3
3
90
0
0
3
ln 5 0
4
x
xx
x
fx
x
x
x
= −
−=
=
=⇔⇔
=
+=
= −
Bảng xét dấu:
Dựa vào bảng xét dấu ta thấy
( )
43
0
03
x
fx
x
− ≤ ≤−
≤⇔
≤≤
.
Vì
{ }
1;2;3xx
+
∈ ⇒∈
.
Câu 163: Có bao nhiêu giá trị nguyên dương của
y
để tập nghiệm của bất phương trình
(
)
( )
2
log 2 2 0
x
xy− −<
có ít nhất
1
số nguyên và không quá
6
số nguyên?
A.
2048
. B.
2016
. C.
1012
. D.
2023
.
Lời giải
Điều kiện:
0.x >
Ta có
( )
( )
2
2
2
2
2
log 2 0
4
log
20
log 2 2 0 .
log 2 0
4
log
20
x
x
x
x
x
xy
y
xy
x
x
xy
y
−<
<
>
−>
− − <⇔ ⇔
−>
>
<
−<
TH1. Nếu
2
4
.
log
x
xy
<
>
Để bất phương trình có ít nhất
1
số nguyên và không quá
6
số nguyên

CHUYÊN ĐỀ VI – TOÁN – 11 – HÀM SỐ MŨ – HÀM SỐ LOGARIT
Page 40
Sưu tầm và biên soạn
thì
2
1
3 log 3 8.
8
yy
−≤ < ⇔ ≤ <
Suy ra có
7
giá trị nguyên dương của
y
thỏa mãn.
TH2. Nếu
2
4
.
log
x
xy
>
<
Để bất phương trình có ít nhất
1
số nguyên và không quá
6
số nguyên
thì
2
5 log 11 32 2048.yy< ≤ ⇔ <≤
Suy ra có
2048 33
1 2016
1
−
+=
giá trị nguyên dương của
y
thỏa mãn.
Từ, suy ra có
2023
giá trị nguyên dương của
y
thỏa mãn yêu cầu bài toán.
Bấm Tải xuống để xem toàn bộ.




