Chuyên đề hệ thức lượng trong tam giác – Lê Bá Bảo

Tài liệu gồm 55 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, bao gồm lý thuyết, bài tập tự luận và bài tập trắc nghiệm chuyên đề hệ thức lượng trong tam giác môn Toán 10.

I. LÝ THUYẾT.
1. Định lí côsin.
2. Định lí sin.
3. Độ dài trung tuyến.
4. Diện tích tam giác.
5. Giải tam giác.

126 63 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Hệ thức lượng trong tam giác (KNTT)

Môn: Toán 10

Thông tin:

55 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 1
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
CHUY£N §Ò TR¾C NGHIÖM
M«n: To¸n 10
Chuyên đề:
HỆ THỨC LƯỢNG TRONG TAM GIÁC
Líp To¸n thÇy L£ B¸ B¶O
Trường THPT Đặng Huy Trứ S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ Trung tâm Km 10 Hương Trà, Huế
Chủ đề 2: HỆ THỨC LƯỢNG TRONG TAM GIÁC
I. LÝ THUYẾT
1. Định lí côsin
c
b
a
C
A
Xét tam giác
ABC
với
,BC a AC b
và
AB c
.
Ta có:
2 2 2 2 2 2 2 2 2
2 .cos ; 2 .cos ; 2 .cosa b c bc A b c a ca B c a b ab C
Hệ quả:
2 2 2 2 2 2 2 2 2
cos ; cos ; cos
2 2 2
b c a c a b a b c
A B C
bc ca ab
2. Định lí sin
R
O
C
B
A
Xét tam giác
ABC
với
,BC a AC b
,
AB c
với
R
là bán kính đường tròn ngoại tiếp.
Ta có:
2
sin sin sin
a b c
R
A B C
3. Độ dài trung tuyến
m
c
m
b
m
a
c
b
a
C
B
A
Xét tam giác
ABC
với
,,
abc
m m m
lần lượt là các trung tuyến kẻ từ
, , .A B C
Ta có:
2 2 2 2 2 2 2 2 2
222
222
;;
444
a b c
b c a a c b a b c
mmm

[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 2
4. Diện tích tam giác
Với tam giác
ABC
ta kí hiệu
,,
a b c
h h h
là độ dài đường cao lần lượt tương ứng với các cạnh
BC, CA, AB; R, r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp tam giác;
2
a b c
p

là
nửa chu vi tam giác; S là diện tích tam giác
ABC
.
Khi đó ta có:
C«ng thøc Herong
1 1 1
2 2 2
1 1 1
sin sin sin
2 2 2
4
( )( )( )
a b c
S ah bh ch
bc A ca B ab C
abc
R
pr
p p a p b p c
5. Giải tam giác
Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một số yếu tố của tam giác đó
được gọi là giải tam giác.
II. BÀI TẬP TỰ LUẬN
Câu 1: Cho tam giác
ABC
có
120A 
và
5, 8AB AC
. Tính độ dài cạnh
BC
.
Câu 2: Cho tam giác
ABC
có
8, 9, 6.a b c
a) Tính số đo các góc của tam giác.
b) Tính diện tích, bán kính đường tròn ngoại tiếp, bán kính đường tròn nội tiếp, độ dài các
đường cao của tam giác.
Câu 3: Cho tam giác
ABC
có
o
15 , 6Ac
và
o
120B
.
a) Tính độ dài các cạnh
,ab
;
b) Tính bán kính đường tròn ngoại tiếp và diện tích của tam giác;
c) Tính độ dài đường cao
a
h
.
Câu 4: Cho tam giác
ABC
có
14, 18, 20a b c
. Tính gần đúng góc
.ABC
Câu 5: Giải tam giác
ABC
, biết
14, 60 ,
ˆˆ
40c A B
.
Câu 6: Cho tam giác
ABC
có
OO
60 , 45 , 5B C AB
. Tính độ dài cạnh
.AC
Câu 7: Cho tam giác
ABC
có
10BC
,
30A 
. Tính bán kính đường tròn ngoại tiếp tam giác
.ABC
Câu 8: Cho tam giác có ba cạnh là
6,10,8
. Tính bán kính đường tròn nội tiếp tam giác đó.
Câu 9: Cho tam giác
ABC
vuông tại
A
có
6AB
cm,
10BC
cm. Tính bán kính đường tròn nội
tiếp tam giác đó.
Câu 10: Tính diện tích
S
của tam giác
ABC
có
4, 6, 150
ˆ
c b A
.
Câu 11: Tính diện tích tam giác có ba cạnh lần lượt là
5
,
12
,
13
.
Câu 12: Cho tam giác
ABC
có góc
B
tù,
3AB
,
4AC
và có diện tích bằng
3 3.
Tính số đo góc
.BAC
Câu 13: Tính diện tích tam giác đều nội tiếp đường tròn bán kính
4R
cm.
Câu 14: Cho tam giác
ABC
có
1, 3, 60 AB AC A
. Tính bán kính đường tròn ngoại tiếp
ABC
.
Câu 15: Cho tam giác
ABC
có
8AB
cm,
18AC
cm và có diện tích bằng
64
cm
2
. Tính
sin .A
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 3
Câu 16: Cho tam giác
ABC
có
9AB
cm,
12AC
cm và
15BC
cm. Tính độ dài đường trung
tuyến
AM
của tam giác
.ABC
Câu 17: Cho tam giác
ABC
có
5AB
,
9AC
và đường trung tuyến
6AM
. Tính độ dài cạnh
BC
.
Câu 18: Cho tam giác
ABC
có
5AB
,
8BC
,
6CA
. Gọi
G
là trọng tâm tam giác. Tính độ dài đoạn
thẳng
.CG
Câu 19: Cho tam giác có ba cạnh lần lượt là
5
,
6
,
7
. Tính độ dài đường cao ứng với cạnh có độ dài
bằng
6.
Câu 20: Cho tam giác
ABC
có các góc
105A 
,
45B 
. Tính tỉ số
AB
AC
.
Câu 21: Cho tam giác có ba cạnh lần lượt là
5,12,13.
Tính độ dài đường cao ứng với cạnh lớn nhất.
Câu 22: Cho tam giác có ba cạnh lần lượt là
2,3,4
. Góc bé nhất của tam giác có sin bằng bao nhiêu?
Câu 23: Cho tam giác
ABC
có
3AB
,
4AC
và
tan 2 2A
. Tính độ dài cạnh
.BC
Câu 24: Cho tam giác
ABC
vuông cân tại
.A
Gọi
,rR
lần lượt là bán kính đường tròn nội tiếp, ngoại
tiếp tam giác
ABC
. Tính tỉ số
.
R
r
Câu 25: Cho tam giác
ABC
có các cạnh
, , a b c
thỏa mãn
3a b c a b c ab
. Tính số đo của góc
.C
Câu 26: Tính góc
C
của tam giác
ABC
biết
ab
và
2 2 2 2
a a c b b c
.
Câu 27: Cho tam giác
ABC
có
10BC
và
sin sin sin
.
5 4 3
A B C

Tính chu vi của tam giác đó.
Câu 28: Cho tam giác
ABC
có các góc thỏa mãn
sin sin sin
12
3
A B C

. Tính số đo các góc của tam giác.
Câu 29: Cho tam giác
ABC
có
7AB
,
5AC
và
1
cos
5
BC
. Tính độ dài cạnh
.BC
Câu 30: Cho tam giác
ABC
, các đường cao
,,
a b c
h h h
thỏa mãn
32
a b c
h h h
. Chứng minh rằng:
3 2 1
.
a b c
Câu 31: Cho tam giác
ABC
. Chứng minh rằng:
a)
2 2 2
2
24
a
b c a
m

; b)
1 1 1 1
a b c
h h h r
.
Câu 32: Cho tam giác
ABC
có các góc thỏa mãn
sin 2.sin .cosC B A
. Chứng minh rằng tam giác
ABC
là một tam giác cân.
Câu 33: Cho tam giác
ABC
. Chứng minh rằng:
a)
2 2 2
cot cot cot
4
abc
A B C
S

. b)
2 2 2 2 2 2
3
4
a b c
m m m a b c
.
Câu 34: Cho tam giác
ABC
có hai trung tuyến kẻ từ
A
và
B
vuông góc. Chứng minh rằng:
a)
2 2 2
5a b c
. b)
cot 2 cot cotC A B
.
Câu 35: Cho tam giác
ABC
có
2
2 sin sinS R A B
. Chứng minh rằng tam giác
ABC
là một tam giác
vuông.
Câu 36: Cho tam giác
ABC
vuông cân tại
A
có
30AB AC
cm. Hai đường trung tuyến
BF
và
CE
cắt nhau tại
G
. Tính diện tích tam giác
.GFC
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 4
Câu 37: Cho hình bình hành có hai cạnh là
5
và
9
, một đường chéo bằng
11
. Tìm độ dài đường chéo
còn lại.
Câu 38: Cho hình bình hành
ABCD
có
,2AB a BC a
và
45BAD
. Tính diện tích hình bình
hành
.ABCD
Câu 39: Cho tam giác
ABC
vuông tại
A
có
AB AC a
. Điểm
M
nằm trên cạnh
BC
sao cho
3
BC
BM
. Tính độ dài đoạn thẳng
.AM
Câu 40: Cho hình vuông
ABCD
có cạnh bằng
a
. Gọi
E
là trung điểm cạnh
BC
,
F
là trung điểm
cạnh
AE
. Tính độ dài đoạn thẳng
DF
.
Câu 41: Cho tam giác
ABC
nội tiếp đường tròn bán kính
,R
,AB R
2.AC R
Tính góc
A
biết
A
là góc tù.
Câu 42: Cho tam giác vuông, trong đó có một góc bằng trung bình cộng của hai góc còn lại. Cạnh lớn
nhất của tam giác đó bằng
.a
Tính diện tích tam giác đã cho.
Câu 43: Cho tam giác
ABC
vuông cân tại
A
và điểm
M
trong tam giác sao cho
1,MA
2MB
,
2MC
. Tính góc
AMC
.
Câu 44: Cho góc
30xOy 
. Gọi
A
và
B
là hai điểm di động lần lượt trên
Ox
và
Oy
sao cho
2AB
.
Tính độ dài lớn nhất của đoạn
.OB
Câu 45: Để đo chiều cao của một tòa nhà, người ta chọn hai điểm
A
và
B
thẳng hàng với chân
C
của
tòa nhà, cách nhau
15
m. Sử dụng giác kế, từ
A
và
B
tương ứng nhìn thấy đỉnh
D
của tòa
nhà dưới các góc
35
và
40
so với phương nằm ngang.
Hỏi chiều cao của tòa nhà đo được là bao nhiêu mét?
Câu 46: Một tàu cá xuất phát từ đảo
A
, chạy
50
km theo hướng
24NE
đến đảo
B
để lấy thêm ngư
cụ, rồi chuyển hướng
36NW
chạy tiếp
130
km đến ngư trường
C
.
a) Tính khoảng cách từ vị trí xuất phát
A
đến
C
(làm tròn đến hàng đơn vị theo đơn vị đo
kilômét).
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 5
b) Tìm hướng từ
A
đến
C
(làm tròn đến hàng đơn vị, theo đơn vị độ).
Câu 47: Một tàu du lịch xuất phát từ bãi biển Đồ Sơn (Hải Phòng), chạy theo hướng
80NE
với vận
tốc
20
km/h. Sau khi đi được
30
phút, tàu chuyển sang hướng
20ES
giữ nguyên vận tốc và
chạy tiếp
36
phút nữa đến đảo Cát Bà.
Hỏi khi đó tàu du lịch cách vị trí xuất phát bao nhiêu kilômet?
Câu 48: Một cây cổ thụ mọc thẳng đứng bên lề một con dốc có độ dốc
10
so với phương nằm ngang.
Từ một điểm dưới chân dốc, cách gốc cây
31
m người ta nhìn đỉnh ngọn cây dưới một góc
40
so với phương nằm ngang.
Hãy tính chiều cao của cây.
Câu 49: Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình
tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính
của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả
như hình vẽ (
4,3AB
cm;
3,7BC
cm;
7,5CA
cm).
Tính gần đúng bán kính của chiếc đĩa này.
Câu 50: Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất
sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24m,
63CAD 
;
48CBD 
.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 6
Tính gần đúng chiều cao h của khối tháp.
III. BÀI TẬP TRẮC NGHIỆM
Câu 1: Cho tam giác
ABC
, khẳng định nào sau đây đúng?
A.
2 2 2
2 .cosa b c bc A
. B.
2 2 2
2 .cosa b c bc A
.
C.
2 2 2
.cosa b c bc A
. D.
2 2 2
.cosa b c bc A
.
Câu 2: Xét tam giác
ABC
tùy ý có
,,BC a AC b AB c
. Mệnh đề nào dưới đây đúng?
A.

2 2 2
cos .
2
a c b
B
ac
B.

2 2 2
cos .
2
a c b
B
ac
C.

2 2 2
cos .
a c b
B
ac
D.

2 2 2
cos .
4
a c b
B
Câu 3: Cho tam giác
ABC
có
120 .A
Đẳng thức nào sau đây đúng?
A.
2 2 2
3a b c bc
. B.
2 2 2
a b c bc
.
C.
2 2 2
3a b c bc
. D.
2 2 2
a b c bc
.
Câu 4: Cho tam giác
ABC
có
;BC a
;AB c
AC b
và có
R
là bán kính đường tròn ngoại tiếp.
Hệ thức nào sau đây là sai?
A.
2.
sin
a
R
A
B.
sin .
2
a
A
R
C.
.sin 2 .b B R
D.
.sin
sin .
cA
C
a
Câu 5: Xét tam giác
ABC
, hệ thức nào sau đây sai?
A.
.sin
sin
bA
a
B
. B.
.sin
sin
cA
C
a
. C.
2 .sina R A
. D.
.tanb R B
.
Câu 6: Cho tam giác
ABC
có
,.AB c AC b
Diện tích của tam giác
ABC
bằng
A.
cos .bc A
B.
sin .bc A
C.
1
cos .
2
bc A
D.
1
sin .
2
bc A
Câu 7: Nếu tam giác
ABC
có
2 2 2
a b c
thì:
A.
A
là góc nhọn. B.
A
là góc tù.
C.
A
là góc vuông. D.
A
là góc nhỏ nhất.
Câu 8: Cho tam giác
ABC
có
, , BC a CA b AB c
. Mệnh đề nào sau đây là đúng?
A. Nếu
2 2 2
0b c a
thì góc
A
nhọn. B. Nếu
2 2 2
0b c a
thì góc
A
tù.
C. Nếu
2 2 2
0b c a
thì góc
A
nhọn. D. Nếu
2 2 2
0b c a
thì góc
A
vuông.
Câu 9: Mệnh đề nào sau đây sai?
A. Nếu
2 2 2
a b c
thì
A
là góc tù.
B. Nếu tam giác
ABC
có một góc tù thì
2 2 2
a b c
.
C. Nếu
2 2 2
a b c
thì
A
là góc nhọn.
D. Nếu
2 2 2
a b c
thì
A
là góc vuông.
Câu 10: Cho tam giác
ABC
thỏa mãn
4 4 4
.a b c
Khẳng định nào sau đây đúng?
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 7
A. Tam giác ABC vuông tại A. B. Tam giác ABC vuông tại B.
C. Tam giác ABC tù. D. Tam giác ABC nhọn.
Câu 11: Cho tam giác
ABC
, các đường cao
,,
a b c
h h h
thỏa mãn hệ thức
32
a b c
h h h
. Tìm hệ thức giữa
, , a b c
.
A.
3 2 1
a b c

. B.
32a b c
. C.
32a b c
. D.
3 2 1
a b c

.
Câu 12: Trung tuyến
AM
của tam giác
ABC
có độ dài bằng
A.
2 2 2
b c a
. B.
2 2 2
1
22
2
b c a
. C.
2 2 2
3 2 2abc
. D.
2 2 2
22b c a
.
Câu 13: Cho tam giác
ABC
có
3 3, 3, 6AC AB BC
. Tính số đo góc
B
.
A.
60
. B.
45
. C.
30
. D.
120
.
Câu 14: Cho tam giác
ABC
có
7b
;
5c
và
3
cos
5
A
. Tính
a
.
A.
42
. B.
2
. C.
2
. D.
3
.
Câu 15: Cho tam giác
ABC
có
33AB
và bán kính đường tròn ngoại tiếp
3R
. Số đo góc
C
là
A.
60
. B.
30
. C.
90
. D.
45
.
Câu 16: Cho tam giác
ABC
có
60B 
,
45C 
,
3AB
. Tính độ dài
AC
.
A.
36
2
. B.
32
2
. C.
6
. D.
26
3
.
Câu 17: Cho tam giác
ABC
có
105BAC 
,
45ACB 
và
8AC
. Tính độ dài cạnh
AB
.
A.
86
3
. B.
42
. C.
82
. D.
4 1 3
.
Câu 18: Cho tam giác
ABC
có
9, 18AB AC
và
60A 
. Bán kính của đường tròn ngoại tiếp tam
giác
ABC
là
A.
3
. B.
93
. C.
9
. D.
6
.
Câu 19: Cho hình vuông
ABCD
có cạnh bằng
6
,
E
là trung điểm của
CD
. Tính bán kính đường tròn
ngoại tiếp tam giác
ACE
.
A.
3 10
2
. B.
35
2
. C.
3 10
. D.
35
.
Câu 20: Cho
ABC
có
45 , 75AB
. Tính tỉ số
AB
BC
.
A.
6
2
. B.
13
2
. C.
6 3 2
6
. D.
6
3
.
Câu 21: Cho tam giác
ABC
có
3, 5, 6. BC AC AB
Độ dài đường trung tuyến kẻ từ đỉnh
C
bằng
A.
2 2.
B. 5. C.
10.
D. 3.
Câu 22: Cho tam giác
ABC
có
4BC
,
5AC
và
60ACB 
. Độ dài đường trung tuyến hạ từ đỉnh
C
là
A.
61
2
. B.
51
2
. C.
3
. D.
2
.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 8
Câu 23: Cho tam giác
ABC
có chu vi bằng
32
và bán kính đường tròn nội tiếp của
ABC
bằng
5
.
Tính diện tích tam giác
ABC
.
A.
32
.
5
S
B.
40.S
C.
160.S
D.
80.S
Câu 24: Cho tam giác
ABC
có
5, 12, 13.a b c
Bán kính đường tròn ngoại tiếp
R
của tam giác
bằng
A.
13.
B.
6,5.
C.
26.
D.
7,5.
Câu 25: Cho tam giác
ABC
có
60 , 3, 4. A AB AC
Tính độ dài đường cao kẻ từ
A
của tam giác
ABC
.
A.
2 39
.
13
a
h
B.
39
.
13
a
h
C.
6 39
.
13
a
h
D.
3 39
.
13
a
h
Câu 26: Cho tam giác
ABC
có
9AB
cm,
12AC
cm và
15BC
cm. Khi đó, đường trung tuyến
AM
của tam giác
ABC
có độ dài bằng
A.
8
cm. B.
10
cm. C.
9
cm. D.
75,
cm.
Câu 27: Cho tam giác
DEF
có
10DE DF
cm và
12EF
cm. Gọi
I
là trung điểm của cạnh
EF
.
Đoạn thẳng
DI
có độ dài bằng
A.
65,
cm. B.
7
cm. C.
8
cm. D.
4
cm.
Câu 28: Cho tam giác
ABC
có
8AB
cm,
18AC
cm và có diện tích bằng
64
cm
2
. Giá trị
sin A
bằng
A.
3
2
. B.
3
8
. C.
4
5
. D.
8
9
.
Câu 29: Cho tam giác
ABC
có các góc
105A 
,
45B 
. Tính tỉ số
AB
AC
.
A.
2
2
. B.
2
. C.
2
2
. D.
6
3
.
Câu 30: Cho tam giác
ABC
có
O
5, 8, 60AB AC A
. Tính độ dài cạnh
.BC
A.
129
. B.
7
. C.
49
. D.
69
.
Câu 31: Tính diện tích tam giác có ba cạnh lần lượt là
3
,
2
và
1.
A.
3
2
. B.
3
. C.
6
2
. D.
2
2
.
Câu 32: Cho tam giác
ABC
nội tiếp đường tròn bán kính
,R
,AB R
3.AC R
Tính góc
A
, biết
B
là góc tù.
A.
30
. B.
45
. C.
60
. D.
90
.
Câu 33: Tam giác
ABC
có
14, 18, 20a b c
. Khẳng định nào sau đây đúng?
A.
42 50'B
. B.
60 56'B
. C.
119 04'B
. D.
90B
.
Câu 34: Cho tam giác
ABC
có
4AB
cm,
7BC
cm,
9CA
cm. Giá trị
cos A
bằng
A.
2
3
. B.
1
3
. C.
2
3
. D.
1
2
.
Câu 35: Cho tam giác
ABC
có
4AB
,
5AC
,
6BC
. Tính
cos .BC
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 9
A.
1
8
. B.
1
4
. C.
–0,125
. D.
0,75
.
Câu 36: Tính bán kính đường tròn nội tiếp tam giác có ba cạnh lần lượt là
5, 12, 13.
A.
2.
B.
2.
C.
2 2.
D.
3.
Câu 37: Cho tam giác
ABC
có
10BC
,
30A
. Bán kính đường tròn ngoại tiếp tam giác
ABC
bằng
A. 5. B. 10. C.
10
3
. D.
10 3
.
Câu 38: Tính diện tích tam giác có ba cạnh lần lượt là
5
,
12
,
13
.
A.
60
. B.
30
. C.
34
. D.
75
.
Câu 39: Cho tam giác
ABC
có
OO
60 , 45 , 5B C AB
. Tính độ dài cạnh
.AC
A.
53
. B.
52
. C.
56
2
. D.
10
.
Câu 40: Tam giác đều nội tiếp đường tròn bán kính
4R
cm thì có diện tích bằng
A.
2
13 cm
. B.
2
13 2 cm
. C.
2
12 3 cm
. D.
2
15 cm
.
Câu 41: Cho hình bình hành
ABCD
có
,2AB a BC a
và
45BAD 
. Tính diện tích hình bình hành
.ABCD
A.
2
2a
. B.
2
2a
. C.
2
a
. D.
2
3a
.
Câu 42: Cho hình bình hành có một cạnh là
5
hai đường chéo là
6
và
8
. Tính độ dài cạnh kề với cạnh
có độ dài bằng
5.
A.
3
. B.
1
. C.
56
. D.
5
.
Câu 43: Cho hình bình hành có hai cạnh là
5
và
9
, một đường chéo bằng
11
. Tìm độ dài đường chéo
còn lại.
A.
9,5
. B.
46
. C.
91
. D.
3 10
.
Câu 44: Cho tam giác
ABC
vuông tại
A
có
6AB
cm,
10BC
cm. Tính bán kính đường tròn nội
tiếp tam giác đó.
A. 1 cm. B.
2
cm. C. 2 cm. D. 3 cm.
Câu 45: Tính diện tích tam giác
ABC
biết
60A
,
10b
,
20c
.
A.
50 3
. B.
50
. C.
50 2
. D.
50 5
.
Câu 46: Cho tam giác
ABC
có
5AB
,
9AC
và đường trung tuyến
6AM
. Tính độ dài cạnh
BC
.
A.
2 17
. B.
17
. C.
129
. D.
22
.
Câu 47: Cho tam giác
ABC
có các góc
75 , 45AB
. Tính tỉ số
AB
AC
.
A.
6
3
. B.
6
. C.
6
2
. D.
1,2
.
Câu 48: Cho tam giác
ABC
vuông tại
A
,
AC b
,
AB c
. Lấy điểm
M
trên cạnh
BC
sao cho góc
30 .BAM 
Tính tỉ số
.
MB
MC
A.
3
3
b
c
. B.
3
3
c
b
. C.
3c
b
. D.
bc
bc
.
Câu 49: Trong tam giác
ABC
, nếu
2
a b c
h h h
thì dẳng thức nào sau đây đúng?
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 10
A.
2 1 1
sin sin sinA B C

. B.
2sin sin sinA B C
.
C.
sin 2sin 2sinA B C
. D.
2 1 1
sin sin sinA B C

.
Câu 50: Cho tam giác
.ABC
Khẳng định nào sau đây đúng?
A.
2 2 2 2 2 2
2
.
3
a b c
m m m a b c
B.
2 2 2 2 2 2
4
.
3
a b c
m m m a b c
C
.
2 2 2 2 2 2
3
.
4
a b c
m m m a b c
D.
2 2 2 2 2 2
1
.
3
a b c
m m m a b c
Câu 51: Xét tam giác
ABC
, khẳng định nào sau đây đúng?
A.
2
a
bc
m
. B.
2
a
bc
m
. C.
2
a
bc
m
. D.
a
m b c
.
Câu 52: Trong tam giác
ABC
, điều kiện để hai trung tuyến kẻ từ
A
và
B
vuông góc với nhau là
A.
2 2 2
2 2 5a b c
. B.
2 2 2
3 3 5a b c
. C.
2 2 2
2 2 3a b c
. D.
2 2 2
5a b c
.
Câu 53: Cho tam giác
ABC
có ba góc nhọn,
BC a
,
AC b
,
AB c
và diện tích là
S
. Tổng
cot cot cotA B C
bằng
A.
2 2 2
2 abc
S

. B.
2 2 2
abc
S

. C.
2 2 2
2
abc
S

. D.
2 2 2
4
abc
S

.
Câu 54: Xét tam giác
ABC
, nếu có
2
.a b c
thì đẳng thức nào dưới đây đúng?
A.
2
1 1 1
a b c
h h h

. B.
2
.
a b c
h h h
. C.
2
1 1 1
a b c
h h h

. D.
2
1 2 2
a b c
h h h

.
Câu 55: Tính bán kính đường tròn ngoại tiếp tam giác
ABC
biết
AB c
và
1
os
3
c AB
.
A.
2
2
c
. B.
32
8
c
. C.
92
8
c
. D.
3
2
c
.
Câu 56: Cho tam giác
ABC
vuông cân tại
A
và nội tiếp trong đường tròn tâm
O
bán kính
R
. Gọi
r
là bán kính đường tròn nội tiếp tam giác
ABC
. Khi đó, tỉ số
R
r
bằng
A.
12
. B.
22
2
. C.
21
2
. D.
12
2
.
Câu 57: Cho tam giác
ABC
vuông cân tại
A
có
30AB AC
cm. Hai đường trung tuyến
BF
và
CE
cắt nhau tại
G
. Diện tích tam giác
GFC
bằng
A. 50 cm
2
. B.
50 2
cm
2
. C. 75 cm
2
. D.
15 105
cm
2
.
Câu 58: Cho tam giác
ABC
có diện tích
S
. Nếu tăng độ dài mỗi cạnh
BC
và
AC
lên hai lần đồng
thời giữ nguyên độ lớn của góc
C
thì diện tích của tam giác mới được tạo nên bằng
A.
2S
. B.
3S
. C.
4S
. D.
5S
.
Câu 59: Cho hình vuông
ABCD
có cạnh bằng
a
. Gọi
E
là trung điểm cạnh
BC
,
F
là trung điểm
cạnh
AE
. Tính độ dài đoạn thẳng
DF
.
A.
13
4
a
. B.
5
4
a
. C.
3
2
a
. D.
3
4
a
.
Câu 60: Cho tam giác
ABC
có
135BC
và
.BC a
Tính bán kính đường tròn ngoại tiếp tam giác.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 11
A.
2
2
a
. B.
2a
. C.
3
2
a
. D.
3a
.
Câu 61: Cho tam giác
ABC
có
9AB
,
10BC
,
11CA
. Gọi
M
là trung điểm
BC
và
N
là trung
điểm
AM
. Tính độ dài
BN
.
A.
6
. B.
42
. C.
5
. D.
34
.
Câu 62: Cho tam giác
ABC
có
5AB
,
8BC
,
6CA
. Gọi
G
là trọng tâm tam giác
ABC
. Độ dài
đoạn thẳng
CG
bằng
A.
57
2
. B.
57
3
. C.
57
6
. D.
13
3
.
Câu 63: Cho tam giác
ABC
có
2AB
cm,
1AC
cm,
O
60A
. Tính độ dài cạnh
.BC
A. 1 cm. B. 2 cm. C.
3
cm. D.
5
cm.
Câu 64: Cho tam giác có ba cạnh lần lượt là
5
,
6
,
7
. Tính độ dài đường cao ứng với cạnh có độ dài
bằng
6.
A.
6
. B.
26
. C.
5
. D.
53
2
.
Câu 65: Cho tam giác có ba cạnh lần lượt là
5,12,13.
Tính độ dài đường cao ứng với cạnh lớn nhất.
A.
60
13
. B.
120
13
. C.
30
13
. D.
12
.
Câu 66: Cho tam giác
ABC
có
12BC
,
9CA
,
6AB
. Trên cạnh
BC
lấy điểm
M
sao cho
4BM
.
Tính độ dài đoạn thẳng
.AM
A.
25
. B.
32
. C.
20
. D.
19
.
Câu 67: Cho tam giác cân
ABC
có
120A 
và
AB AC a
. Lấy điểm
M
trên cạnh
BC
sao cho
2
5
BC
BM
. Tính độ dài
.AM
A.
3
3
a
. B.
11
5
a
. C.
7
5
a
. D.
6
4
a
.
Câu 68: Cho tam giác
ABC
có các cạnh
, , a b c
thỏa mãn điều kiện
3a b c a b c ab
. Tính số
đo của góc
.C
A.
120
. B.
30
. C.
45
. D.
60
.
Câu 69: Cho tam giác
ABC
có
.
4
a b c a b c
S
Khẳng định nào sau đây đúng?
A. Tam giác ABC vuông tại A. B. Tam giác ABC vuông tại B.
C. Tam giác ABC tù. D. Tam giác ABC nhọn.
Câu 70: Cho tam giác
ABC
thỏa mãn
sin sin
sin .
cos cos
BC
A
BC
Khẳng định nào sau đây đúng?
A. Tam giác
ABC
cân. B. Tam giác
ABC
đều.
C. Tam giác
ABC
vuông. D. Tam giác
ABC
có góc
60 .A 
Câu 71: Một tam giác có độ dài các cạnh là
1, ,2m
với
m
. Giá trị của
m
là
A.
1
. B. 2. C.
3
. D.
4
.
Câu 72: Cho tam giác
ABC
có
7AB
,
5AC
và
1
cos
5
BC
. Tính độ dài cạnh
.BC
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 12
A.
2 15
. B.
4 22
. C.
4 15
. D.
2 22
.
Câu 73: Tam giác
ABC
có
1
cos A B
8
,
4AC
,
5BC
. Tính cạnh
.AB
A.
46
. B.
11
. C.
52
. D.
6
.
Câu 74: Tính bán kính đường tròn ngoại tiếp tam giác
ABC
biết
12AB
và
1
cot( )
3
AB
.
A.
2 10
. B.
9 10
5
. C.
5 10
. D.
32
.
Câu 75: Tính bán kính đường tròn ngoại tiếp tam giác
ABC
biết
10AB
và
1
tan( )
3
AB
.
A.
5 10
9
. B.
10
3
. C.
10
5
. D.
5 10
.
Câu 76: Tìm chu vi tam giác
ABC
, biết rằng
6AB
và
2sin 3sin 4sinA B C
.
A.
26
. B.
13
. C.
5 26
. D.
10 6
.
Câu 77: Cho tam giác
ABC
có
10BC
và
sin sin sin
5 4 3
A B C

. Tìm chu vi của tam giác đó.
A.
12
. B.
36
. C.
24
. D.
22
.
Câu 78: Tam giác
ABC
có các cạnh
,,a b c
thỏa mãn điều kiện
.
6 5 7
a b b c a c

Tính
cos .A
A.
1
.
4
B.
1
.
3
C.
1
.
3
D.
1
.
3
Câu 79: Tính góc
C
của tam giác
ABC
biết
ab
và
2 2 2 2
a a c b b c
.
A.
150C 
. B.
120C 
. C.
60C 
. D.
30C 
.
Câu 80: Cho góc
O
30xOy
. Gọi
A
và
B
là hai điểm di động lần lượt trên
Ox
và
Oy
sao cho
1AB
.
Độ dài lớn nhất của đoạn
OB
bằng
A.
1,5
. B.
3
. C.
22
. D.
2
.
Câu 81: Cho góc
30xOy 
. Gọi
A
và
B
là hai điểm di động lần lượt trên
Ox
và
Oy
sao cho
2AB
.
Độ dài lớn nhất của đoạn
OB
bằng
A. 2. B. 3. C. 4. D. 5.
Câu 82: Hai chiếc tàu thủy cùng xuất phát từ một vị trí
A
, đi thẳng theo hai hướng tạo với nhau góc
60
. Tàu
B
chạy với tốc độ
20
hải lí một giờ. Tàu
C
chạy với tốc độ
15
hải lí một giờ.
Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí? Kết quả gần nhất với số nào sau đây?
A.
61
hải lí. B.
36
hải lí. C.
21
hải lí. D.
18
hải lí.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 13
Câu 83: Để đo khoảng cách từ một điểm
A
trên bờ sông đến gốc cây
C
trên cù lao giữa sông, người ta
chọn một điểm
B
cùng ở trên bờ với
A
sao cho từ
A
và
B
có thể nhìn thấy điểm
C
. Ta đo được
khoảng cách
m40AB
,
0
45CAB
và
70CBA 
(tham khảo hình vẽ)
Vậy sau khi đo đạc và tính toán được khoảng cách
AC
gần nhất với giá trị nào sau đây?
A.
m53
. B.
m30
. C.
m41,5
. D.
m41
.
Câu 84: Từ vị trí
A
người ta quan sát một cây cao (hình vẽ).
Biết
m m 4 , 20 , 45AH HB BAC
.
Chiều cao của cây gần nhất với giá trị nào sau đây?
A.
m17,5
. B.
m17
. C.
m16,5
. D.
m16
.
Câu 85: Giả sử
CD h
là chiều cao của tháp trong đó
C
là chân tháp. Chọn hai điểm
,AB
trên mặt
đất sao cho ba điểm
,AB
và
C
thẳng hàng. Ta đo được
m24AB
,
63 , 48CAD CBD
(tham khảo hình vẽ)
Chiều cao
h
của tháp gần với giá trị nào sau đây?
A.
m18
. B.
m18,5
. C.
m60
. D.
m61,4
.
Câu 86: Trên nóc một tòa nhà có một cột ăng-ten cao
m5
. Từ vị trí quan sát
A
cao
m7
so với mặt
đất, có thể nhìn thấy đỉnh
B
và chân
C
của cột ăng-ten dưới góc
50
và
40
so với phương
nằm ngang (tham khảo hình vẽ)
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 14
Chiều cao của tòa nhà gần nhất với giá trị nào sau đây?
A.
m12
. B.
m19
. C.
m24
. D.
m29
.
Câu 87: Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng đứng
cách chân tháp một khoảng
m60CD
, giả sử chiều cao của giác kế là
m1OC
. Quay thanh
giác kế sao cho khi ngắm theo thanh ta nhình thấy đỉnh
A
của tháp. Đọc trên giác kế số
đo của góc
60AOB
(tham khảo hình vẽ)
60
°
1
m
60
m
O
C
D
A
B
Chiều cao của ngọn tháp gần với giá trị nào sau đây?
A.
m40
. B.
m114
. C.
m105
. D.
m110
.
Câu 88: Một thợ lặn có vị trí cách mặt nước 8m, một con tàu đắm ở góc
0
70 .
Sau khi cùng xuống tới
một điểm cao hơn 14m so với đáy đại dương, thợ lặn nhìn thấy con tàu đắm ở góc
0
57
. Chiều
sau của con tàu đắm gần giá trị nào nhất?
A. 24,979 m. B. 32,964 m. C. 32,979 m. D. 33,25 m.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 15
Câu 89: Đầu của các tổng thống ở Mount Rushmore cao 18 mét. Một du khách nhìn thấy đỉnh đầu
của George Washington ở góc cao
48
và cằm của ông ở góc cao
44,76 .
Chiều cao của múi
Rushmore gần giá trị nào nhất?
A. 182,753 m. B. 99,649 m. C. 99,9 m. D. 168,055 m.
Câu 90: Từ hai vị trí
A
và
B
của một tòa nhà, người ta quan sát đỉnh
C
của ngọn núi. Biết rằng độ
cao
m70AB
, phương nhìn
AC
tạo với phương nằm ngang góc
30
, phương nhìn
BC
tạo
với phương nằm ngang góc
15 30'
(tham khảo hình vẽ)
Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây?
A.
m135
. B.
m234
. C.
m165
. D.
m195
.
________________HẾT________________
Huế, 10h58’ ngày 29 tháng 8 năm 2022
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 16
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
CHUY£N §Ò TR¾C NGHIÖM
M«n: To¸n 10
Chuyên đề:
HỆ THỨC LƯỢNG TRONG TAM GIÁC
LỜI GIẢI CHI TIẾT
II. BÀI TẬP TỰ LUẬN
Câu 1: Cho tam giác
ABC
có
120A 
và
5, 8AB AC
. Tính độ dài cạnh
BC
.
Lời giải:
Áp dụng Định lí côsin cho tam giác
ABC
, ta có:
2 2 2
2. . .cos120BC AB AC AB AC
22
1
5 8 2.5.8. 129
2



.
Vậy
129BC
.
Câu 2: Cho tam giác
ABC
có
8, 9, 6.a b c
a) Tính số đo các góc của tam giác.
b) Tính diện tích, bán kính đường tròn ngoại tiếp, bán kính đường tròn nội tiếp, độ dài các
đường cao của tam giác.
Lời giải:
a) Áp dụng định lí côsin, ta có
2 2 2
81 36 64 53
cos .
2 2.9.6 108
b c a
A
bc
Suy ra
60 36 39 .A

Hoàn toàn tương tự, tính được
78 35 5B

,
40 48 16C


.
b) Do
8a
,
9b
,
6c
nên tam giác
ABC
có nửa chu vi
8 9 6 23
22
p


.
Suy ra
7
2
pa
,
5
2
pb
,
11
2
pc
.
Từ đó, theo công thức Heron ta được diện tích của tam giác là
23 7 5 11 8855
...
2 2 2 2 4
S 
.
Suy ra bán kính đường tròn nội tiếp
8855
46
S
r
p

và bán kính đường tròn ngoại tiếp
432
4
8855
abc
R
S

.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 17
Câu 3: Cho tam giác
ABC
có
o
15 , 6Ac
và
o
120B
.
a) Tính độ dài các cạnh
,ab
;
b) Tính bán kính đường tròn ngoại tiếp và diện tích của tam giác;
c) Tính độ dài đường cao
a
h
.
Lời giải:
a) Do
oo
15 , 120AB
nên
oo
120 45C A B
.
Áp dụng định lí sin ta được:
o
o
6
.sin .sin15 3 3 1
sin sin 45
c
aA
C
,
o
o
6
.sin .sin120 3 6
sin sin45
c
bB
C
.
b) Theo định lí sin, bán kính đường tròn ngoại tiếp của tam giác là
o
6
32
2sin
2sin45
c
R
C
.
Do
3 3 1 , 3 6, 6a b c
và
32R
nên
3 3 1 .3 6.6 9 3 3 1
42
4.3 2
abc
S
R

.
c) Từ kết quả của phần b), suy ra
9 3 3 1
2
33
3 3 1
a
S
h
a
.
Câu 4: Cho tam giác
ABC
có
14, 18, 20a b c
. Tính gần đúng góc
.ABC
Lời giải:
Ta có
2 2 2 2 2 2
14 20 18 17
cos
2 2.14.20 35
a c b
B
ac
.
Suy ra:
60 56'B 
.
Câu 5: Giải tam giác
ABC
, biết
14, 60 ,
ˆˆ
40c A B
.
Lời giải:
Ta có
ˆˆ
180 80
ˆ
C A B
.
Áp dụng Định lí
sin,
ta có:
14
sin60 sin40 sin80

ab
Suy ra
14sin60 14sin40
12,3; 9,14.
sin80 sin80


ab
Câu 6: Cho tam giác
ABC
có
OO
60 , 45 , 5B C AB
. Tính độ dài cạnh
.AC
Lời giải:
Áp dụng định lí sin cho tam giác
,ABC
ta có:
.sin 5 6
sin sin sin 2
AB AC AB B
AC
C B C
.
Câu 7: Cho tam giác
ABC
có
10BC
,
30A 
. Tính bán kính đường tròn ngoại tiếp tam giác
.ABC
Lời giải:
Gọi
R
là bán kính đường tròn ngoại tiếp tam giác
ABC
, ta có:
10
2 10
sin 2.sin 2.sin30
BC BC
RR
AA
.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 18
Câu 8: Cho tam giác có ba cạnh là
6,10,8
. Tính bán kính đường tròn nội tiếp tam giác đó.
Lời giải:
Gọi
,pr
lần lượt là nửa chu vi và bán kính đường tròn nội tiếp tam giác đã cho, ta có:
6 8 10
12
2
p


.
Diện tích tam giác là
( 6)( 8)( 10) 24S p p p p
(đvdt).
Suy ra
24
2
12
S
r
p
.
Nhận xét: Tam giác đã cho là tam giác vuông.
Câu 9: Cho tam giác
ABC
vuông tại
A
có
6AB
cm,
10BC
cm. Tính bán kính đường tròn nội
tiếp tam giác đó.
Lời giải:
Ta có
22
8AC BC AB
(cm).
Diện tích tam giác
ABC
là:
2
1
. 24
2
S AB AC cm
Nửa chu vi của tam giác là
6 8 10
12
2
p


Suy ra:
24
2
12
S
r
p
(cm).
Câu 10: Tính diện tích
S
của tam giác
ABC
có
4, 6, 150
ˆ
c b A
.
Lời giải:
Ta có:
sin sin
11
.6.4. 150 6
22
S bc A
.
Câu 11: Tính diện tích tam giác có ba cạnh lần lượt là
5
,
12
,
13
.
Lời giải:
Nửa chu vi của tam giác là:
5 12 13
15
2
p


Diện tích của tam giác là:
5 12 13 15 15 5 15 12 15 13 30S p p p p
.
Câu 12: Cho tam giác
ABC
có góc
B
tù,
3AB
,
4AC
và có diện tích bằng
3 3.
Tính số đo góc
.BAC
Lời giải:
Ta có:
1 2 2.3 3 3
. . .sin sin
2 . 3.4 2
S
S AB AC A A
AB AC
Vì góc
B
tù nên
A
là góc nhọn
60A
.
Câu 13: Tính diện tích tam giác đều nội tiếp đường tròn bán kính
4R
cm.
Lời giải:
Gọi
a
là độ dài cạnh và
S
là diện tích của tam giác, ta có:
2
3 . .
44
a a a a
S
R

3 4 3aR
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 19
Vậy diện tích tam giác đã cho là:
2
2
4 3 . 3
12 3
4
S cm
.
Câu 14: Cho tam giác
ABC
có
1, 3, 60 AB AC A
. Tính bán kính đường tròn ngoại tiếp
ABC
.
Lời giải:
Ta có:
2 2 2 2
2. . .cos 3 1 2.3.1.cos60 7 7BC AC AB AC AB A BC
Ta lại có:
7 21
2
sin 2.sin 2.sin60 3
BC BC
RR
AA
.
Câu 15: Cho tam giác
ABC
có
8AB
cm,
18AC
cm và có diện tích bằng
64
cm
2
. Tính
sin .A
Lời giải:
Ta có:
1 2 8
. .sin sin
2 . 9
S
S AB AC A A
AB AC
.
Câu 16: Cho tam giác
ABC
có
9AB
cm,
12AC
cm và
15BC
cm. Tính độ dài đường trung
tuyến
AM
của tam giác
.ABC
Lời giải:
Cách 1: Ta có
2 2 2 2 2 2
9 12 15
7,5
2 4 2 4
AB AC BC
AM

.
Cách 2: Tam giác
ABC
vuông tại
A
nên
7,5
2
BC
AM 
.
Câu 17: Cho tam giác
ABC
có
5AB
,
9AC
và đường trung tuyến
6AM
. Tính độ dài cạnh
BC
.
Lời giải:
5
9
6
M
A
B
C
Ta có:
2 2 2
2
24
AC AB BC
AM

2 2 2 2
2 2 2
95
4 4 6
22
AC AB
BC AM

68 2 17.BC
Câu 18: Cho tam giác
ABC
có
5AB
,
8BC
,
6CA
. Gọi
G
là trọng tâm tam giác. Tính độ dài đoạn
thẳng
.CG
Lời giải:
M
G
C
B
A
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 20
Gọi
M
là trung điểm
AB
, ta có
2 2 2
2
175
2 4 4
CB AC AB
CM
.
Suy ra:
2 2 175 5 7
3 3 4 3
CG CM
.
Câu 19: Cho tam giác có ba cạnh lần lượt là
5
,
6
,
7
. Tính độ dài đường cao ứng với cạnh có độ dài
bằng
6.
Lời giải:
Nửa chu vi của tam giác là:
5 6 7
9
2
p


.
Diện tích tam giác là:
5 6 7 6 6S p p p p
.
Đặt
5a
,
6b
,
7c
.
Độ dài đường cao ứng với cạnh có độ dài bằng 6 là:
2 2.6 6
26
6
b
S
h
b
.
Câu 20: Cho tam giác
ABC
có các góc
105A 
,
45B 
. Tính tỉ số
AB
AC
.
Lời giải:
Ta có:
sin sin(180 105 45 ) 2
sin sin sin sin45 2
b c AB c C
B C AC b B
.
Câu 21: Cho tam giác có ba cạnh lần lượt là
5,12,13.
Tính độ dài đường cao ứng với cạnh lớn nhất.
Lời giải:
Đặt
5a
,
12b
,
13c
. Ta có:
Nửa chu vi của tam giác là:
5 12 13
15
2
p


Diện tích của tam giác là:
5 12 13 15 15 5 15 12 15 13 30S p p p p
.
Đường cao ứng với cạnh lớn nhất là:
2 2.30 60
13 13
c
S
h
c
.
Câu 22: Cho tam giác có ba cạnh lần lượt là
2,3,4
. Góc bé nhất của tam giác có sin bằng bao nhiêu?
Lời giải:
Góc bé nhất ứng với cạnh có số đo bé nhất.
Giả sử
4,3,2 cba
. Ta có
8
7
..2
cos
222
cb
acb
A
.
Do đó
8
15
8
7
1sin
2
A
.
Câu 23: Cho tam giác
ABC
có
3AB
,
4AC
và
tan 2 2A
. Tính độ dài cạnh
.BC
Lời giải:
Từ giả thiết
tan 2 2 0A 
, ta suy ra
A
là góc nhọn
2
2
2
1 1 1 1
tan 2 2 cos cos
1 tan 9 3
1 2 2
A A A
A
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 21
Suy ra:
2 2 2 2
1
2 . .cos 3 4 2.3.4. 17
3
BC AB AC AB AC A
.
Câu 24: Cho tam giác
ABC
vuông cân tại
.A
Gọi
,rR
lần lượt là bán kính đường tròn nội tiếp, ngoại
tiếp tam giác
ABC
. Tính tỉ số
.
R
r
Lời giải:
Giả sử
2
2
2
a
AB AC a BC a R
.
Mặt khác
2
. 2 2
.
2 2 2
22
AB AC a a a a
S pr r r
Suy ra
12
R
r

.
Câu 25: Cho tam giác
ABC
có các cạnh
, , a b c
thỏa mãn
3a b c a b c ab
. Tính số đo của góc
.C
Lời giải:
Trong tam giác
ABC
ta luôn có:
2 2 2
2 .cosc a b ab C
.
Hệ thức
2
2
33a b c a b c ab a b c ab
2 2 2
c a b ab
Suy ra:
1
2.cos 1 cos 60
2
C C C
.
Câu 26: Tính góc
C
của tam giác
ABC
biết
ab
và
2 2 2 2
a a c b b c
.
Lời giải:
Ta có:
2 2 2 2
a a c b b c
3 3 2
0a b c a b
2 2 2
0a b a ab b c a b
2 2 2
0a ab b c
2 2 2
cos
2
a b c
C
ab


1
2

. Do đó:
120C 
.
Câu 27: Cho tam giác
ABC
có
10BC
và
sin sin sin
.
5 4 3
A B C

Tính chu vi của tam giác đó.
Lời giải:
Do
sin sin sin
5 4 3
A B C

nên
8; 6
5 4 3
a b c
bc
(do
10a BC
).
Chu vi tam giác
ABC
bằng
24
.
Câu 28: Cho tam giác
ABC
có các góc thỏa mãn
sin sin sin
12
3
A B C

. Tính số đo các góc của tam giác.
Lời giải:
Áp dụng định lí sin, ta có
: : 1: 2: 3abc
.
Đáp số:
30A 
,
90B 
,
60C
.
Câu 29: Cho tam giác
ABC
có
7AB
,
5AC
và
1
cos
5
BC
. Tính độ dài cạnh
.BC
Lời giải:
Vì trong tam giác
ABC
ta có
BC
bù với góc
A
nên
1
cos
5
BC
1
cos
5
A
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 22
Lúc đó:
2 2 2 2
1
2 . .cosA 7 5 2.7.5. 2 15
5
BC AB AC AB AC
.
Câu 30: Cho tam giác
ABC
, các đường cao
,,
a b c
h h h
thỏa mãn
32
a b c
h h h
. Chứng minh rằng:
3 2 1
.
a b c
Lời giải:
Kí hiệu
ABC
SS
. Ta có:
32
a b c
h h h
3.2 2.2 2S S S
a b c
3 2 1
a b c
.
Câu 31: Cho tam giác
ABC
. Chứng minh rằng:
a)
2 2 2
2
24
a
b c a
m

; b)
1 1 1 1
a b c
h h h r
.
Lời giải:
a) Gọi
M
là trung điểm của
BC
. Khi đó
a
m AM
.
Có hai trường hợp sau xảy ra:
Trường hợp 1.
bc
. Trong trường hợp này
AM
cũng chính là đường cao kẻ từ
A
của tam
giác. Do đó
2 2 2 2
2 2 2 2
4 2 4
a
a b c a
m AC CM b
.
Trường hợp 2.
bc
. Không mất tính tổng quát, xét trường hợp
bc
(H.3.2), trường hợp còn
lại chứng minh tương tự.
Gọi
D
là chân đường cao kẻ từ
A
. Do
bc
nên
D
thuộc tia
MC
.
Áp dụng định lí Pythagore trong tam giác
ADB
, ta có:
2
2 2 2 2
AB BD AD BM MD AD
2 2 2
2.BM BM MD MD AD
.
Suy ra
2 2 2
2.AB BM BM MD AM
1
.
Một cách tương tự, áp dụng định lí Pythagore trong tam giác
ADC
, cũng được
2
2 2 2 2
2.AC AD MC MD MC MC MD AM
2
.
Từ
1
và
2
suy ra:
2 2 2 2 2
2 . . 2AB AC BM CM BM MD CM MD AM
2 2 2
2BM CM AM
.
Hay
2 2 2
2
24
a
b c a
m

.
b) Từ công thức tính diện tích tam giác ta suy ra
1 1 1 1
222
a b c
p a b c
r S S S S h h h
.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 23
Câu 32: Cho tam giác
ABC
có các góc thỏa mãn
sin 2.sin .cosC B A
. Chứng minh rằng tam giác
ABC
là một tam giác cân.
Lời giải:
Áp dụng định lý sin và côsin, ta có:
sin 2.sin .cos 2 cosC B A c b A
2 2 2
2.
2
b c a
cb
bc


2 2 2 2
c b c a
ab
.
Vậy tam giác
ABC
cân tại
C
.
Câu 33: Cho tam giác
ABC
. Chứng minh rằng:
a)
2 2 2
cot cot cot
4
abc
A B C
S

. b)
2 2 2 2 2 2
3
4
a b c
m m m a b c
.
Lời giải:
a) Từ định lí côsin và công thức tính diện tích tam giác, suy ra:
2 2 2 2 2 2
cos
cot
sin 2. . .sin 4
A b c a b c a
A
A b c A S
.
Tương tự cũng có
2 2 2
cot
4
c a b
B
S

,
2 2 2
cot
4
a b c
C
S

.
Từ đó
2 2 2
cot cot cot
4
abc
A B C
S

.
b) Áp dụng công thức tính độ dài trung tuyến.
Câu 34: Cho tam giác
ABC
có hai trung tuyến kẻ từ
A
và
B
vuông góc. Chứng minh rằng:
a)
2 2 2
5a b c
. b)
cot 2 cot cotC A B
.
Lời giải:
a) Gọi
M
,
N
theo thứ tự là trung điểm của các cạnh
BC
,
CA
; gọi
G
là trọng tâm tam giác
ABC
(Hình vẽ). Khi đó
2
3
AG AM
,
2
3
BG BN
.
Từ đó theo định lí Pythagore ta có:
2 2 2 2 2 2
2 2 2 2
44
9 2 4 9 2 4
b c a c a b
c AB AG BG

22
2
4
94
ab
c




.
Suy ra
2 2 2
5c a b
.
b) Do
2 2 2
5a b c
nên
2 2 2 2
cot
4
a b c c
C
SS


.
Mà
2 2 2 2 2 2 2
2 cot cot 2
44
b c a c a b c
AB
S S S





.
Suy ra
cot 2 cot cotC A B
.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 24
Câu 35: Cho tam giác
ABC
có
2
2 sin sinS R A B
. Chứng minh rằng tam giác
ABC
là một tam giác
vuông.
Lời giải:
Từ định lí sin và công thức tính diện tích, suy ra diện tích của tam giác bằng
2
2 sin 2 sin 2 sin
2 sin sin sin
44
R A R B R C
abc
S R A B C
RR
.
Từ đó, do
2
2 sin sinS R A B
, suy ra
sin 1C
và do đó
90C
.
Suy ra điều phải chứng minh.
Câu 36: Cho tam giác
ABC
vuông cân tại
A
có
30AB AC
cm. Hai đường trung tuyến
BF
và
CE
cắt nhau tại
G
. Tính diện tích tam giác
.GFC
Lời giải:
H
G
E
F
C
B
A
Nối
AG
cắt
BC
tại
H
ta có:
1 1 1
.
2 3 6
GFC AGC AHC ABC
S S S S
Mà
2
1
.30.30 450
2

ABC
S cm
nên
2
1
.450 75
6

GFC
S cm
.
Câu 37: Cho hình bình hành có hai cạnh là
5
và
9
, một đường chéo bằng
11
. Tìm độ dài đường chéo
còn lại.
Lời giải:
5
9
9
11
C
A
D
B
Gọi hình bình hành là
ABCD
,
5AD
,
9AB
.
Gọi
là góc đối diện với đường chéo có độ dài
11
.
Ta có:
2 2 2
5 9 11 1
cos
2.5.9 6

là góc tù
BAD

11BD
2 2 2 2 2
2. . .cos 2. . .cosAC AD DC AD DC ADC AD DC AD DC BAD
(vì
BAD
và
ADC
bù nhau
cos cosADC BAD
)
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 25
2 2 2
1
5 9 2.5.9. 91 91
6
AC AC



.
Câu 38: Cho hình bình hành
ABCD
có
,2AB a BC a
và
45BAD
. Tính diện tích hình bình
hành
.ABCD
Lời giải:
a
D
A
B
C
H
Gọi
BH
là đường cao của hình bình hành
ABCD
.
Tam giác
BHA
vuông tại
H
, góc
45BAH BAC
,
2
.sin45
2
a
BH AB
.
Diện tích hình bình hành
ABCD
là:
2
2
. . 2
2
a
S BH AD a a
.
Câu 39: Cho tam giác
ABC
vuông tại
A
có
AB AC a
. Điểm
M
nằm trên cạnh
BC
sao cho
3
BC
BM
. Tính độ dài đoạn thẳng
.AM
Lời giải:
B
A
C
M
Ta có:
2 2 2 2
2BC AB AC a a a
;
22BC AB a
2
3
a
BM
2
2 2 0 2
2 2 2 5
2 . .cos45 2 . .
3 3 2 3
a a a
AM AB BM AB BM a a




.
Câu 40: Cho hình vuông
ABCD
có cạnh bằng
a
. Gọi
E
là trung điểm cạnh
BC
,
F
là trung điểm
cạnh
AE
. Tính độ dài đoạn thẳng
DF
.
Lời giải:
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 26
F
E
C
D
A
B
Ta có:
2
2
5
22
aa
AE DE a



Dùng công thức độ dài trung tuyến:
2
2
2 2 2 2 2
2
5
5 13
4
2 4 2 16 16
a
a
DA DE AE a a
DF
13
4
a
DF
.
Câu 41: Cho tam giác
ABC
nội tiếp đường tròn bán kính
,R
,AB R
2.AC R
Tính góc
A
biết
A
là góc tù.
Lời giải:
Góc
A
tù, suy ra
,BC
đều là góc nhọn.
Ta có:
1
2 2 sin 30 .
sin sin 2
AB R
R R C C
CC
(vì
C
nhọn)
Tương tự:
22
2 2 sin 45
sin sin 2
AC R
R R B B
BB
(do
B
nhọn).
Suy ra:
180 30 45 105 .A
Câu 42: Cho tam giác vuông, trong đó có một góc bằng trung bình cộng của hai góc còn lại. Cạnh lớn
nhất của tam giác đó bằng
.a
Tính diện tích tam giác đã cho.
Lời giải:
Gọi tam giác thỏa đề là
ABC
(với
A B C
).
Đề cho tam giác vuông nên ta suy ra
90A 
.
Ta có:
180 ,A B C
mà theo đề:
2,A C B
Suy ra
60B 
.
Ta tính:
.cos60 .
2
a
AB BC
Diện tích tam giác:
2
13
. .sin .
28
a
S AB BC B
Câu 43: Cho tam giác
ABC
vuông cân tại
A
và điểm
M
trong tam giác sao cho
1,MA
2MB
,
2MC
. Tính góc
AMC
.
Lời giải:
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 27
B
A
C
M
Áp dụng định lý cosin trong tam giác ta có:
2 2 2
2 2 2
2 2 2
2 . .cos
2 . .cos
2 . .cos
AB AM BM AM BM AMB
BC BM CM BM CM BMC
AC CM AM CM AM CMA
2
2
2
5 4.cos
2 6 4 2.cos
3 2 2.cos
AB AMB
AB BMC
AB CMA


2
2
2
5 4.cos
2 6 4 2.cos
3 2 2.cos
AB AMB
AB BMC
AB CMA


1 2.cos 2.cos 0
cos cos
AMB CMA
CMA BMC
Câu 44: Cho góc
30xOy 
. Gọi
A
và
B
là hai điểm di động lần lượt trên
Ox
và
Oy
sao cho
2AB
.
Tính độ dài lớn nhất của đoạn
.OB
Lời giải:
Đặt
OA x
,
OB y
,0xy
Áp dụng công thức định lý hàm số cosin cho ta giác
OAB
ta có:
2 2 2 2 2
2 cos30 2 3 4 0x y xy x y xy
*
Tìm điều kiện để tồn tại
x
, ta coi phương trình trên là phương trình ẩn
x
, tham số
y
.
Khi đó, phương trình
*
có nghiệm
2
2
0 3 4 4 0 4 4y y y
.
Do đó
max 4.y
Câu 45: Để đo chiều cao của một tòa nhà, người ta chọn hai điểm
A
và
B
thẳng hàng với chân
C
của
tòa nhà, cách nhau
15
m. Sử dụng giác kế, từ
A
và
B
tương ứng nhìn thấy đỉnh
D
của tòa
nhà dưới các góc
35
và
40
so với phương nằm ngang.
Hỏi chiều cao của tòa nhà đo được là bao nhiêu mét?
Lời giải:
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 28
Do
40CBD 
,
35BAD 
nên
40 35 5ABD
(H.3.3). Áp dụng định lí sin cho tam giác
ABD
ta được
15
.sin .sin35
sin sin5
AB
BD A
D
.
Từ đó suy ra chiều cao của tòa nhà bằng
15
.sin .sin35 63,45 m
sin5
h CD BD CBD
Câu 46: Một tàu cá xuất phát từ đảo
A
, chạy
50
km theo hướng
24NE
đến đảo
B
để lấy thêm ngư
cụ, rồi chuyển hướng
36NW
chạy tiếp
130
km đến ngư trường
C
.
a) Tính khoảng cách từ vị trí xuất phát
A
đến
C
(làm tròn đến hàng đơn vị theo đơn vị đo
kilômét).
b) Tìm hướng từ
A
đến
C
(làm tròn đến hàng đơn vị, theo đơn vị độ).
Lời giải:
a) Từ giả thiết suy ra
90 24 90 36 120ABC
(H.3.7).
Áp dụng định lí côsin cho tam giác
,ABC
ta được:
2 2 2
2 . .cosAC AB BC AB BC ABC
1
2500 16900 2.50.130. 25900
2



.
Suy ra
10 259 161 kmAC
.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 29
Hình 3.7
b) Áp dụng định lí sin cho tam giác
ABC
ta được
sin .sin 0,6993
BC
CAB ABC
AC

.
Suy ra
44CAB 
và do đó
AC
chếch về hướng tây một góc
44 24 20
so với phương
bắc.
Vậy hướng từ
A
tới
C
là
20NW
.
Câu 47: Một tàu du lịch xuất phát từ bãi biển Đồ Sơn (Hải Phòng), chạy theo hướng
80NE
với vận
tốc
20
km/h. Sau khi đi được
30
phút, tàu chuyển sang hướng
20ES
giữ nguyên vận tốc và
chạy tiếp
36
phút nữa đến đảo Cát Bà.
Hỏi khi đó tàu du lịch cách vị trí xuất phát bao nhiêu kilômet?
Lời giải:
Coi điểm xuất phát là
A
, điểm tàu chuyển hướng là
B
và đích đến là
C
(H3.8).
Theo giả thiết
180 10 20 150ABC
.
Hình 3.8
Do tàu chạy từ
A
tới
B
với vận tốc
20km/h
trong
30
phút, nên
30
20. 10 km
60
AB 
.
Do tàu chạy từ
B
đến
C
với vận tốc
20km/h
trong
36
phút, nên
36
20. 12 km
60
BC 
.
Áp dụng định lí côsin cho tam giác
,ABC
ta được:
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 30
2 2 2 2 2
3
2. . .cos 10 12 2.10.12. 452
2
AC AB BC AB BC ABC




.
Suy ra
452 21 kmAC 
.
Câu 48: Một cây cổ thụ mọc thẳng đứng bên lề một con dốc có độ dốc
10
so với phương nằm ngang.
Từ một điểm dưới chân dốc, cách gốc cây
31
m người ta nhìn đỉnh ngọn cây dưới một góc
40
so với phương nằm ngang.
Hãy tính chiều cao của cây.
Lời giải:
Áp dụng định lí sin cho tam giác
ABC
(H.3.9).
Hình 3.9
Đáp số: Chiều cao của cây là
20,23 mh
.
Câu 49: Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình
tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính
của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả
như hình vẽ (
4,3AB
cm;
3,7BC
cm;
7,5CA
cm).
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 31
Tính gần đúng bán kính của chiếc đĩa này.
Lời giải:
Bán kính
R
của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác
ABC
.
Nửa chu vi của tam giác
ABC
là:
4,3 3,7 7,5 31
2 2 4
AB BC CA
p
cm.
Diện tích tam giác
ABC
là:
5,2S p p AB p BC p CA
cm
2
.
Mà
. . . .
5,73
44
AB BC CA AB BC CA
SR
RS
cm.
Câu 50: Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất
sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24m,
63CAD
;
48CBD
.
Tính gần đúng chiều cao h của khối tháp.
Lời giải:
Ta có
63 117 180 117 48 15CAD BAD ADB
Áp dụng định lý sin trong tam giác ABD ta có:
.sin
sin sin sin
AB BD AB BAD
BD
ADB BAD ADB
Tam giác BCD vuông tại C nên có:
sin .sin
CD
CBD CD BD CBD
BD
Vậy
.sin .sin 24.sin117 .sin48
61,4
sin15
sin
AB BAD CBD
CD m
ADB

.
III. BÀI TẬP TRẮC NGHIỆM
Câu 1: Cho tam giác
ABC
, khẳng định nào sau đây đúng?
A.
2 2 2
2 .cosa b c bc A
. B.
2 2 2
2 .cosa b c bc A
.
C.
2 2 2
.cosa b c bc A
. D.
2 2 2
.cosa b c bc A
.
Lời giải:
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 32
Áp dụng định lí hàm số cos tại đỉnh
A
ta có:
2 2 2
2 .cosa b c bc A
.
Chọn đáp án B.
Câu 2: Xét tam giác
ABC
tùy ý có
,,BC a AC b AB c
. Mệnh đề nào dưới đây đúng?
A.

2 2 2
cos .
2
a c b
B
ac
B.

2 2 2
cos .
2
a c b
B
ac
C.

2 2 2
cos .
a c b
B
ac
D.

2 2 2
cos .
4
a c b
B
Câu 3: Cho tam giác
ABC
có
120 .A
Đẳng thức nào sau đây đúng?
A.
2 2 2
3a b c bc
. B.
2 2 2
a b c bc
.
C.
2 2 2
3a b c bc
. D.
2 2 2
a b c bc
.
Lời giải:
Áp dụng định lí hàm số cos tại đỉnh
A
ta có:
2 2 2
2 .cosa b c bc A
.
2 2 2
2 . os120a b c bc c
2 2 2
a b c bc
.
Chọn đáp án B.
Câu 4: Cho tam giác
ABC
có
;BC a
;AB c
AC b
và có
R
là bán kính đường tròn ngoại tiếp.
Hệ thức nào sau đây là sai?
A.
2.
sin
a
R
A
B.
sin .
2
a
A
R
C.
.sin 2 .b B R
D.
.sin
sin .
cA
C
a
Lời giải:
Theo định lý
sin
trong tam giác
2.
sin sin sin
a b c
R
A B C
Nên ta suy ra đáp án sai là
.sin 2 .b B R
Chọn đáp án C.
Câu 5: Xét tam giác
ABC
, hệ thức nào sau đây sai?
A.
.sin
sin
bA
a
B
. B.
.sin
sin
cA
C
a
. C.
2 .sina R A
. D.
.tanb R B
.
Lời giải:
Theo định lí hàm số sin ta có:
2
sin sinB sinC
a b c
R
A
Suy ra:
+
.sin
sin sinB sin
a b b A
a
AB
.
+
.sin
sin
sin sinC
a c c A
C
Aa
.
+
2 2 .sin
sin
a
R a R A
A
.
+
2 sin tan
sinB 2 2cosB
b b b
R R B R B
.
Chọn đáp án D.
Câu 6: Cho tam giác
ABC
có
,.AB c AC b
Diện tích của tam giác
ABC
bằng
A.
cos .bc A
B.
sin .bc A
C.
1
cos .
2
bc A
D.
1
sin .
2
bc A
Câu 7: Nếu tam giác
ABC
có
2 2 2
a b c
thì:
A.
A
là góc nhọn. B.
A
là góc tù.
C.
A
là góc vuông. D.
A
là góc nhỏ nhất.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 33
Lời giải:
Ta có:
2 2 2
cos
2
b c a
A
bc

. Vì
2 2 2
a b c
cos 0A
. Do đó
A
nhọn.
Chọn đáp án A.
Câu 8: Cho tam giác
ABC
có
, , BC a CA b AB c
. Mệnh đề nào sau đây là đúng?
A. Nếu
2 2 2
0b c a
thì góc
A
nhọn. B. Nếu
2 2 2
0b c a
thì góc
A
tù.
C. Nếu
2 2 2
0b c a
thì góc
A
nhọn. D. Nếu
2 2 2
0b c a
thì góc
A
vuông.
Lời giải:
Áp dụng định lí cô sin ta có:
2 2 2 2 2 2
2 cos 2 cosa b c bc A bc A b c a
.
Suy ra: Nếu
2 2 2
0 cos 0b c a A
nên
A
nhọn.
Chọn đáp án A.
Câu 9: Mệnh đề nào sau đây sai?
A. Nếu
2 2 2
a b c
thì
A
là góc tù.
B. Nếu tam giác
ABC
có một góc tù thì
2 2 2
a b c
.
C. Nếu
2 2 2
a b c
thì
A
là góc nhọn.
D. Nếu
2 2 2
a b c
thì
A
là góc vuông.
Lời giải:
Ta có :
2 2 2
cos
2
b c a
A
bc

.
Do đó :
*
2 2 2
a b c
thì
cos 0A
do đó
A
là góc tù nên A. đúng.
*
2 2 2
a b c
thì
cos 0A
do đó
A
là góc nhọn nên C. đúng.
*
2 2 2
a b c
thì
cos 0A
do đó
A
là góc vuông nên D. đúng.
* Nếu tam giác
ABC
có góc
B
tù thì
2 2 2
b a c
; nếu góc
C
tù thì
2 2 2
c a b
do đó B. sai.
Chọn đáp án B.
Câu 10: Cho tam giác
ABC
thỏa mãn
4 4 4
.a b c
Khẳng định nào sau đây đúng?
A. Tam giác ABC vuông tại A. B. Tam giác ABC vuông tại B.
C. Tam giác ABC tù. D. Tam giác ABC nhọn.
Lời giải:
Do
4 4 4
a b c
nên
a
là cạnh lớn nhất,
A
là góc lớn nhất của tam giác
.ABC
Ta có:
2
2 2 4 4
b c b c
(do
22
20bc
)
Lúc đó:
22
2 2 4 4 4 2 2 4 2 2 2 2 2 2
00 b c b c a b c a b c a b c a
2 2 2 o
0 cos 0 90 . b c a A A
Chọn đáp án D.
Câu 11: Cho tam giác
ABC
, các đường cao
,,
a b c
h h h
thỏa mãn hệ thức
32
a b c
h h h
. Tìm hệ thức giữa
, , a b c
.
A.
3 2 1
a b c

. B.
32a b c
. C.
32a b c
. D.
3 2 1
a b c

.
Lời giải:
Kí hiệu
ABC
SS
. Ta có:
32
a b c
h h h
3.2 2.2 2S S S
a b c
3 2 1
a b c
.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 34
Chọn đáp án D.
Câu 12: Trung tuyến
AM
của tam giác
ABC
có độ dài bằng
A.
2 2 2
b c a
. B.
2 2 2
1
22
2
b c a
. C.
2 2 2
3 2 2abc
. D.
2 2 2
22b c a
.
Lời giải:
Theo công thức tính độ dài đường trung tuyến
2 2 2
2
2
4
b c a
AM

.
Chọn đáp án B.
Câu 13: Cho tam giác
ABC
có
3 3, 3, 6AC AB BC
. Tính số đo góc
B
.
A.
60
. B.
45
. C.
30
. D.
120
.
Lời giải:
2 2 2
cos
2.
AB BC AC
B
AB BC

9 36 27 1
36 2


. Vậy số đo góc
B
là
60
.
Chọn đáp án A.
Câu 14: Cho tam giác
ABC
có
7b
;
5c
và
3
cos
5
A
. Tính
a
.
A.
42
. B.
2
. C.
2
. D.
3
.
Lời giải:
Áp dụng định lí hàm số Cosin vào tam giác
ABC
có
2 2 2
3
2 . .Cos 25 49 2.5.7. 32
5
BC AB AC AB AC A
4 2.BC
Chọn đáp án A.
Câu 15: Cho tam giác
ABC
có
33AB
và bán kính đường tròn ngoại tiếp
3R
. Số đo góc
C
là
A.
60
. B.
30
. C.
90
. D.
45
.
Lời giải:
Áp dụng định lý sin trong tam giác
ABC
ta có:
3 3 3
sin 60 .
2 2.3 2
AB
CC
R
Chọn đáp án A.
Câu 16: Cho tam giác
ABC
có
60B 
,
45C 
,
3AB
. Tính độ dài
AC
.
A.
36
2
. B.
32
2
. C.
6
. D.
26
3
.
Lời giải:
Ta có:
.sin 3.sin60 3 6
sin sin sin sin45 2
AC AB AB B
AC
B C C
.
Chọn đáp án A.
Câu 17: Cho tam giác
ABC
có
105BAC 
,
45ACB 
và
8AC
. Tính độ dài cạnh
AB
.
A.
86
3
. B.
42
. C.
82
. D.
4 1 3
.
Lời giải:
Ta có:
180 180 105 45 30ABC BAC ACB
.
Áp dụng định lý sin trong tam giác
ABC
ta có
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 35
8.sin45
82
sin45 sin30 sin30
AB AC
AB
.
Chọn đáp án C.
Câu 18: Cho tam giác
ABC
có
9, 18AB AC
và
60A 
. Bán kính của đường tròn ngoại tiếp tam
giác
ABC
là
A.
3
. B.
93
. C.
9
. D.
6
.
Lời giải:
Trong tam giác
ABC
ta có
2 2 2
2 . .cos 243BC AB AC AB AC A
93BC
.
Mặt khác
93
29
sin 2sin 2sin60
BC BC
RR
AA
.
Chọn đáp án C.
Câu 19: Cho hình vuông
ABCD
có cạnh bằng
6
,
E
là trung điểm của
CD
. Tính bán kính đường tròn
ngoại tiếp tam giác
ACE
.
A.
3 10
2
. B.
35
2
. C.
3 10
. D.
35
.
Lời giải:
6
E
D
C
A
B
Ta có
22
36 9 3 5 AE AD DE
Áp dụng định lý sin cho tam giác
ACE
ta được:
3 5 3 10
2.
2
2
sin
2.
2
AE
R R R
ACE
Chọn đáp án A.
Câu 20: Cho
ABC
có
45 , 75AB
. Tính tỉ số
AB
BC
.
A.
6
2
. B.
13
2
. C.
6 3 2
6
. D.
6
3
.
Lời giải:
Áp dụng định lí hàm số sin trong tam giác
ABC
, ta có
sin 180 45 75
sin sin60 6
sin sin sin sin45 sin 45 2
AB BC AB C
C A BC A

.
Chọn đáp án A.
Câu 21: Cho tam giác
ABC
có
3, 5, 6. BC AC AB
Độ dài đường trung tuyến kẻ từ đỉnh
C
bằng
A.
2 2.
B. 5. C.
10.
D. 3.
Lời giải:
Gọi
M
là trung điểm của
AB
. Áp dụng công thức độ dài trung tuyến, ta có:
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 36
2 2 2 2 2 2
2
2 2 5 3 6
8
44
CA CB AB
CM
. Suy ra
22CM
.
Vậy độ dài trung tuyến kẻ từ đỉnh
C
của tam giác
ABC
bằng
2 2.
Chọn đáp án A.
Câu 22: Cho tam giác
ABC
có
4BC
,
5AC
và
60ACB 
. Độ dài đường trung tuyến hạ từ đỉnh
C
là
A.
61
2
. B.
51
2
. C.
3
. D.
2
.
Lời giải:
Ta có:
2 2 2 2 2
1
2 . .cos 4 5 2.4.5. 21 21
2
AB AC BC AC BC ACB AB
.
Do đó
2 2 2 2 2
2
2 2 2.5 2.4 21 61
4 4 4
c
CA CB AB
m
. Vậy
61
2
c
m
.
Chọn đáp án D.
Câu 23: Cho tam giác
ABC
có chu vi bằng
32
và bán kính đường tròn nội tiếp của
ABC
bằng
5
.
Tính diện tích tam giác
ABC
.
A.
32
.
5
S
B.
40.S
C.
160.S
D.
80.S
Câu 24: Cho tam giác
ABC
có
5, 12, 13.a b c
Bán kính đường tròn ngoại tiếp
R
của tam giác
bằng
A.
13.
B.
6,5.
C.
26.
D.
7,5.
Lời giải:
Ta có:
5 12 13
15.
22
abc
p
Do đó
15. 15 5 15 12 15 13 30.
ABC
S p p a p b p c
Mà
5.12.13
6,5.
4 4 4.30
ABC
abc abc
SR
RS
Chọn đáp án B.
Câu 25: Cho tam giác
ABC
có
60 , 3, 4. A AB AC
Tính độ dài đường cao kẻ từ
A
của tam giác
ABC
.
A.
2 39
.
13
a
h
B.
39
.
13
a
h
C.
6 39
.
13
a
h
D.
3 39
.
13
a
h
Lời giải:
Áp dụng định lý côsin vào tam giác
ABC
ta có:
22
2 . .cosA 25 12 13BC AB AC AB AC
Diện tích của tam giác
ABC
:
1 1 3
. .sinA .3.4. 3 3
2 2 2
S AB AC
Gọi
a
h
là đường cao kẻ từ
A
của tam giác
.ABC
Ta có:
2
ABC
a
S
h
BC
6 3 6 39
.
13
13

Chọn đáp án C.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 37
Câu 26: Cho tam giác
ABC
có
9AB
cm,
12AC
cm và
15BC
cm. Khi đó, đường trung tuyến
AM
của tam giác
ABC
có độ dài bằng
A.
8
cm. B.
10
cm. C.
9
cm. D.
75,
cm.
Lời giải:
Cách 1: Ta có
2 2 2 2 2 2
9 12 15
7,5
2 4 2 4
AB AC BC
AM

.
Cách 2: Tam giác
ABC
vuông tại
A
nên
7,5
2
BC
AM 
.
Chọn đáp án D.
Câu 27: Cho tam giác
DEF
có
10DE DF
cm và
12EF
cm. Gọi
I
là trung điểm của cạnh
EF
.
Đoạn thẳng
DI
có độ dài bằng
A.
65,
cm. B.
7
cm. C.
8
cm. D.
4
cm.
Lời giải:
Cách 1: Ta có
2 2 2 2 2 2
10 10 12
8
2 4 2 4
DE DF EF
DI

.
Cách 2: Tam giác
DIE
vuông tại
I
nên
2 2 2 2
10 6 8DI DE EI
Chọn đáp án C.
Câu 28: Cho tam giác
ABC
có
8AB
cm,
18AC
cm và có diện tích bằng
64
cm
2
. Giá trị
sin A
bằng
A.
3
2
. B.
3
8
. C.
4
5
. D.
8
9
.
Lời giải:
Ta có:
1 2 8
. .sin sin
2 . 9
S
S AB AC A A
AB AC
.
Chọn đáp án D.
Câu 29: Cho tam giác
ABC
có các góc
105A 
,
45B 
. Tính tỉ số
AB
AC
.
A.
2
2
. B.
2
. C.
2
2
. D.
6
3
.
Lời giải:
Ta có:
sin sin(180 105 45 ) 2
sin sin sin sin45 2
b c AB c C
B C AC b B
.
Chọn đáp án A.
Câu 30: Cho tam giác
ABC
có
O
5, 8, 60AB AC A
. Tính độ dài cạnh
.BC
A.
129
. B.
7
. C.
49
. D.
69
.
Lời giải:
Ta có:
2 2 2 2
1
2 . .cos 5 8 2.5.8. 49 7
2
BC AB AC AB AC A
.
Chọn đáp án B.
Câu 31: Tính diện tích tam giác có ba cạnh lần lượt là
3
,
2
và
1.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 38
A.
3
2
. B.
3
. C.
6
2
. D.
2
2
.
Lời giải:
Nửa chu vi của tam giác là:
3 2 1
2
p

.
Diện tích tam giác là:
2
3 2 1
2
S p p p p
.
Chọn đáp án D.
Câu 32: Cho tam giác
ABC
nội tiếp đường tròn bán kính
,R
,AB R
3.AC R
Tính góc
A
, biết
B
là góc tù.
A.
30
. B.
45
. C.
60
. D.
90
.
Lời giải:
Góc
B
là góc tù nên
A
,
C
là góc nhọn.
Ta có:
1
2 2 sin 30 .
sin sin 2
AB R
R R C C
CC
(vì
C
nhọn)
Tương tự:
33
2 2 sin 120
sin sin 2
AC R
R R B B
BB
(do
B
tù).
Suy ra:
180 30 120 30 .A
Chọn đáp án A.
Câu 33: Tam giác
ABC
có
14, 18, 20a b c
. Khẳng định nào sau đây đúng?
A.
42 50'B
. B.
60 56'B
. C.
119 04'B
. D.
90B
.
Lời giải:
Ta có
2 2 2 2 2 2
14 20 18 17
cos
2 2.14.20 35
a c b
B
ac
. Suy ra:
60 56'
o
B
.
Chọn đáp án B.
Câu 34: Cho tam giác
ABC
có
4AB
cm,
7BC
cm,
9CA
cm. Giá trị
cos A
bằng
A.
2
3
. B.
1
3
. C.
2
3
. D.
1
2
.
Lời giải:
Ta có:
2 2 2
2 2 2
2
2 . .cos cos
2 . 3
AB AC BC
BC AB AC AB AC A A
AB AC

.
Chọn đáp án A.
Câu 35: Cho tam giác
ABC
có
4AB
,
5AC
,
6BC
. Tính
cos .BC
A.
1
8
. B.
1
4
. C.
–0,125
. D.
0,75
.
Lời giải:
Ta có
4 ABc
,
5 ACb
,
6 BCa
. Tính
8
1
..2
cos
222
cb
acb
A
.
Để ý
125,0
8
1
cos)cos( ACB
.
Chọn đáp án C.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 39
Câu 36: Tính bán kính đường tròn nội tiếp tam giác có ba cạnh lần lượt là
5, 12, 13.
A.
2.
B.
2.
C.
2 2.
D.
3.
Lời giải:
Nhận xét: Đây là tam giác vuông với cạnh huyền là 13.
Diện tích tam giác:
1
.5.12 30.
2
S 
Bán kính đường tròn nội tiếp tam giác:
30
2.
15
S
r
p
Chọn đáp án B.
Câu 37: Cho tam giác
ABC
có
10BC
,
30A
. Bán kính đường tròn ngoại tiếp tam giác
ABC
bằng
A. 5. B. 10. C.
10
3
. D.
10 3
.
Lời giải:
Gọi
R
là bán kính đường tròn ngoại tiếp tam giác
ABC
, ta có:
10
2 10
sin 2.sin 2.sin30
BC BC
RR
AA
.
Chọn đáp án B.
Câu 38: Tính diện tích tam giác có ba cạnh lần lượt là
5
,
12
,
13
.
A.
60
. B.
30
. C.
34
. D.
75
.
Lời giải:
Nửa chu vi của tam giác là:
5 12 13
15
2
p


Diện tích của tam giác là:
5 12 13 15 15 5 15 12 15 13 30S p p p p
.
Chọn đáp án B.
Câu 39: Cho tam giác
ABC
có
OO
60 , 45 , 5B C AB
. Tính độ dài cạnh
.AC
A.
53
. B.
52
. C.
56
2
. D.
10
.
Lời giải:
Áp dụng định lí sin cho tam giác
ABC
ta có:
.sin 5 6
sin sin sin 2
AB AC AB B
AC
C B C
.
Chọn đáp án C.
Câu 40: Tam giác đều nội tiếp đường tròn bán kính
4R
cm thì có diện tích bằng
A.
2
13 cm
. B.
2
13 2 cm
. C.
2
12 3 cm
. D.
2
15 cm
.
Lời giải:
Gọi
a
là độ dài cạnh và
S
là diện tích của tam giác, ta có:
2
3 . .
44
a a a a
S
R

3 4 3aR
Vậy diện tích tam giác đã cho là:
2
2
4 3 . 3
12 3
4
S cm
.
Chọn đáp án C.
Câu 41: Cho hình bình hành
ABCD
có
,2AB a BC a
và
45BAD 
. Tính diện tích hình bình hành
.ABCD
A.
2
2a
. B.
2
2a
. C.
2
a
. D.
2
3a
.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 40
Lời giải:
a
D
A
B
C
H
Gọi
BH
là đường cao của hình bình hành
ABCD
.
Tam giác
BHA
vuông tại
H
, góc
45BAH BAC
,
2
.sin45
2
a
BH AB
.
Diện tích hình bình hành
ABCD
là:
2
2
. . 2
2
a
S BH AD a a
.
Chọn đáp án C.
Câu 42: Cho hình bình hành có một cạnh là
5
hai đường chéo là
6
và
8
. Tính độ dài cạnh kề với cạnh
có độ dài bằng
5.
A.
3
. B.
1
. C.
56
. D.
5
.
Lời giải:
5
8
6
C
A
D
B
Gọi hình bình hành là
ABCD
. Ta có:
2 2 2
3 4 25 5
AC BD
ABCD
là hình thoi
5AB AD
.
Chọn đáp án D.
Câu 43: Cho hình bình hành có hai cạnh là
5
và
9
, một đường chéo bằng
11
. Tìm độ dài đường chéo
còn lại.
A.
9,5
. B.
46
. C.
91
. D.
3 10
.
Lời giải:
5
9
9
11
C
A
D
B
Gọi hình bình hành là
ABCD
,
5AD
,
9AB
.
Gọi
là góc đối diện với đường chéo có độ dài
11
. Ta có:
2 2 2
5 9 11 1
cos
2.5.9 6

là góc tù
BAD

11BD
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 41
2 2 2 2 2
2. . .cos 2. . .cosAC AD DC AD DC ADC AD DC AD DC BAD
(vì
BAD
và
ADC
bù nhau
cos cosADC BAD
)
2 2 2
1
5 9 2.5.9. 91 91
6
AC AC



.
Chọn đáp án C.
Câu 44: Cho tam giác
ABC
vuông tại
A
có
6AB
cm,
10BC
cm. Tính bán kính đường tròn nội
tiếp tam giác đó.
A. 1 cm. B.
2
cm. C. 2 cm. D. 3 cm.
Lời giải:
Ta có
22
8AC BC AB
(cm). Diện tích tam giác
ABC
là:
2
1
. 24
2
S AB AC cm
Nửa chu vi
6 8 10
12.
2

p
Suy ra
24
2
12
S
r
p
(cm).
Chọn đáp án C.
Câu 45: Tính diện tích tam giác
ABC
biết
60A
,
10b
,
20c
.
A.
50 3
. B.
50
. C.
50 2
. D.
50 5
.
Lời giải:
Áp dụng công thức :
1
. .sin
2
S bc A
1
.10.20.sin60
2

50 3
.
Chọn đáp án A.
Câu 46: Cho tam giác
ABC
có
5AB
,
9AC
và đường trung tuyến
6AM
. Tính độ dài cạnh
BC
.
A.
2 17
. B.
17
. C.
129
. D.
22
.
Lời giải:
5
9
6
M
A
B
C
Ta có:
2 2 2
2
24
AC AB BC
AM

2 2 2 2
2 2 2
95
4 4 6
22
AC AB
BC AM

68 2 17.BC
Chọn đáp án A.
Câu 47: Cho tam giác
ABC
có các góc
75 , 45AB
. Tính tỉ số
AB
AC
.
A.
6
3
. B.
6
. C.
6
2
. D.
1,2
.
Lời giải:
Ta có:
sin sin(180 75 45 ) 6
sin sin sin sin 45 2
b c AB c C
B C AC b B
.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 42
Chọn đáp án C.
Câu 48: Cho tam giác
ABC
vuông tại
A
,
AC b
,
AB c
. Lấy điểm
M
trên cạnh
BC
sao cho góc
30 .BAM 
Tính tỉ số
.
MB
MC
A.
3
3
b
c
. B.
3
3
c
b
. C.
3c
b
. D.
bc
bc
.
Lời giải:
60
°
30
°
B
A
C
M
.
Ta có
.sin30
sin30 sin sin 2.sin
MB AM AM AM
MB
B B B
.
.sin60 3
sin60 sin sin 2.sin
MC AM AM AM
MC
C C C
. Do đó
sin 3
3
3sin 3
MB C c c
MC b
Bb
.
Chọn đáp án B.
Câu 49: Trong tam giác
ABC
, nếu
2
a b c
h h h
thì dẳng thức nào sau đây đúng?
A.
2 1 1
sin sin sinA B C

. B.
2sin sin sinA B C
.
C.
sin 2sin 2sinA B C
. D.
2 1 1
sin sin sinA B C

.
Lời giải:
Ta có:
2
a b c
h h h
2 2 2
2.
S S S
a b c
2 1 1
a b c
2 1 1
2 .sin 2 .sin 2 .sinR A R B R C
2 1 1
sin sin sinA B C
.
Chọn đáp án A.
Câu 50: Cho tam giác
.ABC
Khẳng định nào sau đây đúng?
A.
2 2 2 2 2 2
2
.
3
a b c
m m m a b c
B.
2 2 2 2 2 2
4
.
3
a b c
m m m a b c
C
.
2 2 2 2 2 2
3
.
4
a b c
m m m a b c
D.
2 2 2 2 2 2
1
.
3
a b c
m m m a b c
Lời giải:
Sử dụng công thức trung tuyến của tam giác, ta có:
2 2 2 2 2 2 2 2 2
2 2 2 2 2 2
2 2 2 2 2 2 3
.
4 4 4 4
a b c
b c a c a b a b c
m m m a b c
Chọn đáp án C.
Câu 51: Xét tam giác
ABC
, khẳng định nào sau đây đúng?
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 43
A.
2
a
bc
m
. B.
2
a
bc
m
. C.
2
a
bc
m
. D.
a
m b c
.
Lời giải:
Ta có:
2 2 2
2
24
a
b c a
m

22
2
4
b c b c a
Vì
2
2
b c a b c a
2
2
4
a
bc
m

2
a
bc
m

.
Chọn đáp án B.
Câu 52: Trong tam giác
ABC
, điều kiện để hai trung tuyến kẻ từ
A
và
B
vuông góc với nhau là
A.
2 2 2
2 2 5a b c
. B.
2 2 2
3 3 5a b c
. C.
2 2 2
2 2 3a b c
. D.
2 2 2
5a b c
.
Lời giải:
Vì hai trung tuyến vẽ từ
A
và
B
vuông góc với nhau nên
ABG
vuông tại
G
với
G
là
trọng tâm tam giác
ABC
.
Khi đó:
2 2 2
c GA GB
2 2 2 2 2 2
2
4
9 2 4 2 4
b c a a c b
c




22
22
4
9 4 4
ab
cc



2 2 2
5c a b
.
Chọn đáp án D.
Câu 53: Cho tam giác
ABC
có ba góc nhọn,
BC a
,
AC b
,
AB c
và diện tích là
S
. Tổng
cot cot cotA B C
bằng
A.
2 2 2
2 abc
S

. B.
2 2 2
abc
S

. C.
2 2 2
2
abc
S

. D.
2 2 2
4
abc
S

.
Lời giải:
Từ công thức
12
sin sin
2
S
S bc A A
bc
, và
2 2 2
cos
2
b c a
A
bc

.
Suy ra
2 2 2
2 2 2
cos
2
cot
2
sin 4
b c a
A b c a
bc
A
S
AS
bc


.
Tương tự ta cũng có
2 2 2
cot
4
a c b
B
S

,
2 2 2
cot
4
a b c
C
S

.
Vậy
2 2 2 2 2 2 2 2 2 2 2 2
cot cot cot
4 4 4 4
b c a a c b a b c a b c
A B C
S S S S
.
Chọn đáp án D.
Câu 54: Xét tam giác
ABC
, nếu có
2
.a b c
thì đẳng thức nào dưới đây đúng?
A.
2
1 1 1
a b c
h h h

. B.
2
.
a b c
h h h
. C.
2
1 1 1
a b c
h h h

. D.
2
1 2 2
a b c
h h h

.
Lời giải:
Ta có :
2
.a b c
2
2 2 2
.
a b c
S S S
h h h

2
1 1 1
.
a b c
h h h

2
.
a b c
h h h
.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 44
Chọn đáp án B.
Câu 55: Tính bán kính đường tròn ngoại tiếp tam giác
ABC
biết
AB c
và
1
os
3
c AB
.
A.
2
2
c
. B.
32
8
c
. C.
92
8
c
. D.
3
2
c
.
Lời giải:
Ta có
1
cos cos( )
3
C A B
. Do đó
2
1 2 2
sin 1
33
C



.
32
2
sin 2sin 8
AB AB c
RR
CC
.
Chọn đáp án B.
Câu 56: Cho tam giác
ABC
vuông cân tại
A
và nội tiếp trong đường tròn tâm
O
bán kính
R
. Gọi
r
là bán kính đường tròn nội tiếp tam giác
ABC
. Khi đó, tỉ số
R
r
bằng
A.
12
. B.
22
2
. C.
21
2
. D.
12
2
.
Lời giải:
Giả sử
2
2
2
a
AB AC a BC a R
.
Mặt khác
2
. 2 2
.
2 2 2
22
AB AC a a a a
S pr r r
Suy ra
12
R
r

.
Chọn đáp án A.
Câu 57: Cho tam giác
ABC
vuông cân tại
A
có
30AB AC
cm. Hai đường trung tuyến
BF
và
CE
cắt nhau tại
G
. Diện tích tam giác
GFC
bằng
A. 50 cm
2
. B.
50 2
cm
2
. C. 75 cm
2
. D.
15 105
cm
2
.
Lời giải:
Nối
AG
cắt
BC
tại
H
ta có:
1 1 1
2 3 6
GFC AGC AHC ABC
S S S S
Mà
2
1
.30.30 450
2

ABC
S cm
nên
2
1
.450 75
6

GFC
S cm
.
Chọn đáp án C.
Câu 58: Cho tam giác
ABC
có diện tích
S
. Nếu tăng độ dài mỗi cạnh
BC
và
AC
lên hai lần đồng
thời giữ nguyên độ lớn của góc
C
thì diện tích của tam giác mới được tạo nên bằng
A.
2S
. B.
3S
. C.
4S
. D.
5S
.
Lời giải:
Ta có
1
. .sin
2
S BC AC C
Khi
BC
,
AC
tăng 2 lần, ta có
1
11
.2 .2 .sin 4 . sin 4
22
S BC AC C BC AC C S



.
Chọn đáp án C.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 45
Câu 59: Cho hình vuông
ABCD
có cạnh bằng
a
. Gọi
E
là trung điểm cạnh
BC
,
F
là trung điểm
cạnh
AE
. Tính độ dài đoạn thẳng
DF
.
A.
13
4
a
. B.
5
4
a
. C.
3
2
a
. D.
3
4
a
.
Lời giải:
F
E
C
D
A
B
Ta có:
2
2
5
22
aa
AE DE a



Dùng công thức độ dài trung tuyến:
2
2
2 2 2 2 2
2
5
5 13
4
2 4 2 16 16
a
a
DA DE AE a a
DF
13
4
a
DF
.
Chọn đáp án A.
Câu 60: Cho tam giác
ABC
có
135BC
và
.BC a
Tính bán kính đường tròn ngoại tiếp tam giác.
A.
2
2
a
. B.
2a
. C.
3
2
a
. D.
3a
.
Lời giải:
Ta có
180 135 45 A
2
2
sin 2sin 2sin45 2
BC BC a a
RR
AA
.
Chọn đáp án A.
Câu 61: Cho tam giác
ABC
có
9AB
,
10BC
,
11CA
. Gọi
M
là trung điểm
BC
và
N
là trung
điểm
AM
. Tính độ dài
BN
.
A.
6
. B.
42
. C.
5
. D.
34
.
Lời giải:
Ta có
2 2 2
2
76
24
AB AC BC
AM
2 2 2
2
34
24
BA BM AM
BN
.
Chọn đáp án D.
Câu 62: Cho tam giác
ABC
có
5AB
,
8BC
,
6CA
. Gọi
G
là trọng tâm tam giác
ABC
. Độ dài
đoạn thẳng
CG
bằng
A.
57
2
. B.
57
3
. C.
57
6
. D.
13
3
.
Lời giải:
Gọi
M
là trung điểm
AB
, ta có:
2 2 2
2
175
2 4 4
CB AC AB
CM
2 2 175 5 7
3 3 4 3
CG CM
.
Chọn đáp án B.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 46
Câu 63: Cho tam giác
ABC
có
2AB
cm,
1AC
cm,
O
60A
. Tính độ dài cạnh
.BC
A. 1 cm. B. 2 cm. C.
3
cm. D.
5
cm.
Lời giải:
Áp dụng định lí Cô – sin cho tam giác
ABC
ta có:
2 2 2
2. . .cosBC AB AC AB AC A
22
1 2 2.1.2.cos60 3
o
. Suy ra:
3BC
(cm).
Chọn đáp án C.
Câu 64: Cho tam giác có ba cạnh lần lượt là
5
,
6
,
7
. Tính độ dài đường cao ứng với cạnh có độ dài
bằng
6.
A.
6
. B.
26
. C.
5
. D.
53
2
.
Lời giải:
Nửa chu vi của tam giác là:
5 6 7
9
2
p


.
Diện tích tam giác là:
5 6 7 6 6S p p p p
. Đặt
5a
,
6b
,
7c
.
Độ dài đường cao ứng với cạnh có độ dài bằng 6 là:
2 2.6 6
26
6
b
S
h
b
.
Chọn đáp án B.
Câu 65: Cho tam giác có ba cạnh lần lượt là
5,12,13.
Tính độ dài đường cao ứng với cạnh lớn nhất.
A.
60
13
. B.
120
13
. C.
30
13
. D.
12
.
Lời giải:
Đặt
5a
,
12b
,
13c
. Ta có: Nửa chu vi của tam giác là:
5 12 13
15
2
p


Diện tích của tam giác là:
5 12 13 15 15 5 15 12 15 13 30S p p p p
.
Đường cao ứng với cạnh lớn nhất là:
2 2.30 60
13 13
c
S
h
c
.
Chọn đáp án A.
Câu 66: Cho tam giác
ABC
có
12BC
,
9CA
,
6AB
. Trên cạnh
BC
lấy điểm
M
sao cho
4BM
.
Tính độ dài đoạn thẳng
.AM
A.
25
. B.
32
. C.
20
. D.
19
.
Lời giải:
2 2 2 2 2 2
6 12 9 11
cos
2 . 2.6.12 16
AB BC AC
B
AB BC
2 2 2 2
11
2 . .cosB 6 4 2.6.4. 19.
16
AM AB BM AB BM
Chọn đáp án D.
Câu 67: Cho tam giác cân
ABC
có
120A 
và
AB AC a
. Lấy điểm
M
trên cạnh
BC
sao cho
2
5
BC
BM
. Tính độ dài
.AM
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 47
A.
3
3
a
. B.
11
5
a
. C.
7
5
a
. D.
6
4
a
.
Lời giải:
30
a
a
A
B
C
M
2 2 2 2
1
2 cos120 2 . . 3
2



BC AB AC ABAC a a a a a
23
5
a
BM
2
2 2 2
2 3 2 3 3 7
2 . .cos30 2 . .
5 5 2 5




a a a
AM AB BM AB BM a a
.
Chọn đáp án C.
Câu 68: Cho tam giác
ABC
có các cạnh
, , a b c
thỏa mãn điều kiện
3a b c a b c ab
. Tính số
đo của góc
.C
A.
120
. B.
30
. C.
45
. D.
60
.
Lời giải:
Trong tam giác
ABC
ta luôn có:
2 2 2
2 .cosc a b ab C
.
Hệ thức
2
2
33a b c a b c ab a b c ab
2 2 2
c a b ab
Suy ra:
1
2.cos 1 cos 60
2
C C C
.
Chọn đáp án D.
Câu 69: Cho tam giác
ABC
có
.
4
a b c a b c
S
Khẳng định nào sau đây đúng?
A. Tam giác ABC vuông tại A. B. Tam giác ABC vuông tại B.
C. Tam giác ABC tù. D. Tam giác ABC nhọn.
Lời giải:
Nửa chu vi của tam giác là
.
2
a b c
p

Ta có:
22
2
16
4
a b c a b c
S S a b c a b c
22
p p a p b p c p c p b
22
p p a p c p b p pa p p b c bc
2 2 2
2.p c b a bc b c a c b a bc b c a
Chọn đáp án A.
Câu 70: Cho tam giác
ABC
thỏa mãn
sin sin
sin .
cos cos
BC
A
BC
Khẳng định nào sau đây đúng?
A. Tam giác
ABC
cân. B. Tam giác
ABC
đều.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 48
C. Tam giác
ABC
vuông. D. Tam giác
ABC
có góc
60 .A 
Lời giải:
Ta có:
2 sin ; sin ; sin .
sin sin sin 2 2 2
a b c a b c
R A B C
A B C R R R
Và
2 2 2 2 2 2
cos ; cos .
22
a c b a b c
BC
ac ab

Ta có:
sin sin
sin sin cos cos sin sin
cos cos
BC
A A B C B C
BC
2 2 2 2 2 2
2 2 2 2 2
a a c b a b c b c
R ac ab R R



2 2 2 2 2 2
2 2 2 2 2 2
2
22
a c b a b c
b c b a c b c a b c bc b c
cb
2 2 3 2 2 3 2 2
22ba bc b ca cb c b c bc
3 3 2 2 2 2
0b c b c bc ba ca
2 2 2
0b c b bc c bc b c a b c
2 2 2 2 2 2 2 2 2
0 0 .b c b c a b c a b c a
Chọn đáp án C.
Câu 71: Một tam giác có độ dài các cạnh là
1, ,2m
với
m
. Giá trị của
m
là
A.
1
. B. 2. C.
3
. D.
4
.
Lời giải:
Ta có 1,
m
, 2 là độ dài 3 cạnh tam giác mà một cạnh luôn lớn hơn hiệu 2 cạnh và nhỏ hơn tổng 2
cạnh nên ta có
2 1 2 1 m
13 m
Mặt khác,
m
nên
2m
.
Chọn đáp án B.
Câu 72: Cho tam giác
ABC
có
7AB
,
5AC
và
1
cos
5
BC
. Tính độ dài cạnh
.BC
A.
2 15
. B.
4 22
. C.
4 15
. D.
2 22
.
Lời giải:
Vì trong tam giác
ABC
ta có
BC
bù với góc
A
nên
1
cos B C
5
1
cos
5
A
2 2 2 2
1
2 . .cosA 7 5 2.7.5. 2 15
5
BC AB AC AB AC
.
Chọn đáp án A.
Câu 73: Tam giác
ABC
có
1
cos A B
8
,
4AC
,
5BC
. Tính cạnh
.AB
A.
46
. B.
11
. C.
52
. D.
6
.
Lời giải:
Vì trong tam giác
ABC
ta có
AB
bù với góc
C
nên
11
cos cos
88
A B C
2 2 2 2
1
2 . .cos 4 5 2.4.5. 6
8
AB AC BC AB BC C
.
Chọn đáp án D.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 49
Câu 74: Tính bán kính đường tròn ngoại tiếp tam giác
ABC
biết
12AB
và
1
cot( )
3
AB
.
A.
2 10
. B.
9 10
5
. C.
5 10
. D.
32
.
Lời giải:
Ta có:
1
cot( )
3
AB
nên
1
cot
3
C 
, suy ra
3cos sinCC
.
Mà
22
sin cos 1CC
3 3 10
sin
10
10
C
2 2 10
sin 2sin
AB AB
RR
CC
.
Chọn đáp án A.
Câu 75: Tính bán kính đường tròn ngoại tiếp tam giác
ABC
biết
10AB
và
1
tan( )
3
AB
.
A.
5 10
9
. B.
10
3
. C.
10
5
. D.
5 10
.
Lời giải:
Ta có:
1
tan( )
3
AB
nên
1
tan
3
C 
.
Do đó
3sin cosCC
, mà
22
sin cos 1CC
1 10
sin
10
10
C
.
2 5 10
sin 2sin
AB AB
RR
CC
.
Chọn đáp án D.
Câu 76: Tìm chu vi tam giác
ABC
, biết rằng
6AB
và
2sin 3sin 4sinA B C
.
A.
26
. B.
13
. C.
5 26
. D.
10 6
.
Lời giải:
Vì
2sin 3sin 4sinA B C
nên ta có:
2 3 4 24a b c
(do
6c AB
).
Do đó:
12, 8, 6a b c
. Chu vi tam giác
ABC
bằng
26
.
Chọn đáp án A.
Câu 77: Cho tam giác
ABC
có
10BC
và
sin sin sin
5 4 3
A B C

. Tìm chu vi của tam giác đó.
A.
12
. B.
36
. C.
24
. D.
22
.
Lời giải:
Vì
sin sin sin
5 4 3
A B C

, nên
8, 6
5 4 3
abc
bc
(do
10a BC
).
Chu vi tam giác
ABC
bằng
24
.
Chọn đáp án C.
Câu 78: Tam giác
ABC
có các cạnh
,,a b c
thỏa mãn điều kiện
.
6 5 7
a b b c a c

Tính
cos .A
A.
1
.
4
B.
1
.
3
C.
1
.
3
D.
1
.
3
Lời giải:
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 50
Ta có:
6
5 9 .
6 5 7
7
a b t
a b b c a c
t b c t a b c t
a c t


Vậy
4
2.
3
at
bt
ct
Theo định lí côsin:
2 2 2 2 2 2
4 9 16 1
cos .
2 2.2 .3 4
b c a t t t
A
bc t t
Tương tự, ta tính được:
7 11
cos ;cos .
8 16
BC
Chọn đáp án A.
Câu 79: Tính góc
C
của tam giác
ABC
biết
ab
và
2 2 2 2
a a c b b c
.
A.
150C 
. B.
120C 
. C.
60C 
. D.
30C 
.
Lời giải:
Ta có:
2 2 2 2
a a c b b c
3 3 2
0a b c a b
2 2 2
0a b a ab b c a b
2 2 2
0a ab b c
2 2 2
cos
2
a b c
C
ab


1
2

. Do đó:
120C 
.
Chọn đáp án B.
Câu 80: Cho góc
O
30xOy
. Gọi
A
và
B
là hai điểm di động lần lượt trên
Ox
và
Oy
sao cho
1AB
.
Độ dài lớn nhất của đoạn
OB
bằng
A.
1,5
. B.
3
. C.
22
. D.
2
.
Lời giải:
Xét tam giác
OAB
có
2 2 1
sin
AB
RR
O
. Với
R
là bán kính đường tròn ngoại tiếp tam
giác
OAB
. Vậy
OB
lớn nhất khi
OB
là đường kính của đường tròn ngoại tiếp tam giác
OAB
.
Khi đó
2OB
.
Chọn đáp án D.
Câu 81: Cho góc
30xOy 
. Gọi
A
và
B
là hai điểm di động lần lượt trên
Ox
và
Oy
sao cho
2AB
.
Độ dài lớn nhất của đoạn
OB
bằng
A. 2. B. 3. C. 4. D. 5.
Lời giải:
Đặt
OA x
,
OB y
. Áp dụng công thức định lý hàm số cosin cho tam giác
OAB
ta có:
2 2 2 2 2
2 cos30 2 3 4 0x y xy x y xy
*
Tìm điều kiện để tồn tại
x
, ta coi phương trình trên là phương trình ẩn
x
, tham số
y
.
Khi đó, phương trình
*
có nghiệm
2
2
0 3 4 4 0 4 4y y y
.
Do đó
max 4y
.
Chọn đáp án C.
Câu 82: Hai chiếc tàu thủy cùng xuất phát từ một vị trí
A
, đi thẳng theo hai hướng tạo với nhau góc
60
. Tàu
B
chạy với tốc độ
20
hải lí một giờ. Tàu
C
chạy với tốc độ
15
hải lí một giờ (tham
khảo hình vẽ)
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 51
Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí?
Kết quả gần nhất với số nào sau đây?
A.
61
hải lí. B.
36
hải lí. C.
21
hải lí. D.
18
hải lí.
Lời giải:
Sau
2
giờ tàu
B
đi được
40
hải lí, tàu
C
đi được
30
hải lí. Vậy tam giác
ABC
có
40, 30AB AC
và
60 .A 
Áp dụng định lí côsin vào tam giác
,ABC
ta có
2 2 2
2 cosa b c bc A
22
30 40 2.30.40.cos60 900 1600 1200 1300.
Vậy
1300 36BC 
(hải lí).
Sau
2
giờ, hai tàu cách nhau khoảng
36
hải lí.
Chọn đáp án B.
Câu 83: Để đo khoảng cách từ một điểm
A
trên bờ sông đến gốc cây
C
trên cù lao giữa sông, người ta
chọn một điểm
B
cùng ở trên bờ với
A
sao cho từ
A
và
B
có thể nhìn thấy điểm
C
. Ta đo được
khoảng cách
m40AB
,
0
45CAB
và
70CBA 
(tham khảo hình vẽ)
Vậy sau khi đo đạc và tính toán được khoảng cách
AC
gần nhất với giá trị nào sau đây?
A.
m53
. B.
m30
. C.
m41,5
. D.
m41
.
Lời giải:
Áp dụng định lí sin vào tam giác
,ABC
ta có
sin sin
AC AB
BC
Vì
sin sinC


nên
m
.sin 40.sin70
41,47 .
sin115
sin
AB
AC

Chọn đáp án C.
Câu 84: Từ vị trí
A
người ta quan sát một cây cao (hình vẽ).
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 52
Biết
m m 4 , 20 , 45AH HB BAC
.
Chiều cao của cây gần nhất với giá trị nào sau đây?
A.
m17,5
. B.
m17
. C.
m16,5
. D.
m16
.
Lời giải:
Trong tam giác
AHB
, ta có
41
tan 11 19'
20 5
AH
ABH ABH
BH

.
Suy ra
0
90 78 41'ABC ABH
. Suy ra
180 56 19'ACB BAC ABC
.
Áp dụng định lý sin trong tam giác
ABC
, ta được:
m.
.sin
17
sin sin sin
AB CB AB BAC
CB
ACB BAC ACB

Chọn đáp án B.
Câu 85: Giả sử
CD h
là chiều cao của tháp trong đó
C
là chân tháp. Chọn hai điểm
,AB
trên mặt
đất sao cho ba điểm
,AB
và
C
thẳng hàng. Ta đo được
m24AB
,
63 , 48CAD CBD
(tham khảo hình vẽ)
Chiều cao
h
của tháp gần với giá trị nào sau đây?
A.
m18
. B.
m18,5
. C.
m60
. D.
m61,4
.
Lời giải:
Áp dụng định lí sin vào tam giác
,ABD
ta có
.
sin sin
AD AB
D
Ta có
D


nên
63 48 15 .D

Do đó
m
.sin 24.sin48
68,91 .
sin15
sin
AB
AD

Trong tam giác vuông
,ACD
có
m.sin 61,4 .h CD AD
Chọn đáp án D.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 53
Câu 86: Trên nóc một tòa nhà có một cột ăng-ten cao
m5
. Từ vị trí quan sát
A
cao
m7
so với mặt
đất, có thể nhìn thấy đỉnh
B
và chân
C
của cột ăng-ten dưới góc
50
và
40
so với phương
nằm ngang (tham khảo hình vẽ)
Chiều cao của tòa nhà gần nhất với giá trị nào sau đây?
A.
m12
. B.
m19
. C.
m24
. D.
m29
.
Lời giải:
Từ hình vẽ, suy ra
10BAC 
và
180 180 50 90 40ABD BAD ADB
.
Áp dụng định lí sin trong tam giác
ABC
, ta có
= m
.sin 5.sin40
18,5
sin10
sin sin sin
BC AC BC ABC
AC
BAC ABC BAC

.
Trong tam giác vuông
ADC
, ta có
m.sin .sin 11,9
CD
CAD CD AC CAD
AC

Vậy
m.11,9 7 18,9CH CD DH
Chọn đáp án B.
Câu 87: Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng đứng
cách chân tháp một khoảng
m60CD
, giả sử chiều cao của giác kế là
m1OC
. Quay thanh
giác kế sao cho khi ngắm theo thanh ta nhình thấy đỉnh
A
của tháp. Đọc trên giác kế số
đo của góc
60AOB
(tham khảo hình vẽ)
60
°
1
m
60
m
O
C
D
A
B
Chiều cao của ngọn tháp gần với giá trị nào sau đây?
A.
m40
. B.
m114
. C.
m105
. D.
m110
.
Lời giải:
Tam giác
OAB
vuông tại
,B
có
tan tan60 . 60 3 m.
AB
AOB AB OB
OB
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 54
Vậy chiều cao của ngọn tháp là
m m.60 3 1 105h AB OC
Chọn đáp án C.
Câu 88: Một thợ lặn có vị trí cách mặt nước 8m, một con tàu đắm ở góc
0
70 .
Sau khi cùng xuống tới
một điểm cao hơn 14m so với đáy đại dương, thợ lặn nhìn thấy con tàu đắm ở góc
0
57
. Chiều
sau của con tàu đắm gần giá trị nào nhất?
A. 24,979 m. B. 32,964 m. C. 32,979 m. D. 33,25 m.
Lời giải:
Đặt
,.CD x AB y
Xét tam giác BCD:
tan 14.tan33
14
x
CBD x
Xét tam giác ACD:
tan
14
x
CAD
y
14 tan20yx
14.tan33
14 10,979
tan20
y
Chiều sâu của con tàu đắm bằng:
14.tan33
8 32,979 .
tan20
m

Chọn đáp án C.
Câu 89: Đầu của các tổng thống ở Mount Rushmore cao 18 mét. Một du khách nhìn thấy đỉnh đầu
của George Washington ở góc cao
48
và cằm của ông ở góc cao
44,76 .
Chiều cao của múi
Rushmore gần giá trị nào nhất?
A. 182,753 m. B. 99,649 m. C. 99,9 m. D. 168,055 m.
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 55
Lời giải:
Đặt
,.AB y BC x
Ta có:
tan44,76
tan44,76
xx
y
y
Lại có:
18 18
tan48
tan48
xx
y
y

18
tan44,76 tan48
xx


18.tan44,76
18 168,055
tan48 tan44,76
x
(m).
Chọn đáp án D.
Câu 90: Từ hai vị trí
A
và
B
của một tòa nhà, người ta quan sát đỉnh
C
của ngọn núi. Biết rằng độ
cao
m70AB
, phương nhìn
AC
tạo với phương nằm ngang góc
30
, phương nhìn
BC
tạo
với phương nằm ngang góc
15 30'
(tham khảo hình vẽ)
Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây?
A.
m135
. B.
m234
. C.
m165
. D.
m195
.
Lời giải:
Từ giả thiết, ta suy ra tam giác
ABC
có
60 , 105 30CAB ABC
và
70.c
Khi đó
180 180 180 165 30 14 30 .A B C C A B

Theo định lí sin, ta có
sin sin
bc
BC
hay
70
sin105 30 sin14 30
b


Do đó
m
70.sin105 30
269,4 .
sin14 30
AC b
Gọi
CH
là khoảng cách từ
C
đến mặt đất. Tam giác vuông
ACH
có cạnh
CH
đối diện với
góc
30
nên
m
269,4
134,7 .
22
AC
CH
Vậy ngọn núi cao khoảng
m135 .
Chọn đáp án A.
________________HẾT________________
Huế, 10h58’ ngày 29 tháng 8 năm 2022
| 1/55
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TR¾C NGHIÖM M«n: To¸n 10 Chuyên đề:
HỆ THỨC LƯỢNG TRONG TAM GIÁC Líp To¸n thÇy L£ B¸ B¶O
Trường THPT Đặng Huy Trứ
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ
Trung tâm Km 10 Hương Trà, Huế Chủ đề 2:
HỆ THỨC LƯỢNG TRONG TAM GIÁC I. LÝ THUYẾT 1. Định lí côsin A b c B a C
Xét tam giác ABC với BC a, AC b và AB c . Ta có: 2 2 2 2 2 2 2 2 2
a b c  2bc.cos A; b c a  2c .
a cos B; c a b  2a . b cosC 2 2 2 2 2 2 2 2 2
b c a
c a b
a b c
Hệ quả: cos A  ; cos B  ; cosC 2bc 2ca 2ab 2. Định lí sin A R O C B
Xét tam giác ABC với BC a, AC b , AB c với R là bán kính đường tròn ngoại tiếp. a b c Ta có:    2R sin A sin B sinC
3. Độ dài trung tuyến A b c mc mb ma B a C
Xét tam giác ABC với m , m , m lần lượt là các trung tuyến kẻ từ A, B,C. a b c Ta có: 2 2 2 b c  2  a 2 2 2 a c  2  b 2 2 2 a b  2  c 2 2 2 m  ; m  ; m a 4 b 4 c 4
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 1
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
4. Diện tích tam giác
Với tam giác ABC ta kí hiệu h , h , h là độ dài đường cao lần lượt tương ứng với các cạnh a b c
a b c
BC, CA, AB; R, r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp tam giác; p  là 2
nửa chu vi tam giác; S là diện tích tam giác ABC . Khi đó ta có: 1 1 1
S ah bh ch 2 a 2 b 2 c 1 1 1
bcsin A casin B absinC 2 2 2 abc  4Rpr  (
p p a)(p b)(p c) C«ng thøc Herong 5. Giải tam giác
Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một số yếu tố của tam giác đó
được gọi là giải tam giác.
II. BÀI TẬP TỰ LUẬN Câu 1:
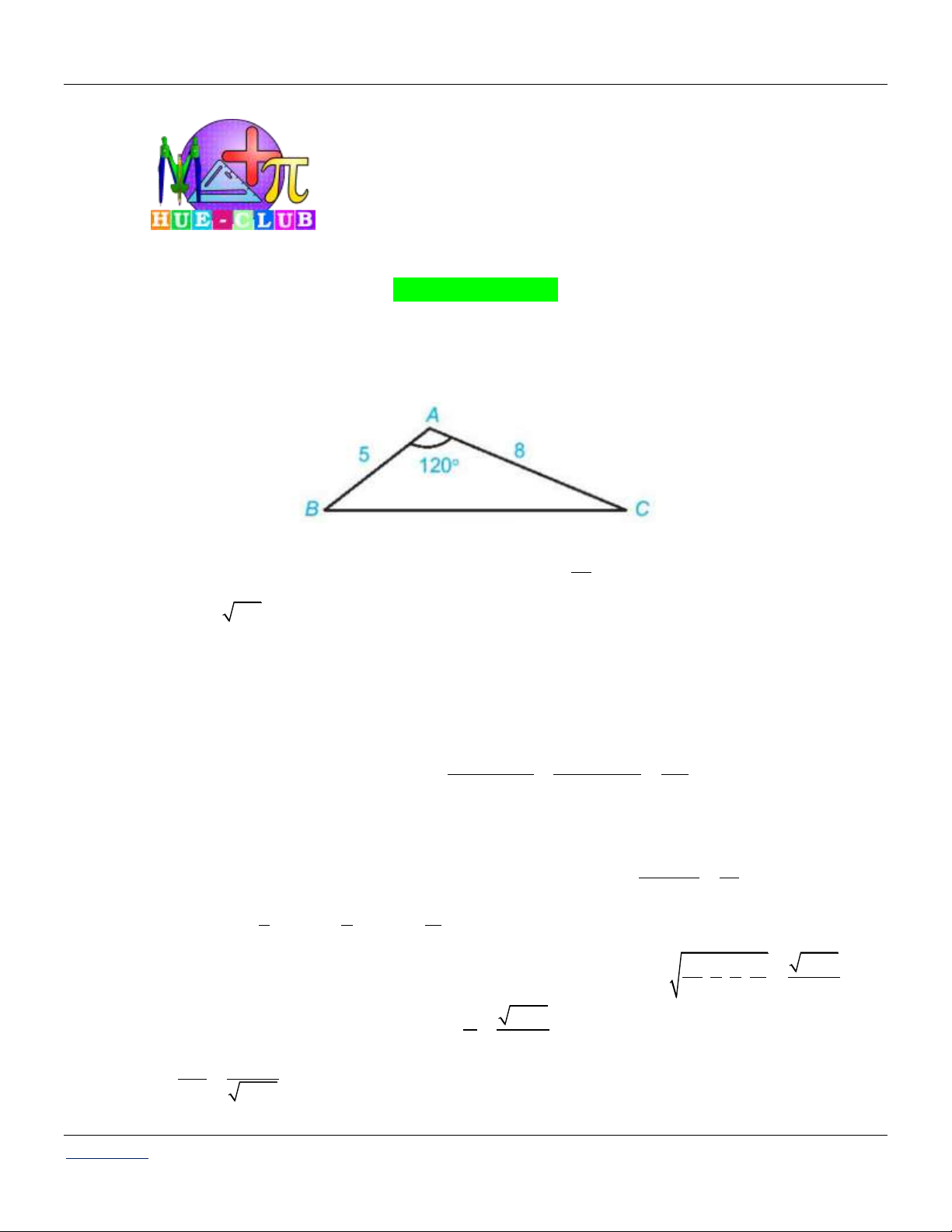
Cho tam giác ABC có A  120 và AB  5, AC  8 . Tính độ dài cạnh BC . Câu 2:
Cho tam giác ABC có a  8,b  9, c  6.
a) Tính số đo các góc của tam giác.
b) Tính diện tích, bán kính đường tròn ngoại tiếp, bán kính đường tròn nội tiếp, độ dài các
đường cao của tam giác. Câu 3: Cho tam giác ABC có o
A  15 , c  6 và o B  120 .
a) Tính độ dài các cạnh a, b ;
b) Tính bán kính đường tròn ngoại tiếp và diện tích của tam giác;
c) Tính độ dài đường cao h . a Câu 4:
Cho tam giác ABC có a  14, b  18, c  20 . Tính gần đúng góc ABC. Câu 5:
Giải tam giác ABC , biết c  14, ˆ
A  60, ˆB  40 . Câu 6: Cho tam giác ABC có O O
B  60 , C  45 , AB  5 . Tính độ dài cạnh AC. Câu 7:
Cho tam giác ABC có BC  10 , A  30 . Tính bán kính đường tròn ngoại tiếp tam giác ABC. Câu 8:
Cho tam giác có ba cạnh là 6,10,8 . Tính bán kính đường tròn nội tiếp tam giác đó. Câu 9:
Cho tam giác ABC vuông tại A có AB  6 cm, BC  10 cm. Tính bán kính đường tròn nội tiếp tam giác đó.
Câu 10: Tính diện tích S của tam giác ABC có  4,  6, ˆ c b A  150 .
Câu 11: Tính diện tích tam giác có ba cạnh lần lượt là 5 , 12 , 13 .
Câu 12: Cho tam giác ABC có góc B tù, AB  3 , AC  4 và có diện tích bằng 3 3. Tính số đo góc BAC.
Câu 13: Tính diện tích tam giác đều nội tiếp đường tròn bán kính R  4 cm.
Câu 14: Cho tam giác ABC có AB  1, AC  3, A  60 . Tính bán kính đường tròn ngoại tiếp ABC .
Câu 15: Cho tam giác ABC có AB  8 cm, AC  18 cm và có diện tích bằng 64 cm2. Tính sin . A
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 2
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Câu 16: Cho tam giác ABC có AB  9 cm, AC  12 cm và BC  15 cm. Tính độ dài đường trung
tuyến AM của tam giác ABC.
Câu 17: Cho tam giác ABC có AB  5 , AC  9 và đường trung tuyến AM  6 . Tính độ dài cạnh BC .
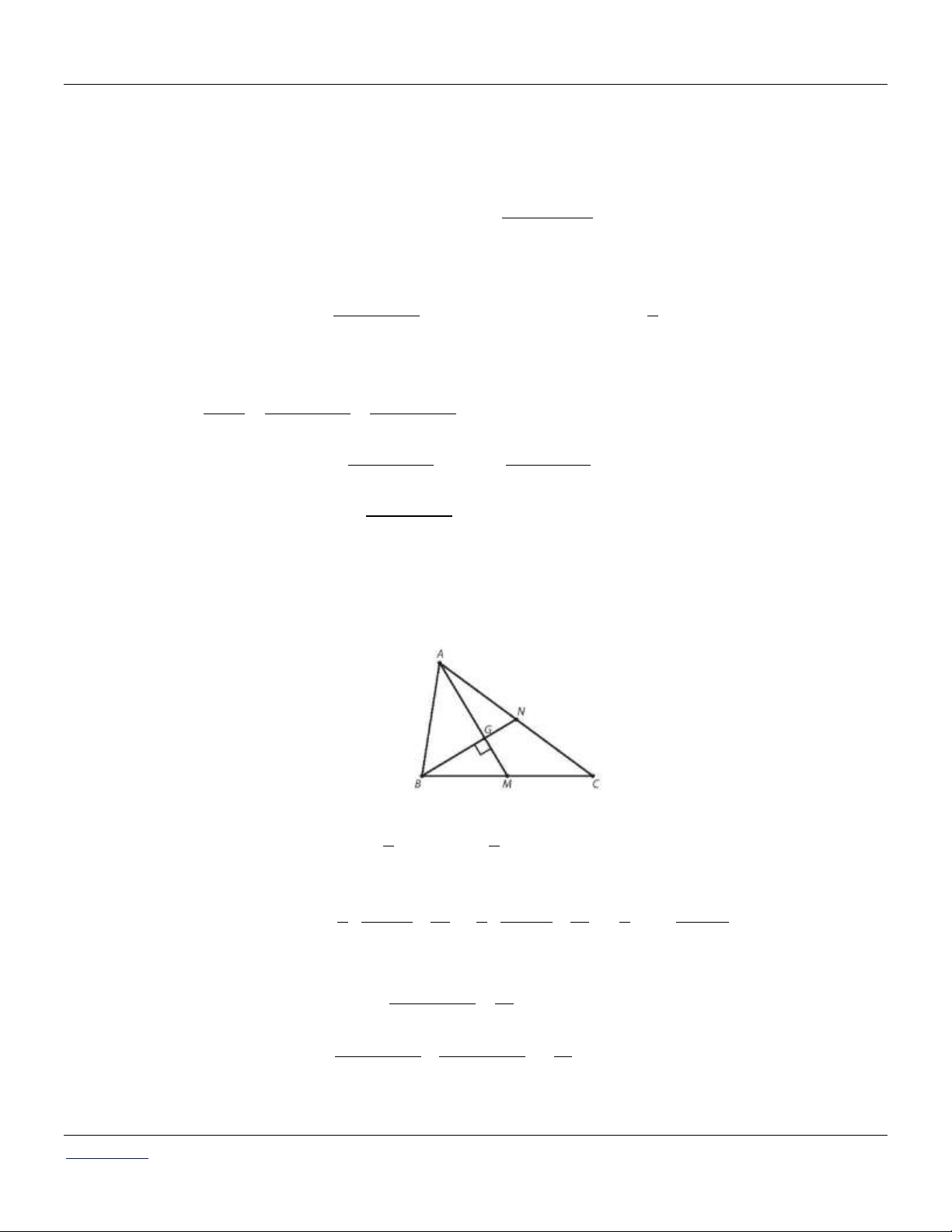
Câu 18: Cho tam giác ABC có AB  5 , BC  8 , CA  6 . Gọi G là trọng tâm tam giác. Tính độ dài đoạn thẳng CG.
Câu 19: Cho tam giác có ba cạnh lần lượt là 5 , 6 , 7 . Tính độ dài đường cao ứng với cạnh có độ dài bằng 6. AB
Câu 20: Cho tam giác ABC có các góc A  105 , B  45 . Tính tỉ số . AC
Câu 21: Cho tam giác có ba cạnh lần lượt là 5,12,13. Tính độ dài đường cao ứng với cạnh lớn nhất.
Câu 22: Cho tam giác có ba cạnh lần lượt là 2, 3, 4 . Góc bé nhất của tam giác có sin bằng bao nhiêu?
Câu 23: Cho tam giác ABC có AB  3 , AC  4 và tan A  2 2 . Tính độ dài cạnh BC.
Câu 24: Cho tam giác ABC vuông cân tại .
A Gọi r, R lần lượt là bán kính đường tròn nội tiếp, ngoại R
tiếp tam giác ABC . Tính tỉ số . r
Câu 25: Cho tam giác ABC có các cạnh a, b, c thỏa mãn a b ca b c  3ab . Tính số đo của góc C.
Câu 26: Tính góc C của tam giác ABC biết a b và  2 2     2 2 a a c b b c  . sin A sin B sinC
Câu 27: Cho tam giác ABC có BC  10 và  
. Tính chu vi của tam giác đó. 5 4 3 sin A sin B sinC
Câu 28: Cho tam giác ABC có các góc thỏa mãn  
. Tính số đo các góc của tam giác. 1 2 3
Câu 29: Cho tam giác ABC có AB  7 , AC  5 và B C 1 cos
  . Tính độ dài cạnh BC. 5
Câu 30: Cho tam giác ABC , các đường cao h , h , h thỏa mãn 3h  2h h . Chứng minh rằng: a b c a b c 3 2 1   . a b c
Câu 31: Cho tam giác ABC . Chứng minh rằng: 2 2 2 b c a 1 1 1 1 a) 2 m   ; b)    . a 2 4 h h h r a b c
Câu 32: Cho tam giác ABC có các góc thỏa mãn sin C  2.sin .
B cos A . Chứng minh rằng tam giác
ABC là một tam giác cân.
Câu 33: Cho tam giác ABC . Chứng minh rằng: 2 2 2
a b c 3
a) cot A  cot B  cot C  . b) 2 2 2
m m m
a b c . a b c  2 2 2 4S 4
Câu 34: Cho tam giác ABC có hai trung tuyến kẻ từ A và B vuông góc. Chứng minh rằng: a) 2 2 2
a b  5c .
b) cot C  2cot A  cot B .
Câu 35: Cho tam giác ABC có 2
S  2R sin Asin B . Chứng minh rằng tam giác ABC là một tam giác vuông.
Câu 36: Cho tam giác ABC vuông cân tại A có AB AC  30 cm. Hai đường trung tuyến BF và CE
cắt nhau tại G . Tính diện tích tam giác GFC.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 3
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
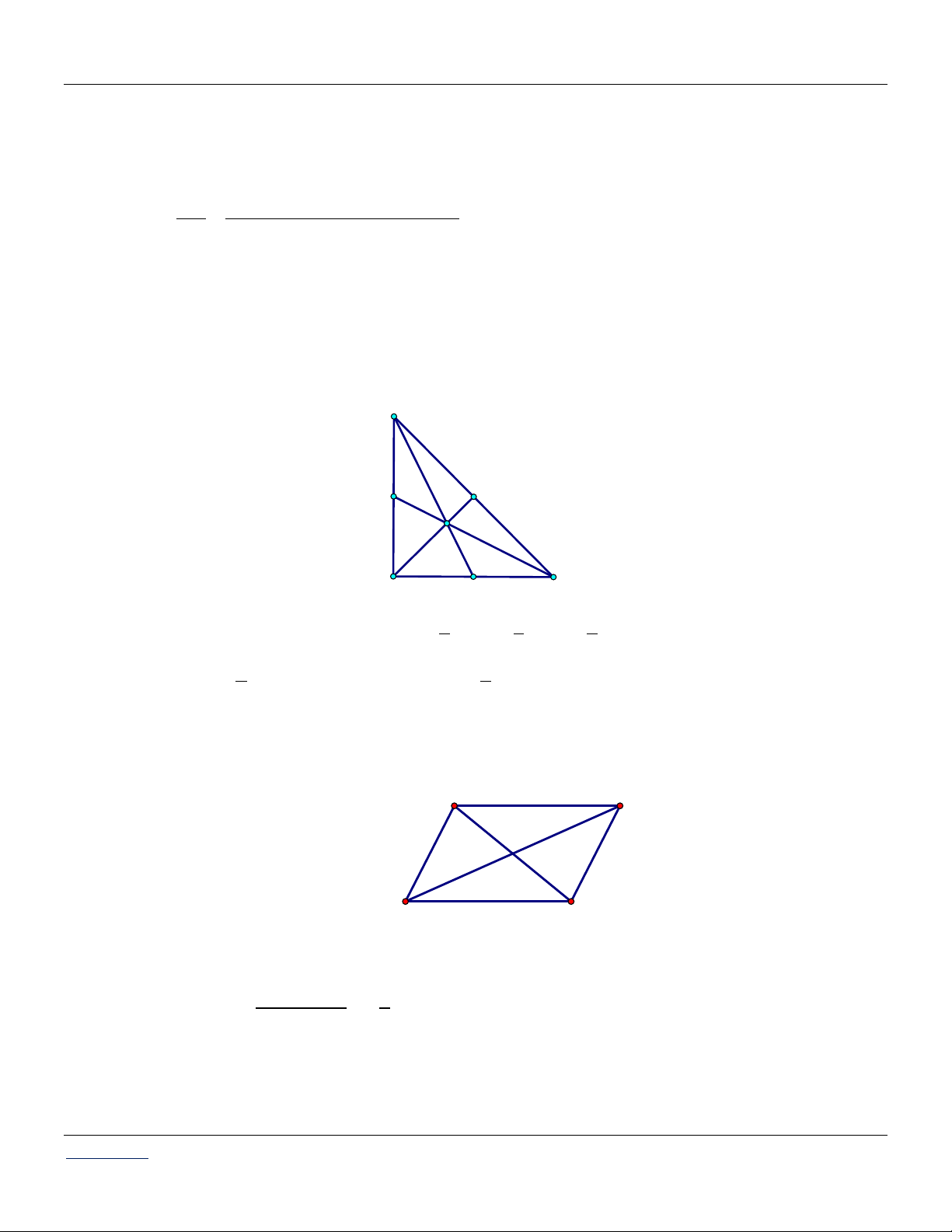
Câu 37: Cho hình bình hành có hai cạnh là 5 và 9 , một đường chéo bằng11. Tìm độ dài đường chéo còn lại.
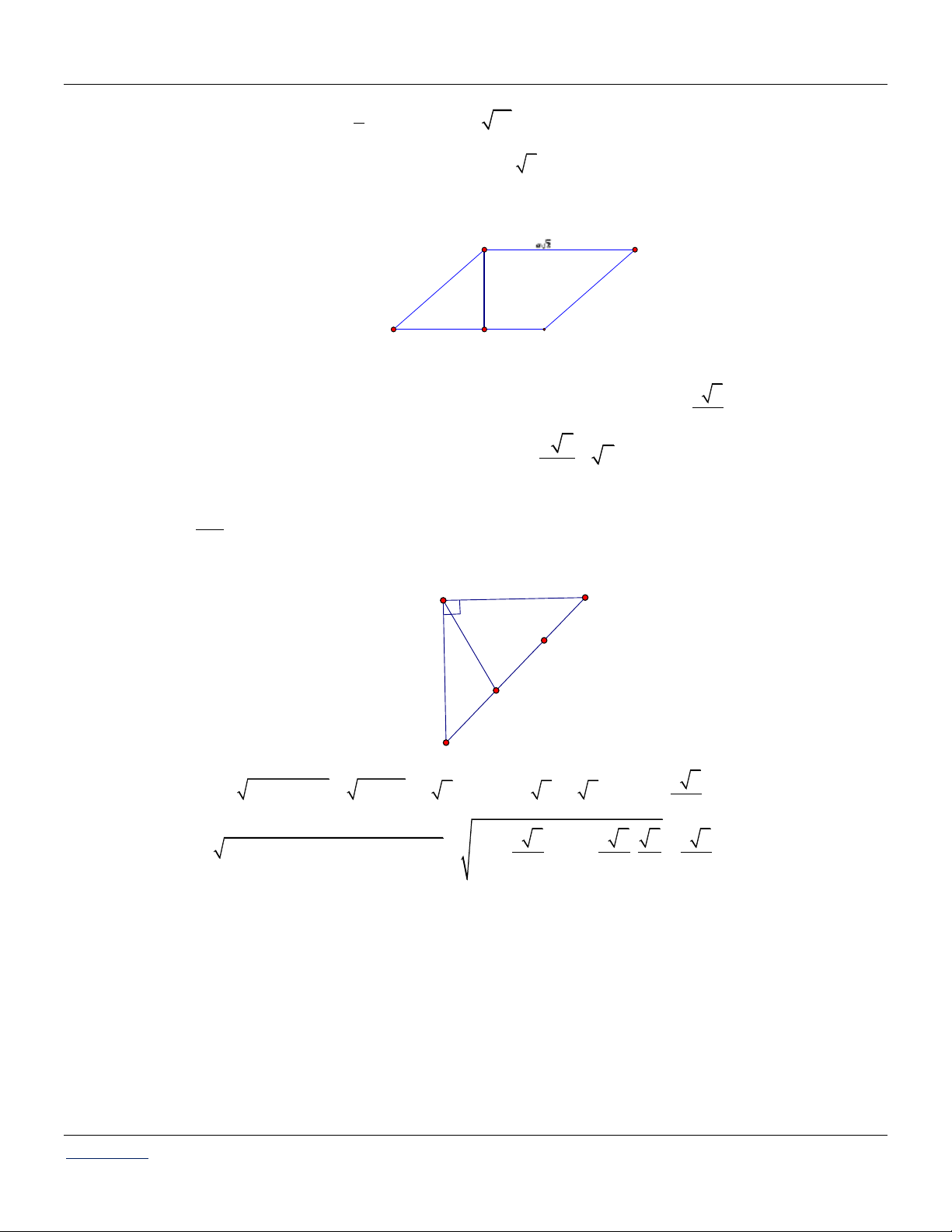
Câu 38: Cho hình bình hành ABCD có AB a, BC a 2 và BAD  45 . Tính diện tích hình bình hành ABCD.
Câu 39: Cho tam giác ABC vuông tại A có AB AC a . Điểm M nằm trên cạnh BC sao cho BC BM
. Tính độ dài đoạn thẳng AM. 3
Câu 40: Cho hình vuông ABCD có cạnh bằng a . Gọi E là trung điểm cạnh BC , F là trung điểm
cạnh AE . Tính độ dài đoạn thẳng DF .
Câu 41: Cho tam giác ABC nội tiếp đường tròn bán kính R, AB R, AC R 2. Tính góc A biết A là góc tù.
Câu 42: Cho tam giác vuông, trong đó có một góc bằng trung bình cộng của hai góc còn lại. Cạnh lớn
nhất của tam giác đó bằng .
a Tính diện tích tam giác đã cho.
Câu 43: Cho tam giác ABC vuông cân tại A và điểm M trong tam giác sao cho MA  1, MB  2 , MC  2 . Tính góc AMC .
Câu 44: Cho góc xOy  30 . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB  2 .
Tính độ dài lớn nhất của đoạn . OB
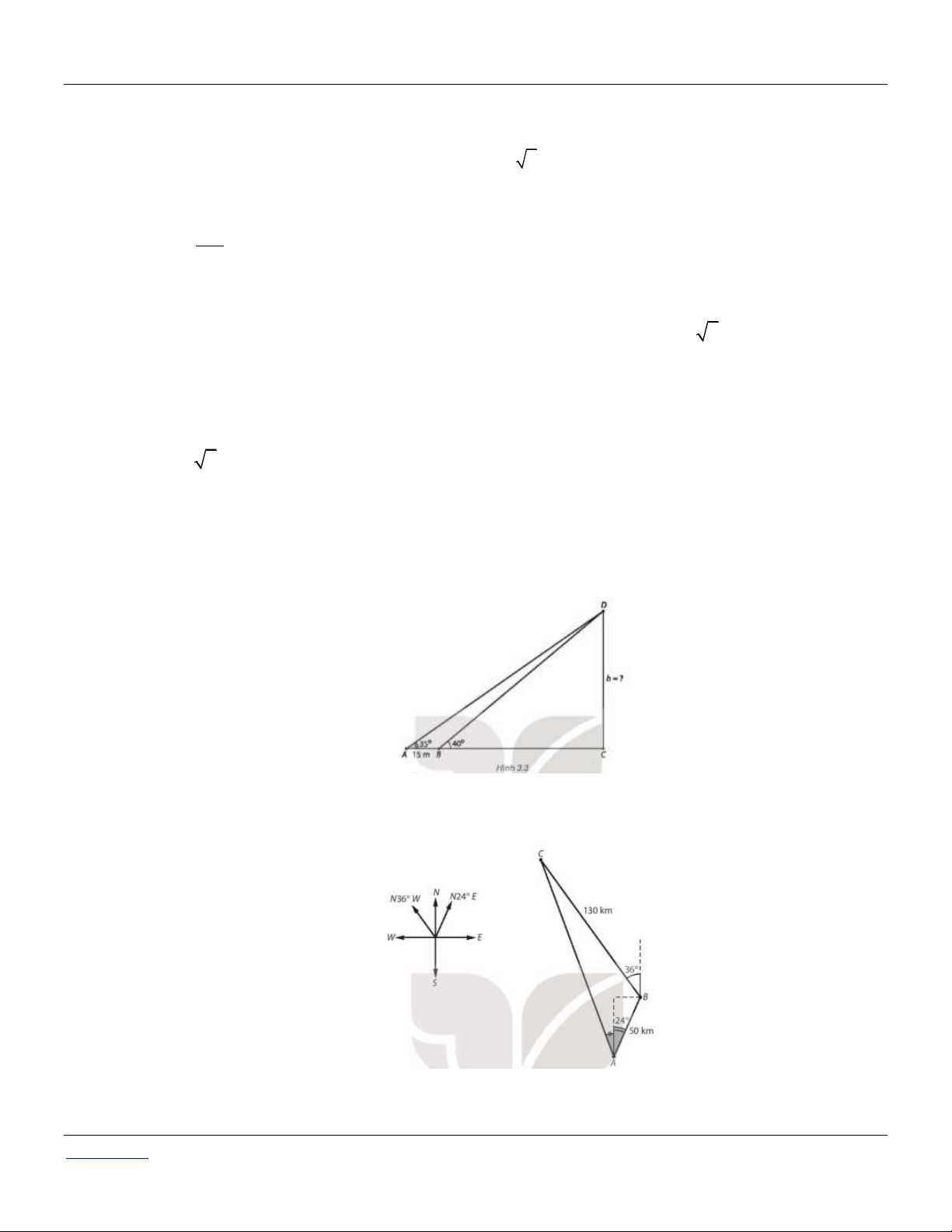
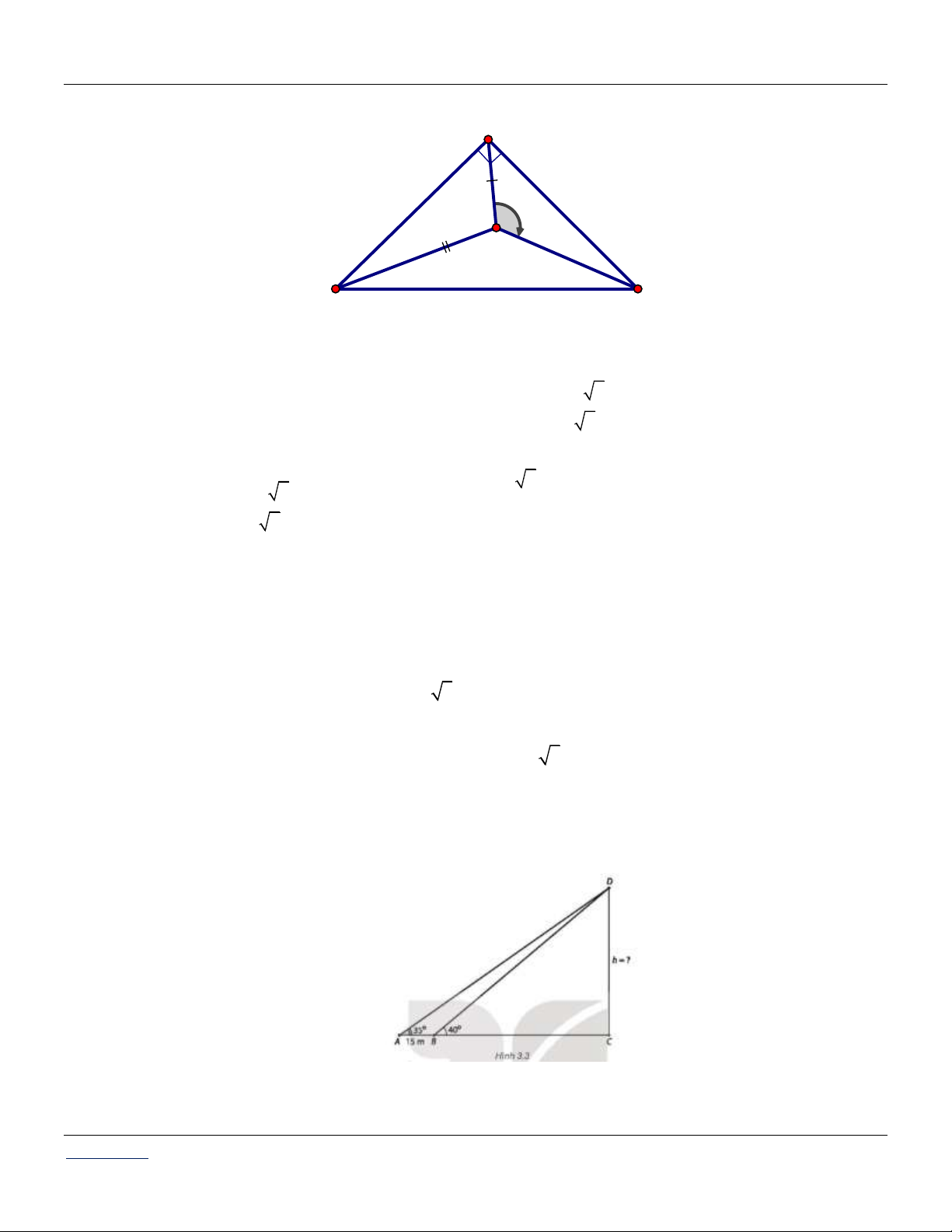
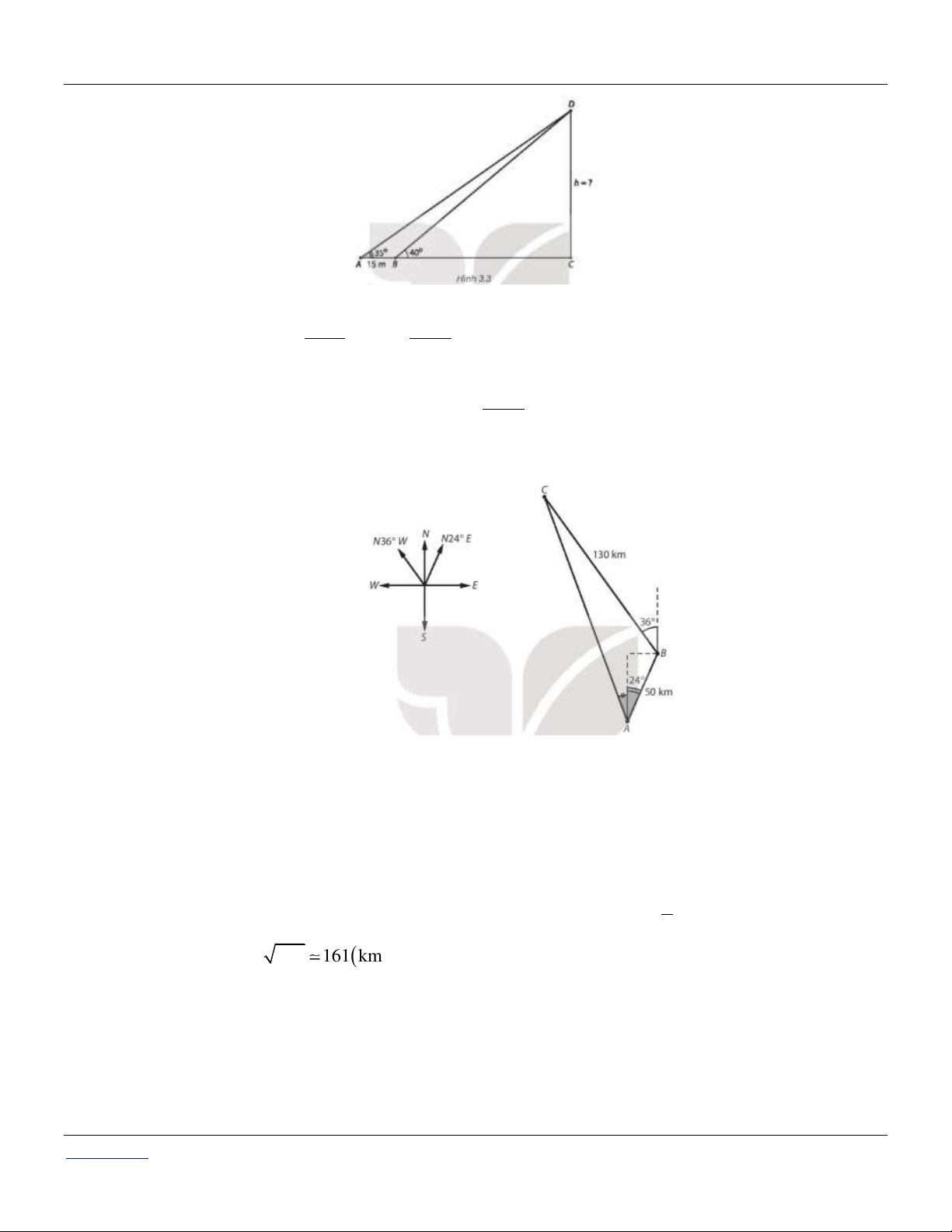
Câu 45: Để đo chiều cao của một tòa nhà, người ta chọn hai điểm A và B thẳng hàng với chân C của
tòa nhà, cách nhau 15 m. Sử dụng giác kế, từ A và B tương ứng nhìn thấy đỉnh D của tòa
nhà dưới các góc 35 và 40 so với phương nằm ngang.
Hỏi chiều cao của tòa nhà đo được là bao nhiêu mét?
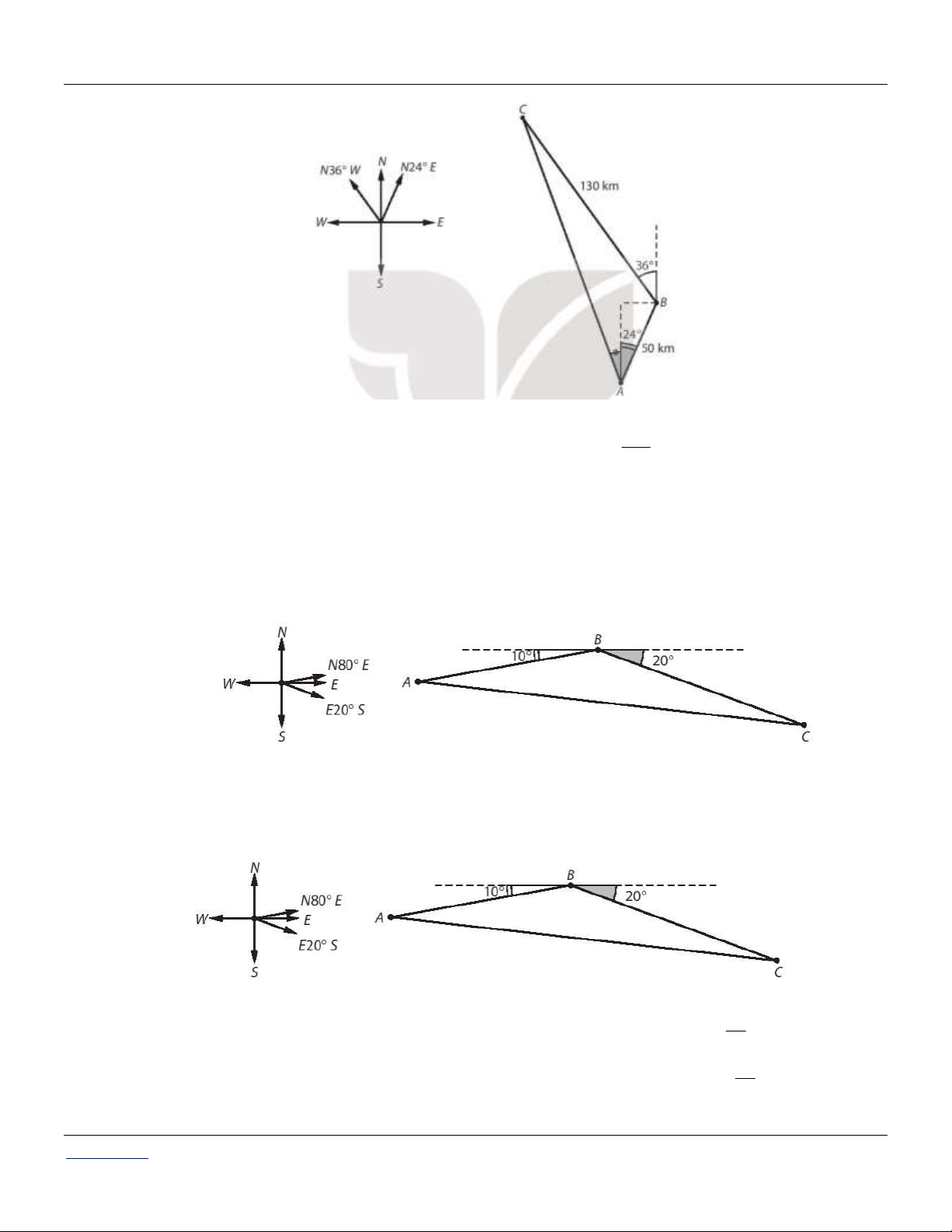
Câu 46: Một tàu cá xuất phát từ đảo A , chạy 50 km theo hướng N 24E đến đảo B để lấy thêm ngư
cụ, rồi chuyển hướng N 36 W
 chạy tiếp 130 km đến ngư trường C .
a) Tính khoảng cách từ vị trí xuất phát A đến C (làm tròn đến hàng đơn vị theo đơn vị đo kilômét).
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 4
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
b) Tìm hướng từ A đến C (làm tròn đến hàng đơn vị, theo đơn vị độ).
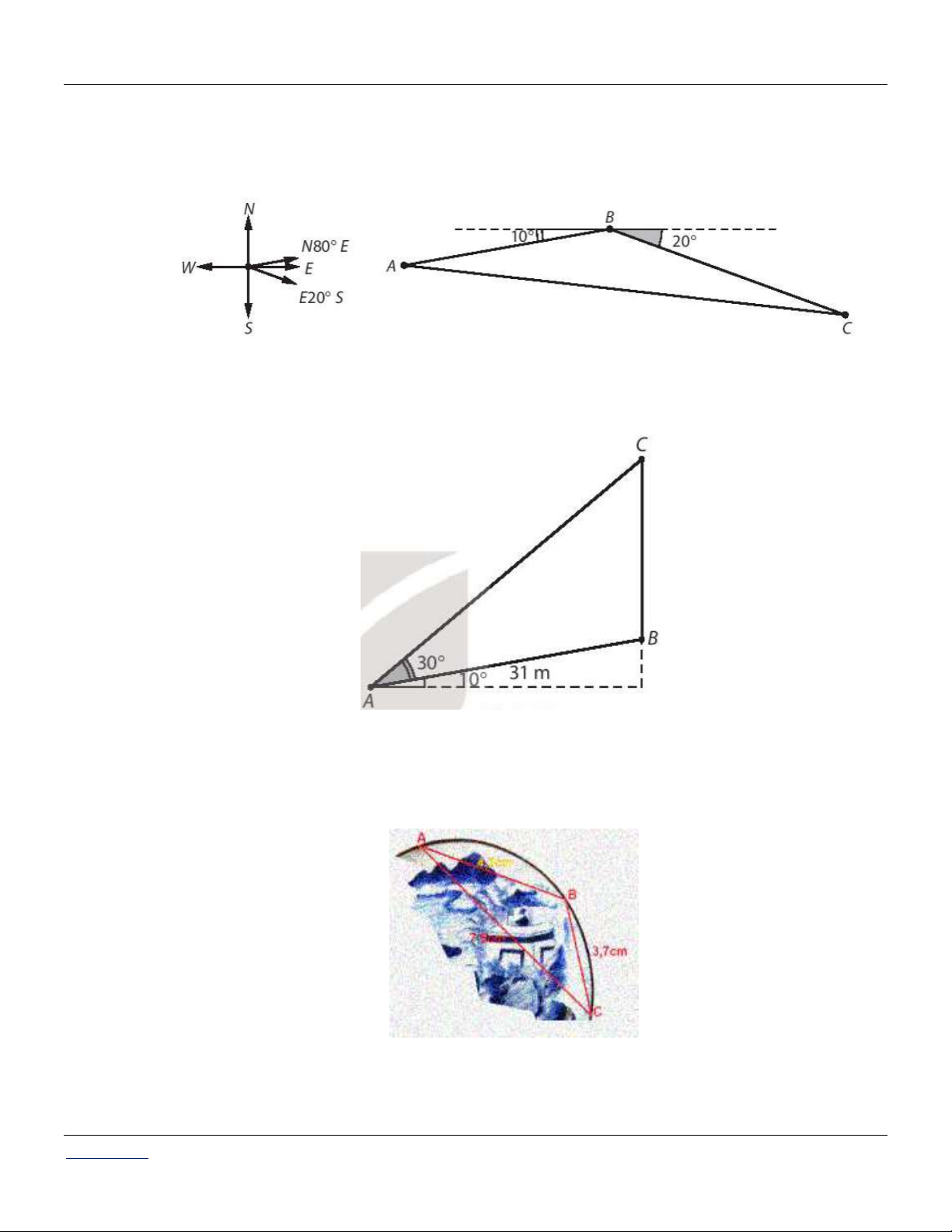
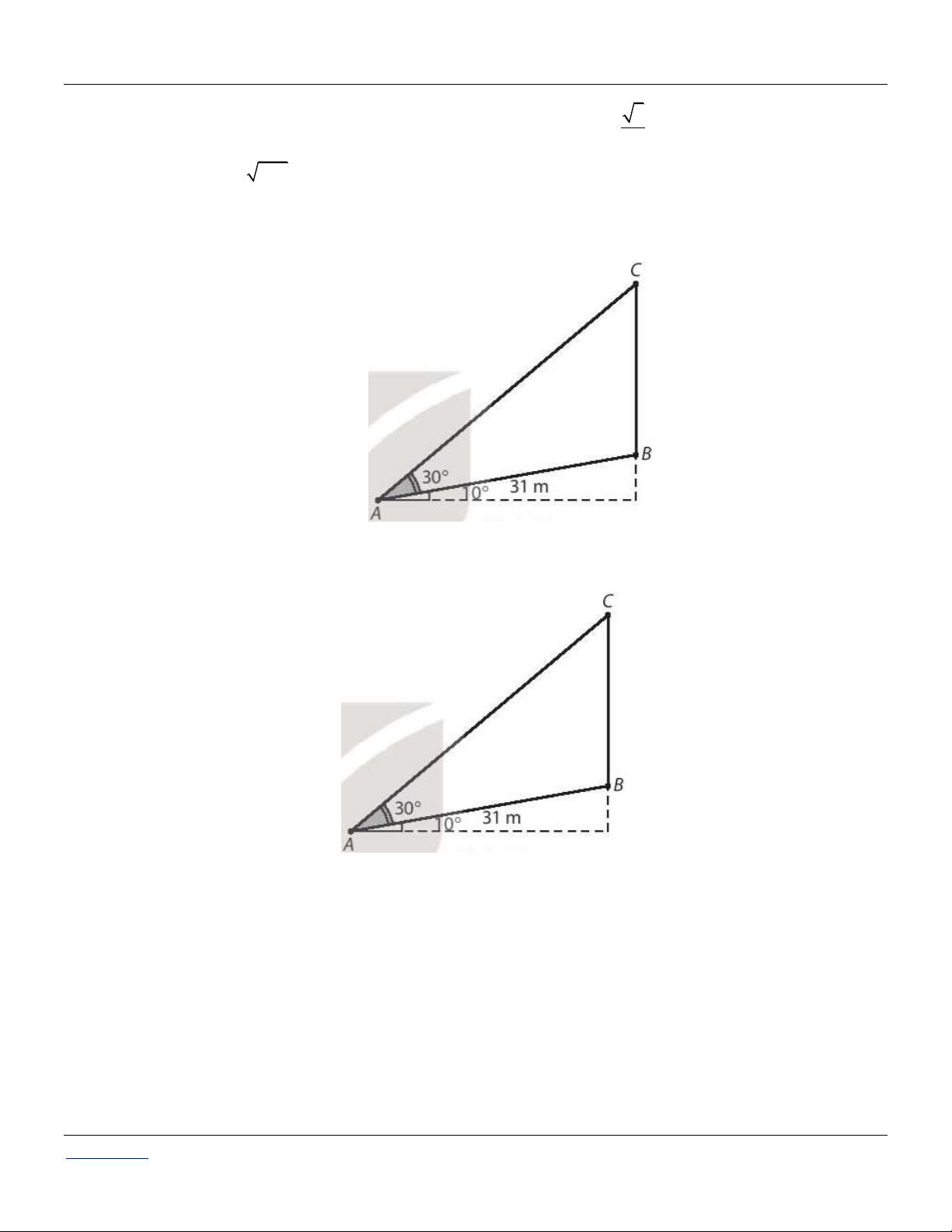
Câu 47: Một tàu du lịch xuất phát từ bãi biển Đồ Sơn (Hải Phòng), chạy theo hướng N80E với vận
tốc 20 km/h. Sau khi đi được 30 phút, tàu chuyển sang hướng E20S giữ nguyên vận tốc và
chạy tiếp 36 phút nữa đến đảo Cát Bà.
Hỏi khi đó tàu du lịch cách vị trí xuất phát bao nhiêu kilômet?
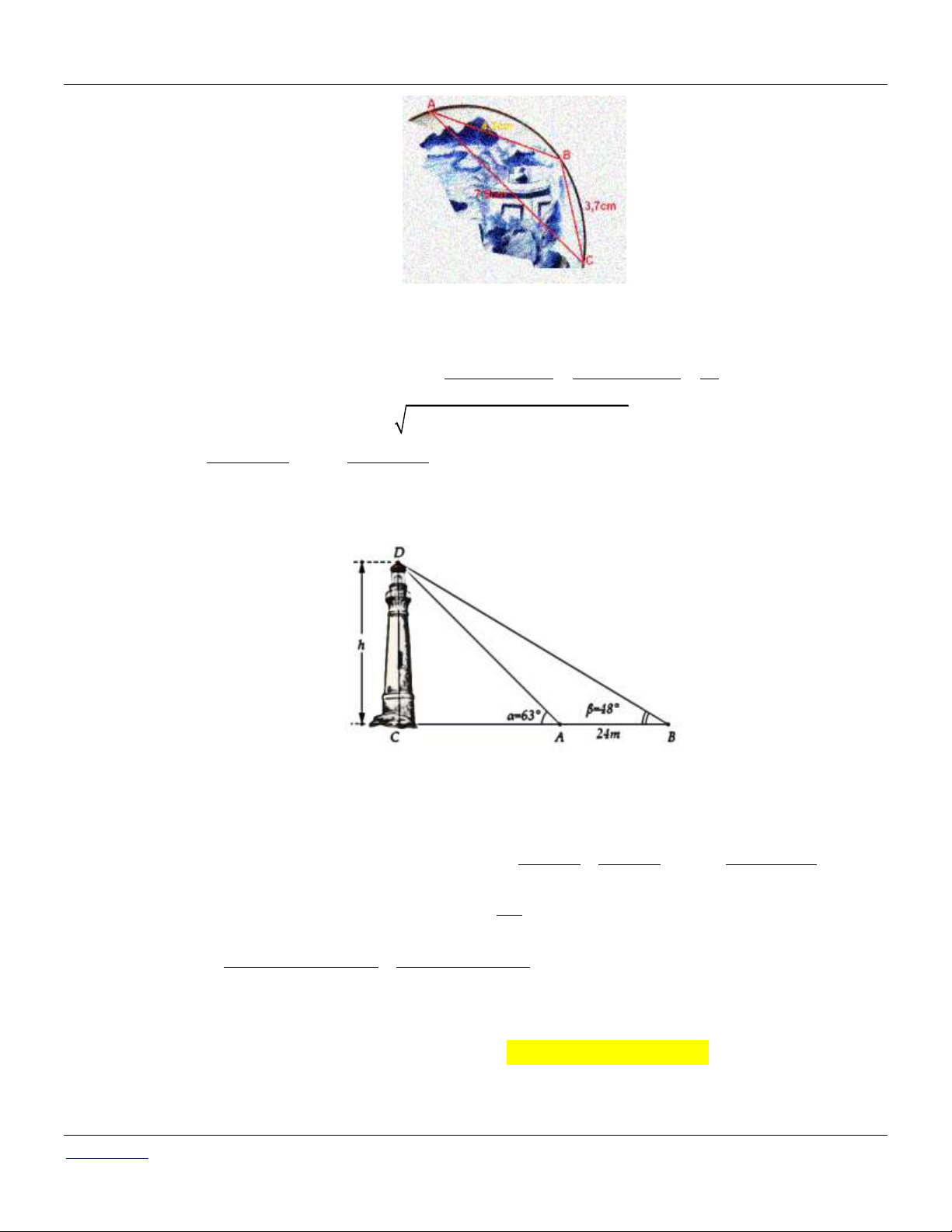
Câu 48: Một cây cổ thụ mọc thẳng đứng bên lề một con dốc có độ dốc 10 so với phương nằm ngang.
Từ một điểm dưới chân dốc, cách gốc cây 31m người ta nhìn đỉnh ngọn cây dưới một góc
40 so với phương nằm ngang.
Hãy tính chiều cao của cây.
Câu 49: Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình
tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính
của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả
như hình vẽ ( AB  4,3 cm; BC  3, 7 cm; CA  7,5 cm).
Tính gần đúng bán kính của chiếc đĩa này.
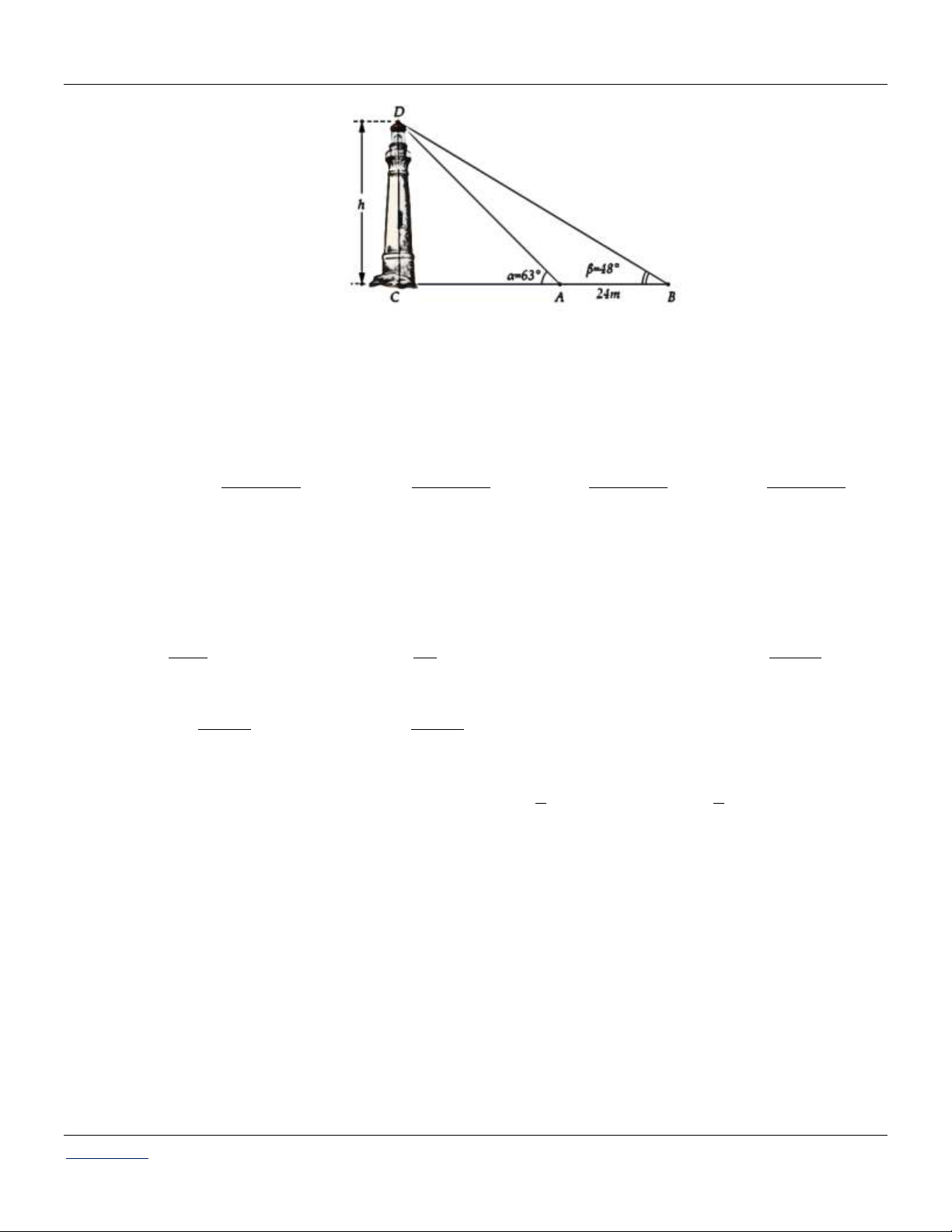
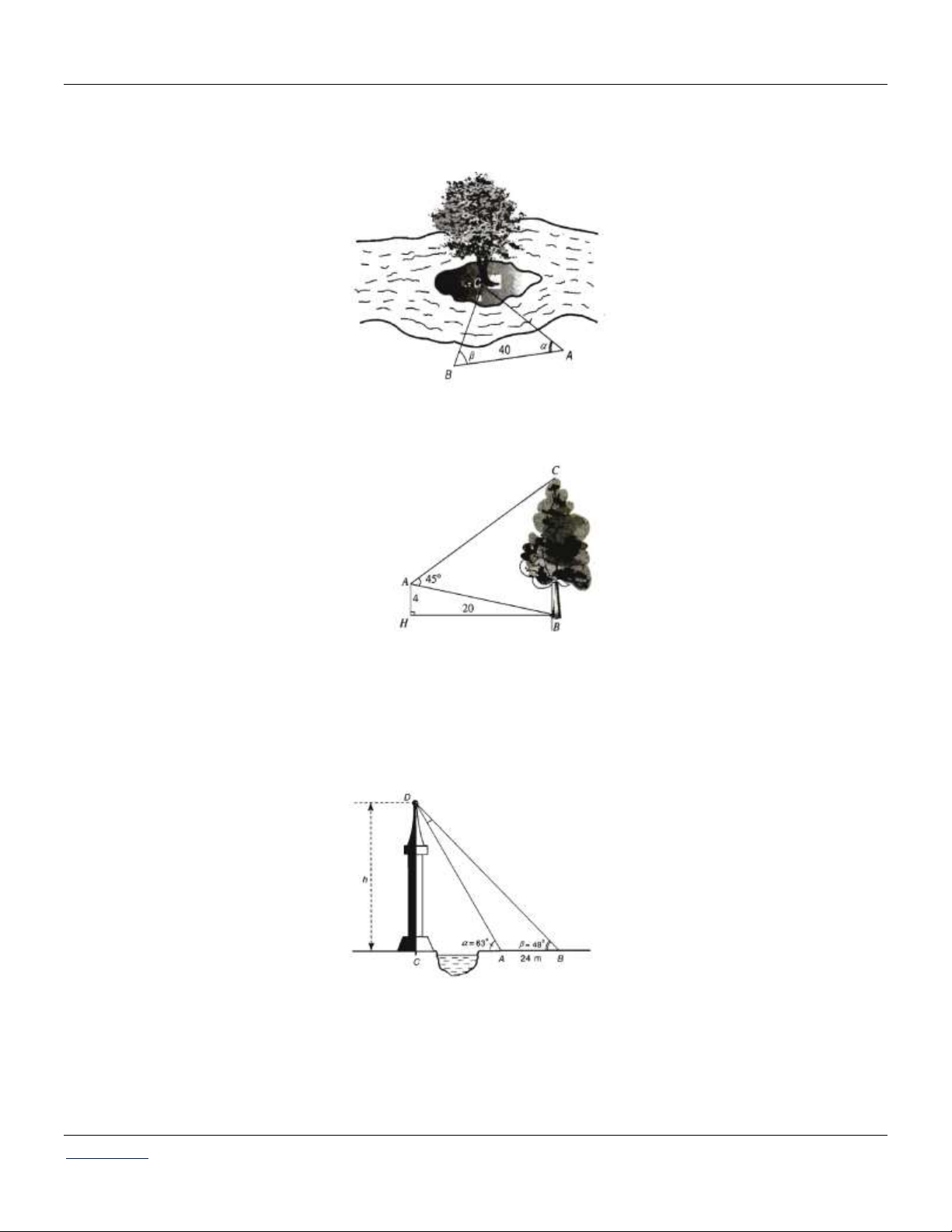
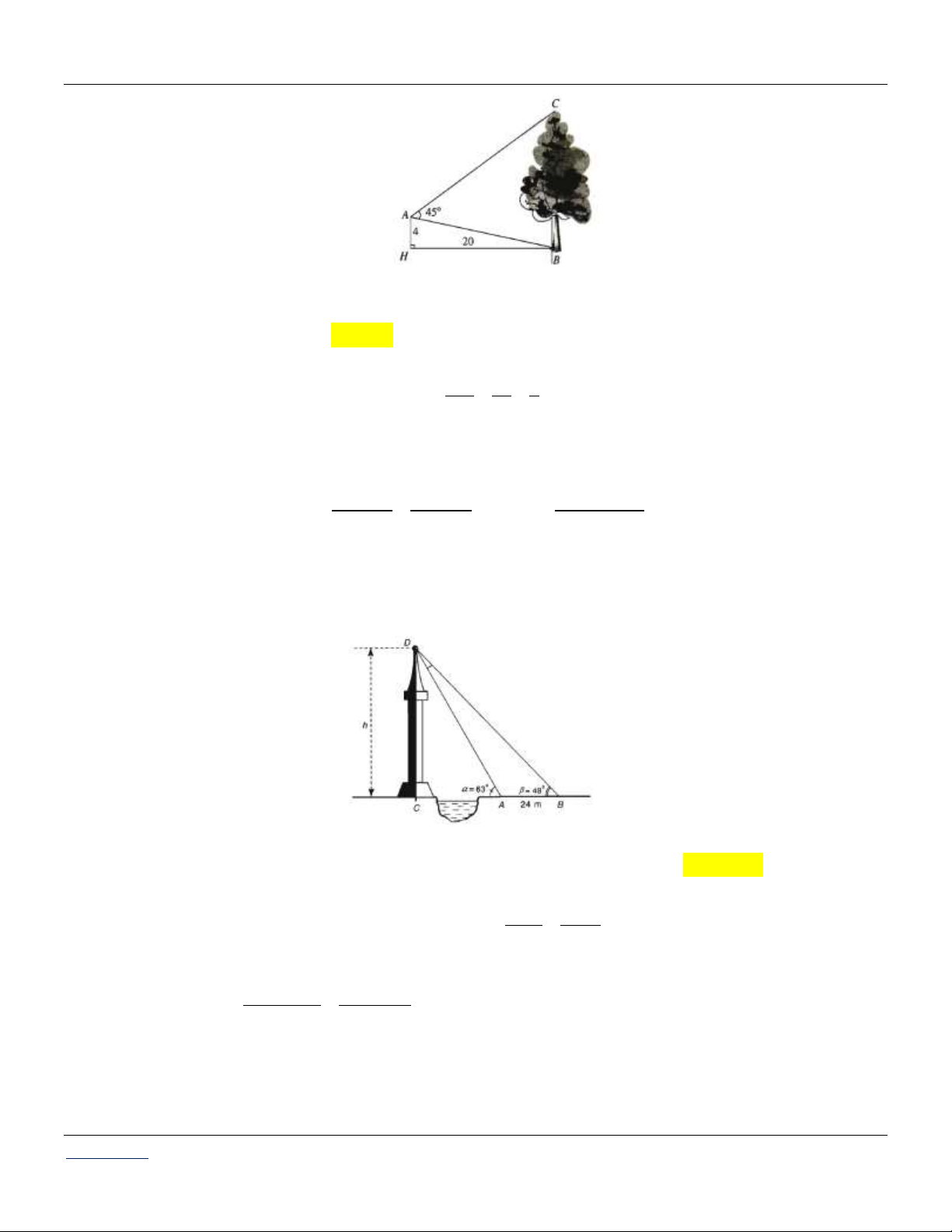
Câu 50: Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất
sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24m, CAD  63 ; CBD  48 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 5
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Tính gần đúng chiều cao h của khối tháp.
III. BÀI TẬP TRẮC NGHIỆM Câu 1:
Cho tam giác ABC , khẳng định nào sau đây đúng? A. 2 2 2
a b c  2b . c cos A. B. 2 2 2
a b c  2b .
c cos A . C. 2 2 2
a b c b .
c cos A . D. 2 2 2
a b c b .
c cos A . Câu 2:
Xét tam giác ABC tùy ý có BC a, AC b, AB c . Mệnh đề nào dưới đây đúng? 2 a  2 c  2 b 2 a  2 c  2 b 2 a  2 c  2 b 2 a  2 c  2 b A. cos B
. B. cos B
. C. cos B
. D. cos B  . 2ac 2ac ac 4 Câu 3:
Cho tam giác ABC có A  120 .
 Đẳng thức nào sau đây đúng? A. 2 2 2
a b c  3bc . B. 2 2 2
a b c bc . C. 2 2 2
a b c  3bc . D. 2 2 2
a b c bc . Câu 4:
Cho tam giác ABC có BC a; AB c; AC b và có R là bán kính đường tròn ngoại tiếp.
Hệ thức nào sau đây là sai? a .sin A.  2 . R B. sin  a A . C. . b sin B  2 . R D. sin  c A C . sin A 2R a Câu 5:
Xét tam giác ABC , hệ thức nào sau đây sai? . b sin A . c sin A A. a . B. sin C . C. a  2 .
R sin A . D. b  . R tan B . sin B a Câu 6:
Cho tam giác ABC có AB c, AC  .
b Diện tích của tam giác ABC bằng 1 1 A. bc cos . A B. bc sin . A C. bc cos . A D. bc sin . A 2 2 Câu 7:
Nếu tam giác ABC có 2 2 2
a b c thì:
A. A là góc nhọn.
B. A là góc tù.
C. A là góc vuông.
D. A là góc nhỏ nhất. Câu 8:
Cho tam giác ABC có BC a, CA  ,
b AB c . Mệnh đề nào sau đây là đúng? A. Nếu 2 2 2
b c a  0 thì góc A nhọn. B. Nếu 2 2 2
b c a  0 thì góc A tù. C. Nếu 2 2 2
b c a  0 thì góc A nhọn. D. Nếu 2 2 2
b c a  0 thì góc A vuông. Câu 9:
Mệnh đề nào sau đây sai? A. Nếu 2 2 2
a b c thì A là góc tù.
B. Nếu tam giác ABC có một góc tù thì 2 2 2
a b c . C. Nếu 2 2 2
a b c thì A là góc nhọn. D. Nếu 2 2 2
a b c thì A là góc vuông.
Câu 10: Cho tam giác ABC thỏa mãn 4 4 4
a b c . Khẳng định nào sau đây đúng?
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 6
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
A. Tam giác ABC vuông tại A. B. Tam giác ABC vuông tại B.
C. Tam giác ABC tù.
D. Tam giác ABC nhọn.
Câu 11: Cho tam giác ABC , các đường cao h , h , h thỏa mãn hệ thức 3h  2h h . Tìm hệ thức giữa a b c a b c a, , b c . 3 2 1 3 2 1 A.   .
B. 3a  2b c .
C. 3a  2b c . D.   . a b c a b c
Câu 12: Trung tuyến AM của tam giác ABC có độ dài bằng 1 A. 2 2 2
b c a . B. 2 2 2
2b  2c a . C. 2 2 2
3a  2b  2c . D. 2 2 2
2b  2c a . 2
Câu 13: Cho tam giác ABC có AC  3 3, AB  3, BC  6 . Tính số đo góc B . A. 60 . B. 45 . C. 30 . D. 120 . 3
Câu 14: Cho tam giác ABC có b  7 ; c  5 và cos A  . Tính a . 5 A. 4 2 . B. 2 . C. 2 . D. 3 .
Câu 15: Cho tam giác ABC có AB  3 3 và bán kính đường tròn ngoại tiếp R  3 . Số đo góc C là A. 60 . B. 30 . C. 90 . D. 45 .
Câu 16: Cho tam giác ABC có B  60 , C  45 , AB  3 . Tính độ dài AC . 3 6 3 2 2 6 A. . B. . C. 6 . D. . 2 2 3
Câu 17: Cho tam giác ABC có BAC  105 , ACB  45 và AC  8 . Tính độ dài cạnh AB . 8 6 A. . B. 4 2 . C. 8 2 . D. 41 3 . 3
Câu 18: Cho tam giác ABC có AB  9, AC  18 và A  60 . Bán kính của đường tròn ngoại tiếp tam giác ABC là A. 3 . B. 9 3 . C. 9 . D. 6 .
Câu 19: Cho hình vuông ABCD có cạnh bằng 6 , E là trung điểm của CD . Tính bán kính đường tròn
ngoại tiếp tam giác ACE . 3 10 3 5 A. . B. . C. 3 10 . D. 3 5 . 2 2 AB
Câu 20: Cho ABC có A  45 ,
B  75 . Tính tỉ số . BC 6 1 3 6  3 2 6 A. . B. . C. . D. . 2 2 6 3
Câu 21: Cho tam giác ABC có BC  3, AC  5, AB  6. Độ dài đường trung tuyến kẻ từ đỉnh C bằng A. 2 2. B. 5. C. 10. D. 3.
Câu 22: Cho tam giác ABC có BC  4 , AC  5 và ACB  60 . Độ dài đường trung tuyến hạ từ đỉnh C là 61 51 A. . B. . C. 3 . D. 2 . 2 2
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 7
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Câu 23: Cho tam giác ABC có chu vi bằng 32 và bán kính đường tròn nội tiếp của ABC bằng 5 .
Tính diện tích tam giác ABC . A. S  32 .
B. S  40.
C. S  160.
D. S  80. 5
Câu 24: Cho tam giác ABC có a  5, b  12, c  13. Bán kính đường tròn ngoại tiếp R của tam giác bằng A. 13. B. 6,5. C. 26. D. 7,5.
Câu 25: Cho tam giác ABC có A  60 ,
AB  3, AC  4. Tính độ dài đường cao kẻ từ A của tam giác ABC . 2 39 39 6 39 3 39 A. h  . B. h  . C. h  . D. h  . a 13 a 13 a 13 a 13
Câu 26: Cho tam giác ABC có AB  9 cm, AC  12 cm và BC  15 cm. Khi đó, đường trung tuyến
AM của tam giác ABC có độ dài bằng A. 8 cm. B. 10 cm. C. 9 cm. D. 7,5 cm.
Câu 27: Cho tam giác DEF có DE DF  10 cm và EF  12 cm. Gọi I là trung điểm của cạnh EF .
Đoạn thẳng DI có độ dài bằng A. 6,5 cm. B. 7 cm. C. 8 cm. D. 4 cm.
Câu 28: Cho tam giác ABC có AB  8 cm, AC  18 cm và có diện tích bằng 64 cm2. Giá trị sin A bằng 3 3 4 8 A. . B. . C. . D. . 2 8 5 9 AB
Câu 29: Cho tam giác ABC có các góc A  105 , B  45 . Tính tỉ số . AC 2 2 6 A. . B. 2 . C. . D. . 2 2 3
Câu 30: Cho tam giác ABC có O
AB  5, AC  8, A  60 . Tính độ dài cạnh BC. A. 129 . B. 7 . C. 49 . D. 69 .
Câu 31: Tính diện tích tam giác có ba cạnh lần lượt là 3 , 2 và 1. 3 6 2 A. . B. 3 . C. . D. . 2 2 2
Câu 32: Cho tam giác ABC nội tiếp đường tròn bán kính R, AB R, AC R 3. Tính góc A , biết B là góc tù. A. 30 . B. 45 . C. 60 . D. 90 .
Câu 33: Tam giác ABC có a  14, b  18, c  20 . Khẳng định nào sau đây đúng? A. B  42 50  ' . B. B  60 56  ' . C. B  119 04  ' .
D. B  90 .
Câu 34: Cho tam giác ABC có AB  4 cm, BC  7 cm, CA  9 cm. Giá trị cos A bằng 2 1 2 1 A. . B. . C. . D. . 3 3 3 2
Câu 35: Cho tam giác ABC có AB  4 , AC  5 , BC  6 . Tính cos  B C .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 8
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống 1 1 A. . B. . C. –0,125 . D. 0, 75 . 8 4
Câu 36: Tính bán kính đường tròn nội tiếp tam giác có ba cạnh lần lượt là 5, 12, 13. A. 2. B. 2. C. 2 2. D. 3.
Câu 37: Cho tam giác ABC có BC  10 , A  30 . Bán kính đường tròn ngoại tiếp tam giác ABC bằng 10 A. 5. B. 10. C. . D. 10 3 . 3
Câu 38: Tính diện tích tam giác có ba cạnh lần lượt là 5 , 12 , 13 . A. 60 . B. 30 . C. 34 . D. 7 5 .
Câu 39: Cho tam giác ABC có O O
B  60 , C  45 , AB  5 . Tính độ dài cạnh AC. 5 6 A. 5 3 . B. 5 2 . C. . D. 10 . 2
Câu 40: Tam giác đều nội tiếp đường tròn bán kính R  4 cm thì có diện tích bằng A. 2 13 cm . B. 2 13 2 cm . C. 2 12 3 cm . D. 2 15 cm .
Câu 41: Cho hình bình hành ABCD có AB a, BC a 2 và BAD  45 . Tính diện tích hình bình hành ABCD. A. 2 2a . B. 2 a 2 . C. 2 a . D. 2 a 3 .
Câu 42: Cho hình bình hành có một cạnh là 5 hai đường chéo là 6 và 8 . Tính độ dài cạnh kề với cạnh có độ dài bằng 5. A. 3 . B. 1. C. 5 6 . D. 5 .
Câu 43: Cho hình bình hành có hai cạnh là 5 và 9 , một đường chéo bằng11. Tìm độ dài đường chéo còn lại. A. 9,5 . B. 4 6 . C. 91 . D. 3 10 .
Câu 44: Cho tam giác ABC vuông tại A có AB  6 cm, BC  10 cm. Tính bán kính đường tròn nội tiếp tam giác đó. A. 1 cm. B. 2 cm. C. 2 cm. D. 3 cm.
Câu 45: Tính diện tích tam giác ABC biết A  60 , b  10 , c  20 . A. 50 3 . B. 50 . C. 50 2 . D. 50 5 .
Câu 46: Cho tam giác ABC có AB  5 , AC  9 và đường trung tuyến AM  6 . Tính độ dài cạnh BC . A. 2 17 . B. 17 . C. 129 . D. 22 . AB
Câu 47: Cho tam giác ABC có các góc A  75, B  45 . Tính tỉ số . AC 6 6 A. . B. 6 . C. . D. 1, 2 . 3 2
Câu 48: Cho tam giác ABC vuông tại A , AC b , AB c . Lấy điểm M trên cạnh BC sao cho góc MB BAM  30 .  Tính tỉ số . MC b 3 3c 3c b c A. . B. . C. . D. . 3c 3b b b c
Câu 49: Trong tam giác ABC , nếu 2h h h thì dẳng thức nào sau đây đúng? a b c
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 9
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống 2 1 1 A.   .
B. 2sin A  sin B  sin C . sin A sin B sin C 2 1 1
C. sin A  2sin B  2sin C . D.   . sin A sin B sin C
Câu 50: Cho tam giác ABC. Khẳng định nào sau đây đúng? 2 4 A. 2 2 2
m m m
a b c B. 2 2 2
m m m
a b c a b c  2 2 2. a b c  2 2 2. 3 3 3 1 C 2 2 2 2 2 2 2 2 2 2 2 2
. m m m
a b c
D. m m m
a b c a b c  . a b c  . 4 3
Câu 51: Xét tam giác ABC , khẳng định nào sau đây đúng? b c b c b c A. m . B. m . C. m .
D. m b c . a 2 a 2 a 2 a
Câu 52: Trong tam giác ABC , điều kiện để hai trung tuyến kẻ từ A và B vuông góc với nhau là A. 2 2 2
2a  2b  5c . B. 2 2 2
3a  3b  5c . C. 2 2 2
2a  2b  3c . D. 2 2 2
a b  5c .
Câu 53: Cho tam giác ABC có ba góc nhọn, BC a , AC b , AB c và diện tích là S . Tổng
cot A  cot B  cot C bằng  2 2 2
2 a b c  2 2 2
a b c 2 2 2
a b c 2 2 2
a b c A. . B. . C. . D. . S S 2S 4S
Câu 54: Xét tam giác ABC , nếu có 2 a  .
b c thì đẳng thức nào dưới đây đúng? 1 1 1 1 1 1 1 2 2 A.   . B. 2
h h .h . C.   . D.   . 2 h h h a b c 2 h h h 2 h h h a b c a b c a b c
Câu 55: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết AB c và c  AB 1 os  . 3 c 2 3c 2 9c 2 3c A. . B. . C. . D. . 2 8 8 2
Câu 56: Cho tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R . Gọi r R
là bán kính đường tròn nội tiếp tam giác ABC . Khi đó, tỉ số bằng r 2  2 2 1 1 2 A. 1 2 . B. . C. . D. . 2 2 2
Câu 57: Cho tam giác ABC vuông cân tại A có AB AC  30 cm. Hai đường trung tuyến BF và CE
cắt nhau tại G . Diện tích tam giác GFC bằng A. 50 cm2. B. 50 2 cm2. C. 75 cm2. D. 15 105 cm2.
Câu 58: Cho tam giác ABC có diện tích S . Nếu tăng độ dài mỗi cạnh BC và AC lên hai lần đồng
thời giữ nguyên độ lớn của góc C thì diện tích của tam giác mới được tạo nên bằng A. 2S . B. 3S . C. 4S . D. 5S .
Câu 59: Cho hình vuông ABCD có cạnh bằng a . Gọi E là trung điểm cạnh BC , F là trung điểm
cạnh AE . Tính độ dài đoạn thẳng DF . a 13 a 5 a 3 3a A. . B. . C. . D. . 4 4 2 4
Câu 60: Cho tam giác ABC có B C  135 và BC  .
a Tính bán kính đường tròn ngoại tiếp tam giác.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 10
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống a 2 a 3 A. . B. a 2 . C. . D. a 3 . 2 2
Câu 61: Cho tam giác ABC có AB  9 , BC  10 , CA  11. Gọi M là trung điểm BC và N là trung
điểm AM . Tính độ dài BN . A. 6 . B. 4 2 . C. 5 . D. 34 .
Câu 62: Cho tam giác ABC có AB  5 , BC  8 , CA  6 . Gọi G là trọng tâm tam giác ABC . Độ dài
đoạn thẳng CG bằng 5 7 5 7 5 7 13 A. . B. . C. . D. . 2 3 6 3
Câu 63: Cho tam giác ABC có AB  2 cm, AC  1 cm, O
A  60 . Tính độ dài cạnh BC. A. 1 cm. B. 2 cm. C. 3 cm. D. 5 cm.
Câu 64: Cho tam giác có ba cạnh lần lượt là 5 , 6 , 7 . Tính độ dài đường cao ứng với cạnh có độ dài bằng 6. 5 3 A. 6 . B. 2 6 . C. 5 . D. . 2
Câu 65: Cho tam giác có ba cạnh lần lượt là 5,12,13. Tính độ dài đường cao ứng với cạnh lớn nhất. 60 120 30 A. . B. . C. . D. 12 . 13 13 13
Câu 66: Cho tam giác ABC có BC  12 , CA  9 , AB  6 . Trên cạnh BC lấy điểm M sao cho BM  4 .
Tính độ dài đoạn thẳng AM . A. 2 5 . B. 3 2 . C. 20 . D. 19 .
Câu 67: Cho tam giác cân ABC có A  120 và AB AC a . Lấy điểm M trên cạnh BC sao cho 2BC BM
. Tính độ dài AM . 5 a 3 11a a 7 a 6 A. . B. . C. . D. . 3 5 5 4
Câu 68: Cho tam giác ABC có các cạnh a, b, c thỏa mãn điều kiện a b ca b c  3ab . Tính số đo của góc C. A.120 . B. 30 . C. 45 . D. 60 .
abcabc
Câu 69: Cho tam giác ABC có S
. Khẳng định nào sau đây đúng? 4
A. Tam giác ABC vuông tại A. B. Tam giác ABC vuông tại B.
C. Tam giác ABC tù.
D. Tam giác ABC nhọn. sin B  sinC
Câu 70: Cho tam giác ABC thỏa mãn sin A
. Khẳng định nào sau đây đúng? cos B  cosC
A. Tam giác ABC cân.
B. Tam giác ABC đều.
C. Tam giác ABC vuông.
D. Tam giác ABC có góc A  60 . 
Câu 71: Một tam giác có độ dài các cạnh là 1, m, 2 với m  . Giá trị của m là A. 1. B. 2. C. 3 . D. 4 .
Câu 72: Cho tam giác ABC có AB  7 , AC  5 và B C 1 cos
  . Tính độ dài cạnh BC. 5
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 11
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống A. 2 15 . B. 4 22 . C. 4 15 . D. 2 22 .
Câu 73: Tam giác ABC có    1 cos A B  
, AC  4 , BC  5 . Tính cạnh . AB 8 A. 46 . B. 11. C. 5 2 . D. 6 . 1
Câu 74: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết AB  12 và cot( A B)  . 3 9 10 A. 2 10 . B. . C. 5 10 . D. 3 2 . 5 1
Câu 75: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết AB  10 và tan( A B)  . 3 5 10 10 10 A. . B. . C. . D. 5 10 . 9 3 5
Câu 76: Tìm chu vi tam giác ABC , biết rằng AB  6 và 2sin A  3sin B  4sin C . A. 26 . B. 13 . C. 5 26 . D. 10 6 . sin A sin B sin C
Câu 77: Cho tam giác ABC có BC  10 và  
. Tìm chu vi của tam giác đó. 5 4 3 A. 12 . B. 36 . C. 24 . D. 22 . a b b c a c
Câu 78: Tam giác ABC có các cạnh a, b, c thỏa mãn điều kiện   . Tính cos . A 6 5 7 1 1 1 1 A.  . B. . C.  . D. . 4 3 3 3
Câu 79: Tính góc C của tam giác ABC biết a b và  2 2     2 2 a a c b b c  .
A. C  150 .
B. C  120 .
C. C  60 .
D. C  30 . Câu 80: Cho góc O
xOy  30 . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB  1.
Độ dài lớn nhất của đoạn OB bằng A. 1,5 . B. 3 . C. 2 2 . D. 2 .
Câu 81: Cho góc xOy  30 . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB  2 .
Độ dài lớn nhất của đoạn OB bằng A. 2. B. 3. C. 4. D. 5.
Câu 82: Hai chiếc tàu thủy cùng xuất phát từ một vị trí A , đi thẳng theo hai hướng tạo với nhau góc
60 . Tàu B chạy với tốc độ 20 hải lí một giờ. Tàu C chạy với tốc độ 15 hải lí một giờ.
Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí? Kết quả gần nhất với số nào sau đây? A. 61 hải lí. B. 36 hải lí. C. 21 hải lí. D. 18 hải lí.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 12
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
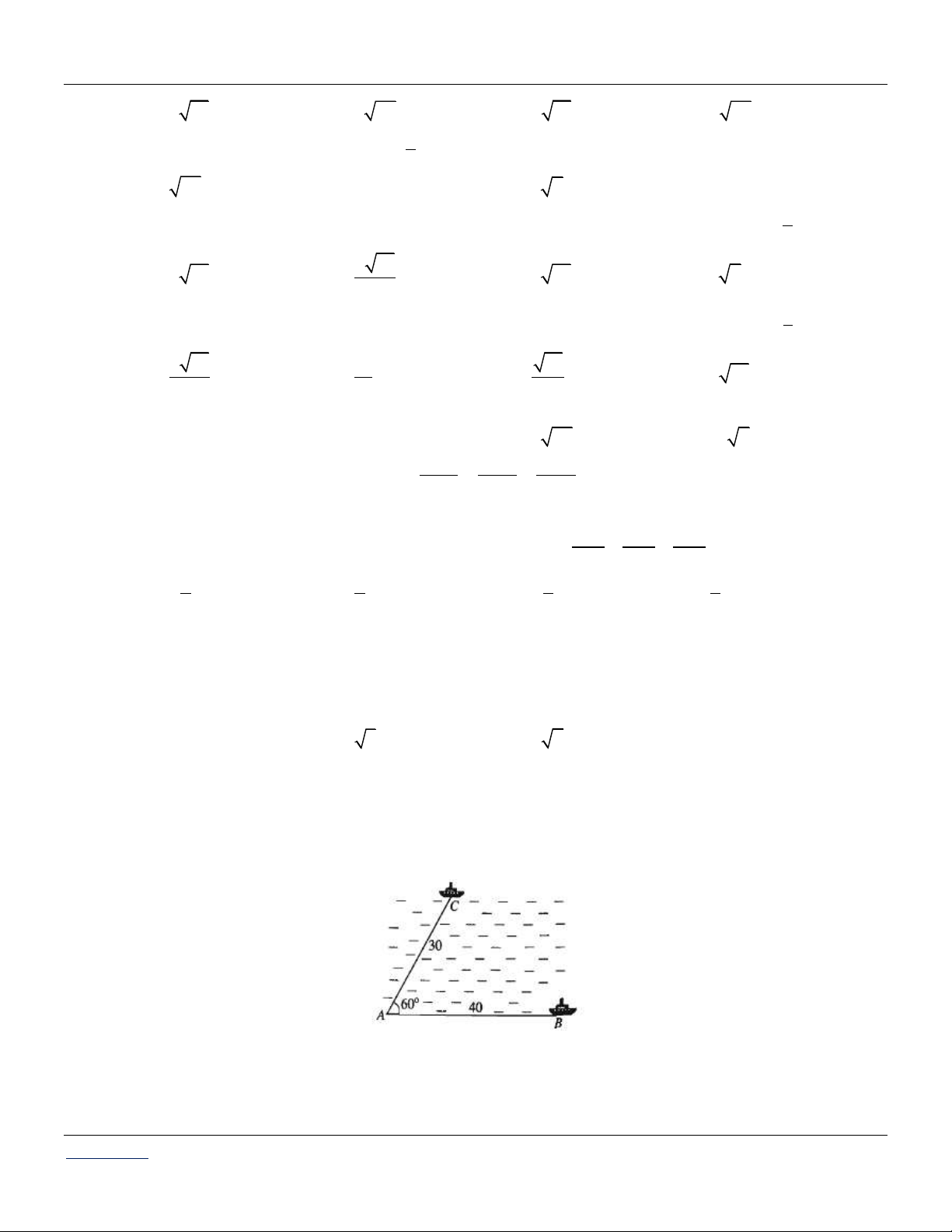
Câu 83: Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta
chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C . Ta đo được
khoảng cách AB  40m , 0
CAB  45 và CBA  70 (tham khảo hình vẽ)
Vậy sau khi đo đạc và tính toán được khoảng cách AC gần nhất với giá trị nào sau đây? A. 53 m . B. 30 m . C. 41,5 m . D. 41 m .
Câu 84: Từ vị trí A người ta quan sát một cây cao (hình vẽ).
Biết AH  4m, HB  20m, BAC  45 .
Chiều cao của cây gần nhất với giá trị nào sau đây? A. 17,5m . B. 17m . C. 16,5m . D. 16m .
Câu 85: Giả sử CD h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt
đất sao cho ba điểm A, B và C thẳng hàng. Ta đo được AB  24 m , CAD  63, CBD  48 (tham khảo hình vẽ)
Chiều cao h của tháp gần với giá trị nào sau đây? A. 18m . B. 18,5m . C. 60m . D. 61,4m .
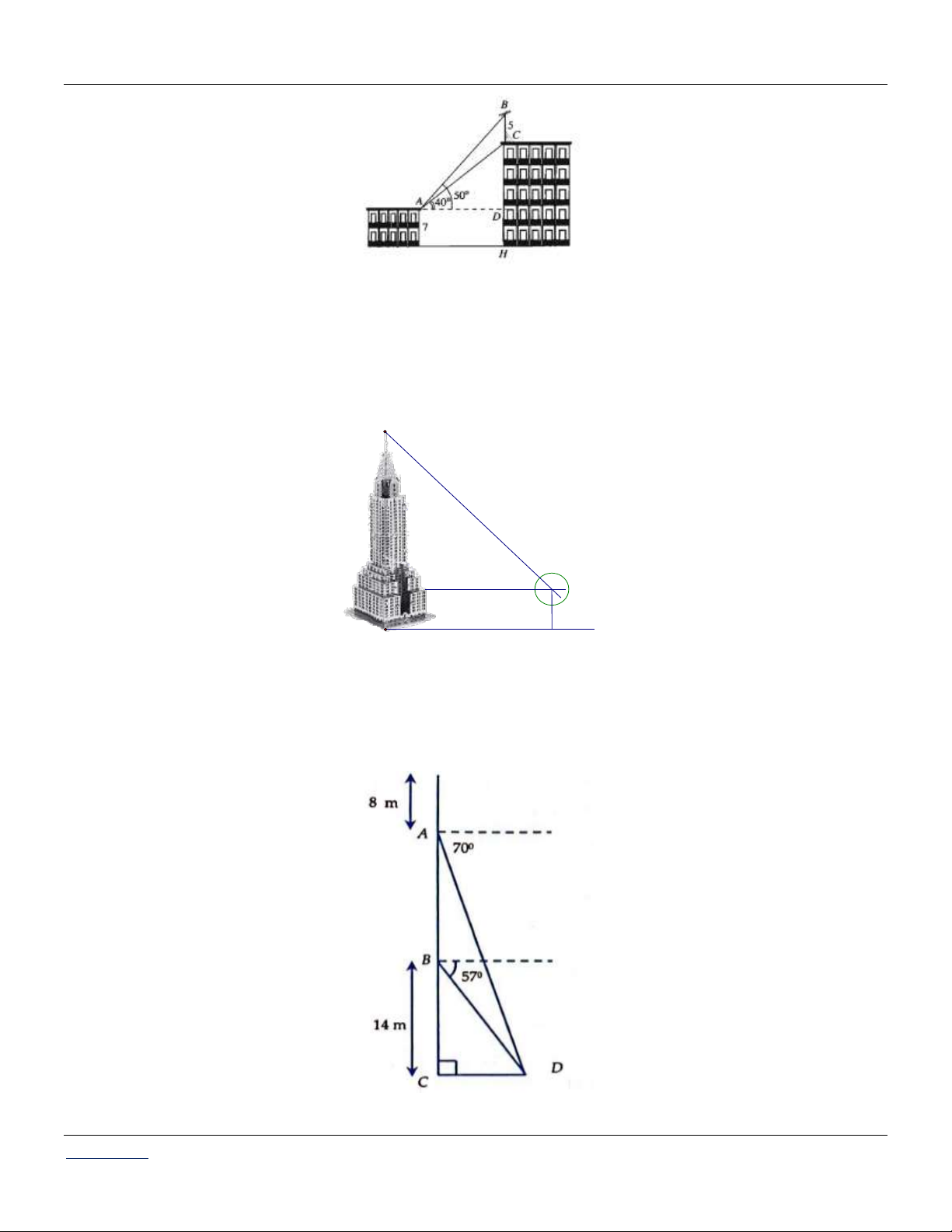
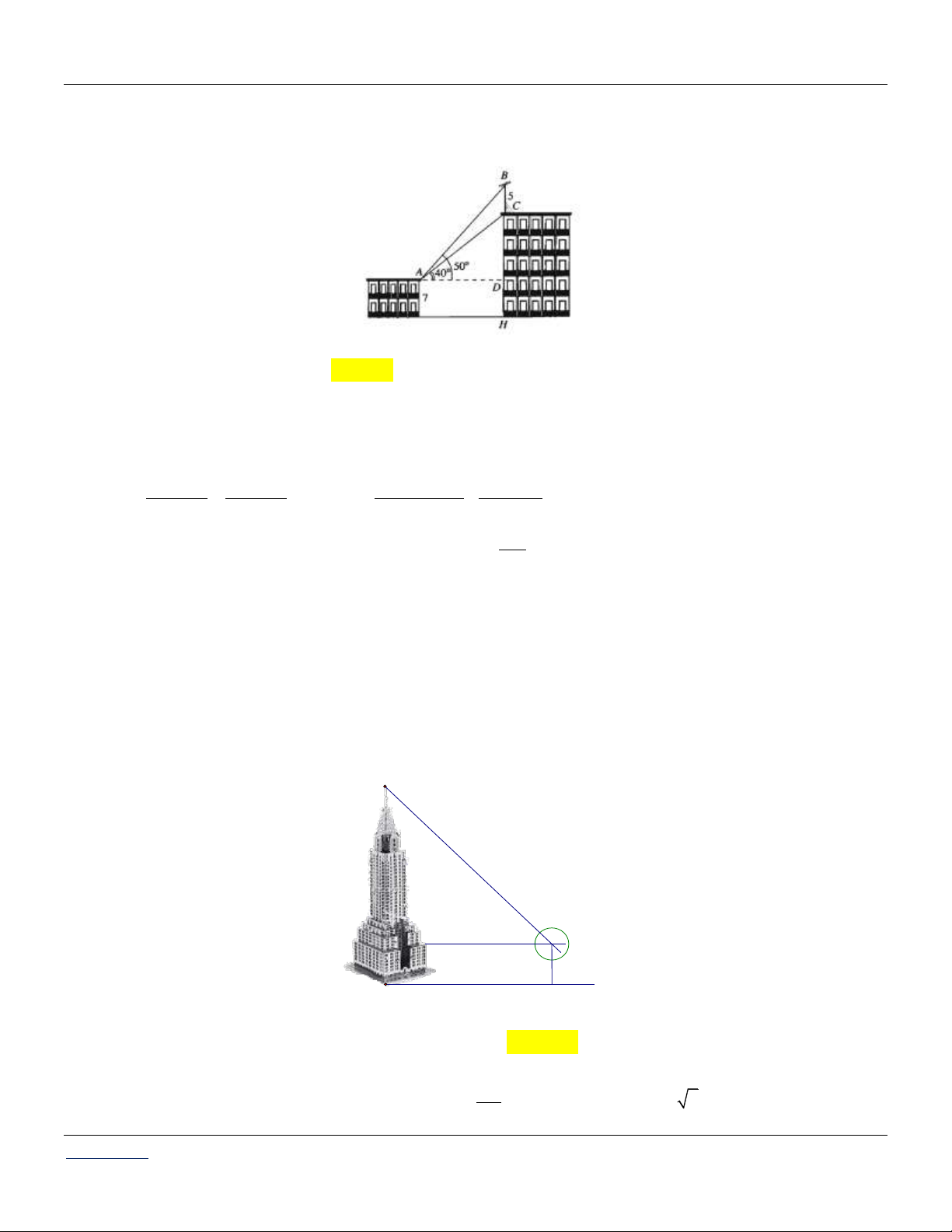
Câu 86: Trên nóc một tòa nhà có một cột ăng-ten cao 5 m . Từ vị trí quan sát A cao 7 m so với mặt
đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50 và 40 so với phương
nằm ngang (tham khảo hình vẽ)
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 13
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Chiều cao của tòa nhà gần nhất với giá trị nào sau đây? A. 12m . B. 19m . C. 24m . D. 29m .
Câu 87: Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng đứng
cách chân tháp một khoảng CD  60m , giả sử chiều cao của giác kế là OC  m 1 . Quay thanh
giác kế sao cho khi ngắm theo thanh ta nhình thấy đỉnh A của tháp. Đọc trên giác kế số
đo của góc AOB  60 (tham khảo hình vẽ) A 60° B O 1m D C 60m
Chiều cao của ngọn tháp gần với giá trị nào sau đây? A. 40m . B. 114m . C. 105m . D. 110m .
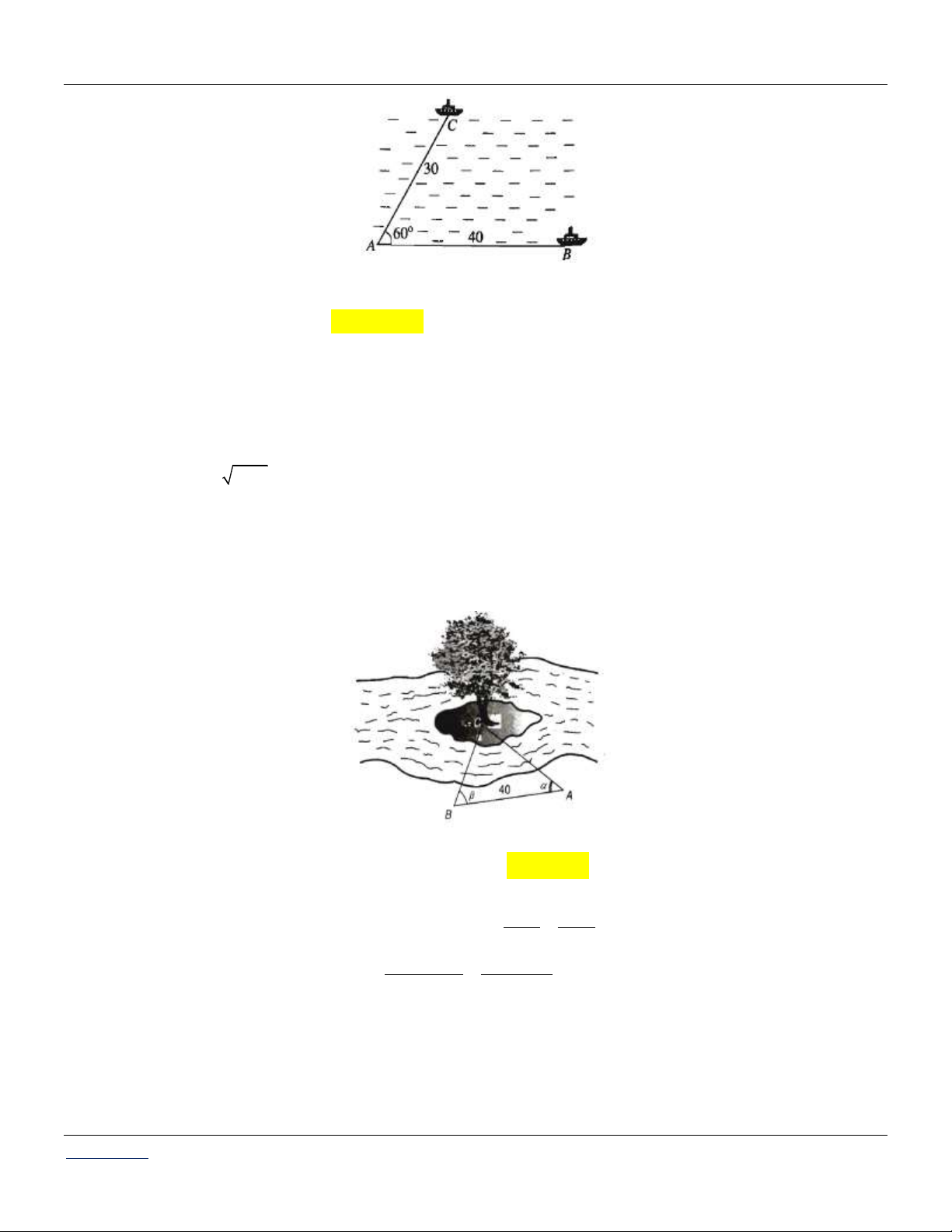
Câu 88: Một thợ lặn có vị trí cách mặt nước 8m, một con tàu đắm ở góc 0
70 . Sau khi cùng xuống tới
một điểm cao hơn 14m so với đáy đại dương, thợ lặn nhìn thấy con tàu đắm ở góc 0 57 . Chiều
sau của con tàu đắm gần giá trị nào nhất? A. 24,979 m. B. 32,964 m. C. 32,979 m. D. 33,25 m.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 14
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
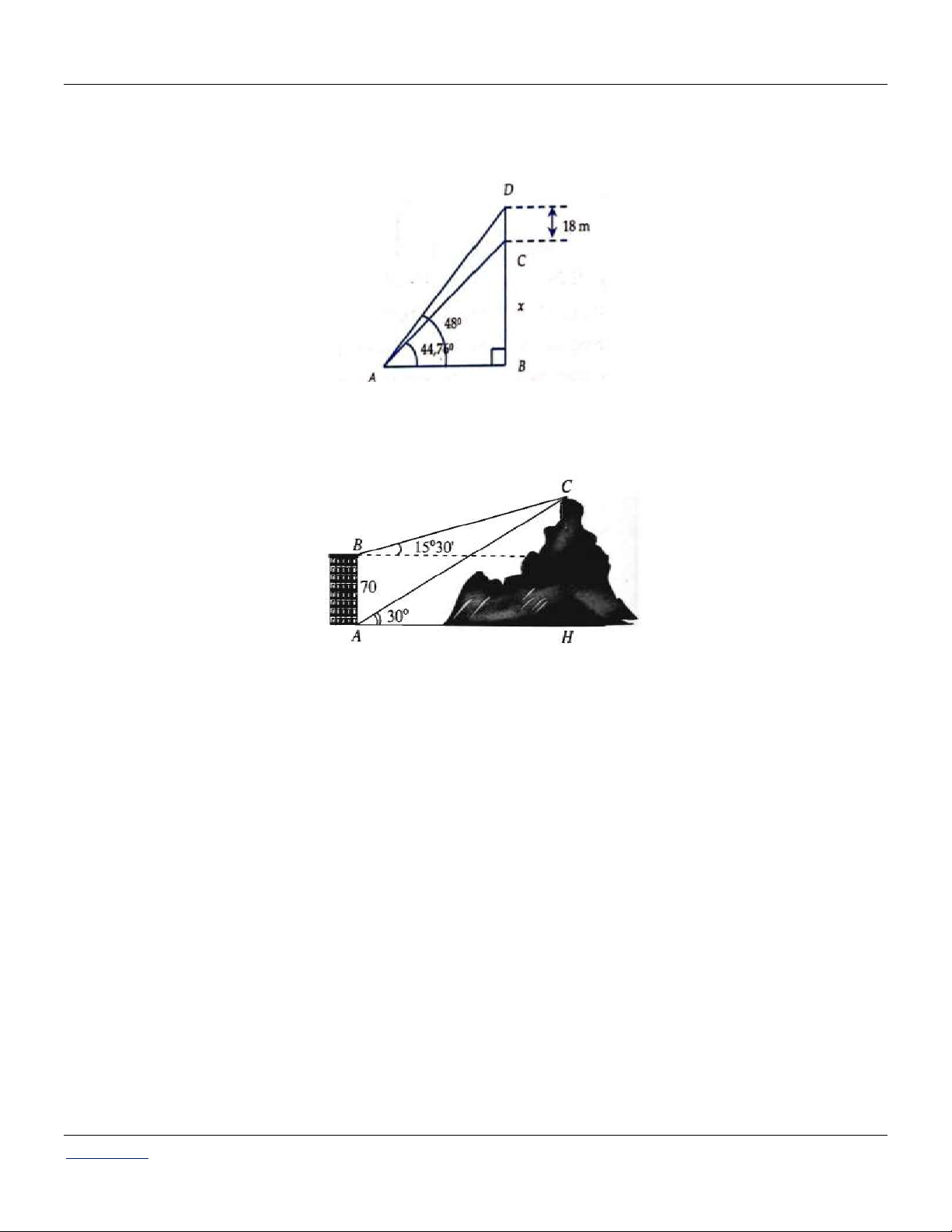
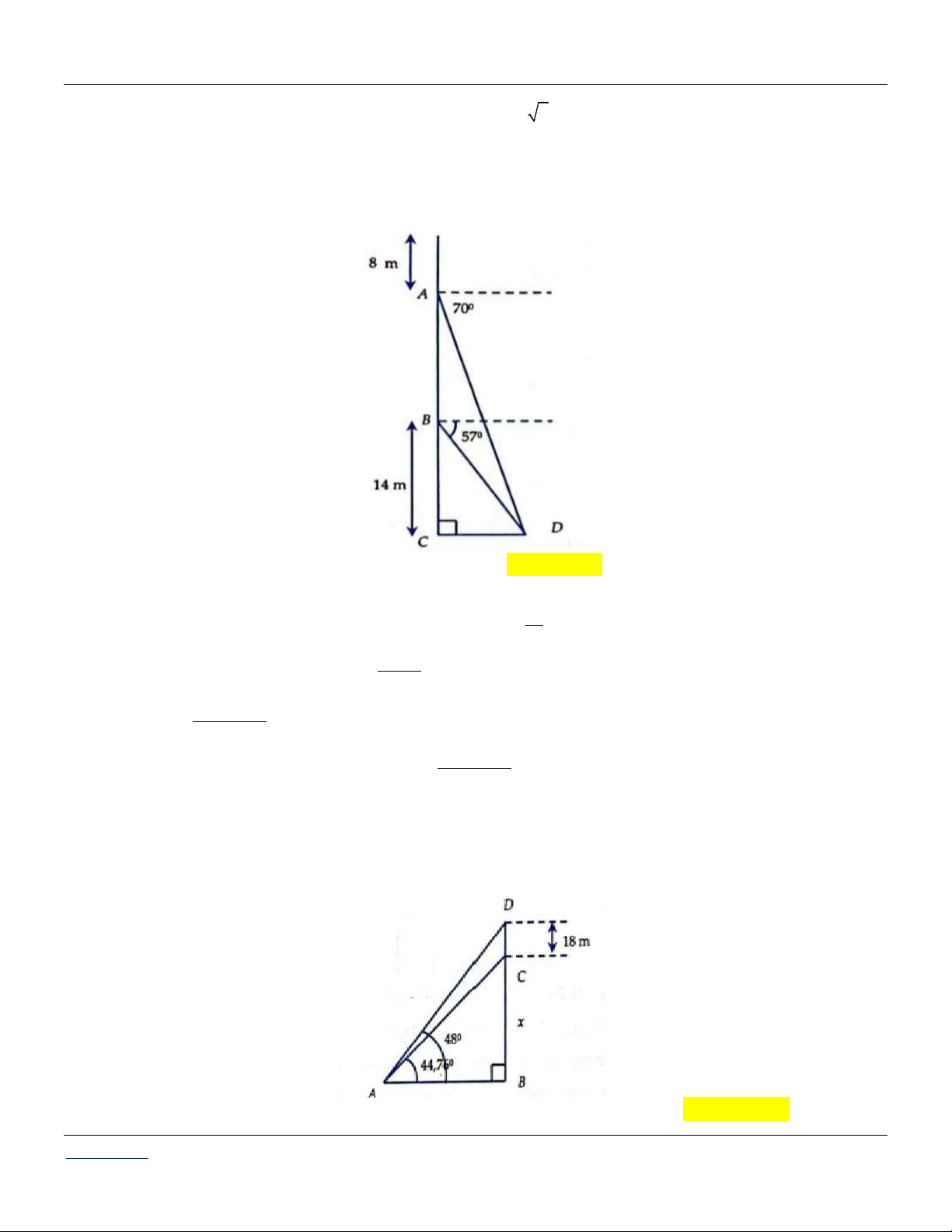
Câu 89: Đầu của các tổng thống ở Mount Rushmore cao 18 mét. Một du khách nhìn thấy đỉnh đầu
của George Washington ở góc cao 48 và cằm của ông ở góc cao 44,76 .  Chiều cao của múi
Rushmore gần giá trị nào nhất? A. 182,753 m. B. 99,649 m. C. 99,9 m. D. 168,055 m.
Câu 90: Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ
cao AB  70m , phương nhìn AC tạo với phương nằm ngang góc 30 , phương nhìn BC tạo
với phương nằm ngang góc 15 3
 0' (tham khảo hình vẽ)
Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây? A. 135m . B. 234m . C. 165m . D. 195m .
________________HẾT________________
Huế, 10h58’ ngày 29 tháng 8 năm 2022
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 15
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TR¾C NGHIÖM M«n: To¸n 10 Chuyên đề:
HỆ THỨC LƯỢNG TRONG TAM GIÁC
LỜI GIẢI CHI TIẾT
II. BÀI TẬP TỰ LUẬN Câu 1:
Cho tam giác ABC có A  120 và AB  5, AC  8 . Tính độ dài cạnh BC . Lời giải:
Áp dụng Định lí côsin cho tam giác ABC , ta có:  1   2 2 2
BC AB AC  2. . AB AC.cos120 2 2  5  8  2.5.8. 129   .  2  Vậy BC  129 . Câu 2:
Cho tam giác ABC có a  8,b  9, c  6.
a) Tính số đo các góc của tam giác.
b) Tính diện tích, bán kính đường tròn ngoại tiếp, bán kính đường tròn nội tiếp, độ dài các
đường cao của tam giác. Lời giải: 2 2 2
b c a 81 36  64 53
a) Áp dụng định lí côsin, ta có cos A    . 2bc 2.9.6 108 Suy ra A  60 36  39   .
Hoàn toàn tương tự, tính được B  78 35
 5 , C  40 4  816 . 8  9  6 23
b) Do a  8 , b  9 , c  6 nên tam giác ABC có nửa chu vi p   . 2 2 7 5 11
Suy ra p a  , p b  , p c  . 2 2 2 23 7 5 11 8855
Từ đó, theo công thức Heron ta được diện tích của tam giác là S  . . .  . 2 2 2 2 4 S 8855
Suy ra bán kính đường tròn nội tiếp r  
và bán kính đường tròn ngoại tiếp p 46 abc 432 R   . 4S 8855
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 16
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống Câu 3: Cho tam giác ABC có o
A  15 , c  6 và o B  120 .
a) Tính độ dài các cạnh a, b ;
b) Tính bán kính đường tròn ngoại tiếp và diện tích của tam giác;
c) Tính độ dài đường cao h . a Lời giải: a) Do o o
A  15 , B  120 nên o o
C  120  A B  45 .
Áp dụng định lí sin ta được: c 6 o a  .sin A  .sin15  3 3 1 , o   sin C sin 45 c 6 o b  .sin B  .sin120  3 6 . o sin C sin 45
b) Theo định lí sin, bán kính đường tròn ngoại tiếp của tam giác là c 6 R    3 2 . o 2sinC 2sin 45 3   abc  3 1.3 6.6 9 3 3 1
Do a  3 3 1,b  3 6,c  6 và R  3 2 nên S    . 4R 4.3 2 2 9 3  S  3 1 2 
c) Từ kết quả của phần b), suy ra h    . a a    3 3 3 3 1 Câu 4:
Cho tam giác ABC có a  14, b  18, c  20 . Tính gần đúng góc ABC. Lời giải: 2 2 2 2 2 2
a c b 14  20 18 17 Ta có cos B    . 2ac 2.14.20 35 Suy ra: B  60 56  ' . Câu 5:
Giải tam giác ABC , biết c  14, ˆ
A  60, ˆB  40 . Lời giải: Ta có ˆ C  ˆ 180 ˆ 
  A B  80. a b 14
Áp dụng Định lí sin, ta có:   sin60 sin40 sin80 14sin60 14sin40 Suy ra a  12,3; b   9,14. sin80 sin80 Câu 6: Cho tam giác ABC có O O
B  60 , C  45 , AB  5 . Tính độ dài cạnh AC. Lời giải: AB AC A . B sin B 5 6
Áp dụng định lí sin cho tam giác ABC, ta có:   AC   . sinC sin B sinC 2 Câu 7:
Cho tam giác ABC có BC  10 , A  30 . Tính bán kính đường tròn ngoại tiếp tam giác ABC. Lời giải:
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC , ta có: BC BC 10  2R R    10 . sin A 2.sin A 2.sin 30
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 17
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống Câu 8:
Cho tam giác có ba cạnh là 6,10,8 . Tính bán kính đường tròn nội tiếp tam giác đó. Lời giải: Gọi ,
p r lần lượt là nửa chu vi và bán kính đường tròn nội tiếp tam giác đã cho, ta có: 6  8 10 p  12. 2
Diện tích tam giác là S
p( p  6)( p  8)( p 10)  24 (đvdt). S 24 Suy ra r    2 . p 12
Nhận xét: Tam giác đã cho là tam giác vuông. Câu 9:
Cho tam giác ABC vuông tại A có AB  6 cm, BC  10 cm. Tính bán kính đường tròn nội tiếp tam giác đó. Lời giải: Ta có 2 2
AC BC AB  8 (cm). 1
Diện tích tam giác ABC là: S A . B AC  24 2 cm  2 6  8 10
Nửa chu vi của tam giác là p  12 2 S 24 Suy ra: r    2 (cm). p 12
Câu 10: Tính diện tích S của tam giác ABC có  4,  6, ˆ c b A  150 . Lời giải: 1 1 Ta có: S  s
bc inA  .6.4 s . in150  6 . 2 2
Câu 11: Tính diện tích tam giác có ba cạnh lần lượt là 5 , 12 , 13 . Lời giải: 5 12 13
Nửa chu vi của tam giác là: p  15 2
Diện tích của tam giác là: S
p p  5 p 12 p 13  1515  515 1215 13  30 .
Câu 12: Cho tam giác ABC có góc B tù, AB  3 , AC  4 và có diện tích bằng 3 3. Tính số đo góc BAC. Lời giải: 1 2S 2.3 3 3
Ta có: S  .A .
B AC.sin A  sin A    2 A . B AC 3.4 2
Vì góc B tù nên A là góc nhọn  A  60 .
Câu 13: Tính diện tích tam giác đều nội tiếp đường tròn bán kính R  4 cm. Lời giải:
Gọi a là độ dài cạnh và S là diện tích của tam giác, ta có: 2 a 3 . a . a a S  
a R 3  4 3 4 4R
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 18
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống 4 32. 3
Vậy diện tích tam giác đã cho là: S   12 3  2 cm . 4
Câu 14: Cho tam giác ABC có AB  1, AC  3, A  60 . Tính bán kính đường tròn ngoại tiếp ABC . Lời giải: Ta có: 2 2 2 2
BC AC AB  2.AC.A .
B cos A  3 1 2.3.1.cos 60  7  BC  7 BC BC 7 21 Ta lại có:  2R R    . sin A 2.sin A 2.sin 60 3
Câu 15: Cho tam giác ABC có AB  8 cm, AC  18 cm và có diện tích bằng 64 cm2. Tính sin . A Lời giải: 1 2S 8 Ta có: S A .
B AC.sin A  sin A   . 2 A . B AC 9
Câu 16: Cho tam giác ABC có AB  9 cm, AC  12 cm và BC  15 cm. Tính độ dài đường trung
tuyến AM của tam giác ABC. Lời giải: 2 2 2 2 2 2 AB AC BC 9 12 15
Cách 1: Ta có AM      7,5 . 2 4 2 4 BC
Cách 2: Tam giác ABC vuông tại A nên AM   7,5 . 2
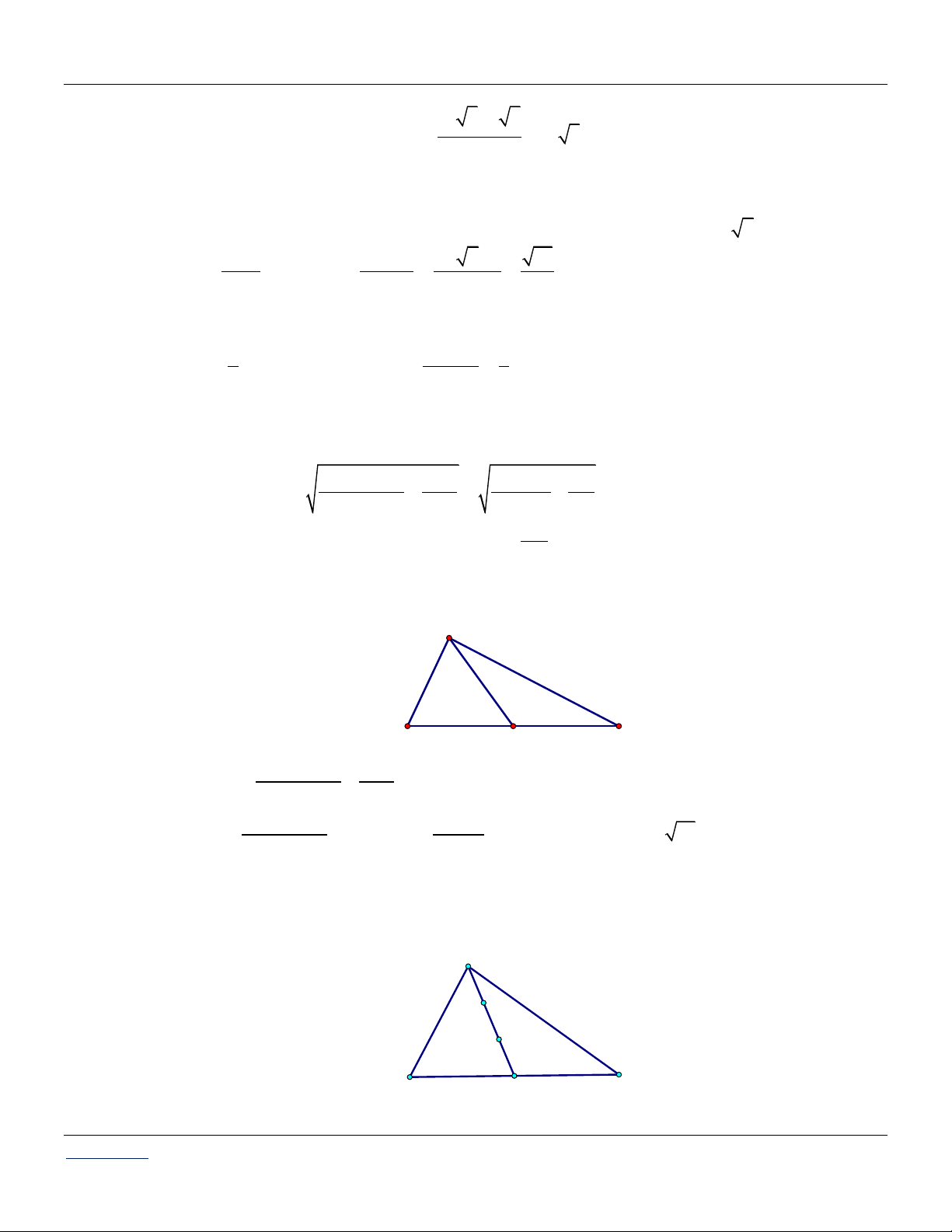
Câu 17: Cho tam giác ABC có AB  5 , AC  9 và đường trung tuyến AM  6 . Tính độ dài cạnh BC . Lời giải: A 5 9 6 B M C 2 2 2 AC AB BC Ta có: 2 AM   2 4 2 2 2 2  AC AB   9  5  2 2 2  BC  4  AM   4
 6    68  BC  2 17.  2   2 
Câu 18: Cho tam giác ABC có AB  5 , BC  8 , CA  6 . Gọi G là trọng tâm tam giác. Tính độ dài đoạn thẳng CG. Lời giải: C G B A M
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 19
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống 2 2 2 CB AC AB 175
Gọi M là trung điểm AB , ta có 2 CM    . 2 4 4 2 2 175 5 7
Suy ra: CG CM   . 3 3 4 3
Câu 19: Cho tam giác có ba cạnh lần lượt là 5 , 6 , 7 . Tính độ dài đường cao ứng với cạnh có độ dài bằng 6. Lời giải: 5  6  7
Nửa chu vi của tam giác là: p   9 . 2
Diện tích tam giác là: S
p p  5 p  6 p  7  6 6 .
Đặt a  5 , b  6 , c  7 . 2S 2.6 6
Độ dài đường cao ứng với cạnh có độ dài bằng 6 là: h    2 6 . b b 6 AB
Câu 20: Cho tam giác ABC có các góc A  105 , B  45 . Tính tỉ số . AC Lời giải: b c AB c sin C sin(180 105  45 )  2 Ta có:       . sin B sin C AC b sin B sin 45 2
Câu 21: Cho tam giác có ba cạnh lần lượt là 5,12,13. Tính độ dài đường cao ứng với cạnh lớn nhất. Lời giải:
Đặt a  5 , b  12 , c  13. Ta có: 5 12 13
Nửa chu vi của tam giác là: p  15 2
Diện tích của tam giác là: S
p p  5 p 12 p 13  1515  515 1215 13  30 . 2S 2.30 60
Đường cao ứng với cạnh lớn nhất là: h    . c c 13 13
Câu 22: Cho tam giác có ba cạnh lần lượt là 2, 3, 4 . Góc bé nhất của tam giác có sin bằng bao nhiêu? Lời giải:
Góc bé nhất ứng với cạnh có số đo bé nhất. 2 2 2
b c a 7 Giả sử a  , 2 b  ,
3 c  4 . Ta có cos A   . . 2 . b c 8 2   Do đó 7 15 sin A  1     .  8  8
Câu 23: Cho tam giác ABC có AB  3 , AC  4 và tan A  2 2 . Tính độ dài cạnh BC. Lời giải:
Từ giả thiết tan A  2 2  0, ta suy ra A là góc nhọn 1 1 1 1 2
tan A  2 2  cos A     cos A  2 1 tan A   2 9 3 1 2 2
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 20
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống 1 Suy ra: 2 2 2 2 BC
AB AC  2A .
B AC.cos A  3  4  2.3.4.  17 . 3
Câu 24: Cho tam giác ABC vuông cân tại .
A Gọi r, R lần lượt là bán kính đường tròn nội tiếp, ngoại R
tiếp tam giác ABC . Tính tỉ số . r Lời giải: a 2
Giả sử AB AC a BC a 2  R  . 2 2 A . B AC 2a a 2 a a R
Mặt khác S pr   r   r  . Suy ra 1 2 . 2 2 2 2  2 r
Câu 25: Cho tam giác ABC có các cạnh a, b, c thỏa mãn a b ca b c  3ab . Tính số đo của góc C. Lời giải:
Trong tam giác ABC ta luôn có: 2 2 2
c a b  2 . ab cos C .
Hệ thức a b ca b c  ab  a b2 2 3  c  3ab 2 2 2
c a b ab 1 Suy ra: 2  .cosC  1
  cosC   C  60 . 2
Câu 26: Tính góc C của tam giác ABC biết a b và  2 2     2 2 a a c b b c  . Lời giải: Ta có:  2 2     2 2 a a c b b c  3 3 2
a b c a b  0
 a b 2 2
a ab b  2
c a b  0 2 2 2
a b c 2 2 2
a ab b c  0  cosC  1
  . Do đó: C 120 . 2ab 2 sin A sin B sinC
Câu 27: Cho tam giác ABC có BC  10 và  
. Tính chu vi của tam giác đó. 5 4 3 Lời giải: sin A sin B sinC a b c Do   nên 
  b  8;c  6 (do a BC  10 ). 5 4 3 5 4 3
Chu vi tam giác ABC bằng 24 . sin A sin B sinC
Câu 28: Cho tam giác ABC có các góc thỏa mãn  
. Tính số đo các góc của tam giác. 1 2 3 Lời giải:
Áp dụng định lí sin, ta có a : b : c  1: 2 : 3 .
Đáp số: A  30 , B  90 , C  60 .
Câu 29: Cho tam giác ABC có AB  7 , AC  5 và B C 1 cos
  . Tính độ dài cạnh BC. 5 Lời giải: 1
Vì trong tam giác ABC ta có B C bù với góc A nên B C 1 cos    cos A  5 5
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 21
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống 1 Lúc đó: 2 2 2 2 BC
AB AC  2A .
B AC.cosA  7  5  2.7.5.  2 15 . 5
Câu 30: Cho tam giác ABC , các đường cao h , h , h thỏa mãn 3h  2h h . Chứng minh rằng: a b c a b c 3 2 1   . a b c Lời giải: S S S
Kí hiệu S S
. Ta có: 3h  2h  3.2 2.2 2 h    3 2 1    . ABC a b c a b c a b c
Câu 31: Cho tam giác ABC . Chứng minh rằng: 2 2 2 b c a 1 1 1 1 a) 2 m   ; b)    . a 2 4 h h h r a b c Lời giải:
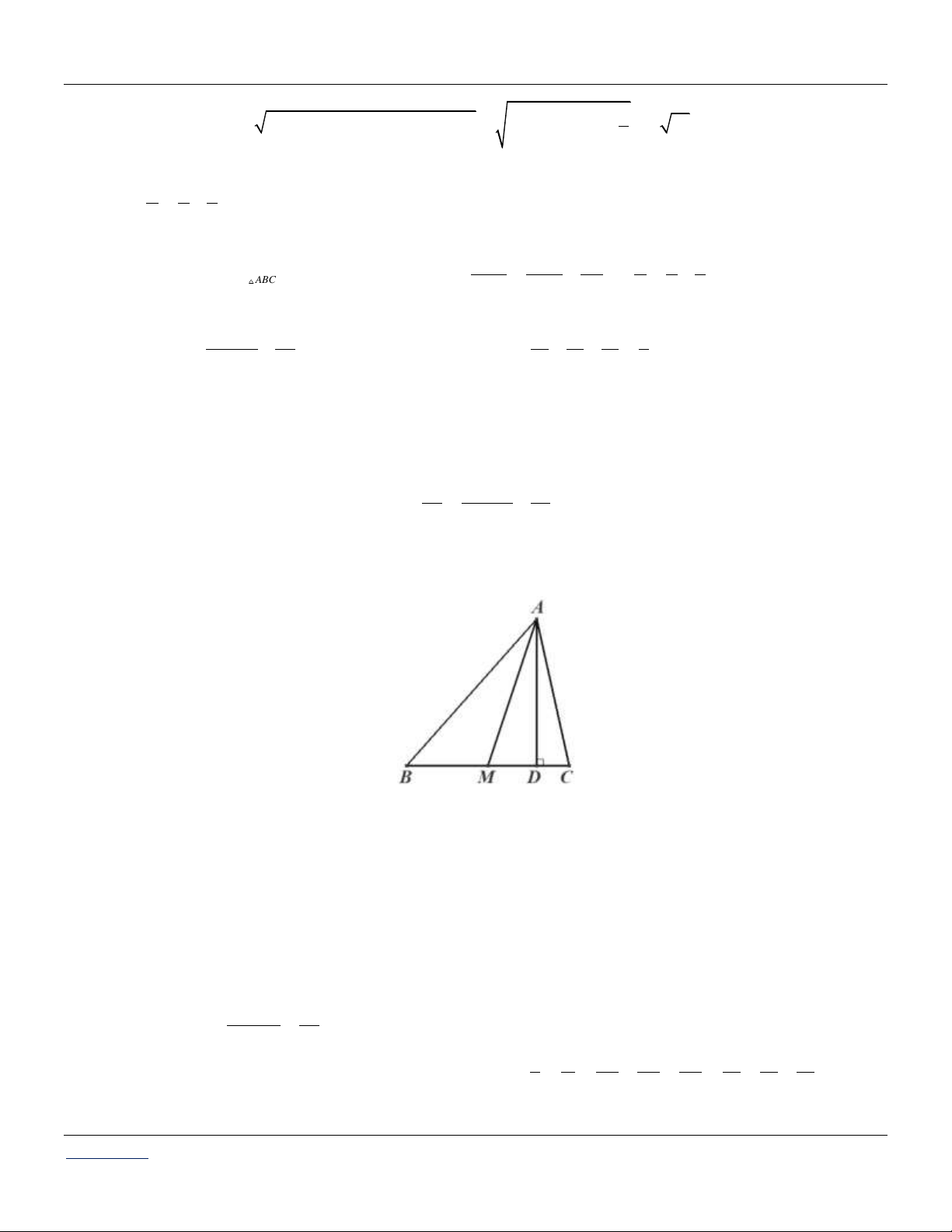
a) Gọi M là trung điểm của BC . Khi đó m AM . a
Có hai trường hợp sau xảy ra:
Trường hợp 1. b c . Trong trường hợp này AM cũng chính là đường cao kẻ từ A của tam 2 2 2 2 a b c a giác. Do đó 2 2 2 2
m AC CM b    . a 4 2 4
Trường hợp 2. b c . Không mất tính tổng quát, xét trường hợp b c (H.3.2), trường hợp còn
lại chứng minh tương tự.
Gọi D là chân đường cao kẻ từ A . Do b c nên D thuộc tia MC .
Áp dụng định lí Pythagore trong tam giác ADB , ta có:      2 2 2 2 2 AB BD AD BM MDAD 2 2 2
BM  2BM.MD MD AD . Suy ra 2 2 2
AB BM  2BM .MD AM   1 .
Một cách tương tự, áp dụng định lí Pythagore trong tam giác ADC , cũng được
AC AD  MC MD2 2 2 2 2
MC  2MC.MD AM 2 . Từ   1 và 2 suy ra: 2 2
AB AC   2 2
BM CM   BM MD CM MD 2 2 . .  2AM   2 2 BM CM  2  2AM . 2 2 2 b c a Hay 2 m   . a 2 4 1 p a b c 1 1 1
b) Từ công thức tính diện tích tam giác ta suy ra        . r S 2S 2S 2S h h h a b c
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 22
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Câu 32: Cho tam giác ABC có các góc thỏa mãn sin C  2.sin .
B cos A . Chứng minh rằng tam giác
ABC là một tam giác cân. Lời giải:
Áp dụng định lý sin và côsin, ta có: 2 2 2
b c a sin C  2.sin .
B cos A c  2b cos A c  2 . b 2 2 2 2
c b c a a b . 2bc
Vậy tam giác ABC cân tại C .
Câu 33: Cho tam giác ABC . Chứng minh rằng: 2 2 2
a b c 3
a) cot A  cot B  cot C  . b) 2 2 2
m m m
a b c . a b c  2 2 2 4S 4 Lời giải:
a) Từ định lí côsin và công thức tính diện tích tam giác, suy ra: 2 2 2 2 2 2 cos A
b c a
b c a cot A    . sin A 2. . b . c sin A 4S 2 2 2
c a b 2 2 2
a b c
Tương tự cũng có cot B  , cot C  . 4S 4S 2 2 2
a b c
Từ đó cot A  cot B  cot C  . 4S
b) Áp dụng công thức tính độ dài trung tuyến.
Câu 34: Cho tam giác ABC có hai trung tuyến kẻ từ A và B vuông góc. Chứng minh rằng: a) 2 2 2
a b  5c .
b) cot C  2cot A  cot B . Lời giải:
a) Gọi M , N theo thứ tự là trung điểm của các cạnh BC , CA ; gọi G là trọng tâm tam giác 2 2
ABC (Hình vẽ). Khi đó AG AM , BG BN . 3 3
Từ đó theo định lí Pythagore ta có: 2 2 2 2 2 2 4  b c a  4  c a b  2 2 4  a b  2 2 2 2
c AB AG BG         2  c   . 9  2 4  9  2 4  9  4  Suy ra 2 2 2
5c a b . 2 2 2 2
a b c c b) Do 2 2 2
a b  5c nên cot C   . 4S S
b c a
c a b c Mà  A B 2 2 2 2 2 2 2 2 cot cot  2    . 4S 4S S  
Suy ra cot C  2cot A  cot B .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 23
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Câu 35: Cho tam giác ABC có 2
S  2R sin Asin B . Chứng minh rằng tam giác ABC là một tam giác vuông. Lời giải:
Từ định lí sin và công thức tính diện tích, suy ra diện tích của tam giác bằng abc
2Rsin A2Rsin B2RsinC 2 S  
 2R sin Asin Bsin C . 4R 4R Từ đó, do 2
S  2R sin Asin B , suy ra sin C  1 và do đó C  90 .
Suy ra điều phải chứng minh.
Câu 36: Cho tam giác ABC vuông cân tại A có AB AC  30 cm. Hai đường trung tuyến BF và CE
cắt nhau tại G . Tính diện tích tam giác GFC. Lời giải: B H E G C A F 1 1 1
Nối AG cắt BC tại H ta có: SSSS .  GFCAGCAHC  2 3 6 ABC 1 1 Mà 2 S  .30.30  450 S    cm nên 2 .450 75cm . ABC  2 GFC 6
Câu 37: Cho hình bình hành có hai cạnh là 5 và 9 , một đường chéo bằng11. Tìm độ dài đường chéo còn lại. Lời giải: A 9 B 11 5 D 9 C
Gọi hình bình hành là ABCD , AD  5 , AB  9 .
Gọi  là góc đối diện với đường chéo có độ dài 11. 2 2 2 5 9 11 1 Ta có: cos   
   là góc tù   BAD BD 11 2.5.9 6 2 2 2 2 2
AC AD DC  2.A .
D DC.cos ADC AD DC  2.A . D DC.cos BAD
(vì BAD và ADC bù nhau  cos ADC   cos BAD )
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 24
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống  1  2 2 2
AC  5  9  2.5.9.   91 AC  91   .  6 
Câu 38: Cho hình bình hành ABCD có AB a, BC a 2 và BAD  45 . Tính diện tích hình bình hành ABCD. Lời giải: B C a A H D
Gọi BH là đường cao của hình bình hành ABCD . a 2
Tam giác BHA vuông tại H , góc BAH BAC  45 , BH A . B sin 45  . 2 a 2
Diện tích hình bình hành ABCD là: 2
S BH.AD  .a 2  a . 2
Câu 39: Cho tam giác ABC vuông tại A có AB AC a . Điểm M nằm trên cạnh BC sao cho BC BM
. Tính độ dài đoạn thẳng AM. 3 Lời giải: A C M B a Ta có: 2 2 2 2
BC AB AC a a a 2 ; BC AB 2  2 a 2  BM  3 2   2 2 0 2 a 2 a 2 2 a 5
AM AB BM  2 .
AB BM.cos 45  a     2 . a .   . 3  3 2 3  
Câu 40: Cho hình vuông ABCD có cạnh bằng a . Gọi E là trung điểm cạnh BC , F là trung điểm
cạnh AE . Tính độ dài đoạn thẳng DF . Lời giải:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 25
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống A B F E D C 2  a a 5 Ta có: 2 AE DE a      2  2
Dùng công thức độ dài trung tuyến: 2 5a 2  2 2 2 a 2 2 a 13 DA DE AE 5a 13a   2 4 DF . DF      4 2 4 2 16 16
Câu 41: Cho tam giác ABC nội tiếp đường tròn bán kính R, AB R, AC R 2. Tính góc A biết A là góc tù. Lời giải:
Góc A tù, suy ra B, C đều là góc nhọn. AB R 1 Ta có:  2R
 2R  sin C   C  30 .  (vì C nhọn) sin C sin C 2 AC R 2 2 Tương tự:  2R
 2R  sin B
B  45 (do B nhọn). sin B sin B 2
Suy ra: A  180  30  45  105 . 
Câu 42: Cho tam giác vuông, trong đó có một góc bằng trung bình cộng của hai góc còn lại. Cạnh lớn
nhất của tam giác đó bằng .
a Tính diện tích tam giác đã cho. Lời giải:
Gọi tam giác thỏa đề là ABC (với A B C ).
Đề cho tam giác vuông nên ta suy ra A  90 .
Ta có: A B C  180 ,
 mà theo đề: A C  2B, Suy ra B  60. a
Ta tính: AB BC.cos 60  . 2 2 1 a 3
Diện tích tam giác: S A . B BC.sin B  . 2 8
Câu 43: Cho tam giác ABC vuông cân tại A và điểm M trong tam giác sao cho MA  1, MB  2 , MC  2 . Tính góc AMC . Lời giải:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 26
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống A M B C
Áp dụng định lý cosin trong tam giác ta có:  2 2 2
AB AM BM  2AM.BM.cos AMB  2    AB 5 4.cos AMB   2 2 2
BC BM CM  2BM.CM.cos BMC 2
 2AB  6  4 2.cosBMC   2 2 2
AC CM AM  
2CM.AM.cosCMA 2    AB 3 2 2.cosCMA   2
AB  5  4.cos AMB  1
  2.cos AMB  2.cosCMA  0 2
 2AB  6  4 2.cosBMC   
cosCMA  cosBMC 2 AB  3   2 2.cosCMA
Câu 44: Cho góc xOy  30 . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB  2 .
Tính độ dài lớn nhất của đoạn . OB Lời giải:
Đặt OA x , OB y x, y  0
Áp dụng công thức định lý hàm số cosin cho ta giác OAB ta có: 2 2 2 2 2
x y  2xy cos 30  2  x y  3xy  4  0 *
Tìm điều kiện để tồn tại x , ta coi phương trình trên là phương trình ẩn x , tham số y . 2
Khi đó, phương trình * có nghiệm      y   2 0 3
4 y  4  0  4   y  4. Do đó max y  4.
Câu 45: Để đo chiều cao của một tòa nhà, người ta chọn hai điểm A và B thẳng hàng với chân C của
tòa nhà, cách nhau 15 m. Sử dụng giác kế, từ A và B tương ứng nhìn thấy đỉnh D của tòa
nhà dưới các góc 35 và 40 so với phương nằm ngang.
Hỏi chiều cao của tòa nhà đo được là bao nhiêu mét? Lời giải:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 27
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Do CBD  40 , BAD  35 nên ABD  40  35  5 (H.3.3). Áp dụng định lí sin cho tam giác AB 15
ABD ta được BD  .sin A  .sin 35 . sin D sin 5
Từ đó suy ra chiều cao của tòa nhà bằng 15
h CD B . D sin CBD  .sin 35  63, 45m sin 5
Câu 46: Một tàu cá xuất phát từ đảo A , chạy 50 km theo hướng N 24E đến đảo B để lấy thêm ngư
cụ, rồi chuyển hướng N 36 W
 chạy tiếp 130 km đến ngư trường C .
a) Tính khoảng cách từ vị trí xuất phát A đến C (làm tròn đến hàng đơn vị theo đơn vị đo kilômét).
b) Tìm hướng từ A đến C (làm tròn đến hàng đơn vị, theo đơn vị độ). Lời giải:
a) Từ giả thiết suy ra ABC  90  24  90  36  120 (H.3.7).
Áp dụng định lí côsin cho tam giác ABC, ta được:   2 2 2
AC AB BC  1 2 A .
B BC.cos ABC  2500 16900  2.50.130.   25900   .  2 
Suy ra AC  10 259 161km .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 28
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống Hình 3.7 BC
b) Áp dụng định lí sin cho tam giác ABC ta được sin CAB  .sin ABC  0, 6993. AC
Suy ra CAB  44 và do đó AC chếch về hướng tây một góc 44  24  20 so với phương bắc.
Vậy hướng từ A tới C là N 20 W  .
Câu 47: Một tàu du lịch xuất phát từ bãi biển Đồ Sơn (Hải Phòng), chạy theo hướng N80E với vận
tốc 20 km/h. Sau khi đi được 30 phút, tàu chuyển sang hướng E20S giữ nguyên vận tốc và
chạy tiếp 36 phút nữa đến đảo Cát Bà.
Hỏi khi đó tàu du lịch cách vị trí xuất phát bao nhiêu kilômet? Lời giải:
Coi điểm xuất phát là A , điểm tàu chuyển hướng là B và đích đến là C (H3.8).
Theo giả thiết ABC  180  10  20  150 . Hình 3.8 30
Do tàu chạy từ A tới B với vận tốc 20 km/h trong 30 phút, nên AB  20. 10km . 60 36
Do tàu chạy từ B đến C với vận tốc 20 km/h trong 36 phút, nên BC  20. 12km . 60
Áp dụng định lí côsin cho tam giác ABC, ta được:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 29
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống  3  2 2 2 2 2
AC AB BC  2.A .
B BC.cos ABC  10 12  2.10.12.    452   . 2  
Suy ra AC  452  21km .
Câu 48: Một cây cổ thụ mọc thẳng đứng bên lề một con dốc có độ dốc 10 so với phương nằm ngang.
Từ một điểm dưới chân dốc, cách gốc cây 31m người ta nhìn đỉnh ngọn cây dưới một góc
40 so với phương nằm ngang.
Hãy tính chiều cao của cây. Lời giải:
Áp dụng định lí sin cho tam giác ABC (H.3.9). Hình 3.9
Đáp số: Chiều cao của cây là h  20, 23m .
Câu 49: Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình
tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính
của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả
như hình vẽ ( AB  4,3 cm; BC  3, 7 cm; CA  7,5 cm).
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 30
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Tính gần đúng bán kính của chiếc đĩa này. Lời giải:
Bán kính R của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác ABC .
AB BC CA 4, 3  3, 7  7, 5 31
Nửa chu vi của tam giác ABC là: p    cm. 2 2 4
Diện tích tam giác ABC là: S
p p AB p BC  p CA  5, 2 cm2. A . B BC.CA A . B BC.CA Mà S   R   5,73 cm. 4R 4S
Câu 50: Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất
sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24m, CAD  63 ; CBD  48 .
Tính gần đúng chiều cao h của khối tháp. Lời giải:
Ta có CAD  63  BAD  117  ADB  180  117  48  15 AB BD A . B sin BAD
Áp dụng định lý sin trong tam giác ABD ta có:   BD  sin ADB sin BAD sin ADB CD
Tam giác BCD vuông tại C nên có: sinCBD   CD B . D sinCBD BD A . B sin BA . D sinCBD 24.sin117 .  sin48 Vậy CD    61,4m . sin15 sin ADB
III. BÀI TẬP TRẮC NGHIỆM Câu 1:
Cho tam giác ABC , khẳng định nào sau đây đúng? A. 2 2 2
a b c  2b . c cos A. B. 2 2 2
a b c  2b .
c cos A . C. 2 2 2
a b c b .
c cos A . D. 2 2 2
a b c b .
c cos A . Lời giải:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 31
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Áp dụng định lí hàm số cos tại đỉnh A ta có: 2 2 2
a b c  2b . c cos A .
Chọn đáp án B. Câu 2:
Xét tam giác ABC tùy ý có BC a, AC b, AB c . Mệnh đề nào dưới đây đúng? 2 a  2 c  2 b 2 a  2 c  2 b 2 a  2 c  2 b 2 a  2 c  2 b A. cos B
. B. cos B
. C. cos B
. D. cos B  . 2ac 2ac ac 4 Câu 3:
Cho tam giác ABC có A  120 .
 Đẳng thức nào sau đây đúng? A. 2 2 2
a b c  3bc . B. 2 2 2
a b c bc . C. 2 2 2
a b c  3bc . D. 2 2 2
a b c bc . Lời giải:
Áp dụng định lí hàm số cos tại đỉnh A ta có: 2 2 2
a b c  2b . c cos A . 2 2 2
a b c  2b . c o c s120 2 2 2
a b c bc .
Chọn đáp án B. Câu 4:
Cho tam giác ABC có BC a; AB c; AC b và có R là bán kính đường tròn ngoại tiếp.
Hệ thức nào sau đây là sai? a .sin A.  2 . R B. sin  a A . C. . b sin B  2 . R D. sin  c A C . sin A 2R a Lời giải: a b c
Theo định lý sin trong tam giác    2 . R sin A sin B sin C
Nên ta suy ra đáp án sai là . b sin B  2 . R
Chọn đáp án C. Câu 5:
Xét tam giác ABC , hệ thức nào sau đây sai? . b sin A . c sin A A. a . B. sin C . C. a  2 .
R sin A . D. b  . R tan B . sin B a Lời giải: a b c
Theo định lí hàm số sin ta có:    2R sin A sinB sinC Suy ra: a b . b sin A +   a  . sin A sinB sin B a c . c sin A +   sin C  . sin A sinC a a +
 2R a  2 . R sin A . sin A b b b +
 2R   R sin B   R tan B . sinB 2 2 cosB
Chọn đáp án D. Câu 6:
Cho tam giác ABC có AB c, AC  .
b Diện tích của tam giác ABC bằng 1 1 A. bc cos . A B. bc sin . A C. bc cos . A D. bc sin . A 2 2 Câu 7:
Nếu tam giác ABC có 2 2 2
a b c thì:
A. A là góc nhọn.
B. A là góc tù.
C. A là góc vuông.
D. A là góc nhỏ nhất.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 32
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống Lời giải: 2 2 2
b c a Ta có: cos A  . Vì 2 2 2
a b c  cos A  0 . Do đó A nhọn. 2bc
Chọn đáp án A. Câu 8:
Cho tam giác ABC có BC a, CA  ,
b AB c . Mệnh đề nào sau đây là đúng? A. Nếu 2 2 2
b c a  0 thì góc A nhọn. B. Nếu 2 2 2
b c a  0 thì góc A tù. C. Nếu 2 2 2
b c a  0 thì góc A nhọn. D. Nếu 2 2 2
b c a  0 thì góc A vuông. Lời giải:
Áp dụng định lí cô sin ta có: 2 2 2 2 2 2
a b c  2bc cos A  2bc cos A b c a . Suy ra: Nếu 2 2 2
b c a  0  cos A  0 nên A nhọn.
Chọn đáp án A. Câu 9:
Mệnh đề nào sau đây sai? A. Nếu 2 2 2
a b c thì A là góc tù.
B. Nếu tam giác ABC có một góc tù thì 2 2 2
a b c . C. Nếu 2 2 2
a b c thì A là góc nhọn. D. Nếu 2 2 2
a b c thì A là góc vuông. Lời giải: 2 2 2
b c a Ta có : cos A  . 2bc Do đó : * 2 2 2
a b c thì cos A  0 do đó A là góc tù nên A. đúng. * 2 2 2
a b c thì cos A  0 do đó A là góc nhọn nên C. đúng. * 2 2 2
a b c thì cos A  0 do đó A là góc vuông nên D. đúng.
* Nếu tam giác ABC có góc B tù thì 2 2 2
b a c ; nếu góc C tù thì 2 2 2
c a b do đó B. sai.
Chọn đáp án B.
Câu 10: Cho tam giác ABC thỏa mãn 4 4 4
a b c . Khẳng định nào sau đây đúng?
A. Tam giác ABC vuông tại A. B. Tam giác ABC vuông tại B.
C. Tam giác ABC tù.
D. Tam giác ABC nhọn. Lời giải: Do 4 4 4
a b c nên a là cạnh lớn nhất, A là góc lớn nhất của tam giác ABC. Ta có: b c 2 2 2 4 4 
b c (do 2 2 2b c  0 ) 2 2 Lúc đó:  2 2 b c  4 4 4
b c a   2 2 b c  4  a    2 2 2
b c a  2 2 2 0
b c a   0 2 2 2 o
b c a  0  cos A  0  A  90 .
Chọn đáp án D.
Câu 11: Cho tam giác ABC , các đường cao h , h , h thỏa mãn hệ thức 3h  2h h . Tìm hệ thức giữa a b c a b c a, , b c . 3 2 1 3 2 1 A.   .
B. 3a  2b c .
C. 3a  2b c . D.   . a b c a b c Lời giải: S S S
Kí hiệu S S
. Ta có: 3h  2h  3.2 2.2 2 h    3 2 1    . ABC a b c a b c a b c
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 33
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Chọn đáp án D.
Câu 12: Trung tuyến AM của tam giác ABC có độ dài bằng 1 A. 2 2 2
b c a . B. 2 2 2
2b  2c a . C. 2 2 2
3a  2b  2c . D. 2 2 2
2b  2c a . 2 Lời giải: 2 b ca 2  2 2 2
Theo công thức tính độ dài đường trung tuyến AM . 4
Chọn đáp án B.
Câu 13: Cho tam giác ABC có AC  3 3, AB  3, BC  6 . Tính số đo góc B . A. 60 . B. 45 . C. 30 . D. 120 . Lời giải: 2 2 2
AB BC AC   cos B  9 36 27 1 
 . Vậy số đo góc B là 60 . 2A . B BC 36 2
Chọn đáp án A. 3
Câu 14: Cho tam giác ABC có b  7 ; c  5 và cos A  . Tính a . 5 A. 4 2 . B. 2 . C. 2 . D. 3 . Lời giải:
Áp dụng định lí hàm số Cosin vào tam giác ABC có 3 2 2 2 BC AB AC 2A . B AC.Cos A 25 49 2.5.7. 32 BC 4 2. 5
Chọn đáp án A.
Câu 15: Cho tam giác ABC có AB  3 3 và bán kính đường tròn ngoại tiếp R  3 . Số đo góc C là A. 60 . B. 30 . C. 90 . D. 45 . Lời giải: AB 3 3 3
Áp dụng định lý sin trong tam giác ABC ta có: sin C     C  60 .  2R 2.3 2
Chọn đáp án A.
Câu 16: Cho tam giác ABC có B  60 , C  45 , AB  3 . Tính độ dài AC . 3 6 3 2 2 6 A. . B. . C. 6 . D. . 2 2 3 Lời giải: AC AB A . B sin B 3.sin 60 3 6 Ta có:   AC    . sin B sin C sin C sin 45 2
Chọn đáp án A.
Câu 17: Cho tam giác ABC có BAC  105 , ACB  45 và AC  8 . Tính độ dài cạnh AB . 8 6 A. . B. 4 2 . C. 8 2 . D. 41 3 . 3 Lời giải:
Ta có: ABC  180  BAC ACB  180 105  45  30 .
Áp dụng định lý sin trong tam giác ABC ta có
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 34
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống AB AC 8.sin 45   AB   8 2 sin 45 sin 30 sin 30 .
Chọn đáp án C.
Câu 18: Cho tam giác ABC có AB  9, AC  18 và A  60 . Bán kính của đường tròn ngoại tiếp tam giác ABC là A. 3 . B. 9 3 . C. 9 . D. 6 . Lời giải:
Trong tam giác ABC ta có 2 2 2
BC AB AC  2 .
AB AC.cos A  243  BC  9 3 . BC BC 9 3 Mặt khác  2R R    9 sin A 2sin A 2sin 60 .
Chọn đáp án C.
Câu 19: Cho hình vuông ABCD có cạnh bằng 6 , E là trung điểm của CD . Tính bán kính đường tròn
ngoại tiếp tam giác ACE . 3 10 3 5 A. . B. . C. 3 10 . D. 3 5 . 2 2 Lời giải: A B 6 C D E Ta có 2 2 AE
AD DE  36  9  3 5 AE 3 5 3 10
Áp dụng định lý sin cho tam giác ACE ta được:  2R R   R  . sin ACE 2 2 2. 2
Chọn đáp án A. AB
Câu 20: Cho ABC có A  45 ,
B  75 . Tính tỉ số . BC 6 1 3 6  3 2 6 A. . B. . C. . D. . 2 2 6 3 Lời giải:
Áp dụng định lí hàm số sin trong tam giác ABC , ta có AB BC AB sin C
sin 180  45  75 sin 60 6       . sin C sin A BC sin A sin 45 sin 45 2
Chọn đáp án A.
Câu 21: Cho tam giác ABC có BC  3, AC  5, AB  6. Độ dài đường trung tuyến kẻ từ đỉnh C bằng A. 2 2. B. 5. C. 10. D. 3. Lời giải:
Gọi M là trung điểm của AB . Áp dụng công thức độ dài trung tuyến, ta có:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 35
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống 2 2 2 CA CB  2  AB 2 2 2 5  3  2  6 2 CM  
 8 . Suy ra CM  2 2 . 4 4
Vậy độ dài trung tuyến kẻ từ đỉnh C của tam giác ABC bằng 2 2.
Chọn đáp án A.
Câu 22: Cho tam giác ABC có BC  4 , AC  5 và ACB  60 . Độ dài đường trung tuyến hạ từ đỉnh C là 61 51 A. . B. . C. 3 . D. 2 . 2 2 Lời giải: 1 Ta có: 2 2 2 2 2
AB AC BC  2AC.BC.cos ACB  4  5  2.4.5.  21 AB  21 . 2 2 2 2 2 2
2CA  2CB AB 2.5  2.4  21 61 61 Do đó 2 m    . Vậy m  . c 4 4 4 c 2
Chọn đáp án D.
Câu 23: Cho tam giác ABC có chu vi bằng 32 và bán kính đường tròn nội tiếp của ABC bằng 5 .
Tính diện tích tam giác ABC . A. S  32 .
B. S  40.
C. S  160.
D. S  80. 5
Câu 24: Cho tam giác ABC có a  5, b  12, c  13. Bán kính đường tròn ngoại tiếp R của tam giác bằng A. 13. B. 6,5. C. 26. D. 7,5. Lời giải:
a b c 5 12 13 Ta có: p   15. 2 2 Do đó S
pp a p b p c       
15.15 515 1215 13 30. ABC abc abc 5.12.13 Mà S   R    6,5. ABC  4R 4S 4.30
Chọn đáp án B.
Câu 25: Cho tam giác ABC có A  60 ,
AB  3, AC  4. Tính độ dài đường cao kẻ từ A của tam giác ABC . 2 39 39 6 39 3 39 A. h  . B. h  . C. h  . D. h  . a 13 a 13 a 13 a 13 Lời giải:
Áp dụng định lý côsin vào tam giác ABC ta có: 2 2 BC
AB AC  2A . B AC.cos A  25 12  13 1 1 3
Diện tích của tam giác ABC : S A . B AC.sin A  .3.4.  3 3 2 2 2 2S
Gọi h là đường cao kẻ từ A của tam giác ABC. Ta có: ABC h   6 3 6 39   . a a BC 13 13
Chọn đáp án C.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 36
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Câu 26: Cho tam giác ABC có AB  9 cm, AC  12 cm và BC  15 cm. Khi đó, đường trung tuyến
AM của tam giác ABC có độ dài bằng A. 8 cm. B. 10 cm. C. 9 cm. D. 7,5 cm. Lời giải: 2 2 2 2 2 2 AB AC BC 9 12 15
Cách 1: Ta có AM      7,5 . 2 4 2 4 BC
Cách 2: Tam giác ABC vuông tại A nên AM   7,5 . 2
Chọn đáp án D.
Câu 27: Cho tam giác DEF có DE DF  10 cm và EF  12 cm. Gọi I là trung điểm của cạnh EF .
Đoạn thẳng DI có độ dài bằng A. 6,5 cm. B. 7 cm. C. 8 cm. D. 4 cm. Lời giải: 2 2 2 2 2 2 DE DF EF 10 10 12
Cách 1: Ta có DI      8 . 2 4 2 4
Cách 2: Tam giác DIE vuông tại I nên 2 2 2 2 DI
DE EI  10  6  8
Chọn đáp án C.
Câu 28: Cho tam giác ABC có AB  8 cm, AC  18 cm và có diện tích bằng 64 cm2. Giá trị sin A bằng 3 3 4 8 A. . B. . C. . D. . 2 8 5 9 Lời giải: 1 2S 8 Ta có: S A .
B AC.sin A  sin A   . 2 A . B AC 9
Chọn đáp án D. AB
Câu 29: Cho tam giác ABC có các góc A  105 , B  45 . Tính tỉ số . AC 2 2 6 A. . B. 2 . C. . D. . 2 2 3 Lời giải: b c AB c sin C sin(180 105  45 )  2 Ta có:       . sin B sin C AC b sin B sin 45 2
Chọn đáp án A.
Câu 30: Cho tam giác ABC có O
AB  5, AC  8, A  60 . Tính độ dài cạnh BC. A. 129 . B. 7 . C. 49 . D. 69 . Lời giải: 1 Ta có: 2 2 2 2 BC
AB AC  2A .
B AC.cos A  5  8  2.5.8.  49  7 . 2
Chọn đáp án B.
Câu 31: Tính diện tích tam giác có ba cạnh lần lượt là 3 , 2 và 1.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 37
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống 3 6 2 A. . B. 3 . C. . D. . 2 2 2 Lời giải: 3  2 1
Nửa chu vi của tam giác là: p  . 2
Diện tích tam giác là: S p p
p p  2 3 2 1  . 2
Chọn đáp án D.
Câu 32: Cho tam giác ABC nội tiếp đường tròn bán kính R, AB R, AC R 3. Tính góc A , biết B là góc tù. A. 30 . B. 45 . C. 60 . D. 90 . Lời giải:
Góc B là góc tù nên A , C là góc nhọn. AB R 1 Ta có:  2R
 2R  sin C   C  30 .
 (vì C nhọn) sin C sin C 2 AC R 3 3 Tương tự:  2R
 2R  sin B
B 120 (do B tù). sin B sin B 2
Suy ra: A  180  30 120  30 . 
Chọn đáp án A.
Câu 33: Tam giác ABC có a  14, b  18, c  20 . Khẳng định nào sau đây đúng? A. B  42 50  ' . B. B  60 56  ' . C. B  119 04  ' .
D. B  90 . Lời giải: 2 2 2 2 2 2
a c b 14  20 18 17 Ta có cos B    . Suy ra: 60o B  56 ' . 2ac 2.14.20 35
Chọn đáp án B.
Câu 34: Cho tam giác ABC có AB  4 cm, BC  7 cm, CA  9 cm. Giá trị cos A bằng 2 1 2 1 A. . B. . C. . D. . 3 3 3 2 Lời giải: 2 2 2
AB AC BC 2 Ta có: 2 2 2
BC AB AC  2A .
B AC.cos A  cos A   . 2A . B AC 3
Chọn đáp án A.
Câu 35: Cho tam giác ABC có AB  4 , AC  5 , BC  6 . Tính cos  B C . 1 1 A. . B. . C. –0,125 . D. 0, 75 . 8 4 Lời giải: 2 2 2
b c a 1
Ta có c AB  4 , b AC  5 , a BC  6 . Tính cos A   . . 2 . b c 8 1
Để ý cos(B C)   cos A     125 , 0 . 8
Chọn đáp án C.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 38
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Câu 36: Tính bán kính đường tròn nội tiếp tam giác có ba cạnh lần lượt là 5, 12, 13. A. 2. B. 2. C. 2 2. D. 3. Lời giải:
Nhận xét: Đây là tam giác vuông với cạnh huyền là 13. 1 S 30
Diện tích tam giác: S  .5.12  30. Bán kính đường tròn nội tiếp tam giác: r    2. 2 p 15
Chọn đáp án B.
Câu 37: Cho tam giác ABC có BC  10 , A  30 . Bán kính đường tròn ngoại tiếp tam giác ABC bằng 10 A. 5. B. 10. C. . D. 10 3 . 3 Lời giải:
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC , ta có: BC BC 10  2R R   10. sin A 2.sin A 2.sin 30
Chọn đáp án B.
Câu 38: Tính diện tích tam giác có ba cạnh lần lượt là 5 , 12 , 13 . A. 60 . B. 30 . C. 34 . D. 7 5 . Lời giải: 5 12 13
Nửa chu vi của tam giác là: p  15 2
Diện tích của tam giác là: S
p p  5 p 12 p 13  1515  515 1215 13  30 .
Chọn đáp án B.
Câu 39: Cho tam giác ABC có O O
B  60 , C  45 , AB  5 . Tính độ dài cạnh AC. 5 6 A. 5 3 . B. 5 2 . C. . D. 10 . 2 Lời giải: AB AC A . B sin B 5 6
Áp dụng định lí sin cho tam giác ABC ta có:   AC   . sin C sin B sin C 2
Chọn đáp án C.
Câu 40: Tam giác đều nội tiếp đường tròn bán kính R  4 cm thì có diện tích bằng A. 2 13 cm . B. 2 13 2 cm . C. 2 12 3 cm . D. 2 15 cm . Lời giải: 2 a 3 . a . a a
Gọi a là độ dài cạnh và S là diện tích của tam giác, ta có: S  
a R 3  4 3 4 4R 4 32. 3
Vậy diện tích tam giác đã cho là: S   12 3  2 cm  . 4
Chọn đáp án C.
Câu 41: Cho hình bình hành ABCD có AB a, BC a 2 và BAD  45 . Tính diện tích hình bình hành ABCD. A. 2 2a . B. 2 a 2 . C. 2 a . D. 2 a 3 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 39
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống Lời giải: B C a A H D
Gọi BH là đường cao của hình bình hành ABCD . a 2
Tam giác BHA vuông tại H , góc BAH BAC  45 , BH A . B sin 45  . 2 a 2
Diện tích hình bình hành ABCD là: 2
S BH.AD  .a 2  a . 2
Chọn đáp án C.
Câu 42: Cho hình bình hành có một cạnh là 5 hai đường chéo là 6 và 8 . Tính độ dài cạnh kề với cạnh có độ dài bằng 5. A. 3 . B. 1. C. 5 6 . D. 5 . Lời giải: A 5 B 8 6 D C
Gọi hình bình hành là ABCD . Ta có: 2 2 2
3  4  25  5
AC BD ABCD là hình thoi AB AD  5 .
Chọn đáp án D.
Câu 43: Cho hình bình hành có hai cạnh là 5 và 9 , một đường chéo bằng11. Tìm độ dài đường chéo còn lại. A. 9,5 . B. 4 6 . C. 91 . D. 3 10 . Lời giải: A 9 B 11 5 D 9 C
Gọi hình bình hành là ABCD , AD  5 , AB  9 . 2 2 2 5 9 11 1
Gọi  là góc đối diện với đường chéo có độ dài 11. Ta có: cos      2.5.9 6
 là góc tù   BAD BD 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 40
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống 2 2 2 2 2
AC AD DC  2.A .
D DC.cos ADC AD DC  2.A .
D DC.cos BAD
(vì BAD và ADC bù nhau  cos ADC   cos BAD )  1  2 2 2
AC  5  9  2.5.9.   91 AC  91   .  6 
Chọn đáp án C.
Câu 44: Cho tam giác ABC vuông tại A có AB  6 cm, BC  10 cm. Tính bán kính đường tròn nội tiếp tam giác đó. A. 1 cm. B. 2 cm. C. 2 cm. D. 3 cm. Lời giải: 1 Ta có 2 2 2 AC
BC AB  8 (cm). Diện tích tam giác ABC là: S A .
B AC  24cm 2 6  8 10 S 24 Nửa chu vi p  12. Suy ra r    2 (cm). 2 p 12
Chọn đáp án C.
Câu 45: Tính diện tích tam giác ABC biết A  60 , b  10 , c  20 . A. 50 3 . B. 50 . C. 50 2 . D. 50 5 . Lời giải: 1
Áp dụng công thức : S  1 .b . c sin A  .10.20.sin 60  50 3 . 2 2
Chọn đáp án A.
Câu 46: Cho tam giác ABC có AB  5 , AC  9 và đường trung tuyến AM  6 . Tính độ dài cạnh BC . A. 2 17 . B. 17 . C. 129 . D. 22 . Lời giải: A 5 9 6 B M C 2 2 2 AC AB BC Ta có: 2 AM   2 4 2 2 2 2  AC AB   9  5  2 2 2  BC  4  AM   4
 6    68  BC  2 17.  2   2 
Chọn đáp án A. AB
Câu 47: Cho tam giác ABC có các góc A  75, B  45 . Tính tỉ số . AC 6 6 A. . B. 6 . C. . D. 1, 2 . 3 2 Lời giải: b c AB c sin C sin(180  75  45 )  6 Ta có:       . sin B sin C AC b sin B sin 45 2
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 41
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Chọn đáp án C.
Câu 48: Cho tam giác ABC vuông tại A , AC b , AB c . Lấy điểm M trên cạnh BC sao cho góc MB BAM  30 .  Tính tỉ số . MC b 3 3c 3c b c A. . B. . C. . D. . 3c 3b b b c Lời giải: B M 30° 60° A C . MB AM AM .sin 30 AM Ta có   MB   . sin 30 sin B sin B 2.sin B MC AM AM .sin 60 AM 3   MB sin C c 3c MC   . Do đó    . sin 60 sin C sin C 2.sin C MC 3 sin B 3b 3b
Chọn đáp án B.
Câu 49: Trong tam giác ABC , nếu 2h h h thì dẳng thức nào sau đây đúng? a b c 2 1 1 A.   .
B. 2sin A  sin B  sin C . sin A sin B sin C 2 1 1
C. sin A  2sin B  2sin C . D.   . sin A sin B sin C Lời giải: S S S
Ta có: 2h h  2 2 2 h  2.   2 1 1    2 1 1    a b c a b c a b c 2 . R sin A 2 . R sin B 2 . R sin C 2 1 1    . sin A sin B sin C
Chọn đáp án A.
Câu 50: Cho tam giác ABC. Khẳng định nào sau đây đúng? 2 4 A. 2 2 2
m m m
a b c B. 2 2 2
m m m
a b c a b c  2 2 2. a b c  2 2 2. 3 3 3 1 C 2 2 2 2 2 2 2 2 2 2 2 2
. m m m
a b c
D. m m m
a b c a b c  . a b c  . 4 3 Lời giải:
Sử dụng công thức trung tuyến của tam giác, ta có: 2 2 2 2 2 2 2 2 2
2b  2c a
2c  2a b
2a  2b c 3 2 2 2
m m m    
a b c a b c  2 2 2. 4 4 4 4
Chọn đáp án C.
Câu 51: Xét tam giác ABC , khẳng định nào sau đây đúng?
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 42
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống b c b c b c A. m . B. m . C. m .
D. m b c . a 2 a 2 a 2 a Lời giải: 2 2 2 2 2 b c a
b c b c 2  a Ta có: 2 m    a 2 4 4 b c b c 2  2 Vì      2 2 b c a b ca m   m  . a 4 a 2
Chọn đáp án B.
Câu 52: Trong tam giác ABC , điều kiện để hai trung tuyến kẻ từ A và B vuông góc với nhau là A. 2 2 2
2a  2b  5c . B. 2 2 2
3a  3b  5c . C. 2 2 2
2a  2b  3c . D. 2 2 2
a b  5c . Lời giải:
Vì hai trung tuyến vẽ từ A và B vuông góc với nhau nên ABG vuông tại G với G là
trọng tâm tam giác ABC . 2 2 2 2 2 2 4  b c a a c b  Khi đó: 2 2 2
c GA GB 2  c       9 2 4 2 4   2 2 4  a b  2 2
c  c    2 2 2
 5c a b . 9 4 4  
Chọn đáp án D.
Câu 53: Cho tam giác ABC có ba góc nhọn, BC a , AC b , AB c và diện tích là S . Tổng
cot A  cot B  cot C bằng  2 2 2
2 a b c  2 2 2
a b c 2 2 2
a b c 2 2 2
a b c A. . B. . C. . D. . S S 2S 4S Lời giải: 1 2S 2 2 2
b c a
Từ công thức S bc sin A  sin A  , và cos A  . 2 bc 2bc 2 2 2
b c a 2 2 2 cos A
b c a Suy ra 2 cot bc A    . sin A 2S 4S bc 2 2 2
a c b 2 2 2
a b c
Tương tự ta cũng có cot B  , cot C  . 4S 4S 2 2 2 2 2 2 2 2 2 2 2 2
b c a
a c b
a b c
a b c
Vậy cot A  cot B  cot C     . 4S 4S 4S 4S
Chọn đáp án D.
Câu 54: Xét tam giác ABC , nếu có 2 a  .
b c thì đẳng thức nào dưới đây đúng? 1 1 1 1 1 1 1 2 2 A.   . B. 2
h h .h . C.   . D.   . 2 h h h a b c 2 h h h 2 h h h a b c a b c a b c Lời giải: 2  2S
 2S   2S  1 1 1 Ta có : 2 a  . b c      .    . 2
h h .h . h h hh h h a b c a
b   c  2 a b c
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 43
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Chọn đáp án B.
Câu 55: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết AB c và c  AB 1 os  . 3 c 2 3c 2 9c 2 3c A. . B. . C. . D. . 2 8 8 2 Lời giải: 2 1  1  2 2
Ta có cos C   cos(A B)   . Do đó sin C  1     . 3  3  3 AB AB 3 2c  2R R   . sin C 2sin C 8
Chọn đáp án B.
Câu 56: Cho tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R . Gọi r R
là bán kính đường tròn nội tiếp tam giác ABC . Khi đó, tỉ số bằng r 2  2 2 1 1 2 A. 1 2 . B. . C. . D. . 2 2 2 Lời giải: a 2
Giả sử AB AC a BC a 2  R  . 2 2 A . B AC 2a a 2 a a R
Mặt khác S pr   r   r  . Suy ra 1 2 . 2 2 2 2  2 r
Chọn đáp án A.
Câu 57: Cho tam giác ABC vuông cân tại A có AB AC  30 cm. Hai đường trung tuyến BF và CE
cắt nhau tại G . Diện tích tam giác GFC bằng A. 50 cm2. B. 50 2 cm2. C. 75 cm2. D. 15 105 cm2. Lời giải: 1 1 1
Nối AG cắt BC tại H ta có: SSS   S GFCAGCAHC  2 3 6 ABC 1 1 Mà 2 S  .30.30  450 S    cm nên 2 .450 75cm . ABC  2 GFC 6
Chọn đáp án C.
Câu 58: Cho tam giác ABC có diện tích S . Nếu tăng độ dài mỗi cạnh BC và AC lên hai lần đồng
thời giữ nguyên độ lớn của góc C thì diện tích của tam giác mới được tạo nên bằng A. 2S . B. 3S . C. 4S . D. 5S . Lời giải: 1 Ta có S
BC.AC.sin C 2 1  1 
Khi BC , AC tăng 2 lần, ta có S  .2BC.2AC.sin C  4
BC.AC sin C  4S . 1   2  2 
Chọn đáp án C.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 44
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Câu 59: Cho hình vuông ABCD có cạnh bằng a . Gọi E là trung điểm cạnh BC , F là trung điểm
cạnh AE . Tính độ dài đoạn thẳng DF . a 13 a 5 a 3 3a A. . B. . C. . D. . 4 4 2 4 Lời giải: A B F E D C 2  a a 5 Ta có: 2 AE DE a      2  2
Dùng công thức độ dài trung tuyến: 2 5a 2  2 2 2 a 2 2 a 13 DA DE AE 5a 13a   2 4 DF . DF      4 2 4 2 16 16
Chọn đáp án A.
Câu 60: Cho tam giác ABC có B C  135 và BC  .
a Tính bán kính đường tròn ngoại tiếp tam giác. a 2 a 3 A. . B. a 2 . C. . D. a 3 . 2 2 Lời giải: BC BC a a 2
Ta có A  180 135  45   2R R    . sin A 2sin A 2sin 45 2
Chọn đáp án A.
Câu 61: Cho tam giác ABC có AB  9 , BC  10 , CA  11. Gọi M là trung điểm BC và N là trung
điểm AM . Tính độ dài BN . A. 6 . B. 4 2 . C. 5 . D. 34 . Lời giải: 2 2 2 AB AC BC 2 2 2 BA BM AM Ta có 2 AM    76  2 BN    34. 2 4 2 4
Chọn đáp án D.
Câu 62: Cho tam giác ABC có AB  5 , BC  8 , CA  6 . Gọi G là trọng tâm tam giác ABC . Độ dài
đoạn thẳng CG bằng 5 7 5 7 5 7 13 A. . B. . C. . D. . 2 3 6 3 Lời giải: 2 2 2 CB AC AB
Gọi M là trung điểm AB , ta có: 2 175 CM     2 2 175 5 7 CG CM   . 2 4 4 3 3 4 3
Chọn đáp án B.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 45
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Câu 63: Cho tam giác ABC có AB  2 cm, AC  1 cm, O
A  60 . Tính độ dài cạnh BC. A. 1 cm. B. 2 cm. C. 3 cm. D. 5 cm. Lời giải:
Áp dụng định lí Cô – sin cho tam giác ABC ta có: 2 2 2
BC AB AC  2. .
AB AC.cos A 2 2 1 2 2.1.2.cos 60o   
 3 . Suy ra: BC  3 (cm).
Chọn đáp án C.
Câu 64: Cho tam giác có ba cạnh lần lượt là 5 , 6 , 7 . Tính độ dài đường cao ứng với cạnh có độ dài bằng 6. 5 3 A. 6 . B. 2 6 . C. 5 . D. . 2 Lời giải: 5  6  7
Nửa chu vi của tam giác là: p   9 . 2
Diện tích tam giác là: S
p p  5 p  6 p  7  6 6 . Đặt a  5 , b  6 , c  7 . 2S 2.6 6
Độ dài đường cao ứng với cạnh có độ dài bằng 6 là: h    2 6 . b b 6
Chọn đáp án B.
Câu 65: Cho tam giác có ba cạnh lần lượt là 5,12,13. Tính độ dài đường cao ứng với cạnh lớn nhất. 60 120 30 A. . B. . C. . D. 12 . 13 13 13 Lời giải: 5 12 13
Đặt a  5 , b  12 , c  13. Ta có: Nửa chu vi của tam giác là: p  15 2
Diện tích của tam giác là: S
p p  5 p 12 p 13  1515  515 1215 13  30 . 2S 2.30 60
Đường cao ứng với cạnh lớn nhất là: h    . c c 13 13
Chọn đáp án A.
Câu 66: Cho tam giác ABC có BC  12 , CA  9 , AB  6 . Trên cạnh BC lấy điểm M sao cho BM  4 .
Tính độ dài đoạn thẳng AM . A. 2 5 . B. 3 2 . C. 20 . D. 19 . Lời giải: 2 2 2 2 2 2
AB BC AC 6 12  9 11 cos B    2A . B BC 2.6.12 16 11 2 2 2 2 AM
AB BM  2A .
B BM .cosB  6  4  2.6.4.  19. 16
Chọn đáp án D.
Câu 67: Cho tam giác cân ABC có A  120 và AB AC a . Lấy điểm M trên cạnh BC sao cho 2BC BM
. Tính độ dài AM . 5
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 46
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống a 3 11a a 7 a 6 A. . B. . C. . D. . 3 5 5 4 Lời giải: A C a a M 30 B  1  2 2 2 2 2a 3 BC
AB AC  2ABAC cos120  a a  2 . a . a   a 3    BM   2  5 2  2a 3  2a 3 3 a 7 2 2 2 AM AB BM  2 . AB BM .cos 30  a     2 . a .    . 5 5 2 5  
Chọn đáp án C.
Câu 68: Cho tam giác ABC có các cạnh a, b, c thỏa mãn điều kiện a b ca b c  3ab . Tính số đo của góc C. A.120 . B. 30 . C. 45 . D. 60 . Lời giải:
Trong tam giác ABC ta luôn có: 2 2 2
c a b  2 .
ab cos C .
Hệ thức a b ca b c  ab  a b2 2 3  c  3ab 2 2 2
c a b ab 1 Suy ra: 2  .cosC  1
  cosC   C  60 . 2
Chọn đáp án D.
abcabc
Câu 69: Cho tam giác ABC có S
. Khẳng định nào sau đây đúng? 4
A. Tam giác ABC vuông tại A. B. Tam giác ABC vuông tại B.
C. Tam giác ABC tù.
D. Tam giác ABC nhọn. Lời giải:
a b c
Nửa chu vi của tam giác là p  . 2
abca bc 2 2 Ta có: 2 S
 16S  a b c a b c 4
           2   2 p p a p b p c p c p b
          2 2 p p a
p c p b p pa p pb c  bc
pc b a  bc  b c ac b a 2 2 2
 2bc b c a .
Chọn đáp án A. sin B  sinC
Câu 70: Cho tam giác ABC thỏa mãn sin A
. Khẳng định nào sau đây đúng? cos B  cosC
A. Tam giác ABC cân.
B. Tam giác ABC đều.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 47
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
C. Tam giác ABC vuông.
D. Tam giác ABC có góc A  60 .  Lời giải: a b c a b c Ta có:  
 2R  sin A  ; sin B  ; sinC  . sin A sin B sinC 2R 2R 2R 2 2 2 2 2 2
a c b
a b c Và cos B  ; cosC  . 2ac 2ab sin B  sinC Ta có: sin A
 sin AcosB  cosC  sinB  sinC cos B  cosC 2 2 2 2 2 2
a a c b
a b c b c       2R  2ac 2ab  2R 2R 2 2 2 2 2 2
a c b
a b c  
b c b 2 2 2
a c b   c 2 2 2
a b c   2bcb c 2c 2b 2 2 3 2 2 3 2 2
ba bc b ca cb c  2b c  2bc   3 3 b c  2 2 2 2
b c bc ba ca  0
 b c 2 2
b bc c   bcb c 2
a b c  0
 b c 2 2 2
b c a  2 2 2 2 2 2
 0  b c a  0  b c a .
Chọn đáp án C.
Câu 71: Một tam giác có độ dài các cạnh là 1, m, 2 với m  . Giá trị của m là A. 1. B. 2. C. 3 . D. 4 . Lời giải:
Ta có 1, m , 2 là độ dài 3 cạnh tam giác mà một cạnh luôn lớn hơn hiệu 2 cạnh và nhỏ hơn tổng 2
cạnh nên ta có 2 1  m  2 1  1  m  3 Mặt khác, m  nên m  2 .
Chọn đáp án B.
Câu 72: Cho tam giác ABC có AB  7 , AC  5 và B C 1 cos
  . Tính độ dài cạnh BC. 5 A. 2 15 . B. 4 22 . C. 4 15 . D. 2 22 . Lời giải:
Vì trong tam giác ABC ta có B C bù với góc A nên    1 cos B C   1
 cos A 5 5 1 2 2 2 2 BC
AB AC  2A .
B AC.cosA  7  5  2.7.5.  2 15 . 5
Chọn đáp án A.
Câu 73: Tam giác ABC có    1 cos A B  
, AC  4 , BC  5 . Tính cạnh . AB 8 A. 46 . B. 11. C. 5 2 . D. 6 . Lời giải:
Vì trong tam giác ABC ta có A B bù với góc C nên  1 A B 1 1 cos    cosC  2 2 2 2 AB
AC BC  2A .
B BC.cos C  4  5  2.4.5.  6 . 8 8 8
Chọn đáp án D.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 48
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống 1
Câu 74: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết AB  12 và cot( A B)  . 3 9 10 A. 2 10 . B. . C. 5 10 . D. 3 2 . 5 Lời giải: 1 1
Ta có: cot( A B) 
nên cot C   , suy ra 3cos C   sin C . 3 3 AB AB Mà 2 2
sin C  cos C  3 3 10 1  sin C     2R R   2 10 . 10 10 sin C 2sin C
Chọn đáp án A. 1
Câu 75: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết AB  10 và tan( A B)  . 3 5 10 10 10 A. . B. . C. . D. 5 10 . 9 3 5 Lời giải: 1 1
Ta có: tan( A B) 
nên tan C   . 3 3
Do đó 3sin C   cos C , mà 2 2
sin C  cos C  1 10 1  sin C   . 10 10 AB AB  2R R   5 10 . sin C 2sin C
Chọn đáp án D.
Câu 76: Tìm chu vi tam giác ABC , biết rằng AB  6 và 2sin A  3sin B  4sin C . A. 26 . B. 13 . C. 5 26 . D. 10 6 . Lời giải:
Vì 2sin A  3sin B  4sin C nên ta có: 2a  3b  4c  24 (do c AB  6 ).
Do đó: a  12,b  8, c  6 . Chu vi tam giác ABC bằng 26 .
Chọn đáp án A. sin A sin B sin C
Câu 77: Cho tam giác ABC có BC  10 và  
. Tìm chu vi của tam giác đó. 5 4 3 A. 12 . B. 36 . C. 24 . D. 22 . Lời giải: sin A sin B sin C a b c Vì   , nên
   b  8,c  6 (do a BC  10 ). 5 4 3 5 4 3
Chu vi tam giác ABC bằng 24 .
Chọn đáp án C. a b b c a c
Câu 78: Tam giác ABC có các cạnh a, b, c thỏa mãn điều kiện   . Tính cos . A 6 5 7 1 1 1 1 A.  . B. . C.  . D. . 4 3 3 3 Lời giải:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 49
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
a b  6ta  4t a b b c a c   Ta có:  
t  b c  5t a b c  9t. Vậy b  2t. 6 5 7  
a c  7tc  3t  2 2 2 2 2 2
b c a
4t  9t  16t 1
Theo định lí côsin: cos A     . 2bc 2.2t.3t 4 7 11
Tương tự, ta tính được: cos B  ;cosC  . 8 16
Chọn đáp án A.
Câu 79: Tính góc C của tam giác ABC biết a b và  2 2     2 2 a a c b b c  .
A. C  150 .
B. C  120 .
C. C  60 .
D. C  30 . Lời giải: Ta có:  2 2     2 2 a a c b b c  3 3 2
a b c a b  0
 a b 2 2
a ab b  2
c a b  0 2 2 2
a b c 2 2 2
a ab b c  0  cosC  1
  . Do đó: C 120 . 2ab 2
Chọn đáp án B. Câu 80: Cho góc O
xOy  30 . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB  1.
Độ dài lớn nhất của đoạn OB bằng A. 1,5 . B. 3 . C. 2 2 . D. 2 . Lời giải: AB
Xét tam giác OAB có
 2  2R R 1. Với R là bán kính đường tròn ngoại tiếp tam sin O
giác OAB . Vậy OB lớn nhất khi OB là đường kính của đường tròn ngoại tiếp tam giác OAB .
Khi đó OB  2 .
Chọn đáp án D.
Câu 81: Cho góc xOy  30 . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB  2 .
Độ dài lớn nhất của đoạn OB bằng A. 2. B. 3. C. 4. D. 5. Lời giải:
Đặt OA x , OB y . Áp dụng công thức định lý hàm số cosin cho tam giác OAB ta có: 2 2 2 2 2
x y  2xy cos 30  2  x y  3xy  4  0 *
Tìm điều kiện để tồn tại x , ta coi phương trình trên là phương trình ẩn x , tham số y . 2
Khi đó, phương trình * có nghiệm      y   2 0 3
4 y  4  0  4   y  4. Do đó max y  4 .
Chọn đáp án C.
Câu 82: Hai chiếc tàu thủy cùng xuất phát từ một vị trí A , đi thẳng theo hai hướng tạo với nhau góc
60 . Tàu B chạy với tốc độ 20 hải lí một giờ. Tàu C chạy với tốc độ 15 hải lí một giờ (tham khảo hình vẽ)
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 50
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí?
Kết quả gần nhất với số nào sau đây? A. 61 hải lí. B. 36 hải lí. C. 21 hải lí. D. 18 hải lí. Lời giải:
Sau 2 giờ tàu B đi được 40 hải lí, tàu C đi được 30 hải lí. Vậy tam giác ABC có
AB  40, AC  30 và A  60 . 
Áp dụng định lí côsin vào tam giác ABC, ta có 2 2 2
a b c  2bc cos A 2 2
 30  40  2.30.40.cos60  900  1600  1200  1300.
Vậy BC  1300  36 (hải lí).
Sau 2 giờ, hai tàu cách nhau khoảng 36 hải lí.
Chọn đáp án B.
Câu 83: Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta
chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C . Ta đo được
khoảng cách AB  40m , 0
CAB  45 và CBA  70 (tham khảo hình vẽ)
Vậy sau khi đo đạc và tính toán được khoảng cách AC gần nhất với giá trị nào sau đây? A. 53 m . B. 30 m . C. 41,5 m . D. 41 m . Lời giải: AC AB
Áp dụng định lí sin vào tam giác ABC, ta có  sin B sinC . AB sin  40.sin70
Vì sinC  sin    nên AC    sin    41,47 m. sin115
Chọn đáp án C.
Câu 84: Từ vị trí A người ta quan sát một cây cao (hình vẽ).
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 51
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Biết AH  4m, HB  20m, BAC  45 .
Chiều cao của cây gần nhất với giá trị nào sau đây? A. 17,5m . B. 17m . C. 16,5m . D. 16m . Lời giải: AH 4 1
Trong tam giác AHB , ta có tan ABH      ABH  11 1  9' . BH 20 5 Suy ra 0
ABC  90  ABH  78 41
 ' . Suy ra ACB  180  BAC ABC  56 1  9' .
Áp dụng định lý sin trong tam giác ABC , ta được: AB CB A . B sin BAC   CB   17m. sin ACB sin BAC sin ACB
Chọn đáp án B.
Câu 85: Giả sử CD h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt
đất sao cho ba điểm A, B và C thẳng hàng. Ta đo được AB  24 m , CAD  63, CBD  48 (tham khảo hình vẽ)
Chiều cao h của tháp gần với giá trị nào sau đây? A. 18m . B. 18,5m . C. 60m . D. 61,4m . Lời giải: AD AB
Áp dụng định lí sin vào tam giác ABD, ta có  . sin  sin D
Ta có   D   nên D      63  48  15 .  . AB sin  24.sin 48 Do đó AD    sin    68,9 m 1 . sin15
Trong tam giác vuông ACD, có h CD  . AD sin  61,4 m.
Chọn đáp án D.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 52
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Câu 86: Trên nóc một tòa nhà có một cột ăng-ten cao 5 m . Từ vị trí quan sát A cao 7 m so với mặt
đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50 và 40 so với phương
nằm ngang (tham khảo hình vẽ)
Chiều cao của tòa nhà gần nhất với giá trị nào sau đây? A. 12m . B. 19m . C. 24m . D. 29m . Lời giải:
Từ hình vẽ, suy ra BAC  10 và ABD  180  BAD ADB  180  50  90  40 .
Áp dụng định lí sin trong tam giác ABC , ta có BC AC
BC.sin ABC 5.sin 40    AC  =  18,5 m . sin10 sin BAC sin ABC sin BACCD
Trong tam giác vuông ADC , ta có sinCAD  
CD AC.sinCAD  11,9 m. AC
Vậy CH CD DH  11,9  7  18,9 m.
Chọn đáp án B.
Câu 87: Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng đứng
cách chân tháp một khoảng CD  60m , giả sử chiều cao của giác kế là OC  m 1 . Quay thanh
giác kế sao cho khi ngắm theo thanh ta nhình thấy đỉnh A của tháp. Đọc trên giác kế số
đo của góc AOB  60 (tham khảo hình vẽ) A 60° B O 1m D C 60m
Chiều cao của ngọn tháp gần với giá trị nào sau đây? A. 40m . B. 114m . C. 105m . D. 110m . Lời giải: AB
Tam giác OAB vuông tại B, có tan AOB   AB  tan60 .  OB  60 3 m. OB
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 53
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống
Vậy chiều cao của ngọn tháp là h AB OC  60 3  1m  105m.
Chọn đáp án C.
Câu 88: Một thợ lặn có vị trí cách mặt nước 8m, một con tàu đắm ở góc 0
70 . Sau khi cùng xuống tới
một điểm cao hơn 14m so với đáy đại dương, thợ lặn nhìn thấy con tàu đắm ở góc 0 57 . Chiều
sau của con tàu đắm gần giá trị nào nhất? A. 24,979 m. B. 32,964 m. C. 32,979 m. D. 33,25 m. Lời giải: x
Đặt CD x, AB y. Xét tam giác BCD: tanCBD   x  14.tan33 14 x
Xét tam giác ACD: tanCAD
 14  ytan 20  x y  14 14.tan 33  y   14  10,979 tan 20 14.tan 33
Chiều sâu của con tàu đắm bằng: 8   32,979 . m tan 20
Chọn đáp án C.
Câu 89: Đầu của các tổng thống ở Mount Rushmore cao 18 mét. Một du khách nhìn thấy đỉnh đầu
của George Washington ở góc cao 48 và cằm của ông ở góc cao 44,76 .  Chiều cao của múi
Rushmore gần giá trị nào nhất? A. 182,753 m. B. 99,649 m. C. 99,9 m. D. 168,055 m.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 54
[...Các chuyên đề Trắc nghiệm Toán THPT...] Đại số 10_Kết nối tri thức với cuộc sống Lời giải: x x
Đặt AB y, BC  .
x Ta có: tan 44,76   y y tan 44,76 x  18 x  18 Lại có: tan 48   y y tan 48 x x  18    18.tan 44,76  x   18  168,055 (m). tan 44,76 tan 48 tan 48  tan 44,76
Chọn đáp án D.
Câu 90: Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ
cao AB  70m , phương nhìn AC tạo với phương nằm ngang góc 30 , phương nhìn BC tạo
với phương nằm ngang góc 15 3
 0' (tham khảo hình vẽ)
Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây? A. 135m . B. 234m . C. 165m . D. 195m . Lời giải:
Từ giả thiết, ta suy ra tam giác ABC có CAB  60, ABC  105 3  0 và c  70.
Khi đó A B C  180  C  180  A B  180 165 3  0  14 3  0 . b c b 70 Theo định lí sin, ta có  hay  sin B sinC sin105 3  0 sin14 3  0 70.sin105 3  0
Do đó AC b   269,4 m. sin14 3  0
Gọi CH là khoảng cách từ C đến mặt đất. Tam giác vuông ACH có cạnh CH đối diện với AC 269,4 góc 30 nên CH    134,7 m. 2 2
Vậy ngọn núi cao khoảng 135 m.
Chọn đáp án A.
________________HẾT________________
Huế, 10h58’ ngày 29 tháng 8 năm 2022
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 55