Chuyên đề hệ thức lượng trong tam giác Toán 10

Tài liệu gồm 42 trang, được biên soạn bởi tác giả Toán Từ Tâm, bao gồm lý thuyết, các dạng bài tập và bài tập luyện tập chuyên đề hệ thức lượng trong tam giác môn Toán 10. Mời bạn đọc đón xem!

30 15 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

TÁC GIẢ

TOÁN TỪ TÂM

ttt

HỆ THỨC LƯỢNG

trong tam giác

Trang 1

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04

MỤC LỤC

Bài 1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0° ĐẾN 180°

A. Lý thuyết

1. Giá trị lượng giác của một góc ..............................................................................................................2

2. Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau ...................................................... 3

3. Mối quan hệ giữa các giá trị lượng giác của hai góc phụ nhau ................................................... 3

4. Giá trị lượng giác của các góc đặc biệt ............................................................................................. 3

7. Các hệ thức lượng giác cơ bản .............................................................................................................. 3

B. Các dạng bài tập

 Dạng 1. Tính giá trị biểu thức lượng giác .............................................................................................. 4

 Dạng 2. Tính giá trị biểu thức lượng giác khi biết một giá trị lượng giác ......................................... 7

 Dạng 3. Chứng minh/rút gọn đẳng thức/biểu thức lượng giác ........................................................ 11

C. Luyện tập

A. Câu hỏi – Trả lời trắc nghiệm ..................................................................................................................... 14

B. Câu hỏi – Trả lời Đúng/sai ......................................................................................................................... 16

C. Câu hỏi – Trả lời ngắn ................................................................................................................................ 18

Bài 2. ĐỊNH LÝ SIN - COS, GIẢI TAM GIÁC & THỰC TẾ

A. Lý thuyết

1. Định lý hàm cos ....................................................................................................................................... 20

2. Định lý hàm sin ....................................................................................................................................... 20

3. Đường trung tuyến ................................................................................................................................. 21

4. Diện tích tam giác .................................................................................................................................. 21

5. Giải tam giác ............................................................................................................................................ 21

B. Các dạng bài tập

 Dạng 1. Giải tam giác .............................................................................................................................. 22

 Dạng 2. Chứng minh hệ thức trong tam giác ...................................................................................... 25

 Dạng 3. Ứng dụng thực tế ...................................................................................................................... 29

C. Luyện tập

A. Câu hỏi – Trả lời trắc nghiệm ..................................................................................................................... 32

B. Câu hỏi – Trả lời Đúng/sai ......................................................................................................................... 36

C. Câu hỏi – Trả lời ngắn ................................................................................................................................ 37

Trang 2

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04

1. Giá trị lượng giác của một góc

GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0° ĐẾN 180°

Bài 1.

Chương 04

Lý thuyết

Định nghĩa

» Trong mặt phẳng , nửa đường tròn tâm nằm phía trên trục hoành bán

kính được gọi là nửa đường tròn đơn vị.

» Với mỗi góc ta xác định một điểm trên nửa đường tròn

đơn vị sao cho và giả sử điểm có tọa độ .

Khi đó:

⓵ . ⓶ . ⓷ . ⓸ .

» Các số được gọi là

các giá trị lượng giác của góc .

Với ta có

Góc

Chú ý

Trang 3

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04

2. Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau

 

180

sin sin

cos cos

tan tan

cot cot



  

Sin – bù

3. Mối quan hệ giữa các giá trị lượng giác của hai góc phụ nhau

 

sin cos

cos sin

tan cot

cot tan



Phụ – chéo

4. Giá trị lượng giác của các góc đặc biệt

Góc

sin

cos

tan



cot



7. Các hệ thức lượng giác cơ bản

⑴

1sin cos

⑵

1tan .cot 

⑶

sin

tan

cos



⑷

cos

cot

sin



⑸

1 tan

cos



⑹

1 cot

sin



Trang 4

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04



Dạng 1.

Tính giá trị biểu thức lượng giác

 Lời giải

........................................................................................................................................................

Các dạng bài tập

⑴

⑵

⑶ ⑷

⑸ ⑹

Có thể sử dụng thêm: Sin – bù;Phụ - chéo

Phương pháp

Ví dụ 1.1.

Tính giá trị các biểu thức sau:

⑴

⑵

⑶

Trang 5

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04

 Lời giải

........................................................................................................................................................

 Lời giải

........................................................................................................................................................

Ví dụ 1.2.

Tính giá trị các biểu thức sau:

⑴

⑵

⑶

Ví dụ 1.3.

Thực hiện các yêu cầu sau:

⑴ Cho . Tính

⑵ Cho . Tính

Trang 6

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04

........................................................................................................................................................

Trang 7

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04



Dạng 2.

Tính giá trị biểu thức lượng giác khi biết một giá trị lượng giác

 Lời giải

........................................................................................................................................................

⑴

⑵

⑶ ⑷

⑸ ⑹

Cần đánh giá được dấu của và/hoặc .

Phương pháp

Ví dụ 2.1.

Thực hiện các yêu cầu sau:

⑴ Cho với . Tính và

⑵ Cho và . Tính và

⑶ Cho tính giá trị lượng giác còn lại.

Trang 8

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04

........................................................................................................................................................

 Lời giải

........................................................................................................................................................

Ví dụ 2.2.

Biết

⑴ và . Tính giá trị của và .

⑵ và . Tính

⑶ và . Tính và .

⑷ tính giá trị của biểu thức

Trang 9

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04

........................................................................................................................................................

 Lời giải

........................................................................................................................................................

 Lời giải

........................................................................................................................................................

Ví dụ 2.3.

Cho biểu thức .

⑴ Với góc bằng bao nhiêu thì không xác định.

⑵ Tìm giá trị của biết .

Ví dụ 2.4.

Cho biểu thức .

⑴ Với góc bằng bao nhiêu thì không xác định.

⑵ Tìm giá trị của biết .

Trang 10

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04

........................................................................................................................................................

 Lời giải

........................................................................................................................................................

Ví dụ 2.5.

Biết

⑴ Tìm

⑵ Chứng minh rằng .

Trang 11

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04



Dạng 3.

Chứng minh/rút gọn đẳng thức/biểu thức lượng giác

 Lời giải

........................................................................................................................................................

⑴

⑵

⑶ ⑷

⑸ ⑹

Sử dụng thêm tính chất.

Phương pháp

Ví dụ 3.1.

Chứng minh các đẳng thức sau(giả sử các biểu thức sau đều có nghĩa)

⑴

⑵

⑶

Trang 12

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04

 Lời giải

........................................................................................................................................................

Ví dụ 3.2.

Rút gọn biểu thức

⑴

⑵

⑶

⑷

⑸

⑹

Trang 13

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04

 Lời giải

........................................................................................................................................................

 Lời giải

........................................................................................................................................................

Ví dụ 3.3.

Đơn giản các biểu thức sau(giả sử các biểu thức sau đều có nghĩa)

⑴

⑵ với

Ví dụ 3.4.

Chứng minh biểu thức sau không phụ thuộc vào .

Trang 14

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04

A. Câu hỏi – Trả lời trắc nghiệm

» Câu 1. Khẳng định nào sau đây đúng?

90 100



sin sin .

95 100



cos cos .

85 125



tan tan .

145 125



cos cos .

» Câu 2. Khẳng định nào sau đây đúng?

90 150



sin sin .

9015 90 30





sin sin .

90 30 100





cos cos .

150 120



cos cos .

» Câu 3. Cho biết

31cos sin

0 90 .

Giá trị của

tan

bằng

tan .

» Câu 4. Cho góc

 

90 180  ;.

Khẳng định nào sau đây đúng?

sin

và

cot

cùng dấu. B. Tích

sin .cot

mang dấu âm.

C. Tích

sin .cos

mang dấu dương. D.

sin

và

tan

cùng dấu.

» Câu 5. Cho là góc tù. Mệnh đề nào đúng trong các mệnh đề sau?

0tan .

0cot .

0sin .

0cos .

» Câu 6. Cho

0º 90º

. Khẳng định nào sau đây đúng?

 

90º  cot tan

. B.

 

90ºcos sin

 

90º  sin cos

. D.

 

90º  tan cot

» Câu 7. Trong các đẳng thức sau đây, đẳng thức nào đúng?

 

180



  sin sin

. B.

 

180



cos cos

 

180



tan tan

. D.

 

180



  cot cot

» Câu 8. Cho và là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào

sai?

sin sin

. B.

cos cos

. C.

tan tan

. D.

cot cot

» Câu 9. Cho hai góc nhọn và (

 )

. Khẳng định nào sau đây là sai?

cos cos

. B.

sin sin

. C.

0tan tan

. D.

cot cot

» Câu 10. Cho

ABC

vuông tại

, góc

bằng



. Khẳng định nào sau đây là sai?

cosB

. B.

sinC

. C.

cosC

. D.

sinB

» Câu 11. Biết

cos

 

0 90   

. Khi đó

tan

bằng

. B.



. C.

. D.



» Câu 12. Cho

sin x

và

90 180

thì

cos

. B.

cos

. C.

cos

. D.

cos

Luyện tập

Trang 15

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04

» Câu 13. Cho

90 180

và thỏa mãn

sin

. Giá trị của

cos

bằng.

 .

» Câu 14. Cho

 

90 180



    sin ;

. Giá trị của

tan

bằng

23

. B.

23

. C.

23

. D.

23

» Câu 15. Cho góc thỏa mãn

sin

và

90 180

. Tính

cos

cos =

. B.

cos

. C.

cos

. D.

cos

» Câu 16. Cho

sin

, với

90 180   

. Tính

cos

cos

. B.

cos

. C.

cos

. D.

cos

» Câu 17. Cho biết

cos

. Tính

tan

. B.



. C.

. D.



» Câu 18. Cho biết

tan

. Tính

cot

2cot

. B.

2cot

. C.

cot

. D.

cot

» Câu 19.

cos

bằng bao nhiêu nếu

cot



. B.

. C.



. D.



» Câu 20. Nếu

3tan

thì

cos

bằng bao nhiêu?



. B.

. C.



. D.

» Câu 21. Biết

cot a

0a

. Tính

cos





cos

. B.





cos

. C.





cos

. D.





cos

» Câu 22. Cho

cosx

. Tính biểu thức

34sin cosP x x

. B.

. C.

. D.

» Câu 23. Cho

sin ,

với

90 180   

. Tính giá trị của





sin cos

cos

M

175

M

. C.

M

. D.

M

» Câu 24. Cho biết

5cot

. Tính giá trị của

2 5 1  cos sin cosE

Trang 16

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04

. B.

100

. C.

. D.

101

» Câu 25. Cho biết

cos

. Giá trị của biểu thức







cot tan

bằng bao nhiêu?



. B.



. C.



. D.



» Câu 26. Cho

2tan

. Tính giá trị của biểu thức







sin cos

là



. B.

. C.

. D.



» Câu 27. Cho

cosx

. Tính biểu thức

34sin cosP x x

. B.

. C.

. D.

» Câu 28. Rút gọn biểu thức

21





cos

sin cos

sin cosaa

. B.

sin cosaa

. C.

cos sinaa

. D.

tan cosaa

» Câu 29. Giá trị của biểu thức

sin cosA x x

bằng

4 .cosa b x

. Giá trị của

2ab

là

. B.

. C.

. D.

» Câu 30. Biểu thức

 

cot tanaa

bằng



sin cos

. B.

2cot tanaa

. C.



sin cos

. D.

2cot tanaa

» Câu 31. Giá trị của biểu thức

1 2 3 88 89

    

 tan tan tan ...tan tanA

là

. B.

. C.

. D.

» Câu 32. Tổng

2 2 2 2 2 2

2 4 6 84 86 88

     

     sin sin sin ... sin sin sin

bằng

. B.

. C.

. D.

     

2 2 2 2 2 2

2 2 4 4 44 44 22

     

       sin cos sin cos ... sin cos

» Câu 33. Biểu thức:

 

4 2 2 2

  cos cos sin sinf x x x x x

có giá trị bằng

. B.

. C.

2

. D.

1

» Câu 34. Biểu thức

2 2 2 2

tan sin tan sinx x x x

có giá trị bằng

1

. B.

. C.

. D.

» Câu 35. Cho hai góc và với





. Tính giá trị của biểu thức

sin cos sin cosP

0 .P

1 .P

1 .P

2 .P

B. Câu hỏi – Trả lời Đúng/sai

» Câu 36. Cho

tan

. Khi đó:

Mệnh đề

Đúng

Sai

(a)

 

90 180



 ;

(b)

cos

Trang 17

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04

(c)

cot

(d)

sin

» Câu 37. Cho biết

90 180



   tan ,

. Khi đó:

Mệnh đề

Đúng

Sai

(a)

0cos

(b)

cos

(c)

cot

(d)

sin

» Câu 38. Cho

 

0 90



   cos

. Khi đó:

Mệnh đề

Đúng

Sai

(a)

sin

(b)

0sin

(c)

sin

(d)

cot

» Câu 39. Cho

 

0 90



  sin

. Khi đó:

Mệnh đề

Đúng

Sai

(a)

0cos

(b)

1cos sin

(c)

tan

(d)

cot

» Câu 40. Cho

 

0 90



  sin

. Khi đó:

Mệnh đề

Đúng

Sai

(a)

0cos

(b)

cos

(c)

cos

(d)







sin cos

Trang 18

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04

» Câu 41. Cho

sin

. Khi đó:

Mệnh đề

Đúng

Sai

(a)

cos

(b)

  sin cosA

(c)

   sin cosB

(d)

2 2 2 2

3 7 2    sin cos cos sinC

» Câu 42. Cho

 

2 0 180



   cot ,

. Khi đó:

Mệnh đề

Đúng

Sai

(a)

0sin

(b)

sin

(c)

cos

(d)

tan

C. Câu hỏi – Trả lời ngắn

» Câu 43. Cho

cosx

. Tính giá trị biểu thức

34sin cosP x x

 Điền đáp số:

» Câu 44. Cho

cot

. Tính giá trị của biểu thức







sin cos

 Điền đáp số:

» Câu 45. Biết

2sin cosaa

. Tính giá trị của

sin cosaa

 Điền đáp số:

» Câu 46. Cho

1tan

. Tính







sin

cos sin

 Điền đáp số:

» Câu 47. Cho

4cot

. Tính giá trị biểu thức





sin cos

sin

 Điền đáp số:

» Câu 48. Cho

cosx

. Tính giá trị biểu thức

34sin cosP x x

 Điền đáp số:

» Câu 49. Cho góc thỏa mãn

cos

. Tính giá trị của biểu thức

3





tan cot

Trang 19

» TOÁN TỪ TÂM – 0901.837.432

HỆ THỨC LƯỢNG TRONG TAM GIÁC

Chương 04

 Điền đáp số:

» Câu 50. Cho biết

sin cos a

. Tính giá trị của

sin cos

ta thu được kết quả

am

với

;mn

là các số tự nhiên. Tính

mn

 Điền đáp số:

» Câu 51. Cho

sin cosxx

. Tính

sin cosP x x

 Điền đáp số:

» Câu 52. Giá trị của biểu thức:

60 2 30 3 45

  





sin cos sin

với

;ab

là các số nguyên

dương. Khi đó giá trị

S a b

bằng bao nhiêu?

 Điền đáp số:

» Câu 53. Cho các góc

thoả mãn

0 180



,

và





. Tính giá trị của biểu thức

6 6 2 2

3  sin sin sin sinT

 Điền đáp số:

» Câu 54. Tính giá trị biểu thức sau:

1 2 3 180

   

   cos cos cos cosD

 Điền đáp số:

» Câu 55. Cho

cot

. Tính giá trị của biểu thức







sin cos

 Điền đáp số:

----------------------------------- Hết -----------------------------------

Bấm Tải xuống để xem toàn bộ.

| 1/42

| | Tải xuống

Preview text:

ttt TOÁN TỪ TÂM HỆ THỨC LƯỢNG trong tam giác TÁC GIẢ Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC MỤC LỤC
Bài 1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0° ĐẾN 180° A. Lý thuyết
1. Giá trị lượng giác của một góc ..............................................................................................................2
2. Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau ...................................................... 3
3. Mối quan hệ giữa các giá trị lượng giác của hai góc phụ nhau ................................................... 3
4. Giá trị lượng giác của các góc đặc biệt ............................................................................................. 3
7. Các hệ thức lượng giác cơ bản .............................................................................................................. 3
B. Các dạng bài tập
 Dạng 1. Tính giá trị biểu thức lượng giác .............................................................................................. 4
 Dạng 2. Tính giá trị biểu thức lượng giác khi biết một giá trị lượng giác ......................................... 7
 Dạng 3. Chứng minh/rút gọn đẳng thức/biểu thức lượng giác ........................................................ 11 C. Luyện tập
A. Câu hỏi – Trả lời trắc nghiệm ..................................................................................................................... 14
B. Câu hỏi – Trả lời Đúng/sai ......................................................................................................................... 16
C. Câu hỏi – Trả lời ngắn ................................................................................................................................ 18
Bài 2. ĐỊNH LÝ SIN - COS, GIẢI TAM GIÁC & THỰC TẾ A. Lý thuyết
1. Định lý hàm cos ....................................................................................................................................... 20
2. Định lý hàm sin ....................................................................................................................................... 20
3. Đường trung tuyến ................................................................................................................................. 21
4. Diện tích tam giác .................................................................................................................................. 21
5. Giải tam giác ............................................................................................................................................ 21
B. Các dạng bài tập
 Dạng 1. Giải tam giác .............................................................................................................................. 22
 Dạng 2. Chứng minh hệ thức trong tam giác ...................................................................................... 25
 Dạng 3. Ứng dụng thực tế ...................................................................................................................... 29 C. Luyện tập
A. Câu hỏi – Trả lời trắc nghiệm ..................................................................................................................... 32
B. Câu hỏi – Trả lời Đúng/sai ......................................................................................................................... 36
C. Câu hỏi – Trả lời ngắn ................................................................................................................................ 37
» TOÁN TỪ T ÂM – 0901.837.432 Trang 1 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC Chương 04
GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0° ĐẾN 180° Bài 1. Lý thuyết
1. Giá trị lượng giác của một góc Định nghĩa » Trong mặt phẳng , nửa đường tròn tâm
nằm phía trên trục hoành bán kính
được gọi là nửa đường tròn đơn vị. » Với mỗi góc
ta xác định một điểm trên nửa đường tròn đơn vị sao cho và giả sử điểm có tọa độ . Khi đó: ⓵ . ⓶ . ⓷ . ⓸ . » Các số
được gọi là các giá trị lượng giác của góc . Chú ý Với ta có Góc + + + - + - + -
» TOÁN TỪ T ÂM – 0901.837.432 Trang 2 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC
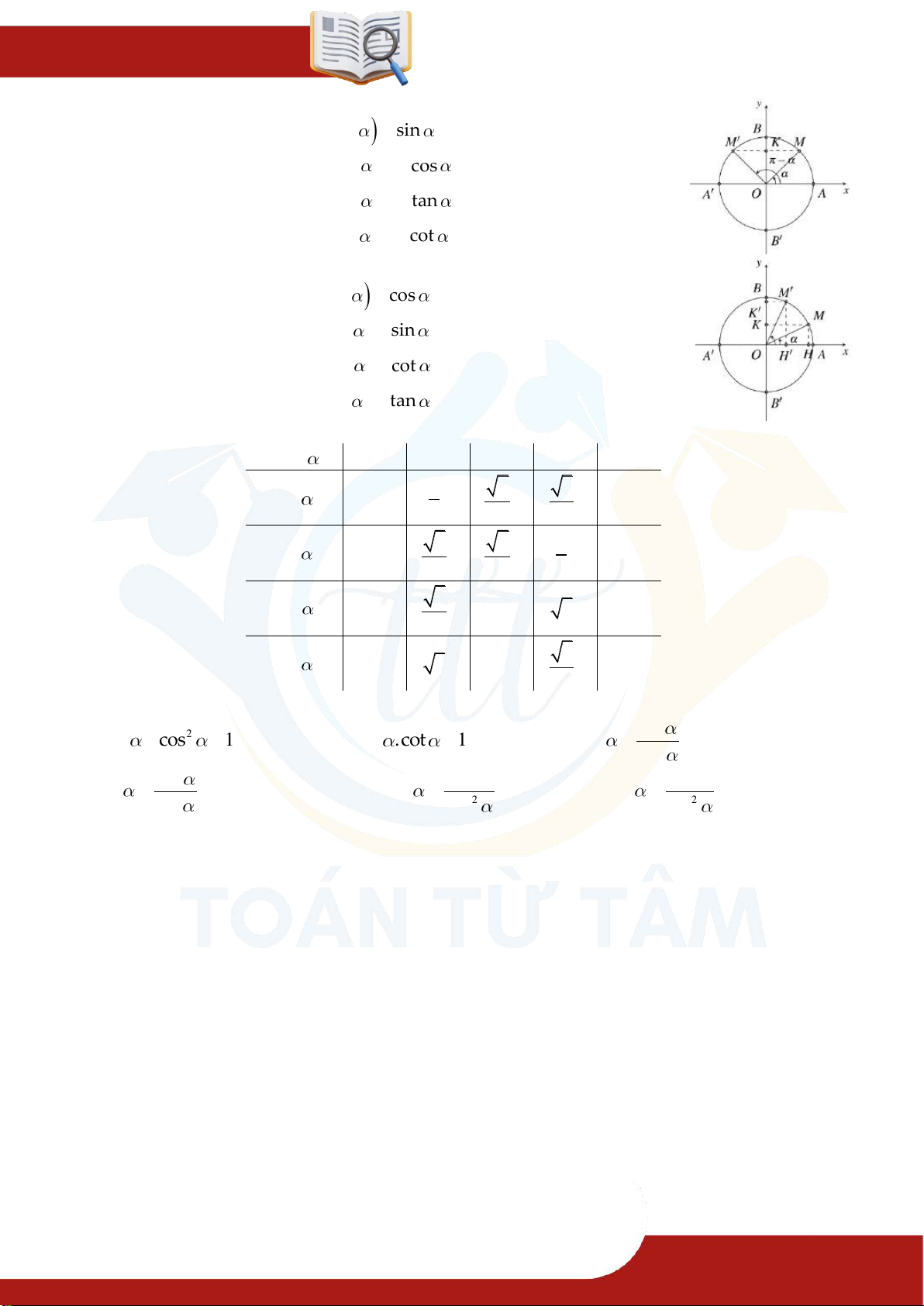
2. Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau sin 180o    sin
cos 180o     cos Sin – bù
tan 180o     tan
cot 180o     cot
3. Mối quan hệ giữa các giá trị lượng giác của hai góc phụ nhau sin 90o    cos cos 90o    sin Phụ – chéo tan 90o    cot cot 90o    tan
4. Giá trị lượng giác của các góc đặc biệt Góc 00 300 450 600 900 1 sin 2 3 0 1 2 2 2 3 2 1 cos 1 0 2 2 2 3 tan 0 1 3  3 3 cot  3 1 0 3
7. Các hệ thức lượng giác cơ bản ⑴ sin 2 2 sin  cos 1
⑵ tan .cot 1 ⑶ tan  cos ⑷ cos 1 1 cot  ⑸ 2 1 tan  ⑹ 2 1 cot  sin 2 cos 2 sin
» TOÁN TỪ T ÂM – 0901.837.432 Trang 3 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC Các dạng bài tập
 Dạng 1. Tính giá trị biểu thức lượng giác Phương pháp ⑴ ⑵ ⑶ ⑷ ⑸ ⑹
Có thể sử dụng thêm: Sin – bù;Phụ - chéo Ví dụ 1.1.
Tính giá trị các biểu thức sau: ⑴ ⑵ ⑶
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 4 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC Ví dụ 1.2.
Tính giá trị các biểu thức sau: ⑴ ⑵ ⑶
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................ Ví dụ 1.3.
Thực hiện các yêu cầu sau: ⑴ Cho . Tính ⑵ Cho . Tính
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 5 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 6 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC
 Dạng 2. Tính giá trị biểu thức lượng giác khi biết một giá trị lượng giác Phương pháp ⑴ ⑵ ⑶ ⑷ ⑸ ⑹
Cần đánh giá được dấu của và/hoặc . Ví dụ 2.1.
Thực hiện các yêu cầu sau: ⑴ Cho với . Tính và ⑵ Cho và . Tính và ⑶ Cho
tính giá trị lượng giác còn lại.
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 7 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC
........................................................................................................................................................ Ví dụ 2.2. Biết ⑴ và . Tính giá trị của và . ⑵ và . Tính ⑶ và . Tính và . ⑷
tính giá trị của biểu thức
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 8 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................ Ví dụ 2.3. Cho biểu thức .
⑴ Với góc bằng bao nhiêu thì không xác định.
⑵ Tìm giá trị của biết .
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................ Ví dụ 2.4. Cho biểu thức .
⑴ Với góc bằng bao nhiêu thì không xác định.
⑵ Tìm giá trị của biết .
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 9 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................ Ví dụ 2.5. Biết ⑴ Tìm
⑵ Chứng minh rằng .
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 10 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC
 Dạng 3. Chứng minh/rút gọn đẳng thức/biểu thức lượng giác Phương pháp ⑴ ⑵ ⑶ ⑷ ⑸ ⑹
Sử dụng thêm tính chất. Ví dụ 3.1.
Chứng minh các đẳng thức sau(giả sử các biểu thức sau đều có nghĩa) ⑴ ⑵ ⑶
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 11 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC Ví dụ 3.2. Rút gọn biểu thức ⑴ ⑵ ⑶ ⑷ ⑸ ⑹
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 12 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC Ví dụ 3.3.
Đơn giản các biểu thức sau(giả sử các biểu thức sau đều có nghĩa) ⑴ ⑵ với
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................ Ví dụ 3.4.
Chứng minh biểu thức sau không phụ thuộc vào .
 Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 13 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC Luyện tập
A. Câu hỏi – Trả lời trắc nghiệm
» Câu 1. Khẳng định nào sau đây đúng? A. sin90 sin100  . B. cos95 cos100  . C. tan85 tan125  . D. cos145 cos125  .
» Câu 2. Khẳng định nào sau đây đúng? A. sin90 sin150  . B. sin90 1  5  sin90 3   0. C. cos9030 cos100   . D. cos150 cos120  .
» Câu 3. Cho biết 3cos  sin 1, 0 0 0 
 90 . Giá trị của tan bằng 4 3 4 5 A. tan  . B. tan  . C. tan  . D. tan  . 3 4 5 4
» Câu 4. Cho góc 90;180. Khẳng định nào sau đây đúng?
A. sin và cot cùng dấu.
B. Tích sin .cot mang dấu âm.
C. Tích sin .cos mang dấu dương.
D. sin và tan cùng dấu.
» Câu 5. Cho là góc tù. Mệnh đề nào đúng trong các mệnh đề sau? A. tan  0. B. cot  0. C. sin  0. D. cos  0. » Câu 6. Cho 0º 
 90º . Khẳng định nào sau đây đúng?
A. cot 90º    tan .
B. cos90º    sin .
C. sin90º    cos .
D. tan90º    cot .
» Câu 7. Trong các đẳng thức sau đây, đẳng thức nào đúng?
A. sin 180     sin .
B. cos 180    cos
C. tan 180    tan .
D. cot 180     cot
» Câu 8. Cho và là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai? A. sin  sin . B. cos   cos . C. tan   tan .
D. cot  cot .
» Câu 9. Cho hai góc nhọn và (
 ) . Khẳng định nào sau đây là sai? A. cos  cos . B. sin  sin .
C. tan  tan  0 . D. cot  cot . » Câu 10. Cho
ABC vuông tại A , góc B bằng 30 . Khẳng định nào sau đây là sai? 1 3 1 1 A. cos B  . B. sin C  . C. cosC  . D. sin B  3 2 2 2 2 » Câu 11. Biết cos
 0   90 . Khi đó tan bằng 3 5 5 2 2 A. . B.  . C. . D.  . 2 2 5 5 1
» Câu 12. Cho sin x 
và 90o  180o x thì 3 2 2 2 2 2 2 A. cos  . B. cos   . C. cos  . D. cos   . 3 3 3 3
» TOÁN TỪ T ÂM – 0901.837.432 Trang 14 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC 3 » Câu 13. Cho 0 0 90 
180 và thỏa mãn sin  . Giá trị của cos bằng. 5 4 4 2 1 A.  . B. . C. . D. . 5 5 5 5 6  2 » Câu 14. Cho sin 
; 90  180 . Giá trị của tan bằng 4 A. 2  3 . B. 2  3 . C. 2  3 . D. 2  3 . 12
» Câu 15. Cho góc thỏa mãn sin  và 90  180 . Tính cos . 13 1 5 1 5 A. cos = . B. cos   . C. cos   . D. cos  . 13 13 13 13 1 » Câu 16. Cho sin
 , với 90  180 . Tính cos . 3 2 2 2 2 2 2 A. cos  .
B. cos   . C. cos  . D. cos   . 3 3 3 3 2
» Câu 17. Cho biết cos   . Tính tan ? 3 5 5 5 5 A. . B.  . C. . D.  . 4 2 2 2 1
» Câu 18. Cho biết tan  . Tính cot . 2 1 1 A. cot  2 . B. cot  2 . C. cot  . D. cot  . 4 2 1 » Câu 19. cos
bằng bao nhiêu nếu cot   ? 2 5 5 5 1 A.  . B. . C.  . D.  . 5 2 5 3
» Câu 20. Nếu tan  3 thì cos bằng bao nhiêu? 10 1 10 10 A.  . B. . C.  . D. . 10 3 10 10 » Câu 21. Biết cot
 a , a  0. Tính cos a 1 1 a A. cos  . B. cos  . C. cos   . D. cos   . 2 1 a 2 1 a 2 1 a 2 1 a 1
» Câu 22. Cho cos x  . Tính biểu thức 2 2
P  3sin x  4cos x 2 13 7 11 15 A. . B. . C. . D. . 4 4 4 4 4  » Câu 23. Cho sin
 , với 90  180 . Tính giá trị của M  sin cos 5 3 cos 25 175 35 25 A. M  B. M  . C. M  . D. M   . 27 27 27 27
» Câu 24. Cho biết cot  5. Tính giá trị của 2 E  2cos 5sin cos 1?
» TOÁN TỪ T ÂM – 0901.837.432 Trang 15 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC 10 100 50 101 A. . B. . C. . D. . 26 26 26 26 2 cot  3tan
» Câu 25. Cho biết cos
  . Giá trị của biểu thức E  bằng bao nhiêu? 3 2 cot  tan 25 11 11 25 A.  . B.  . C.  . D.  . 3 13 3 13 3sin  2cos
» Câu 26. Cho tan  2 . Tính giá trị của biểu thức A  là 2 sin  cos 2 4 3 3 A.  . B. . C. . D.  . 5 5 2 2 1
» Câu 27. Cho cos x  . Tính biểu thức 2 2
P  3sin x  4cos x . 2 13 7 11 15 A. . B. . C. . D. . 4 4 4 4 2 2 cos a 1
» Câu 28. Rút gọn biểu thức A  sin a  cos a
A. sina  cosa .
B. sina cosa .
C. cosa sina .
D. tan a  cos a .
» Câu 29. Giá trị của biểu thức 6 6
A  sin x  cos x bằng a  .
b cos4x . Giá trị của a  2b là 9 11 13 15 A. . B. . C. . D. . 8 8 8 8
» Câu 30. Biểu thức cot a tan a2  bằng 1 1 1 1 A.  . B. 2 2
cot a  tan a2 . C.  . D. 2 2
cot a tan a  2. 2 2 sin cos 2 2 sin cos     
» Câu 31. Giá trị của biểu thức A  tan1 tan 2 tan3 ...tan88 tan89 là A. 0 . B. 2 . C. 3 . D. 1.       » Câu 32. Tổng 2 2 2 2 2 2
sin 2  sin 4  sin 6  ...  sin 84  sin 86  sin 88 bằng A. 21. B. 23. C. 22 . D. 24 .  2  2  sin cos   2  2  sin cos  ...  2  2 2 2 4 4 sin 44 cos 44          22 .
» Câu 33. Biểu thức: f x 4 2 2 2
 cos x  cos xsin x  sin x có giá trị bằng A. 1. B. 2 . C. 2  . D. 1.
» Câu 34. Biểu thức 2 2 2 2
tan xsin x  tan x  sin x có giá trị bằng A. 1. B. 0 . C. 2 . D. 1.
» Câu 35. Cho hai góc và với 90  
. Tính giá trị của biểu thức P  sin cos  sin cos A. P  0. B. P 1. C. P  1  . D. P  2.
B. Câu hỏi – Trả lời Đúng/sai 5 » Câu 36. Cho tan   . Khi đó: 12 Mệnh đề Đúng Sai   (a) 90 ;180  12 (b) cos  13
» TOÁN TỪ T ÂM – 0901.837.432 Trang 16 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC 12 (c) cot  5 5 (d) sin  13 3  
» Câu 37. Cho biết tan
  ,90  180 . Khi đó: 4 Mệnh đề Đúng Sai (a) cos  0 4
(b) cos   5 4
(c) cot   3 3
(d) sin   5 3   » Câu 38. Cho cos
  0   90 . Khi đó: 4 Mệnh đề Đúng Sai 7 (a) 2 sin  16 (b) sin  0 7 (c) sin   4 3 7 (d) cot   7 12   » Câu 39. Cho sin 
0  90 . Khi đó: 13 Mệnh đề Đúng Sai (a) cos  0 (b) 2 cos  1 sin 12 (c) tan   5 5 (d) cot   12 2   » Câu 40. Cho sin
 0   90 . Khi đó: 3 Mệnh đề Đúng Sai (a) cos  0 5 (b) 2 cos  9 5 (c) cos   3 sin  5 cos 7 (d)  2 sin  cos 4  5
» TOÁN TỪ T ÂM – 0901.837.432 Trang 17 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC 1 » Câu 41. Cho sin  . Khi đó: 3 Mệnh đề Đúng Sai 8 (a) 2 cos  9 35 (b) 2 2 A  sin  3cos  9 1 (c) 2 2 B  5sin  cos   3 (d) 2 2 2 2 C  sin  3cos  cos  7sin  2   » Câu 42. Cho cot
  2,0  180 . Khi đó: Mệnh đề Đúng Sai (a) sin  0 1 (b) sin   3 6 (c) cos   3 1 (d) tan  2
C. Câu hỏi – Trả lời ngắn 1
» Câu 43. Cho cos x 
. Tính giá trị biểu thức 2 2
P  3sin x  4cos x ? 2
 Điền đáp số: 1 3sin  4cos » Câu 44. Cho cot
 . Tính giá trị của biểu thức A  ? 3 2 sin  5cos
 Điền đáp số:
» Câu 45. Biết sin a  cos a  2 . Tính giá trị của 4 4
sin a  cos a ?
 Điền đáp số: 2 sin 1
» Câu 46. Cho tan 1. Tính B  . 2 2 2 cos  sin
 Điền đáp số:  » Câu 47. Cho cot
 4. Tính giá trị biểu thức P  sin cos . sin
 Điền đáp số: 1
» Câu 48. Cho cos x 
. Tính giá trị biểu thức 2 2
P  3sin x  4cos x . 2
 Điền đáp số: 2 tan  3cot
» Câu 49. Cho góc thỏa mãn cos 
. Tính giá trị của biểu thức A  . 4 tan  cot
» TOÁN TỪ T ÂM – 0901.837.432 Trang 18 .. Ch ương 04
HỆ THỨC LƯỢNG TRONG TAM GIÁC
 Điền đáp số: 2 a  m
» Câu 50. Cho biết sin  cos  a . Tính giá trị của sin cos ta thu được kết quả với ; m n n
là các số tự nhiên. Tính m  n
 Điền đáp số: 1
» Câu 51. Cho sin x  cos x 
. Tính P  sin x  cos x . 5
 Điền đáp số:    a  3 b
» Câu 52. Giá trị của biểu thức: A  sin 60  2 cos 30  3sin 45 
với a; b là các số nguyên 2 dương. Khi đó giá trị 2
S  a  b bằng bao nhiêu?
 Điền đáp số:
» Câu 53. Cho các góc , thoả mãn 0 , 180   và 90  
. Tính giá trị của biểu thức 6 6 2 2 T  sin  sin 3sin sin .
 Điền đáp số:    
» Câu 54. Tính giá trị biểu thức sau: D  cos1  cos 2  cos3  cos180 .
 Điền đáp số: 1 3sin  4cos » Câu 55. Cho cot
 . Tính giá trị của biểu thức A  ? 3 2 sin  5cos
 Điền đáp số:
----------------------------------- Hết -----------------------------------
» TOÁN TỪ T ÂM – 0901.837.432 Trang 19 ..

Chuyên đề hệ thức lượng trong tam giác Toán 10

Thông tin :

Tài liệu liên quan:

Chuyên đề một số phương pháp đếm trong các bài toán tổ hợp

Các dạng toán vectơ Toán 10 thường gặp

Các dạng toán mệnh đề và tập hợp Toán 10 thường gặp

Đề cương giữa học kỳ 1 Toán 10 năm 2024 – 2025 trường THPT Hoàng Văn Thụ – Hà Nội

Đề cương giữa học kỳ 1 Toán 10 năm 2024 – 2025 trường THPT Xuân Đỉnh – Hà Nội