










































































Preview text:
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC G
ƠN IV HỆ THỨC LƯỢNG HƯ TRONG TAM GIÁC C
BÀI 1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0 ĐẾN 180. I LÝ THUYẾT.
1. ĐỊNH NGHĨA GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC.
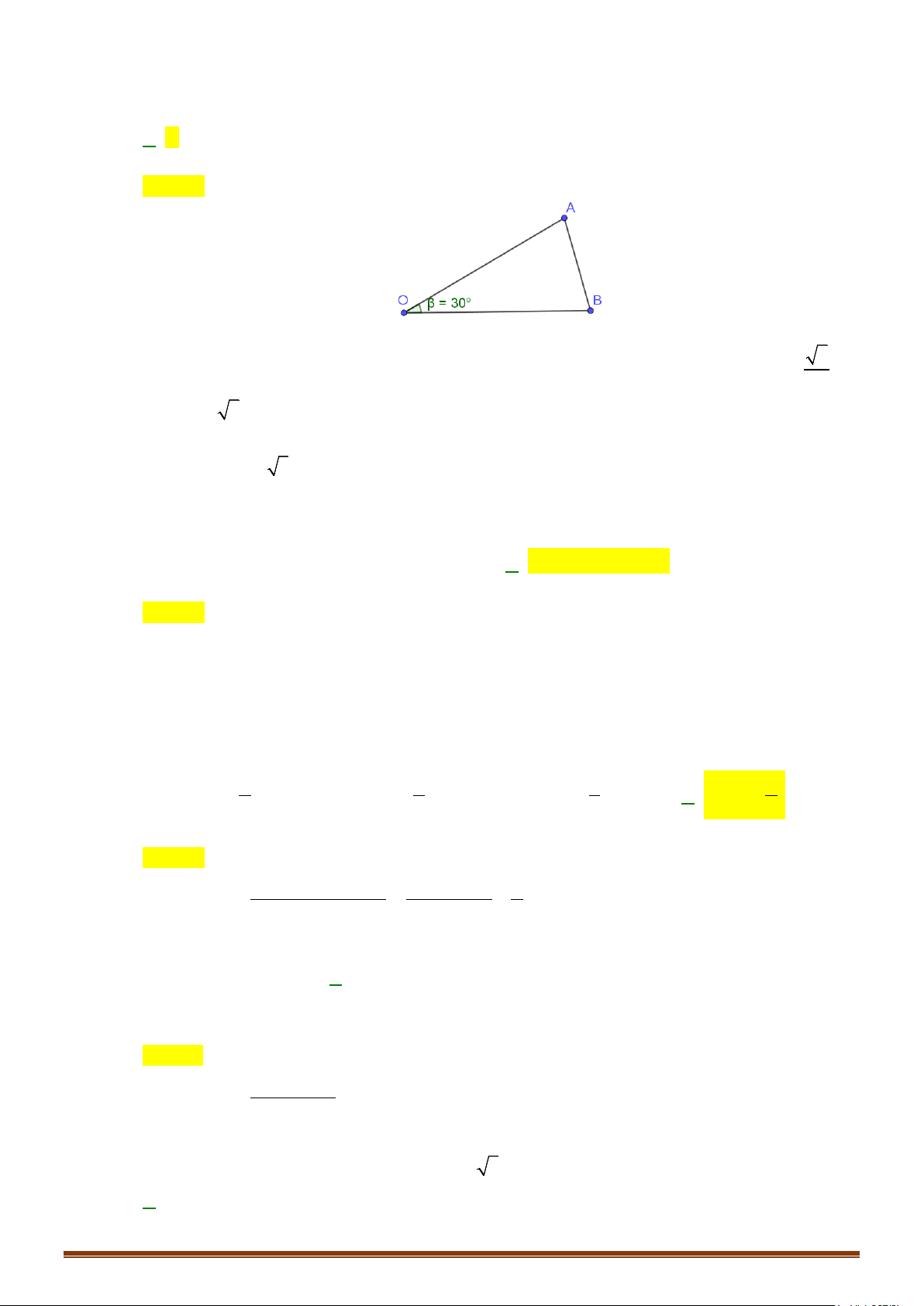
Trong mặt phẳng tọa độ Oxy .Với góc α ( o o
0 ≤ α ≤180 ) , ta xác định được duy nhất điểm M
trên trên đường nửa đường tròn đơn vị tâm O , sao cho α =
xOM , biết M ( ; x y). Khi đó: y o x o o sinα = y; cosα = ; x
tanα = (α ≠ 90 ); cotα = (α ≠ 0 ,180 ) x y
Các số sinα,cosα,tanα,cot β được gọi là giá trị lượng giác của góc α . y M ( x;y ) Q O P x Hình 2.1 Chú ý: Với o o
0 ≤ α ≤180 ta có 0 ≤ sinα ≤ 1; −1 ≤ cosα ≤ 1 Góc 0o o o 90 180 sin + + cos + - tan + - cot + - Page 73
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
2. MỐI QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU o
sin(180 ) sin o
cos(180 ) cos o
tan(180 ) tan o
cot(180 ) cot
3. MỐI QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC PHỤ NHAU (BỔ SUNG) o
sin(90 ) cos o
cos(90 ) sin o
tan(90 ) cot o
cot(90 ) tan
4. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC GÓC ĐẶC BIỆT
Góc 00 300 450 600 900 sin 0 1 2 2 3 1 2 2 cos 1 3 1 2 0 2 2 2 tan 0 3 1 3 | 3 cot | 3 1 3 0 3
5. CÁC HỆ THỨC LƯỢNG GIÁC CƠ BẢN (BỔ SUNG – KẾT QUẢ CỦA BÀI TẬP 5 SGK) sinα tanα = (α ≠ 90o) ; cosα cosα cotα = (α ≠ 0o; 180o) sinα
tanα.cotα =1 (α ≠ 0o; 90o; 180o) 2 2 sin α + cos α =1 2 1 1+ tan α = (α ≠ 90o) 2 cos α 2 1 1+ cot α = (α ≠ 0o; 180o) 2 sin α Page 74
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
II HỆ THỐNG BÀI TẬP.
DẠNG 1: TÍNH CÁC GIÁ TRỊ BIỂU THỨC LƯỢNG GIÁC 1 PHƯƠNG PHÁP. · S
ử dụng định nghĩa giá trị lượng giác của một góc
· Sử dụng tính chất và bảng giá trị lượng giác đặc biệt
· Sử dụng các hệ thức lượng giác cơ bản 2
BÀI TẬP TỰ LUẬN.
Câu 1. Tính giá trị các biểu thức sau: a) 2 o 2 o 2 o
A = a sin 90 + b cos90 + c cos180 b) 2 o 2 o 2 o
B = 3− sin 90 + 2cos 60 − 3tan 45 c) 2 0 2 o 2 o 2 o o o
C = sin 45 − 2sin 50 + 3cos 45 − 2sin 40 + 4 tan 55 .tan 35
Câu 2. Tính giá trị các biểu thức sau: a) 2 o 2 o 2 o 2 o
A = sin 3 + sin 15 + sin 75 + sin 87 b) o o o o o
B = cos0 + cos 20 + cos 40 +...+ cos160 + cos180 c) o o o o o
C = tan 5 tan10 tan15 ...tan80 tan85 3
BÀI TẬP TRẮC NGHIỆM.
Câu 1: G iá trị của o o
cos60 + sin 30 bằng bao nhiêu? A. 3 B. 3 C. 3 D. 1. 2 3
Câu 2: Giá trị của o o
tan 30 + cot 30 bằng bao nhiêu? + A. 4 B. 1 3 C. 2 D. 2 3 3 3
Câu 3: Trong các đẳng thức sau đây, đẳng thức nào sai? A. o o sin 0 + cos0 =1 B. o o sin 90 + cos90 =1 C. o o sin180 + cos180 = 1 − D. o o sin 60 + cos60 =1
Câu 4: Trong các khẳng định sau, khẳng định nào sai? A. o o cos60 = sin 30 . B. o o cos60 = sin120 . C. o o cos30 = sin120 . D. o o sin 60 = −cos120 .
Câu 5: Đẳng thức nào sau đây sai? A. o o sin 45 + sin 45 = 2 . B. o o sin 30 + cos60 =1. C. o o sin 60 + cos150 = 0 . D. o o sin120 + cos30 = 0 . Câu 6: Giá trị o o
cos 45 + sin 45 bằng bao nhiêu? A. 1. B. 2 . C. 3 . D. 0 .
Câu 7: Trong các đẳng thức sau, đẳng thức nào đúng? A. ( o sin 180 −α ) = −cosα . B. ( o sin 180 −α ) = −sinα . C. ( o sin 180 −α ) = sinα . D. ( o sin 180 −α ) = cosα .
Câu 8: Trong các đẳng thức sau, đẳng thức nào sai? Page 75
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. o o sin 0 + cos0 = 0. B. o o sin 90 + cos90 =1. C. o o sin180 + cos180 = 1 − . D. o o 3 +1 sin 60 + cos60 = . 2
Câu 9: Cho α là góc tù. Điều khẳng định nào sau đây là đúng? A. sinα < 0 . B. cosα > 0 . C. tanα < 0. D. cotα > 0 .
Câu 10: Giá trị của o o o o
E = sin 36 cos6 sin126 cos84 là A. 1 . B. 3 . C. 1. D. 1 − . 2 2
Câu 11: Giá trị của biểu thức 2 o 2 o 2 o 2 o
A = sin 51 + sin 55 + sin 39 + sin 35 là A. 3. B. 4 . C. 1. D. 2 .
Câu 12: Giá trị của biểu thức o o o o o
A = tan1 tan 2 tan 3 . .tan88 tan89 là A. 0 . B. 2 . C. 3. D. 1. Câu 13: Tổng 2 o 2 o 2 o 2 o 2 o 2 o
sin 2 + sin 4 + sin 6 +. .+ sin 84 + sin 86 + sin 88 bằng A. 21. B. 23. C. 22 . D. 24 .
Câu 14: Giá trị của o o o o o
A = tan 5 .tan10 .tan15 ...tan80 .tan85 là A. 2 . B. 1. C. 0 . D. 1 − .
Câu 15: Giá trị của 2 ° 2 ° 2 ° 2 B cos 73 cos 87 cos 3 cos 17° = + + + là A. 2 . B. 2 . C. 2 − . D. 1.
DẠNG 2: TÍNH GIÁ TRỊ CỦA MỘT BIỂU THỨC LƯỢNG GIÁC , KHI BIẾT TRƯỚC MỘT GIÁ
TRỊ LƯỢNG GIÁC. 1 PHƯƠNG PHÁP. · D
ựa vào các hệ thức lượng giác cơ bản
· Dựa vào dấu của giá trị lượng giác
· Sử dụng các hằng đẳng thức đáng nhớ 2
BÀI TẬP TỰ LUẬN. Câu 1. Cho 1 sinα = với 0 0
90 < α < 180 . Tính cosα và tanα 3 Câu 2. Cho 2
cosα = − và sinα > 0 . Tính sinα và cotα 3 Câu 3. Cho tan γ = 2 −
2 tính giá trị lượng giác còn lại. α + α Câu 4. Cho 3 cosα = với 0 0 0 < α < 90 . Tính tan 3cot A = . 4 tanα + cotα α − α
Câu 5. Cho tanα = 2 . Tính sin cos B = 3 3 sin α + 3cos α + 2sinα
Câu 6. Biết sin x + cos x = m a) Tìm 4 4
sin x − cos x .
b) Chứng minh rằng m ≤ 2 . 3
BÀI TẬP TRẮC NGHIỆM. Page 76
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Câu 1: Cho 1
cos x = . Tính biểu thức 2 2
P = 3sin x + 4 cos x 2 A. 13 . B. 7 . C. 11. D. 15 . 4 4 4 4 Câu 2: Biết 1
cosα = . Giá trị đúng của biểu thức 2 2
P = sin α + 3cos α là: 3 A. 1 . B. 10 . C. 11. D. 4 . 3 9 9 3 Câu 3: Cho biết 1 tanα = . Tính cotα . 2 A. cotα = 2. B. cotα = 2 . C. 1 cotα = . D. 1 cotα = . 4 2 2 cosα π = − 0 < α < Câu 4: Cho biết 3 và 2 . Tính tanα ? A. 5 . B. 5 − . C. 5 . D. 5 − . 4 2 2 2
Câu 5: Cho α là góc tù và 5 sinα =
. Giá trị của biểu thức 3sinα + 2cosα là 13 A. 3. B. 9 − . C. 3 − . D. 9 . 13 13
Câu 6: Cho biết sinα + cosα = a . Giá trị của sinα.cosα bằng bao nhiêu? A. 2 sinα.cosα = a .
B. sinα.cosα = 2a . 2 2 C. 1 sin .cos a α α − = . D. a 1 sinα.cosα − = . 2 2 α + α Câu 7: Cho biết 2
cosα = − . Tính giá trị của biểu thức cot 3tan E = ? 3 2cotα + tanα A. 19 − . B. 19 . C. 25 . D. 25 − 13 13 13 13
Câu 8: Cho biết cotα = 5 . Tính giá trị của 2
E = 2cos α + 5sinα cosα +1? A. 10 . B. 100 . C. 50 . D. 101. 26 26 26 26 α + α Câu 9: Cho 1
cotα = . Giá trị của biểu thức 3sin 4cos A = là: 3 2sinα − 5cosα A. 15 − . B. 13 − . C. 15 . D. 13. 13 13 α − α Câu 10: Cho biết 2
cosα = − . Giá trị của biểu thức cot 3tan E = bằng bao nhiêu? 3 2cotα − tanα A. 25 − . B. 11 − . C. 11 − . D. 25 − . 3 13 3 13
Câu 11: Biết sin a + cos a = 2 . Hỏi giá trị của 4 4
sin a + cos a bằng bao nhiêu? A. 3 . B. 1 . C. 1 − . D. 0 . 2 2
Câu 12: Cho tanα + cotα = m . Tìm m để 2 2 tan α + cot α = 7 . Page 77
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. m = 9 . B. m = 3 . C. m = 3 − . D. m = 3 ± .
Câu 13: Cho biết 3cosα − sinα =1, o o
0 < α < 90 Giá trị của tanα bằng A. 4 tanα = B. 3 tanα = C. 4 tanα = D. 5 tanα = 3 4 5 4
Câu 14: Cho biết 2cosα + 2 sinα = 2 , 0 0
0 < α < 90 . Tính giá trị của cotα. A. 5 cotα = B. 3 cotα = C. 2 cotα = D. 2 cotα = 4 4 4 2 Câu 15: Cho biết 1
cosα + sinα = . Giá trị của 2 2
P = tan α + cot α bằng bao nhiêu? 3 A. 5 P = . B. 7 P = . C. 9 P = . D. 11 P = . 4 4 4 4 Câu 16: Cho biết 1 sinα − cosα = . Giá trị của 4 4
P = sin α + cos α bằng bao nhiêu? 5 A. 15 P = B. 17 P = C. 19 P = D. 21 P = 5 5 5 5
DẠNG 3: CHỨNG MINH CÁC ĐẲNG THỨC, RÚT GỌN CÁC BIỂU THỨC LƯỢNG GIÁC 1 PHƯƠNG PHÁP. · S
ử dụng các hệ thức lượng giác cơ bản
· Sử dụng tính chất của giá trị lượng giác
· Sử dụng các hằng đẳng thức đáng nhớ . 2
BÀI TẬP TỰ LUẬN. Câu 1. Chứng
minh các đẳng thức sau(giả sử các biểu thức sau đều có nghĩa) a) 4 4 2 2
sin x + cos x = 1− 2sin . x cos x + +
b) 1 cot x tan x 1 =
1− cot x tan x −1 + c) cos x sin x 3 2
= tan x + tan x + tan x +1 3 cos x 3 B 3 sin cos B cos( A + C)
Câu 2. Cho tam giác ABC . Chứng minh 2 2 + − .tan B = 2 A + C A + C sin cos sin B 2 2
Câu 3. Đơn giản các biểu thức sau(giả sử các biểu thức sau đều có nghĩa) a) o o 2 2 2
A = sin(90 − x) + cos(180 − x) + sin x(1+ tan x) − tan x b) 1 1 1 B = . + − 2
sin x 1+ cos x 1− cos x
Câu 4. Chứng minh biểu thức sau không phụ thuộc vào x . 4 2 4 4 2 4
P = sin x + 6cos x + 3cos x + cos x + 6sin x + 3sin x 3
BÀI TẬP TRẮC NGHIỆM.
Câu 1: Tr ong các hệ thức sau hệ thức nào đúng? Page 78
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC α A. 2 2 sin α + cosα = 1. B. 2 2 sin α + cos = 1. 2 C. 2 2 sinα + cosα = 1. D. 2 2 sin 2α + cos 2α = 1.
Câu 2: Trong các hệ thức sau hệ thức nào đúng? α A. 2 2 sin α + cosα = 1. B. 2 2 sin α + cos = 1. C. 2 2 sinα + cosα = 1. D. 2 2 sin α + cos α = 1. 2
Câu 3: Trong các hệ thức sau hệ thức nào đúng?
A. sin 2α + cos 2α = 1. B. 2 2 sinα + cosα = 1. C. 2 2 sin α + cosα = 1. D. 2 2 sin α + cos α = 1.
Câu 4: Rút gọn biểu thức sau A = ( x + x)2 − ( x − x)2 tan cot tan cot A. A = 4 . B. A =1. C. A = 2 . D. A = 3
Câu 5: Đơn giản biểu thức G = ( 2 − x) 2 2 1 sin
cot x +1− cot x . A. 2 sin x . B. 2 cos x . C. 1 . D. cos x . cos x
Câu 6: Khẳng định nào sau đây là sai? A. 2 2 1 sin α + cos α =1. B. 2 1+ cot α = sinα ≠ 0 . 2 ( ) sin α C. tanα.cotα = 1 − (sinα.cosα ≠ 0) . D. 2 1 1+ tan α = cosα ≠ 0 . 2 ( ) cos α 2
Câu 7: Rút gọn biểu thức 1− sin x P = ta được 2sin .xcos x A. 1 P = tan x . B. 1 P = cot x .
C. P = 2cot x .
D. P = 2 tan x . 2 2
Câu 8: Đẳng thức nào sau đây là sai? A. ( x + x)2 + ( x − x)2 cos sin cos sin = 2, x ∀ . B. 2 2 2 2
tan x sin x tan x sin x, x 90° − = ∀ ≠ C. 4 4 2 2
sin x + cos x = 1− 2sin x cos x, x ∀ . D. 6 6 2 2
sin x − cos x = 1− 3sin x cos x, x ∀
Câu 9: Đẳng thức nào sau đây là sai? A. 1− cos x sin x =
(x ≠ 0°,x ≠180°). sin x 1+ cos x B. 1 tan x cot x (x 0°,90°,180° + = ≠ ) sin x cos x C. 2 2 1 tan x cot x 2 x 0°,90°,180° + = − ≠ 2 2 ( ) sin x cos x D. 2 2
sin 2x + cos 2x = 2 . Câu 10: Biểu thức 2 2 2 2
tan xsin x − tan x + sin x có giá trị bằng A. 1 − . B. 0 . C. 2 . D. 1.
Câu 11: Biểu thức ( a + a)2 cot tan bằng A. 1 1 − . B. 2 2 1 1
cot a + tan a2 . C. + . D. 2 2
cot a tan a + 2 . 2 2 sin α cos α 2 2 sin α cos α
Câu 12: Đơn giản biểu thức sin = cot x E x + ta được 1+ cos x A. sin x . B. 1 . C. 1 . D. cos x . cos x sin x Page 79
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 2 2
Câu 13: Rút gọn biểu thức sau
cot x − cos x sin .xcos x A = + . 2 cot x cot x A. A =1. B. A = 2 . C. A = 3. D. A = 4 .
Câu 14: Biểu thức f (x) = ( 4 4 x + x) − ( 6 6 3 sin cos
2 sin x + cos x) có giá trị bằng: A. 1. B. 2 . C. 3 − . D. 0 .
Câu 15: Biểu thức: f (x) 4 2 2 2
= cos x + cos xsin x + sin x có giá trị bằng A. 1. B. 2 . C. 2 − . D. 1 − .
Câu 16: Trong các mệnh đề sau, mệnh đề nào sai? A. ( x x)2 sin cos
= 12sin x cos x . B. 4 4 2 2
sin x + cos x =12sin x cos x . C. ( x + x)2 sin cos
= 1+ 2sin x cos x . D. 6 6 2 2
sin x + cos x =1sin x cos x . Page 80
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC G
ƠN IV HỆ THỨC LƯỢNG HƯ TRONG TAM GIÁC C
BÀI 1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0 ĐẾN 180. I LÝ THUYẾT.
1. ĐỊNH NGHĨA GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC.
Trong mặt phẳng tọa độ Oxy .Với góc α ( o o
0 ≤ α ≤180 ) , ta xác định được duy nhất điểm M
trên trên đường nửa đường tròn đơn vị tâm O , sao cho α =
xOM , biết M ( ; x y). Khi đó: y o x o o sinα = y; cosα = ; x
tanα = (α ≠ 90 ); cotα = (α ≠ 0 ,180 ) x y
Các số sinα,cosα,tanα,cot β được gọi là giá trị lượng giác của góc α . y M ( x;y ) Q O P x Hình 2.1 Chú ý: Với o o
0 ≤ α ≤180 ta có 0 ≤ sinα ≤ 1; −1 ≤ cosα ≤ 1 Góc 0o o o 90 180 sin + + cos + - tan + - cot + - Page 1
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
2. MỐI QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU o
sin(180 ) sin o
cos(180 ) cos o
tan(180 ) tan o
cot(180 ) cot
3. MỐI QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC PHỤ NHAU (BỔ SUNG) o
sin(90 ) cos o
cos(90 ) sin o
tan(90 ) cot o
cot(90 ) tan
4. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC GÓC ĐẶC BIỆT
Góc 00 300 450 600 900 sin 0 1 2 2 3 1 2 2 cos 1 3 1 2 0 2 2 2 tan 0 3 1 3 | 3 cot | 3 1 3 0 3
5. CÁC HỆ THỨC LƯỢNG GIÁC CƠ BẢN (BỔ SUNG – KẾT QUẢ CỦA BÀI TẬP 5 SGK) sinα tanα = (α ≠ 90o) ; cosα cosα cotα = (α ≠ 0o; 180o) sinα
tanα.cotα =1 (α ≠ 0o; 90o; 180o) 2 2 sin α + cos α =1 2 1 1+ tan α = (α ≠ 90o) 2 cos α 2 1 1+ cot α = (α ≠ 0o; 180o) 2 sin α Page 2
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
II HỆ THỐNG BÀI TẬP.
DẠNG 1: TÍNH CÁC GIÁ TRỊ BIỂU THỨC LƯỢNG GIÁC 1 PHƯƠNG PHÁP.
· Sử dụng định nghĩa giá trị lượng giác của một góc
· Sử dụng tính chất và bảng giá trị lượng giác đặc biệt
· Sử dụng các hệ thức lượng giác cơ bản 2
BÀI TẬP TỰ LUẬN.
Câu 1. Tính giá trị các biểu thức sau: a) 2 o 2 o 2 o
A = a sin 90 + b cos90 + c cos180 b) 2 o 2 o 2 o
B = 3− sin 90 + 2cos 60 − 3tan 45 c) 2 0 2 o 2 o 2 o o o
C = sin 45 − 2sin 50 + 3cos 45 − 2sin 40 + 4 tan 55 .tan 35 Lời giải a) 2 o 2 o 2 o
A = a sin 90 + b cos90 + c cos180 2 2 2
= a + b + c (− ) 2 2 .1 .0 . 1 = a − c . 2 2 b) 2 o 2 o 2 o
B = 3− sin 90 + 2cos 60 − 3tan 45 = − ( )2 1 2 3 1 + 2 − 3 = 1. 2 2 c) 2 0 2 o 2 o 2 o o o
C = sin 45 − 2sin 50 + 3cos 45 − 2sin 40 + 4 tan 55 .tan 35 2 2 2 2 C = + − ( 2 0 2 0 + ) 1 3 3 2 sin 50
cos 40 + 4 = + − 2 + 4 = 4 . 2 2 2 2
Câu 2. Tính giá trị các biểu thức sau: a) 2 o 2 o 2 o 2 o
A = sin 3 + sin 15 + sin 75 + sin 87 b) o o o o o
B = cos0 + cos 20 + cos 40 +...+ cos160 + cos180 c) o o o o o
C = tan 5 tan10 tan15 ...tan80 tan85 Lời giải: a) A = ( 2 o 2 o sin 3 + sin 87 ) + ( 2 o 2 o sin 15 + sin 75 ) = ( 2 o 2 o + )+( 2 o 2 o sin 3 cos 3 sin 15 + cos 15 ) =1+1= 2 b) B = ( o o + )+( o o + )+ +( o o cos0 cos180 cos 20 cos160 ... cos80 + cos100 ) = ( o o − )+( o o − )+ +( o o cos0 cos0 cos 20 cos 20 ... cos80 − cos80 ) = 0 Page 3
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC c) C = ( o o )( o o ) ( o o
tan 5 tan85 tan15 tan 75 ... tan 45 tan 45 ) = ( o o )( o o ) ( o o
tan 5 cot 5 tan15 cot 5 ... tan 45 cot 5 ) =1 3
BÀI TẬP TRẮC NGHIỆM.
Câu 1: Giá trị của o o
cos60 + sin 30 bằng bao nhiêu? A. 3 B. 3 C. 3 D. 1. 2 3 Lời giải Chọn D Ta có o o 1 1 cos60 + sin 30 = + =1. 2 2
Câu 2: Giá trị của o o
tan 30 + cot 30 bằng bao nhiêu? + A. 4 B. 1 3 C. 2 D. 2 3 3 3 Lời giải Chọn A o o 3 4 3 tan 30 + cot 30 = + 3 = . 3 3
Câu 3: Trong các đẳng thức sau đây, đẳng thức nào sai? A. o o sin 0 + cos0 =1 B. o o sin 90 + cos90 =1 C. o o sin180 + cos180 = 1 − D. o o sin 60 + cos60 =1 Lời giải Chọn D
Giá trị lượng giác của góc đặc biệt.
Câu 4: Trong các khẳng định sau, khẳng định nào sai? A. o o cos60 = sin 30 . B. o o cos60 = sin120 . C. o o cos30 = sin120 . D. o o sin 60 = −cos120 . Lời giải Chọn B
Giá trị lượng giác của góc đặc biệt.
Câu 5: Đẳng thức nào sau đây sai? A. o o sin 45 + sin 45 = 2 . B. o o sin 30 + cos60 =1. C. o o sin 60 + cos150 = 0 . D. o o sin120 + cos30 = 0 . Lời giải Chọn D Page 4
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
Giá trị lượng giác của góc đặc biệt. Câu 6: Giá trị o o
cos 45 + sin 45 bằng bao nhiêu? A. 1. B. 2 . C. 3 . D. 0 . Lời giải Chọn B Ta có o o cos 45 + sin 45 = 2 .
Câu 7: Trong các đẳng thức sau, đẳng thức nào đúng? A. ( o sin 180 −α ) = −cosα . B. ( o sin 180 −α ) = −sinα . C. ( o sin 180 −α ) = sinα . D. ( o sin 180 −α ) = cosα . Lời giải Chọn C
Câu 8: Trong các đẳng thức sau, đẳng thức nào sai? A. o o sin 0 + cos0 = 0. B. o o sin 90 + cos90 =1. C. o o sin180 + cos180 = 1 − . D. o o 3 +1 sin 60 + cos60 = . 2 Lời giải Chọn A Ta có o o sin 0 + cos0 =1.
Câu 9: Cho α là góc tù. Điều khẳng định nào sau đây là đúng? A. sinα < 0 . B. cosα > 0 . C. tanα < 0. D. cotα > 0 . Lời giải Chọn C
Góc tù có điểm biểu diễn thuộc góc phần tư thứ II, có giá trị sinα > 0, còn cosα , tanα
và cotα đều nhỏ hơn 0 .
Câu 10: Giá trị của o o o o
E = sin 36 cos6 sin126 cos84 là A. 1 . B. 3 . C. 1. D. 1 − . 2 2 Lời giải Chọn A o o E = ( o o + ) ( o o − ) o o o o o 1
sin 36 cos6 sin 90 36 cos 90 6 = sin 36 cos6 − cos36 sin 6 = sin 30 = 2
Câu 11: Giá trị của biểu thức 2 o 2 o 2 o 2 o
A = sin 51 + sin 55 + sin 39 + sin 35 là Page 5
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. 3. B. 4 . C. 1. D. 2 . Lời giải Chọn D A = ( 2 o 2 o + )+( 2 o 2 o + ) = ( 2 o 2 o + )+( 2 o 2 o sin 51 sin 39 sin 55 sin 35 sin 51 cos 51 sin 55 + cos 55 ) = 2.
Câu 12: Giá trị của biểu thức o o o o o
A = tan1 tan 2 tan 3 . .tan88 tan89 là A. 0 . B. 2 . C. 3. D. 1. Lời giải Chọn D A = ( o o ) ( o o ) ( o o ) o
tan1 .tan89 . tan 2 .tan88 . . tan 44 .tan 46 .tan 45 =1. Câu 13: Tổng 2 o 2 o 2 o 2 o 2 o 2 o
sin 2 + sin 4 + sin 6 +. .+ sin 84 + sin 86 + sin 88 bằng A. 21. B. 23. C. 22 . D. 24 . Lời giải Chọn C 2 o 2 o 2 o 2 o 2 o 2 o
S = sin 2 + sin 4 + sin 6 +. .+ sin 84 + sin 86 + sin 88 = ( 2 o 2 o + )+( 2 o 2 o sin 2 sin 88 sin 4 + sin 86 ) +...+ ( 2 o 2 o sin 44 + sin 46 ) = ( 2 o 2 o sin 2 + cos 2 ) + ( 2 o 2 o sin 4 + cos 4 ) +...+ ( 2 o 2 o sin 44 + cos 44 ) = 22.
Câu 14: Giá trị của o o o o o
A = tan 5 .tan10 .tan15 ...tan80 .tan85 là A. 2 . B. 1. C. 0 . D. 1 − . Lời giải Chọn B
A (tan5 .°tan85° ).(tan10 .°tan80° ). .(tan 40° tan50° ).tan 45° = = 1.
Câu 15: Giá trị của 2 ° 2 ° 2 ° 2 B cos 73 cos 87 cos 3 cos 17° = + + + là A. 2 . B. 2 . C. 2 − . D. 1. Lời giải Chọn B B = ( 2 o 2 o cos 73 + cos 17 ) + ( 2 o 2 o cos 87 + cos 3 ) = ( 2 o 2 o cos 73 + sin 73 ) + ( 2 o 2 o cos 87 + sin 87 ) = 2 .
DẠNG 2: TÍNH GIÁ TRỊ CỦA MỘT BIỂU THỨC LƯỢNG GIÁC , KHI BIẾT TRƯỚC MỘT GIÁ
TRỊ LƯỢNG GIÁC. 1 PHƯƠNG PHÁP.
· Dựa vào các hệ thức lượng giác cơ bản
· Dựa vào dấu của giá trị lượng giác
· Sử dụng các hằng đẳng thức đáng nhớ Page 6
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 2
BÀI TẬP TỰ LUẬN. Câu 1. Cho 1 sinα = với 0 0
90 < α < 180 . Tính cosα và tanα 3 Câu 2. Cho 2
cosα = − và sinα > 0 . Tính sinα và cotα 3 Câu 3. Cho tan γ = 2 −
2 tính giá trị lượng giác còn lại. Lời giải: Câu 1. Vì 0 0
90 < α < 180 nên cosα < 0 mặt khác 2 2 sin α + cos α = 1 suy ra 2 1 2 2
cosα = − 1− sin α = − 1− = − 9 3 1 α Do đó sin 3 1 tanα = = = − cosα 2 2 2 2 − 3 Câu 2. Vì 2 2
sin α + cos α = 1 và sinα > 0 , nên 2 4 5 sinα = 1− cos α = 1− = và 9 3 2 cosα − 3 2 cotα = = = − sinα 5 5 3 Câu 3. Vì 1 tanα = 2 −
2 < 0 ⇒ cosα < 0 mặt khác 2 tan α +1 = 2 cos α Nên 1 1 1 cosα = − = − = − 2 tan +1 8 +1 3 α Ta có sin 1 2 2 tanα = ⇒ sinα = tanα.cosα = 2 − 2. − = cosα 3 3 1 cosα − 3 1 ⇒ cotα = = = − sinα 2 2 2 2 3 α + α Câu 4. Cho 3 cosα = với 0 0 0 < α < 90 . Tính tan 3cot A = . 4 tanα + cotα α − α
Câu 5. Cho tanα = 2 . Tính sin cos B = 3 3 sin α + 3cos α + 2sinα Lời giải: Page 7
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 1 1 tanα + 3 2 + 2 2 Câu 4. tanα tan α + 3 Ta có cos α 2 A = = = = 1+ 2cos α 2 1 tan α +1 1 tanα + 2 tanα cos α Suy ra 9 17 A = 1+ 2. = 16 8 sinα cosα − tanα ( 2 tan α + ) 1 − ( 2 3 3 tan α α α + ) 1 Câu 5. cos cos B = = 3 3 3 sin α 3cos α 2sinα tan α + 3 + 2 tanα ( 2 tan α + ) 1 + + 3 3 3 cos α cos α cos α 2 (2 + ) 1 − (2 + ) 1 3( 2 − )1 Suy ra B = = . 2 2 + 3 + 2 2 (2 + ) 1 3 + 8 2
Câu 6. Biết sin x + cos x = m a) Tìm 4 4
sin x − cos x .
b) Chứng minh rằng m ≤ 2 . Lời giải: a) Ta có ( x + x)2 2 2 sin cos
= sin x + 2sin x cos x + cos x = 1+ 2sin x cos x (*) 2
Mặt khác sin x + cos x = m nên 2 m m 1
= 1+ 2sinα cosα hay sinα cosα − = 2 Đặt 4 4
A = sin x − cos x . Ta có A = ( 2 2 x + x)( 2 2 sin cos
sin x − cos x) = (sin x + cos x)(sin x − cos x) ⇒ A = ( x + x)2 ( x − x)2 2 sin cos sin cos
= (1+ 2sin x cos x)(1− 2sin x cos x) 2 2 2 4 − − 2 4 2 m 1 m 1 3 + 2 ⇒ = 3 2m m 1+ 1 m − m A − = .Vậy A + − = 2 2 4 2 b) Ta có 2 2
2sin x cos x ≤ sin x + cos x = 1 Kết hợp với (*) suy ra ( x + x)2 sin cos
≤ 2 ⇒ sin x + cos x ≤ 2 3
BÀI TẬP TRẮC NGHIỆM. Câu 1: Cho 1
cos x = . Tính biểu thức 2 2
P = 3sin x + 4 cos x 2 A. 13 . B. 7 . C. 11. D. 15 . 4 4 4 4 Lời giải Chọn A Ta có P = x + x = ( x + x) 2 2 2 2 2 2 1 13 3sin 4cos 3 sin cos + cos x = 3 + = . 2 4 Câu 2: Biết 1
cosα = . Giá trị đúng của biểu thức 2 2
P = sin α + 3cos α là: 3 Page 8
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. 1 . B. 10 . C. 11. D. 4 . 3 9 9 3 Lời giải Chọn C 1 2 2 α = ⇒ P = α + c α = ( 2 2 α + α ) 2 2 11 cos sin 3 os sin cos + 2cos α = 1+ 2cos α = . 3 9 Câu 3: Cho biết 1 tanα = . Tính cotα . 2 A. cotα = 2. B. cotα = 2 . C. 1 cotα = . D. 1 cotα = . 4 2 Lời giải Chọn A 1 tanα.cotα = 1 ⇒ cotα = = 2 . tanα 2 cosα π = − 0 < α < Câu 4: Cho biết 3 và 2 . Tính tanα ? A. 5 . B. 5 − . C. 5 . D. 5 − . 4 2 2 2 Lời giải Chọn D π
Do 0 < α < ⇒ tanα < 0. Ta có: 2 1 1+ tan α = 2 5 ⇔ tan α = 5 ⇒ tanα = − . 2 2 cos α 4 2
Câu 5: Cho α là góc tù và 5 sinα =
. Giá trị của biểu thức 3sinα + 2cosα là 13 A. 3. B. 9 − . C. 3 − . D. 9 . 13 13 Lời giải Chọn B Ta có 2 2 144 12 cos α = 1− sin α = ⇒ cosα = ± 169 13
Do α là góc tù nên cosα < 0 , từ đó 12 cosα = − 13 Như vậy 5 12 9 3sinα + 2cosα = 3⋅ + 2 − = − . 13 13 13
Câu 6: Cho biết sinα + cosα = a . Giá trị của sinα.cosα bằng bao nhiêu? A. 2 sinα.cosα = a .
B. sinα.cosα = 2a . 2 2 C. 1 sin .cos a α α − = . D. a 1 sinα.cosα − = . 2 2 Lời giải Chọn D Page 9
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 2 a ( α α )2 2 a 1 sin cos 1 2sinα cosα sinα cosα − = + = + ⇒ = . 2 α + α Câu 7: Cho biết 2
cosα = − . Tính giá trị của biểu thức cot 3tan E = ? 3 2cotα + tanα A. 19 − . B. 19 . C. 25 . D. 25 − 13 13 13 13 Lời giải Chọn B cotα + 3tanα 1+ 3tan α 3( 3 2 2 tan α ) − + − 2 2 1 2 2 cos α 3 − 2cos α 19 E = = = = = = . 2 2cotα + tanα 2 + tan α 1+ ( 2 1+ tan α ) 2 1 1+ cos α 13 +1 2 cos α
Câu 8: Cho biết cotα = 5 . Tính giá trị của 2
E = 2cos α + 5sinα cosα +1? A. 10 . B. 100 . C. 50 . D. 101. 26 26 26 26 Lời giải Chọn D 2 2 1 1 E = α α + α + = ( 2 101 sin 2cot 5cot 3cot α + 5cotα +1 = . 2 2 ) sin α 1+ cot α 26 α + α Câu 9: Cho 1
cotα = . Giá trị của biểu thức 3sin 4cos A = là: 3 2sinα − 5cosα A. 15 − . B. 13 − . C. 15 . D. 13. 13 13 Lời giải Chọn D
3sinα + 4sinα.cotα 3 + 4cotα A = = = 13 .
2sinα − 5sinα.cotα 2 − 5cotα α − α Câu 10: Cho biết 2
cosα = − . Giá trị của biểu thức cot 3tan E = bằng bao nhiêu? 3 2cotα − tanα A. 25 − . B. 11 − . C. 11 − . D. 25 − . 3 13 3 13 Lời giải Chọn C cotα − 3tanα 1− 3tan α 4 − 3( 3 2 2 tan α + ) 4 − 2 1 2 cos α 4cos α − 3 11 E = = = = = = − . 2 2cotα − tanα 2 − tan α 3 − ( 2 1+ tan α ) 2 1 3cos α −1 3 3 − 2 cos α
Câu 11: Biết sin a + cos a = 2 . Hỏi giá trị của 4 4
sin a + cos a bằng bao nhiêu? A. 3 . B. 1 . C. 1 − . D. 0 . 2 2 Lời giải Chọn B
Ta có: sin a + cos a = 2 1 ⇒ = ( a + a)2 2 sin cos ⇒ sin . a cos a = . 2 Page 10
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC a + a = ( a + a) 2 4 4 2 2 2 2 1 1 sin cos sin cos
− 2sin a cos a = 1− 2 = . 2 2
Câu 12: Cho tanα + cotα = m . Tìm m để 2 2 tan α + cot α = 7 . A. m = 9 . B. m = 3 . C. m = 3 − . D. m = 3 ± . Lời giải Chọn D = α + α = ( α + α )2 2 2 7 tan cot tan cot − 2 2
⇒ m = 9 ⇔ m = 3 ± .
Câu 13: Cho biết 3cosα −sinα =1, o o
0 < α < 90 Giá trị của tanα bằng A. 4 tanα = B. 3 tanα = C. 4 tanα = D. 5 tanα = 3 4 5 4 Lời giải Chọn A Ta có α − α = ⇔ α = α + → α = ( α + )2 2 3cos sin 1 3cos sin 1 9cos sin 1 2 2 ⇔ α = α + α + ⇔ ( 2 − α ) 2 9cos sin 2sin 1 9 1 sin = sin α + 2sinα +1 sinα = 1 − 2 10sin α 2sinα 8 0 ⇔ + − = ⇔ 4 . • sinα = 1 − : không thỏa mãn vì o o 0 < α < 90 sinα = 5 α • 4 3 sin 4 sinα = ⇒ cosα = → tanα = = . 5 5 cosα 3
Câu 14: Cho biết 2cosα + 2 sinα = 2 , 0 0
0 < α < 90 . Tính giá trị của cotα. A. 5 cotα = B. 3 cotα = C. 2 cotα = D. 2 cotα = 4 4 4 2 Lời giải Chọn C Ta có α + α = ⇔ α = − α → α = ( − α )2 2 2cos 2 sin 2 2 sin 2 2cos 2sin 2 2cos 2 2
⇔ 2sin α = 4 − 8cosα + 4cos α ⇔ 2( 2 1− cos α ) 2 = 4 − 8cosα + 4cos α cosα = 1 2 6cos α 8cosα 2 0 ⇔ − + = ⇔ 1. cosα = 3
• cosα = 1: không thỏa mãn vì o o 0 < α < 90 • 1 2 2 cosα 2 cosα = ⇒ sinα = → cotα = = . 3 3 sinα 4 Câu 15: Cho biết 1
cosα + sinα = . Giá trị của 2 2
P = tan α + cot α bằng bao nhiêu? 3 A. 5 P = . B. 7 P = . C. 9 P = . D. 11 P = . 4 4 4 4 Page 11
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Lời giải Chọn B Ta có 1 α + α = → ( α + α )2 1 cos sin cos sin = 1 4
⇔ 1+ 2sinα cosα = ⇔ sinα cosα = − . 3 9 9 9 2 Ta có α α P α α ( α α )2 2 2 sin cos tan cot tan cot 2 tanα cotα = + = + − = + − 2 cosα sinα 2 2 2 2 2 sin α + cos α 1 9 7 = − 2 = − 2 = − − 2 = . sinα cosα sinα cosα 4 4 Câu 16: Cho biết 1 sinα − cosα = . Giá trị của 4 4
P = sin α + cos α bằng bao nhiêu? 5 A. 15 P = B. 17 P = C. 19 P = D. 21 P = 5 5 5 5 Lời giải Chọn B Ta có 1 α 1 2 − α = → ( α − α )2 1 sin cos sin cos
= ⇔ 1− 2sinα cosα = ⇔ sinα cosα = . 5 5 5 5 P = α + α = ( α + α )2 4 4 2 2 2 2 sin cos sin cos − 2sin α cos α = − ( αcosα )2 17 1 2 sin = . 5 Page 12
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
DẠNG 3: CHỨNG MINH CÁC ĐẲNG THỨC, RÚT GỌN CÁC BIỂU THỨC LƯỢNG GIÁC 1 PHƯƠNG PHÁP.
· Sử dụng các hệ thức lượng giác cơ bản
· Sử dụng tính chất của giá trị lượng giác
· Sử dụng các hằng đẳng thức đáng nhớ . 2
BÀI TẬP TỰ LUẬN.
Câu 1. Chứng minh các đẳng thức sau(giả sử các biểu thức sau đều có nghĩa) a) 4 4 2 2
sin x + cos x = 1− 2sin . x cos x + +
b) 1 cot x tan x 1 =
1− cot x tan x −1 + c) cos x sin x 3 2
= tan x + tan x + tan x +1 3 cos x Lời giải a) 4 4 4 4 2 2 2 2
sin x + cos x = sin x + cos x + 2sin x cos x − 2sin x cos x
= (sin x + cos x)2 2 2 2 2
− 2sin x cos x 2 2
= 1− 2sin x cos x 1 tan x +1 1+ b) 1+ cot x t anx t anx tan x +1 = = = 1− cot x 1
tan x −1 tan x −1 1− tan x tan x + c) cos x sin x 1 sin x = + 2 = x + + x ( 2 tan 1 tan tan x + ) 1 3 2 3 cos x cos x cos x 3 2
= tan x + tan x + tan x +1 3 B 3 sin cos B cos( A + C)
Câu 2. Cho tam giác ABC . Chứng minh 2 2 + − .tan B = 2 A + C A + C sin cos sin B 2 2 Lời giải: Vì 0
A + B + C = 180 nên 3 B 3 sin cos B cos( 0 180 − B) 2 2 VT = + − .tan B 0 0 180 − B 180 − B sin B cos sin 2 2 Page 13
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 3 B 3 sin cos B 2 2 − cos B 2 B 2 = + − .tan = sin + cos B B +1 = 2 = VP B B sin B 2 2 sin cos 2 2
Suy ra điều phải chứng minh.
Câu 3. Đơn giản các biểu thức sau(giả sử các biểu thức sau đều có nghĩa) a) o o 2 2 2
A = sin(90 − x) + cos(180 − x) + sin x(1+ tan x) − tan x b) 1 1 1 B = . + − 2
sin x 1+ cos x 1− cos x Lời giải: a) 2 1 2
A = cos x − cos x + sin . x − tan x = 0 2 cos x b) 1 1− cos x +1+ cos = . x B − x ( − x)( + x) 2 sin 1 cos 1 cos 1 2 1 2 = . − 2 = . − 2 2 2 sin x 1− cos x sin x sin x 1 2 = 2 −1 = 2 cot x 2 sin x
Câu 4. Chứng minh biểu thức sau không phụ thuộc vào x . 4 2 4 4 2 4
P = sin x + 6cos x + 3cos x + cos x + 6sin x + 3sin x Lời giải P = ( − x)2 + x + x + ( − x)2 2 2 4 2 2 4 1 cos 6cos 3cos 1 sin
+ 6sin x + 3sin x
= 4cos x + 4cos x +1 + 4sin x + 4sin x +1 = (2cos x + )2 1 + (2sin x + )2 4 2 4 2 2 2 1 2 2
= 2cos x +1+ 2sin x +1 = 3
Vậy P không phụ thuộc vào x . 3
BÀI TẬP TRẮC NGHIỆM.
Câu 1: Trong các hệ thức sau hệ thức nào đúng? α A. 2 2 sin α + cosα = 1. B. 2 2 sin α + cos = 1. 2 C. 2 2 sinα + cosα = 1. D. 2 2 sin 2α + cos 2α = 1. Lời giải Chọn D
Công thức lượng giác cơ bản.
Câu 2: Trong các hệ thức sau hệ thức nào đúng? Page 14
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC α A. 2 2 sin α + cosα = 1. B. 2 2 sin α + cos = 1. C. 2 2 sinα + cosα = 1. D. 2 2 sin α + cos α = 1. 2 Lời giải Chọn D
Công thức lượng giác cơ bản.
Câu 3: Trong các hệ thức sau hệ thức nào đúng?
A. sin 2α + cos 2α = 1. B. 2 2 sinα + cosα = 1. C. 2 2 sin α + cosα = 1. D. 2 2 sin α + cos α = 1. Lời giải Chọn D
Công thức lượng giác cơ bản.
Câu 4: Rút gọn biểu thức sau A = ( x + x)2 − ( x − x)2 tan cot tan cot A. A = 4 . B. A =1. C. A = 2 . D. A = 3 Lời giải Chọn A A = ( 2 2 x + x x + x) −( 2 2 tan 2 tan .cot cot tan x − 2 tan .
x cot x + cot x) = 4.
Câu 5: Đơn giản biểu thức G = ( 2 − x) 2 2 1 sin
cot x +1− cot x . A. 2 sin x . B. 2 cos x . C. 1 . D. cos x . cos x Lời giải Chọn A G = ( 2 − x) 2 2 2 2 2 1 sin
−1 cot x +1 = −sin .
x cot x +1 =1− cos x = sin x .
Câu 6: Khẳng định nào sau đây là sai? A. 2 2 1 sin α + cos α =1. B. 2 1+ cot α = sinα ≠ 0 . 2 ( ) sin α C. tanα.cotα = 1 − (sinα.cosα ≠ 0) . D. 2 1 1+ tan α = cosα ≠ 0 . 2 ( ) cos α Lời giải Chọn C sin x cos tanα.cotα = . x =1. cos x sin x 2
Câu 7: Rút gọn biểu thức 1− sin x P = ta được 2sin .xcos x A. 1 P = tan x . B. 1 P = cot x .
C. P = 2cot x .
D. P = 2 tan x . 2 2 Lời giải Chọn B 2 2 1− sin x cos x cos x 1 P = = = = cot x .
2sin .xcos x 2sin .xcos x 2sin x 2
Câu 8: Đẳng thức nào sau đây là sai? A. ( x + x)2 + ( x − x)2 cos sin cos sin = 2, x ∀ . B. 2 2 2 2
tan x sin x tan x sin x, x 90° − = ∀ ≠ C. 4 4 2 2
sin x + cos x = 1− 2sin x cos x, x ∀ . D. 6 6 2 2
sin x − cos x = 1− 3sin x cos x, x ∀ Page 15
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Lời giải Chọn D 6 6 x − x = ( 2 2 x − x)( 2 2 sin cos sin cos
1− sin x cos x) .
Câu 9: Đẳng thức nào sau đây là sai? A. 1− cos x sin x =
(x ≠ 0°,x ≠180°). sin x 1+ cos x B. 1 tan x cot x (x 0°,90°,180° + = ≠ ) sin x cos x C. 2 2 1 tan x cot x 2 x 0°,90°,180° + = − ≠ 2 2 ( ) sin x cos x D. 2 2
sin 2x + cos 2x = 2 . Lời giải Chọn D 2 2
sin 2x + cos 2x = 1. Câu 10: Biểu thức 2 2 2 2
tan xsin x − tan x + sin x có giá trị bằng A. 1 − . B. 0 . C. 2 . D. 1. Lời giải Chọn B − + = ( − ) 2 2 2 2 2 2 2 2 sin tan sin tan sin tan sin 1 + sin x x x x x x x x = ( 2 − cos x) 2 + sin x = 0 . 2 cos x
Câu 11: Biểu thức ( a + a)2 cot tan bằng A. 1 1 − . B. 2 2 1 1
cot a + tan a2 . C. + . D. 2 2
cot a tan a + 2 . 2 2 sin α cos α 2 2 sin α cos α Lời giải Chọn C ( a + a)2 2 2 = a + a a +
a = ( 2 a + ) + ( 2 a + ) 1 1 cot tan cot 2cot .tan tan cot 1 tan 1 = + . 2 2 sin a cos a
Câu 12: Đơn giản biểu thức sin = cot x E x + ta được 1+ cos x A. sin x . B. 1 . C. 1 . D. cos x . cos x sin x Lời giải Chọn C sin x cos x sin x
cos x(1+ cos x) + sin .xsin x E = cot x + = + =
1+ cos x sin x 1+ cos x sin x(1+ cos x) x( + x) + ( 2 cos 1 cos
1− cos x) cos x(1+ cos x) + (1+ cos x)(1− cos x) 1 = = = . sin x(1+ cos x) sin x(1+ cos x) sin x 2 2
Câu 13: Rút gọn biểu thức sau
cot x − cos x sin .xcos x A = + . 2 cot x cot x A. A =1. B. A = 2 . C. A = 3. D. A = 4 . Lời giải Page 16
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Chọn A 2 2 2
cot x − cos x sin .xcos x
cos x sin .xcos x 2 2 A = + = 1− +
= 1− sin x + sin x =1. 2 2 cot x cot x cot x cot x
Câu 14: Biểu thức f (x) = ( 4 4 x + x) − ( 6 6 3 sin cos
2 sin x + cos x) có giá trị bằng: A. 1. B. 2 . C. 3 − . D. 0 . Lời giải Chọn A 4 4 2 2
sin x + cos x = 1− 2sin x cos x . 6 6 2 2
sin x + cos x = 1− 3sin x cos x . f (x) = ( 2 2 − x x) − ( 2 2 3 1 2sin cos
2 1− 3sin x cos x) = 1.
Câu 15: Biểu thức: f (x) 4 2 2 2
= cos x + cos xsin x + sin x có giá trị bằng A. 1. B. 2 . C. 2 − . D. 1 − . Lời giải Chọn A f (x) 2 = x( 2 2 x + x) 2 2 2 cos cos sin
+ sin x = cos x + sin x =1.
Câu 16: Trong các mệnh đề sau, mệnh đề nào sai? A. ( x x)2 sin cos
= 12sin x cos x . B. 4 4 2 2
sin x + cos x =12sin x cos x . C. ( x + x)2 sin cos
= 1+ 2sin x cos x . D. 6 6 2 2
sin x + cos x =1sin x cos x . Lời giải Chọn D x + x = ( x)3 + ( x)3 = ( x + x)3 6 6 2 2 2 2 − ( 2 2 x + x) 2 2 sin cos sin cos sin cos 3 sin cos .sin . x cos x 2 2 = 1− 3sin . x cos x . Page 17
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC G
ƠN IV HỆ THỨC LƯỢNG HƯ TRONG TAM GIÁC C
BÀI 1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0 ĐẾN 180.
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM. III
DẠNG 1. DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC. GIÁ TRỊ LƯỢNG GIÁC
Câu 1: Cho góc α ∈(90 ;°180°). Khẳng định nào sau đây đúng?
A. sinα và cotα cùng dấu.
B. Tích sinα.cotα mang dấu âm.
C. Tích sinα.cosα mang dấu dương.
D. sinα và tanα cùng dấu.
Câu 2: Cho α là góc tù. Mệnh đề nào đúng trong các mệnh đề sau?
A. tanα < 0.
B. cotα > 0.
C. sinα < 0.
D. cosα > 0.
Câu 3: Cho 0º < α < 90º . Khẳng định nào sau đây đúng? A. cot (90º α − ) = − tanα . B. cos(90º α − ) = sinα . C. sin(90º α − ) = −cosα . D. tan (90º α − ) = −cotα .
Câu 4: Đẳng thức nào sau đây đúng? A. ( o
tan 180 + a) = − tan a . B. ( o
cos 180 + a) = −cosa . C. ( o
sin 180 + a) = sin a . D. ( o
cot 180 + a) = −cot a .
Câu 5: Trong các đẳng thức sau đây, đẳng thức nào đúng?
A. sin (180° −α ) = −sinα .
B. cos(180° −α ) = cosα
C. tan (180° −α ) = tanα .
D. cot (180° −α ) = −cotα
Câu 6: Cho α và β là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai? A. sinα = sin β . B. cosα = −cos β .
C. tanα = − tan β .
D. cotα = cot β .
Câu 7: Cho góc α tù. Điều khẳng định nào sau đây là đúng? A. sinα < 0 . B. cosα > 0 . C. tanα > 0. D. cotα < 0 .
Câu 8: Hai góc nhọn α và β phụ nhau, hệ thức nào sau đây là sai? A. sinα = cos β . B. tanα = cot β . C. 1 cot β = . D. cosα = −sin β . cotα
Câu 9: Trong các đẳng thức sau đây, đẳng thức nào đúng? A. ° 3 sin150 = − . B. ° 3 cos150 = . C. ° 1 tan150 = − . D. cot150° = 3 2 2 3 Page 82
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
Câu 10: Bất đẳng thức nào dưới đây là đúng? A. sin 90° sin100° < . B. cos95° cos100° > . C. tan85° tan125° < . D. cos145° cos125° > .
Câu 11: Giá trị của tan 45° cot135° + bằng bao nhiêu? A. 2 . B. 0 . C. 3 . D. 1.
Câu 12: Giá trị của cos30° sin 60° + bằng bao nhiêu? A. 3 . B. 3 . C. 3 . D. 1. 3 2
Câu 13: Giá trị của cos60° sin 30° + bằng bao nhiêu? A. 3 . B. 3 . C. 3 . D. 1 2 3
Câu 14: Giá trị của tan 30° cot 30° + bằng bao nhiêu? + A. 4 . B. 1 3 . C. 2 . D. 2 . 3 3 3
Câu 15: Trong các đẳng thức sau đây, đẳng thức nào sai? A. sin 0° cos0° + =1. B. sin 90° cos90° + =1. C. sin180° cos180° + = 1 − . D. sin 60° cos60° + =1.
Câu 16: Tính giá trị của biểu thức P = sin 30°cos60° + sin 60°cos30°. A. P =1.
B. P = 0 .
C. P = 3 . D. P = − 3 .
Câu 17: Trong các khẳng định sau, khẳng định nào sai? A. cos60° sin 30° = . B. cos60° sin120° = . C. cos30° sin120° = . D. sin 60° cos120° = − .
Câu 18: Đẳng thức nào sau đây sai? A. sin 45° sin 45° + = 2 . B. sin 30° cos60° + =1. C. sin 60° cos150° + = 0 . D. sin120° cos30° + = 0 .
Câu 19: Cho hai góc nhọn α và β (α < β ) . Khẳng định nào sau đây là sai? A. cosα < cos β . B. sinα < sin β .
C. tanα + tan β > 0. D. cotα > cot β . Câu 20: Cho A
∆ BC vuông tại A , góc B bằng 30° . Khẳng định nào sau đây là sai? A. 1 cos B = . B. 3 sin C = . C. 1 cosC = . D. 1 sin B = 3 2 2 2
Câu 21: Tìm khẳng định sai trong các khẳng định sau: A. cos75° cos50° > . B. sin80° sin 50° > . C. tan 45° tan 60° < . D. cos30° sin 60° = .
DẠNG 2. CHO BIẾT MỘT GIÁ TRỊ LƯỢNG GIÁC, TÍNH CÁC GIÁ TRỊ LƯỢNG GIÁC CÒN LẠI Câu 22: Cho 1
sinα = , với 90° < α <180°. Tính cosα . 3 A. 2 cosα = . B. 2 cosα = − . C. 2 2 cosα = . D. 2 2 cosα = − . 3 3 3 3 Câu 23: Cho biết 2 cosα = − . Tính tanα ? 3 A. 5 . B. 5 − . C. 5 . D. 5 − . 4 2 2 2 Page 83
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Câu 24: Cho biết 1 tanα = . Tính cotα . 2 A. cotα = 2. B. cotα = 2 . C. 1 cotα = . D. 1 cotα = . 4 2
Câu 25: cosα bằng bao nhiêu nếu 1 cotα = − ? 2 A. 5 ± . B. 5 . C. 5 − . D. 1 − . 5 2 5 3
Câu 26: Nếu tanα = 3 thì cosα bằng bao nhiêu? A. 10 − . B. 1 . C. 10 ± . D. 10 . 10 3 10 10
Câu 27: Cho α là góc tù và 5 sinα =
. Giá trị của biểu thức 3sinα + 2cosα là 13 A. 9 . B. 3. C. 9 − . D. 3 − . 13 13
Câu 28: Biết cotα = −a , a > 0 . Tính cosα A. cos a α = . B. 1 cosα = . C. 1 cosα = − . D. cos a α = − . 2 1+ a 2 1+ a 2 1+ a 2 1+ a Câu 29: Cho 1
cos x = . Tính biểu thức 2 2
P = 3sin x + 4cos x 2 A. 13 . B. 7 . C. 11. D. 15 . 4 4 4 4 4
Câu 30: Cho α là góc tù và sinα = . Giá trị của biểu thức A = 2sinα − cosα bằng 5 7 − 7 11 A. . B. . C. 1. D. . 5 5 5 Câu 31: Cho 4 α + α
sinα = , với 90° ≤ α ≤180° . Tính giá trị của sin cos M = 5 3 cos α A. 25 M = B. 175 M = . C. 35 M = . D. 25 M = − . 27 27 27 27 α + α Câu 32: Cho biết 2
cosα = − . Tính giá trị của biểu thức cot 3tan E = ? 3 2cotα + tanα A. 19 − . B. 19 . C. 25 . D. 25 − 13 13 13 13
Câu 33: Cho biết cotα = 5 . Tính giá trị của 2
E = 2cos α + 5sinα cosα +1? A. 10 . B. 100 . C. 50 . D. 101. 26 26 26 26 α + α Câu 34: Cho 1
cotα = . Giá trị của biểu thức 3sin 4cos A = là: 3 2sinα − 5cosα A. 15 − . B. 13 − . C. 15 . D. 13. 13 13 α − α Câu 35: Cho biết 2
cosα = − . Giá trị của biểu thức cot 3tan E = bằng bao nhiêu? 3 2cotα − tanα Page 84
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. 25 − . B. 11 − . C. 11 − . D. 25 − . 3 13 3 13 Câu 36: Biết 1
cosα = . Giá trị đúng của biểu thức 2 2
P = sin α + 3cos α là: 3 A. 11. B. 4 . C. 1 . D. 10 . 9 3 3 9
DẠNG 3. CHỨNG MINH, RÚT GỌN BIỂU THỨC LƯỢNG GIÁC
Câu 37: Đẳng thức nào sau đây là sai? A. ( x + x)2 + ( x − x)2 cos sin cos sin = 2, x ∀ . B. 2 2 2 2
tan x sin x tan xsin x, x 90° − = ∀ ≠ C. 4 4 2 2
sin x + cos x =1− 2sin xcos x, x ∀ . D. 6 6 2 2
sin x − cos x =1−3sin xcos x, x ∀
Câu 38: Đẳng thức nào sau đây là sai? A. 1− cos x sin x =
(x ≠ 0°,x ≠180°). sin x 1+ cos x B. 1 tan x cot x (x 0°,90°,180° + = ≠ ) sin xcos x C. 2 2 1 tan x cot x 2 x 0°,90°,180° + = − ≠ 2 2 ( ) sin xcos x D. 2 2
sin 2x + cos 2x = 2 .
Câu 39: Trong các hệ thức sau hệ thức nào đúng? α A. 2 2 sin α + cosα =1. B. 2 2 sin α + cos =1. 2 C. 2 2 sinα + cosα =1. D. 2 2 sin 2α + cos 2α =1.
Câu 40: Trong các hệ thức sau hệ thức nào đúng? α A. 2 2 sin α + cosα =1. B. 2 2 sin α + cos =1. C. 2 2 sinα + cosα =1. D. 2 2 sin α + cos α =1. 2 2 2
Câu 41: Rút gọn biểu thức sau
cot x − cos x sin .xcos x A = + 2 cot x cot x
A. A = 4 .
B. A = 2 . C. A =1. D. A = 3.
Câu 42: Biểu thức ( a + a)2 cot tan bằng A. 1 1 − . B. 2 2
cot a + tan a2 . C. 1 1 + . D. 2 2
cot a tan a + 2. 2 2 sin α cos α 2 2 sin α cos α
Câu 43: Rút gọn biểu thức sau A = ( x + x)2 − ( x − x)2 tan cot tan cot A. A = 4 . B. A =1. C. A = 2 . D. A = 3
Câu 44: Đơn giản biểu thức G = ( 2 − x) 2 2 1 sin
cot x +1− cot x . A. 2 sin x . B. 2 cos x . C. 1 . D. cos x . cos x
Câu 45: Đơn giản biểu thức sin = cot x E x + ta được 1+ cos x A. sin x . B. 1 . C. 1 . D. cos x . cos x sin x
Câu 46: Khẳng định nào sau đây là sai? Page 85
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. 2 2 sin α + cos α =1. B. 2 1 1+ cot α = sinα ≠ 0 . 2 ( ) sin α C. tanα.cotα = 1 − (sinα.cosα ≠ 0) . D. 2 1 1+ tan α = cosα ≠ 0 . 2 ( ) cos α 2
Câu 47: Rút gọn biểu thức 1− sin x P = ta được 2sin . x cos x 1 1
A. P = tan x . B. P = cot x .
C. P = 2cot x .
D. P = 2 tan x . 2 2
DẠNG 4. TÍNH GIÁ TRỊ BIỂU THỨC LƯỢNG GIÁC
Câu 48: Biểu thức A = cos 20° + cos 40° + cos60° +...+ cos160° + cos180° có giá trị bằng A. 1. B. 1 − . C. 2 . D. 2 − .
Câu 49: Cho tanα − cotα = 3. Tính giá trị của biểu thức sau: 2 2 A = tan α + cot α . A. A =12. B. A =11. C. A =13. D. A = 5.
Câu 50: Giá trị của biểu thức A tan1° tan 2° tan 3 .° .tan88° tan89° = là A. 0 . B. 2 . C. 3. D. 1. Câu 51: Tổng 2 ° 2 ° 2 ° 2 ° 2 ° 2
sin 2 sin 4 sin 6 . . sin 84 sin 86 sin 88° + + + + + + bằng A. 21. B. 23. C. 22 . D. 24 .
Câu 52: Biết sin a + cos a = 2 . Hỏi giá trị của 4 4
sin a + cos a bằng bao nhiêu? A. 3 . B. 1 . C. 1 − . D. 0 . 2 2
Câu 53: Biểu thức f (x) = ( 4 4 x + x) − ( 6 6 3 sin cos
2 sin x + cos x) có giá trị bằng: A. 1. B. 2 . C. 3 − . D. 0 .
Câu 54: Biểu thức: f (x) 4 2 2 2
= cos x + cos xsin x + sin x có giá trị bằng A. 1. B. 2 . C. 2 − . D. 1 − . Câu 55: Biểu thức 2 2 2 2
tan xsin x − tan x + sin x có giá trị bằng A. 1 − . B. 0 . C. 2 . D. 1.
Câu 56: Giá trị của A tan 5 .°tan10 .°tan15 ... ° tan80 .°tan85° = là A. 2 . B. 1. C. 0 . D. 1 − .
Câu 57: Giá trị của 2 ° 2 ° 2 ° 2
B cos 73 cos 87 cos 3 cos 17° = + + + là A. 2 . B. 2 . C. 2 − . D. 1.
Câu 58: Cho tanα + cotα = m . Tìm m để 2 2 tan α + cot α = 7 . A. m = 9 . B. m = 3 . C. m = 3 − . D. m = 3 ± .
Câu 59: Giá trị của E sin 36° cos6° sin126° cos84° = là A. 1 . B. 3 . C. 1. D. 1 − . 2 2
Câu 60: Giá trị của biểu thức 2 ° 2 ° 2 ° 2
A sin 51 sin 55 sin 39 sin 35° = + + + là A. 3. B. 4 . C. 1. D. 2 .
Câu 61: Cho sin x + cos x = m . Tính theo m M = x x giá trị của sin .cos . Page 86
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 2 2 A. 2 m m −1 m +1 −1. B. . C. . D. 2 m +1. 2 2 Page 87
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC G
ƠN IV HỆ THỨC LƯỢNG HƯ TRONG TAM GIÁC C
BÀI 1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0 ĐẾN 180.
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM. III
DẠNG 1. DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC. GIÁ TRỊ LƯỢNG GIÁC
Câu 1: Cho góc α ∈(90 ;°180°). Khẳng định nào sau đây đúng?
A. sinα và cotα cùng dấu.
B. Tích sinα.cotα mang dấu âm.
C. Tích sinα.cosα mang dấu dương.
D. sinα và tanα cùng dấu. Lời giải Chọn B
Với α ∈(90 ;°180°), ta có sinα > 0,cosα < 0 suy ra: tanα < 0,cotα < 0 Vậy sinα.cotα < 0
Câu 2: Cho α là góc tù. Mệnh đề nào đúng trong các mệnh đề sau?
A. tanα < 0.
B. cotα > 0.
C. sinα < 0.
D. cosα > 0. Lời giải Chọn C tanα < 0.
Câu 3: Cho 0º < α < 90º . Khẳng định nào sau đây đúng? A. cot (90º α − ) = − tanα . B. cos(90º α − ) = sinα . C. sin(90º α − ) = −cosα . D. tan (90º α − ) = −cotα . Lời giải Chọn B Vì α và (90º α
− ) là hai cung phụ nhau nên theo tính chất giá trị lượng giác của hai cung phụ
nhau ta có đáp án B đúng.
Câu 4: Đẳng thức nào sau đây đúng? A. ( o
tan 180 + a) = − tan a . B. ( o
cos 180 + a) = −cosa . Page 1
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC C. ( o
sin 180 + a) = sin a . D. ( o
cot 180 + a) = −cot a . Lời giải Chọn B
Lý thuyết “cung hơn kém 180°”
Câu 5: Trong các đẳng thức sau đây, đẳng thức nào đúng?
A. sin (180° −α ) = −sinα .
B. cos(180° −α ) = cosα
C. tan (180° −α ) = tanα .
D. cot (180° −α ) = −cotα Lời giải Chọn D
Mối liên hệ hai cung bù nhau.
Câu 6: Cho α và β là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai? A. sinα = sin β . B. cosα = −cos β .
C. tanα = − tan β .
D. cotα = cot β . Lời giải Chọn D
Mối liên hệ hai cung bù nhau.
Câu 7: Cho góc α tù. Điều khẳng định nào sau đây là đúng? A. sinα < 0 . B. cosα > 0 . C. tanα > 0. D. cotα < 0 . Lời giải Chọn D
Câu 8: Hai góc nhọn α và β phụ nhau, hệ thức nào sau đây là sai? A. sinα = cos β . B. tanα = cot β . C. 1 cot β = . D. cosα = −sin β . cotα Lời giải Chọn D cosα cos(90° = − β ) = sin β .
Câu 9: Trong các đẳng thức sau đây, đẳng thức nào đúng? A. ° 3 sin150 = − . B. ° 3 cos150 = . C. ° 1 tan150 = − . D. cot150° = 3 2 2 3 Lời giải Chọn C
Giá trị lượng giác của góc đặc biệt.
Câu 10: Bất đẳng thức nào dưới đây là đúng? A. sin 90° sin100° < . B. cos95° cos100° > . C. tan85° tan125° < . D. cos145° cos125° > . Lời giải Chọn B
Câu 11: Giá trị của tan 45° cot135° + bằng bao nhiêu? A. 2 . B. 0 . C. 3 . D. 1. Lời giải Chọn B tan 45° cot135° + =1−1 = 0
Câu 12: Giá trị của cos30° sin 60° + bằng bao nhiêu? A. 3 . B. 3 . C. 3 . D. 1. 3 2 Page 2
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Lời giải Chọn C ° ° 3 3 cos30 + sin 60 = + = 3 . 2 2
Câu 13: Giá trị của cos60° sin30° + bằng bao nhiêu? A. 3 . B. 3 . C. 3 . D. 1 2 3 Lời giải Chọn D Ta có ° ° 1 1 cos60 + sin 30 = + =1. 2 2
Câu 14: Giá trị của tan30° cot 30° + bằng bao nhiêu? + A. 4 . B. 1 3 . C. 2 . D. 2 . 3 3 3 Lời giải Chọn A ° ° 3 4 3 tan 30 + cot 30 = + 3 = . 3 3
Câu 15: Trong các đẳng thức sau đây, đẳng thức nào sai? A. sin 0° cos0° + =1. B. sin 90° cos90° + =1. C. sin180° cos180° + = 1 − . D. sin 60° cos60° + =1. Lời giải Chọn D
Giá trị lượng giác của góc đặc biệt.
Câu 16: Tính giá trị của biểu thức P = sin30°cos60° + sin 60°cos30°. A. P =1.
B. P = 0 .
C. P = 3 . D. P = − 3 . Lời giải Chọn A Ta có: 1 1 3 3
P = sin 30°cos60° + sin 60°cos30° = . + . = 1. 2 2 2 2
Câu 17: Trong các khẳng định sau, khẳng định nào sai? A. cos60° sin 30° = . B. cos60° sin120° = . C. cos30° sin120° = . D. sin 60° cos120° = − . Lời giải Chọn B
Giá trị lượng giác của góc đặc biệt.
Câu 18: Đẳng thức nào sau đây sai? A. sin 45° sin 45° + = 2 . B. sin 30° cos60° + =1. C. sin 60° cos150° + = 0 . D. sin120° cos30° + = 0 . Lời giải Chọn D
Giá trị lượng giác của góc đặc biệt.
Câu 19: Cho hai góc nhọn α và β (α < β) . Khẳng định nào sau đây là sai? Page 3
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. cosα < cos β . B. sinα < sin β .
C. tanα + tan β > 0. D. cotα > cot β . Lời giải Chọn B
Biểu diễn lên đường tròn. Câu 20: Cho A
∆ BC vuông tại A , góc B bằng 30° . Khẳng định nào sau đây là sai? A. 1 cos B = . B. 3 sin C = . C. 1 cosC = . D. 1 sin B = 3 2 2 2 Lời giải Chọn A ° 3 cos B = cos30 = . 2
Câu 21: Tìm khẳng định sai trong các khẳng định sau: A. cos75° cos50° > . B. sin80° sin 50° > . C. tan 45° tan 60° < . D. cos30° sin 60° = . Lời giải Chọn A Lý thuyết.
DẠNG 2. CHO BIẾT MỘT GIÁ TRỊ LƯỢNG GIÁC, TÍNH CÁC GIÁ TRỊ LƯỢNG GIÁC CÒN LẠI Câu 22: Cho 1
sinα = , với 90° < α <180°. Tính cosα . 3 A. 2 cosα = . B. 2 cosα = − . C. 2 2 cosα = . D. 2 2 cosα = − . 3 3 3 3 Lời giải Chọn D 2 Ta có 2 2 cos α =1−sin α 1 8 = 1− = . 3 9
Mặt khác 90° < α <180° nên 2 2 cosα = − . 3 Câu 23: Cho biết 2 cosα = − . Tính tanα ? 3 A. 5 . B. 5 − . C. 5 . D. 5 − . 4 2 2 2 Lời giải Chọn D
Do cosα < 0 ⇒ tanα < 0. Ta có: 2 1 1+ tan α = 2 5 ⇔ tan α = 5 ⇒ tanα = − . 2 cos α 4 2 Câu 24: Cho biết 1 tanα = . Tính cotα . 2 A. cotα = 2. B. cotα = 2 . C. 1 cotα = . D. 1 cotα = . 4 2 Lời giải Page 4
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Chọn A 1
tanα.cotα =1⇒ cot x = = 2 . tan x
Câu 25: cosα bằng bao nhiêu nếu 1 cotα = − ? 2 A. 5 ± . B. 5 . C. 5 − . D. 1 − . 5 2 5 3 Lời giải Chọn A Ta có 1 cotα = − ⇒ tanα = 2 − . 2 2 1 2 1 1 1 1+ tan α = ⇔ cos α = = = 2 2 cos α 1+ tan α . 1+ ( 2 − )2 5 Suy ra 5 cosα = ± . 5
Câu 26: Nếu tanα = 3 thì cosα bằng bao nhiêu? A. 10 − . B. 1 . C. 10 ± . D. 10 . 10 3 10 10 Lời giải Chọn C Ta có 2 1 2 1 1 1 1+ tan α = ⇔ cos α = = = . 2 2 2 cos α 1+ tan α 1+ 3 10 Suy ra 10 cosα = ± . 10
Câu 27: Cho α là góc tù và 5 sinα =
. Giá trị của biểu thức 3sinα + 2cosα là 13 A. 9 . B. 3. C. 9 − . D. 3 − . 13 13 Lời giải Chọn C Ta có 2 2 144 12 cos α =1− sin α = ⇒ cosα = ± 169 13
Do α là góc tù nên cosα < 0 , từ đó 12 cosα = − 13 Như vậy 5 12 9 3sinα + 2cosα = 3⋅ + 2 − = − . 13 13 13
Câu 28: Biết cotα = −a , a > 0 . Tính cosα Page 5
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. cos a α = . B. 1 cosα = . C. 1 cosα = − . D. cos a α = − . 2 1+ a 2 1+ a 2 1+ a 2 1+ a Lời giải Chọn D
Do cotα = −a , a > 0 nên 0 0
90 < α <180 suy ra cosα < 0 . Mặt khác, 1 tanα = 1 tanα − ⇔ = . cotα a 2 Mà ta lại có 2 1 1+ tan α = 2 1 ⇔ cos α = 2 ⇔ cos a α = . 2 cos α 2 1+ tan α 2 1+ a a Khi đó cosα = − và do a a > 0 nên cosα = − . 2 1+ a 2 1+ a Câu 29: Cho 1
cos x = . Tính biểu thức 2 2
P = 3sin x + 4cos x 2 A. 13 . B. 7 . C. 11. D. 15 . 4 4 4 4 Lời giải Chọn A Ta có P = x + x = ( x + x) 2 2 2 2 2 2 1 13 3sin 4cos 3 sin cos + cos x = 3+ = . 2 4 4
Câu 30: Cho α là góc tù và sinα = . Giá trị của biểu thức A = 2sinα − cosα bằng 5 7 − 7 11 A. . B. . C. 1. D. . 5 5 5 Lời giải Chọn D 2 4 4 9 Ta có: 2 2
sinα = ⇒ cos α =1− sin α =1− = . 5 5 25 3
Do α là góc tù nên cosα 0 cosα − < ⇒ = . 5 2.4 3 11 A 2sinα cosα − = − = − = . 5 5 5 Câu 31: Cho 4 α + α
sinα = , với 90° ≤ α ≤180° . Tính giá trị của sin cos M = 5 3 cos α A. 25 M = B. 175 M = . C. 35 M = . D. 25 M = − . 27 27 27 27 Chọn D Page 6
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 2 Ta có 2 2 4 9 cos α =1− sin α =1− = . 5 25 Mà 3 90 α 180 cosα 0 cosα − ° ≤ ≤ ° ⇒ ≤ ⇒ = . 5 Từ đó sinα + cosα 25 M − = = . 3 cos α 27 α + α Câu 32: Cho biết 2
cosα = − . Tính giá trị của biểu thức cot 3tan E = ? 3 2cotα + tanα A. 19 − . B. 19 . C. 25 . D. 25 − 13 13 13 13 Lời giải Chọn B cotα + 3tanα 1+ 3tan α 3( 3 2 2 tan α ) − + − 2 2 1 2 2 cos α 3− 2cos α 19 E = = = = = = . 2 2cotα + tanα 2 + tan α 1+ ( 2 1+ tan α ) 2 1 1+ cos α 13 +1 2 cos α
Câu 33: Cho biết cotα = 5 . Tính giá trị của 2
E = 2cos α + 5sinα cosα +1? A. 10 . B. 100 . C. 50 . D. 101. 26 26 26 26 Lời giải Chọn D 2 2 1 1 E = α α + α + = ( 2 101 sin 2cot 5cot 3cot α + 5cotα +1 = . 2 2 ) sin α 1+ cot α 26 α + α Câu 34: Cho 1
cotα = . Giá trị của biểu thức 3sin 4cos A = là: 3 2sinα − 5cosα A. 15 − . B. 13 − . C. 15 . D. 13. 13 13 Lời giải Chọn D
3sinα + 4sinα.cotα 3+ 4cotα A = = =13 .
2sinα − 5sinα.cotα 2 − 5cotα α − α Câu 35: Cho biết 2
cosα = − . Giá trị của biểu thức cot 3tan E = bằng bao nhiêu? 3 2cotα − tanα A. 25 − . B. 11 − . C. 11 − . D. 25 − . 3 13 3 13 Lời giải Chọn C
cotα − 3tanα 1− 3tan α 4 − 3( 3 2 2 tan α + ) 4 − 2 1 2 cos α 4cos α − 3 11 E = = = = = = − . 2 2cotα − tanα 2 − tan α 3− ( 2 1+ tan α ) 2 1 3cos α −1 3 3− 2 cos α Câu 36: Biết 1
cosα = . Giá trị đúng của biểu thức 2 2
P = sin α + 3cos α là: 3 Page 7
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. 11. B. 4 . C. 1 . D. 10 . 9 3 3 9 Lời giải Chọn A 1 2 2 α = ⇒ P = α + c α = ( 2 2 α + α ) 2 2 11 cos sin 3 os sin cos + 2cos α =1+ 2cos α = . 3 9
DẠNG 3. CHỨNG MINH, RÚT GỌN BIỂU THỨC LƯỢNG GIÁC
Câu 37: Đẳng thức nào sau đây là sai? A. ( x + x)2 + ( x − x)2 cos sin cos sin = 2, x ∀ . B. 2 2 2 2
tan x sin x tan xsin x, x 90° − = ∀ ≠ C. 4 4 2 2
sin x + cos x =1− 2sin xcos x, x ∀ . D. 6 6 2 2
sin x − cos x =1−3sin xcos x, x ∀ Lời giải Chọn D 6 6 x − x = ( 2 2 x − x)( 2 2 sin cos sin cos
1− sin x cos x).
Câu 38: Đẳng thức nào sau đây là sai? A. 1− cos x sin x =
(x ≠ 0°,x ≠180°). sin x 1+ cos x B. 1 tan x cot x (x 0°,90°,180° + = ≠ ) sin xcos x C. 2 2 1 tan x cot x 2 x 0°,90°,180° + = − ≠ 2 2 ( ) sin xcos x D. 2 2
sin 2x + cos 2x = 2 . Lời giải Chọn D 2 2
sin 2x + cos 2x =1.
Câu 39: Trong các hệ thức sau hệ thức nào đúng? α A. 2 2 sin α + cosα =1. B. 2 2 sin α + cos =1. 2 C. 2 2 sinα + cosα =1. D. 2 2 sin 2α + cos 2α =1. Lời giải Chọn D
Công thức lượng giác cơ bản.
Câu 40: Trong các hệ thức sau hệ thức nào đúng? α A. 2 2 sin α + cosα =1. B. 2 2 sin α + cos =1. C. 2 2 sinα + cosα =1. D. 2 2 sin α + cos α =1. 2 Lời giải Chọn D
Công thức lượng giác cơ bản. 2 2
Câu 41: Rút gọn biểu thức sau
cot x − cos x sin .xcos x A = + 2 cot x cot x
A. A = 4 .
B. A = 2 . C. A =1. D. A = 3. Lời giải Chọn C Page 8
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 2 cos x 2 2 2 − cos x 2
cot x − cos x sin .xcos x sin x sin .xcos x A = + = + 2 2 cot x cot x cos x cos x 2 sin x sin x 2 cos x( 2 1− sin x) 2 2 2 =
+ sin x =1− sin x + sin x =1. 2 cos x
Câu 42: Biểu thức ( a + a)2 cot tan bằng A. 1 1 − . B. 2 2
cot a + tan a2 . C. 1 1 + . D. 2 2
cot a tan a + 2. 2 2 sin α cos α 2 2 sin α cos α Lời giải Chọn C ( a + a)2 2 2 = a + a a +
a = ( 2 a + ) + ( 2 a + ) 1 1 cot tan cot 2cot .tan tan cot 1 tan 1 = + . 2 2 sin a cos a
Câu 43: Rút gọn biểu thức sau A = ( x + x)2 − ( x − x)2 tan cot tan cot A. A = 4 . B. A =1. C. A = 2 . D. A = 3 Lời giải Chọn A A = ( 2 2 x + x x + x) −( 2 2 tan 2 tan .cot cot tan x − 2 tan .
x cot x + cot x) = 4.
Câu 44: Đơn giản biểu thức G = ( 2 − x) 2 2 1 sin
cot x +1− cot x . A. 2 sin x . B. 2 cos x. C. 1 . D. cos x . cos x Lời giải Chọn A G = ( 2 − x) 2 2 2 2 2 1 sin
−1 cot x +1 = −sin .xcot x +1 =1− cos x = sin x .
Câu 45: Đơn giản biểu thức sin = cot x E x + ta được 1+ cos x A. sin x . B. 1 . C. 1 . D. cos x . cos x sin x Lời giải Chọn C sin x cos x sin x
cos x(1+ cos x) + sin .xsin x E = cot x + = + =
1+ cos x sin x 1+ cos x sin x(1+ cos x) x( + x) + ( 2 cos 1 cos
1− cos x) cos x(1+ cos x) + (1+ cos x)(1− cos x) 1 = = = . sin x(1+ cos x) sin x(1+ cos x) sin x
Câu 46: Khẳng định nào sau đây là sai? A. 2 2 sin α + cos α =1. B. 2 1 1+ cot α = sinα ≠ 0 . 2 ( ) sin α C. tanα.cotα = 1 − (sinα.cosα ≠ 0) . D. 2 1 1+ tan α = cosα ≠ 0 . 2 ( ) cos α Lời giải Chọn C Page 9
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC sin x cos tanα.cotα = . x =1. cos x sin x 2
Câu 47: Rút gọn biểu thức 1− sin x P = ta được 2sin . x cos x A. 1 P = tan x . B. 1 P = cot x .
C. P = 2cot x .
D. P = 2 tan x . 2 2 Lời giải Chọn B 2 2 1− sin x cos x cos x 1 P = = = = cot x . 2sin . x cos x 2sin .
x cos x 2sin x 2
DẠNG 4. TÍNH GIÁ TRỊ BIỂU THỨC LƯỢNG GIÁC
Câu 48: Biểu thức A = cos 20° + cos 40° + cos60° +...+ cos160° + cos180° có giá trị bằng A. 1. B. 1 − . C. 2 . D. 2 − . Lời giải Chọn B
Ta có cosα = −cos(180° −α ) (0° ≤ α ≤180°) nên suy ra cosα + cos(180° −α ) = 0.
Do đó: A = (cos 20° + cos160°) + (cos 40° + cos140°) + (cos60° + cos120°)
+(cos80° + cos100°) + cos180° = cos180° = 1 − .
Câu 49: Cho tanα − cotα = 3. Tính giá trị của biểu thức sau: 2 2 A = tan α + cot α . A. A =12. B. A =11. C. A =13. D. A = 5. Lời giải Chọn B α − α = ⇔ ( α − α )2 2 2 tan cot 3 tan cot
= 9 ⇔ tan α + cot α − 2 tanα.cotα = 9 2 2 2 2
⇔ tan α + cot α − 2 = 9 ⇔ tan α + cot α =11.
Câu 50: Giá trị của biểu thức A tan1° tan 2° tan3 .° .tan88° tan89° = là A. 0 . B. 2 . C. 3. D. 1. Lời giải Chọn D
A (tan1.°tan89° ).(tan 2 .°tan88° ). .(tan 44 .°tan 46° ).tan 45° = = 1. Câu 51: Tổng 2 ° 2 ° 2 ° 2 ° 2 ° 2
sin 2 sin 4 sin 6 . . sin 84 sin 86 sin 88° + + + + + + bằng A. 21. B. 23. C. 22 . D. 24 . Lời giải Chọn C 2 ° 2 ° 2 ° 2 ° 2 ° 2
S sin 2 sin 4 sin 6 . . sin 84 sin 86 sin 88° = + + + + + + ( 2 ° 2 ° ) ( 2 ° 2 ° ) ( 2 ° 2 sin 2 sin 88 sin 4 sin 86 ... sin 44 sin 46° = + + + + + + ) ( 2 ° 2 ° ) ( 2 ° 2 ° ) ( 2 ° 2 sin 2 cos 2 sin 4 cos 4 ... sin 44 cos 44° = + + + + + + ) = 22.
Câu 52: Biết sin a + cosa = 2 . Hỏi giá trị của 4 4
sin a + cos a bằng bao nhiêu? Page 10
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. 3 . B. 1 . C. 1 − . D. 0 . 2 2 Lời giải Chọn B Ta có: 1
sin a + cos a = 2 ⇒ = ( a + a)2 2 sin cos ⇒ sin . a cos a = . 2 a + a = ( a + a) 2 4 4 2 2 2 2 1 1 sin cos sin cos
− 2sin a cos a =1− 2 = . 2 2
Câu 53: Biểu thức f (x) = ( 4 4 x + x) − ( 6 6 3 sin cos
2 sin x + cos x) có giá trị bằng: A. 1. B. 2 . C. 3 − . D. 0 . Lời giải Chọn A 4 4 2 2
sin x + cos x =1− 2sin xcos x . 6 6 2 2
sin x + cos x =1−3sin xcos x . f (x) = ( 2 2 − x x) − ( 2 2 3 1 2sin cos
2 1− 3sin x cos x) =1.
Câu 54: Biểu thức: f (x) 4 2 2 2
= cos x + cos xsin x + sin x có giá trị bằng A. 1. B. 2 . C. 2 − . D. 1 − . Lời giải Chọn A f (x) 2 = x( 2 2 x + x) 2 2 2 cos cos sin
+ sin x = cos x + sin x =1. Câu 55: Biểu thức 2 2 2 2
tan xsin x − tan x + sin x có giá trị bằng A. 1 − . B. 0 . C. 2 . D. 1. Lời giải Chọn B − + = ( − ) 2 2 2 2 2 2 2 2 sin tan sin tan sin tan sin 1 + sin x x x x x x x x = ( 2 − cos x) 2 + sin x = 0 . 2 cos x
Câu 56: Giá trị của A tan5 .°tan10 .°tan15 ... ° tan80 .°tan85° = là A. 2 . B. 1. C. 0 . D. 1 − . Lời giải Chọn B
A (tan5 .°tan85° ).(tan10 .°tan80° ). .(tan 40° tan50° ).tan 45° = = 1.
Câu 57: Giá trị của 2 ° 2 ° 2 ° 2
B cos 73 cos 87 cos 3 cos 17° = + + + là A. 2 . B. 2 . C. 2 − . D. 1. Lời giải Chọn B B ( 2 ° 2 ° ) ( 2 ° 2 ° ) ( 2 ° 2 ° ) ( 2 ° 2 cos 73 cos 17 cos 87 cos 3 cos 73 sin 73 cos 87 sin 87° = + + + = + + + ) = 2.
Câu 58: Cho tanα + cotα = m . Tìm m để 2 2 tan α + cot α = 7 . A. m = 9 . B. m = 3 . C. m = 3 − . D. m = 3 ± . Lời giải Chọn D = α + α = ( α + α )2 2 2 7 tan cot tan cot − 2 2
⇒ m = 9 ⇔ m = 3 ± .
Câu 59: Giá trị của E sin36° cos6° sin126° cos84° = là Page 11
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. 1 . B. 3 . C. 1. D. 1 − . 2 2 Lời giải Chọn A E ° ° = ( ° ° + ) ( ° ° − ) ° ° ° ° ° 1
sin 36 cos6 sin 90 36 cos 90 6 = sin 36 cos6 − cos36 sin 6 = sin 30 = 2
Câu 60: Giá trị của biểu thức 2 ° 2 ° 2 ° 2
A sin 51 sin 55 sin 39 sin 35° = + + + là A. 3. B. 4 . C. 1. D. 2 . Lời giải Chọn D A ( 2 ° 2 ° ) ( 2 ° 2 ° ) ( 2 ° 2 ° ) ( 2 ° 2 sin 51 sin 39 sin 55 sin 35 sin 51 cos 51 sin 55 cos 55° = + + + = + + + ) = 2.
Câu 61: Cho sin x + cos x = m . Tính theo m M = x x giá trị của sin .cos . 2 2 A. 2 m m −1 m +1 −1. B. . C. . D. 2 m +1. 2 2 Lời giải Chọn B x + x = m ⇒( x + x)2 2 = m ⇔( 2 2 x + x) 2 sin cos sin cos sin cos + 2sin .
x cos x = m 2 2 m 1 1 2sin .xcos x m sin .xcos x − ⇔ + = ⇔ = . 2 2 Vậy m 1 M − = . 2 Page 12
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC G
ƠN IV HỆ THỨC LƯỢNG HƯ TRONG TAM GIÁC C
BÀI 2. ĐỊNH LÝ COSIN VÀ ĐỊNH LÝ SIN
BÀI 3. GIẢI TAM GIÁC VÀ ỨNG DỤNG THỰC TẾ I LÝ THUYẾT. Cho tam giác ABC, BC = a, CA = b, ,
AB = c S là diện tích tam giác. Giả sử h h h lần lượt a , b , c
là độ dài các đường cao đi qua ba đỉnh ,
A B,C; m m m lần lượt là các đường trung tuyến đi a , b , c qua ba đỉnh ,
A B,C. R và r lần lượt là bán kính đường tròn ngoại tiếp và nột tiếp của tam giác
ABC . Ta có kết quả sau đây:
1. Định lí côsin trong tam giác 2 2 2
a = b + c − 2 . bc cos , A 2 2 2
b = c + a − 2c . a cos B, 2 2 2
c = a + b − 2 . ab cosC.
*Hệ quả của định lí côsin 2 2 2 2 2 2 2 2 2 cos
b + c − a = , cos
a + c − b = ,cos
b + a − c A B C = . 2bc 2ac 2ab
2. Định lí sin trong tam giác: a b c = = = 2 . R sin A sin B sinC
*Hệ quả của định lí sin a = 2 . R sin A b = 2 . R sin B c = 2 . R sin C sin a A = 2R sin b B = 2R sin c C = 2R
3. Các công thức tính diện tích tam giác: 1) 1 1 1
S = ah = bh = ch a b c . 2 2 2 1 1 1
2) S = bcsin A = casin B = absin C 2 2 2 Page 88
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 3) abc S = 4R 1
4) S = pr với p = (a + b + c) 2
5) Công thức Hê- Rông S = p( p − a)( p − b)( p − c) 4. Giải tam giác.
Giải tam giác là tìm số đo các cạnh còn lại và các góc còn lại của tam giác khi biết một số yếu tố cho trước.
Để giải tam giác ta sử dụng một cách hợp lý các công cụ là: Định lý cosin, định lý sin và công
thức về diện tích tam giác.
5. Áp dụng giải tam giác vào thực tế.
Vận dụng giải tam giác giúp chúng ta giải quyết rất nhiều bài toán trong thực tế, đặc biệt là trong thiết kế và xây dựng.
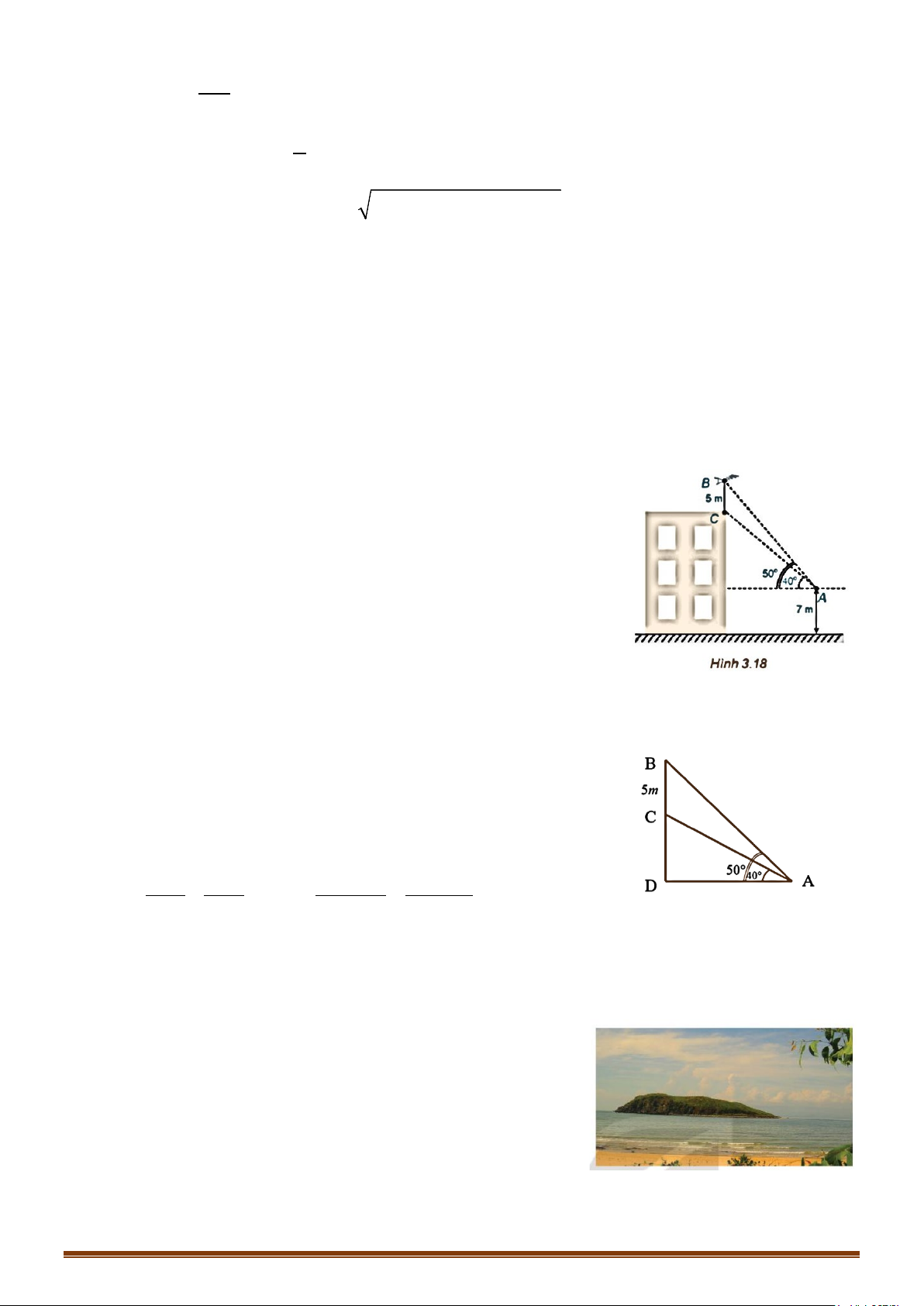
Ví dụ 1. Trên nóc một tòa nhà có một cột ăng-ten
cao 5 m. Từ một vị trí quan sát A cao 7 m so
với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-
ten, với các góc tương ứng
là 50° và 40° so với phương nằm ngang (H.3.18).
a) Tính các góc của tam giác ABC.
b) Tính chiều cao của tòa nhà.
Ví dụ 2. Từ bãi biển Vũng Chùa, Quảng Bình, ta có thể ngắm được
Đảo Yến. Hãy đề xuất một cách xác định bề rộng của hòn
đảo (theo chiều ta ngắm được). Đảo Yến nhìn từ bãi biển
Vũng Chùa, Quảng Bình
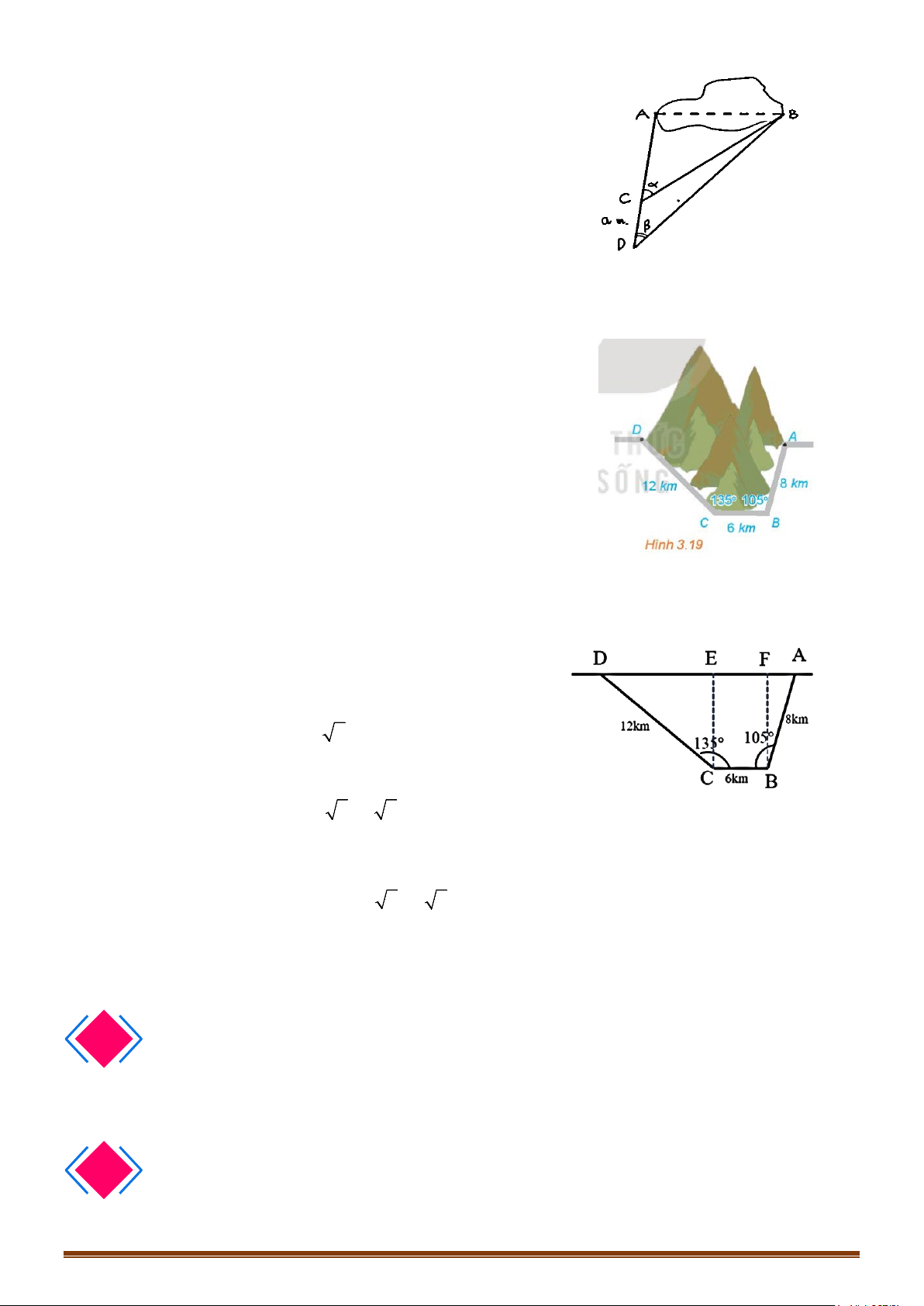
Ví dụ 3. Để tránh núi, đường giao thông hiện tại
phải đi vòng như mô hình trong Hình 3.19.
Để rút ngắn khoảng cách và tránh sạt lở núi,
người ta dự định làm đường hầm xuyên núi,
nối thẳng từ A tới D . Hỏi độ dài đường mới
sẽ giảm bao nhiêu kilômét so với đường cũ? Page 89
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
II HỆ THỐNG BÀI TẬP.
DẠNG 1: GIẢI TAM GIÁC
{Tìm một số yếu tố của tam giác khi cho biết các yếu tố khác.} 1 PHƯƠNG PHÁP.
+ Á p dụng các công thức sách giáo khoa như: định lí cosin, hệ quả của định lí cosin, định lí sin,
các công thức liên quan đến diện tích để vận dụng vào làm bài. 2
BÀI TẬP TỰ LUẬN.
Câu 1. Cho tam giác ABC có = = 0
AB 4, AC 6, A =120 . Tính độ dài cạnh BC
Câu 2. Cho tam giác ABC có a = 7;b = 8;c = 5 . Tính , A S,h R a , .
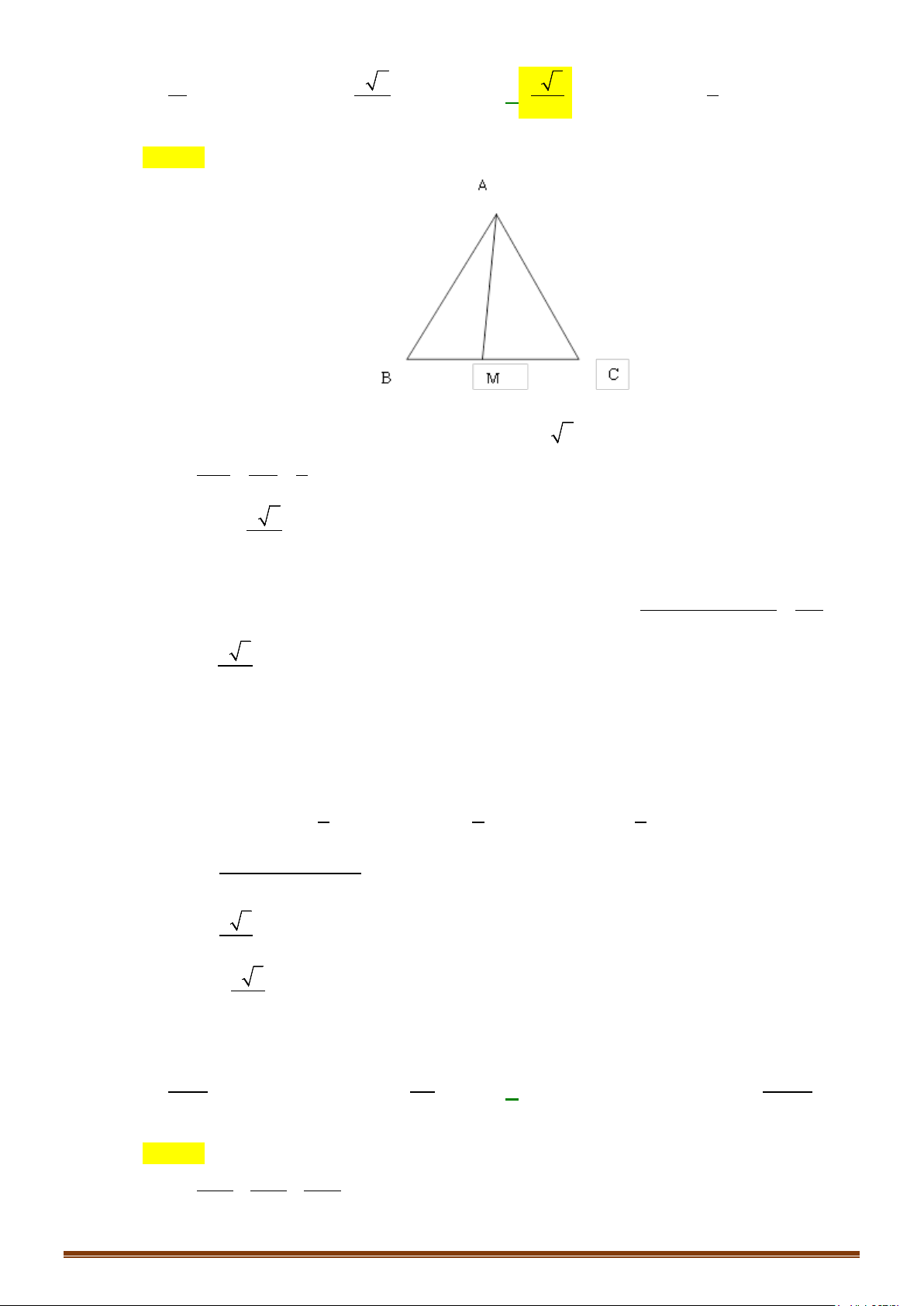
Câu 3. Cho tam giác ABC có độ dài ba cạnh là AB = 2 , BC = 5 , CA = 6. Tính độ dài đường trung tuyến
MA, với M là trung điểm của BC .
Câu 4. Tam giác ABC vuông tại A có AC = 6 cm , BC =10 cm . Tính bán kính đường tròn nội tiếp tam giác ABC .
Câu 5. Cho tam giác ABC có b = 7 , c = 5 , 3
cos A = . Tính độ dài đường cao h của tam giác ABC . 5 a 3
BÀI TẬP TRẮC NGHIỆM. Câu 1: Cho A
∆ BC có BC = a ,
BAC =120° . Bán kính đường tròn ngoại tiếp A ∆ BC là A. a 3 a R = . B. R = . C. a 3 R = .
D. R = a . 2 2 3
Câu 2: Tam giác ABC có a = 8, c = 3, B = 60°. Độ dài cạnh b bằng bao nhiêu? A. 49 . B. 97 . C. 7 . D. 61 . Câu 3: Cho A
∆ BC có a = 4, c = 5 , B =150°. Tính diện tích tam giác ABC . A. S =10 . B. S =10 3 . C. S = 5. D. S = 5 3 .
Câu 4: Một tam giác có ba cạnh là 52, 56, 60 . Bán kính đường tròn ngoại tiếp tam giác đó là A. 65 . B. 40 . C. 32,5. D. 65,8 . 4
Câu 5: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta
xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 60°. Biết
CA = 200(m) , CB =180(m) . Khoảng cách AB bằng bao nhiêu? A. 228(m) . B. 20 91(m) . C. 112(m) . D. 168(m).
Câu 6: Tam giác ABC có góc A nhọn, AB = 5, AC = 8, diện tích bằng 12. Tính độ dài cạnh BC. A. 2 3 . B. 4 . C. 5. D. 3 2 .
Câu 7: Tam giác ABC có AB = 4 , AC = 6 và trung tuyến BM = 3 . Tính độ dài cạnh BC . A. 17 . B. 2 5 . C. 4 . D. 8 .
Câu 8: Tam giác ABC có AB = 4 , AC =10 và đường trung tuyến AM = 6 . Tính độ dài cạnh BC . A. 2 6 . B. 5. C. 22 . D. 2 22 .
Câu 9: Tam giác ABC có = °
A 75 , B = 45°, AC = 2 . Tính cạnh AB . Page 90
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. 2 . B. 6 . C. 6 . D. 6 . 2 2 3
Câu 10: Tam giác ABC có B = 60°, C = 45° , AB = 3. Tính cạnh AC . A. 3 6 . B. 3 2 . C. 6 . D. 2 6 . 2 2 3
Câu 11: Tam giác ABC có các góc = °
A 75 , B = 45°. Tính tỉ số AB . AC A. 6 . B. 6 . C. 6 . D. 1,2 . 3 2
Câu 12: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết AB = c và os(A + B) 1 c = . 3 A. c 2 . B. 3c 2 . C. 9c 2 . D. 3c . 2 8 8 2
Câu 13: Tam giác ABC có các góc A =105°, B = 45°. Tính tỉ số AB . AC A. 2 . B. 2 . C. 2 . D. 6 . 2 2 3
Câu 14: Tam giác ABC có AB = 4 , AC = 5, BC = 6 . Tính cos(B + C) . A. 1 . B. 1 − . C. –0,125. D. 0,75. 8 4
Câu 15: Tam giác có ba cạnh lần lượt là 2,3,4 . Góc bé nhất của tam giác có sin bằng bao nhiêu? A. 15 . B. 7 . C. 1 . D. 14 . 8 8 2 8
Câu 16: Tam giác có ba cạnh lần lượt là 3, 8, 9. Góc lớn nhất của tam giác có cosin bằng bao nhiêu? A. 1 . B. 1 − . C. 17 . D. 4 − . 6 6 4 25
Câu 17: Hình vuông ABCD có cạnh bằng a . Gọi E là trung điểm cạnh BC , F là trung điểm cạnh AE
. Tìm độ dài đoạn thẳng DF .
A. a 13 . B. a 5 . C. a 3 . D. 3a . 4 4 2 4
Câu 18: Tam giác ABC có BC =12 ,CA = 9 , AB = 6. Trên cạnh BC lấy điểm M sao cho BM = 4. Tính
độ dài đoạn thẳng AM A. 2 5 . B. 3 2 . C. 20 . D. 19 .
Câu 19: Tam giác ABC vuông tại A có AB = AC = a . Điểm BC
M nằm trên cạnh BC sao cho BM = . 3
Độ dài AM bằng bao nhiêu?
A. a 17 . B. a 5 .
C. 2a 2 . D. 2a . 3 3 3 3
Câu 20: Tam giác ABC có ( + ) 1
cos A B = − , AC = 4 , BC = 5 . Tính cạnh AB 8 A. 46 . B. 11. C. 5 2 . D. 6 . Page 91
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
Câu 21: Tam giác ABC có AB = 7 , AC = 5 và (B +C) 1 cos
= − . Tính BC 5 A. 2 15 . B. 4 22 . C. 4 15 . D. 2 22 .
Câu 22: Tam giác ABC có BC = 5 , AC = 3 và cot C = 2 . Tính cạnh AB A. 6 . B. 2 . C. 9 . D. 2 10 . 5
Câu 23: Tam giác ABC có AB = 3, AC = 4 và tan A = 2 −
2 . Tính cạnh BC A. 3 2 . B. 4 3 . C. 33 . D. 7 .
Câu 24: Cho tam giác ABC có cạnh BC = a , cạnh CA = b . Tam giác ABC có diện tích lớn nhất khi góc C bằng: A. o 60 . B. o 90 . C. o 150 . D. o 120 .
Câu 25: Cho tam giác MPQ vuông tại P . Trên cạnh MQ lấy hai điểm E, F sao cho các góc MPE , EPF ,
FPQ bằng nhau. Đặt MP = q, PQ = , m PE = x,
PF = y . Trong các hệ thức sau, hệ thức nào đúng?
A. ME = EF = FQ . B. 2 2 2
ME = q + x − xq . C. 2 2 2
MF = q + y − yq . D. 2 2 2
MQ = q + m − 2qm .
Câu 26: Tính góc C của tam giác ABC biết a ≠ b và ( 2 2 − ) = ( 2 2 a a c b b − c ) . A. C =150° .
B. C =120° . C. C = 60° .
D. C = 30°.
Câu 27: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết AB =12 và 1 cot(A + B) = . 3 9 10 A. 2 10 . B. . C. 5 10 . D. 5 3 2 .
Câu 28: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết AB =10 và 1 tan(A + B) = . 3 5 10 10 A. . B. 10 . C. . D. 5 10 . 9 3 5
Câu 29: Tam giác ABC có AB = 4 , AC = 6 , 1 cos B = , 3
cosC = .Tính cạnh BC . 8 4 A. 7 . B. 5. C. 3 3. D. 2.
Câu 30: Cho tam giác cân ABC có 0
A =120 và AB = AC = a . Lấy điểm M trên cạnh BC sao cho 2BC BM =
. Tính độ dài AM 5 A. a 3 . B. 11a . C. a 7 . D. a 6 . 3 5 5 4
DẠNG 2: HỆ THỨC LIÊN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC, NHẬN DẠNG TAM GIÁC 1 PHƯƠNG PHÁP. Áp d
ụng các công thức sách giáo khoa như: định lí cosin, hệ quả của định lí cosin, định lí sin,
các công thức liên quan đến diện tích để vận dụng vào làm bài. Page 92
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 2
BÀI TẬP TỰ LUẬN.
Câu 1. Cho tam giác ABC thỏa sin A = 2cosC . Tam giác ABC là tam giác gì? sin B
Câu 2. Chứng minh trong tam giác ABC ta có: h = R B C a 2 .sin .sin
Câu 3. Cho tam giác ABC . Chứng minh S = .
R r.(sin A+ sin B + sinC) . 3 3 3
b + c − a 2
Câu 4. Cho tam giác ABC thỏa = a
b + c − a
. Chứng minh tam giác ABC là tam giác đều.
a = 2 .bcosC
Câu 5. Chứng minh trong tam giác ABC ta có: sin .
B cosC + sin C.cos B = sin A 3
BÀI TẬP TRẮC NGHIỆM.
Câu 1: Cho tam giác ABC , chọn công thức đúng trong các đáp án sau: 2 2 2 b c a 2 2 2 a c b A. 2 m + = + 2 m + = − a 2 4 . B. a 2 4 . 2 2 2 c b a 2 2 2 a b c C. 2 2 2 m + − = 2 m + = − a 4 . D. a 2 4 .
Câu 2: Trong tam giác ABC , câu nào sau đây đúng? A. 2 2 2
a = b + c + 2 .
bc cos A. B. 2 2 2
a = b + c − 2 .
bc cos A. C. 2 2 2
a = b + c + . bc cos A. D. 2 2 2
a = b + c − .
bc cos A .
Câu 3: Nếu tam giác ABC có 2 2 2
a < b + c thì: A. A là góc tù. B.
A là góc vuông. C. A là góc nhọn. D.
A là góc nhỏ nhất.
Câu 4: Tam giác ABC có ba cạnh thoả mãn điều kiện (a + b + c)(a + b − c) = 3ab . Khi đó số đo của C là A. 120°. B. 30° . C. 45°. D. 60°.
Câu 5: Cho tam giác ABC . Khẳng định nào sau đây là đúng? 2 4 A. 2 2 2
m + m + m = a + b + c 2 2 2 2 2 2
m + m + m = a + b + c a b c ( 2 2 2) 3 . B. a b c ( ) 3 . 1 3 C. 2 2 2
m + m + m = a + b + c 2 2 2 2 2 2
m + m + m = a + b + c a b c ( 2 2 2). D. a b c ( ). 3 4
Câu 6: Cho tam giác ABC thỏa mãn c = .
a cos B . Khẳng định nào sau đây là đúng?
A. Tam giác ABC là tam giác cân.
B. Tam giác ABC là tam giác nhọn.
C. Tam giác ABC là tam giác vuông.
D. Tam giác ABC là tam giác tù.
Câu 7: Diện tích S của tam giác sẽ thỏa mãn hệ thức nào trong hai hệ thức sau đây? I. 2
S = p( p − a)( p −b)( p − c) . II. 2
16S = (a + b + c)(a + b − c)(a −b + c)(−a + b + c) . A. Chỉ I. B. Chỉ II. C. Cả I và II. D. Không có. Page 93
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
Câu 8: Cho tam giác ABC , các đường cao h h h h = h + h
a , b , c thỏa mãn hệ thức 3 a
2 b c. Tìm hệ thức giữa
a, b, c . A. 3 2 1 = − .
B. 3a = 2b + c .
C. 3a = 2b − c . D. 3 2 1 = + . a b c a b c
Câu 9: Trong tam giác ABC , hệ thức nào sau đây sai? A. . b sin A a = . B. .sin sin c A C = . C. a = 2 . R sin A . D. b = . R tan B . sin B a
Câu 10: Cho tam giác ABC thỏa mãn hệ thức b + c = 2a . Trong các mệnh đề sau, mệnh đề nào đúng?
A. cos B + cosC = 2cos A .
B. sin B + sin C = 2sin A . C. 1
sin B + sin C = sin A .
D. sin B + cosC = 2sin A. 2
Câu 11: Tam giác ABC có A =120° thì câu nào sau đây đúng? A. 2 2 2
a = b + c − 3bc . B. 2 2 2
a = b + c + bc . C. 2 2 2
a = b + c + 3bc . D. 2 2 2
a = b + c − bc .
Câu 12: Trong tam giác ABC , điều kiện để hai trung tuyến vẽ từ A và B vuông góc với nhau là: A. 2 2 2
2a + 2b = 5c . B. 2 2 2
3a + 3b = 5c . C. 2 2 2
2a + 2b = 3c . D. 2 2 2
a + b = 5c .
Câu 13: Trong tam giác ABC , nếu có 2 a = . b c thì : 1 1 1 1 1 1 1 2 2 A. = − . B. 2 h = h h = + = + a b. . C. . D. . 2 h h h c 2 h h h 2 h h h a b c a b c a b c
Câu 14: Trong tam giác ABC , nếu có 2h = h + h a b c thì : A. 2 1 1 = + .
B. 2sin A = sin B + sin C .
sin A sin B sin C
C. sin A = 2sin B + 2sin C . D. 2 1 1 = − .
sin A sin B sin C
Câu 15: Trong tam giác ABC , câu nào sâu đây đúng? A. b c m + = . B. b c m + > . C. b c m + < .
D. m = b + c . a 2 a 2 a 2 a
Câu 16: Tam giác ABC có các cạnh a, b , c thỏa mãn điều kiện (a + b + c)(a + b − c) = 3ab . Tính số đo của góc C . A. 45°. B. 60° . C. 120°. D. 30° .
Câu 17: Cho tam giác ABC , xét các bất đẳng thức sau:
I. a − b < c .
II. a < b + c .
III. m + m + m < a + b + c . a b c
Hỏi khẳng định nào sau đây đúng?
A. Chỉ I, II.
B. Chỉ II, III.
C. Chỉ I, III.
D. Cả I, II, III.
Câu 18: Tam giác ABC có các cạnh a , b , c thỏa mãn điều kiện 2 2 2
b + c − a = 3bc . Tính số đo của góc A . A. 45°. B. 60°. C. 120°. D. 30° .
Câu 19: Tam giác ABC . a cos B = .
b cos A . Tam giác ABC là tam giác gì? A. Tam giác vuông. B. Tam giác đều.
C. Tám giác vuông cân D. Tam giác cân.
Câu 20: Cho tam giác ABC vuông tại A , AC = b , AB = c . Lấy điểm M trên cạnh BC sao cho góc
BAM = 30° Tính tỉ số MB . MC Page 94
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. b 3 . B. 3c . C. 3c .
D. b − c . 3c 3b b b + c
Câu 21: Mệnh đề nào sau đây sai? A. Nếu 2 2 2
a > b + c thì A là góc tù.
B. Nếu tam giác ABC có một góc tù thì 2 2 2
a > b + c . C. Nếu 2 2 2
a < b + c thì A là góc nhọn. D. Nếu 2 2 2
a = b + c thì A là góc vuông.
DẠNG 3: ỨNG DỤNG THỰC TẾ 1 PHƯƠNG PHÁP. Áp d
ụng các công thức sách giáo khoa như: định lí cosin, hệ quả của định lí cosin, định lí sin,
các công thức liên quan đến diện tích để vận dụng vào làm bài. 2
BÀI TẬP TỰ LUẬN.
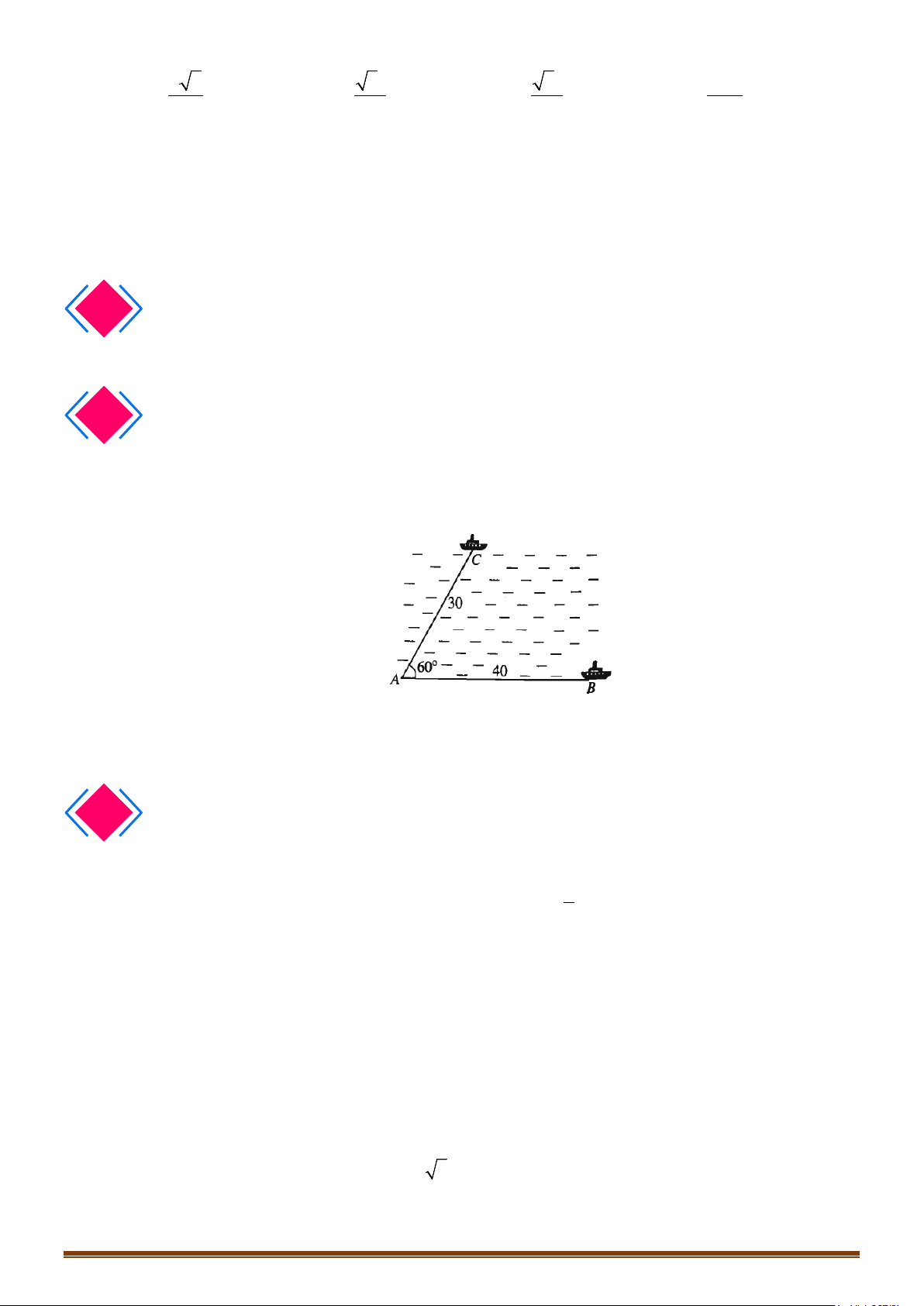
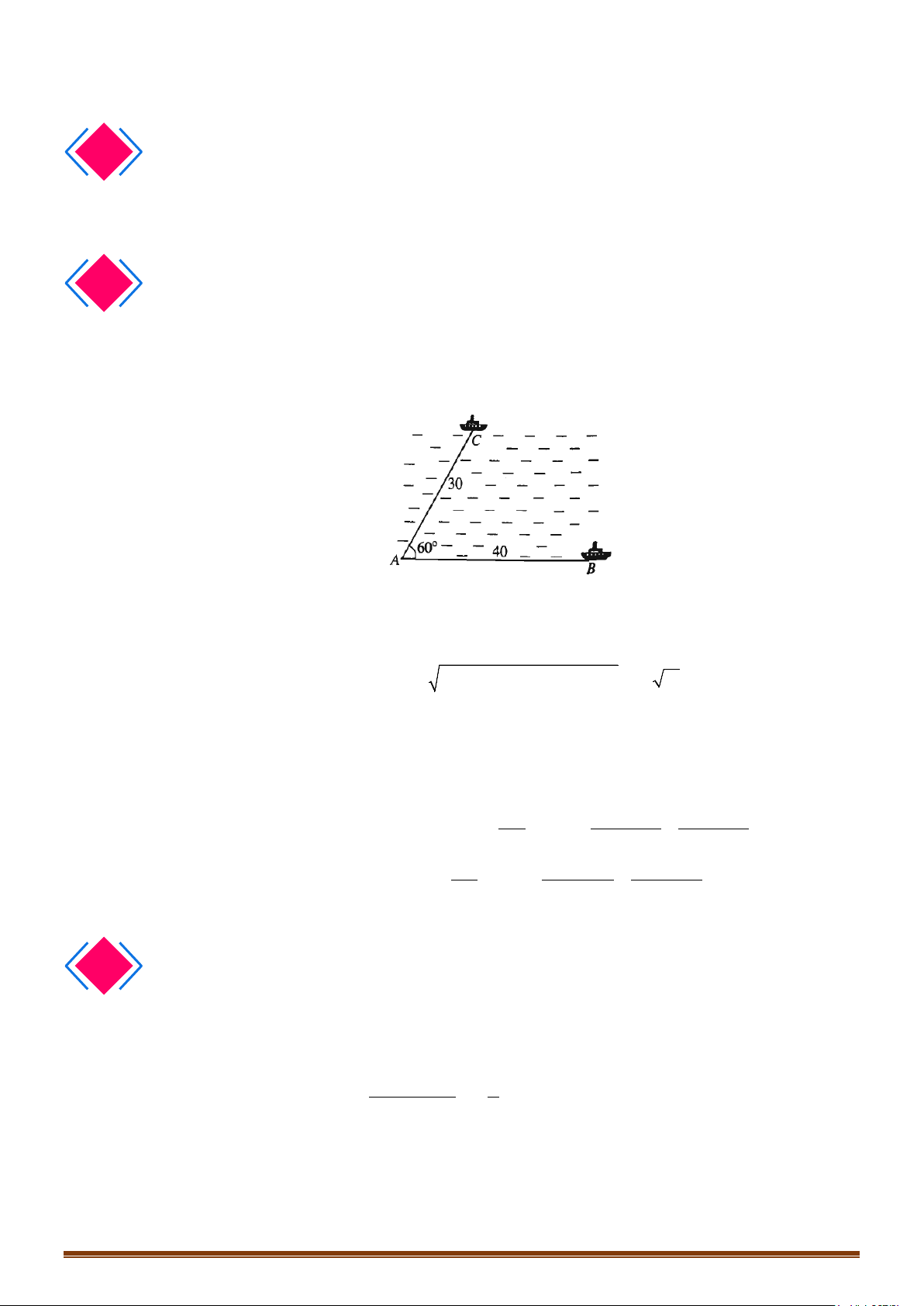
Câu 1: Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 0 60
. Tàu thứ nhất chạy với tốc độ 30km / h , tàu thứ hai chạy với tốc độ 40km / h . Hỏi sau 2 giờ hai
tàu cách nhau bao nhiêu km ?
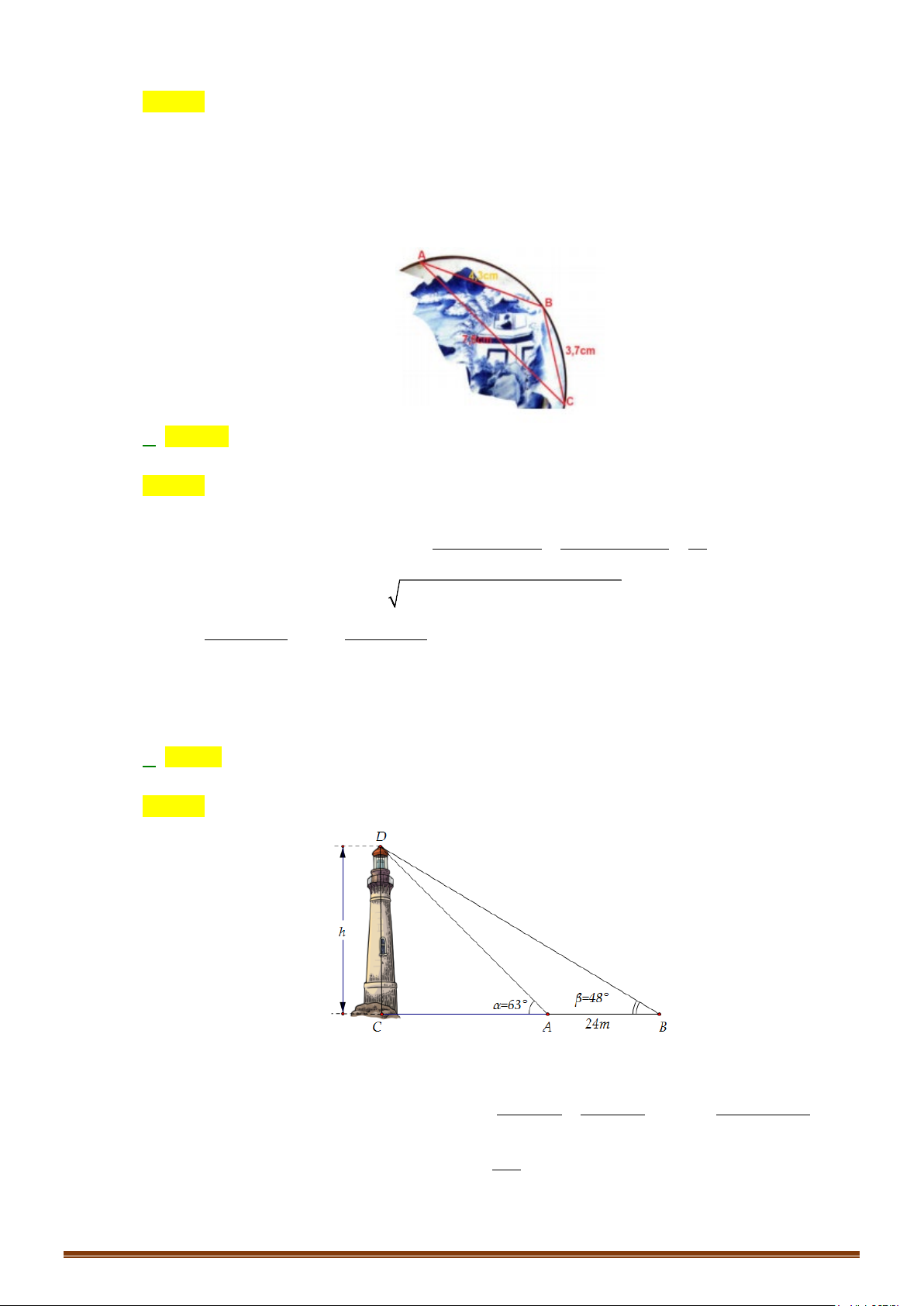
Câu 2: Từ một đỉnh tháp chiều cao CD = 80m , người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là 0 72 12' và 0
34 26' so với phương nằm ngang. Ba điểm ,
A B, D thẳng hàng. Tính
khoảng cách AB (chính xác đến hàng đơn vị)?
BÀI TẬP TỰ LUẬN TỔNG HỢP.
Câu 3: C ho tam giác ABC có a =13,b = 8,c = 7 . Tính góc A, suy ra S, ha, R, r, ma. Câu 4: Cho tam giác 3
ABC có AB 4, AC 5 và cosA . Tính cạnh BC, và độ dài đường cao 5 kẻ từ A .
Câu 5: Cho tam giác ABC có AB , 10 AC 4 và A 0 60 .
a) Tính chu vi của tam giác b) Tính tanC
Câu 6: Giải tam giác ABC biết 0 A B 0 60 , 40 và c 14 .
Câu 7: Giải tam giác ABC , biết: 0 b A C 0 4,5; 30 ; 75
Câu 8: Cho tam giác ABC cân tại A biết a = B = 0 3;
C = 30 . Tính R, r, cạnh c, b, suy ra S Page 95
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
Câu 9: Cho tam giác ABC nội tiếp đường tròn bán kính bằng 3, biết 0 0
A 30 , B 45 . Tính độ dài
trung tuyến kẻ từ A và bán kính đường tròn nội tiếp tam giác.
Câu 10: Cho tam giác ABC thỏa mãn 2
sin A sin B.sinC . Chứng minh rằng a) 2 a bc b) 1 cos A 2
Câu 11: Tam giác ABC có BC a, CA ,
b AB c và trung tuyến AM AB c chứng minh rằng: 2 2 2 a)
a 2(b c ) 2 2 2 b)
sin A 2(sin B sin C )
Câu 12: Cho tam giác ABC . Chứng minh rằng điều kiện cần và đủ để hai trung tuyến kẻ từ B và C vuông góc với nhau là 2 2 2
b c 5a .
Câu 13: Chứng minh rằng trong mọi tam giác ABC ta có; a) a . b cosC . c cos B
b) sinA sinB cosC sinC cosB
Câu 14: Chứng minh rằng trong mọi tam giác ABC ta có: h 2R sinB sinC a
Câu 15: Tìm tính chất đặc biệt của tam giác ABC biết: 2acos A = .
b cosC + .ccos B a
2b cosC (1)
Nhận dạng tam giác ABC biết: 3 3 3 2 a b c a (2) Câu 16:
a b c
Câu 17: Nhận dạng tam giác ABC biết: a.sinA b sinB c sinC h h h a b c
Câu 18: Cho tam giác ABC . Chứng minh tam giác ABC cân nếu h . c sin A a Page 96
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC G
ƠN IV HỆ THỨC LƯỢNG HƯ TRONG TAM GIÁC C
BÀI 2. ĐỊNH LÝ COSIN VÀ ĐỊNH LÝ SIN
BÀI 3. GIẢI TAM GIÁC VÀ ỨNG DỤNG THỰC TẾ I LÝ THUYẾT. Cho tam giác ABC, BC = a, CA = b, ,
AB = c S là diện tích tam giác. Giả sử h h h lần lượt a , b , c
là độ dài các đường cao đi qua ba đỉnh ,
A B,C; m m m lần lượt là các đường trung tuyến đi a , b , c qua ba đỉnh ,
A B,C. R và r lần lượt là bán kính đường tròn ngoại tiếp và nột tiếp của tam giác
ABC . Ta có kết quả sau đây:
1. Định lí côsin trong tam giác 2 2 2
a = b + c − 2 . bc cos , A 2 2 2
b = c + a − 2c . a cos B, 2 2 2
c = a + b − 2 . ab cosC.
*Hệ quả của định lí côsin 2 2 2 2 2 2 2 2 2 cos
b + c − a = , cos
a + c − b = ,cos
b + a − c A B C = . 2bc 2ac 2ab
2. Định lí sin trong tam giác: a b c = = = 2 . R sin A sin B sinC
*Hệ quả của định lí sin a = 2 . R sin A b = 2 . R sin B c = 2 . R sin C sin a A = 2R sin b B = 2R sin c C = 2R
3. Các công thức tính diện tích tam giác: 1) 1 1 1
S = ah = bh = ch a b c . 2 2 2 1 1 1
2) S = bcsin A = casin B = absin C 2 2 2 Page 1
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 3) abc S = 4R 1
4) S = pr với p = (a + b + c) 2
5) Công thức Hê- Rông S = p( p − a)( p − b)( p − c) 4. Giải tam giác.
Giải tam giác là tìm số đo các cạnh còn lại và các góc còn lại của tam giác khi biết một số yếu tố cho trước.
Để giải tam giác ta sử dụng một cách hợp lý các công cụ là: Định lý cosin, định lý sin và công
thức về diện tích tam giác.
5. Áp dụng giải tam giác vào thực tế.
Vận dụng giải tam giác giúp chúng ta giải quyết rất nhiều bài toán trong thực tế, đặc biệt là trong thiết kế và xây dựng.
Ví dụ 1. Trên nóc một tòa nhà có một cột ăng-ten
cao 5 m. Từ một vị trí quan sát A cao 7 m so
với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-
ten, với các góc tương ứng
là 50° và 40° so với phương nằm ngang (H.3.18).
a) Tính các góc của tam giác ABC.
b) Tính chiều cao của tòa nhà. Lời giải a) Ta có
BAC = 50° − 40° =10°, = °− = ° ⇒ = ° − − ABC 90 BAD 40 ACB 180 ABC BAC =130°
b) Áp dụng định lý sin trong tam giác ABC ta có BC AC
BC.sin B 5.sin 40 AC ° = ⇒ = = ≈ 18,51. sin A sin B sin A sin10°
Xét tam giác ACD vuông tại D có CD = AC.sin 40° ≈11,9
Vậy chiều cao của tòa nhà là: 11,9 + 7 =18,9 . m
Ví dụ 2. Từ bãi biển Vũng Chùa, Quảng Bình, ta có thể ngắm được
Đảo Yến. Hãy đề xuất một cách xác định bề rộng của hòn
đảo (theo chiều ta ngắm được). Đảo Yến nhìn từ bãi biển
Vũng Chùa, Quảng Bình Lời giải Page 2
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Gọi ,
A B là hai vị trí ngoài cùng mà ta quan sát khi nhìn từ bãi biển
Từ một điểm C trên bãi biển dùng giác kế ta xác định được góc ACB = α .
Lấy điểm D trên bãi biển sao cho ,
A C, D thẳng hàng và
có độ dài đoạn CD = a mét. Ta xác định được ADB = β .
Từ đó áp dụng định lí sin cho hai tam giác BCD và ABC ta xác định được bề rộng AB của hòn đảo.
Ví dụ 3. Để tránh núi, đường giao thông hiện tại
phải đi vòng như mô hình trong Hình 3.19.
Để rút ngắn khoảng cách và tránh sạt lở núi,
người ta dự định làm đường hầm xuyên núi,
nối thẳng từ A tới D . Hỏi độ dài đường mới
sẽ giảm bao nhiêu kilômét so với đường cũ? Lời giải
Dựng CE, BF vuông góc với AD .
Xét tam giác CDE vuông tại E có = D C = 45° ⇒ DE = C .
D sin 45° = 6 2 k . m
Xét tam giác ABF vuông tại F có B =15° ⇒ AF = A .
B sin15° = (2 6 − 2 2 )k . m
Mặt khác EF = BC = 6km
⇒ AD = DE + EF + FA = 6 + 4 2 + 2 6 ≈16,56k . m
Vậy độ dài đường mới sẽ giảm 9,44km so với đường cũ.
II HỆ THỐNG BÀI TẬP.
DẠNG 1: GIẢI TAM GIÁC
{Tìm một số yếu tố của tam giác khi cho biết các yếu tố khác.} 1 PHƯƠNG PHÁP. Page 3
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
+ Áp dụng các công thức sách giáo khoa như: định lí cosin, hệ quả của định lí cosin, định lí sin,
các công thức liên quan đến diện tích để vận dụng vào làm bài. 2
BÀI TẬP TỰ LUẬN.
Câu 1. Cho tam giác ABC có = = 0
AB 4, AC 6, A =120 . Tính độ dài cạnh BC Lời giải 2 2 2 2 2 0
BC = AB + AC − 2 .
AB AC.cosA = 6 + 4 − 2.6.4.cos120 2 2 1 6 4 2.6.4. − = + −
= 76 ⇒ BC = 76 = 2 19. 2
Câu 2. Cho tam giác ABC có a = 7;b = 8;c = 5 . Tính , A S,h R a , . Lời giải 2 2 2 2 2 2 +
b + c − a 8 + 5 − 7 1 cos A = = = ⇒ A = 60° . 2bc 2.8.5 2 + 1 1 S = .
b .csin A = .8.5.sin 60° =10 3 . 2 2 + Ta có: 1 2S 2.10 3 20 3 S = . a h ⇒ h = = = . 2 a a a 7 7 + Ta có: . a . b c . a . b c 7.8.5 7 3 S = ⇒ R = = = . 4R 4S 4.10 3 3
Câu 3. Cho tam giác ABC có độ dài ba cạnh là AB = 2 , BC = 5 , CA = 6. Tính độ dài đường trung tuyến
MA, với M là trung điểm của BC . Lời giải
Áp dụng công thức tình độ dài trung tuyến ta có: 2 2 2 AB AC BC 2 2 2 MA + + = − 2 6 5 55 = − = . 2 4 2 4 2
Câu 4. Tam giác ABC vuông tại A có AC = 6 cm , BC =10 cm . Tính bán kính đường tròn nội tiếp tam giác ABC . Lời giải
Do tam giác ABC vuông tại A có AC = 6 cm , BC =10 cm nên 2 2
AB = BC − AC 2 2 = 10 − 6 = 8 .
Diện tích tam giác ABC là 1 S = = 24 . ∆ AB AC ABC . 2
Bán kính đường tròn nội tiếp tam giác ABC là 2S 2.24 ABC r ∆ = = = 2 .
AB + BC + CA 6 + 8 +10
Câu 5. Cho tam giác ABC có b = 7 , c = 5 , 3
cos A = . Tính độ dài đường cao h của tam giác ABC . 5 a Page 4
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Lời giải A c b ha B H a C
Theo định lí hàm cos ta có 2 2 2
a = b + c − 2bccos A 3
= 49 + 25 − 2.7.5. = 32 ⇒ a = 4 2 . 5 Ta lại có: 3 cos A = 4 ⇒ sin A = . 5 5
Diện tích tam giác ABC là 1 S = 1 4 = .7.5. =14 . ∆ bc A ABC sin 2 2 5 Vì 1 S = nên 2S 7 2 ABC h ∆ = 28 = = ∆ a h ABC . 2 a a a 4 2 2 Vậy 7 2 h = . a 2 3
BÀI TẬP TRẮC NGHIỆM. Câu 1: Cho A
∆ BC có BC = a ,
BAC =120° . Bán kính đường tròn ngoại tiếp A ∆ BC là A. a 3 a R = . B. R = . C. a 3 R = .
D. R = a . 2 2 3 Lời giải Chọn D
Theo định lý sin trong tam giác ta có 2 BC 1 a a 3 R = ⇒ = = . R . sin BAC 2 sin120° 3
Câu 2: Tam giác ABC có a = 8, c = 3, B = 60°. Độ dài cạnh b bằng bao nhiêu? A. 49 . B. 97 . C. 7 . D. 61 . Lời giải Chọn C 2 2 2
b = a + c − 2accos B 2 2
= 8 + 3 − 2.8.3cos60° = 49 ⇒ b = 7 . Câu 3: Cho A
∆ BC có a = 4, c = 5 , B =150°. Tính diện tích tam giác ABC . A. S =10 . B. S =10 3 . C. S = 5. D. S = 5 3 . Lời giải Page 5
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Chọn C
Diện tích tam giác ABC là 1 = S acsin B 1 = .4.5sin150° = 5 . 2 2
Câu 4: Một tam giác có ba cạnh là 52, 56, 60 . Bán kính đường tròn ngoại tiếp tam giác đó là A. 65 . B. 40 . C. 32,5. D. 65,8 . 4 Lời giải Chọn C Ta có: 52 56 60 p + + = = 84 . 2
Áp dụng hệ thức Hê – rông ta có: S = 84(84 −52)(84 −56)(84 − 60) =1344 . Mặt khác abc S = abc ⇒ R = 52.56.60 = = 32,5. 4R 4S 4.1344
Câu 5: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta
xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 60°. Biết
CA = 200(m) , CB =180(m) . Khoảng cách AB bằng bao nhiêu? A. 228(m) . B. 20 91(m) . C. 112(m) . D. 168(m). Lời giải Chọn B 2 2 2
AB = CA + CB − 2 . CA .
CB cos60° = 36400 ⇒ AB = 20 91(m) .
Câu 6: Tam giác ABC có góc A nhọn, AB = 5, AC = 8, diện tích bằng 12. Tính độ dài cạnh BC. A. 2 3 . B. 4 . C. 5. D. 3 2 . Lời giải Chọn C Ta có: 1 2S 2.12 3 = ⇒ = = = ⇒ S .A . B AC.sin A sin A A = 36 52 ° 12 ′ ′′ 2 A . B AC 5.8 5 2 2 2 2 2
BC = AB + AC − 2.A .
B AC.cos A = 5 + 8 − 2.5.8.cos36 52 ° 12
′ ′′ ≈ 25 ⇒ BC ≈ 5 .
Câu 7: Tam giác ABC có AB = 4 , AC = 6 và trung tuyến BM = 3 . Tính độ dài cạnh BC . Page 6
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. 17 . B. 2 5 . C. 4 . D. 8 . Lời giải Chọn B B 4 3 A 6 M C 2 2 2 Ta có: 2 AB BC AC BM + = − 2 4 2 2 2 AC 2
⇒ BC = 2 BM + − AB 4 2 2 6 2
= 23 + − 4 = 20 ⇒ BC = 2 5 . 4
Câu 8: Tam giác ABC có AB = 4 , AC =10 và đường trung tuyến AM = 6 . Tính độ dài cạnh BC . A. 2 6 . B. 5. C. 22 . D. 2 22 . Lời giải Chọn D A 4 10 6 B M C 2 2 2 Ta có: 2 AC AB BC AM + = − 2 4 2 2 2 2 + + 2 AC AB 2 10 4 2 ⇒ BC = 4 − AM = 4
− 6 = = 88 ⇒ BC = 2 22 . 2 2
Câu 9: Tam giác ABC có = °
A 75 , B = 45°, AC = 2 . Tính cạnh AB . A. 2 . B. 6 . C. 6 . D. 6 . 2 2 3 Lời giải Chọn B Ta có: b c .
b sin C AC.sin C 2.sin(180 − 75 − 45 ) = ⇒ AB = c = = = = 6 . sin B sin C sin B sin B sin 45 Page 7
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC .
Câu 10: Tam giác ABC có B = 60°, C = 45° , AB = 3. Tính cạnh AC . A. 3 6 . B. 3 2 . C. 6 . D. 2 6 . 2 2 3 Lời giải Chọn A Ta có: b c . c sin B A . B sin B 3.sin 60 3. 6 = ⇒ AC = b = = = = . sin B sin C sin C sin C sin 45 2
Câu 11: Tam giác ABC có các góc = °
A 75 , B = 45°. Tính tỉ số AB . AC A. 6 . B. 6 . C. 6 . D. 1,2 . 3 2 Lời giải Chọn C Ta có: b c
AB c sin C sin(180° − 75° − 45 ) ° 6 = ⇒ = = = = . sin B sin C AC b sin B sin 45° 2
Câu 12: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết AB = c và os(A + B) 1 c = . 3 A. c 2 . B. 3c 2 . C. 9c 2 . D. 3c . 2 8 8 2 Lời giải Chọn B Ta có 1
cosC = −cos(A + B) = − . 3 2 Do đó 1 2 2 sin C = 1− − = . 3 3 AB AB 3 2 = 2 c R ⇒ R = = . sin C 2sin C 8
Câu 13: Tam giác ABC có các góc A =105°, B = 45°. Tính tỉ số AB . AC A. 2 . B. 2 . C. 2 . D. 6 . 2 2 3 Lời giải. Chọn A Page 8
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Ta có: b c
AB c sin C sin(180° −105° − 45 ) ° 2 = ⇒ = = = = . sin B sin C AC b sin B sin 45° 2
Câu 14: Tam giác ABC có AB = 4 , AC = 5, BC = 6 . Tính cos(B + C) . A. 1 . B. 1 − . C. –0,125. D. 0,75. 8 4 Lời giải. Chọn C
Ta có c = AB = 4 , b = AC = 5 , a = BC = 6. 2 2 2 Tính
b + c − a 1 cos A = = . . 2 . b c 8 Để ý 1
cos(B + C) = − cos A = − = − 125 , 0 . 8
Câu 15: Tam giác có ba cạnh lần lượt là 2,3,4 . Góc bé nhất của tam giác có sin bằng bao nhiêu? A. 15 . B. 7 . C. 1 . D. 14 . 8 8 2 8 Lời giải. Chọn A
Góc bé nhất ứng với cạnh có số đo bé nhất. 2 2 2 Giả sử a + − = , 2 b = , 3 c = 4. Ta có b c a 7 cos A = = . 2. . b c 8 2 Do đó 7 15 sin A = 1 − = . 8 8
Câu 16: Tam giác có ba cạnh lần lượt là 3, 8, 9. Góc lớn nhất của tam giác có cosin bằng bao nhiêu? A. 1 . B. 1 − . C. 17 . D. 4 − . 6 6 4 25 Lời giải Chọn B 2 2 2
Góc lớn nhất tương ứng với cạnh lớn nhất: 3 8 9 1 cosα + − = = − . 2.3.8 6
Câu 17: Hình vuông ABCD có cạnh bằng a . Gọi E là trung điểm cạnh BC , F là trung điểm cạnh AE
. Tìm độ dài đoạn thẳng DF .
A. a 13 . B. a 5 . C. a 3 . D. 3a . 4 4 2 4 Lời giải Chọn A Page 9
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A B F E D C 2 Ta có: 2 a a 5 AE DE a = = + = 2 2
Dùng công thức độ dài trung tuyến: 2 2 5a 2 2 2 a + 2 2 a 13 2 DA + DE AE 4 5a 13a DF = − = − = ⇒ DF = . 2 4 2 16 16 4
Câu 18: Tam giác ABC có BC =12 ,CA = 9 , AB = 6. Trên cạnh BC lấy điểm M sao cho BM = 4.
Tính độ dài đoạn thẳng AM A. 2 5 . B. 3 2 . C. 20 . D. 19 . Lời giải Chọn D 2 2 2 2 2 2
AB + BC − AC 6 +12 − 9 11 cos B = = = 2A . B BC 2.6.12 16 2 2 2 2 11
AM = AB + BM − 2A .
B BM.cosB = 6 + 4 − 2.6.4. = 19 . 16
Câu 19: Tam giác ABC vuông tại A có AB = AC = a . Điểm BC
M nằm trên cạnh BC sao cho BM = . 3
Độ dài AM bằng bao nhiêu? A a 17 . B. a 5 .
C. 2a 2 . D. 2a . 3 3 3 3 Lời giải Chọn B A C M B Page 10
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 2 2 2 2
BC = AB + AC = a + a = a 2 a 2
BC = AB 2 = a 2 ⇒ BM = 3 2 2 2 0 2 a 2 a 2 2 a 5
AM = AB + BM − 2A .
B BM.cos 45 = a + − 2 . a . = . 3 3 2 3
Câu 20: Tam giác ABC có ( + ) 1
cos A B = − , AC = 4 , BC = 5 . Tính cạnh AB 8 A. 46 . B. 11. C. 5 2 . D. 6 . Lời giải Chọn A
Vì trong tam giác ABC ta có A+ B bù với góc C nên ( A+ B) 1 1 cos = − ⇒ cosC = 8 8 2 2 2 2 1
AB = AC + BC − 2A .
B BC.cosC = 4 + 5 − 2.4.5. = 6 . 8
Câu 21: Tam giác ABC có AB = 7 , AC = 5 và (B +C) 1 cos
= − . Tính BC 5 A. 2 15 . B. 4 22 . C. 4 15 . D. 2 22 . Lời giải Chọn A
Vì trong tam giác ABC ta có B + C bù với góc A nên ( + ) 1 cos B C = − 5 1 ⇒ cos A = 5 2 2 2 2 1
BC = AB + AC − 2A .
B AC.cosA = 7 + 5 − 2.7.5. = 2 15 . 5
Câu 22: Tam giác ABC có BC = 5 , AC = 3 và cot C = 2 . Tính cạnh AB A. 6 . B. 2 . C. 9 . D. 2 10 . 5 Lời giải Chọn B
Từ giả thiết cot C = 2 , ta suy ra C là góc nhọn 1 2 1 1 4 2
cot C = 2 ⇒ tan C = ⇒ cos C = = = ⇒ cosC = 2 2 2 1+ tan C 1 5 5 1+ − 2 2 2 2 2 2
AB = AC + BC − 2A .
B BC.cosC = 3 + 5 − 2.3. 5. = 2 . 5 Page 11
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
Câu 23: Tam giác ABC có AB = 3, AC = 4 và tan A = 2 −
2 . Tính cạnh BC A. 3 2 . B. 4 3 . C. 33 . D. 7 . Lời giải Chọn C
Từ giả thiết tan A = 2 −
2 , ta suy ra A là góc tù 2 1 1 1 1 tan A = 2 − 2 ⇒ cos A = = = ⇒ cos A = − 2 2 1+ tan A 1+ (2 2) 9 3 2 2 2 2 1 BC AB AC 2A . B AC.cosA 3 4 2.3.4. = + − = + − − = 33 . 3
Câu 24: Cho tam giác ABC có cạnh BC = a , cạnh CA = b . Tam giác ABC có diện tích lớn nhất khi góc C bằng: A. o 60 . B. o 90 . C. o 150 . D. o 120 . Lờigiải Chọn B
Diện tích của tam giác ABC là: 1 S = . a . b sin C 2
S lớn nhất khi sin C lớn nhất, hay = ⇒ sin 1 = 90o C C .
Câu 25: Cho tam giác MPQ vuông tại P . Trên cạnh MQ lấy hai điểm E, F sao cho các góc MPE , EPF ,
FPQ bằng nhau. Đặt MP = q, PQ = , m PE = x,
PF = y . Trong các hệ thức sau, hệ thức nào đúng?
A. ME = EF = FQ . B. 2 2 2
ME = q + x − xq . C. 2 2 2
MF = q + y − yq . D. 2 2 2
MQ = q + m − 2qm . Lờigiải Chọn C M E q x F y m P Q
Từ giả thiết, suy ra = = MPQ MPE EPF FPQ = = 30o 3
Tam giác MPF có = + = 60o MPF MPE EPF ; Page 12
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 2 2 2 = + − MF MP PF 2. . MP PF.cosMPF 2 2 1 2 2 = q + y − 2. . y .
q = q + y − yq . 2
Câu 26: Tính góc C của tam giác ABC biết a ≠ b và ( 2 2 − ) = ( 2 2 a a c b b − c ) . A. C =150° .
B. C =120° . C. C = 60° .
D. C = 30°. Lời giải Chọn C Ta có: ( 2 2 − ) = ( 2 2 a a c b b − c ) 3 3 2
⇔ a −b − c (a −b) = 0 ⇔ (a − b)( 2 2
a + ab + b ) 2
− c (a − b) = 0 2 2 2
a + b − c 2 2 2
⇔ a + ab + b − c = 0 ⇒ cosC = 1 2 C = ° . ab = − . Do đó: 120 2
Câu 27: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết AB =12 và 1 cot(A + B) = . 3 9 10 A. 2 10 . B. . C. 5 10 . D. 5 3 2 . Lời giải Chọn A Ta có: 1
cot(A + B) = nên 1
cot C = − , suy ra 3cosC = −sin C . 3 3 Mà 3 3 10 2 2
sin C + cos C = 1 ⇒ sin C = = . 10 10 AB = 2 AB R ⇒ R = = 2 10 . sin C 2sin C
Câu 28: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết AB =10 và 1 tan(A + B) = . 3 5 10 10 A. . B. 10 . C. . D. 5 10 . 9 3 5 Lời giải Chọn D Ta có: 1
tan(A + B) = nên 1 tan C = − . 3 3
Do đó 3sin C = −cosC , mà 1 10 2 2
sin C + cos C = 1 ⇒ sin C = = . 10 10 AB = 2 AB R ⇒ R = = 5 10 . sin C 2sin C
Câu 29: Tam giác ABC có AB = 4 , AC = 6 , 1 cos B = , 3
cosC = .Tính cạnh BC . 8 4 Page 13
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. 7 . B. 5. C. 3 3. D. 2. Lời giải. Chọn B 2 63
sin B = 1− cos B = , 2 7
sin C = 1− cos C = . 8 4 9
cos A = − cos(B + C) = sin .
B sin C − cos . B cosC = . 16 Do đó 2 2
BC = AB + AC − . 2 .
AB AC.cos A = 5.
Câu 30: Cho tam giác cân ABC có 0
A =120 và AB = AC = a . Lấy điểm M trên cạnh BC sao cho 2BC BM =
. Tính độ dài AM 5 A. a 3 . B. 11a . C. a 7 . D. a 6 . 3 5 5 4 Lời giải Chọn C A a C a M 30 B 2a 3 2 2 0 2 2 1 BC AB AC 2ABAC cos120 a a 2 . a . a = + − = + − − = a 3 ⇒ BM = 2 5 2 2 2 0 2 2a 3 2a 3 3 a 7
AM = AB + BM − 2A .
B BM.cos30 = a + − 2 . a . = . 5 5 2 5
DẠNG 2: HỆ THỨC LIÊN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC, NHẬN DẠNG TAM GIÁC 1 PHƯƠNG PHÁP.
Áp dụng các công thức sách giáo khoa như: định lí cosin, hệ quả của định lí cosin, định lí sin,
các công thức liên quan đến diện tích để vận dụng vào làm bài. 2
BÀI TẬP TỰ LUẬN.
Câu 1. Cho tam giác ABC thỏa sin A = 2cosC . Tam giác ABC là tam giác gì? sin B Lời giải Page 14
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 2 2 2
a + b − c
Ta có: sin A = 2cosC a ⇔
= 2cosC ⇔ a = 2 .
b cosC ⇔ a = 2 .b sin B b 2ab 2 2 2 2
⇔ a = a + b − c ⇔ b = c
Tam giác ABC cân tại A.
Câu 2. Chứng minh trong tam giác ABC ta có: h = R B C a 2 .sin .sin Lời giải
Áp dụng định lí sin trong tam giác ta có: b = 2R ⇒ 2 .
R sin B = b sin B
Do đó: h = R
B C ⇔ h = b C a .sin a 2 .sin .sin ( đúng)
Câu 3. Cho tam giác ABC . Chứng minh S = .
R r.(sin A+ sin B + sinC) . Lời giải a b c
a + b + c Ta có : VP = . R r. + + = r. = r.p = S ( đpcm).
2R 2R 2R 2 3 3 3
b + c − a 2
Câu 4. Cho tam giác ABC thỏa = a
b + c − a
. Chứng minh tam giác ABC là tam giác đều.
a = 2 .bcosC Lời giải 3 3 3 3 3 3 2 2 3
b + c − a b
+ c − a = a b + a c − a 2 2 2 2 = a
(b + c)(b −bc +c −a ) = 0 Ta có: + − ⇔ 2 2 2 b c a ⇔ 2 2 2
a = 2 . a + b − c
a + b − c = 2 .cos b a b C 2ab a = a 1 bc − + 2 . bc cosA = 0 cos A = A = 60° ⇔ ⇔ 2 ⇔ 2 2 b = c b = c b = c
Vì tam giác ABC cân có 1 góc bằng 60° nên tam giác ABC là tam giác đều.
Câu 5. Chứng minh trong tam giác ABC ta có: sin .
B cosC + sin C.cos B = sin A Lời giải 2 2 2 2 2 2 b 2 2 2 2 2 2 2 + − + − =
. a + b − c c +
. a + c −b VT a b c a c b 2a a = + = = = sin A 2 R 2ab 2R 2ac 4aR 4aR 4aR 2R 3
BÀI TẬP TRẮC NGHIỆM.
Câu 1: Cho tam giác ABC , chọn công thức đúng trong các đáp án sau: 2 2 2 b c a 2 2 2 a c b A. 2 m + = + 2 m + = − a 2 4 . B. a 2 4 . 2 2 2 c b a 2 2 2 a b c C. 2 2 2 m + − = 2 m + = − a 4 . D. a 2 4 . Lời giải Chọn C 2 2 2 2 2 2 b c a b c a
Theo công thức đường trung tuyến ta có 2 2 2 m + + − = − = a 2 4 4 .
Câu 2: Trong tam giác ABC , câu nào sau đây đúng? A. 2 2 2
a = b + c + 2 .
bc cos A. B. 2 2 2
a = b + c − 2 .
bc cos A. Page 15
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC C. 2 2 2
a = b + c + . bc cos A. D. 2 2 2
a = b + c − .
bc cos A . Lời giải Chọn B
Áp dụng định lí hàm số cos tại đỉnh A ta có: 2 2 2
a = b + c − 2 . bc cos A.
Câu 3: Nếu tam giác ABC có 2 2 2
a < b + c thì: A. A là góc tù. B.
A là góc vuông. C. A là góc nhọn. D.
A là góc nhỏ nhất. Lời giải Chọn C 2 2 2
b + c − a Ta có 2 2 2
a = b + c − 2bc cos A ⇒ cos A = 2 nên cos A > 0 bc do 2 2 2
a < b + c
Câu 4: Tam giác ABC có ba cạnh thoả mãn điều kiện (a + b + c)(a + b − c) = 3ab . Khi đó số đo của C là A. 120°. B. 30° . C. 45°. D. 60°. Lời giải Chọn D
Ta có: (a + b + c)(a + b − c) = ab ⇔ (a + b)2 2 2 2 2 3
− c = 3ab ⇔ a + b − c = ab . 2 2 2
a + b − c ab 1
Theo hệ quả của định lí hàm cosin: = = = ⇒ cos C C = 60° 2 . ab 2ab 2
Câu 5: Cho tam giác ABC . Khẳng định nào sau đây là đúng? 2 4 A. 2 2 2
m + m + m = a + b + c 2 2 2 2 2 2
m + m + m = a + b + c a b c ( 2 2 2) 3 . B. a b c ( ) 3 . 1 3 C. 2 2 2
m + m + m = a + b + c 2 2 2 2 2 2
m + m + m = a + b + c a b c ( 2 2 2) 3 . D. a b c ( ) 4 . Lời giải
Sử dụng công thức trung tuyến, ta có: 2 2 2 2 2 2 2 2 2 2 2 2
2b + 2c − a
2c + 2a − b
2a + 2b − c 3
m + m + m = + + = a + b + c a b c ( 2 2 2) 4 4 4 4
Câu 6: Cho tam giác ABC thỏa mãn c = .
a cos B . Khẳng định nào sau đây là đúng?
A. Tam giác ABC là tam giác cân.
B. Tam giác ABC là tam giác nhọn.
C. Tam giác ABC là tam giác vuông.
D. Tam giác ABC là tam giác tù Lời giải 2 2 2 2 2 2
a + c −b
a + c −b
Ta có: c = .acos B ⇔ c = .a ⇔ c = 2ac 2c 2 2 2
⇔ c + b = a
Theo định lí pi ta go tam giác ABC vuông tại A .
Câu 7: Diện tích S của tam giác sẽ thỏa mãn hệ thức nào trong hai hệ thức sau đây? I. 2
S = p( p − a)( p −b)( p − c) . Page 16
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC II. 2
16S = (a + b + c)(a + b − c)(a −b + c)(−a + b + c) . A. Chỉ I. B. Chỉ II. C. Cả I và II. D. Không có. Lời giải Chọn C
Ta có: I. đúng vì là công thức Hê-rông tính diện tích tam giác.
Khi đó: 2 a b c . a b c . a b c . a b c S + + + − − + − + + = 2 2 2 2 2
⇔ 16S = (a + b + c)(a + b − c)(a −b + c)(−a + b + c). Do đó II. đúng
Câu 8: Cho tam giác ABC , các đường cao h h h h = h + h
a , b , c thỏa mãn hệ thức 3 a
2 b c. Tìm hệ thức giữa
a, b, c . A. 3 2 1 = − .
B. 3a = 2b + c .
C. 3a = 2b − c . D. 3 2 1 = + . a b c a b c Lời giải Chọn D
Kí hiệu S = SABC .
Ta có: 3h = h + h 3.2S 2.2S 2S a 2 b c ⇔ = + 3 2 1 ⇔ = + . a b c a b c
Câu 9: Trong tam giác ABC , hệ thức nào sau đây sai? A. . b sin A a = . B. .sin sin c A C = . C. a = 2 . R sin A . D. b = . R tan B . sin B a Lời giải Chọn D
Theo định lí hàm số sin ta có: a b c = = = 2R sin A sinB sinC Suy ra: + a b . b sin A = ⇒ a = . sin A sinB sin B + a c . c sin = ⇒ sin A C = . sin A sinC a
+ a = 2R ⇒ a = 2 . R sin A. sin A + b = 2 b ⇒ = sin b R R B ⇒ = R tan B . sinB 2 2cosB
Câu 10: Cho tam giác ABC thỏa mãn hệ thức b + c = 2a . Trong các mệnh đề sau, mệnh đề nào đúng?
A. cos B + cosC = 2cos A .
B. sin B + sin C = 2sin A . C. 1
sin B + sin C = sin A .
D. sin B + cosC = 2sin A. 2 Lời giải Chọn B
a = 2Rsin A a b c Ta có = = = 2R ⇔ b = 2Rsin B .
sin A sin B sin C c = 2Rsin C Page 17
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
Mà b + c = 2a ⇔ 2Rsin B + 2Rsin C = 4Rsin A ⇔ sin B + sin C = 2sin A.
Câu 11: Tam giác ABC có A =120° thì câu nào sau đây đúng? A. 2 2 2
a = b + c − 3bc . B. 2 2 2
a = b + c + bc . C. 2 2 2
a = b + c + 3bc . D. 2 2 2
a = b + c − bc . Lời giải Chọn B
Áp dụng định lí hàm số cos tại đỉnh A ta có: 2 2 2
a = b + c − 2 . bc cos A. 2 2 2
⇒ a = b + c − 2 . bc os c 120° 2 2 2
⇒ a = b + c + bc .
Câu 12: Trong tam giác ABC , điều kiện để hai trung tuyến vẽ từ A và B vuông góc với nhau là: A. 2 2 2
2a + 2b = 5c . B. 2 2 2
3a + 3b = 5c . C. 2 2 2
2a + 2b = 3c . D. 2 2 2
a + b = 5c . Lời giải Chọn D
Vì hai trung tuyến vẽ từ A và B vuông góc với nhau nên ABG vuông tại G với G là trọng tâm tam giác ABC . 2 2 2 2 2 2 Khi đó: + + 2 2 2
c = GA + GB 2 4 b c a a c b ⇔ c = − + − 9 2 4 2 4 2 2 2 4 2 a b ⇔ c = c + + 2 2 2
⇔ 5c = a + b . 9 4 4
Câu 13: Trong tam giác ABC , nếu có 2 a = . b c thì : 1 1 1 1 1 1 1 2 2 A. = − . B. 2 h = h h = + = + a b. . C. . D. . 2 h h h c 2 h h h 2 h h h a b c a b c a b c Lời giải Chọn B 2 1 1 1 Ta có: 2 a = . b c 2S 2S 2 2 ⇔ = . S ⇔ = . ⇔ h = h h a b. . h 2 c h h h h h a b c a b c
Câu 14: Trong tam giác ABC , nếu có 2h = h + h a b c thì : A. 2 1 1 = + .
B. 2sin A = sin B + sin C .
sin A sin B sin C
C. sin A = 2sin B + 2sin C . D. 2 1 1 = − .
sin A sin B sin C Lời giải Chọn A Ta có :
2h = h + h 2 2 2 a b c ⇔ 2. S S S = + 2 1 1 ⇔ = + 2 1 1 ⇔ = + a b c a b c 2 . R sin A 2 . R sin B 2 . R sin C 2 1 1 ⇔ = + .
sin A sin B sin C
Câu 15: Trong tam giác ABC , câu nào sâu đây đúng? A. b c m + = . B. b c m + > . C. b c m + < .
D. m = b + c . a 2 a 2 a 2 a Lời giải Chọn C 2 2 2 b c a 2 2 2
b + c + b − c − a Ta có: 2 m + = − ( ) ( ) a = 2 4 4 Page 18
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC b + c 2 ( )2 Vì − < ⇒ ( − )2 2 b c a
b c < a ⇒ m < b c a 4 m + ⇔ < . a 2
Câu 16: Tam giác ABC có các cạnh a, b , c thỏa mãn điều kiện (a + b + c)(a + b − c) = 3ab . Tính số đo của góc C . A. 45°. B. 60° . C. 120°. D. 30° . Lời giải Chọn B
Ta có: (a + b + c)(a + b − c) = 3ab ⇔ (a + b)2 2
− c = 3ab ⇔ 2 2 2
a + b − c = ab . 2 2 2 Mà
a + b − c 1 cosC = = ⇒ C = 60° . 2ab 2
Câu 17: Cho tam giác ABC , xét các bất đẳng thức sau:
I. a − b < c .
II. a < b + c .
III. m + m + m < a + b + c . a b c
Hỏi khẳng định nào sau đây đúng?
A. Chỉ I, II.
B. Chỉ II, III.
C. Chỉ I, III.
D. Cả I, II, III. Lời giải Chọn D
Ta có I. và II. đúng vì đây là bất đẳng thức tam giác 2 2 2
(b + c)2 +(b −c)2 2 − a Ta có: 2 b c a m + = − = . a 2 4 4 b + c 2 ( )2 Vì − < ⇒ ( − )2 2 b c a
b c < a ⇒ m < b c m + ⇔ < . a 4 a 2 Tương tự ta có: a c m + < ; a c m + < . b 2 c 2
Do đó: m + m + m < a + b + c . a b c Vậy III. Đúng.
Câu 18: Tam giác ABC có các cạnh a , b , c thỏa mãn điều kiện 2 2 2
b + c − a = 3bc . Tính số đo của góc A . A. 45°. B. 60°. C. 120°. D. 30° . Lời giải Chọn D Ta có: 2 2 2
b + c − a = 3bc ⇔ 2bc cos A = 3bc ⇔ 3 cos A = ⇒ A = 30° . 2 2 2 2 Mà
a + b − c 1 cosC = = ⇒ C = 60° . 2ab 2
Câu 19: Tam giác ABC . a cos B = .
b cos A . Tam giác ABC là tam giác gì? A. Tam giác vuông. B. Tam giác đều.
C. Tám giác vuông cân D. Tam giác cân. Page 19
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Lời giải Chọn D 2 2 2 2 2 2 Ta có: + − + − . a c b b c a a cos B = . b cos A ⇔ . a = . b ⇔ 2 2
a = b ⇔ a = b . 2ac 2bc Vậy tam giác ABC cân.
Câu 20: Cho tam giác ABC vuông tại A , AC = b , AB = c . Lấy điểm M trên cạnh BC sao cho góc
BAM = 30° Tính tỉ số MB . MC A. b 3 . B. 3c . C. 3c .
D. b − c . 3c 3b b b + c Lời giải Chọn B B M 30° 60° A C . Ta có MB AM AM.sin 30° AM = ⇒ MB = = . sin 30° sin B sin B 2.sin B MC AM AM.sin 60° AM 3 = ⇒ MC = = . sin 60° sin C sin C 2.sin C Do đó MB sin C c 3c = = = . MC 3 sin B 3b 3b
Câu 21: Mệnh đề nào sau đây sai? A. Nếu 2 2 2
a > b + c thì A là góc tù.
B. Nếu tam giác ABC có một góc tù thì 2 2 2
a > b + c . C. Nếu 2 2 2
a < b + c thì A là góc nhọn. D. Nếu 2 2 2
a = b + c thì A là góc vuông. Lời giải Chọn B 2 2 2 Ta có : cos
b + c − a A = . 2bc Do đó : * 2 2 2
a > b + c thì cos A < 0 do đó A là góc tù nên A. đúng. * 2 2 2
a < b + c thì cos A > 0 do đó A là góc nhọn nên C. đúng. * 2 2 2
a = b + c thì cos A = 0 do đó A là góc vuông nên D. đúng.
* Nếu tam giác ABC có góc B tù thì 2 2 2
b > a + c ; nếu góc C tù thì 2 2 2
c > a + b do đó B. sai. Page 20
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
DẠNG 3: ỨNG DỤNG THỰC TẾ 1 PHƯƠNG PHÁP.
Áp dụng các công thức sách giáo khoa như: định lí cosin, hệ quả của định lí cosin, định lí sin,
các công thức liên quan đến diện tích để vận dụng vào làm bài. 2
BÀI TẬP TỰ LUẬN.
Câu 1: Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 0 60
. Tàu thứ nhất chạy với tốc độ 30km / h , tàu thứ hai chạy với tốc độ 40km / h . Hỏi sau 2 giờ hai
tàu cách nhau bao nhiêu km ? Lời giải
Ta có: Sau 2h quãng đường tàu thứ nhất chạy được là: 1S = 30.2 = 60k . m
Sau 2h quãng đường tàu thứ hai chạy được là: S2 = 40.2 = 80k . m
Vậy: sau 2h hai tàu cách nhau là: 2 2 0 S = 1 S + S2 − 2 1
S .S2.cos60 = 20 13.
Câu 2: Từ một đỉnh tháp chiều cao CD = 80m , người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là 0 72 12' và 0
34 26' so với phương nằm ngang. Ba điểm ,
A B, D thẳng hàng. Tính
khoảng cách AB (chính xác đến hàng đơn vị)? Lời giải
Ta có: Trong tam giác vuông CDA: 0 CD CD 80 tan 72 12' = ⇒ AD = = 25,7. 0 0 AD tan 72 12' tan 72 12'
Trong tam giác vuông CDB : 0 CD CD 80 tan34 26' = ⇒ BD = = 116,7. 0 0 BD tan34 26' tan34 26'
Suy ra: khoảng cách AB =116,7 − 25,7 = 91 . m
BÀI TẬP TỰ LUẬN TỔNG HỢP.
Câu 3: Cho tam giác ABC có a =13,b = 8,c = 7 . Tính góc A, suy ra S, ha, R, r, ma. Lời giải 2 2 2 2 2 2
b + c − a 1 0
a = b + c − 2bc cos A ⇒ cos A =
= − ⇒ A =120 2bc 2 Page 21
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 1 1 3
S = bcsin A = 56. = 14 3 2 2 2 1 2S 28 3 S = . a h ⇒ h = = 2 a a a 13 abc abc 7.8.13 13 3 S = ⇒ R = = = 4R 4S 4.14 3 3 2S 2.14 3 S = . p r ⇒ r = = = 3
a + b + c 7 + 8 +13 2 2 2 2 b + c a 57 m = − ⇒ m = a 2 4 a 2 Câu 4: Cho tam giác 3
ABC có AB 4, AC 5 và cosA . Tính cạnh BC, và độ dài đường cao 5 kẻ từ A . Lời giải
Áp dụng định lí côsin ta có 3 2 2 2 2 2
BC AB AC 2AB.AC.cos A 4 5 2.4.5. 17 Suy ra BC 17 5 Vì 9 4 2 A 2 sin
cos A 1 nên sin A 1 2 cos A 1 25 5
Theo công thức tính diện tích ta có 1 1 4 S AB AC .
.sin A .4.5. 8 (1) ABC 2 2 5 Mặt khác 1 1 S
a.h . 17.h (2) ABC 2 a 2 a Từ (1) và (2) suy ra 1 16 17
. 17.h 8 h 2 a a 17
Vậy độ dài đường cao kẻ từ A là 16 17 h a 17
Câu 5: Cho tam giác ABC có AB , 10 AC 4 và A 0 60 .
a) Tính chu vi của tam giác b) Tính tanC Lời giải
a) Theo định lí côsin ta có BC 2 2 2 . . cos 0 10 4 2 10 4 60 76 BC , 8 72
Suy ra chu vi tam giác là 2p 10 4 8,72 , 22 72 b) (Hình 2.23a) Page 22
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A 10 4 C H B Hình 2.23a Kẻ đường cao BH ta có AH AB cos 0 60 5 .
HC 5 4 1 BH AB.sin 0 60 5 3 . Vậy tan tan HB C BCH 5 3 HC
Câu 6: Giải tam giác ABC biết 0 A B 0 60 , 40 và c 14 . Lời giải Ta có 0 C A B 0 0 0 0 180 180 60 40 80 Theo định lí sin ta có c sin A 0 14.sin 60 a a 12, 3 sinC 0 sin 80 c sin B 0 14.sin 40 b b 9,1 sinC 0 sin 80
Câu 7: Giải tam giác ABC , biết: 0 b A C 0 4,5; 30 ; 75 Lời giải Ta có 0 0 0 0 0
B 180 A C 180 30 75 75 C
suy ra tam giác ABC cận tại A ⇒ c = b = 4,5 . Theo định lí sin ta có b sin A 0 4,5.sin 30 a a 2, 33 . sin B 0 sin 75
Câu 8: Cho tam giác ABC cân tại A biết a = B = 0 3;
C = 30 . Tính R, r, cạnh c, b, suy ra S Lời giải Áp dụng định lí sin: a a 3 = 2R ⇒ R = = = 1 sin A 2sin A 3 2 2 0
⇒ b = c = 2R sin 30 =1 Page 23
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 1 3 S = . b csin A = 2 4 S 3 r = = (2 − 3) . p 2
Câu 9: Cho tam giác ABC nội tiếp đường tròn bán kính bằng 3, biết 0 0
A 30 , B 45 . Tính độ dài
trung tuyến kẻ từ A và bán kính đường tròn nội tiếp tam giác. Lời giải Ta có 0 C A B 0 0 0 0 180 180 30 45 105
Theo định lí sin ta có a R A 0 2 sin 2.3.sin 30 3 , 2 b R 2 sin B 0 2.3.sin 45 6. 3 2 2 c R C 0 2 sin 2.3.sin105 5,796
Theo công thức đường trung tuyến ta có
2b2 c2 a2 218 2 5,796 9 2 m 23,547 a 4 4
Theo công thức tính diện tích tam giác ta có 1 bc sin A S
pr bc sin A r ABC 2 2p 0 3 2.5,796 sin 30 0,943 3 3 2 5,796
Câu 10: Cho tam giác ABC thỏa mãn 2
sin A sin B.sinC . Chứng minh rằng a) 2 a bc b) 1 cos A 2 Lời giải
a) Áp dụng định lí sin ta có a b c sin A , sin B , sinC 2R 2R 2R 2 Suy ra 2 a b c 2
sin A sin B.sinC . a bc đpcm 2R 2R 2R
b) Áp dụng định lí côsin và câu a) ta có 2 2 2 2 2
b c a
b c bc 2bc bc 1 cos A đpcm 2bc 2bc 2bc 2
Câu 11: Tam giác ABC có BC a, CA ,
b AB c và trung tuyến AM AB c chứng minh rằng: Page 24
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 2 2 2 a)
a 2(b c ) 2 2 2 b)
sin A 2(sin B sin C ) Lời giải
a) Áp dụng công thức đường trung tuyến 2 2 Ta có 2 2 a 2 a 2 2 2 2 b c 2AM
2c a 2(b c ) (*) 2 2
b) Theo định lí sin ta có a b c 2R sin A sin B sinC 2 2 2 a 4R sin A 2 2 2 b
4R sin B 2 2 2 c 4R sin C Thay vào (*) ta có đpcm
Câu 12: Cho tam giác ABC . Chứng minh rằng điều kiện cần và đủ để hai trung tuyến kẻ từ B và C vuông góc với nhau là 2 2 2
b c 5a . Lời giải
Gọi G là trọng tâm của tam giác ABC .
Khi đó hai trung tuyến kẻ từ B và C vuông góc với nhau khi và chỉ khi tam giác GBC vuông tại G 2 2 2 2 2 2 2 2
GB GC BC m
m a (*) 3 b 3 c
Mặt khác theo công thức đường trung tuyến ta có 2 2 2 2 2 2 2 2(a c ) b 2 2(a b ) c m , m b 4 c 4 Suy ra 4
(*) m2 m2 a2 b c 9 2 2 2 a c 2 b 2 4 2 2 a b 2 c 2 a 2 2 2 2
4a b c 9a 2 2 2
b c 5a 9 4 4
Câu 13: Chứng minh rằng trong mọi tam giác ABC ta có; a) a . b cosC . c cos B
b) sinA sinB cosC sinC cosB Lời giải
a) Áp dụng định lí côsin ta có: Page 25
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 2 2 2 2 2 2
a b c
c a b VP . b . c 2ab 2ca 2 2 2 2 2 2
a b c c a b a VT 2a b) a b c
sin A sin B cosC sinC cos B .cosC .cos B 2R 2R 2R
a b.cosC c.cos B
Câu 14: Chứng minh rằng trong mọi tam giác ABC ta có: h 2R sinB sinC a Lời giải 2S b
h 2R sin B sinC 2R sinC a a 2R 1
S ab sinC (đúng) 2
Câu 15: Tìm tính chất đặc biệt của tam giác ABC biết: 2acos A = .
b cosC + .ccos B Lời giải
Yêu cầu bài toán tương đương với: 2(2Rsin )
A cos A = (2Rsin B)cosC + 2Rsin C cos B ⇔ 2sin .
A cos A = sin(B + C) = sin A 1 ⇔ = ≠ ⇔ 0 cos A (do sin A 0) A = 60 2 a
2b cosC (1)
Nhận dạng tam giác ABC biết: 3 3 3 2 a b c a (2) Câu 16:
a b c Lời giải
Áp dụng định lí cosin ở (1) và thế vào (2) 2 2 2
a b c (1) a b c a 2 2 2
(2) a b c bc 1 0 cos A A 60 2 KL: Tam giác ABC đều.
Câu 17: Nhận dạng tam giác ABC biết: a.sinA b sinB c sinC h h h a b c Lời giải
Áp dụng công thức diện tích ta có 1 1
S bc sin A ah suy ra 2 2 a S S S S S S
a.sin A b sin B c sinC h h h 2 2 2 2 2 2 a. . b . c a b c bc ca ab a b c Page 26
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 2 2 2
a b c ab bc ca
a b2 b c2 c a2 0
a b c
Vậy tam giác ABC đều.
Câu 18: Cho tam giác ABC . Chứng minh tam giác ABC cân nếu h . c sin A a Lời giải Sử dụng công thức 1 1
S ah bc sin A thay h .
c sin A vào (*) được: a * 2 2 a
bh ah a b suy ra tam giác ABC cân tại C a a Page 27
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC G
ƠN IV HỆ THỨC LƯỢNG HƯ TRONG TAM GIÁC C
BÀI 2. ĐỊNH LÝ COSIN VÀ ĐỊNH LÝ SIN
BÀI 3. GIẢI TAM GIÁC VÀ ỨNG DỤNG THỰC TẾ
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM. III
DẠNG 1. ĐỊNH LÝ COSIN, ÁP DỤNG ĐỊNH LÝ COSIN ĐỂ GIẢI TOÁN
Câu 1: Cho tam giác ABC , mệnh đề nào sau đây đúng? A. 2 2 2
a = b + c + 2bccos A . B. 2 2 2
a = b + c − 2bccos A. C. 2 2 2
a = b + c − 2bccosC . D. 2 2 2
a = b + c − 2bccos B .
Câu 2: Cho tam giác ABC , có độ dài ba cạnh là BC = a, AC = b, AB = c . Gọi m là độ dài đường trung a
tuyến kẻ từ đỉnh A , R là bán kính đường tròn ngoại tiếp tam giác và S là diện tích tam giác đó.
Mệnh đề nào sau đây sai? 2 2 2 A. 2 b c a m + = − . B. 2 2 2
a = b + c + 2bccos A. a 2 4 abc a b c C. S = . D. = = = 2R . 4R
sin A sin B sinC
Câu 3: Cho tam giác ABC có a = 8,b =10 , góc C bằng 0
60 . Độ dài cạnh c là? A. c = 3 21 . B. c = 7 2 . C. c = 2 11 . D. c = 2 21.
Câu 4: Cho ∆ABC có = = 0
b 6,c 8, A = 60 . Độ dài cạnh a là: A. 2 13. B. 3 12. C. 2 37. D. 20.
Câu 5: Cho ∆ABC có 0
B = 60 ,a = 8,c = 5. Độ dài cạnh b bằng: A. 7. B. 129. C. 49. D. 129 . Câu 6: Cho A
∆ BC có AB = 9; BC = 8; 0
B = 60 . Tính độ dài AC . A. 73 . B. 217 . C. 8 . D. 113 .
Câu 7: Cho tam giác ABC có AB = 2, AC =1 và 0
A = 60 . Tính độ dài cạnh BC. A. BC = 2. B. BC =1. C. BC = 3. D. BC = 2.
Câu 8: Tam giác ABC có = = 0
a 8,c 3, B = 60 . Độ dài cạnh b bằng bao nhiêu? A. 49. B. 97 C. 7. D. 61.
Câu 9: Tam giác ABC có 0
C =150 , BC = 3, AC = 2. Tính cạnh AB ? A. 13 . B. 3. C. 10. D. 1. Page 97
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Câu 10: Cho ; a ;c
b là độ dài 3 cạnh của tam giác ABC . Biết b = 7 ; c = 5 ; 4
cos A = . Tính độ dài của a . 5 A. 3 2 . B. 7 2 . C. 23 . D. 6 . 2 8 Câu 11: Cho xOy = 30°.Gọi ,
A B là 2 điểm di động lần lượt trên Ox,Oy sao cho AB = 2 . Độ dài lớn
nhất của OB bằng bao nhiêu? A. 4. B. 3. C. 6. D. 2. Câu 12: Cho ; a ;c
b là độ dài 3cạnh của một tam giác. Mệnh đề nào sau đây không đúng? A. 2
a < ab + ac . B. 2 2 2
a + c < b + 2ac . C. 2 2 2
b + c > a + 2bc . D. 2
ab + bc > b .
Câu 13: Cho tam giác ABC có AB = 4 cm, BC = 7 cm, AC = 9cm. Tính cos A. A. 2 cos A = − . B. 1 cos A = . C. 1 cos A = . D. 2 cos A = . 3 2 3 3
Câu 14: Cho tam giác ABC có 2 2 2
a + b − c > 0 . Khi đó: A. Góc 0 C > 90 B. Góc 0 C < 90 C. Góc 0 C = 90
D. Không thể kết luận được gì về góc C.
Câu 15: Cho tam giác ABC thoả mãn: 2 2 2
b + c − a = 3bc . Khi đó: A. 0 A = 30 . B. 0 A = 45 . C. 0 A = 60 . D. 0 A = 75 .
Câu 16: Cho các điểm (
A 1;1), B(2;4),C(10; 2 − ). Góc
BAC bằng bao nhiêu? A. 0 90 . B. 0 60 . C. 0 45 . D. 0 30 .
Câu 17: Cho tam giác ABC , biết a = 24,b =13,c =15. Tính góc A? A. 0 33 34'. B. 0 117 49'. C. 0 28 37'. D. 0 58 24'.
Câu 18: Cho tam giác ABC , biết a =13,b =14,c =15. Tính góc B ? A. 0 59 49'. B. 0 53 7'. C. 0 59 29'. D. 0 62 22'.
Câu 19: Cho tam giác ABC biết độ dài ba cạnh BC, ,
CA AB lần lượt là a, ,
b c và thỏa mãn hệ thức ( 2 2 − ) = ( 2 2 b b a
c c − a ) với b ≠ c . Khi đó, góc BAC bằng A. 45°. B. 60°. C. 90° . D. 120°.
Câu 20: Tam giác ABC có AB = c, BC = a, CA = b . Các cạnh a, ,
b c liên hệ với nhau bởi đẳng thức ( 2 2 − ) = ( 2 2 b b a
c a − c ) . Khi đó góc
BAC bằng bao nhiêu độ. A. 30 . B. 60. C. 90 . D. 45.
Câu 21: Cho tam giác ABC vuông cân tại A và M là điểm nằm trong tam giác ABC sao cho
MA: MB : MC =1: 2 :3 khi đó góc AMB bằng bao nhiêu? A. 135° . B. 90°. C. 150° . D. 120° .
Câu 22: Cho tam giác ABC , chọn công thức đúng trong các đáp án sau: 2 2 2 2 2 2 A. 2 b c a m + = + B. 2 a c b m + = − a . a . 2 4 2 4 2 2 2 2 2 2 C. 2 a b c m + = −
D. 2 2c 2b a m + − = a . a . 2 4 4
Câu 23: Tam giác ABC có AB = 9 cm, BC =15 cm, AC =12cm. Khi đó đường trung tuyến AM của
tam giác có độ dài là A. 10 cm . B. 9 cm . C. 7,5 cm . D. 8 cm . Page 98
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
Câu 24: Cho tam giác ABC có AB = 3, BC = 5 và độ dài đường trung tuyến BM = 13 . Tính độ dài AC . A. 11 . B. 4 . C. 9 . D. 10 . 2 Câu 25: Cho A ∆ BC vuông ở ,
A biết C = 30 ,° AB = 3. Tính độ dài trung tuyến AM ? A. 3 B. 4 C. 5 D. 7 2 2
Câu 26: Tam giác ABC có a = 6,b = 4 2,c = 2. M là điểm trên cạnh BC sao cho BM = 3. Độ dài đoạn AM bằng bao nhiêu? A. 9 . B. 9. C. 3. D. 1 108. 2 Câu 27: Gọi 2 2 2 S = a m + b m + c
m là tổng bình phương độ dài ba trung tuyến của tam giác ABC . Trong các
mệnh đề sau mệnh đề nào đúng? A. 3 2 2 2 3
S = (a + b + c ) . B. 2 2 2
S = a + b + c . C. 2 2 2
S = (a + b + c ) . D. 2 2 2
S = 3(a + b + c ) . 4 2 Câu 28: Cho A
∆ BC có AB = 2 ; AC = 3; 0
A = 60 . Tính độ dài đường phân giác trong góc A của tam giác ABC . A. 12 . B. 6 2 . C. 6 3 . D. 6 . 5 5 5 5
DẠNG 2. ĐỊNH LÝ SIN, ÁP DỤNG ĐỊNH LÝ SIN ĐỂ GIẢI TOÁN
Câu 29: Cho tam giác ABC . Tìm công thức sai:
A. a = 2R. B. sin a A = .
C. bsin B = 2R. D. csin sin A C = . sin A 2R a Câu 30: Cho A
∆ BC với các cạnh AB = c, AC = ,
b BC = a . Gọi R,r, S lần lượt là bán kính đường tròn
ngoại tiếp, nội tiếp và diện tích của tam giác ABC . Trong các phát biểu sau, phát biểu nào sai? A. abc S = . B. a R = . 4R sin A C. 1
S = absin C . D. 2 2 2
a + b − c = 2abcosC . 2
Câu 31: Cho tam giác ABC có góc
BAC = 60° và cạnh BC = 3 . Tính bán kính của đường tròn ngoại tiếp tam giác ABC . A. R = 4 . B. R =1. C. R = 2 . D. R = 3.
Câu 32: Trong mặt phẳng, cho tam giác ABC có AC = 4 cm , góc A = 60°, B = 45°. Độ dài cạnh BC là A. 2 6 . B. 2 + 2 3 . C. 2 3 − 2 . D. 6 . Câu 33: Cho A
∆ BC có AB = 5; A = 40°; B = 60°. Độ dài BC gần nhất với kết quả nào? A. 3,7 . B. 3,3 . C. 3,5 . D. 3,1.
Câu 34: Cho tam giác ABC thoả mãn hệ thức b + c = 2a . Trong các mệnh đề sau, mệnh đề nào đúng?
A. cos B + cosC = 2cos . A
B. sin B + sinC = 2sin . A C. 1
sin B + sin C = sin A .
D. sin B + cosC = 2sin . A 2
Câu 35: Tam giác ABC có a =16,8 ; 0 B = 56 13'; 0
C = 71 . Cạnh c bằng bao nhiêu? Page 99
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. 29,9. B. 14,1. C. 17,5. D. 19,9.
Câu 36: Tam giác ABC có 0 A = 68 12' , 0
B = 34 44' , AB =117. Tính AC ? A. 68. B. 168. C. 118. D. 200.
DẠNG 3. DIỆN TÍCH TAM GIÁC, BÁN KÍNH ĐƯỜNG TRÒN
Câu 37: Chọn công thức đúng trong các đáp án sau: A. 1
S = bcsin A. B. 1
S = acsin A. C. 1
S = bcsin B. D. 1
S = bcsin B. 2 2 2 2
Câu 38: Cho hình thoi ABCD có cạnh bằng a . Góc
BAD = 30° . Diện tích hình thoi ABCD là 2 2 2 A. a . B. a . C. a 3 . D. 2 a . 4 2 2
Câu 39: Tính diện tích tam giác ABC biết AB = 3, BC = 5, CA = 6. A. 56 . B. 48 . C. 6 . D. 8 .
Câu 40: Cho ∆ABC có a = 6,b = 8,c =10. Diện tích S của tam giác trên là: A. 48. B. 24. C. 12. D. 30.
Câu 41: Cho ∆ABC có 0
a = 4,c = 5, B =150 .Diện tích của tam giác là: A. 5 3. B. 5. C. 10. D. 10 3.
Câu 42: Một tam giác có ba cạnh là 13,14,15. Diện tích tam giác bằng bao nhiêu? A. 84. B. 84 . C. 42. D. 168.
Câu 43: Cho các điểm ( A 1; 2 − ), B( 2;
− 3),C(0;4). Diện tích ABC ∆ bằng bao nhiêu? A. 13. B. 13. C. 26. D. 13. 2 4
Câu 44: Cho tam giác ABC có ( A 1; 1 − ), B(3; 3
− ),C(6;0). Diện tích ABC ∆ là A. 12. B. 6. C. 6 2. D. 9.
Câu 45: Cho tam giác ABC có a = 4,b = 6,c = 8 . Khi đó diện tích của tam giác là: A. 9 15. B. 3 15. C. 105. D. 2 15. 3
Câu 46: Cho tam giác ABC . Biết AB = 2 ; BC = 3 và
ABC = 60° . Tính chu vi và diện tích tam giác ABC . A. 5 + 7 và 3 . B. 5 + 7 và 3 3 . C. 5 7 và 3 3 . D. 5 + 19 và 3 . 2 2 2 2
Câu 47: Tam giác ABC có các trung tuyến m = , m = , m = .Diện tích S của tam giác c 9 b 12 a 15 ABC bằng A. 72 . B. 144. C. 54. D. 108.
Câu 48: Cho tam giác ∆ ABC có 3
b =7;c =5;cos A = . Độ dài đường cao h của tam giác ∆ ABC là. 5 a A. 7 2 . B. 8 . C. 8 3 D. 80 3 2
Câu 49: Cho tam giác ABC có AB = 2a; AC = 4a và
BAC =120° . Tính diện tích tam giác ABC ? A. 2 S = 8a . B. 2
S = 2a 3 . C. 2
S = a 3 . D. 2 S = 4a .
Câu 50: Cho tam giác ABC đều cạnh a . Bán kính đường tròn ngoại tiếp tam giác ABC bằng A. a 3 . B. a 3 . C. a 3 . D. a 2 . 2 3 4 2 Page 100
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
Câu 51: Cho tam giác ABC có chu vi bằng 12 và bán kính đường tròn nội tiếp bằng 1. Diện tích của tam giác ABC bằng A. 12. B. 3. C. 6 . D. 24 .
Câu 52: Cho tam giác ABC đều cạnh 2a . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC . A. 2a . B. 4a . C. 8a . D. 6a . 3 3 3 3
Câu 53: Cho tam giác ABC có BC = 6 , AC = 2 và AB = 3 +1. Bán kính đường tròn ngoại tiếp tam giác ABC bằng: A. 5 . B. 3 . C. 2 . D. 2 .
Câu 54: Cho tam giác ABC có AB = 3, AC = 4 , BC = 5 . Bán kính đường tròn nội tiếp tam giác bằng A. 1. B. 8 . C. 4 . D. 3 . 9 5 4
Câu 55: Cho ∆ABC có S = 84,a =13,b =14,c =15. Độ dài bán kính đường tròn ngoại tiếp R của tam giác trên là: A. 8,125. B. 130. C. 8. D. 8,5.
Câu 56: Cho ∆ABC có S =10 3 , nửa chu vi p =10. Độ dài bán kính đường tròn nội tiếp r của tam giác trên là: A. 3. B. 2. C. 2. D. 3.
Câu 57: Một tam giác có ba cạnh là 26,28,30. Bán kính đường tròn nội tiếp là: A. 16. B. 8. C. 4. D. 4 2.
Câu 58: Một tam giác có ba cạnh là 52,56,60. Bán kính đường tròn ngoại tiếp là: A. 65. B. 40. C. 32,5. D. 65. 8 4
Câu 59: Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn ngoại tiếp là? A. 6. B. 8. C. 13 . D. 11. 2 2
Câu 60: Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu? A. 2. B. 2 2. C. 2 3. D. 3.
Câu 61: Tam giác với ba cạnh là 6;8;10 có bán kính đường tròn ngoại tiếp bằng bao nhiêu? A. 5. B. 4 2. C. 5 2. D. 6 .
Câu 62: Cho hình chữ nhật ABCD có cạnh AB = 4, BC = 6, M là trung điểm của BC, N là điểm trên
cạnh CD sao cho ND = 3NC . Khi đó bán kính của đường tròn ngoại tiếp tam giác AMN bằng A. 3 5 . B. 3 5 . C. 5 2 . D. 5 2 . 2 2
Câu 63: Cho tam giác đều ABC ;gọi D là điểm thỏa mãn DC = 2BD . Gọi R và r lần lượt là bán kính
đường tròn ngoại tiếp và nội tiếp của tam giác ADC. Tính tỉ số R . r A. 5 . B. 5 + 7 7 . C. 7 + 5 5 . D. 7 + 5 7 . 2 9 9 9
DẠNG 4. ỨNG DỤNG THỰC TẾ
Câu 64: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta
xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 78o24'. Biết CA = 250 ,
m CB =120m . Khoảng cách AB bằng bao nhiêu? Page 101
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. 266 . m B. 255 . m C. 166 . m D. 298 . m
Câu 65: Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 0 60
. Tàu thứ nhất chạy với tốc độ 30km / h , tàu thứ hai chạy với tốc độ 40km / h . Hỏi sau 2 giờ hai
tàu cách nhau bao nhiêu km ? A. 13. B. 20 13. C. 10 13. D. 15.
Câu 66: Từ một đỉnh tháp chiều cao CD = 80m , người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là 0 72 12' và 0 34 26' . Ba điểm ,
A B, D thẳng hàng. Tính khoảng cách AB ? A. 71 . m B. 91 . m C. 79 . m D. 40 . m
Câu 67: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta
xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 0 56 16' . Biết
CA = 200m , CB =180m . Khoảng cách AB bằng bao nhiêu? A. 180 . m B. 224 . m C. 112 . m D. 168 . m
Câu 68: Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn
bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính của
chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như
hình vẽ ( AB = 4,3cm; BC = 3,7 cm; CA = 7,5 cm). Bán kính của chiếc đĩa này bằng.
A. 5,73 cm.
B. 6,01cm.
C. 5,85cm. D. 4,57cm.
Câu 69: Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất
sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24m, 0 CAD = 63 ; 0 CBD = 48 . Chiều cao
h của khối tháp gần với giá trị nào sau đây? A. 61,4 m. B. 18,5 m. C. 60 m. D. 18 m. Page 102
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC G
ƠN IV HỆ THỨC LƯỢNG HƯ TRONG TAM GIÁC C
BÀI 2. ĐỊNH LÝ COSIN VÀ ĐỊNH LÝ SIN
BÀI 3. GIẢI TAM GIÁC VÀ ỨNG DỤNG THỰC TẾ
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM. III
DẠNG 1. ĐỊNH LÝ COSIN, ÁP DỤNG ĐỊNH LÝ COSIN ĐỂ GIẢI TOÁN
Câu 1: Cho tam giác ABC , mệnh đề nào sau đây đúng? A. 2 2 2
a = b + c + 2bccos A . B. 2 2 2
a = b + c − 2bccos A. C. 2 2 2
a = b + c − 2bccosC . D. 2 2 2
a = b + c − 2bccos B . Lời giải Chọn B
Theo định lý cosin trong tam giác ABC , ta có 2 2 2
a = b + c − 2bccos A.
Câu 2: Cho tam giác ABC , có độ dài ba cạnh là BC = a, AC = b, AB = c. Gọi m là độ dài đường trung a
tuyến kẻ từ đỉnh A , R là bán kính đường tròn ngoại tiếp tam giác và S là diện tích tam giác đó.
Mệnh đề nào sau đây sai? 2 2 2 A. 2 b c a m + = − . B. 2 2 2
a = b + c + 2bccos A. a 2 4 abc a b c C. S = . D. = = = 2R . 4R
sin A sin B sinC Lời giải Chọn B
Theo định lý hàm số cosin trong tam giác ta có 2 2 2
a = b + c − 2bccos A
Câu 3: Cho tam giác ABC có a = 8,b =10 , góc C bằng 0
60 . Độ dài cạnh c là? A. c = 3 21 . B. c = 7 2 . C. c = 2 11 . D. c = 2 21. Lời giải Chọn D Ta có: 2 2 2 2 2 0
c = a + b − 2 . a .
b cosC = 8 +10 − 2.8.10.cos60 = 84 ⇒ c = 2 21 .
Câu 4: Cho ∆ABC có = = 0
b 6,c 8, A = 60 . Độ dài cạnh a là: A. 2 13. B. 3 12. C. 2 37. D. 20. Lời giải Chọn A Ta có: 2 2 2 0
a = b + c − 2bccos A = 36 + 64 − 2.6.8.cos60 = 52 ⇒ a = 2 13 .
Câu 5: Cho ∆ABC có 0
B = 60 ,a = 8,c = 5. Độ dài cạnh b bằng: Page 1
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. 7. B. 129. C. 49. D. 129 . Lời giải Chọn A Ta có: 2 2 2 2 2 0
b = a + c − 2accos B = 8 + 5 − 2.8.5.cos60 = 49 ⇒ b = 7 . Câu 6: Cho A
∆ BC có AB = 9; BC = 8; 0
B = 60 . Tính độ dài AC . A. 73 . B. 217 . C. 8 . D. 113 . Lời giải Chọn A Theo định lý cosin có: 2 2 2 = + − AC BA BC 2B .
A BC.cos ABC = 73 ⇒ AC = 73 . Vậy AC = 73 .
Câu 7: Cho tam giác ABC có AB = 2, AC =1 và 0
A = 60 . Tính độ dài cạnh BC. A. BC = 2. B. BC =1. C. BC = 3. D. BC = 2. Lời giải Chọn C
Theo định lý cosin ta có: 2 2 0
BC = AB + AC − 2A . B AC.cos60 2 2 1 = 2 +1 − 2.2.1. = 3. 2
Câu 8: Tam giác ABC có = = 0
a 8,c 3, B = 60 . Độ dài cạnh b bằng bao nhiêu? A. 49. B. 97 C. 7. D. 61. Lời giải Chọn C Ta có: 2 2 2 2 2 0
b = a + c − 2accos B = 8 + 3 − 2.8.3.cos60 = 49 ⇒ b = 7 .
Câu 9: Tam giác ABC có 0
C =150 , BC = 3, AC = 2. Tính cạnh AB ? A. 13 . B. 3. C. 10. D. 1. Lời giải Chọn A
Theo định lí cosin trong ∆ABC ta có: 2 2 2
AB = CA + CB − 2 . CA .
CB cosC =13 ⇒ AB = 13 . Chọn A Câu 10: Cho ; a ;c
b là độ dài 3 cạnh của tam giác ABC . Biết b = 7 ;c = 5 ; 4
cos A = . Tính độ dài của a 5 . A. 3 2 . B. 7 2 . C. 23 . D. 6 . 2 8 Lời giải Chọn A
Áp dụng định lí cosin cho tam giác ABC ta có: 2 2 2 2 2 4
a = b + c − 2 .
bc cos A = 7 + 5 − 2.7.5. = 18. 5 Suy ra: a = 18 = 3 2 . Page 2
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Câu 11: Cho xOy = 30°.Gọi ,
A B là 2 điểm di động lần lượt trên Ox,Oy sao cho AB = 2 . Độ dài lớn
nhất của OB bằng bao nhiêu? A. 4. B. 3. C. 6. D. 2. Lời giải Chọn A Áp dụng định lí cosin: 2 2 2 2 2 3
AB = OA + OB − 2 . OA .
OB cos30° ⇔ 4 = OA + OB − 2 . OA . OB 2 2 2 ⇔ OA − 3. .
OB OA + OB − 4 = 0 .
Coi phương trình là một phương trình bậc hai ẩn OA. Để tồn tại giá trị lớn nhất của OB thì 2 2 2 ∆ ≥ 0 ⇔ ( 3 ) − 4(OB − 4) ≥ 0 ⇔ ≤ 16 ⇔ ≤ 4 (*) OB OB OB . Vậy max OB = 4 .
Câu 12: Cho a; ;c
b là độ dài 3cạnh của một tam giác. Mệnh đề nào sau đây không đúng? A. 2
a < ab + ac . B. 2 2 2
a + c < b + 2ac . C. 2 2 2
b + c > a + 2bc . D. 2
ab + bc > b . Lời giải Chọn C Do 2 2 2 + − = b c a 2 .
bc cos A ≤ 2bc ⇒ 2 2 2
b + c ≤ a + 2bc nên mệnh đề C sai.
Áp dụng bất đẳng thức tam giác ta có 2
a < b + c ⇒ a < ab + ac ;đáp án A đúng. Tương tự 2
a + c > b ⇒ ab + bc > b ;mệnh đề D đúng. Ta có: 2 2 2
a + c −b = 2 .
ac cos B < 2ac 2 2 2
⇒ a + c < b + 2ac ;mệnh đề B đúng.
Câu 13: Cho tam giác ABC có AB = 4 cm, BC = 7 cm, AC = 9cm. Tính cos A. A. 2 cos A = − . B. 1 cos A = . C. 1 cos A = . D. 2 cos A = . 3 2 3 3 Lời giải Chọn D 2 2 2 2 2 2 Ta có cos
AB + AC − BC A + − = 4 9 7 2 = = . 2.A . B AC 2.4.9 3
Câu 14: Cho tam giác ABC có 2 2 2
a + b − c > 0 . Khi đó: A. Góc 0 C > 90 B. Góc 0 C < 90 C. Góc 0 C = 90
D. Không thể kết luận được gì về góc C. Lời giải Chọn B 2 2 2 Ta có: cos
a + b − c C = . 2ab Mà: 2 2 2
a + b − c > 0 suy ra: 0
cosC > 0 ⇒ C < 90 .
Câu 15: Cho tam giác ABC thoả mãn: 2 2 2
b + c − a = 3bc . Khi đó: A. 0 A = 30 . B. 0 A = 45 . C. 0 A = 60 . D. 0 A = 75 . Lời giải Page 3
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Chọn A 2 2 2 Ta có:
b + c − a 3bc 3 0 cos A = = = ⇒ A = 30 . 2bc 2bc 2
Câu 16: Cho các điểm (
A 1;1), B(2;4),C(10; 2 − ). Góc
BAC bằng bao nhiêu? A. 0 90 . B. 0 60 . C. 0 45 . D. 0 30 . Lời giải Chọn A
Ta có: AB = (1;3) , AC = (9; 3) − . . AB AC Suy ra:
= = ⇒ 0 cos BAC 0 BAC = 90 . AB . AC
Câu 17: Cho tam giác ABC , biết a = 24,b =13,c =15. Tính góc A? A. 0 33 34'. B. 0 117 49'. C. 0 28 37'. D. 0 58 24'. Lời giải Chọn B 2 2 2 2 2 2 Ta có:
b + c − a 13 +15 − 24 7 0 cos A = = = − ⇒ A 117 49'. 2bc 2.13.15 15
Câu 18: Cho tam giác ABC , biết a =13,b =14,c =15. Tính góc B ? A. 0 59 49'. B. 0 53 7'. C. 0 59 29'. D. 0 62 22'. Lời giải Chọn C 2 2 2 2 2 2 Ta có:
a + c − b 13 +15 −14 33 0 cos B = = = ⇒ B 59 29'. 2ac 2.13.15 65
Câu 19: Cho tam giác ABC biết độ dài ba cạnh BC, ,
CA AB lần lượt là a, ,
b c và thỏa mãn hệ thức ( 2 2 − ) = ( 2 2 b b a
c c − a ) với b ≠ c . Khi đó, góc BAC bằng A. 45°. B. 60°. C. 90° . D. 120°. Lời giải Chọn D Ta có b( 2 2
b − a ) = c( 2 2 c − a ) 3 2 3 2 3 3 2
⇔ b − ba = c − ca ⇔ b − c − a (b − c) = 0 ⇔ (b − c)( 2 2 2
b + bc + c − a ) 2 2 2
= 0 ⇔ b + c − a = bc − . 2 2 2 + − − Mặt khác b c a bc 1 = = = − ⇒ cos BAC BAC =120°. 2bc 2bc 2
Câu 20: Tam giác ABC có AB = c, BC = a, CA = b . Các cạnh a, ,
b c liên hệ với nhau bởi đẳng thức ( 2 2 − ) = ( 2 2 b b a
c a − c ) . Khi đó góc
BAC bằng bao nhiêu độ. A. 30 . B. 60. C. 90 . D. 45. Lời giải Chọn B
Theo bài ra, ta có: b( 2 2
b − a ) = c( 2 2 a − c ) 3 2 2 3 3 3 2 2
⇔ b − a b = a c − c = 0 ⇔ b + c − a b − a c = 0 ⇔ (b + c)( 2 2
b − bc + c ) 2
− a (b + c) = ⇔ (b + c)( 2 2 2
b − bc + c − a ) 2 2 2 0
= 0 ⇔ b − bc + c − a = 0 2 2 2 2 2 2
b + c − a 1 ⇔ + − = ⇔ = ⇔ 1 = ⇒ b c a bc cos BAC BAC = 60°. 2bc 2 2 Page 4
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
Câu 21: Cho tam giác ABC vuông cân tại A và M là điểm nằm trong tam giác ABC sao cho
MA: MB : MC =1: 2 :3 khi đó góc AMB bằng bao nhiêu? A. 135° . B. 90°. C. 150° . D. 120° . Lời giải
MB = x ⇔ MA = 2x ; MC = 3x với 0 < x < BC = 2 . Ta có 2 2 2 1+ 4x − x 3x +1 cos BAM = = 2.1.2x 4x 2 2 2 1+ 4x − 9x 1− 5 cos x MAC = = . 4x 4x 2 2 2 2
3x +1 1− 5x ⇒ + =1 4 2 2 4
⇒ 9x + 6x +1+1−10x + 25x =16 . 4x 4x 2 5+ 2 2 1 x = > (l) 4 2
⇒ 34x − 20x + 2 = 0 17 5 ⇔ . 2 5− 2 2 x = 17 2 2 + − ⇒ 2 2 2 cos
AM + BM − AB AMB = 4x x 1 = 2AM.BM 2.2 .xx 2 5x −1 25 −10 2 20 −8 2 − 2 = = −1 : = . 2 4x 17 17 2 Vậy AMB =135° .
Câu 22: Cho tam giác ABC , chọn công thức đúng trong các đáp án sau: 2 2 2 2 2 2 A. 2 b c a m + = + B. 2 a c b m + = − a . a . 2 4 2 4 2 2 2 2 2 2 C. 2 a b c m + = −
D. 2 2c 2b a m + − = a . a . 2 4 4 Lời giải Chọn D 2 2 2 2 2 2 Ta có: 2 b + c a
2b + 2c − a a m = − = . 2 4 4
Câu 23: Tam giác ABC có AB = 9 cm, BC =15 cm, AC =12cm. Khi đó đường trung tuyến AM của
tam giác có độ dài là A. 10 cm . B. 9 cm . C. 7,5 cm . D. 8 cm . Lời giải Chọn C 2 2 2 2 2 2 Ta có 2 AB AC BC 15 AM + + = − 9 12 15 225 = − = ⇒ AM = . 2 4 2 4 4 2
Câu 24: Cho tam giác ABC có AB = 3, BC = 5 và độ dài đường trung tuyến BM = 13 . Tính độ dài AC . A. 11 . B. 4 . C. 9 . D. 10 . 2 Lời giải Chọn B Page 5
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A 3 M 13 B C 5
Theo công thức tính độ dài đường trung tuyến;ta có: 2 2 2 BA + BC AC = − ⇔ ( ) 2 2 2 2 2 3 + 5 13 AC BM = − ⇔ AC = 4 . 2 4 2 4 Câu 25: Cho A ∆ BC vuông ở ,
A biết C = 30 ,° AB = 3. Tính độ dài trung tuyến AM ? A. 3 B. 4 C. 5 D. 7 2 2 Lời giải Chọn A
AM là trung tuyến ứng với cạnh huyền nên 1
AM = BC = BM = MC . 2 Xét B
∆ AC có B = 90° − 30° = 60°.
Xét tam giác ABM có BM = AM và B = 60° suy ra A
∆ BM là tam giác đều.
⇒ AM = AB = 3.
Câu 26: Tam giác ABC có a = 6,b = 4 2,c = 2. M là điểm trên cạnh BC sao cho BM = 3. Độ dài đoạn AM bằng bao nhiêu? A. 9 . B. 9. C. 3. D. 1 108. 2 Lời giải Chọn C
Ta có: Trong tam giác ABC có a = 6 ⇒ BC = 6 mà BM = 3 suy ra M là trung điểm BC. 2 2 2 Suy ra: 2 2 b + c a AM = a m = − = 9 ⇒ AM = 3 . 2 4 Câu 27: Gọi 2 2 2 S = a m + b m + c
m là tổng bình phương độ dài ba trung tuyến của tam giác ABC . Trong các
mệnh đề sau mệnh đề nào đúng? A. 3 2 2 2
S = (a + b + c ) . B. 2 2 2
S = a + b + c . 4 C. 3 2 2 2
S = (a + b + c ) . D. 2 2 2
S = 3(a + b + c ) . 2 Lời giải Chọn A 2 2 2 2 2 2 2 2 2 Ta có: 2 2 2 b + c a a + c b a + b c 3 2 2 2 S = a m + b m + c m = − + − + −
= (a + b + c ). 2 4 2 4 2 4 4 Câu 28: Cho A
∆ BC có AB = 2 ; AC = 3; 0
A = 60 . Tính độ dài đường phân giác trong góc A của tam giác ABC . Page 6
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. 12 . B. 6 2 . C. 6 3 . D. 6 . 5 5 5 5 Lời giải Chọn C
Gọi M là chân đường phân giác góc A. Ta có 2 2 2
BC = AB + AC − 2A .
B AC.cos A = 7 ⇒ BC = 7. Lại có BM AB 2 = = . CM AC 3 Suy ra 2 7 BM = . 5
Áp dụng định lý cosin trong tam giác ABM ta được: = + − 2 2 2 2 2 2 2 2
AB + BC − AC 108 AM AB BM 2A .
B BM.cos ABC = AB + BM − 2A . B BM. = . 2.A . B BC 25 6 3 ⇒ AM = . 5 CÁ CH 2
Gọi M là chân đường phân giác trong của góc A .
Vì đoạn thẳng AM chia tam giác ABC thành hai phần nên ta có: 1 = + ⇔ 1 = 1 + S S S AB AC BAC AB AM BAM AC AM MAC ABC ABM ACM . .sin . .sin . .sin 2 2 2 A . B AC.sin 60 AM ° ⇔ = .
( AB + AC).sin30° 6 3 ⇔ AM = . 5 Vậy 6 3 AM = . 5
DẠNG 2. ĐỊNH LÝ SIN, ÁP DỤNG ĐỊNH LÝ SIN ĐỂ GIẢI TOÁN
Câu 29: Cho tam giác ABC . Tìm công thức sai:
A. a = 2R. B. sin a A = .
C. bsin B = 2R. D. csin sin A C = . sin A 2R a Lời giải Chọn C Ta có: a b c = = = 2 . R
sin A sin B sinC Page 7
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Câu 30: Cho A
∆ BC với các cạnh AB = c, AC = ,
b BC = a . Gọi R,r, S lần lượt là bán kính đường tròn
ngoại tiếp, nội tiếp và diện tích của tam giác ABC . Trong các phát biểu sau, phát biểu nào sai? A. abc S = . B. a R = . 4R sin A C. 1
S = absin C . D. 2 2 2
a + b − c = 2abcosC . 2 Lời giải Chọn B
Theo định lí Sin trong tam giác, ta có a = 2R . sin A
Câu 31: Cho tam giác ABC có góc
BAC = 60° và cạnh BC = 3 . Tính bán kính của đường tròn ngoại tiếp tam giác ABC . A. R = 4 . B. R =1. C. R = 2 . D. R = 3. Lời giải Chọn B Ta có: BC BC 3 = 2R ⇔ R = = = 1. sin A 2sin A 3 2. 2
Câu 32: Trong mặt phẳng, cho tam giác ABC có AC = 4 cm , góc A = 60°, B = 45°. Độ dài cạnh BC là A. 2 6 . B. 2 + 2 3 . C. 2 3 − 2 . D. 6 . Lời giải Chọn A 3 4. Ta có BC AC = 2 ⇔ BC = = 2 6 . sin A sin B 2 2 Câu 33: Cho A
∆ BC có AB = 5; A = 40°; B = 60°. Độ dài BC gần nhất với kết quả nào? A. 3,7 . B. 3,3 . C. 3,5 . D. 3,1. Lời giải Chọn B = ° − −
C 180 A B =180° − 40° − 60° = 80°
Áp dụng định lý sin: BC AB AB 5 = ⇒ BC = .sin A = sin 40° ≈ 3,3. sin A sin C sin C sin80°
Câu 34: Cho tam giác ABC thoả mãn hệ thức b + c = 2a . Trong các mệnh đề sau, mệnh đề nào đúng?
A. cos B + cosC = 2cos .
A B. sin B + sinC = 2sin . A C. 1
sin B + sin C = sin A .
D. sin B + cosC = 2sin . A 2 Lời giải Chọn B Ta có: b + c a b c 2 = = = 2 b c b + c b + c R ⇒ = = ⇔ =
⇔ sin B + sinC = 2sin . A
sin A sin B sinC
sin A sin B sinC
2sin A sin B + sinC Page 8
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
Câu 35: Tam giác ABC có a =16,8 ; 0 B = 56 13'; 0
C = 71 . Cạnh c bằng bao nhiêu? A. 29,9. B. 14,1. C. 17,5. D. 19,9. Lời giải Chọn D
Ta có: Trong tam giác ABC : + + 0 = ⇒ 0 0 0 0 A B C 180
A =180 − 71 − 56 13' = 52 47' . 0 Mặt khác a b c a c .
a sinC 16,8.sin 71 = = ⇒ = ⇒ c = = 19,9. 0
sin A sin B sinC sin A sinC sin A sin52 47'
Câu 36: Tam giác ABC có 0 A = 68 12' , 0
B = 34 44' , AB =117. Tính AC ? A. 68. B. 168. C. 118. D. 200. Lời giải Chọn A
Ta có: Trong tam giác ABC : + + 0 = ⇒ 0 0 0 0 A B C 180
C =180 − 68 12'− 34 44' = 77 4'. 0 Mặt khác a b c AC AB .
AB sin B 117.sin34 44' = = ⇒ = ⇒ AC = = 68. 0
sin A sin B sinC sin B sinC sinC sin 77 4'
DẠNG 3. DIỆN TÍCH TAM GIÁC, BÁN KÍNH ĐƯỜNG TRÒN
Câu 37: Chọn công thức đúng trong các đáp án sau: A. 1
S = bcsin A. B. 1
S = acsin A. C. 1
S = bcsin B. D. 1
S = bcsin B. 2 2 2 2 Lời giải Chọn A Ta có: 1 1 1
S = bcsin A = acsin B = absin C . 2 2 2
Câu 38: Cho hình thoi ABCD có cạnh bằng a . Góc
BAD = 30° . Diện tích hình thoi ABCD là 2 2 2 A. a . B. a . C. a 3 . D. 2 a . 4 2 2 Lời giải Chọn B Ta có 1 = S AB AD BAD 2 = . a .
a sin 30° = a . ABCD . .sin 2
Câu 39: Tính diện tích tam giác ABC biết AB = 3, BC = 5, CA = 6. A. 56 . B. 48 . C. 6 . D. 8 . Lời giải Chọn A Ta có: AB AC BC 3 5 6 p + + + + = = = 7 . 2 2
Vậy diện tích tam giác ABC là:
S = p( p − AB)( p − AC)( p − BC) = 7(7 − 3)(7 − 6)(7 − 5) = 56 .
Câu 40: Cho ∆ABC có a = 6,b = 8,c =10. Diện tích S của tam giác trên là: A. 48. B. 24. C. 12. D. 30. Lời giải Chọn B Ta có: Nửa chu vi a + b + c ABC ∆ : p = . 2 Page 9
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
Áp dụng công thức Hê-rông: S = p( p − a)( p − b)( p − c) = 12(12 − 6)(12 −8)(12 −10) = 24 .
Câu 41: Cho ∆ABC có 0
a = 4,c = 5, B =150 .Diện tích của tam giác là: A. 5 3. B. 5. C. 10. D. 10 3. Lời giải Chọn B Ta có: 1 1 0 S ABC ∆ = . a .
c sin B = .4.5.sin150 = 5. 2 2
Câu 42: Một tam giác có ba cạnh là 13,14,15. Diện tích tam giác bằng bao nhiêu? A. 84. B. 84 . C. 42. D. 168. Lời giải Chọn A Ta có:
a + b + c 13 +14 +15 p = = = 21 . 2 2
Suy ra: S = p( p − a)( p − b)( p − c) = 21(21−13)(21−14)(21−15) = 84 .
Câu 43: Cho các điểm ( A 1; 2 − ), B( 2;
− 3),C(0;4). Diện tích ABC ∆ bằng bao nhiêu? A. 13. B. 13. C. 26. D. 13. 2 4 Lời giải Chọn A Ta có: AB = ( 3
− ;5) ⇒ AB = 34 , AC = ( 1
− ;6) ⇒ AC = 37 , BC = (2;1) ⇒ BC = 5 . Mặt khác
AB + AC + BC 37 + 34 + 5 p = = . 2 2 Suy ra: 13
S = p( p − AB)( p − AC)( p − BC) = . 2
Câu 44: Cho tam giác ABC có ( A 1; 1 − ), B(3; 3
− ),C(6;0). Diện tích ABC ∆ là A. 12. B. 6. C. 6 2. D. 9. Lời giải Chọn B Ta có: AB = (2; 2
− ) ⇒ AB = 2 2 , AC = (5;1) ⇒ AC = 26 , BC = (3;3) ⇒ BC = 3 2 . Mặt khác .
AB BC = 0 ⇒ AB ⊥ BC . Suy ra: 1 S ABC ∆ = . AB BC = 6. 2
Câu 45: Cho tam giác ABC có a = 4,b = 6,c = 8 . Khi đó diện tích của tam giác là: A. 9 15. B. 3 15. C. 105. D. 2 15. 3 Lời giải Chọn B Ta có:
a + b + c 4 + 6 + 8 p = = = 9. 2 2
Suy ra: S = p( p − a)( p − b)( p − c) = 3 15.
Câu 46: Cho tam giác ABC . Biết AB = 2 ; BC = 3 và
ABC = 60° . Tính chu vi và diện tích tam giác ABC . A. 5 + 7 và 3 . B. 5 + 7 và 3 3 . 2 2 Page 10
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC C. 5 7 và 3 3 . D. 5 + 19 và 3 . 2 2 Lời giải A I K J C B Chọn B Ta có: 2 2 2 = + − AC AB BC 2.A .
B BC.cosABC = 4 + 9 − 2.2.3.cos60° =13− 6 = 7 . Suy ra AC = 7 .
Chu vi tam giác ABC là AB + AC + BC = 2 + 3+ 7 .
Diện tích tam giác ABC là 1 = 1 3 3 S = ° = . ∆ AB BC ABC ABC . .sin .2.3.sin 60 2 2 2
Câu 47: Tam giác ABC có các trung tuyến m = , m = , m = .Diện tích S của tam giác c 9 b 12 a 15 ABC bằng A. 72 . B. 144. C. 54. D. 108. Lời giải 1 Chọn A Theo bài toán ta có 2 2 2 2 b + c a 2 m = − = a 15 2 4 2 2 2
2b + 2c − a = 900 a =10 2 2 2 + 2 a c b 2 2 2 2 m = − =
⇔ a + c −b = ⇔ b = b 12 2 2 576 4 13 2 4 2 2 2 2 2 2
2a + 2b − c = 324 + c = 2 73 2 a b c 2 m = − = c 9 2 4 Ta có a b c p + + =
= 5 + 2 13 + 73 , áp dụng công thức He-rong ta có 2 S
= p p − a p − b p − c = . ABC ( )( )( ) 72 Cách 2:
Đặt BC = a,CA = , b AB = c ,
Theo định lý trung tuyến có: 2 2
4m + a = b + c 2 2 2 2 2 a 2( 2 2 ) = =
−a + 2b + 2c = 900 a =100 a 100 a 10 2 2 4m + b = a + c 2 2 2
⇒ 2a − b + 2c = 576 2 ⇒ b = 208 2 ⇒ b = 208 ⇒ b = 4 13 b 2( 2 2 ) 2 2 2 2 2 2 2
4m + c = b + a
2a + 2b − c = 324 c = 291 c = 292 c = 2 73 c 2 ( 2 2) Có S 1
= p p − a p − b p − c , p = (a + b + c) Suy ra S = ABC 72 ABC ( )( )( ) 2
Câu 48: Cho tam giác ∆ ABC có 3
b =7;c =5;cos A = . Độ dài đường cao h của tam giác ∆ ABC là. 5 a A. 7 2 . B. 8 . C. 8 3 D. 80 3 2 Page 11
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Lời giải Chọn A 2 2 2 2 3
a = b + c − 2bccos A = 7 + 5 − 2.7.5. = 32 = 4 2 5 4 2 sin A = 2 2 3 16
sin A=1− cos A=1− = 5 . Suy ra vì ≤ 0 0 A ≤180 nên 4 sin A= 5 25 4 sin A 5 = − 5 1 1 4
S = bcsin A = .7.5. =14 mà 1 1 7 2 S = . a h ⇔ = h ⇔ h = a 14 .4 2. 2 2 5 2 2 a a 2
Câu 49: Cho tam giác ABC có AB = 2a; AC = 4a và
BAC =120° . Tính diện tích tam giác ABC ? A. 2 S = 8a . B. 2
S = 2a 3 . C. 2
S = a 3 . D. 2 S = 4a . Lời giải Chọn B
Diện tích của tam giác ABC là 1 = 1 2 S AB AC BAC = a a ° = a . ABC . .sin .2 .4 .sin120 2 3 2 2
Câu 50: Cho tam giác ABC đều cạnh a . Bán kính đường tròn ngoại tiếp tam giác ABC bằng A. a 3 . B. a 3 . C. a 3 . D. a 2 . 2 3 4 2 Lời giải Chọn B Gọi a a
G là trọng tâm ABC . Bán kính đường tròn ngoại tiếp 2 3 3 R = AG = = . 3 2 3
Câu 51: Cho tam giác ABC có chu vi bằng 12 và bán kính đường tròn nội tiếp bằng 1. Diện tích của tam giác ABC bằng A. 12. B. 3. C. 6 . D. 24 . Lời giải Chọn C
Theo đề bài tam giác ABC có chu vi bằng 12 nên nửa chu vi là 12 p = ; bán kính đường tròn 2
nội tiếp bằng 1, tức là ta có: r =1.
Diện tích tam giác ABC là: S = . p r = 6.1 = 6 .
Câu 52: Cho tam giác ABC đều cạnh 2a . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC . A. 2a . B. 4a . C. 8a . D. 6a . 3 3 3 3 Lời giải Chọn A Page 12
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A K I B H C
Gọi H, K lần lượt là trung điểm cạnh AB, BC;
I là giao điểm của AH và CK .
Lúc đó, I là tâm đường tròn ngoại tiếp tam giác ABC. Ta có: 2a 3 AH = = a 3 . 2 Do đó: 2 2 2 = = = 3 a R AI AH a = . 3 3 3
Câu 53: Cho tam giác ABC có BC = 6 , AC = 2 và AB = 3 +1. Bán kính đường tròn ngoại tiếp tam giác ABC bằng: A. 5 . B. 3 . C. 2 . D. 2 . Lời giải Chọn C 2 2 2
Áp dụng định lý cosin ta có
b + c − a 1 cos A = = suy ra A = 60°. 2bc 2
Áp dụng định lý sin ta có a R = = 2 . 2sin A
Câu 54: Cho tam giác ABC có AB = 3, AC = 4 , BC = 5 . Bán kính đường tròn nội tiếp tam giác bằng A. 1. B. 8 . C. 4 . D. 3 . 9 5 4 Lời giải Chọn A Vì 2 2 2
AB + AC = BC nên tam giác ABC vuông tại A . 1 A .BAC
Do đó bán kính đường tròn nội tiếp S 2 3.4 r = = = = 1.
p 1 (AB + AC + BC) 3+4+5 2
Câu 55: Cho ∆ABC có S = 84,a =13,b =14,c =15. Độ dài bán kính đường tròn ngoại tiếp R của tam giác trên là: A. 8,125. B. 130. C. 8. D. 8,5. Lời giải Chọn A Ta có: . a . b c . a . b c 13.14.15 65 S ABC ∆ = ⇔ R = = = . 4R 4S 4.84 8
Câu 56: Cho ∆ABC có S =10 3 , nửa chu vi p =10. Độ dài bán kính đường tròn nội tiếp r của tam giác trên là: Page 13
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC A. 3. B. 2. C. 2. D. 3. Lời giải Chọn D Ta có: S 10 3
S = pr ⇒ r = = = 3. p 10
Câu 57: Một tam giác có ba cạnh là 26,28,30. Bán kính đường tròn nội tiếp là: A. 16. B. 8. C. 4. D. 4 2. Lời giải Chọn B Ta có:
a + b + c 26 + 28 + 30 p = = = 42. 2 2 S
p( p − a)( p − b)( p − c)
42(42 − 26)(42 − 28)(42 − 30)
S = pr ⇒ r = = = = 8. p p 42
Câu 58: Một tam giác có ba cạnh là 52,56,60.Bán kính đường tròn ngoại tiếp là: A. 65. B. 40. C. 32,5. D. 65. 8 4 Lời giải Chọn C Ta có:
a + b + c 52 + 56 + 60 p = = = 84. 2 2
Suy ra: S = p( p − a)( p − b)( p − c) = 84(84 − 52)(84 − 56)(84 − 60) =1344 . Mà abc abc 52.56.60 65 S = ⇒ R = = = . 4R 4S 4.1344 2
Câu 59: Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn ngoại tiếp là? A. 6. B. 8. C. 13 . D. 11. 2 2 Lời giải Chọn C Ta có: 2 2 2 13 5 +12 =13 ⇒ R = . . 2
Câu 60: Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu? A. 2. B. 2 2. C. 2 3. D. 3. Lời giải Chọn A Ta có: 5 +12 +13 p = =15 . Mà 2 2 2 1
5 +12 =13 ⇒ S = .5.12 = 30. 2 2 Mặt khác = . S
S p r ⇒ r = = 2. p
Câu 61: Tam giác với ba cạnh là 6;8;10 có bán kính đường tròn ngoại tiếp bằng bao nhiêu? A. 5. B. 4 2. C. 5 2. D. 6 . Lời giải Chọn A Ta có: 2 2 2 10 6 + 8 =10 ⇒ R = = 5.. 2 Page 14
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC
Câu 62: Cho hình chữ nhật ABCD có cạnh AB = 4, BC = 6, M là trung điểm của BC, N là điểm trên
cạnh CD sao cho ND = 3NC . Khi đó bán kính của đường tròn ngoại tiếp tam giác AMN bằng A. 3 5 . B. 3 5 . C. 5 2 . D. 5 2 . 2 2 Lời giải Chọn D Ta có
MC = 3, NC =1⇒ MN = 10
BM = 3, AB = 4 ⇒ AM = 5
AD = 6, ND = 3 ⇒ AN = 45 AM AN MN 10 5 45 p + + + + = = 2 2 S
= p p − AM p − AN p − MN = AMN ( )( )( ) 152
Bán kính của đường tròn ngoại tiếp của tam giác AMN là:
AM.AN.MN 5 2 R = = 4SAMN 2
Câu 63: Cho tam giác đều ABC ;gọi D là điểm thỏa mãn DC = 2BD . Gọi R và r lần lượt là bán kính
đường tròn ngoại tiếp và nội tiếp của tam giác ADC. Tính tỉ số R . r A. 5 . B. 5 + 7 7 . C. 7 + 5 5 . D. 7 + 5 7 . 2 9 9 9 Lời giải Chọn D
Ta có DC = 2BD ⇔ DC = 2
− DB . Do đó DC = 2DB .
Gọi S là diện tích của tam giác ACD và E là trung điểm của BC . Page 15
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 2 2 2 2 a 3 a 3 S = S = = ABC . 3 3 4 6
Đặt AB = a . Suy ra 2 . 2 2 2 a 3 a 2a 7
AD = AE + ED = + = 2 6 6
AD + DC + AC 5 + 7 S = .r = . a r 5 + 7 ar.2a 7 7 5 + 7 2 6 a r 2 ( ) 3 ( ) 4 Hơn nữa ⇒ S = = . 3 A .
D DC.BC 2a 7 6.36R 108R S = = 4R 36R a ( + ) 4 4 7 5 7 a r 7 R (5+ 7).12 7 R (5+ 7) Hay = ⇔ = ⇔ = . 12 108R r 108 r 9
DẠNG 4. ỨNG DỤNG THỰC TẾ
Câu 64: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta
xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 78o24'. Biết CA = 250 ,
m CB =120m . Khoảng cách AB bằng bao nhiêu? A. 266 . m B. 255 . m C. 166 . m D. 298 . m Lời giải Chọn B Ta có: 2 2 2 2 2 = +
− 2 . .cos = 250 +120 − 2.250.120.cos78o AB CA CB CB CA C
24' 64835 ⇒ AB 255.
Câu 65: Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 0 60
. Tàu thứ nhất chạy với tốc độ 30km / h , tàu thứ hai chạy với tốc độ 40km / h . Hỏi sau 2 giờ hai
tàu cách nhau bao nhiêu km ? A. 13. B. 20 13. C. 10 13. D. 15. Lời giải Chọn B
Ta có: Sau 2h quãng đường tàu thứ nhất chạy được là: 1 S = 30.2 = 60k . m
Sau 2h quãng đường tàu thứ hai chạy được là: S2 = 40.2 = 80k . m
Vậy: sau 2h hai tàu cách nhau là: 2 2 0 S = 1 S + S2 − 2 1
S .S2.cos60 = 20 13.
Câu 66: Từ một đỉnh tháp chiều cao CD = 80m , người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là 0 72 12' và 0 34 26' . Ba điểm ,
A B, D thẳng hàng. Tính khoảng cách AB ? A. 71 . m B. 91 . m C. 79 . m D. 40 . m Lời giải Chọn B
Ta có: Trong tam giác vuông CDA: 0 CD CD 80 tan 72 12' = ⇒ AD = = 25,7. 0 0 AD tan 72 12' tan 72 12'
Trong tam giác vuông CDB : 0 CD CD 80 tan34 26' = ⇒ BD = = 116,7. 0 0 BD tan34 26' tan34 26'
Suy ra: khoảng cách AB =116,7 − 25,7 = 91 . m
Câu 67: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta
xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 0 56 16' . Biết
CA = 200m , CB =180m . Khoảng cách AB bằng bao nhiêu? A. 180 . m B. 224 . m C. 112 . m D. 168 . m Page 16
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC Lời giải Chọn A Ta có: 2 2 2 2 2 0
AB = CA + CB − 2C . B C .
A cosC = 200 +180 − 2.200.180.cos56 16' 32416 ⇒ AB 180.
Câu 68: Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn
bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính của
chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như
hình vẽ ( AB = 4,3cm; BC = 3,7 cm; CA = 7,5 cm). Bán kính của chiếc đĩa này bằng.
A. 5,73 cm.
B. 6,01cm.
C. 5,85cm. D. 4,57cm. Lời giải Chọn A
Bán kính R của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác ABC .
Nửa chu vi của tam giác ABC là: AB BC CA 4,3 3,7 7,5 31 p + + + + = = = cm. 2 2 4
Diện tích tam giác ABC là: S = p( p − AB)( p − BC)( p −CA) ≈ 5,2cm2. Mà A . B BC.CA A . B BC.CA S = ⇒ R = ≈ 5,73 cm. 4R 4S
Câu 69: Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất
sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24m, 0 CAD = 63 ; 0 CBD = 48 . Chiều cao
h của khối tháp gần với giá trị nào sau đây? A. 61,4 m. B. 18,5 m. C. 60 m. D. 18 m. Lời giải Chọn A Ta có 0 = ⇒ 0 = ⇒ 0 CAD BAD ADB = − ( 0 0 + ) 0 63 117 180 117 48 =15
Áp dụng định lý sin trong tam giác ABD ta có: AB BD A . B sin BAD = ⇒ BD = sin ADB sin BAD sin ADB
Tam giác BCD vuông tại C nên có: CD = ⇒ = sin CBD CD B . D sin CBD BD Page 17
CHUYÊN ĐỀ IV – TOÁN 10 – CHƯƠNG IV – HỆ THỨC LƯỢNG TRONG TAM GIÁC 0 0 Vậy A . B sin BA .
D sin CBD 24.sin117 .sin 48 CD = = = 61,4m 0 sin ADB sin15 Page 18
Document Outline
- 1_TOAN-10_B1_C4_GIÁ-TRỊ-LƯỢNG-GIÁC-CỦA-MỘT-GÓC_TU-LUAN_DE
- DẠNG 1: TÍNH CÁC GIÁ TRỊ BIỂU THỨC LƯỢNG GIÁC
- DẠNG 2: TÍNH GIÁ TRỊ CỦA MỘT BIỂU THỨC LƯỢNG GIÁC , KHI BIẾT TRƯỚC MỘT GIÁ TRỊ LƯỢNG GIÁC.
- DẠNG 3: CHỨNG MINH CÁC ĐẲNG THỨC, RÚT GỌN CÁC BIỂU THỨC LƯỢNG GIÁC
- 1_TOAN-10_B1_C4_GIÁ-TRỊ-LƯỢNG-GIÁC-CỦA-MỘT-GÓC_TU-LUAN_HDG
- DẠNG 1: TÍNH CÁC GIÁ TRỊ BIỂU THỨC LƯỢNG GIÁC
- DẠNG 2: TÍNH GIÁ TRỊ CỦA MỘT BIỂU THỨC LƯỢNG GIÁC , KHI BIẾT TRƯỚC MỘT GIÁ TRỊ LƯỢNG GIÁC.
- DẠNG 3: CHỨNG MINH CÁC ĐẲNG THỨC, RÚT GỌN CÁC BIỂU THỨC LƯỢNG GIÁC
- 2_TOAN-10_B1_C4_GIÁ-TRỊ-LƯỢNG-GIÁC-CỦA-MỘT-GÓ_TRAC-NGHIEM_DE
- DẠNG 1. DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC. GIÁ TRỊ LƯỢNG GIÁC
- DẠNG 2. CHO BIẾT MỘT GIÁ TRỊ LƯỢNG GIÁC, TÍNH CÁC GIÁ TRỊ LƯỢNG GIÁC CÒN LẠI
- DẠNG 3. CHỨNG MINH, RÚT GỌN BIỂU THỨC LƯỢNG GIÁC
- A. . B. . C. . D. .
- DẠNG 4. TÍNH GIÁ TRỊ BIỂU THỨC LƯỢNG GIÁC
- 2_TOAN-10_B1_C4_GIÁ-TRỊ-LƯỢNG-GIÁC-CỦA-MỘT-GÓC_TRAC-NGHIEM_HDG
- DẠNG 1. DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC. GIÁ TRỊ LƯỢNG GIÁC
- DẠNG 2. CHO BIẾT MỘT GIÁ TRỊ LƯỢNG GIÁC, TÍNH CÁC GIÁ TRỊ LƯỢNG GIÁC CÒN LẠI
- DẠNG 3. CHỨNG MINH, RÚT GỌN BIỂU THỨC LƯỢNG GIÁC
- DẠNG 4. TÍNH GIÁ TRỊ BIỂU THỨC LƯỢNG GIÁC
- 3_TOAN-10_B2,3_C4_DINH-LY-COSIN-SIN-GIAI-TAM-GIAC_TU-LUAN_DE
- DẠNG 1: GIẢI TAM GIÁC
- DẠNG 2: HỆ THỨC LIÊN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC, NHẬN DẠNG TAM GIÁC
- DẠNG 3: ỨNG DỤNG THỰC TẾ
- 3_TOAN-10_B2,3_C4_DINH-LY-COSIN-SIN-GIAI-TAM-GIAC_TU-LUAN_HDG
- DẠNG 1: GIẢI TAM GIÁC
- DẠNG 2: HỆ THỨC LIÊN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC, NHẬN DẠNG TAM GIÁC
- DẠNG 3: ỨNG DỤNG THỰC TẾ
- 4_TOAN-10_B2,3_C4_DINH-LY-COSIN-SIN-GIAI-TAM-GIAC_TRAC-NGHIEM_DE
- DẠNG 1. ĐỊNH LÝ COSIN, ÁP DỤNG ĐỊNH LÝ COSIN ĐỂ GIẢI TOÁN
- DẠNG 2. ĐỊNH LÝ SIN, ÁP DỤNG ĐỊNH LÝ SIN ĐỂ GIẢI TOÁN
- DẠNG 3. DIỆN TÍCH TAM GIÁC, BÁN KÍNH ĐƯỜNG TRÒN
- DẠNG 4. ỨNG DỤNG THỰC TẾ
- 4_TOAN-10_B2,3_C4_DINH-LY-COSIN-SIN-GIAI-TAM-GIAC_TRAC-NGHIEM_HDG
- DẠNG 1. ĐỊNH LÝ COSIN, ÁP DỤNG ĐỊNH LÝ COSIN ĐỂ GIẢI TOÁN
- DẠNG 2. ĐỊNH LÝ SIN, ÁP DỤNG ĐỊNH LÝ SIN ĐỂ GIẢI TOÁN
- DẠNG 3. DIỆN TÍCH TAM GIÁC, BÁN KÍNH ĐƯỜNG TRÒN
- DẠNG 4. ỨNG DỤNG THỰC TẾ



