




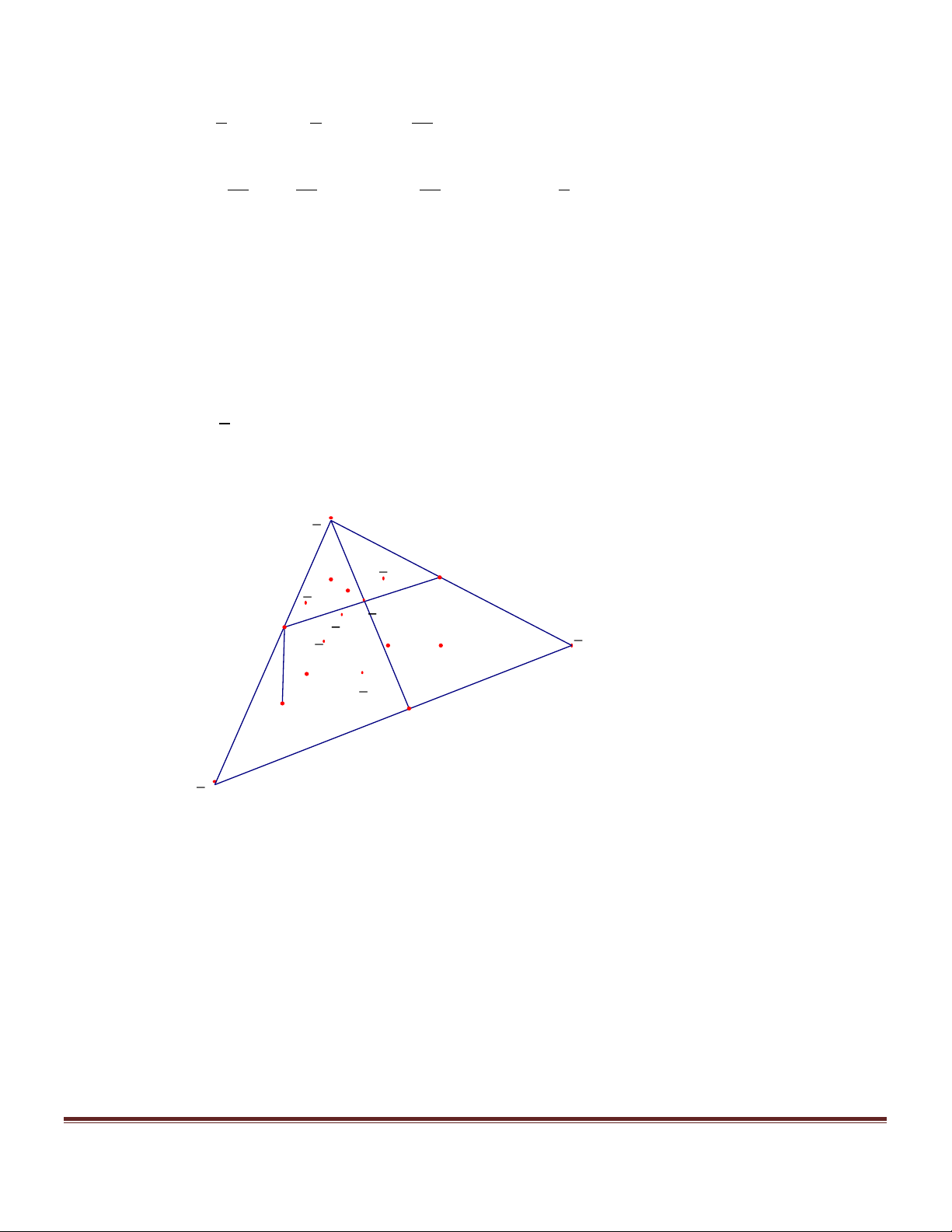


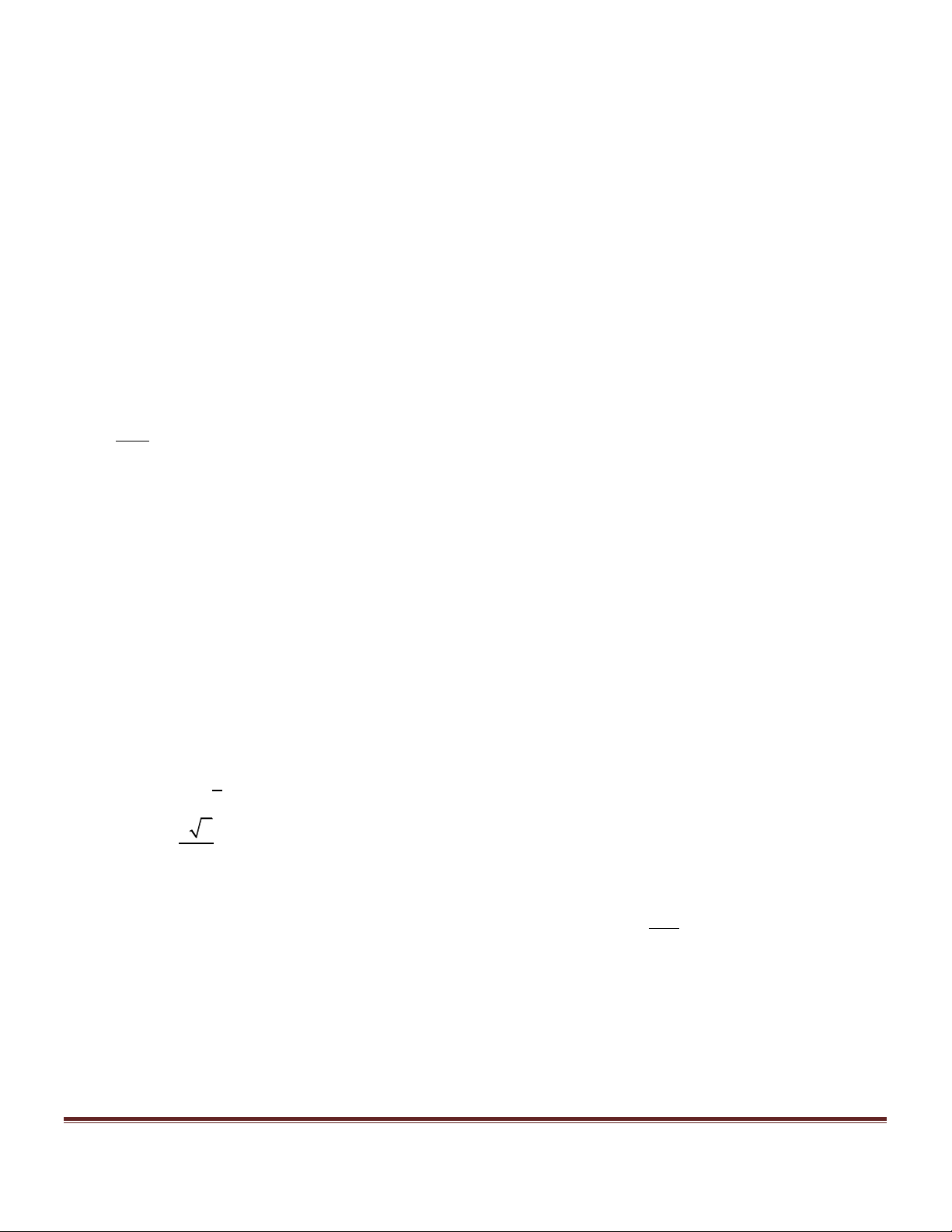












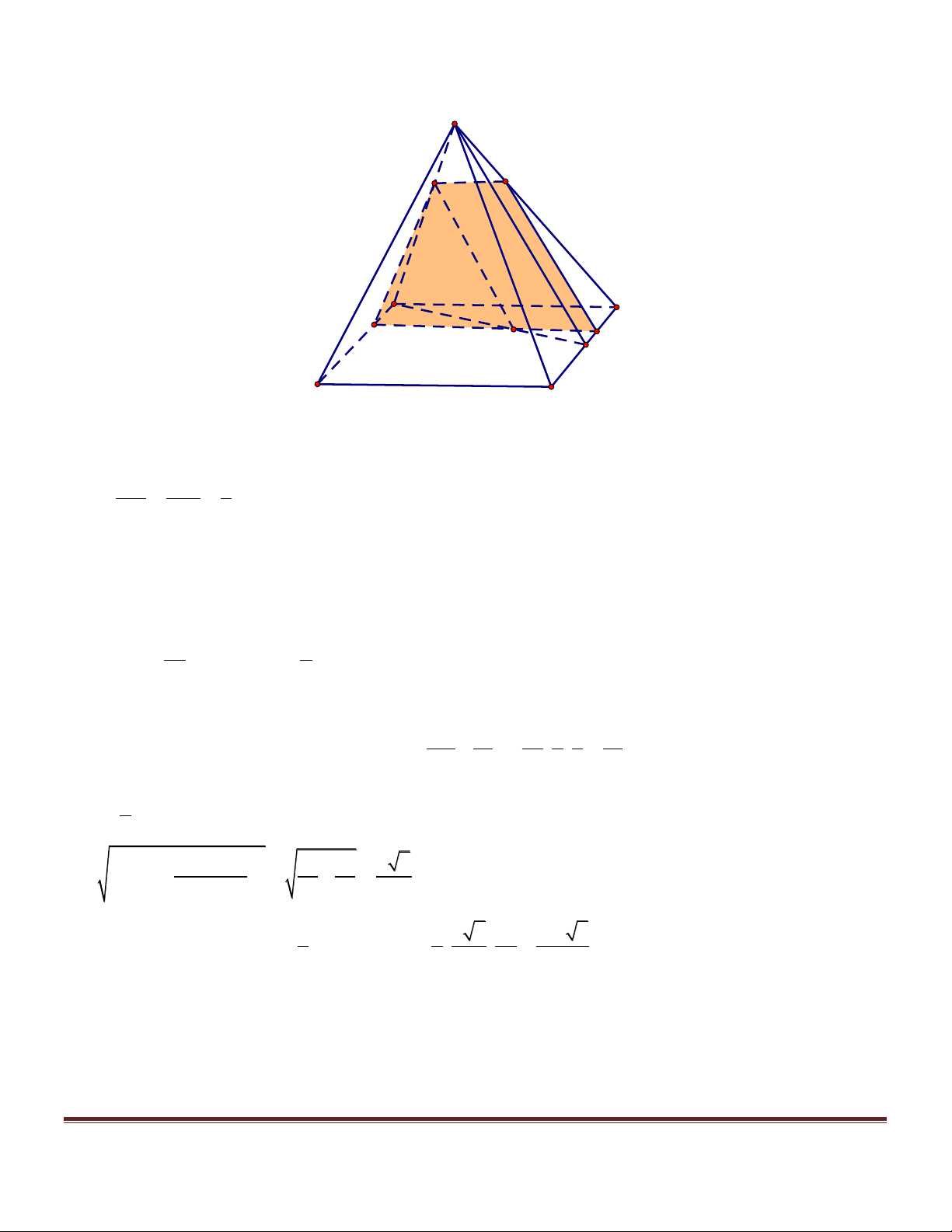









Preview text:
CHUYÊN ĐỀ HÌNH HỌC KHÔNG GIAN BỒI DƯỠNG HỌC SINH GIỎI Bài 1.
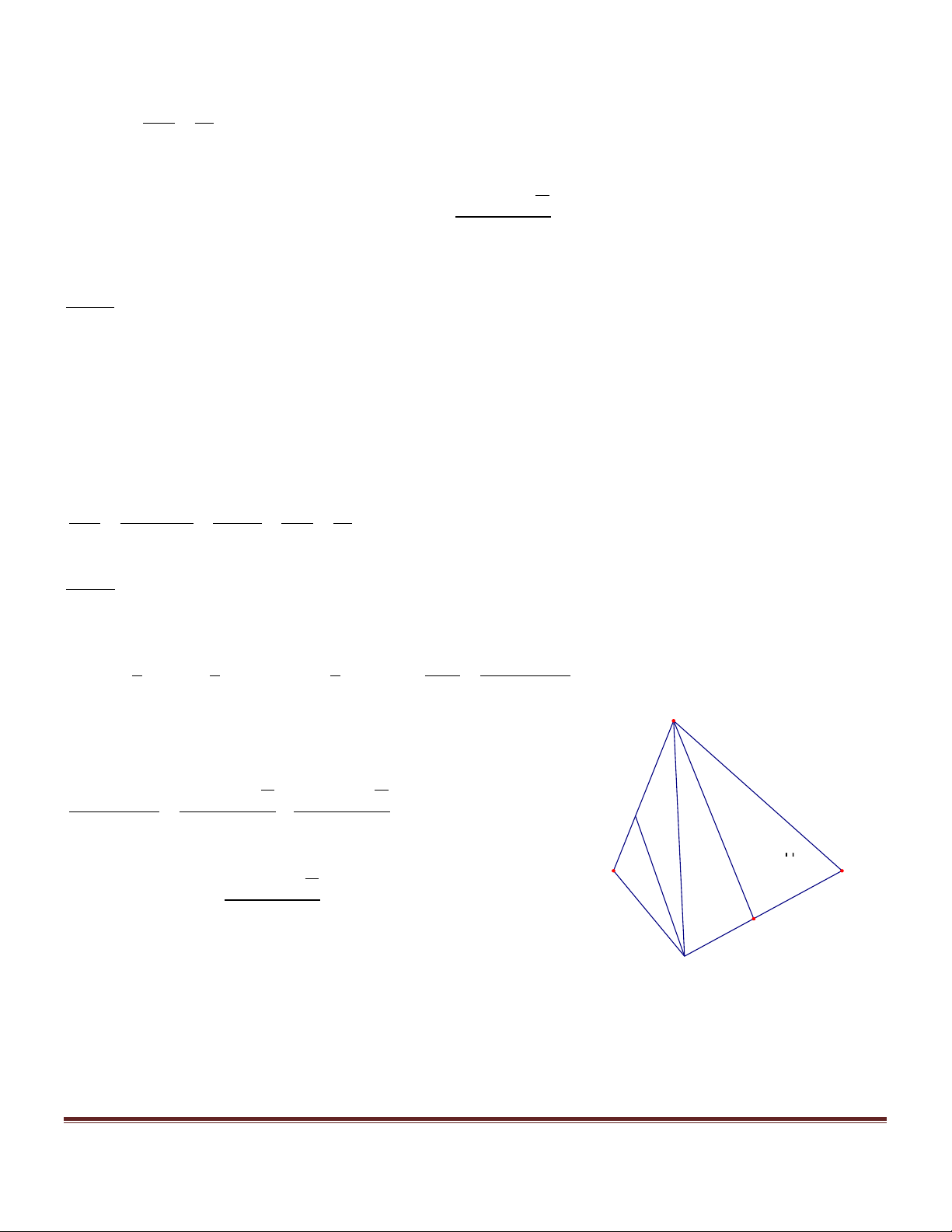
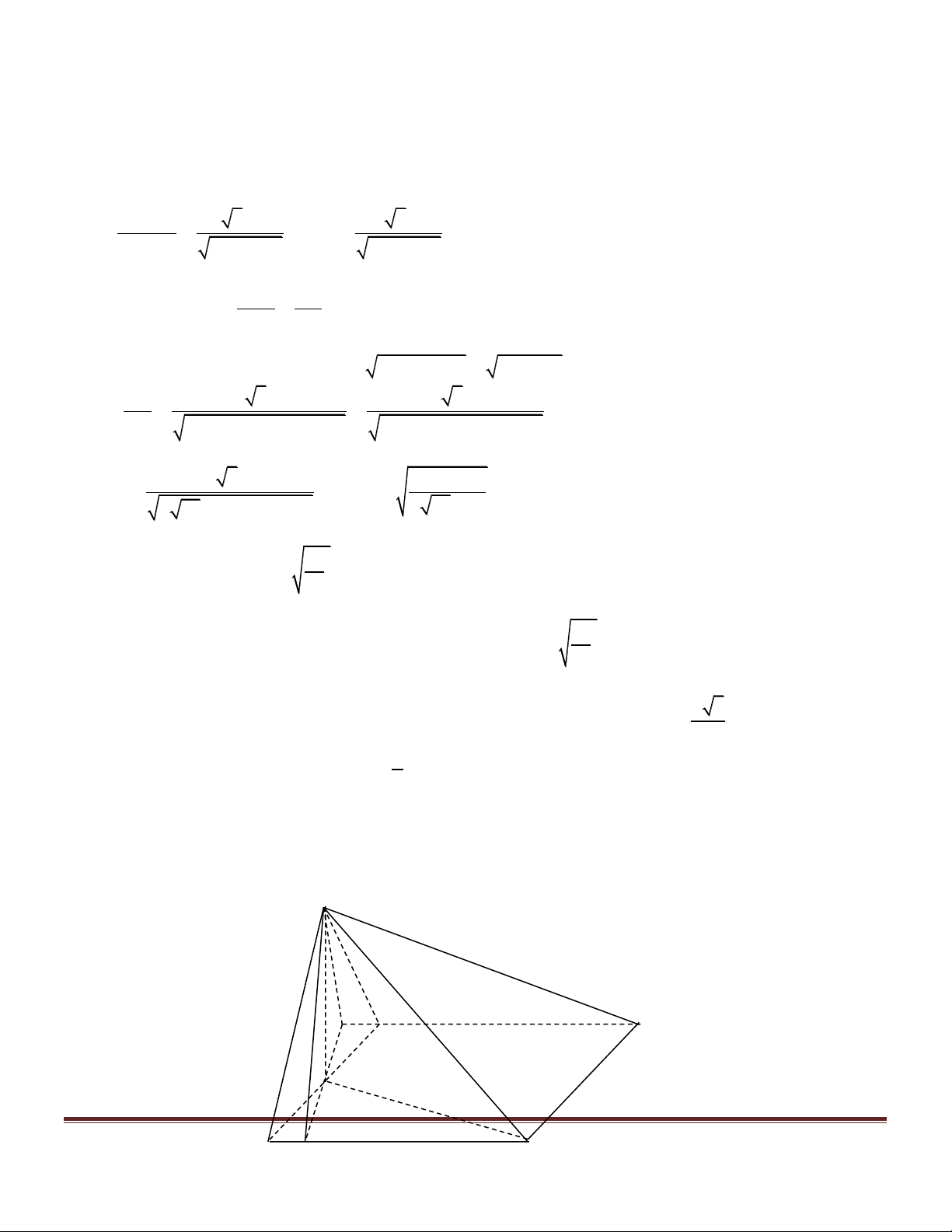
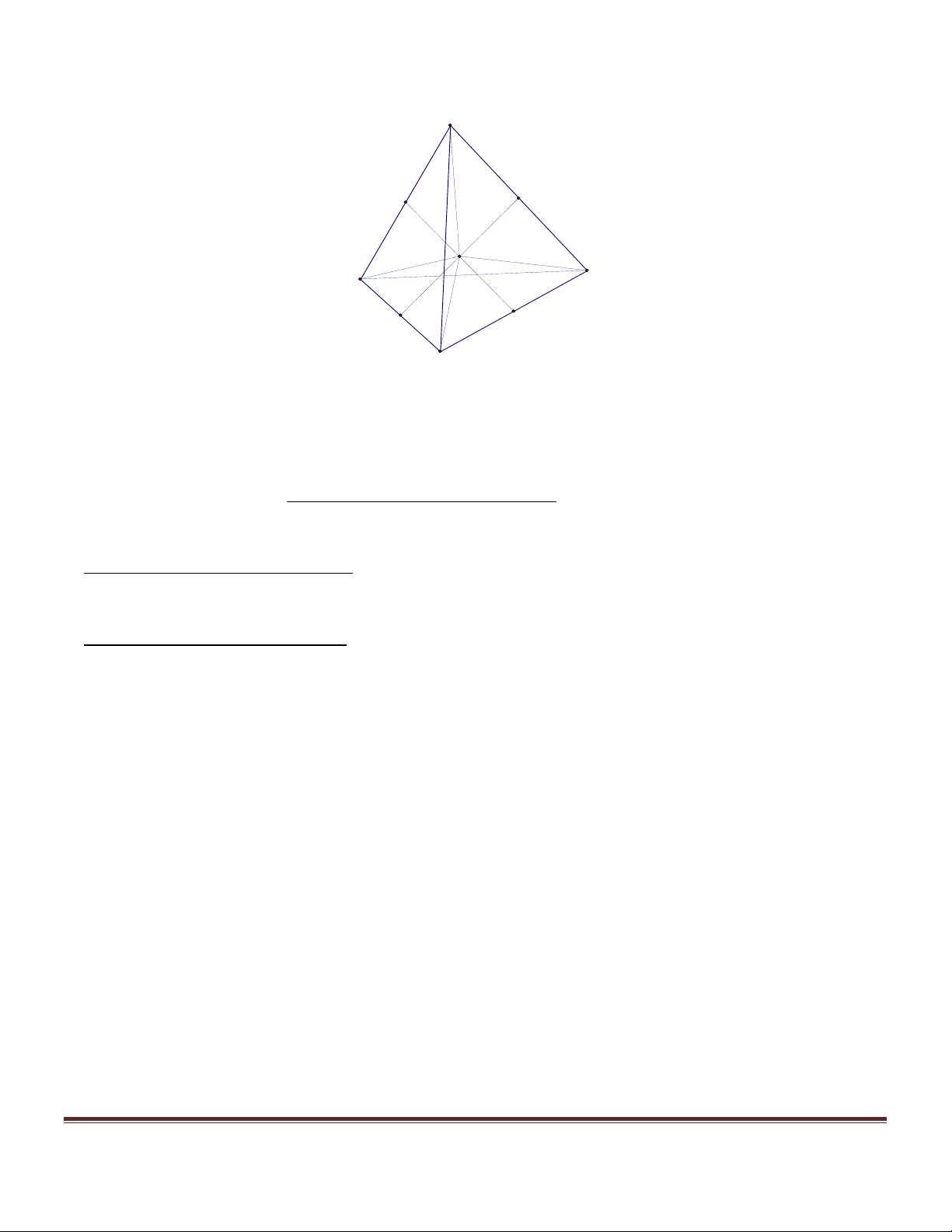
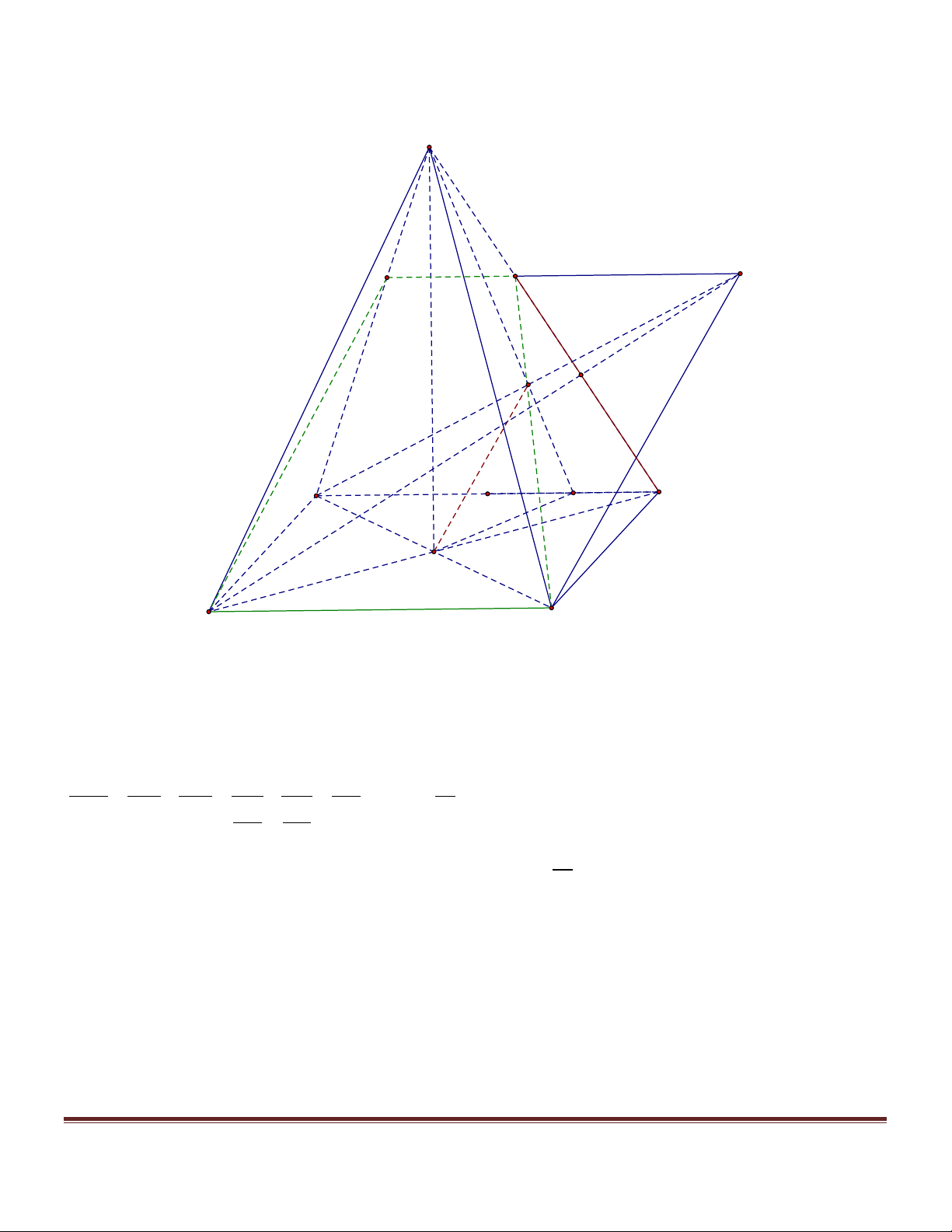
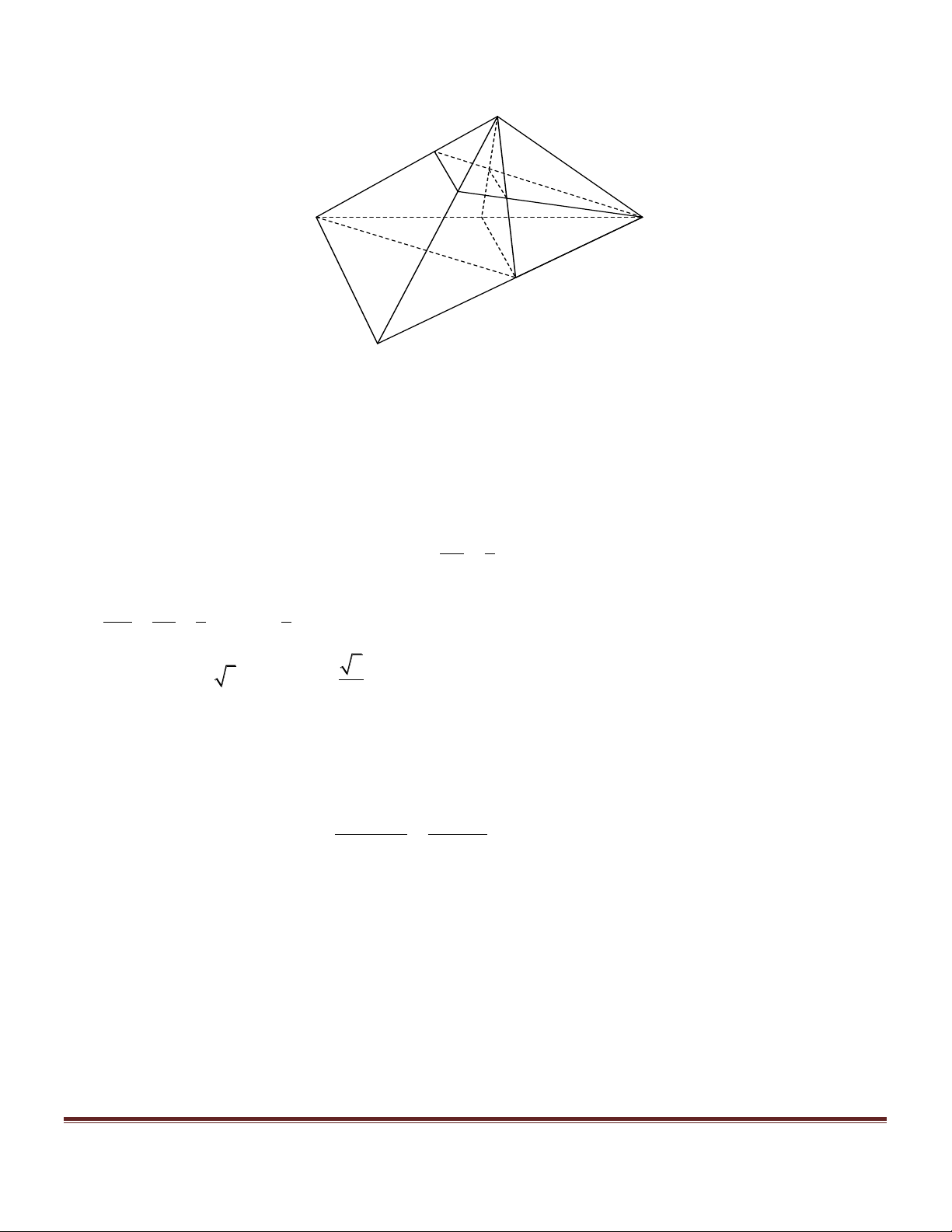
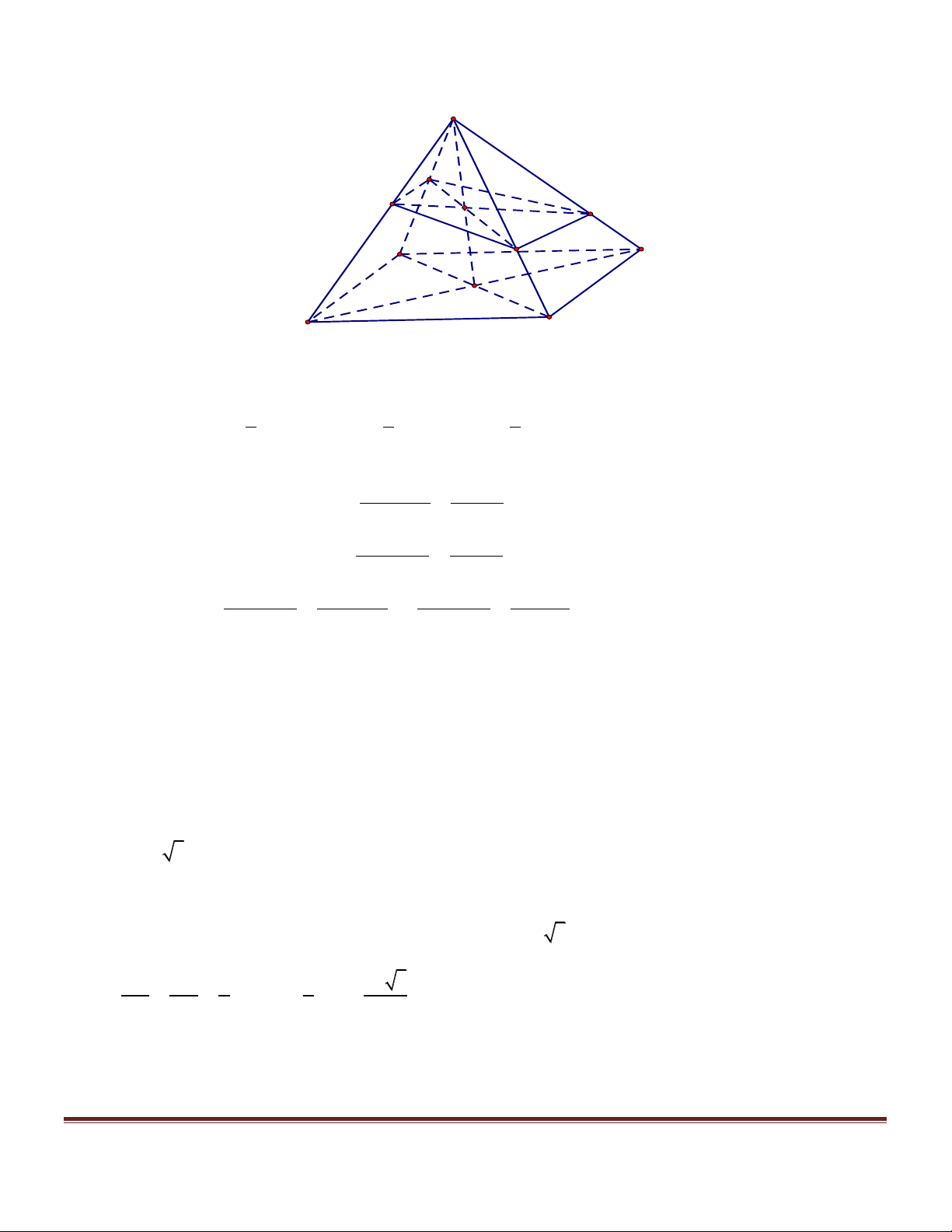
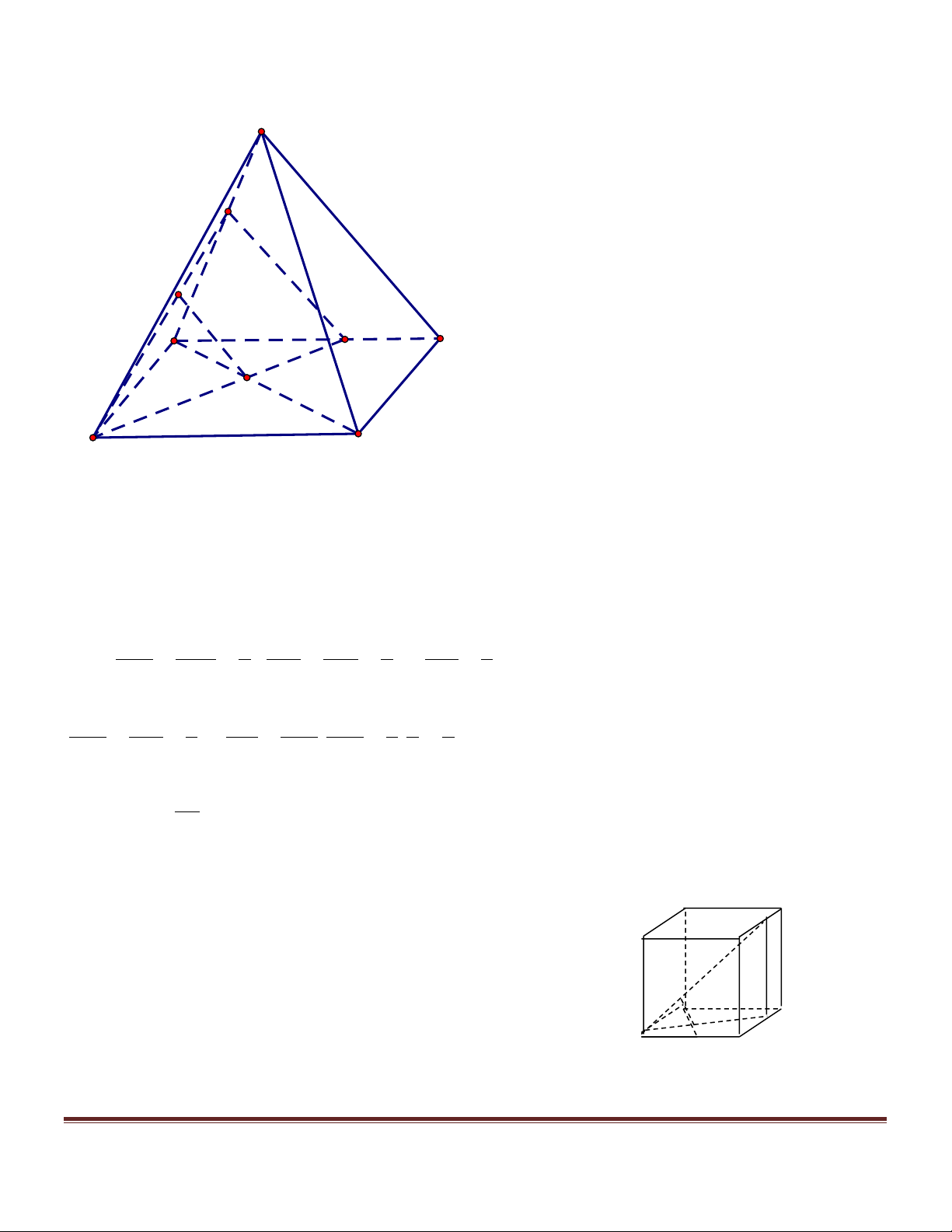
Xét các hình chóp n – giác S.A A ...A ( n là số tự nhiên tùy ý lớn hơn 2 ) thỏa mãn đồng thời 1 2 n các điều kiện sau:
a/ Đáy A A ...A có tất cả các cạnh đều bằng 1. 1 2 n b/ ∑ ∑ ∑ 0 SA A = SA A = ... = SA A = 60 1 2 2 3 n 1
Tìm giá trị lớn nhất, nhỏ nhất độ dài đường cao SH của hình chóp nêu trên. Hướng dẫn giải
Chứng minh nếu hình chóp S.A A ...A tồn tại thì khi đó hình chóp là đều: 1 2 n
Chứng minh rằng các cạnh bên bằng nhau
Đặt : SA = x ; SA = x ; ..... ; SA = x . 1 1 2 2 n n
Dùng định lý cosin trong các tam giác SA A ; SA A ; ...; SA A ta có: 1 2 2 3 n 1 2 2 0 2
x = 1+ x - 2x cos 60 = 1+ x - x 2 1 1 1 1 2 2 0 2
x = 1+ x - 2x o
c s60 = 1+ x - x 3 2 2 2 2
....................................................... 2 2 0 2 x = 1+ x - 2x os6 c 0 = 1+ x - x n n- 1 n- 1 n- 1 n- 1 2 2 0 2
x = 1+ x - 2x o
c s60 = 1+ x - x . 1 n n n n 2 Ï x Ô = f (x ) 2 1 Ô Ô Ô 2 x Ô = f (x ) 1 3 3 2 Ô Ô È 3 ˆ Đặt 2 2
f (x) = x - x + 1 = (x - ) + , ta có hệ: ............... Ô ˜ Ì
với x , x , ..., x Í Œ ;+ • ˜ 2 4 Ô 1 2 n ˜ Í Ô 2 ˜ Í ¯ 2 x Ô = f (x ) Î Ô n n- 1 Ô Ô 2 x Ô = f (x ) Ô Ó 1 n é 3 ö Trên ê
;+¥÷ f (x) đồng biến. 2 ÷ ë ø
Do đó: x ¹ x thì vô lý. 1 2
Thật vậy: nếu x < x Þ f x < f x Þ 2 2
x < x Þ x < x Þ ... Þ x < x x < x 1 2 ( 1) ( 2) . Ta có ( vô lý) 2 3 2 3 n 1 1 1
Tương tự nếu x > x cũng suy ra điều vô lý: x > x . Vậy x = x . 1 2 1 1 1 2 Trang 1
Do x = x ta được 2 2 x = x - x +1 Û x = . T
1 ừ đó ta được: x = x = ... = x = . 1 1 2 1 1 1 1 1 2 n
Chứng minh đáy A A ...A là đa giác đều. Từ SA = SA = ... = SA =1 suy ra hình vuông góc H của S lên 1 2 n 1 2 n
đáy cách đều các đỉnh của đáy. Đa giác A A ...A có các cạnh bằng nhau và nội tiếp trong một đường tròn nên 1 2 n là đa giác đều.
a) Tìm SH lớn nhất, nhỏ nhất.
b) Chứng minh n < 6 .Ta có các mặt bên của hònh chóp là các tam giác đều cạnh 1. Ngoài ra: 0
60 = A SA < A HA ; 0
60 = A SA < A HA ; ...; 0
60 = A SA < A HA . 1 2 1 2 2 3 2 3 n 1 n 1 Do đó: 0 0 .6
n 0 < 360 Û n < 6 (n > 2). •
Tính SH và tìm giá trị lớn nhất, nhỏ nhất của SH : 1
Xét tam giác vuông SHA : 2 SH = 2 2 SA - HA .SA =1;HA = . 1 1 1 1 1 p 2sin n 1 1 æ p ö 1 æ p ö 1 p 2 2 2 2 SH = 1- =1- 1+ cot g = 3 - cot g , SH= 3 - cot g n = 3;4;5. ç ÷ ç ÷ p 2 4 è 4 ø 4 è 4 ø 2 4 4sin n
n = 3: SH = 2 ; n = 4 : SH =
2 ; n = 5: SH = 1 1 - . 3 2 2 2 5 • 2 1 1
Do đó giá trị lớn nhất của SH là
, giá trị nhỏ nhất của SH là - . 3 2 2 5 Bài 2.
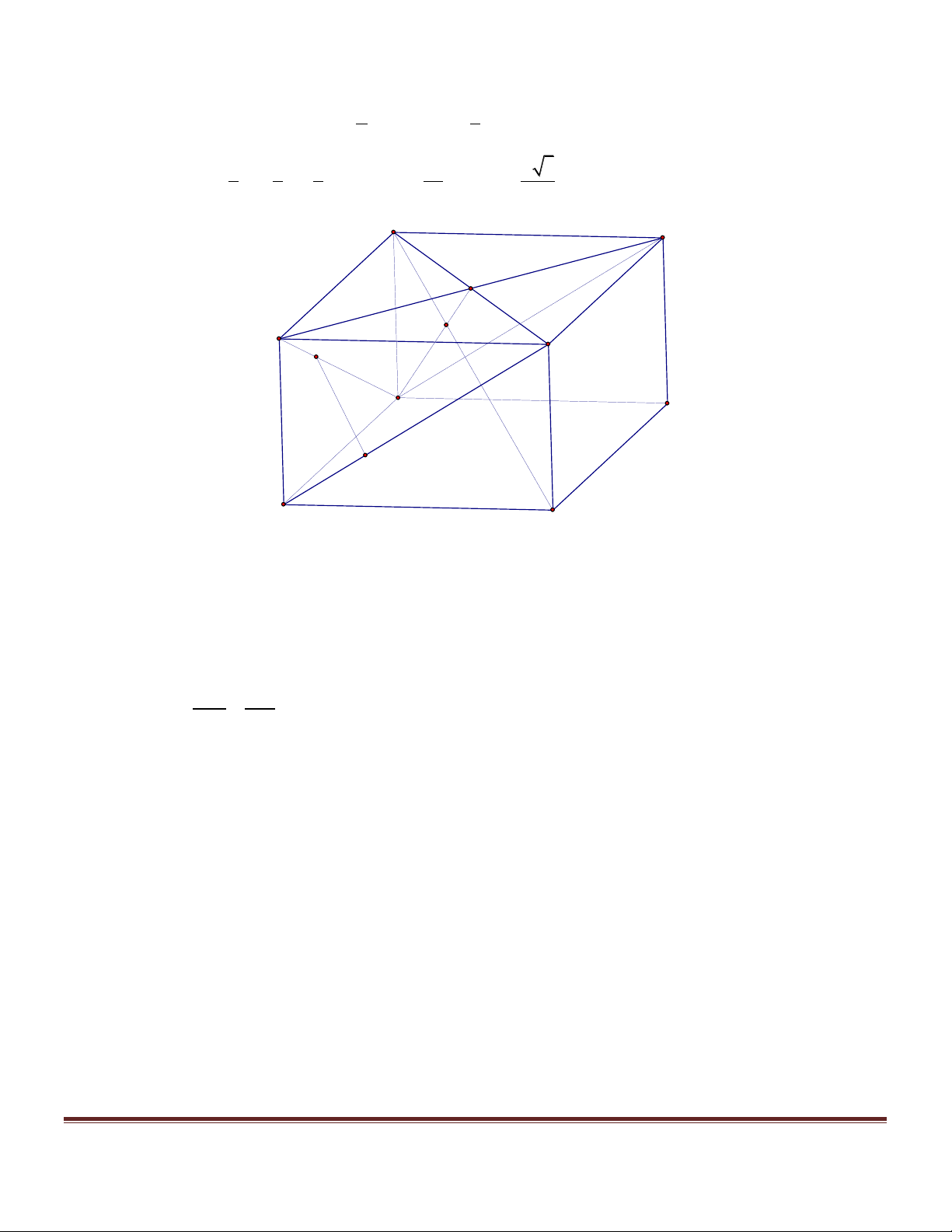
Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh a .Gọi E, G, K lần lượt là trung điểm của các cạnh
A' D ', B 'C 'và AA'. H là tâm của hình vuông DCDC '. M , N là hai điểm lần lượt ở trên hai đường thẳng
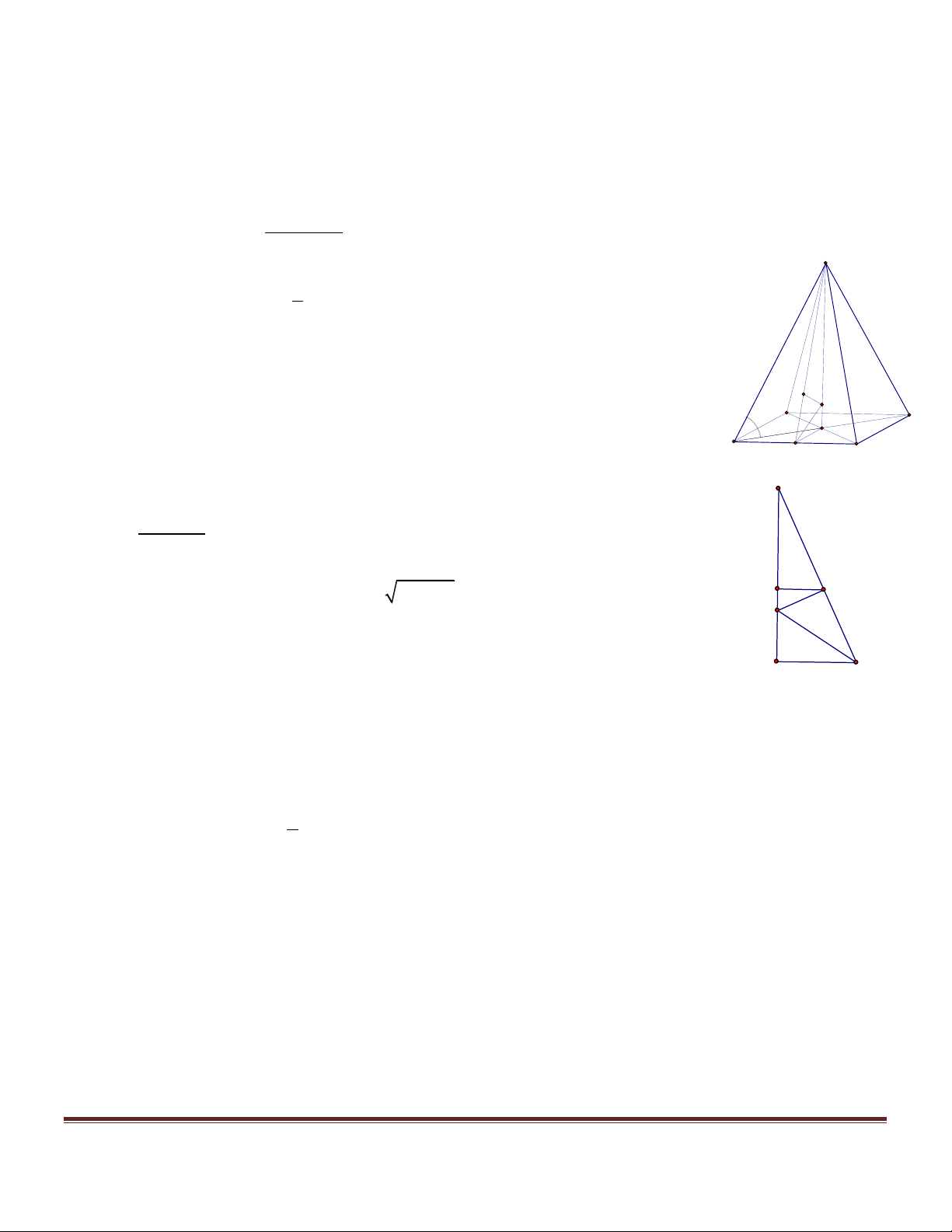
AD và EG sao cho MN vuông góc với KH và cắt KH .Tính độ dài đoạn MN theo a. Hướng dẫn giải D’ C’ E H D 1 C G A’ B’ M H I1 I E1 G1 N1 M D H1 C E1 G I1 N1 1 A B A B
Xác định đoạn MN Trang 2
Gọi E , N , G , H là hình chiếu vuông góc của E, N, G, H trên mặt phẳng ( ABCD). 1 1 1 1
Do KH ^ MN (gt) và K KH ^ NN suy ra KH ^ MN , suy ra AH ^ MN tại I . 1 1 1 1 1
Mà theo giả thiết MN cắt KH tại I suy ra II // NN mà I là trung điểm của đoạn MN nên I phải là 1 1 1
trung điểm của MN . 1
Từ đó suy ra cách dựng hai điểm M , N . Tính độ dài MN
Đặt a = DAH Þ H AN = E N M = a . 1 1 1 1 1 1 3 AE 5
Xét tam giác vuông DAH , ta có: sina = 1 Þ tga = Þ os c 2a = Þ AN = 1 = a. 5 2 5 1 cos 2a 6 5 1 a 5 a 5
Xét tam giác vuông AIN , ta có: IN = AN . sina = a. = Þ MN = . 1 1 1 1 6 5 6 3 2
(Cách khác: Gọi P là trung điểm của CG , suy ra được N ở trên AP , suy ra E N = a .) 1 1 1 1 3 E N a 5 5 14 a 14 1 1 2 2 2 2 2 2 MN = = Þ MN = NN + MN = a + a = a Þ MN = . 1 1 1 cos a 3 9 9 3
Cách khác: Dùng phương pháp tọa độ trong không gian.... Bài 3.
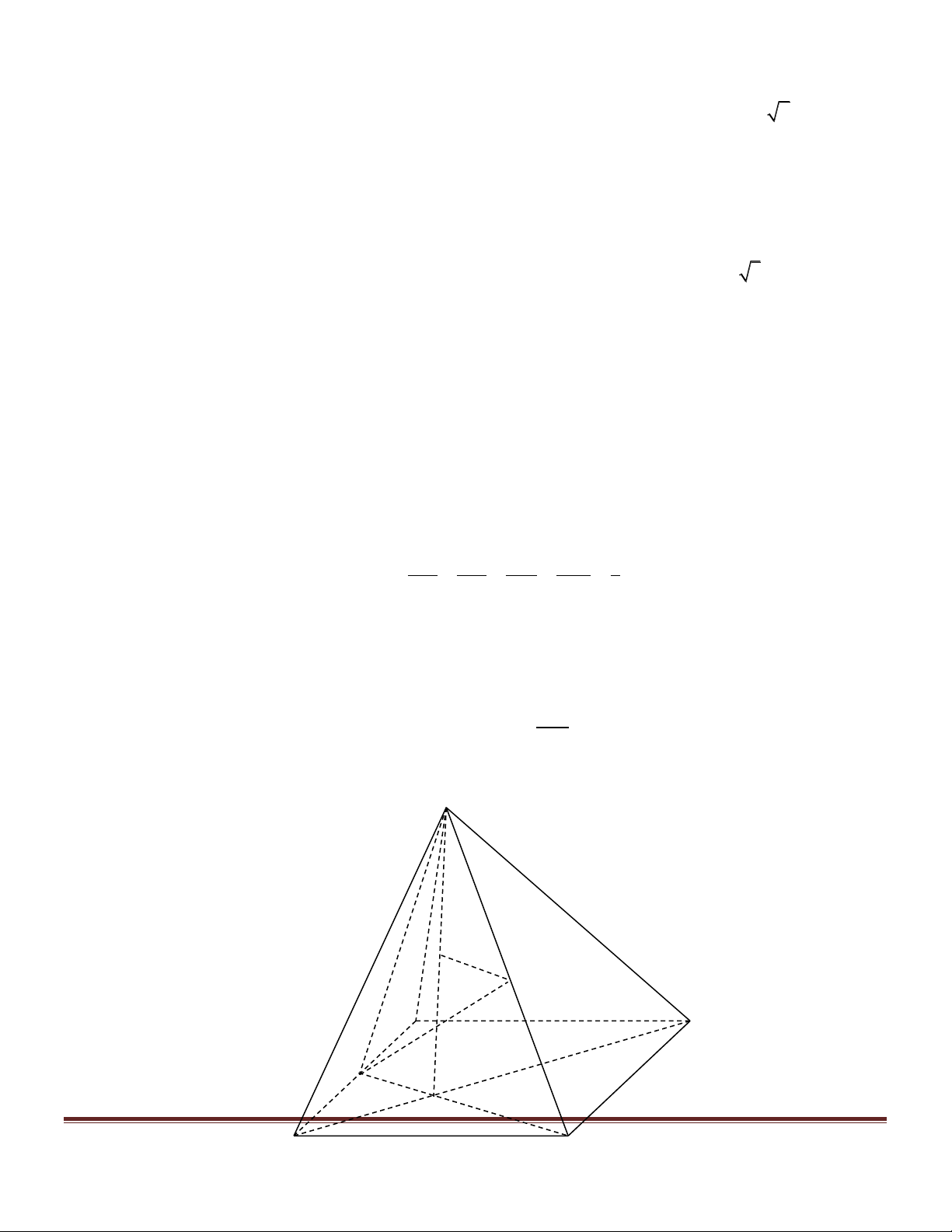
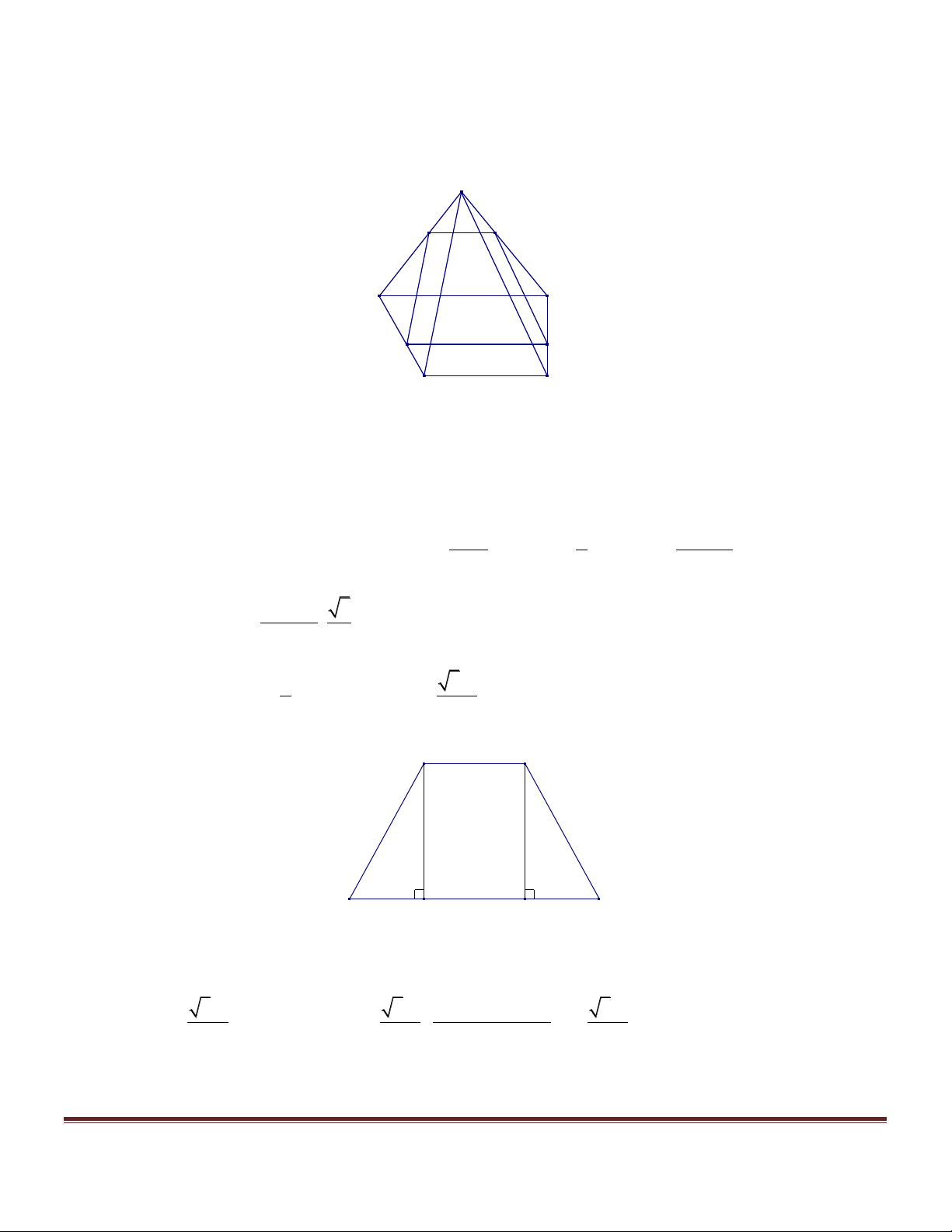
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy a =12,54(c )
m ,các cạnh bên nghiên với đáy một góc 0
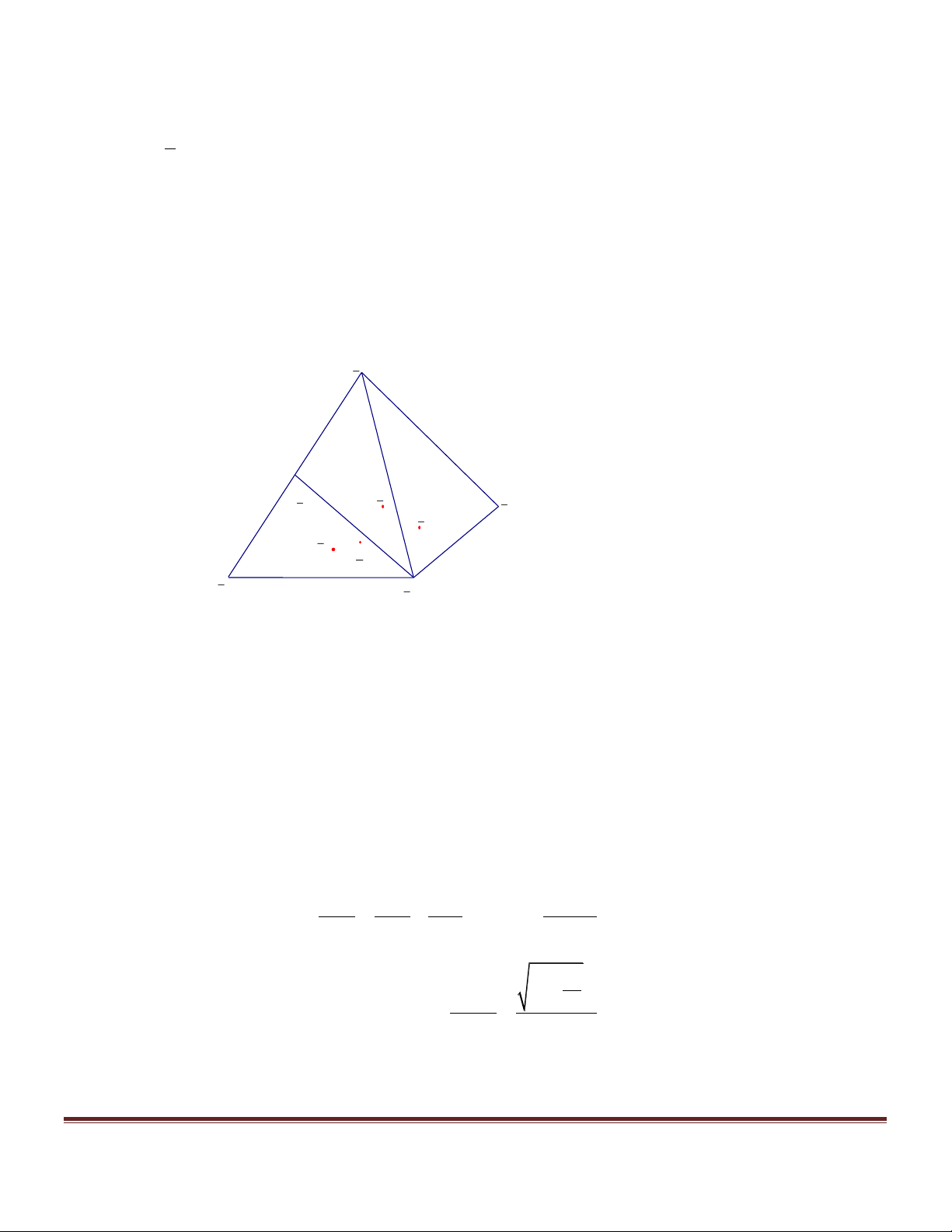
a = 72 . Tính thể tích và diện tích xung quanh của hình chóp S.ABCD . Hướng dẫn giải a 2
Chiều cao của hình chóp: 0 SH = 72 tg » 27,29018628 2 1 Thể tích của hình chóp: 2
V = a h » 1430,475152( 3 cm ) 3
Trung đoạn của hình chóp 2 d = a 2 SH + » 28,00119939 4 1
Diện tích xung quanh của hình chóp: S = .4 .
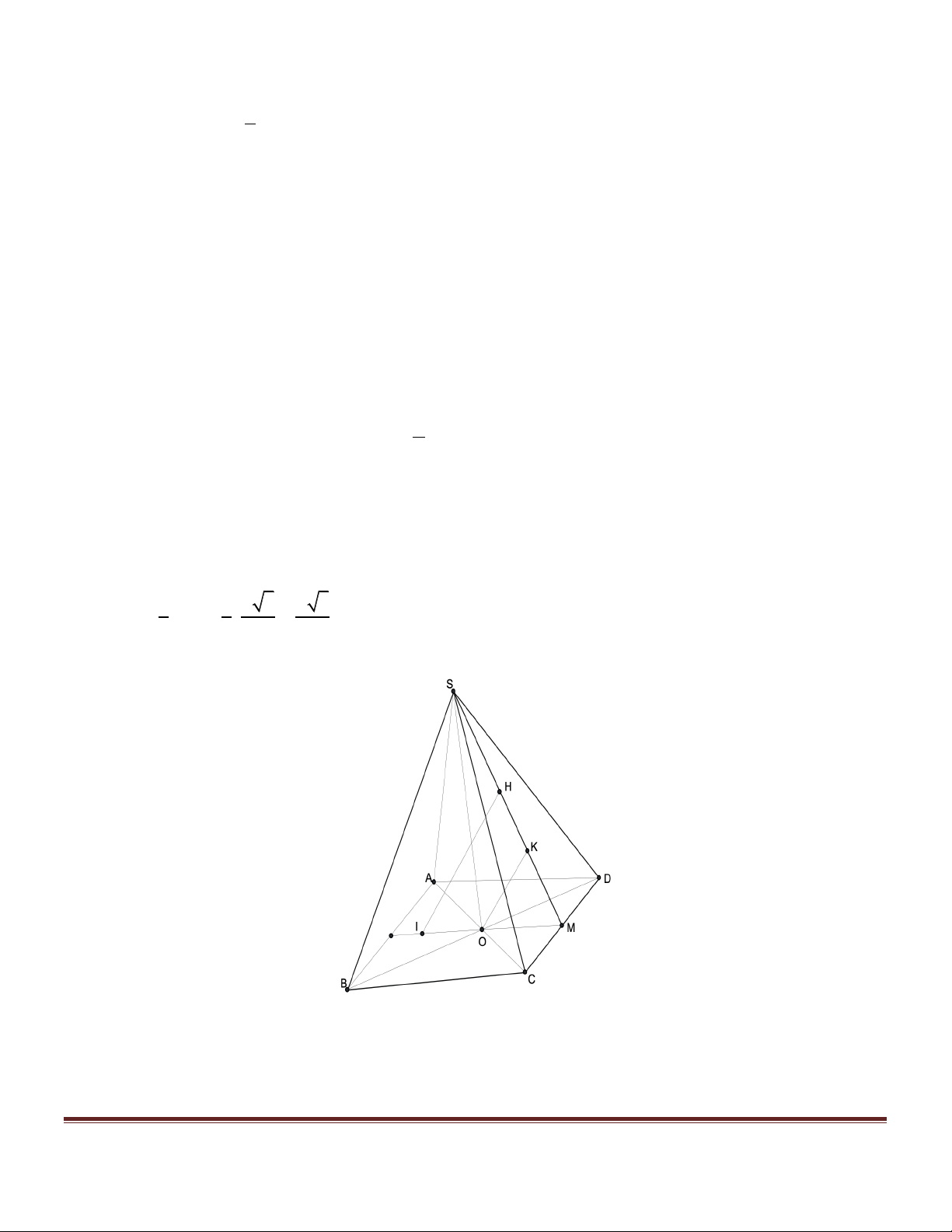
a d » 702,2700807 cm xq ( 2) 2 Bài 4.
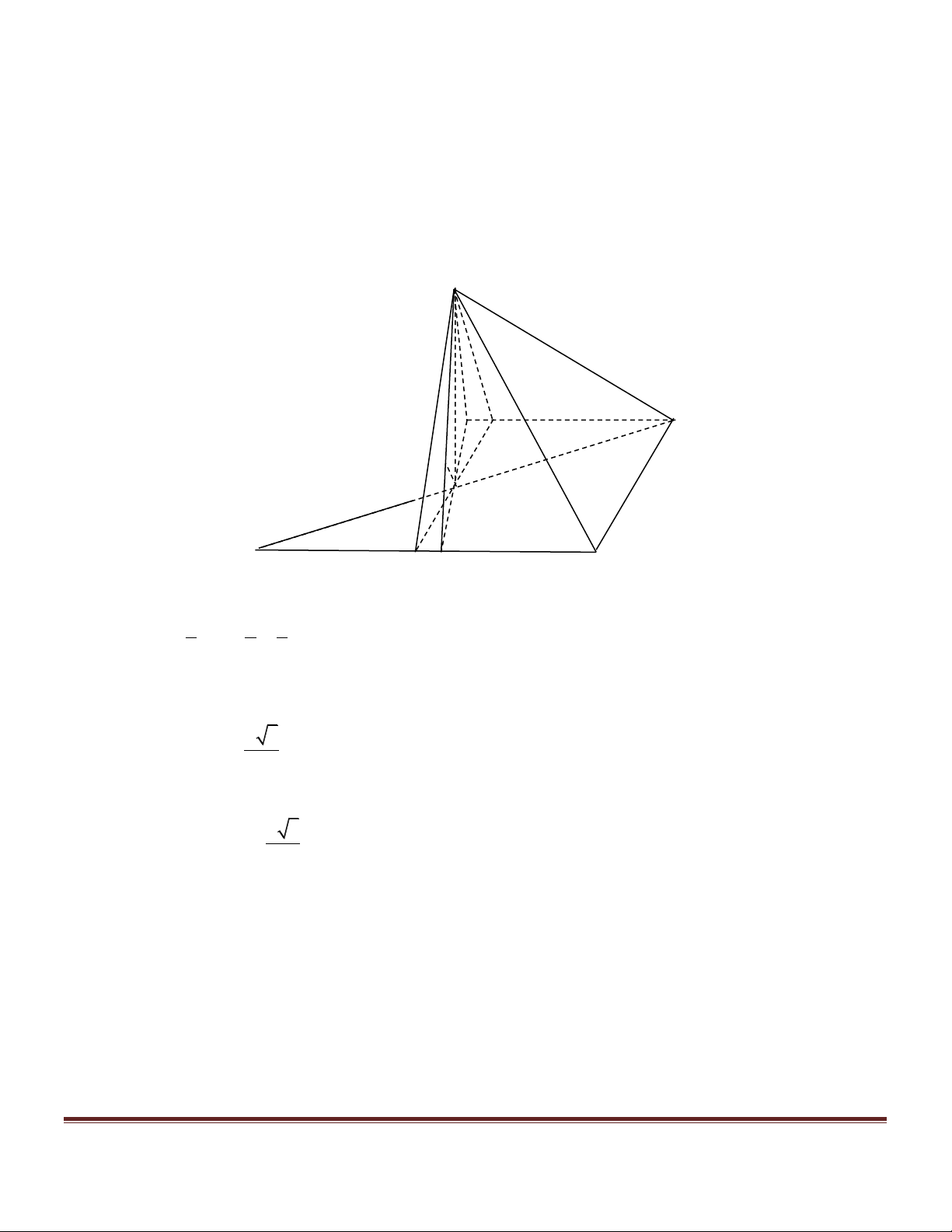
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy a =12,54(c )
m , a = 12,54(c ) m ,các cạnh bên nghiên với đáy một góc 0 a = 72 .
a) Tính thể tích hình cầu (S S.ABCD 1 ) nội tiếp hình chóp . Trang 3
b) Tính diện tích của hình tròn thiết diện của hình cầu (S1) cắt bởi mặt phẳng đi qua các tiếp điểm của mặt cầu (S S.ABCD
2 ) với các mặt bên của hình chóp . Hướng dẫn giải SH.MH
SH = 27.29018628; IH =
= 4.992806526 = R (bán kính mặt cầu nội tiếp) MH + MS S 4
Thể tích hình chóp (S 3 3
V = p R » 521.342129(cm ) 1 ) : 3 SM » 28,00119939
MH = 6, 27; IK = IH K I A 720 D H
Khoảng cách từ tâm I đến mặt phẳng đi qua các tiếp điểm của (S B 1 ) với các mặt bên M C của hình chóp: S 2 IH d = EI = = 4.866027997 SH - IH E K
Bán kính đường tròn giao tuyến: 2 2
r = EK = R - d » 1,11798414 1 I
Diện tích hình tròn giao tuyến: 2
S » 74,38733486(cm ) H M Bài 5.
Một thùng hình trụ có đường kính đáy ( bên trong) bằng12,24(cm) đựng nước
cao lên 4,56(cm) so với mặt trong của đáy. Một viên bi hình cầu được thả vào trong thùng thì mực nước
dâng lên sát với điểm cao nhất của viên bi (nghĩa là mặt nước là tiếp diện của mặt cầu). Hãy tính bán kính của viên bi. Hướng dẫn giải 4 Ta có phương trình : 2 3 2 3 2 2
p R h + p x = p R .2x Û 4x - 6R x + 3R h = 0 (0 < x < R) 3
Với R, x, h lần lượt là bán kính đáy của hình trụ, hình cầu và chiều cao ban đầu của cột nước.
Bấm máy giải phương trình: 3
4x - 224,7264x + 512,376192 = 0(0 < x £ 6,12)
Ta có: x » 2,588826692; x » 5,857864771 1 2
(AB) : 5x - 3y + 8 = 0; (AC) : 3x - 8y + 42 = 0;
(BC) : 2x + 5y - 3 = 0
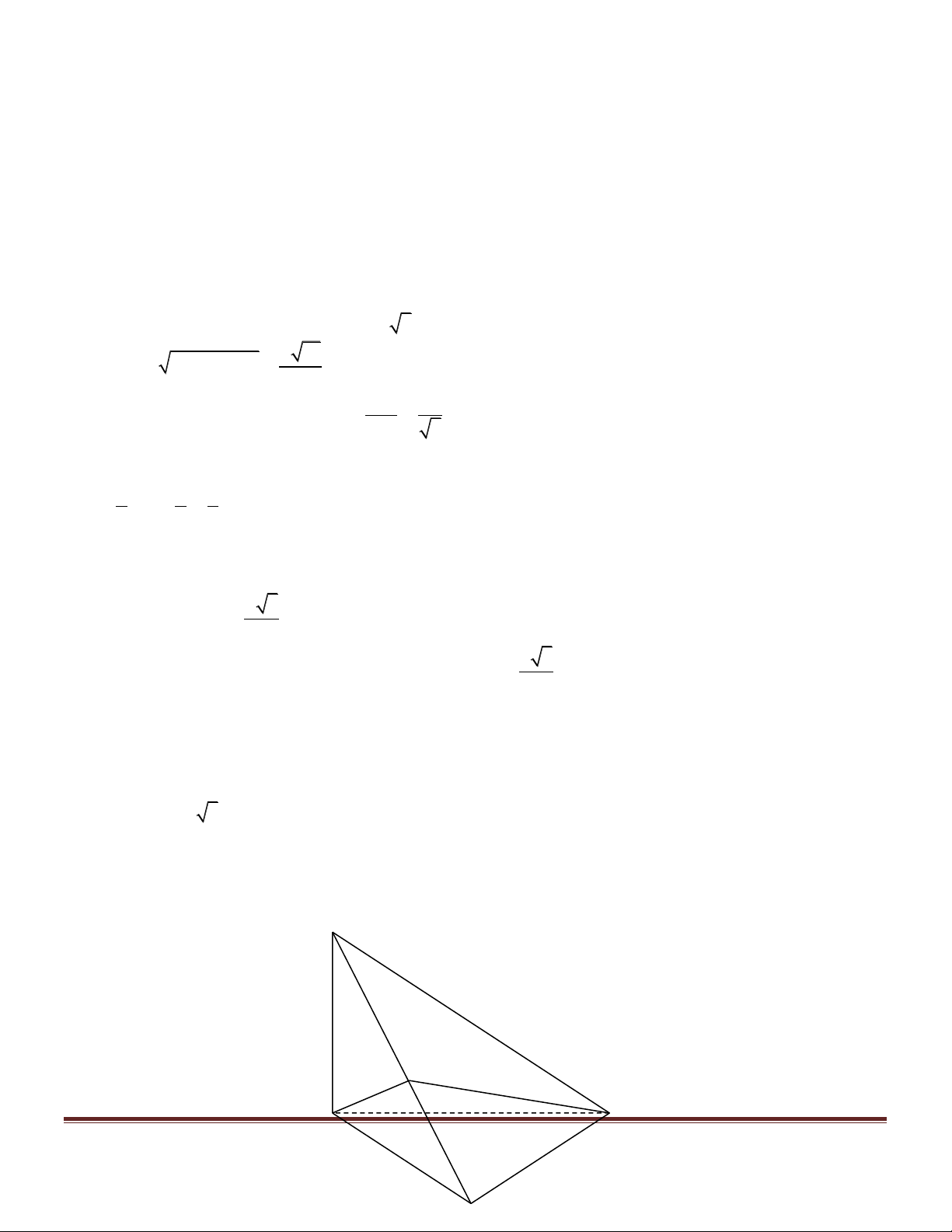
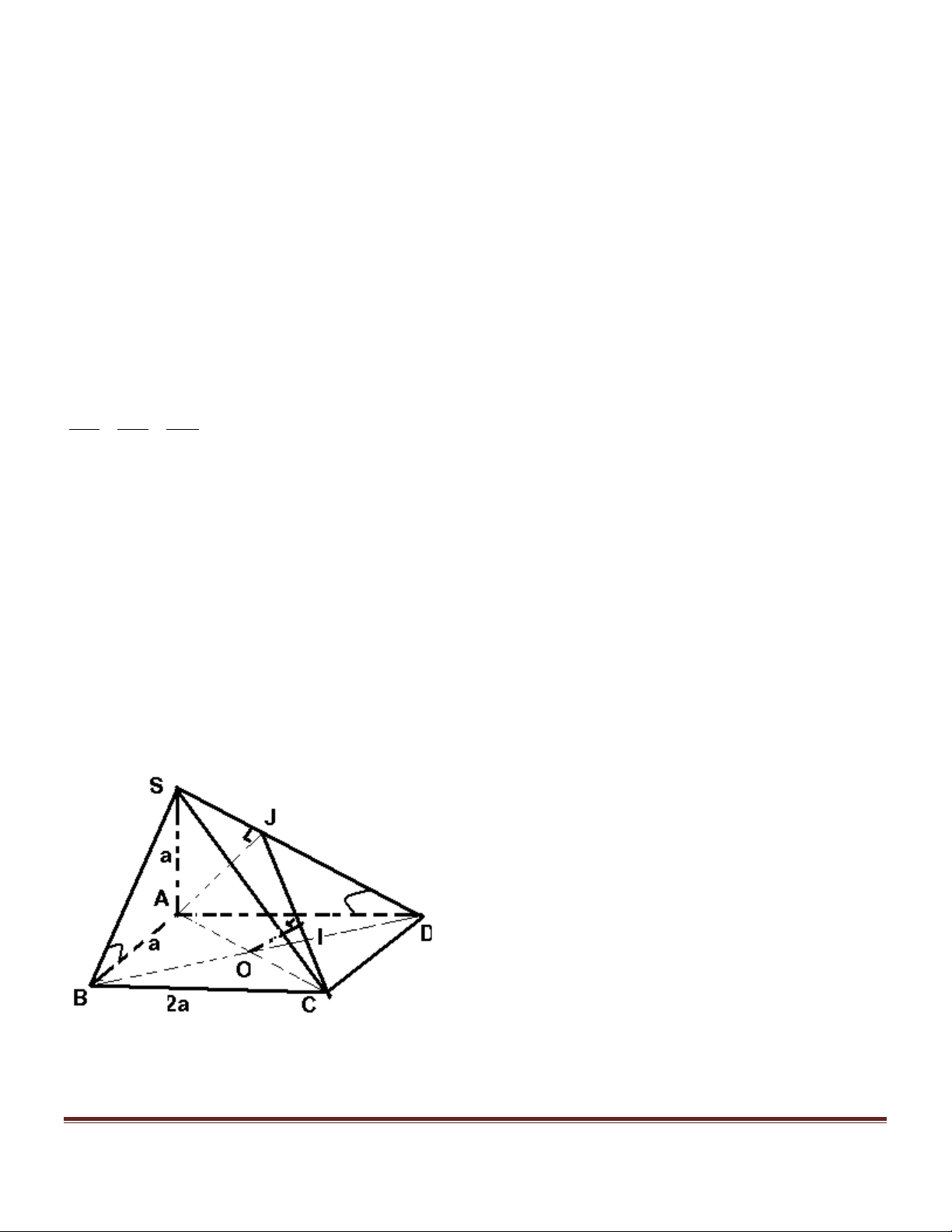
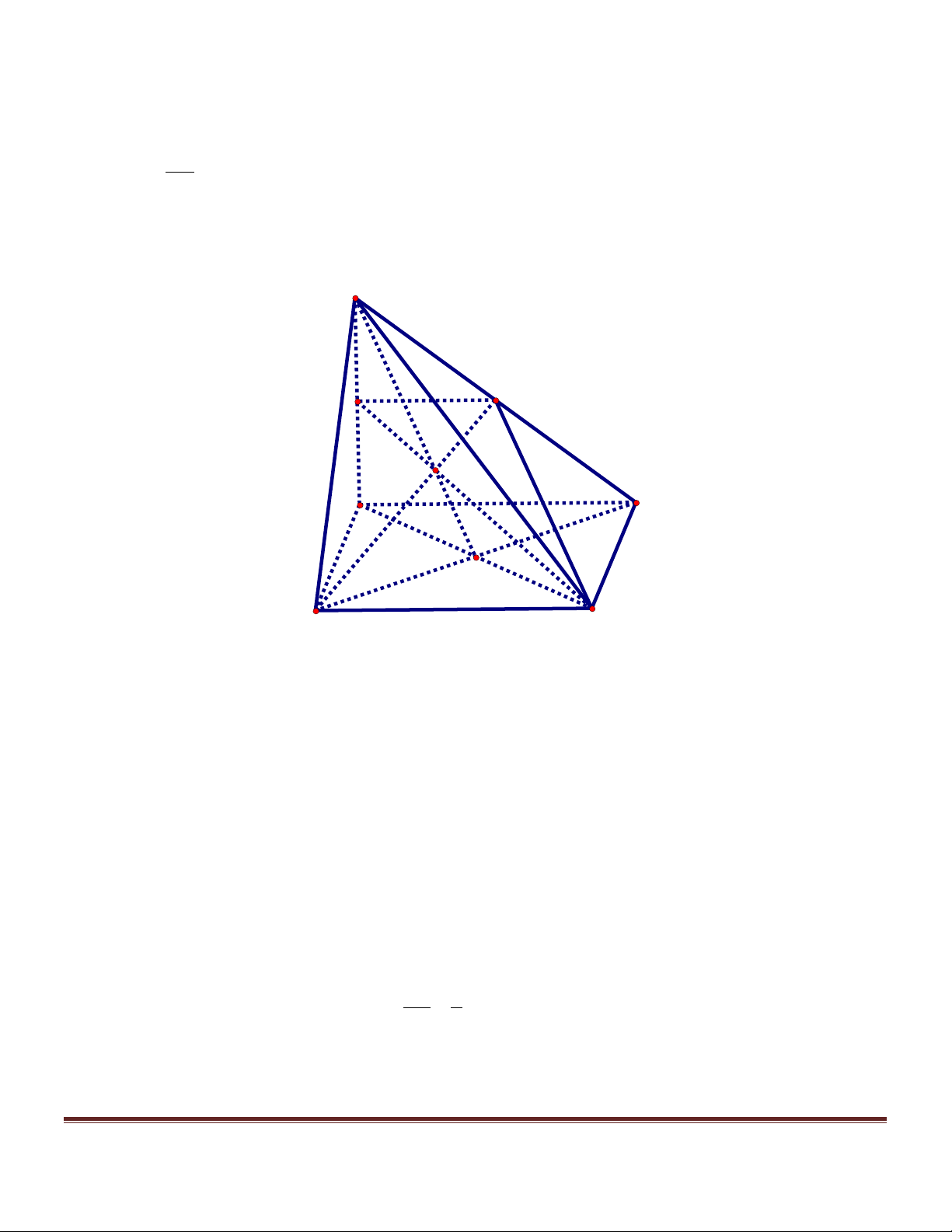
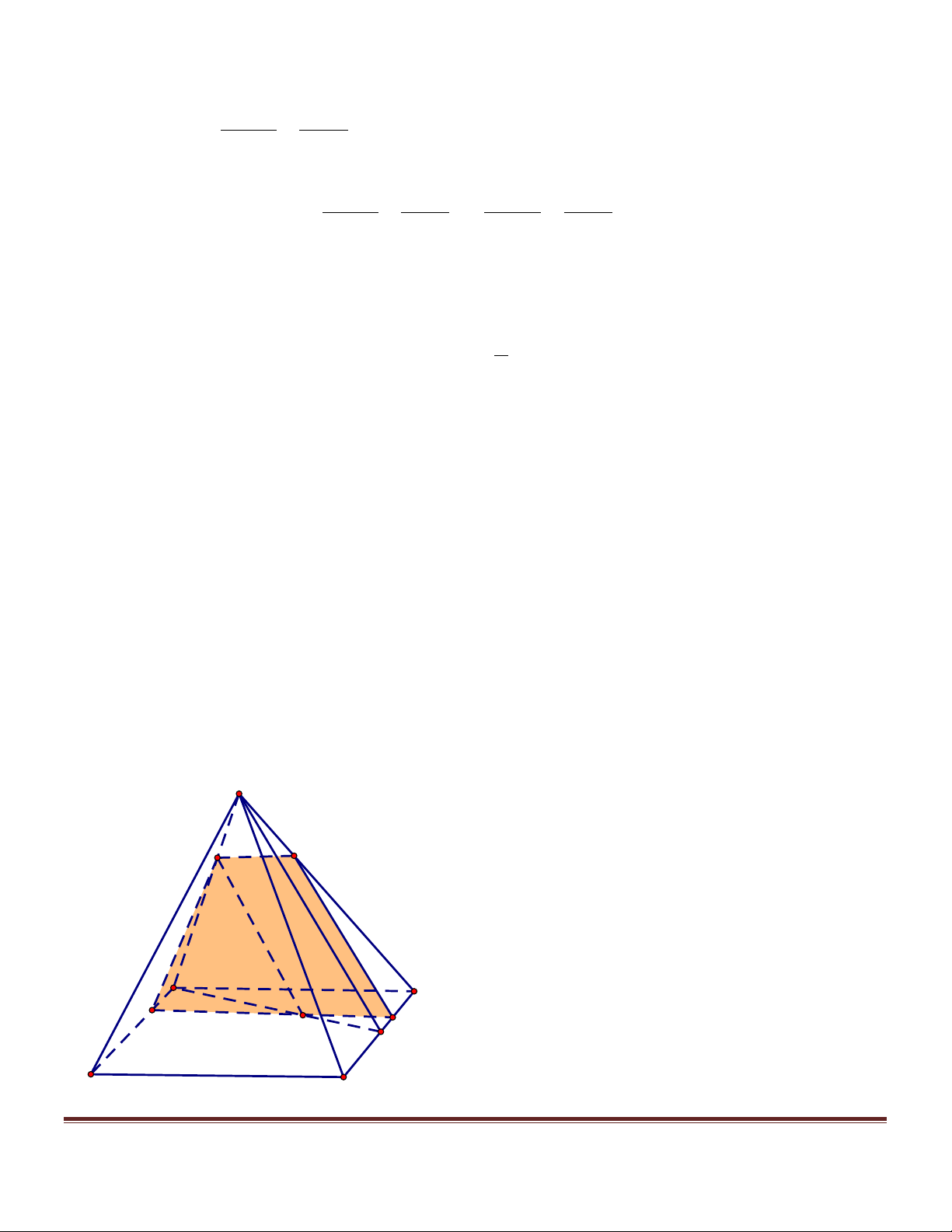
B. Xét hai độ dài khác nhau a, b . Tìm điều kiện của a, b để tồn tại tứ diện (T ) có một cạnh bằng a và các
cạnh còn lại đều bằng b .Với tứ diện (T ) này, hãy xác định mặt phẳng (a ) sao cho thiết diện của mặt phẳng
(a) và tứ diện (T ) là một hình vuông (V ) .Tính diện tích của hình vuông (V ) theo a và b. Trang 4
Điều kiện độ dài a, b :
+ Giả sử tứ diện (T ) tồn tại. Gọi AB là cạnh bằng a , các cạnh AC, AD, BC, ,
BD CD đều cùng bằng b .
Gọi I là trung điểm cạnh CD .Tam giác AIB là tam giác cân: b 3 AB = ;
a AI = BI =
. Từ AB < AI + BI Suy ra: 0 < a < b 3 2
+Ngược lại với: 0 < a < b 3 .Dựng tam giác đều BCD cạnh b với chiều cao BI . (BCD)
Dựng tam giác cân AIB có AB = a , nằm trong mặt phẳng chứa BI và vuông góc với mặt phẳng .Ta có: A Ï (BCD) ABCD mp . Tứ diện
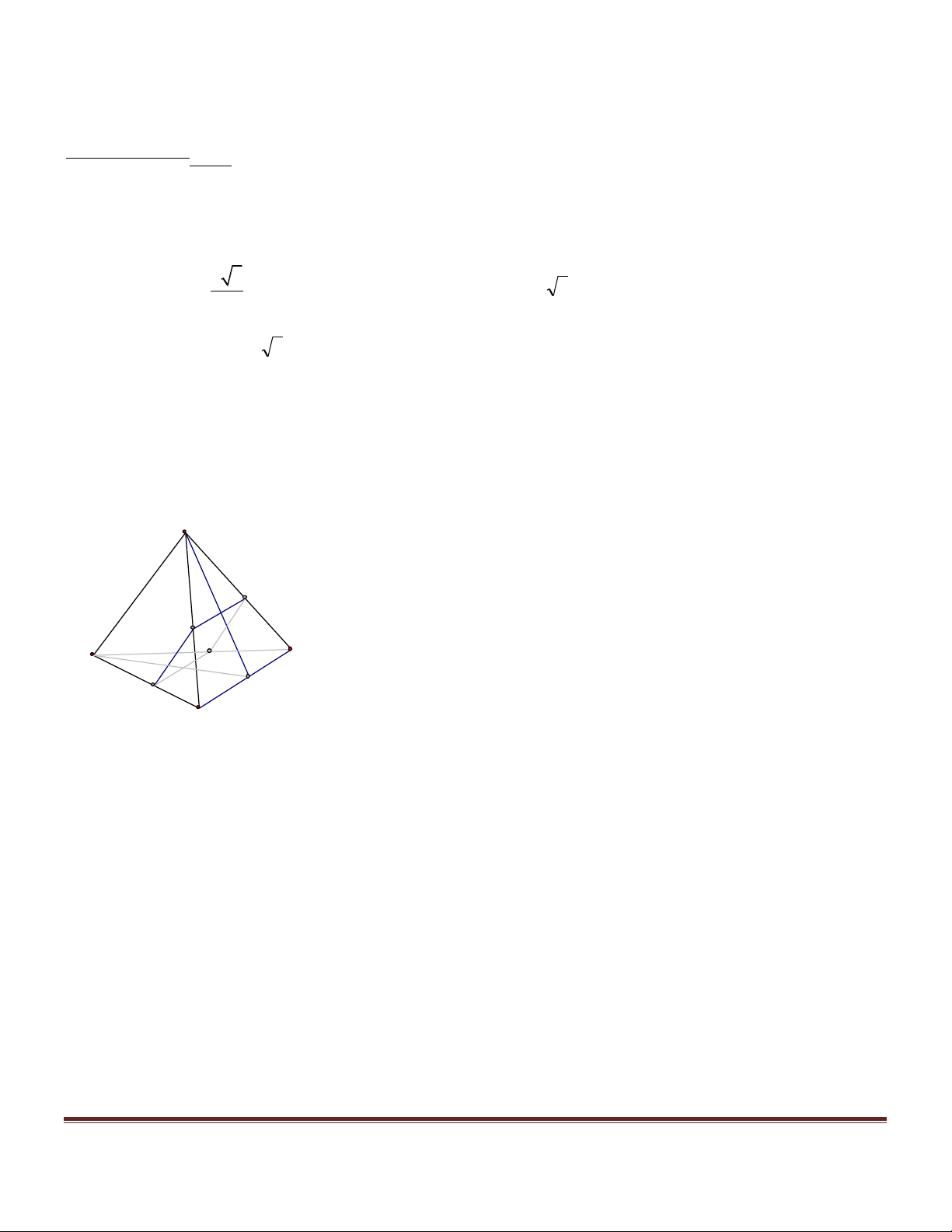
thỏa điều kiện bài toán. A a Q M P D B N I C
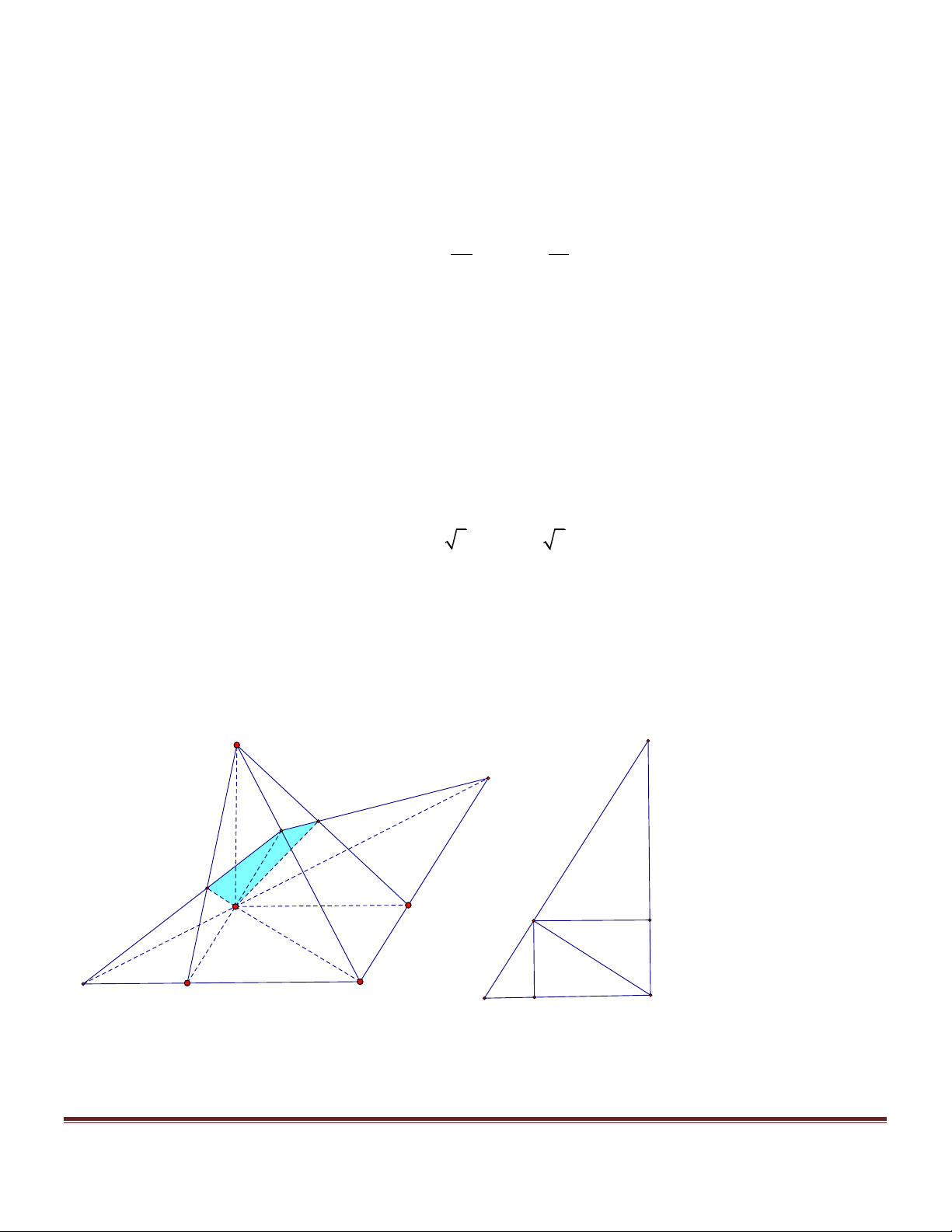
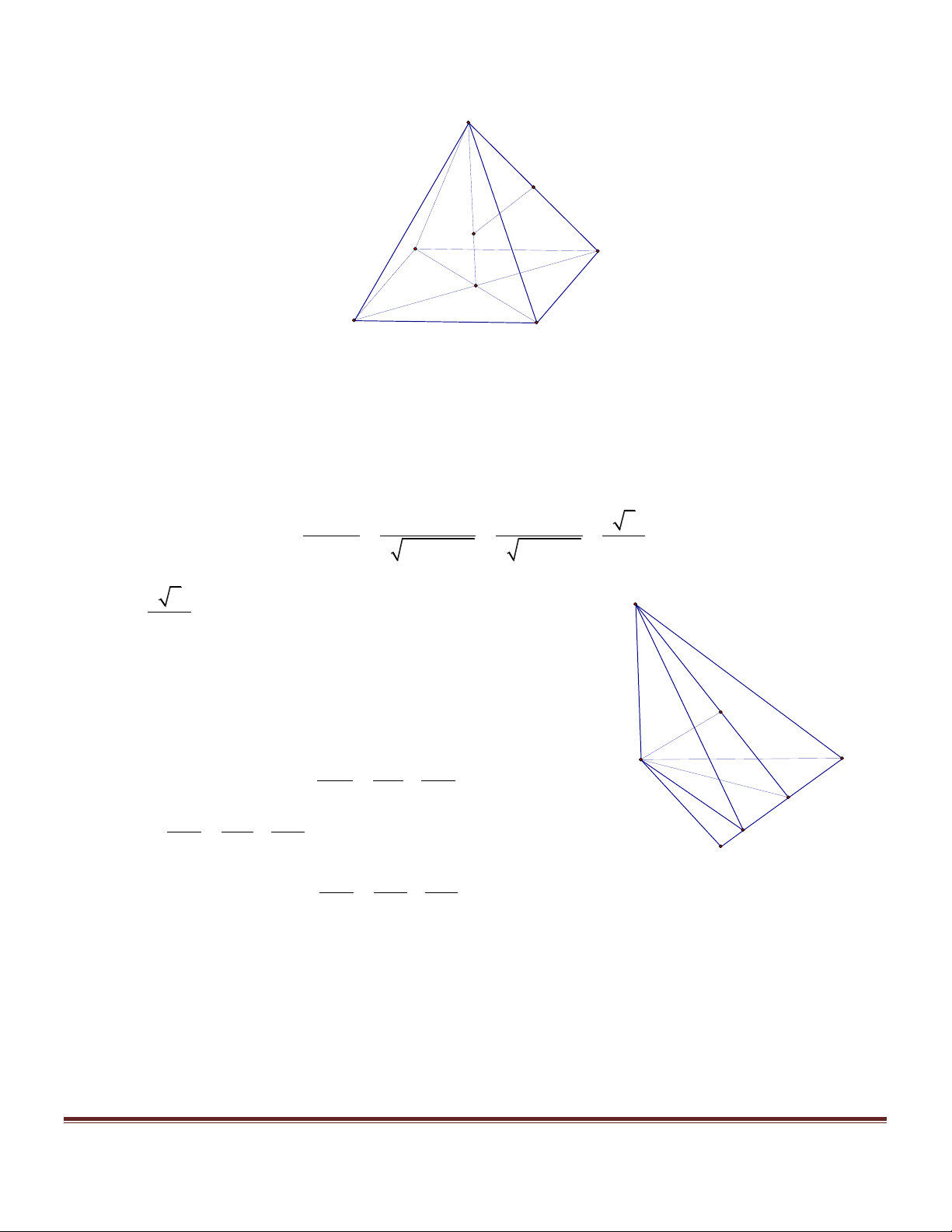
Xác định mặt phẳng (a ):
+ Giả sử thiết diện MNPQ là hình vuông . Các mặt của tứ diện (T )lần lượt chứa các đoạn giao tuyến
MN, NP, PQ, QM được gọi tên là mặt (I ) , mặt (II ), mặt (III ), mặt (IV ). Do MN // P ;
Q MQ // NP nên cạnh chung của mặt (I ) và mặt (III ) ; cạnh chung của mặt (II ) và mặt (IV )
nằm trên hai đường thẳng song song với mp (a ).
Ngoài ra hai đường thẳng này vuông góc với nhau, vì MN vuông góc MQ.
+ Do a khác b nên tứ diện (T ) AB CD
chỉ có một cặp cạnh đối vuông góc , đó là và . Trang 5 Vì vậy mặt phẳng (a ) AB CD phải song song với và . MA
+ Gọi giao điểm của mp (a ) AC, BC, , BD AD
M , N, P, Q k = với , lần lượt là .Đặt: . MC a kb a Ta có: MN = ; MQ =
. Từ MN = MQ ta có : k = . 1+ k 1+ k b ab
+ Diện tích của hình vuông MNPQ là : 2 ( ) a + b
........................................................................................................................................ Bài 6.
Cho hình chóp tứ giác S.ABCD , có đáy là một hình bình hành. Gọi G là trọng tâm tam giác SAC .
M là một điểm thay đổi trong miền hình bình hành ABCD .Tia MG cắt mặt bên của hình chóp tại điểm N MG NG .Đặt Q = + NG MG
1/ Tìm tất cả các vị trí của điểm M sao cho Q đạt giá trị nhỏ nhất.
2/ Tìm giá trị lớn nhất của Q . Hướng dẫn giải s N N' D' H C' G D A M O C B 1/ MG NG NG + Q = + ³ MG
2 .Dấu bằng khi và chỉ khi = = 1 . NG MG NG MG Trang 6
+ SG cắt mp ( ABCD) tại tâm O của hình bình hành ABCD . Gọi K là trung điểm của SG . Từ K dựng
mặt phẳng song song với mp ( ABCD) cắt , SA ,
SB SC, SD lần lượt tại A , B , C , D . Từ N dựng mặt 1 1 1 1
phẳng song song với mp ( ABCD) cắt SG tại N '. NG N 'G NG Ta có : = ;
=1 Û N ' trùng K Û N thuộc cạnh hình bình hành A B C D MG OG MG 1 1 1 1
Nối NK cắt cạnh hình bình hành A B C D P PM // SG 1 1 1 1 tại , ta có : . + Từ đó ' ' ' '
Q = 2 khi và chỉ khi M thuộc cạnh hình bình hành A B C D 1 1 1 1 ' ' ' '
A B C D là hình chiếu song song của hình bình hành A B C D lên mp ( ABCD) 1 1 1 1 1 1 1 1 theo phương SG . 2/
+ Miền hình bình hành ABCD hợp bởi các miền tam giác OAB, OBC, OC , D ODA
M thuộc miền hình bình hành ABCD nên M thuộc một trong bốn miền tam giác này. Chẳng hạn M thuộc miền O
D AB . M º A Þ N º C '; M º B Þ N º D '; M º O Þ N º S .
Do đó N thuộc miền SC D
' D ' và N ' thuộc đoạn SH , với C ', D ' và H lần lượt là trung điểm của
SC, SD và SO . HG N 'G SG 1 NG
Do đó: HG £ N 'G £ SG . Vì vậy: £ £ hay £ £ 2. OG OG OG 2 MG NG 1 é1 ù +Đặt : x =
Ta có : Q = + x với x Î ; 2 . MG x ê 2 ú ë û æ 1 ö ì æ 1 ö ü 5
Q ' = 0 vàø x Î ; 2 Û x = 1 . MaxQ = Max Q í ;Q ç ÷ (2);Q( )1ý = . ç ÷ è 2 ø î è 2 ø þ 2 5
+Giá trị lớn nhất của Q là : . Đạt khi M trùng với O hoặc các đỉnh ,
A B, C, D . 2 Bài 7.
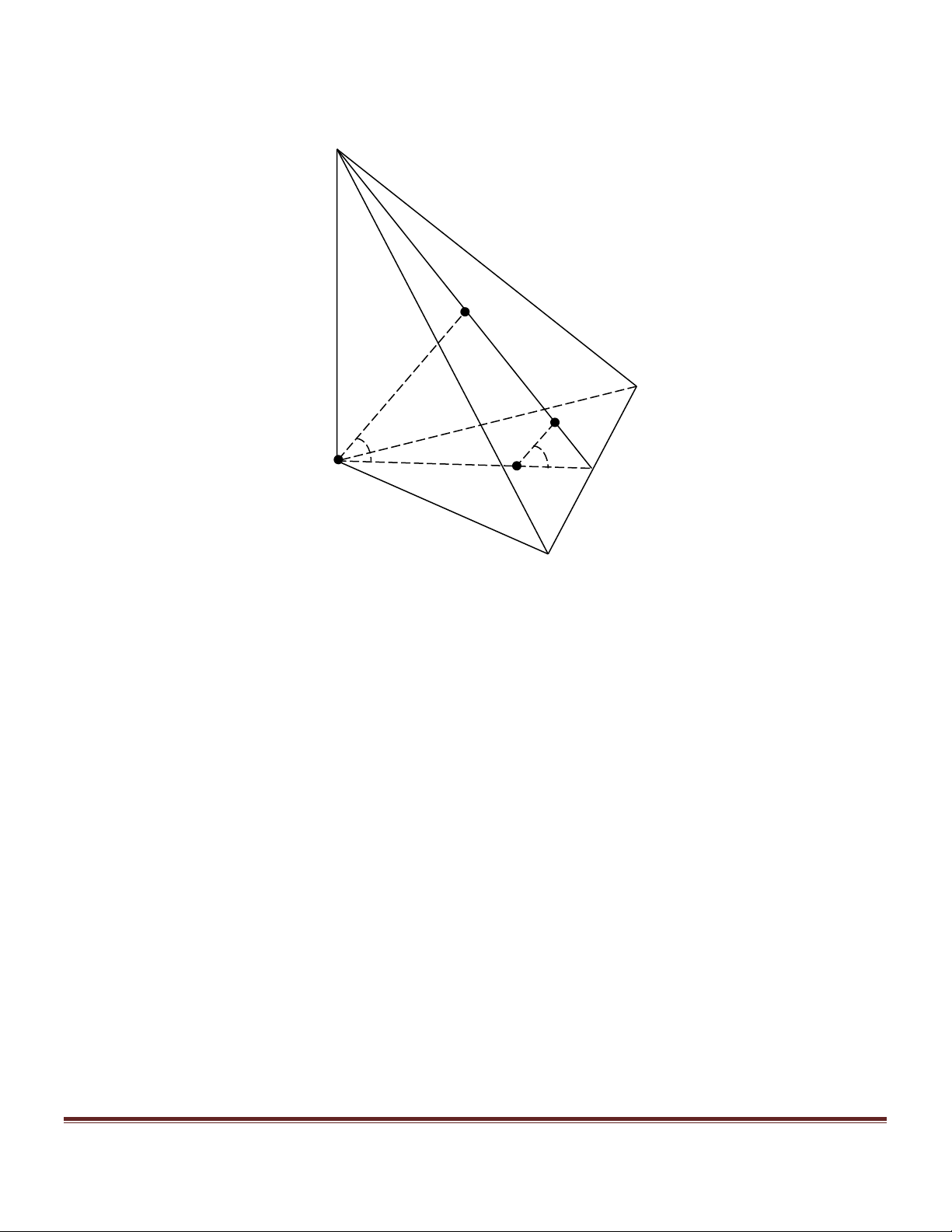
Cho tứ diện ABCD có diện tích các tam giác ADB và ADC là S và S . Mặt phẳng phân giác của b c
nhị diện tạo bởi hai mặt ( ADB) và ( ADC)cắt BC tại M . a là góc giữa hai mặt ( ADB) và ( ADC). Chứng minh: Trang 7 MB S a/ b = MC Sc a 2S .S .cos b c
b/ Diện tích S của tam giác ADM là: 2 S = . m m S + S b c Hướng dẫn giải Câu a:
+ Do M ở trên mặt phẳng phân giác của góc nhị
diện cạnh AD nên khoảng cách từ M đến hai mặt phẳng
(ADB), (ADC) bằng nhau và kí hiệu là d . + Do đó: MB dt(DBM) V S .d S ADBM b b = = = = MC dt(DCM) V S .d S ADCM c c Câu b:
+ Tính công thức thể tích tứ diện: 1 1 1 sina 2S .S .sin a b c V
= S .BH = S .BK.sin a = S .BK.AD. = ABCD c c c 3 3 3 AD 3AD A + V = V + V
, áp dụng công thức tính thể tích trên ta suy ra: ABCD ADBM ADCM a a 2S .S .sin 2S .S .sin b m c m 2S .S .sin a b c 2 2 = + 3AD 3AD 3AD K a 2S .S .cos D C b c Rút gọn, được: 2 S = . m S + S b c M S Bài 8.
Với hai đường thẳng MN, PQ chéo nhau trong không gian, kí hiệu d (MN, PQ)và (MN, PQ)lần
lượt là khoảng cách và góc giữa hai đường thẳng MN, PQ.
a/ Chứng minh rằng nếu tứ diện ABCD thỏa điều kiện: d ( A ,
B CD) = d ( AC, BD) = d ( A , D BC) Trang 8 thì trong ba số: cotg( ,
AB CD); cotg( AC, BD); cotg( ,
AD BC)có một số bằng tổng hai số còn lại.
b/ Chứng minh rằng nếu tứ diện ABCD thỏa điều kiện: d ( A ,
B CD) = d ( AC, BD) = d ( A , D BC)và ( ,
AB CD) = ( AC, BD) = ( ,
AD BC) thì nó là hình chóp tam giác đều. Hướng dẫn giải C a / D B1
• Dựng hình hộp ngoại tiếp tứ diện AC BD B DAC . 1 1 1 1 A1
• Giả thiết d ( A ,
B CD) = d ( AC, BD) = d ( A , D BC)
suy ra các mặt của hình hộp cùng diện tích S . D1 Đặt a = A , B a = C , D AC = ,
b BC = b , AD = , c 1 1
BC = c , AD = z, AC = y, AB = x. 1 1 1 1 A C1
• Từ hình bình hành AC BD ta có: 1 1 4 2 a a1 2 + - y 4 4 B 2 2 a + a = 2( 2 2 y + z ; cos AB,CD = 1 ) ( ) 1 a.a1 2 2 2 ( ) y - z cos AB,CD = a.a1 2 2 y - z
• Chú ý: S = dtAC BD = a asin A , B CD cot g (AB,CD) = 1 1 1 ( ). Do đó: 2S 2 2 z - x 2 2 x - y Tương tự: cot g (AC,BD) = ; = 2S 2S
• Nếu x £ y £ zthì cotg( ,
AB CD) + cotg( AC, BD) + cotg( , AD BC) = cotg( , AD BD).
• Các trường hợp khác cũng có kết quả như thế. b/
• Từ các kết quả câu a/ nếu thêm ( ,
AB CD) = ( AC, BD) = ( , AD BC) thì cotg( ,
AB CD) = cotg( AC, BD) = cotg( , AD BC) = 0.
• Suy ra các cặp cạnh đối của tứ diện ABCD vuông góc đôi một. 2 2 2 2 2 2 a ì + a = b + b = c + c • Lúc này ta cũng có: 1 1 1 í (Do x = y = z) a.a = b.b = c.c î 1 1 1 Trang 9 • Suy ra { , a a } = , b b = , c c ABCD 1
{ }1 { }. Vì vậy phải có ít nhất một mặt của tứ diện là một tam giác 1
đều. Từ đó ABCD là hình chóp tam giác đều. Bài 9.
Trong không gian cho ba tia Ox, Oy, Oz không đồng phẳng và ba điểm ,
A B, C ( khác điểm O )
lần lượt trên Ox, Oy, Oz .Dãy số (an) (a a > 0 d > 0 n
n ) là một cấp số cộng có và công sai . Với mỗi số 1
nguyên dương, trên các tia Ox, Oy, Oz theo thứ tự lấy các điểm A , B , C sao cho n n n
OA = a .OA ; OB = a .OB ; OB = a .OC .Chứng minh các mặt phẳng ( A , B ,C n n
n ) luôn luôn đi qua một n n n 1 + n n+2 n
đường thẳng cố định. Hướng dẫn giải
+ Phát biểu và chứng minh mệnh đề:
Nếu hai điểm X ,Y phân biệt. Điều kiện cần và đủ để điểm S thuộc đường thẳng XY là tồn tại cặp
số thực x, y thỏa: !!!" !!!" !!!" O ìï S = xOX + yOY í
, với điểm O tùy ý. ïîx + y =1 a a +Từ giả thiết: (a d > 0 n 1 + n a = a + d - =1
n ) là cấp số cộng công sai nên: . n 1 + n d d
+ áp dụng nhận xét trên, ta có: !!" a !!!!" a !!!!" n 1 + n OI = OB -
OA thì I Î A B . n n d d n n !!!" !!!!" !!!" !!!!"
và OA = a OA ; OB = a OB ( do a ,a > 0) n n n 1 + n n n 1 + !!!" !!!" !!" OB OA 1 !!!"
Thế vào trên ta được: OI = - = AB , n
" =1,2...suy ra I cố định, nên đường thẳng A B d d d n n
luôn đi qua một điểm cố định I .
+ Tương tự, chứng minh được: !!" !!!" • 1
B B luôn đi qua một điểm cố định J xác định bởi: OJ = BC. n n d !!!" !!!" • 1
A C luôn đi qua một điểm cố định K xác định bởi: OK = AC n n 2d
Vậy các đường thẳng A B , B C , A C lần lượt đi qua ba điểm I, J , K cố định. n n n n n n
+Chứng minh ba điểm thẳng hàng: Trang 10
!!" 1 !!!" !!" 1 !!!" !!!" 1 !!!"
Ta có: OI = AB, OJ = BC , OK = AC. d d 2d !!!" 1 !!!" 1 !!!" !!!" 1 !!" !!" 1 !!" !!" Do đó: OK = AC = (AB + BC) = (d.OI + d.OJ) = (OI + OJ) 2d 2d 2d 2
Vậy I, J , K thẳng hàng. Điều này chứng tỏ mặt phẳng A B C luôn đi qua một đường thẳng cố định. n n n
Bài 10. Trong không gian cho ba mặt phẳng cố định có một điểm chung duy nhất. M là một điểm của
không gian, các đường thẳng đi qua M song song với hai mặt phẳng cắt mặt phẳng còn lại lần lượt tại ,
A B, C . Biết MA + MB + MC = 1998 .Tìm tập hợp các trọng tâm của tam giác ABC . Hướng dẫn giải
+ Gọi O là giao điểm của 3 mặt phẳng. a, ,
b c là 3 giao tuyến . Dùng tính chất hình hộp và tính chất trọng uuuur 2 uuur tâm, ta có: OM ' =
OM , với M " là trọng tâm của ABC D . 3 _ U _ B _ C _ M _ M' _ _ O C _ A _ V
+ Tìm tập hợp các điểm M :
Ba mặt phẳng chia không gian làm 8 miền. Ta chỉ cần xét một miền: Gọi U, V, ÷ thuộc , a , b c:
OU = ‘ = OV = 1998. uuur uuur uuur uuur
Chứng minh được: M thuộc miền trong tam giác UV÷ khi và chỉ khi: OM = xOU + yOV + zOW với
x + y + z =1.
Mà MA + MB + MC =1998 Û x + y + z =1.
Do đó: Tập các điểm M là miền trong của tam giác UV÷ . Trang 11
Suy ra các điểm M ' ( trọng tâm của tam giác ABC ) là ảnh của miền trong tam giác UV÷ qua phép vị 2 tựtâm O tỉ 3
Bài 11. Cho hình chóp S.ABCD , đáy ABCD là hình chữ nhật có AB = a, BC = b, SA = SB = SC = SD = c .
K là hình chiếu vuông góc của P xuống AC .
a/ Tính độ dài đoạn vuông góc chung của SA và BK .
b/ Gọi M , N lần lượt là trung điểm của đoạn thẳng AK và CD . Chứng minh: Các đường thẳng BM và MN vuông góc nhau. _ S Hướng dẫn giải _ D _ N _ C _ K _ M _ O _ A _ B
a) + Theo giả thiết ta được: SO ^ ( ABCD) Þ (SAC) ^ ( ABCD).
Mà BK Ì (SAC)và B BK ^ AC Þ BK ^ SA .
+ Gọi H là hình chiếu của K xuống SA
Þ HK ^ SA và HK ^ BK ( vì HK Ì (SAC))
Þ HK là đoạn vuông góc chung của SA và BK .
Suy ra được: BH ^ SA và H
D BK vuông tại K . 2 2 1 1 1 a b + Do ABC D
vuông đỉnh A nên: 2 = + Þ BK = . 2 2 2 2 2 BK AB BC a + b 2 2 a c - .a SI.AB + SA
D B cân đỉnh S , BH là đường cao nên 4 HB = = SA c + Do H
D BK vuông tại K nên: Trang 12 2 2 2 2 2 (4c - a )a a b 2 2 2 HK = HB - BK = - 2 2 2 4c a + b 2 2 2 4 2 2 2 2 (4c - a - b )a a (4c - a - b ) 2 HK = Þ HK = 2 2 2 2 2 4c (a + b ) 2c (a + b ) !!!!" !!!" !!!"
b) + 2BM = BA + BK ( vì M là trung điểm của AK )
!!!!" !!!" !!!" !!!" 1 !!!" !!!" !!!" 1 !!!"
+ MN = MB + BC + CN = (AB + KB) + BC + BA 2 2 !!!!" 1 !!!" !!!" + MN = KB + BC. 2 + Do đó: !!!!" !!!!" !!!" !!!" !!!" !!!" 4BM.MN = (BA + BK).(KB + 2BC) !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
= BA.KB + 2BA.BC + BK.KB + 2BK.BC !!!" !!!" !!!" !!!" !!!" !!!" = BA.KB + BK.KB + 2BK.BC ! " !! !!!" !!!" !!!" = KB.(BA + BK - 2.BC) !!!" !!!" !!!" !!!" !!!" = KB.(BA - BC + BK - BC) !!!" !!!" !!!" !!!" !!!" !!!" !!!"
= KB.(CA + CK) = KB.CA + KB.CK = 0
Vậy: BK ^ MN .
( Có thể tính và áp dụng định lý Pythagor).
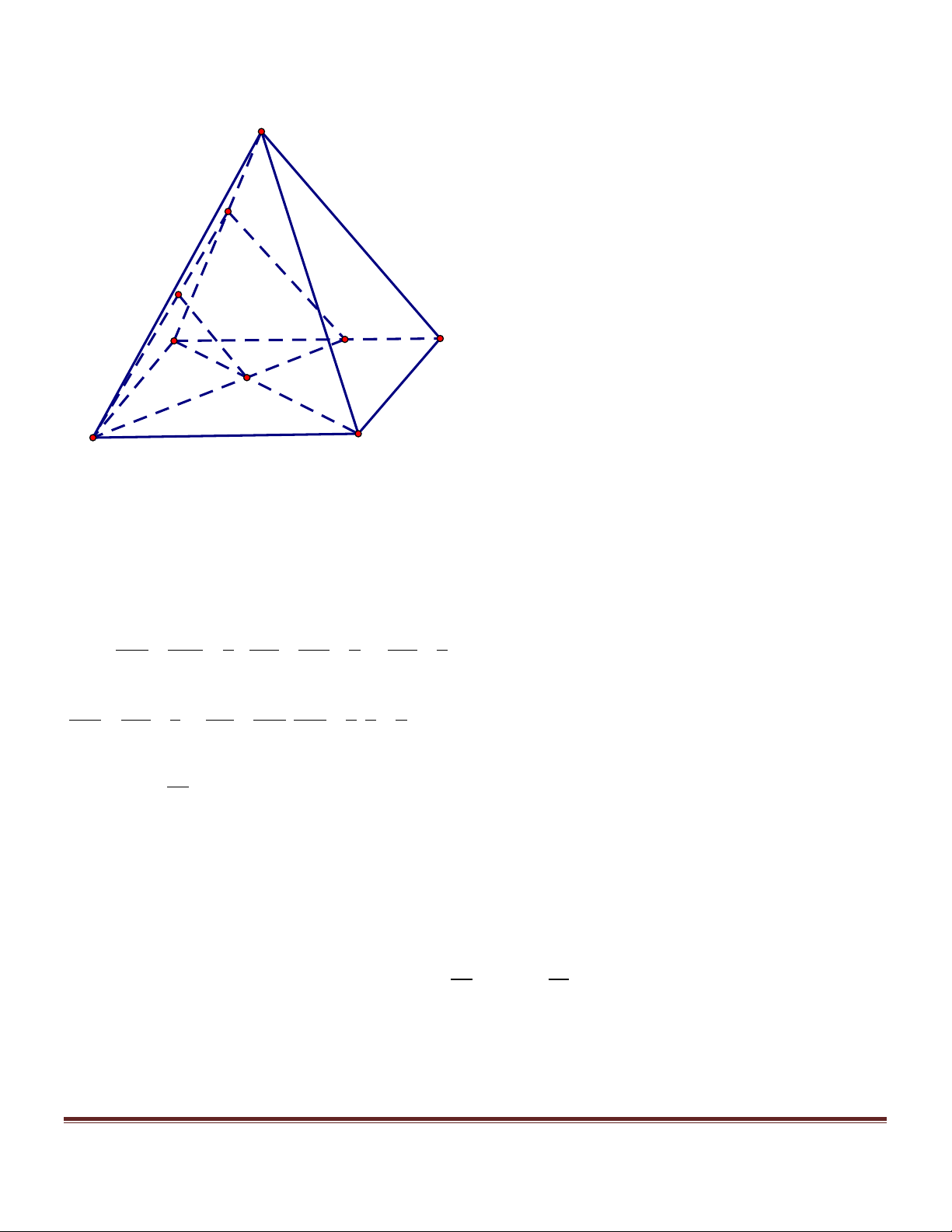
Bài 12. Cho tứ diện ABCD cóhai cạnh đối bằng b, c và các cạnh còn lại bằng a .
a/ Tìm giá trị nhỏ nhất của tổng các khoảng cách từ một điểm tùy ý trong không gian đến các đỉnh của tứ diện.
b/ Giả sử tứ diện ABCD thay đổi vị trí trong không gian nhưng có ba đỉnh ,
A B, C lần lượt ở trên mặt
cầu cố định và đồng tâm.Chứng minh rằng đỉnh D luôn ở trong một hình cầu cố định khi độ dài a, , b c
thay đổi thỏa các giả đã cho. Hướng dẫn giải D a)
• Ta có thể giả sử AD = ,
b BC = c và các cạnh còn lại D’
bằng a . Gọi I, J lần lượt là trung điểm của các cạnh I A’ ,
AD BC . Ta dễ dàng suy ra I vuông góc với AD và K0 A TrCang 13 J B
BC và IJ chính là trục đối xứng của tứ diện.
• Lấy M tùy ý trong không gian, M ' là điểm đối xứng
của M qua IJ suy ra trung điểm K của MM ' chính là
hình chiếu của M trên đường thẳng IJ và ta có:
• 2(MA+ MB + MC + MD) = MA+ MB + MC + MD+ M ' A+ M 'B + M 'C + M 'D
= (MA+ M ' A)+(MB + M 'B)+(MC + M 'C)+(MD+ M 'D)
£ 2KA+ 2KB + 2KC + 2KD ( ) 1 .
( Do tính chất: trung tuyến của một tam giác thì bé hơn nữa tổng
của hai cạnh cùng xuất phát từ một đỉnh của nó). • Do đó:
MA + MB + MC + MD £ KA + KB + KC + KD
• Bài toán trở thành tìm điểm K trên IJ sao cho KA + KB + KC + KD bé nhất.
• Trong mặt phẳng (BCI )dựng hình thang BCD' A' sao cho IJ là trung điểm của hai đáy và
IA = IA', ID = ID '. Ta thấy rằng: với K tùy ý trên I thì KA = KA' và KD = KD ' . Do đó:
KA+ KB + KC + KD = KA'+ KB + KC + KD' = (KA'+ KC) + (KB + KD') £ A'C + BD'.
• Vậy KA + KB + KC + KD nhỏ nhất khi K chính là giao điểm K của hai đường chéo A'C và BD ' . 0 2 2 2 2 • c b c b Tính 2 2 2 2 2 2 2 2
IJ : IJ = DJ - ID = DC - JC - ID = a - - Þ IJ = a - - . 4 4 4 4 2 2 2 2 æ + ö æ + • BC A 'D ' b c ö c b bc Tính 2 2 2 2 BD ' : BD ' = + IJ = + a - - = a + . ç ÷ ç ÷ è 2 ø è 2 ø 4 4 2
• Tổng các khoảng cách nhỏ nhất là: 2 d = 2BD' = 4a + 2bc . b)
• Gọi r , r , r là bán kính các mặt cầu tâm O và lần lượt đi qua các đỉnh ,
A B, C. Ta có: 1 2 3
• OD < OC + DC < OC + AB < OC + OA+ OB = r + r + r . Do đó D ở trong hình cầu cố định tâm O , bán 1 2 3
kính R = r + r + r . 1 2 3
Bài 13. Cho tam giác ABC có góc A nhọn. M là điểm di động trên BC . P, Qlần lượt là hình chiếu
vuông góc của M lên AB, AC.Tìm tập hợp các điểm S không phụ thuộc mặt phẳng ( ABC)sao cho: g (S ,
A PQ) = g (S ,
P AQ) = g (S , Q AP).
( ký hiệu g (a,b)là góc giữa hai đường thẳng a, b ) Hướng dẫn giải
+ Với tứ diện ABCD ta chứng minh: Trang 14 g ( A ,
B CD) = g ( A ,
D BC) = g ( AC, BD) Û AB ^ CDvà AD ^ BC, AC ^ BD. !!!" !!!" !!!" !!!" !!!" !!!"
Thật vậy ta có đẳng thức: AB.CD+ AC.DB+ AD.BC = . T 0 ừ đó nếu: g ( A ,
B CD) = g ( A ,
D BC) = g ( AC, BD) =j thì ( . AB CD +e . AC DB +e . AD BC o c sj = 0 1 2 )
Với e , e nhận giá trị1 hay 1
- . Mặt khác ta có bất đẳng thức đối với các cạnh của tứ diện là: 1 2 . AB CD + e . AC DB + e . AD BC ¹ 0 , nên 0 j = 90 . 1 2
+ g (SA PQ) = g (SP AQ) = g (SQ AP) 0 , , ,
= 90 khi và chỉ khi hình chiếu S lên ( ABC) là trực tâm tam giác APQ. BM + Đặt
= t . Gọi E, F là hình chiếu của B và C lên AC, AB. Ta có: BC
!!!!" !!!" !!!!" !!!" !!!" !!!" !!!"
MH = MP + MQ = MB + BP + MC + CQ mà ta có: !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!!" !!!!" !!!" !!!"
BP = tBE, CQ = (1- t)CE, MB = (1- t)BC, BH = BM + MH = tBF + (1- t)BE !!!" !!!" !!!" !!"
+Suy ra: EH = BH - BE = tEF. Tập hợp các điểm H là đoạn EF .
Vậy tập hợp các điểm S là dải mặt phẳng ở giữa hai đường thẳng a, b lần lượt đi qua E, F và vuông góc mặt phẳng ( ABC).
Bài 14. Cho tứ diện đều ABCD . Mặt phẳng (P) chứa cạnh BC và cắt cạnh AD của tứ diện tại E . Gọi
x, y lần lượt là góc tạo bởi (P) với các mặt phẳng (BCD) và ( ABC)
a, cm c (x + y) 1 os = 3 5 2 b, Cho tan x =
. Tính tỉ số thể tích 2 tứ diện ABCE và BCDE 7
Bài 15. Cho hình chóp S.ABCD đáy ABCD là hình thang ( AD ! BC) và AD = 2BC . Gọi M , N lần CP
lượt là trung điểm của ,
SA SB. Mặt phẳng (DMN ) cắt SC tại P . Tính tỉ số . CS
Bài 16. Cho tam giác đều ABC :
1. M là điểm nằm trong tam giác sao cho 2 2 2
MA = MB + MC . Hãy tính góc ∑ BM . C Trang 15
2. Một điểm S nằm ngoài mặt phẳng ( ABC) sao cho tứ diện SABC đều, gọi I, K là trung điểm
của các cạnh AC và SB . Trên đường thấng AS và CK ta chọn các điểm P, Q sao cho
PQ // BI . Tính độ dài PQ biết cạnh của tứ diện có độ dài bằng 1.
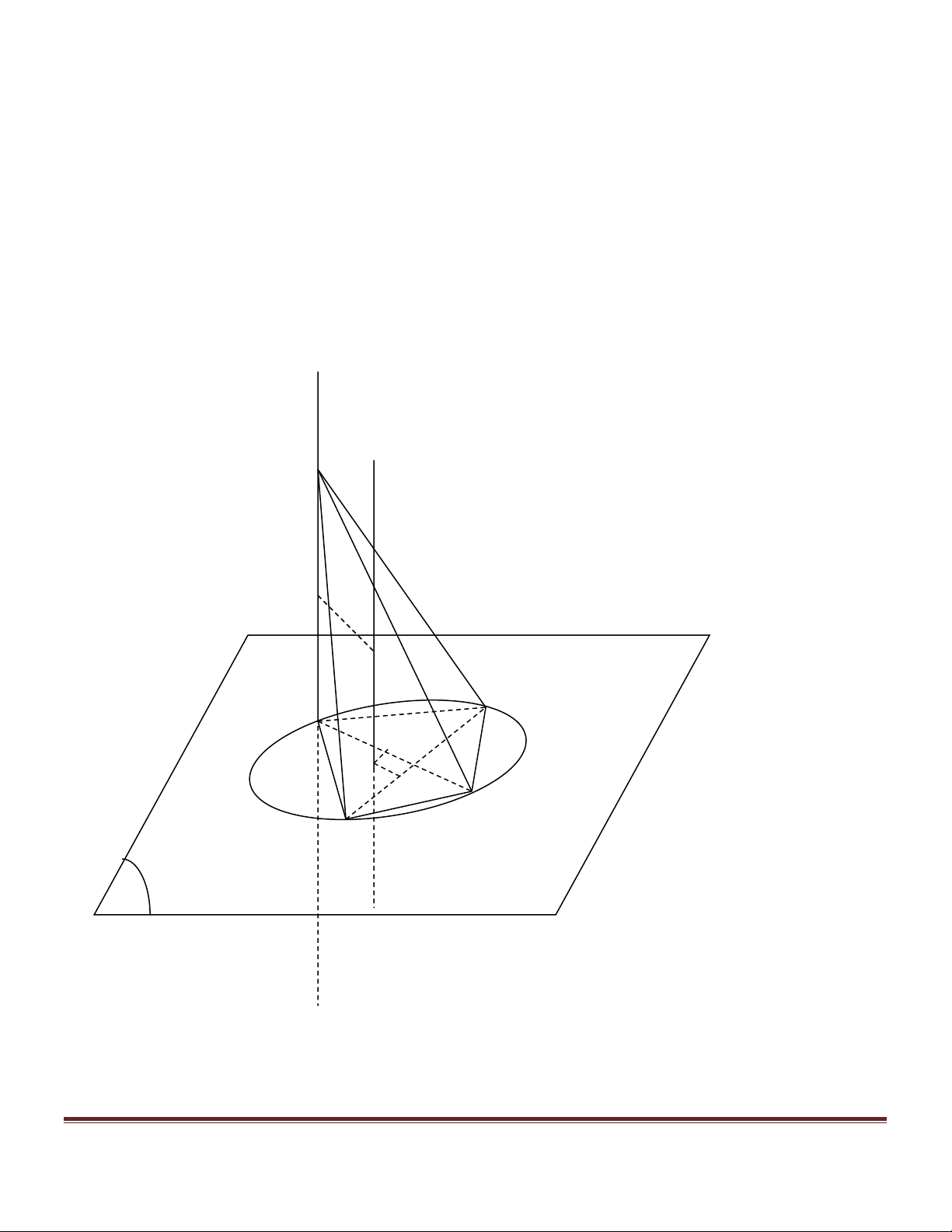
Bài 17. Trong mặt phẳng (a) cho đường tròn (C) Đường kính AB cố định và điểm M di động trên (C).
Gọi S là điểm cố định trên đường thẳng vuông góc với mp (a) tại A . Hạ các đường AI, AJ lần lượt vuông
góc với SM và SB .
2.1 Chứng minh rằng AI ^ IJ .
2.2 Tìm quỹ tích của điểm I khi M di động trên (C .)
Bài 18. Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ cạnh a .
a. Tính góc giữa hai đường thẳng AC¢ và A¢B .
b. Gọi M , N , P lần lượt là các điểm thuộc các cạnh A¢B¢ , BC , DD¢ sao cho A¢M = BN = DP .
Chứng minh rằng trọng tâm tam giác MNP luôn thuộc một đường thẳng cố định khi M , N , P thay đổi.
Bài 19. Cho hình lăng trụ ABC .
D A B C D có đáy ABCD là hình thoi M , N lần lượt là trung điểm của 1 1 1 1
BB và CD . Mặt phẳng ( A MC AB E 1 ) cắt tại . 1
a. Chứng minh tam giác ACE là tam giác vuông. KC b. Mặt phẳng ( A MN CC K 1 ) cắt tại . Tính tỉ số . 1 KC1
Bài 20. Cho lăng trụ đứng OA .
B O A B có đáy là tam giác vuông cân tại O , OA = OB = a , AA = a 2 . 1 1 1 1
Gọi M là trung điểm của OA.
a. Xác định thiết diện giữa lăng trụ và mặt phẳng (P) đi qua M , vuông góc với A B. 1
b. Tính diện tích thiết diện vừa tìm được theo a .
Bài 21. Cho tứ diện ABCD có AB vuông góc với AC và chân đường vuông góc hạ từ A đến mặt phẳng
(BCD) là trực tâm của tam giác BCD. Chứng minh rằng (BC +CD+ DB)2 £ ( 2 2 2
6 AB + AD + AC ).
Bài 22. Cho tứ diện ABCD . Gọi M , N, ,
P Q lần lượt là trung điểm , AB , AD C , D BC .
a. Chứng minh tứ giác MNPQ là hình bình hành. Tìm điều kiện của tứ diện để MNPQ là hình thoi.
b. Mặt phẳng a đi qua N và song song với AB,CD . Xác định thiết diện của (a )và tứ diện ABCD . Thiết diện là hình gì? Trang 16 Hướng dẫn giải 1/ (1,5 A điểm) 0,5 M N 0,5 F B E D 0,25 P Q 0,25 C 0,5 MN // BDü * ý Þ MN // PQ PQ // BD þ * Tương tự MQ // NP
Kết luận: Tứ giác MNPQ là hình bình hành
* MNPQ là hình thoi khi AC = BD 2 / (1
* (a ) Ç( ABD) = NE Þ NE // AB 0,25 điểm)
* (a ) Ç( ACD) = NF Þ NF // CD 0,25
Þ Thiết diện là tứ giác NEQF 0,25
* Tứ giác NEQF là hình bình hành 0,25
Bài 23. Cho hình chóp S.ABCD có đáy là nửa lục giác đều với cạnh a ( a > 0 ). Cạnh SA vuông góc với SM
đáy và SA = a 3 . M là một điểm khác B trên SB sao cho AM ^ MD . Tính tỉ số . SB Hướng dẫn giải S H A D B C Trang 17
Đặt hình chóp vào hệ trục toạ độ như hình vẽ. Suy ra ta có: A = (0;0;0), D = (2 ; a 0;0), æ a a 3 ö
S = (0;0;a 3) và Bç ;
;0÷. Suy ra phương trình của SB là ç 2 2 ÷ è ø 2x 2y z - a 3 = = a a 3 -a 3
Gọi M (x ; y ; z SB 0 0 0 ) thuộc cạnh , ta có: ìïy = 3x 0 0 í .
ïz = a 3 - 2 3x î 0 0 !!!!" !!!!"
Mặt khác AM ^ DN Û AM .DM = 0 3a 2 2 2
Û x - 2ax + y + z = 0 Û x = 0 0 0 0 0 8
æ 3a 3a 3 a 3 ö !!!" 3 !!" Û SM 3 M ç ; ;
÷ Þ SM = SB hay = ç 8 8 4 ÷ 4 è ø SB 4
Bài 24. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành tâm O và các cạnh bên có độ
dài bằng nhau. Một mặt phẳng (a ) thay đổi và luôn cắt các cạnh bên của chóp, gọi giao điểm của (a ) với các cạnh bên ,
SA SB, SC, SD lần lượt là M , N, ,
P Q . Đặt x = SM , y = SN , z = SP , t = SQ . Chứng 1 1 1 1 minh rằng: + = + . x z y t
Bài 25. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh bằng a , mặt bên SAB là tam
giác đều và mp (SAB) vuông góc với mp ( ABCD).
a. Tính các khoảng cách: d é , O
ë (SBC)ù , d é ,
A SCD ù, d AC, SB . û ë ( )û ( )
b. Xác định tâm và tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD .
c. Mặt phẳng (P) chứa AB và vuông góc với mặt phẳng (SCD) cắt hình chóp đã cho theo
thiết diện hình gì? Tính diện tích thiết diện theo a .
Bài 26. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a , SA vuông góc với mặt phẳng
(ABC) và SA = 3a . Gọi O là trọng tâm của tam giác ABC , H là hình chiếu vuông góc của điểm
O lên mặt phẳng (SBC).
1/. Chứng minh rằng : H là trực tâm của tam giác SBC .
2/. Tính góc giữa đường thẳng OH và mặt phẳng ( ABC). Trang 18 Hướng dẫn giải S 3a K C H A M O 2a B
1/. Gọi M là trung điểm của cạnh BC . Do ABC D
đều, G là trọng tâm của ABC D
nên ta có AM ^ BC .
Do SA ^ ( ABC) nên AM là hình chiếu vuông góc của SM lên ( ABC).
Theo Định lí ba đường vuông góc ta có SM ^ BC .
Mặt khác do H là hình chiếu vuông góc của O lên (SBC)nên OH ^ BC và OM ^ BC Suy ra HM ^ BC .
Suy ra SH ^ BC (1) * Do ABC D
đều nên ta có CO ^ AB
Do SA ^ ( ABC) nên SA ^ OC .
Từ đó suy ra OC ^ (SAB).
Suy ra SB ^ OC .
Mặt khác OH ^ (SBC) Þ OH ^ SB Trang 19
Từ đó ta có SB ^ (COH ) .
Suy ra CH ^ SB (2)
Từ (1) và (2) suy ra H là trực tâm của SB D C .
2/. Gọi K là hình chiếu vuông góc của điểm A lên (SBC) .
Do đó ta có OH // AK .
Ta có đường thẳng AM là hình chiếu vuông góc của đường thẳng AK lên ( ABC).
Vì vậy góc giữa đường thẳng OH và ( ABC) bằng góc giữa đường thẳng AK và ( ABC) bằng góc giữa hai
đường thẳng ( AK, AM ) bằng góc ∑ KAM . Do ∑ ∑ 0
KAM + AMS = 90 và ∑ ∑ 0
ASM + AMS = 90 nên ∑ ∑ KAM = SM A Xét SA
D M vuông tại A có AM = a 3, SA = 3a . AM 3 Suy ra ∑ ∑ ∑ 0 tan SM A = Û tan SM A = Û SM A = 30 S A 3
Từ đó ta có góc (OH ( ABC)) 0 , = 30 .
Kết luận: (OH ( ABC)) 0 , = 30 .
Bài 27. Cho tứ diện ABCD có các cặp cạnh đối bằng nhau từng đôi một AB = C ; D AC = ; BD AD = BC .
Chứng minh với mọi điểm M trong không gian ta đều có: 2 2 2 2
MA + MB + MC ³ MD
Bài 28. Cho hai đường thẳng d,d¢ chéo nhau và vuông góc với nhau nhận OI làm đường vuông góc
chung ( O thuộc d và I thuộc d¢ ). Trên d lấy điểm A cố định, trên d¢ lấy hai điểm M , N di
động sao cho mặt phẳng (d,M ) vuông góc với mặt phẳng (d, N ) .
a/. Chứng minh trực tâm tam giác AMN cố định.
b/. Xác định M , N để diện tích tam giác AMN là nhỏ nhất.
Bài 29. Cho tứ diện S.ABC có SA = SB = SC = 1, mặt phẳng (P) đi qua trọng tâm M của tứ diện, cắt cạnh ,
SA SB, SC lần lượt tại D, E, F (khác S ).
!!!" 1 æ 1 !!!" 1 !!" 1 !!!"ö
Chứng minh rằng: SM = SD + SE + SF . ç ÷ 4 è SD SE SF ø 1 1 1
Tìm giá trị lớn nhất của biểu thức : + + . . SD SE SE.SF SF.SD Trang 20
Bài 30. Cho hình chóp S.ABCD , có đáy ABCD là hình chữ nhật với AB = a 2, BC = a và
SA = SB = SC = SD = 2a . Gọi K là hình chiếu vuông góc của B trên AC và H là hình chiếu
vuông góc của K trên SA .
1/. Chứng minh rằng SA ^ BK .
2/. Tính góc giữa đường thẳng SB và mặt phẳng (BKH ) .
Bài 31. Cho góc tam diện Sxyz thỏa mãn góc ∂ 0 ∂ 0
xSy =121 ; xSz = 59 . Trên tia Sx lấy điểm A sao cho
SA = a cho trước. Trên tia phân giác của góc ∂
xSylấy điểm B thỏa mãn SB = a 3.
Tính các góc của tam giác SAB .
Bài 32. Cho hình thang vuông ABCD có 0
A = D = 90 , AB = 2a,CD = a, AD = 3a và M là điểm bất kỳ
thuộc đoạn thẳng AD .
1/. Xác định vị trí của điểm M để hai đường thẳng BM và CM vuông góc với nhau.
2/. Lấy điểm S thuộc đường thẳng vuông góc với mp(BCD) tại M sao cho SM = AM , xét mặt
phẳng (P) qua điểm M và vuông góc với SA. Mặt phẳng (P)cắt hình chóp SABCD theo thiết
diện là hình gì ? Tính diện tích của thiết diện theo a, x biết x = AM và 0 < x £ 3a ?.
Bài 33. Cho tứ diện ABCD có các đường cao AA', BB',CC ', DD ' đồng qui tại một điểm thuộc miền trong
của tứ diện. Các đường thẳng AA', BB',CC ', DD ' lại cắt mặt cầu ngoại tiếp tứ diện ABCD theo
thứ tự tại A , B ,C , D 1 1 1 1. Chứng minh: AA¢ BB¢ CC¢ DD¢ 8 + + + ³ AA BB CC DD 3 1 1 1 1
Bài 34. Cho hình chóp SABCD có đáy ABCD là hình bình hành. M , N lần lượt là trung điểm của AB , SC .
a/. Tìm giao tuyến của (SMN ) và (SBD). MI
b/. Tìm giao điểm I của MN và (SBD , t ) ính tỷ số . MN Hướng dẫn giải S J N A D I M K Trang 21 B C
a/. Trªn ( ABCD) gäi K lµ giao ®iÓm cña MC vµ BD.
Ta cã: S lµ ®iÓm chung thø nhÊt cña 2 mp (SMN ) vµ (SBD .) MÆt kh¸c:
- K Î BD nªn K ( Î SBD)
- C Î SN nªn C Î(SMN ) do ®ã MC Ì( SMN ).
- K Î MC nªn K Î(SMN ) .
Þ K lµ ®iÓm chung thø 2 cña 2 mp (SMN)vµ (SBD .)
VËy: giao tuyÕn cña (SMN )vµ (SBD)lµ SK .
b/. Trªn (SMN ) gäi I lµ giao ®iÓm cña SK vµ MN .
Ta cã: I Î SK , mµ SK Ì (SBD) nªn I Î(SBD .)
VËy I lµ giao ®iÓm cña MN vµ (SBD .) 1
Gäi J lµ trung ®iÓm cña SK th× JN lµ ®-êng trung b×nh cña tam gi¸c SKC nªn JN // = KC . 2 1
MÆt kh¸c dÔ thÊy K lµ träng t©m tam gi¸c ABC nªn MK = KC . Do ®ã: JN // = MK . 2 IM MK MI Suy ra: = = 1 1 nªn : = . IN JN MN 2
Bài 35. Cho hình thoi ABCD có ∑ = 60o BAD , AB = 2 .
a Gọi H là trung điểm AB . Trên đường thẳng d
vuông góc với mặt phẳng ( ABCD) tại H lấy điểm S thay đổi khác H . Trên tia đối của tia BC 1
lấy điểm M sao cho BM = BC. 4 a 3 a/. Khi SH =
.Chứng minh đường thẳng SM vuông góc với mặt phẳng (SAD ). 2
b/. Tính theo a độ dài của SH để góc giữa SC và (SAD )có số đo lớn nhất. Trang 22 Hướng dẫn giải S B M C K H I A N D 1 a 1 a/. Ta có ∑ ∑ 0 MB = BC =
= HB, HBM = HAD = 60 4 2 2 Þ H
D BM vuông tại M . a o 3 Þ HM = . HB sin 60 = . 2
Gọi N là giao của HM và AD . a 3
Ta có: HN = HM = SH = Þ SM D
N vuông tại S . 2
ìSH ^ AD(SH ^ (ABCD)) í
Þ AD ^ (SMN) Þ AD ^ SM
îMN ^ DA(AD / /BC)
Kết hợp với SM ^ SN Þ SM ^ (SAD)
b/. Gọij là góc giữa SC và (SAD ); K là hình chiếu vuông góc của H lên SN ; I là giao của HC với AD
. Lấy E đối xứng với I qua K .
Vì AD ^ (SMN) Þ AD ^ HK . Kết hợp với HK ^ SN Þ KH ^ (SAD).
Mà HK là đường trung bình của tam giác ICE nên HK // CE . Trang 23
Suy ra CE ^ (SAD)tại E . Suy ra SE
D C vuông tại E và SE là hình chiếu của SC trên(SAD). Ta có ∑ j = CSE .
Đặt x = SH (x > 0). Tam giác SHN vuông tại H và HK là đường cao nên SH.HN 3ax 2 3ax HK = = Þ CE = . 2 2 2 2 SN 3a + 4x 3a + 4x 2 2 25a 3a 2 2 2 2
CH = CM + MC = + = 7a 4 4
Tam giác SHC vuông tại H nên 2 2 2 2
SC = SH + CH = x + 7a . EC 2 3ax 2 3ax sinj = = = . 2 2 2 2 4 4 2 2 SC
(4x + 3a )(x + 7a )
(4x + 21a ) + 31a x 2 3ax 12 Þ sinj £ Þ sinj £ . 2 2 2 2
4 21.a x + 31.a x 4 21 + 31 21
Dấu đẳng thức xảy ra khi 4 x = .a. 4 21
Vậy j lớn nhất khi và chỉ khi sinj lớn nhất khi và chỉ khi 4 SH = . . a 4
Bài 36. Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Hình chiếu vuông góc của S trên mặt phẳng ( a 3
ABCD) là trung điểm H của cạnh AB . ∑ 0
BAD = 60 , AB = 2a, SH = . Trên tia đối của tia 2 1
BC lấy điểm M sao cho BM = BC. 4
a/. Tính côsin của góc giữa đường thẳng SD và mặt phẳng ( ABCD).
b/. Chứng minh rằng đường thẳng SM vuông góc với mặt phẳng (SAD). S Hướng dẫn giải B M C H A N D Trang 24
a/. Vì H là hình chiếu của S trên ( ABCD)nên
góc giữa SD và ( ABCD)là ∑ SDH
( vì tam giác SDH vuông tại H nên ∑ SDH nhọn)
Tam giác ABD đều cạnh 2a nên DH = a 3 a 15 Ta có 2 2
SD = SH + HD = . 2 DH
Trong tam giác SHD ta có: ∑ 2 os c SDH = = . SD 5 b/. Ta có 1 a 1 ∑ ∑ 0 MB = BC =
= HB, HBM = HAD = 60 4 2 2 Þ H
D BM vuông tại M . a o 3 Þ HM = . HB sin 60 = . 2 a 3
Gọi N là giao của HM và AD . Suy ra HN = HM = SH = Þ SM D
N vuông tại S . 2
ìSH ^ AD(SH ^ (ABCD)) í
Þ AD ^ (SMN) Þ AD ^ SM
îMN ^ DA(AD / /BC)
Kết hợp với SM ^ SN Þ SM ^ (SAD)
Bài 37. Cho hình chóp S.ABC có đáy là tam giác vuông tại B , cạnh bên SA vuông góc với đáy.
SA = a 3, AB = BC = .
a Gọi H là hình chiếu của A trên SB .
a/. Chứng minh rằng đường thẳng BC vuông góc với mặt phẳng (SAB).
b/. Tính độ dài đoạn thẳng HC theo a . Hướng dẫn giải S H A C Trang 25 B
a/. Ta có BC ^ AB (Vì ABC vuông tại B ) (1)
BC ^ SA (Vì SA ^ (ABC)) (2)
Từ (1) và (2) suy ra BC ^ (SAB).
b/. Ta có AH ^ SB (theo giả thiết) (3) ìBC ^ (SAB) í Þ BC ^ AH (4) îAH Î(SAB)
Từ (3) và (4) suy ra AH ^ (SBC) Þ AH ^ HC hay tam giác AHC vuông tại H . 2 1 1 1 1 1 4 3a
Tam giác SAC vuông tại A có AH là đường cao nên 2 = + = + = Þ AH = . 2 2 2 2 2 2 AH SA AB 3a a 3a 4
Tam giác ABC vuông tại B nên 2 2 2 2
AC = AB + BC = 2a . a 5 Do đó, 2 2
HC = AC - AH = . 2
Bài 38. Cho hình chóp ABCD , M là điểm nằm trong hình chóp. Kéo dài DM cắt mặt phẳng ( ABC) tại N . Chứng minh: a) ∑ ∑ ∑ ∑ ∑ ∑
ADN + BDN + CDN < ADB + BDC + CDA ∑ ∑ ∑ ∑ ∑ ∑
DMA+ DMB + DMC + AMB + BMC + CMA > 3p
Bài 39. Cho tứ diện ABCD . Gọi M , N, P,Q, R, S lần lượt là trung điểm của ,
DA DB, DC, BC,C , A A . B
a) Tính góc giữa AB và CD biết AB = CD = 2a , MQ = a 3 .
b) Giả sử MQ = NR + SP. Chứng minh rằng: DA DB DC = = ∑ ∑ ∑ cos BDC cosCDA cos ADB Trang 26
Bài 40. Cho hình lập phương ABCD ’ A ’ B C’ ’
D . Một mặt phẳng (P) bất kì đi qua ’ BD và cắt cạnh ’ AA ở
E , cắt cạnh CC’ ở F .
a) Chứng minh rằng tứ giác BE ’
D F là hình bình hành và ’ A E = CF .
b) Tìm E để diện tích tứ giác BE ’ D F đạt GTNN.
Bài 41. Cho đường thẳng d vuông góc với mặt phẳng tam giác ABC tại A . Trên d lấy điểm N và điểm
M sao cho BN vuông góc với CM .
!!!!" !!!" !!!" !!!" !!!" !!!!"
a) Chứng minh rằng BM.CN = .
BACA+ AN.AM .
b) Tìm điều kiện cần và đủ để M , N nằm cùng phía đối với A trên đường thẳng d .
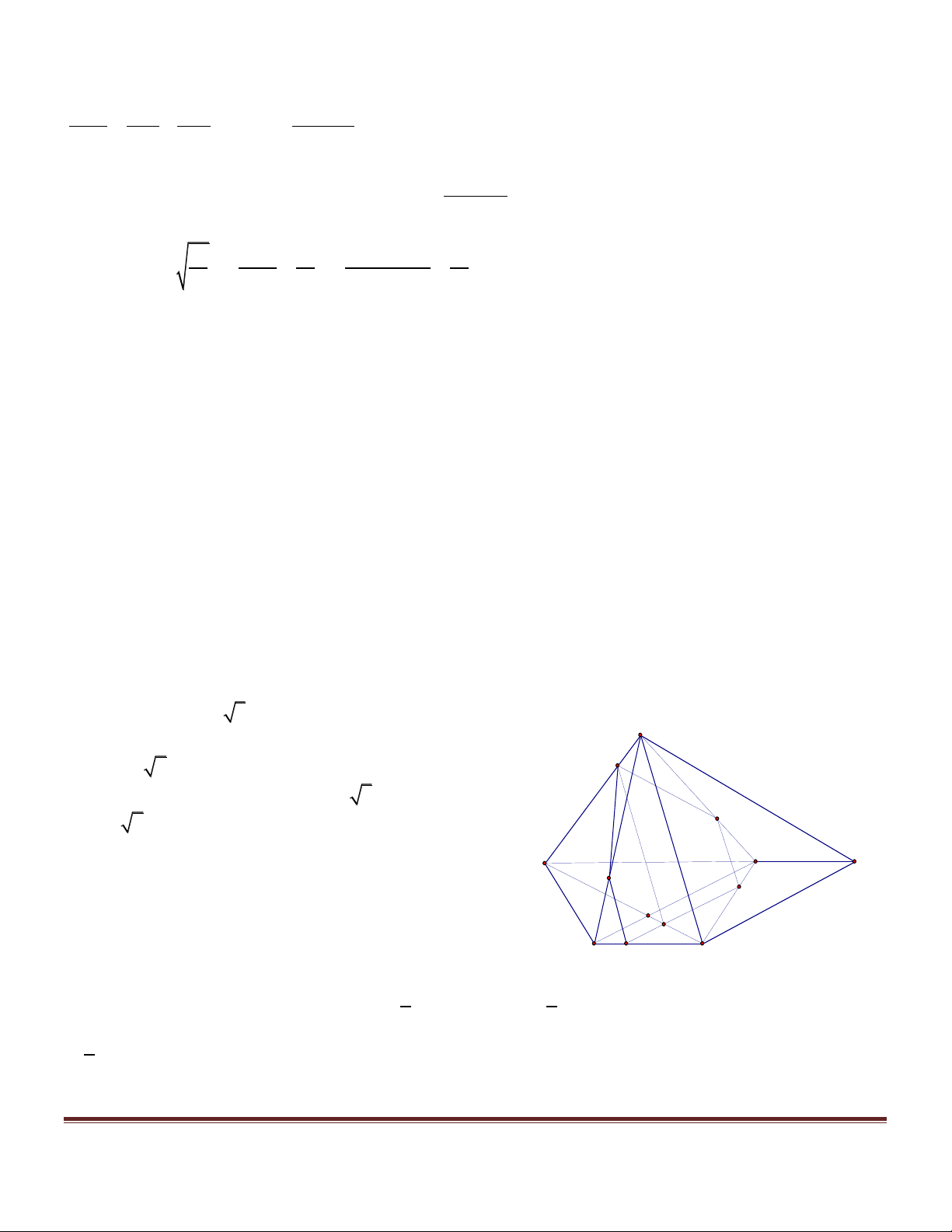
Bài 42. Cho hình chóp đáy là đa giác đều S.ABCD . M cố định trên SC . Mặt phẳng (a ) quay quanh trục
AM cắt SB, SD tại P, . Q
a) Xác định mặt phẳng (a ) để diện tích tứ giác APMQ nhỏ nhất.
b) Cho AB = 1; SA = 2 3 3; CM =
. Tính diện tích tứ giác SPMQ. 3
Bài 43. Cho tứ diện ABCD có AB = CD = ; c AD = BC = ; b AC = BD = .
a Gọi A , C lần lượt là trọng tâm 1 1
của các mặt đối diện với đỉnh A và đỉnh C . a) Chứng minh rằng: 2 2 2
AA ^ CC Û a + c = 3b . 1 1
b) Gọi AH là đường cao của tứ diện, H thuộc mặt phẳng(BCD), H là trực tâm BCD D . Kéo dài CH cắt 1 1
BD tại K . Chứng minh 2
AH = 4CH .H K . 1 1
Bài 44. Cho 2 đường thẳng D, ’
D chéo nhau và vuông góc với nhau. Gọi AB là đường vuông góc chung (AÎD, B ’
ÎD .) M và N là 2 điểm di động trên ’ D sao cho 0 MA Ð
N = 90 không đổi. I là điểm cố định trên D .
a) Chứng minh rằng trực tâm H của tam giác MIN cố định.
b) Tìm tập hợp hình chiếu K của M trên IN .
Bài 45. Cho góc tam diện vuông Oxyz , tia Ot bất kì nằm trong góc tam diện. Gọi a, b ,g theo thứ tự là
góc hợp bởi tia Ot với các tia , Ox Oy, . Oz 2
Chứng minh rằng: cot ga.cot gb.cot gg £ 4
Bài 46. Chứng minh rằng nếu một tứ diện MNPQ thỏa mãn điều kiện MN vuông góc với PQ và MP
vuông góc với NQ thì MQ vuông góc với NP .
Bài 47. Cho hình chóp S.ABCD . đáy ABCD là hình bình hành, AC cắt BD tại H và: ∑ ∑ ∑ ∑ ASB = CS ;
D BSC = DSA. Chứng minh: SH vuông góc với mặt phẳng ( ABCD). Bài 48.
a)Cho tứ diện ABCD và M là Một điểm nằm trong BCD D . Chứng minh: ∑ ∑ ∑ ∑ ∑ ∑
MAB + MAC + MADáBAD + DAC + CAB Trang 27 S
b)Gọi S và R là tổng độ dài các cạnh và bán kính mặt cầu ngoại tiếp tứ diện. Hỏi tứ diện nào có tỉ số lớn R
nhất. Tìm giá trị lớn nhất đó. Hướng dẫn giải
a) Gọi K là giao điểmcủa BM và CD , ta có : ∑ ∑ ∑ ∑ ∑ ∑ ∑
MAB + MACáMAB + MAK + KAC = KAB + KAC ∑ ∑ ∑ ∑ ∑ ∑ ∑ A
KAB + KACáBAD + DAK + KAC = BAD + DAC Hay : ∑ ∑ ∑ ∑
MAB + MACáBAD + DAC(1) tương tự : ∑ ∑ ∑ ∑
MAB + MADáBAC + CAD (2) ∑ ∑ ∑ ∑
MAD + MACáDAB + BAC (3)
Cộng (1), (2), (3) theo từng vế ta có đpcm.
b) Gọi G và O lần lượt là trọng tâm và tâm mặt cầu ngoại tiếp tứ diện ABCD ta có :
S = (BC + CA + AB + DA + DB + DC)2 2 £ ( 2 2 2 2 2 2
6 BC + CA + AB + DA + DB + DC ) (1) Mặt khác ta có : !!!" !!!" !!!" !!!" !!!" !!!"
BC + CA + AB + DA + DB + DC = (OC -OB)2 + (OA-OC)2 + (OB -OA)2 2 2 2 2 2 2 + !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
+(OA-OD)2 +(OB -OD)2 +(OC -OD)2 =16R -(OA+OB +OC +OD)2 2 = 2 2 2
=16R -16OG ³16R (2) S
ìBC = CA = AB = DA = DB = DC Từ (1) và (2) 2 2
Þ S £ 6.16R hay £ 4 6 . đẳng thức xảy ra Û í R G î º O
Û ABCD là tứ diện đều. S Và khi đó (max) = 4 6. R
Bài 49. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ^ ( ABCD) và độ dài SA = a .
Một mặt phẳng đi qua CD cắt cạnh ,
SA SB lần lượt ở M , N . Đặt AM = x .
a)Tính diện tích tứ giác MNCD theo a, x . 2
b) Xác định x để thể tích hình chóp S.MNCD bằng lần thể tích hình chóp S.ABCD . 9 Hướng dẫn giải Trang 28
a) Gọi K là giao điểm của AE và MN ; H là giao điểmcủa AC và BD. Áp dụng định lý cosin trong tam
giác ACE ta có : AE = 2 Þ AC = AE = 2. ∑ ∑ 0
Þ MEN = BCD = 90 Þ MN = 2EK.
Theo Tính chất đường phân giác SK trong SA D E ta có : AE 2 S EK = = . 4 4 1 Þ S = . AMEN 2 L
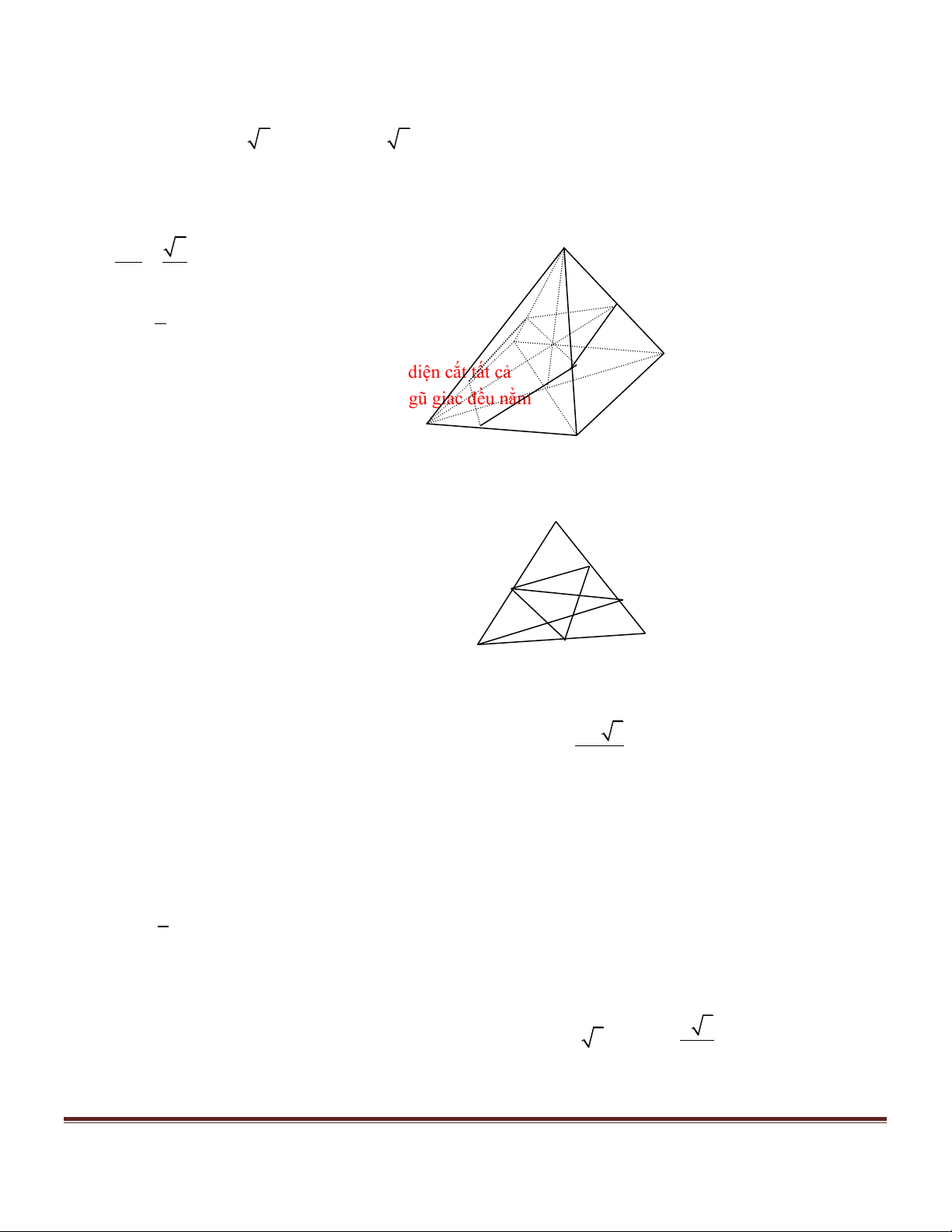
b) Gọi hình chóp đều đó là S.ABCD , vì thiết diện cắt tất cả M P
các mặt bên nên các đỉnh K, M , ,
L N, P của ngũ gi ác đ ềNu n ằm
trên các cạnh AB, SB, SC, S , D AD tương ứng K
Không mất tính tổng quát, hình chiếu trên mặt phẳng vuông D C
góc với cạnh BC .(xem hình 3) S’ Giả sử ’ B K’: ’ A ’ B = . p
VÌ M’K’ / /N’ ’ P ; M’ ’ P / /K’ ’ L nên ’ B M’: ’ B S’ = ’ A ’ P : ’
A S’ = S’N’: ’ A S’ = . p N’
Þ P S A S = - p Þ S N A S = ( - p)2 ’ ’: ’ ’ 1 ’ ’: ’ ’ 1 M’ Hình 3
(vì M’N’ / / ’ L ’ P ) - Þ 3 5
p = S N A S = ( - p)2 ’ ’: ’ ’ 1 . 1- 3p ¹ 0 2
Þ p - 3p +1 = 0 Û p = . 2 Giả sử ∑
SA =1; ASB = 2a T . a có : 2 2 2
NP = p + (1- p) - 2 p(1- p)cosa và 2 2 2
KP = p + 4(1- p )sin 2a - 4 p(1- p)sin 2a ( 2 cos 2a =1- 2sin a ) 2
Þ1-3p = 4(1-3p)sin a (Do 1- 3p ¹ 0 ) Û 1 2 0
sin a = Þ a = 30 . Vậy mặt bên của hình chóplà tam giác đều. 4
Bài 50. a) Cho hình chóp tứ giác đều S.ABCD . Trên cạnh SC lấy điểm E . Thiết diện tạo thành do mặt
phẳng đi qua AE và song song với BD cắt ,
SB SD lần lượt tại M , N. 2 3
Tính diện tích thiết diện đó khi cho cạnh đáy bằng 1, cạnh bên bằng 3 và CE = . 3 Trang 29
b) Giả sử thiết diện của hình chóp tứ giác đều là một ngũ giác đều. Hãy chứng minh rằng mặt bên của hình
chóp này là các tam giác đều.
Bài 51. Cho hình chóptam giác đều S.ABC , cạnh đáy bằng a và mỗi mặt của góc tam diện đỉnh S bằng 0 30 .
a. Hỏi phải cắt hình chóp bằng một mặt phẳng đi qua A như thế nào để thiết diện tam giác ’ AB C’ ( ’ B Î SB, ’
C Î SC) thu được có chu vi nhỏ nhất.
b. Tính giá trị chu vi nhỏ nhất đó theo a . 1
Bài 52. Cho lăng trụ ABC.A¢B C
¢ ¢. Trên tia đối của tia AB lấy điểm M sao cho AM = AB. Gọi E là 2 trung điểm AC .
a)Xác định thiết diện của lăng trụ cắt bởi mặt phẳng (MEB¢). CD AK
b) Gọi D = BC Ç(MEB¢), K = AA¢Ç(MEB¢). Tính tỉ số và . CB AA' Hướng dẫn giải
+) Xác định được điểm D và suy ra hai giao tuyến DE và DD¢
+) Xác định được điểm K ; suy rađược đoạn giao tuyến EK và ’ KB
+) Kết luận thiết diện là tứ giác D ’ EKB b,(1,25) AK MA 1 AK 1 +) Xét tam giác M ’ BB có = = Þ = BB ' MB 3 AA' 3
+) Trong ( ABC) .Dựng EN / / AB(N Î 1
BC), khi đó EN = AB 2 DN NE 1 1
+) Xét tam giác DBM có: = = Þ DN = BN DB BM 3 2 CD 1
Suy ra D là trung điểm CN . Vậy = CB 4
Bài 53. Cho hình chóp S.ABCD có đáy là hình thang AD / /BC và AD > BC . Gọi M , N, E lần lượt là
trung điểm của AB,CD, SA.
a)Chứng minh rằng: (MNE) / / (SBC).
b) Chứng minh: SC / / (MNE) và AF không song song với (SBC).
c) Xác định thiết diện của hình chóp cắt bởi (MNE). Thiết diện là hình gì? Trang 30
Bài 54. Trong mặt phẳng (P) cho đường tròn tâm O bán kính R và 1 điểm A cố định trên (O). Tứ giác
ABCD biến thiên nội tiếp trong (O).sao cho 2 đường chéo luôn vuông góc với nhau. Trên đường thẳng d
vuông góc với mặt phẳng (P)tại A lấy1 điểm S . Nối S với ,
A B,C, D .
a. Chứng minh 2 cạnh BD, SC vuông góc với nhau.
b. Nêu cách xác định điểm I cách đều 5 điểm ,
A B,C, D, S .
c. Tứ giác ABCD là hình gì để diện tích của nó lớn nhất. Tìm GTLN đó theo R Hướng dẫn giải d d’ S I B A H O K C D P
a, Vì SA ^ (P) nên AC là hình chiếu của SC trên mp (P) Trang 31
Theo gt AC ^ BD nên theo định lí 3 đường vuông góc ta có SC ^ BD . b, Cách dựng:
Qua O kẻ đường thẳng d’ vuông góc với mp (P).
Dựng mp (Q) là mp trung trực của SA.
Giao của mp (Q)và đường thẳng d’ là điểm I cần xác định CM:
Vì I Î d ' nên I cách đều ,
A B,C, D .
Vì I Î mp(Q)nên I cách đều S và A.
Vậy điểm I vừa dựng cách đều 5 điểm , A B,C, , D S . 1 c, S
= AC.BD. Kẻ OH ^ AC tại H . Kẻ OK ^ BDtại K ! ABCD 2 Ta có 2 2 2 2
AC = 2 AO -OH = 2 R -OH 2 2 2 2
BD = 2 BO -OK = 2 R -OK
Để tứ giác ABCD có diện tích lớn nhất thì độ dài AC và BD lớn nhất khi và chỉ khi OH = OK = 0 ìH º O Þ í îK º O 1
Vậy tứ giác ABCD là hình vuông. Khi đó 2 S = .2 .2 R R = 2R ! ABCD 2
Bài 55. Cho hình vuông cạnh a tâm O . gọi S là điểm nằm ngoài mặt phẳng ( ABCD) sao cho SB = SD ,
M là điểm tùy ý trên AO với AM = x . Mặt phẳng (a ) qua M và song song SA và BD cắt , SO SB, AB
lân lượt tại N, P,Q.
a)Tứ giác MNPQ là hình gì?
b) SA = a . Tính diện tích MNPQ theo a và x . Tìm x để diện tích lớn nhất.
Bài 56. Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ cạnh a . Trang 32
a) Tính góc giữa hai đường thẳng AC¢ và A¢B .
b) Gọi M , N, P lần lượt là các điểm thuộc các cạnh A B
¢ ,¢ BC, DD¢ sao cho A¢M = BN = DP . Chứng minh
rằng trọng tâm tam giác MNP luôn thuộc một đường thẳng cố định khi M , N, P thay đổi.
Bài 57. Cho hình chóp cố định S.ABC có các góc tam diện đỉnh A ba mặt vuông. Hình lăng trụ
AMN.A¢M N
¢ ¢ thay đổi sao cho MN / /BC(M Î A ;
B N Î AC) ; các điểm A ,¢ M ,¢ N¢ lần lượt thuộc ,
SA SB, SC . Tìm giá trị lớn nhất của thể tích khối lăng trụ AMN.A¢M N
¢ ¢ theo thể tích khối chóp S.ABC
Bài 58. Cho hính chóp S.ABC có SA = SB = AB = AC = a ,diện tích tam giác SBC là S .Gọi M là điểm 0
di động trên SB , N là trung điểm của BC . Biết AN vuông góc với mặt phẳng (SBC). Tìm giá trị nhỏ nhất
của diện tích tam giác AMN theo a và S . 0
Bài 59. Cho hình chóp OABC . Xét các điểm A , B ,C theo thứ tự thuộc các cạnh ,
OA OB,OC sao cho 1 1 1 OA OB OC + +
= 3. Chứng minh rằng khi các điểm A , B ,C thay đổi thì mặt phẳng (A B C ) đi qua một OA OB OC 1 1 1 1 1 1 1 1 1 điểm cố định.
Bài 60. Cho hình hộp ABCDA B C D . Hãy xác định các điểm M , N theo thứ tự thuộc các đoạn thẳng 1 1 1 1
AC và B D sao cho MN song song với A D. 1 1 1 1
Bài 61. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Biết SA = a, AB = a, BC = 2a, cạnh bên
SA vuông góc với mf ( ABCD).
a)Tính góc giữa các mặt phẳng (SBC) và (SCD) với ( ABCD).
b) Gọi O là giao điểm của hai đường chéo AC và BD .Tính khoảng cách từ O đến mf (SCD). Hướng dẫn giải Hình vẽ ; a). Trang 33
Góc giữa (SCD) với ( ABCD)chính là góc ∑ SDA
Góc giữa (SBC) với ( ABCD)là góc ∑ SBA Ta có ∑ 1 tan SDA = 2 ∑ tan SB A = 1
b). Từ A kẻ AJ ^ SD Þ AJ ^ mf (SDC). Nối CJ và từ O kẻ OI / / AJ Þ OI ^ mf (SCD).
Vậy OI chính là khoảng cách cần tìm 1 1 1 1 Ta có OI = AJ ; = + 2 2 2 2 AJ SA AD a 5
Từ đó ta có kết quả ; OJ = 5
Bài 62. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA = a 2 vuông góc với mặt đáy ( ABCD).
a) Gọi M là trung điểm SD . Tính góc giữa SA và CM .
b) Xác định thiết diện của hình chóp S.ABCD cắt bởi mp (a )đi qua A và vuông góc với SC . Tính diện tích của thiết diện đó.
Bài 63. Cho hình tứ diện ABCD có đáy ABC là tam giác đều cạnh a , mặt bên DBC là tam giác cân đỉnh
D , cạnh bên DBC tạo với mặt đáy một góc bằng 0 60 .
a) Chứng minh rằng AD vuông góc với BC .
b) Gọi H là hình chiếu vuông góc của D trên mặt phẳng ( ABC).Chứng minh H nằm trên
trung tuyến AM của tam giác ABC . Tính DH , biết tam giác HBC vuông.
c) Gọi E là trung điểm AC . Xác định thiết diện của hình chóp cắt bởi mp(P) đi qua E và vuông góc với AB .
Bài 64. Cho tứ diện ABCD có AB = CD = a , AC = BD = b , AD = BC = c . M là điểm tùy ý trên cạnh
AB , (P) là mặt phẳng qua M và song song với AC và BD cắt BC,CD, DA lần lượt tại N, P, . Q Tìm vị
trí của M và điều kiện của a,b, c để thiết diện MNPQ là hình vuông, tính diện tích thiết diện trong trường hợp đó.
Bài 65. Cho tứ diện ABCD . Tìm M trong không gian sao cho 2 2 2 2
MA + MB + MC + MD đạt giá trị nhỏ nhất.
Bài 66. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O . Gọi M là trung điểm SC .
1) Tìm giao điểm F của đường thẳng SD và mặt phẳng ( ABM ). Trang 34
2) Gọi I là giao điểm của AM và SO . Chứng minh ba điểm B, I, F thẳng hàng BF 3) Tính tỉ số BI S F M I D C O ` A B
1) Trong mp (SDC) dựng đường thẳng qua M song song với CD cắt SD tại F , suy ra F là trung điểm của SD ìMF ! CD Do í
Þ MF ! AB Suy ra F thuộc mp ( ABM ) . îAB ! CD
2) Ta có BI là giao tuyến của ( ABM )và mp (SBD) .
ìF Î SD Ì (SBD) ìF Î(SBD) Mặt khác í Þ í
suy ra F nằm trên giao tuyến của mp (SBD) và mp ( ABM ) . îF Î(ABM ) îF Î(ABM )
Vậy B, I, F thẳng hàng. BF 3
3) Xét tam giác SBD có I là trọng tâm nên = . BI 2 Trang 35
Bài 67. Cho hình chóp S.ABCD , có đáy ABCD là hình chữ nhật với AB = a 2, BC = a và
SA = SB = SC = SD = 2 .
a . Gọi K là hình chiếu vuông góc của B trên AC và H là hình chiếu vuông góc
của K trên SA.
a)Tính độ dài HK theo a .
b)Gọi M , N lần lượt là trung điểm của đoạn thẳng AK,CD. CMR các đoạn thẳng BM và MN vuông góc với nhau.
Bài 68. (HSG Nghệ An 2016) Cho hình thoi ABCD có ∑
BAD=60o, AB = 2 .
a Gọi H là trung điểm AB .
Trên đường thẳng d vuông góc với mặt phẳng (ABCD) tại H lấy điểm S thay đổi khác H . Trên tia đối của 1
tia BC lấy điểm M sao cho BM = BC. 4 a 3 a) Khi SH =
. Chứng minh đường thẳng SM vuông góc với mặt phẳng (SAD). 2
b) Tính theo a độ dài của SH để góc giữa SC và (SAD) có số đo lớn nhất. Hướng dẫn giải
Bài 69. (HSG Hà Tĩnh 2008) Cho hình thang cân ABCD có đáy lớn AD = 2a , đáy nhỏ BC = a , các cạnh
bên AB = CD = a . Trên nửa đường thẳng At vuông góc với mặt phẳng (ABCD) lấy điểm S (không trùng với
A). Mặt phẳng (P) đi qua điểm A và vuông góc với SD cắt các cạnh SB, SC, SD tại B ,C ,D . 1 1 1
a. Chứng minh rằng: AB C D là tứ giác nội tiếp được trong một đường tròn. 1 1 1
b. Khi điểm S chạy trên nửa đường thẳng At , chứng minh đường thẳng C D đi qua một điểm cố 1 1 định. Hướng dẫn giải
Bài 70. (HSG Nghệ An Bảng B 2016) Cho hình chóp tam giác S.ABC có đáy là tam giác đều cạnh a .
Đường thẳng SA vuông góc với mặt phẳng (ABC). Gọi †M là trung điểm của đoạn AB , H là hình chiếu
vuông góc của C lên SB .
a) Chứng minh đường thẳng SB vuông góc với mp (HCM).
b) Biết góc tạo bởi đường thẳng AB và mp (HMC) bằng 300. Tính diện tích tam giác HMC . Trang 36
Bài 71. (HSG Quảng Bình 2011) Cho tứ diện đều ABCD cạnh a . Gọi I, J lần lượt là trọng tâm các tam
giác ABC và DBC . Mặt phẳng (a ) qua IJ cắt các cạnh AB, AC, DC, DB lần lượt tại các điểm M, N, ,
P Q với AM = x , AN = y ( 0 < , x y < a).
a) Chứng minh MN, P ,
Q BC đồng qui hoặc song song và MNPQ là hình thang cân. 4a 3a
b) Chứng minh rằng: a(x + y) = 3xy. Suy ra: £ x + y < . 3 2
c) Tính diện tích tứ giác MNPQ theo a và s = x + y .
Bài 72. (HSG Vĩnh Phúc 2011) Cho hình hộp ABCD.A B ¢ C ¢ D
¢ ¢ có tất cả các mặt đều hình vuông cạnh a
1. Chứng minh rằng AC¢ vuông góc với mặt phẳng (A B
¢ D) và đường thẳng AC¢ đi qua trọng tâm của tam giác A BD ¢ .
2. Hãy xác định các điểm M, N lần lượt nằm trên các cạnh A D
¢ , CD¢sao cho MN vuông góc với mặt phẳng (CB D
¢ ¢). Tính độ dài đoạn MN theoa .
Bài 73. (HSG Vĩnh Phúc 2016) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA vuông
góc với mặt phẳng ( ABCD). Biết AB = a, BC = a 3 và SD = a 5.
a) Đường thẳng qua A vuông góc với AC cắt các đường thẳng CB,CD lần lượt tại I, J . Gọi H là hình
chiếu vuông góc của A trên SC . Hãy xác định các giao điểm K , L của ,
SB SD với (HIJ ) và chứng minh
rằng AK ^ (SBC) .
b) Tính diện tích tứ giác . AKHL Hướng dẫn giải S J J L H K D A A D I B C I B C
Trong (SCD) gọi L = SD Ç JH Þ L = SD Ç( IJ H )
Trong (SBC) gọi K = SB Ç IH Þ K = SB Ç( IJ H ) Trang 37 ìIJ ^ AC Ta có í
Þ IJ ^ (SAC) Þ IJ ^ SC, mà AH ^ SC . Suy ra SC ^ (IJH). î ^ IJ SA
Suy ra AK ^ SC . Mà BC ^ (SAB) Þ BC ^ AK .Vậy AK ^ (SBC) . . SA AC 2a . SA AB 2a b) Ta có 2 2
SA = SD - AD = a 2 ; AH = = ; AK = = 2 2 SA + AC 3 2 2 SA + AB 6 2
Do AK ^ (SBC) Þ AK ^ KH , do đó 2 2 = - = a KH AH AK . 6
Tương tự phần (a) thì AL ^ (SCD) Þ AL ^ HL. Từ đó tính được 2 2 2 = - = a LH AH AL . 15 2 1 1 8a Suy ra S = S + S
= AK.KH + A . L LH = . AKHL AKH ALH 2 2 15
Bài 74. (Bình Sơn Vĩnh Phúc) Cho hình chóp tứ giác đều S.ABCD có đường cao SH . Mặt phẳng (a ) SH 1
đi qua A và vuông góc với †SC , cắt SH tại †H sao cho: 1 = và cắt các cạnh 1 SH 3
bên SB,SC,SD lần lượt tại B ,¢C ,¢D¢ .
a) Tính tỷ số diện tích thiết diện AB C ¢ D
¢ ¢ và diện tích đáy hình chóp.
b) Cho biết cạnh đáy của hình chóp là a . Tính SH .
Bài 75. (HSG Vĩnh Phúc 2012) 1. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng
a 2, các cạnh bên bằng nhau và bằng 3a ( a > 0 ). Hãy xác định điểm O sao cho O cách đều tất cả các đỉnh
của hình chóp S.ABCD và tính độ dài SO theo a .
2. Cho hình chóp S.ABC có đường thẳng SA vuông góc với mặt phẳng (SBC). Gọi H là hình chiếu của S
lên mặt phẳng (ABC). Chứng minh rằng đường thẳng SB vuông góc với đường thẳng SC, biết rằng 1 1 1 1 = + + . 2 2 2 2 SH SA SB SC
3. Cho tứ diện ABCD thỏa mãn điều kiện AB = CD, BC = AD, AC = BD và một điểm X thay đổi trong
không gian. Tìm vị trí của điểm X sao cho tổng XA + XB + XC + XD đạt giá trị nhỏ nhất. Hướng dẫn giải Trang 38 S M O D C I A B
Gọi I = AC Ç BD . Do SA = SB = SC = SD nên các tam giác SAC, SBD cân tại đỉnh S nên SI vuông góc với
AC, BD suy ra SI vuông góc với mặt phẳng (ABCD). Dễ thấy mọi điểm nằm trên đường thẳng SI cách đều
các đỉnh A, B, C, D.
Trong tam giác SIC, dựng trung trực của cạnh SC cắt đường thẳng SI tại O suy ra OS = OA = OB = OC = OD . 2 SM .SC 3 .3 a a 9a 9 2a Ta có SM .SC = . SO SI Þ SO = = = = . 2 2 2 2 SI 2 SA - IA 2 9a - a 8 9 2 A Vậy = a SO . 8
Gọi K là giao điểm của đường thẳng AH và BC; trong mặt phẳng (SBC)
gọi D là giao điểm của đường thẳng qua S, vuông góc với SC. Ta có BC
vuông góc với SH và SA nên BC vuông góc với mặt phẳng (SAH) suy ra H
BC vuông góc với SK. 1 1 1 S C
Trong tam giác vuông SAK ta có = + , kết hợp với giả 2 2 2 SH SA SK K 1 1 1 thiết ta được = + (1) 2 2 2 SK SB SC B D 1 1 1
Trong tam giác vuông SDC ta có = + (2) 2 2 2 SK SD SC
Từ (1) và (2) ta được SB = SD , từ đó suy ra B º D hay suy ra SB vuông góc với SC. Trang 39 A M Q G D B P N C
Gọi G là trọng tâm của tứ diện; M, N, P, Q lần lượt là trung điểm của các cạnh AB, CD, BC, AD. Ta có tam
giác ACD bằng tam giác BCD nên AN = BN suy ra MN ^ AB , tương tự ta chứng minh được MN ^ CD và
đường thẳng PQ vuông góc với cả hai đường thẳng BC, AD. Từ đó suy GA = GB = GC = GD . . + . + . + . Ta có + + +
= XAGA XB GB XC GC XD GD XA XB XC XD GA
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" . XA GA + .
XB GB + XC.GC + . ³ XD GD GA !!!" (!!!" !!!" !!!" !!!"
XG GA + GB + GC + GD) 2 . + 4.GA =
= 4GA. Dấu bằng xảy ra khi và chỉ khi X trùng với điểm G. Vậy GA
XA + XB + XC + XD nhỏ nhất khi và chỉ khi X là trọng tâm của tứ diện ABCD.
Bài 76. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tất cả các cạnh bên đều bằng a. Gọi
điểm M thuộc cạnh SD sao cho SD = 3SM , điểm G là trọng tâm tam giác BCD .
a) Chứng minh rằng MG song song với mp (SBC)
b) Gọi (a ) là mặt phẳng chứa MG và song với CD . Xác định và tính diện tích thiết diện của hình chóp với mp(a )
c) Xác định điểm P thuộc MA và điểm Q thuộc BD sao cho PQ song song với SC . Tính PQ theo a . Hướng dẫn giải Trang 40 S M H D C E G F I A B
a) Gọi I là trung điểm của BC DG DM 2 Ta có =
= Þ MG / /SI mà SI Ì (SBC) nên MG / / (SBC) DI DS 3
b) Qua G kẻ đường thẳng song song với CD cắt AD và BC lần lượt tại E và F . Qua M kẻ đường thẳng
song song với CD cắt SC tại H . Thiết diện của hình chóp với mp(a ) là tứ giác EFHM .
Ta có HM / / EF vì cùng song song với CD 2a a ! ! 0 MD = HC =
, DE = CF = , MDE = HCF = 60 nên tam giác DME bằng tam giác CHF suy ra ME 3 3
= HF do đó EFHM là hình thang cân 2 2 2 4a a 2a a 1 a Ta có 2 2 2 0
EM = DM + DE - 2DM.D . E o c s60 = + - 2 . . = 9 9 3 3 2 3 = a MH
, EF = a .Gọi h là độ dài đường cao của hình thang ta có 3 2 2 2 æ EF - HM ö a a a 2 2 h = EM - = - = ç ÷ è 2 ø 3 9 3 2 1 1 a 2 4a 2a 2
Diện tích thiết diện là S = . .( h EF + HM ) = . . = EFHM 2 2 3 3 9 Trang 41 S M P D C N Q A B
c) Qua M dựng đường thẳng song song với SC cắt CD tại N. Nối A với N cắt BD tại Q. Trong mp (AMN)
từ Q dựng đường thẳng song song với MN cắt AM tại P.
Ta có PQ//MN, MN//SC nên PQ//MN
Suy ra hai điểm P, Q thỏa mãn điều kiện bài toán. MN DM 2 AQ AB 3 AQ 3 Ta có = = , = = Þ = SC DS 3 QN DN 2 AN 5 PQ AQ 3 PQ PQ MN 3 2 2 = = , = . = . = MN AN 5 SC MN SC 5 3 5 2 Suy ra = a PQ 5
Bài 77. Cho tứ diện đều ABCD cạnh a . Gọi I, J lần lượt là trọng tâm các tam giác ABC và DBC . Mặt
phẳng (a ) qua IJ cắt các cạnh AB, AC, DC, DB lần lượt tại các điểm M, N, ,
P Q với AM = x, AN = y ( 0 < , x y < a ).
a) Chứng minh MN, P ,
Q BC đồng qui hoặc song song và MNPQ là hình thang cân.
b) Chứng minh rằng: 4a 3a
a(x + y) = 3xy. Suy ra: £ x + y < . 3 2
c) Tính diện tích tứ giác MNPQ theo a và s = x + y . Trang 42 Hướng dẫn giải
a) Ta có: (a) Ç (ABC) = MN , (a) Ç (BCD) = PQ, (ABC) Ç (BCD) = BC , (a),(ABC),( D BC ) phân biệt nên MN, P ,
Q BC song song hoặc đồng qui. KI KJ
Gọi K là trung điểm BC , ta có: =
nên AD / /IJ , do đó AD / /(P) KA D K
Các mặt phẳng (ABD),(ADC) đi qua AD cắt (a)theo các giao tuyến lần lượt là , MQ NP nên :
MQ / / AD, NP / / AD . Suy ra : MQ / / NP hay MNPQ là hình thang.
Ta có: DBAD, DCAD là các tam giác đều, MQ / / AD, NP / / AD Nên AM = D ,
Q AN = DP. Suy ra : DAMN = DDQP Þ MN = PQ, hay MNPQ là hình thang cân. ax 3 ay 3 b) Ta có: 0 0 0 S = S + S Û xy sin 60 = sin 30 +
sin 30 Û 3xy = a(x + y) AMN AMI ANI 3 3 2 ( + ) 2 3(x + y) 4a Vì : £ x y xy
nên ; a(x + y) £ Û x + y ³ 4 4 3 Mặt khác: 0 < , x y < a 2
Þ (a - x)(a - y) > 0 Þ a - a(x + y) + xy > 0 a(x + y) 3a 4a 3a 2
Þ a - a(x + y) +
> 0 Þ x + y < . Vậy : £ x + y < . 3 2 3 2
c) Ta có: MQ = BM = a - x , NP = CN = a - y , 2 2 2
MN = x + y - xy
Gọi h là chiều cao hình thang cân MNPQ, ta có: a x + 2 ( y) 2 2 2 2 æ x + y - MQ - NP ö
3(x + y ) - 2xy
3(x + y) - 8xy 3( ) 8 2 9s -8as 2 2 h = MN - = = 3 = = ç ÷ è 2 ø 4 4 4 12 MQ + NP 2a - s 8as Vậy: 2 S = . h = 3s - MNPQ 2 4 3
Bài 78. (HSG Hà Tĩnh 2013) Cho hình chóp SABC có SC ^ ( ABC) và tam giác ABC vuông tại B . Biết
AB = a; AC = a 3 và góc giữa hai mặt phẳng (SAB), (SAC) bằng a 13 với sina = . Tính độ dài SC 19 theo a.
Gọi H, K là hình chiếu của C lên , SA SB . Ta chứng minh được
CK ^ (SAB), SA ^ (CHK). Suy ra DCHK vuông tại K và SA ^ KH . Do đó a = ÐCHK. S
Đặt SC = x > 0 . Trong tam giác vuông SAC ta có H x K Trang 43 C A a B 2 2 1 1 1 3a x 2 = + Þ CH = . 2 2 2 2 2 CH CA CS 3a + x 2 2 2a x
Tương tự, trong tam giác vuông SBC ta có 2 CK = . 2 2 2a + x 2 13 CK 13 2 2 2(3a + x ) 13 Ta có sina = Û = Û =
Û x = 6a , vì x > 0. Vậy SC = 6a 2 19 CH 19 2 2 3(2a + x ) 19
Bài 79. (HSG Quảng Bình 2013) Cho hình chóp S.ABCD , có đáy ABCD là hình thang cân (AD / /BC)
và BC = 2a , AB = AD = DC = a(a > 0). Mặt bên SBC là tam giác đều. Gọi O là giao điểm của AC và BD .
Biết SD vuông góc với AC . a) Tính SD .
b) Mặt phẳng (a ) qua điểm M thuộc đoạn OD ( M khácO, D ) và song song với hai đường thẳng SD và AC .
Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (a ). Biết MD = x . Tìm x để diện tích
thiết diện lớn nhất.
a) Dễ thấy đáy ABCD là nữa hình lục giác đều cạnh a .
Kẻ DT / / AC ( T thuộc BC ). Suy ra CT = AD = a và DT vuông góc SD .
Ta có: DT = AC = a 3 . S
Xét tam giác SCT có SC = 2 , a CT = , a 0 ÐSCT =120 Þ ST = a 7 K
Xét tam giác vuông SDT có DT = a 3 , Q
ST = a 7 Þ SD = 2a
b) Qua M kẻ đường thẳng song song với AC cắt B C T
†AD, DC lần lượt tại N, P. J
Qua M, N, P kẻ các đường thẳng song song với SD cắt P O SB, ,
SA SC lần lượt tại K, J, Q . Thiết diện là ngũ giác NPQKJ . M A D N
Ta có: NJ, MK, PQ cùng vuông góc với NP . 1 1
dt (NPQKJ) = dt(NMKJ)+ dt(MPQK) = (NJ + MK)MN + (MK + PQ)MP 2 2 1
= (NJ + MK).NP (do NJ = PQ .) 2 Trang 44 NP MD AC.MD . x a 3 Ta có: = Þ NP = = = 3x . AC OD OD a 3 æ a ö 2 . a - x NJ AN OM S . ç ÷ D OM è 3 ø = = Þ NJ = = = 2(a - x 3) SD AD OD OD a 3 2 . a (a 3 . - x KM BM SD BM ) 2 = Þ KM = = = (a 3 - x) SD BD BD a 3 3 æ ö
Suy ra: dt (NPQKJ) = 1 2 2(a - x 3) +
(a 3 - x) 3x = 2(3a - 2 3x)x 2 ç ÷ è 3 ø 2 1 1 3 3 2 =
(3a - 2 3x)2 3x £
é(3a - 2 3x) + 2 3xù = a 3 4 3 ë û 4 3 3 3
Diện tích NPQKJ lớn nhất bằng 2 a khi x = a 4 4
Bài 80. (HSG Đà Nẵng 2011) 1) Cho hình hộp ABC .
D A' B 'C ' D '. Trên cạnh AB lấy điểm M khác A và B.
Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (ACD ').
a) Trình bày cách dựng thiết diện của hình hộp và mặt phẳng (P).
b) Xác định vị trí của M để thiết diện nói trên có diện tích lớn nhất.
2) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M là trung điểm của SC. Một mặt phẳng
(P) chứa AM và lần lượt cắt các cạnh SB, SD tại các điểm B', D' khác S. Chứng minh rằng: 4 SB ' SD ' 3 £ + £ . 3 SB SD 2 I D' Q R C' F A' P D B' C S K O A E N J M B Trang 45
Trong mp(ABCD), qua M vẽ đường thẳng song song với AC cắt DB, BC lần lượt tại E, N.
Trong mp(BDD’B’), qua E vẽ đường thẳng song song với D’O (O=ACÇBD) cắt B’D’ tại F.
Trong mp(A’B’C’D’), qua F vẽ đường thẳng song song với AC cắt A’D’, D’C’ lần lượt tại R, Q.
Trong mp(AA’D’D), qua R vẽ đường thẳng song song với AD’ cắt AA’ tại S.
Trong mp(CC’D’D), qua Q vẽ đường thẳng song song với CD’ cắt CC’ tại P.
Thiết diện là lục giác MNPQRS
Do các mặt đối diên của hình hộp song song nên các cạnh đối của lục giác thiết diên MNPQRS song song và
3 cặp cạnh đó lần lượt song song với các cạnh tam giác ACD’.
Þ Các tam giác JKI, ACD’, RQI, JMS, NKP đồng dạng Þ MJ MA NC NK PC PK QD ' QI = = = = = = =
Þ MJ=NK và PK=QI MN MB NB NM PC ' PQ QC ' QP
Þ Các tam giác RQI, JMS, NKP bằng nhau (gọi diện tích của chúng là S1 và gọi diện tích các tam giác JKI,
ACD’ lần lượt là S2, S) AM Đặt
= k; ta có điều kiện 0 < k <1 và có: AB 2 2 2 S æ JM ö æ AM ö æ AM ö 1 2 = ç ÷ = = ç ÷ ç
÷ = k Þ S1 = k2S S è AC ø è DC ø è AB ø 2 2 2 S æ JK ö æ JM + MK ö æ JM MK ö = ç ÷ = ç ÷ = ç + ÷ = (k + )2 2
1 Þ S2 =( k2 + 2k +1)SÞ Diện tích thiết diện: S è AC ø è AC ø è AC AC ø
S = S - 3S td 2 1 2 1 é3 1 ù æ ö 3S 2
S = 2S(-k + k + ) = 2S k td ê - - ç ÷ ú £ (dấu bằng 2 ê4 è 2 ø ë ú 2 û S 1 xảy ra Û k = ) 2
Lấy I = AMÇB'D' và O = ACÇBD, D' M
ta có: S, O, I là các điểm chung của 2 mặt phẳng (SAC) và (SBD) I D P C O Trang 46 B' A N B
Þ S, O, I thẳng hàng.
Và I là trọng tâm các mặt chéo SAC Þ SI 2 = SO 3 SD SB
Vẽ BP // B'I và DN // D'I ( ,
P N Î SO)Þ OP = ON . Đặt x = ; y = SD ' SB ' Þ SB SD SP SN 2SO 3 x + y = + = + =
= 2 = 3 Þ x, y Î[1;2] (*) SB ' SD ' SI SI SI 2 2 2 1 1 3 æ 2 ö 4 1 1 3 æ 2 ö 4 Suy ra: + = ³ 3 = Suy ra: + = ³ 3 = ç ÷ ç ÷ x y xy è x + y ø 3 x y xy è x + y ø 3
Bài 81. Cho tứ diện đều ABCD có độ dài cạnh bằng 1. Gọi M, N lần lượt là hai điểm thuộc các cạnh
AB, AC sao cho mặt phẳng (DMN) vuông góc với mặt phẳng(ABC). Đặt AM = x, AN = y. Tìm x, y để
diện tích toàn phần của tứ diện †DAMN nhỏ nhất.
Kẻ DH ^ MN , do (DMN) ^ (ABC) suy ra DH ^ (ABC) .
Mà ABCD là tứ diện đều, nên suy ra H là tâm của tam giác đều ABC . 3 D Ta có: S = 1 . 0 . AM AN.sin60 = xy ; S = S + S AMN 2 4 AMN AMH ANH 1 = 0 . AM AH.sin30 + 1 0
AN.AH.sin30 †= 1 3 . (x+y). 2 2 4 3 3 1 3 C B Suy ra xy = .
(x+y) Þ †x + y = 3xy 0 £ x, y £ 1 4 4 3 H N M
Diện tích toàn phần của tứ diện DAMN : A S = S + S + S + S †= 1 0 . AD . AM sin60 + 1 0 . AD AN.sin60 AMD AND DMN AMN 2 2 1 1 6 + DH.MN + 0 .
AM AN.sin60 . = 3 xy + 3xy(3xy -1) . 2 2 6 2 4
Từ 3xy = x + y ³ 2 xy Þ xy ³ Þ xy ³ . 3 9 Trang 47 3(4 + 2) 2 Suy ra min S = , khi x = y = . 9 3 Câu 1.
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi C’ là trung điểm của SC,
M là điểm thuộc cạnh SA. Mặt phẳng (a ) chứa C’M cắt các cạnh SB, SD lần lượt tại B’, D’.
a) Khi (a ) song song với BC. Xác định vị trí của M để tứ giác B’C’D’M là hình bình hành. SB SD
b) Khi (a ) thay đổi. Xác định vị trí của M để + = . 3 SB ' SD' Hướng dẫn giải S M B' D' I C' A B O D C (a ) a) (2.5 điểm) Khi
song song với BC. Xác định vị trí của M để tứ giác B’C’D’M là hình bình hành.
Gọi O là tâm hình bình hành ABCD. Gọi I = C 'M Ç SO Þ I Î B ' D ' . Ta có: ìB'C'/ / BC BC / /(a) Þ í Þ B'C'/ / D'M.
îD'M / /BC 1 1
Mặt khác, vì C’ là trung điểm SC nên B 'C ' = BC = D A . 2 2 1
Khi đó tứ giác B’C’D’M là hình bình hành khi D'M = B 'C ' = D A . 2 Trang 48
Vậy M là trung điểm của SA. b, S C' I M E A C O F SB SD
b) Khi (a ) thay đổi. Xác định vị trí của M để + = . 3 SB ' SD' Xét ta giác SAC:
Qua A, C lần lượt kẻ các đường thẳng song song với C’M, cắt SO tại E, F. Ta có: SA SE SC SF = SA SC SO ; = Þ + = 2 . SM SI SC ' SI SM SC ' SI
Tương tự, xét ta, giác SBD, ta có: SB D S SO + = SB D S SA SC SA 2 Þ + = + = + 2. SB ' D S ' SI SB ' D S ' SM SC ' SM SB D S SA Vậy + = 3 Û
= 1 Û M º A. SB ' D S ' SM Câu 2.
Cho hình chóp S.ABCD đáy là hình thoi tâm O, cạnh a, góc BAD=600; SO
vuông góc với mặt phẳng (ABCD); 3a SO =
. Gọi E là trung điểm của AD, F là trung điểm 4 của DE.
1/ Chứng minh (SOF) ^ (SAD).
2/ Tính khoảng cách từ O và C đến mặt phẳng (SAD).
3/ Gọi (a )là mặt phẳng qua BC và vuông góc với mặt phẳng (SAD). Xác định thiết diện của
hình chóp với mặt phẳng (a ). Tính diện tích của thiết diện này. Trang 49 Hướng dẫn giải S N M K H E F A D O B C
1/ Tam giác ABD đều nên BE ^ AD ; OF//BE Þ OF ^ AD (1).
SO ^ (ABCD) Þ SO ^ AD(2).
Từ (1) và (2) Þ AD ^ ( O
S F) Þ (SAD) ^ ( O S F).
2/ Kẻ OH ^ SF tại H Þ OH ^ (SAD) Þ d( ;
O (SAD)) = OH . 1 1 1 1 1 64 3a = + = + = Þ OH = . 2 2 2 2 2 2 OH SO OF 9a 3a 9a 8 16 16
O là trung điểm của AC nên 3a
d(C;(SAD)) = 2d( ; O (SAD)) = . 4
3/ Gọi K là hình chiếu của C trên mp(SAD) ÞH là trung điểm của AK.
mp(a) º mp(BCK) ; BC//AD nên mp(BCK) cắt mp(SAD) theo giao tuyến song song với AD.
Từ K kẻ đường thẳng song song với AD cắt SD, SA tại M và N. Thiết diện tạo thành là hình thang BCMN. Trang 50 2 12a a 12 2 2 2 SF = SO + OF = Þ SF = . 16 4 2 SH SO 3 2
SO = SH.SF Þ = = . 2 SF SF 4
Þ MN cắt SF tại trung điểm I ÞMN là đường trung bình của tam giác SAD. AD a Þ MN = = 2 2 a 3a ( + a) 2
(MN + BC)CK 9 2 4 a Þ S = = = . td 2 2 16
Bài 82. [VĨNH PHÚC -2010-2011] Cho hình hộp ABC .
D A' B 'C ' D ' có tất cả các mặt đều là hình vuông cạnh a .
a) Chứng minh rằng AC ' vuông góc với mặt phẳng ( A' BD) và đường thẳng AC ' đi qua trọng tâm của tam giác A' BD .
b) Hãy xác định các điểm M , N lần lượt nằm trên các cạnh A' ,
D CD' sao cho MN vuông góc với mặt
phẳng (CB' D') . Tính độ dài đoạn MN theo a . Hướng dẫn giải
a) Ta có BD ^ AC và BD ^ AA' nên BD ^ ( ACC ' A') Þ AC ' ^ BD.
Tương tự ta chứng minh được AC ' ^ A' D . Từ đó ta suy ra AC ' ^ ( A' BD).
Gọi I là giao điểm của AC và BD . Khi đó G = AC 'Ç A' I chính là giao điểm của AC ' và mặt phẳng (A'BD). GI AI
Do AC / / A'C ' Þ =
= 2 suy ra G là trọng tâm của tam giác A' BD . GA' A'C ' !!!!" !" !!!!!" " !!!!!" !" !" " !" !" " " !" !" !"
b) Đặt A' A = m, A' D ' = n, A' B ' = p Þ m = n = p = a; . m n = . n p = . p m = 0 !!!!!" !!!!" !!!!!" !!!!" và A' M = .
x A' D; D ' N = y.D 'C !!!!!" !" " !!!!!" !" !" !!!!" !!!!" !!!!!" !!!!!" !" " !" Ta có A' M = . x m + .
x n; D ' N = y.m + y.p Þ MN = MA' + A' D ' + D ' N = ( y - x)m + (1- x)n + y p
Do đường thẳng MN vuông góc với mặt phẳng (CB’D’) nên ta có ì !" " !" !" " !!!!" !!!!" ìï = ï( - ) + ( - ) + )( + ) ì 2 1 = 0 = . ' 0 1 ì + - 2 = 0 x y x m x n y p m n MN B C y x ïï 3 í!!!!" !!!!" Û í !" " !" !" !" Û í Û í
ïîMN.D'C = 0
ïî( y - x)m + (1- x)n + y p)(m + p) = î2y - x = 0 1 0 ï y = ïî 3 Trang 51 !!!!!" 2 !!!!" !!!!!" 1 !!!!"
Vậy M, N là các điểm sao cho A' M = A' ;
D D ' N = D 'C 3 3 2 !!!!" 1 !" 1 " 1 !" a a 3 Do đó ta có 2
MN = - m + n + p Þ MN = Þ MN = . 3 3 3 3 3 A B I G D C M A' B' N D' C'
Bài 83. [Cao Văn Bá – THPT Diễn Châu 3 – 2009-2010] Cho hình chóp S.ABCD , có đáy là hình thang
với AD / / BC. M là một điểm di động bên trong tứ giác ABCD . Qua M vẽ những đường thẳng lần lượt song song với ,
SA SB cắt các mặt phẳng (SBC) và (SAD) theo thứ tự tại N và P .
a) Nêu cách dựng các điểm N , P . MN MP b) Chứng minh: + không đổi. SA SB
c) Tìm tập hợp điểm M sao cho diện tích của tam giác MNP có giá trị lớn nhất.
Bài 84. [TRƯỜNG THPT CẨM THUỶ I 2008-2009] Cho tam giác S.ABCD đáy là hình thang, đáy lớn
BC = 2a , đáy bé AD = ,
a AB = b . Mặt bên SAD là tam giác đều. M là một điểm di động trên AB , mp
(P) qua điểm M và song song với , SA BC .
a) Tìm thiết diện của S.ABCD với mặt phẳng mp (P). Thiết diện là hình gì?
b) Tính diện tích thiết diện theo a và x = AM ( 0 < x < b) . Tìm giá trị của x để diện tích thiết diện lớn nhất Hướng dẫn giải
a) Từ M kẻ đường thẳng song song BC và SA , lần lượt cắt DC tại N , SQ tại Q . Trang 52
Từ Q kẻ đường thẳng song song với BC cắt SC tại P suy ra được MNPQ là thiết diện. Dễ dàng chứng
minh được là hình thang cân. S Q P 2a C B M b N x D A a
b) * Tính diện tích thiết diện MNPQ b - x x ab + ax
Sử dụng định lý Talets ta suy ra được MQ = NP =
.a ; PQ = .2a, MN = b b b ba - ax 3
Từ đó tính ra được QK = . b 2 2 1 3a
Áp dụng công thức S = MN + PQ QK =
b - x b + x MNPQ ( ). 3 2 ( )( ) 2 4b P Q N M H K *Tìm x để S
đạt giá trị lớn nhất MNPQ 2 2 2 2 3a
3a æ 3b - 3x + b + 3x ö 3a S =
3b - 3x b + 3x £ = MNPQ 2 ( )( ) 2 ç ÷ 12b 12b è 2 ø 12 Trang 53 b
Dấu "=" xảy ra khi x = . 3
Bài 85. [THPT Quảng Xương 2 THANH HOÁ 2009- 2010] Cho hình chóp tứ giác đều S.ABCD có
cạnh đáy bằng a và đường cao SO = a .
a) Tính góc tạo bởi hai mặt phẳng ( ABCD) và (SCD).
b) Gọi I là trọng tâm tam giác ABO , xác định hình chiếu H của I lên mp (SCD) và tính độ dài IH theo a . Hướng dẫn giải
a) Gọi M là trung điểm CD suy ra góc giữa ( ABCD) và (SCD) là góc SMO , a
Tam giác SMO vuông tại O , SO = a, OM = suy ra tan SMO = 2 hay SMO = 63,4°. 2
b) Kẻ OK là đường cao tam giác SOM suy ra OK vuông góc mp (SCD), từ I kẻ đường thẳng song
song với OK trong mp (SOM )cắt SM tại H thì H là điểm cần tìm. 5 5 a 5 a 5
Ta có IH = .OK = . = 3 3 5 3 Trang 54
Bài 86. Cho tứ diện ABCD có các đường cao AA', BB', CC ', DD' đồng qui tại một điểm thuộc miền
trong của tứ diện. Các đường thẳng AA', BB', CC ', DD' lại cắt mặt cầu ngoại tiếp tứ diện ABCD theo thứ
AA' BB ' CC ' DD ' 8
tự tại A , B ,C , D . Chứng minh: + + + ³ . 1 1 1 1 AA BB CC DD 3 1 1 1 1 Bài 87.
a. Cho tứ diện ABCD . Gọi I và J lần lượt là trung điểm của AC và BC . Trên cạnh BD lấy điểm K
sao cho BK = 2 KD . Tìm giao điểm E của đường thẳng CD với mặt phẳng ( IJK ). Chứng minh rằng DE = DC .
b. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Hai điểm M và N lần lượt thay đổi trên các BM NC đoạn thẳng , SB AC sao cho =
= x,(x > 0, x ¹ )
1 , Gọi G là trọng tâm tam giác SCD . Chứng MS NA
minh rằng MN luôn song song với một mặt phẳng cố định khi x thay đổi và tìm x để NG / / ( SAD ).
Bài 88. [ÔN THI ĐỘI TUYỂN FESTIVAL – ĐỀ SỐ 3] Cho hình chóp S.ABC đều cạnh a , cạnh bên a 3 bằng
. Gọi (P) là mặt phẳng qua A song song với BC và vuông góc với mặt phẳng (SBC). Gọi I 2
là trung điểm của BC .
a) Xác định thiết diện của hình chóp với (P).Tính khoảng cách từ điểm I đến (P).
b) Tính sina với a là góc giữa AB và (P).
Bài 89. [ÔN THI ĐỘI TUYỂN FESTIVAL – ĐỀ SỐ 2] Cho hình lăng trụ ABC.A' B 'C ' có
AB = a , AC = 2a, ’
AA = 2a 5 và góc 120O BAC =
. Gọi M là trung điểm của CC ' .
a) CMR: MB ^ MA' .
b) Tính khoảng cách từ A đến mặt phẳng ( ’ A BM ) .
Bài 90. [HỌC SINH GIỎI TỈNH NAM ĐỊNH, LỚP 11, 2005] Cho tứ diện OABC có , OA , OB OC
đôi một vuông góc với nhau tại O . Gọi A , B , C thứ tự là trung điểm của các cạnh BC, C , A AB . 1 1 1
a) Chứng minh tam giác A B C là tam giác nhọn. 1 1 1
b) Biết số đo 3 góc của tam giác ABC là , A ,
B C . Gọi a là số đo của góc nhị diện [C ,OA , B 1 1 1] , tìm
cosa theo B và C .
c) Gọi d là độ dài lớn nhất trong độ dài 3 cạnh , OA ,
OB OC và gọi h là độ dài lớn nhất trong độ dài 3 6
đường cao của tam giác ABC . Chứng minh rằng:
h £ d < h 3
Bài 91. [HỌC SINH GIỎI TỈNH NAM ĐỊNH, LỚP 11, 2004] Cho hình chóp tam giác đều S.ABC có
cạnh đáy bằng a .
a) Ta coi hình chóp đã cho là tứ diện SABC có trọng tâm O , gọi a là góc giữa mp (SAB) và mp ( ABC).
Hãy tính cosa để O cách đều tất cả các mặt của SABC . Trang 55 b) Biết ∑
ASB = 30° . Xét mặt phẳng (P) thay đổi đi qua A , sao cho mp(P) cắt các đoạn thẳng , SB SC thứ
tự tại B ', C ' . Tìm giá trị nhỏ nhất của chu vi tam giác AB 'C ' theo a .
Bài 92. [HỌC SINH GIỎI LỚP 11 TỈNH QUẢNG NGÃI NĂM HỌC 2011-2012] Cho tứ diện đều
S.ABC . Gọi (P) là mặt phẳng đi qua đường cao SO của tứ diện; mặt phẳng (P) cắt các mặt phẳng (SBC), (SC )
A và (SAB) lần lượt theo các giao tuyến SM, SN, SP . Các giao tuyến này lần lượt tạo với
mặt phẳng ( ABC) các góc a, b ,g . Chứng minh: 2 2 2
tan a + tan b + tan g = 12
Bài 93. [NGHỆ AN 2015-2016] Cho hình thoi ABCD có góc ∑ 0
BAD = 60 , AB = 2a . Gọi H là trung
điểm AB . Trên đường thẳng d vuông góc với mặt phẳng ( ABCD) tại H lấy điểm S thay đổi khác H . 1
Trên tia đối của tia BC lấy điểm M sao cho BM = BC . 4 a 3 a) Khi SH =
, chứng minh rằng đường thẳng SM vuông góc với mặt phẳng (SAD) . 2
b) Tính SH theo a để góc giữa SC và (SAD) có số đo lớn nhất.
Bài 94. [TRƯỜNG THPT TRƯNG VƯƠNG - BÌNH ĐỊNH] Trong không gian cho khối đa diện có số
cạnh qua mỗi đỉnh là một số chẵn .Một thiết diện tạo bởi mặt phẳng không đi qua đỉnh nào của khối đa diện
với khối đa diện .Chứng minh số cạnh của thiết diện là một số chẵn. Hướng dẫn giải
Giả sử số đỉnh của thiết diện là m ;Ta xét một tron 2k .
Tổng các cạnh đi qua m đỉnh mới là 3m . 2k + 3m
Vậy số cạnh của khối đa diện này bằng
Î Z Þ m là số chẵn 2
Bài 95. [VĨNH PHÚC 2009-2010] Cho hình chóp S.ABCD , có đáy ABCD là hình chữ nhật với
AB = a 2, BC = a và SA = SB = SC = SD = 2a . Gọi K là hình chiếu vuông góc của B trên AC và H là
hình chiếu vuông góc của K trên SA.
a) Tính độ dài HK theo a .
b) Gọi M , N lần lượt là trung điểm của đoạn thẳng AK, CD . Chứng minh rằng các đoạn thẳng BM và
MN vuông góc với nhau.
Bài 96. [TRƯỜNG THPT QUỲNH LƯU NGHỆ AN 2016 - 2017] Cho tứ diện S.ABC đều, gọi I, K
là trung điểm của các cạnh AC và SB . Trên đường thẳng AS và CK ta chọn các điểm P,Q sao cho
PQ / /BI . Tính độ dài PQ biết cạnh của tứ diện có độ dài bằng 1. Hướng dẫn giải Trang 56 S P E Q A K I C B F
Ta có PQ là giao tuyến của hai mặt phẳng : Mặt phẳng chứa CK và song song với BI và mặt phẳng chứa
SA và song song với BI .
Trong mặt phẳng (SBI ) kẻ KE / / BI, CE cắt SA ở P .
Qua A kẻ A F / / BI ( F thuộc BC ) , CK cắt SF tại Q . Vậy PQ / / BI . SP 1
Ta có I , E là các trung điểm của AC và SI Þ = SA 3 PQ SP 1 1 Mà = = Û PQ = AF AF SA 3 3
Ta có AF = 2BI = 3 3 . Vậy PQ = . 3
Bài 97. [TRƯỜNG THPT QUỲNH LƯU NGHỆ AN 2016 - 2017] Cho hình chóp S.ABCD , đáy
ABCD là hình vuông và SA = SB = SC = SD . Mặt phẳng (P) thay đổi nhưng luôn cắt các cạnh , SA ,
SB SC, SD lần lượt tại A ,¢ B ,¢C ,¢ D¢ ( A ,¢ B ,¢C ,¢ D¢ không trùng với đầu mút các đoạn thẳng SB¢ + SD¢ SB .¢SD¢ , SA ,
SB SC, SD. Chứng minh rằng: = . SA¢ + SC¢ SA .¢SC¢ Hướng dẫn giải
Gọi O là tâm đáy ABCD , O¢ = A¢C¢ Ç B D ¢ ¢ . Ta có S, ,
O O¢thẳng hàng (do chúng thuộc giao tuyến hai mặt
phẳng (SAC)và (SBD)). Trang 57 S D' A' O' C' D C B' O A B Đặt ∑ ∑
ASC = BSD =2a. Trong tam giác SA¢C¢, ta có: 1 1 1 S = S + S
Û SA.¢SC¢sin 2 = ¢ ¢ + ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ a SA .SO sina SO .SC sina SA C SA O SC O 2 2 2 ¢ + ¢ a Û SA¢ SC¢
a = SO¢(SA¢+ SC¢) SA SC 2cos 2 . cos Û = (1). SA .¢SC¢ SO¢ SB¢ + SD¢ a
Tương tự với tam giác SB D ¢ ¢ 2cos ta được = (2). SB .¢SD¢ SO¢
SB¢ + SD¢ SA¢ + SC¢
SB¢ + SD¢ SB .¢SD¢ Từ (1) và (2) ta suy = Û = .Ta có ĐPCM. SB .¢SD¢ SA .¢SC¢ SA¢ + SC¢ SA .¢SC¢
Bài 98. [THPT QUỲNH LƯU – HOÀNG MAI NGHỆ AN 2016 - 2017] Cho hình chóp S.ABCD , đáy
ABCD là nửa lục giác đều với BC = 2a , AB = AD = DC = a (a > 0). Mặt bên SBC là tam giác đều. Gọi
O là giao điểm của AC và BD . Cho biết SD vuông góc với AC . a) Tính SD .
b) Mặt phẳng (a ) qua điểm M thuộc đoạn OB ( M không trùng với B ), song song với SD và
AC . Xác định thiết diện của hình chóp S.ABCD với mặt phẳng (a ). Tính diện tích thiết diện theo a và x
biết BM = x 3 . Tìm x để diện tích thiết diện đó lớn nhất. Hướng dẫn giải a) Tính SD
+) Dựng OI song song SD ( I thuộc cạnh SB ); AC = BD = a 3 OA AD 1 2 2a 3 Ta có: = = Þ OC = AC = OC BC 2 3 3 Trang 58 ì 1 2a SI = BS = OI BI BO 2 ïï +) Mặt khác: 3 3 = = = Þ í SD BS BD 3 3 ïSD = OI ïî 2 2 a
+) Áp dụng định lý cosin trong tam giác SIC , tính được 2 28 IC = 9
+) Do SD ^ AC và OI / /SD nên OI ^ AC . 4a
Trong tam giác vuông OIC , tính được OI = 3
Þ SD = OI = 2a. 3 2
b) Xác định thiết diện của hình chóp S.ABCD với mặt phẳng (a ).
+) Xác định được thiết diện là tam giác NPQ (với N, P, Q lần lượt nằm trên các cạnh BA, BC, BS)
ìMQ / /SD, NP / / AC +) Ta có: í Þ NP ^ MQ îSD ^ AC 1
ÞDiện tích thiết diện: S = N . P MQ NPQ 2
+) Trong tam giác SBD , tính được MQ = 2x 3
+) Trong tam giác BAC , tính được NP = x 3 2 2 3 3x
+) Diện tích thiết diện: S = NPQ 2 a a
+) Vì M thuộc đoạn BO ( M ¹ 2 3 2
B ) nên 0 < x 3 £ BO = Û 0 < x £ 3 3 2 2 3 3 æ 2a ö 2a 3 2 2a 3 Do đó, S £ . = . Vậy, min S = . NPQ ç ÷ 2 è 3 ø 3 NPQ 3 AB AC
Bài 99. Cho tứ diện SABC. Hai điểm I, J thứ tự chuyển động trên AB, AC sao cho + = 3. Chứng AI AJ
minh rằng mặt phẳng (SIJ) luôn đi qua một đường thẳng cố định. Hướng dẫn giải !!!" " !!!" " Đặt AB = ;
b AC = c. Gọi M là trung điểm BC, gọi G là trọng tâm tam giác ABC. Gỉa sử !!" " AB 1 AC 1 3k -1 !!!" k !!" !!!" !!" k " " " AI = kb Þ = Þ = 3 - = Þ AJ =
c Þ IJ = AJ - AI = c - kb AI k AJ k k 3k -1 3k -1 . Trang 59 r r uur uur uur uuur r 2 uuur r 2 b + c r 3k -1 r 1 r
Ta có: GI = GA + AI = -AG + kb = - AM + kb = - . + kb =
b - c. Ta thấy 3 3 2 3 3 !!" 3k -1 " 1 1- 3k é k " " " ù 1- 3k !!" GI = b - c = c - kb =
IJ. Vậy G, I, J thẳng hàng. Hay IJ luôn đi qua 3 3 3k êë3k 1 ú - û 3k
điểm G cố định, hay mặt phẳng (SIJ) luôn đi qua đường thẳng cố định SG. Bài 100.
Cho tứ diện OABC có OA, OB, OC vuông góc với nhau từng đôi một. Gọi A, B, C là ba góc
của tam giác ABC và a, b,g lần lượt là góc tạo bởi OA, OB, OC với mặt phẳng (ABC). Chứng minh rằng: 2 2 2 os c a os c b os c g = = .
sin 2A sin 2B sin 2C Hướng dẫn giải
Gọi H là hình chiếu vuông góc của O trên mặt phẳng (ABC)
Þ H là trực tâm của tam giác ABC. Þ ∑ ∑ ∑
OAH = a ;OBH = b; OCH = g 2 2 AH AH AH
Gọi AK là đường cao của tam giác ABC. Ta có: 2 os c a = = = 1 2 ( ) OA AH.AK AK 2 2 2 2
AB + AC - BC 2OA Mặt khác: cos A = = > 0 2 . AB AC 2 . AB AC Tương tự: cos ,
B cosC > 0 nên tam giác ABC nhọn.
- Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC, ta có: BC BC ∑
= 2R ; sin A = sin BHC Þ
= 2R Þ R cũng là bán kính đường tròn ngoại tiếp tam sin A ∑ sin BHC giác BHC. - Trong tam giác ABH: ∑ AH = 2 . R sin ABH = 2 . R cos A BC AH BC.AH Nên: sin 2A = 2sin . A cos A = 2 . = 2 2 ( ) 2R 2R R Trang 60 2 2 os c A R Từ (1) và (2) ta có: = sin 2A S ABC D 2 2 2 2 os c B R os c C R
Chứng minh tương tự ta cũng có: = ; = sin 2B S sin 2C S ABC D ABC D Vậy ta có ĐPCM.
Bài 101. Cho tam giác ABC vuông tại A có AB=c, AC=b.Gọi (P) là mặt phẳng qua BC và vuông
góc với mặt phẳng (ABC) ; S là một điểm di động trên (P) sao cho S.ABC là hình chóp có hai mặt bên SAB, p
SAC hợp với đáy ABC hai góc có số đo lần lượt là a và -a . Gọi H, I, J lần lượt là hình chiếu vuông góc 2 của S trên BC, AB, AC. a. Chứng minh rằng 2
SH = HI.HJ .
b. Tìm giá trị lớn nhất của SH và khi đó hãy tìm giá trị của a . Hướng dẫn giải
Bài 102. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tất cả các cạnh bên đều bằng a. Gọi
điểm M thuộc cạnh SD sao cho SD = 3SM, điểm G là trọng tâm tam giác BCD.
a) Chứng minh rằng MG song song với mp(SBC)
b) Gọi (a ) là mặt phẳng chứa MG và song với CD. Xác định và tính diện tích thiết diện của hình chóp với mp(a )
c) Xác định điểm P thuộc MA và điểm Q thuộc BD sao cho PQ song song với SC. Tính PQ theo a. Hướng dẫn giải S M H D C E G F I A B Trang 61
Gọi I là trung điểm của BC DG DM 2 Ta có = = Þ MG / /SI DI DS 3
Mà SI Ì (SBC) nên MG //(SBC)
Qua G kẻ đường thẳng song song với CD cắt AD và BC lần lượt tại E và F. Qua M kẻ đường thẳng song
song với CD cắt SC tại H
Thiết diện của hình chóp với mp(a ) là tứ giác EFHM
Ta có HM//EF vì cùng song song với CD 2a a 0 MD = HC = , DE = CF = , MD Ð E = H
Ð CF = 60 nên tam giác DME bằng tam giác CHF 3 3
suy ra ME = HF do đó EFHM là hình thang cân 2 2 2 4a a 2a a 1 a Ta có: 2 2 2 0
EM = DM + DE - 2DM.DE. os c 60 = + - 2 . . = 9 9 3 3 2 3 a MH = ,EF = a 3 2 2 2 æ EF - HM ö a a a 2
Gọi h là độ dài đường cao của hình thang ta có 2 h = EM - = - = ç ÷ è 2 ø 3 9 3 2 1 1 a 2 4a 2a 2
Diện tích thiết diện là S = . . h (EF + HM ) = . . = EFHM 2 2 3 3 9 Trang 62 S M P D C N Q A B
Qua M dựng đường thẳng song song với SC cắt CD tại N. Nối A với N cắt BD tại Q. Trong mp (AMN) từ Q
dựng đường thẳng song song với MN cắt AM tại P.
Ta có PQ//MN, MN//SC nên PQ//MN
Suy ra hai điểm P, Q thỏa mãn điều kiện bài toán. MN DM 2 AQ AB AQ Ta có = = 3 3 , = = Þ = SC DS 3 QN DN 2 AN 5 PQ AQ 3 PQ PQ MN 3 2 2 = = , = . = . = MN AN 5 SC MN SC 5 3 5 2a Suy ra PQ = . 5
Bài 103. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi M, N lần lượt là trung điểm của AB
và B’C’. Dựng và tính đoạn vuông góc chung của AN và DM. D’ C’ A’ B’ N
Gọi I là trung điểm của BC.
NI ^ mp(ABCD) Þ NI ^ DM (1đ) K D C
Chứng minh được: AI ^ DM H I A M B
Þ DM ^ mp(AIN) Trang 63
Gọi H là giao điểm của AI và DM, từ H hạ HK ^ AN ,HK là đoạn vuông góc chung của AN và DM, Tính được a AH = 5 a 5 AI = 2 3a AN = 2 êAKH đồng dạng êAIN KH AH = IN AN a a 2a KH = . = 5 3a 3 5 2 2a 5
Vậy khoảng cách AN và DM là: 15
Bài 104. Cho tứ diện ABCD, Chứng minh rằng 6 mặt phẳng ,mỗi mặt phẳng đi qua trung điểm một cạnh và
vuông góc với cạnh đối diện đồng quy tại một điểm. Bài 105.
Cho hình chóp SABC có SC ^ ( ABC) và tam giác ABC vuông tại B. Biết AB = a; AC = a 3
và góc giữa hai mặt phẳng (SAB), (SAC) bằng a 13 với sina =
. Tính độ dài SC theo a. 19 Hướng dẫn giải Xét hai trường hợp:
+) B và C không tù. Khi đó 2 2 1 cos CB Ð B ' = Þ sin C = ,cosC = 5 5 5 BB ' 5 BC = = cos CB Ð B ' 2 CC ' 4 3 Suy ra sin B = = ,cos B = BC 5 5 Trang 64 A B’ C’ H C B 2 BB ' 5 1 5
Þ sin A = sin BcosC + sinC cos B = Þ AB = = Þ S = A . B CC ' = . 5 sin A 2 2 2 +) B hoặc C tù.
Do BB ' > CC ' nên B < 2 1
C và C tù Þ sin C = ,cosC = - . 5 5 4 3
Còn sin B = ,cos B = 2 25
(giống trường hợp 1) Þ sin A = , AB = 25 Suy ra S = . 5 5 5 5 2 2 Bài 106.
Cho tứ diện ABCD , O là điểm bất kì nằm trong miền tam giác BCD . Từ O kẻ các đường
thẳng song song với AB, AC, AD cắt các mặt phẳng ( ACD), ( ABD), ( ABC) lần lượt tai M , N, P. OM ON OP Chứng minh rằng: + + không đổi. AB AC AD Bài 107. Cho hình hộp ABC . D ’ A ’ B C’ ’
D có tất cả các mặt đều là hình vuông cạnh a .
a) Chứng minh rằng AC’ vuông góc với mặt phẳng ( ’
A BD) và đường thẳng ’
A C đi qua trọng tâm tam giác ’ A BD .
b) Hãy xác định các điểm M , N lần lượt nằm trên các cạnh ’ A , D C ’
D sao cho MN vuông góc với mặt phẳng ( ’ CB ’
D ). Tính độ dài đoạn MN theo a. Bài 108.
Cho hình chóp S.ABCD . Tứ giác đáy có AB và CD cắt nhau tại E . AD và BC cắt nhau tại
F . AC và BD cắt nhau tại G . (P) là mặt phẳng cắt ,
SA SB, SC lần lượt tại ’, A ’, B C . ’ a) Tìm giao điểm ’
D của SD và (P).
b) Với điều kiện nào của (P) thì ’ A ’ B C’ ’
D là hình bình hành. Bài 109.
Cho tứ diện ABCD , mặt phẳng (a ) song song với hai đường thẳng AD và BC . Gọi M , N, ,
P Q tương ứng là giao điểm của (a ) với các đường thẳng AB, AC, C ,
D DB . Xác định tất cả các vị trí của (a ) để:
a) Tứ giác MNPQ là hình thoi.
b) Diện tích thiết diện giữa (a ) và tứ diện ABCD là lớn nhất. Bài 110.
Cho tam giác ABC vuông tại A có AB = c, AC = b .Gọi (P) là mặt phẳng qua BC và
vuông góc với mặt phẳng ( ABC); S là một điểm di động trên (P)sao cho S.ABC là hình chóp có hai mặt Trang 65 p
bên SAB , SAC hợp với đáy ABC hai góc có số đo lần lượt là a và
-a . Gọi H, I, J lần lượt là hình 2
chiếu vuông góc của S trên BC, AB, AC. a) Chứng minh rằng 2
SH = HI.HJ .
b) Tìm giá trị lớn nhất của SH và khi đó hãy tìm giá trị của a . Bài 111.
Cho hình lăng trụ tứ giác ABC . D ’ A ’ B C’ ’
D . Một mặt phẳng (P) thay đổi song song với hai đáy
của lăng trụ, cắt các đoạn thẳng AB’, BC’, CD’, DA’ tương ứng lần lượt tại các điểm M, N, P, Q. Hãy xác
định vị trí của mặt phẳng (P) sao cho tứ giác MNPQ có diện tích lớn nhất. Bài 112.
Cho hình chóp S.ABCD, ABCD là hình vuông và SAB là tam giác đều, mặt phẳng đi qua ba
điểm A, B, C vuông góc với mặt phẳng chứa tam giác SAB. Gọi M là một điểm di động trên đoạn AB và P là
hình chiếu vuông góc của S lên CM.
a) Tìm quỹ tích của điểm P khi M di động.
b) Xác định vị trí của điểm M để độ dài đoạn thẳng nối M với trung điểm của đoạn SC đạt giá trị lớn nhất. Bài 113.
Gọi O là một điểm trên cạnh AB của tứ diện ABCD (O không trùng với A và B). Mặt cầu
ngoại tiếp tứ diện AOCD cắt các cạnh BC và BD của tứ diện ABCD lần lượt tại M và N (M ¹ C, N ¹ D). Mặt
cầu ngọai tiếp tứ diện BOCD cắt các cạnh AC và AD của tứ diện ABCD lần lượt tại P và Q (P ¹ C, Q ¹ D).
Chứng minh rằng tam giác OMN đồng dạng với tam giác OQP. Bài 114.
Cho P là một điểm cố định nằm bên trong một hình cầu cho trước. Ba đoạn thẳng PA, PB, PC
đôi một vuông góc với nhau, có ba đầu mút A, B, C nằm trên mặt cầu. Gọi G là trọng tâm tam giác ABC.
a) Tính PG theo PA, PB, PC.
b) Tìm quỹ tích điểm G khi A, B, C thay đổi. Bài 115.
Cho hình chóp tứ giác đều S.ABCD đỉnh S, cạnh đáy của hình chóp có độ dài bằng 2, chiều
cao bằng h. Gọi C ( ;
O r) là hình cầu tâm O bán kính r nội tiếp hình chóp; gọi C (K;R) là hình cầu tâm K bán 1 2
kính R tiếp xúc với 8 cạnh của hình chóp. Biết rằng khoảng cách từ O đến mặt phẳng (ABCD) bằng khoảng
cách từ K đến mặt phẳng (ABCD). 2 1+ h -1
a) Chứng minh rằng: r = . h
b) Tính giá trị của h, từ đó suy ra thể tích hình chóp. Bài 116.
Cho hình lăng trụ đứng ABC.A’B’C’, có các cạnh bằng a. Xét các đoạn thẳng MN có hai đầu
mút M, N lần lượt nằm trên các đoạn thẳng BC’, CA’ và song song với mặt phẳng(ABB’A’). Tìm theo a độ
dài của đoạn thẳng ngắn nhất trong các đoạn thẳng ấy. Khi MN ngắn nhất hỏi MN có vuông góc với BC’ và
CA’ hay không? Chứng minh. Bài 117.
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Gọi H là chân
được vuông góc hạ từ O đến (ABC).
a) Chứng minh rằng H là trực tâm tam giác ABC. abc 3 b) Chứng minh rằng . a S + . b S + . c S £ . HBC HAC HAB 2 Bài 118.
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB=2CD=2AD, SA
vuông góc với đáy tại A. Gọi M là trung điểm của SC, K là điểm di động trên AB. Tìm tập hợp hình chiếu của H của M lên CK. Bài 119.
Cho tứ diện ABCD có trọng tâm G . Tìm điểm M sao cho tổng: MA MB MC MD + + +
đạt giá trị bé nhất. . GB GC.GD . GAGC.GD . GA . GB GD . GA . GB GC Trang 66




