











































































































































Preview text:
Chương 1
ỨNG DỤNG CỦA ĐẠO HÀM ĐỂ KHẢO SÁT
VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Bài 1: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
1.1 TÓM TẮT LÝ THUYẾT 1. Định nghĩa :
Giả sử là một khoảng , một đoạn hoặc một nửa khoảng . Hàm số xác định
trên được gọi là
• Đồng biến trên nếu với mọi ∈ < ⇒ < ; ( ) ( )
• Nghịch biến trên nếu với mọi ∈
< ⇒ > . ( ) ( )
2. Điều kiện cần để hàm số đơn điệu : Giả sử hàm số
có đạo hàm trên khoảng
• Nếu hàm số đồng biến trên khoảng thì ( ) ≥ với mọi ∈ ;
• Nếu hàm số nghịch biến trên khoảng thì ( ) ≤ với mọi ∈ .
3. Điều kiện đủ để hàm số đơn điệu :
Giả sử là một khoảng hoặc nửa khoảng hoặc một đoạn , là hàm số liên tục
trên và có đạo hàm tại mọi điểm trong của ( tức là điểm thuộc nhưng
không phải đầu mút của ) .Khi đó :
• Nếu ( ) > với mọi ∈ thì hàm số đồng biến trên khoảng ;
• Nếu ( ) < với mọi ∈ thì hàm số nghịch biến trên khoảng ;
• Nếu ( ) = với mọi ∈ thì hàm số không đổi trên khoảng . Chú ý :
• Nếu hàm số liên tục trên
và có đạo hàm ( ) > trên khoảng
( )thì hàm số đồng biến trên .
• Nếu hàm số liên tục trên
và có đạo hàm ( ) < trên khoảng
( )thì hàm số nghịch biến trên .
• Giả sử hàm số liên tục trên đoạn .
Nếu hàm số đồng biến trên khoảng (
) thì nó đồng biến trên đoạn . 5
Nếu hàm số nghịch biến trên khoảng ( ) thì nó nghịch biến trên đoạn .
Nếu hàm số không đổi trên khoảng ( ) thì không đổi trên đoạn .
4. Định lý mở rộng
Giả sử hàm số có đạo hàm trên khoảng .
• Nếu ≥ với ∀ ∈ và = chỉ tại một số hữu hạn điểm thuộc
thì hàm số đồng biến trên khoảng ;
• Nếu ≤ với ∀ ∈ và = chỉ tại một số hữu hạn điểm thuộc
thì hàm số nghịch biến trên khoảng .
1.2 DẠNG TOÁN THƯỜNG GẶP
Dạng 1 : Xét chiều biến thiên của hàm số .
Xét chiều biến thiên của hàm số =
( ) ta thực hiện các bước sau:
• Tìm tập xác định của hàm số .
• Tính đạo hàm = ( ) .
• Tìm các giá trị của thuộc để ( ) = hoặc () không xác định
( ta gọi đó là điểm tới hạn hàm số ).
• Xét dấu = ( ) trên từng khoảng thuộc .
• Dựa vào bảng xét dấu và điều kiện đủ suy ra khoảng đơn điệu của hàm số.
Ví dụ 1: Xét chiều biến thiên của các hàm số sau: +
− + − = = − + Giải: + = −
Hàm số đã cho xác định trên khoảng ( − ∞ ) ∪( +∞). Ta có: =
< ∀ ≠ ( − ) Bảng biến thiên:
−∞ +∞ − − +∞ −∞ 6
Vậy hàm số đồng biến trên mỗi khoảng (− ∞ )và (+∞) .
− + − = +
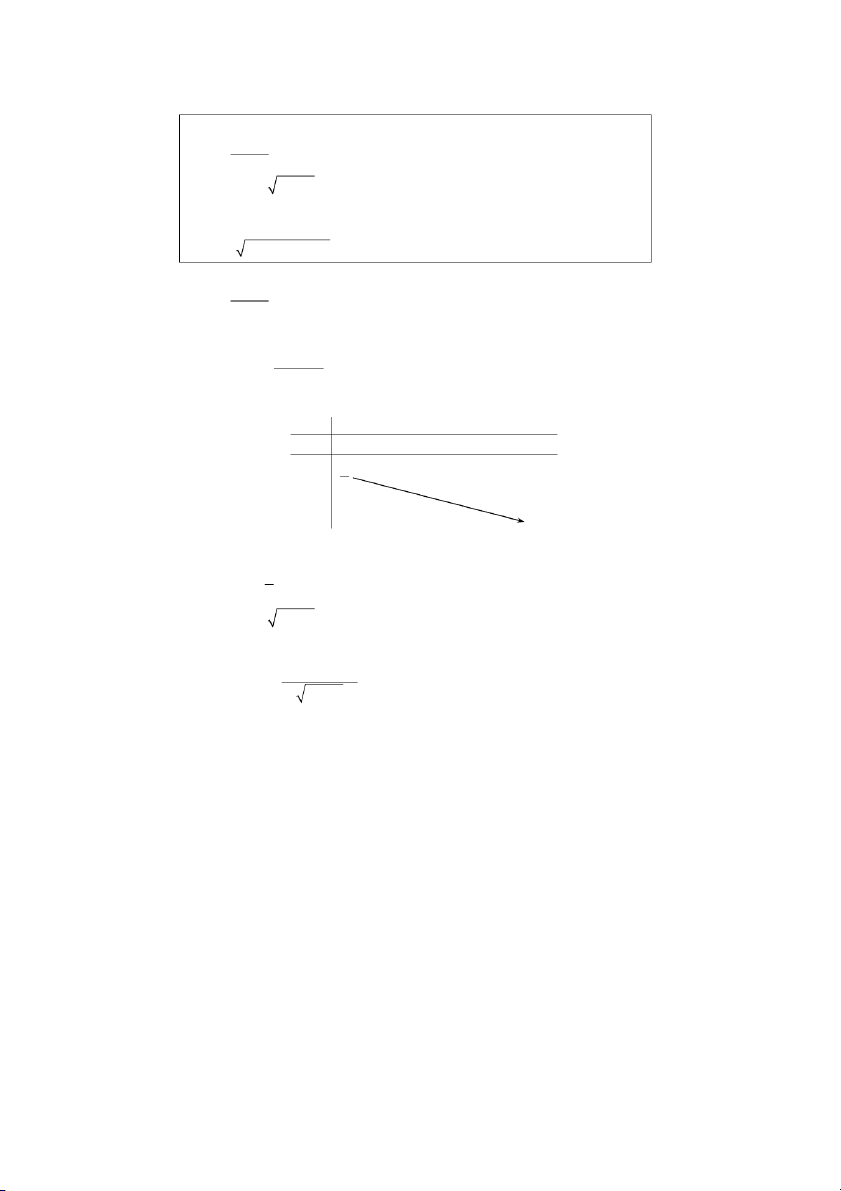
Hàm số đã cho xác định trên khoảng ( − ∞ − ) ∪( − +∞). − − + Ta có: = ∀ ≠ − ( + ) = − = ⇔ = Bảng biến thiên : −∞ −
− +∞
− + + − +∞ +∞ −∞ −∞
Vậy, hàm số đồng biến trên các khoảng ( − − ) và (− )
, nghịch biến trên các khoảng (− ∞ − ) và ( + ) ∞ . Nhận xét: + * Đối với hàm số =
≠ luôn đồng biến hoặc luôn nghịch +
biến trên từng khoảng xác định của nó. + + * Đối với hàm số =
luôn có ít nhất hai khoảng đơn điệu.
+
* Cả hai dạng hàm số trên không thể luôn đơn điệu trên ℝ . Bài tập tương tự :
Xét chiều biến thiên của các hàm số sau: − = = + +
+ + − + = = +
− − + + + = =
+ +
Ví dụ 2: Xét chiều biến thiên của các hàm số sau:
= − − + +
= − + + 7 Giải: = −
− + +
Hàm số đã cho xác định trên ℝ . Ta có : =
− − + = −
= ⇔ − − + = ⇔ =
Bảng xét dấu của : −∞ − +∞ − + − + Trên khoảng(
− ) : > ⇒ đồng biến trên khoảng ( − ) ,
+ Trên mỗi khoảng (−
∞ −) (+∞) : < ⇒ nghịch biến trên các khoảng(−
∞ −) ( +∞ ) .
Hoặc ta có thể trình bày :
Hàm số đã cho xác định trên ℝ . Ta có : =
− − + = −
= ⇔ − − + = ⇔ = Bảng biến thiên : −∞ − +∞ − + − +∞ −∞
Vậy, hàm số đồng biến trên khoảng (−) , nghịch biến trên các khoảng (− ∞ − ) và ( +∞) .
= − + +
Hàm số đã cho xác định trên ℝ . Ta có:
= − + = − + = −
= ⇔ − + = ⇔ = Bảng xét dấu: −∞ − +∞ − + + 8
Vậy,hàm số đồng biến trên khoảng − +
∞ và nghịch biến trên khoảng − ∞ − . Nhận xét:
Ta thấy tại = thì = , nhưng qua đó không đổi dấu.
Đối với hàm bậc bốn
= + + + + luôn có ít nhất một
khoảng đồng biến và một khoảng nghịch biến. Do vậy với hàm bậc bốn
không thể đơn điệu trên ℝ .
Bài tập tương tự :
Xét chiều biến thiên của các hàm số sau:
= − +
= − + +
= + + + = − + − = −
+ −
= + −
= − + +
Ví dụ 3 : Xét chiều biến thiên của các hàm số sau:
= −
= −
= −
= + − + + Giải:
= − .
Hàm số đã cho xác định trên mỗi nửa khoảng (− ∞ ∪ +∞ ). − Ta có: = ∀ ∈ (− ∞ ) ∪ ( +∞) . −
Hàm số không có đạo hàm tại các điểm = = . Cách 1 : + Trên khoảng (−
∞ ) : < ⇒ hàm số nghịch biến trên khoảng (− ∞ ) ,
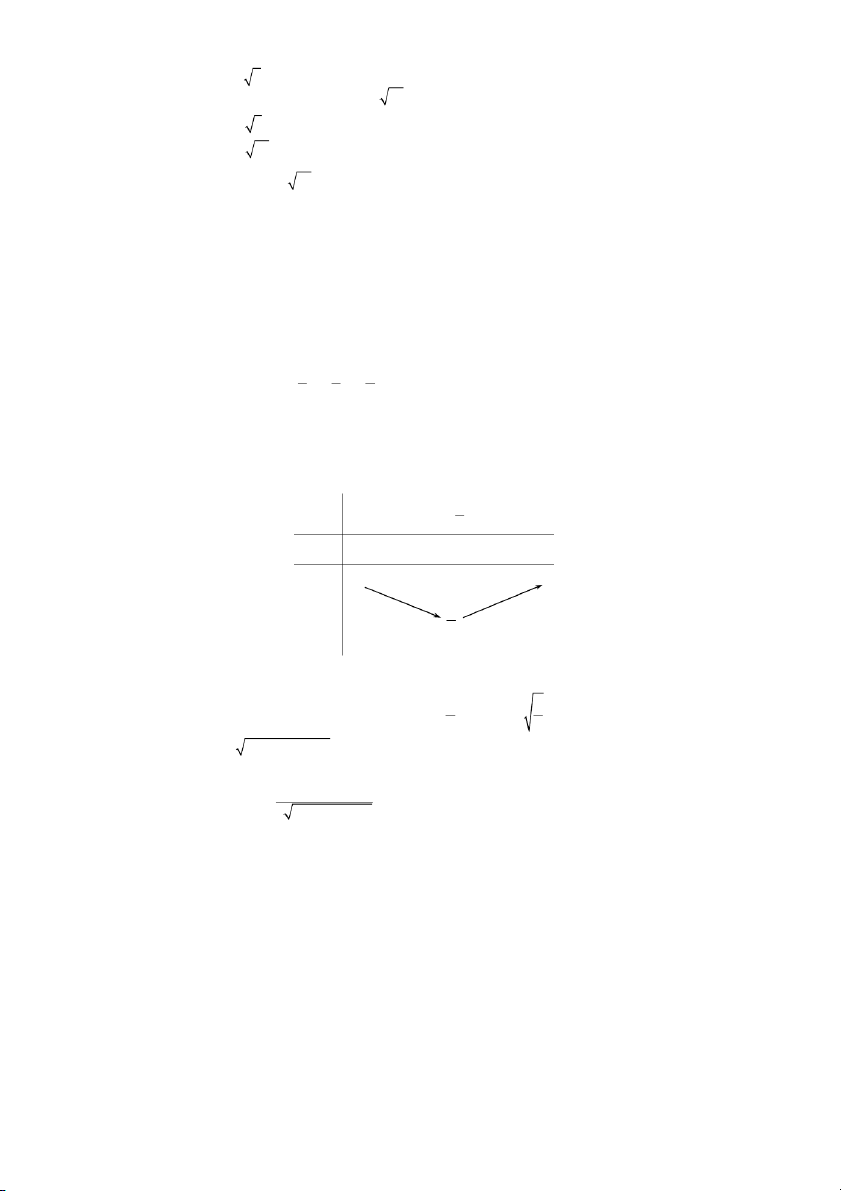
+ Trên khoảng ( +∞) : > ⇒ hàm số đồng biến trên khoảng ( +∞) . Cách 2 : Bảng biến thiên : −∞ +∞ − + 9
Vậy , hàm số nghịch biến trên khoảng (−∞)và đồng biến trên khoảng (+∞) = −
Hàm số đã cho xác định trên nửa khoảng −∞ .
− Ta có: = ∀ ∈ (− ∞ ) ∪ () .
−
Hàm số không có đạo hàm tại các điểm = = .
Suy ra, trên mỗi khoảng (−
∞ ) và () : = ⇔ = Bảng biến thiên: −∞ +∞ − || + − ||
Hàm số đồng biến trên khoảng , nghịch biến trên các khoảng −∞ và .
= −
Hàm số đã cho xác định trên đoạn − . − Ta có: = ∀ ∈ ( − ) −
Hàm số không có đạo hàm tại các điểm =− = .
Trên khoảng (−):
= ⇔ = ± Bảng biến thiên: −∞ − − +∞ || − + − ||
Hàm số đồng biến trên khoảng −
, nghịch biến trên mỗi khoảng −− và . 10
= + − + +
Hàm số đã cho xác định trên ℝ . +
Ta có: = −
+ + ≥ − = ⇔
+ + = + ⇔ ⇔ = −
+ + = ( + ) Bảng biến thiên : −∞ − +∞ + −
Hàm số đồng biến trên khoảng −∞− , nghịch biến trên khoảng −+∞. Bài tập tương tự :
Xét chiều biến thiên của các hàm số sau:
= − = ( − ) +
= + − − +
− + = = − + +
= − =
− +
Ví dụ 4 :Xét chiều biến thiên của các hàm số sau:
= − − Giải:
− − ≤ − ∨ ≥
= − − =
− + + − < <
Hàm số đã cho xác định trên ℝ .
− <
− ∨ > Ta có: =
− + − < <
Hàm số không có đạo hàm tại =− và = . + Trên khoảng (
− ) : = ⇔ = ; + Trên khoảng (− ∞ − ) : < ;
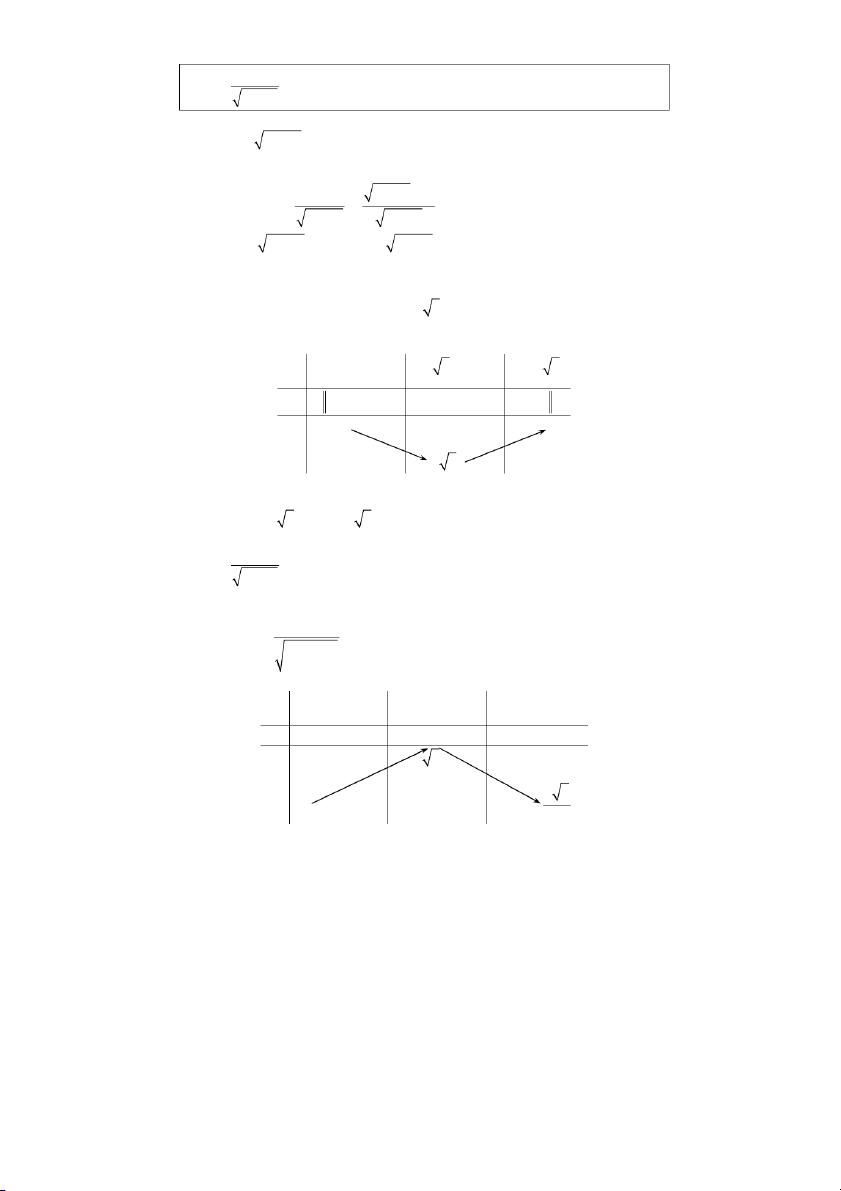
+ Trên khoảng (+∞) : > . 11 Bảng biến thiên: −∞ − +∞
− + − +
Hàm số đồng biến trên mỗi khoảng
− và +∞, nghịch biến trên mỗi khoảng − ∞ − và .
Bài tập tương tự :
Xét chiều biến thiên của các hàm số sau:
= − + =
− + − + −
= − + + − +
= + − + Ví dụ 5 :
Xét chiều biến thiên của hàm số sau: = + trên đoạn π . Giải :
Hàm số đã cho xác định trên đoạn π
Ta có: = ( − ) ∈ π . ∈ π = π π π Trên đoạn π
: = ⇔ ⇔ = ∨ = ∨ = . = Bảng biến thiên: π π π π + − + − π
Dựa vào bảng biến thiên suy ra : hàm số đồng biến trên các khoảng và π π π π π
, nghịch biến trên các khoảng và π . Bài tập tương tự :
Xét chiều biến thiên của các hàm số sau: 12 π
1. = trên khoảng . 2. =
trên khoảng ( π ) . π 3. = −
( − ) trên khoảng . π π
4. = − + + trên đoạn π .
Ví dụ 6: Chứng minh rằng hàm số =
+ đồng biến trên đoạn π π
và nghịch biến trên đoạn π . Giải :
Hàm số đã cho xác định trên đoạn π
Ta có: = ( − )
∈ ( π) π
Vì ∈ (π ) ⇒ > nên trên ( π )
= ⇔ = ⇔ = . π π
+ Trên khoảng : > nên hàm số đồng biến trên đoạn ; π π
+ Trên khoảng π : < nên hàm số nghịch biến trên đoạn π . Bài tập tương tự :
1. Chứng minh rằng hàm số () = ( − ) (π − − ) đồng biến trên π đoạn .
2. Chứng minh rằng hàm số = − + nghịch biến trên ℝ.
3. Chứng minh rằng hàm số =
đồng biến trên các khoảng (π ) và (ππ) π
4. Chứng minh rằng hàm số
= +
đồng biến trên khoảng và π π
nghịch biến trên khoảng 13
Dạng 2 : Tùy theo tham số khảo sát tính đơn điệu của hàm số .
Ví dụ : Tùy theo khảo sát tính đơn điệu của hàm số: = −
( + )
+ + + Giải:
Hàm số đã cho xác định trên ℝ . Ta có
= − ( + )
+ và % = ( − )
+ = thì
= ≥ ∀ ∈ ℝ và = chỉ tại điểm = . Hàm số đồng
biến trên mỗi nửa khoảng ( − ∞ và + ) ∞
. Do đó hàm số đồng biến trên ℝ .
+ = thì = ( − ) ≥
∀ ∈ ℝ và = chỉ tại điểm = . Hàm số
đồng biến trên mỗi nửa khoảng (−∞ và +∞
). Do đó hàm số đồng biến trên ℝ . =
+ ≠ ≠ khi đó = ⇔ . =
⋅ Nếu <
hoặc > thì <
Bảng xét dấu : −∞ +∞
+ − +
Dựa vào bảng xét dấu, suy ra hàm số đồng biến trên các khoảng (− ∞ ) và (
+∞) , giảm trên khoảng (
) .
⋅ Nếu < < thì >
Bảng xét dấu : −∞ +∞
+ − +
Dựa vào bảng xét dấu, suy ra hàm số đồng biến trên các khoảng ( − ∞ ) và (+ )
∞ , giảm trên khoảng (
) .
Bài tập tự luyện:
Tùy theo khảo sát tính đơn điệu của hàm số: = −
+ + − =
( − ) − ( − ) + + + 14
Dạng 3 : Hàm số đơn điệu trên ℝ .
Sử dụng định lý về điều kiện cần
• Nếu hàm số () đơn điệu tăng trên ℝ thì ( ) ≥ ∀ ∈ ℝ .
• Nếu hàm số () đơn điệu giảm trên ℝ thì ( ) ≤ ∀ ∈ ℝ .
Ví dụ 1 : Tìm để các hàm số sau luôn nghịch biến trên mỗi khoảng xác định .
+ −
− + ( + ) − + = = + − Giải :
+ − = +
Hàm số đã cho xác định trên khoảng ( − ∞ − ) ∪ ( − +∞)
+ − Ta có : = ≠ − . ( +) Cách 1 :
Bảng xét dấu −∞ − +∞ + − +
Dựa vào bảng xét dấu ta thấy
Nếu − < < thì < ⇒ hàm số nghịch biến trên mỗi khoảng (− ∞ −) , ( − + ) ∞ . Cách 2 :
Hàm số nghịch biến trên tập xác định khi : <
∀ ∈ (−∞ − )
∪ (− +∞ )
⇔ + − < ⇔ − < <
− + ( + ) − + − =
= − + + − −
Hàm số đã cho xác định trên khoảng ( − ∞ ) ∪( +∞). −
Ta có : = − + ≠ ( −) + ≤
⇒ < ≠ , do đó hàm số nghịch biến trên mỗi khoảng (− ∞ ), (+ ) ∞ . 15 + >
khi đó phương trình = có hai nghiệm < < ⇒ hàm số đồng
biến trên mỗi khoảng ( và ( , trường hợp này không thỏa . ) ) Vậy ≤
thỏa mãn yêu cầu của bài toán.
Bài tập tương tự :
Tìm để các hàm số sau luôn nghịch biến trên . mỗi khoảng xác định
− + − ( − )
+ + = = − + ( − )
+ + −
− ( + ) + − = = + −
Ví dụ 2 : Tìm để các hàm số sau luôn nghịch biến trên ℝ.
= − + + ( + ) − + = +
− + + ( − )
+ − Giải:
= − + + ( + ) − +
Hàm số đã cho xác định trên ℝ . Ta có : = −
+ + + và có % = + Bảng xét dấu % −∞ +∞ − % − + +
= − thì = − ( − ) ≤ với mọi ∈ ℝ và = chỉ tại điểm =
Do đó hàm số nghịch biến trên ℝ . +
< − thì < ∀ ∈ ℝ . Do đó hàm số nghịch biến trên ℝ . +
> − thì = có hai nghiệm
. Hàm số đồng biến trên ( < ) khoảng (
. Trường hợp này không thỏa mãn . ) = +
− + + ( − )
+ −
Hàm số đã cho xác định trên ℝ . 16 Ta có
= + − + + − . + =
− , khi đó =
− ≤ ∀ ∈ ℝ ⇒ hàm số luôn nghịch biến trên ℝ .
+ ≠ − tam thức
= + − + + − có % = + Bảng xét dấu % −∞ − +∞ % − + +
< − thì < với mọi ∈ ℝ . Do đó hàm số nghịch biến trên ℝ . + >
− thì = có hai nghiệm
. Hàm số đồng biến trên ( < ) khoảng (
. Trường hợp này không thỏa mãn . ) Vậy ≤
− là những giá trị cần tìm.
Bài tập tương tự :
Tìm để các hàm số sau luôn nghịch biến trên . mỗi khoảng xác định = + + =
− + − + = ( − ) − − =
− + − +
Ví dụ 3 : Tìm để các hàm số sau luôn đồng biến trên ℝ . =
+ + + = ( − )
+ ( + )
+ + ɩ Giải : =
+ + +
Hàm số đã cho xác định trên ℝ . Ta có
= + + và có % = − Bảng xét dấu % −∞ − +∞ % + − +
+ Nếu − < <thì > với mọi ∈ ℝ . Hàm số đồng biến trênℝ .
+ Nếu = thì = ( + )
, ta có : = ⇔ = − > ≠ − . Hàm
số đồng biến trên mỗi nửa khoảng ( − ∞
− và −+∞
)nên hàm số đồng biến trên ℝ .
+ Tương tự nếu =
− . Hàm số đồng biến trên ℝ . 17 + Nếu <
− hoặc > thì = có hai nghiệm phân biệt . Giả sử
< . Khi đó hàm số nghịch biến trên khoảng ( ,đồng biến trên mỗi ) khoảng (−
∞ và ( +∞ . Do đó <
− hoặc > không thoả mãn yêu ) ) cầu bài toán .
Vậy hàm số đồng biến trên ℝ khi và chỉ khi − ≤ ≤ . = ( − )
+ ( + )
+ +
Hàm số đã cho xác định trên ℝ .
Ta có : = ( − )
+ ( + )
+ và có % = ( − + + )
Hàm số đồng biến trênℝ khi và chỉ khi ⇔ ≥ ∀ ∈ ℝ ( ) + Xét
− = ⇔ = ± i
= ⇒ = + ⇒
≥ ⇔ ≥ −
⇒ = không thoả yêu cầu bài toán. i
= − ⇒ = > ∀ ∈ℝ ⇒
= − thoả mãn yêu cầu bài toán. + Xét
− ≠ ⇔ ≠ ± Bảng xét dấu % −∞ − +∞ % − + − + Nếu <
− ∨ > thì > với mọi ∈ ℝ. Hàm số đồng biến trên ℝ .
+ Nếu = thì = ( + )
, ta có : = ⇔ =
− > ≠ − . Hàm
số đồng biến trên mỗi nửa khoảng ( − ∞ − − + ) ∞ nên hàm số đồng biến trên ℝ . + Nếu
− < < ≠ thì = có hai nghiệm phân biệt . Giả sử
< . Khi đó hàm số nghịch biến trên khoảng ( ,đồng biến trên mỗi ) khoảng (−
∞ và ( +∞ . Do đó
− < < ≠ không thoả mãn yêu cầu ) ) bài toán .
Do đó hàm số đồng biến trên ℝ khi và chỉ khi < − ∨ ≥ .
Vậy với ≤ ≤ thì hàm số đồng biến trên ℝ .
Bài tập tương tự : Tìm
để các hàm số sau luôn đồng biến trên mỗi khoảng xác định . = − + (
− ) − =
− + ( + ) + 18 = ( + ) − ( − )
+ − = ( − ) − ( − )
+ ( − ) + Chú ý : Phương pháp:
* Hàm số = tăng trên ℝ ⇔ ≥ ∀ ∈ ℝ
⇔ ≥ . ∈ℝ
* Hàm số = giảm trên ℝ ⇔ ≤ ∀ ∈ℝ
⇔ ≤ . ∈ ℝ Chú ý: 1) Nếu
= + + thì = = ≥ *
≥ ∀ ∈ℝ ⇔ > % ≤ = = ≤ *
≤ ∀ ∈ ℝ ⇔ < % ≤
2) Hàm đồng biến trên ℝ thì nó phải xác định trên ℝ .
Dạng 4 : Hàm số đơn điệu trên tập con của ℝ . Phương pháp:
* Hàm số = tăng
∀ ∈ ⇔ ≥ ∀ ∈ ⇔ ≥ . ∈ * Hàm số = giảm
∀ ∈ ⇔ ≤
∀ ∈ ⇔ !" ≤ . ∈
Ví dụ 1 : Tìm để các hàm số sau + =
luôn nghịch biến khoảng (−∞ ) . +
= + + ( + )
+ nghịch biến trên khoảng ( − ) . Giải : + 1. =
luôn nghịch biến khoảng ( −∞ ). +
Hàm số đã cho xác định trên khoảng ( −∞ ) . 19 − Ta có = ≠ − ( + ) < ∀ ∈ (− ∞ )
Hàm số nghịch biến trên khoảng (
−∞ ) khi và chỉ khi − ∉ (−∞ ) − < − < < − < < ⇔ ⇔ ⇔ ⇔ − < ≤ − − ∉ ( − ∞ ) − ≥ ≤ − Vậy : với − < ≤
− thì thoả yêu cầu bài toán . 2.
= + + ( + ) + nghịch biến trên khoảng ( − ) .
Hàm số đã cho xác định trên khoảng ( − ) . Ta có :
= + + + Cách 1 :
Hàm số đã cho nghịch biến trên khoảng (−) khi và chỉ khi
≤ ∀ ∈ (− ) hay.
Xét hàm số () = −(
+ + ) ∀ ∈( − )
⇒ ( ) =
− − < ∀ ∈(
− ) ⇒ ( ) nghịch biến trên khoảng (− )
và # ( ) =
− # ( = − + − ) →− → Bảng biến thiên. − () − − ( ) − Vậy ≤ −
thoả yêu cầu bài toán . Cách 2 :
( ) = +
Nghiệm của phương trình ( ) = là =
− < . Do đó, hàm số đã
cho nghịch biến trên khoảng (
− ) khi và chỉ khi ≤ # ( = − . − ) → Vậy ≤ −
thoả yêu cầu bài toán . 20 Bài tập tự luyện:
Tìm để các hàm số sau: − 1. =
luôn nghịch biến khoảng (+∞ ) . − − 2. = (
luôn nghịch biến khoảng ().
+ ) − − 3. =
luôn nghịch biến khoảng (− ∞ ) . − ( − ) + 4. =
luôn nghịch biến khoảng () . +
Ví dụ 2 : Tìm để các hàm số sau
= − + − đồng biến trên khoảng (+∞ ) .
= − + + − đồng biến trên khoảng (−). =
+ ( − )
+ ( − ) + đồng biến trên khoảng ( +∞). Giải :
= − + − đồng biến trên khoảng (+∞ ) .
Hàm số đã cho xác định trên khoảng ( +∞ ) . Ta có :
= − +
Hàm số đã cho đồng biến trên khoảng (+∞ ) khi và chỉ khi
≥ ∀ ∈ (+∞ ) ⇔ ( )
= − ≥ − >
Xét hàm số ()
= − liên tục trên khoảng (+∞ ) , ta có
() = − >
∀ > ⇔ () đồng biến trên khoảng ( +∞)
và # ( ) = # (
− ) = # ( = +∞ + + ) →+∞ → → Bảng biến thiên. − +∞ () + +∞ () −
Dựa vào bảng biến thiên suy ra ≥ − ⇔ ≥ − 21
= − + + − đồng biến trên khoảng (−).
Hàm số đã cho xác định trên khoảng ( − ) . Ta có :
= − +
Hàm số đã cho đồng biến trên khoảng (− )
khi và chỉ khi ≥ ∀ ∈ ( − ) . − Hay − + ≥ ∀ ∈ (− ) ⇔ ≥ ∀ ∈ − ( ) −
Xét hàm số ( ) =
liên tục trên khoảng (− ) , ta có ( − + ) = < ∀ ∈
− ⇒ nghịch biến trên khoảng(−) ( ) ( ) và ( ) # = −
# ( = −∞ + − ) →− → Bảng biến thiên. − () − − ( ) −∞
Dựa vào bảng biến thiên suy ra ≥ − =
+ ( − )
+ ( − ) + đồng biến trên khoảng ( +∞).
Hàm số đã cho xác định trên khoảng (+∞ ) . Ta có :
= + ( − ) + −
Hàm số đồng biến trên khoảng ( ) +∞ khi và chỉ khi ≥ ∀ ∈ ( +∞) ⇔ + (
− ) + − ≥ ∀ ∈ (+∞ ) ⇔ ( +
+ + ) ≥ + ∀ ∈ ( +∞) ⇔ ≥
∀ ∈ +∞ ( )
+ + +
Xét hàm số ( ) =
∈ +∞ ( )
+ + 22 − + ⇒ ( ) ( ) = <
∀ ∈ +∞ ⇒ nghịch biến trên khoảng ( ) ( )
( + +) (
+∞) và # ( ) =
# ( = + ) →+∞ → Bảng biến thiên. +∞ () − () Vậy ≥
thoả yêu cầu bài toán .
Bài tập tự luyện:
Tìm để các hàm số sau:
+ ( + ) − 1. =
đồng biến trên khoảng ( + ) ∞ . − 2.
= − − (
− + ) + ( − ) ( − ) đồng biến trên khoảng (+∞) . 3. =
− − + − + đồng biến trên khoảng ( +∞) .
Ví dụ 3 : Tìm để các hàm số sau :
+ − =
nghịch biến trên nửa khoảng +∞ ) . +
= − + − − + + − đồng biến trên nửa khoảng +∞ ) . Giải :
+ − =
nghịch biến trên nửa khoảng +∞ ) + .
Hàm số đã cho xác định trên nửa khoảng +∞)
+ + Ta có = + 23
Hàm nghịch biến trên nửa khoảng $ + ∞
⇔ = + + ≤ , ∀ ∈ +∞ ) ( ).
Cách 1: Dùng tam thức bậc hai
• Nếu = khi đó () không thỏa mãn.
• Nếu ≠ . Khi đó có
% = − Bảng xét dấu % −∞ +∞ % + − +
• Nếu < < thì >
∀ ∈ ℝ , nếu có hai nghiệm thì
≤ ⇔ ∈ nên () không thỏa mãn.
• Nếu < hoặc > . Khi đó = có hai nghiệm
− + −
− − − = ≤
Vì < hoặc >
⇒ < ⇒ ≤ ⇔ ≥
Do đó ≤ ∀ ∈ +∞ ) ⇔ ≤ ⇔
− ≥ − < ⇔ ⇔ ≤ − .
+ ≥ −
Cách 2: ⇔ ≤ =
∀ ∈ +∞
) ⇔ ≤ + ≥ Ta có = = − ⇒ ≤ − . ≥
= − + − − + + − đồng biến trên nửa khoảng +∞ ) .
Hàm số đã cho xác định trên nửa khoảng +∞ ) Ta có
= − + − − +
Hàm đồng biến trên nửa khoảng + ) ∞
. ⇔ ≥ ∀ ∈ + ) ∞ 24
⇔ = − + − − + ≥ ∀ ∈ +∞ )
Vì tam thức có
% = − + >
∀ ∈ℝ nên có hai nghiệm + − % + + % = = . ≤
Vì < nên
⇔ . ≥
Do đó ≥ ∀ ∈ +∞
) ⇔ ≤ ⇔ % ≤ − ≤ ≤ ⇔ ⇔ ⇔ − ≤ ≤
% ≤ −
+ − ≤ Bài tập tự luyện :
Tìm để các hàm số sau :
+ ( − ) − 1. =
đồng biến trên nửa khoảng (− ∞ + . 2. =
+ ( − )
− ( − ) + nghịch biến trên nửa khoảng ( − ∞ − . 3. =
− ( − )
+ ( − ) + đồng biến trên nửa khoảng +∞ ).
+ − + + 4. =
đồng biến trên nửa khoảng +∞ ) . −
Ví dụ 4 : Tìm tất cả các tham số để hàm số
= + + + nghịch
biến trên đoạn có độ dài bằng ?. Giải :
Hàm số đã cho xác định trên ℝ . Ta có :
= + + có % = −
i Nếu ≥ thì ≥ ∀ ∈ ℝ , khi đó hàm số luôn đồng biến trên ℝ , do đó
≥ không thoả yêu cầu bài toán .
i Nếu < , khi đó = có hai nghiệm phân biệt < và hàm số ( )
nghịch biến trong đoạn
= − với độ dài Theo Vidét, ta có :
+ = − = 25
Hàm số nghịch biến trên đoạn có độ dài bằng ⇔ =
⇔ ( − ) = ⇔ ( + )
− = ⇔ − = ⇔ = . Bài tập tương tự :
1. Tìm tất cả các tham số để hàm số
= − + + − nghịch
biến trên đoạn có độ dài bằng ?.
2. Tìm tất cả các tham số để hàm số = −
+ + + + đồng
biến trên đoạn có độ dài bằng ?.
Ví dụ 5: Tìm để hàm số = + đồng biến trên ℝ . Giải:
Hàm số đã cho xác định trên ℝ .
Ta có = − .
Cách 1: Hàm đồng biến trên ℝ
⇔ ≥ ∀ ∈ ℝ ⇔ − ≥
∀ ∈ ℝ ⇔ ≤ ∀ ∈ℝ
* = thì luôn đúng * > thì
⇔ ≤
∀ ∈ ℝ ⇔ ≤
⇔ < ≤ . * < thì
⇔ ≥
∀ ∈ ⇔ − ≥
⇔ − ≤ < .
Vậy − ≤ ≤ là những giá trị cần tìm.
Cách 2: Hàm đồng biến trên ℝ ⇔ ≥ ∀ ∈ ℝ − ≥
⇔ = % − + & ≥ ⇔ ⇔ − ≤ ≤ . + ≥
Bài tập tự luyện:
1. Tìm để hàm số = ( − ) + nghịch biến trên ℝ .
2. Tìm để hàm số = + đồng biến trên ℝ.
Dạng 5 : Sử dụng tính đơn điệu của hàm số CM bất đẳng thức.
• Đưa bất đẳng thức về dạng ( ) ≥ ∈() .
• Xét hàm số = ( ) ∈ ( ).
• Lập bảng biến thiên của hàm số trên khoảng ().
• Dựa vào bảng biến thiên và kết luận. 26 π
Ví dụ 1 : Với ∈ .Chứng minh rằng :
+ > < < π Giải :
+ > π
Xét hàm số ( ) = + − liên tục trên nửa khoảng . π
Ta có : ( ) = +
− > + − > ∀ ∈ π π
⇒ ( )là hàm số đồng biến trên
và ( ) > ( ) ∀ ∈ π
hay + > ∀ ∈ (đpcm).
⊕ Từ bài toán trên ta có bài toán sau : Chứng minh rằng tam giác có ba
góc nhọn thì + + + ! + ! + ! > π < < π
Với > thì < (xem ví dụ 2 ) π
Xét hàm số ( ) =
liên tục trên nửa khoảng .
− π
Ta có ( ) =
∀ ∈ . π
Xét hàm số () =
− liên trục trên đoạn và có π
() =
− <
∀ ∈ ⇒ () liên tục và nghịch biến trên đoạn π π
và ta có ( ) < () = ∀ ∈ π
Từ đó suy ra ( ) ( ) = <
∀ ∈ ⇒ liên tục và nghịch ( ) π π π
biến trên nửa khoảng , ta có ( )
> = ∀ ∈ . π 27
Bài tập tương tự : π
Chứng minh rằng với mọi ∈ ta luôn có:
! >
+ ! > <
! > + +
Ví dụ 2 : Chứng minh rằng : π π
≤ ∀ ∈ < − + ∀ ∈ π
> − ∀ ∈ π ' > ∀ ∈ .
Giải : π
≤ ∀ ∈ π
Xét hàm số = − liên tục trên đoạn ∈ π
Ta có: = − ≤ ∀ ∈ ⇒
là hàm nghịch biến trên π đoạn . π
Suy ra ≤ = ⇔ ≤ ∀ ∈ (đpcm). π
> −
∀ ∈ ' π
Xét hàm số = − +
liên tục trên nửa khoảng ∈ . π
Ta có: = − +
⇒ ( = − + ≥ ∀ ∈ (theo câu 1) π π
⇒ ≥ = ∀ ∈
⇒ ≥ = ∀ ∈ 28 π
⇒ > −
∀ ∈ (đpcm). ' π
< − +
∀ ∈ π Xét hàm số
= − + −
liên tục trên nửa khoảng ∈ . π
Ta có: = − + −
≤ ∀ ∈ (theo câu π
2) ⇒ ≤ = ∀ ∈ π
⇒ < − +
∀ ∈ (Đpcm). π
> ∀ ∈ . π
Theo kết quả câu 2, ta có:
> − ∀ ∈ ⇒ > − ⇒ > − = − + − ⇒ > − + + − π Vì ∈ ⇒ − > ⇒ > − + π Mặt khác, theo câu 3: − +
> ∀ ∈ π Suy ra
> ∀ ∈ (đpcm). π Nhận xét: Ta có
< < ⇒ < < ∀ ∈ nên 29 α ≥ α
∀ ≤ . Do đó, ta có kết quả sau α π Chứng minh rằng: với α ∀ ≤ , ta luôn có:
≥ ∀ ∈ .
Bài tập tương tự : Chứng minh rằng : > − ∀ > −
< < − +
∀ ≠ π
Ví dụ 3 : Chứng minh rằng < + − ∀ ∈ π Giải : π
Xét hàm số = −
liên tục trên nửa khoảng ∈ .
− +
Ta có: = − + = .
π
Theo kết quả câu 4 d ví dụ 2 , ta có:
> ∀ ∈ π π ⇒
− + >
∀ ∈ ⇒ > ∀ ∈ π π
⇒ ≤ = − ∀ ∈ π π Do vậy: < + − ∀ ∈ (đpcm). π
Bài tập tương tự : π
1. Chứng minh rằng : <
(π − ) với mọi ∈ . π π
2. Chứng minh rằng : > + − với mọi ∈ . π π ( π ) π +
Ví dụ 4 : Với ≤ <
. Chứng minh rằng + > Giải : 30
+ Ta có: + ≥ =
+ π Ta chứng minh: ≥
⇔ + ≥ ∀ ∈ . π
Xét hàm số ()
= + −
liên tục trên nửa khoảng .
− +
Ta có: ( ) = + − =
− + π =
≥ ∀ ∈ .
⇒ đồng biến trên π π
$ ⇒ ≥ = ⇒ + ! ≥ , ∀ ∈ (đpcm).
Ví dụ 5 : Chứng minh bất đẳng thức sau với mọi số tự nhiên > + + − < Giải : Đặt = ∈ () ∀ ∈ .
Bất đẳng thức cần chứng minh là:
+ + − < ∀ ∈ () Xét hàm ( ) =
+ + − ∈ $
⇒ ( ) = − < ∀ ∈( ) ( − − + )
( − )
Vậy ( ) giảm trên () nên () < () = ∀ ∈() . Ví dụ 6:
Cho ≥ ≥ ≥ .Chứng minh rằng : + + ≥ + +
Cho > .Chứng minh rằng:
+ + +
+ + ≥
+ +
+ +
+ Giải : 31
Cho ≥ ≥ ≥ .Chứng minh rằng : + + ≥ + +
≥ ≥ ≥
Xét hàm số : = + + − + + .
Ta có: = − − −
= − −
≥ ∀ ≥
⇒ () là hàm số đồng biến
∀ ≥ ⇒ ≥ = ⇒ đpcm.
Cho > Chứng minh rằng:
+ + +
+ + ≥
+ +
+ +
+ .
Không mất tính tổng quát ta giả sử: ≥ ≥ > . Xét hàm số
= + + + + + −
+ − + − + Ta có
= − +
+ +
+ +
− +
⇒ ( = − + +
⇒ ( > (do ≥ ≥ )
⇒ ≥ = − = − ≥ nên
là hàm số đồng biến.
⇒ ≥ = − + = − ≥ ⇒ đpcm. Ví dụ 7:
Cho > . Chứng minh rằng: + + ≥ . + + +
Cho < ≤ ≤ . Chứng minh rằng:
− + + ≤ + . + + + + Giải :
Cho > . Chứng minh rằng: + + ≥ + + +
Đặt = = =
⇒ = và bất đẳng thức đã cho ⇔ + + ≥ . + + + 32
Giả sử ≤ ⇒ ≥ nên có: + ≥ = + + + + ⇒ + + ≥ + = +
= với + + + + + + +
= ≤ −
Ta có: = − ≤ ≤ + + +
⇒ ≥ = ∀ ≤ ⇒đpcm. −
Cho < ≤ ≤ . Chứng minh rằng: + + ≤ + + + +
+ Đặt = α
= ≤ α ≤ . Khi đó bất đẳng thức cần chứng minh trở α + + thành + + ≤ α + + + α + +
+
⇔ + + ≥ + α + α + + α + + Xét hàm số
= + + − + α + ≤ α ≤ α + + α + α −
Ta có: = + − − α + + α )
= α − − ≥ ≤ α ≤ α) + α
Như vậy hàm là đồng biến do đó
≥ α = α − α + − α
Nhưng α = α − + = α + α + − ≥ αα − = α α α
⇒ ≥ α ≥ = ⇒ đpcm.
Bài tập tự luyện: 1.
Cho hàm số ( ) = + − 33 π
Chứng minh rằng hàm số đồng biến trên nửa khoảng . π
Chứng minh rằng + > với mọi ∈ . 2. π
Chứng minh rằng > với mọi ∈ . π
Chứng minh rằng > +
với mọi ∈ . 3. π
Cho hàm số ( ) =
− với mọi ∈ π π
Xét chiều biến thiên của hàm số trên đoạn . π
Từ đó suy ra rằng
≥ với mọi ∈ . π 4.
Chứng minh rằng các bất đẳng thức sau :
< với mọi >
> với mọi <
> −
với mọi ≠
> −
với mọi >
< −
với mọi < π
+ > với mọi ∈ .
Dạng 6 : Dùng đơn điệu hàm số để giải và biện luận phương trình và bất phương trình . Chú ý 1 :
Nếu hàm số = ( ) luôn đơn điệu nghiêm cách trên ( hoặc luôn đồng biến
hoặc luôn nghịch biến trên ) thì số nghiệm của phương trình : () = sẽ
không nhiều hơn một và ( ) = ( ) khi và chỉ khi = . 34 Chú ý 2:
• Nếu hàm số = () luôn đơn điệu nghiêm cách trên ( hoặc luôn đồng
biến hoặc luôn nghịch biến trên ) và hàm số = () luôn đơn điệu nghiêm
ngoặc ( hoặc luôn đồng biến hoặc luôn nghịch biến ) trên , thì số nghiệm trên
của phương trình ( ) = ( ) không nhiều hơn một.
• Nếu hàm số = ( )có đạo hàm đến cấp trên và phương trình −
= có nghiệm, khi đó phương trình
= có nhiều nhất là + nghiệm. Chú ý 3:
Nếu hàm số = ( )xác định trên và có ′ () > hoặc ′ ( ) < trên
thì ( ) đồng biến hoặc luôn luôn nghịch biến trên nên ( ) = nhiều
nhất nghiệm trên suy ra ( ) nhiều nhất nghiệm trên .
Ví dụ : Giải phương trình :
+ + = + + . Giải :
Điều kiện : ≥
Xét hàm số ( ) = + + − (
+ + ) trên nửa khoảng +∞ ).
Ta có : ′() = + − − +
Và ′ () = − − − <
∀ > , suy ra phương trình ( + )
( ) = nhiều nhất nghiệm và () = ( )
= ⇒ = = là
nghiệm của phương trình.
Ví dụ 1 : Giải các phương trình
+ + + + + + + =
− − + = + − Giải :
+ + + + + + + = Phương trình ⇔ (− )
+ − + = + + + + 35 Đặt =
− = + > Phương trình
⇔ + + = + + Xét hàm số
= + + liên tục trên khoảng (+∞) +
Ta có = +
> ∀ > ⇒ () đồng biến trên khoảng + (+∞). Khi đó phương trình
⇔ = ⇔ = ⇔ − = + ⇔ = − Vậy
= − là nghiệm duy nhất của phương trình.
− − + =
+ − . Đặt y = =
+ − . Khi đó phương trình cho −
− + = ⇔
+ − =
− − + =
− − + = ⇔ ⇔
+ = + + + + = ( +) + + ( ) ( )
() có dạng ( ) = ( + ) ()
Xét hàm ()
= + ∈ ℝ
Vì ( )
= + >
∀ ∈ ℝ nên hàm số đồng biến trên tập số thực ℝ .
Khi đó ( ) ⇔ = +
− − + =
− − + = Hệ ( ) ( ) ⇔ ⇔ = + = + − + − −
Giải phương trình ( ) ta có tập nghiệm : = .
Ví dụ 2 : Chứng minh rằng phương trình:
− = có nghiệm duy nhất Giải : Cách 1 : Xét hàm số =
− liên tục trên nửa khoảng +∞ ). 36
( − ) Ta có: =
> ∀ ∈ (+∞) = − = +∞ →+∞ →+∞ ( # # ) − Bảng biến thiên : +∞ + +∞
Dựa vào bảng biến thiên ta thấy đồ thị của hàm số =
− luôn cắt
đường thẳng = tại duy nhất một điểm. Do đó phương trình
− = có nghiệm duy nhất . Cách 2:
Xét hàm số = ()
= − − liên tục trên nửa khoảng +∞) .
Ta có () = − ( )
= . Vì ( ) () =
− < ⇒ () = có ít nhất
một nghiệm trong khoảng (). − ( ) ( ) = >
∀ ∈ ( +∞) ⇒ ( ) liên tục và đồng biến trên khoảng − ().
Vậy phương trình cho có nghiệm duy nhất thuộc khoảng ( ).
Ví dụ 3 : Giải bất phương trình sau : − + + ≥ Giải :
Điều kiện : ≥
Xét hàm số = − + + liên tục trên nửa khoảng +∞
Ta có : = + > ∀ > ⇒ ( ) − −
là hàm số đồng biến trên nửa khoảng +∞ và = , khi đó bất phương
trình cho ⇔ ≥ ⇔ ≥
Vậy bất phương trình cho có nghiệm là ≥ . 37
Ví dụ 4 : Giải bất phương trình sau − + − ≤ − Giải : Điều kiện: < ≤ Bất phương trình cho
⇔ − +
≤ + ⇔ ≤ − Xét hàm số
= − +
liên tục trên nửa khoảng − −
Ta có : = − < ∀ ∈ ⇒ là hàm − −
nghịch biến trên nửa đoạn .
Hàm số = + là hàm đồng biến trên ℝ và = =
i Nếu > ⇒ < = = < ⇒ đúng
i Nếu < ⇒ > = = > ⇒ vô nghiệm.
Vậy nghiệm của bất phương trình đã cho là: ≤ ≤ .
Ví dụ 5 : Giải bất phương trình sau
+ − − + ≤ − + − + + Giải : Điều kiện: ≥ .
Bất phương trình cho ⇔ + + + − − ≤ ()
i Nếu − − ≤ ⇔ ≤ ⇒ luôn đúng. i Nếu >
Xét hàm số = + + + − − liên tục trên khoảng (+∞) Ta có: + + +
= +
− − +
> ∀ > + + −
⇒ ( ) đồng biến trên khoảng (+∞) và = , do đó
() ⇔ ≤ ⇔ ≤ . 38
Vậy nghiệm của bất phương trình đã cho là: ≤ ≤ .
Ví dụ 6 : Giải bất phương trình sau
+ + + < + − Giải :
+ + + ≥ Điều kiện: ⇔
− ≤ ≤ . − ≥ Bất phương trình cho
⇔ + + + − − < ⇔ < () Xét hàm số
= + + + − − liên tục trên đoạn − .
+ +
Ta có: = +
> ∀ ∈ (−) ⇒ () + + + −
đồng biến trên nửa khoảng (
− ) và = , do đó
() ⇔ < ⇔ < .
Vậy nghiệm của bất phương trình đã cho là: − ≤ < .
Ví dụ 7 : Chứng minh rằng
− + > ∀ ∈ ℝ Giải : Xét hàm số
= − + liên tục trên ℝ . Ta có
= − và = ⇔ = .
Vì đổi dấu từ âm sang dương khi qua , do đó
= = − + >
Vậy > ∀ .
Ví dụ 8 : Chứng minh rằng phương trình : + − = có −
đúng hai nghiệm dương phân biệt. Giải :
Điều kiện: > (do > ). 39 Xét hàm số :
= +
− với > . − Ta có
= − −
⇒ ( = + > ∀ > −
⇒ = có nhiều nhất một nghiệm ⇒ = có nhiều nhất là hai nghiệm.
Mà: # = +
∞ < # = +∞ ⇒ = có hai nghiệm + →+∞ → ∈
và > . ( )
Ví dụ 9 : Giải hệ phương trình
+ + − =
− = −
+ + − =
+ = + = ( )
+ = ( ) Giải :
+ + − =
+ + − = − ≤ ≤ Điều kiện: . − ≤ ≤ Cách 1:
Trừ và ta được: + − − = + − − ( )
Xét hàm số = + − − liên tục trên đoạn − . 40 Ta có: * = + > ∀ ∈ − + −
⇒ ⇔ = ⇔ = .
Thay = vào ,ta được: + +
− = ⇔ + + + − = = − ≥ ⇔ − + + = − ⇔ ⇔
− + = = = =
Vậy hệ phương trình có nghiệm phân biệt . = = Cách 2:
Trừ và ta được:
( + − + ) +( − − − ) =
+ − +
− − − ⇔ + =
+ + +
− + − ⇔ − + = ( ) .
+ + +
− + − Vì +
> nên ( ) ⇔ = + + + − + −
Thay = vào ,ta được: + +
− = ⇔ + + + − = = − ≥ ⇔ − + + = − ⇔ ⇔
− + = = = =
Vậy hệ phương trình có nghiệm phân biệt . = = + = ( )
+ = ( ) Cách 1 : 41 Xét hàm số *
= + ⇒ = + > ∀ ∈ ℝ .
=
Hệ phương trình trở thành .
=
+ Nếu > ⇒
>
⇒ > (do và dẫn đến mâu thuẫn).
+ Nếu < ⇒ <
⇒ < (mâu thuẫn).
Suy ra = , thế vào hệ ta được + = ⇔ ( + )
= ⇔ = +
+ > =
Vậy hệ có nghiệm duy nhất . = Cách 2:
Trừ và ta được:
− + − = ⇔ −
+ + + = ⇔ − + +
+ = ⇔ =
Thế = vào và ta được: + = ⇔ (
+ ) = ⇔ = =
Vậy hệ phương trình có nghiệm duy nhất . =
− = −
+ =
Từ và suy ra − ≤ ≤
⇔ = Xét hàm số
= − liên tục trên đoạn $− , ta có
= − ≤
∀ ∈ $− ⇒ ( ) nghịch biến trên đoạn $−
Do đó: ⇔ = thay vào ta được nghiệm của hệ là: = = ± .
Ví dụ 10 : Giải hệ phương trình −
= − −
= −
− − =
= + Giải : 42 −
= −
− − =
Điều kiện: ≠ ≠ . Ta có: = ⇔ − + = ⇔ = −
i = phương trình
⇔ − = ⇔ = ± .
i = − phương trình vô nghiệm.
= = −
Vậy hệ phương trình có nghiệm phân biệt . = = − Bình luận: −
= −
Cách giải sau đây sai: .
− − =
Điều kiện: ≠ ≠ . Xét hàm số *
= − ∈ ℝ , %& ⇒ = + > ∀ ∈ ℝ , %& .
Suy ra ⇔ = ⇔ = !
Sai do hàm số đơn điệu trên khoảng rời nhau (cụ thể
( −) = () = ). −
= −
= + Cách 1:
Điều kiện: ≠ ≠ = − ⇔ − + = ⇔ − + = ⇔ = − = i
= phương trình ⇔ − ± = 43
i = − phương trình
⇔ + + = − Xét hàm số *
= + + ⇒ = + = ⇔ = − = −
> # = # = +∞ →−∞ →+∞
⇒ >
∀ ∈ ℝ ⇒ + + = vô nghiệm. Cách 2:
Điều kiện: ≠ ≠ = − ⇔ − + = ⇔ − + = ⇔ = − = i
= phương trình ⇔ − ± =
i = − phương trình
⇔ + + = i Với
< ⇒ + > ⇒ + + > . i Với
≥ ⇒ ≥ ≥
− ⇒ + + > .
Suy ra phương trình vô nghiệm.
Vậy hệ phương trình có nghiệm phân biệt − + − − = = = ∨ ∨ . = − + − − = =
Bài tập tự luyện:
1. Giải phương trình:
+ + + + =
− + − + =
2. Giải phương trình:
+ = ( )
3. Giải bất phương trình:
+ − − + ≤ − + − + +
Dạng 7 : Dùng đơn điệu hàm số để giải và biện luận phương trình và
bất phương trình chứa tham số.
Cho hàm số ( ) = xác định với mọi ∈ ( ) 44
• Biến đổi () về dạng ( ) = ()
• Xét hàm số = ( ) liên tục trên
• Dùng tính chất đơn điệu của hàm số và kết luận.
Ví dụ 1: Tìm tham số thực để ptrình
+ + = có nghiệm thực . Giải :
Xét hàm số ( )
= + + và =
Hàm số ( )
= + + liên tục trên ℝ .
+ +
Ta có : ( ) = + = + + < ( )
= ⇔ + = − ⇔
+ = < − − ⇔ ± ± ⇔ = = = =
Bảng biến thiên : suy ra () ≥
mà ( ) = do đó ≥ thì phương
trình cho có nghiệm thực .
Ví dụ 2 : Tìm tham số thực để phương trình :
+ − = ( ) có nghiệm thực . Giải :
Xét hàm số ()
= + − liên tục trên nửa khoảng +∞ ).
Ta có : ( ) = − < ( ) + Vì < = ⇒ − < nên
( +) ( +)
( ) <
∀ > ⇒ ( ) nghịch biến trên nửa khoảng +∞ ) và
# = , nên < ≤ ∀ ∈ +∞ ) . → + ∞
Vậy, phương trình () có nghiệm thực trên nửa khoảng + )
∞ ⇔ < ≤ 45
Ví dụ 3: Tìm tham số thực để phương trình :
( −) + + ( −) − + − = () có nghiệm thực. Giải :
Điều kiện: − ≤ ≤ .
+ + − +
Phương trình ⇔ =
+ + − + Nhận thấy rằng: ( + ) +( + − − ) = ⇔ + = π ϕ
Nên tồn tại góc ϕ ∈ = ∈ sao cho: −
+ = ϕ =
và − = ϕ = + +
+ + − +
− + + = ⇔ = = ( ) ( )
− + + + + − +
− + +
Xét hàm số: =
liên tục trên đoạn ∈ − . Ta có
+ +
− − −
=
< ∀ ∈ ⇒ nghịch biến trên đoạn [ 0; ] 1 ( ) (
− + + )
và = =
Suy ra phương trình () có nghiệm khi phương trình ( )có nghiệm trên
đoạn ∈
khi và chỉ khi: ≤ ≤ .
Ví dụ 4: Tìm tham số thực để bất phương trình
− + ≤ − + có nghiệm thực trong đoạn − . Giải : Đặt =
− + , ∀ ∈ − ⇒ ∈
Bài toán trở thành tìm tham số thực để bất phương trình
+ − ≤ có
nghiệm thực ∈ 46
Xét hàm số ()
= + − liên tục trên đoạn .
Ta có : = + >
∀ ∈ ⇒
( ) liên tục và đồng biến trên đoạn
Vậy bất phương trình cho có nghiệm thực trên đoạn khi
!" ≤ ⇔ ≤ ⇔ ≤ ⇔ ≥ ∈
Bài tập tự luyện:
1. Tìm tham số thực để phương trình : + ( − ) + = có nghiệm
thực trên đoạn .
2. Tìm tham số thực để bất phương trình:
− + ≥ − + có
nghiệm thực trên đoạn .
Dạng 8 : Dùng đơn điệu hàm số để chứng minh hệ thức lượng giác
Ví dụ : Chứng minh rằng : nếu tam giác thoả mãn hệ thức
+ + + =
thì tam giác đều.
+ + Giải :
Đặt : = + + = + ⇒ < ≤ . Xét hàm số ( )
= + hàm số liên tục trên nửa khoảng .
Ta có : ( ) = − > ∀ ∈ ⇒
đồng biến trên nửa khoảng ( )
,suy ra : < () ≤ .
Đẳng thức ( ) = xảy ra khi
= + + = hay tam giác đều.
Bài đọc thêm : HỆ HOÁN VỊ VÒNG QUANH 47
=
=
Định nghĩa: Là hệ có dạng: (I)
=
Định lí 1: Nếu là các hàm cùng tăng hoặc cùng giảm trên và
là nghiệm của hệ trên thì = = =
Định lí 2:Nếu khác tính đơn điệu trên và là nghiệm của = = =
hệ trên thì = = = nếu lẻ và −
nếu chẵn .
= = =
Ví dụ 1: Giải các hệ phương trình
− + − = = −
− + − = =
− + − = − = − Giải : = − = − = −
Giả sử > > Xét hàm số : ( ) =
,xác định trên = ℝ , {± } .Ta có − + ( ) = >
∀ ∈ ⇒ luôn đồng biến trên . ( ) −
Do đó : > > ⇒ ( ) > ( ) > ( ) ⇒ > > . Mâu thuẫn, do đó điều giả sử sai .
Tương tự < < không thoả .
Vậy = =
Hệ cho có nghiệm : (
) = () 48
− + − =
− + − =
− + − =
− + − =
= + −
− + − = ⇔
= + −
− + − =
= + −
Xét hàm số đặc trưng :
= − + ⇒ = −
> ∀ >
= ⇔ − = ⇔ = ⇒ () < ∀ <
Hàm số đồng biến trên khoảng
+∞ và nghịch biến trên khoảng −
∞ .Hàm số đạt giá trị nhỏ nhất tại = ⇒ = Và
≥
⇔ − + ≥ ≥ > ⇒ ≥ ⇒ ≥ > ⇒ ≥ >
= Vậy
thuộc miền đồng biến, suy ra hệ phương trình = là hệ hoán
= vị vòng quanh.
Không mất tính tổng quát giả sử
≥ ⇒ ≥ ⇒ ≥ ⇒ ≥
⇒ ≥ ⇒ ≥ ⇒ ≥
⇒ ≥ ≥ ≥ ⇒ = = Thay vào hệ ta có:
− + − = ⇒ = .
Suy ra: = = = 49
Ví dụ 2: Giải hệ phương trình :
− = − π
+ =
>
#- + = #- +
#- +
= #- + Giải :
− = − π
+ =
> π Từ ( )
() ⇒ ∈
() ⇔ − = − ( ). π
Xét hàm số () = − ∈ ta có π
( ) = − < ∈ ⇒ ( ) là hàm nghịch biến trên khoảng π
∈ nên (
) ⇔ ( ) = ( ) ⇔ = π
Với = thay vào () ta tìm được = = π π
Vậy ( ) = là nghiệm của hệ.
#- + = #- +
#- +
= #- +
> Điều kiện : > 50
#- + = #- + ( )
Đặt = = , ta có hệ:
#- + = #- + ( )
trừ vế theo vế ta được
#- + + #- = #- + + #- ⇔ = ( )
Xét hàm số = #- + + #- , dễ thấy là hàm đồng biến nên
() ⇔ = . +
Thay vào () ta được : #- + − #- = ⇔ = ⇔ = = α + π = Vậy hệ đã cho ⇔ ⇔
= π − α + π , trong đó = = ± β + π α = β = . − + =
Ví dụ 3: Giải hệ phương trình : +
#- + + = #- + + + Giải : − + = +
#- + + = #- + + +
+ + > Điều kiện :
+ + > − + Lấy #
vế của phương trình : = , ta được + +
− = #
= #( + ) − #( + ) + ⇔ + + ( + ) = + + ( # # + )( ) 51
Phương trình () có dạng (
+ ) = ( + ) ( )
Xét hàm số : ( ) = # + liên tục trên nửa khoảng +∞ ), ta có () = + >
∀ ≥ ⇒ () đồng biến trên nửa khoảng +∞ ). Do đó ( )
⇔ + = + ⇔ = ± .
• Với = − thay vào phương trình #- + + = #- + + + , ta được <
#- − = ⇔
⇔ = ⇒ = − thoả mãn bài toán . − =
• Với = thay vào phương trình #- + + = #- + + + , ta được
#- + = #- + > − . + =
Đặt #- + = #- + = ⇒
+ = ⇒ + = ⇔ + =
Xét hàm số () = +
là hàm số đồng biến trên ℝ và () = nên
= là nghiệm duy nhất của phương trình + = .
Với = ⇒ ( ) = () thoả mãn hệ phương trình .
Ví dụ 4: Hãy xác định tất cả các nghiệm của hệ phương trình (ẩn () ) sau: + =
#- #- = + = ()
. Học sinh giỏi Quốc Gia năm 2008 .
#- #- = ( )
Dễ thấy, nếu ( )là các nghiệm của hệ cho thì > > ( ) 52 Đặt #- =
> (do () ). Ki đó, =
và từ phương trình () có = . Khi đó phương trình () ⇔ + = ( ) .
Số nghiệm của hệ bằng số nghiệm dương của phương trình () − Xét hàm số ( )
= +
liên tục trên khoảng ( +∞) . Ta có ( ) # = # − Trên khoảng (+∞ ) , = # và =
là các hàm nghịch biến và chỉ nhận giá trị dương. #
Do đó trên khoảng ( +∞) , =
là hàm đồng biến. Suy ra, () là hàm
số đồng biến trên khoảng ( +∞ ). Vì
= # − # # − # < nên ∃ ∈ sao cho ( )
( = . )
Do đó, ta có bảng biến thiên của hàm số () trên khoảng (+∞). +∞ ( ) − + ( ) +∞ +∞ − ( )
Từ bảng biến thiên ta thấy phương trình () có đúng hai nghiệm dương. Vì vậy,
hệ phương trình cho có tất cả hai nghiệm.
Bài 2: CỰC TRỊ HÀM SỐ 53
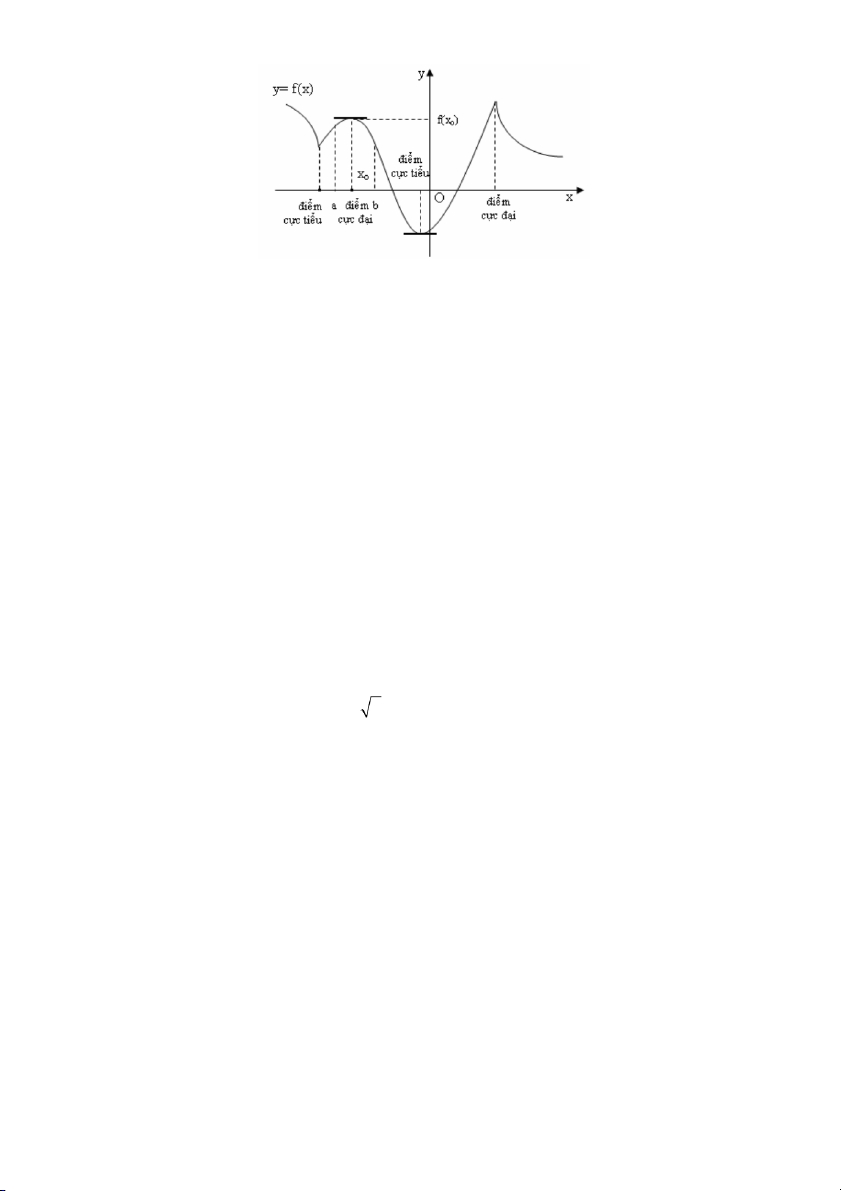
2.1 TÓM TẮT LÝ THUYẾT
1. Khái niệm cực trị hàm số :
Giả sử hàm số xác định trên tập hợp ( ⊂ ℝ ) và ∈ được gọi là một của hàm số điểm cực đại
nếu tồn tại một khoảng ( )
( ) ⊂
chứa điểm sao cho:
. Khi đó ( được )
<
∀ ∈ , ( ) { }
gọi là giá trị cực đại của hàm số .
được gọi là một điểm cực tiểu của hàm số nếu tồn tại một khoảng ( )
( ) ⊂
chứa điểm sao cho:
. Khi đó ( được )
<
∀ ∈ , ( ) { }
gọi là giá trị cực tiểu của hàm số .
Giá trị cực đại và giá trị cực tiểu được gọi chung là cực trị
Nếu là một điểm cực trị của hàm số thì người ta nói rằng hàm số đạt cực
trị tại điểm .
Như vậy : Điểm cực trị phải là một điểm trong của tập hợp ( ⊂ ℝ)
Nhấn mạnh : ∈
⊂ nghĩa là là một điểm trong của : ( )
Ví dụ : Xét hàm số =
xác định trên +∞
). Ta có > ()
với mọi > nhưng = không phải là điểm cực tiểu vì tập hợp +∞ )
không chứa bất kì một lân cận nào của điểm . Chú ý : 54
• Giá trị cực đại ( cực tiểu) nói chung không phải là GTLN (GTNN) của
trên tập hợp .
• Hàm số có thể đạt cực đại hoặc cực tiểu tại nhiều điểm trên tâp hợp .
Hàm số cũng có thể không có điểm cực trị.
• là một điểm cực trị của hàm số thì điểm ( được gọi là điểm )
cực trị của đồ thị hàm số .
2. Điều kiện cần để hàm số đạt cực trị:
Định lý 1: Giả sử hàm số đạt cực trị tại điểm . Khi đó , nếu có đạo hàm
tại điểm thì ( = ) Chú ý :
• Đạo hàm có thể bằng tại điểm nhưng hàm số không đạt cực trị tại điểm .
• Hàm số có thể đạt cực trị tại một điểm mà tại đó hàm số không có đạo hàm
. • Hàm số chỉ có thể đạt cực trị tại một điểm mà tại đó đạo hàm của hàm số
bằng , hoặc tại đó hàm số không có đạo hàm .
• Hàm số đạt cực trị tại và nếu đồ thị hàm số có tiếp tuyến tại điểm
( thì tiếp tuyến đó song song với trục hoành. )
Ví dụ : Hàm số = và hàm số
=
3. Điều kiện đủ để hàm số đạt cực trị:
Định lý 2: Giả sử hàm số liên tục trên khoảng () chứa điểm và có đạo
hàm trên các khoảng ( và ( . Khi đó : ) )
( < ∈ ) ( ) Nếu
thì hàm số đạt cực tiểu tại điểm . Nói một
( > ∈ ) ( )
cách khác , nếu ( )đổi dấu từ âm sang dương khi qua điểm thì hàm số
đạt cực tiểu tại điểm .
( ) − +
() ( ) ( ) ( ) 55 ( > ∈ ) ( ) Nếu
thì hàm số đạt cực đại tại điểm . Nói một
( < ∈ ) ( )
cách khác , nếu ( )đổi dấu từ dương sang âm khi qua điểm thì hàm số
đạt cực đại tại điểm .
( ) + − ( ) ()
() ( )
Định lý 3: Giả sử hàm số có đạo hàm cấp một trên khoảng (
) chứa điểm
, ( = và có đạo hàm cấp hai khác tại điểm . )
Nếu ( < thì hàm số đạt cực đại tại điểm . )
Nếu ( > thì hàm số đạt cực tiểu tại điểm . ) Chú ý:
Không cần xét hàm số có hay không có đạo hàm tại điểm = nhưng không
thể bỏ qua điều kiện " hàm số liên tục tại điểm " − ≤
Ví dụ : Hàm số =
không đạt cực trị tại = . Vì >
hàm số không liên tục tại = .
2.1 DẠNG TOÁN THƯỜNG GẶP.
Dạng 1 : Tìm các điểm cực trị của hàm số .
Quy tắc 1: Áp dụng định lý 2
• Tìm ( )
• Tìm các điểm ( = ) tại đó đạo hàm bằng hoặc hàm số liên tục
nhưng không có đạo hàm.
• Xét dấu của () . Nếu ( )đổi dấu khi qua điểm thì hàm số có cực
trị tại điểm . 56
Quy tắc 2: Áp dụng định lý 3
• Tìm ( )
• Tìm các nghiệm ( = )của phương trình ( ) = .
• Với mỗi tính ( )
− Nếu ( ) < thì hàm số đạt cực đại tại điểm .
− Nếu ( ) > thì hàm số đạt cực tiểu tại điểm .
Ví dụ 1 : Tìm cực trị của các hàm số :
= + + +
= −
+ − + Giải :
= + + +
Hàm số đã cho xác định và liên tục trên ℝ . Ta có:
= + + = + ≥ ∀ ⇒ Hàm số không có cực trị. Chú ý:
* Nếu không đổi dấu thì hàm số không có cực trị.
* Đối với hàm bậc ba thì = có hai nghiệm phân biệt là điều cần và đủ để hàm có cực trị.
= − + − +
Hàm số đã cho xác định và liên tục trên ℝ . Ta có: =
− + − =
− − +
= ⇔ − − + = ⇔ = ∨ = − Bảng biến thiên −∞ − +∞ + + − −∞ −∞
Vậy, hàm đạt cực đại tại =
− với giá trị cực đại của hàm số là − = ,
hàm số không có cực tiểu.
Bài tập tự luyện:
Tìm cực trị của các hàm số : −
+ − 1. = 2. = −
+ +
Ví dụ 2 : Tìm cực trị của các hàm số :
= −
= + − − 57
= − − = − − =
− + Giải : = ( )
= −
Hàm số đã cho xác định và liên tục trên đoạn − − Ta có = ∈ ( − ) −
Hàm số không có đạo hàm tại các điểm =− = . Suy ra, trên khoảng (
− ) : = ⇔ = − =
Bảng xét dấu − −
− + −
đổi dấu từ âm sang dương khi qua điểm − thì hàm số đạt cực tiểu tại
điểm = − (− ) = −;
đổi dấu từ dương sang âm khi qua điểm thì hàm số đạt cực đại tại
điểm = ( ) = .
= − −
Hàm số đã cho xác định và liên tục trên ( −∞ − ∪ +∞ . )
− −
Ta có: = − = ∈ (−
∞ − ) ∪ ( +∞). − −
Hàm số không có đạo hàm tại các điểm =− = .
Suy ra, trên mỗi khoảng (
−∞ − ) ( +∞ ): = ∈
(−∞− ) ∪( +∞) ≤ < ⇔ ⇔ ⇔ = . − = − =
Tương tự trên suy ra hàm số đạt cực tiểu tại điểm = = , hàm số không có cực đại. =
− +
Hàm số đã cho xác định và liên tục trên nửa khoảng −∞ . 58
− − Ta có: =
< ≠
− +
Hàm số không có đạo hàm tại các điểm = = .
Suy ra, trên mỗi khoảng (
−∞ ) : = ⇔ = Bảng biến thiên: −∞ − || + 0 − || +∞
Hàm số đạt cực đại tại điểm =
= và đạt cực tiểu tại điểm
= = . Chú ý:
* Ở bài 2 ví dụ 2 mặc dù = ± là điểm mà tại đó hàm số không có đạo hàm
tuy nhiên hàm số lại không xác định trên bất kì khoảng nào của hai điểm
này nên hai điểm này không phải là điểm cực trị của hàm số.
* Tương tự vậy thì = của hàm số ở câu 3 cũng không phải là điểm cực trị
nhưng = lại là điểm cực trị của hàm số.
= + − −
Hàm số đã cho xác định và liên tục trên nửa khoảng ( −∞ − ) +∞ .
Ta có: = − ∈ ( −∞ − ) ∪ ( +∞) . −
Hàm số không có đạo hàm tại các điểm =− = .
Suy ra, trên các khoảng ( −∞
− ) ( +∞) : = ∈
(−∞− ) ∪ (+∞) ≤ < ⇔ ⇔ ⇔ = .
− = = Bảng biến thiên:
−∞ − +∞
+ || || − + 59
Trên khoảng ( ) < , trên khoảng ( +∞) > điểm cực tiểu là ( +). = − −
Hàm số đã cho xác định và liên tục trên đoạn − . − + Ta có: = ∀ ∈ ( − ) −
Hàm số không có đạo hàm tại các điểm =− = . Suy ra, trên khoảng (
− ) : = ∈ ( − ) − < ≤ ⇔ ⇔ ⇔ = −
− = − = Bảng biến thiên: −∞ − − +∞
|| − + || Trên khoảng (−− )
< , trên khoảng (
− ) > suy ra điểm cực tiểu là (−− ) .
Bài tập tương tự :
Tìm cực trị của các hàm số : 1.
= + + − 3.
= + + + 2. =
+ +
4. = − + ( − )
Ví dụ 3 : Tìm cực trị của các hàm số :
= ( ) =
= () = ( + ) = () = ( − ) Giải :
= ( ) = 60
Hàm số đã cho xác định và liên tục trên ℝ . ≥ = . − < >
Ta có = − < Trên khoảng (
−∞ ): < ,trên khoảng ( +∞) : > . Bảng biến thiên −∞ +∞ − + +∞ +∞
Hàm số đạt điểm cực tiểu tại điểm = () = . + ≥
= ( ) = ( + ) ( ) = −
( + ) <
Hàm số đã cho xác định và liên tục trên ℝ .
+ > >
Ta có =
− − <
Hàm số liên tục tại = , không có đạo hàm tại = . Trên khoảng (
−∞ ): = ⇔ = − ,trên khoảng (+∞) : > . Bảng biến thiên −∞ − +∞ + − + +∞ −∞
Vậy hàm số đạt cực đại tại điểm = − (
− ) = , hàm số đạt cực tiểu tại điểm
= ( ) = . = () = ( − )
Hàm số đã cho xác định và liên tục trên ℝ . − ≥
= ( )
( ) = . −
( − ) < 61 ( − ) > Ta có =
− + − < − Trên khoảng (
−∞ ): > ,trên khoảng ( +∞) : = ⇔ = Bảng biến thiên −∞ +∞ + − + +∞ −∞ −
Hàm số đạt điểm cực đại tại điểm = ( )
= , hàm số đạt điểm cực tiểu tại
điểm = ( ) = − .
Bài tập tương tự :
Tìm cực trị của các hàm số :
= + +
= − + −
= + − −
= + + +
= + −
=
− + + − + −
Ví dụ 4 : Tìm cực trị của các hàm số sau
= −
= − − Giải :
= −
Hàm số đã cho xác định và liên tục trên ℝ .
Ta có = π π
= ⇔ = ⇔ =
+ ∈ ℤ , = − π π π − =
+ = − + π = = + π π
Vậy hàm số đạt cực đại tại các điểm =
+ π + π = − và đạt cực π π π π đại tại =
+ ( +) + ( +) = − 62
= − −
Hàm số đã cho xác định và liên tục trên ℝ .
Ta có = + = ( + ) = = π π = ⇔ ⇔ π ∈ ℤ . = − = = ± + π
= + π π π ±
+ π = = − <
. Hàm số đạt cực đại tại = ± + π , π ± + π =
(π ) = π + >
∀ ∈ ℤ . Hàm số đạt cực tiểu tại = π
( π ) = ( − π )
Bài tập tương tự:
Tìm cực trị của các hàm số : 1.
= − . 5.
= − .
2. = .
6. = . 3.
= . 7.
= .
4. = + .
8. = + . π
Ví dụ 5: Tìm cực trị của hàm số : = trên đoạn . Giải: π
Hàm số đã cho xác định và liên tục đoạn .
−
Ta có : = − + = . π π ∈ Trên khoảng : = ⇔ ⇔ = ( ) =
Tồn tại góc β sao cho β =
, khi đó () ⇔ = β . 63 Với β = thì β = và ( β) = β β =
Bảng xét dấu : π β + −
Hàm số đạt cực đại tại = β (β ) = với β = .
Bài tập tương tự:
Tìm cực trị của các hàm số : π π
1. = ( + )
trên khoảng − .
2. =
+ trên khoảng ( π ). π π
3. = + trên đoạn − . + + 4.
=
trên khoảng (−π π) . − +
Ví dụ 6: Tìm cực trị của hàm số :
= + + . Giải:
= + + = ( + )(−
) +
Vì − = (
− ) = (
− ) >
Nên = + ( − ) + −
Đặt = + ⇒
=
≤ ≤
Khi đó = ( )
= − + + − , ≤ ≤ Ta có : ( ) ( ) = − + + = − − > ∀ ∈ , suy ra hàm số không có cực trị .
Ví dụ 7: Tính đạo hàm của hàm số tại điểm = và chứng minh rằng hàm
số đạt cực tiểu tại = , biết rằng hàm số xác định bởi : 64
+ − ≠
= . = Giải : − + − ( )
= # = # → → ( )
= # → (
+ )
+ + + ( )
= # = → (
+ )
+ + +
Mặt khác ≠ , ta có : ( ) =
⇒ ( ) ≥ = () (
+ )
+ + +
Vì hàm số liên tục trên ℝ nên hàm số đạt cực tiểu tại = . ≠
Ví dụ 8 : Cho hàm số = . Chứng minh rằng =
= nhưng hàm số không đạt cực trị tại điểm . Giải :
− ( ) Ta có
= với mọi ≠ .
− ( )
Với mọi ≠ :
≤ và # = nên # = . Do đó → →
hàm số có đạo hàm tại = và = . Lấy một dãy =
, khi đó =
π = ∀ . π (π) Giả sử (
) là một khoảng bất kỳ chứa điểm .
Vì # = nên với đủ lớn ∈ ( và do = = ∀ , theo () ) →
định nghĩa cực trị của hàm số , = không phải là một điểm cực trị của .
Dạng 2 : Tìm điều kiện để hàm số có cực trị. 65 Cách 2:
Hàm số đạt cực đại tại = −
− +
( ) ( ) = = = ⇔ ⇔ ⇔ ( ) − + − ( < ) < <
Với < thì () ⇒ < .
− +
Xét hàm số : ( ) = < − − + − + # ( ) = # = − # = = −∞ →−∞ →−∞ − ( ) # → − − → − −
Ta có ( =
< ∀ ∈ −∞ ) ( ) ( − )
− + Bảng biến thiên : −∞
( ) −
( ) − −∞ Phương trình (
) có nghiệm < ⇔ < − ⇔ < − Ví dụ 12 : Tìm các hệ số
sao cho hàm số ( )
= + + + đạt cực trị
bằng tại điểm =
− và đồ thị của hàm số đi qua điểm ( ) . + + Tìm các hệ số
sao cho hàm số ( ) = đạt cực trị tại +
điểm = và = . Giải :
Hàm số đã cho xác định và liên tục trên ℝ .
Ta có ()
= + + 73
Hàm số đạt cực trị bằng tại điểm = − khi và chỉ khi ( − ) =
− = ⇔ ( − ) ( ) =
− + =
Đồ thị của hàm số đi qua điểm () khi và chỉ khi
() = ⇔ + + + = ( ) Từ ( )
() suy ra = = = − .
Hàm số đã cho xác định khi + ≠
+ + −
Ta có đạo hàm = ( +) • Điều kiện cần :
Hàm số đạt cực trị tại điểm = và = khi và chỉ khi − = ( ) = ( ) ⇔ + + − = = ( +) − = = > ≠ = − ⇔
⇔ + = ⇔ ( )
+ + − = =
+ ≠
+ ≠ • Điều kiện đủ : = − − = ⇒ = = ⇔ = ( = − + ) Bảng biến thiên
−∞ +∞ + − − + +∞ +∞ −∞ −∞
Từ bảng biến thiên :hàm số đạt cực trị tại điểm = và = . Vậy =
− = là giá trị cần tìm.
Bài tập tự luyện: 74
Ví dụ 13: Tìm các hệ số
sao cho hàm số ( )
= + + +
đạt cực tiểu tại điểm = () = và đạt cực đại tại điểm = () = . Giải :
Hàm số đã cho xác định và liên tục trên ℝ .
Ta có ()
= + +
() = +
i Hàm số ( )đạt cực tiểu tại = khi và chỉ khi
() = = = ⇔ ⇔ . () () > > >
i Hàm số ( )đạt cực đại tại = khi và chỉ khi ( ) =
+ + = ⇔ () () <
+ < ( ) = = = ⇒ ⇔ . ( ) ( ) =
+ + + =
+ + = Từ ( )
()( )suy ra =
− = = = .
Ta kiểm tra lại () =
− +
Ta có ( ) =
− +
( ) = − +
() = > . Hàm số đạt cực tiểu tại = () =
− < . Hàm số đạt cực đại tại = Vậy : =
− = = = .
Bài tập tự luyện:
Dạng 3 : Tìm điều kiện để các điểm cực trị của hàm số thỏa mãn điều kiện cho trước. Phương pháp:
• Trước hết ta tìm điều kiện để hàm số có cực trị,
• Biểu diễn điều kiện của bài toán thông qua tọa độ các điểm cực trị của đồ thị
hàm số từ đó ta tìm được điều kiện của tham số. Chú ý:
* Nếu ta gặp biểu thức đối xứng của hoành độ các điểm cực trị và hoành độ các
điểm cực trị là nghiệm của một tam thức bậc hai thì ta sử dụng định lí Viét .
* Khi tính giá trị cực trị của hàm số qua điểm cực trị ta thường dùng các kết quả sau: 75
Định lí 1: Cho hàm đa thức = () , giả sử = ( + ) /
( ) + ( ) khi đó
nếu là điểm cực trị của hàm số thì giá trị cực trị của hàm số là:
( = và = ( ) gọi là phương trình quỹ tích của các điểm cực trị. ) ( )
Chứng minh: Giả sử là điểm cực trị của hàm số, vì
là hàm đa thức
nên ( = ⇒ ( = + + = (đpcm) . ) ( ) ( ) ( ) ) ()
Định lí 2: Cho hàm phân thức hữu tỉ =
khi đó nếu là điểm cực ()
( )
trị của hàm số thì giá trị cực trị của hàm số: = .
( ) ( ) Và =
là phương trình quỹ tích của các điểm cực trị. ( )
( ) ( ) − ( ) ( )
Chứng minh: Ta có = ( )
⇒ = ⇔ ( ) ( ) − ( ) ( ) = (*). Giả sử là điểm cực trị của ( ) ( )
hàm số thì là nghiệm của phương trình (*) ⇒ = = . ( ) ( ) ( ) Ví dụ 1 : Tìm
để đồ thị của hàm số =
− + ( − ) + có điểm cực trị dương. Giải :
Hàm số đã cho xác định và liên tục trên ℝ . Ta có
= − + −
= ⇔ − + − =
Hàm số có hai điểm cực trị dương ⇔ có hai nghiệm dương phân biệt % =
− + > >
⇔ = > ⇔ . ≠
= − > 76 > Vậy
là những giá trị cần tìm. ≠
Bài tập tương tự :
1. Tìm để đồ thị của hàm số
= − + ( + ) + có điểm cực trị dương.
− + −
2. Tìm để đồ thị của hàm số =
có điểm cực trị âm. +
+ + +
Ví dụ 2 : Tìm để đồ thị của hàm số = có cực đại, −
cực tiểu và điểm đó nằm về hai phía với trục . Giải :
Hàm số đã cho xác định và liên tục trên ℝ ,{ } .
− − − Ta có = −
= ⇔ − − − = ( ≠ ) ()
Hàm số có hai điểm cực trị ⇔ () có nghiệm phân biệt ≠ ≠ < −
⇔ + > ⇔ . >
− − ≠
Hai điểm cực trị của đồ thị hàm số nằm về hai phía trục
⇔ ( < . ) ( )
Áp dụng kết quả định lí 2 ta có: ( = − , ( = − ) ( ) ) ( )
⇒ ( ) ( ) =
− + + = − − . ( ) ( ) ( < −
< ⇔ − − < ⇔ . ) ( ) > < − Vậy
là những giá trị cần tìm. >
Bài tập tương tự : 77
1. Tìm để đồ thị của hàm số = −
+ ( − ) + có cực đại, cực
tiểu và điểm đó nằm về hai phía với trục . ( + )
2. Tìm để đồ thị của hàm số = −
− + − có cực đại,
cực tiểu và điểm đó nằm về hai phía với trục .
+ + +
3. Cho hàm số = ≠
. Tìm để hàm số có cực đại, −
cực tiểu và hai điểm cực trị đó nằm về hai phía của trục hoành.
Ví dụ 3 : Tìm để đồ thị của hàm số
= + − − có
điểm cực đại, cực tiểu và các điểm này cách đều trục . Giải:
Hàm số đã cho xác định và liên tục trên ℝ Ta có
= + − ⇒ = ⇔ + − =
Vì (2) luôn có hai nghiệm phân biệt nên đồ thị hàm số luôn có hai cực trị. Gọi
là hoành độ hai cực trị, hai điểm cực trị cách đều trục tung
⇔ = ⇔ = −
⇔ + = (vì ≠ ) − − ⇔ = = = ⇔ = .
Vậy = là giá trị cần tìm.
Bài tập tương tự :
1. Tìm để đồ thị của hàm số
= − + ( − )
− ( − )
có điểm cực đại, cực tiểu và các điểm này cách đều trục .
− ( − ) + +
2. Tìm để đồ thị của hàm số = có điểm cực −
đại, cực tiểu và các điểm này cách đều trục .
Ví dụ 4 : Tìm để đồ thị của hàm số
= − ( + ) + (
− + ) + có hai điểm cực đại và cực tiểu
nằm về hai phía trục tung . Giải :
Hàm số cho xác định và liên tục trên ℝ Ta có :
= − ( + )
+ − +
Hàm số có hai điểm cực đại và cực tiểu nằm về hai phía trục tung khi và chỉ khi
phương trình = có hai nghiệm phân biệt thoả mãn < <
⇔ ( ) <
⇔ − + < ⇔ < < 78
Vậy giá trị cần tìm là < < .
Bài tập tương tự :
1. Tìm để đồ thị của hàm số
= − + (
+ − )
− có hai
điểm cực đại và cực tiểu nằm về hai phía trục tung .
2. Tìm để đồ thị của hàm số
= − + ( − ) + (
+ + ) +
có hai điểm cực đại và cực tiểu nằm về hai phía trục hoành .
Ví dụ 5 : Xác định giá trị tham số để hàm số
= − + ( + ) − − đạt cực đại và cực tiểu đồng thời hai giá trị cực trị cùng dấu. Giải :
Hàm số đã cho xác định và liên tục trên ℝ Ta có :
= − + ( + ).
Hàm số có cực đại , cực tiểu khi = có hai nghiệm phân biệt
⇔ % = − ( + ) > ⇔ − > ⇔ < = ( − )
− + ( + ) +
( −) + − =
( − )+ ( − ) + −
Gọi ( là các điểm cực trị của đồ thị hàm số thì ) ( )
là nghiệm của phương trình ()
= − + ( + ) = . Trong đó : =
−
+ − + − ( ) ( ) ( ) ( = ) ⇒
= − + − ( ) =
−
+ − + − ( ) ( ) ( ) ( = )
⇒ = − + − ( )
Theo định lý Vidét , ta có : + = = +
Theo bài toán : > ⇔ − + − − + − > ( ) ( )
⇔ ( − ) ( + + > )( ) 79
⇔ ( − ) + + + > ( )
⇔ ( − )
+ ( + ) + > ⇔ ( − ) + > ( ) > − ⇔ ≠
So với điều kiện bài toán , vậy −
< < là giá trị cần tìm .
Bài tập tương tự :
− ( + ) + +
Ví dụ 6 : Xác định giá trị tham số để hàm số = có −
hai điểm cực đại và cực tiểu cùng dấu . Giải :
Hàm số đã cho xác định trên = ℝ , { }
− − −
Ta có đạo hàm ( ) = ≠ ( −) Cách 1:
Hàm số có cực đại và cực tiểu khi ( ) = có hai nghiệm phân biệt
≠ hay phương trình ()
= − − − = có hai nghiệm % >
+ >
phân biệt ≠ , khi đó ⇔ ⇔ > − ( ) () ≠
− − ≠
Gọi ( là các điểm cực trị của đồ thị hàm số thì ) ( )
là nghiệm của ( ) =
= − + ⇒ = − − + Khi đó: = ⇔
= + + ⇒ = − + +
Hai giá trị cực trị cùng dấu khi
> ⇔ − − + − + + > ( )( ) ⇔ ( − ) − ( + ) >
⇔ − − > ⇔ < − ∨ > + ( ) Từ ( )
và () suy ra − < < − ∨ > + 80 Cách 2 :
Hàm số đã cho xác định trên = ℝ ,{ } và có đạo hàm − − − ( ) = ≠ ( − )
Hàm số có cực đại và cực tiểu khi ( ) = có hai nghiệm phân biệt
≠ hay phương trình ( )
= − − − = có hai nghiệm % >
+ > phân biệt ⇔ ⇔ ⇔ > − ( ) ≠ − − ≠
Hai giá trị cực trị cùng dấu khi đồ thị của hàm số = cắt trục hoành tại
hai điểm phân biệt ≠ hay phương trình − ( + )
+ + = ( ≠ )có hai nghiệm phân biệt ≠ . % = ( + ) − ( + ) >
− − > Tức là ⇔ ⇔ ( ) + ≠ − + + + ≠
< −
⇔ > + ≠ −
− < < −
So với điều kiện suy ra là giá trị cần tìm . > +
Bài tập tương tự :
+ + − +
Ví dụ 7 : Tìm tham số > để hàm số = đạt
cực tiểu tại ∈ (). Giải :
Hàm số đã cho xác định và liên tục trên khoảng ( ) − + − ( ) Ta có : = =
≠ , ( )
= − + − 81
Hàm số đạt cực tiểu tại ∈ ( ) ⇔ ( ) = có hai nghiệm phân biệt >
< thoả < < < ⇔ < ( ) ( ) ( )> > > < < <
⇔ − + − < ⇔ ⇔ . >
+ − > > < − >
Vậy giá trị cần tìm là < < ∨ > .
Bài tập tương tự :
1. Tìm tham số để hàm số
= − − + đạt cực tiểu tại ∈ ( ) .
2. Tìm tham số để hàm số
= − ( − )
− đạt cực đại tại
∈ ( + ) .
Ví dụ 8 : Tìm tham số thực để đồ thị của hàm số : =
+ + ( +) − có cực đại tại ∈ (−). Giải :
Hàm số đã cho xác định và liên tục trên ℝ . Ta có
= + + +
+ Nếu = thì = >
∀ ∈ ℝ ⇒hàm số luôn tăng ∀ ∈ ℝ , do đó hàm số không có cực trị.
+ Nếu ≠ , ta có % = ( − ) . Bảng xét dấu −∞ +∞ % + − + 82
i Nếu < < thì > ∀ ∈ ℝ ⇒ hàm số luôn tăng ∀ ∈ ℝ , do đó
hàm số không có cực trị.
i Nếu = thì = + + = ( + ) ≥
∀ ∈ ℝ ⇒ hàm số luôn
tăng ∀ ∈ ℝ , do đó hàm số không có cực trị.
i Với < hoặc > , khi đó tam thức có hai nghiệm phân biệt % = − ± < . ( ) +
< . Ta có bảng xét dấu −∞ +∞ − + −
Dựa vào bảng xét dấu, suy ra là hoành độ cực đại của hàm số. %
Theo bài toán, ta có − < < ⇔ − < − −
< ⇔ % < −
⇔ ( − )
< ⇔ + > ⇔ < − ( < ) + > , tương tự.
Bài tập tự luyện: +
1. Tìm tham số thực
để đồ thị của hàm số : = có cực đại tại − +
∈() và có cực tiểu ở ngoài khoảng đó.
+ ( + )
2. Tìm tham số thực để đồ thị của hàm số : = có cực đại tại + ∈
và có cực tiểu ở ngoài đoạn đó.
3. Tìm tham số thực để đồ thị của hàm số : = ( + )
+ − có một
cực trị tại ∈ (− ) .
+ ( + )
Ví dụ 9 : Cho hàm số =
, hãy tìm tham số để hàm số đạt +
cực đại , cực tiểu tại các điểm có hoành độ thỏa mãn hệ thức :
+ = − + . 83 Giải :
Hàm số đã cho xác định và liên tục trên ( −∞ − ) ∪ ( − +∞).
+ + Ta có = ≠ − ( + )
Để hàm số đạt cực đại , cực tiểu tại các điểm có hoành độ thì phương
trình ( )
= + + = có hai nghiệm phân biệt khác − khi đó
% = − > ⇔ < .
(− ) = (− ) + (− ) + ≠
+ =
Theo định lý Vidét , ta có : .
= +
+ = − +
⇔ ( + )
− = − = − =
− + = ⇔ ⇔ ⇔ = ⇔ = . ≠ < ≠ < ≠ <
Bài tập tương tự :
1. Tìm để đồ thị của hàm số: = − ( − )
+ ( − ) có cực
đại, cực tiểu đồng thời hoành độ cực đại, cực tiểu thỏa mãn hệ thức :
= + . 2. Tìm
để đồ thị của hàm số: =
− + (
− ) − có cực đại,
cực tiểu đồng thời hoành độ cực đại, cực tiểu thỏa mãn hệ thức :
= − + . ( ) ( − )
3. Tìm để đồ thị của hàm số: = + + +
≠ có cực đại, −
cực tiểu đồng thời hoành độ cực đại, cực tiểu thỏa mãn hệ thức :
− = − . 84
4. Tìm < ∈ ℤ để đồ thị của hàm số: =
− ( − ) + ( − ) +
có cực đại, cực tiểu đồng thời hoành độ
cực đại, cực tiểu thỏa mãn hệ thức : ≤ − < . 5. Tìm +
∈ ℤ để đồ thị của hàm số:
= − ( + ) + ( + ) + ( + )
có cực đại ( , cực tiểu )
( thỏa mãn hệ thức : ( − ) ( − )
> − . ( ) )
Ví dụ 10 : Tìm tham số để hàm số = ( − )(
− − − ) có cực
đại và cực tiểu thỏa = . ! ð Giải:
Hàm số đã cho xác định và liên tục trên ℝ . Ta có
= − ( + ) + −
= ⇔ − ( + )
+ − =
Hàm số có hai điểm cực trị thỏa mãn
= ⇔ (1) có hai nghiệm ð !
% = + > =
thỏa mãn: = ⇔ ⇔ . − = = = = −
Vậy = hoặc = − là giá trị cần tìm.
Bài tập tương tự :
1. Tìm tham số để hàm số
= − − có cực đại ( −)và cực
+ − tiểu
sao cho < .
2. Tìm tham số để hàm số
= − + có cực đại ( ) và cực tiểu
sao cho > (
+ + . )
Ví dụ 11 : Tìm tham số để hàm số =
− ( −)
+ ( −) + có cực đại , cực tiểu đồng thời
hoành độ cực đại cực tiểu thỏa + = . Giải:
Hàm số đã cho xác định và liên tục trên ℝ . 85 Ta có
= − ( − )
+ ( − )
Hàm số có cực đại , cực tiểu khi đổi dấu hai lần qua nghiệm , tức là phương trình
− ( − )
+ ( − ) = có hai nghiệm phân biệt ≠ ≠ ⇔ %
= ( − ) − ( − ) >
− + + > ≠ ⇔ − + < <
Theo định lý Vi – ét và yêu cầu bài toán, ta có: −
+ = = ( ) ( −) − + = ⇔ = ( − ) − − ( − ) = = =
⇔ − + = ( ≠ ) ⇔ =
So với điều kiện bài toán , vậy = ∨
= là giá trị cần tìm .
Bài tập tương tự :
1. Tìm tham số để hàm số
= − − có cực đại ( −)và cực tiểu
sao cho − < (
− . )
2. Tìm tham số để hàm số
= − + có cực đại ( ) và cực tiểu
sao cho − > (
− . ) + + −
Ví dụ 12: Tìm tham số
để hàm số =
có điểm cực đại +
và cực tiểu tại các điểm có hoành độ thỏa mãn ( − = ) ( ) Giải :
+ + − = = − + + + 86
Hàm số đã cho xác định và liên tục trên = ℝ ,{− } Với ≠
− ≠ , ta có
+ − = − = =
= + − + + +
Đồ thị hàm số có cực đại , cực tiểu khi = có nghiệm phân biệt và đổi
dấu khi qua các nghiệm đó , khi đó phương trình ( ) = có hai nghiệm
+ = >
phân biệt khác − ⇔ ⇔ >
− + − ≠ Khi đó ta có
( = + ) ⇒ − = + − + = − ( ) ( ) ( ) = +
( ) − ( )
= ⇔ − = ⇔ + − = ( ) + = − Mà − ( ) = − Từ ( ) 0 ( ) suy ra − −
− = ⇔ =
Bài tập tương tự : 1. Tìm tham số để hàm số =
+ ( − )
− có điểm cực đại và cực
tiểu tại các điểm có hoành độ thỏa mãn ( − < . ) ( )
2. Tìm tham số để hàm số = ( + )
− ( − )
có điềm cực tiểu
khác () và hoành độ của cực tiểu thỏa mãn ( + > . ) ( ) − + 3. Tìm tham số
để hàm số =
có điểm cực đại và cực tiểu tại −
các điểm có hoành độ thỏa mãn ( − > . ) ( ) 4.
Ví dụ 13: Tìm tất cả các giá trị của tham số thì hàm số
+ ( + ) + + =
có giá trị cực trị , đồng thời + > . + ! Giải : 87
Hàm số đã cho xác định trên = ℝ , {− } . + − ( ) Ta có : = =
≠ −
= + − ( ) ( + ) ( +)
Hàm số có cực đại , cực tiểu khi phương trình () = ≠ −có hai % > + >
nghiệm phân biệt khác − ⇔ ⇔ ⇔ > − (− ) ≠
− − ≠
Gọi ( = + + = + + là các điểm cực trị của ) ( )
đồ thị hàm số thì là nghiệm của phương trình () = ≠ −
Theo định lý Vid ét + =
− = − Theo bài toán : +
= + = + + + + + CÑ ! ( ) ( )
+ = ( + ) + ( + )( + ) + ( + )
+ = ( + ) − + ( + )
( + ) + ( + )
+ = ( + ) − ( + ) + ( + )
= + + Xét ()
= + + > −
() = + > ∀ > −
Do đó hàm số () đồng biến trên khoảng
∈ − +∞ và ( )
> − = ∈ − +∞ Vậy + > ∈ CÑ − +∞ !
+ ( + ) + +
Ví dụ 14 : Cho hàm số = . Gọi
là hai điểm +
cực trị , định để diện tích tam giác bằng . Với giá trị vừa tìm
được , tính khoảng cách từ đến đường thẳng . Giải :
Hàm số đã cho xác định và liên tục trên = ℝ , {− } . 88 + Ta có = ≠ − ( +) i Với
∀ ∈ ℝ hàm số đã cho có điểm cực đại (− − ) và điểm cực tiểu
( +) . i Ta có :
( − − )
⇒ = − + ( + ) ⇒ = + và
= − + ( − ) ( + ) = ( − ) ( + )
. = (
) − ( )
⇒ = − = i Diện tích ( = = − % ) ( ) ( ) = − ( =
= + ⇒ = ⇔ + = ⇔ % ) ( % ) =
i Gọi là khoảng cách từ đến đường thẳng khi đó = và + (
= ⇒ = . % ) + = − ⇒ = . + = ⇒ = .
Bài tập tự luyện:
1. Định để đồ thị của hàm số
= − + ( − )
− − có cực trị
sao cho tam giác diện tích bằng , biết () .
2. Định để đồ thị của hàm số
= − + có cực trị
sao cho
tam giác diện tích bằng .
Ví dụ 15 : Tìm tham số để hàm số
= − + có điểm cực trị
là đỉnh của một tam giác vuông cân. Giải:
Hàm số đã cho xác định và liên tục ℝ. Ta có
= − = − . 89
Với ≠ hàm số có ba cực trị .Khi đó tọa độ các điểm cực trị của đồ thị hàm số là:
− −
− .
Dễ thấy = nên tam giác ABC vuông cân
⇔ + =
⇔ + = ⇔ = ±
Vậy = ± là những giá trị cần tìm.
Bài tập tự luyện:
1. Tìm tham số để hàm số =
− + ( − )
+ có điểm cực trị
sao cho một tam giác vuông cân , với là gốc tọa độ.
2. Tìm tham số để hàm số = − ( − )
+ − có điểm cực trị
là đỉnh của một tam giác vuông.
Ví dụ 16: Tìm để đồ thị của hàm số
= − + + có cực đại ,
cực tiểu đồng thời các điểm cực trị lập thành tam giác đều. Giải :
Hàm số đã cho xác định và liên tục ℝ. Ta có
= − = ( − ) = = ⇔ = ()
Đồ thị hàm số có cực đại , cực tiểu khi = có nghiệm phân biệt và đổi
dấu khi qua các nghiệm đó , khi đó phương trình () có hai nghiệm phân biệt
khác ⇔ >
= ⇒ (
+ ) Khi đó : = ⇔ (
− − + ) = ± ⇒ (
− + )
Hàm số có cực trị
lập thành tam giác đều
= ⇔
⇔ = ⇔ + = = ⇔ ( − )
= ⇔ = ( > ) Vậy
= là giá trị cần tìm .
Bài tập tự luyện: 1. Tìm
để đồ thị của hàm số = − ( − )
+ − có cực đại ,
cực tiểu đồng thời các điểm cực trị lập thành tam giác đều. 90
2. Tìm để đồ thị của hàm số = −
+ có cực đại , cực tiểu
đồng thời các điểm cực trị lập thành tam giác đều, biết ( − ) .
Ví dụ 17: Tìm để đồ thị của hàm số
= − + ( )có điểm cực đại
và điểm cực tiểu của đồ thị ( )ở về hai phía khác nhau của đường tròn (phía
trong và phía ngoài): ( )
+ − − + − = . Giải :
Hàm số đã cho xác định và liên tục ℝ. Ta có :
= − = ⇒ = = ⇔
= ⇒ = − Cách 1:
Đồ thị hàm số có hai điểm cực trị (
) ( − ) . Hai điểm
() (−) ở về hai phía của hai đường tròn ( khi ) ⇔ < ⇔ − + + + < ( )( * * ) ( ) ( )
⇔ − + < ⇔ < < Cách 2 :
( ) ( − ) + ( − ) = có tâm ( ) và bán kính =
Ta có : = ( − ) + ( + )
= + + = + + ≥
> = ⇒ điểm B nằm ngoài ( , )
do đó điểm nằm trong đường tròn
( ⇔ < ⇔ + − < ⇔ − + < ⇔ < < ) ( )
Bài tập tự luyện:
1. Tìm để đồ thị của hàm số = − +
+ ( )có điểm cực đại và
điểm cực tiểu của đồ thị () ở về một phía khác nhau của đường tròn (phía
trong hoặc phía ngoài): ( )
+ + + + − = . 91
2. Tìm để đồ thị của hàm số
= + + − ( có điểm cực đại )
và điểm cực tiểu của đồ thị ( ở về hai phía khác nhau của đường tròn (phía )
trong và phía ngoài): ( )
+ = .
Ví dụ 18 : Tìm để đồ thị của hàm số:
= − + − có ba cực trị.
Đồng thời các điểm cực trị
của đồ thị tạo thành một tam giác có
bán kính đường tròn ngoại tiếp bằng . Giải :
Hàm số đã cho xác định và liên tục trên ℝ . Ta có :
= − = ( − ) = = ⇔ =
Với > : = có ba nghiệm phân biệt và đổi dấu khi đi qua các nghiệm đó.
Khi đó ba điểm cực trị của đồ thị hàm số là: ( − ) ( − −
+ − ) ( − + − ).
= = +
= và =
− − = △ ( + )
= = ⇔ =
⇔ − + = △ = ⇔ − =
Bài tập tương tự :
Tìm để đồ thị của hàm số: =
− + + có ba cực trị
sao cho tam giác nội tiếp được trong đường tròn có bán kính = .
Ví dụ 19: Tìm để đồ thị của hàm số
= − + + có cực đại,
cực tiểu và các điểm cực đại, cực tiểu của đồ thị hàm số đối xứng nhau qua
đường thẳng : = − . Giải :
Hàm số đã cho xác định và liên tục trên ℝ . Cách 1 : 92 Ta có
= − + ⇒ = ⇔ − + = .
hàm số có cực trị ⇔ (1) có 2 nghiệm phân biệt ⇔ % = −
> ⇔ − < < .
phương trình đường thẳng đi qua các điểm cực trị là :
= − +
+ ⇒ các điểm cực trị là :
− + +
1 − + + .
Gọi là giao điểm của hai đường thẳng và
+ + + − ⇒ . − −
và đối xứng qua d thì trước hết
⊥ ⇔ − = − ⇔ = khi
đó ( − )và (
−
− ⇒ I là trung điểm của ⇒ A và B ) ( )
đối xứng nhau qua .
Vậy = là giá trị cần tìm. Cách 2 :
Hàm số đã cho xác định trên ℝ và có đạo hàm
= − + .
Hàm số có cực đại , cực tiểu khi phương trình = có hai nghiệm
phân biệt
⇔ % = − > ⇔ − < < . Vidét, ta có
+ = = .
Gọi ( là các điểm cực trị của đồ thị hàm số và I là ) ( )
trung điểm của đoạn AB.
Đường thẳng AB có hệ số góc − − − −
+ − ( ) ( ) = = − −
= ( + ) − − + + ( ) − = − − + = Đường thẳng = −
(%) có hệ số góc =
Hai điểm ( đối xứng nhau qua đường thẳng (%) ) ( ) 93 ⊥ % khi và chỉ khi ∈ %
− i
⊥ % ⇔ = − ⇔ = − ⇔ = i
= ⇒ = −
= ⇒ = ⇒ ( ) = ⇔ ⇒ −
= ⇒ = − ⇒ − ( ) ( )
Dễ thấy ( − ) ∈ %
Vậy = thoả mãn yêu cầu bài toán .
Bài tập tương tự :
Tìm để đồ thị của hàm số
= + ( − )
− ( − ) + + có cực
đại, cực tiểu và các điểm cực đại, cực tiểu của đồ thị hàm số đối xứng nhau qua
đường thẳng : = . + Ví dụ 20: Tìm
để đồ thị của hàm số = có cực trị và khoảng −
cách giữa hai điểm cực trị bằng . Giải :
Hàm số đã cho xác định và liên tục trên = ℝ , { } .
− + + Ta có = −
= ⇔ − − = ≠
% = + >
Đồ thị hàm số có cực trị ⇔ ⇔ > −.
− − ≠
Đường thẳng đi qua các điểm cực trị có phương trình =
− − ⇒ các điểm cực trị là: − − − −
⇒ = − = ⇔ + − − =
⇔ + − = ⇔ = .
Vậy = là giá trị cần tìm.
Bài tập tương tự : + − + 1. Tìm
để đồ thị của hàm số =
có cực trị và khoảng cách −
giữa hai điểm cực trị bằng . 94
2. Tìm để đồ thị của hàm số
= − + − + có cực trị và khoảng
cách giữa hai điểm cực trị bé hơn . + +
Ví dụ 21: Tìm giá trị của để đồ thị hàm số = () = có +
điểm cực đại, điểm cực tiểu và khoảng cách từ hai điểm đó đến đường thẳng
% + + = bằng nhau. Giải :
Hàm số đã cho xác định và liên tục trên = ℝ ,{− }
+ + − Ta có = ≠ − ( + )
Hàm số có cực đại , cực tiểu khi ( ) đổi dấu hai lần qua nghiệm hay
phương trình ( )
= + + − = có hai nghiệm phân biệt khác − % >
− > ⇔ ⇔ ⇔ < ( − ) ≠ − ≠
Gọi ( = + = + là các điểm cực trị của đồ thị ) ( )
hàm số thì là nghiệm của phương trình ( ) = ≠ . Theo định lý Vi
ét + = − = − + + + +
Theo yêu cầu bài toán (
%) = (%) ⇔ =
⇔ + + = + + ⇔ ( + + )
= ( + + )
⇔ ( + + ) − ( + + ) =
⇔ ( − + + + = ) ( )
⇔ ( + + + = ≠ ⇔ (− )
+ + = ⇔ = ) ( )
So với điều kiện, vậy = là giá trị cần tìm .
Bài tập tương tự :
+ − +
1. Tìm giá trị của để đồ thị hàm số = có điểm cực đại, −
điểm cực tiểu và khoảng cách từ hai điểm đó đến đường thẳng % − = bằng nhau. 95
2. Tìm giá trị của để đồ thị hàm số
= − ( + )
− + có điểm
cực đại, điểm cực tiểu và khoảng cách từ cực đại đến đường thẳng
() − = nhỏ hơn . + +
Ví dụ 22: Tìm giá trị của
để đồ thị hàm số = có điểm cực −
tiểu nằm trên Parabol ( )
= + − Giải :
Hàm số đã cho xác định và liên tục trên = ℝ ,{ }
− − − Ta có =
≠ . Đặt ( )
= − − − . ( − )
Hàm số có cực đại , cực tiểu khi phương trình ( ) = có hai nghiệm
% = − ( − − ) > + > phân biệt khác ⇔ ⇔ ⇔ > − ( ) = − − ≠ ≠ −
= − + ⇒ = + − + Khi đó : = ⇔
= + + ⇒ = + + + Bảng xét dấu :
−∞ +∞
+ − − +
Dựa vào bảng xét dấu suy ra ( + + + + + ) là
điểm cực tiểu của đồ thị hàm số .
∈ ( ) ⇔ + + + = ( + + )
+ + + −
⇔ + = ⇔ = −
So với điều kiện bài toán, ta có =
− là giá trị cần tìm.
Bài tập tương tự :
1. Tìm giá trị của
để đồ thị hàm số = −
+ ( − ) có điểm
cực tiểu nằm trên đường thẳng ( ) = . 96
2. Tìm giá trị của để đồ thị hàm số = − ( + )
+ − có điểm
cực tiểu nằm trên Parabol ( ) = .
Ví dụ 23: Tìm giá trị của để đồ thị hàm số
= − + ( + ) − ( + − )
+ − có điểm cực tiểu tại một
điểm có hoành độ nhỏ hơn Giải :
Hàm số đã cho xác định và liên tục trên ℝ . Ta có
= − + ( + ) − (
+ − ) .
Hàm số đạt cực tiểu tại một điểm có hoành độ nhỏ hơn
⇔ = − + ( + ) − (
+ − ) = có hai nghiệm thoả mãn điều kiện :
() ⇔ −() <
< < % > ( ) ⇔
< ≤ ⇔
− ≥ ( ) ( ) ( ) < (
+ − ) < − < <
⇔ ( + ) − (
+ − ) >
− + > ⇔ (
+ − ) ≥
+ − ≥ + < < − < < < − < < ⇔ ⇔ ⇔ <
≤ − ∨ ≥ ≤ − <
Bài tập tương tự :
1. Tìm giá trị của để đồ thị hàm số
= − + ( + )
− có điểm
cực tiểu tại một điểm có hoành độ âm.
2. Tìm giá trị của
để đồ thị hàm số =
( − ) − ( − ) + +
có điểm cực tiểu tại một điểm có hoành độ lớn hơn .
Ví dụ 24: Tìm giá trị của để đồ thị hàm số 97 − ( + )
− + − =
có cực trị đồng thời tích các giá trị cực −
đại và cực tiểu đạt giá trị nhỏ nhất. Giải :
Hàm số đã cho xác định và liên tục trên = ℝ ,{ } . − + − + ( ) Ta có = = ≠ ( − ) ( − ) ( )
= − + − +
Hàm số có cực đại , cực tiểu khi phương trình () = ≠
có hai nghiệm phân biệt khác . % > −
+ − > ⇔ ( ⇔ ⇔ < < ) ≠
− + ≠
Gọi ( là các điểm cực trị của đồ thị hàm số thì ) ( )
là nghiệm của phương trình () = ≠ . = − −
+ − ⇒ = − + − + − Khi đó = ⇔ = + −
+ − ⇒ = − − − + − = (
− + − + − ) (
− − − + − )
= ( − ) − (
− + − )
= − + = − − ≥ −
⇒ = − =
So với điều kiện , vậy = là giá trị cần tìm .
Bài tập tương tự :
1. Tìm giá trị của để đồ thị hàm số
= − + + − có cực trị
đồng thời tích các giá trị cực đại và cực tiểu đạt giá trị nhỏ nhất.
2. Tìm giá trị của
để đồ thị hàm số = − +
+ − + có cực trị
đồng thời tích các giá trị cực đại và cực tiểu đạt giá trị lớn nhất. 98
Ví dụ 25: Với giá trị nào của thì đồ thị của hàm số + ( + )
+ + =
tương ứng có một điểm cực trị thuộc góc +
phần tư thứ ( ) và một điểm cực trị thuộc góc phần tư thứ (" ) của mặt phẳng tọa độ. Giải :
Hàm số đã cho xác định trên = ℝ , { − }
+ − Ta có : =
≠ − ( + )
Gọi ( là các điểm cực trị của đồ thị hàm số thì ) ( )
< là nghiệm của phương trình ( ) ( )
= + − = ≠ −
Đồ thị của hàm số có một điểm cực trị thuộc góc phần tư thứ ( )và
một điểm cực trị thuộc góc phần tư thứ (" ) của mặt phẳng tọa độ khi ( ) ⇔ ( )
< ⇔ − < ⇔ ≠ ( )
() ⇔Đồ thị của hàm số không cắt trục
⇔ + ( + )
+ + = ( ≠ − ) vô nghiệm ≠ ≠ ⇔ % = ( ⇔ + )
− ( + ) <
− − + < ≠ < − ⇔ ⇔ ( ) > >
() ⇔ < ( ) Từ () ( ) ( ) suy ra < − là giá trị cần tìm.
Ví dụ 25: Chứng tỏ rằng chỉ có một điểm duy nhất trên mặt phẳng toạ độ sao
− + + +
cho nó là điểm cực đại của đồ thị () ( ) = ứng với − 99
một giá trị thích hợp của và cũng là điểm cực tiểu của đồ thị ứng với một giá
trị thích hợp khác. Tìm toạ độ của . Giải :
Hàm số đã cho xác định trên = ℝ , { } .
− + − Ta có =
≠ ( − )
Tam thức ()
= − + − có % = > ∀ .
= − Do đó = ⇔ = + ( ) = −
+ − ⇒ (
− − + − ) ⇒ ( ) = −
+ + ⇒ ( + − + + )
Đặt ( .Giả sử ứng với giá trị = thì là điểm cực đại và ứng với )
giá trị = thì là điểm cực tiểu của đồ thị hàm số
= − = + Ta có: .
= − + −
= − + +
− = + Theo bài toán , ta có : −
+ − = − + +
− =
− = ⇔ ( ⇔ −
+ − = − + = − ) ( ) = = − ⇔ ⇒ ⇒ − − . = − = −
Vậy − − là điểm duy nhất cần tìm thoả yêu cầu bài toán .
Dạng 4 : Ứng dụng cực trị của hàm số trong bài toán đại số .
Ví dụ : Tìm tất cả các giá trị thực của để phương trình sau có một số lẻ nghiệm thực:
− + − − − − − = . Giải : 100
= ( − )( − ) ( − )
= − + −
= ( − + )
− ( − )
( ) là đa thức bậc với hệ số của là −.
= − + = (
− + ) ( − )−
− ( − ) = −
= ⇔ = = =
= = =
Bảng biến thiên của () . −∞ +∞
+ − + − ( ) −∞ −∞
Từ bảng biến thiên cho thấy phương trình
= có một số lẻ nghiệm
khi và chỉ khi: = = =
Bài 4 : GIÁ TRỊ LỚN NHẤT
GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ.
4.1 TÓM TẮT LÝ THUYẾT
1. Định nghĩa: Cho hàm số xác định trên
• Số gọi là giá trị lớn nhất (GTLN) của hàm số = ( ) trên
≤ ∀∈ nếu
, ta kí hiệu = !" .
∃ ∈ = ∈
Chú ý : Nếu ≤ ∀∈ thì ta chưa thể suy ra = !" ∈
• Số gọi là giá trị nhỏ nhất (GTNN) của hàm số = () trên
≥ ∀∈ nếu
, ta kí hiệu = .
∃ ∈ = ∈
Chú ý : Nếu ≥ ∀∈ thì ta chưa thể suy ra = . ∈
2. Phương pháp tìm GTLN, GTNN của hàm số 101
Phương pháp chung: Để tìm GTLN, GTNN của hàm số = ( ) trên ta
tính , tìm các điểm mà tại đó đạo hàm triệt tiêu hoặc không tồn tại và lập bảng
biến thiên. Từ bảng biến thiên ta suy ra GTLN, GTNN. Chú ý:
• Nếu hàm số = ( ) luôn tăng hoặc luôn giảm trên
thì !" = !"% & =
% & . $!2 $!2
• Nếu hàm số = ( ) liên tục trên thì luôn có GTLN, GTNN trên
đoạn đó và để tìm GTLN, GTNN ta làm như sau
Tính và tìm các điểm mà tại đó triệt tiêu hoặc hàm số không có đạo hàm.
Tính các giá trị .Khi đó +
!" ( ) = !" ∈ ∈
{ ( ) (
) ( ) ( ) ( )}
+ ( ) = ∈ ∈
{ ( ) (
) ( ) ( ) ( )}
• Nếu hàm số = () là hàm tuần hoàn chu kỳ T thì để tìm GTLN, GTNN
của nó trên ta chỉ cần tìm GTLN, GTNN trên một đoạn thuộc có độ dài bằng ! .
* Cho hàm số = ( ) xác định trên . Khi đặt ẩn phụ = , ta tìm được
∈ # với
∀∈ , ta có = ( )
thì Max, Min của hàm trên chính là
Max, Min của hàm trên # .
* Khi bài toán yêu cầu tìm giá trị lớn nhất, giá trị nhỏ nhất mà không nói trên tập
nào thì ta hiểu là tìm GTLN, GTNN trên tập xác định của hàm số.
* Ngoài phương pháp khảo sát để tìm Max, Min ta còn dùng phương pháp miền
giá trị hay Bất đẳng thức để tìm Max, Min.
* Ta cần phân biệt hai khái niệm cơ bản :
+ Giá trị lớn nhất của hàm số = ( ) trên với cực đại của hàm số .
+ Giá trị nhỏ nhất của hàm số = () trên với cực tiểu của hàm số .
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số = () trên mang tính toàn
cục , còn giá trị cực đại và giá trị cực tiểu của hàm số chỉ mang tính địa phương.
4.2 DẠNG TOÁN THƯỜNG GẶP
Để tìm giá trị lớn nhất và nhỏ nhất của hàm số = () trên ta có thể sử
dụng đạo hàm và kết hợp với việc so sánh giá trị cực đại, cực tiểu với giá trị đặc
biệt ( ta gọi đó là các giá trị tới hạn ) . Giá trị tới hạn này thường là các giá trị 102
tại các đầu mút của các đoạn hoặc là giá trị của hàm số tại các điểm mà không tồn tại đạo hàm.
Ví dụ 1 : Tìm giá trị lớn nhất và nhỏ nhất của các hàm số: − = trên đoạn . −
= − + trên đoạn .
= + ( − )
trên đoạn − . = − + +
trên đoạn $− . Giải : − = −
Hàm số đã cho xác định và liên tục trên đoạn . − Ta có =
< ∀ ∈ ( − ) Bảng biến thiên − −
Từ bảng biến thiên suy ra : ( ) !" =
= ( ) = − =
= − +
Hàm số đã cho xác định và liên tục trên đoạn .
− + Ta có : =
∈ + = = ⇔ = 103 = − = − !" = −
∈ ⇒ = − = −
∈ = − Vậy !" =
− khi = , =
− khi = . ∈ ∈
= + ( − )
Hàm số đã cho xác định và liên tục trên đoạn − . Đặt
= ∈ − ⇒ ∈
Hàm số đã cho viết lại () = + ( − )
∈
Ta có () = − ( − ) = (
− + − ) ( = = ) = ⇔ =
( ) = () = Bảng biến thiên
( ) − + ( )
Từ bảng biến thiên suy ra :
( ) = = ( ) !" = = ± − − = − + +
Hàm số đã cho xác định và liên tục trên đoạn $ − . − + Ta có =
− + + 104
= ⇔ = ∈$ − − = ( ) = = .
Vậy : =
= − = và !" = = . ∈ −
∈ − Tương tự:
1. Tìm giá trị lớn nhất và nhỏ nhất của các hàm số: ( )
= − + trên đoạn − + + ( ) =
+ +
2. Tìm giá trị lớn nhất và nhỏ nhất của các hàm số: = − +
trên đoạn $ − . () = − + +
trên đoạn $− . + +
Ví dụ 2 : Tìm giá trị lớn nhất của các hàm số: = > . + Giải :
Hàm số đã cho xác định và liên tục trên khoảng ( +∞) + +
+ − = = = +
+ ( + − )
+ −
Hàm số đạt giá trị lớn nhất trên khoảng (+∞ ) khi hàm số
= + − đạt giá trị nhỏ nhất trên khoảng ( +∞ ). () = − + > ( )
= ⇔ + = ⇔ ⇔ = =
() = = ⇒ = = = . > >
Ví dụ 3: Tìm giá trị lớn nhất và nhỏ nhất của các hàm số:
= + − trên đoạn − . 105 + =
trên đoạn ∈ − . + Giải :
= + −
Hàm số đã cho xác định và liên tục trên đoạn − .
− −
Ta có = − =
∈ (−) − −
− − =
− = = ⇔ ⇔ ∈ ( − ) ∈ ( − )
< < < < ⇔ ⇔ ⇔ =
− = = Bảng biến thiên − − + −
Từ bảng biến thiên , ta được
!" ( ) =
= ( ) = − = − ∈ − ∈ − + =
trên đoạn ∈ − . +
Hàm số đã cho xác định và liên tục trên đoạn − . − + Ta có =
⇒ = ⇔ = ( + ) Bảng biến thiên . − + − 106
Từ bảng biến thiên , ta được
!" =
= = = − ∈ − ∈ −
Ví dụ 4 : Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
= − + trên đoạn − Giải :
Hàm số đã cho xác định và liên tục trên đoạn − .
Đặt ( )
= − + ∈ − () = − = () = ⇔
= ∉ − ( − ) =
− () = () =
− , suy ra !" () = ( ) = − . − −
∈ − ⇒
()∈ − ⇒
() = () ∈ ( ) ( )
< ⇒ ∃ ∈ ! = ( ) ( )
Vậy !" () = ( ) = − − Tương tự:
1. Tìm giá trị lớn nhất của các hàm số: ()
= + − + trên đoạn − .
2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số ( ) = − + trên đoạn 3 . Ví dụ 5:
Tìm để giá trị lớn nhất của hàm số
= + + − trên đoạn −
đạt giá trị nhỏ nhất . Tìm giá trị
$ % để giá trị lớn nhất của hàm số
= + $ + % trên đoạn − là bé nhất . Giải :
Hàm số đã cho xác định và liên tục trên đoạn − . 107
= + + − = ( + ) + −
Đặt = ( + ) ∈
− ⇒ ∈
Ta có () = + − ∈
!" ⇔ !" () = !" = − − ∈− ∈ ∈
{ ( ) { }
!" { } ∈
• − ≥ − ⇔ ≤ ⇒ !" () = − = − ∈
• − ≤ − ⇔ ≥ ⇒ !" () = − = − ∈
− ≥ − = ∀ ≤ Mặt khác
⇒ !" ( ) ≥ ∀ ∈ ℝ
− ≥ − = ∀ ≥ ∈
Vậy giá trị nhỏ nhất của !" () = = ∈ Xét hàm số ( )
= + $ + %
Hàm số đã cho xác định và liên tục trên đoạn −
⇒ = ( ) (
− ) = − $ +% () = % () = + $ + %
Giả sử !" = (α )
⇒ + ≥ − = + $ , − + ≥ − − = − $ > $
• > ⇒ + $ > ⇒ ⇒ (α ) > > − > $
• < ⇒ − $ > ⇒ ⇒ (α ) > > $
!" = !" −
− ∈ − $
• = ⇒ ( ) $ = +
% ( ) = − = % (
− ) = () = + %
Giá trị lớn nhất của là một trong hai giá trị % + % %
• > − ⇒ + % > ⇒ ± >
⇒ α > 108 % • < − ⇒ % > ⇒ >
⇒ α > %
• = − ⇒ () = − ≤
⇒ !" =
⇔ = = ±
cũng là giá trị nhỏ nhất của (α ). Vậy
$ = % = − thoả mãn bài toán . +
Ví dụ 6 : Tìm các giá trị
sao cho hàm số = có giá trị lớn nhất +
bằng và có giá trị nhỏ nhất bằng − . Giải :
Hàm số đã cho xác định và liên tục trên ℝ .
• Hàm số có giá trị lớn nhất bằng khi và chỉ khi + ≤ ∀ ∈ ℝ +
− + − ≥ ∀ ∈ ℝ ⇔ + − + − = ∃ co ùnghieäm x ∈ ℝ = 0 + % = − (
− ) ≤ ⇔
⇔ + − = % = − ( − ) ( ) ≥
• Hàm số có giá trị nhỏ nhất bằng khi và chỉ khi +
≥ −∀ ∈ ℝ +
+ + + ≥ ∀ ∈ ℝ ⇔ ⇔ + + + + = ∃ co ùnghieäm x ∈ ℝ = − 0 +
% = − ( + ) ≤ ⇔
⇔ − − = % = − ( + ) ( ) ≥ Từ () 0 ( ) ta có hệ
+ − = ( ) = = − = ⇔⇔ ⇔ ∨
− − = ( ) = = = = − = Vậy giá trị
cần tìm là : ∨ = =
Ví dụ 7 : Tìm giá trị lớn nhất và nhỏ nhất của các hàm số: 109
= + + π
= − trên đoạn − π + =
+ +
+ =
+ Giải :
= + +
= + + = − +
Hàm số đã cho xác định và liên tục trên ℝ . Đặt
= ≤ ≤
Xét hàm số ()
= − + liên tục trên đoạn
Ta có ( ) = − , ∈ ( ) = ⇔ =
( ) = ( ) = = =
( ) =
= !" = " ( ) = ∈ ∈ π
= − trên đoạn − π π
Hàm số đã cho xác định và liên tục trên đoạn đoạn − π π
Ta có : () = − − < < π π π π ( )
= ⇔ = − π π π π − = − + = − 110


