
















































































Preview text:
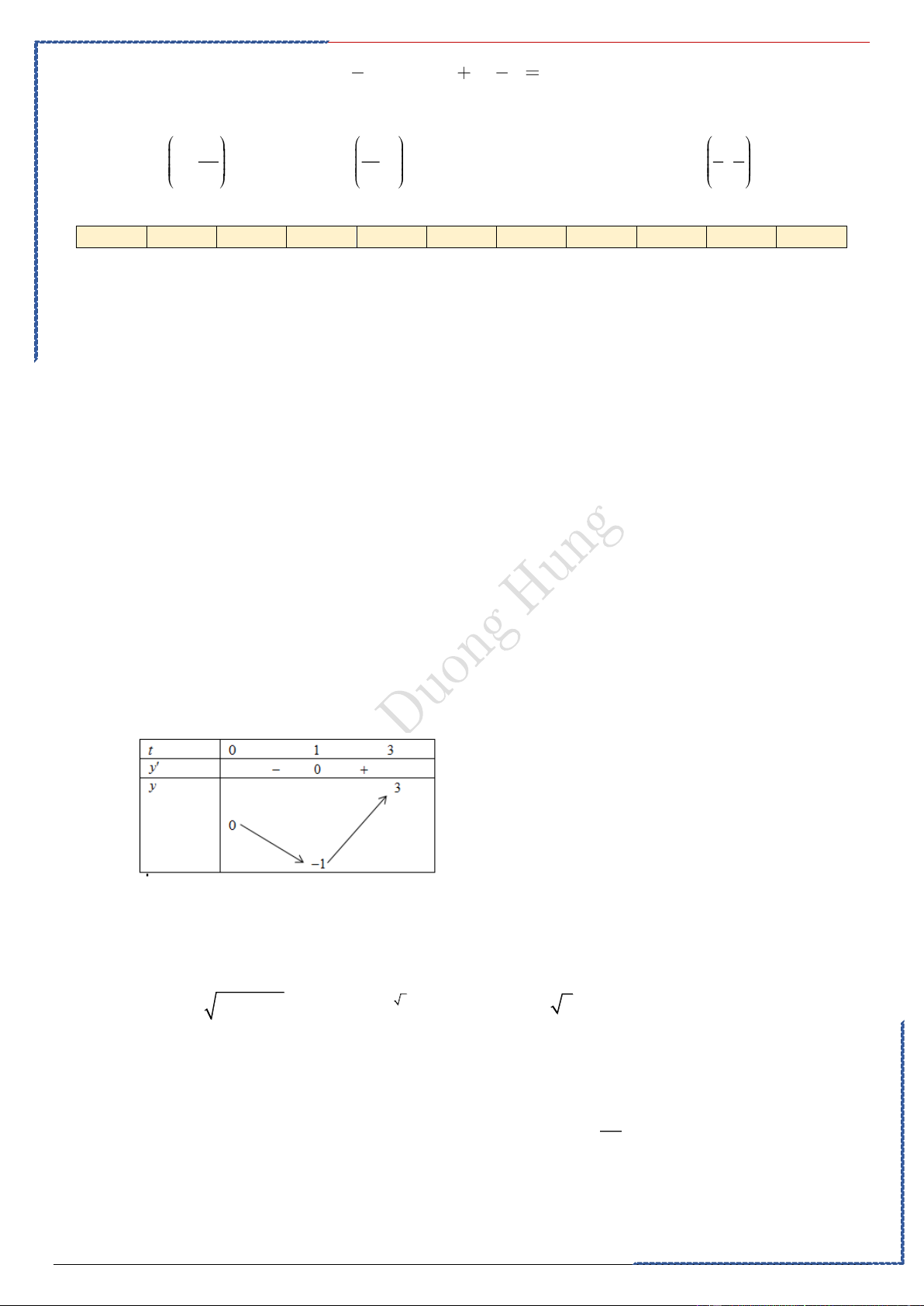
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 1
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Full 50 Chuyên đề 12 new 2020-2021 CHƯƠNG ②: FB: Duong Hung
Bài 1: MŨ – LŨY THỪA
Dạng ①: Mũ – Lũy Thừa
_ Dạng 1: Tính giá trị biểu thức
- Phương pháp: Công thức mũ, lũy thừa cơ bản: ⬧
- Phương pháp: Casio.
⬧ Xét hiệu Calc đặc biết hóa: Chọn giá trị thích hợp để thử đáp án.
A - Bài tập minh họa:
Câu 1: Tính giá trị của biểu thức 3 7 A = 2 .2 . Ⓐ. 10 2 . Ⓑ. 4 2− . Ⓒ. 4 2 . Ⓓ. 21 2 . Lời giải
PP nhanh trắc nghiệm Chọn Ⓐ.
Casio: Nhập ấn = Ta có: 3 7 3+7 10 A = 2 .2 = 2 = 2
Câu 2: Chọn mệnh đề nào đúng. Ⓐ. ( )5 2 7 3 = 3 . Ⓑ. ( )5 2 10 3 = 3 . Ⓒ. ( )5 2 3 3 3− = . Ⓓ. ( )5 2 3 3 = 3 . Lời giải PP nhanh trắc nghiệm Chọn B Casio: Nhập ấn = Ta có: ( )5 2 2.5 10 3 = 3 = 3
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 2
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 3: Giá trị của biểu thức 2 1 − 2 1− 2 C = 3 .9 .27 bằng Ⓐ.1 Ⓑ. 27 Ⓒ. 3 Ⓓ. 9 Lời giải
PP nhanh trắc nghiệm
Chọn D
Casio: nhập biểu thức Calc và nhấn phím =
rồi so sánh kết quả. Ta có: 2 1 − 2 1− 2 C = 3 .9 .27 − (31− 2 2 1 2. 2 ) = 3 .3 .3 2 1 − +2. 2+ ( 3 1− 2 ) 2 = 3 = 3 = 9 2
Câu 4. Cho a là số thực dương. Giá trị của biểu thức 3 P = a a bằng 5 2 7 Ⓐ. 6 a . Ⓑ. 5 a . Ⓒ. 3 a . Ⓓ. 6 a . Chọn D
Casio: nhập biểu thức xét hiệu Calc a=2 và
nhấn phím = 0 chọn kết quả. 2 2 1 7
Với a 0 , ta có 3 3 2 6 P = a
a = a a = a . Hoặc: Câu 5. Biểu thức 3 3 2 6 5 P =
x . x . x ( x 0) viết dưới dạng lũy thừa với số mũ hữu tỷ là 8 5 1 Ⓐ. 3 P = x . Ⓑ. 6 P = x . Ⓒ. 3 P = x . Ⓓ. 3 P = x . Lời giải
Casio: nhập biểu thức xét hiệu Calc x=2 và
nhấn phím = 0 chọn kết quả. Chọn A
Nếu lấy log sẽ có kết quả là số mũ nhanh hơn. 1 5 3 1 5 8 2 Ta có: P = x ( x) 2 3 6 2 3 6 3 3
.x = x .x .x = x .
B - Bài tập rèn luyện:
Câu 1: Với giá trị nào của x thì đẳng thức 2020 2020 x = x đúng Ⓐ. x . Ⓑ. x 0 . Ⓒ. x = 0 .
Ⓓ. Không có giá trị x nào.
Câu 2: Tính giá trị của biểu thức 2 9 A = 3 .3 Ⓐ. 18 3 . Ⓑ. 11 3 . Ⓒ. 7 3 . Ⓓ. 7 3− .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 3
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 3: Tính giá trị của biểu thức 3 5 C = 4 . 5 3 Ⓐ. 8 4 . Ⓑ. 3 4 . Ⓒ. 2 4 . Ⓓ. 5 4 .
Câu 4: Cho x, y là những số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là sai? Ⓐ. m+n n m n . n x y = ( xy) . . Ⓑ. ( ) n = . n xy x y . . Ⓒ. m. n m n x x x + = . . Ⓓ. ( m ) m.n x = x ..
Câu 5: Cho 0 a 1; , m n +
. Trong các đẳng thức sau, đẳng thức nào đúng? Ⓐ. m n m−n a = a . Ⓑ. m n m+n a = a . Ⓒ. m n m/ n a = a . Ⓓ. m n m.n a = a .
Câu 6: Viết dưới dạng lũy thừa thì số 5 3 2 2 2 bằng 3 7 17 11 Ⓐ. 10 2 . Ⓑ. 10 2 . Ⓒ. 10 2 . Ⓓ. 30 2 . 3
Câu 7: Viết biểu thức 2 4 về dạng lũy thừa 2m ta được m = ? 0,75 16 Ⓐ. 13 − . Ⓑ. 13 . Ⓒ. 5 . Ⓓ. 5 − . 6 6 6 6 4
Câu 8: Viết biểu thức 9. 81 về dạng lũy thừa 2a ta được a = ? 2 27 Ⓐ. − − 3 . Ⓑ. 1 . Ⓒ. 3 . Ⓓ. 1 . 2 2 2 2 2 2
Câu 9: Viết biểu thức về dạng 2 8 2x và biểu thức
về dạng 2y . Ta có 2 2
x + y = ? 4 8 3 4 Ⓐ. 2017 . Ⓑ. 11 . Ⓒ. 53 . Ⓓ. 2017 . 567 6 24 576 3 1 + 2− 3
Câu 10: Rút gọn biểu thức a .a P = ( . + a − ) a 0 2 2 2 2
Ⓐ. P = a . Ⓑ. 3 P = a . Ⓒ. 4 P = a . Ⓓ. 5 P = a .
Câu 11: Giá trị của biểu thức − − P − ( ) 4 − − = + + + ( ) 5 ( )5 10 3 2 1 9 3 .27 0, 2 .25 128 .2 0,1 . 0, 2 là Ⓐ. P = 38 . Ⓑ. P = 30 . Ⓒ. P = 40 . Ⓓ. P = 32 . x 1 − 1 Câu 12: Cho x 2
9 −12 = 0 , tính giá trị của biểu thức 2 P = −8.9 +19 − . x 1 3 − Ⓐ. 31. Ⓑ. 23. Ⓒ. 22 . Ⓓ. 15.
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 4
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung 1 2 2 1 − 1 a b Câu 13: Cho 1
a 0 , b 0 , giá trị của biểu thức T = 2(a + b) .(ab)2 . 1 + − 4 b a bằng Ⓐ. 1 2 1 1. Ⓑ. . Ⓒ. . Ⓓ. . 2 3 3
Câu 14: Cho a là số thực dương, khi đó 3 3
a a a viết dưới dạng lũy thừa là 1 5 1 1 Ⓐ. 6 a . Ⓑ. 18 a . Ⓒ. 2 a . Ⓓ. 12 a .
Câu 15: Giá trị của biểu thức 4log 2 5 a a
(với 0 a 1) bằng Ⓐ. 25. Ⓑ. 625. Ⓒ. 5. Ⓓ. 125. 4 1 2 − 3 3 3
a a + a Câu 16: Cho
a là số thực dương. Đơn giản biểu thức P = . 1 3 1 − 4 4 4
a a + a
Ⓐ. P = a(a + ) 1 .
Ⓑ. P = a −1. Ⓒ. P = . a .
Ⓓ. P = a +1. 2020 2019
Câu 17: Giá trị của biểu thức (1+ 2) .( 2 − ) 1 bằng
Ⓐ. Không xác định. Ⓑ. 1+ 2 . Ⓒ. 3 − 2 2 . Ⓓ. 2 −1.
Câu 18: Với số thực bất kỳ, mệnh đề nào sai? Ⓐ. 2 ( )2 10 = 100 . Ⓑ. 10 = ( 10) . Ⓒ. 2 10 = 10 . Ⓓ. (10 ) 2 = 10 . m m
Câu 19: Cho biểu thức 5 3 8 2 2 2 n = , trong đó
là phân số tối giản. Gọi 2 2
P = m + n . n
Khẳng định nào sau đây đúng?
Ⓐ. P(330;340).
Ⓑ. P(350;360). Ⓒ. P(260;370) . Ⓓ. P(340;350). 2020 2021
Câu 20: Cho P = (5− 2 6) (5+ 2 6) . Ta có
Ⓐ. P (2;7).
Ⓑ. P (6;9).
Ⓒ. P (0;3).
Ⓓ. P (8;10). BẢNG ĐÁP ÁN 1.B 2.B 3.B 4.A 5.D 6.D 7.A 8.B 9.D 10.D 11.C 12.B 13.A 14.C 15.A 16.C 17.B 18.D 19.D 20.D
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 5
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Dạng ②: So sánh các lũy thừa.
-Phương pháp:
_Sử dụng công thức về tính chất của lũy thừa. ; ; ; ; Đặc biệt:
_Casio: Xét hiệu với chức năng Calc đặc biết hóa.
A - Bài tập minh họa:
Câu 1: Cho các số nguyên dương m, n và số thực dương a . Mệnh đề nào sau đây sai? Ⓐ. (n a)m n m = a . Ⓑ. m n n.m a = a . Ⓒ. n m . a. m n m n a a + =
. Ⓓ. n .m n+m a a = a . Lời giải
PP nhanh trắc nghiệm Chọn D
Cả 4 mệnh đề đều xác định với điều kiện m, n
Casio: Thử trực tiếp 4 đáp án với giá trị
nguyên dương và a là số thực dương.
a = 2, n = 2, m = 3 ta thấy ở đáp án D cho hiệu
hai vế của mệnh đề khác 0 nên sai. 1 1 m+n +
Đáp án D sai vì n m n m m. . n a a = a = a khác với 1 n+m m+n a = a . m m m
Đáp án A đúng vì ( n ) 1 n m n n a
= a = a = a
Đáp án B đúng vì 1 1 n 1 m m n n m m.n m.n a = a = a = a = a .
Đáp án C đúng vì 1 1 m+n + n m m. n m m. . n m+n n a a = a = a == a .
Câu 2: Cho số thực a 1 và số thực , . Kết luận nào sau đây đúng? Ⓐ. 1 , . Ⓑ. . Ⓒ. . Ⓓ. a 1, a 1, a a a . Lời giải
PP nhanh trắc nghiệm Chọn D
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 6
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu D đúng theo lý thuyết.
a 1nên dễ thấy D đúng.
Câu 3: Cho các số thực a,b thỏa mãn 0 a b. Mệnh đề nào sau đây đúng? Ⓐ. x x
a b với x 0. Ⓑ. x x
a b với x 0 . Ⓒ. x x
a b với x 0 . Ⓓ. x x
a b với x . Lời giải
PP nhanh trắc nghiệm Chọn B
Casio: xét hiệu và calc a,b thỏa điều kiện. Lấy 1 a = , b =1, x = 1 − . Ta có 2 1 − 1 1 = 2; 1− =1
. Suy ra các khẳng định “ 2 x x
a b với x 0”, “ x x
a b với x 0 ”, “ x x
a b với x ” sai.
Câu 4: Cho a 1. Mệnh đề nào sau đây đúng? 3 2 1 Ⓐ. 1 a 3 1 1 a . Ⓑ. 1. Ⓒ. 3 a a . Ⓓ. . 5 2018 2019 a a a a Lời giải
PP nhanh trắc nghiệm Chọn A 1 Ta có 5 a .
Casio: xét hiệu và calc a thỏa điều kiện. 5 a Lại có 3 5 1 3 5 3 a a a . 5 a 1 a Chọn Ⓐ.
B - Bài tập rèn luyện: 4 Câu 1: Cho 2 5 a a và 2 log
0 . Khẳng định nào sau đây là đúng? b e
Ⓐ. a 1,b 1.
Ⓑ. 0 a 1 b .
Ⓒ. 0 b 1 a .
Ⓓ. 0 b a 1.
Câu 2: Cho số thực a thỏa mãn 3
a a . Mệnh đề nào sau đây đúng? Ⓐ. 0 a 1. Ⓑ. a 0 . Ⓒ. a 1. Ⓓ. a =1. 1 1
Câu 3: Nếu (a − )4 (a − )3 2 2
thì khẳng định nào sau đây là đúng?
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 7
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 2 a 3. Ⓑ. a 2 . Ⓒ. a 3. Ⓓ. a 3. 3 − 5 −
Câu 4: Cho ( m − ) 4 ( m − ) 4 2 1 2 1
. Khẳng định nào sau đây đúng? Ⓐ. m 1.
Ⓑ. 1 m 1. Ⓒ. m 1.
Ⓓ. 1 m 1. 2 2 3 − 5 −
Câu 5: Cho ( m − ) 4 ( m − ) 4 2 1 2 1
. Khẳng định nào sau đây đúng? Ⓐ. m 1.
Ⓑ. 1 m 1. Ⓒ. m 1.
Ⓓ. 1 m 1. 2 2
Câu 6: Cho a 1. Khẳng định nào dưới đây đúng? 3 2 1 Ⓐ. a 1 1 − 1 1 . Ⓑ. . Ⓒ. 3 a . Ⓓ. 3 a a . a 2017 2018 a a 5 a 1 1
Câu 7: Nếu (a − )4 (a − )3 2
2 thì khẳng định nào sau đây là đúng? Ⓐ. 2 a 3. Ⓑ. a 2 . Ⓒ. a 3. Ⓓ. a 3. 1 1
Câu 8: Nếu (a − )4 (a − )3 2 2
thì khẳng định nào sau đây là đúng? Ⓐ. 2 a 3. Ⓑ. a 2 . Ⓒ. a 3. Ⓓ. a 3.
Câu 9: Cho số thực a 1. Mệnh đề nào sau đây sai? 3 4 1 Ⓐ. a 1 1 − 1 1. Ⓑ. 3 a a . Ⓒ. . Ⓓ. 2 a . a 2020 2021 a a 3 a
Câu 10: Khẳng định nào sau đây đúng? Ⓐ. 2 − 019 2 − 020 ( 5 + 2) ( 5 + 2) . Ⓑ. 2018 2019 ( 5 + 2) ( 5 + 2) . Ⓒ. 2020 2021 ( 5 − 2) ( 5 − 2) . Ⓓ. 2018 2019 ( 5 − 2) ( 5 − 2) . BẢNG ĐÁP ÁN 1.B 2.A 3.D 4.D 5.D 6.C 7.D 8.D 9.B 10.C
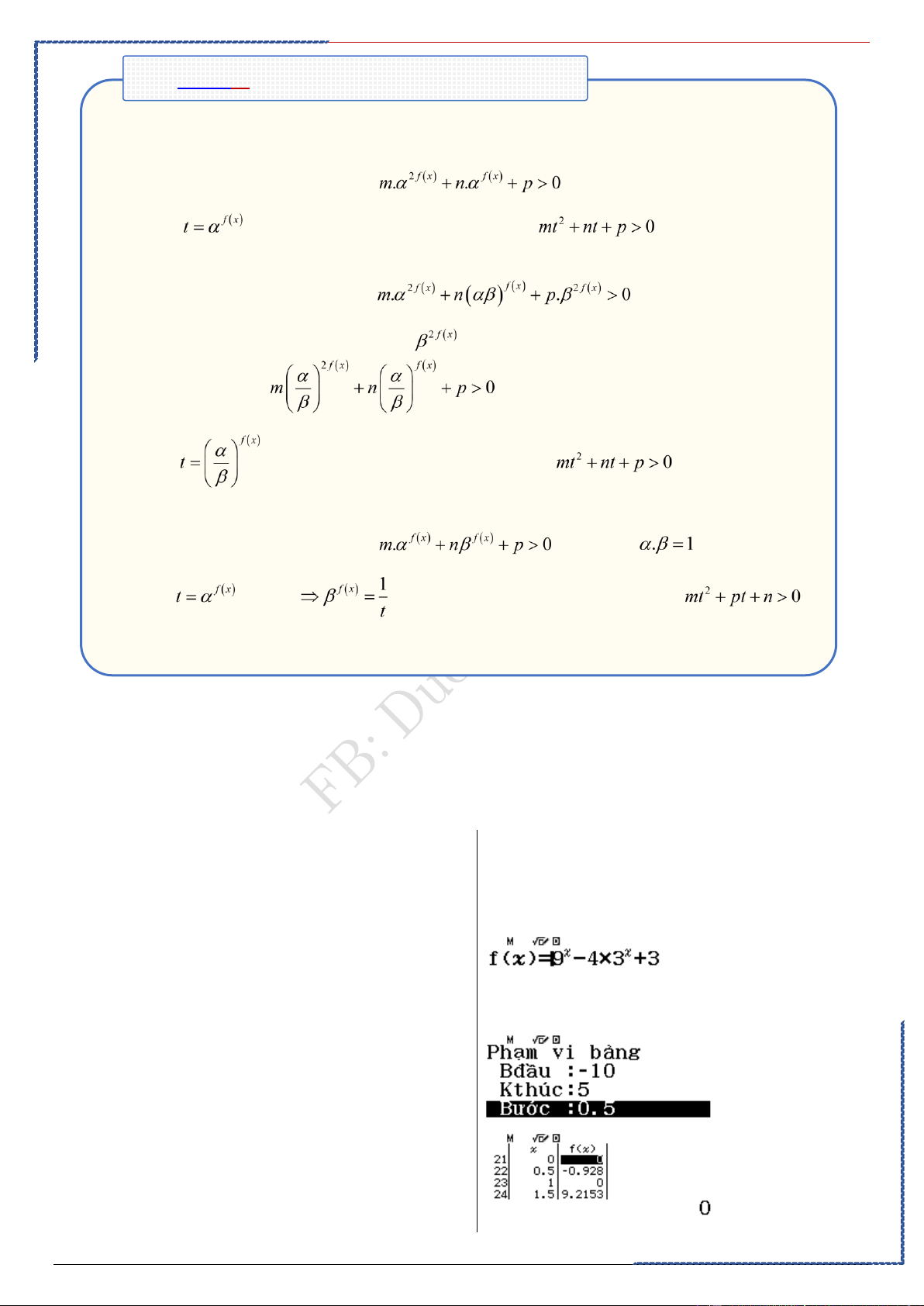
Dạng ③: Biến đổi, rút gọn, biểu diễn các biểu
thức chứa lũy thừa.
-Phương pháp:
_Sử dụng công thức, tính chất của mũ, lũy thừa.
_Casio: Xét hiệu với chức năng Calc
A - Bài tập minh họa:
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 8
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung 1
Câu 1: Cho a là số thực dương. Giá trị rút gọn của biểu thức 3 P = a a bằng 2 5 1 Ⓐ. 3 a . Ⓑ. 5 a . Ⓒ. 6 a . Ⓓ. 6 a . Lời giải
PP nhanh trắc nghiệm Chọn Ⓒ.
Casio: lấy log ra mũ ngay chọn C 1 1 1 1 1 5 + Ta có: 3 3 2 3 2 6 P = a
a = a .a = a = a .
Câu 2: Biểu diễn biểu thức 3 2 4 3 Q = x x
x dưới dạng lũy thừa số mũ hữu tỉ. 23 1 23 12 Ⓐ. 12 Q = x . Ⓑ. 4 Q = x . Ⓒ. 24 Q = x . Ⓓ. 23 Q = x . Lời giải
PP nhanh trắc nghiệm Chọn C
Casio: lấy log ra mũ ngay chọn C Ta có: 3 2 4 3 Q = x x x 1 1 3 23 1+ 2+ 2 3 4 24 = x = x 1 1 5 3 2 2
a a − a
Câu 3: Cho số thực dương
a 0 và khác 1. Hãy rút gọn biểu thức R = . 1 7 19 4 12 12
a a − a Ⓐ. R =1+ a . Ⓑ. R =1 . Ⓒ. R = a .
Ⓓ. R =1− a . Lời giải
PP nhanh trắc nghiệm Chọn A
Casio: Nhập biểu thức R với a = 2 ta được Q = 3 Ta có:
Suy ra đáp án là A 1 1 5 3 2 2
a a − a R = 1 7 19 4 12 12
a a − a 1 1
a a (1− a ) 5 2 3 2 6 a (1+ a) = = =1+ a 1 7 5 4 12
a a (1− a) 6 a
B - Bài tập rèn luyện: 1
Câu 1: Cho a là số thực dương. Giá trị rút gọn của biểu thức 2 4 P = a a bằng
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 9
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung 1 3 5 1 Ⓐ. 2 a . Ⓑ. 4 a . Ⓒ. 4 a . Ⓓ. 4 a .
Câu 2: Cho a là số thực dương. Biểu thức 2 3
a . a được viết dưới dạng lũy thừa với số mũ hữu tỉ là 4 7 5 2 Ⓐ. 3 a . Ⓑ. 3 a . Ⓒ. 3 a . Ⓓ. 3 a . 1
Câu 3: Rút gọn biểu thức 6 3
P = x . x với x 0. 1 2 Ⓐ. 8 P = x . . Ⓑ. 9 P = x . Ⓒ. 2 P = x .
Ⓓ. P = x. 3
Câu 4: Cho a là một số thực dương. Viết biểu thức 3 2 5
P = a . a dưới dạng lũy thừa với số mũ hữu tỉ. 1 2 1 19 Ⓐ. − 15 P = a . Ⓑ. 5 P = a . Ⓒ. 15 P = a . Ⓓ. 15 P = a .
Câu 5: Rút gọn biểu thức 3 5 2
P = x : x với x 0. 13 2 Ⓐ. 5 P = x . Ⓑ. 9 P = x . Ⓒ. 2 P = x .
Ⓓ. P = x. 2 1 −
Câu 6: Đơn giản biểu thức 1 2 P = a .
được kết quả là a Ⓐ. 2 a . Ⓑ. 2 2 1 a − . Ⓒ. 1 2 a − . Ⓓ. a . 1
Câu 7: Rút gọn biểu thức 3 6
P = x . x với x 0 . 1 2 Ⓐ. 2 P = x .
Ⓑ. P = x . Ⓒ. 8 P = x . Ⓓ. 9 P = x . 5
Câu 8: Rút gọn biểu thức 3 3
Q = b : b với b 0 . 5 4 4 Ⓐ. − 2 Q = b . Ⓑ. 9 Q = b . Ⓒ. 3 Q = b . Ⓓ. 3 Q = b . 3
Câu 9: Cho a là một số thực dương. Viết biểu thức 3 2 5
P = a : a dưới dạng lũy thừa với số mũ hữu tỉ. 1 2 1 19 Ⓐ. − 15 P = a . Ⓑ. 5 P = a . Ⓒ. 15 P = a . Ⓓ. 15 P = a . ( + a − ) 3 1 3 1
Câu 10: Cho biểu thức P =
, với a 0 . Mệnh đề nào dưới đây đúng? 5 −3 4− 5 a .a 1 3 Ⓐ. 2 P = a .
Ⓑ. P = a . Ⓒ. 2 P = a . Ⓓ. 3 P = a . 4 − a ( 1 2 3 3 3 a + a )
Câu 11: Cho số thực dương a . Biểu thức thu gọn của biểu thức P = là 1 − a ( 3 1 4 4 4 a + a )
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 10
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. a . Ⓑ. a +1. Ⓒ. 2a . Ⓓ. 1. 3 1 + 2− 3
Câu 12: Rút gọn của biểu thức a .a ( là: + a − ) 2 1 2 1 Ⓐ. a . Ⓑ. 2 a . Ⓒ. 1. Ⓓ. 3 a . ( + a − ) 3 1 3 1
Câu 13: Rút gọn biểu thức: P =
(a 0). Kết quả là − 3+2 2+ 3 a .a 1 Ⓐ. 1 1. Ⓑ. 2 a . Ⓒ. 4 a . Ⓓ. . 4 a
Câu 14: Viết biểu thức 3 4 P = . x
x ( x 0 ) dưới dạng luỹ thừa với số mũ hữu tỷ. 1 5 1 5 Ⓐ. 12 P = x . Ⓑ. 12 P = x . Ⓒ. 7 P = x . Ⓓ. 4 P = x .
Câu 15: Cho biểu thức 3 6 5 P =
x. x. x ( x 0 ). Mệnh đề đúng là 5 7 5 2 Ⓐ. 3 P = x . Ⓑ. 3 P = x . Ⓒ. 2 P = x . Ⓓ. 3 P = x .
Câu 16: Cho biểu thức 6 4 5 3 P = . x
x . x , với x 0 . Mệnh đề nào dưới đây đúng? 47 15 7 5 Ⓐ. 48 P = x . Ⓑ. 16 P = x . Ⓒ. 16 P = x . Ⓓ. 42 P = x .
Câu 17: Cho biểu thức 4 3 2 3 Q = . x
x . x , x 0 . Mệnh đề nào dưới đây đúng? 13 17 15 15 Ⓐ. 24 Q = x . Ⓑ. 12 Q = x . Ⓒ. 6 Q = x . Ⓓ. 24 Q = x . 1 1 1 1 − − 3 3 3 3 −
Câu 18: Cho biểu thức a b a b P = , với ,
a b 0 . Mệnh đề nào dưới đây đúng? 3 2 3 2 a − b Ⓐ. 1 1 P = . Ⓑ. 3 P = ab . Ⓒ. = ( )23 P ab . Ⓓ. P = − . 3 ab (ab)2 3 3 4 3 4 +
Câu 19: Cho biểu thức b a a b P =
, với a 0 , b 0. Mệnh đề nào sau đây đúng? 3 3 a + b 1 1 1 1
Ⓐ. P = b + a .
Ⓑ. P = 2ab . Ⓒ. 3 3
P = a .b . Ⓓ. 2 2
P = a .b . 1 1 2 3 2 3 + Câu 20: Cho a b b a
a, b là hai số thực dương. Rút gọn biểu thức . 6 6 a + b 1 2 2 2 2 1 Ⓐ. 3 3 a b . Ⓑ. 3 3 a b . Ⓒ. 3 ab . Ⓓ. 3 3 a b .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 11
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung BẢNG ĐÁP ÁN 1.C 2.B 3.D 4.D 5.A 6.D 7.B 8.D 9.C 10.B 11.A 12.B 13.B 14.B 15.A 16.C 17.A 18.A 19.A 20.C
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 12
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021 CHƯƠNG ②: FB: Duong Hung
Bài 2: HÀM SỐ LŨY THỪA
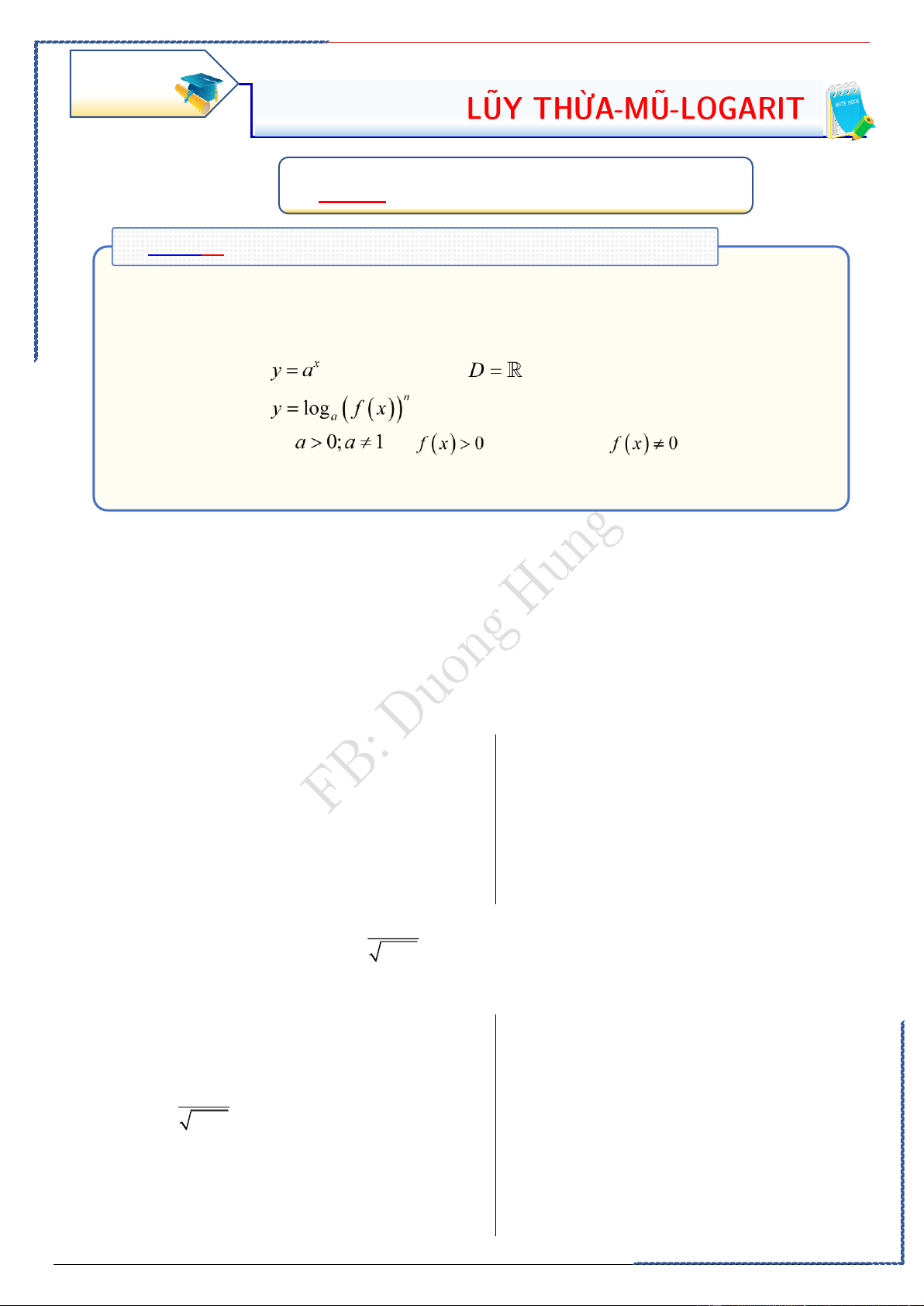
Dạng ①: Tìm tập xác định của hàm số.
-Phương pháp: Xét hàm số
⬧. Khi nguyên dương: hàm số xác định khi và chỉ khi xác định.
⬧. Khi nguyên âm: hàm số xác định khi và chỉ khi .
⬧. Khi không nguyên: hàm số xác định khi và chỉ khi . . Casio: table NHẬP HÀM START: a END: b STEP khéo tý.
Lưu ý: Chỉ dùng MTCT để loại trừ là chính, và không dùng MTCT để chọn trực tiếp
đáp án. Đối với TXĐ hàm số lũy thừa an toàn nhất vẫn là giải theo công thức.
A - Bài tập minh họa:
Câu 1: Hàm số y = ( x − )12 2
có tập xác định là
Ⓐ. D = 2;+). Ⓑ. D = . Ⓒ. D = (2;+) . Ⓓ. D = \ 2 . Lời giải
PP nhanh trắc nghiệm
Chọn C Casio:
Hàm số y = ( x − )12 2
xác định khi x − 2 0 x 2 .
Tập xác định của hàm số là D = (2;+) .
Chú ý biểu thức f (x) 0 nên chọn C 1
Câu 2: Tìm tập xác định của hàm số 2 3
y = (x − 3x + 2) . Ⓐ. D = (0;+ ) . Ⓑ. D = (1;2). Ⓒ. D = (− ; 1) (2;+ ) . Ⓓ. D = \{1;2}. Lời giải
PP nhanh trắc nghiệm Chọn C Casio: INEQ
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 13
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung x 1
Điều kiện: 2
x − 3x + 2 0 x 2
Từ điều kiện suy ra tập xác định của hàm số là D = (− ; 1) (2;+ ) −
Câu 3: Cho hàm số y = ( x − ) 5 1
. x . Tập xác định của hàm số là Ⓐ. D = (1;+).
Ⓑ. D = 0;+) \ 1 .
Ⓒ. D = 0;+) . Ⓓ. D = . Lời giải
PP nhanh trắc nghiệm
Chọn B x 0 x 0 Casio:
Hàm số xác định khi và chỉ khi . x −1 0 x 1
Vậy: Tập xác định của hàm số là D = 0;+) \ 1 . Chọn B khá dễ dàng
Chọn Satrt, end thích hợp dựa vào đáp án
B - Bài tập rèn luyện:
Câu 1: Tìm tập xác định D của hàm số n
y = x , với n là một số nguyên âm. Ⓐ. D = .. Ⓑ. D = \{0}. Ⓒ. D = (−;0).
Ⓓ. D = (0;+ ).
Câu 2: Tìm điều kiện của + x để hàm số 1 y = x có nghĩa. Ⓐ. x .. Ⓑ. x 0. Ⓒ. x 0. Ⓓ. x 0.
Câu 3: Tập xác định D của hàm số y = ( x − x − )3 2 6 5 là Ⓐ. D = ( 4 − ) ;1 . Ⓑ. D = 1;7. Ⓒ. D = 1;7. Ⓓ. D = . R
Câu 4: Hàm số y = ( x − )12 2
có tập xác định là Ⓐ. D = 2;+). Ⓑ. D = . Ⓒ. D = (2;+) . Ⓓ. D = \ 2 .
Câu 5: Tập xác định của hàm số y = ( − x)13 2 là Ⓐ. (2;+) . Ⓑ. \ 2 . Ⓒ. . Ⓓ. ( ; − 2) .
Câu 6: Tìm tập xác định của hàm số 2 y (x 1)− = − Ⓐ. \{1}. Ⓑ. (1;+). Ⓒ. 1;+) . Ⓓ. \{0}.
Câu 7: Tập xác định − D của hàm số 2 y = x là Ⓐ. D = (−;0) .
Ⓑ. D = (−; + ) \
0 . Ⓒ. D = (−; + ). Ⓓ. D = (0;+) .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 14
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung 1
Câu 8: Tập xác định D của hàm số 3
y = x là Ⓐ. D = (−;0) .
Ⓑ. D = (−; + ) \
0 . Ⓒ. D = (−; + ). Ⓓ. D = (0;+) .
Câu 9: Tập xác định D của hàm số e
y = x là Ⓐ. D = (−;0) .
Ⓑ. D = (−; + ) \
0 .Ⓒ. D = (−; + ). Ⓓ. D = (0;+) .
Câu 10: Tập xác định D của hàm số 5 y = x là Ⓐ. D = (−;0) .
Ⓑ. D = (−; + ) \
0 .Ⓒ. D = (−; + ). Ⓓ. D = (0;+) .
Câu 11: Tìm tập xác định D của hàm số 4 2 y =
x − 3x − 4 . Ⓐ. D = 1 − ;4. Ⓑ. D = (− ;
− 14;+) .Ⓒ. D = ( 1 − ;4) . Ⓓ. D = (− ; − )1(4;+) .
Câu 12: Tập xác định D của hàm số y = ( + x − x ) 2019 2 5 4 . Ⓐ. D = \ 1 − ; 5 . Ⓑ. D = (− ;
− )1(5;+).Ⓒ. D = (1;5) . Ⓓ. D = ( 1 − ;5) . −
Câu 13: Tìm tập xác định của hàm số y = (x − x + ) 3 2 7 10 Ⓐ. \2; 5 . Ⓑ. (− ; 2)(5;+) . Ⓒ. . Ⓓ. (2;5) .
Câu 14: Tập xác định của hàm số y = ( 3 x − 8) là Ⓐ. \ 2 . Ⓑ. ( ; − 2) . Ⓒ. . Ⓓ. (2;+) . 3 −
Câu 15: Tập xác định 2x 3
D của hàm số y = là 2
x −3x + 2 Ⓐ. D = . R Ⓑ. D = R 1; 2 . Ⓒ. 3 D = ; + . Ⓓ. D = (0;+). 2 3 2 x − 4
Câu 16: Tìm tập xác định của hàm số y = . x 1 + Ⓐ. D = \{−1}. Ⓑ. D = (− ; 1 − )[4;+ ) . Ⓒ. D = ( 1 − ;4). Ⓓ. D = (− ; 1 − )(4;+ ) . −
Câu 17: Tìm tập xác định D của hàm số y = (x − x) 6cos 2 4 . Ⓐ. D = (− ;
0)(1;+) .Ⓑ. D = \0 ;1 . Ⓒ. D = (0; ) 1 . Ⓓ. D = .
Câu 18: Hàm số nào sau đây có tập xác định là ? 3 + Ⓐ. x 2 − y = ( x + ) 2 2 4 .
Ⓑ. y = ( x + )12 4 . Ⓒ. y = .
Ⓓ. y = (x + x − ) 2 2 2 3 . x 0 2 1− x
Câu 19: Tập xác định hàm số f ( x) = là 4 − x Ⓐ. (− ; 4) \1;− 1 . Ⓑ.(− ; + ) \ 1 − ;1 . Ⓒ. (− ; 4) . Ⓓ. ( 1 − ) ;1 . −
Câu 20: Tập xác định của hàm số = ( x y − ) 2 3 9 là
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 15
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. D = (− ; 2).. Ⓑ.(2;+) . Ⓒ. D = (− ;
+). Ⓓ. D = (− ; +) \ 2 . BẢNG ĐÁP ÁN 1.B 2.D 3.D 4.C 5.C 6.A 7.B 8.D 9.D 10.C 11.B 12.D 13.A 14.D 15.B 16.D 17.A 18.A 19.A 20.D
Dạng ②: Đạo hàm của hàm số luỹ thừa
. Phương pháp giải:
✓Dựa vào công thức đạo hàm ⬧. ⬧.
✓Và các công thức tính đạo hàm đã học. . Casio: ⬧.
(thường ra số có dạng với nguyên dương)
A - Bài tập minh họa:
Câu 1: Tính đạo hàm của hàm số 1 2 − = x y . 1− x − 1− x Ⓐ. −ln 2 ln 2 2 2 1 = .2 −x y . Ⓑ. 1 = .2 −x y . Ⓒ. y = . Ⓓ. y = . 2 1− x 2 1− x 2 1− x 2 1− x Lời giải
PP nhanh trắc nghiệm Chọn A
Casio: Xét hiệu x 1 − 1
y = 2 − .ln 2.( 1− x ) 1− x ( ) = .2 .ln 2. 2 1− x −ln 2 Hay 1 = .2 −x y 2 1− x
Chú ý điều kiện xác định. Chọn A.
Câu 2: Tính đạo hàm của hàm số 6 1 3 + = x y . Ⓐ. 6 x+2 y = 3 .2 . Ⓑ. 6 = (6 +1).3 x y x Ⓒ. 6 x+2 y = 3 .2 ln 3 . Ⓓ. 6 1 3 + = x y .ln 3 Lời giải
PP nhanh trắc nghiệm Chọn C Ta có: Casio: Xét hiệu 6 x 1 + y =
y = ( x + ) 6x 1+ 6 x 1 + 6 x+2 3 6 1 3 ln 3 = 6 3 ln 3 = 3 2 ln 3
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 16
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Câu 3: Cho hàm số x − = + x y e
e . Tính y( ) 1 = ? Ⓐ. 1 e + . Ⓑ. 1 e − . Ⓒ. 1 −e + . Ⓓ. 1 −e − . e e e e Lời giải
PP nhanh trắc nghiệm
Chọn A Ta có:
f '( x + x − f ' x 0 ) ( 0) Với lim = f ' (x 0 ) x −x x −x →
y = e − e
y = e + e x 0 x x Casio: y ( ) 1 1 = e + e d -Tính ( f (x)) x 0 x dx = d - Tính ( f (x)) 6 − x= + 0 x 10 dx Ans − Pr eans - Tính 6 10− Xấp xỉ.
B - Bài tập rèn luyện:
Câu 1: Đạo hàm của hàm số 5 y x − = bằng Ⓐ. 1 4 y ' x − = − . Ⓑ. 6 y ' 5x − = − . Ⓒ. 6 y ' 5x − = . y x − = 4 Ⓓ. 4 ' 5 .
Câu 2: Tính đạo hàm của hàm số y = (x + )3 2 2 1 . 1 Ⓐ. 3 ( 3 3 x + )1 2 2 1 . Ⓑ. 4 x . Ⓒ. (2x)12 . Ⓓ. 3x(x + )1 2 2 1 . 2 4 2 1
Câu 3: Đạo hàm của hàm số 3
y = (x −1) tại điểm x = 2 là Ⓐ. 1 . Ⓑ.1. Ⓒ. 3. Ⓓ. 0. 3
Câu 4: Đạo hàm của hàm số 3 y = (5 − x)
tại điểm x = 4 là Ⓐ. − 3. Ⓑ.1. Ⓒ. 3. Ⓓ. 0. 1 −
Câu 5: Tính đạo hàm của hàm số 3 y = x . 2 4 − 2 4 − Ⓐ. 2 4 1 1 3 y = x . Ⓑ. 3 y = − x . Ⓒ. 3
y = − x . Ⓓ. 3 y = − x . 3 3 3 3
Câu 6: Đạo hàm của hàm số 5 y = x là
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 17
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung 4 Ⓐ. 1 1 − 5 Ⓑ. Ⓒ. 1 5 x . Ⓓ. 5 5 x 5 4 5 x 5 5 4 x
Câu 7: Đạo hàm của hàm số 3 y = x là 4 Ⓐ. 1 1 1 1 3 x . Ⓑ. Ⓒ. Ⓓ. 3 3 2 3 x 3 2 x 3 2 x
Câu 8: Đạo hàm của hàm số y = ( x + )2 3 1 là − Ⓐ. − 3 y = (3x + ) 1 .
Ⓑ. y = ( x + ) 1 2 3 1 . Ⓒ. 2 y = 3 . Ⓓ. y = (3x + ) 22 1 . 2 2 2
Câu 9: Đạo hàm của hàm số y = ( − x) 3 5 là Ⓐ. −
y = 3 (5 − x) . Ⓑ. y = ( − x) 3 1 3 5 . Ⓒ. − − y = ( − x)1 3 3 5 . Ⓓ. y = − ( − x) 3 1 3 5 . 1 Câu 10: Hàm số 3
y = (x −1) có đạo hàm là 2 3 − 3 − Ⓐ. 1 1 (x 1) (x 1) y ' = Ⓑ. y ' = Ⓒ. y ' = Ⓓ. y ' = 2 3 3 (x −1) 3 3 (x −1) 3 3
Câu 11: Tính đạo hàm của hàm số y = ( x + x + )4 2 3 3 2 1 . Ⓐ. 4 4 y ' =
(6x + 2)(3x + 2x +1)2 2 3 .
Ⓑ.y ' = (3x + 2x + 1)2 2 3 . 3 3 Ⓒ. 4 4 y ' =
(6x + 2)(3x + 2x +1)1 2 3 .
Ⓓ. y ' = (3x + 2x + 1)1 2 3 . 3 3
Câu 12: Tính đạo hàm của hàm số y = (x − x + )1 2 3 1 Ⓐ. 2x −1 2x −1 y = . Ⓑ. y = . 3 2 3 x − x +1 3 ( x − x + )2 2 3 1 Ⓒ. 2x −1 1 y = . Ⓓ. y = . (x − x+ )2 2 3 1 3 ( x − x + )2 2 3 1
Câu 13: Đạo hàm của hàm số 5
y = sin 3x + 2 là Ⓐ. cos 3x − . Ⓑ. cos 3x . Ⓒ. 3cos3x . Ⓓ. 3cos 3x . 5 5 5 (sin 3x + 2)6 5 2 sin 3x + 2 5 sin 3x + 2 5 (sin 3x + 2)4 5
Câu 14: Cho hàm số f (x ) = 3 2
x + x + 1. Giá trị f ' (0) là Ⓐ. 3. Ⓑ.1. Ⓒ. 1 . Ⓓ. 2 . 3 3 x −1
Câu 15: Cho hàm số f (x) 5 = . Tính f '(0). x +1 Ⓐ. f ( ) 1 ' 0 = . Ⓑ. f ( ) 1 ' 0 = − . Ⓒ. f ( ) 2 ' 0 = . Ⓓ. f ( ) 2 ' 0 = − . 5 5 5 5 Câu 16: Cho hàm số 3
y = 1 + 2 sin 2x. Đạo hàm tại của hàm số đã cho tại điểm x = 0.
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 18
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ.y ( ) 4 ' 0 = . Ⓑ.y ( ) 1 ' 0 = .
Ⓒ. y ' (0) = 1. Ⓓ. y ( ) 2 ' 0 = − . 3 3 3
Câu 17: Đạo hàm của hàm số 1 y = là 4 x x Ⓐ. 5 5 5 5 y = Ⓑ. y = − Ⓒ. 4 y = x. Ⓓ. y = − x 4 9 4 x 4 4 5 4 x
Câu 18: Đạo hàm của hàm số: = ( 2 y x + x) là Ⓐ. − 1 −
y = ( x + x) 1 2 2 . Ⓑ. y = ( 2 x + x) (2x + ) 1 . Ⓒ. + −
y = ( x + x) 1 2 (2x + ) 1 . Ⓓ. = ( + ) 1 2 y x x . 1
Câu 19: Đạo hàm của hàm số y =
tại điểm x =1 là ( − 1+ x − x ) 5 2 3 Ⓐ. y( ) 5 1 = − Ⓑ. y( ) 5 1 = Ⓒ. y( ) 1 = 1. Ⓓ. y( ) 1 = 1 − . 3 3 −
Câu 20: Cho hàm số y = ( x + ) 2 2
. Hệ thức nào sau đây đúng? Ⓐ. 2 y − y = 0. Ⓑ. 2
y − 6 y = 0. Ⓒ. 4
y − 8y = 0.
Ⓓ. y − y = 0. BẢNG ĐÁP ÁN 1.B 2.D 3.A 4.B 5.D 6.B 7.B 8.D 9.D 10.A 11.C 12.B 13.D 14.C 15.C 16.A 17.B 18.B 19.A 20.B
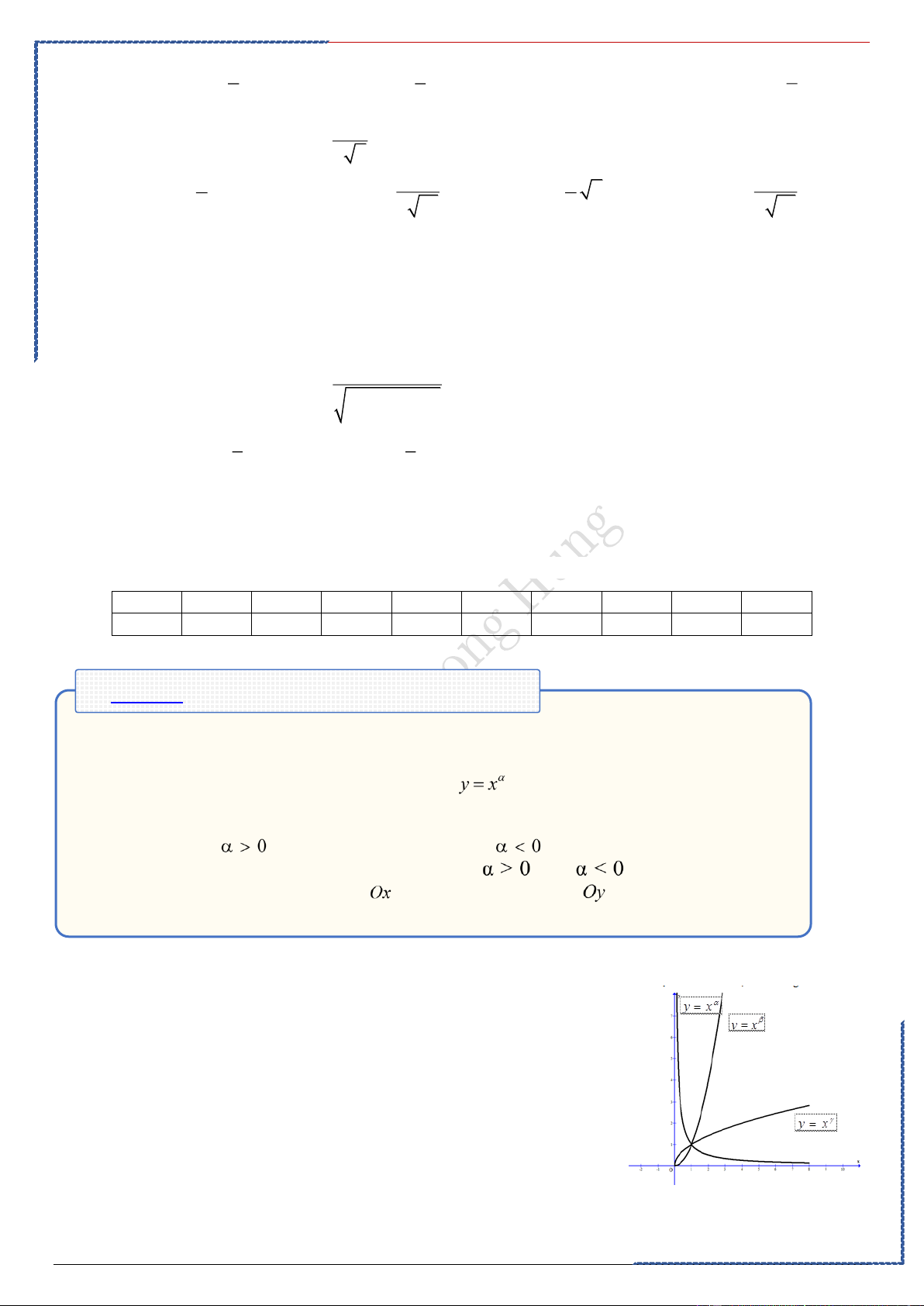
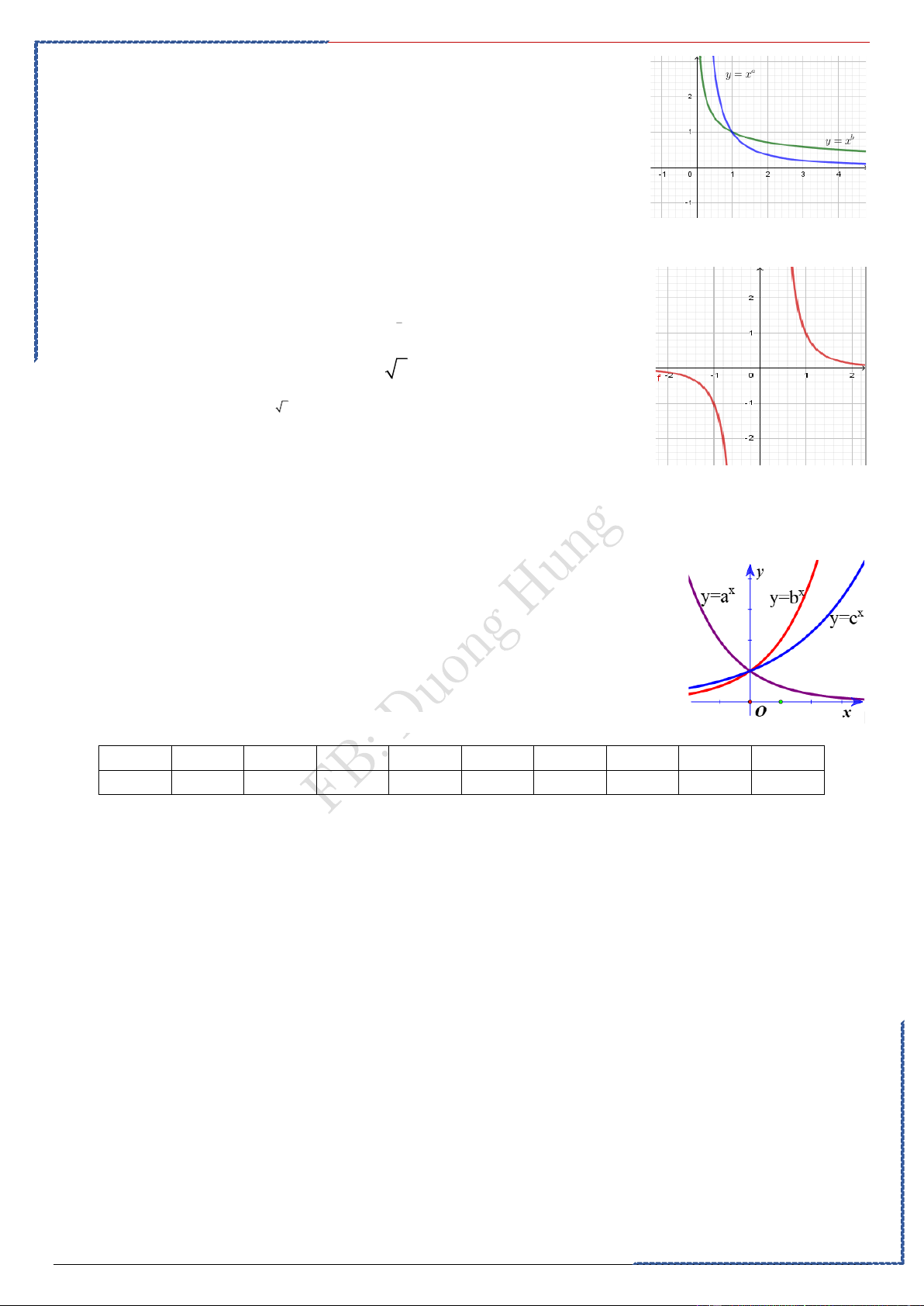
Dạng ③: Tính chất, đồ thị của hàm số luỹ
. Phương pháp giải:
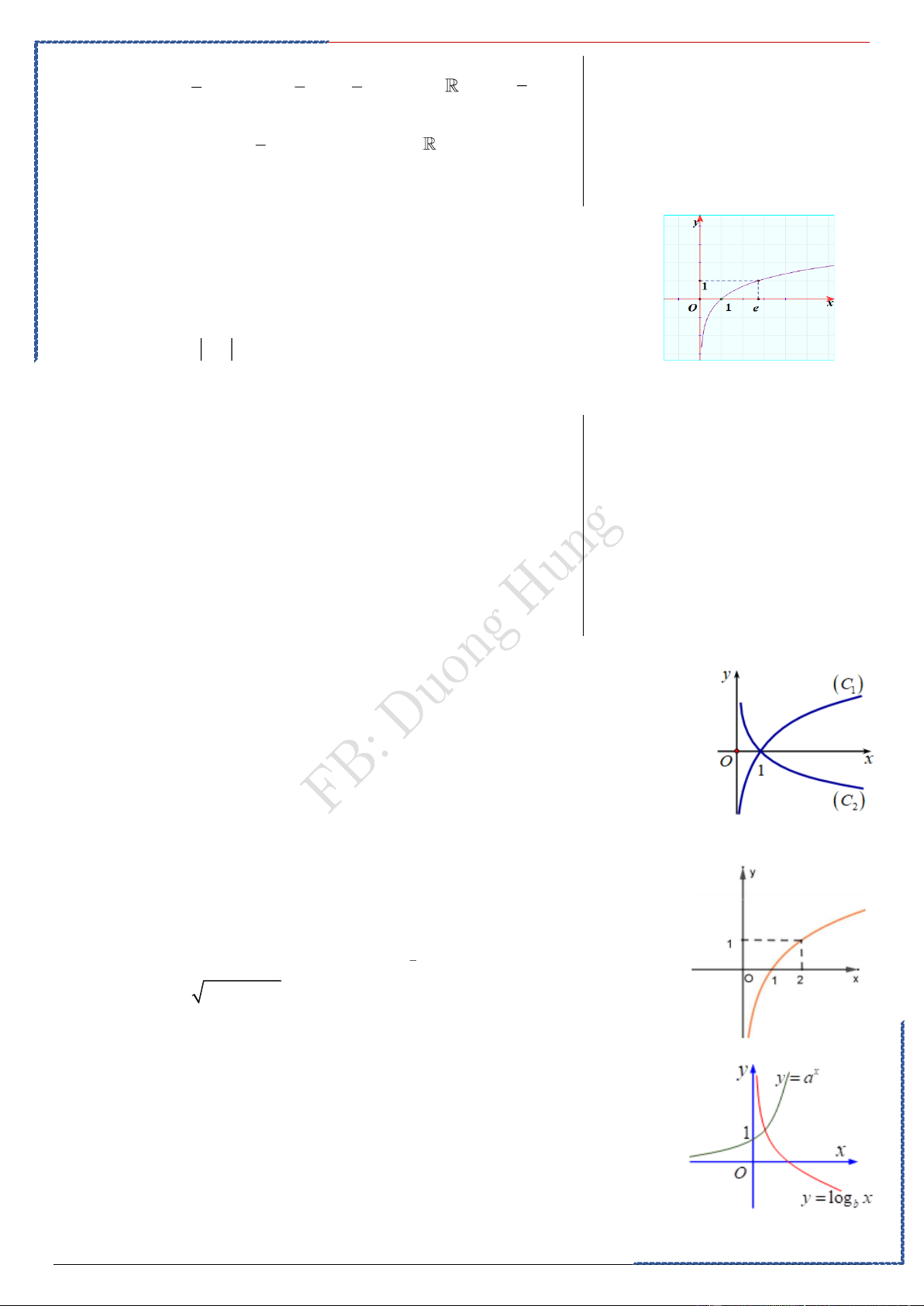
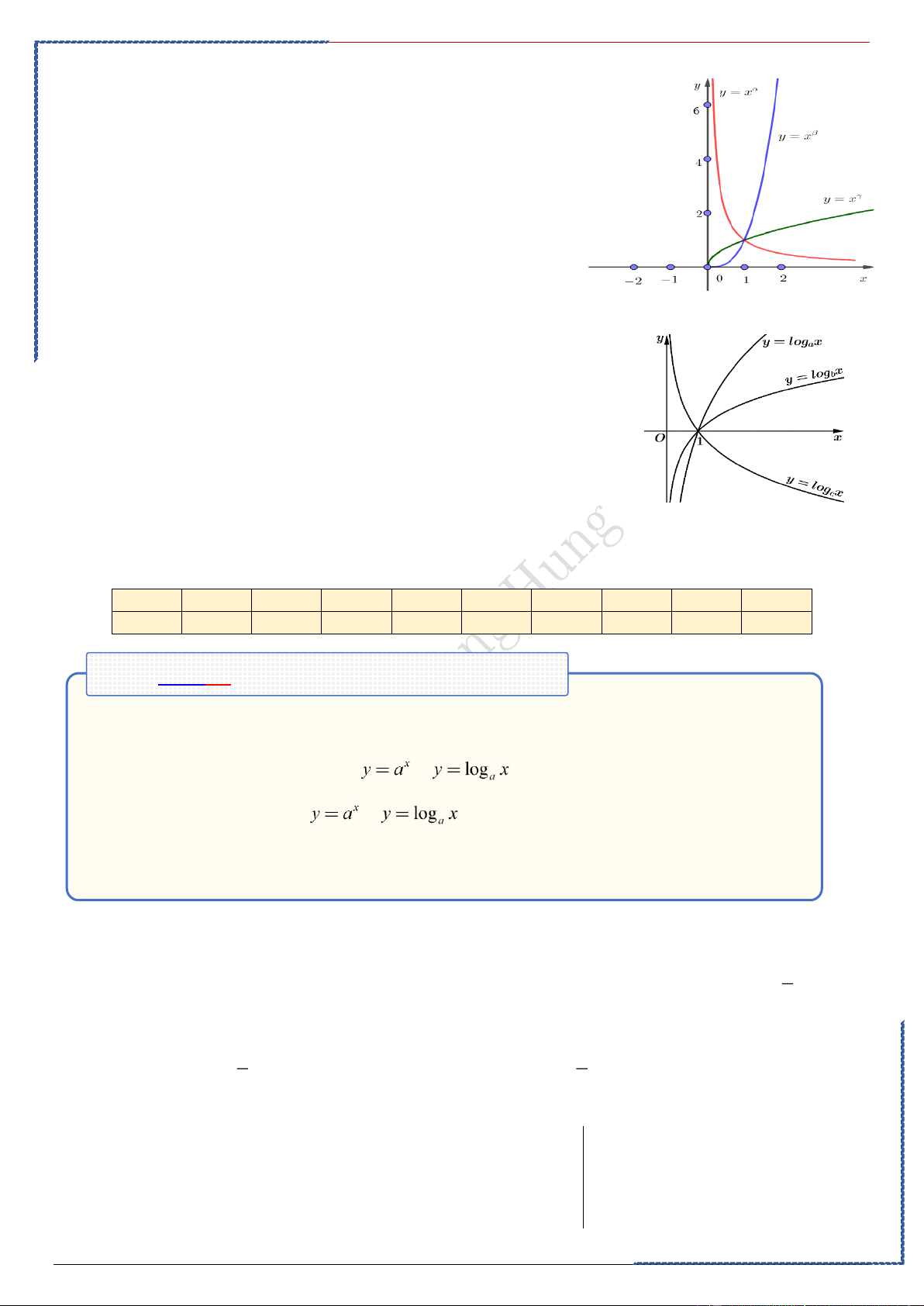
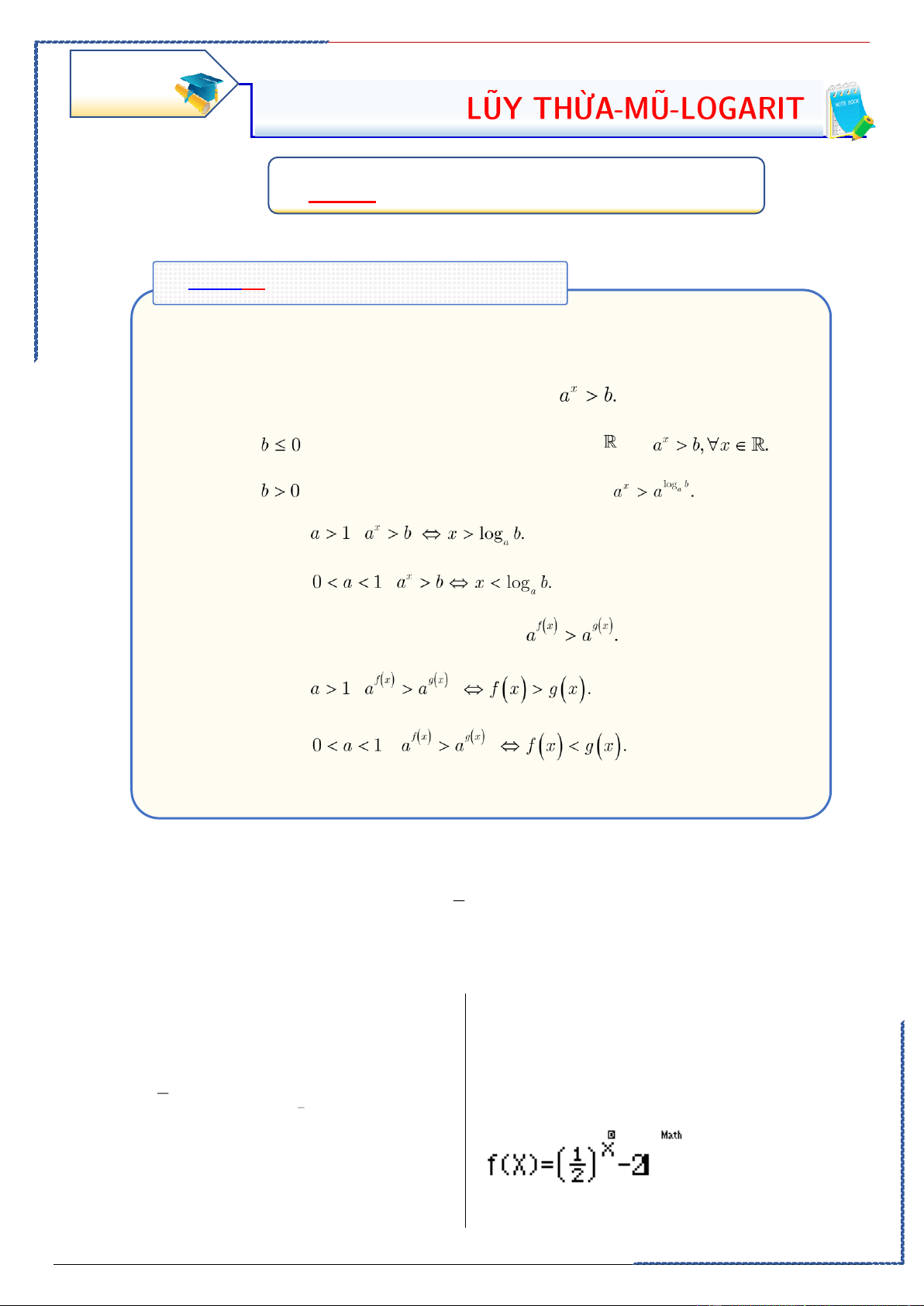
Lưu ý: Những đặc điểm sau của đồ thị hàm số :
• Đồ thị luôn đi qua điểm (1; 1). • Khi
hàm số luôn đồng biến, khi
hàm số luôn nghịch biến
• Đồ thị hàm số không có tiệm cận khi ; khi đồ thị hàm số có tiệm cận ngang là trục
, tiệm cận đứng là trục .
A - Bài tập minh họa:
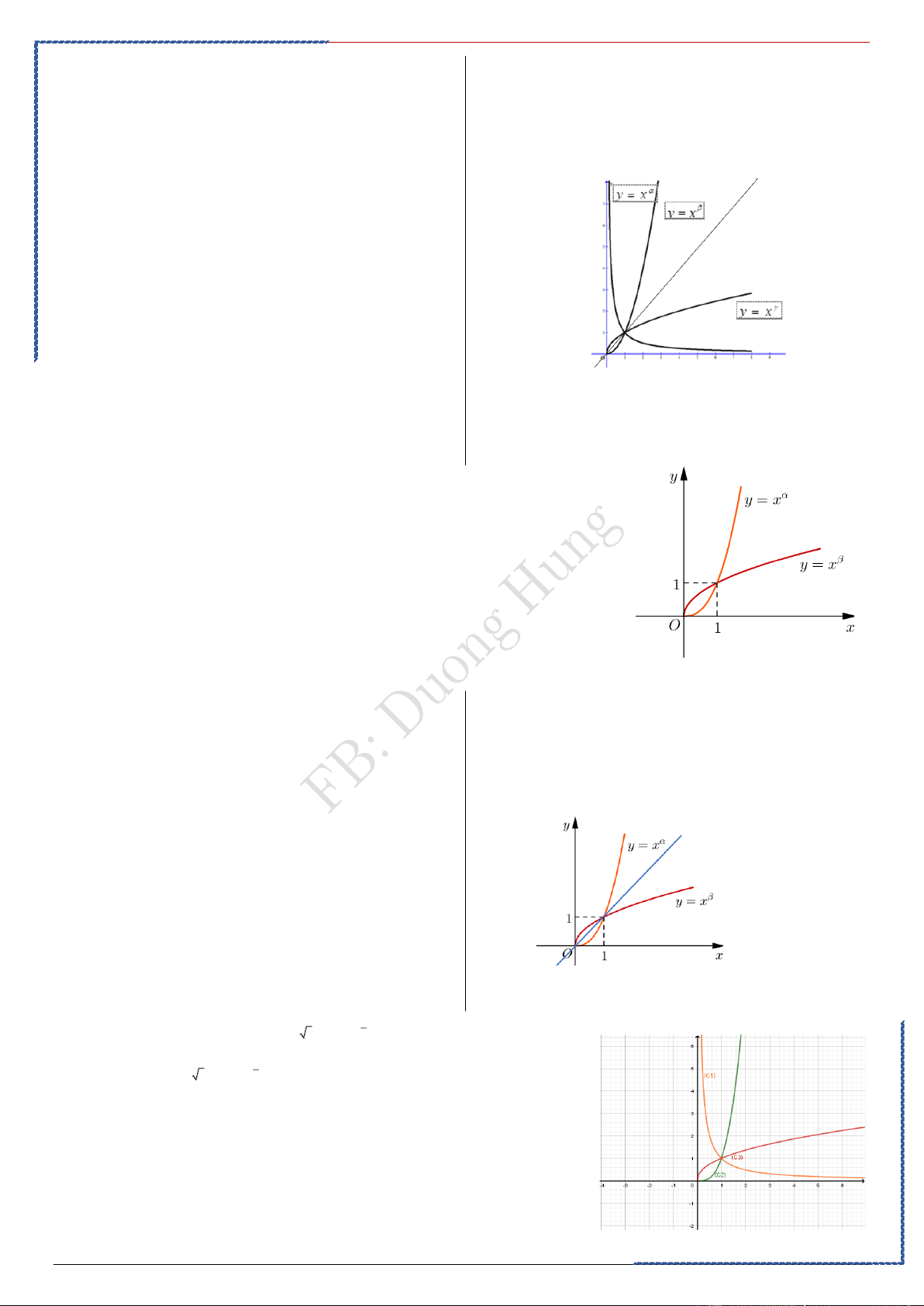
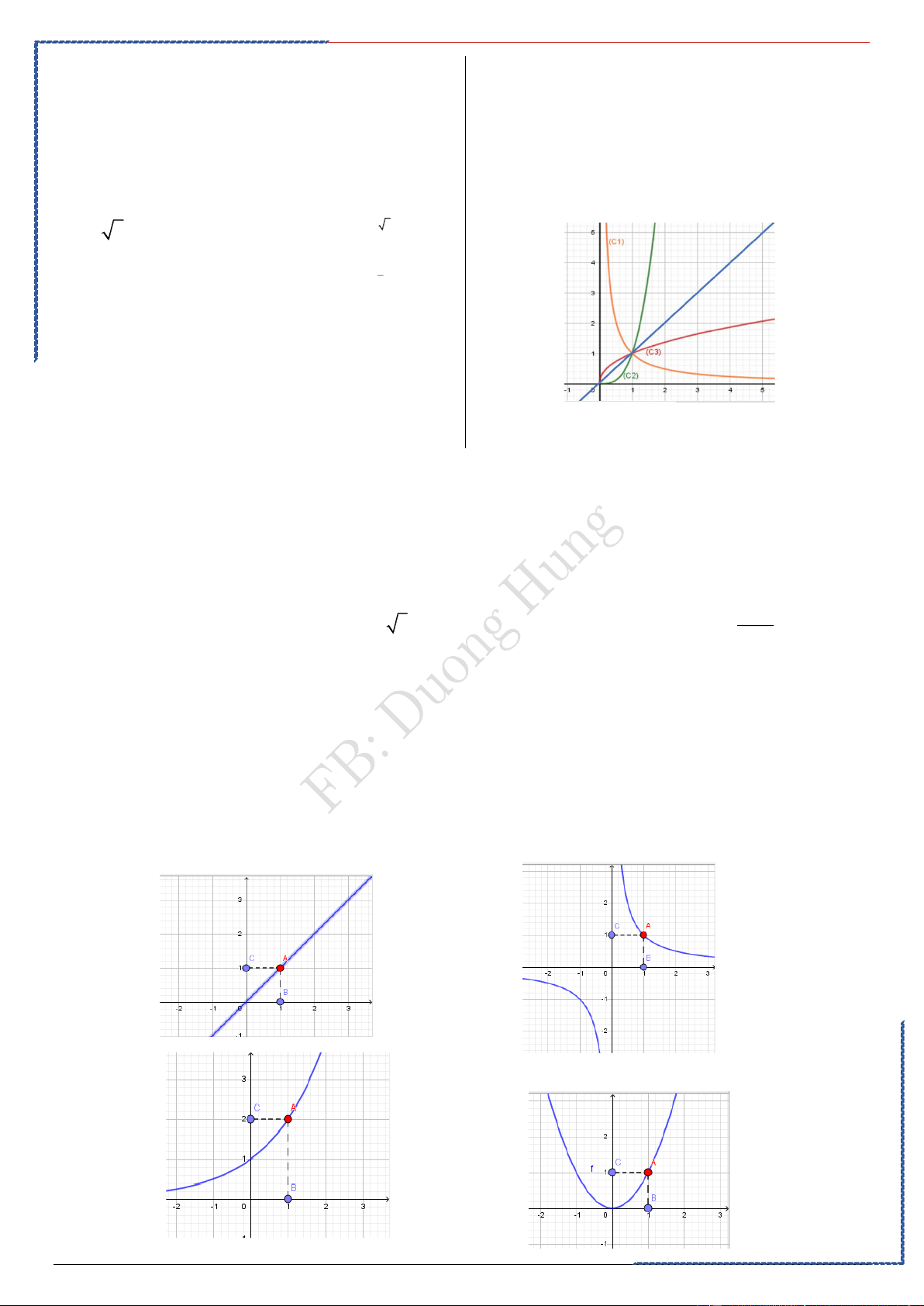
Câu 1: Cho các hàm số lũy thừa
y = x , y = x , y = x có đồ thị như
hình vẽ. Mệnh đề đúng là Ⓐ. . Ⓑ. .
Ⓒ. .
Ⓓ. .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 19
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm Chọn C
Vẽ đường thẳng y=x quan sát đồ thị thấy ngay
gia trị tương ứng và chọn C
Từ đồ thị hàm số ta có Hàm số
y = x nghịch biến trên (0; +) nên 0. Hàm số
y = x , y = x đồng biến trên (0; +) nên 0, 0 . Đồ thị hàm số
y = x nằm phía trên đồ thị hàm
số y = x khi x 1 nên 1. Đồ thị hàm số
y = x nằm phía dưới đồ thị hàm
số y = x khi x 1 nên 1.
Vậy 0 1
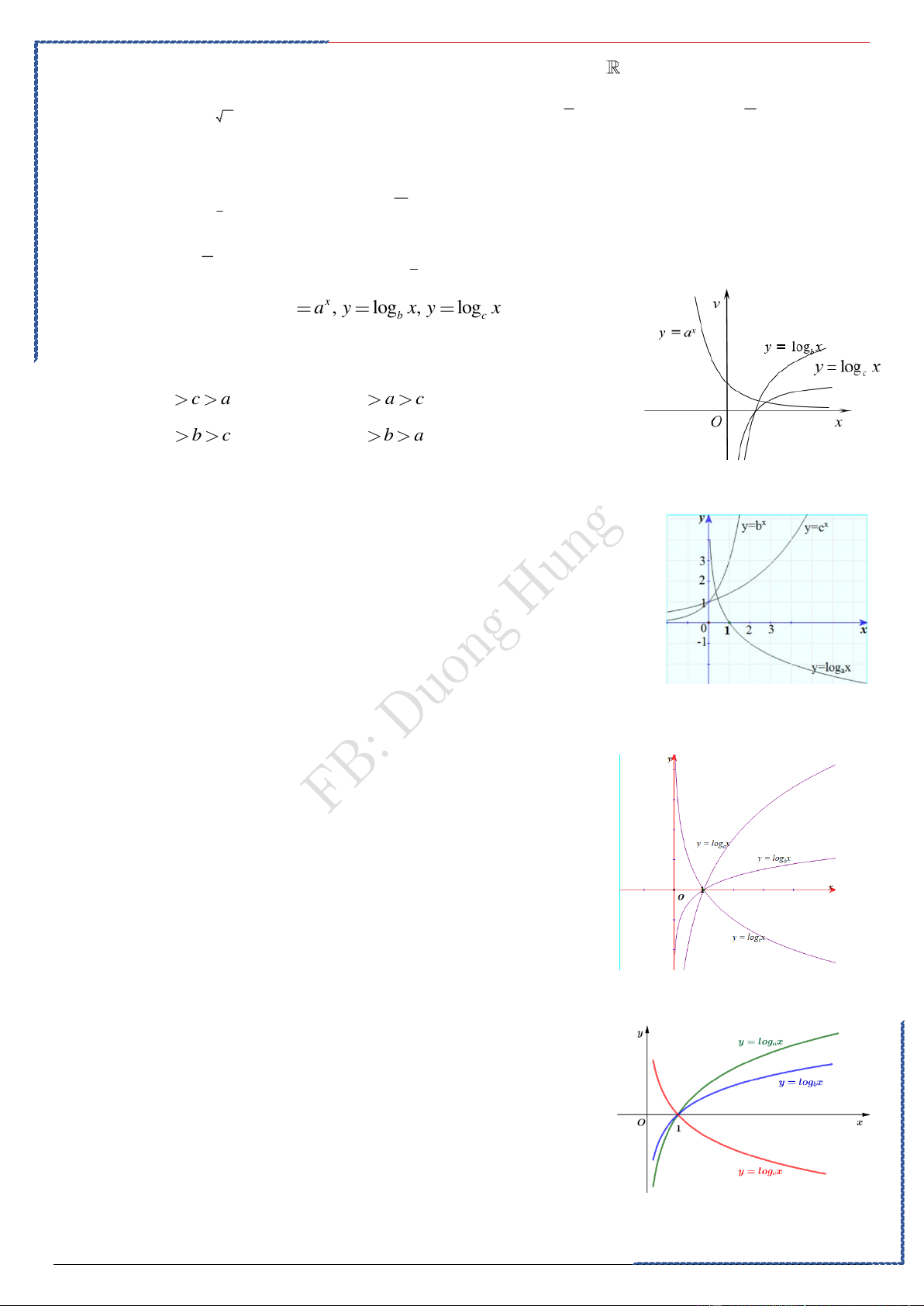
Câu 2: Cho , là các số thực. Đồ thị các hàm số
y = x , y = x
trên khoảng (0; +) được cho trong hình vẽ bên. Khẳng định nào sau đây là đúng?
Ⓐ. 0 1 Ⓑ. 0 1 .
Ⓒ. 0 1 . Ⓓ. 0 1 . Lời giải
PP nhanh trắc nghiệm Chọn A. Với
x 1 ta có: x 1 0; x 1 0 Mắt nhanh vẽ đường thẳng y=x quan sát đồ 0 0 0
thị thấy ngay giá trị tương ứng và loại B,C,D
x x 0 0
Mặt khác, dựa vào hình dáng đồ thị ta suy ra
1 và 1. Suy ra A là phương án đúng 1
Câu 3: Cho ba hàm số 3 2 5 y x , y x , y x− = = = . Khi đó đồ thị của 1 ba hàm số 3 2 5 y x , y x , y x− = = = lần lượt là Ⓐ. (C3),(C2),(C1) . Ⓑ. (C2),(C3),(C1) . Ⓒ. (C2),(C1),(C3) . Ⓓ. (C1),(C3),(C2) .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 20
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm
Chọn B
Nhìn vào đồ thị (C ) ta thấy nó đi xuống từ
Vẽ đường thẳng y = x quan sát đồ thị thấy 1
trái sang phải. Là đồ thị của hàm số nghịch biến
ngay giá trị tương ứng chọn B.
nên nó là đồ thị của hàm số 2 y x− = .
(C ) tăng; (C ) giảm; (C ) giảm 2 3 1
Vì 3 1 nên đồ thị của hàm số 3
y = x là (C ) 2 1
Do đó (C ) là đồ thị của hàm số 5 y = x ; 3
Vậy đáp án là: B
B - Bài tập rèn luyện:
Câu 1: Hàm số nào sau đây là hàm số lũy thừa? Ⓐ. − y = x . Ⓑ. = x y . Ⓒ. − = x y . Ⓓ. = x y e
Câu 2: Hàm số nào sau đây là hàm luỹ thừa? − Ⓐ. x x 3 y = x . Ⓑ. y = ( )2 3 .
Ⓒ. y = 2sin x − 1 1. Ⓓ. y = . x + 3
Câu 3: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai? Ⓐ.Hàm số
y = x có tập xác định tùy theo . Ⓑ.Đồ thị hàm số
y = x với 0 có tiệm cận. Ⓒ. Hàm số
y = x với 0 nghịch biến trên khoảng (0; ) + . Ⓓ. Đồ thị hàm số
y = x với 0 có hai tiệm cận.
Câu 4: Đồ thị nào dưới đây không là đồ thị của hàm số y = x ? Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ.
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 21
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Câu 5: Cho hàm số − 2 y = x
. Mệnh đề nào sau đây là sai?
Ⓐ.Đồ thị hàm số không cắt trục hoành.
Ⓑ.Hàm số nghịch biến trên khoảng (0; + ) .
Ⓒ. Hàm số có tập xác định là (0; + ) .
Ⓓ. Đồ thị hàm số không có tiệm cận. Câu 6: Cho hàm số 2 y x− =
. Hỏi khẳng định nào dưới đây là khẳng định đúng?
Ⓐ.Đồ thị hàm số đã cho không có tiệm cận.
Ⓑ.Đồ thị hàm số đã cho có một tiệm cận ngang và không có tiệm cận đứng.
Ⓒ. Đồ thị hàm số đã cho không có tiệm cận ngang và có một tiệm cận đứng.
Ⓓ. Đồ thị hàm số đã cho có một tiệm cận ngang và một tiệm cận đứng. Câu 7: Cho hàm số 4
y = x . Khẳng định nào sau đây là sai?
Ⓐ.Tập xác định D = (0;+)
Ⓑ.Hàm số đồng biến trên (0;+)
Ⓒ. Đồ thị hàm số đi qua điểm M (1 ) ;1
Ⓓ. Đồ thị hàm số có tiệm cận ngang. 3 Câu 8: Cho hàm số − 4 y = x
. Khẳng định nào sau đây là sai?
Ⓐ.Đồ thị hàm số có 2 đường tiệm cận.
Ⓑ.Hàm số nghịch biến trên .
Ⓒ. Hàm số không có điểm cực trị.
Ⓓ. Đồ thị hàm số đi qua điểm A(1; ) 1 . Câu 9: Cho hàm số 4 − y = x
. Khẳng định nào sau đây là sai?
Ⓐ.Đồ thị hàm số có một trục đối xứng.
Ⓑ.Đồ thị hàm số đi qua điểm A(1; ) 1 .
Ⓒ. Đồ thị hàm số có hai đường tiệm cận.
Ⓓ. Đồ thị hàm số có một tâm đối xứng. Câu 10: Cho hàm số y = x ,
. Khẳng định nào dưới đây là sai?
Ⓐ.Tập xác định của hàm số luôn chứa khoảng (0;+) .
Ⓑ.Trên khoảng (0;+) thì hàm số đồng biến khi 0 và nghịch biến khi 0 .
Ⓒ. Đồ thị của hàm số luôn có đường tiệm cận ngang là trục Ox, tiệm cận đứng là trục Oy.
Ⓓ. Đạo hàm của hàm số trên khoảng (0;+) là 1 y .x − = . 2 5 3 2 1 1
Câu 11: Cho a = , b = , 6 3 c = 7 , 3 6 d = 7
. Chọn kết quả đúng? 3 3 Ⓐ. a ,
b c d . Ⓑ. a ,
b c d . Ⓒ. a ,
b c d . Ⓓ. a ,
b c d .
Câu 12: Cho hàm số y = f ( x) 1
= x 3 . Khẳng định nào dưới đây là sai?
Ⓐ.Hàm số có đồ thị nhận trục tung làm trục đối xứng.
Ⓑ. lim f (x) = . x→
Ⓒ. Hàm số đồng biến trên ( ;
− 0) và nghịch biến (0;+) .
Ⓓ. Hàm số không có đạo hàm tại x = 0 .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 22
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 13: Hình dưới đây là đồ thị của hai hàm số = a y x và = b y x . Hãy
chọn khẳng định đúng.
Ⓐ. a b 0 .
Ⓑ. b a 0.
Ⓒ. a b 0.
Ⓓ. b a 0 .
Câu 14: Đường cong trong hình bên là đồ thị của một hàm số trong bốn
hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? 1 Ⓐ. − 3 y x− = Ⓑ. 3 y = x Ⓒ. 3 y = x Ⓓ. 3 y = x Câu 15: Cho hàm số − 2 y = x
. Mệnh đề nào sau đây là sai?
Ⓐ.Đồ thị hàm số không cắt trục hoành. Ⓑ.Hàm số nghịch
biến trên khoảng (0; + ) .
Ⓒ. Hàm số có tập xác định là (0; + ) .
Ⓓ. Đồ thị hàm số không có tiệm cận.
Câu 16: Cho ba số thực dương a , b , c khác 1. Đồ thị các hàm số x y = a , x y = b , x
y = c được cho trong hình vẽ dưới đây. Mệnh đề nào dưới đây đúng?
Ⓐ.1 a c b .
Ⓑ. a 1 c b .
Ⓒ. a 1 b c .
Ⓓ. 1 a b c . BẢNG ĐÁP ÁN 1.A 2.A 3.B 4.C 5.D 6.D 7.D 8.B 9.D 10.C 11.C 12.C 13.C 14.A 15.D 16.B
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 23
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021 CHƯƠNG ②: FB: Duong Hung Bài 3: LOGARIT
Dạng ①: Tính giá trị biểu thức.
Phương pháp:
.Sử dụng công thức, tính chất và các quy tắc về logarit
.Casio: Xét hiệu kết hợp Calc đặc biệt hóa.
A - Bài tập minh họa:
Câu 1: Cho a 0,a 1, biểu thức D = log a có giá trị bằng bao nhiêu? 3 a A. 3 − . B. 3 . C. 1 . D. 1 − . 3 3 Lời giải
PP nhanh trắc nghiệm Chọn C Casio: Ta có: 1 1 D = log a = log a = . 3 3 a a 3
Câu 2: Với a và b là hai số thực dương, a 1. Giá trị của 3 loga b a bằng 1 1 A. 3 b . B. b . C. 3b . D. 3 b . 3 Lời giải
PP nhanh trắc nghiệm Chọn D
Áp dụng công thức: logab a = b Casio: Ta có: 3 log 3 a b a = b .
Câu 3: Cho hai số thực dương a, b và a 1. Khẳng định nào đúng ? A. 1 log ab = + log b . B. 2021
2021log ab = 1+ log b . 2 a a a a
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 24
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung C. 2020 log a
b = 2020 + log b . D. 2018 log a
b = 2018(1+ log b . a a ) a a Lời giải
PP nhanh trắc nghiệm
Chọn C. log
ab = 2(log a + log b Casio: a a ) a = 2 + 2log . b a ab = b a ( 2018 2018log 2018 + loga ) 2020 log a
b = 2020.log a + log b a a a
Chú ý: 2020 ta chọn số 2 đại diện là OK = 2020 + log b a
B - Bài tập rèn luyện:
Câu 1: Với a là số thực dương tùy ý. Chọn khẳng định đúng Ⓐ. 1 1 3 log a = 3 + log . a Ⓑ. 3 log a = 3.log . a Ⓒ. 3 log a = log . a Ⓓ. 3 log a = + log . a 2 2 2 2 2 2 3 2 2 3 3 a
Câu 2: Cho a là số thực dương khác 4 . Tính I = log . a 64 4 Ⓐ 1 1 . I = − .
Ⓑ. I = 3 − .
Ⓒ. I = 3.
Ⓓ. I = . 3 3
Câu 3: Cho 2 số thực a và b với a 0,a 1,b 0 . Khẳng định nào sau đây là sai? Ⓐ 1 . 1 1 1 log b = log b . Ⓑ. 2 log a = 1 . Ⓒ. 2
log b = log b . Ⓓ. 2 log b = log b . 2 a a 2 a 2 a a 2 a a 2 2 3 2 5 4 Câu 4: Tính a a a log . a 15 7 a 2 3 2 5 4 2 3 2 5 4 Ⓐ a a a . a a a 12 log = 3 . Ⓑ. log = . a 15 7 a a 15 7 5 a 2 3 2 5 4 2 3 2 5 4 Ⓒ a a a . a a a 9 log = . Ⓓ. log = 2. a a 15 7 5 a 15 7 a
Câu 5: Cho các số thực dương a b c d , a , b ,
c d và biểu thức: M = lg
+ lg + lg + lg . Khẳng định nào sau b c d a đây đúng? Ⓐ. M = 1.
Ⓑ. M = 0 . Ⓒ a b c d
. M = lg (abcd ) .
Ⓓ. M = lg + + + . b c d a
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 25
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 6: Biểu thức log 2sin + log cos
có giá trị bằng: 2 2 12 12 Ⓐ. 1 − . Ⓑ. −2 . Ⓒ. 1.
Ⓓ. log 3 −1. 2
Câu 7: Tính giá trị của biểu thức ( )3log 4 log 4 = − a a P a a
, với (a 0,a ) 1 . Ⓐ. P = 24 .
Ⓑ. P = 8 − .
Ⓒ. P = 8.
Ⓓ. P =12.
Câu 8: Nếu log b = p thì 2 4 log a b bằng a a Ⓐ. 4 p + 2.
Ⓑ. 4 p + 2a . Ⓒ. 2 4 a p . Ⓓ. 4 p + 2a .
Câu 9: Cho các số thực a, , b c thỏa mãn: lo 3 g 7 log711 lo 11 g 25 a = 27,b = 49,c
= 11 . Giá trị của biểu thức 2 2 (log 25) 2 (log 11) 11 (log 7) 7 3 A = a + b + c là Ⓐ. A = 519.
Ⓑ. A = 729 .
Ⓒ. A = 469 .
Ⓓ. A =129. a
Câu 10: Tính giá trị của biểu thức 10 2 2 P = log a b + log + log −
b ( với 0 a 1;0 b 1). 2 a ( ) 3 a b b Ⓐ. P = 2 .
Ⓑ. P =1.
Ⓒ. P = 3 .
Ⓓ. P = 2 .
Câu 11: Giá trị của biểu thức M = log 2 + log 4 + log 8 +...+ log 256 bằng 2 2 2 2 Ⓐ. 56.
Ⓑ. 8.log 256 . Ⓒ. 48 . Ⓓ. 36. 2 Câu 12: Giả sử p
p, q là các số thực dương sao cho log p = log q = log
p + q . Tìm giá trị của . 9 12 16 ( ) q Ⓐ. 1 (− 1 1+ 5 ) . Ⓑ. (1+ 5). Ⓒ. 4 . Ⓓ. 8 . 2 2 3 5
Câu 13: Cho a, b là các số thực dương khác 1, thoả log b + log a =1. Mệnh đề nào dưới đây là đúng? 2 2 a b Ⓐ. 1 1 a = .
Ⓑ. a = b . Ⓒ. a = . Ⓓ. 2 a = b . b 2 b a Câu 14: Cho ,
a b là các số thực dương và ab 1 thỏa mãn 2
log a = 3 thì giá trị của 3 log bằng ab ab b Ⓐ. 3 . Ⓑ. 3 . Ⓒ. 8 . Ⓓ. 2 . 8 2 3 3
Câu 15: Cho a 0 , b 0 thỏa mãn 2 2
a + 4b = 5ab . Khẳng định nào sau đây đúng? a + b a + Ⓐ 2 log log b . log = .
Ⓑ. 5log(a + 2b) = log a − logb . 3 2
Ⓒ. 2log(a + 2b) = 5(log a + logb).
Ⓓ. log(a + ) 1 + log b = 1 .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 26
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 16: Cho a , b là hai số thực dương, khác 1. Đặt log b = m , tính theo m giá trị của a 3
P = log b − log a . 2 a b 2 2 2 2 Ⓐ − − − − . 4 3 = m 12 12 3 P . Ⓑ. = m P . Ⓒ. = m P . Ⓓ. = m P . 2m 2m m 2m
Câu 17: Cho P = log 16m và a = log m với m là số dương khác 1.Mệnh đề nào dưới đây đúng? m 2 Ⓐ + . 2
P = 3 − a . Ⓑ. 4 = a P . . Ⓒ. 3 + = a P .
Ⓓ. P = 3+ . a a . a a
Câu 18: Rút gọn biểu thức A = (log b + log a + 2 b b a
ta được kết quả là a b )(log −log a ab )log −1 b Ⓐ. 1 Ⓑ. − a log a .
Ⓒ. log a . Ⓓ. logb log a . b b 3 b .
Câu 19: Kết quả rút gọn của biểu thức C = log b + log a + 2 b b b là a b (log −log a ab ) loga Ⓐ. 3 log b .
Ⓑ. . log b . Ⓒ. ( b .
Ⓓ. log b . a )3 log a a a Câu 20: Cho ,
a b là các số thực dương thoả mãn 2 2
a + b = 14ab . Khẳng định nào sau đây là sai? Ⓐ a + b a + . ln ln b ln = .
Ⓑ. 2log a + b = 4 + log a + log b . 2 ( ) 4 2 2 2 Ⓒ a + . b 2 log
a + b = 4 + log a + log b . Ⓓ. 2log
= log a + log b . 4 ( ) 4 4 4 BẢNG ĐÁP ÁN 1.B 2.C 3.D 4.A 5.B 6.A 7.C 8.A 9.C 10.B 11.D 12.B 13.B 14.D 15.A 16.B 17.B 18.A 19.C 20.C
Dạng ②: Biến đổi, rút gọn, biểu diễn biểu thức chứa logarit, mũ, lũy thừa.
. Phương pháp: áp dụng các tính chất, quy tắc tính logarit, đổi cơ số
. Casio: Xét hiệu kết hợp Calc đặc biệt hóa; Sto, Alpha khi biểu diễn
A - Bài tập minh họa:
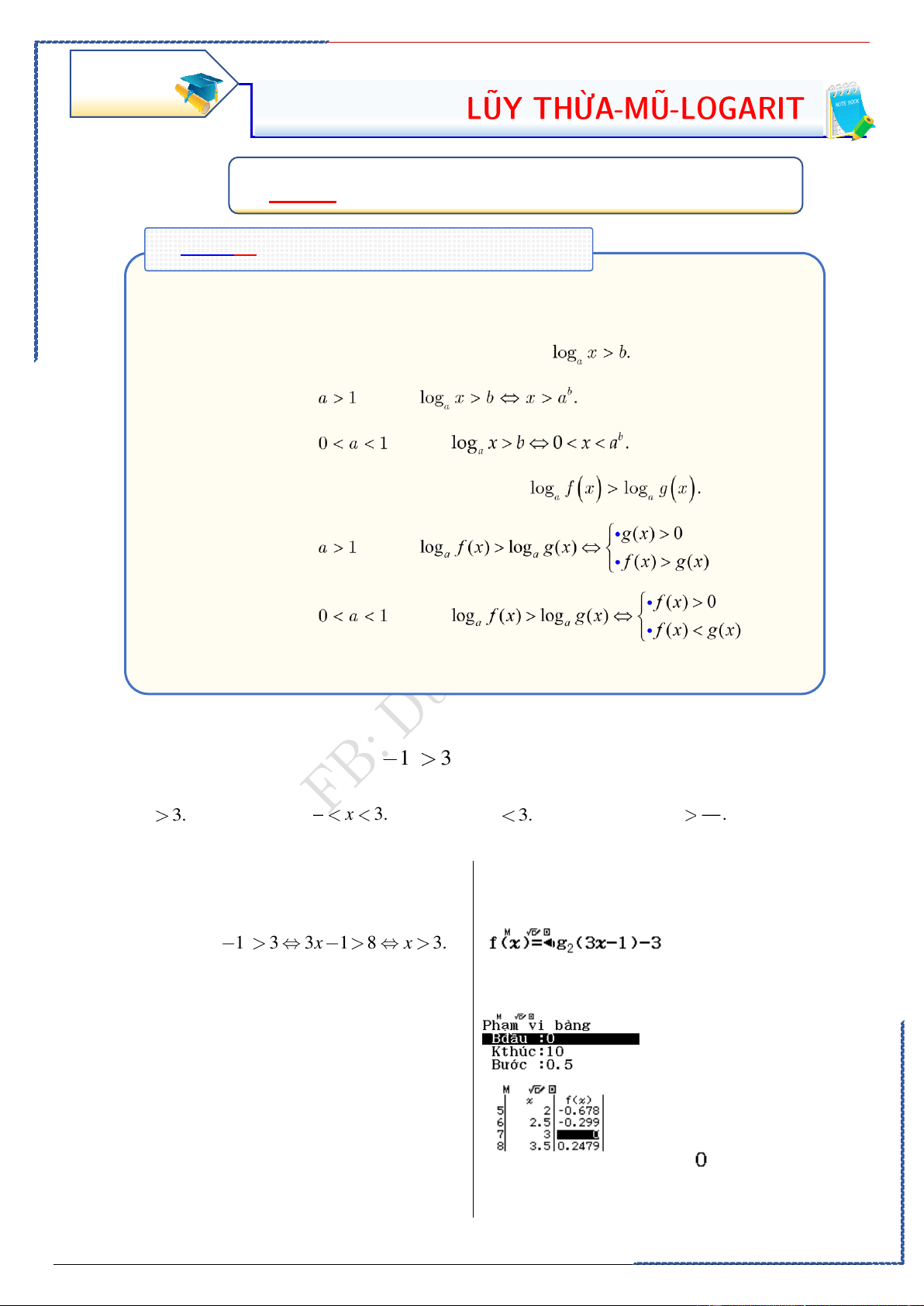
Câu 1: Cho a 0;a 1. Tìm mệnh đề đúng trong các mệnh đề sau? A. log n
x = n log x .
B. log x có nghĩa x . a a a C. log a = 0 . D. log x y = x y x . a ( . ) log .log ; 0 a a a
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 27
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm Chọn A
log x có nghĩa x 0 câu B sai
Casio: Xét hiệu với Calc đặc biệt hóa. a
log a = 1 câu C sai. a log ( .
x y) = log x + log ; y x 0 câu D sai. a a a Calc A=2, x=5, m=3 Chọn A
Câu 2: Cho a là số thực dương bất kì. Tìm khẳng định đúng trong các khẳng định sau: A. 1 3 log a = log a .
B. log (3a) = 3log a . 3 C. ( a) 1 log 3 = log a . D. 3
log a = 3log a . 3 Lời giải
PP nhanh trắc nghiệm Chọn D 3
log a = 3log a A sai, D đúng.
Casio: Xét hiệu với Calc đặc biệt hóa.
log (3a) = log3+ loga B, C sai. Calc A=2 Chọn D
Câu 3: Cho a là số thực dương khác 1. Tính I = log a . a 1
A. I = . B. I = 2 − . C. I = 0. D. I = 2 . 2 Lời giải
PP nhanh trắc nghiệm Chọn D
Ta có: I = log a = 2log a = 2. Casio: a a
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 28
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Câu 4: Cho ,
a b 0 , a 1 thỏa log b = 3 . Tính 3 P = log b . a 2 a 9 1 A. P =18. B. P = 2 . C. P = . D. P = . 2 2 Lời giải
PP nhanh trắc nghiệm Chọn C 3 3 9 Casio: Vì ,
a b 0 nên ta có: P = log b = .3 = . 2 a 2 2 Chọn A=2, tìm B=8.
B - Bài tập rèn luyện:
Câu 1: Cho b là số thực dương tùy ý, log b bằng 2 3 Ⓐ 1 1 . 2log b .
Ⓑ. log b . Ⓒ. 2 − log b .
Ⓓ. − log b . 3 3 2 3 3 2
Câu 2: Với a là số thực dương bất kỳ, khẳng định nào dưới đây đúng? 1
Ⓐ. log(4a) = 4loga . Ⓑ. ( 4
log a ) = 4loga . Ⓒ. log( 4
a ) = loga . Ⓓ. ( a) 1 log 4 = log a . 4 4
Câu 3: Với a , b là hai số thực khác 0 tùy ý, ( 2 4 ln a b ) bằng
Ⓐ. 2ln a + 4ln b .
Ⓑ. 4(ln a + ln b ) . Ⓒ. 2lna +4lnb .
Ⓓ. 4ln a + 2lnb .
Câu 4: Với a là một số thực dương bất kì, mệnh đề nào dưới đây đúng?
Ⓐ. log(3a) 0.
Ⓑ. log(3a) = 3log . a Ⓒ. 3 log a = 3log . a Ⓓ. 3 log a 0 . 2018 2018
Câu 5: Với các số thực a,b,c 0 và a,b 1 bất kì. Mệnh đề nào dưới đây Sai? Ⓐ. 1 log b = .
Ⓑ. log b c = b + c . a ( . ) log log a log a a a b Ⓒ. log .
b log c = log c .
Ⓓ. log b = c b . c log a b a a a
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 29
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 6: Với số dương a tùy ý, ta có log (8a) − log(2a) bằng Ⓐ. 6log . a Ⓑ. ( 2 log 16a ).
Ⓒ. log(6a).
Ⓓ. log 4.
Câu 7: Cho a > 0; b > 0. Tìm đẳng thức sai. Ⓐ. 2 log (a ) b = 2log (a ) b .
Ⓑ. log a + log b = log ab . 2 2 2 ( ) 2 2 Ⓒ. a
log a − log b = log .
Ⓓ. log a + log b = log (a + ) b . 2 2 2 b 2 2 2 Câu 8: Với , a b
0 tùy ý, mệnh đề nào dưới đây đúng?
Ⓐ. log ab log . a log b . Ⓑ. 2 log ab 2 log a 2 log b . Ⓒ. 2 log ab log a 2 log b .
Ⓓ. log ab log a log b .
Câu 9: Cho a , b là hai số thực dương tùy ý và b 1. Tìm kết luận đúng.
Ⓐ. ln a + ln b = ln (a + b) .
Ⓑ. ln (a + b) = ln . a ln b . Ⓒ. a
ln a − ln b = ln (a − b) . Ⓓ. ln log a = . b ln b
Câu 10: Với a là số thực dương bất kỳ, khẳng định nào sau đây đúng?
Ⓐ. log 4a 4 log a . Ⓑ. 4 log a 4 log a . Ⓒ 1 1 . 4 log a log a .
Ⓓ. log 4a log a . 4 4
Câu 11: Với a,b là các số thực dương tùy ý và a khác 1 , đặt P = 3 b + 6 log log b . Mệnh đề 2 a a nào dưới đây đúng?
Ⓐ. P = 27log b.
Ⓑ. P = 15log b .
Ⓒ. P = 9log b .
Ⓓ. P = 6log b . a a a a
Câu 12: Với a và b là hai số thực dương tùy ý, ( 2 3 log a b ) bằng. Ⓐ. 1 1 log a + log b .
Ⓑ. 2(log a + logb) . Ⓒ. 1 log a + log b .
Ⓓ. 2log a + 3logb. 2 3 3
Câu 13: Cho ba số thực dương a, , b c với a 1 và
. Mệnh đề nào sau đây sai?
Ⓐ. log c a c .
Ⓑ. log (b c) log b log c . a a a a Ⓒ. log b
log b . Ⓓ. log a 1. a a a
Câu 14: Cho a 0;a 1 ; x, y là hai số thực dương. Đẳng thức nào sau đây là đúng?
Ⓐ. log (xy) = log .xlog y .
Ⓑ. log xy = x + y . a ( ) log log a a a a a
Ⓒ. log (x + y) = log x + log y .
Ⓓ. log x + y = x y a ( ) log .log a a a a a
Câu 15: Với a , b là hai số thực dương tuỳ ý, ( 3 4
log a b ) bằng
Ⓐ. 2log a + 3logb .
Ⓑ. 3log a + 4logb . Ⓒ 1 1
. 2(3log a + 2logb) .
Ⓓ. log a + logb . 3 4
Câu 16: Với a , b là hai số thực tuỳ ý, ( 2 4
log a b ) bằng
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 30
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Ⓐ. 2log a + 4logb.
Ⓑ. 2log a + 4logb . Ⓒ. 2log a + 4log b . Ⓓ. 2log a + 4log b .
Câu 17: Cho a 0;a 1 ; x, y là hai số thực dương. Đẳng thức nào sau đây là đúng? Ⓐ. x log ( xy) = log . x log y . Ⓑ. log
= log x − log y . a a a a a a y
Ⓒ. log (x + y) = log x + log y .
Ⓓ. log x + y = x y a ( ) log .log a a a a a
Câu 18: Cho log 2 = a . Tính 125 log
theo a được kết quả là 4
Ⓐ. 3−5a.
Ⓑ. 4(1+ a).
Ⓒ. 6 + 7a .
Ⓓ. 2(a + 5) .
Câu 19: Tính giá trị của biểu thức log2 P = 2 a + log ( b a
(a 0,a ) 1 . a )
Ⓐ. P = a −b. Ⓑ. = 2a P + b .
Ⓒ. P = a +b .
Ⓓ. P = 2a +b .
Câu 20: Cho a là số thực dương bất kỳ. Mệnh đề nào dưới đây đúng?
Ⓐ. log 5a 1 log a .
Ⓑ. log 5a 1 a . 5 5 5
Ⓒ. log 5a log a .
Ⓓ. log 5a 5 log a . 5 5 5 5
Câu 21: Cho các số thực a , b sao cho a b 0. Mệnh đề nào sau đây sai? Ⓐ. a 2 log
= log a − log b .
Ⓑ. log(a −b) = 2log(b − a) . b Ⓒ. ( 2 2 2
log a b ) = 2(log a + log b ) . Ⓓ. ( 3
log a b) = 4log a + 2log (ab) .
Câu 22: Cho a là số thực dương tùy ý, mệnh đề nào sau đây đúng?
Ⓐ. log 8a = 3− log a .
Ⓑ. log 8a = 3+ log a . 2 ( ) 2 ( ) 2 2
Ⓒ. log 8a = 3log a .
Ⓓ. log 8a = 8log a . 2 ( ) 2 ( ) 2 2 = = Câu 23: Biết log 3 , a log 5 . b I = log 5 6 6 Tính 3 theo , a . b Ⓐ. b b b b I = . Ⓑ. I = . Ⓒ. I = . Ⓓ. I = . a 1+ a 1− a a −1 Câu 24: Với ,
a b là hai số thực dương và a 1, log a b bằng a ( )
Ⓐ. 2 + 2log b .
Ⓑ. 2 + log b. Ⓒ. 1 1 + log b .
Ⓓ. 1 + log b . a a 2 2 a 2 a
Câu 25: Với a là số thực dương bất kì, mệnh đề nào dưới đây đúng? Ⓐ. ( a) 1 log 3 = log a . Ⓑ. 3 loga = 3log a . 3 Ⓒ. 1
log (3a) = 3log a . Ⓓ. 3 loga = log a . 3
Câu 26: Cho a,b là các số thực dương; a 1, là số thực bất kì. Mệnh đề nào sau đây đúng? Ⓐ. 2 log = .
Ⓑ. (log b = b . a )2 2 b log b log 2 a a a Ⓒ.
log b = log b . Ⓓ. log b = b . a ( 2 ) 2log a a a
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 31
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 27: Cho các số thực dương a b c d , a , b ,
c d và biểu thức: M = lg + lg + lg + lg . Khẳng b c d a
định nào sau đây đúng? Ⓐ. M =1.
Ⓑ. M = 0 . Ⓒ . a b c d
M = lg (abcd ) .
Ⓓ. M = lg + + + . b c d a
Câu 28: Với a , b là hai số thực dương tuỳ ý, ( 2 log ab ) bằng Ⓐ 1
. 2log a + log b .
Ⓑ. log a + 2logb .
Ⓒ. 2(log a + logb) . Ⓓ. log a + logb . 2
Câu 29: Cho log 3 = a . Hãy tính log 54 theo a . 2 4 Ⓐ. 1 1 log 54 = 1 + 3a . Ⓑ. log 54 = 1 + 6a . 4 ( ) 4 ( ) 2 2 Ⓒ. 1 log 54 = 1 + 12a .
Ⓓ. log 54 = 2 1+ 6a . 4 ( ) 4 ( ) 2
Câu 30: Cho biểu thức 2 A = log
a + log 4a với a 0, a 1. Khẳng định nào sau đây đúng? 1 a 2
Ⓐ. A =1+ 2a .
Ⓑ. A = 4+ 2a .
Ⓒ. A =1− 2a .
Ⓓ. A = 4− 2a . BẢNG ĐÁP ÁN 1.B 2.B 3.A 4.C 5.D 6.D 7.D 8.C 9.D 10.B 11.D 12.D 13.B 14.B 15.B 16.D 17.B 18.A 19.C 20.A 21.A 22.B 23.A 24.B 25.B 26.C 27.B 28.B 29.A 30.D
Dạng ③: Biểu diễn các biểu thức chứa logarit theo biểu thức khác
-Phương pháp:
. Sử dụng công thức, tính chất của mũ, lũy thừa.
. Casio: Xét hiệu với chức năng Calc sau khi Sto và Alpha vào các tham số a,b,c….
A - Bài tập minh họa: 3 a Câu 1. Cho , a ,
b c 0,c 1 và đặt log a = m , log b = n , T = log
. Tính T theo m, n . c c c 4 3 b A. 3 3 T = m − n . B. 3 T = 6n − m . C. 3 3 T = m + n . D. 3 T = 6m − n . 2 8 2 2 8 2 Lời giải
PP nhanh trắc nghiệm Chọn D
Casio: Cho a = 2,b = 3,c = 5.
Bấm log 2 = 0, 4306765581lưu vào A 5
Bấm log 3 = 0,6826061945lưu vào B 5
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 32
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung 3 a 3 3 3 2 4 3 T = log = log a − log b = 6 log a − log b Bấm log
trừ đáp án nếu bằng 0 c c c 4 3 c c 2 5 b 4 3 3 3 thì nhận đáp án đó = 6m − n 2
Lưu ý: m thay bởi A, n thay bởi B.
Câu 2. Nếu log 4 = a thì log 4000 bằng A. 3+ a . B. 4 + a . C. 3+ 2a . D. 4 + 2a . Lời giải
PP nhanh trắc nghiệm Chọn A Casio: Ta có = ( 3) 3 log 4000 log 4.10
= log 4 + log10 = log 4 + 3 = a + 3 .
Câu 3. Đặt a = log 15;b = log 10. Hãy biểu diễn log 50 theo a và b. 3 3 3
A. log 50 = (a + b − ) 1 . B. log
50 = 3(a + b − ) 1 . 3 3
C. log 50 = 2(a + b − ) 1 .
D. log 50 = 4(a + b − ) 1 3 3 Lời giải
PP nhanh trắc nghiệm Chọn C Casio:
Ta có log 50 = log 50 = 2 log 50 = 2 log 10.5 1 3 3 ( ) 3 2 3 = 2(log 10 + log 5 3 3 ) = 2(log 10 + log 15− log 3 3 3 3 ) = 2(a + b − ) 1 Chọn C.
B - Bài tập rèn luyện:
Câu 1: Đặt a = log 4, b = log 4. Hãy biểu diễn log 80 theo a và . b 3 5 12 2 Ⓐ a − + . 2 2ab 2 log 80 = . Ⓑ. log 80 = a ab . 12 ab + b 12 ab
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 33
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung 2 Ⓒ a + − . 2ab 2 2 log 80 = . Ⓓ. log 80 = a ab . 12 ab + b 12 ab
Câu 2: Cho a = log 20. Tính log 5 theo a. 2 20 + − + Ⓐ 5a a 1 a 2 a 1 . . Ⓑ. . Ⓒ. . Ⓓ. . 2 a a a − 2
Câu 3: Cho log 3 = a ; log 7 = b . Tính log 2016 theo a và b . 2 2 2
Ⓐ. 5+ 2a +b .
Ⓑ. 5+3a + 2b.
Ⓒ. 2+ 2a +3b .
Ⓓ. 2+3a + 2b .
Câu 4: Cho a , b là hai số thực dương, khác 1. Đặt log b = m , tính theo m giá trị của a 3
P = log b − log a . 2 a b 2 2 2 2 Ⓐ m − m − m − m − . 4 3 . Ⓑ. 12 . Ⓒ. 12 . Ⓓ. 3 . 2m 2m m 2m
Câu 5: Đặt log 5 = a . Mệnh đề nào sau đây đúng? 3 Ⓐ a + a + a − a + . 1 2 1 2 1 2 1 log 75 = . Ⓑ. log 75 = . Ⓒ. log 75 = . Ⓓ. log 75 = . 15 2a +1 15 a +1 15 a +1 15 a −1
Câu 6: Cho log 5 = a , log 5 = b . Khi đó log 5 tính theo a và b là 2 3 6 Ⓐ. 1 . Ⓑ. ab .
Ⓒ. a + b . Ⓓ. 2 2 a + b . a + b a + b
Câu 7: Nếu a = log 3 b = log 5 30 và 30 thì
Ⓐ. log 1350 = 2a + b + 2 .
Ⓑ. log 1350 = 2a + b +1. 30 30
Ⓒ. log 1350 = a + 2b +1.
Ⓓ. log 1350 = a + 2b + 2 . 30 30 =
Câu 8: Cho log 27 a log 16 12 thì 6
tính theo a là Ⓐ − a + a + − . 3 a . Ⓑ. 3 . Ⓒ. 3 . Ⓓ. 4(3 a) . 3 + a 4(3 − a) a − 3 3 + a
Câu 9: Cho P = log 16m và a = log m với m là số dương khác 1.Mệnh đề nào dưới đây đúng? m 2 Ⓐ + . 2
P = 3 − a . Ⓑ. 4 = a P . . Ⓒ. 3 + = a P . Ⓓ. P = 3+ . a a . a a
Câu 10: Cho a = log m với 0 m 1. Đẳng thức nào dưới đây đúng? 2 Ⓐ + − . 3 a a log 8m = .
Ⓑ. log 8m = (3− a a . Ⓒ. 3 log 8m = . Ⓓ. m ) m a m a
log 8m = (3 + a a . m )
Câu 11: Cho a = log 3, b = log 2 . Hãy tính log 150 , a . b 60 theo 4 25 + + + + Ⓐ 1 2 2b ab 1 b 2ab . log 150 = . log 150 = . 60 Ⓑ. 60 2 1+ 4b + 2ab 1+ 4b + 4ab + + + + Ⓒ 1 1 b 2ab 1 b 2ab . log 150 = . log 150 = 4 . 60 Ⓓ. 60 4 1+ 4b + 2ab 1+ 4b + 4ab = = =
Câu 12: Cho a log 3; b log 5; c log 2 log 63 2 3 7 . Hãy tính 140 theo a, , b c .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 34
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ ac + ac + ac + ac − . 2 1 . Ⓑ. 2 1 . Ⓒ. 2 1 . Ⓓ. 2 1 . abc + 2c +1 abc + 2c −1 abc − 2c +1 abc + 2c +1 = = = Câu 13: Cho log 5 , a log 7 , b log 3 c log 35 27 8 2 . Tính 12 Ⓐ b + b + b + b + . 3 3ac . Ⓑ. 3 2ac . Ⓒ. 3 2ac . Ⓓ. 3 3ac . c + 2 c + 2 c + 3 c +1
Câu 14: Cho a = log 3, b = log 5, c = log 7 log 1050 2 2 2 . Biểu thức biểu diễn 60 là Ⓐ + a + b + + a + b + . 1 2c 1 2 c log 1050 = . Ⓑ. log 1050 = . 60 1+ 2a + b 60 2 + a + b Ⓒ + a + b + + a + b + . 1 2 c 1 2 c log 1050 = . Ⓓ. log 1050 = . 60 1+ 2a + b 60 2 + a + b Câu 15: Cho ,
a b là các số thực dương thoả mãn 2 2
a + b = 14ab . Khẳng định nào sau đây là sai? Ⓐ a + b a + . ln ln b ln =
. Ⓑ. 2log a + b = 4 + log a + log b . 2 ( ) 4 2 2 2 Ⓒ a + . b 2 log
a + b = 4 + log a + log b . Ⓓ. 2log
= log a + log b . 4 ( ) 4 4 4
Câu 16: Cho các số dương a,b thỏa mãn 2 2
4a − 9b = 13ab . Chọn mệnh đề đúng? Ⓐ a + b . 2 3 1 1 log = (loga +logb) .
Ⓑ. log(2a + 3b) = 3log a + 2logb . 5 2 4 Ⓒ a + b . 2 3 1
log 2a + 3b = log a + 2log b . Ⓓ. log = (loga +logb) . 4 2
Câu 17: Cho a 0;b 0 thỏa mãn 2 2
a + b = 14a .
b Chọn mệnh đề đúng trong các mệnh đề sau? Ⓐ a + . b 1 log
= (log a + logb) .
Ⓑ. 2(log a + logb) = log(14ab). 4 2 Ⓒ. 1
log (a + b) = 2(log a + log b) .
Ⓓ. log(a + b) − 4 = (log a + logb) . 2 1 1
Câu 18: Với a 0, a 1 , cho biết: 1−log u 1−log t a t = a ; a v = a
. Chọn khẳng định đúng Ⓐ − . 1 u = a . Ⓑ. 1 u = a . Ⓒ. 1 u = a . Ⓓ. 1 u = a . 1− log v 1+ log t 1+ log v 1− log v a a a a
Câu 19: Biết log 5 = a, log 7 = ,
b log 3 = c thì log 35 tính theo , a , b c bằng 27 8 2 12 3(b + ac) + + 3(b + ac) Ⓐ 3b 2ac 3b 2ac . . Ⓑ. . Ⓒ. . Ⓓ. . c + 2 c +1 c + 2 c +1 = = = Câu 20: Cho log 5 , a log 2 , b log 11 c log 495 3 5 3 . Khi đó 216 bằng Ⓐ a + a + c + a + c + a + c + . c . Ⓑ. 2 . Ⓒ. 2 . Ⓓ. 2 . 3ab + 3 3ab ab + 3 3ab + 3 BẢNG ĐÁP ÁN 1.C 2.C 3.A 4.B 5.B 6.B 7.B 8.D 9.B 10.A 11.B 12.A 13.A 14.D 15.C 16.A 17.A 18.D 19.A 20.D
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 35
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 36
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021 CHƯƠNG ②: FB: Duong Hung
Bài 4: HÀM SỐ MŨ-LOGARIT
Dạng ①: Tìm tập xác định của hàm số mũ , hàm số logarit
Phương pháp:
. Tìm điều kiện của hàm số và giải điều kiện ta thu được tập xác định của hàm số. ⬧.Với hàm số có tập xác định ⬧.Với hàm số Xác định khi và khi n lẻ hoặc khi n chẵn.
. Casio: Table , Calc rất hiệu quả.
A - Bài tập minh họa:
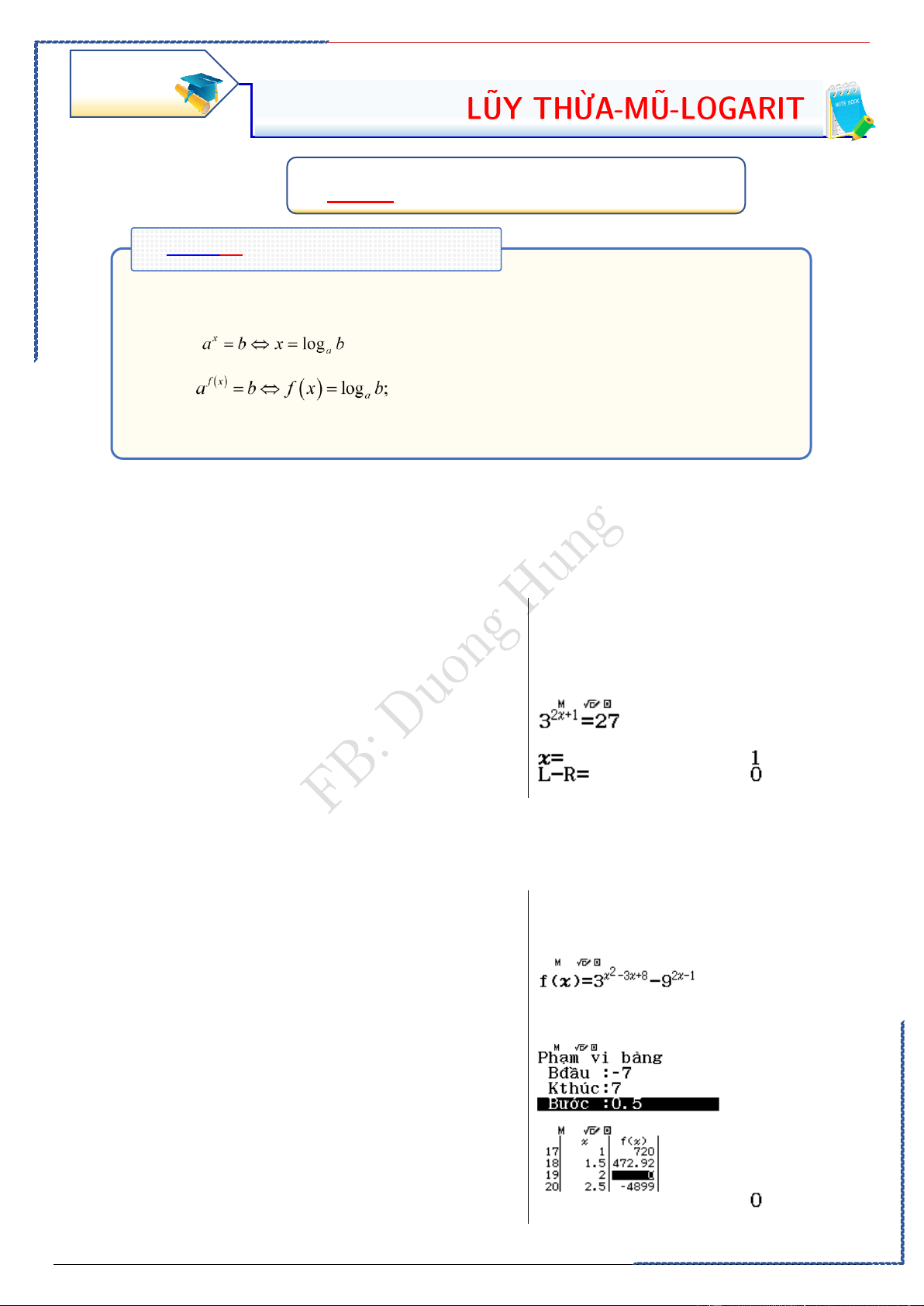
Câu 1: Tập xác định D của hàm số y = log ( 2 x − 2x − 3 2 ) Ⓐ. D = ( 1 − ;3) Ⓑ. D = (− ; − ) 1 (3;+) Ⓒ. D = 1 − ; 3 Ⓓ. D = (− ; − 1 3;+) Lời giải
PP nhanh trắc nghiệm Chọn B Casio: Table
Hàm số xác định khi 2
x − 2x − 3 0 x (− ; − ) 1 (3;+) . 1
Câu 2: Tập xác định của hàm số y = + ln(x −1) là 2 − x
A. D = (1;2)
Ⓑ. D = (1;+) Ⓒ. D = (0;+ )
Ⓓ. D = [1;2] Lời giải
PP nhanh trắc nghiệm Chọn A Casio: Table 1
Hàm số y =
+ ln(x −1) xác định khi 2 − x 2 − x 0 1 x 2 . x −1 0
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 37
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 3: Tập xác định của hàm số y = ( 2
log 2x − x ) là Ⓐ. D = 0;2 Ⓑ. D = (− ; 02;+) Ⓒ. D = (− ; 0)(2;+) Ⓓ. D = (0;2) Lời giải
PP nhanh trắc nghiệm Chọn D Casio: Table Điều kiện: 2
2x − x 0 0 x 2 .
Vậy tập xác định của hàm số là D = (0;2) .
Câu 4: Tìm tập xác định D của hàm số y = log (x − 2) − 3 . 3 Ⓐ. D = [29;+ ) Ⓑ. D = (29;+ )
Ⓒ. D = (2;29) Ⓓ. D = (2;+ ) Lời giải
PP nhanh trắc nghiệm Chọn A Casio: Table
Hàm số xác định khi x − 2 0 x − 2 0 x log (x − 2) 29 3 − 3 0 x − 2 3
Tập xác định D = 29;+)
B - Bài tập rèn luyện:
Câu 1: Tập xác định của hàm số y = log ( 2 3 − 2x − x là 2 ) Ⓐ. D = ( 1 − ) ;1 . Ⓑ. D = ( 1 − ;3) . Ⓒ. D = ( 3 − ; ) 1 . Ⓓ. D = (0; ) 1 .
Câu 2: Tìm tập xác định của hàm số y = log x −1 . 2 ( ) Ⓐ. D = (− ) ;1 .
Ⓑ. D = (1;+ ) . Ⓒ. D = 1 .
Ⓓ. D = .
Câu 3: Tập xác định của hàm số y = (x − )2 log 2 là Ⓐ. . Ⓑ. \ 2 . Ⓒ.(2;+) . Ⓓ. 2;+) .
Câu 4: Tập xác định của hàm số y = ( 2 log x − ) 1 là Ⓐ. (−;− )
1 (1; + ) . Ⓑ. (− ) ;1 . Ⓒ.(1;+ ) . Ⓓ. ( 1; − ) 1 .
Câu 5: Tìm tập xác định D của hàm số y = log 3 − x . 3 ( ) Ⓐ. D = \ 3 .
Ⓑ. D = (− ;3 . Ⓒ. D = (− ;3 ).
Ⓓ. D = (3;+).
Câu 6: Tìm tập xác định D của hàm số 2 ln x 2x 1 .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 38
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. D . Ⓑ. D (1; ) . Ⓒ. D . Ⓓ. D \{1}.
Câu 7: Tìm tập xác định D của hàm số y log (x 2) . 2021 Ⓐ. D . Ⓑ. D ; 2 . Ⓒ. D \ 2 . Ⓓ. D 2; . − Câu 8: x 1
Tập xác định của hàm số y = log là 2 x Ⓐ. \ 0 . Ⓑ. (1;+). Ⓒ. (0; ) 1 . Ⓓ. (− ; 0) (1;+) .
Câu 9: Tìm tập xác định của hàm số y = log ( 2
x − 3x là: 3 ) Ⓐ. D = (− ; 0)(3;+ ) .
Ⓑ. D = 0; 3 . Ⓒ. D = (0;3) . Ⓓ. D = (− ; 0)3;+ ) . x
Câu 10: Tập xác định D của hàm số 1 y = là 2 Ⓐ. D = . Ⓑ. D = (− ; 0) .
Ⓒ. D = (0;+) .
Ⓓ. D = \ 0 .
Câu 11: Trong các hàm số sau, hàm số nào không xác định trên . Ⓐ. 3x y = . Ⓑ. y = ( 2 log x ) .
Ⓒ. y = ln ( x + ) 1 . Ⓓ. 0,3x y = . 1+ x
Câu 12: Hàm số y = có tập xác định là log x −1 Ⓐ.0;+) \1 0 .
Ⓑ. 0;+) \ e . Ⓒ.(0;+) \ e . Ⓓ. (0;+) \1 0 .
Câu 13: Tìm tập xác định D của hàm số y = log(x + ) 1 −1 . Ⓐ. D = (10;+) .
Ⓑ. D = 9;+) . Ⓒ.( ;9 − .
Ⓓ. D = \ 1 . 1
Câu 14: Tìm tập xác định của hàm số y = . 1 − ln x Ⓐ. (0;+ ) \ e .
Ⓑ. (e;+ ) . Ⓒ. \ e . Ⓓ. (0;+ ) .
Câu 15: Điều kiện xác định của hàm số y log 1 5x 2 là 0,2 Ⓐ. 1 29 ; . Ⓑ. 24 ; . Ⓒ. 26 ; . Ⓓ. 24 1 ; . 5 125 125 125 125 5 x + Câu 16: 2
Tập xác định D của hàm số y = log là 13 x − 5
Ⓐ. D = (−;0 (5;+ ) . Ⓑ. D = 2 − ;5) .
Ⓒ. D = (−;− 25;+ ) .
Ⓓ. D = (−;− 2) (5;+ ) . − Câu 17: 3x 1
Tìm tập xác định D của hàm số y = . log (3x) Ⓐ. 1 D = (0; + ) . Ⓑ. 1 D = ; + .
Ⓒ. D = (0;+ ) . Ⓓ. 1 D = ; + . 3 3 3
Câu 18: Tập xác định của hàm số y = log 4 − x là 2 ( ) Ⓐ.(−;4) . Ⓑ. 2;4) . Ⓒ.(−;2. Ⓓ. (−;2) .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 39
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung x
Câu 19: Tập xác định của hàm số 2 9 y = − là 3 4 Ⓐ.(− ; − 2). Ⓑ. 2; − + ) . Ⓒ.(− ; − 2. Ⓓ. ( 2; − + ) .
Câu 20: Tập xác định của hàm số y = 2 − ln (ex) là Ⓐ.(1;+). Ⓑ. (0; ) 1 . Ⓒ. (0; ] e . Ⓓ. (1;2) . BẢNG ĐÁP ÁN 1.C 2.B 3.B 4.A 5.C 6.D 7.D 8.D 9.A 10.A 11.B 12.D 13.B 14.A 15.D 16.D 17.D 18.A 19.C 20.C
Dạng ②: Đạo hàm của hàm số mũ, logarit
. Phương pháp: Đối với bài toán tính đạo hàm hoặc chứng minh đẳng thức chứa đạo hàm
Dùng các công thức tính đạo hàm
Thay vào các đẳng thức chứa đạo hàm ta thu được kết quả . Casio: Nhập
thay cho đạo hàm và ấn ; kiểm tra giá trị CALC
vào kết quả A, B, C, D và so sánh các kết quả. Xét hiệu
kiểm tra mệnh đề đúng.
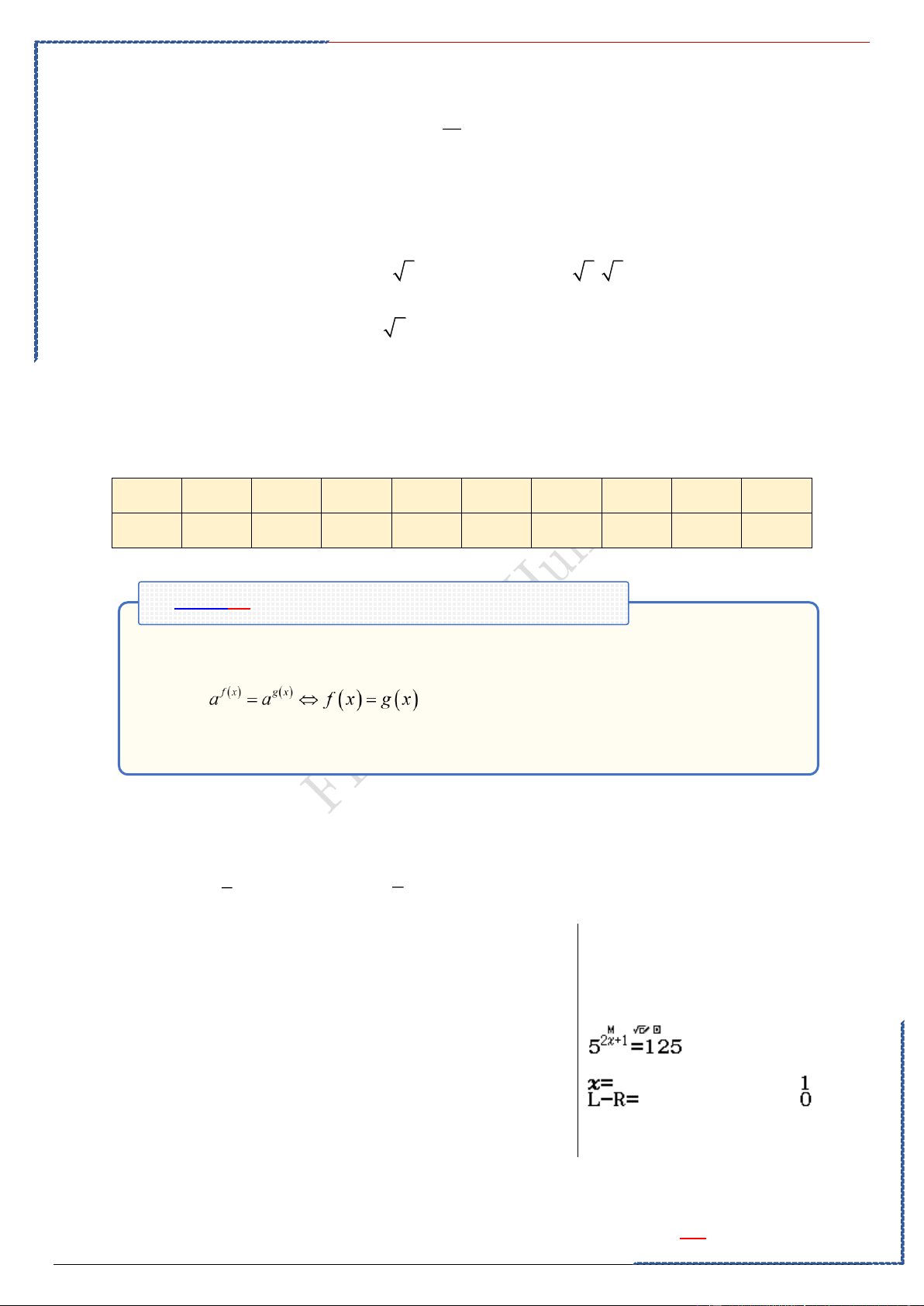
A - Bài tập minh họa:
Câu 1: Đạo hàm của hàm số y = log −x − 3 . 2 ( ) Ⓐ. 1 1 ( . Ⓑ. . Ⓒ.(−x −3) . Ⓓ. (x + 3) . − ln 2 ln 2 x − 3) ln 2 (x +3)ln 2 Lời giải
PP nhanh trắc nghiệm Chọn B Casio: f ' x
Điều kiện: x 3 − . 0 ( −x − 3 1 log −x − 3 = = . 2 ( )) ( )
(−x −3)ln 2 (x +3)ln 2
Câu 2: Tính đạo hàm của hàm số = ( 2 + 2 − 2).5x y x x Ⓐ. = ( 2 + 2).5x y x . Ⓑ. = (2 + 2).5x y x .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 40
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓒ. = (2 + 2).5x y x ln 5 .
Ⓓ. = ( + ) x + ( 2 2 2 .5 + 2 − 2).5x y x x x ln 5 . Lời giải
PP nhanh trắc nghiệm Chọn D Casio: f ' x 0 = ( 2 + − ) x +( x y x x ) ( 2 2 2 .5 5 . x + 2x − 2) = ( + ) x + ( 2 2 2 .5 + 2 − 2).5x x x x ln 5
Câu 3: Tính đạo hàm của hàm số 6x y = . x Ⓐ. 6x y = . Ⓑ. 6x y = ln 6 . Ⓒ. 6 y = . Ⓓ. 1 .6x y x − = . ln 6 Lời giải
PP nhanh trắc nghiệm
Chọn B
Casio: Xét hiệu
Ta có = 6x = 6x y y ln 6 . f ' x 0
Câu 4: Chọn công thức đúng? Ⓐ.( 1 x) 1 ln 4 = ; (x 0). Ⓑ. (ln x) = ; ( x 0). x x ln a Ⓒ.( x x) 1 log = ; (x 0). Ⓓ. (log x = x a ) ; ( 0). a x ln a Lời giải
PP nhanh trắc nghiệm Chọn A
Casio: Xét hiệu 4x 4 1 Ta có: ( ln 4x) ( ) = =
= ; (x 0).A đúng. f ' x 0 4x 4x x 1 (
ln x) = ; ( x 0) . B sai. x 1 ( log x = x C sai. a ) ; ( 0). x ln a 1 ( log x = x D sai. a ) ; ( 0). x ln a
Câu 5: Tính đạo hàm của hàm số 2 3 2 x y + = ? A. 2 x+2 y = 2 ln 4 . Ⓑ. x+2 y = 4 ln 4 . C. 2 x+2 y = 2 ln16 . Ⓓ. 2 x+3 y = 2 ln 2 .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 41
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm Chọn C
Casio: Xét hiệu 2 x+3 1 − 2 x+2 y = 2.2 ln 2 = 2 ln 4 f ' x 0
B - Bài tập rèn luyện: Câu 1: Hàm số 2 ( ) 2 x f x = có đạo hàm. Ⓐ. ( ) 2 ' 2 x f x = ln 2 + . Ⓑ. ( ) 2 1 ' 2 x f x − = . Ⓒ. f (x) 2 x 1 ' = 2 ln 2 . Ⓓ. ( ) 2 ' = 2 2 x f x x . Câu 2:
Tính đạo hàm của hàm số 2 y = log (x +1). 5 Ⓐ. 2x 2x 1 2x y = . Ⓑ. y = . Ⓒ. y = y = . ln 5 2 x +1 2 (x + . Ⓓ. 1) ln 5 2 (x +1) ln 5 2 Câu 3:
Tính đạo hàm của hàm số 1 4x x y + + = .
(2x ) 2x+x 1+ + Ⓐ. 1 4 y
( x ) 2x+x 1 2 1 4 + = + .ln 4 . Ⓑ. y = . ln 4 Ⓒ. ( ) 2 1 2 + + 2 1 4x x y x + + = + . Ⓓ. x x 1 y = 4 .ln 4 . Câu 4: Hàm số 3 . x 2x y = có đạo hàm là: Ⓐ. 3 . x 2 .x y = ln 2.ln 3 . Ⓑ. 3x 2x y = + . Ⓒ. 5x y = ln 5 . Ⓓ. 6x y = ln 6 . Câu 5:
Đạo hàm của hàm số y = log x là 5 Ⓐ. ln 5 x y = . Ⓑ. y = . Ⓒ. 1 y = . Ⓓ. . x ln 5 . x ln 5 . x ln 5 Câu 6: Hàm số y = log ( 3
x − x có đạo hàm là 3 ) 2 2 − Ⓐ. 3x −1 3x 1 1 3x −1 y = ( . Ⓑ. y = y = . Ⓓ. y = . 3 x − x)ln 3 3 x − . Ⓒ. x ( 3x − x)ln3 ( 3x − x)ln3 Câu 7: Cho hàm số ( ) 2 1 e x f x + =
. Ta có f (0) bằng Ⓐ. 3 2e . Ⓑ. 2 . Ⓒ. 2e . Ⓓ. e . Câu 8: Hàm số y = ( 2
log x + 2x) có đạo hàm là (2x + 2) + Ⓐ. ln10 2x 2 y = y = 2 x + . Ⓑ. 2x 2 x + . 2x + Ⓒ. 2x 2 1 y = ( . Ⓓ. y = 2 x + 2x)ln10 2 x + . 2x Câu 9: Đạo hàm của hàm số 1 3 6 x f x là:
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 42
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 1 3 3.6 . x f x ln 6 . Ⓑ. 1 3 6 . x f x ln 6 . Ⓒ. 1 3 .6 . x f x x ln 6 . Ⓓ. 3 1 3 .6 x f x x . 2
Câu 10: Tính đạo hàm của hàm số 2x y . 2 1+ x 1+ x Ⓐ. .2 x 2 .2 x y = . Ⓑ. 1 .2 x y x + = .ln 2 . Ⓒ. 2 . x ln 2x y = . Ⓓ. y = . ln 2 ln 2 2 Câu 11: Hàm số 1 e x f x có đạo hàm là Ⓐ. 2 x x x 1 2 f x .e . Ⓑ. x 1 f x .e . 2 2 x 1 2 x 1 Ⓒ. 2 2x x x 1 2 f x .e . Ⓓ. x 1 f x .e .ln 2 . 2 x 1 2 x 1
Câu 12: Đạo hàm của hàm số = (2 − ) 1 3x y x là Ⓐ. x ( x ) x 1 2.3 2 1 . x 3 − + − . Ⓑ. 2.3 .xln3.
Ⓒ. 3x (2 + 2xln3− ln3) .
Ⓓ. 3x (2 − 2xln3+ ln3) .
Câu 13: Cho hàm số f ( x) = ( 4 ln x + )
1 . Đạo hàm f (0) bằng: Ⓐ.1. Ⓑ. 0. Ⓒ.3. Ⓓ. 2.
Câu 14: Tính đạo hàm của hàm số 2 3 2 x y + = . Ⓐ. 2 x+2 y = 2 ln 4 + + + . Ⓑ. x 2 y = 4 ln 4 . Ⓒ. 2 x 2 y = 2 ln16 . Ⓓ. 2 x 3 y = 2 ln 2
Câu 15: Tính đạo hàm của hàm số sin 2 x y = . sin x Ⓐ. cos .2 x sin 1 sin .2 x y x − = . Ⓑ. sin 2 . x y = ln 2 . Ⓒ. y = . Ⓓ. sin = cos .2 .x y x ln 2 . ln 2
Câu 16: Tính đạo hàm của hàm số y = x ln x . Ⓐ. 1 y = ln x +1. Ⓑ. y ln x . Ⓒ. y ln x 1. Ⓓ. y = . x
Câu 17: Tính đạo hàm của hàm số y = log (2x +1). 2 Ⓐ. 2 1 2 y = . Ⓑ. y = . Ⓒ. 1 y = . Ⓓ. y = . 2x +1 2x +1 (2x +1) ln 2 (2x +1) ln 2 BẢNG ĐÁP ÁN 1.C 2.D 3.A 4.D 5.C 6.A 7.C 8.C 9.A 10.B 11.B 12.C 13.B 14.C 15.D 16.A 17.D
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 43
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Dạng ③: Sự biến thiên và đồ thị của hàm số mũ- logarit
-Phương pháp:
_ Nếu là hàm số dạng ;
thì dựa vào cơ số a để xác định tính đơn điệu hàm số.
_ Nếu là các hàm số khác ta xét sự biến thiên của hàm số theo các bước: TXĐ⇒BBT⇒Kết luận Casio:
Dùng table để khảo sát tính tăng giảm, giảm của hàm số để chọn được đáp án.
A - Bài tập minh họa:
Câu 1: Tìm mệnh đề đúng trong các mệnh đề sau . Ⓐ.Hàm số x
y = a với a 1 nghịch biến trên khoảng ( – ; +). Ⓑ. Hàm số x
y = a với 0 a 1 đồng biến trên khoảng ( – ; +).
Ⓒ.Hàm số y = log x với a 1 đồng biến trên khoảng (0;+). a
Ⓓ. Hàm số y = log x với 0 a 1 nghịch biến trên khoảng (– ; +). a Lời giải
PP nhanh trắc nghiệm
Chọn C
Quan sát cơ số
Câu hỏi nhận biết.
Hàm số y = log x với a 1 đồng biến trên khoảng (0;+) . a
Phương án A sai vì Hàm số x
y = a với a 1 đồng biến trên khoảng (– ; +).
Phương án B sai vì Hàm số x
y = a với 0 a 1 nghịch biến trên khoảng (– ; +).
Phương án D sai vì Hàm số y = log x với 0 a 1 nghịch biến a trên khoảng (0;+) .
Câu 2: Hàm số nào sau đây nghịch biến trên ? Ⓐ. 2021x y = . Ⓑ. 3 x y − = . Ⓒ. = ( )x y . Ⓓ. x y = e . Lời giải
PP nhanh trắc nghiệm Chọn B Dễ thấy 3 x y − =
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 44
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung x x Do − x 1 y = 3 = có 1 1 y ' = ln 0, x do 1 0 1. 3 3 3 3 x Vậy hàm số − x 1 y = 3
= nghịch biến trên . 3
Câu 3: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây ? Ⓐ. y = ln x . Ⓑ. ex y = − . Ⓒ. y = ln x . Ⓓ. ex y = . Lời giải
PP nhanh trắc nghiệm Chọn A
Quan sát giao điểm đặc biệt
Đồ thị hàm số đi qua các điểm (1;0) và (e ) ;1 nên loại đáp án B; D.
Mặt khác với x (0; )
1 thì đồ thị nằm dưới trục Ox nên loại đáp án C.
B - Bài tập rèn luyện:
Câu 1: Cho hai hàm số y = log x , y = log x với a , b là hai số thực dương, a b
khác 1 có đồ thị lần lượt là (C , (C như hình vẽ. Khẳng định nào 2 ) 1 ) sau đây SAI?
Ⓐ. 0 b a 1.
Ⓑ. a 1.
Ⓒ. 0 b 1 a .
Ⓓ. 0 b 1.
Câu 2: Hình bên là đồ thị của hàm số nào sau
Ⓐ. y = log x .
Ⓑ. y = log x . 2 1 2 Ⓒ. 2 y = x − 2x +1 . Ⓓ. 2x y = − 2.
Câu 3: Cho a 0,b 0, a 1,b 1 . Đồ thị hàm số x
y = a và y = log x được b
xác định như hình vẽ bên. Mệnh đề nào sau đây là đúng?
Ⓐ. a 1,b 1.
Ⓑ. a 1,0 b 1.
Ⓒ. 0 a 1,b 1.
Ⓓ. 0 a 1,0 b 1.
Câu 4: Hình bên là đồ thị của hàm số nào trong các hàm số sau đây?
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 45
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung x Ⓐ. 7 . Ⓑ. log x . 7 5 x Ⓒ. 5 . Ⓓ. log x . 7 0,7
Câu 5: Đường cong trong hình sau là đồ thị của hàm số nào?
Ⓐ. y = log 4x . Ⓑ. 2x y = . 2 ( ) Ⓒ. x y = x +1. Ⓓ. y = ( 2) .
Câu 6: Đồ thị sau đây là đồ thị của hàm số nào? Ⓐ. x y = e .
Ⓑ. y = log x . 4 Ⓒ. x y e− = .
Ⓓ. y = log x . 2
Câu 7: Đồ thị hình bên dưới là đồ thị của hàm số nào? Ⓐ. ( x y = 3 ) . Ⓑ. 3 x y − = . −x Ⓒ. 3 1 y = .
Ⓓ. y = . 1 3x− 3
Câu 8: Trong các hàm số sau, hàm số nào đồng biến trên tập xác định của nó?
Ⓐ. f (x) = ln(1− x) .
Ⓑ. f (x) = log (x +1) . 2 1 −
Ⓒ. f (x) = −log x .
Ⓓ. f (x) = log (x +1) . 3 2
Câu 9: Trong các hàm số sau đây hàm số nào là hàm số nghịch biến trên ? x x Ⓐ. − 2 e y = log x . Ⓑ. y = . Ⓒ. y = ( 3 log x ) . Ⓓ. y = . 3 4 4
Câu 10: Trong các hàm số dưới đây, hàm nào nghịch biến trên tập số thực ? x x Ⓐ. 2 y = .
Ⓑ. y = log x .
Ⓒ. y = log (2x + . Ⓓ. 2 y = . )1 1 3 e 2 4
Câu 11: Tìm mệnh đề đúng trong các mệnh đề sau: x Ⓐ. Đồ thị các hàm số x y = a và 1
y = với 0 a 1 đối xứng nhau qua trục Oy . a
Ⓑ. Đồ thị các hám số x
y = a với 0 a 1 luôn đi qua điểm có tọa độ ( ; a 1) . Ⓒ. x
y = a với a 1 là hàm số nghịch biến trên (− ; + ) . Ⓓ. x
y = a với 0 a 1 là hàm số đồng biến trên (− ; + ) .
Câu 12: Hàm số nào dưới đây đồng biến trên khoảng (0; + ) ?
Ⓐ. y = log x .
Ⓑ. y = log x .
Ⓒ. y = log x .
Ⓓ. y = log x . 3 e 1 6 3 4
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 46
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 13: Trong các hàm số dưới đây, hàm số nào đồng biến trên tập 2 x x Ⓐ. e y = log x . Ⓑ. y = log ( 2
x − x . Ⓒ. y = . Ⓓ. y = . 2 ) 10 −3 3 3
Câu 14: Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số thực !?. x Ⓐ. y = log x . Ⓑ. y = 1 3 2 x Ⓒ. 2 y = . Ⓓ. y = log ( 2 2x + . )1 e 4
Câu 15: Cho các hàm số x y a , y log , x y
log x có đồ thị như b c
hình vẽ bên. Chọn khẳng định đúng? Ⓐ. b c a . Ⓑ. b a c . Ⓒ. a b c . Ⓓ. c b a .
Câu 16: Cho các hàm số y = log x , x y = b , x
y = c có đồ thị như hình bên. Chọn khẳng định đúng. a
Ⓐ. c b a .
Ⓑ. a b c.
Ⓒ.b c a .
Ⓓ. b a c .
Câu 17: Hình bên là đồ thị của ba hàm số y = log x , y = log x , a b
y = log x , (0 a, , b c )
1 được vẽ trên cùng một hệ trục tọa c
độ. Khẳng định nào sau đây đúng
Ⓐ.b a c.
Ⓑ. b c a .
Ⓒ. a b c.
Ⓓ. a c b.
Câu 18: Từ các đồ thị y = log x , y = log x , y = log x đã cho ở hình vẽ. Khẳng định nào sau đây a b c đúng?
Ⓐ. 0 c 1 a b .
Ⓑ. 0 a b 1 c .
Ⓒ. 0 c a 1 b .
Ⓓ. 0 c 1 b a .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 47
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 19: Cho các hàm số lũy thừa
y = x , y = x , y = x có đồ thị
như hình vẽ. Chọn đáp án đúng. Ⓐ. .
Ⓑ. . Ⓒ. .
Ⓓ. .
Câu 20: Cho a, ,
b c là các số thực dương khác 1. Hình vẽ bên là
đồ thị của ba hàm số y = log , x y = log ,
x y = log x . a b c
Khẳng định nào sau đây là đúng?
Ⓐ. a c b .
Ⓑ. a b c .
Ⓒ. c b a .
Ⓓ. c a b . BẢNG ĐÁP ÁN 1.A 2.A 3.B 4.C 5.B 6.D 7.D 8.D 9.B 10.D 11.A 12.A 13.D 14.C 15.D 16.C 17.A 18.A 19.B 20.D
Dạng ④: Tìm GTLN-GTNN của hàm số
-Phương pháp:
. Nếu cho đồ thị hàm số dạng ;
thì dựa vào dáng đồ thị.
. Nếu cho hàm số dạng ;
thì dùng quy tắc tìm GTLN-GTNN
Casio: Dùng table để khảo sát tính tăng giảm, giảm của hàm số để chọn được đáp án
A - Bài tập minh họa: Câu 1: Gọi ,
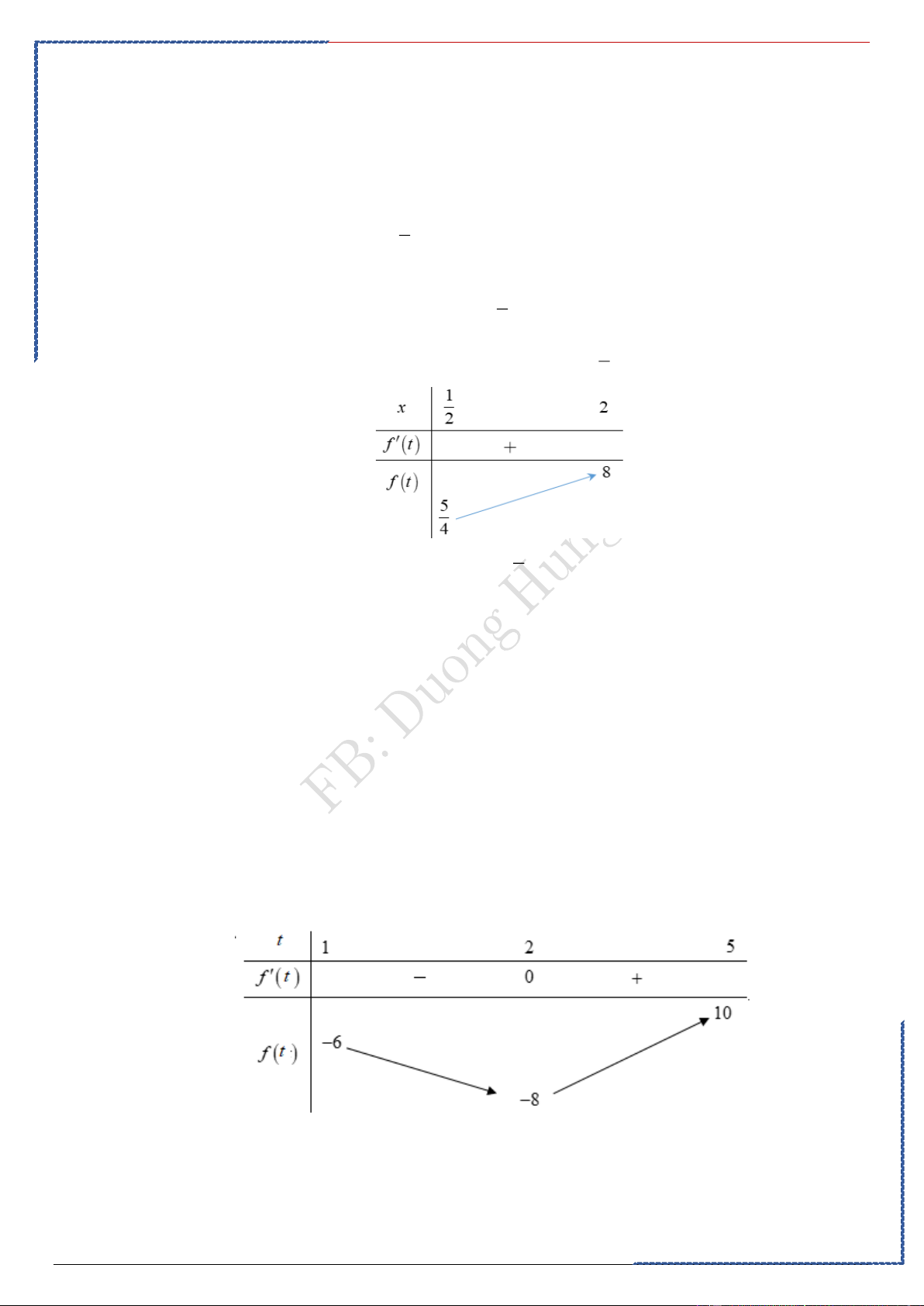
m M lần lượt là giá trị nhỏ nhất, lớn nhất của hàm số y = x − ln x trên đoạn 1 ; e . Giá 2
trị của M − m là Ⓐ. 1 e − ln 2 − . Ⓑ. e −1. Ⓒ. 1 ln 2 − . Ⓓ. e − 2. 2 2 Lời giải
PP nhanh trắc nghiệm
Chọn D
Casio: table
Điều kiện: x 0 .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 48
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Ta có 1 y = 1− ; 1 1 y = 0 1− = 0 x =1 ; e . x x 2 1 1 y = + ln 2 ; y ( )
1 = 1; y (e) = e −1. 2 2
giá trị nhỏ nhất của hàm số trên đoạn 1 ;e là m =1 đạt 2
được khi x =1;giá trị lớn nhất của hàm số trên đoạn 1 ;e là 2
M = e −1 đạt được khi x = e ;
Vậy M − m = e − 2 .
Câu 2: Giá trị nhỏ nhất của hàm số x 1 y xe + = trên 2 − ;0 bằng Ⓐ. 2 e . Ⓑ. 0 . Ⓒ. 2 − . Ⓓ. 1 − . e Lời giải
PP nhanh trắc nghiệm Chọn B
Casio: table
Ta có y = ( x + ) x 1 1 e +
y = 0 x = 1 − . y ( ) 1 2 2e− − = − , y (− ) 1 = 1 − , y (0) = 0 .
Giá trị nhỏ nhất của hàm số x 1 y xe + = trên 2 − ;0 bằng 1 − .
Câu 3: Gọi M là giá trị lớn nhất của hàm số x
y = e .ln x trên 1;e , khẳng định nào sau đây đúng? Ⓐ.15 M 16 . Ⓑ. M 10. Ⓒ. M 20 .
Ⓓ. M là số hữu tỉ. Lời giải
PP nhanh trắc nghiệm Chọn C Casio: table Xét hàm số x
y = e .ln x trên 1;e . x x 1
Ta có y = e ln x + x 1 e . = e ln x + . x x
Vì x 1;e nên ln x 0
;1 y 0 với x 1;e.
Ta có bảng biến thiên:
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 49
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Suy ra M = max y = y (e) e = e 15,15. 1;e
B - Bài tập rèn luyện:
Câu 1: Giá trị nhỏ nhất của hàm số x 1 y xe + = trên 2 − ;0 bằng Ⓐ. 2 e . Ⓑ. 0 . Ⓒ. 2 − . Ⓓ. 1 − . e 2 Câu 2: ln x
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = trên đoạn 3 1 ;e . x Ⓐ. 4 4 9 4 4 9 M = ; m = 0 . Ⓑ. M = ; m = 0 . Ⓒ. M = ; m = . Ⓓ. M = ; m = . 2 e 2 e 2 2 e e 2 2 e e Câu 3: Cho hàm số 2 a x y x e − =
( a là tham số). Giá trị lớn nhất của hàm số trên đoạn 0; 3 bằng: Ⓐ. a 3 9e − . Ⓑ. 0 . Ⓒ. 2 4 a e − . Ⓓ. a 1 e − . Lời giải
Câu 4: Giá trị nhỏ nhất của hàm số x
y = xe trên đoạn 2 − ;2 bằng Ⓐ. 1 − . Ⓑ. 0. Ⓒ. 2 − . Ⓓ. −e . e 2 e 2 Câu 5: ln x
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = trên đoạn 3 1 ;e lần lượt là x Ⓐ. 9 4 3 e và 1. Ⓑ. và 0 . Ⓒ. 2 e và 0 . Ⓓ. và 0 . 3 e 2 e
Câu 6: Giá trị nhỏ nhất của hàm số x x+3 f (x) = 4 − 2 trên đoạn 0; 3 là − − Ⓐ. 9 16. − Ⓑ. 15. − Ⓒ. 3999 . Ⓓ. . 250 4
Câu 7: Giá trị lớn nhất của hàm số ( ) = (2 − 3) x f x x
e trên đoạn 0; 3 ? Ⓐ. 3 2e . Ⓑ. 3 5e . Ⓒ. 3 4e . Ⓓ. 3 3e .
Câu 8: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = ln x trên đoạn 1;e lần lượt là: Ⓐ.1 và 0 . Ⓑ. 0 và 1 − . Ⓒ. 1 và 0 . Ⓓ. ln 2 và 0 . ln 2 Câu 9: 1 Cho hàm số 2 y = ln x −
x +1 . Tìm giá trị lớn nhất M của hàm số trên 1 ; 2 2 2 Ⓐ. 1 M = . Ⓑ. 7 M = + ln 2 . Ⓒ. 7 M = − ln 2 .
Ⓓ. M = ln 2 −1. 2 8 8 Câu 10: 1
Gọi giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = .
x ln x trên đoạn ;
e lần lượt là m và 2 e
M . Tích M.m bằng − Ⓐ. 2 . Ⓑ. 1 − . Ⓒ. 2e . Ⓓ. 1. e BẢNG ĐÁP ÁN 1.D 2 3.C 4.A 5.D 6.A 7.D 8.A 9.C 10.B
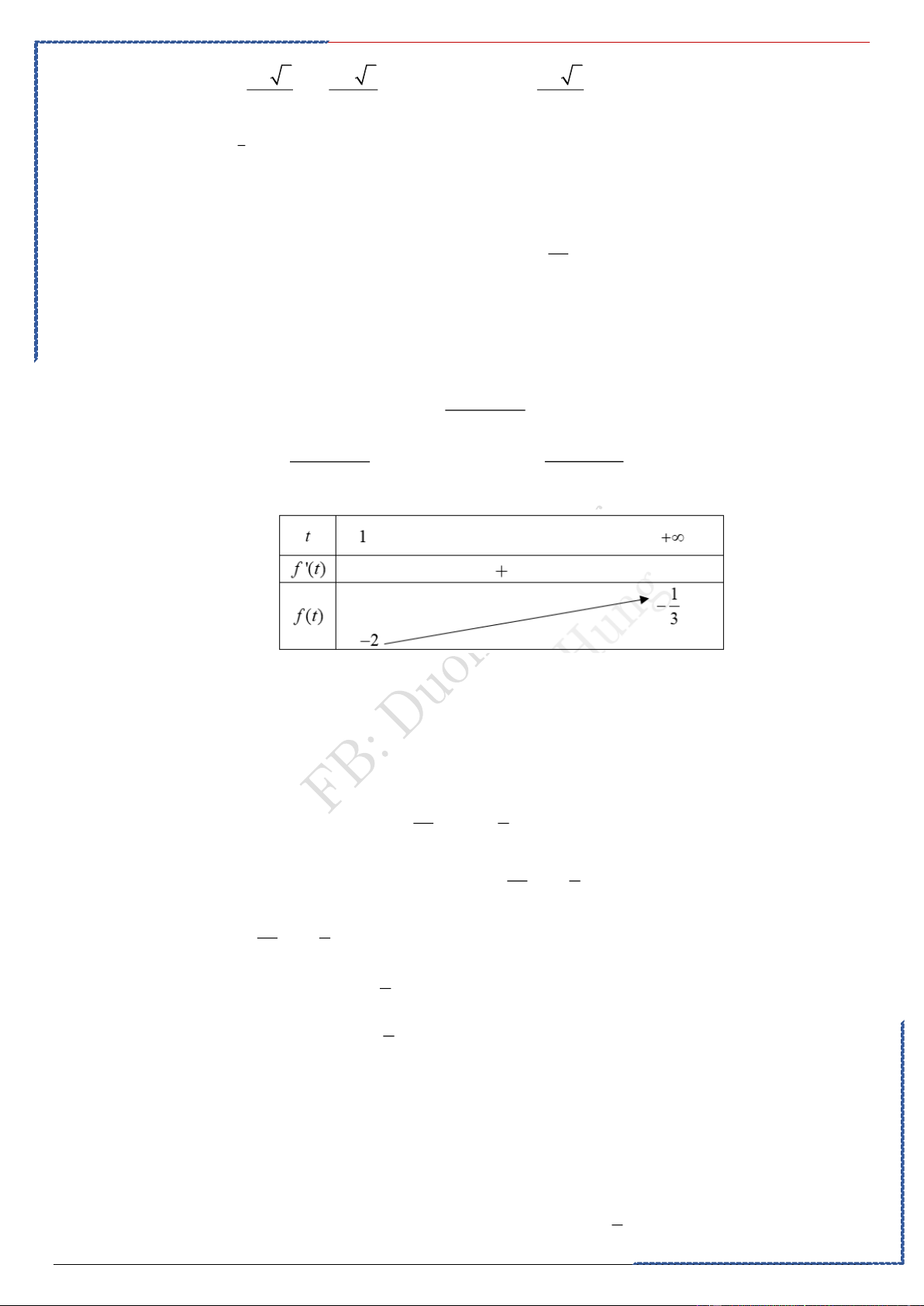
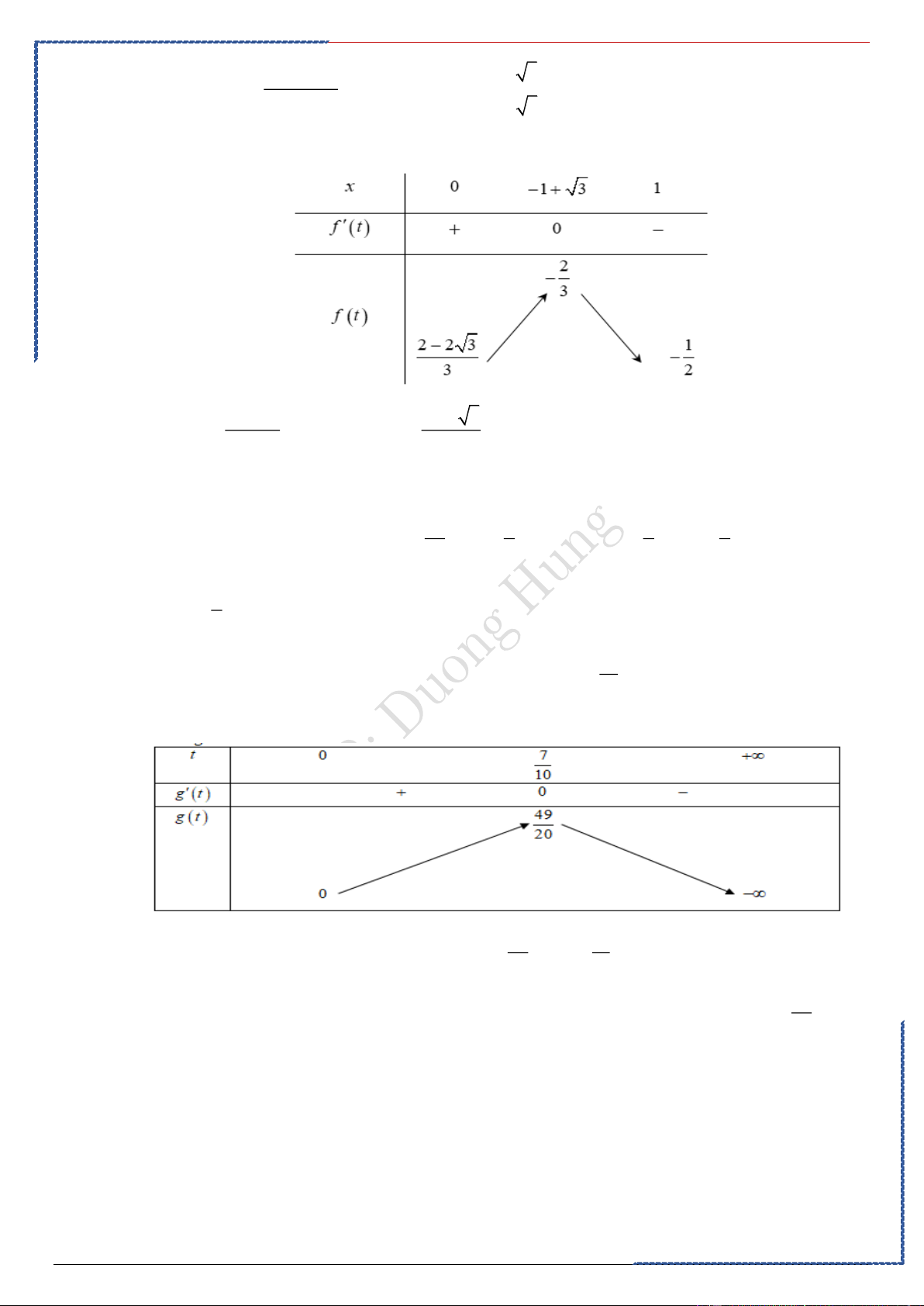
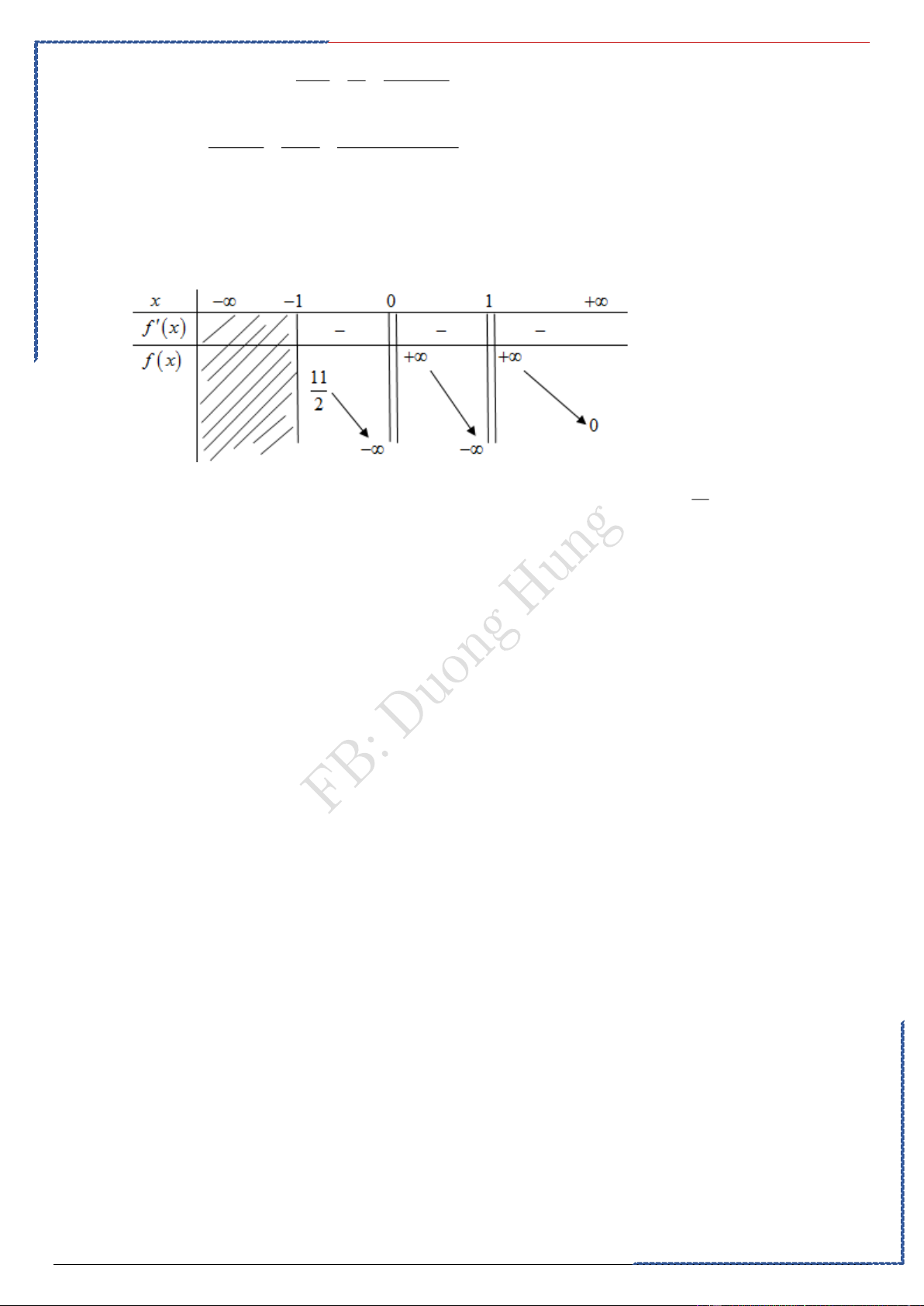
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 50
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Dạng ⑤: Toán thực tế.
-Phương pháp:
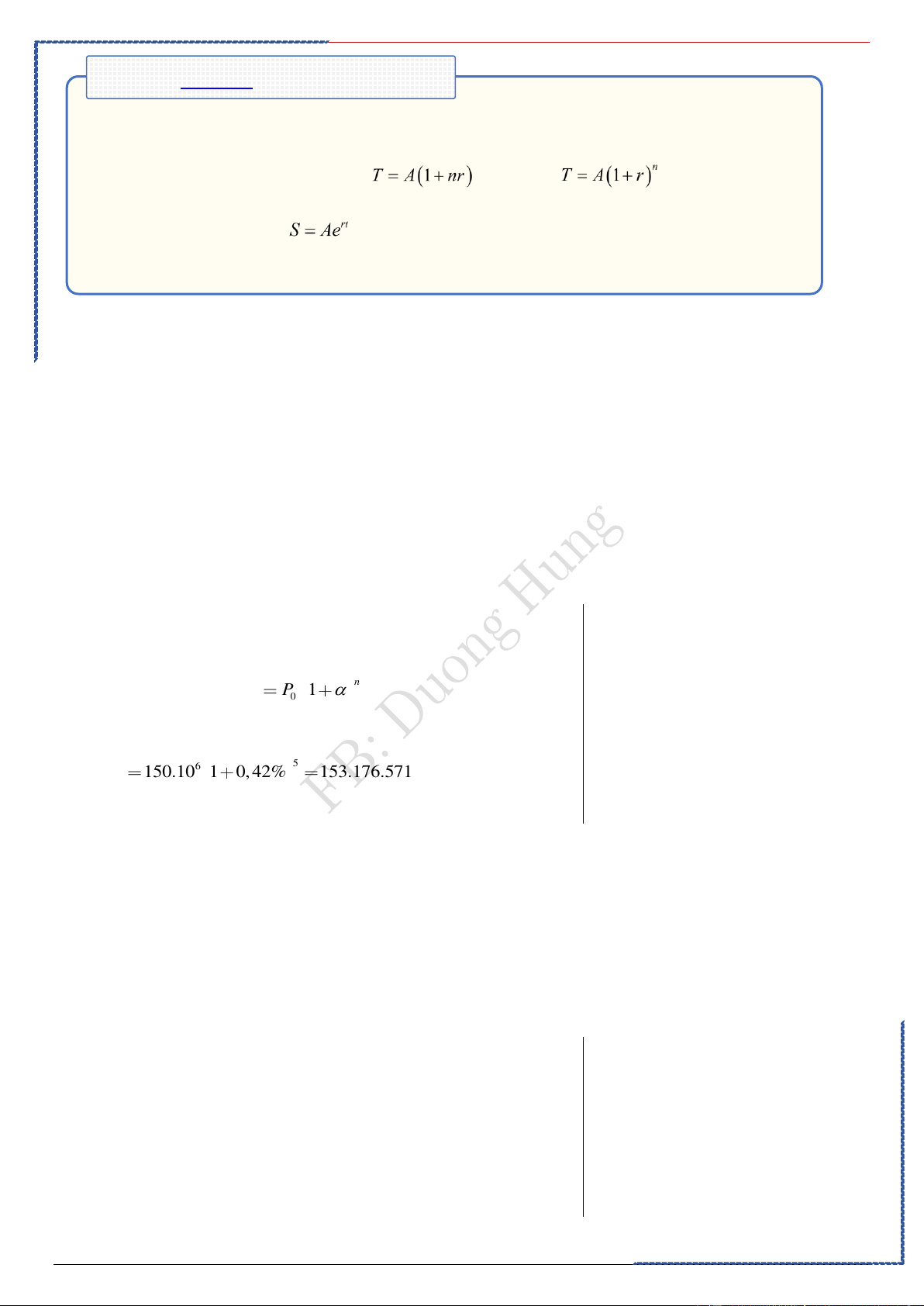
. Lãi suất ngân hàng: Lãi đơn: , Lãi kép: , . Toán tăng trưởng:
Casio: Table, Calc, Solve
A - Bài tập minh họa:
Câu 1: Một người gửi 150 triệu đồng vào một ngân hàng với lãi suất 0, 42% /tháng. Biết rằng nếu
không rút tiền khỏi ngân hàng thì cứ sau mỗi tháng số tiền lãi sẽ được nhập vào vốn ban
đầu để tính lãi cho tháng tiếp theo. Hỏi sau đúng 5 tháng người đó được lĩnh số tiền (cả
vốn ban đầu và lãi) gần nhất với số tiền nào dưới đây, nếu trong khoảng thời gian đó người
đó không rút tiền ra và lai suất không thay đổi?
Ⓐ.153.636.000 đồng.
Ⓑ. 153.820.000. Ⓒ.152.536.000.
Ⓓ. 153.177.000 đồng. Lời giải
PP nhanh trắc nghiệm Chọn D Casio:
Áp dụng công thức n P P 1 . n 0
Ta có tổng số tiền (cả gốc và lãi) người đó nhận được là: 5 6 P 150.10 1 0, 42%
153.176.571, 37 đồng. 5
Câu 2: Ông An gửi 100 triệu đồng vào tiết kiệm ngân hàng theo thể thức lãi kép trong một thời gian
khá lâu mà không rút ra với lãi suất ổn định trong mấy chục năm qua là 10% /1 năm. Tết
năm nay do ông kẹt tiền nên rút hết ra để gia đình đón Tết. Sau khi rút cả vốn lẫn lãi, ông
trích ra gần 10 triệu để sắm sửa đồ Tết trong nhà thì ông còn 250 triệu. Hỏi ông đã gửi tiết kiệm bao nhiêu lâu? Ⓐ.10 năm. Ⓑ. 17 năm. Ⓒ.15 năm. Ⓓ. 20 năm. Lời giải
PP nhanh trắc nghiệm Chọn B Casio:
Gọi x là số năm ông An đã gửi tiết kiệm.
Sau x năm ông An có được số tiền cả vốn lẫn lãi là x 100.(1+ 0, ) 1 ( triệu đồng).
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 51
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Theo giả thiết ta có: x 100.(1+ 0, ) 1 10 + 250 x 100.(1+ 0, ) 1 260 x 10 .
Câu 3: Một người gửi100triệu đồng vào một ngân hàng với lãi suất 0,65% / tháng . Biết rằng nếu
không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu để
tính lãi cho tháng tiếp theo. Hỏi sau12 tháng, người đó lĩnh được số tiền (cả vốn lẫn lãi) là bao
nhiêu? Biết rằng trong khoảng thời gian này người đó không rút tiền ra, số phần trăm lãi hằng tháng không thay đổi. Ⓐ.108.085.000đồng.
Ⓑ. 108.000.000đồng. Ⓒ.108.084.980đồng.
Ⓓ. 108.084.981đồng. Lời giải
PP nhanh trắc nghiệm Chọn D Casio:
Sau12 tháng, người đó lĩnh được số tiền (cả vốn lẫn lãi) là = ( + )n T A r = ( + )12 1 100 1 0, 65% =108084981 (đồng
Câu 4: Dân số thế giới được ước tính theo công thức n. = . i S
A e , trong đó A là dân số của năm lấy làm
mốc, S là dân số sau n năm, i là tỉ lệ tăng dân số hằng năm. Theo thống kê dân số thế giới
tính đến 01/ 2017 , dân số Việt Nam có khoảng 94,970 triệu người và tỉ lệ tăng dân số là
1, 03% . Nếu tỉ lệ tăng dân số không đổi thì đến năm 2020 dân số nước ta có bao nhiêu triệu
người, chọn đáp án gần nhất. Ⓐ.100 triệu.
Ⓑ. 102 triệu người. Ⓒ. 98 triệu người. Ⓓ. 104 triệu người Lời giải
PP nhanh trắc nghiệm Chọn C Casio:
Áp dụng công thức ta có: 3.1,03% S = 94,970.e 97,95 triệu (dân).
B - Bài tập rèn luyện:
Câu 1: Anh Bảo gửi 27 triệu đồng vào ngân hàng theo thể thức lãi kép, kỳ hạn là một quý, với lãi
suất 1,85 % một quý. Hỏi thời gian tối thiểu bao nhiêu để anh Bảo có được ít nhất 36 triệu
đồng tính cả vốn lẫn lãi? Ⓐ.19 quý. Ⓑ. 15 quý. Ⓒ.16 quý. Ⓓ. 20 quý.
Câu 2: Một người gửi 100 triệu đồng vào một ngân hàng với lãi suất 0, 4% /tháng. Biết rằng nếu
không rút tiền khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu
để tính lãi cho tháng tiếp theo. Hỏi sau ít nhất bao nhiêu tháng, người đó được lĩnh số tiền
(cả vốn ban đầu và lãi) lớn hơn hai lần số tiền ban đầu, nếu người đó không rút tiền ra và lãi suất không thay đổi? Ⓐ.174 tháng. Ⓑ. 173 tháng. Ⓒ.176 tháng. Ⓓ. 175 tháng.
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 52
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 3: Một người gửi tiết kiệm vào ngân hàng với lãi suất 8, 4% /năm và tiền lãi hàng năm được nhập
vào tiền vốn. Tính số năm tối thiểu người đó cần gửi để số tiền thu được nhiều hơn 3 lần số tiền gửi ban đầu. Ⓐ.10 năm. Ⓑ. 14 năm. Ⓒ.8 năm. Ⓓ. 11 năm.
Câu 4: Ông An muốn sở hữu khoản tiền 20.000.000 đồng vào ngày 10/7/2020 ở một tài khoản với lãi
suất năm 6,05% . Hỏi ông An đã đầu tư tối thiểu bao nhiêu tiền trên tài khoản này vào ngày
10/7/2015 để được mục tiêu đề ra?
Ⓐ.14.059.373,18 đồng. Ⓑ. 15.812.018,15 đồng.
Ⓒ.14.909.000 đồng. Ⓓ. 14.909.965,26 đồng.
Câu 5: Một người gởi 75 triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn 1 năm với lãi suất
5, 4% một năm. Giả sử lãi suất không thay đổi, hỏi 6 năm sau người đó nhận về số tiền là bao
nhiêu kể cả gốc và lãi? (đơn vị đồng, làm tròn đến hàng nghìn) Ⓐ.97.860.000. Ⓑ. 150.260.000. Ⓒ.102.826.000. Ⓓ. 120.826.000.
Câu 6: Một người gửi tiết kiệm vào ngân hàng với lãi suất 8, 4% /năm và tiền lãi hàng năm được nhập
vào tiền vốn. Tính số năm tối thiểu người đó cần gửi để số tiền thu được nhiều hơn 2 lần số tiền gửi ban đầu. Ⓐ.10 năm. Ⓑ. 9 năm. Ⓒ.8 năm. Ⓓ. 11 năm.
Câu 7: Một người gửi tiết kiệm với số tiền gửi là A đồng với lãi suất 6% một năm, biết rằng nếu
không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính
gốc cho năm tiếp theo. Sau 10 năm người đó rút ra được số tiền gốc lẫn lãi nhiều hơn số tiền
ban đầu là 100 triệu đồng? Hỏi người đó phải gửi số tiền A bằng bao nhiêu? Ⓐ.145037058,3đồng.
Ⓑ. 55839477,69 đồng. Ⓒ.126446589 đồng.
Ⓓ. 111321563,5 đồng.
Câu 8: Một người gửi ngân hàng 100 triệu đồng theo hình thức lãi kép, lãi xuất r = 0,5% một tháng
(kể từ tháng thứ 2 , tiền lãi được tính theo phần trăm tổng tiền có được của tháng trước đó
với tiền lãi của tháng trước đó). Sau ít nhất bao nhiêu tháng, người đó có nhiều hơn 125 triệu. Ⓐ. 45 tháng. Ⓑ. 46 tháng. Ⓒ. 47 tháng. Ⓓ. 44 tháng.
Câu 9: Cường độ của ánh sáng I khi đi qua môi trường khác với không khí, chẳng hạn như sương
mù hay nước,.sẽ giảm dần tùy theo độ dày của môi trường và một hằng số gọi là khả năng
hấp thu ánh sáng tùy theo bản chất môi trường mà ánh sáng truyền đi và được tính theo công thức − = . x I I e
với x là độ dày của môi trường đó và tính bằng mét, I là cường độ ánh sáng 0 0
tại thời điểm trên mặt nước. Biết rằng nước hồ trong suốt có =1,4 . Hỏi cường độ ánh sáng
giảm đi bao nhiêu lần khi truyền trong hồ đó từ độ sâu 3m xuống đến độ sâu 30m (chọn giá
trị gần đúng với đáp số nhất). Ⓐ. 30 e lần. Ⓑ. 16 2, 6081.10 lần. Ⓒ. 27 e lần. Ⓓ. 16 2, 6081.10− lần.
Câu 10: E.coli là vi khuẩn đường ruột gây tiêu chảy, đau bụng dữ dội. Cứ sau 20 phút thì số lượng vi
khuẩn E. coli tăng gấp đôi. Ban đầu, chỉ có 40 vi khuẩn E. coli trong đường ruột. Hỏi sau bao
nhiêu giờ, số lượng vi khuẩn E.coli lớn hơn 671088640 con? Ⓐ. 48 giờ. Ⓑ. 24 giờ. Ⓒ.12 giờ. Ⓓ. 8 giờ.
Câu 11: Sự tăng trưởng của một loại vi khuẩn tuân theo công thức: = .ert S A
, trong đó A là số vi
khuẩn ban đầu, r là tỉ lệ tăng trưởng, t là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn
ban đầu là 100 con và sau 5 giờ có 300 con. Để số lượng vi khuẩn ban đầu tăng gấp đôi thì
thời gian tăng trưởng t gần với kết quả nào sau đây nhất:
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 53
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ.3 giờ 9 phút. Ⓑ. 3 giờ 2 phút. Ⓒ.3 giờ 30 phút. Ⓓ. 3 giờ 18 phút.
Câu 12: Cho biết sự rằng tỉ lệ tăng dân số thế giới hàng năm là 1,32% , nếu tỉ lệ tăng dân số không
thay đổi thì đến tăng trưởng dân số được tính theo công thức tăng trưởng liên tục = .eNr S A
trong đó A là dân số tại thời điểm mốc, S là số dân sau N năm, r là tỉ lệ tăng dân số hàng
năm. Năm 2013 dân số thể giới vào khoảng 7095 triệu người. Biết năm 2020 dân số thế giới
gần nhất với giá trị nào sau đây?
Ⓐ. 7879 triệu người. Ⓑ. 7680 triệu người. Ⓒ.7782 triệu người. Ⓓ. 7777 triệu người.
Câu 13: Dân số thế giới được dự đoán theo công thức ( ) = ebt P t a
, trong đó a , b là các hằng số, t là
năm tính dân số. Theo số liệu thực tế, dân số thế giới năm 1950 là 2560 triệu người; dân số
thế giới năm 1980 là 3040 triệu người. Hãy dự đoán dân số thế giới năm 2020 ? Ⓐ.3823 triệu. Ⓑ. 5360 triệu. Ⓒ.3954 triệu. Ⓓ. 4017 triệu.
Câu 14: Sự tăng dân số được ước tính theo công thức .
P = P en r , trong đó P là dân số của năm lấy n 0 0
làm mốc tính, P là dân số sau n năm, r là tỉ lệ tăng dân số hàng năm. Biết rằng năm 2001, n
dân số Việt Nam là 78.685.800 triệu và tỉ lệ tăng dân số năm đó là 1,7% . Hỏi cứ tăng dân số
với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 100 triệu người? Ⓐ. 2018 . Ⓑ. 2017 . Ⓒ. 2015 . Ⓓ. 2016 . BẢNG ĐÁP ÁN 1.C 2.A 3.B 4.D 5.C 6.B 7.C 8.A 9.B 10.D 11.A 12.C 13.A 14.D Hướng dẫn giải
Câu 1: Chọn C
Áp dụng công thức lãi kép P = P + r với P = 27 , r = 0,0185 , tìm n sao cho P 36 . n ( n 1 ) n Ta có 4
27.1, 0185n 36 n log n =16 . 1,0185 3
Câu 2: Chọn A
Áp dụng công thức lãi kép ta có: n n
P = P 1+ r
=100 1+ 0,4% 200 n 173,6331381 0 ( ) ( )
Vậy sau ít nhất 174 tháng thì số tiền lĩnh được lớn hơn hai lần số tiền ban đầu.
Câu 3: Chọn B
Gọi số tiền gửi ban đầu là A và số năm tối thiểu thỏa ycbt là n . Ta có ( n
1+ 8, 4%) 3 1, 084n A A 3 n log 3 = 13, 62064 . 1,084
Vậy số năm tối thiểu là 14 năm.
Câu 4: Chọn D
Gọi A là số tiền tối thiểu mà ông An đầu tư. 6 6 Ta có 20.10 20.10 A( + r )5 6 1 = 20.10 A = A = 14.909.65,26 . 5 5 6.05 6, 05 1+ 1+ 100 100
Câu 5: Chọn C 6
Số tiền người đó nhận về sau 6 năm là: 5, 4 75000000 1+ 102826000 . 100
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 54
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 6: Chọn B
Gọi số tiền gửi ban đầu là A và số năm tối thiểu thỏa ycbt là n . Ta có ( n
1+ 8, 4%) = 2 1, 084n A A = 2 n = log 2 = 8, 59 . 1,084
Vậy số năm tối thiểu là 9 năm.
Câu 7: Chọn C
Từ công thức lãi kép ta có A = A + r . n ( n 1 ) Theo đề bài ta có n = 10 100 r = 0,06 + A = A( + )10 100 1 0, 06 = A( 10 100 1, 06 − ) 1 A = 10 1.06 −1 A = A +100 n
A =126446597 (đồng).
Câu 8: Chọn A
Theo công thức lãi kép số tiền có được sau n
n tháng là T = T 1+ r . 0 ( )
Áp dụng vào ta có: 100.000.000 1,005n
125.000.000 n 45.
Câu 9: Chọn B
Cường độ ánh sáng ở độ sâu 3m là 1 − ,4.3 4 − ,2 I = I .e = I .e 1 0 0
Cường độ ánh sáng ở độ sâu 30m là 1 − ,4.30 4 − 2 I = I .e = I .e 2 0 0 4 − ,2 I e Ta có 1 16 =
= 2,6081.10 nên cường độ ánh sáng giảm đi 16 2, 6081.10 lần. 42 − I e 2
Câu 10: Chọn D 1
Vì cứ sau 20 phút (bằng giờ) số lượng vi khuẩn tăng gấp đôi nên số lượng vi khuẩn tăng 3
theo quy luật N = N .2n = 40.2n 671088640 n 4 2 . n 0 1
Vậy sau ít nhất 24. = 8 giờ thì số vi khuẩn đạt mức lớn hơn 671088640 con. 3
Câu 11: Chọn A 1 Ta có 5 300 100.e r = r = ln 3 . 5 1 t. ln 3 5 2.A = . A e
t = 5log 2 3,1546 giờ. ChọnA 3
Câu 12: Chọn C
Áp dụng công thức = .eNr S A
với A = 7095 , N = 7 ; r = 0.0132 ta có 7.0,0132 S = 7095.e 7782 triệu người.
Câu 13: Chọn A 1950 . b a e = 2560 ( ) 1
Từ giả thiết ta có hệ phương trình: . 1980 . b a e = 3040 (2) b 19 19 1 19 Chia (2) cho ( ) 1 ta được 30 e = 30b = ln b = ln . 16 16 30 16 Thay vào ( ) 2560 1 ta được: a = . 65 19 16
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 55
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung 1 19 2020. ln 2560 Vậy P (2020) 30 16 = .e 3823 (triệu) 65 19 16
Câu 14: Chọn D 1000000 ln .
P = P en r n.1,7% 100000000 = 78685800e 786858 n = 14.1. n 0 1, 7%
Sau 15 năm thì dân số nước ta ở mức 100 triệu người.
Do đó năm 2016 dân số nước ta ở mức 100 triệu người.
Dạng ⑥: Toán tìm tham số m để hàm số xác định
-Phương pháp:
. Sử dụng điều kiện xác định của hàm số trên dạng 1. . Casio: table
A - Bài tập minh họa:
Câu 1: Tìm tất cả các giá trị của tham số m để hàm số y = log ( 2
x − 2x + m có tập xác định là . 2 )
Ⓐ. m 1.
Ⓑ. m 1. Ⓒ. m 1. Ⓓ. m 1 − Lời giải
PP nhanh trắc nghiệm
Chọn C
' 0 1− m 0 m 1
Hàm số có tập xác định là 2
x − 2x + m 0, x .
Tam thức vế trái có hệ số bậc hai dương nên để thỏa mãn
yêu cầu bài toán thì ' 0 1− m 0 m 1.
Vậy m 1
Câu 2: Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số 1 y = + log
x − m xác định trên khoảng (2;3) ? 3 2m +1− x Ⓐ.1. Ⓑ. 2 . Ⓒ. 4 . Ⓓ. 3 . Lời giải
PP nhanh trắc nghiệm Chọn B
Hàm số y xác định trên khoảng (2;3)
2m +1− x 0 , x (2;3) x − m 0 2m x −1 , x (2;3) m x
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 56
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
2m max (x − ) 1 2; 3 m 1 1 m 2. m min x m 2 2; 3
Vậy có 2 giá trị nguyên dương của m thỏa mãn yêu cầu bài toán.
Câu 3: Hàm số y = ( 2
ln x − 2mx + 4) có tập xác định D = khi các giá trị của tham số m là Ⓐ. m 2. Ⓑ. m 2 − hoặc m 2 . Ⓒ. m = 2 . Ⓓ. 2 − m 2 . Lời giải
PP nhanh trắc nghiệm Chọn D a =1 0 2 − m 2 Hàm số y = ( 2
ln x − 2mx + 4) có tập xác định khi 0 2
x − 2mx + 4 0, x ( ) 1 ( ) a =1 0 2 1 m − 4 0 2 − m 2. 0
B - Bài tập rèn luyện:
Câu 1: Hàm số y = ( 2 ln x + mx + )
1 xác định với mọi giá trị của x khi. − Ⓐ. m 2 . Ⓑ. m 2 . Ⓒ. 2 − m 2 . Ⓓ. m 2 . m 2
Câu 2: Tìm tất cả các giá trị của m để hàm số y = log ( 2
−x + mx + 2m +1 xác định với mọi x (1;2) . 3 ) Ⓐ. 1 − 1 m . Ⓑ. 3 m . Ⓒ. 3 m . Ⓓ. m 3 4 4 3
Câu 3: Tìm tất cả các giá trị của tham số m để hàm số y = ln(m −1)x − m + 2 xác định trên đoạn 0;2 . Ⓐ. 0 m 2.
Ⓑ. 1 m 2 . Ⓒ. m 2 . Ⓓ. m 1 .
Câu 4: Tìm tất cả các giá trị thực của tham số m để hàm số y = ( 2
log x − 2mx + 4) có tập xác định là
Ⓐ. m 2 m 2 − . Ⓑ. m = 2. Ⓒ. m 2 . Ⓓ. 2 − m 2. 1
Câu 5: Số các giá trị nguyên của tham số m để hàm số y = log(mx − m + 2) xác định trên ;+ là 2 Ⓐ.4. Ⓑ. 5. Ⓒ.Vô số. Ⓓ. 3.
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 57
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 6: Số các giá trị nguyên của tham số m để hàm số y = log(mx - m + 2) xác định trên 1 ;+ là 2 Ⓐ. 4 . Ⓑ. 5 . Ⓒ.vô số. Ⓓ. 3 2
Câu 7: Tìm tất cả các giá trị của m để hàm số = log 2018x x y − x −
− m xác định với mọi giá trị 2018 2 x thuộc 0; + ) Ⓐ. m 9. Ⓑ. m 1.
Ⓒ. 0 m 1. Ⓓ. m 2.
Câu 8: Tìm tất cả các giá trị thực của tham số m để hàm số y = ( 2
log x − 2mx + 4) có tập xác định là . m Ⓐ. 2 − m 2 . Ⓑ. 2 − m 2 . Ⓒ. 2 . Ⓓ. m = 2 . m 2 − BẢNG ĐÁP ÁN 1.C 2.B 3.A 4.D 5.A 6.A 7.B 8.B Hướng dẫn giải
Câu 1: Yêu cầu bài toán 2
x + mx +1 0 , x 2 m − 4 0 2 − m 2. Câu 2: Yêu cầu bài toán 2
−x + mx + 2m +1 0, x (1;2) ( x −
m x + 2) x −1, x (1;2) 2 1 2 m , x (1;2) x + 2 −
Xét hàm số f ( x) 2 x 1 = , với x (1; 2) x + 2 2 + + x = 2 − − 3 x x (1;2 4 1 ) f '(x) =
, f ' x = 0 . 2 ( ) (x + 2) x = 2 − + 3 (1;2)
f (x) 0, x (1;2), x 1 2 + f /(x) 3 f(x) 0 4 2 − 3 3
Dựa vào bảng biến thiên có x 1
f ( x) ,(1; 2) , nên m , x
(1;2) khi m . 4 x + 2 4 3 Vậy m . 4 Câu 3:
Yêu cầu bài toán (m − )
1 x − m + 2 0, x 0;2
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 58
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Bài toán tương đương với tìm m để đồ thị hàm số nằm phía trên trục Ox
ĐK hàm số y = (m −1)x − m + 2,0 x 2 có hai đầu mút y(0) 0 và y (2) 0. y
(0) = −m + 2 0 m 2 y ( m 2) = 2(m − ) 0 2 1 − m + 2 0 m 0 Câu 4:
Điều kiện xác định của hàm số: 2
x − 2mx + 4 0 .
Để hàm số có tập xác định là thì 2 2
x − 2mx + 4 0,x m − 4 0 2 − m 2. Câu 5:
YCBT mx − m + 2 0 thỏa 1 x ; + 2 a = 0 m = 0 m = 0 b 0 −m + 2 0 m = 0 m 0 a m m 0 0 m 4 0 0 m − 4 b m − 0 0 m 4 1 2 1 − 2 m a 2 m 2
Vì m nên m0;1;2; 3 . Câu 6:
YCBT mx − m + 2 0 thỏa 1 x ; + 2 a = 0 m = 0 m = 0 b 0 −m + 2 0 m = 0 m 0 a m m 0 0 m 4 0 0 m − 4 b m − 0 0 m 4 1 2 1 − 2 m a 2 m 2
Vì m nên m0;1;2; 3 . Câu 7:
Hàm số đã cho xác định x 0;+ ) 2 2018x x − x − − m 0 x 0;+ ) 2 2 2018x x − x − , m x 0;+ )( )1 2 Đặt ( ) 2 = 2018x x f x − x − , x 0; + ) 2 ( ) = 2018x f x ln(2018) −1− x ( ) = x f x ( )2 2018 ln2018 −1
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 59
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung 2
Có 2018x (ln2018) −1 0, x 0,+ ) // f (x) 0 Bảng biến thiên: x 0 +∞ y // + +∞ y / m>0 + y 1
Có y 0 . Suy ra y = f (x) đồng biến trong 0;+
), có f(0) = ln(2018)−1 0
Suy ra y = f (x) đồng biến trong 0;+ ), có f (0) =1
Dựa vào BBT để có ( ) 1 m 1. Câu 8:
Điều kiện để hàm số y = ( 2
log x − 2mx + 4) xác dịnh trên là a =1 0 2
x − 2mx + 4 0, x 2 m − 4 0 2 − m 2 . 0
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 60
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021 CHƯƠNG ②: FB: Duong Hung
Bài 5: PHƯƠNG TRÌNH MŨ
Dạng ①: Phương trình mũ cơ bản.
-Phương pháp:
-Casio: Slove, Calc nghiệm, Table.
A - Bài tập minh họa:
Câu 1: Phươg trình 2x 1 3 + = 27 có nghiệm là Ⓐ. x = 2 . Ⓑ. x = 3 − . Ⓒ. x = 3. Ⓓ. x =1. Lời giải
PP nhanh trắc nghiệm
Chọn D Casio 2x 1 3 + = 27 2 x 1 + 3 3
= 3 2x +1= 3 2x = 2 x =1 Solve nghiệm
Câu 2: Phươg trình có 2x−3x+8 2 x 1 3 9 − =
có tổng các nghiệm bằng Ⓐ. S = 5. Ⓑ. S = 7 . Ⓒ. S = 3. Ⓓ. S = 2 . Lời giải
PP nhanh trắc nghiệm
Chọn B
Casio Solve hoặc table 2 2 x −3x+8 2 x 1 − x −3x+8 4 x−2 2 3 = 9 3 = 3
x − 3x + 8 = 4x − 2 x = 5 2
x − 7x +10 = 0 x = 2 S = 5 + 2 = 7
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 61
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
S = 5 + 2 = 7 . Chọn Ⓑ.
Câu 3: Tích các nghiệm của phương trình ( ) 2 8− x 3 − 5−5 2.5 =10 .10 x Ⓐ. 3. Ⓑ. 6
− . Ⓒ. 2 . Ⓓ. 6 . Lời giải
PP nhanh trắc nghiệm
Chọn B
Casio Solve hoặc table ( −x 2.5) 2 2 8 3 − 5−5 x 8−x 2−5 =10 .10 10 =10 x x = 1 − 2
8 − x = 2 − 5x x = 6
B - Bài tập rèn luyện:
Câu 1. Phươg trình 2x 1 5 + = 625 có nghiệm là Ⓐ. 5 x = . Ⓑ. 3 x = . Ⓒ. x = 3. Ⓓ. x =1. 2 2
Câu 2. Phương trình: x 1 2 3 có nghiệm là 9 Ⓐ. −2 . Ⓑ. 1. − Ⓒ.1. Ⓓ. 2 .
Câu 3. Tìm tập nghiệm − +
S của phương trình 2 x 3x 2 9 =1.
Ⓐ. S = 1 . Ⓑ. S = 0; 1 . Ⓒ. S = 1;− 2 . Ⓓ. S = 1; 2 .
Câu 4. Nghiệm của phương trình 2 5 −x =125 là Ⓐ. x = 1 − . Ⓑ. x = 5 − . Ⓒ. x = 3. Ⓓ. x =1.
Câu 5. Phương trình 2017 2 8x − = 0 có nghiệm là Ⓐ. 2017 x = . Ⓑ. 2017 x = . Ⓒ. 2017 x = . Ⓓ. 2017 x = . 4 5 6 3
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 62
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 6. Cho phương trình x x 1 4 2 + + −3 = 0. Khi đặt 2x t =
ta được phương trình nào sau đây Ⓐ. 2
2t − 3t = 0 .
Ⓑ. 4t −3 = 0. Ⓒ. 2
t + t − 3 = 0 Ⓓ. 2
t + 2t − 3 = 0 .
Câu 7. Phương trình 2x 1
5 + = 125 có nghiệm là Ⓐ. 5 x = . Ⓑ. x =1. Ⓒ. x = 3. Ⓓ. 3 x = . 2 2
Câu 8. Phương trình 3 2 2 x + x x + x 1 3 9 − =
có tích tất cả các nghiệm bằng Ⓐ. 2 . Ⓑ. 2 2 . Ⓒ. −2 2 . Ⓓ. −2 . 2 x +2 x− 1
Câu 9. Phương trình 2 3 27
= có tập nghiệm là 3 Ⓐ. 1 − ; 7 . Ⓑ. 1 − ;− 7 . Ⓒ.1; 7 . Ⓓ.1; 7 − .
Câu 10. Tập nghiệm của phương trình: x 1 x 1 4 4 272 là Ⓐ. 3;2 . Ⓑ. 2 . Ⓒ. 3 . Ⓓ. 3;5 .
Câu 11. Tổng các nghiệm của phương trình 2x+2x 2 2
= 8 −x bằng Ⓐ. 6 − . Ⓑ. 5 − . Ⓒ. 5 . Ⓓ. 6 .
Câu 12. Phương trình 2x 1 − x 1 6 5.6 − −
+1= 0 có hai nghiệm x ; x . Khi đó tổng hai nghiệm x + x là 1 2 1 2 Ⓐ. 5. Ⓑ. 3. Ⓒ.2. Ⓓ.1.
Câu13. Nghiệm của phương trình 7x 1 − 2x 1 − 2 = 8 là Ⓐ. x = 2 Ⓑ. x =1. Ⓒ. x = 2 − . Ⓓ. x = 3 − . 2 x −2 x−3
Câu 14. Tập nghiệm của phương trình 1 x 1 = 7 + là 7 Ⓐ. S = 2 . Ⓑ. S = − 1 . Ⓒ. S = 1 − ; 2 . Ⓓ. S = 1 − ; 4 .
Câu 15. Nghiệm của phương trình x+ x− 1 1 1 2 .4 . =16x là 1 8 −x Ⓐ. x = 3. Ⓑ. x =1. Ⓒ. x = 4. Ⓓ. x = 2. 2 − x
Câu 16. Tổng bình phương các nghiệm của phương trình x− 1 3 2 5 = bằng 5 Ⓐ. 2. Ⓑ. 5. Ⓒ.0. Ⓓ.3. 2 − x
Câu 17. Tổng các nghiệm của phương trình x− 1 3 2 3 = bằng 3
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 63
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 0. Ⓑ. 2. Ⓒ. 5. Ⓓ. 3.
Câu 18. Tập nghiệm của phương trình 2x−x− 1 4 2 = là 16 Ⓐ. 2 − ; 2 . Ⓑ. 1 − ;1 . Ⓒ.2; 4 . Ⓓ.0; 1 .
Câu 19. Tìm tập nghiệm S của phương trình 2 2 x −3 3 = 27 . Ⓐ. S = 3 . Ⓑ. S = 3.
Ⓒ. S = − 3; 3. Ⓓ.S = 3 − ; 3 . x − x+
Câu 20. Tập nghiệm của phương trình ( ) 2 2 1 2 = 4 là Ⓐ. 1;− 3 . Ⓑ. − 1 . Ⓒ. 1 − ; 3 . Ⓓ. 3 . BẢNG ĐÁP ÁN 1.D 2.B 3.D 4.B 5.D 6.D 7.B 8.D 9.D 10.C 11.B 12.D 13.C 14.C 15.D 16.B 17.D 18.D 19.C 20.C
Dạng ②: Phương trình mũ đưa về cùng cơ số.
-Phương pháp:
-Casio: Slove, Calc nghiệm, Table.
A - Bài tập minh họa:
Câu 1: Phươg trình 2x 1 5 + = 125 có nghiệm là Ⓐ. 5 x = . Ⓑ. 3 x = . Ⓒ. x = 3. Ⓓ. x =1 2 2 Lời giải
PP nhanh trắc nghiệm
Chọn D 2x 1 + 2 x 1 + 3 5 =125 5
= 5 2x +1= 3 x =1. Casio: Solve
Câu 2: Tìm tập nghiệm − +
S của phương trình 2 x 3x 2 9 =1. Ⓐ. S = 1 . Ⓑ. S = 0; 1 . Ⓒ. S = 1;− 2 . Ⓓ. S = 1; 2 .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 64
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm
Chọn D Casio: Solve x =1 2x−3x+2 2 9
=1 x − 3x + 2 = 0 . x = 2
Câu 3: Nghiệm của phương trình 2 5 −x = 125 là Ⓐ. x = 1 − . Ⓑ. x = 5 − . Ⓒ. x = 3. Ⓓ. x =1. Lời giải
PP nhanh trắc nghiệm
Chọn A 2−x 2−x 3 5 =125 5
= 5 2 − x = 3 x = 1 − .
Casio: Calc, Solve hoặc table
Câu 4: Phương trình 3 2 2 x + x x + x 1 3 9 − =
có tích tất cả các nghiệm bằng Ⓐ. 2 . Ⓑ. 2 2 . Ⓒ. −2 2 . Ⓓ. −2 . Lời giải
PP nhanh trắc nghiệm
Chọn D Casio: Solve Phương trình 3 2 2 x + x x + x 1 3 9 − = . + ( 2 3 2 2 x + x− x x )1 3 = 3 3 2 x + x = 2( 2 x + x − ) 1 x =1 3 2
x − x − 2x + 2 = 0 (x − ) 1 ( 2
x − 2) = 0 x = 2 x = − 2
Suy ra tích tất cả các nghiệm bằng −2 .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 65
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
B - Bài tập rèn luyện: 2 x +2 Câu 1: x− 1 Phương trình 2 3 27
= có tập nghiệm là 3 Ⓐ. 1 − ; 7 . Ⓑ. 1 − ;− 7 . Ⓒ.1; 7 . Ⓓ.1; 7 − .
Câu 2: Tập nghiệm của phương trình: x 1 x 1 4 4 272 là Ⓐ. 3;2 . Ⓑ. 2 . Ⓒ. 3 . Ⓓ. 3;5 .
Câu 3: Tính tổng các nghiệm của phương trình 2 2 x +5 x+4 2 = 4 . − Ⓐ. 5 . Ⓑ. 1 − . Ⓒ.1. Ⓓ. 5 . 2 2
Câu 4: Tìm tập nghiệm +
S của phương trình x 1 2 = 8. Ⓐ. S = 4 . Ⓑ. S = 1 . Ⓒ. S = 3 . Ⓓ. S = 2 .
Câu 5: Tổng tất cả các nghiệm của phương trình 2x−4x+5 2 = 8 là Ⓐ. −2 . Ⓑ. −4 . Ⓒ. 4 . Ⓓ. 2 .
Câu 6: Phương trình 2
log x + 3log x + 2 = 0 có tổng tất cả các nghiệm là 2 1 2 Ⓐ. 6 . Ⓑ. 8 . Ⓒ. 9 . Ⓓ. 5 . x+ x +
Câu 7: Tập nghiệm S của phương trình ( + ) = ( + ) 2 2017 1008 1 2 3 2 2 là Ⓐ. 1 S = ; 1 − . Ⓑ. 1 S = 1 ;− .
Ⓒ. S = 1008;201 7 . Ⓓ. S = 1; 2 . 2 2
Câu 8: Tính tổng các nghiệm của phương trình 2 2 x +5 x+4 2 = 4 . − Ⓐ. 5 . Ⓑ. 1 − . Ⓒ.1. Ⓓ. 5 . 2 2
Câu 9: Số nghiệm của phương trình 2 2 x 7 x 5 3 1 0 là Ⓐ. 1. Ⓑ. 3 . Ⓒ. 2 . Ⓓ. 0 .
Câu 10: Biết phương trình 2x−3 x 1 8 32 + =
có 2 nghiệm x , x . Tính x .x . 1 2 1 2 Ⓐ. 14 7 5 x .x = − . Ⓑ. x .x = 4 − . Ⓒ. x .x = . Ⓓ. x .x = . 1 2 3 1 2 1 2 3 1 2 3
Câu 11: Biết phương trình 2x−3 x 1 8 32 + =
có 2 nghiệm x , x . Tính x .x . 1 2 1 2
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 66
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 14 7 5 x .x = − . Ⓑ. x .x = 4 − . Ⓒ. x .x = . Ⓓ. x .x = . 1 2 3 1 2 1 2 3 1 2 3 1 3 x+ x+ Câu 12: 1
Biết phương trình x 2x 1 2 2 9 2 2 3 − − = −
có nghiệm là a . Tính giá trị P = a + log 2 . 9 2 2 Ⓐ. 1 P = 1− log 2 . Ⓑ. P =1 . Ⓒ. P =1− log 2 . Ⓓ. 1 P = . 9 2 9 2 2 2
Câu 13: Tập nghiệm của phương trình 2x−3 3 x = 27 là Ⓐ. 1 − ; 3 . Ⓑ. 9 . Ⓒ. 3 . Ⓓ. .
Câu 14: Tìm tích các nghiệm của phương trình 2x−4 2 = 32 . Ⓐ. P = 16 − . Ⓑ. P = 9. Ⓒ. P = 9 − . Ⓓ. P = 4 − .
Câu 15: Biết phương trình 2x−3 x 1 8 32 + =
có 2 nghiệm x , x . Tính x .x . 1 2 1 2 Ⓐ. 14 7 5 x .x = − . Ⓑ. x .x = 4 − . Ⓒ. x .x = . Ⓓ. x .x = . 1 2 3 1 2 1 2 3 1 2 3
Câu 16: Tìm số nghiệm của phương trình 8x 4 + 2 x e = e . Ⓐ. 0 . Ⓑ. 2 . Ⓒ. 3 . Ⓓ.1. Câu 17: +
Nghiệm của phương trình x x 1 3 .2 = 72.6a là Ⓐ. x = a +1. Ⓑ. x = 2 . a Ⓒ. x = a + 2. Ⓓ. x = . a x 3 Câu 18: x x 1 Tính tổng S x
x biết x , x là các giá trị thực thỏa mãn đẳng thức 2 6 1 2 1 2 1 2 4 Ⓐ. S 4 . Ⓑ. S 8. Ⓒ. S 5. Ⓓ. S 2 . BẢNG ĐÁP ÁN 1.D 2.C 3.A 4.D 5.C 6.A 7.B 8.A 9.C 10.A 11.A 12.B 13.A 14.C 15.A 16.A 17.C 18.A
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 67
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Dạng ③: Đặt ẩn phụ
-Phương pháp: . Với , . . Dạng 1: Đặt đưa phương trình
về dạng phương trình bậc 2: .
Giải phương trình tìm nghiệm và kiểm tra điều kiện .
Sau đó thế vào phương trình tìm nghiệm . . Dạng 2: , trong đó . Đặt . . suy ra . Hoặc có dạng . Dạng 3: . Chia hai vế cho và đặt .
Đưa phương trình
về dạng phương trình bậc 2 giải
A - Bài tập minh họa:
Câu 1: Phương trình 2.4x − 7.2x + 3 = 0 có tích tất cả các nghiệm bằng
Ⓐ. x = − log 3 Ⓑ. x = log 3 2 2 Ⓒ. x = 1 −
Ⓓ. x = 1, x = log 3 2 Lời giải
PP nhanh trắc nghiệm Chọn D _Casio : Solve
2.4x − 7.2x + 3 = 0 Đặt 2x t =
, t 0. Phương trình trở thành 2
2t − 7t + 3 = 0 Với 1 − t = , ta được x 1 2 = 2 x = 1 − 2
Với t = 3 , ta được 2x = 3 x = log 3 2 Vậy S = log 3; 1
− .nên. P = x x = −log 3 2 1 2 2
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 68
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 2: Tổng các nghiệm của phương trình 2x−3 x−2 2 −3.2 +1= 0 là Ⓐ. 6 . Ⓑ. 1. Ⓒ. 3 . Ⓓ. −4 Lời giải
PP nhanh trắc nghiệm Chọn A Công thức tính nhanh: 2 x−3 x−2 2 − 3.2 +1 = 0 2 . x + . x A a
B a + C = 0 có 2 2 2 x 3 = − 2x +1 = 0
nghiệm phân biệt x , x 1 2 8 4 C Đặt = 2x t
,t 0 . Phương trình trở thành
suy ra x + x = log A 1 2 a t = 4 2
t − 6t + 8 = 0 Casio: Solve t = 2
Với t = 4, ta được 2x = 4 x = 2
Với t = 2, ta được 2x = 2 x =1
Vậy phương trình có nghiệm x = 2 , x =1. S = 3 .
Câu 3: Phương trình 6.4x 13.6x 6.9x − + = 0. có nghiệm là Ⓐ. S = 1 − ;1 . Ⓑ. S = 1 ;1 . Ⓒ. S = 2 − ;1 . Ⓓ. S = 1 − ; 3
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 69
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm Chọn A Casio: Solve 2 x x x x x 3 3 6.4 −13.6 + 6.9 = 0 6 −13 + 6 = 0 2 2 x 3 3 = 2 2 x = 1 x x = −1 3 2 = 2 3 Vậy S = 1 − ;1
B - Bài tập rèn luyện:
Câu 1. Gọi x , x là các nghiệm của phương trình: 2x 9 2x −
+8 = 0. Tính S = x + x . 1 2 1 2 Ⓐ. S = 8. Ⓑ. S = 6 . Ⓒ. S = 9 − . Ⓓ. S = 9 .
Câu 2. Nghiệm của phương trình 9x 4.3x − − 45 = 0 là Ⓐ. x = 9 . Ⓑ. x = 5
− hoặc x = 9 .
Ⓒ. x = 2 hoặc x = log 5 . Ⓓ. x = 2 . 3
Câu 3. Nghiệm của phương trình: 9x 10.3x − + 9 = 0 là
Ⓐ. x = 2 ; x =1.
Ⓑ. x = 9 ; x =1.
Ⓒ. x = 3; x = 0 .
Ⓓ. x = 2 ; x = 0 .
Câu 4. Cho phương trình x 1
25 + − 26.5x +1 = 0 . Đặt 5x t =
, t 0 thì phương trình trở thành Ⓐ. 2
t − 26t +1 = 0 . Ⓑ. 2
25t − 26t = 0 . Ⓒ. 2
25t − 26t +1 = 0 . Ⓓ. 2 t − 26t = 0 .
Câu 6 . Cho phương trình x x 1 25 5 + − + 4 = 0 , khi đặt 5x t =
ta được phương trình nào dưới đây ? Ⓐ. 2
2t − t + 4 = 0 . Ⓑ. 2
t − t + 4 = 0 . Ⓒ. 2
t − 5t + 4 = 0 . Ⓓ. 2
2t − 5t + 4 = 0 .
Câu 6. Nghiệm của phương trình 25x 15x 6.9x − − = 0 là Ⓐ. 3 x = − log 2 . Ⓑ. x = − g lo 3. Ⓒ. x = log 3. Ⓓ. x = log . 3 5 5 3 5 5 3
Câu 7. Cho phương trình 1−2 13
x −13−x −12 = 0 . Bằng cách đặt 13x t = phương trình trở thành
phương trình nào sau đây? Ⓐ. 2
12t − t −13 = 0 . Ⓑ. 2
13t − t −12 = 0 . Ⓒ. 2
12t + t −13 = 0 . Ⓓ. 2
13t + t − 2 = 0 . x x
Câu 8. Cho phương trình ( 7+ 4 3) +( 7−4 3 ) =14 (*). Tìm khẳng định đúng trong các khẳng định sau: x
Ⓐ. Đặt t = ( 7 + 4 3 ) thì phương trình (*) trở thành 2t −14t −1= 0.
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 70
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung x
Ⓑ. Đặt t = ( 7 −4 3 ) thì phương trình (*) trở thành 2t +t −14 = 0. x
Ⓒ.Đặt t = ( 7−4 3) thì phương trình (*) trở thành 2t −14t +1= 0. x
Ⓓ.Đặt t = ( 7 + 4 3 ) thì phương trình (*) trở thành 2t +t −14 = 0. x
Câu 9. Cho phương trình x 2
3 − 8.3 +15 = 0 . Phương trình đã cho có bao nhiêu nghiệm? Ⓐ. 0 . Ⓑ. 3 . Ⓒ.1. Ⓓ. 2 . x
Câu 10. Phương trình − x 1 1 3
= 2 + có bao nhiêu nghiệm âm? 9 Ⓐ. 0 . Ⓑ. 1. Ⓒ. 2 . Ⓓ. 3 .
Câu 11. Nghiệm phương trình 9x 4.3x − − 45 = 0 là Ⓐ. x = 9 . Ⓑ. x = 5 − hoặc x = 9 .
Ⓒ. x = 2 hoặc x = log 5 . Ⓓ. x = 2 . 3
Câu 12. Tính tổng tất cả các nghiệm của phương trình sau 2x+8 x+5 3 − 4.3 + 27 = 0 . Ⓐ. 4 . Ⓑ. 4 − . Ⓒ. 5 − . Ⓓ. 5 . 27 27
Câu 13. Tổng tất cả các nghiệm của phương trình 2 3 x 4.3x − + 3 = 0 bằng: Ⓐ. 4 . Ⓑ. 3 . Ⓒ. 4 . Ⓓ.1. 3
Câu 14. Tổng tất cả các nghiệm của phương trình 2x x+2 3 − 2.3 + 27 = 0 bằng Ⓐ. 9 . Ⓑ. 18. Ⓒ. 3 . Ⓓ. 27 .
Câu 15 . Phương trình x x 2 x 1 9 6 2 + − = có bao nhiêu nghiệm âm? Ⓐ. 3 Ⓑ. 0 . Ⓒ.1. Ⓓ. 2 . x x
Câu 16. Gọi x , x là nghiệm của phương trình (2 − 3) +(2 + 3) = 4 . Khi đó 2 2
x + 2x bằng 1 2 1 2 Ⓐ. 2. Ⓑ. 3 . Ⓒ.5. Ⓓ.4.
Câu 17. Tìm tổng cácnghiệm của phương trình 2x 1 2 + − 5.2x + 2 = 0. Ⓐ. 0. Ⓑ. 5 . Ⓒ.1. Ⓓ.2. 2
Câu 18. Biết rằng phương trình x 1 − 3 5
+5 −x = 26 có hai nghiệm x , x . Tính tổng x + x . 1 2 1 2 Ⓐ. 2 . Ⓑ. 5 . Ⓒ. 4 . Ⓓ. −2 .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 71
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Câu 19. Gọi + +
x ; x là 2 nghiệm của phương trình x 1 x 1 4
−5.2 + 4 = 0 . Khi đó giá trị S = x + x là 1 2 1 2 Ⓐ. S = 1 − . Ⓑ. S = 0 . Ⓒ. S =1. Ⓓ. S = 2 .
Câu 20. Cho phương trình 2x+1 x 7
−8.7x +1 = 0có 2 nghiệm x , x ( x x . Khi đó 2 có giá trị là: 1 2 ) 1 2 x1 Ⓐ. 4. Ⓑ. 2. Ⓒ. 1 − . Ⓓ.0. BẢNG ĐÁP ÁN 1B 2D 3D 4C 5C 6C 7C 8C 9D 10D 11D 12C 13D 14C 15D 16B 17A 18C 19B 20D
Dạng ⑤: PT chứa tham số m thỏa mãn ĐK
-Phương pháp:
. Sử dụng các phương phá giải PT mũ và các kiến thức có liên quan để tìm tham số m .Casio: Table, Solve
Bài tập vận dụng rèn luyện:
Câu 1: Cho phương trình .16x − 2( − 2).4x m m
+ m −3 = 0 . Tập hợp tất cả các giá trị dương của m để
phương trình đã cho có hai nghiệm phân biệt là khoảng ( ;
a b) . Tổng T = a + 2b bằng Ⓐ. 14 . Ⓑ. 10. Ⓒ.11. Ⓓ. 7 .
Câu 2: Giá trị của tham số m để phương trình x x 1 4 . m 2 + −
+ 2m = 0 có hai nghiệm x , x thỏa mãn 1 2
x + x = 3 là: 1 2 Ⓐ. m = 3. Ⓑ. m =1. Ⓒ. m = 4 . Ⓓ. m = 2 .
Câu 3: Tìm tất cả các giá trị của tham số m để phương trình sinx 1+sin 4 + 2
x − m = 0 có nghiệm.
Ⓐ. 5 m 8 .
Ⓑ. 5 m 8.
Ⓒ. 5 m 7 .
Ⓓ. 5 m 9 . 3 4 4 4 Câu 4: Gọi ( ; a )
b là tập các giá trị của tham số m để phương trình 2
2e x − 8ex − m = 0 có đúng hai
nghiệm thuộc khoảng (0;ln 5). Tổng a + b bằng Ⓐ. 2 . Ⓑ. 4. Ⓒ. 6. − Ⓓ. 14. −
Câu 5: Tất cả các giá trị thực của m để phương trình 9x + 6x − .4x m = 0 có nghiệm là Ⓐ. m 0. Ⓑ. m 0. Ⓒ. m 0. Ⓓ. m 0.
Câu 6: Có bao nhiêu giá trị nguyên của tham số m để phương trình 25x − 3.5x + m −1 = 0 có hai nghiệm phân biệt? Ⓐ. 2 Ⓑ. 1. Ⓒ. 4 . Ⓓ.5 .
Câu 7: Tìm m để phương trình x (m ) x x 1 9 1 6 4 + − + +
= 0 có hai nghiệm trái dấu. Ⓐ. m 3. Ⓑ. 3 m 5 . Ⓒ. m . Ⓓ. m 4 .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 72
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 8: Số giá trị nguyên của m để phương trình x x 1 4 . m 2 2m
0 có hai nghiệm phân biệt x , x 1 2 và x x 3là 1 2 Ⓐ. 0 . Ⓑ. 2 . Ⓒ.3. Ⓓ.1.
Câu 9: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 + −x −( + ) 2 1 1 1+ 1 9 3 .3 −x m
+ 2m +1= 0 có nghiệm thực? Ⓐ. 5 . Ⓑ. 7 . Ⓒ.Vô số. Ⓓ. 3 .
Câu 10: Cho phương trình 2 2 x 2 x 1 x 2 x 2 4 . m 2 3m 2
0 . Tìm tất cả giá trị của tham số m để
phương trình có 4 nghiệm phân biệt. Ⓐ. m 1 . Ⓑ. m 2 . Ⓒ. m 2 . Ⓓ. m 1. m 2
Câu 11: Có bao nhiêu giá trị nguyên của tham số m để phương trình 25x 3.5x m 1 0 có hai nghiệm phân biệt? Ⓐ. 2 Ⓑ. 1. Ⓒ. 4 . Ⓓ.5 .
Câu 12: Tổng tất cả các giá trị của tham số m x x
để 25 − (m +1).5 + m = 0 có hai nghiệm phân biệt x , x 1 2 thỏa mãn 2 2 x + x = 4 1 2 bằng Ⓐ. 626 . Ⓑ. 0 . Ⓒ. 26 . Ⓓ. 26 . 25 25 5
Câu 13: Tìm m để phương trình 32x 1 + −10m 3 . x + 3 2
m = 0 có 2 nghiệm x , x sao cho x + x = 0 : 1 2 1 2 Ⓐ. 1 m = 1. Ⓑ. m = 1 Ⓒ. m = 1 − . Ⓓ. . 3 BẢNG ĐÁP ÁN 1.C 2.C 3.B 4.D 5.A 6.A 7.D 8.D 9.B 10.C 11.A 12.A 13.A
Hướng dẫn giải chi tiết. Câu 1: Đặt 4x t =
0, phương trình đã cho trở thành : 2
mt − 2(m − 2)t + m − 3 = 0 ( ) * . Phương trình
đã cho có hai nghiệm phân biệt khi phương trình (*) có hai nghiệm dương phân biệt. m 0 (
m − 2)2 − m(m − 3) 0 Suy ra 2(m − 2) 3 m 4 0 m m−3 0 m
Vậy T = a + 2b = 3+ 2.4 =11. Câu 2:
Có 4x − 2 .2x m + 2m = 0 ( ) 1 . Đặt = 2x t (t 0). Khi đó ( ) 1 trở thành 2 t − 2 .
m t + 2m = 0 (2) .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 73
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Để ( )
1 có hai nghiệm x , x thỏa mãn x + x = 3 thì (2) có hai nghiệm t ,t 0 thỏa mãn 1 2 1 2 1 2 2
' = m − 2m 0
t .t = 8 t
+ t = 2m 0 m = 4 . 1 2 1 2
t .t = 2m = 8 1 2 Câu 3: Đặt sin 2 x t = , với 1 1
− sin x 1 t 2 2 Phương trình sinx 1+sin 4 + 2
x − m = 0 có nghiệm khi và chỉ khi phương trình 2 2
t + 2t − m = 0 t + 2t = m có nghiệm 1 t ; 2 2 Đặt f (t) 2
= t + 2t , có f (t) = 2t + 2 , f (t) 1 = 0 t = 1 − ; 2
, ta có bảng biến thiên 2
Vậy để phương trình có nghiệm khi và chỉ khi 5 m 8 4 Câu 4: Đặt: = x t
e (t (1;5) vì x (0;ln 5) )
Khi đó, phương trình trở thành: 2
2t − 8t − m = 0(*)
Bài toán trở thành: Tìm giá trị của tham m để phương trình có đúng hai nghiệm thuộc khoảng (1;5). Xét hàm: 2
g(t) = 2t − 8t Ta có: g (
t) = 4t −8. g (
t) = 0 4t −8 = 0 t = 2(1;5). Bảng biến thiên
Dựa vào bảng biến thiên, để phương trình có đúng hai nghiệm thuộc khoảng (1;5). thì 8 − m 6 − . Suy ra: a = 8 − ;b = 6 − .
Vậy : a + b = ( 8 − ) + ( 6 − ) = 1 − 4.
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 74
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Câu 5: 2 x x x x x 3 3 9 + 6 − . m 4 = 0 + − m = 0 . 2 2 x Đặt 3 t = 0 . 2
Phương trình trở thành 2
t + t − m = 0 ( ) 1 .
Phương trình đã cho có nghiệm khi và chỉ khi phương trình ( ) 1 có nghiệm dương: 0 1 + 4m 0 S 0 1 − 0 (KTM ) m 0 . P 0 −m 0 ac 0 −m 0 Câu 6: Đặt = 5x t
(t 0) . Phương trình đã cho trở thành: 2t −3t + m−1= 0 ( ) 1 .
Phương trình đã cho có hai nghiêm phân biệt ( )
1 có hai nghiệm dương phân biệt 0 13 b − 13 4m 0 m 13 − 0 4 1 m . a m −1 0 4 m 1 c 0 a 13 1 m Ta có 4 m 2; 3 . m Câu 7: x x x ( 9 3 m ) x x 1 9 1 6 4 + − + + = 0 − (m+ ) 1 + 4 = 0 (1) 4 2 x Đặt 3 t = , (t 0) 2
Phương trình trở thành 2 t − (m + ) 1 t + 4 = 0 (2) .
YCBT: Phương trình có hai nghiệm trái dấu x 0 x 1 2 x x 1 2 có hai nghiệm 3 3
t , t thỏa mãn 0 t = 1 à v t = 1 . 1 2 1 2 2 2 = (m + )2 1 −16 0
= (m + )2 − − 1 16 0 m 3 m 5 P 0 à v S 0 m +1 0 m 1 − m 4 . (
t −1 t −1 0
t t − t − t +1 0 4 − (m + ) 1 +1 0 1 )( 2 ) 1 2 1 2 Câu 8: x x 1 4 . m 2 2m 0 Đặt 2x t ,t 0 được phương trình 2 t 2mt 2m 0
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 75
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung x x x x 1 2 3 1 2 x x 3 2 2 2 2 8 t .t 8 . 1 2 1 2
Phương trình có hai nghiệm phân biệt x , x và x x 3 1 2 1 2 2 ' m 2m 0
Phương trình có hai nghiệm dương phân biệt t ,t và t .t 8 b 1 2 1 2 2m 0 a c 2m 8 a m 4 .
Vậy chỉ có một giá trị nguyên m 4 thỏa mãn yêu cầu bài toán. Câu 9: Ta có 2 2 2 1 1 0 1 1 1 1 1 2 3 3 x x x + − − + − 9 Đặt 2 1 1 3 x t + − = phương trình trở thành 2
t − (m + 3).t + 2m +1 = 0 ( ) 1 Phương trình 2 + −x −( + ) 2 1 1 1+ 1 9 3 .3 −x m
+ 2m +1= 0 có nghiệm thực phương trình ( ) 1 có
nghiệm t 3;9 ( ) 2 t − 3t +1 1 1 m =
m = t −1− vì t − 2 0 t − 2 t − 2 1 Xét f (t) 1 = t −1−
liên tục trên đoạn 3;9 có f (t) =1+ 0 t 3;9 f t 2 ( ) t − 2 (t −2)
đồng biến trên đoạn 3;9 .Có f ( ) = f ( ) 55 3 1; 9 = 7 Vậy phương trình 2 + −x −( + ) 2 1 1 1+ 1 9 3 .3 −x m
+ 2m +1= 0 có nghiệm thực 55 m 1; 7 m Có 7 giá trị nguyên. Câu 10: 2 2 Ta có 2 2 x 2 x 1 x 2x 2 x 1 x 1 4 . m 2 3m 2 0 4 2 . m 2 3m 2 0 1 . 2 Đặt x 1 t 2 , t
1. Phương trình 1 trở thành 2 t 2mt 3m 2 0 2 .
Phương trình 1 có 4 nghiệm phân biệt
phương trình 2 có 2 nghiệm phân biệt t ; t 1 1 2 0 m 2 t t 2 m 1 m 2 . 1 2 t 1 t 1 0 m 1 1 2 Câu 11: Đặt 5x t t
0 . Phương trình đã cho trở thành: 2 t 3t m 1 0 1 .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 76
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Phương trình đã cho có hai nghiêm phân biệt
1 có hai nghiệm dương phân biệt 0 13 b 13 4m 0 m 13 0 4 1 m . a m 1 0 4 m 1 c 0 a 13 1 m Ta có 4 m 2;3 . m Câu 12: x x
Ta có 25 − (m +1).5 + m = 0 (1). 5x =1
(5x −1).(5x − m) = 0 . 5x = m
Để phương trình (1) có hai nghiệm phân biệt thì m 0 và m 1. 1 5x =1 x = 0
Khi đó hai nghiệm x , x của (1) 1 . 1 2 là: 2 5x = m x = log m 2 5 m = 25 log m = 2 2 2 2
Theo bài ra ta có: x + x = 4 0 + log m = 4 1 . 1 2 ( 5 )2 5 log m = 2 − m = 5 25 1 626
Tổng tất cả các giá trị của tham số m là: 25+ = . 25 25 Câu 13:
Phương trình đã cho tương đương với 3 . 3 2x −10m 3 . x + 3 2 m = 0 .
Đặt t = 3x (t ) 0 2 2 ta có pt ẩn t : . 3 t −10m 3 . t + 3m = 0
Giả sử x , x
t , t là các nghiệm của pt , khi đó 1 x x2 t = 3 ,t = 3 1
2 là các nghiệm của pt , 1 2 1 2 Theo bài ra : x + x x x 1 2 1 2 x + x = = 3 .3 = 1 = 1 2 0 3 1 1 t .t2 1
Yêu cầu bài toán xảy ra khi và chỉ khi pt có 2 nghiệm dương phân biệt sao cho t .t = 1 1 2 / 2 =16m 0 m 0 10m
Do đó , giá trị của m cần tìm thỏa mãn S = 0 m = 1. 3 m = 1 2 P = m =1
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 77
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021 CHƯƠNG ②: FB: Duong Hung
Bài 6: PHƯƠNG TRÌNH LOGARIT
Dạng ①: Phương trình logarit cơ bản.
-Phương pháp:
-Casio: Slove, Calc nghiệm, Table.
A - Bài tập minh họa:
Câu 1: Tìm nghiệm của phương trình log x −1 = 3. 2 ( ) Ⓐ. x = 9 . Ⓑ. x = 7 . Ⓒ. x = 8.
Ⓓ. x =10 . Lời giải
PP nhanh trắc nghiệm Chọn A
log ( x − ) 3
1 = 3 x −1 = 2 x = 9
Casio: Calc, Solve 2
Nhập: log X −1 − 3 CALC X = 9 → 0 2 ( ) (nhận A) 1
Câu 2: Tìm nghiệm của phương trình log x 1 . 9 2 Ⓐ. 7 x 2 . Ⓑ. x 4 . Ⓒ. x 4 . Ⓓ. x 2 Lời giải
PP nhanh trắc nghiệm
Chọn A 1
Casio : Solve.
log ( x + ) 1 2 1 =
x +1 = 9 x = 2 9 2
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 78
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 3: Phương trình 2
log (x + 4x +12) = 2 có tích hai nghiệm là 3 Ⓐ. 3 Ⓑ. 3 − C. 4 Ⓓ. −4 Lời giải
PP nhanh trắc nghiệm
Chọn B 2 2 2
log (x + 4x +12) = 2 x + 4x +12 = 3
Casio: table, Solve 3 x = 1 − 2
x + 4x + 3 = 0 x = 3−
B - Bài tập rèn luyện: 1
Câu 1: Tìm nghiệm của phương trình log x 1 . 9 2 Ⓐ. 7 x 2 . Ⓑ. x 4 . Ⓒ. x 4 . Ⓓ. x . 2
Câu 2: Giải phương trình log x −1 = 2 . 3 ( ) Ⓐ. x =10 . Ⓑ. x =11. Ⓒ. x = 8. Ⓓ. x = 7 .
Câu 3: Tìm tập nghiệm S của phương trình log x = 3. 4 Ⓐ. S = 12 . Ⓑ. S = . Ⓒ. S = 64 . Ⓓ. S = 81 .
Câu 4: Nghiệm của phương trình log 2x −1 = 2 là 3 ( ) 7 9 Ⓐ. x = 4. Ⓑ. x = . Ⓒ. x = . Ⓓ. x = 5 . 2 2
Câu 5: Tìm tập nghiệm của phương trình log ( 2 2x + x + 3 = 1. 3 ) Ⓐ. 1 0;− . Ⓑ. 0 . Ⓒ. 1 − . Ⓓ. 1 0; . 2 2 2
Câu 6: Tìm nghiệm phương trình log 2x +1 = 3 . 3 ( ) Ⓐ. 4 . Ⓑ. 0 . Ⓒ.13. Ⓓ. 12 .
Câu 7: Nghiệm của phương trình log x −1 = 3 là 4 ( ) Ⓐ. x = 80. Ⓑ. x = 82. Ⓒ. x = 65. Ⓓ. x = 63.
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 79
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 8: Tập nghiệm của phương trình log ( 2
x − 3x + 3 = 1 là 3 ) Ⓐ. 3 . Ⓑ. 3 − ; 0 . Ⓒ.0; 3 . Ⓓ. 0 .
Câu 9: Tập nghiệm của phương trình 2
log(x + x + 4) = 1 là Ⓐ. 3 − ; 2 . Ⓑ. − 3 . Ⓒ. 2 . Ⓓ. 2 − ; 3 .
Câu 10: Tập nghiệm của phương trình 2
ln(2x − x +1) = 0 là Ⓐ. 0 . Ⓑ. 1 0 ; . Ⓒ. 1 . Ⓓ. . 2 2
Câu 11: Số nghiệm của phương trình log ( 2 x + x = 1 là 2 ) Ⓐ. 0 . Ⓑ. 1. Ⓒ. 2 . Ⓓ. 3.
Câu 12: Gọi x , x là 2 nghiệm của phương trình log ( 2
x − x − 5 = log
2x + 5 . Khi đó x − x bằng 3 ) 3 ( ) 1 2 1 2 Ⓐ. 5 . Ⓑ. 3 . Ⓒ. 7 . Ⓓ. −2 .
Câu 13: Tìm số nghiệm của phương trình log 2x −1 = 2 . 3 ( ) Ⓐ. 1. Ⓑ. 5. Ⓒ.2. Ⓓ. 0.
Câu 14: Tập nghiệm của phương trình 2 log (x 3x 11) 2 là 1 3 Ⓐ. 1 . Ⓑ. 1; 2 . Ⓒ. 1 − ; 2 . Ⓓ. .
Câu 15: Nghiệm của phương trình log x −1 = 2 là 2 ( ) Ⓐ. x = 5.
Ⓑ. x =1. Ⓒ. x = 4 .
Ⓓ. x = 3.
Câu 16: Giải phương trình 2
log x = 2 được kết quả là 6 Ⓐ. x 36 .
Ⓑ. x 6 . Ⓒ. x 6. Ⓓ. x = 6 .
Câu 17: Tìm nghiệm của phương trình: log (4 − 3x) = 2 x Ⓐ. x = 1. Ⓑ. x = 4 . Ⓒ. x .
Ⓓ. x 1;− 4 .
Câu 18: Tìm x biết log x − 3 = 2 . 5 ( ) Ⓐ. x =1. Ⓑ. x = 28 . Ⓒ. x =13. Ⓓ. x = 22 .
Câu 19: Phương trình log 3x − 2 = 3 có nghiệm là 3 ( ) Ⓐ. 25 x = . Ⓑ. x = 87 . Ⓒ. 29 x = . Ⓓ. 11 x = . 3 3 3
Câu 20: Nghiệm của phương trình log 2x − 3 = 2 là 3 ( ) Ⓐ. 11 . Ⓑ. 6 . Ⓒ.5 . Ⓓ. 9 . 2 2 BẢNG ĐÁP ÁN 1.A 2.A 3.C 4.D 5.A 6.C 7.C 8.C 9.A 10.B 11.C 12.C 13.A 14.B 15.A 16.B 17.C 18.B 19.C 20.B
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 80
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Dạng ②: Phương trình logarit đưa về cùng cơ số
-Phương pháp:
-Casio: Slove, Calc nghiệm, Table.
A - Bài tập minh họa:
Câu 1: Phương trình log (5x − ) 3 + log ( 2
x + 1 = 0 có 2 nghiệm x ; x trong đó x x . Giá trị của 3 1 ) 1 2 1 2 3
P = 2x + 3x là 1 2 Ⓐ. 13. Ⓑ. 14. Ⓒ. 3 . Ⓓ. 5 . Lời giải
PP nhanh trắc nghiệm
Chọn B
Phương trình tương đương với log (5x − 3) = log ( 2 x + 1
Casio: Solve hoặc table 3 3 ) 2
x + 1 = 5x - 3 x = 1
, do x x nên x = 1; x = 4 1 2 1 2 5x − 3 0 x = 4
Suy ra P = 2x + 3x = 2 + 12 = 14 . 1 2
Câu 2: Cho phương trình 2log x + log 10 − x = log 9.log 2 . Hỏi phương trình đã cho có mấy 9 3 ( ) 2 3 nghiêm Ⓐ. 4 . Ⓑ. 3 . Ⓒ.1. Ⓓ. 2 . Lời giải
PP nhanh trắc nghiệm
Chọn D
Casio: table_mode 8
Điều kiện 0 x 10 Ta có :
2 log x + log (10 − x) = log 9.log 2 log x + log (10 − x) = 2 9 3 2 3 3 3
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 81
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung x = 1 tháa m·n log x 10 x 2 x 10x 9 0 3 ( ( − )) ( ) = − 2 + − = x = 9 (tháa m·n) .
Vậy tập nghiệm của phương trình là S = 1; 9 .
Câu 3: Số nghiệm của phương trình log .
x log (2x −1) = 2 log x 3 3 3
Ⓐ. 2. Ⓑ. 0. Ⓒ.1. Ⓓ. 3. Lời giải
PP nhanh trắc nghiệm
Chọn A
Casio: Solve hoặc table x 0 1 Điều kiện: x . 2x −1 0 2 log .
x log (2x −1) = 2 log x log .
x (log (2x −1) − 2) = 0 3 3 3 3 3 log x = 0 x =1 x = 1(TM) 3 . log (2x −1) = 2 2x −1 = 9 x = 5 (TM) 3
Vậy phương trình có 2 nghiệm.
B - Bài tập rèn luyện:
Câu 1: Tìm số nghiệm của phương trình ln (4x + 2) = ln x + ln ( x − ) 1 Ⓐ. 2 . Ⓑ. 0 . Ⓒ. 3 . Ⓓ. 1.
Câu 2: Phương trình log (x +1) + log 3 = log (4x +1) có nghiệm là 3 3 3 Ⓐ. x = 3 Ⓑ. x = 3 − Ⓒ. x = 4
Ⓓ. x = 2
Câu 3: Nghiệm của phương trình log x +1 =1+ log x −1 là 2 ( ) 2 ( ) Ⓐ. x =1. Ⓑ. x = 2 − . Ⓒ. x = 3. Ⓓ. x = 2 .
Câu 4: Với a , b , x là các số thực dương thỏa mãn log x = 5log a + 3log b . Mệnh đề nào dưới đây 2 2 2
là mệnh đề đúng?
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 82
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Ⓐ. x = 3a +5b . Ⓑ. 5 3
x = a + b . Ⓒ. 5 3 x = a b .
Ⓓ. x = 5a +3b .
Câu 5: Tập nghiệm của phương trình log x −1 = log
2x + 3 tương ứng là 2021 ( ) 2021 ( ) Ⓐ. 4 − . Ⓑ. . Ⓒ. 2 4; − . Ⓓ. 2 . 3
Câu 6: Số nghiệm thực của phương trình 3 3log 2x 1 log x 5 3 là 3 1 3 Ⓐ. 3 . Ⓑ. 1. Ⓒ. 2 . Ⓓ. 0 .
Câu 7: Số nghiệm thực của phương trình 3log (2x − )
1 − log ( x − 5)3 = 3 là 3 1 3 Ⓐ. 3. Ⓑ. 1 Ⓒ.2 Ⓓ. 0
Câu 8: Phương trình log (5x − ) 3 + log ( 2
x + 1 = 0 có 2 nghiệm x ; x trong đó x x . Giá trị của 3 1 ) 1 2 1 2 3
P = 2x + 3x là 1 2 Ⓐ. 13. Ⓑ. 14. Ⓒ.3 . Ⓓ. 5 .
Câu 9: Cho phương trình 2log x + log 10 − x = log 9.log 2 . Hỏi phương trình đã cho có mấy 9 3 ( ) 2 3 nghiêm Ⓐ. 4 . Ⓑ. 3 . Ⓒ.1. Ⓓ. 2 .
Câu 10: Gọi P là tích tất cả các nghiệm của phương trình: log ( 3 x + x + ) 1 = log ( 2
2x +1 . Tính P . 2 2 ) Ⓐ. P =1 . Ⓑ. P = 3. Ⓒ. P = 6 . Ⓓ. P = 0 .
Câu 11: Số nghiệm của phương trình log .
x log (2x −1) = 2 log x 3 3 3 Ⓐ. 2. Ⓑ. 0. Ⓒ.1. Ⓓ. 3.
Câu 12: Biết phương trình log ( 2
x − 5x + 1 = log 9 có hai nghiệm thực x , x . Tích x .x bằng 2 ) 4 1 2 1 2 Ⓐ. 8 − . Ⓑ. −2 . Ⓒ.1. Ⓓ. 5 .
Câu 13: Tổng các nghiệm của phương trình 2
log x − log 3 = 1 là 4 2 Ⓐ. 6 . Ⓑ. 5 . Ⓒ. 4 . Ⓓ. 0 .
Câu 14: Phương trình 2 log x = log 7 có tập nghiệm là 4 2 Ⓐ. . Ⓑ. 7 − . Ⓒ. 7 . Ⓓ. 7; 7 − . Câu 15: 2 3
Cho phương trình log x +1 + 2 = log
4 − x + log 4 + x . Tổng các nghiệm của phương 4 ( ) 8 ( ) 2 trình trên là Ⓐ. 4 + 2 6 . Ⓑ. −4 . Ⓒ. 4 − 2 6 . Ⓓ. 2 − 2 3 . 4 −2 2.
Câu 16: Tổng các nghiệm của phương trình log . x log x = 8 bằng 3 3 Ⓐ. 82. Ⓑ. 6562 . Ⓒ. 82 . Ⓓ. 0. 81 9
Câu 17: Tổng các nghiệm của phương trình 2
log x − log 3 = 1 là: 4 2
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 83
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 6 . Ⓑ. 5 . Ⓒ. 4 . Ⓓ. 0 . Câu 18: 1
Số nghiệm của phương trình 2 log(x +10) +
log x = 2 − log 4 là 2 Ⓐ. 2 . Ⓑ. 1 . Ⓒ. 4 . Ⓓ. 3 .
Câu 19: Giải phương trình log x − 3 − log x − 5 =1 3 ( ) 1 ( ) 3 Ⓐ. S = 2 .
Ⓑ. S = 2; 6 . Ⓒ. S = 6 . Ⓓ. S = .
Câu 20: Số nghiệm của phương trình ln x ln 3x 2 0 là Ⓐ. 0 . Ⓑ. 1. Ⓒ. 2 . Ⓓ. 3 . BẢNG ĐÁP ÁN 1.D 2.D 3.C 4.C 5.B 6.B 7.B 8.B 9.D 10.D 11.A 12.B 13 14.D 15.C 16.C 17.D 18.A 19.C 20.B
Dạng ③: Đặt ẩn phụ
-Phương pháp: . Dạng: Đặt .
Khi đó, phương trình trở thành : .
Giải phương trình tìm , thay vào cách đặt để tìm thỏa ĐK.
Chú ý : Nếu đặt thì
A - Bài tập minh họa:
Câu 1: Tích tất cả các nghiệm của phương trình 2
log x − 2log x − 7 = 0 là 3 3 Ⓐ. 9 Ⓑ. 7 − Ⓒ.1 . Ⓓ. 2 Lời giải
PP nhanh trắc nghiệm
Chọn A
Công thức nhanh:
Điều kiện : x 0 . Nếu 2 . A log x + .
B log x + C = 0 có hai nghiệm a a − Đặt B
t = log x . Khi đó pt trở thành : 3
phân biệt x ; x thì A x x = a 1 2 1 2 t =1+ 2 2 Casio: 2
t − 2t − 7 = 0 t =1− 2 2 1+2 2 log x =1+ 2 2 x = 3 ( ) n Với 3 1 1−2 2 log x =1− 2 2 x = 3 ( ) n 3 2
x .x = 9 1 2
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 84
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 2: Số nghiệm của phương trình 2 2
log x + 8log x + 4 = 0 là 2 2 Ⓐ. x = 2 .
Ⓑ. x = 3. Ⓒ. x =1. Ⓓ. x = 0 . Lời giải
PP nhanh trắc nghiệm Chọn D
Điều kiện : x 0 . Casio: table 2 2
log x + 8log x + 4 = 0 2 2
(2log x)2 +8log x + 4 = 0 2 2
4(log x)2 +8log x + 4 = 0 2 2
Đặt t = log x . Khi đó pt trở thành : 2 2
4t + 8t + 4 = 0 t = 1 − 1 log x = 1 − x = n . 2 ( ) 2
Câu 3: Gọi x ; x là hai nghiệm của phương trình 2
log x − 3log x + 2 = 0 .Giá trị biểu thức 2 2
P = x + x 1 2 3 3 1 2 bằng bao nhiêu ? Ⓐ. x = 20 . Ⓑ. x = 92 . Ⓒ. x = 90 . Ⓓ. x = 9 . Lời giải
PP nhanh trắc nghiệm
Chọn C
Điều kiện : x 0 . Casio: Solve
Đặt t = log x . Khi đó pt trở thành : 3 t = 1 log x = 1 x = 3 n 2 3 ( )
t − 3t + 2 = 0 t = 2 log x = 2 x = 9 n 3 ( ) 2 2 2 2
P = x + x = 3 + 9 = 90. 1 2
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 85
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
B - Bài tập rèn luyện:
Câu 1: Cho phương trình (log x )2 2
− 5log x + 2 = 0 . Bằng cách đặt t = log x 2 2 2 phương trình trở thành
phương trình nào dưới đây? Ⓐ. 2
2t − 5t +1 = 0 . Ⓑ. 4
t − 5t +1 = 0 . Ⓒ. 2
4t − 5t +1 = 0 . Ⓓ. 4
2t − 5t +1 = 0 .
Câu 2: Phương trình log2 x − 5log x + 4 = 0 có hai nghiệm x , x . Khi đó tích x .x bằng 2 2 1 2 1 2 Ⓐ. 36. Ⓑ. 64. Ⓒ.32. Ⓓ. 16.
Câu 3: Tích tất cả các nghiệm của phương trình 2
log x − 2log x − 7 = 0 là 3 3 Ⓐ. 9 . Ⓑ. 7 − . Ⓒ.1. Ⓓ. 2 .
tổng các nghiệm bằng 0.
Câu 4: Số nghiệm của phương trình 2 2
log x + 8log x + 4 = 0 là 2 2 Ⓐ. 2 . Ⓑ. 3 . Ⓒ. 0 . Ⓓ. 1.
Câu 5: Tích tất cả các nghiệm của phương trình 2 log x 2log x 7 0 là 3 3 Ⓐ. 9 . Ⓑ. 7 . Ⓒ.1. Ⓓ. 2 . Câu 6: 17
Tích tất cả các nghiệm của phương trình 2 log x + log x = bằng 2 2 4 Ⓐ. 3 . Ⓑ. 17 . Ⓒ. 1 . Ⓓ. 1 . 2 4 4 2
Câu 7: Số nghiệm của phương trình 2 2 log x 8log x 4 0 là 2 2 Ⓐ. 2 . Ⓑ. 3 . Ⓒ. 0 . Ⓓ. 1.
Câu 8: Tích tất cả các nghiệm của phương trình log 12 − 2x = 5 − x bằng 2 ( ) Ⓐ. 2 . Ⓑ. 1. Ⓒ. 6 . Ⓓ. 3 .
Câu 9: Tập nghiệm của phương trình: log 9 ( x + ) 8 = x + 2 là 3 Ⓐ. 0 . Ⓑ. 8 ; 1 . Ⓒ. ; 0 log . Ⓓ. ; 0 log . 3 8 3 4
Câu 10: Phương trình 2
log x + 3log x + 2 = 0 có tổng tất cả các nghiệm là 2 1 2 Ⓐ. 6 . Ⓑ. 8 . Ⓒ.9 . Ⓓ. 5 .
Câu 11: Tổng tất cả các nghiệm của phương trình 2 log x 4log . x log 2 3 0 bằng 3 2 3 Ⓐ. 81. Ⓑ. 9 . Ⓒ.30. Ⓓ. 4 .
Câu 12: Tổng các nghiệm của phương trình 2 4 log x −1 − 3log
x −1 + 2 = 0 là 4 ( ) 2 ( ) Ⓐ. 8 . Ⓑ. 3 . Ⓒ. 2 . Ⓓ. 15.
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 86
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 13: Gọi x , x là các nghiệm của phương trình 2
log x − 3log x + 2 = 0 . Giá trị của biểu thức 1 2 2 2 2 2
P = x + x bằng bao nhiêu? 1 2 Ⓐ. 20. Ⓑ. 5. Ⓒ.36. Ⓓ. 25. + Câu 14: a b
Biết nghiệm lớn nhất của phương trình log
4x − 2x + 2 = x + 2 có dạng x = log với 2 ( ) 2 c a, ,
b c là số nguyên tố. Tính P = a + b + c . Ⓐ. 23. Ⓑ. 24. Ⓒ.25. Ⓓ. 26.
Câu 15: Biết phương trình 2
ln x + ln x −12 = 0 có hai nghiệm phân biệt x và x . Tính tích x x . 1 2 1 2 Ⓐ. 1 1 1 x x = Ⓑ. x x = . Ⓒ. x x = . Ⓓ. 3 x x = e . 1 2 4 e 1 2 12 e 1 2 e 1 2
Câu 16: P là tích các nghiệm của phương trình 2 2 3
log x − 4log x + 8 = 0 , giá trị của P là 2 2 Ⓐ. P = 8.
Ⓑ. P = 6 . Ⓒ. P = 64 .
Ⓓ. P = 4 . Lời giải
Câu 17: Tổng tất cả các nghiệm của phương trình log 7 − 3x = 2 − x bằng 3 ( ) Ⓐ. 2 . Ⓑ. 1. Ⓒ. 7 . Ⓓ. 3.
Câu 18: Phương trình 2
log x + 3log x + 2 = 0 có tổng tất cả các nghiệm là 2 1 2 Ⓐ. 6 . Ⓑ. 8 . Ⓒ.9 . Ⓓ. 5 .
Câu 19: Gọi x , x là các nghiệm của phương trình 2
log x − 3log x + 2 = 0 . Giá trị của biểu thức 1 2 2 2 2 2
P = x + x bằng bao nhiêu? 1 2 Ⓐ. 20. Ⓑ. 5. Ⓒ.36. Ⓓ. 25.
Câu 20: Phương trình 2
log x − log 8x + 3 = 0 tương đương với phương trình nào sau đây? 2 2 ( ) Ⓐ. 2
log x + log x = 0 . Ⓑ. 2
log x − log x − 6 = 0 . 2 2 2 2 Ⓒ. 2
log x − log x = 0 . Ⓓ. 2
log x − log x + 6 = 0 2 2 2 2 BẢNG ĐÁP ÁN 1.C 2.C 3.A 4.D 5.A 6.D 7.D 8.C 9.D 10.A 11.C 12.A 13.A 14.B 15.C 16.A 17.A 18.A 19.A 20.C
Dạng ⑤: PT chứa tham số m
-Phương pháp:
. Sử dụng các phương phá giải PT logarit và các kiến thức có liên quan để tìm tham số m .Casio: Table, Solve
Bài tập vận dụng rèn luyện:
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 87
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 1: Tìm tất cả các giá trị của m để phương trình 2 2
log x − log x − m + 2 = 0 có 2 nghiệm phân biệt 3 3 thuộc đoạn 1;27 . Ⓐ. m(1;2.
Ⓑ. m1;2 . Ⓒ. m(1;2) .
Ⓓ. m(1;+) .
Câu 2: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 2
log x + log x +1 − 2m −1 = 0 có 5 5 nghiệm thuộc đoạn 2 2 1 ;5 Ⓐ. 6 . Ⓑ. 5 . Ⓒ. 7 . Ⓓ. 8 .
Câu 3: Tìm tất cả các giá trị của tham số m để phương trình 2
log 3x + log x + m −1 = 0 có đúng 2 3 3
nghiệm phân biệt thuộc khoảng (0; ) 1 . Ⓐ. 9 m . Ⓑ. 1 0 m . Ⓒ. 9 0 m . Ⓓ. 9 m − . 4 4 4 4
Câu 4: Giả sử phương trình 2
log x − m + 2 log x + 2m = 0 có hai nghiệm thực phân biệt x , x thỏa 2 ( ) 2 1 2
mãn x + x = 6 . Giá trị của biểu thức x − x là 1 2 1 2 Ⓐ. 3 . Ⓑ. 8 . Ⓒ. 2 . Ⓓ. 4 . Câu 5: x
Có bao nhiêu giá trị của tham số m để phương trình 2 4 log x m log 2 0 có hai nghiệm 36 6 6
phân biệt x , x thỏa mãn x .x 72 x .x 1296 0 1 2 1 2 1 2 Ⓐ. 0 . Ⓑ. 1. Ⓒ. 2. Ⓓ. 3.
Câu 6: Với giá trị nào của m thì phương trình: 2
log x − m + 2 .log x + 3m −1 = 0 có hai ngiệm x , x 3 ( ) 3 1 2
thỏa mãn x .x = 27 ? 1 2 Ⓐ. m =1. Ⓑ. 28 m = . Ⓒ. 4 m = . Ⓓ. m = 25. 3 3
Câu 7: Tìm tất cả các giá trị thực của tham số m để phương trình 2 2
log x + log x − 3 = m ( 2
log x − 3 có nghiệm thuộc 32; +) 2 1 4 ) 2 Ⓐ. m (− 3;1 . Ⓑ. 1 − ; 3 ). Ⓒ. 1; 3 ).
Ⓓ. m (1; 3.
Câu 8: Có bao nhiêu giá trị nguyên của tham số k để phương trình 2 2
log x + log x +1 − 2k −1 = 0 có 3 3 nghiệm thuộc 3 1 ;3 ? Ⓐ. 0 . Ⓑ. 4 . Ⓒ.3 . Ⓓ. 7 .
Câu 9: Biết rẳng phương trình 2
log x − m + 2 log x + 3m −1 = 0 có hai nghiệm phân biệt x ; x thỏa 3 ( ) 3 1 2
mãn x .x = 27 . Khi đó tổng ( x + x bằng: 1 2 ) 1 2 Ⓐ. 6 . Ⓑ. 34 . Ⓒ.12 . Ⓓ. 1 . 3 3
Câu 10: Cho phương trình 2 2 log x + log
x + 2 - m -1 = 0 . Tìm tất cả các giá trị tham số m để phương 2 2 trình có nghiệm 2 x 1 ;2 . Ⓐ. 13 − m 3 .
Ⓑ. −1+ 2 m 3 . Ⓒ. 13 − m 3 .
Ⓓ. −1+ 2 m 3 4 4
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 88
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 11: Cho phương trình 2 log 2x 2m log x m 1
0. Gọi S là tập hợp tất cả các giá trị của 2 2
m để tích hai nghiệm của phương trình bằng 16. Tổng tất cả các phần tử của S nằm trong khoảng nào sau đây? Ⓐ. 35 11 5 7 16; . Ⓑ. ;6 . Ⓒ. 5;9 . Ⓓ. ; . 2 2 2 2 BẢNG ĐÁP ÁN 1.A 2.A 3.C 4.C 5.A 6.A 7.D 8.C 9.C 10.D 11.D
Hướng dẫn giải chi tiết. Câu 1:
Điều kiện: x 0 2 2 2
log x − log x − m + 2 = 0 log x − 2 log x − m + 2 = 0 1 3 3 3 3 ( )
Đặt: log x = t . 3 Pt ( ) 1 trở thành: 2
t − 2t = m − 2 (2) . Phương trình ( )
1 có 2 nghiệm phân biệt x 1;27 pt (2) có 2 nghiệm phân biệt t 0; 3 đồ thị hàm số 2
y = t − 2t và y = m − 2 có 2 giao điểm phân biệt với t 0; 3 . Xét hàm số 2
y = t − 2t trên t 0; 3
Có y = 2t − 2 ; y = 0 t =10; 3 . BBT
Nhìn BBT ta thấy YCBT m − 2( 1
− ;0 m(1;2. Câu 2:
Điều kiện: x 0 Đặt 2
t = log x +1 , khi 2 2 x 1 ;5 2
log x 0; 2 2 log x +1 1;9 t 1;3 5 thì 5 5
Bài toán trở thành: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2
t + t − 2m − 2 = 0( )
* có nghiệm thuộc đoạn 1; 3 . −
Phương trình (*) có nghiệm 9
0 8m + 9 0 m . 8
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 89
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung 1 − − 8m + 9 t = 0 1 Khi đó, phương trình ( 2 *) có 2 nghiệm: 1 − + 8m + 9 t = 2 2
phương trình (*) có nghiệm thuộc đoạn 1; 3 khi và chỉ khi: 1 − + 8m + 9 1 3 2 1
− + 8m + 9 6 9 8m + 9 49 0 m 5 . 2
Vì m m0;1;2;3;4; 5 . Câu 3:
Phương trình đã cho tương đương với: 2
log 3x + log 3x + m − 2 = 0 3 3
Đặt t = log 3x , phương trình có dạng: 2
t + t + m − 2 = 0 ( ) * 3 Với x (0; )
1 0 3x 3 log 3x 1 t 1. 3
Yêu cầu đề bài tương đương với tìm tham số m đề phương trình (*) có đúng hai nghiệm
phân biệt t ,t nhỏ hơn 1 2 1 0 0 1 − 4m + 8 0 ( 9 − 4m 0 9
t −1 t −1 0 t
t − t + t +1 0 m − 2 +1+1 0 0 m 1 )( 2 ) 1 2 ( 1 2 ) m 0 4
t + t − 2 0
t + t − 2 0 1 − − 2 0 1 2 1 2 Câu 4:
Điều kiện: x 0 .
Đặt t = log x . 2 t = 2 log x = 2 x = 4
Khi đó phương trình đã cho có dạng: 2 t − (m + 2) 2 t + 2m = 0 . t = m log x = m x = 2m 2 Do + = 64 + 2m x x = 6m =1. 1 2 Vậy 1
x − x = 4 − 2 = 2 . 1 2 Câu 5: x 2 4 log x m log 2 0 2 log x mlog x m 2 0 36 6 6 6 6 m 2 2 3
Phương trình có hai nghiệm phân biệt khi 2 m 4 m 2 0 m 2 2 3 x .x 72 x .x 1296 0 x .x 36 x .x 1296 1 2 1 2 1 2 1 2 log x .x 4 log x log x 4 m 4 6 1 2 6 1 6 2 Câu 6:
Điều kiện: x 0 .
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 90
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Giả sử phương trình có hai nghiệm x , x . 1 2
Theo Viet, ta có: log x + log x = m + 2 log x .x = m + 2 log 27 = m + 2 3 1 3 2 3 ( 1 2 ) 3
3 = m + 2 m =1.
Thử lại với m =1 ta có: log x =1 x = 3 2 3
log x − 3.log x + 2 = 0 . 3 3 log x = 2 x = 9 3 Câu 7: x 0 x 0 x 0 Điều kiện − 2 2 log x 1
log x + log x − 3 0 2 2 1 − − log x 2 log x 3 0 2 2 2 2 log x 3 2 2 2
log x + log x − 3 = m ( 2 log x − 3 2
log x − 2log x −3 = m log x −3 2 2 ( 2 ) 2 1 4 ) 2
Đặt t = log x . 2
Với x 32;+) log x 5 t 5. 2
Suy ra phương trình đã cho trở thành m 0 m 0 2
t − 2t − 3 = m(t − 3) t +1 t
− 2t − 3 = m (t −3)2 2 2 2 m = t − 3 + f (t ) t 1 = , t 5 . t − 3 − f (t) 4 = . (t −3)2 Bảng biến thiên m 0
Yêu cầu bài toán 1 m 3 . 2 1 m 3 Câu 8: Đặt 2
t = log x +1 , suy ra t 1; 2 . 3 2 t + t − 2
Phương trình trở thành 2
t + t − 2k − 2 = 0 k = . 2
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 91
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung t + t − Đặt 1 f (t ) 2 2 = ; f (t) 1
= t + ; f (t) = 0 t = − 1;2; f ( ) 1 = 0 ; f (2) = 2 . 2 2 2
Suy ra 0 m 2 .
Vậy có ba giá trị nguyên của m là: 0;1;2 . Câu 9:
Điều kiện; x 0
Đặt log x = t 3
Phương trình đã cho trở thành 2
t − (m + 2)t + 3m −1 = 0 ( ) 1
Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình ( ) 1 có 2 nghiệm phân biệt 2
0 m − 8m + 8 0 m(− ;
4 − 2 2 )(4+ 2 2;+)
Ta có x .x = 27 log x .x = log 27 t + t = 3 1 2 3 ( 1 2 ) 3 1 2
Theo Vi-ét ta được m + 2 = 3 m =1 t = 2 Với m = 1 x + x =12 . t =1 1 2 Câu 10: 2 2 2 2 log x + log
x + 2 - m -1 = 0 log x + log
x + 2 -1 = m 1 2 2 2 2 ( ) Đặt 2 2 2 t = log
x + 2 log x = t − 2. 2 2 2 2 2 x 1
;2 0 log x 2 0 log x 2 2 log x + 2 2 t 2;2 2 2 2 Pt ( ) 1 trở thành 2
t + t - 3 = m (2) Pt ( ) 1 có nghiệm 2 x 1 ;2 pt (2) có nghiệm t 2;2 Đặt f (t) 1 2
= t + t − 3, f ' (t) = 2t +1= 0 t = − . 2 BBT t 2 2 f'(t) + f(t) 3 -1+ 2
Dựa vào BBT ta có pt (2) có nghiệm t 2;2 1 − + 2 m 3 . Câu 11: Điều kiện pt: x 0. 2 Đặt t log x. Pt trở thành 2 1 t 2mt m 1 0 t 2 1 m t m 0 1 . 2
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 92
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Phương trình đã cho có 2 nghiệm x ; x khi phương trình 1 có 2 nghiệm t ; t . 1 2 1 2 3 5 m Khi đó 2 2 ' 0 m 3m 1 0 . 3 5 m 2 2 1 m
Theo giả thiết x x 16 log x x log 16 t t 4 4 m 3 TM . 1 2 2 1 2 2 1 2 1
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 93
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021 CHƯƠNG ②: FB: Duong Hung
Bài 7: BẤT PHƯƠNG TRÌNH MŨ
Dạng ①: Bất phương trình mũ cơ bản.
-Phương pháp:
①. Xét bất phương trình mũ cơ bản có dạng . Nếu
, tập nghiệm của bất phương trình là , vì . Nếu
thì bất phương trình tương đương với . Với , . Với ,
②. Xét bất phương trình mũ cùng cơ số: . Với , . Với ,
-Casio: Table, Calc
A - Bài tập minh họa: 1 x
Câu 1: Tìm tập nghiệm của bất phương trình 2. 2
Ⓐ. (−,− 1. Ⓑ. − + 1, ). Ⓒ. (−,−1). Ⓓ.(−1,+). Lời giải
PP nhanh trắc nghiệm
Chọn A
Casio: Table 1 x Ta có
2 x log 2 x − 1. 2 1 2
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 94
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Dò trên đoạn -5 đến 5 step 1 Chọn đáp án A
Chú ý: Miền giá trị âm loại hết. x
Câu 2: Tập nghiệm của bất phương trình 1 4 là 2 Ⓐ. ( 2; − +) . Ⓑ.(− ; 2 − ) . Ⓒ. ( ; − 2) . Ⓓ.(2;+) . Lời giải
PP nhanh trắc nghiệm Chọn B
Điều kiện xác định:
Casio: Table x . x x x 2 − 1 1 1 1 4 2 2 2 2 2 2 x 2. −
Vậy bất phương trình có tập nghiệm là S = (− ; 2 − ). Thỏa mãn chọn A − 1 3x 2 25
Câu 3: Tìm tập nghiệm S của bất phương trình . 5 4 1 Ⓐ. S ;1 . Ⓑ. 1 S ; . Ⓒ. S ; . Ⓓ.S 1; . 3 3 Lời giải
PP nhanh trắc nghiệm Chọn D Ta có
Casio: Table − x 2 1 3 25 25
1 − 3x log2 5 4 4 5 1 − 3x −2 x 1.
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 95
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Quan sát đáp án,ta thiết lập từ -3 đến 3 step 1/3,
dò tìm ,chọn đáp án D
B - Bài tập rèn luyện: 2 x −2x 1 1
Câu 1: Bất phương trình:
có tập nghiệm là S = (a; b) . Khi đó giá trị của a – b là 2 8 Ⓐ. −2. Ⓑ.−4. Ⓒ. 2. Ⓓ. 4 . 2 x −25 x 134 + Câu 2: 1
Giải bất phương trình 25. 5 Ⓐ. 1 x . Ⓑ. 1 x .
Ⓒ. 8 x 17.
Ⓓ.x 8,x 17. 25 25 2 x −2 x Câu 3: 1 1
Tìm số x nhỏ nhất thỏa mãn bất phương trình . 5 125 Ⓐ. 3 − . Ⓑ. −2. Ⓒ. 2. Ⓓ.−1. Câu 4: x+ 1
Nghiệm của bất phương trình 2 3 là 9 Ⓐ. x 4 − . Ⓑ. x 0 . Ⓒ. x 0 . Ⓓ. x 4 .
Câu 5: Tập nghiệm của bất phương trình x+1 x − 2 4 8 là Ⓐ. + 8; ). Ⓑ.. Ⓒ. (0;8). Ⓓ.(−;8 .
Câu 6: Tìm tập nghiệm S của bất phương trình x x 1 4 2 + . Ⓐ. S = (0 ) ;1 . Ⓑ. S = (1;+ ).
Ⓒ. S = (−;+) . Ⓓ. S = (− ) ;1 . x
Câu 7: Tập nghiệm của bất phương trình 1 4 là 2 Ⓐ. ( 2; − +) . Ⓑ.(− ; 2 − ) . Ⓒ. ( ; − 2) . Ⓓ.(2;+) . 2 x 3x Câu 8: 1
Tập nghiệm của bất phương trình 4 là 2 − + Ⓐ. 3 17 3 17 S = ; . Ⓑ. S = (− ;1 2; +) . 2 2 − + Ⓒ. 3 17 3 17 S = − ; ; + . Ⓓ. S = 1;2. 2 2
Câu 9: Tập nghiệm của bất phương trình 2x 1 2 − 8 là Ⓐ. S = (− ; 4) . Ⓑ. S = (2;+ ) . Ⓒ. S = (− ;3 ). Ⓓ. S = (− ; 2) .
Câu 10: Tập nghiệm S của bất phương trình 3x ex là
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 96
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Ⓐ. S = (0;+) . Ⓑ. S = \ 0 . Ⓒ. S = (− ; 0) . Ⓓ. S = . 2 − x +3x 1 1
Câu 11: Tìm tập nghiệm S của bất phương trình . 2 4
Ⓐ. S = 1;2. Ⓑ. S = (− ) ;1 .
Ⓒ. S = (1;2) . Ⓓ. S = (2;+ ).
Câu 12: Tập nghiệm của bất phương trình: 2x−3 2 x 16 là Ⓐ. (− ; − ) 1 (4; +). Ⓑ.(0;4). Ⓒ. (− ; 4 − ) (1;+). Ⓓ.( 1 − ;4). x−
Câu 13: Bất phương trình ( − ) 2 3 1 1 có tập nghiệm là Ⓐ. (2;+). Ⓑ. 2;+ ). Ⓒ. ( ;2 − ). Ⓓ.( ;2 − . 2 4 x 1 − 5x 1 + 3 4−3x Câu 14: 1 1
Cho bất phương trình
. Tập nghiệm của bất phương trình là 2 2 Ⓐ. 3 3 ; + . Ⓑ. . Ⓒ. \ . Ⓓ.. 2 2
Câu 15: Tập nghiệm của bất phương trình 2x−2 3 x 27 là Ⓐ. (− ; 1 − ) . Ⓑ.(3; ) + . Ⓒ. ( 1 − ;3) . Ⓓ.(− ; 1 − ) (3;+ ) . BẢNG ĐÁP ÁN 1.B 2.C 3.D 4.A 5.A 6.D 7.B 8.D 9.D 10.C 11.C 12.D 13.D 14.C 15.C
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 97
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Dạng ②: Bất phương trình mũ đặt ẩn phụ
-Phương pháp:
. Bất phương trình có dạng : Đặt
, t > 0. Bất phương trình trở thành . Giải bất phương trình tìm t suy ra x.
. Bất phương trình có dạng :
Chia hai vế của phương trình cho
, bất phương trình trở thành: . Đặt
, t > 0. Bất phương trình trở thành . Giải bất
phương trình tìm t suy ra x.
. Bất phương trình có dạng : , trong đó . Đặt , t > 0
. Khi đó bất phương trình trở thành .
Giải bất phương trình tìm t suy ra x.
A - Bài tập minh họa:
Câu 1: Tìm tập nghiệm S của bất phương trình 9x 4.3x − + 3 0. Ⓐ. S = (0; ) 1 . Ⓑ. S = 1; 3 . Ⓒ. S = (− ;1 . Ⓓ. S = 0 ;1 . Lời giải
PP nhanh trắc nghiệm Chọn D
9x − 4.3x + 3 0 Casio: table
(3x )2 − 4.3x +3 0 .
13x 3 0 x1.
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 98
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Câu 1:
Câu 2: Tập nghiệm của bất phương trình: x x 1 2 x 1 3 2 4 8 0 Ⓐ. 1 ; . Ⓑ. 1 ; . Ⓒ. ; 4 . Ⓓ. 4; . 4 4 Lời giải
PP nhanh trắc nghiệm Chọn A
Casio: Table x x 1 2 x 1 x 1 2 x 1 3 2 4 8 0 4 8 0 3 3 2 x 2 x 2 x 2 4.2 8. 2 0 2. 2 2 x 0(*) Đặt 2 2 x t, t 0 , suy ra bpt trở thành: 2 t 0 3 2 2.t t 0 2 t 2 2 Giao với Đk t 0 ta được: t 2 1 x 2 x 1 1 2 2 2 2 2 2 2x x 2 2 4
Vậy tập nghiệm của BPT đã cho là 1 T ; . 4
Câu 3: Bất phương trình 6.4x 13.6x 6.9x − +
0 có tập nghiệm là? Ⓐ. S = (− ; 2 − )(1;+) . Ⓑ. S = (− ; − ) 1 (1;+) . Ⓒ. S = (− ; 2 − 2;+) . Ⓓ. S = (− ; − ) 1 (2;+) Lời giải
PP nhanh trắc nghiệm Chọn B
Casio: Table
Chia cả 2 vế của bất phương trình cho 9x ta được 2 x x 2 2 6. −13. + 6 0 . 3 3 x Đặ 2 t = t
(t 0) . Ta được bất phương trình mới: 3 2 t 2 3
6t −13t + 6 0 . 3 t 2
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 99
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung x 2 2 3 3 x 1 Suy ra . x x 1 2 3 − 3 2
Vậy tập nghiệm của bất phương trình là S = (− ; − ) 1 (1;+) .
B - Bài tập rèn luyện: 2 − 2 −
Câu 1: Tập nghiệm của bất phương trình 9 x + 3 x 12 là Ⓐ. (− ; 2 − ). Ⓑ.( 2; − +) . Ⓒ. ( 2 − ;0) . Ⓓ.(0;2) .
Câu 2: Tập nghiệm của bất phương trình 3.9x 10.3x −
+ 3 0 có dạng S = ;
a b , trong đó a,b là các số
nguyên. Giá trị của biểu thức 5b − 2a bằng Ⓐ. 43 . Ⓑ. 8 . Ⓒ. 7 . Ⓓ.3. 3 3
Câu 3: Nghiệm nguyên dương lớn nhất của bất phương trình: x 1 − x−2 4 − 2 3 là Ⓐ. 1. Ⓑ.2. Ⓒ. 3. Ⓓ.4.
Câu 4: Tập nghiệm của bất phương trình: 2x 1
3 + −10.3x + 3 0 là Ⓐ. 1 − ;0) . Ⓑ.( 1 − ) ;1 . Ⓒ. (0 ;1 . Ⓓ. 1 − ;1 .
Câu 5: Giải bất phương trình: 32.16x 18.4x − +1 0 . Ⓐ. 4 − x 1 − . Ⓑ. 1 2 − x . Ⓒ. 1 1 x . Ⓓ. 1 2 − x − . 2 16 2 2
Câu 6: Nghiệm của bất phương trình x − x 5 e + e là 2 Ⓐ. 1 x hoặc x 2 . Ⓑ. 1 x 2. 2 2
Ⓒ. −ln2 x ln2.
Ⓓ. x −ln2 hoặc x ln 2.
Câu 7: Nghiệm của bất phương trình x 1 − x−3 9 −36.3 +3 0 là
Ⓐ. x 1. Ⓑ. x 3.
Ⓒ. 1 x 3. Ⓓ.1 x 2.
Câu 8: Bất phương trình 9x − 3x − 6 0 có tập nghiệm là Ⓐ. ( ) ;1 − . Ⓑ.(− ; 2
− ) (3;+) . Ⓒ. (1;+). Ⓓ.( 2 − ;3) . Câu 9: x− 1 2
Tập hợp nghiệm của bất phương trình 3 2 3 + là 27x 3 Ⓐ. (0; ) 1 . Ⓑ.(1;2). Ⓒ. 1 . Ⓓ.(2;3). 3
Câu 10: Tìm tập nghiệm của bất phương trình 2x 1
6 + −13.6x + 6 0 . Ⓐ. 2 3 1 − ;1 . Ⓑ.(− ; − )
1 (1; +) . Ⓒ. log ; log . Ⓓ. ( ; − log 2 . 6 ) 6 6 3 2 BẢNG ĐÁP ÁN 1.C 2.C 3 4.D 5.D 6.C 7.D 8.A 9.C 10.C
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 100
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Dạng ③: Bất PT mũ chứa tham số
-Phương pháp:
.Sử dụng PP giải bất PT mũ kết hợp công thức, tính chất của mũ, lũy thừa, logarit
.Khai thác điều kiện bài toán
.Xử lý bài toán và chọn giá trị m thỏa ĐK bài toán.
B - Bài tập Vận dụng Cao rèn luyện:
Câu 1: Cho bất phương trình: 9x + ( − ) 1 .3x m + m 0 ( )
1 . Tìm tất cả các giá trị của tham số m để bất phương trình ( ) 1 nghiệm đúng x 1. Ⓐ. 3 m − . Ⓑ. 3 m − .
Ⓒ. m 3+ 2 2. Ⓓ. m 3+ 2 2. 2 2
Câu 2: Tìm m để bất phương trình .9x − (2 +1).6x + .4x m m m
0 nghiệm đúng với mọi x (0 ) ;1 .
Ⓐ. 0 m 6 Ⓑ. m 6. Ⓒ. m 6. Ⓓ. m 0.
Câu 3: Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình sau có tập nghiệm là ( x+ x x ; − 0 : 1 m2 + (2m + ) 1 (1− 5) + (3+ 5) 0 . Ⓐ. 1 m − . Ⓑ. 1 m . Ⓒ. 1 m . Ⓓ. 1 m − . 2 2 2 2
Câu 4: Tất cả các giá trị của m để bất phương trình (3 +1)12x + (2 − )6x + 3x m m 0 có nghiệm đúng x 0 là: Ⓐ. ( 2; − +) . Ⓑ.(− ; 2 − ] . Ⓒ. 1 − ; − . Ⓓ. 1 2; − − . 3 3
Câu 5: Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 2 2 sin x cos x cos 4 + 5 .7 x m có nghiệm. Ⓐ. 6 m − . Ⓑ. 6 m . Ⓒ. 6 m . Ⓓ. 6 m − . 7 7 7 7
Câu 6: Tìm tất cả các giá trị thực của tham số m để bất phương trình 9x − 2( + ) 1 .3x m − 3− 2m 0
nghiệm đúng với mọi x .
Ⓐ. m tùy ý. Ⓑ. 4 m − . Ⓒ. 3 m − . Ⓓ. 3 m − . 3 2 2
Câu 7: Tìm tất cả các giá trị của tham số m để bất phương trình x 1 4 − − (2x m + ) 1 0 nghiệm đúng với mọi x .
Ⓐ. m(−;0)(1;+) .
Ⓑ. m(−;0.
Ⓒ. m(0;+) . Ⓓ. m(0; ) 1 . x x
Câu 8: Cho bất phương trình x 1 .
m 3 + + (3m + 2)(4 − 7 ) + (4 + 7 ) 0, với m là tham số. Tìm tất cả
các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x (− ; 0. Ⓐ. 2 − 2 3 2 − 2 3 2 − 2 3 2 + 2 3 m − . Ⓑ. m . Ⓒ. m . Ⓓ.m . 3 3 3 3
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 101
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 9: Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để bất phương trình
5.4x + .25x − 7.10x m
0 có nghiệm. Số phần tử của S là Ⓐ. 3. Ⓑ.Vô số. Ⓒ. 2 . Ⓓ.1. Câu 10: 1 2 3
Tìm tất cả các giá trị m để phương trình + +
= m có ba nghiệm phân biệt. x −1 3x ln ( x + ) 1 Ⓐ. 11 m . Ⓑ. 11 0 m . Ⓒ. m 0. Ⓓ. 11 0 m . 2 2 2 BẢNG ĐÁP ÁN 1.A 2.B 3.D 4.B 5.B 6.D 7.B 8.C 9.C 10.B Hướng dẫn giải Câu 1: Đặt 3x t =
Vì x 1 t 3 Bất phương trình đã cho thành: 2 t + (m − )
1 .t + m 0 nghiệm đúng t 3 2 t − t
−m nghiệm đúng t 3. t +1
Xét hàm số g (t) 2 = t − + t g (t) 2 2 , 3, ' =1− t
. Hàm số đồng biến trên t +1 (t + ) 0, 3 2 1 3;+) và g ( ) 3 3 = . 2
Yêu cầu bài toán tương đương 3 3
−m m − . 2 2 x x Câu 2: Ta có 9 3 .9x − (2 + ) 1 .6x + .4x m m m 0 . m − (2m+ ) 1 + m 0 . 4 2 x Đặt 3
t = . Vì x (0 ) ;1 nên 3 1 t 2 2
Khi đó bất phương trình trở thành t 2 . m t − (2m + )
1 t + m 0 m . (t − )2 1 Đặt ( ) = t f t . (t − )2 1 −t −
Ta có f (t) 1 =
, f (t) = t = − . ( 0 1 t − )3 1 Bảng biến thiên. t 1 − 1 3 2 f (t ) + 0 − − + f (t ) 6
Dựa vào bảng biến thiên ta có m lim f (t) = 6 . 3 t → 2
Câu 3: Phương trình đã cho tương đương
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 102
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung x + x
m + ( m + ) 1− 5 3 + 5 2 2 1 + 0 ( ) 1 . Đặt 1 5 t = 0 , ta được: 2 2 2 m + ( m + )1 2 2 1
+ t 0 f (t) 2
= t + 2mt + 2m +1 0 (2) t
BPT nghiệm đúng x 0 nên BPT có nghiệm 0 t 1, suy ra
Phương trình f (t) = 0 có 2 nghiệm t ,t thỏa t 0 1 t 1 2 1 2 f (0) 0 2m +1 0 m 0 − ,5 − . Vậy 1 m thỏa Ycbt. f ( ) 1 0 4m + 2 0 m 0 − ,5 2 Câu 4:
Đặt 2x = t . Do x 0 t 1. Khi đó ta có: 2
(3m+1) t + (2 − m) t+1 0, t 1 2 −t − 2t −1 2 2
(3t − t) m − t − 2t −1 t 1 m t 1 2 3t − t 2 −t − t − 2 t + t − Xét hàm số 2 1 7 6 1 f (t) =
trên 1; + f '(t) = 0 t (1;+) 2 ( ) 3t − t 2 2 (3 t − t) BBT
Do đó m lim f (t) = 2
− thỏa mãn yêu cầu bài toán + t 1 → Ghi chú:
+ m f (x)x D m maxf (x)x D Sử dụng
+ m f (x)x D m minf (x)x D Câu 5: 2 2 cos x cos x x x x Ta có 2 2 2 1 5 sin cos cos 4 + 5 . m 7 4 + m . 28 7 t t Đặt 2
t = cos x,t 0 ;1 thì BPT trở thành: 1 5 4 + m . 28 7 t t Xét f (t) 1 5 = 4. +
là hàm số nghịch biến trên 0; 1 . 28 7
Suy ra: f ( ) f (t) f ( ) 6 1 0
f (t) 5. 7 Từ đó BPT có nghiệm 6 m . 7 Câu 6: Đặt = 3x t , t 0
Phương trình trở thành 2 t − 2(m + )
1 t − 3 − 2m 0 ycbt 2
t − 2(m + )
1 t − 3 − 2m 0, t 0, ( ) 1 ta có = (m + )2 2 , m Nếu = 0 m = 2 − , khi đó từ ( ) 1 ta có ( t + )2 1 2 1 0,t − 2
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 103
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Nếu m 2 − ta có 0 0 m 2 − S khi đó ( ) 3
1 có hai nghiệm thỏa mãn ycbt khi và chỉ khi 0 m 1 − m − 2 2 3 P 0 m − 2 Kết luận Vậy 3 m − . 2 Câu 7:
Bất phương trình x 1 4 − − (2x m + ) 1 0 ( ) 1 .
Bất phương trình trở thành: 1 2
t − m(t + ) 1 0 2
t − 4mt − 4m 0 (2) . 4 Đặt f (t) 2
= t − 4mt − 4m .
Đồ thị hàm số y = f (t) có đồ thị là một Parabol với hệ số a dương, đỉnh I ( 2
2m; − 4m − 4m) . Bất phương trình ( )
1 nghiệm đúng với mọi x
Bất phương trình (2) nghiệm đúng với
mọi t 0 hay f (t) 0, t 0 .
TH1: m 0 f (0) = 4
− m 0 m 0 thỏa mãn. TH2: m 0 2 4
− m − 4m 0 nên m 0 không thỏa mãn. Vậy m 0 . Câu 8: x x x 1 .
m 3 + + (3m + 2)(4 − 7 ) + (4 + 7 ) 0 x x − +
m + ( m + ) 4 7 4 7 3 3 2 + 0( ) 1 3 3 x + Đặt 4 7 t = (t 0)
. Bất phương trình trở thành: 3 3m + (3m + 2)1 2
+ t 0 t + 3mt + 3m + 2 0(2) . t Ta có x (− ;
0 t (0 ;1
Để bất phương trình đã cho nghiệm đúng với mọi x (− ;
0 thì bất phương trình nghiệm
đúng với mọi t (0; 1 2 t + 2 m − (
t + ) , t (0; 1 3 1 2 t + 2
Xét hàm số f (t) = − trên (0 ;1 3(t + ) 1
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 104
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung 2 + − t = 1 − − 3 0;1
Ta có f (t) t 2t 2 = − . f (t) ( = 0 . 3(t + )2 1 t = 1 − + 3 Bảng biến thiên 2 + − Vậy t 2 2 2 3 m − ( . t + ) , t (0 ;1 m 3 1 3
Câu 9: x x 2x x x x x 4 2 2 2 Ta có: 5.4 + .
m 25 − 7.10 0 5. − 7. + m 0 5. − 7. + m 0 . 25 5 5 5 x 2 Đặt t = , t 0.
Bất phương trình trở thành: 2 2
5t − 7t + m 0 m 5
− t + 7t = g (t). 5
Ta lại có: g(t) = − t + g(t) 7 10 7 = 0 1
− 0t + 7 = 0 t = . 10 Bảng biến thiên:
Quan sát bảng biến thiên ta thấy g (t) 49 max = khi 7 t = . t ( 0;+) 20 10
Để bất phương trình đề bài cho thỏa mãn điều kiện có nghiệm m g (t) 49 max = . t ( 0;+) 20
Do m là số nguyên dương nên m 1; 2 .
Câu 10: Chọn B x +1 0 x 1 − Đk: ln ( x + )
1 0 x 0 D = ( 1 − ;+) \0 ;1 x −1 0 x 1
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 105
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Xét hàm số f ( x) 1 2 3 = + + trên D . x −1 3x ln ( x + ) 1 f ( x) 1 2 ln 3 3 = − − − . (x − ) 0, x D 2 x 1 3 (x + ) 2 1 ln ( x + ) 1
Nên hàm số f ( x) nghịch biến trên D .
Ta có BBT của hàm số f ( x) 11
Dựa vào BBT ta có phương trình có ba nghiệm phân biệt khi 0 m . 2
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 106
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021 CHƯƠNG ②: FB: Duong Hung
Bài 8: BẤT PHƯƠNG TRÌNH LOGARIT
Dạng ①: Bất phương trình logarit cơ bản.
-Phương pháp:
①. Xét bất phương trình logarit cơ bản có dạng . Trường hợp , ta có: . Trường hợp , ta có:
②. Xét bất phương trình logarit cùng cơ số: . Trường hợp , ta có: . Trường hợp , ta có:
-Casio: Table, Calc
A - Bài tập minh họa:
Câu 1: Giải bất phương trình : log 3x 1 3. 2 10 Ⓐ. x 3. Ⓑ. 1 x 3. Ⓒ. x 3. Ⓓ. x . 3 3 Lời giải
PP nhanh trắc nghiệm
Chọn A
Casio: Table
Ta có log 3x 1 3 3x 1 8 x 3. 2 Thỏa mãn chọn A
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 107
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 2: Tập nghiệm của bất phương trình log x −1 0 là 0,2 ( ) Ⓐ. ( ; − 2) . Ⓑ.(2;+) . Ⓒ.( ) ;1 − . Ⓓ. (1;2) . Lời giải
PP nhanh trắc nghiệm Chọn B Casio: Calc, table
Ta có log ( x − ) 0
1 0 x −1 0, 2 x 2 . 0,2
Vậy tập nghiệm của bất phương trình là S = (2; +) .
Câu 3: Tập nghiệm của bất phương trình log ( 2
x − 5x + 7 0 là 1 ) 2 Ⓐ. (− ;
2)(3;+ ) . Ⓑ.(3;+ ) . Ⓒ.( ; − 2). Ⓓ. (2;3). Lời giải
PP nhanh trắc nghiệm Chọn D Casio: Calc, table log ( 2 x − 5x + 7) 2
0 0 x − 5x + 7 1. 1 2 2
x − 5x + 6 0 2
x − 5x + 7 0 2 x 3.
Câu 4: Bất phương trình log 3x +1 log x + 7 có bao nhiêu nghiệm nguyên ? 3 ( ) 3 ( ) Ⓐ. 2 . Ⓑ.3. Ⓒ. 4 . Ⓓ. 1. Lời giải
PP nhanh trắc nghiệm Chọn B Casio: Calc, table Ta có: 3
x +1 x + 7 log 3x +1 log x + 7 3 ( ) 3 ( ) 3 x +1 0 x 3 1 1 − x 3 . x − 3 3
Vì x là số nguyên nên x 0;1; 2 .
Vậy bất phương trình có 3 nghiệm nguyên.
B - Bài tập rèn luyện:
Câu 1: Tập nghiệm S của bất phương trình log x 1 là
Ⓐ. S = (−;10) . Ⓑ. S = (0;10). Ⓒ. S = (− ) ;1 .
Ⓓ. S = (10;+ ).
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 108
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 2: Tìm tập nghiệm S của bất phương trình log x 0 . 1 2 Ⓐ. 1 S = ; + . Ⓑ. S = 1;+) . Ⓒ. 1 S = 0; . Ⓓ. S = (0 ;1 . 2 2
Câu 3: Tập nghiệm của bất phương trình log x − 9 0 là 2 ( ) Ⓐ. 9;+). Ⓑ.10;+) . Ⓒ.(9;+). Ⓓ. (10;+).
Câu 4: Tập nghiệm của bất phương trình log x −1 4 là 2 ( ) Ⓐ. ( ;17 − . Ⓑ.( ;17 − ). Ⓒ.1;17). Ⓓ. (1;17) .
Câu 5: Tập nghiệm của bất phương trình 1 ln 0 là x Ⓐ. ( ; − 1) . Ⓑ.(0;1) . Ⓒ.(1; ) + . Ⓓ. .
Câu 6: Giải bất phương trình log 5x − 3 2 − , ta có nghiệm là 1 ( ) 5 Ⓐ. 28 28 28 x . Ⓑ. 3 28 x . Ⓒ. 3 x . Ⓓ. x . 5 5 5 5 5 5
Câu 7: Bất phương trình log ( 2
x − 2x + 3 1 có tập nghiệm là 2 ) Ⓐ. \ 1 . Ⓑ. . Ⓒ. 1 . Ⓓ. .
Câu 8: Tập nghiệm của bất phương trình 3 log x 4 là 2 Ⓐ. (8;16). Ⓑ.(0;16) . Ⓒ.(8;+) . Ⓓ. .
Câu 9: Tìm tập nghiệm S của bất phương trình log (2x − ) 1 2 − 0,5 Ⓐ. 1 5 S = ; . Ⓑ. 1 5 S = ; . Ⓒ. 5 S = − ; . Ⓓ. 5 S = ; + . 2 2 2 2 2 2
Câu 10: Tập nghiệm của bất phương trình 2 log x 1 − là 1 2 Ⓐ. 2;+ − ). Ⓑ. 2; 0 ) (0; 2 . Ⓒ. − 2; 2. Ⓓ. (0; 2 .
Câu 11: Tìm tập nghiệm của bất phương trình log ( 2
x − 3x + 2 1 − . 1 ) 2 Ⓐ. ( ; − ) 1 . Ⓑ.0; ) 1 (2; 3 . Ⓒ.0; 2)(3; 7. Ⓓ. 0; 2) .
Câu 12: Bất phương trình log ( 2
2x − x +1 0 có tập nghiệm là 2 ) 3 Ⓐ. 3 S = 0; . Ⓑ. 3 S = 1 − ; . 2 2 Ⓒ. S ( ) 1 = − ;0 ; + .
Ⓓ. S = (− ) 3 ;1 ; + . 2 2
Câu 13: Tập nghiệm của bất phương trình: log x − 3 −1 0 có dạng ( ;
a b) . Khi đó giá trị a + 3b bằng 1 ( ) 3 Ⓐ. 15. Ⓑ.13. Ⓒ. 37 . Ⓓ. 30. 3
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 109
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 14: Bất phương trình log x + log x 1 có nghiệm là 2 3 Ⓐ. log log 6 log 2 2 6 x 3 . Ⓑ. 3 x 2 . Ⓒ. x 6 . Ⓓ. 6 x 3 .
Câu 15: Cho hàm số f ( x) = log ( 2
x − 5x + 7 . Nghiệm của bất phương trình f ( x) 0 là 1 ) 3 Ⓐ. x 3.
Ⓑ. x 2 hoặc x 3. Ⓒ. 2 x 3. Ⓓ. x 2 .
Câu 16: Tập nghiệm của bất phương trình: log (5x + 2) log 3x + 6 là 0,4 0,4 ( ) Ⓐ. ( ; − 2). Ⓑ.(0;2). Ⓒ. 2 − ;2 . Ⓓ. (2;+). 5
Câu 17: Cho bất phương trình: log f x log g x . Khi đó bất phương trình tương đương: 1 ( ) 1 ( ) 3 3
Ⓐ. f (x) g (x).
Ⓑ. g (x) f (x) 0. Ⓒ. g (x) f (x) 0. Ⓓ. f (x) g (x)
Câu 18: Nghiệm của bất phương trình log ( x + 2) log (5 − x) là Ⓐ. 3 3 2 − x . Ⓑ. 3 x 5 . Ⓒ. 3 x . Ⓓ. x . 2 2 2 2
Câu 19: Tập nghiệm của bất phương trình log 3x −1 log x +1 là 2 ( ) 2 ( ) Ⓐ. ( ) ;1 − . Ⓑ. 1 ;1 . Ⓒ.(1;+). Ⓓ. (0; ) 1 . 3
Câu 20: Tập nghiệm của bất phương trình log 7 − x + log x −1 0 là 2 ( ) 1 ( ) 2
Ⓐ. S = (1;4.
Ⓑ. S = (−;4.
Ⓒ. S = 4;+ ) .
Ⓓ. S = 4;7).
Câu 21: Tập nghiệm của bất phương trình log ( 2 x + x log 2 − x + 4 là 0,5 ) 0,5 ( ) Ⓐ. (− ; 4
− ) (1;2). Ⓑ.Đáp án khác. Ⓒ.( 4 − ;− ) 1 . Ⓓ. (− ; 4 − ) (1;+) .
Câu 22: Tập nghiệm của bất phương trình log x −1 + log 11− 2x 0 là 1 ( ) 3 ( ) 3 Ⓐ. S = (1;4 Ⓑ. S = (1;4) Ⓒ. S = (− ; 4 Ⓓ. 11 S = 3; 2
Câu 23: Tập nghiệm của bất phương trình log ( 2
x − 4 log 3x là 2 ) 2 Ⓐ. (2;4. Ⓑ. 1 − ;4. Ⓒ.( 2 − ;4. Ⓓ. (− ; 2 − 4;+) .
Câu 24: Giải bất phương trình log 3x − 2 log 6 − 5x được tập nghiệm là ( ;
a b) . Hãy tính tổng 2 ( ) 2 ( )
S = a + b Ⓐ. 8 S = . Ⓑ. 28 S = . Ⓒ. 11 S = . Ⓓ. 31 S = . 3 15 5 6
Câu 25: Tập nghiệm của bất phương trình 2log x −1 log 5 − x +1. 2 ( ) 2 ( ) Ⓐ. 3; 5 . Ⓑ.(1; 3 . Ⓒ.1; 3 . Ⓓ. (1;5) .
Câu 26: Tìm tập nghiệm S của bất phương trình log x −1 log 2x −1 0,5 ( ) 0,5 ( )
Ⓐ. S = (0;+) .
Ⓑ. S = (1;+) . Ⓒ. S = (− ; 0) .
Ⓓ. S = (− ) ;1 .
Câu 27: Tập nghiệm S của bất phương trình log x − 3 log 4 là 1 ( ) 1 2 2
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 110
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Ⓐ. S =(−;7. Ⓑ. S =(3;7. Ⓒ. S =3;7.
Ⓓ. S =7;+) 2 x − Câu 28: 1
Điều kiện xác định của bất phương trình ln 0 là x Ⓐ. 1 − x 0 x −1 . Ⓑ. x 1 − . Ⓒ. x 0 . Ⓓ. . x 1 x 1 2
Câu 29: Tìm tập nghiệm S của bất phương trình: log 2 . 1 x −1 2
Ⓐ. S = (1;1+ 2) . Ⓑ. S = (1; 9).
Ⓒ. S = (1+ 2; +) . Ⓓ. S = (9; +). x + Câu 30: 4 6
Tập nghiệm của bất phương trình log 0 là 3 x Ⓐ. 3 S = 2; − − . Ⓑ. S = 2 − ;0) . Ⓒ. S = (− ; 2. Ⓓ. 3 S = \ − ;0 . 2 2 BẢNG ĐÁP ÁN 1.B 2.D 3.D 4.D 5.B 6.B 7.A 8.A 9.A 10.B 11.B 12.C 13.B 14.D 15.C 16.C 17.C 18.A 19.B 20.D 21 22.A 23.A 24.C 25.B 26.B 27.B 28.A 29.D 30.A
Dạng ②: Bất phương trình logarit đặt ẩn phụ.
-Phương pháp:
. Bất phương trình có dạng : .Đặt
. Bất phương trình trở thành .
.Giải bất phương trình tìm t suy ra x thỏa ĐK
-Casio: Table, Calc
A - Bài tập minh họa:
Câu 1: Tìm tập nghiệm S của bất phương trình 2
log x − 5log x + 4 0. 2 2 Ⓐ. S = (− ; 2][16;+ ) . Ⓑ. S = [2;16].
Ⓒ. S = (0;2] [16;+ ) . Ⓓ. S = (− ; 1] [4;+ ) . Lời giải
PP nhanh trắc nghiệm Chọn C Casio
Điều kiện: x 0 .
Với điều kiện trên bất phương trình tương đương log x 1 0 x 2 2
log x −5log x + 4 0 2 . 2 2 log x 4 x 16 2
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 111
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 2: Tập nghiệm của phương trình 2 log x 3log x 2 0 là khoảng ;
a b . Giá trị biểu 2 2 thức 2 2 a b bằng Ⓐ. 16. Ⓑ.5. Ⓒ. 20 . Ⓓ. 10. Lời giải
PP nhanh trắc nghiệm Chọn C Casio: Table 2 log x 3log x 2 0 log x 1 log x 2 0 2 2 2 2 1 log x 2 2 x 4 x 2; 4 2 a 2 Vậy 2 2 a b 20 b 4
Câu 3: Bất phương trình 2 log x + 6 5log
x có tập nghiệm là 0,5 0,5 Ⓐ. 1 ( 2; 3) . Ⓑ. 1 1; . Ⓒ. 1 1 ; . Ⓓ. ; + . 3 8 4 8 Lời giải
PP nhanh trắc nghiệm Chọn C
Casio: Table
Điều kiện: x 0. Ta có: 2 2 log x + 6 5log x log x − 5log x + 6 0 0,5 0,5 0,5 0,5 1 1
2 log x 3 x . 0,5 4 8
So điều kiện, ta được: 1 1 x . 8 4
B - Bài tập rèn luyện:
Câu 1: Bất phương trình 2 log x − 5log x 6 − có tập nghiệm là 0,2 0,2 Ⓐ. 1 1 S = ; . Ⓑ. S = (2;3) . Ⓒ. 1 S = 0; .
Ⓓ. S = (0;3) . 125 25 25
Câu 2: Xác định tập nghiệm S của bất phương trình 2
log x + log 2x − 3 0 2 2 Ⓐ. 1 S = 0; (2;+ ). Ⓑ. S = (2;+) . 4
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 112
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓒ. 1 S = − ; (2;+ ).
Ⓓ. S = (1;+) . 4
Câu 3: Bất phương trình 2 log
x + 3log x + 2 0 có tập nghiệm S = ;
a b . Giá trị của 2 a b bằng 1 1 2 2 Ⓐ. 16. Ⓑ.12. Ⓒ.8. Ⓓ. 4.
Câu 4: Tập nghiệm của bất phương trình (log x)2 − 4log x + 3 0 là 2 2 Ⓐ. (0;2)(8;+) Ⓑ.(− ; 2)(8;+) Ⓒ.(2;8) Ⓓ. (8;+)
Câu 5: Nghiệm của bất phương trình 2 log x − log
2x − 5 0 là 1 2 ( ) 2 Ⓐ. 1 1 x 0; (9;+ ).
Ⓑ. x 0; 8;+ ). 4 4 Ⓒ. 1 1 x − ; 8;+ ) . Ⓓ. x − ; 9;+ ) . 4 4 3 x Câu 6: 32
Nếu đặt t = log x thì bất phương trình 4 2 2 log x − log + 9log 4log x trở thành 1 2 1 2 2 − ( ) 2 2 8 x 2 bất phương trình nào? Ⓐ. 4 2
t +13t + 36 0 . Ⓑ. 4 2
t − 5t + 9 0 . Ⓒ. 4 2
t −13t + 36 0 . Ⓓ. 4 2
t −13t − 36 0 .
Câu 7: Tập nghiệm S của bất phương trình 2 log x 3log x 2 0 là 3 3
Ⓐ. S = 3;9.
Ⓑ. S = 1;9.
Ⓒ. S = 0;9.
Ⓓ. S = 1;2. 3 x Câu 8: 32
Nghiệm nguyên lớn nhất của bất phương trình 4 2 2 log x − log + 9log 4log x là 1 2 1 2 2 − ( ) 2 8 x 2 Ⓐ. x = 7 . Ⓑ. x = 8. Ⓒ. x = 4 . Ⓓ. x =1. 3
Câu 9: Tập nghiệm của bất phương trình log x x x là x (125 ) 2 .log + log 25 5 2
Ⓐ. S = (1; 5) . Ⓑ. S = ( 1 − ; 5) . Ⓒ. S = (− 5 ) ;1 .
Ⓓ. S = (− 5;− )1 .
Câu 10: Xác định tập nghiệm S của bất phương trình 2
log x + log 2x − 3 0 2 2 Ⓐ. 1 S = 0; (2;+ ). Ⓑ. S = (2;+) . 4 Ⓒ. 1 S = − ; (2;+ ).
Ⓓ. S = (1;+) . 4 BẢNG ĐÁP ÁN 1.A 2.A 3.C 4.A 5.B 6.C 7.A 8.A 9.A 10.A
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 113
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Dạng ③: Bất PT logarit chứa tham số
-Phương pháp:
. Sử dụng PP giải BPT logarit kết hợp công thức, tính chất của mũ, lũy thừa, logarit
. Khai thác điều kiện bài toán
. Xử lý bài toán và chọn giá trị m thỏa ĐK bài toán.
B - Bài tập Vận dụng Cao rèn luyện:
Câu 1: Tìm tất cả các giá trị thực của tham số m để bất phương trình log (5x −1) m có nghiệm x 1 2 ? Ⓐ. m 2. Ⓑ. m 2 . Ⓒ. m 2. Ⓓ. m 2.
Câu 2: Tìm tất cả các giá trị thực của tham số m để phương trình log ( 2 mx − x = 2 vô nghiệm? 2 ) Ⓐ. m m 4. Ⓑ. 4 − m 4 . Ⓒ. 4 . Ⓓ. m 4 − . m 4 −
Câu 3: Tìm tất cả giá trị thực của tham số m để bất phương trình log ( 2
x + 4x + m 1 nghiệm đúng 3 ) với mọi x .? Ⓐ. m 7. Ⓑ. m 7 . Ⓒ. m 4.
Ⓓ. 4 m 7.
Câu 4: Tìm tất cả giá trị thực của tham số m để bất phương trình log ( 2 mx − x log 4 vô nghiệm? 1 ) 1 5 5 Ⓐ. m 4 − m 4 . Ⓑ. 4 . Ⓒ. m 4. Ⓓ. 4 − m 4 . m 4 −
Câu 5: Tìm tất cả các giá trị thực của tham số m sao cho khoảng (2;3) thuộc tập nghiệm của bất phương trình log ( 2 x + ) 1 log ( 2
x + 4x + m −1 (1) . 5 5 ) Ⓐ. m 1 − 2;1 3 . Ⓑ. m12 ;13 . Ⓒ. m 1 − 3;12 . Ⓓ. m 1 − 3; 1 − 2 .
Câu 6: Tìm m để bất phương trình 1+ log ( 2 x + ) 1 log ( 2
mx + 4x + m) thoã mãn với mọi x . 5 5 Ⓐ. 1
− m 0 . Ⓑ. 1
− m 0 . Ⓒ. 2 m 3.
Ⓓ. 2 m 3.
Câu 7: Số giá trị nguyên của tham số m sao cho bất phương trình: + ( 2x + ) ( 2 log 5 log 1
log mx + 4x + m) nghiệm đúng với mọi x thuộc . Ⓐ. 0.
Ⓑ.m và m 3. Ⓒ.1. Ⓓ. 2.
Câu 8: Hỏi có bao nhiêu giá trị nguyên của m để bất phương trình 2
log x + mlog x − m 0 nghiệm 2 2
đúng với mọi giá trị của x (0; + ) .
Ⓐ. Có 4 giá trị nguyên. Ⓑ.Có 5 giá trị nguyên. Ⓒ.Có 6 giá trị nguyên.
Ⓓ. Có 7 giá trị nguyên.
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 114
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 9: Tìm tất cả các giá trị thực của tham số m để bất phương trình log (5x −1).log (2.5x − 2) m 2 2 có nghiệm x 1? Ⓐ. m 6. Ⓑ. m 6. Ⓒ. m 6. Ⓓ. m 6.
Câu 10: Trong tất cả các cặp ( ; x y ) thỏa mãn log
4x + 4 y − 4 1 . Tìm m để tồn tại duy nhất 2 2 ( ) x + y +2 cặp ( ; x y ) sao cho 2 2
x + y + 2x − 2 y + 2 − m = 0 . Ⓐ. ( − )2 10 2 . Ⓑ. 10 − 2 và 10 + 2 . Ⓒ.( − )2 10 2 và ( + )2 10 2 . Ⓓ. 10 − 2 .
Câu 11: Tất cả các giá trị thực của m để bất phương trình x x + x +12 . m log 3 có nghiệm là 5− 4− x
Ⓐ. m 2 3 . Ⓑ. m 2 3 . Ⓒ. m 12log 5 .
Ⓓ. 2 m 12log 5 . 3 2 BẢNG ĐÁP ÁN 1.A 2.B 3.A 4.D 5.A 6.C 7.C 8.B 9.C 10.A 11.B Hướng dẫn giải
Câu 1: Tìm tất cả các giá trị thực của tham số m để bất phương trình log (5x −1) m có nghiệm x 1 2 ? Ⓐ. m 2. Ⓑ. m 2 . Ⓒ. m 2. Ⓓ. m 2. Lời giải
1 5x −1 4 log 5x x −1 2 m 2 2 ( )
Câu 2: Tìm tất cả các giá trị thực của tham số m để phương trình log ( 2 mx − x = 2 vô nghiệm? 2 ) Ⓐ. m m 4. Ⓑ. 4 − m 4 . Ⓒ. 4 . Ⓓ. m 4 − . m 4 − Lời giải log ( 2 mx − x ) 2
= 2 −x + mx − 4 = 0(*) 2
Phương trình vô nghiệm 2
0 m −16 0 4 − m 4
Câu 3: Tìm tất cả giá trị thực của tham số m để bất phương trình log ( 2
x + 4x + m 1 nghiệm đúng 3 ) với mọi x .? Ⓐ. m 7. Ⓑ. m 7 . Ⓒ. m 4.
Ⓓ. 4 m 7. Lời giải log ( 2
x + 4x + m) 2
1 x x + 4x + m − 3 0 x 0 m 7 3
Câu 4: Tìm tất cả giá trị thực của tham số m để bất phương trình log ( 2 mx − x log 4 vô nghiệm? 1 ) 1 5 5 Ⓐ. m 4 − m 4 . Ⓑ. 4 . Ⓒ. m 4. Ⓓ. 4 − m 4 . m 4 − Lời giải log ( 2 mx − x ) 2 2
log 4 mx − x 4 x − mx + 4 0 1 1 5 5 2
x − mx + 4 0 vô nghiệm 2
x − mx + 4 0 x R 0 4 − m 4
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 115
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 5: Tìm tất cả các giá trị thực của tham số m sao cho khoảng (2;3) thuộc tập nghiệm của bất phương trình log ( 2 x + ) 1 log ( 2
x + 4x + m −1 (1) . 5 5 ) Ⓐ. m 1 − 2;1 3 . Ⓑ. m12 ;13 . Ⓒ. m 1 − 3;12 . Ⓓ. m 1 − 3; 1 − 2 . Lời giải 2
x + 4x + m 2 2 x +1
m −x − 4x = f (x) (1) 5 2
m x − x + = 2 4 4 5 g(x)
x + 4x + m 0
m Max f (x) = 1 − 2 khi x = 2 Hệ trên thỏa mãn x x (2;3) 2 3 1 − 2 m 13.
m Min f (x) = 13 khi x = 2 2x3
Câu 6: Tìm m để bất phương trình 1+ log ( 2 x + ) 1 log ( 2
mx + 4x + m) thoã mãn với mọi x . 5 5 Ⓐ. 1
− m 0 . Ⓑ. 1
− m 0 . Ⓒ. 2 m 3.
Ⓓ. 2 m 3. Lời giải 2
mx + 4x + m 0
BPT thoã mãn với mọi x . ( x ) 5 ( 2 x + ) 2
1 mx + 4x + m m 0 m 0 m −2 2 2
mx + 4x + m 0 1 6 − 4m 0 m 2 ( x ) m . ( 2 3 5 − m) 2
x − 4x + 5 − m 0 5 − m 0 m 5 1
6 − 4(5 − m)2 0 m 3 m 7
Câu 7: Số giá trị nguyên của tham số m sao cho bất phương trình: + ( 2x + ) ( 2 log 5 log 1
log mx + 4x + m) nghiệm đúng với mọi x thuộc . Ⓐ. 0.
Ⓑ.m và m 3. Ⓒ.1. Ⓓ. 2. Lời giải
Bất phương trình xác định với mọi x thuộc khi: 2
mx + 4x + m 0,x m 0 m 0 m 2 ( ) 1 2 0 4 − m 0
Bất phương trình nghiệm đúng với mọi x thuộc khi: 2 2
5x + 5 mx + 4x + , m x (5− m) 2
x − 4x + 5 − m 0, x 5 − m 0 m 5 m 3 (2) 2 0
−m +10m − 21 0
Từ và ta được 2 m 3, m m = 3 . Vậy có 1 giá trị m.
Câu 8: Hỏi có bao nhiêu giá trị nguyên của m để bất phương trình 2
log x + mlog x − m 0 nghiệm 2 2
đúng với mọi giá trị của x (0; + ) .
Ⓐ. Có 4 giá trị nguyên. Ⓑ.Có 5 giá trị nguyên. Ⓒ.Có 6 giá trị nguyên.
Ⓓ. Có 7 giá trị nguyên. Lời giải
Đặt t = log x (x 0) 2
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 116
Tài liệu giảng dạy Ôn thi TN-HS TB-Yếu hiệu quả cao – FB Duong Hung
Bất phương trình trở thành: 2
t + mt − m 0,t 0 2
m + 4m 0 4 − m 0
Vì m nguyên nên m 4 − ; 3 − ; 2 − ; 1 − ;
0 . Vậy có 5 giá trị nguyên của m thỏa ycbt.
Câu 9: Tìm tất cả các giá trị thực của tham số m để bất phương trình log (5x −1).log (2.5x − 2) m 2 2 có nghiệm x 1? Ⓐ. m 6. Ⓑ. m 6. Ⓒ. m 6. Ⓓ. m 6. Lời giải
BPT log (5x −1).log (2.5x − 2) m log (5x −1). 1
+ log (5x −1) m 2 2 2 2 Đặt t = log ( 2
x + x −1 do x 1 t 2; +) 6 ) BPT 2
t(1+ t) m t + t m f (t) m Với 2
f (t) = t + t ,
f (t) = 2t +1 0 với t 2; +) nên hàm đồng biến trên t 2; +)
Nên Minf (t) = f (2) = 6
Do đó để để bất phương trình log (5x −1).log (2.5x − 2) m có nghiệm x 1thì: 2 2
m Minf (t) m 6
Câu 10: Trong tất cả các cặp ( ; x y ) thỏa mãn log
4x + 4 y − 4 1 . Tìm m để tồn tại duy nhất 2 2 ( ) x + y +2 cặp ( ; x y ) sao cho 2 2
x + y + 2x − 2 y + 2 − m = 0 . Ⓐ. ( − )2 10 2 . Ⓑ. 10 − 2 và 10 + 2 . Ⓒ.( − )2 10 2 và ( + )2 10 2 . Ⓓ. 10 − 2 . Lời giải Ta có log
4x + 4 y − 4 1 2 2
x + y − 4x − 4y + 6 0 ( ) 1 . 2 2 ( ) x + y +2 Giả sử M ( ; x y) thỏa mãn pt ( )
1 , khi đó tập hợp điểm M là hình tròn (C tâm I (2; 2) 1 ) bán kính R = 2 . 1
Các đáp án đề cho đều ứng với m 0. Nên dễ thấy 2 2
x + y + 2x − 2 y + 2 − m = 0 là phương
trình đường tròn (C tâm J ( 1 − ) ;1 bán kính R = m . 2 ) 2
Vậy để tồn tại duy nhất cặp ( ;
x y ) thỏa đề khi chỉ khi (C và (C tiếp xúc ngoài 2 ) 1 )
IJ = R + R 10 = m + 2 m = ( 10 − 2)2 . 1 2
Câu 11: Tất cả các giá trị thực của m để bất phương trình x x + x +12 . m log 3 có nghiệm là 5− 4− x
Ⓐ. m 2 3 . Ⓑ. m 2 3 . Ⓒ. m 12log 5 .
Ⓓ. 2 m 12log 5 . 3 2 Lời giải
Điều kiện: x 0;4. Ta thấy 4 − x 4 5 − 4 − x 3 log 3 0 5− 4− x
Khi đó bất phương trình đã cho trở thành m f ( x) = (x x + x +12).log 5− 4 − x (*) . 3 ( ) Với 3 x 1
u = x x + x +12 u = + và 2 2 x +12 1
v = log 5 − 4 − x v = . 3 ( )
2 4 − x (5 − 4 − x ).ln 3
Suy ra f (x) 0;x (0;4) f (x) là hàm số đồng biến trên đoạn 0;4 .
Để bất phương trình có nghiệm m min f ( x) = f (0) = 2 3 0;4
St-bs: Duong Hung – Zalo 0774.860.155 – Full 50 chuyền đề word xinh 117




