
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM
Dạng 1. Rút gọn, biến đổi, tính toán biểu thức lũy thừa
Công thức lũy thừa
Cho các số dương
,a b
và
,m n
. Ta có:
0
1a
. ...........
n
n thöøa soá
a a a a
với
*
n
1
n
n
a
a
( ) ( )
m n mn n m
a a a
.
m n m n
a a a
m
m n
n
a
a
a
( )
n n n
a b ab
n
n
n
a a
b b
1
2
*
1
3
3
( , )
n
m n
m
a a
a a m n
a a
Câu 1. (Nhân Chính Hà Nội 2019) Cho
0, ,a m n
. Khẳng định nào sau đây đúng?
A.
.
m n m n
a a a
B.
. .
m n m n
a a a
C.
( ) ( ) .
m n n m
a a
D.
.
m
n m
n
a
a
a
Câu 2. (THPT Minh Khai - 2019) Với
0a
,
0b
,
,
là các số thực bất kì, đẳng thức nào sau đây
sai?
A.
a
a
a
. B.
.a a a
. C.
a a
b b
. D.
.a b ab
.
Câu 3. (Sở Quảng Trị 2019) Cho
, 0x y
và
,
. Tìm đẳng thức sai dưới đây.
A.
.xy x y
. B.
x y x y
. C.
x x
. D.
.x x x
.
Câu 4. (Nho Quan A - Ninh Bình - 2019) Cho các số thực
, , , , 0a b m n a b
. Khẳng định nào sau đây
là đúng?
A.
m
n
m
n
a
a
a
. B.
n
m m n
a a
. C.
m
m m
a b a b
. D.
.
m n m n
a a a
.
Câu 5. (Cụm 8 Trường Chuyên 2019) Với
là số thực bất kì, mệnh đề nào sau đây sai?
A.
10 10
. B.
2
10 10
. C.
2
10 100
. D.
2
2
10 10
.
Câu 6. (Mã 105 2017) Rút gọn biểu thức
5
3
3
:Q b b
với
0b
.
A.
4
3
Q b
B.
4
3
Q b
C.
5
9
Q b
D.
2
Q b
Câu 7. (Mã 110 2017) Rút gọn biểu thức
1
6
3
.P x x
với
0x
.
A.
P x
B.
1
8
P x
C.
2
9
P x
D.
2
P x
Câu 8. (SGD Nam Định 2019) Cho
a
là số thực dương. Giá trị rút gọn của biểu thức
4
3
P a a
bằng
A.
7
3
a . B.
5
6
a . C.
11
6
a . D.
10
3
a .
Câu 9. (Mã 102 2017) Cho biểu thức
4
3
2 3
. .P x x x
, với
0x
. Mệnh đề nào dưới đây đúng?
LŨY THỪA - HÀM SỐ LŨY THỪA
Chuyên đề 16

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
3
P x
B.
1
2
P x
C.
13
24
P x
D.
1
4
P x
Câu 10. (THPT Lương Thế Vinh Hà Nội 2019) Cho biểu thức
1
1
6
3
2
. . x
P x x
với
0
x
. Mệnh đề nào
dưới đây đúng?
A.
P x
B.
11
6
P x
C.
7
6
P x
D.
5
6
P x
Câu 11. (THPT Lê Quy Đôn Điện Biên 2019) Rút gọn biểu thức
1
3
6
P x x
với
0
x
.
A.
1
8
P x
B.
P x
C.
2
9
P x
D.
2
P x
Câu 12. (THPT Sơn Tây Hà Nội 2019) Cho a là số thực dương. Viết và rút gọn biểu thức
3
2018
2018
.
a a
dưới dạng lũy thừa với số mũ hữu tỉ. Tìm số mũ của biểu thức rút gọn đó.
A.
2
1009
. B.
1
1009
. C.
3
1009
. D.
2
3
2018
.
Câu 13. (Cụm Liên Trường Hải Phòng 2019) Rút gọn biểu thức
3 1 2 3
2 2
2 2
.a a
P
a
với
0
a
.
A.
P a
. B.
3
P a
. C.
4
P a
. D.
5
P a
.
Câu 14. (THPT Yên Khánh - Ninh Bình 2019) Biểu thức
3
2
5
P x x x x
(với
0
x
), giá trị của
là
A.
1
2
. B.
5
2
. C.
9
2
. D.
3
2
.
Câu 15. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Cho
a
là số thực dương khác
1
. Khi đó
2
4
3
a
bằng
A.
3
2
a
. B.
8
3
a
. C.
3
8
a
. D.
6
a
.
Câu 16. (Cụm Liên Trường Hải Phòng 2019) Rút gọn biểu thức
3 1 2 3
2 2
2 2
.a a
P
a
với
0a
A.
P a
B.
3
P a
C.
4
P a
D.
5
P a
Câu 17. (THPT Lương Tài Số 2 2019) Cho biểu thức
3
5
4
.
P x x
,
0
x
. Khẳng định nào sau đây là
đúng?
A.
2
P x
B.
1
2
P x
C.
1
2
P x
D.
2
P x
Câu 18. (Bỉm Sơn - Thanh Hóa - 2019) Cho biểu thức
5 1 2 5
2 2
2 2
.a a
P
a
. Rút gọn
P
được kết quả:
A.
5
a
. B.
a
. C.
3
a
. D.
4
a
.
Câu 19. (Chuyên Vĩnh Phúc 2019) Cho biểu thức
3
3
4
.
P x x x
, với
0.
x
Mệnh đề nào dưới đây
đúng?
A.
1
2
.P x
B.
7
12
.P x
C.
5
8
.P x
D.
7
24
.P x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 20. (THPT Thiệu Hóa – Thanh Hóa 2019) Cho hai số thực dương
,a b
. Rút gọn biểu thức
1 1
3 3
6 6
a b b a
A
a b
ta thu được
.
m n
A a b
. Tích của
.m n
là
A.
1
8
B.
1
21
C.
1
9
D.
1
18
Câu 21. (Sở Quảng Ninh 2019) Rút gọn biểu thức
11
3 7
3
7
4 5
.
.
a a
A
a a
với
0
a
ta được kết quả
m
n
A a
trong
đó
,m n
*
N
và
m
n
là phân số tối giản. Khẳng định nào sau đây đúng?
A.
2 2
312
m n
. B.
2 2
543
m n
. C.
2 2
312
m n
. D.
2 2
409.
m n
Câu 22. (Sở Vĩnh Phúc 2019) Cho
a
là số thực dương. Đơn giản biểu thức
4 1 2
3 3 3
1 3 1
4 4 4
a a a
P
a a a
.
A.
1
P a a
. B.
1P a
. C.
P a
. D.
1P a
.
Câu 23. Cho
, a b
là các số thực dương. Rút gọn
4 4
3 3
3 3
a b ab
P
a b
ta được
A.
P ab
. B.
P a b
. C.
4 4
P a b ab
. D.
P ab a b
.
Câu 24. (KTNL GV Thpt Lý Thái Tổ 2019) Cho biểu thức
5
3
8 2 2 2
m
n
, trong đó
m
n
là phân số tối
giản. Gọi
2 2
P m n
. Khẳng định nào sau đây đúng?
A.
330;340
P
. B.
350;360
P
. C.
260;370
P
. D.
340;350
P
.
Câu 25. (Sở Bắc Ninh 2019) Cho
0
a
,
0
b
, giá trị của biểu thức
1
2
2
1
1
2
1
2 . . 1
4
a b
T a b ab
b a
bằng
A.
1
. B.
1
2
. C.
2
3
. D.
1
3
.
Câu 26. (Đề Tham Khảo 2017) Tính giá trị của biểu thức
2017 2016
7 4 3 4 3 7P
A.
2016
7 4 3P
B.
1P
C.
7 4 3
P
D.
7 4 3
P
Câu 27. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho biểu thức
3
3
2 2 2
3 3 3
P . Mệnh đề nào trong các
mệnh đề sau là đúng?
A.
1
8
2
3
P
. B.
18
2
3
P
. C.
1
18
2
3
P
. D.
1
2
2
3
P
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 28. (THPT An Lão Hải Phòng 2019) Cho hàm số
1
3 4
3
3
1
8 8
3 1
8
a a a
f a
a a a
với
0, 1
a a
. Tính
giá trị
2016
2017M f
A.
1008
2017 1
M
B.
1008
2017 1
M
C.
2016
2017 1
M
D.
2016
1 2017
M
Câu 29. (THPT Trần Phú 2019) Giá trị của biểu thức
3 1 3 4
0
3 2
2 .2 5 .5
10 :10 0,1
P
là
A.
9
. B.
10
. C.
10
. D.
9
.
Câu 30. (THPT Ngô Quyền – 2017) Cho hàm số
2
3
2
3
3
1
8 8
3 1
8
a a a
f a
a a a
với
0, 1
a a
. Tính giá trị
2018
2017M f
.
A.
2018
2017 1.
B.
1009
2017 1.
C.
1009
2017 .
D.
1009
2017 1.
Câu 31. Cho biểu thức
5
12
3
4
f x x x x
. Khi đó, giá trị của
2,7
f
bằng
A.
0,027
. B.
27
. C.
2,7
. D.
0, 27
.
Câu 32. Tính giá trị biểu thức
2018 2017
2019
4 2 3 . 1 3
1 3
P
.
A.
2017
2P
. B.
1
. C.
2019
2
. D.
2018
2
.
Câu 33. (Chuyên Nguyễn Du-ĐăkLăk 2019) Giá trị biểu thức
2018 2019
3 2 2 . 2 1
bằng
A.
2019
2 1
. B.
2017
2 1
. C.
2019
2 1
. D.
2017
2 1
.
Câu 34. Cho
0, 0
a b
giá trị của biểu thức
1
2
1
1
2
2
1
1
4
2
a b
b
T a b b
a
a
bằng
A.
1
. B.
1
3
. C.
2
3
. D.
1
2
.
Dạng 2. So sánh các biểu thức chứa lũy thừa
Nếu
1
a
thì a a
;
Nếu
0 1a
thì a a
.
Với mọi
0
a b
, ta có:
0
m m
a b m
0
m m
a b m
Câu 1. (Bạc Liêu – Ninh Bình 2019) Cho
2 1 2 1
m n
. Khi đó
A.
m n
. B.
m n
. C.
m n
. D.
m n
.
Câu 2. Cho
1
a
. Mệnh đề nào sau đây là đúng?
A.
3
5
1
.
a
a
B.
1
3
.a a
C.
3
2
1.
a
a
D.
2016 2017
1 1
a a
.
Câu 3. (THPT Yên Phong Số 1 Bắc Ninh 2019) Trong các mệnh đề sau, mệnh đề nào SAI?

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
2018 2017
3 1 3 1
. B.
3
2 1
2 2
.
C.
2017 2018
2 1 2 1
. D.
2019 2018
2 2
1 1
2 2
.
Câu 4. (THPT Sơn Tây Hà Nội 2019) Khẳng định nào sau đây đúng?
A.
2017 2018
( 5 2) ( 5 2)
. B.
2018 2019
( 5 2) ( 5 2)
.
C.
2018 2019
( 5 2) ( 5 2)
. D.
2018 2019
( 5 2) ( 5 2)
.
Câu 5. (THPT Lê Quý Đôn Đà Nẵng 2019) Khẳng định nào dưới đây là đúng?
A.
3 3
3 5
.
7 8
B.
1 1
2 3
. C.
2
2
1
3
5
. D.
50
100
1
2
4
.
Câu 6. (Nam Định - 2018) Trong các khẳng định sau, khẳng định nào sai?
A.
2018 2017
2 2
1 1
2 2
. B.
2017 2018
2 1 2 1
.
C.
2018 2017
3 1 3 1
. D.
2 1 3
2 2
.
Câu 7. (THPT Tiên Lãng 2018) Tìm tập tất cả các giá trị của
a
để
7
5 2
21
a a
?
A.
0
a
.
B.
0 1a
.
C.
1
a
. D.
5 2
21 7
a
.
Câu 8. So sánh ba số:
0,3 3,2
0,2 , 0,7
và
0,3
3
.
A.
0,3
3,2 0,3
0,7 0,2 3
. B.
0,3
0,3 3,2
0,2 0,7 3
.
C.
0,3
0,3 3,2
3 0,2 0,7
. D.
0,3
0,3 3,2
0,2 3 0,7
.
Câu 9. (THPT Cộng Hiền 2019) Cho
, 0
a b
thỏa mãn
1 2
1 3
3 3
2 4
,
a a b b
. Khi đó khẳng định nào
đúng?
A.
0 1,0 1
a b
. B.
0 1, 1a b
. C.
1,0 1a b
. D.
1, 1
a b
.
Câu 10. So sánh ba số
64
1001 2
1000 , 2
a b
và
1 2 3 1000
1 2 3 ... 1000c
?
A.
c a b
. B.
b a c
. C.
c b a
. D.
a c b
.
Dạng 3. Tìm tập xác định của hàm số lũy thừa
Dạng:
y x
y u
với
u
là đa thức đại số.
Tập xác định:
Nếu
.
ÑK
u
Nếu
0.
0
ÑK
u
Nếu
0.
ÑK
u
Câu 1. (Mã 123 2017) Tập xác định D của hàm số
1
3
1
y x
là:.
A.
1;D
B.
D
C.
\ 1
D
D.
;1
D
Câu 2. (Mã 104 2017) Tìm tập xác định
D
của hàm số
3
2
2
y x x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
; 1 2;D
B.
\ 1;2
D
C.
D
D.
0;D
Câu 3. (Chuyên Bắc Giang 2019) Tập xác định của hàm số
1
5
1
y x
là
A.
1;
B.
\ 1
C.
1;
D.
0;
Câu 4. Tìm tập xác định
D
của hàm số
4
2
3
y x x
.
A.
0;3
. B.
\ 0;3
D
.
C.
;0 3;D
. D.
D R
Câu 5. (KSCL THPT Nguyễn Khuyến 2019) Tìm tập xác định của hàm số:
2
2
3
4
y x
là
A.
2;2
D
B.
\ 2; 2
D R
C.
D R
D.
2;D
Câu 6. (Thpt Lương Tài Số 2 2019) Trong các hàm số sau đây, hàm số nào có tập xác định
D
?
A.
2
y x
B.
2
1
2y
x
C.
2
2
y x
D.
2
y x
Câu 7. (Chuyên Vĩnh Phúc 2019) Tìm tập xác định
D
của hàm số
1
2
3
3 1
y x
.
A.
1 1
; ;
3 3
D
B.
D
C.
1
\
3
D
D.
1 1
; ;
3 3
D
Câu 8. (THPT An Lão Hải Phòng 2019) Hàm số nào dưới đây đồng biến trên tập xác định của nó?
A.
1
π
x
y
B.
2
3
x
y
C.
3
x
y
D.
0,5
x
y
Câu 9. (THPT An Lão Hải Phòng 2019) Tìm tập xác định
D
của hàm số
2
2
2 3
y x x
.
A.
D
B.
; 3 1;D
C.
0;D
D.
\ 3;1
D
Câu 10. (Chuyên KHTN 2019) Tập xác định của hàm số
1
2
1
y x
là
A.
0;
. B.
1;
. C.
1;
. D.
;
.
Câu 11. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Tập xác định của hàm số
2019
2
2020
4 y x x
là
A.
4 )
;0 ;( ] [
B.
4 )
;0 ;( ) (
C.
0;4
D.
\ 0;4
Câu 12.
(THPT Gang Thép Thái Nguyên 2019) Tập xác định của hàm số
2 2
( 6 8)
y x x
là
A.
(2;4)
D
. B.
;2
. C.
4;
. D.
D
.
Câu 13. (KTNL GV THPT Lý Thái Tổ 2019) Tìm tập xác định của hàm số
3
2
7 10
y x x
A.
\ 2;5
. B.
;2 5;
. C.
. D.
2;5
.
Câu 14. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Tìm tập xác định
D
của hàm số
3
2
4 1
y x
.
A.
1 1
\ ;
2 2
D
. B.
1 1
; ;
2 2
D
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
C.
D
. D.
1 1
;
2 2
D
.
Câu 15. (Hsg Tỉnh Bắc Ninh 2019) Tập xác định của hàm số
2019
2
4 3y x x
là
A.
\ 4;1 .
B.
.
C.
4;1 .
D.
4;1 .
Câu 16. (Chuyên Lê Quý Đôn Điện Biên 2019) Tìm tập xác định của
1
2
3
3x 2
y x
A.
;1 2;
. B.
\ 1;2
. C.
2
2
2 ln 5
x
y
x
. D.
.
Câu 17. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Tập xác định của hàm số
2
3 2
y x x
là
A.
1;2 .
. B.
;1 2;
. C.
\ 1;2
. D.
;1 2;
Câu 18. (Sở Bắc Ninh 2019) Tìm tập xác định
D
của hàm số
2 3
2
3 4
y x x
.
A.
\ 1;4
D
. B.
; 1 4;
D
.
C.
D
. D.
; 1 4;
D
.
Câu 19. (Gia Lai 2019) Tìm tập xác định
D
của hàm số
2
2
6 9
y x x
.
A.
\ 0
D
. B.
3;D
. C.
\ 3
D
. D.
D
.
Câu 20. (chuyên Hà Tĩnh 2019)Tìm tập xác định của hàm số
1
2
3
3 2
y x x
là
A.
\ 1;2
. B.
;1 2;
. C.
1;2
. D.
.
Câu 21. (Chu Văn An - Hà Nội - 2019) Tập xác định
D
của hàm số
3
2
27
y x
là
A.
D 3;
. B.
D 3;
. C.
D \ 3
. D.
D
.
Câu 22. (Bắc Ninh 2019) Tập xác định của hàm số
3
2
2
5
3 2 3
y x x x
là
A.
; \ 3
D
B.
;1 2; \ 3
D
.
C.
; \ 1;2
D
. D.
;1 2;D
.
Dạng 4. Đạo hàm hàm số lũy thừa
Đạo hàm:
1
1
.
y x y x
y u y u u
Câu 1. (Sở Quảng Trị 2019) Tìm đạo hàm của hàm số:
3
2
2
( 1)
y x
A.
1
2
3
(2 )
2
x
B.
1
4
3
4
x
C.
1
2
2
3 ( 1)
x x
D.
1
2
2
3
( 1)
2
x
Câu 2. (Kiểm tra năng lực - ĐH - Quốc Tế - 2019) Đạo hàm của hàm số
2
2
3
3
y x
tại
1x
là
A.
3
4
3
. B.
3
2 4
3
. C.
3
2
3
. D. 3 lựa chọn kia đều sai.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 3. (THPT Lý Nhân Tông – 2017) Hàm số
2
2
5
1
y x
có đạo hàm là.
A.
3
2
5
4
5 1
x
y
x
. B.
2
2 1
y x x
. C.
5 2
4 1
y x x
. D.
2
2
5
4
1
y
x
.
Câu 4. (THPT Nguyễn Đăng Đạo – 2017) Đạo hàm của hàm số
1
3
2 1
y x
trên tập xác định là.
A.
4
3
1
2 1
3
x
. B.
1
3
2 2 1 ln 2 1
x x
.C.
1
3
2 1 ln 2 1
x x
. D.
4
3
2
2 1
3
x
.
Câu 5. (Chuyên Vinh 2018) Đạo hàm của hàm số
1
2
3
1
y x x
là
A.
8
2
3
1
1
3
y x x
. B.
3 2
2 1
2 1
x
y
x x
.C.
2
2
3
2 1
3 1
x
y
x x
. D.
2
2
3
1
1
3
y x x
.
Câu 6. (THPT Chuyen LHP Nam Dinh – 2017) Tính đạo hàm của hàm số
6
1 cos3y x
.
A.
5
' 6sin3 1 cos3y x x
. B.
5
' 6sin3 cos3 1
y x x
.
C.
5
' 18sin3 cos3 1
y x x
. D.
5
' 18sin3 1 cos3y x x
.
Câu 7. (THPT Chuyên LHP – 2017) Tìm đạo hàm của hàm số
2
2
1
e
y x
trên
.
A.
1
2
2
2 1
e
y x x
. B.
2
2
1
e
y ex x
.
C.
1
2
2
1
2
e
e
y x
. D.
2 2
2
1 ln 1
e
y x x
.
Câu 8. (THPT Tứ Kỳ - Hải Dương - 2018) Cho hàm số
e e e e
y x
,
0
x
. Đạo hàm của
y
là:
A.
15 31
16 32
e .y x
. B.
32 31
e e e e
32.
y
x
. C.
15 31
16 32
e .y x
. D.
e e e e
2
y
x
.
Câu 9. (Xuân Trường - Nam Định - 2018) Tính đạo hàm của hàm số
sin 2 3
x
y x
A.
1
2cos 2 3
x
y x x
. B.
cos2 3
x
y x
.
C.
2cos 2 3 ln 3
x
y x
. D.
2cos 2 3 ln 3
x
y x
.
Câu 10. (THPT Thuận Thành - Bắc Ninh - 2018) Đạo hàm của hàm số
1
3
2 1
y x
là:
A.
2
3
1
2 1
3
y x
. B.
1
3
2 1 ln 2 1y x x
.
C.
4
3
2
2 1
3
y x
. D.
2
3
2
2 1
3
y x
.
Câu 11. (THPT Nghen - Hà Tĩnh - 2018) Đạo hàm của hàm số
.2
x
y x
là
A.
1 ln 2 2
x
y x
. B.
1 ln 2 2
x
y x
. C.
1 2
x
y x
. D.
2 1
2 2
x x
y x
.
Dạng 5. Khảo sát hàm số lũy thừa
Khảo sát hàm số lũy thừa
y x
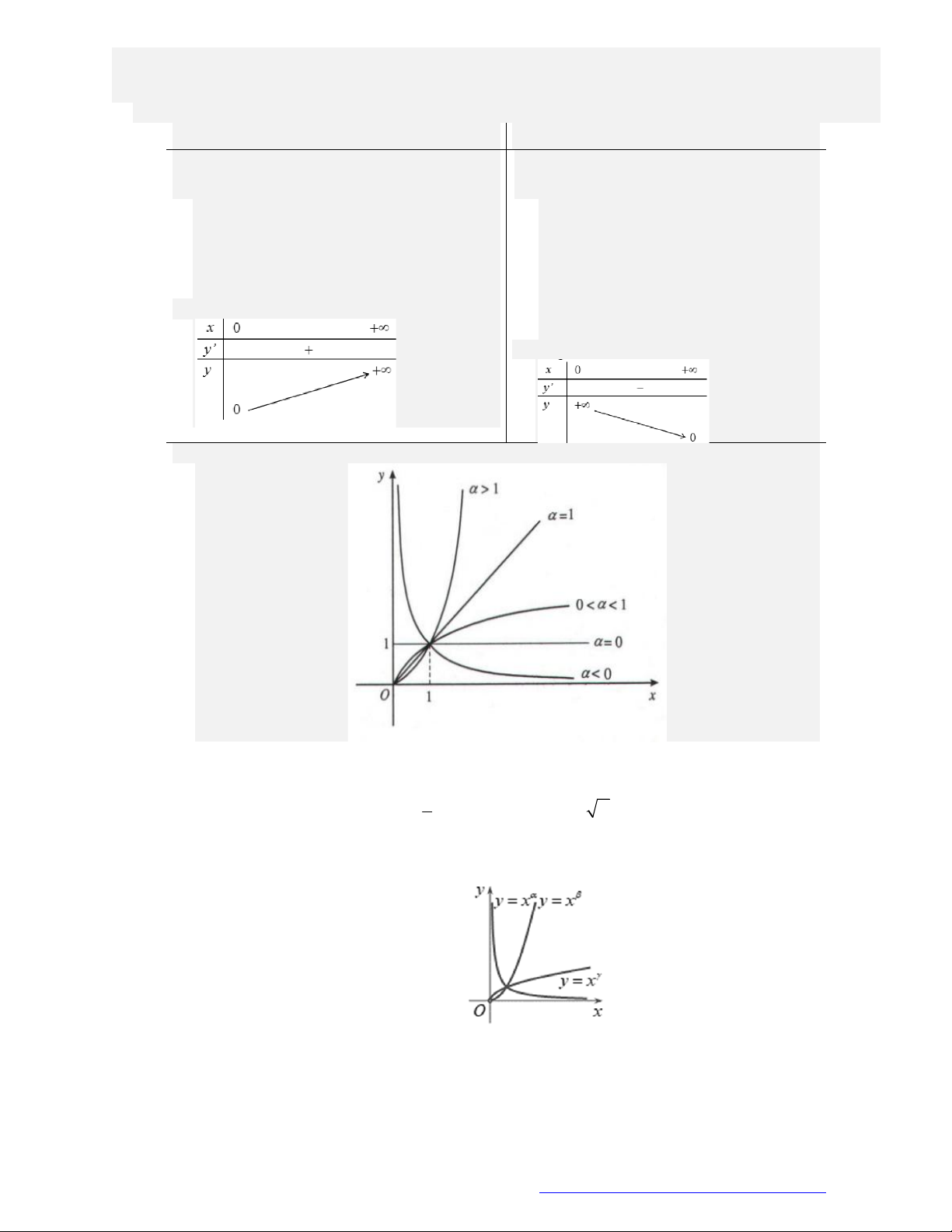
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Tập xác định của hàm số lũy thừa y x
luôn chứa khoảng
0;
với mọi
.
Trong trường hợp
tổng quát, ta khảo sát hàm số
y x
trên khoảng này.
, 0.y x
, 0.y x
1. Tập xác định:
0; .
2. Sự biến thiên
1
' . 0 0.y x x
Giới hạn đặc biệt:
0
lim 0, lim .
x
x
x x
Tiệm cận: không có.
3. Bảng biến thiên.
1. Tập xác định:
0; .
2. Sự biến thiên
1
' . 0 0.y x x
Giới hạn đặc biệt:
0
lim , lim 0.
x
x
x x
Tiệm cận:
Ox là tiệm cận ngang.
Oy là tiệm cận đứng.
3. Bảng biến thiên.
Đồ thị của hàm số.
Câu 1. (THPT Phan Chu Trinh - Đắc Lắc - 2018) Hàm số nào sau đây nghịch biến trên
?
A.
2
x
y
. B.
1
3
x
y
. C.
x
y
. D.
e
x
y
.
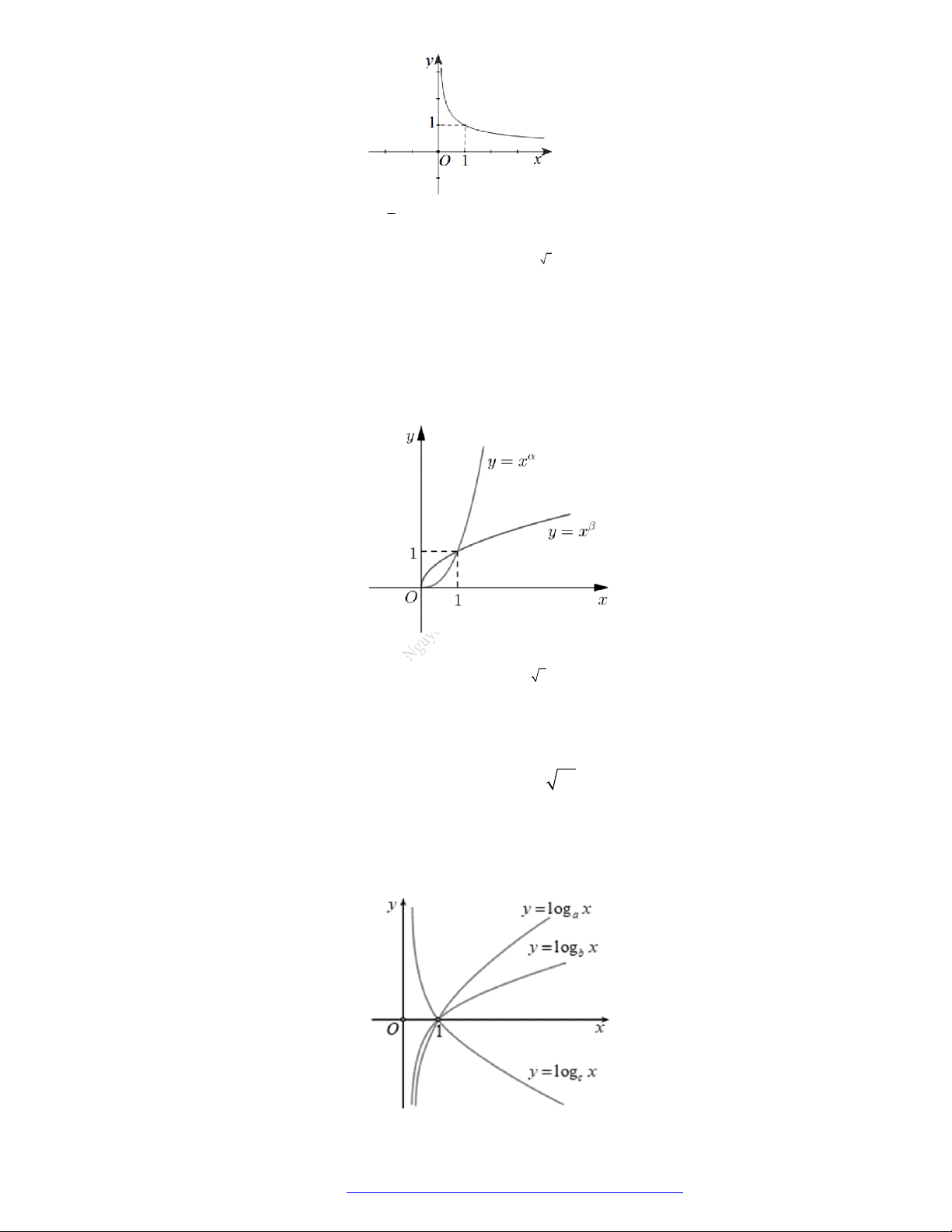
Câu 2. Cho các hàm số lũy thừa
y x ,
y x ,
y x có đồ thị như hình vẽ. Mệnh đề đúng là
A.
.
B.
.
C.
.
D.
.
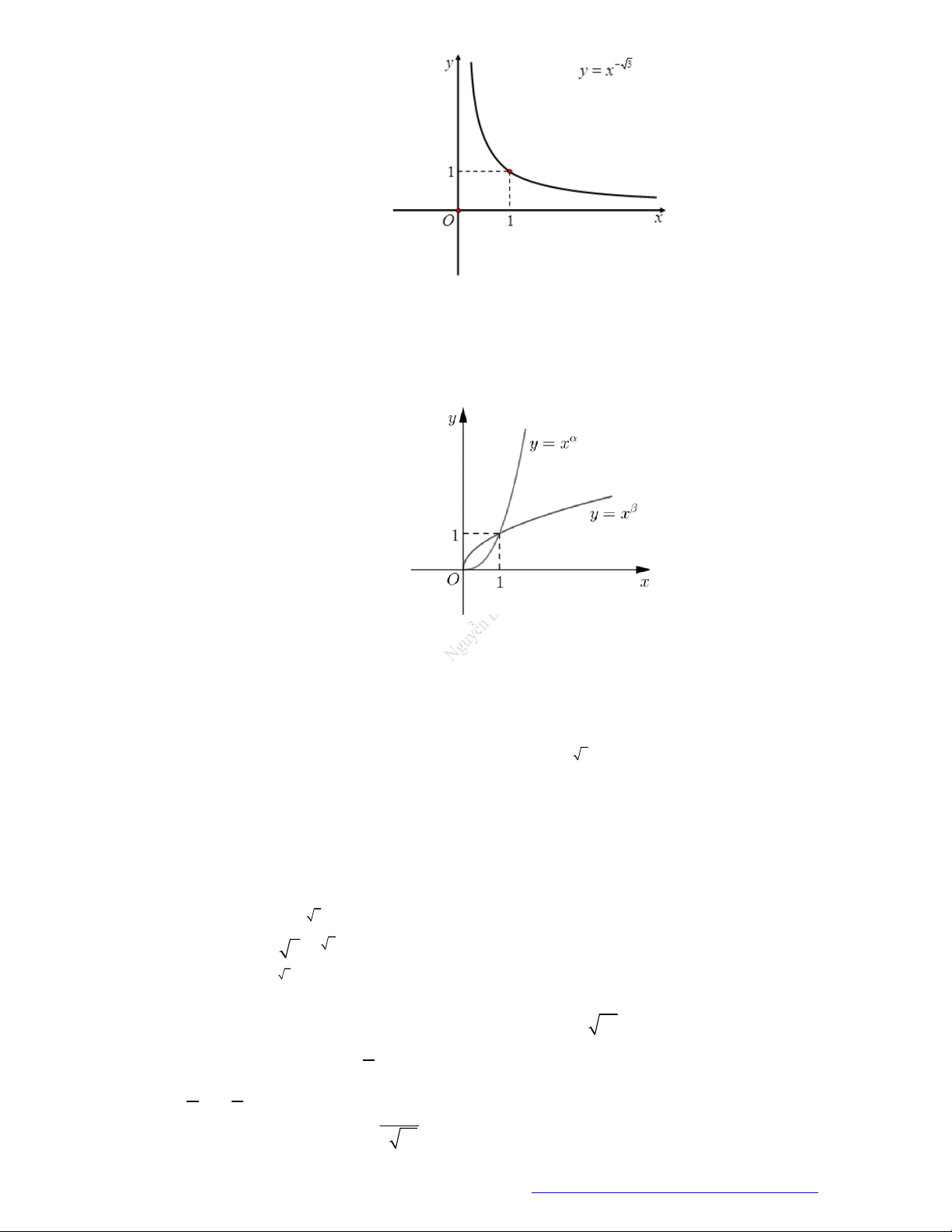
Câu 3. Đường cong ở hình vẽ dưới đây là đồ thị của hàm số nào dưới đây?
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
2 .
x
y
B.
1
2
.
y x
C.
1
.y x
D.
2
log 2y x
.
Câu 4. (THPT Quốc Oai - Hà Nội - 2017) Cho hàm số
3
y x
khẳng định nào sau đây đúng?
A. Đồ thị hàm số cắt trục
Ox
.
B. Đồ thị hàm số không có tiệm cận.
C. Đồ thị hàm số có một tiệm cận đứng và không có tiệm cận ngang.
D. Đồ thị hàm số có một tiệm cận đứng và một tiệm cận ngang.
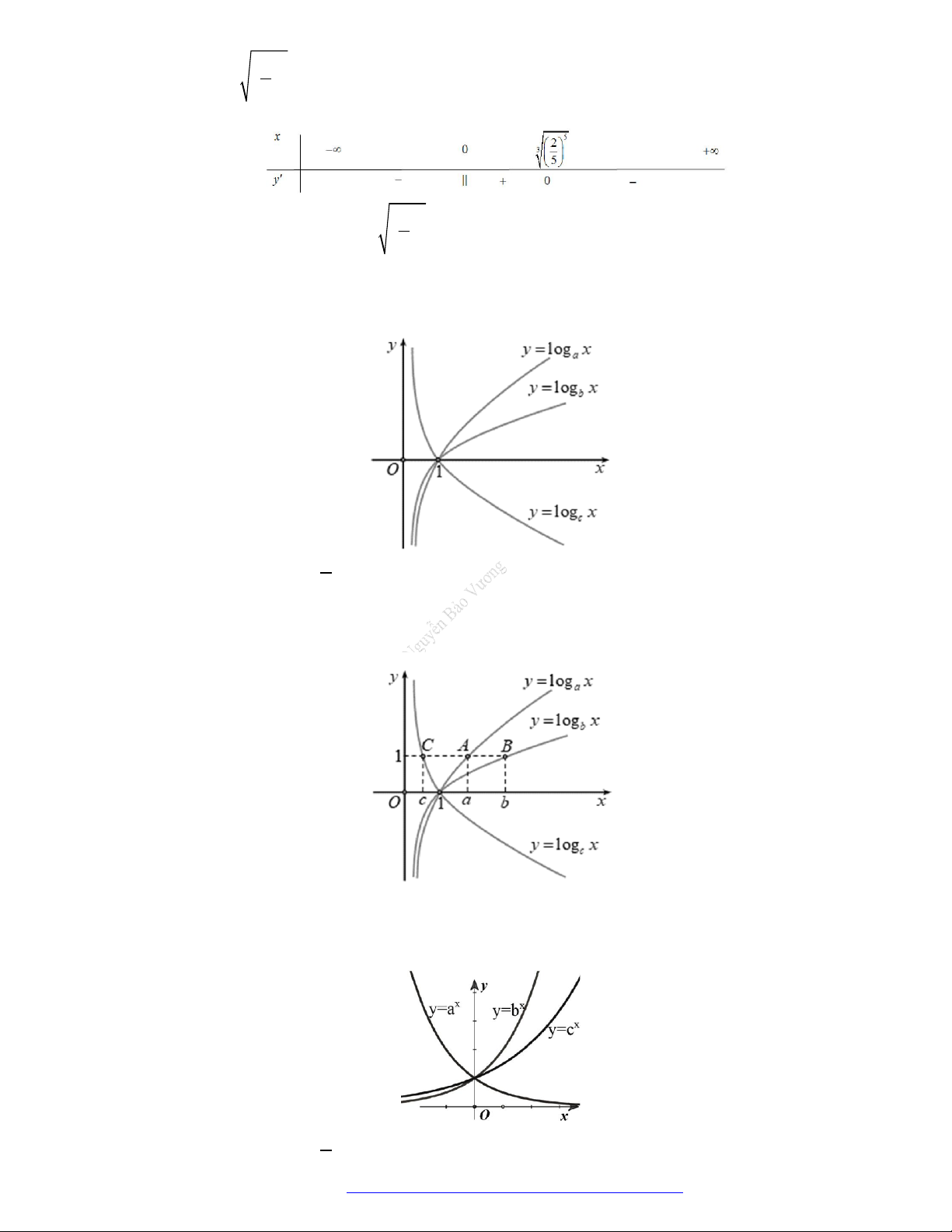
Câu 5. (Chuyên Vinh 2017) Cho là các số
,
là các số thực. Đồ thị các hàm số
, y x y x
trên
khoảng
0; +
được cho trong hình vẽ bên. Khẳng định nào sau đây là đúng?
.
A.
0 1
. B.
0 1
. C.
0 1
. D.
0 1
.
Câu 6. (THPT – THD Nam Dinh- 2017) Cho hàm số
2
y x
. Mệnh đề nào sau đây là sai?
A. Hàm số có tập xác định là
0;
. B. Đồ thị hàm số không có tiệm cận.
C. Hàm số nghịch biến trên khoảng
0;
. D. Đồ thị hàm số không cắt trục hoành.
Câu 7. (Chuyên Nguyễn Huệ 2019) Số cực trị của hàm số
25
y x x là
A.
1
. B.
2
. C.
3
. D.
0
.
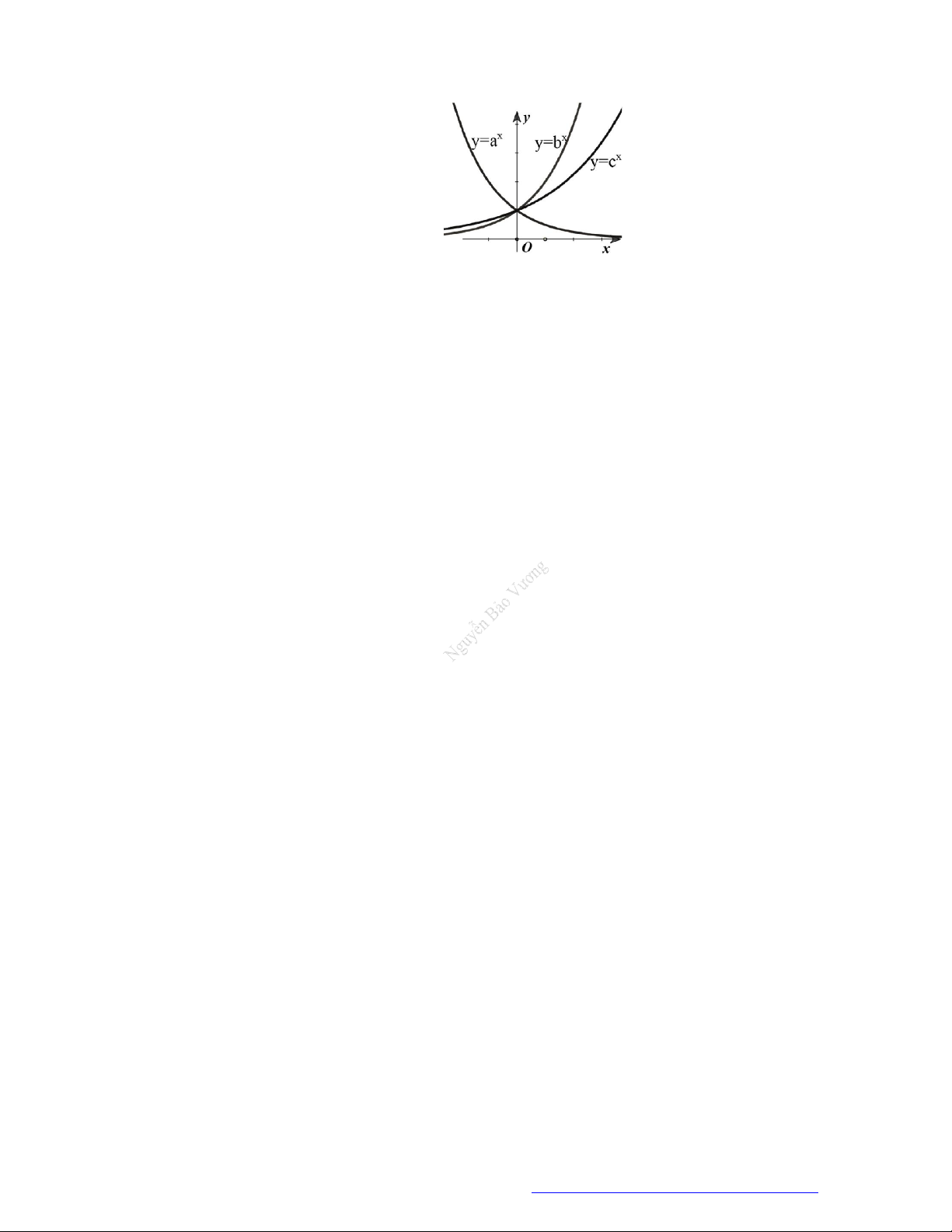
Câu 8. (THPT Lương Văn Tụy - Ninh Bình - 2018) Cho
a
,
b
,
c
là ba số dương khác
1
. Đồ thị các
hàm số log
a
y x , log
b
y x , log
c
y x được cho trong hình vẽ bên. Mệnh đề nào dưới đây là
mệnh đề đúng?
A.
a b c
. B.
c a b
. C.
c b a
. D.
b c a
.
T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu
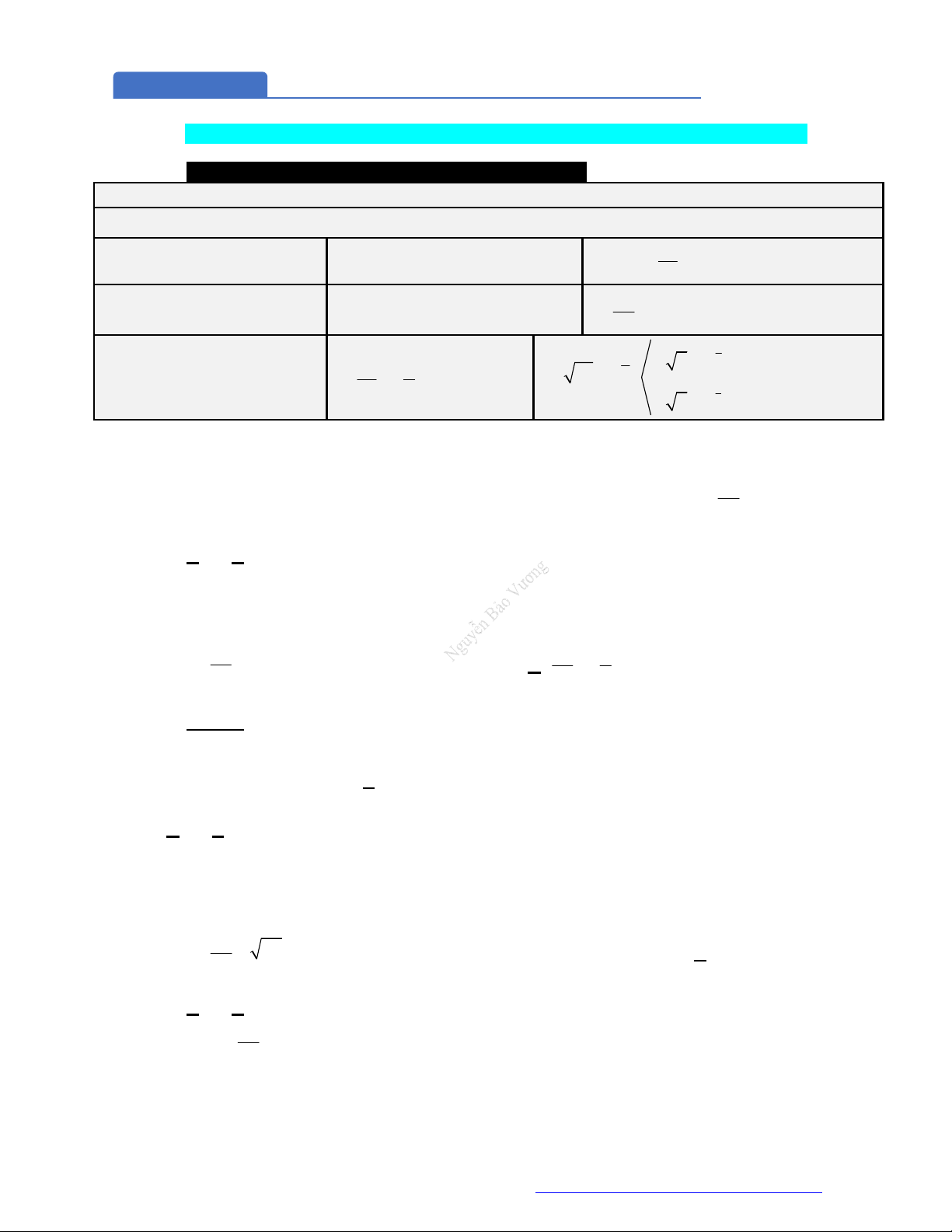
9. (THPT Nghen - Hà Tĩnh - 2018) Cho ba số thực dương
a
,
b
,
c
khá
c
1
.
Đồ thị các hàm số
x
y
a ,
x
y
b ,
x
y
c được cho trong hình vẽ dưới đây. Mệnh đề nào dưới đây đúng?
A.
1 a c b
. B.
1a c b
. C.
1a b c
. D.
1 a b c
.
Câu
10. (THPT Yên Lạc - 2018) Hàm số
2
2
e
x
y x nghịch biến trên khoảng nào?
A.
;
0
. B.
2
;0
. C.
1
;
. D.
1
;0
.
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM
Dạng 1. Rút gọn, biến đổi, tính toán biểu thức lũy thừa
Công thức lũy thừa
Cho các số dương
,a b
và
,m n
. Ta có:
0
1a
. ...........
n
n thöøa soá
a a a a
với
*
n
1
n
n
a
a
( ) ( )
m n mn n m
a a a
.
m n m n
a a a
m
m n
n
a
a
a
( )
n n n
a b ab
n
n
n
a a
b b
1
2
*
1
3
3
( , )
n
m n
m
a a
a a m n
a a
Câu 1. (Nhân Chính Hà Nội 2019) Cho
0, ,a m n
. Khẳng định nào sau đây đúng?
A.
.
m n m n
a a a
B.
. .
m n m n
a a a
C.
( ) ( ) .
m n n m
a a
D.
.
m
n m
n
a
a
a
Lời giải
Chọn C.
Tính chất lũy thừa
Câu 2. (THPT Minh Khai - 2019) Với
0a
,
0b
,
,
là các số thực bất kì, đẳng thức nào sau đây
sai?
A.
a
a
a
. B.
.a a a
. C.
a a
b b
. D.
.a b ab
.
Lời giải
Chọn C
Câu 3. (Sở Quảng Trị 2019) Cho
, 0x y
và
,
. Tìm đẳng thức sai dưới đây.
A.
.xy x y
. B.
x y x y
. C.
x x
. D.
.x x x
.
Lời giải
Chọn B
Theo tính chất của lũy thừa thì đẳng thức
x y x y
Sai.
Câu 4. (Nho Quan A - Ninh Bình - 2019) Cho các số thực
, , , , 0a b m n a b
. Khẳng định nào sau đây
là đúng?
A.
m
n m
n
a
a
a
. B.
n
m m n
a a
. C.
m
m m
a b a b
. D.
.
m n m n
a a a
.
Lời giải
Chọn D
Ta có:
m
m n
n
a
a
a
Loại A
.
n
m m n
a a
Loại B
2
2 2
1 1 1 1
Loại C
.
m n m n
a a a
Chọn D
LŨY THỪA - HÀM SỐ LŨY THỪA
Chuyên đề 16

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 5. (Cụm 8 Trường Chuyên 2019) Với
là số thực bất kì, mệnh đề nào sau đây sai?
A.
10 10
. B.
2
10 10
. C.
2
10 100
. D.
2
2
10 10
.
Lời giải
Theo định nghĩa và các tính chất của lũy thừa, ta thấy A, B, C là các mệnh đề đúng.
Xét mệnh đề D: với
1
, ta có:
2
2
1
1
10 100 10 10
nên mệnh đề D sai.
Câu 6. (Mã 105 2017) Rút gọn biểu thức
5
3
3
:Q b b
với
0b
.
A.
4
3
Q b
B.
4
3
Q b
C.
5
9
Q b
D.
2
Q b
Lời giải
Chọn B
5 5 1 4
3
3 3 3 3
: :
Q b b b b b
Câu 7. (Mã 110 2017) Rút gọn biểu thức
1
6
3
.P x x
với
0
x
.
A.
P x
B.
1
8
P x
C.
2
9
P x
D.
2
P x
Lời giải
Chọn A
Ta có:
1 1 1 1 1 1
6
3 3 6 3 6 2
. .
P x x x x x x x
Câu 8. (SGD Nam Định 2019) Cho
a
là số thực dương. Giá trị rút gọn của biểu thức
4
3
P a a
bằng
A.
7
3
a
. B.
5
6
a
. C.
11
6
a
. D.
10
3
a
.
Lời giải
Chọn C
Ta có:
4 4 4 1 11
1
3 3 3 2 6
2
.
P a a a a a a
.
Câu 9. (Mã 102 2017) Cho biểu thức
4
3
2 3
. .
P x x x
, với
0x
. Mệnh đề nào dưới đây đúng?
A.
2
3
P x
B.
1
2
P x
C.
13
24
P x
D.
1
4
P x
Lời giải
Chọn C
Ta có, với
0 :
x
7 13
3 7 13
4 4
3 3
4 4
4
3
2 3 2
6 6
2 2 24
. . . . . .
P x x x x x x x x x x x x
.
Câu 10. (THPT Lương Thế Vinh Hà Nội 2019) Cho biểu thức
1
1
6
3
2
. . x
P x x
với
0
x
. Mệnh đề nào
dưới đây đúng?
A.
P x
B.
11
6
P x
C.
7
6
P x
D.
5
6
P x
Lời giải
Chọn A
1 1 1 1
1
6
3 2 3 6
2
. . x
P x x x x
Câu 11. (THPT Lê Quy Đôn Điện Biên 2019) Rút gọn biểu thức
1
3
6
P x x
với
0
x
.
A.
1
8
P x
B.
P x
C.
2
9
P x
D.
2
P x
Lời giải
Chọn B
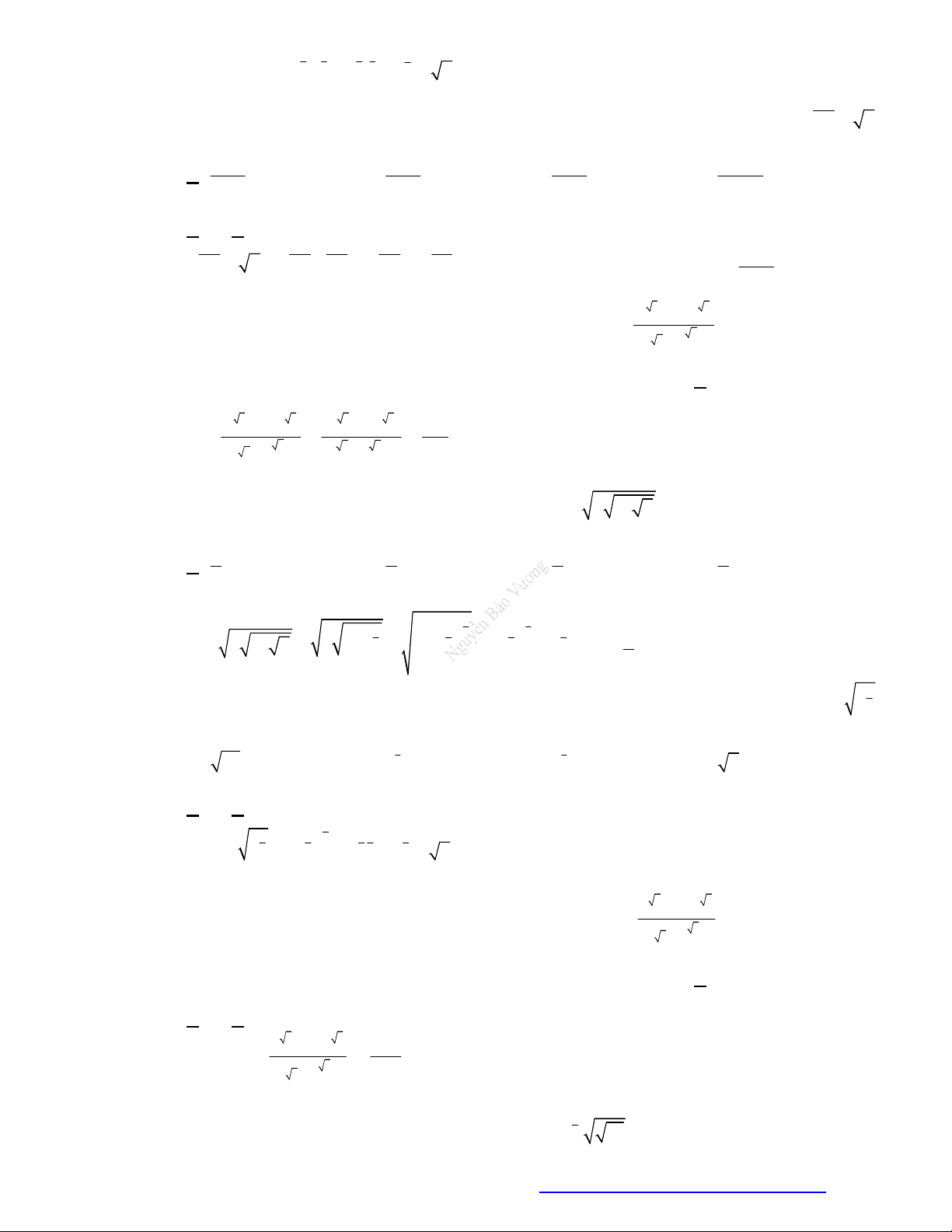
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Với
1 1 1 1
1
6 3 6 3 2
0; .
x P x x x x x
Câu 12. (THPT Sơn Tây Hà Nội 2019) Cho a là số thực dương. Viết và rút gọn biểu thức
3
2018
2018
.
a a
dưới dạng lũy thừa với số mũ hữu tỉ. Tìm số mũ của biểu thức rút gọn đó.
A.
2
1009
. B.
1
1009
. C.
3
1009
. D.
2
3
2018
.
Lời giải
Chọn A
3 3 1 4 2
2018
2018 2018 2018 2018 1009
. .
a a a a a a
. Vậy số mũ của biểu thức rút gọn bằng
2
1009
.
Câu 13. (Cụm Liên Trường Hải Phòng 2019) Rút gọn biểu thức
3 1 2 3
2 2
2 2
.a a
P
a
với
0
a
.
A.
P a
. B.
3
P a
. C.
4
P a
. D.
5
P a
.
Lời giải
3 1 2 3 3 1 2 3 3
5
2
2 2
2 2 2 2
2 2
.a a a a
P a
a
a
a
.
Câu 14. (THPT Yên Khánh - Ninh Bình 2019) Biểu thức
3
2
5
P x x x x
(với
0
x
), giá trị của
là
A.
1
2
. B.
5
2
. C.
9
2
. D.
3
2
.
Lời giải
1 1
1 5 3 1
5 3
3
5
3
2 25
2 2 2 2
3
1
. . .
2
P x x x x x x x x x x
Câu 15. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Cho
a
là số thực dương khác
1
. Khi đó
2
4
3
a
bằng
A.
3
2
a
. B.
8
3
a
. C.
3
8
a
. D.
6
a
.
Lời giải
Chọn D
Ta có:
1
2 2 2 1 1
4
.
4
6
3 3 3 4 6
a a a a a
Câu 16. (Cụm Liên Trường Hải Phòng 2019) Rút gọn biểu thức
3 1 2 3
2 2
2 2
.a a
P
a
với
0a
A.
P a
B.
3
P a
C.
4
P a
D.
5
P a
Lời giải
Chọn D
Ta có
3 1 2 3 3
5
2 4
2 2
2 2
.a a a
P a
a
a
Câu 17. (THPT Lương Tài Số 2 2019) Cho biểu thức
3
5
4
.
P x x
,
0
x
. Khẳng định nào sau đây là
đúng?
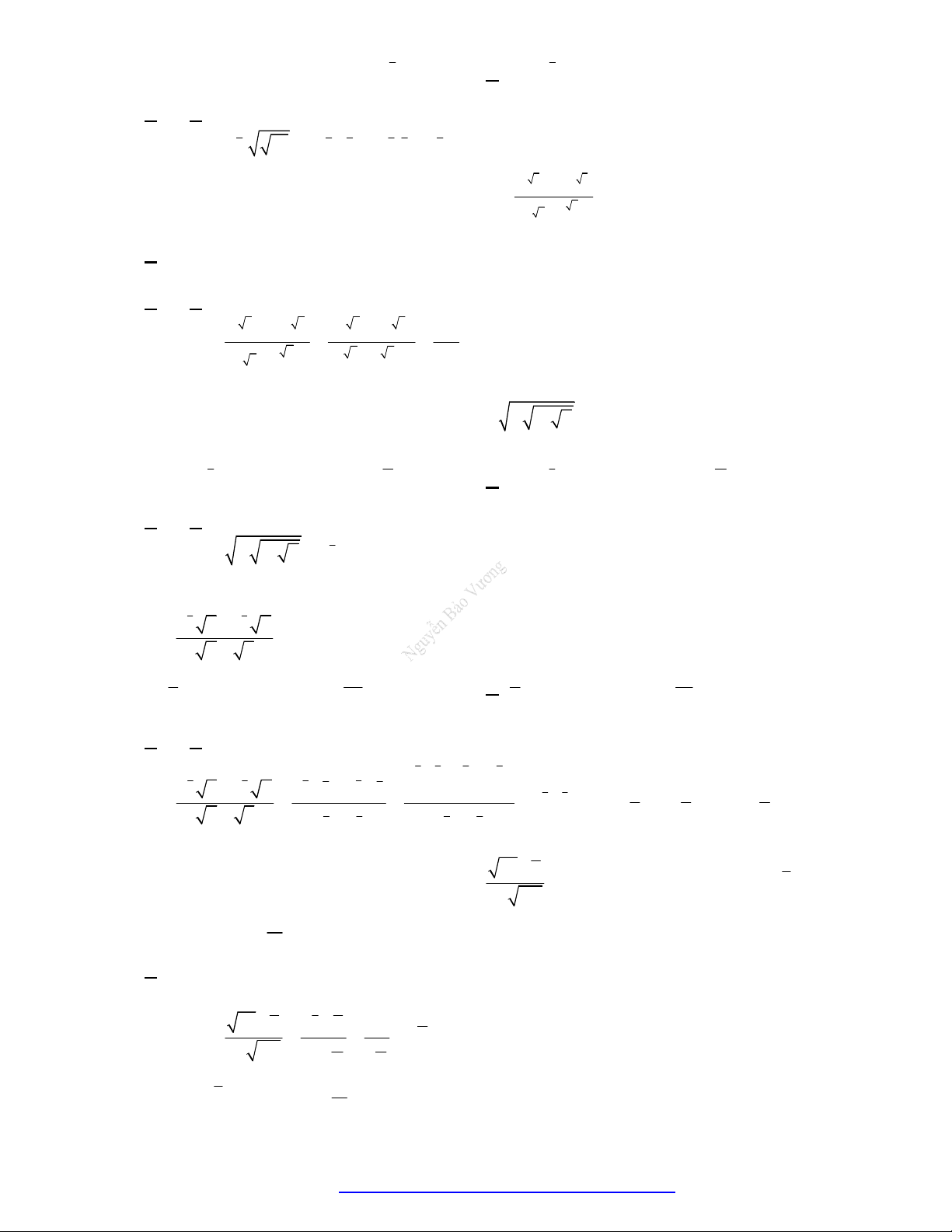
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
P x
B.
1
2
P x
C.
1
2
P x
D.
2
P x
Lời giải
Chọn C
Ta có
3
5
4
.
P x x
3 5 3 5 1
4 4 4 4 2
.
x x x x
.
Câu 18. (Bỉm Sơn - Thanh Hóa - 2019) Cho biểu thức
5 1 2 5
2 2
2 2
.a a
P
a
. Rút gọn
P
được kết quả:
A.
5
a
. B.
a
. C.
3
a
. D.
4
a
.
Lời giải
Chọn A
Ta có:
5 1 2 5 5 1 2 5 3
5
2
2 2
2 2 2 2
2 2
.a a a a
P a
a
a
a
.
Câu 19. (Chuyên Vĩnh Phúc 2019) Cho biểu thức
3
3
4
.
P x x x
, với
0.
x
Mệnh đề nào dưới đây
đúng?
A.
1
2
.P x
B.
7
12
.P x
C.
5
8
.P x
D.
7
24
.P x
Lời giải
Chọn C
Ta có:
5
3
3
4
8
.
P x x x x
Câu 20. (THPT Thiệu Hóa – Thanh Hóa 2019) Cho hai số thực dương
,a b
. Rút gọn biểu thức
1 1
3 3
6 6
a b b a
A
a b
ta thu được
.
m n
A a b
. Tích của
.m n
là
A.
1
8
B.
1
21
C.
1
9
D.
1
18
Lời giải
Chọn C
1 1 1 1
3 3 6 6
1 1 1 1
1 1
1 1
3 3 3 3
2 2
3 3
1 1 1 1
6 6
6 6 6 6
.
. .
.
a b b a
a b b a a b b a
A a b
a b
a b a b
1
3
m
,
1
3
n
1
.
9
m n
.
Câu 21. (Sở Quảng Ninh 2019) Rút gọn biểu thức
11
3 7
3
7
4 5
.
.
a a
A
a a
với
0
a
ta được kết quả
m
n
A a
trong
đó
,m n
*
N
và
m
n
là phân số tối giản. Khẳng định nào sau đây đúng?
A.
2 2
312
m n
. B.
2 2
543
m n
. C.
2 2
312
m n
. D.
2 2
409.
m n
Lời giải
Ta có:
11 7 11
19
3
7 6
3 3 3
7
5 23
74 5
4
7 7
. .
.
.
a a a a a
A a
a a
a a a
Mà
m
n
A a
,
,m n
*
N
và
m
n
là phân số tối giản
2 2
19, 7
312
m n
m n

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 22. (Sở Vĩnh Phúc 2019) Cho
a
là số thực dương. Đơn giản biểu thức
4 1 2
3 3 3
1 3 1
4 4 4
a a a
P
a a a
.
A.
1
P a a
. B.
1P a
. C.
P a
. D.
1P a
.
Lời giải
4 1 2
3 3 3
4 1 4 2
2
3 3 3 3
1 3 1 1
1 3 1
4 4 4 4
4 4 4
1
1 1
.
. .
a a a
a a
a a a a a a
P a
a a
a a a a
a a a
.
Câu 23. Cho
, a b
là các số thực dương. Rút gọn
4 4
3 3
3 3
a b ab
P
a b
ta được
A.
P ab
. B.
P a b
. C.
4 4
P a b ab
. D.
P ab a b
.
Lời giải
1 1
3 3
4 4 1 1
3 3 3 3
1 1 1 1
3 3
3 3 3 3
. .
.
ab a b
a b ab a a b ab b
P ab
a b
a b a b
Câu 24. (KTNL GV Thpt Lý Thái Tổ 2019) Cho biểu thức
5
3
8 2 2 2
m
n
, trong đó
m
n
là phân số tối
giản. Gọi
2 2
P m n
. Khẳng định nào sau đây đúng?
A.
330;340
P
. B.
350;360
P
. C.
260;370
P
. D.
340;350
P
.
Lời giải
Chọn D
Ta có
3 1 1 3 1 1 11
5 5
3
3 3
5 10 30 5 10 30 15
8 2 2 2 2 2 2 .2 .2 2 2
2 2 2 2
11
11
11 15 346
15
15
m
m
P m n
n
n
.
Câu 25. (Sở Bắc Ninh 2019) Cho
0
a
,
0
b
, giá trị của biểu thức
1
2
2
1
1
2
1
2 . . 1
4
a b
T a b ab
b a
bằng
A.
1
. B.
1
2
. C.
2
3
. D.
1
3
.
Lời giải
Cách 2:
Ta có
1
2
2
1
1
2
1
2 . . 1
4
a b
T a b ab
b a
1
2
2
1
1
2
1
2 . . 1
4
a b
a b ab
ab
1
2
2
1
1
2
2 . . 1
4
a b
a b ab
ab

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
1
2
2
1
1
2
2 . .
4
a b
a b ab
ab
1
2
1
2
1
2 . . 1
2
a b
ab
a b
ab
.
Câu 26. (Đề Tham Khảo 2017) Tính giá trị của biểu thức
2017 2016
7 4 3 4 3 7P
A.
2016
7 4 3P
B.
1P
C.
7 4 3
P
D.
7 4 3
P
Lời giải
Chọn D
2016
2017 2016
2016
7 4 3 4 3 7 7 4 3 . 7 4 3 4 3 7
7 4 3 1 7 4 3.
P
Câu 27. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho biểu thức
3
3
2 2 2
3 3 3
P
. Mệnh đề nào trong các
mệnh đề sau là đúng?
A.
1
8
2
3
P
. B.
18
2
3
P
. C.
1
18
2
3
P
. D.
1
2
2
3
P
.
Lời giải
Cách 1:
Ta có:
3
3
2 2 2
3 3 3
P
3
2
3
3
2 2
3 3
3 1 3 1
. 1
2 3 2 2
3 3
2 2 2
3 3 3
.
Câu 28. (THPT An Lão Hải Phòng 2019) Cho hàm số
1
3 4
3
3
1
8 8
3 1
8
a a a
f a
a a a
với
0, 1
a a
. Tính
giá trị
2016
2017M f
A.
1008
2017 1
M
B.
1008
2017 1
M
C.
2016
2017 1
M
D.
2016
1 2017
M
Lời giải
Chọn B
1
3 4
3
3
1
8 83 1
8
1
1
1
a a a
a
f a a
a
a a a
nên
2016 2016 1008
2017 1 2017 1 2017
M f
Câu 29. (THPT Trần Phú 2019) Giá trị của biểu thức
3 1 3 4
0
3 2
2 .2 5 .5
10 :10 0,1
P
là
A.
9
. B.
10
. C.
10
. D.
9
.
Lời giải
Chọn B
Ta có
3 1 3 4 3 1 3 4
0
3 2 1
3 2
2 .2 5 .5 2 5 4 5 9
10.
1
10 1 10 1
10 :10 0,1
1
10
P
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 30. (THPT Ngô Quyền – 2017) Cho hàm số
2
3 2
3
3
1
8 8
3 1
8
a a a
f a
a a a
với
0, 1
a a
. Tính giá trị
2018
2017M f
.
A.
2018
2017 1.
B.
1009
2017 1.
C.
1009
2017 .
D.
1009
2017 1.
Lời giải
Chọn B
Ta có
2 2 1
3 3 3
1
2
1
1 3 1
2
8 8 8
1
1
1
a a a
a
f a a
a
a a a
.
Do đó
1
2018 2018 1009
2
2017 1 2017 1 2017
M f
.
Câu 31. Cho biểu thức
5
12
3
4
f x x x x
. Khi đó, giá trị của
2,7
f
bằng
A.
0,027
. B.
27
. C.
2,7
. D.
0, 27
.
Lời giải
Chọn C.
5
12
3 4
2,7 2,7. 2,7. 2,7 2,7
f x
.
Câu 32. Tính giá trị biểu thức
2018 2017
2019
4 2 3 . 1 3
1 3
P
.
A.
2017
2P
. B.
1
. C.
2019
2
. D.
2018
2
.
Lời giải
Chọn A
Ta có:
2.2018 2017
2017
2017
2019
1 3 . 1 3
1 3 1 3 2
1 3
P
.
Câu 33. (Chuyên Nguyễn Du-ĐăkLăk 2019) Giá trị biểu thức
2018 2019
3 2 2 . 2 1
bằng
A.
2019
2 1
. B.
2017
2 1
. C.
2019
2 1
. D.
2017
2 1
.
Lời giải
Chọn D
Ta có
2018 2019
3 2 2 . 2 1
2018
2 2019
2 1 . 2 1
2018 2018 2018
2 1 . 2 1 . 2 1 . 2 1
=
2019
2017
2 1 . 2 1 2 1
2017
2 1
.
Câu 34. Cho
0, 0
a b
giá trị của biểu thức
1
2
1
1
2
2
1
1
4
2
a b
b
T a b b
a
a
bằng
A.
1
. B.
1
3
. C.
2
3
. D.
1
2
.
Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn A
Ta có
1
1
2
1 1
2
1 1
2 2
1
1
2 2
1 1 1
2
2
1 1 1
2 2
1
2
2
2
1
2 2 1 2
4
1 2
2 2 2 1.
4 4 2
1
1
4
2
4
a b
T a b ab a b ab
b a
a b
a b a b ab
a b ab a b
a b
b
ab a b ab
b a
a
a b
ab
Dạng 2. So sánh các biểu thức chứa lũy thừa
Nếu
1
a
thì a a
;
Nếu
0 1a
thì a a
.
Với mọi
0
a b
, ta có:
0
m m
a b m
0
m m
a b m
Câu 1. (Bạc Liêu – Ninh Bình 2019) Cho
2 1 2 1
m n
. Khi đó
A.
m n
. B.
m n
. C.
m n
. D.
m n
.
Lời giải
Chọn C
Do
0 2 1 1
nên
2 1 2 1
m n
m n
.
Câu 2. Cho
1
a
. Mệnh đề nào sau đây là đúng?
A.
3
5
1
.
a
a
B.
1
3
.a a
C.
3
2
1.
a
a
D.
2016 2017
1 1
a a
.
Lời giải
Chọn A
Vì
1; 3 5
a
3 5 3
5
1
.
a a a
a
Câu 3. (THPT Yên Phong Số 1 Bắc Ninh 2019) Trong các mệnh đề sau, mệnh đề nào SAI?
A.
2018 2017
3 1 3 1
. B.
3
2 1
2 2
.
C.
2017 2018
2 1 2 1
. D.
2019 2018
2 2
1 1
2 2
.
Lời giải
Chọn A
A.
2018 2017
3 1 3 1
. Cùng cơ số,
0 3 1 1
, hàm nghịch biến, số mũ lớn hơn nên bé
hơn. Sai
B.
3
2 1
2 2
. Cùng cơ số,
2 1
, hàm đồng biến, số mũ
2 2
2 1 3 2 2 3 3
nên lớn
hơn. Đúng
C.
2017 2018
2 1 2 1
. Cùng cơ số,
0 2 1 1
, hàm nghịch biến, số mũ bé hơn nên lớn
hơn. Đúng.
D.
2019 2018
2 2
1 1
2 2
. Cùng cơ số,
2
0 1 1
2
, hàm nghịch biến, số mũ lớn hơn nên
bé hơn. Đúng

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 4. (THPT Sơn Tây Hà Nội 2019) Khẳng định nào sau đây đúng?
A.
2017 2018
( 5 2) ( 5 2)
. B.
2018 2019
( 5 2) ( 5 2)
.
C.
2018 2019
( 5 2) ( 5 2)
. D.
2018 2019
( 5 2) ( 5 2)
.
Lời giải
Chọn C
2018 2019
0 5 2 1
( 5 2) ( 5 2)
2018 2019
C
đúng.
2017 2018
5 2 1
( 5 2) ( 5 2)
2017 2018
A
sai
2018 2019
5 2 1
( 5 2) ( 5 2)
2018 2019
B
sai
2018 2019
0 5 2 1
( 5 2) ( 5 2)
2018 2019
D
sai.
Câu 5. (THPT Lê Quý Đôn Đà Nẵng 2019) Khẳng định nào dưới đây là đúng?
A.
3 3
3 5
.
7 8
B.
1 1
2 3
. C.
2
2
1
3
5
. D.
50
100
1
2
4
.
Lời giải
Ta có:
3 3
3 5 3 5
7 8 7 8
(vì
3 0
). Phương án A Sai.
1 1 1 1
2 3 2 3
(vì
0
). Phương án B Đúng.
2
2 2 2
1
3 5 3 5 3
5
(vì
2 0
). Phương án C Sai.
50
100
50
100
2 100 100
1
2 2 2 2 2
4
( Mệnh đề sai ). Phương án D Sai.
Câu 6. (Nam Định - 2018) Trong các khẳng định sau, khẳng định nào sai?
A.
2018 2017
2 2
1 1
2 2
. B.
2017 2018
2 1 2 1
.
C.
2018 2017
3 1 3 1
. D.
2 1 3
2 2
.
Hướng dẫn giải
Chọn C
+)
0 2 1 1
2017 2018
2017 2018
2 1 2 1
nên A đúng.
+)
0 3 1 1
2018 2017
2018 2017
3 1 3 1
nên B sai.
+)
2 1
2 1 3
2 1 3
2 2
nên C đúng.
+)
2
0 1 1
2
2018 2017
2018 2017
2 2
1 1
2 2
nên D đúng.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 7. (THPT Tiên Lãng 2018) Tìm tập tất cả các giá trị của
a
để
7
5 2
21
a a
?
A.
0
a
.
B.
0 1a
.
C.
1
a
. D.
5 2
21 7
a
.
Lời giải
Chọn B
7
2 6
21
a a
.
Ta có
7
5 2 5 6
21 21 21
a a a a
mà
5 6
vậy
0 1a
.
Câu 8. So sánh ba số:
0,3 3,2
0,2 , 0,7
và
0,3
3
.
A.
0,3
3,2 0,3
0,7 0,2 3
. B.
0,3
0,3 3,2
0,2 0,7 3
.
C.
0,3
0,3 3,2
3 0,2 0,7
. D.
0,3
0,3 3,2
0,2 3 0,7
.
Lời giải
Chọn D
Ta có
0,3
0,3
0,2 3 0,2 3
nên loại đáp án
Câu 9. (THPT Cộng Hiền 2019) Cho
, 0
a b
thỏa mãn
1 2
1 3
3 3
2 4
,
a a b b
. Khi đó khẳng định nào
đúng?
A.
0 1,0 1
a b
. B.
0 1, 1a b
. C.
1, 0 1a b
. D.
1, 1
a b
.
Lời giải
Chọn C
Ta có
1
1
32
2
3
3
4
1 1 1
ln ln ln 0 1
2 3 6
2 3 1
ln ln 0 ln 0 1
3 4 12
a a a a a a
b b b b b b
Lưu ý: Ta có thể sử dụng máy tính Casio để thử các đáp án bằng cách cho
,a b
các giá trị cụ thể.
Câu 10. So sánh ba số
64
1001 2
1000 , 2
a b
và
1 2 3 1000
1 2 3 ... 1000c
?
A.
c a b
. B.
b a c
. C.
c b a
. D.
a c b
.
Lời giải
Chọn A
Ta có:
1 1000 2 1000 999 1000
1 1000 ; 2 1000 ...999 1000
1 2 3 1000 1000
1 2 3 ... 1000 1000.1000
c c a
Mặt khác:
10
2 1000
64
4
6
64 10 10 6 2 1001
2
2 .ln2 . 2 .ln2 1000 .ln1000 1001.ln1000 2 1000
10
a b
Vậy
.c a b
Dạng 3. Tìm tập xác định của hàm số lũy thừa
Dạng:
y x
y u
với
u
là đa thức đại số.
Tập xác định:
Nếu
.
ÑK
u
Nếu
0.
0
ÑK
u

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Nếu
0.
ÑK
u
Câu 1. (Mã 123 2017) Tập xác định D của hàm số
1
3
1
y x
là:.
A.
1;D
B.
D
C.
\ 1
D
D.
;1
D
Lời giải
Chọn A
Hàm số xác định khi
1 0 1x x
. Vậy
1;D
.
Câu 2. (Mã 104 2017) Tìm tập xác định
D
của hàm số
3
2
2
y x x
.
A.
; 1 2;D
B.
\ 1;2
D
C.
D
D.
0;D
Lời giải
Chọn B
Vì
3
nên hàm số xác định khi
2
2 0 1; 2
x x x x
. Vậy
\ 1;2
D
.
Câu 3. (Chuyên Bắc Giang 2019) Tập xác định của hàm số
1
5
1
y x
là
A.
1;
B.
\ 1
C.
1;
D.
0;
Lời giải
Chọn C
Vì
1
5
nên hàm số xác định khi và chỉ khi
1 0 1x x
Vậy tập xác định của hàm số
1;D
Câu 4. Tìm tập xác định
D
của hàm số
4
2
3
y x x
.
A.
0;3
. B.
\ 0;3
D
.
C.
;0 3;D
. D.
D R
Lời giải
Chọn B
Hàm số
2
2
3
y x x
xác định khi
2
3 0
x x
0
3
x
x
.
Vậy tập xác định của hàm số là
\ 0;3
D
.
Câu 5. (KSCL THPT Nguyễn Khuyến 2019) Tìm tập xác định của hàm số:
2
2
3
4
y x
là
A.
2;2
D
B.
\ 2; 2
D R
C.
D R
D.
2;D
Lời giải
Chọn A
Điều kiện:
2
4 0
x
2;2
x
. Vậy TXĐ:
2;2
D
.
Câu 6. (Thpt Lương Tài Số 2 2019) Trong các hàm số sau đây, hàm số nào có tập xác định
D
?
A.
2
y x
B.
2
1
2y
x
C.
2
2
y x
D.
2
y x
Lời giải
Chọn C
Đáp án A: Điều kiện
0
x
. Tập xác định
0;D
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đáp án B: Điều kiện
0
x
. Tập xác định
\ 0
D
.
Đáp án C: Điều kiện
2
2 0
x
(luôn đúng). Tập xác định
D
.
Đáp án D: Điều kiện
2 0 2
x x
. Tập xác định
2;D
.
Câu 7. (Chuyên Vĩnh Phúc 2019) Tìm tập xác định
D
của hàm số
1
2
3
3 1
y x
.
A.
1 1
; ;
3 3
D
B.
D
C.
1
\
3
D
D.
1 1
; ;
3 3
D
Lời giải
Chọn A
Điều kiện xác định:
2
1
3
3 1 0
1
3
x
x
x
Tập xác định
1 1
; ;
3 3
D
Câu 8. (THPT An Lão Hải Phòng 2019) Hàm số nào dưới đây đồng biến trên tập xác định của nó?
A.
1
π
x
y
B.
2
3
x
y
C.
3
x
y
D.
0,5
x
y
Lời giải
Chọn C
Hàm số
x
y a
đồng biến trên
khi và chỉ khi
1
a
.
Thấy các số
1 2
; ; 0,5
π 3
nhỏ hơn
1
, còn
3
lớn hơn 1 nên chọn
.C
Câu 9. (THPT An Lão Hải Phòng 2019) Tìm tập xác định
D
của hàm số
2
2
2 3
y x x
.
A.
D
B.
; 3 1;D
C.
0;D
D.
\ 3;1
D
Lời giải
Chọn B
Hàm số xác định khi
2
1
2 3 0
3
x
x x
x
.
Vậy
; 3 1;D
.
Câu 10. (Chuyên KHTN 2019) Tập xác định của hàm số
1
2
1
y x
là
A.
0;
. B.
1;
. C.
1;
. D.
;
.
Lời giải
Điều kiện để hàm số xác định:
1 0 1x x
.
Tập xác định:
1;D
.
Câu 11. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Tập xác định của hàm số
2019
2
2020
4 y x x
là
A.
4 )
;0 ;( ] [
B.
4 )
;0 ;( ) (
C.
0;4
D.
\ 0;4
Lời giải
Điều kiện
2
0
4 0 .
4
x
x x
x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 12.
(THPT Gang Thép Thái Nguyên 2019) Tập xác định của hàm số
2 2
( 6 8)
y x x
là
A.
(2;4)
D
. B.
;2
. C.
4;
. D.
D
.
Lời giải
Hàm số xác định khi và chỉ khi:
2
6 8 0 2 4
x x x
.
Vậy tập xác định của hàm số là
2;4
D
.
Câu 13. (KTNL GV THPT Lý Thái Tổ 2019) Tìm tập xác định của hàm số
3
2
7 10
y x x
A.
\ 2;5
. B.
;2 5;
. C.
. D.
2;5
.
Lời giải
Chọn A
ĐKXĐ:
2
2
7 10 0
5
x
x x
x
.
Vậy TXĐ:
\ 2;5
D
.
Câu 14. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Tìm tập xác định
D
của hàm số
3
2
4 1
y x
.
A.
1 1
\ ;
2 2
D
. B.
1 1
; ;
2 2
D
.
C.
D
. D.
1 1
;
2 2
D
.
Lời giải
Điều kiện xác định của hàm số là
2
4 1 0
x
1
2
x
.
Câu 15. (Hsg Tỉnh Bắc Ninh 2019) Tập xác định của hàm số
2019
2
4 3y x x
là
A.
\ 4;1 .
B.
.
C.
4;1 .
D.
4;1 .
Lờigiải
Vì
2019
2
4 3y x x
là hàm số lũy thừa có số mũ nguyên âm nên điều kiện xác định là
2
1
4 3 0 .
4
x
x x
x
Vậy tập xác định của hàm số là
\ 4;1 .
D
Câu 16. (Chuyên Lê Quý Đôn Điện Biên 2019) Tìm tập xác định của
1
2
3
3x 2
y x
A.
;1 2;
. B.
\ 1;2
. C.
2
2
2 ln 5
x
y
x
. D.
.
Lời giải
Vì
1
3
không nguyên nên
1
2
3
3x 2
y x
xác định khi
2
3x 2 0
x
;1 2;x
.
Câu 17. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Tập xác định của hàm số
2
3 2
y x x
là
A.
1;2 .
. B.
;1 2;
. C.
\ 1;2
. D.
;1 2;
Lời giải
Chọn B
Hàm số
2
3 2
y x x
xác định
2
3 2 0
x x
1
2
x
x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tập xác định
;1 2;D
Câu 18. (Sở Bắc Ninh 2019) Tìm tập xác định
D
của hàm số
2 3
2
3 4
y x x
.
A.
\ 1;4
D
. B.
; 1 4;
D
.
C.
D
. D.
; 1 4;
D
.
Lời giải
Hàm số xác định khi
2
3 4 0
x x
1
4
x
x
.
Vậy tập xác định
D
của hàm số là:
; 1 4;
D
.
Câu 19. (Gia Lai 2019) Tìm tập xác định
D
của hàm số
2
2
6 9
y x x
.
A.
\ 0
D
. B.
3;D
. C.
\ 3
D
. D.
D
.
Lời giải
Chọn C
Do
2
nên ta có điều kiện:
2
2
6 9 0 3 0 3
x x x x
Vậy tập xác định của hàm số là
\ 3
D
Câu 20. (chuyên Hà Tĩnh 2019)Tìm tập xác định của hàm số
1
2
3
3 2
y x x
là
A.
\ 1;2
. B.
;1 2;
.
C.
1;2
. D.
.
Lời giải
Chọn B
Điều kiện xác định là
2
3 2 0 ;1 2;x x x
.
Vậy tập xác định của hàm số là
;1 2;D
.
Câu 21. (Chu Văn An - Hà Nội - 2019) Tập xác định
D
của hàm số
3
2
27
y x
là
A.
D 3;
. B.
D 3;
. C.
D \ 3
. D.
D
.
Lời giải
Chọn A
Điều kiện xác định của hàm số:
3
27 0 3
x x
.
Do đó tập xác định của hàm số là
D 3;
.
Câu 22. (Bắc Ninh 2019) Tập xác định của hàm số
3
2
2
5
3 2 3
y x x x
là
A.
; \ 3
D
B.
;1 2; \ 3
D
.
C.
; \ 1;2
D
. D.
;1 2;D
.
Lời giải
Chọn B
Hàm số đã cho xác định khi
2
1
3 2 0
2
3 0
3
x
x x
x
x
x
Vậy tập xác định của hàm số là
;1 2; \ 3
D
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Dạng 4. Đạo hàm hàm số lũy thừa
Đạo hàm:
1
1
.
y x y x
y u y u u
Câu 1. (Sở Quảng Trị 2019) Tìm đạo hàm của hàm số:
3
2
2
( 1)
y x
A.
1
2
3
(2 )
2
x
B.
1
4
3
4
x
C.
1
2
2
3 ( 1)
x x
D.
1
2
2
3
( 1)
2
x
Lời giải
Chọn C
Áp dụng công thức đạo hàm hợp hàm số lũy thừa :
'
'
1
( ) . . ( )u x u u x
Ta có :
'
3 1 1
2 2 2
2 2 2
3
' ( 1) .2x.( 1) 3x.( 1)
2
y x x x
Câu 2. (Kiểm tra năng lực - ĐH - Quốc Tế - 2019) Đạo hàm của hàm số
2
2
3
3
y x
tại
1x
là
A.
3
4
3
. B.
3
2 4
3
. C.
3
2
3
. D. 3 lựa chọn kia đều sai.
Lời giải
Chọn B
Ta có
2
2
3
3
y x
.
1 1 1
2 2 2 2
3 3 3
2 2 4
3 3 3 2 3
3 3 3
x
y x x x x x
.
1
3
3
3
4 4 2 4
1 .2
3 3
3. 2
y
.
Vậy
3
2 4
1
3
y
.
Câu 3. (THPT Lý Nhân Tông – 2017) Hàm số
2
2
5
1
y x
có đạo hàm là.
A.
3
2
5
4
5 1
x
y
x
. B.
2
2 1
y x x
. C.
5 2
4 1
y x x
. D.
2
2
5
4
1
y
x
.
Lời giải
Chọn A
Vì Áp dụng công thức
1
. .
n n
u n u u
.
Câu 4. (THPT Nguyễn Đăng Đạo – 2017) Đạo hàm của hàm số
1
3
2 1
y x
trên tập xác định là.
A.
4
3
1
2 1
3
x
. B.
1
3
2 2 1 ln 2 1
x x
.
C.
1
3
2 1 ln 2 1
x x
. D.
4
3
2
2 1
3
x
.
Lời giải
Chọn D
Ta có:
1 1 4
1
3 3 3
1 2
2 1 2 1 2 1 2 1
3 3
y x x x x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 5. (Chuyên Vinh 2018) Đạo hàm của hàm số
1
2
3
1
y x x
là
A.
8
2
3
1
1
3
y x x
. B.
3 2
2 1
2 1
x
y
x x
.C.
2
2
3
2 1
3 1
x
y
x x
. D.
2
2
3
1
1
3
y x x
.
Lời giải
Chọn C
Ta có
1
1
2 2
3
2
2
3
1 2 1
1 1
3
3 1
x
y x x x x
x x
.
Câu 6. (THPT Chuyen LHP Nam Dinh – 2017) Tính đạo hàm của hàm số
6
1 cos3y x
.
A.
5
' 6sin3 1 cos3y x x
. B.
5
' 6sin3 cos3 1
y x x
.
C.
5
' 18sin3 cos3 1
y x x
. D.
5
' 18sin3 1 cos3y x x
.
Lời giải
Chọn D
Ta có
6 5
1 cos3 6 1 cos3 . 1 cos3 'y x y x x
.
5 5
6 1 cos 3 .3sin 3 18sin 3 1 cos3x x x x
.
Câu 7. (THPT Chuyên LHP – 2017) Tìm đạo hàm của hàm số
2
2
1
e
y x
trên
.
A.
1
2
2
2 1
e
y x x
. B.
2
2
1
e
y ex x
.
C.
1
2
2
1
2
e
e
y x
. D.
2 2
2
1 ln 1
e
y x x
.
Lời giải
Chọn B
Ta có:
1 1 2
2 2 2 2
2 2 2
1 .2 1 1 1
2
e e e
e
e
y x x x ex x ex x
.
Câu 8. (THPT Tứ Kỳ - Hải Dương - 2018) Cho hàm số
e e e e
y x
,
0
x
. Đạo hàm của
y
là:
A.
15 31
16 32
e .y x
. B.
32 31
e e e e
32.
y
x
. C.
15 31
16 32
e .y x
. D.
e e e e
2
y
x
.
Lời giải
Ta có:
1
32
e e e e .y x
1
1
32
1
e e e e .
32
y x
31
32
1
e e e e .
32
x
32 31
e e e e
32. x
.
Câu 9. (Xuân Trường - Nam Định - 2018) Tính đạo hàm của hàm số
sin 2 3
x
y x
A.
1
2cos 2 3
x
y x x
. B.
cos2 3
x
y x
.
C.
2cos 2 3 ln 3
x
y x
. D.
2cos 2 3 ln 3
x
y x
.
Lời giải
Hàm số
sin 2 3
x
y x
có tập xác định
D
và có đạo hàm:
2cos 2 3 ln 3
x
y x
.
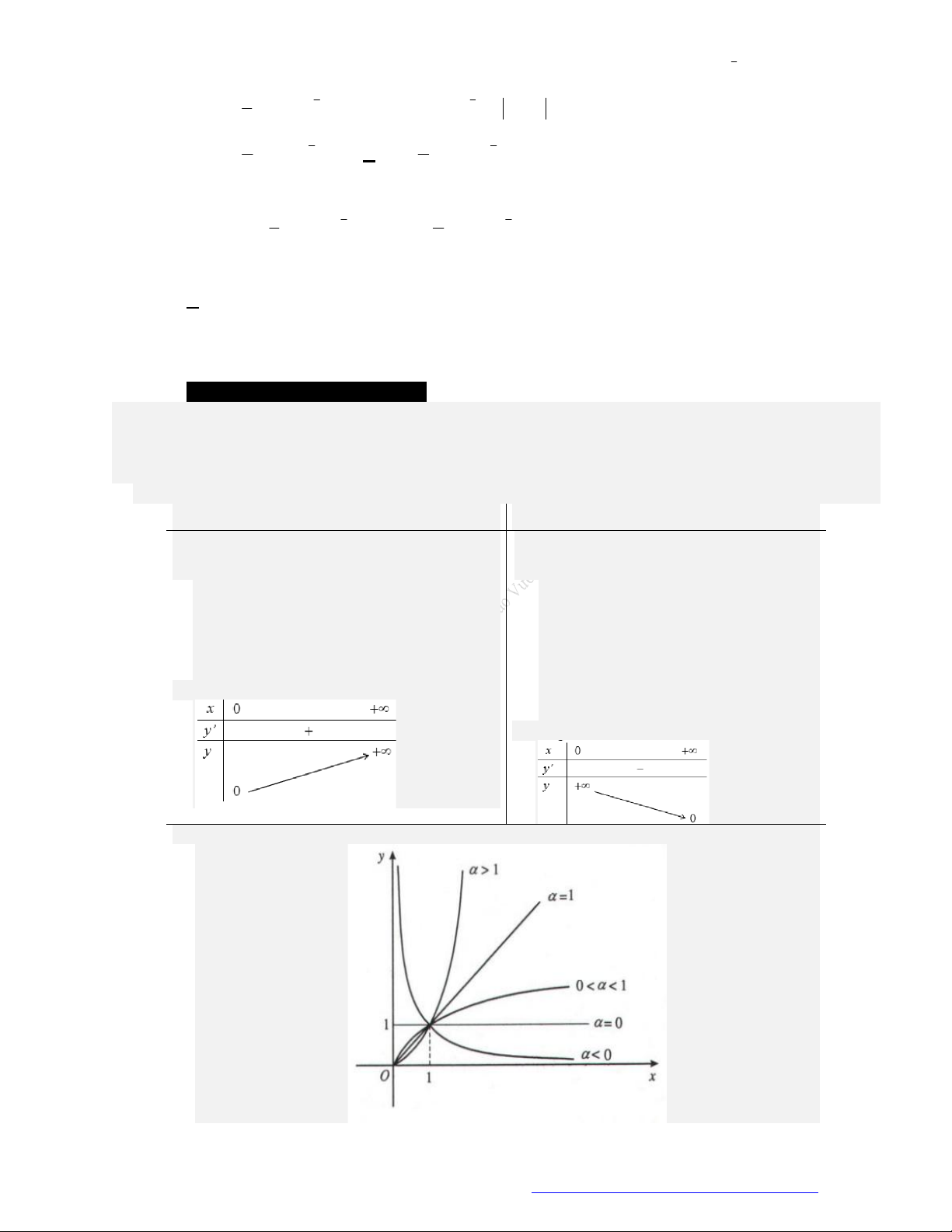
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Câu 10. (THPT Thuận Thành - Bắc Ninh - 2018) Đạo hàm của hàm số
1
3
2 1y x
là:
A.
2
3
1
2 1
3
y x
. B.
1
3
2 1 ln 2 1y x x
.
C.
4
3
2
2 1
3
y x
. D.
2
3
2
2 1
3
y x
.
Lời giải
Ta có:
2 2
3 3
1 2
2 1 2 1 2 1
3 3
y x x x
.
Câu 11. (THPT Nghen - Hà Tĩnh - 2018) Đạo hàm của hàm số .2
x
y x là
A.
1 ln 2 2
x
y x
. B.
1 ln 2 2
x
y x
. C.
1 2
x
y x
. D.
2 1
2 2
x x
y x
.
Lời giải
2 .2 .ln 2
x x
y x
1 ln 2 2
x
x
.
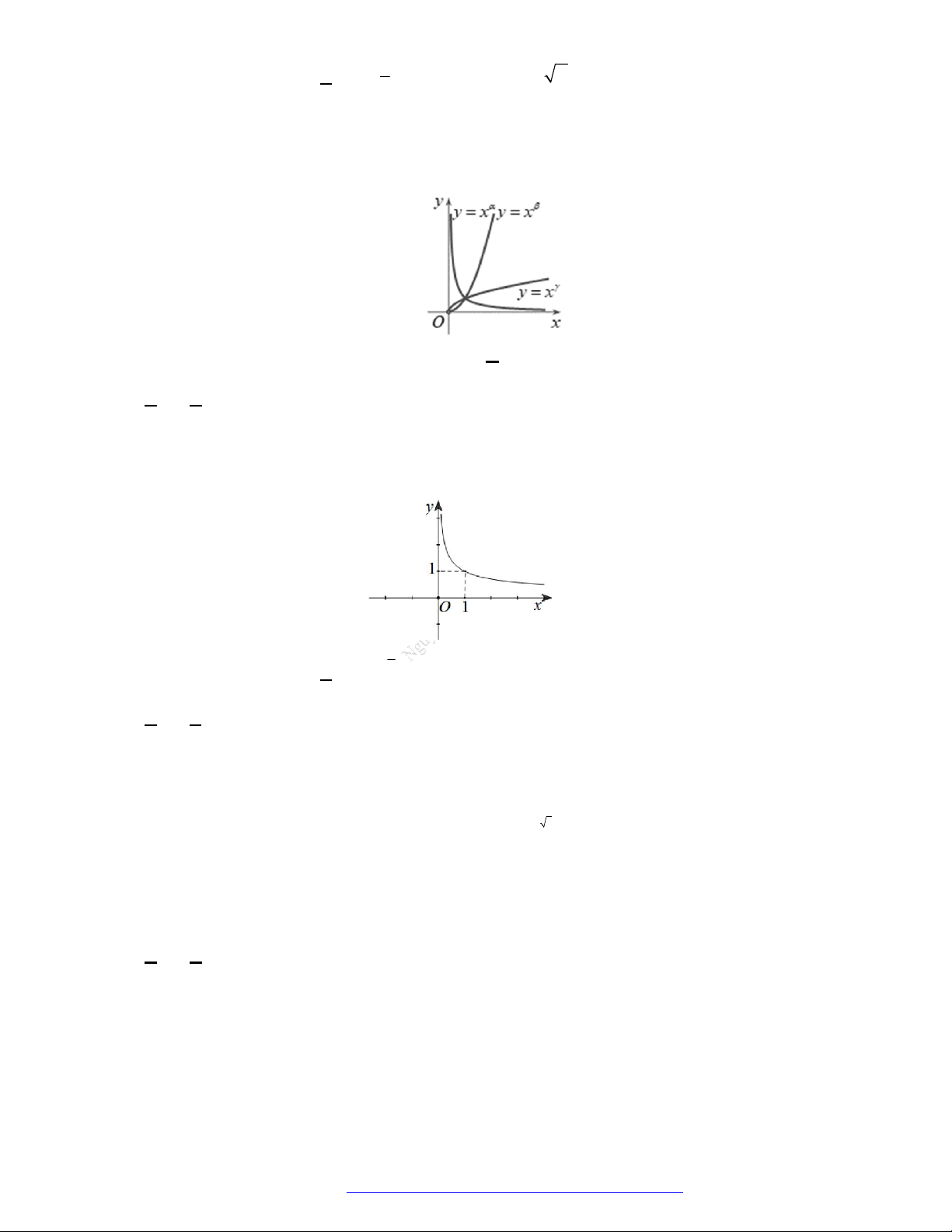
Dạng 5. Khảo sát hàm số lũy thừa
Khảo sát hàm số lũy thừa y x
Tập xác định của hàm số lũy thừa y x
luôn chứa khoảng
0;
với mọi
.
Trong trường hợp
tổng quát, ta khảo sát hàm số y x
trên khoảng này.
, 0.y x
, 0.y x
1. Tập xác định:
0; .
2. Sự biến thiên
1
' . 0 0.y x x
Giới hạn đặc biệt:
0
lim 0, lim .
x
x
x x
Tiệm cận: không có.
3. Bảng biến thiên.
1. Tập xác định:
0; .
2. Sự biến thiên
1
' . 0 0.y x x
Giới hạn đặc biệt:
0
lim , lim 0.
x
x
x x
Tiệm cận:
Ox là tiệm cận ngang.
Oy là tiệm cận đứng.
3. Bảng biến thiên.
Đồ thị của hàm số.
Câu 1. (THPT Phan Chu Trinh - Đắc Lắc - 2018) Hàm số nào sau đây nghịch biến trên
?
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A. 2
x
y . B.
1
3
x
y
. C.
x
y
. D. e
x
y .
Lời giải
Hàm số
x
y a nghịch biến trên
khi và chỉ khi
0 1a
.
Câu 2. Cho các hàm số lũy thừa
y x ,
y x ,
y x có đồ thị như hình vẽ. Mệnh đề đúng là
A.
.
B.
.
C.
.
D.
.
Lời giải
Chọn C
Dựa vào đồ thị ta có
0
,
1
;
0 1
.
Vậy
.
Câu 3. Đường cong ở hình vẽ dưới đây là đồ thị của hàm số nào dưới đây?
A.
1
2 .
x
y
B.
1
2
.
y x
C.
1
.y x
D.
2
log 2y x
.
Lời giải
Chọn B
Dựa vào đồ thị ta thấy TXĐ của hàm số là
D= 0;
loại A, C.
Hàm số nghịch biến trên TXĐ của nó mà hàm số
2
log 2y x
đồng biến trên TXĐ của nó nên ta
loại đáp án D. chọn B.
Câu 4. (THPT Quốc Oai - Hà Nội - 2017) Cho hàm số
3
y x
khẳng định nào sau đây đúng?
A. Đồ thị hàm số cắt trục
Ox
.
B. Đồ thị hàm số không có tiệm cận.
C. Đồ thị hàm số có một tiệm cận đứng và không có tiệm cận ngang.
D. Đồ thị hàm số có một tiệm cận đứng và một tiệm cận ngang.
Lời giải
Chọn D
* TXĐ:
0;D
.
* Đồ thị hàm số:
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Từ đồ thị hàm số ta thấy đồ thị hàm số có một tiệm cận đứng là trục
Oy
và một tiệm cận ngang là
trục
Ox
. Đáp án đúng là
D.
Câu 5. (Chuyên Vinh 2017) Cho là các số
,
là các số thực. Đồ thị các hàm số
, y x y x
trên
khoảng
0; +
được cho trong hình vẽ bên. Khẳng định nào sau đây là đúng?
.
A.
0 1
. B.
0 1
. C.
0 1
. D.
0 1
.
Lời giải
Chọn C
Với
0
1x
ta có:
0 0
1 0; 1 0x x
.
0 0
x x
.
Câu 6. (THPT – THD Nam Dinh- 2017) Cho hàm số
2
y x
. Mệnh đề nào sau đây là sai?
A. Hàm số có tập xác định là
0;
. B. Đồ thị hàm số không có tiệm cận.
C. Hàm số nghịch biến trên khoảng
0;
. D. Đồ thị hàm số không cắt trục hoành.
Lời giải
Chọn B
Tập xác định:
0;D
, suy ra C đúng.
Do
0x
nên
2
0x
, suy ra A đúng.
Ta có:
2 1
2. 0; 0y x x
, suy ra B đúng.
Ta có
2
0
lim
x
x
nên đồ thị hàm số nhận
Oy
làm tiệm cận đứng, đáp án D đúng.
Câu 7. (Chuyên Nguyễn Huệ 2019) Số cực trị của hàm số
2
5
y x x là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn B
Tập xác định:
. Xét
5 3
2
1
5
y
x
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
5
3
2
0
5
y x
;
y
không xác định khi
0x
.
Ta có bảng biến thiên:
y
đổi dấu khi qua
0x
và
5
3
2
5
x
nên hàm số có 2 cực trị.
Câu 8. (THPT Lương Văn Tụy - Ninh Bình - 2018) Cho
a
,
b
,
c
là ba số dương khác
1
. Đồ thị các
hàm số
log
a
y x
,
log
b
y x
,
log
c
y x
được cho trong hình vẽ bên. Mệnh đề nào dưới đây là
mệnh đề đúng?
A.
a b c
. B.
c a b
. C.
c b a
. D.
b c a
.
Lời giải
* Đồ thị các hàm số log
a
y x , log
b
y x , log
c
y x lần lượt đi qua các điểm
;1A a
,
;1B b
,
;1C c
.
* Từ hình vẽ ta có:
c a b
.
Câu 9. (THPT Nghen - Hà Tĩnh - 2018) Cho ba số thực dương
a
,
b
,
c
khác
1
. Đồ thị các hàm số
x
y a ,
x
y b ,
x
y c được cho trong hình vẽ dưới đây. Mệnh đề nào dưới đây đúng?
A.
1 a c b
. B.
1a c b
. C.
1a b c
. D.
1 a b c
.

T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Lờ
i giải
Đồ thị của hàm số
x
y
a có hướng đi xuống nên
1a
.
Đồ
thị của các hàm số
x
y
b và
x
y
c có hướng đi lên nên
1b
và
1c
.
Hơn nữa đồ thị hàm
số
x
y
b ở phía trên đồ thị hàm số
x
y
c nên
b c
.
Vậ
y
1a c b
.
Câu
10. (THPT Yên Lạc - 2018) Hàm số
2
2
e
x
y
x nghịch biến trên khoảng nào?
A.
;
0
. B.
2
;0
. C.
1
;
. D.
1
;0
.
Lời
giải
Ta có
2
2 e 1
x
y x x
; giải
phương trình
0y
0
1
x
x
.
Do
0y
với
1;0x
nê
n hàm số nghịc biến trên khoảng
1;0
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM
Dạng 1. Câu hỏi lý thuyết
Công thức logarit:
Cho các số
, 0, 1a b a
và
,m n
. Ta có:
log
a
b a b
10
lg log logb b b
ln log
e
b b
log 1 0
a
log 1
a
a
log
n
a
a n
1
log log
m
a
a
b b
m
log log
n
a a
b n b
log log
m
n
a
a
n
b b
m
log ( ) log log
a a a
bc b c
log log log
a a a
b
b c
c
log
log log
a
b b
b
c a
a b
a c
log .log log
a b a
b c c
,
1b
log
log
log
a
b
a
c
c
b
,
1b
1
log
log
a
b
b
a
,
1b
Câu 1. (Đề Minh Họa 2017). Cho hai số thực
a
và
b
, với
1 a b
. Khẳng định nào dưới đây là khẳng
định đúng?
A. log 1 log
b a
a b B. 1 log log
a b
b a C. log log 1
b a
a b D. log 1 log
a b
b a
Câu 2. (Mã 110 2017) Cho
a
là số thực dương khác
1
. Mệnh đề nào dưới đây đúng với mọi số dương
, x y
?
A. log log log
a a a
x
x y
y
B.
log log
a a
x
x y
y
C. log log log
a a a
x
x y
y
D.
log
log
log
a
a
a
x
x
y y
Câu 3. (THPT Minh Khai Hà Tĩnh 2019) Với mọi số thực dương
, , ,a b x y
và
, 1a b
, mệnh đề nào
sau đây sai?
A.
1 1
log
log
a
a
x x
. B.
log log log
a a a
xy x y
.
C. log .log log
b a b
a x x . D. log log log
a a a
x
x y
y
.
Câu 4. (Chuyên Hạ Long 2019) Trong các mệnh đề sau, mệnh đề nào đúng?
A.
log log
a a
b b
với mọi số ,a b dương và
1a
.
B.
1
log
log
a
b
b
a
với mọi số ,a b dương và
1a
.
C. log log log
a a a
b c bc với mọi số ,a b dương và
1a
.
D.
log
log
log
c
a
c
a
b
b
với mọi số , ,a b c dương và
1a
.
Câu 5. (THPT-Thang-Long-Ha-Noi- 2019) Cho
,a b
là hai số thực dương tùy ý và
1b
.Tìm kết luận
đúng.
CÔNG THỨC, BIẾN ĐỔI LOGARIT
Chuyên đề 17
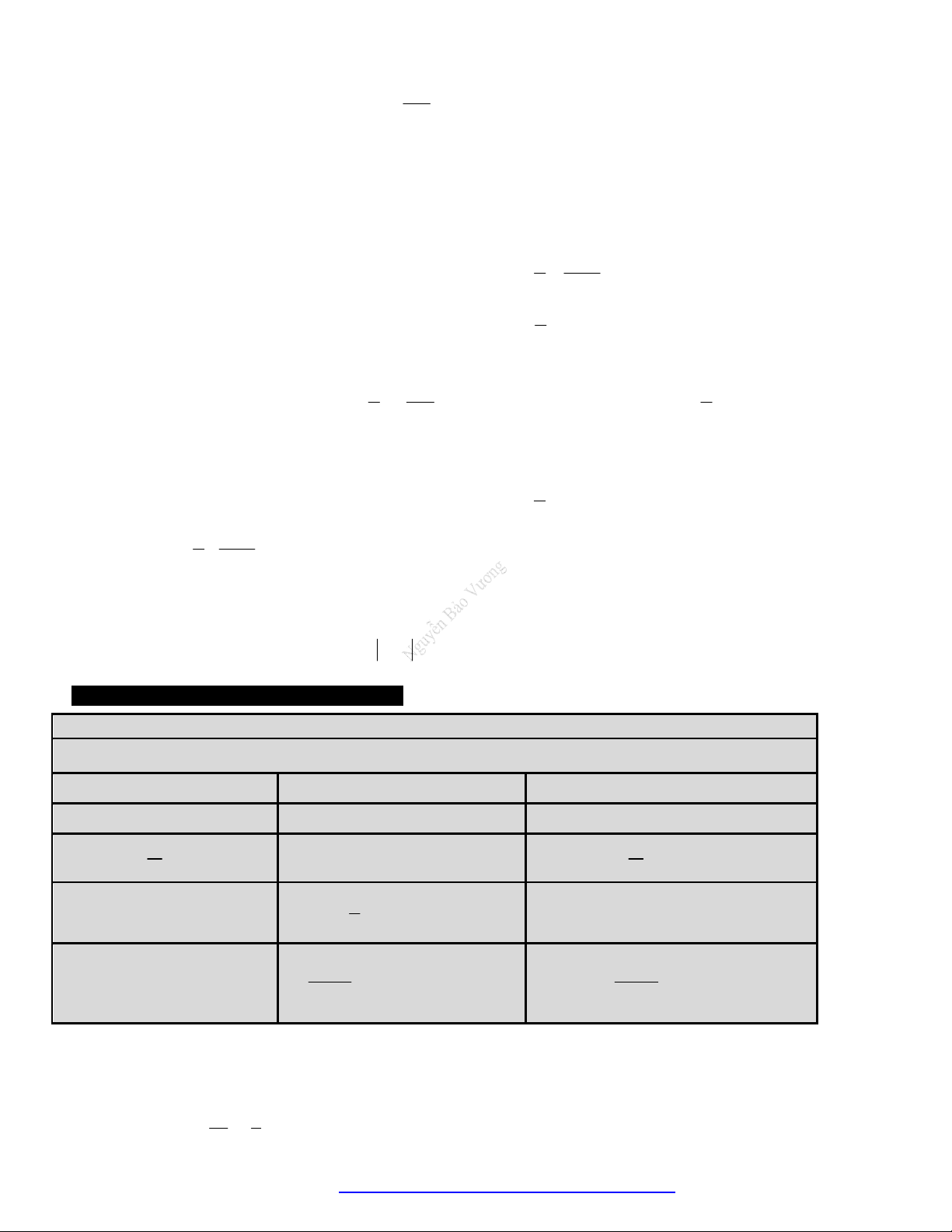
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
ln ln ln
a b a b
. B.
ln a b ln a.ln b
.
C.
lna ln b ln a b
. D.
b
lna
log a
ln b
.
Câu 6. (THPT Yên Phong Số 1 Bắc Ninh 2019) Cho hai số dương
, 1 .
a b a
Mệnh đề nào dưới đây
SAI?
A.
log 2a a
a
. B.
log a
a
. C.
log 1 0
a
. D.
log b
a
a b
.
Câu 7. (Sở Thanh Hóa 2019) Với các số thực dương
,a b
bất kì. Mệnh đề nào dưới đây đúng?
A.
log log .logab a b
. B.
log
log
log
a a
b b
.
C.
log log logab a b
. D.
log logb loga
a
b
.
Câu 8. (VTED 03 2019) Với các số thực dương
,a b
bất kì. Mệnh đề nào dưới đây đúng?
A.
ln ln lnab a b
B.
ln
ln
ln
a a
b b
C.
ln ln .lnab a b
D.
ln ln ln
a
b a
b
Câu 9. (Chuyên Lê Hồng Phong Nam Định 2019) Với các số thực dương
a
,
b
bất kì. Mệnh đề nào sau
đây đúng?
A.
log log .logab a b
. B.
log log log
a
b a
b
.
C.
log
log
log
a a
b b
. D.
log log logab a b
.
Câu 10. Cho
, , 0
a b c
,
1
a
và số
, mệnh đề nào dưới đây sai?
A.
log
c
a
a c
B.
log 1
a
a
C.
log log
a a
b b
D.
log log log
a a a
b c b c
Dạng 2. Tính, rút gọn biểu thức chứa logarit
Công thức logarit:
Cho các số
, 0, 1a b a
và
,m n
. Ta có:
log
a
b a b
10
lg log logb b b
ln log
e
b b
log 1 0
a
log 1
a
a
log
n
a
a n
1
log log
m
a
a
b b
m
log log
n
a a
b n b
log log
m
n
a
a
n
b b
m
log ( ) log log
a a a
bc b c
log log log
a a a
b
b c
c
log
log log
a
b b
b
c a
a b
a c
log .log log
a b a
b c c
,
1
b
log
log
log
a
b
a
c
c
b
,
1
b
1
log
log
a
b
b
a
,
1
b
Câu 11. [THPT An Lão Hải Phòng 2019) Cho
, ,a b c
là các số dương
, 1
a b
. Trong các mệnh đề sau,
mệnh đề nào là mệnh đề đúng?
A.
3
1
log log .
3
a a
b
b
a
B.
log
.
b
a
a b

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
C.
log log 0 .
a
a
b b
D. log log .log .
a b a
c c b
Câu 12. (Mã 101 - 2020 Lần 1) Với
,a b
là các số thực dương tùy ý và
1a
,
5
log
a
b
bằng:
A. 5log
a
b . B.
1
log
5
a
b
. C. 5 log
a
b . D.
1
log
5
a
b
.
Câu 13. (Mã 102 - 2020 Lần 1) Với , là các số thực dương tùy ý và , bằng
A. . B. . C. . D. .
Câu 14. (Mã 103 - 2020 Lần 1) Với a,b là các số thực dương tùy ý và
1a
,
3
log
a
b
bằng
A. 3 log
a
b B. 3log
a
b C.
1
3
log
a
b
D.
1
3
log
a
b
Câu 15. (Mã 102 - 2020 Lần 2) Với
a
là số thực dương tùy ý,
5
log 5a
bằng
A.
5
5 log a
. B.
5
5 log a
. C.
5
1 log a
. D.
5
1 log a
.
Câu 16. (Mã 103 - 2020 Lần 2) Với
a
là số thực dương tùy ý,
2
log 2a
bằng
A.
2
1 log a
. B.
2
1 log a
. C.
2
2 log a
. D.
2
2 log a
.
Câu 17. (Đề Minh Họa 2020 Lần 1) Với
a
là số thực dương tùy ý,
2
2
log a
bằng:
A.
2
2 log a
. B.
2
1
log
2
a
. C.
2
2log a
. D.
2
1
log
2
a
.
Câu 18. (Đề Tham Khảo 2020 Lần 2) Với
a
là hai số thực dương tùy ý,
3
2
log a
bằng
A.
2
3
log
2
a
. B.
2
1
log
3
a
. C.
2
3 log a
. D.
2
3log a
.
Câu 19. (Mã 103 2019) Với
a
là số thực dương tùy ý,
3
2
log a
bằng
A.
2
3 log .a B.
2
3log .a C.
2
1
log .
3
a
D.
2
1
log .
3
a
Câu 20. (Mã 102 2019) Với
a
là số thực dương tùy ý,
3
5
log a
bằng
A.
5
1
log
3
a
. B.
5
1
log
3
a
. C.
5
3 log a
. D.
5
3log a
.
Câu 21. (Mã 104 2017) Cho
a
là số thực dương tùy ý khác
1
. Mệnh đề nào dưới đây đúng?
A.
2
log log 2
a
a B.
2
2
1
log
log
a
a
C.
2
1
log
log 2
a
a
D.
2
log log 2
a
a
Câu 22. (Mã 104 2019) Với
a
là số thực dương tùy ý,
2
2
log a
bằng:
A.
2
1
log
2
a
. B.
2
2 log a
C.
2
2log a
. D.
2
1
log
2
a
.
Câu 23. (Đề Tham Khảo 2019) Với
a
,
b
là hai số dương tùy ý,
2
log ab
bằng
A.
2 log loga b
B.
1
log log
2
a b
C.
2log loga b
D.
log 2loga b
Câu 24. (Đề Tham Khảo 2017) Cho
a
là số thực dương
1a
và
3
3
log
a
a . Mệnh đề nào sau đây đúng?
A.
1
3
P
B.
3P
C.
1P
D.
9P
Câu 25. (Mã 101 2019) Với
a
là số thực dương tùy ý, bằng
2
5
log a
A.
5
1
log .
2
a
B.
5
2 log .a C.
5
1
log .
2
a
D.
5
2log .a
a
b
1
a
2
log
a
b
1
log
2
a
b
1
log
2
a
b
2 log
a
b
2log
a
b

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 26. (Mã 103 2018) Với
a
là số thực dương tùy ý,
ln 7 ln 3a a
bằng
A.
ln 7
ln 3
B.
7
ln
3
C.
ln 4a
D.
ln 7
ln 3
a
a
Câu 27. (Mã 101 2018) Với
a
là số thực dương tùy ý,
ln 5 ln 3a a
bằng:
A.
5
ln
3
B.
ln5
ln3
C.
ln 5
ln 3
a
a
D.
ln 2a
Câu 28. (Mã 102 2018) Với
a
là số thực dương tùy ý,
3
log 3a
bằng:
A.
3
1 log a
B.
3
3log a
C.
3
3 log a
D.
3
1 log a
Câu 29. Với các số thực dương
,a b
bất kì. Mệnh đề nào dưới đây đúng.
A.
ln ln ln .ab a b
B.
ln ln .ln .ab a b
C.
ln
ln .
ln
a a
b b
D.
ln ln ln .
a
b a
b
Câu 30. (Mã 123 2017) Cho
a
là số thực dương khác
1
. Tính
log .
a
I a
A.
2.I
B.
2I
C.
1
2
I
D.
0I
Câu 31. (Mã 104 2018) Với
a
là số thực dương tùy ý,
3
3
log
a
bằng:
A.
3
1 log a
B.
3
3 log a
C.
3
1
log a
D.
3
1 log a
Câu 32. Với các số thực dương
, ba
bất kì. Mệnh đề nào dưới đây đúng?
A.
3
2 2 2
2
log 1 3log log
a
a b
b
. B.
3
2 2 2
2 1
log 1 log log
3
a
a b
b
.
C.
3
2 2 2
2
log 1 3log log
a
a b
b
. D.
3
2 2 2
2 1
log 1 log log
3
a
a b
b
.
Câu 33. (Mã 110 2017) Cho
log 2
a
b
và
log 3
a
c
. Tính
2 3
log
a
P b c
.
A.
13
P
B.
31
P
C.
30
P
D.
108
P
Câu 34. (Mã 102 2019) Cho
a
và
b
là hai số thực dương thỏa mãn
3 2
32
a b
. Giá trị của
2 2
3log 2loga b
bằng
A.
4
. B.
5
. C.
2
. D.
32
.
Câu 35. (Đề Tham Khảo 2017) Cho
,a b
là các số thực dương thỏa mãn
1
a
,
a b
và
log 3
a
b
.
Tính
P log
b
a
b
a
.
A.
5 3 3
P
B.
1 3
P
C.
1 3
P
D.
5 3 3
P
Câu 36. (Mã 103 2019) Cho
a
và
b
là hai số thực dương thỏa mãn
2 3
16
a b
. Giá trị của
2 2
2log 3loga b
bằng
A.
2
. B.
8
. C.
16
. D.
4
.
Câu 37. (Mã 104 2017) Với các số thực dương
x
,
y
tùy ý, đặt
3
log x
,
3
log y
. Mệnh đề nào
dưới đây đúng?

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
3
27
log
2
x
y
B.
3
27
log 9
2
x
y
C.
3
27
log
2
x
y
D.
3
27
log 9
2
x
y
Câu 38. (Mã 101 2019) Cho
a
và
b
là hai số thực dương thỏa mãn
4
16
a b
.
Giá trị của
2 2
4log loga b
bằng
A.
4
. B.
2
. C.
16
. D.
8
.
Câu 39. (Dề Minh Họa 2017) Cho các số thực dương
,a b
với
1
a
. Khẳng định nào sau đây là khẳng
định đúng ?
A.
2
1
log log
4
a
a
ab b
B.
2
1 1
log log
2 2
a
a
ab b
C.
2
1
log log
2
a
a
ab b
D.
2
log 2 2log
a
a
ab b
Câu 40. (Mã 123 2017) Với
a
,
b
là các số thực dương tùy ý và
a
khác
1
, đặt
2
3 6
log log
a
a
P b b
.
Mệnh đề nào dưới đây đúng?
A.
6 log
a
P b
B.
27 log
a
P b
C.
15log
a
P b
D.
9 log
a
P b
Câu 41. (Đề Tham Khảo 2018) Với
a
là số thực dương bất kì, mệnh đề nào dưới đây đúng?
A.
1
log 3 log
3
a a
B.
log 3 3log
a a
C.
3
1
log log
3
a a
D.
3
log 3log
a a
Câu 42. (Mã 105 2017) Cho
3
log 2
a
và
2
1
log
2
b
. Tính
2
3 3 1
4
2 log log 3 log
I a b
.
A.
5
4
I
B.
0I
C.
4I
D.
3
2
I
Câu 43. (Mã 105 2017) Cho
a
là số thực dương khác
2
. Tính
2
2
log
4
a
a
I
.
A.
2I
B.
1
2
I
C.
2I
D.
1
2
I
Câu 44. (Mã 104 2017) Với mọi
a
,
b
,
x
là các số thực dương thoả mãn
2 2 2
log 5log 3logx a b
.
Mệnh đề nào dưới đây đúng?
A.
5 3x a b
B.
5 3
x a b
C.
5 3
x a b
D.
3 5x a b
Câu 45. (Mã 104 2019) Cho
a
và
b
là hai số thực dương thỏa mãn
3
8
ab
. Giá trị của
2 2
log 3loga b
bằng
A.
6
. B.
2
. C.
3
. D.
8
.
Câu 46. (Mã 105 2017) Với mọi số thực dương
a
và
b
thỏa mãn
2 2
8a b ab
, mệnh đề nào dưới đây
đúng?
A.
1
log log log
2
a b a b
B.
1
log log log
2
a b a b
C.
1
log 1 log log
2
a b a b
D.
log 1 log loga b a b
Câu 47. (Mã 123 2017) Cho
log 3,log 4
a b
x x
với
,a b
là các số thực lớn hơn 1. Tính
log .
ab
P x
A.
12P
B.
12
7
P
C.
7
12
P
D.
1
12
P

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 48. (Mã 110 2017) Cho
, x y
là các số thực lớn hơn
1
thoả mãn
2 2
9 6x y xy
. Tính
12 12
12
1 log log
2log 3
x y
M
x y
.
A.
1
2
M
. B.
1
3
M
. C.
1
4
M
. D.
1M
Câu 49. (Đề Minh Họa 2020 Lần 1) Xét tất cả các số dương
a
và
b
thỏa mãn
2 8
log log ( )a ab . Mệnh
đề nào dưới đây đúng?
A.
2
a b
. B.
3
a b
. C.
a b
. D.
2
a b
.
Câu 50. (Đề Tham Khảo 2020 Lần 2) Xét số thực
a
và
b
thỏa mãn
3 9
log 3 .9 log 3
a b
. Mệnh đề nào
dưới đây đúng
A.
2 2a b
. B.
4 2 1a b
. C.
4 1ab
. D.
2 4 1a b
.
Câu 51. (Mã 102 - 2020 Lần 1) Cho và
là các số thực dương thỏa mãn . Giá trị của
bằng
A. . B. . C. . D. .
Câu 52. (Mã 103 - 2020 Lần 1) Cho a và b là hai số thực dương thỏa mãn
3
log ( )
9 4
ab
a
. Giá trị của
2
ab
bằng
A.
3
. B. 6. C. 2 D. 4
Câu 53. (Mã 102 - 2020 Lần 2) Với
,a b
là các số thực dương tùy ý thỏa mãn
3 9
log 2log 2a b , mệnh
đề nào dưới đây đúng?
A.
2
9a b
. B.
9a b
. C.
6a b
. D.
2
9a b
.
Câu 54. (Mã 103 - 2020 Lần 2) Với
,a b
là các số thực dương tùy ý thỏa mãn
3 9
log 2log 3a b
, mệnh
đề nào dưới đây đúng?
A.
27a b
. B.
9a b
. C.
4
27a b
. D.
2
27a b
.
Câu 55. (Mã 104 - 2020 Lần 2) Với
,a b
là các số thực dương tùy ý thỏa mãn
2 4
log 2log 4a b , mệnh
đề nào dưới đây đúng?
A.
2
16a b
. B.
8a b
. C.
16a b
. D.
4
16a b
.
Câu 56. (Chuyên Bắc Giang 2019) Cho các số thực dương
,a b
thỏa mãn
ln ;lna x b y
. Tính
3 2
ln a b
A.
2 3
P x y
B.
6P xy
C.
3 2P x y
D.
2 2
P x y
Câu 57. (Chuyên Vĩnh Phúc 2019) Giá trị của biểu thức
2 2 2 2
log 2 log 4 log 8 ... log 256M
bằng
A.
48
B.
56
C.
36
D.
2
8log 256
Câu 58. (THCS - THPT Nguyễn Khuyến 2019) Cho
8
log c m và
3
log 2
c
n
. Khẳng định đúng là
A.
2
1
log
9
mn c
. B.
9mn
. C.
2
9logmn c . D.
1
9
mn
.
Câu 59. (THPT Lương Thế Vinh Hà Nội 2019) Cho
0, 1a a
và
log 1,log 4
a a
x y
. Tính
2 3
log
a
P x y
A.
18P
. B.
6P
. C.
14P
. D.
10P
.
Câu 60. (Sở Bình Phước 2019) Với
a
và
b
là hai số thực dương tùy ý;
3 4
2
log a b
bằng
A.
2 2
1 1
log log
3 4
a b
B.
2 2
3log 4loga b
C.
2 4
2 log loga b
D.
2 2
4log 3loga b
a
b
2
log ( )
4 3
ab
a
2
ab
3
6
2
12

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 61. (Chuyên Hạ Long -2019) Cho
20
7
4
3 27 243
P
. Tính
3
log P
?
A.
45
28
. B.
9
112
. C.
45
56
. D. Đáp án khác.
Câu 62. (THPT Cẩm Giàng 2 2019) Cho các số dương
, , ,a b c d
. Biểu thức
ln ln ln ln
a b c d
S
b c d a
bằng
A. 1. B. 0. C.
ln
a b c d
b c d a
. D.
ln
abcd
.
Câu 63. Cho
x
,
y
là các số thực dương tùy ý, đặt
3
log
x a
,
3
log
y b
. Chọn mệnh đề đúng.
A.
1
3
27
1
log
3
x
a b
y
. B.
1
3
27
1
log
3
x
a b
y
.
C.
1
3
27
1
log
3
x
a b
y
. D.
1
3
27
1
log
3
x
a b
y
.
Câu 64. (THPT Bạch Đằng Quảng Ninh 2019) Với
,a b
là các số thực dương tùy ý và
a
khác
1
, đặt
2
3 6
log log
a
a
P b b
. Mệnh đề nào dưới đây đúng?
A.
27log
a
P b
. B.
15log
a
P b
. C.
9log
a
P b
. D.
6log
a
P b
.
Câu 65. (THPT Quang Trung Đống Đa Hà Nội 2019) Với các số thực dương
,a b
bất kỳ
1
a
. Mệnh
đề nào dưới đây đúng?
A.
3
2
1
log 2log .
3
a a
a
b
b
B.
3
2
1
log 3 log .
2
a a
a
b
b
C.
3
2
1 1
log log .
3 2
a a
a
b
b
D.
3
2
log 3 2log .
a a
a
b
b
Câu 66. (Chuyên Lê Hồng Phong Nam Định 2019) Cho các số thực dương
, ,a b c
với
a
và
b
khác
1
.
Khẳng định nào sau đây là đúng?
A.
2
log .log log
a a
b
b c c
. B.
2
1
log .log log
4
a a
b
b c c
.
C.
2
log .log 4log
a a
b
b c c
. D.
2
log .log 2log
a a
b
b c c
.
Câu 67. (Chuyên Bắc Giang -2019) Giả sử
,a b
là các số thực dương bất kỳ. Mệnh đề nào sau đây sai?
A.
2 2
log 10 2 log
ab ab
B.
2 2
log 10 1 log logab a b
C.
2
log 10 2 2log
ab ab
D.
2
log 10 2 1 log logab a b
Câu 68. (THPT Lương Thế Vinh Hà Nội 2019) Cho
log 3,log 2
a a
b c
. Khi đó
3 2
log
a
a b c
bằng
bao nhiêu?
A.
13
B.
5
C.
8
D.
10
Câu 69. (THPT Lê Quy Đôn Điện Biên 2019) Rút gọn biểu thức
9 1
3
3
3log 6log 3 log .
9
x
M x x
A.
3
log 3M x
B.
3
2 log
3
x
M
C.
3
log
3
x
M
D.
3
1 logM x
Câu 70. (Chuyên Lê Thánh Tông 2019) Cho
2
8 4
log log 5
x y
và
2
8 4
log log 7
y x
. Tìm giá trị
của biểu thức
P x y
.
A.
56
P
. B.
16
P
. C.
8
P
. D.
64
P
.
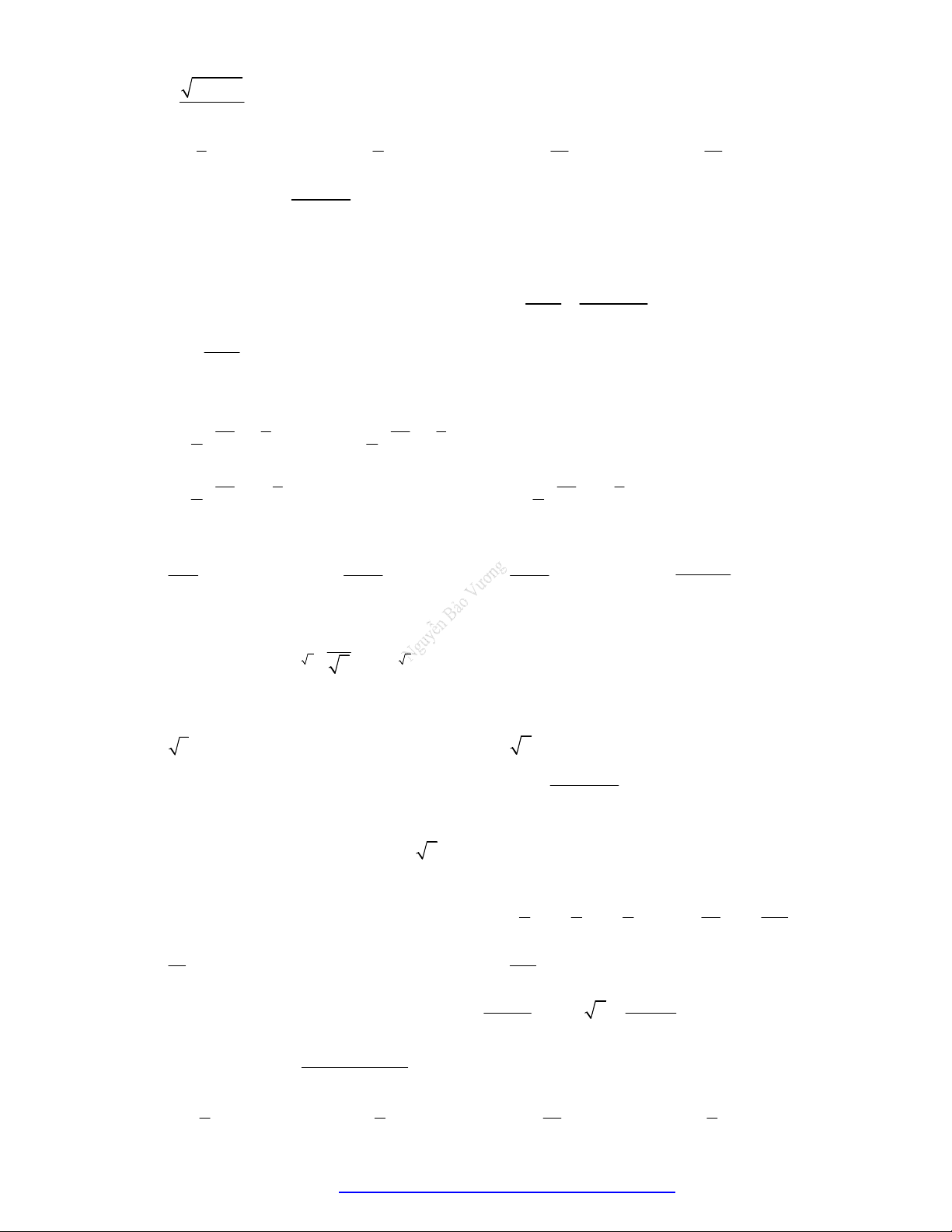
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 71. (Hsg Bắc Ninh 2019) Cho hai số thực dương
,a b
.Nếu viết
6 3 2
2 2 4
64
log 1 log log ( , )
a b
x a y b x y
ab
thì biểu thức
P xy
có giá trị bằng bao nhiêu?
A.
1
3
P
B.
2
3
P
C.
1
12
P
D.
1
12
P
Câu 72. Cho
700
log 490
log7
b
a
c
với
, ,a b c
là các số nguyên. Tính tổng
T a b c
.
A.
7
T
. B.
3
T
. C.
2T
. D.
1T
.
Câu 73. Cho
, a b
là hai số thưc dương thỏa mãn
2 2
14a b ab
. Khẳng định nào sau đây sai?
A.
2 2 2
2log 4 log loga b a b
. B.
ln ln
ln
4 2
a b a b
.
C.
2log log log
4
a b
a b
. D.
4 4 4
2log 4 log loga b a b
.
Câu 74. Cho
,x y
là các số thực dương tùy ý, đặt
3
log
x a
,
3
log
y b
. Chọn mệnh đề đúng.
A.
1
3
27
1
log
3
x
a b
y
. B.
1
3
27
1
log
3
x
a b
y
.
C.
1
3
27
1
log
3
x
a b
y
. D.
1
3
27
1
log
3
x
a b
y
.
Câu 75. (Sở Vĩnh Phúc 2019) Cho
log
a
x
,
log
b
x
. Khi đó
2
2
log
ab
x
bằng.
A.
αβ
α+β
. B.
2
αβ
2
α+β
. C.
2
2
α+β
. D.
2
α+β
α+2β
.
Câu 76. (THPT Bạch Đằng Quảng Ninh 2019) Tính giá trị biểu thức
2
3
10 2 2
log log log
a b
a
a
P a b b
b
(với
0 1;0 1a b
).
A.
3
. B.
1
. C.
2
. D.
2
.
Câu 77. (Toán Học Tuổi Trẻ 2019) Đặt
3
6
3
log 7
log 56,
log 2
b
M N a
c
với
, ,
a b c R
. Bộ số
, ,a b c
nào dưới đây để có
?M N
A.
3, 3, 1
a b c
. B.
3, 2, 1
a b c
.
C.
1, 2, 3
a b c
. D.
1, 3, 2
a b c
.
Câu 78. (THPT Yên Phong 1 Bắc Ninh 2019) Tính
1 2 3 98 99
log log log ... log log .
2 3 4 99 100
T
A.
1
10
. B.
2
. C.
1
100
. D.
2
.
Câu 79. Cho
, , 0; và , 1
a b x a b b x
thỏa mãn
2
2 1
log log
3 log
x x
b
a b
a
x
.
Khi đó biểu thức
2 2
2
2 3
( 2 )
a ab b
P
a b
có giá trị bằng:
A.
5
4
P
. B.
2
3
P
. C.
16
15
P
. D.
4
5
P
.
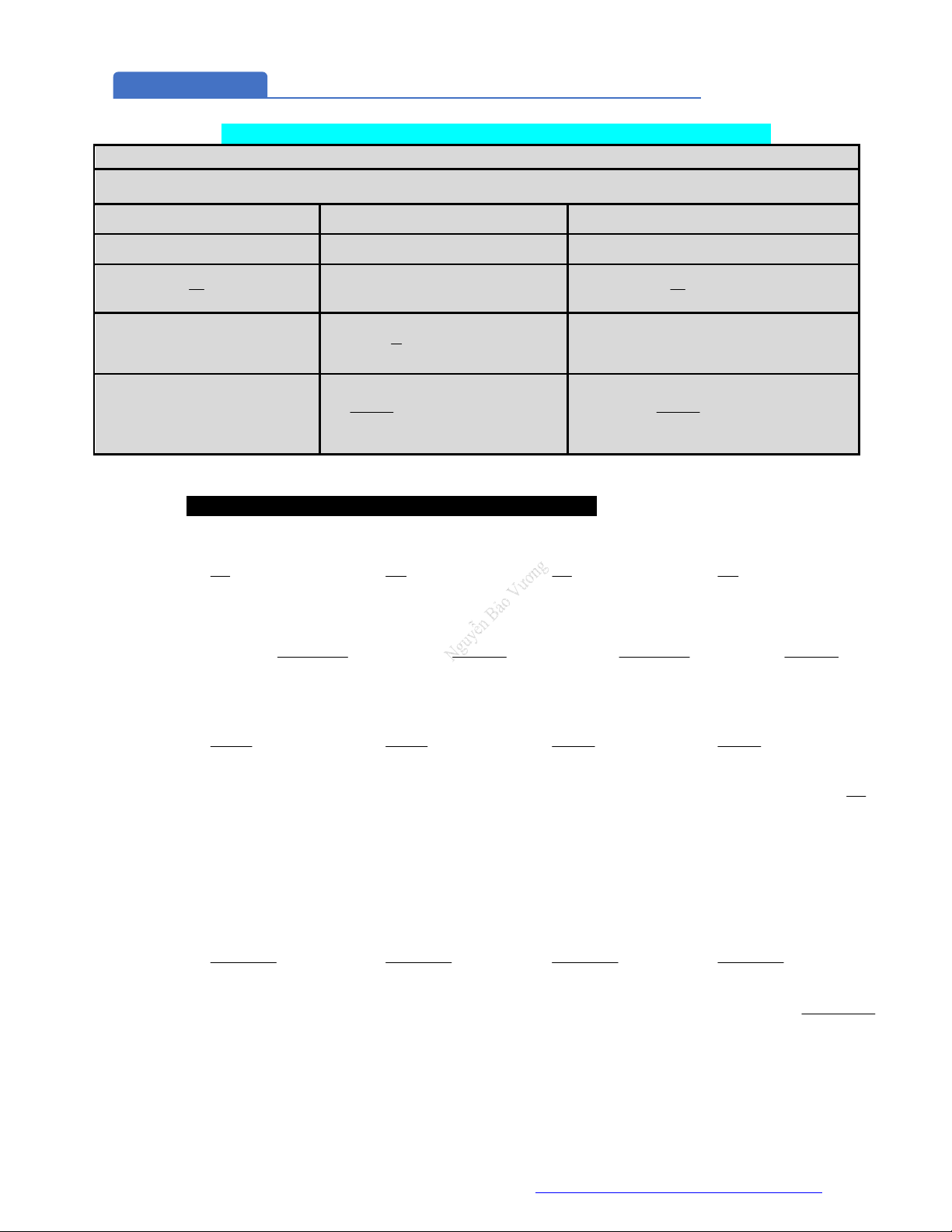
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ MỨC 7-8 ĐIỂM
Công thức logarit:
Chocácsố
, 0, 1a b a
và
,m n
.Tacó:
log
a
b a b
10
lg log logb b b
ln log
e
b b
log 1 0
a
log 1
a
a
log
n
a
a n
1
log log
m
a
a
b b
m
log log
n
a a
b n b
log log
m
n
a
a
n
b b
m
log ( ) log log
a a a
bc b c
log log log
a a a
b
b c
c
log
log log
a
b b
b
c a
a b
a c
log .log log
a b a
b c c
,
1b
log
log
log
a
b
a
c
c
b
,
1b
1
log
log
a
b
b
a
,
1b
Dạng. Biểu diễn biểu thức logarit này theo logarit khác
Câu 1. (ĐềThamKhảo2019)Đặt
3
log 2 a khiđó
16
log 27 bằng
A.
3
4
a
B.
3
4a
C.
4
3a
D.
4
3
a
Câu 2. (ĐềMinhHọa2017)Đặt
2 5
log 3, log 3.a b Hãybiểudiễn
6
log 45theo
a
và
b
.
A.
2
6
2 2
log 45
a ab
ab
B.
6
2
log 45
a ab
ab b
C.
2
6
2 2
log 45
a ab
ab b
D.
6
2
log 45
a ab
ab
Câu 3. (ChuyênĐạiHọcVinh2019)Đặt
3
log 2a=
,khiđó
6
log 48
bằng
A.
3 1
1
a
a
-
-
B.
3 1
1
a
a
+
+
C.
4 1
1
a
a
-
-
D.
4 1
1
a
a
+
+
Câu 4. (Chuyên Phan Bội Châu -2019) Cho
3
log 5 ,a
3
log 6 ,b
3
log 22 c . Tính
3
90
log
11
P
theo
,a
,b
c
?
A.
2P a b c
. B.
2P a b c
. C.
2P a b c
. D.
2P a b c
.
Câu 5. (LươngThếVinhHàNội2019)Với
27
log 5 a
,
3
log 7 b
và
2
log 3 c
,giátrịcủa
6
log 35
bằng
A.
3
1
a b c
c
B.
3
1
a b c
b
C.
3
1
a b c
a
D.
3
1
b a c
c
Câu 6. (THPTNguyễnKhuyến2019)Đặt
2
log 3a ;
5
log 3b . Nếubiểudiễn
6
log 45
a m nb
b a p
thì
m n p
bằng
A.
3
B.
4
C.
6
D.
3
Câu 7. (THPTThiệu Hóa – Thanh Hóa 2019) Cho các số thực dương
a
,
b
thỏa mãn
3
log a x ,
3
log b y .Tính
4 5
3
log 3P a b
.
CÔNG THỨC, BIẾN ĐỔI LOGARIT
Chuyên đề 17

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
4 5
3
P x y
B.
4 5
3
P x y
C.
60P xy
D.
1 4 5P x y
Câu 8. (THPTAnLãoHảiPhòng2019)Biết
6 6
log 3 ,log 5
a b
.Tính
3
log 5
theo
,a b
A.
b
a
B.
1
b
a
C.
1
b
a
D.
1
b
a
Câu 9. Cho
12
log 3
a
.Tính
24
log 18
theo
a
.
A.
3 1
3
a
a
. B.
3 1
3
a
a
. C.
3 1
3
a
a
. D.
3 1
3
a
a
.
Câu 10. (THPTGiaLộcHảiDương2019)Đặt
2
log 3
a
và
5
log 3
b
.Hãybiểudiễn
6
log 45
theo
a
và
b
.
A.
2
6
2 2
log 45
a ab
ab
.B.
6
2
log 45
a ab
ab
. C.
6
2
log 45
a ab
ab b
. D.
2
6
2 2
log 45
a ab
ab b
.
Câu 11. (HSG Bắc Ninh 2019) Đặt
ln 2, ln 5
a b
, hãy biểu diễn
1 2 3 98 99
ln ln ln ... ln ln
2 3 4 99 100
I
theo
a
và
b
.
A.
2
a b
B.
2
a b
C.
2
a b
D.
2
a b
Câu 12. (ChuyênBắcNinh2019)Đặt
2 3
log 3; log 5
a b
Biểudiễnđúngcủa
20
log 12
theo
,a b
là
A.
1
2
ab
b
. B.
2
a b
b
. C.
1
2
a
b
. D.
2
2
a
ab
.
Câu 13. (SởBìnhPhước2019)Cho
2 2
log 3 , log 5
a b
,khiđó
15
log 8
bằng
A.
3
a b
B.
1
3( )a b
C.
3( )a b
D.
3
a b
Câu 14. (ChuyênLêQuýĐônĐiệnBiên2019)Giảsử
27 8 2
log 5 ; log 7 ; log 3
a b c
.Hãybiểudiễn
12
log 35
theo
, ,a b c
?
A.
3 3
2
b ac
c
. B.
3 3
1
b ac
c
. C.
3 2
3
b ac
c
. D.
3 2
2
b ac
c
.
Câu 15. (Chuyen Phan Bội Châu Nghệ An 2019) Cho
3
log 5
a
,
3
log 6
b
,
3
log 22
c
. Tính
3
90
log
11
P
theo
a
,
b
,
c
.
A.
2
P a b c
. B.
2
P a b c
. C.
2
P a b c
. D.
2
P a b c
.
Câu 16. (THPT-YênĐịnhThanhHóa2019)Đặt
2 3
log 3; log 5
a b
.Biểudiễn
20
log 12
theo
,a b
.
A.
20
log 12
2
a b
b
. B.
20
1
log 12
2
ab
b
. C.
20
1
log 12
2
a
b
. D.
20
2
log 12
2
a
ab
.
Câu 17. (SởHàNội2019)Nếu
2
log 3
a
thì
72
log 108
bằng
A.
2
3
a
a
. B.
2 3
3 2
a
a
. C.
3 2
2 3
a
a
. D.
2 3
2 2
a
a
.
Câu 18. (Chuyên Trần Phú Hải Phòng 2019) Cho
30 30
log 3 ;log 5
a b
. Tính
30
log 1350
theo
,a b
;
30
log 1350
bằng
A.
2
a b
B.
2 1a b
C.
2 1a b
D.
2 2
a b
Câu 19. (THPT Quang Trung Đống Đa Hà Nội 2019) Đặt
2m log
và
7n log
. Hãy biểu diễn
6125 7
log
theo
m
và
n
.
A.
6 6 5
2
m n
. B.
1
(6 6 5 )
2
n m
. C.
5 6 6
m n
. D.
6 5 6
2
n m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 20. (LươngThếVinhHàNội2019)Cho
27
log 5
a
,
3
log 7
b
,
2
log 3
c
.Tính
6
log 35
theo
a
,
b
và
c
.
A.
3
1
a b c
c
. B.
3
1
a b c
b
. C.
3
1
a b c
a
. D.
3
1
b a c
c
.
Câu 21. (SởThanhHóa2019)Cho
2
loga m
và
log 16
m
A m
,với
0 1
m
.Mệnhđềnàosauđây
đúng?
A.
4
.
a
A
a
B.
4
.
a
A
a
C.
(4 ) .A a a
D.
(4 ) .A a a
Câu 22. (THPTNgôSĩLiênBắcGiang2019)Biết
3
15
log a
,tính
25
81
P log
theo
a
tađược
A.
2 1
P a
B.
2( 1)
P a
C.
2
1
P
a
D.
2
1a
Câu 23. (ChuyênPhanBộiChâu2019)Cho
3
log 5
a
,
3
log 6
b
,
3
log 22
c
.Tính
3
90
log
11
P
theo
, ,a b c
.
A.
2
P a b c
B.
2
P a b c
C.
2
P a b c
D.
2
P a b c
Câu 24. (ChuyênĐHSPHàNội2019)Nếu
3
log 5
a
thì
45
log 75
bằng
A.
2
1 2
a
a
. B.
1
2
a
a
. C.
1 2
2
a
a
. D.
1 2
1
a
a
.
Câu 25. (Chuyên Phan Bội Châu Nghệ An 2019) Cho
3
log 5 ,a
3
log 6 ,b
3
log 22 .c
Tính
3
90
log
11
P
theo
,a
,b
.c
A.
2
P a b c
. B.
2
P a b c
. C.
2
P a b c
. D.
2
P a b c
.
Câu 26. (ChuyênNguyễnTấtThànhYênBái2019)Cho
12
log 3
a
.Tính
24
log 18
theo
a
.
A.
3 1
3
a
a
. B.
3 1
3
a
a
. C.
3 1
3
a
a
. D.
3 1
3
a
a
.
Câu 27. (THPTNghĩaHưngNđ-2019)Đặt
log ,log
a b
b m c n
.Khiđó
2 3
log
a
ab c
bằng
A.
1 6mn
. B.
1 2 3m n
. C.
6mn
. D.
1 2 3m mn
.
Câu 28. (CụmLiênTrườngHảiPhòng2019)Đặt
2
log 3
a
và
5
log 3
b
.Hãybiểudiễn
6
log 45
theo
a
và
b
A.
6
2a
log 45
a b
ab b
B.
6
2a
log 45
a b
ab
C.
2
6
2 2a
log 45
a b
ab
D.
2
6
2 2a
log 45
a b
ab b
Câu 29. (THPT Thiệu Hóa – Thanh Hóa 2019) Cho
9 4 2
log 5 ; log 7 ; log 3
a b c
.Biết
24
log 175
mb nac
pc q
.Tính
2 3 4A m n p q
.
A.
27
B.
25
C.
23
D.
29
Câu 30. (ChuyênKHTN2019)Vớicácsố
, 0
a b
thỏamãn
2 2
6a b ab
,biểuthức
2
log
a b
bằng
A.
2 2
1
3 log log
2
a b
. B.
2 2
1
1 log log
2
a b
.
C.
2 2
1
1 log log
2
a b
. D.
2 2
1
2 log log
2
a b
.
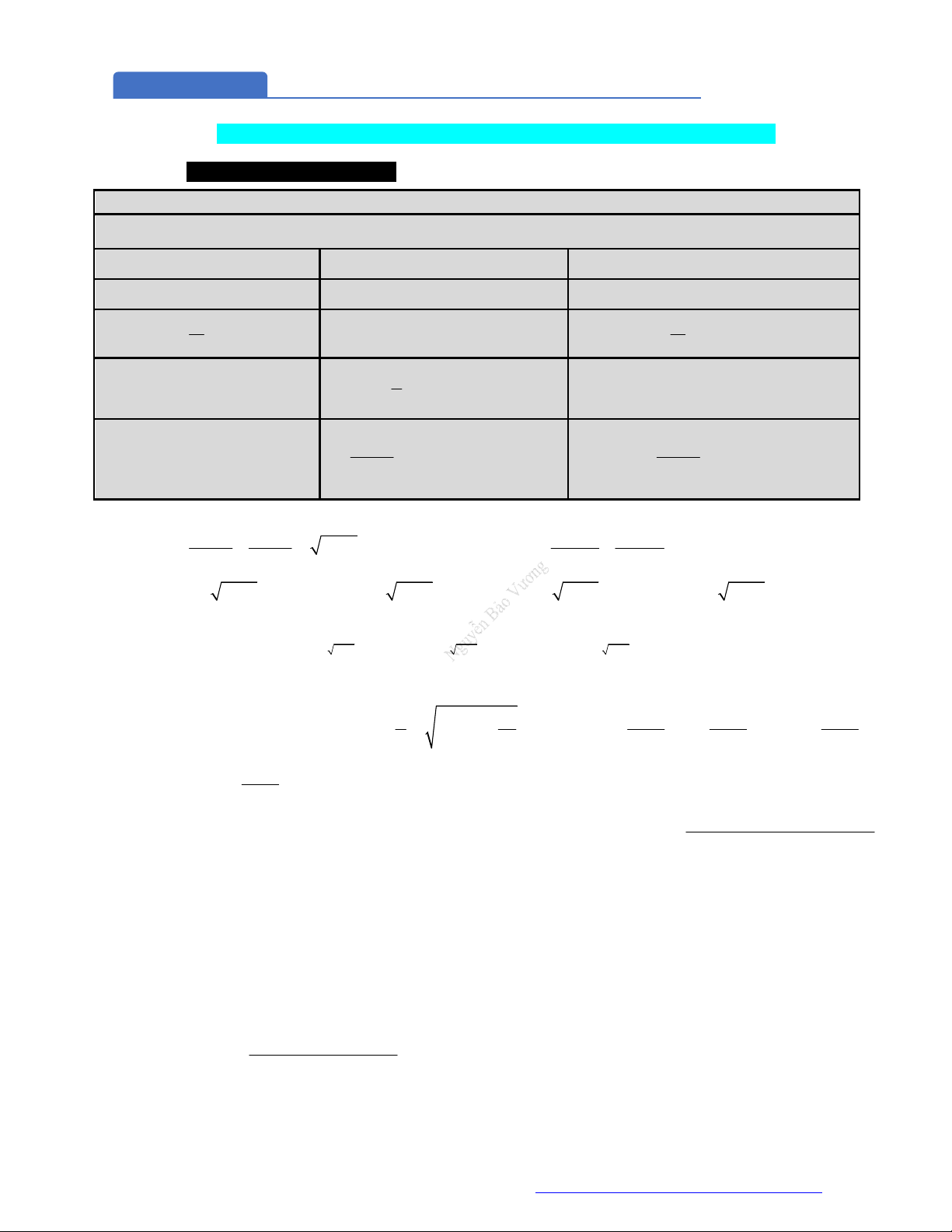
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI MỨC 9-10 ĐIỂM
Dạng. Một số bài toán KHÓ
Công thức logarit:
Cho các số
, 0, 1a b a
và
,m n
. Ta có:
log
a
b a b
10
lg log logb b b
ln log
e
b b
log 1 0
a
log 1
a
a
log
n
a
a n
1
log log
m
a
a
b b
m
log log
n
a a
b n b
log log
m
n
a
a
n
b b
m
log ( ) log log
a a a
bc b c
log log log
a a a
b
b c
c
log
log log
a
b b
b
c a
a b
a c
log .log log
a b a
b c c
,
1b
log
log
log
a
b
a
c
c
b
,
1b
1
log
log
a
b
b
a
,
1b
Câu 1. (Chuyên Lam Sơn - 2020) Cho các số thực
a
,
b
thỏa mãn
1a b
và
1 1
2020
log log
b a
a b
. Giá trị của biểu thức
1 1
log log
ab ab
P
b a
bằng
A.
2014
. B.
2016
. C.
2018
. D.
2020
.
Câu 2. (Liên Trường Thpt Tp Vinh Nghệ 2019) Tìm số nguyên dương n sao cho
3
2 2 2 2 2
2018 2018
2018
2018 2018
log 2019 2 log 2019 3 log 2019 ... log 2019 1010 .2021 log 2019
n
n
A.
2021n
. B.
2019n
. C.
2020n
. D.
2018.n
.
Câu 3. Cho hàm số
2
2
1 17
( ) log
2 4
f x x x x
. Tính
1 2 2018
...
2019 2019 2019
T f f f
A.
2019
2
T
. B.
2019T
. C.
2018T
. D.
1009T
.
Câu 4. (THPT Nguyễn Khuyến 2019) Gọi
a
là giá trị nhỏ nhất của
3 3 3 3
log 2.log 3.log 4...log
9
n
n
f n
với
n
và
2n
. Hỏi có bao nhiêu giá trị của
n
để
f n a
.
A. 2 B. 4 C. 1 D. vô số
Câu 5. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho
x
,
y
và
z
là các số thực lớn hơn
1
và gọi
w
là
số thực dương sao cho log 24
x
w ,
log 40
y
w
và
log 12
xyz
w
. Tính log
z
w .
A.
52
. B.
60
. C.
60
. D.
52
.
Câu 6. Cho
1 1f
,
f m n f m f n mn
với mọi
*
,m n
. Tính giá trị của biểu thức
96 69 241
log
2
f f
T
.
A.
9T
. B.
3T
. C.
10T
. D.
4T
.
CÔNG THỨC, BIẾN ĐỔI LOGARIT
Chuyên đề 17

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 7. (Chuyên Lê Quý Dôn Quảng Trị 2019) Cho các số thực dương
, ,x y z
thỏa mãn đồng thời
2 2 2
1 1 1 1
log log log 2020
x y z
và
2
log ( ) 2020
xyz
. Tính
2
log 1
xyz x y z xy yz zx
A.
4040
. B.
1010
. C. 2020. D.
2
2020
.
Câu 8. (Bạc Liêu – Ninh Bình 2019) Cho ba số thực dương
, , x y z
theo thứ tự lập thành một cấp số
nhân, đồng thời với mỗi số thực dương
( 1)
a a
thì
3
log , log , log
a
a a
x y z
theo thứ tự lập
thành một cấp số cộng. Tính giá trị của biểu thức
1959 2019 60x y z
P
y z x
.
A.
60
. B.
2019
. C.
4038
. D.
2019
2
.
Câu 9. (THPT Hai Bà Trưng - Huế - 2019) Cho hàm số
2
1 2
log
2 1
x
f x
x
và hai số thực
, m n
thuộc khoảng
0;1
sao cho
1 m n
. Tính
f m f n
.
A.
2
. B.
0
. C.
1
. D.
1
2
.
Câu 10. (Chuyên - Vĩnh Phúc - 2019) Gọi
n
là số nguyên dương sao cho
2 3
3 3
3 3 3
1 1 1 1 190
...
log log log log log
n
x x x x x
đúng với mọi
x
dương,
1x
. Tìm giá trị của biểu
thức
2 3P n
.
A.
32
P
. B.
23
P
. C.
43
P
. D.
41P
.
Câu 11. Cho
x
,
y
,
z
là ba số thực dương lập thành cấp số nhân;
log
a
x
,
log
a
y
,
3
log
a
z
lập thành cấp
số cộng, với
a
là số thực dương khác 1. Giá trị của
9 3x y z
p
y z x
là
A. 13. B. 3. C. 12. D. 10.
Câu 12. (Chuyên Nguyễn Huệ 2019) Cho
(1) 1;
f
( ) ( ) ( )
f m n f m f n mn
với mọi
*
,
m n N
.
Tính giá trị của biểu thức
2019 2009 145
log
2
f f
T
A.
3
. B.
4
. C.
5
. D.
10
.
Câu 13. Có bao nhiêu số nguyên dương
n
để
log 256
n
là một số nguyên dương?
A.
2.
B.
3.
C.
4
. D.
1
.
Câu 14. Cho tam giác
ABC
có
BC a
,
CA b
,
AB c
. Nếu
a
,
b
,
c
theo thứ tự lập thành một cấp số
nhân thì
A.
2
ln sin .ln sin ln sin
A C B
. B.
lnsin .lnsin 2lnsinA C B
.
C.
lnsin lnsin 2lnsinA C B
. D.
ln sin lnsin ln 2sinA C B
.
Câu 15. (Chuyên Lương Văn Chánh - Phú Yên - 2018) Cho
2018!
x
. Tính
2018 2018 2018 2018
2 3 2017 2018
1 1 1 1
...
log log log log
A
x x x x
.
A.
1
2017
A
. B.
2018
A
. C.
1
2018
A
. D.
2017
A
.
Câu 16. ( Chuyên Hùng Vương - Gia Lai - 2018) Tìm bộ ba số nguyên dương
( ; ; )a b c
thỏa mãn
log1 log(1 3) log(1 3 5) ... log(1 3 5 ... 19) 2log5
040 log 2 log3
a b c

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
(
2;6;4)
. B.
(
1;3;2)
. C.
(
2;4;4)
. D.
(
2;4;3)
.
Câu 17. (Phan Đìn
h Phùng - Hà Tĩnh - 2018) Tổng
3
2018
2
2 2
2 2 2
1
2 log 2 3 log 2 .... 2018 log 2
S
dưới
đây.
A.
2 2
10
08 .2018
. B.
2 2
10
09 .2019
. C.
2 2
10
09 .2018
. D.
2
2019
.
Câu 18. (ChuyêN KHTN - 2018) Số
20162017
20172018
c
ó bao nhiêu chữ số?
A.
1
47278481.
B.
1
47278480.
C.
1
47347190.
D.
1
47347191.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM
Dạng 1. Câu hỏi lý thuyết
Công thức logarit:
Cho các số
, 0, 1a b a
và
,m n
. Ta có:
log
a
b a b
10
lg log logb b b
ln log
e
b b
log 1 0
a
log 1
a
a
log
n
a
a n
1
log log
m
a
a
b b
m
log log
n
a a
b n b
log log
m
n
a
a
n
b b
m
log ( ) log log
a a a
bc b c
log log log
a a a
b
b c
c
log
log log
a
b b
b
c a
a b
a c
log .log log
a b a
b c c
,
1b
log
log
log
a
b
a
c
c
b
,
1b
1
log
log
a
b
b
a
,
1b
Câu 1. (Đề Minh Họa 2017). Cho hai số thực
a
và
b
, với
1 a b
. Khẳng định nào dưới đây là khẳng
định đúng?
A. log 1 log
b a
a b B. 1 log log
a b
b a C. log log 1
b a
a b D. log 1 log
a b
b a
Lời giải
Chọn A
Cách 1- Tự luận: Vì
log log log 1
1 log 1 log
log log 1 log
a a a
b a
b b b
b a b
b a a b
b a a
Cách 2- Casio: Chọn
3 2
2; 3 log 2 1 log 3a b Đáp án
D.
Câu 2. (Mã 110 2017) Cho
a
là số thực dương khác
1
. Mệnh đề nào dưới đây đúng với mọi số dương
, x y
?
A.
log log log
a a a
x
x y
y
B.
log log
a a
x
x y
y
C. log log log
a a a
x
x y
y
D.
log
log
log
a
a
a
x
x
y y
Lời giải
Chọn A
Theo tính chất của logarit.
Câu 3. (THPT Minh Khai Hà Tĩnh 2019) Với mọi số thực dương
, , ,a b x y
và
, 1a b
, mệnh đề nào
sau đây sai?
A.
1 1
log
log
a
a
x x
. B.
log log log
a a a
xy x y
.
CÔNG THỨC, BIẾN ĐỔI LOGARIT
Chuyên đề 17

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
C.
log .log log
b a b
a x x
. D.
log log log
a a a
x
x y
y
.
Lời giải
Với mọi số thực dương
, , ,a b x y
và
, 1a b
. Ta có:
1
1 1
log log
log
a a
a
x
x x
. Vậy
A
sai.
Theo các tính chất logarit thì các phương án
,B C
và
D
đều đúng.
Câu 4. (Chuyên Hạ Long 2019) Trong các mệnh đề sau, mệnh đề nào đúng?
A.
log log
a a
b b
với mọi số
,a b
dương và
1
a
.
B.
1
log
log
a
b
b
a
với mọi số
,a b
dương và
1
a
.
C.
log log log
a a a
b c bc
với mọi số
,a b
dương và
1
a
.
D.
log
log
log
c
a
c
a
b
b
với mọi số
, ,a b c
dương và
1
a
.
Lời giải
Chọn A.
Câu 5. (THPT-Thang-Long-Ha-Noi- 2019) Cho
,a b
là hai số thực dương tùy ý và
1b
.Tìm kết luận
đúng.
A.
ln ln ln
a b a b
. B.
ln a b ln a.ln b
.
C.
lna ln b ln a b
. D.
b
lna
log a
ln b
.
Lời giải
Theo tính chất làm Mũ-Log.
Câu 6. (THPT Yên Phong Số 1 Bắc Ninh 2019) Cho hai số dương
, 1 .
a b a
Mệnh đề nào dưới đây
SAI?
A.
log 2a a
a
. B.
log a
a
. C.
log 1 0
a
. D.
log b
a
a b
.
Lời giải
Chọn A
Câu 7. (Sở Thanh Hóa 2019) Với các số thực dương
,a b
bất kì. Mệnh đề nào dưới đây đúng?
A.
log log .logab a b
. B.
log
log
log
a a
b b
.
C.
log log logab a b
. D.
log logb loga
a
b
.
Lời giải
Ta có
log log logab a b
.
Câu 8. (VTED 03 2019) Với các số thực dương
,a b
bất kì. Mệnh đề nào dưới đây đúng?
A.
ln ln lnab a b
B.
ln
ln
ln
a a
b b
C.
ln ln .lnab a b
D.
ln ln ln
a
b a
b
Lời giải
Chọn A.
Câu 9. (Chuyên Lê Hồng Phong Nam Định 2019) Với các số thực dương
a
,
b
bất kì. Mệnh đề nào sau
đây đúng?
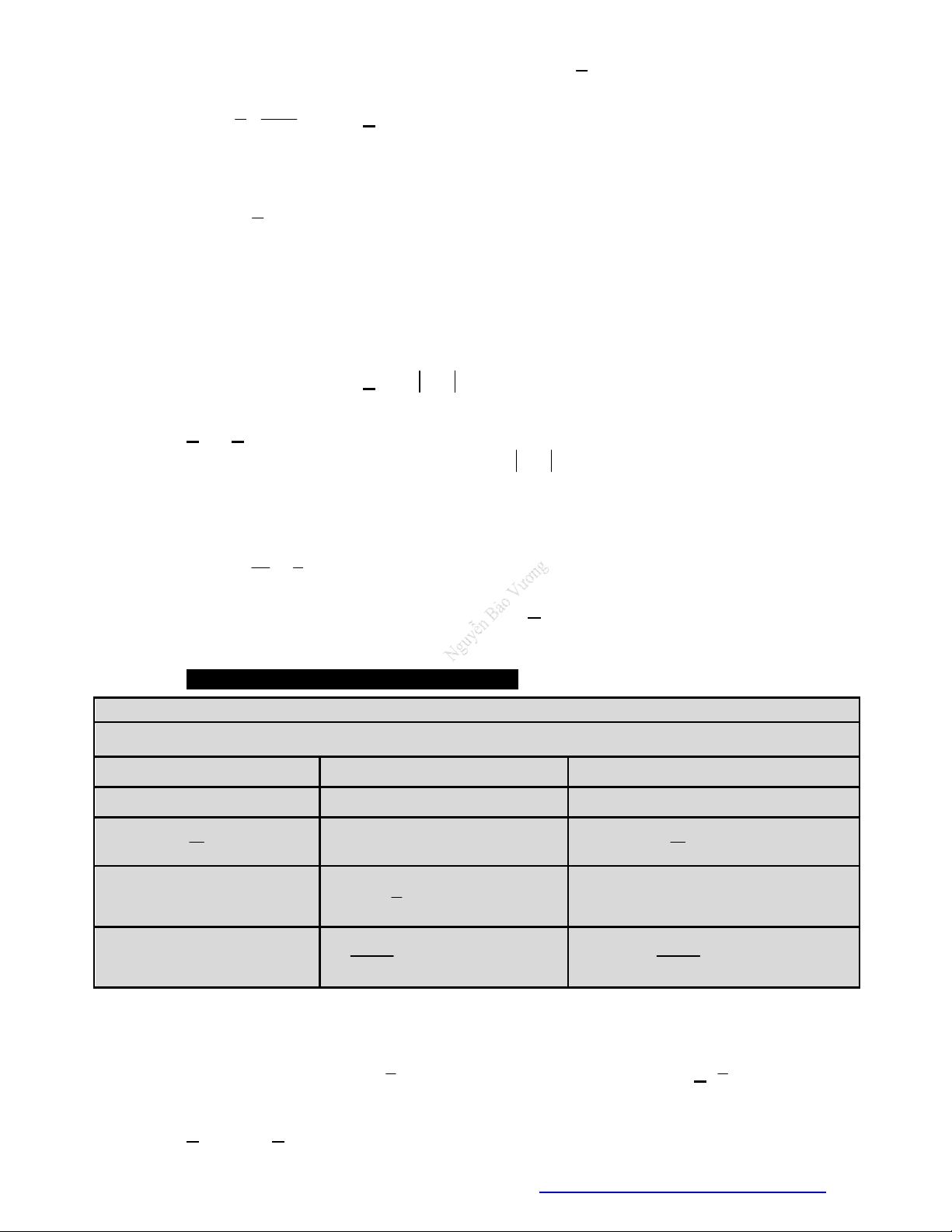
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
log log .logab a b
. B.
log log log
a
b a
b
.
C.
log
log
log
a a
b b
. D.
log log logab a b
.
Lời giải
Với các số thực dương
a
,
b
bất kì ta có:
)log log log
a
a b
b
nên B, C sai.
)log log logab a b
nên A sai, D đúng.
Vậy chọn D.
Câu 10. Cho
, , 0
a b c
,
1
a
và số
, mệnh đề nào dưới đây sai?
A.
log
c
a
a c
B.
log 1
a
a
C.
log log
a a
b b
D.
log log log
a a a
b c b c
Lời giải
Chọn D
Theo tính chất của logarit, mệnh đề sai là
log log log
a a a
b c b c
.
Câu 11. [THPT An Lão Hải Phòng 2019) Cho
, ,a b c
là các số dương
, 1
a b
. Trong các mệnh đề sau,
mệnh đề nào là mệnh đề đúng?
A.
3
1
log log .
3
a a
b
b
a
B.
log
.
b
a
a b
C.
log log 0 .
a
a
b b
D.
log log .log .
a b a
c c b
Lời giải
Dạng 2. Tính, rút gọn biểu thức chứa logarit
Công thức logarit:
Cho các số
, 0, 1a b a
và
,m n
. Ta có:
log
a
b a b
10
lg log logb b b
ln log
e
b b
log 1 0
a
log 1
a
a
log
n
a
a n
1
log log
m
a
a
b b
m
log log
n
a a
b n b
log log
m
n
a
a
n
b b
m
log ( ) log log
a a a
bc b c
log log log
a a a
b
b c
c
log
log log
a
b b
b
c a
a b
a c
log .log log
a b a
b c c
,
1
b
log
log
log
a
b
a
c
c
b
,
1
b
1
log
log
a
b
b
a
,
1
b
Câu 12. (Mã 101 - 2020 Lần 1) Với
,a b
là các số thực dương tùy ý và
1
a
,
5
log
a
b
bằng:
A.
5log
a
b
. B.
1
log
5
a
b
. C.
5 log
a
b
. D.
1
log
5
a
b
.
Lời giải
Chọn D.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 13. (Mã 102 - 2020 Lần 1) Với
a
,
b
là các số thực dương tùy ý và
1
a
,
2
log
a
b
bằng
A.
1
log
2
a
b
. B.
1
log
2
a
b
. C.
2 log
a
b
. D.
2log
a
b
.
Lời giải
Chọn B
Ta có
2
1
log log
2
a
a
b b
.
Câu 14. (Mã 103 - 2020 Lần 1) Với a,b là các số thực dương tùy ý và
1
a
,
3
log
a
b
bằng
A. 3
log
a
b
B. 3
log
a
b
C.
1
3
log
a
b
D.
1
3
log
a
b
Lời giải
Chọn D
Ta có:
3
1
log log .
3
a
a
b b
Câu 15. (Mã 102 - 2020 Lần 2) Với
a
là số thực dương tùy ý,
5
log 5a
bằng
A.
5
5 log a
. B.
5
5 log a
. C.
5
1 log a
. D.
5
1 log a
.
Lời giải
Chọn C
Ta có:
5
log 5a
5 5
log 5 log a
5
1 log a
.
Câu 16. (Mã 103 - 2020 Lần 2) Với
a
là số thực dương tùy ý,
2
log 2a
bằng
A.
2
1 log a
. B.
2
1 log a
. C.
2
2 log a
. D.
2
2 log a
.
Lời giải
Chọn A
2 2 2 2
log 2 log 2 log 1 loga a a
.
Câu 17. (Đề Minh Họa 2020 Lần 1) Với
a
là số thực dương tùy ý,
2
2
log
a
bằng:
A.
2
2 log a
. B.
2
1
log
2
a
. C.
2
2log a
. D.
2
1
log
2
a
.
Lời giải
Chọn C
Với
0; 0; 1.
a b a
Với mọi
. Ta có công thức:
log log .
a a
b b
Vậy:
2
2 2
log 2loga a
.
Câu 18. (Đề Tham Khảo 2020 Lần 2) Với
a
là hai số thực dương tùy ý,
3
2
log
a
bằng
A.
2
3
log
2
a
. B.
2
1
log
3
a
. C.
2
3 log a
. D.
2
3log a
.
Lời giải
Chọn D
Ta có:
3
2 2
log 3log .a a

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 19. (Mã 103 2019) Với
a
là số thực dương tùy ý,
3
2
log
a
bằng
A.
2
3 log .a
B.
2
3log .a
C.
2
1
log .
3
a
D.
2
1
log .
3
a
Lời giải
Chọn B
Ta có
3
2 2
log 3log .a a
Câu 20. (Mã 102 2019) Với
a
là số thực dương tùy ý,
3
5
log
a
bằng
A.
5
1
log
3
a
. B.
5
1
log
3
a
. C.
5
3 log a
. D.
5
3log a
.
Lời giải
Chọn D
3
5 5
log 3loga a
Câu 21. (Mã 104 2017) Cho
a
là số thực dương tùy ý khác
1
. Mệnh đề nào dưới đây đúng?
A.
2
log log 2
a
a
B.
2
2
1
log
log
a
a
C.
2
1
log
log 2
a
a
D.
2
log log 2
a
a
Lời giải
Chọn C
Áp dụng công thức đổi cơ số.
Câu 22. (Mã 104 2019) Với
a
là số thực dương tùy ý,
2
2
log
a
bằng:
A.
2
1
log
2
a
. B.
2
2 log a
C.
2
2log a
. D.
2
1
log
2
a
.
Lời giải
Chọn C
Vì
a
là số thực dương tùy ý nên
2
2 2
log 2loga a
.
Câu 23. (Đề Tham Khảo 2019) Với
a
,
b
là hai số dương tùy ý,
2
log
ab
bằng
A.
2 log loga b
B.
1
log log
2
a b
C.
2log loga b
D.
log 2loga b
Lời giải
Chọn D
Có
2 2
log log log log 2 logab a b a b
.
Câu 24. (Đề Tham Khảo 2017) Cho
a
là số thực dương
1
a
và
3
3
log
a
a
. Mệnh đề nào sau đây đúng?
A.
1
3
P
B.
3
P
C.
1P
D.
9
P
Lời giải
Chọn D
1
3
3
3 3
log log 9
a
a
a a
.
Câu 25. (Mã 101 2019) Với
a
là số thực dương tùy ý, bằng
2
5
log
a
A.
5
1
log .
2
a
B.
5
2 log .a
C.
5
1
log .
2
a
D.
5
2log .a
Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn D
Vì
a
là số thực dương nên ta có
2
5 5
log 2 log .a a
Câu 26. (Mã 103 2018) Với
a
là số thực dương tùy ý,
ln 7 ln 3a a
bằng
A.
ln 7
ln 3
B.
7
ln
3
C.
ln 4a
D.
ln 7
ln 3
a
a
Lời giải
Chọn B
ln 7 ln 3a a
7
ln
3
a
a
7
ln
3
.
Câu 27. (Mã 101 2018) Với
a
là số thực dương tùy ý,
ln 5 ln 3a a
bằng:
A.
5
ln
3
B.
ln5
ln3
C.
ln 5
ln 3
a
a
D.
ln 2a
Lời giải
Chọn A
ln 5 ln 3a a
5
ln
3
.
Câu 28. (Mã 102 2018) Với
a
là số thực dương tùy ý,
3
log 3a
bằng:
A.
3
1 log a
B.
3
3log a
C.
3
3 log a
D.
3
1 log a
Lời giải
Chọn D
Câu 29. Với các số thực dương
,a b
bất kì. Mệnh đề nào dưới đây đúng.
A.
ln ln ln .ab a b
B.
ln ln .ln .ab a b
C.
ln
ln .
ln
a a
b b
D.
ln ln ln .
a
b a
b
Lời giải
Chọn A
Theo tính chất của lôgarit:
0, 0 : ln ln lna b ab a b
Câu 30. (Mã 123 2017) Cho
a
là số thực dương khác
1
. Tính
log .
a
I a
A.
2.I
B.
2I
C.
1
2
I
D.
0I
Lời giải
Chọn B
Với
a
là số thực dương khác
1
ta được:
1
2
log log 2 log 2
a
a
a
I a a a
Câu 31. (Mã 104 2018) Với
a
là số thực dương tùy ý,
3
3
log
a
bằng:
A.
3
1 log a
B.
3
3 log a
C.
3
1
log a
D.
3
1 log a
Lời giải
Chọn A

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Ta có
3 3 3
3
log log 3 log a
a
3
1 log a
.
Câu 32. Với các số thực dương
, ba
bất kì. Mệnh đề nào dưới đây đúng?
A.
3
2 2 2
2
log 1 3log log
a
a b
b
. B.
3
2 2 2
2 1
log 1 log log
3
a
a b
b
.
C.
3
2 2 2
2
log 1 3log log
a
a b
b
. D.
3
2 2 2
2 1
log 1 log log
3
a
a b
b
.
Lời giải
Chọn A
Ta có:
3
3 3
2 2 2 2 2 2 2
2
log log 2 log log 2 log log 1 3log log
a
a b a b a b
b
.
Câu 33. (Mã 110 2017) Cho
log 2
a
b
và
log 3
a
c
. Tính
2 3
log
a
P b c
.
A.
13
P
B.
31
P
C.
30
P
D.
108
P
Lời giải
Chọn A
Ta có:
2 3
log 2log 3log 2.2 3.3 13
a a a
b c b c
.
Câu 34. (Mã 102 2019) Cho
a
và
b
là hai số thực dương thỏa mãn
3 2
32
a b
. Giá trị của
2 2
3log 2loga b
bằng
A.
4
. B.
5
. C.
2
. D.
32
.
Lời giải
Chọn B
Ta có:
3 2
2 2 2 2
log log 32 3log 2log 5
a b a b
Câu 35. (Đề Tham Khảo 2017) Cho
,a b
là các số thực dương thỏa mãn
1
a
,
a b
và
log 3
a
b
.
Tính
P log
b
a
b
a
.
A.
5 3 3
P
B.
1 3
P
C.
1 3
P
D.
5 3 3
P
Lời giải
Chọn C
Cách 1: Phương pháp tự luận.
1 1
log
log 1 3 1
3 1
2 2
1
log 1 3 2
log 1
log
2
a
a
a
a
a
b
b
a
P
b b
b
a
1 3
.
Cách 2: Phương pháp trắc nghiệm.
Chọn
2
a
,
3
2
b
. Bấm máy tính ta được
1 3
P
.
Câu 36. (Mã 103 2019) Cho
a
và
b
là hai số thực dương thỏa mãn
2 3
16
a b
. Giá trị của
2 2
2log 3loga b
bằng
A.
2
. B.
8
. C.
16
. D.
4
.
Lời giải
Chọn D

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
2 3
2 2 2 2
2log 3log log log 16 4
a b a b
Câu 37. (Mã 104 2017) Với các số thực dương
x
,
y
tùy ý, đặt
3
log x
,
3
log y
. Mệnh đề nào
dưới đây đúng?
A.
3
27
log
2
x
y
B.
3
27
log 9
2
x
y
C.
3
27
log
2
x
y
D.
3
27
log 9
2
x
y
Lời giải
Chọn D
3
27
log
x
y
27 27
3
log 3log
2
x y
3 3
1
log log
2 2
x y
.
Câu 38. (Mã 101 2019) Cho
a
và
b
là hai số thực dương thỏa mãn
4
16
a b
.
Giá trị của
2 2
4log loga b
bằng
A.
4
. B.
2
. C.
16
. D.
8
.
Lời giải
Chọn A
4 4 4
2 2 2 2 2 2 2
4log log log log log log 16 log 2 4
a b a b a b
.
Câu 39. (Dề Minh Họa 2017) Cho các số thực dương
,a b
với
1
a
. Khẳng định nào sau đây là khẳng
định đúng ?
A.
2
1
log log
4
a
a
ab b
B.
2
1 1
log log
2 2
a
a
ab b
C.
2
1
log log
2
a
a
ab b
D.
2
log 2 2log
a
a
ab b
Lời giải
Chọn B
Ta có:
2 2 2
1 1 1 1
log log log .log .log .log
2 2 2 2
a a a
a a a
ab a b a b b
.
Câu 40. (Mã 123 2017) Với
a
,
b
là các số thực dương tùy ý và
a
khác
1
, đặt
2
3 6
log log
a
a
P b b
.
Mệnh đề nào dưới đây đúng?
A.
6 log
a
P b
B.
27 log
a
P b
C.
15 log
a
P b
D.
9 log
a
P b
Lời giải
Chọn A
2
3 6
6
log log 3log log 6 log
2
a a a a
a
P b b b b b
.
Câu 41. (Đề Tham Khảo 2018) Với
a
là số thực dương bất kì, mệnh đề nào dưới đây đúng?
A.
1
log 3 log
3
a a
B.
log 3 3log
a a
C.
3
1
log log
3
a a
D.
3
log 3log
a a
Lời giải
Chọn D

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 42. (Mã 105 2017) Cho
3
log 2
a
và
2
1
log
2
b
. Tính
2
3 3 1
4
2 log log 3 log
I a b
.
A.
5
4
I
B.
0I
C.
4I
D.
3
2
I
Lời giải
Chọn D
2
2
3 3 1 3 3 3
2
4
2 log log 3 log 2 log log 3 log 2log
I a b a b
1 3
2
2 2
.
Câu 43. (Mã 105 2017) Cho
a
là số thực dương khác
2
. Tính
2
2
log
4
a
a
I
.
A.
2I
B.
1
2
I
C.
2I
D.
1
2
I
Lời giải
Chọn A
2
2
2 2
log log 2
4 2
a a
a a
I
Câu 44. (Mã 104 2017) Với mọi
a
,
b
,
x
là các số thực dương thoả mãn
2 2 2
log 5log 3logx a b
.
Mệnh đề nào dưới đây đúng?
A.
5 3x a b
B.
5 3
x a b
C.
5 3
x a b
D.
3 5x a b
Lời giải
Chọn C
Có
5 3 5 3 5 3
2 2 2 2 2 2
log 5log 3log log log log
x a b a b a b x a b
.
Câu 45. (Mã 104 2019) Cho
a
và
b
là hai số thực dương thỏa mãn
3
8
ab
. Giá trị của
2 2
log 3loga b
bằng
A.
6
. B.
2
. C.
3
. D.
8
.
Lời giải
Chọn C
Ta có
3 3
2 2 2 2 2 2
log 3log log log log log 8 3
a b a b ab
.
Câu 46. (Mã 105 2017) Với mọi số thực dương
a
và
b
thỏa mãn
2 2
8a b ab
, mệnh đề nào dưới đây
đúng?
A.
1
log log log
2
a b a b
B.
1
log log log
2
a b a b
C.
1
log 1 log log
2
a b a b
D.
log 1 log loga b a b
Lời giải:
Chọn C
Ta có
2
2 2
8 10a b ab a b ab
.
Lấy log cơ số
10
hai vế ta được:
2
log log 10 2log log10 log loga b ab a b a b
.
Hay
1
log 1 log log
2
a b a b
.
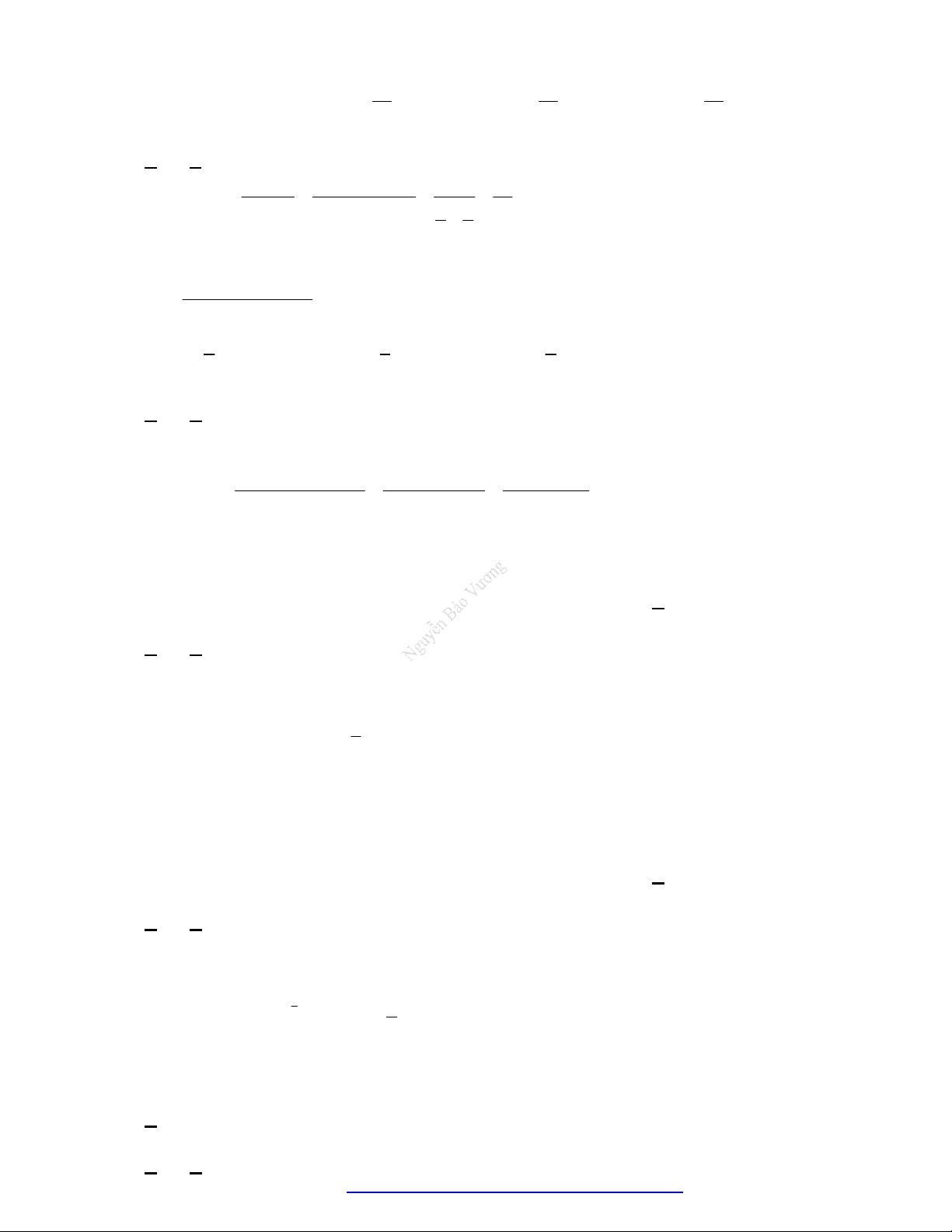
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 47. (Mã 123 2017) Cho
log 3,log 4
a b
x x
với
,a b
là các số thực lớn hơn 1. Tính
log .
ab
P x
A.
12P
B.
12
7
P
C.
7
12
P
D.
1
12
P
Lời giải
Chọn B
1 1 1 12
log
1 1
log log log 7
3 4
ab
x x x
P x
ab a b
Câu 48. (Mã 110 2017) Cho
, x y
là các số thực lớn hơn
1
thoả mãn
2 2
9 6x y xy
. Tính
12 12
12
1 log log
2log 3
x y
M
x y
.
A.
1
2
M
. B.
1
3
M
. C.
1
4
M
. D.
1M
Lời giải
Chọn D
Ta có
2
2 2
9 6 3 0 3x y xy x y x y
.
Khi đó
2
12
12
12 12
2
2
12
12
12
log 36
log 12
1 log log
1
2log 3
log 36
log 3
y
xy
x y
M
x y
y
x y
.
Câu 49. (Đề Minh Họa 2020 Lần 1) Xét tất cả các số dương
a
và
b
thỏa mãn
2 8
log log ( )a ab
. Mệnh
đề nào dưới đây đúng?
A.
2
a b
. B.
3
a b
. C.
a b
. D.
2
a b
.
Lời giải
Chọn D
Theo đề ta có:
2 8 2 2 2 2
3 3 2
2 2
1
log log ( ) log log ( ) 3log log ( )
3
log log ( )
a ab a ab a ab
a ab a ab a b
Câu 50. (Đề Tham Khảo 2020 Lần 2) Xét số thực
a
và
b
thỏa mãn
3 9
log 3 .9 log 3
a b
. Mệnh đề nào
dưới đây đúng
A.
2 2
a b
. B.
4 2 1
a b
. C.
4 1ab
. D.
2 4 1
a b
.
Lời giải
Chọn D
Ta có:
2
2
3 9 3
3
1
2
2
3 3
log 3 .9 log 3 log 3 .3 log 3
1
log 3 log 3 2 2 4 1.
2
a b a b
a b
a b a b
Câu 51. (Mã 102 - 2020 Lần 1) Cho
a
và
b
là các số thực dương thỏa mãn
2
log ( )
4 3
ab
a
. Giá trị của
2
ab
bằng
A.
3
. B.
6
. C.
2
. D.
12
.
Lời giải
Chọn A

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Từ giả thiết ta có :
2
log ( )
4 3
ab
a
2 2 2
log ( ).log 4 log (3 )ab a
2 2 2 2
2(log log ) log log 3
a b a
2 2 2
log 2log log 3
a b
2
2 2
log ( ) log 3
ab
2
3
ab
Câu 52. (Mã 103 - 2020 Lần 1) Cho a và b là hai số thực dương thỏa mãn
3
log ( )
9
4
ab
a
. Giá trị của
2
ab
bằng
A.
3
. B. 6. C. 2 D. 4
Lời giải
Chọn D
Ta có :
3
log
3 3
9 4 2log log 4
ab
a ab a
2 2
3 3
log log 4 a b a
2 2
4 a b a
2
4
ab
.
Câu 53. (Mã 102 - 2020 Lần 2) Với
,a b
là các số thực dương tùy ý thỏa mãn
3 9
log 2log 2
a b
, mệnh
đề nào dưới đây đúng?
A.
2
9a b
. B.
9a b
. C.
6a b
. D.
2
9a b
.
Lời giải
Chọn B
Ta có:
3 9
log 2log 2
a b
3 3
log log 2
a b
3
log 2
a
b
9a b
.
Câu 54. (Mã 103 - 2020 Lần 2) Với
,a b
là các số thực dương tùy ý thỏa mãn
3 9
log 2log 3
a b
, mệnh
đề nào dưới đây đúng?
A.
27a b
. B.
9a b
. C.
4
27a b
. D.
2
27a b
.
Lời giải
Chọn A
Ta có:
3 9 3 3 3
log 2log 3 log log 3 log 3 27 27
a a
a b a b a b
b b
.
Câu 55. (Mã 104 - 2020 Lần 2) Với
,a b
là các số thực dương tùy ý thỏa mãn
2 4
log 2log 4
a b
, mệnh
đề nào dưới đây đúng?
A.
2
16a b
. B.
8a b
. C.
16a b
. D.
4
16a b
.
Lời giải
Chọn C
Ta có
2 4
log 2log 4
a b

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
2
2 2
2 2
2
4
log 2log 4
1
log 2. log 4
2
log log 4
log 4
2
16
a b
a b
a b
a
b
a
b
a b
Câu 56. (Chuyên Bắc Giang 2019) Cho các số thực dương
,a b
thỏa mãn
ln ;ln
a x b y
. Tính
3 2
ln
a b
A.
2 3
P x y
B.
6P xy
C.
3 2P x y
D.
2 2
P x y
Lời giải
Chọn C
Ta có
3 2 3 2
ln ln ln 3ln 2ln 3 2a b a b a b x y
Câu 57. (Chuyên Vĩnh Phúc 2019) Giá trị của biểu thức
2 2 2 2
log 2 log 4 log 8 ... log 256
M
bằng
A.
48
B.
56
C.
36
D.
2
8log 256
Lời giải
Chọn C
Ta có
1 2 3 8
2 2 2 2 2 2
log 2 log 4 log 8 ... log 256 log 2.4.8...256 log 2 .
2 .2 ...2
M
1 2 3 ... 8
2 2
log 2 1 2 3 ... 8 log 2 1 2 3 ... 8 36
.
Câu 58. (THCS - THPT Nguyễn Khuyến 2019) Cho
8
log
c m
và
3
log 2
c
n
. Khẳng định đúng là
A.
2
1
log
9
mn c
. B.
9
mn
. C.
2
9logmn c
. D.
1
9
mn
.
Lời giải
3
8 2
1 1 1
log .log 2 log . log 2
3 3 9
c
c
mn c c
.
Câu 59. (THPT Lương Thế Vinh Hà Nội 2019) Cho
0, 1
a a
và
log 1,log 4
a a
x y
. Tính
2 3
log
a
P x y
A.
18
P
. B.
6
P
. C.
14P
. D.
10
P
.
Lời giải
Ta có
2 3 2 3
log . log log
a a a
x y x y
2log 3log
a a
x y
2.( 1) 3.4 10
.
Câu 60. (Sở Bình Phước 2019) Với
a
và
b
là hai số thực dương tùy ý;
3 4
2
log
a b
bằng
A.
2 2
1 1
log log
3 4
a b
B.
2 2
3log 4loga b
C.
2 4
2 log log
a b
D.
2 2
4log 3loga b
Lời giải
Chọn B
Ta có:
3 4 3 4
2 2 2 2 2
log log log 3log 4loga b a b a b
nên B đúng.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 61. (Chuyên Hạ Long -2019) Cho
20
7
4
3 27 243
P
. Tính
3
log P
?
A.
45
28
. B.
9
112
. C.
45
56
. D. Đáp án khác.
Lời giải
Ta có:
20
7
4
3 27 243
P
1 1 1 1 1 1
9
. . .
20 20 7 20 7 4
112
3 .27 .243 3
P
9
112
3 3
9
log log 3
112
P
.
Câu 62. (THPT Cẩm Giàng 2 2019) Cho các số dương
, , ,a b c d
. Biểu thức
ln ln ln ln
a b c d
S
b c d a
bằng
A. 1. B. 0. C.
ln
a b c d
b c d a
. D.
ln
abcd
.
Lời giải
Cách 1:
Ta có
ln ln ln ln ln ln1 0
a b c d a b c d
S
b c d a b c d a
.
Cách 2:
Ta có:
ln ln ln ln ln ln ln ln ln ln ln ln 0
a b c d
S a b b c c d d a
b c d a
.
Câu 63. Cho
x
,
y
là các số thực dương tùy ý, đặt
3
log
x a
,
3
log
y b
. Chọn mệnh đề đúng.
A.
1
3
27
1
log
3
x
a b
y
. B.
1
3
27
1
log
3
x
a b
y
.
C.
1
3
27
1
log
3
x
a b
y
. D.
1
3
27
1
log
3
x
a b
y
.
Lời giải
Do
x
,
y
là các số thực dương nên ta có:
1 3
3 3
27
1
log log
3
x x
y y
3
3 3
1
log log
3
x y
3 3
1
log 3log
3
x y
3 3
1
log log
3
x y
1
3
a b
.
Câu 64. (THPT Bạch Đằng Quảng Ninh 2019) Với
,a b
là các số thực dương tùy ý và
a
khác
1
, đặt
2
3 6
log log
a
a
P b b
. Mệnh đề nào dưới đây đúng?
A.
27log
a
P b
. B.
15log
a
P b
. C.
9log
a
P b
. D.
6log
a
P b
.
Lời giải
Ta có
2
3 6
1
log log 3log 6. log 6log .
2
a a a a
a
P b b b b b
Câu 65. (THPT Quang Trung Đống Đa Hà Nội 2019) Với các số thực dương
,a b
bất kỳ
1
a
. Mệnh
đề nào dưới đây đúng?
A.
3
2
1
log 2log .
3
a a
a
b
b
B.
3
2
1
log 3 log .
2
a a
a
b
b

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
C.
3
2
1 1
log log .
3 2
a a
a
b
b
D.
3
2
log 3 2log .
a a
a
b
b
Lời giải
Ta có:
3
2
3
2
1
3
log log log
=log 2log
1 1
= log 2log 2log
3 3
a a a
a a
a a a
a
a b
b
a b
a b b
Câu 66. (Chuyên Lê Hồng Phong Nam Định 2019) Cho các số thực dương
, ,a b c
với
a
và
b
khác
1
.
Khẳng định nào sau đây là đúng?
A.
2
log .log log
a a
b
b c c
. B.
2
1
log .log log
4
a a
b
b c c
.
C.
2
log .log 4log
a a
b
b c c
. D.
2
log .log 2log
a a
b
b c c
.
Lời giải
Chọn C
Ta có:
1
2
2
log .log 2log .log
a a
b
b
b c b c
2log .2log
a b
b c
4log .log
a b
b c
4log
a
c
.
Câu 67. (Chuyên Bắc Giang -2019) Giả sử
,a b
là các số thực dương bất kỳ. Mệnh đề nào sau đây sai?
A.
2 2
log 10 2 log
ab ab
B.
2 2
log 10 1 log logab a b
C.
2
log 10 2 2log
ab ab
D.
2
log 10 2 1 log logab a b
Lời giải
Chọn B
2 2 2
2
log 10 log10 log 2 log
ab ab ab A
đúng
2 2
2
1 log log log 10 1 log log log 10 log 10
a b ab a b ab ab B
sai
2 2
2
log 10 log10 log 2 2log
ab ab ab C
đúng
2 2
2
log 10 log10 log 2 2log 2 1 log log
ab ab ab a b D
đúng
Câu 68. (THPT Lương Thế Vinh Hà Nội 2019) Cho
log 3,log 2
a a
b c
. Khi đó
3 2
log
a
a b c
bằng
bao nhiêu?
A.
13
B.
5
C.
8
D.
10
Lời giải
Chọn C
Ta có
3 2
log
a
a b c
3 2
log log log
a a a
a b c
1
3 2log log
2
a a
b c
1
3 2.3 .2 8
2
.
Câu 69. (THPT Lê Quy Đôn Điện Biên 2019) Rút gọn biểu thức
9 1
3
3
3log 6log 3 log .
9
x
M x x
A.
3
log 3M x
B.
3
2 log
3
x
M
C.
3
log
3
x
M
D.
3
1 logM x
Lời giải
Chọn A

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
ĐK:
0
x
.
3 3 3 3 3 3
3log 3 1 log log 2 1 log 1 log log 3 .M x x x x x x
Câu 70. (Chuyên Lê Thánh Tông 2019) Cho
2
8 4
log log 5
x y
và
2
8 4
log log 7
y x
. Tìm giá trị
của biểu thức
P x y
.
A.
56
P
. B.
16
P
. C.
8
P
. D.
64
P
.
Lời giải
Điều kiên:
, 0
x y
Cộng vế với vế của hai phương trình, ta được:
2 2
8 4 2
log log 12 log 9 512
xy x y xy xy
(1)
Trừ vế với vế của hai phương trình, ta được:
2
8 4 2
2
log log 2 log 3 8 8
x y x x
x y
y y y
x
. (2)
Từ (1) và (2) suy ra
8 64 56
y x P
.
Câu 71. (Hsg Bắc Ninh 2019) Cho hai số thực dương
,a b
.Nếu viết
6 3 2
2 2 4
64
log 1 log log ( , )
a b
x a y b x y
ab
thì biểu thức
P xy
có giá trị bằng bao nhiêu?
A.
1
3
P
B.
2
3
P
C.
1
12
P
D.
1
12
P
Lời giải
Ta có
1
6 3 2
6
2 2 2 2 2 2
64 1 1
log log 64 log log log log
2 3
a b
a b a b
ab
2 4
1 4
1 log log
2 3
a b
. Khi đó
1 4 2
; y
2 3 3
x P xy
Câu 72. Cho
700
log 490
log7
b
a
c
với
, ,a b c
là các số nguyên. Tính tổng
T a b c
.
A.
7
T
. B.
3
T
. C.
2T
. D.
1T
.
Lời giải
Ta có:
700
log 490 log10 log 49 1 2log 7 4 2log7 3 3
log 490 2
log700 log100 log 7 2 log 7 2 log 7 2 log 7
Suy ra
2, 3, 2
a b c
Vậy
1T
.
Câu 73. Cho
, a b
là hai số thưc dương thỏa mãn
2 2
14a b ab
. Khẳng định nào sau đây sai?
A.
2 2 2
2log 4 log loga b a b
. B.
ln ln
ln
4 2
a b a b
.
C.
2log log log
4
a b
a b
. D.
4 4 4
2log 4 log loga b a b
.
Lời giải
Ta có
2
2 2
14 16a b ab a b ab
.
Suy ra
2
4 4 4 4 4
log log 16 2log 2 log loga b ab a b a b
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 74. Cho
,x y
là các số thực dương tùy ý, đặt
3
log
x a
,
3
log
y b
. Chọn mệnh đề đúng.
A.
1
3
27
1
log
3
x
a b
y
. B.
1
3
27
1
log
3
x
a b
y
.
C.
1
3
27
1
log
3
x
a b
y
. D.
1
3
27
1
log
3
x
a b
y
.
Lời giải
3
3
1 3 3 3 3 3
3 3 3
3
27
1 1 1 1
log log log log log log log
3 3 3 3
x x x
x y x y a b
y y y
.
Câu 75. (Sở Vĩnh Phúc 2019) Cho
log
a
x
,
log
b
x
. Khi đó
2
2
log
ab
x
bằng.
A.
αβ
α+β
. B.
2
αβ
2
α+β
. C.
2
2
α+β
. D.
2
α+β
α+2β
.
Lời giải
Ta có :
2 2
2
log 2log
ab ab
x x
2
1
2.
log
x
ab
2
2
log log
x x
a b
2
1 1
2.
log log
a b
x x
2 2
1 2
2
.
Câu 76. (THPT Bạch Đằng Quảng Ninh 2019) Tính giá trị biểu thức
2
3
10 2 2
log log log
a b
a
a
P a b b
b
(với
0 1;0 1a b
).
A.
3
. B.
1
. C.
2
. D.
2
.
Lời giải
Ta có:
2
3
10 2 2
log log log 5 log 2 log 6 1
a a
a b
a
a
P a b b b b
b
.
Câu 77. (Toán Học Tuổi Trẻ 2019) Đặt
3
6
3
log 7
log 56,
log 2
b
M N a
c
với
, ,
a b c R
. Bộ số
, ,a b c
nào dưới đây để có
?M N
A.
3, 3, 1
a b c
. B.
3, 2, 1
a b c
.
C.
1, 2, 3
a b c
. D.
1, 3, 2
a b c
.
Lời giải
Ta có:
3
3 3
3 3 3 3 3
6
3 3 3 3 3
3 1 log 2 log 7 3
log 56 log 2 .7 3log 2 log 7 log 7 3
log 56 3
log 6 1 log 2 1 log 2 1 log 2 log 2 1
M
Vậy
3
3
1
a
M N b
c

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Câu 78. (THP
T Yên Phong 1 Bắc Ninh 2019) Tính
1
2 3 98 99
log log log ... log log .
2 3 4 99 100
T
A.
1
10
. B.
2
. C.
1
10
0
. D.
2
.
Lờ
i giải
2
1
2 3 98 99 1 2 3 98 99 1
l
og log log ... log log log . . ... . log log10 2
2
3 4 99 100 2 3 4 99 100 100
T
.
Câu 79. Cho
, , 0; và , 1
a b x a b b x
thỏa
mãn
2
2
1
lo
g log
3 log
x
x
b
a
b
a
x
.
Khi
đó biểu thức
2
2
2
2 3
( 2 )
a ab b
P
a
b
c
ó giá trị bằng:
A.
5
4
P
. B.
2
3
P
. C.
1
6
15
P
. D.
4
5
P
.
Lờ
i giải
2
2 1 2
log log log log log
3 log 3
x
x x x x
b
a b a b
a a b
x
2
2
2
3 5 4 0 4 0 4a b ab a ab b a b a b a b
(do
a b
).
2 2 2 2 2
2 2
2
3 32 12 5
( 2 ) 36 4
a
ab b b b b
P
a b b
.
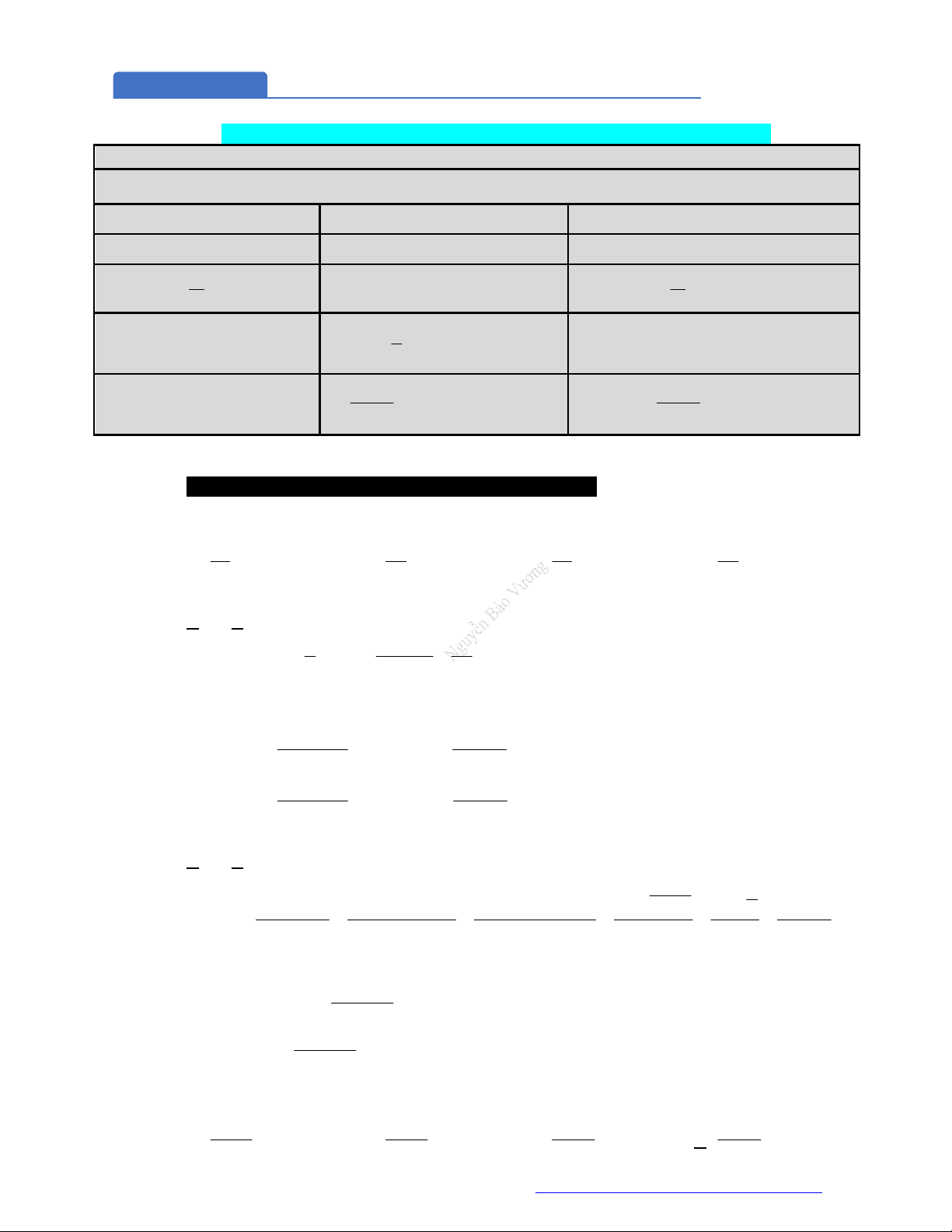
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ MỨC 7-8 ĐIỂM
Công thức logarit:
Chocácsố
, 0, 1a b a
và
,m n
.Tacó:
log
a
b a b
10
lg log logb b b
ln log
e
b b
log 1 0
a
log 1
a
a
log
n
a
a n
1
log log
m
a
a
b b
m
log log
n
a a
b n b
log log
m
n
a
a
n
b b
m
log ( ) log log
a a a
bc b c
log log log
a a a
b
b c
c
log
log log
a
b b
b
c a
a b
a c
log .log log
a b a
b c c
,
1b
log
log
log
a
b
a
c
c
b
,
1b
1
log
log
a
b
b
a
,
1b
Dạng. Biểu diễn biểu thức logarit này theo logarit khác
Câu 1. (ĐềThamKhảo2019)Đặt
3
log 2 a khiđó
16
log 27 bằng
A.
3
4
a
B.
3
4a
C.
4
3a
D.
4
3
a
lờigiải
ChọnB
Tacó
16 2
3
3 3 3
log 27 log 3
4 4.log 2 4a
Câu 2. (ĐềMinhHọa2017)Đặt
2 5
log 3, log 3.a b Hãybiểudiễn
6
log 45theo
a
và
b
.
A.
2
6
2 2
log 45
a ab
ab
B.
6
2
log 45
a ab
ab b
C.
2
6
2 2
log 45
a ab
ab b
D.
6
2
log 45
a ab
ab
Lờigiải
ChọnB
2
2
2
2 3 5
2 2
6
2 2
log 3
2
2
log 3 .5
2 log 3.log 5 log 3
2log 3 log 5 2
log 45
log 2.3 1 log 3 1 1 1
a
a
a
a
a ab
b
a a a ab b
CASIO:Sto\Gán
2 5
log 3, log 3A B bằngcách:Nhập
2
log 3\shift\Sto\
A
tươngtự
B
ThửtừngđápánA:
6
2
log 45 1,34
A AB
AB
(Loại)
ThửđápánC:
6
2
log 45 0
A AB
AB
(chọn).
Câu 3. (ChuyênĐạiHọcVinh2019)Đặt
3
log 2a=
,khiđó
6
log 48
bằng
A.
3 1
1
a
a
-
-
B.
3 1
1
a
a
+
+
C.
4 1
1
a
a
-
-
D.
4 1
1
a
a
+
+
CÔNG THỨC, BIẾN ĐỔI LOGARIT
Chuyên đề 17

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lờigiải
ChọnD
Cách1:Giảitrựctiếp
( )
3
6 6 6 6
8
2
2
1 1 1
log 48 log 6.8 log 6 log 8 1 1 1
1
log 6 log 2.3
1 log 3
3
= = + = + = + = +
+
( )
2
2
1
4
1 log 3 3
4 1
1
1
1 log 3
1
a
a
a
a
+
+ +
+
= = =
+
+
+
.ChọnđápánD
Cách2:DùngmáytínhCasio
Tacó
6
log 48 2.1605584217
=
.Thay
3
log 2 0.63092975375
a= =
vào4đápánthìtachọnđáp
ánDvì
4 1
2.1605584217
1
a
a
+
=
+
Câu 4. (Chuyên Phan Bội Châu -2019) Cho
3
log 5 ,a
3
log 6 ,b
3
log 22
c
. Tính
3
90
log
11
P
theo
,a
,b
c
?
A.
2
P a b c
. B.
2
P a b c
. C.
2
P a b c
. D.
2
P a b c
.
Lờigiải
Tacó
3 3 3
log 6 log 2 1 log 2 1b b b
,
3 3 3
log 22 log 2 log 11
c c
3 3
log 11 log 2 1c c b
.
Khiđó
3 3 3 3 3 3
90
log log 90 log 11 2 log 2 log 5 log 11 2
11
P b a c
.
Câu 5. (LươngThếVinhHàNội2019)Với
27
log 5
a
,
3
log 7
b
và
2
log 3
c
,giátrịcủa
6
log 35
bằng
A.
3
1
a b c
c
B.
3
1
a b c
b
C.
3
1
a b c
a
D.
3
1
b a c
c
Lờigiải
ChọnA
Tacó:
27 3 3 5
1 1
log 5 log 5 3 log 5 log 3
3 3
a a a
a
3 7
1
log 7 log 3b
b
;
2 3 2 7
1
log 3.log 7 log 7 log 2bc
bc
;
3 2 2 5
1
3 log 5.log 3 log 5 log 2
3
ac
ac
6 6 6
5 7 5 5 7 7
1 1 1 1
log 35 log 5 log 7
log 6 log 6 log 2 log 3 log 3 log 2
3
1 1
1 1 1 1
1
3 3
a b c
c
ac a b bc

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 6. (THPTNguyễnKhuyến2019)Đặt
2
log 3
a
;
5
log 3
b
.Nếubiểudiễn
6
log 45
a m nb
b a p
thì
m n p
bằng
A.
3
B.
4
C.
6
D.
3
Lờigiải
ChọnB
3 3 3
6
3 3 3
1
2
2 1
log 45 log 9 log 5
log 45
1
log 6 log 2 log 3 1
1
a b
b
b a
a
Suyra
1, 2, 1 4
m n p m n p
Câu 7. (THPT Thiệu Hóa – Thanh Hóa 2019) Cho cácsố thực dương
a
,
b
thỏa mãn
3
log
a x
,
3
log
b y
.Tính
4 5
3
log 3
P a b
.
A.
4 5
3
P x y
B.
4 5
3
P x y
C.
60P xy
D.
1 4 5P x y
Lờigiải
ChọnD
4 5 4 5
3 3 3 3 3 3
log 3 log 3 log log 1 4log 5log 1 4 5P a b a b a b x y
.
Câu 8. (THPTAnLãoHảiPhòng2019)Biết
6 6
log 3 ,log 5
a b
.Tính
3
log 5
theo
,a b
A.
b
a
B.
1
b
a
C.
1
b
a
D.
1
b
a
Lờigiải
ChọnA
6 6 3
6
log 3 3 6 ,log 5 5 6 log 5 log 6
a
a b b
b
a b
a
Câu 9. Cho
12
log 3
a
.Tính
24
log 18
theo
a
.
A.
3 1
3
a
a
. B.
3 1
3
a
a
. C.
3 1
3
a
a
. D.
3 1
3
a
a
.
Lờigiải
ChọnB
Tacó:
12
log 3
a
2
2
log 3
log 12
2
2
2
log 3
log 2 .3
2
2
2 2
log 3
log 2 log 3
2
2
log 3
2 log 3
2
2
log 3
1
a
a
.
Tacó:
2
24
2
log 18
log 18
log 24
2
2
3
2
log 2.3
log 2 .3
2
2
1 2log 3
3 log 3
2
1 2.
1
2
3
1
a
a
a
a
3 1
3
a
a
.
Vậy
24
log 18
3 1
3
a
a
.
Câu 10. (THPTGiaLộcHảiDương2019)Đặt
2
log 3
a
và
5
log 3
b
.Hãybiểudiễn
6
log 45
theo
a
và
b
.
A.
2
6
2 2
log 45
a ab
ab
.B.
6
2
log 45
a ab
ab
.
C.
6
2
log 45
a ab
ab b
. D.
2
6
2 2
log 45
a ab
ab b
.
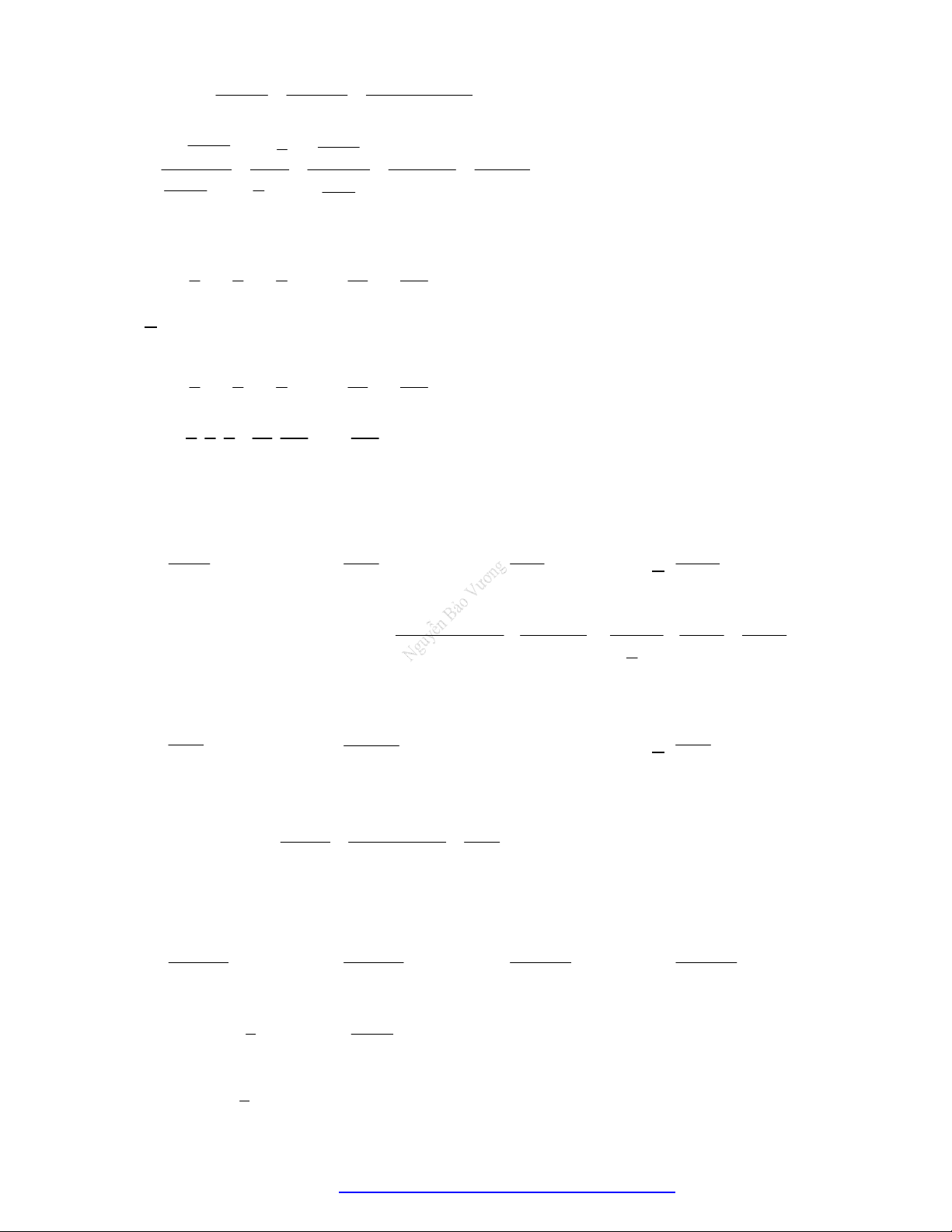
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lờigiải
2 2
3 3 3 3
6
3 3 3 3
5
2
log 45 log 3 .5 log 3 log 5
log 45
log 6 log 2.3 log 2 log 3
1
2 1
1
2
2
2 1
log 3
2
1 1
1
1
1 1
log 3
b
b a
a ab
b
b
a
b a b ab
a
a
Câu 11. (HSG Bắc Ninh 2019) Đặt
ln 2, ln 5
a b
, hãy biểu diễn
1 2 3 98 99
ln ln ln ... ln ln
2 3 4 99 100
I
theo
a
và
b
.
A.
2
a b
B.
2
a b
C.
2
a b
D.
2
a b
Lờigiải
1 2 3 98 99
ln ln ln ... ln ln
2 3 4 99 100
I
2
1 2 3 98 99 1
ln . . ... . ln ln10
2 3 4 99 100 100
2 ln10 2 ln 2 ln 5 2
a b
.
Câu 12. (ChuyênBắcNinh2019)Đặt
2 3
log 3; log 5
a b
Biểudiễnđúngcủa
20
log 12
theo
,a b
là
A.
1
2
ab
b
. B.
2
a b
b
. C.
1
2
a
b
. D.
2
2
a
ab
.
Lờigiải
Tacó
20 20 20
3 3 2
1 2
log 12 log 3 2log 2
2log 2 log 5 log 5 2
1 2 2
1
2 2
2.
a
ab ab
b
a
.
Câu 13. (SởBìnhPhước2019)Cho
2 2
log 3 , log 5
a b
,khiđó
15
log 8
bằng
A.
3
a b
B.
1
3( )a b
C.
3( )a b
D.
3
a b
Lờigiải
ChọnD
15 15
2 2 2
3 3 3
log 8 3log 2
log 15 log 3 log 5
a b
Câu 14. (ChuyênLêQuýĐônĐiệnBiên2019)Giảsử
27 8 2
log 5 ; log 7 ; log 3
a b c
.Hãybiểudiễn
12
log 35
theo
, ,a b c
?
A.
3 3
2
b ac
c
. B.
3 3
1
b ac
c
. C.
3 2
3
b ac
c
. D.
3 2
2
b ac
c
.
Lờigiải
2
27 3 2
2
log 5
1
log 5 log 5 3 log 5 3 .
3 log 3
a a a ac
8 2 2
1
log 7 log 7 log 7 3 .
3
b b b

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Xét
2
2 2 2
12
2
2 2
2
log 5.7
log 35 log 5 log 7
3 3
log 35 .
log 12 log 3 2 2
log 3.2
ac b
c
Câu 15. (Chuyen Phan Bội Châu Nghệ An 2019) Cho
3
log 5
a
,
3
log 6
b
,
3
log 22
c
. Tính
3
90
log
11
P
theo
a
,
b
,
c
.
A.
2
P a b c
. B.
2
P a b c
. C.
2
P a b c
. D.
2
P a b c
.
Lờigiải
Tacó:
3
90
log
11
P
3
180
log
22
3 3
log 180 log 22
3 3
log 36.5 log 22
3 3 3
log 36 log 5 log 22
2
3 3 3
log 6 log 5 log 22
3 3 3
2log 6 log 5 log 22
2
a b c
.
Vậy
2
P a b c
.
Câu 16. (THPT-YênĐịnhThanhHóa2019)Đặt
2 3
log 3; log 5
a b
.Biểudiễn
20
log 12
theo
,a b
.
A.
20
log 12
2
a b
b
. B.
20
1
log 12
2
ab
b
. C.
20
1
log 12
2
a
b
. D.
20
2
log 12
2
a
ab
.
Lờigiải
Tacó
2 2 2 2
20
2 2 2 2 3
log 12 log 4.3 2 log 3 2 log 3
2
log 12
log 20 log 4.5 2 log 5 2 log 3.log 5 2
a
ab
.
Câu 17. (SởHàNội2019)Nếu
2
log 3
a
thì
72
log 108
bằng
A.
2
3
a
a
. B.
2 3
3 2
a
a
. C.
3 2
2 3
a
a
. D.
2 3
2 2
a
a
.
Lờigiải
Tacó
2
72
2
log 108
log 108
log 72
2 3
2
3 2
2
log 2 .3
log 2 .3
2
2
2 3log 3
3 2log 3
2 3
3 2
a
a
.
Câu 18. (Chuyên Trần Phú Hải Phòng 2019) Cho
30 30
log 3 ;log 5
a b
. Tính
30
log 1350
theo
,a b
;
30
log 1350
bằng
A.
2
a b
B.
2 1a b
C.
2 1a b
D.
2 2
a b
Lờigiải
Tacó
2
1350 30.45 30.9.5 30.3 .5
Nên
2
30 30
log 1350 log 30.3 .5
2
30 30 30
log 30 log 3 log 5
30 30
1 2log 3 log 5
1 2
a b
Câu 19. (THPT Quang Trung Đống Đa Hà Nội 2019) Đặt
2m log
và
7n log
. Hãy biểu diễn
6125 7
log
theo
m
và
n
.
A.
6 6 5
2
m n
. B.
1
(6 6 5 )
2
n m
. C.
5 6 6
m n
. D.
6 5 6
2
n m
.
Lờigiải
Tacó
5
3
2
5 10 5
log6125 7 log5 7 3log5 log7 3log log7
2 2 2
5 6 5 6
3(l log2) log
5
7
2
3 1
22
m
n m
n
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy
6 5 6
log6125 7
2
n m
.
Câu 20. (LươngThếVinhHàNội2019)Cho
27
log 5
a
,
3
log 7
b
,
2
log 3
c
.Tính
6
log 35
theo
a
,
b
và
c
.
A.
3
1
a b c
c
. B.
3
1
a b c
b
. C.
3
1
a b c
a
. D.
3
1
b a c
c
.
Lờigiải
Chọn D.
Theogiảthiết,tacó
27 3 3
1
log 5 log 5 log 5 3
3
a a a
.
Tacó
2 2 3
log 5 log 3 log 5 3ac
và
2 2 3
log 7 log 3 log 7
bc
.
Vậy
2 2 2
6
2 2 2
3
log 35 log 5 log 7 3
log 35
log 6 log 2 log 3 1 1
a b c
ac bc
c c
.
Câu 21. (SởThanhHóa2019)Cho
2
loga m
và
log 16
m
A m
,với
0 1
m
.Mệnhđềnàosauđây
đúng?
A.
4
.
a
A
a
B.
4
.
a
A
a
C.
(4 ) .A a a
D.
(4 ) .A a a
Lờigiải
Tacó
2 2 2
2 2
log 16 log 16 log
4
log 16 .
log log
m
m m
a
A m
m m a
Câu 22. (THPTNgôSĩLiênBắcGiang2019)Biết
3
15
log a
,tính
25
81
P log
theo
a
tađược
A.
2 1
P a
B.
2( 1)
P a
C.
2
1
P
a
D.
2
1a
Lờigiải
ChọnD
Tacó
3 3 3
log 15 1 5 5 1a log a log a
3
25
3 3
81
4 4 2
= log 81
25 2 5 2 1 1
log
P
log log a a
Câu 23. (ChuyênPhanBộiChâu2019)Cho
3
log 5
a
,
3
log 6
b
,
3
log 22
c
.Tính
3
90
log
11
P
theo
, ,a b c
.
A.
2
P a b c
B.
2
P a b c
C.
2
P a b c
D.
2
P a b c
Lờigiải
Tacó:
3 3 3 3 3 3
log 90 log 11 log 90 log 2 log 11 log 2
P
3 3 3 3 3 3 3
log 180 log 2 log 5.36 log 2 log 5 2log 6 log 2 2a b c
Câu 24. (ChuyênĐHSPHàNội2019)Nếu
3
log 5
a
thì
45
log 75
bằng
A.
2
1 2
a
a
. B.
1
2
a
a
. C.
1 2
2
a
a
. D.
1 2
1
a
a
.
Lờigiải
Tacó
45 45 45
log 75 2.log 5 log 3
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Và
45 45
5 5 3 3
1 1 1 1 1 1
log 5 ;log 3
2
log 45 2log 3 1 2 log 45 2 log 5 2
1
a
a a
a
.
Dođó
45
2 1 1 2
log 75
2 2 2
a a
a a a
.
Câu 25. (Chuyên Phan Bội Châu Nghệ An 2019) Cho
3
log 5 ,a
3
log 6 ,b
3
log 22 .c
Tính
3
90
log
11
P
theo
,a
,b
.c
A.
2
P a b c
. B.
2
P a b c
. C.
2
P a b c
. D.
2
P a b c
.
Lờigiải.
Tacó
2
3 3 3 3 3 3
90 180 5.6
log log log log 5 2log 6 log 22 2
11 22 22
P a b c
.
Câu 26. (ChuyênNguyễnTấtThànhYênBái2019)Cho
12
log 3
a
.Tính
24
log 18
theo
a
.
A.
3 1
3
a
a
. B.
3 1
3
a
a
. C.
3 1
3
a
a
. D.
3 1
3
a
a
.
Lờigiải
Tacó
12 2
3 3
1 1 2
log 3 log 3
log 12 1 2log 2 1
a
a
a
.
Khiđó:
2
2
2
24
3
2
2
2
1 2.
log 3 .2
1 2 log 3
1 3
1
log 18
2
3 log 3 3
log 2 .3
3
1-
a
a
a
a
a
a
.
Câu 27. (THPTNghĩaHưngNđ-2019)Đặt
log ,log
a b
b m c n
.Khiđó
2 3
log
a
ab c
bằng
A.
1 6mn
. B.
1 2 3m n
. C.
6mn
. D.
1 2 3m mn
.
Lờigiải
2 3
log log 2log 3log
a a a a
ab c a b c
log
1 2 3 1 2 3log .log 1 2 3
log
b
a b
b
c
m m b c m mn
a
.
Câu 28. (CụmLiênTrườngHảiPhòng2019)Đặt
2
log 3
a
và
5
log 3
b
.Hãybiểudiễn
6
log 45
theo
a
và
b
A.
6
2a
log 45
a b
ab b
B.
6
2a
log 45
a b
ab
C.
2
6
2 2a
log 45
a b
ab
D.
2
6
2 2a
log 45
a b
ab b
Lờigiải
ChọnA
2
2
2 2 3
6
2 2
2a
log 3 .5
2log 3 log 3.log 5
2a
log 45
log 2.3 1 log 3 1
a
b a
b
a ab b
Câu 29. (THPT Thiệu Hóa – Thanh Hóa 2019) Cho
9 4 2
log 5 ; log 7 ; log 3
a b c
.Biết
24
log 175
mb nac
pc q
.Tính
2 3 4A m n p q
.
A.
27
B.
25
C.
23
D.
29

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lờigiải
ChọnB
T
acó
2
2
24 24 24 24
7 5
1
2
log 175 log 7.5 log 7 2log 5
l
og 24 log 24
3
3
7 7 5 5
3 2 3 2
1 2 1 2
1 3 1 3
log 3 log 2 log 3 log 2
l
og 7 log 7 log 5 log 5
2
3 2 3 2 3
1
2 1 2
1 3 1 3 1 3 1 3
1
l
og 7.log 2 log 7 log 5 log 3.log 5 2 2a c.2a
2 .
b
b
c
1 2 2 4a 2 4a
3
3
3 3 3
2 2 2ac 2ac
b c b c
c
c
c c c
b b
.
2
3 4 2 8 3 12 25
A
m n p q
Câu
30. (ChuyênKHTN2019)Vớicácsố
,
0
a
b
thỏa
mãn
2
2
6a
b ab
,
biểuthức
2
l
og
a
b
bằng
A.
2
2
1
3 log log
2
a
b
. B.
2
2
1
1 log log
2
a
b
.
C.
2
2
1
1
log log
2
a
b
.D.
2
2
1
2
log log
2
a
b
.
Lờigiải
T
acó:
2
2
2 2 2
6
2 6 2 8a b ab a b ab ab ab a b ab
*
.
Do
0
,
0
0
a
b
a b
a b
,lấylogaritcơsố2haivếcủa
*
ta
được:
2
2
2 2 2 2
l
og log 8 2 log 3 log loga b ab a b a b
2
2 2
1
l
og 3 log log
2
a
b a b
.
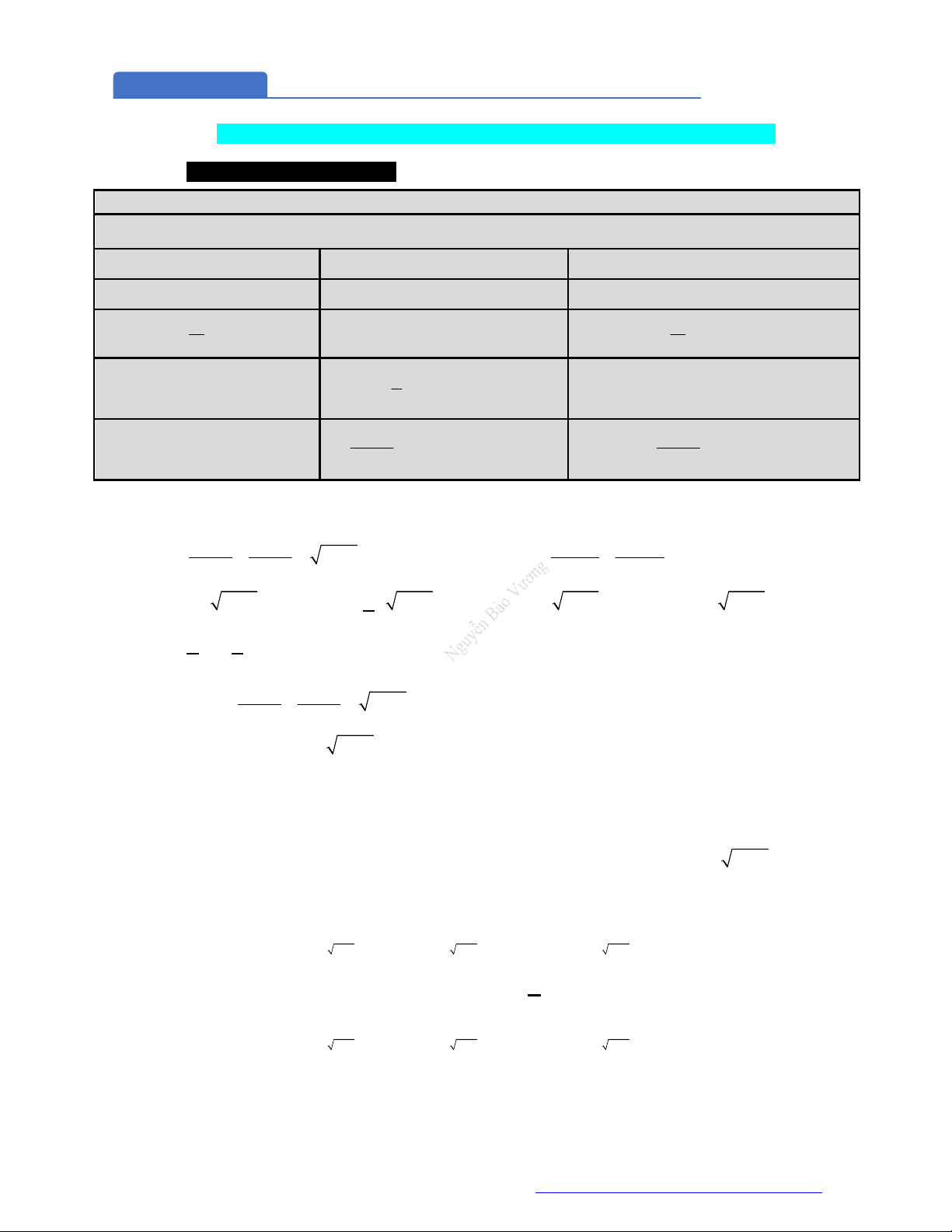
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI MỨC 9-10 ĐIỂM
Dạng. Một số bài toán KHÓ
Công thức logarit:
Cho các số
, 0, 1a b a
và
,m n
. Ta có:
log
a
b a b
10
lg log logb b b
ln log
e
b b
log 1 0
a
log 1
a
a
log
n
a
a n
1
log log
m
a
a
b b
m
log log
n
a a
b n b
log log
m
n
a
a
n
b b
m
log ( ) log log
a a a
bc b c
log log log
a a a
b
b c
c
log
log log
a
b b
b
c a
a b
a c
log .log log
a b a
b c c
,
1b
log
log
log
a
b
a
c
c
b
,
1b
1
log
log
a
b
b
a
,
1b
Câu 1. (Chuyên Lam Sơn - 2020) Cho các số thực
a
,
b
thỏa mãn
1a b
và
1 1
2020
log log
b a
a b
. Giá trị của biểu thức
1 1
log log
ab ab
P
b a
bằng
A. 2014 . B. 2016 . C. 2018 . D. 2020 .
Lời giải
Chọn B
Do
1a b
nên log 0
a
b , log 0
b
a và log log
b a
a b .
Ta có:
1 1
2020
log log
b a
a b
log log 2020
b a
a b
2 2
log log 2 2020
b a
a b
2 2
log log 2018
b a
a b
(*)
Khi đó, log log log log log log log log
b a b b a a b a
P ab ab a b a b a b
Suy ra:
2
2 2 2
log log log log 2 2018 2 2016 2016
b a b a
P a b a b P
Câu 2. (Liên Trường Thpt Tp Vinh Nghệ 2019) Tìm số nguyên dương n sao cho
3
2 2 2 2 2
2018 2018
2018 2018 2018
log 2019 2 log 2019 3 log 2019 ... log 2019 1010 .2021 log 2019
n
n
A.
2021n
. B.
2019n
. C.
2020n
. D.
2018.n
.
Lời giải
3
2 2 2 2 2
2018 2018
2018 2018 2018
log 2019 2 log 2019 3 log 2019 ... log 2019 1010 .2021 log 2019
n
n
3 3 3 2 2
2018 2018 2018 2018 2018
log 2019 2 log 2019 3 log 2019 ... log 2019 1010 .2021 log 2019n
3 3 3 2 2
2018 2018
1 2 3 ... log 2019 1010 .2021 log 2019n
3 3 3 2 2
1 2 3 ... 1010 .2021n
CÔNG THỨC, BIẾN ĐỔI LOGARIT
Chuyên đề 17
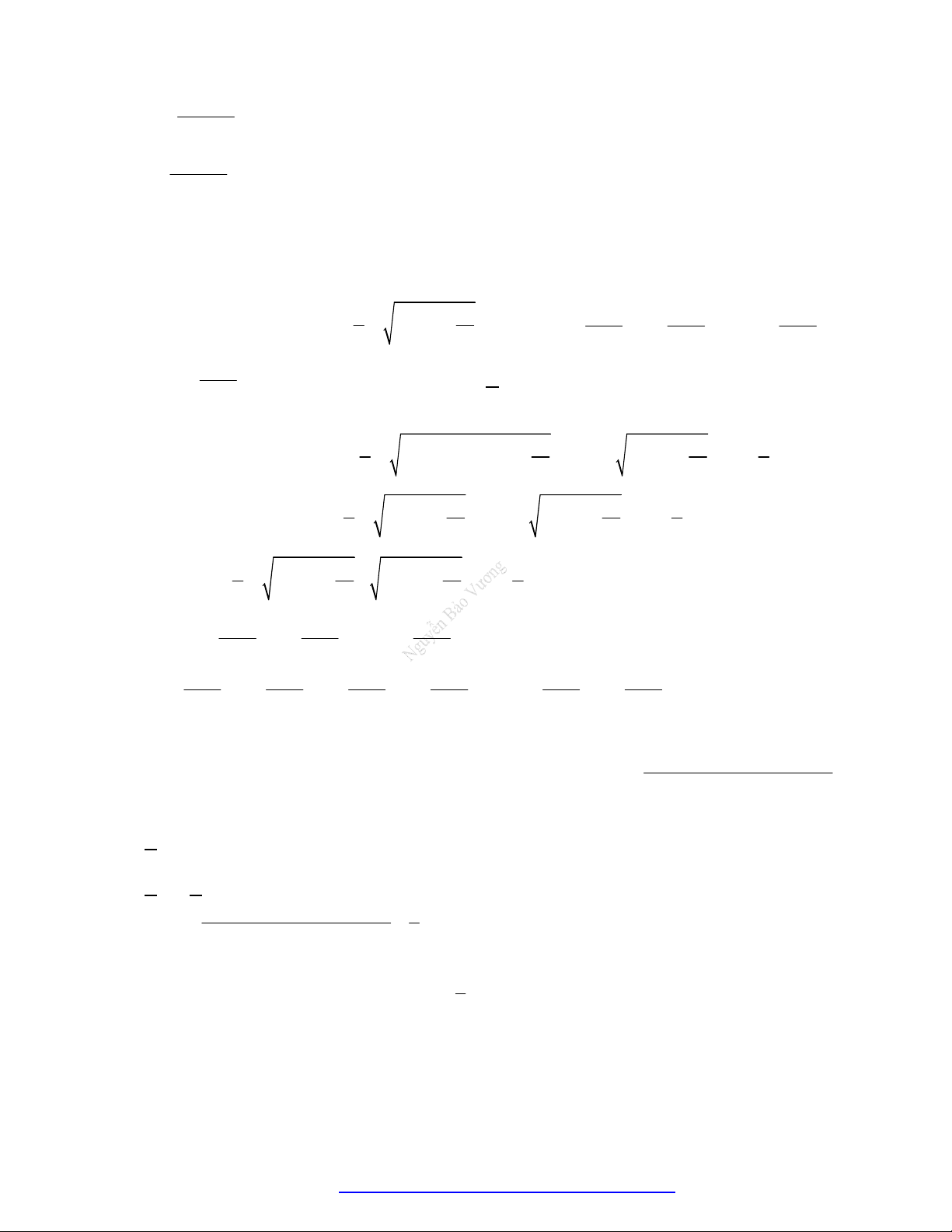
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2 2
1 2 ... 1010 .2021
n
2
2 2
1
1010 .2021
2
n n
1
1010.2021
2
n n
2
2020.2021 0
n n
2020
2021
n
n
Câu 3. Cho hàm số
2
2
1 17
( ) log
2 4
f x x x x
. Tính
1 2 2018
...
2019 2019 2019
T f f f
A.
2019
2
T
. B.
2019
T
. C.
2018
T
. D.
1009
T
.
Lời giải
Ta có:
2
2
2 2
1 17 17 1
(1 ) log 1 1 1 log
2 4 4 2
f x x x x x x x
2 2
2 2
1 17 17 1
1 log log
2 4 4 2
f x f x x x x x x x
2 2
2
1 17 17 1
log
2 4 4 2
x x x x x x
2
log 4 2
1 2 2018
...
2019 2019 2019
T f f f
1 2018 2 2017 1009 1010
...
2019 2019 2019 2019 2019 2019
f f f f f f
1009.2 2018
Câu 4. (THPT Nguyễn Khuyến 2019) Gọi
a
là giá trị nhỏ nhất của
3 3 3 3
log 2.log 3.log 4...log
9
n
n
f n
với
n
và
2
n
. Hỏi có bao nhiêu giá trị của
n
để
f n a
.
A. 2 B. 4 C. 1 D. vô số
Lời giải
Chọn A
9 9 9 9
3 3 3 3
3 3 3 3
log 2.log 3.log 4...log
1
log 2.log 3.log 4...log
9 9
n
n
f n n
Ta có:
- Nếu
9 9 9 9 9
8 8
3 3 3 3 3
1
2 3 0 log 1 log 2.log 3.log 4...log 3
9
n k f n n f
- Nếu
9
9 9 8 9 8
3
3 3 3 .log 3 3
n f f f
- Nếu
9 9 9
9 9 9 9
3 3 3
3 log 1 3 .log 3 1 ...log 3
n n f n f n f
Từ đó suy ra
9 8
3 3
Min f n f f
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 5. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho
x
,
y
và
z
là các số thực lớn hơn
1
và gọi
w
là
số thực dương sao cho
log 24
x
w
,
log 40
y
w
và
log 12
xyz
w
. Tính
log
z
w
.
A.
52
. B.
60
. C.
60
. D.
52
.
Lời giải
Chọn C
log 24
x
w
1
log
24
w
x
log 40
y
w
1
log
40
w
y
.
Lại do
log 12
xyz
w
1
12
log
w
xyz
1
12
log log log
w w w
x y z
1
12
log log log
w w w
x y z
1
12
1 1
log
24 40
w
z
1
log
60
w
z
log 60
z
w
.
Câu 6. Cho
1 1
f
,
f m n f m f n mn
với mọi
*
,m n
. Tính giá trị của biểu thức
96 69 241
log
2
f f
T
.
A.
9
T
. B.
3
T
. C.
10
T
. D.
4T
.
Lời giải
Chọn B
Có
1 1
f
,
f m n f m f n mn
96 95 1 95 1 95 95 96 94 95 96 ... 1 2 ... 95 96
f f f f f f f
96.97
96 1 2 ... 95 96 4656
2
f
.
Tương tự
69.70
69 1 2 ... 68 69 2415
2
f
.
Vậy
96 69 241
4656 2415 241
log log log1000 3
2 2
f f
T
.
Câu 7. (Chuyên Lê Quý Dôn Quảng Trị 2019) Cho các số thực dương
, ,x y z
thỏa mãn đồng thời
2 2 2
1 1 1 1
log log log 2020
x y z
và
2
log ( ) 2020
xyz
. Tính
2
log 1
xyz x y z xy yz zx
A.
4040
. B.
1010
. C. 2020. D.
2
2020
.
Lời giải
Chọn A
Đặt
2 2 2
log ; log ; loga x b y c z
.
Ta có
1 1 1 1
2020a b c
và
2020
a b c
2 2 2 2 2 2
1 1 1
1
0
0
a b c a b c ab ac bc abc
a b c
a b ab abc abc b c bc a c ac
a b b c c a

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vì vai trò
, ,a b c
như nhau nên giả sử
2020
0 2020 2
a b c z
và
1xy
.
2 2
2
2 2
log 1 log ( ) 1 1
log 2log 4040
xyz x y z xy yz zx z x y z yz zx
z z
Câu 8. (Bạc Liêu – Ninh Bình 2019) Cho ba số thực dương
, , x y z
theo thứ tự lập thành một cấp số
nhân, đồng thời với mỗi số thực dương
( 1)
a a
thì
3
log , log , log
a
a a
x y z
theo thứ tự lập
thành một cấp số cộng. Tính giá trị của biểu thức
1959 2019 60x y z
P
y z x
.
A.
60
. B.
2019
. C.
4038
. D.
2019
2
.
Lời giải
Chọn C
Ta có:
, , x y z
là ba số thực dường, theo thứ tự lập thành một cấp số nhân thì
2
. (1)y x z
.
Với mỗi số thực
( 1),
a a
3
log , log , log
a
a a
x y z
theo thứ tự lập thành một cấp số cộng thì
3
2log log log 4log log 3log (2)
a a a a
a a
y x z y x z
.
Thay
(1)
vào
(2)
ta được
2log . log 3log log log
a a a a a
x z x z x z x z
.
Từ
(1)
ta suy ra
y x z
.
Thay vào giả thiết thì
1959 2019 60 4038
P
.
Câu 9. (THPT Hai Bà Trưng - Huế - 2019) Cho hàm số
2
1 2
log
2 1
x
f x
x
và hai số thực
, m n
thuộc khoảng
0;1
sao cho
1 m n
. Tính
f m f n
.
A.
2
. B.
0
. C.
1
. D.
1
2
.
Lời giải
Chọn C
2 2
1 2 1 2
log log
2 1 2 1
m n
f m f n
m n
2 2
1 2 2
log log
2 1 1
m n
m n
2
1 2 2
log .
2 1 1
m n
m n
2
1 4
log
2 1
mn
m n mn
, vì
1 m n
2 2
1 4 1 1
log log 4 .2 1
2 2 2
mn
mn
.
Câu 10. (Chuyên - Vĩnh Phúc - 2019) Gọi
n
là số nguyên dương sao cho
2 3
3 3
3 3 3
1 1 1 1 190
...
log log log log log
n
x x x x x
đúng với mọi
x
dương,
1x
. Tìm giá trị của biểu
thức
2 3P n
.
A.
32
P
. B.
23
P
. C.
43
P
. D.
41P
.
Lời giải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Chọn D
2 3
3 3
3 3 3
1 1 1 1 190
...
log log log log log
log 3 2log 3 3log 3 ... log 3 190log 3
log 3 1 2 3 ... 190log 3
1 2 3 ... 190
1
190
2
n
x x x x x
x x
x x x x x
n
n
n
n n
2
380 0
n n
19
19
20
n
n
n
(do
n
nguyên dương)
2 3 41
P n
Câu 11. Cho
x
,
y
,
z
là ba số thực dương lập thành cấp số nhân;
log
a
x
,
log
a
y
,
3
log
a
z
lập thành cấp
số cộng, với
a
là số thực dương khác 1. Giá trị của
9 3x y z
p
y z x
là
A. 13. B. 3. C. 12. D. 10.
Lời giải
Chọn A
x
,
y
,
z
là ba số thực dương lập thành cấp số nhân nên ta có
2
xz y
(1).
log
a
x
,
log
a
y
,
3
log
a
z
lập thành cấp số cộng nên:
3
log log 2log
a
a a
x z y
log 3log 4log
a a a
x z y
3 4
xz y
(2).
Từ (1) và (2) ta suy ra
x y z
.
Vậy
9 3
9 1 3 13
x y z
p
y z x
.
Câu 12. (Chuyên Nguyễn Huệ 2019) Cho
(1) 1;
f
( ) ( ) ( )
f m n f m f n mn
với mọi
*
,
m n N
.
Tính giá trị của biểu thức
2019 2009 145
log
2
f f
T
A.
3
. B.
4
. C.
5
. D.
10
.
Lời giải
Chọn B
Ta có
(2019) (2009 10) (2009) (10) 20090
f f f f
Do đó
(2019) (2009) 145 (10) 20090 145
f f f

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
(10) (9) (1) 9
(9) (8) (1) 8
...................
(3) (2) (1) 2
(2) (1) (1) 1
f f f
f f f
f f f
f f f
Từ đó cộng vế với vế ta được:
(10) 10. (1) 1 2 .... 8 9 55.
f f
Vậy
(2019) (2009) 145 20090 145 55
log log log10000 4.
2 2
f f
Câu 13. Có bao nhiêu số nguyên dương
n
để
log 256
n
là một số nguyên dương?
A.
2.
B.
3.
C.
4
. D.
1
.
Lời giải
Chọn C
2
8
log 256 8.log 2
log
n n
n
là số nguyên dương
2
log 1;2;4;8 2;4;16;256
n n
.
Vậy có
4
số nguyên dương.
Câu 14. Cho tam giác
ABC
có
BC a
,
CA b
,
AB c
. Nếu
a
,
b
,
c
theo thứ tự lập thành một cấp số
nhân thì
A.
2
ln sin .ln sin ln sin
A C B
. B.
lnsin .lnsin 2lnsinA C B
.
C.
lnsin lnsin 2lnsinA C B
. D.
ln sin lnsin ln 2sinA C B
.
Lời giải
Chọn C
Theo định lý sin trong tam giác
ABC
ta có:
2 sin
2 sin
2 sin
a R A
b R B
c R C
, với
R
là bán kính đường tròn ngoại
tiếp tam giác
ABC
.
Vì
a
,
b
,
c
theo thứ tự lập thành một cấp số nhân nên ta có:
2
2
. 2 sin . 2 sin 2 sin
a c b R A R C R B
2
sin .sin sin
A C B
.
Do
0 sin A
,
sin B
,
sin 180
C
nên
sin A
,
sin B
,
sin 0
C
.
Vì thế ta có thể suy ra
2
ln sin .sin ln sinA C B
lnsin lnsin 2lnsinA C B
.
Câu 15. (Chuyên Lương Văn Chánh - Phú Yên - 2018) Cho
2018!
x
. Tính
2018 2018 2018 2018
2 3 2017 2018
1 1 1 1
...
log log log log
A
x x x x
.
A.
1
2017
A
. B.
2018
A
. C.
1
2018
A
. D.
2017
A
.
Lời giải
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
2018 2018 2018 2018
2 3 2017 2018
1 1 1 1
...
log log log log
A
x x x x
2018 2018 2018 2018
log 2 log 3 ... log 2017 log 2018
x x x x
2018.log 2 2018.log 3 ... 2018.log 2017 2018.lo
g 2018
x x x x
2018. log 2 log 3 ... log 2017 log 2018
x x x x
2018.log 2.3.....2017.2018
x
Câu 16. ( Chuyên Hùng Vương - Gia Lai - 2018) Tìm bộ ba số nguyên dương
( ; ; )a b c
thỏa mãn
log1 log(1 3) log(1 3 5) ... log(1 3 5 ... 19) 2log5
040 log2 log3
a b c
A.
(2;6;4)
. B.
(1;3;2)
. C.
(2;4;4)
. D.
(2;4;3)
.
Lời giải
Ta có
log1 log(1 3) log(1 3 5) ... log(1 3 5 ... 19) 2log5
040 log2 log3
a b c
2 2 2
log1 log 2 log3 ... log10 2log5040 log 2 log3
a b c
2 2 2
log 1.2 .3 .10 2log5040 log 2 log3
a b c
2
log 1.2.3.10 2log5040 log2 log3
a b c
2log 1.2.3.10 2 log5040 log 2 log 3
a b c
2 log10! log 7! log 2 log 3 2log 8.9.10 log 2 log3
a b c a b c
2 6log2 4log3 log 2 log3
a b c
.
Vậy
2
a
,
6
b
,
4
c
.
Câu 17. (Phan Đình Phùng - Hà Tĩnh - 2018) Tổng
3 2018
2 2 2
2 2 2
1 2 log 2 3 log 2 .... 2018 log 2
S
dưới đây.
A.
2 2
1008 .2018
. B.
2 2
1009 .2019
. C.
2 2
1009 .2018
. D.
2
2019
.
Lời giải
Ta có
2
3 3 3 3
1
1 2 3 ...
4
n n
n
.
Mặt khác
3 2018
2 2 2
2 2 2
1 2 log 2 3 log 2 .... 2018 log 2
S
1 1 1
2 3 2018
2 2 2
2 2 2
1 2 log 2 3 log 2 .... 2018 log 2
3 3 3
2 2 2
1 2 log 2 3 log 2 .... 2018 log 2
3 3 3
1 2 3 ... 2018
2
2018 2018 1
2
2 2
1009 .2019
.
Câu 18. (ChuyêN KHTN - 2018) Số
20162017
20172018
có bao nhiêu chữ số?
A.
147278481.
B.
147278480.
C.
147347190.
D.
147347191.
Lời giải
Số chữ số của một số tự nhiên
x
là:
log 1
x
(
log x
là phần nguyên của
log x
).
Vậy số chữ số của số
20162017
20172018
là
20162017
log20172018 1 20162017log 20172018 1 147278481.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM
Dạng 1. Tìm tập xác định
Hàm số mũ
Dạng:
x
u
y a
y a
với
0
.
1
a
a
Tập xác định:
.D
Hàm số logarit
Dạng:
log
log
a
a
y x
y u
với
0
.
1
a
a
Đặc biệt:
ln ;a e y x 10 log lga y x x
.
Điều kiện xác định:
0u
.
Câu 1. (Đề Tham Khảo 2020 Lần 2) Tập xác định của hàm số
2
logy x
là
A.
0; .
B.
; .
C.
0; .
D.
2; .
Câu 2. (Mã 101 - 2020 Lần 1) Tập xác định của hàm số
5
logy x là
A.
0;
. B.
;0
. C.
0;
. D.
;
.
Câu 3. (Mã 102 - 2020 Lần 1) Tập xác định của hàm số là
A. . B. . C. . D. .
Câu 4. (Mã 103 - 2020 Lần 1) Tập xác định của hàm số
3
logy x là
A.
( ;0)
B.
(0; )
C.
( ; )
D.
[0; )
Câu 5. (Mã 104 - 2020 Lần 1) Tập xác định của hàm số
4
logy x là
A.
( ;0)
. B.
0;
. C.
0;
. D.
;
.
Câu 6. (Mã 102 - 2020 Lần 2) Tập xác định của hàm số
5
x
y
là
A.
. B.
0;
. C.
\ 0
. D.
0;
.
Câu 7. (Mã 103 - 2020 Lần 2) Tập xác định của hàm số
2
x
y
là
A.
. B.
0;
. C.
0;
. D.
\ 0
.
Câu 8. (Mã 123 2017) Tìm tập xác định
D
của hàm số
5
3
log .
2
x
y
x
A.
( ; 2) (3; )D
B.
( 2; 3)D
C.
( ; 2) [3; )D
D.
\{ 2}D
Câu 9. (Đề Minh Họa 2017) Tìm tập xác định D của hàm số
2
2
log 2 3y x x
A.
; 1 3;D
B.
1;3D
C.
; 1 3;D
D.
1;3D
Câu 10. (Mã 104 2017) Tìm tập xác định
D
của hàm số
2
3
log 4 3y x x
.
HÀM SỐ MŨ - HÀM SỐ LOGARIT
Chuyên đề 18
6
log
y x
0;
0;
;0
;

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1;3
D
B.
;1 3;D
C.
;2 2 2 2;D
. D.
2 2;1 3;2 2
D
Câu 11. (THPT Lương Thế Vinh Hà Nội 2019) Tìm tập xác định của hàm số
2
2018
log 3
y x x
.
A.
D
B.
0;D
C.
; 0 3;D
D.
0; 3
D
Câu 12. (Chuyên Vĩnh Phúc 2019) Tập xác định của
2
ln 5 6
y x x
là
A.
2; 3
B.
2; 3
C.
; 2 3;
D.
; 2 3;
Câu 13. (THPT Lê Quy Đôn Điện Biên 2019) Tìm tập xác định của hàm số
5
1
log
6
y
x
.
A.
;6
B.
C.
0;
D.
6;
Câu 14. (THPT Lương Thế Vinh Hà Nội 2019) Tập xác định của hàm số
2
2
log 3 2
y x x
là
A.
( 1;1)D
. B.
( 1;3)D
. C.
( 3;1)D
. D.
(0;1)D
.
Câu 15. (Sở Vĩnh Phúc 2019) Tập xác định của hàm số
2
2
log 2 3
y x x
là
A.
1;3
. B.
1;3
.
C.
; 1 3;
. D.
; 1 3;
.
Câu 16. (Chuyên Lê Hồng Phong Nam Định 2019) Tìm tập xác định của hàm số:
x
y x
2 log 3
A.
0;
. B.
0;3
. C.
;3
. D.
0;3
.
Câu 17. (Chuyên Nguyễn Trãi Hải Dương 2019) Tập xác định của hàm số
ln 2
y x
là
A.
. B.
3;
. C.
0;
. D.
2;
.
Câu 18. (THPT Ba Đình 2019) Tìm tập xác định D của hàm số
2019
2
2019
y log 4 x 2x 3 .
A.
3 3
D 2; ;2
2 2
. B.
3 3
D 2; ;2
2 2
.
C.
3
D ;2
2
. D.
D 2;2
.
Câu 19. Tìm tập xác định của hàm số
0
2
2
2 log 9
y x x
là
A.
2;3 .
D
B.
3;3 \ 2 .
D
C.
3; .
D
. D.
3;3 .
D
.
Dạng 2. Tìm đạo hàm
Đạo hàm hàm số mũ
ln
ln .
x x
u u
y a y a a
y a y a a u
.
Đặc biệt:
( )
( ) .
x x
u u
e e
e e u
với
2,71828...e
Đạo hàm hàm số logarit

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
1
log
ln
log
ln
a
a
y x y
x a
u
y u y
u a
.
Đặc biệt:
1
(ln )
(ln )
x
x
u
u
u
.
Câu 1. (Đề Tham Khảo 2017) Tìm đạo hàm của hàm số
logy x
.
A.
ln10
y
x
B.
1
ln10
y
x
C.
1
10ln
y
x
D.
1
y
x
Câu 2. (Mã 103 - 2019) Hàm số
2
2
x x
y
có đạo hàm là
A.
2
2 .ln 2
x x
. B.
2
(2 1).2 .ln 2
x x
x
.
C.
2
2 1
( ).2
x x
x x
. D.
2
(2 1).2
x x
x
.
Câu 3. (Mã 104 - 2019) Hàm số
2
3
x x
y
có đạo hàm là
A.
2
2 1 .3
x x
x
. B.
2
2 1
.3
x x
x x
. C.
2
2 1 .3 .ln 3
x x
x
. D.
2
3 .ln3
x x
.
Câu 4. (Đề Minh Họa 2017) Tính đạo hàm của hàm số
13
x
y
A.
13
ln13
x
y
B.
1
.13
x
y x
C.
13 ln13
x
y
D.
13
x
y
Câu 5. (Mã 110 2017) Tính đạo hàm của hàm số
2
log 2 1
y x
.
A.
2
2 1 ln 2
y
x
B.
1
2 1 ln 2
y
x
C.
2
2 1
y
x
D.
1
2 1
y
x
Câu 6. (Đề Minh Họa 2017) Tính đạo hàm của hàm số
1
4
x
x
y
A.
2
1 2 1 ln 2
'
2
x
x
y
B.
2
1 2 1 ln 2
'
2
x
x
y
C.
2
1 2 1 ln 2
'
2
x
x
y
D.
2
1 2 1 ln 2
'
2
x
x
y
Câu 7. (Đề Tham Khảo 2019) Hàm số
2
2
log 2x
f x x
có đạo hàm
A.
2
ln 2
'
2x
f x
x
B.
2
1
'
2x ln 2
f x
x
C.
2
2x 2 ln 2
'
2x
f x
x
D.
2
2x 2
'
2x ln 2
f x
x
Câu 8. (Mã 101 - 2019) Hàm số
2
3
2
x x
y
có đạo hàm là
A.
2
3
2 3 2 ln 2
x x
x
. B.
2
3
2 ln 2
x x
.
C.
2
3
2 3 2
x x
x
. D.
2
2 3 1
3 2
x x
x x
.
Câu 9. (Mã 102 - 2019) Hàm số
2
3
3
x x
y
có đạo hàm là
A.
2
3
2 3 .3
x x
x
. B.
2
3
3 .ln3
x x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
C.
2
2 3 1
3 .3
x x
x x
. D.
2
3
2 3 .3 .ln 3
x x
x
.
Câu 10. Tính đạo hàm của hàm số
y = ln 1+ x +1
.
A.
1
1 1 1
y
x x
B.
2
1 1 1
y
x x
C.
1
2 1 1 1
y
x x
D.
1
1 1
y
x
Câu 11. (Chuyên Vĩnh Phúc 2019) Đạo hàm của hàm số
1 2x
y e
là
A.
1 2
2
x
y e
B.
1 2
2
x
y e
C.
1 2
2
x
e
y
D.
1 2 x
y e
Câu 12. (Chuyên Lam Sơn Thanh Hóa 2019) Đạo hàm của hàm số
2
3
log 1
y x x
là:
A.
2
2 1 ln 3
'
1
x
y
x x
B.
2
2 1
'
1 ln 3
x
y
x x
C.
2
2 1
'
1
x
y
x x
D.
2
1
'
1 ln 3
y
x x
Câu 13. (THPT Lê Quy Đôn Điện Biên 2019) Tính đạo hàm của hàm số
2
x x
y e
.
A.
2 1
x
x e
B.
2
2 1
x x
x e
C.
2 1
2 1
x
x e
D.
2 2 1x
x x e
Câu 14. (THPT Hùng Vương Bình Phước 2019) Cho hàm số
2
2
log 1
f x x
, tính
1
f
A
1 1
f
. B.
1
1
2ln 2
f
. C.
1
1
2
f
. D.
1
1
ln 2
f
.
Câu 15. (THPT-Thang-Long-Ha-Noi- 2019) Tìm đạo hàm của hàm số
2
ln 1
x
y e
.
A.
2
2
2
2
1
x
x
e
y
e
. B.
2
2
1
x
x
e
y
e
. C.
2
1
1
x
y
e
. D.
2
2
2
1
x
x
e
y
e
.
Câu 16. (Chuyen Phan Bội Châu Nghệ An 2019) Tính đạo hàm của hàm số
1
2
x
x
y
A.
2
2
x
x
y
. B.
2
ln 2. 1 1
2
x
x
y
.
C.
2
2
x
x
y
. D.
ln 2. 1 1
2
x
x
y
.
Câu 17. (Chuyên Lê Quý Đôn Quảng Trị 2019) Tính đạo hàm của hàm số
2
9
log 1
y x
.
A.
2
1
1 ln9
y
x
. B.
2
1 ln3
x
y
x
. C.
2
2 ln 9
1
x
y
x
. D.
2
2ln 3
1
y
x
.
Câu 18. (KTNL GV THPT Lý Thái Tổ 2019) Tính đạo hàm hàm số
.sin2
x
y e x
A.
sin 2 cos 2
x
e x x
. B.
.cos2
x
e x
.
C.
sin 2 cos 2
x
e x x
. D.
sin 2 2cos 2
x
e x x
.
Câu 19. (VTED 2019) Đạo hàm của hàm số
1
4
x
x
y
là
A.
2
1 2 1 ln 2
2
x
x
B.
2
1 2 1 ln 2
2
x
x
C.
2
1 2 1 ln 2
2
x
x
D.
2
1 2 1 ln 2
2
x
x
Câu 20. (Chuyên Hùng Vương Gia Lai 2019) Cho hàm số
1
1 ln
y
x x
với
0
x
. Khi đó
2
'y
y
bằng
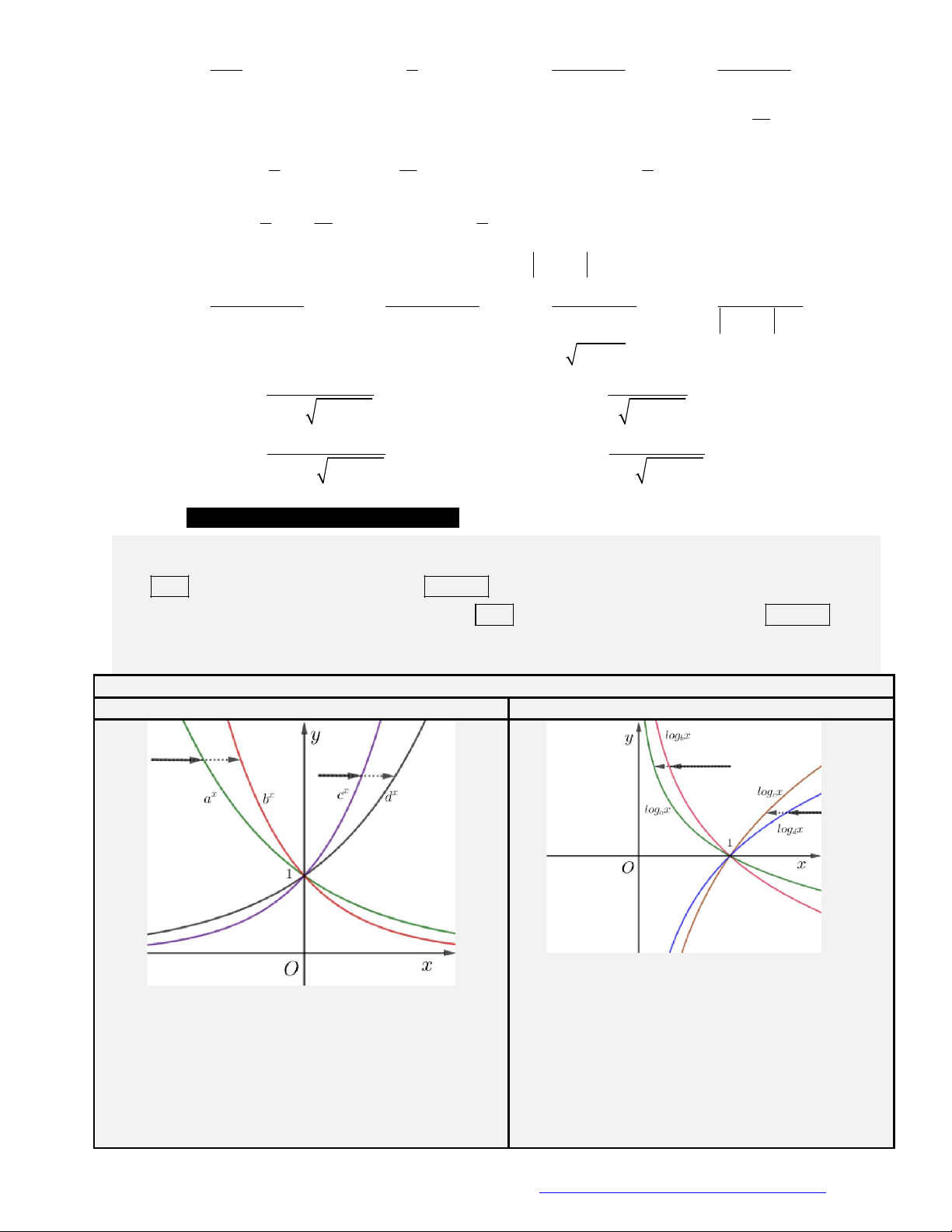
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
1
x
x
. B.
1
1
x
. C.
1 ln
x
x x
. D.
1
1 ln
x
x x
.
Câu 21. (Chuyên Lê Quý Đôn Điện Biên 2019) Tính đạo hàm của hàm số
x
1
2 ln
e
x
y x
.
A.
1 1
2 ln2 ln
e
x
x
y x
x
. B.
1
2 ln 2 e
x x
y
x
.
C.
x
1 1
2 ln 2
e
x
y
x
. D.
x
1
2 ln2 e
x
y
x
.
Câu 22. (VTED 2019) Đạo hàm của hàm số
2
2
( ) log 2f x x x
là
A.
2
2 2
2 ln 2
x
x x
B.
2
2 l 2
1
nx x
C.
2
(2 2)ln
2
2
x
x
x
D.
2
2 2
2 ln2
x
x x
Câu 23. (Chuyên KHTN 2019) Đạo hàm của hàm số
(x) ln(lnx)f
là:
A.
1
( )
x ln ln ln
f x
x x
. B.
1
( )
2 ln ln
f x
x
C.
1
( )
2x lnx ln ln
f x
x
. D.
1
( )
lnx ln ln
f x
x
.
Dạng 3. Khảo sát hàm số mũ, logarit
Sự biến thiên hàm số mũ:
x
y a
.
Nếu
1a
thì hàm đồng biến trên
. Nếu
0 1a
thì hàm nghịch biến trên
.
Sự biến thiên hàm số logarit:
log
a
y x
. Nếu
1a
: hàm đồng biến trên
(0; )
. Nếu
0 1a
: hàm
nghịch biến trên
(0; ).
Đồ thị hàm số mũ và logarit
ĐỒ THỊ HÀM SỐ MŨ ĐỒ THỊ HÀM SỐ LOGARIT
Ta thấy:
0 1; 0 1
x x
a a b b
.
Ta thấy:
1; 1.
x x
c c d d
So sánh a với b: Đứng trên cao, bắn mũi tên từ trái
sang phải, trúng
x
a
trước nên
a b
.
So sánh c với d: Đứng trên cao, bắn mũi tên từ trái
sang phải, trúng
x
c
trước nên
.c d
Vậy
0 1 .b a d c
Ta thấy:
log 0 1; log 0 1
a b
x a x b
.
Ta thấy:
log 1; log 1.
c d
x c x d
So sánh a với b: Đứng trên cao, bắn mũi tên
từ phải sang trái, trúng
log
b
x
trước:
.b a
So sánh c với d: Đứng trên cao, bắn mũi tên
từ phải sang trái, trúng
log
d
x
trước:
.d c
Vậy
0 1a b c d
.
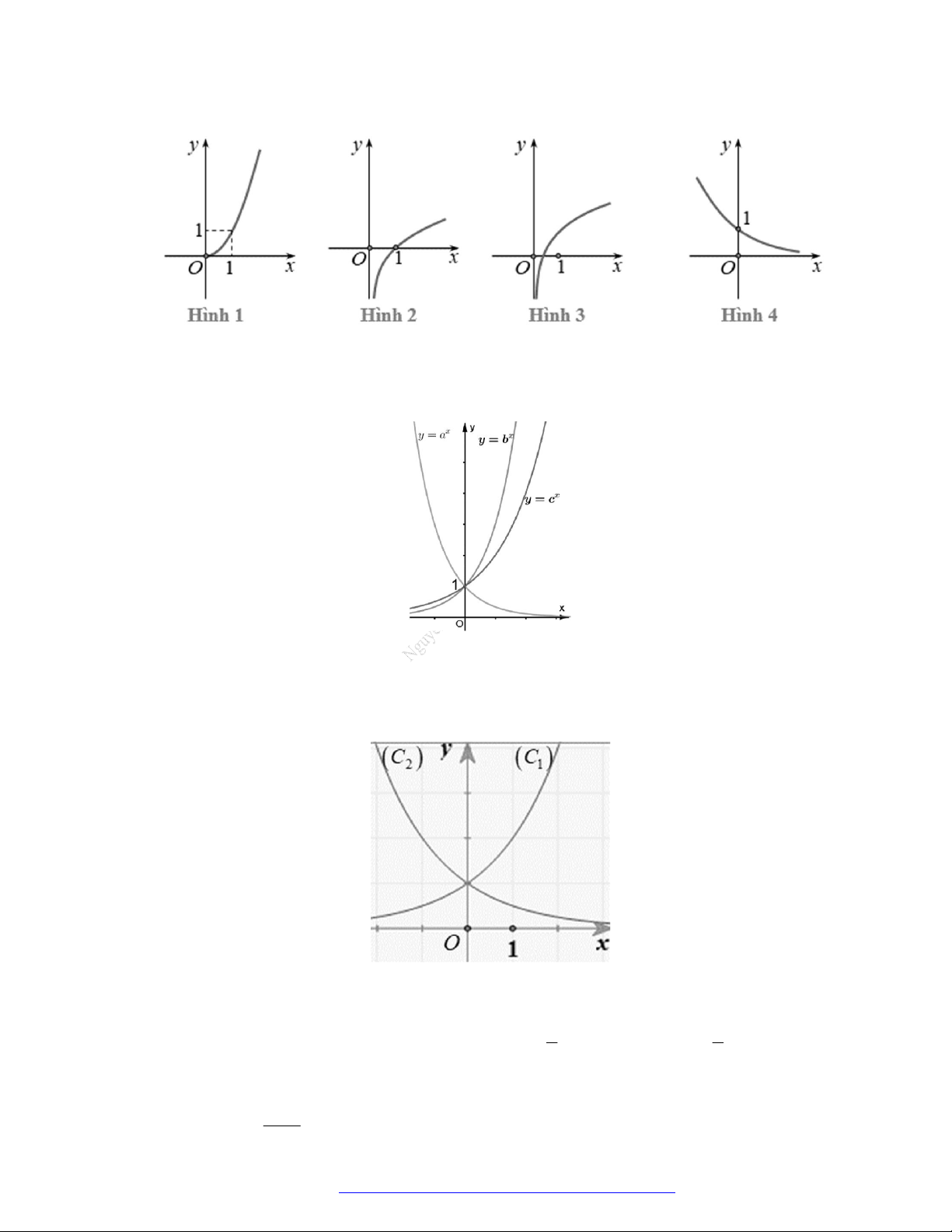
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 1. (Đề Tham Khảo 2017) Cho hàm số
lnf x x x
. Một trong bốn đồ thị cho trong bốn phương
án A, B, C, D dưới đây là đồ thị của hàm số
y f x
. Tìm đồ thị đó?
A. Hình 2 B. Hình 3 C. Hình 4 D. Hình 1
Câu 2. Cho ba số thực dương
, ,a b c
khác
1
. Đồ thị các hàm số , ,
x x x
y a y b y c được cho trong hình
vẽ bên
Mệnh đề nào dưới đây đúng?
A.
b c a
B.
c a b
C.
a b c
D.
a c b
Câu 3. (Mã 105 2017) Cho hàm số
,
x x
y a y b
với
, a b
là hai số thực dương khác 1, lần lượt có đồ
thị là
1
C
và
2
C
như hình bên. Mệnh đề nào dưới đây đúng
?
A.
0 1b a
B.
0 1a b
C.
0 1b a
D.
0 1a b
Câu 4. (Chuyên Bắc Giang 2019) Trong các hàm số sau hàm số nào nghịch biến trên
?
A.
2
3
log x
B.
3
logy x
C.
e
4
x
y
D.
2
5
x
y
Câu 5. Mệnh đề nào trong các mệnh đề dưới đây sai?
A. Hàm số
2
1
2018
x
y
đồng biến trên
.
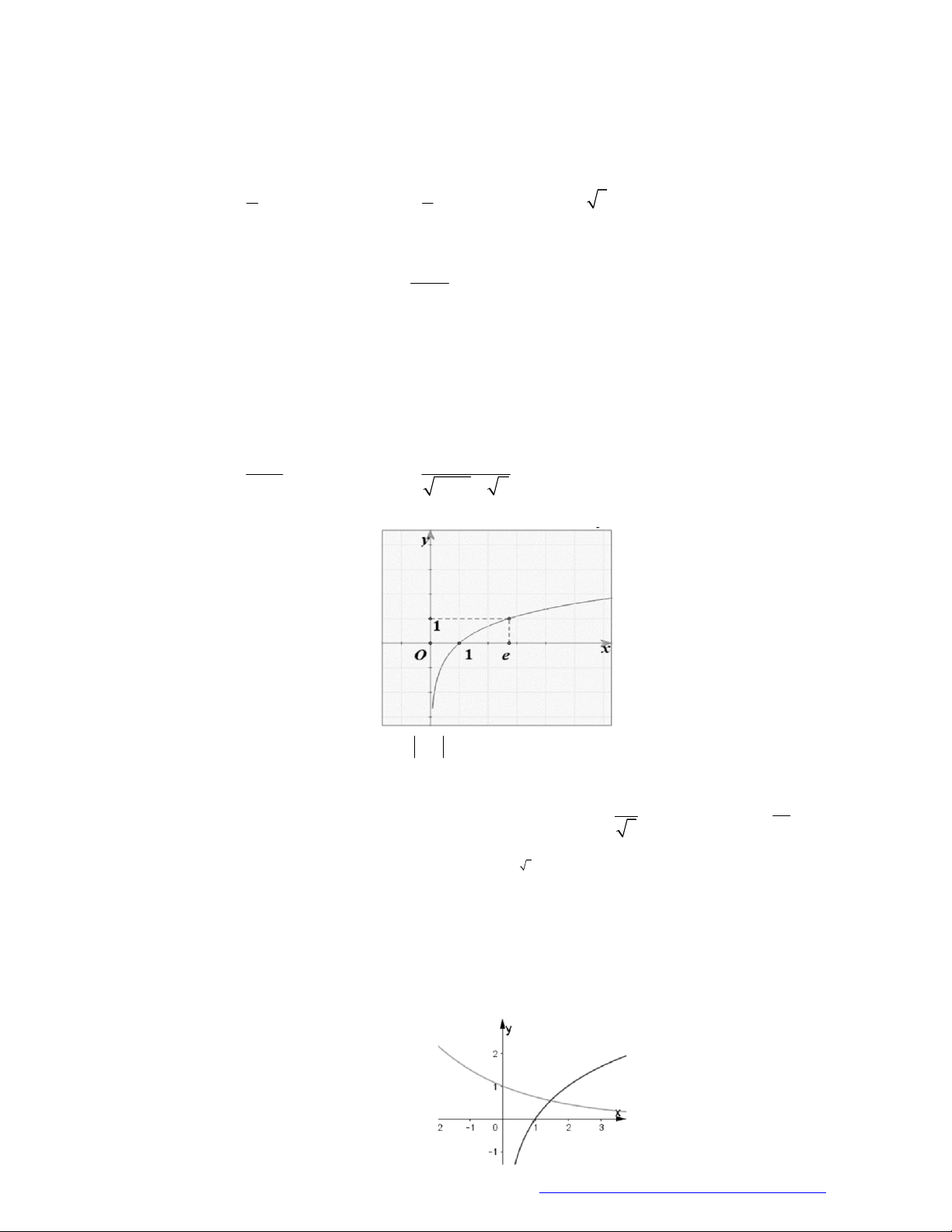
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
B. Hàm số
logy x
đồng biến trên
0;
.
C. Hàm số
lny x
nghịch biến trên khoảng
;0
.
D. Hàm số 2
x
y đồng biến trên
.
Câu 6. (THPT An Lão Hải Phòng 2019) Hàm số nào dưới đây đồng biến trên tập xác định của nó?
A.
1
π
x
y
B.
2
3
x
y
C.
3
x
y
D.
0,5
x
y
Câu 7. (THPT An Lão Hải Phòng 2019) Cho hàm số
2
logy x . Mệnh đề nào dưới đây sai?
A. Đạo hàm của hàm số là
1
ln 2
y
x
B. Đồ thị hàm số nhận trục
Oy
làm tiệm cận đứng
C. Tập xác định của hàm số là
;
D. Hàm số đồng biến trên khoảng
0;
Câu 8. (THPT Lê Quy Đôn Điện Biên 2019) Trong các hàm số sau, hàm số nào luôn đồng biến trên
?
A.
2015
y
2016
x
B.
3
y
2016 2
x
C.
2x
y (0,1) D.
2
(2016)
x
y
Câu 9. Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
e
x
y
. B.
lny x
. C.
lny x
. D.
e
x
y
.
Câu 10. (Chuyên Lê Thánh Tông 2019) Tìm hàm số đồng biến trên
.
A.
3
x
f x
. B.
3
x
f x
. C.
1
3
x
f x
. D.
3
3
x
f x
.
Câu 11. (Chuyên Bắc Ninh 2019) Cho hàm số
5
logy x
. Mệnh đề nào dưới đây là mệnh đề sai?
A. Hàm số đã cho đồng biến trên tập xác định.
B. Hàm số đã cho có tập xác định
0\D
.
C. Đồ thị hàm số đã cho có một tiệm cận đứng là trục tung.
D. Đồ thị hàm số đã cho không có tiệm cận ngang.
Câu 12. Cho đồ thị hàm số
x
y a
và
log
b
y x
như hình vẽ.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khẳng định nào sau đây đúng?
A.
1
0
2
a b
. B.
0 1a b
. C.
0 1b a
. D.
0 1a
,
1
0
2
b
.
Câu 13. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong các hàm số sau, hàm số nào nghịch biến?
A.
ln .y x
B.
2018
1
2019
logy x
C.
log .y x
D.
4 3
log .y x
Câu 14. (Sở Hà Nội 2019) Đồ thị hàm số
lny x
đi qua điểm
A.
1; 0
. B.
2
2; e
. C.
2 ; 2e
. D.
0;1
.
Câu 15. (Chuyên Lương Thế Vinh Đồng Nai 2019) Trong các hàm số sau,hàm số nào luôn nghịch biến
trên tập xác định của nó?
A.
2
1
2
y
. B.
logy x
. C.
2
x
y
. D.
2
3
x
y
.
Câu 16. (Chuyên Lương Thế Vinh Đồng Nai 2019) Chọn khẳng định sai trong các khẳng định sau:
A. Hàm số
2
logy x
đồng biến trên
.
B. Hàm số
1
2
logy x
nghịch biến trên tập xác định của nó.
C. Hàm số
2
x
y
đồng biến trên
.
D. Hàm số
2
y x
có tập xác định là
0;
.
Câu 17. (KTNL GV Bắc Giang 2019) Hàm số nào dưới đây đồng biến trên khoảng
(0; )
?
A.
3
logy x
. B.
6
logy x
. C.
3
log
e
y x
. D.
1
4
logy x
.
Câu 18. (Chuyên Lê Hồng Phong Nam Định 2019) Trong các mệnh đề sau, mệnh đề nào đúng?
A. Đồ thị của hàm số
2
x
y
và
2
logy x đối xứng với nhau qua đường thẳng
y x
.
B. Đồ thị của hai hàm số
x
y e và
lny x
đối xứng với nhau qua đường thẳng
y x
.
C. Đồ thị của hai hàm số 2
x
y và hàm số
1
2
x
y
đối xứng với nhau qua trục hoành.
D. Đồ thị của hai hàm số
2
logy x và
2
1
logy
x
đối xứng với nhau qua trục tung.
Câu 19. (Chuyên Lê Hồng Phong Nam Định 2019) Hàm số nào sau đây có đồ thị như hình bên?
A.
3
logy x . B.
2
log 1y x . C.
2
log 1y x
. D.
3
log 1y x
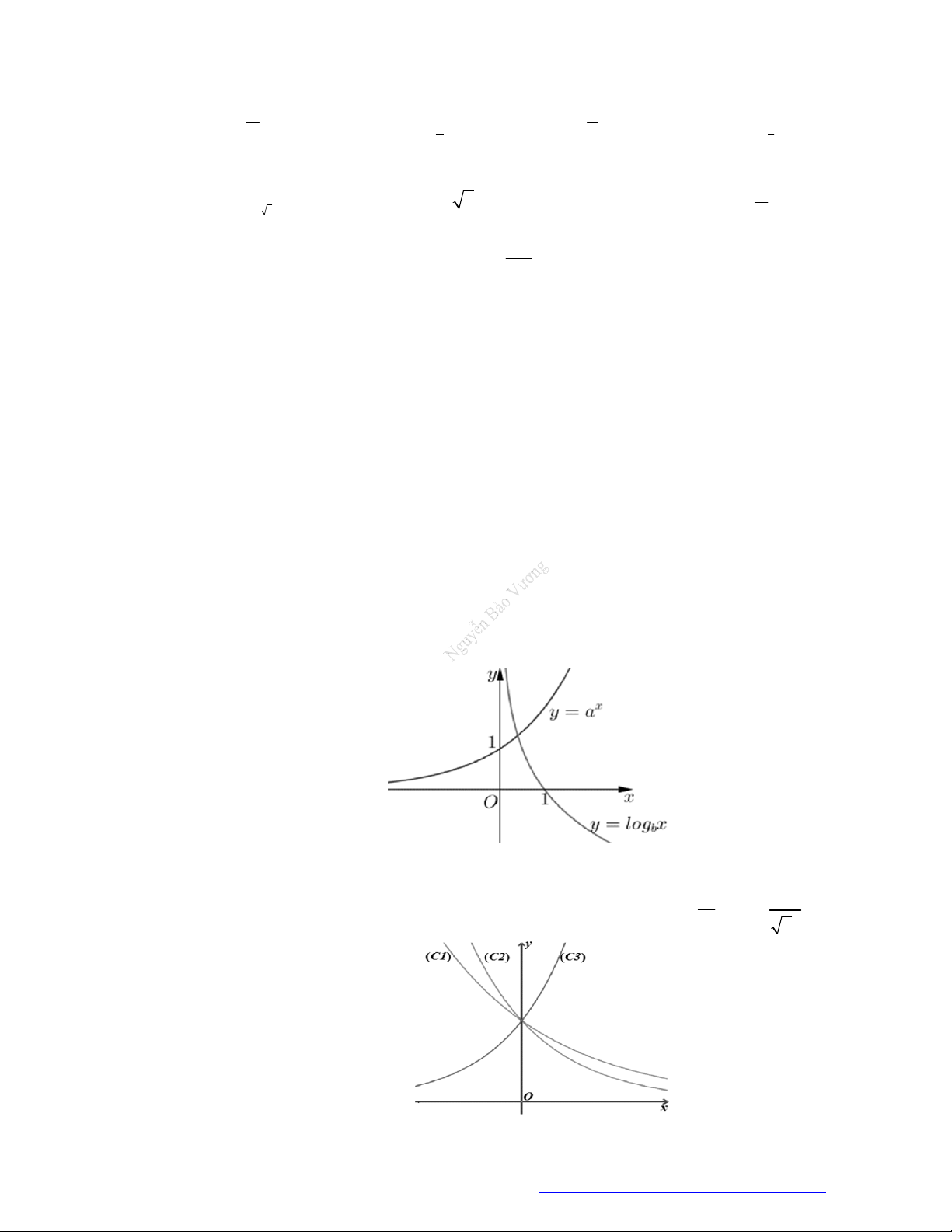
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 20. (Chuyên Quốc Học Huế 2019) Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số
thực
R
.
A.
3
x
y
B.
2
4
log 2 1
y x
C.
2
x
y
e
D.
2
3
logy x
Câu 21. (Chuyên Vĩnh Phúc 2019) Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
A.
3
logy x
B.
2
log 1y x C.
4
logy x
D.
3
x
y
Câu 22. (Chuyên Bắc Giang -2019 Cho hàm số
3
9 17
ln3
x
y x
. Mệnh đề nào sau đây sai?
A. Hàm số nghịch biến trên khoảng
;0
B. Hàm số đồng biến trên khoảng
0;
C. Hàm số đạt cực trị tại
2x
D. Hàm số có giá trị cực tiểu là
9
1
ln3
y
Câu 23. (THPT Lê Quy Đôn Điện Biên -2019) Đồ thị
L
của hàm số
lnf x x
cắt trục hoành tại
điểm
A
, tiếp tuyến của
L
tại
A
có phương trình là:
A.
2 1y x
B.
1y x
C.
3y x
D.
4 3y x
Câu 24. (THCS - THPT Nguyễn Khuyến 2019) Hàm số
3x
y xe
đạt cực đại tại
A.
1
3
x
e
. B.
1
3
x
. C.
1
x
e
. D.
0x
.
Câu 25. (THPT Gia Lộc Hải Dương 2019) Hàm số
2
3
log 2y x x
nghịch biến trên khoảng nào?
A.
2;
. B.
;0
. C.
1;
. D.
0;1
.
Câu 26. Cho đồ thị hàm số
x
y a và log
b
y x như hình vẽ. Trong các khẳng định sau, đâu là khẳng
định đúng
A.
0 1,0 1a b
. B.
1, 1a b
. C.
0 1b a
. D.
0 1a b
.
Câu 27. Hình vẽ bên thể hiện đồ thị của ba trong bốn hàm số
6
x
y
,
8
x
y
,
1
5
x
y
và
1
.
7
x
y
Hỏi (C
2
) là đồ thị hàm số nào?

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
6
x
y
. B.
1
7
x
y
. C
.
1
5
x
y
. D
.
8
x
y
Câu
28. (Chuyên Lê Hồng Phong Nam Định 2019) Giá trị nhỏ nhất của hàm số
ln x
y
x
trên
đoạ
n
2
;3
bằng
A.
ln 2
2
. B.
ln 3
3
. C
.
2
3
e
. D
.
1
e
.
Câu
29. (Sở Ninh Bình 2019) Cho hàm số
ln
f x x x
. Khẳng định nà
o dưới đây đúng?
A. Hàm số đồng biến trên khoảng
0
;1
.
B. Hàm số đồng biến trên khoảng
0
;
.
C. Hà
m số đồng biến trên các khoảng
;0
và
1;
.
D. Hà
m số đồng biến trên khoảng
1
;
.
Câu
30. (HSG Bắc Ninh 2019) Giá trị nhỏ nhất của hàm số
2
2
2
x
f
x x e
trên
đoạn
1
;2
bằng:
A.
4
2e
B.
2
e
C.
2
2e
D.
2
2e
Câu
31. Giá trị nhỏ nhất của hàm số
1
4
2
8
3
x
x
y
t
rên
1
;0
bằng
A.
4
9
. B.
5
6
. C
.
2
2
3
. D.
2
3
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ – MỨC 7-8 ĐIỂM
Dạng 1. Tìm tập xác định hàm số mũ - logarit
Hàm số mũ
Dạng:
x
u
y a
y a
với
0
.
1
a
a
Tập xác định:
.D
Hàm số logarit
Dạng:
log
log
a
a
y x
y u
với
0
.
1
a
a
Đặc biệt:
ln ;a e y x 10 log lga y x x
.
Điều kiện xác định:
0u
.
Câu 1. (Mã 105 2017) Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
log 2 1y x x m có
tập xác định là
.
A.
2m
B.
2m
C.
0m
D.
0m
Câu 2. (Mã 104 2017) Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
ln 2 1y x x m
có
tập xác định là
.
A.
0 3m
B.
1m
hoặc
0m
C.
0m
D.
0m
Câu 3. Hàm số
2
ln 1y x mx
xác định với mọi giá trị của
x
khi.
A.
2
2
m
m
. B.
2m
. C.
2 2m
. D.
2m
.
Câu 4. (THPT Cẩm Giàng 2 2019) Tìm tất cả các giá trị của tham số
m
để hàm số
2
3 3
1
log 4log 3
y
m x x m
xác định trên khoảng
0;
A.
; 4 1;m
. B.
1;m
.
C.
4;1m
. D.
1;m
.
Câu 5. Tìm tất cả các giá trị của
m
để hàm số
2
ln 2 1y x mx m
xác định với mọi
1; 2x
.
A.
1
3
m
. B.
3
4
m
. C.
3
4
m
. D.
1
3
m
.
Câu 6. (Chuyên Lê Quý Đôn Điện Biên -2019) Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
log( 4 1)y x x m có tập xác định là
.
A.
4m
. B.
0m
. C.
4m
. D.
3m
.
Câu 7. (Chuyên Vĩnh Phúc 2019) Có bao nhiêu giá trị nguyên của tham số
m
trên
2018; 2018
để
hàm số
2
ln 2 1y x x m
có tập xác định là
?
A.
2019
B.
2017
C.
2018
D.
1009
Câu 8. (THPT Nghĩa Hưng Nđ- 2019) Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
log 2 4y x mx
có tập xác định là
.
HÀM SỐ MŨ - HÀM SỐ LOGARIT
Chuyên đề 18

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2 2
m
. B.
2
m
. C.
2
2
m
m
. D.
2 2
m
.
Câu 9. Số các giá trị nguyên của tham số
m
để hàm số
log 2
y mx m
xác định trên
1
;
2
là
A.
4
B.
5
C. Vô số D.
3
Câu 10. (Gia Bình 2019) Tìm tất cả các giá trị của
m
để hàm số
2
2018
log 2018
2
x
x
y x m
xác
định với mọi giá trị
x
thuộc
0;
A.
9
m
B.
1
m
C.
0 1
m
D.
2
m
Câu 11. Hàm số
2
log 4 2
x x
y m
có tập xác định là
thì
A.
1
4
m
. B.
0
m
. C.
1
4
m
. D.
1
4
m
.
Câu 12. (Chuyên Bắc Ninh 2019) Tập hợp tất cả các giá trị của tham số
m
để hàm số
2 2
2018
3 5
log 2 4 5
x
y
x x m m
xác định với mọi
x
là
A.
;1 3;
. B.
(1;3) \ 2
. C.
;1
. D.
1;3 \ 2
.
Câu 13. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
2018
log 2017 1
2
x
x
y x m
xác
định với mọi
x
thuộc
0;
?
A.
1
. B.
2
. C.
2018
. D. Vô số.
Câu 14. (Sở Vĩnh Phúc 2019) Có tất cả bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
3
1
log
2 1
y x m
m x
xác định trên khoảng
2;3
?
A.
1
. B.
2
. C.
4
. D.
3
.
Câu 15. (Chuyên Vĩnh Phúc - 2020) Tìm tất cả các giá trị của tham số
m
để hàm số
2020
log 2
y mx m
xác định trên
1;
.
A.
0
m
. B.
0
m
. C.
1
m
. D.
1
m
.
Câu 16. (Chuyên Lương Thế Vinh Đồng Nai 2019) Tập xác định của hàm số
2020 2019 2018 2017
log log log log
y x
là
; .
D a
Giá trị của
a
bằng
A.
2019
2018
. B.
2020
2019
. C.
2018
2017
. D.
0
.
Dạng 2. Tính đạo hàm mũ – logarit
Đạo hàm hàm số mũ
ln
ln .
x x
u u
y a y a a
y a y a a u
.
Đặc biệt:
( )
( ) .
x x
u u
e e
e e u
với
2,71828...e
Đạo hàm hàm số logarit

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
1
log
ln
log
ln
a
a
y x y
x a
u
y u y
u a
.
Đặc biệt:
1
(ln )
(ln )
x
x
u
u
u
.
Câu 1. (Đề Tham Khảo 2017) Cho hàm số
ln x
y
x
, mệnh đề nào dưới đây đúng?
A.
2
1
2y xy
x
. B.
2
1
y xy
x
. C.
2
1
y xy
x
. D.
2
1
2y xy
x
.
Câu 2. (Chuyên Bắc Giang 2019) Cho hàm số
ln 2018 ln
1
x
f x
x
. Tính
' 1 ' 2 ' 3 ' 2017 .
S f f f f
A.
4035
2018
S
B.
2017
2018
S
C.
2016
2017
S
D.
2017
S
Câu 3. (Sở Vĩnh Phúc 2019) Cho hàm số
2018
ln
1
x
f x
x
. Tính tổng
1 2 ... 2018
S f f f
.
A.
ln 2018
. B.
1
. C.
2018
. D.
2018
2019
.
Câu 4. Cho hàm
cos ln s ln
y x x in x
. Khẳng định nào sau đây đúng?
A.
2
2 4 0
x y xy y
. B.
2
2 0
x y xy xy
.
C.
2
2 2 5 0
x y xy y
. D.
2
2 0
x y xy y
.
Câu 5. (THPT Bạch Đằng Quảng Ninh 2019) Tính đạo hàm của hàm số
2019
log , 0
xy x
.
A.
1
ln 2019
y
x
. B.
1
y
x
. C.
1
ln 2019
y
x
. D.
ln 2019
y x
.
Câu 6. (THPT An Lão Hải Phòng 2019) Cho hàm số
2
x x
f x e
. Biết phương trình
0
f x
có hai
nghiệm
1
x
,
2
x
. Tính
1 2
.x x
.
A.
1 2
1
.
4
x x
B.
1 2
. 1
x x
C.
1 2
3
.
4
x x
D.
1 2
. 0
x x
Câu 7. (Sở Bắc Ninh - 2020) Cho hàm số
ln .
2
x
f x
x
Tổng
' ' ' '
1 3 5 ... 2021
f f f f
bằng
A.
4035
.
2021
. B.
2021
2022
. C.
2021.
. D.
2022
.
2023
Câu 8. (Kiểm tra năng lực - ĐH - Quốc Tế - 2019) Phương trình
0
f x
với
4 3 2
1
ln 4 4
2
f x x x x
có bao nhiêu nghiệm?
A.
0
nghiệm. B.
1
nghiệm. C.
2
nghiệm. D.
3
nghiệm.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 9. Cho hàm số
1
ln
4
x
f x
x
. Tính giá trị của biểu thức
0 3 6 ... 2019P f f f f
.
A.
1
4
. B.
2024
2023
. C.
2022
2023
. D.
2020
2023
.
Câu 10. (THPT Minh Khai - 2019) Cho hàm số
2 1 3
x
y f x m e
. Giá trị của
m
để
5
' ln 3
3
f
là
A.
7
9
m
. B.
2
9
m
. C.
3m
. D.
3
2
m
.
Dạng 3. Khảo sát hàm số mũ, logarit
Sự biến thiên hàm số mũ:
x
y a
.
Nếu
1a
thì hàm đồng biến trên
. Nếu
0 1a
thì hàm nghịch biến trên
.
Sự biến thiên hàm số logarit:
log
a
y x
. Nếu
1a
: hàm đồng biến trên
(0; )
. Nếu
0 1a
: hàm
nghịch biến trên
(0; ).
Đồ thị hàm số mũ và logarit
ĐỒ THỊ HÀM SỐ MŨ ĐỒ THỊ HÀM SỐ LOGARIT
Ta thấy:
0 1; 0 1
x x
a a b b
.
Ta thấy:
1; 1.
x x
c c d d
So sánh a với b: Đứng trên cao, bắn mũi tên từ trái
sang phải, trúng
x
a
trước nên
a b
.
So sánh c với d: Đứng trên cao, bắn mũi tên từ trái
sang phải, trúng
x
c
trước nên
.c d
Vậy
0 1 .b a d c
Ta thấy:
log 0 1; log 0 1
a b
x a x b
.
Ta thấy:
log 1; log 1.
c d
x c x d
So sánh a với b: Đứng trên cao, bắn mũi tên từ phải
sang trái, trúng
log
b
x
trước:
.b a
So sánh c với d: Đứng trên cao, bắn mũi tên từ phải
sang trái, trúng
log
d
x
trước:
.d c
Vậy
0 1a b c d
.
Câu 1. (Mã 103 - 2020 Lần 2) Hàm số
log
a
y x
và
log
b
y x
có đồ thị như hình bên.
x
y
3
O
1
x
2
x
log
b
y x
log
a
y x
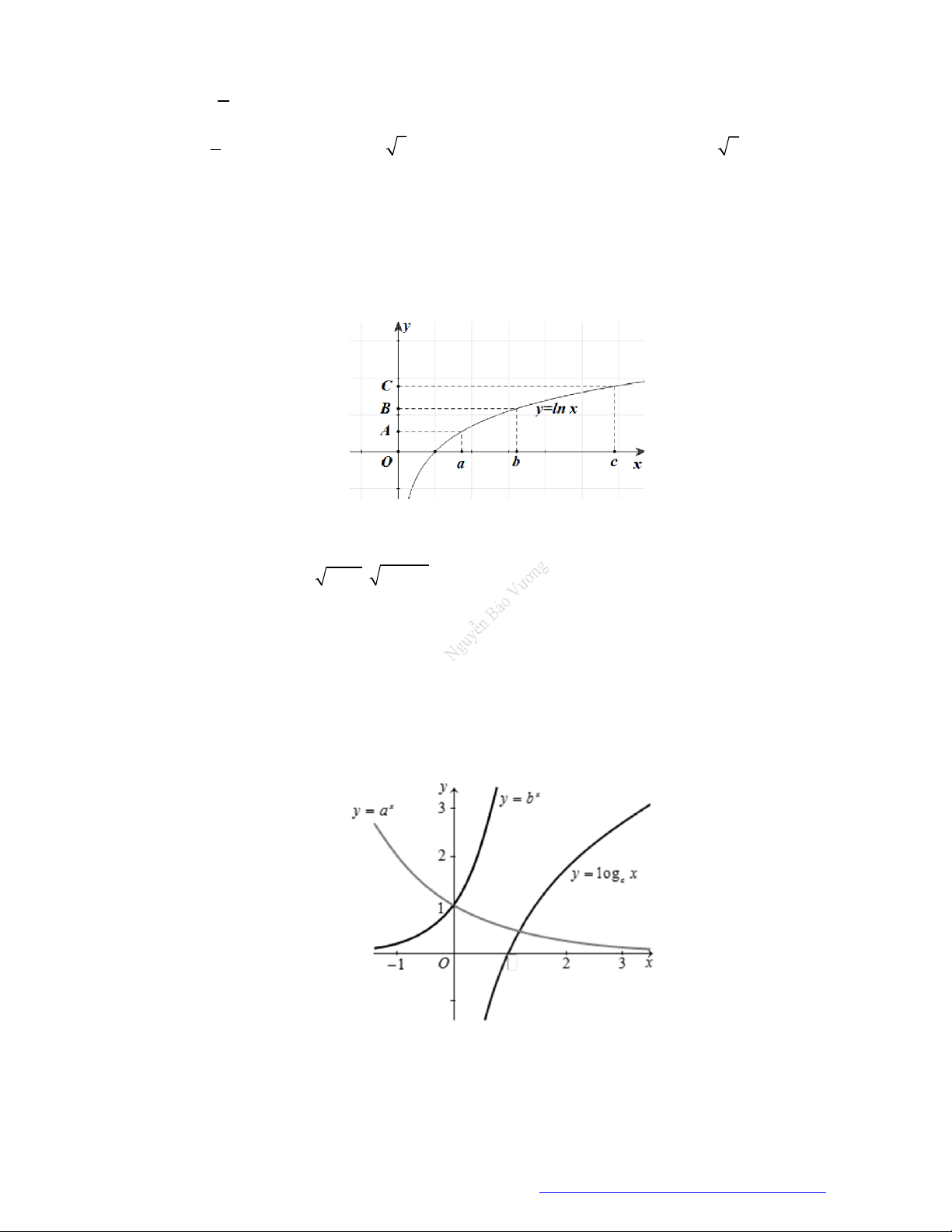
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Đường thẳng
3y
cắt hai đồ thị tại các điểm có hoành độ là
1 2
;x x
. Biết rằng
1 2
2x x
. Giá trị
của
a
b
bằng
A.
1
3
. B.
3
. C.
2
. D.
3
2
.
Câu 2. Tìm tập hợp tất cả các giá trị thực của tham số
m
để hàm số
2
y ln 1 1x mx
đồng biến trên
khoảng
;
A.
1;
B.
; 1
C.
1;1
D.
; 1
Câu 3. (Chuyên ĐHSP Hà Nội 2019) Trong hình dưới đây, điểm
B
là trung điểm của đoạn thẳng
AC
.
Khẳng định nào sau đây là đúng?
A.
2a c b
. B.
2
ac b
. C.
2
2ac b
. D.
ac b
.
Câu 4. Cho các số thực
,a b
sao cho
0 , 1a b
, biết rằng đồ thị các hàm số
x
y a
và log
b
y x cắt
nhau tại điểm
5 1
2018; 2019M
. Mệnh đề nào dưới đây đúng?
A.
1, 1a b
B.
1,0 1a b
C.
0 1, 1a b
D.
0 1,0 1a b
Câu 5. (Sở Hà Nội 2019) Tập tất cả các giá trị của tham số
m
để hàm số
2
ln 1 1y x mx
đồng
biến trên
là
A.
1;1
. B.
; 1
. C.
1;1
. D.
; 1
.
Câu 6. (THPT Đông Sơn Thanh Hóa 2019) Trong hình vẽ bên có đồ thị các hàm số
, , log
x x
c
y a y b y x
. Hãy chọn mệnh đề đúng trong các mệnh đề sau đây?
A.
a c b
. B.
c a b
. C.
a b c
. D.
b c a
.
Câu 7. (Lương Thế Vinh Hà Nội 2019) Cho đồ thị của ba hàm số , ,
x x x
y a y b y c như hình vẽ
bên. Khẳng định nào sau đây đúng?
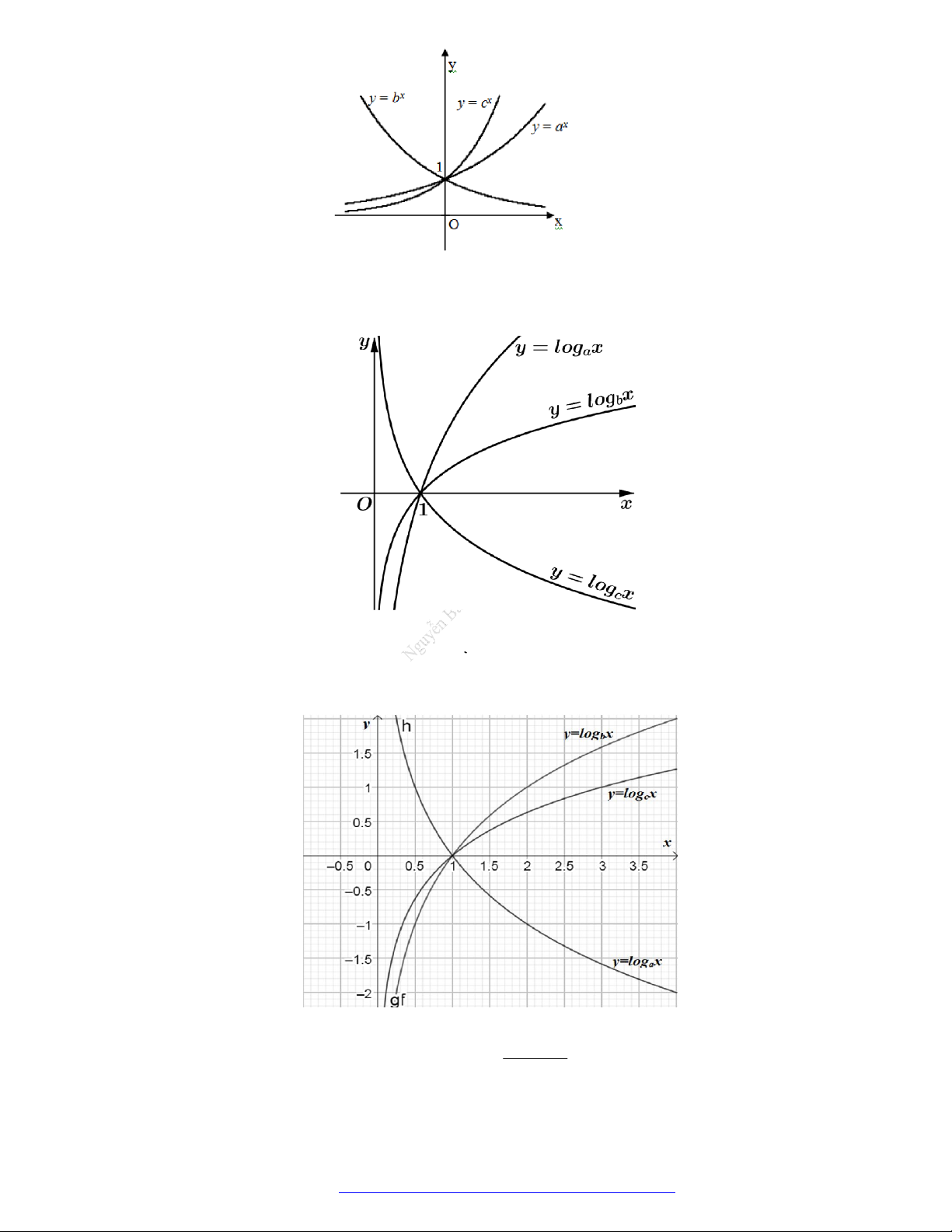
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
b a c
. B.
a c b
. C.
c a b
. D.
c b a
.
Câu 8. (KTNL GV Thpt Lý Thái Tổ 2019) Cho
, ,a b c
là các số thực dương khác 1. Hình vẽ bên là đồ
thị của ba hàm số
log , log , log
a b c
y x y x y x
.
Khẳng định nào sau đây là đúng?
A.
a c b
. B.
a b c
. C.
c b a
. D.
c a b
.
Câu 9. (Chuyên Thái Bình 2019) Cho
, ,a b c
là các số thực dương khác 1. Hình vẽ bên là đồ thị hàm số
log , log , log
a b c
y x y y x y x . Khẳng định nào sau đây là đúng?
A.
a b c
. B.
a c b
. C.
b a c
. D.
b a c
.
Câu 10. (THPT Nguyễn Khuyến 2019) Cho hàm số
ln 6
ln 2
x
y
x m
với
m
là tham số. Gọi
S
là tập hợp
các giá trị nguyên dương của
m
để hàm số đồng biến trên khoảng
1; e
. Tìm số phần tử của
S
.
A.
3
B.
1
C.
2
D.
4
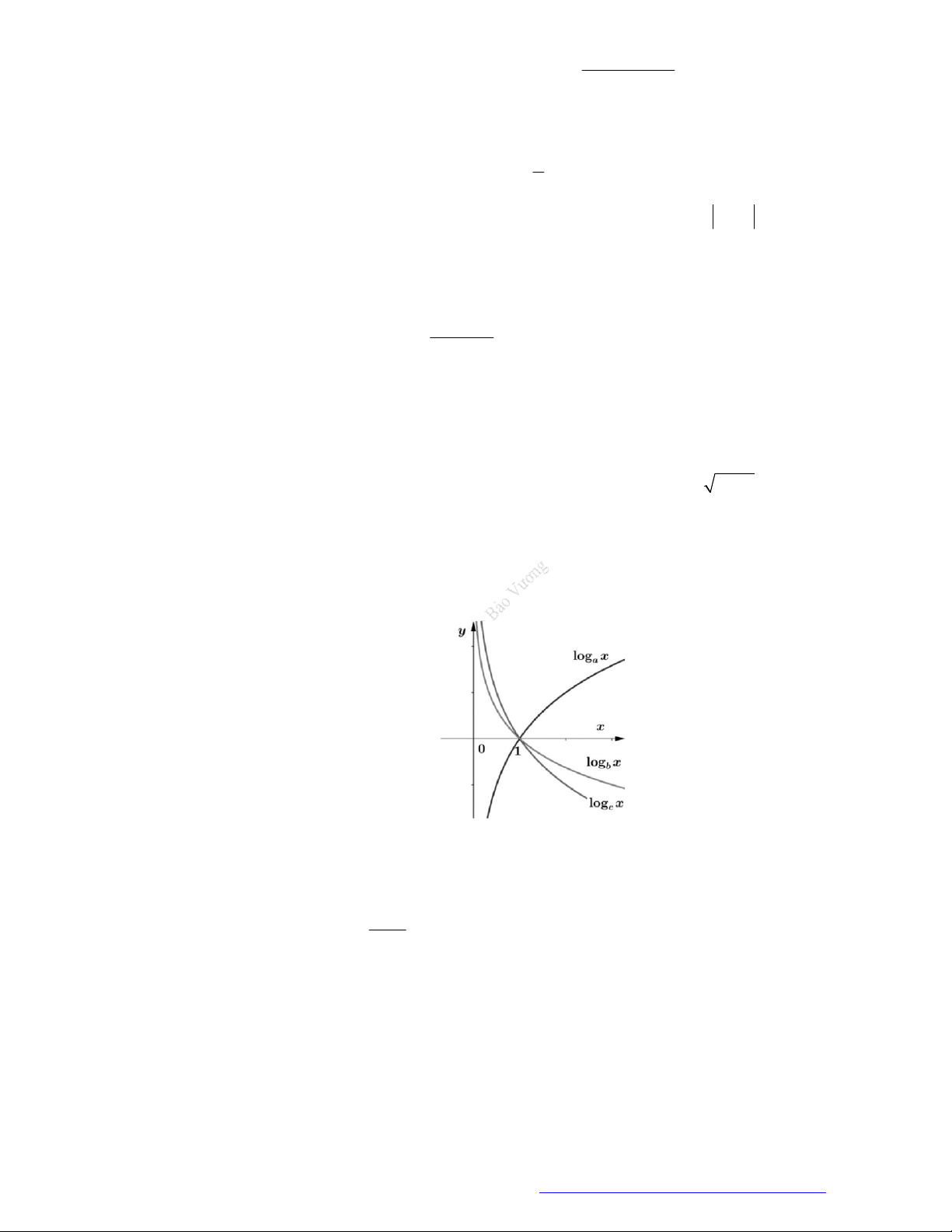
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 11. Tìm tất cả các giá trị thực của tham số m để hàm số
2
2
log 2
log 1
m x
y
x m
nghịch biến trên
4;
A.
2m
hoặc
1m
. B.
2m
hoặc
1m
.
C.
2m
hoặc
1m
. D.
2m
.
Câu 12. (HSG Bắc Ninh 2019) Cho hàm số
2018
1
logy
x
có đồ thị
1
C
và hàm số
y f x
có đồ thị
2
C
. Biết
1
C
và
2
C
đối xứng nhanh qua gốc tọa độ. Hỏi hàm số
y f x
nghịch biến trên
khoảng nào dưới đây?
A.
0;1
B.
1;0
C.
; 1
D.
1;
Câu 13. (THPT Bạch Đằng Quảng Ninh 2019) Có bao nhiêu giá trị nguyên của tham số
2019;2019m
để hàm số
ln 6
ln 3
x
y
x m
đồng biến trên khoảng
6
1;e
?
A.
2020
. B.
2021
. C.
2018
. D.
2019
.
Câu 14. (Chuyên Hưng Yên 2019) Có bao nhiêu giá trị nguyên của tham số thực
m
thuộc đoạn
2018;2018
để hàm số
1 ln 2 y f x x x m x
đồng biến trên khoảng
2
0;e
.
A.
2016
. B.
2022
. C.
2014
. D.
2023
.
Câu 15. (THPT Quang Trung Đống Đa Hà Nội 2019) Cho
2
ln 1 sin 6f x a x x b x
với
,a b
. Biết rằng
log log 2f e
. Tính giá trị của
log ln10f
.
A.
10
. B.
2
. C.
4
. D.
8
.
Câu 16. (Sở Bắc Ninh 2019) Cho
, ,a b c
dương và khác 1. Các hàm số log
a
y x , log
b
y x , log
c
y x
có đồ thị như hình vẽ
Khẳng định nào dưới đây đúng?
A.
a c b
. B.
a b c
. C.
c b a
. D.
b c a
.
Câu 17. Đồ thị hàm số
y f x
đối xứng với đồ thị hàm số
0, 1
x
y a a a
qua điểm
1;1I
. Giá trị
của biểu thức
1
2 log
2018
a
f
bằng
A.
2016
. B.
2016
. C.
2020
. D.
2020
.
Câu 18. (Chuyên Hùng Vương - Phú Thọ - 2020) Trong hình vẽ bên các đường cong
1 2 3
: , : , :
x x x
C y a C y b C y c
và đường thẳng
4; 8y y
tạo thành hình vuông
MNPQ
có cạnh bằng
4
.
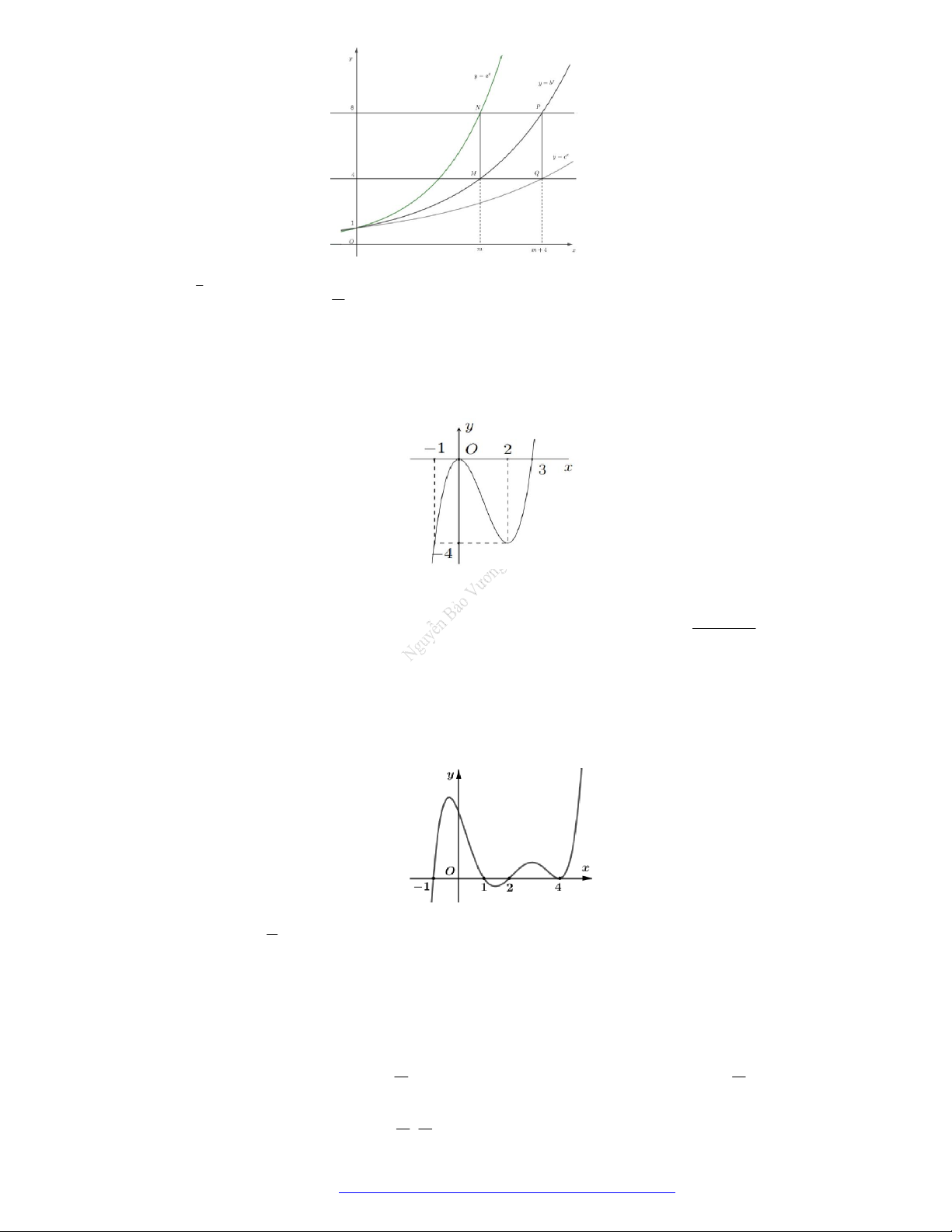
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Biết rằng
2
x
y
abc
với ;x y
và
x
y
tối giản, giá trị của
x y
bằng
A.
34
. B.
5
. C.
43
. D.
19
.
Câu 19. ( Bạc Liêu – Ninh Bình 2019) Cho hàm số
y f x
. Hàm số
'y f x
có đồ thị như hình vẽ.
Hàm số
2 e
x
y f
nghịch biến trên khoảng
A.
1; 3
. B.
2; 1
. C.
; 0
. D.
0; +
.
Câu 20. Có bao nhiêu giá trị nguyên của tham số
2019;2019m
để hàm số
ln 6
ln 3
x
y
x m
đồng biến
trên khoảng
6
1;e
?
A.
2020
. B.
2021
. C.
2018
. D.
2019
.
Câu 21. (Chuyên Lê Hồng Phong Nam Định 2019) Cho hàm số
.y f x
Đồ thị hàm số
y f x
như hình bên dưới
Hàm số
1 2
1
2
f x
g x
nghịch biến trên khoảng nào trong các khoảng sau?
A.
;0 .
B.
0;1 .
C.
1;0 .
D.
1; .
Câu 22. (Kiểm tra năng lực - ĐH - Quốc Tế - 2019) Xét hàm số
sin
cos
x
f x x
. Mệnh đề nào sau đây
là đúng?
A. Hàm số
f
tăng trên khoảng
0;
2
. B. Hàm số
f
tăng trên khoảng
;0
2
.
C. Hàm số
f
giảm trên khoảng
;
2 2
. D.
3
lựa chọn kia đều sai.
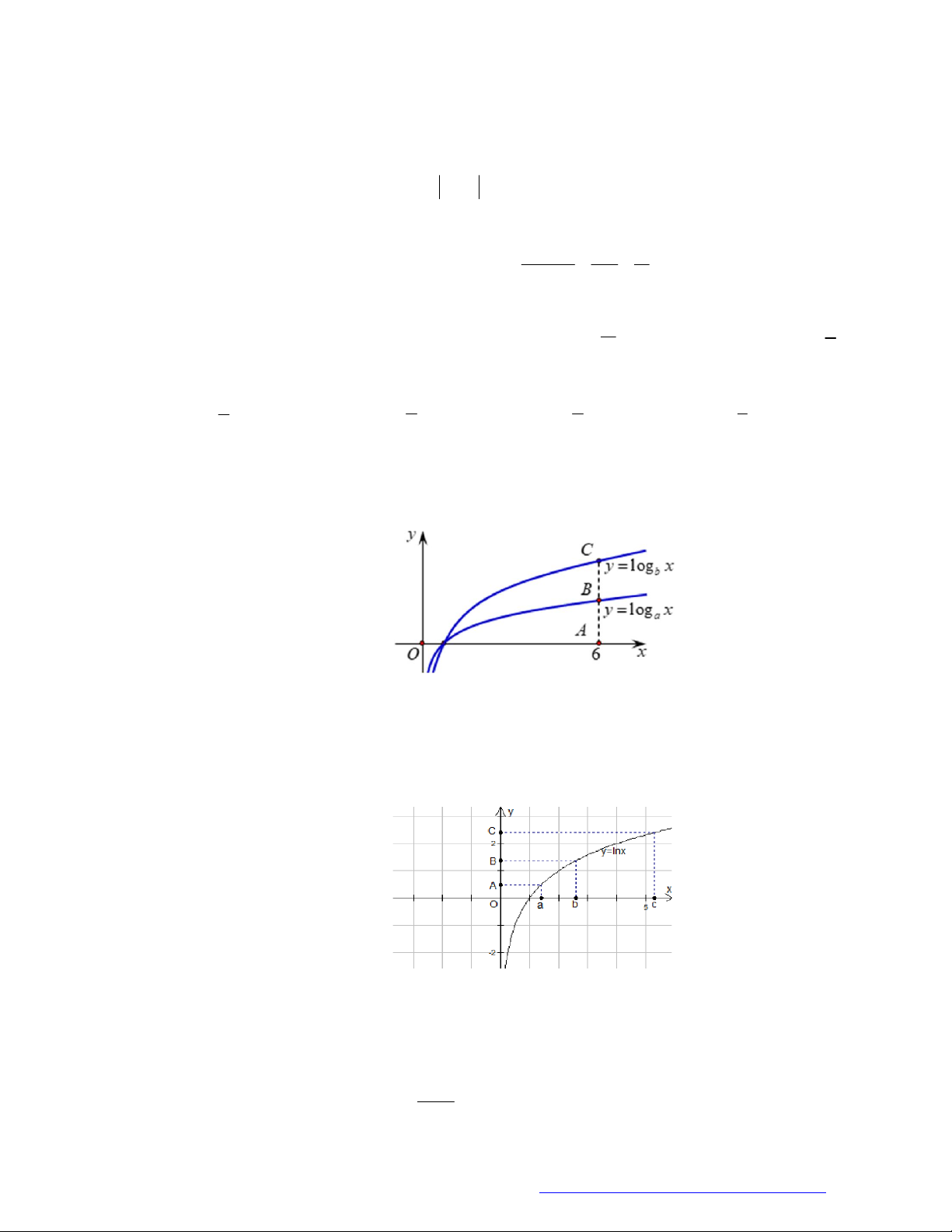
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 23. Có bao nhiêu giá trị nguyên của tham số
m
trong đoạn
2019;2019
để hàm số
2
ln 2 1y x mx
đồng biến trên
.
A.
2019
. B.
2020
. C.
4038
. D.
1009
.
Câu 24. Gọi
C
là đồ thị của hàm số
2018
logy x và
C
là đồ thị hàm số
y f x
,
C
là đối xứng
với
C
qua trục tung. Hàm số
y f x
đồng biến trên khoảng nào sau đây?
A.
0;1
. B.
; 1
. C.
1;0
. D.
1;
.
Câu 25. Có bao nhiêu giá trị thực
m
để hàm số
2
2019 6
2
ln 2019 ln 6 2
x x
m
g x x x
đồng biến trên
.
A. Duy nhất. B. Không tồn tại. C.
2019
. D. Vô số.
Câu 26. Tập các giá trị của tham số
m
để hàm số
ln 3 1 2
m
y x
x
đồng biến trên khoảng
1
;
2
là
A.
2
;
9
. B.
4
;
3
. C.
7
;
3
. D.
1
;
3
.
Câu 27. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho các hàm số log
a
y x và log
b
y x có đồ thị như
hình vẽ bên.
Đường thẳng
6x
cắt trục hoành, đồ thị hàm số log
a
y x và log
b
y x lần lượt tại
,A B
và
C
.
Nếu
2
log 3AC AB thì
A.
3 2
b a
. B.
2 3
b a
. C.
3 2
log logb a
. D.
2 3
log logb a
.
Câu 28. Trong hình dưới đây, điểm
B
là trung điểm của đoạn thẳng
AC
.
Khẳng định nào sau đây là đúng?
A.
2a c b
. B.
2
ac b
. C.
2
2ac b
. D.
ac b
Câu 29.
Đồ thị hàm số
y f x
đối xứng với đồ thị của hàm số
0, 1
x
y a a a
qua điểm
1;1I
.
Giá trị của biểu thức
1
2 log
2018
a
f
bằng
A.
2016
.
B.
2020
.
C.
2016
.
D.
2020
.
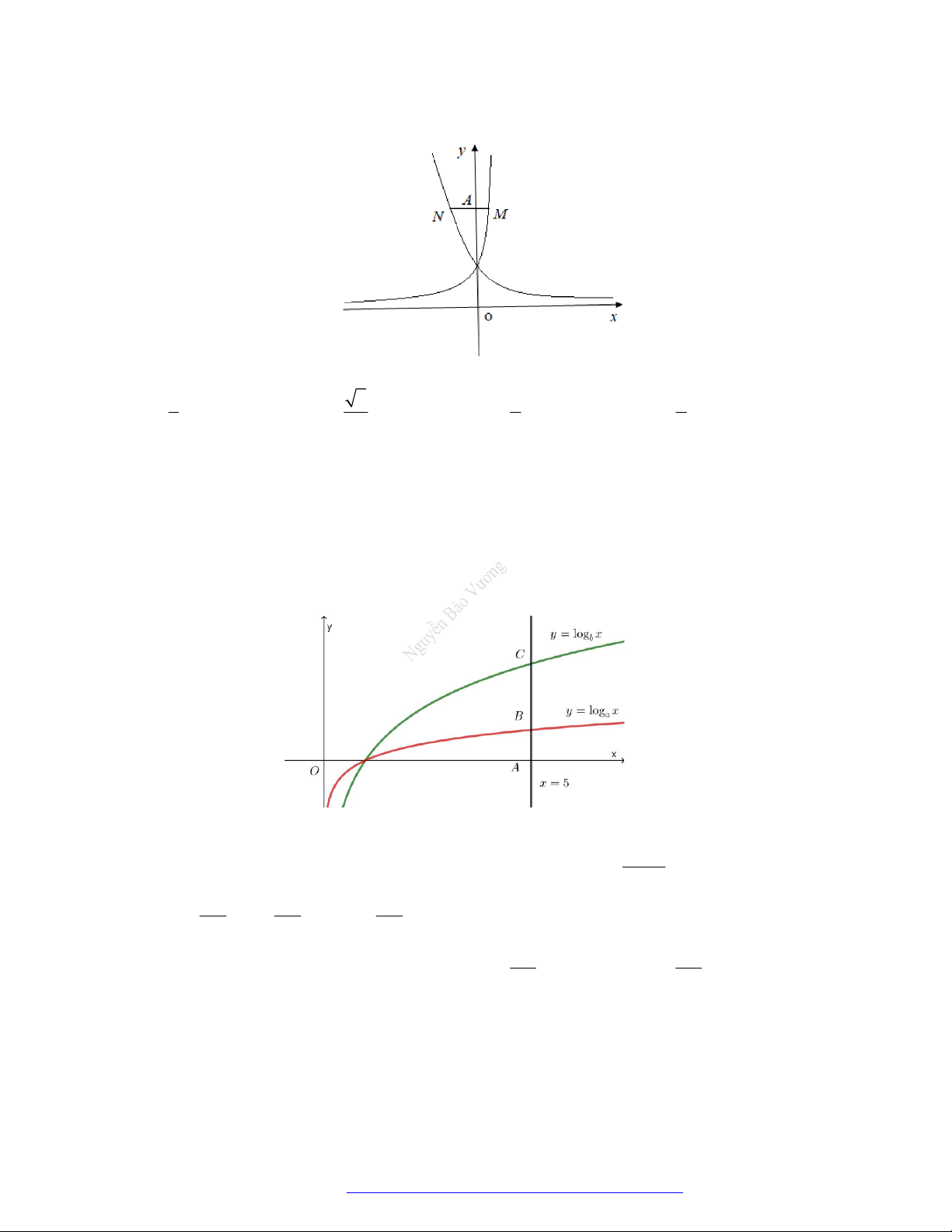
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 30. (Hội 8 trường chuyên ĐBSH - 2019) Cho số thực dương
a
khác
1
. Biết rằng bất kỳ đường
thẳng nào song song với trục
Ox
mà cắt các đường
4 ,
x x
y y a
, trục tung lần lượt tại
,M N
và
A
thì
2AN AM
( hình vẽ bên). Giá trị của
a
bằng
A.
1
3
. B.
2
2
. C.
1
4
. D.
1
2
.
Câu 31. (THPT Ngô Quyền - Ba Vì - Hải Phòng 2019) Đồ thị hàm số
y f x
đối xứng với đồ thị
hàm số
log
a
y x
,
0 1a
qua điểm
2;1I
. Giá trị của biểu thức
2019
4f a
bằng
A.
2023
. B.
2023
. C.
2017
. D.
2017
.
Câu 32. Cho các hàm số
log
a
y x
và
log
b
y x
có đồ thị như hình vẽ bên. Đường thẳng
5x
cắt trục
hoành, đồ thị hàm số
log
a
y x
và
log
b
y x
lần lượt tại
,A B
và
C
. Biết rằng
2CB AB
. Mệnh
đề nào sau đây là đúng?
A.
5a b
. B.
2
a b
. C.
3
a b
. D.
3
a b
.
Câu 33. (THPT Đông Sơn 1 - Thanh Hóa - 2019) Cho hàm số
4
.
4 2
x
x
f x
Tính giá trị biểu thức
1 2 100
... ?
100 100 100
A f f f
A.
50
. B.
49
. C.
149
3
. D.
301
6
.
Câu 34. Tìm tập hợp tất cả các giá trị của tham số thực
m
đề hàm số
2
ln 1 1y x mx
đồng biến
trên
.
A.
1; 1 .
B.
1; 1 .
C.
; 1 .
D.
; 1 .
Câu 35. Có bao nhiêu giá trị nguyên của
m
thuộc khoảng
2019;2019
để hàm số sau có tập xác định là
D
?
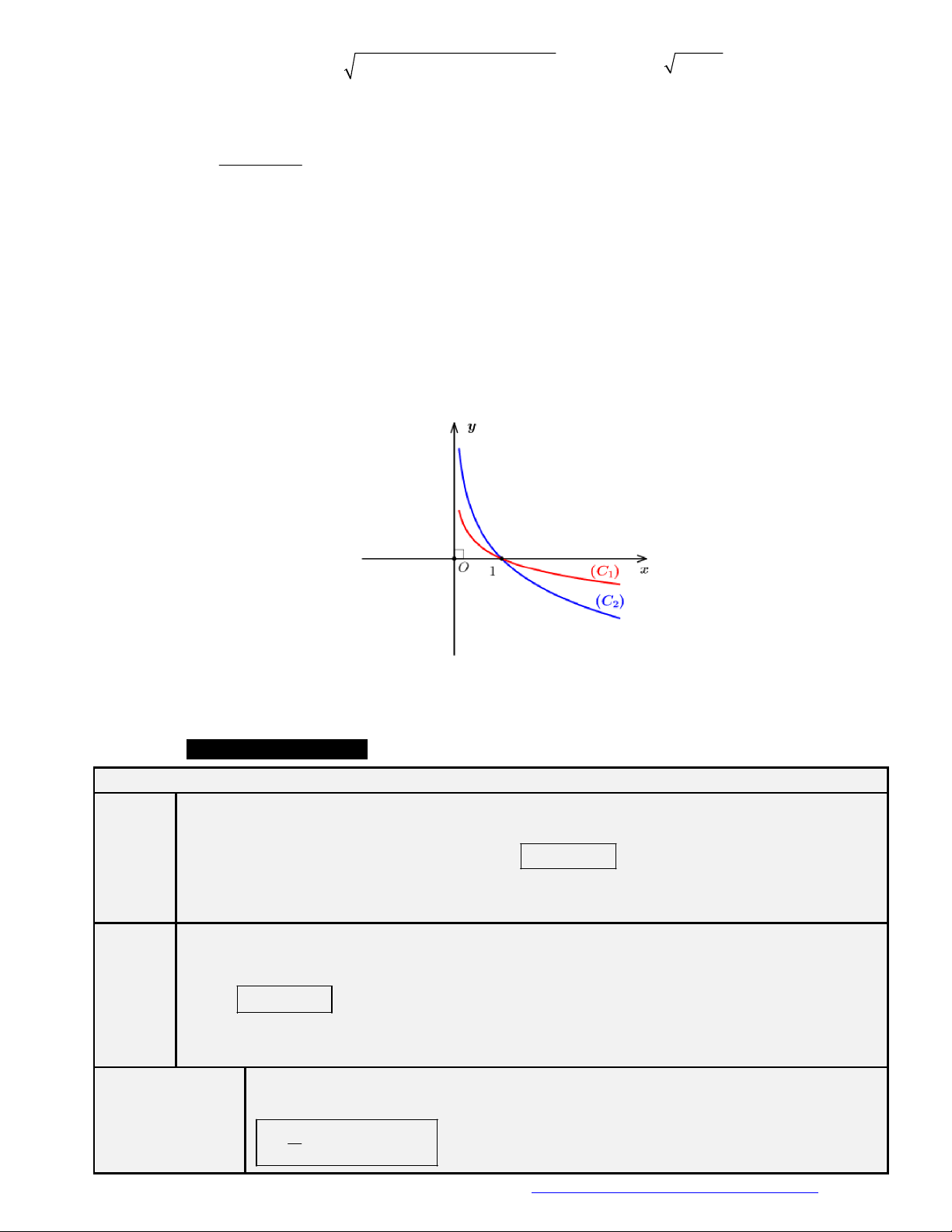
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
2 2 2
2
2 1 2 4 log 2 1y x m x m x m m x m x
A.
2020
. B.
2021
. C.
2018
. D.
2019
.
Câu 36. (THPT Yên Dũng 2-Bắc Giang 2019) Tập tất cả các giá trị của tham số
m
để hàm số
ln 2
ln 1
m x
y
x m
nghịch biến trên
2
;e
là:
A.
2
1
m
m
. B.
2
1
m
m
. C.
2
1
m
m
. D.
2m
.
Câu 37. (Chuyên Bắc Giang 2019) Có bao nhiêu giá trị nguyên của
m
thuộc khoảng
2019;2019
để
hàm số
3 2
1
2019
x x mx
y
nghịch biến trên
1;2
A.
2020
. B.
2019
. C.
2010
. D.
2011
.
Câu 38. (Hậu Lộc 2-Thanh Hóa -2019) Cho
a
,
b
là các số thực dương khác
1
, đồ thị hàm số log
a
y x
và log
b
y x lần lượt là
1
C
,
2
C
như hình vẽ.
Khẳng định nào sau đây là đúng
A.
e.e .
a b
b a
. B.
e.e .
a b
b a
. C.
e.e .
a b
b a
. D.
e.e .
a b
a b
.
Dạng 4. Bài toán thực tế
BÀI TOÁN NGÂN HÀNG
1. Công
thức
tính lãi
đơn
Nếu ta gởi tiền vào ngân hàng theo hình thức tiền lãi chỉ được tính dựa vào tiền gốc ban đầu
(tức là tiền lãi của kỳ hạn trước không gộp vào vốn để tính lãi cho kỳ hạn kế tiếp),
đây gọi là hình thức lãi đơn. Ta có:
(1 )T A nr
với A: tiền gởi ban đầu; r: lãi suất;
n: kỳ hạn gởi; T: tổng số tiền nhận sau kỳ hạn n. Lưu ý: r và n phải khớp đơn vị; T bao
gồm cả A, muốn tính số tiền lời ta lấy T – A.
2. Công
thức lãi
kép
Nếu ta gởi tiền vào ngân hàng theo hình thức: hàng tháng tiền lãi phát sinh sẽ được cộng vào
tiền gốc cũ để tạo ra tiền gốc mới và cứ tính tiếp như thế, đây gọi là hình thức lãi kép.
Ta có: (1 )
n
T A r với A: tiền gởi ban đầu; r: lãi suất; n: kỳ hạn gởi; T: tổng số tiền nhận sau
kỳ hạn n. Lưu ý: r và n phải khớp đơn vị; T bao gồm cả A, muốn tính số tiền lời ta lấy T
– A.
3. Mỗi tháng gởi
đúng số tiền
giống nhau theo
hình thức lãi kép
Nếu đầu mỗi tháng khách hàng luôn gởi vào ngân hàng số tiền A đồng với lãi kép
%r
/tháng thì số tiền họ nhận được cả vốn lẫn lãi sau n tháng là:
1 1 1
n
A
T r r
r
.
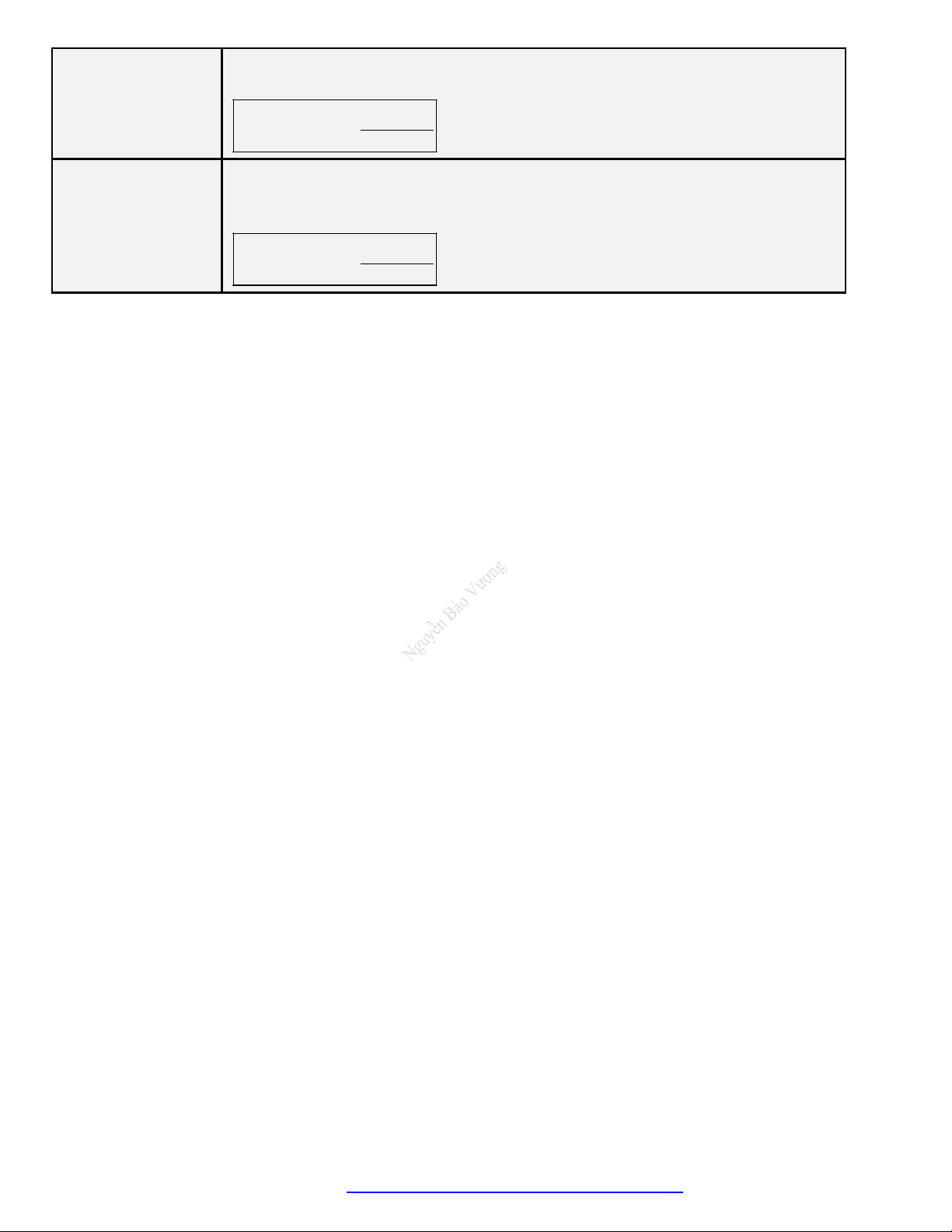
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
4. Gởi tiền vào ngân
hàng rồi rút ra hàng
tháng số tiền cố
định
Nếu khách hàng gởi vào ngân hàng số tiền A đồng với lãi suất
%r
/tháng. Vào ngày
ngân hàng tính lãi mỗi tháng thì rút ra X đồng. Số tiền thu được sau n tháng là:
1 1
1
n
n
r
T A r X
r
5. Vay vốn và trả
góp (tương tự bài
toán 4)
Nếu khách hàng vay ngân hàng số tiền A đồng với lãi suất r%/tháng. Sau đúng một
tháng kể từ ngày vay bắt đầu hoàn nợ, hai lần hoàn nợ cách nhau đúng một tháng, mỗi
lần hoàn nợ đúng số tiền X đồng. Số tiền khách hàng còn nợ sau n tháng là:
1 1
1
n
n
r
T A r X
r
Câu 1. (Mã 101 - 2020 Lần 1) Trong năm 2019, diện tích rừng trồng mới của tỉnh
A
là
600 ha
. Giả sử
diện tích rừng trồng mới của tỉnh
A
mỗi năm tiếp theo đều tăng
6%
so với diện tích rừng trồng
mới của năm liền trước. Kể từ sau năm 2019, năm nào dưới đây là năm đầu tiên tỉnh
A
có diện
tích rừng trồng mới trong năm đó đạt trên
1000 ha
?
A. Năm 2028. B. Năm 2047. C. Năm 2027. D. Năm 2046.
Câu 2. (Mã 102 - 2020 Lần 1) Trong năm 2019, diện tích rừng trồng mới của tỉnh A là
1000
ha. Giả sử
diện tích rừng trồng mới của tỉnh A mỗi năm tiếp theo đều tăng
%6
so với diện tích rừng trồng
mới của năm liền trước. Kể từ sau năm 2019, năm nào dưới đây là năm đầu tiên tỉnh A có diện
tích rừng trồng mới trong năm đó đạt trên
1400
ha.
A.
2043
. B.
2025
. C.
2024
. D.
2042
.
Câu 3. (Mã 103 - 2020 Lần 1) Trong năm
2019
, diện tích rừng trồng mới của tỉnh
A
là
900
ha. Giả sử
diện tích rừng trồng mới của tỉnh
A
mỗi năm tiếp theo đều tăng
6%
so với diện tích rừng trồng
mới của năm liền trước. Kể từ sau năm 2019, năm nào dưới đây là năm đầu tiên của tỉnh
A
có
diện tích rừng trồng mới trong năm đó đạt trên
1700
ha?
A. Năm
2029.
B. Năm
2051.
C. Năm
2030.
D. Năm
2050.
Câu 4. (Mã 104 - 2020 Lần 1) Trong năm
2019
, diện tích rừng trồng mới của tỉnh A là
800ha
. Giả sử
diện tích rừng trồng mới của tỉnh A mỗi năm tiếp theo đều tăng
6%
so với diện tích rừng trồng
mới của năm liền trước. Kể từ sau năm
2019
, năm nào dưới đây là năm đầu tiên tỉnh A có diện
tích rừng trồng mới trong năm đó đạt trên
1400ha
?
A. Năm
2029
. B. Năm
2028
. C. Năm
2048
. D. Năm
2049
.
Câu 5. (Mã 102 - 2020 Lần 2) Năm
2020
một hãng xe niêm yết giá bán loại xe X là
750.000.000
đồng
và dự định trong
10
năm tiếp theo, mỗi năm giảm
2%
giá bán so với giá bán của năm liền trước.
Theo dự định đó năm
2025
hãng xe ô tô niêm yết giá bán loại xe X là bao nhiêu ( kết quả làm
tròn đến hàng nghìn )?
A.
677.941.000
đồng. B.
675.000.000
đồng.
C.
664.382.000
đồng. D.
691.776.000
đồng.
Câu 6. (Mã 103 - 2020 Lần 2) Năm 2020, một hãng xe ô tô niêm yết giá bán loại xe X là 800.000.000
đồng và dự định trong 10 năm tiếp theo, mỗi năm giảm 2% giá bán so với giá bán của năm liền
trước. Theo dự định đó, năm 2025 hãng xe ô tô niêm yết giá bán loại xe X là bao nhiêu (kết quả
làm tròn đến hàng nghìn)?
A. 708.674.000 đồng. B. 737.895.000 đồng. C. 723.137.000 đồng. D. 720.000.000 đồng.
Câu 7. (Đề Tham Khảo 2018) Một người gửi
100
triệu đồng vào ngân hàng với lãi suất
0,4%/
tháng.
Biết rằng nếu không rút tiền ta khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được lập vào
vốn ban đầu để tính lãi cho tháng tiếp theo. Hỏi sau
6
tháng, người đó được lĩnh số tiền ( cả vốn
ban đầu và lãi) gần nhất với số tiền nào dưới đây, nếu trong khoảng thời gian này người đó không
rút tiền ra và lãi xuất không thay đổi?

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
A.
102.16.000
đồng B.
102.017.000
đồng C.
102.424.000
đồng D.
102.423.000
đồng
Câu 8. (Mã 104 2018) Một người gửi tiết kiệm vào một ngân hàng với lãi suất
6,1% /
năm. Biết rằng
nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính
lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó thu được (cả số tiền gửi ban đầu và
lãi) gấp đôi số tiền gửi ban đầu, giả định trong khoảng thời gian này lãi suất không thay đổi và
người đó không rút tiền ra?
A.
11
năm B.
12
năm C.
13
năm D.
10
năm
Câu 9. Anh An gửi số tiền 58 triệu đồng vào một ngân hàng theo hình thức lãi kép và ổn định trong 9
tháng thì lĩnh về được 61758000đ. Hỏi lãi suất ngân hàng hàng tháng là bao nhiêu? Biết rằng lãi
suất không thay đổi trong thời gian gửi.
A.
0,8 %
B.
0,6 %
C.
0,7 %
D.
0,5 %
Câu 10. (Chuyên Bắc Giang 2019) Một người gửi
100
triệu đồng vào một ngân hàng với lãi suất
0,6%
/tháng. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ
được nhập làm vốn ban đầu để tính lãi cho tháng tiếp theo. Hỏi sau ít nhất bao nhiêu tháng, người
đó được lĩnh số tiền không ít hơn
110
triệu đồng (cả vốn ban đầu và lãi), biết rằng trong suốt thời
gian gửi tiền người đó không rút tiền và lãi suất không thay đổi?
A.
18
tháng B.
16
tháng C.
17
tháng D.
15
tháng
Câu 11. Một người lần ầu gửi vào ngân hàng
100
triệu ồng theo thể thức lãi kép (tức là tiền lãi của
kỳ trước ược cộng vào vốn của kỳ kế tiếp) với kì hạn
3
tháng, lãi suất
2%
một quý. Sau
úng
6
tháng, người ó gửi thêm
100
triệu ồng với kỳ hạn và lãi suất như trước ó. Tổng
số tiền người ó nhận ược sau
1
năm gửi tiền vào ngân hàng gần bằng với kết quả nào sau
ây? Biết rằng trong suốt thời gian gửi tiền lãi suất ngân hàng không thay ổi và người ó
không rút tiền ra.
A.
212
triệu ồng
B.
216
triệu ồng
C.
210
triệu ồng
D.
220
triệu ồng
Câu 12. (KTNL Gia Bình 2019) Ông An gửi tiết kiệm
50
triệu đồng vào ngân hàng với kỳ hạn
3
tháng,
lãi suất
8,4%
một năm theo hình thức lãi kép. Ông gửi được đúng
3
kỳ hạn thì ngân hàng thay
đổi lãi suất, ông gửi tiếp
12
tháng nữa với kỳ hạn như cũ và lãi suất trong thời gian này là
12%
một năm thì ông rút tiền về. Số tiền ông An nhận được cả gốc lẫn lãi là: (làm tròn đến chữ số
hàng đơn vị)
A.
62255910
đồng. B.
59895767
đồng. C.
59993756
đồng. C.
63545193
đồng.
Lời giải
Chọn B
Đợt I, ông An gửi số tiền
0
50
P
triệu, lãi suất
8,4%
một năm tức là
2,1%
mỗi kỳ hạn. Số tiền
cả gốc và lãi ông thu được sau
3
kỳ hạn là:
3
3
50000000. 1.021
P
.
Đợt II, do ông không rút ra nên số tiền
3
P
được xem là số tiền gửi ban đầu của đợt II, lãi suất đợt
II là
3%
mỗi kỳ hạn. Ông gửi tiếp
12
tháng bằng
4
kỳ hạn nên số tiền thu được cuối cùng là:
4 3 4
3
1.03 50000000. 1.021 . 1.03 59895767
P P
đồng.
Câu 13. (THPT An Lão Hải Phòng 2019) Ngày 01 tháng 01năm 2017, ông An đem 800
triệu đồng gửi vào một ngân hàng với lãi suất 0,5% một tháng. Từ đó, cứ tròn mỗi tháng, ông đến
ngân hàng rút 6 triệu để chi tiêu cho gia đình. Hỏi đến ngày 01tháng 01 năm 2018, sau khi rút
tiền, số tiền tiết kiệm của ông An còn lại là bao nhiêu? Biết rằng lãi suất trong suốt thời gian ông
An gửi không thay đổi
A.
11
800.(1,005) 72
(triệu đồng) B.
12
1200 400.(1,005)
(triệu đồng)
C.
12
800.(1,005) 72
(triệu đồng) D.
11
1200 400.(1,005)
(triệu đồng)

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 14. (THPT Lê Quy Đôn Điện Biên 2019) Ông An gửi
100
triệu vào tiết kiệm ngân hàng theo thể
thức lãi kép trong một thời gian khá lâu mà không rút ra với lãi suất ổn định trong mấy chục năm
qua là
10% /1
năm. Tết năm nay do ông kẹt tiền nên rút hết ra để gia đình đón Tết. Sau khi rút cả
vốn lẫn lãi, ông trích ra gần
10
triệu để sắm sửa đồ Tết trong nhà thì ông còn
250
triệu. Hỏi ông
đã gửi tiết kiệm bao nhiêu lâu?
A.
10
năm B.
17
năm C.
15
năm D.
20
năm
Câu 15. Một học sinh
A
khi
15
tuổi được hưởng tài sản thừa kế
200 000 000
VNĐ. Số tiền này được bảo
quản trong ngân hàng
B
với kì hạn thanh toán
1
năm và học sinh
A
chỉ nhận được số tiền này
khi
18
tuổi. Biết rằng khi
18
tuổi, số tiền mà học sinh
A
được nhận sẽ là
231 525 000
VNĐ.
Vậy lãi suất kì hạn một năm của ngân hàng
B
là bao nhiêu?
A.
8% /
năm. B.
7% /
năm. C.
6% /
năm. D.
5% /
năm.
Câu 16. (THPT Minh Khai Hà Tĩnh 2019) Ông Anh gửi vào ngân hàng
60
triệu đồng theo hình thức
lãi kép. Lãi suất ngân hàng là
8%
trên năm. Sau
5
năm ông An tiếp tục gửi thêm
60
triệu đồng
nữa. Hỏi sau
10
năm kể từ lần gửi đầu tiên ông An đến rút toàn bộ tiền gốc và tiền lãi được là bao
nhiêu? (Biết lãi suất không thay dổi qua các năm ông gửi tiền).
A.
231,815
(triệu đồng). B.
197,201
(triệu đồng).
C.
217,695
(triệu đồng). D.
190,271
(triệu đồng).
Câu 17. (Chuyên Vĩnh Phúc 2019) Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền
T
theo hình thức lãi kép với lãi suất
0,6%
mỗi tháng. Biết sau
15
tháng người đó có số tiền là
10
triệu đồng. Hỏi số tiền
T
gần với số tiền nào nhất trong các số sau.
A.
613.000
đồng B.
645.000
đồng C.
635.000
đồng D.
535.000
đồng
Câu 18. (Chuyên Hùng Vương Gia Lai 2019) Anh Nam gửi 100 triệu đồng vào ngân hàng theo thể thức
lãi kép kì hạn là một quý với lãi suất 3% một quý. Sau đúng 6 tháng anh Nam gửi thêm 100 triệu
đồng với kì hạn và lãi suất như trước đó.Hỏi sau 1 năm số tiền (cả vốn lẫn lãi) anh Nam nhận
được là bao nhiêu? ( Giả sử lãi suất không thay đổi).
A.
218,64
triệu đồng. B.
208,25
triệu đồng.
C.
210,45
triệu đồng. D.
209,25
triệu đồng.
Câu 19. (Chuyên Sơn La 2019) Ông A gửi vào ngân hàng
50
triệu đồng với lãi suất
0, 5% /
tháng. Hỏi
sau ít nhất bao nhiêu tháng thì ông A có được số tiền cả gốc lẫn lãi nhiều hơn 60 triệu đồng? Biết
rằng trong suốt thời gian gửi, lãi suất ngân hàng không đổi và ông A không rút tiền ra.
A.
36
tháng. B.
38
tháng. C.
37
tháng. D.
40
tháng.
Câu 20. (Chuyên Lê Hồng Phong Nam Định 2019) Một người gửi
300
triệu đồng vào một ngân hàng
với lãi suất
7% /
năm. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi
sẽ được nhập vào gốc để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó nhận
được số tiền nhiều hơn
600
triệu đồng bao gồm cả gốc và lãi? Giả định trong suốt thời gian gửi,
lãi suất không đổi và người đó không rút tiền ra.
A.
9
năm. B.
10
năm. C.
11
năm. D.
12
năm.
Câu 21. (THPT Gia Lộc Hải Dương 2019) Anh Bảo gửi 27 triệu đồng vào ngân hàng theo thể thức lãi
kép, kỳ hạn là một quý, với lãi suất
1,85%
một quý. Hỏi thời gian tối thiểu bao nhiêu để anh Bảo
có được ít nhất 36 triệu đồng tính cả vỗn lẫn lãi?
A. 16 quý. B. 20 quý. C. 19 quý. D. 15 quý.
Câu 22. (Sở Bắc Giang 2019) Ông An gửi 100 triệu đồng vào một ngân hàng với lãi suất 0,8%/ tháng.
Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng số tiền lãi sẽ được nhập vào
gốc để tính lãi cho tháng tiếp theo và từ tháng thứ hai trở đi, mỗi tháng ông gửi them vào tài
khoản với số tiền 2 triệu đồng. Hỏi sau đúng 2 năm số tiền ông An nhận được cả gốc lẫn lãi là bao

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
nhiêu? Biết rằng trong suốt thời gian gửi lãi suất không thay đổi và ông An không rút tiền ra (kết
quả được làm tròn đến hàng nghìn).
A.
169.871.000
đồng. B.
171.761.000
đồng. C.
173.807.000
đồng. D.
169.675.000
đồng.
Câu 23. Năm 2020, một hãng xe ô tô niêm yết giá bán loại xe X là 900.000.000 đồng và dự định trong 10
năm tiếp theo, mỗi năm giảm 2% giá bán so với giá bán năm trước. Theo dự định đó, năm 2025
hãng xe ô tô niêm yết giá bán loại xe X là bảo nhiêu ( kết quả làm tròn đến hàng nghìn)?
A. 810.000.000. B. 813.529.000. C. 797.258.000. D. 830.131.000.
Câu 24. (Mã 104 - 2020 Lần 2) Năm
2020
, một hãng xe ô tô niêm yết giá bán loại xe
X
là
850.000.000
đồng và dự định trong
10
năm tiếp theo, mỗi năm giảm
2%
giá bán của năm liền trước. Theo dự
định đó, năm
2025
hãng xe ô tô niêm yết giá bán xe
X
là bao nhiêu (kết quả làm tròn đến hàng
nghìn)?
A.
768.333.000
đồng. B.
765.000.000
đồng. C.
752.966.000
đồng. D.
784.013.000
đồng.
Câu 25. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Một ngân hàng
X
, quy định về số tiền nhận
được của khách hàng sau
n
năm gửi tiền vào ngân hàng tuân theo công thức
( ) (1 8%)
P n A
,
trong đó
A
là số tiền gửi ban đầu của khách hàng. Hỏi số tiền ít nhất mà khách hàng B phải gửi
vào ngân hàng
X
là bao nhiêu để sau ba năm khách hàng đó rút ra được lớn hơn
850
triệu đồng
(Kết quả làm tròn đến hàng triệu)?.
A.
675
triệu đồng. B.
676
triệu đồng.
C.
677
triệu đồng. D.
674
triệu đồng.
Câu 26. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Ông tuấn gửi 100 triệu vào ngân hàng với
hình thức lãi kép, kỳ hạn 1 năm với lãi suất
8%
. Sau 5 năm ông rút toàn bộ tiền và dùng một nữa
để sửa nhà, số tiền còn lại ông tiếp tục gửi ngân hàng với lãi suất như lần trước. Số tiền lãi ông
tuấn nhận được sau 10 năm gửi gần nhất với giá trị nào dưới đây?
A.
46,933
triệu. B.
34,480
triệu. C.
81, 413
triệu. D.
107,946
triệu.
Câu 27. (Nguyễn Huệ - Phú Yên - 2020) Dân số thế giới được ước tính theo công thức
.
ni
S Ae
, trong
đó
A
là dân số của năm lấy mốc,
S
là dân số sau
n
năm,
i
là tỷ lệ tăng dân số hàng năm. Biết
năm
2005
dân số của thành phố Tuy Hòa là khoảng
202.300
người và tỉ lệ tăng dân số là
1,47%
.
Hỏi với mức tăng dân số không đổi thì đến năm bao nhiêu dân số thành phố Tuy Hòa đạt được
255.000
người?
A.
2020
. B.
2021
. C.
2023
. D.
2022
.
Câu 28. (Tiên Du - Bắc Ninh - 2020) Số ca nhiễm Covid – 19 trong cộng đồng ở một tỉnh vào ngày thứ
x
trong một giai đoạn được ước tính theo công thức
.e
rx
f x A
trong đó
A
là số ca nhiễm ở
ngày đầu của giai đoạn,
r
là tỷ lệ gia tăng số ca nhiễm hàng ngày của giai đoạn đó và trong cùng
một giai đoạn thì
r
không đổi. Giai đoạn thứ nhất tính từ ngày tỉnh đó có 9 ca bệnh đầu tiên và
không dùng biện pháp phòng chống lây nhiễm nào thì đến ngày thứ 6 số ca bệnh của tỉnh là 180
ca. Giai đoạn thứ hai (kể từ ngày thứ 7 trở đi) tỉnh đó áp dụng các biện pháp phòng chống lây
nhiễm nên tỷ lệ gia tăng số ca nhiễm hàng ngày giảm đi 10 lần so với giai đoạn trước. Đến ngày
thứ 6 của giai đoạn hai thì số ca mắc bệnh của tỉnh đó gần nhất với số nào sau đây?
A.
242
. B.
16
. C.
90
. D.
422
.
Câu 29. (Kìm Thành - Hải Dương - 2020) Anh Việt vay tiền ngân hàng
500
triệu đồng mua nhà và trả
góp hàng tháng. Cuối mỗi tháng bắt đầu từ tháng thứ nhất anh trả
10
triệu đồng và chịu lãi suất là
0,9%
/ tháng cho số tiền chưa trả. Với hình thức hoàn nợ như vậy thì sau bao lâu anh Việt sẽ trả
hết số nợ ngân hàng?
A.
65
tháng. B.
66
tháng. C.
67
tháng. D.
68
tháng.
Câu 30. (Thanh Chương 1 - Nghệ An - 2020) Dân số thế giới được ước tính theo công thức
.
ni
S Ae
,
trong đó
A
là dân số của năm lấy làm mốc,
S
là dân số sau
n
năm,
i
là tỉ lệ tăng dân số hằng

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
năm.
Dân số Việt Nam năm 2019 là
9
5,5
triệu
người, tỉ lệ tăng dân số hằng năm từ 2009 đến nay
là
1
,14%
. Hỏi dân
số Việt Nam năm 2009 gần với số nào nhất trong các số sau?
A.
9
4,4
t
riệu người. B.
8
5,2
triệ
u người. C.
8
6,2
triệ
u người. D.
83
,9
t
riệu người.
Câu 31. (Tiên Lãng - Hải Phòng - 2020) Ông An dự định gửi vào ngân hàng một số tiền với lãi suất
không đổi là 7% một năm. Biết rằng cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu để
tính lãi cho năm kế tiếp. Tính số tiền tối thiểu
x
(tr
iệu đồng,
x
)
ông An gửi vào ngân hàng để
sau 3 năm số tiền lãi đủ mua một chiếc xe gắn máy giá trị 45 triệu đồng.
A. 200. B. 190. C. 250. D. 150.
Câu 32. (Đề Minh Họa 2020 Lần 1) Để dự báo dân số của một quốc gia, người ta sử dụng công thức
;
nr
S
Ae
trong
đó
A
là dân số của năm lấy làm mốc tính,
S
là dân số sau
n
năm,
r
là tỉ lệ tăng
dân số hàng năm. Năm 2017, dân số Việt nam là
93.671.600
người
(Tổng cục Thống kê, Niên
giám thống kê 2017, Nhà xuất bản Thống kê, Tr 79). Giả sử tỉ lệ tăng dân số hàng năm không đổi
là
0,81%,
dự bá
o dân số Việt nam năm 2035 là bao nhiêu người (kết quả làm tròn đến chữ số
hàng trăm)?
A.
1
09.256.100
. B.
1
08.374.700
. C
.
1
07.500.500
. D
.
1
08.311.100
.
Câu
33. (Đề Tham Khảo 2020 Lần 2) Để quảng bá cho sản phẩm A, một công ty dự định tổ chức quảng
cáo theo hình thức quảng cáo trên truyền hình. Nghiên cứu của công ty cho thấy: nếu sau
n
lần
quảng
cáo được phát thì tỉ lệ người xem quảng cáo đó mua sản phẩm A tuân theo công thức
0
,015
1
1 49e
n
P
n
.
Hỏi cần phát ít nhất bao nhiêu lần quảng cáo để tỉ lệ người xem mua sản
phẩm đạt trên
3
0%?
A.
2
02
. B.
2
03
. C
.
2
06
. D
.
2
07
.
Câu
34. (Sở Hà Nội 2019) Cường độ ánh sáng đi qua môi trường nước biển giảm dần theo công thức
0
e
x
I
I
,
với
0
I
là
cường độ ánh sáng lúc ánh sáng bắt đầu đi vào môi trường nước biển và
x
là
độ dà
y của môi trường đó (
x
t
ính theo đơn vị mét). Biết rằng môi trường nước biển có hằng số
hấp thụ là
1
,4
.
Hỏi ở độ sâu 30 mét thì cường độ ánh sáng giảm đi bao nhiêu lần so với
cường độ ánh sáng lúc ánh sáng bắt đầu đi vào nước biển?
A.
2
1
e
lầ
n. B.
42
e
lầ
n. C.
21
e
lầ
n. D.
4
2
e
lần
Câu
35. (Chuyên Lê Quý Đôn Điện Biên 2019) Một người thả một lá bèo vào một chậu nước. Sau 12
giờ, bèo sinh sôi phủ kín mặt nước trong chậu. Biết rằng sau mỗi giờ lượng bèo tăng gấp 10 lần
lượng bèo trước đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì bèo phủ kín
1
5
mặt
nước trong
chậu (kết quả làm tròn đến 1 chữ số phần thập phân).
A.
9
,1
giờ
. B.
9
,7
giờ. C
.
1
0,9
giờ. D.
1
1,3
giờ.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI MỨC 9-10 ĐIỂM
Dạng 1. Tính toán liên quan đến logarit dùng đẳng thức
Định nghĩa logarit:
Cho hai số thực dương
,a b
với
1, log
α
a
a α b a b
:
Các tính chất logarit: Cho ba số thực dương
, ,a b c
với
0 , , 1 a b c
log log
log ; log log log ; log log ;
log log
log .log log .
c a
a a a a a a
a a
a b a
b b
b b c bc b c
a c
b c c
Phương trình mũ cơ bản nhất
log 0 1; 0
x
a
a b x b a b
.
Cách giải phương trình mũ có dạng
2 2
1 2 3
0
x
x x
α a α ab α b
trong đó
1,2,3
i
α i
là hệ số,
cơ số
0 , 1 a b
B1: Biến đổi phương trình về dạng:
2
1 2 3
2 0 *
x x
a a
α α α
b b
.
B2: Đặt ẩn phụ
, 0
x
a
t t
b
, phương trình
*
trở thành
2
1 2 3
0 α t α t α
.
B3: Giải tìm t thỏa mãn
0t
.
B4: Giải phương trình mũ cơ bản
x
a
t
b
. Tìm được
x
.
Câu 1. (Đề Minh Họa 2020 Lần 1) Cho
x
,
y
là các số thực dương thỏa mãn
9 6 4
log log log 2x y x y
. Giá trị của
x
y
bằng
A.
2
. B.
1
2
. C.
2
3
log
2
. D.
3
2
log 2
.
Câu 2. (Chuyên Lào Cai - 2020) các số thực
a
,
b
,
c
thỏa mãn
2 2 2
( 2) ( 2) ( 2) 8a b c
và
2 3 6
a b c
. Khi đó
a b c
bằng
A.
2
. B.
4
. C.
2 2
. D.
8
.
Câu 3. (Chuyên Thái Nguyên - 2020) Cho
4 4 7
x x
. Khi đó biểu thức
5 2 2
8 4.2 4.2
x x
x x
a
P
b
với
a
b
là phân số tối giản và
,a b
. Tích
.a b
có giá trị bằng
A.
10
. B.
8
. C.
8
. D.
10
.
Câu 4. (Sở Ninh Bình 2019) Cho
a
,
b
,
c
là các số thực khác
0
thỏa mãn
4 9 6
a b c
. Khi đó
c c
a b
bằng
A.
1
2
. B.
1
6
. C.
6
. D.
2
.
HÀM SỐ MŨ - HÀM SỐ LOGARIT
Chuyên đề 18
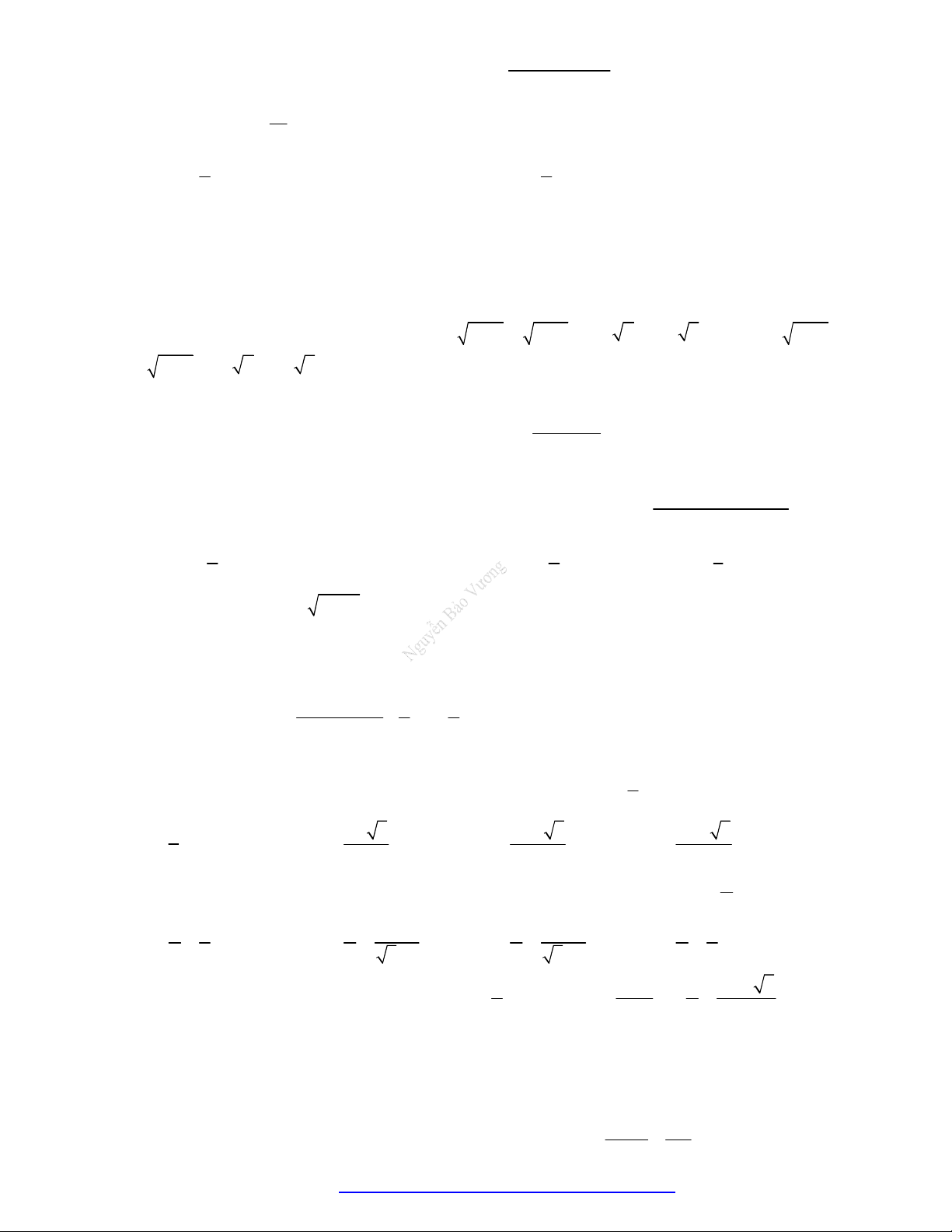
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 5. Biết
30
log 10
a
,
30
log 150
b
và
1 1 1
2000
2 2 2
log 15000
x a y b z
x a y b z
với
1 1 1 2 2 2
; y ;z ; ; y ;z
x x
là các số
nguyên, tính
1
2
x
S
x
.
A.
1
2
S
. B.
2
S
. C.
2
3
S
. D.
1
S
.
Câu 6. Cho các số thực dương
,x y
khác 1 và thỏa mãn
log log
log log
x y
x y
y x
x y x y
.
Giá trị của
2 2
x xy y
bằng
A. 0. B. 3. C. 1. D. 2.
Câu 7. Cho các số thực dương
a
,
b
thỏa mãn
log log log log 100
a b a b
và
log a
,
logb
,
log
a
,
log
b
đều là các số nguyên dương. Tính
P ab
.
A.
164
10 .
B.
100
10 .
C.
200
10 .
D.
144
10 .
Câu 8. Cho
9 4 2
log 5 ; log 7 ; log 3
a b c
.Biết
24
log 175
mb nac
pc q
.Tính
2 3 4 A m n p q
A.
27
B.
25
C.
23
D.
29
Câu 9. Cho
x
,
y
là các số thực lớn hơn
1
thoả mãn
2 2
6
x y xy
. Tính
12 12
12
1 log log
2log 3
x y
M
x y
.
A.
1
4
M
. B.
1M
. C.
1
2
M
. D.
1
3
M
.
Câu 10. Cho
2
ln 1 sin 6
f x a x x b x
với
a
,
b
. Biết
log log e 2
f
. Tính
log ln10
f
.
A.
4
. B.
10
. C.
8
. D.
2
.
Câu 11. Cho
x -x
9 + 9 = 14
và
x -x
x+1 1-x
6+3(3 +3 ) a
=
2-3 -3 b
với
a
b
là phân số tối giản. Tính
. .P a b
A.
10.
P
B.
45.
P
C.
10.
P
D.
45.
P
Câu 12. Cho hai số thực dương
,a b
thỏa
4 6 9
log log log
a b a b
. Tính
a
b
.
A.
1
2
. B.
1 5
2
. C.
1 5
2
. D.
1 5
2
.
Câu 13. Cho các số thực dương
,x y
thỏa mãn
6 9 4
log log log 2 2x y x y
. Tính tỉ số
x
y
?
A.
2
3
x
y
. B.
2
3 1
x
y
. C.
2
3 1
x
y
. D.
3
2
x
y
.
Câu 14. Cho
x
,
y
là các số thực dương thỏa mãn
25 15 9
log log log
2 4
x x y
y
và
2
x a b
y
, với
a
,
b
là các số nguyên dương, tính
a b
.
A.
14
a b
. B.
3
a b
. C.
21
a b
. D.
34
a b
.
Câu 15. Cho dãy số
n
u
thỏa mãn
3 5 4
log 2 63 2log 8 8
n
u u n
,
*
n
. Đặt
1 2
...
n n
S u u u
. Tìm số nguyên dương lớn nhất
n
thỏa mãn
2
2
.
148
. 75
n n
n n
u S
u S
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
18
. B.
17
. C.
16
. D.
19
.
Dạng 2. Bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất mũ – loagrit (sử dụng phương pháp
bất đẳng thức – biến đổi)
Bất đẳng thức Cauchy (AM – GM)
, 0,
a b
thì
2 .a b ab
Dấu
" "
xảy ra khi:
.a b
, , 0,
a b c
thì
3
3. .a b c abc
Dấu
" "
xảy ra khi
.a b c
Nhiều trường hợp đánh giá dạng:
2
.
2
a b
a b
và
3
. .
3
a b c
a b c
Bất đẳng thức Cauchy – Schwarz (Bunhiaxcôpki)
, , , ,a b x y
thì:
2 2 2 2 2
( . . ) ( )( ) .a x b y a b x y
Dấu
" "
khi
a b
x y
,b,c, x, y,z
a
thì:
2 2 2 2 2 2 2
( . . . ) ( )( ) .a x b y c z a b c x y z
Dấu
" "
xảy ra khi và chỉ khi:
a b c
x y z
Nhiều trường hợp đánh giá dạng:
2 2 2 2
. . ( )(x ).a x b y a b y
Hệ quả. Nếu
, ,a b c
là các số thực và
, ,x y z
là các số dương thì:
2 2 2
( )a b a b
x y x y
và
2 2 2 2
( )a b c a b c
x y z x y z
: bất đẳng thức cộng mẫu số.
Câu 1. (Đề Tham Khảo 2020 Lần 2) Xét các số thực dương
, , ,a b x y
thoả mãn
1, 1a b
và
x y
a b ab
. Giá trị nhỏ nhất của biểu thức
2P x y
thuộc tập hợp nào dưới đây?
A.
1;2
. B.
5
2;
2
. C.
3;4
. D.
5
;3
2
.
Câu 2. (Đề Tham Khảo 2020 Lần 2) Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
2 2
3 4
log ( ) log
x y x y
?
A.
3
. B.
2
. C.
1
. D. Vô số.
Câu 3. (Mã 103 2018) Cho
0, 0
a b
thỏa mãn
2 2
4 5 1 8a 1
log 16 1 log 4 5 1 2
a b b
a b a b
. Giá
trị của
a 2b
bằng
A.
6
B.
27
4
C.
20
3
D.
9
Câu 4. (Mã 101 - 2020 Lần 1) Xét các số thực không âm
x
và
y
thỏa mãn
1
2 .4 3
x y
x y
. Giá trị
nhỏ nhất của biểu thức
2 2
4 6P x y x y
bằng
A.
33
4
. B.
65
8
. C.
49
8
. D.
57
8
.
Câu 5. Xét các số thực
,x y
thỏa mãn
2 2
1 2 2
2 2 2 4
x y x
x y x
. Giá trị nhỏ nhất của biểu thức
4
2 1
y
P
x y
gần nhất với số nào dưới đây?
A.
2
. B.
3
. C.
5
. D.
4
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 6. Cho các số thực
,x y
thỏa mãn bất đẳng thức
2 2
4 9
log 2 3 1
x y
x y
. Giá trị lớn nhất của biểu
thức
3P x y
là
A.
3
2
. B.
2 10
4
. C.
5 10
4
. D.
3 10
4
.
Câu 7. (Chuyên Lam Sơn Thanh Hóa 2019) Cho các số thực
,a b
thay đổi, thỏa mãn
1
, 1.
3
a b
Khi
biểu thức
4 2
3
log log 9 81
a b
P b a a
đạt giá trị nhỏ nhất thì tổng
a b
bằng
A.
2
3 9
B.
3
9 2
C.
2 9 2
D.
3 3 2
Câu 8. (Chuyên Trần Phú Hải Phòng 2019) Cho các số thực
, ,ca b
thỏa mãn
1 3
0 1; 1; 1
8 8
a b c
. Gọi
M
là giá trị nhỏ nhất của biểu thức
3 1 1 3 1
log log log
16 2 16 4 2 16 3
a b c
b c
P a
. Khẳng định nào sau đây đúng?
A.
3 2
M
. B.
2M
. C.
2 3
M . D.
2
M
.
Câu 9. Cho các số thực
, , ,a b m n
sao cho
2 0
m n
và thoả mãn điều kiện:
2 2
2 2
4
2
2
log 9 1 log 3 2
9 .3 .3 ln 2 2 1 81
m n
m n
a b a b
m n
Tìm giá trị nhỏ nhất của biểu thức
2 2
P a m b n
A.
2 5 2
. B.
2
. C.
5 2
. D.
2 5
Câu 10. Cho các số thực
, ,ca b
thỏa mãn
1 3
0 1; 1; 1
8 8
a b c
. Gọi
M
là giá trị nhỏ nhất của
biểu thức
3 1 1 3 1
log log log
16 2 16 4 2 16 3
a b c
b c
P a
. Khẳng định nào sau đây đúng?
A.
3 2
M
. B.
2M
. C.
2 3
M
. D.
2
M
.
Câu 11. (Chuyên Lam Sơn - 2020) Xét các số thực dương
, ,a b c
lớn hơn
1
( với
a b
) thỏa mãn
4 log log 25log
a b ab
c c c
. Giá trị nhỏ nhất của biểu thức
log log log
b a c
a c b
bằng
A.
5
. B.
8
. C.
17
4
. D.
3
.
Câu 12. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Xét các số thực dương
a
,
b
,
x
,
y
thỏa mãn
a 1
,
b 1
và
2x 3y 6 6
a b a b
. Biết giá trị nhỏ nhất của biểu thức
4 2
P xy x y
có dạng
165
m n (với
,m n
là các số tự nhiên), tính
S m n
.
A.
58
. B.
54
. C.
56
. D.
60
Câu 13. (Chuyên Lê Hồng Phong - Nam Định - 2020) Xét các số thực
,x y
thỏa mãn
2 2
log 1 log 1 1
x y
. Khi biểu thức
2 3P x y
đạt giá trị nhỏ nhất thì
3 2 3x y a b
với
,a b
. Tính
T ab
?
A.
9
T
. B.
7
3
T
. C.
5
3
T
. D.
7
T
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 14. (Chuyên Phan Bội Châu - Nghệ An - 2020) Cho
0, 0a b
thỏa mãn
2 2
4 5 1 8a 1
log 16 1 log 4 5 1 2
a b b
a b a b
. Giá trị của
2a b
bằng
A.
27
4
. B.
6
. C.
20
3
. D.
9
.
Câu 15. (Chuyên Sơn La - 2020) Cho
, ,a b c
là các số thực lớn hơn
1
. Giá trị nhỏ nhất của biểu thức
3
4040 1010 8080
log
log 3log
ac ab
bc
P
a
b c
bằng
A.
2020
. B.
16160
. C.
20200
. D.
13130
.
Câu 16. (Chuyên Vĩnh Phúc - 2020) Cho
, ,a b c
là các số thực dương khác
1
thỏa mãn
2 2
log log log 2log 3
a b a b
c c
b c
b b
. Gọi
,M m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
log log
a b
P b c . Giá trị của biểu thức
3S m M
bằng
A.
16
. B.
4
. C.
6
. D.
6
.
Câu 17. (Sở Hưng Yên - 2020) Cho các số thực
, 1x y
và thỏa mãn điều kiện
4xy
. Biểu thức
2
2
4
2
log 8 log
2
x
y
y
P x
đạt giá trị nhỏ nhất tại
0 0
,x x y y
. Đặt
4 4
0 0
T x y
mệnh đề nào
sau đây đúng
A.
131T
. B.
132T
. C.
129T
. D.
130T
.
Câu 18. (Sở Hà Tĩnh - 2020) Cho các số thực dương
, ,a b c
thỏa mãn
10abc
. Biết giá trị lớn nhất của
biểu thức
5log .log 2log .log log .logF a b b c c a
bằng
m
n
với
,m n
nguyên dương và
m
n
tối
giản. Tổng m n bằng
A.
13.
B.
16.
C.
7.
D.
10.
Câu 19. (Lê Lai - Thanh Hóa - 2020) Cho thỏa mãn
. Giá trị biểu thức bằng?
A. 6. B. . C. . D. 22.
Câu 20. (Liên trường Nghệ An - 2020) Cho các số thực dương
; ;a b c
khác
1
thỏa mãn
2 2
3
log log 2log log
a b b a
c c
b c
b a b
. Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
log log
a b
P ab bc . Tính giá trị biểu thức
2 2
2 9S m M
.
A.
28S
. B.
25S
. C.
26S
. D.
27S
.
Câu 21. (Lý Nhân Tông - Bắc Ninh - 2020) Cho
0, 0a b
thỏa mãn
2 2
4 5 1 8 1
log (16 1) log (4 5 1) 2
a b ab
a b a b
. Giá trị của
2a b
bằng
A.
9
. B.
6
. C.
27
4
. D.
20
3
.
Câu 22. (Nguyễn Huệ - Phú Yên - 2020) Xét các số thực
, , ,a b x y
thỏa mãn
1, 1a b
và
x y
a
a b
b
. Giá trị lớn nhất của biểu thức
2P x y
thuộc tập nào dưới đây?
0, 0
a b
2 2
10 3 1 10 1
log 25 1 log 10 3 1 2
a b ab
a b a b
2a b
11
2
5
2

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
0;
2
. B.
1
1;
2
. C.
3
1;
2
. D.
3 5
;
2 2
.
Câu 23. (Tiên Du - Bắc Ninh - 2020) Cho biểu thức
2 3 2 1 2 1
3 (1 4 ) 2
y x x y x y
P
và biểu thức
3 2
log 3
y x
Q y
. Giá trị nhỏ nhất của y để tồn tại x đồng thời thỏa mãn
1P
và
1
Q
là số
0
y
.
Khẳng định nào sau đây là đúng ?
A.
0
4 1
y
là số hữu tỷ. B.
0
y
là số vô tỷ.
C.
0
y
là số nguyên dương. D.
0
3 1
y
là số tự nhiên chẵn.
Câu 24. (Trường VINSCHOOL - 2020) Cho dãy số
n
u
có số hạng đầu
1
1
u thỏa mãn
2 2 2 2
2 1 2 1 2 2
log 5 log 7 log 5 log 7
u u
và
1
7
n n
u u
với mọi
1n
. Giá trị nhỏ nhất của
n
để
1111111
n
u bằng:
A.
11
. B.
8
. C.
9
. D.
10
.
Câu 25. (Chuyên Lê Hồng Phong - Nam Định - 2020) Xét các số thực
,x y
thỏa mãn
2 2
log 1 log 1 1
x y
. Khi biểu thức
2 3P x y
đạt giá trị nhỏ nhất thì
3 2 3x y a b
với
,a b
. Tính
T ab
.
A.
9
T
. B.
7
3
T
. C.
5
3
T
. D.
7
T
.
Câu 26. Xét các số thực
a
,
b
,
0
c
thỏa mãn
3 5 15
a b c
. Giá trị nhỏ nhất của biểu thức
2 2 2
4( ) P a b c a b c
thuộc tập hợp nào dưới đây?
A.
1;2
. B.
5; 1
. C.
2;4
. D.
4;6
.
Câu 27. Xét các số thực dương
a
,
b
,
c
,
x
,
y
,
z
thỏa mãn
1
a
,
1b
,
1c
và
x y z
a b c abc
.
Giá trị nhỏ nhất của biểu thức
1
2
P x y z
thuộc tập hợp nào dưới đây?
A.
10;13
. B.
7;10
. C.
3;5
. D.
5;7
.
Câu 28. Xét các số thực dương
, , ,a b x y
thỏa mãn
1, 1
a b
và
2 2
.
x y
a b a b
. Giá trị nhỏ nhất của
biểu thức
.P x y
là
A.
9
4
P
. B.
6
2
P
. C.
3
2
P
. D.
4
9
P
.
Câu 29. Xét các số thực dương
, , ,a b x y
thỏa mãn
1, 1
a b
và
2
2
x
y
y
x
a b ab
. Giá trị nhỏ nhất của biểu
thức
.P x y
là
A.
2P
. B.
4P
. C.
3
P
. D.
1P
.
Câu 30. Xét các số thực dương
, , , , ,a b c x y z
thỏa mãn
1, 1, 1, 2
a b c y
và
1 2 1x y z
a b c abc
.
Giá trị nhỏ nhất của biểu thức
P x y z
là
A.
13
P
. B.
3
P
. C.
9
P
. D.
1P
.
Dạng 3. Sử dụng phương pháp hàm số (hàm đặc trưng) giải các bài toán logarit
1. Định lý: Nếu hàm số
y f x
đồng biến (hoặc luôn nghịch biến) và liên tục trên
;a b
thì
*
; ; :
u v a b f u f v u v
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
* Phương trình
f x
k
k const
có nhiều nhất 1 nghiệm trên khoảng
;a b
.
2. Định lý: Nếu hàm số
y f x
đồng biến (hoặc nghịch biến) và liên tục trên
;a b
, đồng thời
lim . lim ( ) 0
x a x b
f x f x
thì phương trình
f x k k const
có duy nhất nghiệm trên
;a b
.
3. Tính chất của logarit:
1.1. So sánh hai logarit cũng cơ số:
Cho số dương
1
a
và các số dương
,b c
.
Khi
1
a
thì
log log
a a
b c b c
.
Khi
0 1a
thì
log log
a a
b c b c
.
1.2. Hệ quả:
Cho số dương
1
a
và các số dương
,b c
.
Khi
1
a
thì
log 0 1
a
b b
.
Khi
0 1a
thì
log 0 1
a
b b
.
log log
a a
b c b c
.
2. Logarit của một tích:
Cho 3 số dương
1 2
, ,a b b
với
1
a
, ta
có
1 2 1 2
log ( . ) log log
a a a
b b b b
3. Logarit của một thương:
Cho 3 số dương
1 2
, ,a b b
với
1
a
, ta
có
1
1 2
2
log log log
a a a
b
b b
b
Đặc biệt: với
, 0, 1
a b a
1
log log
a a
b
b
.
4. Logarit của lũy thừa:
Cho
, 0, 1
a b a
, với mọi
, ta có
log log
a a
b b
.
Đặc biệt:
1
log log
n
a a
b b
n
(
n
nguyên dương).
5. Công thức đổi cơ số:
Cho 3 số dương
, ,a b c
với
1, 1a c
, ta có
log
log
log
c
a
c
b
b
a
.
Đặc biệt:
1
log
log
a
c
c
a
và
1
log log
a
a
b b
với
0
.
Câu 1. (Mã 102 - 2020 Lần 1) Có bao nhiêu số nguyên
x
sao cho ứng với mỗi
x
có không quá
242
số
nguyên
y
thỏa mãn
2
4 3
log log
x y x y
?
A.
55
. B.
28
. C.
29
. D.
56
.
Câu 2. (Mã 101 - 2020 Lần 1) Có bao nhiêu số nguyên
x
sao cho ứng với mỗi
x
có không quá
728
số
nguyên
y
thỏa mãn
2
4 3
log log ( )x y x y
?
A.
59
. B.
58
. C.
116
. D.
115
.
Câu 3. (Mã 103 - 2020 Lần 1) Có bao nhiêu số nguyên
x
sao cho ứng với mỗi
x
có không quá
127
số
nguyên
y
thỏa mãn
2
3 2
log log
x y x y
?
A.
89
. B.
46
. C.
45
. D.
90
.
Câu 4. (Mã 102 - 2020 Lần 1) Xét các số thực không âm
x
và
y
thỏa mãn
1
2 .4 3
x y
x y
. Giá trị nhỏ
nhất của biểu thức
2 2
6 4P x y x y
bằng
A.
65
8
. B.
33
4
. C.
49
8
. D.
57
8
.
Câu 5. (Đề Minh Họa 2020 Lần 1) Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
0 2020
x
và
3
log 3 3 2 9
y
x x y
?
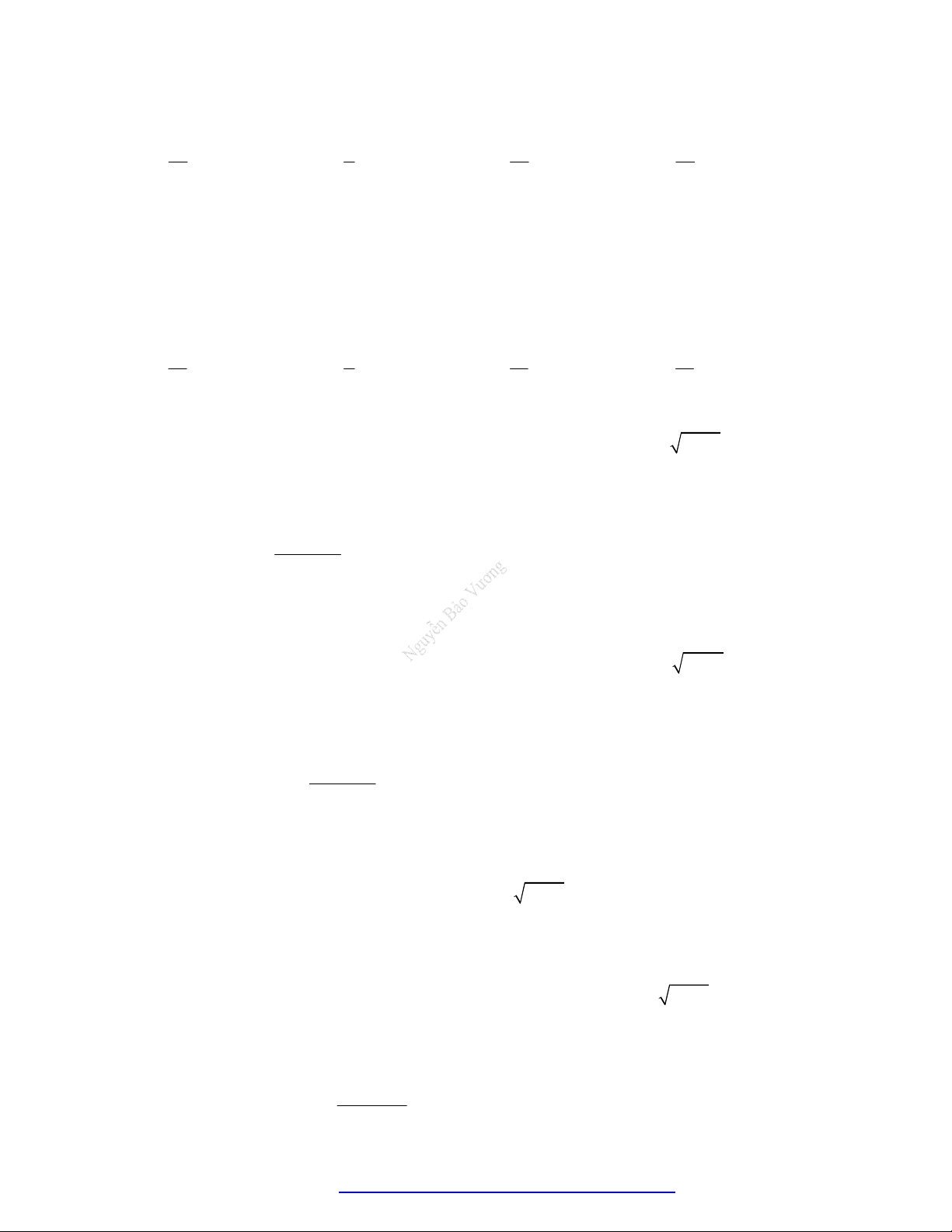
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2019
. B.
6
. C.
2020
. D.
4
.
Câu 6. (Mã 103 - 2020 Lần 1) Xét các số thực không âm
x
và
y
thỏa mãn
1
2 .4 3
x y
x y
. Giá trị
nhỏ nhất của biểu thức
2 2
2 4P x y x y
bằng
A.
33
8
. B.
9
8
. C.
21
4
. D.
41
8
.
Câu 7. (Mã 104 - 2020 Lần 1) Có bao nhiêu số nguyên
x
sao cho ứng với mỗi
x
có không quá
255
số
nguyên
y
thỏa mãn
2
3 2
log log
x y x y
?
A.
80
. B.
79
. C.
157
. D.
158
Câu 8. (Mã 104 - 2020 Lần 1) Xét các số thực không âm
x
và
y
thỏa mãn
1
2 .4 3
x y
x y . Giá trị
nhỏ nhất của biểu thức
2 2
4 2
P x y x y
bằng
A.
33
8
. B.
9
8
. C.
21
4
. D.
41
8
.
Câu 9. (Mã 102 - 2020 Lần 2) Có bao nhiêu cặp số nguyên dương
,m n
sao cho
16
m n
và ứng với
mỗi cặp
,m n
tồn tại đúng
3
số thực
1;1
a
thỏa mãn
2
2 ln 1
m
a n a a
?
A.
16
. B.
14
. C. 15. D.
13
.
Câu 10. (Mã 102 - 2020 Lần 2) Xét các số thực thỏa mãn
2 2
1 2 2
2 2 2 4
x y x
x y x
. Giá trị lớn nhất
của biểu thức
8 4
2 1
x
P
x y
gần với giá trị nào sau đây nhất?
A.
9
B.
6
. C.
7
. D.
8
.
Câu 11. (Mã 103 - 2020 Lần 2) Có bao nhiêu cặp số nguyên dương
;m n
sao cho
10
m n
và ứng với
mỗi cặp
;m n
tồn tại đúng
3
số thực
1;1
a
thỏa mãn
2
2 ln 1
m
a n a a
?
A.
7
. B.
8
. C.
10
. D.
9
.
Câu 12. (Mã 103 - 2020 Lần 2) Xét các số thực
,x y
thỏa mãn
2 2
1 2 2
2 2 2 .4
x y x
x y x
. Giá trị nhỏ
nhất của biểu thức
8 4
2 1
x
P
x y
gần nhất với số nào dưới đây
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 13. Có bao nhiêu cắp số nguyên dương
,m n
sao cho
14
m n
và ứng với mỗi cặp
,m n
tồn tại
đúng ba số thực
1;1
a
thỏa mãn
2
2 ln 1
m
a n a a
?
A.
14
. B.
12
. C.
11
. D.
13
.
Câu 14. (Mã 104 - 2020 Lần 2) Có bao nhiêu cặp số nguyên dương
( , )m n
sao cho
12
m n
và ứng với
mỗi cặp
( , )m n
tồn tại đúng 3 số thực
( 1,1)
a
thỏa mãn
2
2 ln( 1)
m
a n a a
?
A.
12
. B.
10
. C.
11
. D.
9
.
Câu 15. (Mã 104 - 2020 Lần 2) Xét các số thực
x
và
y
thỏa mãn
2 2
1 2 2
2 2 2 4
x y x
x y x
. Giá trị
lớn nhất của biểu thức
4
2 1
y
P
x y
gần nhất với số nào dưới đây?
A.
1
. B.
0
. C.
3
. D.
2
.
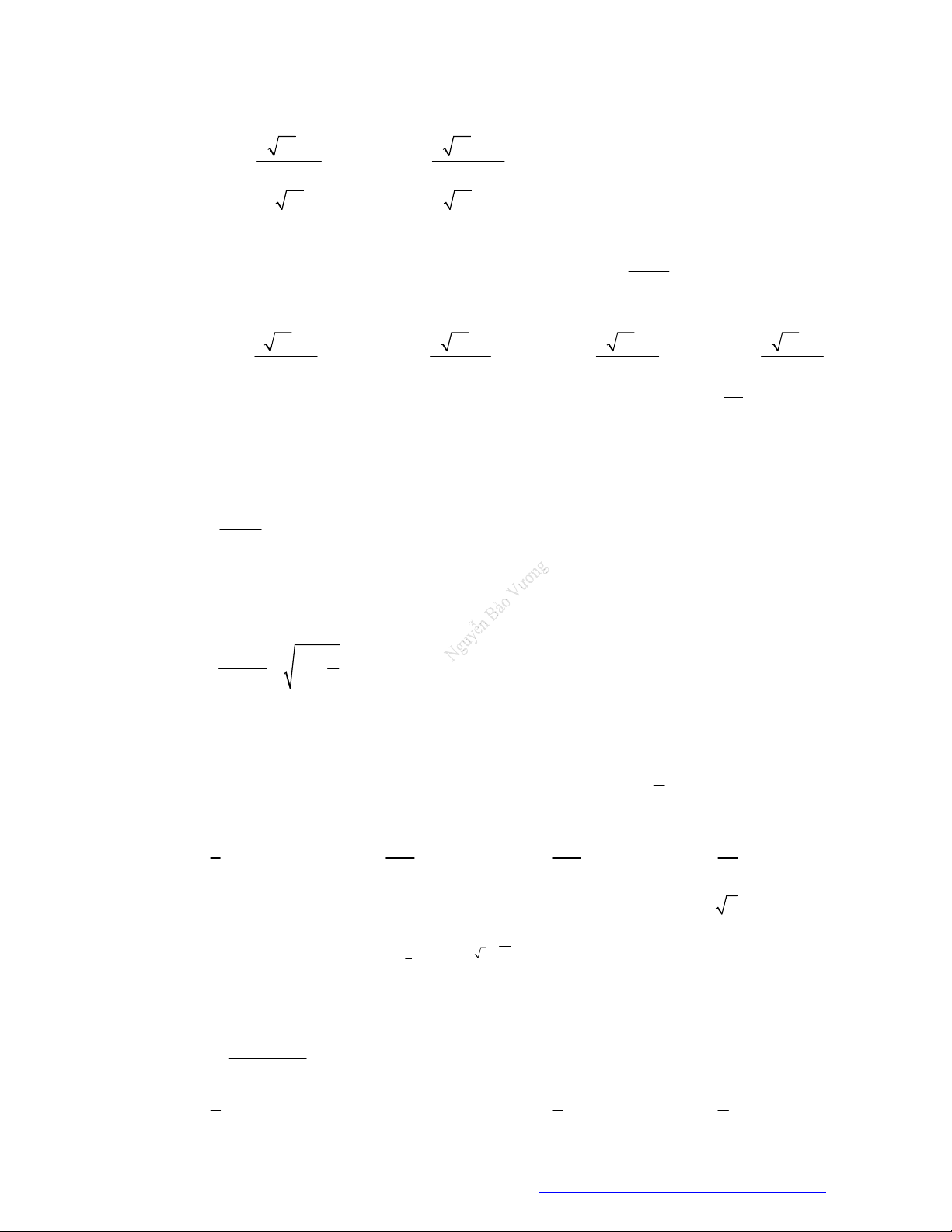
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 16. (Mã 123 2017) Xét các số thực dương
,x y
thỏa mãn
3
1
log 3 2 4
2
xy
xy x y
x y
. Tìm giá trị
nhỏ nhất
min
P
của
P x y
A.
min
2 11 3
3
P
B.
min
9 11 19
9
P
C.
min
18 11 29
21
P
D.
min
9 11 19
9
P
Câu 17. (Mã 110 2017) Xét các số thực dương
, a b
thỏa mãn
2
1
log 2 3
ab
ab a b
a b
. Tìm giá trị
nhỏ nhất
min
P
của
2P a b
.
A.
min
3 10 7
2
P
B.
min
2 10 1
2
P
C.
min
2 10 3
2
P
D.
min
2 10 5
2
P
Câu 18. (Chuyên Lê Thánh Tông 2019) Cho hai số thực dương
, x y
thỏa mãn
ln
ln
ln5
2
2 .5 2
x y
x y
. Tìm
giá trị lớn nhất của biểu thức
( 1)ln ( 1)lnP x x y y
.
A.
max
10
P
. B.
max
0
P
. C.
max
1
P
. D.
max
ln 2
P
.
Câu 19. (THPT Bạch Đằng Quảng Ninh 2019) Cho các số thực
,x y
thỏa mãn
0 , 1
x y
và
3
log 1 1 2 0
1
x y
x y
xy
. Tìm giá trị nhỏ nhất của
2
P x y
.
A.
2
. B.
1
. C.
1
2
. D.
0
.
Câu 20. (Chuyên Hạ Long 2019) Cho các số thực
,a b
thỏa mãn
1.
a b
Biết rằng biểu thức
1
log
log
a
ab
a
P
a b
đạt giá trị lớn nhất khi
.
k
b a
Khẳng định nào sau đây là sai
A.
2;3
k
. B.
0;1
k
. C.
0;1
k
. D.
3
0;
2
k
.
Câu 21. Cho hai số thực
, a b
thỏa mãn
2 2
4 1
log 2 8 1
a b
a b
. Tính
a
P
b
khi biểu thức
4 6 5 S a b
đạt giá trị lớn nhất.
A.
8
5
B.
13
2
C.
13
4
D.
17
44
Câu 22. (Chuyên Vĩnh Phúc 2019) Cho
a
,
b
là các số dương thỏa mãn
1b
và
a b a
. Tìm giá trị
nhỏ nhất của biểu thức
log 2log
a
b
b
a
P a
b
.
A.
6
. B.
7
. C.
5
. D.
4
.
Câu 23. (THPT Đoàn Thượng - Hải Dương 2019) Cho
a
,
b
là hai số thực dương thỏa mãn
5
4 2 5
log 3 4
a b
a b
a b
. Tìm giá trị nhỏ nhất của biểu thức
2 2
T a b
A.
1
2
. B.
1
. C.
3
2
. D.
5
2
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 24. (THPT Lê Quý Đôn Đà Nẵng 2019) Với hai số thực
,a b
bất kì, ta kí
hiệu
,
2 3
a b
f x x a x b x x
.Biết rằng luôn tồn tại duy nhất số thực
0
x
để
0
, ,
min
a b a b
x R
f x f x
với mọi số thực
,a b
thỏa mãn
b a
a b
và
0
a b
. Số
0
x
bằng
A.
2 1e
B.
2,5
C.
e
D.
2e
Câu 25. (Chuyên Lê Hồng Phong Nam Định 2019) Cho hai số thực
1, 1
a b
. Biết phương trình
2
1
1
x x
a b
có hai nghiệm phân biệt
1 2
,x x
. Tìm giá trị nhỏ nhất của biểu thức
2
1 2
1 2
1 2
4
x x
S x x
x x
.
A.
3
3 4
. B.
4
C.
3
3 2
. D.
3
4
.
Câu 26. (Chuyên Quốc Học Huế 2019) Cho
,x y
là các số thực lớn hơn
1
sao cho
y x
e e
x x y y
y e x e
.
Tìm giá trị nhỏ nhất của biểu thức:
log log
x y
P xy x
.
A.
2
2
B.
2 2
C.
1 2 2
2
D.
1 2
2
Câu 27. Xét các số thực dương
,x y
thỏa mãn
3
1
log 3 3 4
3
y
xy x y
x xy
. Tìm giá trị nhỏ nhất
min
P
của
P x y
.
A.
min
4 3 4
3
P
. B.
min
4 3 4
3
P
. C.
min
4 3 4
9
P
. D.
min
4 3 4
9
P
.
Câu 28. (Chuyên Vĩnh Phúc 2019) Xét các số thực dương
x
,
y
thỏa mãn
2
1 1 1
2 2 2
log log log
x y x y
. Tìm giá trị nhỏ nhất
min
P
của biểu thức
3P x y
.
A.
min
9
P
B.
min
8
P
C.
min
25 2
4
P
D.
min
17
2
P
Câu 29. (Chuyên Vĩnh Phúc 2019) Cho
,x y
là các số thực dương thỏa mãn
2019 201 2
2
9 019
log log logx y
x y
. Gọi
min
T
là giá trị nhỏ nhất của biểu thức
2
T x y
. Mệnh
đề nào dưới đây đúng?
A.
min
7;8
T
B.
min
6;7
T
C.
min
5;6
T
D.
min
8;9
T
Câu 30. (Mã 105 2017) Xét hàm số
2
9
9
t
t
f t
m
với
m
là tham số thực. Gọi
S
là tập hợp tất cả các
giá trị của
m
sao cho
1
f x f y
với mọi số thực
,x y
thỏa mãn
x y
e e x y
.Tìm số
phần tử của
S
.
A.
0
B. Vô số C.
1
D.
2
Câu 31. (THCS - THPT Nguyễn Khuyến 2019) Cho hàm số
y f x
liên tục trên
, có bảng biến
thiên như hình vẽ và có đạo hàm cấp hai
0, xf x
.
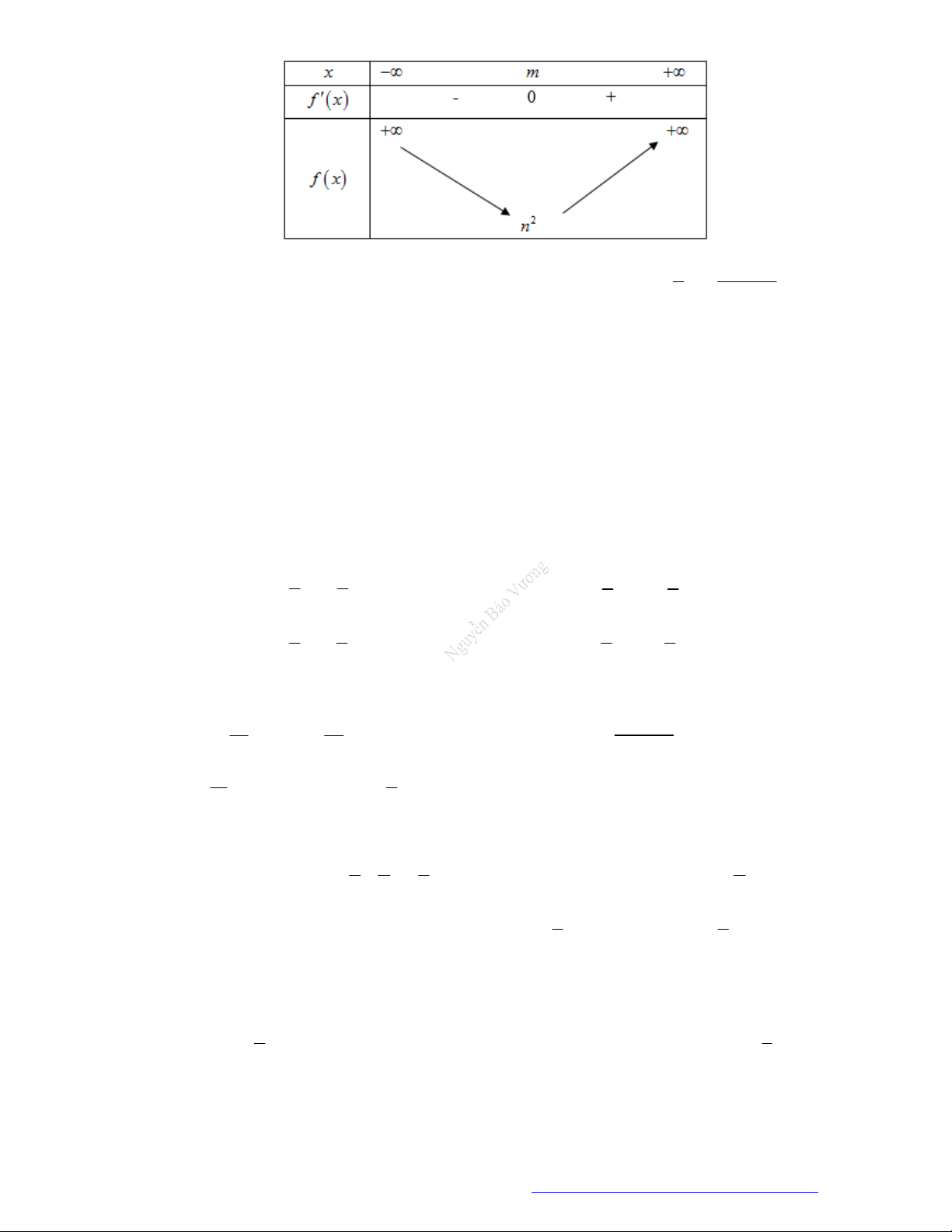
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Gọi
, , ,a b c n
là các số thực và biểu thức:
2
3
e e e 1
2 3
f a f b f c
a b c
P f
. Khẳng
định đúng với mọi
, , ,a b c n
là
A.
0 3P
. B.
7 3e P 0
. C.
3P
. D.
7 3eP
.
Câu 32. (Chuyên Đại Học Vinh 2019) Cho hàm số
( ) 2 2
x x
f x
. Gọi
0
m
là số lớn nhất trong các số
nguyên
m
thỏa mãn
12
( ) (2 2 ) 0f m f m
. Mệnh đề nào sau đây đúng?
A.
0
1513;2019m
B.
0
1009;1513m
C.
0
505;1009m
D.
0
1;505m
Câu 33. (Việt Đức Hà Nội 2019) Tìm tất cả các giá trị của tham số
m
đề đồ thị hàm số
2
2 2
log 2log 2 1 y m x x m
cắt trục hoành tại một điểm duy nhất có hoành độ thuộc khoảng
1;
.
A.
1 1
;
2 2
m
. B.
1 1
;0
2 2
m
.
C.
1 1
;
2 2
m
. D.
1 1
;0
2 2
m
.
Câu 34. (Chuyên Biên Hòa - Hà Nam - 2020) Cho
;x y
là hai số thực dương thỏa mãn
x y
và
1 1
2 2
2 2
y x
x y
x y
. Giá trị nhỏ nhất của biểu thức
2 2
2
3x y
P
xy y
bằng
A.
13
2
. B.
9
2
. C.
2
. D.
6
.
Câu 35. (Chuyên ĐH Vinh - Nghệ An -2020) Xét các số thực dương
,x y
thỏa mãn
2
2 2
2
2 2 1
2 4 log 4
2
x y xy
x y
. Khi
4x y
đạt giá trị nhỏ nhất,
x
y
bằng
A.
2
. B.
4
. C.
1
2
. D.
1
4
.
Câu 36. (Chuyên Hưng Yên - 2020) Biết phương trình
4 3 2
1 0x ax bx cx
có nghiệm. Tìm giá trị
nhỏ nhất của biểu thức
2 2 2
T a b c
A.
min
4
3
T
. B.
min
4T
. C.
min
2T
. D.
min
8
3
T
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 37. (Chuyên KHTN - 2020) Cho
,x y
là các số thực dương thỏa mãn
2
2 2
3 3 4
log 1 2 2 1 4 1
x y
x y x y xy
x y
. Giá trị lớn nhất của biểu thức
5 3 2
2 1
x y
P
x y
.
A.
3
. B.
1
. C.
2
. D.
4
.
Câu 38. (Chuyên Bến Tre - 2020) Cho các số thực
,x y
thỏa mãn
0 , 1x y
và
3
log 1 1 2 0
1
x y
x y
xy
. Tìm giá trị nhỏ nhất của
P
với
2P x y
A.
2
. B.
1
. C.
0
. D.
1
2
.
Câu 39. (Chuyên Chu Văn An - 2020) Cho
,x y
là các số thực dương thỏa mãn
3
4
log 2 1.
x y
x y
x y
Tìm giá trị nhỏ nhất của biểu thức
4 2
2
3 2 2
( )
x y xy y
P
x x y
.
A.
1
.
4
B.
1
.
2
C.
3
.
2
D.
2.
Câu 40. (Chuyên Hùng Vương - Gia Lai - 2020) Xét các số thực dương
, , ,a b x y
thỏa mãn
1, 1
a b
và
2 2
2
x y
a b ab
. Giá trị nhỏ nhất của biểu thức
2 2
P x y
thuộc tập hợp nào dưới đây?
A.
10;15
. B.
6;10
. C.
1;4
. D.
4;6
.
Câu 41. (Chuyên Lào Cai - 2020) Xét các số thực dương
x
,
y
thỏa mãn
2
log log log
x y x y
.
Biểu thức
8P x y
đạt giá trị nhỏ nhất của bằng:
A.
min
16
P
. B.
min
33
2
P
. C.
min
11 2
P
. D.
min
31
2
P
.
Câu 42. (Chuyên Lê Hồng Phong - Nam Định - 2020) Xét các số thực
,x y
thỏa mãn
2 2
log 1 log 1 1
x y
. Khi biểu thức
2 3P x y
đạt giá trị nhỏ nhất thì
3 2 3x y a b
với
,a b
. Tính
T ab
?
A.
9
T
. B.
7
3
T
. C.
5
3
T
. D.
7
T
.
Câu 43. (Chuyên Phan Bội Châu - Nghệ An - 2020) Cho các số thực
, , , a b c d
thỏa mãn
2 2
2
log 4 6 7 1
a b
a b
và
27 .81 6 8 1
c d
c d
. Tìm giá trị nhỏ nhất của biểu thức
2 2
P a c b d
.
A.
49
.
25
B.
64
.
25
C.
7
.
5
D.
8
5
.
Câu 44. (Chuyên Thái Bình - 2020) Cho hai số thực dương
,x y
thỏa mãn
2 2
log log 6 6x x x y y x
. Giá trị nhỏ nhất của biểu thức
3
3T x y
là
A.
16
. B.
18
. C.
12
. D.
20
.
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 45. (Chuyên Thái Nguyên - 2020) Xét các số thực dương
,a b
thoả mãn
2
1
log 2 3
ab
ab a b
a b
. Tìm giá trị nhỏ nhất
min
P
của
P a b
.
A.
min
1 2 5
P
. B.
min
2 5
P
. C.
min
1 5
P
. D.
min
1 2 5
P
.
Câu 46. (ĐHQG Hà Nội - 2020) Cho các số thực x, y thỏa mãn
2 2
2
log log 2 2 5
2
x
y x y xy
x
.
Hỏi giá trị nhỏ nhất của
2 2
P x y xy
là bao nhiêu?
A.
30 20 2
. B.
33 22 2
. C.
24 16 2
. D.
36 24 2
.
Câu 47. (Sở Bình Phước - 2020) Cho
,x y
là các số thực dương thỏa mãn
2
2 2 2
log log 1 log 2x y x y
. Giá trị nhỏ nhất của biểu thức
2x y
bằng
A.
2 2 3
. B.
2 3 2
. C.
3 3
. D.
9
.
Câu 48. (Sở Yên Bái - 2020) Cho các số thực
,x y
thuộc đoạn
0;1
thỏa mãn
2
1
2
2021
2020
2 2022
x y
x
y y
.
Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
3 3 2
2 6 3 9
x y x xy
. Tính
.M m
.
A.
5
2
. B.
5.
C.
5.
D.
3.
Câu 49. (Bỉm Sơn - Thanh Hóa - 2020) Xét các số thực dương
.x y
thỏa mãn
2
1 1 1
2 2 2
log log log
x y x y
. Tìm giá trị nhỏ nhất
min
P
của biểu thức
3P x y
.
A.
min
17
2
P
. B.
min
8
P
. C.
min
9
P
. D.
min
25 2
4
P
.
Câu 50. (Nguyễn Trãi - Thái Bình - 2020) Cho các số thực
x
,
y
thay đổi thỏa mãn
2 2
1x y xy
và
hàm số
3 2
2 3 1
f t t t
. Gọi
M
và
m
tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của
5 2
4
x y
Q f
x y
. Tổng
M m
bằng
A.
4 3 2
. B.
4 5 2
. C.
4 2 2
. D.
4 4 2
.
Câu 51. (Yên Lạc 2 - Vĩnh Phúc - 2020) Cho hai số thực
a
,
b
lớn hơn
1
. Tìm giá trị nhỏ nhất của biểu
thức
2 2
4 1
log
4 4 log
a
ab
a b
S
b
.
A.
5
4
. B.
11
4
. C.
9
4
. D.
7
4
.
Câu 52. (Hải Hậu - Nam Định - 2020) Với các số thực dương
, ,x y z
thay đổi sao cho
2
2 2 2
2 2
log 4 8 8 2
x y z
x x y y z z
x y z
, gọi giá trị lớn nhất và giá trị nhỏ nhất của
biểu thức
2 2 2
4 7 11 8
6 5 86
x y z x y z
T
x y
thứ tự là
M
và
m
. Khi đó
M m
bằng:
A.
3
2
. B.
1
. C.
5
2
. D.
1
2
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 53. (Lương Thế Vinh - Hà Nội - 2020) Cho các số thực
,x y
thỏa mãn
3
ln ln( 2) ln 3
y x
. Tìm
giá trị nhỏ nhất của biểu thức
3
2 2
4 2
( 1) .
2
y x x
x y
H e x y y
A.
1
. B.
0
. C.
e
. D.
1
e
.
Câu 54. (Thanh Chương 1 - Nghệ An - 2020) Cho
,x y
là các số thực dương thỏa mãn
2
8 8
2
xy x y
xy
x y
.
Khi
2
2
P xy xy
đạt giá trị lớn nhất, giá trị của biểu thức
3 2x y
bằng
A.
4
. B.
2
. C.
3
. D.
5
.
Câu 55. (Tiên Lãng - Hải Phòng - 2020) Cho
,x y
là các số dương thỏa mãn
log 2 log log
x y x y
. Khi đó, giá trị nhỏ nhất của biểu thức
2 2
4
1 2 1
x y
P
y x
là:
A.
31
5
. B.
6
. C.
29
5
. D.
32
5
.
Câu 56. (Chuyên Sư Phạm Hà Nội - 2020) Cho các số thực
,x y
thay đổi, thỏa mãn
0x y
và
1
ln ln ln
2
x y xy x y
. Giá trị nhỏ nhất của
M x y
là
A.
2 2
. B. 2. C. 4. D. 16.
Câu 57. (Sở Hà Nội - Lần 2 - 2020) Xét
, ,x y z
là các số thực lớn hơn 1 thỏa mãn điều kiện
2
xyz
. Giá
trị nhỏ nhất của biểu thức
3 3 3
2 2 2
1
log log log
4
S x y z
bằng
A.
1
32
. B.
1
4
. C.
1
16
. D.
1
8
.
Câu 58. Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
2 2
3 4
log ( ) log 2
x y x y
?
A.
1
B.
3
C.
2
D. Vô số
Câu 59. Có bao nhiêu cặp số nguyên dương
;x y
thỏa mãn đồng thời hai điều kiện:
6
1 10
x
và
2
2 2 2
log 10 20 20 10 2 1
y
x x y x x
?
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 60. Có bao nhiêu số nguyên
10
y
sao cho tồn tại số nguyên
x
thỏa mãn
2
2
2 2 1
5 2 5 1
y
y
x x x
x
?
A.
10
B.
1
C.
5
D. Vô số
Câu 61. Có bao nhiêu cặp số nguyên dương
;x y
thoả mãn
1 2020
x
và
1
2
2 2 log 2
y y
y x x
A.
2021
. B.
10
. C.
2020
. D.
11
.
Câu 62. Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
2 2
2 2
3
2log log 1 3 log 1
x y x y
A.
1
B.
3
C.
2
D.
5

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Câu 63. Có ba
o nhiêu cặp số nguyên
;x y
thỏa
mãn
0 2020
y
và
3
2 1
lo
g 1 2 ?
x
x
y
y
A.
20
19
. B.
11
. C.
20
20
. D.
4
.
Câu 64. (Chuyên Lươn
g Văn Chánh - Phú Yên - 2020) Xét các số thực
, ,a b x
thoả mãn
1,
1,0 1a b x
và
2
log
log ( )
b a
x x
a b
. Tìm giá trị nhỏ nhất của biểu thức
2 2
ln ln ln( ).P a b ab
A.
1 3
3
4
. B.
2
e
. C.
1
4
. D.
3 2
2
12
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM
Dạng 1. Tìm tập xác định
Hàm số mũ
Dạng:
x
u
y a
y a
với
0
.
1
a
a
Tập xác định:
.D
Hàm số logarit
Dạng:
log
log
a
a
y x
y u
với
0
.
1
a
a
Đặc biệt:
ln ;a e y x 10 log lga y x x
.
Điều kiện xác định:
0u
.
Câu 1. (Đề Tham Khảo 2020 Lần 2) Tập xác định của hàm số
2
logy x
là
A.
0; .
B.
; .
C.
0; .
D.
2; .
Lời giải
Chọn C
Điều kiện xác định của hàm số
2
logy x
là
0x
.
Vậy tập xác định của hàm số
2
logy x
là
0; .D
Câu 2. (Mã 101 - 2020 Lần 1) Tập xác định của hàm số
5
logy x là
A.
0;
. B.
;0
. C.
0;
. D.
;
.
Lời giải
Chọn C
Điều kiện:
0x
.
Tập xác định:
0;D
.
Câu 3. (Mã 102 - 2020 Lần 1) Tập xác định của hàm số là
A. . B. . C. . D. .
Lời giải
Chọn B
Điều kiện:
Vậy tập xác định của hàm số đã cho là
Câu 4. (Mã 103 - 2020 Lần 1) Tập xác định của hàm số
3
logy x là
A.
( ;0)
B.
(0; )
C.
( ; )
D.
[0; )
Lời giải
Chọn B.
Điều kiện xác định:
0x
.
HÀM SỐ MŨ - HÀM SỐ LOGARIT
Chuyên đề 18
6
log
y x
0;
0;
;0
;
0.
x
0; .
D

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 5. (Mã 104 - 2020 Lần 1) Tập xác định của hàm số
4
logy x
là
A.
( ;0)
. B.
0;
. C.
0;
. D.
;
.
Lời giải
Chọn C
Điều kiện
0
x
.
Câu 6. (Mã 102 - 2020 Lần 2) Tập xác định của hàm số
5
x
y
là
A.
. B.
0;
. C.
\ 0
. D.
0;
.
Lời giải
Chọn A
Tập xác định của hàm số
5
x
y
là
Câu 7. (Mã 103 - 2020 Lần 2) Tập xác định của hàm số
2
x
y
là
A.
. B.
0;
. C.
0;
. D.
\ 0
.
Lời giải
Chọn A
Hàm số mũ
2
x
y
xác định với mọi
x
nên tập xác định là
D
.
Câu 8. (Mã 123 2017) Tìm tập xác định
D
của hàm số
5
3
log .
2
x
y
x
A.
( ; 2) (3; )D
B.
( 2; 3)D
C.
( ; 2) [3; )D
D.
\{ 2}D
Lời giải
Chọn A
Tập xác định của là tập các số
x
để
3
3
0 3 2 0
2
2
x
x
x x
xx
Suy ra
; 2 3;D
.
Câu 9. (Đề Minh Họa 2017) Tìm tập xác định D của hàm số
2
2
log 2 3
y x x
A.
; 1 3;D
B.
1;3
D
C.
; 1 3;D
D.
1;3
D
Lời giải
Chọn C
2
2
log 2 3
y x x
. Hàm số xác định khi
2
2 3 0
x x
1
x
hoặc
3
x
Vậy tập xác định:
; 1 3;D
Câu 10. (Mã 104 2017) Tìm tập xác định
D
của hàm số
2
3
log 4 3
y x x
.
A.
1;3
D
B.
;1 3;D
C.
;2 2 2 2;D
. D.
2 2;1 3;2 2
D
Lời giải
Chọn B

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Điều kiện
2
1
4 3 0
3
x
x x
x
.
Câu 11. (THPT Lương Thế Vinh Hà Nội 2019) Tìm tập xác định của hàm số
2
2018
log 3
y x x
.
A.
D
B.
0;D
C.
; 0 3;D
D.
0; 3
D
Lời giải
Chọn D
Hàm số xác định khi:
2
3 0 0; 3
x x x
Vậy
0; 3
D
Câu 12. (Chuyên Vĩnh Phúc 2019) Tập xác định của
2
ln 5 6
y x x
là
A.
2; 3
B.
2; 3
C.
; 2 3;
D.
; 2 3;
Lời giải
Chọn B
Hàm số xác định khi và chỉ khi
2
5 6 0 2 3.
x x x
Vậy tập xác định của hàm số là
2;3 .
D
Câu 13. (THPT Lê Quy Đôn Điện Biên 2019) Tìm tập xác định của hàm số
5
1
log
6
y
x
.
A.
;6
B.
C.
0;
D.
6;
Lời giải
Chọn A
Điều kiện:
1
0 6 0 6
6
x x
x
. Do đó tập xác định của hàm số là
;6
.
Câu 14. (THPT Lương Thế Vinh Hà Nội 2019) Tập xác định của hàm số
2
2
log 3 2
y x x
là
A.
( 1;1)D
. B.
( 1; 3)D
. C.
( 3;1)D
. D.
(0;1)D
.
Lời giải
Hàm số
2
2
log 3 2
y x x
xác định khi:
2
3 2 0 3 1x x x
.
Vậy tập xác định của hàm số đã cho là:
3;1
D
.
Câu 15. (Sở Vĩnh Phúc 2019) Tập xác định của hàm số
2
2
log 2 3
y x x
là
A.
1;3
. B.
1;3
.
C.
; 1 3;
. D.
; 1 3;
.
Lời giải
Hàm số xác định khi
2
1
2 3 0
3
x
x x
x
.
Vậy
; 1 3;D
.
Câu 16. (Chuyên Lê Hồng Phong Nam Định 2019) Tìm tập xác định của hàm số:
x
y x
2 log 3
A.
0;
. B.
0;3
. C.
;3
. D.
0;3
.
Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn D
Điều kiện xác định:
x x
D
x x
0 0
0;3
3 0 3
Câu 17. (Chuyên Nguyễn Trãi Hải Dương 2019) Tập xác định của hàm số
ln 2
y x
là
A.
. B.
3;
. C.
0;
. D.
2;
.
Lời giải
ĐKXĐ:
ln 2 0
2 1
2 1 3
2 0
2 0
x
x
x x
x
x
.
TXĐ:
3;D
.
Câu 18. (THPT Ba Đình 2019) Tìm tập xác định D của hàm số
2019
2
2019
y log 4 x 2x 3 .
A.
3 3
D 2; ;2
2 2
. B.
3 3
D 2; ;2
2 2
.
C.
3
D ;2
2
. D.
D 2;2
.
Lời giải
Điều kiện có nghĩa của hàm số là
2
2 x 2
4 x 0
3
x
2x 3 0
2
Vậy tập xác định của hàm số là
3 3
D 2; ;2
2 2
Câu 19. Tìm tập xác định của hàm số
0
2
2
2 log 9
y x x
là
A.
2;3 .
D
B.
3;3 \ 2 .
D
C.
3; .
D
. D.
3;3 .
D
.
Lời giải
+ Điều kiện xác định:
2
2 0
2
3 3
9 0
x
x
x
x
+ Vậy tập xác định của hàm số là:
3;3 \ 2 .
D
Dạng 2. Tìm đạo hàm
Đạo hàm hàm số mũ
ln
ln .
x x
u u
y a y a a
y a y a a u
.
Đặc biệt:
( )
( ) .
x x
u u
e e
e e u
với
2,71828...e
Đạo hàm hàm số logarit

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
1
log
ln
log
ln
a
a
y x y
x a
u
y u y
u a
.
Đặc biệt:
1
(ln )
(ln )
x
x
u
u
u
.
Câu 1. (Đề Tham Khảo 2017) Tìm đạo hàm của hàm số
logy x
.
A.
ln10
y
x
B.
1
ln10
y
x
C.
1
10ln
y
x
D.
1
y
x
Lời giải
Chọn B
Áp dụng công thức
1
log
ln
a
x
x a
, ta được
1
ln10
y
x
.
Câu 2. (Mã 103 - 2019) Hàm số
2
2
x x
y
có đạo hàm là
A.
2
2 .ln 2
x x
. B.
2
(2 1).2 .ln 2
x x
x
.
C.
2
2 1
( ).2
x x
x x
. D.
2
(2 1).2
x x
x
.
Lời giải
Chọn B
Ta có
2 2
2
' ( )'.2 .ln 2 (2 1).2 .ln 2
x x x x
y x x x
.
Câu 3. (Mã 104 - 2019) Hàm số
2
3
x x
y
có đạo hàm là
A.
2
2 1 .3
x x
x
. B.
2
2 1
.3
x x
x x
. C.
2
2 1 .3 .ln 3
x x
x
. D.
2
3 .ln3
x x
.
Lời giải
Chọn C
Ta có:
. .ln
u u
a u a a
nên
2 2
3 ' 2 1 .3 .ln3
x x x x
x
.
Câu 4. (Đề Minh Họa 2017) Tính đạo hàm của hàm số
13
x
y
A.
13
ln13
x
y
B.
1
.13
x
y x
C.
13 ln13
x
y
D.
13
x
y
Lời giải
Chọn C
Ta có:
13 ln13
x
y
.
Câu 5. (Mã 110 2017) Tính đạo hàm của hàm số
2
log 2 1
y x
.
A.
2
2 1 ln 2
y
x
B.
1
2 1 ln 2
y
x
C.
2
2 1
y
x
D.
1
2 1
y
x
Lời giải
Chọn A
Ta có
2
2 1
2
log 2 1
2 1 ln 2 2 1 ln 2
x
y x
x x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 6. (Đề Minh Họa 2017) Tính đạo hàm của hàm số
1
4
x
x
y
A.
2
1 2 1 ln 2
'
2
x
x
y
B.
2
1 2 1 ln 2
'
2
x
x
y
C.
2
1 2 1 ln 2
'
2
x
x
y
D.
2
1 2 1 ln 2
'
2
x
x
y
Lời giải
Chọn A
Ta có:
2 2
1 .4 1 . 4
4 1 .4 .ln 4
'
4 4
x x
x x
x x
x x
x
y
2
2
4 . 1 .ln 4 ln 4 1 2 1 ln 2
1 .2ln 2 2ln 2
4 2
4
x
x x
x
x x
x
.
Câu 7. (Đề Tham Khảo 2019) Hàm số
2
2
log 2x
f x x
có đạo hàm
A.
2
ln2
'
2x
f x
x
B.
2
1
'
2x ln 2
f x
x
C.
2
2x 2 ln 2
'
2x
f x
x
D.
2
2x 2
'
2x ln 2
f x
x
Lời giải
Chọn D
2
2 2
2x '
2x 2
'
2x ln 2 2x ln 2
x
f x
x x
Câu 8. (Mã 101 - 2019) Hàm số
2
3
2
x x
y
có đạo hàm là
A.
2
3
2 3 2 ln 2
x x
x
. B.
2
3
2 ln 2
x x
.
C.
2
3
2 3 2
x x
x
. D.
2
2 3 1
3 2
x x
x x
.
Lời giải
Chọn A
2 2
3 3
' 2 ' 2 3 2 ln 2
x x x x
y x
.
Câu 9. (Mã 102 - 2019) Hàm số
2
3
3
x x
y
có đạo hàm là
A.
2
3
2 3 .3
x x
x
. B.
2
3
3 .ln3
x x
.
C.
2
2 3 1
3 .3
x x
x x
. D.
2
3
2 3 .3 .ln 3
x x
x
.
Lời giải
Chọn D
Ta có:
2 2
3 3
3 2 3 .3 .ln 3
x x x x
y x
.
Câu 10. Tính đạo hàm của hàm số
y = ln 1+ x +1
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
A.
1
1 1 1
y
x x
B.
2
1 1 1
y
x x
C.
1
2 1 1 1
y
x x
D.
1
1 1
y
x
Lời giải
Chọn C
Ta có:
1 1
1
ln 1 1
1 1
2 1 1 1
x
y x
x
x x
.
Câu 11. (Chuyên Vĩnh Phúc 2019) Đạo hàm của hàm số
1 2x
y e
là
A.
1 2
2
x
y e
B.
1 2
2
x
y e
C.
1 2
2
x
e
y
D.
1 2 x
y e
Lời giải
Chọn B
1 2 1 2
' . 1 2 ' 2.
x x
y e x e
Câu 12. (Chuyên Lam Sơn Thanh Hóa 2019) Đạo hàm của hàm số
2
3
log 1
y x x
là:
A.
2
2 1 ln 3
'
1
x
y
x x
B.
2
2 1
'
1 ln 3
x
y
x x
C.
2
2 1
'
1
x
y
x x
D.
2
1
'
1 ln 3
y
x x
Lời giải
Chọn B
2
2 2
1 '
2 1
'
1 ln 3 1 ln 3
x x
x
y
x x x x
Câu 13. (THPT Lê Quy Đôn Điện Biên 2019) Tính đạo hàm của hàm số
2
x x
y e
.
A.
2 1
x
x e
B.
2
2 1
x x
x e
C.
2 1
2 1
x
x e
D.
2 2 1x
x x e
Lời giải
Chọn B
2 2 2
'
'
2
. 2 1
x x x x x x
e e x x x e
Câu 14. (THPT Hùng Vương Bình Phước 2019) Cho hàm số
2
2
log 1
f x x
, tính
1
f
A
1 1
f
. B.
1
1
2ln 2
f
. C.
1
1
2
f
. D.
1
1
ln 2
f
.
Lời giải
TXĐ:
D
.
2
2 1
1
ln 2
1 .ln 2
x
f x f
x
.
Câu 15. (THPT-Thang-Long-Ha-Noi- 2019) Tìm đạo hàm của hàm số
2
ln 1
x
y e
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
2
2
2
1
x
x
e
y
e
. B.
2
2
1
x
x
e
y
e
. C.
2
1
1
x
y
e
. D.
2
2
2
1
x
x
e
y
e
.
Lời giải
Ta có:
2
2
2
2 2
1
2
ln 1
1 1
x
x
x
x x
e
e
y e
e e
.
Câu 16. (Chuyen Phan Bội Châu Nghệ An 2019) Tính đạo hàm của hàm số
1
2
x
x
y
A.
2
2
x
x
y
. B.
2
ln 2. 1 1
2
x
x
y
.
C.
2
2
x
x
y
. D.
ln 2. 1 1
2
x
x
y
.
Lời giải
Ta có
2
1 .2 2 . 1
2
x x
x
x x
y
2
1.2 2 .ln 2. 1
2
x x
x
x
ln 2. 1 1
2
x
x
Câu 17. (Chuyên Lê Quý Đôn Quảng Trị 2019) Tính đạo hàm của hàm số
2
9
log 1
y x
.
A.
2
1
1 ln9
y
x
. B.
2
1 ln3
x
y
x
. C.
2
2 ln 9
1
x
y
x
. D.
2
2ln 3
1
y
x
.
Lời giải
Ta có
2
2 2 2 2 2
1
2 2
1 ln9 1 ln3 1 2ln 3 1 ln3
x
x x x
y
x x x x
.
Câu 18. (KTNL GV THPT Lý Thái Tổ 2019) Tính đạo hàm hàm số
.sin2
x
y e x
A.
sin 2 cos 2
x
e x x
. B.
.cos2
x
e x
.
C.
sin 2 cos 2
x
e x x
. D.
sin 2 2cos 2
x
e x x
.
Lời giải
Chọn D
' .sin 2 .sin 2 . sin 2 .sin 2 2 .cos 2 sin 2 2cos 2
x x x x x x
y e x e x e x e x e x e x x
Câu 19. (VTED 2019) Đạo hàm của hàm số
1
4
x
x
y
là
A.
2
1 2 1 ln 2
2
x
x
B.
2
1 2 1 ln 2
2
x
x
C.
2
1 2 1 ln 2
2
x
x
D.
2
1 2 1 ln 2
2
x
x
Lời giải
Chọn A
2
2
1 4 1 4
4
1 2 1 ln 2
2
x x
x
x
x
y
x
x
Câu 20. (Chuyên Hùng Vương Gia Lai 2019) Cho hàm số
1
1 ln
y
x x
với
0
x
. Khi đó
2
'y
y
bằng

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
A.
1
x
x
. B.
1
1
x
. C.
1 ln
x
x x
. D.
1
1 ln
x
x x
.
Lời giải
2
1 1 1 1
1 ln 1 ln 1
1 ln
y
y x x x x
x x y y y x
.
Câu 21. (Chuyên Lê Quý Đôn Điện Biên 2019) Tính đạo hàm của hàm số
x
1
2 ln
e
x
y x
.
A.
1 1
2 ln 2 ln
e
x
x
y x
x
. B.
1
2 ln 2 e
x x
y
x
.
C.
x
1 1
2 ln 2
e
x
y
x
. D.
x
1
2 ln 2 e
x
y
x
.
Lời giải
Ta có
x
2 1 1 1
2 ln2 ln ln 2 ln
e e
x
x
x
y x x
x x
.
Câu 22. (VTED 2019) Đạo hàm của hàm số
2
2
( ) log 2f x x x
là
A.
2
2 2
2 ln 2
x
x x
B.
2
2 l 2
1
n
x x
C.
2
(2 2)ln
2
2
x
x
x
D.
2
2 2
2 ln 2
x
x x
Lời giải
Ta có
2
2 2
2
2 2
( )
2 ln2 2 ln 2
x x
x
f x
x x x x
Câu 23. (Chuyên KHTN 2019) Đạo hàm của hàm số
(x) ln(lnx)
f
là:
A.
1
( )
x ln ln ln
f x
x x
. B.
1
( )
2 ln ln
f x
x
C.
1
( )
2x lnx ln ln
f x
x
. D.
1
( )
lnx ln ln
f x
x
.
Lời giải
Áp dụng các công thức
ln
ln
u
u
u
và
2
u
u
u
ta có
1
( )
2 ln ln(ln )
f x
x x x
.
Dạng 3. Khảo sát hàm số mũ, logarit
Sự biến thiên hàm số mũ:
x
y a
.
Nếu
1
a
thì hàm đồng biến trên
. Nếu
0 1
a
thì hàm nghịch biến trên
.
Sự biến thiên hàm số logarit:
log
a
y x
. Nếu
1
a
: hàm đồng biến trên
(0; )
. Nếu
0 1
a
: hàm
nghịch biến trên
(0; ).
Đồ thị hàm số mũ và logarit
ĐỒ THỊ HÀM SỐ MŨ ĐỒ THỊ HÀM SỐ LOGARIT
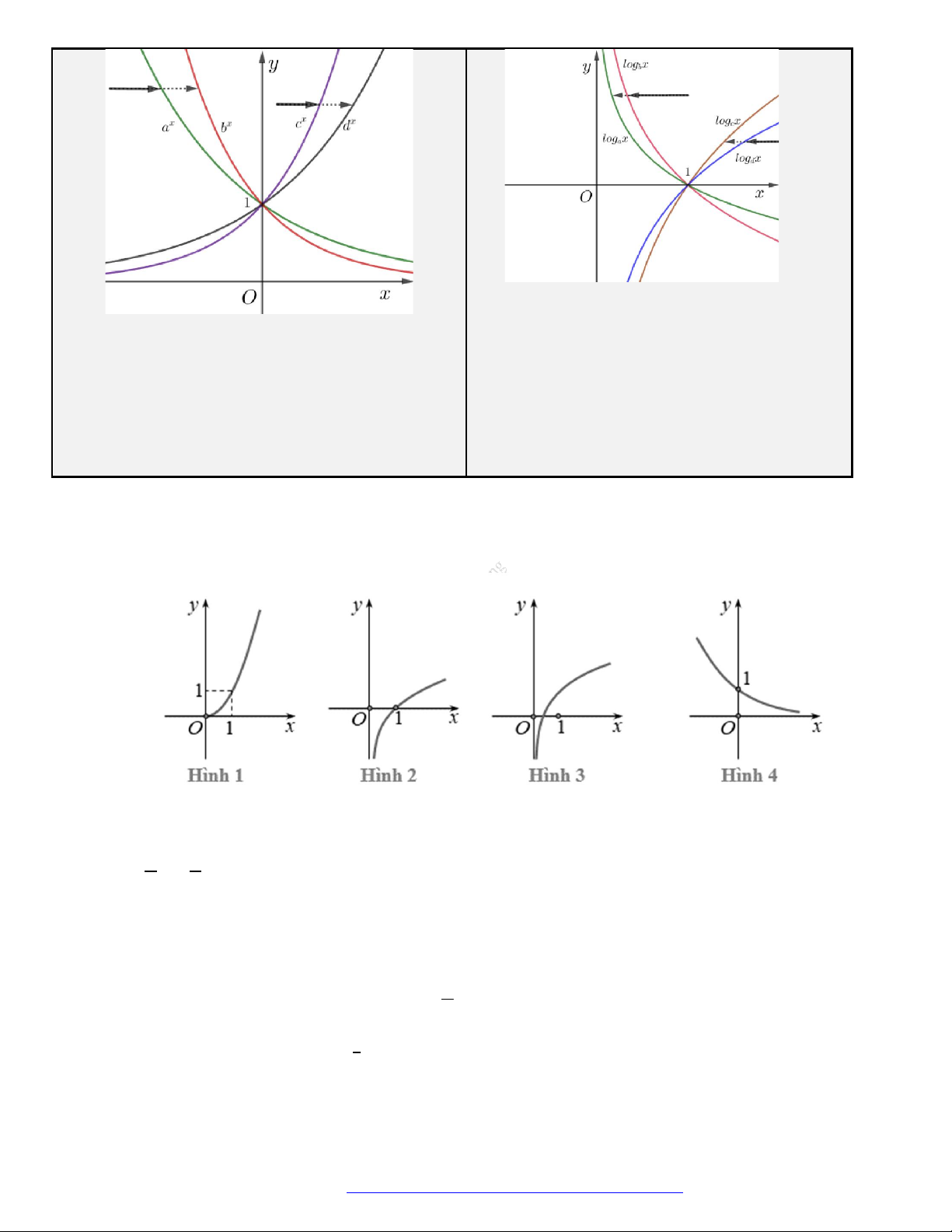
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta thấy:
0 1; 0 1
x x
a a b b
.
Ta thấy:
1; 1.
x x
c c d d
So sánh a với b: Đứng trên cao, bắn mũi tên từ trái
sang phải, trúng
x
a
trước nên
a b
.
So sánh c với d: Đứng trên cao, bắn mũi tên từ trái
sang phải, trúng
x
c
trước nên
.c d
Vậy
0 1 .b a d c
Ta thấy:
log 0 1; log 0 1
a b
x a x b
.
Ta thấy:
log 1; log 1.
c d
x c x d
So sánh a với b: Đứng trên cao, bắn mũi tên
từ phải sang trái, trúng
log
b
x
trước:
.b a
So sánh c với d: Đứng trên cao, bắn mũi tên
từ phải sang trái, trúng
log
d
x
trước:
.d c
Vậy
0 1a b c d
.
Câu 1. (Đề Tham Khảo 2017) Cho hàm số
lnf x x x
. Một trong bốn đồ thị cho trong bốn phương
án A, B, C, D dưới đây là đồ thị của hàm số
y f x
. Tìm đồ thị đó?
A. Hình 2 B. Hình 3 C. Hình 4 D. Hình 1
Lời giải
Chọn B
Tập xác định
0;D
Ta có
ln ln 1f x x x f x g x x
.
Ta có
1 1g
nên đồ thị hàm số đi qua điểm
1;1
. Loại hai đáp án B và D
Và
0 0
lim lim ln 1
x x
g x x
. Đặt
1
t
x
. Khi
0x
thì
t
.
Do đó
0
1
lim lim ln 1 lim ln 1
t t
x
g x t
t
nên loại đáp án A
Câu 2. Cho ba số thực dương
, ,a b c
khác
1
. Đồ thị các hàm số , ,
x x x
y a y b y c được cho trong hình
vẽ bên
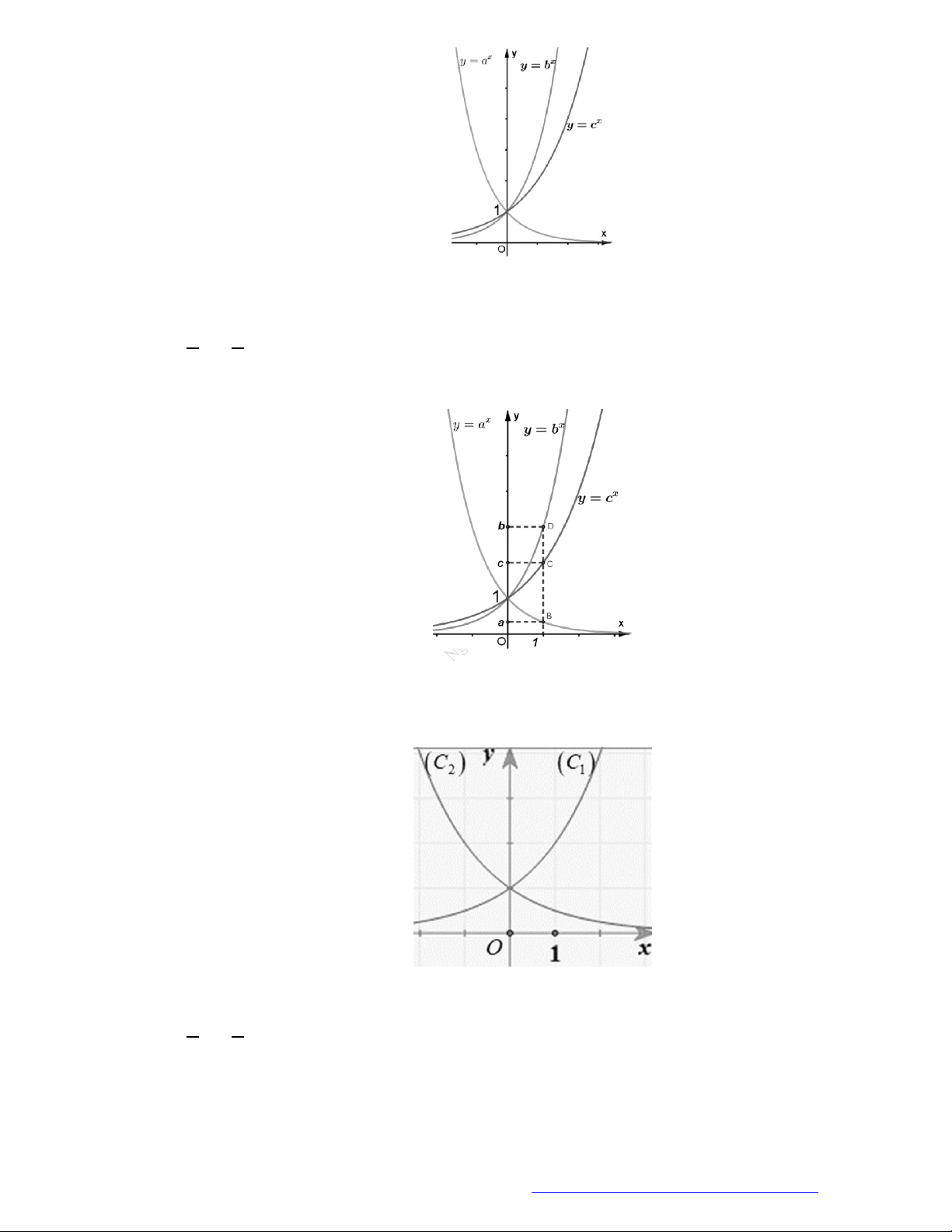
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Mệnh đề nào dưới đây đúng?
A.
b c a
B.
c a b
C.
a b c
D.
a c b
Lời giải
Chọn D
Đường thẳng
1x
đồ thị các hàm số , ,
x x x
y a y b y c tại các điểm có tung độ lần lượt là
, ,y a y b y c
như hình vẽ:
Từ đồ thị kết luận
a c b
Câu 3. (Mã 105 2017) Cho hàm số ,
x x
y a y b với
, a b
là hai số thực dương khác 1, lần lượt có đồ
thị là
1
C
và
2
C
như hình bên. Mệnh đề nào dưới đây đúng
?
A.
0 1b a
B.
0 1a b
C.
0 1b a
D.
0 1a b
Lời giải
Chọn A
Theo hình ta thấy hàm
x
y a
là hàm đồng biến nên
1a
, còn hàm
x
y b
là hàm nghịch biến
nên
0 1b
. Suy ra
0 1 .b a
Câu 4. (Chuyên Bắc Giang 2019) Trong các hàm số sau hàm số nào nghịch biến trên
?

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
3
log
x
B.
3
log
y x
C.
e
4
x
y
D.
2
5
x
y
Lời giải
Chọn C
Hàm số mũ
x
y a
với
0 1a
nghịch biến trên
.
Ta có
e
0 1
4
nên hàm số
e
4
x
y
nghịch biến trên
.
Câu 5. Mệnh đề nào trong các mệnh đề dưới đây sai?
A. Hàm số
2
1
2018
x
y
đồng biến trên
.
B. Hàm số
logy x
đồng biến trên
0;
.
C. Hàm số
ln
y x
nghịch biến trên khoảng
;0
.
D. Hàm số
2
x
y
đồng biến trên
.
Lời giải
Chọn C
Hàm số
ln( )y x
TXĐ
;0
D
Cơ số
1a e
do đó hàm số đồng biết trên
;0
Câu 6. (THPT An Lão Hải Phòng 2019) Hàm số nào dưới đây đồng biến trên tập xác định của nó?
A.
1
π
x
y
B.
2
3
x
y
C.
3
x
y
D.
0,5
x
y
Lời giải
Chọn C
Hàm số
x
y a
đồng biến trên
khi và chỉ khi
1
a
.
Thấy các số
1 2
; ; 0,5
π 3
nhỏ hơn
1
, còn
3
lớn hơn 1 nên chọn
.C
Câu 7. (THPT An Lão Hải Phòng 2019) Cho hàm số
2
logy x
. Mệnh đề nào dưới đây sai?
A. Đạo hàm của hàm số là
1
ln 2
y
x
B. Đồ thị hàm số nhận trục
Oy
làm tiệm cận đứng
C. Tập xác định của hàm số là
;
D. Hàm số đồng biến trên khoảng
0;
Lời giải
Chọn C
Hàm số
2
logy x
có tập xác định là
0;
D =
.
Câu 8. (THPT Lê Quy Đôn Điện Biên 2019) Trong các hàm số sau, hàm số nào luôn đồng biến trên
?
A.
2015
y
2016
x
B.
3
y
2016 2
x
C.
2x
y (0,1)
D.
2
(2016)
x
y
Lời giải
Chọn D
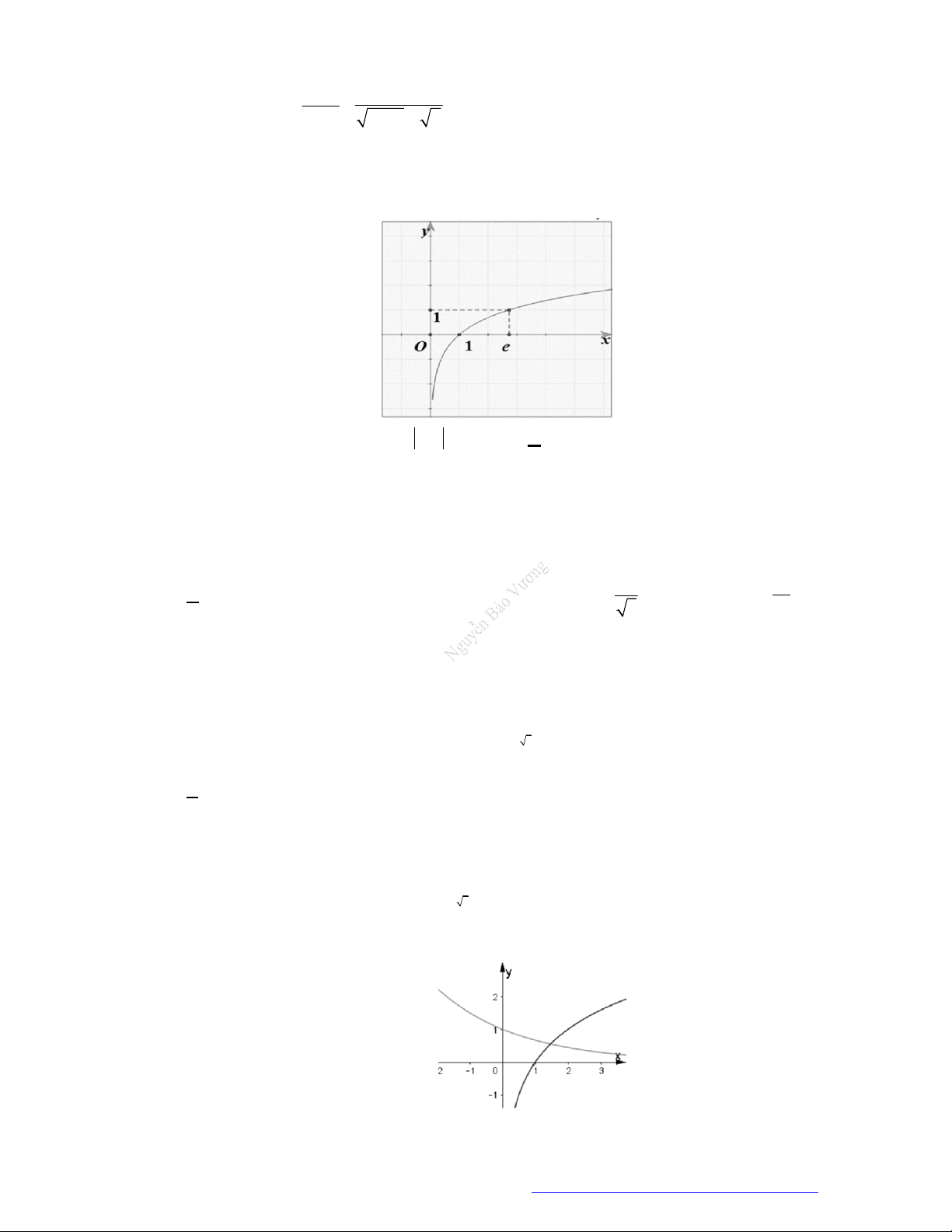
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
2
y 0,01(0,1)
x
x
,
2
40642(2016 56)
x x
y
Ta có các cơ số
2015
2016
;
3
2016 2
;
0,01
đều nhỏ hơn
1
nên các hàm số ở A, B, C nghịch biến
trên
.
Cơ số
4064256 1
nên hàm số
2
(2016)
x
y đồng biến trên
.
Câu 9. Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
e
x
y
. B.
lny x
. C.
lny x
. D.
e
x
y
.
Lời giải
Đồ thị hàm số đi qua điểm
; 1e
và nằm cả trên và dưới trục hoành nên chỉ có hàm số
lny x
thoả mãn.
Câu 10. (Chuyên Lê Thánh Tông 2019) Tìm hàm số đồng biến trên
.
A.
3
x
f x
. B.
3
x
f x
. C.
1
3
x
f x
. D.
3
3
x
f x
.
Lời giải
Hàm số
x
f x a
đồng biến trên
nếu
1a
và nghịch biến trên
nếu
0 1a
.
Vậy hàm số
3
x
f x
là hàm số đồng biến trên
.
Câu 11. (Chuyên Bắc Ninh 2019) Cho hàm số
5
logy x
. Mệnh đề nào dưới đây là mệnh đề sai?
A. Hàm số đã cho đồng biến trên tập xác định.
B. Hàm số đã cho có tập xác định
0\D
.
C. Đồ thị hàm số đã cho có một tiệm cận đứng là trục tung.
D. Đồ thị hàm số đã cho không có tiệm cận ngang.
Lời giải
Ta có tập xác định của hàm số
5
logy x
là
0D ;
. Do đó đáp án B sai.
Câu 12. Cho đồ thị hàm số
x
y a
và
log
b
y x
như hình vẽ.
Khẳng định nào sau đây đúng?

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
0
2
a b
. B.
0 1
a b
. C.
0 1
b a
. D.
0 1a
,
1
0
2
b
.
Lời giải
Chọn B
Xét hàm số
x
y a
đi qua
0;1
suy ra đồ thị hàm số
1
là đồ thị của hàm nghịch biến nên
0 1a
.
Xét đồ thị hàm số
log
b
y x
đi qua
1;0
suy ra đồ thị của hàm số
2
là đồ thị của hàm đồng
biến suy ra
1b
.
Vậy
0 1
a b
.
Câu 13. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong các hàm số sau, hàm số nào nghịch biến?
A.
ln .y x
B.
2018
1
2019
log
y x
C.
log .y x
D.
4 3
log .y x
Lời giải
+)
lny x
; TXĐ:
0;D
1e
suy ra hàm số
lny x
đồng biến trên
D
.
+)
2018
1
2019
log
y x
; TXĐ:
0;D
2018 2018
0 1 0 1 1
2019 2019
suy ra hàm số
2018
1
2019
log
y x
là hàm nghịch biến
D
.
+)
logy x
; TXĐ:
0;D
1
suy ra hàm số
logy x
đồng biến trên
D
.
+)
4 3
log
y x
; TXĐ:
0;D
4 3 1
suy ra hàm số
4 3
log
y x
đồng biến trên
D
.
Câu 14. (Sở Hà Nội 2019) Đồ thị hàm số
lny x
đi qua điểm
A.
1; 0
. B.
2
2; e
. C.
2 ; 2e
. D.
0;1
.
Lời giải
Với
1x
lny x
ln1
0
.
Với
2
x
lny x
ln 2
.
Với
2x e
lny x
ln2e
ln 2 1
.
Với
0
x
, hàm số không xác định.
Câu 15. (Chuyên Lương Thế Vinh Đồng Nai 2019) Trong các hàm số sau,hàm số nào luôn nghịch biến
trên tập xác định của nó?
A.
2
1
2
y
. B.
logy x
. C.
2
x
y
. D.
2
3
x
y
.
Lời giải
Ta thấy hàm số
2
3
x
y
là hàm số mũ có có tập xác định là
cơ số
2
1
3
a
nên nghịch biến
trên tập xác định của nó.
Ngoài ra ta có thể loại các đáp án khác bằng cách giải thích cụ thể đặc điểm các hàm đó như sau:

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Đáp án A loại vì: Hàm số
2
1
2
y
là hàm hằng nên không nghịch biến củng không đồng biến.
Đáp án B loại vì: Hàm số
logy x
là hàm số logarit có tập xác định là
(0; )
D
có cơ số
10 1
a
nên luôn đồng biến trên tập xác định của nó.
Đáp án C loại vì: hàm số
2
x
y
là hàm số mũ có tập xác định là
có cơ số
2 1
a
Câu 16. (Chuyên Lương Thế Vinh Đồng Nai 2019) Chọn khẳng định sai trong các khẳng định sau:
A. Hàm số
2
logy x
đồng biến trên
.
B. Hàm số
1
2
logy x
nghịch biến trên tập xác định của nó.
C. Hàm số
2
x
y
đồng biến trên
.
D. Hàm số
2
y x
có tập xác định là
0;
.
Lời giải
Hàm số
2
logy x
đồng biến trên khoảng
0;
.
Câu 17. (KTNL GV Bắc Giang 2019) Hàm số nào dưới đây đồng biến trên khoảng
(0; )
?
A.
3
log
y x
. B.
6
logy x
. C.
3
log
e
y x
. D.
1
4
logy x
.
Lời giải
Chọn A.
Hàm số
log
a
y x
đồng biến trên khoảng
(0; )
⇔
1
a
⇒ Chọn A
Câu 18. (Chuyên Lê Hồng Phong Nam Định 2019) Trong các mệnh đề sau, mệnh đề nào đúng?
A. Đồ thị của hàm số
2
x
y
và
2
logy x
đối xứng với nhau qua đường thẳng
y x
.
B. Đồ thị của hai hàm số
x
y e
và
lny x
đối xứng với nhau qua đường thẳng
y x
.
C. Đồ thị của hai hàm số
2
x
y
và hàm số
1
2
x
y
đối xứng với nhau qua trục hoành.
D. Đồ thị của hai hàm số
2
logy x
và
2
1
log
y
x
đối xứng với nhau qua trục tung.
Lời giải
Chọn B
Đồ thị hàm số
x
y a
và đồ thị hàm số
log
a
y x
đối xứng với nhau qua đường phân giác góc
phần tư thứ nhất (
y x
), suy ra chọn B.
Câu 19. (Chuyên Lê Hồng Phong Nam Định 2019) Hàm số nào sau đây có đồ thị như hình bên?
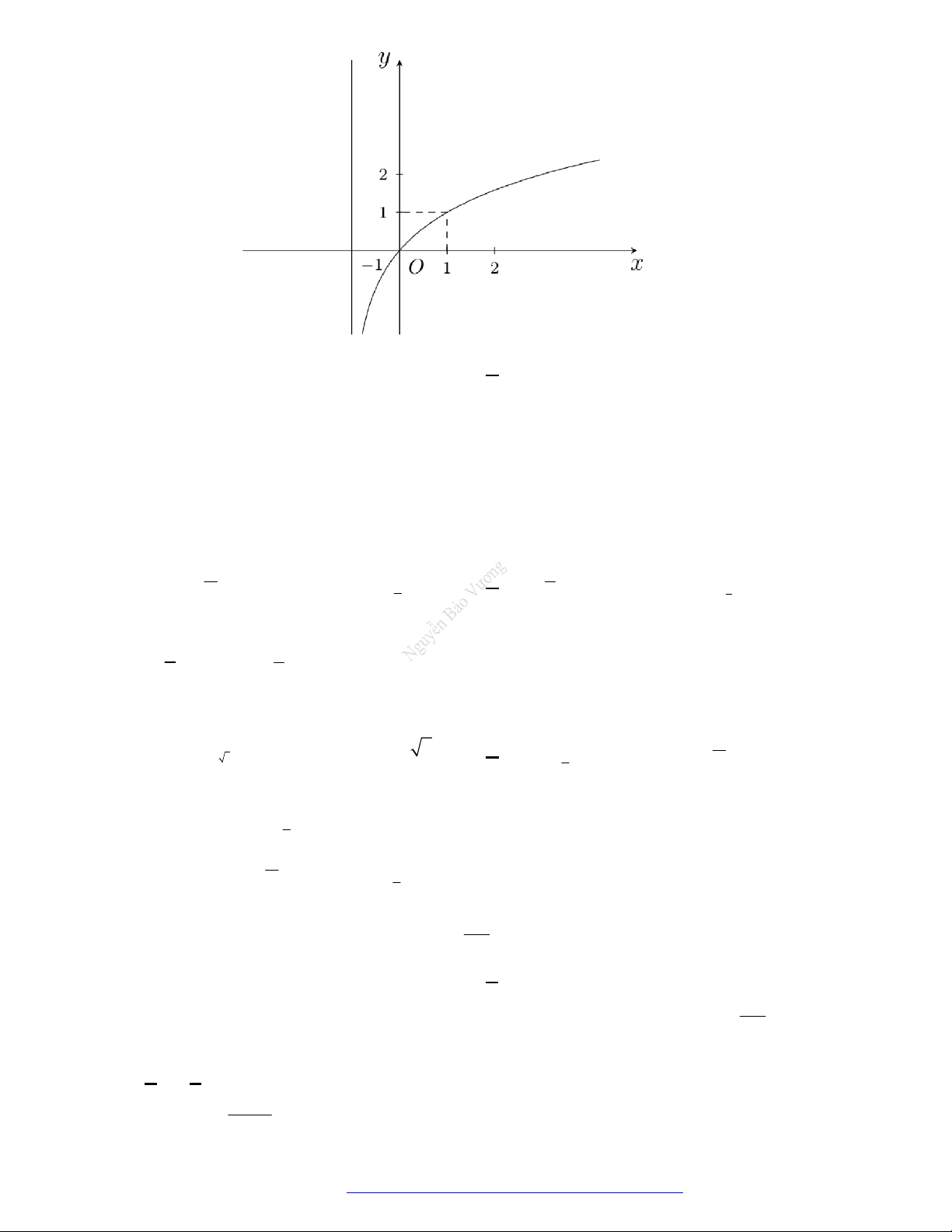
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3
logy x . B.
2
log 1y x . C.
2
log 1y x
. D.
3
log 1y x
Lời giải
Đồ thị hàm số đi qua điểm
0;0
nên loại đáp án A và B.
Đồ thị hàm số đi qua điểm
1;1
nên loại D.
Vậy đáp án C thỏa mãn.
Câu 20. (Chuyên Quốc Học Huế 2019) Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số
thực
R
.
A.
3
x
y
B.
2
4
log 2 1
y x
C.
2
x
y
e
D.
2
3
logy x
Lời giải
Vì
2
1
e
nên
2
x
y
e
nghịch biến trên
R
.
Câu 21. (Chuyên Vĩnh Phúc 2019) Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
A.
3
logy x
B.
2
log 1y x C.
4
logy x
D.
3
x
y
Lời giải
Xét hàm số
4
logy x
có tập xác định:
0;D
.
Nhận thấy cơ số
1
4
nên
4
logy x
nghịch biến trên tập xác định.
Câu 22. (Chuyên Bắc Giang -2019 Cho hàm số
3
9 17
ln3
x
y x
. Mệnh đề nào sau đây sai?
A. Hàm số nghịch biến trên khoảng
;0
B. Hàm số đồng biến trên khoảng
0;
C. Hàm số đạt cực trị tại
2x
D. Hàm số có giá trị cực tiểu là
9
1
ln3
y
Lời giải
Chọn B
Ta có:
3 ln3
' 9 3 9
ln3
x
x
y
' 0 3 9 2
x
y x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Câu 23. (THPT Lê Quy Đôn Điện Biên -2019) Đồ thị
L
của hàm số
lnf x x
cắt trục hoành tại
điểm
A
, tiếp tuyến của
L
tại
A
có phương trình là:
A.
2 1y x
B.
1y x
C.
3y x
D.
4 3y x
Lời giải
Chọn B
TXĐ
0;D
.
1
f x
x
Xét phương trình hoành độ giao điểm:
ln 0 1 1;0x x A
Vậy phương trình tiếp tuyến của đồ thị hàm số
L
tại điểm
A
là:
(1) 1 0 1y f x x
, chọn B.
Câu 24. (THCS - THPT Nguyễn Khuyến 2019) Hàm số
3x
y xe
đạt cực đại tại
A.
1
3
x
e
. B.
1
3
x
. C.
1
x
e
. D.
0x
.
Lời giải
Tập xác định là
.
3
1 3
x
y e x
.
Vì
3
0,
x
e x
nên dấu của
y
là dấu của nhị thức
1 3x
, suy ra
y
đổi dấu từ dương sang
âm khi
x
đi qua
1
3
.
Do đó,
1
3
x
là điểm cực đại của hàm số.
Câu 25. (THPT Gia Lộc Hải Dương 2019) Hàm số
2
3
log 2y x x
nghịch biến trên khoảng nào?
A.
2;
. B.
;0
. C.
1;
. D.
0;1
.
Lời giải
Hàm số
2
3
log 2y x x
có tập xác định
;0 2;D
.
Ta có
2
2 2
2 ln3
x
y
x x
. Khi đó
0y
1x
.
Bảng biến thiên:
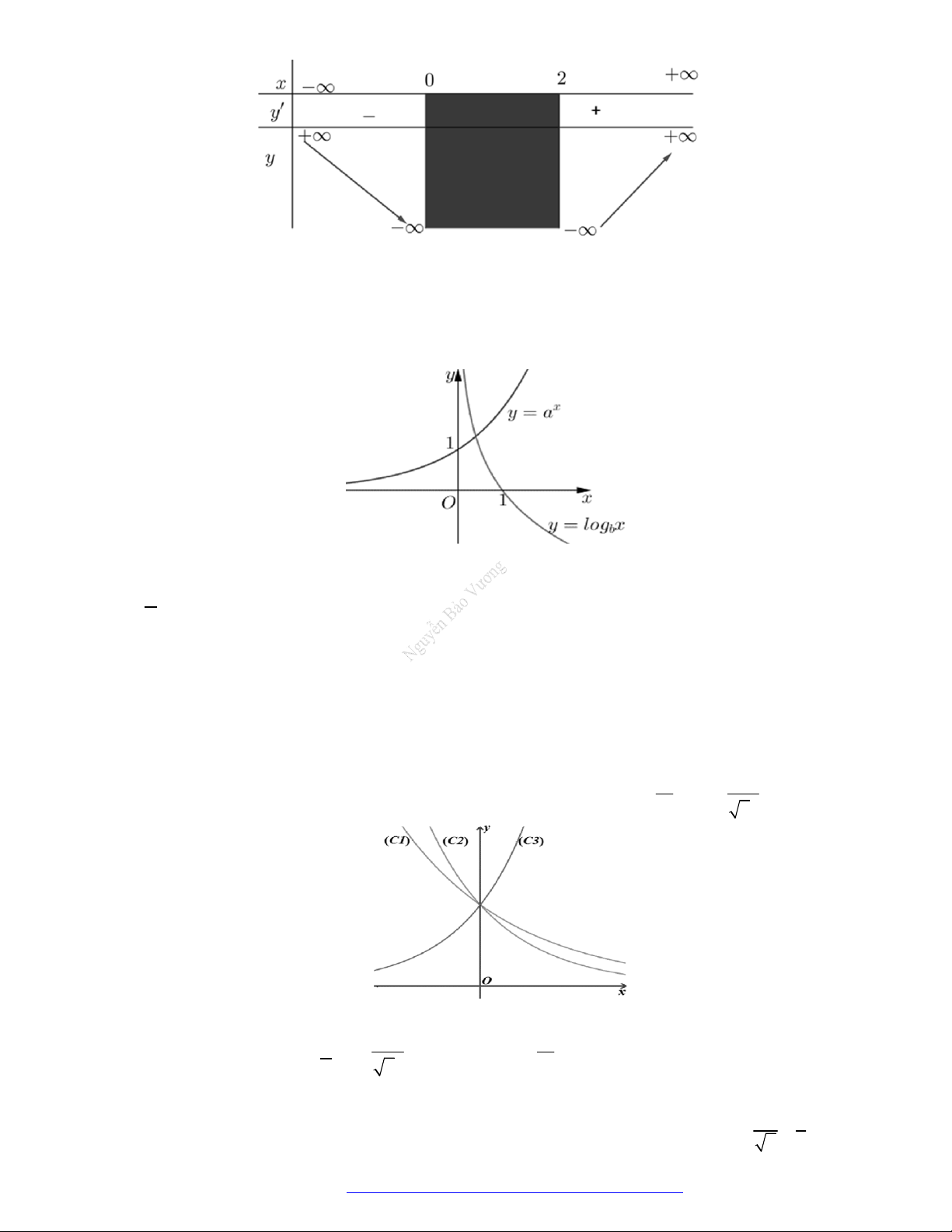
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào bảng biến thiên ta có hàm số
y
nghịch biến trên
;0
.
Câu 26. Cho đồ thị hàm số
x
y a
và log
b
y x như hình vẽ. Trong các khẳng định sau, đâu là khẳng
định đúng
A.
0 1,0 1a b
. B.
1, 1a b
.
C.
0 1b a
. D.
0 1a b
.
Lời giải
Dựa vào đồ thị ta thấy khi
0x y
do đó đồ thị hàm số
x
y a có
1a
. Nên ta loại đáp
án A và. D.
Ở đồ thị hàm số
log
y
b
y x x b
ta thấy khi
x y
do đó ta có
0 1b
.
Câu 27. Hình vẽ bên thể hiện đồ thị của ba trong bốn hàm số
6
x
y
,
8
x
y
,
1
5
x
y
và
1
.
7
x
y
Hỏi (C
2
) là đồ thị hàm số nào?
A.
6
x
y
. B.
1
7
x
y
. C.
1
5
x
y
. D.
8
x
y
Lời giải
Hàm số có đồ thị (C
2
) là hàm số nghịch biến, do đó loại đáp án A,D. Cho
1x
suy ra
1 1
5
7
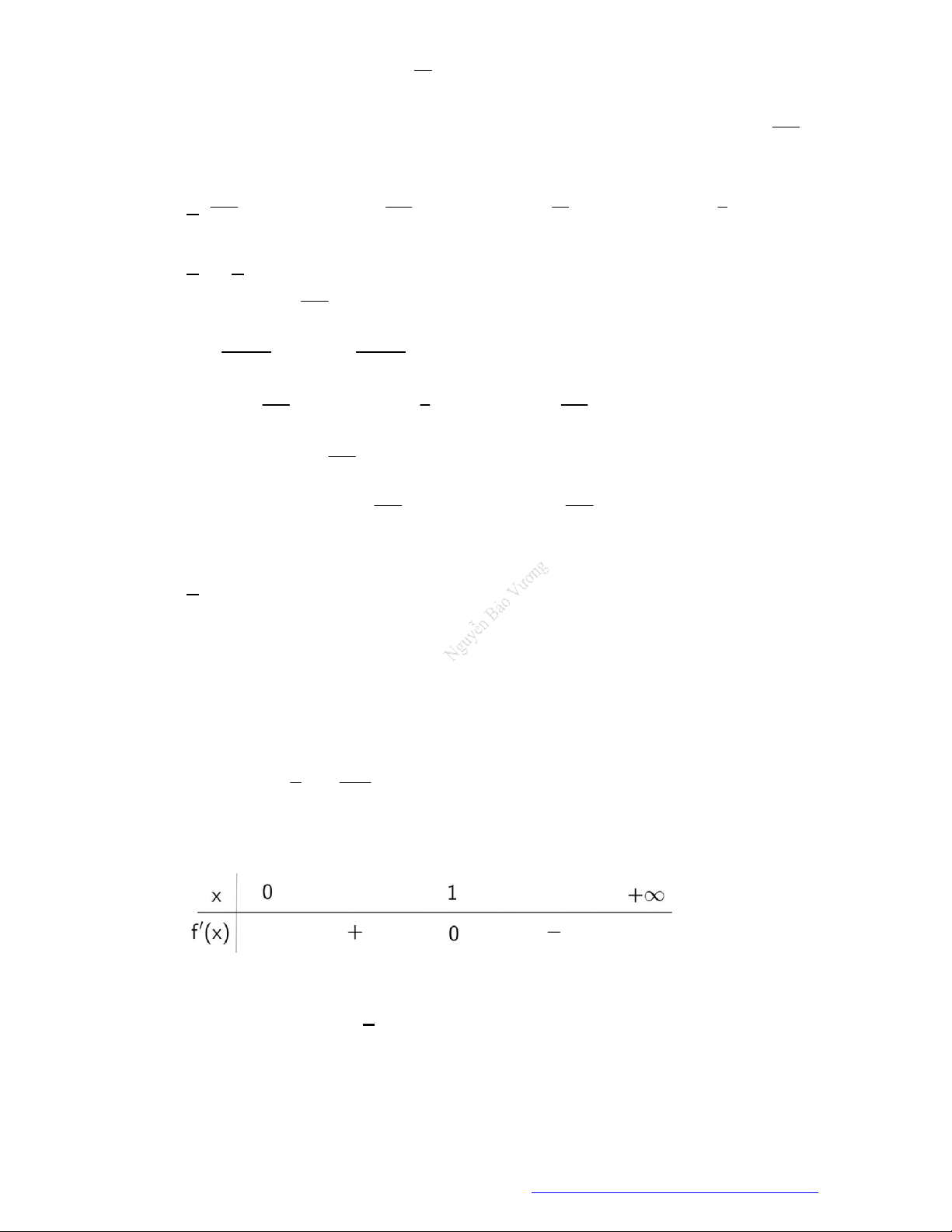
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Do đó đồ thị hàm số (C
2
) là
1
.
5
x
y
Câu 28. (Chuyên Lê Hồng Phong Nam Định 2019) Giá trị nhỏ nhất của hàm số
ln x
y
x
trên đoạn
2;3
bằng
A.
ln 2
2
. B.
ln 3
3
. C.
2
3
e
. D.
1
e
.
Lời giải
Chọn A
Xét
ln x
y f x
x
. Hàm số
y f x
liên tục trên đoạn
2;3
/
2
1 ln x
y
x
;
/
0y
2
1 ln
0
x
x
2;3x e
Có
ln2
2 0,3466
2
f
;
1
0,3679f e
e
;
ln3
3 0,366
3
f
,
Suy ra
2;3
ln2
2
x
Min f x
.
Vậy giá trị nhỏ nhất của hàm số
ln x
y
x
trên đoạn
2;3
bằng
ln 2
2
.
Câu 29. (Sở Ninh Bình 2019) Cho hàm số
lnf x x x
. Khẳng định nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
0;1
.
B. Hàm số đồng biến trên khoảng
0;
.
C. Hàm số đồng biến trên các khoảng
;0
và
1;
.
D. Hàm số đồng biến trên khoảng
1;
.
Lời giải
Tập xác định của hàm số
f x
:
0;D
Ta có
1 1
1
x
f x
x x
0 1f x x
Bảng xét dấu
f x
:
Câu 30. (HSG Bắc Ninh 2019) Giá trị nhỏ nhất của hàm số
2 2
2
x
f x x e
trên đoạn
1;2
bằng:
A.
4
2e
B.
2
e
C.
2
2e
D.
2
2e
Lời giải
Ta có:
2 2 2 2 2
2 2 2 2 2
x x x
f x x e xe x x e
1 1;2
0
2 1;2
x
f x
x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Và
2
1
f
e
;
4
2
2f e
;
2
1
f
e
Giá t
rị nhỏ nhất của hàm số
2 2
2
x
f
x x e
trê
n đoạn
1
;2
bằ
ng
2
e
tại
1x
.
Câu
31. Giá trị nhỏ nhất của hàm số
1
4
2
8
3
x
x
y
trên
1
;0
bằng
A.
4
9
. B.
5
6
. C
.
2
2
3
. D.
2
3
.
Lời giải
Chọn D
3
1
2
0
1
4
2
ln 2 8 ln8 0 2 2 2 0
1
1
/ 2
3
2
2
x
x
x x x
x
x
y
x
Xét
y(-1)=5/6 ; y(-1/2)=0,9428 ; y(0)=2/3
.
Ta có:
m
in
2
3
y
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ – MỨC 7-8 ĐIỂM
Dạng 1. Tìm tập xác định hàm số mũ - logarit
Hàm số mũ
Dạng:
x
u
y a
y a
với
0
.
1
a
a
Tập xác định:
.D
Hàm số logarit
Dạng:
log
log
a
a
y x
y u
với
0
.
1
a
a
Đặc biệt:
ln ;a e y x 10 log lga y x x
.
Điều kiện xác định:
0u
.
Câu 1. (Mã 105 2017) Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
log 2 1y x x m có
tập xác định là
.
A.
2m
B.
2m
C.
0m
D.
0m
Lời giải
Chọn D
Để hàm số có tâp xác định
khi và chỉ khi
2
2 1 0,x x m x
.
0
2
1 1. 1 0m
0m
.
Câu 2. (Mã 104 2017) Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
ln 2 1y x x m
có
tập xác định là
.
A.
0 3m
B.
1m
hoặc
0m
C.
0m
D.
0m
Lời giải
Chọn C
Hàm số có tâp xác định
khi và chỉ khi
2
1 0( )
2 1 0,
1 1 0 0
a ld
x x m x
m m
.
Câu 3. Hàm số
2
ln 1y x mx
xác định với mọi giá trị của
x
khi.
A.
2
2
m
m
. B.
2m
. C.
2 2m
. D.
2m
.
Lời giải
Chọn C
Yêu cầu bài toán
2
1 0x mx
,
x
2
4 0m
2 2m
.
Câu 4. (THPT Cẩm Giàng 2 2019) Tìm tất cả các giá trị của tham số
m
để hàm số
2
3 3
1
log 4log 3
y
m x x m
xác định trên khoảng
0;
HÀM SỐ MŨ - HÀM SỐ LOGARIT
Chuyên đề 18
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
; 4 1;m
. B.
1;m
.
C.
4;1
m
. D.
1;m
.
Lời giải
Cách 1
Điều kiện:
0
x
.
Hàm số xác định khi:
2
3 3
log 4log 3 0
m x x m
2
3 3
log 1 4log 3m x x
3
2
3
4log 3
log 1
x
m
x
,
0;x
.
Để hàm số xác định trên
0;
thì phương trình
3
2
3
4log 3
log 1
x
m
x
vô nghiệm
0;x
Xét hàm số
3
2
3
4log 3
log 1
x
y
x
.
Đặt
3
log
x t
khi đó ta có
2
4 3
1
t
y
t
,
2
2
2
4 6 4
1
t t
y
t
0
y
1
2
2
t
t
.
Ta có BBT:
t
1
2
2
y
0
0
y
1
0
0
4
Để hàm số xác định trên
0;
thì
; 4 1;m
.
Cách 2:
Đề hàm số xác định trên khoảng
0;
thi phương trình
2
3 3
.log 4log 3 0
m x x m
vô
nghiệm.
TH1:
0
m
thì PT trở thành
3
4log 3 0
x
3
3
log
4
x
3
4
3
x
.
Vậy
0
m
không thỏa mãn.
TH2:
0
m
thì để PT vô nghiệm
2
4 4 3 0
m m
2
4 12 16 0
m m
4
1
m
m
.
Để hàm số xác định trên
0;
thì
; 4 1;m
.
Câu 5. Tìm tất cả các giá trị của
m
để hàm số
2
ln 2 1
y x mx m
xác định với mọi
1; 2
x
.
A.
1
3
m
. B.
3
4
m
. C.
3
4
m
. D.
1
3
m
.
Lời giải
Hàm số xác định với mọi
1; 2
x
khi
2
2 1 0, 1; 2
x mx m x
.
2
2 1 0, 1; 2
f x x mx m x
.
0
f x
có
2
nghiệm thỏa mãn
1 2
1 2
x x
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
1 0
3 0
3
4 3 0
4
2 0
f
m
m
m
f
.
Câu 6. (Chuyên Lê Quý Đôn Điện Biên -2019) Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
log( 4 1)
y x x m
có tập xác định là
.
A.
4
m
. B.
0
m
. C.
4
m
. D.
3
m
.
Lời giải
Hàm số
2
log( 4 1)
y x x m
có tập xác định là
khi và chỉ khi
2
4 1 0
x x m
x
Câu 7. (Chuyên Vĩnh Phúc 2019) Có bao nhiêu giá trị nguyên của tham số
m
trên
2018; 2018
để
hàm số
2
ln 2 1
y x x m
có tập xác định là
?
A.
2019
B.
2017
C.
2018
D.
1009
Lời giải
Hàm số
2
ln 2 1
y x x m
có tập xác định là
khi và chỉ khi:
2
2 1 0 x x m x
' 0 1 1 0 0
m m
.
Kết hợp với điều kiện
m
nguyên thuộc
2018; 2018
ta có 2018 giá trị của
m
.
Câu 8. (THPT Nghĩa Hưng Nđ- 2019) Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
log 2 4
y x mx
có tập xác định là
.
A.
2 2
m
. B.
2
m
. C.
2
2
m
m
. D.
2 2
m
.
Lời giải
2
log 2 4
y x mx
Điều kiện xác định của hàm số trên:
2
2 4 0
x mx
.
Để tập xác định của hàm số là
thì
2
1 0,
0
2 2
0
4 0
m
a
m
m
.
Vậy đáp án đúng là đáp án D.
Câu 9. Số các giá trị nguyên của tham số
m
để hàm số
log 2
y mx m
xác định trên
1
;
2
là
A.
4
B.
5
C. Vô số D.
3
Lời giải
Chọn A
Điều kiện xác định
2 0 2 (1)
mx m mx m
Trường hợp 1.
0
m
.
1 2 0
(luôn đúng với
1
;
2
x
).
Trường hợp 2.
0
m
.
2
1
m
x
m
Để hàm số
log 2
y mx m
xác định trên
1
;
2
thì

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 1
0 4.
2
m
m
m
Vì
m
nên
1;2;3 .
m
Trường hợp 3.
0
m
.
2
1
m
x
m
.
Suy ra tập xác định của hàm số
log 2
y mx m
là
2
; .
m
D
m
Do đó
1
;
2
D
suy ra không có giá trị
0
m
nào thỏa yêu cầu bài toán.
Từ
3
trường hợp trên ta được
0;1;2;3 .
m
Câu 10. (Gia Bình 2019) Tìm tất cả các giá trị của
m
để hàm số
2
2018
log 2018
2
x
x
y x m
xác
định với mọi giá trị
x
thuộc
0;
A.
9
m
B.
1
m
C.
0 1
m
D.
2
m
Lời giải
Chọn B
Hàm số đã cho xác định
0;x
2
2018 0, 0;
2
x
x
x m x
2
2018 , 0;
2
x
x
x m x
.
YCBT
0;
min
x
m f x
.
Đặt
2
2018 , 0;
2
x
x
f x x x
2018 ln 2018 1
x
f x x
2
2018 ln 2018 1 0, 0;
x
f x x
Khi đó
f x
đồng biến trên
0;x
và
0 ln 2018 1 0
f
Suy ra
f x
đồng biến trên
0;x
và
0 1
f
Vậy
1
m
thì thỏa YCBT.
Câu 11. Hàm số
2
log 4 2
x x
y m
có tập xác định là
thì
A.
1
4
m
. B.
0
m
. C.
1
4
m
. D.
1
4
m
.
Lời giải
Chọn D
Điều kiện xác định:
4 2 0
x x
m
Hàm số đã cho có tập xác định là
4 2 0, 4 2 ,
x x x x
m x m x
(*)
Đặt
2 , 0
x
t t
Khi đó (*) trở thành
2
, 0
m t t t
0;
max ( )m f t
với
2
( ) , 0f t t t t
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Ta có:
' 2 1f t t
,
1
' 0
2
f t t
Bảng biến thiên của hàm số
2
( ) , 0f t t t t
:
t
0
1
2
'f t
+ 0 -
f t
0
1
4
Từ BBT ta thấy
0;
1
max ( )
4
f t
đạt được khi
1
2
t
Vậy
0;
1
max
4
m f t m
Câu 12. (Chuyên Bắc Ninh 2019) Tập hợp tất cả các giá trị của tham số
m
để hàm số
2 2
2018
3 5
log 2 4 5
x
y
x x m m
xác định với mọi
x
là
A.
;1 3;
. B.
(1;3) \ 2
. C.
;1
. D.
1;3 \ 2
.
Lời giải
Xét hàm số
2 2
2018
3 5
log 2 4 5
x
y
x x m m
ĐKXĐ:
2 2
2 2
2 2
2 2
2018
2 4 5 0
2 4 5 0
log 2 4 5 0
2 4 5 1
x x m m
x x m m
x x m m
x x m m
.
Nên điều kiện để hàm số xác định với mọi
x
là
2 2
2 2
2 4 5 0
2 4 4 0
x x m m
x x m m
với
x
.
Điều này xảy ra khi và chỉ khi :
2
1
2
2
1 4 5 0
1 4 4 0
m m
m m
2
2
4 4 0
4 3 0
m m
m m
2
1
4 3 0
3
m
m m
m
.
Vậy
;1 3;m
.
Câu 13. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
2018
log 2017 1
2
x
x
y x m
xác
định với mọi
x
thuộc
0;
?
A.
1
. B.
2
. C.
2018
. D. Vô số.
Lời giải
Chọn D
Điều kiện
2
2017 1 0, 0;
2
x
x
x m x
2
2017 1, 0;
2
x
x
x m x
.
Xét hàm số
2
2017 , 0;
2
x
x
f x x x
liên tục có
2017 ln 2017 1 , 0;
x
f x x x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2017 ln 2017 1 0, 0;
x
f x x
Vậy hàm số
f x
đồng biến trên
0;
suy ra
0 ln 2017 1 0, 0;f x f x
Vậy hàm số
y f x
đồng biến trên
0;
suy ra
0;
min 0 1
f x f
.
Mặt khác
0;
1 min 0 1 2
m f x f m
.
Vậy có vô số giá trị nguyên
m
thỏa mãn.
Câu 14. (Sở Vĩnh Phúc 2019) Có tất cả bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
3
1
log
2 1
y x m
m x
xác định trên khoảng
2;3
?
A.
1
. B.
2
. C.
4
. D.
3
.
Lời giải
Hàm số xác định
2 1 0 2 1
0
m x x m
x m x m
;2 1
D m m
.
Hàm số đã cho xác định trên khoảng
2;3
nên
2;3 ;2 1
D m m
2 3 2 1
m m
2
1 2
2 1 3
m
m
m
.
Vì
m
nguyên dương nên
1;2
m
.
Câu 15. (Chuyên Vĩnh Phúc - 2020) Tìm tất cả các giá trị của tham số
m
để hàm số
2020
log 2
y mx m
xác định trên
1;
.
A.
0
m
. B.
0
m
. C.
1
m
. D.
1
m
.
Lời giải
Chọn B
Cách 1:
Điều kiện:
2 0 2
mx m mx m
1
Trường hợp 1:
0
m
1
trở thành
0 1
(luôn thỏa mãn).
Trường hợp 2:
0
m
2
1
m
x
m
Tập xác định của hàm số là
2
;
m
D
m
.
Khi đó, yêu cầu bài toán trở thành
2
1
m
m
2 2 0
m m
(luôn thỏa mãn).
Trường hợp 3:
0
m
2
1
m
x
m
Tập xác định của hàm số là
2
;
m
D
m
. Do
đó không tồn tại
m
thỏa mãn yêu cầu bài toán.
Vậy tất cả các giá trị cần tìm là
0
m
.
Cách 2:
Điều kiện:
2 0
mx m
,
1;x
1 2
m x
,
1;x
1
.
Với
1x
, ta được
0 2
m
, đúng với mọi
m
.
Với
1x
, ta được
2
1
1
m
x
,
1;x
2
.
Xét hàm số
2
1
g x
x
với
1x
, ta có:
2
2
0
1
g x
x
,
1x
.
Bảng biến thiên:

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Từ bảng biến thiên, ta được
2 0m
.
Vậy, tất cả các giá trị cần tìm của
m
là
0m
.
Câu 16. (Chuyên Lương Thế Vinh Đồng Nai 2019) Tập xác định của hàm số
2020 2019 2018 2017
log log log logy x là
; .D a
Giá trị của
a
bằng
A.
2019
2018
. B.
2020
2019
. C.
2018
2017
. D.
0
.
Lời giải
Điều kiện xác định của hàm số đã cho là:
2017
2017
2017
2018 2017
2018 2017
2018 2017
2019 2018 2017 2018 2017
0
0
0
log 0
log 0
log 0
log log 0
log log 0
log log 1
log log log 0 log log 1
x
x
x
x
x
x
x
x
x
x x
2018
2017
2018
2017
2017
0
0
0
log 0 2017
log 2018
2017
log 2018
x
x
x
x x
x
x
x
.
Dạng 2. Tính đạo hàm mũ – logarit
Đạo hàm hàm số mũ
ln
ln .
x x
u u
y a y a a
y a y a a u
.
Đặc biệt:
( )
( ) .
x x
u u
e e
e e u
với
2,71828...e
Đạo hàm hàm số logarit
1
log
ln
log
ln
a
a
y x y
x a
u
y u y
u a
.
Đặc biệt:
1
(ln )
(ln )
x
x
u
u
u
.
Câu 1. (Đề Tham Khảo 2017) Cho hàm số
ln x
y
x
, mệnh đề nào dưới đây đúng?
A.
2
1
2y xy
x
. B.
2
1
y xy
x
. C.
2
1
y xy
x
. D.
2
1
2y xy
x
.
Lời giải
Chọn A

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Cách 1.
2 2 2
1
. ln
ln . .ln
1 ln
x x
x x x x
x
x
y
x x x
2 2
4
1 ln . 1 lnx x x x
y
x
2
4
1
. 2 1 lnx x x
x
x
4 3 3
2 1 ln 1 2 1 ln
3 2ln
x x x x
x
x x x
Suy ra:
2 3
1 ln 3 2ln
2 2.
x x
y xy x
x x
2 2
2 2ln 3 2ln 1
x x
x x
.
Cách 2. Ta có
lnxy x
, lấy đạo hàm hai vế, ta được
1
y xy
x
.
Tiếp tục lấy đạo hàm hai vế của biểu thức trên, ta được
2
1
y y xy
x
, hay
2
1
2y xy
x
.
Câu 2. (Chuyên Bắc Giang 2019) Cho hàm số
ln 2018 ln
1
x
f x
x
. Tính
' 1 ' 2 ' 3 ' 2017 .
S f f f f
A.
4035
2018
S
B.
2017
2018
S
C.
2016
2017
S
D.
2017
S
Lời giải
Chọn B
Ta có
ln 2018 ln
1
x
f x
x
1 1 1
1 1
f x
x x x x
Do đó
1 1 1 1 1 1
...
1 2 2 3 2017 2018
S
1 2017
1
2018 2018
.
Câu 3. (Sở Vĩnh Phúc 2019) Cho hàm số
2018
ln
1
x
f x
x
. Tính tổng
1 2 ... 2018
S f f f
.
A.
ln 2018
. B.
1
. C.
2018
. D.
2018
2019
.
Lời giải
Ta có:
2018 1 2018
ln . .
2018
1 1
1
x x
f x
x
x x
x
2
1 2018 1
.
2018 . 1
1
x
x x x
x
Vậy
1 2 ... 2018
S f f f
1 1 1
...
1.2 2.3 2018.2019
1 1 1 1 1 1
...
1 2 2 3 2018 2019
1 2018
1
2019 2019
.
Câu 4. Cho hàm
cos ln s ln
y x x in x
. Khẳng định nào sau đây đúng?
A.
2
2 4 0
x y xy y
. B.
2
2 0
x y xy xy
.
C.
2
2 2 5 0
x y xy y
. D.
2
2 0
x y xy y
.
Lời giải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Chọn D
Ta có
cos ln s ln
y x x in x
cos ln s ln s ln cos ln 2cos lny x in x in x x x
2
sin lny x
x
Từ đó kiểm tra thấy đáp án
D
đúng vì :
2
2 2 sin ln 2 cos ln 2 cos ln sin ln 0
x y xy y y x x x x x x x
.
Câu 5. (THPT Bạch Đằng Quảng Ninh 2019) Tính đạo hàm của hàm số
2019
log , 0
xy x
.
A.
1
ln 2019
y
x
. B.
1
y
x
. C.
1
ln 2019
y
x
. D.
ln 2019
y x
.
Lời giải
2019
2019
2019
log , 0
log
log , 0
x khi x
x
x hi x
y
k
1
, 0
ln 2019
1
, 0
ln 2019
khi x
x
khi x
x
y
1
ln 2019
y
x
.
Câu 6. (THPT An Lão Hải Phòng 2019) Cho hàm số
2
x x
f x e
. Biết phương trình
0
f x
có hai
nghiệm
1
x
,
2
x
. Tính
1 2
.x x
.
A.
1 2
1
.
4
x x
B.
1 2
. 1
x x
C.
1 2
3
.
4
x x
D.
1 2
. 0
x x
Lời giải
Chọn A
Ta có:
2
1 2
x x
f x x e
.
2 2 2
2
2 1 2 1 2 1 4 4
x x x x x x
f x e x x e x x e
2
2 2
0 1 4 4 0 1 4 4 0
x x
f x x x e x x
khi đó
1 2
1
4
c
x x
a
.
Câu 7. (Sở Bắc Ninh - 2020) Cho hàm số
ln .
2
x
f x
x
Tổng
' ' ' '
1 3 5 ... 2021
f f f f
bằng
A.
4035
.
2021
. B.
2021
2022
. C.
2021.
. D.
2022
.
2023
Lời giải
Chọn D
Ta có
'
2 1 1
ln
2 2 2
x
f x f x
x x x x x
Vậy
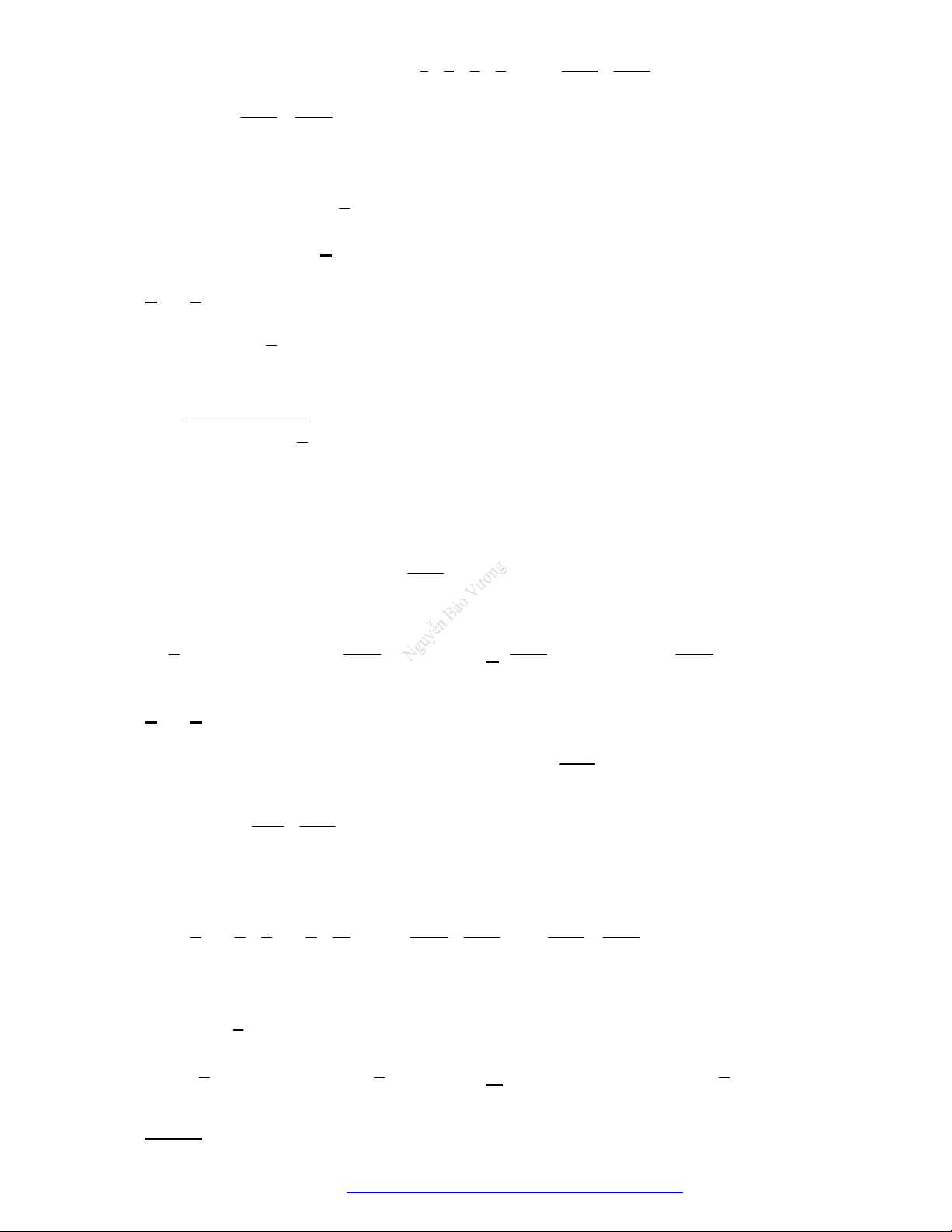
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
' ' ' '
1 1 1 1 1 1
1 3 5 ... 2021 ......
1 3 3 5 2021 2023
1 2022
1 .
2023 2023
f f f f
Câu 8. (Kiểm tra năng lực - ĐH - Quốc Tế - 2019) Phương trình
0
f x
với
4 3 2
1
ln 4 4
2
f x x x x
có bao nhiêu nghiệm?
A.
0
nghiệm. B.
1
nghiệm. C.
2
nghiệm. D.
3
nghiệm.
Lời giải
Chọn B
Điều kiện:
4 3 2
1
4 4 0
2
x x x
.
Ta có:
3 2
4 3 2
4 12 8
0
1
4 4
2
x x x
f x f x
x x x
3 2
0
4 12 8 0 1
2
x
x x x x
x
.
Đối chiếu điều kiện ta được
1x
.
Vậy phương trình
0
f x
có
1
nghiệm.
Câu 9. Cho hàm số
1
ln
4
x
f x
x
. Tính giá trị của biểu thức
0 3 6 ... 2019
P f f f f
.
A.
1
4
. B.
2024
2023
. C.
2022
2023
. D.
2020
2023
.
Lời giải
Chọn C
Với
[0 ; + )
x
ta có
1 0
x
và
4 0
x
nên
1
ln ln 1 ln 4
4
x
f x x x
x
.
Từ đó
1 1
1 4
f x
x x
.
Do đó
0 3 6 ... 2019
P f f f f
1 1 1 1 1 1 1 1 2022
1 ... 1
4 4 7 7 10 2020 2023 2023 2023
.
Câu 10. (THPT Minh Khai - 2019) Cho hàm số
2 1 3
x
y f x m e
. Giá trị của
m
để
5
' ln3
3
f
là
A.
7
9
m
. B.
2
9
m
. C.
3
m
. D.
3
2
m
.
Lời giải
Chọn C
' 2 1
x
f x m e
.
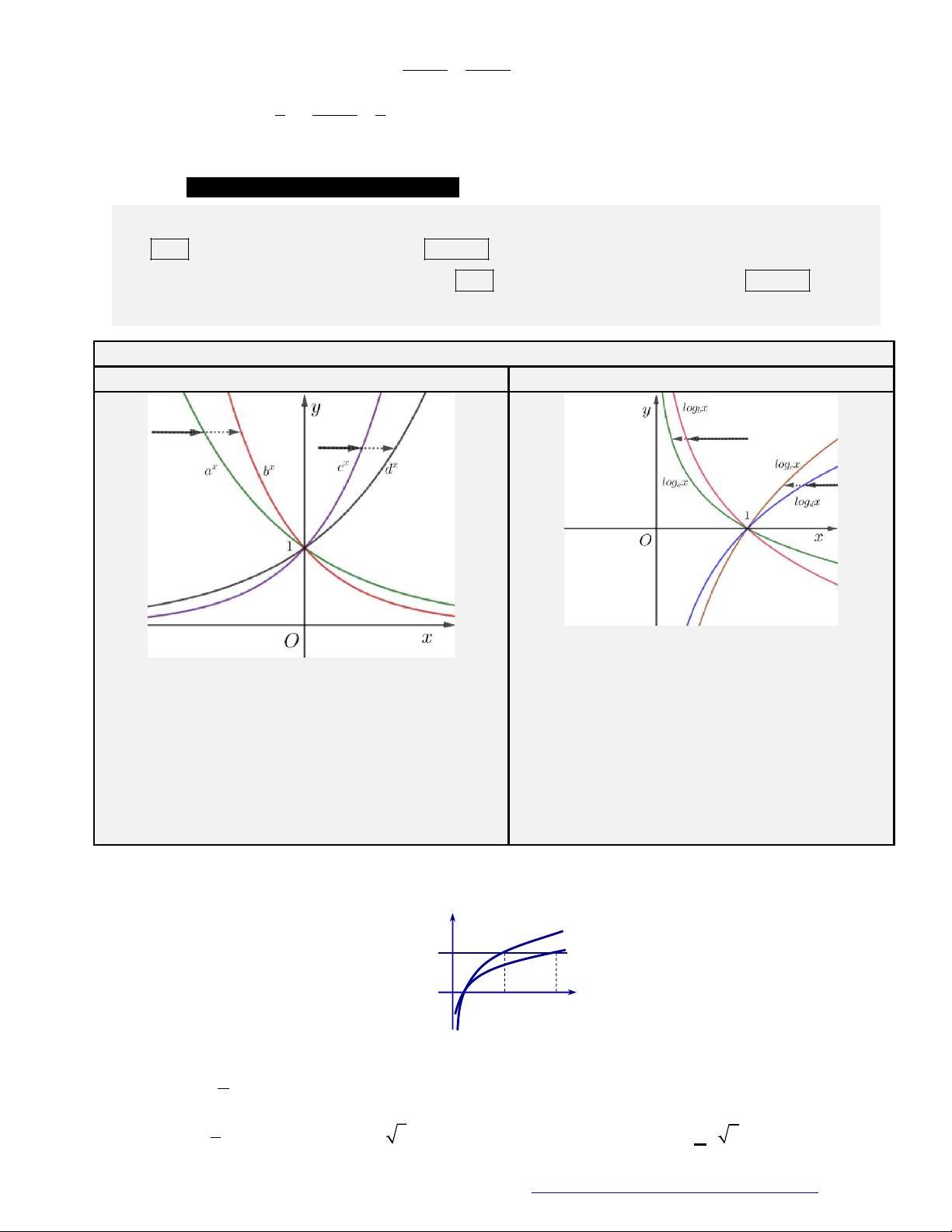
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
ln3
ln3
2 1 2 1
' ln 3 2 1
3
m m
f m e
e
.
5 2 1 5
' ln 3 3
3 3 3
m
f m
.
Dạng 3. Khảo sát hàm số mũ, logarit
Sự biến thiên hàm số mũ:
x
y a
.
Nếu
1a
thì hàm đồng biến trên
. Nếu
0 1a
thì hàm nghịch biến trên
.
Sự biến thiên hàm số logarit:
log
a
y x
. Nếu
1a
: hàm đồng biến trên
(0; )
. Nếu
0 1a
: hàm
nghịch biến trên
(0; ).
Đồ thị hàm số mũ và logarit
ĐỒ THỊ HÀM SỐ MŨ ĐỒ THỊ HÀM SỐ LOGARIT
Ta thấy:
0 1; 0 1
x x
a a b b
.
Ta thấy:
1; 1.
x x
c c d d
So sánh a với b: Đứng trên cao, bắn mũi tên từ trái
sang phải, trúng
x
a
trước nên
a b
.
So sánh c với d: Đứng trên cao, bắn mũi tên từ trái
sang phải, trúng
x
c
trước nên
.c d
Vậy
0 1 .b a d c
Ta thấy:
log 0 1; log 0 1
a b
x a x b
.
Ta thấy:
log 1; log 1.
c d
x c x d
So sánh a với b: Đứng trên cao, bắn mũi tên từ phải
sang trái, trúng
log
b
x
trước:
.b a
So sánh c với d: Đứng trên cao, bắn mũi tên từ phải
sang trái, trúng
log
d
x
trước:
.d c
Vậy
0 1a b c d
.
Câu 1. (Mã 103 - 2020 Lần 2) Hàm số
log
a
y x
và
log
b
y x
có đồ thị như hình bên.
Đường thẳng
3y
cắt hai đồ thị tại các điểm có hoành độ là
1 2
;x x
. Biết rằng
1 2
2x x
. Giá trị
của
a
b
bằng
A.
1
3
. B.
3
. C.
2
. D.
3
2
.
x
y
3
O
1
x
2
x
log
b
y x
log
a
y x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn D
Xét phương trình hoành độ giao điểm
3
1
log 3
a
x x a
, và
3
2
log 3
b
x x b
.
Ta có
3
3 3
3
1 2
2 2 2 2
a a
x x a b
b b
.
Câu 2. Tìm tập hợp tất cả các giá trị thực của tham số
m
để hàm số
2
y ln 1 1x mx
đồng biến trên
khoảng
;
A.
1;
B.
; 1
C.
1;1
D.
; 1
Lời giải
Chọn D
Ta có:
2
2
1
x
y m
x
.
Hàm số
2
ln 1 1y x mx
đồng biến trên khoảng
;
0, ;y x
.
2
2
( ) , ;
1
x
g x m x
x
. Ta có
2
2
2
2 2
( ) 0 1
1
x
g x x
x
Bảng biến thiên:
Dựa vào bảng biến thiên ta có:
2
2
( ) , ;
1
x
g x m x
x
1m
Câu 3. (Chuyên ĐHSP Hà Nội 2019) Trong hình dưới đây, điểm
B
là trung điểm của đoạn thẳng
AC
.
Khẳng định nào sau đây là đúng?
A.
2a c b
. B.
2
ac b
. C.
2
2ac b
. D.
ac b
.
Lời giải
Ta có
0;lnA a
,
0;lnB b
,
0;lnC c
và
B
là trung điểm của
AC
nên
2 2
ln ln 2ln ln lna c b ac b ac b
.
Vậy
2
ac b
.
Câu 4. Cho các số thực
,a b
sao cho
0 , 1a b
, biết rằng đồ thị các hàm số
x
y a và log
b
y x cắt
nhau tại điểm
5 1
2018; 2019M
. Mệnh đề nào dưới đây đúng?
A.
1, 1a b
B.
1,0 1a b
C.
0 1, 1a b
D.
0 1,0 1a b
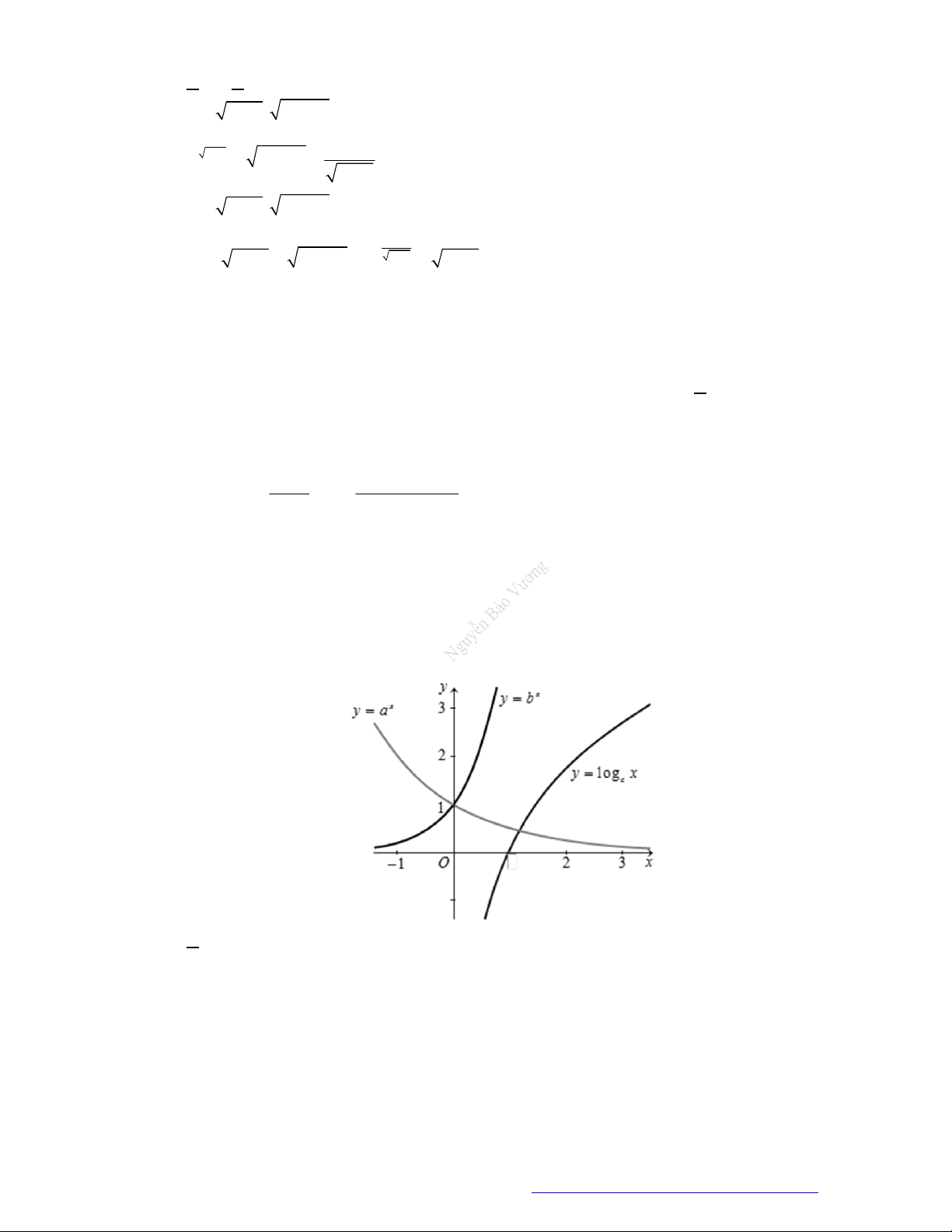
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Lời giải
Chọn C
5 1
2018; 2019M
thuộc đồ thị hàm số
x
y a
nên ta có:
2018 5 1 0
5
1
2019 1 0 1
2019
a a a
5 1
2018; 2019M
thuộc đồ thị hàm số log
b
y x nên ta có:
5
1
5 1 0
2019
log 2018 2019 2018 1 1
b
b b b
Vậy
0 1, 1.a b
Câu 5. (Sở Hà Nội 2019) Tập tất cả các giá trị của tham số
m
để hàm số
2
ln 1 1y x mx
đồng
biến trên
là
A.
1;1
. B.
; 1
. C.
1;1
. D.
; 1
.
Lời giải
Tập xác định:
D
.
Ta có:
2
2 2
2 2
1 1
x mx x m
y m
x x
Để hàm số đồng biến trên
điều kiện là
2
2
0
0; 2 0; ; 1
1 0
m
y x mx x m x m
m
.
Câu 6. (THPT Đông Sơn Thanh Hóa 2019) Trong hình vẽ bên có đồ thị các hàm số
, , log
x x
c
y a y b y x
. Hãy chọn mệnh đề đúng trong các mệnh đề sau đây?
A.
a c b
. B.
c a b
. C.
a b c
. D.
b c a
.
Lời giải
Dựa vào đồ thị các hàm số
, , log
x x
c
y a y b y x
,ta có:
Hàm số
x
y a nghịch biến trên
nên ta có:
0 1a
. (1)
Các hàm số
, log
x
c
y b y x
đồng biến trên tập xác định của nó nên ta có:
1
1
b
c
.(2)
Từ (1),(2)
a b
a c
. Do đó loại hai phương án B, D.
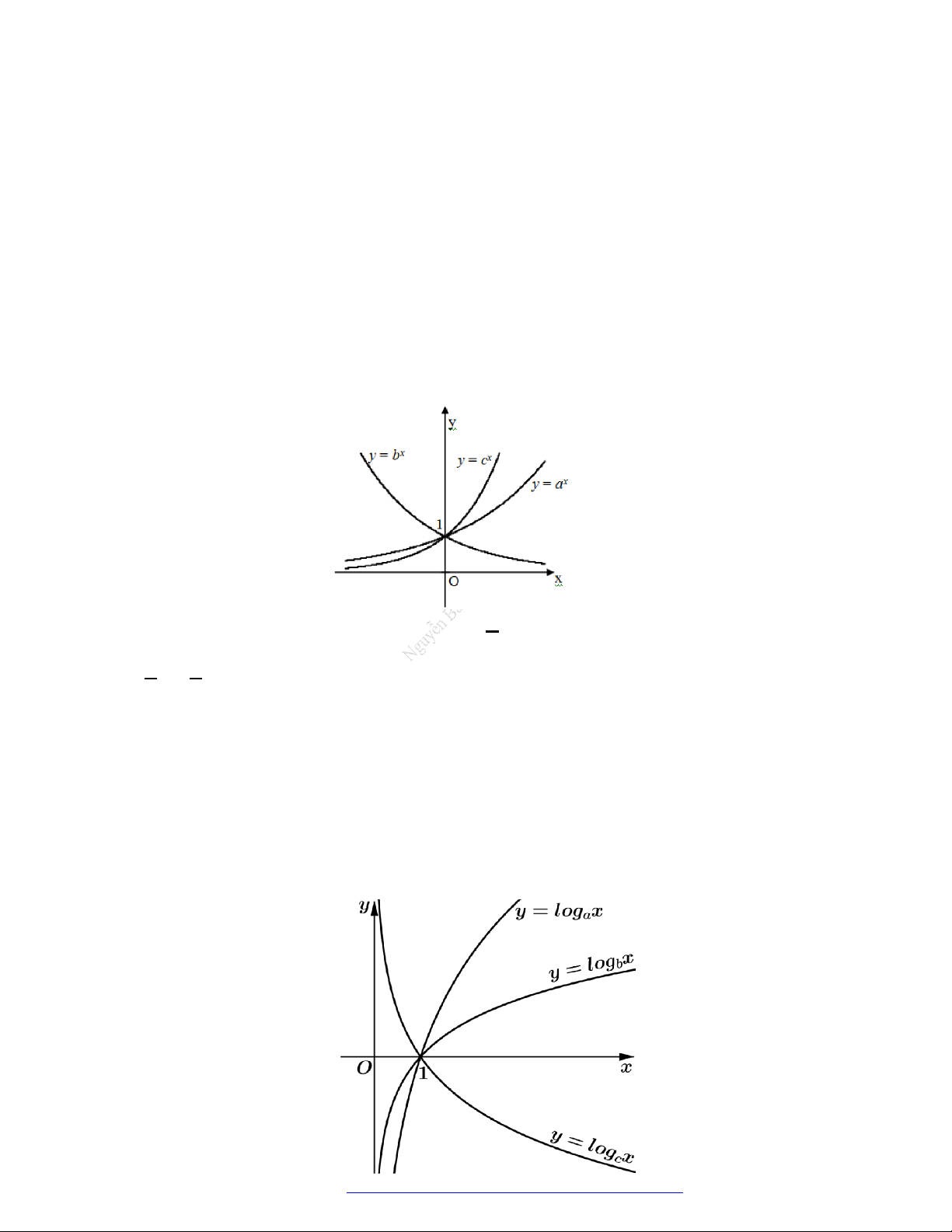
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Nếu
b c
thì ta có đồ thị hai hàm số
, log
x
b
y b y x
đối xứng nhau qua đường thẳng
y x
.
Tuy nhiên nhìn hình dáng hai đồ thị hàm số
, log
x
b
y b y x
không có tính chất đối xứng nhau
qua đường thẳng
y x
. Do đó phương án đúng là A.
Cách khác:
Hàm số
x
y a nghịch biến trên
nên ta có:
0 1a
.
Các hàm số
, log
x
c
y b y x
đồng biến biến trên tập xác định của nó nên ta có:
1
1
b
c
.
Xét đồ thị hàm số log
c
y x , ta có: log 2 1 2
c
c .
Xét đồ thị hàm số
x
y b , ta có:
1
2 2b b
.
Do đó:
0 a c b
.
Câu 7. (Lương Thế Vinh Hà Nội 2019) Cho đồ thị của ba hàm số , ,
x x x
y a y b y c như hình vẽ
bên. Khẳng định nào sau đây đúng?
A.
b a c
. B.
a c b
. C.
c a b
. D.
c b a
.
Lời giải
Chọn C
Xét hàm số
x
y b : Dựa vào hình dáng đồ thị ta thấy
lim 0
x
x
b
, do đó
0 1b
.
Xét hàm số
x
y a : Dựa vào hình dáng đồ thị ta thấy
lim
x
x
a
, do đó
1a
.
Từ đó suy ra:
a b
. Loại đáp án A, D.
Xét tại
1x
đồ thị hàm số
x
y c
có tung độ lớn hơn tung độ của đồ thị hàm số
x
y a
nên
c a
. Vậy
1c a b
.
Câu 8. (KTNL GV Thpt Lý Thái Tổ 2019) Cho
, ,a b c
là các số thực dương khác 1. Hình vẽ bên là đồ
thị của ba hàm số
log , log , log
a b c
y x y x y x
.
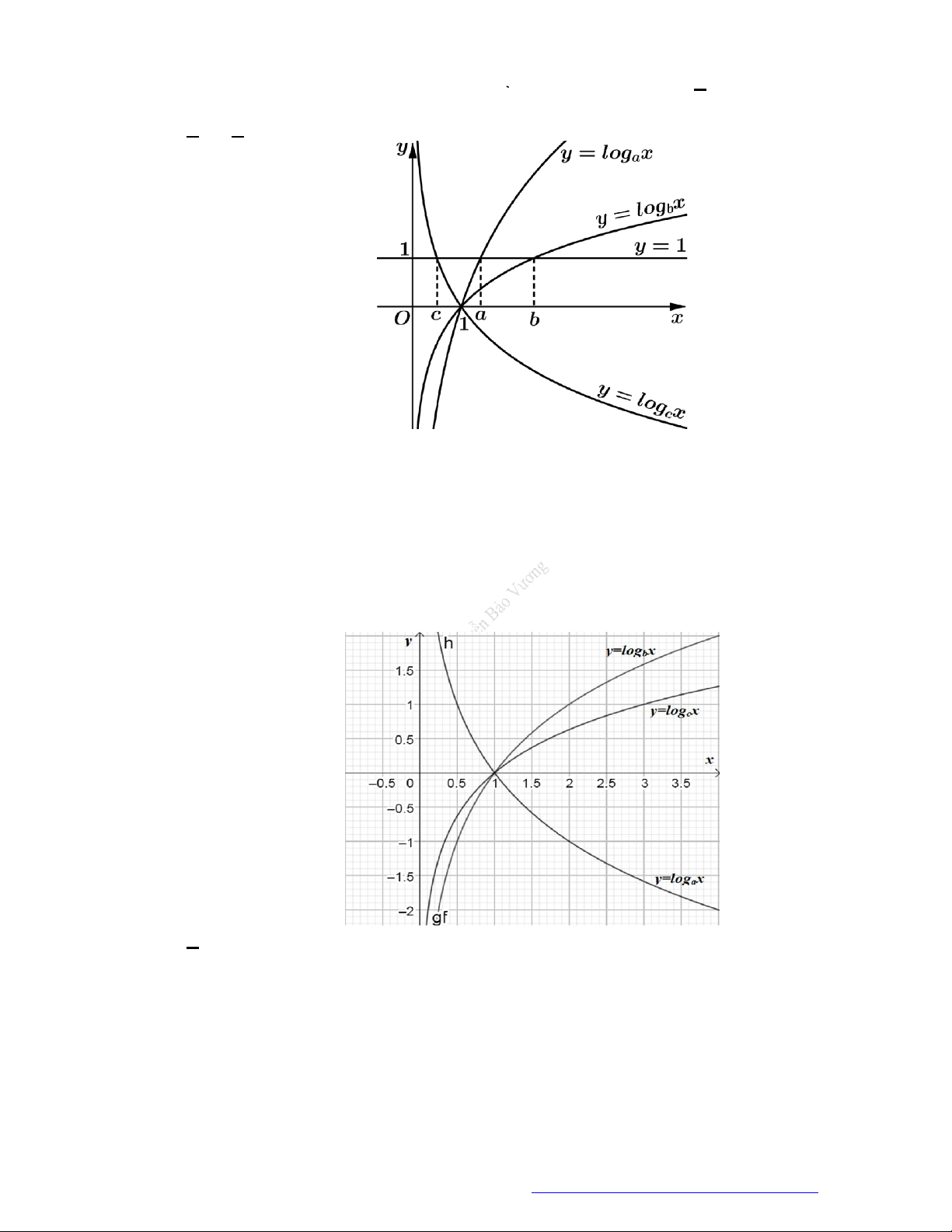
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Khẳng định nào sau đây là đúng?
A.
a c b
. B.
a b c
. C.
c b a
. D.
c a b
.
Lời giải
Chọn D
Theo hình dạng của đồ thị ta có
, 1
0 1
a b
c
.
Vẽ đường thẳng
1y
cắt đồ thị hai hàm số
log , log
a b
y x y x
lần lượt tại 2 điểm
( ;1), ( ;1)M a N b
. Ta thấy điểm
N
bên phải điểm
M
nên
b a
.
Vậy
c a b
.
Câu 9. (Chuyên Thái Bình 2019) Cho
, ,a b c
là các số thực dương khác 1. Hình vẽ bên là đồ thị hàm số
log , log , log
a b c
y x y y x y x . Khẳng định nào sau đây là đúng?
A.
a b c
. B.
a c b
. C.
b a c
. D.
b a c
.
Lời giải
Do log
b
y x và log
c
y x là hai hàm đồng biến nên
, 1b c
.
Do log
a
y x nghịch biến nên
0 1a
. Vậy
a
bé nhất.
Mặt khác: Lấy
y m
, khi đó tồn tại
1 2
, 0x x để
1 1
2
2
log
log
m
b
m
c
x m b x
x m
c x
.
Dễ thấy
1 2
m m
x x b c b c
. Vậy
a b c
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 10. (THPT Nguyễn Khuyến 2019) Cho hàm số
ln 6
ln 2
x
y
x m
với
m
là tham số. Gọi
S
là tập hợp
các giá trị nguyên dương của
m
để hàm số đồng biến trên khoảng
1; e
. Tìm số phần tử của
S
.
A.
3
B.
1
C.
2
D.
4
Lời giải
Chọn C
Điều kiện:
2
ln 2 e
m
x m x
. Có
2
6 2
ln 2
m
y
x x m
Hàm số đồng biến trên
1; e
0 1; e
y x
2
6 2
0 1; e
ln 2
m
x
x x m
2
2
2
6 2 0
6 2 0
e 1
e 1; e
e e
m
m
m
m
m
3
0
0
1
3
1
2
2
m
m
m
m
m
.
Do
m
nguyên dương nên
1; 2
m
. Vậy tập
S
có
2
phần tử.
Câu 11. Tìm tất cả các giá trị thực của tham số m để hàm số
2
2
log 2
log 1
m x
y
x m
nghịch biến trên
4;
A.
2
m
hoặc
1
m
. B.
2
m
hoặc
1
m
.
C.
2
m
hoặc
1
m
. D.
2
m
.
Lời giải
Chọn D
Đặt
2
logt x
.
Ta có
4; 2;x t
.
Hàm số được viết lại
2
1
mt
y
t m
(1).
Vì
2
logt x
đồng biến trên
0;
nên yêu cầu bài toán
(1) nghịch biến trên
2;
2
1 2 0
2
1
1 2
1
m
m m
m
m
m
m
.
Câu 12. (HSG Bắc Ninh 2019) Cho hàm số
2018
1
logy
x
có đồ thị
1
C
và hàm số
y f x
có đồ thị
2
C
. Biết
1
C
và
2
C
đối xứng nhanh qua gốc tọa độ. Hỏi hàm số
y f x
nghịch biến trên
khoảng nào dưới đây?
A.
0;1
B.
1;0
C.
; 1
D.
1;
Lời giải
Ta có
2018
1
logy
x
thì
2
1 1
0
ln 2018
y
x x
hàm số nghịch biến ta vẽ được đồ thị hàm số
1
C
như hình
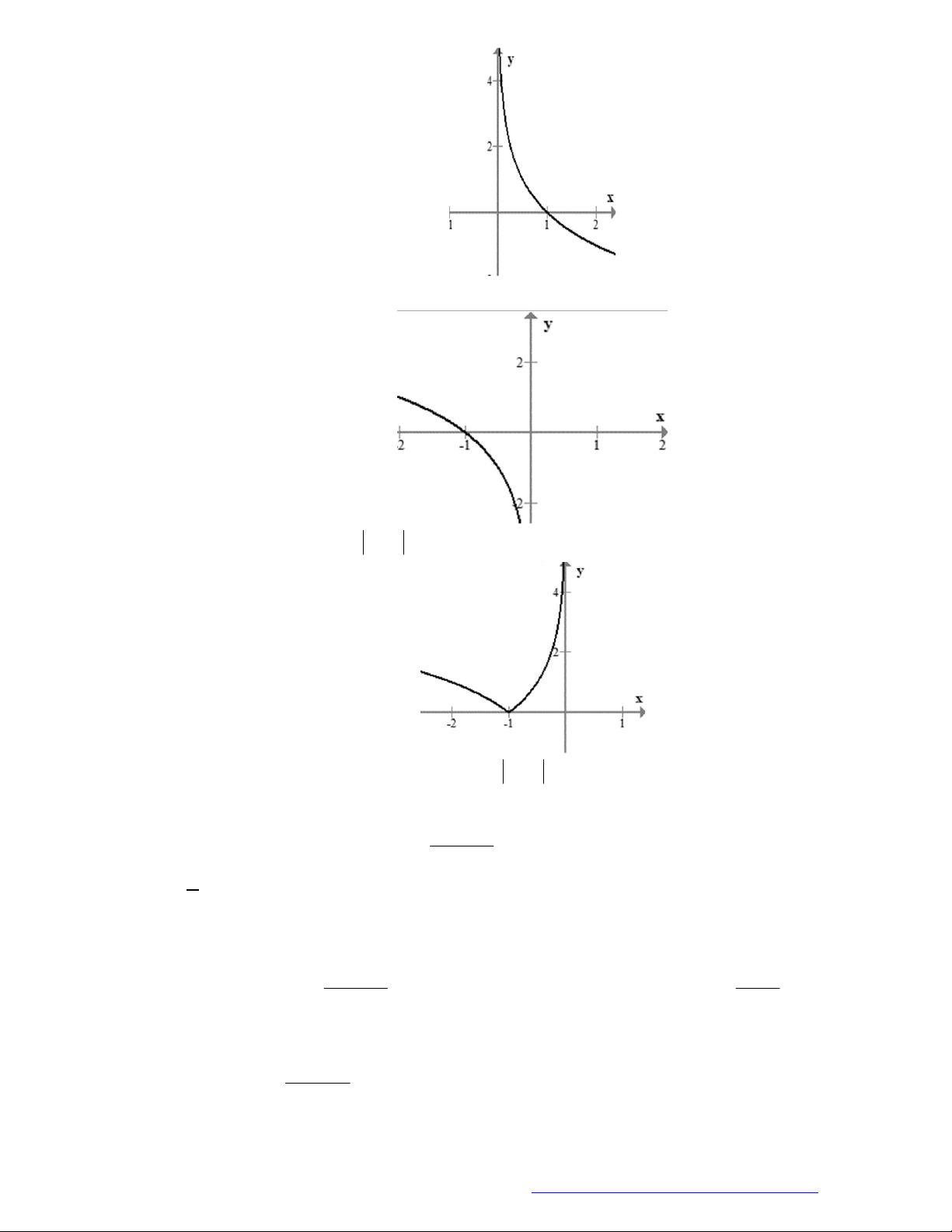
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Do
2
C
đối xứng với
1
C
qua
O
nên có dạng như hình dưới
Từ đó đồ thị hàm số
y f x
là
Dựa vào đồ thị trên ta có hàm số
y f x
nghịch biến trên khoảng
; 1
Câu 13. (THPT Bạch Đằng Quảng Ninh 2019) Có bao nhiêu giá trị nguyên của tham số
2019;2019m
để hàm số
ln 6
ln 3
x
y
x m
đồng biến trên khoảng
6
1;e
?
A.
2020
. B.
2021
. C.
2018
. D.
2019
.
Lời giải
Đặt
lnt x
.
Khi đó hàm số
ln 6
ln 3
x
y
x m
đồng biến trên khoảng
6
1;e
thì hàm số
6
3
t
y t
t m
đồng biến
trên khoảng
0;6
.
Ta có
2
3 6
3
m
y t
t m
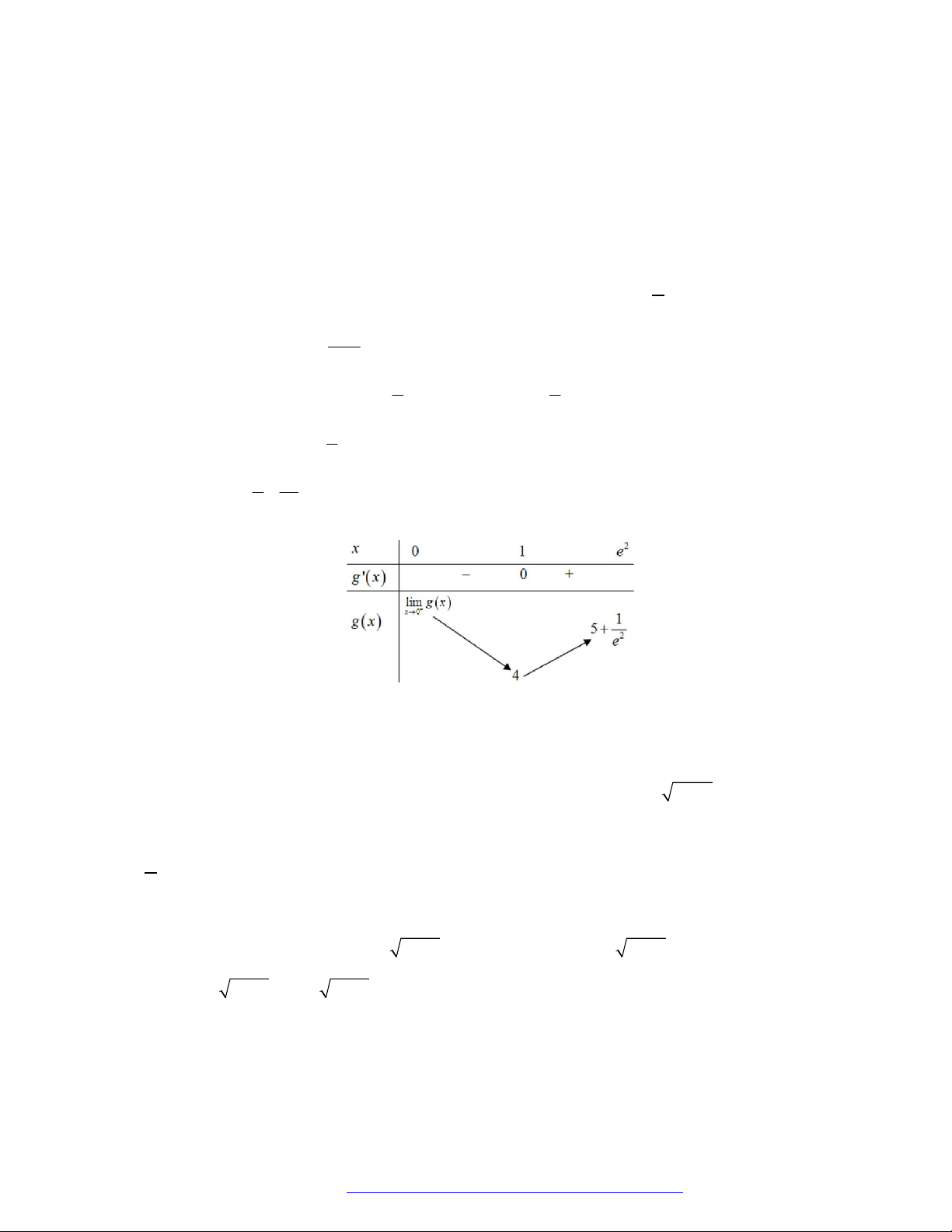
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Để hàm số
y t
đồng biến trên khoảng
0;6
thì
2019;2019
2
3 6 0
0 2019; 2018;... 1;0
0
3 0;6
2
m
m
m
m
m m
m
m
m
.
Vậy có tất cả:
2020
số nguyên
m
thoả mãn yêu cầu bài toán.
Câu 14. (Chuyên Hưng Yên 2019) Có bao nhiêu giá trị nguyên của tham số thực
m
thuộc đoạn
2018;2018
để hàm số
1 ln 2 y f x x x m x
đồng biến trên khoảng
2
0;e
.
A.
2016
. B.
2022
. C.
2014
. D.
2023
.
Lời giải
Ta có:
1
' ' ln 2
x
y f x x m
x
Yêu cầu bài toán
1 1
ln 3 0 ln 3
f x x m x m
x x
;
2
0; x e
.
Xét hàm số:
1
ln 3 g x x
x
với
2
0;x e
.
Ta có:
2
1 1
' 0 1 g x x
x x
.
Bảng biến thiên:
Dựa vào bảng biến thiên suy ra
4g x
với mọi
2
0;x e
.
Từ đó suy ra
2018 4 m
.
Vậy có
2023
giá trị của
m
thỏa mãn.
Câu 15. (THPT Quang Trung Đống Đa Hà Nội 2019) Cho
2
ln 1 sin 6f x a x x b x
với
,a b
. Biết rằng
log log 2f e
. Tính giá trị của
log ln10f
.
A.
10
. B.
2
. C.
4
. D.
8
.
Lời giải
Ta có
log loge log ln10 log1 0
.
Mặt khác
2 2
ln 1 sin 6 ln 1 sin 6f x f x a x x b x a x x b x
2 2
ln 1 1 sin sin 12a x x x x b x b x
ln1 12 12a
x
.
Khi đó suy ra
log log e log ln10 12f f
log ln10 10f
.
Câu 16. (Sở Bắc Ninh 2019) Cho
, ,a b c
dương và khác 1. Các hàm số log
a
y x , log
b
y x , log
c
y x
có đồ thị như hình vẽ
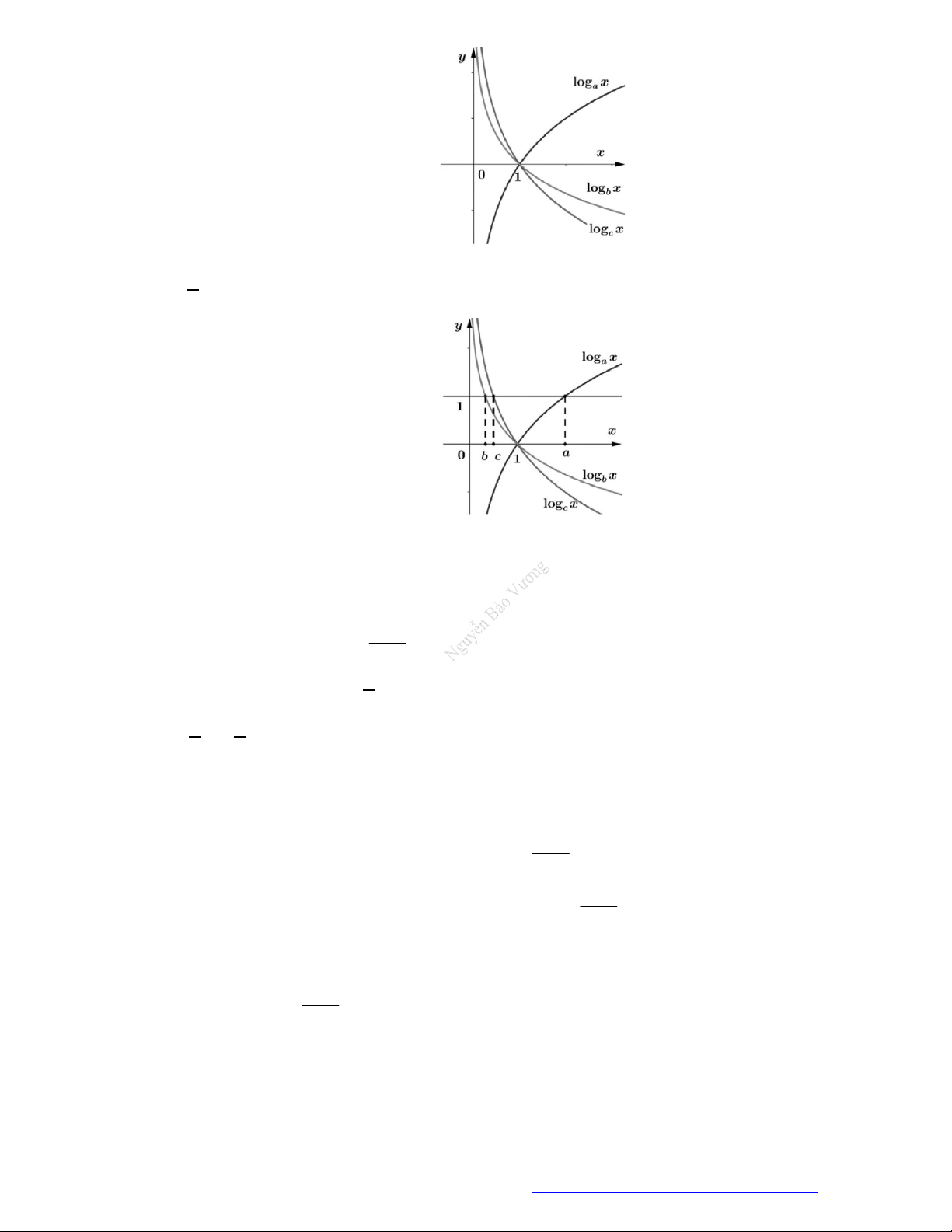
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Khẳng định nào dưới đây đúng?
A.
a c b
. B.
a b c
. C.
c b a
. D.
b c a
.
Lời giải
Kẻ đường thẳng
( ) : 1d y
. Hoành độ giao điểm của
( )d
với các đồ thị hàm số
log
a
y x , log
b
y x , log
c
y x lần lượt là
, ,a b c
. Dựa vào đồ thị hàm số ta thấy
a c b
.
Câu 17. Đồ thị hàm số
y f x
đối xứng với đồ thị hàm số
0, 1
x
y a a a
qua điểm
1;1I
. Giá trị
của biểu thức
1
2 log
2018
a
f
bằng
A.
2016
. B.
2016
. C.
2020
. D.
2020
.
Lờigiải
Chọn B
Gọi
C
là đồ thị hàm số
x
y a
;
1
C
là đồ thị hàm số
y f x
.
1
1
2 log ;
2018
a M
M y C
1
2 log
2018
M a
y f
.
Gọi
N
đối xứng với
M
qua
1;1I
1
log ;2
2018
a M
N y
.
Do đồ thị
1
C
đối xứng
C
qua
1;1I
nên
1
log ;2
2018
a M
N y C
.
N C
1
log
2018
2
a
M
y a
log 2018
2
a
M
y a
2 2018
M
y 2016
M
y
.
Vậy
1
2 log 2016
2018
a
f
.
Câu 18. (Chuyên Hùng Vương - Phú Thọ - 2020) Trong hình vẽ bên các đường cong
1 2 3
: , : , :
x x x
C y a C y b C y c
và đường thẳng
4; 8y y
tạo thành hình vuông
MNPQ
có cạnh bằng
4
.
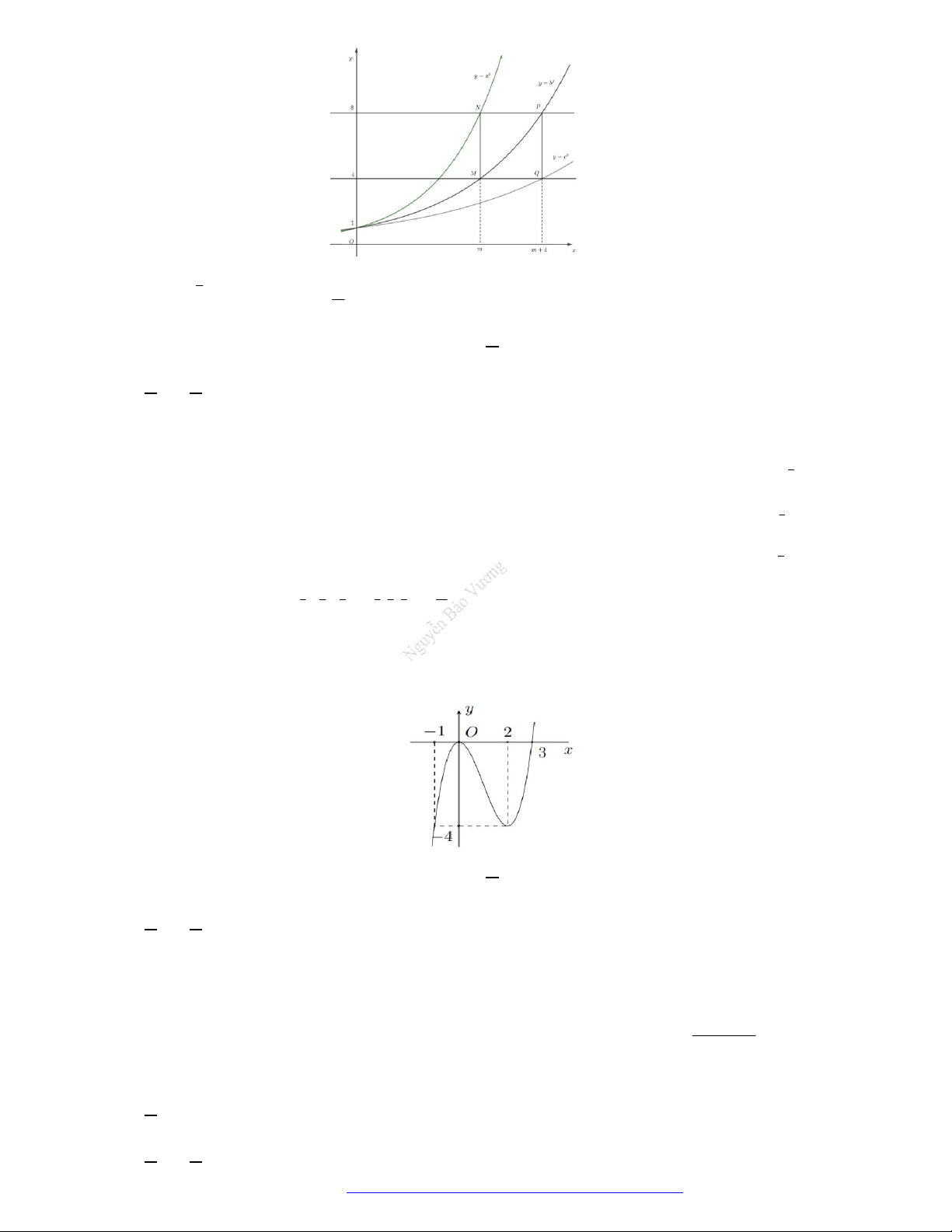
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Biết rằng
2
x
y
abc
với ;x y
và
x
y
tối giản, giá trị của
x y
bằng
A.
34
. B.
5
. C.
43
. D.
19
.
Lời giải
Chọn C
Giả sử hoành độ điểm
M
là
m
, ta suy ra
;4 ; ;8 ; 4;8 ; Q 4; 4M m N m P m m
.
Từ giả thiết ta có
,M P
thuộc đường cong
x
y b nên
1
4 4
4
8
4 4
8 2
2
m m
m
m
b b
b b
b
.
,N Q
lần lượt thuộc đường cong ;
x x
y a y c nên
3
8 8 3
8
12 12 2 1
6
8 2 2
4 2
2
a a a
c c
c
.
Khi đó
3 1 3 1 11 19
8 6 8 4 6
4 24
2 .2 .2 2 2abc
.Vậy
19; 24 43x y x y
.
Câu 19. ( Bạc Liêu – Ninh Bình 2019) Cho hàm số
y f x
. Hàm số
'y f x
có đồ thị như hình vẽ.
Hàm số
2 e
x
y f
nghịch biến trên khoảng
A.
1; 3
. B.
2; 1
. C.
; 0
. D.
0; +
.
Lời giải
Chọn C
Ta có
' e ' 2 e
x x
y f
. Hàm số
2 e
x
y f
nghịch biến khi và chỉ khi
' 0 e ' 2 e 0 ' 2 e 0 2 e 3 e 1 0.
x x x x x
y f f x
Câu 20. Có bao nhiêu giá trị nguyên của tham số
2019;2019m
để hàm số
ln 6
ln 3
x
y
x m
đồng biến
trên khoảng
6
1;e
?
A.
2020
. B.
2021
. C.
2018
. D.
2019
.
Lời giải
Chọn A
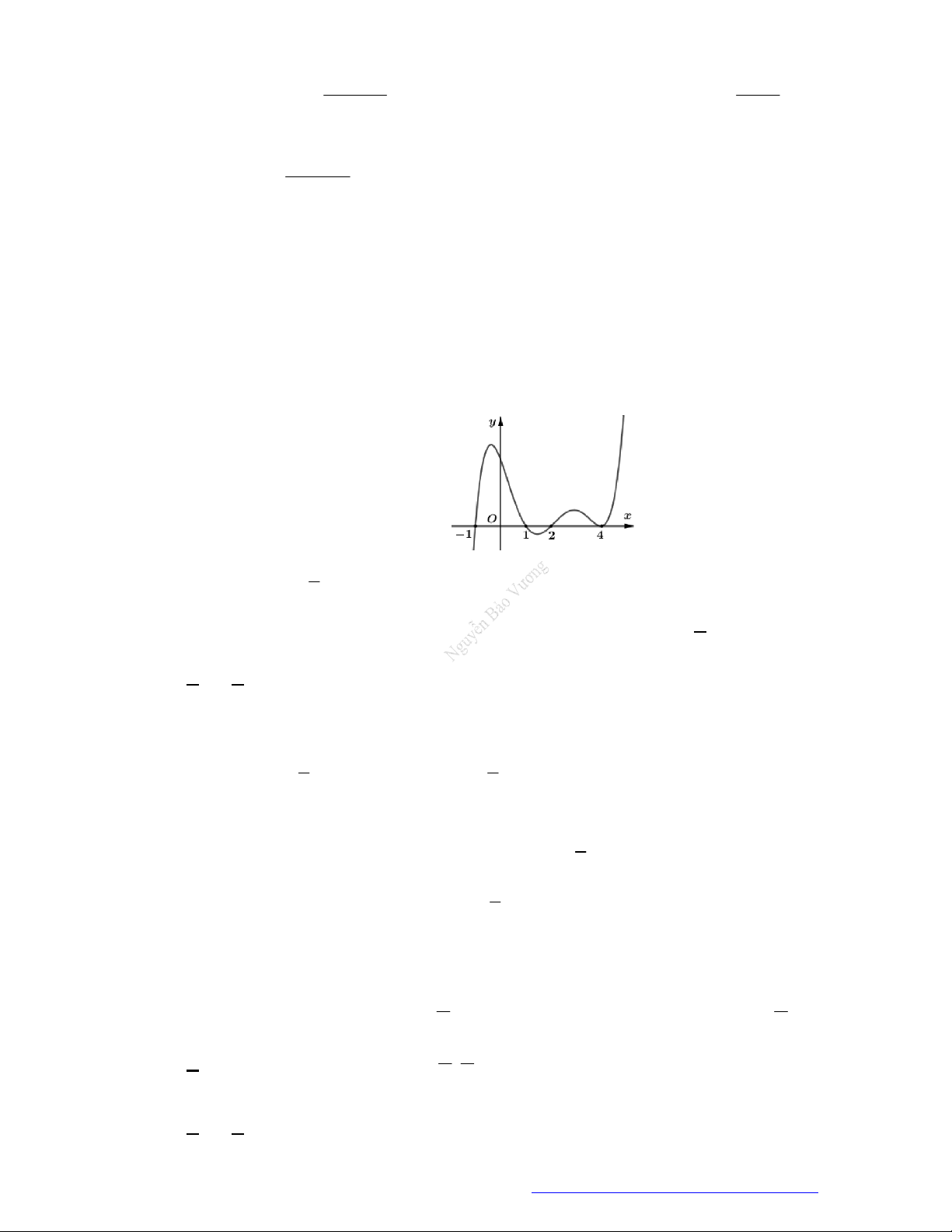
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Đặt
lnt x
.
Khi đó hàm số
ln 6
ln 3
x
y
x m
đồng biến trên khoảng
6
1;e
thì hàm số
6
3
t
y t
t m
đồng biến
trên khoảng
0;6
.
Ta có
2
3 6
3
m
y t
t m
Để hàm số
y t
đồng biến trên khoảng
0;6
thì
2019;2019
2
3 6 0
0 2019; 2018;... 1;0
0
3 0;6
2
m
m
m
m
m m
m
m
m
.
Vậy có tất cả:
2020
số nguyên
m
thoả mãn yêu cầu bài toán.
Câu 21. (Chuyên Lê Hồng Phong Nam Định 2019) Cho hàm số
.y f x
Đồ thị hàm số
y f x
như hình bên dưới
Hàm số
1 2
1
2
f x
g x
nghịch biến trên khoảng nào trong các khoảng sau?
A.
;0 .
B.
0;1 .
C.
1;0 .
D.
1; .
Lời giải
Chọn D
Dựa vào đồ thị, suy ra
1
0
1 2
x
f x
x
.
Ta có
1 2
1 1
1 2 .( 2).ln
2 2
f x
g x f x
.
Xét
1
1 2 1
0 1 2 0
1
1 1 2 2
0
2
x
x
g x f x
x
x
.
Vậy
g x
nghịch biến trên các khoảng
1
;0
2
và
1; .
Câu 22. (Kiểm tra năng lực - ĐH - Quốc Tế - 2019) Xét hàm số
sin
cos
x
f x x
. Mệnh đề nào sau đây
là đúng?
A. Hàm số
f
tăng trên khoảng
0;
2
. B. Hàm số
f
tăng trên khoảng
;0
2
.
C. Hàm số
f
giảm trên khoảng
;
2 2
. D.
3
lựa chọn kia đều sai.
Lời giải
Chọn C
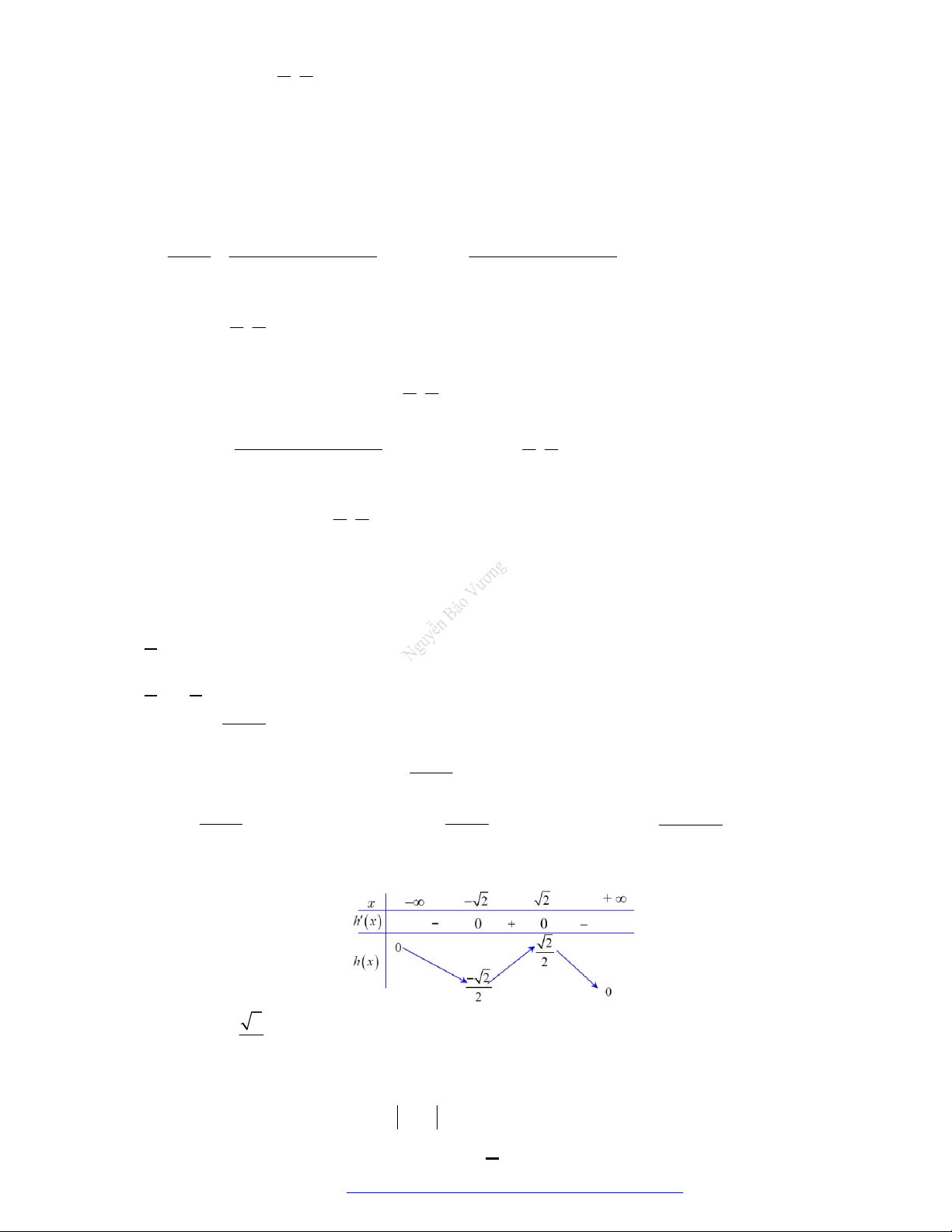
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Nhận xét:
cos 0
;
0
2 2
x
x
f x
.
Ta có:
sin sin
cos ln ln cos sin .ln cos
x x
f x x f x x x x
.
ln sin .ln cosf x x x
.
2 2 2 2
cos .lncos sin cos .ln cos sin
.
cos cos
f x
x x x x x x
f x f x
f x x x
.
Do
; cos 0;1
2 2
x x
. Mặt khác
e 1 lncos 0x
.
2 2
cos .ln cos sin 0, ;
2 2
x x x x
.
2 2
cos .lncos sin
. 0, ;
cos 2 2
x x x
f x f x x
x
(Dấu “=” xảy ra tại
0x
).
y f x
giảm trên
;
2 2
.
Câu 23. Có bao nhiêu giá trị nguyên của tham số
m
trong đoạn
2019;2019
để hàm số
2
ln 2 1y x mx
đồng biến trên
.
A.
2019
. B.
2020
. C.
4038
. D.
1009
.
Lời giải
Chọn A
Ta có
2
2
2
x
y m
x
.
Hàm số đã cho đồng biến trên
2
2
0
2
x
m
x
với mọi
x
.
2
2
2
x
m
x
với mọi
x
. Xét
2
2
2
x
h x
x
với
x
. Có
2
2
2
4 2
2
x
h x
x
Bảng biến thiên:
Suy ra
2
2
m
,
m
là số nguyên trong đoạn
2019;2019
nên có
2019
số.
Câu 24. Gọi
C
là đồ thị của hàm số
2018
logy x và
C
là đồ thị hàm số
y f x
,
C
là đối xứng
với
C
qua trục tung. Hàm số
y f x
đồng biến trên khoảng nào sau đây?
A.
0;1
. B.
; 1
. C.
1;0
. D.
1;
.
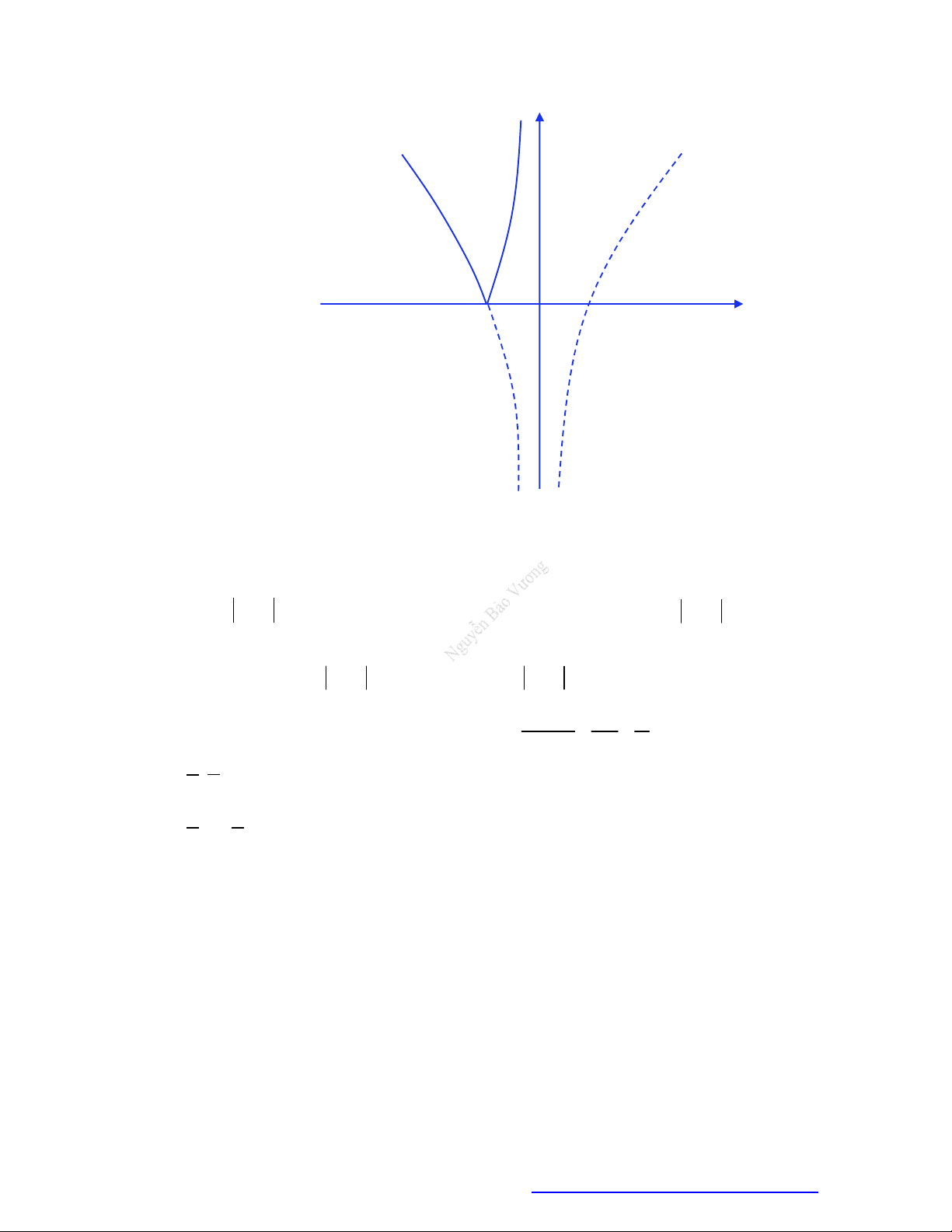
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Lời giải
Chọn C
Ta có hàm số
2018
log
y x
có tập xác định
0;D
là hàm số đồng biến trên
0;
. Vì
C
đối xứng với
C
qua trục tung nên hàm số
y f x
là hàm số nghịch biến trên
;0
.
Ta có
0
0
f x khi f x
f x
f x khi f x
nên suy ra đồ thị hàm số
y f x
:
Dựa vào đồ thị
y f x
ta suy ra hàm số
y f x
đồng biến trên
1;0
.
Câu 25. Có bao nhiêu giá trị thực
m
để hàm số
2
2019 6
2
ln 2019 ln 6 2
x x
m
g x x x
đồng biến trên
.
A. Duy nhất. B. Không tồn tại. C.
2019
. D. Vô số.
Lời giải
Chọn A
Ta có
2019 6 2
x x
g x mx
.
Hàm số
g x
đồng biến trên
khi và chỉ khi
0,g x x
.
Ta có
0 0,g m
.
Nếu
2019 6 2 0, 0
0
2019 6 2 0, 0
x x
x x
g x mx x
m
g x mx x
.
Suy ra hàm số đồng biến trên khoảng
0;
.
0
m
(loại).
Nếu
0
m
Xét
2019 ln 2019 6 ln 6
x x
g x m
là hàm số đồng biến trên
C
x
1
1
O
C
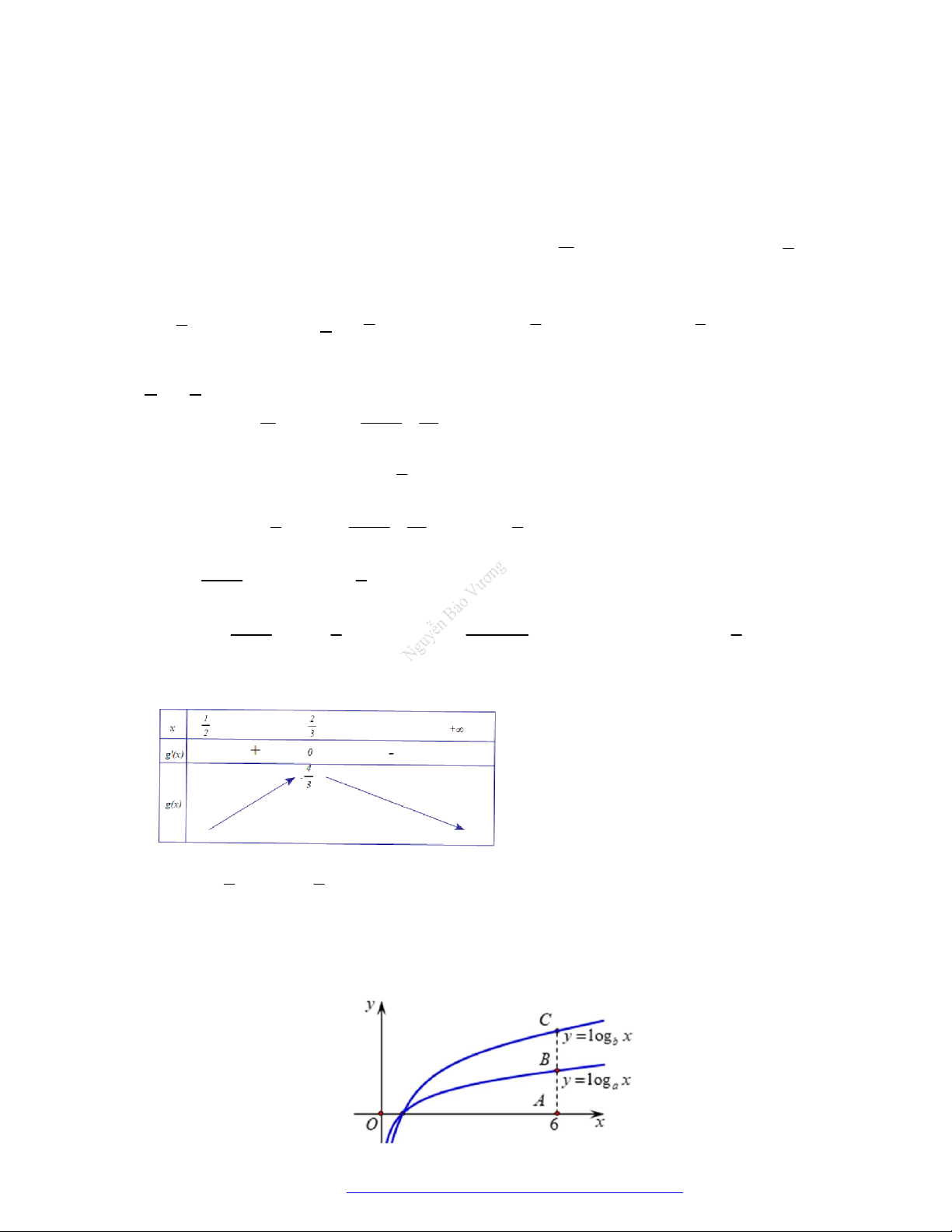
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
lim 2019 ln2019 6 ln6 0
x x
x
phương trình
0g x
có nghiệm duy nhất
0
x x
khi
0m
và
g x
đạt GTNN tại điểm cực tiểu duy nhất tại
0
x x .
Do đó, để
0,g x x
thì
0
0g x
.
Mà
0 0
0
0 0 0 2019 ln 2019 6 ln6g x m
hay
ln 2019 ln 6m
.
Do đó có duy nhất một giá trị thực của
m
thỏa mãn.
Câu 26. Tập các giá trị của tham số
m
để hàm số
ln 3 1 2
m
y x
x
đồng biến trên khoảng
1
;
2
là
A.
2
;
9
. B.
4
;
3
. C.
7
;
3
. D.
1
;
3
.
Lời giải
Chọn B
2
3
ln 3 1 2 '
3 1
m m
y x y
x x
x
.
Để hàm số đồng biến trên khoảng
1
;
2
.
2
2
1 3 1
' 0, x ; 0, x ;
2 3 1 2
3 1
, x ;
1 3 2
m
y
x
x
x
m g x
x
.
Xét
2 2
2
3 1 6 9 2
, x ; ' ' 0 0
1 3 2 3
1 3
x x x
g x g x g x x x
x
x
.
Bảng biến thiên.
.
Vậy
4 4
;
3 3
m m
.
Câu 27. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho các hàm số log
a
y x và log
b
y x có đồ thị như
hình vẽ bên.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Đường thẳng
6x
cắt trục hoành, đồ thị hàm số log
a
y x và log
b
y x lần lượt tại
,A B
và
C
.
Nếu
2
log 3AC AB thì
A.
3 2
b a
. B.
2 3
b a
. C.
3 2
log logb a
. D.
2 3
log logb a
.
Lời giải
Chọn D
Từ các đồ thị hàm số đã cho trên hình ta có
6;0A
,
6;log 6
a
B
,
6;log 6
b
C
,
log 6
C A b
AC y y , log 6
B A a
AB y y .
Vậy
2 2
log 3 log 6 log 6.log 3
b a
AC AB
6 6 6
2 3
6 6 6 6 6
log 3 log 2 log 3
1 1
. log log
log log log 2 log log
b a
b a b a
.
Câu 28. Trong hình dưới đây, điểm
B
là trung điểm của đoạn thẳng
AC
.
Khẳng định nào sau đây là đúng?
A.
2a c b
. B.
2
ac b
. C.
2
2ac b
. D.
ac b
Lời giải
Chọn B
Từ đồ thị ta thấy tọa độ điểm
0;lnA a
,
0;lnbB
,
0;lncC
Theo bài ra
B
là trung điểm của đoạn thẳng
AC
nên ta có:
2
0 0
0
0 (1)
2 2
ln ln
2 ln ln (2)
ln
22
A B
B B
B
A B
B
BB
x x
x x
x
y y a c
y ac b
y b
y
Từ
2
(2) ac b .
Vậy chọn. B.
Câu 29.
Đồ thị hàm số
y f x
đối xứng với đồ thị của hàm số
0, 1
x
y a a a
qua điểm
1;1I
.
Giá trị của biểu thức
1
2 log
2018
a
f
bằng
A.
2016
.
B.
2020
.
C.
2016
.
D.
2020
.
Lời giải
Chọn A
Xét
1 1
2 log ; 2 log
2018 2018
a a
M f
thuộc đồ thị hàm số
y f x
.
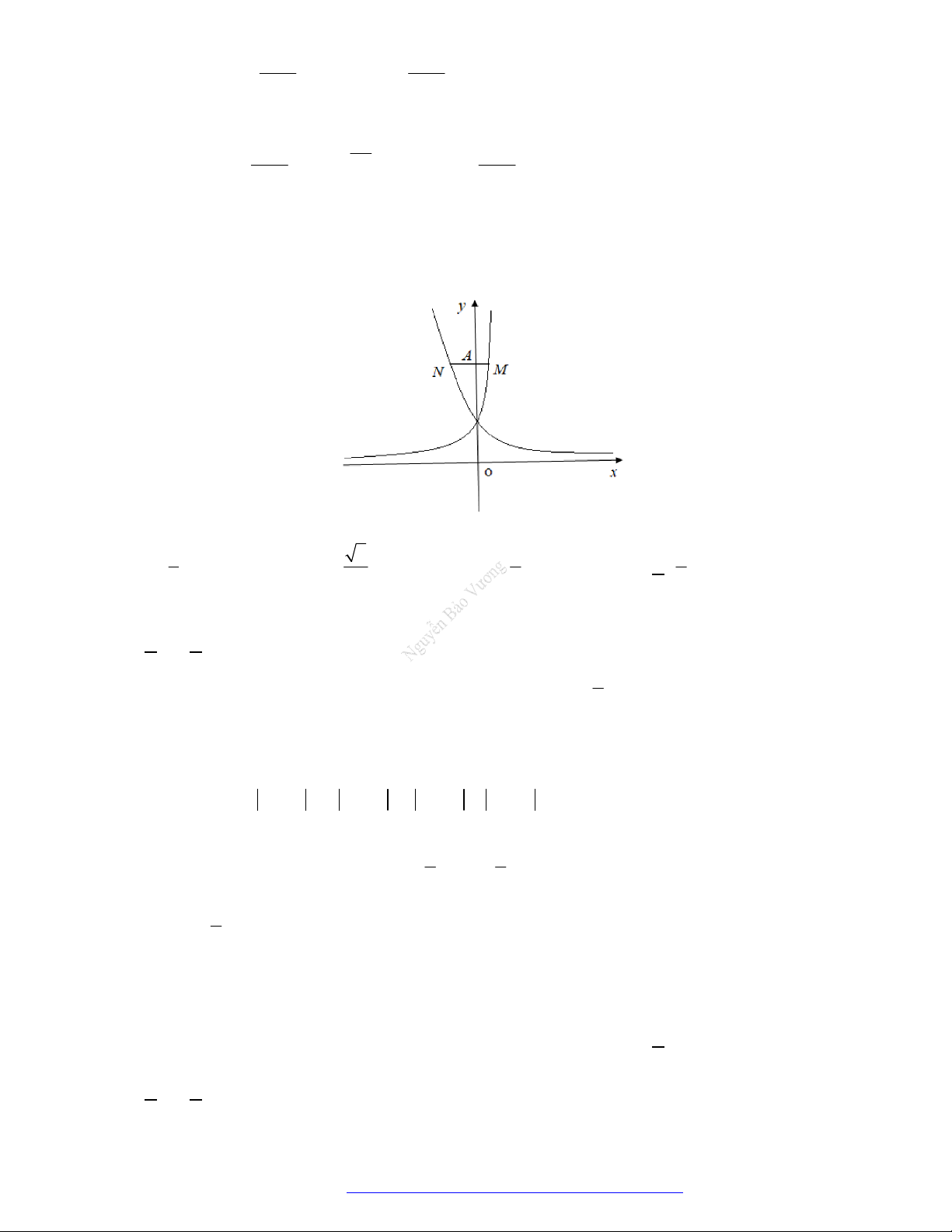
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điểm
1 1
log ;2 2 log
2018 2018
a a
N f
đối xứng với
M
qua
1;1I
thuộc đồ thị hàm số
x
y a
nên ta có:
1
log
log 2018
2018
1 1
2 2 log 2 log 2 2 2018 2016
2018 2018
a
a
a a
f a f a
.
Câu 30. (Hội 8 trường chuyên ĐBSH - 2019) Cho số thực dương
a
khác
1
. Biết rằng bất kỳ đường
thẳng nào song song với trục
Ox
mà cắt các đường
4 ,
x x
y y a
, trục tung lần lượt tại
,M N
và
A
thì
2AN AM
( hình vẽ bên). Giá trị của
a
bằng
A.
1
3
. B.
2
2
. C.
1
4
. D.
1
2
.
Lời giải
Chọn D
Dựa vào ĐTHS ta thấy hàm số
x
y a
nghịch biến nên
1
0
2
a
.
Mọi đường thẳng
(m 0)y m
đều cắt các đường
4 ,
x x
y y a
, trục tung lần lượt tại
4
log ; , log ;
a
M m m N m m
và
(0 ; m)A
, theo bài ra
4 2
2
2
2 log 2 log log log
log log 2
2
log log
1
1
log log
log log
2
2
a a
m m
a
a
m m
AN AM m m m m
a
a
m m
m m
a
a
Vậy
1
.
2
a
Câu 31. (THPT Ngô Quyền - Ba Vì - Hải Phòng 2019) Đồ thị hàm số
y f x
đối xứng với đồ thị
hàm số
log
a
y x
,
0 1a
qua điểm
2;1I
. Giá trị của biểu thức
2019
4f a
bằng
A.
2023
. B.
2023
. C.
2017
. D.
2017
.
Lời giải
Chọn D
Lấy điểm
2019 2019
4 ; 4A a f a
thuộc đồ thị của hàm số
y f x
và điểm
;log
a
B x x
thuộc đồ thị của hàm số
log
a
y x
.
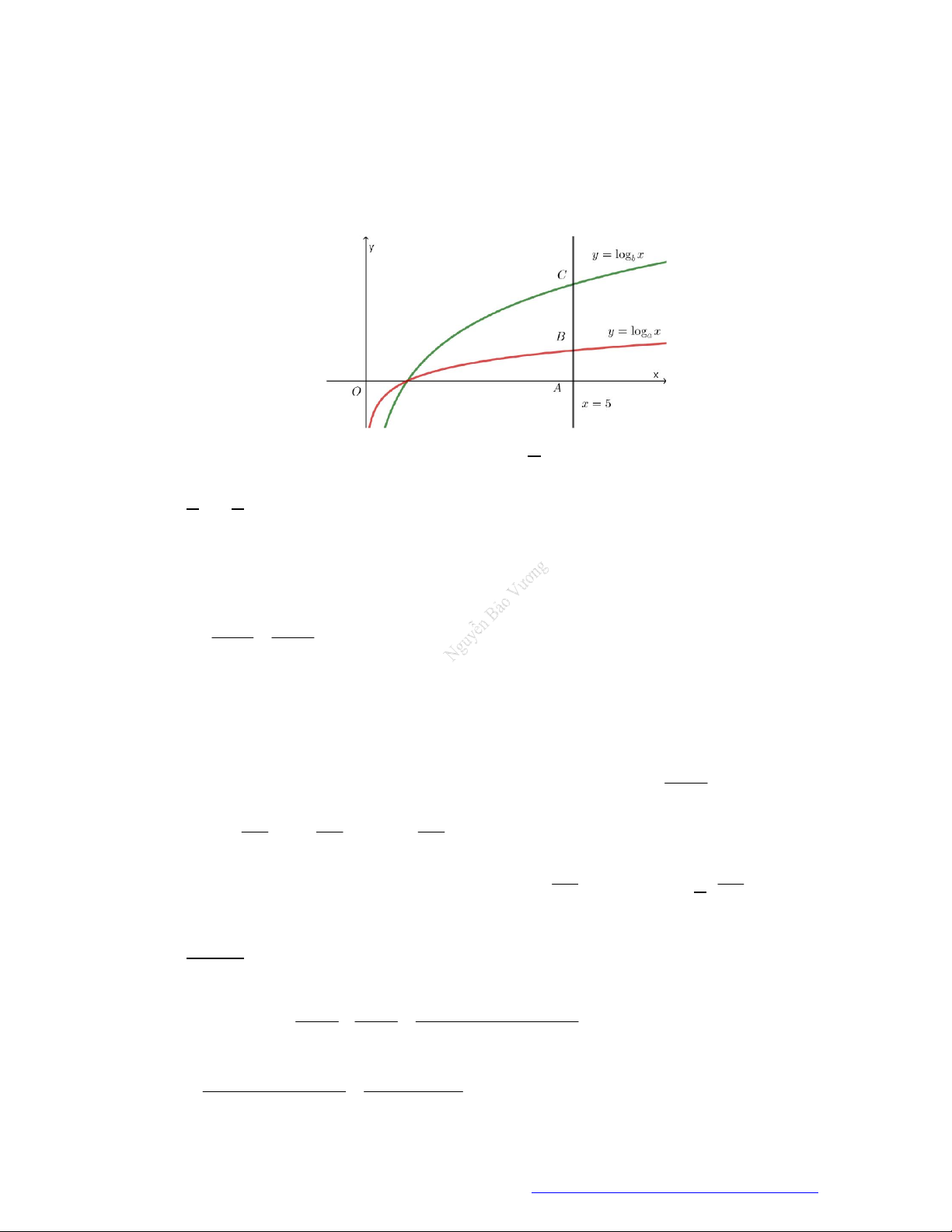
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Hai điểm
A
và
B
đối xứng nhau qua điểm
I
khi và chỉ khi
2019 2019
2019
2019 2019 2019
4 2.2
4 2017
4 log 2.1 4 log 2
a a
a x x a
f a
f a x f a a
.
Câu 32. Cho các hàm số
log
a
y x
và
log
b
y x
có đồ thị như hình vẽ bên. Đường thẳng
5x
cắt trục
hoành, đồ thị hàm số
log
a
y x
và
log
b
y x
lần lượt tại
,A B
và
C
. Biết rằng
2CB AB
. Mệnh
đề nào sau đây là đúng?
A.
5a b
. B.
2
a b
. C.
3
a b
. D.
3
a b
.
Lời giải
Chọn C
Dễ thấy
5;0 , 5;log 5 , 5;log 5
a b
A B C
và
log 5 log 5 0
b a
.
Do
2CB AB
nên ta có
log 5 log 5 2 log 5 0
b a a
.
5 5
5 5
3
5 5
3
log 5 3log 5
1 3
log log
log 3log
log log
.
b a
b a
a b
a b
a b
Câu 33. (THPT Đông Sơn 1 - Thanh Hóa - 2019) Cho hàm số
4
.
4 2
x
x
f x
Tính giá trị biểu thức
1 2 100
... ?
100 100 100
A f f f
A.
50
. B.
49
. C.
149
3
. D.
301
6
.
Lời giải
Chọn D
Xét hai số dương
a
và
b
sao cho
1a b
, ta có
4 4 2 4 4 2
4 4
4 2 4 2
4 2 4 2
a b b a
a b
a b
a b
f a f b
2 4 4 4 2 4 4 4
1
4 2 4 4 4 2 4 4 4
a b a b a b
a b a b a b
.
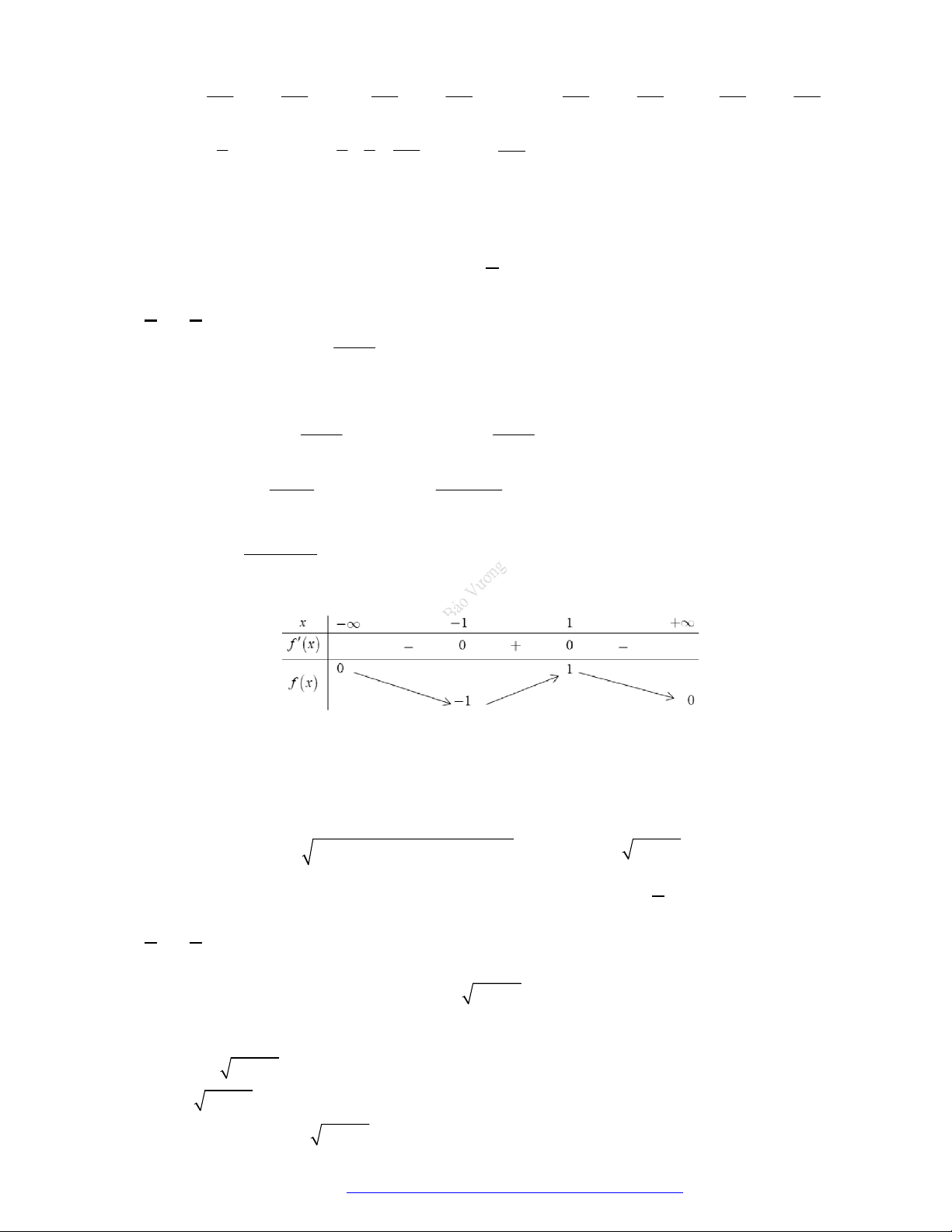
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Do đó
1 99 2 98 49 51 50 100
...
100 100 100 100 100 100 100 100
A f f f f f f f f
1 1 2 301
49 1 49 .
2 2 3 6
f f
Vậy
301
.
6
A
.
Câu 34. Tìm tập hợp tất cả các giá trị của tham số thực
m
đề hàm số
2
ln 1 1y x mx
đồng biến
trên
.
A.
1; 1 .
B.
1; 1 .
C.
; 1 .
D.
; 1 .
Lời giải
Chọn C
TXÐ: .D R
Ta có
2
2
' .
1
x
y m
x
Hàm số
2
ln 1 1y x mx
đồng biến trên R
khi
2 2
2 2
' 0 0 .
1 1
x x
y x R m x R m x R
x x
Xét hàm
2
2
.
1
x
f x
x
Ta có
2
2
2
2 2
' .
1
x
f x
x
2
2
2
2 2
' 0 0 1.
1
x
f x x
x
Bảng biến thiên:
Dựa vào bảng biến thiến suy ra
1 ( ) 1 .f x x R
Từ đó suy ra
1.m
Câu 35. Có bao nhiêu giá trị nguyên của
m
thuộc khoảng
2019;2019
để hàm số sau có tập xác định là
D
?
2 2 2
2
2 1 2 4 log 2 1y x m x m x m m x m x
A.
2020
. B.
2021
. C.
2018
. D.
2019
.
Lời giải
Chọn D
Hàm số xác định với mọi
x
thì
2 2
2
2 1 2 4 0
2 1 0
x m x m m
x m x
luôn đúng với mọi
x
+) Ta có:
2
2 2
2 1 2 4 1 3 0x m x m m x m
,
x
+)
2
2 1 0x m x
,
x
2
2 1 ,x x m x .
Xét hàm số
2
2 1f x x x
với
x
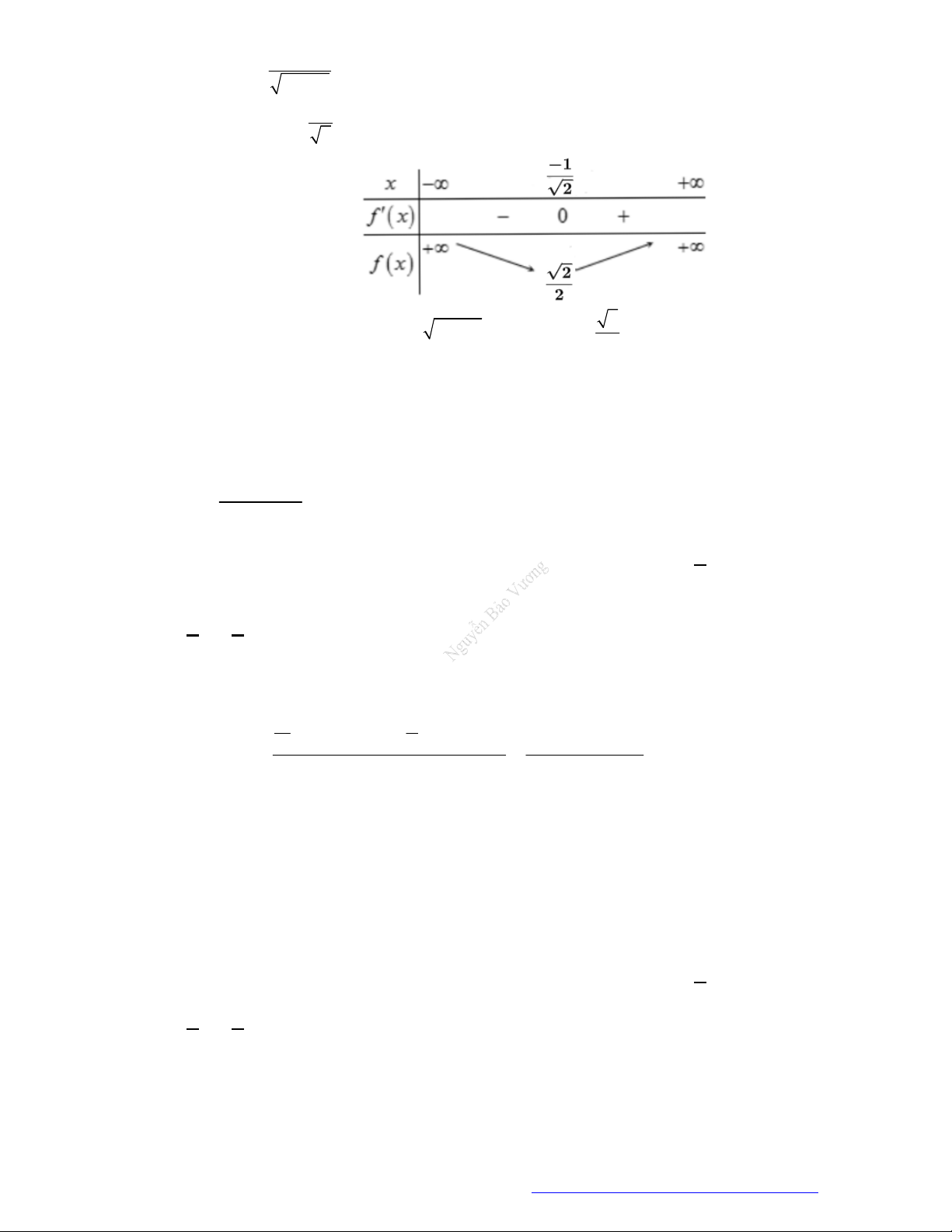
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
2
2
1
2 1
x
f x
x
.
1
0
2
f x x
.
Từ bảng biến thiên ta thấy để
2
2
2 1 ,
2
x x m x m
.
Kết hợp điều kiện
2019;2019
m
m
{ 2018, 2017, 2016,..., 1,0}m
.
Kết luận: có 2019 giá trị của
m
thỏa mãn bài toán.
Câu 36. (THPT Yên Dũng 2-Bắc Giang 2019) Tập tất cả các giá trị của tham số
m
để hàm số
ln 2
ln 1
m x
y
x m
nghịch biến trên
2
;e
là:
A.
2
1
m
m
. B.
2
1
m
m
. C.
2
1
m
m
. D.
2m
.
Lời giải
Chọn D
Điều kiện xác định:
1
0
m
x
x e
Ta có:
2
2 2
1
ln 1 ln 2
2
'
ln 1 ln 1
m
x m m x
m m
x x
y
x m x x m
Hàm số nghịch biến trên
2
;e
khi và chỉ khi
2
1 2
2
2 0
2
1
1 2
m
m
m m
m
m
e e
m
.
Câu 37. (Chuyên Bắc Giang 2019) Có bao nhiêu giá trị nguyên của
m
thuộc khoảng
2019;2019
để
hàm số
3 2
1
2019
x x mx
y
nghịch biến trên
1;2
A.
2020
. B.
2019
. C.
2010
. D.
2011
.
Lời giải
Chọn D
3 2
2 1
' 3 2 .2019 .ln2019
x x mx
y x x m
Hàm số nghịch biến trên
1;2
' 0 1;2y x
2
3 2 0 1;2x x m x
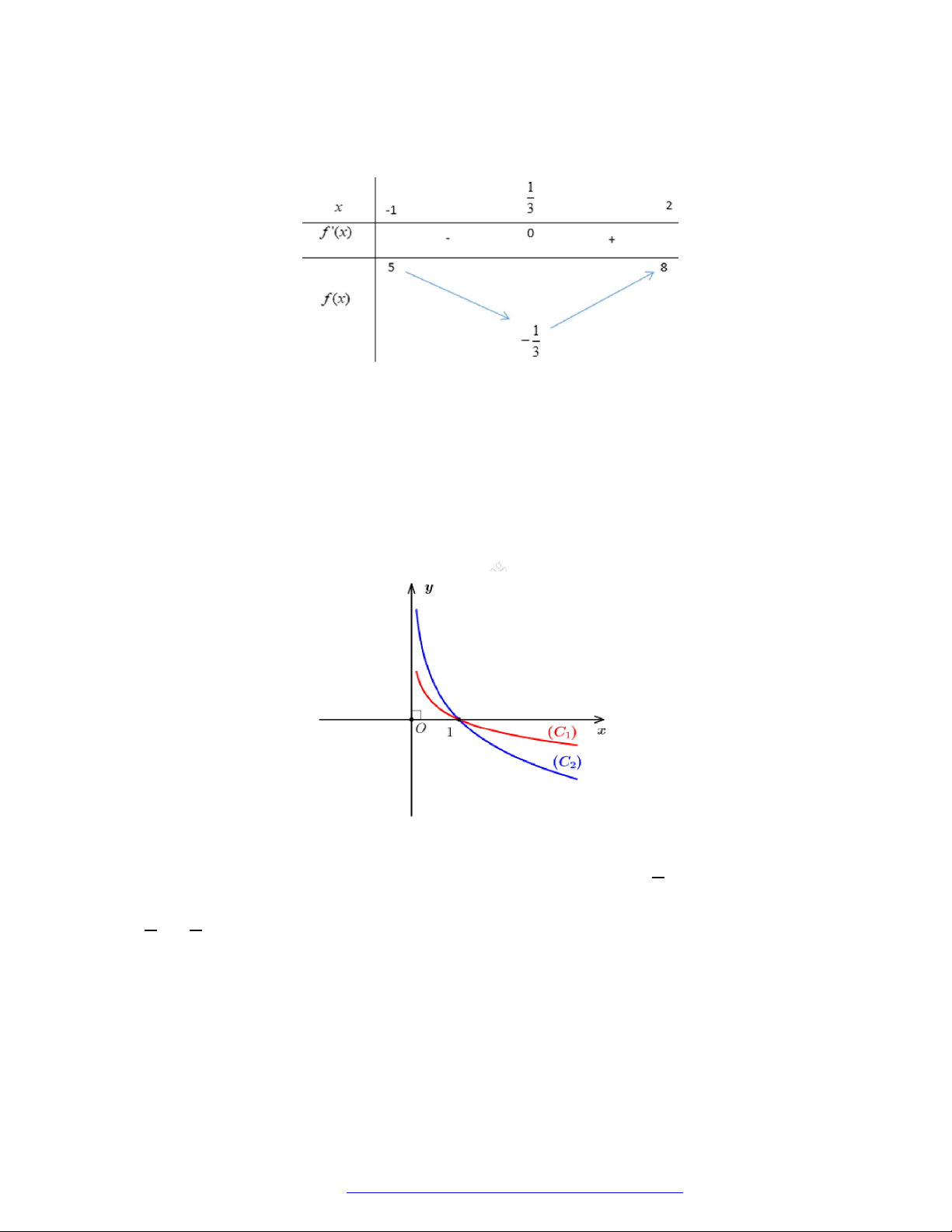
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
3 2 1;2x x m x
Đặt
2
( ) 3 2f x x x
;
'( ) 6 2f x x
.
Bảng biến thiên:
Từ bảng biến thiên suy ra
( ) 8 1;2f x x
.
Do đó ycbt
8m
.
Vì
m
nguyên thuộc khoảng
2019;2019
nên có 2011 giá trị
m
thỏa mãn.
Câu 38. (Hậu Lộc 2-Thanh Hóa -2019) Cho
a
,
b
là các số thực dương khác
1
, đồ thị hàm số log
a
y x
và log
b
y x lần lượt là
1
C
,
2
C
như hình vẽ.
Khẳng định nào sau đây là đúng
A.
e.e .
a b
b a
. B.
e.e .
a b
b a
. C.
e.e .
a b
b a
. D.
e.e .
a b
a b
.
Lời giải
Chọn D
Ta có log 1
a
x x a vàlog 1 .
b
x x b
Nên kẻ đường thẳng
1y
cắt đồ thị
1
C
,
2
C
lần lượt tại các điểm có tọa độ
;1a
và
;1b
.
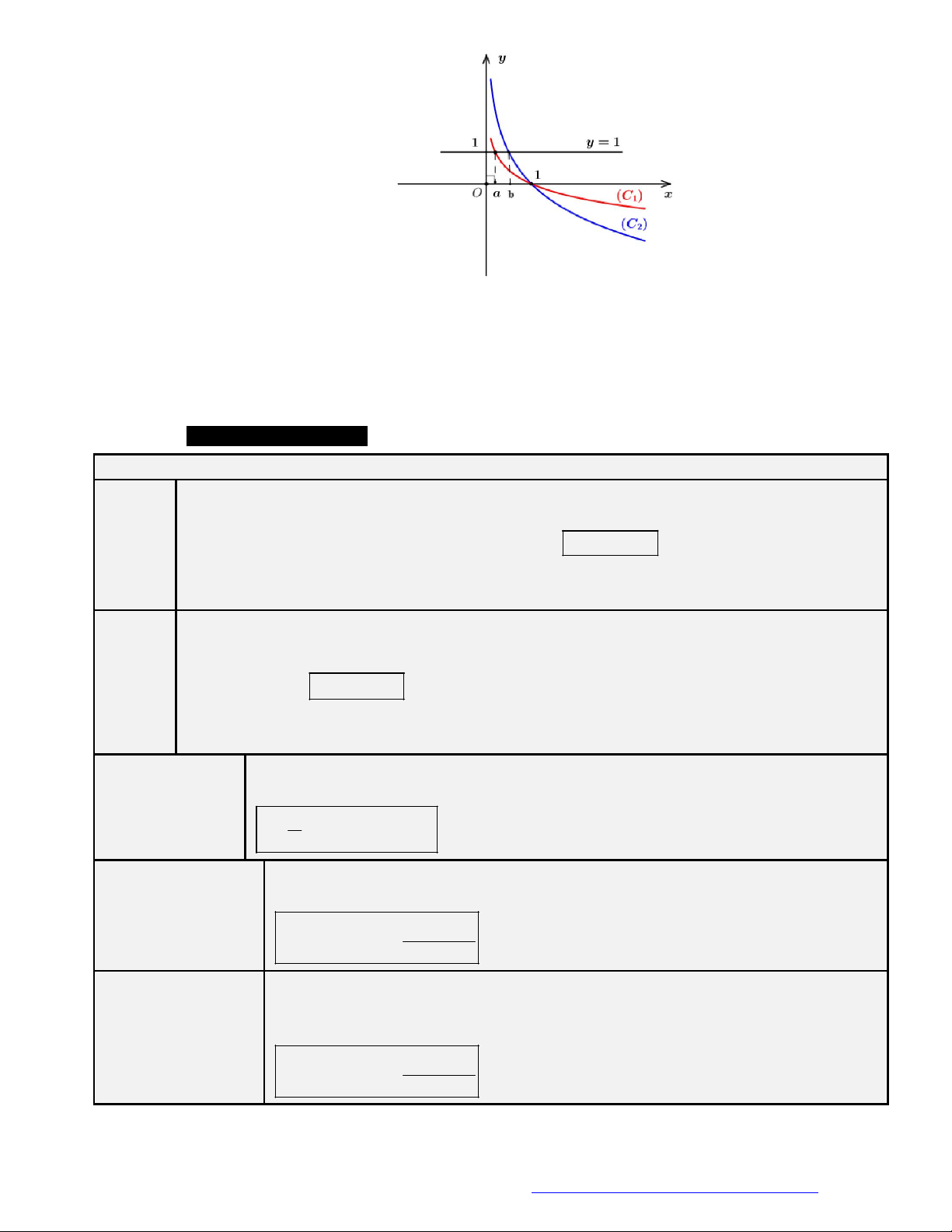
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Nhìn vào đồ thị ta suy ra
.a b
Do
a
,
b
,
a
e
,
b
e
là các số dương và
1e
nên từ
a b
ta suy ra
. .
. .
a. . . .
a b a b
a b
b b b b
e e a e a e
a e b e
e b e a e b e
Dạng 4. Bài toán thực tế
BÀI TOÁN NGÂN HÀNG
1. Công
thức
tính lãi
đơn
Nếu ta gởi tiền vào ngân hàng theo hình thức tiền lãi chỉ được tính dựa vào tiền gốc
ban đầu (tức là tiền lãi của kỳ hạn trước không gộp vào vốn để tính lãi cho kỳ hạn kế
tiếp), đây gọi là hình thức lãi đơn. Ta có:
(1 )T A nr
với A: tiền gởi ban đầu; r: lãi
suất; n: kỳ hạn gởi; T: tổng số tiền nhận sau kỳ hạn n. Lưu ý: r và n phải khớp đơn vị;
T bao gồm cả A, muốn tính số tiền lời ta lấy T – A.
2. Công
thức lãi
kép
Nếu ta gởi tiền vào ngân hàng theo hình thức: hàng tháng tiền lãi phát sinh sẽ được cộng vào
tiền gốc cũ để tạo ra tiền gốc mới và cứ tính tiếp như thế, đây gọi là hình thức lãi kép.
Ta có: (1 )
n
T A r với A: tiền gởi ban đầu; r: lãi suất; n: kỳ hạn gởi; T: tổng số tiền
nhận sau kỳ hạn n. Lưu ý: r và n phải khớp đơn vị; T bao gồm cả A, muốn tính số tiền
lời ta lấy T – A.
3. Mỗi tháng gởi
đúng số tiền
giống nhau theo
hình thức lãi kép
Nếu đầu mỗi tháng khách hàng luôn gởi vào ngân hàng số tiền A đồng với lãi kép
%r
/tháng thì số tiền họ nhận được cả vốn lẫn lãi sau n tháng là:
1 1 1
n
A
T r r
r
.
4. Gởi tiền vào ngân
hàng rồi rút ra hàng
tháng số tiền cố
định
Nếu khách hàng gởi vào ngân hàng số tiền A đồng với lãi suất
%r
/tháng. Vào ngày
ngân hàng tính lãi mỗi tháng thì rút ra X đồng. Số tiền thu được sau n tháng là:
1 1
1
n
n
r
T A r X
r
5. Vay vốn và trả
góp (tương tự bài
toán 4)
Nếu khách hàng vay ngân hàng số tiền A đồng với lãi suất r%/tháng. Sau đúng một
tháng kể từ ngày vay bắt đầu hoàn nợ, hai lần hoàn nợ cách nhau đúng một tháng, mỗi
lần hoàn nợ đúng số tiền X đồng. Số tiền khách hàng còn nợ sau n tháng là:
1 1
1
n
n
r
T A r X
r

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 1. (Mã 101 - 2020 Lần 1) Trong năm 2019, diện tích rừng trồng mới của tỉnh
A
là
600 ha
. Giả sử
diện tích rừng trồng mới của tỉnh
A
mỗi năm tiếp theo đều tăng
6%
so với diện tích rừng trồng
mới của năm liền trước. Kể từ sau năm 2019, năm nào dưới đây là năm đầu tiên tỉnh
A
có diện
tích rừng trồng mới trong năm đó đạt trên
1000 ha
?
A. Năm 2028. B. Năm 2047. C. Năm 2027. D. Năm 2046.
Lời giải
Chọn A.
Diện tích rừng trồng mới của năm
2019 1
là
1
600 1 6%
.
Diện tích rừng trồng mới của năm
2019 2
là
2
600 1 6%
.
Diện tích rừng trồng mới của năm
2019
n
là
600 1 6%
n
.
Ta có
1 6%
5 5
600 1 6% 1000 1 6% log 8,76
3 3
n n
n
Như vậy kể từ năm 2019 thì năm 2028 là năm đầu tiên diện tích rừng trồng mới đạt trên
1000 ha
.
Câu 2. (Mã 102 - 2020 Lần 1) Trong năm 2019, diện tích rừng trồng mới của tỉnh A là
1000
ha. Giả sử
diện tích rừng trồng mới của tỉnh A mỗi năm tiếp theo đều tăng
%6
so với diện tích rừng trồng
mới của năm liền trước. Kể từ sau năm 2019, năm nào dưới đây là năm đầu tiên tỉnh A có diện
tích rừng trồng mới trong năm đó đạt trên
1400
ha.
A.
2043
. B.
2025
. C.
2024
. D.
2042
.
Lời giải
Chọn B
Ta có sau
n
năm thì diện tích rừng trồng mới của tỉnh A là:
. .
n
1000 1 0 06
Khi đó,
. . . . .
n
n
n
1000 1 0 06 1400 1 06 1 4 5 774
.
Vậy vào năm 2025 thì diện tích rừng trong mới trong năm đó đạt trên
1400
ha.
Câu 3. (Mã 103 - 2020 Lần 1) Trong năm
2019
, diện tích rừng trồng mới của tỉnh
A
là
900
ha. Giả sử
diện tích rừng trồng mới của tỉnh
A
mỗi năm tiếp theo đều tăng
6%
so với diện tích rừng trồng
mới của năm liền trước. Kể từ sau năm 2019, năm nào dưới đây là năm đầu tiên của tỉnh
A
có
diện tích rừng trồng mới trong năm đó đạt trên
1700
ha?
A. Năm
2029.
B. Năm
2051.
C. Năm
2030.
D. Năm
2050.
Lời giải
Chọn C.
Trong năm
2019,
diện tích rừng trồng mới của tỉnh A là
900
A
ha.
Trong năm
2020,
diện tích rừng trồng mới của tỉnh A là
1
6% 1 6%
A A A A
ha.
Trong năm
2021,
diện tích rừng trồng mới của tỉnh A là
2
2 1 1 1
6% 1 6% 1 6% 1 6% 1 6%
A A A A A A
ha.
Trong năm
2022,
diện tích rừng trồng mới của tỉnh A là
2 3
3 2 2 2
6% 1 6% 1 6% 1 6% 1 6%
A A A A A A
ha.
…
Trong năm
2019 , n
diện tích rừng trồng mới của tỉnh A là
1 6%
n
n
A A
ha.
Khi đó, diện tích rừng trồng mới đạt trên
1700
ha khi

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
17
1700 1 6% 1700 900.1,06 1700 1,06
9
n
n n
n
A A
1,06 min
17
log 10,9 11.
9
n n
Vậy năm
2030
là năm đầu tiên của tỉnh A có diện tích rừng trồng mới trong năm đó đạt trên
1700
ha.
Câu 4. (Mã 104 - 2020 Lần 1) Trong năm
2019
, diện tích rừng trồng mới của tỉnh A là
800ha
. Giả sử
diện tích rừng trồng mới của tỉnh A mỗi năm tiếp theo đều tăng
6%
so với diện tích rừng trồng
mới của năm liền trước. Kể từ sau năm
2019
, năm nào dưới đây là năm đầu tiên tỉnh A có diện
tích rừng trồng mới trong năm đó đạt trên
1400ha
?
A. Năm
2029
. B. Năm
2028
. C. Năm
2048
. D. Năm
2049
.
Lời giải
Chọn A
Trong năm
2019
, diện tích rừng trồng mới của tỉnh A là
800ha
. Giả sử diện tích rừng trồng mới
của tỉnh A mỗi năm tiếp theo đều tăng
6%
so với diện tích rừng trồng mới của năm liền trước nên
sau
n
(năm) diện tích rừng trồng mới của tỉnh A là
800. 1 6%
n
với
n
.
Ta có
1,06
7 7
800. 1 6% 1400 1,06 log 9,60402
4 4
n
n
n
.
Vì
n
nên giá trị nhỏ nhất thỏa mãn là
10
n
.
Vậy: kể từ sau năm
2019
, năm đầu tiên tỉnh A có diện tích rừng trồng mới trong năm đó đạt trên
1400ha
là năm
2029
.
Câu 5. (Mã 102 - 2020 Lần 2) Năm
2020
một hãng xe niêm yết giá bán loại xe X là
750.000.000
đồng
và dự định trong
10
năm tiếp theo, mỗi năm giảm
2%
giá bán so với giá bán của năm liền trước.
Theo dự định đó năm
2025
hãng xe ô tô niêm yết giá bán loại xe X là bao nhiêu ( kết quả làm
tròn đến hàng nghìn )?
A.
677.941.000
đồng. B.
675.000.000
đồng.
C.
664.382.000
đồng. D.
691.776.000
đồng.
Lời giải
Chọn A
Giá xe năm
2020
là
A
Giá xe năm
2021
là
1
. 1
A A A r A r
.
Giá xe năm
2022
là
2
2 1 1
. 1
A A A r A r
.
Giá xe năm
2023
là
3
3 2 2
. 1
A A A r A r
.
Giá xe năm
2024
là
4
4 3 3
. 1
A A A r A r
.
Giá xe năm
2025
là
5
5
5 4 4
2
. 1 750.000.000 1 677.941.000
100
A A A r A r
đồng.
Câu 6. (Mã 103 - 2020 Lần 2) Năm 2020, một hãng xe ô tô niêm yết giá bán loại xe X là 800.000.000
đồng và dự định trong 10 năm tiếp theo, mỗi năm giảm 2% giá bán so với giá bán của năm liền
trước. Theo dự định đó, năm 2025 hãng xe ô tô niêm yết giá bán loại xe X là bao nhiêu (kết quả
làm tròn đến hàng nghìn)?
A. 708.674.000 đồng. B. 737.895.000 đồng. C. 723.137.000 đồng. D. 720.000.000 đồng.
Lời giải
Chọn C

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Giá bán loại xe X năm 2021 là:
800.000.000 800.000.000 2% 800.000.000 1 2%
Giá bán loại xe X năm 2022 là:
2
800.000.000 1 2% 800.000.000 1 2% 2% 800.000.00
0 1 2%
.
Tương tự ta có: giá bán loại xe X năm 2025 sẽ là:
5
800.000.000 1 2% 723.137.000
đồng.
Câu 7. (Đề Tham Khảo 2018) Một người gửi
100
triệu đồng vào ngân hàng với lãi suất
0,4%/
tháng.
Biết rằng nếu không rút tiền ta khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được lập vào
vốn ban đầu để tính lãi cho tháng tiếp theo. Hỏi sau
6
tháng, người đó được lĩnh số tiền ( cả vốn
ban đầu và lãi) gần nhất với số tiền nào dưới đây, nếu trong khoảng thời gian này người đó không
rút tiền ra và lãi xuất không thay đổi?
A.
102.16.000
đồng B.
102.017.000
đồng C.
102.424.000
đồng D.
102.423.000
đồng
Lời giải
Chọn C
Ta có
6
0
0,4
1 100.000.000 1 102.424.128
100
n
n
A A r
Câu 8. (Mã 104 2018) Một người gửi tiết kiệm vào một ngân hàng với lãi suất
6,1% /
năm. Biết rằng
nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính
lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó thu được (cả số tiền gửi ban đầu và
lãi) gấp đôi số tiền gửi ban đầu, giả định trong khoảng thời gian này lãi suất không thay đổi và
người đó không rút tiền ra?
A.
11
năm B.
12
năm C.
13
năm D.
10
năm
Lời giải
Chọn B
Gọi
x
số tiền gửi ban đầu.
Theo giả thiết
6,1 6,1
2 1 2 1
100 100
N N
x x
1,061
6,1
2 1 log 2 11,7
100
N
N
Vậy sau ít nhất 12 năm người đó thu được số tiền thỏa yêu cầu.
Câu 9. Anh An gửi số tiền 58 triệu đồng vào một ngân hàng theo hình thức lãi kép và ổn định trong 9
tháng thì lĩnh về được 61758000đ. Hỏi lãi suất ngân hàng hàng tháng là bao nhiêu? Biết rằng lãi
suất không thay đổi trong thời gian gửi.
A.
0,8 %
B.
0,6 %
C.
0,7 %
D.
0,5 %
Lời giải
Chọn C
Áp dụng công thức
0
1
n
n
A A r
với
n
là số kỳ hạn,
0
A
là số tiền ban đầu,
n
A
là số tiền có
được sau
n
kỳ hạn,
r
là lãi suất.
Suy ra
9
9
9
9 0
0
1 1 0,7%
A
A A r r
A
.
Câu 10. (Chuyên Bắc Giang 2019) Một người gửi
100
triệu đồng vào một ngân hàng với lãi suất
0,6%
/tháng. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ
được nhập làm vốn ban đầu để tính lãi cho tháng tiếp theo. Hỏi sau ít nhất bao nhiêu tháng, người

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
đó được lĩnh số tiền không ít hơn
110
triệu đồng (cả vốn ban đầu và lãi), biết rằng trong suốt thời
gian gửi tiền người đó không rút tiền và lãi suất không thay đổi?
A.
18
tháng B.
16
tháng C.
17
tháng D.
15
tháng
Lời giải
Chọn B
Sau
n
tháng, người đó lĩnh được số tiền là:
100. 1 0,6%
n
(triệu đồng).
Sau
n
tháng, người đó được lĩnh số tiền không ít hơn
110
triệu đồng (cả vốn ban đầu và lãi)
1 0,6%
11
100. 1 0,6% 110 log 15,9
10
n
n
.
Câu 11. Một người lần ầu gửi vào ngân hàng
100
triệu ồng theo thể thức lãi kép (tức là tiền lãi của
kỳ trước ược cộng vào vốn của kỳ kế tiếp) với kì hạn
3
tháng, lãi suất
2%
một quý. Sau
úng
6
tháng, người ó gửi thêm
100
triệu ồng với kỳ hạn và lãi suất như trước ó. Tổng
số tiền người ó nhận ược sau
1
năm gửi tiền vào ngân hàng gần bằng với kết quả nào sau
ây? Biết rằng trong suốt thời gian gửi tiền lãi suất ngân hàng không thay ổi và người ó
không rút tiền ra.
A.
212
triệu ồng
B.
216
triệu ồng
C.
210
triệu ồng
D.
220
triệu ồng
Lời giải
Chọn A
Ta có:
2% 0,02
r
Số tiền
100
triệu ồng gửi lần ầu thì sau 1 năm (4 quý) nhận ược cả vốn lẫn lãi là:
4
1
100 1 0,02 108,24
T
triệu ồng
Số tiền
100
triệu ồng gửi lần thứ hai thì sau 6 tháng (2 quý) nhận ược cả vốn lẫn lãi là:
2
2
100 1 0,02 104,04
T
triệu ồng
Vậy tổng số tiền nhận được là:
1 2
212,28
T T T
triệu ồng.
Câu 12. (KTNL Gia Bình 2019) Ông An gửi tiết kiệm
50
triệu đồng vào ngân hàng với kỳ hạn
3
tháng,
lãi suất
8,4%
một năm theo hình thức lãi kép. Ông gửi được đúng
3
kỳ hạn thì ngân hàng thay
đổi lãi suất, ông gửi tiếp
12
tháng nữa với kỳ hạn như cũ và lãi suất trong thời gian này là
12%
một năm thì ông rút tiền về. Số tiền ông An nhận được cả gốc lẫn lãi là: (làm tròn đến chữ số
hàng đơn vị)
A.
62255910
đồng. B.
59895767
đồng. C.
59993756
đồng. C.
63545193
đồng.
Lời giải
Chọn B
Đợt I, ông An gửi số tiền
0
50
P
triệu, lãi suất
8,4%
một năm tức là
2,1%
mỗi kỳ hạn. Số tiền
cả gốc và lãi ông thu được sau
3
kỳ hạn là:
3
3
50000000. 1.021
P
.
Đợt II, do ông không rút ra nên số tiền
3
P
được xem là số tiền gửi ban đầu của đợt II, lãi suất đợt
II là
3%
mỗi kỳ hạn. Ông gửi tiếp
12
tháng bằng
4
kỳ hạn nên số tiền thu được cuối cùng là:
4 3 4
3
1.03 50000000. 1.021 . 1.03 59895767
P P
đồng.
Câu 13. (THPT An Lão Hải Phòng 2019) Ngày 01 tháng 01năm 2017, ông An đem 800 triệu đồng gửi
vào một ngân hàng với lãi suất 0,5% một tháng. Từ đó, cứ tròn mỗi tháng, ông đến ngân hàng rút
6 triệu để chi tiêu cho gia đình. Hỏi đến ngày 01tháng 01 năm 2018, sau khi rút tiền, số tiền tiết

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
kiệm của ông An còn lại là bao nhiêu? Biết rằng lãi suất trong suốt thời gian ông An gửi không
thay đổi
A.
11
800.(1,005) 72
(triệu đồng) B.
12
1200 400.(1,005)
(triệu đồng)
C.
12
800.(1,005) 72
(triệu đồng) D.
11
1200 400.(1,005)
(triệu đồng)
Lời giải
Chọn B
Gửi ngân hàng số tiền là A đồng với lãi suất
%r
./tháng. Mỗi tháng vào ngày ngân hàng tính lãi,
rút ra số tiền là X đồng. Sô tiền còn lại sau n tháng đươc tính theo công thức:
12
1
12
2
1 1 1,005 1
1 800 1,005 6. 775.3288753
0
1200 400.(1,0
%
5
,5
0 )
n
n
n
r
S A r X
r
Câu 14. (THPT Lê Quy Đôn Điện Biên 2019) Ông An gửi
100
triệu vào tiết kiệm ngân hàng theo thể
thức lãi kép trong một thời gian khá lâu mà không rút ra với lãi suất ổn định trong mấy chục năm
qua là
10% /1
năm. Tết năm nay do ông kẹt tiền nên rút hết ra để gia đình đón Tết. Sau khi rút cả
vốn lẫn lãi, ông trích ra gần
10
triệu để sắm sửa đồ Tết trong nhà thì ông còn
250
triệu. Hỏi ông
đã gửi tiết kiệm bao nhiêu lâu?
A.
10
năm B.
17
năm C.
15
năm D.
20
năm
Lời giải
Chọn A
Số tiền ông An tích lũy được gồm cả vốn và lãi là
260
triệu
Công thức tính lãi kép
1
n
n
A A r
6 6
260.10 100.10 1 10%
n
10
n
Câu 15. Một học sinh
A
khi
15
tuổi được hưởng tài sản thừa kế
200 000 000
VNĐ. Số tiền này được bảo
quản trong ngân hàng
B
với kì hạn thanh toán
1
năm và học sinh
A
chỉ nhận được số tiền này
khi
18
tuổi. Biết rằng khi
18
tuổi, số tiền mà học sinh
A
được nhận sẽ là
231 525 000
VNĐ.
Vậy lãi suất kì hạn một năm của ngân hàng
B
là bao nhiêu?
A.
8% /
năm. B.
7% /
năm. C.
6% /
năm. D.
5% /
năm.
Lời giải
Ta có: số tiền nhận được của gốc và lãi là:
3
200 000 000 1 231 525 000
r
5%
r
/năm
Câu 16. (THPT Minh Khai Hà Tĩnh 2019) Ông Anh gửi vào ngân hàng
60
triệu đồng theo hình thức
lãi kép. Lãi suất ngân hàng là
8%
trên năm. Sau
5
năm ông An tiếp tục gửi thêm
60
triệu đồng
nữa. Hỏi sau
10
năm kể từ lần gửi đầu tiên ông An đến rút toàn bộ tiền gốc và tiền lãi được là bao
nhiêu? (Biết lãi suất không thay dổi qua các năm ông gửi tiền).
A.
231,815
(triệu đồng). B.
197,201
(triệu đồng).
C.
217,695
(triệu đồng). D.
190,271
(triệu đồng).
Lời giải
Số tiền ông An nhận được sau
5
năm đầu là:
5
60 1 8% 88,160
(triệu đồng)
Số tiền ông An nhận được (toàn bộ tiền gốc và tiền lãi) sau
10
năm là:

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
5
88,16 60 1 8% 217,695
(triệu đồng).
Câu 17. (Chuyên Vĩnh Phúc 2019) Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền
T
theo hình thức lãi kép với lãi suất
0,6%
mỗi tháng. Biết sau
15
tháng người đó có số tiền là
10
triệu đồng. Hỏi số tiền
T
gần với số tiền nào nhất trong các số sau.
A.
613.000
đồng B.
645.000
đồng C.
635.000
đồng D.
535.000
đồng
Lời giải
Ta có: Số tiền cả lãi lẫn gốc sau
15
tháng gửi:
15
15
1 1 1
T
S r r
r
Vậy:
15
10.000.000 1 0,006 1 0,00
635.301
6 1
0,006
T
T
Câu 18. (Chuyên Hùng Vương Gia Lai 2019) Anh Nam gửi 100 triệu đồng vào ngân hàng theo thể thức
lãi kép kì hạn là một quý với lãi suất 3% một quý. Sau đúng 6 tháng anh Nam gửi thêm 100 triệu
đồng với kì hạn và lãi suất như trước đó.Hỏi sau 1 năm số tiền (cả vốn lẫn lãi) anh Nam nhận
được là bao nhiêu? ( Giả sử lãi suất không thay đổi).
A.
218,64
triệu đồng. B.
208,25
triệu đồng.
C.
210,45
triệu đồng. D.
209,25
triệu đồng.
Lời giải
• Số tiền anh Nam nhận được sau 6 tháng (tức 2 quý) là:
2
0
1 0
100 1 3 / 106,09
T
triệu đồng.
• Số tiền anh Nam nhận được sau một năm (tức 2 quý còn lại của năm) là:
2
0
2 0
106,09 100 1 3 / 218,64
T
triệu đồng.
Câu 19. (Chuyên Sơn La 2019) Ông A gửi vào ngân hàng
50
triệu đồng với lãi suất
0, 5% /
tháng. Hỏi
sau ít nhất bao nhiêu tháng thì ông A có được số tiền cả gốc lẫn lãi nhiều hơn 60 triệu đồng? Biết
rằng trong suốt thời gian gửi, lãi suất ngân hàng không đổi và ông A không rút tiền ra.
A.
36
tháng. B.
38
tháng. C.
37
tháng. D.
40
tháng.
Lời giải
Gọi
A
là số tiền gửi vào ngân hàng,
r
là lãi suất,
T
là số tiền cả gốc lẫn lãi thu được sau
n
tháng. Ta có
1
n
T A r
.
Theo đề
1,005
6
50. 1,005 60 log 36,6
5
n
T n
.
Vậy sau ít nhất
37
tháng thì ông A thu được số tiền cả gốc lẫn lãi hơn 60 triệu.
Câu 20. (Chuyên Lê Hồng Phong Nam Định 2019) Một người gửi
300
triệu đồng vào một ngân hàng
với lãi suất
7%/
năm. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi
sẽ được nhập vào gốc để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó nhận
được số tiền nhiều hơn
600
triệu đồng bao gồm cả gốc và lãi? Giả định trong suốt thời gian gửi,
lãi suất không đổi và người đó không rút tiền ra.
A.
9
năm. B.
10
năm. C.
11
năm. D.
12
năm.
Lời giải
Kí hiệu số tiền gửi ban đầu là
A
, lãi suất một kì hạn là
m
thì số tiền cả gốc và lãi có được sau
n
kì hạn là
. 1
n
A m
.
Do đó, số tiền cả gốc và lãi người đó nhận được sau
n
năm là
300.1,07
n
triệu đồng.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Số tiền cả gốc và lãi nhận được nhiều hơn
600
triệu đồng
300.1,07 600
n
1,07
log 2 10,245
n
.
Vậy sau ít nhất
11
năm thì người đó nhận được số tiền nhiều hơn
600
triệu đồng bao gồm cả gốc
và lãi.
Câu 21. (THPT Gia Lộc Hải Dương 2019) Anh Bảo gửi 27 triệu đồng vào ngân hàng theo thể thức lãi
kép, kỳ hạn là một quý, với lãi suất
1,85%
một quý. Hỏi thời gian tối thiểu bao nhiêu để anh Bảo
có được ít nhất 36 triệu đồng tính cả vỗn lẫn lãi?
A. 16 quý. B. 20 quý. C. 19 quý. D. 15 quý.
Lời giải
Bài toán lãi kép:
Kí hiệu số tiền gửi ban đầu là
A
, lãi suất một kì hạn là
%r
thì số tiền cả gốc và lãi có được sau
n
kì hạn là
. 1 %
n
n
S A r
.
Anh Bảo nhận được số tiền ít nhất 36 triệu đồng tính cả vốn và lãi nên ta có:
27 1 1,85% 36 15.693
n
n
.
Vậy thời gian tối thiểu để anh Bảo nhận được ít nhất 36 triệu đồng tính cả vốn lẫn lãi là 16 quý.
Câu 22. (Sở Bắc Giang 2019) Ông An gửi 100 triệu đồng vào một ngân hàng với lãi suất 0,8%/ tháng.
Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng số tiền lãi sẽ được nhập vào
gốc để tính lãi cho tháng tiếp theo và từ tháng thứ hai trở đi, mỗi tháng ông gửi them vào tài
khoản với số tiền 2 triệu đồng. Hỏi sau đúng 2 năm số tiền ông An nhận được cả gốc lẫn lãi là bao
nhiêu? Biết rằng trong suốt thời gian gửi lãi suất không thay đổi và ông An không rút tiền ra (kết
quả được làm tròn đến hàng nghìn).
A.
169.871.000
đồng. B.
171.761.000
đồng. C.
173.807.000
đồng. D.
169.675.000
đồng.
Lời giải
Với 100 triệu ban đầu số tiền cả lãi và gốc thu được sau hai năm là
24
6
1
100. 1 0,8% .10 121074524
T
Mỗi tháng tiếp theo gửi 2 triệu thì tổng số tiền cả lãi và gốc là
23
6
2
2
. 1 0,008 1 . 1 0,008 10 50686310
0,008
T
Vậy tổng số tiền là
1 2
171.761.000
T T T
Câu 23. Năm 2020, một hãng xe ô tô niêm yết giá bán loại xe X là 900.000.000 đồng và dự định trong 10
năm tiếp theo, mỗi năm giảm 2% giá bán so với giá bán năm trước. Theo dự định đó, năm 2025
hãng xe ô tô niêm yết giá bán loại xe X là bảo nhiêu ( kết quả làm tròn đến hàng nghìn)?
A. 810.000.000. B. 813.529.000. C. 797.258.000. D. 830.131.000.
Lời giải
Chọn B
Ta có:
2
900.000.000,
100
A r
Năm 2021 giá xe niêm yết là:
1
T A Ar
Năm 2022 giá xe niêm yết là
2
2
1
T A Ar A Ar r A r
.
Năm 2025 giá xe niêm yết là:
5
5 4 4
1
T T T r A r
5
5
2
900.000.000 1 813.529.000
100
T

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
Câu 24. (Mã 104 - 2020 Lần 2) Năm
2020
, một hãng xe ô tô niêm yết giá bán loại xe
X
là
850.000.000
đồng và dự định trong
10
năm tiếp theo, mỗi năm giảm
2%
giá bán của năm liền trước. Theo dự
định đó, năm
2025
hãng xe ô tô niêm yết giá bán xe
X
là bao nhiêu (kết quả làm tròn đến hàng
nghìn)?
A.
768.333.000
đồng. B.
765.000.000
đồng. C.
752.966.000
đồng. D.
784.013.000
đồng.
Lời giải
Chọn A
Giá bán xe năm đầu tiên:
1
850.000.000
A
đồng.
Giá bán xe năm thứ hai:
2 1 1 1
. 1
A A A r A r
đồng, với
2%
r
.
Giá bán xe năm thứ ba:
2
3 2 2 2 1
1 1
A A A r A r A r
đồng.
…
Giá bán xe năm thứ
n
:
1
1
1
n
n
A A r
đồng.
Vậy giá bán xe năm thứ 6 là
5 5
6 1
1 850.000.000. 1 2% 768.333.000
A A r
đồng.
Câu 25. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Một ngân hàng
X
, quy định về số tiền nhận
được của khách hàng sau
n
năm gửi tiền vào ngân hàng tuân theo công thức
( ) (1 8%)
P n A
,
trong đó
A
là số tiền gửi ban đầu của khách hàng. Hỏi số tiền ít nhất mà khách hàng B phải gửi
vào ngân hàng
X
là bao nhiêu để sau ba năm khách hàng đó rút ra được lớn hơn
850
triệu đồng
(Kết quả làm tròn đến hàng triệu)?.
A.
675
triệu đồng. B.
676
triệu đồng.
C.
677
triệu đồng. D.
674
triệu đồng.
Lời giải
Chọn A
Ta có
( ) (1 8%)
n
P n A
.
Sau 3 năm số tiền khách hàng rút về lớn hơn
850
triệu đồng là:
3
3
850
850 (1 8%) 674,8
(1 8%)
A A
.
Vậy số tiền ít nhất mà khách hàng B phải gửi vào ngân hàng
X
là
675
triệu đồng.
Câu 26. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Ông tuấn gửi 100 triệu vào ngân hàng với
hình thức lãi kép, kỳ hạn 1 năm với lãi suất
8%
. Sau 5 năm ông rút toàn bộ tiền và dùng một nữa
để sửa nhà, số tiền còn lại ông tiếp tục gửi ngân hàng với lãi suất như lần trước. Số tiền lãi ông
tuấn nhận được sau 10 năm gửi gần nhất với giá trị nào dưới đây?
A.
46,933
triệu. B.
34,480
triệu. C.
81, 413
triệu. D.
107,946
triệu.
Lời giải
Chọn C
Năm năm đầu ông Tuấn có số tiền cả gốc và lãi là
5
1
100. 1 0.08 146,933
T
Sau khi sửa nhà số tiền còn lại gửi vào ngân hàng trong 5 năm thì số tiền cả gốc và lãi là
5
2
146,932
1 0.08 107,946.
2
T
Số tiền lãi trong 10 năm là
146,933 100 107,946 73,466 81,413.
L
Câu 27. (Nguyễn Huệ - Phú Yên - 2020) Dân số thế giới được ước tính theo công thức
.
ni
S Ae
, trong
đó
A
là dân số của năm lấy mốc,
S
là dân số sau
n
năm,
i
là tỷ lệ tăng dân số hàng năm. Biết
năm
2005
dân số của thành phố Tuy Hòa là khoảng
202.300
người và tỉ lệ tăng dân số là
1,47%
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hỏi với mức tăng dân số không đổi thì đến năm bao nhiêu dân số thành phố Tuy Hòa đạt được
255.000
người?
A.
2020
. B.
2021
. C.
2023
. D.
2022
.
Lời giải
Chọn B
Lấy năm
2005
làm mốc, khi đó
202.300
A
.
Giả sử sau
n
năm thì dân số thành phố Tuy Hòa đạt được
255.000
người, tức là ta có
1,47
100
255.000 202.300
n
e
255000
100 ln 15,75
202300
n
năm.
Vậy đến năm
2021
thì dân số thành phố Tuy Hòa đạt được
255.000
người.
Câu 28. (Tiên Du - Bắc Ninh - 2020) Số ca nhiễm Covid – 19 trong cộng đồng ở một tỉnh vào ngày thứ
x
trong một giai đoạn được ước tính theo công thức
.e
rx
f x A
trong đó
A
là số ca nhiễm ở
ngày đầu của giai đoạn,
r
là tỷ lệ gia tăng số ca nhiễm hàng ngày của giai đoạn đó và trong cùng
một giai đoạn thì
r
không đổi. Giai đoạn thứ nhất tính từ ngày tỉnh đó có 9 ca bệnh đầu tiên và
không dùng biện pháp phòng chống lây nhiễm nào thì đến ngày thứ 6 số ca bệnh của tỉnh là 180
ca. Giai đoạn thứ hai (kể từ ngày thứ 7 trở đi) tỉnh đó áp dụng các biện pháp phòng chống lây
nhiễm nên tỷ lệ gia tăng số ca nhiễm hàng ngày giảm đi 10 lần so với giai đoạn trước. Đến ngày
thứ 6 của giai đoạn hai thì số ca mắc bệnh của tỉnh đó gần nhất với số nào sau đây?
A.
242
. B.
16
. C.
90
. D.
422
.
Lời giải
Chọn A
* Giai đoạn 1:
Ta có:
6
1
180 9.e ln 20
6
r
r
* Giai đoạn 2:
Đến ngày thứ 6 số ca mắc bệnh của tỉnh là
. 6
10
( ) 180.e 242
r
f x
Câu 29. (Kìm Thành - Hải Dương - 2020) Anh Việt vay tiền ngân hàng
500
triệu đồng mua nhà và trả
góp hàng tháng. Cuối mỗi tháng bắt đầu từ tháng thứ nhất anh trả
10
triệu đồng và chịu lãi suất là
0,9%
/ tháng cho số tiền chưa trả. Với hình thức hoàn nợ như vậy thì sau bao lâu anh Việt sẽ trả
hết số nợ ngân hàng?
A.
65
tháng. B.
66
tháng. C.
67
tháng. D.
68
tháng.
Lời giải
Chọn C
Gọi A là số tiền vay ngân hàng;
r
là lãi suất hàng tháng cho số tiền còn nợ;
m
là số tiền trả nợ
hàng tháng;
n
là thời gian trả hết nợ.
Để trả hết nợ thì
1 1 1 0
n n
m
A r r
r
10
500 1 0,9% 1 0,9% 1 0
0,9%
n n
20
1 0,9%
11
n
1 0,9%
20
log 66,72
11
n

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
Vậy sau 67 tháng anh Việt trả hết nợ.
Câu 30. (Thanh Chương 1 - Nghệ An - 2020) Dân số thế giới được ước tính theo công thức
.
ni
S Ae
,
trong đó
A
là dân số của năm lấy làm mốc,
S
là dân số sau
n
năm,
i
là tỉ lệ tăng dân số hằng
năm. Dân số Việt Nam năm 2019 là
95,5
triệu người, tỉ lệ tăng dân số hằng năm từ 2009 đến nay
là
1,14%
. Hỏi dân số Việt Nam năm 2009 gần với số nào nhất trong các số sau?
A.
94,4
triệu người. B.
85,2
triệu người. C.
86,2
triệu người. D.
83,9
triệu người.
Lời giải
Chọn B
Áp dụng công thức
.
ni
S Ae
trong đó:
95,5
S
triệu người,
10
n
năm,
1,14%
i
Ta có số dân Việt Nam năm 2009 là:
10.1,14%
95,5
85,2
ni
S
A
e e
triệu người
Câu 31. (Tiên Lãng - Hải Phòng - 2020) Ông An dự định gửi vào ngân hàng một số tiền với lãi suất
không đổi là 7% một năm. Biết rằng cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu để
tính lãi cho năm kế tiếp. Tính số tiền tối thiểu
x
(triệu đồng,
x
) ông An gửi vào ngân hàng để
sau 3 năm số tiền lãi đủ mua một chiếc xe gắn máy giá trị 45 triệu đồng.
A. 200. B. 190. C. 250. D. 150.
Lời giải
Chọn A
Áp dụng công thức
1 .
n
o
P P r
Số tiền ông An có được sau 3 năm là:
3
1 0,07 .
P x
Tiền lãi ông An có được sau 3 năm là:
3 3
1 0,07 1 0,07 1 .
P x x x x
Số tiền lãi trên là 45 triệu đồng nên:
3
1 0,07 1 45 199,96
x x
Câu 32. (Đề Minh Họa 2020 Lần 1) Để dự báo dân số của một quốc gia, người ta sử dụng công thức
;
nr
S Ae
trong đó
A
là dân số của năm lấy làm mốc tính,
S
là dân số sau
n
năm,
r
là tỉ lệ tăng
dân số hàng năm. Năm 2017, dân số Việt nam là
93.671.600
người (Tổng cục Thống kê, Niên
giám thống kê 2017, Nhà xuất bản Thống kê, Tr 79). Giả sử tỉ lệ tăng dân số hàng năm không đổi
là
0,81%,
dự báo dân số Việt nam năm 2035 là bao nhiêu người (kết quả làm tròn đến chữ số
hàng trăm)?
A.
109.256.100
. B.
108.374.700
. C.
107.500.500
. D.
108.311.100
.
Lời giải
Chọn B
Lấy năm 2017 làm mốc, ta có
93.671.600; 2035 2017 18
A n
Dân số Việt Nam vào năm 2035 là
.
0,
1
81
100
8
93.671.600. 108.374.700
S e
Câu 33. (Đề Tham Khảo 2020 Lần 2) Để quảng bá cho sản phẩm A, một công ty dự định tổ chức quảng
cáo theo hình thức quảng cáo trên truyền hình. Nghiên cứu của công ty cho thấy: nếu sau
n
lần
quảng cáo được phát thì tỉ lệ người xem quảng cáo đó mua sản phẩm A tuân theo công thức
0,015
1
1 49e
n
P n
. Hỏi cần phát ít nhất bao nhiêu lần quảng cáo để tỉ lệ người xem mua sản
phẩm đạt trên
30%?
A.
202
. B.
203
. C.
206
. D.
207
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn B
Theo bài ra ta có
0,015
1
0,3
1 49e
n
0,015
10
1 49e
3
n
0,015
7
e
147
n
7
0,015 ln
147
n
1 7
ln 202,97
0,015 147
n
.
Vậy ít nhất 203 lần quảng cáo.
Câu 34. (Sở Hà Nội 2019) Cường độ ánh sáng đi qua môi trường nước biển giảm dần theo công thức
0
e
x
I I
, với
0
I
là cường độ ánh sáng lúc ánh sáng bắt đầu đi vào môi trường nước biển và
x
là
độ dày của môi trường đó (
x
tính theo đơn vị mét). Biết rằng môi trường nước biển có hằng số
hấp thụ là
1,4
. Hỏi ở độ sâu 30 mét thì cường độ ánh sáng giảm đi bao nhiêu lần so với
cường độ ánh sáng lúc ánh sáng bắt đầu đi vào nước biển?
A.
21
e
lần. B.
42
e
lần. C.
21
e
lần. D.
42
e
lần
Lời giải:
Khi mới bắt đầu đi vào môi trường nước biển thì
0
x
1
.e
o
o
I I
Ở độ sâu 30 mét thì
.30
2
e.
o
I I
Vậy ta có:
.30
42
2
2 1
1
e
e
e
.
.
.
o
o
o
I
I
I I
I I
, vậy
2
I
tăng
42
e
lần so với
1
I
, nói cách khác,
2
I
giảm
42
e
lần so với
1
I
Câu 35. (Chuyên Lê Quý Đôn Điện Biên 2019) Một người thả một lá bèo vào một chậu nước. Sau 12
giờ, bèo sinh sôi phủ kín mặt nước trong chậu. Biết rằng sau mỗi giờ lượng bèo tăng gấp 10 lần
lượng bèo trước đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì bèo phủ kín
1
5
mặt nước trong
chậu (kết quả làm tròn đến 1 chữ số phần thập phân).
A.
9,1
giờ. B.
9,7
giờ. C.
10,9
giờ. D.
11,3
giờ.
Lời giải
Gọi
S
là diện tích lá bèo thả ban đầu.
Vì sau mỗi giờ, lượng bèo tăng gấp 10 lần lượng bèo trước đó nên sau 12 giờ, tổng diện tích các lá
bèo trong chậu là
12
10 S
.
Theo đề bài: Sau 12 giờ, bèo phủ kín mặt nước trong chậu nên diện tích mặt nước trong chậu là
12
10 S
. Giả sử sau
x
giờ thì bèo phủ kín
1
5
mặt nước trong chậu.
Ta có:
12
1
10 .10
5
x
S S
12
10 5
x
12 log5 11,3
x
.
Vậy sau
11,3
giờ thì bèo phủ kín
1
5
mặt nước trong chậu.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
Câu 36. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Cho biết sự tăng dân số được ước tính theo công
thức
.
Nr
S A e
(trong đó
A
là dân số của năm lấy làm mốc tính,
S
là dân số sau
N
năm,
r
là tỉ
lệ tăng dân số hằng năm). Đầu năm 2010 dân số tỉnh Bắc Ninh là
1.038.229
người tính đến đầu
năm 2015 dân số của tỉnh là
1.153.600
người. Hỏi nếu tỉ lệ tăng dân số hằng năm giữ nguyên thì
đầu năm 2020 dân số của tỉnh nằm trong khoảng nào?
A.
1.281.600;1.281.700
. B.
1.281.700;1.281.800
.
C.
1.281.800;1.281.900
. D.
1.281.900;1.282.000
.
Lời giải
Chọn B
Áp dụng công thức
.
Nr
S A e
từ đầu năm 2010 đến đầu năm 2015 ta có:
5
1
1038229. ln
5 10
1153600
11536
9
00
3822
r
e r
.
Đầu năm 2020 dân số của tỉnh Bắc Ninh là
115361 0
ln
5 1038
0
2
.
2 9
10
10382
. 1281792
29S e
người.
Vậy Chọn B.
Câu 37. (Chuyên Bắc Ninh - 2020) Anh Dũng đem gửi tiết kiệm số tiền là 400 triệu đồng ở hai loại kỳ
hạn khác nhau. Anh gửi 250 triệu đồng theo kỳ hạn 3 tháng với lãi suất
%x
một quý. Số tiền còn
lại anh gửi theo kỳ hạn 1 tháng với lãi suất
0,25%
một tháng. Biết rằng nếu không rút lãi thì số
lãi sẽ được nhập vào số gốc để tính lãi cho kỳ hạn tiếp theo. Sau một năm số tiền cả gốc và lãi của
anh là 416.780.000 đồng. Tính
x
.
A.
1,2
. B.
0,8
. C.
0,9
. D. 1,5.
Lời giải
Chọn A
+ Xét bài toán ông B gửi tiết kiệm số tiền
A
đồng với lãi suất
r
cho 1 kỳ hạn. Biết rằng nếu
không rút lãi thì số lãi sẽ được nhập vào số gốc để tính lãi cho kỳ hạn tiếp theo. Hỏi sau
n
kỳ hạn
số tiền cả gốc và lãi của ông B là bao nhiêu nếu trong thời gian gửi lãi suất không thay đổi?
- Sau 1 kì hạn số tiền cả gốc và lãi mà ông B có được là
1
. 1
T A A r A r
.
- Sau 2 kì hạn số tiền cả gốc và lãi mà ông B có được là
2 1 1 1
. 1
T T T r T r
2
1
A r
.
- Tổng quát ông B có số tiền cả gốc và lãi sau
n
kì hạn là
1
n
n
T A r
1
.
+ Áp dụng công thức
1
cho bài toán đề cho, gọi S là số tiền cả gốc và lãi anh Dũng có sau một
năm gửi, ta có :
4 12
250 1 % 150 1 0,25%
S x
(triệu đồng).
416,78
S
(triệu đồng)
4 12
250 1 % 150 1 0,25% 416,78
x
1,2
x
.
Vậy
1,2
x
.
Câu 38. (Chuyên Lê Quý Đôn – Điện Biên 2019) Một người thả một lá bèo vào một chậu nước. Sau 12
giờ bèo sinh sôi phủ kín mặt nước trong chậu. Biết rằng sau mỗi giờ lượng bèo tăng gấp 10 lần
lượng bèo trước đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì bèo phủ kín
1
5
mặt nước trong
chậu (kết quả làm tròn đến một chữ số phần thập phân)?
A. 9,1 giờ. B. 9,7 giờ. C. 10,9 giờ. D. 11,3 giờ.
Lời giải
Chọn D
Sau mỗi giờ, lượng lá bèo phủ trên mặt nước là:
10 1 12
n
n
.
Lượng lá bèo phủ kín mặt nước trong chậu (sau 12 giờ) là:
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
13
2 12
10 1
1 10 10 ... 10
9
S
Do đó, lượng lá bèo cần để phủ
1
5
mặt nước trong chậu là
13
10 1
.
45
Giả sử sau
t
giờ, lá bèo phủ kín được
1
5
mặt nước trong chậu, ta có
1 13
2
10 1 10 1
1 10 10 ... 10
9 45
t
t
13
1
10 4
10 11,3.
5
t
t
Câu 39. (Bình Giang-Hải Dương 2019) Một công ty vừa tung ra thị trường sản phẩm mới và họ tổ chức
quảng cáo trên truyền hình mỗi ngày. Một nghiên cứu thị trường cho thấy, nếu sau
x
lần quảng
cáo được phát thì số
%
người xem mua sản phẩm là
0.015
100
, 0
1 49e
x
P x x
. Hãy tính số lần
quảng cáo được phát tối thiểu để số
%
người xem mua sản phẩm đạt hơn
75%
.
A.
323
. B.
343
. C.
330
. D.
333
.
Lời giải
Chọn D
Theo yêu cầu bài toán ta có:
0.015 0.015
0.015
100 4 1
75 1 49e e
1 49e 3 147
1
ln
1
147
0.015 ln 332.7
147 0.015
x x
x
P x
x x
Vậy số lần quảng cáo tối tiểu là
333
lần.
Câu 40. Áp suất không khí
P
(đo bằng milimet thủy ngân, kí hiệu là mmHg) suy giảm mũ so với độ cao
x
(so với mặt nước biển)(đo bằng mét) theo công thức
0
.
xi
P P e
, trong đó
0
760mmHg
P
là áp
suất ở mực nước biển
0
x
,
i
là hệ số suy giảm. Biết rằng ở độ cao
1000 m
thì áp suất của
không khí là
672,71mmHg
. Hỏi áp suất không khí ở độ cao
3343m
là bao nhiêu (làm tròn đến
hàng phần trăm)?
A.
505, 45 mmHg
. B.
530,23mmHg
. C.
485,36 mmHg
. D.
495,34 mmHg
.
Lời giải
Chọn A
Ở độ cao
1
1000m
x
thì áp suất không khí
1
672,71mmHg
P
. Suy ra
1
1 0
.
x i
P P e
1
1
0
ln
P
x i
P
1
0
1
ln
P
P
i
x
4
1,22.10
.
Áp suất không khí
2
P
ở độ cao
2
3343m
x
là:
2
2 0
.
x i
P P e
4
3343.( 1.22.10 )
760.e
505,46 mmHg
.
Câu 41. Số lượng loại vi khuẩn
A
trong một phòng thí nghiệm được tính theo công thức
( ) (0).2
t
s t s
,
trong đó
(0)s
là số lượng vi khuẩn
A
lúc ban đầu,
( )s t
là số lượng vi khuẩn
A
có sau
t
phút.
Biết sau 3 phút thì số vi khuẩn
A
là 625 nghìn con. Hỏi sau bao lâu kể từ lúc ban đầu, số lượng
loại vi khuẩn
A
là 20 triệu con.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
A. 7 phút. B. 12 phút. C. 48 phút. D. 8 phút.
Lời giải
Chọn D
Theo giả thiết ta có:
3
(3) 625000 (0).2 625000 (0) 78125
s s s .
Số lượng loại vi khuẩn
A
là 20 triệu con khi
20000000 20000000
( ) 20000000 (0).2 20000000 2 256 8
(0) 78125
t t
s t s t
s
.
Vậy, sau 8 phút thì số lượng vi khuẩn
A
là 20 triệu con.
NHỮNG CÂU HỎI KHÓ HƠN VỀ BÀI TOÁN THỰC TẾ
Câu 1. (Đề Minh Họa 2017) Ông A vay ngắn hạn ngân hàng 100 triệu đồng, với lãi suất 12%/năm. Ông
muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn
nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là như nhau và
trả hết tiền nợ sau đúng 3 tháng kể từ ngày vay. Hỏi, theo cách đó, số tiền
m
mà ông A sẽ phải trả
cho ngân hàng trong mỗi lần hoàn nợ là bao nhiêu? Biết rằng, lãi suất ngân hàng không thay đổi
trong thời gian ông A hoàn nợ.
A.
3
3
120.(1,12)
(1,12) 1
m
(triệu đồng) B.
3
100.(1,01)
3
m
(triệu đồng)
C.
3
3
(1,01)
(1,01) 1
m
(triệu đồng) D.
100.1,03
3
m
(triệu đồng)
Lời giải
Chọn C
Theo đề ta có: ông A trả hết tiền sau 3 tháng vậy ông A hoàn nợ 3 lần
Với lãi suất 12%/năm suy ra lãi suất một tháng là 1%
Hoàn nợ lần 1:
-Tổng tiền cần trả (gốc và lãi) là :
100.0, 01 100 100.1, 01
(triệu đồng)
- Số tiền dư :
100.1, 01 m
(triệu đồng)
Hoàn nợ lần 2:
- Tổng tiền cần trả (gốc và lãi)
là :
2
100.1,01 .0,01 100.1,01 100.1,01 .1,01 100. 1,
01 1,01.m m m m
(triệu đồng)
- Số tiền dư:
2
100. 1,01 1,01.
m m
(triệu đồng)
Hoàn nợ lần 3:
- Tổng tiền cần trả (gốc và lãi) là :
2 3 2
100. 1,01 1,01. .1,01 100. 1,01 1,01 1,01m m m m
(triệu đồng)
- Số tiền dư:
3 2
100. 1,01 1,01 1,01
m m m
(triệu đồng)
3
3 2
2
100. 1,01
100. 1,01 1,01 1,01 0
1,01 1,01 1
m m m m
3 3
3
2
100. 1,01 . 1,01 1 1,01
1,01 1
1,01 1,01 1 . 1,01 1
m
(triệu đồng).
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 2. (Đề Tham Khảo 2019) Ông A vay ngân hàng 100 triệu đồng với lãi suất 1%/tháng. Ông ta muốn
hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai
lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi tháng là như nhau và ông
A trả hết nợ sau đúng năm năm kể từ ngày vay. Biết rằng mỗi tháng ngâng hàng chỉ tính lãi trên
số dư nợ thực tế của tháng đó. Hỏi số tiền mỗi tháng ông ta cần trả cho ngâng hàng gần nhất với
số tiền nào dưới đây?
A.
2,20
triệu đồng B.
2,22
triệu đồng C.
3,03
triệu đồng D.
2,25
triệu đồng
Lời giải
Chọn B
Ta xây dựng bài toán tổng quát như sau
Gọi số tiền người đó vay ngâng hàng là
0
V
triệu đồng
Số tiền hàng tháng người đó phải trả là
a
triệu đồng
Lãi suất là
r
%/ tháng
Vậy số tiền nợ ngân hàng sau tháng thứ nhất là
0
1 0,0V r
Số tiền người đó còn nợ ngân hàng sau khi trả tiền tháng 1 là
1 0
1 0,0
T V r a
Số tiền người đó còn nợ ngân hàng sau khi trả tiền tháng 2 là
2 1
2
1 0,0
1 0,0 1 0,0
1 0,0 1 0,0
o
o
T T r a
V r a r a
V r a r a
Số tiền người đó còn nợ ngâng hàng sau tháng thứ n là
1
1 0,0 1 0,0 ... 1 0, 0
n n
n o
T V r a r a r a
Vì sau n tháng thì trả hết tiền nên ta có
1
1
0 1 0,0 1 0,0 ... 1 0,0 0
1 0,0 1 0,0 ... 1 0,0 1
1 0,0 1
1 0,0
1 0,0 1
.0,0 . 1 0,0
1 0,0 1
n n
n o
n n
o
n
n
o
n
o
n
T V r a r a r a
V r a r r
r
V r a
r
V r r
a
r
Áp dụng
60
60
100.0,01 1,01
2,224444768
1,01 1
a
Câu 3. (Đại Học Hà Tĩnh - 2020) Đầu mỗi tháng anh A gửi vào ngân hàng 3 triệu đồng với lãi suất kép
là
0,6%
mỗi tháng. Hỏi sau ít nhất bao nhiêu tháng (khi ngân hàng đã tính lãi) thì anh A có được
số tiền cả lãi và gốc nhiều hơn 100 triệu, biết lãi suất không đổi trong qua trình gửi.
A.
31
tháng. B.
40
tháng. C.
35
tháng. D.
30
tháng.
Lời giải
Chọn A
+ Đặt
1a r
và M. Trong đó M là số tiền góp vào hàng tháng, r là lãi suất hàng tháng.
Tiền gốc và lãi anh A nhận trong tháng thứ nhất là:
1
. .T M M r M a
.
Tiền gốc và lãi anh A nhận trong tháng thứ hai là:
2
2
. .
T M a M M a M r Ma Ma

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
…
Tương tự tiền gốc và lãi anh A nhận trong tháng thứ n là:
1 1 2
1
... ... 1 . 1 1 1
1
n
n
n n n n
n
a M
T Ma Ma Ma Ma a a Ma r r
a r
+ Sau tháng thứ n anh A gửi vào ngân hàng 3 triệu đồng với lãi suất kép là
0,6%
mỗi tháng và
nhận được số tiền nhiều hơn 100 triệu, khi đó ta có:
3
1 0,6% 1 1 0,6% 100 30,3
0,6%
n
n
Vậy sau ít nhất 31 tháng thì anh A mới có được số tiền nhiều hơn 100 triệu.
Câu 4. (Sở Hà Tĩnh - 2020) Một người vay tiền ở một ngân hàng theo hình thức lãi kép với lãi suất
0,7%
/ tháng với tổng số tiền vay là 1 tỉ đồng. Mỗi tháng người đó đều trả cho ngân hàng một số
tiền như nhau để trừ vào tiền gốc và lãi. Biết rằng đúng 25 tháng thì người đó trả hết gốc và lãi
cho ngân hàng. Hỏi số tiền của người đó trả cho ngân hàng ở mỗi tháng gần nhất với số nào sau
đây?
A.
43.730.000
đồng. B.
43.720.000
đồng.
C.
43.750.000
đồng. D.
43.740.000
đồng.
Lời giải
Chọn D
Gọi
M
là số tiền vay ban đầu.
Gọi
A
là số tiền mà hàng tháng người đó trả cho ngân hàng.
Sau tháng 1 dư nợ còn lại là:
.1,007
M A
Sau tháng 2 dư nợ còn lại là:
2
.1,007 .1,007 .1,007 .1,007
M A A M A A
Sau tháng 3 dư nợ còn lại là:
2
2 3
.1,007 .1,007 .1,007 .1,007 . 1,007 1,007 1
M A A A M A
.
Sau tháng thứ
n
dư nợ còn lại là:
1
2
.1,007 . 1,007 1,007 ... 1,007 1
n
n n
M A
.
Vì đúng 25 tháng thì trả hết nợ nên:
24
25 23
1.1,007 . 1,007 1,007 ... 1,007 1 0
A
25
24
25 23 25
1,007 1
1,007 . 1,007 1,007 ... 1,007 1 1,007 .
0,007
A A
.
25
25
1,007 .0,007
0,04374151341
1,007 1
A
tỉ đồng
43.741.513
đồng
43.740.000
đồng.
Câu 5. (Sở Bình Phước - 2020) Một sinh viên ra trường đi làm ngày 1/1/2020 với mức lương khởi điểm
là
a
đồng mỗi tháng và cứ sau 2 năm lại được tăng thêm 10% và chi tiêu hàng tháng của anh ta là
40% lương. Anh ta dự định mua một căn hộ chung cư giá rẻ có giá trị tại thời điểm 1/1/2020 là 1
tỷ đồng và cũng sau 2 năm thì giá trị căn hộ tăng thêm 5%. Với a bằng bao nhiêu thì sau đúng 10
năm anh ta mua được căn hộ đó, biết rằng mức lương và mức tăng giá trị ngôi nhà là không đổi (
kết quả quy tròn đến hàng nghìn đồng).
A. 11.487.000 đồng. B. 14.517.000 đồng. C. 55.033.000 đồng. D. 21.776.000 đồng.
Lời giải
Chọn B
Áp dụng công thức
1 .
n
o
P P r
Ta được giá trị ngôi nhà sau 10 năm là:
5 5
9 9
10 1 0,05 10 . 1,05 .
P

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Sau khi chi tiêu hàng tháng thì số tiền Người sinh viên còn lại của mỗi tháng là 60% lương. Trong
hai năm 2020 - 2021, Người sinh viên có được số tiền là:
24 0, 6 .a
Trong hai năm 2022 - 2023, anh sinh viên có được số tiền là:
24 0,6 1 0,1 .a
Trong hai năm 2024 - 2025, anh sinh viên có được số tiền là:
2
24 0,6 1 0,1 .a
Trong hai năm 2026 - 2027, anh sinh viên có được số tiền là:
3
24 0,6 1 0,1 .a
Trong hai năm 2028 - 2029, anh sinh viên có được số tiền là:
4
24 0,6 1 0,1 .a
Tổng số tiền anh sinh viên có được sau 10 năm là:
2 3 4
2 3 4
5
24 0,6 24 0,6 1 0,1 24 0,6 1 0,1 24 0,6 1 0,1 24 0,6 1 0,1
24 0,6 1 1 0,1 1 0,1 1 0,1 1 0,1
1 1 0,1
0,61051
24 0,6 24 0,6 87,91344
1 1 0,1 0,1
a a a a a
a
a a a
Số tiền trên bằng giá trị của ngôi nhà sau 10 năm:
5
9
10 . 1, 05 87,91344 14.517.000a a
Câu 6. (Bỉm Sơn - Thanh Hóa - 2020) Một người vay ngân hàng
100
triệu đồng với lãi suất là
0,7% /
tháng theo thỏa thuận cứ mỗi tháng người đó sẽ trả cho ngân hàng
5
triệu đồng và cứ trả
hàng tháng như thế cho đến khi hết nợ (tháng cuối cùng có thể trả dưới
5
triệu). Hỏi sau bao
nhiêu tháng thì người đó trả được hết nợ ngân hàng?
A.
21
. B.
22
. C.
23
. D.
24
.
Lời giải
Chọn B
Gọi số tháng là
n
(
*n
). Đặt
5a
,
1,007q
. Đến lần nộp tiền thứ
n
:
Khoản tiền
a
đầu tiên trở thành
1
.
n
a q
. Khoản tiền
a
thứ hai trở thành
2
.
n
a q
. … Giả sử khoản
tiền cuối cùng vẫn là
a
thì tổng số tiền đã trả cả vốn lẫn lãi là
1 1,007 1
. 5.
1 0,007
n n
q
a
q
.
Số tiền
100
triệu đồng với lãi suất là
0,7% /
tháng, sau
n
tháng, sẽ trở thành
100. 1,007
n
.
Ta có phương trình
1,007 1
5. 100.1,007 21,6
0,007
n
n
n
.
Theo đề bài, tháng cuối cùng có thể trả dưới
5
triệu đồng nên số tháng phải làm tròn là
22
tháng.
Câu 7. (Lê Lai - Thanh Hóa - 2020) COVID19 là một loại bệnh viêm đường hô hấp cấp do chủng mới
của virus corona (nCoV) bắt nguồn từ Trung Quốc (đầu tháng 12/2019) gây ra với tốc độ truyền
bệnh rất nhanh (tính đến 7/4/2020 đã có 1 360 039 người nhiễm bệnh). Giả sử ban đầu có 1 người
bị nhiễm bệnh và cứ sau 1 ngày sẽ lây sang 4 người khác. Tất cả những người nhiễm bệnh lại tiếp
tục lây sang những người khác với tốc độ như trên (1 người lây 4 người). Hỏi sau 7 ngày sẽ có
tổng cộng bao nhiêu người nhiễm bệnh? (Biết rằng những người nhiễm bệnh không phát hiện bản
thân bị bệnh và không phòng tránh cách li, do trong thời gian ủ bệnh vẫn lây bệnh sang người
khác).
A. người. B. người. C. người. D. người.
Lời giải
Chọn D
Sau 1 ngày, tổng số người nhiễm bệnh là người.
Sau 2 ngày, tổng số người nhiễm bệnh là người.
77760
16384
62500
78125
1 4 5
2
1 4 1 4 .4 1 4

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
Sau 3 ngày, tổng số người nhiễm bệnh là người.
Sau 7 ngày, tổng số người nhiễm bệnh là người.
Ngoài ra chúng ta có thể áp dụng công thức lãi kép để tính nhanh:
, với , , .
Câu 8. (Liên trường Nghệ An - 2020) Ông
A
có số tiền
100000000
đồng gửi tiết kiệm theo thể thức
lãi kép, có hai loại kì hạn: loại kì hạn
12
tháng với lãi suất
12%
/năm và loại kì hạn
1
tháng với
lãi suất
1%
/tháng. Ông
A
muốn gửi
10
năm. Theo anh chị, kết luận nào sau đây đúng (làm tròn
đến hàng nghìn)?
A. Gửi theo kì hạn
1
tháng có kết quả nhiều hơn kì hạn
1
năm là
16186000
đồng sau
10
năm.
B. Cả hai loại kì hạn đều có cùng số tiền như nhau sau
10
năm.
C. Gửi theo kì hạn
1
tháng có kết quả nhiều hơn kì hạn
1
năm là
19454000
đồng sau
10
năm.
D. Gửi theo kì hạn
1
tháng có kết quả nhiều hơn kì hạn
1
năm là
15584000
đồng sau
10
năm.
Lời giải
Chọn C
Tổng số tiền ông
A
nhận được sau
10
năm khi gửi theo kì hạn
12
tháng là:
1
8 10
1 0 1
. 1 10 .1,12 310585000
n
T T r
(đồng).
Tổng số tiền ông
A
nhận được sau
10
năm khi gửi theo kì hạn
1
tháng là
2
8 120
2 0 2
. 1 10 .1,01 330039000
n
T T r
(đồng).
Như vậy, sau
10
năm, gửi theo kì hạn
1
tháng có kết quả nhiều hơn kì hạn
1
năm là:
2 1
330039000 310585000 19454000T T T
(đồng).
Câu 9. (Trần Phú - Quảng Ninh - 2020) Một người vay vốn ở ngân hàng với số tiền
50
triệu đồng, thời
hạn
50
tháng với lãi suất
1,15%
trên tháng, tính theo dư nợ trả đúng ngày quy định. Hỏi hàng
tháng người đó phải trả đều đặn vào ngân hàng một khoản tiền là bao nhiêu để đến cuối tháng thứ
50 thì người đó trả hết cả gốc lẫn lãi cho ngân hàng (làm tròn đến trăm đồng) ?
A.
1.018.500
đồng. B.
1.320.800
đồng. C.
1.320.500
đồng. D.
1.771.300
đồng.
Lời giải
Chọn C
Gọi
N
là số tiền vay ban đầu,
r
là lãi suất theo tháng,
A
là số tiền phải trả hàng tháng, ta có:
+ Số dư nợ sau 1 tháng là:
r 1N N A N r A
.
+ Số dư nợ sau 2 tháng là:
2 2
1 1 1 1 1
A
N r A N r A r A N r r
r
.
+ Số dư nợ sau 3 tháng là:
3 3
1 1 1
A
N r r
r
.
…
+ Số dư nợ sau n tháng là:
1 1 1
n n
A
N r r
r
.
Giả sử sau
n
tháng thì dư nợ bằng 0, ta có
1 .
1 1 1 0
1 1
n
n n
n
N r r
A
N r r A
r
r
.
Áp dụng với
50.000.000N
đồng,
r 1,15%
và
50n
tháng ta có:
1.320.500A
đồng.
Câu 10. (Chuyên Lam Sơn Thanh Hóa 2019) Để đủ tiền mua nhà, anh An vay ngân hàng
500
triệu theo
phương thức trả góp với lãi suất
0,85%
/tháng. Nếu sau mỗi tháng, kể từ thời điểm vay, anh An
trả nợ cho ngân hàng số tiền cố định là
10
triệu đồng bao gồm cả tiền lãi vay và tiền gốc. Biết
2 2 3
1 4 1 4 .4 1 4
7
1 4 78125
7
1 1. 1 4 78125
n
n
S A r
1A
4r
7
n

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
rằng phương thức trả lãi và gốc không thay đổi trong suốt quá trình anh An trả nợ. Hỏi sau bao
nhiêu tháng thì anh trả hết nợ ngân hàng? (Tháng cuối có thể trả dưới
10
triệu đồng).
A.
68
B.
66
C.
65
D.
67
Lời giải
Chọn B
Giả sử anh An vay số tiền là
A
với lãi suất
r
trên tháng và trả nợ cho ngân hàng số tiền cố định là
x. Anh An sau các tháng còn nợ ngân hàng với số tiền là:
Tháng thứ
1
:
1
A r x
Tháng thứ 2:
2
2 2
1 1
1 1 1 1 1 1 .
r
A r x r x A r r x A r x
r
Tháng thứ
3
:
3
3
1 1
1 .
r
A r x
r
…
Tháng thứ
n
:
1 1
1 .
n
n
r
A r x
r
Áp dụng công thức ta có:
500; 0,0085; 10
A r x
và sau
n
tháng trả hết nợ ta có:
1 0,0085 1
500. 1 0,0085 10. 0
0,0085
n
n
1,0085
1,0085 1
40 40
50. 1,0085 1,0085 log 65,4
0,0085 23 23
n
n n
n
Câu 11. (THPT Đoàn Thượng - Hải Dương 2019) Ông Chính gửi 200 triệu đồng vào một ngân hàng với
lãi suất
7%
năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ
được nhập vào gốc để tính lãi cho năm tiếp theo và từ năm thứ 2 trở đi, mỗi năm ông gửi thêm
vào tài khoản với số tiền 20 triệu đồng. Hỏi sau 18 năm số tiền ông Chính nhận được cả gốc lẫn
lãi là bao nhiêu? Giả định trong suốt thời gian gửi lãi suất không thay đổi và ông Chính không rút
tiền ra (kết quả được làm tròn đến hàng nghìn).
A.
1.686.898.000
VNĐ. B.
743.585.000
VNĐ.
C.
739.163.000
VNĐ. D.
1.335.967.000
VNĐ.
Lời giải
Gọi
200
a
triệu;
20
b
triệu;
7%
.
Số tiền sau 1 năm:
1a
.
Số tiền sau 2 năm:
2
1 1a b
.
Số tiền sau 3 năm:
3 2
1 1 1a b b
.
……………………
Số tiền sau 18 năm:
18 17 16
1 1 1 ... 1a b
17
18
1 1
1 1 .a b

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
Vậy số tiền ông Chính nhận sau 18 năm là:
1.335.967.000
VNĐ.
Câu 12. (Chuyên Vĩnh Phúc 2019) Một người gửi tiết kiệm số tiền
80000000
đồng với lãi suất
6,9%
/
năm. Biết rằng tiền lãi hàng năm được nhập vào tiền gốc, hỏi sau đúng 5 năm người đó rút được
cả tiền gốc lẫn tiền lãi gần với con số nào sau đây?
A.
105370000
đồng B.
111680000
đồng C.
107667000
đồng D.
116570000
đồng
Lời giải
Gọi
0
P
là số tiền gửi ban đầu,
r
là lãi suất / năm.
Số tiền gốc và lãi sau năm thứ nhất:
1 0 0 0
. 1
P P P r P r
.
Số tiền gốc và lãi sau năm thứ hai:
2
2 1 1 0
. 1
P P P r P r
.
….
Số tiền gốc và lãi người đó rút ra được sau 5 năm là
5 5
5 0
. 1 80000000. 1 6,9% 111680799
P P r
(đồng).
Câu 13. (Chuyên Vĩnh Phúc 2019) Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền
T
theo hình thức lãi kép với lãi suất
0,6%
mỗi tháng. Biết sau
15
tháng, người đó có số tiền là
10
triệu đồng. Hỏi số tiền
T
gần với số tiền nào nhất trong các số sau.
A.
613.000
đồng B.
645.000
đồng C.
635.000
đồng D.
535.000
đồng
Lời giải
Chọn C
Số tiền nhận được khi gửi khoản tiền
T
ở tháng đầu tiên là
15 15
(1 0,006) .1,006
T T
.
Số tiền nhận được khi gửi khoản tiền
T
ở tháng thứ 2 là
14 14
(1 0,006) .1,006
T T
.
Cứ như vậy, số tiền nhận được khi gửi khoản tiền
T
ở tháng thứ 14 là
(1 0,006) .1,006
T T
.
Vậy tổng số tiền nhận được sau
15
tháng là:
15
15 14 2
1,006 1
(1,006 1,006 ... 1,006 1,006) .1,006.
0,006
T T
.
Theo giả thiết có:
15
1,006 1
10000000 .1,006. 635301,46
0,006
T T
.
Câu 14. Một người muốn có
1
tỉ tiền tiết kiệm sau
6
năm gửi ngân hàng bằng cách bắt đầu từ ngày
01/01/2019 đến 31/12/2024, vào ngày 01/01 hàng năm người đó gửi vào ngân hàng một số tiền
bằng nhau với lãi suất ngân hàng là
7% /1
năm (tính từ ngày 01/01 đến ngày 31/12) và lãi suất
hàng năm được nhập vào vốn. Hỏi số tiền mà người đó phải gửi vào ngân hàng hàng năm là bao
nhiêu (với giả thiết lãi suất không thay đổi và số tiền được làm tròn đến đơn vị đồng)?
A.
130 650 280
(đồng). B.
130 650 000
(đồng).
C.
139 795 799
(đồng). D.
139 795 800
(đồng).
Lời giải
Chọn A
Gọi
0
T
là số tiền người đó gửi vào ngân hàng vào ngày 01/01 hàng năm,
n
T
là tổng số tiền cả vốn
lẫn lãi người đó có được ở cuối năm thứ
n
, với
*
n
,
r
là lãi suất ngân hàng mỗi năm.
Ta có:
1 0 0 0
1
T T rT T r
.
Đầu năm thứ
2
, người đó có tổng số tiền là:
2 2
0 0
0 0 0
1 1 1 1 1 1 1
1 1
T T
T r T T r r r
r
r
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 52 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Do đó:
2 2
2
0 0 0
2
. 1 1 . 1 1 . . 1 1 1
T T T
T r r r r r
r r r
.
……
Ta có:
0
. 1 1 1
n
n
T
T r r
r
.
Áp dụng vào bài toán, ta có:
6
0
0
10 . 1 0,07 1 1 0,07 130 650 280
0,07
T
T
đồng.
Câu 15. (THPT Ba Đình 2019) Một người vay ngân hàng
100
triệu đồng với lãi suất là
0,7%
/tháng theo
thỏa thuận cứ mỗi tháng người đó sẽ trả cho ngân hàng
5
triệu đồng và cứ trả hàng tháng như thế
cho đến khi hết nợ (tháng cuối cùng có thể trả dưới
5
triệu). Hỏi sau bao nhiêu tháng thì người đó
trả được hết nợ ngân hàng.
A.
22
. B.
23
. C.
24
. D.
21
.
Lời giải
Gọi số tiền vay ban đầu là
M
, số tiền hoàn nợ mỗi tháng là
m
, lãi suất một tháng là
r
.
Hết tháng thứ nhất, số tiền cả vốn lẫn nợ ngân hàng là
1
M Mr M r
(triệu đồng).
Sau khi hoàn nợ lần thứ nhất, số tiền còn nợ là
1
M r m
(triệu đồng).
Sau khi hoàn nợ lần thứ hai, số tiền còn nợ là
2
1 1 1 1
M r m M r m r m M r m r m
(triệu đồng).
Sau khi hoàn nợ lần thứ ba, số tiền còn nợ là
2 2
1 1 1 1
M r m r m M r m r m r m
3 2
1 1 1
M r m r m r m
(triệu đồng).
Lập luận tương tự, sau khi hoàn nợ lần thứ
n
, số tiền còn nợ là
1 2
1 1 1 ... 1
n n n
M r m r m r m r m
1
1 1
1
n
n
m r
M r
r
.
Sau tháng thứ
n
trả hết nợ thì ta có
1
1 1
1 0
n
n
m r
M r
r
1
1 1
n
n
Mr r
m
r
1
n
m m Mr r
1
n
m
r
m Mr
1
log
r
m
n
m Mr
Thay số với
100.000.000
M
,
0,7%
r
,
5.000.000
m
ta tính được
21,62
n
(tháng).
Vậy sau
22
tháng người đó trả hết nợ ngân hàng.
Câu 16. (HSG Bắc Ninh 2019) Vào ngày
15
hàng tháng ông An đều đến gửi tiết kiệm tại ngân hàng
SHB
số tiền
5
triệu đồng theo hình thức lãi kép với kì hạn một tháng, lãi suất tiết kiệm không đổi
trong suốt quá trình gửi là
7,2% /
năm. Hỏi sau đúng
3
năm kể từ ngày bắt đầu gửi ông An thu
được số tiền cả gốc và lãi là bao nhiêu (làm tròn đến nghìn đồng)?.
A.
195251000
(đồng) B.
201453000
(đồng) C.
195252000
(đồng) D.
201452000
(đồng)
Lời giải
Gọi
n
T
là số tiền cả gốc lẫn lãi sau
n
tháng,
a
là số tiền gốc,
r
là lãi xuất, ta có:
Cuối tháng thứ
1
ông An có số tiền là:
1
1
T a r
Đầu tháng thứ
2
ông An có số tiền là:
2
1
T a r a

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53
Cuối tháng thứ
2
ông An có số tiền là:
2
2
1 1 1 1
T a r a a r a r a r a r
……………………………………………………………
Cuối tháng thứ
n
ông An có số tiền là::
2
1 1 ... 1
n
n
T a r a r a r
2
1 1 1 1 1 1
1 1 ... 1 . 1
1 1
n n
n
r r a r r
a r r r a
r r
.
Với kì hạn một tháng, suy ra 3 năm có 36 kỳ. Lãi xuất của một năm là
7,2%
, suy ra lãi xuất của 1
tháng là:
7,2
% 0.6%
12
. Áp dụng
1
ta có:
5000000; 0.6% 0.072; 36
a r n
36
36
5000000 1 0.6% 1 0.6% 1
201453000
0.6%
T
Câu 17. (THPT-Thang-Long-Ha-Noi- 2019) Anh Bình gửi
200
triệu vào ngân hàng VB với kì hạn cố
định
12
tháng và hưởng lãi suất
0,65% /
tháng. Tuy nhiên sau khi gửi được tròn 8 tháng anh phải
dùng đến
200
triệu trên. Anh đến ngân hàng định rút tiền thì được nhân viên ngân hàng tư vấn:
“Nếu rút tiền trước kì hạn, toàn bộ số tiền anh gửi chỉ có lãi suất không kỳ hạn là
0,02% /
thángAnh nên thế chấp sổ tiết kiệm đó tại ngân hàng để vay ngân hàng
200
triệu với lãi
suất
0,7% /
tháng. Khi sổ của anh đến kì hạn, anh có thể rút tiền để trả nợ ngân hàng”. Nếu làm
theo tư vấn của nhân viên ngân hàng anh Bình sẽ đỡ thiệt một số tiền gần nhất với con số nào
dưới đây (biết ngân hàng tính lãi theo thể thức lãi kép).
A.
10,85
triệu đồng. B.
10,51
triệu đồng. C.
10,03
triệu đồng. D.
10,19
triệu đồng.
Lời giải
Số tiền trả cho ngân hàng nếu vay 200 triệu trong 4 tháng
4
200. 1 0,7% 200 5,65907
N
Tổng số tiền lãi nếu anh Bình gửi đúng kì hạn là
12
1
200. 1 0,65% 200 16,16996
L
Số tiền lãi nếu anh Bình làm theo tư vấn của nhân viên ngân hàng
16,16996 5,65907 10,51089.
L
Số tiền lãi nếu gửi 8 tháng theo hình thức lãi suất không kì hạn
8
2
200. 1 0,02% 200 0,32022.
L
Số tiền anh Bình đỡ thiệt nếu làm theo tư vấn của nhân viên ngân hàng
16,16996 5,65907 0,32022 10,19067.
Câu 18. (Chuyên Lê Quý Đôn Điện Biên 2019) Một thầy giáo cứ đầu mỗi tháng lại gửi ngân hàng 8 000
000 VNĐ với lãi suất
0,5%
/ tháng. Hỏi sau bao nhiêu tháng thầy giáo có thể tiết kiệm tiền để
mua được một chiếc xe ô tô trị giá
400 000 000 VNĐ?
A.
60
. B.
50
. C.
55
. D.
45
.
Lời giải
Đặt
8 000 000
T
Số tiền thầy giáo thu được sau tháng thứ nhất, thứ 2, thứ 3,., thứ
n
lần lượt là
1 2 3
, , ,...,
n
T T T T
Ta có:

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 54 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
1
1
T T r
2
2 1
1 1 1
T T T r T r T r
3 2
3 2
1 1 1 1
T T T r T r T r T r
.
1
1 1
1 1 ... 1 1
n
n n
n
r
T T r T r T r T r
r
Theo bài ra ta có
1 1
400 000 000 1 400 000 000
n
n
r
T T r
r
1.005
251 251
1 log 44,54
201 201
n
r n
Vậy sau 45 tháng thầy giáo sẽ mua được một chiếc xe ô tô trị giá 400 000 000 VNĐ.
Câu 19. (Chuyên Lương Thế Vinh Đồng Nai 2019) Một người vay ngân hàng số tiền
400
triệu đồng,
mỗi tháng trả góp
10
triệu đồng và lãi suất cho số tiền chưa trả là
1%
mỗi tháng. Kỳ trả đầu tiên
là cuối tháng thứ nhất. Biết lãi suất không đổi trong suốt quá trình gửi, hỏi số tiền còn phải trả ở
kỳ cuối là bao nhiêu để người này hết nợ ngân hàng? (làm tròn đến hàng nghìn).
A.
2.921.000
. B.
3.387.000
. C.
2.944.000
. D.
7.084.000
.
Lời giải
Cuối tháng thứ nhất, tiền gốc và lãi là
400 1,01
triệu đồng. Sau khi trả
10
triệu thì số tiền người
đó còn nợ ngân hàng là
400 1,01 10
triệu đồng.
Cuối tháng thứ hai, tiền gốc và lãi là:
2
400 1,01 10 1,01
triệu đồng. Sau khi trả
10
triệu thì số
tiền người đó còn nợ ngân hàng là
2
400 1,01 10 1,01 10
triệu đồng.
Như vậy ở cuối tháng thứ
1
n n
người đó nếu còn nợ thì số tiền nợ là:
1 2
400 1,01 10 1,01 10 1,01 10
n n n
triệu đồng.
Xét
1 2
400 1,01 10 1,01 10 1,01 10 0
n n n
1,01 1
400 1,01 10 0
0,01
n
n
600 1,01 1000
n
1,01
5
log 51,33
3
n
Do vậy kỳ cuối cùng người đó phải trả tiền là tháng thứ
52
. Cuối tháng thứ
51
, số tiền còn nợ lại
là
51
51
1,01 1
400 1,01 10 3,3531596
0,01
triệu đồng.
Vậy kỳ cuối người đó phải trả số tiền là
3,3531596 1,01 3,386647
triệu đồng
3387000
đồng.
Câu 20. (Chuyên Lê Quý Đôn Quảng Trị 2019) Một người gửi
100
triệu đồng vào ngân hàng với lãi
suất
0,5% /
tháng và ông ta rút đều đặn mỗi tháng một triệu đồng kể từ sau ngày gửi một tháng
cho đến khi hết tiền ( tháng cuối cùng có thể không còn đủ một triệu đồng). Hỏi ông ta rút hết tiền
sau bao nhiêu tháng?
A.
139
. B.
140
. C.
100
. D.
138
.
Lời giải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 55
Gọi số tiền lúc đầu người đó gửi là
A
(triệu đồng), lãi suất gửi ngân hàng một tháng là
r
,
n
S
là
số tiền còn lại sau
n
tháng.
Sau 1 tháng kể từ ngày gửi tiền, số tiền còn lại của người đó là:
1
1 1
S A r
.
Sau 2 tháng kể từ ngày gửi tiền, số tiền còn lại của người đó là:
2
2
1 1 1 1 1 1 1
S A r r A r r
.
…
Sau
n
tháng kể từ ngày gửi tiền, số tiền còn lại của người đó là:
1 2
1 1 1 1 1
n n n
n
S A r r r r
1 1
1
n
n
r
A r
r
.
Giả sử sau
n
tháng người đó rút hết tiền. Khi đó ta có
1 1
0 1 0
n
n
n
r
S A r
r
1 1 1 0
n
r Ar
1 1
1
log log 1
1
r r
n n Ar
Ar
.
Câu 21. (THPT Quỳnh Lưu 3 Nghệ An 2019) Một bà mẹ Việt Nam anh hùng được hưởng số tiền là
4
triệu đồng trên
1
tháng (chuyển vào tài khoản ngân hàng của mẹ ở ngân hàng vào đầu tháng). Từ
tháng
1
năm
2019
mẹ không đi rút tiền mà để lại ngân hàng và được tính lãi
1%
trên
1
tháng.
Đến đầu tháng
12
năm
2019
mẹ đi rút toàn số tiền ( gồm số tiền của tháng
12
và số tiền gửi từ
tháng
1
). Hỏi khi đó mẹ lĩnh về bao nhiêu tiền? (kết quả làm tròn theo đơn vị nghìn đồng).
A.
50970000
đồng. B.
50560000
đồng. C.
50670000
đồng. D.
50730000
đồng.
Lời giải
Gọi sô tiền mẹ gửi vào ngân hàng vào đầu tháng hàng tháng là
A
đồng.
Số tiền mẹ lĩnh vào đầu tháng
12
là T đồng.
Lãi suất hàng tháng mẹ gửi tại ngân hàng là r %.
Vì mẹ rút tiền vào đầu tháng
12
năm
2019
nên thời gian được tính lãi suất là
11
tháng.
Ta có:
+) Đầu tháng
1
mẹ gửi vào
A
đồng.
cuối tháng
1
số tiền của mẹ là:
1
A Ar A r
đồng.
+) Đầu tháng
2
số tiền của mẹ gửi vào là:
1
A A r
đồng.
cuối tháng
2
số tiền của mẹ là:
2
+ 1 1 1 1
A A r r A r A r
đồng.
+) Đầu tháng
3
số tiền mẹ gửi vào là:
2
1 1
A A r A r
.
cuối tháng
3
số tiền của mẹ
là:
2 2 3
1 1 1 1 1 1
A A r A r r A r A r A r
.
Cứ như vậy đến cuối tháng thứ
11
số tiền của mẹ là:
2 11 2 11
1
1 1 ... 1 1 1 ... 1
A r A r A r A r r r T
.
Ta thấy
2 11
1 1 ... 1r r r
là tổng của 1 cấp số nhân với
1
1 ,n 11,q 1u r r
.
11
1
1
1
1
u q
T A
q
. Ta có:

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 56 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
4000000
1% 0.01
A
r
1
46730000
T
đồng.
Vì mẹ rút tiền vào đầu tháng
12
năm
2019
1
4000000 50730000
T T
đồng.
Câu 22. (Sở Thanh Hóa 2019) Bạn H trúng tuyển vào trường Đại học Ngoại Thương nhưng vì do không
đủ tiền nộp học phí nên H quyết định vay ngân hàng trong bốn năm mỗi năm 4 triệu đồng để nộp
học phí với lãi suất ưu đãi 3%/năm (theo thể thức lãi suất kép) biết rằng tiền vay mỗi năm H nhận
được từ ngày đầu tiên của năm học và trong suốt bốn năm học H không trả tiền cho ngân hàng.
Ngay sau khi tốt nghiệp Đại học (tròn 4 năm kể từ khi bạn H bắt đầu vay ngân hàng) bạn H thực
hiện trả góp hàng tháng cho ngân hàng số tiền (không đổi và tiền trả vào ngày cuối của tháng) với
lãi suất theo cách tính mới là 0,25%/tháng và lãi suất được tính theo dư nợ thực tế, bạn H trả đúng
5 năm thì hết nợ. Tính số tiền hàng tháng mà bạn H phải trả cho ngân hàng (kết quả làm tròn đến
hàng đơn vị).
A. 323.582 (đồng). B. 398.402 (đồng). C. 309.718 (đồng. D. 312.518 (đồng).
Lời giải
Xét bài toán 1: Vay nhận vốn định kì lãi suất kép.
Gọi
A
là số tiền mỗi năm bạn H vay ngân hàng,
1
r
là lãi suất theo năm.
Cuối năm thứ nhất, H nợ ngân hàng với số tiền là
1
. 1
A r
.
Đầu năm thứ hai, H nợ ngân hàng với số tiền là
1
. 1
A A r
.
Cuối năm thứ hai, H nợ ngân hàng với số tiền là
2
1 1 1 1 1
. 1 1 1 1
A A r A A r r A r A r
.
Tiếp tục như vậy, cuối năm thứ n số tiền mà H nợ ngân hàng là:
1 1
2
1 1 1
1
1 1 1
1 1 ... 1
n
n
A r r
B A r A r A r
r
.
Xét bài toán 2: Vay trả góp, lãi suất dư nợ thực tế.
Gọi
a
là số tiền mà bạn H phải trả hàng tháng sau khi ra trường,
2
r
là lãi suất mỗi tháng, số tiền
H nợ ngân hàng là B.
Cuối tháng thứ nhất bạn H còn nợ ngân hàng số tiền là:
2 2
. . 1
B B r a B r a
.
Cuối tháng thứ hai bạn H còn nợ ngân hàng số tiền là:
2 2 2
. 1 . 1
B r a B r a r a
=
2
2 2
. 1 1
B r a a r
.
Cứ tiếp tục như vậy ta có công thức tổng quát.
Cuối tháng thứ m bạn H còn nợ ngân hàng số tiền là
2 1
2 2 2 2
. 1 1 1 ... 1
m m
B r a r a r a r a
=
2
2
2
1 1
. 1
m
m
r
B r a
r
.
Áp dụng 2 bài toán trên vào câu 42, ta có phương trình.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 57
4
60
60
4.1,03 1,03 1
1,0025 1
1,0025 . 0 0,309718
0,03 0,0025
a a
(triệu đồng).
Vậy số tiền mà H cần phải trả hàng tháng là 309.718 triệu đồng.
Câu 23. (Sở Phú Thọ 2019) Ông A muốn mua một chiếc ôtô trị giá 1 tỉ đồng nhưng vì chưa đủ tiền nên
chọn mua bằng hình thức trả góp hàng tháng (số tiền trả góp mỗi tháng như nhau) với lãi suất
12%
/năm và trả trước
500
triệu đồng. Hỏi mỗi tháng ông phải trả số tiền gần nhất với số tiền nào
dưới đây để sau đúng 2 năm, kể từ ngày mua xe, ông trả hết nợ, biết kì trả nợ đầu tiên sau ngày
mua ôtô đúng một tháng và chỉ tính lãi hàng tháng trên số dư nợ thực tế của tháng đó?
A.
23 537 000
đồng B.
24 443 000
đồng C.
22 703 000
đồng D.
23 573 000
đồng
Lời giải
Chọn A
Gọi
a
là số tiền trả hàng tháng.
Sau tháng thứ 1, số tiền còn lại:
1
500 1
P r a
.
Sau tháng thứ 2, số tiền còn lại:
2 1
1
P P r a
2
500 1 1
r a r a
.
.
Sau tháng thứ
n
, số tiền còn lại:
1
500 1 1 ... 1
n n
n
P r a r a r a
.
Vậy sau 24 tháng:
24
24
1 1
500 1 0
r
r a
r
24
24
500 1 .
1 1
r r
a
r
24
24
500 1 1% .1%
1 1% 1
a
23,537
triệu đồng.
Câu 24. (Chuyên Thái Nguyên 2019) Một người vay ngân hàng
50
triệu đồng, mỗi tháng trả ngân hàng
4
triệu đồng và phải trả lãi suất cho số tiền còn nợ là
1,1%
một tháng theo hình thức lãi kép. Giả
sử sau
n
tháng người đó trả hết nợ. Khi đó
n
gần nhất với số nào sau?
A.
14
. B.
13
. C.
16
. D.
15
.
Lời giải
Phương pháp:Sử dụng công thức trả góp
(1 ) (1 ) 1
n n
M
P r r
r
, trong đó:
P
: là số tiền phải trả sau
n
tháng
r
: Lãi suất/ tháng
M
: số tiền phải trả mỗi tháng
Áp dụng công thức ta có:
(1 ) (1 ) 1
n n
M
P r r
r
4
50(1 1,1%) (1 1,1%) 1
1,1%
n n
4 4
50(1 1,1%) (1 1,1%)
1,1% 1,1%
n n
4 3450
(1 1,1%)
1,1% 11
n
1 1,8
80 80
(1 1,1%) log 13, 52
69 69
n
n

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 58 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 25. Ông
A
vay ngân hàng
100
triệu đồng với lãi suất
1%
/tháng. Ông ta muốn hoàn nợ cho ngân
hàng theo cách: Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên
tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi tháng là như nhau và sau đúng một năm kể
từ ngày vay ông
A
còn nợ ngân hàng tổng số tiền
50
triệu đồng. Biết rằng mỗi tháng ngân hàng
chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi số tiền mỗi tháng ông ta cần trả cho ngân hàng
gần nhất với số tiền nào dưới đây?
A.
4,95
triệu đồng B.
4,42
triệu đồng C.
4,5
triệu đồng D.
4,94
triệu đồng
Lời giải
Gọi
X
là số tiền mỗi tháng ông
A
trả cho ngân hàng.
Số tiền còn nợ sau
n
kì hạn là
1 1
. 1 .
n
n
n
r
T T r X
r
(triệu đồng), trong đó
100
T
(triệu
đồng) là số tiền mà ông
A
vay.
Sau đúng một năm, số tiền ông còn nợ là
50
triệu đồng nên ta có
12
12
1 0,01 1
50 100. 1 0,01 .
0,01
X
12
12
100.1,01 50 .0,01
4,94
1,01 1
X
(triệu đồng).
Vậy mỗi tháng ông ta cần trả cho ngân hàng gần nhất với số tiền
4,94
triệu đồng.
Câu 26. (Chuyên ĐHSP Hà Nội 2019) Một người nhận hợp đồng dài hạn làm việc cho một công ty với
mức lương khởi điểm của mỗi tháng trong ba năm đầu tiên là
6
triệu đồng/ tháng. Tính từ ngày
đầu làm việc, cứ sau đúng ba năm liên tiếp thì tăng lương
10%
so với mức lương một tháng
người đó đang hưởng. Nếu tính theo hợp đồng thì tháng đầu tiên của năm thứ
16
người đó nhận
được mức lương là bao nhiêu?
A.
4
6.1,1
(triệu đồng). B.
6
6.1,1
(triệu đồng).
C.
5
6.1,1
(triệu đồng). D.
16
6.1,1
(triệu đồng).
Lời giải
Sau
3
năm, bắt đầu từ tháng đầu tiên của năm thứ
4
số tiền lương người đó nhận được sau mỗi
tháng là
6 6.10% 6.1,1
(triệu đồng).
Sau
6
năm (
2.3
năm), bắt đầu từ tháng đầu tiên của năm thứ
7
số tiền lương người đó nhận
được sau mỗi tháng là
2
6.1,1 6.1,1.10% 6.1,1. 1 10% 6.1,1
(triệu đồng).
Tương tự như vậy sau
15
năm (
5.3
năm), bắt đầu từ tháng đầu tiên của năm thứ
16
số tiền người
đó nhận được sau mỗi tháng là
5
6.1,1
(triệu đồng).
Vậy tháng đầu tiên của năm thứ
16
, người đó nhận được mức lương là
5
6.1,1
(triệu đồng).
Câu 27. (Đề Thi Công Bằng KHTN 2019) Một người gửi
50
triệu đồng vào một ngân hàng với lãi suất
6% /
năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được
nhập vào gốc để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó nhận được số
tiền nhiều hơn 100 triệu đồng bao gồm gốc và lãi?
A.
11
năm. B.
12
năm. C.
13
năm. D.
14
năm.
Lời giải
Dạng toán lãi kép:
Bài toán tổng quát: gửi
a
đồng vào ngân hàng với lãi suất
%r
(sau mỗi kì hạn không rút tiền lãi
ra).
Gọi
n
A
là số tiền có được sau
n
năm.
Sau
1
năm:
1
%. 1 %A a r a a r
.
Sau
2
năm:
2
2
1 % 1 % . % 1 %
A a r a r r a r
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 59
Sau
3
năm:
2 2 3
3
1 % 1 % . % 1 %
A a r a r r a r
.
Sau
n
năm:
1 %
n
n
A a r
.
Người đó nhận được số tiền hơn
100
triệu. Suy ra:
1,06
50 1 6% 100
50.1,06 100
1,06 2
log 2 11,9
n
n
n
n
Vậy
12
n
.
Câu 28. (THPT Nghĩa Hưng NĐ 2019) Anh
C
đi làm với mức lương khởi điểm là
x
(triệu đồng)/
tháng, và số tiền lương này được nhận vào ngày đầu tháng. Vì làm việc chăm chỉ và có trách
nhiệm nên sau
36
tháng kể từ ngày đi làm, anh
C
được tăng lương thêm
10%
. Mỗi tháng, anh ta
giữ lại
20%
số tiền lương để gửi tiết kiệm ngân hàng với kì hạn
1
tháng và lãi suất là
0,5%
/tháng, theo hình thức lãi kép (tức tiền lãi của tháng này được nhập vào vốn để tính lãi cho
tháng tiếp theo). Sau
48
tháng kể từ ngày đi làm, anh
C
nhận được số tiền cả gốc và lãi là
100
triệu đồng. Hỏi mức lương khởi điểm của người đó là bao nhiêu?
A.
8.991.504
đồng. B.
9.991.504
đồng. C.
8.981.504
đồng. D.
9.881.505
đồng.
Lời giải
Gọi số tiền mỗi tháng anh gửi tiết kiệm ngân hàng trong
36
tháng đầu là
A
; số tiền mỗi tháng
anh gửi tiết kiệm sau tháng thứ
36
là
B
.
Đặt
1 0,5% 1,005
q
Gọi
n
S
là số tiền sau tháng thứ
n
ta có
1
.0,5% . S A A A q
2
2 1 1 1
.0,5% .
S S A S A S A q Aq Aq
.
….
36
36 35
36 35 35 35
1
.0,5% . .
1
q
S S A S A S A q Aq Aq Aq Aq
q
.
37 36 36 36 36
.0,5% . . .
S S B S B S B q S q B q
.
2 2
38 37 37 37 36
.0,5% .
S S B S B S B q S q Bq Bq
.
….
36 12
12 12 11 13
48 36
1 1
. ... . .
1 1
q q
S S q Bq Bq Bq Aq Bq
q q
.
Theo giả thiết ta có
20% 0,2 A x x
;
20% 10% 0,22
B x x x
;
8
48
10
S
.
Vậy
36 12
13 8
1 1
0,2 . 0,22 . . 10
1 1
q q
xq x q
q q
36 12
8 13
1 1
10 : 0,2 . 0,22. .
1 1
q q
x q q
q q
8991504
x
đồng.
Câu 29. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Bạn Nam vừa trúng tuyển đại học, vì hoàn cảnh
gia đình khó khăn nên được ngân hàng cho vay vốn trong 4 năm học đại học, mỗi năm
10
triệu
đồng vào đầu năm học để nạp học phí với lãi suất
7,8%
/năm (mỗi lần vay cách nhau đúng 1
năm). Sau khi tốt nghiệp đại học đúng 1 tháng, hàng tháng Nam phải trả góp cho ngân hàng số

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 60 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
tiền là
m
đồng/tháng với lãi suất
0,7%
/tháng trong vòng
4
năm. Số tiền
m
mỗi tháng Nam cần
trả cho ngân hàng gần nhất với số nào sau đây (ngân hàng tính lãi trên số dư nợ thực tế).
A.
1.468.000
(đồng). B.
1.398.000
(đồng). C.
1.191.000
(đồng). D.
1.027.000
(đồng).
Lời giải
Bài toán được chia làm hai giai đoạn
* Giai đoạn 1: vay vốn để học đại học trong 4 năm. Đặt
7,8
0,078
100
r
Ở năm thứ nhất:
4
1
10(1 )M r
(triệu đồng)
Ở năm thứ hai:
3
2
10(1 )M r
(triệu đồng)
Ở năm thứ ba:
2
3
10(1 )M r
(triệu đồng)
Ở năm thứ tư:
1
4
10(1 )M r
(triệu đồng)
Như vậy tổng số tiền mà Nam đã vay trong 4 năm là
4
0
1
48, 4324
i
i
M M
(triệu đồng)
* Giai đoạn 2: trả góp cho ngân hàng số tiền đã vay hàng tháng
Sau tháng thứ nhất, người đó còn số nợ là:
1
0,7
1
100
o
P M m
. Đặt
0,7
1
100
y
Sau tháng thứ hai người đó còn nợ:
2
2 2
2 1
1
( 1)
1
o o a
y
P P y m M y m y m M y m y M y m
y
Sau tháng thứ ba người đó còn nợ:
3
3 2 3
3 2
1
1
1
o o
y
P P y m M y m y y M y m
y
Bằng phương pháp quy nạp, sau
n
tháng số tiền trả hết sẽ là
( 1)
1
0
1
1
n
n
o
o
n
M y y
y
M y m m
y
y
Đồng thời ta có:
48n
tháng và
0,7
1 1,007
100
y
suy ra
1,914m
(triệu đồng).
Câu 30. (Chuyên Phan Bội Châu -2019) Một anh sinh viên nhập học đại học vào tháng
8
năm
2014
.
Bắt đầu từ tháng
9
năm
2014
, cứ vào ngày mồng một hàng tháng anh vay ngân hàng
3
triệu
đồng với lãi suất cố định
0,8%
/tháng. Lãi tháng trước được cộng vào số nợ để tiếp tục tính lãi cho
tháng tiếp theo (lãi kép). Vào ngày mồng một hàng tháng kể từ tháng
9 / 2016
về sau anh không
vay ngân hàng nữa và anh còn trả được cho ngân hàng
2
triệu đồng do việc làm thêm. Hỏi ngay
sau khi kết thức ngày anh ra trường
30 / 6 / 2018
anh còn nợ ngân hàng bao nhiêu tiền (làm tròn
đến hàng nghìn đồng)?
A.
49.024.000
đồng B.
47.401.000
đồng C.
47.024.000
đồng D.
45.401.000
đồng
Lời giải
Chọn
Anh sinh viên vay hàng tháng
3
a
triệu đồng từ
9
/
2014
đến
8 / 2016
, tổng cộng
24
tháng.
Cuối tháng thứ 1:
1
ar 1
T a a r
Cuối tháng thứ 2:
2
2 1 1
. . 1 . 1
T T a T a r a r a r
….

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 61
Cuối tháng n:
1
. 1
. 1 ... . 1
n n
n
T a
r a r a r
Suy ra
1 1
. 1 .
n
n
r
T a
r
r
Vậy tổng số tiền vay đến cuối tháng 8/2016 là
24
24
1 0
,8% 1
3. 1
0,8% . 79,662
0,8%
T
triệu
Tính t
ừ cuối tháng 8/2016 Anh sinh viên thiếu ngân hàng
79,662
A
và bắt đầu trả đầu hàng
tháng
2
m
triệu từ
9 /
2016
đến
6 /
2018
, tổng cộng được
22
thá
ng
Đầu tháng
9 / 2016
: c
òn nợ
79
,662 2 77,662
A m
triệu
Cu
ối tháng
9 /
2016
: t
iền nợ có lãi đến cuối tháng:
1
77,
662 1
T r
Đầu tháng
10
/ 2016
sau khi tr
ả nợ
m
thì
còn nợ
77,
662 1
r m
Cuối tháng
10 / 2016
: còn nợ
2
2
77
,662 1 1 77,662 1 1
T r
m r r m r
Cuối tháng
11
/ 2016
: còn n
ợ
3 2
3
77,662 1 1 1
T r m r m r
….
Cuối tháng
6 /
2018
còn nợ
22 21 20
22
21
22
77,662
1 1 1 ... 1
1 1
77,662 1 . 1
T r
m r m r m r
r
r m
r
r
21
2
2
1 0
,8% 1
77,
662. 1 0,8% 2. 1 0,8% . 46,64
0,8%
triệu
đồng.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI MỨC 9-10 ĐIỂM
Dạng 1. Tính toán liên quan đến logarit dùng đẳng thức
Địnhnghĩalogarit:
Chohaisốthựcdương
,a b
với
1, log
α
a
a α b a b
:
Cáctínhchấtlogarit:Chobasốthựcdương
, ,a b c
với
0 , , 1 a b c
log log
log ; log log log ; log log ;
log log
log .log log .
c a
a a a a a a
a a
a b a
b b
b b c bc b c
a c
b c c
Phươngtrìnhmũcơbảnnhất
log 0 1; 0
x
a
a b x b a b
.
Cáchgiảiphươngtrìnhmũcódạng
2 2
1 2 3
0
x
x x
α a α ab α b
trongđó
1,2,3
i
α i
làhệsố,
cơsố
0 , 1 a b
B1:Biếnđổiphươngtrìnhvềdạng:
2
1 2 3
2 0 *
x x
a a
α α α
b b
.
B2:Đặtẩnphụ
, 0
x
a
t t
b
,phươngtrình
*
trởthành
2
1 2 3
0 α t α t α
.
B3:Giảitìmt thỏamãn
0t
.
B4:Giảiphươngtrìnhmũcơbản
x
a
t
b
.Tìmđược
x
.
Câu 1. (Đề Minh Họa 2020 Lần 1) Cho
x
,
y
là các số thực dương thỏa mãn
9 6 4
log log log 2x y x y
.Giátrịcủa
x
y
bằng
A.
2
. B.
1
2
. C.
2
3
log
2
. D.
3
2
log 2
.
Lời giải
Chọn B
Đặt
9 6 4
log log log 2t x y x y
.Khiđó
9
6
2 4
t
t
t
x
y
x y
2.9 6 4
t t t
9 3
2. 1 0
4 2
t t
3
1
2
3 1
2 2
t
t
3 1
2 2
t
.
Dođó:
9 3 1
6 2 2
t t
x
y
.
HÀM SỐ MŨ - HÀM SỐ LOGARIT
Chuyên đề 18
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 2. (Chuyên Lào Cai - 2020) các số thực
a
,
b
,
c
thỏa mãn
2 2 2
( 2) ( 2) ( 2) 8
a b c
và
2 3 6
a b c
.Khiđó
a b c
bằng
A.
2
. B.
4
. C.
2 2
. D.
8
.
Lời giải
Chọn A
Tacó
2
log 6
a c
và
3
log 6
b c
.Suyra
1 1 1
a b c
.Hay
1 1 1
0
a b c
.
Hay
0
ab bc ca
.Suy ra
2 2 2 2
( )a b c a b c
nên
2
( ) 4( ) 4 0.
a b c a b c
Vậy
2
a b c
.
Câu 3. (Chuyên Thái Nguyên - 2020) Cho
4 4 7
x x
.Khiđóbiểuthức
5 2 2
8 4.2 4.2
x x
x x
a
P
b
với
a
b
làphânsốtốigiảnvà
,a b
.Tích
.a b
cógiátrịbằng
A.
10
. B.
8
. C.
8
. D.
10
.
Lời giải
ChọnA
Tacó
2 2 2
4 4 7 2 2.2 .2 2 2 7 2 2 9 2 2 3
x x x x x x x x x x
.
Dođó
5 2 2
5 2 2 5 3 2 1
8 4.3 20 10
8 4.2 4.2
8 4. 2 2
x x
x x
x x
x x
P
.
Suyra
1, 10
a b
.
Vậy
. 10
a b
.
Câu 4. (Sở Ninh Bình 2019) Cho
a
,
b
,
c
làcácsốthựckhác
0
thỏamãn
4 9 6
a b c
.Khiđó
c c
a b
bằng
A.
1
2
. B.
1
6
. C.
6
. D.
2
.
Lời giải
Chọn D
Đặt
4
9
6
log
4 9 6 log
log
a b c
a t
t b t
c t
.
Khiđó
6 6
6 6 6
4 9
log log
log .log 4 log .log 9 log log 4 log 9
log log
t t t t
t t
c c
t t t
a b t t
2
6 6 6
log .log 36 log 36 log 6 2
t
t
.
Câu 5. Biết
30
log 10
a ,
30
log 150
b và
1 1 1
2000
2 2 2
log 15000
x a y b z
x a y b z
với
1 1 1 2 2 2
; y ;z ; ; y ;z
x x làcácsố
nguyên,tính
1
2
x
S
x
.
A.
1
2
S
. B.
2
S
. C.
2
3
S
. D.
1
S
.
Lời giải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Chọn A
Tacó
30 30 30
2000
30 30 30
log 15000 log 150 2log 10
log 15000
log 2000 log 2 3log 10
1
Tacó
30 30 30 30 30
log 10 log 5 log 2 log 2 log 5
a a
2
30 30 30
log 150 1 log 5 log 5 1 b b
thayvào
2
tađược
30
log 2 1
a b
Tacó
2000
2 2
log 1500
1 3 4 1
b a a b
a b a a b
Suyra
1
2
2 1
4 2
x
S
x
.
Câu 6. Chocácsốthựcdương
,x y
khác1vàthỏamãn
log log
log log
x y
x y
y x
x y x y
.
Giátrịcủa
2 2
x xy y
bằng
A. 0. B. 3. C. 1. D. 2.
Lời giải
Chọn D
ĐK:
x y
.
Tacó
1
1
1
log
log log
log
log log
log log
log log
x
x y
x
x y
x y
x
x
y
y
y x
x
y
x y
x y x y
x y x y
x y x y
2 2
2 2
2 2
1
1
1
2
1
log log 0 log 0
x x x
y
xy
y
x
x
x xy y
x y
x y x y x y
.
Câu 7. Cho các số thực dương
a
,
b
thỏa mãn
log log log log 100
a b a b
và
log a
,
logb
,
log
a
,
log
b
đềulàcácsốnguyêndương.Tính
P ab
.
A.
164
10 .
B.
100
10 .
C.
200
10 .
D.
144
10 .
Lời giải
Chọn A
Tacó:
log log log log 100
a b a b
log log 2 log 2 log 200
a b a b
2 2
log 1 log 1 202 81 121
a b
*
Mà
log a
,
logb
,
log
a
,
log
b
đềulàcácsốnguyêndươngnên
64
100
100
64
log 1 9
log 64 10
log 1 11
log 100 10
*
log 100
10
log 1 11
log 64
10
log 1 9
a
a a
b
b b
a
a
a
b
b
b

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy:
64 100 164
10 .10 10 .
P ab
Câu 8. Cho
9 4 2
log 5 ; log 7 ; log 3
a b c
.Biết
24
log 175
mb nac
pc q
.Tính
2 3 4 A m n p q
A.
27
B.
25
C.
23
D.
29
Lời giải
Chọn B
Tacó
2
24 24 24 24
7 5
1 2
log 175 log 7.5 log 7 2log 5
log 24 log 24
3 3
7 7 5 5
3 2 3 2
1 2 1 2
1 3 1 3
log 3 log 2 log 3 log 2
log 7 log 7 log 5 log 5
2 3 2 3 2 3
1 2 1 2
1 3 1 3 1 3 1 3
1
log 7.log 2 log 7 log 5 log 3.log 5 2 2a c.2a
2 .
b
b
c
1 2 2 4a 2 4a
3 3
3 3 3
2 2 2ac 2ac
b c b c
c c
c c c
b b
.
2 3 4 2 8 3 12 25.
A m n p q
Câu 9. Cho
x
,
y
làcácsốthựclớnhơn
1
thoảmãn
2 2
6
x y xy
.Tính
12 12
12
1 log log
2log 3
x y
M
x y
.
A.
1
4
M
. B.
1M
. C.
1
2
M
. D.
1
3
M
.
Lời giải
Chọn B
Tacó
2 2 2 2
6 6 0 *
x y xy x xy y
.
Do
x
,
y
làcácsốthựcdươnglớnhơn
1
nêntachiacả2vếcủa
*
cho
2
y
ta
được
2
3
3
6 0
2
2
x
x y n
y
x x
x
y y
x y l
y
Vậy
3x y
(1).
Mặtkhác
12 12
12
1 log log
2log 3
x y
M
x y
12
2
12
log 12
log 3
xy
x y
(2).
Thay(1)vào(2)tacó
2
12
2
12
log 36
1
log 36
y
M
y
.
Câu 10. Cho
2
ln 1 sin 6
f x a x x b x
với
a
,
b
. Biết
log log e 2
f
. Tính
log ln10
f
.
A.
4
. B.
10
. C.
8
. D.
2
.
Lờigiải
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
ChọnB
Đặt
0
log loge
x
Có:
2
0 0 0 0
ln 1 sin 6 2
f x a x x b x
Tacó
0
1
log ln10 log log loge
loge
f f f f x
2
0 0 0 0
ln 1 sin 6
f x a x x b x
2
0 0 0
ln 1 sin 6
a x x b x
2
0 0 0 0
ln 1 sin 6 12 12 10
a x x b x f x .
Câu 11. Cho
x -x
9 + 9 = 14
và
x -x
x+1 1-x
6+3(3 +3 ) a
=
2-3 -3 b
với
a
b
làphânsốtốigiản.Tính
. .P a b
A.
10.
P
B.
45.
P
C.
10.
P
D.
45.
P
Lờigiải
ChọnB
Tacó
2 2 2 2
2
9 9 14 3 2.3 .3 3 16
3 3 16 3 3 4.
x x x x x x
x x x x
1 1
6 3(3 3 ) 6 3(3 3 ) 6 3(3 3 )
2 3 3 2 3.3 3.3
2 3. 3 3
6 3.4 18 9
45.
2 3.4 10 5
x x x x x x
x x x x
x x
a
ab
b
Câu 12. Chohaisốthựcdương
,a b
thỏa
4 6 9
log log log
a b a b
.Tính
a
b
.
A.
1
2
. B.
1 5
2
. C.
1 5
2
. D.
1 5
2
.
Lờigiải
Chọn D
Đặt
4 6 9
log log log
t a b a b
.
4
6 4 6 9
9
t
t t t t
t
a
b
a b
2
2 1 5
3 2
2 2
1 0
3 3
2 1 5
( )
3 2
t
t t
t
L
.
4 2 1 5
6 3 2
t
t
t
a
b
.
Câu 13. Chocácsốthựcdương
,x y
thỏamãn
6 9 4
log log log 2 2x y x y
.Tínhtỉsố
x
y
?

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
3
x
y
. B.
2
3 1
x
y
. C.
2
3 1
x
y
. D.
3
2
x
y
.
Lờigiải
Chọn B
Giảsử
6 9 4
log log log 2 2
x y x y t
.Tacó:
6 (1)
9 (2)
2 2 4 (3)
t
t
t
x
y
x y
.
Khiđó
6 2
0
9 3
t
t
t
x
y
.
Lấy(1),(2)thayvào(3)tacó
2.6 2.9 4
t t t
2
2 2
2. 2 0
3 3
t t
2 2
1 3
3
3 1
2
1 3
3
t
t
(thoûa)
(loaïi)
.
Câu 14. Cho
x
,
y
làcácsốthựcdươngthỏamãn
25 15 9
log log log
2 4
x x y
y
và
2
x a b
y
,với
a
,
b
làcácsốnguyêndương,tính
a b
.
A.
14
a b
. B.
3
a b
. C.
21
a b
. D.
34
a b
.
Lờigiải
Chọn D
Tacó
25
25
log
2
log
25 15 9
2
9 25
15
log log log
2 4
15
log log
4 2
x
x
y
x x y
y
x x
Đặt
25
log 2.25
2
t
x
t x
,tađược
2.25 15 4.9
t t t
2
5 5
2 4
3 3
t t
5
3
1 33
log
4
t
2.25 5 1 33
2.
15 3 2
t
t
t
x
y
.
Dođó
1
a
,
33
b
nên
34
a b
.
Câu 15. Chodãysố
n
u
thỏamãn
3 5 4
log 2 63 2log 8 8
n
u u n
,
*
n
.Đặt
1 2
...
n n
S u u u
.Tìmsốnguyêndươnglớnnhất
n
thỏamãn
2
2
.
148
. 75
n n
n n
u S
u S
.
A.
18
. B.
17
. C.
16
. D.
19
.
Lờigiải
Chọn A
Tacó
*
n
,
3 5 4
log 2 63 2log 8 8
n
u u n
3 5 2
log 2 63 log 8 8
n
u u n
.
Đặt
3 5
log 2 63
t u
5
2 63 3
8 8 2
t
t
n
u
u n
5
5
2 63 3
32 2
t
t
u
u
(với
5
n
)
1 3 2.2
t t
2
t
8 4
n
u n
.Khiđó
5
36
u

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Với
8 4
n
u n
và
5
36
u
,tacó:
3 5 4 3 4
log 2 63 2log 8 8 log 2.36 63 2log 8 4 8 8
n
u u n n n
3 4
log 9 2log 4 2 2
đúng
*
n
.
Tacó:
1
8 1 4 8 4 8
n n
u u n n
.Vậy
n
u
làcấpsốcộngcósốhạngđầu
1
4
u
,công
sai
8
d
.
1
2
1 2
.
... 4
2
n
n n
u u n
S u u u n
.
Dođó
2
2
2
2
8 4 .16
.
148
. 16 4 .4 75
n n
n n
n n
u S
u S n n
19
n
.
Dạng 2. Bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất mũ – loagrit (sử dụng phương pháp
bấtđẳng thức – biến đổi)
Bất đẳng thức Cauchy (AM – GM)
, 0,
a b
thì
2 .a b ab
Dấu
" "
xảyrakhi:
.a b
, , 0,
a b c
thì
3
3. .a b c abc
Dấu
" "
xảyrakhi
.a b c
Nhiềutrườnghợpđánhgiádạng:
2
.
2
a b
a b
và
3
. .
3
a b c
a b c
Bất đẳng thức Cauchy – Schwarz (Bunhiaxcôpki)
, , , ,a b x y
thì:
2 2 2 2 2
( . . ) ( )( ) .a x b y a b x y
Dấu
" "
khi
a b
x y
,b,c, x, y,z
a
thì:
2 2 2 2 2 2 2
( . . . ) ( )( ) .a x b y c z a b c x y z
Dấu
" "
xảyrakhivàchỉkhi:
a b c
x y z
Nhiềutrườnghợpđánhgiádạng:
2 2 2 2
. . ( )(x ).a x b y a b y
Hệ quả.Nếu
, ,a b c
làcácsốthựcvà
, ,x y z
làcácsốdươngthì:
2 2 2
( )a b a b
x y x y
và
2 2 2 2
( )a b c a b c
x y z x y z
:bấtđẳngthứccộngmẫusố.
Câu 1. (Đề Tham Khảo 2020 Lần 2) Xét các số thực dương
, , ,a b x y
thoả mãn
1, 1a b
và
x y
a b ab
.Giátrịnhỏnhấtcủabiểuthức
2P x y
thuộctậphợpnàodướiđây?
A.
1;2
. B.
5
2;
2
. C.
3;4
. D.
5
;3
2
.
Lời giải
Chọn D
Đặt
log
a
t b
.Vì
, 1a b
nên
0t
.
Tacó:
1 1
log 1 log 1
2 2
x
a a
a ab x ab b t
.
1 1 1
log 1 log 1
2 2
y
b b
b ab y ab a
t
.
Vậy
1 1
2 1 1
2
P x y t
t
3 1 3
2
2 2 2
t
t
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dấuđẳngthứcxảyrakhivàchỉkhi
2
1
2
t
b a
t
.
Giátrịnhỏnhấtcủabiểuthức
2P x y
bằng
3
2
2
thuộcnửakhoảng
5
;3
2
.
Câu 2. (Đề Tham Khảo 2020 Lần 2) Cóbaonhiêusốnguyên
x
saochotồntạisốthực
y
thỏamãn
2 2
3 4
log ( ) log
x y x y
?
A.
3
. B.
2
. C.
1
. D. Vôsố.
Lời giải
Chọn B
Cách 1:
Đặt
2 2
3 4
2 2
3
log ( ) log 1
4
t
t
x y
t x y x y
x y
.
ÁpdụngbấtđẳngthứcCauchy,tacó
2
2 2
9
2
9
9 2 4 2 log 2
4
t
t t
t
x y x y t
Nhưvậy,
9
4
log 2
2 2 2
4 4 4 1,89 1;0;1
t t
x y x x
Trườnghợp1:
2
3 0
0
1
4
t
t
y t
x
y
y
.
Trườnghợp2:
2
3 1 0
1
0
4 1
t
t
y t
x
y
y
.
Trườnghợp3:
2 2
2
0
3 1
1 5
3 1 2
1 4 1
t
t
t
t
y
x x y
y
y
mâuthuẫnvới
3
2
o
2 2
l g 2
4x y
suyraloại
1
x
.
Vậycóhaigiátrị
0;1
x
Cách 2:
Đặt
2 2
3 4
2 2
3
log ( ) log 1
4
t
t
x y
t x y x y
x y
.
Suyra
,x y
làtọađộcủađiểm
M
với
M
thuộcđườngthẳng
: 3
t
d x y
vàđườngtròn
2 2
: 4
t
C x y
.
Đểtồntại
y
tứctồntại
M
nên
,
d C
cóđiểmchung,suyra
,
d O d R
trongđó
0;0 , 2
t
O R
nên
3
2
3
2 log 2
2
t
t
t
.
Khiđó
3
2
3
2
2 2
log 2
log 2
0 3
1
4
x y
x y
.
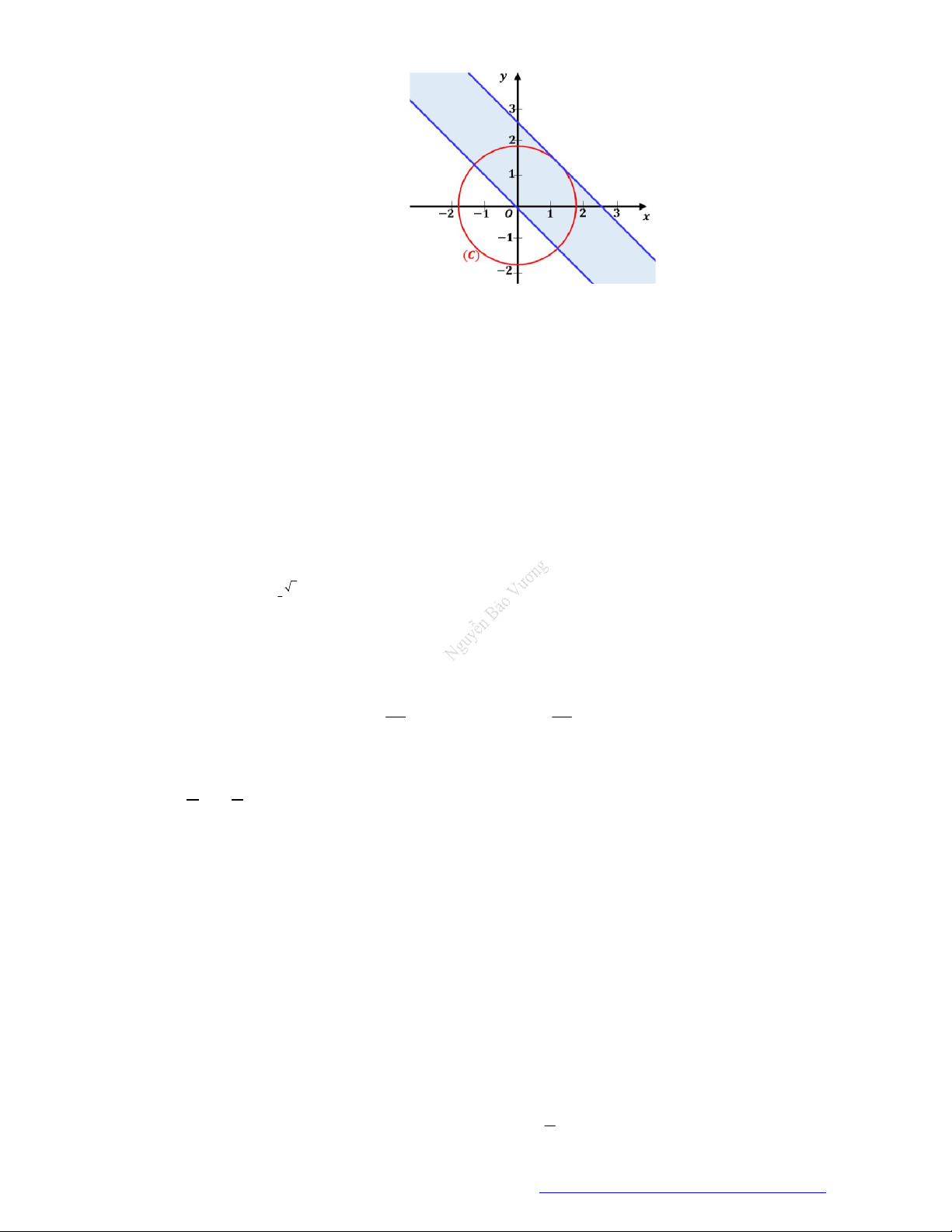
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Minhhọaquỹtíchđiểm
M
nhưhìnhvẽsau
Tathấycó3giátrị
x
cóthểthỏamãnlà
1; 0; 1x x x
.
Thửlại:
Trườnghợp1:
2
3 0
0
1
4
t
t
y t
x
y
y
.
Trườnghợp2:
2
3 1 0
1
0
4 1
t
t
y t
x
y
y
.
Trườnghợp3:
2 2
2
0
3 1
1 5
3 1 2
1 4 1
t
t
t
t
y
x x y
y
y
mâuthuẫnvới
3
2
o
2 2
l g 2
4x y
suyraloại
1x
.
Câu 3. (Mã1032018)Cho
0, 0a b
thỏamãn
2 2
4 5 1 8a 1
log 16 1 log 4 5 1 2
a b b
a b a b
.Giá
trịcủa
a 2b
bằng
A.
6
B.
27
4
C.
20
3
D.
9
Lờigiải
ChọnB
Từgiảthiếtsuyra
2 2
4 5 1
log 16 1 0
a b
a b
và
8a 1
log 4 5 1 0
b
a b
.
ÁpdụngBĐTCôsitacó
2 2
4 5 1 8a 1
log 16 1 log 4 5 1
a b b
a b a b
2 2
4 5 1 8a 1
2log 16 1 .log 4 5 1
a b b
a b a b
8a 1
2 2
2log 16 1
b
a b
.
Mặtkhác
2
2 2
16 1 4 8a 1 8a 1 , 0a b a b b b a b
,
suyra
8a 1
2 2
2log 16 1 2
b
a b
.
Khiđó
2 2
4 5 1 8a 1
log 16 1 log 4 5 1 2
a b b
a b a b
4 5 1 8a 1
log 8 1 log 4 5 1
4
a b b
ab a b
b a
2
24 1
log 32 1 1
4
a
a
b a
2
3
32 24
4
4
3
a
a a
b a
b
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy
3 27
2 6
4 4
a b
.
Câu 4. (Mã 101 - 2020 Lần 1) Xétcácsốthựckhôngâm
x
và
y
thỏamãn
1
2 .4 3
x y
x y
.Giátrị
nhỏnhấtcủabiểuthức
2 2
4 6P x y x y
bằng
A.
33
4
. B.
65
8
. C.
49
8
. D.
57
8
.
Lời giải
Chọn B.
Cách 1:
Nhận xét:Giátrịcủa
,x y
thỏamãnphươngtrình
1
2 4 3 1
x y
x y
sẽlàmchobiểuthức
P
nhỏnhất.Đặt
a x y
,từ
1
tađượcphươngtrình
1
2 3
4 . 2 0
a
a
y y
.
Nhậnthấy
1
2 3
4 . 2
a
y a
y y
làhàmsốđồngbiếntheobiến
a
,nênphươngtrìnhtrêncó
nghiệmduynhất
3 3
2 2
a x y
.
Taviếtlạibiểuthức
2
1 1 65
4 2
4 8 8
P x y x y y
.Vậy
min
65
8
P
.
Cách 2:
Vớimọi
,x y
khôngâmtacó
3 3
1
2 2
3 3
2 .4 3 .4 . 4 1 0
2 2
x y x y
x y
x y x y x y y
(1)
Nếu
3
0
2
x y
thì
3
0
2
3
. 4 1 0 . 4 1 0
2
x y
x y y y
(vôlí)
Vậy
3
2
x y
.
ÁpdụngbấtđẳngthứcBunhyakovskitađược
2 2
2 2
4 6 3 2 13
P x y x y x y
2
2
1 1 3 65
5 13 5 13
2 2 2 8
x y
Đẳngthứcxảyrakhi
5
3
4
2
1
3 2
4
y
x y
x y
x
.
Vậy
65
min
8
P
.
Câu 5. Xét các số thực
,x y
thỏa mãn
2 2
1 2 2
2 2 2 4
x y x
x y x
. Giá trị nhỏ nhất của biểu thức
4
2 1
y
P
x y
gần nhấtvớisốnàodướiđây?
A.
2
. B.
3
. C.
5
. D.
4
.
Lời giải
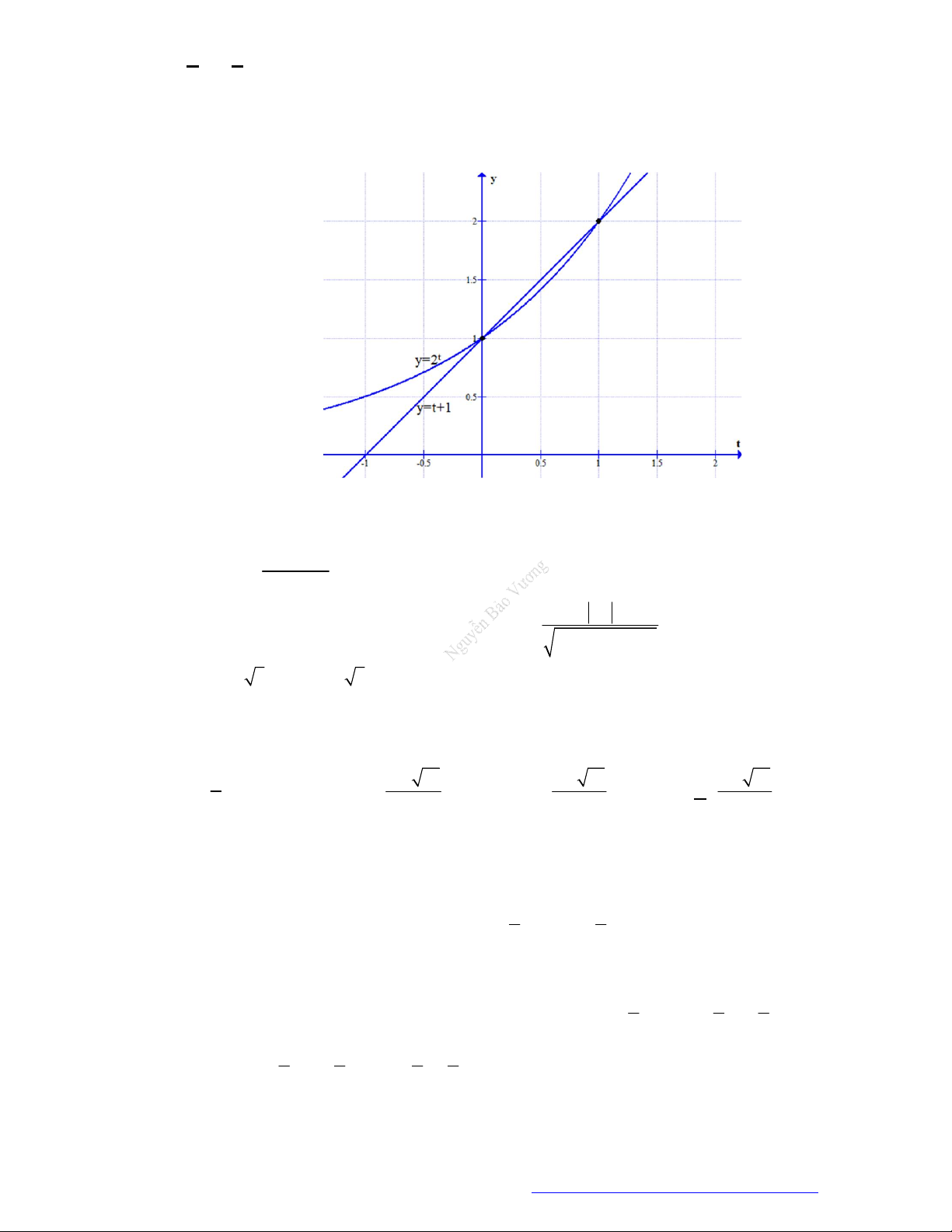
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Chọn B
Tacó
2 2 2 2
1 2 2 1 2 2 2
2 2 2 4 2 2 2
x y x x y x
x y x x y x
2
2
2
1
2
2 1 1
x y
x y
.Đặt
2
2
1 0t x y t
,tađượcBPT:
2 1
t
t
.
Đồthịhàmsố
2
t
y
vàđồthịhàmsố
1y t
nhưsau:
Từđồthịsuyra
2
2
2 1 0 1 1 1
t
t t x y
.Dođótậphợpcáccặpsố
;x y
thỏa
mãnthuộchìnhtròn
C
tâm
1;0 , 1I R
.
Tacó
4
2 4 0
2 1
y
P Px P y P
x y
làphươngtrìnhcủađườngthẳng
d
.
Do
d
và
C
cóđiểmchung
2
2
2
3
, 1 4 8 16 0
4 4
P
d I d R P P
P P
1 5 1 5P
,suyragiátrịnhỏnhấtcủa
P
gần nhấtvới
3
.
Câu 6. Chocácsốthực
,x y
thỏamãnbấtđẳngthức
2 2
4 9
log 2 3 1
x y
x y
.Giátrịlớnnhấtcủabiểu
thức
3P x y
là
A.
3
2
. B.
2 10
4
. C.
5 10
4
. D.
3 10
4
.
Lờigiải
Điềukiện
2 2
4 9 1x y .
Trườnghợp1:
2 2
4 9 1x y .
Tacó
2 2
2 1
2 3 1
3 1
x
x y
y
1 3
3 1
2 2
x y P
.
1
Trườnghợp2:
2 2
4 9 1x y
.
Khiđó
2 2
2 2
4 9
log 2 3 1 2 3 4 9
x y
x y x y x y
2 2
1 1 1
2 3
2 2 2
x y
.
1 1 1 3
3 2 3
2 2 2 4
P x y x y
.
ÁpdụngBĐTBunhiacopskitađược:

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2 2
1 1 1 1 1 1 5
2 3 1 2 3
2 2 2 4 2 2 8
x y x y
.
Suyra
1 1 1 3 3 10
2 3
2 2 2 4 4
P x y
.
2
Dấubằngxẩyrakhivàchỉkhi
1 1
5 10
2 2 3
8 6 1
2 2
20
4 12 3 10
5 2 10
3 10
3
30
4
x y
x
x y
x y
y
x y
.Từ
1
và
2
suyragiátrịlớnnhấtcủa
P
là
3 10
4
.
Câu 7. (ChuyênLamSơnThanhHóa2019)Chocácsốthực
,a b
thayđổi,thỏamãn
1
, 1.
3
a b
Khi
biểuthức
4 2
3
log log 9 81
a b
P b a a
đạtgiátrịnhỏnhấtthìtổng
a b
bằng
A.
2
3 9
B.
3
9 2
C.
2 9 2
D.
3 3 2
Lờigiải
ChọnA
Do
2
4 2 2 2
9 81 9 9 0
a a a a
đúng
1
;
3
a
Dấubằngxảyrakhi
3
a
Suyra
2
3 3
log log 3 log 2log 3 2 2
a b a b
P b a b a
Dấubằngxảyrakhivàchỉkhi
2
3
3
3
log 2log 3
9
a b
a
a
b a
b
Vậy,khi
P
đạtgiátrịnhỏnhấtthì
2
3 9 .
a b
Câu 8. (Chuyên Trần Phú Hải Phòng 2019) Cho các số thực
, ,ca b
thỏa mãn
1 3
0 1; 1; 1
8 8
a b c
. Gọi
M
là giá trị nhỏ nhất của biểu thức
3 1 1 3 1
log log log
16 2 16 4 2 16 3
a b c
b c
P a
.Khẳngđịnhnàosauđâyđúng?
A.
3 2
M
. B.
2M
. C.
2 3
M . D.
2
M
.
Lờigiải
Tacó:
1 8 1 1 8 1
.
2 16 16 4 4
b b b
2
2
2
2
b
b
.
3 8 3 1 1 1 8 3
. . .
2 16 16 2 2 2 2
c c c
4
4
4
4
c
c
.
Suyra
3 1 1 3 1
log log log
16 2 16 4 2 16 3
a b c
b c
P a
2 4
3 1 1
log log log
16 4 3
a b a
b c c
3
2 3
3.
16 2
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Vậy
min
3
2
P
1
4
8 1 1
1
8 3 1
2
3 1
log log log
2
8 3
4
a b c
b
b
c c
b c a
a
.
Câu 9. Chocácsốthực
, , ,a b m n
saocho
2 0m n
vàthoảmãnđiềukiện:
2 2
2 2
4
2
2
log 9 1 log 3 2
9 .3 .3 ln 2 2 1 81
m n
m n
a b a b
m n
Tìmgiátrịnhỏnhấtcủabiểuthức
2 2
P a m b n
A. 2 5 2 . B.
2
. C. 5 2 . D. 2 5
Lờigiải
2 2 2 2 2 2
2 2
log 9 1 log 3 2 9 6 4 6 4 9 0a b a b a b a b a b a b
1
Gọi
;A a b
.Từ
1
tasuyrađiểm
A
thuộcđiểmđườngtròn
C
cótâm
3;2I
,bánkính
2R
.
4 4
2
2 2
2 2
9 .3 .3 ln 2 2 1 81 ln 2 2 1 81 3
m n
m n
m n m n
m n m n
TheobấtđẳngthứcCô-si:
4 4
2 2 2 . 4
2 2
m n m n
m n m n
4
2
2
3 81
m n
m n
.
(Đẳngthứcxảyrakhi:
4
2 2 2
2
m n m n
m n
)
Từ
2 2 2
ln 2 2 1 0 2 2 1 1 2 2 0m n m n m n
2 2 0 2m n
.
Gọi
;B m n
.Từ
2
tasuyrađiểm
B
thuộcđườngthẳng
:
2 2 0x y
Tacó:
2 2
P a m b n AB
2 2
3.2 2 2
min min ; 2 2 5 2.
2 1
P AB d I R
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 10. Chocácsốthực
, ,ca b
thỏamãn
1 3
0 1; 1; 1
8 8
a b c
.Gọi
M
làgiátrịnhỏnhấtcủa
biểuthức
3 1 1 3 1
log log log
16 2 16 4 2 16 3
a b c
b c
P a
.Khẳngđịnhnàosauđâyđúng?
A.
3 2
M
. B.
2M
. C.
2 3
M
. D.
2
M
.
Lờigiải
ChọnC
Tacó:
1 8 1 1 8 1
.
2 16 16 4 4
b b b
2
2
2
2
b
b
.
3 8 3 1 1 1 8 3
. . .
2 16 16 2 2 2 2
c c c
4
4
4
4
c
c
.
Suyra
3 1 1 3 1
log log log
16 2 16 4 2 16 3
a b c
b c
P a
2 4
3 1 1
log log log
16 4 3
a b a
b c c
3
2 3
3.
16 2
.
Vậy
min
3
2
P
1
4
8 1 1
1
8 3 1
2
3 1
log log log
2
8 3
4
a b c
b
b
c c
b c a
a
.
Câu 11. (Chuyên Lam Sơn - 2020) Xét các số thực dương
, ,a b c
lớn hơn
1
( với
a b
) thỏa mãn
4 log log 25log
a b ab
c c c
.Giátrịnhỏnhấtcủabiểuthức
log log log
b a c
a c b
bằng
A.
5
. B.
8
. C.
17
4
. D.
3
.
Lời giải
Chọn A
Đặt
log ,log
c c
a x b y
.
Vì
, , 1a b c
và
a b
nênsuyra
log log
c c
a b
hay
0
x y
.
Từgiảthiếtsuyra:
1 1 1
4 25.
log log log
c c c
a b ab
4 4 25
x y x y
2
25
4
x y
xy
17
4
x y
y x
4
1
4
x
y
x
y
4x y
(vì
x y
).
Tacó:
log
1
log log log log
log log
c
b a c c
c c
a
a c b b
b a
1x
y
y x
1 1
4 2 . 5
4 4
x
y y
y y y
.
Dấubằngxảyrakhivàchỉkhi
1
2
y
và
2
x
,tứclà
2 2
;
a c c b
Vậygiátrịnhỏnhấtcủabiểuthứcđãchobằng
5
.
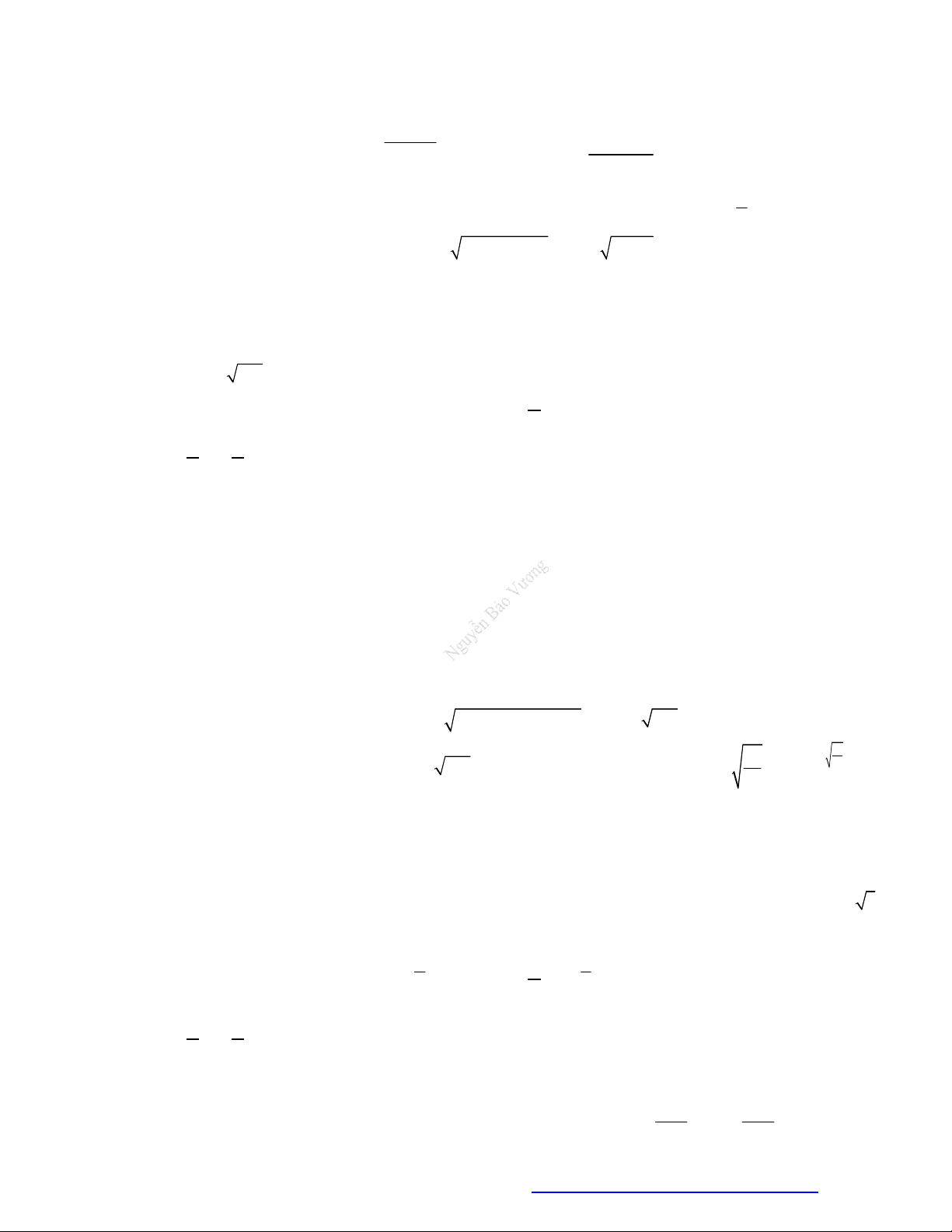
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Cách khác
Từgiảthiếtsuyra:
4 log .log log 25.log .log
a b b ab b
b c c b c
log
4log log 1 25
log
b
b a
b
c
c b
ab
log 0
25
4 log 1
log 1
b
a
b
c
b
a
.
Do
, , 1a b c
nên
log 0
b
c
;suyra
4 1 log 1 log 25
a b
b a
1
log
4
a
b
.
Khiđó:
log log log 4 2 log .log 4 2 log 5
b a c a c a
a c b c b b
.
Vậygiátrịnhỏnhấtcủabiểuthứcbằng
5
đạtđượckhivàchỉkhi
4 2 2
, ,
a b a c c b
.
Câu 12. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Xét các số thực dương
a
,
b
,
x
,
y
thỏamãn
a 1
,
b 1
và
2x 3y 6 6
a b a b
. Biết giá trị nhỏ nhất của biểu thức
4 2
P xy x y
có dạng
165
m n (với
,m n
làcácsốtựnhiên),tính
S m n
.
A.
58
. B.
54
. C.
56
. D.
60
Lời giải
Chọn C
Theobàiratacó:
2x 3y 6 6
a b a b
2x 6 6
3y 6 6
a a b
b a b
6 6
a
6 6
b
2x log a b
3y log a b
a
b
2x 6 6log b
3y 6 6log a
a
b
x 3 1 log b
y 2 1 log a
Vì
a
,
b 1
nên
a a
log b log 1 0
.
Dođó:
4 2 24(1 log )(1 log ) 6 6log 2 2log
a b a b
P xy x y b a b a
52 30log 22log 52 2 30log .22log 52 4 165
a b a b
b a b a
Vậy
P
đạtgiátrịnhỏnhấtlà
165
m n
khi
11
15
11
30log 22log log
15
a b a
b a b b a
Tacó:
52
56
4
m
m n
n
.
Câu 13. (Chuyên Lê Hồng Phong - Nam Định - 2020) Xét các số thực
,x y
thỏa mãn
2 2
log 1 log 1 1
x y
.Khibiểuthức
2 3P x y
đạtgiátrịnhỏnhấtthì
3 2 3x y a b
với
,a b
.Tính
T ab
?
A.
9
T
. B.
7
3
T
. C.
5
3
T
. D.
7
T
.
Lời giải
Chọn C
Điềukiện:
1 0 1
1 0 1
x x
y y
Khiđó:
2 2
2 2
log 1 log 1 1 1 1 2 1 1
1 1
x y x y y y
x x
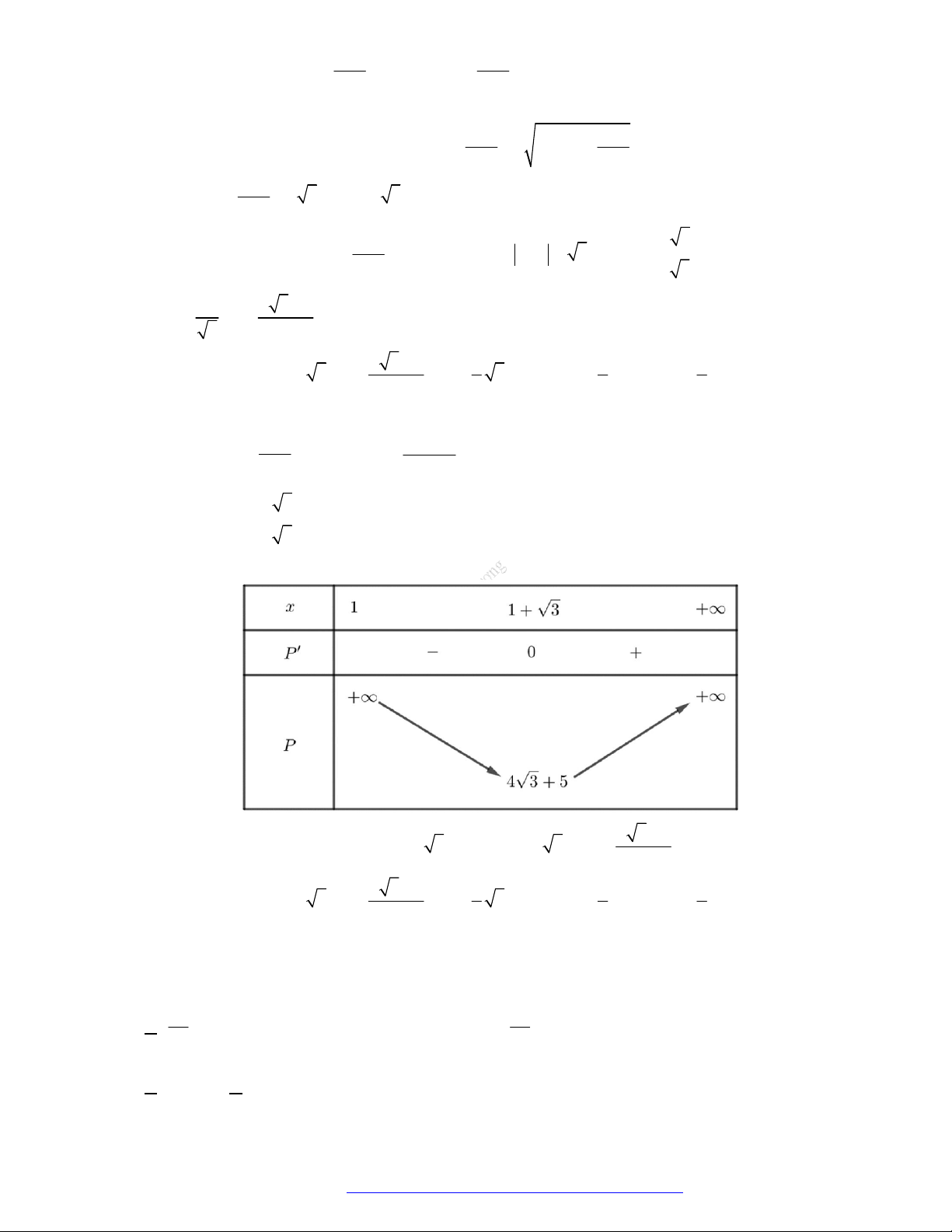
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Suyra:
6 6
2 3 2 3 2 1 5
1 1
P x y x x
x x
Cách 1:Dùngbấtđẳngthức
ÁpdụngbấtđẳngthứcCôsi,tacó:
6 6
2 1 2 2 1 .
1 1
x x
x x
6
2 1 4 3 4 3 5
1
x P
x
Dấu“=”xảyra
2
1 3
6
2 1 1 3 1 3
1
1 3
x N
x x x
x
x L
2 2 3 3
1
3
3
y
.
Dođó:
2 3 3 5 5 5
3 2 3 1 3 2 1 3 1;
3 3 3 3
x y a b T ab
.
Cách 2:Dùngbảngbiếnthiên
Tacó:
6
2 3
1
P x
x
2
6
' 2
1
P
x
1 3
' 0
1 3
x N
P
x L
Bảngbiếnthiên
Dựavàobảngbiếnthiên,tacó:
min
2 3 3
4 3 5 1 3
3
P x y
.
Dođó:
2 3 3 5 5 5
3 2 3 1 3 2 1 3 1;
3 3 3 3
x y a b T ab
.
Câu 14. (Chuyên Phan Bội Châu - Nghệ An - 2020) Cho
0, 0a b
thỏa mãn
2 2
4 5 1 8a 1
log 16 1 log 4 5 1 2
a b b
a b a b
.Giátrịcủa
2a b
bằng
A.
27
4
. B.
6
. C.
20
3
. D.
9
.
Lời giải
Chọn A.
Tacó:
0, 0a b

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Nên
2 2
4 5 1
8 1
log 16 1 0
4 5 1 1
8 1 1
log 4 5 1 0
a b
ab
a b
a b
ab
a b
2 2 2 2
4 5 1 8 1 4 5 1 8 1
2 2
8 1
log 16 1 log 4 5 1 2 log 16 1 .log 4 5 1
2 log 16 1
a b ab a b ab
ab
P a b a b a b a b
P a b
Mặtkhác:
2 2 2 2
8 1
16 1 2 16 1 8 1 2 log 8 1 2
ab
a b a b ab P ab
Dấubằngxảyrakhivàchỉkhi:
2 2
2
3
4
16
4
8 1 4 5 1 2 1 6 1
3
a b
a
a b
ab a b b b
b
Dođó
27
2
4
a b
.
Câu 15. (Chuyên Sơn La - 2020) Cho
, ,a b c
làcácsốthựclớnhơn
1
.Giátrịnhỏnhấtcủabiểuthức
3
4040 1010 8080
log
log 3log
ac ab
bc
P
a
b c
bằng
A.
2020
. B.
16160
. C.
20200
. D.
13130
.
Lời giải
Chọn C
Tacó
3
4040 1010 8080 4040 1010 8080
1 1
log 2log
log 3log
log 3. log
2 3
bc
ac ab
bc
ac ab
P
a a
b c
b c
2020log 2020log 8080log
a b c
bc ac ab
2020 log log 2020 log log 8080 log log
a a b b c c
b c a c a b
2020log 2020log 2020log 8080log 2020log 8080l
og
a b a c b c
b a c a c b
Vì
, , 1a b c
nêncácsố
log ,log ,log ,log ,log ,log 0
a b a c b c
b a c a c b
Khiđótacó
2
2020log 2020log 2 2020 log log 4040
a b a b
b a b a
2
2020log 8080log 2 4040 log log 8080
a c a c
c a c a
2
2020log 8080log 2 4040 log log 8080
b c b c
c b c b
Suyra
4040 8080 8080 20200
P
Câu 16. (Chuyên Vĩnh Phúc - 2020) Cho
, ,a b c
là các số thực dương khác
1
thỏa mãn
2 2
log log log 2log 3
a b a b
c c
b c
b b
.Gọi
,M m
lầnlượtlàgiátrịlớnnhất,giátrịnhỏnhấtcủa
log log
a b
P b c
.Giátrịcủabiểuthức
3
S m M
bằng
A.
16
. B.
4
. C.
6
. D.
6
.
Lời giải
Chọn C
Biếnđổiđẳngthứcđềbàitađược
2 2 2 2
2 2
log log log 2log 3 log log log log 2log 1
log log log .log log 2log 1
a b a b a b a a b
a b a b a b
c c
b c b c c b c
b b
b c b c b c

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đặt
log ; log
a b
u b v c
tacóphươngtrình
2 2
2 1u v uv u v
2 2 2 2
2 2 1 4 4 3
u uv v u u v v
2 2 2
( ) ( 1) ( 2) 3(*)
u v u v
Tacóbấtđẳngthứcquenthuộc
2 2 2
1
( )
2
x y x y
dấubằngxảyrakhi
x y
,ápdụngbất
đẳngthứcnàytacó
2 2 2 2 2 2
1 1
( 1) ( 2) ( 1 2) ( 1) ( 2) ( 1)
2 2
u v u v u v u v
(**)
Từ(*)và(**)tacó
2 2
1
3 ( ) ( 1)
2
u v u v
hay
2 2 2
1 5
3 ( 1) 3 2 5 0 1
2 3
P P P P P
Vậy
5
1,
3
m M
suyra
3 6
S m M
.
Câu 17. (Sở Hưng Yên - 2020) Cho các số thực
, 1x y
và thỏa mãn điều kiện
4xy
. Biểu thức
2
2
4
2
log 8 log
2
x
y
y
P x
đạtgiá trị nhỏ nhấttại
0 0
,
x x y y
.Đặt
4 4
0 0
T x y
mệnh đềnào
sauđâyđúng
A.
131T
. B.
132T
. C.
129T
. D.
130T
.
Lời giải
Chọn D
Tacó
2
2
4
2
log 8 log
2
x
y
y
P x
2
2
2
2
2 2
log
log 8
2
log 4 log 2
y
x
x y
2 2
2 2
3 log 2log 1
2 log 2log 1
x y
x y
.
Đặt
2
log
x a
,
2
log
y b
(
, 0
a b
),tađược
3 2 1
2 2 1
a b
P
a b
1 2
2 2 1a b
.
Vì
4xy
suyra
2 2
log log 2
x y
2 0 2a b a b
Suyra
1 2 1 2
2 2 1 4 2 1
P
a b b b
.
Xéthàm
1 2
( )
4 2 1
f b
b b
trên
0;2
,tacó:
2 2
1 4
( )
4 2 1
f b
b b
2
2
0 2 1 4(4 ) 0
f b b b
7
4
b
.
Tacó:
9 9 7 8
0 , 2 ,
4 10 4 9
f f f
.
Suyratrênđoạn
0;2
tacó:
8
min
9
P
2
2
1
log
4
7
log
4
x
y
1
4
7
4
2
2
x
y
1
4
0
7
4
0
2
2
x
y

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Vậy
4 4
1 7
4 4
4 4
0 0
2 2 130T x y
.
Câu 18. (Sở Hà Tĩnh - 2020) Chocácsốthựcdương
, ,a b c
thỏamãn
10abc
.Biếtgiátrịlớnnhấtcủa
biểuthức
5log .log 2log .log log .logF a b b c c a
bằng
m
n
với
,m n
nguyêndươngvà
m
n
tối
giản.Tổngm n bằng
A.
13.
B.
16.
C.
7.
D.
10.
Lời giải
Chọn C
Đặt
10
log
log 10
log
10
x
y
z
a
a x
b y b
c z
c
,mà
10 10 .10 .10 10 1 *
x y z
abc x y z
.
Tacó
5log .log 2log .log log .log 5 2F a b b c c a xy yz zx
.
Từ
* 1y x z
,thayvàobiểuthức
F
,tađược:
2 2
5 1 2 1 2 5 6 2 5F x x z x z z xz z x xz z x
2 2 2
9 1 1 5
2 6 2 3 2 2
2 2 2 2
z x xz z x x x
2 2 2
9 1 3 1 5
2 3 4 4
4 4 2 2 2
z x xz z x x x
2
2
3 1 1 5 5
2 2
2 2 2 2 2
z x x
.
Vậy
5
max
2
F
khivàchỉkhi
3
1
2
3 1
0 2
2 2
5
2 0
2
x y z
y
z x x
x
z
.
Vậy
5, 2 5 2 7.m n m n
Câu 19. (Lê Lai - Thanh Hóa - 2020) Cho thỏa mãn
.Giátrịbiểuthức bằng?
A. 6. B. . C. . D. 22.
Lời giải
Chọn B
Với
0, 0a b
tacó
2 2
25 1 10 1a b ab
,dấu“=”xảyrakhivàchỉkhi
5b a
.
Suyra
2 2
10 3 1 10 3 1
log 25 1 log 10 1
a b a b
a b ab
,dấu“=”xảyrakhivàchỉkhi
5b a
.
Mặtkhác,talạicóvới
0, 0a b
thì
10 3 1 10 1
log 10 1 0,log 10 3 1 0
a b ab
ab a b
.
Dođó:
2 2
10 3 1 10 1 10 3 1 10 1
log 25 1 log 10 3 1 log 10 1 log 10 3 1
a b ab a b ab
a b a b ab a b
10 3 1 10 1
2 log 10 1 .log 10 3 1 2
a b ab
ab a b
Dấu“=”xảyrakhivàchỉkhi
0, 0
a b
2 2
10 3 1 10 1
log 25 1 log 10 3 1 2
a b ab
a b a b
2a b
11
2
5
2

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
10 3 1 10 1
5
5
5
2
log 10 1 log 10 3 1
10 3 1 10 1 1
2
a b ab
b
b a
b a
ab a b
a b ab
a
11
2
2
a b
Câu 20. (Liên trường Nghệ An - 2020) Cho các số thực dương
; ;a b c
khác
1
thỏa mãn
2 2
3
log log 2log log
a b b a
c c
b c
b a b
.Gọi
,M m
lầnlượtlàgiátrịlớnnhấtvàgiátrịnhỏnhấtcủa
log log
a b
P ab bc
.Tínhgiátrịbiểuthức
2 2
2 9
S m M
.
A.
28
S
. B.
25
S
. C.
26
S
. D.
27
S
.
Lời giải
Chọn D
Đặt
log ; log , ; 0 log log log
a b a a b
x b y c x y c xy P ab bc x y x P y
Khiđótacó
2 2 2 2
3
2
2
2 2
log log 2log log 2 2 3
2 2 3
3 1 0
a b b a
c c
b c x y y xy x
b a b
P y y y P y y P y
y P y P P
.
Phươngtrìnhcónghiệmkhi
2
5 5
0 3 2 5 0 1 1; 27
3 3
P P P m M S
Nêngiátrịnhỏnhấtcủa
P
là
1
1
4
4
2
0
4 4
0 0
7 7
4 4
2
0
1
log
2
2
8
4
130
7
9
log
2 2
4
x
x
x
T x y
y
y y
Câu 21. (Lý Nhân Tông - Bắc Ninh - 2020) Cho
0, 0a b
thỏa mãn
2 2
4 5 1 8 1
log (16 1) log (4 5 1) 2
a b ab
a b a b
.Giátrịcủa
2a b
bằng
A.
9
. B.
6
. C.
27
4
. D.
20
3
.
Lời giải
Chọn C
TheobấtđẳngthứcCôsivới
0, 0a b
tacó:
2 2 2 2 2 2
16 1 2 16 1 8 1 16 1 8 1
a b a b ab a b ab
(*)
Do
4 5 1 1a b
nêntừ(*)có:
2 2
4 5 1 8 1 4 5 1 8 1
log (16 1) log (4 5 1) log (8 1) log (4 5 1)
a b ab a b ab
a b a b ab a b
2 2
4 5 1 8 1 4 5 1
4 5 1
1
log (16 1) log (4 5 1) log (8 1)
log (8 1)
a b ab a b
a b
a b a b ab
ab
Mặtkhác
4 5 1 1a b
và
8 1 1ab
nên:
4 5 1
4 5 1
1
log (8 1) 2
log (8 1)
a b
a b
ab
ab
.
Suyra
2 2
4 5 1 8 1
log (16 1) log (4 5 1) 2
a b ab
a b a b
.
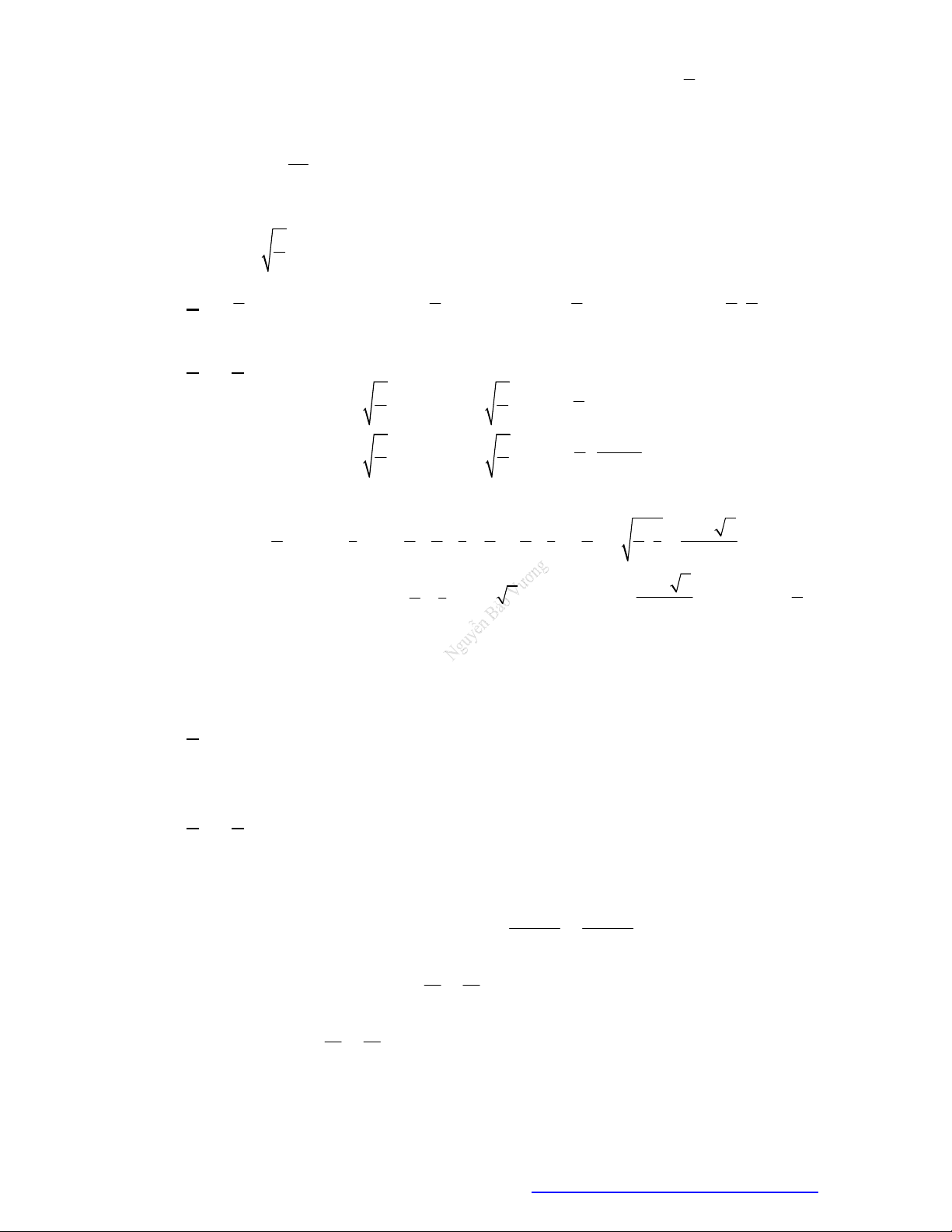
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Đẳngthứcxảyrakhi
2 2
2
4
16
3
4 5 1 8 1 2 6 0
4
3
, 0 , 0
b a
a b
a
a b ab b b
b
a b a b
.
Vậy
27
2
4
a b
.
Câu 22. (Nguyễn Huệ - Phú Yên - 2020) Xét các số thực
, , ,a b x y
thỏa mãn
1, 1
a b
và
x y
a
a b
b
.Giátrịlớnnhấtcủabiểuthức
2P x y
thuộctậpnàodướiđây?
A.
1
0;
2
. B.
1
1;
2
. C.
3
1;
2
. D.
3 5
;
2 2
.
Lời giải
Chọn A
Từgiảthiếttacó:
1
1 log
log
2
1 1
1
log
2 log
x
a
a
y
b
a
a a
x b
a x
b b
a a
y
b y
b
b b
Đặt
log
a
t b
.Vì
1, 1
a b
,nên
0t
.
Khiđó:
1 1 3 1 3 1 3 1 3 2 2
1 1 2.
2 2 2 2 2 2 2 2
t t t
P t
t t t t
Dấubằngxảyrakhivàchỉkhi
1
2 0
2
t
t t
t
.
max
3 2 2 1
0,086 0;
2 2
P
.
Câu 23. (Tiên Du - Bắc Ninh - 2020) Cho biểu thức
2 3 2 1 2 1
3 (1 4 ) 2
y x x y x y
P
và biểu thức
3 2
log 3
y x
Q y
.Giátrịnhỏnhấtcủa yđểtồntạix đồngthờithỏamãn
1P
và
1
Q
làsố
0
y
.
Khẳngđịnhnàosauđâylàđúng?
A.
0
4 1
y
làsốhữutỷ. B.
0
y
làsốvôtỷ.
C.
0
y
làsốnguyêndương. D.
0
3 1
y
làsốtựnhiênchẵn.
Lời giải
Chọn A
Điềukiện
2 3 0
.
0
y x
y
2 1 2 1 2 1 2 1
2 1 2 1
1 1
3 .(1 4 ) 2 3 .(1 ) .
4 2
y x x y x y y x
x y y x
P
Đặt
2 1t y x
tacó
1 1
3 (1 ) .
4 2
t
t t
P
Cho
1 1
1 3 (1 ) 1 12 3 4 2 (1).
4 2
t t t t t
t t
P
*Với
0t
thỏamãn(1).
*Với
0t
tacó
12 4
12 3 4 2 (1)
3 2
t t
t t t t
t t
thỏamãn.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
*Với
0t
tacó
12 4
12 3 4 2 (1)
3 2
t t
t t t t
t t
khôngthỏamãn.
Vậy
(1) 0t
hay
2 1 0y x
(a).
Vì
2 1 0y x
2 3 2 1y x
nên
2 1
log 3 1 3 2 3 2 2 3
y x
Q y y y x x y
(b).
Từ(a),(b)vàđiềukiệntacó
2 1 0
2 2 3 .
0
y x
x y
y
Cặpsố
( ; )x y
thỏamãnhệđượcbiểudiễnởmiềnkhôngbịgạchởhìnhbên.ĐiểmAthuộcmiền
khôngbịgạchvàcó
min
2
.
3
y
Vậy
0
2
.
3
y
Dođó
0
11
4 1 .
3
y
Câu 24. (Trường VINSCHOOL - 2020) Cho dãy số
n
u
có số hạng đầu
1
1u thỏa mãn
2 2 2 2
2 1 2 1 2 2
log 5 log 7 log 5 log 7 u u
và
1
7
n n
u u với mọi
1n
. Giá trị nhỏ nhất của
n
để
1111111
n
u bằng:
A.
11
. B.
8
. C.
9
. D.
10
.
Lời giải
Chọn D
Tacó
1
7 , 1
n n n
u u n u
làmộtcấpsốnhânvớisốhạngđầulà
1
u ,côngbội
7q
.
2 2
2 2
2 1 2 1 2 2 1 2 2 1
log 5 log 7 log 5 log log 7 log u u u u
2 2 2 2
2 2 2 1 2 1 2 2 2 1 2 1
log 5 2.log 5.log log log 7 2.log 7.log log u u u u
2 2 2
2 1 2 2 2 1 2 2
2log 2. log 5 log 7 .log log 5 log 7 u u
2 2 2 2 2
2 1 2 2 1 2 2 2 2
2log 2.log 35.log log 5 log 7 log 5 log 7 u u
2
2 1 2 2 1 2 1 2 1 2
2log 2.log 35.log 0 2log . log log 35 0 u u u u
12 1
1
2 1 2
2 1 2
1 loailog 0
1
nhan
log log 35 0
35
log log 35
uu
u
u
u
.
Sốhạngtổngquátcủadãysốlà
1 1 1 2
1
1 1 1
. .7 .7 .7
35 5.7 5
n n n n
n
u u q
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
2 2
7
1
1111111 .7 1111111 7 5555555 2 log 5555555
5
n n
n
u n
7
log 5555555 2
n
.Vì
n
nêngiátrịnhỏnhấtcủa
n
bằng
10
.
Câu 25. (Chuyên Lê Hồng Phong - Nam Định - 2020) Xét các số thực
,x y
thỏa mãn
2 2
log 1 log 1 1
x y
.Khibiểuthức
2 3P x y
đạtgiátrịnhỏnhấtthì
3 2 3x y a b
với
,a b
.Tính
T ab
.
A.
9
T
. B.
7
3
T
. C.
5
3
T
. D.
7
T
.
Lời giải
Chọn C
Tacó
2 2
, 1 1
log 1 log 1 1
2 2
1 1
1 1
x y x
x y
y y
x x
.
Khiđó
2 6
2 3 2 3 1 2 1 5 2 12 5
1 1
P x y x x
x x
,dấubằngxảyrakhivàchỉ
khi
1
1 3
6 2 5 3
2 1 3 2 3 1 3 2 1 1
2
1 3
1
3
3
2
1
1
x
x
x x y
x
y
y
x
.
Vậy
5
1,
3
a b
nên
5
3
T
.
Câu 26. Xét các số thực
a
,
b
,
0
c
thỏa mãn
3 5 15
a b c
. Giá trị nhỏ nhất của biểu thức
2 2 2
4( ) P a b c a b c
thuộctậphợpnàodướiđây?
A.
1;2
. B.
5; 1
. C.
2;4
. D.
4;6
.
Lời giải
Chọn B
Đặt
3
5
15
log
3 5 15 0 log
log
a b c
a t
t b t
c t
.Khiđó
2 2 2
3 5 15 3 5 15
log log log 4(log log log )
P t t t t t t
2 2 2
3 5 15 3 5 15
log 1 log 3 log 3 4log 1 log 3 log 3
t t
2 2 2
5 15 5 15
1 log 3 log 3 4 1 log 3 log 3
X X ,(với
3
logX t
)
5 15
min
2 2
5 15
2 1 log 3 log 3
4
1 log 3 log 3
P P
,
khi
2 1 log 3 log 3
5 15
2 2
1 log 3 log 3
5 15
5
15
3
2 2
5 15
2 1 log 3 log 3
log 3
1 log 3 log 3
t t
Suyra

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
5 15
2 2
5 15
2 1 log 3 log 3
5 15
2 2
1 log 3 log 3
5
15
5
2 1 log 3 log 3
5 15
2 2
1 log 3 log 3
5
15
15
2 1 log 3 log 3
1 log 3 log 3
log 3
log 3
a
b
c
.
Câu 27. Xétcácsốthựcdương
a
,
b
,
c
,
x
,
y
,
z
thỏamãn
1
a
,
1b
,
1c
và
x y z
a b c abc
.
Giátrịnhỏnhấtcủabiểuthức
1
2
P x y z
thuộctậphợpnàodướiđây?
A.
10;13
. B.
7;10
. C.
3;5
. D.
5;7
.
Lời giải
Chọn D
Từgiảthiếttacó
1
1 log log
2
a a
x b c
,
1
1 log log
2
b b
y a c
,
1
1 log log
2
c c
z b a
.Khiđótacó
2 4 log log log log log log
a b a c b c
P b a c a c b
.
Vì
1
a
,
1b
,
1c
nên
log 0
a
b
,
log 0
b
c
,
log 0
c
a
,
log 0
b
a
,
log 0
c
b
,
log 0
a
c
.
ÁpdụngbấtđẳngthứcCôSitađược
log log 2 log .log
a b a b
b a b a
hay
log log 2
a b
b a
.
Tươngtự
log log 2
a c
c a
và
log log 2
b c
c b
.
Dođó
2 10P
hay
5P
.Dấu
" "
xảyrakhivàchỉkhi
a b c
.
Vậygiátrịnhỏnhất
min
5
P
.
Câu 28. Xétcácsốthựcdương
, , ,a b x y
thỏamãn
1, 1
a b
và
2 2
.
x y
a b a b
.Giátrịnhỏnhấtcủa
biểuthức
.P x y
là
A.
9
4
P
. B.
6
2
P
. C.
3
2
P
. D.
4
9
P
.
Lời giải
Chọn B
2 2
2
2
1 1
log
2 2
.
1 1
log
2 2
a
x y
b
x b
a b a b
y a
+)
2
1 1 1 1
log log
2 2 2 2
a b
xy b a
1 1 1
log log
4 2 4
a b
b a
3
2
(
, 1 log 0,log 0
a b
a b b a
).
Vì
6
0, 0
2
x y xy
.Dấubằngxảyrakhivàchỉkhi
a b
.
Câu 29. Xétcácsốthựcdương
, , ,a b x y
thỏamãn
1, 1
a b
và
2
2
x
y
y
x
a b ab
.Giátrịnhỏnhấtcủabiểu
thức
.P x y
là

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
A.
2P
. B.
4P
. C.
3
P
. D.
1P
.
Lời giải
Chọn B
2
2
2
2
1 log
1 log
x
a
y
y
x
b
x
b
y
a b ab
y
a
x
.
Tacó
2 2
. 1 log 1 log
a a
x y
xy b b
y x
1 1 log log
a b
b a
4
(
, 1 log 0,log 0
a b
a b b a
).
Dấubằngxảyrakhivàchỉkhi
a b
.
Câu 30. Xétcácsốthựcdương
, , , , ,a b c x y z
thỏamãn
1, 1, 1, 2
a b c y
và
1 2 1x y z
a b c abc
.
Giátrịnhỏnhấtcủabiểuthức
P x y z
là
A.
13
P
. B.
3
P
. C.
9
P
. D.
1P
.
Lời giải
Chọn C
1 2 1
1 1 log log
2 1 log log
1 1 log log
a
b
c
a
x y z
b
c
x b c
a b c abc y a c
z b a
.
Tacó:
1 2 1 3 log log log log log log
a c
a b b c
x y z b c c a b a
3 6
x y z
9
P
(
, , 1 log 0,log 0,log 0,log 0,log 0,log 0
a a b b c c
a b c b c a c a b
).
Dấubằngxảyrakhivàchỉkhi
a b c
.
Dạng 3. Sử dụng phương pháp hàm số (hàm đặc trưng) giải các bài toán logarit
1. Định lý:Nếuhàmsố
y f x
đồngbiến(hoặcluônnghịchbiến)vàliêntụctrên
;a b
thì
*
; ; :
u v a b f u f v u v
.
*Phươngtrình
f x
k
k const
cónhiềunhất1nghiệmtrênkhoảng
;a b
.
2.Định lý: Nếuhàmsố
y f x
đồngbiến(hoặcnghịchbiến)vàliêntụctrên
;a b
,đồngthời
lim . lim ( ) 0
x a x b
f x f x
thìphươngtrình
f x k k const
códuynhấtnghiệmtrên
;a b
.
3. Tính chất của logarit:
1.1. So sánh hai logarit cũng cơ số:
Chosốdương
1
a
vàcácsốdương
,b c
.
Khi
1
a
thì
log log
a a
b c b c
.
Khi
0 1a
thì
log log
a a
b c b c
.
1.2. Hệ quả:
Chosốdương
1
a
vàcácsốdương
,b c
.
Khi
1
a
thì
log 0 1
a
b b
.
Khi
0 1a
thì
log 0 1
a
b b
.
log log
a a
b c b c
.
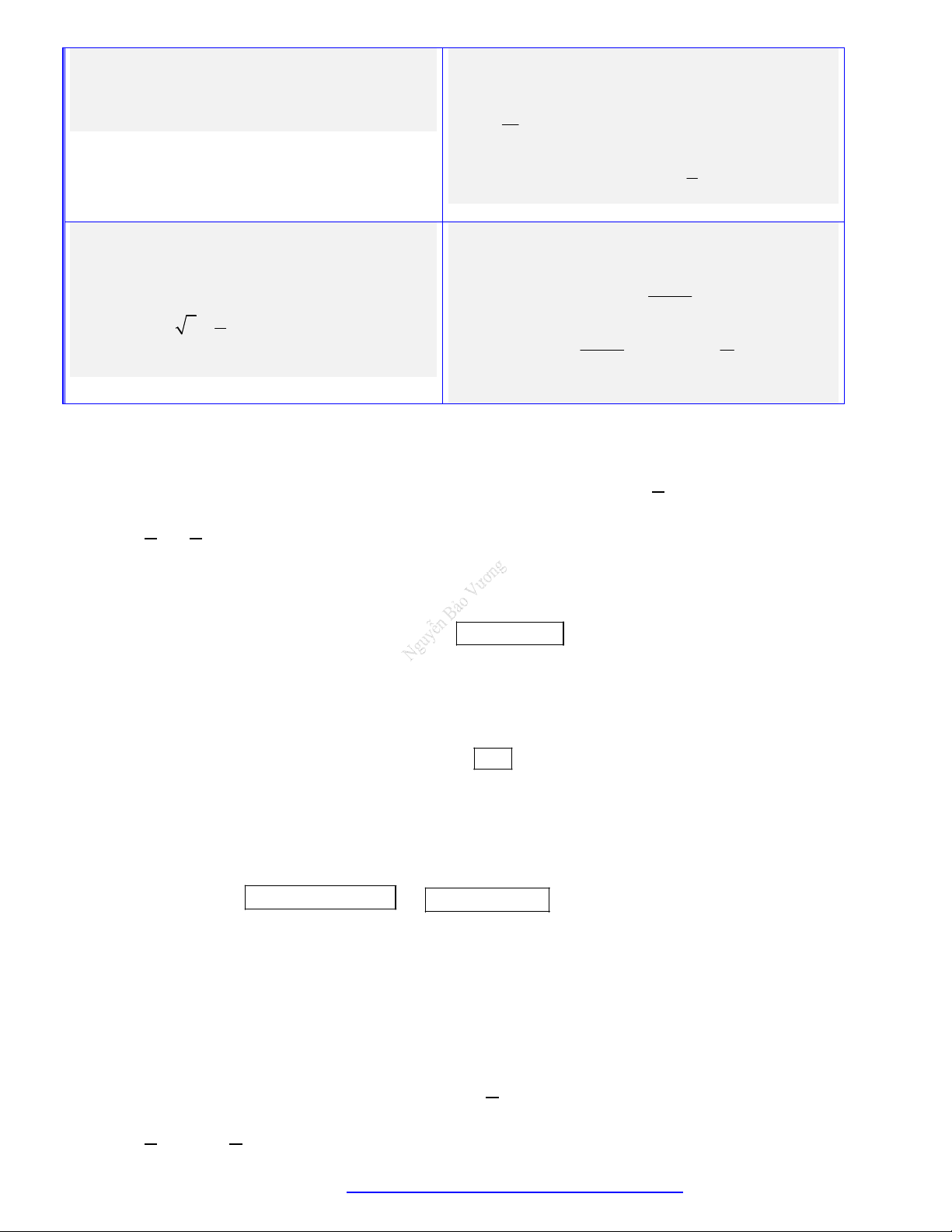
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2. Logarit của một tích:
Cho3sốdương
1 2
, ,a b b
với
1
a
,ta
có
1 2 1 2
log ( . ) log log
a a a
b b b b
3. Logarit của một thương:
Cho3sốdương
1 2
, ,a b b
với
1
a
,ta
có
1
1 2
2
log log log
a a a
b
b b
b
Đặcbiệt:với
, 0, 1
a b a
1
log log
a a
b
b
.
4. Logarit của lũy thừa:
Cho
, 0, 1
a b a
,vớimọi
,tacó
log log
a a
b b
.
Đặcbiệt:
1
log log
n
a a
b b
n
(
n
nguyêndương).
5. Công thức đổi cơ số:
Cho3sốdương
, ,a b c
với
1, 1a c
,tacó
log
log
log
c
a
c
b
b
a
.
Đặcbiệt:
1
log
log
a
c
c
a
và
1
log log
a
a
b b
với
0
.
Câu 1. (Mã 102 - 2020 Lần 1) Cóbaonhiêusốnguyên
x
saochoứngvớimỗi
x
cókhôngquá
242
số
nguyên
y
thỏamãn
2
4 3
log log
x y x y
?
A.
55
. B.
28
. C.
29
. D.
56
.
Lời giải
Chọn D
Điềukiện:
2
0
0
x y
x y
.
Đặt
3
log
x y t
,tacó
2
4
3
t
t
x y
x y
2
4 3 *
3
t t
t
x x
y x
.
Nhậnxétrằnghàmsố
4 3
t t
f t
đồngbiếntrênkhoảng
0;
và
0
f t
vớimọi
0t
Gọi
n
thỏa
2
4 3
n n
x x
,khiđó
*
t n
Từđó,tacó
3 3
t n
x y x x
.
Mặtkhác,vìcókhôngquá
242
sốnguyên
y
thỏamãnđềbàinên
3
3 242 log 242
n
n
.
Từđó,suyra
3
log 242
2
4 242
x x
27,4 28,4
x
.
Mà
x
nên
27, 26, ..., 27, 28
x
.
Vậycó
56
giátrịnguyêncủa
x
thỏayêucầuđềbài.
Câu 2. (Mã 101 - 2020 Lần 1) Cóbaonhiêusốnguyên
x
saochoứngvớimỗi
x
cókhôngquá
728
số
nguyên
y
thỏamãn
2
4 3
log log ( )x y x y
?
A.
59
. B.
58
. C.
116
. D.
115
.
Lời giải
Chọn C.
Vớimọi
x
tacó
2
x x
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Xéthàmsố
2
3 4
( ) log ( ) log
f y x y x y
.
Tậpxácđịnh
D ( ; )
x
(do
2
y x y x
).
2
1 1
'( ) 0,
( )ln 3
ln 4
f y x D
x y
x y
(do
2
0
x y x y
,
ln 4 ln 3
)
f
tăngtrên
D
.
Tacó
2
3 4
( 1) log ( 1) log 1 0
f x x x x x
.
Cókhôngquá728sốnguyên
y
thỏamãn
0
f y
2
3 4
( 729) 0 log 729 log 729 0
f x x x
2 6
729 4 0
x x
2
3367 0
x x
57,5 58,5
x
Mà
x
nên
57, 56,...,58
x
.
Vậycó
58 ( 57) 1 116
sốnguyên
x
thỏa.
Câu 3. (Mã 103 - 2020 Lần 1) Cóbaonhiêusốnguyên
x
saochoứngvớimỗi
x
cókhôngquá
127
số
nguyên
y
thỏamãn
2
3 2
log log
x y x y
?
A.
89
. B.
46
. C.
45
. D.
90
.
Lời giải
Chọn D
Tacó
2
3 2
log log 1
x y x y
Đặt
*
t x y
(do
, , 0
x y x y
)
2 2
3 2 2 3
(1) log log ( ) log log 0 2
x x t t g t t x x t
Đạohàm
2
1 1
( ) 0
ln 2
ln3
g t
t
x x t
vớimọi
y
.Dođó
g t
đồngbiếntrên
1;
Vìmỗi
x
nguyêncókhôngquá
127
giátrị
*
t
nêntacó
2
2 3
(128) 0 log 128 log 128 0
g x x
2 7
128 3 44,8 45,8
x x x
Nhưvậycó
90
giátrịthỏayêucầubàitoán
Câu 4. (Mã 102 - 2020 Lần 1) Xétcácsốthựckhôngâm
x
và
y
thỏamãn
1
2 .4 3
x y
x y
.Giátrịnhỏ
nhấtcủabiểuthức
2 2
6 4P x y x y
bằng
A.
65
8
. B.
33
4
. C.
49
8
. D.
57
8
.
Lời giải
Chọn A
Tacó
1 2 2 2
2 .4 3 .2 3 2
x y x y
x y y x
2 3 2
2 .2 3 2 .2 *
y x
y x
Hàmsố
.2
t
f t t
đồngbiếntrên
,nêntừ
*
tasuyra
2 3 2 2 2 3 0 1
y x x y
Tathấy
1
bấtphươngtrìnhbậcnhấtcómiềnnghiệmlànửamặtphẳngcóbờlàđườngthẳng
: 2 2 3 0
d x y
(phầnkhôngchứagốctọađộ
O
),kểcảcácđiểmthuộcđườngthẳng
d
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Xétbiểuthức
2 2
2 2
6 4 3 2 13 2
P x y x y x y P
Để
P
tồntạithìtaphảicó
13 0 13
P P
.
Trườnghợp1:Nếu
13
P
thì
3; 2
x y
khôngthỏa
1
.Dođó,trườnghợpnàykhôngthể
xảyra.
Trường hợp 2: Với
13
P
, ta thấy
2
là đường tròn
C
có tâm
3; 2
I
và bán kính
13
R P
.
Để
d
và
C
cóđiểmchungthì
13 65
; 13
8
2 2
d I d R P P
.
Vậy
65
min
8
P
Câu 5. (Đề Minh Họa 2020 Lần 1) Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
0 2020
x
và
3
log 3 3 2 9
y
x x y
?
A.
2019
. B.
6
. C.
2020
. D.
4
.
Lời giải
Chọn D
Cách 1:
Tacó:
2
3 3
log 3 3 2 9 log 1 1 2 3
y y
x x y x x y
.
1
Đặt
3
log 1 1 3
t
x t x
.
Phươngtrình
1
trởthành:
2
3 2 3
t y
t y
2
Xéthàmsố
3
u
f u u
trên
.
1 3 ln 3 0,
u
f u u
nênhàmsố
f u
đồngbiếntrên
.
Dođó
2 2 2f t f y t y
3
log 1 2 1 9 9 1
y y
x y x x
Vì
9
0 2020 0 9 1 2020 1 9 2021 0 log 2021
y y
x y
3
log 2021 3,464
Do
0;1;2;3
y y
,có4giátrịcủaynêncũngcó4giátrịcủa
x
Vậycó4cặpsốnguyên
;x y
.
Cách 2:
Tacó:
2
3 3
log 3 3 2 9 log 1 1 2 3
y y
x x y x x y

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
Xéthàmsố
3
log 1 1
f x x x
với
0;2020
x
.
Tacó
1
1 0, 0;2020
1 ln3
f x x x
x
Hàmsố
f x
đồngbiếntrênđoạn
0;2020
.
Suyra
3 2
0 log 1 1 2020 1 log 2021 2021
f f x x x f f x
3
1 2 9 log 2021 2021 2028
y
y
Nếu
0
0 2 9 9 9 1
y y
y y
0
y
Khiđó
2 9 2 9 2027 9 2027 2 2027
y y y
y y y y
9
log 2027 3,465
y
3
y
0 3
y
0;1; 2;3
y
.Do
f x
làhàmsốluônđồngbiếnnênvớimỗigiátrịcủa
y
chỉcho1giátrị
của
x
.
+)
3
0 log 1 1 1 0
y x x x
+)
3 3
1 log 1 1 11 log 1 10 8
y x x x x x
+)
3 3
2 log 1 1 85 log 1 84 80
y x x x x x
+)
3 3
3 log 1 1 735 log 1 734 729
y x x x x x
Vậycó4cặpsốnguyên
;x y
.
Câu 6. (Mã 103 - 2020 Lần 1) Xétcácsốthựckhôngâm
x
và
y
thỏamãn
1
2 .4 3
x y
x y
.Giátrị
nhỏnhấtcủabiểuthức
2 2
2 4P x y x y
bằng
A.
33
8
. B.
9
8
. C.
21
4
. D.
41
8
.
Lời giải
Chọn D
Tacó
1 1 2 3 2
2 .4 3 2 3 .4 .4 0 2 .2 3 2 2
x y x y y x
x y x y y x
(1)
XétTH:
3
3 2 0
2
x x
.(1)đúngvớimọigiátrị
2 2
3
21
2 4
2
4
0
x
P x y x y
y
(2)
XétTH:
3
3 2 0 0
2
x x
.
Xéthàmsố
.2
t
f t t
với
0t
2 .2 .ln 2 0
t t
f t t
vớimọi
0t
(1)
2 3 2
f y f x
3
2 3 2
2
y x y x
.Khiđó:

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2 2 2 2
3 33
2 4 2 2 3 2 2 5
2 4
P x y x y x x x x x x
2
5 41 41
2
4 8 8
x
(3)
Sosánh(2)và(3)tathấyGTNNcủa
P
là
41
8
khi
5 1
,
4 4
x y
.
Câu 7. (Mã 104 - 2020 Lần 1) Cóbaonhiêusốnguyên
x
saochoứngvớimỗi
x
cókhôngquá
255
số
nguyên
y
thỏamãn
2
3 2
log log
x y x y
?
A.
80
. B.
79
. C.
157
. D.
158
Lời giải
Chọn D
Tacó:
2
3 2
log log
x y x y
2
log
2
3
x y
x y
2
log 3
2
x y x y
1
Đk:
1x y
(do
,x y
,
0
x y
)
Đặt
1t x y
,nêntừ
2
log 3
2
1
x x t t
2
Để
1
khôngcóquá255nghiệmnguyên
y
khivàchỉkhibấtphươngtrình
2
cókhôngquá255
nghiệmnguyêndương
t
.
Đặt
255
M f
với
2
log 3
f t t t
.
Vì
f
làhàmđồngbiếntrên
1,
nên
2
1 2
1
t f x x
khi
2
0
x x
.
Vậy
2
cókhôngquá255nghiệmnguyên
1 2
255
f x x
2
255
x x
78 79
x
x
.
Vậycó158sốnguyên
x
thỏamãnyêucầubàitoán.
Câu 8. (Mã 104 - 2020 Lần 1) Xétcácsốthựckhôngâm
x
và
y
thỏamãn
1
2 .4 3
x y
x y .Giátrị
nhỏnhấtcủabiểuthức
2 2
4 2
P x y x y
bằng
A.
33
8
. B.
9
8
. C.
21
4
. D.
41
8
.
Lời giải
Chọn D
Tacó
1 1 2 3 2
2 .4 3 2 3 .4 .4 0 2 .2 3 2 2
x y x y y x
x y x y y x
(1)
XétTH
3
3 2 0
2
x x
.(1)đúngvớimọigiátrị
2 2
3
33
4 2
2
4
0
x
P x y x y
y
(2)
XétTH
3
3 2 0 0
2
x x
.
Xéthàmsố
.2
t
f t t
với
0t
2 .2 .ln 2 0
t t
f t t
vớimọi
0t
(1)
2 3 2
f y f x
2 3 2
3
2
y x
y x
2
2 2 2 2
3 21
4 2 4 3 2 2
2 4
P x y x y x x x x x x
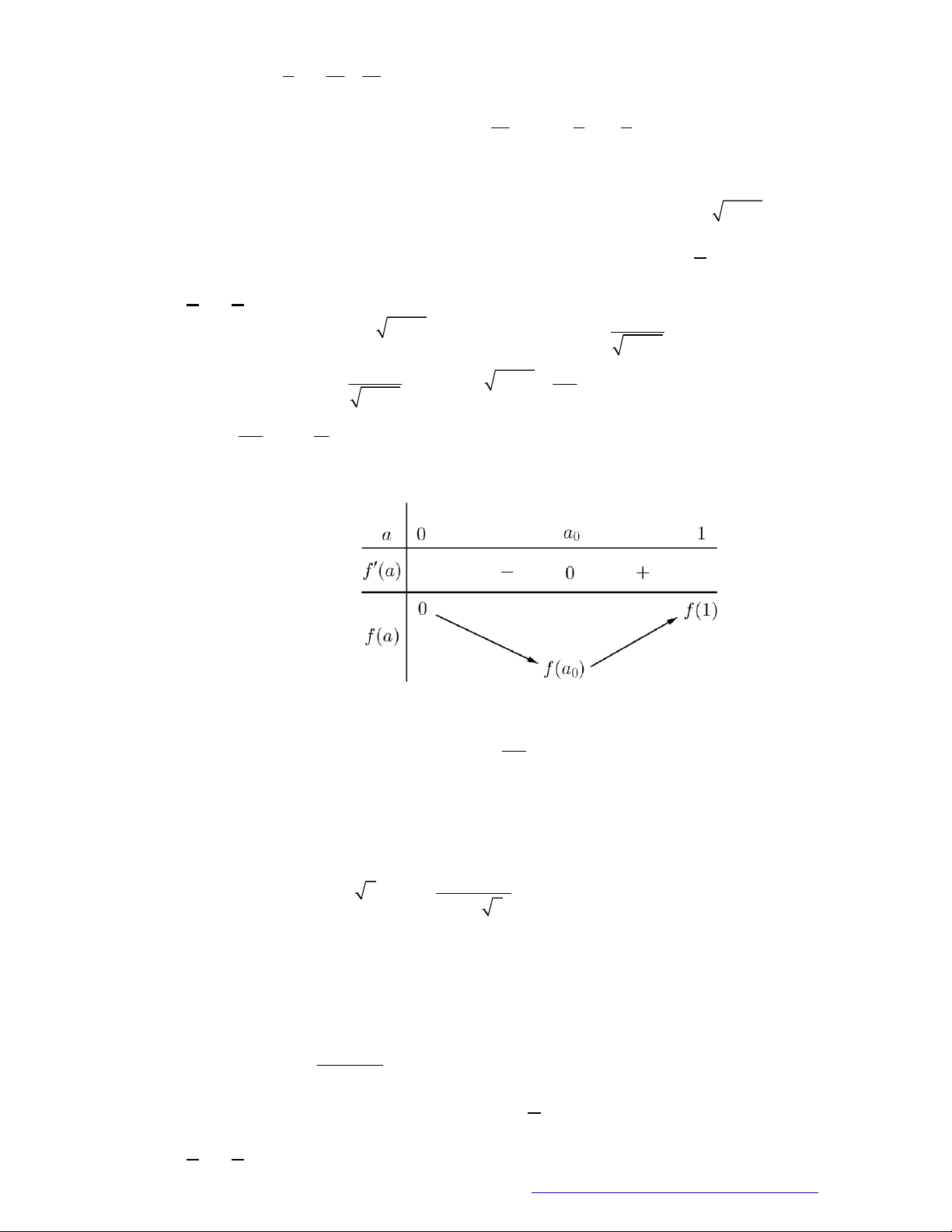
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
2
1 41 41
2
4 8 8
P x
(3)
Sosánh(2)và(3)tathấyGTNNcủa
P
là
41
8
khi
1 5
,
4 4
x y
Câu 9. (Mã 102 - 2020 Lần 2) Cóbaonhiêucặpsốnguyêndương
,m n
saocho
16m n
vàứngvới
mỗicặp
,m n
tồntạiđúng
3
sốthực
1;1a
thỏamãn
2
2 ln 1
m
a n a a
?
A.
16
. B.
14
. C. 15. D.
13
.
Lời giải
Chọn D
Đặt
2
2 ln 1
m
f a a n a a
,tacó
1
2
2
1
m
n
f a ma
a
.
1 1 2
2
0 2 0 1
2
1
m m
n n
f a ma a a
m
a
phảicómộtnghiệm
0
1a .
Suyra
2 4
2
n n
m m
suyra
0
a lànghiệmduynhất.
Tacóbảngbiếnthiên
Tathấy
0
làmộtnghiệmcủaphươngtrình
0f a
.
Nếu
1m
suyrađểcónghiệmduynhấtthì
1 2
2
n
n
m
(loại)
Nếu
m
lẻvà
1m
thìtacó
a
làmộtnghiệmthì
a
cũnglàmộtnghiệm,dođócóđủ3nghiệm.
Nếu
m
chẵnthìphươngtrìnhchỉcótốida2nghiệm(vìkhôngcónghiệmâm).
Suyra
m
lẻ.
Đểcó1nghiệmdươngthìtheoBBTtacó
2
ln 1 2 2,2
ln
2
2
0
1
1f n n
.
Suyra
1;2n
suyra
3;5; ;15m
.
Suyracó
13
cặp
,m n
(do
15 2 17 16
).
Câu 10. (Mã 102 - 2020 Lần 2) Xétcácsốthựcthỏamãn
2 2
1 2 2
2 2 2 4
x y x
x y x
.Giátrịlớnnhất
củabiểuthức
8 4
2 1
x
P
x y
gầnvớigiátrịnàosauđâynhất?
A.
9
B.
6
. C.
7
. D.
8
.
Lời giải
Chọn C
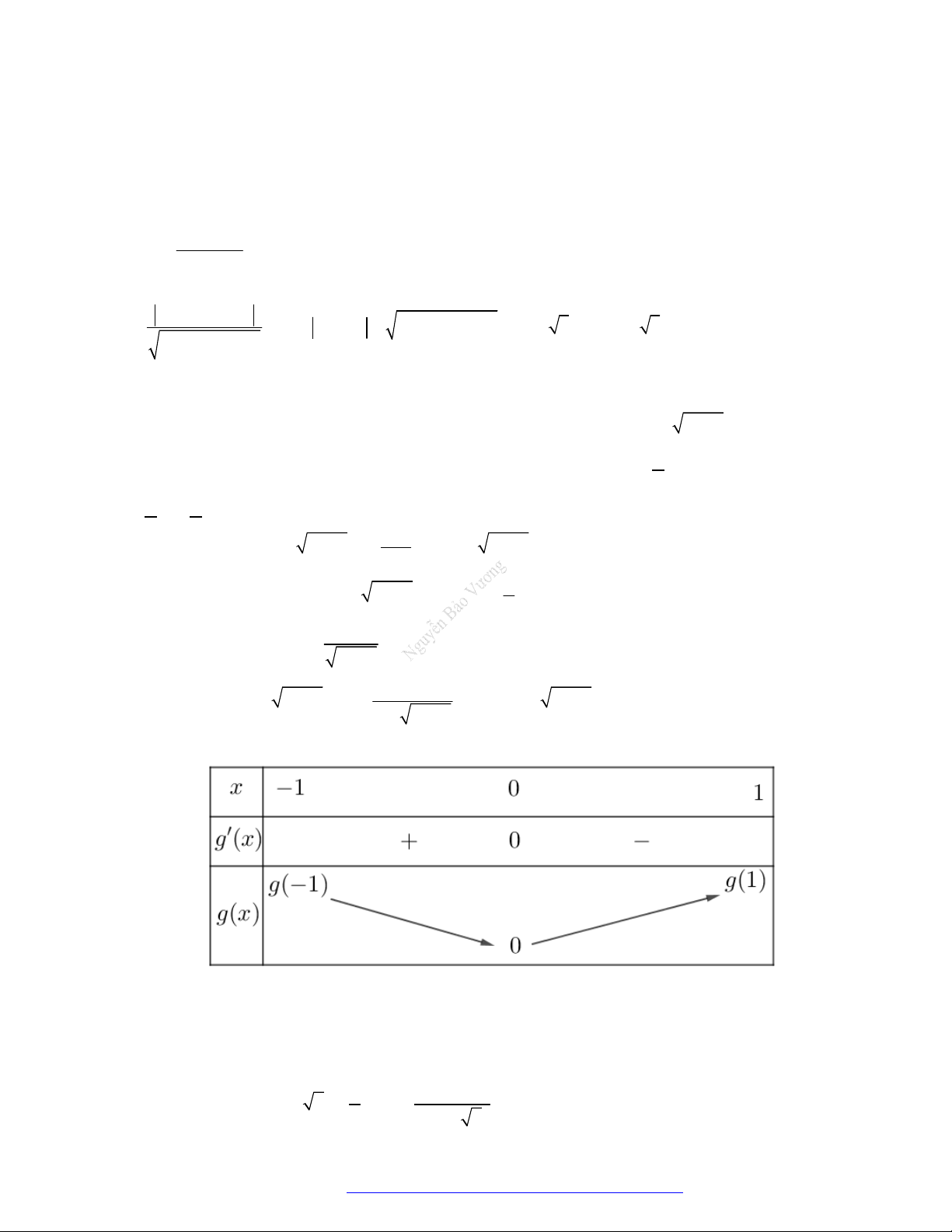
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2
1 2 2
2 2 2 .4
x y x
x y x
2 2
1 2 22
2 2 2
xx y
x y x
2
2
2
1
2
1 12 0 1
x y
x y
Đặt
2
2
1t x y
2
2
1 2 1 0 0 1 1 1
t
t t x y
8 4
2 8 . . 4 0
2 1
x
P P x P y P
x y
Yêucầubàitoántươngđương:
2
2
2
2
2 8 4
1 3 12 2 8 5 5 5 5
2 8
P P
P P P P
P P
Câu 11. (Mã 103 - 2020 Lần 2) Cóbaonhiêucặpsốnguyêndương
;m n
saocho
10m n
vàứngvới
mỗicặp
;m n
tồntạiđúng
3
sốthực
1;1a
thỏamãn
2
2 ln 1
m
a n a a
?
A.
7
. B.
8
. C.
10
. D.
9
.
Lời giải
Chọn D
Tacó
2 2
2
2 ln 1 ln 1
m
m
a
a n a a a a
n
.
Xéthaihàmsố
2
ln 1f x x x
và
2
m
g x x
n
trên
1;1
.
Ta có
2
1
0
1
f x
x
nên
f x
luôn đồng biến và
2 2
2
1
ln 1 ln ln 1
1
f x x x x x f x
x x
nên
f x
làhàmsốlẻ.
+Nếu
m
chẵnthì
g x
làhàmsốchẵnvàcóbảngbiếnthiêndạng
Suyraphươngtrìnhcónhiềunhất
2
nghiệm,dođó
m
lẻ.
+Nếu
m
lẻthìhàmsố
g x
làhàmsốlẻvàluônđồngbiến.
Tathấyphươngtrìnhluôncónghiệm
0x
.Dựavàotínhchấtđốixứngcủađồthịhàmsốlẻ,suy
ra phương trình đã cho có đúng
3
nghiệm trên
1;1
khi có
1
nghiệm trên
0;1
, hay
2 2
1 1 ln 1 2 2,26 1;2
ln 1 2
f g n n
n
.
Đốichiếuđiềukiện,với
1n
suyra
1;3;5;7;9m
,có
5
cặpsốthỏamãn
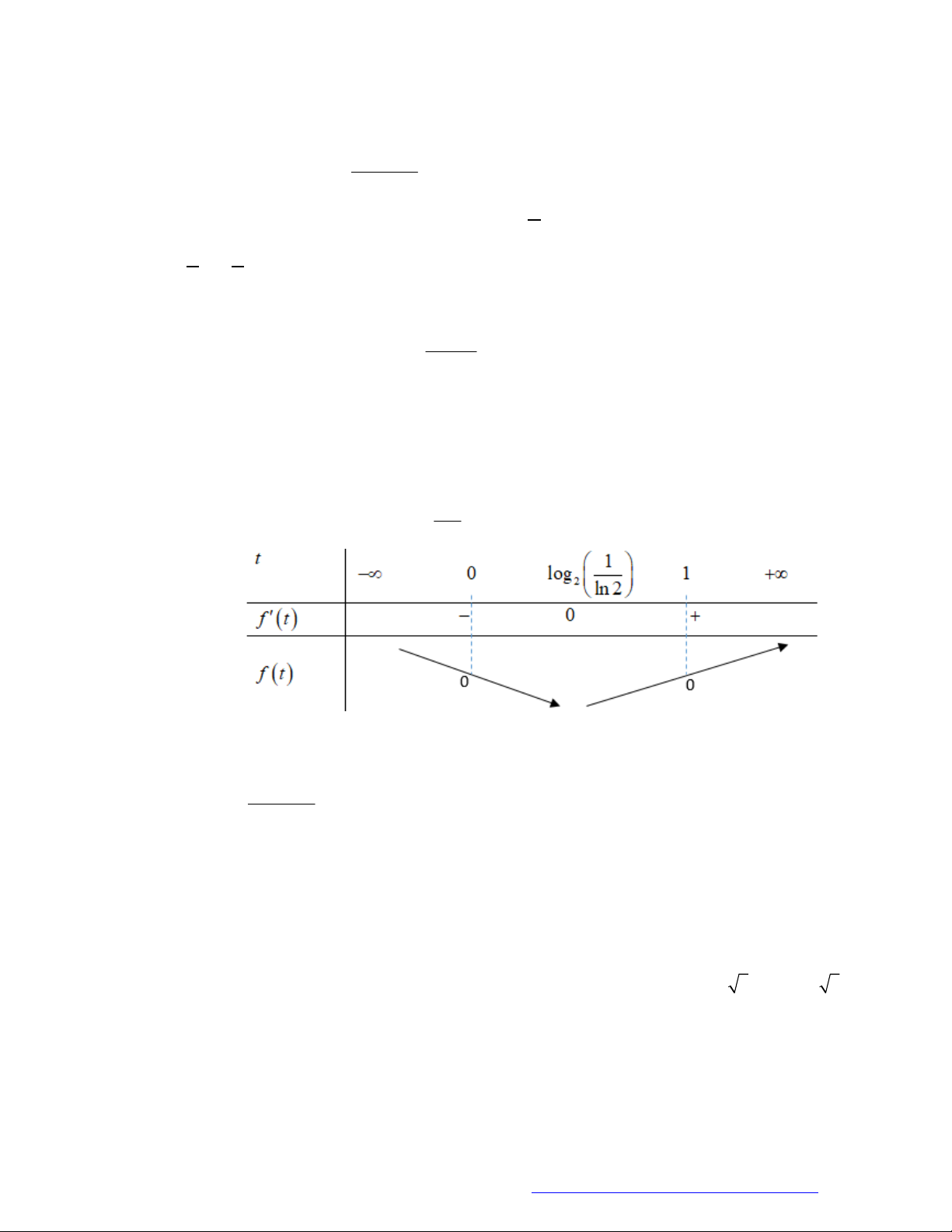
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
Với
2n
thì
1;3;5;7m
có
4
cặpsốthỏamãn.
Vậycó
9
cặpsốthỏamãnbàitoán.
Câu 12. (Mã 103 - 2020 Lần 2) Xétcácsốthực
,x y
thỏamãn
2 2
1 2 2
2 2 2 .4
x y x
x y x
.Giátrịnhỏ
nhấtcủabiểuthức
8 4
2 1
x
P
x y
gần nhất vớisốnàodướiđây
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C
Nhậnxét
2 2
2 2 0 ;x y x x y
Bất phương trình
2 2
1 2 2
2 2 2 .4
x y x
x y x
2 2
1
2 2
2
2
2 2
2
x y
x
x y x
2 2
2 1 2 2
2 2 2
x y x
x y x
.
Đặt
2 2
2 1t x y x
Bấtphươngtrình
2 1
t
t 2 1 0
t
t
Đặt
2 1
t
f t t
.Tathấy
0 1 0f f
.
Tacó
2 ln 2 1
t
f t
2
1
0 2 ln 2 1 log 0,52
ln 2
t
f t t
QuansatsBBTtathấy
0 0 1f t t
2 2
0 2 1 1x y x
2
2
1 1x y
1
Xét
8 4
2 8 4
2 1
x
P Px Py P x
x y
4 8 2P P x Py
4 2 8 8 2 2 8P P P x P Py
3 12 8 2 1P P x Py
2
2 2 2
2 2
3 12 8 2 1 8 2 1P P x Py P P x y
Thế
1
vàotacó
2
3 12P
2
2
8 2P P
2
4 40 80 0P P
5 5 5 5P
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dấu“=”xảyrakhi
2
2
8 2 1 2
5
1 1
P x
P y
x y
2
2
1
5
2
1
5
x y
y
2
1
5
5
3
x y
y
1
3
5
3
5
3
5
3
x
y
x
y
Vậygiátrịnhỏnhấtcủa
P
là
5 5 2,76
gầngiátrị
3
nhất.
Câu 13. Cóbaonhiêucắpsốnguyêndương
,m n
saocho
14
m n
vàứngvớimỗicặp
,m n
tồntại
đúngbasốthực
1;1
a
thỏamãn
2
2 ln 1
m
a n a a
?
A.
14
. B.
12
. C.
11
. D.
13
.
Lời giải
Chọn C.
Xét
2
2
. ln 1
m
f x x x x
n
trên
1;1
Đạohàm
1
2
2 1
0
1
m
m
f x x
n
x
Theođềbài
0
f x
cóbanghiệmnên
1
2
2 1
1
m
m
x
n
x
cóítnhấthainghiệm
Xétđồthịcủahàm
1
2
1
;
1
m
y x y
x
,suyra
1
m
chẵnvà
1 0
m
Suyra
3;5;7;9;11;13
m
.Khiđó
0
f x
cónghiệm
1
2
0
0
x
x
Phươngtrìnhcó3nghiệm
1 0
1 0
f
f
2
ln 2 1
2 1;2
2
ln 2 1
n
n n
n
1;2
n
và
3;5;7;9;11;13
m
,do
14
m n
nêntacó11cặp
;m n
thỏayêucầubài
toán.
Câu 14. (Mã 104 - 2020 Lần 2) Cóbaonhiêucặpsốnguyêndương
( , )m n
saocho
12
m n
vàứngvới
mỗicặp
( , )m n
tồntạiđúng3sốthực
( 1,1)
a
thỏamãn
2
2 ln( 1)
m
a n a a
?
A.
12
. B.
10
. C.
11
. D.
9
.
Lời giải
Chọn D
Tacó
2 2
2
2 ln( 1) ln( 1) (*)
m m
a n a a a a a
n
.
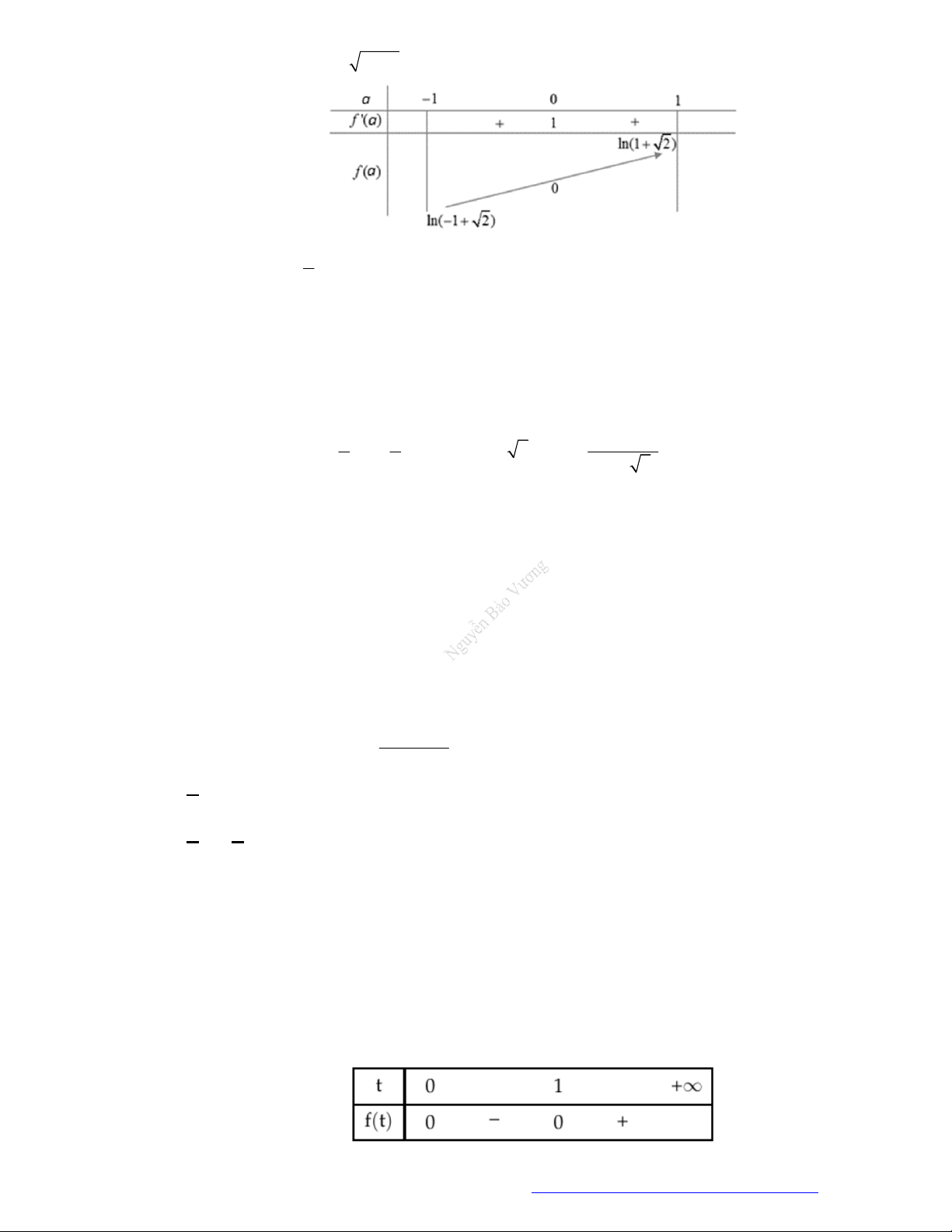
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
Xéthàm
2
( ) ln( 1)f a a a
trên
( 1,1)
(dễthấyhàm
f
lẻ,đồngbiếntrên
R
),cóBBT:
Xéthàm
2
( ) .
m
g a a
n
trên
( 1,1)
.
Với
m
chẵn,
( )g a
làhàmchẵnvà
( ) 0,g a a R
,dođó
(*)
khôngthểcó3nghiệm.
Với
m
lẻ,
( )g a
làhàmlẻ,đồngbiếntrên
R
vàtiếptuyếncủađồthịtạiđiểm
0a
làđường
thẳng
0y
.
Dễthấy
(*)
cónghiệm
0 ( 1;1)a
.Để
(*)
cóđúng3nghiệmtứclàcòncó2nghiệmnữalà
0
a với
0
0 1a .
Muốnvậy,thì
2 2 2
(1) .1 (1) ln(1 2) 2,26 1; 2
ln(1 2)
m
g f n n n
n n
Cụthể:
+
3;5;7;9m
thì
1;2n
:Có
8
cặp
( , )m n
+
11m
thì
1n
:Có
1
cặp
( , )m n
+
1m
:Đồthịhàmsố
( )g a
làđườngthẳng(
( ) ; ( ) 2g a a g a a
)khôngthểcắtđồthịhàmsố
( )f a
tạigiaođiểm
0
0a đượcvìtiếptuyếncủahàmsố
( )f a
tạiđiểmcóhoànhđộ
0a
là
đườngthẳng
y a
.
Vậycócảthảy
9
cặp
( , ).m n
Câu 15. (Mã 104 - 2020 Lần 2) Xétcácsốthực
x
và
y
thỏamãn
2 2
1 2 2
2 2 2 4
x y x
x y x
.Giátrị
lớnnhấtcủabiểuthức
4
2 1
y
P
x y
gần nhấtvớisốnàodướiđây?
A.
1
. B.
0
. C.
3
. D.
2
.
Lời giải
Chọn A
Tacó:
2 2 2 2
1 2 2 2 1 2 2
2 2 2 4 2 2 1 1
x y x x x y
x y x x x y
.
Đặt
2 2
2 1 0t x x y t .Khiđótacó
2 1
t
t
,
0t
.
Đặt
2 1, 0
t
f t t t
,tacó:
2 ln 2 1
t
f t
,cho
0f t
.
Tanhậnthấyphươngtrình
0f t
có mộtnghiệmnênphương trình
0f t
có tối đahai
nghiệm.
Mặtkháctacó
0 1 0f f
.Suyraphươngtrình
0f t
cóhainghiệm
1t
và
0t
.
Khiđótacóbảngxétdấucủahàmsố
f t
nhưsau:
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khiđó
0 0;1
f t t
.Suyra
2
2 2 2
2 1 1 1 1
x x y x y
.
Khiđótậphợpcácđiểm
;M x y
làmộthìnhtròn
S
tâm
1;0
I
,bánkính
1R
.
Tacó:
4
2 4 0
2 1
y
P Px P y P
x y
.
Khiđótacũngcótậphợpcácđiểm
;M x y
làmộtđườngthẳng
: 2 4 0
Px P y P
.
Để
và
S
cóđiểmchung,tasuyra
, 1
d I
.
2
2 2
2
1 3 5 8 16
2 4
P P
P P P
P P
2
4 8 16 0 1 5 1 5
P P P
.
Tasuyra
max
1 5
P
.Dấu
" "
xảyrakhi
1
3
5
3
x
y
Câu 16. (Mã1232017)Xétcácsốthựcdương
,x y
thỏamãn
3
1
log 3 2 4
2
xy
xy x y
x y
.Tìmgiátrị
nhỏnhất
min
P
của
P x y
A.
min
2 11 3
3
P
B.
min
9 11 19
9
P
C.
min
18 11 29
21
P
D.
min
9 11 19
9
P
Lờigiải
ChọnA
Với
,x y
dươngvà kết hợp với điềukiện của biểuthức
3
1
log 3 2 4
2
xy
xy x y
x y
tađược
1 0xy
Biếnđổi
3
1
log 3 2 4
2
xy
xy x y
x y
3 3 3
log 1 log 2 3 1 2 log 3
xy x y xy x y
3 3 3
log 1 log 3 3 1 log 2 2xy xy x y x y
3 3
log 3 1 3 1 log 2 2 1
xy xy x y x y
Xéthàmsố
3
log
f t t t
trên
0;D
1
' 1 0
.ln 3
f t
t
vớimọi
x D
nênhàmsố
3
log
f t t t
đồngbiếntrên
0;D
Từđósuyra
3 2
1 3 1 2 3 2 1 3
1 3
y
xy x y y x y x
y
(do
0y
)
Theogiảthiếttacó
0, 0x y
nêntừ
3 2
1 3
y
x
y
tađược
3
0
2
y
.
2
3 2 3 3
1 3 3 1
y y y
P x y y
y y
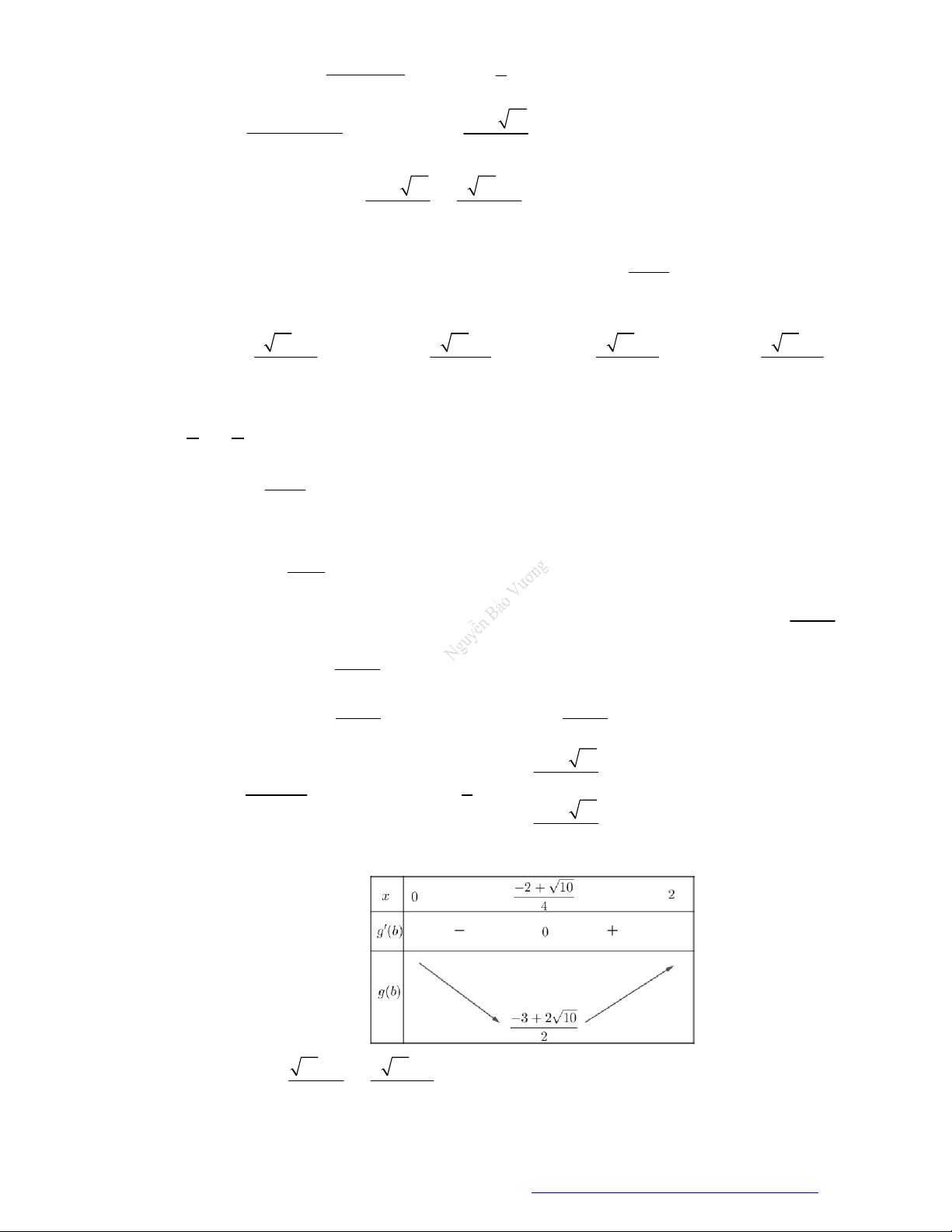
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
Xéthàmsố
2
3 3
3 1
y y
g y
y
với
3
0
2
y
2
2
9 6 10
' 0
3 1
y y
g y
y
tađược
1 11
3
y
.
Từđósuyra
1 11
mi
2 11
.
3
n
3
3
P g
Câu 17. (Mã1102017)Xétcácsốthựcdương
, a b
thỏamãn
2
1
log 2 3
ab
ab a b
a b
.Tìmgiátrị
nhỏnhất
min
P
của
2P a b
.
A.
min
3 10 7
2
P
B.
min
2 10 1
2
P
C.
min
2 10 3
2
P
D.
min
2 10 5
2
P
Lờigiải
ChọnC
Điềukiện:
1ab
.
Tacó
2 2 2
1
log 2 3 log 2 1 2 1 log *
ab
ab a b ab ab a b a b
a b
.
Xéthàmsố
2
logy f t t t
trênkhoảng
0;
.
Tacó
1
1 0, 0
.ln 2
f t t
t
.Suyrahàmsố
f t
đồngbiếntrênkhoảng
0;
.
Dođó
2
* 2 1 2 1 2 1 2
2 1
b
f ab f a b ab a b a b b a
b
.
Do
0, 0a b
nên
2
0 0 2
2 1
b
b
b
.
Khiđó:
2
2 2
2 1
b
P a b b
b
.Xéthàmsố
2
( ) 2
2 1
b
g b b
b
trênkhoảng
0;2
.
2
2
2 10
0;2
5 5
4
2 0 2 1
2
2 1
2 10
0;2
4
b
g b b
b
b
Lậpbảngbiếnthiên
Vậy
min
10 2 2 10 3
4 2
P g
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 18. (ChuyênLêThánhTông2019)Chohaisốthựcdương
,x y
thỏamãn
ln
ln
ln5
2
2 .5 2
x y
x y
.Tìm
giátrịlớnnhấtcủabiểuthức
( 1)ln ( 1)lnP x x y y
.
A.
max
10
P
. B.
max
0
P
. C.
max
1
P
. D.
max
ln 2
P
.
Lờigiải
ln
ln( ) ln 5 ln( ) ln 2 ln( ) ln5 ln( ) ln( ) ln5 ln2
2
2 .5 2 2 .5 2 2 .5 2 .2
x y
x y x y x y x y x y
ln( ) ln10
10 2
x y
ln10 ln( ) ln10.log2
ln( ) log 2 ln( ) ln10.log2
x y
x y x y e e
log2
10 2
x y x y
.
Dođó
1 ln 3 ln 2
P x x x x
.
Xéthàmsố
( ) ( 1)ln (3 )ln(2 )f x x x x x
1 3 2 2
( ) ln ln(2 ) ln
2 2 (2 )
x x x x
f x x x
x x x x x
.
2
2 2
2
1 2 2 4 4
. 0, 0;2
2
2
x x x
f x x
x
x
x x
Dođó
0
f x
cónhiềunhấtmộtnghiệmtrên
0;2
Mà
1x
làmộtnghiệmcủa pt
0
f x
nênphương trình
0
f x
cónghiệmduynhấtlà
1
x
.
Lậpbảngbiếnthiêntađược
max 1 0
f x f
.
Câu 19. (THPT Bạch Đằng Quảng Ninh 2019) Cho các số thực
,x y
thỏa mãn
0 , 1
x y
và
3
log 1 1 2 0
1
x y
x y
xy
.Tìmgiátrịnhỏnhấtcủa
2
P x y
.
A.
2
. B.
1
. C.
1
2
. D.
0
.
Lờigiải
Vớiđiềukiệnbiểuthứcđềbàicónghĩa,tacó
3 3 3
log 1 1 2 0 log log 1 1 0
1
x y
x y x y xy xy x y
xy
3 3
log log 1 1 *
x y x y xy xy
Xéthàmsố
3
log
f x t t
trên
0;2
1
ln3 1 0, 0;2
f t t
t
nênhàmsố
f t
đồngbiếntrên
0;2
.
Dođótừ
*
tacó
1
1 1 1
1
x
x y xy y x x y
x
1
2 2
1
x
P x y x
x
2
2
2 0, 0;1
1
P x x
x
Suyra
min 0 1
P P
đạtđượckhi
0, 1
x y
.
Câu 20. (Chuyên Hạ Long 2019) Cho các số thực
,a b
thỏa mãn
1.
a b
Biết rằng biểu thức
1
log
log
a
ab
a
P
a b
đạtgiátrịlớnnhấtkhi
.
k
b a
Khẳngđịnhnàosauđâylàsai
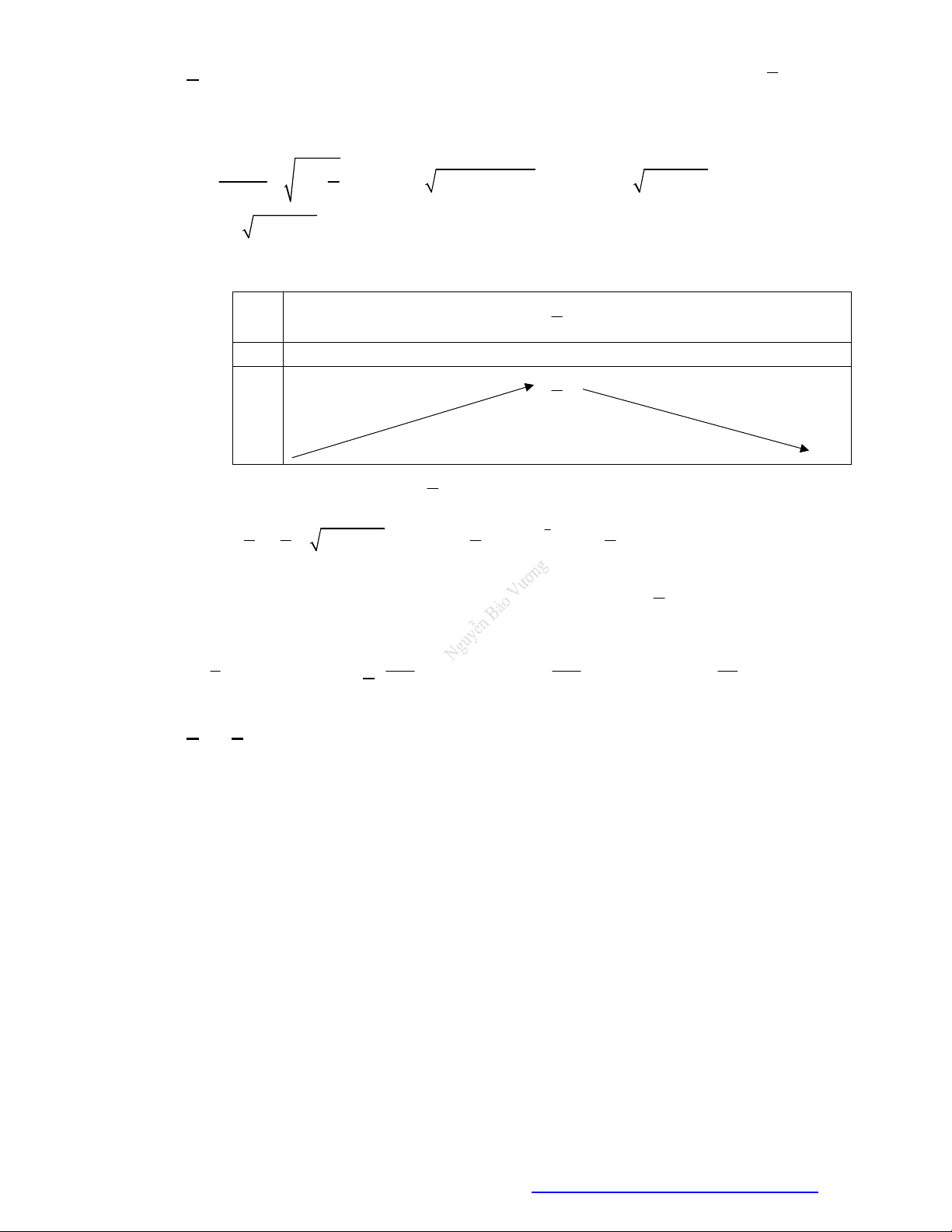
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
A.
2;3
k
. B.
0;1
k
. C.
0;1
k
. D.
3
0;
2
k
.
Lờigiải
Tacó
1 log 0
a
a b b
.
1
log log log log 1 log 1 log .
log
a a a a a a
ab
a
P ab a b b b
a b
Đặt
2
1 log 0 log 1
a a
t b t b t
.Tacó:
2
2P t t
trên
0;
Bảngbiếnthiên
t
1
2
P
9
2
Hàmsốđạtgiátrịlớnnhấttại
1
.
2
t
Với
3
4
1 1 3 3
1 log log .
2 2 4 4
a a
t b b b a k
Câu 21. Chohaisốthực
,a b
thỏamãn
2 2
4 1
log 2 8 1
a b
a b
.Tính
a
P
b
khibiểuthức
4 6 5 S a b
đạtgiátrịlớnnhất.
A.
8
5
B.
13
2
C.
13
4
D.
17
44
Lờigiải
ChọnB
2 2
2 2
4 1
log 2 8 1 2 8 4 1
a b
a b a b a b
Tacó:

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2
2 2
2
2
2 2 2
2 2
2 8 4 1
2 8 4 1
6 5
4 6 5
4
6 5 6 5
2 8 4 1
4 4
6 5
4
8 48 40 128 36 25 12 10 60 64 16
6 5
4
100 2(58 6 ) 2 1 0
a b a b
a b a b
S b
S a b
a
S b S b
b b
S b
a
S b b S b Sb S b b
S b
a
b S b S S
S
a
2 2 2
6 5
4
(58 6 ) 100.(1 ) 0 64 896 3264 0
17 3
b
S S S S
S
GiátrịlớnnhấtcủaSlà:
13
5
3
2
5
a
b
Suyra
13
2
a
b
Câu 22. (ChuyênVĩnhPhúc2019)Cho
a
,
b
làcácsốdươngthỏamãn
1b
và
a b a
.Tìmgiátrị
nhỏnhấtcủabiểuthức
log 2log
a
b
b
a
P a
b
.
A.
6
. B.
7
. C.
5
. D.
4
.
Lờigiải
ChọnD
Tacó:
1 1
4. log 1 4. log 1
1
1 log
1
log
b b
a
b
P a a
b
a
Đặt
log
b
t a
.Vì
log 1 log 1 1 2
2
b b
t
a b a a a t t
.
1
4 1 4 1
1
1
1
t
P t t
t
t
với
1;2
t
.
Xéthàmsố
( ) 4 1
1
t
f t t
t
với
1;2
t
.
2
2
3
1 1
2
( ) 4, ( ) 0 1
1
4
1
2
t tm
f t f t t
t
t l
.
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
Bảngbiếnthiên
Từbảngbiếnthiênsuyra:
1;2
3
minf 5.
2
t f
Vậygiátrịnhỏnhấtcủabiểuthức
P
bằng
5
.
Câu 23. (THPT Đoàn Thượng - Hải Dương 2019) Cho
a
,
b
là hai số thực dương thỏa mãn
5
4 2 5
log 3 4
a b
a b
a b
.Tìmgiátrịnhỏnhấtcủabiểuthức
2 2
T a b
A.
1
2
. B.
1
. C.
3
2
. D.
5
2
.
Lờigiải
5 5 5
4 2 5
log 3 4 log 4 2 5 log 3 4
a b
a b a b a b a b
a b
5 5
log 4 2 5 4 2 5 log 5 5a b a b a b a b
(*).
Xéthàm
5
log , 0f x x x x
.
Đạohàm
1
1 0, 0
.ln5
f x x
x
.Suyrahàmsố
f x
đồngbiếntrên
0;
.
Phươngtrình(*)viếtlại:
4 2 5 5 4 2 5 5 3 5f a b f a b a b a b a b
.
Mặtkhác:
2
2 2 2 2 2 2 2
5
5 3 1 3 .
2
a b a b T a b
.
Dấu
" "
xảyra
1 3
a b
1 3
;
2 2
a b
.
Câu 24. (THPT Lê Quý Đôn Đà Nẵng 2019) Với hai số thực
,a b
bất kì, ta kí
hiệu
,
2 3
a b
f x x a x b x x .Biết rằng luôn tồn tại duy nhất số thực
0
x
để
0
, ,
min
a b a b
x R
f x f x
vớimọisốthực
,a b
thỏamãn
b a
a b
và
0 a b
.Số
0
x bằng
A.
2 1e
B.
2,5
C.
e
D.
2e
Lờigiải
Tacó
b a
a b
ln lnb a a b
ln ln
*
a b
a b
.
Xéthàmsố
lnx
y
x
,trêntậpxácđịnh
0;D
5
6
+∞
+
-
0
3
2
3
2
2
1
+∞
-∞
f(t)
f'(t)
t
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
1 ln x
y
x
,
0y x e
Bảngbiếnthiên
Có
0 a b
f a f b
Kếthợpvớibảngbiếnthiênsuyra
1a e b
.
Talạicó
,
2 3
a b
f x x a b x x x
2 3 1x a b x x x b a
.
Suyra
,
min 1
x
a b
f x b a
2
2 3
a x b
x
Từ
1
và
2
suyrasốthựcduynhấtthỏamãnyêucầubàitoánlà
x e
Thử lại:khi
x e
thì
1f e b a
.
Vậy
0
, , ,
min
a b a b a b
x R
f x f x f e
Câu 25. (Chuyên Lê Hồng Phong Nam Định 2019) Cho hai số thực
1, 1a b
. Biết phương trình
2
1
1
x x
a b
có hai nghiệm phân biệt
1 2
,x x . Tìm giá trị nhỏ nhất của biểu thức
2
1 2
1 2
1 2
4
x x
S x x
x x
.
A.
3
3 4
. B.
4
C.
3
3 2
. D.
3
4
.
Lờigiải
ChọnA
Tacó
2
1 2 2
1 1 log 0 log log 0
x x
a a a
a b x x b b x x b
Dophươngtrìnhcóhainghiệm
1 2
,x x nêntheođịnhlýViettacó:
1 2
1 2
1
log
log
1
b
a
x x a
b
x x
Khiđó
2
1
4log
log
b
b
S a
a
Đặt log
b
t a ,do
1, 1 0a b t
.Khiđó
3
2 2
1 1
4 2 2 3 4S t t t
t t
.
Đẳngthứcxảyrakhi
2
3
1 1
2
2
t t
t
.Vậy
3
min 3 4S
Câu 26. (ChuyênQuốcHọcHuế2019)Cho
,x y
làcácsốthựclớnhơn
1
saocho
y x
e e
x x y y
y e x e
.
Tìmgiátrịnhỏnhấtcủabiểuthức:
log log
x y
P xy x
.
1
e
ba
+
0
x
y
/
y
+∞
0
_
0
e
-∞
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
A.
2
2
B.
2 2
C.
1 2 2
2
D.
1 2
2
Lờigiải
Cách1.
Tacó:
ln ln
y x y x
e e e e
x x y y x x y y
y e x e y e x e
ln ln
ln ln
y x
x y
x y
x y xe y x ye
x e y e
(*)(vì
ln
x
y e x
có
1
' 0; 1
x
y e x
x
nên
1 0
y y e
)
Xéthàmsố:
ln
t
t
f t
t e
trên
1;
tacó
2
ln 1
'
ln
t t
t
t e te
f t
t e
.Vớihàmsố
ln 1
t t
g t t e te
có
1
' ln 1 ' 0, 1
t t t
g t t e te te t
t
Nên
1 1 ' 0; 1g t g f t t
y f t
làhàmnghịchbiếntrên
1;
nênvới(*)
1f x f y y x
Khiđó
1 1 1 1 1 1 1 2 2
log log log 2 log .
2 2 log 2 2 log 2
x y x x
x x
P xy x y y
y y
Dấu“=”xảyrakhi:
2
2
1 1
log log 2
2 log
x x
x
y y y x
y
Vậy:
min
1 2 2
2
P
.
Cách2:
Với
, 1x y
thì
log ;log
x y
y x
làcácsốdương,tacó:
log log
x y
P xy x
1 1 1 1 1 1 1 2 2
log 2 log .
2 2 log 2 2 log 2
x x
x x
y y
y y
Dấu“=”xảyrakhi:
2
2
1 1
log log 2
2 log
x x
x
y y y x
y
,
Thay
2
1
y x
x
vàođiềukiệnthấythỏamãnđiềukiệnbanđầu.
Vậy
min
1 2 2
2
P
.
Câu 27. Xétcácsốthựcdương
,x y
thỏamãn
3
1
log 3 3 4
3
y
xy x y
x xy
.Tìmgiátrịnhỏnhất
min
P
của
P x y
.
A.
min
4 3 4
3
P
. B.
min
4 3 4
3
P
. C.
min
4 3 4
9
P
. D.
min
4 3 4
9
P
.
Lờigiải
Để
1
0
3
y
x xy
màtừgiảthiết
, 0
x y
suyra
1 0 1y y
.VậyĐKXĐ:
0;0 1x y
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tacó:
3
1
log 3 3 4
3
y
xy x y
x xy
3 3 4
1
3
3
xy x y
y
x xy
3 3 3
3 1
3
3
xy x y
y
x xy
3
3 3
3 1
3
3 3
xy x
y
y
x xy
3 3 3
3 3 .3 3 .3 (*)
y xy x
y xy x
Xét
.3
t
f t t
với
0t
.Tacó
3 .3 .ln3 0
t t
f t t
với
0
t
,suyra
f t
đồngbiếntrên
khoảng
0;
. Từ
(*)
ta có
3 3 3
f y f xy x
với
3 3 0,3 0
y xy x
nên
3
3 3 3
3( 1)
x
y xy x y
x
.
Tacó
3 3 1 4
1
3 1 3 1 3 3
x x
P x y x x
x x
4 4 4 4 4 3 4
1 2 1 .
3 1 3 3 1 3 3
P x x
x x
.
Vậy
min
4
1
3 1
2 3 3
4 3 4 3
3
3 3 1
2 3 1
0;0 1
3
x
x
x
x
P y
x
y
x y
.
Câu 28. (Chuyên Vĩnh Phúc 2019) Xét các số thực dương
x
,
y
thỏa mãn
2
1 1 1
2 2 2
log log log
x y x y
.Tìmgiátrịnhỏnhất
min
P
củabiểuthức
3P x y
.
A.
min
9
P
B.
min
8
P
C.
min
25 2
4
P
D.
min
17
2
P
Lờigiải.
Tacó:
2
1 1 1
2 2 2
log log log
x y x y
2 2
1 1
2 2
log log
xy x y xy x y
2
2
1
1
1
y
x
x y y
y
y
(Vì
; 0
x y
).
Tacó:
2
1
3 3 4 1
1 1
y
P x y y y
y y
.
Xéthàmsố:
1
4 1 ; 1
1
f y y y
y
.
Đạohàm:
/
2
1
4
1
f y
y
.
/
3
2
0
1
2
y n
f y
y l
.
Bảngbiếnthiên.
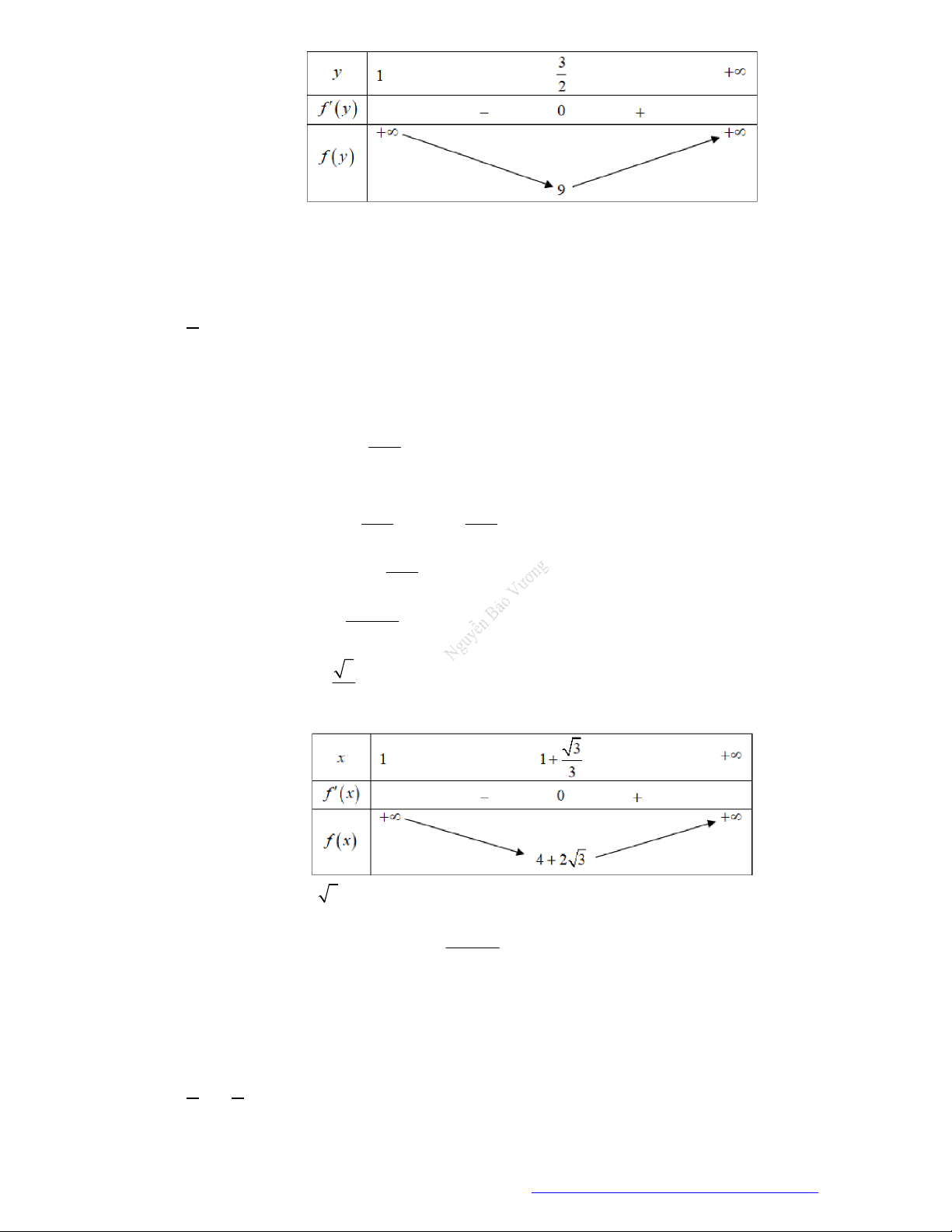
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
Câu 29. (Chuyên Vĩnh Phúc 2019) Cho
,x y
là các số thực dương thỏa mãn
2019 201 2
2
9 019
log log logx y x y
.Gọi
min
T làgiátrịnhỏnhấtcủabiểuthức
2T x y
.Mệnh
đềnàodướiđâyđúng?
A.
min
7;8T
B.
min
6;7T
C.
min
5;6T
D.
min
8;9T
Lờigiải.
Tacó:
2019 201 2
2
9 019
log log logx y x y
2019 2019
2
log logxy x y
2
xy x y
2
1y x x
2
1
1
x
y
x
x
Tacó:
2
1
2 2 3 1
1 1
x
T x y x x
x x
.
Xéthàmsố:
1
3 1 ; 1
1
f x x x
x
.
Đạohàm:
/
2
1
3
1
f x
x
.
/
3
0 1 ( 1)
3
f x x do x
.
Bảngbiếnthiên.
Dođó:
min
4 2 3T
.
Câu 30. (Mã1052017)Xéthàmsố
2
9
9
t
t
f t
m
với
m
làthamsốthực.Gọi
S
làtậphợptấtcảcác
giátrịcủa
m
saocho
1f x f y
vớimọisốthực
,x y
thỏamãn
x y
e e x y
.Tìmsố
phầntửcủa
S
.
A.
0
B. Vôsố C.
1
D.
2
Lờigiải
ChọnD
Tacó
4 4 2
9 3
1 9 log log
x y
f x f y m x y m m
Đặt
, 0x y t t
.Vì
1 ln 1 ln 0, 0
x y
t
e e x y e et t t t t t
(1)
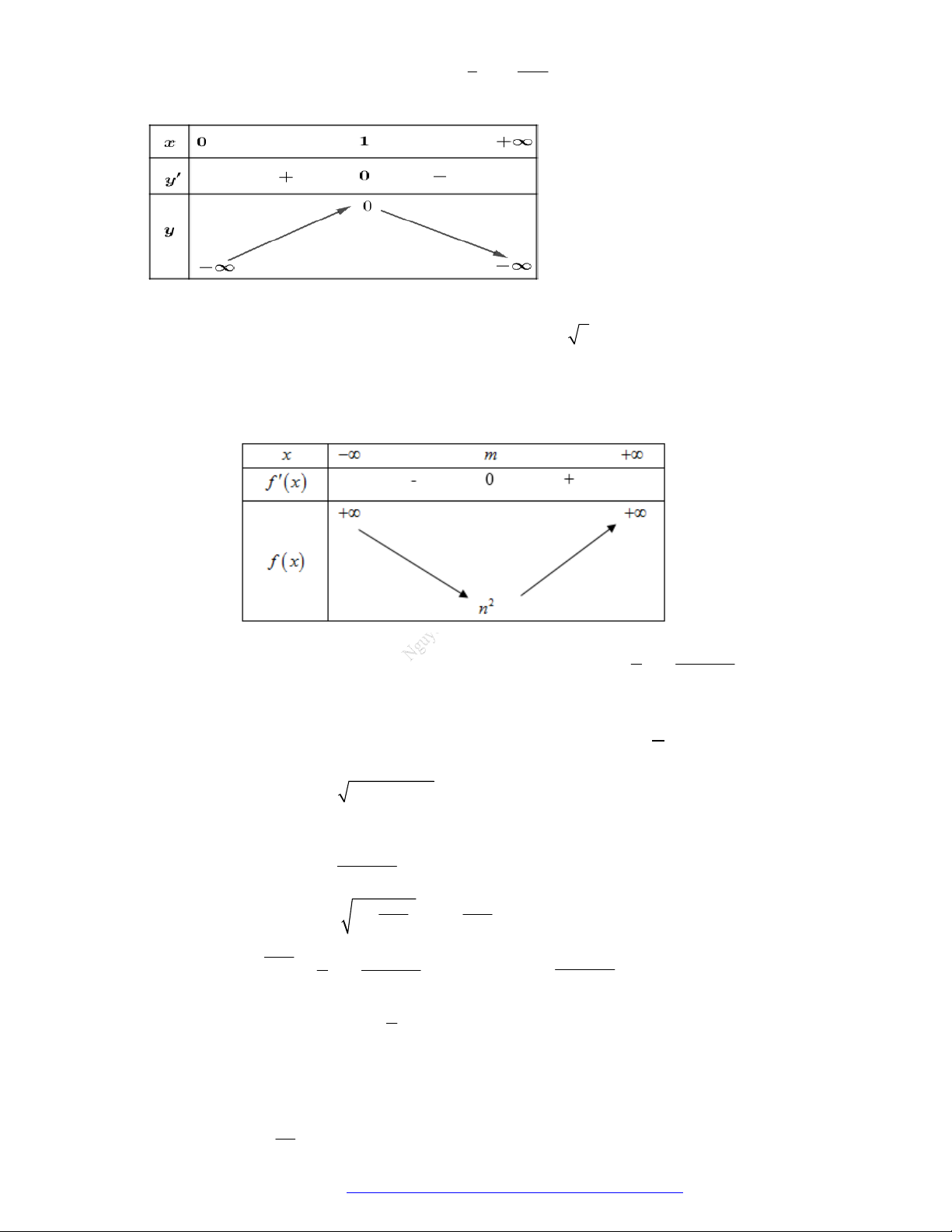
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Xéthàm
ln 1f t t t
với
0t
.
1 1
1 0 0
t
f t t
t t
Bảngbiếnthiên
Dựavàobảngbiếnthiên,tacó
1 , 0f t f t
1 ln 0, 0t t t (2)
Từ
1
và
2
tacó
2 2
3
1 log 1 3 3t m m m
Câu 31. (THCS-THPTNguyễnKhuyến2019)Chohàmsố
y f x
liêntụctrên
,cóbảngbiến
thiênnhưhìnhvẽvàcóđạohàmcấphai
0, xf x
.
Gọi
, , ,a b c n
làcácsốthựcvàbiểuthức:
2
3
e e e 1
2 3
f a f b f c
a b c
P f
.Khẳng
địnhđúngvớimọi
, , ,a b c n
là
A.
0 3P
. B.
7 3e P 0
. C.
3P
. D.
7 3eP
.
Lờigiải
Tacó
3
e e e 3
f a f b f c f a f b f c
e
.
Mặtkhácdo
0, xf x
nên
f x
làhàmlồi,ápdụngbấtđẳngthứclồitacó
3
3
a b c
f a f b f c f
Dođó
3
3
3 3
e e e 3 3
a b c a b c
f f
f a f b f c
e e
Suyra
2
3
3
3 1
2 3
a b c
f
a b c
P e f
.Đặt
2
, 0
3
a b c
t f t n
Tacó
P g t
với
2
3
3 1
2
t
g t e t
3e 3 1 ; " 3e 3 3 e 1 0, 0.
t t t
g t t g t t
Nên
g t
là hàm nghịch biến
trên
0;
.
'( ) (0) 0, 0; ( ) (0)g t g t g t g
Dođó
3
0 7 3e.
2
P g
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
Câu 32. (Chuyên Đại Học Vinh 2019) Chohàmsố
( ) 2 2
x x
f x
.Gọi
0
m
làsốlớnnhấttrongcácsố
nguyên
m
thỏamãn
12
( ) (2 2 ) 0
f m f m
.Mệnhđềnàosauđâyđúng?
A.
0
1513;2019
m
B.
0
1009;1513
m
C.
0
505;1009
m
D.
0
1;505
m
Lờigiải
ChọnB
Hàmsố
( ) 2 2
x x
f x
xácđịnh
x
.
Khiđó
x
,tacó
( ) 2 2 (2 2 ) ( )
x x x x
f x f x
.
Suyra
( )f x
làhàmsốlẻ.
1
Mặtkhác
( ) (2 2 )ln2 0
x x
f x
,
x
.
Dođóhàmsố
( )f x
đồngbiếntrên
.
2
Tacó
12
( ) (2 2 ) 0
f m f m
12
(2 2 ) ( )f m f m
.
Theo
1
suyra
12
(2 2 ) ( )f m f m
.
Theo
2
tađược
12
12 12
2
2 2 3 2
3
m m m m
.
Vì
m
nên
0
1365 1365
m m
.Vậy
0
1009;1513
m
.
Câu 33. (Việt Đức Hà Nội 2019) Tìm tất cả các giá trị của tham số
m
đề đồ thị hàm số
2
2 2
log 2log 2 1
y m x x m
cắttrụchoànhtạimộtđiểmduynhấtcóhoànhđộthuộckhoảng
1;
.
A.
1 1
;
2 2
m
. B.
1 1
;0
2 2
m
.
C.
1 1
;
2 2
m
. D.
1 1
;0
2 2
m
.
Lờigiải
Xétphươngtrìnhhoànhđộgiaođiểm
2
2 2
log 2log 2 1 0
m x x m
.
Ycbt
Phươngtrìnhcóduynhấtmộtnghiệmthuộckhoảng
1;
.
Đặt
2
log 0
t x
1;
x
.
Phươngtrình
2
2 2 1 0
mt t m
2
2 1
2
t
m
t
.
Ycbt
Phươngtrìnhcóduynhấtmộtnghiệm
0;
t
.
Xéthàmsố
2
2 1
2
t
f t
t
trên
0;
.
Tacó
2
2
2 2
2 2
2 2 2 2 1
2 2 4
1 1
t t t
t t
f t
t t
0
f t
2
2 2 4 0
t t
1 0;
2 0;
t
t
.
Bảngbiếnthiên
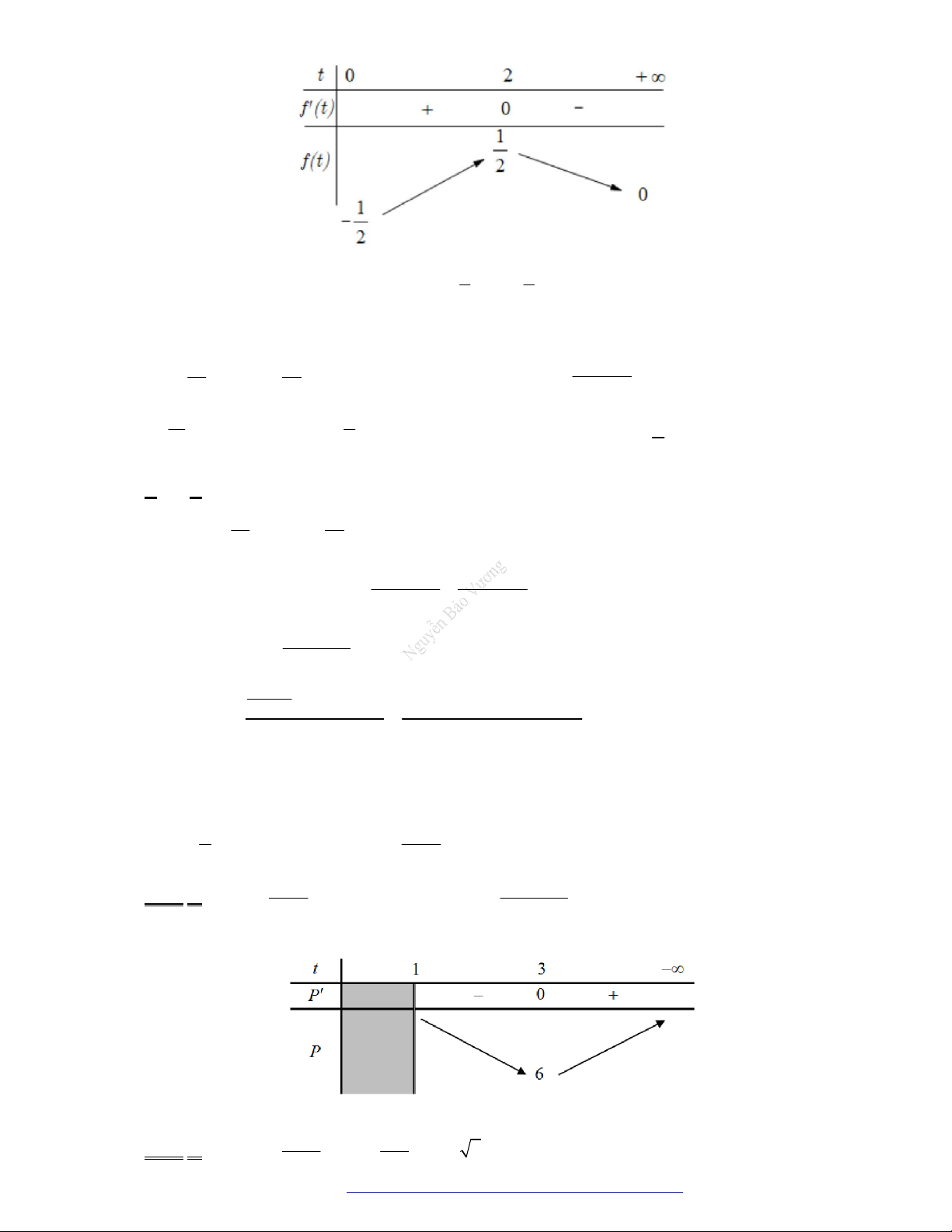
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từbảngbiếnthiêntasuyra:ycbt
1 1
;0
2 2
m
.
Câu 34. (Chuyên Biên Hòa - Hà Nam - 2020) Cho
;x y
là hai số thực dương thỏa mãn
x y
và
1 1
2 2
2 2
y x
x y
x y
.Giátrịnhỏnhấtcủabiểuthức
2 2
2
3x y
P
xy y
bằng
A.
13
2
. B.
9
2
. C.
2
. D.
6
.
Lờigiải
ChọnD
Tacó
1 1
2 2 4 1 4 1
2 2
y x
y x
x y x y
x y
ln 4 1 ln 4 1
ln 4 1 ln 4 1
x y
x y
y x
x y
(vì
, 0x y
).
Xéthàmsố
ln 4 1
t
f t
t
trênkhoảng
0;
.
Tacó
2
2
4 .ln 4
. ln 4 1
4 ln 4 4 1 ln 4 1
4 1
0, 0
4 1
t
t
t t t t
t
t
t
f t t
t
t
f t
luônnghịchbiếntrênkhoảng
0; .
Lạicó
f x f y x y
.
Đặt
x
t
y
,khiđó
1;t
2
3
1
t
P
t
.
Cách1:Xét
2
3
1
t
P
t
với
1;t
,tacó
2
2
1
2 3
; 0
3
1
t
t t
P P
t
t
Bảngbiếnthiên
Từbảngbiếnthiên,suyragiátrịnhỏnhấtcủa
P
bằng
6
khi
3t
hay
3x y
.
Cách2:Tacó
2
3 4
1 2 2 4 2 6
1 1
t
P t
t t
(AM – GM).

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
Suyra,giátrịnhỏnhấtcủa
P
bằng
6
khi
3t
hay
3x y
.
Câu 35. (Chuyên ĐH Vinh - Nghệ An -2020) Xét các số thực dương
,x y
thỏa mãn
2
2 2
2
2 2 1
2 4 log 4
2
x y xy
x y
.Khi
4x y
đạtgiátrịnhỏnhất,
x
y
bằng
A.
2
. B.
4
. C.
1
2
. D.
1
4
.
Lời giải
Chọn A
Tacó:
2
2 2
2
2 2 1
2 4 log 4
2
x y xy
x y
2 2
2 2
1
2 4 8 1 log log 4 8
2
x y xy x y xy xy xy
2
2
2 2
2 log 2 log 1
2 2
xy xy
x y x y
.
Xéthàmsố
2
2
2 logf t t t
,với
0;t
1
4 0, 0
.ln 2
f t t t
t
, suy ra hàm số
f t
đồng biến trên khoảng
0;
. Từ
1 2
2
xy
f x y f x y xy
.
Tacó:
2
2 ( 2) 2 ; 2
2
y
x y xy x y y x y
y
.
2 4 4
4 4 10 4 2 10 2 4 2 . 18
2 2 2
y
P x y y y y
y y y
min
18
P
khi
4
4 2 2 1 3
2
y y y
y
.
2
3 6 2
2
y x
y x
y y
.
Câu 36. (Chuyên Hưng Yên - 2020) Biếtphươngtrình
4 3 2
1 0
x ax bx cx
cónghiệm.Tìmgiátrị
nhỏnhấtcủabiểuthức
2 2 2
T a b c
A.
min
4
3
T
. B.
min
4
T
. C.
min
2
T
. D.
min
8
3
T
.
Lời giải
Chọn A
Tacó
4 3 2
1 0
x ax bx cx
.
Vì
0x
khônglànghiệmcủaphươngtrìnhnênchiahaivếphươngtrìnhcho
2
x
tađược
2 2
2 2 2
2 2 2
1 1 1
0
c c c
x ax b x ax b x ax b
x x x x x x
.
Tacó
2
2 2 2 2
2
1
1
c
ax b a b c x
x x
.(theoBĐTCauchy-Schwarz)
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khiđó
2
2 2 2 2 2
2 2
1 1
1
x a b c x
x x
2
2
2
2 2 2
2
2
1
1
1
x
x
a b c
x
x
.(1)
Đặt
2
2
1
2
t x
x
(theoBĐTCôSi).
Khảosáthàmsố
2
, 2;
1
t
f t t
t
có
2
2
2
' 0, 2;
1
t t
f t t
t
.
Dođó
2;
4
min 2
3
f t f
2 2 2
4
3
a b c
.
Dấu
2
" "
3
a b c
.
Phươngtrìnhcónghiệmthi
2;
min
T f t
.
4 3 2
2 2 2
1 0
3 3 3
x x x x
cónghiệm
1 2x t
thỏamãn.
Vậy
min
4
3
T
.
Câu 37. (Chuyên KHTN - 2020) Cho
,x y
là các số thực dương thỏa mãn
2
2 2
3 3 4
log 1 2 2 1 4 1
x y
x y x y xy
x y
. Giá trị lớn nhất của biểu thức
5 3 2
2 1
x y
P
x y
.
A.
3
. B.
1
. C.
2
. D.
4
.
Lời giải
Chọn C
Tacó:
2
2 2
3 3 4
log 1 2 2 1 4 1
x y
x y x y xy
x y
2 2
2
2 2
3 3 4
log 2 2 3 3 3
x y
x y x y
x y
2 2
2 2
2 2
3 3 3 2 2 2 2
2 2 3 3 3
3 3 4 2
3 3 4 .2 .2
2
x y
x y x y
x y
x y
x y x y
x y
2 2
3 3 3 2 2 2 2
2. 3 3 4 .2 2. .2
x y x y
x y x y
2 2
3 3 4 2 2 2 2
3 3 4 .2 2 2 .2
x y x y
x y x y
1
Đặt
.2 0
t
f t t t
.
Taxét:
2 .2 .ln 2 0, 0
t t
f t t t
.Suyrahàmsố
f t
đồngbiếntrên
0;
.
Lúcđó;
1
códạng:
2 2
3 3 4 2 2
f x y f x y
2 2 2 2 2 2
3 3 4 2 2 2 3 4 2
x y x y x xy y x y x xy y
2 2
3 4
x y x y x y
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
2
3 4 0 1 4 4 0
x y x y x y x y
.
Khiđó:
5 3 2 4
2 2 0 2
2 1 2 1
x y x y
P
x y x y
.
Vậy
P
đạtgiátrịlớnnhấtlà
2
,đạtđượckhi
2 2
4
3 3 4 2 2 2
0
x y
x y x y x y
x y
.
Câu 38. (Chuyên Bến Tre - 2020) Cho các số thực
,x y
thỏa mãn
0 , 1x y
và
3
log 1 1 2 0
1
x y
x y
xy
.Tìmgiátrịnhỏnhấtcủa
P
với
2P x y
A.
2
. B.
1
. C.
0
. D.
1
2
.
Lời giải
Chọn B
Tacó
3 3
log 1 1 2 0 log 1 0
1 1
x y x y
x y xy x y
xy xy
3 3
log log 1 1
x y x y xy xy
Xéthàmsốđặctrưng
3
log
f t t t
với
0
t
Tacó
1
' 1 0, 0
ln3
f t t
t
Hàmsố
f t
đồngbiếnvới
0
t
Có
1
1 1 1 1
1
y
f x y f xy x y xy x y y x
y
Tacó
2 2 4 4
2 3 1 3 2 1 1
1 1 1
y
P x y y y y
y y y
Vậygiátrịnhỏnhấtcủa
P
bằng
1
.
Câu 39. (Chuyên Chu Văn An - 2020) Cho
,x y
làcácsốthựcdươngthỏamãn
3
4
log 2 1.
x y
x y
x y
Tìmgiátrịnhỏnhấtcủabiểuthức
4 2
2
3 2 2
( )
x y xy y
P
x x y
.
A.
1
.
4
B.
1
.
2
C.
3
.
2
D.
2.
Lời giải
Chọn D
Tacó
3 3 3
4
log 2 1 log ( 4 ) (x 4 y) log 3( ) 3( )
x y
x y x y x y x y
x y
(1).
Xéthàmsố
3
( ) log
f t t t
trênkhoảng
(0; )
.
Tacó
1
'( ) 1 0, 0
ln3
f t t
t
.Suyrahàmsố
( )f t
đồngbiếntrênkhoảng
(0; )
.
Từ(1)suyra
( 4 ) (3( ))f x y f x y
và
( 4 ) 0;3( ) 0
x y x y
.
Dođó,
(1) 4 3( ) 2x y x y y x
.
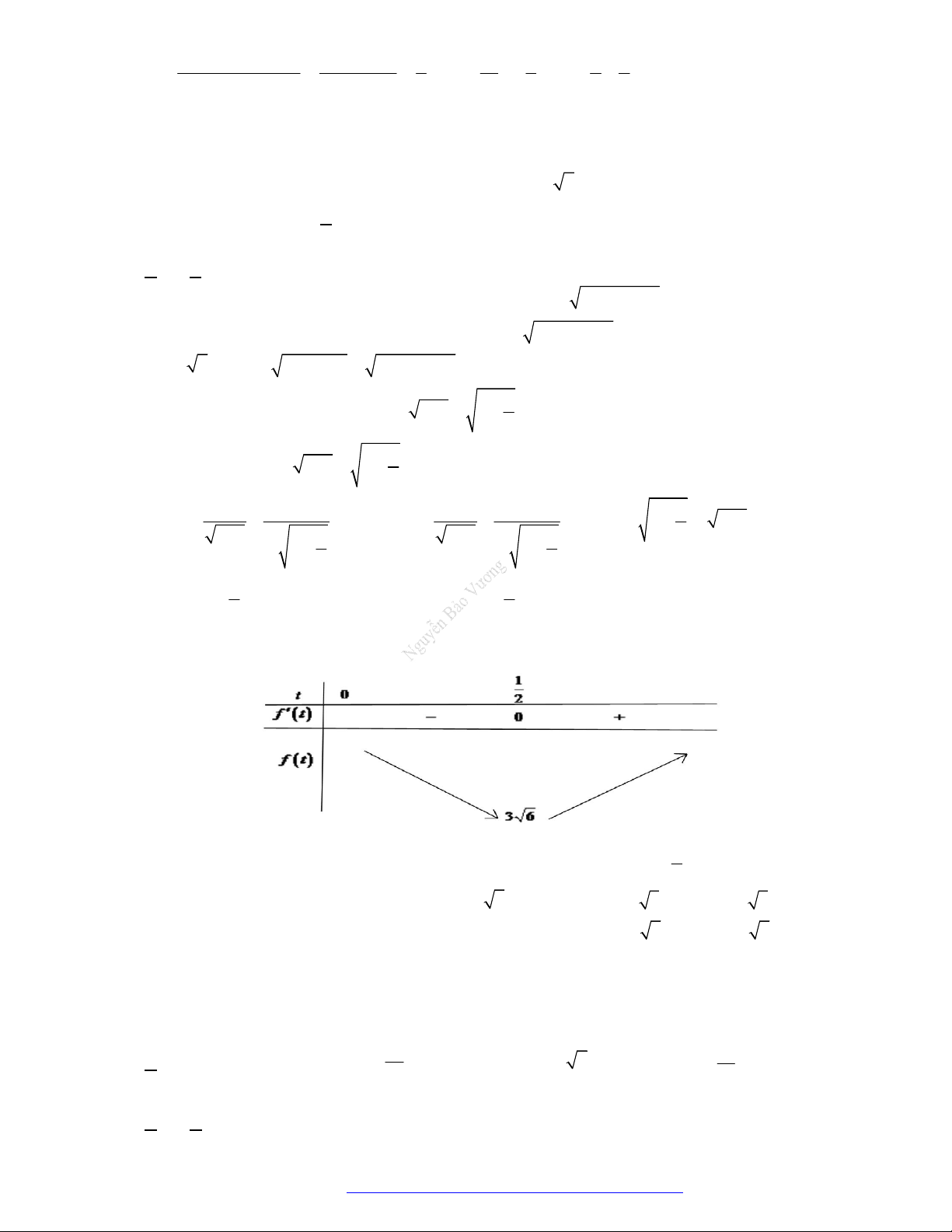
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 52 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
4 2 5 2
2 2
2 3
3 2 2 6 12 1 12 1 6 6
6 6 2.
9 9
( ) 9
x y xy y x x
P x x
x x x
x x y x
Dấu
" "
xảyra
1x
.Vậy 2.
Min
P
Câu 40. (Chuyên Hùng Vương - Gia Lai - 2020) Xétcácsốthựcdương
, , ,a b x y
thỏamãn
1, 1a b
và
2 2
2
x y
a b ab
.Giátrịnhỏnhấtcủabiểuthức
2 2P x y
thuộctậphợpnàodướiđây?
A.
10;15
. B.
6;10
. C.
1;4
. D.
4;6
.
Lời giải
Chọn B
Tacó:
2
2 2
2
log 2 1 log 2 2log
x
a a a
a ab x ab b x b
2
2 2
2
log 2 1 log 2 2log
y
b b b
b ab y ab a y a
2 2 4 1 log 2 2log
a b
P x y b a
.
Đặt
log 0
a
t b t
tađược:
2
4 1 2P t
t
.
Xéthàmsố
2
4 1 2f t t
t
,với
0;t
.
2
2 2
2 1 2 1 2
; 0 0 2 2 1
1 2 1 2
2 2
f t f t t t
t
t t
t t
t t
4 4 3
2 1
4 2 1 8 8 1 0
2
t t t t t t
t
.
Bảngbiếnthiêncủahàmsố
f t
.
Từbảngbiếnthiênsuyra
0;
Min min 3 6 6;10P f t
khi
2
1
log
2
3 3
6 6
a
b
a b
x x
y y
.
Câu 41. (Chuyên Lào Cai - 2020) Xétcácsốthựcdương
x
,
y
thỏamãn
2
log log logx y x y
.
Biểuthức
8P x y
đạtgiátrịnhỏnhấtcủabằng:
A.
min
16P
. B.
min
33
2
P
. C.
min
11 2P
. D.
min
31
2
P
.
Lời giải
Chọn A
Từđềbài
2
xy x y
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53
2
2
1
1
1
y
x
x y y
y
y
(Vì
; 0
x y
).
Tacó:
2
1
8 8 9 1
1 1
y
P x y y y
y y
.
Xéthàmsố:
1
9 1 ; 1
1
f y y y
y
.
Đạohàm:
/
2
1
9
1
f y
y
.
/
4
3
0
2
3
y
f y
y l
.
Bảngbiếnthiên,tathấygiátrịnhỏnhấtcủa
( )f y
là
4
16.
3
f
Vậy
min
16
P
khi
16
3
x
.
Câu 42. (Chuyên Lê Hồng Phong - Nam Định - 2020) Xét các số thực
,x y
thỏa mãn
2 2
log 1 log 1 1
x y
.Khibiểuthức
2 3P x y
đạtgiátrịnhỏnhấtthì
3 2 3x y a b
với
,a b
.Tính
T ab
?
A.
9
T
. B.
7
3
T
. C.
5
3
T
. D.
7
T
.
Lời giải
Chọn C
Điềukiện:
1 0 1
1 0 1
x x
y y
Khiđó:
2 2
2 2
log 1 log 1 1 1 1 2 1 1
1 1
x y x y y y
x x
Suyra:
6 6
2 3 2 3 2 1 5
1 1
P x y x x
x x
Cách 1:Dùngbấtđẳngthức
ÁpdụngbấtđẳngthứcCôsi,tacó:
6 6
2 1 2 2 1 .
1 1
x x
x x
6
2 1 4 3 4 3 5
1
x P
x
Dấu“=”xảyra
2
1 3
6
2 1 1 3 1 3
1
1 3
x N
x x x
x
x L
2 2 3 3
1
3
3
y
.
Dođó:
2 3 3 5 5 5
3 2 3 1 3 2 1 3 1;
3 3 3 3
x y a b T ab
.
Cách 2:Dùngbảngbiếnthiên
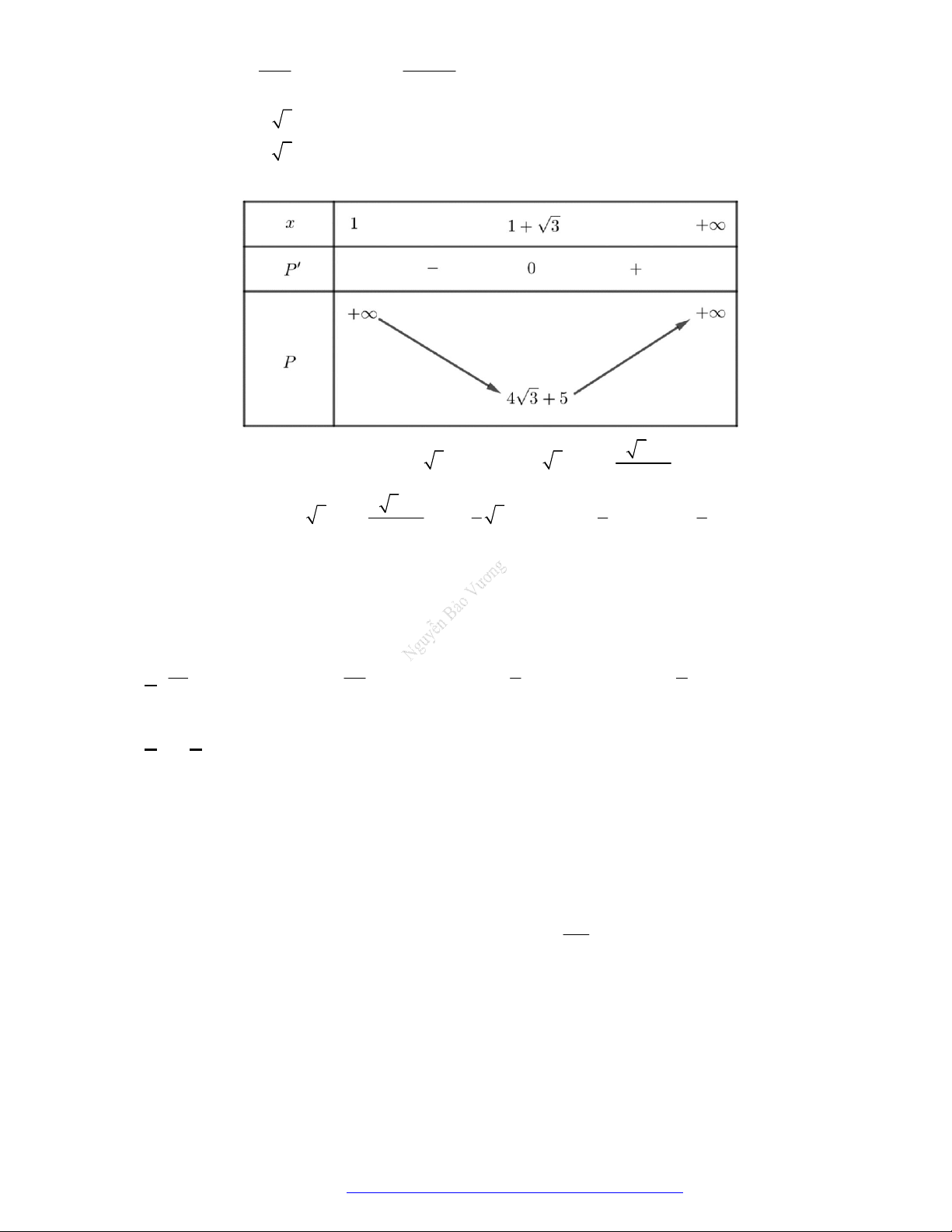
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 54 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tacó:
6
2 3
1
P x
x
2
6
' 2
1
P
x
1 3
' 0
1 3
x N
P
x L
Bảngbiếnthiên
Dựavàobảngbiếnthiên,tacó:
min
2 3 3
4 3 5 1 3
3
P x y
.
Dođó:
2 3 3 5 5 5
3 2 3 1 3 2 1 3 1;
3 3 3 3
x y a b T ab
.
Câu 43. (Chuyên Phan Bội Châu - Nghệ An - 2020) Cho các số thực
, , , a b c d
thỏa mãn
2 2
2
log 4 6 7 1
a b
a b
và
27 .81 6 8 1
c d
c d
. Tìm giá trị nhỏ nhất của biểu thức
2 2
P a c b d
.
A.
49
.
25
B.
64
.
25
C.
7
.
5
D.
8
5
.
Lờigiải
Chọn A
Tacó
2 2
2 2
2 2
2
log 4 6 7 1 2 4 6 7 2 3 4 1
a b
a b a b a b a b
.
Lạicó
3 4
27 .81 6 8 1 3 2 3 4 1 2
c d c d
c d c d
.
Xéthàmsố
3 2 1
t
f t t
trên
.
Khiđó
f t
làhàmsốcóđạohàmliêntụctrên
và
3 .ln 3 2
t
f t
.
Vìphươngtrình
0f t
cóđúngmộtnghiệm
0 3
2
log
ln3
t
nênphươngtrình
0f t
có
tốiđa2nghiệm.Mặtkhác,
0 1 0f f
nên
0;1S
làtậpnghiệmcủaphươngtrình
0f t
.
Dođó,
2
tươngđươngvới
3 4 0c d
hoặc
3 4 1 3c d
.
Trongmặtphẳngvớihệtrụctọađộ
Oxy
,gọiđiểm
M
cótọađộ
,a b
vàđiểm
N
cótọađộ
,c d
.Khiđó,từ
1
suyra
M
thuộcđườngtròntâm
2;3I
,bánkính
2r
vàtừ
3
suyra
N
thuộcđườngthẳng
1
:3 4 0x y hoặc
2
:3 4 1 0x y .
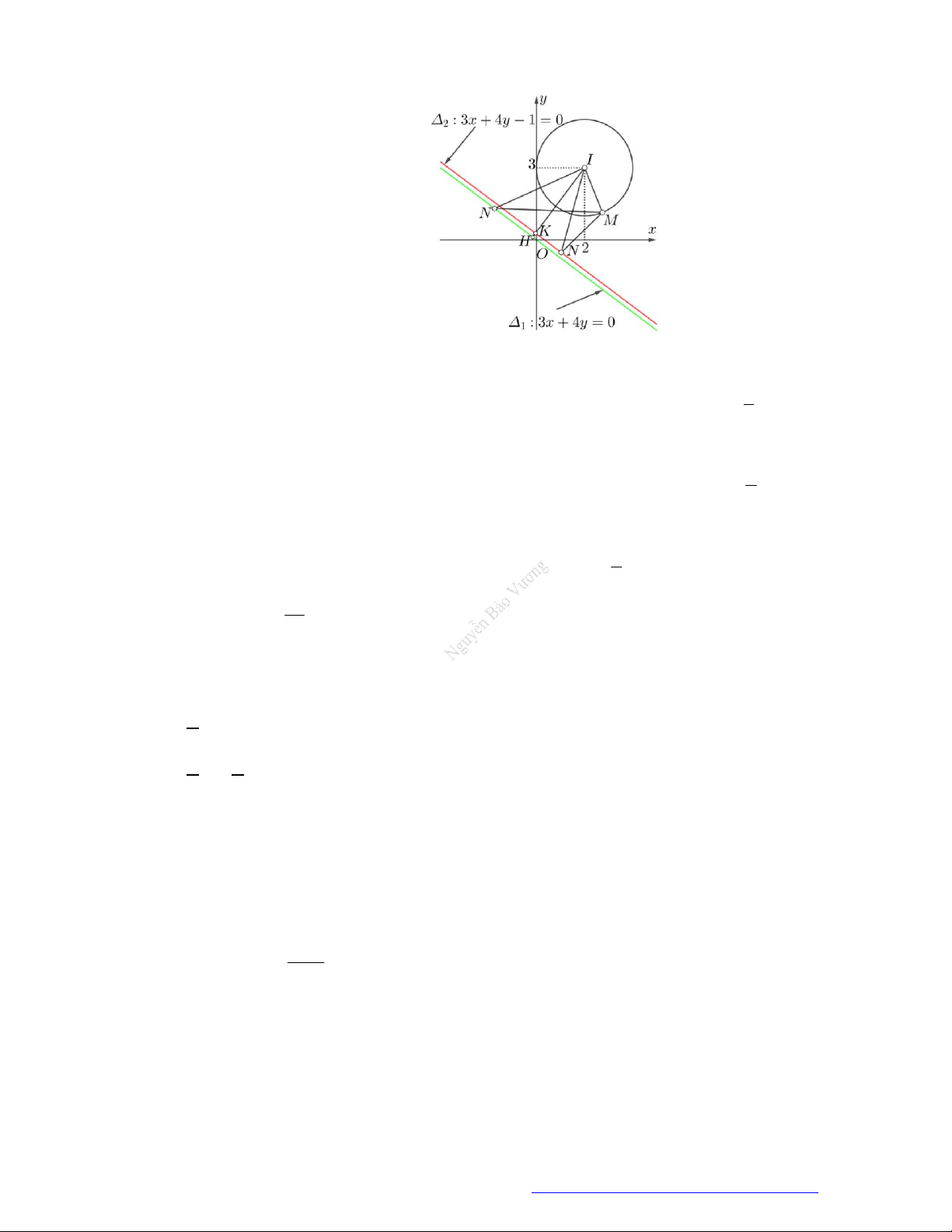
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 55
Tacầntìmgiátrịnhỏnhấtcủabiểuthức
2 2
2
P a c b d MN
.
Gọi
,H K
lầnlượtlàhìnhchiếuvuônggóccủa
I
lêncácđườngthẳng
1
và
2
.
Nếu
N
dichuyểntrênđườngthẳng
1
thì
MN IN IM IH r
nên
8
5
MN
.
Dấuđẳngthứcxảyrakhi
N H
và
M
làgiaođiểmcủađoạnthẳng
IH
vớiđườngtròn.
Nếu
N
dichuyểntrênđườngthẳng
2
thì
MN IN IM IK r
nên
7
5
MN
.
Dấuđẳngthứcxảyrakhi
N K
và
M
làgiaođiểmcủađoạnthẳng
IK
vớiđườngtròn.
Từhaitrườnghợptrên,tacógiátrịnhỏnhấtcủa
MN
bằng
7
5
.Từđó,giátrịnhỏnhấtcủabiểu
thức
P
bằng
49
.
25
Câu 44. (Chuyên Thái Bình - 2020) Cho hai số thực dương
,x y
thỏa mãn
2 2
log log 6 6x x x y y x
.Giátrịnhỏnhấtcủabiểuthức
3
3T x y là
A.
16
. B.
18
. C.
12
. D.
20
.
Lời giải
Chọn A
Điềukiện:
0x
,
0 6y
.
Tacó
2 2
log log 6 6x x x y y x
2
2 2
log log 6 6x x y x xy
2
2 2 2 2
log log log 6 log 6x x x y x x xy
2 2
2 2
log log 6 6x x x y x y
*
Xéthàmsố
2
logf t t t
trên
0;
.
Tacó
1
1 0, 0;
.ln 2
f t t
t
nênhàmsố
f t
đồngbiếntrên
0;
.
Khiđó
2
* 6f x f x y
2
6x x y
6x y 6y x
.
3
3 6T x x
3
3 18x x g x
.
Xéthàmsố
3
3 18g x x x
trên
0;
.
Tacó
2
3 3g x x
;
0g x
1 0;
1 0;
x
x
Bảngbiếnthiên:
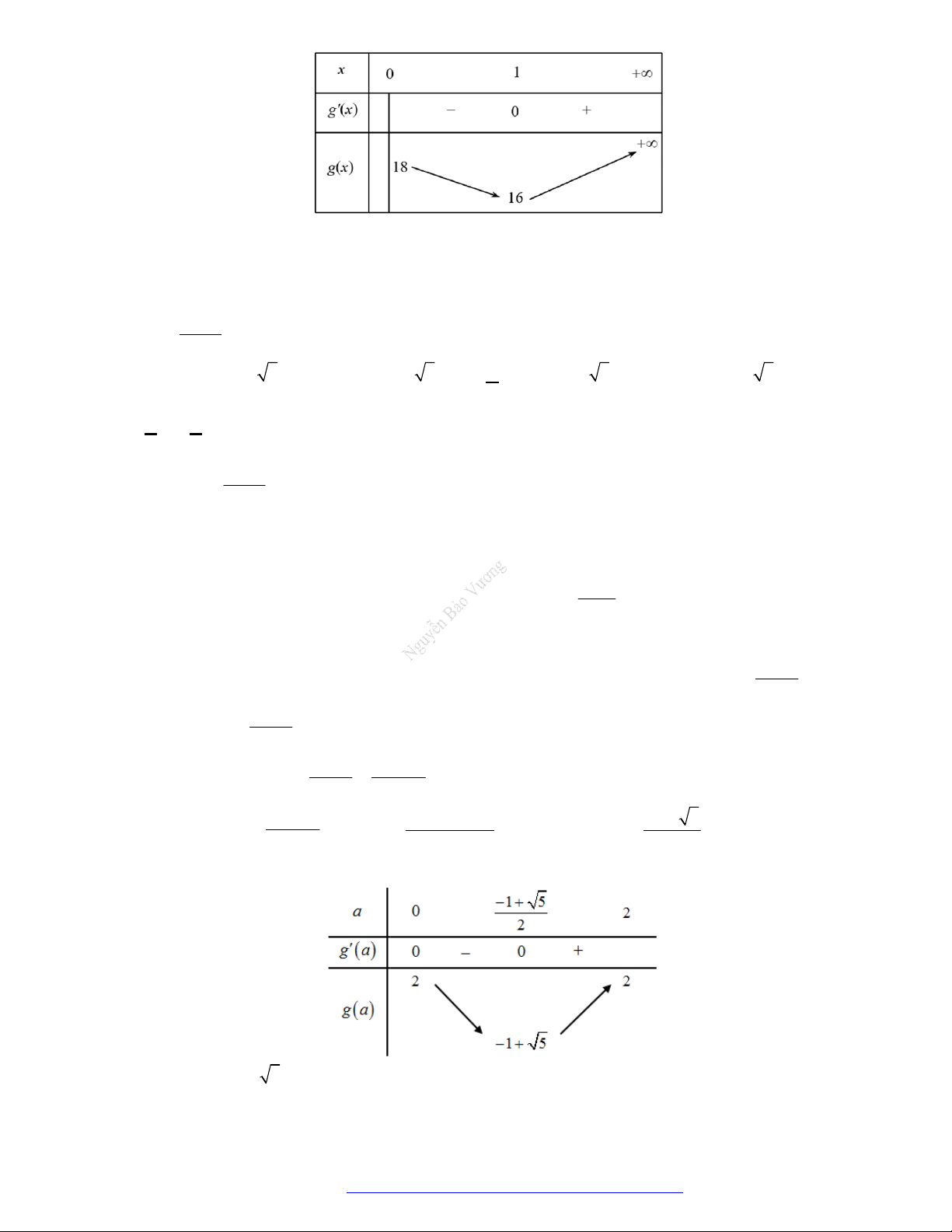
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 56 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từbảngbiếnthiênsuyra
1 16T g x g
.Dấu“=”xảyrakhivàchỉkhi
1
6 5
x
y x
.
Câu 45. (Chuyên Thái Nguyên - 2020) Xét các số thực dương
,a b
thoả mãn
2
1
log 2 3
ab
ab a b
a b
.Tìmgiátrịnhỏnhất
min
P của
P a b
.
A.
min
1 2 5P
. B.
min
2 5P
. C.
min
1 5P
. D.
min
1 2 5P
.
Lời giải
ChọnC
Điềukiện
1 0 1ab ab
.
Tacó
2 2 2
1
log 2 3 log 1 log 2 1 1
ab
ab a b ab a b a b ab
a b
2 2
log 1 1 2 1 logab ab a b a b
2 2
log 2 1 2 1 log . 1ab ab a b a b
Xét hàm số
2
logf t t t
với
0t
có
1
1 0, 0
.ln 2
f t t
t
nên hàm số
2
logf t t t
đồngbiếntrênkhoảng
0;
.
Tacó
2
1 2 1 2 1 2 2 1
2 1
a
f ab f a b ab a b a b a b
a
.
Do
2
, 0 0 0 2
2 1
a
a b a
a
.
Khiđó
2
2 2 2
2 1 2 1
a a
P a b a
a a
Xéthàm
2
2 2
2 1
a
g a
a
2
2
4 4 4 1 5
0
2
2 1
a a
g a g a a
a
.
Bảngbiếnthiên
Vậy
min
1 5P
.
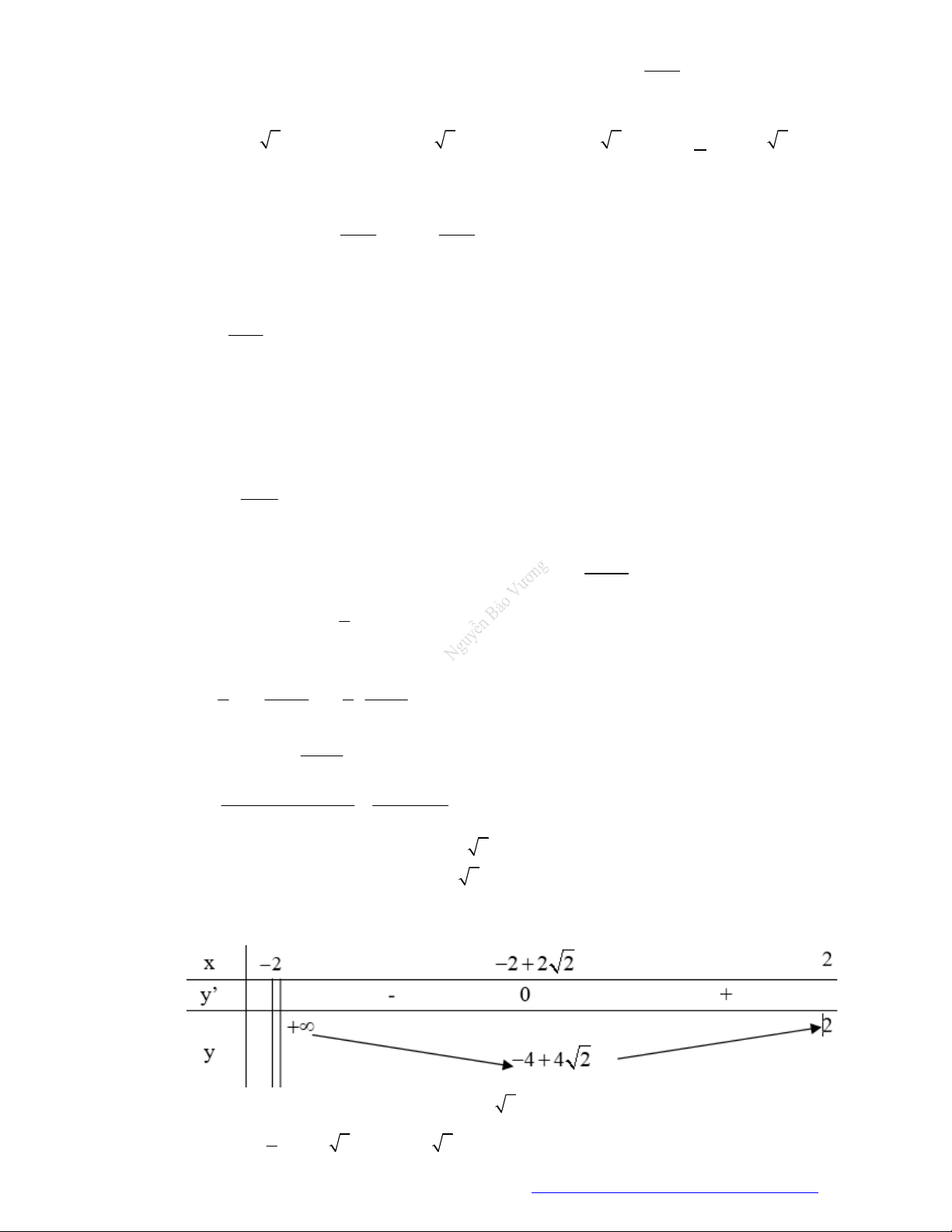
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 57
Câu 46. (ĐHQG Hà Nội - 2020) Chocácsốthựcx,ythỏamãn
2 2
2
log log 2 2 5
2
x
y x y xy
x
.
Hỏigiátrịnhỏnhấtcủa
2 2
P x y xy
làbaonhiêu?
A.
30 20 2
. B.
33 22 2
. C.
24 16 2
. D.
36 24 2
.
Lời giải
Chọn D
Điềukiệnxácđịnh:
2 2
2 2
0 0
2 2
0
0 0
x x
x
x x
y
y y
Theobàiratacó:
2 2
2 2 2
2 2
2 2
2
log log 2 2 5
2
log (2 ) log ( 2) log 2( 2) ( 2) 1
log (2 ) 1 (2 4) log ( 2) ( 2)
log (4 2 ) (4 2 ) log ( 2) ( 2)
x
y x y xy
x
x x y x y x
x x x y y x
x x y x y x
Xéthàmsố
2
( ) log ( 0)f t t t t
:
1
'( ) 1 0 0
.ln 2
f t t
t
Suyra:
( )f t
làhàmđồngbiếntrênkhoàng
(0; )
Mà
(4 2 ) ( 2)f x f y x
nên
4 2
4 2 ( 2)
2
x
x y x y
x
Vì
2 2 2
3
( )
4
P x y xy x y
ThayvàoPtacó:
2
2
2
3 4 2 3 4
4 2 4 2
x x
P x
x x
Xéthàmsố
2
4
2
x
y
x
trênkhoảng
( 2;2)
:
2 2
2 2
2
2 ( 2) ( 4) 4 4
'
( 2) ( 2)
2 2 2
' 0 4 4 0
2 2 2( )
x x x x x
y
x x
x
y x x
x l
(Vì
( 2;2)x
)
Lậpbảngbiếnthiên:
Dựavàobảngbiếnthiên,tacó
min
4 4 2y
Vậy
2
min
3
4 4 2 36 24 2
4
P

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 58 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 47. (Sở Bình Phước - 2020) Cho
,x y
là các số thực dương thỏa mãn
2
2 2 2
log log 1 log 2x y x y
.Giátrịnhỏnhấtcủabiểuthức
2x y
bằng
A.
2 2 3
. B.
2 3 2
. C.
3 3
. D.
9
.
Lời giải
Chọn A
Với
0; 0.
x y
Tacó:
2
2 2 2
2
2
2
log log 1 log 2 1
2 2 2
2 1
1 0
2
1.
x y x y
xy x y
y x x
x
x
y
x
Đặt
2m x y
tacó:
2
2
2
2
1 2
2
.
1
x m x x x m
m x x x
x x
m
x
Xéthàmsố
2
2
1
x x
g x
x
với
1x
.
Tatìmthấy
1;
min 3 2 2
g x
khi
2 2
2
x
.
Vậy
3 2 2
m
,dấubằngxảyrakhi
2 2
2
4 3 2
4
x
y
(thỏamãnđiềukiệnbàitoán).
VậyGTNNcủa
2x y
là
3 2 2
.
Câu 48. (Sở Yên Bái - 2020) Chocácsốthực
,x y
thuộcđoạn
0;1
thỏamãn
2
1
2
2021
2020
2 2022
x y
x
y y
.
Gọi
,M m
lầnlượtlàgiátrịlớnnhấtvàgiátrịnhỏnhấtcủabiểuthức
3 3 2
2 6 3 9
x y x xy
.Tính
.M m
.
A.
5
2
. B.
5.
C.
5.
D.
3.
Lời giải
Chọn D
Tacó
2
1
2
2021
2020
2 2022
x y
x
y y
1 2 2
2020 2 2022 2021
x y
y y x
2
1 2
2020 1 2021 2020 2021
y x
y x
.
Tacó
2
2020 2021
t
f t t
với
0;1
t
có
2
2020 .ln 2020. 2021 2.2020 . 0
t t
f t t t
.
Dovậy
2
2020 2021
t
f t t
đồngbiếntrênkhoảng
0;1
t
.
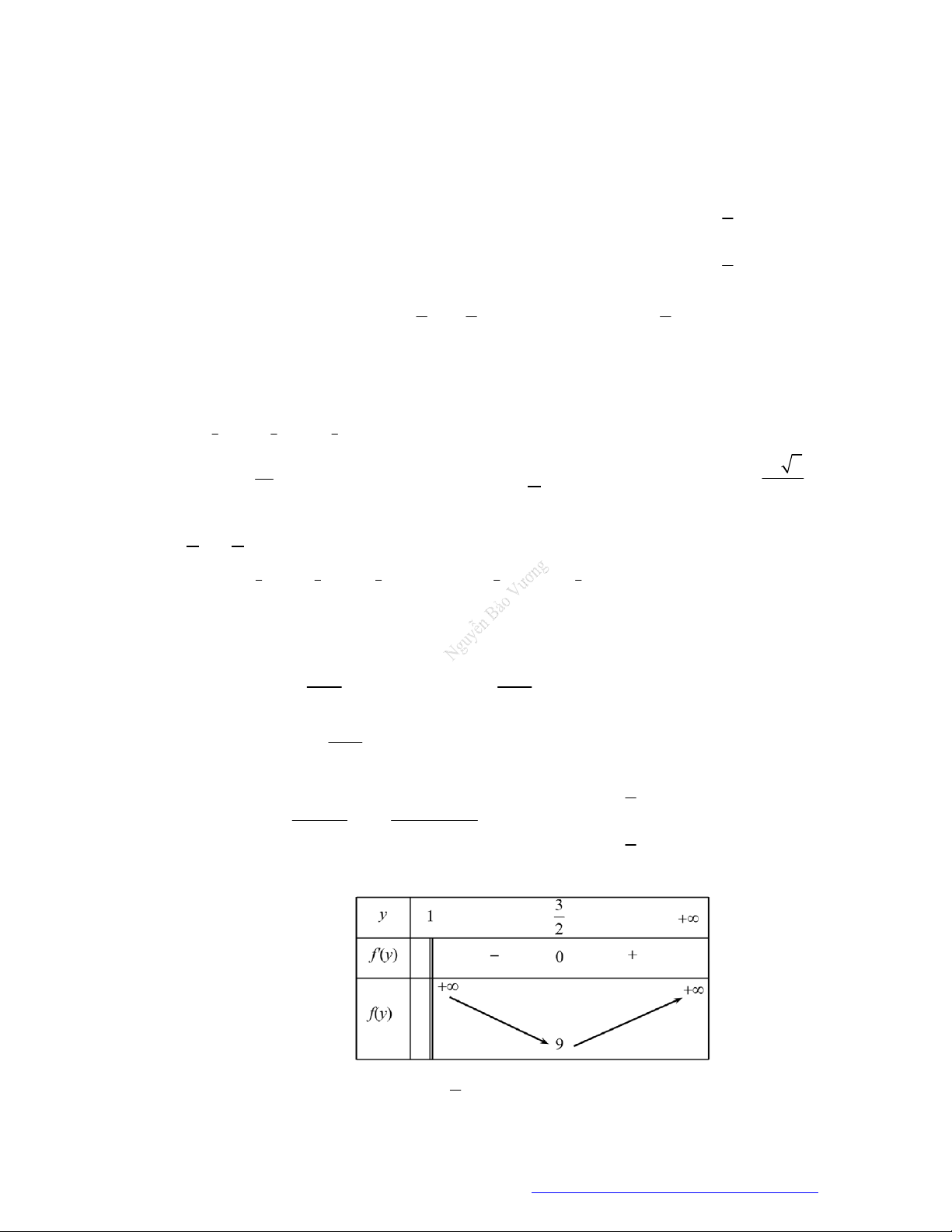
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 59
Suyra
1 1 1 f y f x x y y x
.
Dovậy
3 3 2
2 6 3 9 x y x xy
3
3 2
2 6 1 3 9 1 x x x x x
3 2 3 2 2
2 6 18 18 6 3 9 9 x x x x x x x
3 2
4 30 27 6 x x x
.
Xét
3 2
4 30 27 6 f x x x x
với
0;1x
.
Mà
3 2
4 30 27 6 f x x x x
nên
2
1
2
12 60 27 0
9
(loai)
2
x
f x x x
x
.
Mặtkhác
1 1
0 6, 1 5,
2 2
f f f
.Dovậy
6M
và
1
2
m
.
Vậynên
. 3 M m
.
Câu 49. (Bỉm Sơn - Thanh Hóa - 2020) Xét các số thực dương
.x y
thỏa mãn
2
1 1 1
2 2 2
log log logx y x y
.Tìmgiátrịnhỏnhất
min
P củabiểuthức
3P x y
.
A.
min
17
2
P
. B.
min
8P . C.
min
9P . D.
min
25 2
4
P
.
Lời giải
Chọn C
Tacó
2
1 1 1
2 2 2
log log logx y x y
2
1 1
2 2
log logxy x y
2
xy x y
2
1y x y
.
Do
2
0 0y y
2
1 0y x y
.Mà
0x
nên
1 0y
,hay
1y
.
Khiđótacó
2
1
y
x
y
.Suyra
2
3 3
1
y
P x y y
y
Xéthàmsố
2
3
1
y
f y y
y
trên
1;
.
Tacó
2
2
2
3
1
y y
f y
y
2
2
4 8 3
1
y y
y
;
0f y
1
1;
2
3
1;
2
y
y
Bảngbiếnthiên:
Từbảngbiếnthiênsuyra
3
9
2
f y f
.Vậy
9P f y
.
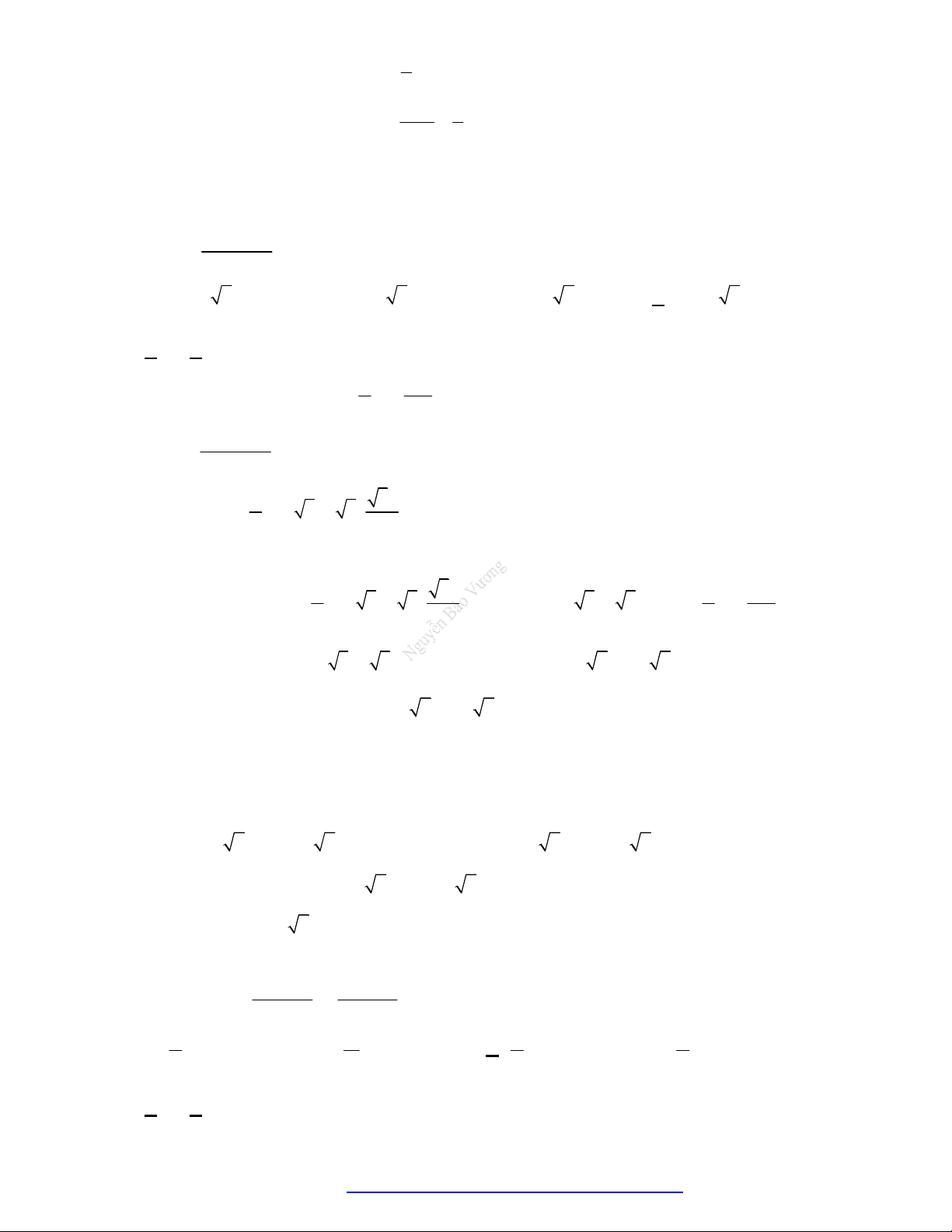
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 60 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dấu
" "
xảyrakhivàchỉkhi
2
3
2
9
1 2
y
y
x
y
.
Câu 50. (Nguyễn Trãi - Thái Bình - 2020) Chocácsốthực
x
,
y
thayđổithỏamãn
2 2
1x y xy
và
hàmsố
3 2
2 3 1
f t t t
.Gọi
M
và
m
tươngứnglàgiátrịlớnnhấtvàgiátrịnhỏnhấtcủa
5 2
4
x y
Q f
x y
.Tổng
M m
bằng
A.
4 3 2
. B.
4 5 2
. C.
4 2 2
. D.
4 4 2
.
Lời giải
Chọn D
Tacó
2
2
2 2
3
1 1
2 4
y y
x y xy x
.
Đặt
5 2
4 5 2 5 1 4 2 0
4
x y
t t x y x y t x t y t
x y
3
5 3 3 2 4
2 2
y y
t x t t
.
ÁpdụngbấtđẳngthứcBunhiacốpxkitacó
2
2
2
2
2 2
3 3
2 4 5 3 3 5 3 3
2 2 2 4
y y y y
t t x t t t x
2
2 2
2
2 4 5 3 3 .1 12 24 0 2 2
t t t t t t
.
Xéthàmsố
3 2
2 3 1
f t t t
với
2 2
t
.
Tacó
2
6 6 6 1
f t t t t t
.
Khiđó
0
0
1
t
f t
t
.
Tacó
2 5 4 2
f
,
0 1
f
,
1 0
f
,
2 5 4 2
f
.
Dođó
0 1
M f
,
2 5 4 2
m f
.
Vậy
4 4 2
M m
.
Câu 51. (Yên Lạc 2 - Vĩnh Phúc - 2020) Chohaisốthực
a
,
b
lớnhơn
1
.Tìmgiátrịnhỏnhấtcủabiểu
thức
2 2
4 1
log
4 4 log
a
ab
a b
S
b
.
A.
5
4
. B.
11
4
. C.
9
4
. D.
7
4
.
Lời giải
Chọn C
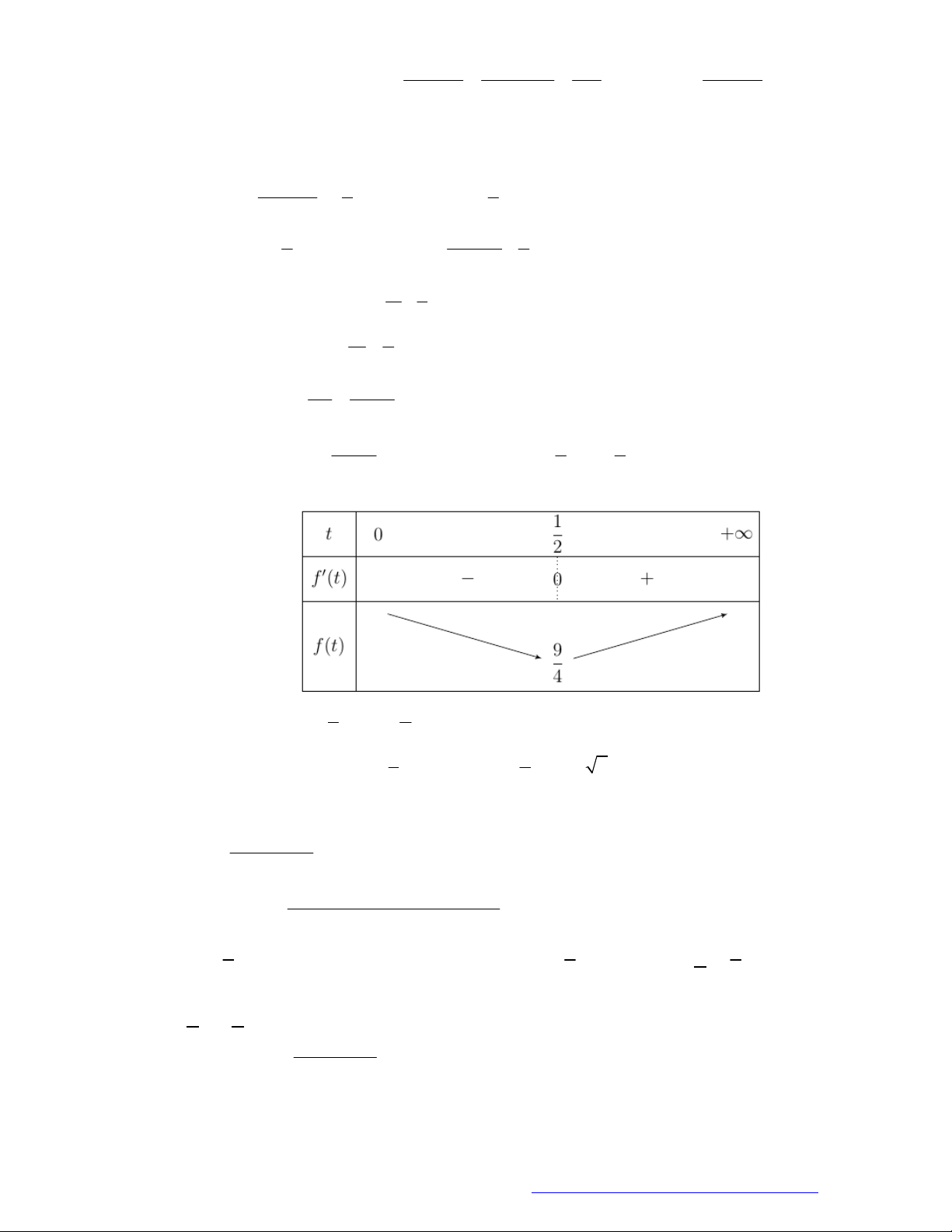
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 61
TheobấtđẳngthứcCôsitacó
2
2
2 2 2 2
2
4 4 4
log log
4 4 4 4
a a
a b
a b ab a b
ab ab
.
Do
a
,
1 log log 1 0
a a
b b
.
Tacó
2 2
4 1 1
log log log log
4 4 4
a b a b
a b
S ab ab ab
1 1 5
1 log log 1 log
4 4log 4
a b a
a
b a b
b
.
Đặt
log
a
t b
,tacó
1 5
4 4
S t
t
.
Xéthàmsố
1 5
4 4
f t t
t
với
0t
.
Tacó
2
2 2
1 4 1
1
4 4
t
f t
t t
.
Khiđó
2
2 2
2
4 1 1 1
0 0 4 1 0
4 4 2
t
f t t t t
t
.
Bảngbiếnthiên
Suyra
0;
9
min
4
t
f t
khi
1
2
t
.
Vậygiátrịnhỏnhấtcủa
9
4
S
khi
1
log
2
a
t b b a
.
Câu 52. (Hải Hậu - Nam Định - 2020) Với các số thực dương
, ,x y z
thay đổi sao cho
2
2 2 2
2 2
log 4 8 8 2
x y z
x x y y z z
x y z
,gọigiátrịlớnnhấtvàgiátrịnhỏnhấtcủa
biểuthức
2 2 2
4 7 11 8
6 5 86
x y z x y z
T
x y
thứtựlà
M
và
m
.Khiđó
M m
bằng:
A.
3
2
. B.
1
. C.
5
2
. D.
1
2
.
Lời giải
Chọn D
+)Tacó
2
2 2 2
2 2
log 4 8 8 2
x y z
x x y y z z
x y z
2 2 2 2 2 2
2 2
log 4 2 2 log 4( 2 2 )x y z x y z x y z x y z
2 2 2 2 2 2
2 2
log 4 2 2 4( 2 2 ) logx y z x y z x y z x y z
(1).

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 62 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
+)Xéthàmđặctrưng
2
log , 0f t t t t
có
1
0, 0
ln 2
f t t t
t
.
+)Tacó
2 2 2 2 2 2
(1) 4 2 2 4 8 8f x y z f x y z x y z x y z
2 2 2
2 4 4 36
x y z
.
+)Thayvàobiểuthức,tađược
4 8 8 4 7 11 8
3 8
6 5 86 6 5 86
x y z x y z
y z
T
x y x y
6 5 86 3 8 6 5 1 3 8 86T x y y z Tx T y z T
.
6 2 5 1 4 3 4 8 86 12 4 5 1 12
T x T y z T T T
6 2 5 1 4 3 4 54T x T y z T
+)TheobấtđẳngthứcBunhiacopxki,tacó
2 2
2
6
6 4 65 5 1 32 4 .3
3
1 TT x T y z T
2 2
2
2
36 6 5 1 3
54 T TT
2
720 360 3
2
160
1
0T T T
.
Suyra
1
2
M m
.
Câu 53. (Lương Thế Vinh - Hà Nội - 2020) Chocácsốthực
,x y
thỏamãn
3
ln ln( 2) ln 3
y x
.Tìm
giátrịnhỏnhấtcủabiểuthức
3
2 2
4 2
( 1) .
2
y x x
x y
H e x y y
A.
1
. B.
0
. C.
e
. D.
1
e
.
Lời giải
Chọn A
Do
3 3 3
ln ln 2 ln 3 2 3 4 2
y x x y y x x y x
2
2
y x
y x
H e y x .
Đặt
t y x
3 3
2 3 2
3 3
x x x
t x g x
với
3
2
x
.
2
3 3
3
x
g x
,
0 1
g x x
1 0
g x g
,suyra
0t
.
Xéthàmsố
2
2
t
t
f t e t
với
0t
.
1
t
f t e t
1
t
f t e
.
0 0
f t e
.
Tacóbảngbiếnthiênnhưsau
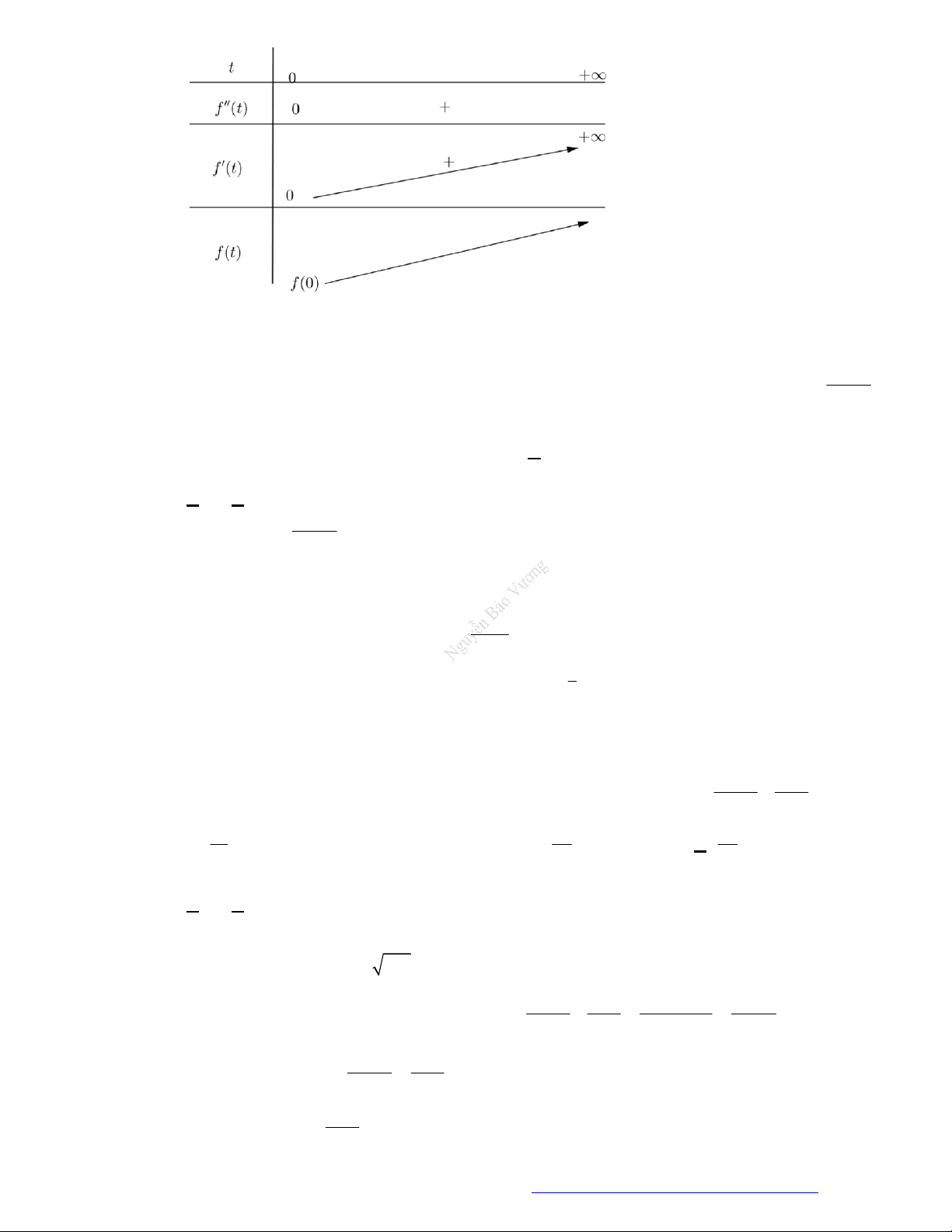
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 63
Suyra
0H f
.
Vậy
min 1H
.
Câu 54. (Thanh Chương 1 - Nghệ An - 2020) Cho
,x y
làcácsốthựcdươngthỏamãn
2
8 8
2
xy x y
xy
x y
.
Khi
2
2P xy xy
đạtgiátrịlớnnhất,giátrịcủabiểuthức
3 2x y
bằng
A.
4
. B.
2
. C.
3
. D.
5
.
Lời giải
Chọn C
Tacó
2
2 2
8 8
2 2 log 8 8 log
xy x y
xy
xy x y xy x y
x y
2 2
log 2 1 2 1 logxy xy x y x y
Xéthàmsố
2
logf t t t
làhàmsốđồngbiếntrên
0;
Dođótừ
*
tacó
2
2 1
2 1
y
xy x y x
y
Suyra
2 2
min
2 2 1P xy xy y y P
khi
1
1
3
y x
.
Dođó
3 2 3x y
Câu 55. (Tiên Lãng - Hải Phòng - 2020) Cho
,x y
là các số dương thỏa mãn
log 2 log logx y x y
.Khiđó,giátrịnhỏnhấtcủabiểuthức
2 2
4
1 2 1
x y
P
y x
là:
A.
31
5
. B.
6
. C.
29
5
. D.
32
5
.
Lời giải
Chọn D
Tacó:
log 2 log log log 2 log 2x y x y x y xy x y xy
Mặtkhác:
2
2 2 2 8 0 8xy x y xy xy xy xy
Ápdụngbấtđẳngthứccauchy-Swattacó:
2 2
2 2
2
4
1 2 1 2 2 2
x y xy
x y
P
y x x y xy
Đặt
xy t
suyra
2
2
2 2
xy
t
P
xy t
Xéthàmsố
2
2
t
f t
t
,với
8;t
.
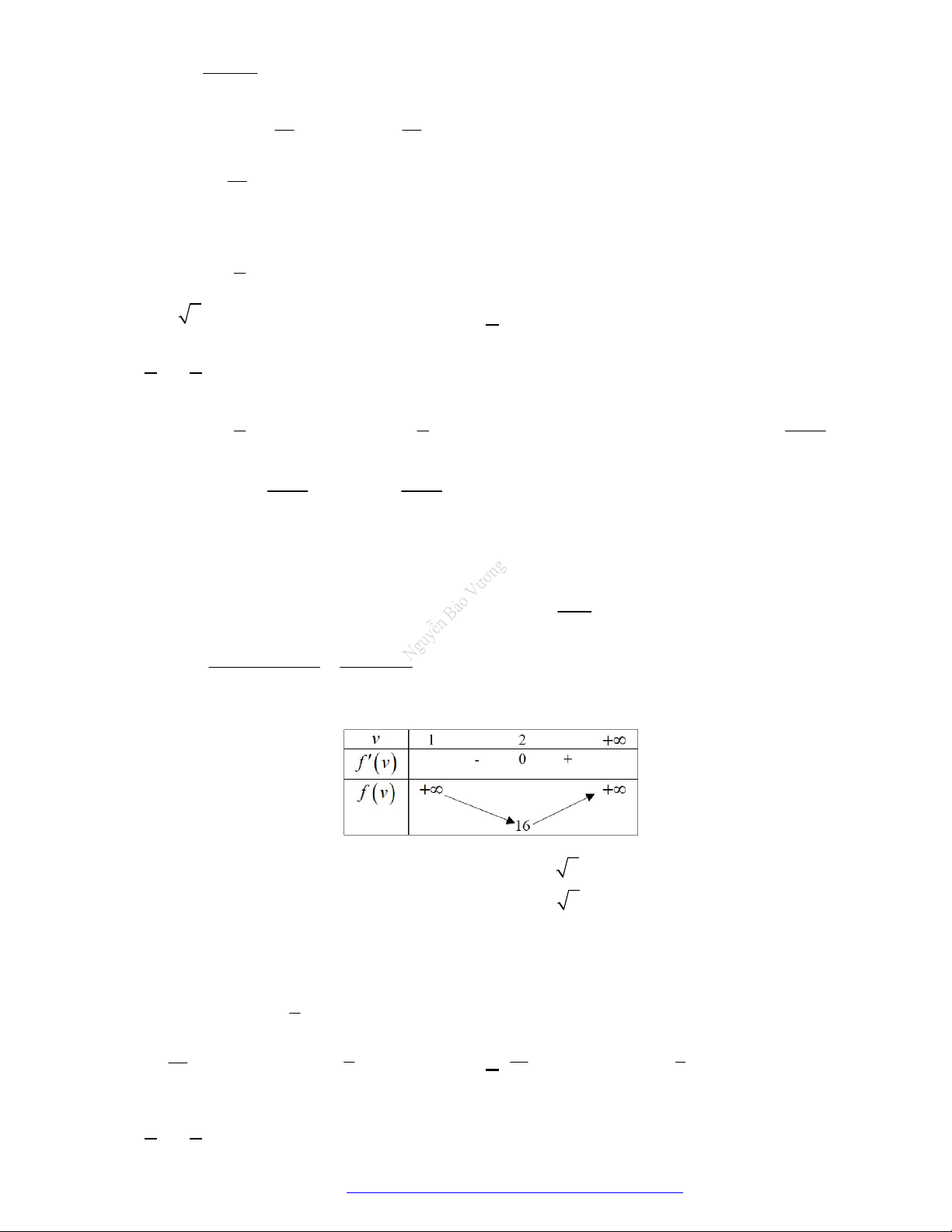
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 64 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
4
0, 8
2
t t
f t t
t
,suyrahàmsố
f t
đồngbiếntrênkhoảng
8;
.
32
8
5
f t f
32
5
P f t
.
32
Min
5
P
khi
2 4
8 2
x y x
xy y
.
Câu 56. (Chuyên Sư Phạm Hà Nội - 2020) Cho các số thực
,x y
thay đổi, thỏa mãn
0x y
và
1
ln ln ln
2
x y xy x y
.Giátrịnhỏnhấtcủa
M x y
là
A.
2 2
. B. 2. C. 4. D. 16.
Lời giải
Chọn C
Với
0x y
, ta có
1
ln ln ln
2
x y xy x y
1
ln ln ln
2
xy x y x y
ln 2ln
x y
xy
x y
2
ln ln
x y
xy
x y
2
x y
xy
x y
2 2
x y xy x y
(*)
Đặt
0
0
u x y
v xy
Tacó(*)
2 2
4u v v u
2 2
1 4v u v
2
2
4
1
v
u f v
v
,
( 1)v
2
2 2
8 1 4 4 2
1 1
v v v v v
f v
v v
,
0 2f v v
do
1v
Bảngbiếnthiên:
Vậy
min( ) min 4x y u
4
2
0
x y
xy
x y
2 2
2 2
x
y
Câu 57. (Sở Hà Nội - Lần 2 - 2020) Xét
, ,x y z
làcácsốthựclớnhơn1thỏamãnđiềukiện
2xyz
.Giá
trịnhỏnhấtcủabiểuthức
3 3 3
2 2 2
1
log log log
4
S x y z
bằng
A.
1
32
. B.
1
4
. C.
1
16
. D.
1
8
.
Lời giải
Chọn C
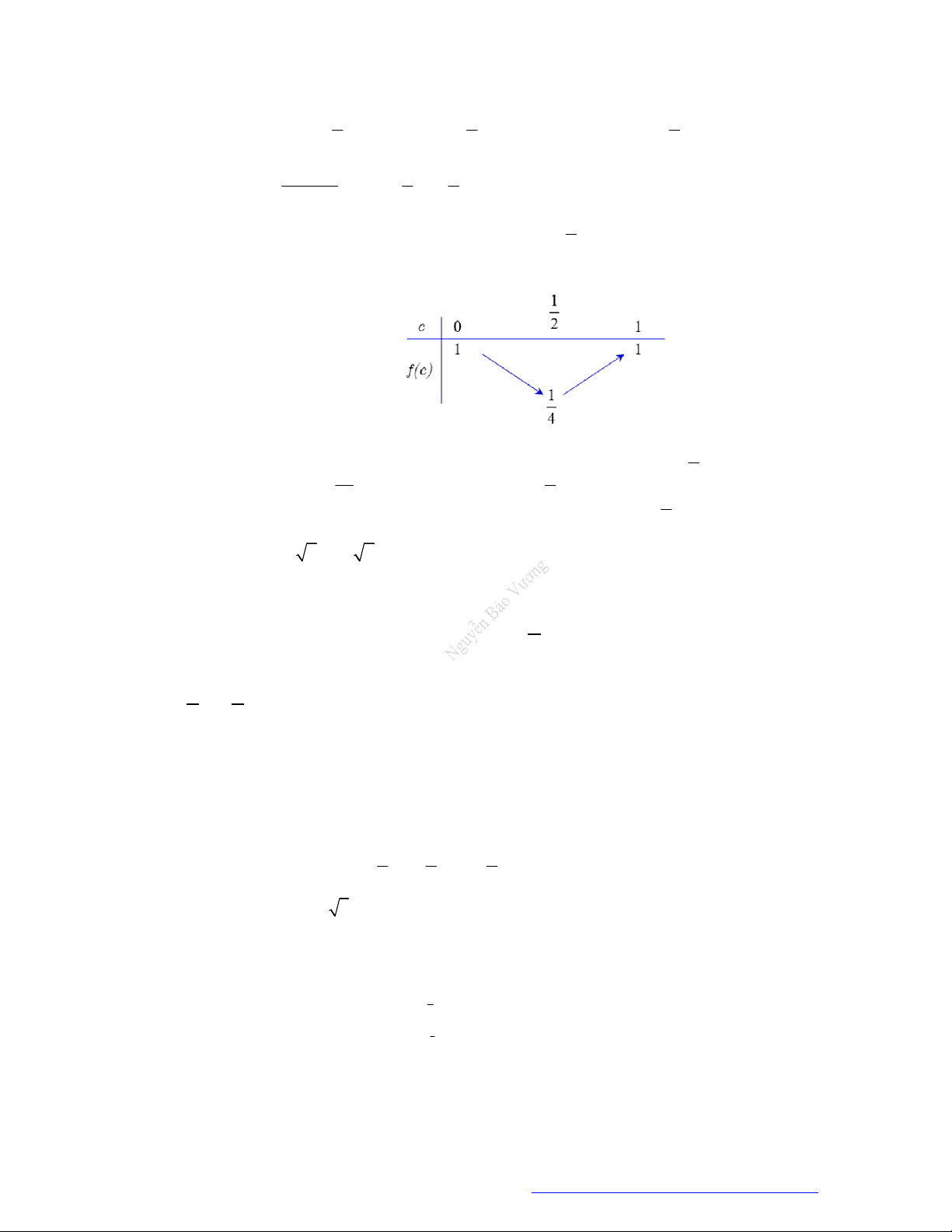
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 65
Tacó
2 2 2 2
log 1 log log log 1xyz x y z
.Đặt
2 2 2
log , log , loga x b y c z .Khiđóta
có
, , 0a b c
và
1a b c
.
3
3 3 3 3 3 3 3
2 2 2
1 1 1
log log log 3 ( )
4 4 4
S x y z a b c a b ab a b c
2
3
3 2
1 1
3 ( ) 3 3 1
4 4 4
a b
a b a b c c c
với
0 1c
.
Đặt
2
( ) 3 3 1f c c c ,
1
( ) 0 6 3 0
2
f c c c
.
Tacóbảngbiếnthiên
Từđâytasuyra
1
16
S
,dấubằngxảyrakhi
1
1
1
4
1
2
2
a b c
a b
c
c
a b
.
Khiđó
4
2, 2x y z
.
Câu 58. Cóbaonhiêusốnguyên
x
saochotồntạisốthực
y
thỏamãn
2 2
3 4
log ( ) log 2x y x y
?
A.
1
B.
3
C.
2
D. Vôsố
Phân tích
Lời giải
Chọn C
Điềukiện:
0x y
.
Đặt
2 2
3 4
log ( ) log 2x y x y t
,suyra
2 2
3
2 4
t
t
x y
x y
2
2
3
3 2 4 1
t
t t
x y
y y
Phươngtrình
1
2
3 2.3 9 4 0
t t t
y y
.Phươngtrìnhphảicónghiệmnên:
2
3 3 1
9 3 9 4 0
2 2 2
t
t t t
t
.
Dođó:
2
2 2
0 3
2
2 2
x y
x
x y
0; 1x
(vì
x
)
Thửlại:
Với
4
9
4
9
2
log 2
log 2
3
0
2 4
3
t
t
t
y
x
y
y
Với
2
1 3 0
1
0
1 2 4
t
t
y t
x
y
y

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 66 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Với
2
3 1
1 2.9 4.3 3 4 0 2
2 1 4
t
t t t
t
y
x
y
Khi
0 9 4
t t
t
nên
2
vônghiệm,khi
0 4 1
t
t
1 4 0
t
nên
2
cũngvônghiệm.
Vậy
0;1
x
.
Câu 59. Có bao nhiêu cặp số nguyên dương
;x y
thỏa mãn đồng thời hai điều kiện:
6
1 10
x
và
2
2 2 2
log 10 20 20 10 2 1
y
x x y x x
?
A.
4
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn D
Điềukiện:
2
10 20 20 0
x x
,đúng
x
.
Ta có
2
2 2 2
log 10 20 20 10 2 1
y
x x y x x
2
2 2 2
2 1 log 10 2 2 10
y
x x x x y
2
2 2 2
2 1 log10 log 2 2 10
y
x x x x y
2
2 2 2
2 2 log 2 2 10
y
x x x x y
2
2
log 2 2
2 2
10 log 2 2 10
x x
y
x x y
(*).
Xéthàm
10
t
f t t
trên
.
Tacó
10 .ln10 1 0
t
f t
,
t
.Dođó
f t
đồngbiếntrên
.
Khi đó
(*)
2 2
log 2 2
f x x f y
2 2
log 2 2
x x y
2
2
2 2 10
y
x x
2
2
1 1 10
y
x
.
Vì
6
1 10
x
nên
2
2
2
6
1 1 1 10 10 1 1
y
x
2
2 6
0 log 10 1 1
y
.
Vì
y
nên
1;2;3
y
.
+Với
1y
2
2 2 10
x x
2
2 8 0
x x
2(ktm)
4(tm)
x
x
.
+Với
2
y
2 4
2 2 10
x x
2
2 9998 0
x x
(khôngcógiátrị
x
nguyênnàothỏamãn).
+Với
3
y
2 9
2 2 10
x x
2
2 999999998 0
x x
(khôngcógiátrị
x
nguyênnàothỏa
mãn).
Vậycómộtcặpnguyêndương
; 4;1
x y
thỏamãnyêucầubàitoán.
Câu 60. Có bao nhiêu số nguyên
10
y
sao cho tồn tại số nguyên
x
thỏa mãn
2
2
2 2 1
5 2 5 1
y
y
x x x
x
?
A.
10
B.
1
C.
5
D. Vôsố
Phân tích
Phươngtrìnhdạng
f u f v
.
Phươngpháp:Chứngminh
y f t
đơnđiệutrên
;a b
.Từphươngtrìnhsuyra
u v
.Từđó
tìmsựliênhệgiữa2biến
,x y
vàchọn
,x y
thíchhợp.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 67
Lời giải
Chọn C
Tacó:
2 2
2
2 2 1 2 2 1 2
5 2 5 1 5 2 1 5
y y
y y
x x x x x x
x x x x
Xét:
1
5
t
f t t
đồngbiếntrên
.Dođótừphươngtrìnhtrênsuyra:
2
2
2 2
2 1 1 2 2 1 2
y y
y y
x x x x x
.
Do
x
nguyênnêntacó
2
2
y
và
10
y
nên
0; 2; 4; 6;8
y
.
Câu 61. Cóbaonhiêucặpsốnguyêndương
;x y
thoảmãn
1 2020
x
và
1
2
2 2 log 2
y y
y x x
A.
2021
. B.
10
. C.
2020
. D.
11
.
Lời giải
Chọn D
Theođềbài,
1
2
2 2 log 2
y y
y x x
2 2
2
2 log 2 2 log
2
y
y y
x x
2 2
2 2
2 2 log 2 2 2 log
2
y
y y y y
x
x
2 2
2 2 2 2
2. 2 log 2 2 log
2 2
y y
y y
x x
1
.
Xéthàmsố
2
2 logf t t t
,
0t
.
Vì
1
2 0
ln 2
f t
t
0
t
f t
đồngbiếntrên
0;
nên
1
2 2 2 2
1 2 2 2.2 2 2 2 2 2
2 2
y y
y y y y y y
x x
f f x x x
.
Do
1 2020
x
nên
2
0 1 log 2020 1 11,98
y y
.
Do
*
y
nên
1;2;3;...;11
y
,vớimỗigiátrị
y
chota1giátrị
x
thoảđề.
Vậycó
11
cặpsốnguyên
;x y
thoảmãnđềbài.
Câu 62. Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
2 2
2 2
3
2log log 1 3 log 1
x y x y
A.
1
B.
3
C.
2
D.
5
Lời giải
Chọn C
Đặt:
2 2
2 2
3
2log log 1 3 log 1
t x y x y
.
Suyra:
2
2
log 1 3
2
2 2
2 2
1 3 .2
2
1 3
1 3
t
t
t
t
x y
x y
x y
x y
Tacó:
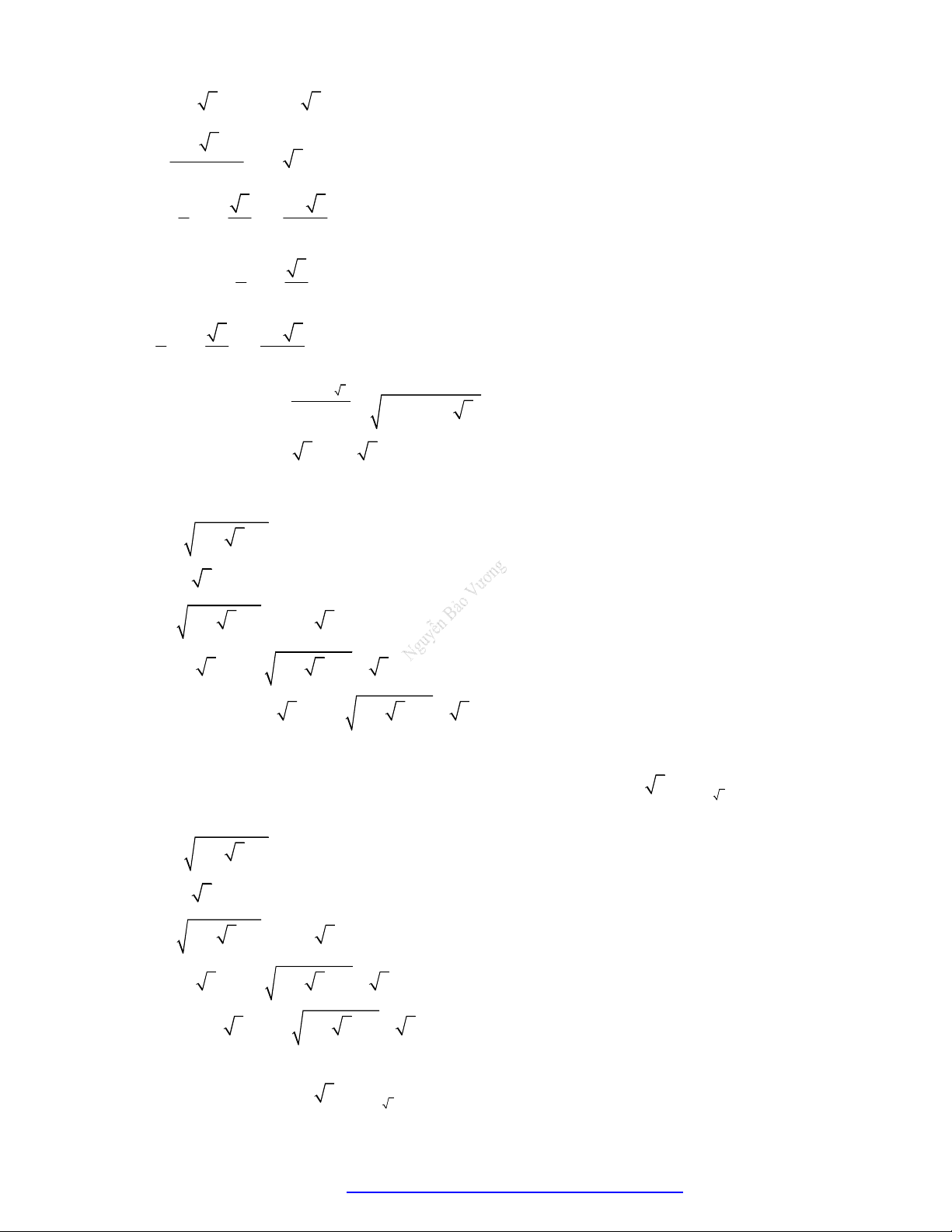
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 68 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2 2
2
1 3 .2 2 1 3
1 3 2
1 3
2
1 3 1 3
2 2 2
t
t
t
t
t
t
x y x y
.
Xét
1 3
2 2
t
t
f t
nghịchbiếntrên
nên
1 3 1 3
1 1
2 2 2
t
t
f t f t
.
Dođó
2
log 1 3
2
2
2 2
0 2 2log 1 3
1 3 1 3
t
t
x y
x y
0; 1
x
(vì
x
)
Thửlại:
Với
1x
:
2
2
1 3 2 1
3
1 3 2 1 3 0
1 3 2 2 1 3 .2 3 1 0
t
t
t
t
t
t t
y
y
Tacó:
1 3 2 2 1 3 .2 3 1
t
t t
g x
liêntụctrên
0;1
thỏamãn
0 1 0
g g
nên
phươngtrìnhcónghiệm
0;1
t
.
Dođóvới
1x
thìtồntạisốthực
y
thỏamãn
2 2
2 2
3
2log log 1 3 log 1
x y x y
Với
1
x
:
2
2
1 3 2 1
3
1 3 2 1 3 0
1 3 2 2 1 3 .2 3 1 0
t
t
t
t
t
t t
y
y
Tacó:
1 3 2 2 1 3 .2 3 1 0, 1
t
t t
t
nênphươngtrìnhvônghiệm.
Dođóvới
1
x
thìkhôngtồntạisốthực
y
thỏamãn
2 2
2 2
3
2log log 1 3 log 1
x y x y
Với
0
x
:

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 69
2
2
1 3 2
1 3
1 3 2 3 1
1 3 2 3 1 0
t
t
t
t
t
t
y
y
Tacó:
1 3 2 3 1
t
t
h x
liêntụctrên
1;0
thỏamãn
1 0 0
h h
nênphươngtrình
cónghiệm
1;0
t
.
Dođóvới
0
x
thìtồntạisốthực
y
thỏamãn
2 2
2 2
3
2log log 1 3 log 1
x y x y
.
Vậy
0;1
x
.
Câu 63. Cóbaonhiêucặpsốnguyên
;x y
thỏamãn
0 2020
y
và
3
2 1
log 1 2 ?
x
x
y
y
A.
2019
. B.
11
. C.
2020
. D.
4
.
Lời giải
Chọn B
Từgiảthiếttacó:
0
2 1
0 2 1 0
0
x
x
y
x
y
y
Tacó:PT
3 3
log 2 1 2 1 log (*)
x x
y y
Xéthàmsố
3
log
f t t t
trên
0;
Khiđó
1
1 0
ln 3
f t
t
dođóhàmsố
3
log
f t t t
đồngbiếntrên
0;
(*)códạng
2 1 2 1
x x
f f y y
Vì
2
0 2020 0 2 1 2020 1 2 2021 0 log 2021
x x
y x
2
0 log 2021
0;1;2;3;4;5;6;7;8;9;10
x
x
x
.Vậycó
11
cặp
;x y
thỏamãn.
Câu 64. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Xét các số thực
, ,a b x
thoả mãn
1, 1, 0 1a b x
và
2
log log ( )
b a
x x
a b
. Tìm giá trị nhỏ nhất của biểu thức
2 2
ln ln ln( ).P a b ab
A.
1 3 3
4
. B.
2
e
. C.
1
4
. D.
3 2 2
12
.
Lời giải
Chọn D
Tacó
2 2
log log ( ) log log ( )
ln ln log .ln 2.log .ln
b a b a
x x x x
b a
a b a b x a x b
2 2
ln
log .ln 2ln .ln 2ln ln 2ln ln 2 ln
ln
b
a
a a b a b a b a b
b
(vì
1, 1
a b
).
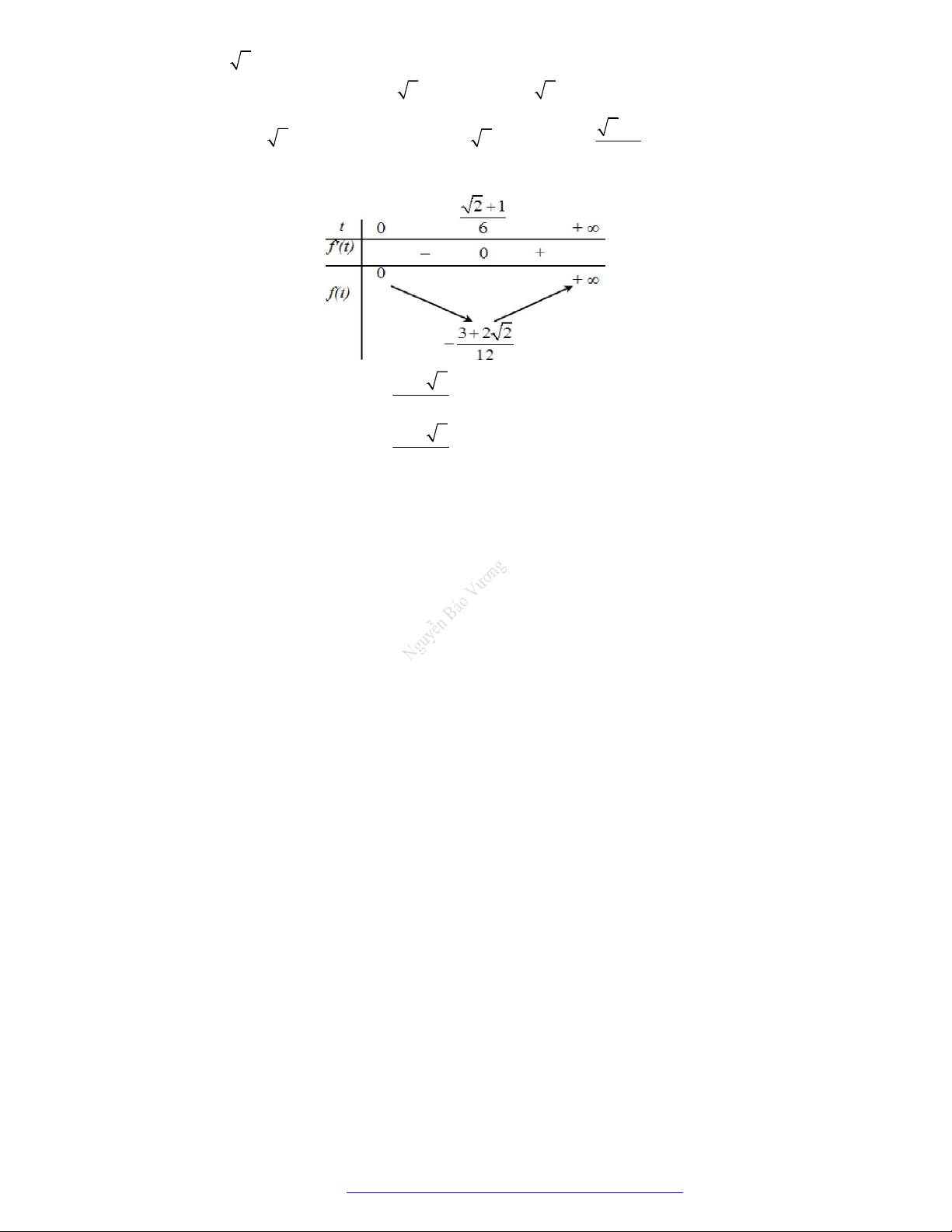
NGUYỄ
N BẢO VƯƠNG - 0946798489
Trang 70 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
T
hay
ln 2 lna b
và
obiểuthức
P
t
ađược
2
2 2 2
l
n ln ln( ) 3ln 2 1 ln 3 2 1P a b ab b b t t (với
l
n 0t b
).
Đặt
2
( ) 3 2 1f t t t .Tacó
2
1
'( ) 6 2 1 0 (0; )
6
f t t t
.
BBT:
DựavàoBBT,suyra
0
;
3
2 2
min ( )
12
f t
.
Vậy
giátrịnhỏnhấtcủa
P
bằ
ng
3
2 2
12
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM
Dạng 1. Phương trình logarit
Phương trình logarit
+ Nếu
0, 1: log
b
a
a a x b x a
+ Nếu
0, 1: log log
a a
a a f x g x f x g x
+ Nếu
0, 1: log
g x
a
a a f x g x f x a
(mũ hóa)
Dạng 1.1 Phương trình cơ bản
Câu 1. (Đề Minh Họa 2020 Lần 1) Nghiệm của phương trình
3
log 2 1 2x
là:
A.
3x
. B.
5x
. C.
9
2
x
. D.
7
2
x
.
Câu 2. (Mã 101 - 2020 Lần 1) Nghiệm của phương trình
3
log 1 2x
là
A.
8x
. B.
9x
. C.
7x
. D.
10x
.
Câu 3. (Mã 102 - 2020 Lần 1) Nghiệm của phương trình là
A. . B. . C. . D. .
Câu 4. (Mã 103 - 2020 Lần 1) Nghiệm của phương trình
2
log 2 3x
là:
A.
6x
. B.
8x
. C.
11x
. D.
10x
.
Câu 5. (Mã 104 - 2020 Lần 1) Nghiệm của phương trình
3
log 2 2x
là
A.
11x
. B.
10x
. C.
7x
. D.
8
.
Câu 6. (Mã 102 - 2020 Lần 2) Nghiệm của phương trình
2
log 9 5x
là
A.
41x
. B.
23x
. C.
1x
. D.
16x
.
Câu 7. (Mã 103 - 2020 Lần 2) Nghiệm của phương trình
2
log 6 5x
là:
A.
4x
. B.
19x
. C.
38x
. D.
26x
.
Câu 8. (Mã 104 - 2020 Lần 2) Nghiệm của phương trình
2
log 7 5x
là
A.
18x
. B.
25x
. C.
39x
. D.
3x
.
Câu 9. (Mã 101 - 2020 Lần 2) Nghiệm của phương trình
2
log ( 8) 5x bằng
A.
17x
. B.
24x
. C.
2x
. D.
40x
.
Câu 10. (Đề Tham Khảo 2019) Tập nghiệm của phương trình
2
2
log 2 1x x
là :
A.
0
B.
0;1
C.
1;0
D.
1
Câu 11. (Đề Minh Họa 2017) Giải phương trình
4
log ( 1) 3. x
A.
65x
B.
80x
C.
82x
D.
63x
Câu 12. (Mã 110 2017) Tìm nghiệm của phương trình
2
log 1 2x
.
A.
5x
. B.
3x
. C.
4x
. D.
3x
.
Câu 13. (Mã 102 2018) Tập nghiệm của phương trình
2
2
log 1 3x
là
A.
10; 10 B.
3;3
C.
3
D.
3
Câu 14. (Mã 104 2017) Tìm nghiệm của phương trình
2
log 5 4x
.
A.
11x
B.
13x
C.
21x
D.
3x
PHƯƠNG TRÌNH MŨ - LOGARIT
Chuyên đề 19
2
log 1 3
x
10
x
8
x
9
x
7
x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 15. (Mã 103 2018) Tập nghiệm của phương trình
2
3
log ( 7) 2x
là
A.
4
B.
4
C.
{ 15; 15}
D.
{ 4;4}
Câu 16. (Mã 105 2017) Tìm nghiệm của phương trình
25
1
log 1
2
x
.
A.
6x
B.
4x
C.
23
2
x
D.
6x
Câu 17. (Chuyên Vĩnh Phúc 2019) Phương trình
3
log 3 2 3x
có nghiệm là
A.
25
3
x
. B.
87x
. C.
29
3
x
. D.
11
3
x
.
Câu 18. (THPT Ba Đình 2019) Tập nghiệm của phương trình là
A. . B. . C. . D. .
Câu 19. (THPT Cù Huy Cận 2019) Tập nghiệm của phương trình
2
3
log 3 1x x
là:
A.
1;0
. B.
0;1
. C.
0
D.
1
.
Câu 20. (Chuyên Vĩnh Phúc 2019) Phương trình
3
log 3 2 3x
có nghiệm là:
A.
25
3
x
B.
87
C.
29
3
x
D.
11
3
x
Câu 21. (Chuyen Phan Bội Châu Nghệ An 2019) Tập nghiệm của phương trình
2
log 2 2 1x x
là
A.
. B.
{ 2;4}
. C.
{4}
. D.
{ 2}
.
Câu 22. (Chuyên Lương Thế Vinh Đồng Nai 2019) Cho phương trình
2
2 2
log (2 1) 2log ( 2).x x
Số
nghiệm thực của phương trình là:
A.
1.
B.
0.
C.
3.
D.
2.
Câu 23. (Chuyên Sơn La 2019) Tập nghiệm của phương trình
2
3
log 2 1x x
là
A.
1; 3
. B.
1;3
. C.
0
. D.
3
.
Câu 24. (THPT Quỳnh Lưu 3 Nghệ An 2019) Tập hợp các số thực
m
để phương trình
2
log x m có
nghiệm thực là
A.
0; .
B.
;0 .
C.
.
D.
0;
Câu 25. (Chuyên Bắc Giang 2019) Tổng bình phương các nghiệm của phương trình
2
1
2
log 5 7 0x x
bằng
A. 6 B. 5 C. 13 D. 7
Câu 26. (THPT-Thang-Long-Ha-Noi- 2019) Tổng các nghiệm của phương trình
2
4 2
log log 3 1x
là
A.
6
B.
5
C.
4
D.
0
Câu 27. (THPT-Thang-Long-Ha-Noi 2019) Tập nghiệm của phương trình
2
0,25
log 3 1x x
là:
A.
4
. B.
1; 4
. C.
3 2 2 3 2 2
;
2 2
. D.
1;4
.
Câu 28. (THPT Yên Phong 1 Bắc Ninh 2019) Nghiệm nhỏ nhất của phương trình
2
5
log 3 5 1x x
là
A.
3
. B.
a
. C.
3
. D.
0
.
Câu 29. (Sở Hà Nội 2019) Số nghiệm dương của phương trình
2
ln 5 0x
là
2
3
log 3 1
x x
1
0;1
1;0
0
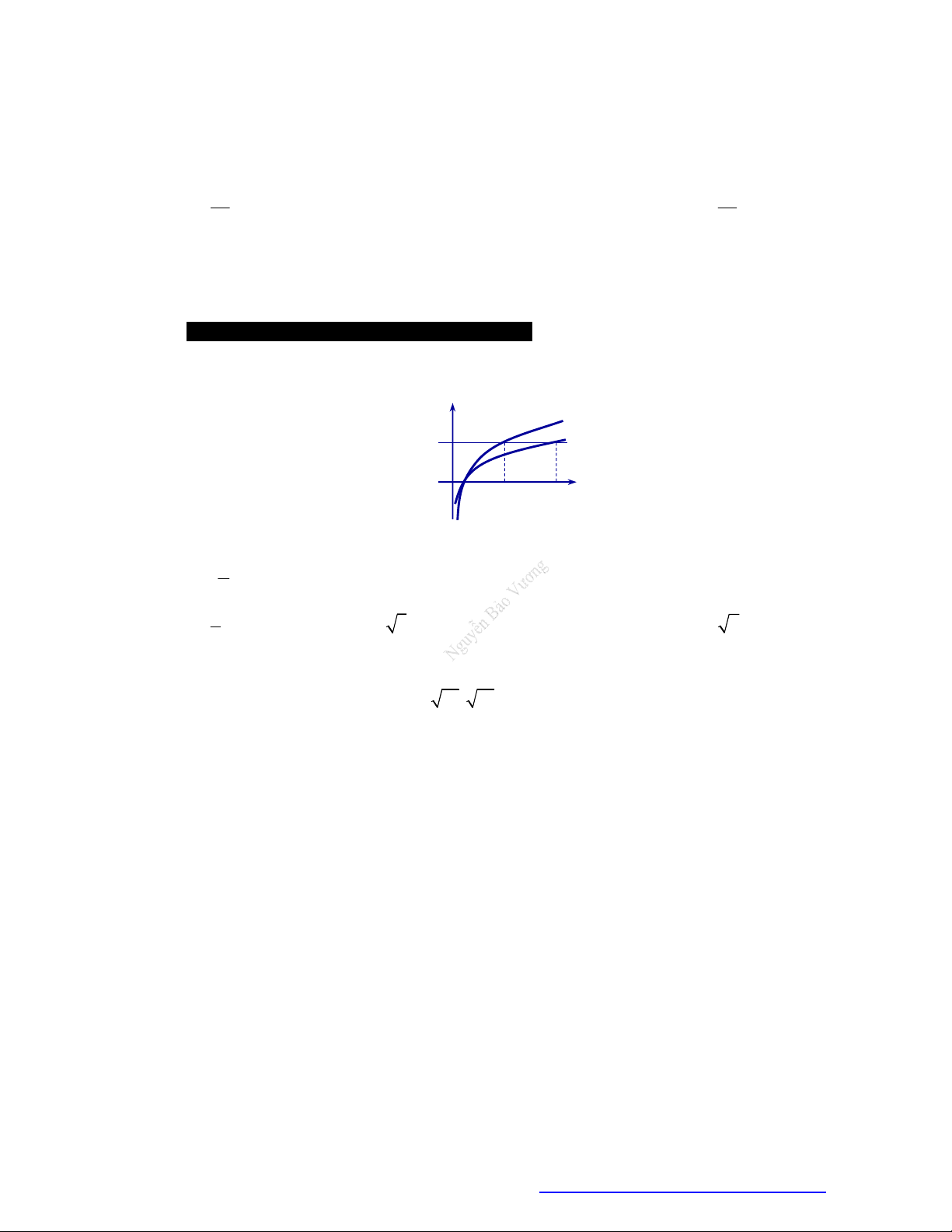
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
2
. B.
4
. C.
0
. D.
1
.
Câu 30. (Chuyên Hạ Long 2019) Số nghiệm của phương trình
2
2
( 3)log (5 ) 0
x x
.
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 31. (THPT Yên Khánh - Ninh Bình - 2019) Tổng tất cả các nghiệm của phương trình
2
2 5 2 log 7 6 2 0
x
x x x
bằng
A.
17
2
. B.
9
. C.
8
. D.
19
2
.
Câu 32. (Chuyên ĐHSP Hà Nội 2019) Tập hợp các số thực
m
để phương trình
2
log
x m
có nghiệm
thực là
A.
0;
. B.
0;
. C.
;0
. D.
.
Dạng 1.2 Biến đổi đưa về phương trình cơ bản
Câu 1. (Mã 103 - 2020 Lần 2) Hàm số
log
a
y x
và
log
b
y x
có đồ thị như hình bên.
Đường thẳng
3
y
cắt hai đồ thị tại các điểm có hoành độ là
1 2
;x x
. Biết rằng
1 2
2x x
. Giá trị
của
a
b
bằng
A.
1
3
. B.
3
. C.
2
. D.
3
2
.
Câu 2. (Đề Tham Khảo 2017) Tìm tập nghiệm
S
của phương trình
2 2
log 1 log 1 3
x x
.
A.
3
S
B.
10; 10
S
C.
3;3
S
D.
4
S
Câu 3. (Mã 103 - 2019) Nghiệm của phương trình
2 2
log 1 1 log 3 1
x x
là
A.
1x
. B.
2
x
. C.
1
x
. D.
3
x
.
Câu 4. (Mã 105 2017) Tìm tập nghiệm
S
của phương trình
3 3
log 2 1 log 1 1
x x
.
A.
3
S
B.
4
S
C.
1
S
D.
2
S
Câu 5. (Mã 101 - 2019) Nghiệm của phương trình
3 3
log 1 1 log 4 1
x x
A.
4
x
. B.
2
x
. C.
3
x
. D.
3
x
.
Câu 6. (Mã 104 - 2019) Nghiệm của phương trình
3 3
log 2 1 1 log 1
x x
là
A.
4
x
. B.
2
x
. C.
1x
. D.
2
x
.
Câu 7. (Mã 102 -2019) Nghiệm của phương trình
2 2
log 1 1 log 1
x x
là
A.
3
x
. B.
2
x
. C.
1x
. D.
2
x
.
Câu 8. (THPT Lê Quy Đôn Điện Biên 2019) Số nghiệm của phương trình
ln 1 ln 3 ln 7
x x x
là
A. 1. B. 0. C. 2. D. 3.
Câu 9. Tìm số nghiệm của phương trình
2 2
log log ( 1) 2
x x
A. 0. B. 1. C. 3. D. 2.
x
y
3
O
1
x
2
x
log
b
y x
log
a
y x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 10. (HSG Bắc Ninh 2019) Số nghiệm của phương trình
3 3
log 6 log 9 5 0
x x
.
A.
0
B.
2
C.
1
D.
3
Câu 11. (THPT Đoàn Thượng - Hải Dương - 2019) Tìm tập nghiệm
S
của phương trình:
3 3
log 2 1 log 1 1
x x
.
A.
3
S
. B.
1
S
. C.
2
S
. D.
4
S
.
Câu 12. (Sở Bắc Giang 2019) Phương trình
2 2
log log 1 1
x x
có tập nghiệm là
A.
1;3
S
. B.
1;3
S
. C.
2
S
. D.
1
S
.
Câu 13. (THPT Gang Thép Thái Nguyên 2019) Tổng các nghiệm của phương trình
2 2 5
log ( 1) log ( 2) log 125
x x
là
A.
3 33
2
. B.
3 33
2
. C. 3. D.
33
.
Câu 14. (THPT Ngô Sĩ Liên Bắc Giang 2019) Tập nghiệm của phương trình
2 2
log log ( 3) 2
x x là
A.
4
S
B.
1,4
S
C.
1
S
D.
4,5
S
Câu 15. (Chuyên Thái Nguyên 2019) Số nghiệm của phương trình
3 3 3
log log 6 log 7
x x
là
A.
0
B.
2
C.
1
D.
3
Câu 16. (Chuyên Sơn La 2019) Cho
0;
2
x
, biết rằng
2 2
log sin log cos 2
x x
và
2 2
1
log sin cos log 1
2
x x n
. Giá trị của
n
bằng
A.
1
4
. B.
5
2
. C.
1
2
. D.
3
4
.
Câu 17. (Mã 110 2017) Tìm tập nghiệm
S
của phương trình
1
2
2
log 1 log 1 1.
x x
A.
3
S
B.
2 5;2 5
S
C.
2 5
S
D.
3 13
2
S
Câu 18. (THPT Hàm Rồng Thanh Hóa 2019) Số nghiệm của phương trình
2
3 1
3
log 4 log 2 3 0
x x x
là
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 19. (Đề Tham Khảo 2018) Tổng giá trị tất cả các nghiệm của phương trình
3 9 27 81
2
log .log .log .log
3
x x x x
bằng
A.
0.
B.
80
.
9
C.
9.
D.
82
.
9
Câu 20. (VTED 2019) Nghiệm của phương trình
2 4 1
2
log log log 3
x x
là
A.
3
1
3
x
. B.
3
3
x
. C.
1
3
x
. D.
1
3
x
.
Câu 21. (THPT Lê Quý Dôn Dà Nẵng -2019) Gọi S là tập nghiệm của phương
trình
2
2
2
log 1 log 2 1
x x
. Số phần tử của tập S là
A. 2 B. 3 C. 1 D. 0

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 22. (Chuyên Lam Sơn Thanh Hóa 2019) Số nghiệm thục của phương trình
3
3 1
3
3log 1 log 5 3x x
là
A.
3
B.
1
C.
2
D.
0
Câu 23. (Chuyên Lê Hồng Phong Nam Định 2019) Tổng các nghiệm của phương trình
2
3
3
log 2 log 4 0x x
là
2S a b
(với
,a b
là các số nguyên). Giá trị của biểu thức
.Q a b
bằng
A. 0. B. 3. C. 9. D. 6.
Dạng 2. Phương trình mũ
Phương pháp đưa về cùng cơ số.
Phương trình mũ
+ Nếu
0, 1a a
thì
f x g x
a a f x g x
+ Nếu a chứa ẩn thì
1
1 0
f x g x
a
a a a f x g x
f x g x
+
log log log .
f x g x f x g x
a a a
a b a b f x b g x (logarit hóa).
Dạng 2.1 Phương trình cơ bản
Câu 1. (Đề Tham Khảo 2020 Lần 2) Nghiệm của phương trình
1
3 27
x
là
A.
4x
. B.
3x
. C.
2x
. D.
1x
.
Câu 2. (Mã 101 - 2020 Lần 1) Nghiệm của phương trình
1
3 9
x
là:
A.
2x
. B.
3x
. C.
2x
. D.
3x
.
Câu 3. (Mã 102 - 2020 Lần 1) Nghiệm của phương trình là
A. . B. . C. . D. .
Câu 4. (Mã 103 - 2020 Lần 1) Nghiệm của phương trình
1
3 9
x
là
A.
1x
. B.
2x
. C.
2x
. D.
1x
.
Câu 5. (Mã 104 - 2020 Lần 1) Nghiệm của phương trình
2
3 27
x
là
A.
2x
. B.
1x
. C.
2x
. D.
1x
.
Câu 6. (Mã 102 - 2020 Lần 2) Nghiệm của phương trình
2 4
2 2
x x
là
A.
16x
. B.
16x
. C.
4x
. D.
4x
.
Câu 7. (Mã 101 - 2020 Lần 2) Nghiệm của phương trình
2 3
2 2
x x
là
A.
8x
. B.
8x
. C.
3x
. D.
3x
.
Câu 8. (Mã 104 - 2020 Lần 2) Nghiệm của phương trình
2 2
2 2
x x
là
A.
2x
. B.
2x
. C.
4x
. D.
4x
.
Câu 9. (Mã 101 - 2019) Nghiệm của phương trình:
2 1
3 27
x
là
A.
1x
. B.
2x
. C.
4x
. D.
5x
.
Câu 10. (Mã 102 - 2019) Nghiệm của phương trình
2 1
3 27
x
là
A.
5
. B.
4
. C.
2
. D.
1
.
Câu 11. Tìm nghiệm của phương trình
1
3 27
x
A.
10x
B.
9x
C.
3x
D.
4x
Câu 12. (Mã 104 2018) Phương trình
2 1
5 125
x
có nghiệm là
A.
5
2
x
B.
1x
C.
3x
D.
3
2
x
2
3 9
x
3
x
3
x
4
x
4
x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 13. (Mã 101 2018) Phương trình
2 1
2 32
x
có nghiệm là
A.
3x
B.
5
2
x
C.
2x
D.
3
2
x
Câu 14. (Mã 104 - 2019) Nghiệm của phương trình
2 1
2 32
x
là
A.
2x
. B.
17
2
x
. C.
5
2
x
. D.
3x
.
Câu 15. (Mã 103 - 2019) Nghiệm của phương trình
2 1
2 8
x
là
A.
2x
. B.
5
2
x
. C.
1x
. D.
3
2
x
.
Câu 16. (Mã 104 2017) Tìm tất cả các giá trị thực của
m
để phương trình
3
x
m
có nghiệm thực.
A.
1m
B.
0m
C.
0m
D.
0m
Câu 17. (THPT An Lão Hải Phòng 2019) Tìm tập nghiệm
S
của phương trình
2
2
5 5
x x
.
A.
S
B.
1
0;
2
S
C.
0;2S
D.
1
1;
2
S
Câu 18. (Chuyên Bắc Ninh 2019) Tìm tập nghiệm
S
của phương trình
1
2 8
x
.
A.
4S
. B.
1S
. C.
3 .S
D.
2S
.
Câu 19. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Phương trình
2
4 6
2
5 log 128
x x
có bao nhiêu
nghiệm?
A.
1
B.
3
C.
2
D.
0
Câu 20. (THPT - Yên Định Thanh Hóa 2019) Tập nghiệm
S
của phương trình
2
2
3 27
x x
.
A.
1;3S
. B.
3;1S
. C.
3; 1S
. D.
1;3S
.
Câu 21. (THPT Quỳnh Lưu 3 Nghệ An 2019) Số nghiệm thực phân biệt của phương trình
2
e 3
x
là:
A. 1. B. 0. C. 3. D. 2.
Câu 22. (Sở Ninh Bình 2019) Phương trình
2
5 1 0
x
có tập nghiệm là
A.
3S
. B.
2S
. C.
0S
. D.
2S
.
Câu 23. (THCS - THPT Nguyễn Khuyến 2019) Họ nghiệm của phương trình
2
cos
4 1 0
x
là
A.
;k k
. B.
;
2
k k
. C.
2 ;k k
. D.
;
3
k k
.
Câu 24. (Chuyên Lê Thánh Tông 2019) Cho biết
2
9 12 0
x
, tính giá trị của biểu thức
1
2
1
1
8.9 19
3
x
x
P
.
A.
31
. B.
23
. C.
22
. D.
15
.
Câu 25. (Chuyên Bắc Ninh 2019) Tính tổng tất cả các nghiệm của phương trình
2
2 5 4
2 4
x x
A.
5
2
. B.
1
. C.
1
. D.
5
2
.
Câu 26. Tìm tất cả các giá trị thực của tham số
m
để phương trình
2 1 2
3 2 3 0
x
m m
có nghiệm.
A.
3
1;
2
m
. B.
1
;
2
m
. C.
0;m
. D.
3
1;
2
m
.
Câu 27. Cho a, b là hai số thực khác 0, biết: . Tỉ số là:
2
2
4
3 8
3
1
625
125
a ab
a ab
a
b

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
A. B. C. D.
Câu 28. Tổng các nghiệm của phương trình
2
2 1
2 8
x x
bằng
A.
0
. B.
2
. C.
2
. D.
1
.
Câu 29. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Phương trình
2
2 5 4
2 4
x x
có tổng tất cả các
nghiệm bằng
A. 1. B.
5
2
. C.
1
. D.
5
2
.
Câu 30. (THPT Ngô Sĩ Liên Bắc Giang 2019) Phương trình
2
2 5 4
5 25
x x
có tổng tất cả các nghiệm
bằng
A.
1
B.
5
2
C.
1
D.
5
2
Câu 31. (Sở Bắc Ninh 2019) Phương trình
2
2 5 4
7 49
x x
có tổng tất cả các nghiệm bằng
A.
5
2
. B.
1
. C.
1
. D.
5
2
.
Dạng 2.2 Biến đổi đưa về phương trình cơ bản
Câu 1. Tập nghiệm của phương trình:
1 1
4 4 272
x x
là
A.
3;2
. B.
2
. C.
3
. D.
3;5
.
Câu 2. (HKI-NK HCM-2019) Phương trình
2
2
2 3
1
27
3
x
x
có tập nghiệm là
A.
1;7
. B.
1; 7
. C.
1;7
. D.
1; 7
.
Câu 3. (THPT Quỳnh Lưu- Nghệ An- 2019) Phương trình
1
3 .2 72
x x
có nghiệm là
A.
5
2
x
. B.
2x
. C.
3
2
x
. D.
3x
.
Câu 4. (Chuyên Bắc Giang 2019) Nghiệm của phương trình
2
2 3
1
1
5
5
x x
x
là
A.
1; 2.x x
B.
1; 2.x x
C.
1; 2.x x
D. Vô nghiệm.
Câu 5. Tập nghiệm của phương trình
2
2 3
1
1
7
7
x x
x
là
A.
1
. B.
1;2
. C.
1;4
. D.
2
.
Câu 6. Tổng các nghiệm của phương trình
2
2 2
2 8
x x x
bằng
A.
6
. B.
5
. C.
5
. D.
6
.
Câu 7. (SGD Điện Biên - 2019) Gọi
1 2
, x x là hai nghiệm của phương trình
2
2 3
1
1
7
7
x x
x
. Khi đó
2 2
1 2
x x
bằng:
A.
17
. B.
1
. C.
5
. D.
3
.
Câu 8. Tổng bình phương các nghiệm của phương trình
2
3 2
1
5
5
x
x
bằng
A.
2
. B.
5
. C.
0
. D.
3
.
Câu 9. Nghiệm của phương trình
7 1 2 1
2 8
x x
là
A.
2.x
B.
3.x
C.
2.x
D.
1.x
8
7
1
7
4
7
4
21

NGUYỄN BẢO VƯƠNG - 0946798489
Câu 10.
(THPT Lương Văn Tụy - Ninh Bình - 2018) Giải phương trình
1
5 7
2
2,
5
5
x
x
.
A.
1x
. B.
1x
. C.
1x
. D.
2
x
.
Câu 11.
(THPT Nguyễn Thị Minh Khai - Hà Tĩnh - 2018) Phương trình
2
3 1
4
1
3
9
x
x
có
hai nghiệm
1
x
,
2
x
.
Tính
1 2
x x
.
A.
6
. B.
5
. C.
6
. D.
2
.
Câu 12.
(Sở Quảng Nam - 2018) Tổng các nghiệm của phương trình
2
2 2
2 8
x x
x
bằng
A.
5
. B.
5
. C.
6
. D.
6
.
Câu 13.
(THPT Thăng Long - Hà Nội - 2018) Tập nghiệm của phương trình
2
1
4
2
x
x x
là
A.
2
0;
3
. B.
1
0;
2
. C.
0;
2
. D.
3
0;
2
.
Câu 14.
(THPT Hải An - Hải Phòng - 2018) Tìm nghiệm của phương trình
2 1
7 4
3 2 3
x
.
A.
1
4
x
. B.
7 4
3
1 log 2 3
x
.
C.
3
4
x
. D.
25 15
3
2
x
.
Câu 15.
(THPT Kim Liên - Hà Nội - 2018) Tính tổng
1 2
S x
x
biết
1
x
,
2
x
là
các giá trị thực thỏa mãn
đẳng thức
2
3
6 1
1
2
4
x
x x
.
A.
5
S
. B.
8
S
. C.
4
S
. D.
2
S
.
Câu 16. (Chuyên Hùng Vương - Bình Dương - 2018) Tập nghiệm S của phương trình
3 1
4 7
16
0
7 4 49
x x
là
A.
1
2
S
B.
2
S
C.
1 1
;
2 2
S
D.
1
;2
2
S
Câu 17. (THPT Nguyễn Thị Minh Khai - Hà Nội - 2018) Tích các nghiệm của phương trình
1
1
1
5 2
5 2
x
x
x
là
A
.
2
. B.
4
. C.
4
. D.
2
.
Câu 18.
(THCS&THPT Nguyễn Khuyến - Bình Dương - 2018) Giải phương trình
2 3
4
4 8
x x
.
A.
6
7
x
. B.
2
3
x
. C.
2
x
. D.
4
5
x
.
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/

T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ + GIỎI MỨC 7-8-9-10 ĐIỂM
DẠNG 1. PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH LOGARIT
Dạng 1.1
Phương pháp đưa về cùng cơ số
+ Nếu
0
, 1: log
b
a
a
a x b x a
1
+ Nếu
0
, 1: log log
a a
a
a f x g x f x g x
2
+ Nếu
0
, 1: log
g
x
a
a
a f x g x f x a
(mũ hóa)
3
Các
bước giải phương trình & bất phương trình mũ – logarit
Bước 1.Đặtđiều
kiện(điềukiệnđạisố
điều
kiệnloga),tacầnchúý:
Đ
0
1
log
0
a
K
a
b
b
và
Đ
Đ
log 0
log 0
K
a
K
a
f x f x
f x f x
.
Bước 2.Dùng
cáccôngthứcvàbiếnđổiđưavềcáccơbảntrên,rồigiải.
Bước 3.S
ovớiđiềukiệnvàkếtluậnnghiệm.
Câu 1. (Mã1102017)Tìmtậpnghiệm
S
của
phươngtrình
1
2
2
l
og 1 log 1 1.x x
A.
3S
B.
2
5;2 5S
C.
2
5S
D.
3
13
2
S
Câu
2. (THPT Hàm Rồng Thanh Hóa 2019) Số nghiệm của phương trình
2
3
1
3
l
og 4 log 2 3 0x x x
là
A.
2
. B.
3
. C.
0
. D.
1
.
Câu
3. (Đề Tham Khảo 2018) Tổng giá trị tất cả các nghiệm của phương trình
3 9 27 81
2
lo
g .log .log .log
3
x x x x
bằng
A.
0.
B.
8
0
.
9
C.
9.
D.
8
2
.
9
Câu
4. Nghiệmcủaphươngtrình
2
4 1
2
l
og log log 3x x
l
à
A.
3
1
3
x
. B.
3
3x
. C.
1
3
x
. D.
1
3
x
.
Câu
5. (THPT Lê Quý Dôn Dà Nẵng 2019) Gọi S là tập nghiệm của phương
trình
2
2
2
log 1 log 2 1x x
.
SốphầntửcủatậpSlà
A. 2 B. 3 C. 1 D. 0
Câu 6. (Chuyên Lam Sơn Thanh Hóa 2019) Số nghiệm thục của phương trình
3
3
1
3
3
log 1 log 5 3x x
là
A.
3
B.
1
C.
2
D.
0
PHƯƠNG
PHÁP GIẢI PHƯƠNG TRÌNH MŨ - LOGARIT
Ch
uyên đề 19
mũlẻ
mũchẵn

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 7. (Chuyên Lê Hồng Phong Nam Định 2019) Tổng các nghiệm của phương trình
2
3
3
log 2 log 4 0
x x
là
2S a b
(với
,a b
làcácsốnguyên).Giátrịcủabiểuthức
.Q a b
bằng
A. 0. B. 3. C. 9. D. 6.
Câu 8. (Chuyên Nguyễn Du-ĐăkLăk 2019) Tổng tất cả các nghiệm của phương trình
2 2
log 1 log 1x x
là
A.
1
. B.
1
. C.
2
. D.
2
.
Câu 9. Tổngtấtcảcácnghiệmthựccủaphươngtrình
2
1
log 4 1 log8 log 4
2
x x x x
bằng
A.
4
. B.
3
. C.
5
. D.
1
.
Câu 10. Gọi
S
làtậpnghiệmcủaphươngtrình
2
2 2
2log 2 2 log 3 2
x x
trên
.Tổngcácphầntử
của
S
bằng
A.
6 2
. B.
8 2
. C.
8
. D.
4 2
.
Câu 11. (SGD Nam Định 2019) Tổng tất cả các nghiệm của phương trình
4
2
3 1 1
3 81
1
log 5 6 log 2 log 3
2
x x x x
bằng
A.
10.
B.
3 10.
C. 0. D. 3.
Câu 12. (SGDGiaLai2019)Chohaisốthựcdương
x
,
y
thỏamãn
2 2
2 2
log 1 log
x y xy
.Mệnh
đềnàodướiđâyđúng?
A.
x y
. B.
x y
. C.
x y
. D.
2
x y
.
Câu 13. Biếtphươngtrình
2
2 4
log 5 1 log 9
x x
cóhainghiệmthực
1
x
,
2
x
.Tích
1 2
.x x
bằng:
A.
8
. B.
2
. C.
1
. D.
5
.
Câu 14. (ChuyênLongAn-2019)Tìmnghiệmphươngtrình
4 2
2log log 3 2
x x
.
A.
4
x
. B.
1x
. C.
3
x
. D.
16
x
.
Câu 15. (Chuyên-KHTN-HàNội-2019)Sốnghiệmcủaphươngtrình
2
3
3
log 1 log 2 1 2
x x
là
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 16. (SởQuảngTrị 2019)Sốnghiệmcủaphươngtrình
2
3 1
3
log 4 log 2 3 0
x x x
là
A.
2
. B.
0
. C.
3
. D.
1
.
Câu 17. Biếtnghiệmlớnnhấtcủaphươngtrình
1
2
2
log log 2 1 1
x x
là
2x a b
(
,a b
làhaisố
nguyên).Giátrịcủa
2a b
bằng
A.
4
. B.
6
. C.
0
. D.
1
.
Câu 18. Tínhtổngtấtcảcácnghiệmthựccủaphươngtrình
2
3
3
log 2 log 4 0
x x
.
A.
6 2
. B.
6
. C.
3 2
. D.
9
.
Câu 19. Gọi
S
làtổngtấtcảcácnghiệmcủaphươngtrình
2
1
log log 10 2 log4
2
x x
.Tính
S
?
A.
10
S
. B.
15
S
. C.
10 5 2
S
. D.
8 5 2
S
.
Câu 20. Cho phương trình
2 3
4 8
2
log 1 2 log 4 log 4
x x x
. Tổng các nghiệm của phương
trìnhtrênlà

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
4
2 6
. B.
4
. C.
4
2 6
. D.
2
2 3
.
Câu 21. Cho
2
8
4
l
og log 5
x
y
và
2
8
4
l
og log 7
y
x
.
Tìmgiátrịcủabiểuthức
P
x y
.
A.
5
6
P
. B.
1
6
P
. C.
8
P
. D.
6
4
P
.
Câu 22. Cho
, , 0; và , 1
a b x a b b x
thỏa
mãn
2
2 1
l
og log
3 log
x
x
b
a b
a
x
.
Khi
đóbiểuthức
2
2
2
2 3
( 2 )
a ab b
P
a b
c
ógiátrịbằng:
A.
5
4
P
. B.
2
3
P
. C.
1
6
15
P
. D.
4
5
P
.
Câu 23. Cho
0
;
2
x
,
biết rằng
2
2
l
og sin log cos 2
x
x
và
2 2
1
l
og sin cos log 1
2
x
x n
.
Giátrịcủa
n
bằng
A.
1
4
. B.
5
2
. C.
1
2
. D.
3
4
.
Câu 24. (Ki
mLiên-HàNội-2018)Biếtrằngphươngtrình
2ln 2 ln 4 ln 4ln 3
x x
cóh
ainghiệm
phânbiệt
1
x
,
2
x
1
2
x
x
.Tính
1
2
x
P
x
.
A.
1
4
. B.
6
4
. C.
1
6
4
. D.
4
.
Câu 25. (THP
T Lê Xoay - 2018) Phương trình
2
2
49
7 7
3
1
log log 1 log log 3
2
x x
có
bao nhiêu
nghiệm?
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 26. (THP
T Lương Văn Tụy - Ninh Bình - 2018) Phương trình
2
3
4
8
2
log 1 2 log 4 log 4
x x x
c
óbaonhiêunghiệm?
A. Vônghiệm. B. Mộtnghiệm. C. Hainghiệm. D. Banghiệm.
Câu 27. (SGD&ĐT BRVT - 2018) Tổng giá trị tất cả các nghiệm của phương t
rình
2
2 4 1
2
l
og 2 log 5 log 8 0
x
x
bằng
A.
6
. B.
3
. C.
9
. D.
1
2
.
Câu 28. (X
uân Trường - Nam Định - 2018) Cho phương trình
2
2 2
2 3 6
l
og 1 .log 1 log 1
x
x x x x x
.
Biếtphươngtrìnhcómộtnghiệmlà
1
và
mộtnghiệmcònlạicódạng
l
og log
1
2
b
b
c
c
x a a
(với
a
,
c
là
cácsốnguyêntốvà
a
c
).
Khi
đógiátrịcủa
2
2
3a b c
bằng:
A.
0
. B.
3
. C.
6
. D.
4
.
Dạng 1.2 Phương phá
p đặt ẩn phụ
L
oại1.
l
og 0
PP
a
P
f x
đặ
t
l
og
a
t
f x
.
L
oại2.Sửdụngcôngthức
lo
g log
b
b
c
a
a
c
để
đặt
lo
g log
b
b
x
a
t
a t x
.
Câu 29. P
hươngtrình
2
5
log 2 log
2
x
x
cóhai
nghiệ
m
1
2 1 2
,
x
x x x
.
Khiđótổng
2
1 2
x x
bằng

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
9
2
. B.
3
. C.
6
. D.
9
4
.
Câu 30. (SGDGiaLai2019)Sốnghiệmcủaphươngtrình
2 2
2 2
log 8log 4 0
x x
là:
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 31. Tíchtấtcảcácnghiệmcủaphươngtrình
2
3 3
log 2log 7 0
x x
là
A.
9
. B.
7
. C.
1
. D.
2
.
Câu 32. (YênDũng2-BắcGiang 2019)Tổngcácnghiệmcủaphươngtrình
2
2 2 3
log log 9.log 3
x x
là
A.
2
. B.
17
2
. C.
8
. D.
2
.
Câu 33. (THPTHaiBàTrưng-Huế-2019)Biếtphươngtrình
2
2 2
log 2 5log 0
x x
cóhainghiệm
phânbiệt
1
x
và
2
x
.Tính
1 2
.x x
.
A.
8
. B.
5
. C.
3
. D.
1
.
Câu 34. (Chuyên Đại học Vinh - 2019) Biết rằng phương trình
2
2 2
log 7 log 9 0
x x
có 2 nghiệm
1 2
,x x
.Giátrịcủa
1 2
x x
bằng
A.
128
. B.
64
. C.
9
. D.
512
.
Câu 35. (Hội8trườngchuyênĐBSH-2019)Chophươngtrình
2
2
2
log 4 log 2 5
x x
.Nghiệmnhỏ
nhấtcủaphươngtrìnhthuộckhoảng
A.
0;1
. B.
3;5
. C.
5;9
. D.
1;3
.
Câu 36. Gọi
T
làtổngcácnghiệmcủaphươngtrình
2
1 3
3
log 5log 4 0
x x
.Tính
T
.
A.
4L
. B.
5
T
. C.
84
T
. D.
5
T
.
Câu 37. (NgôQuyền-HảiPhòng2019)Phươngtrình
2
2 2
log 5log 4 0
x x
cóhainghiệm
1 2
,x x
.Tính
tích
1 2
.x x
.
A.
32
. B.
36
. C.
8
. D.
16
.
Câu 38. (ChuyênĐHVinh 2019)Chocácsốthựca,bthỏamã
1
a b
và
2
log log 3
a b
b a
.Tínhgiá
trịcủabiểuthức
2
log
2
ab
a b
T
.
A.
1
6
. B.
3
2
. C.
6
. D.
2
3
.
Câu 39. Biếtrằngphươngtrình
2
2 2
log log 2018 2019 0
x x
cóhainghiệmthực
1 2
,x x
.Tích
1 2
.x x
bằng
A.
2
log 2018
. B.
0,5
. C.
1
. D.
2
.
Câu 40. Chophươngtrình
2 2 2
3 3
log 3 log 1 0.
x x
Biếtphươngtrìnhcó2nghiệm,tínhtích
P
củahai
nghiệmđó.
A.
9.
P
B.
2
.
3
P
C.
3
9.
P D.
1.
P
Câu 41. (THPT Ba Đình 2019) Biết rằng phương trình
4
2
3 3
x
log x log
3
có hainghiệm
a
và
b
. Khi
đó
ab
bằng
A.
8
. B.
81
. C.
9
. D.
64
.
Câu 42. (Chuyên Quốc Học Huế -2019) Gọi
T
là tổng các nghiệm của phương trình
2
1 3
3
log 5log 4 0
x x
.Tính
T
.
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
4T
B.
4T
C.
84
T
D.
5
T
Câu 43. (Cụm8Trườn
gChuyên2019)Chophươngtrình
2
2
2
log 4 log 2 5
x x
.
Nghiệmnhỏnhất
củaphươngtrìnhthuộckhoảngnàosauđây?
A.
1
; 3
. B.
5
; 9
. C.
0
;1
. D.
3
; 5
.
Câu 44. (THP
T Lương Thế Vinh Hà Nội 2019) Tích tất cả các nghiệm của phương trình
2
3
3
l
og 2log 7 0
x
x
là
A.
9
. B.
7
. C.
1
. D.
2
.
Câu 45. (C
huyên Hùng Vương Gia Lai 2019) Cho 2 số thực dương
a
và
b
t
hỏa mãn
4
9
3
l
og log 8
a
b
và
3
3
3
log log 9
a b
.Giátrịbiểuthức
1P
ab
bằng
A.
8
2
. B.
2
7
. C.
2
43
. D.
2
44
.
Câu 46. (C
huyênĐạiHọcVinh2019)Biếtphươngtrình
2
2
2
l
og 7 log 9 0
x
x
cóhainghiệm
1 2
,x x
.
Giátrị
1
2
.x
x
bằng
A.
12
8
B.
6
4
C.
9
D.
51
2
Câu 47. (Mã104 2017)X
étcácsốnguyêndương
a
,
b
sao
chophươngtrình
2
l
n ln 5 0
a
x b x
c
ó
hainghiệmphânbiệt
1
x
,
2
x
vàphươngtrình
2
5
log log 0
x
b x a
cóhainghiệmphânbiệt
3
x
,
4
x
t
hỏamãn
1
2 3 4
x
x x x
.T
ínhgiátrịnhỏnhất
min
S
của
2
3S a b
.
A.
min
1
7
S
B.
min
3
0
S
C.
min
2
5
S
D.
min
3
3
S
Câu 48. (C
huyên Lê Quý Đôn Điện Biên 2019) Tích các nghiệm của phương trình
2
25
log 125 .log 1
x
x x
.
A.
6
30
. B.
1
1
25
. C.
6
30
625
. D.
7
1
25
Câu 49. (C
huyên Lê Quý Đôn Điện Biên 2019) Tích các nghiệm của phương trình
2
2
5
l
og 125 .log 1
x
x
x
.
A.
6
30
. B.
1
12
5
. C.
6
30
625
. D.
7
12
5
Câu 50. (Kiểmtr
anănglực-ĐH-QuốcTế-2019)Xétphươngtrình
2
3
log 1 log 2 3
x x
.
Mệnh
đềnàosauđâyđúng?
A. Phươngtrìnhtrênvônghiệm.
B. Phươngtrìnhtrêncónghiệmbéhơn
1
.
C. Phươngtrìnhtrê
ncónghiệmlớnhơn
1
vàmột
nghiệmbéhơn
1
.
D. Phươngtrìnhtrê
nchỉcónghiệmhơn
1
.
Câu 51. (Tham k
hảo 2018) Cho dãy số
n
u
thỏa mãn
1
1 10 10
log 2 log 2log 2logu u u u
và
1
2
n
n
u
u
với
mọi
1n
.G
iátrịnhỏnhấtcủa
n
để
10
0
5
n
u
bằng
A.
24
7
. B.
24
8
. C.
2
29
. D.
2
90
.
Câu 52. Cho
a
,
b
l
àcácsốdươngthỏamãn
9 16 12
5
l
og log log
2
b
a
a
b
.
Tínhgiátrị
a
b
.
A.
3
6
4
a
b
. B.
7
2 6
a
b
. C.
7
2 6
a
b
. D.
3
6
4
a
b
.
Câu 53. (THP
T Hai Bà Trưng - Huế - 2019) Cho hai số thực dương
,m
n
thỏa
mãn
4
6 9
l
og log log
2
m
n
m n
.Tínhgi
átrịcủabiểuthức
m
P
n
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2P
. B.
1P
. C.
4P
. D.
1
2
P
.
Câu 54. (Hội 8 trường chuyên ĐBSH - 2019) Giả sử
,p q
là các số thực dương thỏa mãn
16 20 25
log log log
p q p q
.Tínhgiátrịcủa
p
q
.
A.
1
1 5
2
. B.
8
5
. C.
1
1 5
2
. D.
4
5
.
Câu 55. (TT Diệu Hiền - CầnThơ- 2018) Tích các nghiệm của phương trình
2
25
log 125 log 1
x
x x
bằng
A.
7
25
. B.
630
625
. C.
1
125
. D.
630
.
Câu 56. (Đặng Thúc Hứa - Nghệ An - 2018) Tích tất cả các nghiệm của phương trình
2
2 2
log log 1 1
x x
A.
1 5
2
2
. B.
1
. C.
1 5
2
2
. D.
1
2
.
Câu 57. (Lý Nhân Tông - Bắc Ninh - 2020) Gọi
x
,
y
các số thực dương thỏa mãn điều kiện
9 6 4
log log log
x y x y
và
2
x a b
y
, với
,a b
là hai số nguyên dương. Tính
2 2
T a b
.
A.
26.
T
B.
29.
T
C.
20.
T
D.
25.
T
Câu 58. (THPT Nguyễn Viết Xuân - 2020) Cho các số thực dương
,a b
thỏa mãn
4 6 9
log log log 4 5 1
a b a b
.Đặt
b
T
a
.Khẳngđịnhnàosauđâyđúng?
A.
1 2T
. B.
1 2
2 3
T
. C.
2 0
T
. D.
1
0
2
T
.
Dạng 1.3 Phương pháp mũ hóa
+Nếu
0, 1: log
g x
a
a a f x g x f x a
(mũ hóa)
Câu 59. (CầnThơ2019)Tíchtấtcảcácnghiệmcủaphươngtrình
2
log 12 2 5
x
x
bằng
A.
2
. B.
32
. C.
6
. D.
3
.
Câu 60. Phươngtrình
4
log 3.2 1
x
x
cónghiệmlà
0
x
thìnghiệm
0
x
thuộckhoảngnàosauđây
A.
1;2
. B.
2;4
. C.
2;1
. D.
4;
.
Câu 61. Phươngtrình
4
log 3.2 1 1
x
x
cóhainghiệm
1 2
;x x
.Tínhgiátrịcủa
1 2
P x x
.
A.
6 4 2
. B.
12
. C.
2
log 6 4 2
. D.
2
.
Câu 62. (Sở Bạc Liêu - 2018) Gọi
1 2
,x x
(với
1 2
x x
) là nghiệm của phương trình
2 1 1
3
log 3 3 1
x x
x
khiđógiátrịcủabiểuthức
1 2
3 3
x x
là:
A.
1 3
. B.
1 3
. C.
2 3
. D.
2 3
.
Câu 63. (ChuyênTháiBình-2018)Sốnghiệmcủaphươngtrình
5
log 3
2
x
x
là:
A.
0
. B.
1
. C.
3
. D.
2
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 64. (HồngBàng-HảiPhòng-2018)Phươngtrình
2
l
og 5 2 2
x
x
cóhaingiệm
1
x
,
2
x
.Tính
1
2 1 2
P x x x x
.
A.
11
. B.
9
. C.
3
. D.
2
.
Câu 65. (THP
T Cao Bá Quát - 2018) Cho phương trình
4
log 3.2 1 1
x
x
có hai nghiệm
1
2
,x x
.
Tổng
1
2
x x
là:
A.
2
l
og 6 4 2
. B.
2
. C.
4
. D.
6 4 2
.
Dạng 1.4 Phương phá
p hàm số, đánh giá
T
hôngthườngtasẽvậndụngnộidungcácđịnhlý(vàcáckếtquả)sau:
Nế
uhàmsố
y
f x
đơnđiệu
mộtchiềutrênDthìphươngtrình
0
f
x
khôngq
uámột
nghiệm
trênD.
Để
vậndụngđịnhlýnày,tacầnnhẩmđược
1
ng
hiệm
o
x
x
của
phươngtrình,rồichỉrõhàm
đơn
điệumộtchiềutrênD(luônđồngbiếnhoặcluônnghịchbiếntrênD)vàkếtluận
o
x x
l
à
nghiệmduynhất.
Hà
m số
f
t
đơn
điệu một chiều trên khoảng
;a
b
và
tồn tại
;
;u v a b
t
hì
f
u f v u v
".
Để
ápdụngđịnhlýnày,tacầnxâydựnghàmđặctrưng
f
t
.
Câu 66. (Đềth
amkhảo2017)Hỏiphươngtrình
3
2
3
6 ln 1 1 0
x
x x
c
óbaonhiêunghiệmphân
biệt?
A.
2
. B.
1
. C.
3
. D.
4
Câu 67. (ChuyênLamSơn-ThanhHóa-2018)Sốnghiệmcủaphươngtrình
1
l
n 1
2
x
x
là:
A.
1
. B.
0
. C.
3
. D.
2
.
Câu 68. (THP
T Nguyễn Trãi - Đà Nẵng - 2018) Giải phương trình
2
3 3
l
og .log .log 3x x x x
2
3
l
og 3log
x
x x
.Ta
cótổngtấtcảcácnghiệmbằng
A.
3
5
. B.
5
. C.
10
. D.
9
.
Câu 69. Tínhtổngtấtcảc
ácnghiệmcủaphươngtrình
2
2
2
1
l
og 3 log 1 4 2 3
2
x
x x x x
.
A.
2
S
. B.
1
S
. C.
1
S
. D.
1 2
S
.
Câu 70. Biết
phươngtrình
5
3
2
1 1
l
og 2log
2
2
x x
x
x
có
mộtnghiệmdạng
2x
a b
trong
đó
,a b
l
àcácsốnguyên.Tính
2
a
b
.
A.
3
. B.
8
. C.
4
. D.
5
.
Câu 71. Sốnghiệmthực
củaphươngtrình
2
1
2
2 2
2
log 1 4 log 3
x
x
x
x x
.
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 72. (BắcNin
h-2018)Chophươngtrình
2
2
2
1 2 1 1
log 2 3 log 1 2 2
2
x
x x x
x x
,
gọi
S
làtổngtấtcảc
ácnghiệmcủanó.Khiđó,giátrịcủa
S
là
A.
2
S
. B.
1
13
2
S
. C.
2
S
. D.
1
13
2
S
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu
73. (Toán Học Và Tuổi Trẻ - 2018) Biết
1
x
,
2
x
là
hai nghiệm của phương trình
2
2
7
4 4 1
l
og 4 1 6
2
x
x
x
x
x
và
1
2
1
2
4
x x a b
với
a
,
b
l
àhaisốnguyêndương.Tính
.a b
A.
1
6
a
b
. B.
1
1
a
b
. C.
1
4
a
b
. D.
1
3.
a
b
Câu
74. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2018) Số nghiệm của phương trình
2
2
l
n 2 2018
2
x
x x
là
A.
3
. B.
1
. C.
4
. D.
2
.
Câu 75. (THPTLêXoay-2018)Sốnghiệmcủaphươngtrình
2
s
in 2 cos 1 log sinx x x
trênkhoảng
0
;
2
là:
A.
4
. B.
3
. C.
2
. D.
1
.
Câu
76. (THPT Nguyễn Thị Minh Khai - Hà Tĩnh - 2018) Phương trình
2
2
3 3
l
og 2 3 7 log 1
x
x x x x
c
ósốnghiệmlà
T
và
tổngcácnghiệmlà
S
.
Khiđó
T
S
bằng
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 77. (THPTNguyễnTấtThành-YênBái-2018)Biết
1
2 1 2
,
x
x x x
là
hainghiệmcủaphương
trình
2
2
7
4
4 1
l
og 4 1 6
2
x
x
x
x
x
và
1
2
1
3
2
4
x x a b
với
,a
b
là các số nguyên
dương.Tính
a
b
A.
1
4
a
b
. B.
1
6
a
b
. C.
1
7
a
b
. D.
1
5
a
b
.
Câu
78. (THPTLương VănCan-2018)Chobiếtphươngtrình
5
3
2
1 1
l
og 2log
2
2
x x
x
x
c
ó
nghiệmduynhất
2x
a b
.
Hỏi
m
thuộc
khoảngnàodướiđâyđểhàmsố
2
m
x a
y
x
m
c
ó
giátrịlớnnhấttrênđoạn
1
;2
bằ
ng
2
.
A.
7;9
m
. B.
6;7
m
. C.
2;4
m
. D.
4;6
m
.
DẠNG 2. PHƯƠNG
PHÁP GIẢI PHƯƠNG TRÌNH MŨ
Dạn
g 2.1 Phương pháp đưa về cùng cơ số
+ Nếu
0, 1
a a
thì
f
x g x
a
a f x g x
+ Nếuachứa
ẩnthì
1
1
0
f
x g x
a
a
a a f x g x
f x g x
.
+
f
x g x
a
b
l
og log
f
x g x
a
a
a
b
l
og .
a
f
x b g x
(logar
it hóa).
Câu 1. (ChuyênBắcGiang2019)Nghiệmcủaphươngtrình
2
2
3
1
1
5
5
x
x
x
là
A.
1
; 2.
x
x
B.
1
; 2.
x
x
C.
1
; 2.
x
x
D. Vô
nghiệm.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 2. Tậpnghiệmcủa
phươngtrình
2
2
3
1
1
7
7
x
x
x
l
à
A.
1
. B.
1
;2
. C.
1
;4
. D.
2
.
Câu 3. Tổngcácnghiệmcủaphươngtrình
2
2
2
2
8
x
x x
bằng
A.
6
. B.
5
. C.
5
. D.
6
.
Câu 4. (SGDĐiệnBiên-2019)Gọi
1
2
,
x x
l
àhainghiệmcủa phươngtrình
2
2
3
1
1
7
7
x
x
x
.
Khiđó
2
2
1 2
x
x
bằng:
A.
1
7
. B.
1
. C.
5
. D.
3
.
Câu 5. Tổngbình
phươngcácnghiệmcủaphươngtrình
2
3
2
1
5
5
x
x
bằng
A.
2
. B.
5
. C.
0
. D.
3
.
Câu 6. Nghiệm
củaphươngtrình
7
1 2 1
2
8
x
x
là
A.
2.
x
B.
3.
x
C.
2.
x
D.
1.
x
Câu 7. (THPTLươngVănTụy-NinhBình-2018)Giảiphươngtrình
1
5
7
2
2
,5
5
x
x
.
A.
1x
. B.
1x
. C.
1x
. D.
2
x
.
Câu 8. (THP
TNguyễnThịMinhKhai-HàTĩnh-2018)Phươngtrình
2
3
1
4
1
3
9
x
x
có
hainghiệm
1
x
,
2
x
.Tính
1 2
x
x
.
A.
6
. B.
5
. C.
6
. D.
2
.
Câu 9. (SởQ
uảngNam-2018)Tổngcácnghiệmcủaphươngtrình
2
2 2
2
8
x x x
bằng
A.
5
. B.
5
. C.
6
. D.
6
.
Câu 10. (THP
TThăngLong-HàNội-2018)Tậpnghiệmcủaphươngtrình
2
1
4
2
x
x
x
là
A.
2
0
;
3
. B.
1
0
;
2
. C.
0
;2
. D.
3
0
;
2
.
Câu 11. (THP
TKimLiên-HàNội-2018)Tínhtổng
1
2
S x x
biết
1
x
,
2
x
là
cácgiátrịthựcthỏamãn
đẳngthức
2
3
6
1
1
2
4
x
x
x
.
A.
5
S
. B.
8
S
. C.
4
S
. D.
2
S
.
Câu 12. (THP
T Nguyễn Thị Minh Khai - Hà Nội - 2018) Tích các nghiệm của phương trình
1
1
1
5
2 5 2
x
x
x
là
A.
2
. B.
4
. C.
4
. D.
2
.
Câu 13. (THCS&
THPTNguyễnKhuyến-BìnhDương-2018)Giảiphươngtrình
2
3 4
4 8
x
x
.
A.
6
7
x
. B.
2
3
x
. C.
2
x
. D.
4
5
x
.
Câu 14. (THP
TCaoBáQuát-2018)Chophươngtrình
2
2
8
4
1
3
2
16
x
x
.
Khẳngđịnhnàosauđâylàđúng:
A. Nghiệmcủaphươngtrìnhlàcácsốvôtỷ.
B. Tổngcácnghiệmcủamộtphươngtrìnhlàmộtsốnguyên.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
C. Tíchcácnghiệmcủaphươngtrìnhlàmộtsốâm.
D. Phươngtrìnhvônghiệm.
Dạng 2.2 Phương pháp đặt ẩn phụ
Loại1.
0
f x
PP
P a
đặt
, 0
f x
t a t
.
Loại2.
2. 2.
. . .
λ. 0
f x
f x f x
a a b b
PP
Chiahaivếcho
2.
,
f x
b
rồiđặt
0
f x
a
t
b
(chiachocơsốlớnnhấthoặcnhỏnhất).
Loại3.
f x f x
a b c
với
. 1
a b
PP
đặt
1
f x f x
t a b
t
.
Loại4.
.
. . 0
f x g x
f x g x
f x
g x
a a
a a b
a
a
PP
đặt
f x
g x
u a
v a
.
Câu 15. (Mã1232017)Chophươngtrình
1
4 2 3 0.
x x
Khiđặt
2
x
t
tađượcphươngtrìnhnàosau
đây
A.
2
2 3 0t t
B.
4 3 0t
C.
2
3 0t t
D.
2
2 3 0t t
Câu 16. (THPT Hoàng Hoa Thám Hưng Yên 2019) Tập nghiệm của phương trình
2 2 2
4 3 7 6 2 3 9
5 5 5 1
x x x x x x
là
A.
1; 1;3
. B.
1;1;3;6
. C.
6; 1;1;3
. D.
1;3
.
Câu 17. (ChuyênLêQuýĐônĐiệnBiên2019)Phươngtrình
2 1
9 6 2
x x x
cóbaonhiêunghiệmâm?
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 18. (ChuyênNguyễnTrãiHảiDương2019)Tổngcácnghiệmcủaphươngtrình
4 6.2 2 0
x x
bằng
A.
0
. B.
1
. C.
6
. D.
2
.
Câu 19. (Cụm8TrườngChuyên 2019)Tổngcácnghiệmcủaphươngtrình
1 1
3 3 10
x x
là
A. 1. B. 0. C.
1
. D. 3.
Câu 20. Gọi
1 2
,x x
lànghiệmcủaphươngtrình
2 3 2 3 4
x x
.Khiđó
2 2
1 2
2x x
bằng
A. 2. B.
3
. C. 5. D. 4.
Câu 21. (ĐềThiCôngBằngKHTN2019)Tổngtấtcảcácnghiệmcủaphươngtrình
2.4 9.2 4 0
x x
bằng.
A.
2
. B.
1
. C.
0
. D.
1
.
Câu 22. (THPTNghĩaHưngNĐ 2019)Phươngtrình
2 1 1
6 5.6 1 0
x x
cóhainghiệm
1
x
,
2
x
.Khiđó
tổnghainghiệm
1 2
x x
là.
A. 5. B. 3. C. 2. D. 1.
Câu 23. Chophươngtrình
1
25 20.5 3 0
x x
.Khiđặt
5
x
t
,tađượcphươngtrìnhnàosauđây.
A.
2
3 0
t
. B.
2
4 3 0
t t
. C.
2
20 3 0
t t
. D.
20
3 0
t
t
.
Câu 24. (SởBìnhPhước-2019)Tậpnghiệmcủaphươngtrình
9 4.3 3 0
x x
là
A.
0;1
B.
1
C.
0
D.
1;3
Câu 25. (ChuyênTháiNguyên2019)Sốnghiệmthựccủaphươngtrình
1 3
4 2 4 0
x x
là:
A.
1
B.
2
C.
3
D.
4
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu 26. (C
huyênBắcGiang2019)Tậpnghiệmcủaphươngtrình
2
2
3 3 30
x
x
l
à
A.
1
3
;
3
S
B.
1
S
C.
1; 1
S
D.
3;1 .
S
Câu 27. (THP
TNguyễnKhuyến2019)Chohàm số
.
5 .
x
f
x x
Tổng
cácnghiệm củaphương tr
ình
25 ' .5 .ln5 2 0
x
x
f x x
l
à
A.
2
B.
0
C.
1
D.
1
Câu 28. (C
huyênKHTN2019)Tổngtấtcảcácnghiệmcủaphươngtrình
2
2
3
2.3 27 0
x
x
bằng
A.
9
. B.
1
8
. C.
3
. D.
2
7
.
Câu 29. (THP
T-Thang-Long-Ha-Noi- 2019)Phươngtrình
2
1
9
6 2
x
x x
cóbaonhi
êunghiệmâm?
A.
3
B.
0
C.
1
D.
2
Câu 30. (C
huyenPhanBộiChâuNghệAn2019)Phươngtrình
2
1 2 1 2 2 0
x
x
c
ótíc
h
c
ácnghiệmlà?
A.
0.
B.
2.
C.
1.
D.
1
.
Câu 31. (C
huyên Bắc Giang 2019) Gọi
1
2
;x
x
l
à
2
nghiệm
của phương trình
2
2
1
4
2 3
x
x x x
.Tính
1
2
x x
A.
3
B.
0
C.
2
D.
1
Câu 32. (HSGBắcNin
h2019)Giảiphươngtrình:
1
1 2 2
4
4 2 2 2 8
x
x x x
Câu 33. Tínhtổngtấtcảc
ácnghiệmcủaphươngtrình
2
8 5
3
4.3 27 0
x
x
?
A.
5
. B.
5
. C.
4
2
7
. D.
4
2
7
.
Câu 34. Tổngtấtcảcácnghiệmcủaphươngtrình
2
2
3
2.3 27 0
x
x
bằng
A.
0
. B.
18
. C.
3
. D.
27
.
Câu 35. (Hội8trườngc
huyênĐBSH2019)Tổngcácnghiệmcủaphươngtrình
1
1
3
3 10
x
x
là
A.
1
. B.
3
. C.
1
. D.
0
.
Câu 36. (S
GDĐiệnBiên-2019)Tíchtấtcảcácnghiệmcủaphươngtrình
4
3
3 30
x
x
bằng
A.
3
. B.
1
. C.
9
. D.
27
.
Câu 37. (Thi thử hội 8 trường chuyên 2019) Kí hiệu
1
x
,
2
x
l
à hai nghiệm thực của phương trình
2
2
1
4
2 3
x
x x x
.Giá
trịcủa
1
2
x x
bằng
A.
3
. B.
4
. C.
2
. D.
1
.
Câu 38. (Đại học Hồn
g Đức 2019) Cho phương trình
sin
sin
7
4 3 7 4 3 4
x
x
.
Tổng
các
nghiệmcủa
phươngtrìnhtrong
2 ;2
bằng
A.
3
2
. B.
2
. C.
0
. D.
.
Câu 39. (X
uân Trường - Nam Định - 2018) Gọi a là một nghiệm của phương trình
2
log log 2log
4
.2 6 18.3 0
x
x x
.K
hẳngđịnhnàosauđâyđúngkhiđánhgiávề
a
?
A.
2
10
1
a
.
B.
a
cũnglà
nghiệmcủaphươngtr
ình
l
og
2
9
3 4
x
.
C.
2
1
2
a
a
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
D.
2
10
a
.
Câu 40. (THPT Lục Ngạn - 2018) Nghiệm của phương trình
25 2 3 5 2 7 0
x x
x x
nằm trong
khoảngnàosauđây?
A.
5;10
. B.
0;2
. C.
1;3
. D.
0;1
Câu 41. (THPTChuVănAn-TháiNguyên-2018)Sốnghiệmnguyênkhôngâmcủabấtphươngtrình
1 1
15.2 1 2 1 2
x x x
bằngbaonhiêu?
A. 3. B. 0. C. 1. D. 2.
Câu 42. (ToánHọcTuổiTrẻSố6)Chophươngtrình
3
1 3
8 8. 0,5 3.2 125 24. 0,5 .
x x
x x
Khiđặt
1
2
2
x
x
t
,phươngtrìnhđãchotrởthànhphươngtrìnhnàodướiđây?
A.
3
8 3 12 0
t t
. B.
3 2
8 3 10 0
t t t
.C.
3
8 125 0
t
. D.
3
8 36 0
t t
.
Câu 43. (THPT Bình Giang - Hải Dương - 2018) Gọi
S
là tập nghiệm của của phương trình:
2 2 2
3x 2 6x 5 2x 3x 7
4 4 4 1
x x
.Khiđó
S
là
A.
1;2
. B.
1;2; 1
. C.
1;2; 1; 5
. D.
.
Dạng 2.3 Phương pháp logarit hóa
Dạng 1:Phươngtrình:
0 1, 0
log
f x
a
a b
a b
f x b
Dạng 2:Phươngtrình:
log log .log
f x g x f x f x
a a a
a b a b f x g x b
hoặc
log log .log .
f x g x
b b b
a b f x a g x
Câu 44. (THPT ThuậnThành3 - Bắc Ninh 2019) Sốgiaođiểm củacác đồ thị hàmsố
2
1
3
x
y
và
5
y
là
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 45. (SởGDNamĐịnh-2019)Tínhtíchcácnghiệmthựccủaphươngtrình
2
1 2 3
2 3
x x
A.
2
3log 3
. B.
2
log 54
. C.
1
. D.
2
1 log 3
.
Câu 46. Chohaisốthực
1, 1
a b
.Gọi
1 2
,x x
làhainghiệmcủaphươngtrình
2
1
. 1
x x
a b
.Trongtrường
hợpbiểuthức
2
1 2
1 2
1 2
.
4 4
x x
S x x
x x
đạtgiátrịnhỏnhất,mệnhđềnàosauđâylàđúng?
A.
a b
. B.
. 4
a b
. C.
. 2
a b
. D.
a b
.
Câu 47. (TTDiệuHiền-CầnThơ-2018)Cho
x
,
y
,
z
làcácsốthựcthỏamãn
2 3 6 .
x y z
Giátrị
củabiểuthức
M xy yz xz
là:
A.
0.
B.
6.
C.
3.
D.
1.
Câu 48. (Lý Nhân Tông - Bắc Ninh - 2020) Gọi
x
,
y
các số thực dương thỏa mãn điều kiện
9 6 4
log log log
x y x y
và
2
x a b
y
, với
,a b
là hai số nguyên dương. Tính
2 2
T a b
.
A.
26.
T
B.
29.
T
C.
20.
T
D.
25.
T

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 49. (THP
T Nguyễn Viết Xuân - 2020) Cho các số thực dương
,a
b
thỏa
mãn
4
6 9
l
og log log 4 5 1
a
b a b
.Đặt
b
T
a
.Khẳng
địnhnàosauđâyđúng?
A.
1
2T
. B.
1
2
2 3
T
. C.
2 0
T
. D.
1
0
2
T
.
Câu 50. (THP
T Cao Bá Quát - 2018) Phương trình
2
1
1
3
.4 0
3
x
x
x
có
hai nghiệ
m
1
2
,
.x x
Tí
nh
1
2 1 2
.
T x x x x
.
A.
3
log 4
T
. B.
3
log 4
T
. C.
1T
. D.
1T
.
Dạng 2.4 Phương phá
p hàm số, đánh giá
T
hôngthườngtasẽvậndụngnộidungcácđịnhlý(vàcáckếtquả)sau:
Nế
uhàmsố
y f x
đơnđiệu
mộtchiềutrênDthìphươngtrình
0
f x
khôngq
uámột
nghiệm
trênD.
Để
vậndụngđịnhlýnày,tacầnnhẩmđược
1
ng
hiệm
o
x x
của
phươngtrình,rồichỉrõhàm
đơn
điệumộtchiềutrênD(luônđồngbiếnhoặcluônnghịchbiếntrênD)vàkếtluận
o
x x
l
à
nghiệm
duynhất.
Hà
m số
f
t
đơn
điệu một chiều trên khoảng
;a
b
và
tồn tại
;
;u v a b
t
hì
f u f v u v
".
Đểápdụngđịnhlýnày,tacầnxâydựnghàmđặctrưng
f t
.
Câu 51. (SGDNamĐịnh 2019)Tổngtấtcảcácnghiệmthựccủaphươngtrình
1
15 .5 5 27 23
x
x
x x
bằng.
A.
1
. B.
2
. C.
1
. D.
0
.
Câu 52. Cho
số thực
sao
cho phương trình
2 2 2cos
x x
x
có
đúng
2019
nghiệm
thực. Số
nghiệmcủaphươngtrình
2
2 4 2cos
x
x
x
là
A.
2
019
. B.
2
018
. C.
4
037
. D.
4
038
.
Câu 53. Biết
1
x
,
2
x
là
hai nghiệm của phương trình
2
2
7
4
4 1
l
og 4 1 6
2
x
x
x
x
x
và
1 2
1
2
4
x
x a b
với
a
,
b
làhaisốnguyêndương.Tính
a
b
.
A.
1
3
a
b
. B.
1
1
a
b
. C.
1
6
a
b
. D.
14
a
b
.
Câu 54. P
hươngtrình
1
1 2
2 4 2
x
x
x x
cótổngcácnghiệmbằng
A. 7 B. 3 C. 5 D. 6
Câu 55. (ChuyênNgữHàNội2019)Tìmsốnghiệmcủaphươngtrình
2
1
1
e log 2 0
x
x
.
A.
4
. B.
3
. C.
2
. D.
0
.
Câu 56. Tínhsốnghiệmcủaphươngtrình
co
t 2
x
x
trongkhoảng
1
1
;2019
12
.
A.
2
019
. B.
2
018
. C.
1
. D.
2
020
.
Câu 57. Hỏiphư
ơngtrình
3
.2 4.3 5.4 6.5
x x x x
c
ótấtcảbaonhiêunghiệmthực?
A.
0
. B.
1
. C.
3
. D.
2
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu
58. (SPĐồngNai-2019)Phươngtrình
s
in 2
2
019 sin 2 cos
x
x
x
có
baonhiêunghiệmthựctrên
5
;2019 ?
A.
2
025
. B.
2
017
. C.
2
022
. D. Vônghiệm.
Câu 59. (BỉmSơn-ThanhHóa-2019)Sốnghiệmcủaphươngtrình
7
l
og 4
3
x
x
là
A.
1
. B.
0
. C.
2
. D.
3
.
Câu
60. Chocácsốthực
x
,
y
với
0
x
thỏamãn
3
1 1
3
1
e e 1 1 e 3
e
x
y xy xy
x y
x y y
.Gọi
m
là
giátrịnhỏnhấtcủabiểuthức
2 1T x y
.Mệnh
đềnàosauđâylàđúng?
A.
2
;3
m
. B.
1
; 0
m
. C.
0
;1
m
. D.
1
;2
m
.
Câu
61. (Chuyên Vĩnh Phúc - 2018) Số nghiệm của phương trình
2
2
2 3 5 8 3
5
2 8 3 .8 3 5 .8
x
x x
x
x x x x
là
A.
4
. B.
3
. C.
1
. D.
2
.
Câu
62. (THPTChuVăn An - Hà Nội - 2018) Tíchtất cả các giá trị của
x
thỏa
mãn phươngtrình
2 2 2
3 3 4 4 3 4 7
x
x x x
bằng
A. 2. B.
1
. C. 4. D. 3.
Câu
63. (THPTChu VănAn-HàNội-2018)Phươngtrình
2
1 2
1
2 2 1
x
x
e
e x x
có
nghiệm
trongkhoảngnào?
A.
5
2
;
2
. B.
3
;
2
2
. C.
3
1
;
2
. D.
1
;1
2
.
DẠNG 3. PHƯƠNG
TRÌNH TỔ HỢP CỦA MŨ VÀ LOGARIT
Câu 1. (Thamkhảo2019)Tổngtấtcảcácnghiệmcủaphươngtrình
3
l
og 7 3 2
x
x
bằng
A.
2
. B.
1
. C.
7
. D.
3
.
Câu
2. Tíchcácnghiệmcủaphươngtrình
1
1
5
l
og 6 36 2
x
x
bằng
A.
0
. B.
6
lo
g 5
. C.
5
. D.
1
.
Câu
3. Tổngcácnghiệmcủaphươngtrình
2
l
og 5 – 2 2
x
x
bằng
A.
3
. B.
1
. C.
2
. D.
0
.
Câu
4. (ThithửcụmVũngTàu-2019)Sốnghiệmcủaphươngtrình
1
2
1
2
l
og (4 4) log (2 3)
x
x
x
A.
3
. B.
1
. C.
0
. D.
2
Câu
5. Gọi
S
là
tậphợptấtcảcácnghiệmnguyêndươngcủaphươngtrình
2
l
og 2 10
x
x
.
Sốtậpcon
của
S
bằng
A.
4
. B.
1
. C.
2
. D.
0
.
Câu
6. Tổngtấtcảcácnghiệmcủaphươngtrình
2
log 6 2 1
x
x
bằng
A.
1
. B.
2
. C.
0
. D.
3
.
Câu
7. (Chuyên Thái Bình - 2018) Tính tích tất cả các nghiệm thực của phương trình
1
2
2
2
2 1
l
og 2 5
2
x
x
x
x
.
A.
0
. B.
2
. C.
1
. D.
1
2
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Câu 8. (Thi thử hội 8 trườngchuyên2019) Phương trình
2
l
og 5.2 4 2
x
x
có bao nhiêu nghiệm
nguyêndương?
A.
2
. B.
0
. C.
3
. D.
1
.
Câu 9. (S
P Đồng Nai - 2019) Phương trình
2
l
og 5 2 2
x
x
c
ó hai nghiệm thực
1 2
,x
x
.
Tính
1
2 1 2
P
x x x x
A.
2
. B.
9
. C.
3
. D.
1
1
.
Câu 10. P
hươngtrình
2
2
5 log 3 0
x
x
có
hai nghiệm
1
x
,
2
x
(với
1
2
x
x
).
Tính giá trị của biểu
thức
1 2
3K
x x
.
A.
3
32
log 2
K
. B.
2
18
log 5
K
. C.
2
24
log 5
K
. D.
2
32
log 3
K
.
Câu 11. Cho
biết phương trình
1
3
1
3
l
og (3 1) 2 log 2
x
x
có
hai nghiệm
1
2
,x
x
.
Hãy tính tổng
1 2
27 27
x
x
S
.
A.
2
52
S
. B.
4
5
S
. C.
9
S
. D.
1
80
S
.
Câu 12. (THP
T Yên Dũng 2-Bắc Giang 2019) Tính tích tất cả các nghiệm thực của phương trình
1
2
2
2
2
1
l
og 2 5
2
x
x
x
x
.
A.
2
. B.
0
. C.
1
2
. D.
1
.
Câu 13. Sốnghiệmcủa
phươngtrình
2
2
4
l
og 3
2 12
x
x
x
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 14. Tínht
íchtấtcảcácnghiệmthựccủaphươngtrình
1
2
2
2
2
1
l
og 2 5
2
x
x
x
x
.
A.
0
. B.
2
. C.
1
. D.
1
2
.
Câu 15. Tổngtấtcảcácnghiệmcủaphươngtrình
2
l
og 10 2019 2019 4
x
x
bằng
A.
2
019
log 16
. B.
2
019
2log 16
. C.
2
019
log 10
. D.
2
019
2log 10
.
Câu 16. (THPTHòaVang-ĐàNẵng-2018)Biếtrằng
1
2
2
log 14 2 1
x
x
y
y
với
0
x
.
Tí
nh
giátrịcủa
biểuthức
2
2
1P
x y xy
.
A.
3
. B.
1
. C.
2
. D.
4
.
Câu 17. (ToánHọcTuổiTrẻ-2018)Phươngtrình
8
8
l
og
log 4
4
4
x
x
x
x
cótậpn
ghiệmlà
A.
2
;8
. B.
1
;
8
2
. C.
1
1
;
2 8
. D.
1
2
;
8
.
Câu 18. (THP
T Yên Lạc- 2018) Tính tổng
S
tất
cả các nghiệm của phương trình:
1
5 3
l
n 5 5.3 30 10 0
6
2
x
x
x x
x
x
.
A.
1
S
. B.
2
S
. C.
1
S
. D.
3
S

T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI – XUẤT SẮC MỨC 9-10 ĐIỂM
PHƯƠNG
PHÁP CHUNG
Tìm m để
,
0f x m
có nghiệm (hoặc có k nghiệm) trên D ?
— Bước
1. Tách m ra khỏi biến số và đưa về dạng
f
x A m
.
— Bước
2. Khảo sát sự biến thiên của hàm số
f
x
tr
ên D.
— Bước 3. Dựa vào bảng biến thiên để xác định giá trị của tham số
A m
để đường thẳng
y A m
nằm
nga
ng cắt đồ thị hàm số
y
f x
.
— Bước
4. Kết luận các giá trị cần tìm của
A
m
để ph
ương trình
f
x A m
có nghiệm
(hoặc có k
nghiệm
) trên D.
Lưu ý
— Nếu
hàm số
y
f x
có giá
trị lớn nhất và giá trị nhỏ nhất trên D thì giá trị
A
m
cần
tìm là những m
thỏa mãn:
m
in max
x
D
x D
f
x A m f x
.
— Nếu
bài toán yêu cầu tìm tham số để phương trình có k nghiệm phân biệt, ta chỉ cần dựa vào bảng biến
thiên
để xác định sao cho đường thẳng
y A m
nằm
ngang cắt đồ thị hàm số
y f x
tại
k điểm
phâ
n biệt.
Dạn
g 1. Phương trình logarit chứa tham số
Câu 1. (Đề Minh Họa 2020 Lần 1) Cho phương trình
2
2
2
l
og 2 2 log 2 0x m x m
(
m
l
à tham
số thực). Tập hợp tất cả các giá trị của
m
để phư
ơng trình đã cho có hai nghiệm phân biệt thuộc
đoạn
1
;2
là
A.
1;2
. B.
1;2
. C.
1;2
. D.
2;
.
Câu
2. (Chuyên Lam Sơn Thanh Hóa 2019)
Cho
hàm số
2
2
27 1
3
3
log 2 3 1 log 1 3 0x m x m x x m
.
Số các giá trị nguyên của
m
để
phương
trình đã cho có hai nghiệm phân biệt
1
2
,x
x thỏa mãn
1 2
15
x x
là
:
A.
1
4
B.
11
C.
1
2
D.
13
Câu
3. (THPT Yên Phong Số 1 Bắc Ninh 2019) Gọi
S
là
tập tất cả các giá trị nguyên của tham số m
với
6
4m
để phương
trình
1
5
5
l
og log 2 0x m x
có nghiệm. Tính
tổng tất cả các phần tử
của
S
.
A.
2
018.
B.
2
016.
C. 2015. D.
2
013.
Câu 4. (Mã 102 2019) Cho phương trình
2
9
3 3
l
og log 6 1 logx x m
(
m
là tham số thực). Có tất cả
bao nhiêu giá trị nguyên của
m
để phư
ơng trình đã cho có nghiệm?
A.
7
. B.
6
. C.
5
. D. Vô
số.
Câu 5. (Mã 103 2019) Cho phương trình
2
9
3 3
l
og log 5 1 logx x m
(
m
là
tham số thực). Có tất cả
bao nhiêu giá trị nguyên của
m
để phư
ơng trình đã cho có nghiệm?
A.
4
.
B.
6
.
C. Vô
số. D.
5
.
Câu 6. (Mã 101 - 2019) Cho phương trình
2
9
3 3
log log 3 1 logx x m
(
m
là tham số thực). Có
tất cả bao nhiêu giá trị nguyên của tham số
m
để phư
ơng trình đã cho có nghiệm?
A. 2. B. 4. C. 3. D. Vô số.
Câu 7. (Mã 104 2019) Cho phương trình
2
9
3 3
l
og 4log 4 1 logx x m
(
m
là
tham số thực). Có tất
cả bao nhiêu giá trị nguyên của
m
để phư
ơng trình đã cho có nghiệm?
P
HƯƠNG TRÌNH MŨ - LOGARIT
Ch
uyên đề 19
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
5
. B.
3
. C. Vô số. D.
4
.
Câu
8. (THPT Lương Thế Vinh Hà Nội 2019) Cho phương trình
2
5
5
l
og 6 12 log 2
m
x
mx
x
x x
,
gọi
S
là
tập hợp tất cả các giá trị của tham số
m
để
phương trình đã cho có nghiệm duy nhất. Tìm số phần tử của
S
.
A.
2
. B.
0
. C.
3
. D.
1
.
Câu
9. Cho phương trình
2
2 2 2
2 5
5 2
l
og 2 4 2 log 2 0
x
x m m x mx m
.
Hỏi có bao nhiêu
giá trị nguyên của tham số
m
để phư
ơng trình đã cho có hai nghiệm
2
2
1 2
3
x x
?
A. 1 B. 0 C. 3 D. 4
Câu
10. (HSG Bắc Ninh 2019) Tìm tất cả các giá trị của tham số thực m để phương trình
2
2
1
2
4
log log 0
x
x m
có hai nghiệm phân biệt thuộc khoảng
0
;1
.
A.
1
0
4
m
B.
1
0
4
m
C.
1
4
m
D.
1
0
4
m
Câu
11. (THPT Đông Sơn Thanh Hóa 2019) Tìm
m
để p
hương
trình :
2
2
1
1
2 2
1
1
log 2 4 5 log 4 4 0
2
m x m m
x
c
ó nghiệm trên
5
,
4
2
.
A.
m
. B.
7
3
3
m
. C.
m
. D.
7
3
3
m
.
Câu
12. (Chuyên Bắc Giang 2019) Tìm
m
để
phương trình
2
2
2 2
log log 3
x x m
có ngh
iệm
[
1;8]
x
.
A.
6 9
m
B.
2 3
m
C.
2 6
m
D.
3 6
m
Câu
13. (HSG Bắc Ninh-2019) Cho phương trình
2
2
2 2
l
og 2log log *
x
x m x m
.
Có bao nhiêu
giá trị nguyên của tham số
20
19;2019
m
để phương trình (*) có nghiệm?
A.
2
021
. B.
2019
. C.
4038
. D.
202
0
.
Câu
14. (Đề Tham Khảo 2017) Hỏi có bao nhiêu giá trị
m
nguyê
n trong
2017;2017
để phương
trình
l
og 2log 1
mx
x
c
ó nghiệm duy nhất?
A.
4
014.
B.
2
018.
C.
4
015.
D.
2
017
.
Câu
15. (THPT An Lão Hải Phòng 2019) Tìm tập hợp tất cả các giá trị thực của tham số
m
để phương
trình
l
n 0
m
x x
c
ó hai nghiệm phân biệt thuộc khoảng
2
;3
A.
l
n 2 ln 3
;
2
3
B.
l
n 2 ln 3
; ;
2 3
C.
l
n 2 1
;
2
e
D.
l
n 3 1
;
3
e
Câu
16. (THPT Dông Sơn Thanh Hóa 2019) Tổng tất cả các giá trị của tham số
m
sao c
ho phương trình:
2
1
2
2
2
2
.log 2 3 4 .log 2 2
x
m
x
x
x x m
có đúng ba
nghiệm phân biệt là:
A. 2. B.
3
.
2
C. 0. D. 3.
Câu
17. Tìm tất cả các giá trị của
m
để phương trình
l
n ln sin sinm m x x
có nghiệm.
A.
1
1
m e 1.
e
B.
1
m e 1.
C.
1
1
m 1.
e
D.
1
m e 1.
Câu
18. (THPT Yên Dũng 2-Bắc Giang 2019) Số các giá trị nguyên của tham số
m
để phương
trình
2
2
l
og ( 1) log ( 8)
x
mx
c
ó hai nghiệm phân biệt là
A.
5
. B. Vô số. C.
4
. D.
3
.
Câu 19. (THPT Trần Phú - 2019) Có bao nhiêu giá trị nguyên dương của tham số
m
để phương
trình
2
l
n 2 ln 4
e
x
m
m x
có nghiệm thuộc vào đoạn
1
;
1
e
?

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 20. (THP
T Trần Phú - 2019) Có bao nhiêu giá trị của tham số
m
để phương trình
2
36
6
4log log 2 0
6
x
x
m
có ha
i nghiệm phân biệt
1 2
,x x
thỏa m
ãn
1
2 1 2
.
72 . 1296 0
x
x x x
A.
0.
B.
1.
C.
2.
D.
3.
Câu 21. (C
huyên Lê Hồng Phong Nam Định 2019) Tập hợp các giá trị thực của tham số m để phương
trình
2
2019 1
2019
l
og 4 log 2 1 0
x
x m
có
hai nghiệm thực phân biệt là
;T
a b
.
Tính
2
S
a b
.
A.
18
. B.
8
. C.
2
0
. D.
16
.
Câu 22. (THP
T Cẩm Bình 2019) Có bao nhiêu giá trị nguyên của
m
để phươ
ng trình
3
3
l
og 3 log 9 16
x
x
m
có hai nghiệm thỏa mãn
1
2
2
x
x
.
A.
1
7
. B.
1
6
. C.
1
4
. D.
1
5
.
Câu 23. (C
huyên Hoàng Văn Thụ-Hòa Bình 2019) Tập hợp các số thực m để phương trình
2
l
n 3 1 ln 4 3
x
mx x x
c
ó nghiệm là nửa khoảng
;a
b
. Tổng
a
b
bằng
A.
10
.
3
B.
4.
C.
22
.
3
D.
7.
Câu 24. (Cần
Thơ 2019) Cho phương trình
2
2 2 2
log 2 log 4 1 log
x x x m
,
với
m
là
tham số thực.
Số các giá trị nguyên thuộc đoạn
2
019;2019
của
m
để phương trình đã cho có nghiệm là
A. 2021. B. 2024. C. 2023. D. 2020.
Câu 25. (Nam Định - 2019) Tìm tất cả các giá trị thực của tham số
m
để phương trình
2
3
9
l
og 1 log 9 1
m
x
x x
c
ó hai nghiệm phân biệt.
A.
1
;0
m
. B.
2
;0
m
. C.
1;m
. D.
1
;0
m
.
Câu 26. (THPT
Hoàng Hoa Thám - Hưng Yên 2019) Cho
,a
b
là các số thực dương lớn hơn 1, thay đổi
thỏa mãn
20
19
a
b
để phư
ơng trình
5
log .log 4log 3log 2019 0
a
b a b
x
x x x
luôn
có hai
nghiệm phân biệt
1
2
;x
x
.
Biết giá trị lớn nhất của
1
2
l
n .x x
bằng
3 4
ln ln
5
7 5 7
m n
;
với
,m
n
là
c
ác số nguyên dương. Tính
2 S m n
A.
2
2209
. B.
2
0190
. C.
2
019
. D.
1
4133
.
Câu 27.
(Bỉm
Sơn - Thanh Hóa - 2019) Xét các số nguyên dương
,
a b
s
ao cho phương trình
2
l
n ln 5 0
a
x b x
c
ó hai nghiệm phân biệt
1 2
, x x
và
phương trình
2
5log log 0
x b x a
c
ó
hai nghiệm phân biệt
3 4
, x x
thỏa
mãn
1 2 3 4
x x x x
.
Tìm giá trị nhỏ nhất của
2
3S a b
A.
min
3
3
S
. B.
min
3
0
S
. C.
min
1
7
S
. D.
min
2
5
S
.
Câu 28. (THP
T Thuận Thành 3 - Bắc Ninh 2019) Có bao nhiêu giá trị nguyên dương của tham số
m
để
phương trì
nh
2
2
2
2
1
l
og 2 1 2
2
x mx
x mx x
x
có hai nghiệm phân biệt?
A.
3
. B.
1
. C.
4.
D.
2
.
Câu 29. (C
huyên Bắc Giang 2019) Số các giá trị nguyên nhỏ hơn
2
018
của
tham số
m
để phư
ơng trình
6
4
l
og 2018 log 1009x m x
có nghiệm là
A.
2
018
. B.
2
017
. C.
2
020
. D.
2
019
.
Câu 30. (C
huyên ĐH Vinh - Nghệ An -2020) Có bao nhiêu số nguyên
m
để phương trình
2
3
5
l
og 3 2 log 3
x x
m
m
có nghiệm?
A.
3
. B.
4
. C.
2
. D.
5
.
Câu 31. (C
huyên Hưng Yên - 2020) Tìm tất cả các giá trị thực của tham số
m
để phươ
ng trình
3
3
lo
g log 1 2 1 0
x
x m
c
ó ít nhất một nghiệm thực trong đoạn
1
;27
.
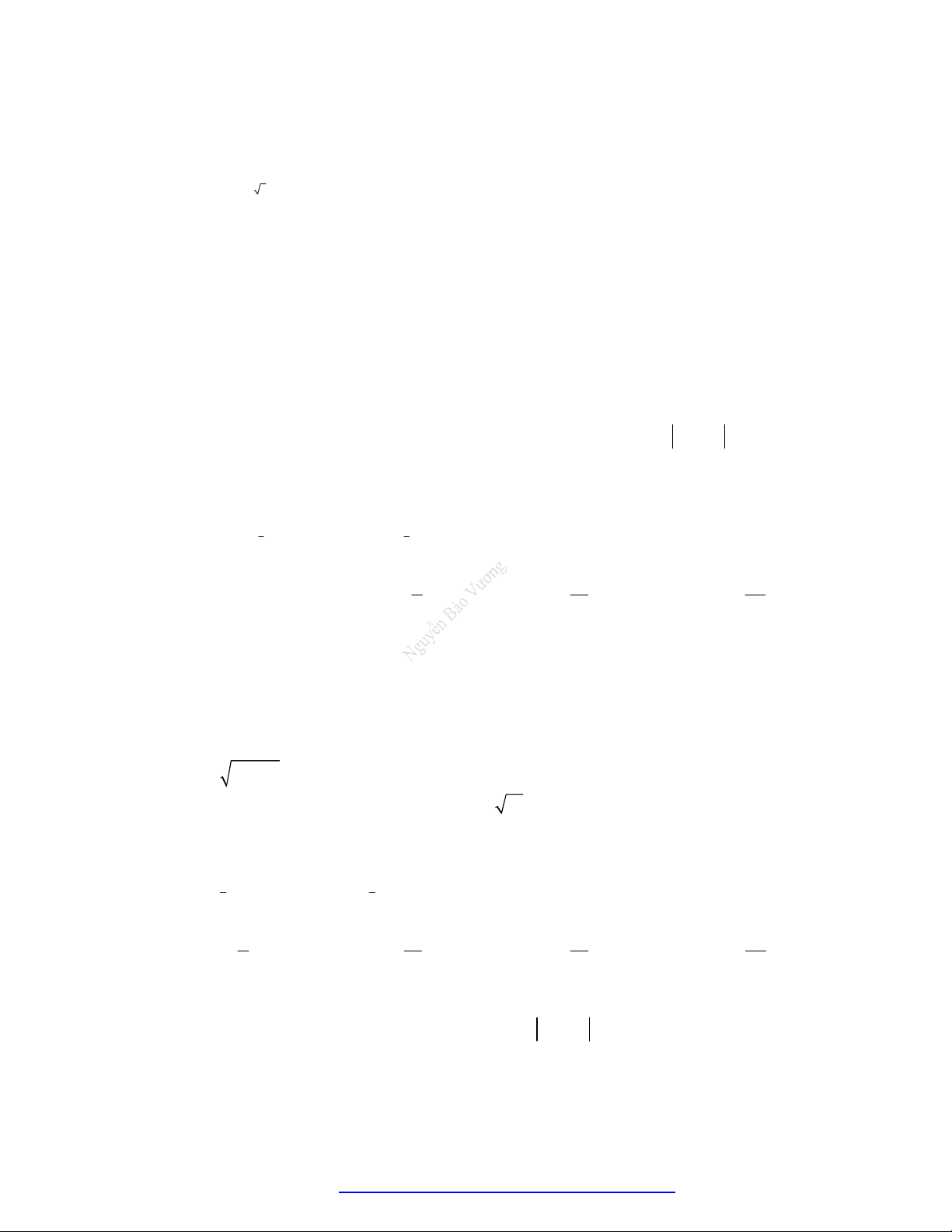
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
0
;2
m
. B.
0
;2
m
. C.
2
;4
m
. D.
0
;4
m
.
Câu
32. (Chuyên KHTN - 2020) Có bao nhiêu giá trị nguyên của tham số
m
để phư
ơng trình
2
2
3 9
l
og log 2 0
x
m x m
c
ó nghiệm
1
;9
x
.
A.
1
. B.
5
. C.
3
. D.
2
.
Câu 33. (Chuyên KHTN - 2020) Có bao nhiêu giá trị nguyên của
m
để phương
trình
2
2
log log 1
mx x
vô nghiệm?
A.
4
. B.
6
. C.
3
. D.
5
.
Câu
34. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Số các giá trị nguyên nhỏ hơn 2020 của tham số
m
để phươ
ng trình
6
4
l
og 2020 log 1010x m x
có nghiệm là
A.
20
20.
B.
2
021.
C.
2
019.
D.
2
022.
Câu
35. (Chuyên Quang Trung - 2020) Xét các số nguyên dương
,a
b
sao
cho phương trình
2
l
n ln 5 0
a
x b x
c
ó hai nghiệm phân biệt
1 2
,x
x
và
phương trình
2
5
log log 0
x
b x a
có
hai
nghiệm phân biệt
3
4
,x
x
sao
cho
1
2 3 4
x
x x x
.
Tìm giá trị nhỏ nhất của
2
3S a b
.
A.
30
. B.
25
. C.
33
. D.
17
.
Câu
36. (Chuyên Thái Bình - 2020) Cho phương trình
2
2
2 2
l
og 5 1 log 4 0
x
m x m m
.
Biết
phương trình có 2 nghiệm phân biệt
1
2
,x
x
thỏa
1
2
1
65
x
x
. G
iá trị của
1
2
x x
bằng
A.
1
6
. B.
1
19
. C.
1
20
. D.
1
59
.
Câu
37.
(Chuyên Thái Nguyên - 2020) Gọi
0
m
là giá trị thực nhỏ nhất của tham số
m
sao cho phương
trình
2
1 1
3 3
1
log 3 5 log 3 1 0
m
x m x m
c
ó nghiệm thuộc
3
;6
.
Khẳng định nào
sau đây là đúng?
A. Không tồn tại
0
m
. B.
0
4
1
;
3
m
. C.
0
1
0
2;
3
m
. D.
0
5
5;
2
m
.
Câu
38. (Chuyên Vĩnh Phúc - 2020) Cho phương trình
l
n 1 2 0
m
x x
. Biết rằng tập hợp tất cả
các giá trị của tham số
m
để phương trình đã cho có hai nghiệm
1
x
,
2
x
thỏa mãn
1
2
0
2 4
x
x
là
khoảng
;a
. Khi đó
a
thuộc khoảng nào dưới
đây?
A.
3,7;3,8
. B.
3,6;3,7
. C.
3,8;3,9
. D.
3,5;3,6
.
Câu 39. (Đại Học Hà Tĩnh - 2020) Tìm tất cả các giá trị của tham số
a
để phương trình
2
3
3 3
l
og log 1 0
x
a x a
c
ó nghiệm duy nhất.
A. Không tồn tại
a
. B.
1
a
hoặ
c
4 2 10
a
.
C.
1
a
. D.
1
a
.
Câu
40. (Sở Ninh Bình 2020) Gọi
0
m
là
giá trị nhỏ nhất của tham số thực
m
sao
cho phương trình
2
1
1
2 2
1
log 2 5 log 2 1 0
m
x m x m
có
nghiệm thuộc khoảng
2
;4
.
Khẳng định
nào dưới đây đúng?
A.
0
4
1
;
3
m
. B.
0
1
0
2
;
3
m
. C.
0
1
6
4
;
3
m
. D.
0
5
5
;
2
m
.
Câu
41.
(Sở Y
ên Bái - 2020) Giả sử phương trình
2
2
2
log ( 2)log 2 0
x m x m
có hai
nghiệm thực
phân biệt
1
2
,x x
thỏa mãn
1
2
6
x x
.
Giá trị biểu thức
1
2
x
x
là
A. 4. B. 3. C. 8. D. 2.
Câu
42. (Bỉm Sơn - Thanh Hóa - 2020) Tìm tất cả các giá trị của
m
để phươ
ng trình
2
2
2
2
l
og log 3
x x m
có nghiệm
1
;8
x
.
A.
2
6
m
B.
3
6
m
C.
6
9
m
D.
2
3
m
.

T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu
43. (Đô Lương 4 - Nghệ An - 2020) Tìm các giá trị thực của tham số
m
để phương
trình
2
3
3
l
og 3log 2 7 0x x m
c
ó hai nghiệm thực
1
x ,
2
x thỏa m
ãn
1
2
3
3 72x x
.
A.
9
2
m
. B.
3m
. C. Không
tồn tại. D.
61
2
m
.
Câu
44. (Đô Lương 4 - Nghệ An - 2020) Số các giá trị nguyên nhỏ hơn
2020
của
tham số
m
để phư
ơng
trình
6
4
l
og 2020 log 1010x m x
có nghiệm là
A.
2022
. B.
2020
. C.
2019
. D.
2
021
.
Câu 45. (Hậu Lộc 2 - Th
anh
Hóa - 2020)
Cho
phương trình
10
log 2log 1 0
x
me
x m mx x
. (
m
l
à tham số ). Có tất cả bao nhiêu giá trị nguyê
n
của
m
để phương
trình đã cho có ba nghiệm thực phân biệt?
A. Vô số. B.
10
. C.
11
. D.
5
.
Câu
46.
(Liên
trường Nghệ An - 2020) Cho phương trình
2
2
2
1
2
2
4 .log 2 3 2 .log 2 2 0
x
m
x x
x x x m
với
m
là tham số. Tổng tất cả các giá trị
của tham số
m
để phươ
ng trình đã cho có ba nghiệm phân biệt là
A.
4
. B.
1
. C.
2
. D.
3
.
Câu
47. (THPT Nguyễn Viết Xuân - 2020) Cho phương trình
2
3
3
l
og 9 5 log 3 10 0x m x m
(với
m
l
à tham số thực). Số giá trị nguyên của tham số
m
để phương
trình đã cho có hai nghiệm phân
biệt thuộc
1
;81
l
à
A.
3
B.
5
C.
4
. D.
2
.
Câu
48. (THPT Nguyễn Viết Xuân - 2020) Cho
,x
y
là hai
số thực dương thỏa mãn
5
4x y
.
Tổng tất
cả giá trị nguyên của tham số
m
để phươ
ng trình
2
2
3
2
l
og 3 1 0
x y m
x x y m
x y
c
ó
nghiệm là
A. 10. B. 5. C. 9. D. 2.
Câu 49.
(Hải
Hậu - Nam Định - 2020) Biết rằng điều kiện cần và đủ của tham số
m
để phương
trình
2
l
og 2 2
x
m
m x
có
nghiệm là
a
m
b
với
,a
b
là
hai số nguyên dương và
7b
.
Hỏ
i
2
a
b b
bằng ba
o nhiêu?
A.
31
. B.
32
. C.
2
1
. D.
23
.
Câu
50. (Lương Thế Vinh - Hà Nội - 2020) Có bao nhiêu giá trị nguyên của tham số
m
để phư
ơng trình
2
2
2
log (4 ) log 2 4 0x m x m có nghiệm thuộc đoạn
1
;8
?
A.
1
.
B.
2
. C.
5
. D.
3
.
Câu
51. (Chuyên Biên Hòa - Hà Nam - 2020) Cho hàm số bậc ba
y
f x
c
ó đồ thị như hình vẽ. Có
bao nhiêu giá trị nguyên của tham số
5
;5m
sao cho phương trình
3
2
2 1
2
2
l
og 1 log 1 2 8 log 1 2 0f x f x m f x m có nghiệm
1;1x
?
A.
7
. B.
5
. C.
6
. D. vô số.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dạn
g 2. Phương trình mũ chứa tham số
Câu 1. (Mã 101 2018) Gọi
S
là
tập hợp tất cả giá trị nguyên của tham số
m
sao
cho phương trình
1
2
16 .4 5 45 0
x
x
m m
c
ó hai nghiệm phân biệt. Hỏi
S
c
ó bao nhiêu phần tử?
A.
6
B.
4
C.
13
D.
3
Câu
2. (Mã 104 2017) Tìm giá trị thực của tham số
m
để phươ
ng trình
1
9
2.3 0
x
x
m
có
hai
nghiệm thực
1
x
,
2
x
t
hỏa mãn
1
2
1
x
x
.
A.
3
m
B.
1
m
C.
6
m
D.
3
m
Câu
3. (Mã 102 2018) Gọi
S
là
tập hợp các giá trị nguyên của tham số
m
s
ao cho phương trình
1
2
25 .5 7 7 0
x
x
m m
có ha
i nghiệm phân biệt. Hỏi
S
c
ó bao nhiêu phần tử.
A.
7
B.
1
C.
2
D.
3
Câu 4. (Mã 103 2018) Gọi
S
là tất cả các giá trị nguyên của tham số
m
sao cho phương trình
1
2
4 .2 2 5 0
x
x
m m
c
ó hai nghiệm phân biệt. Hỏi
S
c
ó bao nhiêu phần tử.
A.
2
B.
1
C.
3
D.
5
Câu
5. (Mã 110 2017) Tìm tất cả các giá trị thực của tham số
m
để phư
ơng trình
1
4
2 0
x
x
m
có
hai nghiệm thực phân biệt
A.
0
;m
B.
;
1
m
C.
0
;1
m
D.
0
;1
m
Câu
6. (Mã 104 2018) Gọi
S
là
tập hợp tất cả các giá trị nguyên của tham số
m
sao
cho phương trình
1
2
9 .3 3 75 0
x
x
m m
c
ó hai nghiệm phân biệt. Hỏi
S
có bao nhi
êu phần tử?
A.
5
B.
8
C.
4
D.
19
Câu
7. (Chuyên Biên Hòa - Hà Nam - 2020) Cho phương trình
0813).32(9
xx
m
(
m
là
tham số
thực). Giá trị của
m
để phư
ơng trình đã cho có hai nghiệm phân biệt
21
, xx
thỏa
mãn
10
2
2
2
1
xx
thuộc khoảng nào
sau đây
A.
10;5
. B.
5;0
. C.
15;10
. D.
;15
.
Câu
8. (Chuyên Lam Sơn Thanh Hóa 2019) Cho phương trình
.16 2 2 .4 3 0 1
x
x
m m m
.
Tập
hợp tất cả các giá trị dương của
m
để phương trình đã cho có hai nghiệm phân biệt là khoảng
;
.a b
Tổng
2T a b
bằng:
A.
1
4
B.
1
0
C.
11
D.
7
Câu 9. (THCS - THPT Nguyễn Khuyến 2019) Phương trình
1
4
3.2 0
x
x
m
có hai nghiệm thực
1 2
,x
x
t
hỏa mãn
1 2
1
x
x
.
Giá trị của
m
thuộc khoảng
nào sau đây?
A.
5
;0
. B.
7
; 5
. C.
0
;1
. D.
5
;7
.
Câu
10. (THPT Lê Xoay Vĩnh Phúc 2019) Với giá trị nào của tham số
m
để phương
trình
1
4
.
2 2 3 0
x
x
m
m
c
ó hai nghiệm
1
2
;x
x
t
hỏa mãn
1
2
4
x x
A.
5
2
m
. B.
2
m
. C.
8
m
. D.
1
3
2
m
.
Câu
11. (THPT Đoàn Thượng - Hải Dương 2019) Phương trình
022.4
1
mm
xx
c
ó hai nghiệm
21
, xx
t
hỏa mãn
3
21
xx
khi
A.
4
m
. B.
3
m
. C.
2
m
. D.
1
m
.
Câu 12. (Chuyên Bắc Giang 2019) Tìm tất cả các giá trị của tham số
m
để phương
trình
2
2 2
2
2 1 2 4 2
4.4 2 2 6 6 3 3 0
x
x x x x x
m m
có hai nghiệm thực phân biệt.
A.
4 3 2 4 3 2
m
B.
4 3 2
m
hoặc
4 3 2
m
C.
1
m
hoặc
1
2
m
D.
1
1
2
m
Câu
13. (Chuyên Vĩnh Phúc 2019) Biết rằng tập các giá trị của tham số
m
để phươ
ng
trình
3
9 2 1 3 1 0
x x
m
m m
c
ó hai nghiệm phân biệt là một khoảng
;a
b
.
Tính tích
.a
b
.
A.
4
B.
3
C.
2
D.
3

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 14. Có
tất cả bao nhiêu số nguyên
m
để phương
trình
4
.2 2 2019 0
x
x
m
m
c
ó hai nghiệm trái
dấu?
A.
10
08
. B.
10
07
. C.
201
8
. D.
201
7
.
Câu 15. Cho
phương trình
4 15 2 1 4 15 6 0
x
x
m
.
Để phương trình có hai nghiệm phân
biệt
1
2
,x
x
t
hỏa mãn
1
2
2
0
x
x
. Ta
có
m
t
huộc khoảng nào?
A.
3
;5
. B.
1
;1
. C.
1
;3
. D.
;
1
.
Câu 16. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Phương trình
2
3 1 2 2 3 4 0
x
x
a
c
ó 2 nghiệm phân biệt
1
2
,x
x
t
hỏa mãn
1
2
2
3
log 3
x x
.
Khi
đó
a
thuộc khoảng
A.
3
;
2
. B.
0
;
. C.
3
;
2
. D.
3
;
2
.
Câu 17. (C
huyên Vĩnh Phúc 2019) Biết rằng tập các giá trị của tham số
m
để phư
ơng
trình
3
9 2 1 3 1 0
x
x
m
m m
có
hai nghiệm phân biệt là một khoảng
;a
b
.
Tính tích
.a
b
.
A.
4
B.
3
C.
2
D.
3
Câu 18. (C
huyên Trần Phú Hải Phòng 2019) Tìm tất cả các giá trị của
mm
để phương
trình
9 2 .3 2 0
x x
m m
c
ó hai nghiệm phân biệt
A.
2
2m
B.
2m
C.
2m
D.
2m
Câu 19. Xá
c định các giá trị của tham số
m
để ph
ương trình
2
9
2 2 6 4 3 4 0
x
x x
m
m m
c
ó hai
nghiệm phân biệt?
A.
2m
.
B.
3m
.
C.
1m
.
D.
2m
.
Câu 20. (KTNL GV TH
PT Lý Thái Tổ 2019) Biết rằng
0
m m
l
à giá trị của tham số
m
sao
cho
phương trình
9 2 2 1 3 3 4 1 0
x
x
m m
có hai nghiệm thực
1
2
,x
x
thỏa
mãn
1
2
2 2 12
x x
.
Khi đó
0
m
thuộc khoảng nào sau
đây
A.
(
3;9)
. B.
9
;+
. C.
1
;3
. D.
-2
;0
.
Câu 21. (Sở Phú T
họ 2019) Có bao nhiêu giá trị nguyên của tham số
m
để phương
trình
16 2 1 4 3 8 0
x
x
m m
c
ó hai nghiệm trái dấu?
A.
6
B.
7
C.
0
D.
3
Câu 22. (C
huyên Thái Nguyên 2019) Gọi
S
là
tập hợp các giá trị thực của tham số
m
để phư
ơng
trình
4
.2 2 1 0
x
x
m
m
c
ó nghiệm. Tập
\ S
c
ó bao nhiêu giá trị nguyên?
A.
1
B.
4
C.
9
D.
7
Câu 23. (THP
T Nghĩa Hưng NĐ- 2019) Cho phương trình
9
2 2 1 3 3 4 1 0
x
x
m
m
có
hai
nghiệm thực
1
2
,x
x
t
hỏa mãn
1
2
2
2 12
x
x
. G
iá trị của
m
thuộc khoảng
A.
9;
. B.
3;9
. C.
2;0
. D.
1;3
.
Câu 24. (Đề Th
am Khảo 2018) Có bao nhiêu giá trị nguyên dương của tham số
m
để ph
ương trình
16 2.12 ( 2).9 0
x
x x
m
c
ó nghiệm dương?
A.
2
B.
4
C.
3
D.
1
Câu 25. (THP
T Ba Đình -2019) Có bao nhiêu giá trị nguyên của tham số
m
để p
hương trình
2
2
4
4
9 4.3 2 1 0
x
x x x
m
c
ó nghiệm?
A.
2
7
. B.
2
5
. C.
23
. D.
24
.
Câu 26. (THP
T-Thang-Long-Ha-Noi- 2019) Gọi
;a
b
là
tập các giá trị của tham số
m
để phương
trình
2
2
8 0
x
x
e
e m
c
ó đúng hai nghiệm thuộc khoảng
0
;ln 5
. Tổng
a
b
l
à
A. 2. B. 4. C.
6
. D.
1
4
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 27. (Sở Bắc Giang 2019) Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình
2 1 2 1 8
x x
m
có hai nghiệm dương phân biệt. Số phần tử của S bằng
A. 8. B. 7. C. 10. D. 9.
Câu 28. (Chuyên Thái Bình 2019) Tìm số giá trị nguyên của tham số
10;10m
để phương
trình
2 2
2
1
10 1 10 1 2.3
x x
x
m
có đúng hai nghiệm phân biệt?
A.
14
. B.
15
. C.
13
. D.
16
.
Câu 29. (Việt Đức Hà Nội 2019) Phương trình
1 1
. 2 1 0
9 3
x x
m m
có nghiệm khi
m
nhận giá trị:
A.
1
2
m
. B.
1
4 2 5
2
m
. C.
4 2 5m
. D.
1
4 2 5
2
m m
.
Câu 30. (THPT Gang Thép Thái Nguyên 2019) Số các giá trị nguyên của tham số
m
để phương trình:
1 .16 2 2 3 .4 6 5 0
x x
m m m
có hai nghiệm trái dấu là
A.
4
. B.
8
. C.
1
. D.
2
.
Câu 31. Phương trình có nghiệm duy nhất. Số giá trị của tham số m thỏa mãn là
A. Vô số B.
1
C.
2
D.
0
Câu 32. (Sở Hà Nội 2019) Cho phương trình
2 .2 .cos 4
x x
m x
, với
m
là tham số. Gọi
0
m
là giá
trị của
m
sao cho phương trình trên có đúng một nghiệm thực. Khẳng định nào sau đây là đúng?
A.
0
5; 1 .m
B.
0
5.m
C.
0
1;0 .m
D.
0
0.m
Câu 33. (HSG Bắc Ninh 2019) Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2 3 3
8 3 .4 3 1 .2 1 1
x x x
x x m x m x
có đúng hai nghiệm phân biệt thuộc
0;10
.
A.
101
B.
100
C.
102
D.
103
Câu 34. (Chuyên Vĩnh Phúc 2019) Tìm tất cả các giá trị thực của tham số
m
để phương trình
3 2 2
2 1 1 1
m m
e e x x x x
có nghiệm.
A.
1
0; ln 2
2
B.
1
; ln 2
2
C.
1
0;
e
D.
1
ln 2;
2
Câu 35. (SP Đồng Nai - 2019) Gọi
A
là tập tất cả các giá trị thực của tham số
m
sao cho tập nghiệm của
phương trình
.2 1 . 2 1
x x
x x x m m
có hai phần tử. Số phần tử của
A
bằng
A. 2. B. 3. C. 1. D. Vô số.
Câu 36. (Nguyễn Huệ- Ninh Bình- 2019)Giá trị của
m
để phương trình
1
4 2 0
x x
m
có nghiệm
duy nhất là:
A.
2m
. B.
0m
. C.
1m
. D.
1m
.
Câu 37. (THPT Thăng Long 2019) Gọi
;a b
là tập hợp tất cả các giá trị thực của tham số
m
để phương
trình
2
2e 8e 0
x x
m
có đúng hai nghiệm thuộc khoảng
0;ln5
. Giá trị của tổng
a b
là
A.
2
. B.
4
. C.
6
. D.
14
.
Câu 38. (Chuyên Long An-2019) Giá trị của tham số
m
thuộc khoảng nào sau đây để phương trình
1
4 .2 2 0
x x
m m
có hai nghiệm
1
x ,
2
x thoả mãn
1 2
3x x .
A.
9
;5
2
m
. B.
2; 1m
. C.
1;3m
. D.
3;5m
.
Câu 39. (THPT Quỳnh Lưu- Nghệ An- 2019) Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
sao cho phương trình
1 2
16 .4 5 44 0
x x
m m
có hai nghiệm đối nhau. Hỏi
S
có bao nhiêu
phần tử?
A.
2
. B.
0
. C.
1
. D.
3
.
4 1 2 . .cos( )
x x
m x
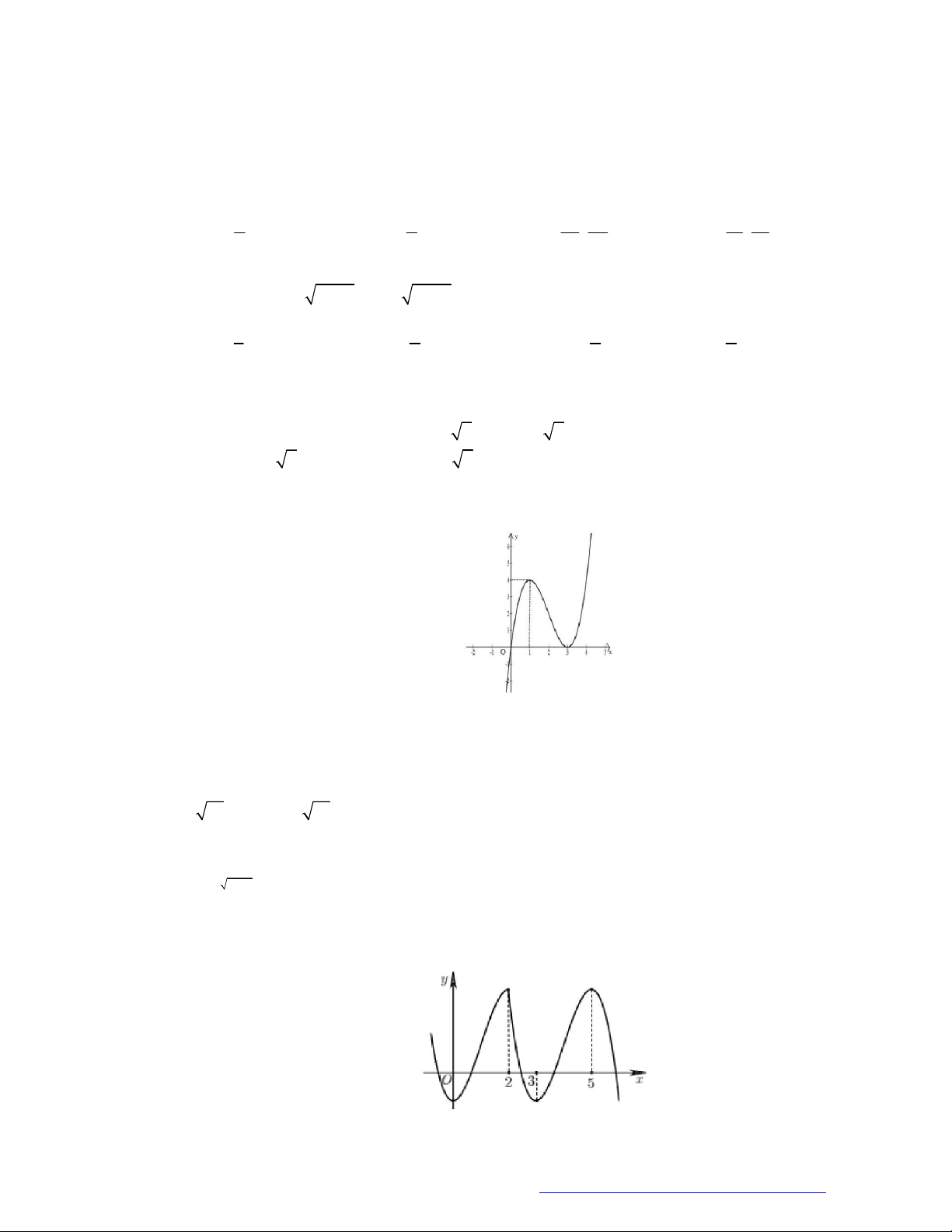
T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu
40. (THPT Hai Bà Trưng - Huế - 2019) Gọi
S
là
tập hợp tất cả các giá trị nguyên của tham số
m
để phương
trình
4
2 .2 6 0
x
x
m
m
có
hai nghiệm thực
1
2
,x
x
sa
o cho
1
2
3x
x
.
Tập hợp
S
có
bao nhiêu phần tử?
A. Vô số. B.
3
. C.
2
. D.
1
.
Câu
41. (THPT Minh Khai - 2019) Giá trị thực của tham số
m
để phươ
ng trình
4
2 3 .2 64 0
x
x
m
c
ó hai nghiệm thực
1
x
,
2
x
t
hỏa mãn
1
2
2
2 24x x
thuộc
khoảng
nào sau đây?
A.
3
0
;
2
. B.
3
;
0
2
. C.
21
29
;
2 2
. D.
11
19
;
2 2
.
Câu
42. (Chuyên - Vĩnh Phúc - 2019) Tìm tất cả các giá trị thực của tham số
m
để phư
ơng trình
3
2 2
2
1 1 1
m
m
e
e x x x x
c
ó nghiệm.
A.
1
0
;
e
. B.
1
0
; ln 2
2
. C.
1
;
ln 2
2
. D.
1
l
n 2;
2
.
Câu 43. (Chuyên Quang Trung- Bình Phước 2019) Tìm tất cả các giá trị thực của tham số
m
để
phương trình
4
1 .2 2 0
x
x
m
c
ó hai nghiệm
1
2
,x
x thoả mãn
1
2
1x
x .
A.
Rm
. B.
1
2 2; 1 2 2m m
.
C.
1
2 2m . D.
1
2 2m
.
Câu
44. (Chuyên Quang Trung- Bình Phước 2019) Cho hàm số
y
f x
li
ên tục trên
và
có đồ thị
như hình vẽ
Tập hợp tất cả các giá trị thực của
m
để p
hương trình
2
x
f
e m
c
ó đúng 2 nghiệm thực là
A.
0
;4
. B.
0
;4
. C.
0
4;
. D.
4
;
.
Câu
45. (Chuyên Thái Bình - 2019) Tìm số giá trị nguyên của tham số
1
0;10m
để phư
ơng trình
2
2
2
1
10 1 10 1 2.3
x
x
x
m
có
đúng hai nghiệm phân biệt.
A.
14
. B.
1
5
. C.
1
3
. D.
1
6
.
Câu
46. (Thi thử cụm Vũng Tàu - 2019) Tổng tất cả các giá trị nguyên của
m
để phươ
ng trình
3
3
3 3 2 3
3
9 24 .3 3 1
x
m x x x
x
x x m
c
ó 3 nghiệm phân biệt.
A.
3
4
. B.
2
7
. C.
3
8
. D.
4
5
.
Câu 47. (Chuyên ĐH Vinh- 2019) Cho số thực
m
và hàm số
y f x
có đồ thị như hình vẽ dưới đây.
Phương trình
2 2
x
x
f m
c
ó nhiều nhất bao nhiêu nghiệm phân biệt thuộc đoạn
1;2
?
A.
2
. B.
3
. C.
4
. D.
5
.
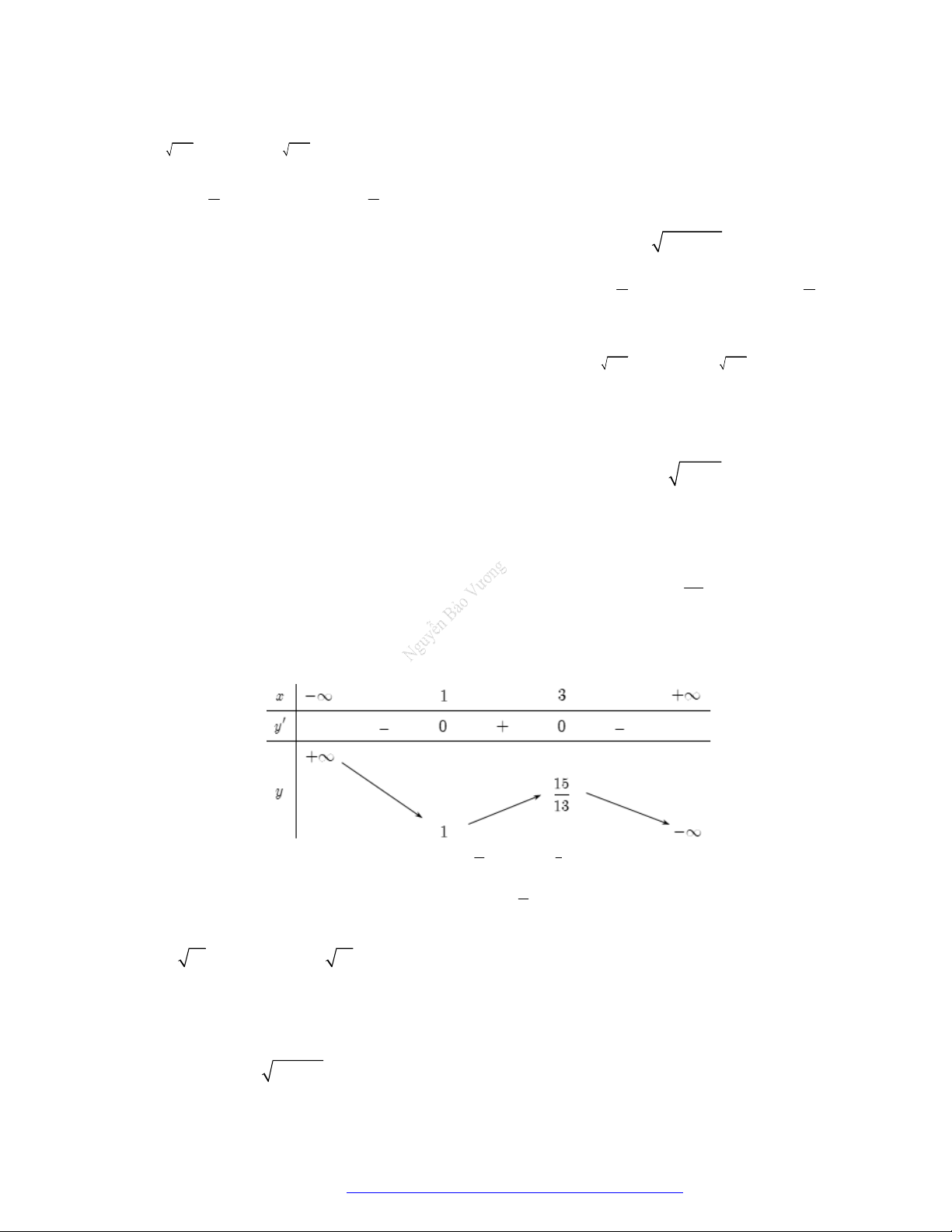
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 48. (THPT Thuận Thành 3 - Bắc Ninh 2019) Gọi
S
là tổng các giá trị nguyên của tham số
m
để
phương trình
3 2
4 7 2 6
x x
m m
có nghiệm
1;3x
. Chọn đáp án đúng.
A.
35S
. B.
20S
. C.
25S
. D.
21S
.
Câu 49. (Chuyên Bắc Giang 2019) Tập các giá trị của
m
để phương trình
2 2
1 1 1 1
4 2 2 2 1 0
x x
m m
có nghiệm là
A.
9
;
2
. B.
9
4;
2
. C.
;4
. D.
4;
.
Câu 50. Cho hàm số
4 7
3 1 .2 – 6 3
x x
f x x x
, khi phương trình
2
7 4 6 9 3 1 0f x x m
có
số nghiệm nhiều nhất thì giá trị nhỏ nhất của tham số
m
có dạng
a
b
(trong đó
a
,
b
và
a
b
là
phân số tối giản). Tính
T a b
.
A.
7T
. B.
11T
. C.
8T
. D.
13T
.
Câu 51. Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2 2
1 1 1 1
9 3 .3 2 1 0
x x
m m
có nghiệm thực?
A.
5
. B.
7
. C. Vô số. D.
3
.
Câu 52. (THPT Thăng Long 2019) Cho hệ phương trình
2 2
2 2 2
1
2 1 2 .2 . 1
x y y
x y
x y
m y
,
m
là tham
số. Gọi
S
là tập các giá trị
m
nguyên để hệ
1
có một nghiệm duy nhất. Tập
S
có bao nhiêu
phần tử?
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 53. Cho
,a b
là các số thực thỏa mãn
0a
và
1a
, biết phương trình
1
2cos
x
x
a bx
a
có
7
nghiệm phân biệt. Tìm số nghiệm thực phân biệt của phương trình
2
2 cos 2 1 0
x x
a a bx
.
A.
28
. B.
14
. C.
0
. D.
7
.
Câu 54. Cho hàm số bậc ba
( )y f x
có bảng biến thiên như sau
Giá trị lớn nhất của
m
để phương trình
3 2
13 3
2 ( ) ( ) 7 ( )
2 2
f x f x f x
e m
có nghiệm trên đoạn
0;2
là
A.
4
e
. B.
3
e
. C.
15
13
e . D.
5
e
.
Câu 55. (Hoàng Hoa Thám - Hưng Yên 2019) Cho phương trình
4 15 2 1 4 15 6 0
x x
m
(
m
là tham số ). Biết phương trình có hai nghiệm phân
biệt
1 2
,x x
thỏa mãn
1 2
2 0x x
. Khi đó
m
thuộc khoảng nào sau đây?
A.
3;5
. B.
1;1
. C.
1;3
. D.
; 1
.
Câu 56. (THPT Minh Khai 2019) Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để phương
trình
5 10 25 4
x x
m
có nghiệm duy nhất. Số tập con của
S
là
A.
3
. B.
4
. C.
16
. D.
15
.
Câu 57. (Sở Quảng Trị 2019) Tìm tập hợp tất cả các giá trị tham số
m
để phương trình
2 2
2 1 2 2
4 .2 3 2 0
x x x x
m m
có 4 nghiệm phân biệt.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
A.
1;
. B.
;1 2;
. C.
2;
. D.
2;
.
Câu 58. Cho phương trình:
3 2 2
2 3
2 2 3 0
x x x m x x
x x m
. Tập các giá trị để bất phương trình có ba
nghiệm phân biệt có dạng
;a b
. Tổng
2a b
bằng:
A.
1.
B.
2.
C.
4.
D.
0.
Câu 59. (Chuyên ĐH Vinh- 2019) Có bao nhiêu số nguyên
m
để phương trình
2 2
4
9.3 4 2 1 3 3 3 1 0
x x
m x x m
có đúng 3 nghiệm thực phân biệt?
A. Vô số. B.
3
. C.
1
. D.
2
.
Câu 60. Có bao nhiêu giá trị nguyên của tham số
2019;2019
m
để phương trình
2 1 2 1
2019 0
1 2
x
x mx m
x x
có đúng 3 nghiệm thực phân biệt?
A.
4038
. B.
2019.
C.
2017.
D.
4039
.
Câu 61. (Chuyên Hưng Yên - 2020) Gọi
S
là tập hợp các giá trị của tham số
m
sao cho hai phương
trình
2
2 1 3
m
x
và
2
3 2 1
x
m x x
có nghiệm chung. Tính tổng các phần tử của
S
.
A.
6
B.
3
. C.
1
. D.
5
2
.
C
ÂU
62. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Giá trị của tham số
m
để phương trình
1
4 .2 2 0
x x
m m
có hai nghiệm
1
,x
2
x
thỏa mãn
1 2
3
x x
là
A.
2
m
. B.
3
m
. C.
4
m
. D.
1
m
.
Câu 63.
(Chuyên Chu Văn An - 2020) Tìm
m
để phương trình
1
4 2 0
x x
m
có hai nghiệm trái dấu.
A.
0
m
. B.
1
m
. C.
1 1
m
. D.
0 1
m
.
Câu 64. (Chuyên Phan Bội Châu - Nghệ An - 2020) Có bao nhiêu giá trị nguyên dương của tham số
m
để phương trình
1
9 2.6 3 .4 0
x x x
m
có hai nghiệm phân biệt?
A.
35
. B.
38
. C.
34
. D.
33
.
Câu 65. (ĐHQG Hà Nội - 2020) Gọi
S
là tập hợp các số nguyên
m
sao cho phương trình
1 2
4 .2 3 500 0
x x
m m
có 2 nghiệm phân biệt. Hỏi tập
S
có bao nhiêu phần tử
A.
1
. B.
4
. C.
3
. D.
2
.
Câu 66. (ĐHQG Hà Nội - 2020) Tìm điều kiện của tham số
a
để phương trình sau có nghiệm:
2 2
1 1 1 1
9 2 .3 2 1 0.
x x
a a
Hãy chọn đáp án đúng nhất?
A.
64
4
7
a
. B.
64
2
9
a
. C.
50
3
3
a
. D.
50
1
3
a
.
Câu 67. (ĐHQG Hà Nội - 2020) Điều kiện của
m
để hệ bất phương trình
2 1 2 1
2
7 7 2020 2020
2 2 3 0
x x x
x
x m x m
có nghiệm là :
A.
3.
m
B.
2 1.
m
C.
1 2.
m
D.
2.
m
Câu 68. (Sở Phú Thọ - 2020) Cho phương trình
2 2
1
16 2.4 10
x x
m
(
m
là tham số). Số giá trị nguyên
của tham
10;10
m
để phương trình đã cho có đúng hai nghiệm thực phân biệt là
A.
7
. B.
9
. C.
8
. D.
1
.
Câu 69. (Sở Hà Tĩnh - 2020) Gọi
S
là tập nghiệm của phương trình
2
2 2 3 0
x
x
x m
(với
m
là
tham số thực). Có tất cả bao nhiêu giá trị nguyên của
2020;2020
m
để tập hợp
S
có hai phần
tử?
A. 2094. B. 2092. C. 2093. D. 2095.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 70. (Sở Ninh Bình 2020) Cho hai số thực bất kỳ
1
a
,
1b
. Gọi
1
x
,
2
x
là hai nghiệm phương trình
2
1
1
x x
a b
. Trong trường hợp biểu thức
2
1 2
1 2
1 2
6 6
x x
S x x
x x
đạt giá trị nhỏ nhất, khẳng định
nào dưới đây đúng?
A.
3
3
a b
. B.
3
6
a b
. C.
3
1
3
a b
. D.
3
1
6
a b
.
Câu 71. (Sở Bắc Ninh - 2020) Gọi
S
là tập tất cả các giá trị của
m
để phương trình
1 2
16 6.8 8.4 .2 0
x x x x
m m
có đúng hai nghiệm phân biệt. Khi đó
S
có
A.
4
tập con. B. Vô số tập con. C.
8
tập con. D.
16
tập con.
Câu 72. (Lý Nhân Tông - Bắc Ninh - 2020) Tìm tập hợp các giá trị của tham số thực
m
để phương trình
6 3 2 0
x x
m m
có nghiệm thuộc khoảng
0;1
.
A.
3;4 .
B.
2;4 .
C.
2;4 .
D.
3;4 .
Câu 73. (Nguyễn Huệ - Phú Yên - 2020) Có bao nhiêu giá trị nguyên
2019;2020
m
sao cho hệ
phương trình sau có nghiệm
2 2 2
2 2 2 2
4 9.3 4 9 .7
2 1 2 2
x y x y y x
x y x m
?
A.
2017
. B.
2021
. C.
2019
. D.
2020
.
Câu 74. (Nguyễn Trãi - Thái Bình - 2020) Tính tổng tất cả các nghiệm của phương trình
sin( )
4
tan
x
e x
thuộc đoạn
0;50
A.
2671
2
. B.
1853
2
. C.
2475
2
. D.
2653
2
.
Câu 75. (Trần Phú - Quảng Ninh - 2020) Tìm tập hợp các giá trị của tham số
m
để phương trình (ẩn
x
):
2
2 2
log log
2
3 2 3 .3 3 0
x x
m m
có hai nghiệm phân biệt thỏa mãn:
1 2
2
x x
.
A.
1; \ 0
. B.
0;
. C.
\ 1;1
. D.
1;
.
Dạng 3. Phương trình kết hợp của mũ và logarit chứa tham số
Câu 1. (Mã 103 -2019) Cho phương trình
2
3 3
2log log 1 5 0
x
x x m
(
m
là tham số thực). Có tất
cả bao nhiêu giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt?
A. Vô số. B.
124.
C.
123.
D.
125.
Câu 2. (Mã 102 - 2019) Cho phương trình
2
2 2
2log 3log 2 3 0
x
x x m
(
m
là tham số thực). Có
tất cả bao nhiêu giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân
biệt?
A. vô số. B. 81. C. 79. D. 80.
Câu 3. (Mã 104 2019) Cho phương trình
2
3 3
2log log 1 4 0
x
x x m (
m
là tham số thực). Có tất
cả bao nhiêu giá trị nguyên dương của
m
để phương trình có đúng hai nghiệm phân biệt?
A.
64
. B. Vô số. C.
62
. D.
63
.
Câu 4. (Mã 101 2019) Cho phương trình
2
2 2
4log log 5 7 0
x
x x m
(
m
là tham số thực). Có tất
cả bao nhiêu giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt?
A.
49
. B.
47
. C. Vô số. D.
48
.
Câu 5. (Mã 102 2018) Cho phương trình
3
3 log ( )
x
m x m
với
m
là tham số. Có bao nhiêu giá trị
nguyên của
15;15
m
để phương trình đã cho có nghiệm?
A.
15
B.
16
C.
9
D.
14

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 6. (Mã 101 2018) Cho phương trình
5
5 log
x
m x m
với
m
là tham số. Có bao nhiêu giá trị
nguyên của
20;20
m
để phương trình đã cho có nghiệm?
A.
19
B.
9
C.
21
D.
20
Câu 7. (Mã 103 -2018) Cho phương trình
7
7 log
x
m x m
với
m
là tham số. Có bao nhiêu giá trị
nguyên của
25;25
m
để phương trình đã cho có nghiệm?
A.
9
B.
25
C.
24
D.
26
Câu 8. Cho phương trình
1
5
5 log 0
x
m x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
tham số
20;20
m
để phương trình đã cho có nghiệm thực?
A.
20
. B.
21
. C.
18
. D.
19
.
Câu 9. (Mã 104 2018) Cho phương trình
2
2 log
x
m x m
với
m
là tham số. Có bao nhiêu giá trị
nguyên của
18;18
m
để phương trình đã cho có nghiệm?
A.
9
B.
19
C.
17
D.
18
Câu 10. (Chuyên Nguyễn Du-ĐăkLăk 2019) Cho phương trình
5
5 log
x
m x m
. Có bao nhiêu giá
trị
m
nguyên trong khoảng
20;20
để phương trình trên có nghiệm?
A.
15
. B.
19
. C.
14
. D.
17
.
Câu 11. Tổng tất cả các giá trị của tham số
m
để phương trình
2 2
2
4 5 2
4 6
2 log 1
x x m
x x
m
có đúng 1
nghiệm là
A.
2
. B.
1
. C.
4
. D.
0
.
Câu 12. Tổng tất cả các giá trị của tham số
m
để phương trình
2
2
2 1 2
2 3
3 log 2 2
x x x m
x x
x m
có
đúng ba nghiệm phân biệt là:
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 13. (Chuyên Lam Sơn - 2020) Có bao nhiêu giá trị nguyên của tham số
a
trên đoạn
10;10
để
phương trình
ln 1 ln 1
x a x
e e x a x
có nghiệm duy nhất.
A.
2
. B.
10
. C.
1
. D.
20
Câu 14. (Chuyên Sơn La - 2020) Có bao nhiêu giá trị nguyên của tham số
m
thuộc
2020;2020
để
phương trình
ln 2 2
x
e x m m
có nghiệm?
A.
2019
. B.
2020
. C.
2021
. D.
4039
.
Dạng 4. Phương trình mũ – logarit chứa nhiều ẩn
Câu 1. (Đề Minh Họa 2020 Lần 1) Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
0 2020
x
và
3
log 3 3 2 9
y
x x y
?
A.
2019
. B.
6
. C.
2020
. D.
4
.
Câu 2. (Đề Tham Khảo 2020 Lần 2) Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
2 2
3 4
log ( ) log
x y x y
?
A.
3
. B.
2
. C.
1
. D. Vô số.
Câu 3. (Mã 103 - 2020 Lần 2) Có bao nhiêu cặp số nguyên dương
;m n
sao cho
10
m n
và ứng với
mỗi cặp
;m n
tồn tại đúng
3
số thực
1;1
a
thỏa mãn
2
2 ln 1
m
a n a a
?
A.
7
. B.
8
. C.
10
. D.
9
.
Câu 4. (Mã 101 - 2020 Lần 2) Có bao nhiêu cắp số nguyên dương
,m n
sao cho
14
m n
và ứng với
mỗi cặp
,m n
tồn tại đúng ba số thực
1;1
a
thỏa mãn
2
2 ln 1
m
a n a a
?
A.
14
. B.
12
. C.
11
. D.
13
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 5.
(Mã 104 - 2020 Lần 2) Có bao nhiêu cặp số nguyên dương
( , )m n
sao cho
12
m n
và ứng với
mỗi cặp
( , )m n
tồn tại đúng 3 số thực
( 1,1)
a
thỏa mãn
2
2 ln( 1)
m
a n a a
?
A.
12
. B.
10
. C.
11
. D.
9
.
Câu 6. (Chuyên Biên Hòa - Hà Nam - 2020) Có tất cả bao nhiêu giá trị thực của tham số
1;1
m
sao
cho phương trình
2
2 2
2
1
log log 2 2 2
m
x y x y
có nghiệm nguyên
;x y
duy nhất?
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 7. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Có bao nhiêu số nguyên
y
để tồn tại số thực
x
thỏa mãn
2 2
11 4
log 3x 4 log
y x y
?
A.
3
B.
2
C.
1
D. vô số.
Câu 8. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Có bao nhiêu cặp số thực
;x y
thỏa mãn
đồng thời các điều kiện
2
3
2 3 log 5
4
3 5
x x
y
và
2
4 1 3 8 ?
y y y
A.
1
. B.
3
. C.
4
. D.
2
.
Câu 9. (Chuyên Bến Tre - 2020) Giả sử
0 0
;x y
là một nghiệm của phương trình
1 1 1
4 2 sin 2 1 2 2 2sin 2 1
x x x x x
y y
. Mệnh đề nào sau đây đúng?
A.
0
7
x
. B.
0
2 4
x
. C.
0
4 7
x
. D.
0
5 2
x
.
Câu 10. (Chuyên Lào Cai - 2020) Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
0 4000
x
và
5
5
5 25 2 log 1 4
y
y x x
?
A.
3
. B.
2
. C.
4
. D.
5
.
Câu 11. (Chuyên Lê Hồng Phong - Nam Định - 2020) Có bao nhiêu bộ
( ; )x y
với
,x y
nguyên và
1 , 2020
x y
thỏa mãn
3 2
2 2 1
2 4 8 log 2 3 6 log
2 3
y x
xy x y x y xy
y x
?
A.
2017
. B.
4034
. C.
2
. D.
2017.2020
.
Câu 12. (Chuyên Sơn La - 2020) Cho x là số thực dương và y là số thực thỏa mãn
1
2
2 log 14 ( 2) 1
x
x
y y
. Giá trị của biểu thức
2 2
2020
P x y xy
bằng
A. 2022. B. 2020. C. 2021. D. 2019.
Câu 13. (Sở Hưng Yên - 2020) Cho phương trình
2
2 2 2
3
log 3 6 6 3 2 1
y
x x y x x
. Hỏi có bao
nhiêu cặp số
;x y
và
0 2020 ; y
x
thỏa mãn phương trình đã cho?
A.
5
. B.
6
. C.
7
. D.
4
.
Câu 14. (Sở Phú Thọ - 2020) Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
2 2021
x
và
1
2
2 log 2 2
y y
x x y
?
A.
2020
. B.
9
. C.
2019
. D.
10
.
Câu 15. (Sở Bắc Ninh - 2020) Có bao nhiêu cặp số nguyên dương
;x y
thảo mãn
2 3
3 3 1 1 3
x y x y
x x x
, với
2020
x
?
A.
13
. B.
15
. C.
6
. D.
7
.
Câu 16. (Sở Bình Phước - 2020) Biết
,a b
là các số thực sao cho
3 3 3 2
.10 .10 ,
z z
x y a b đồng thời
, ,x y z
là các số các số thực dương thỏa mãn
log
x y z
và
2 2
log 1.
x y z
Giá trị của
2 2
1 1
a b
thuộc khoảng
A.
(1;2)
. B.
(2;3)
. C.
(3;4)
. D.
(4;5)
.
Câu 17. (Đặng Thúc Hứa - Nghệ An - 2020) Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
0 2020
y
và
3
3
3 3 6 9 log
x
x y y
.

T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
A.
2020
B.
9
. C.
7
. D.
8
.
Câu 18. (Đô Lương 4 - Nghệ An - 2020) Giả sử
,a b
l
à các số thực sao cho
3
3
3
2
.10
.10
z
z
x
y a b đúng
với mọi các số thực dương
,
,x y z
thỏa
mãn
log( )x y z
và
2
2
l
og( ) 1x y z . Giá trị của
a
b
bằ
ng
A.
25
2
. B.
3
1
2
. C.
31
2
.
D.
29
2
.
Câu
19. (Kim Liên - Hà Nội - 2020) Có bao nhiêu số hữu tỉ
a
t
huộc đoạn
1
;1
sa
o cho tồn tại số thự
c
b
thỏa mãn
2
2
2
2
4 1 1
log 1 2
4 1 2 1 2 4 2
a
a
a a a a
a
b b
.
A.
0
. B.
3
. C.
1
. D. Vô số.
Câu 20. (Lê Lai - Thanh Hóa - 2020) Có bao nhiêu cặp số nguyên thoả mãn
và
?
A. 19. B. 6 C. 10. D. 41.
Câu 21. (Thanh Chương 1 - Nghệ An - 2020) Cho các số thực
x
,
y
thỏa
mãn
1x
,
1y
và
3
3 3 3 3
9
l
og log 6 2log log 2 3 log 2
2
x y x y xy
.
Giá trị của biểu thức
2P
x y
gần
với số nào
nhất trong các số sau
A.
7
. B.
8
. C.
1
0
. D.
9
.
Câu
22. (Tiên Lãng - Hải Phòng - 2020) Có bao nhiêu cặp số nguyên dương
;x
y
với
2
020x
thỏa
m
ãn
3
2
3 3 1 9 log 2 1
y
x
y x
A.
1010
. B.
2020
. C.
3
. D.
4
.
;x
y
0; 20 20
x y x
2
2
2
log 2 2 3 0
x y x y xy x y

T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM
Dạng 1. Phương trình logarit
Phương trình logarit
+ Nếu
0
, 1: log
b
a
a
a x b x a
+ Nếu
0, 1: log log
a
a
a a f x g x f x g x
+ Nếu
0, 1: log
g
x
a
a a f x g x f x a
(mũ hóa)
Dạng 1.1 Phương trình cơ bản
Câu 1. (Đề Minh Họa 2020 Lần 1) Nghiệm của phương trình
3
log 2 1 2x
là
:
A.
3x
. B.
5x
. C.
9
2
x
. D.
7
2
x
.
Lờ
i giải
Chọn B
Điều
kiện:
1
2
1 0
2
x x
Ta
có
3
2
1
l
og 2 1 2
2
2 1 3
x
x
x
1
2
5
x
x
5x
.
Vậy phươ
ng trình có nghiệm
5x
.
Câu
2. (Mã 101 - 2020 Lần 1) Nghiệm của phương trình
3
l
og 1 2x
là
A.
8x
. B.
9x
. C.
7x
. D.
10x
.
Lờ
i giải
Chọn D.
TX
Đ:
1
;D
2
3
l
og 1 2 1 3 10x x x
Câu
3. (Mã 102 - 2020 Lần 1) Nghiệm của phương trình là
A. . B. . C. . D. .
Lờ
i giải
Chọn C
Ta
có .
Câu 4. (Mã 103 - 2020 Lần 1) Nghiệm của phương trình
2
l
og 2 3x
là:
A.
6x
. B.
8x
. C.
1
1x
. D.
1
0x
.
Lờ
i giải
Chọn D
Điều
kiện:
2
0 2x x
.
P
HƯƠNG TRÌNH MŨ - LOGARIT
Ch
uyên đề 19
2
l
og 1 3
x
1
0
x
8
x
9
x
7
x
2
log 1 3
x
3
1
0
1 2
x
x
1
9
x
x
9
x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
log 2 3 2 8 10
x x x
(thỏa).
Vậy phương trình có nghiệm
10
x
.
Câu 5. (Mã 104 - 2020 Lần 1) Nghiệm của phương trình
3
log 2 2
x
là
A.
11
x
. B.
10
x
. C.
7
x
. D.
8
.
Lời giải
Chọn A
Điều kiện:
2
x
Phương trình tương đương với
2
2 3 11
x x
Câu 6. (Mã 102 - 2020 Lần 2) Nghiệm của phương trình
2
log 9 5
x
là
A.
41
x
. B.
23
x
. C.
1x
. D.
16
x
.
Lời giải
Chọn B
ĐK:
9
x
Ta có:
5
2
log 9 5 9 2
x x
23
x
.
Câu 7. (Mã 103 - 2020 Lần 2) Nghiệm của phương trình
2
log 6 5
x
là:
A.
4
x
. B.
19
x
. C.
38
x
. D.
26
x
.
Lời giải
Chọn D
Điều kiện
6 0 6
x x
Ta có:
2
log 6 5
x
5
2 2
log 6 log 2
x
6 32
x
32 6
x
26x T
M
Vậy nghiệm của phương trình:
26
x
Câu 8. (Mã 104 - 2020 Lần 2) Nghiệm của phương trình
2
log 7 5
x
là
A.
18
x
. B.
25
x
. C.
39
x
. D.
3
x
.
Lời giải
Chọn B
5
2
log 7 5 7 2
x x
25
x
.
Câu 9. (Mã 101 - 2020 Lần 2) Nghiệm của phương trình
2
log ( 8) 5
x
bằng
A.
17
x
. B.
24
x
. C.
2
x
. D.
40
x
.
Lời giải
Chọn B
Ta có
5
2
log ( 8) 5 8 2 24
x x x
.
Câu 10. (Đề Tham Khảo 2019) Tập nghiệm của phương trình
2
2
log 2 1
x x
là :
A.
0
B.
0;1
C.
1;0
D.
1
Lời giải
Chọn B

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
2 2
2
0
log 2 1 2 2
1
x
x x x x
x
Câu 11. (Đề Minh Họa 2017) Giải phương trình
4
log ( 1) 3.
x
A.
65
x
B.
80
x
C.
82
x
D.
63
x
Lời giải
Chọn A
ĐK:
1 0 1 x x
Phương trình
4
log 1 3
x
3
1 4 65
x x
.
Câu 12. (Mã 110 2017) Tìm nghiệm của phương trình
2
log 1 2
x
.
A.
5
x
. B.
3
x
. C.
4
x
. D.
3
x
.
Lời giải
Chọn B
Ta có
2
log 1 2
x
1 4
x
3
x
.
Câu 13. (Mã 102 2018) Tập nghiệm của phương trình
2
2
log 1 3
x
là
A.
10; 10
B.
3;3
C.
3
D.
3
Lời giải
Chọn B
2
2
log 1 3
x
2
1 8
x
2
9
x
3
x
.
Câu 14. (Mã 104 2017) Tìm nghiệm của phương trình
2
log 5 4
x
.
A.
11
x
B.
13
x
C.
21
x
D.
3
x
Lời giải
Chọn C
ĐK:
5 0 5
x x
Khi đó
2
log 5 4
x
5 16 21
x x
.
Câu 15. (Mã 103 2018) Tập nghiệm của phương trình
2
3
log ( 7) 2
x
là
A.
4
B.
4
C.
{ 15; 15}
D.
{ 4;4}
Lời giải
Chọn D
2
3
log ( 7) 2
x
2
7 9
x
4
4
x
x
Câu 16. (Mã 105 2017) Tìm nghiệm của phương trình
25
1
log 1
2
x
.
A.
6x
B.
4x
C.
23
2
x
D.
6x
Lời giải
Chọn B
Điều kiện:
1x
Xét phương trình
25 5
1
log 1 log 1 1
2
x x
1 5 4x x
.
Câu 17. (Chuyên Vĩnh Phúc 2019) Phương trình
3
log 3 2 3
x
có nghiệm là

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
25
3
x
. B.
87x
. C.
29
3
x
. D.
11
3
x
.
Lời giải
Chọn C
Ta có:
3
3
29
log 3 2 3 3 2 3 3 29
3
x x x x
.
Vậy phương trình đã cho có nghiệm là
29
3
x
.
Câu 18. (THPT Ba Đình 2019) Tập nghiệm của phương trình là
A. . B. . C. . D. .
Lời giải
ĐKXĐ:
2
3 0x x x
Ta có:
Vậy tập nghiệm của phương trình là .
Câu 19. (THPT Cù Huy Cận 2019) Tập nghiệm của phương trình
2
3
log 3 1x x
là:
A.
1;0
. B.
0;1
. C.
0
D.
1
.
Lời giải
2 2 2
3
0
log 3 1 3 3 0
1
x
x x x x x x
x
Câu 20. (Chuyên Vĩnh Phúc 2019) Phương trình
3
log 3 2 3x
có nghiệm là:
A.
25
3
x
B.
87
C.
29
3
x
D.
11
3
x
Lời giải
Điều kiện:
2
3
x
.
Phương trình tương đương
3
3 2 3x
29
3
x
(nhận).
Vậy
29
3
S
.
Câu 21. (Chuyen Phan Bội Châu Nghệ An 2019) Tập nghiệm của phương trình
2
log 2 2 1x x
là
A.
. B.
{ 2;4}
. C.
{4}
. D.
{ 2}
.
Lời giải
Ta có
2 2 2
2
log 2 2 1 2 2 10 2 8 0
4
x
x x x x x x
x
Câu 22. (Chuyên Lương Thế Vinh Đồng Nai 2019) Cho phương trình
2
2 2
log (2 1) 2log ( 2).x x
Số
nghiệm thực của phương trình là:
A.
1.
B.
0.
C.
3.
D.
2.
Lời giải
Điều kiện:
2.x
2
3
log 3 1
x x
1
0;1
1;0
0
2 2
3
0
log 3 1 3 3
1
x
x x x x
x
0;1
S

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Phương trình đã cho tương đương với:
2 2
2log (2 1) 2log ( 2)
x x
2 1 2 1
x x x
Nghiệm này không thỏa mãn điều kiện của phương trình nên phương trình đã cho vô nghiệm.
Câu 23. (Chuyên Sơn La 2019) Tập nghiệm của phương trình
2
3
log 2 1
x x
là
A.
1; 3
. B.
1;3
. C.
0
. D.
3
.
Lời giải
Phương trình
2 2 1 2
3
1
log 2 1 2 3 2 3 0
3
x
x x x x x x
x
.
Tập nghiệm của phương trình là
1; 3
.
Câu 24. (THPT Quỳnh Lưu 3 Nghệ An 2019) Tập hợp các số thực
m
để phương trình
2
log
x m
có
nghiệm thực là
A.
0; .
B.
;0 .
C.
.
D.
0;
Lời giải
Tập giá trị của hàm số
2
logy x
là
nên để phương trình có nghiệm thực thì
m
Câu 25. (Chuyên Bắc Giang 2019) Tổng bình phương các nghiệm của phương trình
2
1
2
log 5 7 0
x x
bằng
A. 6 B. 5 C. 13 D. 7
Lời giải
Chọn C
2 2 2 2 2
1 1 2 1 2
2
log 5 7 0 5 7 1 5 6 0 2 3 13
x x x x x x x x x x
Câu 26. (THPT-Thang-Long-Ha-Noi- 2019) Tổng các nghiệm của phương trình
2
4 2
log log 3 1
x
là
A.
6
B.
5
C.
4
D.
0
Lời giải
Điều kiện
0
x
. Có
2 2 2 2 2
4 2 2 2 2 2
1
log log 3 1 log 1 log 3 log 2.log 6 6
2
x x x x
Dó đó, tổng các nghiệm sẽ bằng
0
Câu 27. (THPT-Thang-Long-Ha-Noi 2019) Tập nghiệm của phương trình
2
0,25
log 3 1
x x
là:
A.
4
. B.
1; 4
. C.
3 2 2 3 2 2
;
2 2
. D.
1;4
.
Lời giải
Ta có:
2
2
0,25
1
2
2
0
0
3
3 0
3
log 3 1
4
3 0,25
3 4 0
1
x
x
x
x x
x
x x
x n
x x
x x
x n
Vậy tập nghiệm của phương trình là
1; 4
S
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 28. (THPT Yên Phong 1 Bắc Ninh 2019) Nghiệm nhỏ nhất của phương trình
2
5
log 3 5 1
x x
là
A.
3
. B.
a
. C.
3
. D.
0
.
Lời giải
2 2 2
5
3
log 3 5 1 3 5 5 3 0
0
x
x x x x x x
x
. Vậy nghiệm nhỏ nhất của phương
trình
2
5
log 3 5 1
x x
là 0.
Câu 29. (Sở Hà Nội 2019) Số nghiệm dương của phương trình
2
ln 5 0
x
là
A.
2
. B.
4
. C.
0
. D.
1
.
Lời giải
Có
2
ln 5 0
x
2
5 1
x
2
2
5 1
5 1
x
x
6
6
2
2
x
x
x
x
.
Vậy phương trình có
2
nghiệm dương là
6
x ,
2
x
.
Câu 30. (Chuyên Hạ Long 2019) Số nghiệm của phương trình
2
2
( 3)log (5 ) 0
x x
.
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Điều kiện:
2
5 0 5 5
x x .
Phương trình
2
2
2
2
2
3 0
3 3
( 3)log (5 ) 0
log (5 ) 0
5 1 2
x
x x
x x
x
x x
.
Đối chiếu điều kiện ta có
2
x
thỏa mãn yêu cầu bài toán. Vậy phương trình có 2 nghiệm.
Câu 31. (THPT Yên Khánh - Ninh Bình - 2019) Tổng tất cả các nghiệm của phương trình
2
2 5 2 log 7 6 2 0
x
x x x
bằng
A.
17
2
. B.
9
. C.
8
. D.
19
2
.
Lời giải
Điều kiện
0 1
6
1 *
6
7
7
x
x
x
.
Phương trình
2
2
2 5 2 0
2 5 2 log 7 6 2 0
log 7 6 2 0
x
x
x x
x x x
x
.
+ Phương trình
2
2
2 5 2 0
1
2
x
x x
x
. Kết hợp với điều kiện
* 2
x
.
+ Phương trình
2 2
1
log 7 6 2 0 7 6 7 6 0
6
x
x
x x x x x
x
. Kết hợp với
điều kiện
* 6
x
.
Vậy phương trình đã cho có hai nghiệm
2; 6
x x
suy ra tổng các nghiệm bằng
8
.
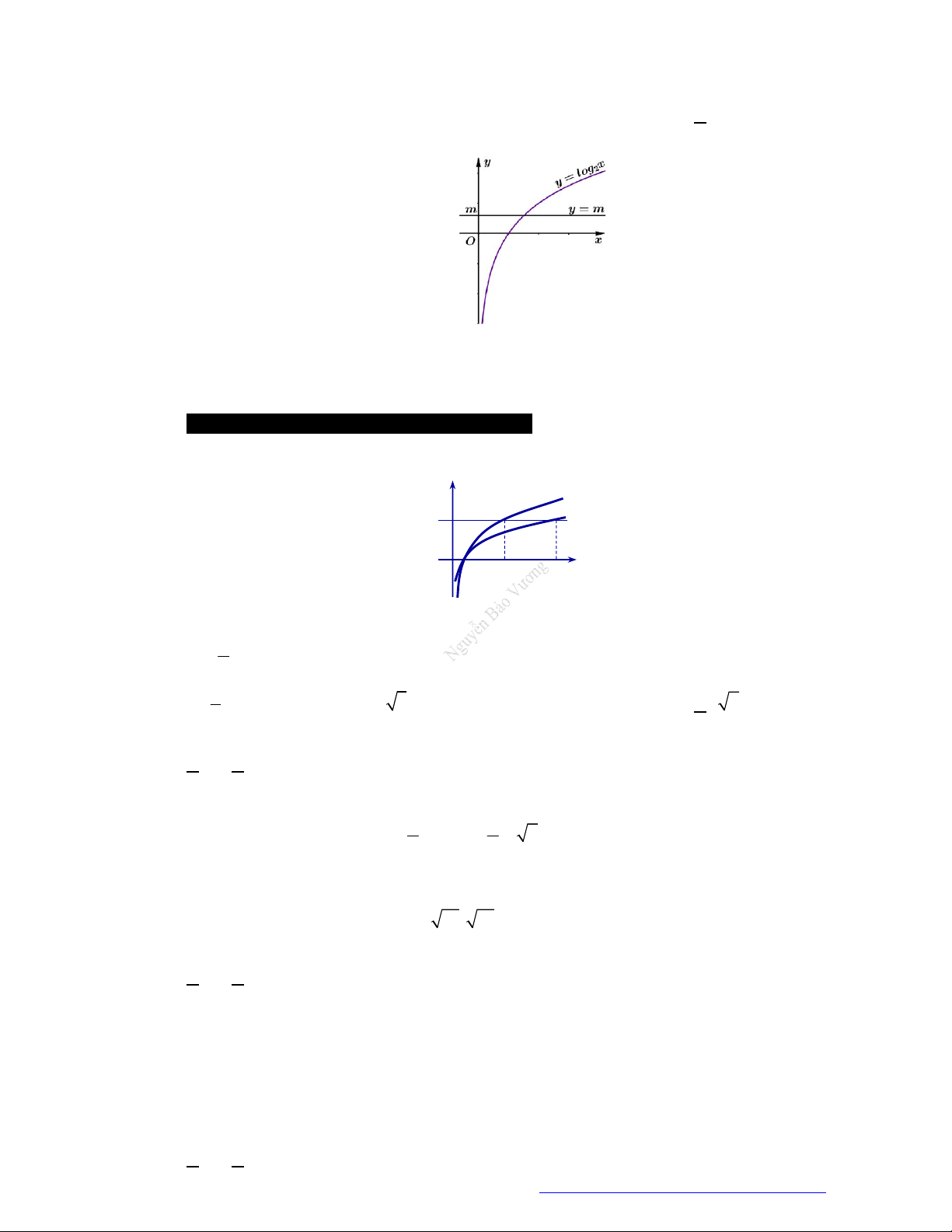
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 32. (Chuyên ĐHSP Hà Nội 2019) Tập hợp các số thực
m
để phương trình
2
log x m
có nghiệm
thực là
A.
0;
. B.
0;
. C.
;0
. D.
.
Lời giải
Điều kiện để phương trình đã cho có nghĩa là
0x
.
Dễ thấy
m
thì đường thẳng
y m
luôn cắt đồ thị hàm số
2
logy x
tại đúng một điểm.
Vậy tập hợp các số thực
m
để phương trình
2
log x m
có nghiệm thực là
m
.
Dạng 1.2 Biến đổi đưa về phương trình cơ bản
Câu 1. (Mã 103 - 2020 Lần 2) Hàm số
log
a
y x
và
log
b
y x
có đồ thị như hình bên.
Đường thẳng
3y
cắt hai đồ thị tại các điểm có hoành độ là
1 2
;x x
. Biết rằng
1 2
2x x
. Giá trị
của
a
b
bằng
A.
1
3
. B.
3
. C.
2
. D.
3
2
.
Lời giải
Chọn D
Xét phương trình hoành độ giao điểm
3
1
log 3
a
x x a
, và
3
2
log 3
b
x x b
.
Ta có
3
3 3
3
1 2
2 2 2 2
a a
x x a b
b b
.
Câu 2. (Đề Tham Khảo 2017) Tìm tập nghiệm
S
của phương trình
2 2
log 1 log 1 3x x
.
A.
3S
B.
10; 10S C.
3;3S
D.
4S
Lời giải
Chọn A
Điều kiện
1x
. Phương trình đã cho trở thành
2
2
log 1 3x
2
1 8x
3x
Đối chiếu điều kiện, ta được nghiệm duy nhất của phương trình là
3 3x S
Câu 3. (Mã 103 - 2019) Nghiệm của phương trình
2 2
log 1 1 log 3 1x x
là
A.
1x
. B.
2x
. C.
1x
. D.
3x
.
Lời giải
Chọn D
x
y
3
O
1
x
2
x
log
b
y x
log
a
y x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điều kiện phương trình:
1
3
x
.
2 2 2 2
log 1 1 log 3 1 log 1 .2 log 3 1 2 1 3 1 3
x x x x x x x
.
Ta có
3
x
( Thỏa mãn điều kiện phương trình)
Vậy nghiệm phương trình là
3
x
.
Câu 4. (Mã 105 2017) Tìm tập nghiệm
S
của phương trình
3 3
log 2 1 log 1 1
x x
.
A.
3
S
B.
4
S
C.
1
S
D.
2
S
Lời giải
Chọn B
ĐK:
1
2 1 0
1.
2
1 0
1
x
x
x
x
x
Ta có
3 3
log 2 1 log 1 1
x x
3
2 1 2 1
log 1 3 4
1 1
x x
x
x x
(thỏa)
Câu 5. (Mã 101 - 2019) Nghiệm của phương trình
3 3
log 1 1 log 4 1
x x
A.
4
x
. B.
2
x
. C.
3
x
. D.
3
x
.
Lời giải
Chọn B
Điều kiện:
1
.
4
x
Ta có:
3 3
log 1 1 log 4 1
1
1
4
2.
4
3 1 4 1
2
x x
x
x
x
x x
x
Vậy: Nghiệm của phương trình là
2.
x
Câu 6. (Mã 104 - 2019) Nghiệm của phương trình
3 3
log 2 1 1 log 1
x x
là
A.
4
x
. B.
2
x
. C.
1x
. D.
2
x
.
Lời giải
Chọn A
Điều kiện:
2 1 0
1
1 0
x
x
x
.
Ta có:
3 3
log 2 1 1 log 1
x x
3 3
log 2 1 log 3 1
x x
2 1 3 3x x
4
x
(nhận).
Câu 7. (Mã 102 -2019) Nghiệm của phương trình
2 2
log 1 1 log 1
x x
là
A.
3
x
. B.
2
x
. C.
1x
. D.
2
x
.
Lời giải
Chọn A

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Điều kiện:
1
1
1
x
x
x
.
Phương trình đã cho tương đương với
2 2
log 1 1 log 1
x x
.
2 2
log 1 log 2. 1
x x
1 2 2 3
x x x
(Thỏa mãn).
Câu 8. (THPT Lê Quy Đôn Điện Biên 2019) Số nghiệm của phương trình
ln 1 ln 3 ln 7
x x x
là
A. 1. B. 0. C. 2. D. 3.
Lời giải
Chọn A
Điều kiện:
1
x
ln 1 3 ln 7
PT x x x
1 3 7
x x x
2
3 4 0
x x
1 ( )
4 ( )
x n
x
Câu 9. Tìm số nghiệm của phương trình
2 2
log log ( 1) 2
x x
A. 0. B. 1. C. 3. D. 2.
Lời giải
Chọn B
Điều kiện:
1x
Ta có:
2 2
log log ( 1) 2
x x
2
2
log [ ( 1)] 2 ( 1) 4 4 0
1 17
2
1 17
2
x x x x x x
x
x
Đối chiếu với điều kiện ta được nghiệm của phương trình là
1 17
2
x
.
Câu 10. (HSG Bắc Ninh 2019) Số nghiệm của phương trình
3 3
log 6 log 9 5 0
x x
.
A.
0
B.
2
C.
1
D.
3
Lời giải
+) Điều kiện
0
x
+) Phương trình
2
3 3 3
log 6 log 3 log 6 3 6 27 0
x x x x x x
3
3
9( )
x
x
x L
. Vậy phương trình có
1
nghiệm.
Vậy số nghiệm của phương trình là
1
.
Câu 11. (THPT Đoàn Thượng - Hải Dương - 2019) Tìm tập nghiệm
S
của phương trình:
3 3
log 2 1 log 1 1
x x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3
S
. B.
1
S
. C.
2
S
. D.
4
S
.
Lời giải
Điều kiện:
2 1 0
1 0
x
x
1x
.
Với điều kiện trên,
3 3
log 2 1 log 1 1
x x
3 3 3
log 2 1 log 1 log 3
x x
3 3
log 2 1 log 3 3
x x
2 1 3 3x x
4
x
(thỏa mãn điều kiện).
Vậy tập nghiệm
4
S
.
Câu 12. (Sở Bắc Giang 2019) Phương trình
2 2
log log 1 1
x x
có tập nghiệm là
A.
1;3
S
. B.
1;3
S
. C.
2
S
. D.
1
S
.
Lời giải
Điều kiện:
1x
.
Với điều kiện trên, ta có:
2
2 2 2
1
log log 1 1 log 1 1 2 0
2
x
x x x x x x
x
.
Kết hợp với điều kiện ta được:
2
x
.
Vậy tập nghiệm của phương trình là
2
S
.
Câu 13. (THPT Gang Thép Thái Nguyên 2019) Tổng các nghiệm của phương trình
2 2 5
log ( 1) log ( 2) log 125
x x
là
A.
3 33
2
. B.
3 33
2
. C. 3. D.
33
.
Lời giải
Điều kiện:
2
x
2
2 2 5 2
log ( 1) log ( 2) log 125 log 3 2 3
x x x x
2
3 33
2
3 6 0 .
3 33
2
x
x x
x
Đối chiếu điều kiện ta thấy nghiệm
3 33
2
x
thỏa mãn.
Vậy tổng các nghiệm của phương trình là
3 33
.
2
Câu 14. (THPT Ngô Sĩ Liên Bắc Giang 2019) Tập nghiệm của phương trình
2 2
log log ( 3) 2
x x là
A.
4
S
B.
1,4
S
C.
1
S
D.
4,5
S
Lời giải
Chọn A
Điều kiện:
3
x
.
PT
2
2
log 3 2 3 4 0
x x x x
4
1
x
x
.
So sánh điều kiện ta được
4
x
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Vậy tập nghiệm của phương trình là
4
S
.
Câu 15. (Chuyên Thái Nguyên 2019) Số nghiệm của phương trình
3 3 3
log log 6 log 7
x x
là
A.
0
B.
2
C.
1
D.
3
Lời giải
Đk:
6
x
Ta có:
2
3 3 3 3 3
1
log log 6 log 7 log 6 log 7 6 7 0
7
x
x x x x x x
x
So với điều kiên vậy phuiwng trình có một nghiệm
7
x
Câu 16. (Chuyên Sơn La 2019) Cho
0;
2
x
, biết rằng
2 2
log sin log cos 2
x x và
2 2
1
log sin cos log 1
2
x x n
. Giá trị của
n
bằng
A.
1
4
. B.
5
2
. C.
1
2
. D.
3
4
.
Lời giải
Vì
0;
2
x
nên
sin 0
x
và
cos 0
x
.
Ta có:
2 2 2
1
log sin log cos 2 log sin .cos 2 sin .cos
4
x x x x x x
.
2
3
sin cos 1 2sin .cos
2
x x x x
.
Suy ra:
2
2 2 2 2
1
log sin cos log 1 log sin cos log 2
2
x x n x x n
2
3 3
sin cos 2 2
2 4
x x n n n
.
Câu 17. (Mã 110 2017) Tìm tập nghiệm
S
của phương trình
1
2
2
log 1 log 1 1.
x x
A.
3
S
B.
2 5;2 5
S
C.
2 5
S
D.
3 13
2
S
Lời giải
Chọn C
Điều kiện
1 0
1 (*)
1 0
x
x
x
.
Phương trình
2 2
2log 1 log 1 1
x x
2 2 2
2log 1 log 1 log 2
x x
2
2 2
log 1 log 2 1
x x
2
2 1 2 2
x x x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2 5
4 1 0
2 5
x L
x x
x
. Vậy tập nghiệm phương trình
2 5
S
Câu 18. (THPT Hàm Rồng Thanh Hóa 2019) Số nghiệm của phương trình
2
3 1
3
log 4 log 2 3 0
x x x
là
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Viết lại phương trình ta được
2
3 3
log 4 log 2 3
x x x
2
2 3 0
4 2 3
x
x x x
3
2
1
3
x
x
x
1x
.
Câu 19. (Đề Tham Khảo 2018) Tổng giá trị tất cả các nghiệm của phương trình
3 9 27 81
2
log .log .log .log
3
x x x x
bằng
A.
0.
B.
80
.
9
C.
9.
D.
82
.
9
Lời giải
Chọn D
Điều kiện
0
x
.
Phương trình đã cho tương đương với
3
4
3 3 3 3 3
3
9
log 2
1 1 1 2
log . .log . log . log (log ) 16
1
log 2
2 3 4 3
9
x
x
x x x x
x
x
Câu 20. (VTED 2019) Nghiệm của phương trình
2 4 1
2
log log log 3
x x
là
A.
3
1
3
x
. B.
3
3
x
. C.
1
3
x
. D.
1
3
x
.
Lời giải
Điều kiện:
0
x
Ta có:
2 4 1 2 2 2
2
1 1
log log log 3 log log log 3
2 2
x x x x
2 2 2 2 2
2log log log 3 0 3log log 3 0
x x x
3 3 3
2 2 2
3
1
log log 3 0 log 3 0 3 1
3
x x x x
.
So với điều kiện, nghiệm phương trình là
3
1
3
x
.
Câu 21. (THPT Lê Quý Dôn Dà Nẵng -2019) Gọi S là tập nghiệm của phương
trình
2
2
2
log 1 log 2 1
x x
. Số phần tử của tập S là
A. 2 B. 3 C. 1 D. 0
Lời giải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
ĐK:
1
x
2
2
2
2
2
0( )
2
log 1 log 2 1 1
4( )
2
x TM
x
x x x
x L
Vậy tập nghiệm có một phần tử
Câu 22. (Chuyên Lam Sơn Thanh Hóa 2019) Số nghiệm thục của phương trình
3
3 1
3
3log 1 log 5 3
x x
là
A.
3
B.
1
C.
2
D.
0
Lời giải
Chọn B
Điều kiện:
5
x
3
3 1
3
3log 1 log 5 3
x x
3 3
3log 1 3log 5 3
x x
3 3
log 1 log 5 1
x x
3
log 1 5 1
x x
1 5 3
x x
2
6 2 0 3 7
x x x
Đối chiếu điều kiện suy ra phương trình có
1
nghiệm
3 7
x
Câu 23. (Chuyên Lê Hồng Phong Nam Định 2019) Tổng các nghiệm của phương trình
2
3
3
log 2 log 4 0
x x
là
2S a b
(với
,a b
là các số nguyên). Giá trị của biểu thức
.Q a b
bằng
A. 0. B. 3. C. 9. D. 6.
Lời giải
Chọn D
Điều kiện:
2 4
x
.
Với điều kiện trên, phương trình đã cho tương đương
3 3 3
2log 2 2log 4 0 log 2 4 0 2 4 1
x x x x x x
2
2
2 4 1
6 7 0
3 2
2 4 1
3
6 9 0
x x
x x
x
x x
x
x x
So lại điều kiện, ta nhận hai nghiệm
1 2
3 2; 3
x x
Ta được:
1 2
6 2 6; 1S x x a b
. Vậy
. 6
Q a b
.
Dạng 2. Phương trình mũ
Phương pháp đưa về cùng cơ số.
Phương trình mũ
+ Nếu
0, 1
a a
thì
f x g x
a a f x g x
+ Nếu a chứa ẩn thì
1
1 0
f x g x
a
a a a f x g x
f x g x
+
log log log .
f x g x f x g x
a a a
a b a b f x b g x
(logarit hóa).
Dạng 2.1 Phương trình cơ bản
Câu 1. (Đề Tham Khảo 2020 Lần 2) Nghiệm của phương trình
1
3 27
x
là
A.
4
x
. B.
3
x
. C.
2
x
. D.
1x
.
Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn A
Ta có:
1
3 27
x
1 3
3 3
x
1 3x 4x
.
Vậy nghiệm của phương trình là
4x
.
Câu 2. (Mã 101 - 2020 Lần 1) Nghiệm của phương trình
1
3 9
x
là:
A.
2x
. B.
3x
. C.
2x
. D.
3x
.
Lời giải
Chọn B.
1
3
3 9 1 log 9 1 2 3
x
x x x
Câu 3. (Mã 102 - 2020 Lần 1) Nghiệm của phương trình là
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có .
Câu 4. (Mã 103 - 2020 Lần 1) Nghiệm của phương trình
1
3 9
x
là
A.
1x
. B.
2x
. C.
2x
. D.
1x
.
Lời giải
Chọn A
Ta có:
1 1 2
3 9 3 3 1 2 1
x x
x x
.
Câu 5. (Mã 104 - 2020 Lần 1) Nghiệm của phương trình
2
3 27
x
là
A.
2x
. B.
1x
. C.
2x
. D.
1x
.
Lời giải
Chọn D
Ta có
2 2 3
3 27 3 3 2 3 1
x x
x x
.
Câu 6. (Mã 102 - 2020 Lần 2) Nghiệm của phương trình
2 4
2 2
x x
là
A.
16x
. B.
16x
. C.
4x
. D.
4x
.
Lời giải
Chọn D
Ta có:
2 4
2 2 2 4 4.
x x
x x x
Câu 7. (Mã 101 - 2020 Lần 2) Nghiệm của phương trình
2 3
2 2
x x
là
A.
8x
. B.
8x
. C.
3x
. D.
3x
.
Lời giải
Chọn C
Ta có
2 3
2 2 2 3 3
x x
x x x
. Vậy phương trình đã cho có một nghiệm
3x
.
Câu 8. (Mã 104 - 2020 Lần 2) Nghiệm của phương trình
2 2
2 2
x x
là
A.
2x
. B.
2x
. C.
4x
. D.
4x
.
Lời giải
Chọn B
2 2
2 2 2 2 2
x x
x x x
.
Câu 9. (Mã 101 - 2019) Nghiệm của phương trình:
2 1
3 27
x
là
A.
1x
. B.
2x
. C.
4x
. D.
5x
.
Lời giải
2
3 9
x
3
x
3
x
4
x
4
x
2
3 9
x
2 2
x
4
x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Chọn B
Ta có:
2 1
3 27
x
2 1 3
3 3
x
2 1 3x
2x
.
Câu 10. (Mã 102 - 2019) Nghiệm của phương trình
2 1
3 27
x
là
A.
5
. B.
4
. C.
2
. D.
1
.
Lời giải
Chọn D
Ta có:
2 1 3 1x x
.
Câu 11. Tìm nghiệm của phương trình
1
3 27
x
A.
10
x
B.
9
x
C.
3
x
D.
4
x
Lời giải
Chọn D
1 3
3 3
x
1 3
x
4
x
.
Câu 12. (Mã 104 2018) Phương trình
2 1
5 125
x
có nghiệm là
A.
5
2
x
B.
1x
C.
3
x
D.
3
2
x
Lời giải
Chọn B
Ta có:
2 1
5 125
x
2 1 3
5 5
x
2 1 3
x
1x
.
Câu 13. (Mã 101 2018) Phương trình
2 1
2 32
x
có nghiệm là
A.
3
x
B.
5
2
x
C.
2
x
D.
3
2
x
Lời giải
Chọn C
Ta có
2 1
2 32
x
2 1 5
2 2
x
2 1 5
x
2
x
.
Câu 14. (Mã 104 - 2019) Nghiệm của phương trình
2 1
2 32
x
là
A.
2
x
. B.
17
2
x
. C.
5
2
x
. D.
3
x
.
Lời giải
Chọn D
2 1 2 1 5
2 32 2 2 2 1 5 3
x x
x x
.
Câu 15. (Mã 103 - 2019) Nghiệm của phương trình
2 1
2 8
x
là
A.
2
x
. B.
5
2
x
. C.
1x
. D.
3
2
x
.
Lời giải
Chọn A
Ta có:
2 1
2 8 2 1 3 2
x
x x
.
Câu 16. (Mã 104 2017) Tìm tất cả các giá trị thực của
m
để phương trình
3
x
m
có nghiệm thực.
A.
1
m
B.
0
m
C.
0
m
D.
0
m
Lời giải
Chọn C
Để phương trình
3
x
m
có nghiệm thực thì
0
m
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 17. (THPT An Lão Hải Phòng 2019) Tìm tập nghiệm
S
của phương trình
2
2
5 5
x x
.
A.
S
B.
1
0;
2
S
C.
0;2
S
D.
1
1;
2
S
Lời giải
Chọn D
2
2 2 2
1
5 5 2 1 2 1 0
1
2
x x
x
x x x x
x
Câu 18. (Chuyên Bắc Ninh 2019) Tìm tập nghiệm
S
của phương trình
1
2 8
x
.
A.
4
S
. B.
1
S
. C.
3 .
S
D.
2
S
.
Lời giải
Ta có:
1 1 3
2 8 2 2 1 3 2
x x
x x
.
Vậy tập nghiệm của phương trình đã cho là
2
S
.
Câu 19. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Phương trình
2
4 6
2
5 log 128
x x
có bao nhiêu
nghiệm?
A.
1
B.
3
C.
2
D.
0
Lời giải
Phương trình đã cho tương đương với:
2 2
5 5
4 6 log 7 4 6 log 7 0
x x x x
Sử dụng máy tính bỏ túi ta thấy phương trình trên có hai nghiệm phân biệt.
Câu 20. (THPT - Yên Định Thanh Hóa 2019) Tập nghiệm
S
của phương trình
2
2
3 27
x x
.
A.
1;3
S
. B.
3;1
S
. C.
3; 1
S
. D.
1;3
S
.
Lời giải
Ta có:
2
2 2
1
3 27 2 3
3
x x
x
x x
x
.
Vậy tập nghiệm
S
của phương trình
2
2
3 27
x x
là
1;3
S
.
Câu 21. (THPT Quỳnh Lưu 3 Nghệ An 2019) Số nghiệm thực phân biệt của phương trình
2
e 3
x
là:
A. 1. B. 0. C. 3. D. 2.
Lời giải
Ta có
2
e 3
x
2
ln 3
x
ln 3
x
.
Vậy phương trình có 2 nghiệm thực phân biệt.
Câu 22. (Sở Ninh Bình 2019) Phương trình
2
5 1 0
x
có tập nghiệm là
A.
3
S
. B.
2
S
. C.
0
S
. D.
2
S
.
Lời giải
Ta có
2 2
5 1 0 5 1 2 0 2
x x
x x
Vậy
2
S
.
Câu 23. (THCS - THPT Nguyễn Khuyến 2019) Họ nghiệm của phương trình
2
cos
4 1 0
x
là

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
A.
;k k
. B.
;
2
k k
. C.
2 ;k k
. D.
;
3
k k
.
Lời giải
Ta có:
2 2
cos cos 2
4 1 0 4 1 cos 0
2
x x
x x k
,
k
Vậy họ nghiệm của phương trình là:
;
2
k k
.
Câu 24. (Chuyên Lê Thánh Tông 2019) Cho biết
2
9 12 0
x
, tính giá trị của biểu thức
1
2
1
1
8.9 19
3
x
x
P
.
A.
31
. B.
23
. C.
22
. D.
15
.
Lời giải
Ta có
2
9 12 0 3 12
x x
.
1 1
3 12
3 8.3 19 3.3 8. 19 3.12 8. 19 23
3 3
x
x x x
P
.
Câu 25. (Chuyên Bắc Ninh 2019) Tính tổng tất cả các nghiệm của phương trình
2
2 5 4
2 4
x x
A.
5
2
. B.
1
. C.
1
. D.
5
2
.
Lời giải
2
2 5 4 2
1
2 4 2 5 2 0
2
2
x x
x
x x
x
.
Vậy tổng hai nghiệm bằng
5
2
.
Câu 26. Tìm tất cả các giá trị thực của tham số
m
để phương trình
2 1 2
3 2 3 0
x
m m
có nghiệm.
A.
3
1;
2
m
. B.
1
;
2
m
. C.
0;m
. D.
3
1;
2
m
.
Lời giải
Chọn A
2 1 2 2 1 2
3 2 3 0 3 3 2
x x
m m m m
Phương trình có nghiệm khi
2
3
3 2 0 1
2
m m m
.
Vậy
3
1;
2
m
.
Câu 27. Cho a, b là hai số thực khác 0, biết: . Tỉ số là:
A. B. C. D.
Lời giải
Ta có :
2
2
2
2
4
4
3 8
3 8
3 4
3
3
1
625 5 5
125
a ab
a ab
a ab
a ab
2 2 2
4 4
3 4 3 8 21 4
3 21
a
a ab a ab a ab
b
2
2
4
3 8
3
1
625
125
a ab
a ab
a
b
8
7
1
7
4
7
4
21

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 28. Tổng các nghiệm của phương trình
2
2 1
2 8
x x
bằng
A.
0
. B.
2
. C.
2
. D.
1
.
Lời giải
Ta có:
2
2 1
2 8
x x
2
2 1 3
2 2
x x
2
2 1 3
x x
2
2 2 0
x x
1 3
1 3
x
x
.
Như vậy phương trình đã cho có hai nghiệm:
1 3
;
1 3
.
Tổng hai nghiệm là:
1 3 1 3
2
.
Câu 29. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Phương trình
2
2 5 4
2 4
x x
có tổng tất cả các
nghiệm bằng
A. 1. B.
5
2
. C.
1
. D.
5
2
.
Lời giải
Chọn D
Cách 1:
Ta có:
2
2 5 4
2 4
x x
2
2 5 4 2
2 2
x x
2
2 5 4 2
x x
2
2 5 2 0
x x
2
1
2
x
x
Tổng tất cả các nghiệm của phương trình đã cho là:
1 5
2
2 2
.
Cách 2:
Ta có:
2
2 5 4
2 4
x x
2
2 5 4 2
2 2
x x
2
2 5 4 2
x x
2
2 5 2 0
x x
(1)
Xét phương trình (1):
9 0
Phương trình (1) có hai nghiệm phân biệt
1 2
; .x x
Theo định lý Viet ta có:
1 2
5
.
2
x x
Tổng tất cả các nghiệm của phương trình đã cho là:
5
.
2
Câu 30. (THPT Ngô Sĩ Liên Bắc Giang 2019) Phương trình
2
2 5 4
5 25
x x
có tổng tất cả các nghiệm
bằng
A.
1
B.
5
2
C.
1
D.
5
2
Lời giải
Chọn D
2
2 5 4 2 2 2
5 5 2 5 4 2 2 5 2 0
x x
x x x x
Tổng các nghiệm là
5
.
2
Câu 31. (Sở Bắc Ninh 2019) Phương trình
2
2 5 4
7 49
x x
có tổng tất cả các nghiệm bằng
A.
5
2
. B.
1
. C.
1
. D.
5
2
.
Lờigiải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
2
2 5 4
7 49
x x
2
2 5 4 2
7 7
x x
2
2 5 4 2
x x
2
2 5 2 0
x x
2
1
2
x
x
.
Vậy tổng tất cả các nghiệm của phương trình bằng:
1 5
2 ( )
2 2
.
Dạng 2.2 Biến đổi đưa về phương trình cơ bản
Câu 1. Tập nghiệm của phương trình:
1 1
4 4 272
x x
là
A.
3;2
. B.
2
. C.
3
. D.
3;5
.
Lời giải
Chọn C
1 1
4 4 272
x x
4
4.4 272
4
x
x
4 64
x
3
x
Vậy phương trình có tập nghiệm
3
S
.
Câu 2. (HKI-NK HCM-2019) Phương trình
2
2
2 3
1
27
3
x
x
có tập nghiệm là
A.
1;7
. B.
1; 7
. C.
1;7
. D.
1; 7
.
Lời giải
Chọn D
Ta có:
2
2
2 3
1
27
3
x
x
2
6 9 2
3 3
x x
2
6 9 2
x x
2
6 7 0
x x
1
7
x
x
.
Vậy tập nghiệm của phương trình là
1; 7
.
Câu 3. (THPT Quỳnh Lưu- Nghệ An- 2019) Phương trình
1
3 .2 72
x x
có nghiệm là
A.
5
2
x
. B.
2
x
. C.
3
2
x
. D.
3
x
.
Lời giải
Chọn B
1
3 .2 72 3 .2 .2 72 6 36 2.
x x x x x
x
Câu 4. (Chuyên Bắc Giang 2019) Nghiệm của phương trình
2
2 3
1
1
5
5
x x
x
là
A.
1; 2.
x x
B.
1; 2.
x x
C.
1; 2.
x x
D. Vô nghiệm.
Lời giải
Chọn A
Ta có:
2
2
2 3
1 ( 2 3) 1 2 2
1
1
5 5 5 2 3 1 2 0 .
2
5
x x
x x x x
x
x x x x x
x
Vậy nghiệm của phương trình là
1; 2.
x x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 5. Tập nghiệm của phương trình
2
2 3
1
1
7
7
x x
x
là
A.
1
. B.
1;2
. C.
1;4
. D.
2
.
Lời giải
Chọn B
Ta có:
2
2
2 3
1 2 3 1 2
1
7 7 7 2 3 1
7
x x
x x x x
x x x
.
2
1
2 0
2
x
x x
x
.
Câu 6. Tổng các nghiệm của phương trình
2
2 2
2 8
x x x
bằng
A.
6
. B.
5
. C.
5
. D.
6
.
Lời giải
Chọn B
Ta có:
2 2
2 2 2 6 3 2
1
2 8 2 2 5 6 0
6
x x x x x x
x
x x
x
.
Vậy tổng hai nghiệm của phương trình bằng
5
.
Câu 7. (SGD Điện Biên - 2019) Gọi
1 2
, x x
là hai nghiệm của phương trình
2
2 3
1
1
7
7
x x
x
. Khi đó
2 2
1 2
x x
bằng:
A.
17
. B.
1
. C.
5
. D.
3
.
Lời giải
Chọn C
2
2
2 3
2 3
1
1 1 2 2
2
1
1
7 7 7 1 2 3 2 0 .
2
7
x x
x x
x x
x
x x x x x
x
Vậy
2 2
1 2
5.
x x
Câu 8. Tổng bình phương các nghiệm của phương trình
2
3 2
1
5
5
x
x
bằng
A.
2
. B.
5
. C.
0
. D.
3
.
Lời giải
Chọn B
Ta có
2
2
3 2 3 2 2
1
1
5 5 5 3 2 0
2
5
x
x x x
x
x x
x
.
Vậy tổng bình phương các nghiệm của phương trình
2
3 2
1
5
5
x
x
bằng
5
.
Câu 9. Nghiệm của phương trình
7 1 2 1
2 8
x x
là
A.
2.
x
B.
3.
x
C.
2.
x
D.
1.
x
Lời giải
Chọn C

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
7 1 2 1 7 1 3.(2 1) 7 1 6 3
2 8 2 2 2 2 7 1 6 3 2
x x x x x x
x x x
.
Câu 10. (THPT Lương Văn Tụy - Ninh Bình - 2018) Giải phương trình
1
5 7
2
2,5
5
x
x
.
A.
1x
. B.
1x
. C.
1x
. D.
2
x
.
Lời giải
Ta có
1 5 7 1
5 7
2 5 5
2,5 5 7 1 1
5 2 2
x x x
x
x x x
.
Câu 11. (THPT Nguyễn Thị Minh Khai - Hà Tĩnh - 2018) Phương trình
2
3 1
4
1
3
9
x
x
có hai nghiệm
1
x
,
2
x
. Tính
1 2
x x
.
A.
6
. B.
5
. C.
6
. D.
2
.
Lời giải
Ta có
2
3 1
4 2 2
1
3 4 2 6 6 6 0
9
x
x
x x x x
.
Áp dụng Vi-ét suy ra phương trình đã cho có hai nghiệm
1
x
,
2
x
thì
1 2
6
x x
.
Câu 12. (Sở Quảng Nam - 2018) Tổng các nghiệm của phương trình
2
2 2
2 8
x x x
bằng
A.
5
. B.
5
. C.
6
. D.
6
.
Lời giải
Phương trình đã cho tương đương:
2
3 2
2 2 2
2 2 2 6 3 5 6 0
x
x x
x x x x x
.
Do đó tổng các nghiệm của phương trình là:
5
b
S
a
.
Câu 13. (THPT Thăng Long - Hà Nội - 2018) Tập nghiệm của phương trình
2
1
4
2
x
x x
là
A.
2
0;
3
. B.
1
0;
2
. C.
0;2
. D.
3
0;
2
.
Lời giải
Ta có
2
1
4
2
x
x x
2
2 2
2 2
x x x
2
2 2
x x x
2
2 3 0
x x
0
3
2
x
x
.
Câu 14. (THPT Hải An - Hải Phòng - 2018) Tìm nghiệm của phương trình
2 1
7 4 3 2 3
x
.
A.
1
4
x
. B.
7 4 3
1 log 2 3
x
.
C.
3
4
x
. D.
25 15 3
2
x
.
Lời giải
Ta có
2 1
7 4 3 2 3
x
4 2 1
2 2 3 2 3
x
4 2 1
x
4 3
x
3
4
x
.
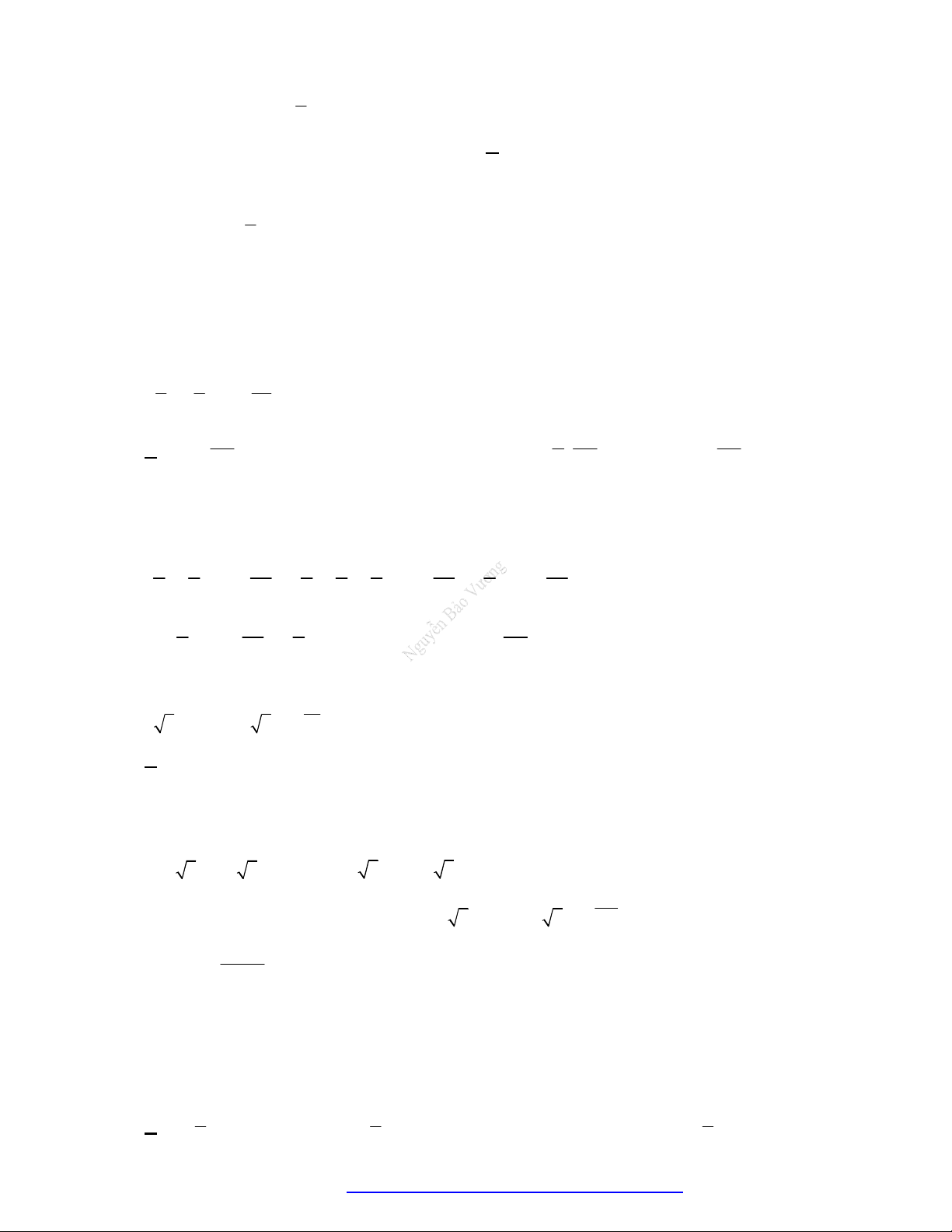
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 15. (THPT Kim Liên - Hà Nội - 2018) Tính tổng
1 2
S x x
biết
1
x
,
2
x
là các giá trị thực thỏa mãn
đẳng thức
2
3
6 1
1
2
4
x
x x
.
A.
5
S
. B.
8
S
. C.
4
S
. D.
2
S
.
Lời giải
Ta có
2 2
3
2 3
6 1 6 1 2
1
2 2 2 6 1 2 6
4
x
x
x x x x
x x x
1
2
1 2
2
1
4 5 0 4
5
x
x x S x x
x
.
Câu 16. (Chuyên Hùng Vương - Bình Dương - 2018) Tập nghiệm S của phương trình
3 1
4 7 16
0
7 4 49
x x
là
A.
1
2
S
B.
2
S
C.
1 1
;
2 2
S
D.
1
;2
2
S
Lời giải
Ta có
3 1 2 1 2 1
2 1 2
4 7 16 4 7 7 16 7 16
0
7 4 49 7 4 4 49 4 49
7 16 7 1
2 1 2 .
4 49 4 2
x x x x x x
x
x x
Câu 17. (THPT Nguyễn Thị Minh Khai - Hà Nội - 2018) Tích các nghiệm của phương trình
1
1
1
5 2 5 2
x
x
x
là
A.
2
. B.
4
. C.
4
. D.
2
.
Lời giải
Chọn. A.
ĐKXĐ :
1
x
Vì
5 2 5 2 1
nên
1
5 2 5 2
.
Khi đó phương trình đã cho tương đương
1
1
1
5 2 5 2
x
x
x
1
1
1
x
x
x
1
2
x
x
. (thỏa điều kiện)
Suy ra tích hai nghiệm là
2
.
Câu 18. (THCS&THPT Nguyễn Khuyến - Bình Dương - 2018) Giải phương trình
2 3 4
4 8
x x
.
A.
6
7
x
. B.
2
3
x
. C.
2
x
. D.
4
5
x
.
Lời giải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
2 3 4
4 8
x x
4 6 12 3
2 2
x x
4
6 12 3x x
6
7
x
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ + GIỎI MỨC 7-8-9-10 ĐIỂM
DẠNG 1. PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH LOGARIT
Dạng 1.1 Phương pháp đưa về cùng cơ số
+Nếu 0, 1: log
b
a
a a x b x a
1
+Nếu
0, 1: log log
a a
a a f x g x f x g x
2
+Nếu
0, 1: log
g x
a
a a f x g x f x a
(mũ hóa)
3
Các bước giải phương trình & bất phương trình mũ – logarit
Bước 1.Đặtđiềukiện(điềukiệnđạisố
điềukiệnloga),tacầnchúý:
Đ
0 1
log
0
a
K
a
b
b
và
Đ
Đ
log 0
log 0
K
a
K
a
f x f x
f x f x
.
Bước 2.Dùngcáccôngthứcvàbiếnđổiđưavềcáccơbảntrên,rồigiải.
Bước 3.Sovớiđiềukiệnvàkếtluậnnghiệm.
Câu 1. (Mã1102017)Tìmtậpnghiệm
S
củaphươngtrình
1
2
2
log 1 log 1 1.x x
A.
3S
B.
2 5;2 5S
C.
2 5S
D.
3 13
2
S
Lờigiải
ChọnC
Điềukiện
1 0
1(*)
1 0
x
x
x
.
Phươngtrình
2 2
2log 1 log 1 1x x
2 2 2
2log 1 log 1 log 2x x
2
2 2
log 1 log 2 1x x
2
2 1 2 2x x x
2
2 5
4 1 0
2 5
x L
x x
x
.Vậytậpnghiệmphươngtrình
2 5S
Câu 2. (THPT Hàm Rồng Thanh Hóa 2019) Số nghiệm của phương trình
2
3 1
3
log 4 log 2 3 0x x x
là
A.
2
. B.
3
. C.
0
. D.
1
.
Lờigiải
Viếtlạiphươngtrìnhtađược
PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH MŨ - LOGARIT
Chuyên đề 19
mũlẻ
mũchẵn

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
3 3
log 4 log 2 3
x x x
2
2 3 0
4 2 3
x
x x x
3
2
1
3
x
x
x
1x
.
Câu 3. (Đề Tham Khảo 2018) Tổng giá trị tất cả các nghiệm của phương trình
3 9 27 81
2
log .log .log .log
3
x x x x
bằng
A.
0.
B.
80
.
9
C.
9.
D.
82
.
9
Lờigiải
ChọnD
Điềukiện
0
x
.
Phươngtrìnhđãchotươngđươngvới
3
4
3 3 3 3 3
3
9
log 2
1 1 1 2
log . .log . log . log (log ) 16
1
log 2
2 3 4 3
9
x
x
x x x x
x
x
Câu 4. Nghiệmcủaphươngtrình
2 4 1
2
log log log 3
x x
là
A.
3
1
3
x
. B.
3
3
x
. C.
1
3
x
. D.
1
3
x
.
Lờigiải
Điềukiện:
0
x
Tacó:
2 4 1 2 2 2
2
1 1
log log log 3 log log log 3
2 2
x x x x
2 2 2 2 2
2log log log 3 0 3log log 3 0
x x x
3 3 3
2 2 2
3
1
log log 3 0 log 3 0 3 1
3
x x x x
.
Sovớiđiềukiện,nghiệmphươngtrìnhlà
3
1
3
x
.
Câu 5. (THPT Lê Quý Dôn Dà Nẵng 2019) Gọi S là tập nghiệm của phương
trình
2
2
2
log 1 log 2 1
x x
.SốphầntửcủatậpSlà
A. 2 B. 3 C. 1 D. 0
Lờigiải
ĐK:
1
x
2
2
2
2
2
0( )
2
log 1 log 2 1 1
4( )
2
x TM
x
x x x
x L
Vậytậpnghiệmcómộtphầntử
Câu 6. (Chuyên Lam Sơn Thanh Hóa 2019) Số nghiệm thục của phương trình
3
3 1
3
3log 1 log 5 3
x x
là
A.
3
B.
1
C.
2
D.
0

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Lờigiải
ChọnB
Điềukiện:
5
x
3
3 1
3
3log 1 log 5 3
x x
3 3
3log 1 3log 5 3
x x
3 3
log 1 log 5 1
x x
3
log 1 5 1
x x
1 5 3
x x
2
6 2 0 3 7
x x x
Đốichiếuđiềukiệnsuyraphươngtrìnhcó
1
nghiệm
3 7
x
Câu 7. (Chuyên Lê Hồng Phong Nam Định 2019) Tổng các nghiệm của phương trình
2
3
3
log 2 log 4 0
x x
là
2S a b
(với
,a b
là các số nguyên). Giá trị của biểu
thức
.Q a b
bằng
A. 0. B. 3. C. 9. D. 6.
Lờigiải
ChọnD
Điềukiện:
2 4
x
.
Vớiđiềukiệntrên,phươngtrìnhđãchotươngđương
3 3 3
2log 2 2log 4 0 log 2 4 0 2 4 1
x x x x x x
2
2
2 4 1
6 7 0
3 2
2 4 1
3
6 9 0
x x
x x
x
x x
x
x x
Solạiđiềukiện,tanhậnhainghiệm
1 2
3 2; 3
x x
Tađược:
1 2
6 2 6; 1S x x a b
.Vậy
. 6
Q a b
.
Câu 8. (Chuyên Nguyễn Du-ĐăkLăk 2019) Tổng tất cả các nghiệm của phương trình
2 2
log 1 log 1x x
là
A.
1
. B.
1
. C.
2
. D.
2
.
Lờigiải
ChọnA
Điềukiện:
0
x
.
Phươngtrìnhtươngđương
2
2
1(N)
log 1 1 1 2 2 0
2(L)
x
x x x x x x
x
Vậytổngcácnghiệmcủaphươngtrìnhbằng
1
.
Câu 9. Tổngtấtcảcácnghiệmthựccủaphươngtrình
2
1
log 4 1 log8 log 4
2
x x x x
bằng
A.
4
. B.
3
. C.
5
. D.
1
.
Lờigiải
ChọnC
Phươngtrình
2
1
log 4 1 log8 log 4
2
x x x x
điềukiện
2 5
x
2
8
log 4 1 2log
4
x
x x
x
2 2
log 4 1 log 2
x x
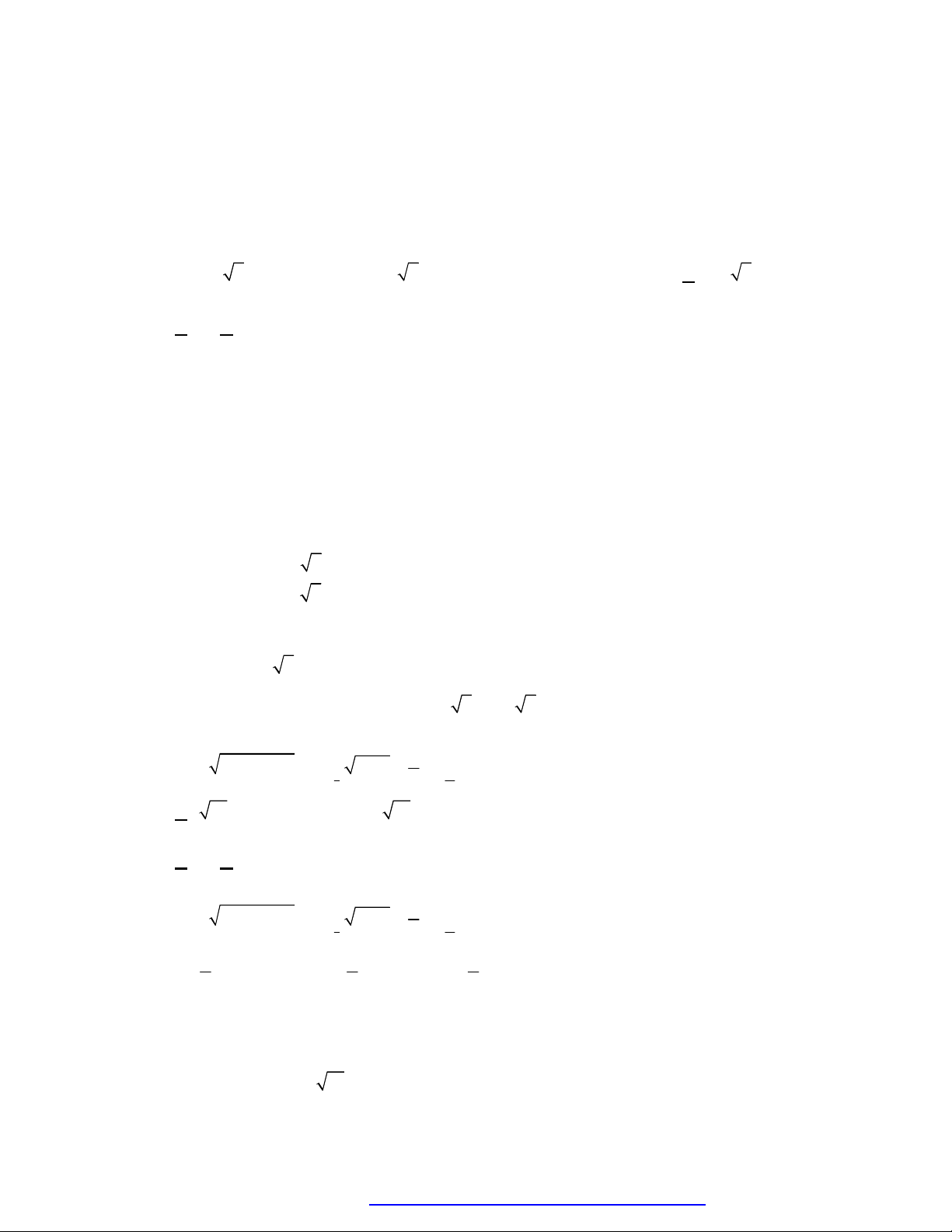
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
4 1 4
x x
1
5
x
x
.
Nghiệm
1
x
loại,
5
x
thỏamãn.
Suyratổngcácnghiệmlà
5
.
Câu 10. Gọi
S
làtậpnghiệmcủaphươngtrình
2
2 2
2log 2 2 log 3 2
x x
trên
.Tổngcácphần
tửcủa
S
bằng
A.
6 2
. B.
8 2
. C.
8
. D.
4 2
.
Lờigiải
ChọnD
Điềukiện:
1
3
x
x
.
2
2 2
2log 2 2 log 3 2
x x
2 2
2 2
log 2 2 log 3 2
x x
.
2
2
log 2 2 3 2
x x
2
2 2
2 8 6 2
x x
.
2
2
2 8 6 2
2 8 6 2
x x
x x
2
2
4 2 0 1
4 4 0 2
x x
x x
.
+)
2 2
1
2 2 ( )
x
x l
.
+)
2 2
x
.
2;2 2
S
.
Vậytổngcácnghiệmcủa
S
là:
2 2 2 4 2
.
Câu 11. (SGD Nam Định 2019) Tổng tất cả các nghiệm của phương trình
4
2
3 1 1
3 81
1
log 5 6 log 2 log 3
2
x x x x
bằng
A.
10.
B.
3 10.
C. 0. D. 3.
Lờigiải
ChọnA
Điềukiện:
3.
x
4
2
3 1 1
3 81
1
log 5 6 log 2 log 3
2
x x x x
2
3 3 3
1 1 1
log 5 6 log 2 log 3
2 2 2
x x x x
2
3 3 3
log 5 6 log 2 log 3 0
x x x x
2
3
log 9 0
x
2
9 1 10
x x (dođiềukiện).
Câu 12. (SGD Gia Lai 2019) Cho hai số thực dương
x
,
y
thỏa mãn
2 2
2 2
log 1 log
x y xy
.
Mệnhđềnàodướiđâyđúng?

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
x y
. B.
x y
. C.
x y
. D.
2
x y
.
Lờigiải
ChọnA
Với
x
,
0
y
tacó:
2 2 2 2
2 2 2 2
log 1 log log log 2x y xy x y xy
.
2 2
2x y xy
.
x y
.
Câu 13. Biếtphươngtrình
2
2 4
log 5 1 log 9
x x
cóhainghiệmthực
1
x
,
2
x
.Tích
1 2
.x x
bằng:
A.
8
. B.
2
. C.
1
. D.
5
.
Lờigiải
ChọnB
Tacó:
2
2 4
log 5 1 log 9
x x
2
2 2
log 5 1 log 3
x x
2
5 1 3 0x x x
2
5 2 0 *
x x
Phươngtrình
*
có
. 2 0
a c
nênluôncó2nghiệmphânbiệt.
Vậy
1 2
. 2
x x
.
Câu 14. (ChuyênLongAn-2019)Tìmnghiệmphươngtrình
4 2
2log log 3 2
x x
.
A.
4
x
. B.
1x
. C.
3
x
. D.
16
x
.
Lờigiải
ChọnA
Điềukiện:
3
x
.
4 2
2 2
2
2
2log log 3 2
log log 3 2
log 3 2
3 4 0
4
1
x x
x x
x x
x x
x
x
Kếthợpđiềukiện,nghiệmcủaphươngtrìnhlà:
4x
.
Câu 15. (Chuyên - KHTN - Hà Nội - 2019) Số nghiệm của phương trình
2
3
3
log 1 log 2 1 2
x x
là
A.
2
. B.
1
. C.
4
. D.
3
.
Lờigiải
ChọnB
Tacó
2
3
3
log 1 log 2 1 2
x x
,điềukiện
1
,x 1
2
x
.
2 2
3 3 3
log 1 log 2 1 log 9
x x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
3 3
log 1 2 1 log 9
x x
2
2
2 3 1 9
x x
2
2
2 3 1 3
2 3 1 3
x x
x x
1
2
2
x
x
Thửlạitacómộtnghiệm
2
x
thỏamãn.
Câu 16. (SởQuảngTrị 2019)Sốnghiệmcủaphươngtrình
2
3 1
3
log 4 log 2 3 0
x x x
là
A.
2
. B.
0
. C.
3
. D.
1
.
Lờigiải
ChọnD
Điềukiện:
2
4
4 0
0
0
2 3 0
3
2
x
x x
x
x
x
x
Tacó
2 2
3 1 3 3
3
2 2
3 3
log 4 log 2 3 0 log 4 log 2 3 0
1
log 4 log 2 3 2 3 0 1.
3( )
x x x x x x
x
x x x x x x
x l
Câu 17. Biếtnghiệmlớnnhấtcủaphươngtrình
1
2
2
log log 2 1 1
x x
là
2x a b
(
,a b
làhaisố
nguyên).Giátrịcủa
2a b
bằng
A.
4
. B.
6
. C.
0
. D.
1
.
Lờigiải
ChọnA
Điềukiện
1
2
x
.
2
2
1 2 2 2
2
2
log log 2 1 1 2log log 2 1 1 log 1 4 2 0
2 1
x
x x x x x x
x
.
Nghiệmlớnnhấtcủaphươngtrìnhlà
2 2 2, 1 2 4
x a b a b
.
Câu 18. Tínhtổngtấtcảcácnghiệmthựccủaphươngtrình
2
3
3
log 2 log 4 0
x x
.
A.
6 2
. B.
6
. C.
3 2
. D.
9
.
Lờigiải
ChọnA

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Điềukiện:
2
4
x
x
.
Tacó:
2
2
3
3
log 2 log 4 0 2 4 1
x x x x
.
2
2
3 2
2 4 1
6 7 0
3 2
2 4 1
6 9 0
3
x nhan
x x
x x
x loai
x x
x x
x nhan
.
Vậytổngtấtcảcácnghiệmthựccủaphươngtrình
2
3
3
log 2 log 4 0
x x
bằng
6 2
.
Câu 19. Gọi
S
làtổngtấtcảcácnghiệmcủaphươngtrình
2
1
log log 10 2 log 4
2
x x
.Tính
S
?
A.
10
S
. B.
15
S
. C.
10 5 2
S
. D.
8 5 2
S
.
Lờigiải
ChọnC
Điềukiệnphươngtrình:
0
10
x
x
.
Phươngtrình:
2
1
log log 10 2 log4 log log 10 log4 2
2
x x x x
log 4 10 2
x x
4 10 100 10 25
x x x x
.
+Khi
10 0
x
:
Phươngtrình
2
10 25 10 25 0 5 t/m
x x x x x
.
+Khi
0
x
:
Phươngtrình
2
5 5 2 t/m
10 25 10 25 0
5 5 2 l
x
x x x x
x
.
Vậy
5 5 5 2 10 5 2
S
.
Câu 20. Chophươngtrình
2 3
4 8
2
log 1 2 log 4 log 4
x x x
.Tổngcácnghiệmcủaphương
trìnhtrênlà
A.
4 2 6
. B.
4
. C.
4 2 6
. D.
2 2 3
.
Lờigiải
ChọnC
Điềukiện:
2
1 0
1
4 0 .
4 4
4 0
x
x
x
x
x
2 3
4 8
2
log 1 2 log 4 log 4
x x x
2 2 2 2
log 1 log 4 log 4 log 4
x x x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2
2 2
log 4 1 log 16 4 1 16
x x x x
2
2
2
2
4 1 16
4 12 0
4 1 16
4 20 0
x x
x x
x x
x x
2
6
2 2 6
2 2 6
x
x
x
x
.
Sovớiđiềukiệnphươngtrìnhtrìnhcó2nghiệp
2; 2 2 6.
x x
Vậytổngcácnghiệmlà
4 2 2.
Câu 21. Cho
2
8 4
log log 5
x y
và
2
8 4
log log 7
y x
.Tìmgiátrịcủabiểuthức
P x y
.
A.
56
P
. B.
16
P
. C.
8
P
. D.
64
P
.
Lờigiải
ChọnA
Tacó:
2 2
8 4 2 2
1 1
log log 5 log log 5
3 2
x y x y
.
3
3
5 5 15
3 3
2 2
log log 5 . 2 . 2 2 1
x y x y x y
.
Tươngtự:
3
2 21
8 4
log log 7 . 2 2
y x y x
.
Lấy
1
nhân
2
được
4 4 36 2 2 18
. 2 . 2 3
x y x y
.
Lấy
1
chia
2
được
2
2 6 2
2 6
1
2 . 4
2
y
x y
x
.
Thay
4
vào
3
được
4
6 4 18 4 12 3 3
2 . 2 2 2 2 8
y y y
.
Thay
8
y
vào
4
được
2
2 6 6 6
2 .64 2 2 64
x x
.Dođó
56
P x y
.
Câu 22. Cho
, , 0; và , 1
a b x a b b x
thỏamãn
2
2 1
log log
3 log
x x
b
a b
a
x
.
Khiđóbiểuthức
2 2
2
2 3
( 2 )
a ab b
P
a b
cógiátrịbằng:
A.
5
4
P
. B.
2
3
P
. C.
16
15
P
. D.
4
5
P
.
Lờigiải
ChọnA
2
2 1 2
log log log log log
3 log 3
x x x x x
b
a b a b
a a b
x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
2 2
2 3 5 4 0 4 0 4a b ab a ab b a b a b a b
(do
a b
).
2 2 2 2 2
2 2
2 3 32 12 5
( 2 ) 36 4
a ab b b b b
P
a b b
.
Câu 23. Cho
0;
2
x
,biếtrằng
2 2
log sin log cos 2
x x
và
2 2
1
log sin cos log 1
2
x x n
.
Giátrịcủa
n
bằng
A.
1
4
. B.
5
2
. C.
1
2
. D.
3
4
.
Lờigiải
ChọnD
Tacó
sin 0
x
;
cos 0
x
,
0;
2
x
.
Theobàira
2 2
log sin log cos 2
x x
2
1
log sin .cos 2 sin .cos
4
x x x x
.
Dođó
2 2
1
log sin cos log 1
2
x x n
.
2
2 2
log sin cos log 1x x n
2 2
2 2
log 1 log sin 2sin .cos cos
n x x x x
.
2 2
3
log 1 log
2
n
.
2 2
3
log log
4
n
.
3
4
n
.
Câu 24. (Kim Liên - Hà Nội - 2018) Biết rằng phương trình
2ln 2 ln 4 ln 4ln 3
x x
có hai
nghiệmphânbiệt
1
x
,
2
x
1 2
x x
.Tính
1
2
x
P
x
.
A.
1
4
. B.
64
. C.
1
64
. D.
4
.
Lờigiải
Điềukiện
2 0
0
0
x
x
x
*
.
Phươngtrình
2 2
4 4
ln 2 ln 4 ln ln3 ln 4 2 ln .3
x x x x
4
2
16
.3 0
1
4 2 81
4
x
x
x
x x
thỏamãn
*
1
1
2
2
1
1
4
64
16
x
x
P
x
x
.
Câu 25. (THPTLêXoay-2018)Phươngtrình
2
2
49 7 7
3
1
log log 1 log log 3
2
x x
cóbaonhiêu
nghiệm?
A.
2
. B.
3
. C.
1
. D.
4
.
Lờigiải

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điềukiện
0
1
x
x
.
2
2
49 7 7
3
1
log log 1 log log 3
2
x x
7 7 7
log log 1 log 2
x x
7 7
log 1 log 2
x x
1 2
1 2
x x
x x
2
2
2 0
2 0
x x
x x
2
1
x
x
.
Câu 26. (THPT Lương Văn Tụy - Ninh Bình - 2018) Phương trình
2 3
4 8
2
log 1 2 log 4 log 4
x x x
cóbaonhiêunghiệm?
A. Vônghiệm. B. Mộtnghiệm. C. Hainghiệm. D. Banghiệm.
Lờigiải
Điềukiện:
4 4
x
và
1
x
.
Tacó
2 3
4 8
2
log 1 2 log 4 log 4
x x x
2 2
log 4 1 log 4 4
x x x
2
4 1 16
x x
2
2
4 1 16
4 1 16
x x
x x
2
2
4 12 0
4 20 0
x x
x x
2
6
2 2 6
2 2 6
x
x
x
x
.
Đốichiếuđiềukiện,phươngtrìnhđãchocóhainghiệm
2
x
và
2 2 6
x
.
Câu 27. (SGD&ĐT BRVT - 2018) Tổng giá trị tất cả các nghiệm của phương trình
2
2 4 1
2
log 2 log 5 log 8 0
x x
bằng
A.
6
. B.
3
. C.
9
. D.
12
.
Lờigiải
Điềukiện
2
5
x
x
*
.
Tacó
2 2 2
log 2 log 5 log 8 0
x x
2 2
log 2 5 log 8
x x
2 5 8
x x
5
2 5 8
2 5
2 5 8
x
x x
x
x x
6
3 17
2
x
x
thỏamãn
*
.
Vậytổngcácnghiệmcủaphươngtrìnhlà
3 17 3 17
6 9
2 2
.
Câu 28. (Xuân Trường - Nam Định - 2018) Cho phương trình
2 2 2
2 3 6
log 1 .log 1 log 1
x x x x x x
.Biếtphươngtrìnhcómộtnghiệmlà
1
vàmộtnghiệmcònlạicódạng
log log
1
2
b b
c c
x a a
(với
a
,
c
làcácsốnguyêntốvà
a c
).
Khiđógiátrịcủa
2
2 3a b c
bằng:
A.
0
. B.
3
. C.
6
. D.
4
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Lờigiải
Điềukiện
2
1 1
1 0
x
x x
*
2 2 2
2 3 6
log 1 .log 1 log 1
x x x x x x
2 2
2 3 6
2
1
log 1 .log log 1
1
x x x x
x x
2 2 2
2 3 6 6
log 1 .log 6.log 1 log 1
x x x x x x
2 2
6 3 2
log 1 log 6.log 1 1 0
x x x x
2
6
2
3 2
log 1 0 1
log 6.log 1 1 0 2
x x
x x
2
1 1 1
x x
2
1 1x x
2
2
1
1 1
x
x x
1x
.
2
2 3
2 log 1 .log 6 1
x x
2
2 6
log 1 log 3
x x
6
log 3
2
1 2x x
6
6
log 3
2
log 3
2
2
1 2
x
x x
6 6
log 3 log 3
1
2 2
2
x
.
6 6
log 2 log 2
1
3 3
2
x
.(thỏamãn
*
)
Nhưvậyphươngtrìnhđãchocócácnghiệmlà
1x
,
6 6
log 2 log 2
1
3 3
2
x
.
Khiđó
3
a
,
6
b
,
2
c
.Vậy
2
2 3 3
a b c
.
Dạng 1.2 Phương pháp đặt ẩn phụ
Loại1.
log 0
PP
a
P f x
đặt
log
a
t f x
.
Loại2.Sửdụngcôngthức
log log
b b
c a
a c
đểđặt
log log
b b
x a
t a t x
.
Câu 29. Phươngtrình
2
5
log 2 log
2
x
x
cóhainghiệm
1 2 1 2
,
x x x x
.Khiđótổng
2
1 2
x x
bằng
A.
9
2
. B.
3
. C.
6
. D.
9
4
.
Lờigiải
ChọnC
Điềukiệnphươngtrình:
0, 1x x
.
2
2
2 2 2 2
2
2
log 2
4
5 1 5 5
log 2 log log log log 1 0
1
2 log 2 2
log
2
2
x
x
x
x x x x
x
x
x
Suyra
1 2
2, 4
x x
.
Suyra
2
1 2
6
x x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 30. (SGDGiaLai2019)Sốnghiệmcủaphươngtrình
2 2
2 2
log 8log 4 0
x x
là:
A.
2
. B.
3
. C.
0
. D.
1
.
Lờigiải
ChọnD
Điềukiện:
0
x
2 2 2
2 2 2 2 2
1
log 8log 4 0 4log 8log 4 0 log 1
2
x x x x x x TM
Câu 31. Tíchtấtcảcácnghiệmcủaphươngtrình
2
3 3
log 2log 7 0
x x
là
A.
9
. B.
7
. C.
1
. D.
2
.
Lờigiải
ChọnA
Điềukiện:
0
x
Đặt
3
logt x
,phươngtrìnhtrởthành:
2
2 7 0
t t
1
Do
. 7 0
a c
nênphươngtrình
1
có
2
nghiệm
1 2
;t t
phânbiệtthỏamãn
1 2
2
t t
.
Khiđó,cácnghiệmcủaphươngtrìnhbanđầulà:
1
1
3 ;
t
x
2
2
3
t
x
.
1 2 1 2
2
1 2
. 3 .3 3 3 9
t t t t
x x
.
Câu 32. (YênDũng2-BắcGiang 2019)Tổngcácnghiệmcủaphươngtrình
2
2 2 3
log log 9.log 3
x x
là
A.
2
. B.
17
2
. C.
8
. D.
2
.
Lờigiải
ChọnB
Tacó
2
2 2
2 2 3 2 2
2
1
log 1
log log 9.log 3 log 2log 3 0
2
log 3
8
x
x
x x x x
x
x
Vậy
1 17
8
2 2
S
.
Câu 33. (THPTHaiBàTrưng-Huế-2019)Biếtphươngtrình
2
2 2
log 2 5log 0
x x
cóhainghiệm
phânbiệt
1
x
và
2
x
.Tính
1 2
.x x
.
A.
8
. B.
5
. C.
3
. D.
1
.
Lờigiải
ChọnA
Điềukiện
0
x
.
Biếnđổiphươngtrìnhđãchovềphươngtrìnhsau:
2
2 2
log 3log 1 0
x x
.
Do
2 1
log
x
và
2 2
log
x
làhainghiệmcủaphươngtrình
2
3 1 0
t t
nên

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
2 1 2 2
log log 3
x x
,mà
2 1 2 2 2 1 2
log log log .x x x x
.
Suyra
2 1 2
log . 3
x x
nên
1 2
. 8
x x
.
Câu 34. (ChuyênĐạihọcVinh-2019)Biếtrằngphươngtrình
2
2 2
log 7 log 9 0
x x
có2nghiệm
1 2
,x x
.Giátrịcủa
1 2
x x
bằng
A.
128
. B.
64
. C.
9
. D.
512
.
Lờigiải
ChọnA
+Điềukiện
0
x
.
+
2
2 2
log 7 log 9 0
x x
2
2
7 13
log
2
7 13
log
2
x
x
7 13
2
7 13
2
2
2
x
x
(thỏamãnđiềukiện
0
x
).
Vậy
7 13 7 13
2 2
1 2
2 .2 128
x x
.
Câu 35. (Hội8trườngchuyênĐBSH-2019)Chophươngtrình
2
2
2
log 4 log 2 5
x x
.Nghiệm
nhỏnhấtcủaphươngtrìnhthuộckhoảng
A.
0;1
. B.
3;5
. C.
5;9
. D.
1;3
.
Lờigiải
ChọnA
Điềukiện:
0.
x
2
2
2 2 2
2
2
2
2
2
log 4 log 2 5 1 log 2 2log 2 5 0
2
log 2 2
log 2 4 .
1
log 2 2
8
x x x x
x
x
x
x
x
Nghiệmnhỏnhấtlà
1
0;1 .
8
x
Câu 36. Gọi
T
làtổngcácnghiệmcủaphươngtrình
2
1 3
3
log 5log 4 0
x x
.Tính
T
.
A.
4L
. B.
5
T
. C.
84
T
. D.
5
T
.
Lờigiải
ChọnC
Điềukiện:
0
x
.
2 2
1 3 3 3
3
log 5log 4 0 log 5log 4 0
x x x x
.
3
4
3
3
log 1
log 4
3 81
x
x
x
x
(thỏamãn).
Vậy
3 81 84
T
.
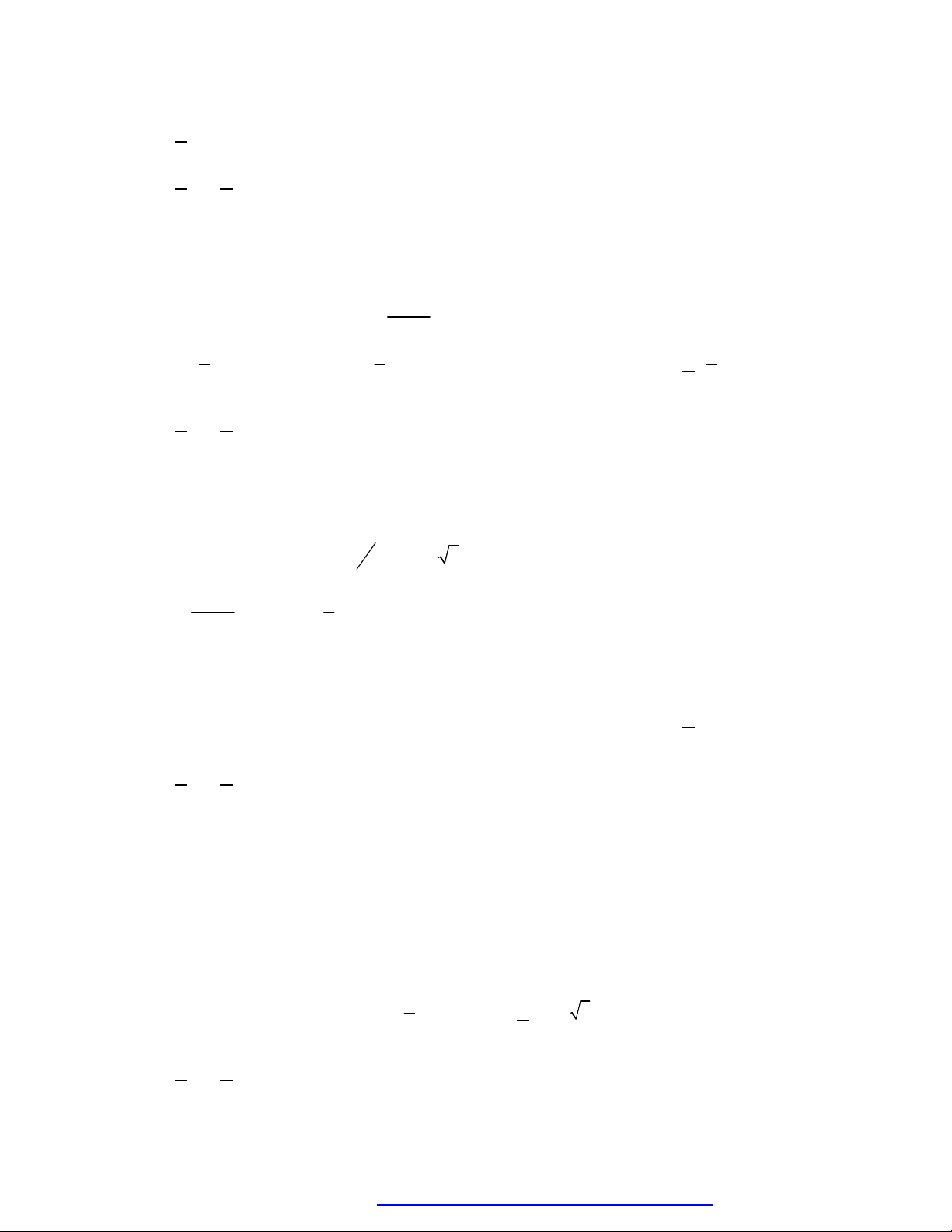
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 37. (NgôQuyền-HảiPhòng2019)Phươngtrình
2
2 2
log 5log 4 0
x x
cóhainghiệm
1 2
,x x
.
Tínhtích
1 2
.x x
.
A.
32
. B.
36
. C.
8
. D.
16
.
Lờigiải
ChọnA
2 1
2
2 2
2 2
log 1 2
log 5log 4 0
log 4 16
x x
x x
x x
.Vậytích
1 2
. 32
x x
.
Câu 38. (ChuyênĐHVinh 2019)Chocácsốthựca,bthỏamã
1
a b
và
2
log log 3
a b
b a
.Tính
giátrịcủabiểuthức
2
log
2
ab
a b
T
.
A.
1
6
. B.
3
2
. C.
6
. D.
2
3
.
Lờigiải
ChọnD
Tacó
2
1
log log 3 2log 3
log
a b b
b
b a a
a
2
log 1
( )
2log 3log 1 0
1
log
( )
2
b
b b
b
a
a b L
a a
a
a b N
2
b a
Vậy
3
2
2
2
log log
2 3
ab
a
a b
T a
nênđápánDđúng.
Câu 39. Biết rằng phương trình
2
2 2
log log 2018 2019 0
x x
có hai nghiệm thực
1 2
,x x
. Tích
1 2
.x x
bằng
A.
2
log 2018
. B.
0,5
. C.
1
. D.
2
.
Lờigiải
ChọnD
ĐKXĐ:
0
x
.
2 2
2 2 2 2 2
log log 2018 2019 0 log log log 2018 2019 0
x x x x
.
Đặt
2
log 2
t
t x x
,tacó
2
2
log 2018 2019 0 *
t t
Gọi
1 2
,t t
làhainghiệmcủa
*
,tacó
1 2
1
1 2
. 2 2 2
t t
x x
.
Câu 40. Chophươngtrình
2 2 2
3 3
log 3 log 1 0.
x x
Biếtphươngtrìnhcó2nghiệm,tínhtích
P
của
hainghiệmđó.
A.
9.
P
B.
2
.
3
P
C.
3
9.
P D.
1.
P
Lờigiải
ChọnC
Tacó
2 2 2
3 3
log 3 log 1 0
x x
(điềukiện
0
x
).
2 2
3 3
1 log 2log 1 0.
x x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Đặt
3
log
x t
tacóphươngtrình
2 2
1 2 1 0
t t
2
2
3 2 0 .
3
0
t
t t
t
Với
3
0 log 0 1.
t x x
Với
2
3
3
3
2 2 1
log 3 .
3 3
9
t x x
Vậy
3 3
1. 9 9.
P
Câu 41. (THPTBaĐình2019)Biếtrằngphươngtrình
4
2
3 3
x
log x log
3
cóhainghiệm
a
và
b
.Khi
đó
ab
bằng
A.
8
. B.
81
. C.
9
. D.
64
.
Lờigiải
Đ/K:
0
x
.
Phươngtrinh
4
2
3 3
x
log x log
3
2
3 3
log 4.log 1 0
x x
3
3
log 2 3
log 2 3
x
x
2 3
2 3
3
3
x
x
.Khiđó
2 3 2 3
. 3 .3 81
a b
.
Câu 42. (Chuyên Quốc Học Huế -2019) Gọi
T
là tổng các nghiệm của phương trình
2
1 3
3
log 5log 4 0
x x
.Tính
T
.
A.
4T
B.
4T
C.
84
T
D.
5
T
Lờigiải
ĐKXĐ:
0
x
Tacó:
2
1 3
3
log 5log 4 0
x x
2
3 3
log 5log 4 0
x x
2
3 3
log 5log 4 0
x x
3
4
3
log 1
3
log 4
3
x
x
x
x
Vậy
4
3 3 84
T
Câu 43. (Cụm 8 Trường Chuyên 2019) Cho phương trình
2
2
2
log 4 log 2 5
x x
. Nghiệm nhỏ
nhấtcủaphươngtrìnhthuộckhoảngnàosauđây?
A.
1; 3
. B.
5 ; 9
. C.
0 ;1
. D.
3; 5
.
Lờigiải
2
2 2
2 2 2 2
2
log 4 log 2 5 1 log 2 2log 2 5 log 2 4
x x x x x
2
2
2
2 4
log 2 2
1
1
2
log 2 2
8
4
xx
x
xx
x
.
Vậynghiệmnhỏnhấtcủaphươngtrìnhthuộckhoảng
0 ;1
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 44. (THPT Lương Thế Vinh Hà Nội 2019) Tích tất cả các nghiệm của phương trình
2
3 3
log 2log 7 0
x x
là
A.
9
. B.
7
. C.
1
. D.
2
.
Lờigiải
Dễthấyphươngtrìnhbậchai:
2
3 3
log 2log 7 0
x x
luôncó2nghiệmphânbiệt
KhiđótheoVi-et,
3 1 3 2 3 1 2 1 2
2
log log log ( . ) 2 . 9
1
x x x x x x
.
Câu 45. (Chuyên Hùng Vương Gia Lai 2019) Cho 2 số thực dương
a
và
b
thỏa mãn
4
9 3
log log 8
a b
và
3
3
3
log log 9
a b
.Giátrịbiểuthức
1P ab
bằng
A.
82
. B.
27
. C.
243
. D.
244
.
Lờigiải
Tacó:
3
4
9 3
3 3 3
3
3 3 3
3
log log 8
2log log 8 log 3
27
log log 9
log 3log 9 log 2 9
a b
a b a
a
a b
a b b b
Nên
1 244
P ab
Câu 46. (ChuyênĐạiHọcVinh2019)Biếtphươngtrình
2
2 2
log 7log 9 0
x x
cóhainghiệm
1 2
,x x
.
Giátrị
1 2
.x x
bằng
A.
128
B.
64
C.
9
D.
512
Lờigiải
ChọnA
Đk:
0
x
;
7 13
2
2
2
2 2
7 13
2
2
7 13
log
2
2
log 7 log 9 0
7 13
log
2
2
x
x
x x
x
x
Vậy
7 13 7 13
7
2 2
1 2
. 2 .2 2 128
x x
Câu 47. (Mã104 2017)Xétcácsốnguyêndương
a
,
b
saochophươngtrình
2
ln ln 5 0
a x b x
có
hainghiệmphânbiệt
1
x
,
2
x
vàphươngtrình
2
5log log 0
x b x a
cóhainghiệmphânbiệt
3
x
,
4
x
thỏamãn
1 2 3 4
x x x x
.Tínhgiátrịnhỏnhất
min
S
của
2 3S a b
.
A.
min
17
S
B.
min
30
S
C.
min
25
S
D.
min
33
S
Lờigiải
ChọnB
Điềukiện
0
x
,điềukiệnmỗiphươngtrìnhcó2nghiệmphânbiệtlà
2
20b a
.
Đặt
ln , logt x u x
khiđótađược
2
5 0 1
at bt
,
2
5 0 2
t bt a
.
Tathấyvớimỗimộtnghiệm
t
thìcómộtnghiệm
x
,một
u
thìcómột
x
.
Tacó
1 2 1 2
1 2
. .
b
t t t t
a
x x e e e e
,
1 2
5
3 4
. 10 10
b
u u
x x
,lạicó
5
1 2 3 4
10
b b
a
x x x x e
5
ln10 3
5 ln10
b b
a a
a
(do
,a b
nguyêndương),suyra
2
60 8
b b
.
Vậy
2 3 2.3 3.8 30
S a b
,suyra
min
30
S
đạtđược
3, 8
a b
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Câu 48. (Chuyên Lê Quý Đôn Điện Biên 2019) Tích các nghiệm của phương trình
2
25
log 125 .log 1
x
x x
.
A.
630
. B.
1
125
. C.
630
625
. D.
7
125
Lờigiải
Điềukiện
0; 1x x
.
Tacó
2
2 2
25 5 5
1
log 125 .log 1 log 125 log log 1 3.log 5 1 log 4
2
x x x x
x x x x x
Đặt
5
log
x t
phươngtrìnhtươngđương:
5
2 2
5
5
log 1
1
3
1 4 3 4 0
1
log 4
4
625
x
x
t
t t t
x
t
t
x
Vậytíchcácnghiệmcủaphươngtrìnhlà
1
125
.
Câu 49. (Chuyên Lê Quý Đôn Điện Biên 2019) Tích các nghiệm của phương trình
2
25
log 125 .log 1
x
x x
.
A.
630
. B.
1
125
. C.
630
625
. D.
7
125
Lờigiải
ChọnB
Điềukiện
0; 1x x
.
Tacó
2
2 2
25 5 5
1
log 125 .log 1 log 125 log log 1 3.log 5 1 log 4
2
x x x x
x x x x x
Đặt
5
log
x t
phươngtrìnhtươngđương:
5
2 2
5
5
log 1
1
3
1 4 3 4 0
1
log 4
4
625
x
x
t
t t t
x
t
t
x
Vậytíchcácnghiệmcủaphươngtrìnhlà
1
125
.
Câu 50. (Kiểmtranănglực- ĐH -QuốcTế- 2019)Xétphươngtrình
2 3
log 1 log 2 3
x x
.
Mệnhđềnàosauđâyđúng?
A. Phươngtrìnhtrênvônghiệm.
B. Phươngtrìnhtrêncónghiệmbéhơn
1
.
C. Phươngtrìnhtrêncónghiệmlớnhơn
1
vàmộtnghiệmbéhơn
1
.
D. Phươngtrìnhtrênchỉcónghiệmhơn
1
.
Lờigiải
ChọnC
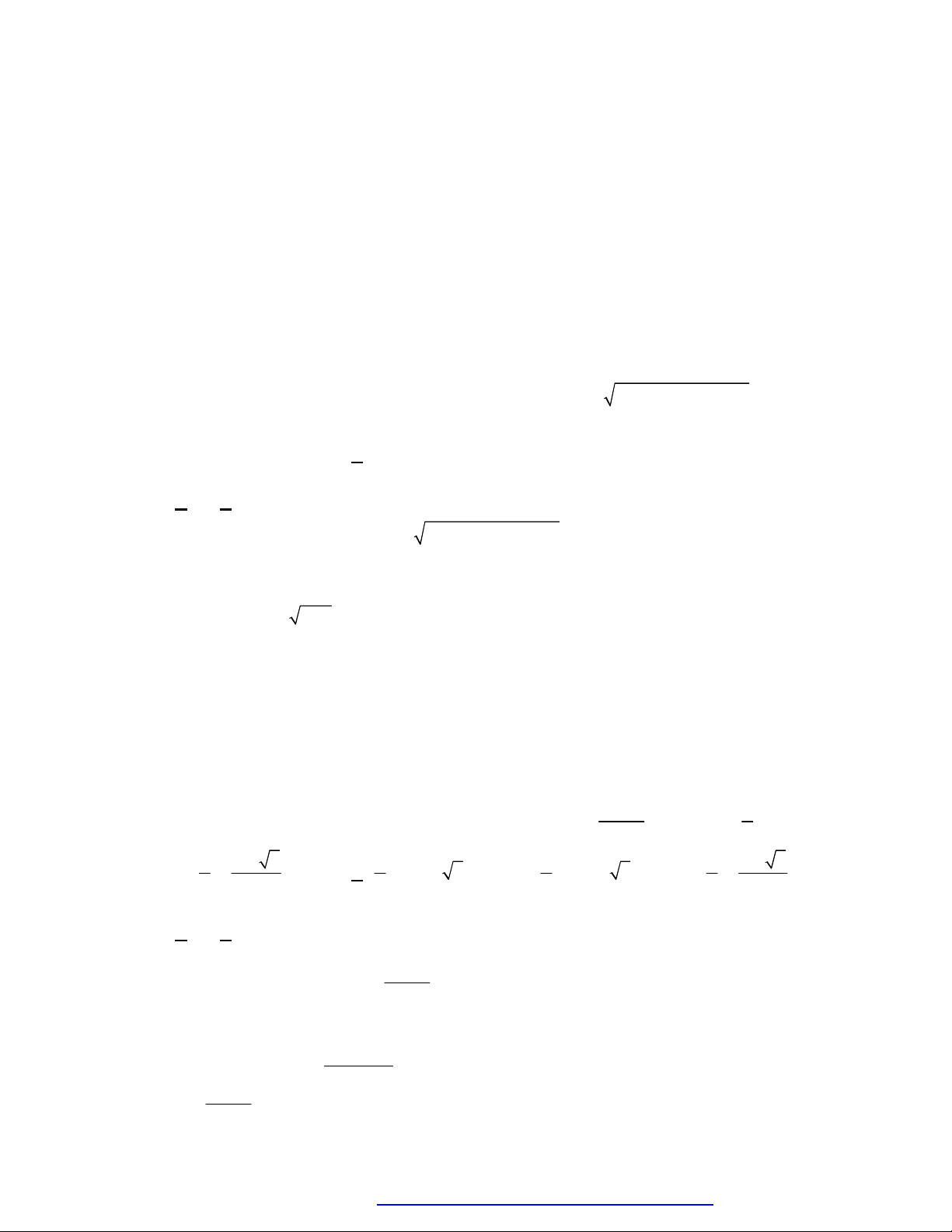
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 3
log 1 log 2 3
x x
,điềukiện
0
x
.
2 3 2
log 1 log 2.log 2 3 0
x x
2
3 2 3 2
log 2. log 2 log 2 log 5 0 1
x x
.
Đặt
2
logt x
.
Phươngtrình
1
trởthành:
2
3 3
log 2 . 2 log 2 5 0 2
t t
.
Phươngtrình
2
có
0
ac
nênluôncóhainghiệm
1 2
0
t t
.
Suyra
0
1
1
2 2 1
t
x
và
0
2
2
2 2 1
t
x
.
Vậyphươngtrình
1
cónghiệmlớnhơn
1
vàmộtnghiệmbéhơn
1
.
Câu 51. (Tham khảo 2018) Cho dãy số
n
u
thỏa mãn
1 1 10 10
log 2 log 2log 2logu u u u
và
1
2
n n
u u
vớimọi
1n
.Giátrịnhỏnhấtcủa
n
để
100
5
n
u
bằng
A.
247
. B.
248
. C.
229
. D.
290
.
Lờigiải
ChọnB
Có
1 1
2 2
n
n n
u u u
.Xét
1 1 10 10
log 2 log 2log 2logu u u u
(*)
Đặt
1 10
log 2logt u u
,điềukiện
2
t
Pt(*)trởthành 2
t t
2
0
2 0
t
t t
1
t
Với
1
t
1 10
log 2log 1
u u
(với
9
10 1 1
log log 2 . 9log 2 logu u u
)
1
log 1 18log 2
u
1 18log 2
1
10u
Mặtkhác
1 1 1 18log 2 18log 2 100
1
2 2 .10 2 .5.10 5
n n n
n
u u
99 18log 2
2
log 5 .10 247,87
n
Vậygiátrịnhỏnhấtcủa
n
là
248
.
Câu 52. Cho
a
,
b
làcácsốdươngthỏamãn
9 16 12
5
log log log
2
b a
a b
.Tínhgiátrị
a
b
.
A.
3 6
4
a
b
. B.
7 2 6
a
b
. C.
7 2 6
a
b
. D.
3 6
4
a
b
.
Lờigiải
ChọnB
+Đặt
9 16 12
5
log log log
2
b a
a b t
9
16
5
12
2
t
t
t
a
b
b a
5.16 9
12
2
t t
t
9 2.12 5.16 0
t t t

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
2
3
1 6
4
3 3
2. 5 0
4 4
3
1 6
4
t
t t
t
l
.
+
2
2
9 3
1 6 7 2 6
16 4
t
t
t
a
b
.
Câu 53. (THPT Hai Bà Trưng - Huế - 2019) Cho hai số thực dương
,m n
thỏa mãn
4 6 9
log log log
2
m
n m n
.Tínhgiátrịcủabiểuthức
m
P
n
.
A.
2P
. B.
1P
. C.
4P
. D.
1
2
P
.
Lờigiải
ChọnB
Đặt
1
2
4 6 9
4
4
2
log log log 6 6
2
9 9
t
t
t t
t t
m
m
m
t n m n n n
m n m n
2
2
3
2
1
3
2 2 2 1 1
2.4 6 9 2. 1 0 log
3 3 3 2 2
2 1
3 2
t
t t t
t t t
t
VN
t
2
3
1
log
2
2.4
4 2 2 1
2. 2. 2. 2. 1
6 3 3 2
6
t t
t
t
m
m
P
n
n
.
Chọn B.
Câu 54. (Hội 8 trường chuyên ĐBSH - 2019) Giả sử
,p q
là các số thực dương thỏa mãn
16 20 25
log log log
p q p q
.Tínhgiátrịcủa
p
q
.
A.
1
1 5
2
. B.
8
5
. C.
1
1 5
2
. D.
4
5
.
Lờigiải
ChọnA
16 20 25
log log log
p q p q
16
20
25
log
log
log
p t
q t
p q t
16
20
25
t
t
t
p
q
p q
16 20 25
t t t
16 4
1 0
25 5
t t
4 1 5
5 2
4 1 5
5 2
t
t
vn

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Suyra
4 1 5
5 2
t
p
q
.
Câu 55. (TTDiệuHiền-CầnThơ-2018)Tíchcácnghiệmcủaphươngtrình
2
25
log 125 log 1
x
x x
bằng
A.
7
25
. B.
630
625
. C.
1
125
. D.
630
.
Lờigiải
Điềukiện:
0 1x
,tacó:
2
25
log 125 log 1
x
x x
2 2
25 25
log log .log 125 1
x
x x
2
25 25
3
log log 1 0
2
x x
25
25
1
log
2
log 2
x
x
2
5
1
25
x
x
.
Vậytíchcácnghiệmcủaphươngtrìnhlà:
1
125
.
Câu 56. (Đặng Thúc Hứa - Nghệ An - 2018) Tích tất cả các nghiệm của phương trình
2
2 2
log log 1 1
x x
A.
1 5
2
2
. B.
1
. C.
1 5
2
2
. D.
1
2
.
Lờigiải
Điềukiện
2
0
log 1 0
x
x
0
1
2
x
x
1
2
x
.
Đặt
2
log 1x t
,
0
t
2
2
log 1
x t
tacóphươngtrình
2
2
1 1t t
4 2
2 0t t t
3
2 1 0
t t t
2
1 2 1 0
t t t t
0 /
1 /
1 5
/
2
1 5
2
t t m
t t m
t t m
t loai
.
Với
0t
thì
1
2
log 1 2
x x
.
Với
1t
thì
0
2
log 0 2
x x
.
Với
1 5
2
t
thì
1 5
2
2
1 5
log 2
2
x x
.
Vậytíchcácnghiệmcủaphươngtrìnhlà
1 5
2
2
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Câu 57. (Lý Nhân Tông - Bắc Ninh - 2020) Gọi
x
,
y
các số thực dương thỏa mãn điều kiện
9 6 4
log log log
x y x y
và
2
x a b
y
, với
,a b
là hai số nguyên dương. Tính
2 2
T a b
.
A.
26.
T
B.
29.
T
C.
20.
T
D.
25.
T
Lời giải
Chọn A
Đặt
9 6 4
log log log
t x y x y
,tacó
9
6
4
t
t
t
x
y
x y
9 6 4
t t t
2
3 1 5
( )
2 2
3 3
1 0
2 2
3 1 5
2 2
t
t t
t
loai
3 1 5
2 2
t
.
Suyra
9 3 1 5
6 2 2
t t
x
y
.
Mà
1 5
1; 5.
2 2
x a b
a b
y
Vậy
2 2 2 2
1 5 26.
T a b
Câu 58. (THPT Nguyễn Viết Xuân - 2020) Cho các số thực dương
,a b
thỏa mãn
4 6 9
log log log 4 5 1
a b a b
.Đặt
b
T
a
.Khẳngđịnhnàosauđâyđúng?
A.
1 2T
. B.
1 2
2 3
T
. C.
2 0
T
. D.
1
0
2
T
.
Lời giải
Chọn D
Giảsử:
4 6 9
1
4
log log log 4 5 1 6
4 5 9
t
t
t
a
a b a b t b
a b
Khiđó
2
4 6 2 2
4.4 5.6 9.9 4. 5. 9 4. 5. 9 0
9 9 3 3
t t t t
t t t
2
3
2 9
3 4
9
log 2
4
2
1
3
t
t
t t
VN
Vậy
2
6 3 4 1
0;
4 2 9 2
t
b
T
a
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dạng 1.3 Phương pháp mũ hóa
+Nếu
0, 1: log
g x
a
a a f x g x f x a
(mũ hóa)
Câu 59. (CầnThơ2019)Tíchtấtcảcácnghiệmcủaphươngtrình
2
log 12 2 5
x
x
bằng
A.
2
. B.
32
. C.
6
. D.
3
.
Lờigiải
ChọnC
Điềukiện
12 2 0(*)
x
Khiđó
5 2
2
log 12 2 5 12 2 2 2 12.2 32 0
x x x x x
x
2 4 2
3
2 8
x
x
x
x
Tathấycảhainghiệmđềuthoảmãnđiềukiện
(*)
,vàtíchbằng
2.3 6
.
Câu 60. Phươngtrình
4
log 3.2 1
x
x
cónghiệmlà
0
x
thìnghiệm
0
x
thuộckhoảngnàosauđây
A.
1;2
. B.
2;4
. C.
2;1
. D.
4;
.
Lờigiải
ChọnB
Tacó
4
log 3.2 1
x
x
1
3.2 4 4 12.2 0
x x x x
2 0,
2 12
x
x
vn
2
log 12 2;4
x
.
Câu 61. Phươngtrình
4
log 3.2 1 1
x
x
cóhainghiệm
1 2
;x x
.Tínhgiátrịcủa
1 2
P x x
.
A.
6 4 2
. B.
12
. C.
2
log 6 4 2
. D.
2
.
Lờigiải
ChọnD
Điềukiện:
1
3.2 1 0 2
3
x x
*
.
2
1
4
2
2
1
log 3.2 1 1 3.2 1 4 2 3.2 1 0
4
log 6 4 2
2 6 4 2 t/m *
2 6 4 2 t/m *
log 6 4 2
x x x x x
x
x
x
x
x
Khiđó
2 2 2 2
log 6 4 2 log 6 4 2 log 6 4 2 6 4 2 log 4 2
P
.
Câu 62. (Sở Bạc Liêu - 2018) Gọi
1 2
,x x
(với
1 2
x x
) là nghiệm của phương trình
2 1 1
3
log 3 3 1
x x
x
khiđógiátrịcủabiểuthức
1 2
3 3
x x
là:
A.
1 3
. B.
1 3
. C.
2 3
. D.
2 3
.
Lờigiải
2 1 1
3
log 3 3 1
x x
x
2 1 1
3 3 1 3
x x x
2
3 4.3 3 0
x x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
3 3 3 1
x x
1 0
x x
.
Do
1 2
x x
nên
1 2
0, 1.
x x
TađượcđápánAlàđúng.
Câu 63. (ChuyênTháiBình-2018)Sốnghiệmcủaphươngtrình
5
log 3
2
x
x
là:
A.
0
. B.
1
. C.
3
. D.
2
.
Lờigiải
Đk:
3
x
Đặt
5
log 3
t x
5 3
t
x
,phươngtrìnhđãchotrởthành
2 5 3
t t
2 3 5
t t
2 1
3. 1
5 5
t t
(1)
Dễthấyhàmsố
2 1
3.
5 5
t t
f t
nghịchbiếntrên
và
1 1
f
nênphươngtrình(1)có
nghiệmduynhất
1t
.
Với
1t
,tacó
5
log 3 1
x
2
x
Vậyphươngtrìnhcónghiệmduynhất
2
x
.
Câu 64. (Hồng Bàng - Hải Phòng - 2018) Phương trình
2
log 5 2 2
x
x
có hai ngiệm
1
x
,
2
x
.
Tính
1 2 1 2
P x x x x
.
A.
11
. B.
9
. C.
3
. D.
2
.
Lờigiải
Điềukiện:
2 5
x
2
log 5 2 2
x
x
2
5 2 2
x x
4
5 2
2
x
x
2 1
2 4
x
x
0
2
x
x
1 2 1 2
2
P x x x x
.
Câu 65. (THPTCaoBáQuát-2018)Chophươngtrình
4
log 3.2 1 1
x
x
cóhainghiệm
1 2
,x x
.
Tổng
1 2
x x
là:
A.
2
log 6 4 2
. B.
2
. C.
4
. D.
6 4 2
.
Lờigiải.
ChọnB
1
4
4
log 3.2 1 1 3.2 1 4 3.2 1 0 1
4
x
x x x x
x
.
Đặt
2 0
x
t t
.PT
2
2
1
3 1 0 2
4
t t
.
Giảsử
2
nghiệmcủaPT
2
là
1 2 1 2
1 2 1 2 1 2
, . 4 2 .2 4 2 4 2.
x x x x
t t t t x x
Dạng 1.4 Phương pháp hàm số, đánh giá
Thôngthườngtasẽvậndụngnộidungcácđịnhlý(vàcáckếtquả)sau:
Nếuhàm số
y f x
đơn điệu một chiềutrênD thì phươngtrình
0
f x
không quámột
nghiệmtrênD.
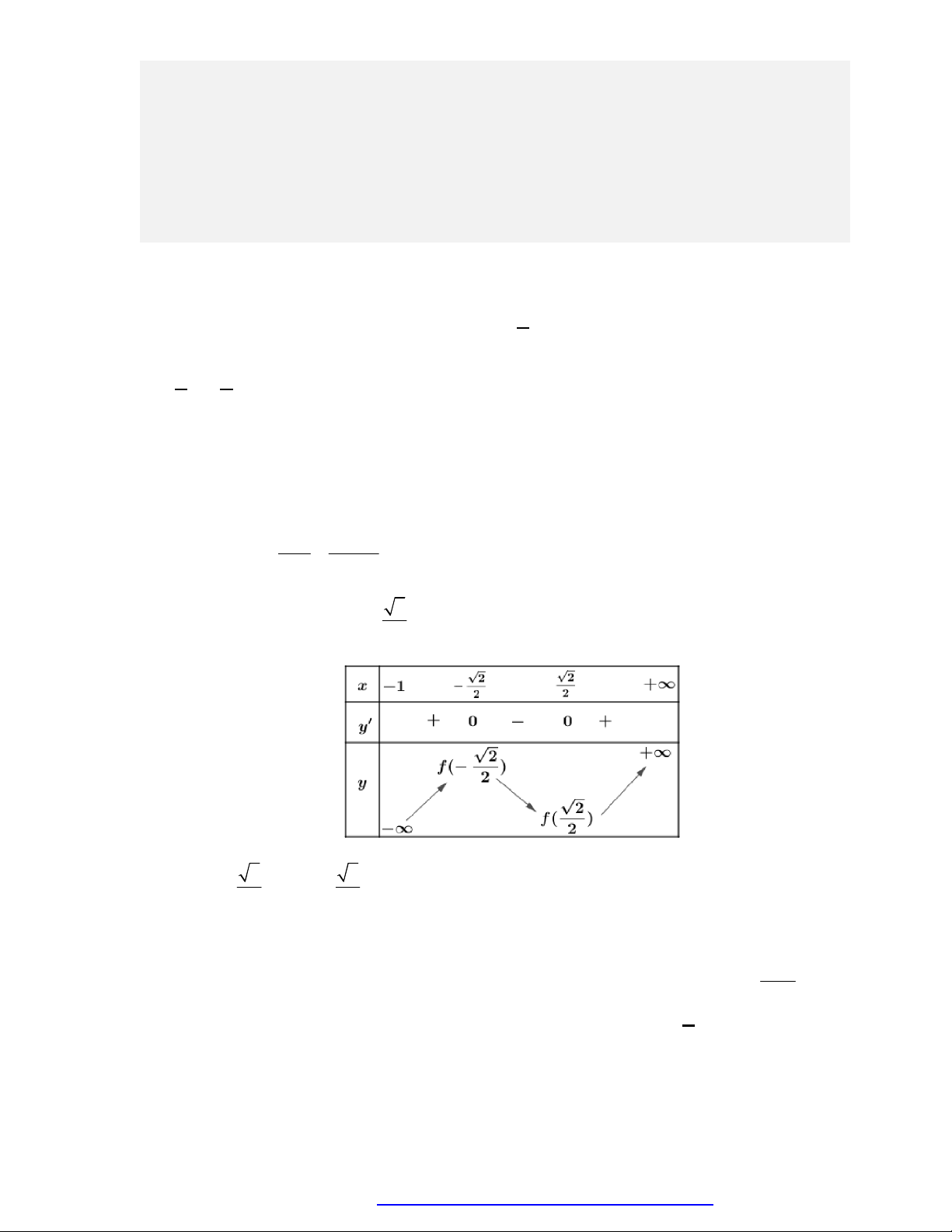
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đểvậndụngđịnhlýnày,tacầnnhẩmđược
1
nghiệm
o
x x
củaphươngtrình,rồichỉrõ
hàmđơn điệu một chiều trên D (luôn đồng biến hoặc luônnghịchbiến trên D) vàkếtluận
o
x x
lànghiệmduynhất.
Hàm số
f t
đơn điệu một chiều trên khoảng
;a b
và tồn tại
; ;u v a b
thì
f u f v u v
".
Đểápdụngđịnhlýnày,tacầnxâydựnghàmđặctrưng
f t
.
Câu 66. (Đề tham khảo 2017) Hỏi phương trình
3
2
3 6 ln 1 1 0
x x x
có bao nhiêu nghiệm
phânbiệt?
A.
2
. B.
1
. C.
3
. D.
4
Lờigiải
ChọnC
Điềukiện:
1
x
.
Phươngtrìnhđãchotươngđươngvới
2
3 6 3ln 1 1 0
x x x
.
Xéthàmsố
2
3 6 3ln 1 1
y x x x
liêntụctrênkhoảng
1;
.
2
3 6 3
6 1
1 1
x
y x
x x
.
2
2
0 2 1 0
2
y x x
(thỏađiềukiện).
Vì
2
0
2
f
,
2
0
2
f
và
lim
x
y
nên đồ thị hàm số cắttrụchoànhtại 3 điểm
phânbiệt.
Câu 67. (ChuyênLamSơn-ThanhHóa-2018)Sốnghiệmcủaphươngtrình
1
ln 1
2
x
x
là:
A.
1
. B.
0
. C.
3
. D.
2
.
Lờigiải
Hàmsố
ln 1
f x x
luônđồngbiếntrênkhoảng
1;
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Hàmsố
1
2
g x
x
có
2
1
0
2
g x
x
,
2
x
nên
g x
luônnghịchbiếntrên
khoảng
1;2
và
2;
.
Vậyphươngtrìnhđãcholuôncóhainghiệm.
Câu 68. (THPT Nguyễn Trãi - Đà Nẵng - 2018) Giải phương trình
2 3 3
log .log .log 3x x x x
2 3
log 3log
x x x
.Tacótổngtấtcảcácnghiệmbằng
A.
35
. B.
5
. C.
10
. D.
9
.
Lờigiải
Điềukiện
0
x
.
2 3 3
log .log .log 3x x x x
2 3
log 3log
x x x
2 3
log 3 log 1 0
x x x
2
3
log 3 0
x
x x
.
Tacóhàmsố
2
log
f x x x
liêntụcvàđồngbiếntrên
0;
và
2 3
f
nênphương
trình
2
log 3 0
x x
cómộtnghiệm
2
x
.
Vậytổngtấtcảcácnghiệmbằng
5
.
Câu 69. Tínhtổngtấtcảcácnghiệmcủaphươngtrình
2
2 2
1
log 3 log 1 4 2 3
2
x x x x x
.
A.
2
S
. B.
1
S
. C.
1
S
. D.
1 2
S
.
Lờigiải
ChọnB
Điềukiện:
1
x
.
Tacó:
2
2 2
2 2 2 2
1
log 3 log 1 4 2 3 log 3 3 1 log 1 *
2
x x x x x x x x x
Xéthàmsố
2
2
log 1
f t t t
trênkhoảng
0;
.
2
2
1
2ln 2. 1 ln 2
1 2ln 2
1
2
2 1 0
ln 2 ln 2 ln 2
t
t t
f t t
t t t
0
t
.
Vậyhàmsố
f t
đồngbiếntrênkhoảng
0;
.
Suyra
* 3 1 3 1f x f x x x
2
1
1
1
1
2 0
2
x
x
x
x
x x
x
.
Vậytổngcácnghiệmcủaphươngtrìnhbằng
1
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 70. Biếtphươngtrình
5 3
2 1 1
log 2log
2
2
x x
x
x
cómộtnghiệmdạng
2x a b
trong
đó
,a b
làcácsốnguyên.Tính
2
a b
.
A.
3
. B.
8
. C.
4
. D.
5
.
Lờigiải
ChọnB
Điềukiện:
0
0
1
1
1
0
2
2
x
x
x
x
x
x
x
.
Tacó:
5 3 5 5 3 3
2 1 1
log 2log log 2 1 log 2log 1 2log 2
2
x x
x x x x
x
x
5 3 5 3
log 2 1 2log 2 log 2log 1 *
x x x x
Xéthàmsố:
5 3
log 1 2log
f t t t
trên
2;
Tacó:
1 2
' 0
1 ln5 .ln3
f t
t t
vớimọi
2;t
.
Suyra
f t
đồngbiếntrên
2;
Từđótacó
1 2
* 2 1 2 1 2 1 0
1 2
x
f x f x x x x x
x
Vậy
1 2 3 2 2 3, 2
x x a b
Câu 71. Sốnghiệmthựccủaphươngtrình
2
1 2
2 2
2 log 1 4 log 3
x x
x x x
.
A.
0
. B.
1
. C.
2
. D.
3
.
Lờigiải
ChọnB
Đk:
0
x
.
Tacó
2
1 1, 0
x x x
dođó
2
1 2
2
2 log 1 0, 0
x
x x x
.
Với
1
0
3
x
thì
2
1 2
2
2
2 log 1 0
4 log 3 0
x
x
x x
x
,dođóphươngtrìnhđãchovônghiệm.
Với
1
3
x
.
2
1 2
2 2
2 log 1 4 log 3
x x
x x x
2
1 2 3
2 2
2 log 1 2 log 3
x x x
x x x
.(*)
Xéthàmsố
2
2 log
t
f t t
,với
1t
.
Có
2
1
2 ln 2log 0, 1;
ln 2
t
f t t f t t
t
.
Suyrahàmsốđồngbiếntrênkhoảng
1;
.
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Dođó(*)
2 2
1 1
1 3 1 3 ;
3
3
f x x f x x x x x
.
Vậyphươngtrìnhđãchocó1nghiệmthực.
Câu 72. (Bắc Ninh -2018)Chophươngtrình
2
2 2
1 2 1 1
log 2 3 log 1 2 2
2
x
x x x
x x
,
gọi
S
làtổngtấtcảcácnghiệmcủanó.Khiđó,giátrịcủa
S
là
A.
2
S
. B.
1 13
2
S
. C.
2
S
. D.
1 13
2
S
.
Lờigiải
Điềukiện
1
2
2
0
x
x
.
Xéthàmsố
2
2
log 1
f t t t
,
0t
.
Tacó
1
2 1
ln 2
f t t
t
2
2ln 2. 2ln 2. 1
0
.ln 2
t t
t
,
0
t
,dođóhàmsố
f t
đồngbiến
trênkhoảng
0;
.
Mặtkháctacó:
2
2 2
1 2 1 1
log 2 3 log 1 2 2
2
x
x x x
x x
2
2
2 2
1 1
log 2 2 1 log 2 2 1
x x
x x
1
2 2f x f
x
1
2 2x
x
3 2
2 4 1 0
x x x
1
3 13
2
3 13
2
x
x
x
Kếthợpvớiđiềukiệntađược
1
3 13
2
x
x
.Vậy
1 13
2
S
.
Câu 73. (Toán Học Và Tuổi Trẻ - 2018) Biết
1
x
,
2
x
là hai nghiệm của phương trình
2
2
7
4 4 1
log 4 1 6
2
x x
x x
x
và
1 2
1
2
4
x x a b
với
a
,
b
làhaisốnguyêndương.
Tính
.a b
A.
16
a b
. B.
11
a b
. C.
14
a b
. D.
13.
a b

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lờigiải
Điềukiện
0
1
2
x
x
Tacó
2
2
2 2
7 7
2 1
4 4 1
log 4 1 6 log 4 4 1 2
2 2
x
x x
x x x x x
x x
2 2
7 7
log 2 1 2 1 log 2 2 1x x x x
Xéthàmsố
7
1
log 1 0
ln7
f t t t f t
t
với
0t
Vậyhàmsốđồngbiến
Phươngtrình
1
trởthành
2 2
3 5
4
2 1 2 2 1 2
3 5
4
x
f x f x x x
x
Vậy
1 2
9 5
4
2 9; 5 9 5 14.
9 5
4
l
x x a b a b
tm
Câu 74. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2018) Số nghiệm của phương trình
2
2
ln 2 2018
2
x
x x
là
A.
3
. B.
1
. C.
4
. D.
2
.
Lờigiải
Xéthàmsố
2
2
ln 2
2
x
f x x x
với
; 2 2;x
.
Tacó
2
2
1
2
x
f x x
x
;
2
2
2
2 4
1 0, ; 2 2;
2
x
f x x
x
.
Nênsuyrahàmsố
2
2
1
2
x
f x x
x
đồngbiếntrênmỗikhoảng
; 2
và
2;
.
Mặkhác
2 . 3 1. 1 3 0
f f
và
8
3 . 2 .1 0
7
f f
nên
f x
cóđúngmột
nghiệm
; 2
a
vàđúngmộtnghiệm
2;b
.
Tacóbảngbiếnthiên
Dựavàobảngbiếnthiênsuyraphươngtrình
2018
f x
cóbốnnghiệmphânbiệt.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
Câu 75. (THPT Lê Xoay - 2018) Số nghiệm của phương trình
2
sin 2 cos 1 log sinx x x
trên
khoảng
0;
2
là:
A.
4
. B.
3
. C.
2
. D.
1
.
Lờigiải
Vì
sin 0
x
và
cos 0
x
, 0;
2
x
nênphươngtrìnhđãchotươngđương
2 2 2
sin 2 cos log cos 1 log sin log cosx x x x x
2 2
log cos cos log sin 2 sin 2 *
x x x x
Xéthàmsố
2
log
f t t t
,với
0;1
t
tacó
1
1 0, 0;1
ln 2
f t t
t
.
Dođó,hàmsố
f t
đồngbiếntrênkhoảng
0;1
.
Từphươngtrình
*
,tacó
cos sin 2 cos sin 2f x f x x x
1
sin
2
x
hay
6
x
.
Câu 76. (THPT Nguyễn Thị Minh Khai - Hà Tĩnh - 2018) Phương trình
2 2
3 3
log 2 3 7 log 1
x x x x x
cósốnghiệmlà
T
vàtổngcácnghiệmlà
S
.Khiđó
T S
bằng
A.
2
. B.
4
. C.
3
. D.
1
.
Lờigiải
*Điềukiện
2
2 3 0
1
1 0
x x
x
x
.
*Tacó
3
x
làmộtnghiệmcủaphươngtrình.
*Khi
1x
,phươngtrìnhđãchođượcviếtlại
2
2
3
2 3
log 7 *
1
x x
x x
x
.
*Phươngtrình
*
cóvếtráilàhàmđồngbiếnvàvếphảilàhàmnghịchbiếnkhi
1x
suyra
3
x
lànghiệmduynhấtcủaphươngtrìnhđãcho.
*Vậy
4
T S
.
Câu 77. (THPTNguyễnTấtThành-YênBái-2018)Biết
1 2 1 2
,
x x x x
làhainghiệmcủaphương
trình
2
2
7
4 4 1
log 4 1 6
2
x x
x x
x
và
1 2
1
3 2
4
x x a b
với
,a b
là các số nguyên
dương.Tính
a b
A.
14
a b
. B.
16
a b
. C.
17
a b
. D.
15
a b
.
Lờigiải
2
2
2 1
4 4 1
0 0
2 2
x
x x
x x
1
2
0
x
x
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
7
4 4 1
log 4 1 6
2
x x
x x
x
2 2
7 7
log 2 1 2 1 log 2 2x x x x
Xéthàm
7
log 0
f t t t t
.
Tacó
1
1 0 0
ln 7
f t t
t
,vậy
7
log 0
f t t t t
làhàmđồngbiếnsuyra
2 2 2
7 7
log 2 1 2 1 log 2 2 2 1 2x x x x x x
2
4 6 1 0
x x
2
4 6 1 0
x x
2
1
3 5
4
3 5
4
x
x
.
1 2
1
3 12 2 5
4
x x
.
Câu 78. (THPTLươngVănCan-2018)Chobiếtphươngtrình
5 3
2 1 1
log 2log
2
2
x x
x
x
có
nghiệmduynhất
2x a b
.Hỏi
m
thuộckhoảngnàodướiđâyđểhàmsố
2
mx a
y
x m
có
giátrịlớnnhấttrênđoạn
1; 2
bằng
2
.
A.
7;9
m
. B.
6;7
m
. C.
2;4
m
. D.
4;6
m
.
Lờigiải
+Điềukiện:
1x
.
Tacó:
5 3
2 1 1
log 2log
2
2
x x
x
x
5 3
2 1 1
log 2log
2
x x
x
x
2
2
5 5 3 3
log 2 1 log log 1 log 2
x x x x
2
2
5 3 5 3
log 2 1 log 2 log log 1
x x x x
(*).
Xéthàmsố
2
5 3
log log 1
f t t t
,với
1t
có
1 2
0, 1
.ln 5 1 .ln 3
f t t
t t
nên
f t
đồngbiếndođó(*)
2 1x x
1 2
x (vì
1x
)
3 2 2
x
.Vậy
3
a
.
+Với
3
a
,taxéthàmsố
1mx
y
x m
TXĐ:
\
D m
2
2
1
' 0
m
y
x m
dođóhàmsốluônnghịchbiến.
Khiđóhàmsốcógiátrịlớnnhấttrênđoạn
1; 2
bằng
2
1; 2
1 2
m
y

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
1; 2
3
1
2
1
m
m
m
m
.
DẠNG 2. PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH MŨ
Dạng 2.1 Phương pháp đưa về cùng cơ số
+Nếu
0, 1
a a
thì
f x g x
a a f x g x
+Nếuachứaẩnthì
1
1 0
f x g x
a
a a a f x g x
f x g x
.
+
f x g x
a b
log log
f x g x
a a
a b
log .
a
f x b g x
(logarit hóa).
Câu 1. (ChuyênBắcGiang2019)Nghiệmcủaphươngtrình
2
2 3
1
1
5
5
x x
x
là
A.
1; 2.
x x
B.
1; 2.
x x
C.
1; 2.
x x
D. Vônghiệm.
Lờigiải
ChọnA
Tacó:
2
2
2 3
1 ( 2 3) 1 2 2
1
1
5 5 5 2 3 1 2 0 .
2
5
x x
x x x x
x
x x x x x
x
Vậynghiệmcủaphươngtrìnhlà
1; 2.
x x
Câu 2. Tậpnghiệmcủaphươngtrình
2
2 3
1
1
7
7
x x
x
là
A.
1
. B.
1;2
. C.
1;4
. D.
2
.
Lờigiải
ChọnB
Tacó:
2
2
2 3
1 2 3 1 2
1
7 7 7 2 3 1
7
x x
x x x x
x x x
.
2
1
2 0
2
x
x x
x
.
Câu 3. Tổngcácnghiệmcủaphươngtrình
2
2 2
2 8
x x x
bằng
A.
6
. B.
5
. C.
5
. D.
6
.
Lờigiải
ChọnB
Tacó:
2 2
2 2 2 6 3 2
1
2 8 2 2 5 6 0
6
x x x x x x
x
x x
x
.
Vậytổnghainghiệmcủaphươngtrìnhbằng
5
.
Câu 4. (SGDĐiệnBiên-2019)Gọi
1 2
, x x
làhainghiệmcủaphươngtrình
2
2 3
1
1
7
7
x x
x
.Khiđó
2 2
1 2
x x
bằng:
A.
17
. B.
1
. C.
5
. D.
3
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lờigiải
ChọnC
2
2
2 3
2 3
1
1 1 2 2
2
1
1
7 7 7 1 2 3 2 0 .
2
7
x x
x x
x x
x
x x x x x
x
Vậy
2 2
1 2
5.
x x
Câu 5. Tổngbìnhphươngcácnghiệmcủaphươngtrình
2
3 2
1
5
5
x
x
bằng
A.
2
. B.
5
. C.
0
. D.
3
.
Lờigiải
ChọnB
Tacó
2
2
3 2 3 2 2
1
1
5 5 5 3 2 0
2
5
x
x x x
x
x x
x
.
Vậytổngbìnhphươngcácnghiệmcủaphươngtrình
2
3 2
1
5
5
x
x
bằng
5
.
Câu 6. Nghiệmcủaphươngtrình
7 1 2 1
2 8
x x
là
A.
2.
x
B.
3.
x
C.
2.
x
D.
1.
x
Lờigiải
ChọnC
7 1 2 1 7 1 3.(2 1) 7 1 6 3
2 8 2 2 2 2 7 1 6 3 2
x x x x x x
x x x
.
Câu 7. (THPTLươngVănTụy-NinhBình-2018)Giảiphươngtrình
1
5 7
2
2,5
5
x
x
.
A.
1x
. B.
1x
. C.
1x
. D.
2
x
.
Lờigiải
Tacó
1 5 7 1
5 7
2 5 5
2,5 5 7 1 1
5 2 2
x x x
x
x x x
.
Câu 8. (THPT Nguyễn Thị Minh Khai - Hà Tĩnh - 2018) Phương trình
2
3 1
4
1
3
9
x
x
có hai
nghiệm
1
x
,
2
x
.Tính
1 2
x x
.
A.
6
. B.
5
. C.
6
. D.
2
.
Lờigiải
Tacó
2
3 1
4 2 2
1
3 4 2 6 6 6 0
9
x
x
x x x x
.
ÁpdụngVi-étsuyraphươngtrìnhđãchocóhainghiệm
1
x
,
2
x
thì
1 2
6
x x
.
Câu 9. (SởQuảngNam-2018)Tổngcácnghiệmcủaphươngtrình
2
2 2
2 8
x x x
bằng
A.
5
. B.
5
. C.
6
. D.
6
.
Lờigiải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
Phươngtrìnhđãchotươngđương:
2
3 2
2 2 2
2 2 2 6 3 5 6 0
x
x x
x x x x x
.
Dođótổngcácnghiệmcủaphươngtrìnhlà:
5
b
S
a
.
Câu 10. (THPTThăngLong-HàNội-2018)Tậpnghiệmcủaphươngtrình
2
1
4
2
x
x x
là
A.
2
0;
3
. B.
1
0;
2
. C.
0;2
. D.
3
0;
2
.
Lờigiải
Tacó
2
1
4
2
x
x x
2
2 2
2 2
x x x
2
2 2
x x x
2
2 3 0
x x
0
3
2
x
x
.
Câu 11. (THPTKimLiên-HàNội-2018)Tínhtổng
1 2
S x x
biết
1
x
,
2
x
làcácgiátrịthựcthỏa
mãnđẳngthức
2
3
6 1
1
2
4
x
x x
.
A.
5
S
. B.
8
S
. C.
4
S
. D.
2
S
.
Lờigiải
Tacó
2 2
3
2 3
6 1 6 1 2
1
2 2 2 6 1 2 6
4
x
x
x x x x
x x x
1
2
1 2
2
1
4 5 0 4
5
x
x x S x x
x
.
Câu 12. (THPT Nguyễn Thị Minh Khai - Hà Nội - 2018) Tích các nghiệm của phương trình
1
1
1
5 2 5 2
x
x
x
là
A.
2
. B.
4
. C.
4
. D.
2
.
Lờigiải
Chọn. A.
ĐKXĐ:
1
x
Vì
5 2 5 2 1
nên
1
5 2 5 2
.
Khiđóphươngtrìnhđãchotươngđương
1
1
1
5 2 5 2
x
x
x
1
1
1
x
x
x
1
2
x
x
.(thỏađiềukiện)
Suyratíchhainghiệmlà
2
.
Câu 13. (THCS&THPTNguyễnKhuyến-BìnhDương-2018)Giảiphươngtrình
2 3 4
4 8
x x
.
A.
6
7
x
. B.
2
3
x
. C.
2
x
. D.
4
5
x
.
Lờigiải

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 3 4
4 8
x x
4 6 12 3
2 2
x x
4 6 12 3x x
6
7
x
.
Câu 14. (THPTCaoBáQuát-2018)Chophươngtrình
2
28
4
1
3
2 16
x
x
.Khẳngđịnhnàosau đâylà
đúng:
A. Nghiệmcủaphươngtrìnhlàcácsốvôtỷ.
B. Tổngcácnghiệmcủamộtphươngtrìnhlàmộtsốnguyên.
C. Tíchcácnghiệmcủaphươngtrìnhlàmộtsốâm.
D. Phươngtrìnhvônghiệm.
Lờigiải.
ChọnC
2 2
28 28
4 4
1 4 4 2
3 3
28
2 16 2 2 4 4 4 1 .
3
x x
x x
x x
TH1:Nếu
3
.
7
x
PT
1 :
2 2
3
28 28
4 4 4 4 8 0
2
3 3
3
x TM
x x x x
x L
TH1:Nếu
3
.
7
x
PT
1 :
2 2
0
28 28
4 4 4 4 0
7
3 3
3
x L
x x x x
x TM
Phươngtrìnhcótậpnghiệm
7
;3
3
S
.
Dạng 2.2 Phương pháp đặt ẩn phụ
Loại1.
0
f x
PP
P a
đặt
, 0
f x
t a t
.
Loại2.
2. 2.
. . .
λ. 0
f x
f x f x
a a b b
PP
Chiahaivếcho
2.
,
f x
b
rồiđặt
0
f x
a
t
b
(chiachocơsốlớnnhấthoặcnhỏnhất).
Loại3.
f x f x
a b c
với
. 1
a b
PP
đặt
1
f x f x
t a b
t
.
Loại4.
.
. . 0
f x g x
f x g x
f x
g x
a a
a a b
a
a
PP
đặt
f x
g x
u a
v a
.
Câu 15. (Mã1232017)Chophươngtrình
1
4 2 3 0.
x x
Khiđặt
2
x
t
tađượcphươngtrìnhnào
sauđây
A.
2
2 3 0t t
B.
4 3 0t
C.
2
3 0t t
D.
2
2 3 0t t
Lờigiải
ChọnD
Phươngtrình
4 2.2 3 0
x x
Câu 16. (THPT Hoàng Hoa Thám Hưng Yên 2019) Tập nghiệm của phương trình
2 2 2
4 3 7 6 2 3 9
5 5 5 1
x x x x x x
là
A.
1; 1;3
. B.
1;1;3;6
. C.
6; 1;1;3
. D.
1;3
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
Lờigiải
2 2 2
4 3 7 6 2 3 9
5 5 5 1
x x x x x x
2 2
2 2
4 3 7 6
4 3 7 6
5 5 5 1
x x x x
x x x x
.
Đặt
2
2
4 3
7 6
a x x
b x x
,tađượcphươngtrình:
5 5 5 1
a b a b
5 5 5 .5 1
a b a b
1 5 1 5 0
a b
5 1
5 1
a
b
0
0
a
b
Khiđó
2
2
4 3 0
7 6 0
x x
x x
1
3
1
6
x
x
x
x
.
Tậpnghiệmcủaphươngtrìnhlà
6; 1;1;3
.
Câu 17. (ChuyênLêQuýĐônĐiệnBiên2019)Phươngtrình
2 1
9 6 2
x x x
cóbaonhiêunghiệmâm?
A.
2
. B.
3
. C.
0
. D.
1
.
Lờigiải
Phươngtrình
2
2 1
3 3
9 6 2 9 6 2.4 2
2 2
x x
x x x x x x
.
Đặt
3
2
x
t
với
0
t
,phươngtrình
trởthành
2
1 (L)
2 0
2
t
t t
t
.
Với
3
2
3
2 2 log 2 0
2
x
t x
.
Vậyphươngtrìnhđãchokhôngcónghiệmâm.
Câu 18. (Chuyên Nguyễn Trãi Hải Dương 2019) Tổng các nghiệm của phương trình
4 6.2 2 0
x x
bằng
A.
0
. B.
1
. C.
6
. D.
2
.
Lờigiải
2
2
2
log 3 7
2 3 7
4 6.2 2 0 2 6.2 2 0
2 3 7
log 3 7
x
x x x x
x
x
x
.
Vậytổnghainghiệmcủaphươngtrình
là
2 2 2 2
log 3 7 log 3 7 log 3 7 3 7 log 2 1
.
Câu 19. (Cụm8TrườngChuyên 2019)Tổngcácnghiệmcủaphươngtrình
1 1
3 3 10
x x
là
A. 1. B. 0. C.
1
. D. 3.
Lờigiải
Tacó:
1 1
3
3 3 10 3.3 10
3
x x x
x
Đặt
3
x
t
0
t
,phươngtrìnhtrởthành:
2
3
3
3 10 3 10 3 0
1
3
t
t t t
t
t
.
Với
3t
tacó
3 3 1
x
x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Với
1
3
t
tacó
1
1
3 3 3 1
3
x x
x
.
Vậytổngcácnghiệmcủaphươngtrìnhlà:
1 1 0
.
Câu 20. Gọi
1 2
,x x
lànghiệmcủaphươngtrình
2 3 2 3 4
x x
.Khiđó
2 2
1 2
2x x
bằng
A. 2. B.
3
. C. 5. D. 4.
Lờigiải
Tacó:
2 3 . 2 3 1
x x
.Đặt
1
2 3 , 0 2 3
x x
t t
t
.
Phươngtrìnhtrởthành:
2
1
4 4 1 0 2 3
t t t t
t
.
Với
2 3 2 3 2 3 1
x
t x
.
Với
1
2 3 2 3 2 3 2 3 2 3 1
x x
t x
.
Vậy
2 2
1 2
2 3
x x
.
Câu 21. (Đề Thi Công Bằng KHTN 2019) Tổng tất cả các nghiệm của phương trình
2.4 9.2 4 0
x x
bằng.
A.
2
. B.
1
. C.
0
. D.
1
.
Lờigiải
Phươngtrình:
2.4 9.2 4 0
x x
(1)
cóTXĐ:
D
.
Đặt
2
x
t
(
0)
t
Khiđópt(1)trởthành:
2
4( )
2 9 4 0 ( 4)(2 1) 0
1
( )
2
t tm
t t t t
t tm
Với
2
4 2 4 2 2 2
x x
t x
Với
1
1 1
2 2 2 1
2 2
x x
t x
Phươngtrìnhcótậpnghiệmlà:
{2; 1}
S
.Vậytổngtấtcảcácnghiệmcủapt(1)là
1
.
Câu 22. (THPTNghĩaHưngNĐ 2019)Phươngtrình
2 1 1
6 5.6 1 0
x x
cóhainghiệm
1
x
,
2
x
.Khi
đótổnghainghiệm
1 2
x x
là.
A. 5. B. 3. C. 2. D. 1.
Lờigiải
1
2
2
2 1 1 2
6 2
6 5.6
6 5.6 1 0 1 0 6 5.6 6 0
6 6
6 3
x
x
x
x x x x
x
.
1 2 1 2
1 2
6 .6 3.2 6 6 1
x x x x
x x
.
Câu 23. Chophươngtrình
1
25 20.5 3 0
x x
.Khiđặt
5
x
t
,tađượcphươngtrìnhnàosauđây.
A.
2
3 0
t
. B.
2
4 3 0
t t
. C.
2
20 3 0
t t
. D.
20
3 0
t
t
.
Lờigiải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
Tacó:
1
25 20.5 3 0
x x
2 2
5
5 20. 3 0 5 4.5 3 0
5
x
x x x
Đặt
5
x
t
,
0t
Khiđóphươngtrìnhtrởthành:
2
4 3 0
t t
.
Câu 24. (SởBìnhPhước-2019)Tậpnghiệmcủaphươngtrình
9 4.3 3 0
x x
là
A.
0;1
B.
1
C.
0
D.
1;3
Lờigiải
ChọnA
Tacó:
9 4.3 3 0
x x
3 1
3 3
x
x
0
1
3 3
3 3
x
x
0
1
x
x
.
Câu 25. (ChuyênTháiNguyên2019)Sốnghiệmthựccủaphươngtrình
1 3
4 2 4 0
x x
là:
A.
1
B.
2
C.
3
D.
4
Lờigiải
pt
1
1 1
2
1
2 8 2 17
4 16.2 4 0 1 log 8 2 7
2 8 2 17
x
x x
x
x
Câu 26. (ChuyênBắcGiang2019)Tậpnghiệmcủaphươngtrình
2 2
3 3 30
x x
là
A.
1
3;
3
S
B.
1
S
C.
1; 1
S
D.
3;1 .
S
Lờigiải
ChọnC
2 2 2
3 3
3 3 30 3.3 10.3 3 0 1
1
3
3
x
x x x x
x
x
Câu 27. (THPTNguyễnKhuyến2019)Chohàmsố
.5 .
x
f x x
Tổngcácnghiệmcủaphươngtrình
25 ' .5 .ln5 2 0
x x
f x x
là
A.
2
B.
0
C.
1
D.
1
lờigiải:
ChọnB
Tacó
.5 ' 5 .5 .ln5
x x x
f x x f x x
Nên
25 ' .5 .ln5 2 0 25 5 2 0
x x x x
f x x
Đặt
5 0
x
t t
Tađượcphươngtrình
2
1
2 0 5 1 0
2
x
t
t t x
t l
Câu 28. (ChuyênKHTN2019)Tổngtấtcảcácnghiệmcủaphươngtrình
2 2
3 2.3 27 0
x x
bằng
A.
9
. B.
18
. C.
3
. D.
27
.
Lờigiải

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
1 3
2
2 2
2 3
log 9 3 6
3 9 3 6
3 2.3 27 0 3 18.3 27 0
3 9 3 6
log 9 3 6
x
x x x x
x
x
x
.
Vậytổngtấtcảcácnghiệmcủaphươngtrìnhđãcholà:
1 2 3 3 3 3
log 9 3 6 log 9 3 6 log 9 3 6 9 3 6 log 27 3
x x
.
Câu 29. (THPT-Thang-Long-Ha-Noi- 2019)Phươngtrình
2 1
9 6 2
x x x
cóbaonhiêunghiệmâm?
A.
3
B.
0
C.
1
D.
2
Lờigiải
Tacó:
2 1
9 6 2
x x x
2
3 3
9 6 2.4 2 0
2 2
x x
x x x
3
1
2
3
2
2
x
x
L
3
2
log 2
x
.
Vậyphươngtrìnhđãchokhôngcónghiệmâm.
Câu 30. (Chuyen Phan Bội Châu Nghệ An 2019) Phương trình
2 1 2 1 2 2 0
x x
có
tíchcácnghiệmlà?
A.
0.
B.
2.
C.
1.
D.
1
.
Lờigiải
Đặt
1
2 1 (t>0) 2 1
x x
t
t
Phươngtrìnhđãchotrởthành
1
2 2 0
t
t
2
2 2 1 0
1 2
1 2
t t
t
t
Với
1 2 2 1 1 2 1
x
t x
Với
1 2 2 1 1 2 1
x
t x
Vậytích2nghiệmcủaphươngtrìnhđãcholà
1
Câu 31. (Chuyên BắcGiang2019)Gọi
1 2
;x x
là
2
nghiệmcủaphương trình
2 2
1
4 2 3
x x x x
.Tính
1 2
x x
A.
3
B.
0
C.
2
D.
1
Lờigiải
ChọnD
Đặt
2
2 ( 0)
x x
t t
.Phươngtrìnhtươngđươngvới
2
1
2 3 0
3
t
t t
t

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
Vì
2
0
0 1 0
1
x
t t x x
x
1 2
1
x x
Câu 32. (HSGBắcNinh2019)Giảiphươngtrình:
1 1 2 2
4 4 2 2 2 8
x x x x
Lờigiải
1 1 2 2 1 1 1 1
4 4 2 2 2 8 4 4 4 2 2 8
x x x x x x x x
Đặt
1 1 2 1 1
2 2 4 4 8
x x x x
t t
Phươngtrìnhtrởthành:
1 1 1 1
2
1 1 2
2
1 1
0
0 2 2 0 2 2
4 2 1 2 ( )
log 1 2
4
2 2 4 2 2.2 1 0
2 1 2
x x x x
x
x x x x
x
x x
x
t
t t VN
x
t
Câu 33. Tínhtổngtấtcảcácnghiệmcủaphươngtrình
2 8 5
3 4.3 27 0
x x
?
A.
5
. B.
5
. C.
4
27
. D.
4
27
.
Lờigiải
ChọnB
Tacó:
2 4
2 8 5 4
3 4.3 27 0 3 12.3 27 0
x
x x x
.
Đặt
4
3 0
x
t t
tađượcphươngtrình
2
3
12 27 0
9
t
t t
t
từđótacó
4
4
3 3 3
2
3 9
x
x
x
x
Vậytổngcácnghiệmphươngtrìnhđãcholà-5.
Câu 34. Tổngtấtcảcácnghiệmcủaphươngtrình
2 2
3 2.3 27 0
x x
bằng
A.
0
. B.
18
. C.
3
. D.
27
.
Lờigiải
ChọnC
Tacó:
2
2 2
3 9 3 6
3 2.3 27 0 3 18.3 27 0
3 9 3 6
x
x x x x
x
3
3
log 9 3 6
log 9 3 6
x
x
Vậytổngcácnghiệmlà
3 3 3 3
log 9 3 6 log 9 3 6 log 9 3 6 9 3 6 log 27 3
.
Câu 35. (Hội8trườngchuyênĐBSH2019)Tổngcácnghiệmcủaphươngtrình
1 1
3 3 10
x x
là
A.
1
. B.
3
. C.
1
. D.
0
.
Lờigiải
ChọnD
Cách1:Tacó
1 1
3
3 3 10 3.3 10
3
x x x
x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đặt
3 , 0
x
t t
phươngtrìnhtrởthành
2
3
3 10 3 0
1
3
t
t t
t
.
Với
3t
tacó
3 3 1
x
x
Với
1
3
t
tacó
1
3 1
3
x
x
Câu 36. (SGDĐiệnBiên-2019)Tíchtấtcảcácnghiệmcủaphươngtrình
4
3 3 30
x x
bằng
A.
3
. B.
1
. C.
9
. D.
27
.
Lờigiải
ChọnA
4
81
3 3 30 3 30
3
x x x
x
.
Đặt
3 0
x
t t
,phươngtrìnhđãchotrởthành:
2
81
30 30 81 0
27 3 27 3
3 3 3 1
x
x
t t t
t
t x
t x
Vậytíchtấtcảcácnghiệmcủaphươngtrìnhlà
1.3 3
.
Câu 37. (Thi thử hội 8trườngchuyên2019)Kíhiệu
1
x
,
2
x
là hai nghiệmthựccủa phươngtrình
2 2
1
4 2 3
x x x x
.Giátrịcủa
1 2
x x
bằng
A.
3
. B.
4
. C.
2
. D.
1
.
Lờigiải
ChọnD
Tacó
2 2 2 2
2
1
4 2 3 2 2.2 3 0
x x x x x x x x
.
Đặt
2
2 0
x x
t
tađược:
2
3
2 3 0
1
t
t t
t
.
Vì
0t
nênnhận
1t
.Suyra
2
2 1
x x
2
0
x x
0
1
x
x
.
Nhưthế
1
2
0
1
x
x
hoặc
1
2
1
0
x
x
.
Vậy
1 2
1
x x
.
Câu 38. (ĐạihọcHồngĐức 2019)Cho phươngtrình
sin sin
7 4 3 7 4 3 4
x x
.Tổngcác
nghiệmcủaphươngtrìnhtrong
2 ;2
bằng
A.
3
2
. B.
2
. C.
0
. D.
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
Lờigiải
ChọnC
sin sin
7 4 3 7 4 3 4
x x
sin sin
2 3 2 3 4
x x
.
Đặt
sin
2 3
x
t
,
0t
.Khiđóphươngtrìnhđãchotrởthành
2
2 3
1
4 4 1 0
2 3
t
t t t
t
t
.
Với
2 3
t
2 ;2
3
sin 1 2 ;
2 2 2
k
x
x x k x
.
Với
2 3
t
2 ;2
3
sin 1 2 ;
2 2 2
k
x
x x k x
.
Vậytổngcácnghiệmbằng
0
.
Câu 39. (Xuân Trường - Nam Định - 2018) Gọi a là một nghiệm của phương trình
2log log 2log
4.2 6 18.3 0
x x x
.Khẳngđịnhnàosauđâyđúngkhiđánhgiávề
a
?
A.
2
10 1
a
.
B.
a
cũnglànghiệmcủaphươngtrình
log
2 9
3 4
x
.
C.
2
1 2
a a
.
D.
2
10
a
.
Lờigiải
Điềukiện
0
x
.
Chiacảhaivếcủaphươngtrìnhcho
2log
3
x
tađược
2log log
3 3
4 18 0
2 2
x x
.
Đặt
log
3
2
x
t
,
0t
.
Tacó
2
4 18 0
t t
9
4
2
t
t L
.
Với
9
4
t
log
3 9
2 4
x
log 2
x
100
x
.
Vậy
2
100 10
a
.
Câu 40. (THPTLụcNgạn-2018)Nghiệmcủaphươngtrình
25 2 3 5 2 7 0
x x
x x
nằmtrong
khoảngnàosauđây?
A.
5;10
. B.
0;2
. C.
1;3
. D.
0;1
Lờigiải
Đặt
5
x
t
,
0t
.
Phươngtrìnhtrởthành:
2
2 3 2 7 0
t x t x
1
2 7
t L
t x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Với
2 7
t x
tacó:
5 2 7
x
x
5 2 7 0
x
x
.
Phươngtrìnhcómộtnghiệm
1x
.
Với
1x
:
5 2 7 5 2 7
x
x
5 2 7 0
x
x
phươngtrìnhvônghiệm.
Với
1x
:
5 2 7 5 2 7
x
x
5 2 7 0
x
x
phươngtrìnhvônghiệm.
Vậyphươngtrìnhcómộtnghiệmduynhất
1 0;2
x
.
Câu 41. (THPTChuVănAn-TháiNguyên- 2018)Số nghiệmnguyênkhông âmcủabấtphương
trình
1 1
15.2 1 2 1 2
x x x
bằngbaonhiêu?
A. 3. B. 0. C. 1. D. 2.
Lờigiải
Với
0
x
thì
1 1
15.2 1 2 1 2 30.2 1 3.2 1
x x x x x
.(1)
Đặt
2 1
x
t
thì
2
1 30 1 3 1 30 1 3 1
t t t t
2
9 36 0 0 4t t t
1 2 4 0;1; 2
x
x
.
Câu 42. (ToánHọcTuổiTrẻSố6)Chophươngtrình
3
1 3
8 8. 0,5 3.2 125 24. 0,5 .
x x
x x
Khi
đặt
1
2
2
x
x
t
,phươngtrìnhđãchotrởthànhphươngtrìnhnàodướiđây?
A.
3
8 3 12 0
t t
. B.
3 2
8 3 10 0
t t t
.C.
3
8 125 0
t
. D.
3
8 36 0
t t
.
Lờigiải
Tacó
3
1 3
8 8. 0,5 3.2 125 24. 0,5
x x
x x
3
3
1 1
8.2 8. 24.2 24. 125 0
2 2
x x
x x
3
3
1 1
8 2 24 2 125 0
2 2
x x
x x
.
Đặt
1
2 2
2
x
x
t t
.Khiđótacó
3 3
3
1
2 3
2
x
x
t t
Phươngtrìnhtrởthành
3 3
8 3 24 125 0 8 125 0
t t t t
.
Câu 43. (THPT Bình Giang - Hải Dương - 2018) Gọi
S
là tập nghiệm của của phương trình:
2 2 2
3x 2 6x 5 2x 3x 7
4 4 4 1
x x
.Khiđó
S
là
A.
1;2
. B.
1;2; 1
. C.
1;2; 1; 5
. D.
.
Lờigiải
Nhậnxét:
Tacó
2 2 2
( 3x 2) ( +6x 5) 2 +3x 7
x x x
dođó
2 2 2
2 +3x 7 3x 2 +6x 5
4 4 .4
x x x
Phươngtrìnhđãchotươngđươngvớiphươngtrìnhsau:
2 2 2 2 2 2
2
2 2
2
3x 2 2 3x 7 x 6x 5 3x 2 x 6x 5 x 6x 5
6x 5 2
x 6x 5 x 3x 2
2
3x 2
(4 4 ) (1 4 ) 0 4 (1 4 ) (1 4 )
4 1 6x 5 0
(1 4 )(4 1) 0
3x 2 0
4 1
x x x
x
x
x
x
Vậy
1;2; 1; 5
S
.
Dạng2.3Phươngpháplogarithóa

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
Dạng 1:Phươngtrình:
0 1, 0
log
f x
a
a b
a b
f x b
Dạng 2:Phươngtrình:
log log .log
f x g x f x f x
a a a
a b a b f x g x b
hoặc
log log .log .
f x g x
b b b
a b f x a g x
Câu 44. (THPTThuậnThành3-BắcNinh 2019)Sốgiaođiểmcủacácđồthịhàmsố
2
1
3
x
y
và
5
y
là
A.
0
. B.
3
. C.
2
. D.
1
.
Lờigiải
ChọnC
Sốgiaođiểmcủahaiđồthịhàmsố
2
1
3
x
y
và
5
y
bằngsốnghiệmcủaphươngtrình
2
1
3 5
x
+)
2
1 2 2
3 3 3
3 5 1 log 5 log 5 1 log 5 1
x
x x x
+)Vậysốgiaođiểmcủahaiđồthịhàmsố
2
1
3
x
y
và
5
y
bằng
2
Câu 45. (SởGDNamĐịnh-2019)Tínhtíchcácnghiệmthựccủaphươngtrình
2
1 2 3
2 3
x x
A.
2
3log 3
. B.
2
log 54
. C.
1
. D.
2
1 log 3
.
Lờigiải
ChọnB
2
2
1 2 3
2
2
2
2 2
2
1 2 3 log 3
2 .log 3 1 3log 3
PT l
0
og 2 log 3
x x
x x
x x
Do
2
1. 1 3log 3 0
nênphươngtrìnhluôncó2nghiệmthựcphânbiệt
1 2
,x x
.
TheoVi-éttacó
1 2 2 2 2 2
1 3log 3 log 2 log 27 log 54
x x
.
Câu 46. Cho hai số thực
1, 1
a b
. Gọi
1 2
,x x
là hai nghiệm của phương trình
2
1
. 1
x x
a b
. Trong
trườnghợpbiểuthức
2
1 2
1 2
1 2
.
4 4
x x
S x x
x x
đạtgiátrịnhỏnhất,mệnhđềnàosauđâylà
đúng?
A.
a b
. B.
. 4
a b
. C.
. 2
a b
. D.
a b
.
Lờigiải
ChọnD
Tacó:
2
1 2
. 1 log 1 0
x x
b
a b x x a
.Nhậnthấyphươngtrìnhluôncóhainghiệmtráidấu.
TheoVi-et:
1 2
log
b
x x a
;
1 2
. 1
x x
.
Khiđó:
2
2
1 2
1 2
1 2
.
4
4 4 log
log
a
a
x x
S x x b
x x b
.
Đặt
log , 0
a
b t t
(Vì
1, 1
a b
),
3
2
3
2 2
4 4 2 4
; 2 ; 0 2
t
S t S t S t
t t t
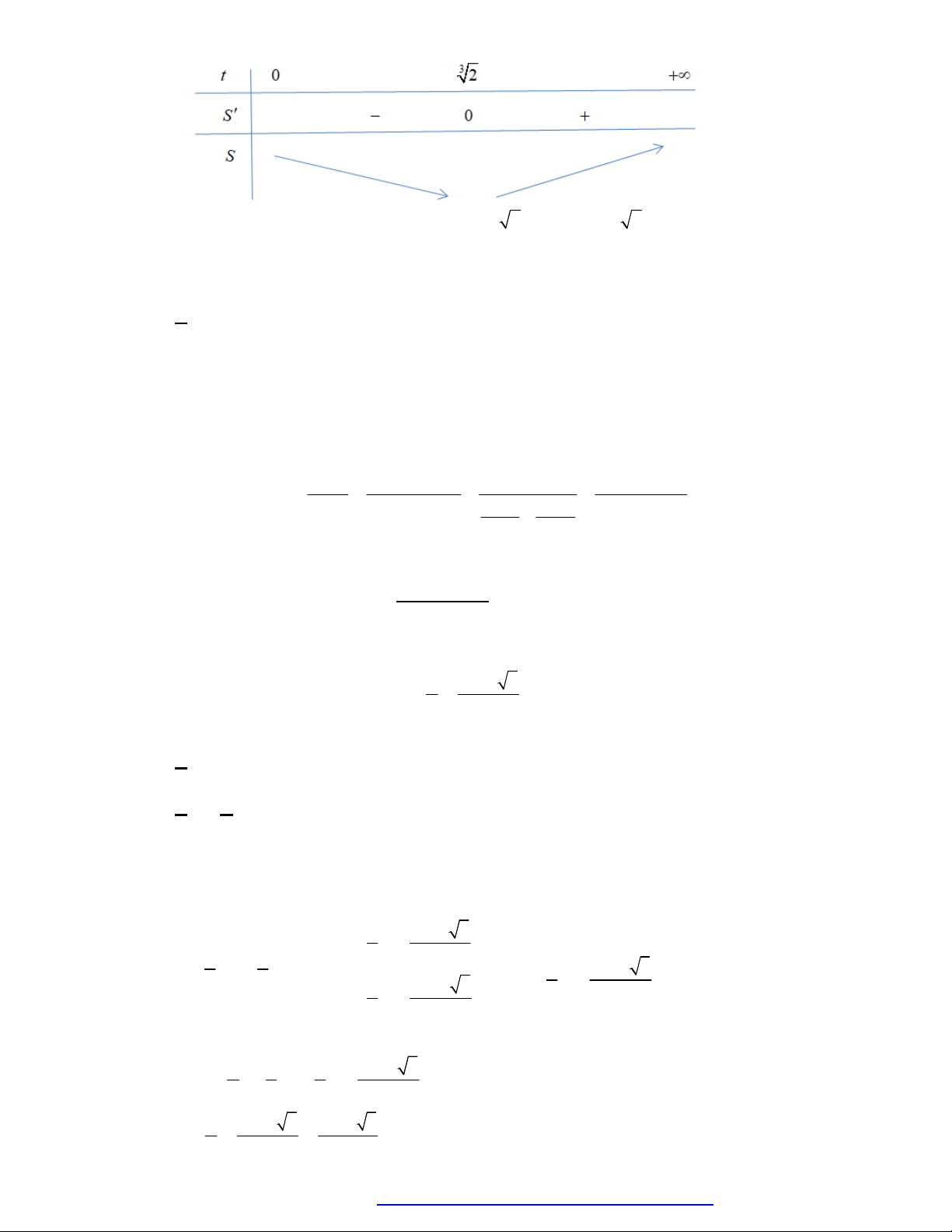
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Suyrabiểuthức
S
đạtgiátrịnhỏnhấttại
3
2
t
hay
3
log 2 1
a
b a b
.
Câu 47. (TTDiệuHiền-CầnThơ-2018)Cho
x
,
y
,
z
làcácsốthựcthỏamãn
2 3 6 .
x y z
Giátrị
củabiểuthức
M xy yz xz
là:
A.
0.
B.
6.
C.
3.
D.
1.
Lờigiải
Đặt
2 3 6
x y z
t
với
0.
t
2
3
6
2
log
3 log .
log
6
x
y
z
t
x t
t y t
z t
t
Mặtkhác:
3 2
6
3 2
3 2
log .log
1 1 1
log
1 1
log 6 log 3 log 2 log log
log log
t t t
t t
t
t t
t t
.
3 2 3 6 6 2
log .log log .log log .logM xy yz xz t t t t t t
3 2 3 2 6
log .log log log .logt t t t t
3 2
3 2 3 2
3 2
log .log
log .log log log . 0.
log log
t t
t t t t
t t
Câu 48. (Lý Nhân Tông - Bắc Ninh - 2020) Gọi
x
,
y
các số thực dương thỏa mãn điều kiện
9 6 4
log log log
x y x y
và
2
x a b
y
, với
,a b
là hai số nguyên dương. Tính
2 2
T a b
.
A.
26.
T
B.
29.
T
C.
20.
T
D.
25.
T
Lời giải
Chọn A
Đặt
9 6 4
log log log
t x y x y
,tacó
9
6
4
t
t
t
x
y
x y
9 6 4
t t t
2
3 1 5
( )
2 2
3 3
1 0
2 2
3 1 5
2 2
t
t t
t
loai
3 1 5
2 2
t
.
Suyra
9 3 1 5
6 2 2
t t
x
y
.
Mà
1 5
1; 5.
2 2
x a b
a b
y

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
Vậy
2 2 2 2
1 5 26.
T a b
Câu 49. (THPT Nguyễn Viết Xuân - 2020) Cho các số thực dương
,a b
thỏa mãn
4 6 9
log log log 4 5 1
a b a b
.Đặt
b
T
a
.Khẳngđịnhnàosauđâyđúng?
A.
1 2T
. B.
1 2
2 3
T
. C.
2 0
T
. D.
1
0
2
T
.
Lời giải
Chọn D
Giảsử:
4 6 9
1
4
log log log 4 5 1 6
4 5 9
t
t
t
a
a b a b t b
a b
Khiđó
2
4 6 2 2
4.4 5.6 9.9 4. 5. 9 4. 5. 9 0
9 9 3 3
t t t t
t t t
2
3
2 9
3 4
9
log 2
4
2
1
3
t
t
t t
VN
Vậy
2
6 3 4 1
0;
4 2 9 2
t
b
T
a
.
Câu 50. (THPT Cao Bá Quát - 2018) Phương trình
2
1
1
3 .4 0
3
x x
x
có hai nghiệm
1 2
, .x x
Tính
1 2 1 2
.
T x x x x
.
A.
3
log 4
T
. B.
3
log 4
T
. C.
1T
. D.
1T
.
Lờigiải
Tacó
2
1
1
3 .4 0
3
x x
x
1
1
1
1
1
1
3
3 .4 1
log 3 .4 0
log3 log 4 0
1 log3 1 log 4 0
1 log3 log4 0
1
log 4
x x
x
x x
x
x x
x
x x x
x x
x
x
Dođó
1 2 1 2 3 3
. log 4 1 log 4 1
T x x x x
Dạng 2.4 Phương pháp hàm số, đánh giá
Thôngthườngtasẽvậndụngnộidungcácđịnhlý(vàcáckếtquả)sau:
Nếuhàm số
y f x
đơn điệu một chiềutrênD thì phươngtrình
0
f x
không quámột
nghiệmtrênD.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đểvậndụngđịnhlýnày,tacầnnhẩmđược
1
nghiệm
o
x x
củaphươngtrình,rồichỉrõ
hàmđơn điệu một chiều trên D (luôn đồng biến hoặc luônnghịchbiến trên D) vàkếtluận
o
x x
lànghiệmduynhất.
Hàm số
f t
đơn điệu một chiều trên khoảng
;a b
và tồn tại
; ;u v a b
thì
f u f v u v
".
Đểápdụngđịnhlýnày,tacầnxâydựnghàmđặctrưng
f t
.
Câu 51. (SGD Nam Định 2019) Tổng tất cả các nghiệm thực của phương trình
1
15 .5 5 27 23
x x
x x
bằng.
A.
1
. B.
2
. C.
1
. D.
0
.
Lờigiải
Chọn D.
Tacó
1 1
15 .5 5 27 23 5 3 1 27 23
x x x
x x x x
(1)
Dễthấy
1
3
x
khôngthỏamãnphươngtrìnhtrênnêntacó
1 1
27 23
5 3 1 27 23 5
3 1
x x
x
x x
x
.(2)
Hàmsố
1
5 5.5
x x
y f x
đồngbiếntrên
.
Hàmsố
27 23
3 1
x
y g x
x
,cóđạohàm
2
96
0
3 1
g x
x
,nênnghịchbiếntrênmỗi
khoảng
1
;
3
và
1
;
3
.
Dođótrênmỗikhoảng
1
;
3
và
1
;
3
,phươngtrình(2)cónhiềunhấtmộtnghiệm.
Tathấy
1
x
và
1x
làcácnghiệmlầnlượtthuộccáckhoảng
1
;
3
và
1
;
3
.
Dođó(2)và(1)cóhainghiệm
1
x
và
1x
.
Tổnghainghiệmnàybằng
0
.
Câu 52. Chosốthực
saochophươngtrình
2 2 2cos
x x
x
cóđúng
2019
nghiệmthực.Số
nghiệmcủaphươngtrình
2 2 4 2cos
x x
x
là
A.
2019
. B.
2018
. C.
4037
. D.
4038
.
Lờigiải
ChọnD
Tacó:
2
2
2 2
2 2 4 2cos 2 2 2.2cos
2
x x
x x
x
x
2 2
2 2
2 2 2cos . (1)
2
2 2 2cos . (2)
2
x x
x x
x
x
.
Tathấy,nếuphươngtrình
2 2 2cos
x x
x
có2019nghiệmthựcthìphươngtrình(1)
cũngcó2019nghiệmthực.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
Nhậnxét:
+
0
x
lànghiệmcủaphươngtrình(1)
0
x
lànghiệmcủaphươngtrình(2).
+
0
0
x
khônglànghiệmcủahaiphươngtrình
1 , 2
.
Dođó,tổngsốnghiệmcủacảhaiphươngtrình
1 , 2
là
4038
.
Vậyphươngtrình
2 2 4 2cos
x x
x
có
4038
nghiệmthực.
Câu 53. Biết
1
x
,
2
x
là hai nghiệm của phương trình
2
2
7
4 4 1
log 4 1 6
2
x x
x x
x
và
1 2
1
2
4
x x a b
với
a
,
b
làhaisốnguyêndương.Tính
a b
.
A.
13
a b
. B.
11
a b
. C.
16
a b
. D.
14
a b
.
Lờigiải
ChọnC
Điềukiện:
1
0,
2
x x
.
Tacó:
2
2 2 2
7 7 7
4 4 1
log 4 1 6 log 4 4 1 4 4 1 log 2 2
2
x x
x x x x x x x x
x
.
Xét hàm số
7
log
f t t t
có
1
1 0
ln 7
f t
t
0
t
nên là hàm số đồng biến trên
0;
.
Dođótacó
2 2
3 5
4 4 1 2 4 6 1 0
4
x x x x x x
.
Khiđó
1 2
3 5 3 5 1
2 2 9 5
4 4 4
x x
hoặc
1 2
3 5 3 5 1
2 2 9 5
4 4 4
x x
.
Vậy
1 2
3 5 3 5
;
4 4
x x
.Dođó
9; 5
a b
và
9 5 14
a b
.
Câu 54. Phươngtrình
1 1 2
2 4 2
x x
x x
cótổngcácnghiệmbằng
A. 7 B. 3 C. 5 D. 6
Lờigiải:
Chọn A.
Tacó
1 1 2 1 1 2
1 1
2 4 2 .2 4.2 4 0
2 ( 4) ( 4) 0 ( 4)(2 ) 0
4
2 2 ( )
x x x x
x x
x
x x x x x
x x x x x
x
x
Giảiphươngtrình(*):
Xéthàmsố
( ) 2 2
x
f x x
có
2
'( ) 2 ln 2 2; ''( ) 2 ln 2 0
x x
f x f x
.Suyraphươngtrình
'( ) 0
f x
códuynhấtmộtnghiệm,suyraphươngtrình
( ) 0
f x
cónhiềunhấtlàhainghiệm.
Màtathấy
(1) (2) 0
f f
nênphươngtrình(*)có2nghiệm
1; 2
x x
Vậytổngcácnghiệmcủaphươngtrìnhlà7.
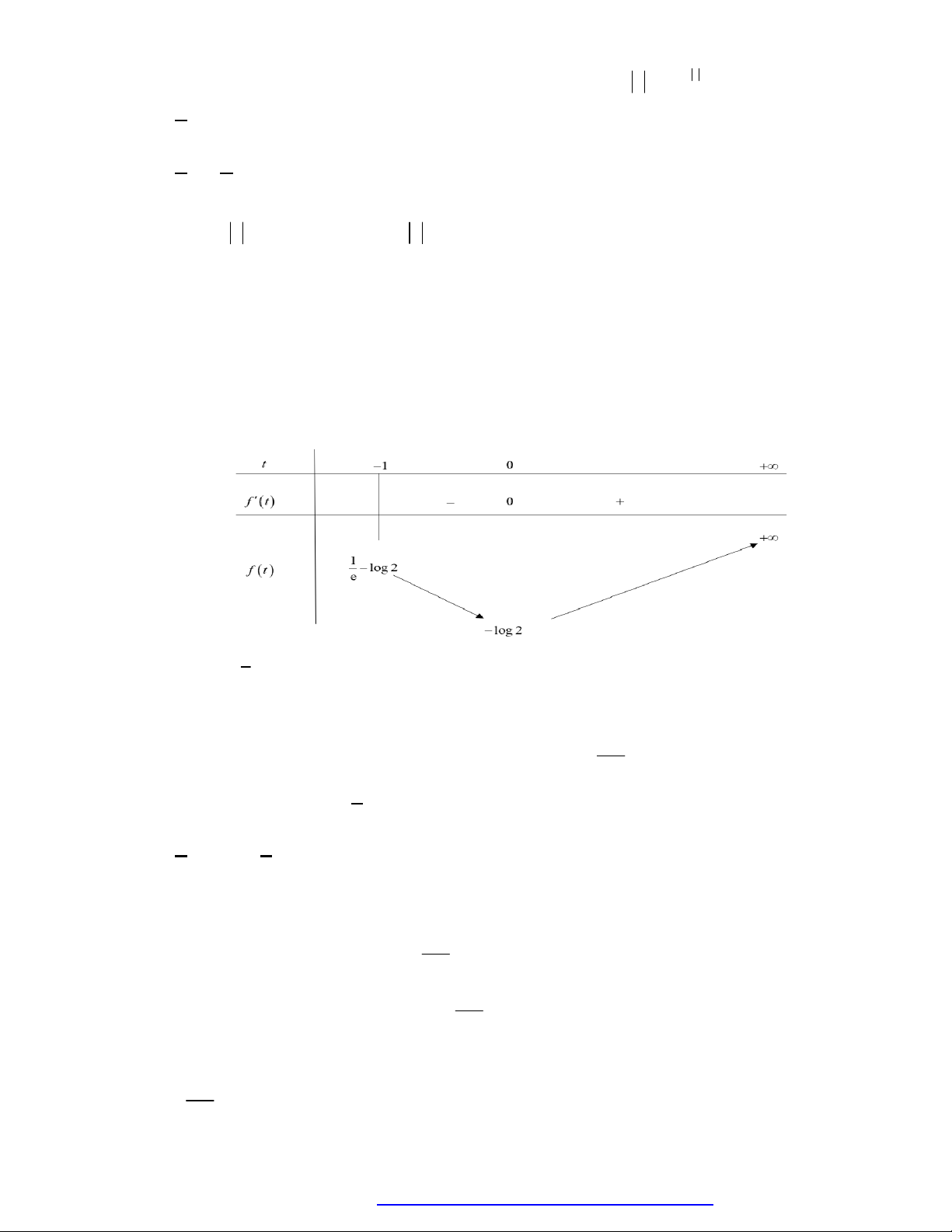
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 55. (ChuyênNgữHàNội2019)Tìmsốnghiệmcủaphươngtrình
2
1
1 e log 2 0
x
x
.
A.
4
. B.
3
. C.
2
. D.
0
.
Lờigiải
ChọnA
Tậpxácđịnh:
D
.
Đặt
1 1
t x
.Với
1
1 1
1
x t
t x t
x t
.
Khiđóphươngtrìnhtrởthành
2
e log2 0 1
t
t
.
Sốnghiệmcủaphươngtrình
1
làsốđiểmchungcủađồthịhàmsố
2
e log2
t
y f t t
và
đườngthẳng
0
y
Tacó:
2
0 ( )
e 2 0
2 ( )
t
t TM
f t t t f t
t L
.
Bảngbiếnthiên
Tacó
1
log 2 0 log 2
e
,dựavàobảngbiênthiêntađượcphươngtrình
1
có2nghiệmphânbiệt
1 2
,t t
thỏamãn
1 2
1
t t
hayphươngtrìnhđãchocó4nghiệm
x
phânbiệt.
Câu 56. Tínhsốnghiệmcủaphươngtrình
cot 2
x
x
trongkhoảng
11
;2019
12
.
A.
2019
. B.
2018
. C.
1
. D.
2020
.
Lờigiải
Chọn B.
Xétphươngtrình
cot 2 1
x
x
.
Điềukiện:
sin 0 ,x x k k
.
Xéthàmsố
11
2 cot , ;2019 \
12
x
f x x x k
,với
k
.
2
2 .ln 2 1 cot 0
x
f x x
11
;2019 \
12
x k
,với
k
.
Suy ra hàm số
f x
liên tục và đồng biến trên mỗi khoảng
11
; ; ;2 ;...; 2018 ;2019
12
.
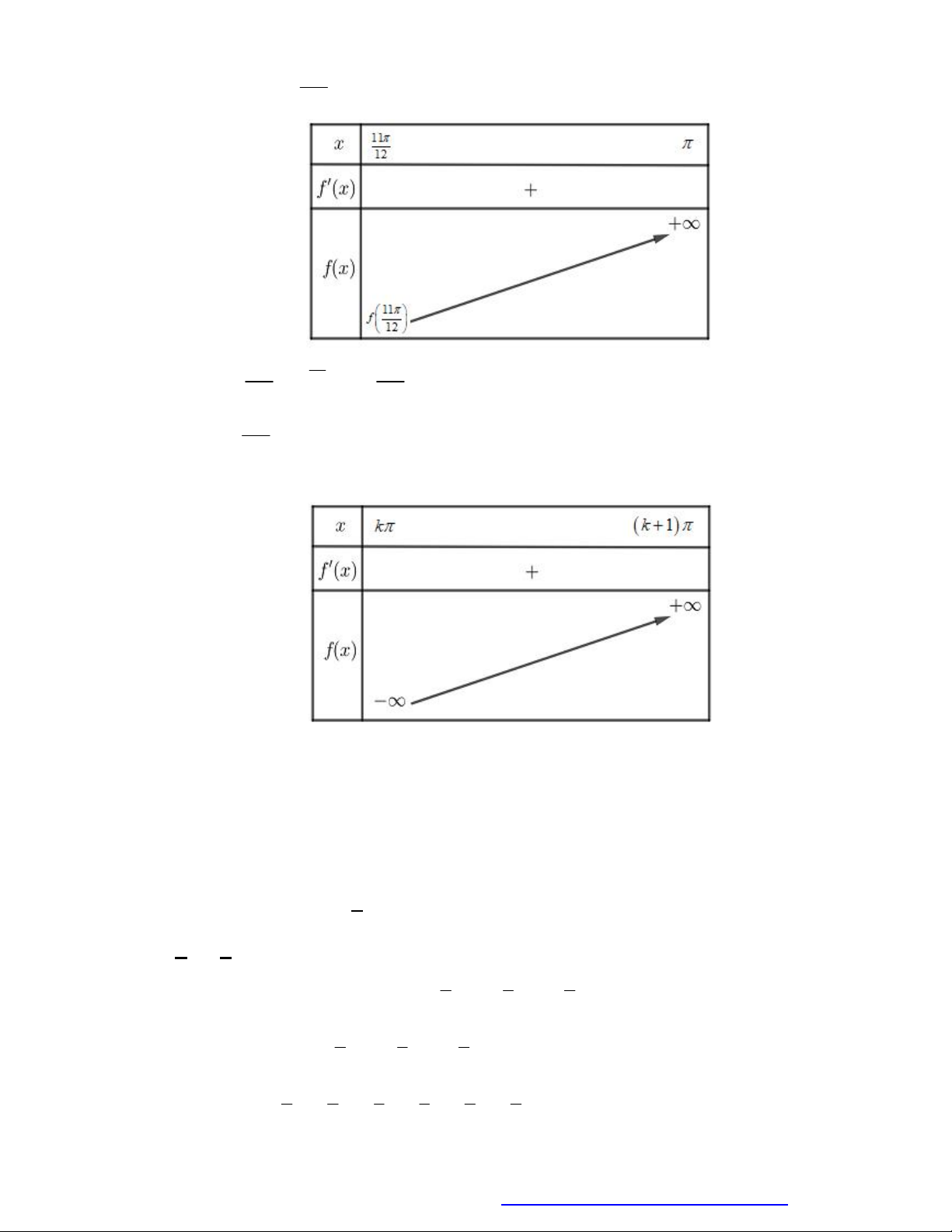
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
+)Trênkhoảng
11
;
12
tacóbảngbiếnthiên
Tacó
11
12
11 11
2 cot 11,0925 0.
12 12
f
Dođóphươngtrình
0
f x
vônghiệmtrên
khoảng
11
;
12
.
+)Trênmỗikhoảng
; 1 , 1;2;....;2018
k k k
tacóbảngbiếnthiên
Dựa vào đồ thị hàm số ta thấy mỗi khoảng
; 1 , 1;2;....;2018
k k k
phương trình
0
f x
cóđúng
1
nghiệm.Màcó
2018
khoảngnênphươngtrình
0
f x
cóđúng2018
nghiệm.
Vậyphươngtrình
0
f x
có
2018
nghiệm.
Câu 57. Hỏiphươngtrình
3.2 4.3 5.4 6.5
x x x x
cótấtcảbaonhiêunghiệmthực?
A.
0
. B.
1
. C.
3
. D.
2
.
Lờigiải
ChọnB
Tacó:
3.2 4.3 5.4 6.5
x x x x
2 3 4
3 4 5 6 0
5 5 5
x x x
.
Xéthàmsố
2 3 4
3 4 5 6
5 5 5
x x x
f x
,
x
.
Có
2 2 3 3 4 4
3 ln 4 ln 5 ln 0
5 5 5 5 5 5
x x x
f x
,
x
nênhàmsố
f x
nghịchbiến
trên
suyraphươngtrình
0
f x
cónhiềunhấtmộtnghiệm
1
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Mặt khác
8 22 176
1 . 2 . 0
5 25 125
f f
nên phương trình có ít nhấtmộtnghiệmthuộc
khoảng
1;2
.
2
.
Từ
1
và
2
suyraphươngtrìnhđãchocónghiệmduynhất.
Câu 58. (SPĐồngNai-2019)Phươngtrình
sin 2
2019 sin 2 cos
x
x x
cóbaonhiêunghiệmthực
trên
5 ;2019 ?
A.
2025
. B.
2017
. C.
2022
. D. Vônghiệm.
Lờigiải
ChọnA
Xét:
sin 2 sin 2
2019 sin 2 cos 2019 sin 1 sin 1 .
x x
x x x x
Đặt:
sin , 1;1 .
t x t
Khiđó
1
trởthành
2 2
2019 1 2019 1 1 2 .
t t
t t t t
Xéthàmsố:
2 2
2
2
2019 1 ( 1 ln 2019 1)
2019 1 , 1;1 .
1
t
t
t t t
f t t t t f t
t
Cho
2
2
1 0
0
1 ln 2019 1 0
t t
f t
t
vônghiệm
0, 1;1 .
f t t
2
cónghiệmduynhất
0 sinx 0 , .t x k k Z
mà
5 ;2019 5 2019 5 2019 5;2019 .
x k k k
Kếtluận:Có2025nghiệmthựctrên
5 ;2019 .
Câu 59. (BỉmSơn-ThanhHóa-2019)Sốnghiệmcủaphươngtrình
7
log 4
3
x
x
là
A.
1
. B.
0
. C.
2
. D.
3
.
Lờigiải
ChọnA
Điềukiệncủaphươngtrình:
4
x
.
Với
0
x
phươngtrìnhđãchotươngđươngvớiphươngtrình
7 3
log 4 log .x x
Đặt
7 3
log 4 log .x x t
Tacó
4 7
3
t
t
x
x
suyra
3 1
7 3 4 7 3 4 4 1 0 1 .
7 7
t t
t t t t
Xéthàmsố
3 1
4 1, .
7 7
t t
f t t
Tacó
3 3 1 1
' ln 4 ln 0, .
7 7 7 7
t t
f t t
Nên
f t
nghịchbiếntrêntập
.
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
Mà
1 0
f
nênphươngtrìnhcónghiệmduynhất
1 3
t x
.
Câu 60. Chocácsốthực
x
,
y
với
0
x
thỏamãn
3 1 1
3
1
e e 1 1 e 3
e
x y xy xy
x y
x y y
.Gọi
m
làgiátrịnhỏnhấtcủabiểuthức
2 1T x y
.Mệnhđềnàosauđâylàđúng?
A.
2;3
m
. B.
1; 0
m
. C.
0;1
m
. D.
1;2
m
.
Lờigiải
ChọnC
Từgiảthiết
3 1 1
3
1
e e 1 1 e 3
e
x y xy xy
x y
x y y
3 1
3 1
1 1
e 3 e 1
e e
x y xy
x y xy
x y xy
(1).
Xéthàmsố
1
= e
e
t
t
f t t
với
t
tacó
1
' = e 1 0,
e
t
t
f t t
f t
làhàmsố
đồngbiếntrên
.
Phươngtrình(1)códạng
1
3 1 3 1 ( 0)
3
x
f x y f xy x y xy y x
x
.
Khiđó
2
2 2
2 2 4 6 5
2 1 1 ' 1 0, 0
3
3 3
x x x
T x y x T x
x
x x
min
2.0 2 1
0 1
0 3 3
T m
.
Câu 61. (Chuyên Vĩnh Phúc - 2018) Số nghiệm của phương trình
2
2 2 3 5 8 3
5 2 8 3 .8 3 5 .8
x x x
x x x x x
là
A.
4
. B.
3
. C.
1
. D.
2
.
Lờigiải
Đặt
2
8 3u x x
,
3 5v x
,phươngtrìnhđãchoviếtlạilà
.8 .8 1 8 8 1 *
v u v u
u v u v u v
Tathấy
0
u
hoặc
0
v
thỏamãnphươngtrình
*
.
Với
0
u
và
0
v
tacó
1 8 8 1
* **
v u
v u
Tathấy:
Nếu
0
u
thì
8 1
0
u
u
vànếu
0
u
thì
8 1
0
u
u
.Dođó
** 0, 0
VP u
.
Nếu
0
v
thì
1 8
0
v
v
vànếu
0
v
thì
1 8
0
v
v
.Dođó
** 0, 0
VT v
.
Từđósuyra
**
vônghiệm.
Nhưvậy,phươngtrìnhđãchotươngđươngvới

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 52 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
4 13
0
8 3 0
4 13
0
3 5 0
5
3
x
u
x x
x
v
x
x
.
Vậy,phươngtrìnhđãchocó
3
nghiệm.
Câu 62. (THPTChuVănAn-HàNội-2018)Tíchtấtcảcácgiátrịcủa
x
thỏamãnphươngtrình
2 2 2
3 3 4 4 3 4 7
x x x x
bằng
A. 2. B.
1
. C. 4. D. 3.
Lờigiải
Phươngtrình
2
3 4 7 3 4 1 3 4 7
x x x x x x
2.4 8 1
3 4 7 2.4 8 0
3 4 7 0 2
x
x x x
x x
Xétphươngtrình
1
:
1 4 4 1
x
x
.
Xétphươngtrình
2
:Xéthàm
3 4 7
x x
f x
trên
.
Hàm
f x
liêntụcvà
3 .ln3 4 .ln 4 0
x x
f x x
nên
f x
làhàmđồngbiếntrên
Khiđó,
2 1 1f x f x
.Vậytíchcácnghiệmcủaphươngtrìnhbằng
1
.
Câu 63. (THPTChuVănAn-HàNội-2018)Phươngtrình
2 1 2
1 2 2 1
x x
e e x x
cónghiệm
trongkhoảngnào?
A.
5
2;
2
. B.
3
;2
2
. C.
3
1;
2
. D.
1
;1
2
.
Lờigiải
ChọnA
ĐK:
1
2
x
2 1 2
1 2 2 1
x x
e e x x
2
2
2 1
1 2 1 1
x x
e e x x
2
2
2 1
1 2 1 1 *
x x
e x e x
Xéthàmsố
2
1
t
f t e t
với
1
2
t
' 2 1 0
t
f t e t
vớimọi
1
2
t
Suyrahàmsốđồngbiếntrên
1
;
2
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53
* 2 1 2 1f x f x x x
2 2
0
0 0
1 2
1 2
2 1 2 1 0
1 2
x
x x
x
x
x x x x
x
.
DẠNG 3. PHƯƠNG TRÌNH TỔ HỢP CỦA MŨ VÀ LOGARIT
Câu 1. (Thamkhảo2019)Tổngtấtcảcácnghiệmcủaphươngtrình
3
log 7 3 2
x
x
bằng
A.
2
. B.
1
. C.
7
. D.
3
.
Lờigiải
ChọnA
Điềukiệnxácđịnhcủaphươngtrìnhlà
3
7 3 0 3 7 log 7
x x
x
.
2
3
9
log 7 3 2 7 3 3 7 3
3
x x x x
x
x
.
Đặt
3
x
t
,với
0 7t
,suyra
3
logx t
.
Tacóphươngtrình
2
7 9 0
t t
cóhainghiệm
1
7 13
2
t
và
2
7 13
2
t
.
Vậycóhainghiệm
1 2
,x x
tươngứng.
Tacó
1 2 3 1 3 2 3 1 2
log log log .x x t t t t
TheođịnhlýVi-éttacó
1 2
. 9
t t
,nên
1 2 3
log 9 2
x x
.
Câu 2. Tíchcácnghiệmcủaphươngtrình
1
1
5
log 6 36 2
x x
bằng
A.
0
. B.
6
log 5
. C.
5
. D.
1
.
Lờigiải
ChọnA
Tacó:
1 1 1
1 5 5
5
log 6 36 2 2log 6 36 2 log 6 36 1
x x x x x x
.
1 2
6
0
6 1
6 36 5 6 6.6 5 0
log 5
6 5
x
x x x x
x
x
x
.
Vậytíchcácnghiệmcủaphươngtrìnhbằng:
6
0.log 5 0
.
Câu 3. Tổngcácnghiệmcủaphươngtrình
2
log 5 – 2 2
x
x
bằng
A.
3
. B.
1
. C.
2
. D.
0
.
Lờigiải
Chọn C.
Điềukiện:
5 2 0.
x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 54 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2
2
4
log 5 2 2 5 2 2 5 2 2 5.2 4 0.
2
2 1 0
.
2
2 4
x x x x x x
x
x
x
x
x
tmdk
x
Vậytổngcácnghiệmcủaphươngtrìnhđãcholàbằng
2
.
Câu 4. (ThithửcụmVũngTàu-2019)Sốnghiệmcủaphươngtrình
1
2 1
2
log (4 4) log (2 3)
x x
x
A.
3
. B.
1
. C.
0
. D.
2
Lờigiải
ChọnB
Điềukiện:
1
3
2 3 0 2
2
x x
.
Tacó:
1 1
2 1 2 2 1
2 2
log (4 4) log (2 3) log (4 4) log 2 log (2 3)
x x x x x
x
1
2 2
log (4 4) log 2 (2 3)
x x x
1
2
4 4 2 (2 3)
(2 ) 3.2 4 0
x x x
x x
2 1(k t/m))
2
2 4(t/m)
x
x
x
.
Đốichiếuđiềukiệntathấy
2
x
thõamãn.Vậyphươngtrìnhđãchocómộtnghiệm.
Câu 5. Gọi
S
làtậphợptấtcảcácnghiệmnguyêndươngcủaphươngtrình
2
log 2 10
x
x
.Sốtập
concủa
S
bằng
A.
4
. B.
1
. C.
2
. D.
0
.
Lờigiải
ChọnC
Xétphươngtrình
2
log 2 10
x
x
,điềukiện
2
2 10 0 2 log 2 log 2
x
x x
.
Tacó
2 2 2
10 2
log 2 10 2 10 10 10 10 2 0 log1 0
10 1
x
x x x x x
x
x x
.
(Vì
10 2 0
x
vônghiệm)
Vậyphươngtrìnhcómộtnghiệm
0
x
thỏamãnđiềukiện.loại
Sốtậpconcủa
S
là
1
2 2
.
Câu 6. Tổngtấtcảcácnghiệmcủaphươngtrình
2
log 6 2 1
x
x
bằng
A.
1
. B.
2
. C.
0
. D.
3
.
Lờigiải
ChọnA
Điềukiệnxácđịnh
2
6 2 0 2 6 log 6
x x
x
Tacó:
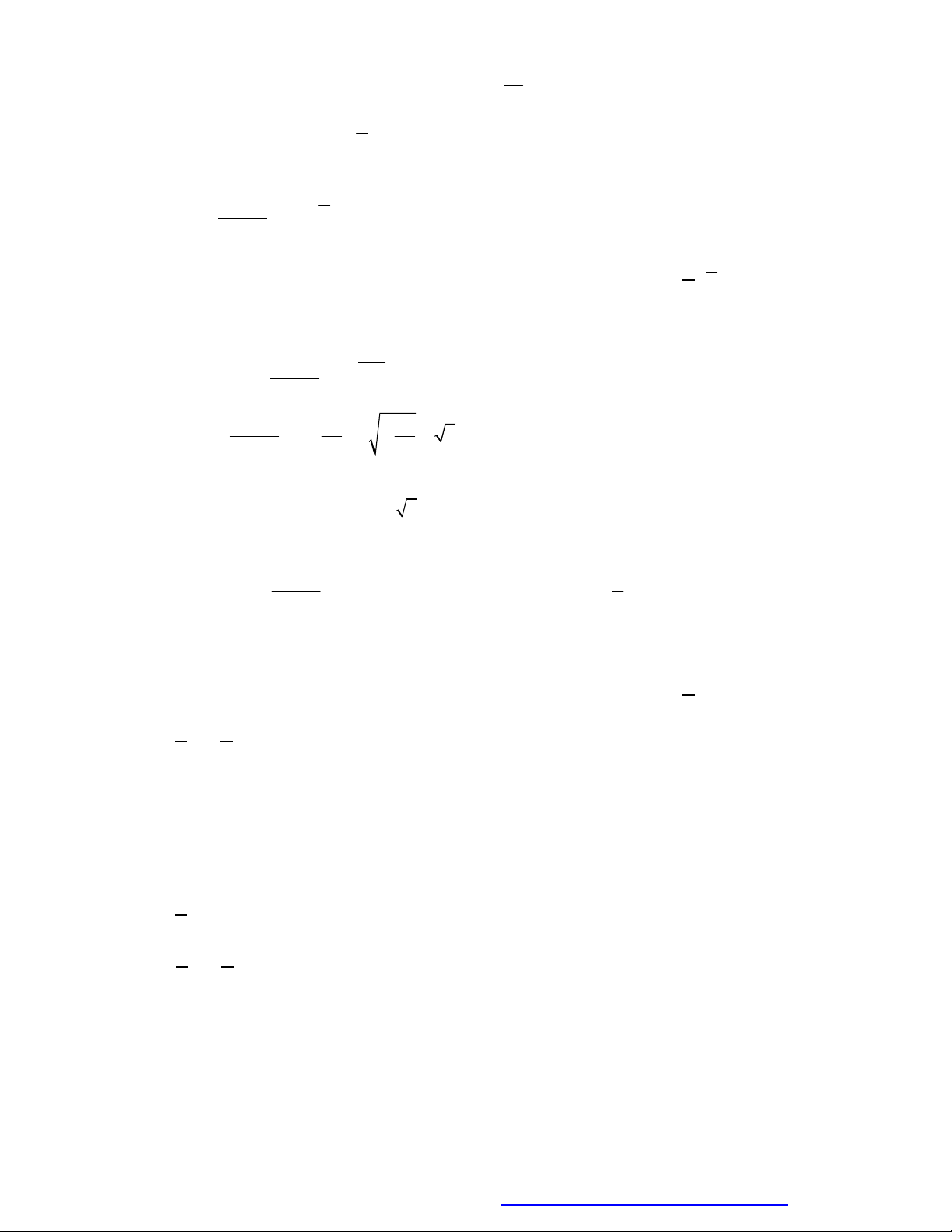
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 55
1 2
2
2
log 6 2 1 6 2 2 6 2 2 6.2 2 0
2
x x x x x x
x
x
Hơnnữa
1 2 1 2
1 2
2 2 .2 2 1
x x x x
c
x x
a
Câu 7. (Chuyên Thái Bình - 2018) Tính tích tất cả các nghiệm thực của phương trình
1
2
2
2
2 1
log 2 5
2
x
x
x
x
.
A.
0
. B.
2
. C.
1
. D.
1
2
.
Lờigiải
Điềukiện:
0
x
.
PT:
2
2 1
2
2
2
2 1
log 2 5 1
2
x
x
x
x
.
Đặt
2
2 1 1 1
2 . 2
2 2 2
x
t x x
x x x
PTtrởthành
2
log 2 5(2)
t
t
.
Xéthàm
2
log 2 2
t
f t t t làhàmđồngbiếnnên:
2 2 2
f t f t
(t/m).
Với
2t
thì
2
2
2 1
2 2 4 1 0
2
x
x x
x
(t/m).Vậy
1 2
1
2
x x
(theoViet).
Câu 8. (Thithửhội8trườngchuyên2019)Phươngtrình
2
log 5.2 4 2
x
x
cóbaonhiêunghiệm
nguyêndương?
A.
2
. B.
0
. C.
3
. D.
1
.
Lờigiải
ChọnD
Phươngtrình
2
2
2 1 0
log 5.2 4 2 2 5.2 4 0
1
2 4
x
x x x
x
x
x
x
.
Vậyphươngtrìnhcómộtnghiệmnguyêndương.
Câu 9. (SP Đồng Nai - 2019) Phương trình
2
log 5 2 2
x
x
có hai nghiệm thực
1 2
,x x
. Tính
1 2 1 2
P x x x x
A.
2
. B.
9
. C.
3
. D.
11
.
Lờigiải
ChọnA
Điềukiện:
2
5 2 0 0 2 5 log 5
x x
x
.
Phươngtrình
2 2
2
2 1 0 ( )
log 5 2 2 5 2 2 2 5.2 4 0 .
2 4 2 ( )
x
x x x x x
x
x n
x
x n
Khiđó
1 2 1 2
2
P x x x x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 56 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 10. Phươngtrình
2
2 5 log 3 0
x
x
cóhainghiệm
1
x
,
2
x
(với
1 2
x x
).Tínhgiátrịcủabiểu
thức
1 2
3K x x
.
A.
3
32 log 2
K
. B.
2
18 log 5
K
. C.
2
24 log 5
K
. D.
2
32 log 3
K
.
Lờigiải
ChọnC
Điềukiện:
0
x
.
2
2 5 log 3 0
x
x
2
2 5 0
log 3 0
x
x
2
2 5
log 3
x
x
2
log 5
8
x
x
1 2
2
log 5
8
x
x
.
Vậy
1 2 2 2
3 log 5 3.8 24 log 5
K x x
.
Câu 11. Cho biết phương trình
1
3
1
3
log (3 1) 2 log 2
x
x
có hai nghiệm
1 2
,x x
. Hãy tính tổng
1 2
27 27
x x
S
.
A.
252
S
. B.
45
S
. C.
9
S
. D.
180
S
.
Lờigiải
ChọnD
Tacó
1
3
1 1 1 2
3 3
log (3 1) 2 log 2 log 2(3 1) 2 2.3 2 3
x x x x
x x
2
3 6.3 2 0
x x
.
Đặt
3 , 0
x
t t
,phươngtrìnhtrởthành
2
6. 2 0
t t
.Phươngtrìnhluôncóhainghiệm
dươngphânbiệt.
Đặt
1 2
1 2
3 , 3
x x
t t
,
1 2 1 2
6, . 2
t t t t
.
Tacó
3 3 3
1 2 1 2 1 2 1 2
( ) ( ) 3 . ( ) 216 3.2.6 180
S t t t t t t t t
Câu 12. (THPT Yên Dũng 2-Bắc Giang 2019)Tính tích tất cả các nghiệmthựccủa phươngtrình
1
2
2
2
2 1
log 2 5
2
x
x
x
x
.
A.
2
. B.
0
. C.
1
2
. D.
1
.
Lờigiải
ChọnC
Điềukiện:
2
2 0
2 1
0
2
x
x
x
0
x
.
Khiđó,
1
2
2
2
2 1
log 2 5
2
x
x
x
x
1
2
2
1
log 2 5
2
x
x
x
x
1
2
2
1
log 5 2
2
x
x
x
x
.
Đặt
1
2
t x
x
1
2 .
2
x
x
2
,phươngtrìnhtrởthành:
2
log 5 2
t
t
,
2
t
.
Xét
2
logf t t
,
2
t
.Tacó:
1
0
.ln 2
f t
t
,
2
t
nên
f t
đồngbiếntrên
2;
.
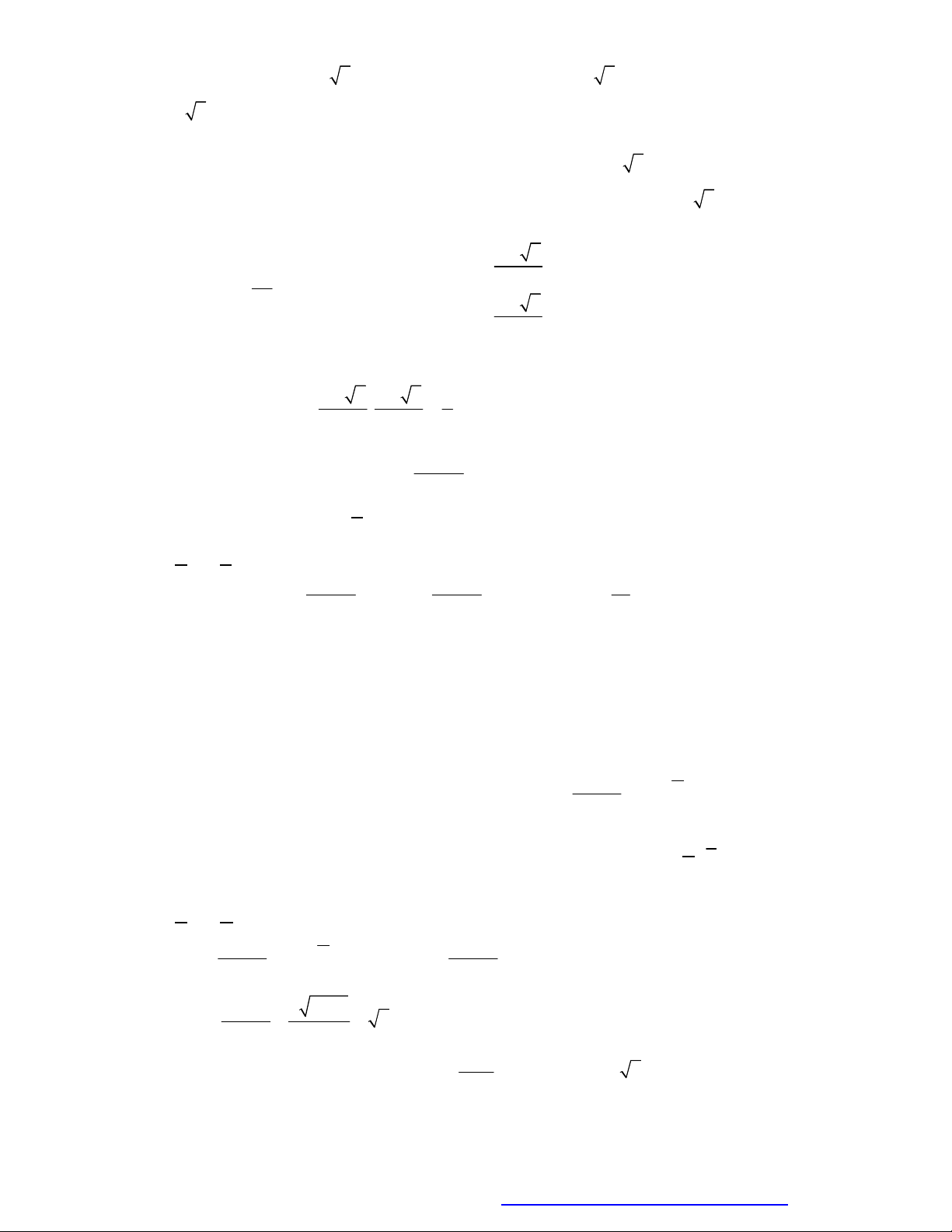
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 57
Xét
5 2
t
g t
,
2
t
.Tacó:
2 .ln 2 0
t
g t
,
2
t
nên
g t
nghịchbiếntrên
2;
.
Từđóphươngtrình
f t g t
cónhiềunhấtmộtnghiệm
2
t
.Tanhậnthấy
2t
là
nghiệm,vàđâylànghiệmduynhấtcủaphươngtrình
2
log 5 2
t
t
trên
2;
.
Suyra
1
2
2
x
x
2
2 4 1 0
x x
2 2
2
2 2
2
x
x
.Cảhaigiátrịnàyđềuthỏamãnđiềukiện
0
x
,nênđềulànghiệmcủaphươngtrìnhđãcho.
Tíchhainghiệmlà:
2 2 2 2
.
2 2
1
2
.
Câu 13. Sốnghiệmcủaphươngtrình
2
2 4
log 3
2 12
x
x
x
A.
0
. B.
1
. C.
2
. D.
3
.
Lờigiải
ChọnB
Phươngtrình
3
2
3
2 4 2 4 2
log 3 2 2 4 2 12
2 12 2 12 2
x x x
x x x
x x
x
2
2 4
2 4 2 32 0
2 8
x
x
x
x
.
.
+Với
2 4 2
x
x
.
+Với
2 8
x
phươngtrìnhvônghiệm.
Vậyphươngtrìnhđãchocó
1
nghiệm.
Câu 14. Tínhtíchtấtcảcácnghiệmthựccủaphươngtrình
1
2
2
2
2 1
log 2 5
2
x
x
x
x
.
A.
0
. B.
2
. C.
1
. D.
1
2
.
Lờigiải
ChọnD
1
2
2
2
2 1
log 2 5
2
x
x
x
x
.Điềukiện
2
2 1
0
2
x
x
0
x
.
Tacó
2 2
2 1 2 2 .1
2
2 2
x x
x x
.
Xéthàmsố
2
1
log 2 ' 2 ln 2 0, 2
ln 2
t t
f t t f t t
t
.
Phươngtrình
2
log 2 5 2 2
t
f t t f t f t
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 58 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy
1
2 2
2
2
2
2 1 2 1
log 2 5 2 2 4 1 0
2 2
x
x
x x
x x
x x
Tacóphươngtrình
2
2 4 1 0
x x
cóhainghiệmdươngphânbiệtcótíchbằng
1
2
.
Câu 15. Tổngtấtcảcácnghiệmcủaphươngtrình
2
log 10 2019 2019 4
x
x
bằng
A.
2019
log 16
. B.
2019
2log 16
. C.
2019
log 10
. D.
2019
2log 10
.
Lờigiải
ChọnB
Tacó
2
log 10 2019 2019 4
x
x
10 2019 2019 16
x
x
(1)
Đặt
2
2019 0
x
t t
tacóPT(1)trởthành
2
10 16
t t
2
10 16 0
t t
2
8
t
t
Với
2t
tacó
2
2019
2019 2 log 2
2
x
x
2019
2log 2
x
Với
8t
tacó
2
2019
2019 8 log 8
2
x
x
2019
2log 8
x
.Dođótổngtấtcảcácnghiệmbằng
2019
2log 2
2019
2log 8
2019 2019
2 log 2 log 8
2019
2 log 2.8
2019
2log 16
.
Câu 16. (THPTHòaVang-ĐàNẵng-2018)Biếtrằng
1
2
2 log 14 2 1
x
x
y y
với
0
x
.
Tínhgiátrịcủabiểuthức
2 2
1P x y xy
.
A.
3
. B.
1
. C.
2
. D.
4
.
Lờigiải
Do
0
x
nên
1 1
2 . 2
x x
x x
1
2
2 2 4
x
x
,dấubằngxảyrakhi
1x
.
Xéthàm
4 2 1, 1
f y y y y
,tacó
2
1
2 1
y
f y y
y
2 2 2
0
2 1
y y
y
0
y
.Lậpbảngbiếnthiên,suyra
1;
max 16
f y
khi
0
y
.
Suyra
2 2
log 14 2 1 log 16 4
y y
.
Dođó
1
2
1
2 log 14 2 1
0
x
x
x
y y
y
.Vậy
2 2
1 2
P x y xy
.
Câu 17. (ToánHọcTuổiTrẻ-2018)Phươngtrình
8
8
log
log 4
4 4
x
x
x x
cótậpnghiệmlà
A.
2;8
. B.
1
;8
2
. C.
1 1
;
2 8
. D.
1
2;
8
.
Lờigiải
Điềukiện:
0
x
.

TÀ
I LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 59
8
8
l
og
log 4
4
4
x
x
x
x
8 8
l
og log
4
4 4
x
x
x
x
8
lo
g
4 2
x
x
8
8 8
l
og log 4 log 2
x x
8
8
2
1
log log
3
3
x x
.
Đặ
t
8
t log x
.
P
hươngtrìnhtrởthành:
2
1
3 3
t t
2
2
1
0
3
3
t
t
1
3
1
t
t
.
8
1
1
l
og
3
3
t
x
2
x
(nhậ
n).
8
1
log 1
t
x
1
8
x
(nhậ
n).
Vậytậpnghiệmlà
1
2;
8
.
C
âu 18. (THPT Yên Lạc- 2018) Tính tổng
S
tất cả các nghiệm của phương trình:
1
5
3
ln 5 5.3 30 10 0
6
2
x x
x x
x
x
.
A
.
1
S
. B.
2
S
. C.
1
S
. D.
3
S
Lờ
igiải
Điềukiện
1
.
3
x
P
hươngtrìnhtươngđương
l
n 5 3 ln 6 2 5 5 3 5 6 2 0
x
x x x
x
x
l
n 5 3 5 5 3 ln 6 2 5 6 2
x
x x x
x
x
(1)
.
Xéthàmsô
l
n 5 , 0f t t t t
.
Có
1
'
5 0
f
t
t
,
0t
nê
n
f
t
đồngbi
ến.Từ
1
suyra
5 3 6 2
x
x
f f x
5
3 6 2
x
x
x
5
3 6 2 0
x
x
x
Xét
5 3 6 2
x
x
g x x
,
' 5 ln 5 3 ln 3 6
x
x
g x
2
2
'
' 5 ln5 3 ln 3 0
x
x
g
x
1
3
x
.
Nê
n
' 0
g x
cókhôngquá
1
nghiệ
msuyra
0
g x
cókhôngquá
2
nghiệmt
rên
1
;
3
.
Mà
0
1 0
g
g
.Vậ
yphươngtrìnhcónghiệm
0,1
.Dođó
1
.
S

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI – XUẤT SẮC MỨC 9-10 ĐIỂM
PHƯƠNG PHÁP CHUNG
Tìm m để
, 0f x m
có nghiệm (hoặc có k nghiệm) trên D ?
— Bước 1. Tách m ra khỏi biến số và đưa về dạng
f x A m
.
— Bước 2. Khảo sát sự biến thiên của hàm số
f x
trên D.
— Bước 3. Dựa vào bảng biến thiên để xác định giá trị của tham số
A m
để đường thẳng
y A m
nằm
ngang cắt đồ thị hàm số
y f x
.
— Bước 4. Kết luận các giá trị cần tìm của
A m
để phương trình
f x A m
có nghiệm (hoặc có k
nghiệm) trên D.
Lưu ý
— Nếu hàm số
y f x
có giá trị lớn nhất và giá trị nhỏ nhất trên D thì giá trị
A m
cần tìm là những m
thỏa mãn:
min max
x D
x D
f x A m f x
.
— Nếu bài toán yêu cầu tìm tham số để phương trình có k nghiệm phân biệt, ta chỉ cần dựa vào bảng biến
thiên để xác định sao cho đường thẳng
y A m
nằm ngang cắt đồ thị hàm số
y f x
tại k điểm
phân biệt.
Dạng 1. Phương trình logarit chứa tham số
Câu 1. (Đề Minh Họa 2020 Lần 1) Cho phương trình
2
2 2
log 2 2 log 2 0x m x m
(
m
là tham
số thực). Tập hợp tất cả các giá trị của
m
để phương trình đã cho có hai nghiệm phân biệt thuộc
đoạn
1;2
là
A.
1;2
. B.
1;2
. C.
1;2
. D.
2;
.
Lời giải
Chọn C
2
2 2
log 2 2 log 2 0x m x m
2
2
1 log 2 log 2 0x m x m
*
Đặt
2
logt x g x
0 1t
và mỗi giá trị của
x
sẽ cho một giá trị của t
*
trở thành
2
1 2 2 0t m t m
2
2 1 2 2 0t t mt t m
2
1 1t m t
1 1 0t t m
1 1
1 2
t m
t
Với
1t
thì phương trình có một nghiệm
2x
Vậy để phương trình ban đầu có hai nghiệm phân biệt thì phương trình
1
phải có một nghiệm
1t
0 1 1m 1 2m
Vậy
1;2m
để thoả mãn yêu cầu bài toán.
PHƯƠNG TRÌNH MŨ - LOGARIT
Chuyên đề 19

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 2. (Chuyên Lam Sơn Thanh Hóa 2019) Cho hàm số
2 2
27 1
3
3log 2 3 1 log 1 3 0
x m x m x x m
. Số các giá trị nguyên của
m
để
phương trình đã cho có hai nghiệm phân biệt
1 2
,x x
thỏa mãn
1 2
15
x x
là:
A.
14
B.
11
C.
12
D.
13
Lời giải
Chọn D
Ta có:
2 2
27 1
3
3log 2 3 1 log 1 3 0
x m x m x x m
2 2
3 3
log 2 3 1 log 1 3x m x m x x m
2
2 2
1 3 0
2 3 1 1 3
x x m
x m x m x x m
2
2
2
1 3 0 *
1 3 0 *
2 2 0 1
2
x x m
x x m
x m
x m x m
x
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân
biệt thỏa mãn (*)
2
2
2
1 3 0
4 1 0
2 1 1 3 0 2 3
4 3 0
2
m m m
m m
m m
m
m
.
Theo giả thiết
2
2
1 2 1 2 1 2
15 4 225 4 221 0 13 17
x x x x x x m m m
Do
đó
13 2 3
m . Vậy số các giá trị nguyên của
m
thỏa mãn là 13.
Câu 3. (THPT Yên Phong Số 1 Bắc Ninh 2019) Gọi
S
là tập tất cả các giá trị nguyên của tham số m
với
64
m
để phương trình
1 5
5
log log 2 0
x m x
có nghiệm. Tính tổng tất cả các phần tử
của
S
.
A.
2018.
B.
2016.
C. 2015. D.
2013.
Lời giải
Chọn C
Ta có:
1 5
5
log log 2 0
x m x
5 5
log log 2
x m x
2
2
2
x
m
x
.
Vì
2
x
nên
2
2 2
2
m
m
.
Kết hợp với
64
m
. Khi đó
2 64
m
.
Vì
m
nên
1;0;1...63
m
có 65 giá trị.
Vậy tổng
S
các giá trị của
m
để phương trình có nghiệm là:
1 63 .65
2015
2
S
.
Câu 4. (Mã 102 2019) Cho phương trình
2
9 3 3
log log 6 1 logx x m
(
m
là tham số thực). Có tất cả
bao nhiêu giá trị nguyên của
m
để phương trình đã cho có nghiệm?
A.
7
. B.
6
. C.
5
. D. Vô số.
Lời giải
Chọn C
Xét phương trình
2
9 3 3
log log 6 1 logx x m
.
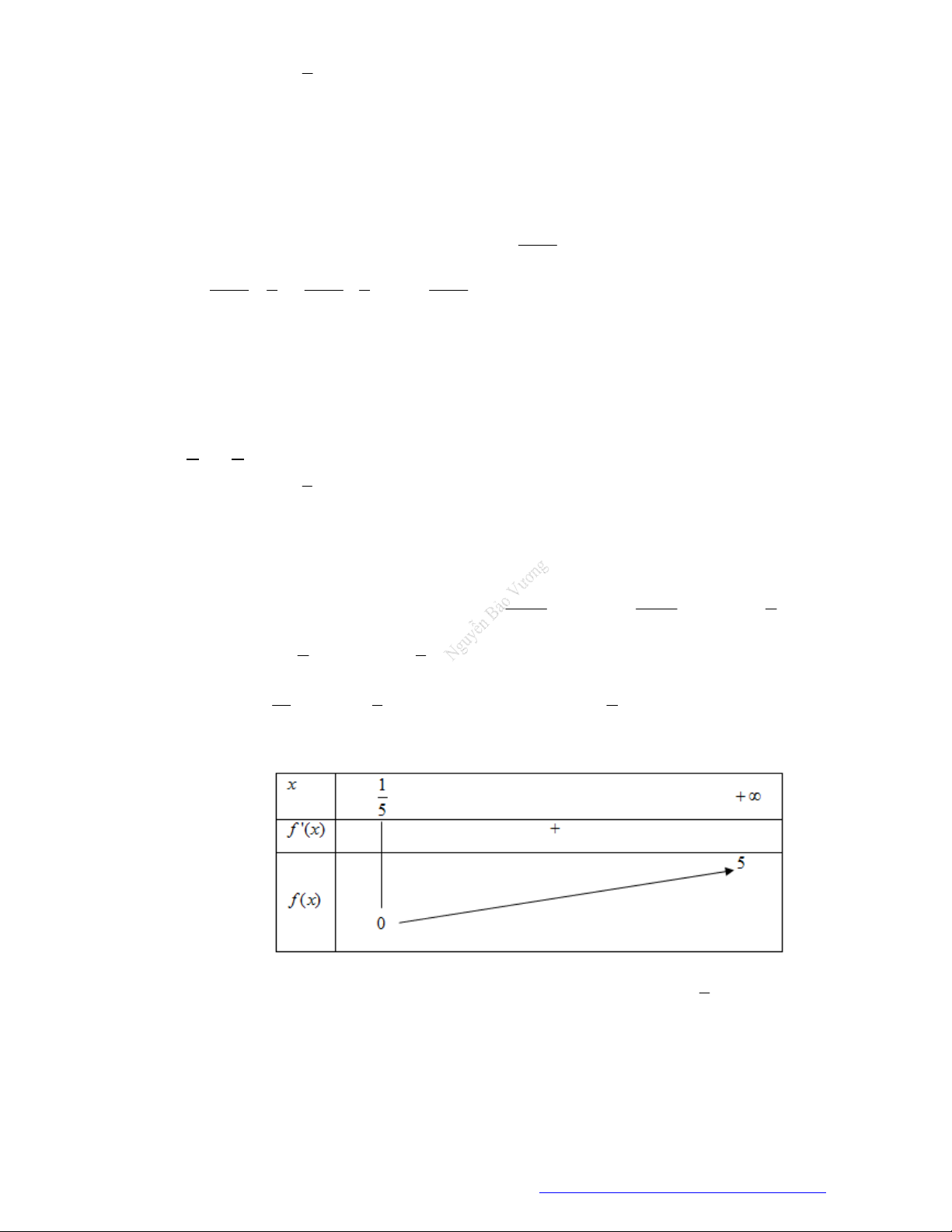
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Điều kiện:
1
6
0
x
m
.
Khi đó
2
9 3 3 3 3 3
log log 6 1 log log log log 6 1
6 1 6 1 1
x x m x m x
mx x x m
+) Với
6m
, phương trình (1) trở thành
0 1
(vô lý).
+) Với
6m
, phương trình (1) có nghiệm
1
6
x
m
1 1 1 1
0
6 6 6 6m m
0 0 6
6
m
m
m
.
Vậy
0 6m
. Mà
1;2;3;4;5m m
. Vậy có 5 giá trị nguyên của
m
thỏa mãn.
Câu 5. (Mã 103 2019) Cho phương trình
2
9 3 3
log log 5 1 logx x m
(
m
là tham số thực). Có tất cả
bao nhiêu giá trị nguyên của
m
để phương trình đã cho có nghiệm?
A.
4.
B.
6.
C. Vô số. D.
5.
Lời giải
Chọn A
Điều kiện:
1
5
0
x
m
.
Xét phương trình:
2
9 3 3
log log 5 1 logx x m
1
.
Cách 1.
3 3 3 3 3
5 1 5 1 1
1 log log 5 1 log log log 5 2
x x
x x m m m m
x x x
.
Xét
1
5f x
x
trên khoảng
1
;
5
.
Có
2
1 1
0, ;
5
f x x
x
và
1
lim lim 5 5
x x
f x
x
.
Ta có bảng biến thiên của hàm số
f x
:
Phương trình
1
có nghiệm khi và chỉ phương trình
2
có nghiệm
1
5
x
.
Từ bảng biến thiên suy ra phương trình
1
có nghiệm khi và chỉ khi
0 5m
.
Mà
m
và
0m
nên
1;2;3;4m
.
Vậy có 4 giá trị nguyên của
m
để phương trình đã cho có nghiệm.
Cách 2.
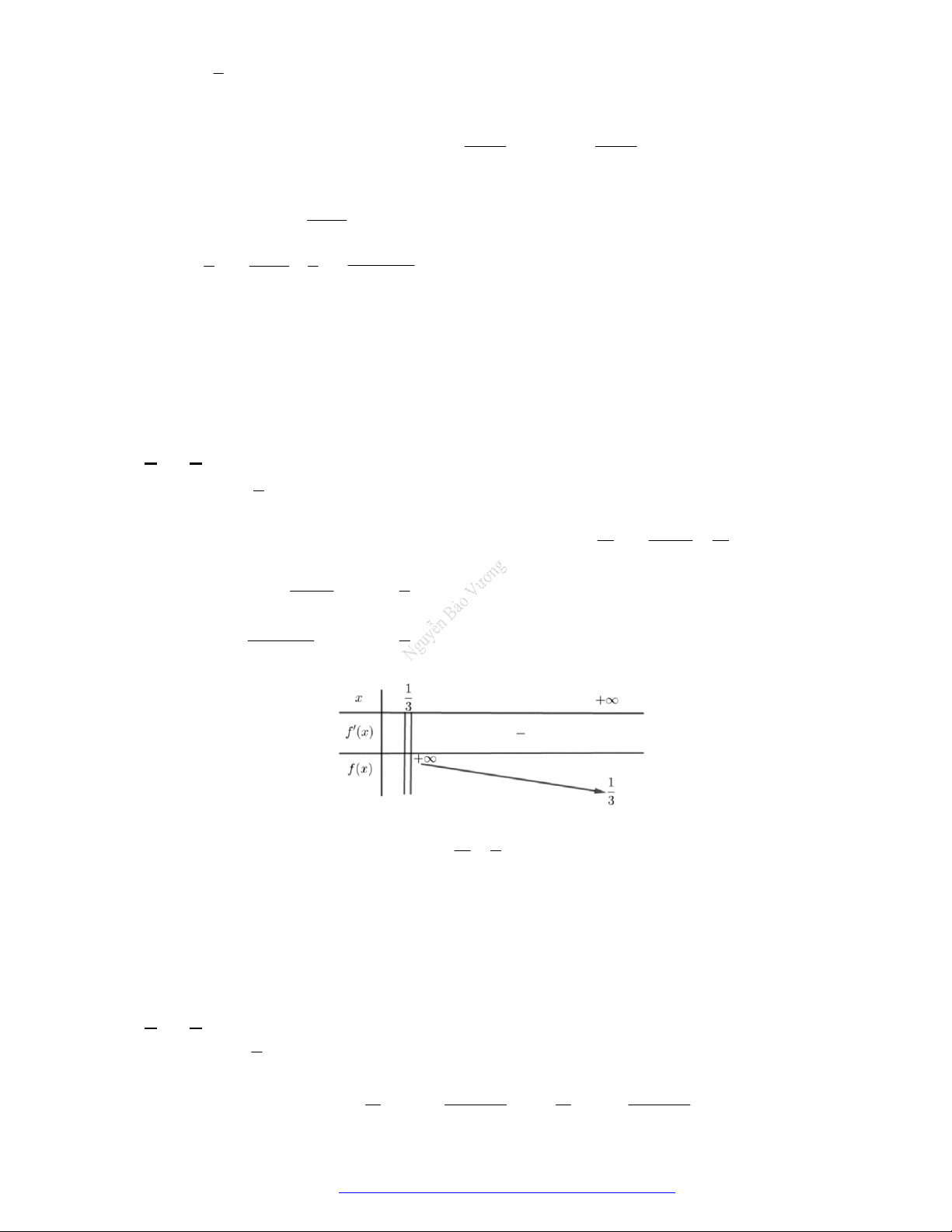
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Với
1
5
0
x
m
, ta có:
3 3 3 3 3
5 1 5 1
1 log log 5 1 log log log 5 1 2
x x
x x m m m m x
x x
Với
5m
, phương trình
2
thành
0. 1x
(vô nghiệm).
Với
5m
,
1
2
5
x
m
.
Xét
1
5
x
1 1
5 5m
0
5. 5
m
m
0 5m
.
Mà
m
và
0m
nên
1;2;3;4m
.
Vậy có 4 giá trị nguyên của
m
để phương trình đã cho có nghiệm.
Câu 6. (Mã 101 - 2019) Cho phương trình
2
9 3 3
log log 3 1 logx x m
(
m
là tham số thực). Có
tất cả bao nhiêu giá trị nguyên của tham số
m
để phương trình đã cho có nghiệm?
A. 2. B. 4. C. 3. D. Vô số.
Lời giải
Chọn A
Điều kiện:
1
3
x
và
0m
.
Phương trình đã cho tương đương:
3 3 3
1
log log 3 1 logx x
m
1
3 1
x
x m
Xét hàm số
3 1
x
f x
x
với
1
3
x
Có
2
1
0,
3 1
f x
x
1
3
x
Dựa vào BBT, phương trình có nghiệm khi
1 1
0 3
3
m
m
Do
1,2 .m m
Câu 7. (Mã 104 2019) Cho phương trình
2
9 3 3
log 4log 4 1 logx x m
(
m
là tham số thực). Có tất
cả bao nhiêu giá trị nguyên của
m
để phương trình đã cho có nghiệm?
A.
5
. B.
3
. C. Vô số. D.
4
.
Lời giải
Chọn C
Điều kiện:
1
4
x
. Phương trình đã cho
3 3 3
log 4log 4 1 logx x m
4
3 3 3
1
log log 4 1 logx x
m
4
3 3
4
4 1
1
log log
4 1
x
x
m f x
m x
x
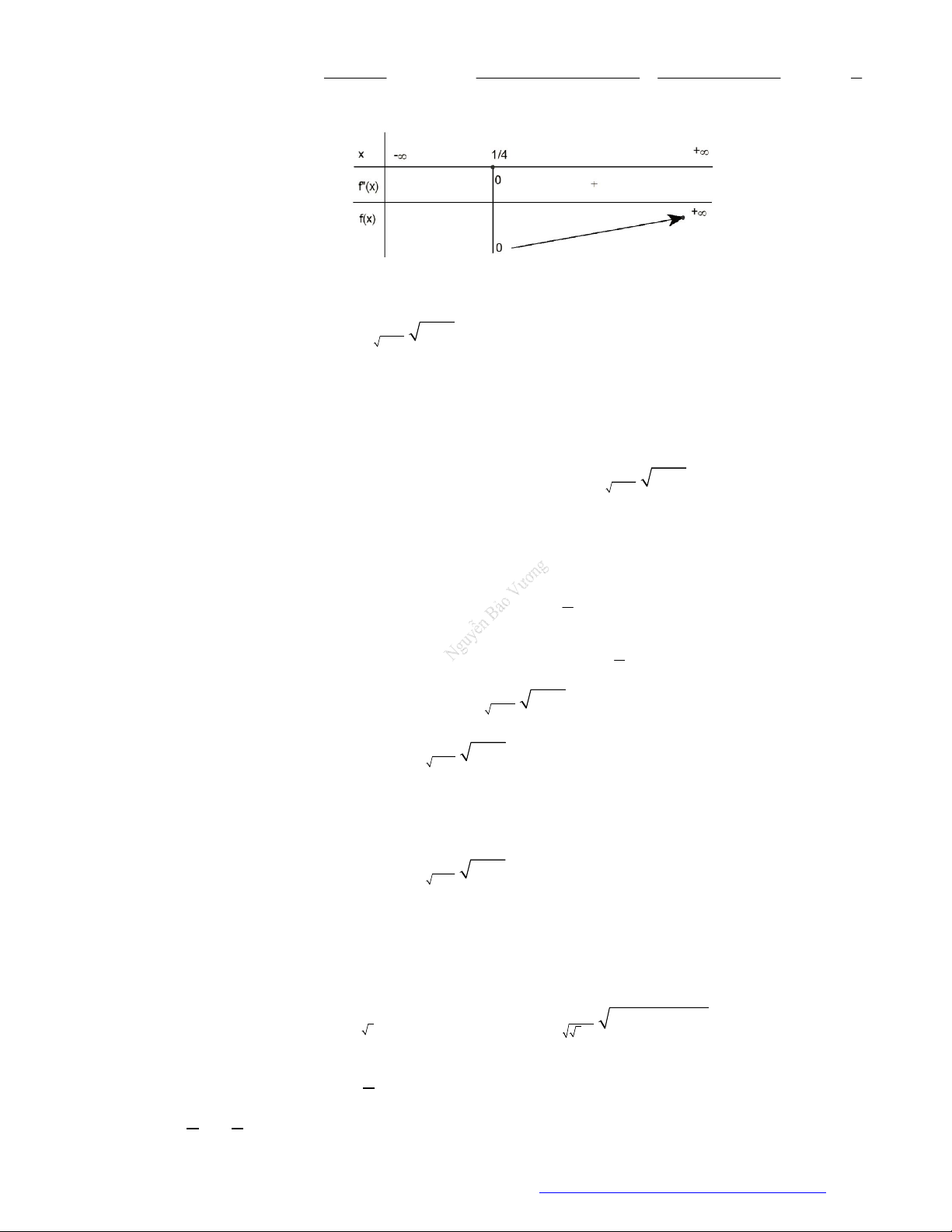
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Xét hàm số
4
4 1
f
x
x
x
có
3 4 3
2 2
16 4 1 4 1 4 1 12 1
1
0,
4
x x x x x
f x x
x x
.
Suy ra bảng biến thiên:
Do đó phương trình có nghiệm khi
0m
. Vậy có vô số giá trị nguyên của
m
.
Câu 8. (THPT Lương Thế Vinh Hà Nội 2019) Cho phương trình
2
5
5
log 6 12 log 2
mx
mx
x x x
, gọi
S
là tập hợp tất cả các giá trị của tham số
m
để
phương trình đã cho có nghiệm duy nhất. Tìm số phần tử của
S
.
A.
2
. B.
0
. C.
3
. D.
1
.
Lời giải
+ Điều kiện
2 0 2
0 5 1 5 6
x x
mx mx
Với điều kiện trên, phương trình
2
5
5
log 6 12 log 2 *
mx
mx
x x x
2
5 5
log 6 12 log 2
mx mx
x x x
2
2
6 12 2
5
x
x x x
x
.
2x
là nghiệm phương trình
*
khi
5
5 2 6 3
2
m m
, vì
m Z
4
m
m Z
.
5x
là nghiệm phương trình
*
khi
6
5 5 6 1
5
m m
, vì
m Z
2
m
m Z
.
+ Phương trình
2
5
5
log 6 12 log 2
mx
mx
x x x
có nghiệm duy nhất khi
2m
hoặc
3m
Thử lại
2m
:
2 2
2 5 2 5 2 5
2 5
log 6 12 log 2 log 6 12 log 2
x x x
x
x x x x x x
2
6 12 2
2 0 5
0 2 5 1
x x x
x x
x
.
3m
:
2 2
3 5 3 5 3 5
3 5
log 6 12 log 2 log 6 12 log 2
x x x
x
x x x x x x
2
6 12 2
2 0 5
0 4 5 1
x x x
x x
x
.
Vậy có hai giá trị
m Z
thỏa mãn ycbt.
Câu 9. Cho phương trình
2 2 2 2
2 5
5 2
log 2 4 2 log 2 0x x m m x mx m
. Hỏi có bao nhiêu
giá trị nguyên của tham số
m
để phương trình đã cho có hai nghiệm
2 2
1 2
3x x
?
A. 1 B. 0 C. 3 D. 4
Lời giải
Chọn B
Phương trình đã cho tương đương với phương trình:

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2 2 2
2 5 5 2
log 2 4 2 log 2 0x x m m x mx m
2 2 2 2
5 2 5 2
log 2 4 2 log 2 0x x m m x mx m
2 2
2 2
2 2
2 2 2 2
2 2 0
2 2 0
1 2 2 0
2 2 4 2
x mx m
x mx m
x m x m m
x x m m x mx m
2 2
1
2
2 0
2
1
x mx m
x m
x m
Phương trình đã cho có hai nghiệm
1 2
,x x thỏa
2 2
1 2
3
x x
2
2
2
2
2 2
2
2 2
2 2 2 0
4 0
1 1 2 0 2 1 0
5 2 2 0
2 1 3
m m m m
m
m m m m m m
m m
m m
0
1 1 11
1
2 5
1 11 1 11
;
5 5
m
m m
m m
Vậy không có giá trị nguyên nào của
m
thỏa yêu cầu đề bài
Câu 10. (HSG Bắc Ninh 2019) Tìm tất cả các giá trị của tham số thực m để phương trình
2
2 1
2
4 log log 0x x m
có hai nghiệm phân biệt thuộc khoảng
0;1
.
A.
1
0
4
m
B.
1
0
4
m
C.
1
4
m
D.
1
0
4
m
Lời giải
Ta có:
2 2
2
2 1 2 2 2 2
2
4 log log 0 2log log 0 log log 1x x m x x m x x m
Đặt
2
logt x với
;0t
.
2
1 t t m
.
Xét
2
f t t t
.
' 2 1
1
' 0
2
f t t
f t t
Bảng biến thiên
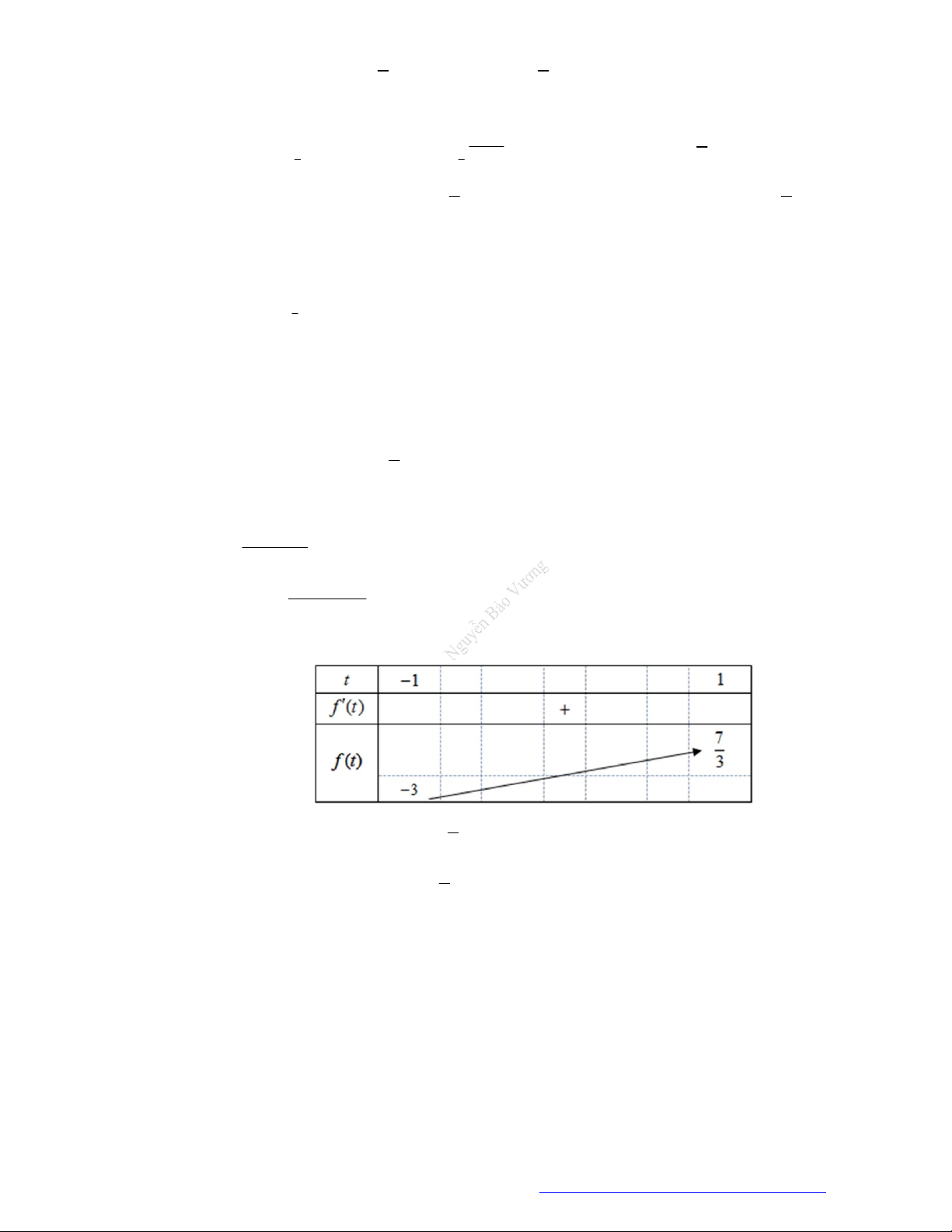
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Dựa vào bảng biến thiên
1 1
0 0
4 4
m m
Câu 11. (THPT Đông Sơn Thanh Hóa 2019) Tìm
m
để phương
trình :
2
2
1 1
2 2
1
1 log 2 4 5 log 4 4 0
2
m x m m
x
có nghiệm trên
5
,4
2
.
A.
m
. B.
7
3
3
m
. C.
m
. D.
7
3
3
m
.
Lời giải
Điều kiện:
2x
. Phương trình đã cho
2
2
1 2
2
1 log 2 4 5 log 2 4 4 0
m x m x m
2
2 2
1 2log 2 4 5 log 2 4 4 0m x m x m
2
2 2
4 1 log 2 4 5 log 2 4 4 0m x m x m
2
2 2
1 log 2 5 log 2 1 0m x m x m
. (1)
Đặt
2
log 2t x
. Vì
5
;4 1;1
2
x t
.
Phương trình (1) trở thành
2
1 5 1 0m t m t m
,
1;1t
. (2)
2
2
5 1
, 1;1
1
t t
m f t t
t t
.
Ta có
2
2
2
2
4 4
' 0
2
1
t
t
f t
t
t t
.
Bảng biến thiên
Phương trình đã cho có nghiệm
5
;4
2
x
khi phương trình (2) có nghiệm
1;1t
.
Từ bảng biến thiên suy ra
7
3
3
m
.
Câu 12. (Chuyên Bắc Giang 2019) Tìm
m
để phương trình
2 2
2 2
log log 3x x m
có nghiệm
[1;8]x
.
A.
6 9m
B.
2 3m
C.
2 6m
D.
3 6m
Lời giải
Chọn C
2 2
2 2
log log 3
x x m
(1)
Điều kiện:
0x
(*)
pt (1)
2
2 2
log 2 log 3
x x m
Cách 1: (Tự luận)
Đặt
2
logt x , với
[1;8]x
thì
[0;3]t
.
Phương trình trở thành:
2
2 3t t m
(2)
Để phương trình (1) có nghiệm
[1;8]x
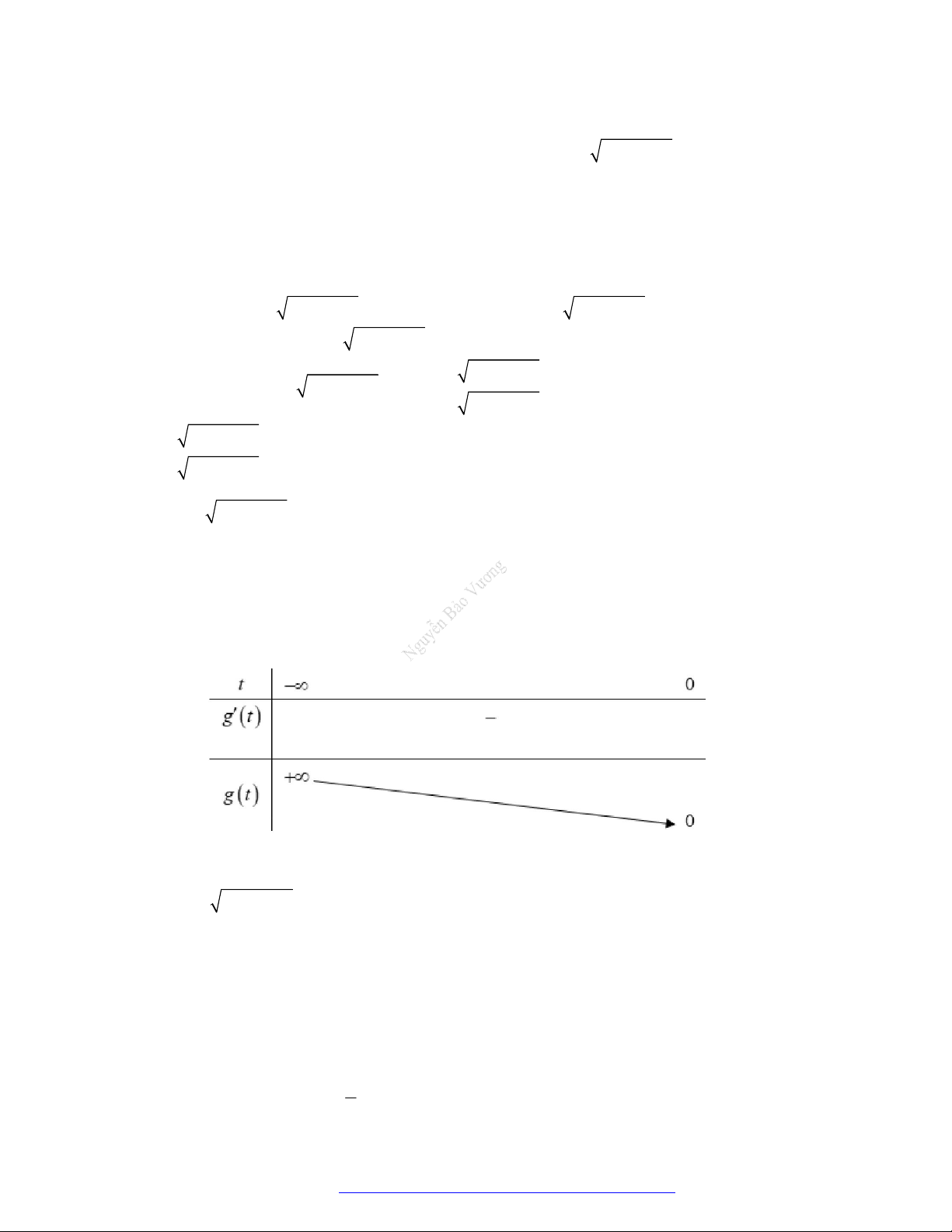
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
phương trình (2) có nghiệm
[0;3]t
[0;3]
[0;3]
min ( ) max ( )f t m f t
, trong đó
2
( ) 2 3f t t t
2 6m
. (bấm máy tính)
Câu 13. (HSG Bắc Ninh-2019) Cho phương trình
2
2 2 2
log 2log log *x x m x m
. Có bao nhiêu
giá trị nguyên của tham số
2019;2019m
để phương trình (*) có nghiệm?
A.
2021
. B.
2019
. C.
4038
. D.
2020
.
Lời giải
Điều kiện:
2
0
log 0
x
m x
.
2 2
2 2 2 2 2 2
log 2log log 4log 8log 4 log 4x x m x m x x m x m
2
2 2 2 2
4log 4log 1 4 log 4 log 1x x m x m x
2
2
2 2
2 2
2 2
2 log 1 2log 1
2log 1 2 log 1
2 log 1 2log 1
m x x
x m x
m x x
2 2
2 2
log log 1
log log
m x x
m x x
* TH
1
:
2 2
log logm x x
2
2
2
2 2
2 2
0 1
log 0
log log 0 1
log log
x
x
x x m
m x x
Đặt:
2
log 0t x t
, phương trình
(1)
trở thành:
2 2
0 2t t m t t m
Đặt:
2
( ) ( ;0g t t t t
.Bài toán trở thành: Tìm giá trị của tham số
m
để phương trình
2
có
ít nhất 1 nghiệm
0t
Ta có:
2
( ) ( ) 2 1 0 0g t t t g t t t
Ta có BBT:
Dựa vào BBT, suy ra: để phương trình
2
có ít nhất 1 nghiệm
0t
thì
0m
(*)
* TH
2
:
2 2
log log 1m x x
2
2
2 2 2
log 1
log log 2log 1
x
m x x x
2
2
2 2
log 1
log 3log 1 0 3
x
x x m
Đặt:
2
log 1t x t
, phương trình
(1)
trở thành:
2 2
3 1 0 3 1 4t t m m t t
Đặt:
2
( ) 1, 1;g t t t t
Ta có:
2
( ) 3 1 ( ) 2 3g t t t g t t
3
( ) 0 2 3 0 1;
2
g t t t
Bài toán trở thành: Tìm giá trị của tham số
m
để phương trình
4
có ít nhất 1 nghiệm
1t
Ta có BBT:
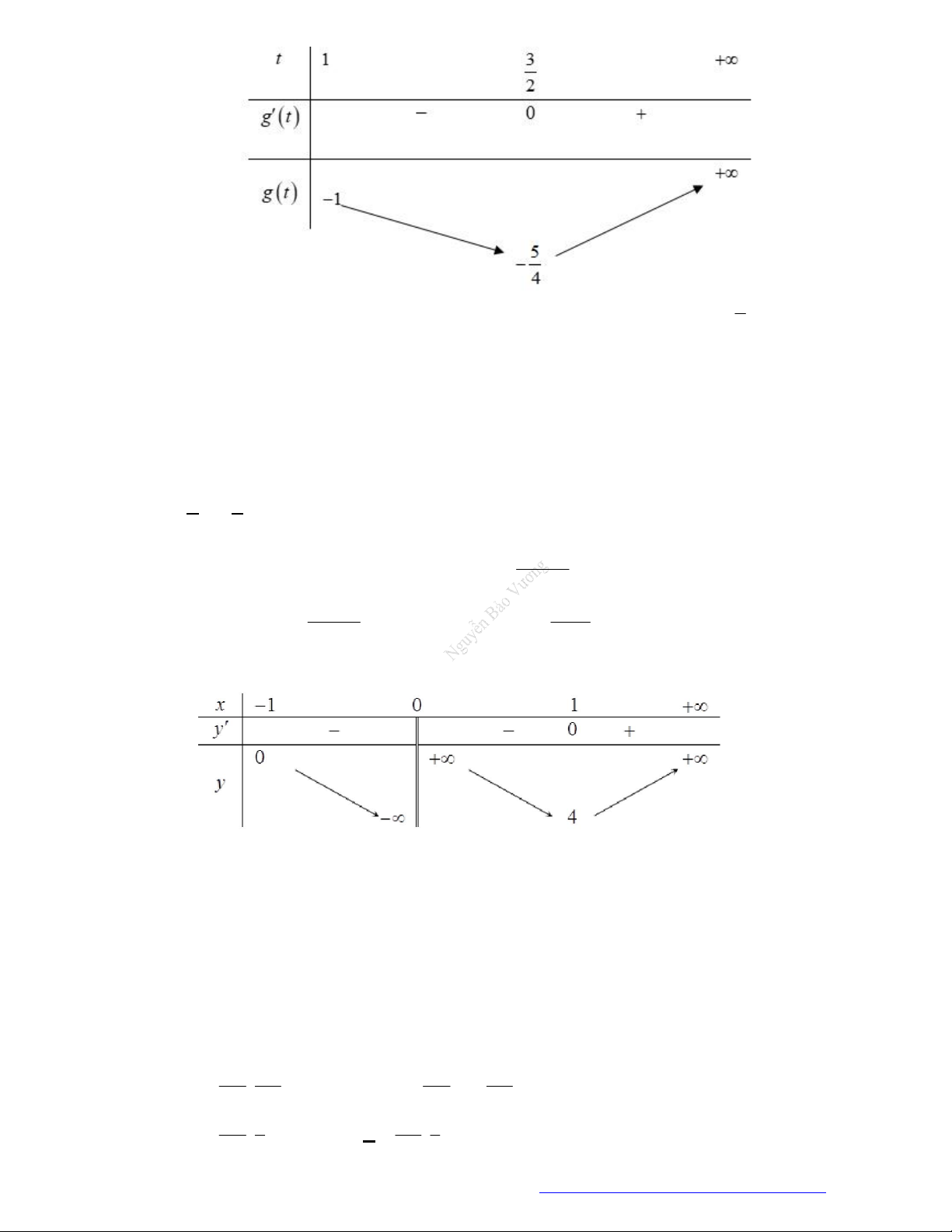
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Dựa vào BBT, suy ra: để phương trình
4
có ít nhất 1 nghiệm
1t
thì
5
4
m
(**)
Kết hợp (*) và (**),
2019;2019m
1;0;1;2;...;2019m
Vậy có tất cả
2021
giá trị của
m
thỏa mãn ycbt
Câu 14. (Đề Tham Khảo 2017) Hỏi có bao nhiêu giá trị
m
nguyên trong
2017;2017
để phương trình
log 2log 1mx x
có nghiệm duy nhất?
A.
4014.
B.
2018.
C.
4015.
D.
2017
.
Lời giải
Chọn B
Điều kiện
1, 0x mx
.
2
2
1
log 2log 1 1
x
mx x mx x m
x
Xét hàm
2
1
1 0,
x
f x x x
x
;
2
2
1
1
0
1
x
x
f x
x l
x
Lập bảng biến thiên
Dựa vào BBT, phương trình có nghiệm duy nhất khi và chỉ khi
4
0.
m
m
Vì
2017;2017m
và
m
nên chỉ có
2018
giá trị
m
nguyên thỏa yêu cầu là
2017; 2016;...; 1;4m
.
Chú ý: Trong lời giải, ta đã có thể bỏ qua điều kiện
0mx
vì với phương trình
log log
a a
f x g x
với
0 1a
ta chỉ cần điều kiện
0f x
.
Câu 15. (THPT An Lão Hải Phòng 2019) Tìm tập hợp tất cả các giá trị thực của tham số
m
để phương
trình
ln 0mx x
có hai nghiệm phân biệt thuộc khoảng
2;3
A.
ln 2 ln 3
;
2 3
B.
ln 2 ln 3
; ;
2 3
C.
ln 2 1
;
2 e
D.
ln 3 1
;
3 e
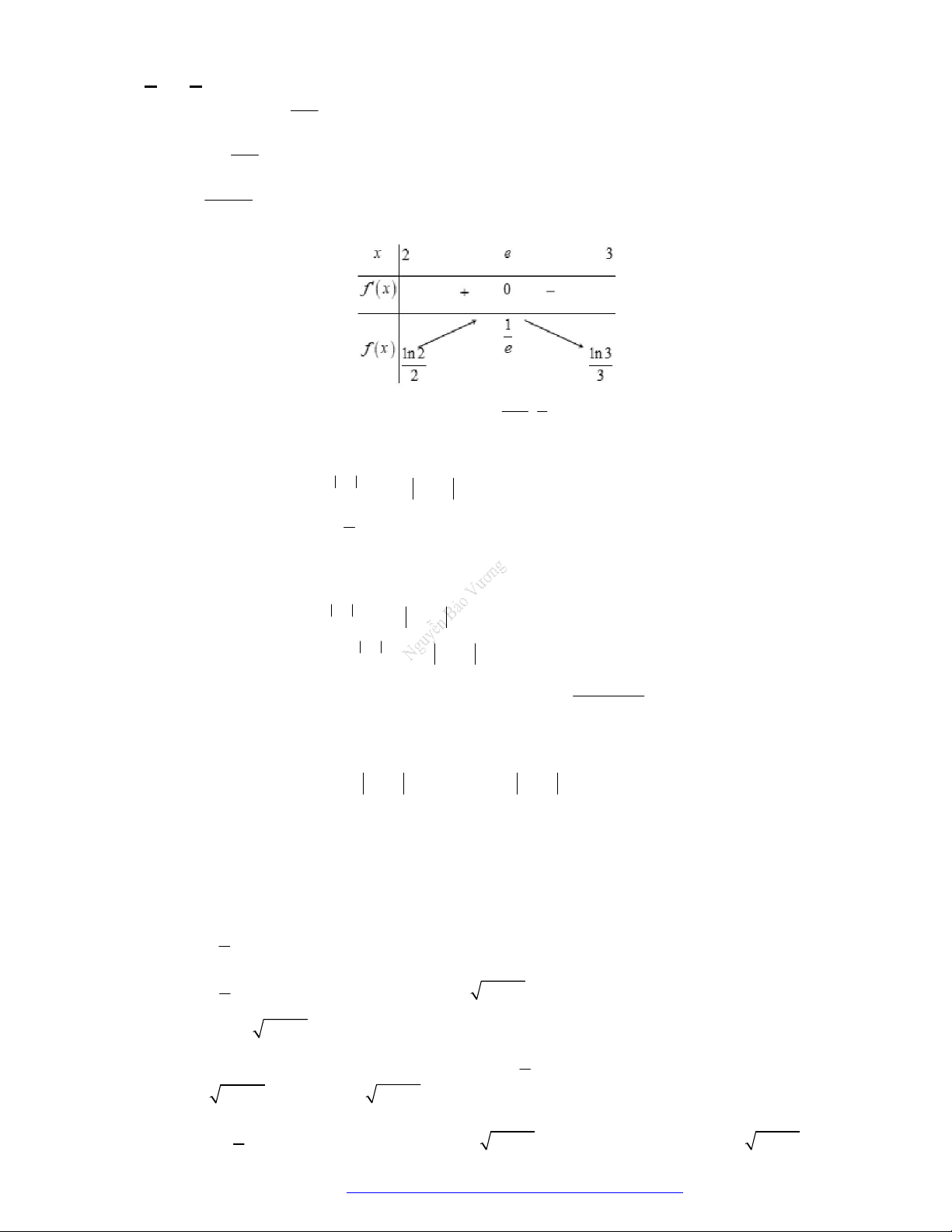
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn D
ln
ln 0 , 2;3
x
mx x m x
x
Đặt
ln
, 2;3
x
f x x
x
2
1 ln x
f x
x
;
0f x x e
BBT
Để phương trình có hai nghiệm phân biệt thì
ln3 1
;
3
m
e
.
Câu 16. (THPT Dông Sơn Thanh Hóa 2019) Tổng tất cả các giá trị của tham số
m
sao cho phương trình:
2
1
2
2 2
2 .log 2 3 4 .log 2 2
x m
x
x x x m
có đúng ba nghiệm phân biệt là:
A. 2. B.
3
.
2
C. 0. D. 3.
Lời giải
Tập xác định
D
2
2
1
2
2 2
2
1
2
2 2
2 . 2 3 4 . 2 2
2 . ( 1) 2 2 . 2 2 (*)
x mx
x m
x
log x x log x m
log x log x m
Đặt
2
( ) 2 log ( 2), 0
t
f t t t
;
2
1
'( ) 2 ln 2.log ( 2) 2 0, 0
( 2) ln 2
t t
f t t t
t
.
Vậy hàm số
2
( ) 2 log ( 2)
t
f t t
đồng biến trên
(0; )
.
Từ (*) ta có
2
2 2
2
2( ) ( 1)
( 1) 2 ( 1) 2
2( ) ( 1)
x m x
f x f x m x x m
x m x
.
2
2
( ) 4 1 2 0 ( )
2 1 ( )
g x x x m a
x m b
Do các phương trình
( )a
và
( )b
là phương trình bậc hai nên để phương trình ban đầu có 3 nghiệm
phân biệt ta có các trường hợp sau:
TH1:
1
2
m
, (b) chỉ có nghiệm kép bằng 0 và (a) có 2 nghiệm phân biệt khác 0 (thỏa mãn).
TH2:
1
2
m
, (b) có 2 nghiệm phân biệt 2 1x m và (a) có 2 nghiệm phân biệt trong đó có 1
nghiệm bằng 2 1m
' 0
( 2 1) 0g m
3
' 0
1
2
( 2 1) 0
1
m
m
g m
m
(thỏa mãn).
+ TH3:
1
2
m
, (b) có 2 nghiệm phân biệt
2 1x m
và (a) có nghiệm kép khác
2 1m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
' 0
( 2 1) 0
g m
3
3
2
2
1
m
m
m
(thỏa mãn).
Vậy tổng các giá trị của
m
là
1 3
1 3.
2 2
Câu 17. Tìm tất cả các giá trị của
m
để phương trình
ln ln sin sinm m x x
có nghiệm.
A.
1
1 m e 1.
e
B.
1 m e 1.
C.
1
1 m 1.
e
D.
1 m e 1.
Lời giải
Đặt
ln sinu m x
ta được hệ phương trình:
sin
ln sin
sin
ln sin
u
x
u m x
e m x
m u x
e m u
Từ hệ phương trình ta suy ra:
sin
sin *
u x
e u e x
Xét hàm số
t
f t e t
có
' 1 0, .
t
f t e t
Hàm số
f t
đồng biến trên
.
* sin sinf u f x u x
Khi đó ta được:
sin
ln sin sin sin **
x
m x x e x m
Đặt
sin , 1;1 .
z x z
Phương trình
**
trở thành:
**
z
e z m
Xét hàm số:
z
g z e z
trên
1;1 .
Hàm số
z
g z e z
liên tục trên
1;1
và có
1;1
1;1
1 1,min 0 1
max g z g e g z g
Hệ phương trình ban đầu có nghiệm
phương trình
**
có nghiệm
1 1.
m e
Câu 18. (THPT Yên Dũng 2-Bắc Giang 2019) Số các giá trị nguyên của tham số
m
để phương trình
2
2
log ( 1) log ( 8)
x mx
có hai nghiệm phân biệt là
A.
5
. B. Vô số. C.
4
. D.
3
.
Lời giải
Chọn D
Điều kiện:
1x
Ta có:
2 2
2 2 2
2
log ( 1) log ( 8) log ( 1) log ( 8) ( 1) 8x mx x mx x mx
2
2 9
x x mx
. Do
1x
nên suy ra
2
2 9
.
x x
m
x
Xét hàm số
2
2 9
( )
x x
f x
x
trên khoảng
(1; ).
2
'
2
9
( )
x
f x
x
,
'
( ) 0 3.
f x x
Bảng biến thiên
Nhìn vào BBT ta thấy yêu cầu của bài toán là
4 8
m
. Do
m
nguyên nên
5;6;7
m
.
Vậy có 3 giá trị của
m
thỏa mãn yêu cầu bài toán.
Câu 19. (THPT Trần Phú - 2019) Có bao nhiêu giá trị nguyên dương của tham số
m
để phương trình
2
ln 2 ln 4
e
x
m m x
có nghiệm thuộc vào đoạn
1
;1
e
?
0
x
'
( )f x
( )f x
1
3
4
8
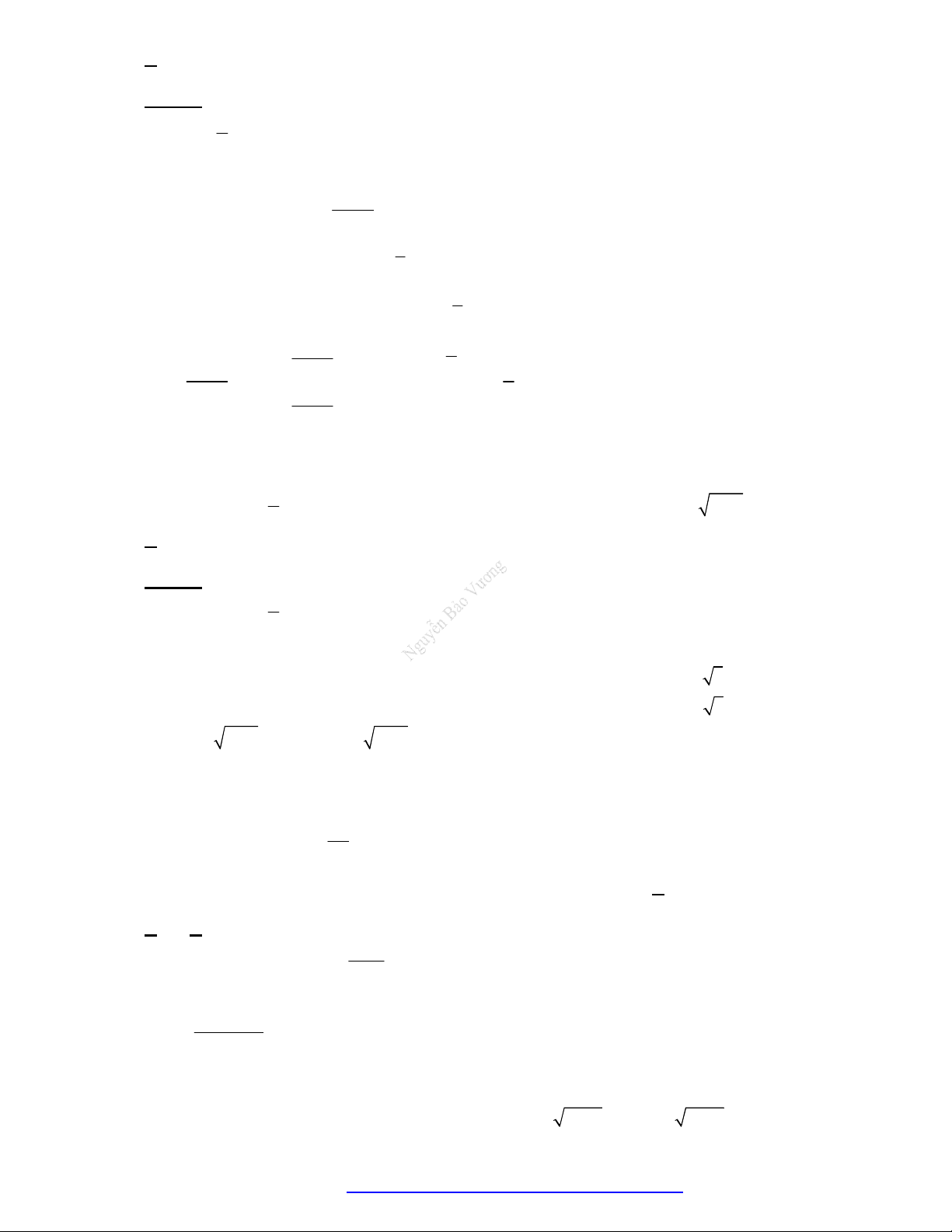
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn A
Có
2
ln 2 ln 4
e
x
m m x
2
ln 1 2 ln 4
m x m x
2 2
2 ln 4
m m x m
1
.
• Với
2
2 0
m m
1
m
0
m
,
1
0ln 3
x
(Vô nghiệm)
Loại
1
m
.
• Với
1
m
,
1
2
ln
1
m
x
m
2
.
+ Hàm số
lny x
đồng biến trên
1
;1
e
ln 1;0
x
.
+ Phương trình
2
có nghiệm thuộc đoạn
1
;1
e
khi
2
1 0
1
m
m
2
1
1
2
0
1
m
m
m
m
3
2
1
1 2
m
m
m
3
2
2
m
2
m
.
Vậy có
1
giá trị nguyên dương của tham số
m
thỏa yêu cầu bài toán.
Câu 20. (THPT Trần Phú - 2019) Có bao nhiêu giá trị của tham số
m
để phương trình
2
36 6
4log log 2 0
6
x
x m
có hai nghiệm phân biệt
1 2
,x x
thỏa mãn
1 2 1 2
. 72 . 1296 0
x x x x
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn A
2
36 6
4log log 2 0
6
x
x m
(Điều kiện
0
x
)
2
66
log log 2 0
x m x m
Phương trình có hai nghiệm phân biệt khi
2
2 2 3
4 2 0
2 2 3
m
m m
m
1 2 1 2 1 2 1 2
. 72 . 1296 0 . 36 . 1296
x x x x x x x x
6 1 2 6 1 6 2
log . 4 log log 4 4
x x x x m
(không thỏa điều kiện của
m
)
Câu 21. (Chuyên Lê Hồng Phong Nam Định 2019) Tập hợp các giá trị thực của tham số m để phương
trình
2
2019 1
2019
log 4 log 2 1 0
x x m
có hai nghiệm thực phân biệt là
;T a b
. Tính
2
S a b
.
A.
18
. B.
8
. C.
20
. D.
16
.
Lời giải
Chọn D
Tập xác định
1
2;2 ;
2
m
D
.
Khi đó, phương trình đã cho trở thành
2
2 2
2019
4
log 0 4 2 1 2 5 0 (*)
2 1
x
x x m x x m
x m
Phương trình
(*)
có 2 nghiệm phân biệt
2
1 1.( 5) 6 0 6 (1)
m m m
Khi đó phương trình
(1)
có 2 nghiệm lần lượt là
1 2
1 6 ; 1 6
x m x m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
TH1:
1
2 5
2
m
m
(2)
2;2
D
.
Phương trình (1) có 2 nghiệm
1 2
,
x x D
1 6 2 6 3
5
1 6 2 6 1
m m
m
m m
(3).
Từ (1), (2) và (3) suy ra
5 6
m
.
TH2:
1
2 2 3 5
2
m
m
(4).
1
;2
2
m
D
.
Phương trình (1) có 2 nghiệm
1 2
,
x x D
3
1 6 2 6 3
5
3
1 3
1 6 6
5
2 2
m
m m
m
m
m m
m m
m
(5).
Từ (4) và (5) suy ra
m
. Vậy
5 6
m
. Suy ra
5, 6
a b
2 16
a b
.
Câu 22. (THPT Cẩm Bình 2019) Có bao nhiêu giá trị nguyên của
m
để phương trình
3
3
log 3 log 9 16
x
x m
có hai nghiệm thỏa mãn
1 2
2
x x
.
A.
17
. B.
16
. C.
14
. D.
15
.
Lời giải
Chọn D
Điều kiện xác định:
3
x
và
2
x
.
Biến đổi phương trình đã cho về phương trình sau:
3
3
log 3 4 log 3 16 0
x
x m
.
2
3 3
log 3 16log 3 4 0 (1)
x x m
.
Đặt
3
log 3
x t
phương trình
1
trở thành:
2
16 4 0 2
t t m
.
Ta có:
3
log 3 3 3
t
x t x
.
Theo điều kiện đề bài thì
2
x
nên
3 3 2 0
t
t
.
Vậy để phương trình
3
3
log 3 log 9 16
x
x m
có hai nghiệm thỏa mãn
1 2
2
x x
thì phương trình
2
phải có hai nghiệm
t
dương phân biệt
1 2
1 2
0
64 4 0
16 0 0 16
4 0
. 4 0
m
t t m
m
t t m
. Vậy có 15 giá trị nguyên
m
thỏa mãn.
Câu 23. (Chuyên Hoàng Văn Thụ-Hòa Bình 2019) Tập hợp các số thực m để phương trình
2
ln 3 1 ln 4 3
x mx x x
có nghiệm là nửa khoảng
;a b
. Tổng
a b
bằng
A.
10
.
3
B.
4.
C.
22
.
3
D.
7.
Lời giải
Chọn D
Ta có:
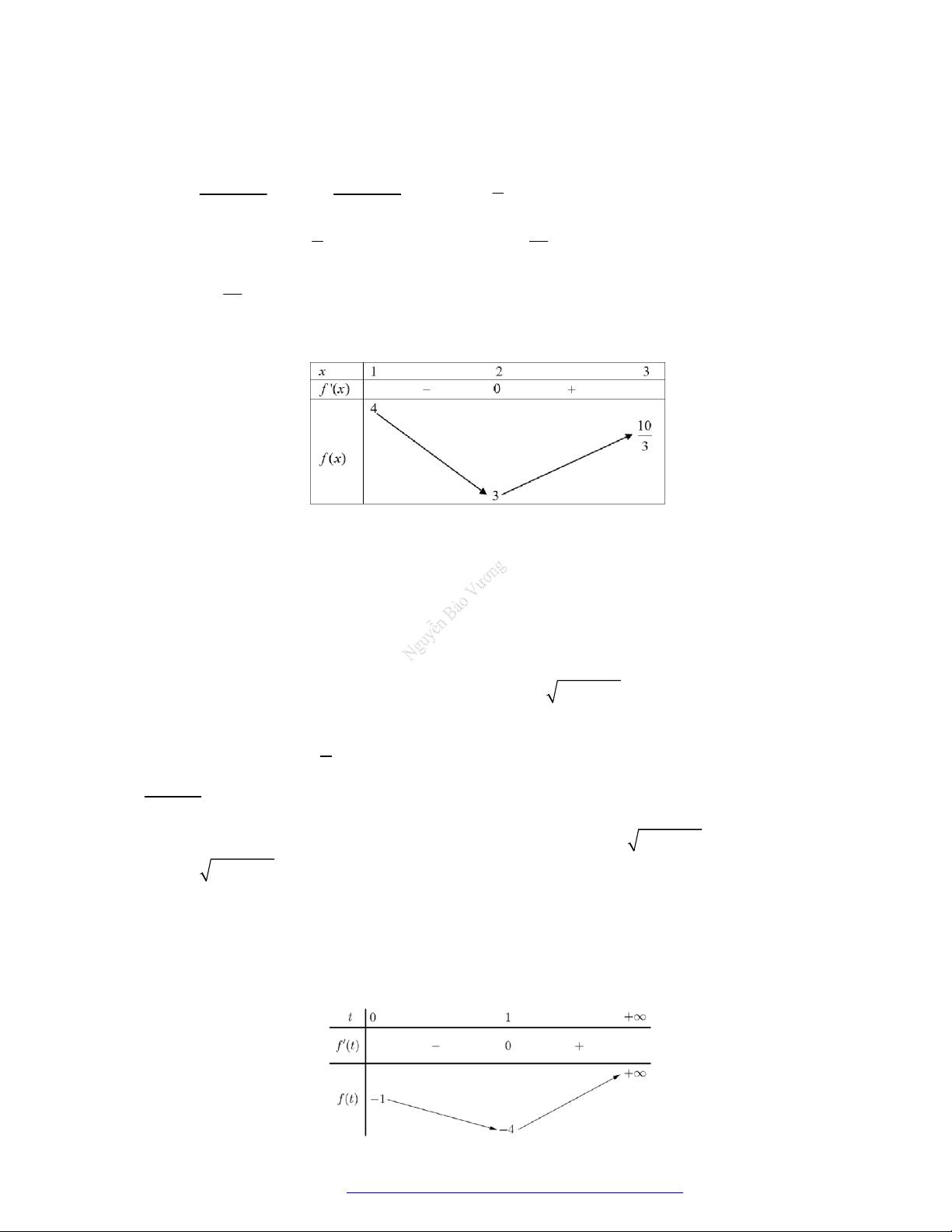
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
2
2
2 2
ln 3 1 ln 4 3 (1)
1 3
4 3 0
4
3 1 4 3
1 3 1 3
1 3
4
4 4
1 (2)
x mx x x
x
x x
x x mx
x mx x x
x x
x
x x x x
x m
m m
x
x x
Xét hàm số:
4
( ) 1; 1;3f x x x
x
có
2
4
'( ) 1f x
x
2
2 1;3 (2) 3
4
'( ) 1 0
2 1;3
x f
f x
x
x
Bảng biến thiên:
Dựa vào bảng biến thiên ta có:
Phương trình (1) có nghiệm.
Phương trình (2) có nghiệm thuộc khoảng
1;3
.
3 4 3;4
m m
.
Suy ra
3
3 4 7
4
a
a b
b
.
Câu 24. (Cần Thơ 2019) Cho phương trình
2
2 2 2
log 2log 4 1 logx x x m
, với
m
là tham số thực.
Số các giá trị nguyên thuộc đoạn
2019;2019
của
m
để phương trình đã cho có nghiệm là
A. 2021. B. 2024. C. 2023. D. 2020.
Lời giải
Chọn B
Điều kiện xác định:
2 2
1 log 0 log 1 0 2x x x
.
Với điều kiện trên thì phương trình tương đương với
2
2 2
1 log 4 1 log 1
x x m
1
.
Đặt
2
1 logt x
, vì
0;2x
nên
0t
. Khi đó,
1
trở thành
4
4 1t t m
2
.
Để
1
có nghiệm
0;2x
thì
2
có nghiệm
0t
.
Xét hàm số
4
4 1f t t t
,
0;t
.
Ta có
3
4 4f t t
. Cho
0 1 0;f t t
.
Ta được bảng biến thiên của
f t
như sau:
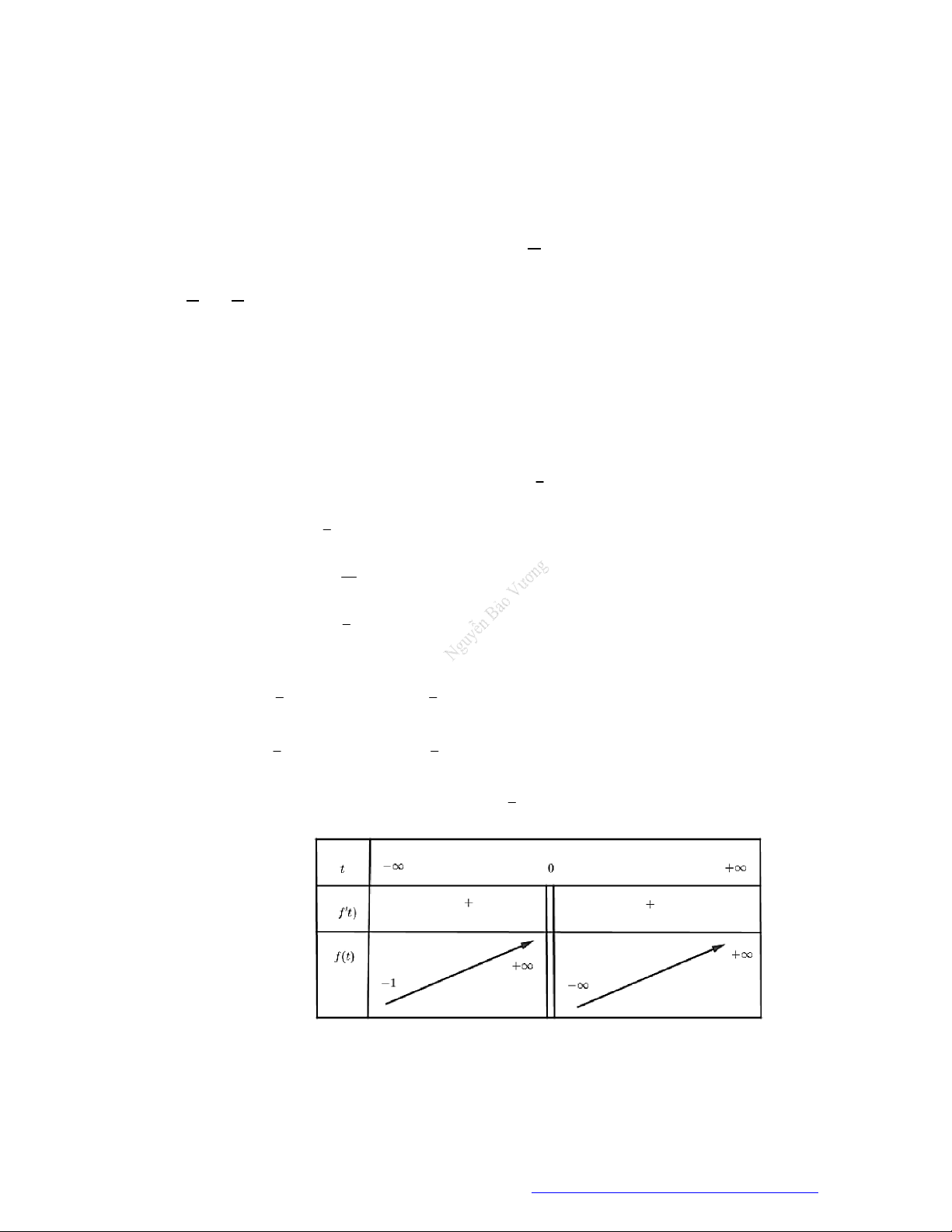
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Theo BBT, để
2
có nghiệm
0t
thì
4m
, mà
2019;2019m
nên tập hợp các giá trị
của
m
cần tìm là
4; 3; 2; 1;0;1; ;2019
.
Vậy có tất cả 2024 giá trị nguyên của
m
thuộc đoạn
2019;2019
để phương trình đã cho có
nghiệm.
Câu 25. (Nam Định - 2019) Tìm tất cả các giá trị thực của tham số
m
để phương trình
2
3 9
log 1 log 9 1
m
x x x
có hai nghiệm phân biệt.
A.
1;0m
. B.
2;0m
. C.
1;m
. D.
1;0m
.
Lời giải
Chọn C
Cách 1.
Điều kiện:
1x
.
Ta có pt:
2
3 9 3 3
log 1 log 9 1 log 1 1 log 1
m
x x x x x m x
3
log 1 1x m x
(1).
Đặt:
3
log 1 3 1
t
x t x
Ta có, Pt (1)
1
3 1 . 1 3 1
t t
m t f t m
t
, với
0t
.
Đặt:
1
3 1
t
f t
t
, với
0t
.
2
1
' 3 .ln3 0, ;0 , 0;
t
f t t
t
.
Suy ra,
1
3 1
t
f t
t
là hàm số đồng biến trên
;0
và
0;
.
Ta xét các giới sau:
1
lim 3 1 1
t
t
t
,
1
lim 3 1
t
t
t
.
0
1
lim 3 1
t
t
t
,
0
1
lim 3 1
t
t
t
.
Ta có bảng biến thiên của hàm số
1
3 1
t
f t
t
, với
;0 , 0;t
.
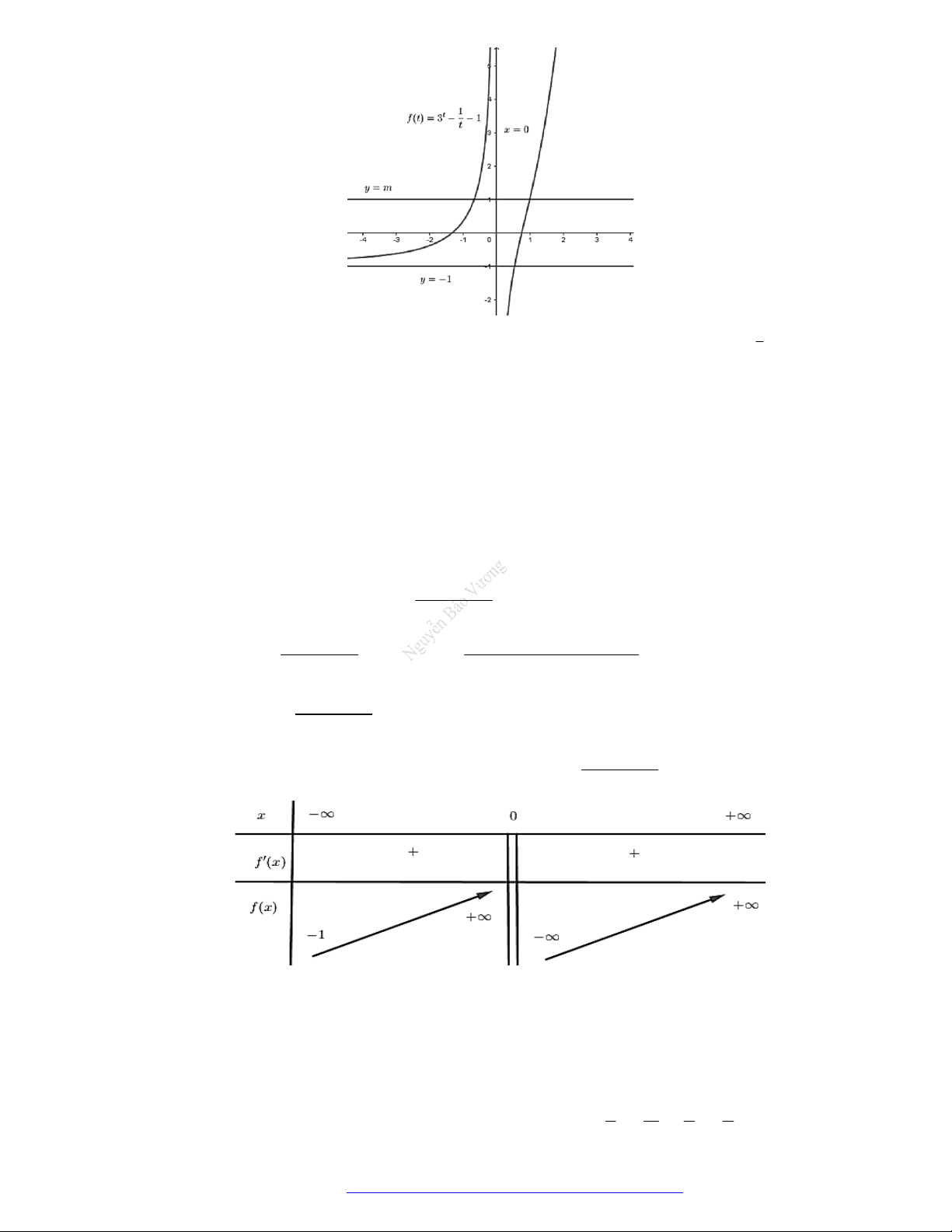
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có, số nghiệm của Pt (1) cũng chính là số nghiệm của đồ thị hàm số (C)
1
3 1
t
f t
t
và đồ thị hàm số
y m
(song song hoặc trùng với trục hoành).
Dựa, vào đồ thị ở hình vẽ trên, để phương trình
2
3 9
log 1 log 9 1
m
x x x
có ba nghiệm khi
1;m
.
Cách 2.
Điều kiện:
1x
.
Ta có:
2
3 9
log 1 log 9 1
m
x x x
(1)
Nhận thấy
0x
không là nghiệm phương trình trên.
Pt (1)
3
3
1
log 1 1
log 1
x m x x m
x
.
Đặt:
2
3
3
1 1
' 1 0, 1;
log 1
1 ln3. log 1
f x x f x x
x
x x
.
Suy ra
3
1
log 1
f x x
x
là hàm số đồng biến
1;x
.
Ta có BBT của hàm số
3
1
log 1
f x x
x
.
Dựa, vào BBT ở hình vẽ trên, để phương trình
2
3 9
log 1 log 9 1
m
x x x
có ba nghiệm khi
1;m
.
Câu 26. (THPT Hoàng Hoa Thám - Hưng Yên 2019) Cho
,a b
là các số thực dương lớn hơn 1, thay đổi
thỏa mãn
2019 a b
để phương trình
5log .log 4log 3log 2019 0
a b a b
x x x x
luôn có hai
nghiệm phân biệt
1 2
;x x
. Biết giá trị lớn nhất của
1 2
ln .x x
bằng
3 4
ln ln
5 7 5 7
m n
; với
,m n
là
các số nguyên dương. Tính
2 S m n
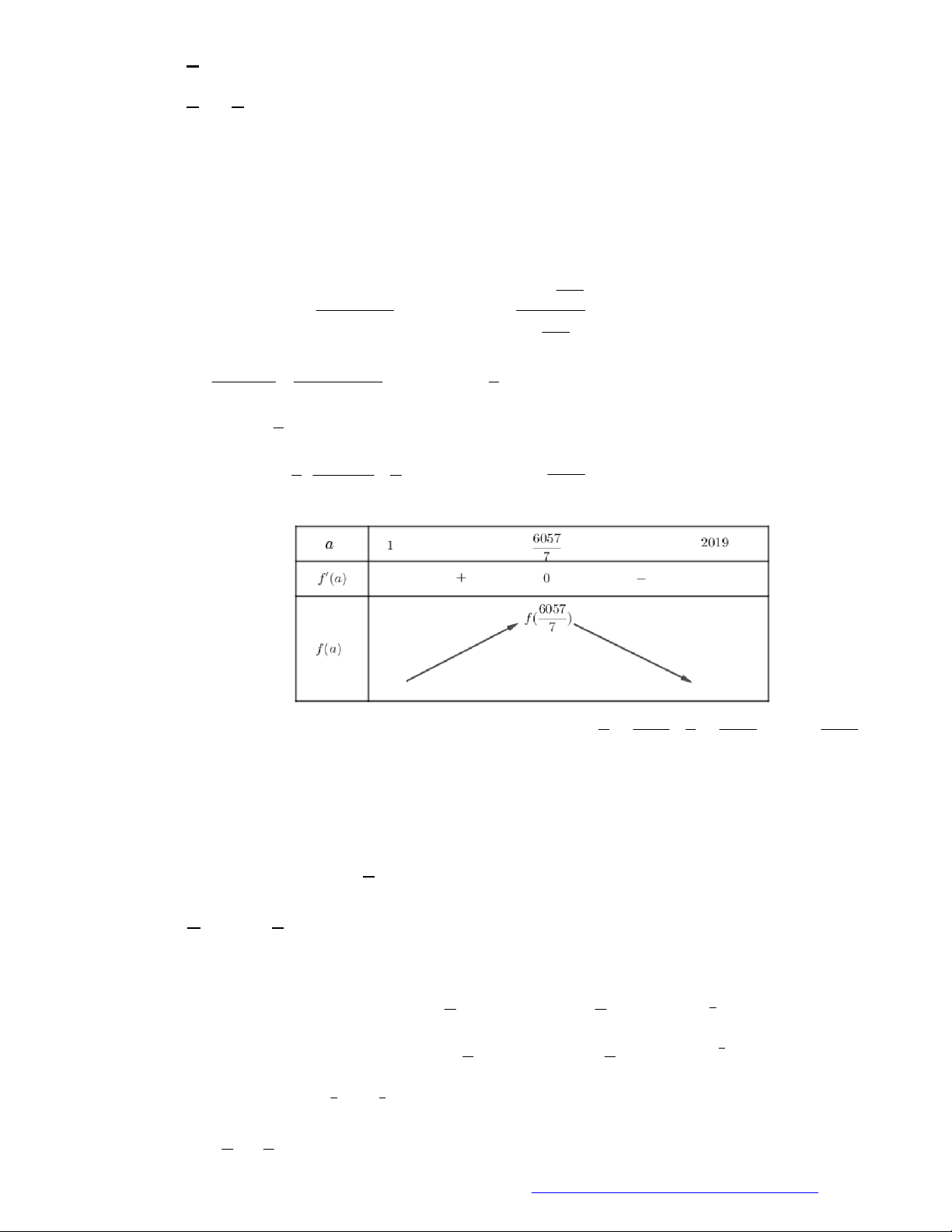
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
A.
22209
. B.
20190
. C.
2019
. D.
14133
.
Lời giải
Chọn A
Theo bài ra ta có
2
5log .log 4log 3log 2019 0
5log . log .log 4log 3 log .log 2019 0
5log . log 4 3log log 2019 0 *
a b a b
a b a a b a
b a b a
x x x x
x a x x a x
a x a x
Vì
, 1 log . 2019 0 *
b
a b a
luôn có hai nghiệm phân biệt
1 2
;x x
Theo Viet ta có:
1 2 1 2
1 2
1 2
ln
4 3.
4 3log
ln
log log log .
ln
5log
5
ln
ln .
4ln 3ln 1
ln . 4ln 2019 3ln
ln 5ln 5
b
a a a
b
a
a
b
x x x x
a
a
b
x x
b a
x x a a
a a
Xét
1
4ln 2019 3ln
5
f a a a
với
1;2019a
Ta có
1 4 3
'
5 2019
f a
a a
;
6057
' 0
7
f a a
Bảng biến thiên
Từ bảng biến thiên ta được giá trị lớn nhất của
1 2
4 8076 3 6057
ln . .ln .ln
5 7 5 7
x x
khi
6057
7
a
.
Từ đó suy ra
6057m
;
8076 2 6057 2.8076 22209 n S m n
Câu 27.
(Bỉm Sơn - Thanh Hóa - 2019) Xét các số nguyên dương
, a b
sao cho phương trình
2
ln ln 5 0a x b x
có hai nghiệm phân biệt
1 2
, x x
và phương trình
2
5log log 0x b x a
có
hai nghiệm phân biệt
3 4
, x x
thỏa mãn
1 2 3 4
x x x x
. Tìm giá trị nhỏ nhất của
2 3S a b
A.
min
33
S
. B.
min
30
S
. C.
min
17
S
. D.
min
25
S
.
Lời giải
Chọn B.
Điều kiện để hai phương trình
2
ln ln 5 0a x b x
và
2
5log log 0x b x a
có hai nghiệm
phân biệt là:
2
20 0b a
.
Theo giả thiết ta có
1 2 1 2
1 2
5
3 4 3 4
3 4
ln ln ln
log log log
10
5 5
b
a
b
b b
x x x x
x x e
a a
b b
x x x x
x x
.
Mà
5
1 2 3 4
10
b b
a
x x x x e
ln10
5
b b
a
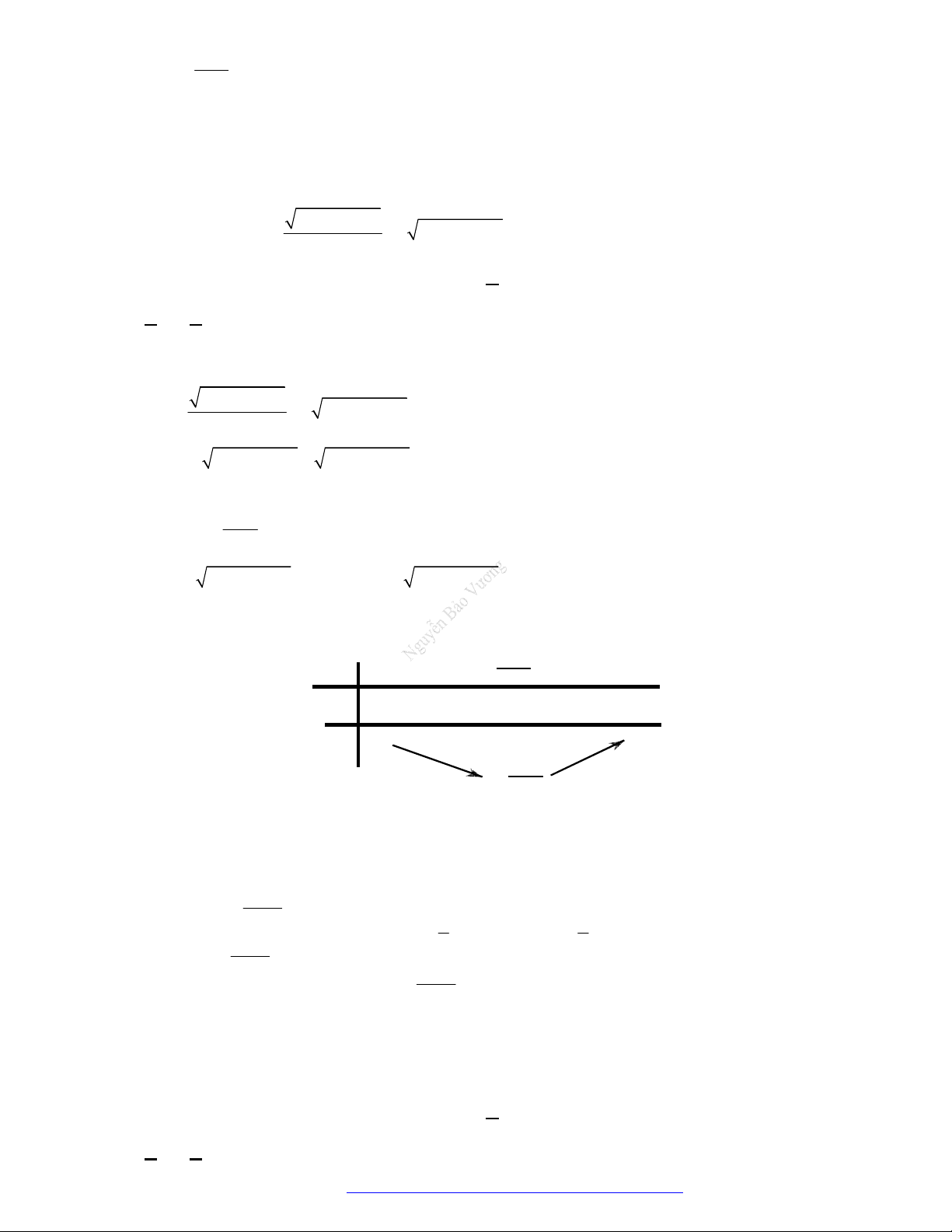
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
5
3
ln10
a a
.
Theo điều kiện có
2 2
20 0 20 60 8b a b a b
.
Từ và suy ra
min
3
2 3 30 30
8
a
S a b S
b
.
Câu 28. (THPT Thuận Thành 3 - Bắc Ninh 2019) Có bao nhiêu giá trị nguyên dương của tham số
m
để
phương trình
2
2
2
2 1
log 2 1 2
2
x mx
x mx x
x
có hai nghiệm phân biệt?
A.
3
. B.
1
. C.
4.
D.
2
.
Lời giải
Chọn C
Điều kiện:
2
2 1 0
2 0
x mx
x
2
2
2
2 1
log 2 1 2
2
x mx
x mx x
x
2 2
2 2
log 2 1 2 1 2 log 2x mx x mx x x
Xét hàm số
2
logf t t t
trên khoảng
0;
,
có
1
1 0, 0;
ln 2
f t t
t
hàm số
f t
đồng biến trên
0;
Mà
2 2
2
2
2 1 2 2 1 2
4 3 0
x
f x mx f x x mx x
x m x
Do
2
4 3f x x m x
là tam thức bậc hai nên có bảng biến thiên
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi phương trình
2
4 3 0f x x m x
có hai nghiệm phân biệt lớn hơn
2.
suy ra:
4
2
2
4
0 9 2
2
m
m
f m
2
8
9 9
.
2 2
4
3 0
2
m
m m
m
Do
*
1;2;3; 4
m m
.Vậy có 4 giá trị của
m
.
Câu 29. (Chuyên Bắc Giang 2019) Số các giá trị nguyên nhỏ hơn
2018
của tham số
m
để phương trình
6 4
log 2018 log 1009x m x
có nghiệm là
A.
2018
. B.
2017
. C.
2020
. D.
2019
.
Lời giải
Chọn C
+∞
f(
4-m
2
)
-∞
+∞
4-m
2
0
+∞
-
+
f(x)
f'(x)
x
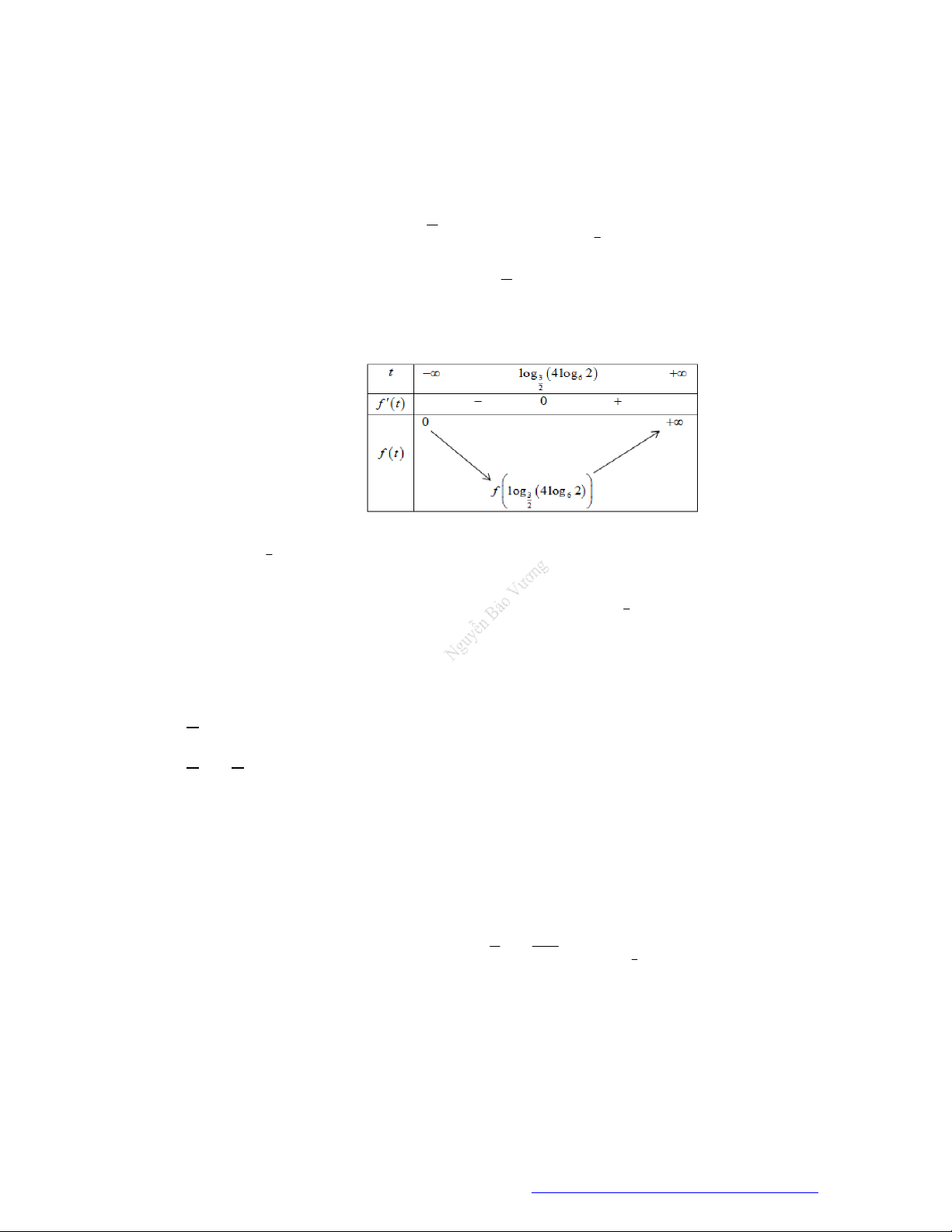
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Đặt
4
log 1009 1009 4
t
x t x
Phương trình đã cho có dạng
6
log 2.4 2.4 6 6 2.4
t t t t t
m t m m
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số
6 2.4
t t
f t
với đường
thẳng
y m
.
Xét hàm số:
6 2.4
t t
f t
6 ln6 2.4 ln 4 2 3 ln 6 2.2 ln 4
t t t t t
f t
.
6 3 6
2
3
0 6 ln 6 2.4 ln 4 4log 2 log 4log 2
2
t
t t
f t t
+)
2
lim lim 6 2.4 lim 6 1 2.
3
t
t t t
t t t
f t
+)
lim lim 6 2.4 0
t t
t t
f t
Ta có bảng biến thiên:
Với
3 6
2
log 4log 2 2,0136f
Từ bảng biến thiên, để phương trình có nghiệm thì
3 6
2
log 4log 2 2,0136
m f
.
Vậy
2 2018m
. Có
2020
số nguyên
m
.
Câu 30. (Chuyên ĐH Vinh - Nghệ An -2020) Có bao nhiêu số nguyên
m
để phương trình
2
3 5
log 3 2 log 3
x x
m m
có nghiệm?
A.
3
. B.
4
. C.
2
. D.
5
.
Lời giải
Chọn A
Đặt
2
3 5
2
3 2 3
log 3 2 log 3
3 5
x t
x x
x t
m
m m t
m
2
2 3 5
t t
m m
2
2 1 3 5 1
t t
m m
(*).
Xét hàm số
3 5 1
t t
f t
với
t
.
Ta có:
3.ln3 5 .ln5
t t
f t
.
Khi đó
3 3 0
5
3 ln5
0 3.ln3 5 .ln5 0 log log 5
5 ln3
t
t t
f t t t
.
Bảng biến thiên
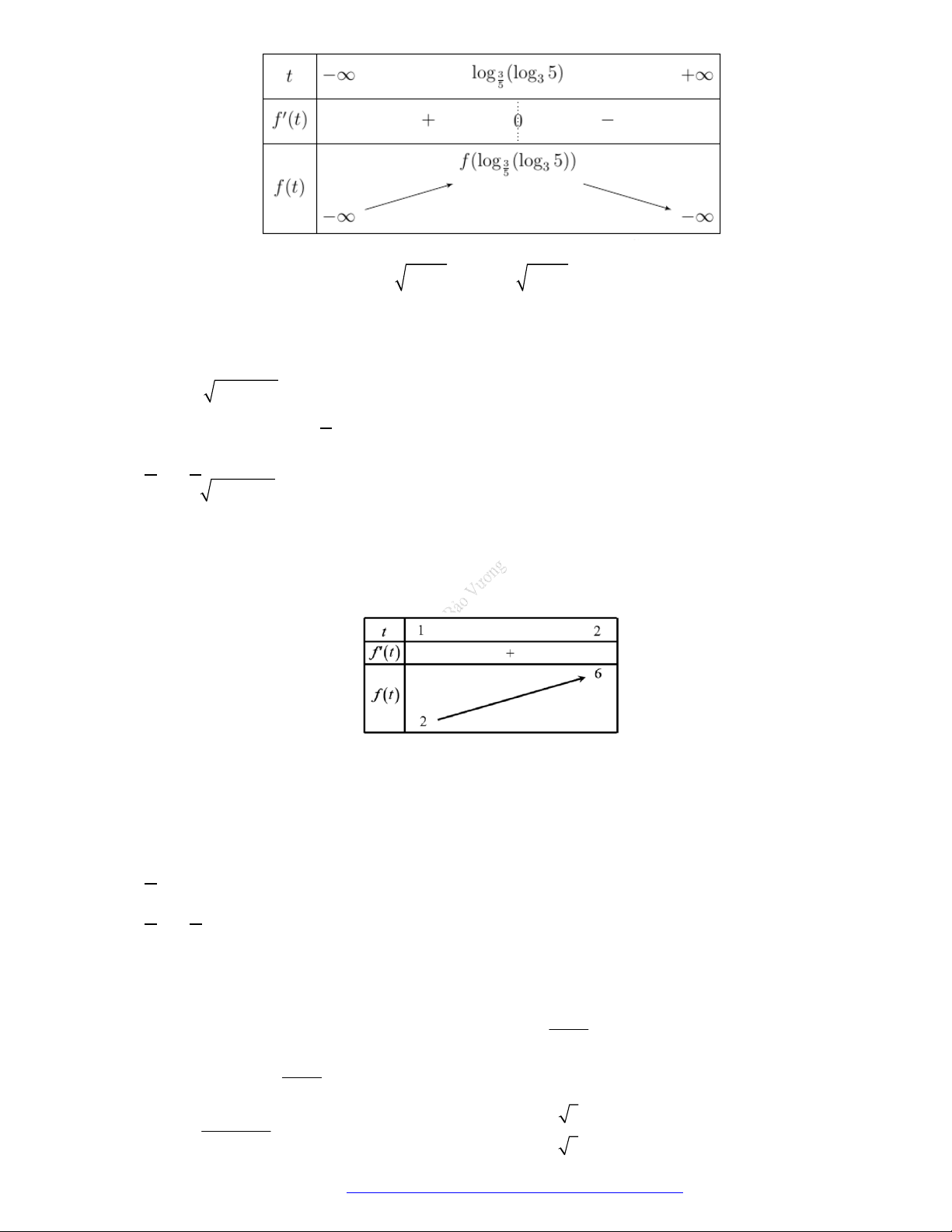
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Phương trình (*) có nghiệm
2
0 0 0
1 1 1 2,068 0,068m f t f t m f t m
.
Do
2; 1;0m m
.
Vậy có
3
giá trị nguyên của
m
thỏa mãn.
Câu 31. (Chuyên Hưng Yên - 2020) Tìm tất cả các giá trị thực của tham số
m
để phương trình
3 3
log log 1 2 1 0x x m
có ít nhất một nghiệm thực trong đoạn
1;27
.
A.
0;2m
. B.
0;2m
. C.
2;4m
. D.
0;4m
.
Lời giải
Chọn B
Đặt
3
log 1t x
. Với
1;27x
thì
1;2t
.
Phương trình đã cho trở thành
2
2 2 0t t m
2
2 2m t t
*
Xét hàm số
2
f t t t
trên đoạn
1;2
.
Ta có
2 1 0, 1;2f t t t
nên hàm số
2
f t t t
đồng biến trên
1;2
.
Bảng biến thiên:
Để phương trình đã cho có ít nhất một nghiệm thực trong đoạn
1;27
thì phương trình
*
phải
có ít nhất một nghiệm thực trong đoạn
1;2
.
Từ bảng biến thiên, suy ra
2 2 2 6m 0 2m
.
Câu 32. (Chuyên KHTN - 2020) Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2 2
3 9
log log 2 0 x m x m
có nghiệm
1;9x
.
A.
1
. B.
5
. C.
3
. D.
2
.
Lời giải
Chọn A
Điều kiện:
0x
.
Ta có:
2 2 2
3 9 3 3
log log 2 0 log log 2 0 x m x m x m x m
.
Đặt
3
logt x , với
1;9 0;2 x t
.
Phương trình đã cho trở thành:
2
2
2
2 0 1
1
t
t mt m m
t
(Do
1, 0;2 t t
).
Xét hàm số
2
2
1
t
f t
t
với
0;2t
ta có:
2
2
2 2
1
t t
f t
t
,
2
1 3 0;2
0 2 2 0
1 3 0;2
t
f t t t
t
.
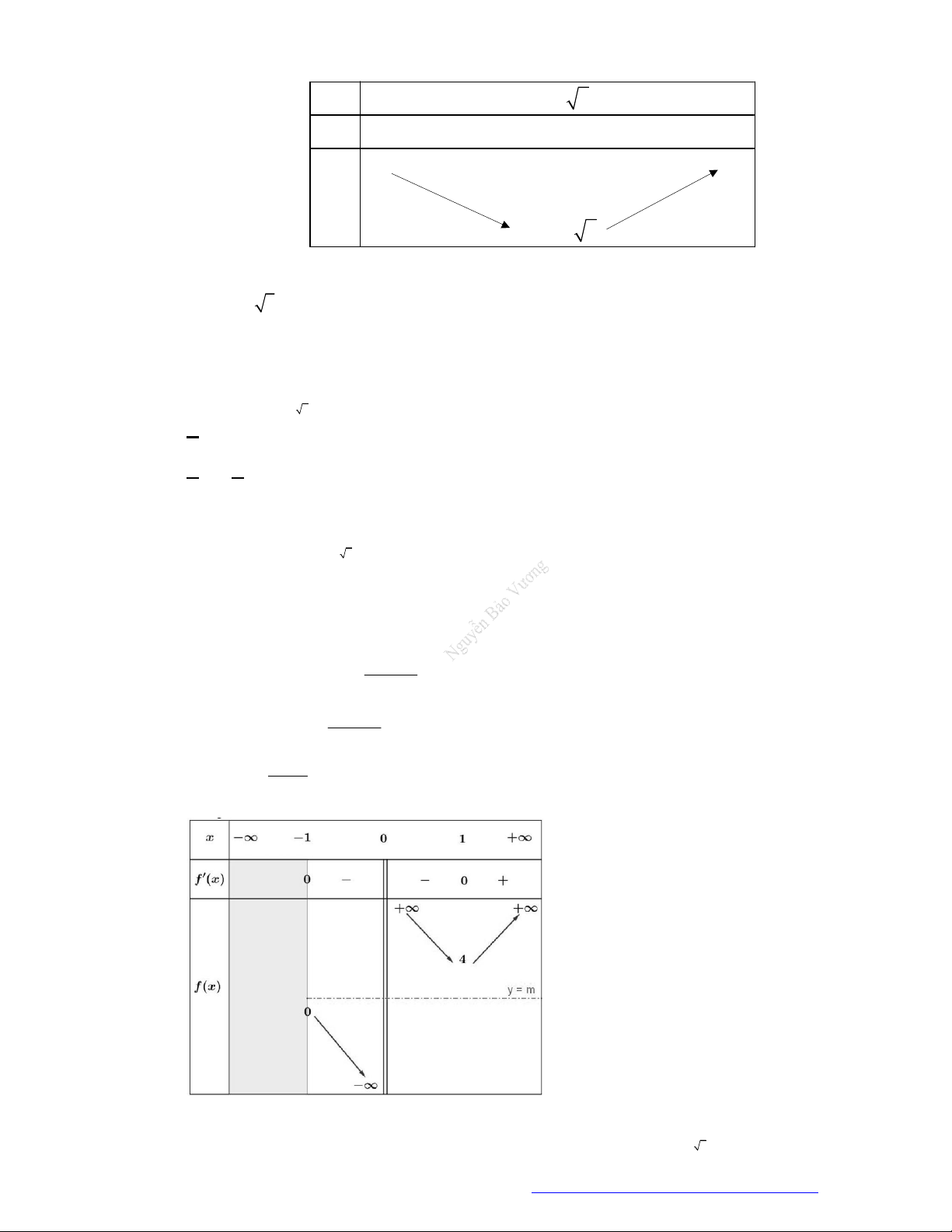
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Bảng biến thiên:
Khi đó: phương trình đã cho có nghiệm
1;9x
Phương trình
1
có nghiệm
0;2t
.
2 2 3 2 m .
Mặt khác, do
m
nên
2m
.
Vậy có một giá trị nguyên của tham số
m
thỏa yêu cầu bài toán.
Câu 33. (Chuyên KHTN - 2020) Có bao nhiêu giá trị nguyên của
m
để phương trình
2
2
log log 1 mx x vô nghiệm?
A.
4
. B.
6
. C.
3
. D.
5
.
Lời giải
Chọn A
Điều kiện
0 0
1 0 1
mx mx
x x
.
Ta có
2 2 2
2
log log 1 log 2log 1 mx x mx x
2
2 22 2
1 0 1
log log 1
1 1 1
x x
mx x
mx x mx x
.
Nhận xét với
0x
không là nghiệm của phương trình (1).
Với
0x
thì
2
1
1
x
m
x
.
Xét hàm số
2
1
x
f x
x
với
1; \ 0 x
có
2
2
1
0 1
x
f x f x x
x
.
Bảng biến thiên
Phương trình đã cho vô nghiệm khi và chỉ khi
0 4 m
. Do
m
nên
0;1;2;3m
.
Vậy có 4 giá trị nguyên của tham số
m
để phương trình
2
2
log log 1 mx x
vô nghiệm.
t
( )f t
( )f t
2
0
1 3
2
2
2 2 3
0
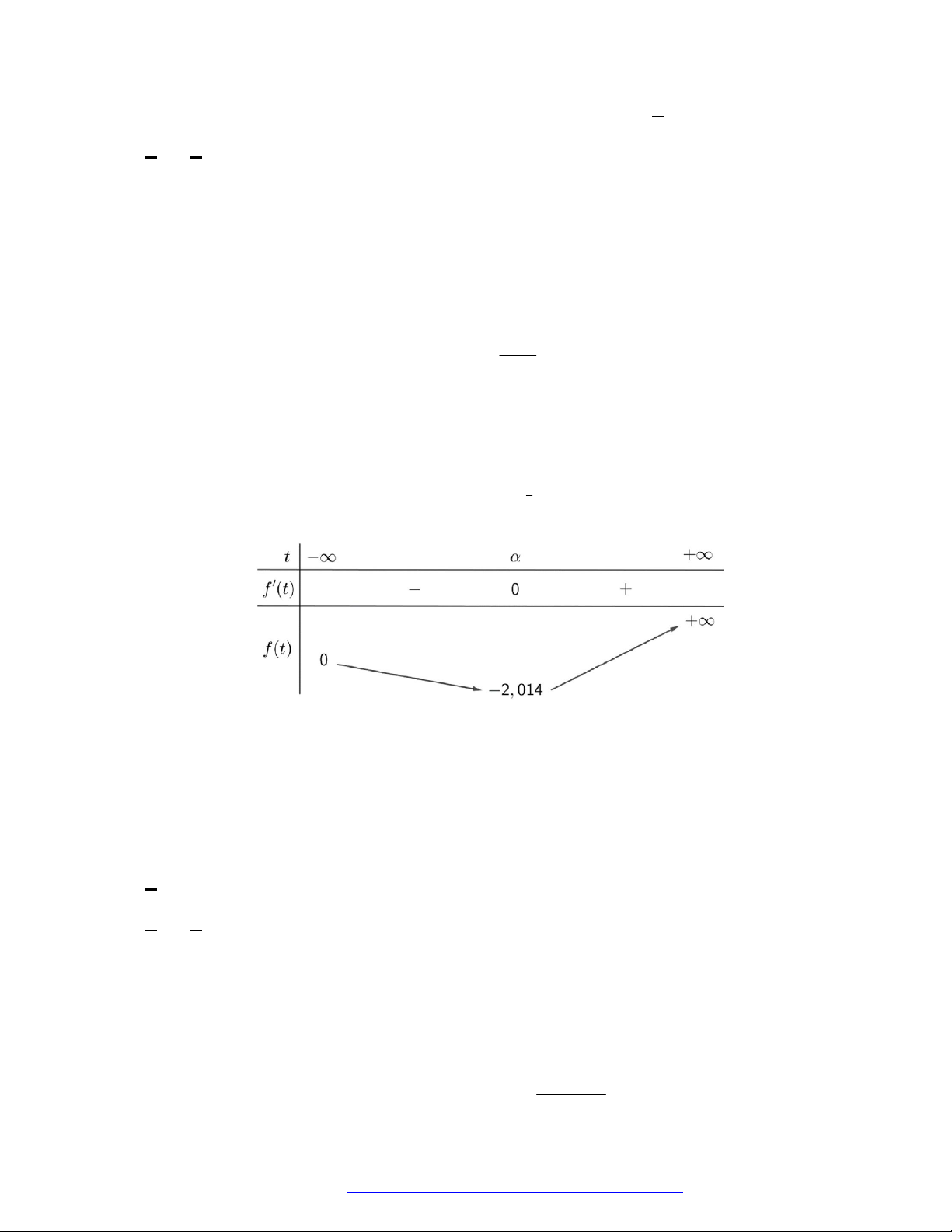
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 34. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Số các giá trị nguyên nhỏ hơn 2020 của tham số
m
để phương trình
6 4
log 2020 log 1010x m x
có nghiệm là
A.
2020.
B.
2021.
C.
2019.
D.
2022.
Lời giải
Chọn D
Điều kiện xác định:
2020 0
1010 0
x m
x
(*)
Đặt
6 4
log 2020 log 1010x m x t
.
Suy ra
2020 6
1
1010 4
t
t
x m
x
.
Từ đó
6 2.4 2
t t
m
.
Với mỗi nghiệm
0
t
của phương trình
2
thì
0
0
4
2010
t
x
là nghiệm của hệ phương trình
1
đồng
thời
0
x
thỏa mãn điều kiện
*
. Do đó
0
x
là nghiệm của phương trình đã cho. Từ đó, điều kiện
cần và đủ để phương trình đã cho có nghiệm là phương trình
2
có nghiệm.
Xét hàm số
6 2.4
t t
f t
trên
.
Ta có
6 .ln6 2.4 .ln 4
t t
f t
và
3 6
2
0 log log 16 :f t t
.
Bảng biến thiên của hàm số
f t
như sau:
Dựa vào bảng biến thiên, ta có phương trình
2
có nghiệm khi và chỉ khi
2 do m m
.
Vậy tất cả các giá trị nguyên của tham số
m
thỏa yêu cầu bài toán là các số nguyên thuộc tập hợp
2. 1,0,1,2,....,2019
, có tất cả 2022 giá trị.
Câu 35. (Chuyên Quang Trung - 2020) Xét các số nguyên dương
,a b
sao cho phương trình
2
ln ln 5 0a x b x
có hai nghiệm phân biệt
1 2
,x x và phương trình
2
5log log 0x b x a có
hai nghiệm phân biệt
3 4
,x x sao cho
1 2 3 4
x x x x . Tìm giá trị nhỏ nhất của
2 3S a b
.
A.
30
. B.
25
. C.
33
. D.
17
.
Lời giải
Chọn A
2
ln ln 5 0 1a x b x
2
5log log 0 2x b x a
Điều kiện để
1
có hai nghiệm phân biệt
1 2
,x x và
2
có hai nghiệm phân biệt
3 4
,x x là:
2 2
20 0 20b a b a
.
Nhận xét:
1 2 3 4
, , , 0x x x x
Do đó:
3 4
1 2 3 4 1 2 3 4 1 2
log
ln ln ln
log
x x
x x x x x x x x x x
e
1 2 3 4
ln ln log log logx x e x x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Mà
1 2 3 4
ln ln ; log log
5
b b
x x x x
a
và
,a b
nguyên dương
Nên
log 5log
5
b b
e a e
a
Vì
a
là số nguyên dương và
5log 2,17
e
nên
3
a
2
20 60 60 60 ( 0)
a b b b
Vì
b
là số nguyên dương và
60 7,75
nên
8
b
Do đó:
2 3 30
S a b
Giá trị nhỏ nhất của
S
là 30 khi
3; 8
a b
.
Câu 36. (Chuyên Thái Bình - 2020) Cho phương trình
2 2
2 2
log 5 1 log 4 0
x m x m m
. Biết
phương trình có 2 nghiệm phân biệt
1 2
,x x
thỏa
1 2
165
x x
. Giá trị của
1 2
x x
bằng
A.
16
. B.
119
. C.
120
. D.
159
.
Lời giải
Chọn D
2 2
2 2
2
2
log 5 1 log 4 0
log
log 4 1
x m x m m
x m
x m
Để phương trình có 2 nghiệm phân biệt khi
1
4 1
3
m m m
Khi đó phương trình có 2 nghiệm
4
4 1
1 2
2 0, 2 2. 2 0
m m m
x x
Vì
4
1 2
165 2 2. 2 165 *
m m
x x
Xét hàm số
4 3
2. 8 1 0 0
f t t t f t t t
Mà
2 3
m
là nghiệm của
*
nên là nghiệm duy nhất. Suy ra
4
1 2
3, 2.3 162
x x
Suy ra
1 2
159
x x
.
Câu 37.
(Chuyên Thái Nguyên - 2020) Gọi
0
m
là giá trị thực nhỏ nhất của tham số
m
sao cho phương
trình
2
1 1
3 3
1 log 3 5 log 3 1 0
m x m x m
có nghiệm thuộc
3;6
. Khẳng định nào
sau đây là đúng?
A. Không tồn tại
0
m
. B.
0
4
1;
3
m
. C.
0
10
2;
3
m
. D.
0
5
5;
2
m
.
Lời giải
Chọn D
Đặt
1
3
log 3
t x
.
Vì
3;6 1
x t
.
Phương trình trở thành:
2
1 5 1 0
m t m t m
(*)
2 2
5 1mt mt m t t
2
2
5 1
1
t t
m
t t
Xét hàm số
2
2
5 1
1
t t
f t
t t
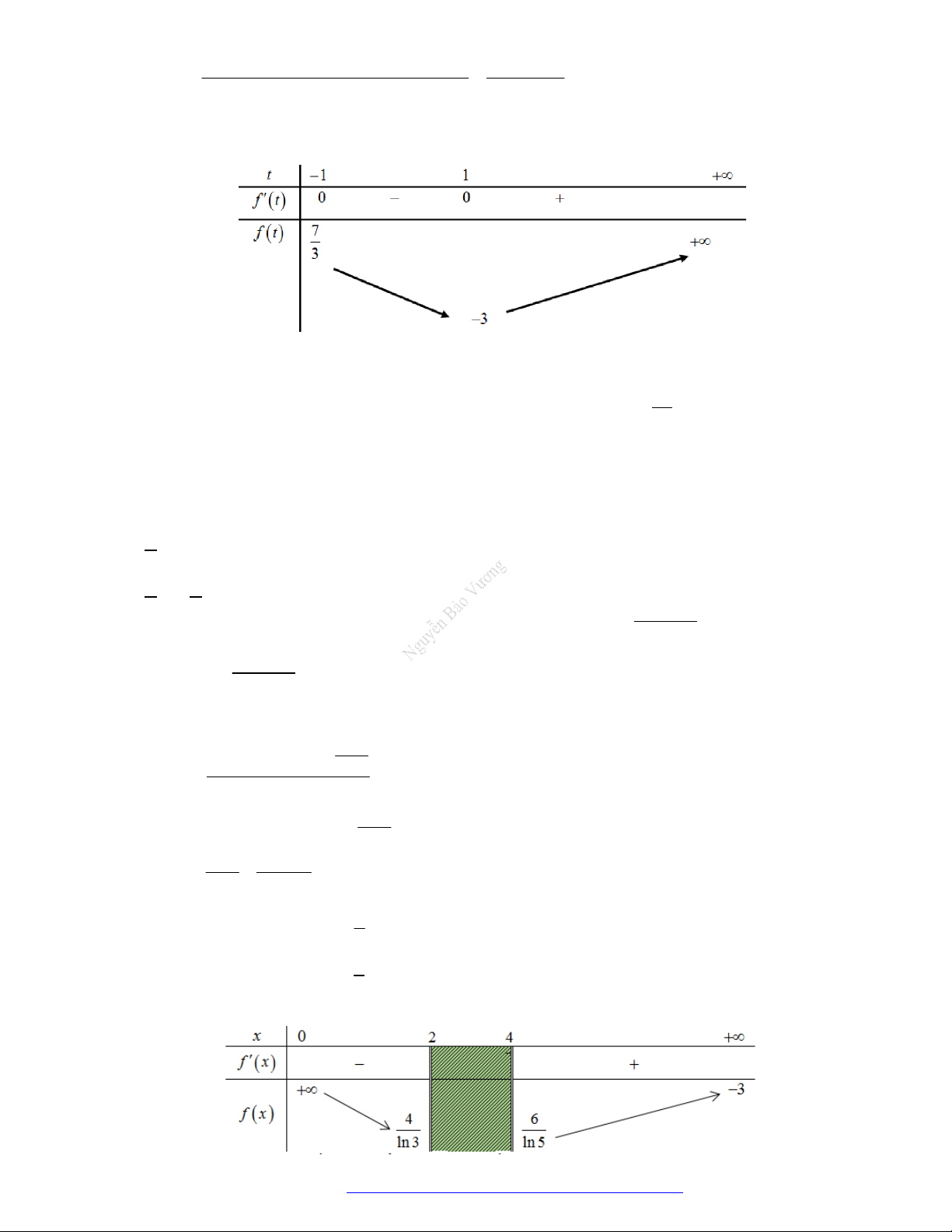
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2
2
2 2
2 2
2 5 1 2 1 5 1
4 4
1 1
t t t t t t
t
f t
t t t t
0 1f t t
.
Bảng biến thiên:
Để phương trình đã cho có nghiệm
3;6x
thì phương trình
*
có nghiệm
1t
.
3
m
.
Vậy giá trị nhỏ nhất của
m
thỏa mãn yêu cầu bài toán là
0
5
3 5;
2
m
.
Câu 38. (Chuyên Vĩnh Phúc - 2020) Cho phương trình
ln 1 2 0m x x
. Biết rằng tập hợp tất cả
các giá trị của tham số
m
để phương trình đã cho có hai nghiệm
1
x ,
2
x thỏa mãn
1 2
0 2 4x x là khoảng
;a
. Khi đó
a
thuộc khoảng nào dưới đây?
A.
3,7;3,8
. B.
3,6;3,7
. C.
3,8;3,9
. D.
3,5;3,6
.
Lời giải
Chọn A
Xét trên khoảng
0;
phương trình:
2
ln 1 2 0
ln 1
x
m x x m
x
Đặt
2
, 1; \ 0
ln 1
x
f x x
x
Với yêu cầu của đề bài ta xét
f x
trên
2
khoảng
0;2
và
4;
2
1
ln 1 2
1
ln 1
x x
x
f x
x
Đặt
1
ln 1 2 , x 0;2 4;
1
g x x x
x
2
1 1
0, 0;2 4;
1
1
g x x
x
x
Suy ra
4
2 ln3 0, 0;2 0, 0;2
3
6
5 ln5 0, 4; 0, 4;
5
g x g x f x x
g x g x f x x
Từ đó ta có bảng biến thiên
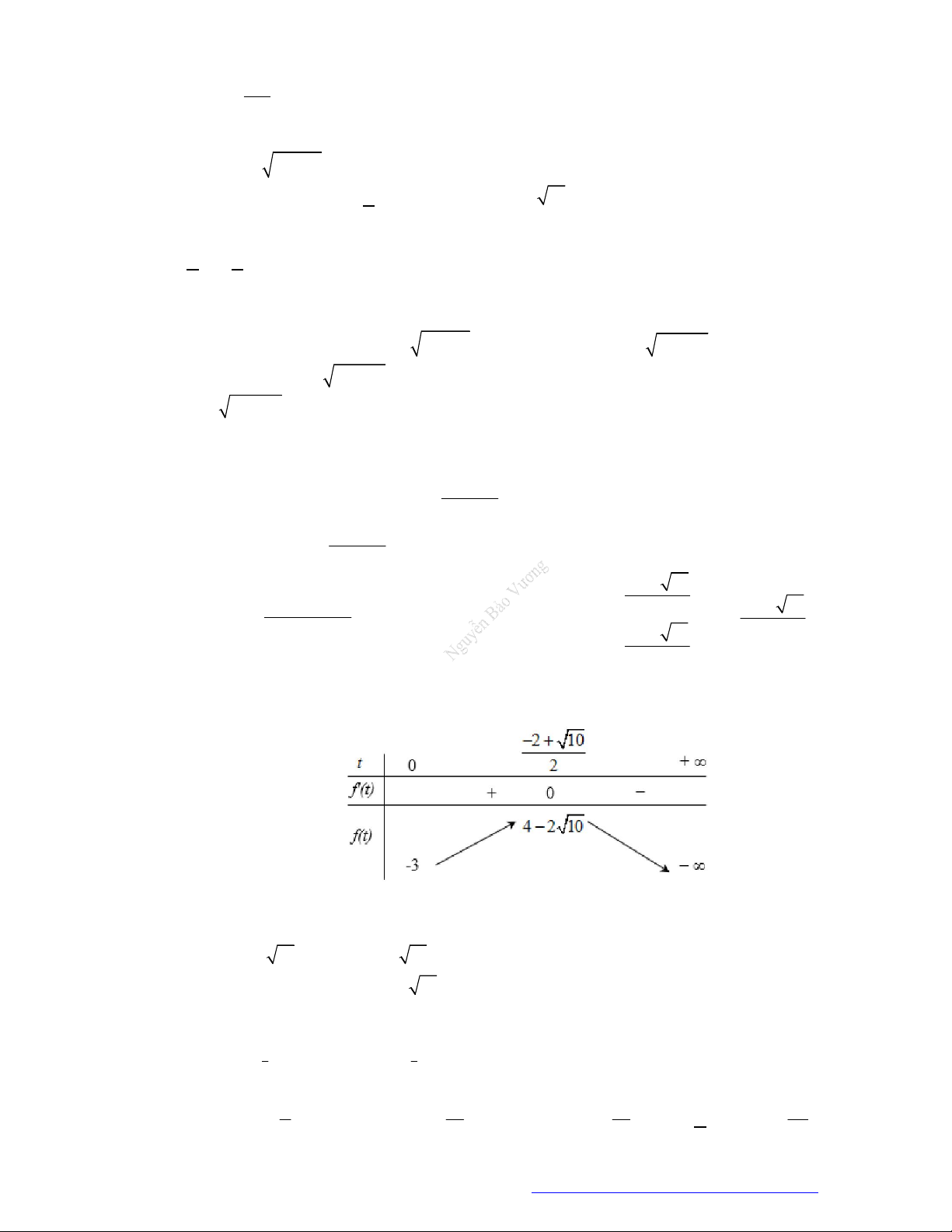
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Dựa vào bảng biến thiên, để phương trình đề bài có
2
nghiệm phân biệt thỏa
1 2
0 2 4x x
6
3,728
ln 5
m
Câu 39. (Đại Học Hà Tĩnh - 2020) Tìm tất cả các giá trị của tham số
a
để phương trình
2 3
3 3
log log 1 0x a x a
có nghiệm duy nhất.
A. Không tồn tại
a
. B.
1a
hoặc
4 2 10a
.
C.
1a
. D.
1a
.
Lời giải
Chọn B
Điều kiện:
3
3
0
0
1
1
log 0
x
x
x
x
x
.
Khi đó phương trình
2 3
3 3 3 3
log log 1 0 2log 3log 1 0x a x a x a x a
3 3
2. 3log 3 3log 3 3 0 1x a x a .
Đặt
3
3log , 0x t t
thì
1
trở thành:
2
2 3 3 3 0t at a
.
Do đó, yêu cầu bài toán trở thành: Tìm tất cả các giá trị của tham số
a
để phương trình
2
2 3 3 3 0t at a
có nghiệm duy nhất thuộc nửa khoảng
0;
.
Ta có:
2
2
2 3
2 3 3 3 0 3 , 0
1
t
t at a a t
t
.
Xét hàm số:
2
2 3
1
t
f t
t
trên nửa khoảng
0;
. Ta có:
+)
2
2
2 4 3
1
t t
f t
t
.
2
2 10
2 10
2
0 2 4 3 0
2
2 10
2
t
f t t t t
t
.
+)
lim
t
f t
.
+) Bảng biến thiên:
Từ bảng biến thiên suy ra phương trình có một nghiệm duy nhất khi
3 3 1
4 2 10 4 2 10
a a
a a
.
Đáp số:
1a
hoặc
4 2 10a
.
Câu 40. (Sở Ninh Bình 2020) Gọi
0
m
là giá trị nhỏ nhất của tham số thực
m
sao cho phương trình
2
1 1
2 2
1 log 2 5 log 2 1 0m x m x m
có nghiệm thuộc khoảng
2;4
. Khẳng định
nào dưới đây đúng?
A.
0
4
1;
3
m
. B.
0
10
2;
3
m
. C.
0
16
4;
3
m
. D.
0
5
5;
2
m
.
Lời giải
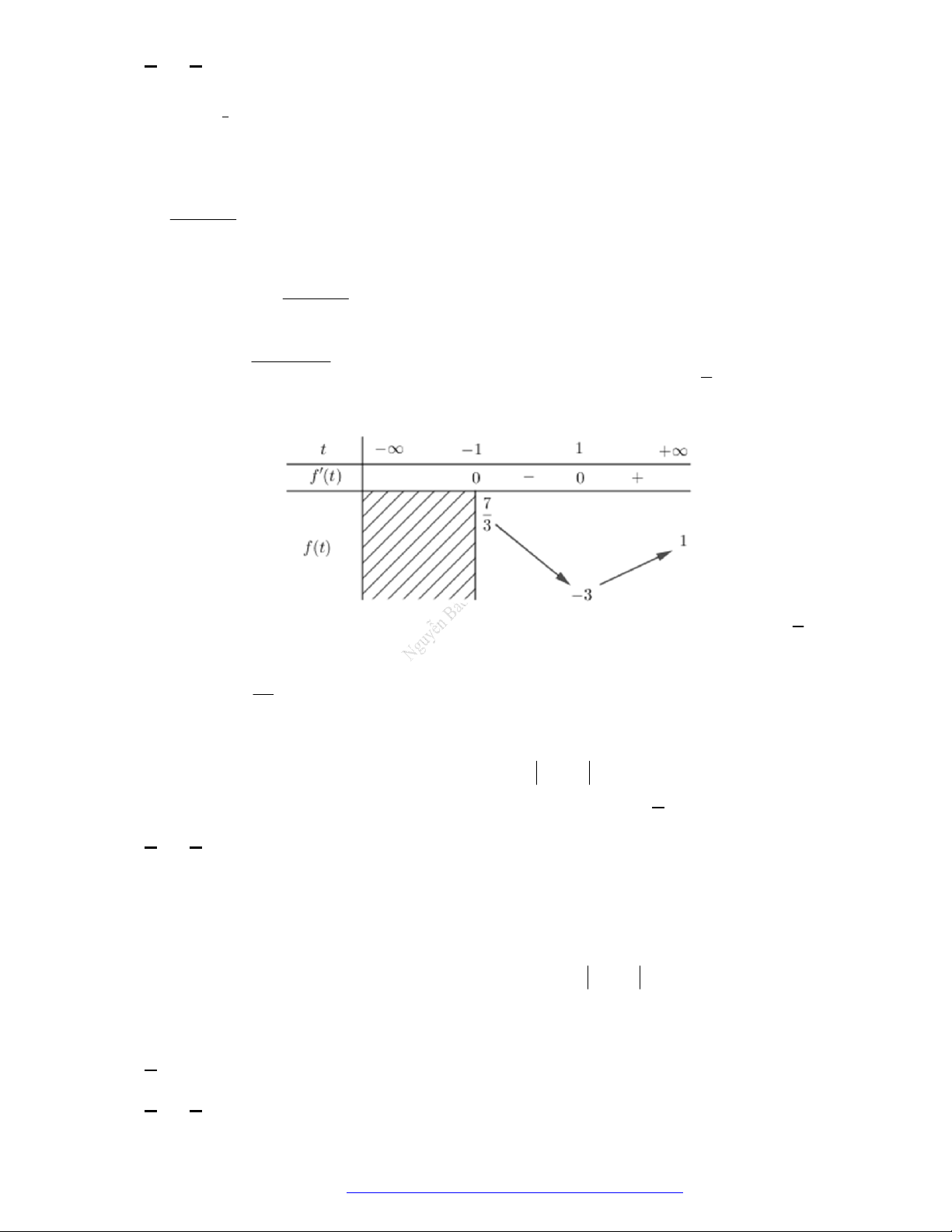
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn D
Điều kiện:
2x
.
Đặt
1
2
log 2t x
, với
2;4x
1;t
.
Phương trình đã cho trở thành:
2
1 5 1 0m t m t m
2 2 2 2
5 1 5 1 1t t mt mt m t t m t t
2
2
2
5 1
1 , 1 0,
1
t t
m t t t
t t
Phương trình đã cho có nghiệm
1
có nghiệm
1t
.
Xét hàm số
2
2
5 1
, 1
1
t t
f t t
t t
Ta có:
2
2
2
4 4
1
t
f t
t t
2
1 1 3
0 4 4 0
7
1 1
3
x f
f t t
x f
Bảng biên thiên hàm số
f t
:
Dựa vào bảng biến thiên, phương trình
f t m
có nghiệm
1t
khi và chỉ khi
7
3
3
m
.
Vậy giá trị nhỏ nhất của tham số thực
m
để phương trình đã cho có nghiệm là
0
5
3 5;
2
m
.
Câu 41.
(Sở Yên Bái - 2020) Giả sử phương trình
2
2 2
log ( 2)log 2 0x m x m
có hai nghiệm thực
phân biệt
1 2
,x x
thỏa mãn
1 2
6x x
. Giá trị biểu thức
1 2
x x
là
A. 4. B. 3. C. 8. D. 2.
Lời giải
Chọn D
Điều kiện
0x
. Phương trình đã cho tương đương
2
2 2 2
2
2 2
2
log log 2log 2 0
log
2
(log )(log 2) 0
log 2
4
m
x m x x m
x m
x
x m x
x
x
Theo giả thiết
1 2 1 2
6 2 4 6 1 2 2
m
x x m x x x
.
Câu 42. (Bỉm Sơn - Thanh Hóa - 2020) Tìm tất cả các giá trị của
m
để phương trình
2
2 2
2
log log 3 x x m
có nghiệm
1;8x
.
A.
2 6 m
B.
3 6 m
C.
6 9 m
D.
2 3 m
.
Lời giải
Chọn A
Đặt
2
logt x . Khi
1;8x
thì
0;3t
. Bài toán trở thành: Tìm
m
để phương trình
2
2 3 t t m
có nghiệm
0;3t
. Xét hàm số
2
2 3 f t t t
với
0;3t
, ta có:

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
2 2 0 1
f t t t
;
0;3
min 1 2
t
f t f
;
0;3
3 6
max
t
f t f
.
Đồ thị hàm số
2
2 3 y f t t t
và đường thẳng
y m
sẽ cắt nhau tại điểm có hoành độ
0;3
t
nếu như
0;3
0;3
ma 6min x 2
t
t
f t m f t m
.
Câu 43. (Đô Lương 4 - Nghệ An - 2020) Tìm các giá trị thực của tham số
m
để phương trình
2
3 3
log 3log 2 7 0
x x m
có hai nghiệm thực
1
x
,
2
x
thỏa mãn
1 2
3 3 72
x x
.
A.
9
2
m
. B.
3
m
. C. Không tồn tại. D.
61
2
m
.
Lời giải
Chọn A
Đặt
3
logt x
.
Phương trình đã cho trở thành
2
3 2 7 0 *
t t m
.
Ứng với mỗi nghiệm
t
của phương trình
*
có một nghiệm
x
.
Vậy phương trình đã cho có hai nghiệm phân biệt khi phương trình
*
có hai nghiệm phân biệt
2
37
0 3 4 2 7 0 9 8 28 0
8
m m m
.
Gọi
1
t
,
2
t
là hai nghiệm phương trình
*
.
Theo định lý Viét ta có:
1 2 3 1 3 2 3 1 2 1 2
3 log log 3 log . 3 . 27
t t x x x x x x
.
Theo đề bài
1 2 1 2 1 2 1 2
3 3 72 . 3 9 72 12
x x x x x x x x
.
Vậy ta có
1 2 1 1
1 2
1 2 2 2
12 9 2
. 2
. 27 3 1
x x x t
t t
x x x t
.
Theo định lý Viét ta có
1 2
9
. 2 2 2 7
2
t t m m
(thỏa mãn).
Kết luận:
9
2
m
thỏa mãn yêu cầu bài toán.
Câu 44. (Đô Lương 4 - Nghệ An - 2020) Số các giá trị nguyên nhỏ hơn
2020
của tham số
m
để phương
trình
6 4
log 2020 log 1010x m x
có nghiệm là
A.
2022
. B.
2020
. C.
2019
. D.
2021
.
Lời giải
Chọn A
Ta đặt
6 4
log 2020 log 1010x m x
t
. Khi đó
2020 6
t
x m
và
1010 4
t
x
. Ta suy ra
2 4 6 6 2 4
t t t t
m m
Đặt
2.4 6
t t
f t
6 ln 6 2.4 .ln 4
t t
f t
0
f t
6 3 6
2
3 2ln 4
log 16 log log 16
2 ln 6
t
t
.
Bảng biến thiên
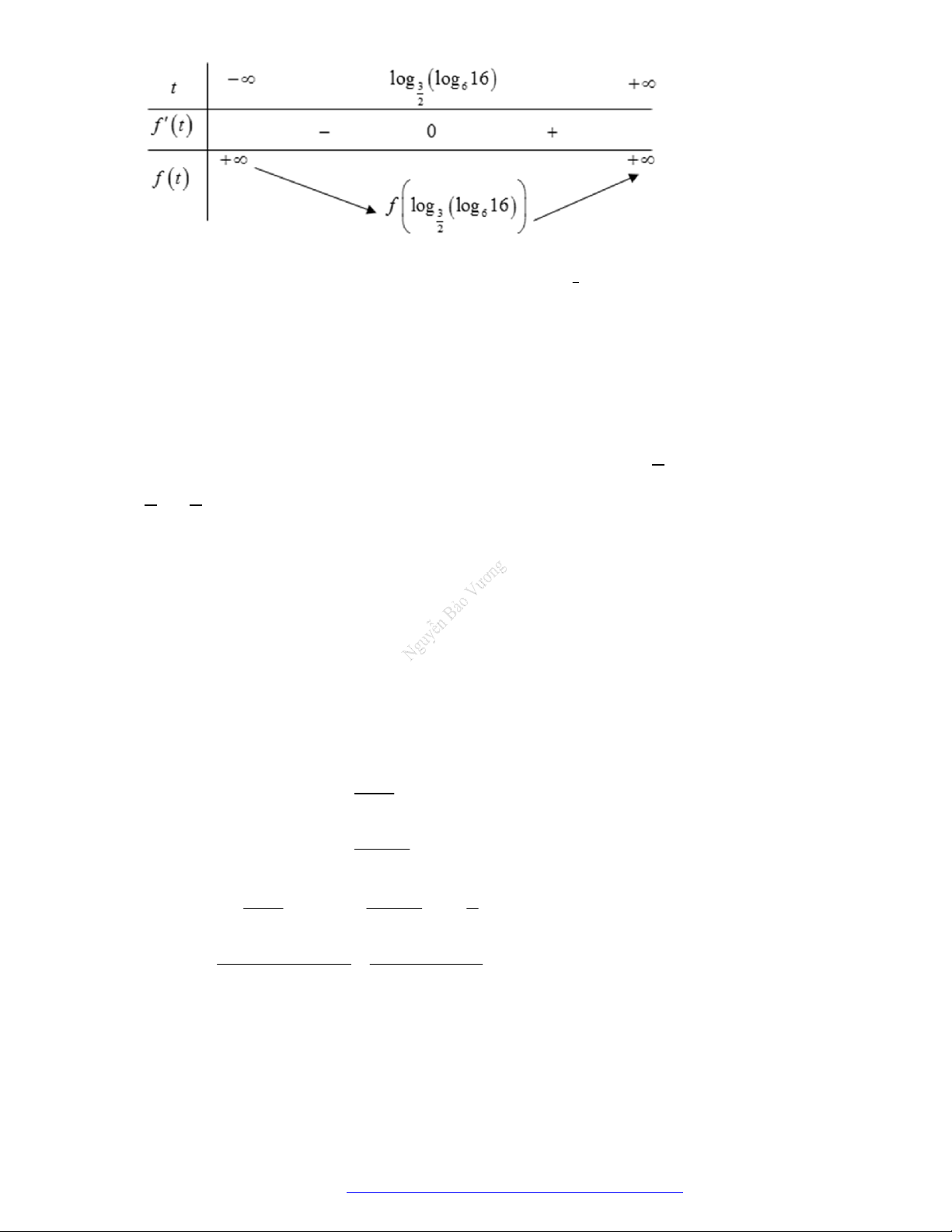
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Phương trình
f t m
có nghiệm khi và chỉ khi
3 6
2
log log 16 2,01m f
.
Hơn nữa,
2020m
m
nên suy ra
2 2019m
m
.
Vậy ta có
2022
giá trị
m
thỏa mãn.
Câu 45. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho phương trình
10 log 2log 1 0
x
me x m mx x
. (
m
là tham số ). Có tất cả bao nhiêu giá trị nguyên
của
m
để phương trình đã cho có ba nghiệm thực phân biệt?
A. Vô số. B.
10
. C.
11
. D.
5
.
Lời giải
Chọn D
10 log 2log 1 0
x
me x m mx x
2
0 1
1 0 2 *
10 0 3
1 4
x
mx
x
me x m
mx x
.
*
0m
thì pt vô nghiệm.
*
0m
thì hệ
2
0
10
*
1
1
x
x
x
m
e
x
m
x
. (Vì
0
1 1 1 0
x x
e e e
)
+Xét
10
1
x
x
f x
e
và
2
1
1
2
x
g x x
x x
.
+
2 2
10 1 .10
10 1 10
.
1 1
x x
x
x x
e e x
e x
f x
e e
Xét
10 1 10 10 10 1 10 0 0;
x x x x
u x e x u x e e x xe x
Suy ra: Hàm số
u x
nghịch biến trong khoảng
0; 0 0u x u
.
0 0;f x x f x
nghịch biến trong khoảng
0;
.
0
lim 10, lim 0
x
x
f x f x
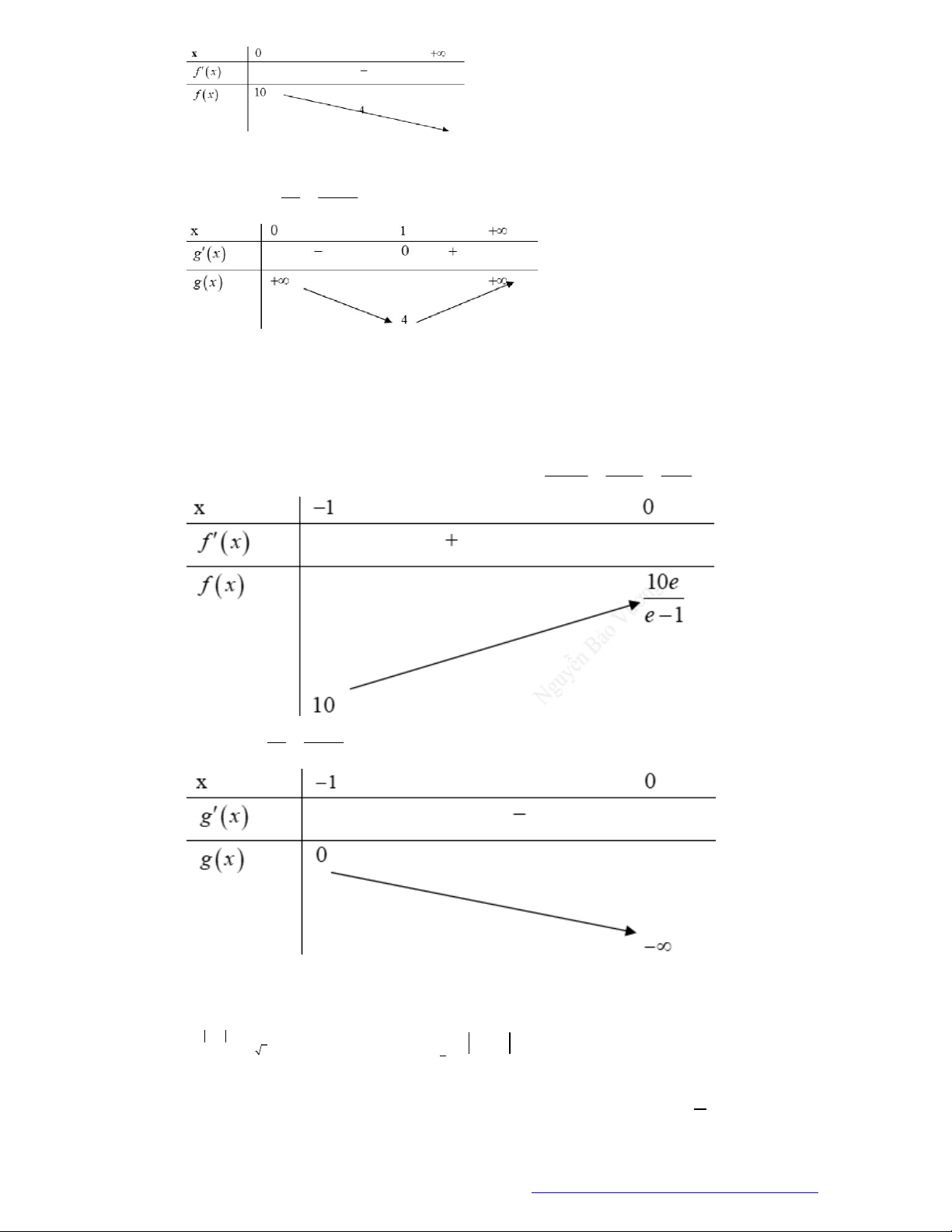
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
+
2
2 2
1
1 1
1 0 .
1
x
x
g x
x
x x
Suy ra phương trình có ba nghiệm thực phân biệt
4 10.m
Vì
5;6;7;8;9m m
*
0m
thì hệ
1 0
*
x
m f x
m g x
.
Tương tự ta có
1
1 0
10 10 10
0 1;0 , lim , lim 10
1 1 1
x x
e e
f x x f x f x
e e e
2
2 2
1
1 1
1 0 .
1
x
x
g x
x
x x
Suy ra phương trình có nhiều nhất 1 nghiệm thực phân biệt, không thỏa mãn yêu cầu bài toán.
Vậy có
5
giá trị
m
.
Câu 46.
(Liên trường Nghệ An - 2020) Cho phương trình
2
2 2
1
2
2
4 .log 2 3 2 .log 2 2 0
x m
x x
x x x m
với
m
là tham số. Tổng tất cả các giá trị
của tham số
m
để phương trình đã cho có ba nghiệm phân biệt là
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn D
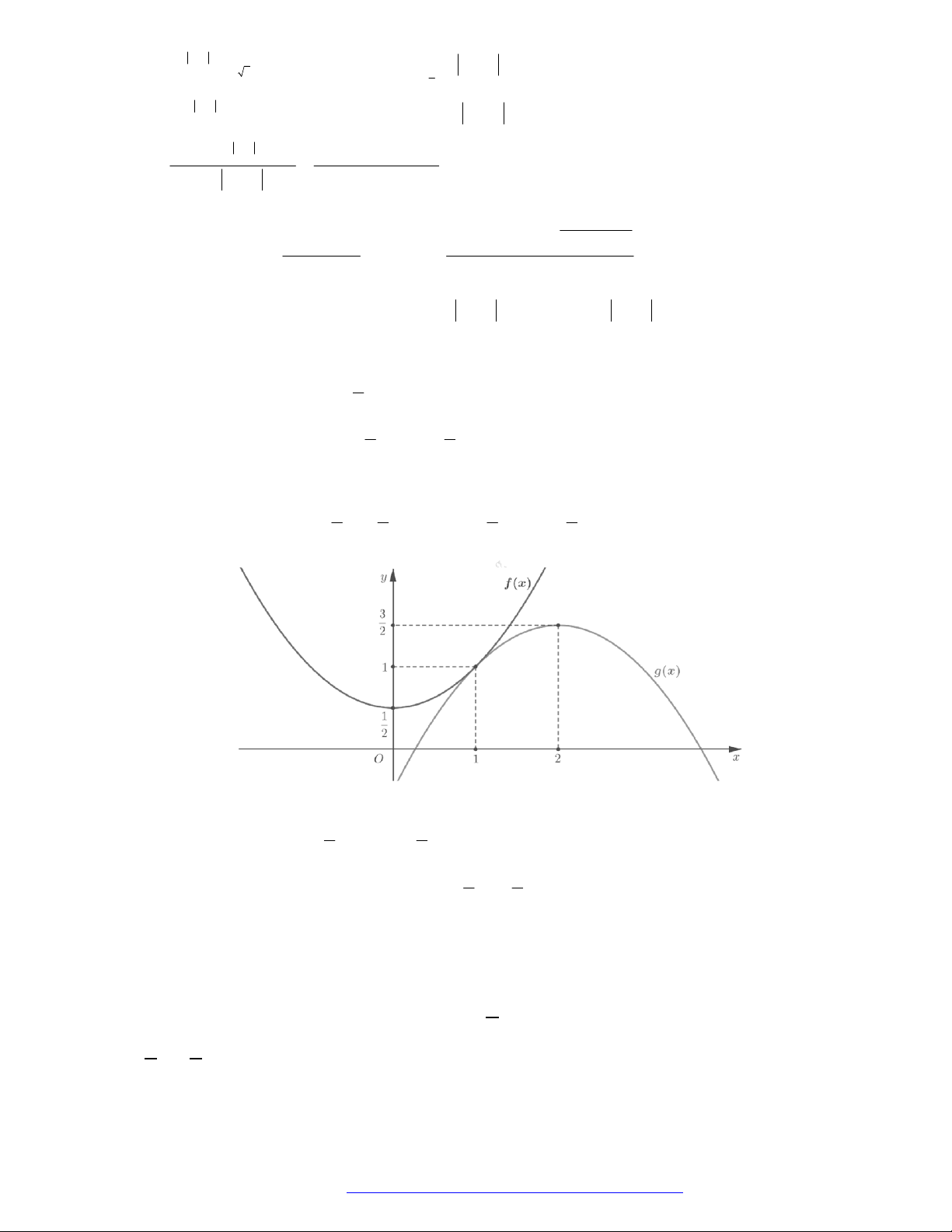
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Có
2
2 2
1
2
2
4 .log 2 3 2 .log 2 2 0
x m
x x
x x x m
2
2
1 2 1 1
2 2
2 .log 1 2 2 .log 2 2 0
x m x
x x m
2
1 2
1 1
2
2
2
2 2
log 2 2
log 1 2
x m
x
x m
x
Xét hàm số
1
2
2
log 2
t
f t
t
có
1
1
2
2
2
2 .ln 2
2 ln 2
0, 2.
log 2
t
t
t
t
f t t
t
Phương trình đã cho
2 2
1 2 1 2f x f x m x x m
2 2
4 1 2 1 2 0x x m x m
2
2
4 2 1 0
1 2 0
x x m
x m
2
2
1
1 1
2
.
1 1
2 2
2 2
x m
x x m
Khi đó
ycbt
phương trình
1
và
2
có tổng cộng
3
nghiệm thực phân biệt.
Vẽ đồ thị hàm số
2
1 1
2 2
f x x
và
2
1 1
2
2 2
g x x x
trên cùng một hệ trục tọa độ (tham
khảo hình vẽ).
Đồ thị hàm số
f x
và
g x
tiếp xúc với nhau tại điểm có hoành độ
1.x
Dựa vào đồ thị ta có
1 3
, 1,
2 2
m m m
thì phương trình đã cho có
3
nghiệm thực phân biệt.
Vậy tổng các giá trị thực của
m
thỏa ycbt là
1 3
1 3.
2 2
Câu 47. (THPT Nguyễn Viết Xuân - 2020) Cho phương trình
2
3 3
log 9 5 log 3 10 0x m x m
(với
m
là tham số thực). Số giá trị nguyên của tham số
m
để phương trình đã cho có hai nghiệm phân
biệt thuộc
1;81
là
A.
3
B.
5
C.
4
. D.
2
.
Lời giải
Chọn C
Ta có
2 2
3 3 3 3
log 9 5 log 3 10 0 log 1 log 3 6 0, 1x m x m x m x m
Đặt
3
logt x , khi
1;81x
thì
0;4t
.
Khi đó ta có phương trình
2
3
1 3 6 0
2
t
t m t m
t m
.
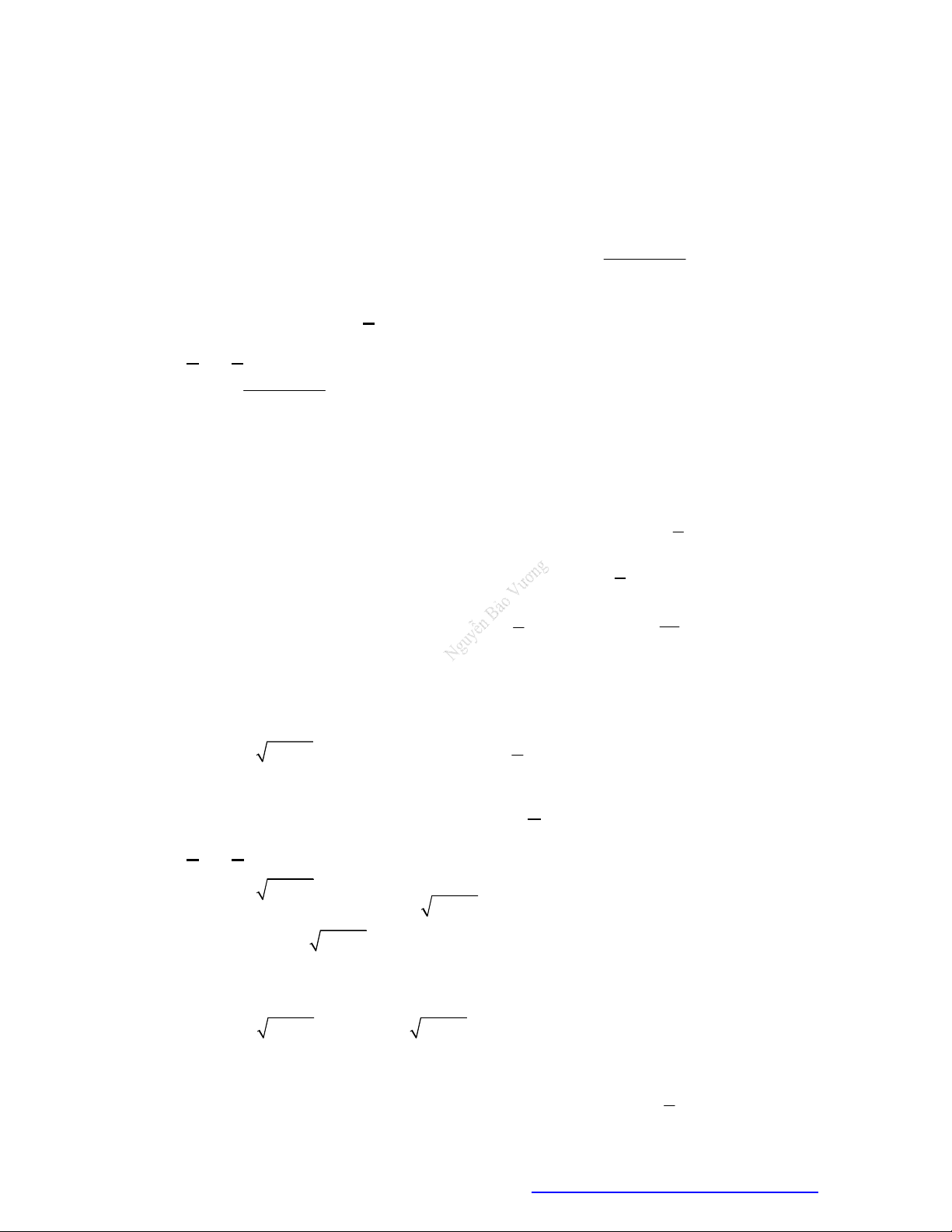
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Phương trình đã cho có hai nghiệm phân biệt thuộc
1;81
phương trình
1
có hai nghiệm
phân biệt
2 3 5
0;4
0 2 4 2 6
m m
t
m m
.
Suy ra có
4
giá trị nguyên của tham số
m
để phương trình đã cho có hai nghiệm phân biệt thuộc
1;81
.
Chọn đáp án C.
Câu 48. (THPT Nguyễn Viết Xuân - 2020) Cho
,x y
là hai số thực dương thỏa mãn
5 4
x y
. Tổng tất
cả giá trị nguyên của tham số
m
để phương trình
2
2
3
2
log 3 1 0
x y m
x x y m
x y
có
nghiệm là
A. 10. B. 5. C. 9. D. 2.
Lời giải
Chọn B
2
2
3
2 2
3 3
2
log 3 1 0
log 2 2 log 3 3 1
x y m
x x y m
x y
x y m x y m x y x y
Vì
, 0
x y
nên
0
x y
. Xét hàm số
3
log
f t t t
là hàm số đồng biến trên
0;
.
Khi đó
1
2 2
2 3 3 3 0 *
x y m x y x x y m
Kết hợp với điều kiện
5 4 4 5x y y x
. Vì
4
, 0 0
5
x y x
.
Ta có
2 2
4
* 2 4 0 2 4, 0;
5
x x m m x x x
.
Hàm số
2
2 4y x x
nghịch biến trên
4
0;
5
(do
1 0
) nên
2
44
2 4 4
25
x x
.
Do vậy
2;3
m
là các giá trị cần tìm.
Vậy tổng tất cả các giá trị
m
thỏa ycbt là 5.
Câu 49.
(Hải Hậu - Nam Định - 2020) Biết rằng điều kiện cần và đủ của tham số
m
để phương trình
2
log 2 2
x
m m x
có nghiệm là
a
m
b
với
,a b
là hai số nguyên dương và
7
b
. Hỏi
2
a b b
bằng bao nhiêu?
A.
31
. B.
32
. C.
21
. D.
23
.
Lời giải
Chọn C
2
2
2 0
log 2 2
2 2 *
x
x
x x
m
m m x
m m
.
2
* 2 2 2 2
x x x x
m m
.
Xét hàm số
2
0
f t t t t
. Ta có
2 1 0
f t t
với mọi
0t
, suy ra hàm số luôn đồng
biến với mọi
0t
.
2
* 2 2 2 2 2 2 **
x x x x x x
f m f m m
.
Đặt
2 0
x
t t
, khi đó phương trình
**
trở thành
2
***
t t m
.
Xét hàm
2
0
g t t t t
, ta có
1
2 1 0
2
g t t g t t
.
Bảng biến thiên
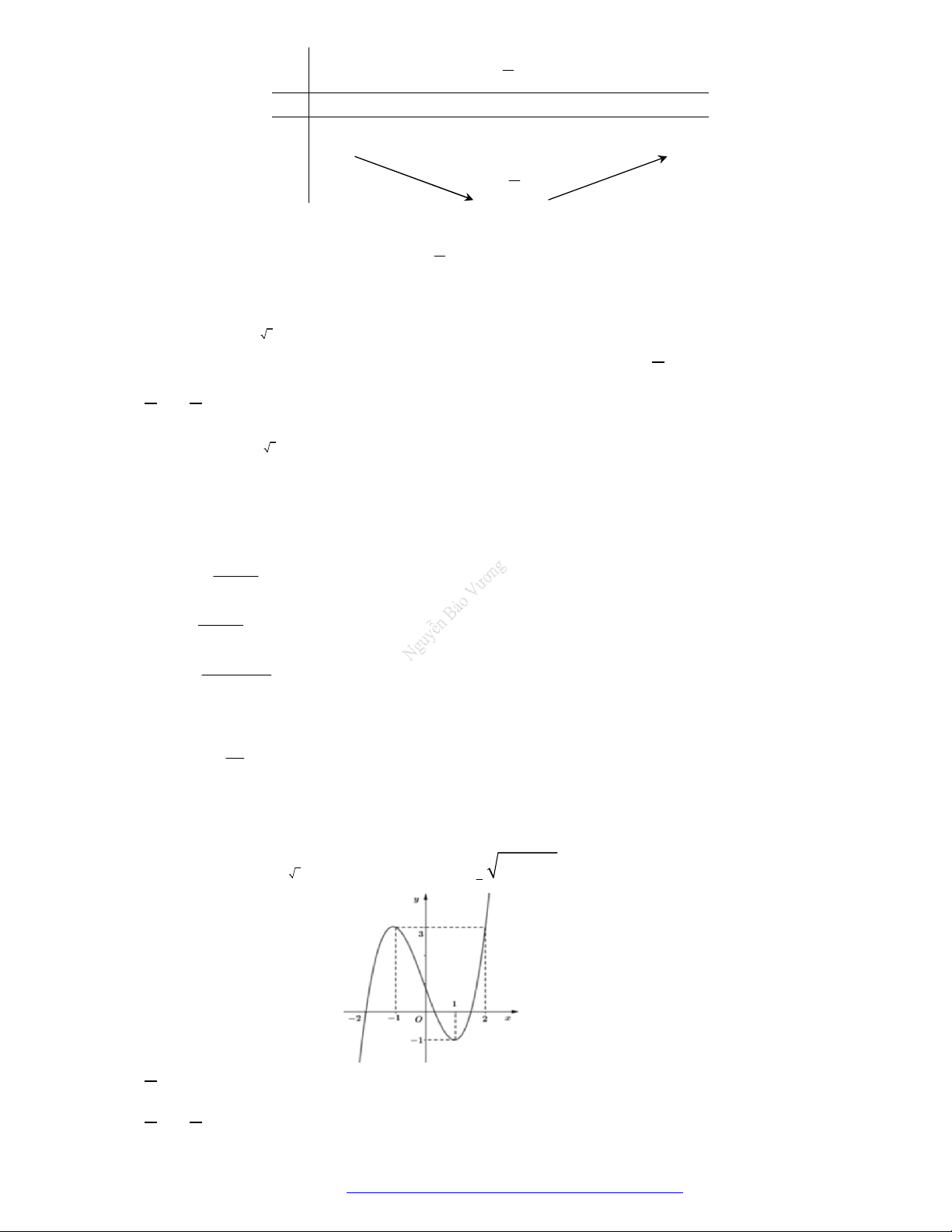
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy để
***
có nghiệm
0t
thì
1
4
m
2
1
21
4
a
a b b
b
.
Câu 50. (Lương Thế Vinh - Hà Nội - 2020) Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
2
2
log (4 ) log 2 4 0x m x m
có nghiệm thuộc đoạn
1;8
?
A.
1.
B.
2
. C.
5
. D.
3.
Lời giải
Chọn D
ĐK:
0x
2
2
2
2
2 2
2
2 2 2
2
2
2
2
2
log 4 log 2 4 0
2 log 2 log 2 4 0
log 4log 2 log 1 1
log ; 1;8 0;3
4
1 2
1
4
; 0;3
1
2 4
0, 0;3
1
x m x m
x m x m
x x m x
x t x t
t t
m
t
t t
f t t
t
t t
f t t
t
0 2 3
21
0 , 0,1,2
8
f m f
m m m
Câu 51. (Chuyên Biên Hòa - Hà Nam - 2020) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ. Có
bao nhiêu giá trị nguyên của tham số
5;5m
sao cho phương trình
3 2
2 1
2
2
log 1 log 1 2 8 log 1 2 0f x f x m f x m có nghiệm
1;1x
?
A.
7
. B.
5
. C.
6
. D. vô số.
Lời giải
Chọn A
Với
1;1 1 3 0 1 4x f x f x
.
t
0
1
2
g
–
0
g
1
4
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
Đặt
2
log 1 ;2 , 1;1
t f x t x
.
Khi đó phương trình đã cho trở thành:
3 2
4 4 2 0
t t m t m
2 2 2
2
2 ;2
2 2 0 2 0 2 *
2 0
t
t t t m t t m t t m
t t m
Để phương trình đã cho có
1;1x
phương trình
*
có nghiệm
;2
t
.
Xét hàm số
2
2f t t t
trên
;2
có
2 2 0 1 ;2
f t t t
.
Ta có bảng biến thiên của hàm số
2
2f t t t
Từ bảng biến thiên suy ra phương trình
*
có nghiệm
;2
t
khi và chỉ khi
1
m
.
Mà
5;5
1;0;1;2;3;4;5
m
m
m
. Vậy có
7
giá trị của
m
thỏa mãn yêu cầu bài toán.
Dạng 2. Phương trình mũ chứa tham số
Câu 1. (Mã 101 2018) Gọi
S
là tập hợp tất cả giá trị nguyên của tham số
m
sao cho phương trình
1 2
16 .4 5 45 0
x x
m m
có hai nghiệm phân biệt. Hỏi
S
có bao nhiêu phần tử?
A.
6
B.
4
C.
13
D.
3
Lời giải
Chọn D
Đặt
4 , 0
x
t t
. Phương trình trở thành:
2 2
4 5 45 0
t mt m
(1).
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân
biệt
0t
.
' 0
0
0
P
S
2
2
45 0
5 45 0
4 0
m
m
m
3 5 3 5
3 3
0
m
m m
m
3 3 5
m .
Vì
m
nguyên nên
4;5;6
m
. Vậy
S
có
3
phần tử.
Câu 2. (Mã 104 2017) Tìm giá trị thực của tham số
m
để phương trình
1
9 2.3 0
x x
m
có hai
nghiệm thực
1
x
,
2
x
thỏa mãn
1 2
1
x x
.
A.
3
m
B.
1
m
C.
6
m
D.
3
m
Lời giải
Chọn A
Ta có
1
9 2.3 0
x x
m
2
3 6.3 0
x x
m
.
Phương trình có hai nghiệm thực
1
x
,
2
x
thỏa mãn
1 2
1
x x
1 2
1 2
9 0
3 3 6 0 3
3 3
x x
x x
m
m
m
.
Câu 3. (Mã 102 2018) Gọi
S
là tập hợp các giá trị nguyên của tham số
m
sao cho phương trình
1 2
25 .5 7 7 0
x x
m m
có hai nghiệm phân biệt. Hỏi
S
có bao nhiêu phần tử.
A.
7
B.
1
C.
2
D.
3
t
1
2
f t
0
f t
1
0

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn C
Xét phương trình
1 2
25 .5 7 7 0 1
x x
m m
.
Đặt
5 0
x
t t
. Phương trình trở thành
2 2
5 7 7 0 2
t mt m
.
YCBT
Phương trình
1
có hai nghiệm phân biệt
Phương trình
2
có hai nghiệm phân biệt
1 2
, 0
t t
2 2
2
25 4 7 7 0
0
0 5 0
0
7 7 0
m m
S m
P
m
2 21
1
3
m
.
Mà
2;3
m m
. Vậy có
2
giá trị nguyên của tham số
m
.
Câu 4. (Mã 103 2018) Gọi
S
là tất cả các giá trị nguyên của tham số
m
sao cho phương trình
1 2
4 .2 2 5 0
x x
m m
có hai nghiệm phân biệt. Hỏi
S
có bao nhiêu phần tử.
A.
2
B.
1
C.
3
D.
5
Lời giải
Chọn B
Ta có:
1 2 2
4 .2 2 5 0 4 2 .2 2 5 0
x x x x
m m m m
(1)
Đặt
2 , 0
x
t t
. Phương trình (1) thành:
2 2
2 . 2 5 0
t m t m
(2)
Yêu cầu bài toán
(2)
có 2 nghiệm dương phânbiệt
2 2
2
' 0 2 5 0 5 5
10
0 2 0 0 5.
2
0
2 5 0
5 5
2 2
m m m
S m m m
P
m
m hoac m
Do
m
nguyên nên
2
m
. Vậy S chỉ có một phần tử
Câu 5. (Mã 110 2017) Tìm tất cả các giá trị thực của tham số
m
để phương trình
1
4 2 0
x x
m
có
hai nghiệm thực phân biệt
A.
0;m
B.
;1
m
C.
0;1
m
D.
0;1
m
Lời giải
Chọn D
Phương trình
2
1
4 2 0 2 2.2 0
x x x x
m m
,
1
.
Đặt
2 0
x
t
. Phương trình
1
trở thành:
2
2 0
t t m
,
2
.
Phương trình
1
có hai nghiệm thực phân biệt
phương trình
2
có hai nghiệm thực phân biệt và lớn hơn
0
1 0
0
2
0 0 0 1
1
0
0
1
m
S m
P
m
.
Câu 6. (Mã 104 2018) Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
sao cho phương trình
1 2
9 .3 3 75 0
x x
m m
có hai nghiệm phân biệt. Hỏi
S
có bao nhiêu phần tử?
A.
5
B.
8
C.
4
D.
19
Lời giải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
Chọn C
1 2
9 .3 3 75 0 1
x x
m m
2
2
3 3 .3 3 75 0
x x
m m
Đặt
3 , 0
x
t t
Phương trình trở thành:
2 2
3 3 75 0 2
t mt m
1
có hai ngiệm phân biệt khi và chỉ khi
2
có hai nghiệm dương phân biệt
2
2
300 3 0 10 10
3 0 0 5 10
5
3 75 0
5
m m
m m m
m
m
m
Do
m
nguyên nên
6;7;8;9
m
Câu 7. (Chuyên Biên Hòa - Hà Nam - 2020) Cho phương trình
0813).32(9
xx
m
(
m
là tham số
thực). Giá trị của
m
để phương trình đã cho có hai nghiệm phân biệt
21
,xx
thỏa mãn
10
2
2
2
1
xx
thuộc khoảng nào sau đây
A.
10;5
. B.
5;0
. C.
15;10
. D.
;15
.
Lời giải
Chọn C
9 (2 3).3 81 0 1
x x
m
2
3 (2 3).3 81 0
x x
m
. Đặt
3 0
x
t t
Phương trình trở thành:
2
(2 3) 81 0 2
t m t
2 2
2 3 4.81 2 3 324
m m
Để phương trình
1
có hai nghiệm phân biệt thì phương trình
2
có hai nghiệm phân biệt
dương:
Điều kiện:
2
15
2 3 18
2
2 3 18
3 3
2 3 324 0
0
15
2 2
2 3 18
0 2 3 0
2
2 3 18 21
3
0 81 0
2
3
2
3
2
2
m
m
m
m
m m
m
S m m
m
m
P
m
m
m
Áp dụng hệ thức Vi-ét:
1 2
1 2
2 3
. 81
t t m
t t
Vì
1 2
4
1 2 1 2
. 81 3 .3 3 4
x x
t t x x
Do đó:
2
2 2 2
1 2 1 2 1 2 1 2 1 2
10 2 . 10 4 2 . 10 . 3
x x x x x x x x x x
Xét hệ phương trình
1 2 1 1
1 2
1 2 2 2
. 3 1 3
30
4 3 27
x x x t
t t
x x x t
Nên
27
2 3 30
2
m m TM
Vậy chọn C.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 8. (Chuyên Lam Sơn Thanh Hóa 2019) Cho phương trình
.16 2 2 .4 3 0 1
x x
m m m
. Tập
hợp tất cả các giá trị dương của
m
để phương trình đã cho có hai nghiệm phân biệt là khoảng
; .a b
Tổng
2T a b
bằng:
A.
14
B.
10
C.
11
D.
7
Lời giải
Chọn C
+) Đặt:
2
4 ( 0) 1 . 2 2 3 0 2
x
t t m t m t m
+) Để
1
có
2
nghiệm phân biệt thì
2
phải có hai nghiệm dương phân biệt
Điều kiện:
2
0
0
4 0
0
2 3 0
2
0 3 4
2
0
0 0( )
0
0
3
3 0
0
m
m
m
m
m m m
m
m
m
m
S m l
m
P
m
m m
m
+) Vậy
3
3 4 2 11
4
a
m a b
b
Câu 9. (THCS - THPT Nguyễn Khuyến 2019) Phương trình
1
4 3.2 0
x x
m
có hai nghiệm thực
1 2
,x x
thỏa mãn
1 2
1
x x
. Giá trị của
m
thuộc khoảng nào sau đây?
A.
5;0
. B.
7; 5
. C.
0;1
. D.
5;7
.
Lời giải
Đặt
2
x
t
. Ta có phương trình
2
6 0
t t m
Phương trình đã cho có hai nghiệm
1 2
,x x
thỏa mãn
1 2
1
x x
pt có hai nghiệm dương
1 2
,t t
thỏa mãn
1 2
1
1 2
1
. 2 2
2
x x
t t
0 9 0
1
0 6 0
2
1 1
0
2 2
m
s m
p m
.
Câu 10. (THPT Lê Xoay Vĩnh Phúc 2019) Với giá trị nào của tham số
m
để phương trình
1
4
.2 2 3 0
x x
m m
có hai nghiệm
1 2
;x x
thỏa mãn
1 2
4
x x
A.
5
2
m
. B.
2
m
. C.
8
m
. D.
13
2
m
.
Lời giải
Phương trình đã cho tương đương
2
2 .2
2 2 3 0 (1)
x x
mm
.
Đặt
2 0
x
t t
, khi đó phương trình
(1)
trở thành:
2
2 . 2 3 0 2
m t mt
.Phương trình
1
có hai nghiệm
1 2
;x x
khi và chỉ khi phương trình
2
có hai nghiệm
1 2
;t t
dương
2
0 2 3 0
0 2 0
0 2 3
3
0
m m
S m m
P m
. Theo định lý Viet ta có
1 2
1 2
.
2
2 3
t t
t t
m
m
Với
2
x
t
ta có:
1
1 2 1 2
2
1
1 2
2
2
13
. 2 .2 2 3 2 16 2 3
2
2
x
x x x x
x
t
t t m m m
t
(thỏa mãn).
Câu 11. (THPT Đoàn Thượng - Hải Dương 2019) Phương trình
022.4
1
mm
xx
có hai nghiệm
21
, xx
thỏa mãn
3
21
xx
khi
A.
4
m
. B.
3
m
. C.
2
m
. D.
1
m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
Lời giải
Đặt
2
x
t
,
0t
. Phương trình viết thành
2
2 2 0 1
t mt m
.
Ta có
1 2 1 2
3
1 2
3 2 2 2 .2 8
x x x x
x x
.
Ycbt tương đương phương trình
1
có hai nghiệm dương
1 2
,t t
thỏa mãn
1 2
. 8
t t
.
2
1 2
1 2
2 0
2 0 4
. 2 8
m m
t t m m
t t m
.
Câu 12. (Chuyên Bắc Giang 2019) Tìm tất cả các giá trị của tham số
m
để phương trình
2 2 2
2 2 1 2 4 2
4.4 2 2 6 6 3 3 0
x x x x x x
m m
có hai nghiệm thực phân biệt.
A.
4 3 2 4 3 2
m
B.
4 3 2
m
hoặc
4 3 2
m
C.
1
m
hoặc
1
2
m
D.
1
1
2
m
Lời giải
Chọn D
2 2 2
2 2 2
2 2
2 2 1 2 4 2
2 1 2 1 2 1
2 1 2 1
4.4 2 2 6 6 3 3 0 (1)
4 2 2 6 6 3 9 0
4 2
2 2 6 3 0 (2)
9 3
x x x x x x
x x x x x x
x x x x
m m
m m
m m
Đặt
2 2
2 1 ( 1) 0
2 2 2
1
3 3 3
x x x
t
. Suy ra
0 1t
Pt (2) trở thành:
2
(2 2) 6 3 0 (3)
t m t m
3 ( )
2 1
t loai
t m
Để phương trình (1) có 2 nghiệm
x
phân biệt
Phương trình
2
(2 2) 6 3 0
t m t m
có đúng một nghiệm
t
thuộc khoảng
0;1
0 2 1 1
m
1
1
2
m
.
Chú ý: Nếu
1t
thì phương trình
2
( 1)
2
1
3
x
chỉ có nghiệm duy nhất là
1
x
.
Câu 13. (Chuyên Vĩnh Phúc 2019) Biết rằng tập các giá trị của tham số
m
để phương
trình
3 9 2 1 3 1 0
x x
m m m
có hai nghiệm phân biệt là một khoảng
;a b
. Tính tích
.a b
.
A.
4
B.
3
C.
2
D.
3
Lời giải
Chọn D
Đặt:
3 ,( 0)
x
t t
. Khi đó phương trình trở thành
2
( 3) 2( 1) 1 0(*)
m t m t m
Phương trình có hai nghiệm phân biệt khi phương trình (*) có hai nghiệm dương phân biệt
( 1)(2 2) 0
0
1
0 0 1
1
3 . 3
1 3
3
0
1
0
3
1
m m
m
S m a b
m
m
P
m
m
m m

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 14. Có tất cả bao nhiêu số nguyên
m
để phương trình
4 .2 2 2019 0
x x
m m
có hai nghiệm trái
dấu?
A.
1008
. B.
1007
. C.
2018
. D.
2017
.
Lời giải
4 .2 2 2019 0
x x
m m
(1 )
Đặt
2 0
x
t t
. Phương trình (1 ) trở thành
2
2 2019 0
t mt m
( 2)
Phương trình ( 1) có hai nghiệm
1 2
;x x
thỏa
1 2
0x x
khi và chỉ khi phương trình ( 2) có hai
nghiệm
1 2
;t t
thỏa
1 2
0 1t t
2
1 2
1 2
1 2 1 2
1 2
4 2 2019 0
0
0
0
0
0
2019
0 2 2019 0
2
1 0
1 1 0
2 2019 1 0
m m
m
S t t
m
P t t m
m
t t t t
t t
m m
2
8 8076 0
0
2019
2018
2019
2
2
2018
m m m
m
m
m
m
. Do
m
nên
1010 2017m
Số giá trị nguyên
m
thỏa đề là
1008
.
Câu 15. Cho phương trình
4 15 2 1 4 15 6 0
x x
m
. Để phương trình có hai nghiệm phân
biệt
1 2
,x x
thỏa mãn
1 2
2 0
x x
. Ta có
m
thuộc khoảng nào?
A.
3;5
. B.
1;1
. C.
1;3
. D.
; 1
.
Lời giải
Đặt
4 15
x
t
,
0t
. Khi đó phương trình ban đầu trở thành:
2
2 1
6 0 6 2 1 0, 0
m
t t t m t
t
(*)
Để phương trình có hai nghiệm phân biệt
1 2
,x x
thỏa mãn
1 2
2 0
x x
khi và chỉ khi phương trình
(*) có hai nghiệm dương phân biệt
1 2
,t t
thỏa mãn
(*)
2
1 2
0
1
0 4
2
0
t t S m
P
Theo Viet, ta có:
1 2
1 2
3
1 2 2
2 2
3
1 2
1
6
6
. 2 1 2 1
2 1
t t
t t
t t m t m
t t
t m
2
3 3 3
7
2 1 2 1 6 2 1 2 3;5
2
m m m m
.
Câu 16. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Phương trình
2 3 1 2 2 3 4 0
x x
a
có 2 nghiệm phân biệt
1 2
,x x
thỏa mãn
1 2
2 3
log 3
x x
.
Khi đó
a
thuộc khoảng
A.
3
;
2
. B.
0;
. C.
3
;
2
. D.
3
;
2
.
Lời giải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
Đặt
2 3 , 0
x
t t
Phương trình trở thành
2
1 2
4 0 4 1 2 0
a
t t t a
t
(1)
GT: Phương trình có 2 nghiệm phân biệt
1 2
,x x
thỏa mãn
1 2
1 2
2 3
log 3 2 3 3
x x
x x
Khi đó
1 2
3t t
YCBT phương trình (1) có 2 nghiệm dương phân biệt thỏa mãn
1 2
3t t
1 2
1
1 2
2
1 2
1 2
1 2
0
3 2 0
0; 0
3
3
4 1
2
1
1
. 1 2
1 2
3
a
t t
t
a
t t a
t
a
t t a
t t a
t t
Câu 17. (Chuyên Vĩnh Phúc 2019) Biết rằng tập các giá trị của tham số
m
để phương
trình
3 9 2 1 3 1 0
x x
m m m
có hai nghiệm phân biệt là một khoảng
;a b
. Tính tích
.a b
.
A.
4
B.
3
C.
2
D.
3
Lời giải
Đặt
3 , ( 0),
x
t t
phương trình đã cho trở thành
2
( 3) ( 1) 1 0 *
2
( )
m t m t m
Để phương trình đã cho có 2 nghiệm phân biệt thì phương trình (*) có hai nghiệm dương phân
biệt.
1 2 2 0
' 0
1
0 0 1 3
3
0
1
0
3
m m
m
S m
m
P
m
m
Khi đó
; 1;3
a b
Tích
. 3
a b
Câu 18. (Chuyên Trần Phú Hải Phòng 2019) Tìm tất cả các giá trị của
mm
để phương trình
9 2 .3 2 0
x x
m m
có hai nghiệm phân biệt
A.
2 2m
B.
2m
C.
2m
D.
2m
Lời giải
Đặt
3 0;
x
t x t
và mỗi
x
cho ta một giá trị
t
tương ứng.
Khi đó phương trình trở thành
2
2 2 0 *
t mt m
Để pt đã cho có 2 nghiệm phân biệt, tương đương phương trình
*
có hai nghiệm dương phân
biệt
2
0 2 0
0 2 0 2
0 2 0
m m
S m m
P m
Câu 19. Xác định các giá trị của tham số
m
để phương trình
2
9 2 2 6 4 3 4 0
x x x
m m m
có hai
nghiệm phân biệt?
A.
2m .
B.
3m .
C.
1m .
D.
2m .
Lời giải
Xét phương trình:
2
9 2 2 6 4 3 4 0
x x x
m m m

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chia cả hai vế của phương trình cho
4
x
ta được
2
2
3 3
2 2 4 3 0
2 2
x x
m m m
Đặt
3
0
2
x
t , t
khi đó phương trình trở thành:
2 2
2 2 4 3 0
t m t m m
Phương trình có
2
nghiệm phân biệt khi và chỉ khi phương trình có
2
nghiệm dương phân biệt
2
2
1 2
2
1 2
2 4 3 0
0 1 0
0 2 2 0 2 1
0
3 1
4 3 0
m m m
t t m m m .
t .t
m ; ;
m m
Câu 20. (KTNL GV THPT Lý Thái Tổ 2019) Biết rằng
0
m m
là giá trị của tham số
m
sao cho
phương trình
9 2 2 1 3 3 4 1 0
x x
m m
có hai nghiệm thực
1 2
,x x
thỏa
mãn
1 2
2 2 12
x x
. Khi đó
0
m
thuộc khoảng nào sau đây
A.
(3;9)
. B.
9;+
. C.
1;3
. D.
-2;0
.
Lời giải
Chọn C
9 2 2 1 3 3 4 1 0 (1)
x x
m m
Đặt
3 , 0
x
t t
. Pt(1) trở thành:
2
2 2 1 3 4 1 0
t m t m
3
.
4 1
t
t m
Để pt(1) có 2 nghiệm thì điều kiện cần và đủ là
1
4 1 0
4
m m
.
Khi đó pt (1) có hai nghiệm
1
1
x
và
2 3
log 4 1
x m
.
Từ giả thiết
1 2
2 2 12
x x
3
3 log 4 -1 2 12
m
3
log 4 1 2
m
2
1 5
. 3 1
4 2
m
. Vậy
1;3 .
m
Câu 21. (Sở Phú Thọ 2019) Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
16 2 1 4 3 8 0
x x
m m
có hai nghiệm trái dấu?
A.
6
B.
7
C.
0
D.
3
Lởi giải
Chọn A
Đặt
4 , 0
x
t t
Phương trình đã cho trở thành
2
2 1 3 8 0
t m t m
*
Yêu cầu bài toán
pt
*
có hai nghiệm
1 2
,t t
thỏa
1 2
0 1
t t
2
1 2
1 2
1 2
0
9 0
0
1 0
8
9
0
3
3 8 0
1 1 0
9 0
m m
t t
m
m
t t
m
t t
m
Vậy
m
có
6
giá trị nguyên.
Câu 22. (Chuyên Thái Nguyên 2019) Gọi
S
là tập hợp các giá trị thực của tham số
m
để phương
trình
4 .2 2 1 0
x x
m m
có nghiệm. Tập
\ S
có bao nhiêu giá trị nguyên?
A.
1
B.
4
C.
9
D.
7
Lời giải
Đặt
2 0
x
t t
, khi đó phương tình có dạng
2
2 1 0 2
t mt m
Để phương trình ban đầu có nghiệm thì phương trình (2) có nghiệm dương

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
TH 1: Pt(2) có 2 nghiệm trái dấu
1
2 1 0
2
m m
TH 2: pt(2) có 2 nghiệm dương
2
8 4 0
0 4 20
2 1 0
m m
m m
m
Nên
1 1
; 4 20; \ ;4 20
2 2
S S
. Vậy các số nguyên thỏa mãn là
0,1,2,3, 4,5,6,7,8
hay đáp án C
Câu 23. (THPT Nghĩa Hưng NĐ- 2019) Cho phương trình
9 2 2 1 3 3 4 1 0
x x
m m
có hai
nghiệm thực
1 2
,x x
thỏa mãn
1 2
2 2 12
x x
. Giá trị của
m
thuộc khoảng
A.
9;
. B.
3;9
. C.
2;0
. D.
1;3
.
Lời giải
Đặt
3
x
t
,
0t
. Phương trình đã cho trở thành:
2
2 2 1 3 4 1 0
t m t m
(1)
Phương trình đã cho có hai nghiệm thực
1 2
,x x
khi và chỉ khi phương trình (1) có hai nghiệm
dương phân biệt
2
1
4 8 4 0
0
1
1
0 2 2 1 0
1
2
0
4
3 4 1 0
1
4
m
m m
m
S m m
m
P
m
m
.
Khi đó phương trình (1) có hai nghiệm là
4 1
t m
và
3t
.
Với
4 1
t m
thì
1
1 3
3 4 1 log 4 1
x
m x m
.
Với
3t
thì
2
2
3 3 1
x
x
.
Ta có
1 2 1
2 2 12 2
x x x
3
log 4 1 2
m
5
2
m
(thỏa điều kiện).
Vậy giá trị
m
cần tìm là
5
2
m
nên
m
thuộc khoảng
1;3
.
Câu 24. (Đề Tham Khảo 2018) Có bao nhiêu giá trị nguyên dương của tham số
m
để phương trình
16 2.12 ( 2).9 0
x x x
m
có nghiệm dương?
A.
2
B.
4
C.
3
D.
1
Lời giải
Chọn A
Phương trình
16 2.12 ( 2).9 0
x x x
m
có nghiệm
0;x
Phương trình tương đương
2
4 4
2. ( 2) 0
3 3
x x
m
có nghiệm
0;x
Đặt
4
, 1;
3
x
t t
2
2. ( 2) 0, 1;t t m t
2
2. 2 , 1;t t m t
Xét
2
2.y t t
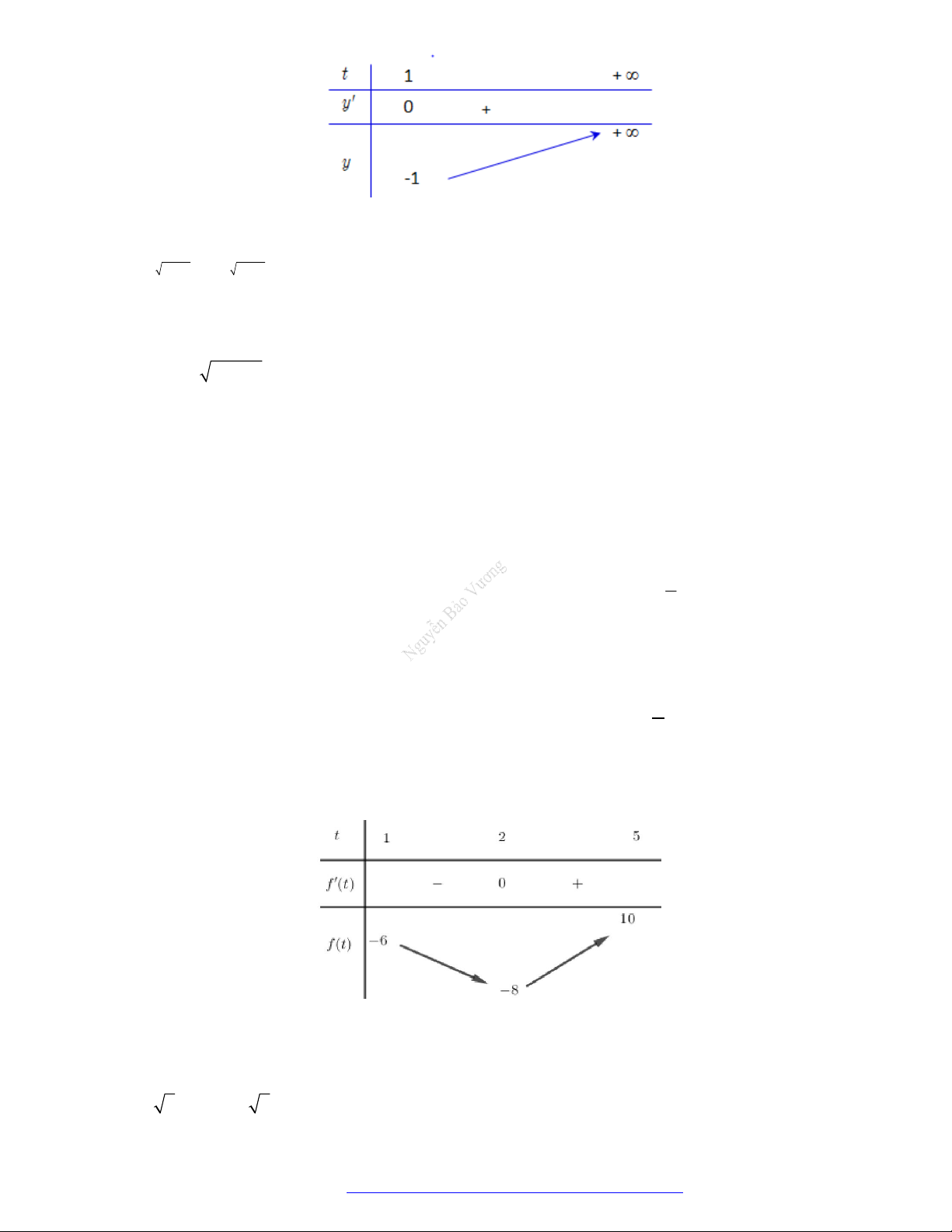
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Phương trình có nghiệm
1;t
khi
2 1 3m m
Câu 25. (THPT Ba Đình -2019) Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2 2
4 4
9 4.3 2 1 0
x x x x
m
có nghiệm?
A.
27
. B.
25
. C.
23
. D.
24
.
Lời giải
ĐKXĐ:
0;4x
.
Đặt
2
4t x x
với
0;4x
thì
0;2t
Đặt
3
t
u
với
0;2t
thì
1;9u
Khi đó, tìm
m
đề phương trình
2
4 2 1 0u u m
có nghiệm thuộc đoạn
1;9
.
2
2 4 1m u u
, với
1;9u
Xét hàm số
2
4 1f u u u
.
2 4 0 2f u u u
.
Ta có,
1 4f
,
2 5f
,
9 44f
.
Do đó, phương trình có nghiệm khi và chỉ khi
5
44 2 5 22
2
m m
.
Vậy có
25
số nguyên của tham số
m
.
Câu 26. (THPT-Thang-Long-Ha-Noi- 2019) Gọi
;a b
là tập các giá trị của tham số
m
để phương trình
2
2 8 0
x x
e e m
có đúng hai nghiệm thuộc khoảng
0;ln 5
. Tổng
a b
là
A. 2. B. 4. C.
6
. D.
14
.
Lời giải
Đặt
x
t e
;
0;ln 5x
tương ứng
1;5t
.
Phương trình thành
2
2 8t t m
.
Xét hàm số
2
2 8f t t t
với
1;5t
có
4 8f t t
Khi đó, phương trình đã cho có hai nghiệm phân biệt thuộc khoảng
0;ln 5
khi phương trình
f t m
có hai nghiệm
1;5t
8 6m
.
Câu 27. (Sở Bắc Giang 2019) Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình
2 1 2 1 8
x x
m
có hai nghiệm dương phân biệt. Số phần tử của S bằng
A. 8. B. 7. C. 10. D. 9.
Lời giải
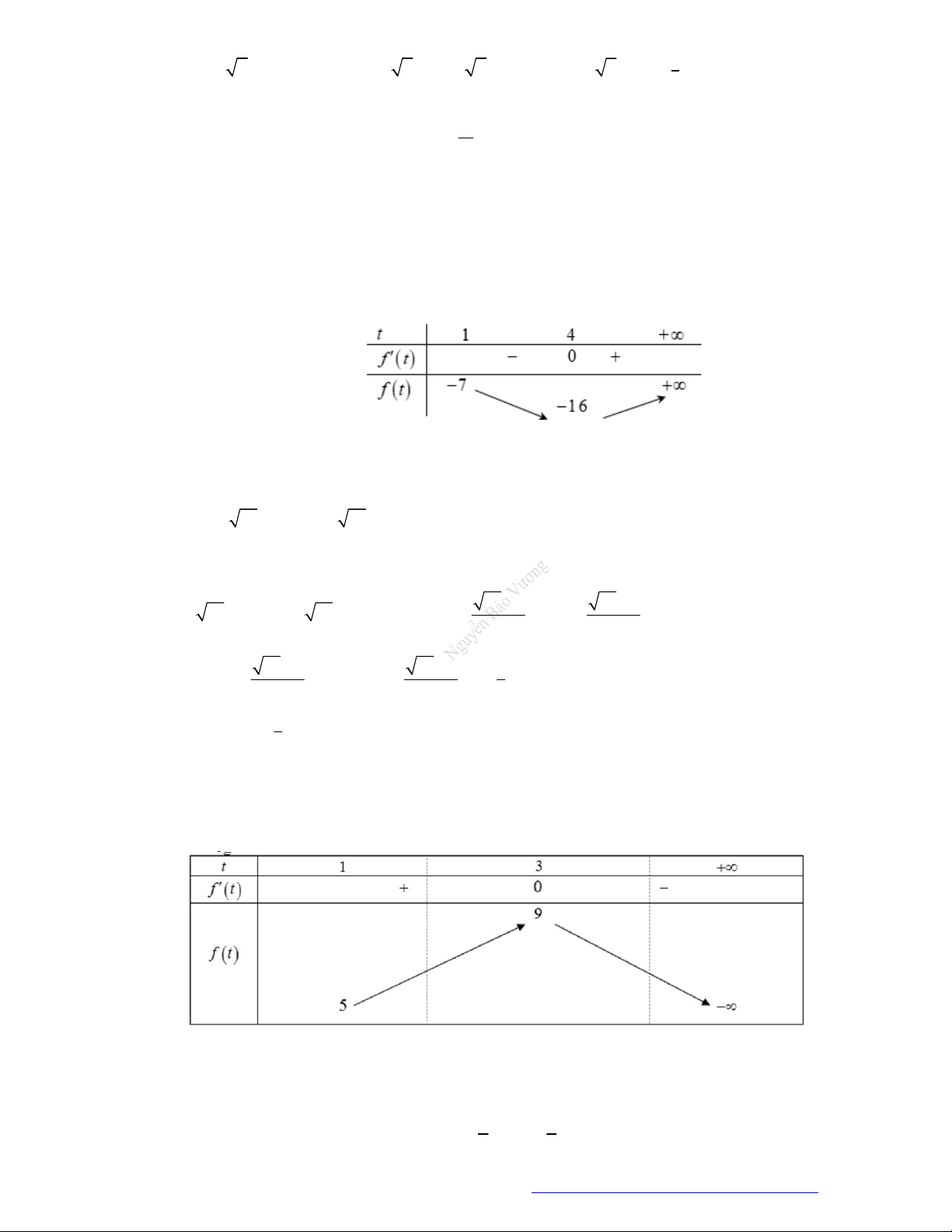
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
Đặt
2 1 , 0
x
t t
. Vì
2 1 . 2 1 1
x x
nên
1
2 1
x
t
.
Phương trình đã cho trở thành
2
8 8
m
t t t m
t
(*).
Phương trình đã cho có hai nghiệm dương phân biệt khi và chỉ khi (*) có hai nghiệm phân biệt lớn
hơn 1.
Xét
2
8f t t t
, trên
1;
.
Ta có
2 8f t t
.
0 4f t t
Bảng biến thiên của hàm
f t
Từ bảng biến thiên ta có (*) có hai nghiệm phân biệt lớn hơn 1 khi và chỉ khi
16 7m
.
Vậy số phần tử của S là 8.
Câu 28. (Chuyên Thái Bình 2019) Tìm số giá trị nguyên của tham số
10;10m
để phương
trình
2 2
2
1
10 1 10 1 2.3
x x
x
m
có đúng hai nghiệm phân biệt?
A.
14
. B.
15
. C.
13
. D.
16
.
Lời giải
2 2
2 2
2
1
10 1 10 1
10 1 10 1 2.3 6
3 3
x x
x x
x
m m
(1)
Đặt
2 2
10 1 10 1 1
, 0
3 3
x x
t t
t
2
1
(1) . 6 6 0
t m t t m
t
(2)
Để
(1)
có đúng hai nghiệm phân biệt khi và chỉ khi
(2)
có một nghiệm lớn hơn 1.
2
(2) 6m t t . Xét hàm số
2
( ) 6f t t t trên khoảng
(1; )
, ta có:
2 6; 0 3f t t f t t
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy
5m
hoặc
9m
là giá trị thỏa mãn yêu cầu bài toán.
Do
10;10m
nên
9; 8; 7; 6; 5; 4; 3; 2; 1;0;1;2;3;4;9m
.
Suy ra có 15 giá trị
m
cần tìm.
Câu 29. (Việt Đức Hà Nội 2019) Phương trình
1 1
. 2 1 0
9 3
x x
m m
có nghiệm khi
m
nhận giá trị:
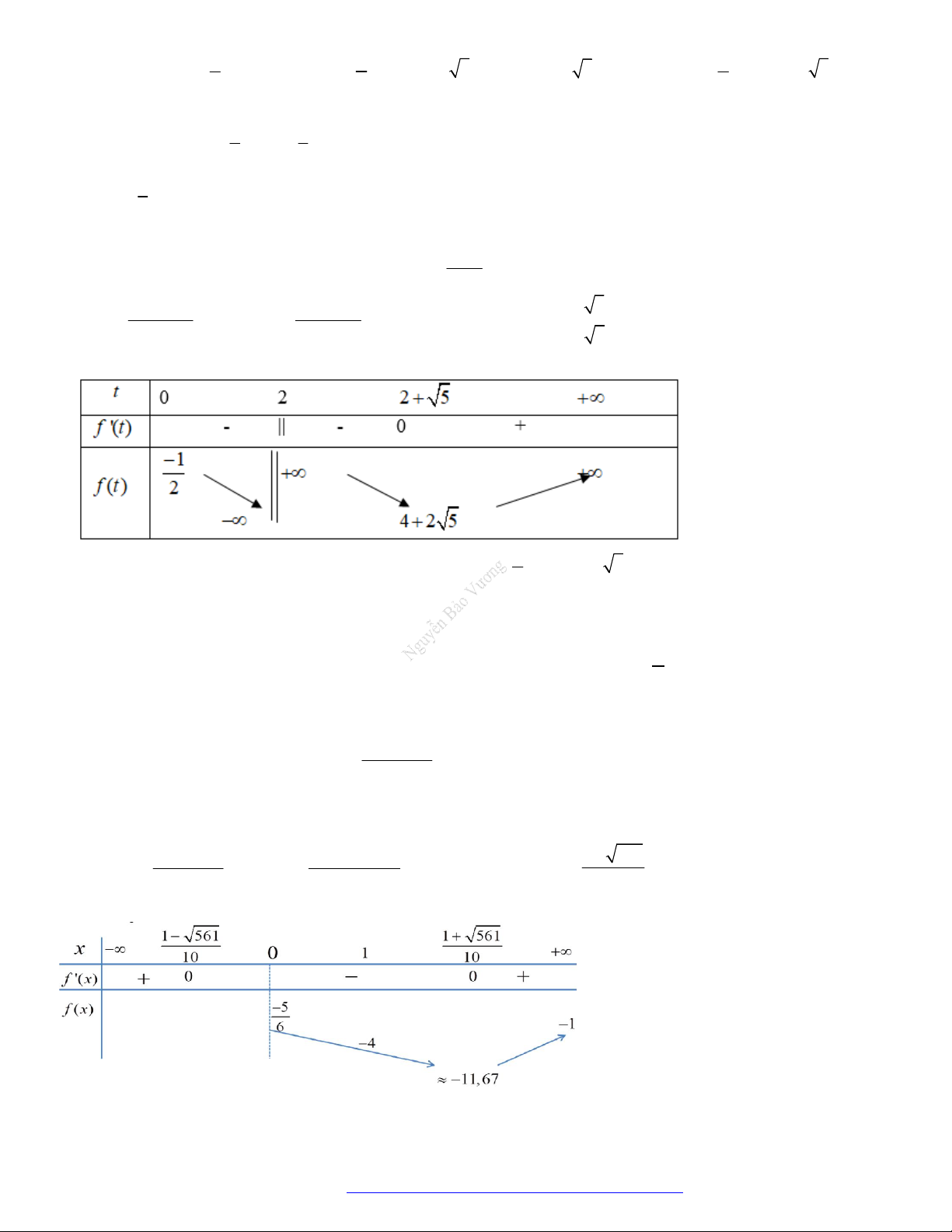
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
2
m
. B.
1
4 2 5
2
m
. C.
4 2 5m
. D.
1
4 2 5
2
m m
.
Lời giải
Ta có phương trình:
1 1
. 2 1 0
9 3
x x
m m
Đặt
1
3
x
t
,
0t
phương trình trở thành:
2
. 2 1 0t m t m
Phương trình có nghiệm
phương trình có nghiệm dương.
2t
không là nghiệm của phương trình nên
2
1
( )
2
t
m f t
t
2
2
4 1
'( )
( 2)
t t
f t
t
,
2
2
2
2 5 ( )
4 1
'( ) 0 0 4 1 0
( 2)
2 5 ( )
t L
t t
f t t t
t
t N
Bảng biến thiên.
Từ bảng biến thiên ta thấy, phương trình có nghiệm khi
1
4 2 5
2
m m
Câu 30. (THPT Gang Thép Thái Nguyên 2019) Số các giá trị nguyên của tham số
m
để phương trình:
1 .16 2 2 3 .4 6 5 0
x x
m m m
có hai nghiệm trái dấu là
A.
4
. B.
8
. C.
1
. D.
2
.
Lời giải
Cách 1.
Đặt 4 , 0
x
t t , phương trình đã cho trở thành:
2
1 2 2 3 6 5 0m t m t m
2
2
6 5
4 6
t t
m
t t
(*).
Phương trình đã cho có hai nghiệm
1 2
,x x trái dấu khi phương trình (*) có hai nghiệm
1 2
,t t thỏa mãn:
1 2
0 1t t .
Đặt
2
2
6 5
4 6
t t
f t
t t
2
'
2
2
10 2 56
4 6
t t
f t
t t
. Suy ra
'
1 561
0
10
f t x
Ta có bảng biến thiên:
Từ bảng biến thiên, ta có phương trình (*) có hai nghiệm
1 2
,t t thỏa mãn:
1 2
0 1t t khi
4 1
m
.
Vậy có hai giá trị nguyên của tham số m thỏa mãn bài toán là
3m
và
2m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
Cách 2:
Đặt
4 , 0
x
t t
, phương trình đã cho trở thành:
2
1 2 2 3 6 5 0m t m t m
(*).
Đặt
2
1 2 2 3 6 5f x m t m t m
.
Phương trình đã cho có hai nghiệm
1 2
,x x trái dấu khi phương trình (*) có hai nghiệm
1 2
,t t thỏa
mãn:
1 2
0 1t t .
Điều đó xảy ra khi:
4 1
1 1 0 1 3 12 0
1
4 1
1 0 0 1 6 5 0
5
6
m
m f m m
m
m
m f m m
m
.
Vậy có hai giá trị nguyên của tham số m thỏa mãn bài toán là
3m
và
2m
.
Câu 31. Phương trình có nghiệm duy nhất. Số giá trị của tham số m thỏa mãn là
A. Vô số B.
1
C.
2
D.
0
Lời giải
Chọn B
Ta có
4 1 2 cos
x x
m x
2 2 cos
x x
m x
Ta thấy nếu
0
x x
là một nghiệm của phương trình thì
0
x x
cũng là nghiệm của phương trình
nên để phương trình có nghiệm duy nhất thì
0
0x
.
Với
0
0x
là nghiệm của phương trình thì
2m
.
Thử lại: Với
2m
ta được phương trình
2
2 2 2cos *
x
x
2; 2VT VP
nên
2
2 2 2
* 0
2cos 2
x
x
x
thỏa mãn. Vậy
2m
.
Câu 32. (Sở Hà Nội 2019) Cho phương trình
2 .2 .cos 4
x x
m x
, với
m
là tham số. Gọi
0
m
là giá
trị của
m
sao cho phương trình trên có đúng một nghiệm thực. Khẳng định nào sau đây là đúng?
A.
0
5; 1 .m
B.
0
5.m
C.
0
1;0 .m
D.
0
0.m
Lời giải
Phương trình
2
4 .2 .cos 4 2 2 .cos
x x x x
m x m x
Điều kiện cần: nếu
0
x
là một nghiệm của phương trình thì
0
2 x
cũng là nghiệm. Vì phương trình
có nghiệm duy nhất nên
0
1x
Thay vào phương trình ta có:
4.m
Điều kiện đủ:
Với
4m
ta có
2
2
4 4.2 cos 4 0 2 2cos 4sin 0
x x x
x x x
2 2 cos
2 2cos
2 2
1
cos 1
cos 1
sin 0
cos 1
x
x
x
x
x
x
x
x
x
x
.
Vậy
4m
thỏa mãn
Câu 33. (HSG Bắc Ninh 2019) Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2 3 3
8 3 .4 3 1 .2 1 1
x x x
x x m x m x
có đúng hai nghiệm phân biệt thuộc
0;10
.
A.
101
B.
100
C.
102
D.
103
Lời giải
4 1 2 . .cos( )
x x
m x
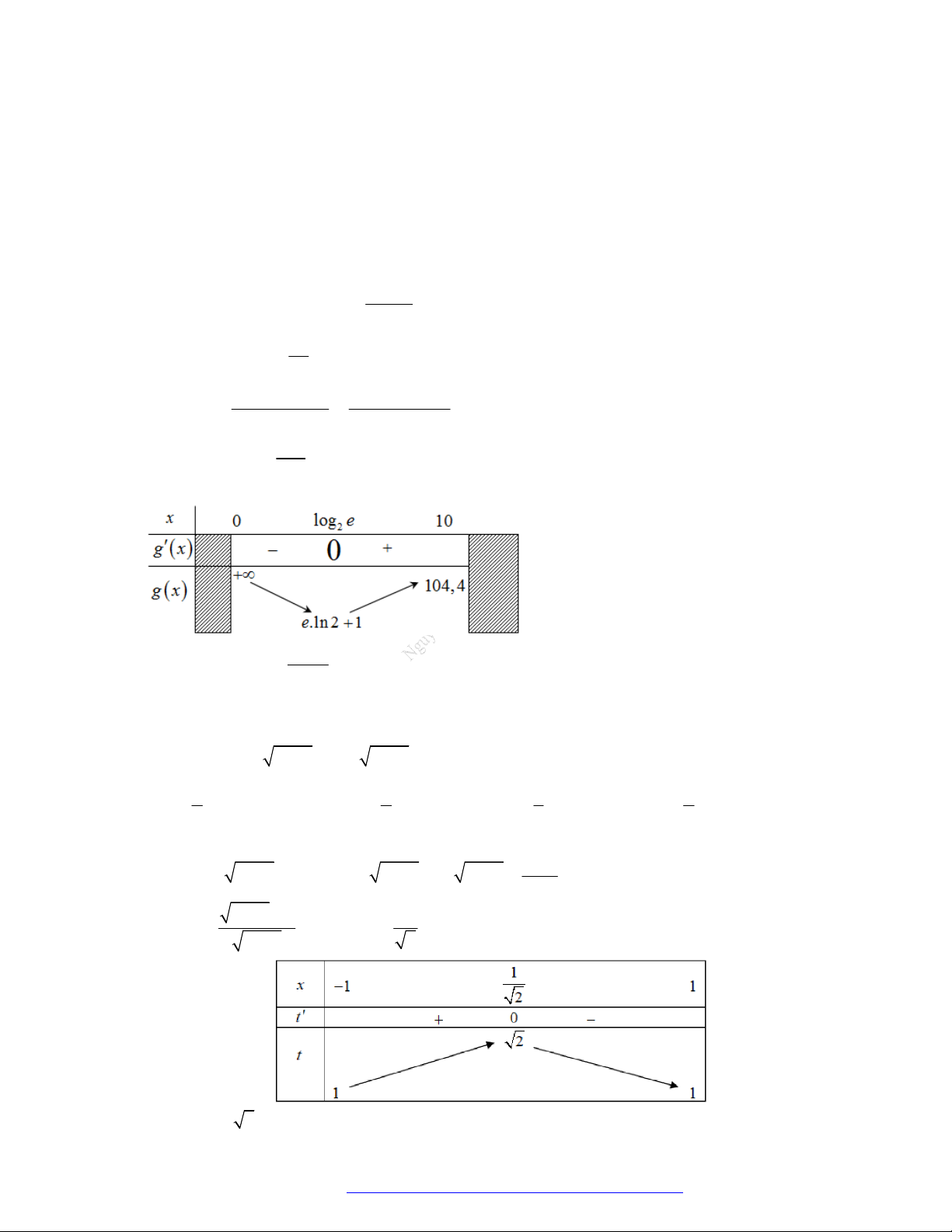
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 3 3
3
3
8 3 .4 3 1 .2 1 1 (1)
2 2
x x x
x x
x x m x m x
x x mx mx
Xét hàm số
3
f t t t
Ta có
2
x
t x
mà
1 2 1024
0 10 1 2 1034 1 1034
0 10
x
x
x x t
x
Xét hàm số
3
, 1;1034 . f t t t t
2
3 1 0, 1;1034
f t t t
hay
3
f t t t
đồng biến trên
1;1034
Suy ra
2
2 2
x
x
x
x mx m
x
Xét hàm số
2
1, 0;10 .
x
g x t
x
2 2
2 .ln 2 1
.2 ln 2 2
x
x x
x
x
g x
x x
2
1
0 log
ln 2
g x x e
BBT
.ln 2 1 104,4ycbt e m
mà
m Z
nên
3,104.m
Có tất cả 102 số nguyên
m
thoả mãn.
Câu 34. (Chuyên Vĩnh Phúc 2019) Tìm tất cả các giá trị thực của tham số
m
để phương trình
3 2 2
2 1 1 1
m m
e e x x x x
có nghiệm.
A.
1
0; ln 2
2
B.
1
; ln 2
2
C.
1
0;
e
D.
1
ln 2;
2
Lời giải
Đặt
2
2 2 2 2
1
1 1 2 1 1
2
t
t x x t x x x x
.
Ta có
2
2
1 1
' , ' 0
2
1
x x
t t x
x
.
Vậy 1; 2t
.
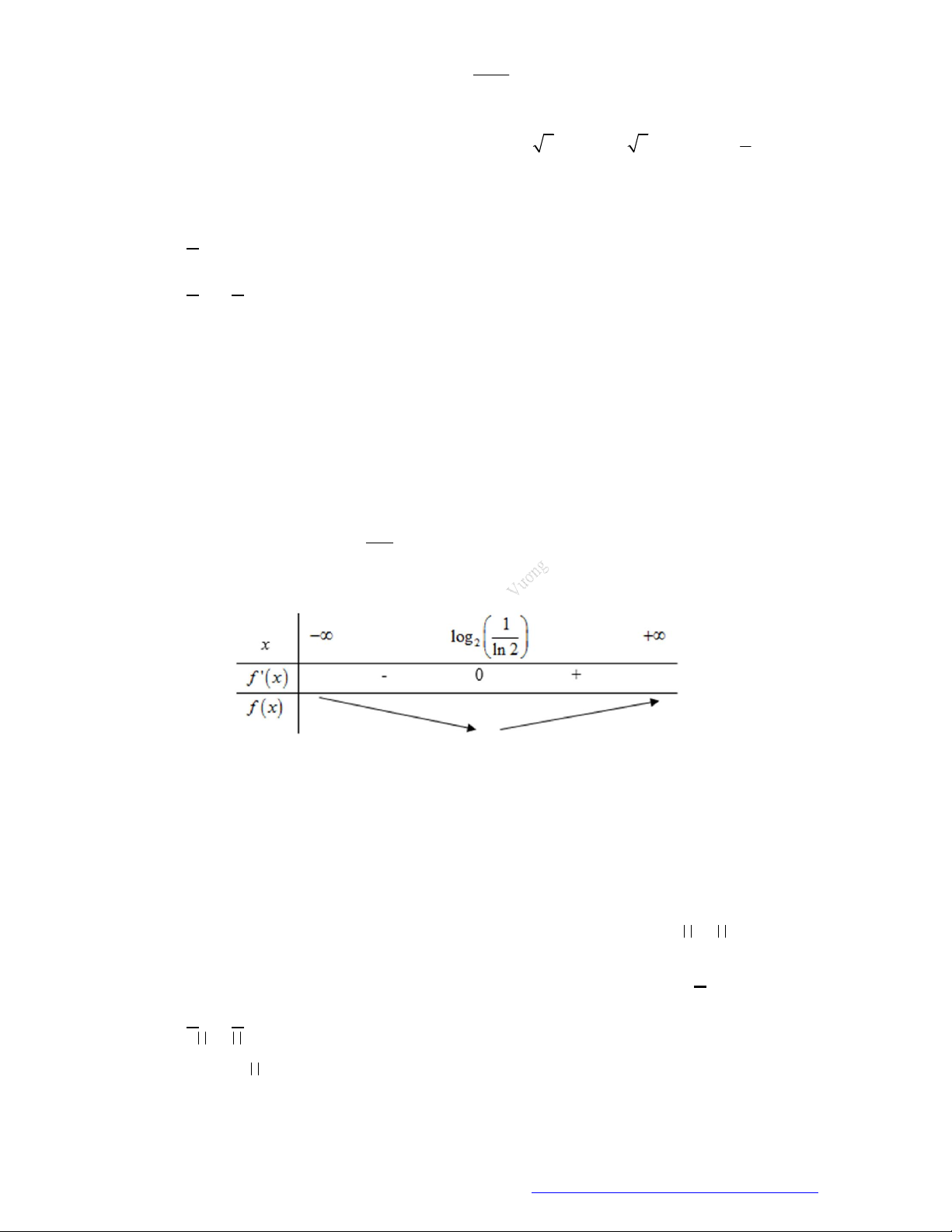
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
Phương trình trở thành
2
3 3 3
1
2 1
2
m m m m m
t
e e t e e t t e t
. (sử dụng hàm đặc
trưng).
Phương trình có nghiệm khi và chi khi
1
1 2 ln 2 ( ; ln 2]
2
m
e m m
.
Câu 35. (SP Đồng Nai - 2019) Gọi
A
là tập tất cả các giá trị thực của tham số
m
sao cho tập nghiệm của
phương trình
.2 1 . 2 1
x x
x x x m m
có hai phần tử. Số phần tử của
A
bằng
A. 2. B. 3. C. 1. D. Vô số.
Lời giải
Chọn A
Phương trình:
.2 1 . 2 1
x x
x x x m m
(1)
2 . 1
x
x m x m x
2 1 0
x
x m x
2 1 0 (2)
x
x m
x
Xét phương trình (2) :2 1 0
x
x
Đặt ( ) 2 1
x
f x x '( ) 2 ln 2 1
x
f x
2
1
'( ) 0 log
ln 2
f x x
Bảng biến thiên của hàm số
( )f x
:
Dựa vào bảng biến thiên ta có phương trình
( ) 0f x
(2)
có nhiều nhất 2 nghiệm.
Mà
(0) (1) 0f f
phương trình
(2)
có đúng 2 nghiệm
0; 1x x
.
phương trình
(1)
có các nghiệm là
0; 1;x x x m
.
Để tập nghiệm của phương trình
(1)
có hai phần tử
0
1
m
m
Số phần tử của
A
bằng 2.
Câu 36. (Nguyễn Huệ- Ninh Bình- 2019)Giá trị của
m
để phương trình
1
4 2 0
x x
m
có nghiệm
duy nhất là:
A.
2m
. B.
0m
. C.
1m
. D.
1m
.
Lời giải
Chọn D
1
4 2 0
x x
m
1
.
Đặt
2
x
t
,
1t
.
Phương trình
1
trở thành:
2 2
2 0 2t t m m t t
2
.
Nhận xét: với
1t
ta có duy nhất
1
nghiệm
x
tương ứng; với mỗi
1t
ta có
2
nghiệm
x
tương
ứng.
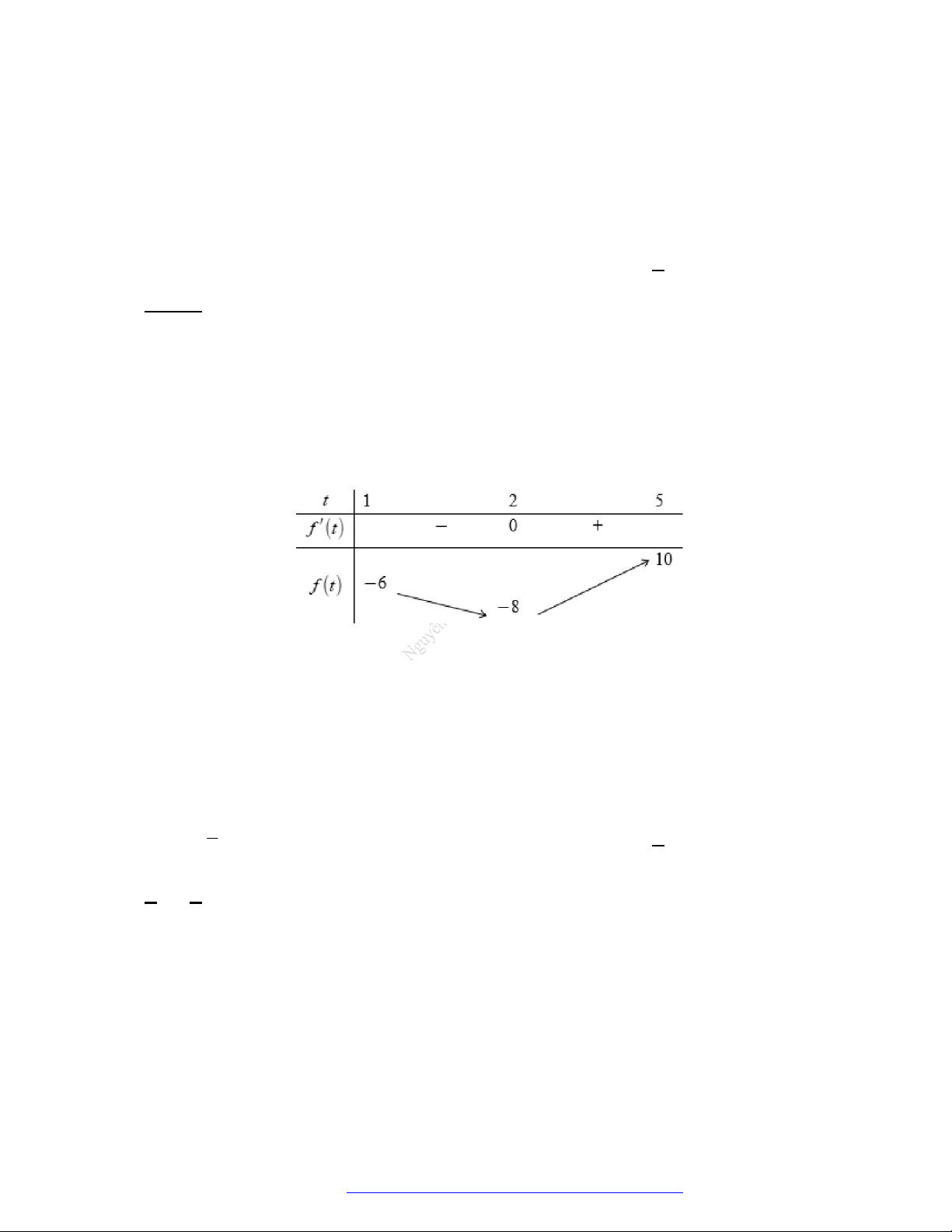
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Phương trình
1
có duy nhất nghiệm
Phương trình
2
có một nghiệm
1
1t và nghiệm còn
lại
2
1t .
1
1t
là nghiệm của phương trình
2
1 0 1m m
.
Khi đó phương trình
2
trở thành:
2
2 1 0 1t t t
(thỏa điều kiện trên).
Vậy phương trình đã cho có nghiệm duy nhất khi và chỉ khi
1m
.
Câu 37. (THPT Thăng Long 2019) Gọi
;a b
là tập hợp tất cả các giá trị thực của tham số
m
để phương
trình
2
2e 8e 0
x x
m
có đúng hai nghiệm thuộc khoảng
0;ln5
. Giá trị của tổng
a b
là
A.
2
. B.
4
. C.
6
. D.
14
.
Lời giải
Chọn D
Đặt
e
x
t
. Khi đó
0 ln5
0;ln5 e ;ex t
hay là
1;5t
.
Phương trình đã cho trở thành
2
2 8t t m
, với
1;5t
.
Vì với mỗi giá trị của
1;5t
ta có một và chỉ một giá trị tương ứng của
0;ln 5x
. Do đó, yêu
cầu bài toán xảy ra khi và chỉ khi phương trình
2
2 8t t m
có hai nghiệm
t
phân biệt thuộc
khoảng
1;5
.
Xét bảng biến thiên của hàm số
2
2 8f t t t
có
4 8f t t
trên đoạn
1;5
:
Dựa vào bảng trên ta thấy, phương trình
2
2 8t t m
có hai nghiệm
t
phân biệt thuộc khoảng
1;5
khi và chỉ khi
8 6m
.
Vậy phương trình
2
2e 8e 0
x x
m
có đúng hai nghiệm thuộc khoảng
0;ln 5
khi và chỉ khi
8; 6m
.
Suy ra
8
a
và
6
b
, do đó
14
a b
.
Câu 38. (Chuyên Long An-2019) Giá trị của tham số
m
thuộc khoảng nào sau đây để phương trình
1
4 .2 2 0
x x
m m
có hai nghiệm
1
x ,
2
x thoả mãn
1 2
3x x .
A.
9
;5
2
m
. B.
2; 1m
. C.
1;3m
. D.
3;5m
.
Lời giải
Chọn D
1
4 .2 2 0
x x
m m
Đặt
2 0
x
t
2
2 2 0t mt m
Giả sử phương trình
có hai nghiệm
1 2
;x x thỏa mãn đều kiện đề bài thì phương trình
**
có
hai nghiệm
1 2
;t t thỏa:
1 2 1 2
1 2
. 8 2 .2 8 2 8 2 8 4
x x x x
t t m m
Thử lại phương trình
ta có
4m
thỏa mãn điều kiện.
Câu 39. (THPT Quỳnh Lưu- Nghệ An- 2019) Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
sao cho phương trình
1 2
16 .4 5 44 0
x x
m m
có hai nghiệm đối nhau. Hỏi
S
có bao nhiêu
phần tử?
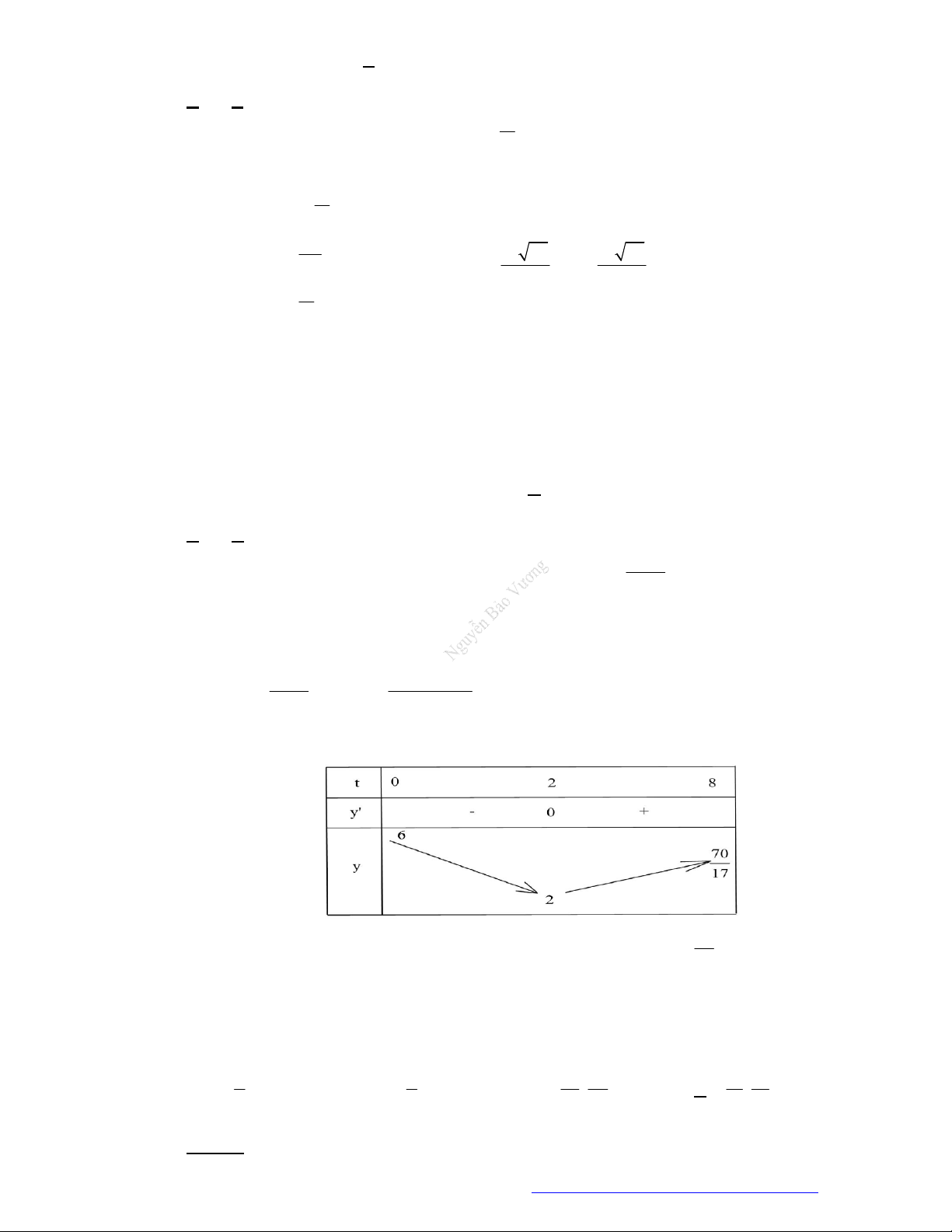
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Chọn B
Ta có
1 2
16 .4 5 44 0
x x
m m
2
2
4 .4 5 44 0
4
x x
m
m
1
.
Đặt
4
x
t
0t
, phương trình có hai nghiệm
1
x
,
2
x
đối nhau
1 2 1 2
0
1 2
4 .4 4 4 1
x x x x
t t
.
Do đó
1
2 2
5 44 0
4
m
t t m
phải có hai nghiệm dương phân biệt
1
t
,
2
t
thỏa
1 2
1t t
0
0
1
S
P
2
2
2
4 5 44 0
16
0
4
5 44 1
m
m
m
m
16 29 16 29
29 29
0
3
m
m
m
m
.
Vậy tập
S
không có phần tử.
Câu 40. (THPT Hai Bà Trưng - Huế - 2019) Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để phương trình
4 2 .2 6 0
x x
m m
có hai nghiệm thực
1 2
,x x
sao cho
1 2
3x x
. Tập hợp
S
có bao nhiêu phần tử?
A. Vô số. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn C
Đặt
2
x
t
,
0t
ta được phương trình
2
2
6
2 6 0 1
2 1
t
t mt m m
t
.
Ta có
1 2
3
1 2
3 2 2 2 8
x x
x x
.
Phương trình
1
có hai nghiệm thỏa mãn
1 2
0 8t t
.
Đặt
2
2
2
2 6
2
6
0
3
2 1
2 1
t t
t
t
f t f t
t
t
t
.
Bảng biến thiên của
f t
trên
0;8
:
Từ bảng biến thiên ta thấy
1
có hai nghiệm
1 2
0 8t t
khi
70
2
17
m
.
Suy ra có hai giá trị nguyên của
m
là
3m
và
4m
.
Câu 41. (THPT Minh Khai - 2019) Giá trị thực của tham số
m
để phương trình
4 2 3 .2 64 0
x x
m
có hai nghiệm thực
1
x
,
2
x
thỏa mãn
1 2
2 2 24x x
thuộc khoảng
nào sau đây?
A.
3
0;
2
. B.
3
;0
2
. C.
21 29
;
2 2
. D.
11 19
;
2 2
.
Lời giải
Chọn D
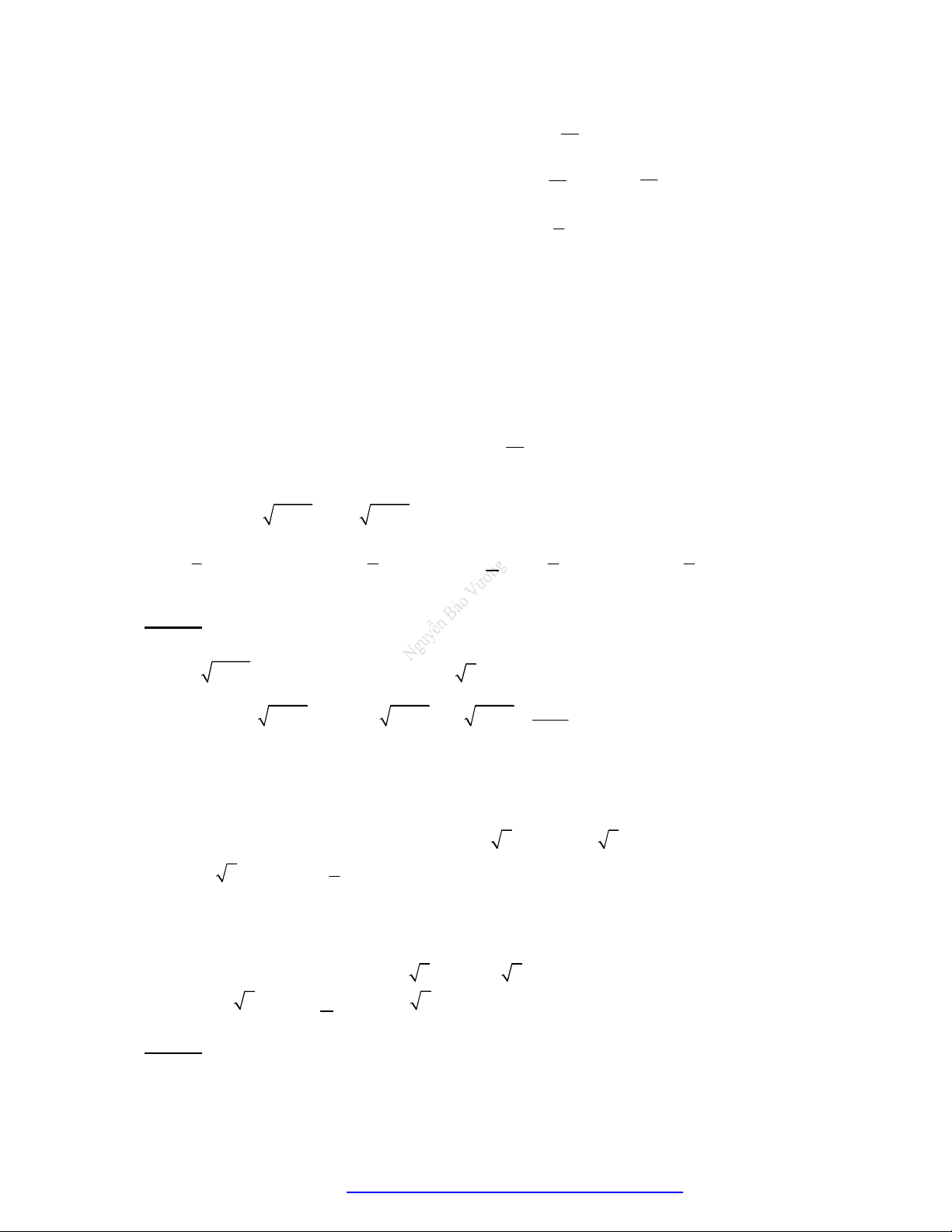
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đặt
2
x
t
, điều kiện
0t
. Phương trình ban đầu trở thành
2
2 3 . 64 0 *
t m t
.
Để phương trình ban đầu có hai nghiệm thực
1
x
và
2
x
thì phương trình
*
phải có hai nghiệm
1
t
,
2
t
dương
0
0
0
S
P
2
4 12 247 0
2 3 0
m m
m
19
2
13
2
3
2
m
m
m
13
2
m
.
Theo định lý Vi-ét, ta có
1 2
. 64
t t
1 2
2 .2 64
x x
1 2
2 64
x x
1 2
6
x x
.
Ta có
1 2
2 2 24
x x
1 2 1 2
. 2 4 24
x x x x
1 2
. 8
x x
.
Từ
1 2
1 2
6
. 8
x x
x x
1
2
1
2
2
4
4
2
x
x
x
x
.
Khi đó, ta có
1 2
1 2
2 2 20 2 3
x x
t t m
17
2
m
.
Câu 42. (Chuyên - Vĩnh Phúc - 2019) Tìm tất cả các giá trị thực của tham số
m
để phương trình
3 2 2
2 1 1 1
m m
e e x x x x
có nghiệm.
A.
1
0;
e
. B.
1
0; ln 2
2
. C.
1
; ln 2
2
. D.
1
ln 2;
2
.
Lời giải
Chọn C
Điều kiện:
1;1
x
Đặt
2
1 .x x t
Vì
1;1 1; 2
x t
Ta có:
2
2
2 2 2 2
1
1 1 2 1 1 .
2
t
t x x x x x x
Phương trình đã cho trở thành:
3 3
.
m m
e e t t
Xét hàm số
3 2
, 3 1 0
f u u u f u u u
do đó hàm số
f
đồng biến trên
.
Phương trình
3 3m m m m
e e t t f e f t e t
.
Phương trình có nghiệm khi và chỉ khi
1 2 0 2
m m
e e
( do
0
m
e
)
1
ln 2 ; ln 2
2
m m
.
Câu 43. (Chuyên Quang Trung- Bình Phước 2019) Tìm tất cả các giá trị thực của tham số
m
để
phương trình
4 1 .2 2 0
x x
m
có hai nghiệm
1 2
,x x
thoả mãn
1 2
1
x x
.
A.
R
m
. B.
1 2 2; 1 2 2
m m
.
C.
1 2 2
m
. D.
1 2 2
m
.
Lời giải
Chọn D
Đặt
2 , 0
x
t t
. Ta có phương trình
2
1 2 0
t m t
(1).
Phương trình đã cho có hai nghiệm
1 2
,x x
khi phương trình (1) có hai nghiệm
1 2
, 0
t t
.
Khi đó
1 2 2 1 2 2 2 1 2
log log log .x x t t t t
.
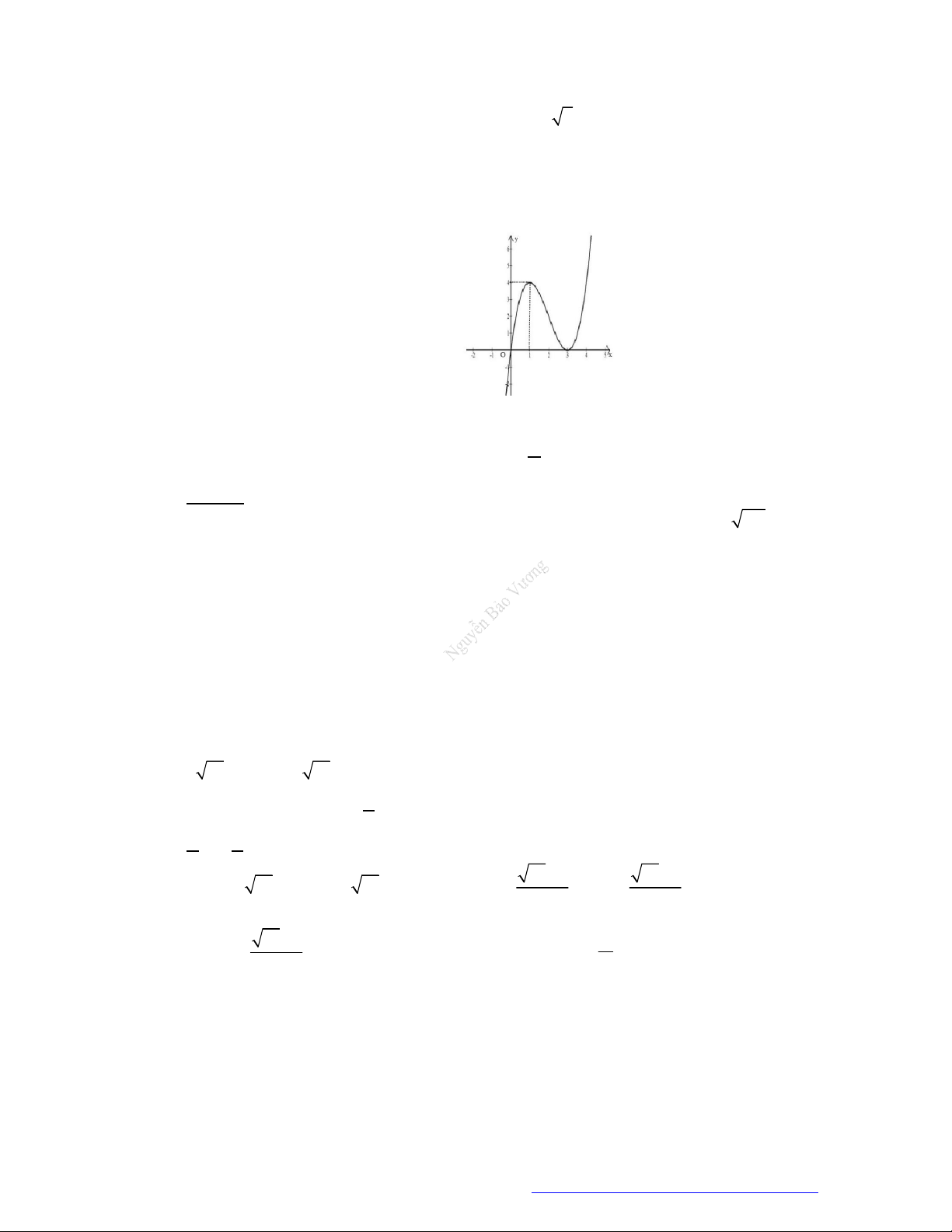
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
Bài toán trở thành tìm
m
để phương trình (1) có hai nghiệm dương phân biệt
1 2
,t t thoả mãn
2 1 2
log . 1t t
2
2 1 2
1 8 0
1 0
log 1
m
m
t t
1 2 2m
.
Câu 44. (Chuyên Quang Trung- Bình Phước 2019) Cho hàm số
y f x
liên tục trên
và có đồ thị
như hình vẽ
Tập hợp tất cả các giá trị thực của
m
để phương trình
2
x
f e m
có đúng 2 nghiệm thực là
A.
0;4
. B.
0;4
. C.
0 4;
. D.
4;
.
Lời giải
Chọn C
Đặt
2
x
t e . Ta có
2
0 1x t
, nếu
1t
thì
0x
và nếu
1t
thì
lnx t
.
Phương trình
2
1
x
f e m
trở thành phương trình
2f t m
.
Sử dụng các nhận xét ở trên và đồ thị của hàm số
y f x
ta có
1
có đúng 2 nghiệm
2
có đúng 1 nghiệm thuộc
1;
và nghiệm này lớn hơn 1.
0
4
m
m
Vậy tập hợp các giá trị nguyên của
m
thỏa yêu cầu bài toán là
0 4;
.
Câu 45. (Chuyên Thái Bình - 2019) Tìm số giá trị nguyên của tham số
10;10m
để phương trình
2 2
2
1
10 1 10 1 2.3
x x
x
m
có đúng hai nghiệm phân biệt.
A.
14
. B.
15
. C.
13
. D.
16
.
Lời giải
Chọn B
Ta có:
2 2
2 2
2
1
10 1 10 1
10 1 10 1 2.3 6
3 3
x x
x x
x
m m
. (1)
Đặt
2
10 1
3
x
t
,
0t
. Phương trình (1) trở thành:
2
6 6
m
t t t m
t
(2).
Phương trình (1) có
2
nghiệm phân biệt phương trình (2) có đúng
1
nghiệm lớn hơn 1.
Xét hàm số:
2
6g t t t
trên khoảng
1;
.
Ta có:
2 6 0 3g t t g t t
.
Bảng biến thiên:
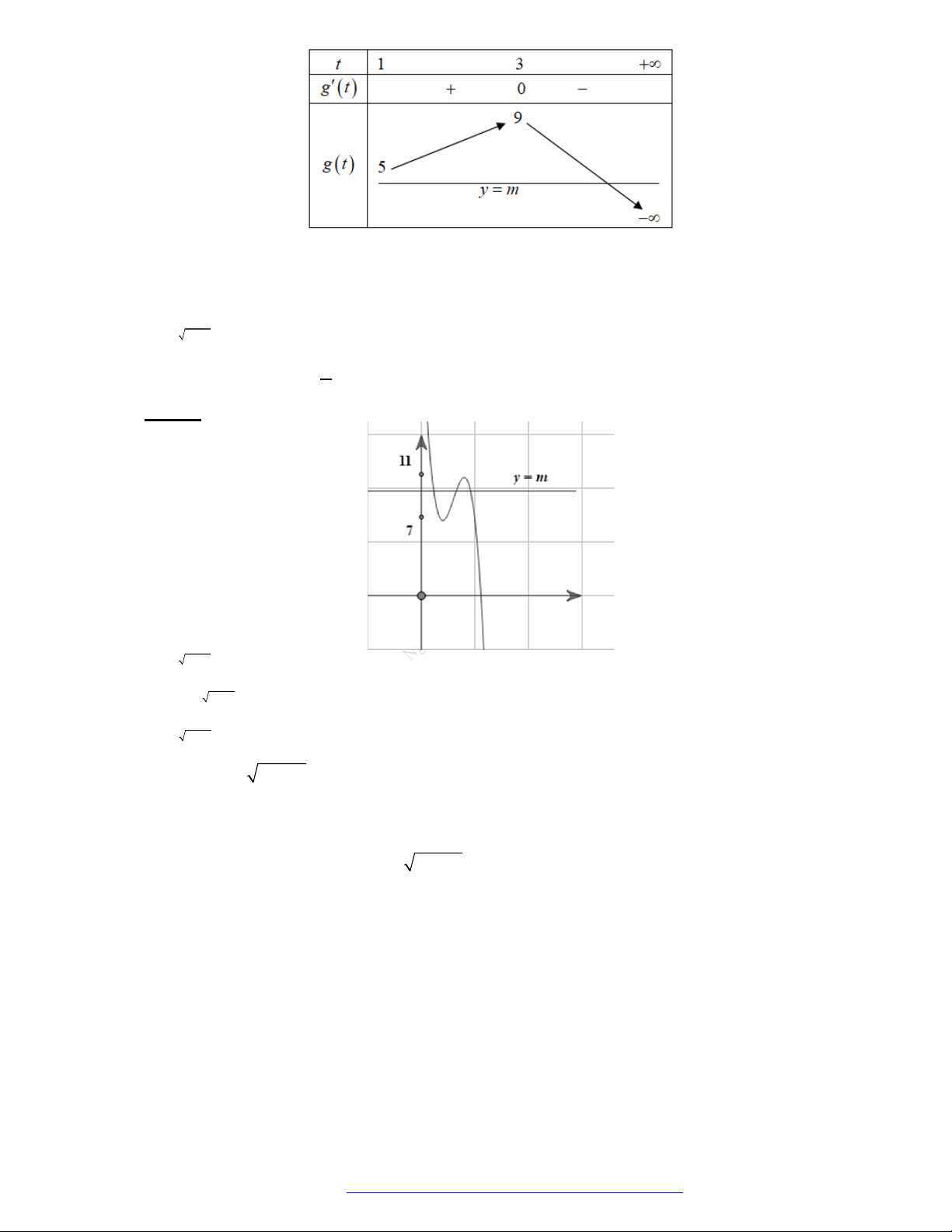
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 52 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Nhìn vào bảng biến thiên ta có: phương trình (2) có đúng
1
nghiệm lớn hơn 1
5m
.
Kết hợp điều kiện m nguyên và
10;10 10;5m m
Có
15
giá trị m thỏa yêu cầu
đề.
Câu 46. (Thi thử cụm Vũng Tàu - 2019) Tổng tất cả các giá trị nguyên của
m
để phương trình
3
3 3 3 2 3
3 9 24 .3 3 1
x m x x x
x x x m
có 3 nghiệm phân biệt.
A.
34
. B.
27
. C.
38
. D.
45
.
Lời giải
Chọn B
3
3
3
3 3 3 2 3
3
3 3 3
3
3 3 3
3
3 3 3 3
3 9 24 .3 3 1
3 3 27 3 .3 3 1
3 3 3 27 3 3 1
3 ; 3
1 3 27 27. 3 3 3
x m x x x
x m x x x
m x x
b a b a
x x x m
x m x
x m x
a x b m x
b a b a
Xét
3 2
3 ' 3 .ln 3 3 0
t t
f t t f t t t R
3
3
3 2
3 3
3 3 9 24 27
f a f b a b x m x
m x x x x x
3 2 2
9 24 27 ' 3 18 x 24
' 0 2 4
f x x x x f x x
f x x x
Dựa vào đồ thị:
7 11 8,9,10.m m
Câu 47. (Chuyên ĐH Vinh- 2019) Cho số thực
m
và hàm số
y f x
có đồ thị như hình vẽ dưới đây.
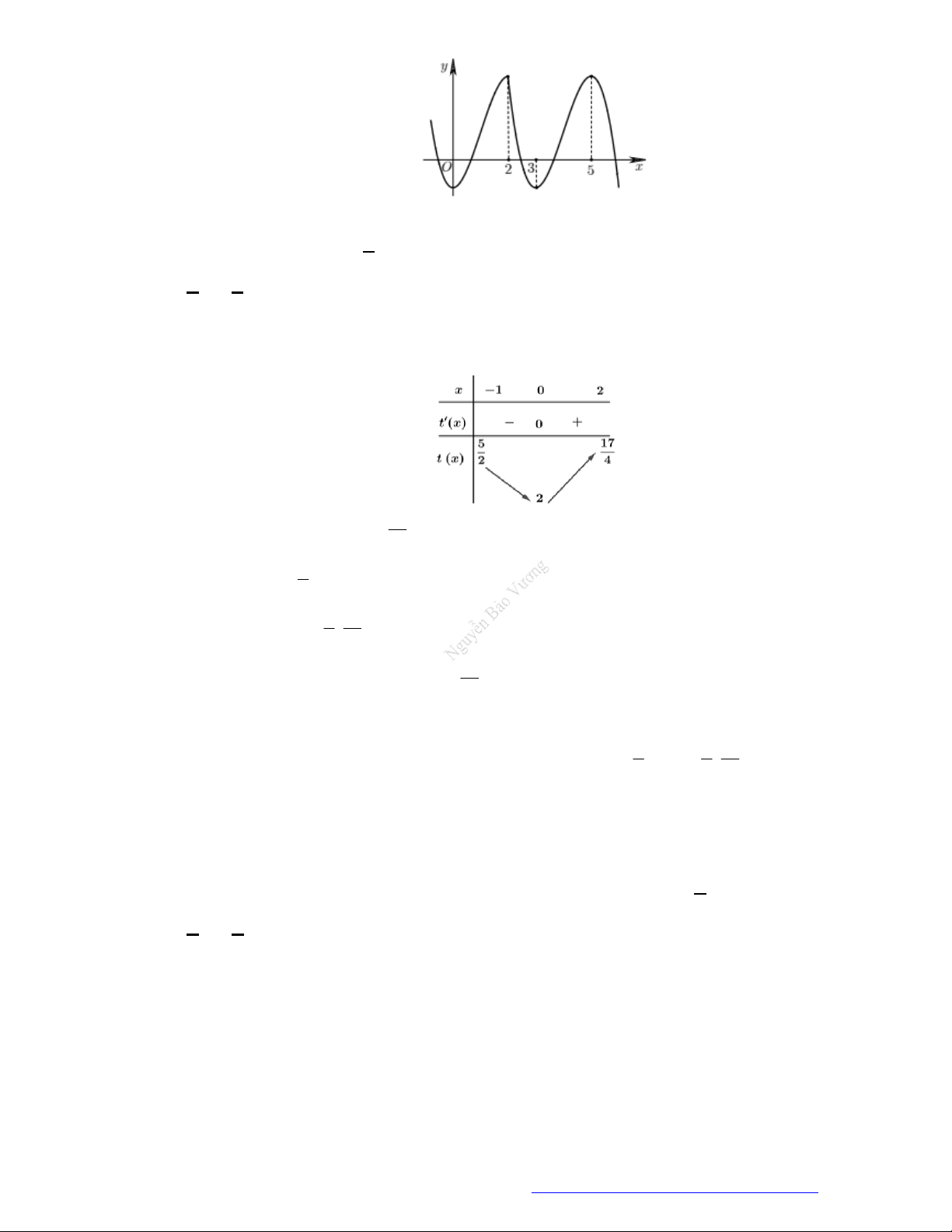
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53
Phương trình
2 2
x x
f m
có nhiều nhất bao nhiêu nghiệm phân biệt thuộc đoạn
1;2
?
A.
2
. B.
3
. C.
4
. D.
5
.
Lời giải
Chọn B
Đặt
2 2
x x
t t x
, với
1;2
x
.
Hàm số
t t x
liên tục trên
1;2
và
' 2 .ln 2 2 .ln 2, ' 0 0
x x
t x t x x
.
Bảng biến thiên:
Vậy với
17
1; 2 2;
4
x t
.
Với mỗi
5
2;
2
t
có 2 giá trị
x
thỏa mãn
2 2
x x
t
.
Với mỗi
5 17
2 ;
2 4
t
có duy nhất 1 giá trị
x
thỏa mãn
2 2
x x
t
.
Xét phương trình
f t m
với
17
2;
4
t
.
Từ đồ thị trên ta thấy phương trình
2 2
x x
f m
có số nghiệm nhiều nhất khi và chỉ khi
phương trình
f t m
có
2
nghiệm
1 2
,t t
, trong đó có
1 2
5 5 17
2; , ;
2 2 4
t t
. Do đó phương
trình
2 2
x x
f m
có nhiều nhất
3
nghiệm phân biệt thuộc đoạn
1;2
.
Câu 48. (THPT Thuận Thành 3 - Bắc Ninh 2019) Gọi
S
là tổng các giá trị nguyên của tham số
m
để
phương trình
3 2
4 7 2 6
x x
m m
có nghiệm
1;3
x
. Chọn đáp án đúng.
A.
35S
. B.
20S
. C.
25S
. D.
21S
.
Lời giải
Chọn D
Đặt
2
x
t
thì phương trình đã cho trở thành
2 2
8 7 6t t m m
với
2 8t
(vì
1 3x
).
Khi đó phương trình
3 2
4 7 2 6
x x
m m
có nghiệm
1; 3x
2
6f t m m
có nghiệm
2; 8t
, với
2
8 7f t t t
.
Ta có
2 8f t t
;
0 4 2; 8
f t t
.
Bảng biến thiên:
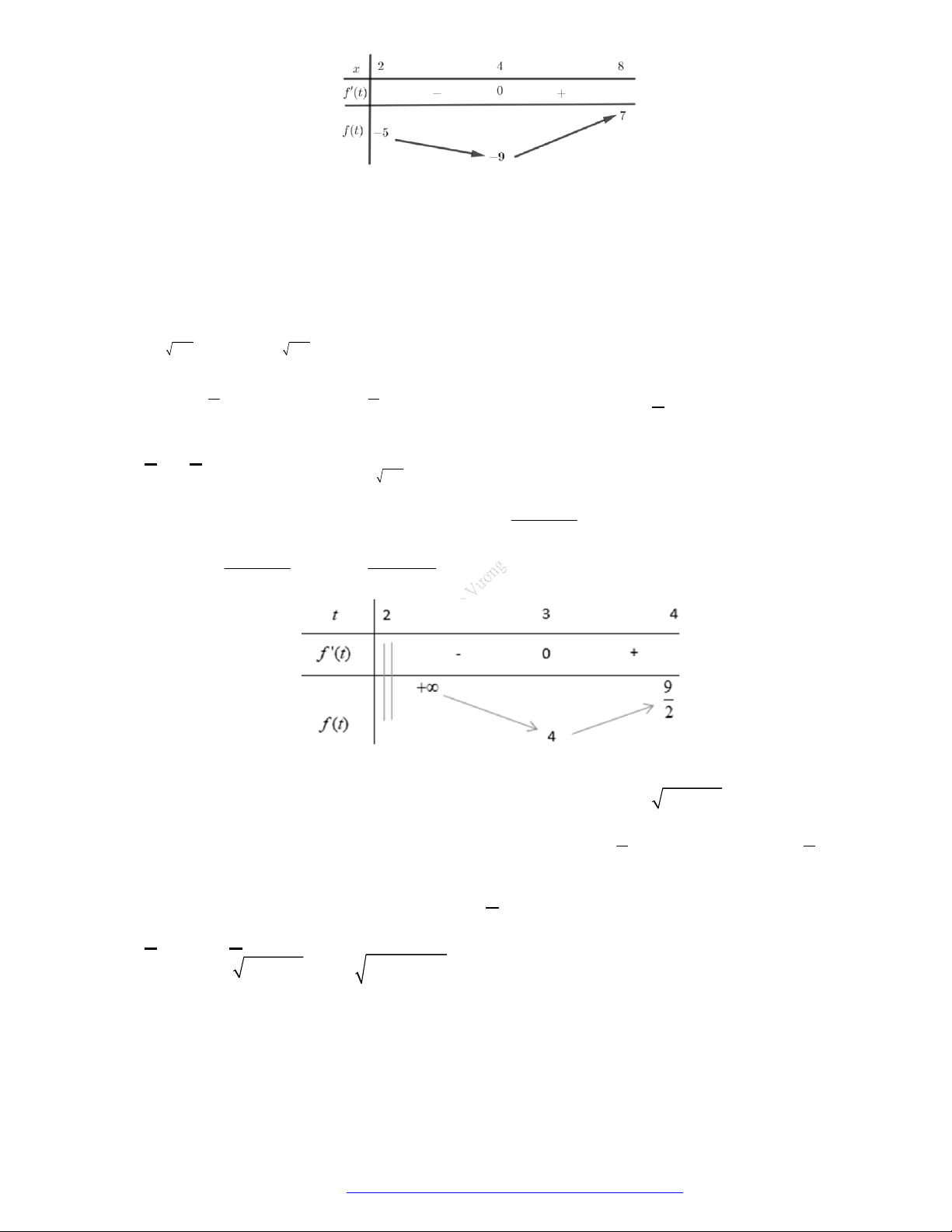
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 54 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào bảng biến thiên ta có:
2
9 6 7m m
2
2
6 9 0
6 7 0
m m
m m
7 1
m
m
7 1m
.
Vì
m
nguyên nên
6; 5; 4; 3; 2; 1;0m
.
Suy ra
6 5 4 3 2 1 0 21
S
.
Câu 49. (Chuyên Bắc Giang 2019) Tập các giá trị của
m
để phương trình
2 2
1 1 1 1
4 2 2 2 1 0
x x
m m
có nghiệm là
A.
9
;
2
. B.
9
4;
2
. C.
;4
. D.
4;
.
Lời giải
Chọn D
Điều kiện:
1 1x
. Đặt
2
1 1
2
x
t
;
1 1 2 4x t
.
Phương trình trở thành:
2
2
2 1
( 2) 2 1 0
2
t t
t m t m m
t
(*)
Đặt
2 2
2
2 1 4 3
( ) '( )
2
2
t t t t
f t f t
t
t
Phương trình có nghiệm
(*) có nghiệm
2;4t
4m
.
Câu 50. Cho hàm số
4 7
3 1 .2 – 6 3
x x
f x x x
, khi phương trình
2
7 4 6 9 3 1 0f x x m
có
số nghiệm nhiều nhất thì giá trị nhỏ nhất của tham số
m
có dạng
a
b
(trong đó
a
,
b
và
a
b
là
phân số tối giản). Tính
T a b
.
A.
7T
. B.
11T
. C.
8T
. D.
13T
.
Lời giải
Chọn C.
Đặt
2
2
7 4 6 9 7 4 1 3 1 3;7 .
t x x x
Khi đó
1 3 .f t m
Xét hàm số
4 7
3 1 2 6 3
t t
f t t t
trên đoạn
3;7 .
Ta có
4 7 7
3 ln3 2 1 2 ln 2 6;
t t t
f t t
2 2
4 7 7 7
3 ln 3 2 ln 2 2 ln 2 1 2 ln 2
t t t t
f t t
2
4 7
0, 3;7
3 ln3 2 1 ln 2 2 ln 2 0.
t t
t
t
Suy ra hàm số
f t
đồng biến trên
3;7 .

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 55
Lại có
3 0
0
7 0
f
f x
f
có nghiệm duy nhất
0
t thuộc
3;7 .
Dựa vào BBT, ta thấy phương trình
1 3f t m
có số nghiệm nhiều nhất
0
0
1
5
1 3 4 .
3 3
f t
f t m m
Suy ra giá trị nhỏ nhất của
m
là
5
5
3
3
a
b
nên
8a b
.
Câu 51. Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2 2
1 1 1 1
9 3 .3 2 1 0
x x
m m
có nghiệm thực?
A.
5
. B.
7
. C. Vô số. D.
3
.
Lời giải
Chọn B
Ta có
2
2 2 1 1
0 1 1 1 1 1 2 3 3 9
x
x x
Đặt
2
1 1
3
x
t
phương trình trở thành
2
3 . 2 1 0 1t m t m
Phương trình
2 2
1 1 1 1
9 3 .3 2 1 0
x x
m m
có nghiệm thực phương trình
1
có nghiệm
3;9t
2
3 1 1
1 1
2 2
t t
m m t
t t
vì
2 0t
Xét
1
1
2
f t t
t
liên tục trên đoạn
3;9
có
2
1
1 0 3;9
2
f t t f t
t
đồng biến trên đoạn
3;9
.Có
55
3 1; 9
7
f f
Vậy phương trình
2 2
1 1 1 1
9 3 .3 2 1 0
x x
m m
có nghiệm thực
55
1;
7
m
m
Có 7 giá trị nguyên.
Câu 52. (THPT Thăng Long 2019) Cho hệ phương trình
2 2
2 2 2
1
2 1 2 .2 . 1
x y y
x y
x y
m y
,
m
là tham
số. Gọi
S
là tập các giá trị
m
nguyên để hệ
1
có một nghiệm duy nhất. Tập
S
có bao nhiêu
phần tử?
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn B
Điều kiện
1 1;1y y
.
Từ phương trình thứ nhất của hệ
1
ta có
2 2 2
x y y
x y y
.
Xét hàm số
2
t
y f t t
với
t
.
Dễ thấy
2 .ln 2 1 0
t
y
với mọi
t
nên hàm số
y f t
đồng biến trên
.
Do đó phương trình
2
tương đương với
2x y y x y
.
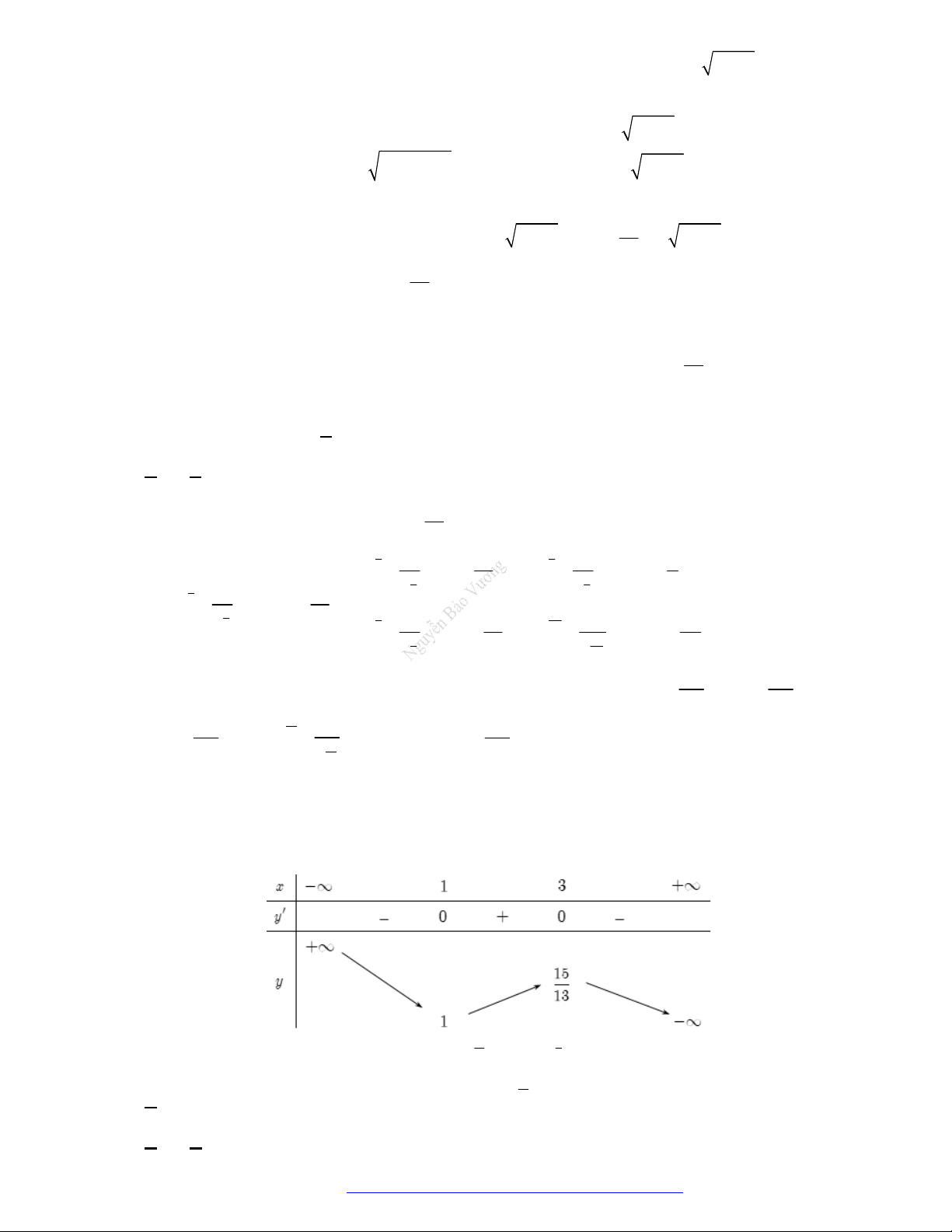
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 56 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Thay
2x y
vào phương trình thứ hai của hệ
1
ta được
2 2
4 1 2 .2 . 1 3
y y
m y
.
Để hệ đã cho có nghiệm duy nhất thì phương trình
3
phải có nghiệm duy nhất
1;1y
.
Giả sử
0
1;1y
là một nghiệm của
3
thì
0 0
2 2
0
4 1 2 .2 . 1
y y
m y
.
Khi đó
0 0 0 0
2
2 2 2
0 0
4 1 2 .2 . 1 4 1 2 .2 . 1
y y y y
m y m y
nên
0
y
cũng là
nghiệm của
3
. Suy ra
0 0 0
0y y y
. Thay
0y
vào
3
ta được
0m
.
Thử lại: với
0m
thì
3
viết thành
2 2
1
4 1 2.2 . 1 2 2 1 4
2
y y y
y
y y
.
Ta có
4 2VT
, dấu bằng khi
1
2 0
2
y
y
y
;
4 2VP
, dấu bằng khi
0y
.
Suy ra phương trình
4
có nghiệm duy nhất là
0y
. Vậy
0m
thỏa mãn.
Câu 53. Cho
,a b
là các số thực thỏa mãn
0a
và
1a
, biết phương trình
1
2cos
x
x
a bx
a
có
7
nghiệm phân biệt. Tìm số nghiệm thực phân biệt của phương trình
2
2 cos 2 1 0
x x
a a bx
.
A.
28
. B.
14
. C.
0
. D.
7
.
Lời giải
Chọn B
Ta có
2
2 cos 2 1 0
x x
a a bx
1
2 2 cos 1
x
x
a bx
a
2
2
2
2
1
4cos
2
x
x
bx
a
a
2
2
2
2
1
2cos
2
1
2cos
2
x
x
x
x
bx
a
a
bx
a
a
2
2
2
2
1
2cos 1
2
1
2cos 2
2
x
x
x
x
x
a b
a
x
a b
a
.
Nếu phương trình
1
và phương trình
2
có nghiệm chung là
0
x thì
0 0
2cos 2cos
2 2
bx bx
0
cos 0
2
bx
0
0
2
0
2
1
0 0
x
x
a x
a
0
cos 1
2
bx
(Vô lí).
Do đó phương trình
1
và phương trình
2
không có nghiệm chung.
Mặt khác theo giả thiết phương trình
1
và phương trình
2
đều có
7
nghiệm phân biệt.
Vậy phương trình đã cho có
14
nghiệm phân biệt.
Câu 54. Cho hàm số bậc ba
( )y f x
có bảng biến thiên như sau
Giá trị lớn nhất của
m
để phương trình
3 2
13 3
2 ( ) ( ) 7 ( )
2 2
f x f x f x
e m
có nghiệm trên đoạn
0;2
là
A.
4
e
. B.
3
e
. C.
15
13
e . D.
5
e
.
Lời giải
Chọn A
Giả sử
2
'( ) ( 1)( 3) ( 4 3)( 0)f x a x x a x x a

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 57
3
2 2
( ) '( )d ( 4 3)d ( 2 3 )
3
x
f x f x x a x x x a x x C
Do
15
(1) 1, (3)
13
f f
nên ta có hệ
4 3
1
3 26
15 15
13 13
a C a
C C
Khi đó hàm số
3 2
1 3 9 15
( )
26 13 26 13
f x x x x
Xét hàm số
( )f x
trên đoạn
0;2
2
1
3
'( ) ( 4 3), '( ) 0
3 0;2
26
x
f x x x f x
x
Ta có:
15 14
(0) , (1) 1, (2)
13 13
f f f
nên
15
1 ( )
13
f x
Đặt
( )f x t
Xét hàm số
3 2
13 3
( ) 2 7
2 2
g t t t t
trên đoạn
15
1;
13
2
1
'( ) 6 13 7, '( ) 0
7 15
1;
6 13
t
g t t t g t
t
Ta có:
15 8778
(1) 4, ( )
13 2197
g g
Suy ra GTLN của
( )g x
trên đoạn
15
1;
13
bằng 4. Theo yêu cầu bài toán thì
4
e
m
.
Câu 55. (Hoàng Hoa Thám - Hưng Yên 2019) Cho phương trình
4 15 2 1 4 15 6 0
x x
m
(
m
là tham số ). Biết phương trình có hai nghiệm phân
biệt
1 2
,x x
thỏa mãn
1 2
2 0
x x
. Khi đó
m
thuộc khoảng nào sau đây?
A.
3;5
. B.
1;1
. C.
1;3
. D.
; 1
.
Lời giải
Chọn A
Đặt
1
4 15 0 4 15
x x
t t
t
Phương trình trở thành:
2
2 1
6 0 6 2 1 0 *
m
t t t m
t
1
1 2
2
2
1
1 2
2
2
2
4 15
2 0 4 15 1 1 1.
4 15
x
x x
x
t
x x
t
Do đó, phương trình đã cho có hai nghiệm phân biệt
1 2
,x x
thỏa mãn
1 2
2 0
x x
khi và chỉ khi
phương trình
*
có hai nghiệm phân biệt dương
1 2
,t t
thỏa mãn
2
1 2
t t
Tức là:
2
1 2
0
0
0
1
S
P
t t
+)
0 8 2 0 4.
m m
+)
6 0
S
luôn đúng.
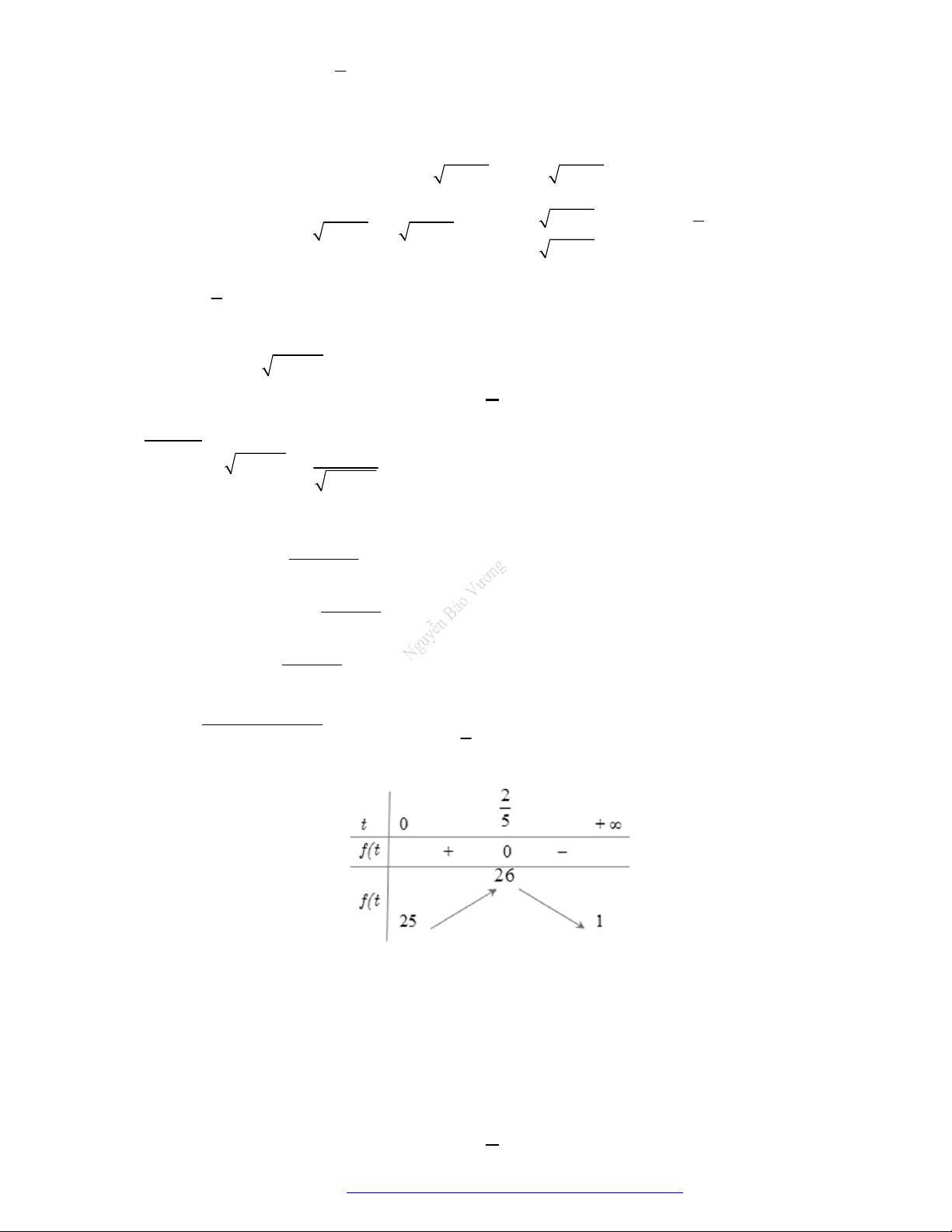
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 58 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
+)
1
2 1 0
2
P m m
.
+) Theo Vi-ét:
1 2
1 2
6 2
. 2 1 3
t t
t t m
Từ
1
và
3
suy ra:
2
3
3 3
2 2 1
2 1 2 1 2 1 .t m t m t m
Thay vào
2
ta được
3
2
3 3
3
7
2 1 2
2
2 1 2 1 6 0
2 1 3
14
m tm
m
m m
m
m ktm
Vậy
7
3;5 .
2
m
Câu 56. (THPT Minh Khai 2019) Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để phương
trình
5 10 25 4
x x
m
có nghiệm duy nhất. Số tập con của
S
là
A.
3
. B.
4
. C.
16
. D.
15
.
Lời giải
Chọn C
5 10
5 10 25 4 1
25 4
x
x x
x
m m
.
TH 1:
0m
. Phương trình
1
vô nghiệm.
TH 2:
0m
.
2
2
5 10
(1)
25 4
x
x
m
Đặt
5
x
t
,
0t
. Ta có:
2
2
2
10
(2)
4
t
m
t
Xét hàm số
2
2
10
4
t
f t
t
trên khoảng
0;
2
2
2
10( )
20 192 80
. ( ) 0 .
2
( )
4
5
t l
t t
f t f t
t tm
t
Bảng biến thiên:
Đề phương trình
1
có đúng một nghiệm
Phương trình
2
có đúng một nghiệm
0t
2
2
26
.
1 25
m
m
Do điều kiện
0
2,3, 4,5
m
m
m
.
Vậy
2,3,4,5S
, do đó số tập con của
S
là
4
2 16
.
Câu 57. (Sở Quảng Trị 2019) Tìm tập hợp tất cả các giá trị tham số
m
để phương trình
2 2
2 1 2 2
4 .2 3 2 0
x x x x
m m
có 4 nghiệm phân biệt.
A.
1;
. B.
;1 2;
. C.
2;
. D.
2;
.
Lời giải
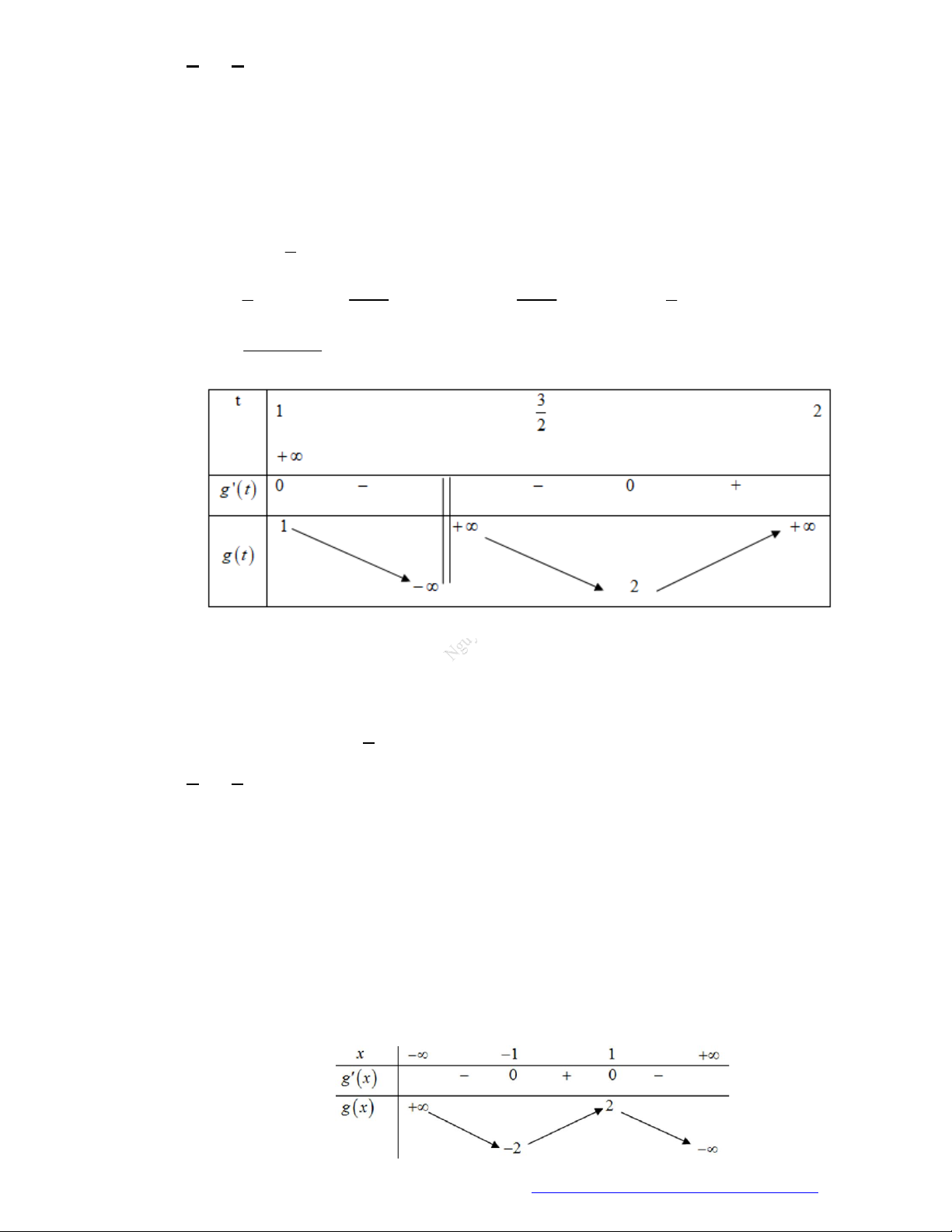
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 59
Chọn C
Xét phương trình:
2 2
1
2 1 2 2
4 .2 3 2 0
x x x x
m m
Đặt
2
2
1
2 1
2 2
x
x x
t
. Do đó, ta có
2
2
1 logx t
. Điều kiện
1t
Ta có phương trình: (1) trở thành:
2
2
2 3 2 0 t mt m
Ta nhận thấy mỗi giá trị
1t
cho hai giá trị
x
tương ứng. Như vậy phương trình (1) có 4 nghiệm
phân biệt khi và chỉ khi phương trình (2) có 2 nghiệm thỏa:
1 2
1 t t .
2
2 2 3 2
t m t
.
Nhận xét:
3
2
t
, không là nghiệm phương trình.
Xét
3
,
2
t
2
2
2
2 3
t
m
t
. Xét hàm
2
2
2 3
t
g t
t
trên
3
1; \
2
2
2
2 6 4
'
2 3
t t
g t
t
;
1
' 0
2
t
g t
t
Dựa vào bảng biến thiên, ta cần
2m
.
Câu 58. Cho phương trình:
3 2 2
2 3
2 2 3 0
x x x m x x
x x m
. Tập các giá trị để bất phương trình có ba
nghiệm phân biệt có dạng
;a b
. Tổng
2a b
bằng:
A.
1.
B.
2.
C.
4.
D.
0.
Lời giải
Chọn B
Ta có:
3 2 2 3 2 2
2 3 2 3 2 2
2 2 3 0 2 2 2 *
x x x m x x x x x m x x
x x m x x x m x x
.
Xét hàm số
2
t
f t t
trên
.
Ta có:
2 ln 2 1 0,
t
f t t
Hàm số
f t
đồng biến trên
.
Mà
3 2 2 3 2 2
* 2 2f x x x m f x x x x x m x x
3 3
3 0 3 **
x x m m x x
.
Xét hàm số
3
3g x x x
trên
.
Ta có:
2
3 3g x x
.
0 1g x x
.
Bảng biến thiên:
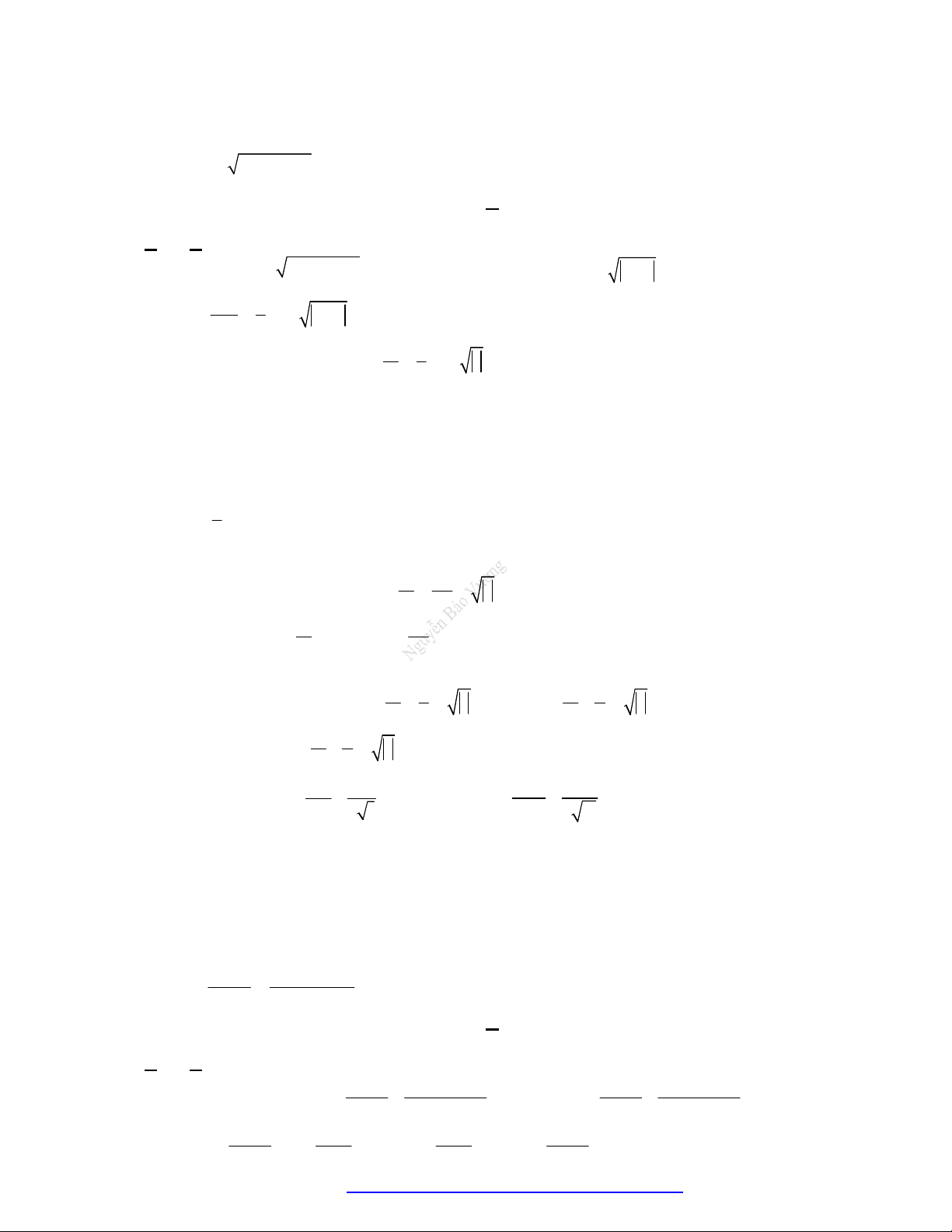
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 60 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Phương trình
3 2 2
2 3
2 2 3 0
x x x m x x
x x m
có 3 nghiệm phân biệt
phương trình (**) có 3
nghiệm phân biệt
2
2 2 2 2
2
a
m a b
b
.
Câu 59. (Chuyên ĐH Vinh- 2019) Có bao nhiêu số nguyên
m
để phương trình
2 2
4
9.3 4 2 1 3 3 3 1 0
x x
m x x m
có đúng 3 nghiệm thực phân biệt?
A. Vô số. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn C
Ta có:
2 2
4
9.3 4 2 1 3 3 .3 1 0
x x
m x x m
2 1
3 4 1 3 3 .3 1 0
x
x
m x m
1
1
1 1
3 4 1 3 3
3 3
x
x
m x m
.
Đặt
1x t
thì PT trở thành
1 1
3 4 3 3
3 3
t
t
m t m
*
Vậy bài toán trở thành tìm
m
để phương trình
*
có đúng 3 nghiệm thực phân biệt.
Nhận thấy, nếu
o
t
là một nghiệm của
*
thì
o
t
cũng là nghiệm của
*
.
Suy ra, điều kiện cần để phương trình
*
có đúng 3 nghiệm thực phân biệt là
*
có nghiệm
0t
.
2
2
1
1 1 . 3 3 2 0
1
3
m
m m m m
m
.
Thử lại:
Với
2
m
thì
*
trở thành
1 2
3 4 3
3 3
t
t
t
.
Nhận thấy,
1
3 2
3
Cauchy
t
t
VT
,
2
. 3 2
3
VP
PT có nghiệm duy nhất
0t
nên
2
m
không thỏa mãn.
Với
1
m
thì
*
trở thành
1 1
3 4 6
3 3
t
t
t
1 2
3 2 3 0
3 3
t
t
t
**
Xét hàm số
1 2
3 2 3
3 3
t
t
f t t
với
0t
.
Ta có,
ln3 2
3 .ln3
3
3
t
t
f t
t
;
2
2
3
ln 3 1
3 ln 3 0
3
3
t
t
f t
t
với mọi
0t
.
f t
đồng biến trên
0; 0
f t
có nhiều nhất 1 nghiệm
0t
.
0
f t
có nhiều nhất 2 nghiệm
0t
.
Lại có,
1 0
f
và
0 0
f
Phương trình
**
có 3 nghiệm là
0t
,
1
t
.
Vậy
1
m
thỏa mãn.
Câu 60. Có bao nhiêu giá trị nguyên của tham số
2019;2019
m
để phương trình
2 1 2 1
2019 0
1 2
x
x mx m
x x
có đúng 3 nghiệm thực phân biệt?
A.
4038
. B.
2019.
C.
2017.
D.
4039
.
Lời giải
Chọn C
Ta có phương trình
2 1 2 1 2 1 ( 2) 1
2019 0 2019 0
1 2 1 2
x x
x mx m x m x
x x x x
2 1 1 1 2 1
2019 0 2019
1 2 2 1
x x
x x
m m
x x x x
.
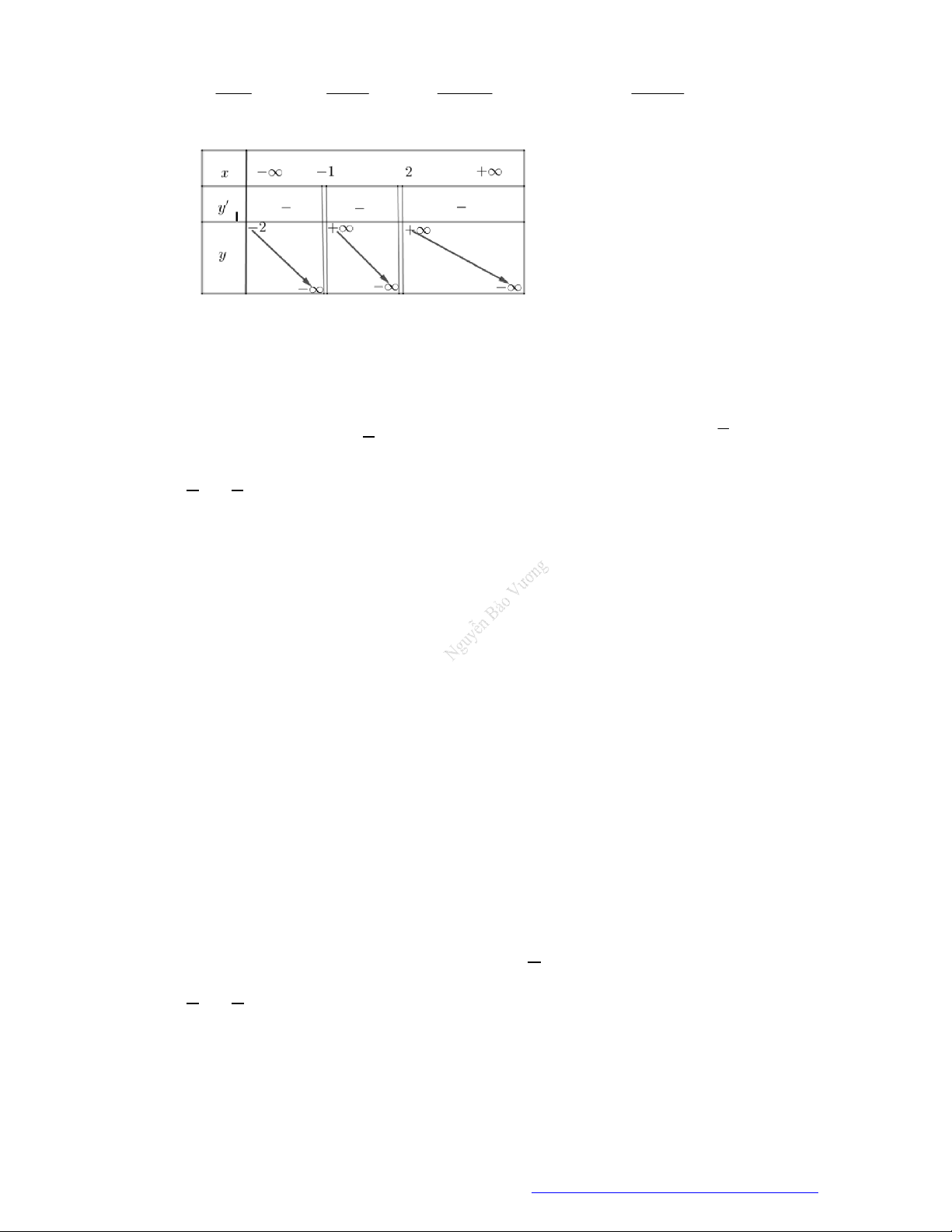
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 61
Xét hàm số
2 2
1 2 1 1 3
2019 ' 2019 ln(2019) 0; \ 1;2
2 1
( 2) ( 1)
x x
x
y y x
x x
x x
.
Ta có bảng biến thiên
Vậy để phương trình có 3 nghiệm phân biệt thì
; 2
m
mà
2019;2019 ;m m
. Vậy
ta có
2017
số nguyên
m
cần tìm.
Câu 61. (Chuyên Hưng Yên - 2020) Gọi
S
là tập hợp các giá trị của tham số
m
sao cho hai phương
trình
2
2 1 3
m
x
và
2
3 2 1
x
m x x
có nghiệm chung. Tính tổng các phần tử của
S
.
A.
6
B.
3
. C.
1
. D.
5
2
.
Lời giải
Chọn B
Vì hai phương trình đã cho có nghiệm chung nên hệ sau có nghiệm
2
2
2 2
3
3
2
2
log 2 1
2 1 3
log 2 1 3 2 1
3 2 1
3 2 1
m
x
x
x
m x
x
x x x
m x x
m x x
2
3
log 2 1
2 2 2
3 3
log 2 1 2 1 3 3 log 2 1 3
x
x x
x x x x x
.
Xét hàm số
3
t
f t t
xác định trên
' 3 .ln3 1 0
t
f t
suy ra hàm
3
t
f t t
đồng
biến trên
suy ra
2 2
3
log 2 1 2 1 3
x
x x x
.
Xét hàm số
2
2 1 3
x
g x x
xác định và liên tục trên
.
Ta có
2 3
' 4 3 ln3 '' 4 3 ln 3 ''' 3 ln 3 0
x x x
g x x g x g x
. Suy ra hàm số
''g x
nghịch biến trên
. Do đó
0g x
có nhiều nhất là 3 nghiệm.
Ta lại có
0 1 2 0g g g
. Suy ra phương trình
2
0 0
2 1 3 1 1
2 2
x
x m
x x m
x m
.
Vậy
3S
.
Câu 62. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Giá trị của tham số
m
để phương trình
1
4 .2 2 0
x x
m m
có hai nghiệm
1
,x
2
x thỏa mãn
1 2
3x x là
A.
2m
. B.
3m
. C.
4m
. D.
1m
.
Lời giải
Chọn C
Đặt
2 ,
x
t
0.t
Phương trình trở thành
2
2 2 0t mt m
(*).
Để phương trình ban đầu có 2 nghiệm thì phương trình (*) phải có 2 nghiệm dương
2
0 2 0
0 2 0 2.
0 2 0
m m
S m m
P m

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 62 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
1 2 1 2
3
1 2 1 2
3 2 2 2 .2 8 . 8 2 8 4.
x x x x
x x t t m m
Kết luận
4.
m
Câu 63.
(Chuyên Chu Văn An - 2020) Tìm
m
để phương trình
1
4 2 0
x x
m
có hai nghiệm trái dấu.
A.
0
m
. B.
1
m
. C.
1 1
m
. D.
0 1
m
.
Lời giải
Chọn D
Đặt
2
x
t
, điều kiện:
0t
.
Phương trình trở thành:
2
2 0
t t m
(*)
Phương trình
1
4 2 0
x x
m
có 2 nghiệm phân biệt trái dấu
2
2 0
t t m
có 2 nghiệm dương phân biệt
1 2
,t t
thỏa mãn:
1 2
1
t t
.
Phương trình (*) có 2 nghiệm dương phân biệt
1 2
1 0
0 1
. 0
m
m
t t m
.
Phương trình có một nghiệm lớn hơn
1
và một nghiệm nhỏ hơn
1
khi và chỉ khi
1 2
1 1 0
t t
1 2 1 2
1 0
t t t t
2 1 0
m
1
m
.
Kết hợp các điều kiện thì ta được
0 1
m
thỏa mãn yêu cầu bài toán.
Câu 64. (Chuyên Phan Bội Châu - Nghệ An - 2020) Có bao nhiêu giá trị nguyên dương của tham số
m
để phương trình
1
9 2.6 3 .4 0
x x x
m
có hai nghiệm phân biệt?
A.
35
. B.
38
. C.
34
. D.
33
.
Lời giải
Chọn A
Phương trình tương đương
2
3 3
12. 3 0
2 2
x x
m
.
Đặt
3
2
x
t
,
0t
.
Phương trình trở thành
2
12. 3 0
t t m
,
0t
(*)
Phương trình đã cho có hai nghiệm phân biệt khi phương trình (*) có hai nghiệm phân biệt dương.
' 0 39 0
39
0 3 0 3 39
3
0 12 0
m
m
P m m
m
S
.
Vậy có 35 giá trị nguyên dương của tham số
m
.
Câu 65. (ĐHQG Hà Nội - 2020) Gọi
S
là tập hợp các số nguyên
m
sao cho phương trình
1 2
4 .2 3 500 0
x x
m m
có 2 nghiệm phân biệt. Hỏi tập
S
có bao nhiêu phần tử
A.
1
. B.
4
. C.
3
. D.
2
.
Lời giải
Chọn C
Đặt
2 0
x
t t
khi đó phương trình
1 2
4 .2 3 500 0 1
x x
m m
trở thành:
2 2
2 . 3 500 0 2
t m t m
. Để
1
có 2 nghiệm phân biệt khi và chỉ khi
2
có 2 nghiệm dương phân biệt hay
0
0
0
P
S
2 2
2
3 500 0
3 500 0
2 0
m m
m
m

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 63
5 10 5 10
10 15 10 15 10 15
5 10
3 3 3
0
m
m m m
m
.
Vậy tập hợp các số nguyên
m
là
13;14;15S
.
Câu 66. (ĐHQG Hà Nội - 2020) Tìm điều kiện của tham số
a
để phương trình sau có nghiệm:
2 2
1 1 1 1
9 2 .3 2 1 0.
x x
a a
Hãy chọn đáp án đúng nhất?
A.
64
4
7
a
. B.
64
2
9
a
. C.
50
3
3
a
. D.
50
1
3
a
.
Lời giải
Chọn A
Đặt
2
1 1
3
x
t
vì
2
0 1 1 3 9x t
. Khi đó bài toán trở thành tìm điều kiện của tham số
a
để phương trình
2
2 . 2 1 0 *t a t a
có nghiệm trên đoạn
3;9
.
Ta có
2
* 2 1 2t t a t
.
Vì
2t
không phải nghiệm của phương trình nên
2
2 1
*
2
t t
a
t
Xét
2 2
' '
1 3;9
2 1 4 3
; 0
2 2
3 3;9
t
t t t t
f t f t f t
t t
t
Ta có
64 64
3 4; 9 4
7 7
f f a
thì phương trình bài ra có nghiệm.
Câu 67. (ĐHQG Hà Nội - 2020) Điều kiện của
m
để hệ bất phương trình
2 1 2 1
2
7 7 2020 2020
2 2 3 0
x x x
x
x m x m
có nghiệm là :
A.
3.m
B.
2 1.m
C.
1 2.m
D.
2.m
Lời giải
Chọn D
2 1 2 1 2 1 2 1
7 7 2020 2020 7 1010. 2 1 7 1010. 2 1 *
x x x x x x
x x x x
Hàm số
( ) 7 1010.
t
f t t
đồng biến trên ℝ.
* 2 1 2 1f x x f x
Suy ra :
2 1 2 1 1 1.x x x x
2
2
2 3
1;1 : 2 2 3 0 .
2
x x
x x m x m m
x
Ycbt
2
2 3
1;1 : **
2
x x
x m
x
Từ bảng biến thiên ta có,
** 2.m
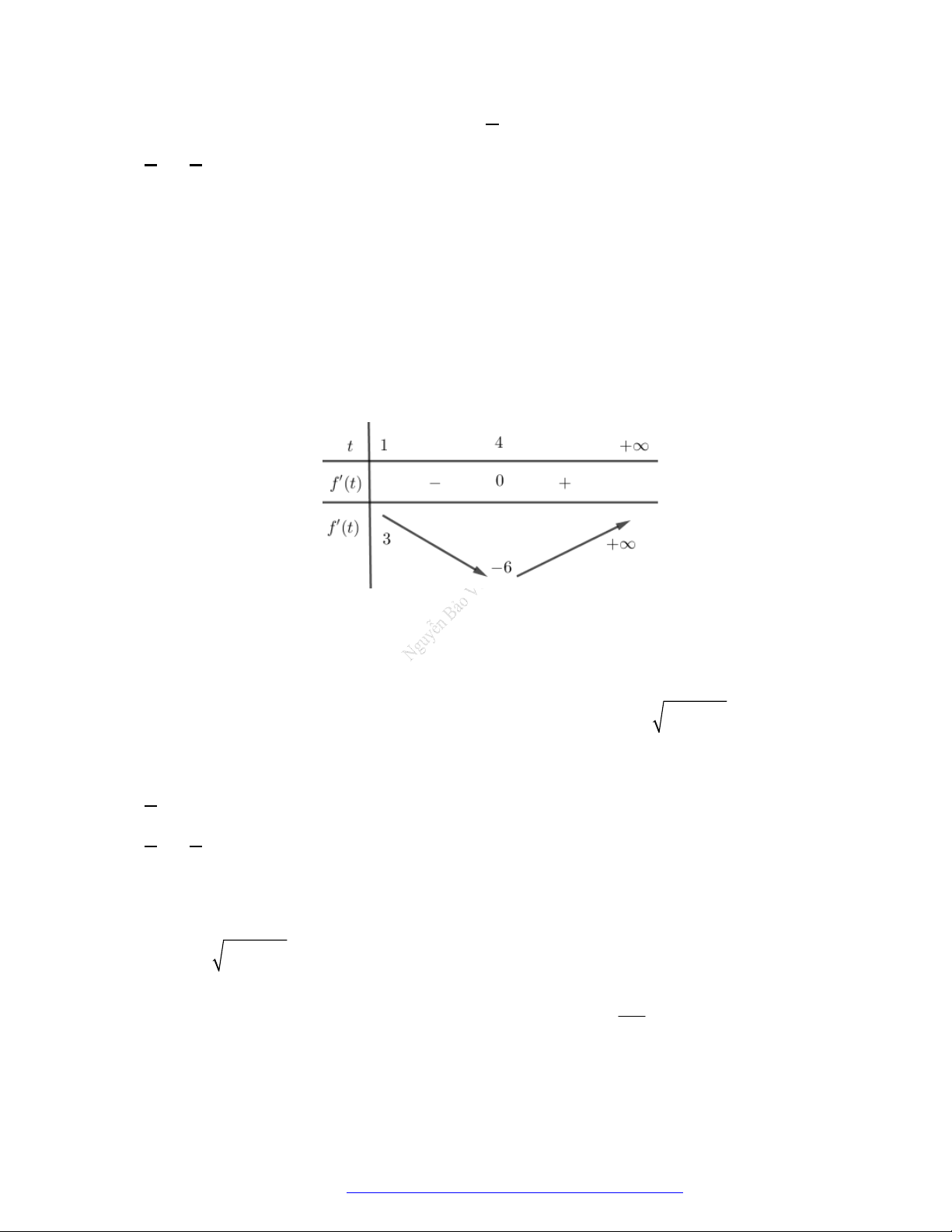
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 64 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 68. (Sở Phú Thọ - 2020) Cho phương trình
2 2
1
16 2.4 10
x x
m
(
m
là tham số). Số giá trị nguyên
của tham
10;10m
để phương trình đã cho có đúng hai nghiệm thực phân biệt là
A.
7
. B.
9
. C.
8
. D.
1
.
Lời giải
Chọn C
Đặt
2
4 , 1
x
t t
.
Khi đó phương trình đã cho trở thành
2
8 10t t m
(1)
Nghiệm
1t
cho một nghiệm
0x
.
Mỗi nghiệm
1t
cho hai nghiệm
x
đối nhau.
Do vậy phương trình đã cho có hai nghiệm thực phân biệt khi và chỉ khi phương trình (1) có đúng
một nghiệm
1t
, nghiệm còn lại (nếu có) phải nhỏ hơn 1.
Xét hàm số
2
8 10f t t t
.
Bảng biến thiên
Từ bảng biến thiên ta có phương trình (1) có một nghiệm lớn hơn 1 khi
3
6
m
m
.
Suy ra số giá trị nguyên
10;10m
là 8.
Câu 69. (Sở Hà Tĩnh - 2020) Gọi
S
là tập nghiệm của phương trình
2
2 2 3 0
x
x
x m
(với
m
là
tham số thực). Có tất cả bao nhiêu giá trị nguyên của
2020;2020m
để tập hợp
S
có hai phần
tử?
A. 2094. B. 2092. C. 2093. D. 2095.
Lời giải.
Chọn A
Gọi
D
là tập xác định của phương trình đã cho.
Nếu
1m
thì
2
3 0
x
m x nên
D
.
Nếu
1m
thì
2 3
log log ;D m
.
2
2
2 2 0
2 2 3
1
0
3 0 2
x
x
x
x
x
x m
m
.
Xét hàm số
2 2
x
f x x
có
2
2 ln 2 2; 0
ln 2
x
f x f x x
do đó phương trình
0f x
có không quá 2 nghiệm.
Mặt khác
1 0; 2 0f f
nên
1
1
2
x
x
.
Lại có với
1m
,
2 3
g2 lo logx m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 65
Nếu
1m
thì
1;2
S
(thỏa mãn yêu cầu bài toán).
Nếu
1m
thì
S
có hai phần tử khi và chỉ khi
2 3
1 log log 2 9 81m m
.
Vậy
S
có hai phần tử khi và chỉ khi
1
*
9 81
m
m
. Số các giá trị nguyên của
2020;2020m
thỏa mãn
*
là
1 2020 1 81 9 2094
.
Câu 70. (Sở Ninh Bình 2020) Cho hai số thực bất kỳ
1a
,
1b
. Gọi
1
x
,
2
x
là hai nghiệm phương trình
2
1
1
x x
a b
. Trong trường hợp biểu thức
2
1 2
1 2
1 2
6 6
x x
S x x
x x
đạt giá trị nhỏ nhất, khẳng định
nào dưới đây đúng?
A.
3
3
a b
. B.
3
6
a b
. C.
3
1
3
a b
. D.
3
1
6
a b
.
Lời giải
Chọn C
Ta có
2
2
ln ln ln ln ln ln 0
x x
a b b x b x a b
.
Phương trình đã cho có hai nghiệm phân biệt
2 2
ln 0 1
ln 4ln 0 1, 1
b b
a b a b
.
Vậy phương trình đã cho luôn có hai nghiệm
1
x
,
2
x
.
Theo định lý Viét ta có
1 2
1 2
ln
log
ln
ln
. 1
ln
b
a
x x a
b
b
x x
b
.
Khi đó ta có
2
2
1 2
1 2
2
1 2
1 1
6 6 6log 6log
log log
b b
b b
x x
S x x a a
x x a a
.
Do
1a
,
1 log log 1 0
b b
b a
.
Áp dụng bất đẳng thức Cauchy ta có
3
3
2 2 2
1 1 1
6log 3log 3log 3 .3log .3log 3 9
log log log
b b b b b
b b b
S a a a a a
a a a
.
Dấu “=” xảy ra khi và chỉ khi
3
1
3
3
3
2
1 1 1
3log log log
log 3 3
b b b
b
a a a a b
a
.
Vậy khẳng định đúng là
3
1
3
a b
.
Câu 71. (Sở Bắc Ninh - 2020) Gọi
S
là tập tất cả các giá trị của
m
để phương trình
1 2
16 6.8 8.4 .2 0
x x x x
m m
có đúng hai nghiệm phân biệt. Khi đó
S
có
A.
4
tập con. B. Vô số tập con. C.
8
tập con. D.
16
tập con.
Lời giải
Chọn D
Đặt
2 , 0
x
t t
, phương trình đã cho trở thành
4 3 2 2
6 8 2 0 * , 0t t t mt m t
.
Phương trình đã cho có đúng hai nghiệm phân biệt khi và chỉ khi phương trình
*
có đúng hai
nghiệm dương phân biệt.
2
4 3 2 2 2
2
4 1
* 6 9 2 0
2 2
m t t
t t t t mt m
m t t
.
2
2 2 2
1
1 1 ln ln
x x
x x x x x x
a b
a b a b b a b b
b
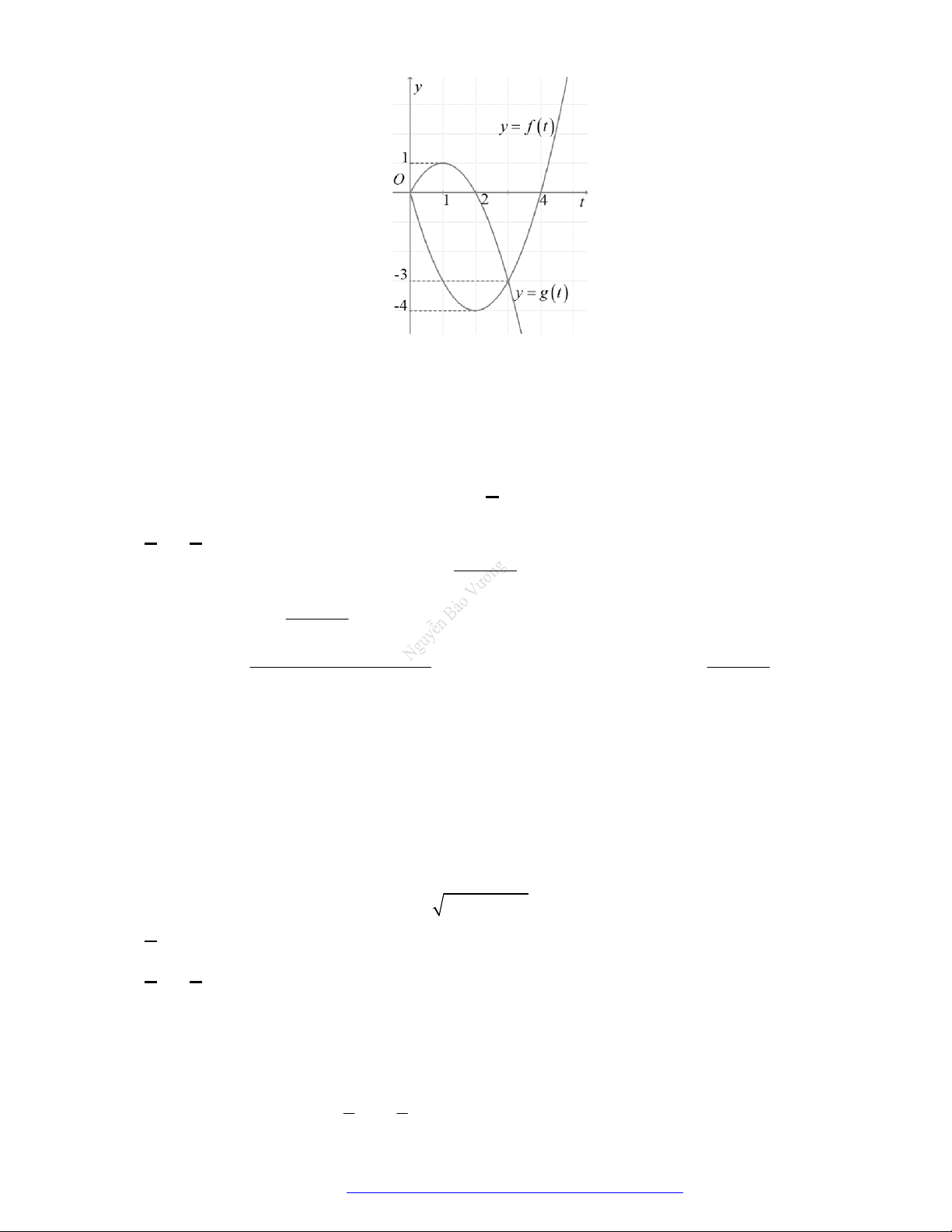
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 66 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Xét hai hàm số
2 2
4 ; 2f t t t g t t t
trên khoảng
0;
có đồ thị như sau
Dựa vào đồ thị hai hàm số này ta suy ra phương trình
*
có đúng hai nghiệm dương phân biệt
khi và chỉ khi
0;1; 3; 4m
hay
S
có 4 phần tử.
Vậy
S
có
4
2 16
tập con.
Câu 72. (Lý Nhân Tông - Bắc Ninh - 2020) Tìm tập hợp các giá trị của tham số thực
m
để phương trình
6 3 2 0
x x
m m
có nghiệm thuộc khoảng
0;1
.
A.
3;4 .
B.
2;4 .
C.
2;4 .
D.
3;4 .
Lời giải
Chọn C
Phương trình
6 3.2
6 3 2 0
1 2
x x
x x
x
m m m
.
Xét hàm số
6 3.2
1 2
x x
x
f x
liên tục trên
0;1
.
Ta có
2
12 ln 3 6 ln 6 3.2 ln 2
' 0, 0;1 .
1 2
x x x
x
f x x
Suy ra hàm số
6 3.2
1 2
x x
x
f x
đồng
biến trên
0;1
.
Do đó phương trình
6 3 2 0
x x
m m
có nghiệm thuộc khoảng
0;1
khi và chỉ khi
0 1f m f
, tức là
2 4.m
Câu 73. (Nguyễn Huệ - Phú Yên - 2020) Có bao nhiêu giá trị nguyên
2019;2020m
sao cho hệ
phương trình sau có nghiệm
2 2 2
2 2 2 2
4 9.3 4 9 .7
2 1 2 2
x y x y y x
x y x m
?
A.
2017
. B.
2021
. C.
2019
. D.
2020
.
Lời giải
Chọn A
Xét phương trình:
2 2 2
2 2 2 2
4 9.3 4 9 .7
x y x y y x
.
Đặt
2
2t x y , phương trình trở thành:
2 2
4 9.3 4 9 .7 4.7 9.3 .7 4.49 49.3
t t t t t t t
2 2 2
4 7 7 3 3 .7 7 .3 *
t t t t
.
Giả sử
2
2 2
3 3
3 .7 7 .3 0 2
7 7
t
t t
t
.
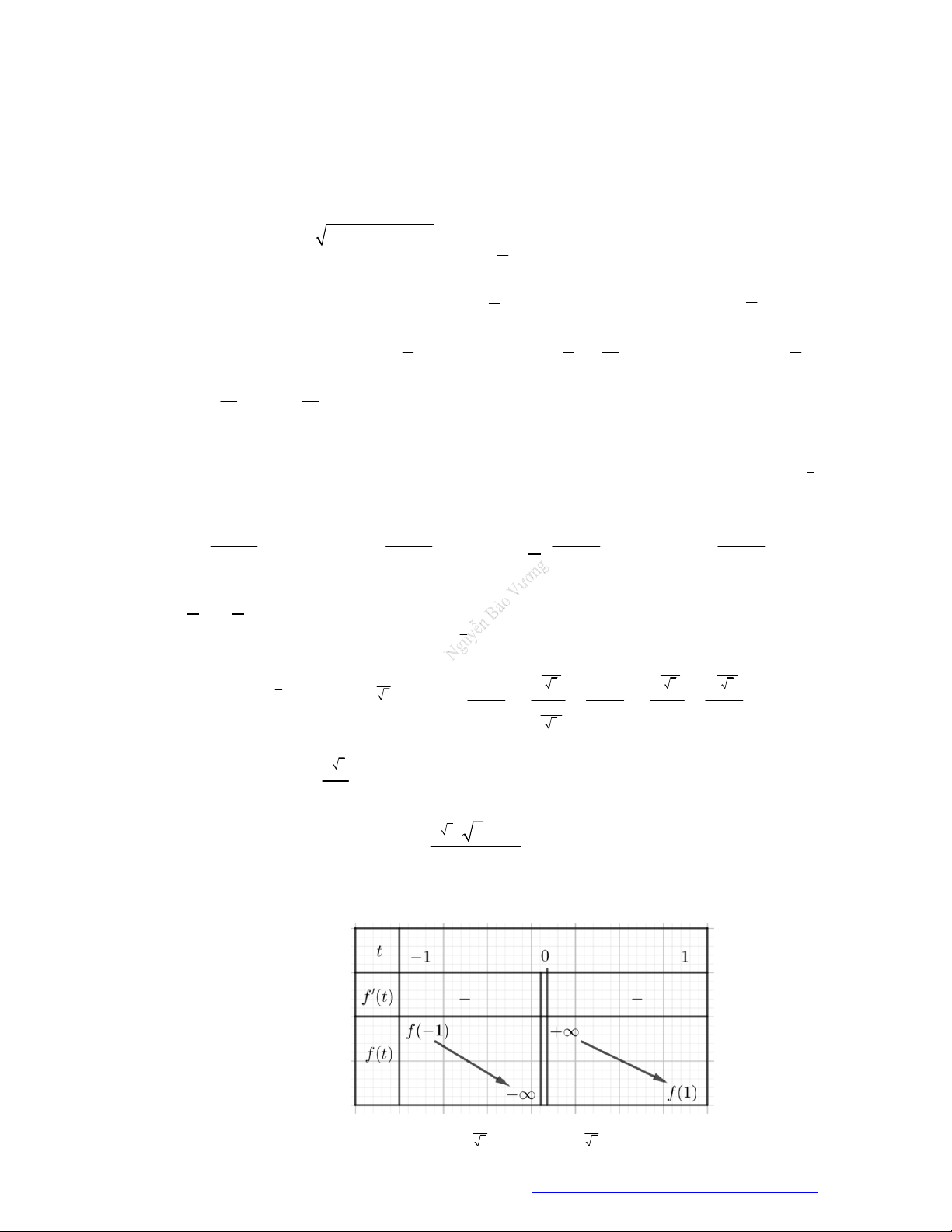
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 67
Nếu
* 0
2 *
* 0
VT
t
VP
vô nghiệm.
Nếu
* 0
2 *
* 0
VT
t
VP
vô nghiệm.
Nếu
2 * *
t VT VP
*
có nghiệm duy nhất
2 2
2 2 2 2 2t x y y x
Ta được:
2
2
3 2 3 1
2 1 2 2
1
2
x x m
x x x m
x
.
Xét hàm số
2
3 2 3f x x x
, với
1
;
2
x
1
6 2 0,
2
f x x x
, suy ra hàm số
f x
đồng biến trên khoảng
1
;
2
1 11
2 4
f x f
1
có nghiệm
1
;
2
x
khi
11 11
;2020
4 4
m m
. Vì
m
nguyên nên
3;4;5;...;2019m
.
Vậy có 2017 giá trị của
m
.
Câu 74. (Nguyễn Trãi - Thái Bình - 2020) Tính tổng tất cả các nghiệm của phương trình
sin( )
4
tan
x
e x
thuộc đoạn
0;50
A.
2671
2
. B.
1853
2
. C.
2475
2
. D.
2653
2
.
Lời giải
Chọn C
Điều kiện:
cos 0x
. Nhận thấy
sin( )
4
0 tan 0
x
e x R x
.
Ta có:
sin sin cos
1
2 2 2
(sin cos )
sin( )
2
4
cos
2
sin sin
tan (*)
cos cos sin cos
x x x
x x
x
x
x e x e e
e x e
x x x x
e
.
Xét hàm số
2
( ) , ( 1;0) (0;1)
t
e
f t t
t
có:
2
2
( 2 2)
'( ) 0, ( 1;0) (0;1)
2
t
e t
f t t
t
( )f t
nghịch biến trên khoảng
( 1;0)
và
(0;1)
.
Bảng biến thiên:
Từ bảng biến thiên ta thấy:
1 1
2 2
( 1) 0, (1) 0f e f e
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 68 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Do đó từ (*) ta có:
(sin ) (cos ) sin cos ,
4
f x f x x x x k k Z
.
Theo giả thiết
1 199
0;50 0 50
4 4 4
x k k
(**)
Do
k Z
nên từ (**) suy ra
0;1;...;49
k
, có 50 giá trị
k
thỏa mãn.
Vậy tổng tất cả các nghiệm của phương trình trên đoạn
0;50
là:
49
0
2475
( )
4 2
k
S k
.
Câu 75. (Trần Phú - Quảng Ninh - 2020) Tìm tập hợp các giá trị của tham số
m
để phương trình (ẩn
x
):
2
2 2
log log
2
3 2 3 .3 3 0
x x
m m
có hai nghiệm phân biệt thỏa mãn:
1 2
2
x x
.
A.
1; \ 0
. B.
0;
. C.
\ 1;1
. D.
1;
.
Lời giải
Chọn A
Điều kiện xác định:
0
x
.
Ta có:
2
2 2
log log
2
3 2 3 .3 3 0
x x
m m
1
2 2
2
log log
2
3 2 3 .3 3 0
x x
m m
Đặt:
2
log
3
x
t
0
t
2 3
log logx t
3
log
2
t
x
Khi đó:
2 2
2 3 3 0
t m t m
2
Phương trình
1
có hai nghiệm phân biệt
Phương trình
2
có hai nghiệm phân biệt dương
1 2
;t t
0
0
0
S
P
2
2
2
3 3 0
2 3 0
3 0
m m
m
m
1
3
m
m
1
m
.
Theo hệ thức Vi-et, ta có:
1 2
2
1 2
2 3
. 3
t t m
t t m
Ta có:
1 2
. 2
x x
3 1 3 2
log log
2 .2 2
t t
3 1 2
log .
2 2
t t
2
3
log 3
2 2
m
2
3
log 3 1
m
2
3 3
m
2
0
m
0
m
Vậy
1
0
m
m
.
Dạng 3. Phương trình kết hợp của mũ và logarit chứa tham số
Câu 1. (Mã 103 -2019) Cho phương trình
2
3 3
2log log 1 5 0
x
x x m
(
m
là tham số thực). Có tất
cả bao nhiêu giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt?
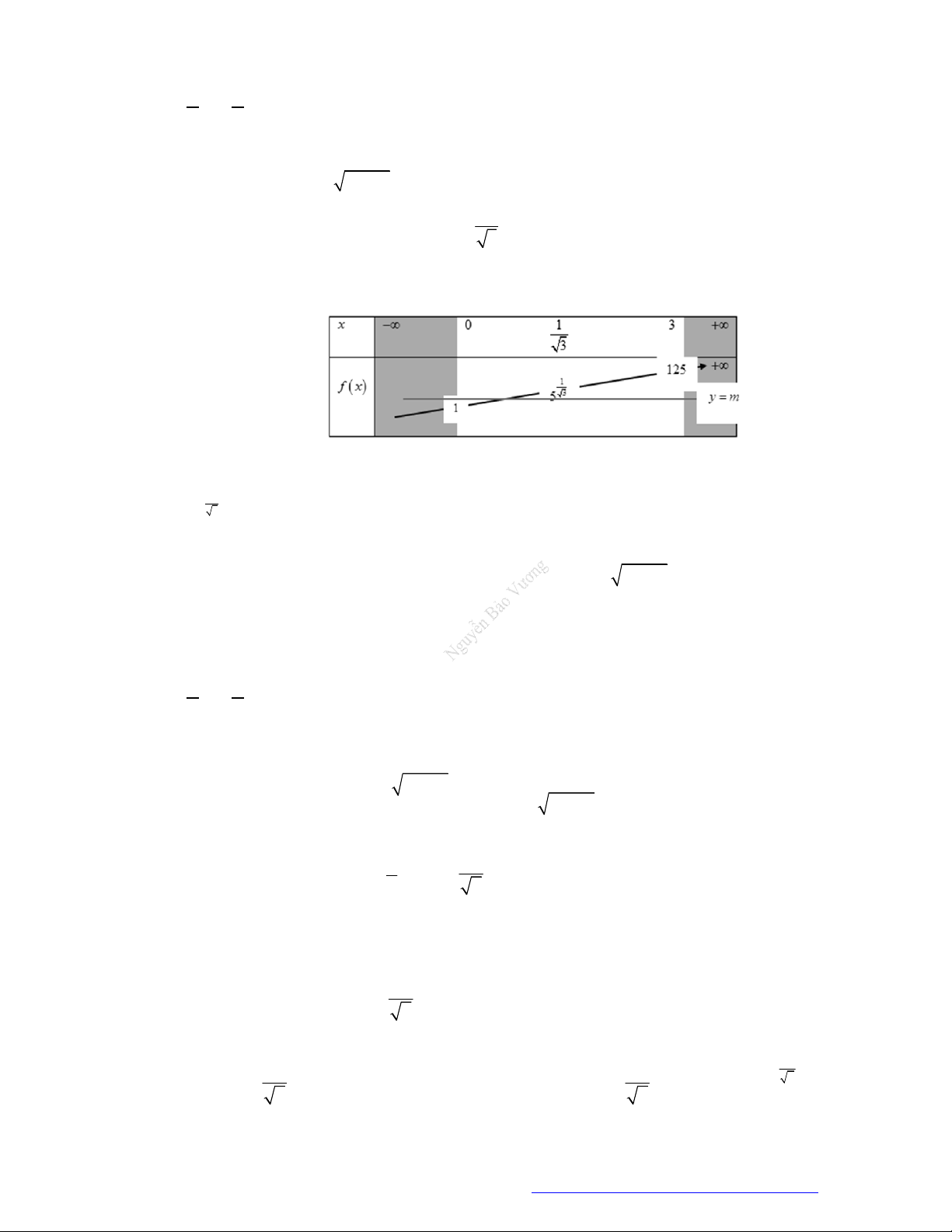
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 69
A. Vô số. B.
124.
C.
123.
D.
125.
Lời giải
Chọn C
Điều kiện:
5
0
0
log
5 0 0
x
x
x
x m
m m
.
2
3 3
2log log 1 5 0
x
x x m (1)
2
3 3
1
3,
2log log 1 0
3
5 0
5
x
x
x x
x x
m
f x m
.
Xét
5
x
f x
hàm số đồng biến trên
.
Dựa vào bảng biến thiên, để phương trình có hai nghiệm phân biệt thì
1
3
1
5 125
m
m
, m
0 1
3 124
m
m
Nên có 123 giá trị m thoả mãn.
Câu 2. (Mã 102 - 2019) Cho phương trình
2
2 2
2log 3log 2 3 0
x
x x m
(
m
là tham số thực). Có
tất cả bao nhiêu giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân
biệt?
A. vô số. B. 81. C. 79. D. 80.
Lời giải
Chọn C
Điều kiện
0 0
3 0 3
x x
x x
m m
(*)
Ta có
2
2 2
2log 3log 2 3 0
x
x x m
2
2 2
2log 3log 2 0 2
1
3 0 3
x
x x
m
.
Trong đó
2
2
4
log 2
2
1
1
log
2
2
x
x
x
x
.(4)
Với
0m
thì
3
3 log
x
m m x
.
Do đó, phương trình (1) có đúng hai nghiệm phân biệt khi và chỉ khi xảy ra các trường hợp sau:
TH1: (3) có nghiệm
3
log 0 0 1x m m
. Kết hợp điều kiện (*) và (4) ta được
1m
thì (1)
có hai nghiệm phân biệt
1
2
x
và
4x
.
TH2:
1m
, khi đó (*)
3
log 0x m
.
Và do
1
4
2
nên (1) có hai nghiệm phân biệt khi và chỉ khi
3
1
log 4
2
m
1
4
2
3 3m
.
Mà
m
nguyên dương nên ta có
3,4,...,80m
, có 78 giá trị của
m
.
Vậy có 79 giá trị nguyên dương của
m
để phương trình có đúng hai nghiệm phân biệt

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 70 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 3. (Mã 104 2019) Cho phương trình
2
3 3
2log log 1 4 0
x
x x m (
m
là tham số thực). Có tất
cả bao nhiêu giá trị nguyên dương của
m
để phương trình có đúng hai nghiệm phân biệt?
A.
64
. B. Vô số. C.
62
. D.
63
.
Lời giải
Chọn C
Ta có điều kiện
4
0
log
x
x m
(*) (với
m
nguyên dương).
Phương trình
2
3 3
2log log 1 4 0 1
x
x x m
2
3 3
2log log 1 0 2
4 3
x
x x
m
.
Phương trình
3
3
3
log 1
2
1
3
log
2
3
x
x
x
x
.
Phương trình
4
3 log
x m
.
Do
m
nguyên dương nên ta có các trường hợp sau:
TH 1:
1
m
thì
4
log 0
m
. Do đó (*) là
0
x
.
Khi đó nghiệm của phương trình
(3)
bị loại và nhận nghiệm của phương trình
2
.
Do đó nhận giá trị
1
m
.
TH 2:
2
m
thì (*) là
4
log
x m
(vì
4
1
log
2
m
)
Để phương trình
1
có đúng hai nghiệm phân biệt
4
3
log 3
3
m
3
3
3
4 4
m
Suy ra
3;4;5; ;63
m
.
Vậy từ cả 2 trường hợp ta có:
63 3 1 1 62
giá trị nguyên dương
m
.
Câu 4. (Mã 101 2019) Cho phương trình
2
2 2
4log log 5 7 0
x
x x m
(
m
là tham số thực). Có tất
cả bao nhiêu giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt?
A.
49
. B.
47
. C. Vô số. D.
48
.
Lời giải
Chọn B
Điều kiện:
0 0
7 0 7
x x
x x
m m
.
* Trường hợp
0
m
thì
2 2
2 2 2 2
4log log 5 7 0 4log log 5 0
x
x x m x x
2 2
log 1 4log 5 0
x x
2
2
log 1
5
log
4
x
x
5
4
2
2
x
x
.
Trường hợp này không thỏa điều kiện
m
nguyên dương.
* Trường hợp
0
m
, ta có
0
7
x
x
m
7
logx m
nếu
1
m
và
0
x
nếu
0 1
m
.
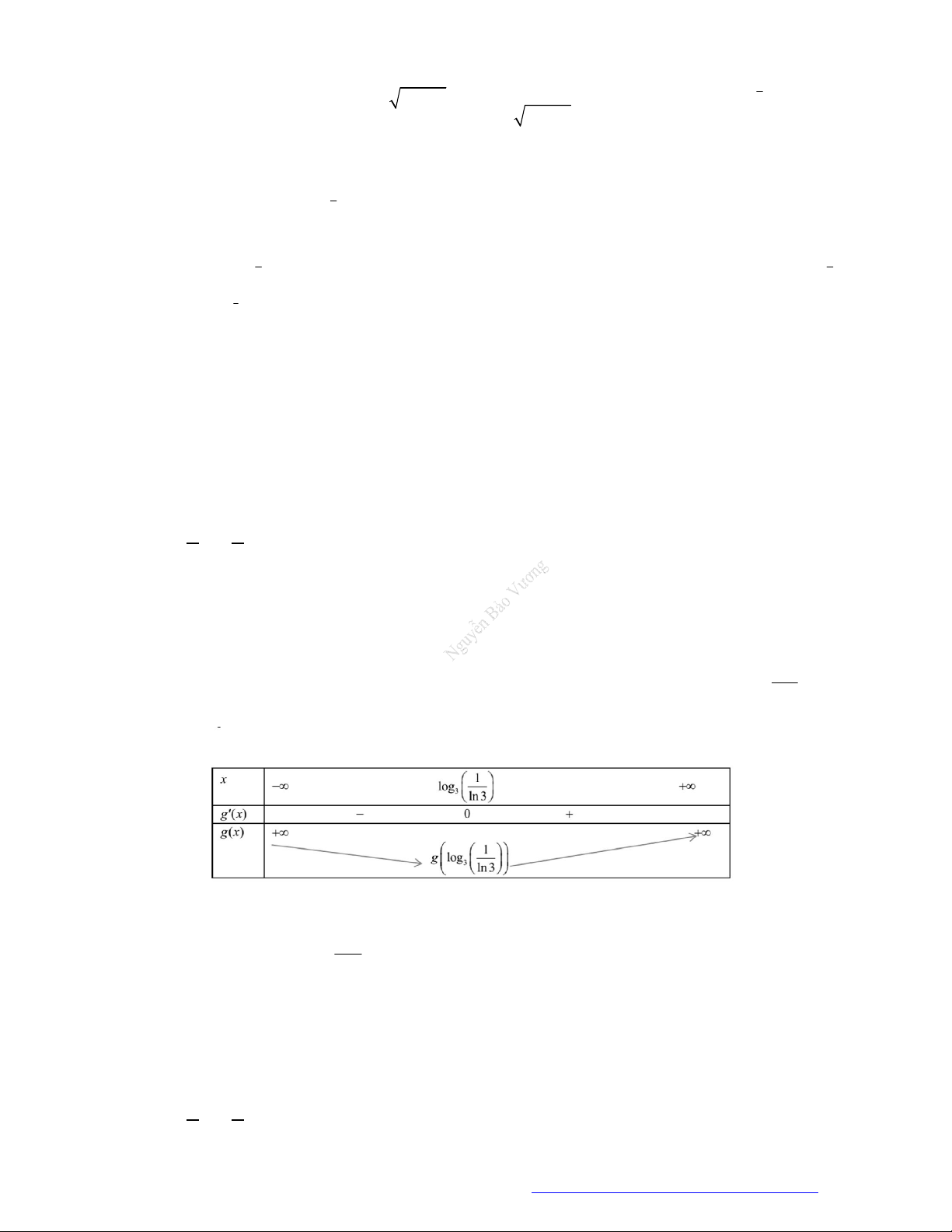
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 71
Khi đó
2
2 2
4log log 5 7 0
x
x x m
2
2 2
4log log 5 0
7 0
x
x x
m
5
4
7
2
2
log
x
x
x m
.
+ Xét
0 1m
thì nghiệm
7
log 0x m nên trường hợp này phương trình đã cho có đúng 2
nghiệm
5
4
2; 2x x
thỏa mãn điều kiện.
+ Xét
1m
, khi đó điều kiện của phương trình là
7
logx m .
Vì
5
4
2 2
nên phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi
5
4
7
2 log 2m
5
4
2 2
7 7m
.
Trường hợp này
3;4;5;...;48m
, có 46 giá trị nguyên dương của
m
.
Tóm lại có 47 giá trị nguyên dương của
m
thỏa mãn.
Chọn phương án
B.
Câu 5. (Mã 102 2018) Cho phương trình
3
3 log ( )
x
m x m
với
m
là tham số. Có bao nhiêu giá trị
nguyên của
15;15 m
để phương trình đã cho có nghiệm?
A.
15
B.
16
C.
9
D.
14
Lời giải
Chọn D
Ta có:
3
3 log
x
m x m
3
3 log ( ) (*)
x
x x m x m
.
Xét hàm số
( ) 3
t
f t t
, với
t
. Có
( ) 3 ln3 1 0,
t
f' t t
nên hàm số
f t
đồng biến
trên tập xác định. Mặt khác phương trình
(*)
có dạng:
3
( ) log ( ) f x f x m
. Do đó ta có
3
( ) log ( ) f x f x m
3
log ( ) x x m
3
x
x m 3
x
x m
Xét hàm số
3
x
g x x
, với
x
. Có ( ) 3 ln 3 1
x
g' x ,
( ) 0g' x
3
1
log
ln3
x
Bảng biến thiên
Từ bảng biến thiên ta thấy các giá trị của tham số để phương trình có nghiệm là:
3
1
; log
ln 3
m g
. Vậy số giá trị nguyên của
15;15 m
để phương trình đã cho có
nghiệm là:
14
.
Câu 6. (Mã 101 2018) Cho phương trình
5
5 log
x
m x m
với
m
là tham số. Có bao nhiêu giá trị
nguyên của
20;20m
để phương trình đã cho có nghiệm?
A.
19
B.
9
C.
21
D.
20
Lời giải
Chọn A
Điều kiện:
x m
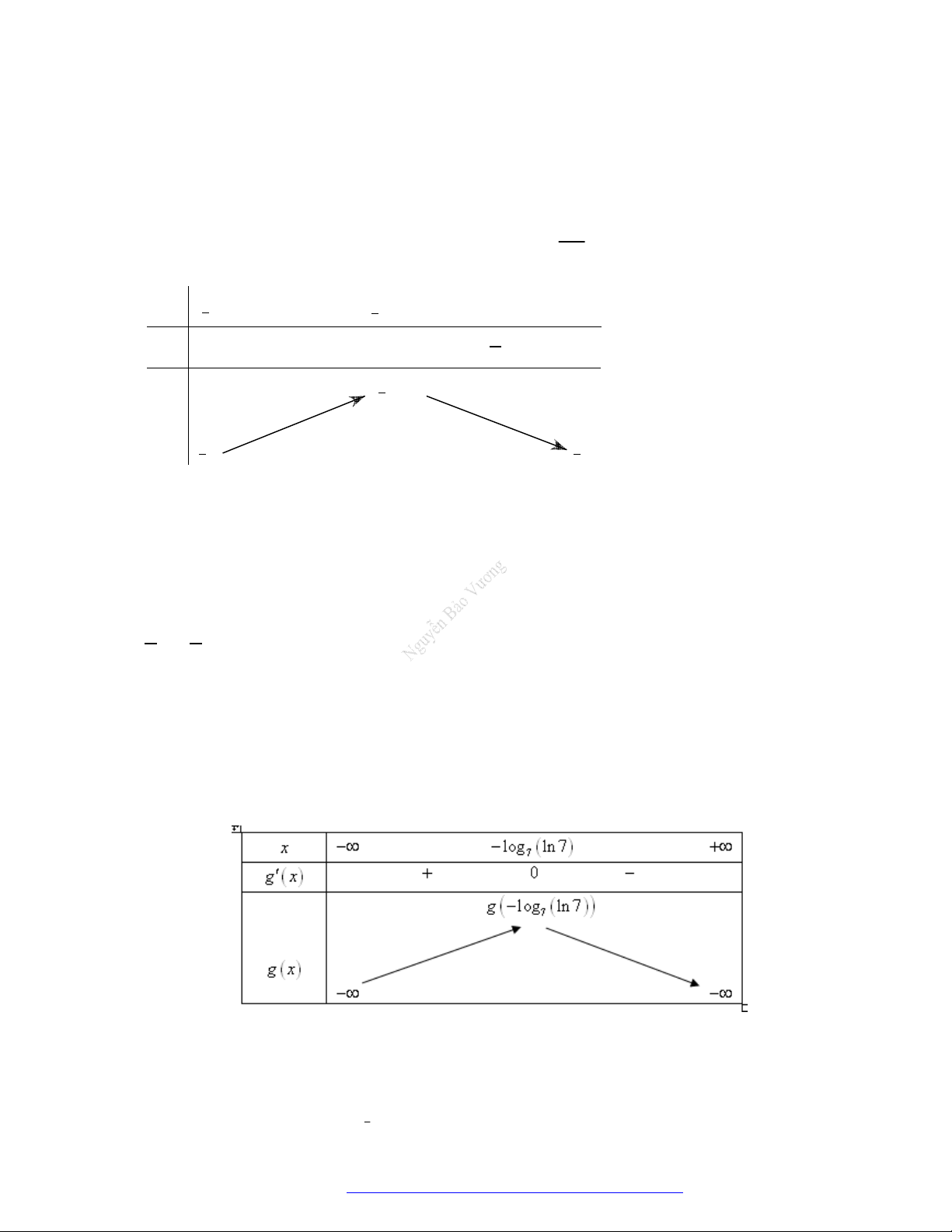
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 72 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đặt:
5
5
log 5 5
5
t
x t
x
x m
t x m x t
m t
1
.
Xét hàm số
5 5 ln5 1 0,
u u
f u u f u u
.
Do đó:
1 5 5
x x
x t x m m x
.
Xét hàm số
5
x
f x x
,
x m
Do:
5 0
x
m x
, suy ra phương trình có nghiệm luôn thỏa điều kiện.
1 5 ln 5
x
f x
,
5
1
0 1 5 ln 5 0 log
ln5
x
f x x
.
Bảng biến thiên:
Dựa vào bảng biến thiên
20;20
0,917 19; 18;...; 1
m
m m
.
Vậy có
19
giá trị nguyên của
m
thỏa ycbt.
Câu 7. (Mã 103 -2018) Cho phương trình
7
7 log
x
m x m
với
m
là tham số. Có bao nhiêu giá trị
nguyên của
25;25 m
để phương trình đã cho có nghiệm?
A.
9
B.
25
C.
24
D.
26
Lời giải
Chọn C
ĐK:
x m
Đặt
7
log t x m
ta có
7
7
x
t
m t
m x
7 7
x t
x t
1
Do hàm số
7
u
f u u
đồng biến trên
, nên ta có
1 t x
. Khi đó:
7 7
x x
m x m x
.
Xét hàm số
7
x
g x x
1 7 ln7 0
x
g x
7
log ln7 x
.
Bảng biến thiên:
Từ đó phương trình đã cho có nghiệm khi và chỉ khi
7
log ln7 0,856 m g
(cácnghiệm
này đều thỏa mãn điều kiện vì
7 0
x
x m
)
Do
m
nguyên thuộc khoảng
25;25
, nên
24; 16;...; 1 m
.
Câu 8. Cho phương trình
1
5
5 log 0
x
m x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
tham số
20;20m
để phương trình đã cho có nghiệm thực?
∞
≈ 0,917
∞
0
≈ 0,295
+∞
∞
y
y'
x
+
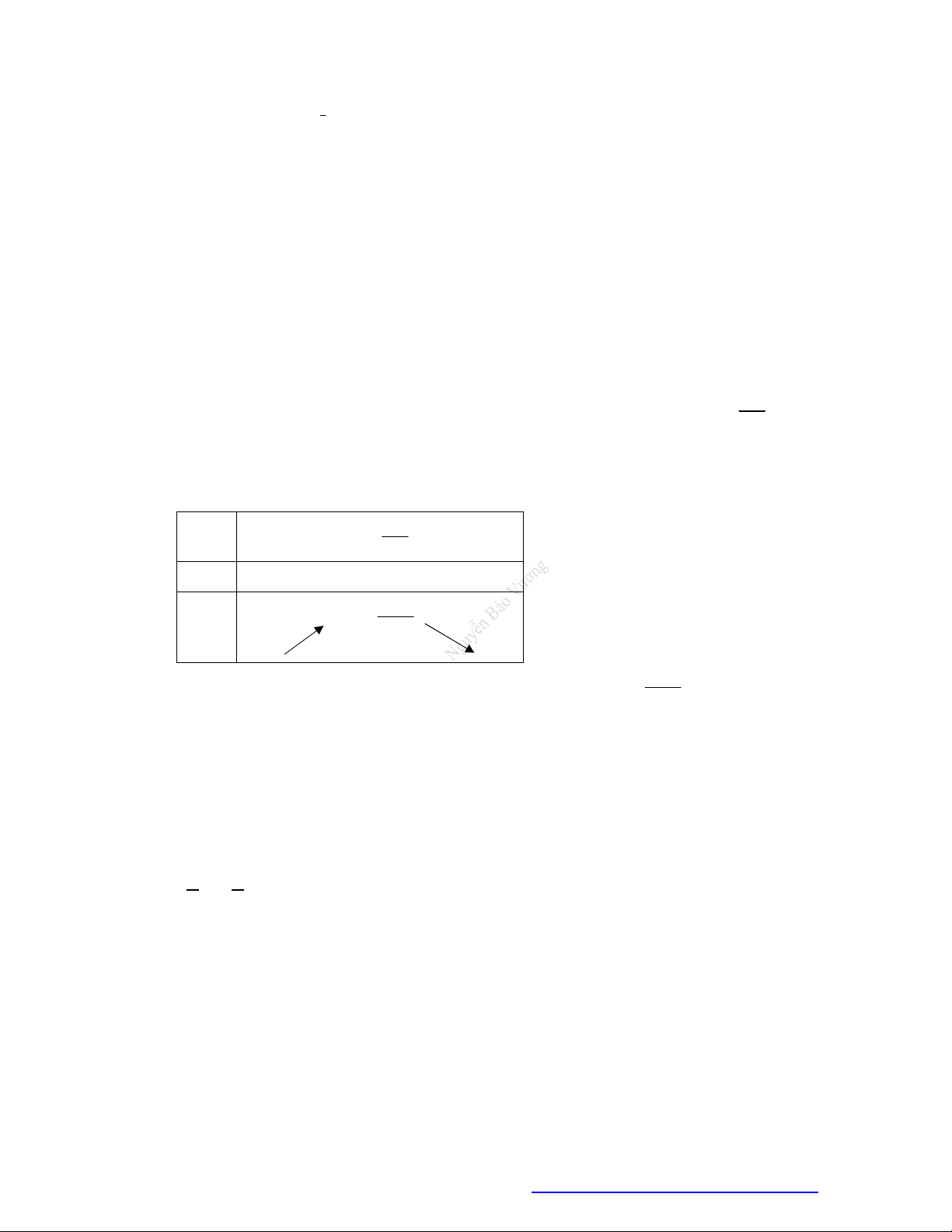
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 73
A.
20
. B.
21
. C.
18
. D.
19
.
Lời giải
Ta có:
1 5
5
5 log 0 5 log 0 1
x x
m x m x m m
.
ĐKXĐ:
x m
.
Đặt
5
log
t x m
, ta có
5
t
x m
.
Khi đó ta có hệ phương trình
5 *
5
5 5 5 2
t
t
x x t
x m
x m
t m x t
.
Xét hàm số
5 ,u .
u
f u u
.
+
5 ln5 1 0,
u
f u u
suy ra hàm số
5
u
f u u
đồng biến trên
.
Do đó
2
f x f t x t
.
Thay vào phương trình
*
ta có
5 3
x
m x
.
Ta có
5 0
x
x m
, do đó phương trình
1
có nghiệm
phương trình
3
có nghiệm
x
.
Xét hàm số
5 ,
x
g x x x
, có
5
1
1 5 ln5, 0 log
ln5
x
g x g x x
.
+
lim 5 ; lim 5
x x
x x
x x
.
BBT
x
5
1
log
ln 5
g x
0
g x
5
1
log
ln 5
e
Từ bảng biến thiên ta thấy phương trình có nghiệm
5
1
log 0,91
ln 5
m
e
.
Vì
20;20
m
và là số nguyên, suy ra
20; 19;...; 1
m
Vậy có
19
giá trị của
m
.
Câu 9. (Mã 104 2018) Cho phương trình
2
2 log
x
m x m
với
m
là tham số. Có bao nhiêu giá trị
nguyên của
18;18
m
để phương trình đã cho có nghiệm?
A.
9
B.
19
C.
17
D.
18
Lời giải
Chọn C
ĐK:
x m
Đặt
2
log
t x m
ta có
2
2
x
t
m t
m x
2 2
x t
x t
1
Do hàm số
2
u
f u u
đồng biến trên
, nên ta có
1
t x
. Khi đó:
2 2
x x
m x m x
.
Xét hàm số
2
x
g x x
g x
1 2 ln 2 0
x
2
log ln 2
x
.
Bảng biến thiên:
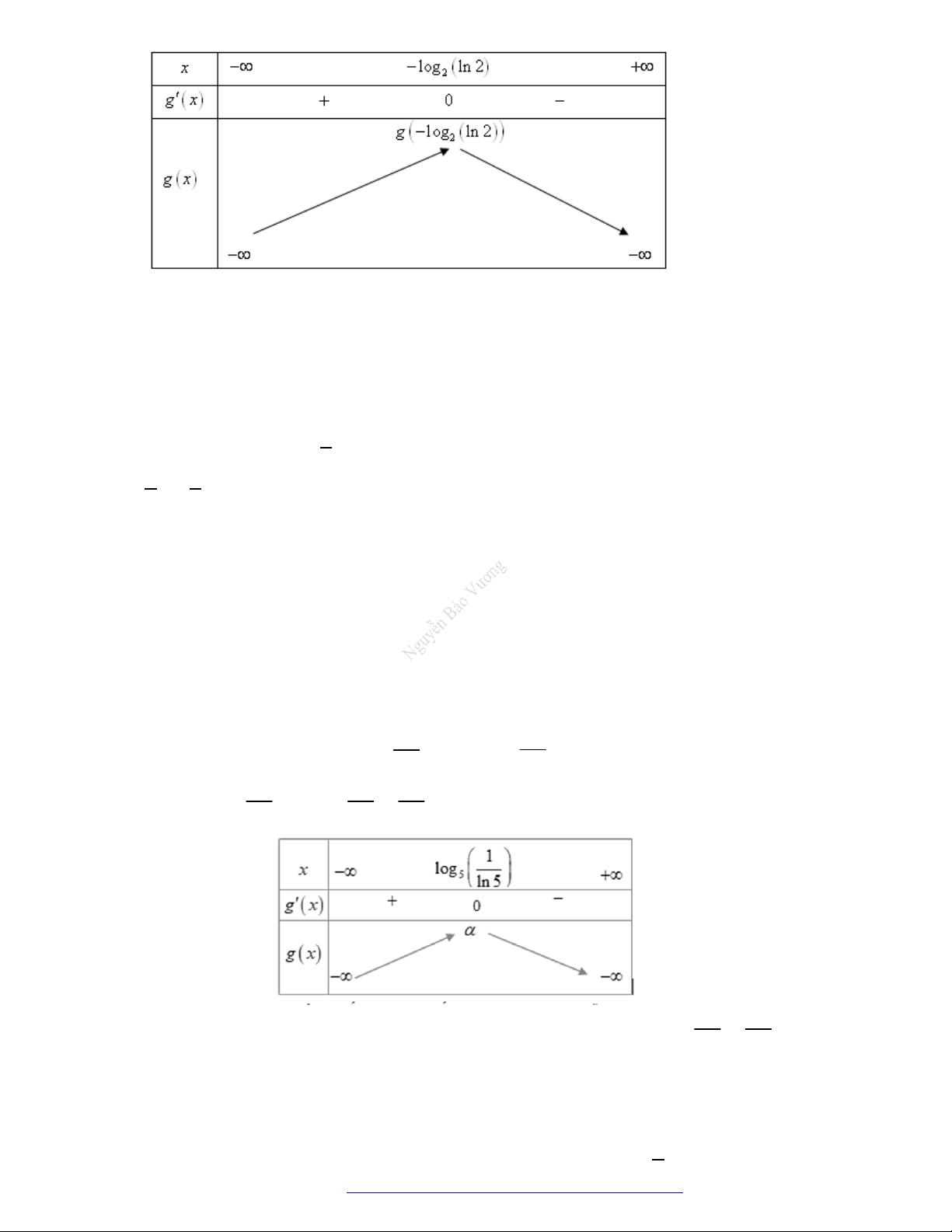
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 74 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ đó phương trình đã cho có nghiệm khi và chỉ khi
2
log ln 2 m g
0,914
(các nghiệm
này đều thỏa mãn điều kiện vì
2 0
x
x m
)
Do
m
nguyên thuộc khoảng
18;18
, nên
17; 16;...; 1 m
.
Câu 10. (Chuyên Nguyễn Du-ĐăkLăk 2019) Cho phương trình
5
5 log
x
m x m
. Có bao nhiêu giá
trị
m
nguyên trong khoảng
20;20
để phương trình trên có nghiệm?
A.
15
. B.
19
. C.
14
. D.
17
.
Lời giải
Chọn B
Ta có phương trình
5
5 log
x
m x m
(1) với điều kiện
0x m
.
Đặt
5
log x m t
5
t
x m
(*) thay vào phương trình (1) ta có
5
x
m t
5 (**)
x
t m
. Từ (*)
và (**) ta có hệ phương trình
5
5
t
x
x m
t m
. Từ hệ phương trình ta suy ra
5 5
t x
x t
5 5
x t
x t
.
Xét hàm số
5
x
f x x
trên
, ta có
1 5 .ln 5 0
x
f x x
nên hàm số
5
x
f x x
luôn đồng
biến trên
, do đó ta có
5 5
x t
x t
f x f t x t
thay vào phương trình (**) ta có
5
x
x m
5
x
x m
. Đặt
5
x
g x x
ta có
1 5 .ln5
x
g x
. Ta có
0 1 5 .ln5 0
x
g x
1
5
ln5
x
5
1
log
ln5
x
.
Ta có BBT với
5 5
1 1 1
log log
ln5 ln5 ln5
g
.
Từ bảng biến thiên ta thấy phương trình
5
x
x m
có nghiệm khi
m
hay
5
1 1
log
ln5 ln5
m
. Ta suy
ra có
19
giá trị nguyên của
m
thỏa mãn.
Câu 11. Tổng tất cả các giá trị của tham số
m
để phương trình
2 2
2
4 5 2
4 6
2 log 1
x x m
x x
m
có đúng 1
nghiệm là
A.
2
. B.
1
. C.
4
. D.
0
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 75
Lời giải
Chọn D
Đặt
2
4 5 t x x
, khi đó
1t
.
Thế vào phương trình đã cho ta được phương trình sau
2
2 2 2 2
2 ln 1 2 ln 1 4 5
t m
t m t m x x m
(Do hàm đặc trưng
2 ln 1
u
f u u
có
2
2 ln 1 .ln 2 0, 0
1
u
u
f u u u f u
u
đồng biến trên
0;
)
Vậy
2 2
2
4 5 2
4 6
2 log 1
x x m
x x
m
có đúng 1 nghiệm
2 2
4 5 0 x x m
có đúng 1 nghiệm
2
1 0
m
1 m
Tổng tất cả các giá trị m bằng
0
.
Câu 12. Tổng tất cả các giá trị của tham số
m
để phương trình
2
2
2 1 2
2 3
3 log 2 2
x x x m
x x
x m
có
đúng ba nghiệm phân biệt là:
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn B
Phương trình tương đương
2
2 3 (2 2)
2
ln 2 2
3
ln 2 3
x x x m
x m
x x
2
2 2
2 3 2
3 .ln 2 3 3 .ln 2 2
x m
x x
x x x m
(*).
Xét hàm đặc trưng
3 .ln , 2
t
f t t t
là hàm số đồng biến nên từ phương trình (*) suy ra
2
2 3 2 2x x x m
2
2 2 1 0g x x x x m
.
Có
2
2
4 2 1 2 4
'
2
2 1
x x m khi x m x khi x m
g x g x
x khi x m
x m khi x m
và
2
' 0
0
x khi x m
g x
x khi x m
.
Xét các trường hợp sau:
TH1:
0m
ta có bảng biến thiên của
g x
như sau:
Phương trình chỉ có tối đa 2 nghiệm nên không có
m
thoả mãn.
TH2:
2m
tương tự.
TH3:
0 2m
, bảng biến thiên
g x
như sau:
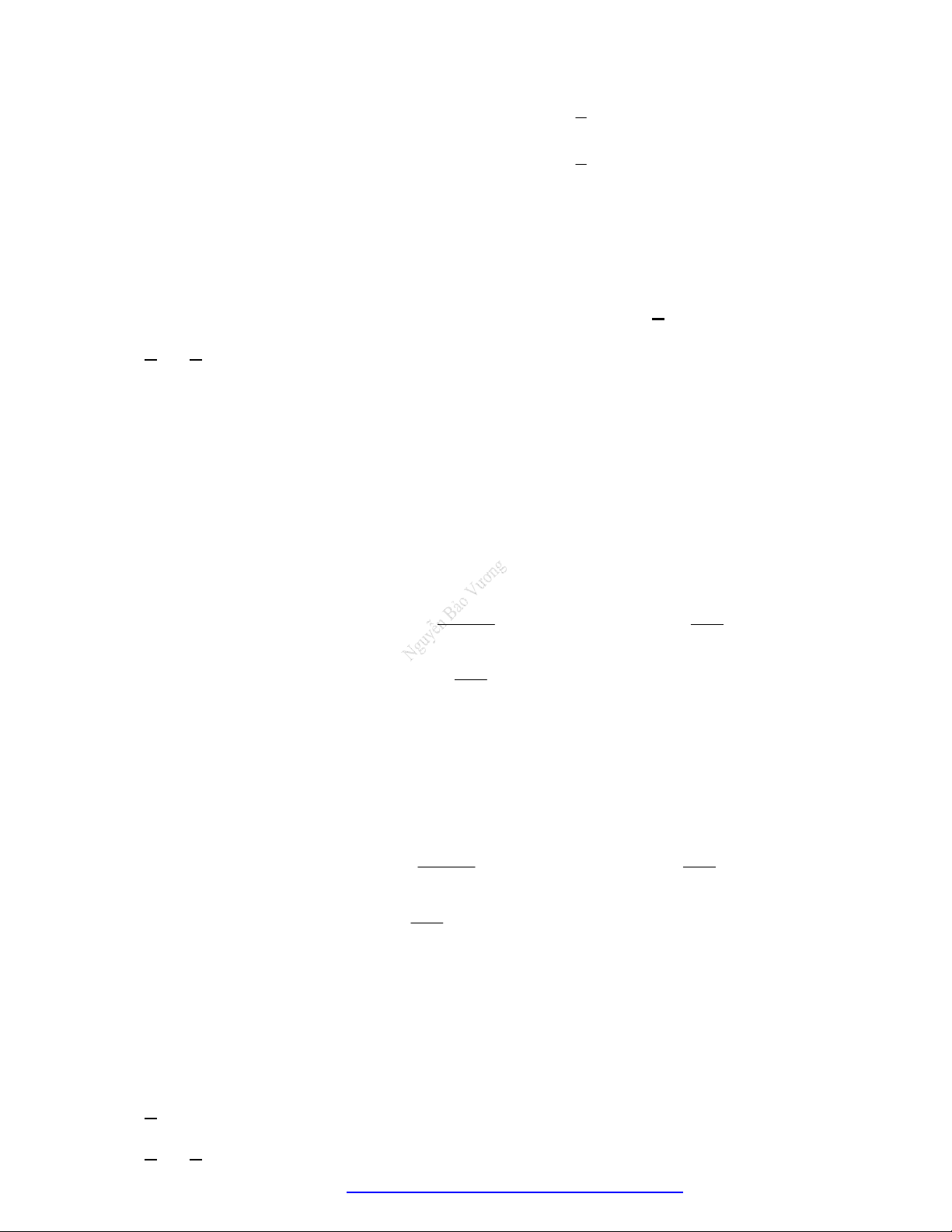
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 76 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Phương trình có 3 nghiệm khi
2
1
1 0
1
2 1 0 2 3
2
2 1 0 2 3
3
2
m
m
m m m
m m
m
.
Cả 3 giá trị trên đều thoả mãn, nên tổng của chúng bằng 3.
Câu 13. (Chuyên Lam Sơn - 2020) Có bao nhiêu giá trị nguyên của tham số
a
trên đoạn
10;10
để
phương trình
ln 1 ln 1
x a x
e e x a x
có nghiệm duy nhất.
A.
2
. B.
10
. C.
1
. D.
20
Lời giải
Chọn D
Điều kiện xác định
1 0
1 0
x a
x
(*)
Phương trình tương đương với
ln 1 ln 1 0
x a x
e e x a x
.
Đặt
e
x a x
f x e
,
ln 1 ln 1
g x x a x
,
Q x f x g x
Phương trình đã cho viết lại thành
0
Q x
+) Với
0
a
thì
0
Q x
(luôn đúng với mọi
x
thoả mãn (*)).
+) Với
0
a
có (*) tương đương với
1
x
,
f x
đồng biến và
g x
nghịch biến với
1
x
Khi đó,
Q x
đồng biến với
1
x
. (1)
Ta có
1 1 1
1
lim lim ln lim ln 1
1 1
lim lim ln
1
1 1
x a x x a x
x x x
x a
x x
x a a
Q x e e e e
x x
a
Q x e
x
e
(2)
Kết hợp (1), (2) thì phương trình
0
Q x
có nghiệm duy nhất.
+) Với
0
a
có (*) tương đương với
1x a
,
g x
đồng biến và
f x
nghịch biến với
1x a
.
Khi đó,
Q x
nghịch biến với
1x a
. (3)
Ta có:
1 1 1
1
lim lim ln lim ln 1
1 1
lim lim ln1 1
1
x a x x a x
x a x a x a
x
x x
a
x a a
Q x e e e e
x x
a
Q x e
x
e
(4)
Kết hợp (3), (4) suy ra
0
Q x
có nghiệm duy nhất.
Do
a
là số nguyên trên đoạn
10;10
nên kết hợp 3 trường hợp trên thấy có 20 giá trị của
a
thoả mãn điều kiện của bài.
Câu 14. (Chuyên Sơn La - 2020) Có bao nhiêu giá trị nguyên của tham số
m
thuộc
2020;2020
để
phương trình
ln 2 2
x
e x m m
có nghiệm?
A.
2019
. B.
2020
. C.
2021
. D.
4039
.
Lời giải
Chọn A
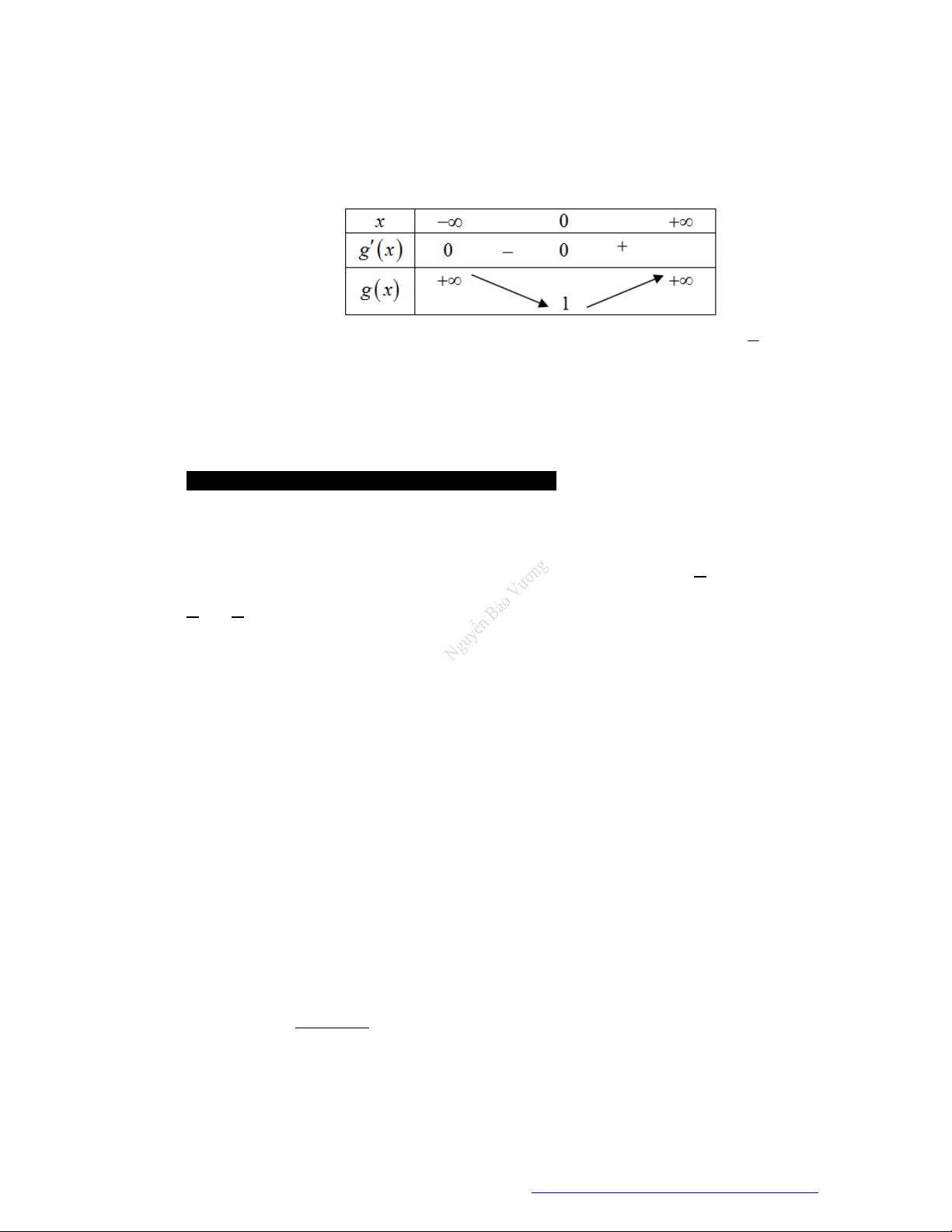
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 77
Ta có
ln 2 2
x
e x m m
ln 2 2
x
e x x m x m
ln 2
ln 2
x m
x
e x e x m
(*).
Xét hàm số
t
f t e t
với
t
1 0,
t
f t e t
. Suy ra hàm số
f t
đồng biến trên
.
Do đó
* ln 2 ln 2 2 2
x x
f x f x m x x m x m e m e x
.
Xét hàm số
1 0 0
x x
g x e x g x e g x x
.
Bảng biên thiên
Từ bảng biên thiên suy ra phương trình có nghiệm khi và chỉ khi
1
2 1
2
m m
.
Mà
, 2020;2020m m
nên
1;2;3;...;2019m
.
Vậy có 2019 giá trị nguyên của tham số
m
thuộc
2020;2020
để phương trình
ln 2 2
x
e x m m
có nghiệm.
Dạng 4. Phương trình mũ – logarit chứa nhiều ẩn
Câu 1. (Đề Minh Họa 2020 Lần 1) Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
0 2020x
và
3
log 3 3 2 9
y
x x y
?
A.
2019
. B.
6
. C.
2020
. D.
4
.
Lời giải
Chọn D
Cách 1:
Ta có:
2
3 3
log 3 3 2 9 log 1 1 2 3
y y
x x y x x y
.
1
Đặt
3
log 1 1 3
t
x t x
.
Phương trình
1
trở thành:
2
3 2 3
t y
t y
2
Xét hàm số
3
u
f u u
trên
.
1 3 ln 3 0,
u
f u u
nên hàm số
f u
đồng biến trên
.
Do đó
2 2 2f t f y t y
3
log 1 2 1 9 9 1
y y
x y x x
Vì
9
0 2020 0 9 1 2020 1 9 2021 0 log 2021
y y
x y
3
log 2021 3,464
Do
0;1;2;3y y
, có 4 giá trị của y nên cũng có 4 giá trị của
x
Vậy có 4 cặp số nguyên
;x y
.
Cách 2:
Ta có:
2
3 3
log 3 3 2 9 log 1 1 2 3
y y
x x y x x y
Xét hàm số
3
log 1 1f x x x
với
0;2020x
.
Ta có
1
1 0, 0;2020
1 ln3
f x x x
x
Hàm số
f x
đồng biến trên đoạn
0;2020
.
Suy ra
3 2
0 log 1 1 2020 1 log 2021 2021f f x x x f f x
3
1 2 9 log 2021 2021 2028
y
y
Nếu
0
0 2 9 9 9 1
y y
y y
0y

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 78 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khi đó
2 9 2 9 2027 9 2027 2 2027
y y y
y y y y
9
log 2027 3,465
y
3
y
0 3
y
0;1; 2;3
y
. Do
f x
là hàm số luôn đồng biến nên với mỗi giá trị của
y
chỉ cho 1 giá trị
của
x
.
+)
3
0 log 1 1 1 0
y x x x
+)
3 3
1 log 1 1 11 log 1 10 8
y x x x x x
+)
3 3
2 log 1 1 85 log 1 84 80
y x x x x x
+)
3 3
3 log 1 1 735 log 1 734 729
y x x x x x
Vậy có 4 cặp số nguyên
;x y
.
Câu 2. (Đề Tham Khảo 2020 Lần 2) Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
2 2
3 4
log ( ) log
x y x y
?
A.
3
. B.
2
. C.
1
. D. Vô số.
Lời giải
Chọn B
Cách 1:
Đặt
2 2
3 4
2 2
3
log ( ) log 1
4
t
t
x y
t x y x y
x y
.
Áp dụng bất đẳng thức Cauchy, ta có
2
2 2
9
2
9
9 2 4 2 log 2
4
t
t t
t
x y x y t
Như vậy,
9
4
log 2
2 2 2
4 4 4 1,89 1;0;1
t t
x y x x
Trường hợp 1:
2
3 0
0
1
4
t
t
y t
x
y
y
.
Trường hợp 2:
2
3 1 0
1
0
4 1
t
t
y t
x
y
y
.
Trường hợp 3:
2 2
2
0
3 1
1 5
3 1 2
1 4 1
t
t
t
t
y
x x y
y
y
mâu thuẫn với
3
2
o
2 2
l g 2
4x y
suy ra loại
1
x
.
Vậy có hai giá trị
0;1
x
Cách 2:
Đặt
2 2
3 4
2 2
3
log ( ) log 1
4
t
t
x y
t x y x y
x y
.
Suy ra
,x y
là tọa độ của điểm
M
với
M
thuộc đường thẳng
: 3
t
d x y
và đường tròn
2 2
: 4
t
C x y
.
Để tồn tại
y
tức tồn tại
M
nên
,
d C
có điểm chung, suy ra
,
d O d R
trong đó
0;0 , 2
t
O R
nên
3
2
3
2 log 2
2
t
t
t
.
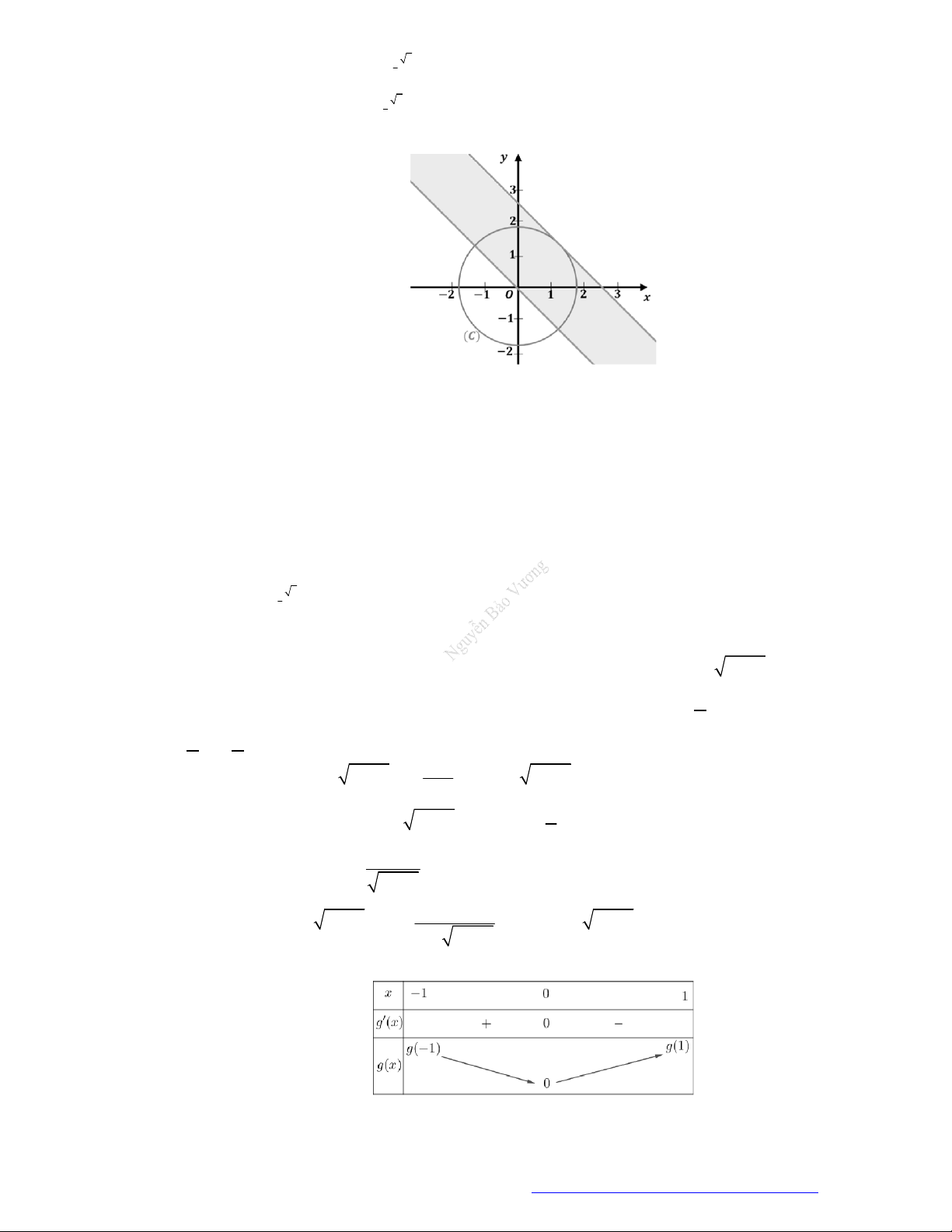
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 79
Khi đó
3
2
3
2
2 2
log 2
log 2
0 3
1
4
x y
x y
.
Minh họa quỹ tích điểm
M
như hình vẽ sau
Ta thấy có 3 giá trị
x
có thể thỏa mãn là
1; 0; 1x x x
.
Thử lại:
Trường hợp 1:
2
3 0
0
1
4
t
t
y t
x
y
y
.
Trường hợp 2:
2
3 1 0
1
0
4 1
t
t
y t
x
y
y
.
Trường hợp 3:
2 2
2
0
3 1
1 5
3 1 2
1 4 1
t
t
t
t
y
x x y
y
y
mâu thuẫn với
3
2
o
2 2
l g 2
4x y suy ra loại
1x
.
Câu 3. (Mã 103 - 2020 Lần 2) Có bao nhiêu cặp số nguyên dương
;m n
sao cho
10m n
và ứng với
mỗi cặp
;m n
tồn tại đúng
3
số thực
1;1a
thỏa mãn
2
2 ln 1
m
a n a a
?
A.
7
. B.
8
. C.
10
. D.
9
.
Lời giải
Chọn D
Ta có
2 2
2
2 ln 1 ln 1
m
m
a
a n a a a a
n
.
Xét hai hàm số
2
ln 1f x x x
và
2
m
g x x
n
trên
1;1
.
Ta có
2
1
0
1
f x
x
nên
f x
luôn đồng biến và
2 2
2
1
ln 1 ln ln 1
1
f x x x x x f x
x x
nên
f x
là hàm số lẻ.
+ Nếu
m
chẵn thì
g x
là hàm số chẵn và có bảng biến thiên dạng
Suy ra phương trình có nhiều nhất
2
nghiệm, do đó
m
lẻ.
+ Nếu
m
lẻ thì hàm số
g x
là hàm số lẻ và luôn đồng biến.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 80 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta thấy phương trình luôn có nghiệm
0
x
. Dựa vào tính chất đối xứng của đồ thị hàm số lẻ, suy
ra phương trình đã cho có đúng
3
nghiệm trên
1;1
khi có
1
nghiệm trên
0;1
, hay
2 2
1 1 ln 1 2 2,26 1;2
ln 1 2
f g n n
n
.
Đối chiếu điều kiện, với
1
n
suy ra
1;3;5;7;9
m
, có
5
cặp số thỏa mãn
Với
2
n
thì
1;3;5;7
m
có
4
cặp số thỏa mãn.
Vậy có
9
cặp số thỏa mãn bài toán.
Câu 4. (Mã 101 - 2020 Lần 2) Có bao nhiêu cắp số nguyên dương
,m n
sao cho
14
m n
và ứng với
mỗi cặp
,m n
tồn tại đúng ba số thực
1;1
a
thỏa mãn
2
2 ln 1
m
a n a a
?
A.
14
. B.
12
. C.
11
. D.
13
.
Lời giải
Chọn C.
Xét
2
2
. ln 1
m
f x x x x
n
trên
1;1
Đạo hàm
1
2
2 1
0
1
m
m
f x x
n
x
Theo đề bài
0
f x
có ba nghiệm nên
1
2
2 1
1
m
m
x
n
x
có ít nhất hai nghiệm
Xét đồ thị của hàm
1
2
1
;
1
m
y x y
x
, suy ra
1
m
chẵn và
1 0
m
Suy ra
3;5;7;9;11;13
m
. Khi đó
0
f x
có nghiệm
1
2
0
0
x
x
Phương trình có 3 nghiệm
1 0
1 0
f
f
2
ln 2 1
2 1;2
2
ln 2 1
n
n n
n
1;2
n
và
3;5;7;9;11;13
m
, do
14
m n
nên ta có 11 cặp
;m n
thỏa yêu cầu bài
toán.
Câu 5.
(Mã 104 - 2020 Lần 2) Có bao nhiêu cặp số nguyên dương
( , )m n
sao cho
12
m n
và ứng với
mỗi cặp
( , )m n
tồn tại đúng 3 số thực
( 1,1)
a
thỏa mãn
2
2 ln( 1)
m
a n a a
?
A.
12
. B.
10
. C.
11
. D.
9
.
Lời giải
Chọn D
Ta có
2 2
2
2 ln( 1) ln( 1) (*)
m m
a n a a a a a
n
.
Xét hàm
2
( ) ln( 1)
f a a a
trên
( 1,1)
(dễ thấy hàm
f
lẻ, đồng biến trên
R
), có BBT:
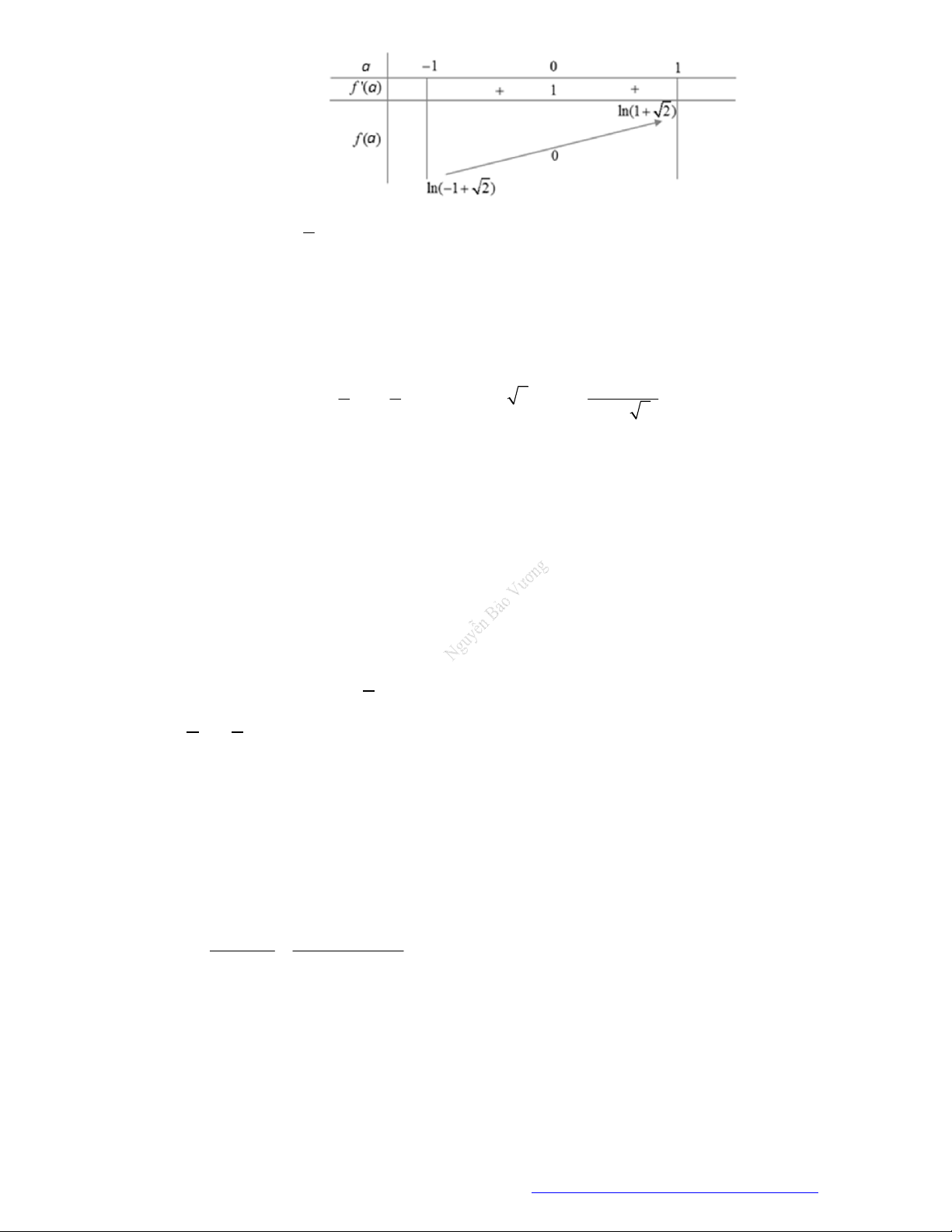
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 81
Xét hàm
2
( ) .
m
g a a
n
trên
( 1,1)
.
Với
m
chẵn,
( )g a
là hàm chẵn và
( ) 0,g a a R
, do đó
(*)
không thể có 3 nghiệm.
Với
m
lẻ,
( )g a
là hàm lẻ, đồng biến trên
R
và tiếp tuyến của đồ thị tại điểm
0a
là đường
thẳng
0y
.
Dễ thấy
(*)
có nghiệm
0 ( 1;1)a
. Để
(*)
có đúng 3 nghiệm tức là còn có 2 nghiệm nữa là
0
a
với
0
0 1a
.
Muốn vậy, thì
2 2 2
(1) .1 (1) ln(1 2) 2,26 1; 2
ln(1 2)
m
g f n n n
n n
Cụ thể:
+
3;5;7;9m
thì
1;2n
: Có
8
cặp
( , )m n
+
11m
thì
1n
: Có
1
cặp
( , )m n
+
1m
: Đồ thị hàm số
( )g a
là đường thẳng (
( ) ; ( ) 2g a a g a a
) không thể cắt đồ thị hàm số
( )f a
tại giao điểm
0
0a
được vì tiếp tuyến của hàm số
( )f a
tại điểm có hoành độ
0a
là
đường thẳng
y a
.
Vậy có cả thảy
9
cặp
( , ).m n
Câu 6. (Chuyên Biên Hòa - Hà Nam - 2020) Có tất cả bao nhiêu giá trị thực của tham số
1;1m
sao
cho phương trình
2
2 2
2
1
log log 2 2 2
m
x y x y
có nghiệm nguyên
;x y
duy nhất?
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn B
Điều kiện:
2 2
0
1 0
x y
x y
.
Nhận xét: Vì
,x y
có vai trò như nhau nên nếu phương trình có nghiệm
0 0
;x y
thì
0 0
;y x
cũng
là một nghiệm của phương trình.
*) Điều kiện cần: Phương trình đã cho có nghiệm duy nhất
0 0
x y
.
Thay vào phương trình ta được
2
2
0 2 0
1
log 2 log 4 2
m
x x
Vì
0 0
4 2 1x x
. Lại có
2 2
2 2
0 0 2 0 0 0
1 1
2 4 2 log 4 2 log 2 log 4 2
m m
x x x x x
0 0
0
0
2
4 2 4 2
2
4 2
4 2
1 1
log 1 log 2
log 2
log 1
x x
x
x
m
m
2 2
1 2 1m m
mà
1;1 1m m
.
*) Điều kiện đủ: Với
1m
thì phương trình đã cho trở thành
2 2
2 2
log log 2 2 2x y x y
2 2
2 2
1
2 2 2 1 1 0
1
x
x y x y x y
y
Suy ra phương trình đã cho có nghiệm duy nhất
1;1 .
Vậy có hai giá trị
m
cần tìm là
1.m
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 82 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 7. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Có bao nhiêu số nguyên
y
để tồn tại số thực
x
thỏa mãn
2 2
11 4
log 3x 4 log
y x y
?
A.
3
B.
2
C.
1
D. vô số.
Lời giải
Chọn B
Đặt
2 2
11 4
2 2
3x 4 11
log 3x 4 log
4
t
t
y
y x y t
x y
(*).
Hệ có nghiệm
đường thẳng
:3x 4 11
t
y
và đường tròn
2 2
: 4
t
C x y
có điểm chung
11
2
11 11
, 2 5 log 5
5 2
t
t
t
d O R t
.
Do
2 2
4
t
x y
nên
11
2
log 5
2 2 1.9239767
t
y
.
Vì
y
nên
1;0;1
y
.
Thử lại:
- Với
1
y
, hệ (*) trở thành
2
2
3x 4 11
11 4
1 4 121 8.11 25 9.4
3
1 4
t
t
t t t t
t
x
(**)
Nếu
0t
thì
2
11 4
4 1 4 1
3
t
t t
.
Nếu
121 4
0 121 4 8 11 4 25 0
8.11 8.4
t t
t t t t
t t
t
.
Vậy (**) vô nghiệm.
- Với
0
y
thì hệ (*) trở thành
11
2
log 3
11
2
2
3x 11
121 11
4 log 3
9 3
4
t
t
t
t
t x
x
.
- Với
1y
thì hệ (*) trở thành
2
2
3x 4 11
11 4
1 4 121 8.11 25 9.4
3
1 4
t
t
t t t t
t
x
.
Xét hàm số
( ) 121 8.11 25 9.4
t t t
f t
, liên tục trên
1
;1
2
có
1
1 0
2
f f
nên phương
trình
( ) 0
f t
luôn có nghiệm thuộc đoạn
1
;1
2
. Khi đó hiển nhiên sẽ tồn tại x thỏa mãn.
Vậy có 2 giá trị nguyên của
y
thỏa mãn là
0, 1y y
.
Câu 8. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Có bao nhiêu cặp số thực
;x y
thỏa mãn
đồng thời các điều kiện
2
3
2 3 log 5
4
3 5
x x
y
và
2
4 1 3 8 ?
y y y
A.
1
. B.
3
. C.
4
. D.
2
.
Lời giải
Chọn D
Ta có:
2 2
3
2 3 log 5 2 3
4 3
3 5 5 3 . (*)
x x x x
y y
Vì
2
2 3
3
0
3 3 5 1 3 0 3.
x x
y
y y
Với
3
y
ta có:
2 2
2
4 1 3 8 4 1 3 8 3 0
y y y y y y y y
3 0
y
. Kết hợp với
3
y
suy ra
3.
y

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 83
Thế
3
y
vào
(*)
ta được:
2
2 3
2
1
3 1 2 3 0 .
3
x x
x
x x
x
Vậy các cặp số thực
;x y
thỏa mãn là
1; 3 ; 3; 3 .
Câu 9. (Chuyên Bến Tre - 2020) Giả sử
0 0
;x y
là một nghiệm của phương trình
1 1 1
4 2 sin 2 1 2 2 2sin 2 1
x x x x x
y y
. Mệnh đề nào sau đây đúng?
A.
0
7
x
. B.
0
2 4
x
. C.
0
4 7
x
. D.
0
5 2
x
.
Lời giải
Chọn B
Ta có
1 1 1
4 2 sin 2 1 2 2 2sin 2 1
x x x x x
y y
1
2
1 2 1 2 1
2
2
1 2 1 2 1
2
1 2 1
4 4.2 4. 2 2 .sin 2 1 4 4 0
2 2 4 2 2 sin 2 1 4 sin 2 1 cos 2 1 0
2 2 2. 2 2 .2sin 2 1 2sin 2 1 4cos 2 1 0
2 2 2sin 2 1 4cos 2 1 0
2 2 2sin 2
x x x x
x x x x x
x x x x x
x x x
x
y
y y y
y y y
y y
1
2 1
1 0
cos 2 1 0
x
x
y
y
.
Vì
2 1 2 1
cos 2 1 0 sin 2 1 1
x x
y y
.
2 1
sin 2 1 1 2 0
x x
y
(vô nghiệm)
2 1
0
sin 2 1 1 2 4 2 2;4
x x
y x x
.
Câu 10. (Chuyên Lào Cai - 2020) Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
0 4000
x
và
5
5
5 25 2 log 1 4
y
y x x
?
A.
3
. B.
2
. C.
4
. D.
5
.
Lời giải
Chọn A
Đặt
5
log 1 5 1
t
x t x
.
Phương trình trở thành:
2 2 1
5 5 2 5 1 5 4 5 2 5 1
y t y t
y t y t
.
Xét hàm số
5 5 .ln5 1 0
u u
f u u f u
nên hàm số luôn đồng biến.
Vậy để
5
2 1 2 1 2 1 log 1
f y f t y t y t x
5
0 2 1 log 4001 0 2 1 5 0;1;2
y y y
Với mỗi nghiệm
y
ta tìm được một nghiệm
x
tương ứng.
Câu 11. (Chuyên Lê Hồng Phong - Nam Định - 2020) Có bao nhiêu bộ
( ; )x y
với
,x y
nguyên và
1 , 2020
x y
thỏa mãn
3 2
2 2 1
2 4 8 log 2 3 6 log
2 3
y x
xy x y x y xy
y x
?
A.
2017
. B.
4034
. C.
2
. D.
2017.2020
.
Lời giải
Chọn B
Từ giả thiết kết hợp ĐKXĐ của bất phương trình ta có:
1 2020;4 2020; ,
y x x y Z
,(1).
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 84 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
3 2
2 2 1
2 4 8 log 2 3 6 log
2 3
y x
xy x y x y xy
y x
3 2
2 2 1
4 (y 2) log 3 (y 2)log 0
2 3
y x
x x
y x
(*).
Xét
2 2
2 1 7
( ) log log 2 0, 4;2020
3 3
x
f x x
x x
(2).
+ Với
1y
thay vào (*) ta được:
3 2
2 2 1
3( 4) log ( 3)log 0
3 3
x
x x
x
( luôn đúng
4; 2020
x
do (1) và (2) ).
Suy ra có 2017 bộ
( ; )x y
.
+ Với
2
y
thay vào (*) ta thấy luôn đúng
4; 2020
x
.
Suy ra có 2017 bộ
( ; )x y
.
+ Với
3 2020 2 0
y y
.
Xét
3 3 3
2 2
g(y) log log log 0, 3
2 2 2
y y y y
y
y y y
(3).
Suy ra (*) vô nghiệm ( Do (2) và (3) ).
Vậy có 4034 bộ
( ; )x y
.
Câu 12. (Chuyên Sơn La - 2020) Cho x là số thực dương và y là số thực thỏa mãn
1
2
2 log 14 ( 2) 1
x
x
y y
. Giá trị của biểu thức
2 2
2020
P x y xy
bằng
A. 2022. B. 2020. C. 2021. D. 2019.
Lời giải
Chọn C
Áp dụng bất đẳng thức Cauchy ta có
1
1 1
2 . 2, 0 2 4
x
x
x x x
x x
.
Đặt
1 , 0y t t
thu được
2 3 2
14 ( 2) 1 14 ( 3) 3 14 16 ( 1) ( 2) 16, 0y y t t t t t t t
.
Dẫn đến
2 2
log 14 ( 2) 1 log 16 4
y y
.
Như vậy hai vế bằng nhau khi dấu đẳng thức xảy ra tức là
2 2
1
1
1; 0 2020 2021
0
t
x x y P x y xy
x
x
.
Câu 13. (Sở Hưng Yên - 2020) Cho phương trình
2
2 2 2
3
log 3 6 6 3 2 1
y
x x y x x
. Hỏi có bao
nhiêu cặp số
;x y
và
0 2020 ; y
x
thỏa mãn phương trình đã cho?
A.
5
. B.
6
. C.
7
. D.
4
.
Lời giải
Chọn D
2 2
2 2 2 2 2 2
3 3
log 3 6 6 3 2 1 log 3 2 2 3 2 1
y y
x x y x x x x y x x
.
2
2 2 2
3
1 log 2 2 3 2 1
y
x x y x x
.
2
2 2 2
3
log 2 2 2 2 3
y
x x x x y
(1).
Đặt
2 2
3
log 2 2 2 2 3
z
x x z x x
thì (1) trở thành:
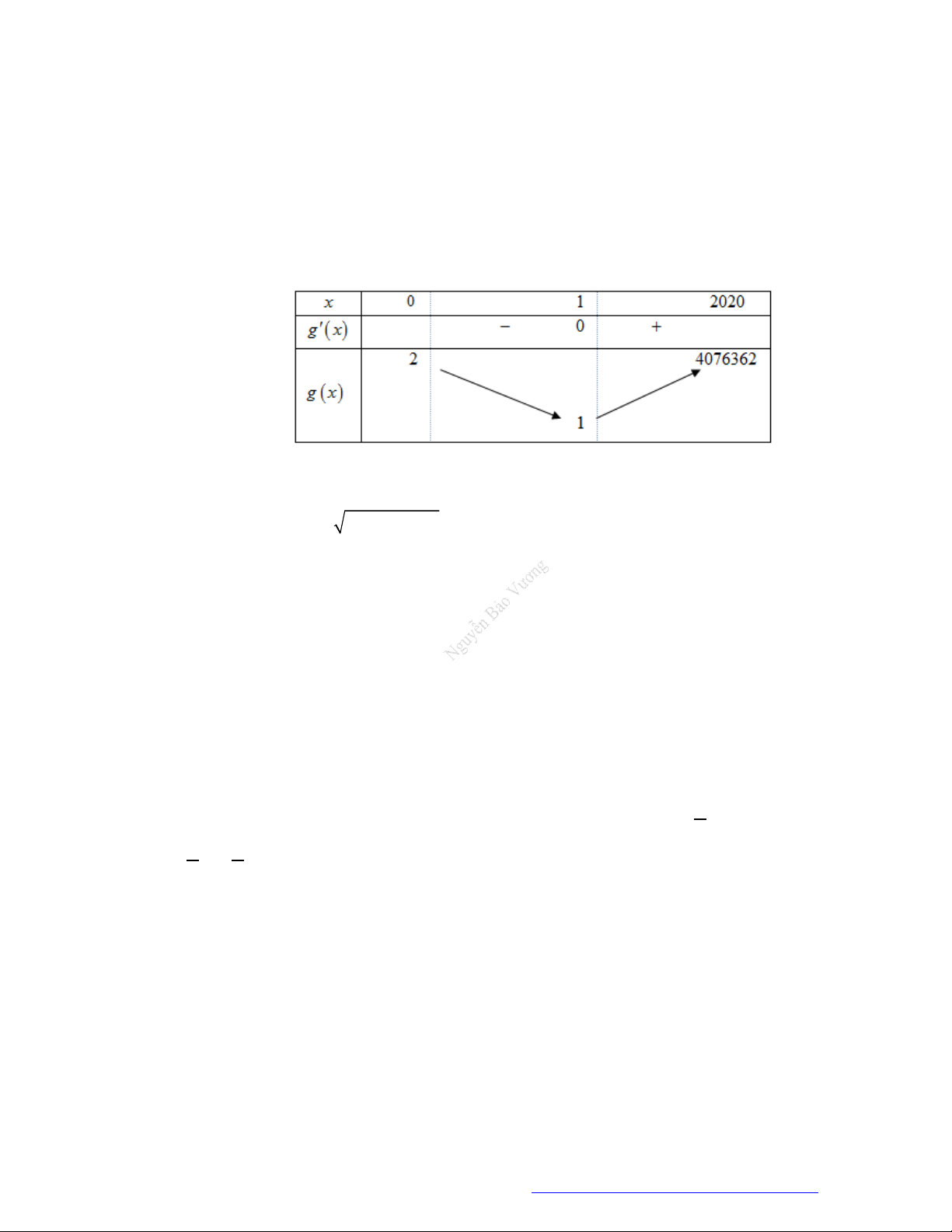
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 85
2
2
3 3
z y
z y
(2).
Xét hàm số
3 3 ln3 1 0, t
t t
f t t f t
.
Suy ra hàm số
f t
đồng biến trên
.
(2)
2 2
f z f y z y
.
Thay trở lại cách đặt ta có:
2
2 2 2
3
log 2 2 2 2 3
y
x x y x x
.
Xét hàm số:
2
2 2, 0;2020 2 2
g x x x x g x x
.
0 1
g x x
.
Bảng biến thiên:
Suy ra:
2
2
3
1 4076362 1 3 4076362 0 log 4076362
y
g x y
.
Do
y
3
0 log 4076362 3,7 y
0;1;2;3 y
.
4
9
1
3
3
3
g x
g x
g x
g x
.
Dựa vào bảng biến thiên của hàm số
g x
ta thấy mỗi phương trình trên có một nghiệm
0 2020x
.
Vậy có 4 cặp số
;x y
thỏa mãn đề bài.
Câu 14. (Sở Phú Thọ - 2020) Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
2 2021x
và
1
2
2 log 2 2
y y
x x y
?
A.
2020
. B.
9
. C.
2019
. D.
10
.
Lời giải
Chọn D
Đặt
1
2
log 2
y
x t
. Suy ra
1
2 2
y t
x
,
1
2 2
t y
x
.
Phương trình đã cho trở thành:
1
2 2 2 2 2.2 2.2
y t y y t
t y y t
.
Xét hàm số
2.2
x
g x x
có
2.2 ln 2 1 0,
x
g x x
nên hàm số
y g x
luôn đồng biến.
Khi đó
2.2 2.2
y t
y t y t
hay
1
2
log 2
y
y x
.
Suy ra
1 1 1
2 2 2 2 2
y y y y y
x x
.
Mà
2 2021x
nên
1
2
2 2 2021 1 1 log 2021
y
y
hay
2
2 log 2021 1y
.
Lại có
y
là số nguyên nên
2,3,...,11y
tức 10 giá trị thỏa mãn.
Xét biểu thức
1
2
y
x
, mỗi giá trị nguyên của
y
cho tương ứng 1 giá trị nguyên của
x
nên có 10
cặp số nguyên
,x y
thỏa mãn yêu cầu đề bài.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 86 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 15. (Sở Bắc Ninh - 2020) Có bao nhiêu cặp số nguyên dương
;x y
thảo mãn
2 3
3 3 1 1 3
x y x y
x x x
, với
2020
x
?
A.
13
. B.
15
. C.
6
. D.
7
.
Lời giải
Chọn D
Ta có
2 3 2 2
3 3 1 1 3 3 3 1 3 1 3 1 3 0
x y x y y x x x y
x x x x x x x x
Ta thấy
2 2
3
3 1 0, 0 3 1 3 0 3 2log 3
x x y y k
x x x x x y x x
.
Vì
6
2020 3 2020 3 3 0;1;2;3;4;5;6
k k
x k
.
Câu 16. (Sở Bình Phước - 2020) Biết
,a b
là các số thực sao cho
3 3 3 2
.10 .10 ,
z z
x y a b
đồng thời
, ,x y z
là các số các số thực dương thỏa mãn
log
x y z
và
2 2
log 1.
x y z
Giá trị của
2 2
1 1
a b
thuộc khoảng
A.
(1;2)
. B.
(2;3)
. C.
(3;4)
. D.
(4;5)
.
Lời giải
Chọn D
Ta có:
2 2
2 2
2 2 1
log
10
10
log 1
10 10.10
z
z z
x y z
x y
x y x y
x y z
x y
Khi đó
3 3 3 2
.10 .10
z z
x y a b
3 2
2 2
. 10 . 10
z z
x y x xy y a b
3 2 2
2 2 2 2
. . . .
x y x xy y a x y b x y x xy y a x y b x y
2 2 2 2 2 2 2 2 2 2
. 2 2 .
10 10
b b
x xy y a x xy y x y x y xy a x y a xy
Đồng nhất hệ số ta được
1
1
10
2
15
2 1
b
a
a
b
a
2 2
1 1 1
4 4,008 4;5 .
225a b
Câu 17. (Đặng Thúc Hứa - Nghệ An - 2020) Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
0 2020
y
và
3
3
3 3 6 9 log
x
x y y
.
A.
2020
B.
9
. C.
7
. D.
8
.
Lời giải
Chọn C
Ta có:
3
2 log
3
3 3 3
3 3 6 9 log 3 3 2 9 3log 3 3 2 3 3log *
y
x x x
x y y x y y x y
.
Xét hàm số:
3 3 2
t
f t t
.
Ta có:
3 .ln3 3 0,
t
f t t
. Suy ra hàm số
y f t
đồng biến trên
.
Khi đó:
2
3 3
* 2 log 2 log 3
x
f x f y x y y
.
Do
0 2020
y
và
,x y
nguyên
nên:
2
3
1 3 2020 2 2 log 2020 2;3;4;5;6;7;8
x
x x
.
Ứng với mỗi giá trị
x
có một giá trị của
y
nên có 7 cặp số
;x y
nguyên thỏa mãn yêu cầu bài
toán.
Câu 18. (Đô Lương 4 - Nghệ An - 2020) Giả sử
,a b
là các số thực sao cho
3 3
3 2
.10 .10
z z
x y a b đúng
với mọi các số thực dương
, ,x y z
thỏa mãn
log( )
x y z
và
2 2
log( ) 1x y z
. Giá trị của
a b
bằng
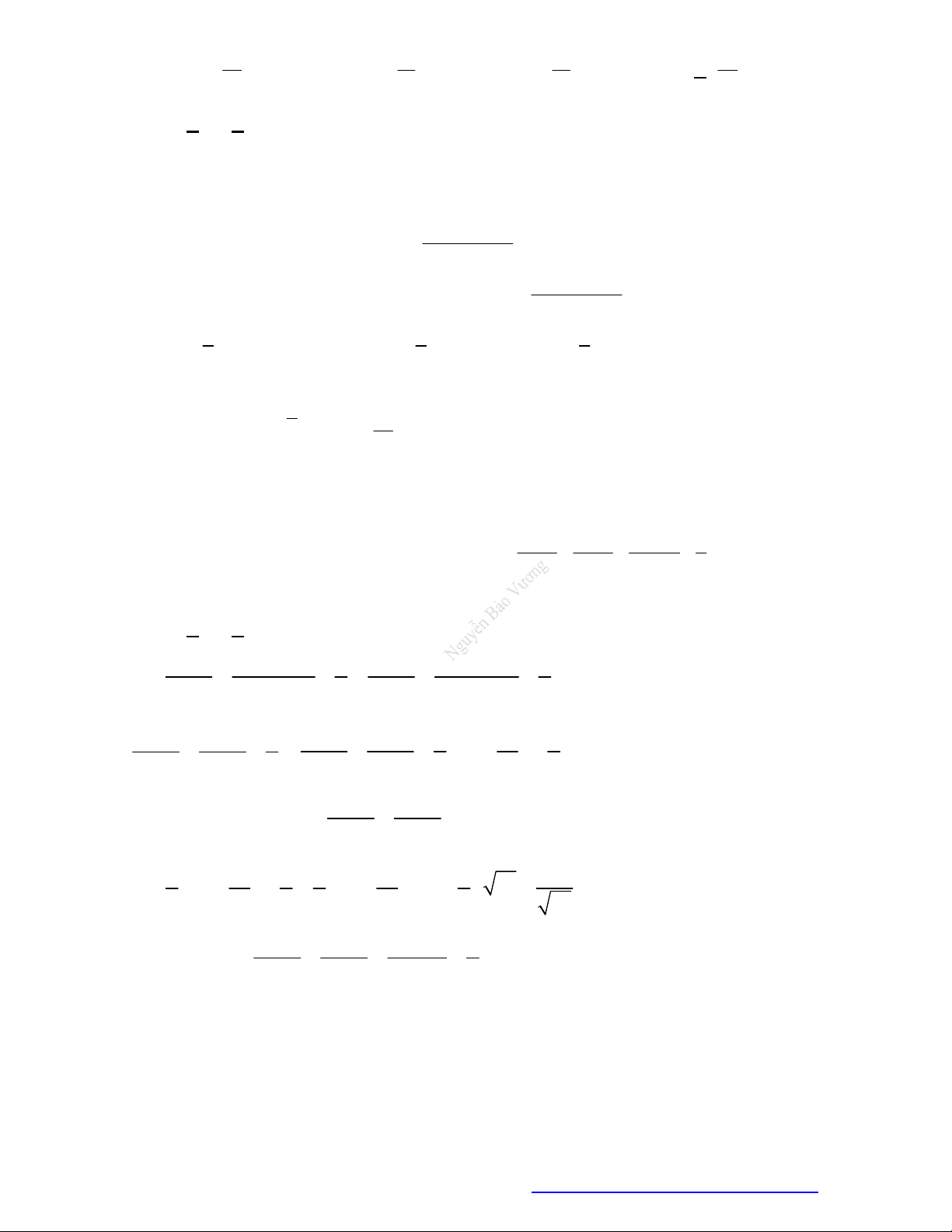
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 87
A.
25
2
. B.
31
2
. C.
31
2
.
D.
29
2
.
Lời giải
Chọn D
2 2
2 2 1 2
log( )
10 10
log( ) 1
10 ( ) 2 10.10
z z
z z
x y z
x y x y
x y z
x y x y xy
2
2
10
10
10 10.10
10 2 10.10
2
z
z
z z
z z
x y
x y
xy
xy
.
Khi đó
2
3 3 3 3
10 10.10
( ) 3 ( ) 10 3. .10
2
z z
z z
x y x y xy x y
3 3 2 3 2 3 2
1 1 1
2.10 3.10 30.10 10 30.10 .10 15.10
2 2 2
z z z z z z z
.
Lại có
3 3 3 2
.10 .10
z z
x y a b .
Suy ra
1
29
2
2
15
a
a b
b
.
Câu 19. (Kim Liên - Hà Nội - 2020) Có bao nhiêu số hữu tỉ
a
thuộc đoạn
1;1
sao cho tồn tại số thực
b
thỏa mãn
2 2
2
2 4 1 1
log 1 2
4 1 2 1 2 4 2
a a
a a a a
a b b
.
A.
0
. B.
3
. C.
1
. D. Vô số.
Lời giải
Chọn C
Ta có:
2 8 1 1 2 4 2 1 1
4 1 2 4 1 2 2
2 1 2
x x x x x
x x x
x x
2 4 1 3
4 1 2 2
x x
x x
2 4 1 3 1 3
2
4 1 4.2 4 2 2
x x
x
x x x
.
Áp dụng bất đẳng thức Cô si:
2 4 1
1 1
4 1 4.2
x x
x x
.
Lại có
2
3 1 3 3 1 3 1
2 2 2 2 0 2
4 2 2 4 2 4
2
x x x
x x
x
.
Từ
1 ; 2
suy ra
2 4 1 1
1
4 1 2 1 2 4 2
x x
x x x x
2 2
2
log 1 2 1
a b b
2 2
1 2 2a b b
2 2
2 1 0a b b
2
2
1 0
a b
0
1
a
b
.
0 1;1
a
nên chọn phương án C.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 88 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 20. (Lê Lai - Thanh Hóa - 2020) Có bao nhiêu cặp số nguyên thoả mãn
và
?
A. 19. B. 6 C. 10. D. 41.
Lờigiải
Chọn C
+ Điều kiện:
+ Ta có:
nên
Xét hàm số: , ta có:
1
' 1 0 0;
ln 2
f t t
t
nên hàm số
đồng
biến trên .
Do đó:
vì
0x y
nên
1 0x y y
+ Do suy ra
19
1
2
y
+ Do
nên
9; 8;...; 1;0y
, với mỗi giá trị cho ta 1 giá trị
thoả mãn YCBT.
Vậy có 10 cặp số nguyên thoả mãn YCBT.
Câu 21. (Thanh Chương 1 - Nghệ An - 2020) Cho các số thực
x
,
y
thỏa mãn
1x
,
1y
và
3 3 3 3 3
9
log log 6 2log log 2 3 log 2
2
x y x y xy
. Giá trị của biểu thức
2P x y
gần với số nào
nhất trong các số sau
A.
7
. B.
8
. C.
10
. D.
9
.
Lời giải
Chọn B
Đặt
3
loga x ,
3
log 2b y . Do
1x
,
1y
nên
0a
,
3
log 2b .
Theo giả thiết ta có:
9
1 2 3
2
a b ab a b
2 2
9
2 2 7 1 0 1
2
a b a b b
Coi
1
là phương trình bậc hai ẩn
a
,
b
là tham số. Để phương trình
1
có nghiệm
0a
thì:
2
2
2
2
0
2 7 1 36 0
2 7 1
0
2 7 1 0
2
b b b
b b
b b
b
4 3 2
2
4 28 45 22 1 0
2 7 1 0
b b b b
b b
2
2
2
2
2
1
1 4 20 1 0
4 20 1 0
2 7 1 0
2 7 1 0
b
b b b
b b
b b
b b
.
Với
2
9 3
1 2 6 0
2 2
b a a a
. Khi đó
3
2
2 3 3 8,1P x y
.
Với
2
2
4 20 1 0
2 7 1 0
b b
b b
: hệ vô nghiệm do
3
log 2b .
;x y
0; 20 20
x y x
2 2
2
log 2 2 3 0
x y x y xy x y
2 0
x y
0
x y
2 2
2
2 2
2
2 2 2 2
2 2
2 2 2 2
2 2
log 2 2 3 0
2
log 2 3 0
log 2 3 log 2 3 0
log 2 3 2 3 log (1)
x y x y xy x y
x y x y
x y xy x y
x y
x y xy x y x y xy x y
x y xy x y xy x y x y
2
log
f t t t
f t
0 ;
2 2 2 2
1 2 3 2 3
f x y xy f x y x y xy x y
2 1 0 1 2x y x y x y
20 20
x
y
y
x
;x y

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 89
Vậ
y giá trị biểu thức
2P
x y
gần
nhất với 8.
Câu 22. (Tiên Lãng - Hải Phòng - 2020) Có bao nhiêu cặp số nguyên dương
;x
y
với
2
020
x
thỏa
mãn
3
2
3 3 1 9 log 2 1
y
x
y x
A.
1
010
. B.
2
020
. C.
3
. D.
4
.
Lờ
i giải
Chọn C
Đặt
3
l
og 2 1 2 3 1
t
x
t x
, t
a được
2
2
3
3 1 2 3 1 3 3.3 3.3 2
t
y t y
y
t t y
(*)
.
Xét hàm số
3
.3 3.3 ln3 1 0,
u
u
f
u u f u u
f
u
đồng
biến trên
.
Do đó (*)
2t
y
, vậy nên
2
2
3 1 9 2 1
y
y
x
x
.
Vì
9
2020 9 4039 log 4039
y
x y
.
Vì
y
nguyên dương nê
n
1
;2;3
y
.
Ta thấy với mỗi
giá trị nguyên của
y
thì tìm được 1 giá trị nguyên của
x
. Vậy có 3 cặp
;x y
thỏa mãn.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM
Dạng 1. Bất phương trình logarit
+ Nếu
1a
thì
log log
a a
f x g x f x g x
(cùng chiều)
+ Nếu
0 1a
thì
log log
a a
f x g x f x g x
(ngược chiều)
+ Nếu a chứa ẩn thì
log 0 1 1 0
log
0 1 1 0
log
a
a
a
B a B
A
A B
B
.
Câu 1. (Đề Tham Khảo 2020 Lần 2) Tập nghiệm của bất phương trình
log 1x
là
A.
10;
. B.
0;
. C.
10;
. D.
;10
.
Câu 2. (Mã 102 - 2020 Lần 2) Tập nghiệm của bất phương trình
2
3
log 13 2x
là
A.
; 2 2:
. B.
;2
. C.
0;2
. D.
2;2
.
Câu 3. (Mã 103 - 2020 Lần 2) Tập nghiệm của bất phương trình
2
3
log 36 3x
là
A.
; 3 3;
. B.
;3
. C.
3;3
. D.
0;3
.
Câu 4. (Mã 101 - 2020 Lần 2) Tập nghiệm của bất phương trình
2
3
log 18 2x
là
A.
;3
. B.
0;3
. C.
3;3
. D.
; 3 3;
.
Câu 5. (Mã 104 - 2020 Lần 2) Tập nghiệm của bất phương trình
2
3
log 31 3x
là
A.
;2
. B.
2;2
. C.
; 2 2;
. D.
0;2
.
Câu 6. (Đề Minh Họa 2017) Giải bất phương trình
2
log 3 1 3x
.
A.
3x
B.
1
3
3
x
C.
3x
D.
10
3
x
Câu 7. (THPT Bạch Đằng Quảng Ninh 2019) Tìm tập nghiệm
S
của bất phương trình
2
ln 0x
.
A.
1;1S
. B.
1;0S
. C.
1;1 \ 0S
. D.
0;1S
.
Câu 8. (THPT Minh Khai Hà Tĩnh 2019) Tìm tập nghiệm
S
của bất phương trình
1 1
2 2
log 1 log 2 1x x
.
A.
2;S
. B.
1;2S
. C.
;2S
. D.
1
;2
2
S
.
Câu 9. (THPT - Yên Định Thanh Hóa 2019) Tập nghiệm S của bất phương trình
2
log 2 3 0x
là
A.
; 1S
. B.
1;S
. C.
; 1S
. D.
;0S
.
Câu 10. (THPT Đông Sơn Thanh Hóa 2019) Tập nghiệm của bất phương trình
0.3 3
10
log 5 2 log 9x
là
A.
5
0;
2
. B.
; 2
. C.
5
2;
2
. D.
2;
.
Câu 11. (Chuyên ĐHSP Hà Nội 2019) Tập nghiệm của bất phương trình
0,5
log 1 1x
là
BẤT PHƯƠNG TRÌNH MŨ - LOGARIT
Chuyên đề 20

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3
;
2
. B.
3
1;
2
. C.
3
;
2
. D.
3
1;
2
.
Câu 12. (HSG Bắc Ninh 2019) Tập nghiệm của bất phương trình
4 4
log ( 1) log (2 5)
x x
là
A.
1;6
B.
5
;6
2
C.
6;
D.
;6
Câu 13. (THPT An Lão Hải Phòng 2019) Tìm tập nghiệm
S
của bất phương trình
3 3
log 2 3 log 1
x x
A.
2
;
3
B.
3 2
;
2 3
C.
3
;1
2
D.
2
;
3
Câu 14. (THPT Cẩm Giàng 2 2019) Tập nghiệm của bất phương trình
3 1
2
log log 1
x
là
A.
0;1
. B.
1
;3
8
. C.
1
;1
8
. D.
1
;
8
.
Câu 15. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Số nghiệm nguyên của bất phương trình
0,8 0,8
log 15 2 log 13 8
x x
là
A. Vô số. B.
4
. C.
2
. D.
3
.
Câu 16. (Sở Vĩnh Phúc 2019) Tập xác định của hàm số
2
log 4 1
y x
là
A.
;4
. B.
2;4
. C.
;2
. D.
;2
.
Câu 17. (Sở Bình Phước 2019) Tập nghiệm của bất phương trình
2
log 3 1 2
x
là
A.
1
;1
3
B.
1 1
;
3 3
C.
1
;1
3
D.
;1
Câu 18. (Chuyen Phan Bội Châu Nghệ An 2019) Tập nghiệm của bất phương trình
2
2
log 1 3
x
là?
A.
2;2
. B.
; 3 3;
. C.
; 2 2;
. D.
3;3
.
Câu 19. (Sở Bắc Giang 2019) Tập nghiệm
S
của bất phương trình
0,8
log 2 1 0
x
là
A.
1
;
2
S
. B.
1;S
. C.
1
;
2
S
. D.
;1
S
.
Câu 20. (Sở Bắc Giang 2019) Tập nghiệm của bất phương trình
2
0,5 0,5
log 5 14 log 6 8
x x x
là
A.
2;2
. B.
;2
. C.
3
\ ;0
2
. D.
3;2
.
Câu 21. (Chuyên Trần Phú Hải Phòng 2019) Bất phương trình
2 2
log (3 2) log (6 5 )x x
có tập
nghiệm là
A.
0;
B.
1
;3 .
2
C.
( 3;1)
D.
6
1;
5
Câu 22. (KTNL GV THPT Lý Thái Tổ 2019) Tập hợp nghiệm của bất phương trình
2
log 1 3
x
là:
A.
1; 8
S
. B.
; 7
S
. C.
; 8
S
. D.
1; 7
S
.
Câu 23. (Sở Thanh Hóa 2019) Tìm tập nghiệm
S
của bất phương trình
2
ln ln 4 4
x x
.
A.
2;S
. B.
1;S
. C.
\ 2
S R
. D.
1; \ 2
S
.
Câu 24. (Chuyên Phan Bội Châu 2019) Tập nghiệm của bất phương trình
2
2
log 1 3
x
là:

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
2;2
. B.
; 3 3;
.
C.
; 2 2;
. D.
3;3
.
Câu 25. (Chuyên KHTN 2019) Tập nghiệm của bất phương trình
2
log 9
1
log 3
x
x
là:
A.
4; 3
. B.
4; 3
. C.
3; 4
. D.
.
Câu 26. (Chuyên Thái Bình 2019) Có tất cả bao nhiêu giá trị của tham số
m
để bất phương trình
2 2
2 2
log 2 log 2
x mx m x
nghiệm đúng
x
?
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 27. (Việt Đức Hà Nội 2019) Giải bất phương trình
2 2
log 3 2 log 6 5x x
được tập nghiệm là
;a b
. Hãy tính tổng
S a b
.
A.
26
5
S
. B.
11
5
S
. C.
28
15
S
. D.
8
3
S
.
Câu 28. (Sở Ninh Bình 2019) Bất phương trình
2
3
log 2 1
x x
có tập nghiệm là
A.
; 1 3;S
. B.
1;3
S
.
C.
3;S
. D.
; 1
S
.
Câu 29. (Hậu Lộc 2-Thanh Hóa 2019) Tập nghiệm của bất phương trình
ln3 ln 2 6
x x
là:
A.
0;6
. B.
0;6
. C.
6;
. D.
;6
.
Câu 30. (Hội 8 trường chuyên ĐBSH - 2019) Tập nghiệm
S
của bất phương trình
2
log 1 3
x
là
A.
1;9
S
. B.
1;10
S
. C.
;9
S
. D.
;10
S
.
Câu 31. (THPT Phan Bội Châu - Nghệ An -2019) Tập nghiệm của bất phương trình
2
2
log 1 3
x
là?
A.
2;2
. B.
; 3 3;
. C.
; 2 2;
. D.
3;3
.
Câu 32. (Bắc Ninh 2019) Bất phương trình
2 2
log (3 2) log (6 5 )
x x
có tập nghiệm là
( ; )a b
. Tổng
a b
bằng
A.
8
3
. B.
28
15
. C.
26
5
. D.
11
5
.
Câu 33. (THPT Hai Bà Trưng - Huế - 2019) Có tất cả bao nhiêu số nguyên
x
thỏa mãn bất phương trình
2
1 2
2
log log 2 0
x
?
A. Vô số. B.
1
. C.
0
. D.
2
.
Câu 34. (THPT Cẩm Bình 2019) Nghiệm của bất phương trình
2 3 2 3
log 2 5 log 1
x x
là
A.
5
4
2
x
. B.
1 4
x
. C.
5
4
2
x
1
. D.
4
x
.
Câu 35. (THPT Hàm Rồng 2019) Bất phương trình
4 2
log 7 log 1
x x
có bao nhiêu nghiệm
nguyên
A.
3
. B.
1
. C.
4
. D.
2
.
Câu 36. (Thi thử cụm Vũng Tàu - 2019) Tập nghiệm của bất phương trình
2
3
5
log 2 1 0
x x
là
A.
3
1;
2
. B.
3
;1 ;
2
. C.
1
;0 ;
2
. D.
1
0;
2
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 37. (Bình Phước - 2019) Tập nghiệm của bất phương trình
2
log 3 1 2 x
là
A.
1
;1
3
. B.
1 1
;
3 3
. C.
1
;1
3
. D.
;1
.
Câu 38. (Ngô Quyền - Hải Phòng -2019) Số nghiệm nguyên của bất phương trình
2
1
2
log 2 8 4x x
là
A. 6. B. Vô số. C. 4. D. 5.
Câu 39. (THPT Thuận Thành 3 - Bắc Ninh 2019) Tập nghiệm
S
của bất phương trình
2
6 6
log log 6x x
là
A.
; 2 3;S
. B.
2;3S
.
C.
3;2 \ 0S
. D.
2;3 \ 0S
.
Câu 40. (Nho Quan A - Ninh Bình - 2019) Bất phương trình
log x
2
2 2
có bao nhiêu nghiệm
nguyên?
A. 4. B. 2. C. 5. D. 3.
Câu 41. (Cần Thơ 2019) Tập nghiệm của bất phương trình
0,2
log 4 1 0x
là
A.
4;
. B.
4;9
. C.
;9
. D.
9;
.
Câu 42. (THPT Cẩm Bình Hà Tỉnh 2019) Tập nghiệm của bất phương
trình
2 1
2
log 7 log 1 0x x
là
A.
1;4S
. B.
;4S
. C.
4;S
. D.
4;7S
.
Câu 43. (NK HCM-2019) Bất phương trình
2
2 2
1 log 2 log 3 2x x x
có các nghiệm là
A.
3; .S
B.
1;3 .S
C.
2; .S
D.
2;3 .S
Dạng 2. Bất phương trình mũ
+ Nếu
1a
thì
f x g x
a a f x g x
. (cùng chiều)
+ Nếu
0 1a
thì
f x g x
a a f x g x . (ngược chiều)
+ Nếu a chứa ẩn thì
1 0
f x g x
a a a f x g x
.
Câu 1. (Đề Minh Họa 2020 Lần 1) Tập nghiệm của bất phương trình
2
1 9
5 5
x x x
là
A.
2;4
. B.
4;2
. C.
; 2 4;
. D.
; 4 2;
.
Câu 2. (Đề Tham Khảo 2020 Lần 2) Tập nghiệm của bất phương trình
9 2.3 3 0
x x
là
A.
0;
. B.
0;
. C.
1;
. D.
1;
.
Câu 3. (Mã 101 - 2020 Lần 1) Tập nghiệm của bất phương trình
2
13
3 27
x
là
A.
4;
. B.
4;4
. C.
;4
. D.
0;4
.
Câu 4. (Mã 102 - 2020 Lần 1) Tập nghiệm của bất phương trình
là
A. . B. . C. . D. .
Câu 5. (Mã 103 - 2020 Lần 1) Tập nghiệm của bất phương trình
2
7
2 4
x
là
A.
( 3;3)
. B.
(0;3)
. C.
( ;3)
. D.
(3; )
.
Câu 6. (Mã 104 - 2020 Lần 1) Tập nghiệm của bất phương trình
2
1
2 8
x
là
2
23
3 9
x
5;5
;5
5;
0;5

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
0;2
. B.
;2
. C.
2;2
. D.
2;
.
Câu 7. (Đề Tham Khảo 2018) Tập nghiệm của bất phương trình
2 6
2 2
x x
là:
A.
; 6
B.
0; 64
C.
6;
D.
0; 6
Câu 8. (Đề Tham Khảo 2019) Tập nghiệm của bất phương trình
2
2
3 27
x x
là
A.
3;
B.
1;3
C.
; 1 3;
D.
; 1
Câu 9. (Dề Minh Họa 2017) Cho hàm số
2
( ) 2 .7 .
x x
f x
Khẳng định nào sau đây là khẳng định sai?
A.
2
2
( ) 1 log 7 0
f x x x
B.
2
( ) 1 ln 2 ln 7 0
f x x x
C.
2
7
( ) 1 log 2 0
f x x x
D.
2
( ) 1 1 log 7 0
f x x
Câu 10. (Đề Tham Khảo 2017) Tìm tập nghiệm
S
của bất phương trình
1
1
5 0
5
x
.
A.
; 2
S
. B.
1;S
. C.
1;S
. D.
2;S
.
Câu 11. (THPT Hoàng Hoa Thám Hưng Yên 2019) Cho hàm số
2
2 3
e 1
x x
y
. Tập nghiệm của bất
phương trình
0
y
là:
A.
; 1
. B.
; 3 1;
.C.
3;1
. D.
1;
.
Câu 12. (Thpt Hùng Vương Bình Phước 2019) Tập nghiệm của bất phương trình
1
9
3
x
trên tập số
thực là
A.
2;
. B.
; 2
. C.
; 2
. D.
2;
.
Câu 13. (THPT Bạch Đằng Quảng Ninh 2019) Tập nghiệm của bất phương trình
1 2
4 8
x x
là
A.
8;
. B.
. C.
0;8
. D.
;8
.
Câu 14. (THPT Cù Huy Cận 2019) Tập nghiệm của bất phương trình
2
2
2 8
x x
là
A.
; 3
. B.
3;1
. C.
3;1
. D.
3;1
.
Câu 15. (Chuyên Vĩnh Phúc 2019) Tập nghiệm
S
của bất phương trình
2
1
5
25
x
x
là
A.
;2
S
B.
;1
S
C.
1;S
D.
2;S
Câu 16. (THPT Gang Thép Thái Nguyên 2019) Tập nghiệm bất phương trình
2
3
2 16
x x
là
A.
; 1
. B.
4;
. C.
1;4
. D.
; 1 4;
.
Câu 17. (THPT Gang Thép Thái Nguyên 2019) Tập nghiệm bất phương trình:
2 8
x
là
A.
;3
. B.
3;
. C.
3;
. D.
;3
.
Câu 18. (Chuyên Quốc Học Huế 2019) Tìm tập nghiệm
S
của bất phương trình
2
3
1 1
2 4
x x
.
A.
1;2
S
B.
;1
S
C.
1;2
S
D.
2;S
Câu 19. (Đề Tham Khảo 2019) Tập nghiệm của bất phương trình
2
2
3 27
x x
là
A.
; 1
B.
3;
C.
1;3
D.
; 1 3;
Câu 20. (Chuyên Vĩnh Phúc 2019) Cho
3
.e
x
f x x
. Tập nghiệm của bất phương trình
0
f x
là

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
;
3
B.
1
0;
3
C.
1
;
3
D.
0;1
Câu 21. (THPT Ba Đình 2019) Số nghiệm nguyên của bất phương trình
2
2 3 7
2 21
1
3
3
x x
x
là
A. 7. B. 6. C. vô số. D. 8.
Câu 22. (THPT Lương Thế Vinh Hà Nội 2019) Tập nghiệm của bất phương trình
2 6
3
1
2
2
x
x
là
A.
0;6
. B.
;6
. C.
0;64
. D.
6;
.
Câu 23. (Chuyên Hùng Vương Gia Lai 2019) Bất phương trình
2
2
1 1
2 8
x x
có tập nghiệm là
A.
3; .
B.
; 1 .
C.
1;3 .
D.
1;3 .
Câu 24. (THPT Yên Phong 1 Bắc Ninh 2019 Nghiệm nguyên lớn nhất của bất phương trình
2
2
4 64
x x
là
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 25. (Sở Hà Nội 2019) Tập nghiệm của bất phương trình
2
3 81
4 256
x
là
A.
; 2
. B.
; 2 2;
. C.
. D.
2;2
.
Câu 26. (Chuyên Sơn La 2019) Tập nghiệm của bất phương trình
2
2
2 8
x x
là
A.
; 1
. B.
1;3
.
C.
3;
. D.
; 1 3;
.
Câu 27. (Chuyên ĐHSP Hà Nội 2019) Tập nghiệm của bất phương trình
e
1
x
là
A.
B.
;0
C.
0;
D.
0;
Câu 28. (Chuyên Lam Sơn Thanh Hóa 2019) Số nghiệm nguyên của bất phương trình
2
3
2 16
x x
là số
nào sau đây ?
A. 5. B. 6. C. 4. D. 3.
Câu 29. (Chuyên Vĩnh Phúc 2019) Tập nghiệm của bất phương trình
2 1
2
1
1
1
x
a
(với
a
là tham số,
0
a
) là:
A.
;0
B.
1
;
2
C.
0;
D.
1
;
2
Câu 30. (Cụm 8 Trường Chuyên 2019) Tập nghiệm
S
của bất phương trình
3 e
x x
là:
A.
\ 0
S
. B.
0 ;S
. C.
S
. D.
; 0
S
.
Câu 31. (Nguyễn Huệ- Ninh Bình- 2019)Bất phương trình
1
2 4
x
có tập nghiệm là:
A.
1:
. B.
;1
. C.
1:
. D.
;1
.
Câu 32. (THPT Minh Khai - 2019) Tìm tập nghiệm
S
của bất phương trình
3 9
x
A.
;2
S
. B.
2;S
. C.
;2
S
. D.
2
S
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 33. (Lômônôxốp - Hà Nội 2019) Tập nghiệm của bất phương trình
1
2
1 1
3 3
x
là:
A.
1
0;
2
. B.
1
;
2
. C.
1
0;
2
. D.
1
;
2
.
Câu 34. ( Đồng Nai - 2019) Tập nghiệm của bất phương trình
2
1
3
9
x
là
A.
4;
. B.
;4
. C.
;0
. D.
0;
.
Câu 35. (Chuyên Long An-2019) Tìm nghiệm của bất phương trình
1
1 1
2 4
x
.
A.
3x
. B.
3x
. C.
3x
. D.
1 3x
.
Câu 36. (Chuyên - Vĩnh Phúc - 2019) Tập nghiệm của bất phương trình
2 1
2
1
1
1
x
a
(với
a
là tham
số,
0a
) là
A.
1
;
2
. B.
0;
. C.
;0
. D.
1
;
2
.
Câu 37. (Chuyên Lam Sơn-2019) Số nghiệm nguyên của bất phương trình
2
3
2 16
x x
là
A.
5
. B.
6
. C.
4
. D.
3
.
Câu 38. (chuyên Hùng Vương Gia Lai 2019) Bất phương trình
2
2
1 1
2 8
x x
có tập nghiệm là
A.
3; .
B.
; 1 .
C.
1;3 .
D.
1;3 .
Câu 39. (Chuyên Hoàng Văn Thụ-Hòa Bình 2019)Cho bất phương trình
2
1 2 1
2 2
3 3
x x x
có tập
nghiệm
;S a b
. Giá trị của
b a
bằng
A.
3
. B.
4
. C.
2
. D.
1
.
Câu 40. (SGD Hưng Yên 2019) Tập nghiệm của bất phương trình
2 1
2
1
3
x
là
A.
( ;0)
. B.
(0; )
. C.
1
;
2
. D.
1
;
2
.
Câu 41. (SGD Điện Biên - 2019) Tập nghiệm của bất phương trình là
A. . B. . C. . D. .
Câu 42. (Ngô Quyền - Ba Vì - Hải Phòng 2019) Tập nghiệm
S
của bất phương trình
2
4
1
8
2
x x
là
A.
;3S
. B.
1;S
. C.
;1 3;S
. D.
1;3S
.
Câu 43. (Cần Thơ - 2019) Nghiệm của bất phương trình
2
2 4
x x
là
A.
1 2 x
. B.
1x
. C.
2x
. D.
2 1 x
.
Câu 44. (Chuyên Lê Quý Đôn Điện Biên 2019) Tìm tập nghiệm của bất phương trình
1 1
2 2 3 3
x x x x
.
A.
2;
. B.
;2
. C.
;2
. D.
2;
.
2 2
x
0;1
; 1
1;

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu
45. (Chuyên Lê Hồng Phong Nam Định 2019) Cho bất phương trình
1
4
5.2 16 0
x x
c
ó tập
nghiệm là đoạn
;a
b
. Tính
2
2
l
og
a
b
A.
2
. B.
1
. C
.
0
. D
.
1
0
.
Câu
46. (Thi thử cụm Vũng Tàu - 2019) Cho bất phương trình
2
1
2 1
2 2
3 3
x
x x
c
ó tập nghiệm
;S a b
. Giá trị của
b a
bằng
A.
2
. B.
1
. C.
1
. D
.
2
.
Câu
47. (Chuyên Quốc Học Huế 2019) Xác định tập nghiệm
S
của bất
phương trình
2
3
1
3
3
x
.
A.
;
1
S
. B.
1
;S
. C
.
1
;S
. D
.
;
1
S
.
Câu
48. (Sở Hà Nam - 2019) Tập nghiệm của bất phương trình
2
2
6
4
1
5
5
x
x
x
là
A.
;1 2;
. B.
2;
. C
.
;1
. D.
1;2
.
Câu
49. (Chu Văn An - Hà Nội - 2019) Bất phương trình
1
2 3
2 2
x
x
c
ó nghiệm là
A.
4
x
. B.
4
x
. C
.
4
x
. D.
4
x
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ-GIỎI MỨC 7-8-9-10 ĐIỂM
DẠNG 1. BẤT PHƯƠNG TRÌNH LOGARIT
Sử dụng các phương pháp giải phương trình logarit đã đưa ra tại Chuyên đề 19. Phương trình mũ
– logarit để giải
Câu 1. (Chuyên Vĩnh Phúc 2019) Tập nghiệm của bất phương trình
2 2
2log 1 log 5 1x x
là
A.
3;5
B.
1;3
C.
1;3
D.
1;5
Câu 2. (THPT Gia Lộc Hải Dương 2019) Tìm tập nghiệm
S
của bất phương trình
3 3
2log 4 3 log 18 27x x
.
A.
3
;3
8
S
. B.
3
;3
4
S
. C.
3
;
4
S
. D.
3;S
.
Câu 3. (THPT Yên Khánh - Ninh Bình -2019) Tập nghiệm của bất phương trình
2
2 2
log 2 log 9
4
x
x
chứa tập hợp nào sau đây?
A.
3
;6
2
. B.
0;3
. C.
1;5
. D.
1
;2
2
.
Câu 4. (Chuyên Đại Học Vinh 2019) Tập nghiệm của bất phương trình
1 3
3
log 1 log 11 2 0 x x
là:
A.
;4
. B.
1;4
. C.
1;4
. D.
11
4;
2
.
Câu 5. (Sở Phú Thọ 2019) Tập nghiệm của bất phương trình
1 3
3
log 1 log 11 2 0 x x
là
A.
;4
B.
1;4
C.
1;4
D.
11
4;
2
Câu 6. (Sở Bắc Ninh 2019) Tập nghiệm của bất phương trình
1 3
3
log 1 log 11 2 0 x x
là:
A.
;4 S
. B.
1;4S
. C.
1;4S
. D.
11
3;
2
S
.
Câu 7. (THPT Nguyễn Khuyến 2019) Tổng tất cả các nghiệm nguyên của bất phương trình
2 2
2log 1 2 log 2x x bằng
A.
12
B.
9
C.
5
D.
3
Câu 8. (Chuyên Bắc Ninh 2019) Tìm tất cả giá trị của tham số
m
để bất phương trình
2 2
log 2 3 log 1x x mx
có tập nghiệm là
.
A.
2 2m
. B.
2 2m
. C.
2 2 2 2m
. D.
2m
.
Câu 9. (Mã 123 2017) Tìm tập nghiệm
S
của bất phương trình
2
2 2
log 5log 4 0x x
.
A.
( ;1] [4; )S
B.
[2 ;16]S
C.
(0; 2] [16; )S
D.
( ; 2] [ 61 ; )
Câu 10. (Mã 105 2017) Tìm tất cả các giá trị thực của tham số
m
để bất phương trình
2
2 2
log 2log 3 2 0x x m
có nghiệm thực.
BẤT PHƯƠNG TRÌNH MŨ - LOGARIT
Chuyên đề 20

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1m
B.
1m
C.
0m
D.
2
3
m
Câu 11. (THPT Đoàn Thượng - Hải Dương 2019)
Biết rằng bất phương trình
5
2
2
log 5 2 2.log 2 3
x
x
có tập nghiệm là
log ;
a
S b
, với
a
,
b
là các số nguyên
dương nhỏ hơn 6 và
1
a
. Tính
2 3P a b
.
A.
7
P
. B.
11.
P
C.
18
P
. D.
16.
P
Câu 12. Tập nghiệm
S
của bất phương trình
2
2 2
0
log 5log 6x x
là
A.
1
;64
2
S
. B.
1
0;
2
S
.
C.
64;S
. D.
2
6
1
0; 4;S
.
Câu 13. (Chuyên Vĩnh Phúc 2019) Kí hiệu
max ;a b
là số lớn nhất trong hai số
, .a b
Tìm tập nghiệm S
của bất phương trình
2 1
3
max log ; log 1.
x x
A.
1
;2 .
3
S
B.
0;2 .
S
C.
1
0; .
3
S
D.
2; .
S
Câu 14. (Sở Bắc Ninh 2019) Tập nghiệm của bất phương trình
2 2 2
2
log 2 4 2 2 1
x x x x x
là
;
a b
.
Khi đó
.a b
bằng
A.
15
16
. B.
12
5
. C.
16
15
. D.
5
12
.
Câu 15. (Chuyên Đại học Vinh - 2019) Bất phương trình
3
9 ln 5 0
x x x
có bao nhiêu nghiệm
nguyên?
A. 4. B. 7. C. 6. D. Vô số.
Câu 16.
(THPT Đoàn Thượng – Hải Dương 2019) Biết rằng bất phương trình
5
2
2
log 5 2 2.log 2 3
x
x
có tập nghiệm là
log ;
a
S b
, với
a
,
b
là các số nguyên
dương nhỏ hơn 6 và
1
a
. Tính
2 3P a b
.
A.
7
P
. B.
11.
P
C.
18
P
. D.
16.
P
Câu 17. (Chuyên Đại học Vinh - 2019) Tính tổng tất cả các nghiệm nguyên của bất phương trình
2 2
2 2
log 3 log 4 1 0
x x x x
.
A.
4
. B.
6
. C.
5
. D.
3
.
Câu 18. (HKI-NK HCM-2019) Biết bất phương trình
2
2
2
1
log 2 1
16 3
x x
x x
x
có tập nghiệm
là
; .S a b
Hãy tính tổng
20 10 .T a b
A.
45 10 2
T
. B.
46 10 2
T
. C.
46 11 2
T
. D.
47 11 2
T
.
Câu 19. (THPT Cẩm Bình Hà Tỉnh 2019) Tập nghiệm của bất phương trình
1
3
log 10 3 1
x
x
chứa
mấy số nguyên.
A.
3
. B.
5
. C.
4
. D. Vô số.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 20. (Chuyên Phan Bội Châu - Nghệ An - 2018) Số nghiệm nguyên của bất phương trình
2 3 2 3
log log 1 log .logx x x x
là
A.
1
. B.
2
. C.
3
. D. Vô số.
Câu 21. (THPT Lý Thái Tổ - Bắc Ninh - 2018) Bất phương trình
2 1
3
3 7
log log 0
3
x
x
có tập nghiệm
là
;a b
. Tính giá trị
3
P a b
.
A.
5
P
. B.
4P
. C.
10
P
. D.
7
P
.
Câu 22. (THPT Ngô Quyền - Hải Phòng - 2018) Tập nghiệm của bất phương trình
1 2
3
log log 0
x
là
A.
0;5
. B.
1;2
. C.
1
;4
4
. D.
1
0;
2
.
Câu 23. (THPT Nam Trực - Nam Định - 2018) Tổng các nghiệm nguyên của bất phương trình
2 5 2
5 5
25 75 0
log logx x
là
A.
70
. B.
64
. C.
62
. D.
66
.
Câu 24. (THPT Lương Văn Can - 2018) Cho bất phương trình
log 1 4 log 0
x x
. Có bao nhiêu số
nguyên
x
thoả mãn bất phương trình trên.
A.
10000
. B.
10001
. C.
9998
. D.
9999
.
DẠNG 2. BẤT PHƯƠNG TRÌNH MŨ
Sử dụng các phương pháp giải phương trình mũ đã đưa ra tại Chuyên đề 19. Phương trình mũ –
logarit để giải
Câu 1. (THPT Trần Phú - 2019) Tập nghiệm của bất phương trình:
1 2 1
3 2 4 8 0
x x x
A.
1
;
4
B.
1
;
4
. C.
;4
D.
4;
.
Câu 2. (Lý Nhân Tông - Bắc Ninh 2019) Bất phương trình
2 1
3 7.3 2 0
x x
có tập nghiệm là
A.
2
; 1 log 3;
. B.
2
; 2 log 3;
.
C.
3
; 1 log 2;
. D.
3
; 2 log 2;
.
Câu 3. (Chuyên ĐH Vinh -2019) Biết tập nghiệm của bất phương trình
2
2 3
2
x
x
là
;a b
. Giá trị
a b
bằng
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 4. (Chuyên Bắc Giang 2019) Tập nghiệm của bất phương trình
3 1 1 2
3 9 3 9.3 0
x x x
là
A.
;1 .
B.
3; .
C.
1; .
D.
;3 .
Câu 5. (THPT Đông Sơn 1 - Thanh Hóa - 2019) Bất phương trình
6.4 13.6 6.9 0
x x x
có tập
nghiệm là?
A.
; 1 1; .
S
B.
; 2 1; .
S
C.
; 1 1; .
S
D.
; 2 2; .
S
Câu 6. (Kinh Môn - Hải Dương 2019) Cho bất phương trình:
2 2
2.5 5.2 133. 10 0
x x x
có tập
nghiệm là:
;S a b
. Biểu thức
1000 5A b a
có giá trị bằng
A. 2021 B. 2020 C. 2019 D. 2018
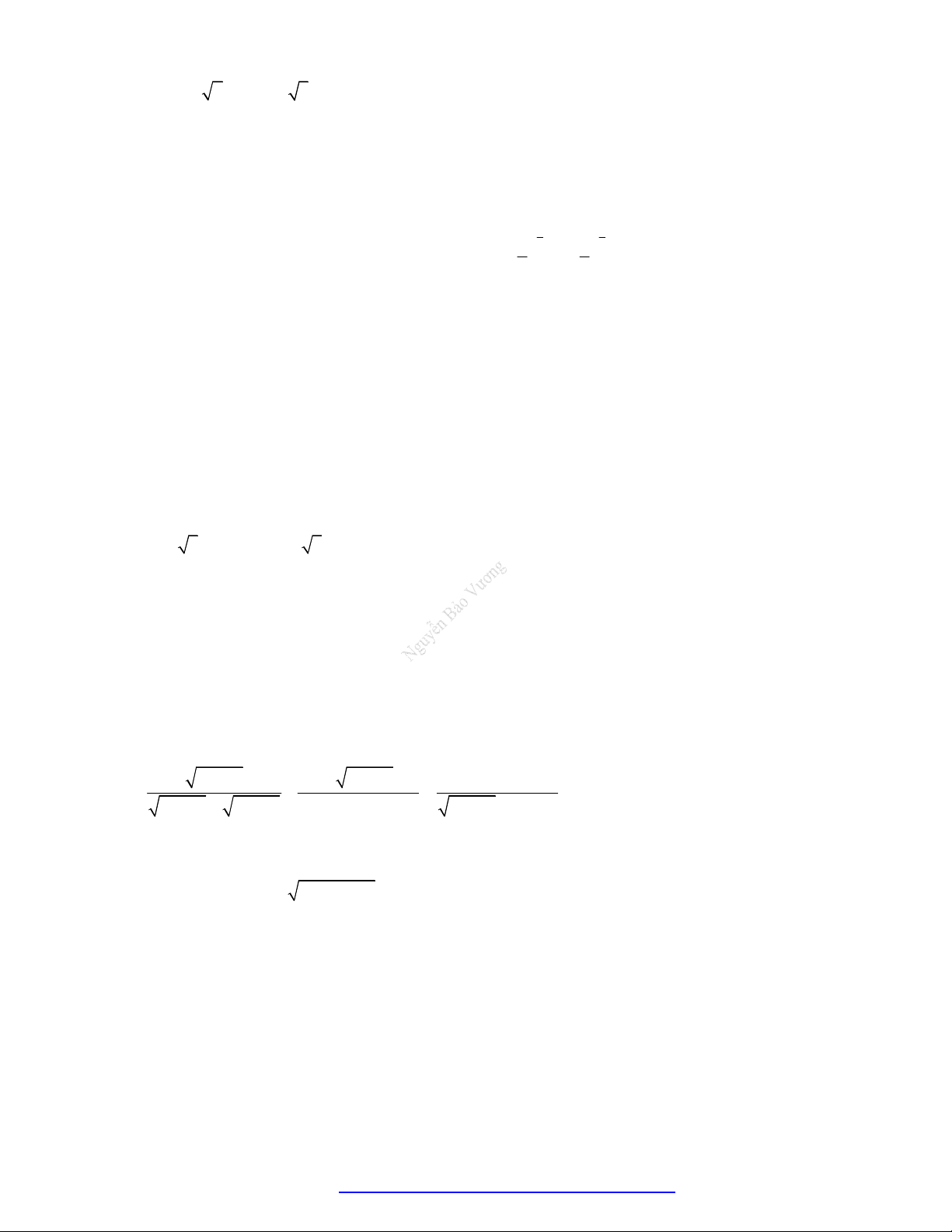
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 7. (Toán Học Tuổi Trẻ Năm 2019) Số nghiệm nguyên của bất phương trình:
2
17 12 2 3 8
x x
là:
A.
3
. B.
1
. C.
2
. D.
4
.
Câu 8. (Chuyên Lê Quý Dôn Diện Biên 2019) Tìm tập nghiệm của bất phương trình
1 1
2 2 3 3
x x x x
.
A.
2;
. B.
;2
. C.
;2
. D.
2;
.
Câu 9. (Chuyên Hưng Yên 2019) Cho bất phương trình
2 1
1
1 1
3 12
3 3
x x
có tập nghiệm
;
S a b
.
Giá trị của biểu thức
3 10 P a b
là
A.
5
. B.
3
. C.
4
. D.
2
.
Câu 10. (Chuyên Hạ Long 2019) Bất phương trình sau có bao nhiêu nghiệm nguyên dương
9 4.3 3 0
x x
.
A. 3. B. 1. C. 0. D. 2.
Câu 11. (THPT Đông Sơn Thanh Hóa 2019) Bất phương trình
6.4 13.6 6.9 0
x x x
có tập nghiệm là?
A.
; 1 1; .
S
B.
; 2 1; .
S
C.
; 1 1; .
S
D.
; 2 2; .
S
Câu 12. (THPT Yên Khánh - Ninh Bình - 2019) Tập nghiệm của bất phương trình
2
4 14
2 3 7 4 3
x x
là:
A.
6;2
. B.
6 2;
. C.
6;2
. D.
; 6 2;
.
Câu 13. (Chuyên Bắc Giang 2019) Tìm số nghiệm nguyên của bất phương trình
1
6 4 2 2.3
x x x
A. 2. B. 3. C. 1. D. 0
Câu 14. (Chuyên Thái Bình 2019) Tập nghiệm của bất phương trình
2
9 2 1
3 9 .5 1
x x
x
là khoảng
;a b
. Tính
b a
A.
6
. B.
3
. C.
8
. D.
4
.
Câu 15. ( Hsg Bắc Ninh 2019) Bất phương trình
2 4 4 2
2
2 2 4 2
2 3 3 4 3 7 3 2
3
2 3 2 3 4 3 2 3
x x x x
x
x x x x
có bao nhiêu nghiệm?
A. Vô số. B. 1. C. 2. D. 3
Câu 16. (KTNL GV Thpt Lý Thái Tổ 2019) Số nghiệm nguyên thuộc đoạn
20; 20
của bất phương
trình:
2 1 2
2 9.2 4 2 3 0
x x
x x
là
A.
38
. B.
36
. C.
37
. D.
19
.
Câu 17. (Chuyên Thái Nguyên 2019) Tập hợp tất cả các số thực
x
không thỏa mãn bất phương trình
2
4 2 2
9 4 .2019 1
x x
x
là khoảng
;a b
. Tính
b a
.
A.
5
. B.
4
. C.
5
. D.
1
.
Câu 18. (THPT Chuyên Thái Bình - 2019) Tập nghiệm của bất phương trình
2
9 2 1
3 9 .5 1
x x
x
là
khoảng
;a b
. Tính
b a
.
A.
6.
B.
3.
C.
8.
D.
4.
Câu 19. (Chuyên Bắc Ninh - 2020) Có bao nhiêu giá trị nguyên của
x
trong đoạn
0;2020
thỏa mãn bất
phương trình sau
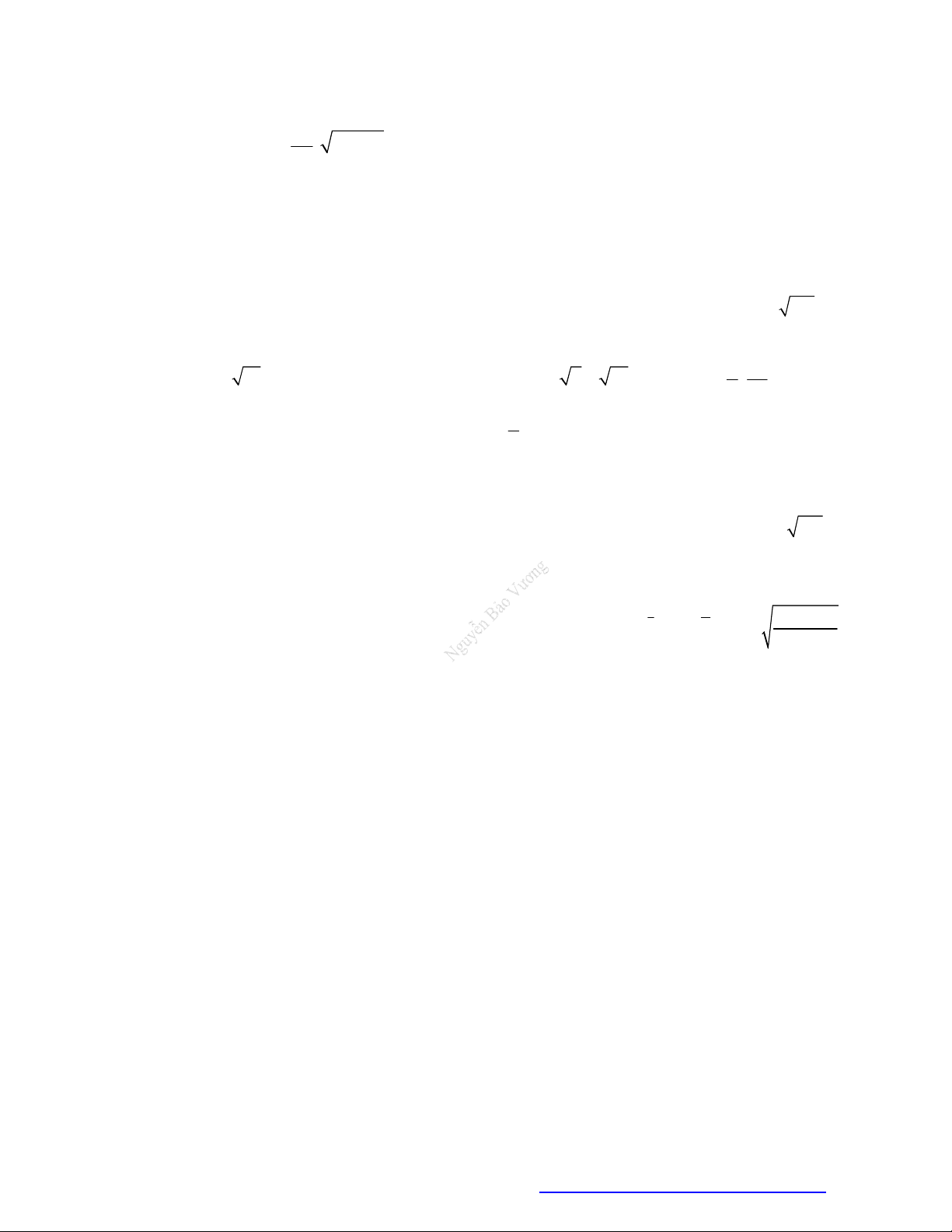
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
1
6 25 36 20 24 30
x
x x x x x
.
A.
3
. B.
2000
. C.
1
. D.
1
000
.
Câu 20. (Hải Hậu - Nam Địn
h - 2020) Tập nghiệm của bất phương trình
2
1
1
(3
9)(3 ) 3 1 0
27
x
x x
c
hứa bao nhiêu số nguyên ?
A. 2. B. 3. C. 4. D. 5.
Câu 21. (THPT Lương Văn Tụy - Ninh Bình - 2018) Tập nghiệm của bất phương trình
9
2 5 .3 9 2 1 0
x
x
x
x
là
A.
0
;1 2;
. B.
;
1 2;
.C
.
1
;2
. D.
;
0 2;
.
Câu 22. (Toán Học Tuổi Trẻ Số 6) Tập
nghiệm của bất phương trình
2
2
2
.7 7.2 351. 14
x
x x
có
dạng
là đoạn
;S
a b
. G
iá trị
2b
a
t
huộc khoảng nào dưới đây?
A.
3; 10
. B.
4;2
. C.
7; 4 10
. D.
2
49
;
9
5
.
Câu 23. (Chuyên ĐHSPHN - 2018) Cho
2
1
1
.
5
2
x
f
x
;
5
4 .ln 5
x
g
x x
.
Tập nghiệm của bất
phương trình
f
x g x
l
à
A.
0
x
. B.
1x
. C.
0
1x
. D.
0
x
.
Câu 24. (THP
T Kinh Môn - Hải Dương - 2018) Bất phương trình
2
2
2
.5 5.2 133. 10
x
x x
có tập
nghiệm là
;S
a b
thì biểu thức
1
000 4 1A b a
có giá
trị bằng
A.
3
992
. B.
4
008
. C.
10
04
. D.
2
017
.
Câu 25. Số nghiệm nguyên thuộc
khoảng
0
;12
của
bất phương trình
1
11
1 2
2
2
2 11
3 3 log
1
x
x
x
x
x x
l
à:
A.
7
. B.
8
. C.
5
. D.
11
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI – MỨC 9-10 ĐIỂM
DẠNG 1. BẤT PHƯƠNG TRÌNH LOGARIT CHỨA THAM SỐ
Câu 1. (Chuyên Lam Sơn Thanh Hóa 2019) Cho
a
là số thực dương,
1a
. Biết bất phương trình
2log 1
a
x x nghiệm đúng với mọi
0x
. Số
a
thuộc tập hợp nào sau đây?
A.
7;8
B.
3;5
C.
2;3
D.
8;
Câu 2. (THPT Cẩm Giàng 2 2019) Cho
a
là số nguyên dương lớn nhất thỏa mãn
3
3 2
3log 1 2loga a a
. Giá trị của
2
log 2017a
xấp xỉ bằng:
A.
19
. B.
26
. C.
25
. D.
23
.
Câu 3. (Chuyên Hưng Yên 2019) Tìm tất cả các giá trị thực của tham số
m
để bất phương trình
0,02 2 0,02
log log 3 1 log
x
m có nghiệm với mọi
;0x
A.
1.m
B.
0 1.m
C.
1.m
D.
2.m
Câu 4. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Gọi
S
là tổng tất cả các giá trị nguyên của
m
để
bất phương trình
2 2
ln 7 7 ln 4x mx x m
nghiệm đúng với mọi
x
thuộc
. Tính
S
.
A.
14S
. B.
0S
. C.
12S
. D.
35S
.
Câu 5. (Chuyên Bắc Giang 2019) Có bao nhiêu giá trị nguyên dương của
m
để bất phương trình
2 2
2 2
log 7 7 log 4x mx x m
nghiệm đúng với mọi
x
.
A.
5
B.
4
C.
0
D.
3
Câu 6. (Chuyên Quang Trung Bình Phước 2019) Tìm tất cả các giá trị thực của tham số
m
để bất
phương trình
3
1 1
2 2
log 1 logx x x m
có nghiệm.
A.
2m
. B.
m
.
C.
2m
. D. Không tồn tại
m
.
Câu 7. (THPT Chuyên Thái Bình - 2019) Có tất cả bao nhiêu giá trị của tham số
m
để bất phương
trình
2 2
2 2
log 2 log 2x mx m x
nghiệm đúng với mọi
x
.
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 8. (Chuyên Vĩnh Phúc - 2019) Tìm tập
S
tất cả các giá trị thực của số
m
để tồn tại duy nhất cặp
số
;x y
thỏa mãn
2 2
2
2
log 4 4 6 1
x y
x y m
và
2 2
2 4 1 0x y x y .
A.
5; 1;1;5S
. B.
1;1S
.
C.
5;5S
. D.
7 5; 1;1;5;7S
.
Câu 9. (Bình Giang-Hải Dương 2019) Xét bất phương trình
2
2 2
log 2 2 1 log 2 0x m x
. Tìm tất
cả các giá trị của tham số
m
để bất phương trình có nghiệm thuộc khoảng
2;
.
A.
3
;0
4
m
. B.
0;m
. C.
;0m
. D.
3
;
4
m
.
Câu 10. Gọi S là tập hợp tất cả các giá trị của tham số m để bất phương trình
2 5 4 4 3
ln 1 0m x x m x x x x
thỏa mãn với mọi
0x
. Tính tổng các giá trị trong
tập hợp S.
BẤT PHƯƠNG TRÌNH MŨ - LOGARIT
Chuyên đề 20

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
. B.
0
. C.
1
. D.
2
.
Câu 11. (Chuyên Thái Bình - 2020) Cho bất phương trình
2 2
7 7
log 2 2 1 log 6 5
x x x x m
.
Có tất cả bao nhiêu giá trị nguyên của
m
để bất phương trình có tập nghiệm chứa khoảng
1;3
?
A.
36
. B.
34
. C.
35
. D. Vô số.
Câu 12. (Chuyên Bắc Ninh - 2020) Gọi
0
m
là giá trị nhỏ nhất để bất phương trình
2 2 2
1 log 2 2log 4 2 2 2 log 1
2
x
x m x x x
có nghiệm. Chọn đáp án
đúng trong các khẳng định sau
A.
0
9;10
m
. B.
0
8;9
m
. C.
0
10; 9
m
. D.
0
9; 8
m
.
Câu 13. (Lương Thế Vinh - Hà Nội - 2020) Gọi
S
là tập hợp tất cả các điểm
;M x y
trong đó
,x y
là
các số nguyên thoả mãn điều kiện
2 2
1
log 2 2 1,
x y
x y m
với
m
là tham số. Có bao nhiêu số
nguyên
m
thuộc đoạn
2020;2019
để tập
S
có không quá
5
phần tử?
A.
1.
B.
2020.
C.
2021.
D.
2019.
Câu 14. (Chuyên Thái Bình - Lần 3 - 2020) Cho bất phương trình
2 2
7 7
log 2 2 1 log 6 5
x x x x m
. Có tất cả bao nhiêu giá trị nguyên của tham số
m
để
bất phương trình trên có tập nghiệm chứa khoảng
1;3 ?
A.
36
. B.
35
. C.
34
. D. Vô số.
Câu 15. (Chuyên Lê Hồng Phong - 2018) Xét bất phương trình
2
2 2
log 2 2 1 log 2 0
x m x
. Tìm tất
cả các giá trị của tham số
m
để bất phương trình có nghiệm thuộc khoảng
2;
.
A.
0;m
. B.
3
;0
4
m
. C.
3
;
4
m
. D.
;0
m
.
Câu 16. (Chuyên Vinh - 2018) Gọi
a
là số thực lớn nhất để bất phương trình
2 2
2 ln 1 0
x x a x x
nghiệm đúng với mọi
x
. Mệnh đề nào sau đây đúng?
A.
2;3
a
. B.
8;a
. C.
6;7
a
. D.
6; 5
a
.
Câu 17. (THPT Lê Xoay - 2018) Giả sử
,S a b
là tập nghiệm của bất phương trình
2 3 4 2 2
2 2
5 6 log log 5 5 6
x x x x x x x x x x
. Khi đó
b a
bằng
A.
1
2
. B.
7
2
. C.
5
2
. D.
2
.
Câu 18. (Chuyên Hà Tĩnh - 2018) Cho bất phương trình
2 2
7 7
log 2 2 1 log 6 5
x x x x m
. Có
bao nhiêu giá trị nguyên của tham số
m
để bất phương trình trên có tập ngiệm chứa khoảng
1;3
?
A.
35
. B.
36
. C.
34
. D.
33
.
Câu 19. (Sở Quảng Nam 2018) Có bao nhiêu giá trị nguyên thuộc khoảng
9;9
của tham số
m
để bất
phương trình
2
3log 2log 1 1
x m x x x x
có nghiệm thực?
A.
6
. B.
7
. C.
10
. D.
11
.
Câu 20. (Yên Phong 1 - 2018) Có bao nhiêu số nguyên
m
sao cho bất phương trình
2 2
ln5 ln 1 ln 4
x mx x m
có tập nghiệm là
.
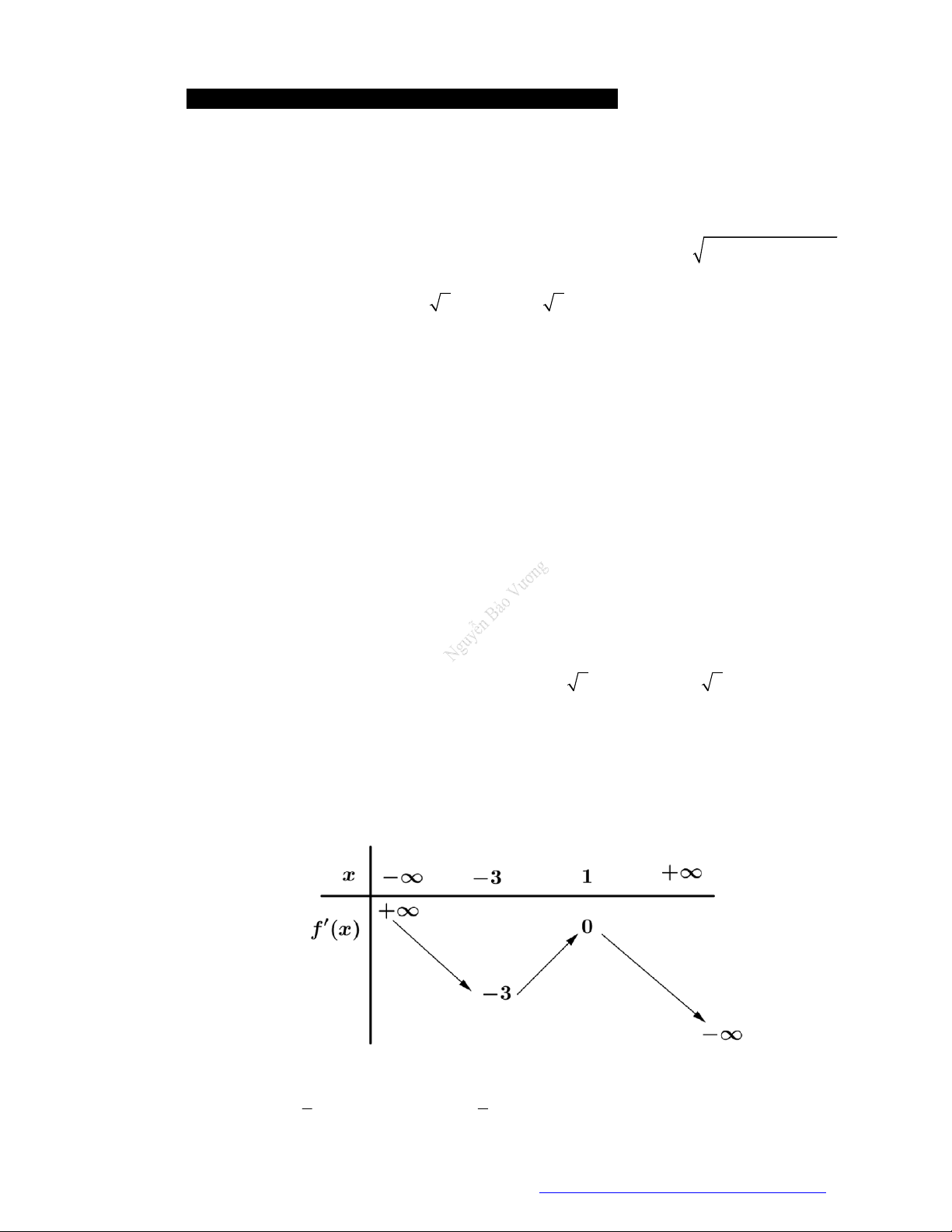
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
3
. B.
4
. C.
1
. D.
2
.
DẠNG 2. BẤT PHƯƠNG TRÌNH MŨ CHỨA THAM SỐ
Câu 1. (VTED 2019) Cho
1a
. Biết khi
0
a a thì bất phương trình
a x
x a
đúng với mọi
1;x
.
Mệnh đề nào dưới đây đúng?
A.
0
1 2a B.
2
0
e a e
C.
0
2 3a D.
2 3
0
e a e
Câu 2. (Chuyên Hạ Long 2019) Tìm
m
để hàm số sau xác định trên
:
4 1 .2
x x
y m m
A. Đáp án khác. B.
1m
.
C.
0m
. D.
3 2 2 3 2 2m
.
Câu 3. Bất phương trình nghiệm đúng với mọi Tập tất cả các giá trị của m
là
A. B. C. D.
Câu 4. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Tìm tất cả các giá trị của tham số
m
để bất phương
trình
1
4 2 1 0
x x
m
nghiệm đúng với mọi
x
.
A.
;0 1;m
. B.
;0m
.
C.
0;m
. D.
0;1m
.
Câu 5. (Chuyên Nguyễn Trãi Hải Dương 2019) Bất phương trình
1
4 1 2 0
x x
m m
nghiệm
đúng với mọi
0x
. Tập tất cả các giá trị của
m
là
A.
;12
. B.
; 1
. C.
;0
. D.
1;16
.
Câu 6. (THPT Hàm Rồng Thanh Hóa 2019) Có bao nhiêu giá trị nguyên của tham số
10;10m
để
bất phương trình sau nghiệm đúng với
x
:
6 2 7 2 3 7 1 2 0
x x
x
m m
A.
10
. B.
9
. C.
12
. D.
11
.
Câu 7. (THPT Lê Quý Đôn Đà Nẵng 2019) Tìm
m
để bất phương trình
2 3 4 5 4
x x x x
mx
có
tập nghiệm là
.
A.
ln120
. B.
ln10
. C.
ln30
. D.
ln14
.
Câu 8. (Đề Tham Khảo 2019) Cho hàm số
y f x
. Hàm số
'y f x
có bảng biến thiên như sau:
Bất phương trình
x
f x e m
đúng với mọi
1;1x
khi và chỉ khi.
A.
1
1m f
e
B.
1
1m f
e
C.
1m f e
D.
1m f e
1
4 ( 1)2 0
x x
m m
0.
x
;12 .
; 1 .
;0 .
1;16 .
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 9. (Chuyên Sơn La 2019) Cho hàm số
y f x
liên tục trên
và có bảng xét dấu đạo hàm như
sau
Bất phương trình
2
x
f x e m
đúng với mọi
1;1x
khi và chỉ khi
A.
0 1.m f
B.
1 .m f e
C.
0 1.m f
D.
1 .m f e
Câu 10. (Phú Thọ 2019) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ
Tổng tất cả các giá trị nguyên của tham số
m
để bất phương trình
2 2
9.6 4 .9 5 .4
f x f x f x
f x m m
đúng
x
là
A.
10
B.
4
C.
5
D.
9
Câu 11. (VTED 2019) Cho hàm số
y f x
. Hàm số
y f x
có bảng biến thiên như sau:
Bất phương trình
2
3.
x
f x e m
có nghiệm
2;2x
khi và chỉ khi:
A.
2 3m f
B.
4
2 3m f e
C.
4
2 3m f e
D.
2 3m f
Câu 12. (THPT-Thang-Long-Ha-Noi- 2019) Cho hàm số
f x
có đồ thị như hình vẽ bên.
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Bất phương trình
3 2019
x x
f e m e
có nghiệm
0;1x
khi và chỉ khi
A.
4
1011
m
. B.
4
3 2019
m
e
. C.
2
1011
m
. D.
3 2019
f e
m
e
.
Câu 13. (THPT Yên Khánh - Ninh Bình - 2019) Cho hàm số
y f x
liên tục trên đoạn
1;9
và có
đồ thị là đường cong trong hình vẽ dưới đây
Có bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
2 2
16.3 2 8 .4 3 .6
f x f x f x
f x f x m m
nghiệm đúng với mọi giá trị thuộc
1;9
?
A.
32
. B.
31
. C.
5.
D.
6
.
Câu 14. (Sở Cần Thơ - 2019) Tất cả giá trị của tham số thực
m
sao cho bất phương trình
9 2 1 .3 3 2 0
x x
m m
có nghiệm đúng với mọi số thực
x
là
A.
3
2
m
. B.
2m
. C.
3
2
m
. D.
m
.
Câu 15. (Sở Nam Định - 2019) Có bao nhiêu giá trị nguyên dương của tham số
m
để tập nghiệm của bất
phương trình
2
3 3 3 2 0
x x
m
chứa không quá 9 số nguyên?
A. 3281. B. 3283. C. 3280. D. 3279.
Câu 16. (THPT Cẩm Bình Hà Tỉnh 2019) Có mấy giá trị nguyên dương của
m
để bất phương trình
2 2 2
9 4 .5
m x m x m x
m
có nghiệm?
A.
10
. B. Vô số. C.
9
. D.
1
.
Câu 17. (Chuyên Nguyễn Trãi Hải Dương 2019) Bất phương trình
1
4 1 2 0
x x
m m
nghiệm
đúng với mọi
0x
. Tập tất cả cá giá trị của
m
là
A.
;12
. B.
; 1
. C.
;0
. D.
1;16
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 18. (THPT Phan Bội Châu - Nghệ An 2019) Cho hàm số
cos2f x x
. Bất phương trình
2019
f x m
đúng với mọi
3
;
12 8
x
khi và chỉ khi
A.
2018
2m
. B.
2018
2m
. C.
2019
2m
. D.
2019
2m
.
Câu 19. (Chuyên Lê Quý Đôn – Điện Biên 2019) Cho hàm số
y f x
. Hàm số
y f x
có bảng
biến thiên như sau:
Bất phương trình
2
x
f x m
đúng với mọi
1;1x
khi và chỉ khi:
A.
1 2m f
. B.
1 2m f
. C.
1
1
2
m f
. D.
1
1
2
m f
.
Câu 20. (Bình Giang-Hải Dương 2019) Số giá trị nguyên dương của tham số
m
để bất phương trình
2 2
3 3 2 2 3
9 2.3 3
x x m x x m x x
có nghiệm là
A.
4
. B.
8
. C.
1
. D.
6
.
Câu 21. (Hậu Lộc 2-Thanh Hóa- 2019) Gọi
S
là tập hợp tất cả các giá trị của tham số
m
để bất phương
trình
2 4 3 3 2 1
0
x
m x x m x x x e
đúng với mọi
x
. Số tập con của
S
là
A. 2. B. 4. C. 3. D. 1.
Câu 22. (Lý Nhân Tông - Bắc Ninh 2019) Cho bất phương trình
1
.3 3 2 4 7 4 7 0
x x
x
m m
, với
m
là tham số thực. Tìm tất cả các giá trị thực của
tham số
m
để bất phương trình đã cho nghiệm đúng với mọi
( ;0]x
.
A.
2 2 3
3
m
. B.
2 2 3
3
m
. C.
2 2 3
3
m
. D.
2 2 3
3
m
.
Câu 23. (Chuyên Hưng Yên - 2020) Có bao nhiêu giá trị nguyên dương của tham số
m
để tập nghiệm
của bất phương trình
2
3 3 3 2 0
x x
m
chứa không quá 9 số nguyên?
A. 1094. B. 3281. C. 1093. D. 3280.
C
ÂU
24. (Chuyên Hùng Vương - Phú Thọ - 2020) Có bao nhiêu
m
nguyên dương để bất phương trình
2 2 2
3 3 3 1 3 0
x x m m
có không quá 30 nghiệm nguyên?
A. 28. B. 29. C. 30. D. 31.
Câu 25. (ĐHQG Hà Nội - 2020) Điều kiện của
m
để hệ bất phương trình
2 1 2 1
2
7 7 2020 2020
2 2 3 0
x x x
x
x m x m
có nghiệm là :
A.
3.m
B.
2 1.m
C.
1 2.m
D.
2.m
Câu 26. (Sở Hà Nội - Lần 2 - 2020) Có bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
2 2
3 9 2 0
x x x
m
có 5 nghiệm nguyên?
A.
65021
. B.
65024
C.
65022
. D.
65023
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 27. (Cụm 5 Trường Chuyên - ĐBSH - 2018) Cho bất phương trình
1
.3 (3 2)(4 7) (4 7) 0
x x x
m m
, với
m
là tham số. Tìm tất cả các giá trị của tham số
m
để bất phương trình đã cho nghiệm đúng với mọi
;0
x
.
A.
2 2 3
3
m
. B.
2 2 3
3
m
. C.
2 2 3
3
m
. D.
2 2 3
3
m
.
Câu 28. (THPT Thái Phiên - Hải Phòng - 2018) Tìm tất cả các giá trị thực của tham số
m
để bất
phương trình
2 3 5 2
x x
m
nghiệm đúng với mọi
2
;log 5
x
.
A.
4
m
. B.
2 2
m
. C.
4
m
. D.
2 2
m
.
Câu 29. (THPT Ngô Quyền - Hải Phòng - 2018) Tìm tất cả các giá trị của
m
để bất phương trình
2 2 2
2 1 2 1 2 1
.4 1 2 .10 .25 0
x x x x x x
m m m
nghiệm đúng với mọi
1
;2
2
x
.
A.
0
m
. B.
100
841
m
. C.
1
4
m
. D.
100
841
m
.
DẠNG 3. BẤT PHƯƠNG TRÌNH NHIỀU ẨN
Câu 1. (Mã 101 - 2020 Lần 1) Có bao nhiêu số nguyên
x
sao cho ứng với mỗi
x
có không quá
728
số
nguyên
y
thỏa mãn
2
4 3
log log ( )x y x y
?
A.
59
. B.
58
. C.
116
. D.
115
.
Câu 2. (Mã 102 - 2020 Lần 1) Có bao nhiêu số nguyên
x
sao cho ứng với mỗi
x
có không quá
242
số
nguyên
y
thỏa mãn
2
4 3
log log
x y x y
?
A.
55
. B.
28
. C.
29
. D.
56
.
Câu 3. (Mã 103 - 2020 Lần 1) Có bao nhiêu số nguyên
x
sao cho ứng với mỗi
x
có không quá
127
số
nguyên
y
thỏa mãn
2
3 2
log log
x y x y
?
A.
89
. B.
46
. C.
45
. D.
90
.
Câu 4. (Mã 104 - 2020 Lần 1) Có bao nhiêu số nguyên
x
sao cho ứng với mỗi
x
có không quá
255
số
nguyên
y
thỏa mãn
2
3 2
log log
x y x y
?
A.
80
. B.
79
. C.
157
. D.
158
Câu 5. (Mã 102 - 2020 Lần 2) Xét các số thực thỏa mãn
2 2
1 2 2
2 2 2 4
x y x
x y x
. Giá trị lớn nhất
của biểu thức
8 4
2 1
x
P
x y
gần với giá trị nào sau đây nhất?
A.
9
B.
6
. C.
7
. D.
8
.
Câu 6. (Mã 103 - 2020 Lần 2) Xét các số thực
,x y
thỏa mãn
2 2
1 2 2
2 2 2 .4
x y x
x y x
. Giá trị nhỏ
nhất của biểu thức
8 4
2 1
x
P
x y
gần nhất với số nào dưới đây
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 7. (Mã 101 - 2020 Lần 2) Xét các số thực
,x y
thỏa mãn
2 2
1 2 2
2 2 2 4
x y x
x y x
. Giá trị nhỏ
nhất của biểu thức
4
2 1
y
P
x y
gần nhất với số nào dưới đây?
A.
2
. B.
3
. C.
5
. D.
4
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 8. (Mã 104 - 2020 Lần 2) Xét các số thực
x
và
y
thỏa mãn
2 2
1 2 2
2 2 2 4
x y x
x y x
. Giá trị
lớn nhất của biểu thức
4
2 1
y
P
x y
gần nhất với số nào dưới đây?
A.
1
. B.
0
. C.
3
. D.
2
.
Câu 9. (Mã 101 - 2020 Lần 1) Xét các số thực không âm
x
và
y
thỏa mãn
1
2 .4 3
x y
x y
. Giá trị
nhỏ nhất của biểu thức
2 2
4 6P x y x y
bằng
A.
33
4
. B.
65
8
. C.
49
8
. D.
57
8
.
Câu 10. (Mã 102 - 2020 Lần 1) Xét các số thực không âm
x
và
y
thỏa mãn
1
2 .4 3
x y
x y
. Giá trị nhỏ
nhất của biểu thức
2 2
6 4P x y x y
bằng
A.
65
8
. B.
33
4
. C.
49
8
. D.
57
8
.
Câu 11. (Mã 103 - 2020 Lần 1) Xét các số thực không âm
x
và
y
thỏa mãn
1
2 .4 3
x y
x y
. Giá trị
nhỏ nhất của biểu thức
2 2
2 4P x y x y
bằng
A.
33
8
. B.
9
8
. C.
21
4
. D.
41
8
.
Câu 12. (Mã 104 - 2020 Lần 1) Xét các số thực không âm
x
và
y
thỏa mãn
1
2 .4 3
x y
x y . Giá trị
nhỏ nhất của biểu thức
2 2
4 2
P x y x y
bằng
A.
33
8
. B.
9
8
. C.
21
4
. D.
41
8
.
Câu 13. (Diệu Hiền - Cần Thơ - 2018) Trong các nghiệm
;x y
thỏa mãn bất phương trình
2 2
2
log 2 1
x y
x y
. Giá trị lớn nhất của biểu thức
2
T x y
bằng:
A.
9
4
. B.
9
2
. C.
9
8
. D.
9
.
Câu 14. (Chuyên Lê Hồng Phong - Nam Định - 2020) Có bao nhiêu bộ
;x y
với
,x y
nguyên và
1 , 2020
x y
thỏa mãn
3 2
2 2 1
2 4 8 log 2 3 6 log
2 3
y x
xy x y x y xy
y x
?
A.
2017
. B.
4034
. C.
2
. D.
2017 2020
.
Câu 15. (THPT Quỳnh Lưu 3 Nghệ An 2019) Cho hai số thực
, 0
a b
thỏa mãn
2 2
log 1 log 1 6
a b
. Giá trị nhỏ nhất của biểu thức
a b
là.
A.
12
. B.
14
. C.
16
. D.
8
.
Câu 16. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Trong các nghiệm
;x y
thỏa mãn bất phương
trình
2 2
2
log 2 1
x y
x y
. Khi đó giá trị lớn nhất của biểu thức
2
T x y
là
A.
9
4
B.
9
C.
9
2
D.
9
8
Câu 17. (Chuyên Vĩnh Phúc 2019) Tìm tập
S
tất cả các giá trị thực của tham số
m
để tồn tại duy nhất
cặp số
;x y
thỏa mãn
2 2
2
2
log 4 4 6 1
x y
x y m
và
2 2
2 4 1 0
x y x y
.
A.
1;1
S
B.
5; 1;1;5
S
C.
5;5
S
D.
7; 5; 1;1;5;7
S

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 18. Tìm tham số
m
để tồn tại duy nhất cặp số
;x
y
thỏa mãn đồng thời các điều kiện sau
2
019
log 0
x y
và
2
1
x
y xy m
A.
1
2
m
. B.
0
m
. C.
2
m
. D.
1
3
m
.
Câu 19. Tr
ong tất cả các cặp
;x y
thỏa
mãn
2
2
2
l
og 4 4 4 1
x
y
x
y
.
Tìm m để tồn tại duy nhất cặp
;x
y
s
ao cho
2 2
2
2 2 0
x
y x y m
.
A.
2
10
2
m
. B.
1
0 2
m
. C.
1
0 2
m
. D.
2
10
2
m
.

T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM
Dạng 1. Bất phương trình logarit
+ Nếu
1a
thì
l
og log
a
a
f
x g x f x g x
(cùng chiều)
+ Nếu
0
1a
t
hì
log log
a
a
f x g x f x g x
(n
gược chiều)
+ Nếu a
chứa ẩn thì
l
og 0 1 1 0
log
0 1 1 0
log
a
a
a
B
a B
A
A B
B
.
Câu
1. (Đề Tham Khảo 2020 Lần 2) Tập nghiệm của bất phương trình
log 1x
l
à
A.
1
0;
. B.
0
;
. C.
1
0;
. D.
;
10
.
Lờ
i giải
Chọn C
0
l
og 1 10.
10
x
x x
x
Vậ
y bất phương trình đã cho có tập nghiệm là
10; .
Câu
2. (Mã 102 - 2020 Lần 2) Tập nghiệm của bất phương trình
2
3
l
og 13 2x
là
A.
;
2 2:
. B.
;
2
.
C.
0
;2
. D.
2
;2
.
Lờ
i giải
Chọn D
Bất
phương trình
2
2
2
3
2 2
13 0 13
log 13 2
13 9 4
x x
x
x x
1
3 13
2 2
2 2
x
x
x
.
Vậy, tập nghiệm của bất phương trình
2
3
l
og 13 2x
là
2
;2
.
Câu
3. (Mã 103 - 2020 Lần 2) Tập nghiệm của bất phương trình
2
3
l
og 36 3x
là
A.
; 3 3;
. B.
;3
. C.
3;3
. D.
0;3
.
Lờ
i giải
Chọn C
Ta
có:
2
2 2
3
log 36 3 36 27 9 0 3 3x x x x
.
Câu
4. (Mã 101 - 2020 Lần 2) Tập nghiệm của bất phương trình
2
3
l
og 18 2x
l
à
A.
;
3
. B.
0
;3
.
C.
3
;3
. D.
;
3 3;
.
Lờ
i giải
Chọn C
B
ẤT PHƯƠNG TRÌNH MŨ - LOGARIT
Chuyên
đề 20

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điều kiện:
2
18 0 3 2 ;3 2
x x
(*).
Khi đó ta có:
2
3
log 18 2
x
2
18 9
x
3 3
x
.
Kết hợp với điều kiện (*) ta được tập ngiệm của bất phương trình đã cho là
3;3
.
Câu 5. (Mã 104 - 2020 Lần 2) Tập nghiệm của bất phương trình
2
3
log 31 3
x
là
A.
;2
. B.
2;2
. C.
; 2 2;
. D.
0;2
.
Lời giải
Chọn B
2 2 2
3
log 31 3 31 27 4 0 2;2
x x x x
.
Câu 6. (Đề Minh Họa 2017) Giải bất phương trình
2
log 3 1 3
x
.
A.
3
x
B.
1
3
3
x
C.
3
x
D.
10
3
x
Lời giải
Chọn A
Đkxđ:
1
3 1 0
3
x x
Bất phương trình
3
3 1 2 3 9 3
x x x
(t/m đk).
Vậy bpt có nghiệm
3
x
.
Câu 7. (THPT Bạch Đằng Quảng Ninh 2019) Tìm tập nghiệm
S
của bất phương trình
2
ln 0
x
.
A.
1;1
S
. B.
1;0
S
. C.
1;1 \ 0
S
. D.
0;1
S
.
Lời giải
Ta có:
2
ln 0
x
2
0 1
x
0
1 1
x
x
. Vậy
1;1 \ 0
S
.
Câu 8. (THPT Minh Khai Hà Tĩnh 2019) Tìm tập nghiệm
S
của bất phương trình
1 1
2 2
log 1 log 2 1
x x
.
A.
2;S
. B.
1;2
S
. C.
;2
S
. D.
1
;2
2
S
.
Lời giải
Ta có
1 1
2 2
log 1 log 2 1
x x
1 2 1
2 1 0
x x
x
1
2
2
x
.
Câu 9. (THPT - Yên Định Thanh Hóa 2019) Tập nghiệm S của bất phương trình
2
log 2 3 0
x
là
A.
; 1
S
. B.
1;S
. C.
; 1
S
. D.
;0
S
.
Lời giải
Ta có
2
log 2 3 0 2 3 1 1
x x x
Vậy tập nghiệm bất phương trình
1;S
Câu 10. (THPT Đông Sơn Thanh Hóa 2019) Tập nghiệm của bất phương trình
0.3 3
10
log 5 2 log 9
x
là

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
5
0
;
2
. B.
;
2
. C.
5
2
;
2
. D.
2
;
.
Lờ
i giải
0.3
3
10
5
5 2 0
5
l
og 5 2 log 9 2
2
5 2 9
2
2
x
x
x
x
x
x
.
Vậy bất phương trì
nh có tập nghiệm là
5
2
;
2
S
.
Câu 11. (C
huyên ĐHSP Hà Nội 2019) Tập nghiệm của bất phương trình
0
,5
log 1 1
x
l
à
A.
3
;
2
. B.
3
1;
2
. C.
3
;
2
. D.
3
1;
2
.
Lờ
i giải
Bất phương trình
3
0
1 0,5 1
2
x
x
.
Vậy tập nghiệm bất phương trình đã cho là:
3
1
; .
2
S
Câu 12. (HSG Bắc Ninh 2019) Tập nghiệm của bất phương trình
4
4
l
og ( 1) log (2 5)
x
x
là
A.
1;6
B.
5
;
6
2
C.
6;
D.
;6
Lời giải
Do
1
4
nê
n
4 4
1 0
l
og ( 1) log (2 5) 6
1 2 5
x
x x x
x x
.
Câu 13. (THPT An Lão Hải Phòng 2019) Tìm tập nghiệm
S
của bất phương trình
3
3
l
og 2 3 log 1
x
x
A.
2
;
3
B.
3
2
;
2
3
C.
3
;1
2
D.
2
;
3
Lời giải
Chọn B
Điề
u kiện :
2
3 0
3
1
1
0
2
x
x
x
.
3
3
log 2 3 log 1
x x
2
2
3 1
3
x
x x
.
S
o với điều kiện, ta được tập nghiệm của bất phương trình là
3 2
;
2
3
S
.
Câu 14. (THP
T Cẩm Giàng 2 2019) Tập nghiệm của bất phương trình
3
1
2
l
og log 1
x
là
A.
0
;1
. B.
1
;
3
8
. C.
1
;1
8
. D.
1
;
8
.
Lờ
i giải

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
3 1
2
log log 1
x
1
1
2
0 log 3
x
0 3
1 1
2 2
x
1
1
8
x
.
Vậy tập nghiệm của bất phương trình là
1
;1
8
S
.
Câu 15. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Số nghiệm nguyên của bất phương trình
0,8 0,8
log 15 2 log 13 8
x x
là
A. Vô số. B.
4
. C.
2
. D.
3
.
Lời giải
Điều kiện
2
15
x
.
Khi đó,
0,8 0,8
log 15 2 log 13 8 15 2 13 8 2 6 3
x x x x x x
.
Tập nghiệm bất phương trình là:
2
;3
15
T
0;1;2
x
.
Câu 16. (Sở Vĩnh Phúc 2019) Tập xác định của hàm số
2
log 4 1
y x
là
A.
;4
. B.
2;4
. C.
;2
. D.
;2
.
Lời giải
Hàm số xác định
2
2
log 4 1
4 2 2
log 4 1 0 2.
4 0 4
4 0
x
x x
x x
x x
x
Vậy tập xác định của hàm số là:
;2
D
.
Câu 17. (Sở Bình Phước 2019) Tập nghiệm của bất phương trình
2
log 3 1 2
x
là
A.
1
;1
3
B.
1 1
;
3 3
C.
1
;1
3
D.
;1
Lời giải
Chọn C
ĐK:
1
3
x
2
log 3 1 2 3 1 4 1 x x x
Kết hợp với điều kiện ta được nghiệm của bất phương trình là
1
1
3
x
Vậy tập nghiệm của bất phương trình
1
;1 .
3
Câu 18. (Chuyen Phan Bội Châu Nghệ An 2019) Tập nghiệm của bất phương trình
2
2
log 1 3
x
là?
A.
2;2
. B.
; 3 3;
.
C.
; 2 2;
. D.
3;3
.
Lời giải
2
2
log 1 3
x
2 2
3
1 8 9
3
x
x x
x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 19. (Sở Bắc Giang 2019) Tập nghiệm
S
của bất phương trình
0,8
log 2 1 0
x
là
A.
1
;
2
S
. B.
1;S
. C.
1
;
2
S
. D.
;1
S
.
Lời giải
Bất phương trình
0
0,8
log 2 1 0 2 1 0,8 2 2 1x x x x
.
Tập nghiệm
S
của bất phương trình
0,8
log 2 1 0
x
là
1;S
.
Câu 20. (Sở Bắc Giang 2019) Tập nghiệm của bất phương trình
2
0,5 0,5
log 5 14 log 6 8
x x x
là
A.
2;2
. B.
;2
. C.
3
\ ;0
2
. D.
3;2
.
Lời giải
Điều kiện:
2
5 14 0
2 *
6 8 0
x
x
x x
Ta có:
2 2
0,5 0,5
log 5 14 log 6 8 5 14 6 8 3 2
x x x x x x x
Kết hợp với điều kiện
*
ta được
2 2
x
.
Vậy tập nghiệm của bất phương trình là
2;2
.
Câu 21. (Chuyên Trần Phú Hải Phòng 2019) Bất phương trình
2 2
log (3 2) log (6 5 )x x
có tập
nghiệm là
A.
0;
B.
1
;3 .
2
C.
( 3;1)
D.
6
1;
5
Lời giải
Vì
2 1
nên
2 2
log (3 2) log (6 5 )x x
1
3 2 6 5
6
1 .
6
6 5 0
5
5
x
x x
x
x
x
Câu 22. (KTNL GV THPT Lý Thái Tổ 2019) Tập hợp nghiệm của bất phương trình
2
log 1 3
x
là:
A.
1; 8
S
. B.
; 7
S
. C.
; 8
S
. D.
1; 7
S
.
Lời giải
Chọn D
Ta có:
3
2
1 0
1
log 1 3 1 7
7
1 2
x
x
x x
x
x
Vậy tập nghiệm của bất phương trình là
1; 7
S
.
Câu 23. (Sở Thanh Hóa 2019) Tìm tập nghiệm
S
của bất phương trình
2
ln ln 4 4
x x
.
A.
2;S
. B.
1;S
. C.
\ 2
S R
. D.
1; \ 2
S
.
Lời giải
2
2
4 4
ln ln 4 4
4 4 0
x x
x x
x
2
2
4 4 0
1
1
x
x x
x
x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy tập
nghiệm của bất phương trình là
1
; \ 2
S
.
Câu
24. (Chuyên Phan Bội Châu 2019) Tập nghiệm của bất phương trình
2
2
l
og 1 3
x
là:
A.
2
;2
. B.
;
3 3;
.
C.
;
2 2;
. D.
3
;3
.
Lời giải
T
a có
2
2
l
og 1 3
x
2
9
0
x
;
3 3;x
Câu
25. (Chuyên KHTN 2019) Tập nghiệm của bất phương trình
2
log 9
1
l
og 3
x
x
là:
A.
4
; 3
. B.
4
; 3
. C.
3
;4
. D
.
.
Lời giải
Đ
K:
2
9
0 3 3
3 0 3
3 1 2
x x x
x x
x x
3
x
.
Với
3
x
suy ra
l
og(3 ) 0
x
nên bất phương trình đã cho tương đương với
2
2
l
og 9 log 3 12 0 4;3
x
x x x x
Kết
hợp điều kiện suy ra tập nghiệm của bất phương trình là
4
; 3
Câu
26. (Chuyên Thái Bình 2019) Có tất cả bao nhiêu giá trị của tham số
m
để bất
phương trình
2
2
2 2
lo
g 2 log 2
x
mx m x
nghiệm
đúng
x
?
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
T
a có :
2
2
2 2
l
og ( 2) log ( 2)
x
mx m x
nghiệm
đúng
x
2 2
2
2,x mx m x x
0
,mx m x
0
m
.
S
uy ra có 1 giá trị m thỏa mãn.
Câu 27. (Việt Đức Hà Nội 2019) Giải bất phương trình
2
2
l
og 3 2 log 6 5x x
được
tập nghiệm là
;a
b
.
Hãy tính tổng
S a b
.
A.
2
6
5
S
. B.
1
1
5
S
. C
.
2
8
15
S
. D
.
8
3
S
.
Lời giải
Điều ki
ện
2
3 2 0
2 6
3
.
6
5 0 6
3 5
5
x
x
x
x
x
T
a có
2
2
l
og 3 2 log 6 5 3 2 6 5 8 8 1.
x
x x x x x
Kết hợp với
điều kiện, ta được
6
1
.
5
x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Vậy, tập nghiệm của bất phương trình là
6
1; .
5
Từ đó,
6 11
1 .
5 5
S a b
Lời giải ngắn gọn như sau:
2 2
1
3 2 6 5
6
log 3 2 log 6 5 1 .
6
6 5 0
5
5
x
x x
x x x
x
x
Câu 28. (Sở Ninh Bình 2019) Bất phương trình
2
3
log 2 1
x x
có tập nghiệm là
A.
; 1 3;S
. B.
1;3
S
.
C.
3;S
. D.
; 1
S
.
Lời giải
2 2 2
3
3
log 2 1 2 3 2 3 0 .
1
x
x x x x x x
x
Vậy tập nghiệm của bất phương trình
; 1 3;S
.
Câu 29. (Hậu Lộc 2-Thanh Hóa 2019) Tập nghiệm của bất phương trình
ln3 ln 2 6
x x
là:
A.
0;6
. B.
0;6
. C.
6;
. D.
;6
.
Lời giải
Chọn B
Bất phương trình
3 0
ln3 ln 2 6 0 6
3 2 6
x
x x x
x x
.
Câu 30. (Hội 8 trường chuyên ĐBSH - 2019) Tập nghiệm
S
của bất phương trình
2
log 1 3
x
là
A.
1;9
S
. B.
1;10
S
. C.
;9
S
. D.
;10
S
.
Lời giải
Chọn A
3
2
log 1 3 0 1 2 1 9
x x x
.
Câu 31. (THPT Phan Bội Châu - Nghệ An -2019) Tập nghiệm của bất phương trình
2
2
log 1 3
x
là?
A.
2;2
. B.
; 3 3;
.
C.
; 2 2;
. D.
3;3
.
Lời giải
Chọn B
2
2
log 1 3
x
2 2
3
1 8 9
3
x
x x
x
.
Câu 32. (Bắc Ninh 2019) Bất phương trình
2 2
log (3 2) log (6 5 )
x x
có tập nghiệm là
( ; )a b
. Tổng
a b
bằng
A.
8
3
. B.
28
15
. C.
26
5
. D.
11
5
.
Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn D
T
a có:
2
2
1
3
2 6 5
6
l
og (3 2) log (6 5 ) 1
6
6 5 0
5
5
x
x x
x x x
x
x
.
Tập
nghiệm của bất phương trình là
6
(1; )
5
.
Vậy
6
11
1
5
5
a b
.
Câu
33. (THPT Hai Bà Trưng - Huế - 2019) Có tất cả bao nhiêu số nguyên
x
thỏa mãn bất phương trình
2
1
2
2
lo
g log 2 0
x
?
A. Vô số. B.
1
. C.
0
. D
.
2
.
Lời
giải
Chọn C
2
1 2
2
lo
g log 2 0
x
2
2
0
log 2 1
x
2
1 2 2
x
2
2
2 2
2
2 0 0
1
1
2
1 1
x x x
x
x
x
Kết hợp với
giả thiết
x
là
số nguyên ta thấy không có số nguyên
x
nào thỏa mãn bất
phương
trình
2
1
2
2
log log 2 0
x
.
Câu
34. (THPT Cẩm Bình 2019) Nghiệm của bất phương trình
2
3 2 3
l
og 2 5 log 1
x
x
là
A.
5
4
2
x
. B.
1 4
x
. C.
5
4
2
x
1
. D
.
4
x
.
Lời
giải
Chọn A
2
3 2 3
4
2
5 1
log 2 5 log 1
5
2
5 0
2
x
x x
x x
x
x
Vậy ng
hiệm của bất phương trình là
5
4
2
x
.
Câu
35. (THPT Hàm Rồng 2019) Bất phương trình
4
2
l
og 7 log 1
x
x
c
ó bao nhiêu nghiệm
nguyên
A.
3
. B.
1
. C.
4
. D.
2
.
Lời giải
Chọn D
Điều ki
ện xác định của bất phương trình là
7 0 7
1
1
0 1
x x
x
x x
Ta có
2
4
2 2 2 2 2
1
log 7 log 1 log 7 log 1 log 7 log 1
2
x x x x x x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
2
6
0 3 2
x
x x
Kế
t hợp điều kiện ta được
1
2
x
Vì
x
nên t
ìm được
0, 1x x
.
Câu 36. (Thi thử cụm
Vũng Tàu - 2019) Tập nghiệm của bất phương trình
2
3
5
l
og 2 1 0
x
x
l
à
A.
3
1
;
2
. B.
3
;1
;
2
.
C
.
1
;
0 ;
2
. D
.
1
0
;
2
.
Lời giải
Chọn C
Ta
có:
2
2
1 0
x
x
,
x
.
Do đó
2
3
5
l
og 2 1 0
x
x
2
2 1 1
x x
2
2 0
x x
0
1
2
x
x
.
Vậ
y tập nghiệm của bất phương trình là
1
;
0 :
2
S
.
Câu 37. (Bình
Phước - 2019) Tập nghiệm của bất phương trình
2
l
og 3 1 2
x
là
A.
1
;
1
3
. B.
1
1
;
3 3
. C.
1
;
1
3
. D.
;1
.
Lờ
i giải
Chọn C
ĐK
:
1
3
x
2
l
og 3 1 2 3 1 4 1 x x x
Kế
t hợp với điều kiện ta được nghiệm của bất phương trình là
1
1
3
x
Vậ
y tập nghiệm của bất phương trình
1
;1
.
3
.
Câu 38. (N
gô Quyền - Hải Phòng -2019) Số nghiệm nguyên của bất phương trình
2
1
2
l
og 2 8 4
x
x
là
A. 6. B. Vô số. C. 4. D. 5.
Lờ
i giải
Chọn C
Ta
có
2
2
4
1
2
2
2
8 0
log 2 8 4
1
2 8
2
x x
x x
x x
2
2
4
2
24 0
x
x
x x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
6 4
4
2 4
6 4
x
x
x
x
x
.
Do đó các nghiệm nguyên của bất phương trình đã cho là
6; 5;3;4
.
Câu 39. (THPT Thuận Thành 3 - Bắc Ninh 2019) Tập nghiệm
S
của bất phương trình
2
6 6
log log 6
x x
là
A.
; 2 3;S
. B.
2;3
S
.
C.
3;2 \ 0
S
. D.
2;3 \ 0
S
.
Lời giải
Chọn D
Điều kiện:
0
.
6
x
x
2 2 2
6 6
log log 6 6 6 0 2 3.
x x x x x x x
Kết hợp với điều kiện, suy ra tập nghiệm
2;3 \ 0 .
S
Câu 40. (Nho Quan A - Ninh Bình - 2019) Bất phương trình
log x
2
2 2
có bao nhiêu nghiệm
nguyên?
A. 4. B. 2. C. 5. D. 3.
Lời giải
Chọn D
log .
x x
x x
x x
2
2 0 2
2 2 2 6
2 4 6
Vậy bất phương trình đã cho có 3 nghiệm nguyên.
Câu 41. (Cần Thơ 2019) Tập nghiệm của bất phương trình
0,2
log 4 1 0
x
là
A.
4;
. B.
4;9
. C.
;9
. D.
9;
.
Lời giải
Chọn B
Ta có
0,2 0,2
log 4 1 0 log 4 1
x x
1
0,2 0,2
log 4 log 0,2x
4 0
4 5
x
x
4
9
x
x
.
Vậy bất phương trình có tập nghiệm là
4;9
.
Câu 42. (THPT Cẩm Bình Hà Tỉnh 2019) Tập nghiệm của bất phương
trình
2 1
2
log 7 log 1 0
x x
là
A.
1;4
S
. B.
;4
S
. C.
4;S
. D.
4;7
S
.
Lời giải
Chọn D
Điều kiện:
1 7.
x
Ta có:

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
2
1 2 2
2
l
og 7 log 1 0 log 7 log 1 0
x
x x x
2
1
7
7 2 8
log 0 1 0
4
1
1 1
x
x x x
x
x x x
.
Kế
t hợp với điều kiện ta có tập nghiệm là
4
;7
.
Câu 43. (N
K HCM-2019) Bất phương trình
2
2
2
1
log 2 log 3 2
x
x x
c
ó các nghiệm là
A.
3
; .
S
B.
1
;3 .
S
C.
2
; .
S
D.
2
;3 .
S
Lờ
i giải
Chọn D
Điều kiện:
2
.
x
2
2
2
1
log 2 log 3 2
x
x x
2
2
2
l
og 3 2 log 2 1
x
x x
2
l
og 1 1 3.
x
x
Đối chi
ếu điều kiện, ta có tập nghiệm là
2;3 .
S
Dạng 2. B
ất phương trình mũ
+ Nếu
1
a
thì
f x g x
a a f x g x
. (cùng chiều)
+ Nếu
0
1a
thì
f
x g x
a a f x g x
. (ngược chiều)
+ Nếu
a chứa ẩn thì
1
0
f
x g x
a
a a f x g x
.
Câu 1. (Đề M
inh Họa 2020 Lần 1) Tập nghiệm của bất phương trình
2
1
9
5
5
x
x x
là
A
.
2;4
. B.
4;2
.
C.
;
2 4;
. D
.
;
4 2;
.
Lờ
i giải
Chọn A
2
1
9 2 2
5
5 1 9 2 8 0 2 4
x
x x
x
x x x x x
.
Vậy Tập nghiệm của bất phương trình là
2;4
.
Câu 2. (Đề Th
am Khảo 2020 Lần 2) Tập nghiệm của bất phương trình
9 2.3 3 0
x
x
l
à
A.
0
;
. B.
0
;
. C.
1
;
. D.
1
;
.
Lờ
i giải
Chọn B
9
2.3 3 0 3 1 3 3 0 3 1
x x x x x
(vì
3
0,
x
x
)
0
x
.
Vậ
y tập nghiệm của bất phương trình đã cho là
0
;
.
Câu 3. (M
ã 101 - 2020 Lần 1) Tập nghiệm của bất phương trình
2
13
3 27
x
l
à
A.
4;
. B.
4;4
. C.
;4
. D.
0;4
.
Lờ
i giải
Chọn B
Ta
có:
2 2
13
13 3 2 2
3 27 3 3 13 3 16 4 4 4
x
x
x x x x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy tập
nghiệm của bất phương trình đã cho là
4
;4
S
.
Câu
4. (Mã 102 - 2020 Lần 1) Tập nghiệm của bất phương trình
2
2
3
3
9
x
là
A
.
5
;5
. B.
;
5
. C.
5
;
. D
.
0
;5
.
Lời
giải
Chọn A
T
a có
2
2
3 2 2
3 9 23 2 25 5 5
x
x x x
.
Vậy nghiệm của
bất phương trình
2
2
3
3
9
x
là
5
;5
.
Câu
5. (Mã 103 - 2020 Lần 1) Tập nghiệm của bất phương trình
2
7
2
4
x
là
A.
(
3;3)
. B.
(0
;3)
. C.
(
;
3)
. D.
(3
;
)
.
Lời giải
Chọn A
Ta có :
2
7
2 4
x
2
7
2
2 2
x
2
7
2
x
2
9
x
3
;3 .
x
Câu 6. (Mã 104 - 2020 Lần 1) Tập nghiệm của bất phương trình
2
1
2 8
x
là
A.
0;2
. B.
;2
. C.
2;2
. D
.
2;
.
Lời giải
Chọn C
Từ phương trì
nh ta có
2
1
3 2 2
x
x
.
Câu
7. (Đề Tham Khảo 2018) Tập nghiệm của bất phương trình
2
6
2
2
x
x
là:
A.
;
6
B.
0
; 64
C.
6
;
D
.
0
; 6
Lời giải
:
Chọn A
Cách 1:
2
6
2
2 2 6 6
x
x
x
x x
Cách 2:
Đặt
2
x
t
,
0t
Bất
phương trình trở thành:
2
64
0t t
0
64t
0
2 64 6
x
x
.
Câu 8. (Đề Tham Khảo 2019) Tập nghiệm của bất phương trình
2
2
3 27
x x
là
A.
3
;
B.
1
;3
C.
; 1 3;
D.
; 1
Lời giải
Chọn B
T
a có
2
2 2 2
3
27 2 3 2 3 0 1 3
x x
x
x x x x
.
Câu
9. (Dề Minh Họa 2017) Cho hàm số
2
(
) 2 .7 .
x
x
f
x
K
hẳng định nào sau đây là khẳng định sai?
A.
2
2
(
) 1 log 7 0
f
x x x
B.
2
(
) 1 ln 2 ln 7 0
f
x x x
C.
2
7
(
) 1 log 2 0
f
x x x
D.
2
( ) 1 1 log 7 0
f x x
Lời giải
Chọn D
Đáp á
n A đúng vì
2
2
2
2 2 2 2
1
log log 1 log 2 .7 0 log 2 log 7 0
x x x x
f
x f x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
2
2
.log 7 0
x x
Đáp án B đúng vì
2 2
1 ln ln1 ln 2 .7 0 ln 2 ln7 0
x x x x
f x f x
2
.ln 2 .ln 7 0
x x
Đáp án C đúng vì
2 2
7 7 7 7 7
1 log log 1 log 2 .7 0 log 2 log 7 0
x x x x
f x f x
2
7
.log 2 0
x x
Vậy D sai vì
2 2
2 2 2 2 2
1 log log 1 log 2 .7 0 log 2 log 7 0
x x x x
f x f x
2
2
log 7 0
x x
.
Câu 10. (Đề Tham Khảo 2017) Tìm tập nghiệm
S
của bất phương trình
1
1
5 0
5
x
.
A.
; 2
S
. B.
1;S
. C.
1;S
. D.
2;S
.
Lời giải
Bất phương trình tương đương
1 1
5 5 1 1 2.
x
x x
Vậy tập nghiệm của bất phương trình là
2;S
.
Câu 11. (THPT Hoàng Hoa Thám Hưng Yên 2019) Cho hàm số
2
2 3
e 1
x x
y
. Tập nghiệm của bất
phương trình
0
y
là:
A.
; 1
. B.
; 3 1;
.
C.
3;1
. D.
1;
.
Lời giải
Ta có
2
2 3
2 2 e
x x
y x
.
0
y
2
2 3
2 2 e 0
x x
x
2 2 0
x
1
x
.
Vậy tập nghiệm của bất phương trình
0
y
là
1;
.
Câu 12. (Thpt Hùng Vương Bình Phước 2019) Tập nghiệm của bất phương trình
1
9
3
x
trên tập số
thực là
A.
2;
. B.
; 2
. C.
; 2
. D.
2;
.
Lời giải
2
1
9 3 3 2 2
3
x
x
x x
.
Vậy tập nghiệm là:
; 2
S
.
Câu 13. (THPT Bạch Đằng Quảng Ninh 2019) Tập nghiệm của bất phương trình
1 2
4 8
x x
là
A.
8;
. B.
. C.
0;8
. D.
;8
.
Lời giải
Ta có:
1 2
4 8
x x
2 2 3 6
2 2
x x
2 2 3 6x x
8
x
.
Vậy tập nghiệm của bất phương trình là
8;S
.
Câu 14. (THPT Cù Huy Cận 2019) Tập nghiệm của bất phương trình
2
2
2 8
x x
là
A.
; 3
. B.
3;1
. C.
3;1
. D.
3;1
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
T
a có :
2
2
2
2 3 2
2
8 2 2 2 3 0 3 1
x
x x x
x
x x
.
Câu
15. (Chuyên Vĩnh Phúc 2019) Tập nghiệm
S
của
bất phương trình
2
1
5
25
x
x
là
A.
;
2
S
B.
;
1
S
C.
1
;S
D.
2
;S
Lời giải
2
2 2
1
5
5 5 2 2 2
2
5
x
x
x x
x
x x
Câu
16. (THPT Gang Thép Thái Nguyên 2019) Tập nghiệm bất phương trình
2
3
2
16
x
x
l
à
A.
; 1
. B.
4;
. C.
1;4
. D
.
; 1 4;
.
Lời giải
2
2
3
3 4 2
2
16 2 2 3 4 1 4
x
x x x
x
x x
.
Câu
17. (THPT Gang Thép Thái Nguyên 2019) Tập nghiệm bất phương trình:
2
8
x
là
A.
;
3
. B.
3
;
. C.
3
;
. D
.
;
3
.
Lời giải
Ta có:
3
2
8 2 2 3
x
x
x
Vậy tập nghiệm
bất phương trình là
3
;
.
Câu
18. (Chuyên Quốc Học Huế 2019) Tìm tập nghiệm
S
của
bất phương trình
2
3
1 1
2 4
x
x
.
A.
1
;2
S
B.
;
1
S
C.
1
;2
S
D
.
2
;S
Lời giải
2
2
3
3 2
2 2
1
1 1 1
3 2 3 2 0 1 2
2
4 2 2
x
x x x
x x x x x
.
Vậy tập
nghiệm của bất phương trìnhđã cho là
1
;2
S
.
Câu
19. (Đề Tham Khảo 2019) Tập nghiệm của bất phương trình
2
2
3
27
x
x
l
à
A.
;
1
B.
3
;
C.
1
;3
D
.
;
1 3;
Lời giải
Chọn C
Ta có
2
2
2 2
3 27 2 3 2 3 0 1 3
x
x
x x x x x
.
Câu 20. (Chuyên Vĩnh Phúc 2019) Cho
3
.
e
x
f
x x
. Tậ
p nghiệm của bất phương trình
0
f
x
là
A
.
1
;
3
B.
1
0
;
3
C.
1
;
3
D.
0
;1
Lời giải
Chọn A
T
a có:
3 3 3
3 . 1 3 .
x x x
f x e x e e x
3
1
0 1 3 0 1 3 0 .
3
x
f
x e x x x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Câu 21. (THPT Ba Đình 2019) Số nghiệm nguyên của bất phương trình
2
2 3 7
2 21
1
3
3
x x
x
là
A. 7. B. 6. C. vô số. D. 8.
Lời giải
Ta có
2
2
2 3 7
2 3 7
2 21 2 21
1
3 3 3
3
x x
x x
x x
2 2
2 3 7 2 21 2 3 7 2 21
x x x x x x
2
7
2 28 0 4
2
x x x
.
Do
x
nên
3; 2; 1;0;1;2;3
x
.
Vậy bất phương trình đã cho có
7
nghiệm nguyên.
Câu 22. (THPT Lương Thế Vinh Hà Nội 2019) Tập nghiệm của bất phương trình
2 6
3
1
2
2
x
x
là
A.
0;6
. B.
;6
. C.
0;64
. D.
6;
.
Lời giải
Ta có
2 6
3 3 2 6
1
2 2 2 3 2 6 6
2
x
x x x
x x x
.
Vậy tập nghiệm của bất phương trình là
;6
S
.
Câu 23. (Chuyên Hùng Vương Gia Lai 2019) Bất phương trình
2
2
1 1
2 8
x x
có tập nghiệm là
A.
3; .
B.
; 1 .
C.
1;3 .
D.
1;3 .
Lời giải
Bất phương trình đã cho tương đương với
2
2 3
2 2
1 1
2 3 2 3 0 1 3
2 2
x x
x x x x x
Vậy, tập nghiệm của bất phương trình đã cho là:
1;3 .
S
Câu 24. (THPT Yên Phong 1 Bắc Ninh 2019 Nghiệm nguyên lớn nhất của bất phương trình
2
2
4 64
x x
là
A.
2
. B.
1
. C.
3
. D.
0
.
Lời giải
Ta có
2
2
4 64
x x
2
2 3 2
4 4 2 3 0 1 3
x x
x x x
. Vậy nghiệm nguyên lớn nhất là
2
x
.
Câu 25. (Sở Hà Nội 2019) Tập nghiệm của bất phương trình
2
3 81
4 256
x
là
A.
; 2
. B.
; 2 2;
. C.
. D.
2;2
.
Lời giải
Ta có:
2 2
4
2 2
3 81 3 3
4 4 0
4 256 4 4
x x
x x x R

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu
26. (Chuyên Sơn La 2019) Tập nghiệm của bất phương trình
2
2
2 8
x
x
là
A.
;
1
. B.
1;
3
.
C.
3;
. D.
; 1 3;
.
Lời giải
Bất phư
ơng trình
2
2
2
2 3 2 2
3
2
8 2 2 2 3 2 3 0
1
x
x x x
x
x
x x x
x
.
Vậy tập nghiệm của bất phương trình là
;
1 3;S
.
Câu
27. (Chuyên ĐHSP Hà Nội 2019) Tập nghiệm của bất phương trình
e
1
x
là
A.
B.
;
0
C.
0
;
D
.
0
;
Lời giải
Vì
e
1
nên
e
e
e
e
1 log log 1 0
x
x
x
.
Vậy tập
nghiệm của bất phương trình là
;
0
S
.
Câu
28. (Chuyên Lam Sơn Thanh Hóa 2019) Số nghiệm nguyên của bất phương trình
2
3
2
16
x
x
là
số
nào sau đây ?
A. 5. B. 6. C. 4. D. 3.
Lời giải
2
2
3
3 4 2
2
16 2 2 3 4 4; 1 .
x
x x x
x
x x
Cá
c nghiệm nguyên của bất phương trình là :
4
; 3; 2; 1;0;1
.
Câu
29. (Chuyên Vĩnh Phúc 2019) Tập nghiệm của bất phương trình
2
1
2
1
1
1
x
a
(với
a
l
à tham số,
0
a
)
là:
A.
;
0
B.
1
;
2
C.
0
;
D
.
1
;
2
Lời giải
T
a có:
2
1 2 1 0
2 2 2
1
1 1
1
1 1 1
x
x
a a a
1
.
Nhận thấy
2
1 1, 0
a a
nên:
2
1
1
1
a
.
Khi đ
ó bất phương trình
1
tương đương
1
2 1 0
2
x x
.
Vậy tập
nghiệm của bất phương trình đã cho :
1
;
2
S
.
Câu
30. (Cụm 8 Trường Chuyên 2019) Tập nghiệm
S
của bất phương trình
3
e
x
x
là:
A.
\
0
S
. B.
0
;S
. C.
S
. D.
;
0
S
.
Lời giải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
3 e
x x
3
1
0
e
x
x
. Tậ
p nghiệm của bất phương trình là
;
0
S
.
Câu 31. (N
guyễn Huệ- Ninh Bình- 2019)Bất phương trình
1
2
4
x
có tập nghiệm là:
A.
1
:
. B.
;
1
. C.
1
:
. D.
;1
.
Lờ
i giải
Chọn D
Ta
có
1
2
4 1 2 1
x
x
x
.
Tập nghiệm của bất phương trình là
;1
.
Câu 32. (THP
T Minh Khai - 2019) Tìm tập nghiệm
S
của
bất phương trình
3
9
x
A.
;2
S
. B.
2;S
. C.
;2
S
. D.
2
S
.
Lờ
i giải
Chọn C
2
3
9 3 3 2
x
x
x
.
Tập nghiệm của
bất phương trình là:
;2
S
.
Câu 33. (Lôm
ônôxốp - Hà Nội 2019) Tập nghiệm của bất phương trình
1
2
1
1
3 3
x
là:
A.
1
0
;
2
. B.
1
;
2
. C.
1
0
;
2
. D.
1
;
2
.
Lờ
i giải
Chọn C
Cơ
số
1
1
3
a
nê
n bất phương trình:
1
2
1
1
3 3
x
1
2
x
1
2 1
0 0
2
x
x
x
.
Câu 34. (
Đồng Nai - 2019) Tập nghiệm của bất phương trình
2
1
3
9
x
là
A
.
4
;
. B.
;
4
. C.
;
0
. D.
0
;
.
Lờ
i giải
Chọn A
Bấ
t phương trình
2
1
3
9
x
2 2
3
3
x
2
2
x
4
x
.
Câu 35. (C
huyên Long An-2019) Tìm nghiệm của bất phương trình
1
1 1
2 4
x
.
A
.
3x
. B.
3x
. C.
3x
. D.
1 3x
.
Lờ
i giải
Chọn A
1
1 2
1 1 1 1
1
2 3
2
4 2 2
x
x
x
x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu
36. (Chuyên - Vĩnh Phúc - 2019) Tập nghiệm của bất phương trình
2
1
2
1
1
1
x
a
(với
a
là
tham
số,
0
a
)
là
A
.
1
;
2
. B.
0
;
. C.
;
0
. D
.
1
;
2
.
Lời
giải
Chọn A
T
a có
2
1
0 1, 0
1
a
a
, nếu
2
1
2
1
1
1
x
a
1 1
2 1 0 ;
2
2
x x x
.
Câu
37. (Chuyên Lam Sơn-2019) Số nghiệm nguyên của bất phương trình
2
3
2 16
x
x
l
à
A.
5
. B.
6
. C.
4
. D
.
3
.
Lời
giải
Chọn B
T
a có
2
2
3
3 4 2 2
2
16 2 2 3 4 3 4 0 4 1
x
x x x
x
x x x x
.
Do
đó số nghiệm nguyên của bất phương trình đã cho là 6.
Câu 38. (chuyên Hùng Vương Gia Lai 2019) Bất phương trình
2
2
1
1
2 8
x
x
c
ó tập nghiệm là
A.
3
; .
B.
;
1 .
C.
1
;3 .
D
.
1
;3 .
Lời
giải
Chọn C
Bất phương trình đã cho tương đương với
2
2
3
2 2
1
1
2
3 2 3 0 1 3
2
2
x
x
x
x x x x
Vậy, tập nghiệm của bất phương trình đã cho là:
1
;3 .
S
Câu 39. (Chuyên Hoàng Văn Thụ-Hòa Bình 2019)Cho bất phương trình
2
1 2 1
2
2
3 3
x x x
có
tập
nghiệm
;S
a b
. Giá t
rị của
b
a
bằng
A
.
3
. B.
4
. C.
2
. D.
1
.
Lời
giải
Chọn A
T
a có:
2
1
2 1
2 2
2
2
1 2 1 3 0 0 3.
3
3
x
x x
x x x x x x
Vậy tập
nghiệm
0
;3
S
, s
uy ra
3
0 3
b
a
.
Câu
40. (SGD Hưng Yên 2019) Tập nghiệm của bất phương trình
2
1
2
1
3
x
là
A.
(
;0)
. B.
(
0; )
. C.
1
;
2
. D
.
1
;
2
.
Lời
giải
Chọn C

T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Ta
có
2
1
2
1
1 2 1 0
3 2
x
x
x
.
Vâ
y: Tập nghiệm của bất phương trình là
1
;
2
.
Câu 41. (SGD Điện Biên - 2019) Tập nghiệm của bất phương trình là
A. . B. . C. . D. .
Lờ
i giải
Chọn A
0
0
2 2 0;1
1
1
x
x
x
x
x
x
Câu 42. (Ngô Quyền - Ba Vì - Hải Phòng 2019) Tập nghiệm
S
của bất phương trình
2
4
1
8
2
x
x
là
A.
;
3S
. B.
1
;S
. C.
;
1 3;S
. D.
1;
3S
.
Lờ
i giải
Chọn C
Bất
phương trình
2
2
4
4 3
2 2
3
1
1 1
8 4 3 4 3 0
1
2 2 2
x
x x x
x
x
x x x
x
.
Nê
n tập nghiệm của bất phương trình
2
4
1
8
2
x
x
là
;1
3;S
.
Câu
43. (Cần Thơ - 2019) Nghiệm của bất phương trình
2
2
4
x
x
l
à
A.
1
2 x
. B.
1x
. C.
2x
. D.
2
1 x
.
Lờ
i giải
Chọn A
2
2
2
2 4 2 2
x
x x x
2
2
0 x x
1 2 x
.
Câu 44. (Chuyên Lê Quý Đôn Điện Biên 2019) Tìm tập nghiệm của bất phương trình
1
1
2
2 3 3
x
x x x
.
A.
2
;
. B.
;
2
. C.
;
2
. D.
2
;
.
Lờ
i giải
Chọn D
Ta
có
1
1 1 2 2
2
2 3 3 3.2 4.3 2 3
x
x x x x x x x
2
2
1
2 0 2
3
x
x
x
.
Câu
45. (Chuyên Lê Hồng Phong Nam Định 2019) Cho bất phương trình
1
4
5.2 16 0
x
x
c
ó tập
nghiệm là đoạn
;a
b
. Tính
2
2
log a b
A.
2
. B.
1
. C.
0
. D.
10
.
Lời giải
2
2
x
0
; 1
;
1
1
;

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn B
Đặt
2 , 0 *
x
t t
Khi đó bất phương trình đã cho trở thành:
2
10 16 0 2 8t t t
(thỏa m
ãn (*))
3
2 2
1
2
2 2 1 3 log 1
3
x
a
x a b
b
.
Câu
46. (Thi thử cụm Vũng Tàu - 2019) Cho bất phương trình
2
1
2 1
2
2
3 3
x
x x
có tập nghiệm
;S
a b
. Giá trị của
b
a
bằng
A.
2
. B.
1
. C.
1
. D
.
2
.
Lời
giải
Chọn C
2
1 2 1
2 2
2
2
1
2 1 3 2 0 1 2 1;2
3
3
x x x
x
x x x x x S
.
Vậy
1
; 2 1a b b a
.
Câu
47. (Chuyên Quốc Học Huế 2019) Xác định tập nghiệm
S
của bất
phương trình
2
3
1
3
3
x
.
A.
;1
S
. B.
1;S
. C.
1;S
. D
.
;1
S
.
Lời
giải
Chọn A
T
a có
2
3
3 2 1
1
3
3 3 3 2 1 1.
3
x
x
x
x
Vậ
y tập nghiệm của bất phương trình là
;1
S
.
Câu
48. (Sở Hà Nam - 2019) Tập nghiệm của bất phương trình
2
2
6
4
1
5
5
x
x
x
là
A.
;
1 2;
. B.
2
;
. C.
;
1
. D.
1
;2
.
Lời
giải
Chọn D
Ta có:
2
2
2 2
6
4
4
6 2 2 2
1
5 5 5 6 4 2 6 4 0
5
x
x
x
x x x
x x x x x
1 2
x
.
Câu
49. (Chu Văn An - Hà Nội - 2019) Bất phương trình
1
2 3
2 2
x
x
có nghiệm là
A.
4
x
. B.
4
x
. C.
4
x
. D.
4
x
.
Lời
giải
Chọn D
T
a có:

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
1
2 3
2
2
1
2x 3
4
x
x
x
x
(vì
1
2
)

T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ-GIỎI MỨC 7-8-9-10 ĐIỂM
BẤT PHƯƠNG TRÌNH LOGARIT
Sử dụng các phương pháp giải phương trình logarit đã đưa ra tại Chuyên đề 19. Phương trình mũ
– logarit để giải
Câu 1. (Chuyên Vĩnh Phúc 2019) Tập nghiệm của bất phương trình
2
2
2
log 1 log 5 1x x
là
A.
3
;5
B.
1
;3
C.
1
;3
D.
1
;5
Lờ
i giải
Chọn B
Điều kiện:
1
5x
.
Ta có
2
2
2
log 1 log 5 1x x
2
2
2
log 1 log 2 5x x
2
1
10 2x x
2
9
0 3 3x x
. Vậy tập nghiệm của bpt là
1
;3S
.
Câu 2. (THPT Gia Lộc Hải Dương 2019) Tìm tập nghiệm
S
của bất phương trình
3
3
2log 4 3 log 18 27x x
.
A.
3
;
3
8
S
. B.
3
;
3
4
S
. C.
3
;
4
S
. D.
3
;S
.
Lời giải
3
3
2
log 4 3 log 18 27 *x x
.
Điều
kiện:
4
3 0
3
18 27 0
4
x
x
x
.
Với điều kiện trên,
2
3
3
*
log 4 3 log 18 27x x
2
4
3 18 27x x
3
3
8
x
.
Kết hợp điều kiện ta được
3
;
3
4
S
.
Câu 3. (THPT Yên Khánh - Ninh Bình -2019) Tập nghiệm của bất phương trình
2
2
2
l
og 2 log 9
4
x
x
chứa tập
hợp nào sau đây?
A.
3
;
6
2
.
B.
0
;3
. C.
1
;5
. D
.
1
;
2
2
.
Lờ
i giải
+
Điều kiện:
0x
.
+ Ta có:
B
ẤT PHƯƠNG TRÌNH MŨ - LOGARIT
Chuyên
đề 20

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2 2
2 2 2 2 2 2
2
5
log 2 log 9 1 log log 2 9 log 3log 10 0
4
1
5 log 2 4
2
x
x x x x x
x x
.
Vậy
5
1
;4
2
x
chứa tập
1
;2
2
.
Câu 4. (Chuyên Đại Học Vinh 2019) Tập nghiệm của bất phương trình
1 3
3
log 1 log 11 2 0
x x
là:
A.
;4
. B.
1;4
. C.
1;4
. D.
11
4;
2
.
Lời giải
Chọn D
ĐK:
1
1 0
11
1;
11
11 2 0
2
2
x
x
x
x
x
Ta có
1 3 3
3
11 2 11 2 11
log 1 log 11 2 0 log 0 0 1;
1 1 2
x x
x x x
x x
Kết luận:
11
1;
2
x
. Vì
11 11
4; 1;
2 2
x
. Ta chọn đáp án D
Câu 5. (Sở Phú Thọ 2019) Tập nghiệm của bất phương trình
1 3
3
log 1 log 11 2 0
x x
là
A.
;4
B.
1;4
C.
1;4
D.
11
4;
2
Lời giải
Chọn B
Điều kiện xác định:
11
1
2
x
.
Khi đó ta có:
1 3
3
log 1 log 11 2 0
x x
3 3
log 11 2 log 1 11 2 1 0
x x x x
1
1;4
4
x
x
x
.
Câu 6. (Sở Bắc Ninh 2019) Tập nghiệm của bất phương trình
1 3
3
log 1 log 11 2 0
x x
là:
A.
;4
S
. B.
1;4
S
. C.
1;4
S
. D.
11
3;
2
S
.
Lời giải
1 3
3
log 1 log 11 2 0
x x
3 3
log 11 2 log 1 0
x x
3 3
log 11 2 log 1
x x
11 2 1
1 0
x x
x
1 4
x
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
S
uy ra tập nghiệm của bất phương trình là
1
;4
S
.
Câu 7. (THP
T Nguyễn Khuyến 2019) Tổng tất cả các nghiệm nguyên của bất phương trình
2
2
2
log 1 2 log 2
x
x
bằng
A.
1
2
B.
9
C.
5
D.
3
Lời giải
Chọn D
Điề
u kiện
1 0 1
2
2
0 2
x x
x
x x
2
2 2 2
4
4
2
log 1 2 log 2 log 1 log 1
2 2
x
x x x
x x
2
2
2
4 6
0
0 ; 2 2;3
2 2
x
x x x
x
x
x
S
uy ra nghiệm của bất phương trình là:
2
;3
x
.
Nghiệ
m nguyên là:
3
x
. Vậy t
ổng tất cả các nghiệm nguyên là
3
Câu 8. (C
huyên Bắc Ninh 2019) Tìm tất cả giá trị của tham số
m
để bất
phương trình
2
2
l
og 2 3 log 1
x
x mx
c
ó tập nghiệm là
.
A
.
2
2
m
. B.
2
2
m
. C.
2
2 2 2
m
. D.
2
m
.
Lờ
i giải
Ta có
2
2
log 2 3 log 1
x x mx
2
2
2
1
0
2
3 1
x
mx
x
x mx
2
2
1
0
2
0
x
mx
x mx
Để
bất phương trình
2 2
l
og 2 3 log 1
x
x mx
c
ó tập nghiệm là
thì hệ
có tập nghi
ệ
m
là
2
1
2
2
4
0
8 0
m
m
2
2
m
.
Câu 9. (Mã 123 2017) T
ìm tập nghiệm
S
của
bất phương trình
2
2
2
log 5log 4 0
x x
.
A.
( ;1] [4; )S
B.
[
2;16]S
C.
(0 ; 2] [16; )S
D
.
( ; 2] [ 61 ; )
Lờ
i giải
Chọn C
Điề
u kiện
0x
Bpt
2
2
log
4
16
log 1 2
x
x
x
x
Kế
t hợp điều kiện ta có
0; 2 16;S
.
Câu 10. (Mã 105 2017) Tì
m tất cả các giá trị thực của tham số
m
để bất
phương trình
2
2
2
lo
g 2 log 3 2 0
x
x m
c
ó nghiệm thực.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1m
B.
1m
C.
0m
D.
2
3
m
Lời giải
Chọn.A
Đặt
2
log 0
t x x
, ta có bất phương trình :
2
2 3 2 0t t m
.
Để BPT luôn có nghiệm thực thì
3 3 0 1m m
.
Câu 11. (THPT Đoàn Thượng - Hải Dương 2019)
Biết rằng bất phương trình
5
2
2
log 5 2 2.log 2 3
x
x
có tập nghiệm là
log ;
a
S b
, với
a
,
b
là các số nguyên
dương nhỏ hơn 6 và
1
a
. Tính
2 3P a b
.
A.
7
P
. B.
11.
P
C.
18
P
. D.
16.
P
Lời giải
Đặt
2
log (5 2)
x
t
. Do
5 2 2
x
với mọi
x
nên
2 2
log (5 2) log 2 1
x
hay
1t
.
Bất phương trình đã cho trở thành:
2
2
3 3 2 0
t t t
t
(do
1t
)
1
2
t
t
.
Đối chiếu với
1t
ta lấy
2t
.
Khi đó
2 5
log (5 2) 2 5 2 log 2
x x
x
.
Vậy bất phương trình có nghiệm là
5
S (log 2; )
, ta có
5, 2 2 3 16
a b a b
.
Câu 12. Tập nghiệm
S
của bất phương trình
2
2 2
0
log 5log 6x x
là
A.
1
;64
2
S
. B.
1
0;
2
S
.
C.
64;S
. D.
2
6
1
0; 4;S
.
Lời giải
2
2 2
1
log 5log 06x x
ĐK:
0 *
x
Đặt
2
log 2
t x
1
thành
2
2
2
1
0 1 6 1 log 6 6
6
2
5
4
t t t x x
So với
*
:
4
1
1
2
6
x
Vậy
1
;64
2
S
.
Câu 13. (Chuyên Vĩnh Phúc 2019) Kí hiệu
max ;a b
là số lớn nhất trong hai số
, .a b
Tìm tập nghiệm S
của bất phương trình
2 1
3
max log ; log 1.
x x
A.
1
;2 .
3
S
B.
0;2 .
S
C.
1
0; .
3
S
D.
2; .
S
Lời giải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Chọn A
2
1 2 3
3
l
og log log logy x x x x
1
1
' 0, 0
ln 2 ln3
y x
x
x
nên phương trình
0
y
c
ó nghiệm duy nhất
Mà phương trình
0
y
c
ó nghiệm
1x
do đó
TH1:
2
1
3
1:log logx x x
Ta
có
2
1 1
3 3
1
m
ax log ; log 1. log 1
3
x
x x x
Do đó
1
1
3
x
TH2:
2
1
3
1:log logx x x
Ta
có
2
1 2
3
max log ; log 1. log 1 2
x x x x
Do đó
1
2
x
Vậ
y
1
;
2 .
3
S
1
;
2 .
3
S
Câu 14. (Sở Bắc Nin
h 2019) Tập nghiệm của bất phương trình
2
2 2
2
l
og 2 4 2 2 1
x
x x x x
là
;
a
b
.
Khi đ
ó
.a
b
bằng
A.
1
5
16
. B.
12
5
. C.
16
1
5
. D.
5
12
.
Lờ
i giải
Ta có:
2
2
2
x x x
2
2
x x x
2
2
2
x
x
x
.
Ta
có:
2
2 2
2
log 2 4 2 2 1
x x x x x
2
2
2
l
og 2 4 2 2 1
x
x x x x
2
2
2
2
log 4 2 2 1
2
x
x x
x x
2
2
2
2
2
3 2 2
l
og 2 2 1, 1
2
x x
x x
x x
Ta
có
2
2
0
x
x
,
x
.
Điều kiện:
2
3
2 2 0
x
x
2
2
2 3 x x
2
2
0
0
4
8 9
x
x
x
x
8
,
*
5
x
Với điều kiện
*
, ta có
2
2 2 2
2 2
1 log 3 2 2 3 2 2 log 2 2 , 2
x x x x x x x x

NGUYỄ
N BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
X
ét hàm số
2
l
og f t t t
với
0t
. Có
1
1
0
.ln 2
f t
t
,
0
; t
.
H
àm số
2
l
og f t t t
đồng
biến trên
0
; ,
2
3
2 2 0; x x
và
2
2
0; x x
N
ên
2
2
2
3 2 2 2 f x x f x x
2
2
3
2 2 2 x x x x
2
2
2 x x
2
2
2 0
2 4
x
x x
2
0
3 2
x
x
2
3
x
.
Kết hợ
p với ĐK ta có tập nghiệm bất phương trình là
8 2
;
5 3
ha
y
1
6
.
15
a b
.
Chọn
đáp án C.
Câu 15. (Chuyên Đại học Vinh - 2019) Bất phương trình
3
9 ln 5 0x x x
c
ó bao nhiêu nghiệm
nguyên?
A
. 4. B. 7. C. 6. D. V
ô số.
Lời giải
Chọn C
Đ
iều kiện:
5x
.
Cho
3
3
3
9
0
0
9 ln 5 0
3
ln 5 0
4
x
x x
x
x x x
x
x
x
.
Bảng xét dấu:
Dựa vào bảng xét dấu ta thấy
4
3
0
0 3
x
f x
x
.
V
ì
4
; 3;0;1;2;3x x
.
Vậy
có 6 giá trị nguyên của
x
thỏa
bài toán.
Câu 16.
(THPT Đoàn Thượng – Hải Dương 2019) Biết rằng bất phương trình
5
2
2
l
og 5 2 2.log 2 3
x
x
c
ó tập nghiệm là
l
og ;
a
S
b
,
với
a
,
b
l
à các số nguyên
dương nhỏ hơn 6 và 1a
. Tính
2
3P a b
.
A
.
7P
. B.
11
.P
C
.
1
8P
. D.
16
.P
Lời giải
Chọn D
Đặt
2
log (5 2)
x
t
. Do
5
2 2
x
với
mọi
x
nên
2
2
log (5 2) log 2 1
x
hay
1t
.
Bấ
t phương trình đã cho trở thành:
2
2
3 3 2 0t t t
t
(d
o
1t
)
1
2
t
t
.
Đối
chiếu với
1t
ta
lấy
2t
.
K
hi đó
2
5
l
og (5 2) 2 5 2 log 2
x
x
x
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Vậy bất phương trình có nghiệm là
5
S (log 2; )
, ta có
5, 2 2 3 16
a b a b
.
Câu 17. (Chuyên Đại học Vinh - 2019) Tính tổng tất cả các nghiệm nguyên của bất phương trình
2 2
2 2
log 3 log 4 1 0
x x x x
.
A.
4
. B.
6
. C.
5
. D.
3
.
Lời giải
Chọn B
Điều kiện:
0
x
.
Ta có
2 2 2 2
2 2 2 2
log 3 log 4 1 0 log 3 3 log 4 4 *
x x x x x x x x
.
Xét hàm số
2
log
f t t t
trên
0;D
. Ta có
1
1 0
ln2
f t t D
t
hàm số
f
đồng biến trên
D
.
Suy ra
2 2
* 3 4 3 4 1 3
f x f x x x x
.
Vậy tập hợp các nghiệm nguyên của bất phương trình là
1; 2; 3
.
Nhận xét: Với cách hỏi và đáp án của câu này ta chỉ cần mở MODE 7 của máy tính cầm tay, nhập
vế trái của bất phương trình và cho biến chạy từ 1 đến 6 là tìm được đáp án ngay.
Câu 18. (HKI-NK HCM-2019) Biết bất phương trình
2
2
2
1
log 2 1
16 3
x x
x x
x
có tập nghiệm
là
; .S a b
Hãy tính tổng
20 10 .T a b
A.
45 10 2
T
. B.
46 10 2
T
. C.
46 11 2
T
. D.
47 11 2
T
.
Lời giải:
Chọn A
Điều kiện:
0
x
.
2
2
2
2 2 2
1
log 2 1 log 1 log 16 3 2 4 3 0
16 3
x x
x x x x x x x
x
2
2
2 2
1 3 1 3 3 3
log 2 log 2 2 2
2 4 2 4 4 4
x x x x
Xét hàm số
2
2
3 3
log 2
4 4
f t t t
với
0t
có
2
2
2 0
3
ln 2
4
t
f t
t
,
0
t
nên
f t
đồng biến trên khoảng
0;
.
Suy ra
2
0
1 3 3 1 3 2 2 3 2 2
2 2
1
2 4 4 2 2 2
3 0
4
x
x x x x x
x x
3 2 2 3 2 2
; 20 10 45 10 2
2 2
a b T a b
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu
19. (THPT Cẩm Bình Hà Tỉnh 2019) Tập nghiệm của bất phương trình
1
3
l
og 10 3 1
x
x
chứa
mấy số nguyê
n.
A
.
3
. B.
5
. C.
4
. D
. Vô số.
Lời giải
Chọn A
T
a có
1
1 1
3
3
l
og 10 3 1 10 3 3 3.3 10 0
3
x
x x x
x
x
(*)
.
Giải (*) ta có
1
3
3 1 1
3
x
x
. Vậy có
3
số nguyên thuộc tập nghiệm của bất phương
trình.
Câu 20. (Chuyên Phan Bội Châu - Nghệ An - 2018) Số nghiệm nguyên của bất phương trình
2
3 2 3
l
og log 1 log .logx x x x
là
A.
1
. B.
2
. C.
3
. D
. Vô số.
Lời giải
Điều ki
ện xác định:
0
x
.
T
a có:
2
3 2 3 2 3
log log 1 log .log log 1 log 1 0
x x x x x x
2
3
2
3
log 1 0
0 2
log 1 0
3
2
3
2
l
og 1 0
0 3
log 1 0
x
x
x
x
x
x
x
x
x
.
Do đó có
2
nghiệ
m nguyên thỏa mãn.
Câu 21. (THPT Lý Thái Tổ - Bắc Ninh - 2018) Bất phương trình
2 1
3
3
7
log log 0
3
x
x
có tập nghiệm
là
;a b
.
Tính giá trị
3
P
a b
.
A.
5
P
. B.
4P
. C.
1
0
P
. D
.
7
P
.
Lời giải
2 1
3
3
7
l
og log 0
3
x
x
1
3
1
3
3
7
0
3
3 7
l
og 0
3
3
7
l
og 1
3
x
x
x
x
x
x
3
7
0
3
3 7
1
3
3
7 1
3 3
x
x
x
x
x
x
3
7
0
3
3 7 1
3 3
x
x
x
x
3
7
0
3
8
3
0
3
3
x
x
x
x
7
;
3 ;
3
7
;3
8
3
3
0 3;3
3 3
x
x
x
x
x
.
S
uy ra
7
3
a
;
3
b
. Vậy
7
3
3. 3 4
3
P
a b
.
Câu
22. (THPT Ngô Quyền - Hải Phòng - 2018) Tập nghiệm của bất phương trình
1
2
3
l
og log 0
x
l
à

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
A.
0
;5
. B.
1;2
. C.
1
;
4
4
. D.
1
0
;
2
.
Lờ
i giải
Điều kiện xác định:
2
0
0
0
1
l
og 0
1
x
x
x
x
x
1
2 2 2
3
1
l
og log 0 log 1 log 1
2
x
x x x
S
o sánh điều kiện, suy ra
1
0
;
2
S
.
Câu 23. (THP
T Nam Trực - Nam Định - 2018) Tổng các nghiệm nguyên của bất phương trình
2
5 2
5 5
25
75 0
l
og logx x
là
A.
70
. B.
64
. C.
62
. D.
66
.
Lờ
i giải
Điều kiện
0
x
.
2
5 2
5 5
25
75 0
l
og logx x
2
5 5
4
4 3 0
log
logx x
5
1 3
2 2
log x
1
125
5
x
.
Nghiệm nguyên của bất phương trình là:
0 1 2 3 4 5 6 7 8 9 10 11; ; ; ; ; ; ; ; ; ; ;
.
11
11 1
1 2 11 66
2
.
.
..S
.
Câu 24. (THP
T Lương Văn Can - 2018) Cho bất phương trình
l
og 1 4 log 0
x
x
.
Có bao nhiêu số
nguyên
x
thoả mãn bất phương trình trên.
A.
1
0000
. B.
1
0001
. C.
9
998
. D.
9
999
.
Lờ
i giải
l
og 1 4 log 0 1
x x
Điề
u kiện:
0
x
.
Khi ấ
y
1
1
1 log 4 10000
10
x x
. Vì
x
nên
1
;2;3;...;9999
x
Vậy có tất cả
9
999
số nguyên
x
t
hoả mãn bất phương trình trên.
BẤT PHƯƠNG TRÌNH MŨ
Sử dụng các
phương pháp giải phương trình mũ đã đưa ra tại Chuyên đề 19. Phương trình mũ –
logarit
để giải
Câu 1. (THPT Trần Phú - 2019) Tập nghiệm của bất phương trình:
1
2 1
3
2 4 8 0
x
x x
A.
1
;
4
B.
1
;
4
. C.
;4
D.
4;
.
Lờ
i giải
Chọn A
1
2 1 1 2 1
3 2 4 8 0 4 8 0
x
x x x x
3
3
2 2 2 2
4.2 8. 2 0 2. 2 2 0(*)
x
x x x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đặt
2
2
, 0
x
t
t
, suy ra
bpt (*) trở thành:
3
2
0
2
2
. 0
2
2
t
t t
t
Giao với Đk
0
t
ta
được:
2
2
t
1
2
2
2
2 1 1
2
2 2 2
2
2 4
x
x
x
x
Vậy tập
nghiệm của BPT đã cho là
1
;
4
T
.
Câu
2. (Lý Nhân Tông - Bắc Ninh 2019) Bất phương trình
2
1
3
7.3 2 0
x
x
có tập nghiệm là
A.
2
;
1 log 3;
. B.
2
;
2 log 3;
.
C
.
3
;
1 log 2;
. D.
3
;
2 log 2;
.
Lời giải
Chọn C
Ta có
2
1
3
7.3 2 0
x
x
2
3. 3 7.3 2 0
x
x
.
Đặt
3
0
x
t
ta
được
2
0
3
7 2 0
t
t
t
1
0
3
2
t
t
.
S
uy ra
1
0
3
3
3
2
x
x
3
1
l
og 2
0
3 3
3
3
x
x
3
1
l
og 2
x
x
.
Vậy bấ
t phương trình có tập nghiệm là
3
;
1 log 2;
.
Câu 3. (Chuyên ĐH Vinh -2019) Biết tập nghiệm của bất phương trình
2
2
3
2
x
x
là
;a
b
.
Giá trị
a b
bằng
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn D
Ta
có:
2
2
2
3 2 3. 2 2 0 1 2 2 0 1
2
x
x x x
x
x
.
Tậ
p nghiệm của bất phương trình là:
0
;1
S
.
Suy ra
0
a
và
1b
nên
1a b
.
Câu 4. (Chuyên Bắc Giang 2019) Tập nghiệm của bất phương trình
3 1 1 2
3
9 3 9.3 0
x x x
l
à
A.
;
1 .
B.
3
; .
C.
1
; .
D
.
;
3 .
Lời giải
Chọn C
T
a có
3 1 1 2 3 2
3
9 3 9.3 0 3.3 9 3.3 9.3 0
x x x x x x
Đặt
3 0
x
t t
.
Ta có bất phương trình
3
2
3
9 3 9 0
t
t t
3 2
3
9 3 9 0
t
t t

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
2
2
3
3 3 3 0
3
3 3 0
3 0
3
t
t t
t t
t
t
Khi đó ta có
3 3 1.
x
x
Vậy tập nghiệm của bất phương trình là
1; .
S
Câu 5. (THP
T Đông Sơn 1 - Thanh Hóa - 2019) Bất phương trình
6
.4 13.6 6.9 0
x
x x
c
ó tập
nghiệm là?
A.
; 1 1; .
S
B.
; 2 1; .
S
C.
;
1 1; .
S
D.
;
2 2; .
S
Lờ
i giải
Chọn C
Ta
có
2
2
3
1
3
2
2 2
6
.4 13.6 6.9 0 6. 13. 6 0 .
1
3
3
2 2
3 3
x
x
x
x x x
x
x
x
Vậ
y tập nghiệm của bất phương trình là
;
1 1; .
S
.
Câu 6. (Ki
nh Môn - Hải Dương 2019) Cho bất phương trình:
2
2
2
.5 5.2 133. 10 0
x
x x
c
ó tập
nghiệm là:
;S
a b
. Biểu
thức
1
000 5A b a
có
giá trị bằng
A. 2021 B. 2020 C. 2019 D. 2018
Lờ
i giải
Chọn B
Ta có:
2
2
2 2
2 2 2 2
2
.5 5.2 133. 10 0 50. 5 133.5 .2 20. 2 0
x
x x x
x x x
2
2 2 2
2.5 5.2 25.5 4.2 0
x
x x x
2
2
2 2 2 2
2.5 5.2 5 2 0
x
x x x
1
2
1
1
2 2 2 2
2
2
2 2
2 2 2 2
1 1 1
2 2 2 2 2
2 2
2 2 2 2
2
5
1
2
2
.5 5.2 0 5 2
5
1
2
5.5 4.2 0 5 2
2
5
2.5 5.2 0 5 2
1
2
2
5.5 4.2 0 5 2
5
2
x
x
x x x
x
x x x x
x x x x x
x x x x
x
2
1
1
0
2
2
0
2
1 0
2
2 0
2
x
x
x
x
2
4
2
4
x
x
x
x
4
2
x
. S
uy ra
4
;2
S
.
Vậy
1
000 5 1000.2 5. 4 2020
A
b a
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 7. (Toán Học Tuổi Trẻ Năm 2019) Số nghiệm nguyên của bất phương trình:
2
17 12 2 3 8
x x
là:
A.
3
. B.
1
. C.
2
. D.
4
.
Lời giải
Ta có:
2
17 12 2 3 8
x x
2
2
3 8 3 8
x x
2
2
3 8 1
x x
2
2 0
x x
2;0
x
.
Vậy bất phương trình đã cho có
3
nghiệm nguyên.
Câu 8. (Chuyên Lê Quý Dôn Diện Biên 2019) Tìm tập nghiệm của bất phương trình
1 1
2 2 3 3
x x x x
.
A.
2;
. B.
;2
. C.
;2
. D.
2;
.
Lời giải
Ta có
1 1 1 2 2
2 2 3 3 3.2 4.3 2 3
x x x x x x x x
2
2
1 2 0 2
3
x
x x
.
Câu 9. (Chuyên Hưng Yên 2019) Cho bất phương trình
2 1
1
1 1
3 12
3 3
x x
có tập nghiệm
;
S a b
.
Giá trị của biểu thức
3 10 P a b
là
A.
5
. B.
3
. C.
4
. D.
2
.
Lời giải
Đặt
1
1
3
x
t
0
t
. Khi đó bất phương trình đã cho trở thành
2
12 3 4 0 3 t t t t t
(vì
0t
).
Từ đó suy ra:
1
1 1
3 1 1 0
3
x
x
x
. Tập nghiệm của bất phương trình là
1;0
.
Vậy
1
a
và
0
b
. Suy ra
3 10 3
P a b
.
Câu 10. (Chuyên Hạ Long 2019) Bất phương trình sau có bao nhiêu nghiệm nguyên dương
9 4.3 3 0
x x
.
A. 3. B. 1. C. 0. D. 2.
Lời giải
Đặt
3 0
x
t
.
Bất phương trình đã cho trở thành
2
4. 3 0
t t
1 3t
1 3 3
x
0 1x
.
Vậy bất phương trình đã cho có tập nghiệm là
0,1
S
nên nó không có nghiệm nguyên dương.
Câu 11. (THPT Đông Sơn Thanh Hóa 2019) Bất phương trình
6.4 13.6 6.9 0
x x x
có tập nghiệm là?
A.
; 1 1; .
S
B.
; 2 1; .
S
C.
; 1 1; .
S
D.
; 2 2; .
S
Lời giải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Ta có
2
2 3
1
3 2
2 2
6.4 13.6 6.9 0 6. 13. 6 0 .
3 3 1
2 2
3 3
x
x x
x x x
x
x
x
Vậy tập nghiệm của bất phương trình là
; 1 1; .
S
Câu 12. (THPT Yên Khánh - Ninh Bình - 2019) Tập nghiệm của bất phương trình
2
4 14
2 3 7 4 3
x x
là:
A.
6;2
. B.
6 2;
. C.
6;2
. D.
; 6 2;
.
Lời giải
Ta có
2
7 4 3 2 3
,
2 3 2 3 1
và
1 2
2 3 2 3 7 4 3 2 3
.
2
4 14
2 3 7 4 3
x x
2
4 14 2
2 3 2 3
x x
2
4 14 2
x x
2
4 12 0
x x
6 2
x
.
Vậy bất phương trình đã cho có tập nghiệm
6;2
.
Câu 13. (Chuyên Bắc Giang 2019) Tìm số nghiệm nguyên của bất phương trình
1
6 4 2 2.3
x x x
A. 2. B. 3. C. 1. D. 0
Lời giải
Chọn C
1
6 4 2 2.3 6 4 2.2 2.3 0
x x x x x x
2 3 2 2 2 3 0
x x x
3 2 2 2 0
x x
3
log 2;1
x
Câu 14. (Chuyên Thái Bình 2019) Tập nghiệm của bất phương trình
2
9 2 1
3 9 .5 1
x x
x
là khoảng
;a b
. Tính
b a
A.
6
. B.
3
. C.
8
. D.
4
.
Lời giải
2
9 2 1
3 9 .5 1
x x
x
1
.
Có
1
5 0
x
x
.
Xét
2
9 0
x
, VT
1
0
3 0 1
(loại).
Xét
2
9 0
x
2
9 0
2 1
3 3 1
9 .5 0
x
x
x
VT
1
1
(loại).
Xét
2
9 0
2
2 1
3 3 1
9 0
9 .5 0
x
x
x
x
VT
1
1
luôn đúng.
Có
2
9 0 3;3
x x
.
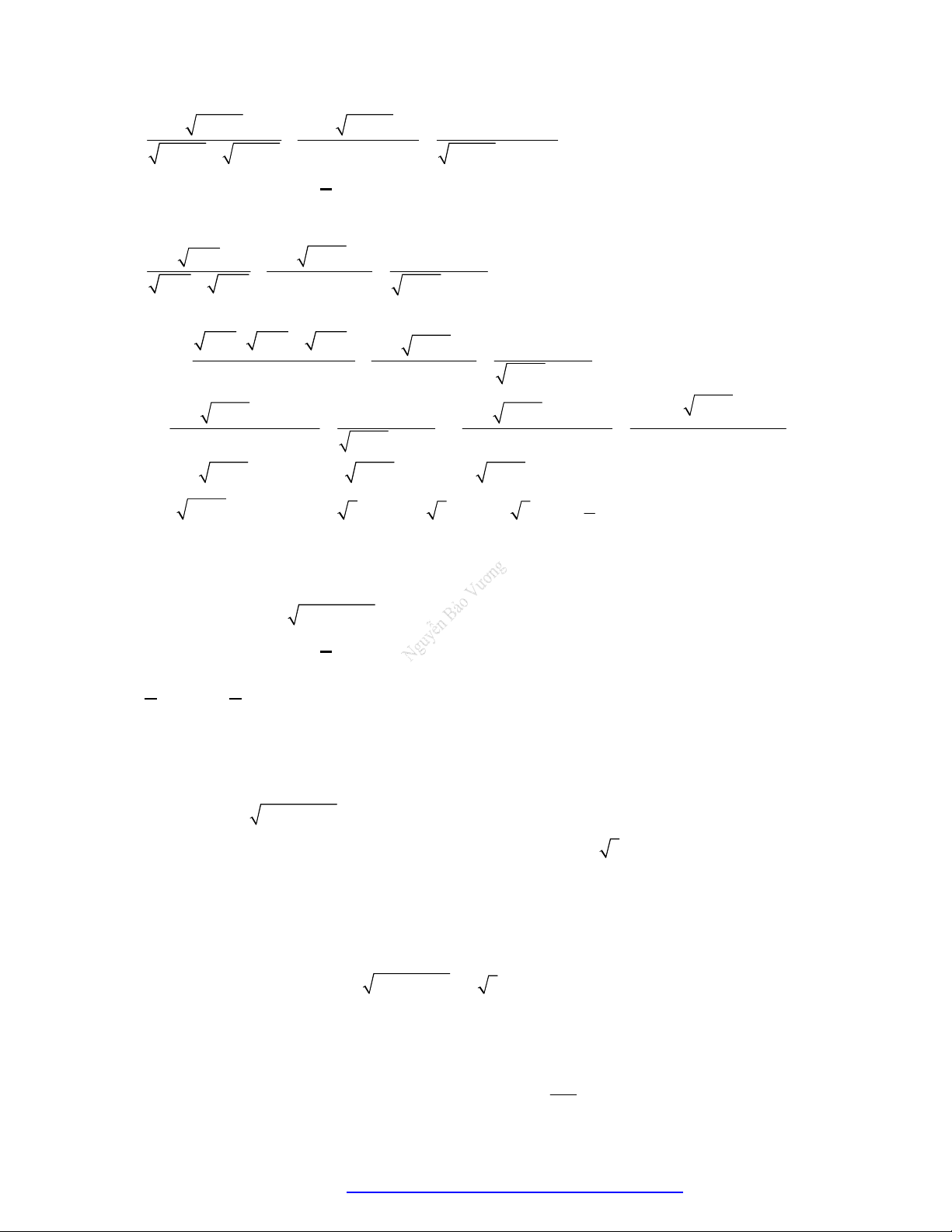
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tập nghiệm
của bất phương trình là:
3
;3 6
b
a
.
Câu
15. ( Hsg Bắc Ninh 2019) Bất phương trình
2
4 4 2
2
2
2 4 2
2
3 3 4 3 7 3 2
3
2
3 2 3 4 3 2 3
x
x x x
x
x
x x x
có bao nhiêu
nghiệm?
A. Vô số. B. 1. C. 2. D. 3
Lời giải
Đặt
2
3
0
x
t
, bấ
t phương trình đã cho trở thành
2
2
2
2
4 7 2
1
2
2
4 2
t t t t
t
t t
t t
Điều ki
ện:
0
2t
2
2
2
2 2 2
4 7 2
1
2
4
2
t t t
t t t
t t
t
t
2
2
2 2 2
2
2
2
4 2
3 4 2 12 2 3 4 2 12
2 2 2 4
4 2
t
t t
t
t t t t t t
t t t t
t t
2
2 2 2 2
3
4 2 12 4 2 4 4 2 10 0
t
t t t t t t
2
2
4
1 0 3
t
t
. Với
2
1
3
3 3 .
4
x
t
x
Vậy bấ
t phương trình có 1 nghiệm duy nhất.
Câu 16. (KTNL GV Thpt Lý Thái Tổ 2019) Số nghiệm nguyên thuộc đoạn
2
0; 20
của
bất
phương
trình:
2
1 2
2
9.2 4 2 3 0
x
x
x
x
là
A.
3
8
. B.
36
. C.
37
. D
.
1
9
.
Lời giải
Chọn B.
Điều ki
ện:
2
2
3 0 3
x
x x
hoặ
c
1x
*
.
Vì
x
l
à số nguyên thuộc đoạn
20; 20
nê
n ta xét các trường hợp sau:
Trường hợp 1.
3
20
x
, khi đó dễ t
hấy
2
1 1
2
9.2 2 2 9 0
x
x x x
nên
2
1 2
2
9.2 4 2 3 0
x
x
x
x
,
do đó trên
3; 20
bất
phương trình có
1
8
nghiệm
nguyên.
Trường hợp 2.
2
x
tha
y trực tiếp vào bất phương trình ta có:
4 5 4 0
(đúng)
.
Do đó
2
x
thỏa
mãn yêu cầu bài toán.
Trường hợp 3.
1
x
t
hay trực tiếp vào bất phương trình ta có:
1
0 0
(sa
i).
Do đó
1
x
không thỏa
mãn yêu cầu bài toán.
Trường hợp 4.
2
0 4
x
. Khi đó, xét hà
m số:
2
2
3f x x x
,
dễ thấy
2
0; 4
m
in 4 5
f
x f
nê
n
2
4
2 3 4 5, 20; 4
x
x x
a
.
Mặt khác
, đặt
2
x
t
, khi đó
2
1 2
2 9.2 2 9
x
x
t t
,
2
0 4
20 4 2 2
x t
.
Khi đ
ó xét hàm số
2
2 9g t t t
với
2
0 4
2
2
t
, dễ thấy
20 4
4
2
; 2
71
m
in 2
1
28
g
t g
b

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Từ
,a
b
suy
ra
2
1 2
20; 4
71
m
in 2 9.2 4 2 3 4 4 5 0
128
x
x
h
x x x h
. Do đó
bấ
t phương trình đã cho nghiệm đúng với mọi
2
0 4
x
, nê
n trên đoạn
20; 4
bấ
t phương
trình có 17 nghiệm nguyên.
Trường hợp
3
x
tha
y trực tiếp vào bất phương trình ta thấy không thỏa mãn.
Vậy số nghiệm nguyên của bất phương trình là: 36.
Câu 17. (Chuyên Thái Nguyên 2019) Tập hợp tất cả các số thực
x
không
thỏa mãn bất phương trình
2
4
2 2
9 4 .2019 1
x
x
x
là
khoảng
;a
b
.
Tính
b a
.
A.
5
. B.
4
. C.
5
. D.
1
.
Lờ
i giải
Xét hai trường hợp:
2
4
0
x
và
2
4
0x
TH1:
2
2
4
0
2
x
x
x
khi đó ta có:
2
2
4
0
4 2 2
2 0
9
9 1
9 4 2019 1
2
0 2019 2019 1
x
x
x
x
x
x
Dấ
u
"
"
xảy r
a
2
4
0
2
2
0
x
x
x
TH2:
2
4 0 2 2x x
, khi đó t
a có:
2
2
4 0
4 2 2
2 0
9
9 1
9
4 2019 1
2
0 2019 2019 1
x
x x
x
x
x
bấ
t phương trình vô nghiệm
Vậy
tập hợp tất cả các số thực
x
k
hông thỏa mãn bất phương trình là
( 2; 2) 2; 2 4a b b a
Câu 18. (THP
T Chuyên Thái Bình - 2019) Tập nghiệm của bất phương trình
2
9
2 1
3
9 .5 1
x
x
x
l
à
khoảng
;a
b
.
Tính
b a
.
A
.
6
.
B.
3
.
C.
8
.
D.
4
.
Lờ
i giải
Chọn A
Với
2
3
9
0 ,
3
x
x
x
ta
có
2
9
0
2 1
3
3 1
9 .5 0
x
x
x
nên
2
9
2 1
3
9 .5 1
x
x
x
không thỏa mãn bất phương trình đã cho, do đó bất phương trình vô nghiệm.
Với
2
9 0 3 3,
x x
ta có
2
9
0
2 1
3
3 1
9 .5 0
x
x
x
nên
2
9
2 1
3 9 .5 1
x
x
x
Bất
phương trình đã cho có tập nghiệm là
3
;3 .
S

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khi đó,
3; 3
a b
nên
6
b a
.
Câu 19. (Chuyên Bắc Ninh - 2020) Có bao nhiêu giá trị nguyên của
x
trong đoạn
0;2020
thỏa mãn bất
phương trình sau
16 25 36 20 24 30
x x x x x x
.
A.
3
. B.
2000
. C.
1
. D.
1000
.
Lời giải
Chọn C
Ta có
2 2 2
16 25 36 20 24 30 4 5 6 4 .5 4 .6 5 .6
x x x x x x x x x x x x x x x
2 2 2
2 4 5 6 2.4 .5 2.4 .6 2.5 .6 0
x x x x x x x x x
2 2 2
4 5 4 6 5 6 0
x x x x x x
4
5
4
6
5
6
1
4 5 0
4 6 0 1 0 0;2020
5 6 0
1
x
x x
x
x x
x x
x
x
.
Vậy có 1 giá trị nguyên của
x
trong đoạn
0;2020
thỏa mãn bất phương trình.
Câu 20. (Hải Hậu - Nam Định - 2020) Tập nghiệm của bất phương trình
2 1
1
(3 9)(3 ) 3 1 0
27
x x x
chứa bao nhiêu số nguyên ?
A. 2. B. 3. C. 4. D. 5.
Lời giải
Chọn B
Điều kiện
1 1
3 1 0 3 1 1
x x
x
.
Ta có
1x
là một nghiệm của bất phương trình.
Với
1x
, bất phương trình tương đương với
2
1
(3 9)(3 ) 0
27
x x
.
Đặt
3 0
x
t
, ta có
2
1
( 9)( ) 0
27
t t
1
( 3)( 3)( ) 0
27
t t t
3
1
3
27
t
t
. Kết hợp
điều kiện
3 0
x
t
ta được nghiệm
1
3
27
t
1
3 3 3 1
27
x
x
. Kết hợp điều
kiện
1x
ta được
1 1x
suy ra trường hợp này bất phương trình có 2 nghiệm nguyên.
Vậy bất phương trình đã cho có tất cả 3 nghiệm nguyên.
Câu 21. (THPT Lương Văn Tụy - Ninh Bình - 2018) Tập nghiệm của bất phương trình
9 2 5 .3 9 2 1 0
x x
x x
là
A.
0;1 2;
. B.
;1 2;
.C.
1;2
. D.
;0 2;
.
Lời giải
Đặt
3
x
t
,
0t
.
Xét phương trình:
2
2 5 9 2 1 0
t x t x
1
.
Ta có
2 2
2
5 9 2 1 8 16 4
x x x x x
nên phương trình
1
luôn có nghiệm.
Nếu
4 0
x
thì phương trình
1
có nghiệm kép
5t x
.
Do đó bất phương trình đã cho trở thành
3 5
x
x
(luôn đúng khi
4
x
).
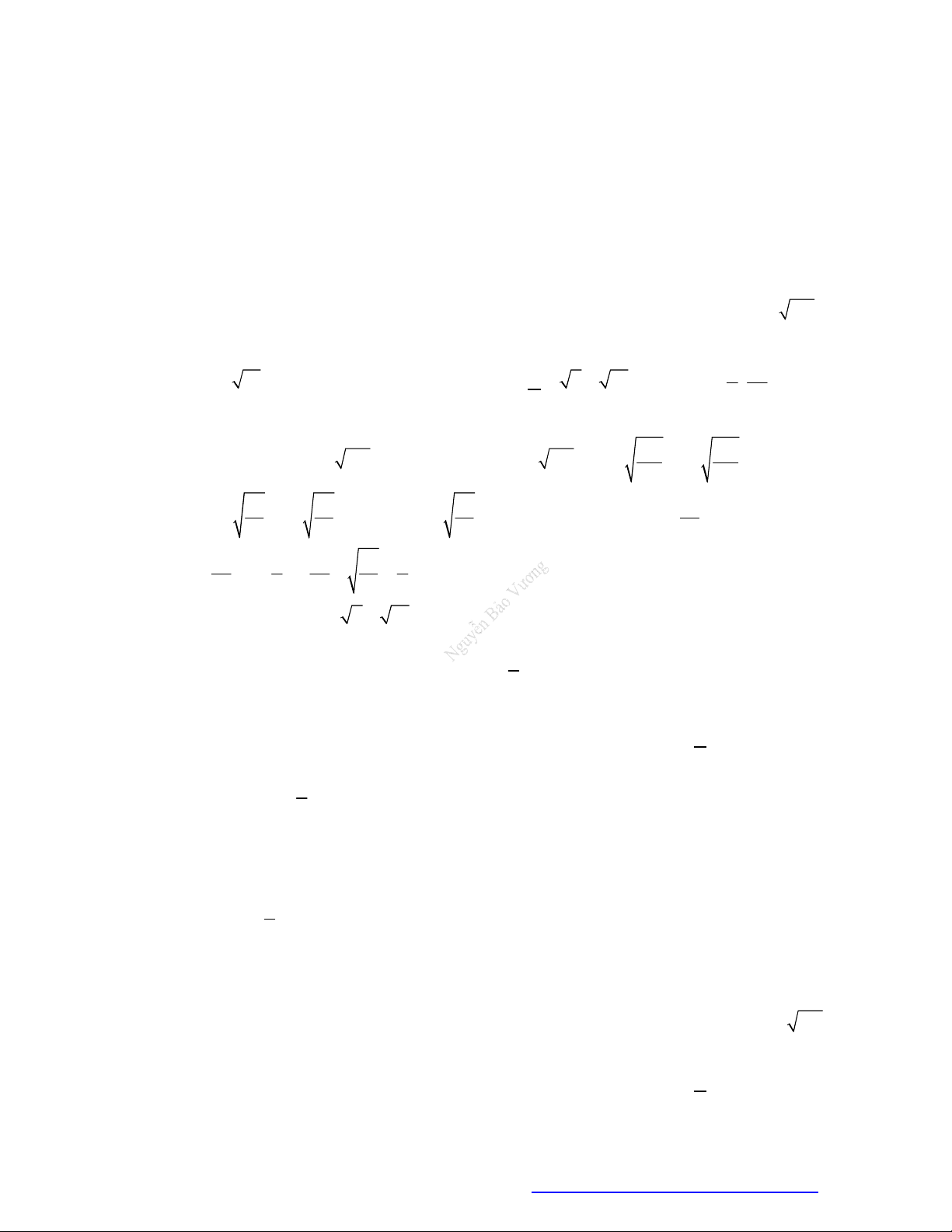
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Nếu
4
0
x
t
hì phương trình
1
c
ó hai nghiệm phân biệt
2 1
9
t x
t
.
Xé
t các phương trình
3
9 2
x
x
1
và
3
2 1 3 2 1 0
x
x
x
x
2
.
Đặt
3
2 1
x
f
x x
;
ta có
3
ln 3 2
x
f
x
là
hàm số đồng biến trên
.
Lại có
0
1 0
f
f
và
0
0
f
,
1
0
f
nê
n
f
x
đổi
dấu một lần duy nhất trong
khoảng
0
;1
.
Vậy phương trình
2
c
ó đúng hai nghiệm
0
x
,
1x
.
Lập
bảng xét dấu cho
1
v
à
2
t
a được tập nghiệm của bất phương trình là:
0;1 2;S
.
Câu 22. (Toán Học Tuổi Trẻ Số 6) Tập
nghiệm của bất phương trình
2
2
2
.7 7.2 351. 14
x
x x
có dạng
là đoạn
;S a b
. G
iá trị
2b a
t
huộc khoảng nào dưới đây?
A.
3
; 10
. B.
4;
2
. C.
7
;4 10
. D.
2
49
;
9
5
.
Lời giải
2
2
2
.7 7.2 351. 14
x
x x
4
9.7 28.2 351. 14
x
x x
2
2
7
2
49
. 28. 351
14
14
x
x
x x
7
2
49.
28. 351
2
7
x
x
x x
. Đặt
7
,
0
2
x
x
t
t
thì bpt trở thành
28
49
351
t
t
4 7
49 2
t
4
7 7
49 2 2
x
x
4
2
x
, khi đó
4
;2
S
.
Giá
trị
2
10
b
a
7
;4 10
.
Câu 23. (C
huyên ĐHSPHN - 2018) Cho
2
1
1
.
5
2
x
f
x
;
5
4 .ln 5
x
g
x x
.
Tập nghiệm của bất
phương trình
f
x g x
l
à
A.
0
x
. B.
1x
. C.
0
1x
. D.
0
x
.
Lờ
i giải
Ta có:
2
1 2 1
1
.
5 . 2 1 .ln5 5 .ln5
2
x
x
f
x x
.
Và
:
5
.ln5 4ln 5 5 4 ln5
x x
g
x
.
Do đó:
f
x g x
2 1
5 .ln5 5 4 ln5
x x
2 1
5
5 4
x x
2
5
.5 5 4 0
x x
4
5
5
5
1
x
x
V
N
5 1
x
0
x
.
Vậ
y nghiệm của bất phương trình đã cho là
0
x
.
Câu 24. (THPT Kinh Môn - Hải Dương - 2018) Bất phương trình
2
2
2
.5 5.2 133. 10
x
x x
c
ó tập
nghiệm là
;S
a b
thì biểu thức
1
000 4 1A b a
có giá trị bằng
A.
3992
. B.
4008
. C.
1004
. D.
2017
.
Lờ
i giải
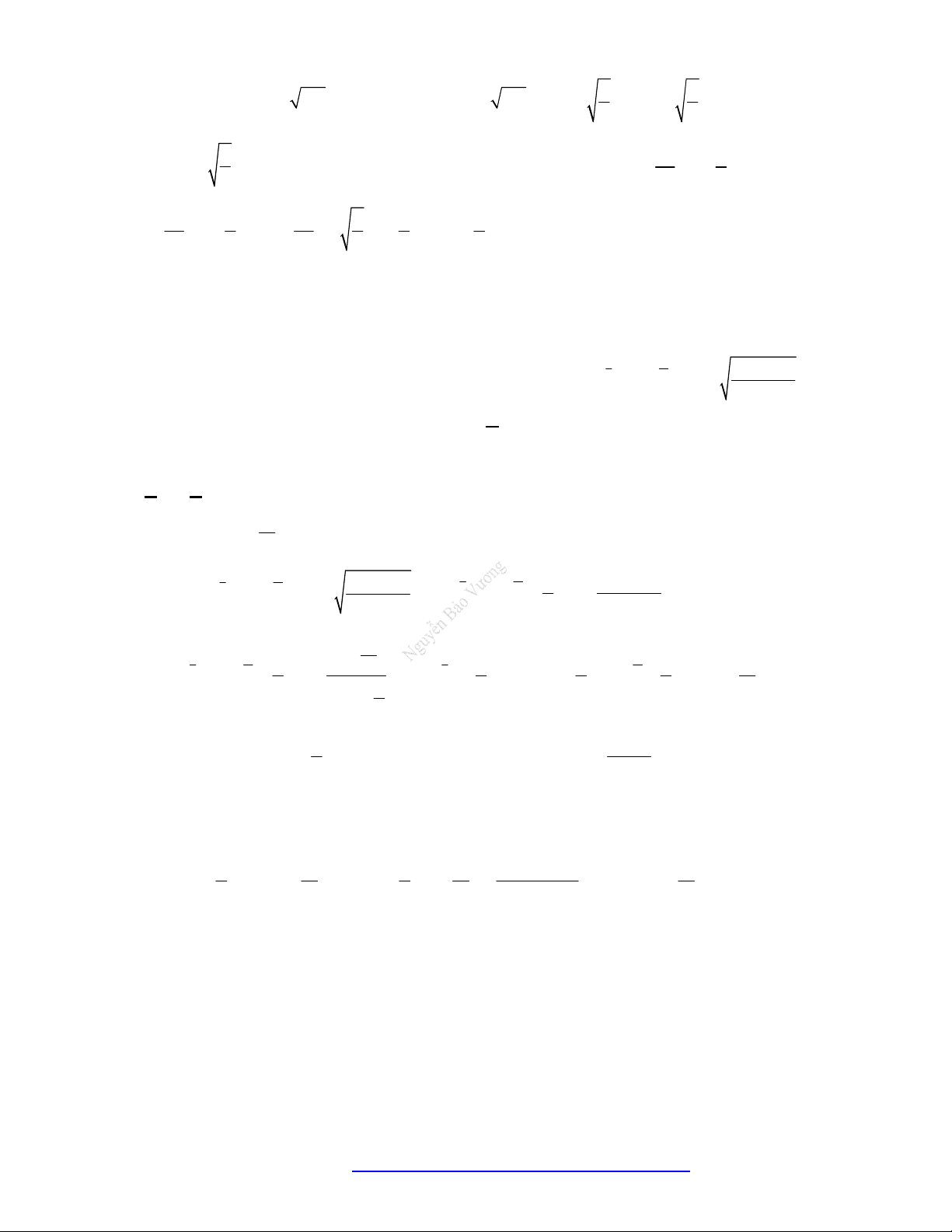
NGUYỄN BẢO VƯƠNG - 0946798489
Ta
có:
2 2
2.5
5.2 133. 10
x x x
50
.5 20.2 133. 10
x x x
5 2
50. 20.
133 0
2 5
x x
.
Đặt
5
2
x
t
,
0t
, ta
được bất phương trình:
2
50
133 20 0
t t
4 5
2
5 2
t
.
Với
4 5
2
5 2
t
, ta có:
4 5
5
25 2 2
x
2 1
2
x
4 2
x
.
Tập nghi
ệm của bất phương trình là
4;
2
S
4
a
,
2
b
.
10
00 4 1A b a
10
00.2 4 4 1
20
17
.
Câu 25.
Số nghiệm nguyên thuộc khoảng
0;
12
của b
ất phương trình
1 11
1
2
2
2
2 11
3 3
log
1
x
x x
x
x x
là:
A.
7
. B.
8
. C.
5
. D.
11
.
Lời giải
Chọn C
Điều kiệ
n
11
2
x
và
0
x
.
Khi đó
1 11
1
2
2
2
2 11
3 3
log
1
x
x x
x
x x
1 1
1
1 2
2
2
1 2
11
3 3
log
2 1
x
x x
x
x x
1 11 1 11
1 2 1 2
2 2 2
11
2
1 1 1
1 11
3 3
log 3 log 1 3 log 2
1
2 2 2
1
x x
x
x x x
x
x
x x
x
x
.
Xét hàm số
2
1
3 l
og
2
t
f t t
với
0t
. Khi đó
1
3 l
n 3 0, 0
2 ln 2
t
f t t
t
nên hàm số đã
cho đồng biến trên
0;
.
Do đó
2
1 11 1 11 3 10 11
1 2 1 2 0 ; 2 0;5
2
x x
f
x f x x
x x x x x
.
Vậy trên khoảng
0;12
có
5
nghiệm nguyên thỏa
yêu cầu bài toán.
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
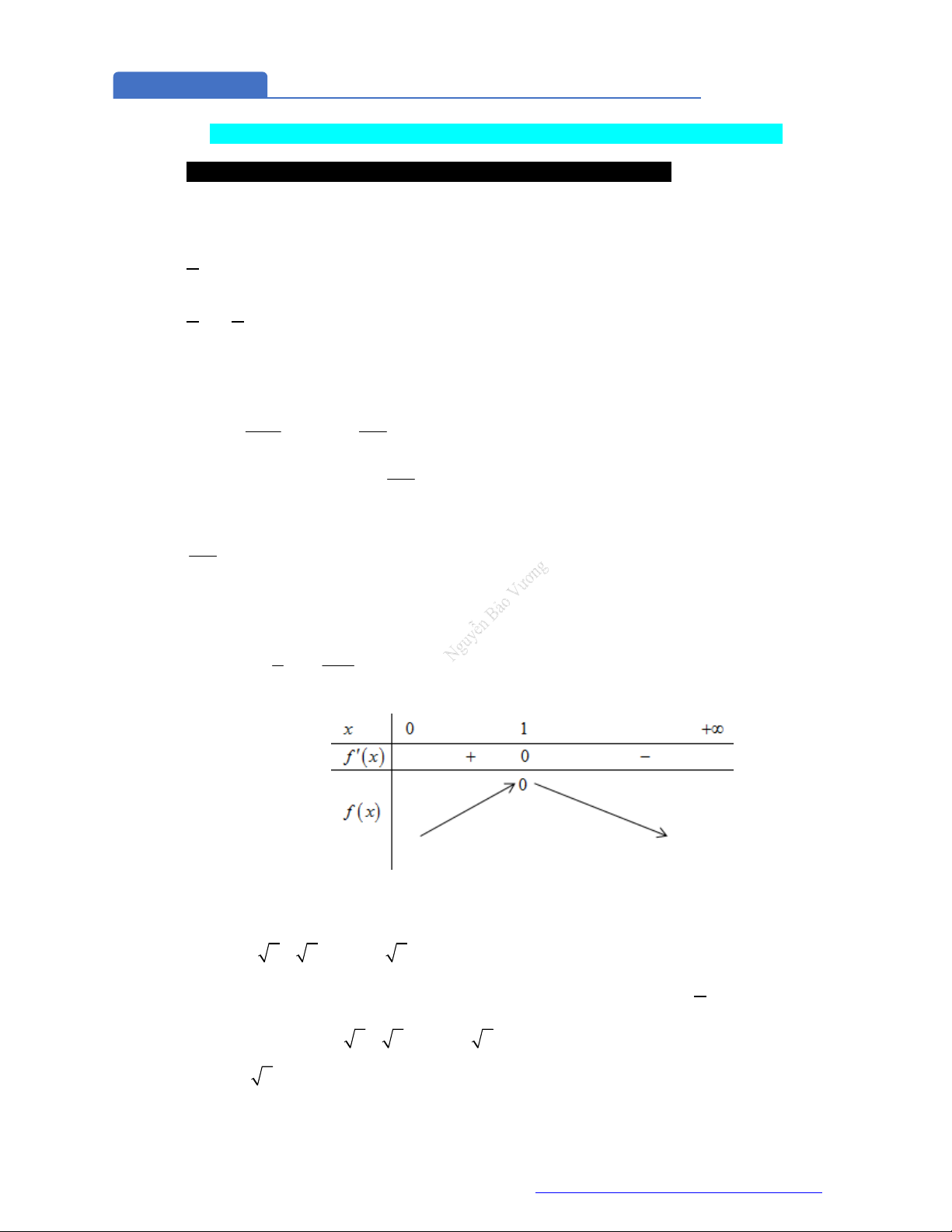
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI – MỨC 9-10 ĐIỂM
DẠNG 1. BẤT PHƯƠNG TRÌNH LOGARIT CHỨA THAM SỐ
Câu 1. (Chuyên Lam Sơn Thanh Hóa 2019) Cho
a
là số thực dương,
1a
. Biết bất phương trình
2log 1
a
x x nghiệm đúng với mọi
0x
. Số
a
thuộc tập hợp nào sau đây?
A.
7;8
B.
3;5
C.
2;3
D.
8;
Lời giải
Chọn A
Ta có: với
1x
thì 2log 1 0 1 1
a
Ta sẽ tìm
a
để đường thẳng
1y x
nhận làm tiếp tuyến của đồ thị hàm số 2log
a
y x tại điểm
1x
Có
2 2
1
lna ln
y y
x a
Phương trình tiếp tuyến
2
1
ln
y x
a
Vậy để đường thẳng
1y x
nhận làm tiếp tuyến của đồ thị hàm số 2log
a
y x thì
2
2
1 ln 2
ln
a a e
a
Thử lại
2
a e
ta sẽ chứng minh
2
2log 1 ln 1
ln 1 0 0
e
x x x x
f x x x x
Có
1 1
1 0 1
x
f x f x x
x x
Bảng biến thiên
Từ bảng biến thiên suy ra
0 ln 1 0f x x x x
Câu 2. (THPT Cẩm Giàng 2 2019) Cho
a
là số nguyên dương lớn nhất thỏa mãn
3
3 2
3log 1 2loga a a
. Giá trị của
2
log 2017a
xấp xỉ bằng:
A.
19
. B.
26
. C.
25
. D.
23
.
Lời giải
Từ giả thiết
3
3 2
3log 1 2loga a a
.
Đặt
2
log 3a x
64
x
a
.
Ta được bất phương trình:
3
3log 1 8 4 6
x x
x
1 8 4 9
x x x
.
BẤT PHƯƠNG TRÌNH MŨ - LOGARIT
Chuyên đề 20

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
1 8 4
1
9 9 9
x x x
.
Đặt
1 8 4
9 9 9
x x x
f x
.
1 1 8 8 4 4
ln ln ln 0
9 9 9 9 9 9
x x x
f x
,
x
.
Vậy
f x
là hàm số nghịch biến trên
. Và ta lại có
2 1f
.
Từ
1 8 4
1
9 9 9
x x x
2f x f
2x
.
Suy ra
2
64 4096a
mà
a
là số nguyên dương lớn nhất thỏa mãn suy ra
4095a
.
Vậy
2 2
log 2017 log 2017 4095 22.97764311 23a
.
Câu 3. (Chuyên Hưng Yên 2019) Tìm tất cả các giá trị thực của tham số
m
để bất phương trình
0,02 2 0,02
log log 3 1 log
x
m có nghiệm với mọi
;0x
A.
1.m
B.
0 1.m
C.
1.m
D.
2.m
Lời giải
Đk:
; 0x m
.
Ta có:
0,02 2 0,02
log log 3 1 log , ;0 .
x
m x
2
log 3 1 , ;0 .
x
m x
3 1 2 , ;0 .
x m
x
Xét hàm
3 1
x
f x
trên
;0
. Ta có
3 .ln3 0, ;0 .
x
f x x
Bảng biến thiên:
Để phương trình có nghiệm với mọi
;0x
ta phải có
2 2
m
1m
.
Câu 4. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Gọi
S
là tổng tất cả các giá trị nguyên của
m
để
bất phương trình
2 2
ln 7 7 ln 4x mx x m
nghiệm đúng với mọi
x
thuộc
. Tính
S
.
A.
14S
. B.
0S
. C.
12S
. D.
35S
.
Lời giải
Chọn C
Ta có:
2 2
ln 7 7 ln 4x mx x m
2 2
2
7 7 4
4 0
x mx x m
mx x m
2
2
7 4 7 0 1
4 0 2
m x x m
mx x m
Bất phương trình đã cho đúng với mọi
x
khi và chỉ khi các bất phương trình
1 , 2
đúng với
mọi
x
.
1
2
0
∞
+
y
y'
x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Xét
2
7 4 7 0
m x x m
1
.
+ Khi
7
m
ta có
1
trở thành
4 0 0
x x
. Do đó
7
m
không thỏa mãn.
+ Khi
7
m
ta có
1
đúng với mọi
x
2
7
7 0 7
' 0 5 9
4 7 0
m
m m
m m
m
5
m
.
Xét
2
4 0
mx x m
2
.
+ Khi
0
m
ta có
2
trở thành
4 0 0
x x
. Do đó
0
m
không thỏa mãn.
+ Khi
0
m
ta có
2
đúng với mọi
x
2
0
0 0
' 0 2 2
4 0
m
m m
m m
m
2
m
.
Từ
và
ta có
2 5
m
. Do
m Z
nên
3;4;5
m
. Từ đó
3 4 5 12
S
.
Câu 5. (Chuyên Bắc Giang 2019) Có bao nhiêu giá trị nguyên dương của
m
để bất phương trình
2 2
2 2
log 7 7 log 4
x mx x m
nghiệm đúng với mọi
x
.
A.
5
B.
4
C.
0
D.
3
Lời giải
Chọn D
Cách 1:
Bpt:
2 2
2 2
log 7 7 log 4
x mx x m
2 2
2
7 7 4
4 0
x mx x m
mx x m
2
2
7 4 7 0
4 0
f x m x x m
g x mx x m
Bpt đã cho nghiệm đúng với mọi
x
0 ,
0 ,
f x x
g x x
Trường hợp 1:
7
m
2
0
4 0
7 4 7 0
0
f x
x
x x
g x
Vậy
7
m
không thỏa yêu cầu bài toán.
Trường hợp 2:
0
m
2
0
7 4 7 0
4 0
0
f x
x x
x
g x
Vậy
0
m
không thỏa yêu cầu bài toán.
Trường hợp 3:
0; 7
m m
Khi đó:
0
,
0,
f x
x
g x x
2
2
0
7 0
0
4 7 0
0
0
0
4 0
f
f
g
g
a
m
m
a
m
m
7
5 9
0
2 2
m
m m
m
m m
2 5
m
Do
m
nên
3;4;5
m
.
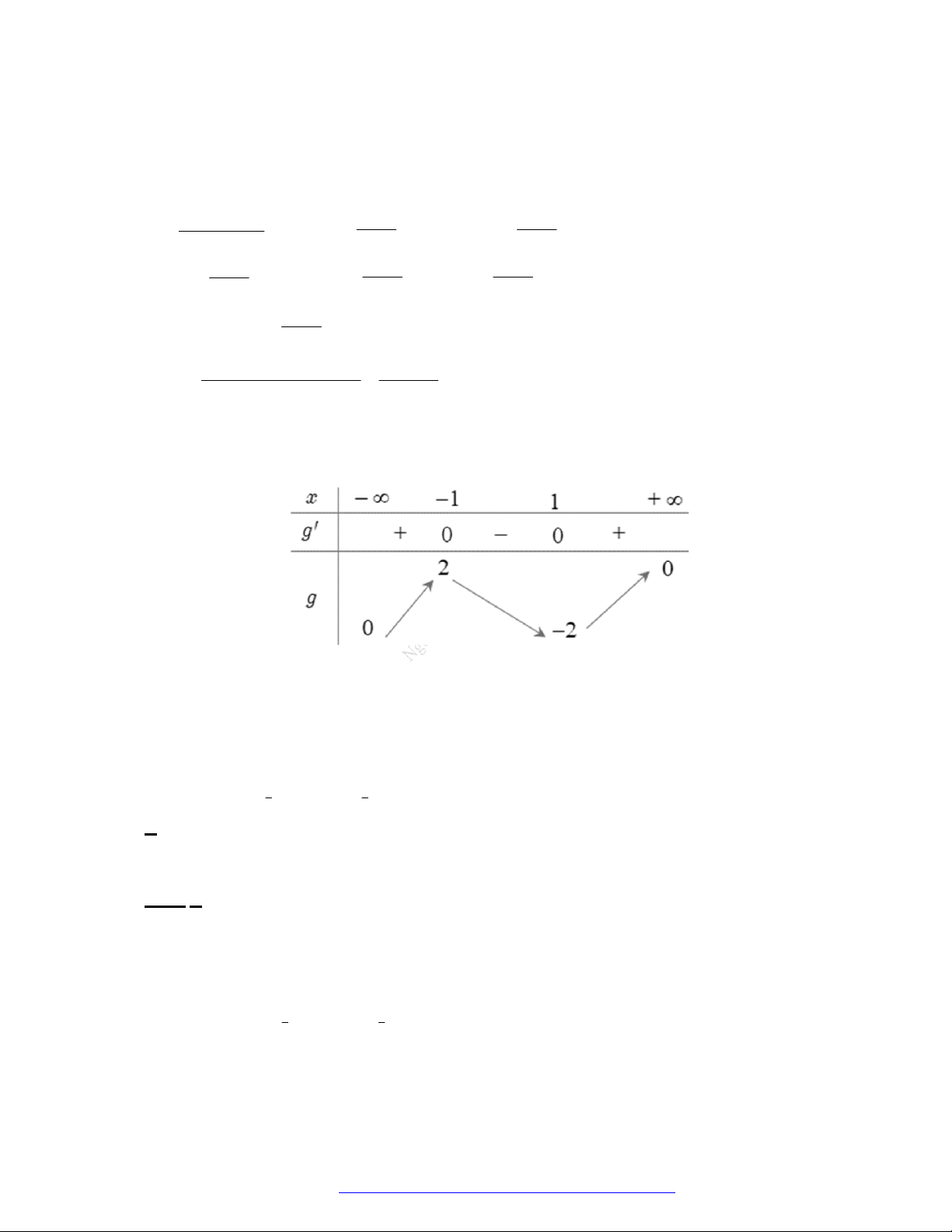
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Cách 2:
2 2
2 2
log 7 7 log 4x mx x m
2 2
2
7 7 4
4 0
x mx x m
mx x m
2
2
7 4 7 0
4 0
m x x m
mx x m
2 2
2
7 4 7 1
1 4
x x m x
m x x
2
2
2
7 4 7
1
4
1
x x
m
x
x
m
x
2 2
2 2
4 4
7 7
1 1
4 4
1 1
x x
m m
x x
x x
m m
x x
(*)
Xét hàm số
2
4
( )
1
x
g x
x
trên
.
2 2 2
2 2 2 2
4( 1) 4 ( 1) 4 4
'( )
( 1) ( 1)
x x x x
g x
x x
1
'( ) 0
1
x
g x
x
Bảng biến thiên
Vậy đk (*)
7 2
2 5
2
m
m
m
Do
m
nên
3;4;5m
.
Câu 6. (Chuyên Quang Trung Bình Phước 2019) Tìm tất cả các giá trị thực của tham số
m
để bất
phương trình
3
1 1
2 2
log 1 logx x x m
có nghiệm.
A. 2m . B.
m
.
C.
2m
. D. Không tồn tại
m
.
Lời giải
Chọn A
Điều kiện
3
1
0
x
x x m
.
Phương trình tương đương
3 3 3
1 1
2 2
log 1 log 1 1x x x m x x x m x m
Khi đó ta có
3
1;
1 , 1 minf x x m x m f x
Ta có
2
3 0 0 1;f x x x
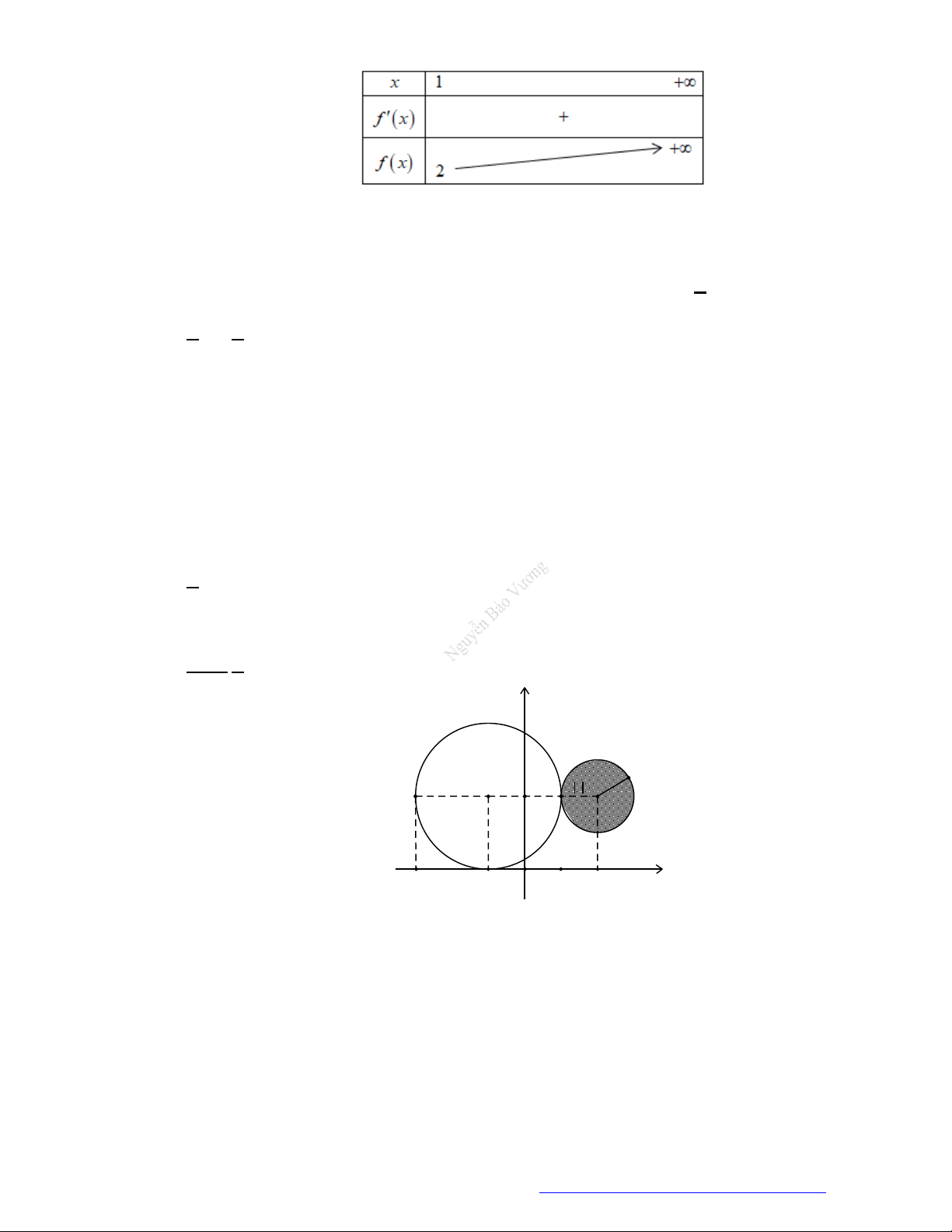
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Bảng biến thiên
Dựa vào bảng biến thiên và đề bài hỏi “có nghiệm” nên ta chọn
m
.
Câu 7. (THPT Chuyên Thái Bình - 2019) Có tất cả bao nhiêu giá trị của tham số
m
để bất phương
trình
2 2
2 2
log 2 log 2x mx m x
nghiệm đúng với mọi
x
.
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn D
Ta thấy
2
2 0x x
Do đó bất phương trình
2 2 2 2
2 2
log 2 log 2 2 2 0x mx m x x mx m x mx m
.
Bất phương trình
2 2
2 2
log 2 log 2x mx m x
nghiệm đúng với mọi
x
khi và chỉ khi
0 0mx m x m
Câu 8. (Chuyên Vĩnh Phúc - 2019) Tìm tập
S
tất cả các giá trị thực của số
m
để tồn tại duy nhất cặp
số
;x y
thỏa mãn
2 2
2
2
log 4 4 6 1
x y
x y m
và
2 2
2 4 1 0x y x y
.
A.
5; 1;1;5S
. B.
1;1S
.
C.
5;5S
. D.
7 5; 1;1;5;7S
.
Lời giải
Chọn A
Nhận thấy
2 2
2 1x y với mọi
,x y
nên:
2 2
2
2
log 4 4 6 1
x y
x y m
2 2 2
4 4 6 2x y m x y
2 2 2
4 4 8 0x y x y m
2 2
2
2 2x y m
(*).
Khi
0m
thì (*)
2
2
x
y
. Cặp
2;2
không là nghiệm của phương trình
2 2
2 4 1 0x y x y .
m
-3
y
x
2
2
1
-1
O
J
I
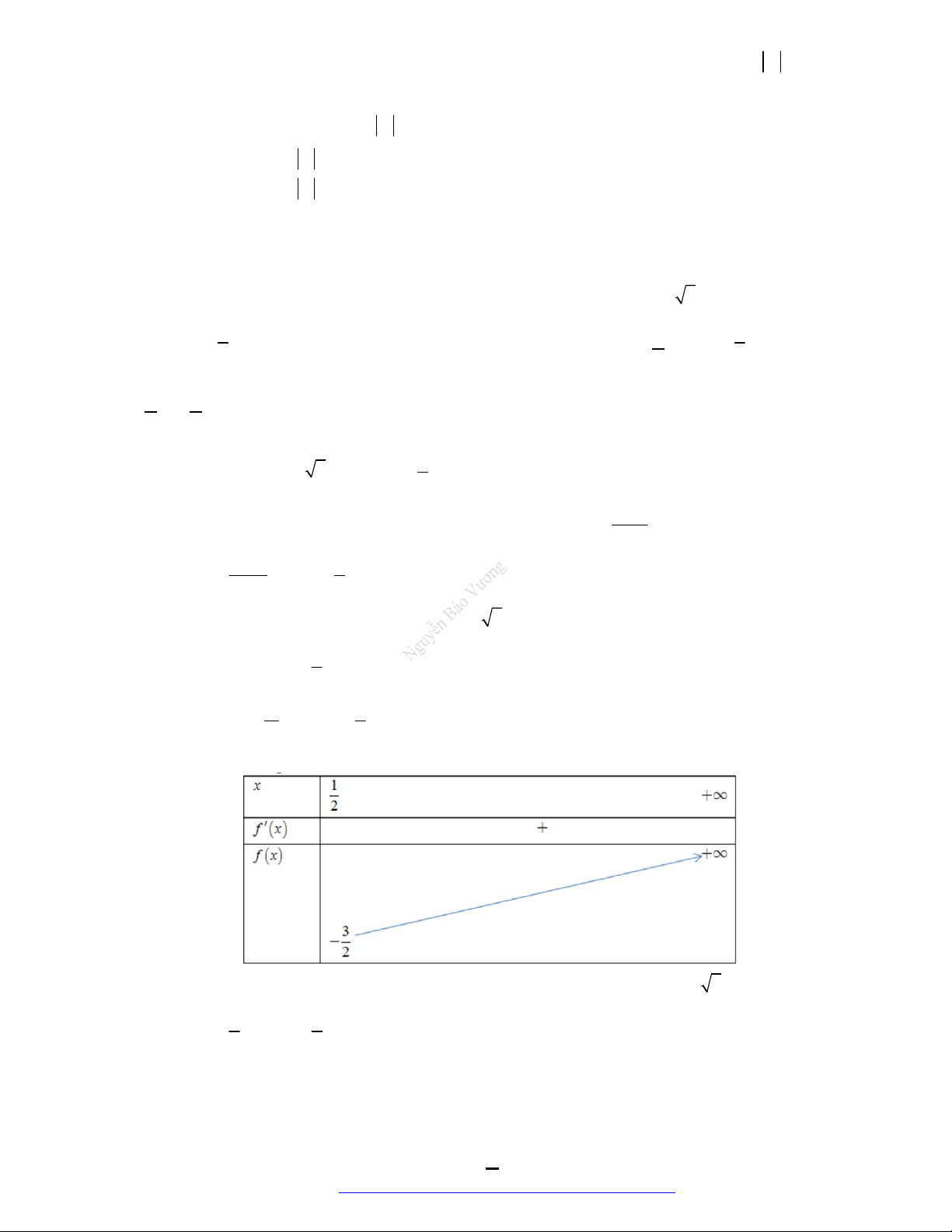
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khi
0m
, tập hợp các điểm
;x y
thỏa mãn (*) là hình tròn tâm
2;2J
, bán kính là
m
.
Trường hợp này, yêu cầu bài toán trở thành tìm
m
để đường tròn tâm
1;2I
, bán kính
2
và
hình tròn tâm
2;2J
, bán kính
m
có đúng một điểm chung (hình vẽ)
Điều này xảy ra khi
1
5
m
m
1
5
m
m
(thỏa mãn
0m
).
Vậy
5; 1;1;5S
.
Câu 9. (Bình Giang-Hải Dương 2019) Xét bất phương trình
2
2 2
log 2 2 1 log 2 0x m x
. Tìm tất
cả các giá trị của tham số
m
để bất phương trình có nghiệm thuộc khoảng
2;
.
A.
3
;0
4
m
. B.
0;m
. C.
;0m
. D.
3
;
4
m
.
Lời giải
Chọn D
Bất phương trình
2 2
2 2 2 2
log 2 2 1 log 2 0 log 2 log 1 0 1x m x x m x
.
Đặt
2
logt x , vì
1
2; ;
2
x t
.
Bất phương trình trở thành
2
2 2
1
2 1 0 2 1 2 2
t
t mt mt t m
t
.
Đặt
2
1t
f t
t
với
1
;
2
t
.
Bất phương trình
1
có nghiệm thuộc khoảng
2;
khi và chỉ khi bất phương trình
2
có
nghiệm thuộc khoảng
1
;
2
.
Ta có
2
1 1
1 0 ;
2
f t t
t
.
Bảng biến thiên
Từ bảng biến thiên suy ra bất phương trình đã cho có nghiệm thuộc khoảng
2;
khi và chỉ
khi
3 3
2
2 4
m m
.
Câu 10. Gọi S là tập hợp tất cả các giá trị của tham số m để bất phương trình
2 5 4 4 3
ln 1 0m x x m x x x x
thỏa mãn với mọi
0x
. Tính tổng các giá trị trong
tập hợp S.
A.
2
. B.
0
. C.
1
. D.
2
.
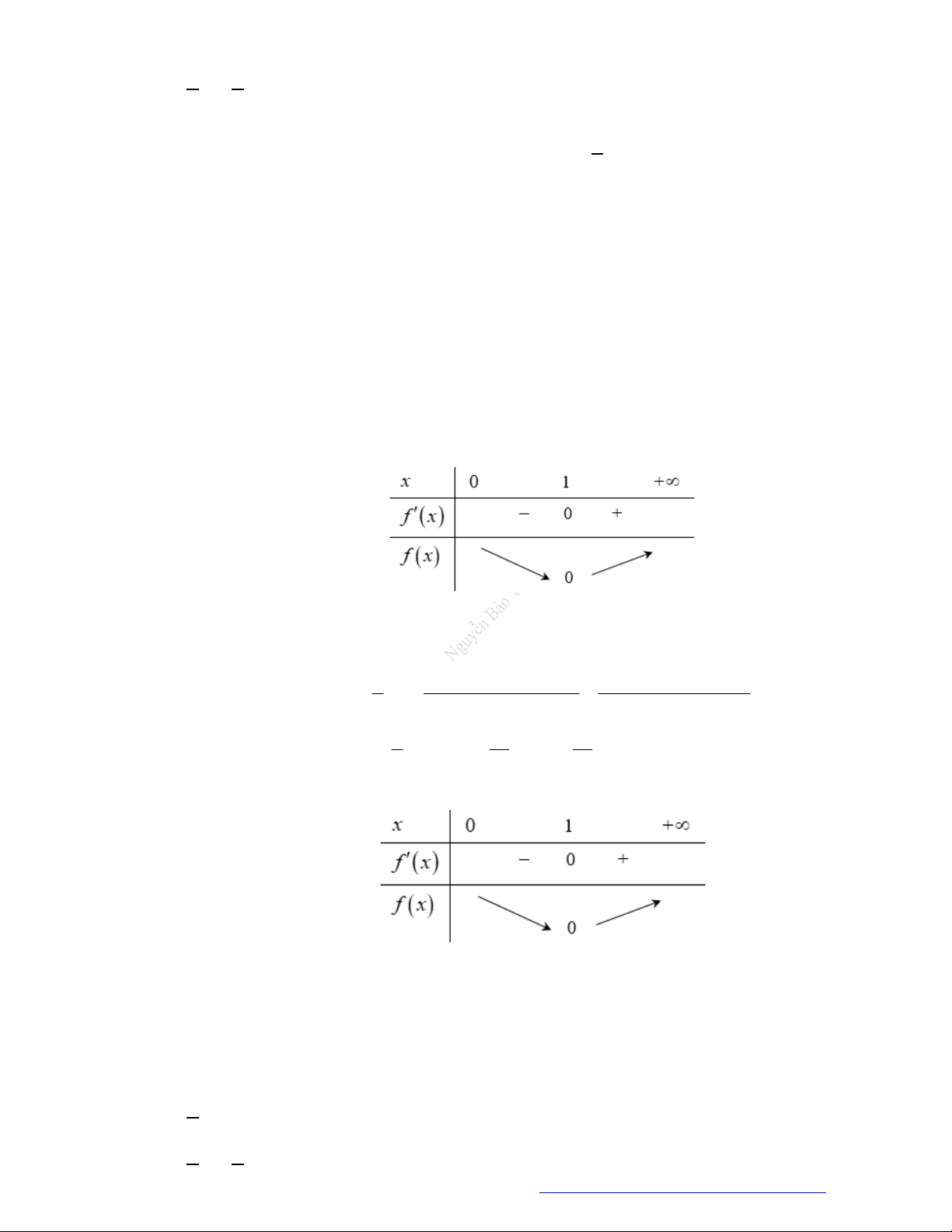
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Lời giải
Chọn C
Đặt
2 5 4 4 3
ln 1f x m x x m x x x x
. Ta có
f x
liên tục, có đạo hàm trên
0;
và
2 4 3 3 2
1
5 4 4 3 1f x m x x m x x
x
.
Bất phương trình đã cho viết thành
0f x
. Giả sử
y f x
có đồ thị là (C).
0f x
với mọi
0x
khi và chỉ khi đồ thị (C) không nằm phía dưới trục Ox.
Mặt khác (C) và Ox có điểm chung là
1;0A
. Nên điều kiện cần để đồ thị (C) không nằm phía
dưới trục Ox là Ox tiếp xúc với (C) tại
1;0A
.
Suy ra,
2
0
' 1 0
1
m
f m m
m
.
Với
0m
ta có bất phương trình đã cho trở thành
ln 1 0f x x x
.
0 1f x x
.
Bảng biến thiên của hàm số
f x
Dựa vào bảng biến thiên ta có
0, 0f x x
. Suy ra
0m
thỏa mãn điều kiện.
Với
1m
ta có bất phương trình đã cho trở thành
5 4 3
2 ln 1 0f x x x x x x
.
4 3
5 4 3
4 3 2
1 5 3 1
1 5 8 3 1
5 8 3 1
x x x
x x x x
f x x x x
x x x
Ta có
2 2 2
4 3 2 2
3 9 9
5 3 1 2 1 0
4 32 32
x x x x x
.
Suy ra
0 1f x x
. Bảng biến thiên của hàm số
f x
như sau
Dựa vào bảng biến thiên ta có
0, 0f x x
. Suy ra
1m
thỏa mãn điều kiện.
Vậy
0;1S
.
Câu 11. (Chuyên Thái Bình - 2020) Cho bất phương trình
2 2
7 7
log 2 2 1 log 6 5x x x x m
.
Có tất cả bao nhiêu giá trị nguyên của
m
để bất phương trình có tập nghiệm chứa khoảng
1;3
?
A.
36
. B.
34
. C.
35
. D. Vô số.
Lời giải
Chọn A
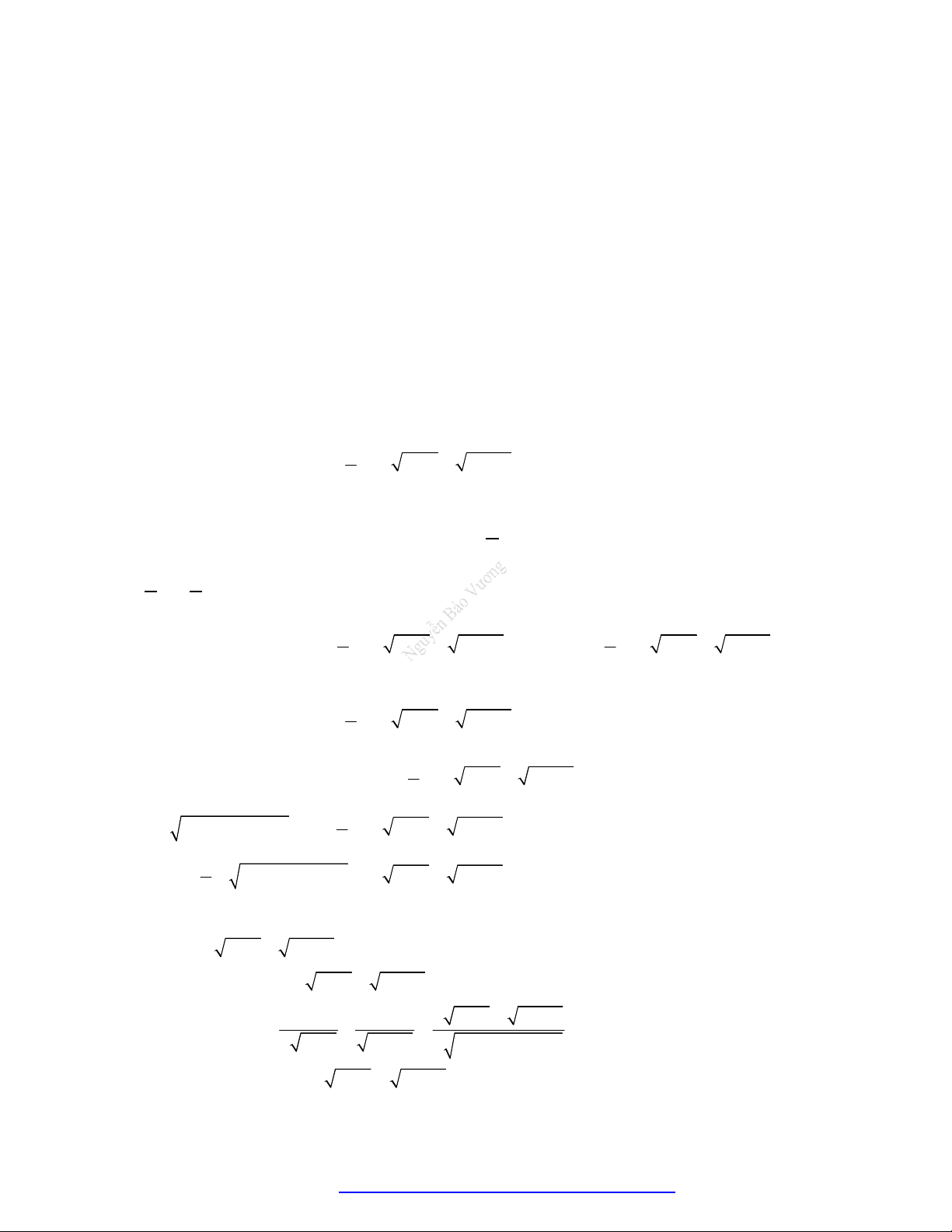
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
2 2
7 7
2 2
7 7
log 2 2 1 log 6 5 , 1;3
log 7 14 14 log 6 5 , 1;3
x x x x m x
x x x x m x
2
2
2
2
6 5 , 1;3 1
6 5 0, 1;3
6 8 9 , 1;3
6 8 9 , 1;3 2
m x x x
x x m x
x x m x
x x m x
Xét
2
6 5 , 1;3
g x x x x
, có
2 2
3 4 1 3 4 12, 1;3
g x x x
Do đó
1 12
m
.
Xét
2
6 8 9, 1;3
h x x x x
, có
2
6.1 8.1 9 23, 1;3
h x x
.
Do đó
2 23
m
.
Do
m
và
12;23
m
nên ta được tập các giá trị của
m
là
12; 11; 10;...;23
.
Vậy có tổng cộng
36
giá trị của
m
thỏa yêu cầu bài toán.
Câu 12. (Chuyên Bắc Ninh - 2020) Gọi
0
m
là giá trị nhỏ nhất để bất phương trình
2 2 2
1 log 2 2log 4 2 2 2 log 1
2
x
x m x x x
có nghiệm. Chọn đáp án
đúng trong các khẳng định sau
A.
0
9;10
m
. B.
0
8;9
m
. C.
0
10; 9
m
. D.
0
9; 8
m
.
Lời giải
Chọn C
+ Điều kiện xác định:
1 2 1 2
*
4 2 2 2 0 4 2 2 2
2 2
x x
x x
m x x m x x
.
+ Với điều kiện trên bất phương trình:
2 2 2
1 log 2 2log 4 2 2 2 log 1
2
x
x m x x x
2
2 2
log 2 2 1 log 4 2 2 2
2
x
x x m x x
2 2 2 4 2 2 2
2
x
x x m x x
2 2 2 4 2 2 2
2
x
m x x x x
1
.
+ Ta thấy các nghiệm của
1
trong khoảng
1;2
luôn thỏa mãn
*
.
+ Đặt
2 2 2 , 0
t x x t
với
1;2
x
.
Xét
2 2 2
f x x x
với
1;2
x
.
1 1 2 2 2 2
2 2 2 2
2 2 2 2
x x
f x
x x
x x
.
0 2 2 2 2 1f x x x x
.
Bảng biến thiên:
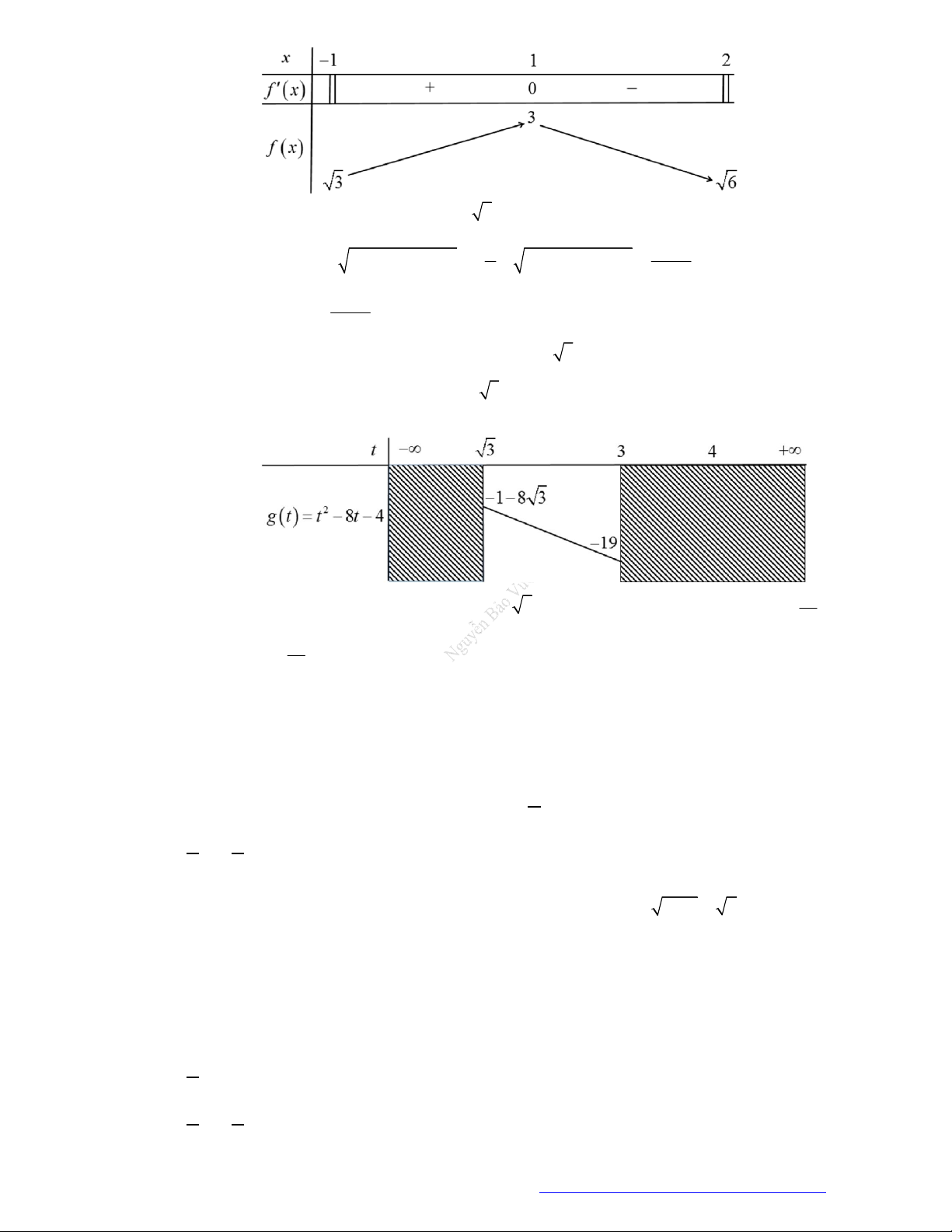
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Suy ra khi
1;2x
thì
3;3t
.
+ Ta có
2
2
4
4 2 2 2 2 2 2 2
2 2
x t
t x x x x x
.
+
1
trở thành
2
2
4
4 2 8 4
2
t
m t m t t
2
.
+
1
có nghiệm
1;2x
2
có nghiệm
3;3t
.
+ Xét hàm số
2
8 4 y g t t t
trên
3;3
.
Bảng biến thiên:
+ Do đó bất phương trình
2
có nghiệm
3;3t
khi và chỉ khi
19
2 19
2
m m
.
Suy ra
0
19
10; 9
2
m
.
Câu 13. (Lương Thế Vinh - Hà Nội - 2020) Gọi
S
là tập hợp tất cả các điểm
;M x y
trong đó
,x y
là
các số nguyên thoả mãn điều kiện
2 2
1
log 2 2 1,
x y
x y m
với
m
là tham số. Có bao nhiêu số
nguyên
m
thuộc đoạn
2020;2019
để tập
S
có không quá
5
phần tử?
A.
1.
B.
2020.
C.
2021.
D.
2019.
Lời giải
Chọn C
2 2
2 2
1
log 2 2 1 2 2 1
x y
x y m x y m x y
2 2
1 1 1x y m
Để bất phương trình có 5 phần tử thì 1 2 1m m
Vậy có 2021 số nguyên
m
thuộc đoạn
2020;2019
để tập
S
có không quá
5
phần tử.
Câu 14. (Chuyên Thái Bình - Lần 3 - 2020) Cho bất phương trình
2 2
7 7
log 2 2 1 log 6 5x x x x m
. Có tất cả bao nhiêu giá trị nguyên của tham số
m
để
bất phương trình trên có tập nghiệm chứa khoảng
1;3 ?
A.
36
. B.
35
. C.
34
. D. Vô số.
Lời giải
Chọn A
Điều kiện xác định
2
6 5 0x x m
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khi đó
2 2
7 7
log 2 2 1 log 6 5
x x x x m
2 2
7 7
log 7 14 14 log 6 5
x x x x m
2 2
7 14 14 6 5
x x x x m
2
6 8 9 0
x x m
.
Khi đó
2
2
6 8 9 0
, 1;3
6 5 0
x x m
ycbt x
x x m
2
2
6.1 8 9 0
1 6 5 0
m
m
12 23
m
.
Vậy có
36
giá trị nguyên của
m
thỏa
.ycbt
Câu 15. (Chuyên Lê Hồng Phong - 2018) Xét bất phương trình
2
2 2
log 2 2 1 log 2 0
x m x
. Tìm tất
cả các giá trị của tham số
m
để bất phương trình có nghiệm thuộc khoảng
2;
.
A.
0;m
. B.
3
;0
4
m
. C.
3
;
4
m
. D.
;0
m
.
Lời giải
Điều kiện:
0
x
2
2 2
log 2 2 1 log 2 0
x m x
2
2 2
1 log 2 1 log 2 0 1
x m x
.
Đặt
2
logt x
.Vì
2
x
nên
2 2
1
log log 2
2
x
. Do đó
1
;
2
t
1
thành
2
1 2 1 2 0
t m t
2
2 1 0
t mt
2
Cách 1: Yêu cầu bài toán tương đương tìm
m
để bpt (2) có nghiệm thuộc
1
;
2
.
Xét bất phương trình (2) có:
2
' 1 0, m m
.
2
2 1 0
f t t mt
có
0
ac
nên (2) luôn có 2 nghiệm phân biệt
1 2
0
t t
.
Khi đó cần
2
2
1 1 3
1
2 2 4
t m m m
.
Cách 2:
2
2
1 1
2 1 0 < m
2 2
t
t mt f t t
t
Khảo sát hàm số
f t
trong
0;
ta được
3
;
4
m
.
Câu 16. (Chuyên Vinh - 2018) Gọi
a
là số thực lớn nhất để bất phương trình
2 2
2 ln 1 0
x x a x x
nghiệm đúng với mọi
x
. Mệnh đề nào sau đây đúng?
A.
2;3
a
. B.
8;a
. C.
6;7
a
. D.
6; 5
a
.
Lời giải
Đặt
2
2
1 3
1
2 4
t x x x
suy ra
3
4
t
Bất phương trình
2 2
2 ln 1 0
x x a x x
ln 1 0
t a t
ln 1a t t
Trường hợp 1:
1t
khi đó
ln 1a t t
luôn đúng với mọi
a
.
Trường hợp 2:
3
1
4
t

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Ta có
3 1 3
ln 1, ;1 , ;1
4 ln 4
t
a t t t a t
t
Xét hàm số
2
1
ln 1
1 3
0, ;1
ln ln 4
t
t
t
f t f t t
t t
do đó
1 3 7
, ;1
3
ln 4
4ln
4
t
a t a
t
Trường hợp 3:
1t
Ta có
1
ln 1, 1; , 1;
ln
t
a t t t a t
t
Xét hàm số
2
1
ln 1
1
, 1;
ln ln
t
t
t
f t f t t
t t
.
Xét hàm số
g t
2
1 1 1
ln 1 0t g t
t t t
Vậy
0g t
có tối đa một nghiệm.
Vì
1 2; lim
t
g g t
vậy
0g t
có duy nhất một nghiệm trên
1;
Do đó
0f t
có duy nhất một nghiệm là
0
t . Khi đó
0
0
0
1
ln
t
t
t
suy ra
0 0
f t t
Bảng biến thiên
Vậy
0
1
, 1;
ln
t
a t a t
t
.
Vậy
0
7
3
4ln
4
t a
.
Vậy số thực
a
thỏa mãn yêu cầu bài toán là:
6;7a
.
Câu 17. (THPT Lê Xoay - 2018) Giả sử
,S a b
là tập nghiệm của bất phương trình
2 3 4 2 2
2 2
5 6 log log 5 5 6x x x x x x x x x x . Khi đó
b a
bằng
A.
1
2
. B.
7
2
. C.
5
2
. D.
2
.
Lời giải
Điều kiện:
2
0
6 0
x
x x
0
2 3
x
x
0;3D
.
2 3 4 2 2
2 2
5 6 log log 5 5 6x x x x x x x x x x
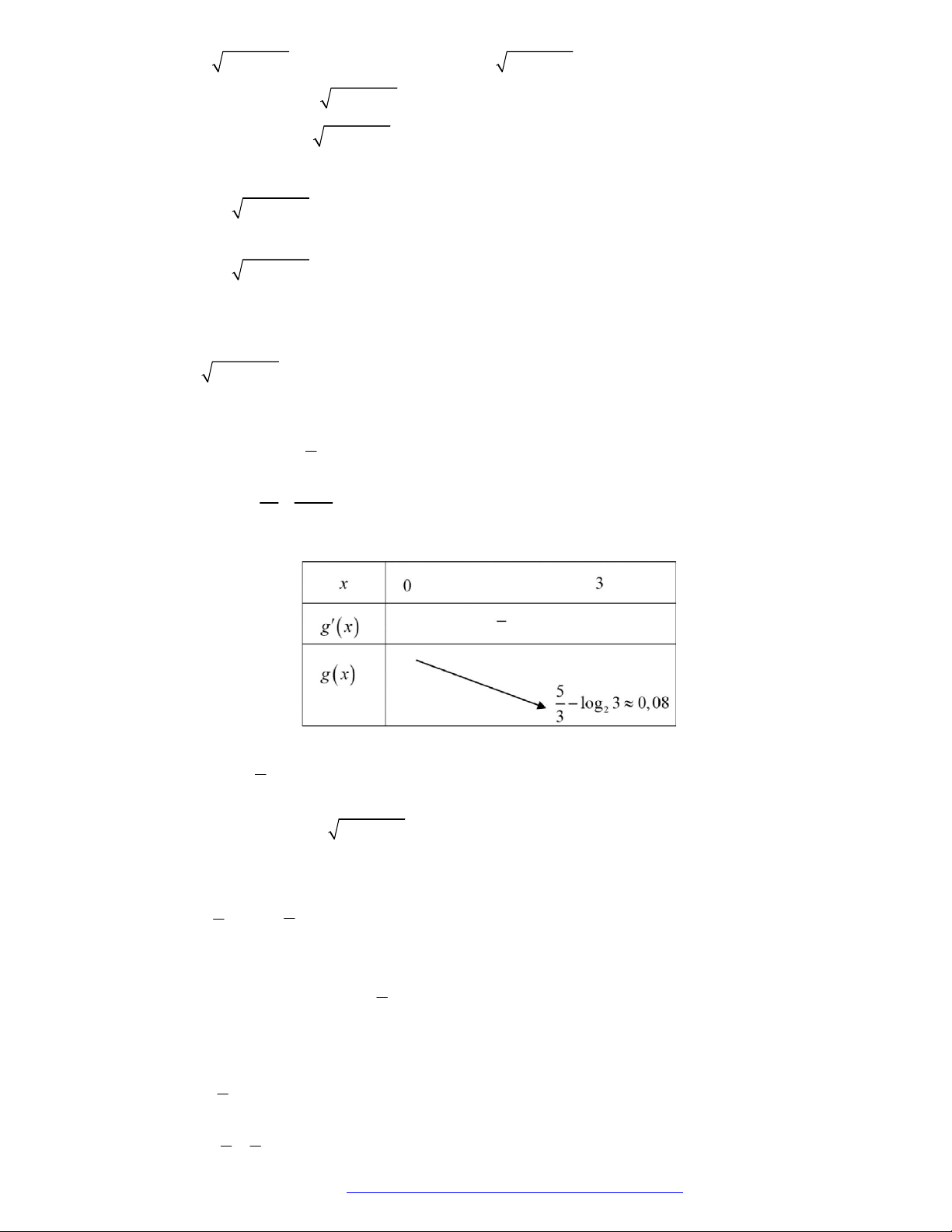
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2
2 2
5 6 log 1 log 5 5 6x x x x x x x x x x
2
2 2
1 5 log 6 log 5 0x x x x x x x
2
2
5 log 1 6 0x x x x x
2
2
2
2
5 log 0
1 6 0
5 log 0
1 6 0
x x
I
x x x
x x
II
x x x
.
Giải hệ (I).
2
2
5 log 0 1
1 6 0 2
x x
x x x
Giải
1
2
5 log 0x x .
Xét hàm số
2
5
logf x x x
x
xg x
với
0;3x
Ta có
2
5 1
0 0;3
ln 2
g x x
x x
.
Lập bảng biến thiên
Vậy
2
5
log 0 0;3f x x x x
x
.
Xét bất phương trình (2):
2
6 1x x x
2
2
6 1
1
x x x
x
2
2 3 5 0
1
x x
x
1
5
2
1
x
x
x
5
2
x
.
Vậy nghiệm của hệ
I
là
5
;3
2
D
.
Hệ
II
vô nghiệm.
Vậy
5
,3
2
S
.
5 1
3
2 2
b a
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 18. (Chuyên Hà Tĩnh - 2018) Cho bất phương trình
2 2
7 7
log 2 2 1 log 6 5
x x x x m
. Có
bao nhiêu giá trị nguyên của tham số
m
để bất phương trình trên có tập ngiệm chứa khoảng
1;3
?
A.
35
. B.
36
. C.
34
. D.
33
.
Lời giải
2
2 2
7 7
6 5 0
log 7 2 2 log 6 5
x x m
bpt
x x x x m
2
2
6 5
6 8 9
m x x
x x m
1;3
1;3
max
min
m f x
m g x
, với
2
6 5f x x x
;
2
6 8 9g x x x
Xét sự biến thiên của hai hàm số
f x
và
g x
2 6 0, 1;3
f x x x
f x
luôn nghịch biến trên khoảng
1;3
1;3
max 1 12
f x f
12 8 0, 1;3
g x x x
g x
luôn đồng biến trên khoảng
1;3
1;3
min 1 23
g x g
Khi đó
12 23
m
Mà
m
nên
11; 10; ...;22
m
Vậy có tất cả
34
giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Câu 19. (Sở Quảng Nam 2018) Có bao nhiêu giá trị nguyên thuộc khoảng
9;9
của tham số
m
để bất
phương trình
2
3log 2log 1 1
x m x x x x
có nghiệm thực?
A.
6
. B.
7
. C.
10
. D.
11
.
Lời giải
Điều kiện
2
0 1
1 1 0
x
m x x x x
0 1
1 0
x
m x x
0 1
1
0
x
x
m
x
.
Bất phương trình đã cho tương đương
2
3 2
log log 1 1
x m x x x x
2
3 2
1 1
x m x x x x
2
1 1
x x m x x x x
2
1 1
1
1
x x x x
x x
m
x x
x x
.
Áp dụng bất đẳng thức cô si ta có
1
1 2 2 1
1
x x
x x x x
x x
.
Vì vậy 1
m x x
.
Khảo sát hàm số
1
f x x x
trên
0;1
ta được
2 1, 414
f x
.
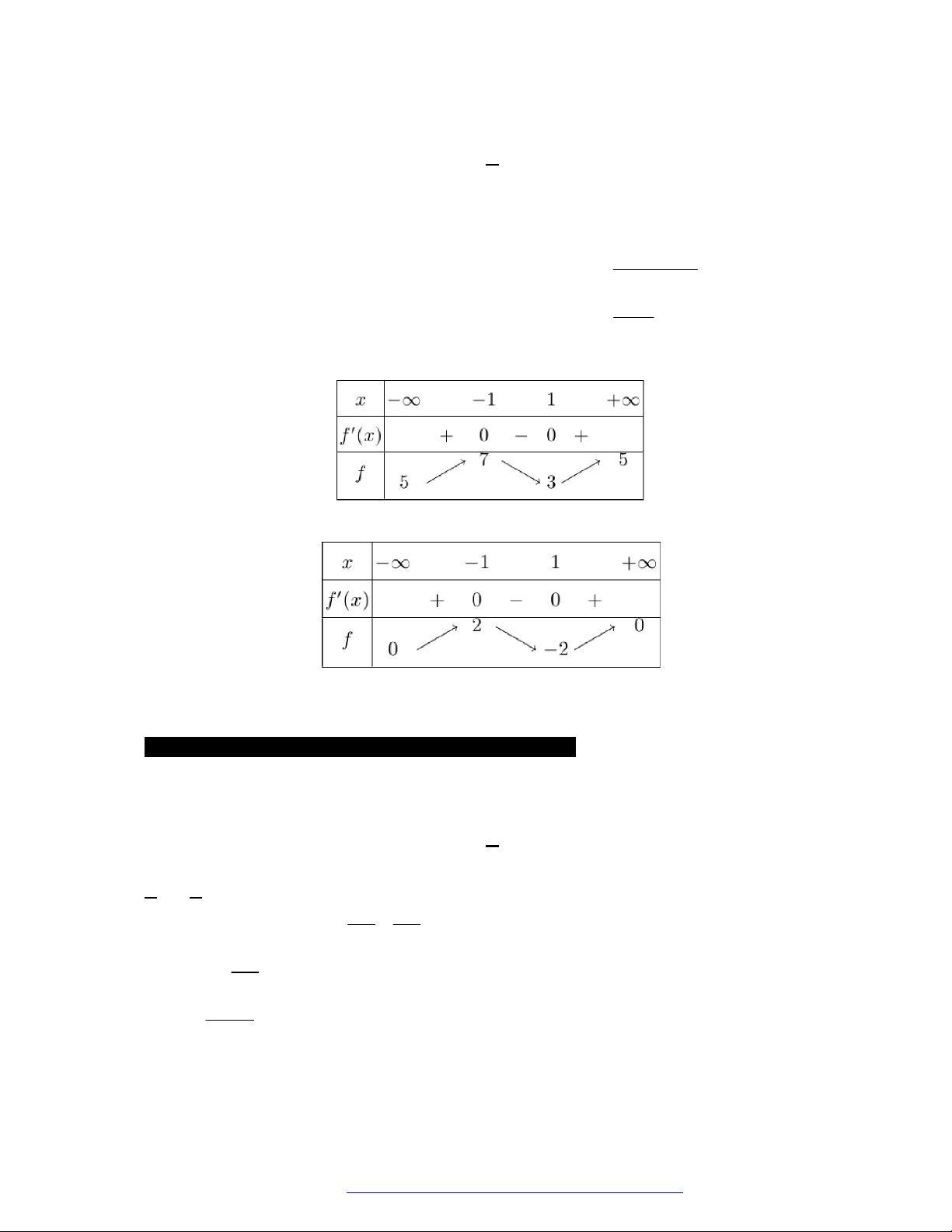
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy
m
có thể nhận được các giá trị
2,3,4,5,6,7,8
.
Câu 20. (Yên Phong 1 - 2018) Có bao nhiêu số nguyên
m
sao cho bất phương trình
2 2
ln5 ln 1 ln 4x mx x m
có tập nghiệm là
.
A.
3
. B.
4
. C.
1
. D.
2
.
Lời giải
Ta có bất phương trình
2 2 2 2
ln5 ln 1 ln 4 ln 5 5 ln 4x mx x m x mx x m
2 2
2
5 5 4
4 0
x mx x m
mx x m
2 2
2
5 5 4 1
1 4
x x m x
m x x
2
2
2
5 5 4
1
4
1
x x
m f x
x
x
m g x
x
.
Hàm số
f x
có bảng biến thiên:
Hàm số
g x
có bảng biến thiên:
Từ bảng biến thiên suy ra để bất phương trình có tập nghiệm là
khi
2 3m
.
Vậy có
1
giá trị nguyên của
m
.
DẠNG 2. BẤT PHƯƠNG TRÌNH MŨ CHỨA THAM SỐ
Câu 1. (VTED 2019) Cho
1a
. Biết khi
0
a a thì bất phương trình
a x
x a
đúng với mọi
1;x
.
Mệnh đề nào dưới đây đúng?
A.
0
1 2a B.
2
0
e a e
C.
0
2 3a D.
2 3
0
e a e
Lời giải
Chọn C
.ln .ln
ln ln
a x
a x
x a a x x a
a x
Đặt
, 1;
ln
x
f x x
x
2
ln 1
ln
x
f x
x
0 .f x x e
Bảng biến thiên:
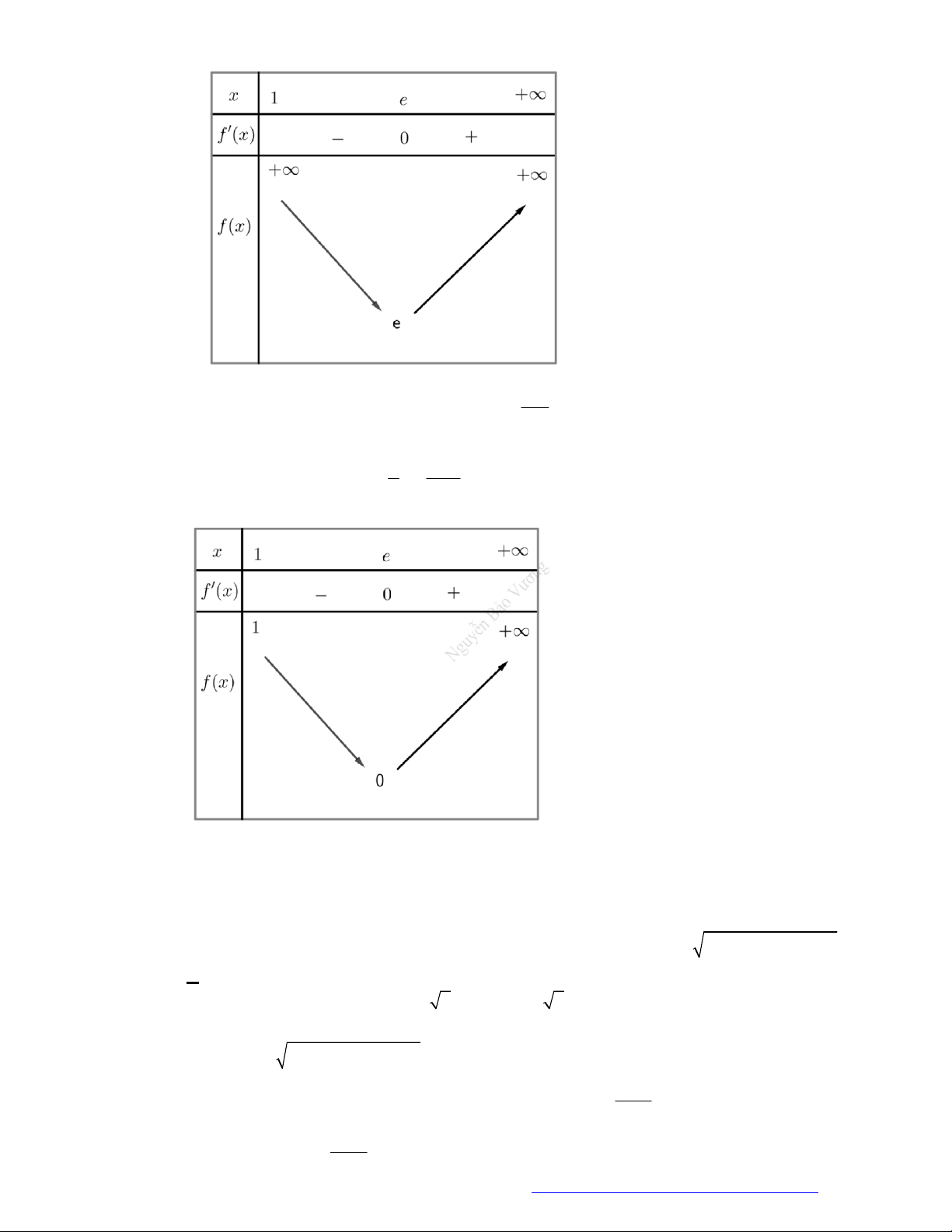
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Bất phương trình nghiệm đúng
1; .ln .ln 0
ln
a
x e a e a a e a
a
* Xét hàm số
.ln ; 1
e x e
g x x e x g x
x x
Vậy
.ln 0a e a
Theo bảng biến thiên, ta có:
.ln 0a e a a e
Vậy
0
2;3a a e
Câu 2. (Chuyên Hạ Long 2019) Tìm
m
để hàm số sau xác định trên
:
4 1 .2
x x
y m m
A. Đáp án khác. B.
1m
.
C.
0m
. D.
3 2 2 3 2 2m
.
Lời giải
Hàm số
4 1 .2
x x
y m m
xác định trên
khi và chỉ khi
4 1 .2 0
x x
m m x
.
Đặt
2 0
x
t t
. Khi đó:
2
1 . 0 0t m t m t
2
0
1
t t
m t
t
.
Xét hàm số:
2
1
t t
f t
t
với
0t
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
2
2
2 1
'
1
t t
f t
t
khi đó:
' 0f t
2
2 1 0 1 2t t t
do
0t
.
Lập bảng biến thiên ta tìm được
0;
min 1 2 3 2 2f t f
.
Để bất phương trình
2
0
1
t t
m t
t
thì
3 2 2m
.
Câu 3. Bất phương trình nghiệm đúng với mọi Tập tất cả các giá trị của m
là
A. B. C. D.
Lời giải
Chọn B
Đặt
2
x
t
. ĐK:
1t
BPT
2
2 2
2
2 1 0 2 1 2 min
2 1
t t
t m t m t m t t m g t m g t
t
Ta có
2
2
2 2 2
' 0, 1 1 1 ; 1
2 1
t t
g t t Min g t g m
t
Câu 4. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Tìm tất cả các giá trị của tham số
m
để bất phương
trình
1
4 2 1 0
x x
m
nghiệm đúng với mọi
x
.
A.
;0 1;m
. B.
;0m
.
C.
0;m
. D.
0;1m
.
Lời giải
Bất phương trình
1
4 2 1 0
x x
m
1
.
Đặt
2
x
t
,
0t
.
Bất phương trình (1) trở thành:
2
1
1 0
4
t m t
2
4 4 0t mt m
2
.
Đặt
2
4 4f t t mt m
.
Đồ thị hàm số
y f t
có đồ thị là một Parabol với hệ số
a
dương, đỉnh
2
2 ; 4 4I m m m
.
Bất phương trình
1
nghiệm đúng với mọi
x
Bất phương trình
2
nghiệm đúng với mọi
0t
hay
0, 0 f t t
.
TH1:
0m
0 4 0f m
0m
thỏa mãn.
TH2:
0m
2
4 4 0m m
nên
0m
không thỏa mãn.
Vậy
0m
.
Câu 5. (Chuyên Nguyễn Trãi Hải Dương 2019) Bất phương trình
1
4 1 2 0
x x
m m
nghiệm
đúng với mọi
0x
. Tập tất cả các giá trị của
m
là
A.
;12
. B.
; 1
. C.
;0
. D.
1;16
.
Lời giải
1
4 1 2 0, 0
x x
m m x
.
2
2 2 1 2 0, 0
x x
m m x (1).
1
4 ( 1)2 0
x x
m m
0.
x
;12 .
; 1 .
;0 .
1;16 .

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Đặt
2 , 0
x
t t
.
(1) trở thành
2
2 1 0, 1t m t m t
(2).
Cách 1:
(2)
2
2
, 1
2 1
t t
m t
t
(3).
Xét hàm số
2
2
2 1
t t
y f t
t
. Ta có hàm số
y f t
liên tục trên
1;
.
2
2
2 2
2 2 2 1 2 2
2 2 2
0, 1
2 1 2 1
t t t t
t t
f t t
t t
.
Suy ra hàm số
f t
đồng biến trên
1;
1 1, 1f t f t
.
Do đó (3)
1;
min
m f t
1
m
.
Cách 2:
2
2 1 0
t m t m
là một bất phương trình bậc hai.
Tam thức bậc hai ở vế trái luôn có
2
1 0,
m m m
nên tam thức luôn có hai nghiệm là
2
1 1
t m m m
và
2
1 1
t m m m
.
Suy ra bất phương trình
2
2 1 0
t m t m
có tập nghiệm là
2 2
; 1 1 1 1;m m m m m m
.
(2)
2 2
2 2
0
1 1 1 1 1
1
m
m m m m m m m
m m m
.
Câu 6. (THPT Hàm Rồng Thanh Hóa 2019) Có bao nhiêu giá trị nguyên của tham số
10;10
m
để
bất phương trình sau nghiệm đúng với
x
:
6 2 7 2 3 7 1 2 0
x x
x
m m
A.
10
. B.
9
. C.
12
. D.
11
.
Lời giải
Ta có:
6 2 7 2 3 7 1 2 0
x x
x
m m
2 3 7 2 3 7 1 2
x x
x x
m m
3 7
3 7 2 1
2
x
x
m m
Đặt
3 7
x
t
,
0t
3 7 1
2
x
t
. Bất phương trình đã cho trở thành:
1
2 . 1
t m m
t
2
2
1
t t
m
t
.
Xét hàm số
2
2
1
t t
f t
t
trên khoảng
0;
, ta có
2
2
2 3
1
t t
f t
t
0
f t
3
0
t
t
. Khi đó, ta có bảng biến thiên sau:
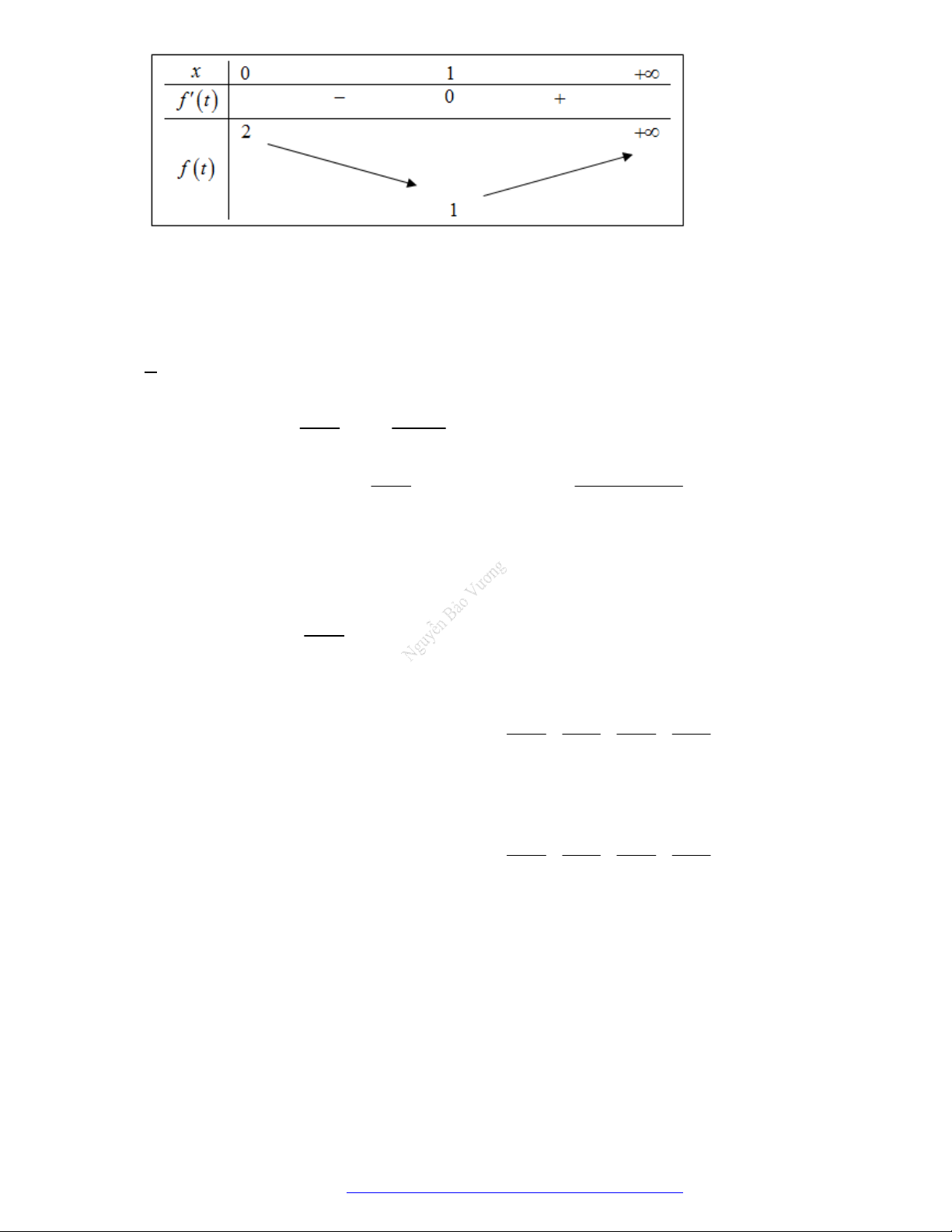
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ bảng biến thiên trên ta suy ra để bất phương trình đã cho nghiệm đúng thì
1m
. Suy ra trong
đoạn
10;10
có tất cả
11
giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Câu 7. (THPT Lê Quý Đôn Đà Nẵng 2019) Tìm
m
để bất phương trình
2 3 4 5 4
x x x x
mx
có
tập nghiệm là
.
A.
ln120
. B.
ln10
. C.
ln30
. D.
ln14
.
Lời giải
+ Với
1a
ta có
ln
0 0
1 1
lim lim .ln ln
ln
x x a
x x
a e
a a
x x a
.
+ Với
1a
xét hàm số
1
0
x
a
f x x
x
, ta có
2
ln 1
x x
xa a a
f x
x
.
Xét hàm số
2 2
ln 1 ln ln ln ln
x x x x x x
g x xa a a g x a a xa a a a xa a
.
Với
0x
ta có
0g x
suy ra
0 0 0, 0g x g g x f x x
.
Với
0x
ta có
0g x
suy ra
0 0 0, 0g x g g x f x x
.
Do đó hàm số
1
1
x
a
f x a
x
đồng biến trên các khoảng
;0
và
0;
.
Trở lại bài toán:
+ Xét
0x
bất phương trình thỏa mãn.
+ Xét
0x
ta có:
2 1 3 1 4 1 5 1
2 3 4 5 4
x x x x
x x x x
mx m h x
x x x x
.
Từ nhận xét trên ta có
h x
đồng biến trên
0;
. Do đó yêu cầu của bài toán tương đương với
0
lim ln 2 ln3 ln 4 ln5 ln120
x
m h x
.
+ Xét
0x
ta có:
2 1 3 1 4 1 5 1
2 3 4 5 4
x x x x
x x x x
mx m h x
x x x x
.
Từ nhận xét trên ta có
h x
đồng biến trên
;0
. Do đó yêu cầu của bài toán tương đương với
0
lim ln 2 ln3 ln 4 ln5 ln120
x
m h x
.
Kết hợp lại ta có
ln120m
.
Câu 8. (Đề Tham Khảo 2019) Cho hàm số
y f x
. Hàm số
'y f x
có bảng biến thiên như sau:
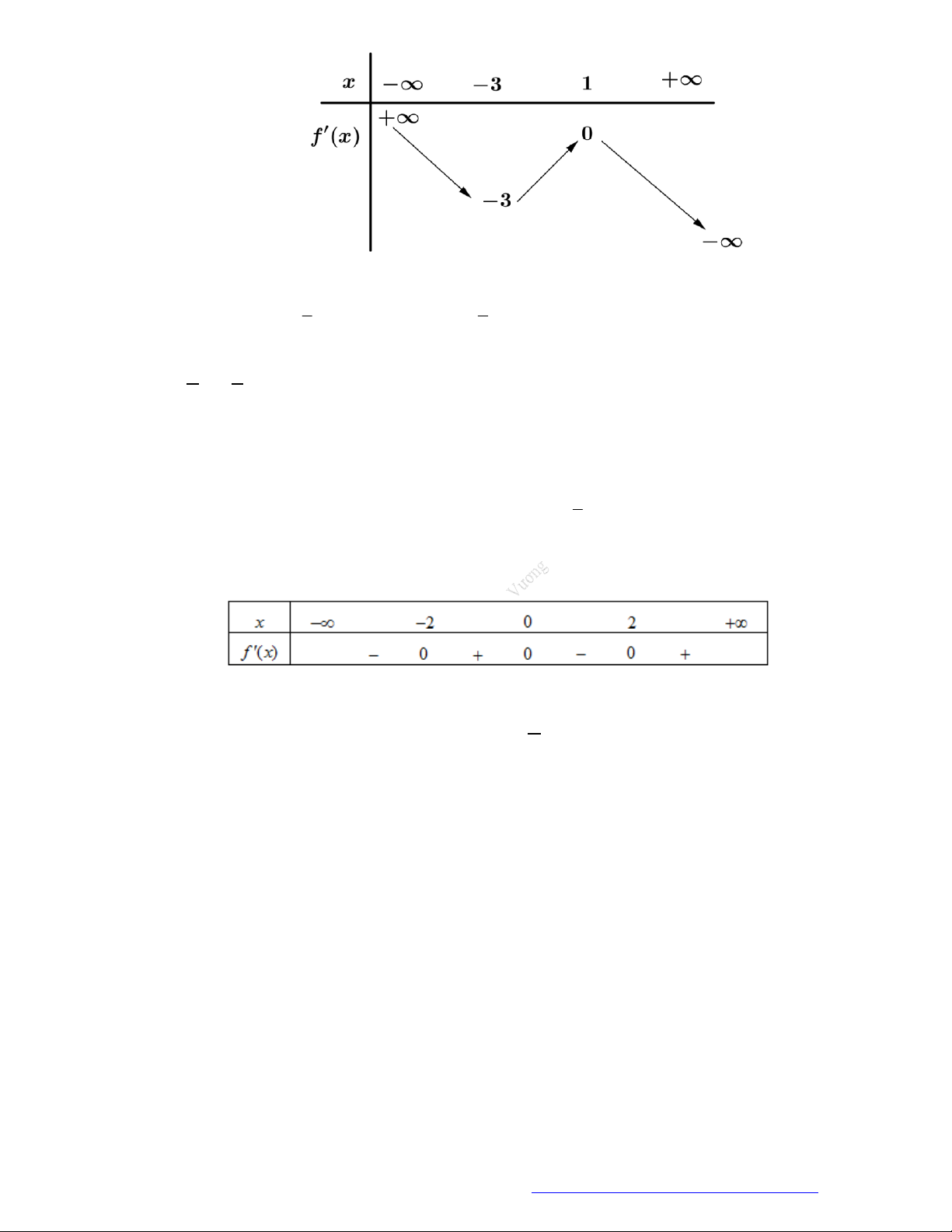
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Bất phương trình
x
f x e m
đúng với mọi
1;1x
khi và chỉ khi.
A.
1
1m f
e
B.
1
1m f
e
C.
1m f e
D.
1m f e
Lời giải
Chọn B
Ta có
x x
e m f x ef mx
.
Xét hàm số
'; ' 0 1;1
x x
g x e g x e xf x f x
.
Suy ra hàm số
g x
nghịch biến trên
1;1
.
Yêu cầu bài toán
ma
1
1x 1m g x g f
e
, chọn C.
Câu 9. (Chuyên Sơn La 2019) Cho hàm số
y f x
liên tục trên
và có bảng xét dấu đạo hàm như
sau
Bất phương trình
2
x
f x e m
đúng với mọi
1;1x
khi và chỉ khi
A.
0 1.m f
B.
1 .m f e
C.
0 1.m f
D.
1 .m f e
Lời giải
2 2
x x
f x e m f x e m
Xét hàm số:
2 2
; 2 .
x x
g x f x e g x f x xe
Trên khoảng
1;0
ta có
0
0, 1;0 .
2 0
f x
g x x
x
Trên khoảng
0;1
ta có
0
0, 0;1 .
2 0
f x
g x x
x
Tại điểm
0x
ta có
2
0
0
2 0
x
f x
g x
xe
.
Suy ra bảng biến thiên của
g x
:
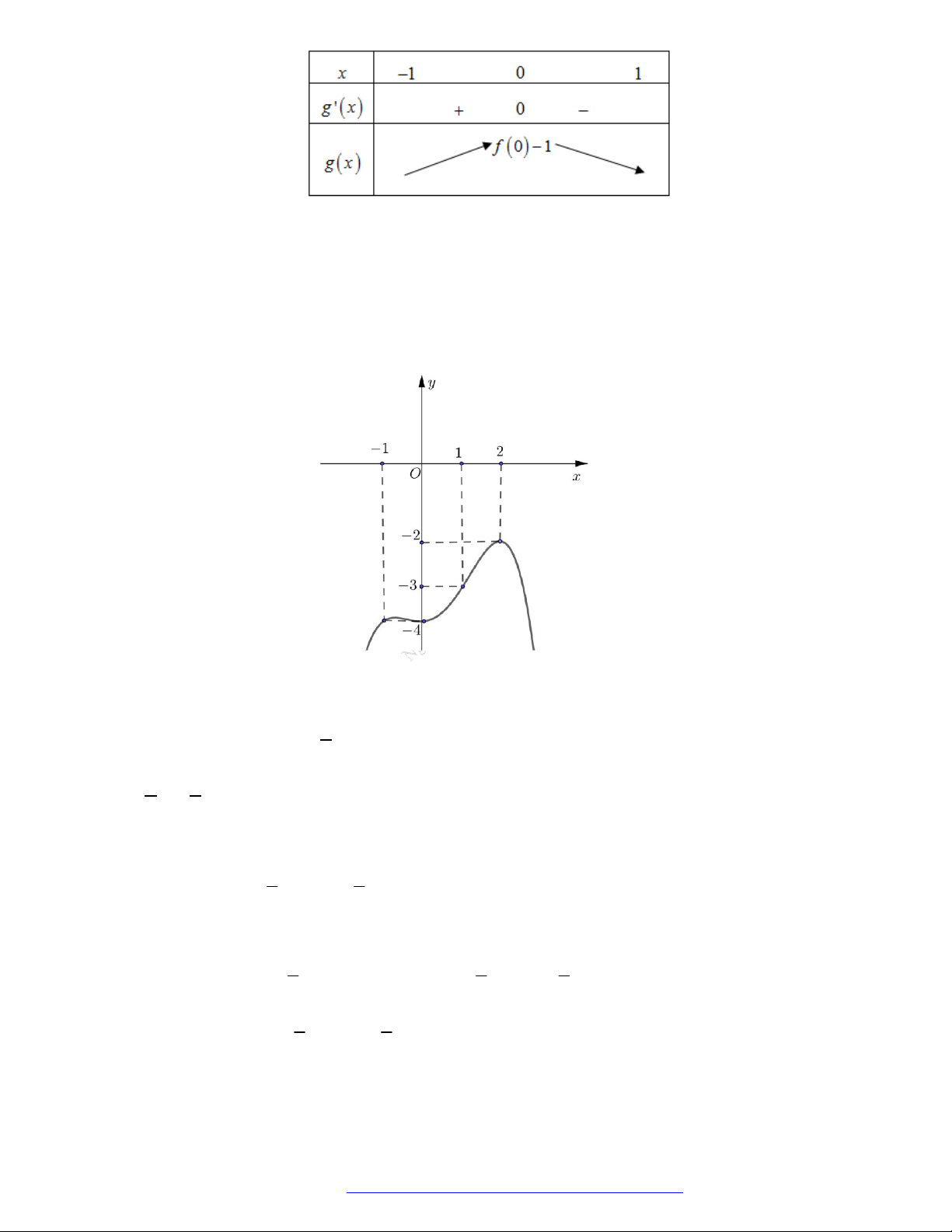
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ bảng biến thiên ta có:
1;1
max 0 1.g x f
Do đó bất phương trình
m g x
đúng với mọi
1;1x
khi và chỉ khi
1;1
max 0 1.m g x f
Câu 10. (Phú Thọ 2019) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ
Tổng tất cả các giá trị nguyên của tham số
m
để bất phương trình
2 2
9.6 4 .9 5 .4
f x f x f x
f x m m
đúng
x
là
A.
10
B.
4
C.
5
D.
9
Lời giải
Chọn B
Ta có
2 2
9.6 4 .9 5 .4
f x f x f x
f x m m
2
2 2
3 3
4 . 9; 5 1
2 2
f x f x
f x m m
Từ đồ thị hàm số suy ra
2, f x x
Do đó
2
2
3
4 0,
2
f x
f x x
và
2
3 3
9. 9. 4,
2 2
f x
x
.
Suy ra
2
2
3 3
4 . 9. 4,
2 2
f x f x
f x x
.
Để
1
có nghiệm đúng
x
thì
2
4 5 1 4 m m m
.
Do
m
là số nguyên nên
1, 2, 3, 4m
.
Câu 11. (VTED 2019) Cho hàm số
y f x
. Hàm số
y f x
có bảng biến thiên như sau:
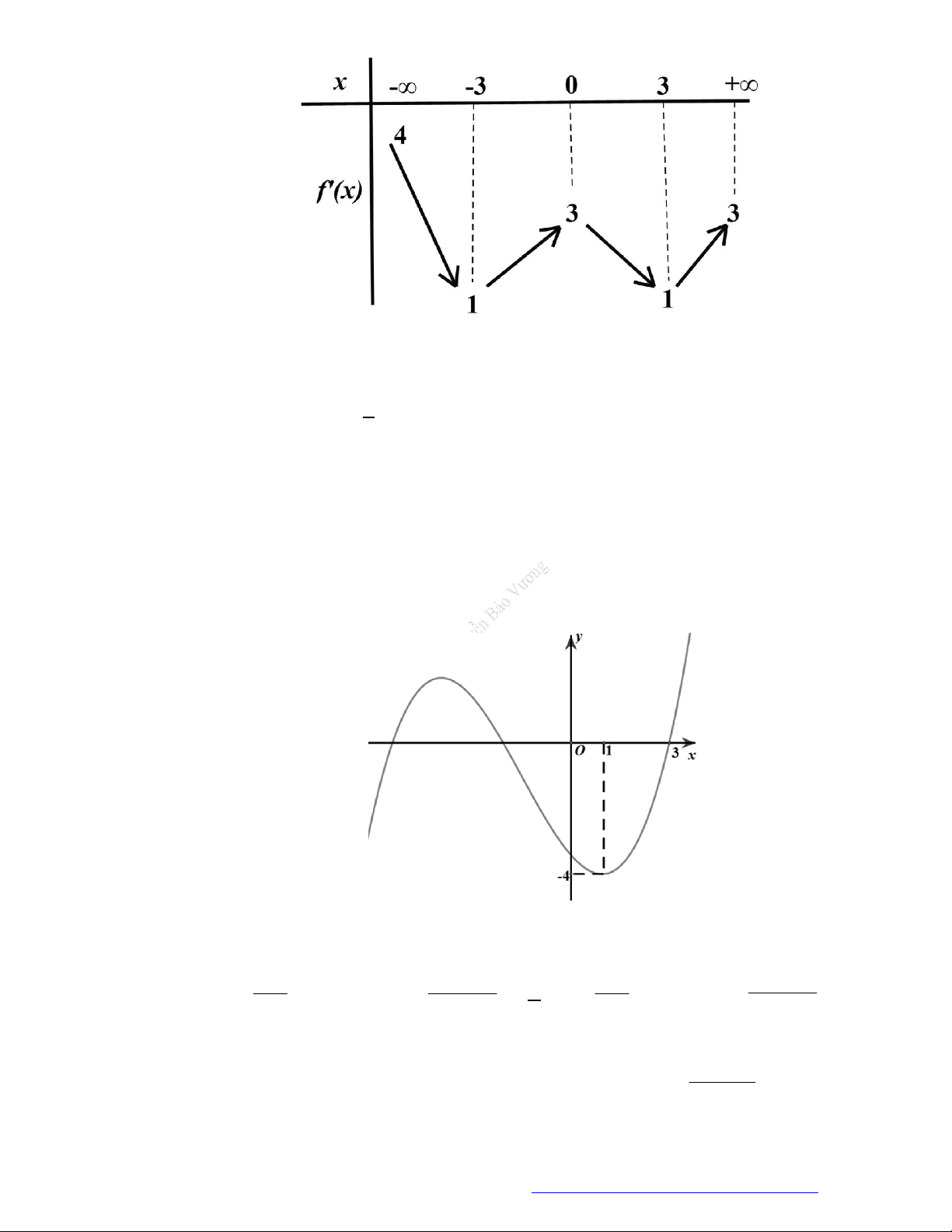
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Bất phương trình
2
3.
x
f x e m
có nghiệm
2;2x
khi và chỉ khi:
A.
2 3m f
B.
4
2 3m f e
C.
4
2 3m f e
D.
2 3m f
Lời giải
Bất phương trình tương đương với
2
3.
x
m g x f x e
.
Ta có
2 2 2
3. 3 3. 0, 2;2
x
g x f x e e x
.
Do đó
4
2 2 3. , 2;2g x g f e x
.
Vậy
4
2 3.m f e
thì phương trình có nghiệm trên khoảng
2;2
.
Câu 12. (THPT-Thang-Long-Ha-Noi- 2019) Cho hàm số
f x
có đồ thị như hình vẽ bên.
Bất phương trình
3 2019
x x
f e m e
có nghiệm
0;1x
khi và chỉ khi
A.
4
1011
m
. B.
4
3 2019
m
e
. C.
2
1011
m
. D.
3 2019
f e
m
e
.
Lời giải
Đặt
x
t e
0t
. Bất phương trình có dạng:
3 2019f t m t
3 2019
f t
m
t
.
Ta có:
0;1x
1;
x
t e e
.
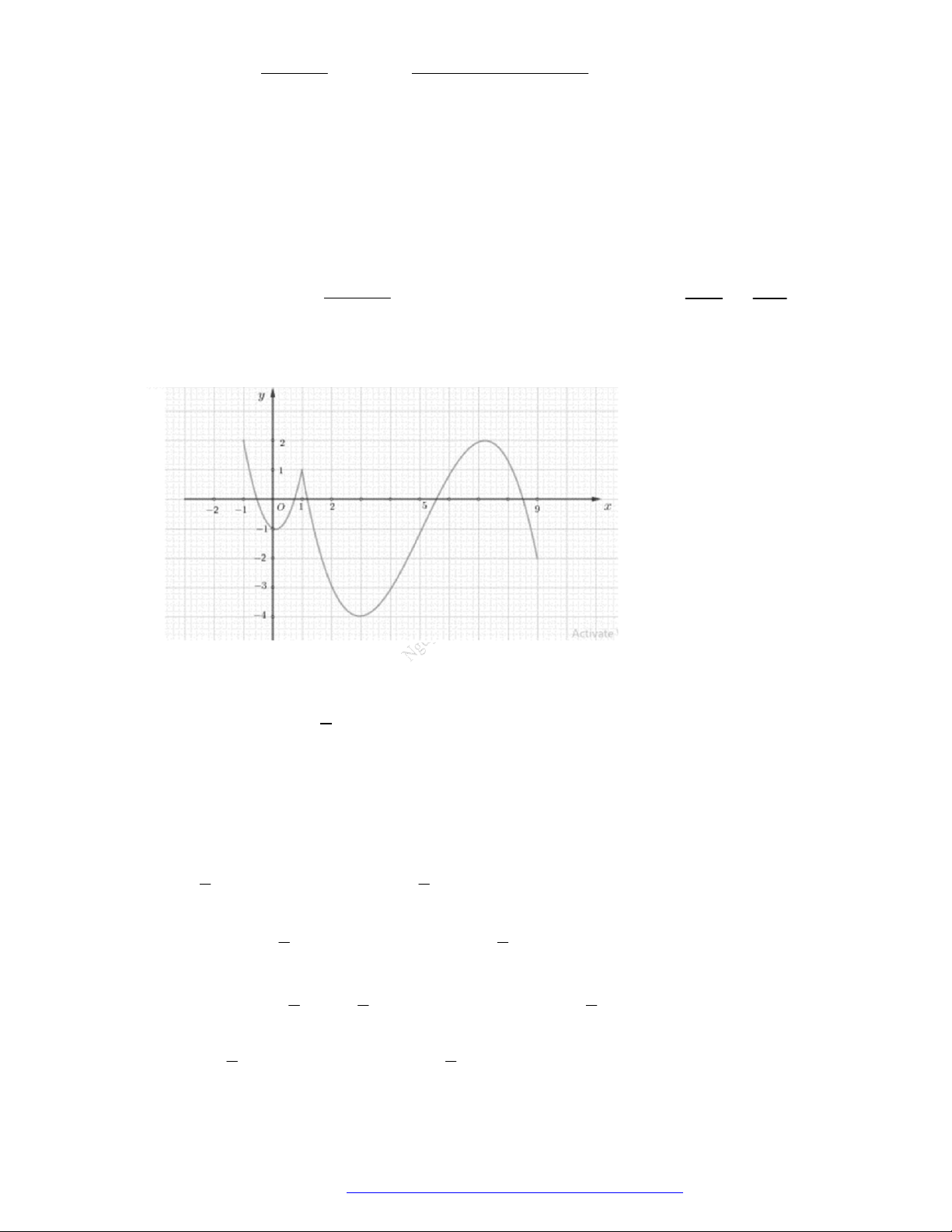
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Xét hàm
3 2019
f t
g t
t
có
2
3 2019 3
3 2019
f t t f t
g t
t
.
Dựa vào đồ thị hàm số
f x
, ta thấy:
f x
đồng biến trên khoảng
1;e
và
0f x
1;x e
0
0
f x
f x
1;x e
.
0g t
1;t e
g t
đồng biến trên khoảng
1;e
1g g t g e
1;t e
.
Vậy bất phương trình
3 2019
x x
f e m e
có nghiệm
0;1x
Bất phương trình
3 2019
f t
m
t
có nghiệm
1;t e
4 2
1
2022 1011
m g
.
Câu 13. (THPT Yên Khánh - Ninh Bình - 2019) Cho hàm số
y f x
liên tục trên đoạn
1;9
và có
đồ thị là đường cong trong hình vẽ dưới đây
Có bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
2 2
16.3 2 8 .4 3 .6
f x f x f x
f x f x m m
nghiệm đúng với mọi giá trị thuộc
1;9
?
A.
32
. B.
31
. C.
5.
D.
6
.
Lời giải
Dễ thấy
4 2, 1;9f x x
(1) nên
4 . 2 0, 1;9f x f x x
.
Do đó
2
2 8 0, 1;9f x f x x
(2).
Ta có
2 2
16.3 2 8 .4 3 .6
f x f x f x
f x f x m m
nghiệm đúng với mọi
1;9x
2 2
1 2
16. 2 8 . 3
2 3
f x f x
f x f x m m
nghiệm đúng với mọi
1;9x
2 2
1; 9
1 2
min 16. 2 8 . 3
2 3
f x f x
x
f x f x m m
(3).
Từ (1) và (2) ta có
2
1 1
2 2
f x
và
2
2
2 8 . 0, 1; 9
3
f x
f x f x x
.
Suy ra
2
1 2
16. 2 8 . 4, 1; 9
2 3
f x f x
f x f x x
.
Dấu “=” xảy ra khi và chỉ khi
2 1 7 8 .f x x x a a
Do đó
4
và (3)
2
4 3 1 4m m m
. Vì
m
nguyên nên
1;0;1;2;3;4m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Câu 14. (Sở Cần Thơ - 2019) Tất cả giá trị của tham số thực
m
sao cho bất phương trình
9 2 1 .3 3 2 0
x x
m m
có nghiệm đúng với mọi số thực
x
là
A.
3
2
m
. B.
2
m
. C.
3
2
m
. D.
m
.
Lời giải
Chọn A
Ta có:
9 2 1 .3 3 2 0
x x
m m
2
3 2.3 3 3 1 .2
x x x
m
3 1 3 3 3 1 .2
x x x
m
3 3 2 3 3 2
x x
m m
Vậy, để
9 2 1 .3 3 2 0,
x x
m m x
khi
3
3 2 0
2
m m
.
Câu 15. (Sở Nam Định - 2019) Có bao nhiêu giá trị nguyên dương của tham số
m
để tập nghiệm của bất
phương trình
2
3 3 3 2 0
x x
m
chứa không quá 9 số nguyên?
A. 3281. B. 3283. C. 3280. D. 3279.
Lời giải
Chọn C
Do
m
là số nguyên dương nên 2m >1 =>
3
log 2 0
m
.
1
2 2
2
3
3 3 0 3 3
2
x x
x
3
3 2 0 log 2
x
m x m
.
Lập bảng biến thiên, ta kết luận:
tập nghiệm bất phương trình này là
3
3
;log 2
2
m
Suy ra,
8
3
6561
log 2 8 2 3 3280.5
2
m m m
=>
Câu 16. (THPT Cẩm Bình Hà Tỉnh 2019) Có mấy giá trị nguyên dương của
m
để bất phương trình
2 2 2
9 4 .5
m x m x m x
m
có nghiệm?
A.
10
. B. Vô số. C.
9
. D.
1
.
Lời giải
Chọn B
Từ giả thiết, ta chỉ xét
m
Ta có:
2 2 2
9 4 .5
m x m x m x
m
2 2
9 4
1
5 5
m x m x
m
Có
2 2 2 2 2
9 4 9 4 6
2 . 2
5 5 5 5 5
m x m x m x m x m x
.
Do đó nếu có
0
x
là nghiệm của bất phương trình
2
6
2
5
m x
m

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
thì
0
x
cũng là nghiệm của
2 2
9 4
5 5
m x m x
m
.
Ta xét các giá trị
m
làm cho bất phương trình
2
6
2 2
5
m x
m
có nghiệm.
Vì
2
6
2
5
m x
m
2
6
5 2
m x
m
,
m
2
6
5
log
2
m
m x
6
2
5
1
log
2
m
x
m
, với
m
.
Vậy với
m
thì bất phương trình
2
có nghiệm tương ứng là
6
2
5
1
log
2
m
x
m
.
Suy ra có vô số giá trị
m
làm cho bất phương trình
1
có nghiệm.
Câu 17. (Chuyên Nguyễn Trãi Hải Dương 2019) Bất phương trình
1
4 1 2 0
x x
m m
nghiệm
đúng với mọi
0x
. Tập tất cả cá giá trị của
m
là
A.
;12
. B.
; 1
. C.
;0
. D.
1;16
.
Lời giải
Chọn B
Bất phương trình
1
4 1 2 0 1
x x
m m
4 2 1 2 0
x x
m m
.
Đặt
2
x
t
bất phương trình trở thành
2
2 1 0 2t m t m
.
Bất phương trình
1
nghiệm đúng với mọi
0x
khi và chỉ khi bất phương trình
2
nghiệm
đúng với mọi
1t
.
2
2
2
2 2 1 2
2 1
t t
t m t t m
t
(do
1t
).
Đặt
2
2
2 1
t t
f t
t
với
1t
.
2
2
2 2 2
' 0 1
2 1
t t
f t t
t
.
Bảng biến thiên
Từ bảng biến thiên ta có
1;f t m t
1m
. Vậy chọn B
Câu 18. (THPT Phan Bội Châu - Nghệ An 2019) Cho hàm số
cos2f x x
. Bất phương trình
2019
f x m đúng với mọi
3
;
12 8
x
khi và chỉ khi
A.
2018
2m
. B.
2018
2m
. C.
2019
2m
. D.
2019
2m
.
Lời giải
Chọn B
Xét hàm số
cos2f x x
, TXĐ:
R
.
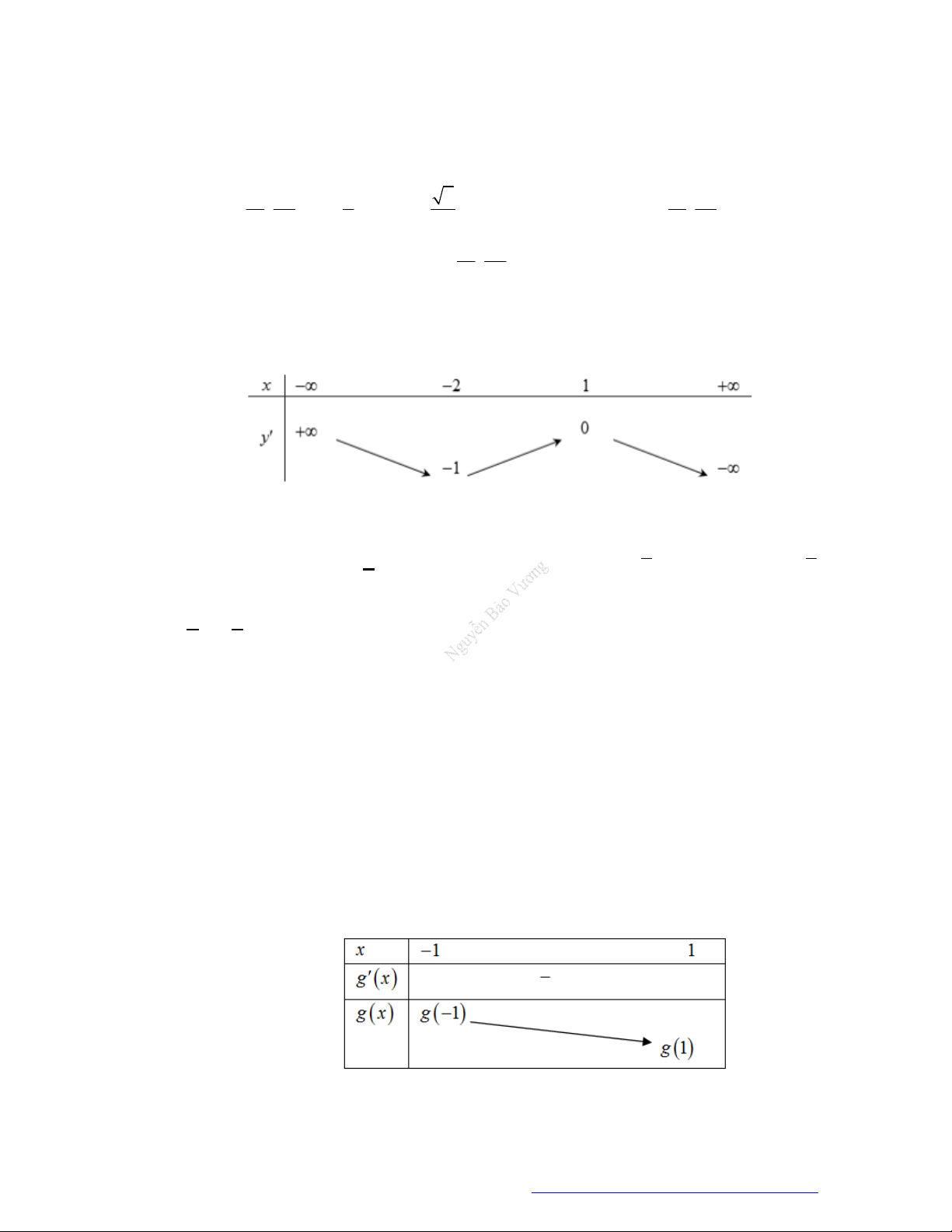
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Ta có
2sin 2f x x
,
2
2 cos 2f x x
,
3
2 sin 2f x x
,
4
4
2 cos2f x x
.
Suy ra
2016
2016
2 cos2f x x
2017
2017
2 sin 2f x x
2018
2018
2 cos 2f x x
2019
2019
2 sin 2f x x .
Vì
3
;
12 8
x
nên
1 2
sin 2
2 2
x
hay
2019
2018
3
2 , ;
12 8
f x x
.
Vậy
2019
f x m đúng với mọi
3
;
12 8
x
khi và chỉ khi
2018
2m
.
Câu 19. (Chuyên Lê Quý Đôn – Điện Biên 2019) Cho hàm số
y f x
. Hàm số
y f x
có bảng
biến thiên như sau:
Bất phương trình
2
x
f x m
đúng với mọi
1;1x
khi và chỉ khi:
A.
1 2m f
. B.
1 2m f
. C.
1
1
2
m f
. D.
1
1
2
m f
.
Lời giải
Chọn B
2
x
f x m
,
1;1x
2
x
f x m
2
x
f x m
.
Xét hàm số
2
x
g x f x
trên
1;1
.
Ta có:
2 .ln 2
x
g x f x
.
Ta thấy:
1;1x
thì
0f x
và
2 .ln 2 0
x
.
Do đó
2 .ln2 0
x
g x f x
,
1;1x
.
Bảng biến thiên
Từ bảng biến thiên ta có:
1 1 2m g m f
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 20. (Bình Giang-Hải Dương 2019) Số giá trị nguyên dương của tham số
m
để bất phương trình
2 2
3 3 2 2 3
9 2.3 3
x x m x x m x x
có nghiệm là
A.
4
. B.
8
. C.
1
. D.
6
.
Lời giải
Chọn C
Đặt
2
3
3
x x m x
t
với
0t
, bất phương trình đã cho trở thành
2
2 1 1
0 3
9 27 9
t t t
.
Do đó
2 2
1
0 3 2 3 2
9
t x x m x x x m x
2
2 2
2
3 0
3 4 4
x
x x m
x x m x x
2
2
3 0
4
x
x x m
x m
(I)
Để bất phương trình đề bài cho có nghiệm thì hệ bất phương trình (I) có nghiệm ta đặt
2
2 (1)
3 0 (2)
4 (3)
x
x x m
x m
.
Điều kiện cần: Từ
(1)
và
(3)
ta có
4 2 2
m m
.
Do
m
là số nguyên dương nên
1
m
.
Điều kiện đủ: Với
1
m
, hệ bất phương trình (I) trở thành
2
2
3 1 0
3
x
x x
x
2 3
3 5 3 5
2 2
x
x x
3 5
3
2
x
. Vậy hệ bất phương trình (I) có nghiệm.
Vậy
1
m
.
Câu 21. (Hậu Lộc 2-Thanh Hóa- 2019) Gọi
S
là tập hợp tất cả các giá trị của tham số
m
để bất phương
trình
2 4 3 3 2 1
0
x
m x x m x x x e
đúng với mọi
x
. Số tập con của
S
là
A. 2. B. 4. C. 3. D. 1.
Lời giải
Chọn B
Xét hàm số
2 4 3 3 2 1x
f x m x x m x x x e
trên
.
Ta có
2 3 2 2 1
4 3 3 2 1
x
f ' x m x x m x x e
liên tục trên
.
Do
1 0
f
nên từ giả thiết ta có
1f x f
,
x
1min f x f .
2
1
1 0 0
0
m
f ' m m
m .
Với
0
m
ta có
1 1
1
x x
f x e x f ' x e .
Cho
0 1f ' x x .
Bảng biến thiên của
f x
:
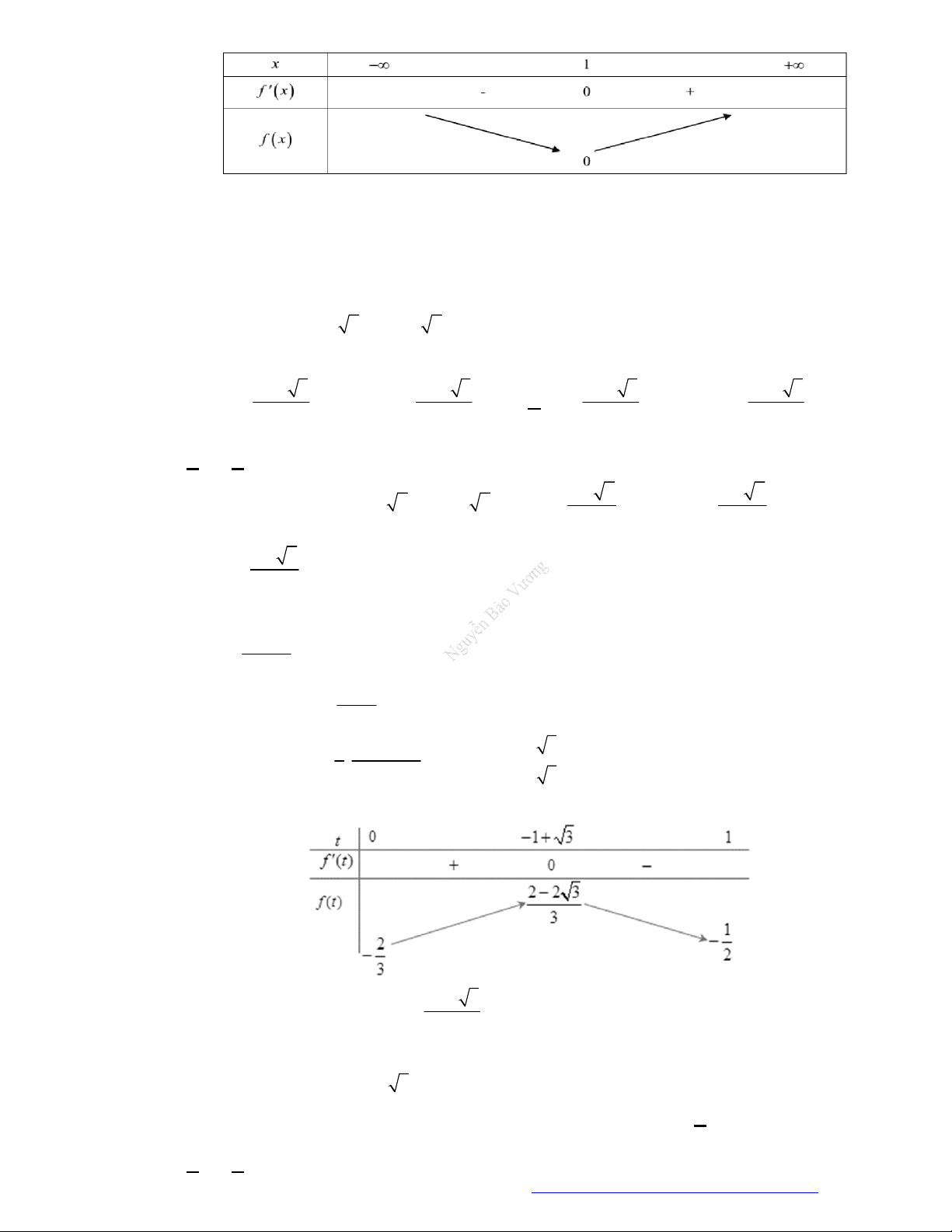
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Trường hợp
0m
, yêu cầu bài toán được thỏa mãn.
Với
1m
ta có
2
4 3 3 2 1 2 1
1 0
x x
f x x x x x e x x e x
,
x .
Trường hợp
1m
yêu cầu bài toán cũng được thỏa mãn.
Câu 22. (Lý Nhân Tông - Bắc Ninh 2019) Cho bất phương trình
1
.3 3 2 4 7 4 7 0
x x
x
m m
, với
m
là tham số thực. Tìm tất cả các giá trị thực của
tham số
m
để bất phương trình đã cho nghiệm đúng với mọi
( ;0]x
.
A.
2 2 3
3
m
. B.
2 2 3
3
m
. C.
2 2 3
3
m
. D.
2 2 3
3
m
.
Lời giải
Chọn C
Ta có
1
.3 3 2 . 4 7 4 7 0
x x
x
m m
4 7 4 7
3 2 3 0
3 3
x x
m m
.
Đặt
4 7
3
x
t
. Ta có
( ;0]x
0 1t
.
Ta tìm tham số
m
sao cho
2
3 3 2 0t mt m
đúng với mọi
0 1t
2
2
, 0;1
3 3
t
m t
t
.
Xét hàm số
2
2
3 3
t
f t
t
trên
0;1
.
Ta có
2
2
1 2 2
0 . 0
3
1
t t
f t
t
1 3
1 3
t
t
.
Lập bảng biến thiên:
Vậy
, 0;1m f t t
2 2 3
3
m
.
Câu 23. (Chuyên Hưng Yên - 2020) Có bao nhiêu giá trị nguyên dương của tham số
m
để tập nghiệm
của bất phương trình
2
3 3 3 2 0
x x
m
chứa không quá 9 số nguyên?
A. 1094. B. 3281. C. 1093. D. 3280.
Lời giải.
Chọn D

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đặt
3 , 0
x
t t
bất phương trình
2
3 3 3 2 0 1
x x
m
trở thành
9 3 2 0 2
t t m
.
Nếu
3
2
9
m
3
1
18
m
thì không có số nguyên dương
m
nào thỏa mãn yêu cầu bài toán.
Nếu
3
2
9
m
3
18
m
thì bất phương trình
3
2 2
9
t m
.
Khi đó tập nghiệm của bất phương trình
1
là
3
3
;log 2
2
S m
.
Để
S
chứa không quá 9 số nguyên thì
8
3
3
log 2 8 0
2
m m
Vậy có 3280 số nguyên dương
m
thỏa mãn.
Câu 24. (Chuyên Hùng Vương - Phú Thọ - 2020) Có bao nhiêu
m
nguyên dương để bất phương trình
2 2 2
3 3 3 1 3 0
x x m m
có không quá 30 nghiệm nguyên?
A. 28. B. 29. C. 30. D. 31.
Lời giải
Chọn B
2 2 2 2
3 3 3 1 3 0 9.3 9.3 .3 3 3 0
9.3 3 3 3 3 0
3 3 9.3 1 0
x x m m x x m x m
x x m x m
x m x
Ta có
3 3 0 .
x m
x m
9.3 1 0 2.
x
x
Bảng xét dấu
x
2
m
VT
+ 0
0 +
Ta có tập nghiệm
2 ; .S m
Tập hợp các nghiệm nguyên là
1; 0; 1; ...; 1 .
m
Để có không quá 30 nghiệm nguyên thì
1 28 29.
m m
Câu 25. (ĐHQG Hà Nội - 2020) Điều kiện của
m
để hệ bất phương trình
2 1 2 1
2
7 7 2020 2020
2 2 3 0
x x x
x
x m x m
có nghiệm là :
A.
3.
m
B.
2 1.
m
C.
1 2.
m
D.
2.
m
Lời giải
Chọn D
2 1 2 1 2 1 2 1
7 7 2020 2020 7 1010. 2 1 7 1010. 2 1 *
x x x x x x
x x x x
Hàm số
( ) 7 1010.
t
f t t
đồng biến trên ℝ.
* 2 1 2 1
f x x f x
Suy ra :
2 1 2 1 1 1.
x x x x
2
2
2 3
1;1 : 2 2 3 0 .
2
x x
x x m x m m
x
Ycbt
2
2 3
1;1 : **
2
x x
x m
x
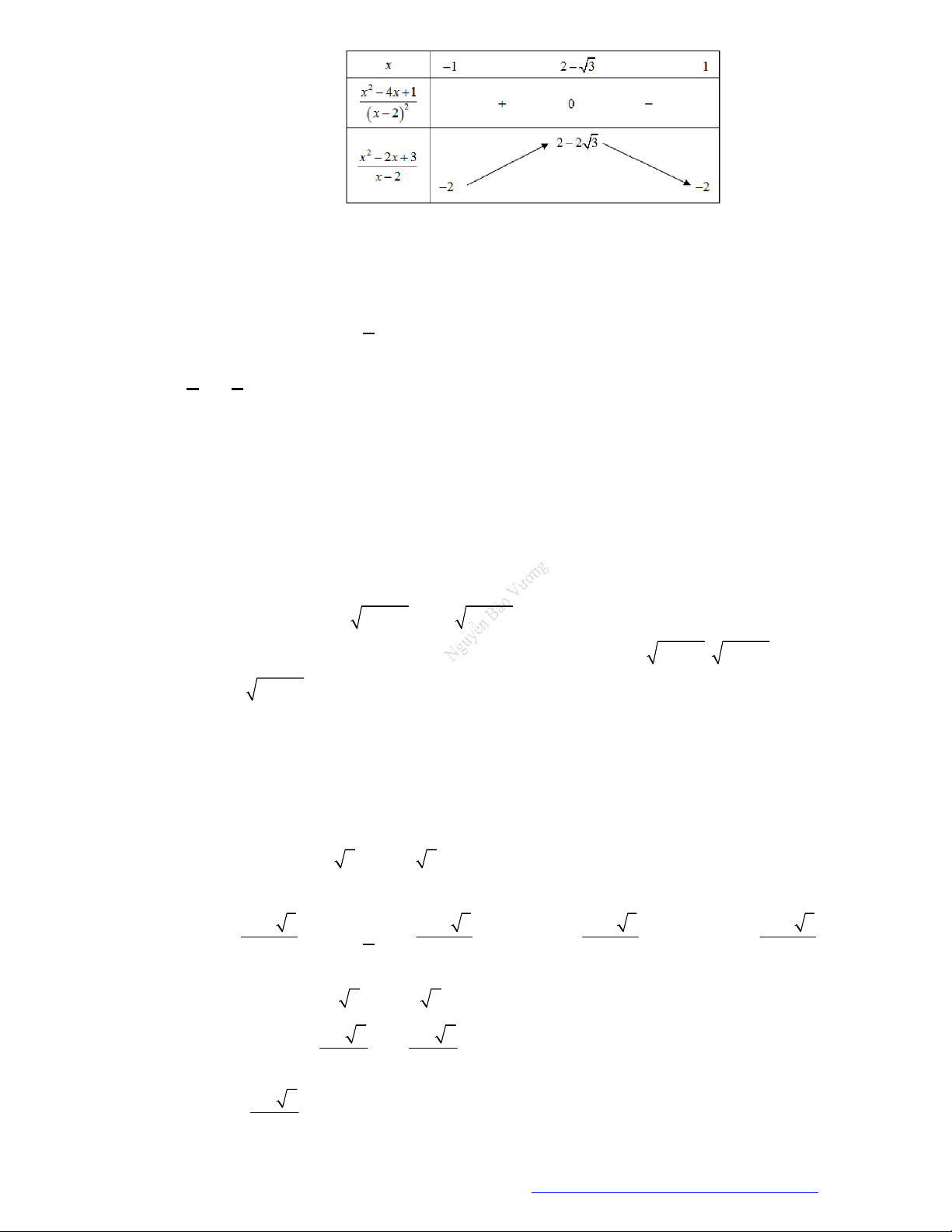
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
Từ bảng biến thiên ta có,
** 2.m
Câu 26. (Sở Hà Nội - Lần 2 - 2020) Có bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
2 2
3 9 2 0
x x x
m
có 5 nghiệm nguyên?
A.
65021
. B.
65024
C.
65022
. D.
65023
.
Lời giải
Chọn B
2 2
3 9 2 0
x x x
m
(1)
Th1: Xét
2
2
1
3 9 0 2
2
x x
x
x x
x
là nghiệm của bất phương trình (1).
Th2: Xét
2
2
1
3 9 0 2
2
x x
x
x x
x
.
Khi đó,
2
2
2
(1) 2 log (2)
x
m x m
Nếu
1m
thì (2) vô nghiệm.
Nếu
1m
thì
2 2
(2) log logm x m .
Do đó, (1) có 5 nghiệm nguyên
2 2
; 1 2; log ; logm m
có 3 giá trị
nguyên
2
log 3;4 512 65536m m (thỏa đk
1m
). Suy ra có 65024 giá trị
m
nguyên
thỏa mãn.
Th3: Xét
2
2
3 9 0 2 1 2
x x
x x x
. Vì
1;2
chỉ có hai số nguyên nên không có
giá trị
m
nào để bất phương trình (1) có 5 nghiệm nguyên.
Vậy có tất cả 65024 giá trị
m
nguyên thỏa ycbt.
Câu 27. (Cụm 5 Trường Chuyên - ĐBSH - 2018) Cho bất phương trình
1
.3 (3 2)(4 7) (4 7) 0
x x x
m m
, với
m
là tham số. Tìm tất cả các giá trị của tham số
m
để bất phương trình đã cho nghiệm đúng với mọi
;0x
.
A.
2 2 3
3
m
. B.
2 2 3
3
m
. C.
2 2 3
3
m
. D.
2 2 3
3
m
.
Lời giải
1
.3 (3 2).(4 7) (4 7) 0
x x x
m m
4 7 4 7
3 (3 2). 0
3 3
x x
m m
Đặt
4 7
3
x
t
Khi
0x
thì
0 1t
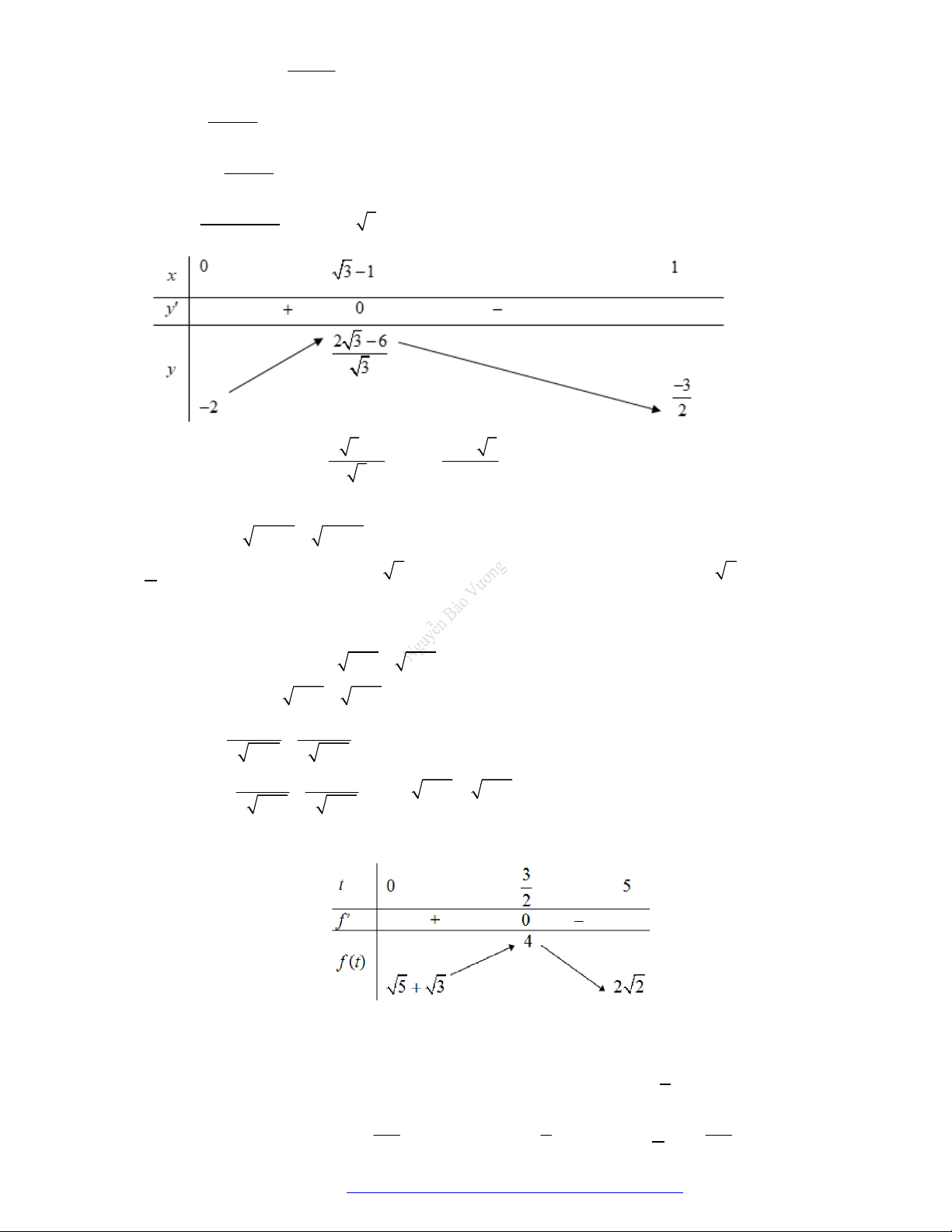
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
BPT trở thành
3 2
3 0,
m
m t
t
0;1t
.
2
2
3 ,
1
t
m
t
0;1t
Xét
2
2
( ) ,
1
t
f t
t
0;1t
2
2 2
( ) 0 3 1
1
t
t t
f t t
t
Vậy ycbt
2 3 6 2 2 3
3 .
3
3
m m
Câu 28. (THPT Thái Phiên - Hải Phòng - 2018) Tìm tất cả các giá trị thực của tham số
m
để bất
phương trình
2 3 5 2
x x
m
nghiệm đúng với mọi
2
;log 5x
.
A.
4m
. B.
2 2m
. C.
4m
. D.
2 2m
.
Lời giải
Đặt
2
x
t
. Vì
2
log 5x
2
log 5
0 2 2
x
0 5t
.
Yêu cầu bài toán trở thành
3 5t t m
,
0;5t
.
Xét hàm số
3 5f t t t với
0;5t
.
Có
1 1
2 2 2 5
f t
t t
.
0f t
1 1
0
2 3 2 5t t
3 5t t
3 5t t 1t
.
Bảng biến thiên
Dựa vào bảng biến thiên ta có:
4m
.
Câu 29. (THPT Ngô Quyền - Hải Phòng - 2018) Tìm tất cả các giá trị của
m
để bất phương trình
2 2 2
2 1 2 1 2 1
.4 1 2 .10 .25 0
x x x x x x
m m m
nghiệm đúng với mọi
1
;2
2
x
.
A.
0m
. B.
100
841
m
. C.
1
4
m
. D.
100
841
m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Lời giải
2 2 2
2 1 2 1 2 1
.4 1 2 .10 .25 0
x x x x x x
m m m
2
2
2 1
2 1 2.
5 5
1 2 . . 0
2 2
x x
x x
m m m
1
Đặt
2
2 1
5
2
x x
t
, Xét
2
2 1u x x x
,
1
;2
2
x
.
2 2
u x x
;
0 1
u x x
1 7
2 4
u
;
1 2; 2 1
u u
1
; 2
2
min 2
u x
,
1
; 2
2
max 1
u x
.
4 2
25 5
t
2
1 1 2 . . 0
m m t m t
2
1 2 0
mt m t m
2
2 1
m t t t
2
2 1
t
m
t t
Xét hàm số
2
2 1
t
f t
t t
,
4 2
;
25 5
t
2
2
1
2 1
t
f t
t t
;
2
1
0 1 0
1
t l
f t t
t l
4 100
25 841
f
;
2 10
5 49
f
.
4 2
;
25 5
100
min
841
f t
.
Vậy
100
841
m
thì bất phương trình nghiệm đúng với mọi
1
;2
2
x
.
DẠNG 3. BẤT PHƯƠNG TRÌNH NHIỀU ẨN
Câu 1. (Mã 101 - 2020 Lần 1) Có bao nhiêu số nguyên
x
sao cho ứng với mỗi
x
có không quá
728
số
nguyên
y
thỏa mãn
2
4 3
log log ( )x y x y
?
A.
59
. B.
58
. C.
116
. D.
115
.
Lời giải
Chọn C.
Với mọi
x
ta có
2
x x
.
Xét hàm số
2
3 4
( ) log ( ) log
f y x y x y
.
Tập xác định
D ( ; )
x
(do
2
y x y x
).
2
1 1
'( ) 0,
( )ln 3
ln 4
f y x D
x y
x y
(do
2
0
x y x y
,
ln 4 ln 3
)
f
tăng trên
D
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
2
3 4
( 1) log ( 1) log 1 0
f x x x x x
.
Có không quá 728 số nguyên
y
thỏa mãn
0
f y
2
3 4
( 729) 0 log 729 log 729 0
f x x x
2 6
729 4 0
x x
2
3367 0
x x
57,5 58,5
x
Mà
x
nên
57, 56,...,58
x
.
Vậy có
58 ( 57) 1 116
số nguyên
x
thỏa.
Câu 2. (Mã 102 - 2020 Lần 1) Có bao nhiêu số nguyên
x
sao cho ứng với mỗi
x
có không quá
242
số
nguyên
y
thỏa mãn
2
4 3
log log
x y x y
?
A.
55
. B.
28
. C.
29
. D.
56
.
Lời giải
Chọn D
Điều kiện:
2
0
0
x y
x y
.
Đặt
3
log
x y t
, ta có
2
4
3
t
t
x y
x y
2
4 3 *
3
t t
t
x x
y x
.
Nhận xét rằng hàm số
4 3
t t
f t
đồng biến trên khoảng
0;
và
0
f t
với mọi
0t
Gọi
n
thỏa
2
4 3
n n
x x
, khi đó
*
t n
Từ đó, ta có
3 3
t n
x y x x
.
Mặt khác, vì có không quá
242
số nguyên
y
thỏa mãn đề bài nên
3
3 242 log 242
n
n
.
Từ đó, suy ra
3
log 242
2
4 242
x x
27,4 28,4
x
.
Mà
x
nên
27, 26, ..., 27, 28
x
.
Vậy có
56
giá trị nguyên của
x
thỏa yêu cầu đề bài.
Câu 3. (Mã 103 - 2020 Lần 1) Có bao nhiêu số nguyên
x
sao cho ứng với mỗi
x
có không quá
127
số
nguyên
y
thỏa mãn
2
3 2
log log
x y x y
?
A.
89
. B.
46
. C.
45
. D.
90
.
Lời giải
Chọn D
Ta có
2
3 2
log log 1
x y x y
Đặt
*
t x y
(do
, , 0
x y x y
)
2 2
3 2 2 3
(1) log log ( ) log log 0 2
x x t t g t t x x t
Đạo hàm
2
1 1
( ) 0
ln 2
ln3
g t
t
x x t
với mọi
y
. Do đó
g t
đồng biến trên
1;

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
Vì mỗi
x
nguyên có không quá
127
giá trị
*
t
nên ta có
2
2 3
(128) 0 log 128 log 128 0
g x x
2 7
128 3 44,8 45,8
x x x
Như vậy có
90
giá trị thỏa yêu cầu bài toán
Câu 4. (Mã 104 - 2020 Lần 1) Có bao nhiêu số nguyên
x
sao cho ứng với mỗi
x
có không quá
255
số
nguyên
y
thỏa mãn
2
3 2
log log
x y x y
?
A.
80
. B.
79
. C.
157
. D.
158
Lời giải
Chọn D
Ta có:
2
3 2
log log
x y x y
2
log
2
3
x y
x y
2
log 3
2
x y x y
1
Đk:
1x y
( do
,x y
,
0
x y
)
Đặt
1t x y
, nên từ
2
log 3
2
1
x x t t
2
Để
1
không có quá 255 nghiệm nguyên
y
khi và chỉ khi bất phương trình
2
có không quá 255
nghiệm nguyên dương
t
.
Đặt
255
M f
với
2
log 3
f t t t
.
Vì
f
là hàm đồng biến trên
1,
nên
2
1 2
1
t f x x
khi
2
0
x x
.
Vậy
2
có không quá 255 nghiệm nguyên
1 2
255
f x x
2
255
x x
78 79
x
x
.
Vậy có 158 số nguyên
x
thỏa mãn yêu cầu bài toán.
Câu 5. (Mã 102 - 2020 Lần 2) Xét các số thực thỏa mãn
2 2
1 2 2
2 2 2 4
x y x
x y x
. Giá trị lớn nhất
của biểu thức
8 4
2 1
x
P
x y
gần với giá trị nào sau đây nhất?
A.
9
B.
6
. C.
7
. D.
8
.
Lời giải
Chọn C
2 2
1 2 2
2 2 2 .4
x y x
x y x
2 2
1 2 22
2 2 2
xx y
x y x
2
2
2
1
2
1 1
2 0 1
x y
x y
Đặt
2
2
1
t x y
2
2
1 2 1 0 0 1 1 1
t
t t x y
8 4
2 8 . . 4 0
2 1
x
P P x P y P
x y
Yêu cầu bài toán tương đương:
2
2
2
2
2 8 4
1 3 12 2 8 5 5 5 5
2 8
P P
P P P P
P P
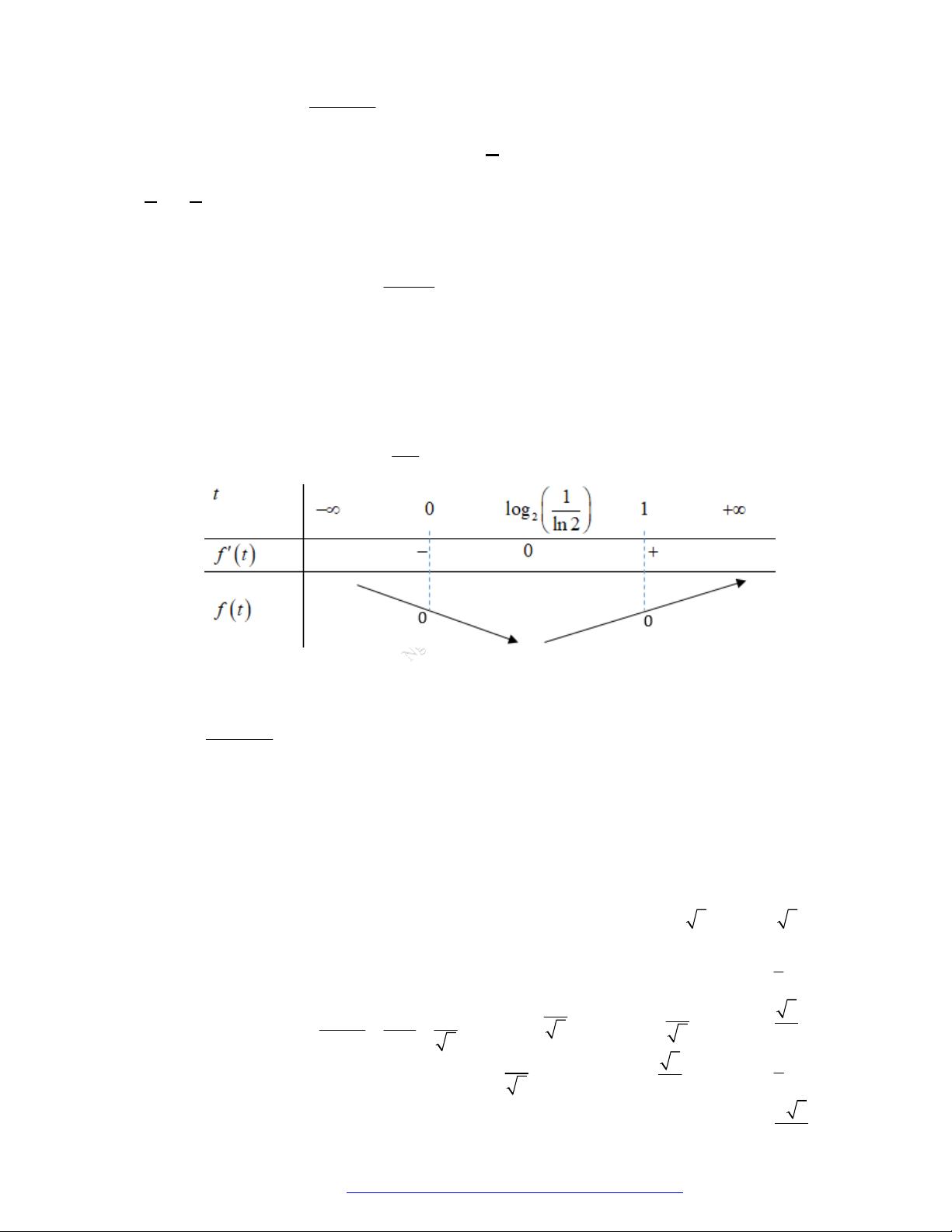
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 6. (Mã 103 - 2020 Lần 2) Xét các số thực
,x y
thỏa mãn
2 2
1 2 2
2 2 2 .4
x y x
x y x
. Giá trị nhỏ
nhất của biểu thức
8 4
2 1
x
P
x y
gần nhất với số nào dưới đây
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C
Nhận xét
2 2
2 2 0 ;x y x x y
Bất phương trình
2 2
1 2 2
2 2 2 .4
x y x
x y x
2 2
1
2 2
2
2
2 2
2
x y
x
x y x
2 2
2 1 2 2
2 2 2
x y x
x y x
.
Đặt
2 2
2 1t x y x
Bất phương trình
2 1
t
t 2 1 0
t
t
Đặt
2 1
t
f t t
. Ta thấy
0 1 0f f
.
Ta có
2 ln 2 1
t
f t
2
1
0 2 ln 2 1 log 0,52
ln 2
t
f t t
Quan sats BBT ta thấy
0 0 1f t t
2 2
0 2 1 1x y x
2
2
1 1x y
1
Xét
8 4
2 8 4
2 1
x
P Px Py P x
x y
4 8 2P P x Py
4 2 8 8 2 2 8P P P x P Py
3 12 8 2 1P P x Py
2
2 2 2
2 2
3 12 8 2 1 8 2 1P P x Py P P x y
Thế
1
vào ta có
2
3 12P
2
2
8 2P P
2
4 40 80 0P P
5 5 5 5P
.
Dấu “=” xảy ra khi
2
2
8 2 1 2
5
1 1
P x
P y
x y
2
2
1
5
2
1
5
x y
y
2
1
5
5
3
x y
y
1
3
5
3
5
3
5
3
x
y
x
y
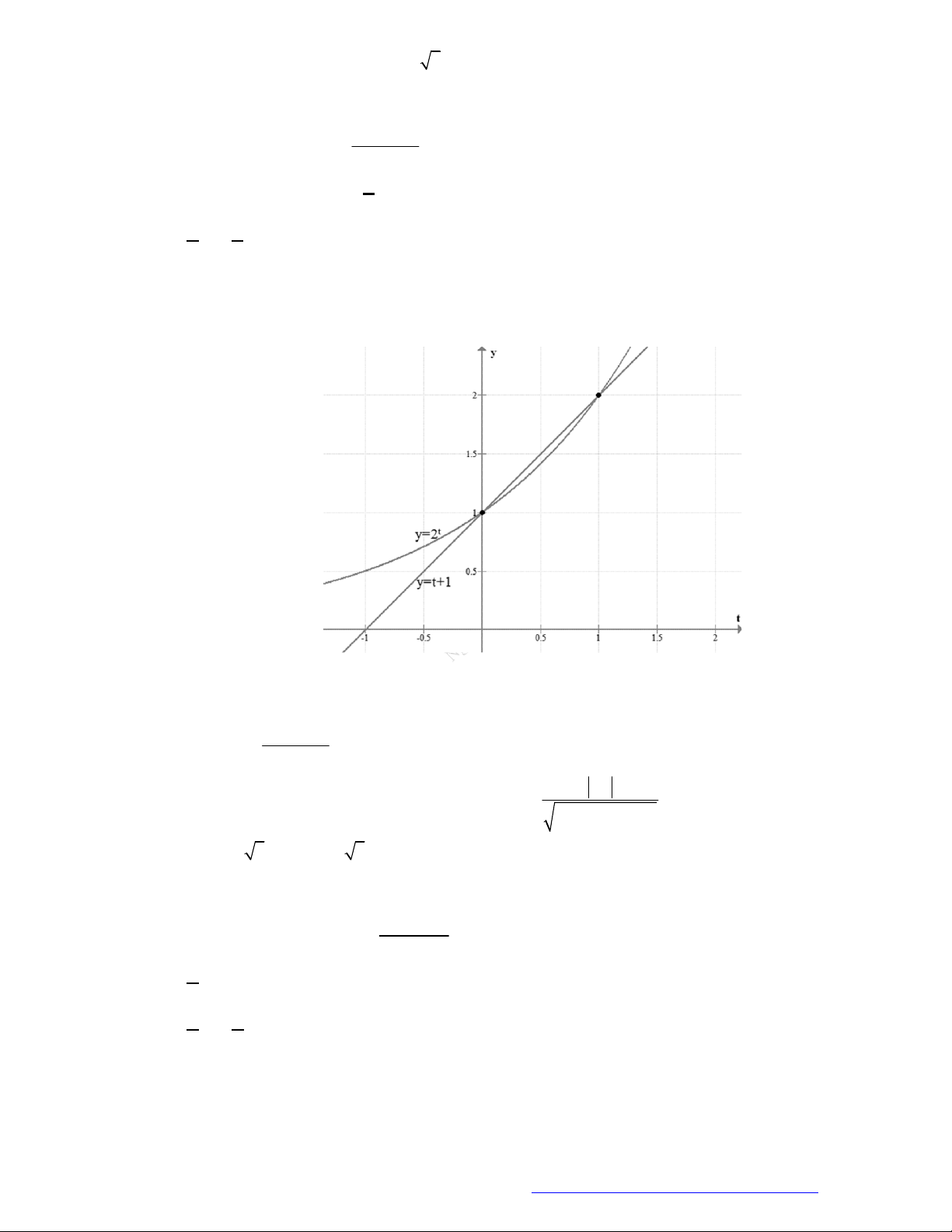
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
Vậy giá trị nhỏ nhất của
P
là
5 5 2,76
gần giá trị
3
nhất.
Câu 7. (Mã 101 - 2020 Lần 2) Xét các số thực
,x y
thỏa mãn
2 2
1 2 2
2 2 2 4
x y x
x y x
. Giá trị nhỏ
nhất của biểu thức
4
2 1
y
P
x y
gần nhất với số nào dưới đây?
A.
2
. B.
3
. C.
5
. D.
4
.
Lời giải
Chọn B
Ta có
2 2 2 2
1 2 2 1 2 2 2
2 2 2 4 2 2 2
x y x x y x
x y x x y x
2
2
2
1
2
2 1 1
x y
x y
. Đặt
2
2
1 0t x y t
, ta được BPT:
2 1
t
t
.
Đồ thị hàm số 2
t
y và đồ thị hàm số
1y t
như sau:
Từ đồ thị suy ra
2
2
2 1 0 1 1 1
t
t t x y
. Do đó tập hợp các cặp số
;x y
thỏa
mãn thuộc hình tròn
C
tâm
1;0 , 1I R
.
Ta có
4
2 4 0
2 1
y
P Px P y P
x y
là phương trình của đường thẳng
d
.
Do
d
và
C
có điểm chung
2
2
2
3
, 1 4 8 16 0
4 4
P
d I d R P P
P P
1 5 1 5P , suy ra giá trị nhỏ nhất của
P
gần nhất với
3
.
Câu 8. (Mã 104 - 2020 Lần 2) Xét các số thực
x
và
y
thỏa mãn
2 2
1 2 2
2 2 2 4
x y x
x y x
. Giá trị
lớn nhất của biểu thức
4
2 1
y
P
x y
gần nhất với số nào dưới đây?
A.
1
. B.
0
. C.
3
. D.
2
.
Lời giải
Chọn A
Ta có:
2 2 2 2
1 2 2 2 1 2 2
2 2 2 4 2 2 1 1
x y x x x y
x y x x x y
.
Đặt
2 2
2 1 0t x x y t . Khi đó ta có
2 1
t
t
,
0t
.
Đặt
2 1, 0
t
f t t t
, ta có:
2 ln 2 1
t
f t
, cho
0f t
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta nhận thấy phương trình
0f t
có một nghiệm nên phương trình
0f t
có tối đa hai
nghiệm.
Mặt khác ta có
0 1 0f f
. Suy ra phương trình
0f t
có hai nghiệm
1t
và
0t
.
Khi đó ta có bảng xét dấu của hàm số
f t
như sau:
Khi đó
0 0;1f t t
. Suy ra
2
2 2 2
2 1 1 1 1x x y x y
.
Khi đó tập hợp các điểm
;M x y
là một hình tròn
S
tâm
1;0I
, bán kính
1R
.
Ta có:
4
2 4 0
2 1
y
P Px P y P
x y
.
Khi đó ta cũng có tập hợp các điểm
;M x y
là một đường thẳng
: 2 4 0Px P y P
.
Để
và
S
có điểm chung, ta suy ra
, 1d I
.
2
2 2
2
1 3 5 8 16
2 4
P P
P P P
P P
2
4 8 16 0 1 5 1 5P P P
.
Ta suy ra
max
1 5P
. Dấu
" "
xảy ra khi
1
3
5
3
x
y
Câu 9. (Mã 101 - 2020 Lần 1) Xét các số thực không âm
x
và
y
thỏa mãn
1
2 .4 3
x y
x y
. Giá trị
nhỏ nhất của biểu thức
2 2
4 6P x y x y
bằng
A.
33
4
. B.
65
8
. C.
49
8
. D.
57
8
.
Lời giải
Chọn B.
Cách 1:
Nhận xét: Giá trị của
,x y
thỏa mãn phương trình
1
2 4 3 1
x y
x y
sẽ làm cho biểu thức
P
nhỏ nhất. Đặt
a x y
, từ
1
ta được phương trình
1
2 3
4 . 2 0
a
a
y y
.
Nhận thấy
1
2 3
4 . 2
a
y a
y y
là hàm số đồng biến theo biến
a
, nên phương trình trên có
nghiệm duy nhất
3 3
2 2
a x y
.
Ta viết lại biểu thức
2
1 1 65
4 2
4 8 8
P x y x y y
. Vậy
min
65
8
P
.
Cách 2:
Với mọi
,x y
không âm ta có

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
3 3
1
2 2
3 3
2 .4 3 .4 . 4 1 0
2 2
x y x y
x y
x y x y x y y
(1)
Nếu
3
0
2
x y
thì
3
0
2
3
. 4 1 0 . 4 1 0
2
x y
x y y y
(vô lí)
Vậy
3
2
x y
.
Áp dụng bất đẳng thức Bunhyakovski ta được
2 2
2 2
4 6 3 2 13
P x y x y x y
2
2
1 1 3 65
5 13 5 13
2 2 2 8
x y
Đẳng thức xảy ra khi
5
3
4
2
1
3 2
4
y
x y
x y
x
.
Vậy
65
min
8
P
.
Câu 10. (Mã 102 - 2020 Lần 1) Xét các số thực không âm
x
và
y
thỏa mãn
1
2 .4 3
x y
x y
. Giá trị nhỏ
nhất của biểu thức
2 2
6 4P x y x y
bằng
A.
65
8
. B.
33
4
. C.
49
8
. D.
57
8
.
Lời giải
Chọn A
Ta có
1 2 2 2
2 .4 3 .2 3 2
x y x y
x y y x
2 3 2
2 .2 3 2 .2 *
y x
y x
Hàm số
.2
t
f t t
đồng biến trên
, nên từ
*
ta suy ra
2 3 2 2 2 3 0 1
y x x y
Ta thấy
1
bất phương trình bậc nhất có miền nghiệm là nửa mặt phẳng có bờ là đường thẳng
: 2 2 3 0
d x y
(phần không chứa gốc tọa độ
O
), kể cả các điểm thuộc đường thẳng
d
.
Xét biểu thức
2 2
2 2
6 4 3 2 13 2
P x y x y x y P
Để
P
tồn tại thì ta phải có
13 0 13
P P
.
Trường hợp 1: Nếu
13
P
thì
3; 2
x y
không thỏa
1
. Do đó, trường hợp này không thể
xảy ra.
Trường hợp 2: Với
13
P
, ta thấy
2
là đường tròn
C
có tâm
3; 2
I
và bán kính
13
R P
.
Để
d
và
C
có điểm chung thì
13 65
; 13
8
2 2
d I d R P P
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy
65
min
8
P
Câu 11. (Mã 103 - 2020 Lần 1) Xét các số thực không âm
x
và
y
thỏa mãn
1
2 .4 3
x y
x y
. Giá trị
nhỏ nhất của biểu thức
2 2
2 4P x y x y
bằng
A.
33
8
. B.
9
8
. C.
21
4
. D.
41
8
.
Lời giải
Chọn D
Ta có
1 1 2 3 2
2 .4 3 2 3 .4 .4 0 2 .2 3 2 2
x y x y y x
x y x y y x
(1)
Xét TH:
3
3 2 0
2
x x
. (1) đúng với mọi giá trị
2 2
3
21
2 4
2
4
0
x
P x y x y
y
(2)
Xét TH:
3
3 2 0 0
2
x x
.
Xét hàm số
.2
t
f t t
với
0t
2 .2 .ln 2 0
t t
f t t
với mọi
0t
(1)
2 3 2
f y f x
3
2 3 2
2
y x y x
. Khi đó:
2
2 2 2 2
3 33
2 4 2 2 3 2 2 5
2 4
P x y x y x x x x x x
2
5 41 41
2
4 8 8
x
(3)
So sánh (2) và (3) ta thấy GTNN của
P
là
41
8
khi
5 1
,
4 4
x y
.
Câu 12. (Mã 104 - 2020 Lần 1) Xét các số thực không âm
x
và
y
thỏa mãn
1
2 .4 3
x y
x y . Giá trị
nhỏ nhất của biểu thức
2 2
4 2
P x y x y
bằng
A.
33
8
. B.
9
8
. C.
21
4
. D.
41
8
.
Lời giải
Chọn D
Ta có
1 1 2 3 2
2 .4 3 2 3 .4 .4 0 2 .2 3 2 2
x y x y y x
x y x y y x
(1)
Xét TH
3
3 2 0
2
x x
. (1) đúng với mọi giá trị
2 2
3
33
4 2
2
4
0
x
P x y x y
y
(2)
Xét TH
3
3 2 0 0
2
x x
.
Xét hàm số
.2
t
f t t
với
0t
2 .2 .ln 2 0
t t
f t t
với mọi
0t
(1)
2 3 2
f y f x
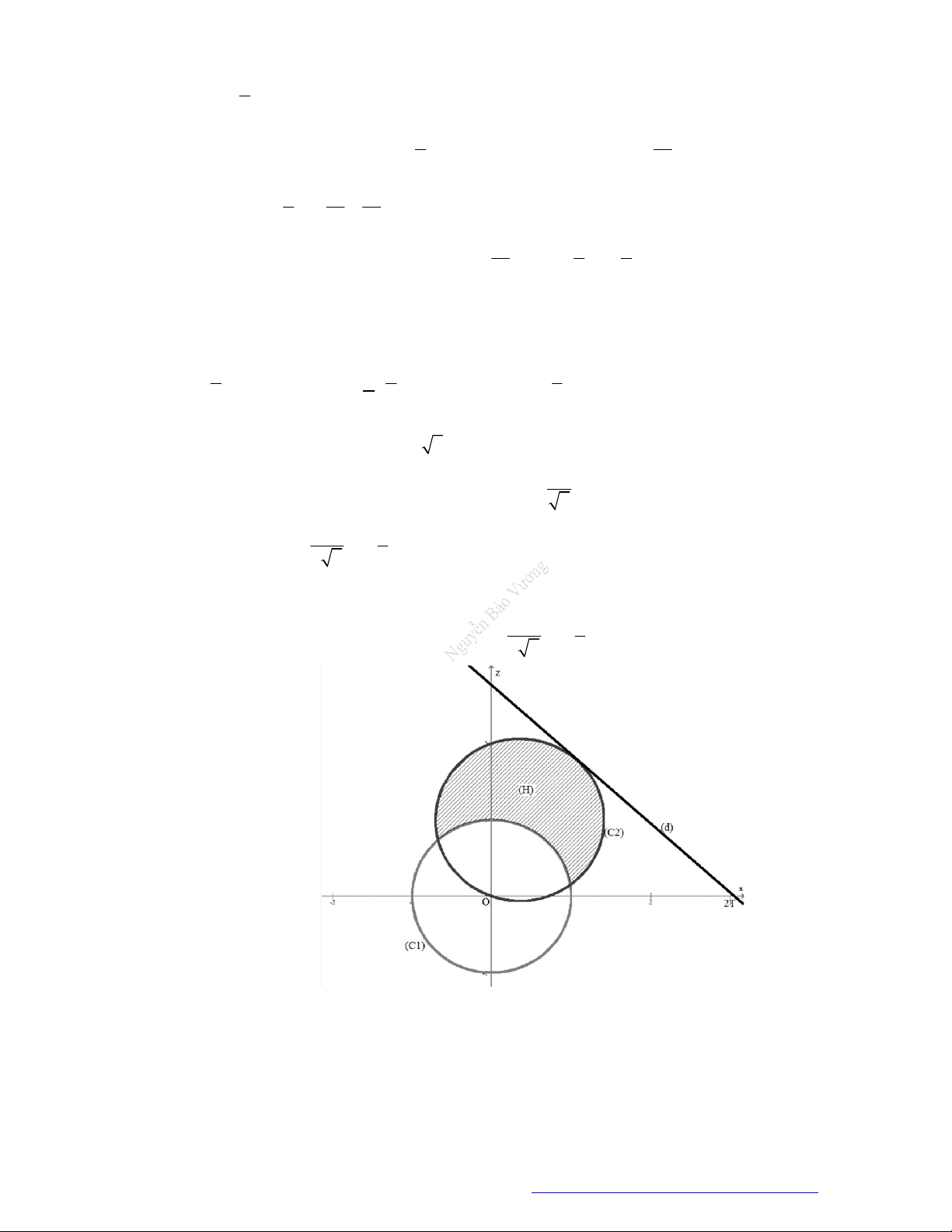
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
2 3 2
3
2
y x
y x
2
2 2 2 2
3 21
4 2 4 3 2 2
2 4
P x y x y x x x x x x
2
1 41 41
2
4 8 8
P x
(3)
So sánh (2) và (3) ta thấy GTNN của
P
là
41
8
khi
1 5
,
4 4
x y
Câu 13. (Diệu Hiền - Cần Thơ - 2018) Trong các nghiệm
;x y
thỏa mãn bất phương trình
2 2
2
log 2 1
x y
x y
. Giá trị lớn nhất của biểu thức
2T x y
bằng:
A.
9
4
. B.
9
2
. C.
9
8
. D.
9
.
Lời giải
Trường hợp 1:
2 2
2 1x y . Đặt
2y z
. Suy ra
2 2
1 1x z
2 2
2
log 2 1
x y
x y
2 2
2 2x y x y
2 2
2
2
z
x x z
2
2
1 9
1 2
8
2 2
x z
Tập hợp các điểm
;M x z
là miền
H
bao gồm miền ngoài của hình tròn
2 2
1
: 1C x z
và
miền trong của hình tròn
2
2
2
1 9
: 1
8
2 2
C x z
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hệ
2
2
2 2
2
2
1 9
1
8
2 2
1
z
T x
x z
x z
có nghiệm khi đường thẳng
:2 0
2
z
d x T
có điểm chung với
miền
H
.
Để T đạt giá trị lớn nhất thì đường thẳng
:2 0
2
z
d x T
tiếp xúc với đường tròn
2
C
3
;
2 2
d I d
với
1
1;
2 2
I
là tâm của đường tròn
2
C
.
1
2
3
4
1 2 2
4
2
T
9 9
4 4
T
0 ( )
9
2
T l
T
Trường hợp 2:
2 2
0 2 1
x y
.
2 2
2
log 2 1
x y
x y
2 2
2 2x y x y
2 1T x y
(loại).
Vậy giá trị lớn nhất của biểu thức
2
T x y
là
9
max
2
T
.
Câu 14. (Chuyên Lê Hồng Phong - Nam Định - 2020) Có bao nhiêu bộ
;x y
với
,x y
nguyên và
1 , 2020
x y
thỏa mãn
3 2
2 2 1
2 4 8 log 2 3 6 log
2 3
y x
xy x y x y xy
y x
?
A.
2017
. B.
4034
. C.
2
. D.
2017 2020
.
Lời giải
Chọn B
+ Điều kiện
*
*
, : , 2020
, : , 2020
2 1 2
0, 0
3, 0
3 2
x y x y
x y x y
x y
x y
x y
.
BPT cho có dạng
2 3
4 2
3 2 log 1 4 2 log 1 0
3 2
x y
x y x y
x y
(*).
+ Xét
1y
thì (*) thành
2 3
4 2
3 log 1 3 4 log 0
3 3
x
x x
x
, rõ ràng BPT này nghiệm
đúng với mọi
3
x
vì
2 2 3
4 2
3 0, log 1 log 0 1 0, 3 4 0, log 0
3 3
x
x x
x
.
Như vậy trường hợp này cho ta đúng 2017 bộ
; ;1x y x
với
4 2020,x x
.
+ Xét
2
y
thì (*) thành
3
4 4 log 1 0
x
, BPT này cũng luôn đúng với mọi x mà
4 2020,x x
.
Trường hợp này cho ta 2017 cặp
;x y
nữa.
+ Với
2, 3
y x
thì
* 0
VT
nên (*) không xảy ra.
Vậy có đúng 4034 bộ số
;x y
thỏa mãn yêu cầu bài toán.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
Câu 15. (THPT Quỳnh Lưu 3 Nghệ An 2019) Cho hai số thực
, 0
a b
thỏa mãn
2 2
log 1 log 1 6
a b
. Giá trị nhỏ nhất của biểu thức
a b
là.
A.
12
. B.
14
. C.
16
. D.
8
.
Lời giải
Ta có
2 2
log 1 log 1 6
a b
2
log 1 1 6
a b
1 1 64
a b
.
Áp dụng bất đẳng thức Cô-si cho hai số dương
1a
và
1b
, ta được
1 1 2 1 1 2 64 16
a b a b
2 16
a b
14
a b
Dấu
" "
xảy ra khi
1 1
a b a b
.
Vậy
min 14
a b
khi
7
a b
.
Câu 16. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Trong các nghiệm
;x y
thỏa mãn bất phương
trình
2 2
2
log 2 1
x y
x y
. Khi đó giá trị lớn nhất của biểu thức
2
T x y
là
A.
9
4
B.
9
C.
9
2
D.
9
8
Lời giải
- TH1:
2 2
2 1
x y
Bất phương trình
2 2
2 2
2
log 2 1 2x 2
x y
x y y x y
2 2
2x 2 1
y x y
Áp dụng bất đẳng thức Bunhia-CopSky ta có
2
2
2 2 2
1
2 2 2x
2
x y y
2
2 2
2 2x
2
9
y
x y
2
2 2x
9 9
2 2 2 0 2 1;
9 2 2
y
x y x y x y x y
Giá trị lớn nhất của
9
2
2
T x y
. Dấu bằng xảy ra khi
1
2;
2
x y
- TH2:
2 2
0 2 1
x y
Bất phương trình
2 2
2 2
2
9
log 2 1 2x 2 1
2
x y
x y y x y
.
Vậy giá trị lớn nhất của
9
2
2
T x y
.
Câu 17. (Chuyên Vĩnh Phúc 2019) Tìm tập
S
tất cả các giá trị thực của tham số
m
để tồn tại duy nhất
cặp số
;x y
thỏa mãn
2 2
2
2
log 4 4 6 1
x y
x y m
và
2 2
2 4 1 0
x y x y
.
A.
1;1
S
B.
5; 1;1;5
S
C.
5;5
S
D.
7; 5; 1;1;5;7
S
Lời giải.
Ta có
2 2
2
2
log 4 4 6 1
x y
x y m
2 2 2
4 4 6 2
x y m x y
2 2 2
4 4 8 0
x y x y m
2 2
2
2 2
x y m
là một hình tròn
1
C
tâm
2;2
I
, bán kính
1
R m
với
0
m
hoặc
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
là điểm
2;2
I
với
0
m
và
2 2
2 4 1 0
x y x y
2 2
1 2 4
x y
là một đường
tròn
2
C
tâm
1;2
J
, bán kính
2
2
R
.
TH1: Với
0
m
ta có:
2
2;2
I C
suy ra
0
m
không thỏa mãn điều kiện bài toán.
TH2: Với
0
m
.
Để hệ
2 2
2
2
2 2
log 4 4 6 1
2 4 1 0
x y
x y m
x y x y
tồn tại duy nhất cặp số
;x y
thì hình tròn
1
C
và đường
tròn
2
C
tiếp xúc ngoài với nhau
1 2
IJ R R
2 2
3 0 2
m
1
m
1
m
.
Câu 18. Tìm tham số
m
để tồn tại duy nhất cặp số
;x y
thỏa mãn đồng thời các điều kiện sau
2019
log 0
x y
và
2 1
x y xy m
A.
1
2
m
. B.
0
m
. C.
2
m
. D.
1
3
m
.
Lời giải
Chọn A
Xét hệ bất phương trình:
2019
log 0 (1)
2 1 (2)
x y
x y xy m
;x y
là nghiệm hệ bất phương trình thì
;y x
cũng là nghiệm của hệ bất phương trình. Do đó hệ
có nghiệm duy nhất
x y
.
Khi đó: (1)
0 2 1x
1
0
2
x
.
Với
1
0
2
x
; (2)
2
2 2 1
x x m
2
2 1 2x m x
2 2
2 1 4 4x m x x
2
2 4 1
x x m
Đặt
2
2 4 1f x x x
f x
nghịch biến trên
1
0;
2
nên
1 1
2 2
f x f
1
0;
2
x
.
Do đó hệ có nghiệm duy nhất
1
2
m
.
Câu 19. Trong tất cả các cặp
;x y
thỏa mãn
2 2
2
log 4 4 4 1
x y
x y
. Tìm m để tồn tại duy nhất cặp
;x y
sao cho
2 2
2 2 2 0
x y x y m
.
A.
2
10 2
m
. B.
10 2
m . C.
10 2
m . D.
2
10 2
m
.
Lời giải
Chọn D
Với mọi
, x y
, ta luôn có
2 2
2 2 1
x y
nên BPT
2 2
2
log 4 4 4 1
x y
x y
2 2
2 2
4 4 4 2 2 2 2
x y x y x y
1
.

TÀI
LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
BPT
1
mô tả
hình tròn tâm
2;2I
và bán kính
1
2R
.
Mặt khá
c, phương trình
2 2
2 2
2 2 2
0 1 1x y x y m x y m
2
nên để
2
có
nghiệm thì
0m
.
TH1:
0m
. Khi đó,
1
2
1
x
y
khôn
g thỏa
1
nên loại
0m
.
TH2:
0m
. Khi đó,
2
là phương trình đường tròn
2
C
tâm
1;1J
và bán kính
2
R m
. Do
đó, yêu
cầu đề bài Hệ BPT
2 2
2 2
2 2 2
1 1
x y
x y m
có nghiệm
duy nhất
2
C
tiếp xúc
với
đường tròn
2 2
1
: 2 2
2C x y
cũng có
tâm
2;2I
và bán
kính
1
2R
. Vì
1
10 2I
J R
nên
1
C
hoặc tiếp xú
c ngoài, hoặc tiếp xúc trong với
2
C
.
TH2a:
1
C
tiếp xúc ngoà
i với
2 1 2
10 2C IJ
R R m
2
10 2 10
2m m .
TH2b:
1
C
tiế
p xúc trong với
2 2 1
10 2C IJ
R R m
2
2 10 10
2m m .
Vậy
2
10 2m
.
Bấm Tải xuống để xem toàn bộ.




