
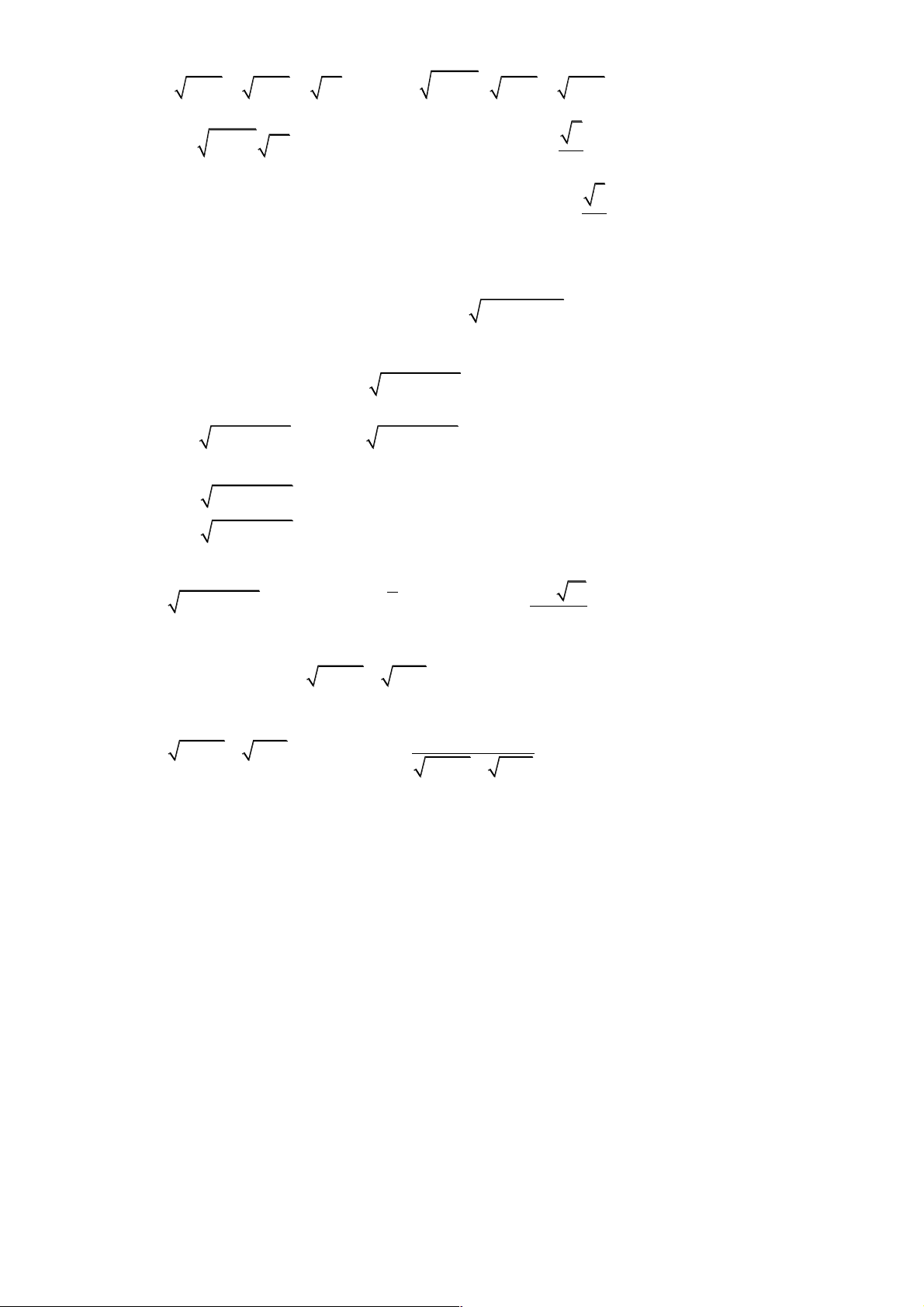






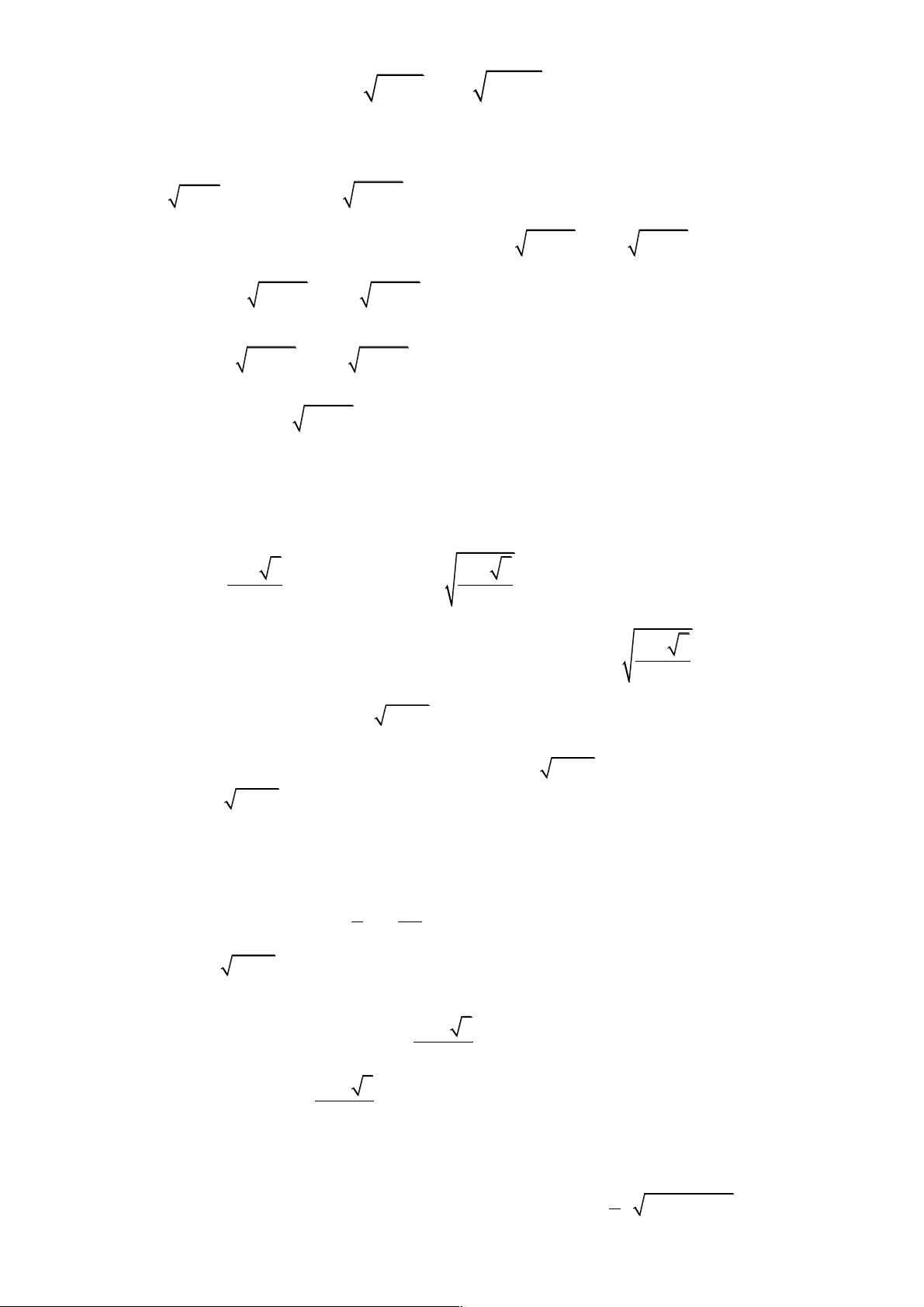

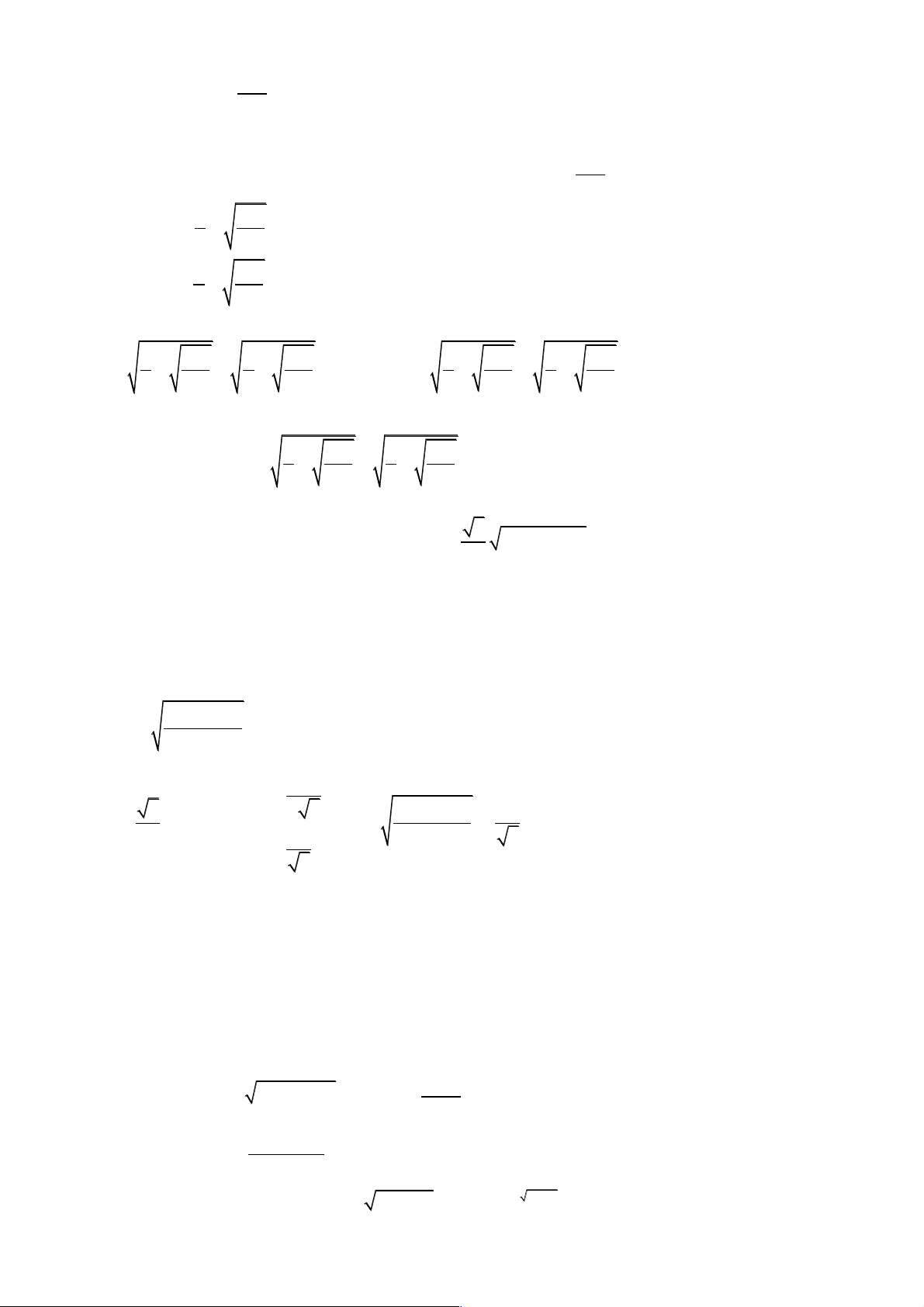

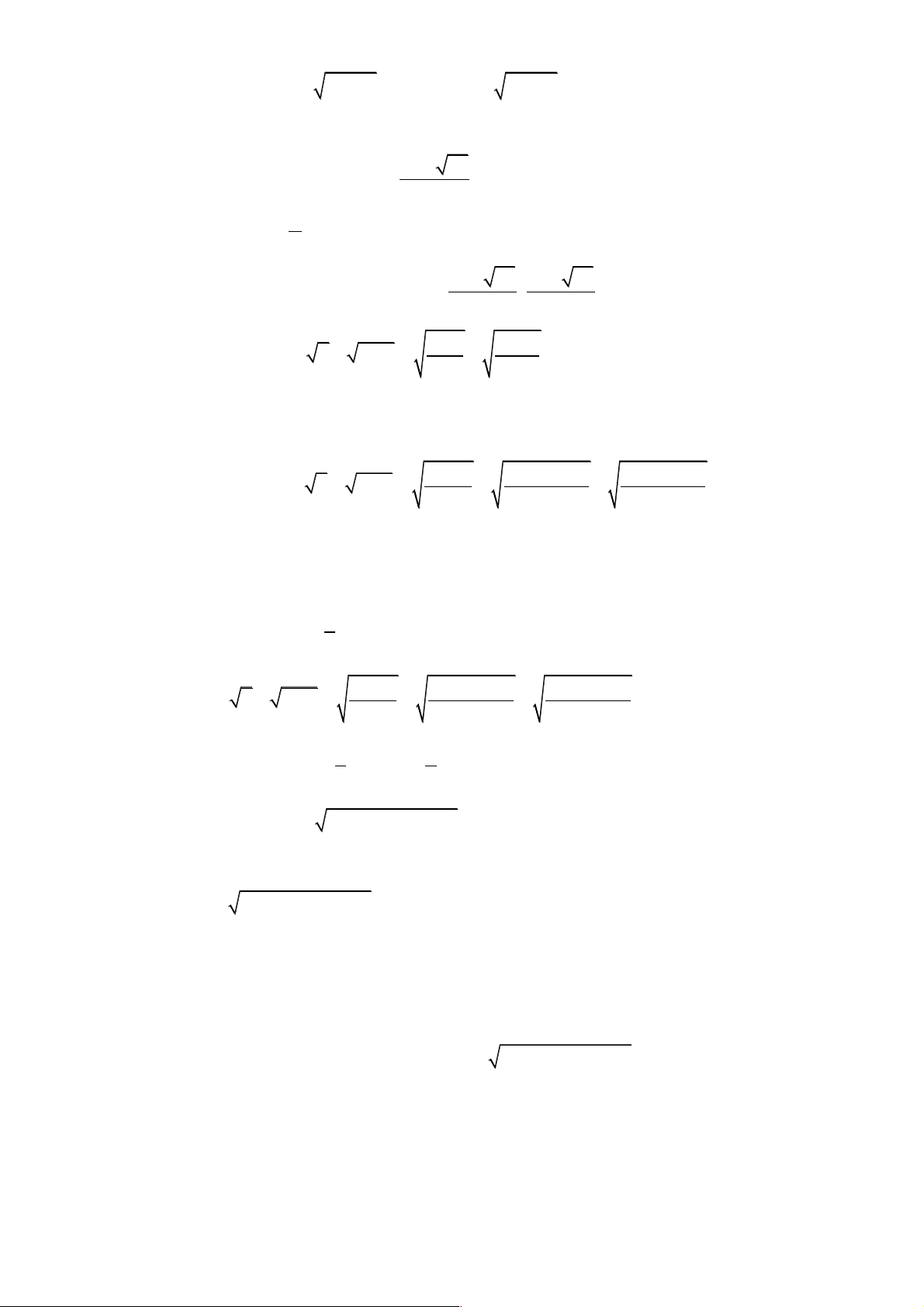

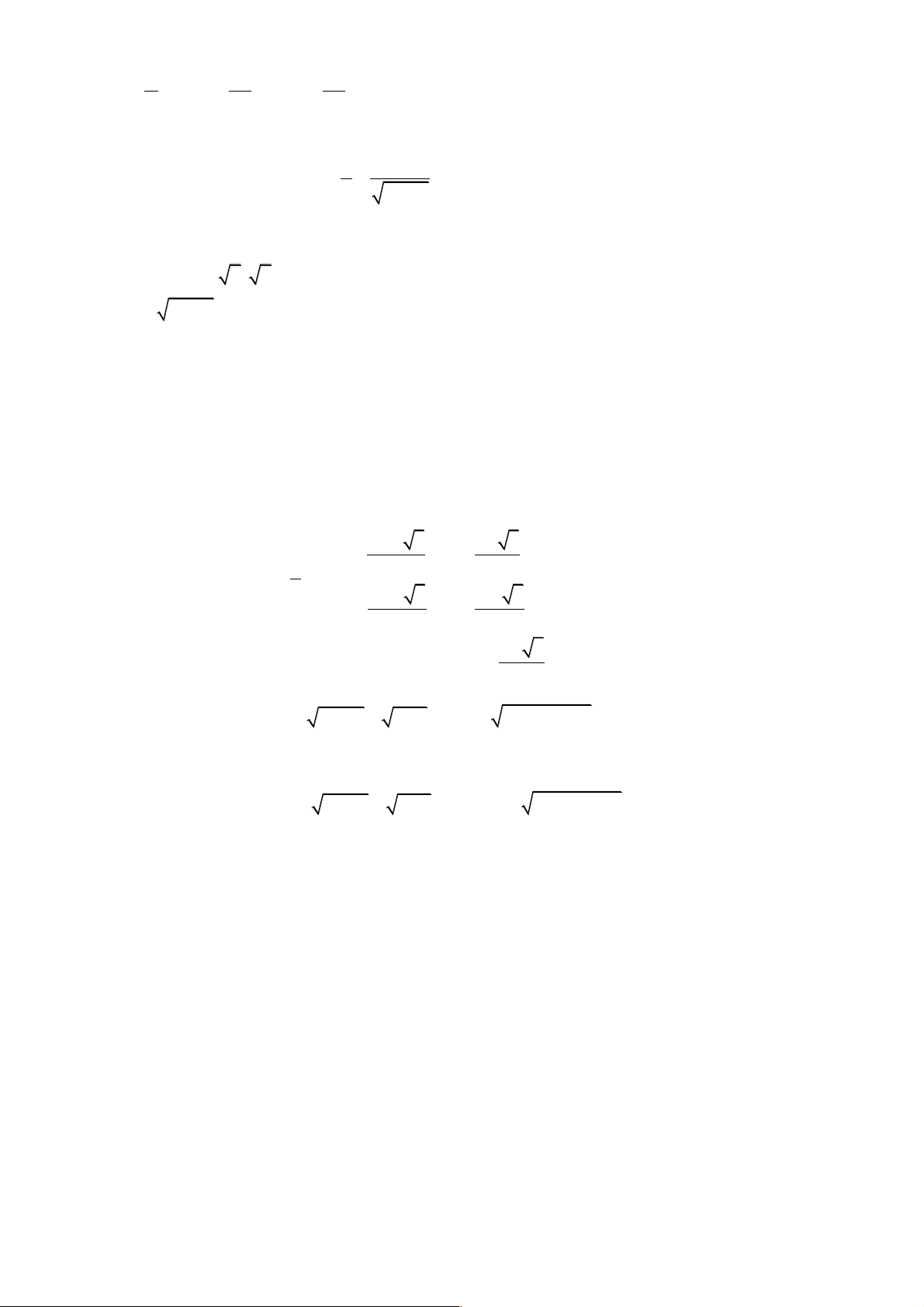



















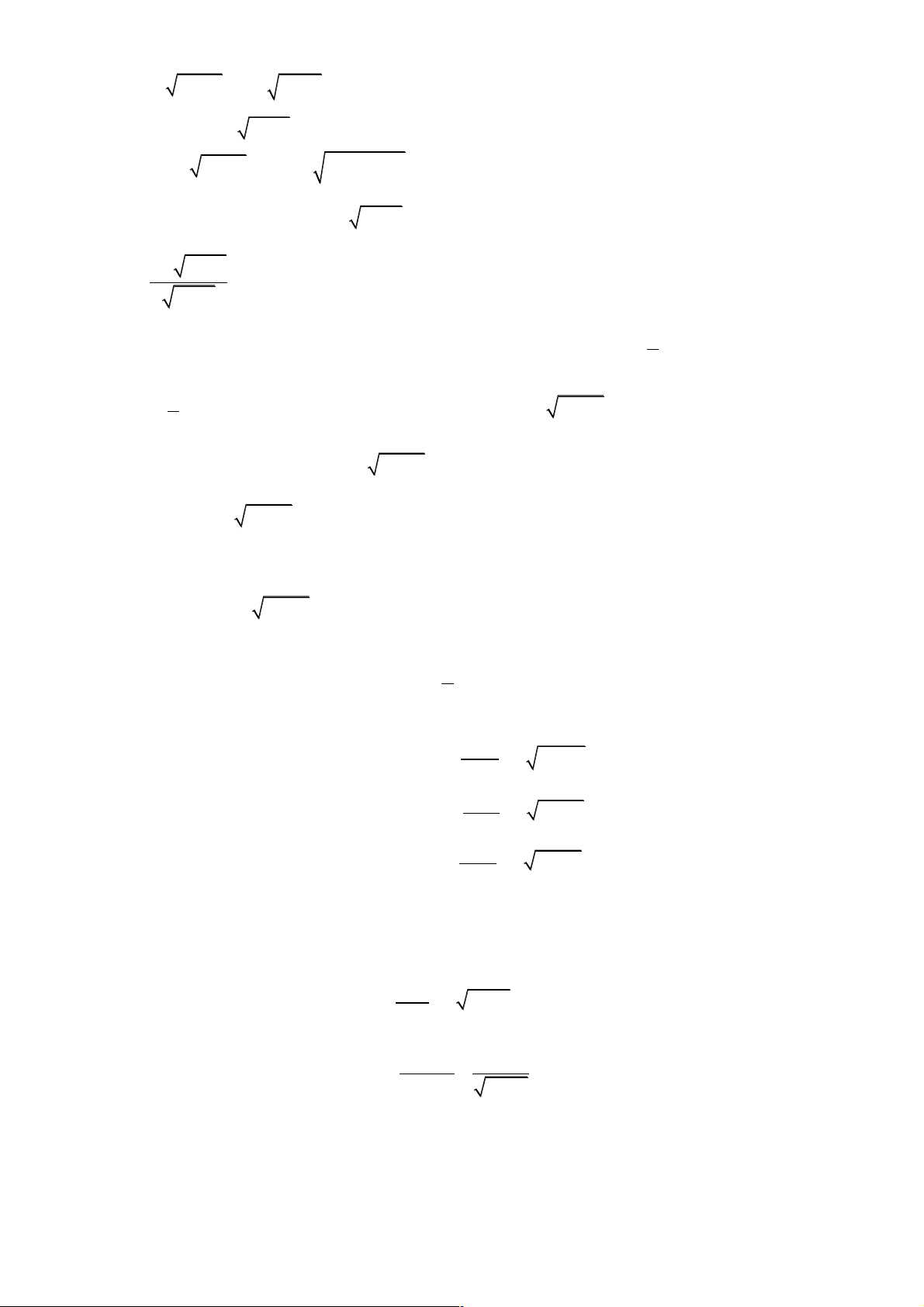
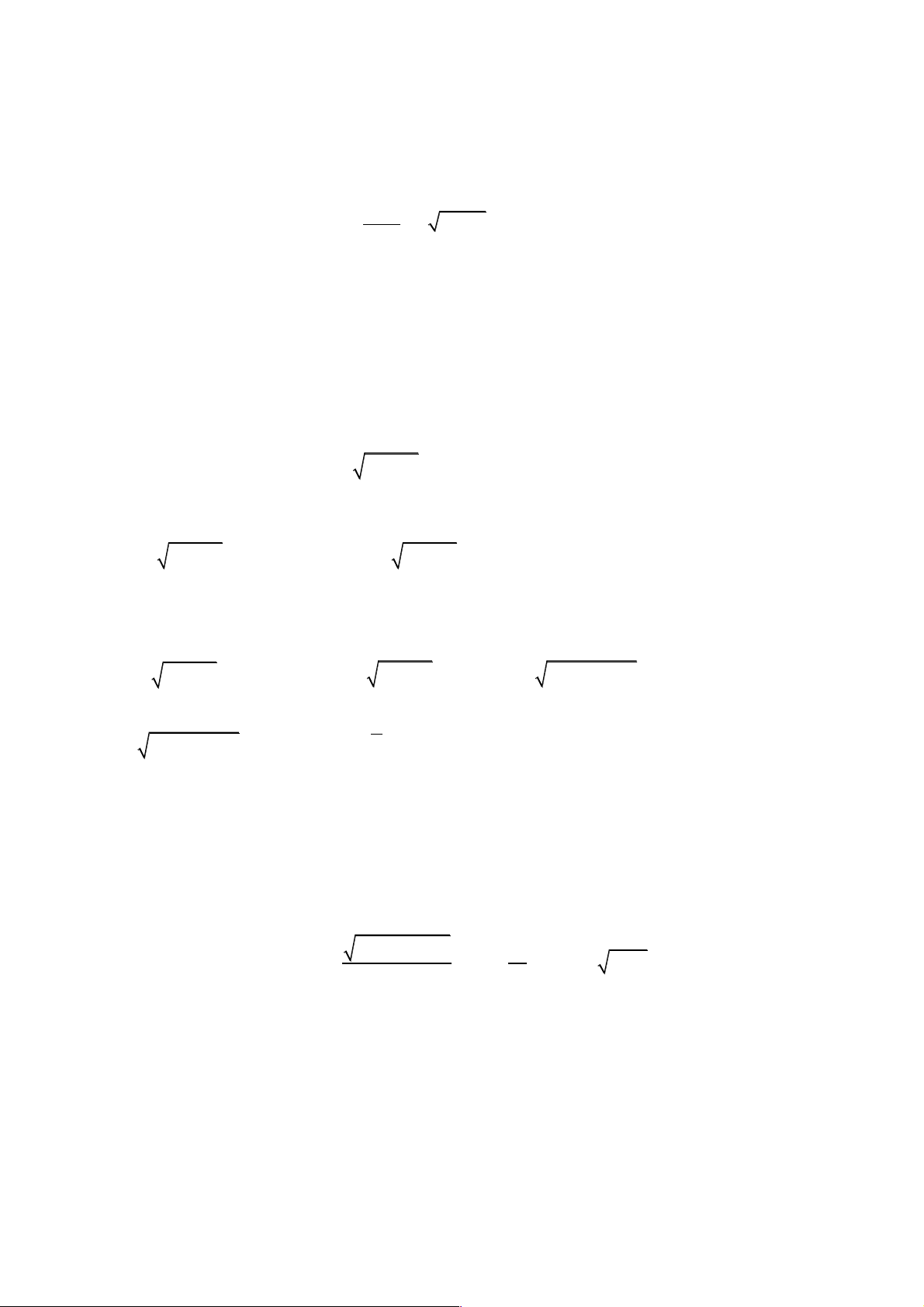



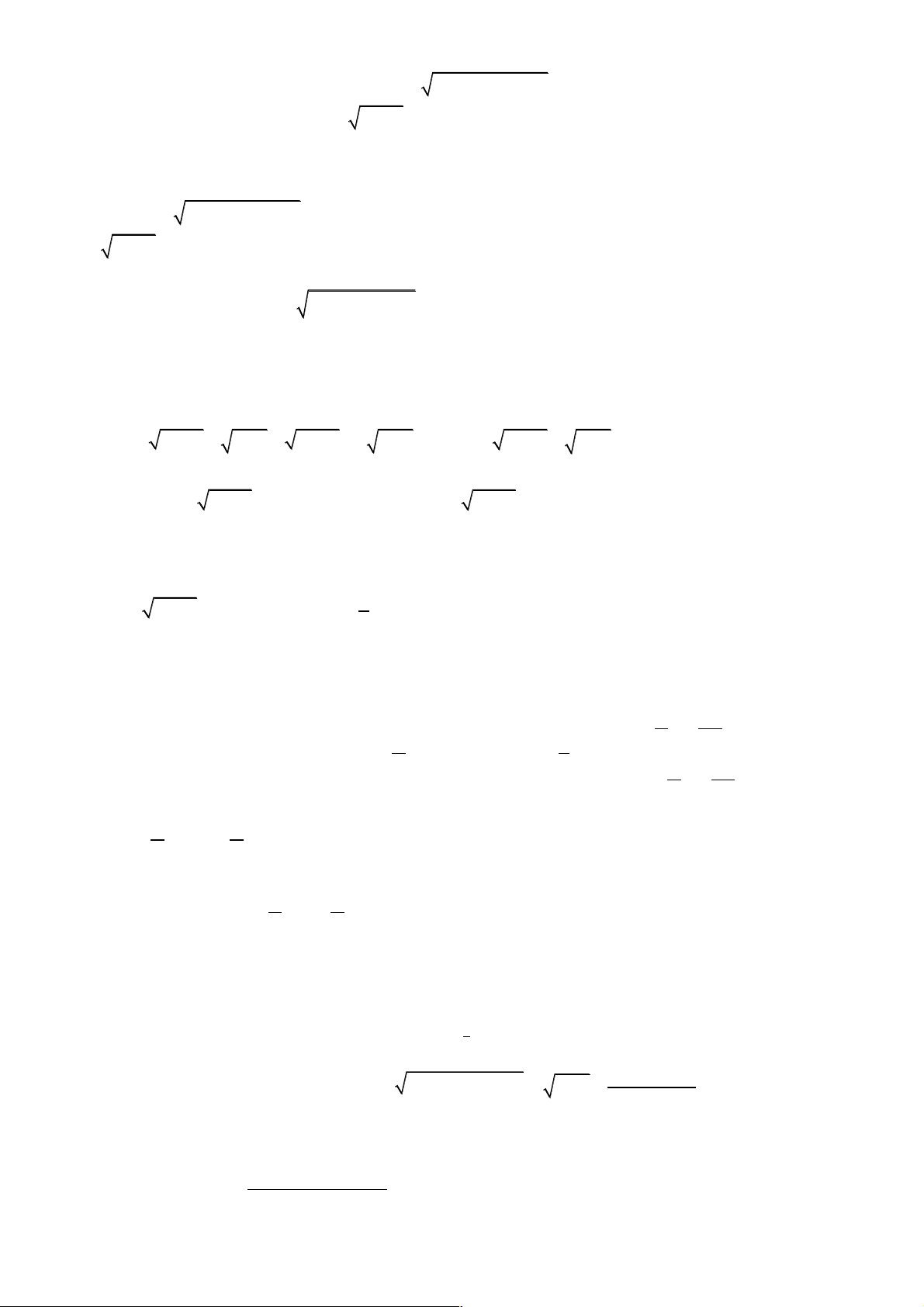

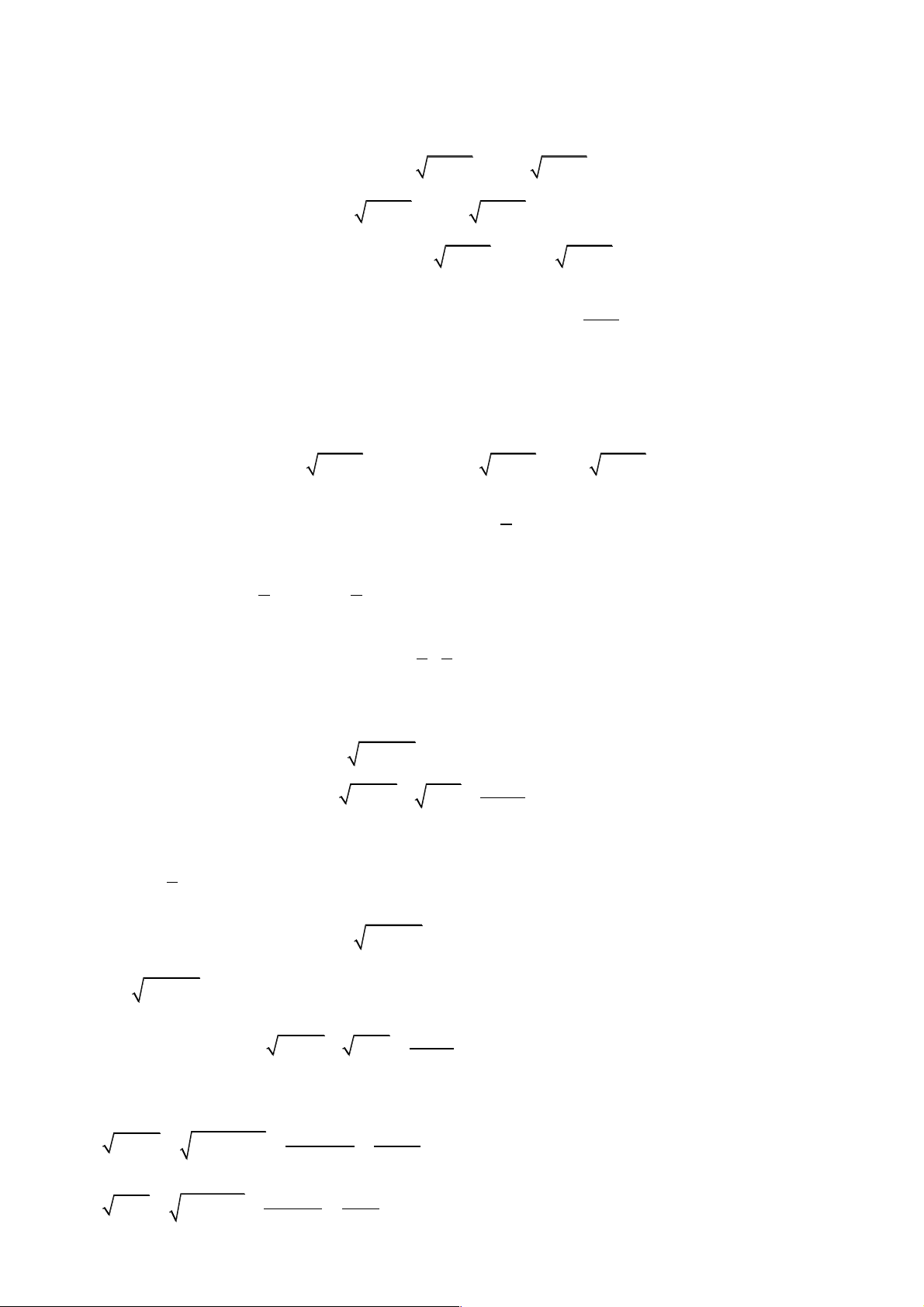














Preview text:
I. PHƯƠNG TRÌNH 1. Không có tham số
Dạng 1: Biến đổi tương đương
Câu 1. Giải phương trình 3 4 2 5 5 2 3 4 5 5
x + x + 2 x + x + 2 = x + 3x - 2 + 2 x + 3x Lời giải
+Biến đổi phương trình tương đương : 2 x - 3x + 2 = 0 éx =1 Û ê ëx = 2
Câu 2. Giải phương trình 2
4 x + 1 + 2 2x + 3 = (x - 1)(x - 2). Lời giải Điều kiện: x ³ 1 - . Nhận thấy x = 1
- là một nghiệm của phương trình. Xét x > 1
- . Khi đó phương trình đã cho tương đương với
( x + - ) + ( x + - ) 3 2 4 1 2 2 2
3 3 = x - x - 2x - 12 4( x - 3) 4( x - 3) 2 Û +
= (x - 3)(x + 2x + 4) x + 1 + 2 2x + 3 + 3 æ ö Û ( x - 3) 4 4 2 + - (x + 1) - 3 = 0. 1 ç ÷ ( ) è x + 1 + 2 2x + 3 + 3 ø 4 4 Vì x > 1
- nên x + 1 > 0 và 2x + 3 > 1. Suy ra + < 3, vì x + 1 + 2 2x + 3 + 3 vậy 4 4 2 + - (x + 1) - 3 < 0. x + 1 + 2 2x + 3 + 3 Do đó phương trình 1
( ) Û x - 3 = 0 Û x = 3.
Vậy phương trình đã cho có 2 nghiệm là x = 1 - hoặc x = 3.
Câu 3. [Đề thi hsg Bắc Sơn, Lạng Sơn] Giải phương trình sau : 3 3 3 x +1 + x -1 = 5x Lời giải 1 3 3 3 3 2
x + 1 + x - 1 = 5x Û 2x + 3 x - 1(3 3 x + 1 + x - 1) = 5x 3 2 3 3 5
Þ x -1 5x = x Þ 4x - 5x = 0 Þ x = 0;x = ± . 2 5
Thˆ lπi ta th y ph≠¨ ng tr◊nh c„ 3 nghi÷m: x = 0; x = ± . 2
Câu 4. Giải phương trình: 2
x + x + = ( x + ) 2 6 1 2 1 x + 2x + 3( )
1 ,với x Î R. Hướng dẫn giải. ( ) 2
Û x + x + -( x + ) 2 1 2 3 2
1 x + 2x + 3 + 4x - 2 = 0 2 2 Û
x + 2x + 3 - 2x +1
x + 2x + 3 - 2 = 0 ( )( ) 2
é x + 2x +3 = 2x -1 Û ê 2
êë x + 2x +3 = 2 ì 1 ïx ³ 3 + 15 2
x + 2x + 3 = 2x -1 Û í 2 Û x = 3 2 3
ïî x -6x -2 = 0
Câu 5. Giải phương trình 2
3x - 2 - x +1 = 2x - x - 3. Hướng dẫn giải. 2x - 3 2
3x - 2 - x +1 = 2x - x - 3 Û = (2x -3)(x+1) 3x - 2 + x +1
Tìm được nghiệm duy nhất x=2/3
Câu 6. Tìm nghiệm nguyên của phương trình 2 2
x - 3y + 2xy - 2x -10y + 4 = 0. Hướng dẫn giải Ta có: 2 2
x - 3y + 2xy - 2x -10y + 4 = 0
Û x + 2x (y - ) 1 + (y - )2 2 1 - ( 2
4y + 8y + 4) == 7
Û (x + y - )2 -( y + )2 1 2 2 = 7 - Û (3y + x + )
1 (y - x +3) = 7
Vì 7 là số nguyên tố nên ta có các trường hợp sau: 3
ì y + y +1 = 7 3 ì y + y +1 = 7 - 3 ì y + y +1 =1 3 ì y + y +1 = 1 - í ; í ; í ; í
î y - x + 3 = 1 î y - x + 3 = 1 -
î y - x + 3 = 7 î y - x + 3 = 7 -
Giải ba hệ phương trình trên ta được: (x; y)Î ( { 3±; )1,(1; 3-),(7; 3-)}. 2
Câu 7. (THPT Quảng Xương 2 – Thanh Hóa, 2009-2010) Giải phương trình: 2 2 =1+ 5+ 6x - x x -1 + 5 - x Hướng dẫn giải 2 2 t - 4
Đặt t = x -1 + 5 - x ta được =1+
Û (t - 2)( 2t + 2t + 2) = 0 t 2
Giải ta được t = 2 suy ra x = 1, x = 5 Dạng 2: Đặt ẩn phụ Bài 1.
Giải phương trình trên tập số thực: 2
x + x +9 = 2x -4+ x +1(1). Hướng dẫn giải Điều kiện: x ³ 1 - .
x + x + = x - + x + Û (x - )2 2 9 2 4 1 2 + 5(x + )
1 = 2(x - 2)+ x +1 !x = -
1 không là nghiệm của phương trình. 2 æ x - 2 ö x - 2 !x > 1: - pt(1) Û ç ÷ + 5 = 2 + . 1 è x +1 ø x +1 x - 2 Đặt t = . x +1 Phương trình trở thành: 2 t +5 = 2t +1 2 Û t = . 3 20 + 4 7 ìï20 + 4 7 üï
Khi đó ta có: 2 x +1 = 3x - 6 Û x = . Vậy S = í . ý 9 ï 9 î ïþ Bài 2.
Giải phương trình sau trên tập số thực: 2
x + x + = (x + ) 2 2 3 7 5 2x +1. Hướng dẫn giải Phương trình (1) 2 Û x + -(x + ) 2 2 1 5
2x +1 + 3x + 6 = 0. Đặt 2
t = 2x +1. Ta có phương trình: 2
t -(x +5)t +3x + 6 = 0(*). D = é- ë ( x + ) 2 ù - û
( x + ) = (x - )2 5 4 3 6 1 . ét = 3 Phương trình (*) Û ê ët = x + 2 ìx + 2 > 0 2
t = 3 Û 2x +1 = 3 Û x = 2 ± 2
t = x + 2 Û 2x +1 = x + 2 Û í 2 îx - 4x - 3 = 0 ìx > 2 - ï Û í Û x = 2 ± 7 . ïîx = 2 ± 7 3 Vậy S = ( 2; ± 2 ± 7 ). Bài 3.
Giải phương trình sau trên tập số thực: ( 2 x - x - ) 2 x + x + + ( 2 2 5 2 2x + x + ) 1 x + 3 = 0.
Hướng dẫn giải ì 2
ìïa = x + x + 2 7 ïa ³ Đặt í . Điều kiện: í 2 . b ïî = x + 3 b ïî ³ 0 Ta có: 2 2 2 2 2 2
2x - x - 5 = 2a -3b ; 2x + x +1 = 2a - b . 3 2 æ b ö æ b ö æ b ö
Thay vào phương trình ta được: ( 2 2
a - b )a +( 2 2 2 3
2a -b )b = 0 Û + 3 - 2 - 2 = 0 ç ÷ ç ÷ ç ÷ è a ø è a ø è a ø éb =1 êa Û ê 2 êæ b ö b + 4 + 2 = 0 êç ÷ ëè a ø a 2 æ b ö b b +)
+ 4 + 2 = 0 : phương trình vô nghiệm do ³ 0. ç ÷ è a ø a a b éx =1 2
+) =1 Û b = a Û x + 3 = x + x + 2 Û . a ê ëx = 1 -
Vậy x = 1; x = 1
- là nghiệm phương trình. Bài 4. Giải phương trình sau 3 2 2 3 3 2
- x +10x -17x +8 = 2x 5x - x Lời giải
Nhận xét rằng x = 0 không là nghiệm của phương trình đã cho. 1
Suy ra x ¹ 0 . Chia cả hai vế của phương trình cho 3
x rồi đặt t = , t ¹ 0, ta có phương trình x 3 2 3 2
8t -17t +10t - 2 = 2 5t -1 Û ( t - )3 + ( t - ) = ( 2t - ) 3 2 2 1 2 2 1 5 1 + 2 5t -1 (*)
Xét hàm số f (t) 3
= t + 2t, t " Î! .
Ta có hàm số f (t) liên tục trên ! và f (t) 2 '
= 3t + 2 > 0, t " .
Suy ra hàm số f (t) luôn đồng biến trên khoảng ( ; -¥ +¥).
Khi đó phương trình đã cho có dạng f ( t - ) 3 2 3 2 2 1 = f
5t -1 Û 2t -1 = 5t -1 ( ) 17 ± 97 3 2
Û 8t -17t + 6t = 0 Û t = (do t ¹ 0) 16 17 - 97 17 + 97
Vậy phương trình đã cho có nghiệm là x = và x = . 1 12 2 12 4 Bài 5.
Giải phương trình sau : ( x - ) 2 2 4 1
x +1 = 2x + 2x + 1 Lời giải Đặt 2 2 2 2
y = x +1 ³1 Û y = x +1Þ 2y + (1- 4x)y + 2x -1 = 0 . 4
Û y = 2x -1 Û x = 3 2 5 - 2 3 3 2 + 5 -1 = x x x . 6 Điều kiện xác định: 2 5x - 2 ³ 0. 2 5x - 2 Đặt t = (t ³ 0). Ta có 2 2 5x = 6t + 2. 6
Phương trình đã cho trở thành 3 3 2 3 2 3
x + 6t + 2 -1 = t Û x + 6t + 2 = (t +1) 3 3
Û x = (t -1) Û x = t -1Û t = x + 1 ìx ³ 1 - 2 5x - 2 ï ìx ³ 1 - 2 Û = x +1 Û í x - Û í 5 2 2 2 6 = (x +1) ï îx +12x + 8 = 0 î 6 Û x = 6 - + 28 (tm đk).
Vậy phương trình đã cho có nghiệm là x = 6 - + 28. Bài 6. Giải phương trình: 2 2 log
(x - 2x -11) = log
(x - 2x -12) (1) 2+ 5 2 2+ 5 2
ìïx - 2x -12 > 0 • Điều kiện: í (*) 2
ïîx - 2x -11> 0 • 2 (2 + 5) = 9 + 4 5 và 2
(2 2 + 5) = 8 + 4 5 do đó 2 + 5 = 9 + 4 5 và 2 2 + 5 = 8+ 4 5 . • (1) Û 2 2 log
(x - 2x -11) = log (x - 2x -12) 9+4 5 8+4 5 Û 2 2 log
(x - 2x -11) = log (x - 2x -12) 9+4 5 8+4 5
• Đặt: a = 8 + 4 5 > 1, t = x2 – 2x -12. Điều kiện: t > 0.
• Do đó: (1) Û lna + 1(t + 1) = lnat ìït = y a
Cách 1: (1) Û lna + 1(t + 1) = lnat Û í (I).
ïît +1= (a +1)y y y • æ a ö æ 1 ö Từ (I) ta được: + =1 (2). ç ÷ ç ÷ è a +1ø è a +1ø
• y = 1: là nghiệm của (2). 5 y y y y • æ a ö æ 1 ö a 1 æ a ö æ 1 ö a 1 y < 1: + > + = 1, y < 1: + < + = . 1 ç ÷ ç ÷ ç ÷ ç ÷ è a +1ø è a +1ø a +1 a +1 è a +1ø è a +1ø a +1 a +1
• Nên (2) có nghiệm duy nhất: y = 1. Do đó: (1) t = a Û x2 – 2x – 12 = 8 + 4 5 ( thỏa *)
Û x2 – 2x – 20 - 4 5 = 0 Û x = 2 + 2 5 hoặc x = -2 5 .
• Vậy phương trình đã cho có hai nghiệm: x = 2 + 2 5 hoặc x = -2 5 .
Cách 2: Xét hàm số y = f(t) = lna + 1(t + 1) - lnat (a >1 • 1 1 Ta được: y ' = -
< 0 vì a > 1, nên hàm số giảm trên (0; +¥) và ta có f(t) = 0 có
(t +1)ln(a +1) t ln a
nghiệm t = a nên f(t) có nghiệm duy nhất t = a.
• Vậy: (1) (1) Û lna + 1(t + 1) = lnat Û t = a x2 – 2x – 12 = 8 + 4 5 ( thỏa *)
Û x2 – 2x – 20 - 4 5 = 0 Û x = 2 + 2 5 hoặc x = -2 5 .
• Vậy phương trình đã cho có hai nghiệm: x = 2 + 2 5 hoặc x = -2 5 . Bài 7. Giải phương trình: 2 3 2
3(x + 2x + 2) =10 x + 2x + 2x +1 (1). • 3 2 2
x + 2x + 2x +1 = (x +1)(x + x +1) nên điều kiện là: x ³ -1.
• x2 + 2x + 2 = (x +1) + (x2 + x + 1), đặt a = x +1, 2
b = x + x +1
• Với điều kiện x ³ -1: (1) trở thành:
3(a2 + b2) = 10ab Û 3a2 – 10ab + 3b2 = 0 Û (a – 3b)(3a – b) = 0 Û a = 3b hay a = b/3. • a = 3b Û x +1=3 2
x + x +1 Û x + 1 = 9(x2 + x + 1) Û 9x2 + 8x + 8 = 0 (vô nghiệm)
• a = b/3 Û 3a = b Û3 x +1 = 2
x + x +1Û9(x + 1) = x2 + x + 1 Û x2 - 8x - 8 = 0 Û x = 4 ± 2 6
Vậy phương trình có hai nghiệm: x = 4 ± 2 6 . Bài 8. Giải phương trình : 3 2
x - 3x + 2 = x +1 Điều kiện: x ³ -1 +) Nếu x > 3 thì:
x 3 - 3x 2 + 2 = (x – 1) 3 - 3(x- 1) > 4(x – 1) – 3(x – 1) = x – 1 >
x + 1 Chứng tỏ x > 3 không thỏa mãn Với -1 £ x £ 3
Đặt x = 2cost + 1 ( 0 £ t £ p )
Khi đó phương trình trở thành:
(2cost + 1) 3 - 3(2cost + 1) 2 + 2 = 2 cos t + 2 Û 8cos 3 t – 6cost = (c 2 os t + ) 1 Û t 2cos3t = 2cos 2 6 Û t cos3t = cos 2 é t é 4 p k ê t 3 = + 2kp t = 2 ê 5 Û ê Û ê ê t 4 p k t 3 2 p êt = ê = - + k ë 2 êë 7 2 - Bài 9. Giải phương trình 3 3 2 5 2 + 5 -1 = x x x 6 Hướng dẫn giải Điều kiện xác định: 2 5x - 2 ³ 0. 2 5x - 2 Đặt
= t(t ³ 0). Ta có 2 2 5x = 6t + 2. 6
Phương trình đã cho trở thành 3 3 2 3 2 3
x + 6t + 2 -1 = t Û x + 6t + 2 = (t +1) 3 3
Û x = (t -1) Û x = t -1 Û t = x + 1 ìx ³ 1 - 2 5x - 2 ï ìx ³ 1 - 2 Û = x +1 Û í - Û í Û x = 6 - + 28 . 5x 2 2 2 6 = (x +1) ï îx +12x + 8 = 0 î 6
Đối chiếu điều kiện ta được nghiệm là x = 6 - + 28 . Bài 10. [Đề chọn hsg tỉnh Trà Vinh, 2014-2015] Giải phương trình : +
- x é ( + x)3 - ( - x)3 2 ù 2 1 1 1 1 = 2 + 1- x êë úû
Bài 11. [Đề thi hsg tỉnh Vĩnh Long, 2015-2016] Giải phương trình 3 3 x +1 = 2 2x -1 Lời giải
Phương trình tương đương với 3 3
x + 2x = 2x -1+ 2 2x -1 Đặt 3
t = 2x -1, ta có phương trình 3 3
x + 2x = t + 2t Û (x -t)( 2 2
x + xt + t ) + 2(x -t) = 0 Û (x -t)( 2 2
x + xt + t + 2) = 0 ( ) 1 2 2 æ t ö 3t Vì 2 2
x + xt + t + 2 = x + +
+ 2 > 0 nên (1) Û x = t ç ÷ è 2 ø 4 é x =1 3 3
Û x = 2x -1 Û x - 2x +1= 0
(x )1( 2x x )1 0 ê Û - + - = Û 1 - ± 5 êx = êë 2 7 ìï 1 - ± 5 üï Tập nghiệm S = 1 í ; ý ï 2 î ïþ
Bài 12. Giải phương trình: 4 2 x + x + + ( 2 1 3 x + )
1 = 3 3x,với xÎ! Hướng dẫn giải. Từ pt ta thấy xñ0 1 æ 1 ö (1) 2 Û x + +1 + 3 x + = 3 3 ç ÷ 2 x è x ø 1
Đặt: t = x + ,t ³ 2 x Pt trở thành: 2
t -1 = 3 (3 - t) t ì £ 3 Û í Û t = 2 2 t î - 9t +14 = 0 1 x + = 2 Û x =1 x Giải phương trình 3 2 3 2
x -5x +12x - 6 = 2 x - x +1
Bài 13. Giải phương trình: 2
-x 2 - 3x + 1- x = x +1. 3- 4x . Hướng dẫn giải. ! ! ! ! ! ! Đặt u = ( x )
;1 ,v = ( 2 - 3x;- 1- x ) từ phương trình ta có .
u v = - u . v ! !
Như vậy: u,v ngược hướng 2 - 3x - 1- x Suy ra: = (1) x 1 1 - - 5
Giải (1) và thử lại ta thấy phương trình đã cho có nghiệm là x = 2
Bài 14. Giải phương trình: x = 10 + 10 + x ,với x Î R Hướng dẫn giải. Đk: x ³ 0
Đặt u =10 + x,u ³10 ì
Ta có: ïx = 10 + u íuïî =10+ x 8
x - u - ( x - u ) = 0 Û ( x - u )( x + u + ) 1 = 0 éx = u Û ê
ë u + x +1 = 0(VL) ìx ³10 21+ 41
x = u Û x = x -10 Û í Û x = 2
îx - 21x +100 = 0 2 21+ 41
Vậy phương trình có một nghiệm: x = , 2 4 Giải phương trình: 3 3 2
81x -8 = x - 2x + x - 2. 3 3x
Bài 15. Giải phương trình: x + = 1 2 x +1 Hướng dẫn giải.
Phương trình đã cho có điều kiện 0 < x < 1 3x 2 3x
Với điều kiện trên ta có: x + = 1 Û x +1 = x2 +1 1- x Û 2 2 2
(1- x) (x +1) = 9x 2 1 æ 1 ö Û x + - 2 x + - 7 = 0 2 ç ÷ x è x ø 1 ét = 1- 10 Đặt t = x + (t ³ 2) ta có: 2
t - 2t - 9 = 0 Û ê Û t = 1+ 10 x êt ë = 1+ 10 é 1+ 10 - 5 - 2 êx = Với t = 1+ 1 10 ta có : x + = 1+ 10 2 Û ê x ê 1+ 10 + 5 + 2 x = êë 2 1 + 10 - 5 - 2
So với điều kiện 0 < x < 1, phương trình đã cho có nghiệm x = 2
Bài 16. Giải phương trình sau trên tập số thực: x +1= (2x +1) x +1 + 2 . Hướng dẫn giải. 1
Điều kiện: x ³ - . Đặt y =
x +1 + 2 ( y > 2 ), 2
ìx +1+ y = 2(x +1)y ï ta thu được hệ í 2 ïîy - x +1 = 2 Suy ra 9 x +1+ y = ( 2
y - x +1)(x +1)y Û ( y x +1+ ) 1 ( 2
y + x +1- y x +1) = 0 Û ( y x +1+ )
1 ( y - 2 x +1) = 0 Û y = 2 x +1 15 - + 33 Do vậy
x +1 + 2 = 2 x +1 Û x = . 32 15 - + 33
Thay vào, thử lại thấy x = thỏa mãn. 32 -15 + 33 Đáp số: x = . 32
Bài 17. Giải phương trình: 2 x + 6 2
x + 4x = x +1. Hướng dẫn giải. ì 2
ïx £ - Ú x ³ 0 ì6 2 x + 4x ³ 0 ï 3 ï 2 ï1 - 5 1 + pt Û 5 íx + 1 - x ³ 0 Û í £ x £ ï 2 2 2 ï 2 2
î6x + 4x = (x + 1 - x ) ï6 2
x + 4x = (x + 1 - 2 x )2 ) 1 ( ï î 4 3 2 ) 1
( Û x + 1 - 2x - 2x - x = 0 2 1 æ 1 ö Û x +
- 2ç x + ÷ - 7 = 0 (x = 0 không là nghiệm) 2 x è x ø 1 ét = 1- 10 Đặt t = x + (t ³ 2) ta được 2
t - 2t - 9 = 0 Û ê x êët = 1+ 10 é 1 + 10 - 5 - 2 êx =
So với điều kiện ta được t = 1 + 10 Û ê 2 ê 1 + 10 + 5 + 2 êx = ë 2 1 + 5 1 + 10 - 5 - 2
So với điều kiện 0 £ x £ , ta được x = 2 2
Bài 18. Giải phương trình sau: 2 2 3 4
4 x + x +1 =1+ 5x + 4x - 2x - x với xÎ R. Hướng dẫn giải. 3 Đặt 2
t = x + x +1, t ³
. Khi đó phương trình trở thành: 2 4 2 4 2 t = t
- + t - Û t - t + -( 2 4 7 5 6 9 t - 4t + 4) = 0 10
Û (t - )2 -(t - )2 2
= Û ( 2t -t - )( 2 3 2 0
1 t + t - 5) = 0(*) 2 ét -t -1= 0 (*) Û ê 2 êët +t -5 = 0 3 + Với t ³ thì 2 t - t -1 = 1 5
0 có một nghiệm là t = 2 2 3 - + Với t ³ thì 2 t + t - 5 = 1 21
0 có một nghiệm là t = 2 2 2 1+ 5 æ1+ 5 ö Khi t = thì 2 2 x + x +1 = ç
÷ Û 2x + 2x -1- 5 = 0 2 ç 2 ÷ è ø 1 - - 3+ 2 5 - + + Û x = 1 3 2 5 hoặc x = . 2 2 2 -1+ 21 æ 1 - + 21 ö Khi t = thì 2 2 x + x +1 = ç
÷ Û 2x + 2x - 9 + 21 = 0 2 ç 2 ÷ è ø 1 - - 19 - 2 21 - + - Û x = 1 19 2 21 hoặc x = . 2 2 x + 2
Bài 19. Giải phương trình -1 = 3(x - 3)2 3 3 + 9(x - 3). 2 Hướng dẫn giải. Điều kiện x ³ 2 - Đặt 3
t = 9( x - 3) ta có 3 3 2 t + 27 x + 2 t + 45 t x = ; = ; 3( x - 3)2 3 = 9 2 18 3
Phương trình đã cho trở thành 3 2 3 t + 45 t t + 45 2 = + t +1 Û = t + 3t + 3 18 3 2 2 æ 3 ö 3 3 t + 45 2 Ta có 2
t + 3t + 3 = t + + > 0 nên ç ÷ = ( 2t + 3t + 3) è 2 ø 4 2 1
Ta được phương trình (2t - )
1 (t + 3)( 2t + 3t + 9) = 0 Û t = Ú t = 3 - 2 1 Với t = 217 thì x = 2 72 Với t = 3 - thì x = 0 11
Bài 20. Giải phương trình 2 2
2x + 1- x + 2x 1- x = 1. Hướng dẫn giải.
Ta có phương trình tương đương với 2 2
1 - x = 1 - 2x - 2x 1 - x 4 2 2 2 2 3 2
fi 1 - x = 1 + 4x + 4x (1 - x ) - 4x - 4x 1 - x + 8x 1 - x 2 2 2
€ x(1 - 4 1 - x + 8x 1 - x ) = 0 x È = 0 Í € Í 2 2 2 1
Í - 4 1 - x + 8x 1 - x = 0(1) Î Xét (1), đặt 2
y = 1 - x , suy ra y ≥ 0 và 2 2 x = 1 - y . Ta được 2 3
1 - 4y + 8y(1 - y ) = 0 € 8y - 4y - 1 = 0 2
€ (2y + 1)(4y - 2y - 1) = 0 1 + 5 5 - 5 € y =
. Từ đó suy ra x = ± . 4 8 5 - 5
Thử lại ta được nghiệm của phương trình là x = 0 và x = - . 8
Bài 21. Giải phương trình 3 3 x +1 = 2 2x -1. Hướng dẫn giải
Phương trình tương đương với 3 3
x + 2x = 2x -1+ 2 2x -1. Đặt 3
t = 2x -1, ta có phương trình 3 3
x + 2x = t + 2t Û (x -t)( 2 2
x + xt + t ) + 2(x -t) = 0 Û (x -t)( 2 2
x + xt + t + 2) = 0 ( ) 1 2 2 æ t ö 3t Vì 2 2
x + xt + t + 2 = x + +
+ 2 > 0 nên (1) Û x = t ç ÷ è 2 ø 4 3 3
Û x = 2x -1 Û x - 2x +1= 0 é x =1
(x )1( 2x x )1 0 ê Û - + - = Û 1 - ± 5 êx = êë 2 ìï 1 - ± 5 üï Tập nghiệm S = 1 í ; ý. ï 2 î ïþ æ 1 ö
Bài 22. (Chuyên Hưng Yên ) Giải phương trình 2 3 2 8x -15x + 9 = 1+ 5x - 2x - 2 ç ÷ è x ø 12 Hướng dẫn giải æ 1 2 ö 3 2 8x -15x + 9 = 1+ 5x - 2x - 2 ç ÷ è x ø 3 2 2 3
Û 8x -15x + 9x = (x +1) (x +1)(2x -1) + 3x - 3x -1(x ¹ 0) 3 2 2 3
Û (2x -1) - (3x - 3x -1) = (x +1) (x +1)(2x -1) + 3x - 3x -1 3 2 u
ìï -(3x -3x -1) = (x +1)v Đặt 3 2
u = 2x – 1, v = 5x - 2x - 2 , ta được hệ: í 3 2 v
ïî -(3x -3x -1) = (x +1)u
Trừ vế với vế hai phương trình trên, ta được: (u - v) ( 2 2
v + uv + u ) = (x + ) (v - u) Û u -v ( 2 2 1 (
) u + uv + v + x + ) 1 = 0 TH1: 3 2 3 2
u = v Û 2x -1= 5x - 2x - 2 Û 8x -17x +8x +1= 0 éx =1 2 (x 1)(8x 9x 1) 0 ê Û - - - = Û 9 ± 113 êx = êë 16 u 3 TH2: 2 2 2 2
u + uv + v + x +1 = 0 Û (v + ) + (2x -1) + x +1 = 0 2 4 u 2 2
Û 4(v + ) +12x -8x + 7 = 0 2 u 2 2 2
Û 4(v + ) + 4x + 2(2x -1) + 5 = 0 phương trình vô nghiệm. 2 9 ± 113
Vậy phương trình đã cho có ba nghiệm: x = 1; x = 16
Bài 23. Giải phương trình : 2
x - 4x + 3 = x + 5. Hướng dẫn giải
Đặt t = x + 5 (t ³ 0) .
Từ phương trình đã cho ta có : 4 2
t -14t - t + 48 = 0 (*)
Ta có : (*) Û (t - )( 3 2
3 t + 3t -5t -16) = 0 ét = 3 Û ê 3 2
ët + 3t -5t -16 = 0 (**)
Với t = 3 ta có x = 4
Đặt y = t +1 ( y ³ )
1 từ phương trình (**) ta có : 3
y -8y - 9 = 0(***)
Dùng máy tính điện tử hoặc khảo sát hàm số f ( y) 3
= y -8y -9 trên [1;+ ¥) ta thấy (***) có một nghiệm duy nhất y 0
Ta biểu diễn y dưới dạng: y = u + v 0 0 0 0 8 Ta có : 3 3
u + v + u + v 3u v -8 - 9 = 0 u ;v u v = 0 0 ( 0 0)( 0 0 ) nên có thể chọn sao cho : 0 0 0 0 3 13 ì 512 3 3 u ï v = Vậy ta có : 0 0 í 27 3 3 u ï + v = 9 î 0 0 512 Như vậy 3 3
u ;v được chọn là nghiệm của phương trình : 2 z + 9z - = 0 0 0 27 ì 9 139 3 u ï = + 0 ï 2 108 Suy ra: í ï 9 139 3 v = - 0 ïî 2 108
Ta tìm được nghiệm của (***) là 2 9 139 9 139 æ 9 139 9 139 ö 3 3 y = + + - .Suy ra : = ç 3 3 x + + - -1÷ - 5 0 2 108 2 108 ç 2 108 2 108 ÷ è ø
Vậy phương trình đã cho có hai nghiệm 2 æ 9 139 9 139 ö x = 4 ; = ç 3 3 x + + - -1÷ - 5 ç 2 108 2 108 ÷ è ø 3
Bài 24. Giải phương trình sau: 2 x - 3x + 1= - 4 x + 2 x + 1 . 3 Hướng dẫn giải: Ta có: 4 x + 2 x + = ( 2 x + x + )( 2 1 1 x ñ x + ) 1 > 0 € 2 x x + = ( 2 x x + ) ( 2 ñ3 1 2 ñ 1 ñ x + x + 1 ) 2 x - x + 1 Đặt t =
, t > 0 . Phương trình trở thành: 2 x + x + 1 È - 3 Ít = < 0 3 Í 2 x x 1 1 2 2 3 - + 2t + t - 1= 0 € Í € = 3 Í 1 2 x + x + 1 Ít = 3 ÍÎ 3 € x = 1
Dạng 3. Sử dụng hàm số
Câu 1. Giải các phương trình sau: a) 3 x + x - + ( 2 8 4 3 ln 4x - 2x + ) 1 = 0. b) ln( 2 x + x + ) 3 2 6
10 + x + 3x + 4x +12 = 0.
Câu 2. Giải phương trình sau: 1 x- x - æ ö a) log
x - 4x + 3 + 2006 + = 2 ( ) 2 4 2 2 2007 ç ÷ è 2007 ø 2 æ 2x + 3 ö b) 4 2 log ç ÷ = x - x - 2 2007 4 2 è x + x +1ø
Câu 3. Giải phương trình log 1 sin 1 2007 x x - - + = -1 2007 ( ) 1 sin . 14 Giải phương trình: 2 x 1 - 2 x 2 .3 x
+ (x -1).3 +1- x - x = 0
• Phương trình đã cho tương đương với: 2 2 x x 1 (x 1).(3 1) . x (3 - - - + -1) = 0
• Xét x = 0; x = ± 1: Thay vào (1) ta thấy đều thỏa nên phương trình có các nghiệm: x = 0; x = ± 1. 2 x x 1 - - - • 3 1 3 1
Xét x ¹ 0; x ¹ ± 1: Khi đó (1) Û + = 0 (2) 2 x x -1 3t -1
Với t ¹ 0, xét hàm số: f (t) = . t
* Với t > 0 thì 3t – 1 > 0 Þf(t) > 0 và với t < 0 thì 3t – 1 < 0 Þ f(t) > 0, do đó:
Vì (2) Û f(x) + f(x2 – 1) = 0 nên (2) vô nghiệm.
• Vậy phương trình đã cho có tất cả là 3 nghiệm: x = 0; x = ± 1.
Câu 4. [Đề chọn hsg tỉnh Trà Vinh, 2014-2015] Giải phương trình : 3 3 2
3x - 5 = 8x - 36x + 53x - 25
Câu 5. Giải phương trình: 3 2 3 2
8x -17x +10x - 2 = 2 5x -1. Ta có 3 2 3 2 3 2 3 2
8x -17x +10x - 2 = 2 5x -1 Û (2x -1) + 2(2x -1) = (5x -1) + 2 5x -1 (1). Đặt 3
f (t) = t + 2t thì 2
f '(t) = 3t + 2 > 0, t
" do đó f đồng biến và liên tục trên ! . Từ đó: 3 2 3 2
(1) Û f (2x -1) = f
5x -1 Û 2x -1 = 5x -1. ( ) éx = 0 2 x(8x 17x 6) 0 ê Û - + = Û . 17 ± 97 êx = êë 16
Vậy phương trình đã cho có 3 nghiệm.
Câu 6. Giải phương trình 3 2 2 3 3 2 - x 1
+ 0x -17 x +8 = 2x 5x - x (1) Hướng dẫn giải
Có x = 0 không là nghiệm của (1)
Xét x ¹ 0 , chia hai vế cho 3 x , được 10 17 8 5 3 2 - + - + = 2 -1 2 3 2 x x x x 1
Đặt y = ( y ¹ 0), khi đó có PT x 3 2 3 2
8y -17y +10y - 2 = 2 5y -1 ( y - )3 2 1 + 2(2y - ) 1 = 2 5y -1+ 3 2 2 5y -1 Suy ra f (2y - ) 3 2 1 = f 5y -1 ( )
Xét hàm số f (t) 3
= t + 2t .Vì f(t) là hàm số đồng biến trên R 15 nên f (2y - ) 3 2 1 = f 5y -1 « 2y - 1 = 3 2 5y -1 ( ) « 3 2
8y -17y + 6y = 0 « y( 2
8y -17y + 6) = 0 17 ± 97
Giải tìm được y = 0 (loại); y = 16 1 Tính x theo x = y 17 ìï - 97 17 + 97 üï
Tập nghiệm của phương trình (1) là í ; ý ï 12 12 î ïþ x + 5 10 - x
Câu 7. Giải phương trình 4 4 4 4 x + 5 - x = + (xÎ! ). 3 3 Hướng dẫn giải.
Điều kiện: 0 £ x £ 5 x + 2x (5 - x) + 2x x + 2(5 - x) Phương trình 4 4 4 4 4 Û 2 x + 5- x = + + (1) 3 3 3
Ta có: x = 0, x = 5 không là nghiệm phương trình.
Xét hàm số f (x) xa = , x > 0; ta có: a 1 - a -2
f '(x) = a x ; f ''(x) = a(a -1)x (*) 1 Áp dụng (*) với a = 4 x + 2x (5 - x) + 2x x + 2(5 - x) Ta có: 4 4 4 4 4 2 x + 5 - x £ + + 3 3 3 5
(1) Û x = 5 - x Û x = 5
. Vậy x = là nghiệm phương trình. 2 2
Câu 8. Giải phương trình 3 3 2 3
5 2x - 3x - 5x - 4 = -x +13x - 2, (x Î ! ) . Hướng dẫn giải. 3 5
ìï a = -x +13x - 2 (1) Đặt 3 3 2
a = 2x -3x -5x - 4 ta được: í 3 3 2
ïîa = 2x -3x -5x - 4 (2 3 3
(1) + (2) Þ a + 5a = (x -1) + 5(x -1) (*) Xét hàm số 3
f (t) = t + 5t trên ! có 2
f '(t) = 3t + 5 > 0 t " Î!
Þ hàm số f (t) đồng biến trên ! ; (*) 3 3 2
Û 2x -3x -5x - 4 = x - 1 16 é êx = 3 ê éx = 3 ê - - 3 3 5
Û x -8x - 3 = 0 Û ê Û x = 2 ëx 3x 1 0 ê + + = 2 ê ê 3 - + 5 x = êë 2 3 - - 5 3 - + 5
Thử lại, ta được: x = 3; x = ; x =
là nghiệm phương trình. 2 2
Câu 9. Giải phương trình : 3 2
x + x - 3x - 2 = 2 x + 2 trên [ 2; - 2]. Hướng dẫn giải
Đặt x = 2cost .Với xÎ[ 2;
- 2] ta có t Î[0;p .] æ t ö
Phương trình đã cho trở thành : 3 2
4cos t - 3cost + 2cos t -1 = 2cos (*) ç ÷ è 2 ø t é é æ ö cos = 0 êt = p ê ç ÷ æ t ö è 2 ø ê
Với t Î[0;p ] Ta có: (*) Û cos3t + cos 2t = 2cos Û ê Û t = 0 ç ÷ è 2 ø ê ê æ 5t ö cos =1 ê ê ç ÷ 4p ë è 2 ø êt = ë 5 p Vậy trên [ 2; - 4
2] phương trình đã cho có nghiệm x = 2
- , x = 2, x = 2cos . 5 2
Câu 10. Giải phương trình: x (2x- )1 2x 1 16 2.4 - - = 0. Lời giải 2 2
Biến đổi phương trình: x (2x- )1 2x 1 - 4x (2x- ) 1 4x 1 - 3 2 16 - 2.4 = 0 Û 2 = 2
Û 8x - 4x - 4x +1= 0 (1) f (x) 3 2 = - - + = f (- ) = - f (0) = æ 1 ö Đa thức 8x 4x
4x 1 0 có tối đa 3 nghiệm và ta có: 1 7; ; 1 f = 1 - ç ÷ è 2 ø f ( ) = f (x) ( 1 - ) f (- ) 1 . f (0) < æ ö æ 1 ö ; 1 . 1 liên tục trên khoảng ;1 và 0, f ( ) 1 0 . f < 0, f . f ç ÷ ( ) 1 < 0 ç ÷ è 2 ø è 2 ø f (x) = ( 1 - ) nên
0 có 3 nghiệm trên khoảng ;1 .
Do f (x) = 0 có đúng 3 nghiệm trong khoảng ( 1 - )
;1 , nên ta có thể đặt x = cos a với 0 < a < p .
Phương trình (1) trở thành: 3 2 a - a - a + = Û a( 2 a - ) = ( 2 8cos 4cos 4cos 1 0 4cos 2cos 1 4 1-sin a)-1 2 3 Û 4cos .
a cos 2a = 3 - 4sin a Û 4sin . a cos .
a cos 2a = 3sin a - 4sin a (do sin a > 0 )
é4a = 3a + k2p
Û sin 4a = sin 3a Û (k Î ê !)
ë4a = p - 3a + k2p
(với 0 < a < p ) 17 p p p Û a = 3 a = 5 a = 7 hay 7 hay 7 . 1 1
Câu 11. Giải phương trình sau: + = 2. 2 x 2 - x Hướng dẫn giải
Điều kiện x Î(- 2; 2) \{ } 0 . Đặt 2
y = 2 - x ;y>0 .
ìx + y = 2xy
Từ phương trình đã cho ,ta có hệ phương trình: í 2 2 îx + y = 2 ìS = 2P
Đặt S = x + y; P = xy đưa đến hệ phương trình: í 2 îS - 2P = 2 éS = 1 - 2
Þ S - S - 2 = 0 Û ê ëS = 2
S = 2; P=1Þ x=y=1 ì 1 - + 3 ì -1- 3 ïx = ïx= 1 ï 2 ï 2 S = 1 - ; P=- Þ í ;í 2 ï 1 - - 3 ï -1+ 3 y = y= ï 2 ï î î 2 -1- 3
Kết hợp với điều kiện, nghiệm pt đã cho là: x = 1 và x= . 2
Câu 12. Giải phương trình: 2
2x + 3 + x +1 = 3x + 2 2x + 5x + 3 -16.(x Î ! ). (Chưa giải)
Câu 13. Giải phương trình: 2
3x - 2 + x -1 = 4x -9 + 2 3x -5x + 2. (Chưa giải)
Dạng 3: Sử dụng hàm số
Bài 1. Cho phương trình: n 2
x - x - x -1 = 0 với n Î • , n > 2. Chứng minh rằng với mỗi số nguyên
n > 2, thì phương trình có một nghiệm dương duy nhất x n Hướng dẫn giải:
Xét hàm số f (x) n 2
= x - x - x -
1 với n nguyên, n > 2 (1) +) Ta có: f (x) n 1 nx - ¢ =
– 2x –1 . Do n > 2, nên khi x > 1 thì f ¢(x) > 0. Vậy f (x) là hàm số đồng biến trên (1;+¥). 18 Lại có: ( ) 1 = 2 - < 0; (2) = 2n f f
– 7 > 0 ( vì n nguyên và n > 2 Þ n ³ 3) Ta có: f ( )
1 f (2) < 0 và f (x) liên tục, đồng biến nên phương trình f (x) = 0 có nghiệm duy nhất trên (1;+¥).
+) Mặt khác với 0 < x < 1 thì n 2
x < x (do n > 2) suy ra f (x) < 0 với mọi 0 < x <1.
Như vậy ta đã chứng minh được (1) có nghiệm dương duy nhất với mọi n nguyên, n > 2. 1
Bài 2. Cho phương trình: 5 4 3 2
x - x - 5x + x + 4x -1 = 0 ( )1. 2
1. Chứng tỏ phương trình (1) có đúng 5 nghiệm. 5 x +1
2. Với x (i =1,5 1 S = å i
) là nghiệm của phương trình nghiệm, tính tổng: 5 4 - - i 1 = 2x x 2 i i Hướng dẫn giải 1
1. Xét hàm số: f (x) 5 4 3
= x - x - 5x + 4x - . 1 2
* f(x) là hàm số xác định và liên tục trên R. æ ö f (- ) 3 2 = 5 - ; f - = 2 ; f ç ÷ (0) = 1 - ; è 2 ø * Ta có: æ 1 ö 5 f = f ( ) 1 = - f ( ) 175 ; 1 ; 3 = ç ÷ è 2 ø 8 2 2 æ ö Þ æ 3 ö æ 1 ö f (- ) 3 2 . f - < 0 ; f - . f ç
÷ (0) < 0 ; f (0). f < 0 ç ÷ ç ÷ è 2 ø è 2 ø è 2 ø æ ö æ 1 ö f f . f ç ÷ ( ) 1 < 0 ; f ( ) 1 . f (3) < 0 ç ÷ è ø è 2 ø
Þ Phương trình f (x) = 0 có 5 nghiệm phân biệt x , x x , x , x , x , x 1 1 2 3 4 5 3 - 1 sao cho: 2 - < x <
< x < 0 < x < < x <1< x < 3 1 2 3 4 5 2 2
* Ta có x là nghiệm của (1) nên: i 1 5 4 3
x - x - 5x + 4x -1 = 0 i 2 i i i 5 4
Û x - x - = ( 3 2 2
2 2 5x - x - 4x i i i i i ) 5 x +1 Do đó: i S = åi=2( 3 2 1
5x - x - 4x i i i ) x +1 x +1
Xét biểu thức: g (x) = = 3 2
5x - x - 4x x(x - ) 1 (5x + 4)
Đồng nhất thức ta được: g (x) 1 2 5 = - + + 4x 9(x - ) 1 36(5x + 4) 19 5 5 5 1 1 1 1 1 1 Do vậy: S = - å + å + å 8 - i= x 9 = x i i 1 72 4 1 1 i i 1 = x + i 5
Mặt khác: f (x) = (x - x x - x x - x x - x x - x 1 ) ( 2 ) ( 3 ) ( 4 ) ( 5 )
f '(x) = (x - x x - x x - x x - x + 2 ) ( 3 ) ( 4 ) ( 5 )
(x - x x - x x - x x - x +... 1 ) ( 3 ) ( 4 ) ( 5 ) f '( x) 5 Þ 1
Với x ¹ x ta được: = å i f ( x) - i 1 = x xi và f (x) 4 3 2 '
= 5x - 2x -15x + 2x + 4 f '( ) 5 5 1 1 1 f '( ) 1 Do đó: = å Þ å = - = -12 f ( ) 1 - - i 1 = 1 x = x f i i 1 1 i ( )1 f '(0) 5 5 1 1 f '(0) = å Þ å = - = 4 f (0) - i 1 = x = x f i i 1 i (0) æ 4 ö æ 4 ö f ' - f ' - ç ÷ 5 5 ç ÷ è 5 ø 1 1 è 5 ø 12900 = å Þ å = - = - æ 4 ö 4 4 = = æ 4 ö i 1 i 1 4789 f - - - x x + f ç ÷ ç ÷ è 5 ø 5 i i 5 è 5 ø 8959 Vậy: S = - . 4789 Dạng 4: Đánh giá Bài 1.
Tìm tất cả các nghiệm nguyên dương của phương trình: 2 2
2x + 3y - 5xy + 3x - 2y - 3 = 0
Hướng dẫn giải
Xem (1) là phương trình bậc hai ẩn x ta có: (1) Û 2 x + ( - y) 2 2
3 5 x + 3y - 2y -3 = 0.
* Để (1) có nghiệm x nguyên điều kiện cần là: D = ( - y)2 - ( 2y - y- ) 2 2 3 5 4.2 3 2
3 = y -14y + 33 = k ( k nguyên, không âm) * Lại xem 2 2
y -14y + 33- k = 0 là phương trình bậc hai ẩn y . Để có nghiệm nguyên y điều kiện cần là d = -( 2 - k ) 2 2 ' 49 33
=16 + k = m là một số chính phương (m nguyên dương). Do 2 2
m - k =16 Û (m + k)(m - k) =16 và 16 = 16.1 = 8.2 = 4.4 nên ta có các trường hợp. ìm + k = 8 ìm = 5 +) TH1: í Û í
suy ra phương trình (1) có nghiệm ( ; x y) = (15;12),(1,2). îm - k = 2 îk = 3 ìm + k = 4 ìm = 4 +) TH2: í Û í
suy ra phương trình (1) có nghiệm ( ; x y) = (13;1 ) 1 ,(3, ) 3 . îm - k = 4 îk = 0 ìm + k =16 +) TH3 : í Loại. îm - k =1 20 Bài 2.
[Đề xuất, Chuyên Hùng Vương Phú Thọ, DHĐBBB, 2015] Giải phương trình 2
4 x +1 + 2 2x + 3 = (x -1)(x - 2). Lời giải Điều kiện: x ³ 1 - . Nhận thấy x = -
1 là một nghiệm của phương trình. Xét x > 1
- . Khi đó phương trình đã cho tương đương với
( x + - ) + ( x + - ) 3 2 4 1 2 2 2
3 3 = x - x - 2x -12 4(x - 3) 4(x - 3) 2 Û +
= (x - 3)(x + 2x + 4) x + 1 + 2 2x + 3 + 3 ( æ ö Û x - 3) 4 4 2 + - (x +1) - 3 = 0. 1 ( ) ç ÷ è x +1 + 2 2x + 3 + 3 ø Vì x > -
1 nên x + 1 > 0 và 2x + 3 > 1. Suy ra 4 4 + < 3, x +1 + 2 2x + 3 + 3 vì vậy 4 4 2 + - (x +1) - 3 < 0. x +1 + 2 2x + 3 + 3 Do đó phương trình 1
( ) Û x - 3 = 0 Û x = 3.
Vậy phương trình đã cho có 2 nghiệm là x = - 1 hoặc x = 3. 2 5x - 2 Bài 3.
[Đề thi hsg tỉnh Nghệ An, bảng A, 2015-2016] 3 3 2 x + 5x - 1 = . 6 Bài 4.
Ký hiệu [x] là số nguyên lớn nhất không vượt quá x. Giải phương trình 2
x -(1+[x]) x + 2015 = 0 . Hướng dẫn giải Ta có x ¹ 0. x - x + x - x + pt Û [x] 2 2 2015 2015 = Û x-1< £ x Û x ³ 2015. x x
[x] = aÎ! (a ³ 2015) 2 Þ x - (a + ) 1 x + 2015 = 0 2 a +1± (a + ) 1 - 8060 Û x = (*) 2 21 2
Do a ³ 2015 Þ x - (a + ) 1 x + 2015 = 0 a +1+ (a + )2 1 - 8060 Û x = ³ 2015 (t/ m); 2 a +1- (a + )2 1 - 8060 a +1- (a + )2 1 - 4a £ < 2015 (loai) 2 2 ì ïa (a )2 1 1 8060 ü + + + - ï Vậy S = í
; a Î !;a ³ 2015ý. 2 ï ï î þ 2. Có tham số Bài 1.
Tìm m để phương trình sau có hai nghiệm phân biệt (m+ ) 2 2
1 x + 2x + 2 + m = 2x + 4x +19, (x Î ! ).(1)
Hướng dẫn giải Đặt 2
t = x + 2x + 2 ; điều kiện: t ³ 1. Ta có: 2
t = x + 2x + 2 Û 2 2 2 2
x + 2x + 2 = t Û x + 2x + 2 - t = 0 (2)
Pt (2) có hai nghiệm phân biệt Û t Î(- ; ¥ - )
1 È(1;+¥).Vậy t >1. 2 2t - t +15
Thay vào phương trình ta được: 2
(m +1)t + m = 2t +15 Û m = t +1 (3) 2 ì 2t - t +15 ïy = (C) Đặt í t +1
ïîy = m (d) .
Ta có: số giao điểm của (C) và (d) là số nghiệm phương trình (3).
Phương trình (1) có hai nghiệm phân biệt khi phương trình (2) có đúng 1 nghiệm t > 1. 18 18
Xét hàm số y = 2t - 3+
; (t Î[1;+ ¥)) ; y ' = 2 - t +1 2 (t +1) .
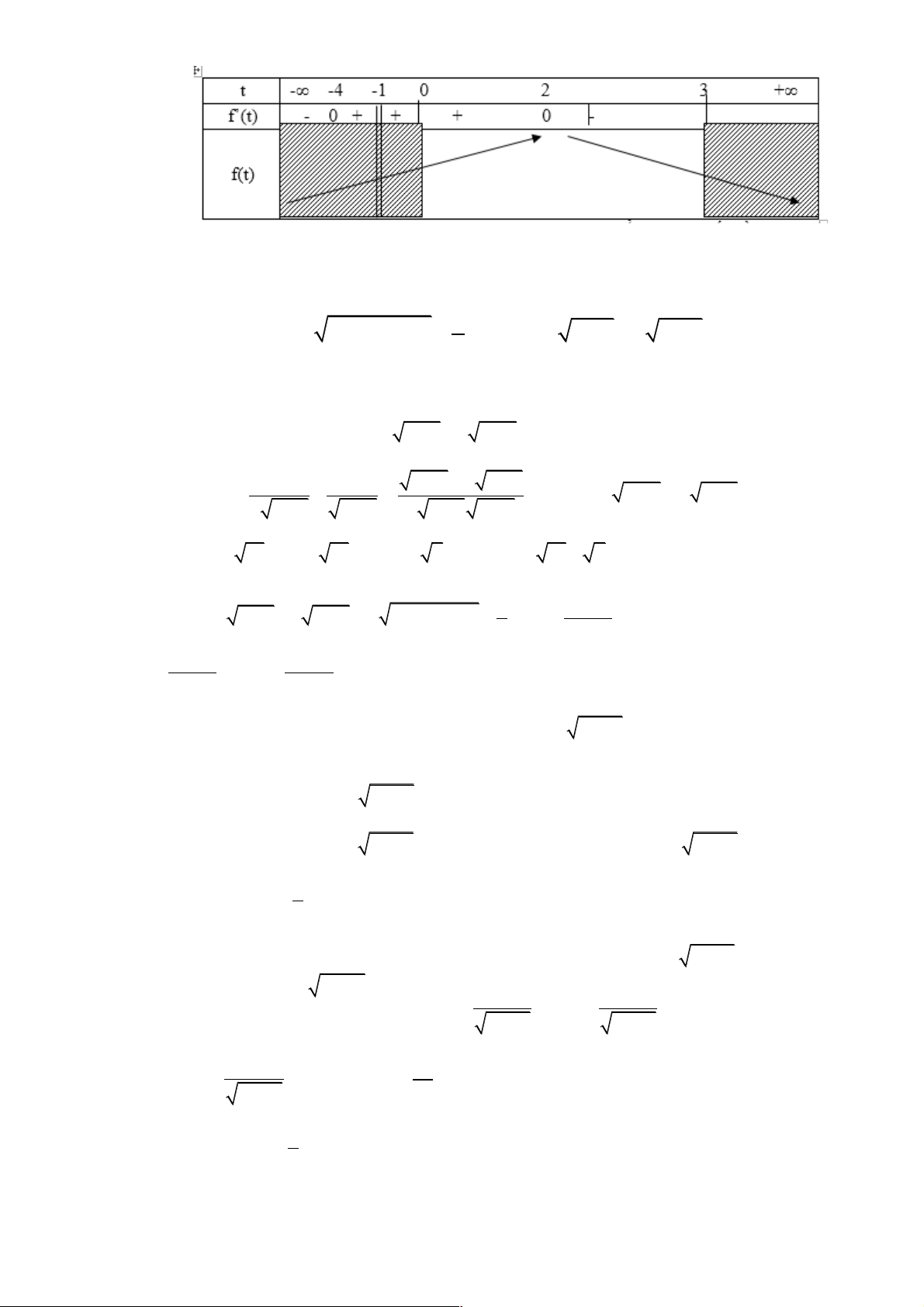
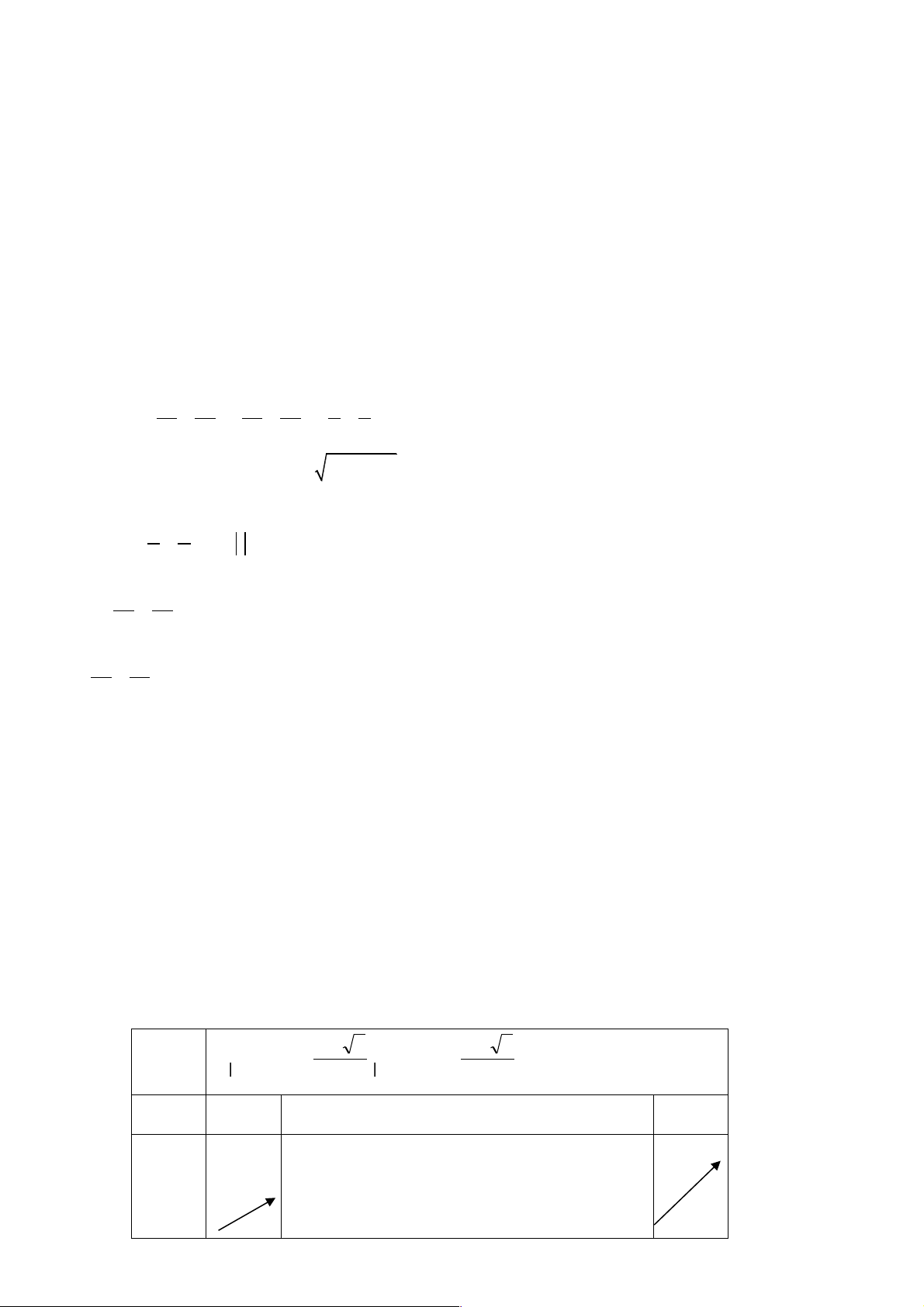
Cho y ' = 0 Û t = 2 Þ y = 7; lim y = +¥ x®+¥ . Bảng biến thiên t 1 2 +∞ y’ - 0 + y 8 +∞ 22 7 ém > 8
Vậy phương trình (1) có hai nghiệm phân biệt Û ê . ëm = 7 3. Bài 2.
Tìm tất cả các giá trị của tham số m để phương trình sau có ba nghiệm phân biệt lập thành một cấp số nhân: 3 2
x - 7x + (m + 6)x - m = 0. Hướng dẫn giải
Phương trình đã cho tương đương: éx =1 2
(x -1)(x - 6x + ) m = 0 Û . ê 2
ëx - 6x + m = 0 (1)
Phương trình đã cho có ba nghiệm phân biệt khi và chỉ khi (1) có hai nghiệm phân biệt khác ìD' = 9 - m > 0 ìm < 9 1, hay: í Û í (*). 2 1 î - 6.1+ m ¹ 0 îm ¹ 5
Khi đó, PT đã cho có ba nghiệm x , x và x = 1, trong đó x , x là nghiệm của (1). 1 2 3 1 2 ìx + x = 6 Theo định lý Viet ta có 1 2 í (2). x .x = m î 1 2
Xét các trường hợp sau: *) Nếu 2 2
x .x = x Û x = x (3). Từ (2) và (3) ta có hệ: 1 3 2 1 2 2 ìx + x = 6 ìx + x - 6 = 0 1 2 2 2 ï ï
éx = 2; x = 4;m = 8 2 2 1
íx .x = m Û íx = x Û . 1 2 1 2 êx = 3; - x = 9;m = 2 - 7 ï ï ë 2 1 2 3 x = x m = x î 1 2 î 2 ìm = 1 ï *) Nếu 2
x .x = x Û x .x = 1 (4). Từ (2) và (4) ta có hệ: íx + x = 6. 1 2 3 1 2 1 2 ïx .x =1 î 1 2
Vậy, có ba giá trị của m thỏa mãn yêu cầu bài toán là: m =1, m = 8, m = 2 - 7 . 2 Bài 3.
Tìm các giá trị của tham số m để phương trình x +
9 - x = - x + 9x + m có nghiệm Hướng dẫn giải. Lời giải:
Điều kiện: 0 £ x £ 9 2
PT (1) € x + 9 - x + 2 x(9 - x) = - x + 9x + m 2 2
€ 9 + 2 - x + 9x = - x + 9x + m (2) 2
Đặt t = - x + 9x 23 ' - 2x + 9 t = ' 9 2 t = 0 € x = Ta có: 2 - x + 9x ; 2 9 Do đó : 0 £ t £ 2
Phương trình (2) trở thành 2 2
9 + 2t = t + m € - t + 2t + 9 = m (3) 9 Xét hàm số 2
f (t) = - t + 2t + 9, 0 £ t £ 2 Ta có : ' '
f (t) = - 2t + 2 ; f (t) = 0 € t = 1 Bảng biến thiên : È 9˘
Phương trình (1) có nghiệm x 0; È 9˘ Œ
€ phương trình (3) có nghiệm t Œ 0; Í Í ˙ Î ˙˚ Í 2˙ Î ˚ 9 € - £ m £ 10 4 Bài 4.
Tìm a để phương trình sau (ẩn x ) chỉ có một nghiệm. 5a - 3 5(2a +1)(1- a) 1+ = x - a
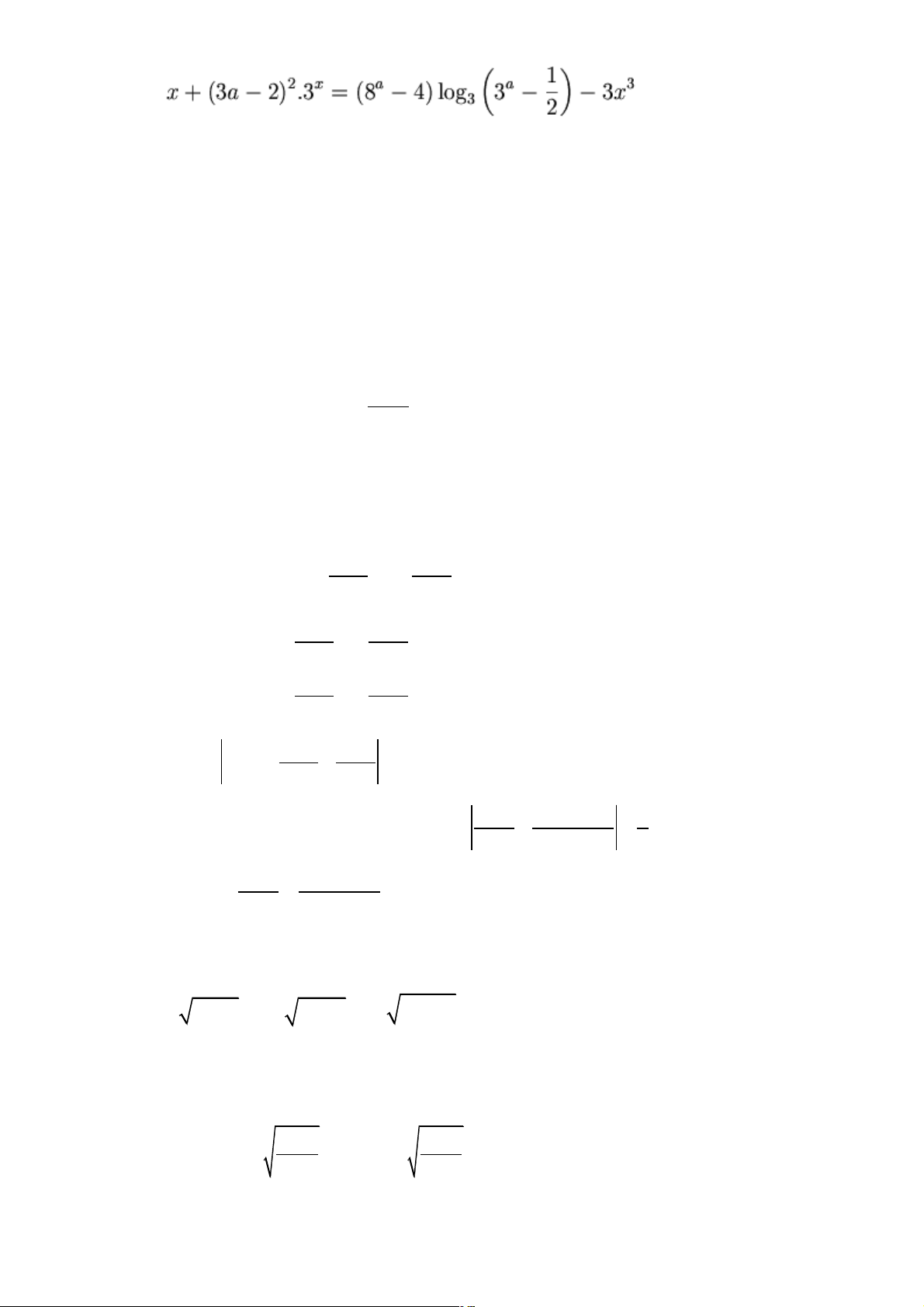
(x - a)(x - 3a +1) Bài 5. Cho hai phương trình sau: (1) 24 (2)
(a là tham số, x là ẩn số)
Tìm a để số nghiệm của phương trình (1) không vượt quá số nghiệm của phương trình (2). Bài 6. Cho phương trình: 2
ax + (2b + c) x + (2d + e) = 0 có một nghiệm không nhỏ hơn 4. Chứng minh rằng phương trình 4 3 2
ax + bx + cx + dx + e = 0 có nghiệm. Bài 7.
Với mỗi số tự nhiên k , gọi N (k) là số nghiệm của phương trình
2016x + 2017 y = k, x ³ 0, y ³ 0 . N(k)
Tính giới hạn sau L = lim k ®+¥ k Lời giải
Giả sử x , y là một nghiệm của phương trình 2016x + 2017 y = k , khi đó mọi nghiệm của 0 0
phương trình trên có dạng x = x + 2017t, y = y - 2016t,t Î! 0 0 y x
Vì x ³ 0 và y ³ 0 nên 0 0 ³ t ³ . 2016 2017
éé y ù é -x ù 0 0 - +1 êê2016ú ê2017ú ë û ë û
Suy ra N (k) = ê
êé y ù é -x ù 0 0 - êê ë 2016ú ê 2017 ú ë û ë û y x Suy ra 0 0 N(k) - - £ 3 . 2016 2017 N k
Kết hợp với 2016x + 2017y = ( ) 1 3 k , ta có - £ . 0 0 k 2016.2017 k N(k) 1 Vậy lim = k ®+¥ k 2016.2017 Bài 8.
Tìm các giá trị của tham số m để phương trình sau có nghiệm 4 2
3 x - 1 + m x + 1 = 2 x - 1. Hướng dẫn giải.
Điều kiện : x ≥ 1 2 Ê Á x 1 ˆ - ˜ x - 1 PT (1) 4 € Á ˜ 4 3Á ˜ + m = 2 (2) Á x + 1˜˜ x + 1 Ë ¯ 25 x - 1 x - 1 2 Đặt 4 t = , Do 4 4 0 £ = 1 -
< 1 fi 0 £ t < 1 x + 1 x + 1 x + 1
Phương trình (2) trở thành : 2 2
3t + m = 2t € m = - 3t + 2t (3) Xét hàm số 2
f (t) = - 3t + 2t , t 0; È Œ 1 Í ) Î Ta có : ' ' 1
f (t) = - 6t + 2 ; f (t) = 0 € t = 3 Bảng biến thiên :
Phương trình (1) có nghiệm x 1; È Œ + • È Í
)€ phương trình (3) có nghiệm t Œ 0;1 Î Í ) Î 1 € - 1 < m £ 3 Bài 9. Cho phương trình 2 x + 2 2
x - 2x + m.(x - 4).
+ 2 8 + 2x - x - 14 - m = 0 . 4 - x
Tìm m để phương trình có nghiệm thực. Hướng dẫn giải.
Với tập xác định D È = - 2;4 , P Í
) hương trình đã cho tương đương với Î 2 2 2
- (- x + 2x + 8) - m 8 + 2x - x + 2 8 + 2x - x - 6 - m = 0. Đặt t = 2
8 + 2x - x thì t Î [ 0; 3) 2 - t + 2t - 6
Xét hàm số f (t ) ;t 0 È;3 ;˘ = Œ t 1 ÍÎ ˙˚ + 2 - t - 2t + 8 f’(t) =
; f’(t) = 0 Û t = - 4 hoặc t = 2. 2 (t + 1)
Bảng biến thiên của hàm số f(t) trên đoạn [ 0; 3 ] 26
Phương trình đã cho có nghiệm x Î [ - 2; 4) Û Đường thẳng y = m cắt đồ thị hàm số f(t), t
Î [ 0; 3 ] Û - 6 ≤ m ≤ - 2 3
Bài 10. Cho phương trình: 2
21+ 4x - x - x + 3 = m( x +3 + 2 7 - x ), với m là tham số. 4
Tìm tham số m để phương trình có nghiệm thực. Hướng dẫn giải. Điều kiện: 3
- £ x £ 7 .Đặt t = x + 3 + 2 7 - x với xÎ[ 3, - 7] 1 1 7 - x - 2 x + 3 Ta có: t ' = - =
; y ' = 0 Û 7 - x = 2 x + 3 Û x = - 1 2 x + 3 7 - x 2 x + 3 7 - x t( 3
- ) = 2 10,t(7) = 10,t( 1
- ) = 5 2 suy ra: t Î é 10,5 2ù ë û 2 3 t -19 Do 2
t = x + 3 + 2 7 - x Û 21+ 4x - x - x + 3 =
nên phương trình trở thành: 4 4 2 2 t -19 t -19 = mt Û = m 4 4t
Bài 11. Tìm m để pt sau có nghiệm 2 2 2
8x + 4x +13 = m (2x +1) x + 3 . Hướng dẫn giải. 2 2 2
8x + 4x +13 = m (2x +1) x + 3 . Ta đưa pt về dạng đẳng cấp 2 2 2 2 2 2 2
8x + 4x +13 = m (2x +1) x + 3 Û (2x +1) + 4(x + 3) = m (2x +1) x + 3 1 Từ pt suy ra x > 2 2 2 2 2
(2x +1) + 4(x + 3) = m (2x +1) x + 3 Chia hai vế pt cho 2 x + 3, ta được 2 æ 2x +1 ö æ 2x +1 ö 2 Û ç ÷ - m ç ÷ + 4 = 0 2 2 è x + 3 ø è x + 3 ø 2x +1 -1 Đặt t =
, lập bbt với x >
tìm được t Î (0;2) 2 x + 3 2 4 P t trở thành 2 t + = m (1) t
Phương trình ban đầu có nghiệm khi và chỉ khi pt (1) có nghiệm thuộc t thuộc (0;2). 27
Tìm được m > 2 Ú m < -2
Bài 12. (Chuyên Hưng Yên). Giả sử với hai số dương a,b thì phương trình 3 2
x - ax + bx - a = 0, n b - 3n
có các nghiệm đều lớn hơn 1. Xác định giá trị của a,b để biểu thức P =
đạt giá trị nhỏ nhất n a
và tìm giá trị nhỏ nhất đó ( n là số nguyên dương cho trước). Hướng dẫn giải
Gọi x , x , x là các nghiệm của phương trình đã cho. 1 2 3
ìx + x + x = a 1 2 3 ï
Theo định lý Vi-et ta có íx x +x x + x x = b 1 2 2 3 3 1 ïx x x = a î 1 2 3
Theo bất đẳng thức AM - GM ta được 3
x + x + x ³ 3 x x x hay 3
a ³ 3 a Û a ³ 3 3 (*) 1 2 3 1 2 3 Theo bất đẳng thức 2
(x + y + z) ³ 3(xy + yz + zx); " ,
x y, z Î R thì 2 2
b = (x x + x x + x x ) ³ 3x x x (x + x + x ) 1 2 2 3 3 1 1 2 3 1 2 3 hay 2 2
b ³ 3a Û b ³ 3 . a n b - 3n 3n n a - 3n n 3n n 3n Suy ra P = ³ = 3 - ³ 3 - , do (*) n n n a a a (3 3)n 3n -1 Do đó ta có P ³ 3n
Đẳng thức xảy ra khi và chỉ khi a = 3 3;b = 3a = 9. Khi đó phương trình có ba nghiệm trùng nhau 3n -1
và đều bằng 3. Vậy giá trị nhỏ nhất của P là
khi a = 3 3;b = 9. 3n 1 1
Bài 13. Giải phương trình 4 2 x - x + - = 0. 4 2 x x
Bài 14. Tìm m để BPT sau vô nghiệm: ( 2 m - ) 2
4 x + 2(m - 2) x +1³ 0 2 1- 1- 4x
Bài 15. Giải bất phương trình < 3 x
Bài 16. Chứng minh phương trình: 4 3 2 2
- x + mx + nx + px + 2011= 0 có ít nhất 2 nghiệm với " , m , n p Î ! Hướng dẫn giải Xét phương trình: 4 3 2 2
- x + mx + nx + px + 2011= 0 (1) Xét hàm số: 4 3 2 f (x) = 2
- x + mx + nx + px + 201 1 28 4 3 2
lim f (x) = lim ( 2
- x + mx + nx + px + 2011) = -¥ Þ b
$ > 0 sao cho f (b) < 0 x®+¥ x®+¥ 4 3 2
lim f (x) = lim ( 2
- x + mx + nx + px + 2011) = -¥ Þ a
$ < 0 sao cho f (a) < 0 x®-¥ x®-¥ f (0) = 2011> 0
Hàm số f (x) liên tục trên các đoạn [ ;0 a ] và [0;b];
ì f (a). f (0) < 0 í
Þ phương trình có ít nhất 1 nghiệm x Î ;0 a x Î 0;b . 2 ( ) 1 ( ) và ít nhất 1 nghiệm
î f (0). f (b) < 0
Vậy phương trình có ít nhất 2 nghiệm.
Bài 17. Cho các phương trình: 2 2
x - (m +1)x + m - 2 = 0 (1) 4 3 2 2
x + mx - x + 2x + m = 0 (2)
trong đó x là ẩn số và m là tham số (0 < m < 1).
1) Chứng tỏ rằng phương trình (1) có đúng 2 nghiệm phân biệt và 1 nằm trong khoảng nghiệm.
2) Chứng minh phương trình (2) có nghiệm. (Chưa giải)
Bài 18. Cho phương trình 3 2
x + 3x + 2mx - m + 2 = 0; mÎ R .
Tìm tất cả các giá trị của m để phương trình trên có 3 nghiệm phân biệt x , x , x thoả mãn điều kiện: 1 2 3
x < x <1< x . 1 2 3 (Chưa giải)
Bài 19. Tìm điều kiện của tham số a, b để phương trình sau có các nghiệm lập thành cấp số cộng: 3 2
x - 3x + ax + b = 0. (Chưa giải)
Bài 20. Tìm m để phương trình sau có nghiệm duy nhất: 2 + x + 5 - x - (2 + x)(5 - x) = m (Chưa giải)
Bài 21. Tìm các giá trị của a để phương trình sau chỉ có một nghiệm: 5a - 3 5(2a +1)(1- a) 1+ = . x - a
(x - a)(x - 3a +1) (Chưa giải)
Bài 22. Giả sử phương trình 3 2
x + x + ax + b = 0 có 3 nghiệm phân biệt.
Hãy xét dấu của biểu thức: 2 a - 3b . Hướng dẫn giải 3 2
y = f (x) = x + x + ax + b = 0. + Tập xác định: R. 2
y ' = 3x + 2x + a là tam thức bậc hai có biệt số D ' = 1- 3 . a + Pt: 3 2
x + x + ax + b = 0có 3 nghiệm phân biệt nên y ' = 0 có 2 nghiệm phân biệt x , x và 1 2 29
f (x ). f (x ) < 0. 1 2 Ï1 Ô - 3a > 0 + Suy ra: Ô Ì
( x , x là hai nghiệm của phương trình 2
3x + 2x + a = 0). f
Ô (x ). f (x ) < 0 1 2 Ô Ó 1 2
+ Thực hiện phép chia đa thức ta được: Ê ˆ 3 2 1 1 1
f (x) = x + x + ax + b = Á Á x ˜
+ ˜ y '+ [(6a - 2)x + 9b - a]. 3 Á Ë 9˜¯ 9 1 1 Suy ra f (x ) =
(6a - 2)x + 9b - a ; f (x ) =
(6a - 2)x + 9b - a . 1 [ 1 ] 2 [ 2 ] 9 9 + 2 2
f (x ). f (x ) < 0 € (6a - 2) x x + (6a - 2)(9b - a)(x + x ) + (9b - a) < 0. 1 2 1 2 1 2 2 a
+ Vì x , x là 2 nghiệm của phương trình: 2
3x + 2x + a = 0nên x + x = - ; x .x = . 1 2 1 2 1 2 3 3 a 2 Do đó: 2 2
(6a - 2) - (6a - 2)(9b - a) + (9b - a) < 0. 3 3 suy ra: 2 2
4(3a - 1)(a - 3b) + (9b - a) < 0. + Vì 2
(9b - a) ≥ 0 và 3a - 1< 0 nên 2
a - 3b > 0.
Bài 23. Cho phương trình: 5 2 4
x - 34x + a -
(x - 1)(x - 33) = . 1
a/ Giải phương trình khi a = 64.
b/ Tìm a để phương trình có nghiệm. Hướng dẫn giải Câu a: +Đặt u = 5 2
x - 34x + a v = 4 (x - 1)(x - 33) . 5 4 Ï u
Ô - (u- 1) = a - 33 +Ta có hệ Ô Ì (I). v Ô = u- 1≥ 0 Ô Ó +Hàm số 5 4
f (u) = u - (u - 1) có 4 3
f '(u) = 5u - 4(u- 1) > 0 " u [ Œ1;+ • ) nên f(u) tăng trên [1; + ¥).
+ a = 64, f (u) = 31= f (2) và f (u) tăng nên hệ (I) chỉ có một nghiệm: (u = 2,v = ) 1 từ đó ta có
nghiệm của phương trình là: x = 17 ± 257. Câu b:
+ f (u ) tăng trên [1; + ¥) mà f ( ) 1 =
1 nên phương trình có nghiệm khi a – 33 ³ 1 hay a ³ 34.
Bài 24. Giải và biện luận phương trình theo tham số m: 2 2 2
(lg cos x) - m log cos x - m + 2 = 0. Hướng dẫn giải 2 2 2
(lg cos x) - m log cos x - m + 2 = 0(1). 30 p p
+Điều kiện: cos x > 0 € -
+ k2p < x < + k2p, k Z Œ . 2 2 2 2 Ï t
Ô - 2mt - m + 2 = 0 (2)
Đặt t = lg cos x. Phương trình trở thành: Ô Ì . t Ô £ 0 Ô Ó S Xét tam thức bậc hai 2 2
f (t) = t - 2mt - m + 2 = 0 có: 2 2 a = 1; = ,
m D ' = 2(m - 1), f (0) = - m + 2. 2
+Trường hợp 1: t = 0 là nghiệm của (2).Khi đó ta có m = ± 2 .
+ m = 2 : (2) € t = 0 hay t = 2 2 nên (1) Û lgcosx = 0 Û cosx = 1Ûx =2kp, kÎZ.
+ m =- 2 : (2) € t = 0 hay t = -2 2 nên (1) lg È cos x = 0 x È = 2kp Û Í Í € , k Z Œ . Í Í -2 2 lg cos x = - 2 2 x Î Í = ± a cco r s10 + 2kp Î
+Trường hợp 2: Phương trình (2) có 2 nghiệm t1, t2 khác 0 (t1 £ t2): 2 2
t = m- 2(m - 1) ; t = m+ 2(m - 1) . 1 2
Với điều kiện (1) có nghiệm nên ta chỉ cần xét 2 trường hợp sau: a/ t £ t < 0; b/ t < 0 < t . 1 2 1 2 2 Ï D Ô ' ≥ 0 Ï 2 Ô (m - 1) ≥ 0 Ô Ô Ô Ô a/ t t 0 Ì S Ô /2 0 Ìm Ô £ < € < € < 0 € - 2 < m £ - 1. 1 2 Ô Ô Ô Ô 2 f Ô (0) > 0 Ô Ô Ó - m - 2 > 0 Ô Ó
Khi đó (2) có hai nghiệm t 2 m± 2(m - 1)
1, t2 âm nên (1) có các họ nghiệm: x = ± arccos10 + 2kp,k Z Œ . b/ 2
t < 0 < t € af (0) < 0 € - m + 2 < 0 € m < - 2 hay m > 2. 1 2 Khi đó (1) Û 2 m- 2(m - 1)
lgcos x = t € x = ± a cco r s10 + 2kp,k Z Œ . 1 +Kết quả:
+ m < - 2 : (1) có nghiệm: 2 m- 2(m - 1) x = ± a cco r s10 + 2kp,k Z Œ .
+ m = - 2 : (1) có nghiệm: -2 2
x = k2p; x = ± a c r cos10 + 2kp,k Z Œ + - 22 m± 2(m - 1) x = ± a cco r s10 + 2kp,k Z Œ + m = 1:
- (1) có nghiệm x = ± a c
r cos0,1+ 2kp,k Z Π.
+ - 1+ m = 2 : (1) có nghiệm x = k2p,k Z Œ .
+ m > 2 : (1) có nghiệm: 2 m- 2(m - 1) x = ± a cco r s10 + 2kp,k Z Œ . 31
BÀI TẬP CHƯA CÓ LỜI GIẢI é2x +1ù 1. Giải phương trình: 2 2
- éx ù = é-x ù. êë 3 ú ë û ë û û 1 1 2. Giải phương trình: + =1 2 2 x (4 - 3x)
3. Cho trước các số nguyên dương a, .
b Chứng minh rằng phương trình 2 x - axy + ( 2 a - b) 2 2 2
4 y + 4by = z có vô số nghiệm nguyên dương. 4. Giải phương trình: 4 3
x –10x – 2(a –1 )
1 + 2(5a + 6-) x + 2a + a = 0. Trong đó a là tham số. 5. Giải phương trình: 1996 1995 1995- x + 1996 - x = 1
6. Giải các phương trình sau: x + 7 1 a) 2
+ + 8 = 2x + 2x -1 ; b) 3 2
x = x + x + . x +1 3 c) 2 2
x -1 = 2x x - 2x 7. Giải phương trình: 2 2
x -3x + 2 + x + x -1 = 0
2. BẤT PHƯƠNG TRÌNH 1. Không có tham số
Dạng 1: Biến đổi tương đương 1 3x Bài 1. Giải bất phương trình: +1 > . 2 2 1- x 1- x (Chưa giải) 9 9 Bài 2.
Giải bất phương trình: 9 - < x - x - x x Lời giải ì 9 9 - ³ 0 ï x ï ï 9 éx ³ 3
Điều kiện: íx - ³ 0 Û x ê ï ë 3 - £ x < 0 ïx ¹ 0 ïî *) Nếu 3 - £ x < 9 9
0 thì x - x - < 0 < 9 - suy ra bất phương trình vô nghiệm. x x 9
*) Nếu x ³ 3 Þ x - x - > 0nên bất phương trình tương đương với x 9 9 9 9 2 2 9 - < x - 2 .
x x - + x - Û x - 9 - 2 .
x x - + x > 0 x x x x 32 ìx ³ 3 ìx ³ 3 ï ï 2 2
( x - 9 - x) > 0 Û í Û í 1± 37 2 ïî x -9 ¹ x ïx ¹ î 2 1± 37
Vậy tập nghiệm là S = [3;+¥)\{ } 2 Bài 3. Giải bất phương trình: 2 2
2(x -1) x + 2x -1 £ x - 2x -1. (1) Hướng dẫn giải éx ³ 1 - + 2 Điều kiện: 2
x + 2x -1 ³ 0 Û ê . êëx £ 1 - - 2
Û x - - x + x - - x + ³ 2 2 Û 2
- - x + 2x -1 2x - x + 2x -1 ³ 0 ( )2 2 2 (1) 1 2 1 ( 1) 0 ( )( ) 2
Û 2x - x + 2x -1 £ 0 (do 2 2
- - x + 2x -1 < 0) 2
Û 2x £ x + 2x -1 (*) +) Với x £ 1 - - 2 thì (*) luôn đúng. +) Với x ³ 1
- + 2, bình phương 2 vế của (*) suy ra vô nghiệm.
Vậy, bất phương trình có nghiệm x £ 1 - - 2. Bài 4. Giải bất phương trình: 2 2
x - 4x + 3 - 2x - 3x + 3 ³ x - . 1 Hướng dẫn giải é êx ³ 3 2
ìïx - 4x + 3 ³ 0 ê +) Điều kiện: í Û x =1 2 ê
ïî2x - 3x +1³ 0 ê 1 êx £ ë 2
+) Với x=1 BPT hiển nhiên đúng suy ra x=1 là nghiệm +) Với x ³
3 suy ra BPT Û (x - 3)(x -1) - (x -1)(2x -1) ³ x - 1 chỉ ra vô nghiệm
+) Với x £ 2 suy ra BPT Û (1- x)(1- 2x) - (1- x)(3 - x) £1- x. 1 Chỉ ra nghiệm x £ 2 33 éx =1
+) Kết luận: BPT có nghiệm ê 1 êx £ ë 2 Bài 5.
Giải bất phương trình sau: 2 2 2
x + x -10x + 9 > x + 2 x -10x + 9. Hướng dẫn giải
Điều kiện x Î(- ;1 ¥ ]È[9;+¥). Với 2 2
x + x -10x + 9 > 0 Û x -10x + 9 > -x suy ra 2 2
x -10x + 9( x -10x + 9 - 2 + 2x) > 0 do đó 2
x -10x + 9 > 0và 2
x -10x + 9 > 2 - 2x . 5
Kết luận tập nghiệm S = (- ;1) È (9;+¥) . 3 Dạng 2: Đặt ẩn phụ Bài 1.
Giải bất phương trình: 3 x +1 + 2x + 4 < 3- x 2. (Chưa giải) Bài 2. Giải bất phương trình: 2
2x - 4x + 6 - 2x -1 > x - 2, xÎ!. Hướng dẫn giải. 1 Điều kiện x ³ . 2
Biến đổi bất phương trình về dạng: 2
2(x - 2) + 2(2x -1) > x - 2 + 2x -1 u ì = x - 2 ï Đặt:
Khi đó, bất phương trình có dạng: 2 2
2u + 2v > u + v (1) í ïv = 2x -1 ³ 0 î Ta có: ( 2 2
2 u + v ) ³ (u + v)2 = u + v ³ u + v
Dấu đẳng thức xảy ra khi u = v
Vậy (1) Û u ¹ v ìx ³ 2 ï
Xét trường hợp u = v , ta có: 2x -1 = x - 2 Û íéx =1 Û x = 5 ïê îëx = 5 é1 ö
Vậy tập nghiệm của bất phương trình là: ;+¥ \ ê ÷ { } 5 . ë2 ø Bài 3. Giải phương trình: 2
x - 3 + 5 - x ³ x -8x +18. 34
Dạng 3: Sử dụng hàm số æ x + y ö 2y Bài 1. Chứng minh rằng: ln > với x > 0 và y > 0. ç ÷
è x ø 2x + y • x + y Đặt t = >1 x • x + y
Vì x > 0 và y > 0 nên: t =
Û tx = x + y Û y = x(t -1) x y x t - t - • 2 2 ( 1) 1 Do đó: = = 2 . 2x + y
2x + x(t -1) t +1 t - • 1
Bài toán trở thành chứng minh: ln t > 2 với mọi t > 1. t +1 • t -1
Xét hàm số y = f(t) = ln t - 2 với mọi t > 1. t +1 (t - )2 1 • y’ =
³ 0 nên hàm số đồng biến trên khoảng (0; +¥). 2 t(t +1) t - • 1
Do đó: t > 1 Þ f(t) > f(1) = 0 Þ ln t - 2 >0. t +1 t - • y 1
Cách giải khác: Đặt t = và đưa đến chứng minh: ln t > 2 . Giải tương tự. x t +1 Bài 2. Giải bpt cos4x+3 2 cos4x+3 2 cos4x+3 (2x) + (1- x ) ³ (1+ x ) , 0 < x < 1 (1).
• (1đ) Biến đổi về dạng: ay + by ³ 1: Chia hai vế của (1) cho (1 + x2)cos4x + 3 > 0 ta được: os c 4x + 3 os c 4x + 3 2 æ 2x ö æ1- x ö (1) Û + ç ÷ ç ÷ ³ 1 (2). 2 2 è1+ x ø è1+ x ø
• (4 đ) Tìm ra nghiệm của (1): 2 2 2 2 æ x ö æ - x ö • 2x 1- x 2 1
Vì 0< x < 1 nên: 0 < <1,0 < <1 và + ç ÷ ç ÷ = 1 2 2 1+ x 1+ x 2 2 è1+ x ø è1+ x ø os4x c + 3 os4x c + 3 2 æ 2 2 x ö æ - x ö 2 æ x ö æ - x ö • 2 1 2 1 Và cos4x + 3 ³ 2 nên: + £ + ç ÷ ç ÷ = . 1 ç 2 ÷ ç 2 ÷ è1+ x ø è1+ x ø 2 2 è1+ x ø è1+ x ø p
• Dấu bằng xảy ra khi chỉ khi: cos4x + 3 = 2 Û cos4x = -1 Û x = (vì 0< x <1). 4 p
Vậy phương trình có nghiệm duy nhất: x = . 4 æ p p ö p
Cách khác: Đặt x = tgt, t Î - ;
nên 0< x <1 Û 0 < t < . ç ÷ è 2 2 ø 4
(2) Û (sin2t)cos4x + 3 + (cos2t)cos4x + 3 ³ 1. Dạng 4: Đánh giá Bài 1.
[Đề chọn HSG Sở Quảng Trị,2010] Giải bất phương trình : 2
x - 3 + 5 - x ³ x -8x +18. 2. Có tham số Bài 1.
Tìm m để bất phương trình sau có nghiệm duy nhất: 35 log 11+ 2
log ( x + mx + 10 + 2
4) log (x + mx + 12) ≥ 0. m 1 m 7 Hướng dẫn giải.
Điều kiện: m > 0 và m π 1, 2 x + mx + 10 ≥ 0.
Bất phương trình đã cho tương đương với: 1- 2
log ( x + mx + 10 + 2
4) log (x + mx + 12) 7 11 ≥ 0. (*) log m 11 Đặt 2
u = x + mx + 10, u ≥ 0.
+ Với 0 < m < 1: (*) € f (u)= log
u + 4 log u + 2 ≥ 1 7 ( ) 11( ) Ta thấy f (9)= 1 và f (u
)là hàm đồng biến nên ta có:
f (u)≥ f ( ) 2 2
9 € u ≥ 9 € x + mx + 10 ≥ 9 € x + mx + 1≥ 0
Vì phương trình trên có 2
D = m - 4 < 0 với 0 < m < 1 nên phương trình trên vô nghiệm Þ bất
phương trình đã cho vô nghiệm.
+ Với m > 1: Ta có: f (u)£ 1= f (9)€ 0 £ u £ 9. ÏÔ 2
x + mx + 10 ≥ 0 (1) 2
€ £ x + mx + 10 £ 9 Ô € Ì . Ô Ô 2 x + mx + 1£ Ó 0 (2) Xét phương trình 2
x + mx + 1= 0 có 2 D = m ñ 4.
Nếu 1< m < 2 € D < 0 Þ (2) vô nghiệm Þ bất phương trình đã cho vô nghiệm.
Nếu m > 2 fi D > 0 fi phương trình trên có 2 nghiệm đều thoả mãn (1) và (2) Þ bất phương trình
đã cho có nhiều hơn một nghiệm.
Nếu m = 2 Þ (2) có nghiệm duy nhất x = - 1 Þ bất phương trình đã cho có nghiệm duy nhất x = - 1.
Vậy giá trị cần tìm của m là: m = - 2. Bài 2.
Tìm m để bất phương trình 2
x - 2x + 4 (4 - x)(x + 2) -18 + m ³ 0 đúng với mọi x Î[- ; 2 .] 4 Bài 3.
[Đề hsg Dương Xá,2008-2009] Cho bất phương trình: 2
x + 4 - x £ 4x - x + m + 3
Xác định m để bất phương trình nghiệm đúng với mọi xÎ[0; ] 4 . Lời giải 0 ì £ x £ 4 0 ì £ x £ 4 Điều kiện í Û í 2 2
î4x - x + m + 3 ³ 0(2)
îm ³ x - 4x -3(2) 36
Điều kiện cần để bpt (1) nghiệm đúng với x
" Î[0;4]thì (2) nghiệm đúng x " Î[0;4] Xét f(x)= x2-4x-3 Bảng biến thiên x 0 2 4 f(x) -3 -3 -7
Từ bảng biến thiên (2) đúng với x " Î[0;4]
Û m ³ max f (x) Û m ³ 3 - [0;4] PT Û 2 2
4 + 2 4x - x £ 4x - x + m + 3 Đặt 2
t = 4x - x Bảng biến thiên x 0 2 4 2 t 0 0
Dựa vào bảng biến thiên suy ra 0 £ t £ 2
Bất phương trình trở thành g(t)=-t2+2t+1 £ m (3)
Để bất phương trình đầu nghiệm đúng với x
" Î[0;4]thì (3) có nghiệm đúng với t
" Î[0;2]. Û m ³ max g(t) [0;2] 37 t 0 1 2 2 g(t) 1 1
Từ BBT suy ra m ³ 2 .
Kết luân m ³ 2 thì bpt (1) nghiệm đúng x " Î[0;4]. III. HỆ PHƯƠNG TRINH 1. Không có tham số
Dạng 1: Biến đổi tương đương
ìïy x -1+5 = 3x (2)
Bài 25. Giải hệ phương trình: í 3 ïîx + (x + ) 2 3
1 y + 2y = y + ( y + ) 2 1 x + 2xy (3) Hướng dẫn giải Điều kiện: x ³ . 1 é y = x -1 é y = x -1
Phương trình (3) Û (x - y - )( 2 2
1 y -2y + x ) = 0 Û ê Û ê 2 2
ë y - 2y + x = 0 êë( y - )2 2 1 + x -1= 0 é y = x -1 ê Û ìx =1 ê Û y = x - .1 í ( ì v x ³1) êëîy =1
(vì (1;1) không thỏa phương trình(2))
Thay vào phương trình (2), ta được : 3 é x -1 =1 éx = 2
( x -1) -3(x - ) 1 + 2 = 0 Û ê Û ê ( ) n .
êë2 x -1 = x -3 êëx = 5+ 2 3 Vậy ( , x y) = (2; ) 1 ;( , x y) = (5+2 3;4+2 3). 2 2
ìï x - y -6 = 2 x - y -3 x + y
Bài 26. Giải hệ phương trình sau trên tập số thực: í 2 3 3
ï x - 2 - 2 y + x + 5y -15 = 0 î Hướng dẫn giải 38 2 2
ìï x - y -6 = 2 x - y -3 x + y (1) Đặt í . 2 3 3
ï x - 2 - 2 y + x + 5y -15 = 0 (2) î ìx - y ³ 0 ï
Điều kiện: íx + y ³ 0. ïx ³ 2 î
(1) Û ( x + y - 2)( x - y + 3) = 0 Û y = 4 - x Thay vào (2) ta được: 3 2
3 x - 2 - 2 4 - x + x -5x + 5 = 0 æ x 3 æ ö 3 ö - - Û x 3 - 2ç
÷ + (x - 3)(x - 2) = 0 ç ÷ è x - + ç 3 2 3 2 1ø
(4 - x) + 4 - x +1÷ è ø éx = 3 ê Û 3 2 ê + + x - 2 = 0 (*) 3 2 3 ê x - 2 +1
(4 - x) + 4 - x +1 ë
Phương trình (*) vô nghiệm do: x ³ 2 Þ x - 2 ³ 0 Þ VT > 0 .
Vậy x = 3 và y = 1 là nghiệm của hệ phương trình. 3 2 2 3
ìx y(1+ y) + x y (2 + y) + xy -30 = 0
Câu 8. Giải hệ phương trình: í 2 2 î
x y + x(1+ y + y ) + y -11 = 0
ìï x + 2y + 4x + y = 5
Câu 9. Giải hệ phương trình: í ( ,x yÎ! ). ïîx - y =1 3 2 ì 3 2 6 4 x xy x +xy y + y + e - e + ln = 0 ï
Câu 10. Giải hệ phương trình: 6 4 y + í y ( y > 0) ï 2
8 3 - 4y = 3+ 24x -16 î x Lời giải 3
Điều kiện: x > 0; 0 < y £ . 4 3 2 x xy x xy y y + - Ta có 3 2 6 4 3 2 + + e - e + ln = 0 x + Û xy e + ln( 3 2 x + xy ) 6 4 y + = y e + ln ( 6 4 y + y 6 4 ) (1). y + y t t 1
Xét hàm số f (t) '
= e + ln t ( t > 0 ) Þ f (t) = e + > 0, t
" > 0, suy ra hàm số g(t) đồng t
biến trên khoảng (0;+¥). Kết hợp với (1) ta có 3 2 6 4 3 6 2
x + xy = y + y Û x - y + y ( 2 x - y ) = Û ( 2 x - y )( 2 2 4 2
x + xy + y + y ) 2 0
= 0 Û x = y (2)
- Thế (2) vào phương trình còn lại của hệ đã cho ta được: 39 2 4 4 2
8 3 - 4y = 3+ 24y -16y Û 16y - 24y + 8 3 - 4y - 3 = 0 (3) Xét hàm số g ( y) 4 2
=16y - 24y + 8 3- 4y - 3 16 16 3 ' Þ g ( y) 3 = 64y - 48y - =16y ( 2 4y - 3) - < 0, 0< " y £ 3 - 4y 3 - 4y 4 æ 3 ö
Suy ra hàm số g ( y) nghịch biến trên khoảng 0;
, từ đó phương trình ( 3) có nghiệm duy ç ÷ è 4 ø 1 1
nhất y = , suy ra x = . 2 2 æ ö
Vậy hệ phương trình có nghiệm duy nhất ( x y) 1 1 , = , . ç ÷ è 2 2 ø 2
ì 4 - x + y +8 = y + 7x -1 ï
Bài 27. Giải hệ phương trình: í
ï 2(x - y)2 + 6y - 2x + 4 - x = y +1. î ì y ³ 1 - Điều kiện : í î0 £ x £ 4
2( x - y)2 + 6y - 2x + 4 - x = y +1 2 2
Û 2x - 4xy + 2y - 2x + 6y + 4 = x + y +1+ 2 x ( y + ) 1
Û 2 éx - 2x( y + ) 1 + ( y + )2 2
1 ù + y +1+ x = 2 x ( y + ) 1 ë û
Û 2( y +1- x) + ( x - y +1)2 = 0 Û y = x -1
Thế vào pt đầu ta được 2
4 - x + x + 7 = x + 5x Û ( 2
x + 3x - 3) + x +1- 4 - x + x + 2 - x + 7 Û ( æ 1 1 ö 2 x + 3x - 3) 1+ + ç ÷ è x +1+ 4 - x x + 2 + x + 7 ø ì 3 - + 21 ïx = ï 2 2
Û x + 3x - 3 = 0 Þ í ï 5 - + 21 y = ïî 2 ì y 2
x - (x + y) = ï Bài 28. Giải hpt 3 x - í y ( , x y Î ! ) . ï 2 2
î2(x + y ) - 3 2x -1 =11 40 1 Điều kiện x ≥ 2
Từ phương trình thứ nhất dễ dàng suy ra được y > 0. y 2
x - (x + y) = 3 x- y 2 2 3
Û x - (x + y)( x - y -1) + x - (x + y) - y = 0 2 2 2
x - (x + y)(x - y -1)
x - (x + y) - y Ta có Û + = 0 3 2 2 3
(x - y) + x - y +1
x - (x + y) - y 2 æ x (x y) ö - + x + Û y (x - y -1)ç + ÷ = 0 ç 3 2 2 3 (x y) x y 1 x (x y) ÷ - + - + - + - è y ø
Û x - y -1 = 0 Û y = x -1
Thay vào phương trình thứ hai ta được 2
4x - 4x + 2 - 3 2x -1 =1 1
Đặt t = 2x -1 ta được t4 – 3t – 10 = 0 Û t = 2 5 3
Từ đó tìm được (x, y) = ( , ) 2 2 ìx, y > 0 ï
Bài 29. Tìm tất cả các số thực x, y thỏa hệ: íx + y = 2 . ï 1+ 1 + î x y x y ³1 Hướng dẫn giải
Ta chứng minh nếu các số x, y thỏa mãn hai điều kiện đầu thì x 1 + y 1 + x y £1Û (x + ) 1 ln x + ( y + ) 1 ln y £ 0
Thay y = 2 - x,ta chứng minh
f (x) = (x + )
1 ln x + (3- x)ln(2 - x) £ 0 với 0 < x < 2
Ta có f (x) = x - ( - x) 1 1 ' ln ln 2 + + x - 2 x é ù f ( x) 1 1 1 1 '' = + - ê + ú 2
x 2 - x ê x (2- x)2 ú ë û 2 1 1 1 æ 1 1 ö (x - )2 1 æ 1 1 ö £ + - + = - ç ÷ x - x è x - x ø x ( - x) + £ 0 ç ÷ 2 2 2 2 è x 2 - x ø
Do đó f '(x)nghịch biến trên (0;2),hơn nữa f '( )
1 = 0nên f '(x)nhận giá trị dương trên (0 ) ;1 và âm
trên (1;2).Suy ra f (x) £ f ( )
1 = 0với mọi xÎ(0;2).
Từ đó,hệ phương trình có nghiệm x = y = 1. 41 4 3 3 2 2
ìïx + x y +9y = y x + x y +9x
Bài 30. Giải hệ phương trình sau: í 3 3
ïîx(y - x ) = 7 Hướng dẫn giải 4 3 3 2 2 2 2
ìïx + x y +9y = y x + x y +9x
ìïx(x - y)(x + y) = 9(x - y)
ìïx(x + y) = 9 í Û í Û í 3 3 3 3 3 3
ïîx(y - x ) = 7
ïîx(y - x ) = 7
ïîx(y - x ) = 7 ì 3 ì 3 y = - x ì 3 ï y = - x x y = - ï ï ï x Û í x Û í Û í x æ 3 ö ï 3 3 3 3 ï ï 3 4
îx(y - x ) = 7 x ( - x) - x = 7 ç ÷
î(3- x x) - x x = 7 ï x î è x ø ì 3 ì 3 y = - x y = - ï ï x Û í x Û í x ï 4 3 ï 4 3
î2x x - 9x + 27x x + 7 x - 27 = 0
î2x x - 9x + 27x x + 7 x - 27 = 0 ì 3 y = - ï x Û í x ï 4 3 3 2 2
î( x -1)(2x + 2x x + 2x - 7x x - 7x - 7x x + 20x + 20 x + 27) = 0 ì 3 ì 3 y = - ï x ïy = - x ìx =1 Û í x Û í x Û í ï ï îy = 2 3
î( x -1)((x + x +1)(2x - 7x x + 20) + 7) = 0 îx =1 2 2
ì x + x - y 9 ï = x 2 2
ï x - x - y 5
Bài 31. Giải hệ phương trình í . ï x 5 + 3 = x ï y 6(5- î y) Hướng dẫn giải ìy ¹ 0 ïy ¹ 5 ï ĐK: í . 2 2 x ³ ï y ï 2 2
x - x - y ¹ 0 î 9 x
Từ (2) suy ra: x = 6 -1 (2'). 5 y
Do y ¹ 0 phương trình (1) tương đương với 2 2 x x - + y y y = x x 6 -1 (1').Đặt = u 2 2 x x - y y y - y y 42 2 u - u -1
* Xét y > 0:phương trình (1')trở thành: = 6u -1. 2 u + u -1 5
Nhân liên hợp của mẫu số đưa về phương trình: 2
u u - 3- u -1 = 0 được nghiệm u = 0;u = . ( ) 3
+ u = 0 suy ra x = 0 không thoả mãn => loại. 5 x 5 + u = Û
= .Thế vào (2') được x = 5; y = 3. 3 y 3 2 u + u -1
* Xét y < 0:phương trình (1')trở thành:
= 6u -1.Phương trình này có nghiệm u=0 suy ra 2 u - u -1
x=0 (Không thoả mãn điều kiện bài toán).
Vậy hệ đã cho có một nghiệm ( ; x y) = (5;3).
ì2( 3x + 2x - y - ) 2 1 = x ( y + ï )1
Bài 32. Giải hệ phương trình : í . 2 2 2
ïx 2x - y + y + 3 = -y + 2x + 2 î Hướng dẫn giải Ta có: 2 2
(1) Û 2x(x + 2) - 2(y +1) = x ( y +1) 2 2
Û 2x(x + 2) = (y +1)(x + 2) Û 2x = y +1 Û y = 2x -1 Thế vào (2) ta có : 2 2 2
x 2x - (2x -1) + 2x -1+ 3 = -(2x -1) + 2x + 2 2 2 Û x 2 - x + 6x +1 = 4 - x + 6x +1
é - x + x + = x Û x 2
- x + 6x +1 = ( 2 - x + 6x + ) 2 2 6 1 2 2 2 2 1 - 2x Û ê 2 êë 2
- x + 6x +1 = -x ìx ³ 0 3 + 15 15 2 2
- x + 6x +1 = 2x Û í Û x = Þ y = 2 2 î 2
- x + 6x +1 = 4x 6 6 ìx £ 0 3- 2 3 3 - 2 3 2 2
- x + 6x +1 = -x Û í Û x = Þ y = 2 2 î 2
- x + 6x +1 = x 3 3 æ 3+ 15 15 ö æ 3- 2 3 3- 2 3 ö
Vậy nghiệm của hệ PT là: ç ; ÷ và ç ; ÷. ç 6 3 ÷ ç ÷ è ø 3 3 è ø 2
ì 4 - x + y +8 = y + 7x -1 ï
Bài 33. Giải hệ phương trình: í
ï 2(x - y)2 + 6y - 2x + 4 - x = y +1. î Hướng dẫn giải 43 ì y ³ 1 - Điều kiện : í . î0 £ x £ 4
2( x - y)2 + 6y - 2x + 4 - x = y +1 2 2
Û 2x - 4xy + 2y - 2x + 6y + 4 = x + y +1+ 2 x ( y + ) 1
Û 2 éx - 2x( y + ) 1 + ( y + )2 2
1 ù + y +1+ x = 2 x ( y + ) 1 ë û
Û 2( y +1- x) + ( x - y +1)2 = 0 Û y = x -1
Thế vào pt đầu ta được : 2
4 - x + x + 7 = x + 5x Û ( 2
x + 3x - 3) + x +1- 4 - x + x + 2 - x + 7 Û ( æ 1 1 ö 2 x + 3x - 3) 1+ + ç ÷ è x +1+ 4 - x x + 2 + x + 7 ø ì 3 - + 21 ïx = ï 2 2
Û x + 3x - 3 = 0 Þ í ï 5 - + 21 y = ïî 2 2 2
ìïx + 2y + xy = 4
Bài 34. Giải hệ phương trình: í 2 2
ïîx - y + 2xy = 2 (Chưa giải) 2 2
ìï x + x + y +1+ x+ y + x+ y +1+ y =18
Bài 35. Giải hệ phương trình: í 2 2
ï x + x + y +1 - x + y + x + y +1 - y = 2 î (Chưa giải) 3 2
ìx + (y - z) = 2 ï
Bài 36. Giải hệ phương trình: 3 2
íy + (z - x) = 30 ï 3 2
z + (x - y) = 16 î (Chưa giải) ì3
ï x - y = x - y
Bài 37. Giải hệ phương trình: í
ïx + y = x + y + 2 î (Chưa giải)
Bài 38. Giải các hệ phương trình ì 8xy 3 2
ìx = 9z - 27(z -1) 2 2 x + y + =16 ï ï a) x + í y b) 3 2
íy = 9x - 27(x -1) ï 2
x + y = x - ï î y 3 2
z = 9y - 27( y -1) î (Chưa giải)
Bài 39. Giải các hệ phương trình: 44 3 2
ìx - 9y + 27y - 27 = 0 3 ìx = 2y -1 ï 2 2 2
ìïx + y + z + 2xy - zx - zy = 3 ï a) 3 2
íy - 9z + 27z - 27 = 0 b) í c) 3 íy = 2z -1 ï 2 2
ïîx + y + yz - zx - 2xy = 1 - 3 2
z - 9x + 27x - 27 = 0 ï 3 î z = 2x -1 î (Chưa giải) 6 3 2 2
ìïx - y + x -9y -30 = 28y
Bài 40. (Trại hè Hùng Vương 2013) Giải hệ phương trình í
ïî 2x +3 + x = y Hướng dẫn giải
Từ phương trình đầu của hệ ta có
( 2x - y- )( 2y + y( 2 + x ) 4 2 3 6
+ x + 3x +10) = 0 2 éx = y + 3 Û ê 2 ê y + ë y ( 2 6 + x ) 4 2
+ x + 3x +10 = 0 (*)
Coi (*) là phương trình bậc 2 ẩn y ta có 4 D = 3
- x - 4 < 0 "x nên (*) vô nghiệm.
Do đó hệ phương trình tương đương với 2 ìïx = y +3 2 í
Þ 2x + 3 + x = x -3
ïî 2x +3 + x = y x x
Û (x - x + )(x + + x + ) é = 2 + 3 2 3 1 2 3 = 0 Û ê
êëx +1+ 2x + 3 = 0
Từ đó ta tìm được nghiệm của hệ là (3;6),(- 2;- ) 1
Bài 41. (Thi cụm Quỳnh Lưu, năm 2016-2017) Giải hệ phương trình sau: 3 2 3 2
ì2x + xy + x = 2y + 4x y + 2y (1) ï í 2
ï 4x + x + 6 - 5 1+ 2y =1- 4y (2) î Hướng dẫn giải 1 Điều kiện: y ³ - 2 (1) 2 2
Û (x - 2y)(2x + y +1) = 0 Û x = 2y .
Thay vào (2) ta có phương trình 2
4x + x + 6 + 2x =1+ 5 x +1 (3) Xét x = 1
- thỏa mãn (3), suy ra y = - 1 x +1 Xét x > 1 - : (3) 2
Û 4x + x + 6 - (1- 2x) = 5 x +1 Û = x +1 2
4x + x + 6 +1- 2x 45
éx +1= 0 Þ x = 1 - (l i oa ) Û ê 2
êë 4x + x + 6 +1- 2x = x +1 (4) ì 1 ïx ³ 2 + 7
Kết hợp (3) và (4) ta được 2 x +1 = 2x -1 Û í 2 Û x = 2 2
ïî4x -8x -3 = 0 1 2 + 7 2 + 7
Kết luận: Hệ phương trình đã cho có 2 nghiệm: ( ; x y) = ( 1 - ;- );( ; ) 2 2 4 Dạng 2: Đặt ẩn phụ (ì2
ï - x)(2 + y) = 8 Bài 1.
Giải hệ phương trình: í 2 2
ïx 4 - y + y 4 - x = 4 î Hướng dẫn giải ìx = 2cos 2u Điều kiện: ;
x y Î[ - 2;2]. Đặt í với u,v [0; p Î ]. îy = 2cos 2v 2 ì
ì(1- cos 2u)(1+ cos 2v) = 2 2 2 u v = si
ì n u cos v =1/ 2 sin cos 1/ 2 ï HPT Û í Û í Û í p
îcos 2u sin 2v + cos 2vsin 2u =1 si î n 2(u + v) =1 ïu + v = î 4 ì p sin
ì (u + v) + sin(u - v) = 2 sin ì (u - v) =1/ 2 u - v = ï ì p ïu = Û ï ï ï í Û í Û 4 í Û í 4 (thỏa). p p ïu + v = ïu + v = p î ï ï 4 î 4 u + v = îv = 0 ïî 4 ì p ïx = 2cos = 0
Kết luận: nghiệm hệ phương trình là í 2 . ïîy = 2cos0 = 2 2 2
ìx +1+ y + xy = 4y ï Bài 2.
Giải hệ phương trình: í y ïx + y - 2 = 2 î x +1
Ta thấy y = 0 không là nghiệm của hệ phương trình đã cho,
ta xét các giá trị y ¹ 0 , chia hai vế của PT thứ nhất cho y ¹ 0 ta được 2
ì x +1 + x+ y = 4 ïï y í
ïx + y - 2 = y ï 2 î x +1 2 x +1 Đặt u =
, v = x + y ta có hệ phương trình y 46 ìu + v = 4 ìv = 4 - u ìu =1 í Û í Û í îu(v - 2) =1
îu(4 - u - 2) =1 îv = 3 2 ì x +1 ìu = 1 ï = 1 Với í ta có í y (*) îv = 3 ï îx + y = 3
Giải hệ PT (*) ta được hai nghiệm (-2; 5) , (1; 2)
Vậy hệ PT ban đầu có hai nghiệm (-2; 5) , (1; 2) ( 2 2 ì x + ï
y )(x + y + 2) = 4( y + 2) Bài 3.
Hệ phương trình tương đương với í 2 2 ïx + y + î
x ( y + 2) + ( y + 2)( y - 2) = 0
+ Với y = -2 thì hệ phương trình vô nghiệm
+ Với y ¹ -2, chia hai vế của hai phương trình cho y + 2 ta có 2 2 ì x + y ï (x + y + 2) = 4 ï y + 2 í 2 2
ï x + y + x + y - 2 = 0 ïî y + 2 2 2 x + y Đặt a =
, b = x + y + 2 y + 2 ìa + b = 4 ìa + b = 4 ï ìa = 2
Khi đó ta có hệ phương trình í Û í Û í îab = 4 ( ï a - 2 î )2 = 0 îb = 2 2 2 ì x + y ï = 2 ìy = -x éx =1, y = 1 - Do đó í y + 2 Û í Û 2 ê ï îx + x - 2 = 0 ëx = 2, - y = 2 îx + y + 2 = 2
Kết hợp với điều kiện thì hệ phương trình có hai nghiệm (x; y): (1; -1), (-2; 2) (
ìï x + 2) 2x -1+( y + 2) 2y -1 = 2. (x + 2)( y + 2) Bài 4.
Giải hệ phương trình: í (x, y Î ! ).
ïîx + y = 2xy
ì (x + 2)(2x - ) 1 ( y + 2)(2y - )1 1 1 ï + = 2
Điều kiện x ³ , y ³ ,(*). Viết lại hệ dưới dạng: í y + 2 x + 2 2 2 ï
îx + y = 2xy ì (x + 2)(2x - )1 ïu = ³ 0 ï y + 2 Đặt í Þ uv = (2x - ) 1 (2y - )
1 = 4xy - 2(x + y) +1 = 1 ï ( y + 2)(2y - )1 ïv = ³ 0 î x + 2 47 ìu + v = 2
Hệ phương trình trở thành : í Û u = v =1 îuv =1 ( ì x + 2 ï )(2x - ) 2 1 = y + 2
ìï2x + 3x - 4 = y (
ìï x - y)(x + y + 2) = 0 hay í Û í Û í ( ï y + 2 î )(2y - ) 2 2 1 = x + 2
ïî2y + 3y - 4 = x
ïî2x + 3x - 4 = y
ìïx - y = 0 do( ) * Û í Û ( ; x y)Î ( { 1; )1,( 2 - ; 2 - )}. 2
ïî2x +3x - 4 = y
Kết hợp điều kiện (*) ta được nghiệm của hệ là: ( ; x y) = (1; ) 1 . Bài 5.
Giải hệ phương trình sau: 4 4 2 2 ì x y æ x y ö x y ï + - ç + ÷ + + = -2 1 4 4 2 2 ( ) í y x è y x ø y x ï 3 2 4
x + x +15y + 30 4 27(1- y) (2) î = Hướng dẫn giải x y Đặt + = t (t ³ 2) y x 2 2 x y 2 Þ + = t - 2 2 2 y x 4 4
x + y = t -2 = t -2t +4 4 4 ( )2 2 4 2 y x ( ) 4 2 Ût - t + -( 2 1 4 2
t - 2)+t + 2 = 0 4 2
Û t - 5t + t + 6 = 0 Û (t + )( 3 2
2 t - 2t -t + ) 3 = 0 ét + 2 = 0 Û ê 3 2
ët - 2t - t + 3 = 0 ét ³ 2 Xét f (t) 3 2
= t - 2t -t + 3 với ê ët £ -2 f (t) 2 ’ = 3t - 4t - 1 t 2 - 7 2 + 7 - ¥ -2 2 +¥ 3 3 f’(t) + + 0 - 0 + + f(t) +¥ -11 1 48 - ¥ Þ f (t)Î(- ; ¥ 1 - ] 1 È[1;+¥).
Þ f (t) = 0 vô nghiệm Þ t = 2 - . Þ x = - y . ( ) 3 2 4
2 Û x + x -15x + 0
3 = 4 27(1- y) , đk: x ³ 1 - . Ta có : 4
4 27(1- y) £ 3+ 3+ 3+ x +1= x +10 . 3 2
Þ x + x -15x + 30 £ x +10 Û (x - )2 2 (x +5) £ 0( ) 3 Do x ³ 1
- Þ x + 5 > 0 ÞVT ( ) 3 ³ 0 Û x = 2 (t/m).
ìï2x + y -1 = 5 Bài 6.
Giải hệ phương trình : í
ïî2y + x -1 = 5 Hướng dẫn giải 2
ìïu = x -1 ³ 0 Þ x = u +1 +) Đặt í 2
ïv = y -1 ³ 0 Þ y = v +1 î 2
ìï2u + v -3 = 0 +) Đưa về hệ: í 2
ïî2v + u -3 = 0 éìu = v êí 2
êî2u + v - 3 = 0
êì2u + 2v -1= 0 êí 2
êëî2u + v -3 = 0
Giải hệ (I) ta được u = v =1Þ x = y = 2 Hệ (II) vô nghiệm
Vậy hệ có nghiệm x = y = 2 . Bài 7.
[Đề xuất, Chyên Lào Cai, DHDDBBB, 2015] Giải hệ phương trình: 3 2
ìïx + xy +( 2 2
x + y - 4)( y + 2) = 0 í 2 2
ïîx + 2y + xy + 2x - 4 = 0 Lời giải ( 2 2 ì x + ï
y )(x + y + 2) = 4( y + 2)
Hệ phương trình tương đương với í 2 2 ïx + y + î
x ( y + 2) + ( y + 2)( y - 2) = 0
+ Với y = -2 thì hệ phương trình vô nghiệm 49
+ Với y ¹ -2, chia hai vế của hai phương trình cho y + 2 ta có 2 2 ì x + y ï (x + y + 2) = 4 ï y + 2 í 2 2
ï x + y + x + y - 2 = 0 ïî y + 2 2 2 x + y Đặt a =
, b = x + y + 2 y + 2 ìa + b = 4 ìa + b = 4 ï ìa = 2
Khi đó ta có hệ phương trình í Û í Û í îab = 4 ( ï a - 2 î )2 = 0 îb = 2 2 2 ì x + y ï = 2 ìy = -x éx =1, y = 1 - Do đó í y + 2 Û í Û 2 ê ï îx + x - 2 = 0 ëx = 2, - y = 2 îx + y + 2 = 2
Kết hợp với điều kiện thì hệ phương trình có hai nghiệm (x; y): (1; -1), (-2; 2) Bài 8.
[Đề thi hsg Ngô Gia Tự, Vp, 2012-2013] Giải hệ phương trình: 3
ìï x - y =10- x + y í 2
ï2x + 2x x + y - y x + y = 25 + î xy Lời giải
ìa = 2x - y ìa + b =10 Đặt : ï khi đó ta có hpt : . í í
ïb = x + x + î y î . a b = 25 Bài 9.
[Đề xuất, Chuyên Thái Bình, DHĐBBB,2015] Giải hệ phương trình sau: 4 2 2 2 3 2 2
ìïx + x y - y = y + x y + x í 5(
ï x y + 7 + (x +1) 2x + y + 8) =13(2x +1) î Lời giải ì2x + y + 8 ³ 0 ĐKXĐ: í î y + 7 ³ 0 2 2 éx + y = 0 2 2 2
Từ (1) ta được: (x + y )(x - y -1) = 0 Û ê 2 ëx = y +1
Trường hợp đầu suy ra x=y=0 nhưng ko là nghiệm của hệ
Do vậy ta được: x2 = y + 1 (1 điểm).
Thay vào phương trình (2) ta được: 2 2
5(x x + 6 + (x +1) x + 2x + 7) =13(2x +1) 50 2 2 b - a -1 2 2 2 2
a = x + 6; b = x + 2x + 7 Þ 2x +1 = b - a Þ x = 2 é Thay êa = b (a b)( ê Þ -
5(a + b)2 - 26(a + b) + 5) = 0 Þ a + b = 5 ê ê 1 êa + b = ë 5
Dễ thấy a + b ³ 2 6 nên trường hợp thứ ba bị loại.
Hai trường hợp đầu ta tính được x=-1/2
KL: Hệ có một nghiệm x=-1/2; y=-3/4
Bài 10. Giải hệ phương trình sau: 2 2 ìx + 2x xy = ï y y í 2 ; x, y Î ! ( 3 3 2 ï 4x + y + 3 î x
x )(15 x + y) = 3 x ( y y + x y + 4x x ) Hướng dẫn giải
Điều kiện: x ³ 0, y ³ 0.
Đặt a = x,b = y ( a ³ 0,b ³ 0).Hệ phương trình đã cho trở thành 4 3 5
ìa + 2a b = b ( ) 1 ï í (ï4a +b +3 î
a )(15a +b ) = 3a(b + a b + 4a )2 6 6 5 2 3 2 3 (2)
Nhận xét: a = 0 Þ b = 0; b = 0 Þ a = 0.Do đó ( ,
a b) = (0,0) là một nghiệm của hệ.
Bây giờ ta xét a > 0,b > 0.Đặt b = ka Þ k > 0 .Với cách đặt này thì
Phương trình (1)trở thành: 1+ 2 5 1+ 2 = Û = k k ak a (3) 5 k
Phương trình (2)trở thành:
( a +a k + a )( a +k a ) = a(k a +a k + a )2 6 6 6 5 2 2 2 3 3 3 3 4 3 15 3 4 (4) 5 æ 3k öæ 1+ 2k 2 ö Thay (3)vào (4)ta được: 6 4 ç + k + 5 ÷ + = ç ÷ ( 3 k + k + 4 3 ) (5) è 1+ 2k øè 3k ø
Áp dụng bất đẳng thức Cauchy - Schwarz cho vế trái của (5)ta được: 2 5 æ 3k öæ 1+ 2 æ k ö 3k 1+ 2 ö k 4 ç + k + 5 ÷ + ³ ç ÷ ç 5 4 + k + . ÷ 3 ( ) 5 6 6 3 è 1+ 2k øè 3k ç ø 1+ 2k 3k ÷ è ø = ( ( + )( +k ) 2 2 2 6 2 1 4
+ k ³ 4 + k + k ) ( )2 3 51
Đẳng thức xảy ra khi và chỉ khi k = 1.Khi đó a = b = 3 hay x = y = 9.
Vậy hệ phương trình đã cho có 2 nghiệm ( ; x y) là (0;0),(9;9). 2 2 ì
2x - 5xy - y = 1 ï
Bài 11. Giải hệ phương trình sau: í . 2 2
ïy( xy - 2y + 4y - xy) =1 î Hướng dẫn giải
+ Điều kiện: 4y ³ x ³ 2y > 0.
+ Trừ vế với vế hai phương trình của hệ ta được: 2 2 2 2
2x - 5xy - y - y
xy - 2y + 4y - xy = 0. ( ) 2 æ x ö æ x ö x x
Chia cả hai vế của PT cho 2 y ,ta được: 2 - 5 -1- - 2 - 4 - = 0. ç ÷ ç ÷ è y ø è y ø y y x + Đặt
= t Þ t Î[2;4] ta có phương trình: y 2
2t - 5t -1- t - 2 - 4 - t = 0.
Û 2t(t - 3) + t - 2( t - 2 -1) + (1- 4 - t ) = 0. æ t - 2 1 ö Û (t -3)ç2t + + ÷ = 0. ç t 2 1 1 4 ÷ - + + - è t ø t - 2 1
Với t Î[2;4] thì 2t + + > 0.
t - 2 +1 1+ 4 - t 1 3
Với t = 3 suy ra x = 3y thay vào PT (1): 2 2y =1Þ y = Þ x = . 2 2 æ 3 1 ö
Kết luận:Nghiệm của hệ phương trình là: ; . ç ÷ è 2 2 ø 2 ìz + 2xyz =1 ï
Bài 12. Giải hệ phương trình: 2 2 2 3 4 3
í x y + 3xy =1+ x y
(x, y, z Î! ). ï 4 3 2
z + zy + 4y = 4y + 6 î y z Hướng dẫn giải 2 ìz + 2xyz =1 ( )1 ï Giải hệ phương trình: 2 2 2 3 4 3
í x y + 3xy =1+ x y (2) . ï 4 3 2
ïz + zy + 4y = 4y + 6y z (3) î 2 1-
Vì z = 0 không thỏa hệ pt nên ( ) 1 Û = z xy . 2z 52 æ æ p p ö ö
Đặt z = tan u u Î - ; \ ç ç ÷ { }
0 thì xy = cot 2u. è 2 2 ÷ è ø ø 2 3cot 2u -1 Từ (2): y = = tan 6 . u 3 cot 2u - 3cot 2u 3
4 tan 6u - 4 tan 6u Vậy x = cot 2 .
u cot 6u .Thay vào (3): z = = tan 24 . u 4 2
1+ tan 6u - 6 tan 6u kp
Vậy tan u = tan 24u Þ u = (k Î!). 23 æ p p ö ì p 11p ü Vì u Î - ; \ ç ÷ { } 0 nên u Î í± ,..., ± ý. è 2 2 ø î 23 23 þ kp
Vậy tan u = tan 24u Þ u = (k Î!). 23 æ p p ö ì p 11p ü Vì u Î - ; \ ç ÷ { } 0 nên u Î í± ,..., ± ý. è 2 2 ø î 23 23 þ ì p 11p ü Vậy hệ có nghiệm: ( ,
x y, z) = (cot 2t.cot 6t;tan 6t;tant) trong đót Îí± ,..., ± ý. î 23 23 þ 3 2
ìïx +1= 2(x - x + y)
Bài 13. Giải hệ phương trình: í 3 2
ïîy +1= 2(y - y + x) (Chưa giải) 2 2 ìx - 2y =1 ï
Bài 14. (Chuyên Vĩnh Phúc 2010 – 2011) Giải hệ phương trình: 2 2
í2y - 3z = 1 ( x, y, z Î ! )
ïxy + yz + zx =1 î Hướng dẫn giải
+) Nếu x = 0 thay vào hệ ta có hệ vô nghiệm
+) Nếu x ¹ 0 ta đặt y = a ;
x z = bx thay vào hệ ta được 2 ìx ( 2 1- 2a ) =1 ï 2 2 2 2 2 ( )ï 1
ìï - 2a = 2a -3b ìï4a -3b =1 2 1 íx ( 2 2
2a - 3b ) =1 Þ í Û í 2 2 1 ï
ïî - 2a = a + ab + b ï2a + a -1+ î b(a + ) 1 = 0 2
ïx (a + ab + b) = 1 î éìa = 1 - êí 2 2 2 2 ìï4a -3b =1 ìï4a -3b =1 êîb = 1 ± Û í Û í Û ( ï a + î
)1(2a - )1+b(a + ) 1 = 0 ( ï a + î ) 1 (2a -1+ b) = 0 êìb =1- 2a êí 2
êëî2a -3a +1= 0 53 ìa = -1 +) Nếu í
thay vào (1) không thỏa mãn îb = ±1 éìa =1 êíb ìb = - a êî = 1 - 1 2 ì ì 1 a = 1 ïa = +) Nếu í Û ê thay í
vào (1) không thỏa mãn, thay í 2 vào (1) ta có 2 ì 1 î2a - 3a +1 = 0 êïa = îb = 1 - ï êí 2 îb = 0 êï ëîb = 0 æ ö æ ö
x = ± 2 . Do đó nghiệm của hệ là ( x y z) 1 1 ; ; = 2; ;0 , - 2; - ;0 ç ÷ ç ÷ è 2 ø è 2 ø
Bài 15. (Chuyên Hoàng Văn Thụ - Hòa Bình, năm 2013) Giải hệ phương trình sau: ì y 2
x - ( x + y) = ï 3 x - í y (x, yÎ! ). ï2 î ( 2 2
x + y ) - 3 2x -1 =11 Hướng dẫn giải 1 Điều kiện x ³ ; 2
x - (x + y) ³ 0; x ¹ y 2 1
Từ phương trình thứ nhất suy ra y và x - y cùng dấu mà y + x - y = x ³ nên y ³ 0. Ta có 2
y = 0 từ phương trình thứ nhất suy ra x = 1 mà (1;0) không thỏa mãn pt thứ 2 nên y > 0 y 2
x - ( x + y) = 3 x- y 2
Û x - (x + y) ( x - y - ) 2 3
1 + x - ( x + y) - y = 0 2
x - ( x + y) ( x - y - ) 2 1
x - ( x + y) 2 - y Û + = 0 (x - y)2 2 3 3 + x - y +1
x - ( x + y) + y æ 2 ö ( )
x - ( x + y) x + y x y 1 ç ÷ Û - - + = 0 ç (x- y)2 2 ÷ 3 3 + x - y +1
x - ( x + y) + è y ø
Û x - y -1 = 0 Û y = x -1
Thay vào phương trình thứ hai ta được 2
4x - 4x + 2 - 3 2x -1 =1 1 æ ö
Đặt t = 2x -1 ta được 4
t - 3t -10 = 0 Û t = 2.Từ đó tìm được ( x y) 5 3 ; = ; ç ÷ è 2 2 ø 3 3 3 1 ìï + x y =19x
Bài 16. Giải hệ phương trình í 2 2 ïîy + xy = 6 - x
Bài 17. Tìm m để hệ phương trình sau có nghiệm duy nhất 54 2
ì x + 2013 + y +1 = ï m í 2 2
ï x y + 2y + 2013 = 2013- x - î m Hướng dẫn giải: 2
ì x + 2013 + y +1 = ï m (I) í 2 2
ï x y + 2y + 2013 = 2013- x - î m 2
ì x + 2013 + z = ï m
* Đặt z = y +1. Ta có (II) í 2 2
ï x z + 2012 = 2013- x - î m
Nhận xét : Hệ (I) có nghiệm duy nhất Û hệ (II) có nghiệm duy nhất
* Điều kiện cần : Giả sử hệ (II) có nghiệm duy nhất ( ; x z). Vì ( ;
x z) là nghiệm của (II) nên ( ; x -z),(- ; x -z),(- ;
x z) cũng là nghiệm của (II)
Do đó để (II) có nghiệm duy nhất thì x = z = 0.
Với x = z = 0, ta có : m = 2013 * Điều kiện đủ : 2
ì x + 2013 + z = 2013 (1) ï
Với m = 2013. Ta có í 2 2
ï x z + 2012 = 2013- x - 2013 (2) î * Vì 2
x + 2013 + z ³ 2013,"x, z, Dấu = xảy ra x = z = 0 nên (1) Û x = z = 0 ( Thỏa mãn (2 ))
Do đó hệ (II) có nghiệm duy nhất x = z = 0 .
* Vậy hệ (I) có nghiệm duy nhất Û hệ (II) có nghiệm duy nhất Û m = 2013 . 2 2 ì
2x - 5xy - y = 1 ï
Bài 18. Giải hệ phương trình sau: í 2 2
ïy( xy - 2y + 4y - xy) =1 î Hướng dẫn giải: 2 2 ì
2x - 5xy - y = 1 (1) ï Ta có: í 2 2
ïy( xy - 2y + 4y - xy) =1 (2) î
+) Điều kiện : 4y ³ x ³ 2y > 0.
+ Trừ vế với vế hai phương trình của hệ ta có: 2 2 2 2
2x - 5xy - y - y
xy - 2y + 4y - xy = 0 ( ) 2 æ x ö æ x ö x x
Chia cả hai vế của PT cho 2 y , ta có: 2 - 5 -1- - 2 - 4 - = 0 ç ÷ ç ÷ è y ø è y ø y y 55 x + Đặt
= t Þ t Î[2;4] ta có phương trình: y 2
2t - 5t -1- t - 2 - 4 - t = 0
Û 2t(t - 3) + t - 2( t - 2 -1) + (1- t - 2 -1) = 0 æ t - 2 1 ö Û (t - 3)ç2t + + ÷ = 0 ç t 2 1 1 t 2 ÷ - + + - è ø t - 2 1
Với t Î[2;4] thì 2t + + > 0
t - 2 +1 1+ t - 2 1 3
Với t = 3 suy ra x = 3y thay vào PT (1): 2 2y =1Þ y = Þ x = 2 2 æ 3 1 ö
Kết luận: Nghiệm của hệ phương trình là: ; ç ÷ è 2 2 ø 4 2 2 2 3 2 2
ìx + x y - y = y + x y + x ( )1 ï
Bài 19. Giải hệ phương trình sau: í 5
î (x y + 7 + ( x + )
1 2x + y + 8) =13(2x + ï )1 (2) Hướng dẫn giải:
ì2x + y + 8 ³ 0 ĐKXĐ: í îy + 7 ³ 0 éx + y = 0
Từ (1) ta được: ( x + y )( x - y - ) 2 2 2 2 2 1 = 0 Û ê 2 ëx = y +1
Trường hợp đầu suy ra x = y = 0 nhưng ko là nghiệm của hệ Do vậy ta được: 2 x = y + 1
Thay vào phương trình (2) ta được: ( 2 x x + + (x + ) 2 5 6 1
x + 2x + 7 =13 2x +1 (*) ) ( ) 2 2 - -1 Đặt 2 2 2 2 = + 6; = + 2 + 7 Þ 2 +1= - Þ = b a a x b x x x b a x 2 é êa = b ê
Thay vào (*) ta được (a - b) é (a + b)2 5
- 26(a + b) + 6ù = 0 Û a + b = 5 ê ë û ê 1 êa + b = ë 5
Dễ thấy a + b ³ 2 6 nên trường hợp thứ ba bị loại. 1
Hai trường hợp đầu ta tính được x = - 2 56 1 3
KL: Hệ có một nghiệm x = - ; y = - . 2 4 (ì 2 x + x +1 ï )( 2 y + y +1) =1 (1)
Bài 20. Giải hệ: í
(x, y Î ! ) 2 ï 1+ 1- x = x( 2 1+ 2 1- y î ) (2) Hướng dẫn giải:
Điều kiện: x £1, y £1 "x, y Î ! ( 2 x + x +1)( 2 -x + x +1) =1 ( 2 y + y +1)( 2 -y + y +1) =1 2 2
ìïy + y +1 = -x + x +1 (3)
Kết hợp với (1) ta được: í 2 2
ïx + x +1 = -y + y +1 (4) î
Cộng (3) và (4) ta được y = -x, thế vào (2) ta được: 2 2
1+ 1- x = x 1+ 2 1- x (5) ( ) é p ù
Đặt x = sin t,t Î 0;
, phương trình (5) trở thành ê 2 ú ë û
1+ cost = sin t(1+ 2cost) t t t é æ t öù 2
Û 2 cos = 2sin .cos . 1+ 2 1- 2sin ê ç ÷ 2 2 2 ë 2 ú è øû é p 4p t = + k t t 2 t p ê 3 6 3 Û 3sin - 4sin = Û sin 3 = sin Û ê 2 2 2 2 4 p 4p êt = + ê k ë 2 3 é p t = é 1 é p ù ê x = Với t Î 0; ta được 6 ê ê Þ 2 ê 2 ú ë û p ê êt = ëx =1 êë 2 æ 1 1 ö
Vậy hệ phương trình có nghiệm (x,y) = ;- ; (x,y) = (1;-1) ç ÷ è 2 2 ø
Dạng 3: Sử dụng hàm số (ì 2 x + x + 4 ï )( 2 y + y +1) = 2 Bài 1.
Giải hệ phương trình sau trên tập số thực: í . 2 3 3
ïî6y -5y +1= x +1 Hướng dẫn giải 57 (ì 2 x + x + 4 ï )( 2
y + y +1) = 2 (2) Đặt í . 2 3 3
ïî6y -5y +1= x +1 (3)
pt ( ) Û x + x + = - y + (- y)2 2 2 4 2 2 + 4
Û f (x) = f ( 2
- y) với f (t) 2
= t + t + 4,t Î! . 2
f ¢(t) t + t + 4 = > 0,"t Î! . 2 t + 4
Suy ra f(t) đồng biến trên ! . Do đó: ( ) = ( 2 - ) Û = 2 - Û = - x f x f y x y y 2 Thế = - x y
vào phương trình (3) ta được: 2 3 3 3x +5x + 2 = 2 x +1 2 Û ( )3 ( ) ( 3 ) 3 3
x +1 + 2 x +1 = x +1 + 2 x +1. Đặt 3 3 u = x +1,v = x +1.
Phương trình trở thành: 3 3
u + u = v + v Û (u -v)( 2 2 2 2
u +uv +v + 2) = 0 éx = 0 3 3 Û u = v Û x +1= x +1 Û ê ëx = 1 - æ ö
Vậy hệ phương trình có 2 nghiệm: ( ) 1 0;0 , 1 - ; . ç 2 ÷ è ø Bài 2. Giải hệ phương trình ì 3 3 x + 4x + 2 = + 4 6 - 2 ï y y - 4 ï ï 3 3 íy + 4y + 2 = + 4 6 - 2z z - 4 ï ï 3 3 z + 4z + 2 = + 4 6 - 2 ï x x - 4 î Hướng dẫn giải
Điều kiện: x, y, z £ 3. 3
Xét các hàm số f (t) 3
= t + 4t + 2, g (t) = + 4 6 - 2t trên ( ] ;3 -¥ . t - 4 3 4
Khi đó ta có f '(t) 2
= 3t + 4 > 0, g '(t) = - - < 0,"t < 3 . (t - 4)2 6 - 2t
Mà f (t), g (t) là các hàm số liên tục trên ( ] ;3
-¥ suy ra f (t) đồng biến trên ( ] ;3
-¥ và g (t) nghịch biến trên ( ] ;3 -¥ .
Không mất tính tổng quát ta giả sử x = min{ , x y, } z . Khi đó ta có: 58
Nếu x < y Þ g (x) > g ( y) Þ f (z) > f (x) Þ z > x Þ g (z) < g (x) Þ f ( y) < f (z)
suy ra y < z Þ g ( y) > g (z) Þ f (x) > f ( y) Þ x > y , vô lí vì x < y .
Do vậy x = y , tương tự lí luận như trên ta được x = z suy ra x = y = z . 3
Thay trở lại hệ ta được 3 x + 4x + 2 = + 4 6 - 2x (1). x - 4
Theo trên, bên trái là hàm đồng biến, bên phải là hàm nghịch biến, nên phương trình có nhiều nhất 1 nghiệm
Mà x = 1 là nghiệm nên nó là nghiệm duy nhất của phương trình (1).
Vậy nghiệm của hệ phương trình đã cho là x = y = z = 1. 3 3 2
ìx - y + 3y + x - 4y = -2 ï Bài 3.
Giải hệ phương trình : í 2 3
ï x + y = 5x - î y Hướng dẫn giải 3 3 2 3 3
ìx - y + 3y + x - 4y = 2 -
ìx + x = (y -1) + (y -1) ï ï Ta có : í Û í . 2 3 2 3
ï x + y = 5x - î y
ï x + y = 5x - î y
Hàm số f(x) = x3 + x là hàm số đồng biến trên R nên phương trình f(x) = f(y - 1) Û x = y – 1. 3 3
ìx + x = (y -1) + (y -1) ìx = y -1 ìx = y -1 ï ï ï Do đó í Û í Û í . 2 3 2 3 2 3
ï x + y = 5x - î y
ï x + y = 5x - î y
ï (y -1) + y = 4y - 5 î ì 5 ïy ³ é y = 2 Ta có 2 3
( y -1) + y = 4y - 5 Û í 4 Û . ê ï ë y =12 3 2
îy -15y + 38y - 24 = 0 ìx =1 ìx =11 Vậy hệ có 2 nghiệm : í ;í . îy = 2 îy =12 Bài 4. Giải hệ phương trình: 3 2x+7 2 ì 64.y + 2 æ 1 ö ïlog + y = +1 + 2. y + 2 ï 2 ç x ÷ 2y +1 í è 2 ø (ï2x - y+ )3 1 + 2x = 1+ ïî y Lời giải.
Phương trình (2) Û ( x - + )3 2 1 + 2x y - y +1 = 2.
Xét hàm số f (t) 3
= t + t,"t Î R, ta có: / f (t) 2
= 3t +1> 0,"t Î R do đó hàm số f (t) đồng biến trên ! . 59
từ (2) ta suy ra f ( )
1 = 2 . Vây 2x - y +1 =1 Û = 2x y Þ y > 0 2 3 2 64.y +128.y æ 1 ö Thay = 2x y vào (1) ta được: log + y = +1 + 2. y + 2 2 ç ÷ 2y +1 è y ø 8y y + 2 1 2 Û log + y = ( +1) 2 + y + 2 2 2y +1 y æ ö Û 1 1 log y + 2 +
y + 2 -1 = log (2 + ) + (2 + ) -1 2 ( ) 2 2 (3) 2 ç ÷ y è y ø
Xét hàm số: f (a) = log a + a -1 2 ( )2, (a>0) 1 1 2 Þ f '(a) = + 2a - 2 ³ 2 .2a - 2 = 2 - 2 > 0 a ln 2 a ln 2 ln 2
Vậy hàm f (a) là hàm đồng biến trên khoảng (0, +¥ ), do đó: Û f ( y + ) æ 1 ö 1 (3) 2 = f 2 + Û y + 2 = 2 + ç ÷ è y ø y é y = 1 - 4 1 3 2 y 2 4 y 2y 4y 1 0 ê Û + = + + Û - - - = Û 2 3 ± 13 y y ê y = êë 2 3 + 13 x 3 + 13 3 + 13
Kết hợp điều kiện ta nhận được y = suy ra 2 = Û x = log 2 2 2 2 æ 3 + 13 3 + 13 ö
Vậy hệ phương trình có nghiệm çlog ; ÷ 2 ç 2 2 ÷ è ø 4008 2004 2 ìïx + x
> 2004 x + 2004x (1) Bài 5. Giải hbpt í (x > 3). 4006 2003 2 ïîx + x
< 2003 x + 2003x (2)
§ (2 đ) Đặt y = 2004. Do x > 0, y > 0 nên ta được:
(1) Û x2y + xy > y2x + yx Û x2y – y2x + xy – yx >0 Û (xy – yx)(xy + yx + 1) > 0
Û xy – yx > 0 Û xy > yx ( do xy + yx + 1 > 0). § ln x ln y ln x ln 2004
(1.5 đ) xy > yx Û ln(xy) > ln(yx) Û ylnx > xlny Û > . Vậy: > (3). x y x 2004 ln 2003 ln
Biến đổi tương tự, bất phương trình (2) trở thành: > x (4). 2003 x ln 2004 ln x ln 2003
Từ (3) và (4), hệ đã cho trở thành: < < (5). 2004 x 2003 § ln x 1- ln x
(1.5 đ) Xét hàm số: y = f(x) = , y’= <0, "x > 3. x 2 x 60 ln 2004 ln x ln 2003
Nên hàm số nghịch biến trên khoảng ( 3; +¥), do đó: < < tương đương với 2004 x 2003 2003 < x < 2004. 3 2 3
ìx - x y = x - x + y +1 ï ( )1 Bài 6.
Giải hệ phương trình: í 3 2 ïx - 9y + 6 î (x -3y) 3 2 -15 = 3 6x + 2 (2) Giải: Ta có ( ) 2 1 Û x (x - ) 1 + (x - ) 1 - y ( 2 x + ) 1 = 0 Û ( 2 x + ) 1 (x - y - ) 1 = 0 Û y = x -1 Thế vào (2) 3 x - 9( x - )2 1 + 6( 2 x - 3x+3) 3 2 -15 = 3 6x + 2 3 2 3 2
Û x - 9x + 6x - 6 = 3 6x + 2 3 2 2 3 2
Û x - 3x + 6x - 4 = 6x + 2 + 3 6x + 2 Û (x - )3 1 + 3( x - ) 1 = ( 2 6x + 2) + ( 3 2 3 6x + 2 ) (*) Xét f (z) 3
= t + 3t trên ! f (z) 2 '
= 3t + 3 > 0"t Î!
Þ f (z)đồng biến trên ! ( ) ** Từ ( ) * và ( ) 3 2 ** Þ x -1 = 6x + 2 Û (x - )3 2 1 = 6x + 2 3 2
Û x - 9x + 3x - 3 = 0 Û 2( 3 2 x - 3x + 3x - ) 1 - ( 3 2 x + 3x + 3x + ) 1 = 0 Û 2(x - )3 1 = ( x + )3 1 3 Û 2 (x - ) 1 = x +1 Û ( 3 2 - ) 3 1 x = 2 +1 3 2 +1 Û x = 3 2 -1 3 3 ì7x + y + 3 ï xy(x - y) 2 =12x -6x +1 (1) Bài 7. Giải hệ phương trình í . 2 2
ï2 x + 3 - 9 - y + y =1 (2) î 61 (Chuyên Bắc Giang) Lời giải Điều kiện xác định: 3 - £ y £ 3.
Phương trình (1) tương đương với phương trình:
(x - y)3 = ( x - )3 2 1 Û y =1- x (3)
Thế (3) vào (2) ta được: 2 2
2 x +3 - 8+ 2x - x - x = 0 2 2
Þ 2 x +3 = 8+2x- x + x Þ ( 2 x + ) 2 4
3 = 2x + 8 + 2x 8 + 2x - x Þ (x - )2 2 2
1 - x 8+ 2x - x - 3 = 0 ( ) Þ (x - ) é x ù 2 1 ê2 + ú = 0 2 ë 8 + 2x - x + 3û éx -1 = 0 ê Þ x . ê2 + = 0 2 êë 8+ 2x - x + 3 Ta có hai trường hợp:
* TH 1: Nếu x = 1 thì y = 0.
Thử lại vào hệ phương trình ban đầu thấy thỏa mãn. x * TH 2: Nếu 2 +
= 0 thì ta có phương trình 2 8+ 2x - x + 3 2
2 8+ 2x - x = -x - 6 ì-x - 6 ³ 0 Û í (vô nghiệm). 2 5
î x + 4x + 4 = 0
Vậy hệ phương trình đã cho có nghiệm duy nhất là ( ; x y) = (1;0). 62
ì2x - 2y + 2x + y + 2xy +1 =1 ïï Bài 8. Giải hệ phương trình: 3 3
í 3y +1 = 8x - 2y -1 ïx > 0 ïî Hướng dẫn giải
ìï2x - 2y + 2x + y + 2xy +1 =1 (1) í 3 3
ï 3y +1 = 8x - 2y -1 (2) î (1) Û (2x + ) 1 - 2( y + ) 1 + (2x + ) 1 ( y + ) 1 = 0 ì2x +1 > 0
ĐK: (2x + 1)(y + 1) ³ 0 Mà x > 0 Þ í îy +1 ³ 0
(1) Û ( 2x +1- y +1)( 2x +1+ 2 y +1) = 0 Û 2x +1- y +1 = 0 Û y = 2x Thay vào (2): 3 3
6x +1 = 8x - 4x -1 Û ( x + ) + x + = ( x)3 3 6 1 6 1 2 + 2x (3)
Hàm số f(t) = t3 + t đồng biến trên R 1 (3) 3 Û 6x +1 = 2x 3 Û 4x - 3x = 2
NX: x >1 không là nghiệm của phương trình é p 2p p a = + ê k
Xét 0 < x £ 1: Đặt x = cosa với 0 £ a < 1 Ta có: cos3a = 9 3 Û ê (kÎ Z ) Do 2 2 p 2p a ê = - + ê k ë 9 3 p p 0 £ a £ Þ a = 2 9 æ p p ö
Vậy hệ có nghiệm cos ;2cos ç ÷ è 9 9 ø Bài 9.
[Đề xuất Chuyên Biên Hòa, DHĐBBB 2014-2015] (4,0 điểm):
Giải hệ phương trình sau trên tập số thực ì = ( + ) 1 1 x y ï x x y í 2 2 1 ï + 4
- x +18x - 20 = y +1 + 2 î 2x - 9x + 8 Lời giải
Điều kiện 𝑦 > −1; 2 ≤ 𝑥 ≤ 5/2.
Đặt 𝑡 = √−4𝑥! + 18𝑥 − 20 → 0 ≤ 𝑡 ≤ 1/2. 63
Phương trình (2) tương đương với 2𝑥! − 9𝑥 + 6 4−4𝑥! + 18𝑥 − 20 + = 4𝑦 + 1 2𝑥! − 9𝑥 + 8 4 𝑓(𝑡) = 𝑡 + 1 + 0 ≤ 𝑡 ≤ 1/2. 𝑡! + 4
Ta có 𝑓(𝑡) đồng biến trên [0; 1/2] nên 1
2 = 𝑓(0) ≤ 𝑓(𝑡) ≤ 𝑓 = > = 83/34 < 5/2 2
Suy ra 4𝑦 + 1 ≥ 2 → 𝑦 + 1 ≥ 4.
Xét phương trình (1) tương đương với 𝑙𝑛𝑥 ln(𝑦 + 1) = 𝑥 𝑦 + 1 𝑙𝑛𝑡 1 − 𝑙𝑛𝑡 𝑔(𝑡) = , 𝑔,(𝑡) =
, 𝑔,(𝑡) > 0 ↔ 𝑡 < 𝑒 𝑡 𝑡!
Xét 2 ≤ 𝑥 ≤ 5/2 ta có hàm số g(x) đồng biến.
Xét 𝑦 + 1 ≥ 4 ta có hàm số g(y+1) nghịch biến
Ta có 2 ≤ 𝑥 ≤ 5/2 nên 𝑔(𝑥) ≥ 𝑔(2) ↔ 𝑔(𝑥) ≥ 𝑙𝑛2/2
𝑦 + 1 ≥ 4 nên 𝑔(𝑦 + 1) ≤ 𝑔(4) = 𝑙𝑛2/2
Mặt khác g(x) liên tục trên (0 ; +∞) nên 𝑔(𝑥) = 𝑔(𝑦 + 1) = 𝑙𝑛2/2
Khi đó 𝑥 = 𝑦 + 1; 𝑥 = 2; 𝑦 = 3
Vậy hệ có nghiệm duy nhất ( 2 ; 3)
Bài 10. [Đề dữ liệu, Chuyên Lê Hồng Phong, DHĐBBB, 2015] Giải hệ phương trình: ì æ 2x + y +1 ö ïlog ï ç ÷ = 3( 2 x + 2 - x - 3 3 2 ) í è x + 2 +1ø (ï2+3x+y x y ï x y î ) 1-( + ) .5 = 7 + - 2 Lời giải x+ y x+ æ ö æ ö y
Điều kiện: 2x + y +1 > 0 Ta có ( ) 1 3 2 Û 10. + 5. - 7x+y + 2 = 0 ç ÷ ç ÷ è 5 ø è 5 ø æ 1 öt æ 3 öt
Đặt t = x + y ta có phương trình 10. + 5. - 7t + 2 = 0 (*) ç ÷ ç ÷ è 5 ø è 5 ø æ öt æ öt Xét hàm số ( ) 1 3 = 10. + 5. - 7t f t + 2 với t Î ! ç ÷ ç ÷ è 5 ø è 5 ø æ öt æ öt Ta có ( ) 1 1 3 3 ' =10. ln + 5. ln - 7t f t ln 7 < 0 "t Î ç ÷ ç ÷ ! è 5 ø 5 è 5 ø 5
Nên hàm số f (t) nghịch biến trên ! 64 Mà f ( )
1 = 0 suy ra phương trình (*) có nghiệm duy nhất t = 1
Với t = 1 ta có x + y = 1
(2) Û log (2x + y + ) 1 - log ( 2x + 2 + ) 2
1 = 3 x + 2 - 3x - 3 3 3 Û log x + 2 - log
x + 2 +1 = 3 x + 2 - 3x - 3 3 ( ) 2 2 3 ( )
Û log (x + 2) + 3(x + 2) = log ( 2x + 2 + )1+3( 2x + 2 +1 ** 3 3 ) ( )
Xét hàm số g (t) = log t +3t với t > 0 ta có g (t) 1 ' = + 3 > 0 "t > 0 3 t ln 3
Þ g (t) đồng biến trên (0; + ¥) Do đó phương trình ( ) ** có dạng
g ( x + 2) = g ( 2x + 2 + ) 2 2
1 Û x + 2 = x + 2 +1 Û x + 2 = x +1 ìx +1³ 0 ï ìx ³ 1 - 1 Û í Û í Û x = ïx + 2 = î (x + )2 2 1 î2x =1 2 1 1
Với x = ta có y = (thỏa mãn điều kiện 2x + y +1 > 0) 2 2 æ ö
Vậy hệ có nghiệm ( x y) 1 1 ; = ; ç ÷ è 2 2 ø
ì xy - y - y + = (x - y)2 8 2 8 4 ï
Bài 11. Giải hệ phương trình: í . 3x - 8
ï 2x - 7 + y -1 = î 2 Hướng dẫn giải 7
+ ĐK: x ³ ; y ³ 1. 2 + Biến đổi ( )
1 được: (xy - y) +
xy - y + = (x + y)2 4 2 8 2 4 .
Û ( xy - y + )2 = (x+ y)2 2 2 2
Û ... Û y = x - 2. 3 - 8
+ Thế vào (2) ta được: 2 - 7 + - 3 = x x x . 2
Áp dụng BĐT Cauchy ta được: x - + x - ▪ x - = ( x - ) 2 7 1 2 6 2 7 2 7 .1 £ = . 2 2 x - + x - ▪ x - = (x - ) 3 1 2 3 3 .1 £ = . 2 2 65 3 -8 Suy ra 2 - 7 + - 3 £ x x x
.Dấu ' = ' xảy ra khi và chỉ khi x = 4. 2 Vậy nghiệm ( ;
x y) cần tìm là (4;2).
Bài 12. Giải hệ phương trình sau: 3 2 x x ( x 1- e ) x 1 1 - ì -
+ + e (2 - y) + xy - 2x - y + 2 = 0 ï í (x, y Î ! ). 2 2
ï 4x + 2y + 8x -14 + x + 2x - y - 2 = 3 î ( x+5+ x+2) Hướng dẫn giải (1) 2 x y ( x 1 ( 2) - Û + - x - e - ) 1 = 0 (3) Xét hàm số x 1 f (x) - = x - e - 1 trên ! ; x 1 f '(x) 1 -
= - e ; f '(x) = 0 Û x = 1 x -¥ 1 +¥ f '(x) + 0 - 1 - f (x)
Từ bảng biến thiên, ta có f (x) £ 1 - ,"x Î ! Do đó 2
(3) Û y = 2 - x
Thế vào phương trình (2) ta được: 2 2
2x + 8x -10 + 2x + 2x - 4 = 3( x +5 + x + 2 + ) 1 (4)
Điều kiện xác định của (4) là: x ³1 (*). Với đk (*), ta có:
(4) Û (2x - 2)(x + 5) + (2x - 2)(x + 2) - 3( x +5 + x + 2) = 3
Û 2x - 2 ( x +5 + x + 2)-3( x +5 + x + 2) = 3
Û ( x +5 + x + 2)( 2x - 2 -3) = 3
Û 2x - 2 - 3 = x + 5 - x + 2
Û ( 2x - 2 - x + 5) + ( x + 2 - 3) = 0 x - 7 x - 7 Û + = 0 2x - 2 + x + 5 x + 2 + 3 æ 1 1 ö Û (x - 7) + = 0 ç ÷
è 2x - 2 + x + 5 x + 2 + 3 ø 1 1
Û x = 7 (tm (*)) ( Vì + > 0 "x ³1) 2x - 2 + x + 5 x + 2 + 3
Với x = 7 Þ y = 4
- 7 (thỏa mãn điều kiện).
Vậy hệ có nghiệm duy nhất ( ; x y) = (7;- 47). 3 3 2
ìx - y + 3y + x - 4y = -2 ï
Bài 13. Giải hệ phương trình : í 2 3
ï x + y = 5x - î y 66 Hướng dẫn giải 3 3 2 3 3
ìx - y + 3y + x - 4y = 2 -
ìx + x = (y -1) + (y -1) ï ï Ta có : í Û í . 2 3 2 3
ï x + y = 5x - î y
ï x + y = 5x - î y
Hàm số f(x) = x3 + x là hàm số đồng biến trên R nên phương trình f(x) = f(y - 1) Û x = y – 1. 3 3
ìx + x = (y -1) + (y -1) ìx = y -1 ìx = y -1 ï ï ï Do đó í Û í Û í 2 3 2 3 2 3
ï x + y = 5x - î y
ï x + y = 5x - î y
ï (y -1) + y = 4y - 5 î ì 5 ïy ³ é y = 2 Ta có 2 3
( y -1) + y = 4y - 5 Û í 4 Û ê ï ë y =12 3 2
îy -15y + 38y - 24 = 0 ìx =1 ìx =11 Vậy hệ có 2 nghiệm : í ;í îy = 2 îy =12 2 3 3 2 3
ìï x y + 2xy - y(y -9) = 27
Bài 14. Giải hệ phương trình : í (x, y Î! ) . 3 2 2 2
ïîx y + 4xy -9y +5y = 9 Hướng dẫn giải +) y = 0 không thỏa mãn ì 9 27 2 3x + 2x -1+ = ï 2 3 ï y y +) y ≠ 0, hệ pt Û í 9 9 3
ïx + 4x + 5- = 2 ïî y y 3 2 3 2 3
ìï x + 2x -1= t -t (1)
Đặt t = , hệ phương trình trở thành í y 3 2
ïîx + 4x + 5 = t + 3t (2)
+) Từ hai phương trình trên suy ra
x3 + 3x2 + 6x + 4 = t3 + 3t Û (x +1)3 + 3(x +1) = t3 + 3t (3)
Xét hàm f(t) = t3 + 3t đồng biến trên ! . Phương trình (3) tương đương x+ 1 = t. 3
Thay vào phương trình (2) và giải phương trình được x = 1, y = . 2 3 Nghiệm của hpt là (1; ). 2 2 2 (
ìï x +1)(y -1) = 3xy
Bài 15. (Olimpic Trại hè Hùng Vương 2013) Giải hệ phương trình : í 2 2
ïîx + y + xy -8x -9y + 23 = 0 Hướng dẫn giải 2 2 (
ìï x +1)(y -1) = 3xy
Hệ phương trình : í 2 2
ïîx + y + xy -8x -9y + 23 = 0 Ta có : 2 2 2 2
x + y + xy -8x - 9y + 23 = 0 Û x + (y -8)x + y - 9y + 23 = 0 14 2 2 2
D = (y -8) - 4(y - 9y + 23) = 3
- y + 20y - 28 ³ 0 Þ 2 £ y £ x 3 Tương tự : 2 2 2 2
x + y + xy -8x - 9y + 23 = 0 Û y + (x - 9)y + x -8x + 23 = 0 11 2 2 2
D = (x - 9) - 4(x -8x + 23) = 3
- x +14x -11³ 0 Þ1£ x £ y 3 67 2 2 x +1 y -1 Ta có : 2 2
(x +1)(y -1) = 3xy Û × = 3 x y 2 x +1 1 é 11ù 1 é 11ù
Xét hàm số f (x) =
= x + với x Î 1;
, ta có : f '(x) = 1- > 0,"x Î 1; nên hàm số f(x) x x ê 3 ú ë û 2 ê x 3 ú ë û é 11ù é 11ù đồng biến trên 1;
, suy ra f (x) ³ f (1) = 2,"x Î 1; ê 3 ú ë û ê 3 ú ë û 2 y -1 1 é 14ù 1 é 14ù
Xét hàm số g(y) =
= y - với y Î 2;
, ta có : g '( y) = 1+ > 0,"y Î 2; nên hàm số y y ê 3 ú ë û 2 ê y 3 ú ë û é 14ù 3 é 14ù g(y) đồng biến trên 2;
, suy ra g( y) ³ g(2) = ,"y Î 2; ê 3 ú ë û 2 ê 3 ú ë û 2 2 x +1 y -1 é 11ù é 14ù Suy ra : × ³ 3;"xÎ 1; ,"y Î 2; ê x y 3 ú ê 3 ú ë û ë û 2 2 x +1 y -1 ìx =1 Do đó phương trình 2 2
(x +1)(y -1) = 3xy Û × = 3 Û í x y îy = 2 ìx = 1 Vì í
không thoả mãn phương trình thứ 2 của hệ nên hệ đã cho vô nghiệm . î y = 2
Bài 16. (Chuyên Nguyễn Tất Thành – Yên Bái) Giải hệ phương trình: 3 2 ìïx + y =1 í 17 ï
5 - x + 3y 4 - y =14 4 - y + 3x 5 î - x Hướng dẫn giải
Điều kiện x £ 5; y £ 4
17 5 - x + 3y 4 - y = 14 4 - y + 3x 5 - x
Û (3(5- x) + 2) 5- x = (3(4 - y) + 2) 4 - y (1)
Xét hàm số f (t) = (3t + 2) t liên tục trên [0; + ¥)có 3t + 2
f '(t) = 3 t + > 0, "t > 0 2 t
Suy ra f(t) là hàm số đồng biến trên [0; + ¥)
Khi đó (1) Û f (5- x) = f (4- y) Û 5- x = 4- y Û y = x - 1
Thay y vào phương trình đầu ta được éx = 0 x (x )2 3 3 2 1 1 x x 2x 0 ê + - = Û + - = Û x =1 ê êx = 2 - ë
Vậy hệ phương trình đã cho có nghiệm là (0;- ) 1 ; (1;0); ( 2; - 3 - ) 68
Bài 17. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2012) Giải hệ phương trình: 2 2 3
ìï x - 2x -5+ 2x x +1 = 2( y + ) 2 1 y + 2y + 2 í 2 2
ïîx + 2y = 2x - 4y + 3 Hướng dẫn giải
Trừ vế với vế của 2 phương trình (1), (2) ta có: 2 2 2
x + x x + = y + y + + ( y + ) 2 2 2 . 1 2 4 2 2 1 y + 2y + 2
Û x + x x + = ( y + )2 + ( y + ) ( y + )2 2 2 1 1 1 1 +1
Đưa về xét hàm số: f (t) 2 2
= t + t t +1 có t + t +1 t 2 ( )2 2 2
f '(t) = 2t + t +1 + = > 0"t 2 2 t +1 t +1
Þ f (t) là hàm số đồng biến trên R, lại có
f (x) = f ( y + ) 1 Þ x = y +1, x + (x - )2 2 = x - (x - ) 2 2 1 2 4
1 + 3 Û 3x - 2x -5 = 0
éx = -1Þ y = -2 ê Û 5 3 êx = Þ y = ë 2 2
Bài 18. (Chuyên Nguyễn Bỉnh Khiêm – Quảng Nam 2014) Giải hệ phương trình sau :
ìï(17 -3x) 5- x + (3y -14) 4- y = 0 (1) í
( x, y Î R) 2
ï2 2x + y + 5 + 3 3x + 2y +11 = x + 6x +13 (2) î Hướng dẫn giải ìx £ 5 ï
§ Điều kiện : íy £ 4 (*)
ï2x + y +5 ³ 0 , 3x + 2y +11³ 0 î
§ Với điều kiện (*), phương trình (1) tương đương :[3(5- x) + 2]. 5- x = [3(4 - y) + 2]. 4 - y (3)
Xét hàm số : f (t) = (3t + 2). t , t ³ 0 3t + 2 '
Þ f (t) = 3 t + > 0 , "t > 0 2 t
f (t) liên tục "t ³ 0 , suy ra f (t) là hàm số luôn đồng biến trên [0;+¥)
Khi đó : pt(3) Û f (5 - x) = f (4 - y) Û 5 - x = 4 - y Û y = x -1 § Thay y = x -
1 vào phương trình (2), ta được : 69 4 2
2 3x + 4 + 3 5x + 9 = x + 6x +13 với x ³ - 3 2
Û é2 3x + 4 - 2(x + 2)ù + é3 5x + 9 - 3(x + 3)ù = x + x ë û ë û 2 2
2 é(3x + 4) - (x + 2) ù 3é(5x + 9) - (x + 3) ù ë û ë û 2 Û + = x + x 3x + 4 + (x + 2) 5x + 9 + (x + 3) 2 - x(x +1) 3 - x(x +1) Û + = x(x +1) 3x + 4 + (x + 2) 5x + 9 + (x + 3) æ 2 3 ö Û x(x +1)ç1+ + ÷ = 0 è 3x + 4 + (x + 2)
5x + 9 + (x + 3) ø éx = 0 Û 2 3 4 ; vì : 1+ + > 0 , "x ³ - ê ëx = 1 - 3x + 4 + (x + 2) 5x + 9 + (x + 3) 3
Với x = 0 suy ra y = - 1 Với x = 1 - suy ra y = -2
Thử lại ta thấy cả hai đều thỏa điều kiện (*)
§ Vậy hệ phương trình có 2 nghiệm : (0; - ) 1 , ( 1 - ; - 2) ì 1 1 16
x + y + x - y + + = ïï x + y x - y 3
Bài 19. Giải hệ phương trình í 1 1 100 2 2
ï(x + y) + (x - y) + + = 2 2 ïî (x + y) (x - y) 9 Hướng dẫn giải 1 1
Đặt a = x + y +
;b = x - y +
(| a |,| b |³ 2) x + y x - y ì 16 a + b = ìa = 2 ì 10 ïï ï ïa = Ta có: 3 í Û í 10 Ú í 3 100 b = 2 2 ïa - 2+ b - 2 ï = î 3 ïîb = 2 ïî 9
Từ đó suy ra hệ phương trình có bốn nghiệm ì 2 ì 2 x = x = ìx = 2 ïï 3 ìx = 2 ïï 3 í Ú í Ú í Ú í îy = 1 - 1 ï îy =1 1 ï y = y = - ïî 3 ïî 3 ì x +1 y +1 ï + = 4 ï x -1 y -1
Bài 20. Giải hệ phương trình: í ï 1 1 + = 3 ïîx -1 y -1 2 2
ìïx + y + xy = 7
Bài 21. Giải hệ phương trình í 4 4 2 2
ïîx + y + x y = 21 70 3
ìïx + 2(x +1) = 3y + 2 y
Bài 22. Giải hệ phương trình sau trên R: í 2 3 ï x - y y = 2 î Hướng dẫn giải: 3 2
Cộng hai phương trình vế theo vế thu được phương trình 3 2
x + 3x + 2x = y + 3 y + 2 y Xét hàm số 3 2
f (x) = x + 3x + 2x với x Î R Ta có 2
f '(x) = 3x + 6x + 2 > 0 nên hàm số đồng biến
nên từ f (x) = f ( y) Þ x = y
từ đó thay vào giải ra được x = y =1 hoặc x = 1+ 3, y = 4 + 2 3 . ìx, y > 0 ï
Bài 23. Tìm tất cả các số thực x, y thỏa hệ: íx + y = 2 . ï 1+ 1 + î x y x y ³1 Hướng dẫn giải:
Ta chứng minh nếu các số x, y thỏa mãn hai điều kiện đầu thì x 1 + y 1 + x y £1Û (x + ) 1 ln x + ( y + ) 1 ln y £ 0
Thay y = 2 - x, ta chứng minh: f (x) = (x + )
1 ln x + (3- x)ln(2 - x) £ 0 với 0 < x < 2
Ta có f (x) = x - ( - x) 1 1 ' ln ln 2 + + x - 2 x 2 1 1 é 1 1 ù 1 1 1 æ 1 1 ö (x - )2 1 æ 1 1 ö f ''( x) = + - ê + ú £ + - + = - + £ 0 2 ç ÷ ç ÷
x 2 - x êë x (2- x)2 ú x 2- x 2 è x 2- x ø
x (2 - x) è x 2 - x ø û
Do đó f ¢(x)nghịch biến trên (0;2),hơn nữa f ¢( )
1 = 0nên f '(x)nhận giá trị dương trên (0 ) ;1 và âm
trên (1;2).Suy ra f (x) £ f ( )
1 = 0với mọi xÎ(0;2).
Từ đó, hệ phương trình có nghiệm x = y = 1. 3 ìïy ( 2 3x + 2x - ) 1 + 4y = 8
Bài 24. Giải hệ phương trình sau: í (x, yÎ! ) 2 3 2 2
ïîy x + 4y x - 6y + 5y = 4 Hướng dẫn giải:
+) y = 0 không thỏa mãn hệ. ì 4 8 2 3x + 2x -1+ = (1) ï 2 3 ï y y
+) Xét y ¹ 0 , hệ tương đương í 4 6 3 ïx + 4x + 5+ = 2 ïî y y 71 3 8 6 æ 2 ö 2
Cộng vế với vế ta được 3 2
x + 3x + 6x + 4 = + Û (x + )3 1 + 3( x + ) 1 = + 3. 3 ç ÷ y y è y ø y Xét hàm số: 3 2
f (t) = t + 3t; f (
¢ t) = 3t +3 > 0 "t ÎR 2
Do đó f (t) là hàm số đồng biến trên ! , suy ra x +1= y
Thế vào (1), kết hợp x ¹ 1
- , ta được (x + )( x - )+(x + )2 = (x + )3 1 3 1 1 1 Û (x - )2 1 = 1 ìx = 1 Do đó í là nghiệm của hệ. î y = 1 3 ì x + 5 - y =1 ï
Bài 25. Giải hệ phương trình: í x -1 3 3 2
x - 3x - y - 6y - 9y - 2 + ln = 0 ï î y +1 Hướng dẫn giải:
Điều kiện: y ³ 0; x > 1.
Ta biến đổi phương trình thứ hai tương đương với: 3 2 3 2
(x -1) + 3(x -1) + ln(x -1) - (y +1) -3( y +1) - ln( y +1) = 0 Nhận thấy hàm số 3 2
f (t) = t + 3t + ln t đồng biến trên khoảng (0;+¥)
nên ta có x -1 = y +1 Û x = y + 2
Thế vào phương trình đầu ta có cặp nghiệm duy nhất của hệ phương trình là x = 3 và y = 1 Dạng 4: Đánh giá 5 4 2
ìx - x + 2x y = 2 ï Bài 1.
Giải hệ phương trình sau: 5 4 2
íy - y + 2y z = 2 ï 5 4 2
z - z + 2z x = 2 î Hướng dẫn giải
Nhận thấy x = y = z =
1 là một nghiệm của phương trình. Ta chứng minh hệ có nghiệm duy nhất.
Giả sử x > 1(*) khi đó 5 4 2 5 4 2
z - z + 2z x > z - z + 2z 5 4 2
Û z - z + 2z - 2 < 0 Û ( 4 z + ) 1 ( z - ) 1 < 0 Û z < 1 Với z < 1 ta có 5 4 2 5 4 2
y - y + 2y z < y - y + 2y 5 4 2
Û y - y + 2y - 2 > 0 Û ( 4 y + ) 1 ( y - ) 1 > 0 Û y > 1 72 Với y > 1 ta có 5 4 2 5 4 2
x - x + 2x y > x - x + 2x 5 4 2
Û x - x + 2x - 2 < 0 Û ( 4 x + ) 1 ( x - ) 1 < 0 Û x < 1
Suy ra x < 1 mâu thuẫn (*).
Tương tự giả sử x < 1 ta cũng dẫn đến điều vô lý.
Vậy hệ phương trình có nghiệm duy nhất x = y = z = . 1 2 2
ì4x + 2xy + x + 6 xy - y + y =15(1) ï Bài 2. Giải hệ phương trình 3 3 í 6(x + y ) 2 2 ïx +
- 2(x + y ) = 3(2) 2 2 î
x + xy + y Hướng dẫn giải ìxy ³ 0 Điều kiện í . 2 2
îx + y + xy ¹ 0
Nếu x = 0 hoặc y = 0 thì hệ vô nghiệm. ìx £ 0 Nếu í
(x,y không đồng thời bằng 0) thì vế trái của (2) âm, phương trình (2) không thoả mãn. î y £ 0 Do đó x > 0, y > 0.
Vì 2 xy £ x + ynên từ phương trình (1) suy ra 2 2 2 2
15 = 4x + 2xy + x + 6 xy - y + y £ (2x + y) + x + 3(x + y) - y =(2x + y) + 4x + 2y 2
Þ (2x + y) + 2(2x + y) ³15Þ 2x + y ³ 3 (3) 2 2 2 2 3 3 3 3 x + y 3(x + y ) 3(x + y ) 2(x + y ) Mặt khác, ta có 2 2 xy £
Þ x + xy + y £ Þ ³ . (4) 2 2 2 2 2 2
x + xy + y x + y 3 3 2(x + y ) Ta chứng minh rằng: 2 2
³ 2(x + y )(5). 2 2 x + y
Thật vậy bất đẳng thức (5) tương đương 3 3 2 2 2 3
2(x + y ) ³ (x + y ) 6 6 3 3 4 2 2 4
Û x + y + 4x y ³ 3x y + 3x y (6)
Áp dụng bất đẳng thức Cauchy, ta có: 6 3 3 3 3 3 12 6 4 2
x + x y + x y ³ 3 x y = 3x y 6 3 3 3 3 3 6 12 2 4
y + x y + x y ³ 3 x y = 3x y
Cộng vế với vế hai đẳng thức trên ta được (5), từ đó suy ra (5) 73 3 3 3(x + y ) Từ (4) và (5) suy ra: 2 2 ³ 2(x + y ) 2 2
x + xy + y
Kết hợp với phương trình (2) và lưu ý rằng 2 2
2(x + y ) ³ x + y, ta được: 3 3 6(x + y ) 2 2 2 2 3 = x +
- 2(x + y ) ³ x + 2(x + y ) ³ x + (x + y) = 2x + y (7) 2 2
x + xy + y
Từ (3) và (7) suy ra 2x + y = 3 và x = y ta được x = y = 1 (thoả mãn các điều kiện của bài toán). Vậy
hệ có nghiệm duy nhất là (1;1). ìïy +(4x - )2 2 3 1 = 4x (8x + ) 1 Bài 3.
Giải hệ phương trình sau: í (I ) 2
ïî40x + x = y 14x -1 Lời giải. 1 æ 2 ö ĐK: x ³
. Đặt t = 4x t ³ . ç ÷ 14 è 7 ø ìy + (t - )2 2 3 1 = t (2t + ) 1 ( ) 1 ( ï I ) Û í 5 t 7 2 ï t + = y t -1(2) î2 4 2
Nhận xét: từ (2) ta có: y > 0 2t +1 2t + +1 2t +1 1
Ta có: 3 t (2t + ) 2 3 1 = 2t. .1 £ = t + 2 3 2 1 1
Do đó, từ (1) suy ra: y + (t - )2 2 2 2
1 £ t + Û y £ t - + 3t - (3) 2 2 2 7 y + t -1 7 Ta có: 2 y t -1 £ 2 2 2 7 y + t -1 5 t Do đó, từ (2) suy ra: 2 2 2 2 t + £
Û 5t -3t +1£ y (4) 2 4 2 1 Từ (3) và (4) suy ra: 2 2
5t - 3t +1 £ t - + 3t - 2 3 3
6t - 6t + £ 0 Û (2t - )2 1 1 1 2
1 £ 0 Û t = Û 4x = Û x = . 2 2 2 2 8 1
Thay x = vào hệ (I ) ta có: 8 ì 1 ì 3 ì 2 2 3 y + = 1 y = ï ï ïy = ± ï 4 ï 4 ï 2 3 í Û í Û í Û y = 3 3 3 ï ï ï 3 2 y = y = y = ïî 2 4 ïî 2 ïî 2 74 æ ö
Vậy hệ phương trình có nghiệm duy nhất: (x y) 1 3 ; = ç ; ÷. ç 8 2 ÷ è ø 2 2 ìx - 2y =1 ï Bài 4. Giải hệ phương trình: 2 2
í2y - 3z = 1 ( x, y, z Î ! )
ïxy + yz + zx =1 î Lời giải
+) Nếu x = 0 thay vào hệ ta có hệ vô nghiệm.
+) Nếu x ¹ 0 ta đặt y = a ;
x z = bx thay vào hệ ta được 2 ìx ( 2 1- 2a ) =1 ï 2 2 2 2 2 ( )ï 1
ìï - 2a = 2a -3b ìï4a -3b =1 2 1 íx ( 2 2
2a - 3b ) =1 Þ í Û í 2 2 1 ï
ïî - 2a = a + ab + b ï2a + a -1+ î b(a + ) 1 = 0 2
ïx (a + ab + b) = 1 î éìa = 1 - êí 2 2 2 2 ìï4a -3b =1 ìï4a -3b =1 êîb = 1 ± Û í Û í Û ( ï a + î
)1(2a - )1+b(a + ) 1 = 0 ( ï a + î ) 1 (2a -1+ b) = 0 êìb =1- 2a êí 2
êëî2a -3a +1= 0 ìa = -1 +) Nếu í
thay vào (1) không thỏa mãn îb = ±1 éìa =1 êíb ìb = - a êî = 1 - 1 2 ì ì 1 a = 1 ïa = +) Nếu í Û ê thay í
vào (1) không thỏa mãn, thay í 2 2 ì 1 î2a - 3a +1 = 0 êïa = îb = 1 - ï êí 2 îb = 0 êï ëîb = 0 æ ö æ ö
vào (1) ta có x = ± 2 . Do đó nghiệm của hệ là (x y z) 1 1 ; ; = 2; ;0 , - 2; - ;0 ç ÷ ç ÷ è 2 ø è 2 ø Bài 5.
Giải hệ phương trình sau:
ì2log (2x + 3y) = log (2 + 2x + 3y) 7 3 ï í (x, y Î ! ). 7 27 2 4
2 27x + 26x + 3y + =1+ x + 6 ï î 3 2 Lời giải
Đặt t = log (2x + 3y), phương trình (1) trở thành: 7
log (7t + 2) = 2 Û 9t = 7t t + 2 Û ... Û t = (S
1 ử dụng tính chất đơn điệu) 3
Û 2x + 3y = 7 Û 3y = 7 - 2x (3) 75
Thế (3) vào (2) ta được: 2 28 27 (9x + 4) 3(9x + 4) 2 4 4 2. 27x + 24x + =1+ x + 6 Û 2. + 4 =1+ (4) 3 2 3 2
Đặt t = 9x + 4 (t ³ 0). Phương trình (4) trở thành: 2 2 t 3t t 3t 4 2. + 4 =1+ Û 4. + 4 =1+ + 6t (5) 3 2 3 2 + 6
Áp dụng bđt AM – GM ta có: 6 £ t t 2 2 t Từ (5) ta có: 2 2 2 4.
+ 4 £ 2t + 4 Û 4t + 48 £ 3t +12t +12 Û (t - 6) £ 0 Û t = 6. 3 2 59 æ 2 59 ö
Từ đó x = Þ y =
. Vậy hệ đã cho có nghiệm duy nhất ( ; x y) = ; . ç ÷ 9 27 è 9 27 ø Bài 6. Giải hệ phương trình : 4 4
ìx + 9y - 6 3xy = 4 - ï 2 í
( x Î R, y Î R ) x xy 5 2 + y + = ï 3 î 3 + 3xy 6 Lời giải
Đặt : 3y = z Ta có : 4 4 2 2
x + z ³ 2x z ,suy ra : 1 £ t = xz £ 2 xz xz
Xét vế trái của phương trình (2) 2 2 x + z + ³ 2xz + 1+ xz 1+ xz t 1
f (t) = 2t +
,t Î[1;2] (t = xz), suy ra 'f(t) = 2 + > 0,"t Î[1;2] 1+ t (1+t)2 5 1
f (t)là hàm số đồng biến trên (1;2) , suy ra : f (t) ³ f (1) = ,suy ra VT = f (t) ³ 5 2 3 6 1 1
Dấu bằng xẩy ra khi t = 1, suy ra : x = 1; y = hoặc x = 1 - ; y = - . 3 3 Bài 7.
Giải hệ phương trình sau: 2 2 ìx + 2x xy = ï y y í 2 ; x, y Î ! ( 3 3 2 ï 4x + y + 3 î x
x )(15 x + y) = 3 x ( y y + x y + 4x x ) Lời giải 76
Điều kiện: x ³ 0, y ³ 0.
Đặt a = x,b = y ( a ³ 0,b ³ 0). Hệ phương trình đã cho trở thành 4 3 5
ìa + 2a b = b ( ) 1 ï í (ï4a +b +3 î
a )(15a +b ) = 3a(b + a b + 4a )2 6 6 5 2 3 2 3 (2)
Nhận xét: a = 0 Þ b = 0; b = 0 Þ a = 0. Do đó ( ,
a b) = (0,0) là một nghiệm của hệ.
Bây giờ ta xét a > 0,b > 0. Đặt b = ka Þ k > 0 . Với cách đặt này thì • 1+ 2
Phương trình (1) trở thành: 5 1+ 2 = Û = k k ak a (3) 5 k
• Phương trình (2) trở thành: ( a + a k + a )( a + k a ) = a(k a + a k + a )2 6 6 6 5 2 2 2 3 3 3 3 4 3 15 3 4 (4) 5 æ 3k öæ 1+ 2k 2 ö
Thay (3) vào (4) ta được: 6 4 ç + k + 5 ÷ + = ç ÷ ( 3 k + k + 4 3 ) (5) è 1+ 2k øè 3k ø
Áp dụng bất đẳng thức Cauchy - Schwarz cho vế trái của (5) ta được: 2 5 5 æ 3k öæ 1+ 2 æ k ö 3k 1+ 2 ö k 6 4 ç + k + 5 ÷ + ³ ç ÷ ç 5( 6 4 + k + . ÷ 3 ) 3 è 1+ 2k øè 3k ç ø 1+ 2k 3k ÷ è ø = ( ( + )( +k ) 2 2 2 6 2 1 4
+ k ³ 4 + k + k ) ( )2 3
Đẳng thức xảy ra khi và chỉ khi k = 1. Khi đó a = b = 3 hay x = y = 9.
Vậy hệ phương trình đã cho có 2 nghiệm ( ; x y) là (0;0),(9;9). 2 2
ì4x + 4xy + x + 6 xy - y + y =15(1) ï Bài 8. Giải hệ phương trình 3 3 í 6(x + y ) 2 2 ïx +
- 2(x + y ) = 3(2) 2 2 î
x + xy + y Bài giải ìxy ³ 0 Điều kiện í 2 2
îx + y + xy ¹ 0
Nếu x = 0 hoặc y = 0 thì hệ vô nghiệm ìx £ 0 Nếu í
(x,y không đồng thời bằng 0) thì vế trái của (2) âm, phương trình (2) không thoả mãn. Do î y £ 0
đó x > 0, y > 0. 1.0 đ 77
Vì 2 xy £ x + ynên từ phương trình (1) suy ra 2 2 2 2
15 = 4x + 4xy + x + 6 xy - y + y £ (2x + y) + x + 3(x + y) - y =(2x + y) + 4x + 2y 1.0 đ 2
Þ (2x + y) + 2(2x + y) ³15Þ 2x + y ³ 3 (3) 2 2 2 2 3 3 3 3 x + y 3(x + y ) 3(x + y ) 2(x + y ) Mặt khác, ta có 2 2 xy £
Þ x + xy + y £ Þ ³ . (4) 2 2 2 2 2 2
x + xy + y x + y 3 3 2(x + y ) Ta chứng minh rằng: 2 2
³ 2(x + y )(5). 1.0 đ 2 2 x + y
Thật vậy bất đẳng thức (5) tương đương 3 3 2 2 2 3
2(x + y ) ³ (x + y ) 6 6 3 3 4 2 2 4
Û x + y + 4x y ³ 3x y + 3x y (6)
Áp dụng bất đẳng thức Cauchy, ta có: 6 3 3 3 3 3 12 6 4 2
x + x y + x y ³ 3 x y = 3x y 6 3 3 3 3 3 6 12 2 4
y + x y + x y ³ 3 x y = 3x y
Cộng vế với vế hai đẳng thức trên ta được (5), từ đó suy ra (5) 3 3 3(x + y ) Từ (4) và (5) suy ra: 2 2 ³ 2(x + y ) 2 2
x + xy + y
Kết hợp với phương trình (2) và lưu ý rằng 2 2
2(x + y ) ³ x + y, ta được: 3 3 6(x + y ) 2 2 2 2 3 = x +
- 2(x + y ) ³ x + 2(x + y ) ³ x + (x + y) = 2x + y (7) 2 2
x + xy + y
Từ (3) và (7) suy ra 2x + y = 3 và x = y ta được x = y = 1 (thoả mãn các điều kiện của bài toán). Vậy
hệ có nghiệm duy nhất là (1;1) ì 3 3 ï
y (2x - y) 2 + x ( 2 2 5y - 4x ) 2 = 4y Bài 9.
Giải hệ phương trình: í ( x, y Î ! ). 2
ï 2 - x + y +1 + 2 = x + y î Hướng dẫn giải
Điều kiện: x £ 2 , y ³ - ; 1 3
y (2x – y) ³ 0 ; 2 2 5y – 4x ³ 0.
+) Sử dụng bất đẳng thức AM-GM cho hai số không âm ta có: 2 2 + - 3 2
y (2x - y) = 2 y ( 2
2xy - y ) £ y xy y 2 ( + - 2 2 5y - 3x 5 - 4 ) 2 2 2 5 4 2 2 2 £ x y x x y x = 2 2 78 2 2 5y - 3x Suy ra: 3 3 +
y (2x - y) 2 x ( 2 2
5y - 4x ) £ 3xy + 2 2 2 5y - 3x Vì vậy, ta phải có: 2 4y £ 3xy + Û (x y)2 3 – £ 0 Û x = y. 2
Vậy phương trình đầu tương đương với x = y.
Thay x = y vào phương trình thứ hai của hệ ta được: 2 - x + x +1 2 2 + = x + x (*).
Do 2 - x + x +1 > 0 nên ta phải có: 2
x + x – 2 > 0 Þ x > 1 ( do x ³ - ). 1
Khi đó phương trình (*) tương đương với: 2
x – x +1+ (x – 1 – 2 - x )+ x - x +1 = 0 Û ( æ 1 1 ö 2 x – x – ) 1 1+ + = 0. ç ÷ è x -1+ 2 - x x + x +1 ø æ ö 2 Û 1 1
x – x –1 = 0 do1 + + > 0 ç ÷ è x -1+ 2 - x x + x +1 ø é 1+ 5 ê x = ( t / m) + ó 2 ê Þ 1 5 x = y = . ê 1- 5 2 êx = ë 2 æ1+ 5 ö
Vậy hệ có nghiệm duy nhất ( ; x y) = ç ÷. ç 2 ÷ è ø
Bài 10. [Đề hsg Dương Xá,2008-2009] Giải hệ phương trình sau: 2 2
ìï x + x + y +1+ x+ y + x+ y +1+ y =18 í 2 2
ï x + x + y +1 - x + y + x + y +1 - y = 2 î Lời giải 2
ìïx + x + y +1³ 0 Điều kiện í 2
ïîy + x + y +1³ 0
Cộng và trừ từng vế tương ứng của hệ phương trình trên ta được 2 2
ìï x + x + y +1 + y + x + y +1 =10 í ïîx + y = 8
Thế y=8-x vào phương trình trên ta được 2 2
x + 9 + x -16x + 73 =10 79 Û 2 2 2
(x + 9)(x -16x + 73) = -x +8x + 9 Û 2 2 2 2
(x + 3 ) é(x -8) + 3 )ù = 9 + x(8 - x) (1) ë û ® ®
Trong hệ trục tọa độ xét a(x;3); b(8 - ; x 3) ® ®
Khi đó | a |.| b |= 2 2 2 2
(x + 3 ) é(x -8) + 3 )ù ë û ® ®
a . b = 9 + x(8 - x) ® ® ® ®
Pt (1) tương đương với | a |.| b |= a . b (2) ® ® ® ®
Ta có | a |.| b | ³ a . b ® ® ® ® ®
Khi đó (2) xảy ra khi và chỉ khi hoặc a = 0 hoặc b = 0 (không xảy ra) hoặc a cùng ® 8 - x hướng b suy ra =1 > 0 Û x=4. x
KL: Nghiệm của hệ là (4;4)
Bài 11. [Đề chọn hsg tỉnh Trà Vinh, 2014-2015] Giải hệ phương trình :
ì x + y + x - y £ 2 1/ í 2 2 î x + y = 1 ì x +1 + y +1 = 3 ï 2/ í
ï x + ( y - 4)2 + 5 = 5 î
Bài 12. [Đề xuất Chuyên Biên Hòa, DHĐBBB 2015-2016]Giải hệ phương trình
ïìx6 + 2x3 -10 y2 = xy - x2 y2 í ïî4x3(2y + )
1 - 28y2 + 3 = 2 x2 + ( 4 y2 + ) 1 - 4xy Lời giải 2 2
ïìxy - x y ³ 0 0 ì £ xy £ 1 Điều kiện : í Û í Û 0 £ xy £ 2 ïîx + ( 4 2 y + ) 1 - 4xy ³ 0 (îx - 2y) 1 2 + 4 ³ 0 1 2 1 æ 1 2 2 ö 1 2 2 1
Ta có : xy - x y = - ç xy - ÷ £ Ü xy - x y £ ( dấu = xảy ra khi xy = ) 4 è 2 ø 4 2 2 Do đó từ (1) Þ 2 6 x + 4 3 x - 20 2
y £ 1 (3) Từ (2) và (3) ta suy ra : 8 3 x y + 4 3 x - 28 2 y + 4 ³ 2 6 x + 4 3 x - 20 2
y + 2 (x - 2y)2 + 4 Û 8 3 x y + 4 ³ 2 6 x + 8 2
y + 2 (x - 2y)2 + 4 80 Û 4 3 x y + 2 6 ³ x + 4 2
y + (x - 2y)2 + 4
Û 2 ³ (x - 2y)2 3
+ (x - 2y)2 + 4 (4)
Ta lại có (x - 2y)2 3
+ (x - 2y)2 + 4 ³ 2 ì ìx = 1 ìx = -1 3 x - 2y = 0 ìx = 0 ï ï Do đó (4) Û í Û í hoặc í 1 hoặc í 1 îx - 2y = 0 îy = 0 ïy = y = - î 2 ïî 2 ìx = 1 ï
Thử lại ta thấy chỉ có í 1 là nghiệm của hpt.0,5 ïy = î 2
Bài 13. Giải hệ phương trình: Hướng dẫn giải Đặt 3 2 3 2
f (t) = 2t + 9t + 12t ; g(t) = t + 3t + 4t + 15 . Ï f
Ô (x)= g (y) 3 2 3 2 Ô
ì2x + 9x +12x = y + 3y + 4y +15 Ô ï Hệ trở thành:Ì f
Ô (y)= g(x). 3 2 3 2
í2y + 9y +12y = z + 3z + 4z +15 Ô Ô
Ôf (z)= g (x) ï 3 2 3 2 Ô Ó
2z + 9z +12z = x + 3x + 4x +15 î Ta có g¢(t) 2
= 3t + 6t + 4 > 0 với mọi t nên hàm g đồng biến. ìx ³ y
ìïg (x) ³ g ( y)
ìïg (x) ³ f (x) Giả sử x = max( , x y, z) thì í hay í suy ra í î x ³ z
ïîg (x) ³ g (z)
ïî f (z) ³ g (z).
ìx + x + x + ³ x + x + x ( ì x - ) 1 ï ( 2 3 2 3 2 x + 7x +15) £ 0 3 4 15 2 9 12 Hay í Û í * . 3 2 3 2
î2z + 9z +12z ³ z + 3z + 4z +15 ï( z - ) 1 î
( 2z +7z -15) ( ) ³ 0 Do 2 2
x + 7x +15 > 0" ,
x z + 7z -15 > 0"z nên từ (*)ta có x £ 1 £ z.
Lại theo giả sử ở trên, x = max( ,
x y, z) nên x = z =1.Thế vào hệ phương trình ban đầu ta được y = 1.
Thử lại thấy x = y = z = 1 là nghiệm.
Kết luận:Hệ đã cho có nghiệm duy nhất x = y = z = 1. 3
ì x + 2 = cos y + cos z ï
Bài 14. Giải hệ phương trình : 3
í y + 2 = cos z + cos x 3
ï z + 2 = cos x +cos î y (Chưa giải) 81 2. Có tham số 3 3 2
ìx - y + 3y -3x - 2 = 0 (4) ï Bài 1.
Tìm m để hpt sau có nghiệm thực: í 2 2 2
ïx + 3 1- x - 2 2y - y + m = 0 (5) î Hướng dẫn giải ì 1 - £ x £1 Điều kiện: í . î0 £ y £ 2
Phương trình (4) Û x - x = ( y - )3 3 3 1 -3( y - ) 1 . Xét hàm số 3
f (t) = t - 3t, với t Î[ 1 - ;1 .] 2
f '(t) = 3t -3 £ 0,"t Î[ 1 - ; ] 1 .
Þ f(t) là hàm số nghịch biến trên [ 1 - ; ]
1 (vì nó liên tục trên đoạn này).
Suy ra: x = y - . 1
Thay vào phương trình (5) ta được: 2 2
x + 1- x + m = 0. Đặt 2
u = 1- x , u Î[0 ]
;1 . Ta có phương trình: g(u) = 2
u - u -1 = m 5
min g(u) = - ;max g(u) = - . 1 [0; ]1 4 [0; ]1 5
Suy ra hệ phương trình đã cho có nghiệm Û - £ m £ - . 1 4 2 2 ìïx + y = 4 Bài 2.
Tìm m để hpt có nghiệm í 2
ïîx - y = m ìx ³ m 2 2 2 ìïx + y = 4
ìïy = x - m ï • í Û í
Û íy = ± x - m 2 2
ïîx - y = m
ïîx - x - (m + 4) = 0 ï 2
x - x - (m + 4) = 0 î
• Do đó hệ có nghiệm khi chỉ khi phương trình:f(x) = x2 + x – (m + 4) = 0 có nghiệm trong [m;+¥) (*) - ± m + • 1 4 17 -17
f(x) = 0 có D = 4m + 17 nên f(x) = 0 có nghiệm x = khi m ³ . 2 4 • 1 - + 4m +17 Do đó: (*) Û m £
Û 2m +1£ 4m +17 2 ì 1 ì2m +1 £ 0 17 1 ïm>- • 17 Û í Û - £ m £ - hay í 2 Û - £ m £ 2 2
î4m +17 ³ (2m +1) 4 2 4 ïî 2 - £ m £ 2
Một số cách giải khác: 82 2 2 2 ìïx + y = 4
ìïy = x - m • Cách 2: í Û í (I) 2 2
ïîx - y = m
ïîx - x - (m + 4) = 0(*)
Hệ (I) có nghiệm Û x2 + x – (m + 4) = 0 có nghiệm trên [-2;2].
Dựa vào đồ thị parabol (P) y = x2 + x – 4 trên [-2;2], và đường thẳng y = m suy ra kết quả.
• Cách 3: Giải theo tam thức bậc hai....
ìï x +1+ y -1 = a Bài 3.
Tìm a để hệ phương trình sau có nghiệm í .
ïîx + y = 2a +1 Hướng dẫn giải Điều kiện x ³ 1 - ; y ³1. ì x +1 + y -1 = ï a
Hệ phương trình tương đương (íï x+1 î
)2 +( y-1)2 = 2a+1 ì x +1 + y -1 = ï a Û í . 1 2
ï x +1 + y -1 = éa - (2a + ) 1 ù 2 ë û î
Do đó x +1 và y -1 là nghiệm của phương trình 1 2 2
T - aT + éa - (2a + ) 1 ù = 0 (*) 2 ë û
Để hệ trên có nghiệm khi phương trình (*) có 2 nghiệm không âm ì 2 ìD ³ ïa - 2( 2 a - 2a - ) 1 ³ 0 0 ï ï
Û íS ³ 0 Û ía ³ 0
Û 1+ 2 £ a £ 2 + 6 . ïP 0 ï ³ 1 î ï ( 2 a - 2a - ) 1 ³ 0 î2 2
ìïu = x -1 ³ 0 Þ x = u +1 Đặt í 2
ïv = y -1 ³ 0 Þ y = v +1 î
ìï2x + y -1 = m Bài 4. Tìm m để hệ: í có nghiệm.
ïî2y + x -1 = m Hướng dẫn giải 2
ìïu = x -1 ³ 0 Þ x = u +1 +) Đặt í 2
ïv = y -1 ³ 0 Þ y = v +1 î 83 2
ìï2u + v + 2 = m +) Đưa về hệ: í (**) 2
ïî2v + u + 2 = m
+) Điều kiện để hệ (**) có nghiệm m ³ 2
Ta xét m ³ 2 hệ có nghiệm hay ko éìu - v = 0 êí (I ) 2
êî2u + v + 2 = m
Biến đổi hệ (**) trở thành:
êì2u + 2v -1= 0 êí (II ) 2
êëî2u + v + 2 = 0 2 - m
+) Xét hệ (I): u=v ta được 2v2+v+2-m=0 có P =
£ 0 với m ³ 2 PT luôn có nghiệm v ³ 0 Þhệ 2 0
có nghiệm u=v=v 2
0 suy ra hệ ban đầu có x=y=vo +1
+) Xét hệ (II): ……….
ìïa(x - a)2 (x-2 2)+1£ 0 Bài 5.
Tìm tham số a để hệ sau có nghiệm: í .
ïîx > a > 0 Lời giải
ìïa(x -a)2 (x- )+ £ (
ìï x - a)2 ax -
a (x - a)2 2 2 1 0 2 2 +1£ 0 í Û í
ïîx > a > 0
ïîx > a > 0 ì 1 ì1 x + £ 2 2 (x -a) 1 + (x - a) 1 + a + £ 2 2 1 ï 2 ï 2 ( ) Û í (x -a) a Û 2 2 í (x -a) a ï
îx > a > 0
ïx > a > 0 î (2)
Do (2)nên x - a và a là hai số dương,áp dụng bất đẳng thức Cô – si cho 4 số dương ta được: 1 (x-a) 1 + (x - a) 1 1 4 + a + ³ 4 = 2 2 3 2 ( ) 2 2 (x -a) a 4 ì 3 2 ïx = 1 1 ï
Do đó (1)chỉ đúng khi dấu đẳng thức xảy ra tại (3)tức là: ( x - a) 2 = a = Û í 2
(x - a)2 a ï 2 a = ïî 2 2 3 2
Vậy hệ có nghiệm khi và chỉ khi a =
và nghiệm của hệ là: x = 2 2 Bài 6.
Tìm giá trị lớn nhất của tham số m để cho hệ phương trình sau có nghiệm: 84 2 2
ìx + xy + y = m ï 2 2 2
íy + yz + z = m (x, y, z Î ! ). ï 3
xy + yz + zx = î m Hướng dẫn giải y 3 3 1
+ Đặt: X = x + ; Y = y; Z =
( y + z); T = (z - y). 2 2 2 2 3 Ta đ ược: 2 2 2 2
x + xy + y = X +Y ; 2 2 2 2
y + yz + z = Z +T ;
(xy + yz + zx) = XZ + YT . 2 ì 2 2
ïX +Y = m ïï Do đó ta có hệ 2 2 2
íZ + T = m . ï 3 3 ïXZ +YT = ï m î 2 + Chú ý: 2 2 2 2 2 2
(X +Y )(Z +T ) = (XZ +YT) + (XT -YZ) .
Do đó:Hệ đã cho có nghiệm thì: 2 æ 3 ö 4 4 2 3 3 3 3 . m m ³ ç
m ÷ £ m (m - ) £ 0 Þ 0 £ m £ ç 2 ÷ 3 3 è ø 4 Suy ra: 3 m £ . 3 ìXT = YZ (1) ï 4 ï 3 + Xét 3 m = .Ta có hệ: 3 íXZ +YT = m (2) 3 2 ï 2 2 2
ïZ +T = m (3) î 3
Từ (1)có thể đặt X = uZ, Y = uT ,thay vào (2)và (3)ta có: u = m. 2 ì 3 ì 2m + 3 ïX = mZ x = y 2 ï ï 2 ï m ï 3 ï m + 2 4
Do đó ta có hệ: íY = mT hay íz = y với 3 m = . 2 ï ï m 3 2 2 2 2
ïZ +T = m ï m 2 ï ïy = 2 î 3m + 4m + 4 ïî 4
+ Từ đó:Đáp số của bài toán là 3 m = . 3 85 ìåpx = 4 ï i i 1 = ï ï p Bài 7. a/ Tìm * p Î • sao cho hệ 1 - íå x = 4 có nghiệm. 1 i 1 = ï
ïx > 0,"iÎ1, ï p i î a
b/ Với p tìm được ở câu a/, hãy xác định tập hợp tất cả các giá trị của tổng: với ai åp i 2 i - 1 = 1 ai > 0 và 2 åpa =1. i i 1 = Hướng dẫn giải Câu a æ p ö æ p 1 ö Do: 2 16 = å x . ç p p i ÷ ç å ÷ ³ Þ £ 4.
è i 1= ø è i 1= xi ø
p = 4 : Khi đó: x =1,i 1
Î ,4.Vậy hệ có nghiệm. i ìx + x = 3
p = 3: Chọn x =1 và 2 3 í
có nghiệm.Nên (x , x , x ) là nghiệm của hệ. 1 x .x = 1 î 1 2 3 2 3 ìx + x = 4 p = 2 : 1 2 í
có nghiệm.Nên (x , x )là nghiệm của hệ. x .x = 1 î 1 2 1 2 p =1:Vô nghiệm.
Vậy hệ có nghiệm khi p = 2; p = 3; p = 4. Câu b 2 a
Ta có: f (a , a ,..., a ) = . p åp i 1 2 2 i a - 1 = (1 a ) i 1 1 2 Xét hàm: 2
g(x) = x(1- x ),0 < x <1; g '(x) = 0 Û x =
. Ta có: max g(x) = . 3 (0;1) 3 3 3 3 3 3 p Do đó: 2
f (a , a ,..., a ) ³ a =1 hay p = 3. p åp =
. Dấu đẳng thức xảy ra khi: 1 2 2 i i 1 = 2 3 a a 1 1 1 2
p = 2 : f (a , a ) = + ³ 2 ³ 2 2 vì 2 2 a + a = .D
1 ấu đẳng thức xảy ra khi a = a = , 1 2 2 2 a a a .a 1 2 1 2 2 1 2 1 2 2 a 1- a 1 1
f (a , a ) = +
liên tục trên (0;1).Khi a ® 0 thì f (a , a ) ® +¥.Vậy p = 2,tập giá trị là: 1 2 2 2 1- a a 1 1 2 1 1 é2 2;+¥ ë ). 1
p = 3: Chọn a = 1- 2x ; a = x ; a = x , 01 2 3 2 86 1- 2x x x 1 2 2 2
a + a + a = 1- 2x + x + x = 1. f (a , a , a ) = + +
= g(x) liên tục trên (0; ); 1 2 3 1 2 3 2x 1- x 1- x 2 æ 1 ö 3 3 é3 3 ö g =
, limg(x)=+¥.Vậy tập giá trị là: ê ;+¥ ÷. ç ÷ x 0 è 3 ø 2 ® 2 ÷ ë ø 3 3
p = 4 : f (a , a ,..., a ) >
. Chọn a = 1- 2x ; a = x ; a = x , a = x thỏa giả thiết: 1 2 p 2 1 2 3 4 2 2 2 2 1
a + a + a + a = 1- 3x + x + x + x = 1 với 0 < x < ; 1 2 3 4 3 1- 2x x x x 1
f (a , a , a , a ) = + + + = g(x) liên tục trên (0; ) ; 1 2 3 4 2x
1- x 1- x 1- x 3 3 3 é3 3 ö lim g(x) =
; lim g(x) = +¥ .Tập giá trị là: ê ;+¥ ÷ . 1 x 0 ÷ x 2 ® ® 2 ë ø 3 Bài 8.
Tìm tất cả các giá trị thực của tham số m để hệ sau có nghiệm thực: 2 ì 4x 2 ïx + ³ 5 2 í (x + 2) ï 4 2
îx + 8x +16mx + 32m +16 = 0 (Chưa giải) Bài 9.
Tìm m để hệ phương trình sau có nghiệm duy nhất: 2 3 ì x - m y +1 =1 ï í 1 . 2 x + y + = ï m 2 y + y +1 î (Chưa giải)
Bài 10. (THPT Quảng Xương 2 – Thanh Hóa, 2009-2010) Tìm các giá trị của m để hệ phương trình sau có nghiệm ( ;
x y) sao cho x > 0, y > 0 ( ì ï x y)æ 1 ö + 1+ = 5 ç ÷ ï è xy ø í (ï æ 1 ö 2 2 x + y ) 1+ = 2m -1 ç 2 2 ÷ ïî è x y ø Hướng dẫn giải 1 1 ìu + v = 5
Đặt u = x + ;v = y + hệ trở thành í x y 2 2
îu + v = 2m + 3
Từ hệ suy ra uv = - m +11 khi đó u, v là nghiệm của phương trình: 87 2
X - 5X – m +11 = 0 ( ) * .
Do x > 0, y > 0 nên u ³ 2, v ³ 2.
Bài toán trở thành tìm m để phương trình (*) có hai nghiệm lớn hơn hoặc bằng 2 .
Đặt t = X - 2 phương trình (*) trở thành: 2
t - t - m + 5 = 0 (* ) * .
Để pt (*) có hai nghiệm lớn hơn hoặc bằng 2 ↔ pt (**) có hai nghiệm không âm 19 Giải được: £ m £ 5. 4
Bài 11. Tìm giá trị của tham số a để hệ phương trình sau có đúng 1 nghiệm: 2 ìï
x + 3 + y = a í 2 2
ï y + 5 + x = x + 5 + 3 - î a 88




