Chuyên đề phương trình và bất phương trình – Mẫn Ngọc Quang

Chuyên đề phương trình và bất phương trình do thầy Mẫn Ngọc Quang biên soạn gồm 140 trang. Tài liệu tổng hợp các phương pháp giải phương trình và bất phương trình điển hình kèm các ví dụ mẫu và bài tập có lời giải chi tiết.

74 37 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 10

Môn: Toán 10

Thông tin:

140 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
1
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
PHƯƠNG TRÌNH
Phương trình căn thức
Dạng 1. Phương pháp nâng lũy thừa.
Kiến thức cơ bản:
Phương trình
2
0g x
f x g x
f x g x
Phương trình
0
0
f x
f x g x g x
f x g x
Ví dụ 1. Giải phương trình
2 5 4x x x
.
Lời giải. Điều kiện:
5
2
x
. Phương trình đã cho tương đương với:
2
2
2
4 0
4
2 5 4
2 5 8 16
2 5 4
4
4
7
3 7 0
10 21 0
x
x
pt x x
x x x
x x
x
x
x
x x
x x
Vậy phương trình đã cho có nghiệm duy nhất là
7x
.
Ví dụ 2. Giải phương trình
2
2 4 2x x x x
.
Lời giải. Điều kiện:
. Phương trình đã cho tương đương với:
2 2
2 2
1
2
2 4 2 3 2 0
x x
x
pt
x
x x x x x
Vậy phương trình đã cho có nghiệm là
1; 2
x
.
Ví dụ 3. Giải phương trình
7 4 1 5 6 2 2 3x x x x x
Lời giải. Điều kiện:
3
2
x
. Nhận xét rằng
4 2 4 5 9x x x x x
, chuyến vế, bình phương phương
trình đã cho ta được:
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
2
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
 

7 2 2 3 5 6 4 1
9 5 2 7 8 12 9 5 2 5 6 4 1
3
7 8 12 5 6 4 1
2
4 13 2 0
pt x x x x
x x x x x x
x
x x x x
x x
Suy ra
13
2;
4
x x
. Thử lại thấy thỏa mãn.
Vậy phương trình đã cho có hai nghiệm kể trên.
Ví dụ 4. Giải phương trình
3
2
1
1 1 3
3
x
x x x x x
x
Lời giải. Điều kiện:
1x
.
Chú ý hằng đẳng thức
3 2
1 1 1
x x x x
, nên phương trình đã cho được viết lại thành:
2
2
1 1
1 1 3
3
x x x
x x x x
x
2
2
2 2
2
1
1 1 1 3
3
1
1 3 1 3
3
1 3 0
1
1
3
x x
x x x x
x
x
x x x x x x
x
x x x
ptvn
x
x
Vậy phương trình đã cho vô nghiệm.
Dạng 2. Phương pháp đặt ẩn phụ hoàn toàn hoặc không hoàn toàn.
Kiến thức cơ bản:
Đặt ẩn phụ hoàn toàn, đặt
t A x
đưa về phương trình ẩn
t
.
Đặt ẩn phụ không hoàn toàn, đặt
t A x
phương trình sau khi biến đổi chứa hai ẩn
,t x
và xét
đenta chính phương.
Phương trình tổng quát dạng:
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
3
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
a A x b B x c A x B x dC x D
A, Đặt ẩn phụ hoàn toàn.
Ví dụ 1. Giải phương trình
2
2 3 1 3 2 2 5 3 16x x x x x x
Lời giải. Điều kiện:
1x
.
Đặt
2 3 1 0
t x x
suy ra
2 2
3 4 2 2 5 3
t x x x
. Khi đó phương trình đã cho trở
thành:
2 2
0
4 16 20 0 5
5 4 0
t
t t t t t
t t
Do đó
2
2 3 1 5 3 4 2 2 5 3 25
x x x x x
2
2
2
21
1
3
2 2 5 3 21 3 3
4 2 5 3 21 3
x
x x x x
x x x
.
Vậy phương trình đã cho có nghiệm duy nhất là
3x
.
Ví dụ 2. Giải phương trình
2
7 7 7 6 2 49 7 42 181 14x x x x x x
Lời giải. Điều kiện:
1x
.
Đặt
7 7 7 6 0
t x x
suy ra
2 2
14 1 2 49 7 42
t x x x
. Khi đó phương trình đã cho trở
thành:
2 2
0
1 181 182 0 13
13 14 0
t
t t t t t
t t
Do đó
2
7 7 7 6 13 14 1 2 49 7 42 169
x x x x x
.
2
2
2
2
6
12
7
49 7 42 84 7 6
49 7 42 84 7
x
x x x x
x x x
.
Vậy phương trình đã cho có nghiệm duy nhất là
6x
.
B, Đặt ẩn phụ không hoàn toàn.
Phương trình tổng quát dạng
2 2
1 1 2 2 2 3 3 3
a x b a x b x c a x b x c
.
Ví dụ 1. Giải phương trình
2 2
1 2 3 1x x x x x
.
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
4
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Lời giải. Điều kiện:
x
.
Bước 1. Đặt
t f x
đưa về phương trình bậc hai ẩn
t
.
Bước 2. Tính
theo
x
và biểu diễn
2
ax b t g x
.
Đặt
2 2 2 2
2 3 1 2 2 1 2 2
t x x x x x t x
, khi đó phương trình đã cho trở thành:
2 2
1 2 2 1 2 2 0x t t x t x t x
Có
2 2
2
1 4 2 2 6 9 3
x x x x x
nên ta được:
2
2
2
1 3
1
2 3 1
2
1 3
2 3 2
2
2
2 1 0 1 2
x x
t x
x x x
x x
x x
t
x x x
Vậy phương trình đã cho có hai nghiệm là
1 2x
.
Ví dụ 2. Giải phương trình
2 2
4 3 1 1 0x x x x x x
.
Lời giải. Điều kiện:
2
1 0
x x
.
Đặt
2 2 2 2 2
1 0 1 1
t x x x x t x t x
.
Khi đó phương trình đã cho trở thành:
2 2
1 4 3 1 0 3 3 0t x x x t t x t x
Ta có
2 2
2
3 4 3 6 9 3 0
x x x x x
nên ta được:
2
2
3 3
1
3
1 3
2
1 41
3 3
1
2
2
x x
x
t
x x
x x
x
x x x
t x
Vậy phương trình đã cho có ba nghiệm là
1 41
1;
2
x
.
Ví dụ 3. Giải phương trình
2 2
3 2 1 1 1 3 8 2 1x x x x x
.
Lời giải. Điều kiện:
x
.
Phương trình đã cho tương đương với:
2 2
3 3 8 3 2 1 0
x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
5
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Đặt
2 2 2 2 2 2
2 1 1 2 1 3 3 3 3
t x t x t x x
.
Khi đó phương trình đã cho trở thành:
2 2
3 8 3 3 0t x t x x
Ta có
2 2
2 2
8 3 12 3 100 60 9 10 3 0
x x x x x x
nên
2
2
3 8 10 3
3 2 1
6 3
0
3 8 10 3
2 1 1 3
1 3
6
x x x
t
x x
x
x x
x x
t x
Vậy phương trình đã cho có nghiệm duy nhất là
0x
.
Ví dụ 4. Giải phương trình
3 3
4 1 1 2 2 1x x x x x
.
Lời giải. Điều kiện:
1x
.
Đặt
3 3 2 3 2
1 0 1 1
t x x t x t
.
Khi đó phương trình đã cho trở thành:
2 2
2 1 4 1 2 1 0 2 4 1 2 1 0t x t x t x t x
Ta có
2 2
2
4 1 8 2 1 16 24 9 4 3 0
x x x x x
nên
3
3
3
4 1 4 3
2
2 1
1 2 1
4
3
4 1 4 3 1
2 1 1
4
4 2
x x
x
t x
x x
x x
x
x
t
Vậy phương trình đã cho có hai nghiệm là
3
3
2;
4
x
.
Dạng 1. Phương trình đưa về tổng các đại lượng không âm hoặc
n n
A B
.
Dấu hiệu: Hệ số trước căn thường là những số chẵn.
1. Đưa về tổng các đại lượng không âm.
Dùng các biến đổi hoặc tách ghép hằng đẳng thức để phương trình đã cho xuất hiện các số
không âm
2 2
0
... 0 0
0
A
A B D C B
C
2. Biến đổi về dạng
n n
A B
.
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
6
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Đưa phương trình về dạng
2 1
,
n n
A B
A B n k
n k
.
Hoặc về dạng
2
0
,
n n
A B A B
A B n k
A B
n k
.
Bài tập ví dụ.
Ví dụ 1. Giải phương trình
2
4 3 2 2 1 4 3 3x x x x x x
Lời giải. Điều kiện:
1
2
x
. Phương trình đã cho tương đương với:
2
2
2 2
4 4 3 3 3 2 2 1 0
4 4 3 3 2 1 2 1 1 0
2 3 2 1 1 0
2 3 0 2 3
1
2 1 1 0 2 1 1
pt x x x x x
x x x x x x
x x x
x x x x
x
x x
Vậy phương trình đã cho có nghiệm duy nhất là
.
Ví dụ 2. Giải phương trình
2
4 6 10 4 14 11x x x x
Lời giải. Điều kiện:
5
3
x
. Phương trình đã cho tương đương với:
2
2
2
2
6 10 4 6 10 4 4 20 25
6 10 2 2 5
6 10 2 2 5
6 10 2 2 5 0
3
6 10 2 3
3 13
2
4
6 10 2 7 0
6 10 2 3
pt x x x x
x x
x x
x x
x
x x
x
x x ptvn
x x
Vậy phương trình đã cho có nghiệm là
3 13
4
x
.
Bài tập vận dụng.
Vận dụng 1. Giải phương trình
2
4 12 1 4 5 1 9 5x x x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
7
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Lời giải. Điều kiện:
9 1
5 5
x
. Phương trình đã cho tương đương với:
2
2 2
4 5 1 4 5 1 13 5 4 9 5 1 0
2 5 1
2 5 1 9 5 2 1 0 9 5 2 1
1 0
x x x x x x x
x x
x x x x x x
x
Vậy phương trình đã cho có nghiệm duy nhất là
.
Vận dụng 2. Giải phương trình
2
6 3 1 9 0x x x x
Lời giải. Điều kiện:
1
3
x
. Phương trình đã cho tương đương với:
2 2
2
2
2
9 6 3 1 2 1 9 6 3 1 3 1
1 3 3 1
1 3 3 1
1 3 1 3
2
3 1 2
7 37
2
3 1 2
3 1 4
pt x x x x x x x
x x
x x
x x
x
x x
x
x x
x x
Vậy phương trình đã cho có nghiệm duy nhất là
7 37
2
x
.
Vận dụng 3. Giải phương trình
3 2
3 1 2 6 4 2 6x x x x x x x
Lời giải. Điều kiện:
2x
. Chú ý
3
3 2
3 3 1 1
x x x x
.
Và
1 2 4 2 3 7 2 1 2 4 2 3 7
x x x x x x x x
3 3
2 3 2 3 2 1 2 1
x x x x
. Khi đó ta được
3
3
2
1 2 1 1 2 1
0
2 2
2
pt x x x x
x
x x x
x x
Vậy phương trình có nghiệm duy nhất là
2x
.
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
8
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Dạng 2. Đặt ẩn phụ đưa về hệ phương trình đối xứng hai ẩn.
Ví dụ. Giải phương trình
2
2 2 2 1x x x x
Lời giải. Điều kiện:
1
2
x
. Đặt
2 1 0
y x
, khi đó
2
2 1
y x
.
Và phương trình đã cho trở thành
2
2
2
2
1 2 1
2 2
2 1
2 1 1
x y
x x y
y x
y x
Với
1a x
thì hệ phương trình trên
2
2 2
2
2 1
2 2
2 1
a y
a y y a
y a
2
2 0 2 0
2 0
1
1 2 1
2 2
1 2 1
1 2 1 0
a y
a y a y a y a y a y
a y
x
x x
x
x x
x x
Vậy phương trình đã cho có nghiệm là
2 2x
.
Bài toán tổng quát.
Giải phương trình
2
ax b c dx e x x
với
e bc
d ac
Chọn
1
2; 1;
2
1
0; ; 1; 1
2
a b c
d e
ta được
2
1 1
2 1 1
2 2
x x
.
Hoặc phương trình
2
1
ax b x cx d x
a
với
2
1
2 2
a c c
b ad
Xét hàm số
2
1
y x cx d
a
có đạo hàm
2
' 0
2
ac
y x c x
a
.
Khi đó bằng phép đặt
2
ac
ax b y
, ta sẽ đưa phương trình về được dạng hệ phương trình
đối xứng quen thuộc.
Ví dụ 1. Giải phương trình
2
29 12 61
3
6 36
x
x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
9
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Làm nháp.
2
29 1
3 ' 6 1 0
6 6
f x x x f x x x
.
Lời giải. Điều kiện:
12 61 0x
.
Đặt
12 61 1
36 6
x
y
suy ra
2
12 61 1 1
36 3 36
x
y y
2 2
12 61 36 12 1 3 5
x y y y y x
Mà theo cách đặt ta có
2 2
29 1
3 3 5
6 6
x x y x x y
.
Do đó phương trình đã cho
2
2 2
2
3 5
3 3
3 5
x x y
x y x y y x
y y x
3 2 0 3 3 2 0
3 2
3
x y
x y x y x y x y x y
x
y
Với
x y
ta được
2
5
3 5
3
x x y
vì
1
6
y
.
Với
3 2
3
x
y
ta được
2
3 2 1 14
3 5
3 3
x
x x x
.
Vậy phương trình đã cho có các nghiệm là
1 14 5
;
3 3
x
.
Dạng 3. Đặt ẩn phụ đưa về hệ phương trình đối xứng hai ẩn bằng phương pháp đồng nhất hệ số.
Ví dụ. Giải phương trình
2
4 4 3 2 5x x x x
Lời giải. Điều kiện:
5
2
x
. Đặt
1
2 5 2 1;
2
x y y
.
Khi đó
2
2 2
2 5 2 1 4 4 1 2 5 4 4 4 2x y y y x y y x
.
Nên phương trình đã cho trở thành
2
2
2 2
4 4 4 2 1
4 4 3 2 1
4 4 4 2 4 4 4 2 2
x x y
x x y
y y x y y x
Lấy
1 2pt pt
ta được
2 2
4 4 4 4 2 2x y x y y x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
10
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

4 6 0 4 4 6 0
2 3
2
x y
x y x y x y x y x y
x
y
Với
x y
ta được
2
1
1 17
2
4
2 2 0
y
x y
y y
.
Với
2 3
2
x
y
ta được
2 5 4 2 0
x x
2
2
9 37
4
2 5 4 2
x
x
x x
.
Vậy phương trình đã cho có ba nghiệm là
9 37 1 17
;
4 4
x
.
Phương pháp tổng quát. Đặt
2 5 0
x Ay B
với mục đích là đưa về hệ phương trình đối
xứng hai ẩn dạng
, 0
, 0
f x y
g x y
Ta có
2
2 2 2
2 5 2 5 2 2 5
x Ay B x Ay B A y ABy B x
Và
2
4 4 3
x x Ay B
, khi đó ta được hệ phương trình:
2 2
2 2 2 2 2 2
4 4 3 4 4 3
2 2 5 2 5 2
x x Ay B x x B Ay
A y ABy B x A y ABy B x
Để đưa về được hệ phương trình đối xứng hai ẩn, tức là hai giá trị
,x y
có vai trò như nhau. Nên
thế
x y
vào hệ phương trình trên ta có được:
2
2
2 2 2 2
4
4 4 3 4 2 2
1
2 5 2 3 5
2
A
x x B Ax AB A
B
A x ABx B x B B
A
Do đó ta có phép đặt
1
2 5 2 1;
2
x y y
và được lời giải như trên.
Bài tập vận dụng.
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
11
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Vận dụng 1. Giải phương trình
2
9 5 3 2 3x x x x
Đáp số: phương trình vô nghiệm.
Vận dụng 2. Giải phương trình
2
2004 1 16032 1x x x x
Đáp số:
4009x
.
Vận dụng 3. Giải phương trình
3 2
3
4
81 8 2 2
3
x x x x x
Đáp số:
3 2 6
0;
3
x
.
Dạng 4. Đặt ẩn phụ phương trình chứa căn bậc ba đưa về hệ đối xứng.
Phương pháp.
Đặt ẩn phụ bằng căn thức bậ ba.
Biến đổi đưa về hệ phương trình đối xứng.
Bài tập ví dụ.
Ví dụ 1. Giải phương trình
3
3 2
3
2. 3 2 3x x x
Lời giải. Điều kiện:
3
3
2
x
.
Đặt
3
3 2 0
y x
suy ra
2 3 3 2
3 2 2 3
y x x y
.
Khi đó phương trình đã cho tương đương với:
3 2 3 2
3
2
3
3 2 3 2
3 2
2 3 2 3
2. 3
2 3 2 3
2 3
y x y x
y x
x y x y
x y
3 3 2 2 2 2
2 2
3 2
2 2 0 2 0
0
2 0 1
2 3
x y y x x y x xy y x y x y
y
x y x xy y x y x y y
y y
Vậy phương trình đã cho có nghiệm duy nhất là
.
Ví dụ 2. Giải phương trình
3
3 2
2 9 3 13x x x x
Lời giải. Điều kiện:
x
.
Đặt
3
3
9
y x
suy ra
3 3
9
x y
.
Khi đó phương trình đã cho tương đương với:
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
12
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
3 3
3 3
3 3
2
2 2
2
2
9
9
9
4 13
2 3 13
2 3 13
x y
x y
x y
x xy y
x y x
x y x
Đặt
a x y
b xy
nên hệ phương trình trên trở thành:
2 3 2
3
2
2 2
3 9 2 3 13 18
2 6 18 3
2
2 13
2 13 2 13
a a b a a a
a ab a
b
b a
a b b a
Từ đó suy ra
3
; 2;1 , 1;2
2
x y
x y
xy
.
Vậy phương trình đã cho nghiệm duy nhất là
1,2
x
.
Ví dụ 3. Giải phương trình
3 33 3
25 25 30x x x x x
Hướng dẫn. Điều kiện:
x
.
Đặt
3
3
25
y x
suy ra
3 3
25
x y
.
Khi đó phương trình đã cho tương đương với:
2
3 3
2 25
25
30
30
x y x y xy
x y
xy x y
xy x y
Ví dụ 4. Giải phương trình
3 3
3 3
4 2 4x x x x x
Hướng dẫn. Điều kiện:
x
.
Đặt
3
3
4
y x
suy ra
3 3
4
x y
.
Khi đó phương trình đã cho tương đương với:
2
3 3
2 4
4
2
2
x y x y xy
x y
x y xy
x y xy
Dạng 5. Đặt ẩn phụ đưa về phương trình đẳng cấp bậc cao.
Phương pháp. Đặt ẩn đưa phương trình vô tỷ về dạng
Đẳng cấp bậc hai
2 2
0aA bAB cB
.
Đẳng cấp bậc ba
3 2 2 3
0aA bA B cAB dB
.
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
13
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Xét các trường hợp để chia cả hai vế của các phương trình trên cho
A
hoặc
B
rồi đưa về ẩn
A
t
B
sau đó sử dụng lược đồ Hoocner.
Bài tập ví dụ.
Ví dụ 1. Giải phương trình
3
3 2
3 2 6 18x x x x x
Lời giải. Điều kiện:
6x
. Phương trình đã cho tương đương với:
3
3
3 6 2 6 0x x x x
Đặt
2
6 0 6
a x x a
nên phương trình
trở thành:
3 2 3
3 2 0x xa a
Nhận xét
6x
không là nghiệm của phương trình đã cho. Nên chia cả hai vế cho
3
a
và đặt
x
t
a
suy ra
3
3 2 0t t
.
Sử dụng lược đồ Hoocner ta có
Từ đó suy ra
2
3
3 2 0 1 2 0
t t t t
3
1 6
2 2
2 2 7
2 6 0
x
t x a x x
t x a
x
x x
Vậy phương trình đã cho có nghiệm là
3;2 2 7
x
.
Ví dụ 2. Giải phương trình
3 3 3
1 2 2 3x x x x
Lời giải. Điều kiện:
x
.
Đặt
3
3 3
3
1
1 2 2 3
2
a x
a b x x x
b x
.
Khi đó phương trình đã cho trở thành:
3
3 3 3 3 3 2 2 3 3 3
3
3
3
3 3
3 3
1 0
0
1; 2
3 0 0 2 0
3
0
2
1 2 0
a b a b a b a b a a b ab b a b
x
a
x x
ab a b b x
x
a b
x x
1
0
3
2
1
1
1
2
0
1
1
2
0
0
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
14
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Vậy phương trình đã cho có các nghiệm là
3
1;2;
2
x
.
Ví dụ 3. Giải phương trình
2 2
2 2 1 3 4 1x x x x x x
Lời giải. Điều kiện:
1
2
x
.
Đặt
2
2 2 2 2
5
2
3 3 2 2 1 3 8 1
2
2 1 0
a x x
a b x x x x x
b x
.
Khi đó phương trình đã cho trở thành:
2
2 2 2 2 2 2 2 2
2 2
2
3 3 3 2
1
2 2 0 0 2 2 1
2
1
a b a b a b a b a b a ab b
x
a ab a a b a b x x x
x
Vậy phương trình đã cho vô nghiệm.
Dạng 6. Đặt ẩn phụ đưa về hệ phương trình đại số.
Phương pháp. Phương trình tổng quát dạng
m n
af x b cf x d k
.
Đặt
m m
m
n n
n
af x b u
af x b u acf x bc cu
cf x d v acf x ad av
cf x d v
m n
cu bc av ad
. Nên phương trình đã cho trở thành:
m n
u v k
cu bc av ad
giải bằng phương pháp thế.
Bài tập ví dụ.
Ví dụ 1. Giải phương trình
3
2 3 2 3 6 5 8x x x
Lời giải. Điều kiện:
6
5
x
.
Đặt
3
3
3 2
2
3 2 2 3
5 2 3 6
6 5
6 5 0
a x a x
a b
b x
b x
.
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
15
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Khi đó phương trình đã cho trở thành:
3 2
2 3 8
5 2 3 6
a b
a b
2
3 2
3
8 2
8 2
3
2
3
4
8 2
5 3 8
5 3 8
3
a
b
a
a
b
b
a
a b
a
Nên suy ra
3
3 2 2
2
6 5 4
x
x
x
là nghiệm duy nhất của phương trình.
Ví dụ 2. Giải phương trình
3
24 12 6x x x
Lời giải. Điều kiện:
12x
.
Đặt
3
3
3 2
2
24 24
36
12
12 0
a x a x
a b
b x
b x
.
Khi đó phương trình đã cho trở thành:
2
3 2
3
6
6
36
6 36
b a
a b
a b
a a
3 2
6
; 0;6 , 3;3 , 4;10
12 0
b a
a b
a a a
Với
; 0;6
a b
nên suy ra
3
24 0
24
12 6
x
x
x
.
Với
; 3;3
a b
nên suy ra
3
24 3
3
12 3
x
x
x
.
Với
; 4;10
a b
nên suy ra
3
24 4
88
12 10
x
x
x
.
Vậy phương trình đã cho có nghiệm là
3; 24; 88
x
.
Ví dụ 3. Giải phương trình
4
4
5 12 3x x x
Lời giải. Điều kiện:
5x
.
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
16
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Đặt
4
4
4 4
4
4
5 5
17
12
12
a x a x
a b
b x
b x
.
Khi đó phương trình đã cho trở thành:
4
4 4
4
3
3
; 1;2 , 2;1
17
3 17
b a
a b
a b
a b
a a
Với
; 1;2
a b
nên suy ra
4
4
5 1
4
12 2
x
x
x
.
Với
; 2;1
a b
nên suy ra
4
4
5 2
11
12 1
x
x
x
.
Vậy phương trình đã cho có nghiệm là
11;4
x
.
Phương trình bậc cao – Kỹ thuật sử dụng lược đồ Hoocner
Lý thuyết. Xét phương trình bậc bốn
4 3 2
1 2 3 4 5
0
a x a x a x a x a
.
Nếu
1 2 3 4 5
0
a a a a a
, phương trình có một nghiệm là
Nếu có tổng hệ số chẵn bằng tổng hệ số lẻ thì phương trình có một nghiệm là
1x
.
Lược đồ Hoocner ( nhân ngang – cộng chéo )
1
a
2
a
3
a
4
a
5
a
0
x
1 1
a A
1 0 2 2
a x a A
2 0 3 3
A x a A
3 0 4 4
A x a A
4 0 5
0
A x a
Khi đó
0
x
là một nghiệm của phương trình đã cho, và ta phân tích phương trình ban đầu được thành
3 2
0 1 2 3 4
0
x x A x A x A x A
.
Phương trình bậc ba còn lại có nghiệm
'
0
x
và tiếp tục sử dụng lược đồ.
Ví dụ 1. Giải phương trình
4 3 2
2 5 3 8 4 0x x x x
Nhận xét: Tổng các hệ số của phương trình bằng
0
nên phương trình có một nghiệm là
1x
.
Lời giải. Do có một nghiệm
1x
nên tách theo lược đồ Hoocner ta có:
2
5
3
8
4
1
2
7
4
4
0
2
2
3
2
0
0
Khi đó phương trình đã cho trở thành

2
1 2 2 3 2 0
x x x x
.
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
17
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Vậy phương trình đã cho có nghiệm là
1
2; ;1
2
x
.
Ví dụ 2. Giải phương trình
5 4 3 2
4 4 21 19 20 12 0x x x x x
.
Nhận xét: Tổng các hệ số chẵn của phương trình bằng tổng các hệ số lẻ nên phương trình có một nghiệm
là
1x
.
Lời giải. Do có một nghiệm
1x
nên tách theo lược đồ Hoocner ta có:
4
4
21
19
20
12
1
4
8
13
32
12
0
2
4
0
13
6
0
0
1
2
4
2
12
0
0
0
Khi đó phương trình đã cho trở thành:

  
2
1 2 2 1 2 6 0
1 2 2 1 2 2 3 0
x x x x x
x x x x x
Vậy phương trình đã cho có nghiệm là
1 3
2; 2; ; 1;
2 2
x
.
Ví dụ 3. Giải phương trình
4 2
9 2 15 0x x x
.
Nhận xét: Đưa phương trình về dạng
2 2
0
f x g x
.
Giả sử, tồn tại số thực
m
thỏa mãn
2
2 2 2 2
2
2 2 2
2 9 2 15 0
2 9 2 15 0
pt x m mx m x x
x m m x x m
Xét đa thức bậc hai
2 2
2 9 2 15
f x m x x m
, ta muốn đưa
f x
về dạng hằng đẳng thức bậc
hai, thì trước hết
'
0
f x
.
Ta có
' 2
1 2 9 15 0 4
f x
m m m
. Do đó phương trình đã cho trở thành
2
2
2 2 2
4 1 0 5 3 0
x x x x x x
.
Lời giải. Phương trình đã cho tương đương với:
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
18
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
2
4 2 2 2
2
2
2 2 2
2
2
8 16 2 1 0 4 1 0
4 1 0 5 3 0
5 0
1 13 1 21
;
2 2
3 0
x x x x x x
x x x x x x
x x
x
x x
Vậy phương trình đã cho có các nghiệm kể trên.
Ví dụ 4. Giải phương trình
2
2
2
1 36
4 2 1 0
2
x
x x
x
x
.
Nhận xét: Đưa về phương trình
 
2
x a x b x c x d Ax
.
Lời giải. Điều kiện:
0
2
x
x
. Phương trình đã cho tương đương với:
2 2
2 3
2
2 2 3
2
4 2 1 2 36 0
4 2 3 2 36 0
2 2
4 3 36 0
pt x x x x x
x x x x x
x x
x x


Đặt
2
t x
x
, phương trình
trở thành:

2
4 3 36 0
t t
.
Vậy phương trình đã cho có các nghiệm kể trên.
Ví dụ 5. Giải phương trình

3
3
2 3 2
1 6 1 1 6 17 5
x x x x x x
Nhận xét: Đưa về phương trình đẳng cấp bậc.
Đẳng cấp bậc hai dạng
2 2
. . . 0a A b AB c B
.
Đẳng cấp bậc ba dạng
2 2 2 3
. . . . 0a A b A B c AB d B
.
Lời giải. Giả sử tồn tại hai số
,m n
thỏa mãn:
2 2
6 6
6 17 5 1 1
17 1
m m
x x m x x n x
n m n
Và hằng đẳng thức
3 2
1 1 1
x x x x
.
Đặt
2
1
1
A x
B x x
, khi đó phương trình đã cho trở thành:
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
19
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

3 3 3 2 2 3
6 6 11 6 11 6 0
2 3 0 2
3
pt A B AB A B A A B AB B
A B
A B A B A B A B
A B
Với
A B
, ta được
2
0
1 1
2
x
x x x
x
.
Với
2A B
, ta được
2
3 13
1 2 1
2
x x x x
.
Với
3A B
, ta được
2
1 3 1 2 6
x x x x
.
Vậy phương trình đã cho có nghiệm là
3 13
0;2;2 6;
2
x
.
Ví dụ 1:
Giải phương trình sau
4
3 4
3
x
x x
x
Lời giải
Điều kiện:
0
x
Phương trình đã cho tương đương
2
3 4 4 3 3 2 0 3 2 3 4 1
x x x x x x x x x x x
Vậy phương trình đã cho có tập nghiệm
1
S
Ví dụ 2: Giải phương trình sau
2
4 2 4 2 1x x x
Lời giải
Điều kiện:
1
2
x
Phương trình đã cho tương đương
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
20
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2 2
2
2 2
4 2 2 1 4 2 1 4 2 1 4 2 1 2 1 2 1 2 1 2 *
x x x x x x x x x x
.
Phương trình
*
tương đương
2 1 2 1 2 1 3
2 1 2 1 2 1 1
x x x x
x x x x
Với
2
2
3
3
2 1 3 4 6
8 10 0
2 1 3
x
x
x x x
x x
x x
Với
2 1 1 2 1 1 0
x x x x vn
Vậy phương trình đã cho có tập nghiệm
4 6
S
Ví dụ 3: Giải phương trình sau
7 1
1 4
2
x x
x
Lời giải
Điều kiện:
1x
Phương trình đã cho tương đương
2
2 2 2 2
2
2
8 7 2 1 2 1 1 9 6 1 1
1 3 1 1 2 1
3 1 1
1 1 3 1 1 4
x x x x x x x x x x x x
x x x x x
x x x
x x x x x
Với
2
2
1 2 1 1 2 1 4 5 2 0
x x x x x x vn
Với
1 1 4 1 4 1 0
x x x x vn
Vậy phương trình đã cho vô nghiệm
Ví dụ 4:
Giải phương trình sau
2
1 13 7
2
2
x
x x
x
Lời giải
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
21
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Điều kiện:
0
x
Phương trình đã cho tương đương
2 2 2 2 2 2
2 2
2
2
2
2 2
2 2 2 13 7 2 2 2 9 12 4
2 3 2 2 4 2
2 3 2
2 2 3 2 2 2
x x x x x x x x x x x x x
x x x x x x x
x x x x
x x x x x x x
Với
2
2
2
2
1
1
2
2 4 2 1
2
15 17 2 0
2 4 2
x
x
x x x x
x x
x x x
Với
2
2
2
2
1
0
9 57
2 2 2
6
3 9 2 0
2 2 2
x
x
x x x x
x x
x x x
Vậy phương trình đã cho có tập nghiệm
9 57
1;
6
S
Ví dụ 5:
Giải phương trình sau
2
2 2
3
2 1
x x
x
x
Lời giải
Điều kiện:
1
2
x
Phương trình đã cho tương đương
2
2 2 2 2 2
2 2
2
2
2
2 2
2 2 1 3 8 4 2 1 2 2 1 3 3 4 4
2 1 3 2 3 3
2 1 3 2
2 1 3 2 3 3 1
x x x x x x x x x x
x x x x x
x x x
x x x x x
Với
2
2
2
3
3
3 3 1
1
3 3
x
x
x x x
x
x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
22
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Với
2
2
2
2
1
1
3
3 3 1 1
3
8 6 2 0
3 3 1
x
x
x x x
x x
x x
Vậy phương trình đã cho có tập nghiệm
1; 1
S
Ví dụ 6: Giải phương trình sau
2 2
2 1 2 1 2 1x x x x x
Lời giải
Điều kiện:
2
2 1 0
x x
Phương trình đã cho tương đương
2 2 2 2 2 2
2 2
2
2
2
2 2
2 1 2 1 2 1 0 2 1 2 1 2 1 2 1 2 1
1 2 1 1 2 1 2
1 2 1 1
1 2 1 1 2 1 2
x x x x x x x x x x x x x x
x x x x x x
x x x x
x x x x x x x
Với
2 2 2
2 1 2 2 1 4 2 5 0 1 6; 1 6
x x x x x x x
Với
2
2 2 2
0 0
2 1 2
2 1 4 3 2 1 0
x x
x x x vn
x x x x x
Vậy phương trình đã cho có tập nghiệm
1 6; 1 6
S
Ví dụ 7: Giải phương trình sau
2 1 3 3
x x x x
Lời giải
Điều kiện:
3 1x
Phương trình đã cho tương đương
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
23
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2 2
2
2
2 2 2
2 2 3 3 2 2 2 3 2 6
2 2 2 2 3 2 3 1 2 2 3 1
x x x x x x x x
x x x x x x x x x
2 2
2 2
2 2 3 1 2 3 1
2 2 3 1 2 3 3
x x x x x x
x x x x x x
Với
2
2
2
2
1
1
2 3 1 1 2
2 1 0
2 3 1
x
x
x x x x
x x
x x x
Với
2
2
2
2
3
3
2 3 3 1
4 3 0
2 3 3
x
x
x x x x
x x
x x x
Vậy phương trình đã cho có tập nghiệm
1 2; 1
S
Ví dụ 8: Giải phương trình sau
4 2 1 2 1 3
x x x
Lời giải
Điều kiện:
1x
Phương trình đã cho tương đương
2 2
1 1 2 1 2
1 2 1 1 2 1 4 2 1 4 1 1 2 1 2
1 1 2 2 1
x x
x x x x x x
x x
Với
1 1 2 1 2 1 3 2 1 1 9 6 1 2 1 6 1 9
x x x x x x x x x
2
2
9
9
27 6 17
54 117 0
36 1 9
x
x
x
x x
x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
24
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Với
2
1 1 2 2 1 1 2 1 1 3 2 2 1 2 1 1 2 2 3 1 3 3x x x x x x x x x x
2 2
2
1
1
1
4 2 3 1 9 1
17 12 5 0
x
x
x
x x x
x x
Vậy phương trình đã cho có tập nghiệm
27 6 17;1
S
Ví dụ 9:
Giải phương trình sau
2
1
1 1 2
4
x x x
Lời giải
Điều kiện:
1 1x
Phương trình đã cho tương đương
2 2 2 4 2 2 2
2
2
2 2
2
1 1 1
1 1 2 2 2 1 4 1 2 1 1 0
4 16 16
1 1 1 0
1 1 0 0
16
0
x x x x x x x x x
x
x x x
x
Vậy phương trình đã cho có tập nghiệm
0
S
Ví dụ 10:
Giải phương trình sau
2 2
1 2 4 1 2 1x x x x
Lời giải
Điều kiện:
1
2
x
Phương trình đã cho tương đương
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
25
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
2
2 2 2
2 2 2
4 1 2 4 1 1 2 1 2 2 1 1 4 1 1 2 1 1
1
2
4 1 2 1 4 1 2 1 4 2 2 0 1
1
1;
2
x x x x x x
x
x x x x x x x
x
Vậy phương trình đã cho có tập nghiệm
1
S
Ví dụ 11: Giải phương trình sau
2
2 7 2 2 1 4 3
x x x x x
Lời giải
Điều kiện:
1
2
x
Phương trình đã cho tương đương
2
2
2 2
2
2 2 2 1 3 4 3 4 0 2 1 2 2 1 1 3 4 3 4 0
2 1 1 0
2 1 1
2 1 1 3 2 0 1
3 4
3 2 0
x x x x x x x x x x x x
x x
x
x x x x
x
x
Vậy phương trình đã cho có tập nghiệm
1
S
Ví dụ 12: Giải phương trình sau
2
13 28 4 4 3 2 2 1x x x x x
Lời giải
Điều kiện:
1
2
x
Phương trình đã cho tương đương
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
26
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
2
2 2
2
4 7 4 4 3 2 1 2 2 1 1 0 4 7 4 3 2 1 1 0
4 3 2 0
3 2
4 3 2 2 1 1 0 1
2 1 1
2 1 1 0
x x x x x x x x x x
x x
x
x x x x
x
x
Vậy phương trình đã cho có tập nghiệm
1
S
Ví dụ 13:
Giải phương trình sau
2
2 1 3 2 2 2 1 2 9 4
x x x x x x
Lời giải
Điều kiện:
3
2
2
x
Phương trình đã cho tương đương
2
2 2
2
1 3 2 2 1 3 2 1 2 1 2 2 2 1 2 2 1 0
1 3 2 2 3 2 1 2 1 2 2 2 1 0
1 3 2 1 0
3 2 1
1 3 2 1 2 1 2 1 0 1
2 1
2 1 2 1 0
x x x x x x x x x x
x x x x x x
x x
x
x x x x x
x
x x
Vậy phương trình đã cho có tập nghiệm
1
S
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
27
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
TUYỂN CHỌN 2016
Bài 1: Giải phương trình:
2
2 1 4 24 29 0
x x x
1
Bài giải:
Điều kiện:
1
2
x
Đặt
2
2 1, 0 2 1
t x t x t
Ta được phương trình:
2
2 2 4 2
1 12 1 29 0 14 42 0
t t t t t t
2
2
3
1 29
2 3 7 0
2
1 29
2
t
t loai
t t t t
t loai
t
Với
3
2
2
t x
Với
1 29 13 29
2 4
t x
Vậy phương trình có nghiệm
3 13 29
; .
2 4
x
Bài 2: Giải phương trình:
2
4 6 1 2 5 1x x x x
1
Bài giải:
Điều kiện:
1
x
2
1
1 1
4 6 1 2
x
x
x x x
2
2
1
4 6 1 2 5 1 3 1
4 6 1 2
x
x x x x x
x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
28
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
1 0 1( )
4 6 1 2 1 2
x x TM
x x x x
Kết hợp (1) và (2) ta được
2
1
2 7
2 1 2 1
2
2
4 8 3 0
x
x x x
x x
( Thỏa mãn )
Vậy phương trình có nghiệm
2 7
1; .
2
x
Bài 3: Giải phương trình:
3 5 3 5x 4 2x 7
x
1
Bài giải:
Điều kiện:
5
5
4
x
3 5 7 3 5x 4 0
x x x
2
2
3 4 5
4 5x
0
3 5 7 5 4
x x
x
x x x x
2
1 3
4 5 0
3 5 7 5 4
x x
x x x x
2
5 4 0
x x
( Do
)
1x
( Không thỏa mãn) hoặc
4
x
( Thỏa mãn )
Vậy phương trình có nghiêm
4.
x
Bài 4: Giải phương trình:
2
3x 8 3 4 1x x x
1
Bài giải:
Điều kiện:
1
x
2
2
2 1 2 1
x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
29
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
2
1
6 3 0
3 2 3
2 1 1
1
5 2 13
2 1 1 3
3
9
9 10 3 0
x
x x
x
x x
x
x x
x
x x
( Thỏa mãn )
Vậy phương trình có nghiệm
5 2 13
;3 2 3 .
9
x
Bài 5: Giải phương trình
2
8 10 11 14 18 11
x x x
1
Bài giải:
ĐK:
11
10
x
2
1 4 2 1 10 11 2 3 14 18 2 4 0
x x x x x x
2 2
2
2 2 1 2 2 1
4 2 1 0
10 11 2 3 14 18 2 4
x x x x
x x
x x x x
2
1
)2 1 0 1
2
x x x x
(tmđk)
1 1
) 2 0
10 11 2 3 14 18 2 4
f x
x x x x
Ta có:
11
' 0
10
f x x
f(x) đồng biến trên
11
;
10

Từ đó
11
0
10
f x f
nên trường hợp này vô nghiệm.
Vậy phương trình có nghiệm
1
1; .
2
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
30
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bài 6: Giải phương trình:
2
3
6 1 2 2 2 8
x x x x x
1
Bài giải:
Điều kiện:
2
x
Xét
2
3
2 1 6 1 2 2 2 3 7 2 8x x x x x x
nên (1) không có nghiệm trên
;1
Xét
1x
, khi đó
2
3
4 2
10 4
6 1 2 2 2 1 1 1
2 2
x
x x
x x x x x
Mà
2
2
2
10 4 3
2 8 2 0
2 2
x x
x x x
. Do đó (3) xảy ra khi và chỉ khi x = 2.
Vậy phương trình có nghiệm
2.
x
Bài 7: Giải phương trình:
2
3 1 6 6
x x x x
1
Bài giải:
Điều kiện:
2
1 0
6 6 0
x
x x
2
2 2
2 2 2 2
3 1 6 6
9( 1) 2 6 6 2 6 6
(15 15 2 ) 4 ( 6 6)
( 5)( 1)(4 5) 0
x x x x
x x x x x x
x x x x x
x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
31
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
1
5
5
4
x
x
x
. Đối chiếu điều kiện ta được
5
5
4
x
x
Vậy phương trình có nghiệm
5
;5 .
4
x
Bài 8 : Giải phương trình;
2 2
1 2 2 6 11 2
x x x x x x
1
Bài giải:
Điều kiện:
2
x
2 3 2
1 6 12 2 2 2x x x x x x
Với x = 0 => phương trình vô nghiệm
Với
0
x
ta có:
2 2
6 12 2 2
1 2
x x
x x x x
2 2
6 2
2 2
1 2
x
x x
x x x
Đặt
2x
t
x
. Ta có:
2 2 3 2 3 2 2
2
1 6 2 6 2 6 2 0 6 3 3 0
3
t t t t t t t t t t t t
2
0
9 377
0
2
3 2 2
8
3
4 9 18 0
9 377
8
x
x
x TM
t x x
x x
x loai
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
32
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Vậy phương trình có nghiệm
9 377
.
8
x
Bài 9: Giải phương trình:
2
2 1 5 2 7 7 0
x x x x
1
Bài giải:
Điều kiện:
1
5
2
x
+) Phương trình
2
2 1 3 1 5 2 7 4 0
x x x x
2 8 4
( 4)(2 1) 0
2 1 3 1 5
x x
x x
x x
4 0
2 1
(2 1) 0
2 1 3 1 5
x
x
x x
Dễ thấy
2 1
(2 1) 0
2 1 3 1 5
x
x x
nên x = 4
Vậy phương trình có nghiệm
4.
x
Bài 10: Giải phương trình:
2
4 2 3 1 2y y y y
1
Bài giải:
Điều kiện:
2
4 2 3 0
1 0
y y
y
*
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
33
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Từ
1 0
y
kết hợp điều kiện
1 13
4
y
2
4 2 3 2 1 1 1 0
y y y y
2
2 2
2
0
1 1
4 2 3 2 1
y
y
y
y y y
2
2 1
2 0
1 1
4 2 3 2 1
y
y
y y y
2
y
( vì
2
2 1
0
1 1
4 2 3 2 1
y
y y y
với
1 13
4
y
)
Vậy phương trình đã cho có nghiệm
2.
y
Bài 11: Giải phương trình:
2
4 6 2 1 5 1x x x x
1
Bài giải:
Điều kiện:
1
x
Với điều kiện
thì :
1
2
2
1
4 6 (1 2 ) 5 1 1
4 6 1 2
x
x x x x x
x x x
2
4 6 1 2 1
1 0 1
(2)
x x x x
x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
34
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Từ
1 , 2
2
1
2 7
2 1 2 1
2
2
4 8 3 0
x
x x x
x x
( Thỏa mãn )
Vậy phương trình đã cho có nghiệm:
2 7
1; .
2
x
Bài 12: Giải phương trình:
3 6 2 4 8x x x
Bài giải:
ĐK:
6 0
6 4
4 0
x
x
x
(1) 6 3 6 2 2 4 0
x x x
2
( 6) 9( 6) 4 4(4 )
0
6 3 6 2 2 4
x x x
x x x
( 3)( 6) 4( 3)
0
6 3 6 2 2 4
x x x
x x x
6 4
( 3) 0
6 3 6 2 2 4
x
x
x x x
3
x
(nhận)
6 4
0 [ 6;4]
6 3 6 2 2 4
x
Do x
x x x
Vậy phương trình có nghiệm :
3
x
Bài 13: Giải phương trình:
3 5 3 5 4 2 7
x x x
Bài giải:
3 5 3 5 4 2 7
x x x
ĐK:
4 5 5/ x
(*)
3 5 7 3 5 4 0
x ( x) ( x x)
2 2
4 5 3 4 5
0
3 5 7 5 4
x x ( x x )
x ( x) x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
35
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
1 3
4 5 0
3 5 7 5 4
( x x )
x ( x) x x
2
5 4 0
x x
( Do (*) )
1
4
x
x
( Thỏa mãn )
Vậy phương trình đã cho có nghiệm
1;4 .
x
Bài 14: Giải phương trình:
3 2
2 3 4 1x x x x x
Bài giải:
3 2
2 3 4 1x x x x x
, Đ/K
2 3
x
3 2 2
2 2 3 2
2 3 3 4 4 1 4
2 3 3
x x
x x x x x x x
x x
2
2 2 3 4
1 4
2 3 3 2 3 2
x x
x x
x x x x
2
2
2 2
2 2
2 3 3 2 3 2
x x
x x x
x x x x
2
0
2
2 2 0
2 3 3 2 3 2
x x x
x x x x

2
2 0 2 1
x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
36
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Vậy phương trình đã cho có nghiệm:
1;2 .
x
Bài 15: Giải phương trình:
2
2 2
1
2 1 3 2 4 2 3 4 4 4 4 3 2 1
4
x x x x x x x
Bài giải:
ĐK:
1 3
2 2
x
. Phương
trình:
2
2 2
2
2 1 2 1
2 1 3 2 2 1 3 2
2 2
x x
x x x x
(*)
Xét hàm số
2
f t t t
trên
0;

có
2 1 0 0;f t t t
nên hàm số f(t)
đồng biến trên
0;

Do đó Phương trình
tương đương với:
2
2 1
2 1 3 2
2
x
f x x f
2
2 1
2 1 3 2
2
x
x x
2
8 2 1 3 2 4 2 1
x x x
2
8 2 1 3 2 2 1 3 2
x x x x
( **)
Đặt
2 1 0
3 2 0
x a
x b
thì phương trình (**) trở thành
2
2 2
2 2
8
4
a b a b
a b
2
2 2 2 2
2 2
8 4 (1)
4 2
a b a b a b
a b
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
37
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Từ (1)
2 2 2 2
8 16 4 2 4
a b a b a b a b
2 2 2 2 4 4
4 2 16 8
a b ab a b a b
(***)
Đặt ab = t
0 2
t
thì pt (***) trở thành
2 4
16 8 16 8
t t t
2
2 2 4 0
t t t t
0t
( Thỏa mãn )
2
t
( Loại )
1 5
t
( Loại )
Vậy t = 0
2 1 3 2 2
2 1. 3 2 0
x x
x x
1
2
3
2
t
t
Chú ý: HS có thể giải theo cách khác như sau
Đặt
2 1 3 2a x x
. Phương trình đã cho trở thành
2 4 2
2 2 4 8 8 8 0
a a a a a a a
Bài 16: Giải phương trình:
2 2
3 2 9 3 4 2 1 1 0
x x x x x
Bài giải:
Phương trình đã cho tương đương với:
2
2
3 2 9 3 2 1 3 2 1 2
x x x x
2
2
3 2 9 3 2 1 2 2 1 3
x x x x
Xét hàm số
2
( ) 3 2
f t t t
ta có
2
2
2
'( ) 3 2 0
3
t
f t t
t
suy ra hàm số đồng
biến
3 2 1
f x f x
Từ đó suy ra
1
3 2 1 .
5
x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
38
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Vậy phương trình đã cho có nghiệm:
1
.
5
x
Bài 17: Giải phương trình:
2
1 (2 3) (2 2) 2
x x x x x
.
Bài giải:
TXĐ D =
1;

Phương trình
1) 1)
3 2
( 1 ( 1 (2 3) (2 3) 2 3 x x x x x x x
(1)
Xét hàm số
3 2 2
( ) ( ) 3 2 1 ( ) 0,
f t t t t f' t t t f' t t
suy ra hàm số f(t) đồng biến
trên
.
Phương trình (1) có dạng
2 3( 1) ( )
f x f x
. Từ hai điều trên phương trình (1)
2
2 2
1 2 3
3 / 2 3 / 2
1 4 12 9 4 13 10 0
x x
x x
x =
x x x x x
Vậy phương trình đã cho có nghiệm
2 .
x
Bài 18: Giải phương trình:
2 3 2
5 5 10 7 3 2 6 2 2 2 5 10
x x x x x x x x
1
Bài giải:
Điều kiện:
2
x
Với điều kiện
thì
2
2
5 5 10 2 6
1 2 2 5
7 3 2 2
x x x
x x x
x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
39
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
2
5 5 10 2 6
2 5 0
7 3 2 2
x x x
x x
x x
2
2
2 0
5 5 10 2 6
5 0
7 3 2 2
x
x x x
x
x x
)
2 0 2
x x
( Thỏa mãn )
)
2 2
2 2
5 5 10 2 6 5 5 10 2 6
5 0 5
7 3 2 2 7 3 2 2
x x x x x x
x x
x x x x
2 2
5 5 10 2 6 5 5 10 2 6
5 2
7 3 2 2
x x x x x x
x x
2
1 1 1 1
5 5 10 2 6 0
5 2
7 3 2 2
x x x
x x
Với điều kiện
thì
1 1
0
5
7 3
2 6 0
1 1
0
2
2 2
x
x
x
và
2
5 5 10 0
x x
x R
Phương trình vô nghiệm.
Vậy phương trình đã cho có nghiệm
2 .
x
Bài 19: Giải phương trình:
2 2
2
1 1 1
. . 13. 1
7 7 7
y y y
y y
y y y
1
Bài giải:
Điều kiện:
7
y
Với điều kiện
thì:
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
40
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bài 20: Giải phương trình:
3 2
2 3 4 1x x x x x
1
Bài giải:
Điều kiện:
2 3
x
Với điều kiện
thì:
3 2 2
2
2
2
2 2 3 2
1 2 3 3 4 4 1 4
2 3 3
2 2 3 4
2 ( 2)
2 3 3 2 3 2
2( 2)
2 2 0
2 3 3 2 3 2
x x
x x x x x x x
x x
x x
x x x
x x x x
x x
x x x
x x x x
)2(0
0
232332
2
22
2
xvi
xxxx
xxx
1
2
02
2
x
x
xx
( Thỏa mãn )
Vậy phương trình đã cho có nghiệm
1;2 .
x
1
2 2 2
2
1 1 7 13 1 7
y y y y y y y
4 3 2
5 33 36 0
y y y y
2
1 3 5 12 0
y y y y
1
3
y
y
( Thỏa mãn )
Vậy phương trình đã cho có nghiệm
1;3 .
y
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
41
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bài 21: Giải phương trình:
2
8 4
1 1 3
4 7
x x
x x
x x
1
Bài giải:
Điều kiện:
1
x
*
Với điều kiện
*
thì
1
2
8 4 1 8
4 7
1 3
x x x x
x x
x
2
8
4 1
2
4 7
1 3
x
x x
x x
x
2
2 1 3 4 1 4 7
x x x x x
2
2
1 3 1 3 2 3 . 2 3
x x x x
(3)
Xét hàm số
2
3 3
f t t t
với
t
có
2
' 3 1 0f t t t
nên
đồng biến trên
.
Do đó
2
2
3 1 2 1 2
1 4 4
x
f x f x x x
x x x
2
2
5 13
2
5 3 0
x
x
x x
( Thỏa mãn )
Vậy phương trình đã cho có nghiệm
5 13
8; .
2
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
42
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bài 22: Giải phương trình:
3
2 15 1x x
1
Bài giải:
Điều kiện:
2
x
Với điều kiện
thì
1
3
2 3 2 15 0
x x
3
2 3 2 15 0
x x
2
3 3
0
1 1
7 0
2 3
4 2 15 15
x
x
x x

7 0 7
x x
( Thỏa mãn )
Vậy phương trình đã cho có nghiệm
7.
x
Bài 13: Giải phương trình
5042444
2
xxxxxx
.
Bài giải:
Điều kiện
4
x
5042244
2
xxxxx
048424
2
xxxx
Giải phương trình 54 xx
Giải phương trình
54: xx
5
x
Vậy phương trình đã cho có nghiệm
5.
x
Bài 23: Giải phương trình:
2
3 8 3 4 1x x x x
1
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
43
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bài giải:
Điều kiện:
1
x
Với điều kiện
thì
2
2
1 2 1 2 1
x x x
2
2
1
6 3 0
3 2 3
2 1 1
1
5 2 13
2 1 1 3
3
9
9 10 3 0
x
x x
x
x x
x
x x
x
x x
Cả 2 nghiêm đều thỏa mãn điều kiện
Vậy phương trình đã cho có nghiệm
5 2 13
;3 2 3 .
9
x
Bài 24: Giải phương trình:
2
4 6 (1 2 ) 5 1x x x x
1
Bài giải:
Điều kiện:
1
x
Với điều kiện
thì:
2
1
1 1
4 6 1 2
x
x
x x x
2
4 6 1 2 1
1 0 1
(2)
x x x x
x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
44
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Kết hợp (1) và (2) ta được
2
1
2 7
2 1 2 1
2
2
4 8 3 0
x
x x x
x x
Thử lại ta có: Phương trình đã cho có 2 nghiệm:
2 7
1;
2
x x
Vậy phương trình đã cho có nghiệm
2 7
1; .
2
x
Bài 25: Giải phương trình:
5 4 3
4 3 2
2 3 14 2
4x 14x 3 2 1
2 2
x x x
x
x x
1
Bài giải:
Điền kiện:
2
x (*).
PT
3 2 4 3 2
2 3 14 4 14 3 2 2 2
x ( x x ) ( x x x ) x
3 4 3 2
3 4 3 2
3 4 3 2
( 2)(2 7) 2 2 (4x 14x 3 2)( 2 4)
( 2)(2 7) 2 2 (4x 14x 3 2)( 2)
2 0 2 ( (*))
(2 7) 2 2 4x 14x 3 2 (1)
x x x x x x
x x x x x x
x x TM
x x x x
3 4 3 4 3 2
1 2 7 2 4 14 4 14 3 2
( ) x ( x ) x x x x x x
3 2
2 7 2 3 2
x ( x ) x x
Nhận thấy
0x
không là nghiệm của phương trình
0x .
Khi đó, PT
3
3 2
2 4 3 2( x ) x
x
x
3
2 3
2 2 2 3 2 2(x ) x x ( )
x
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
45
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Xét hàm số:
3
2 3f(t) t t
với
t .
Ta có:
2
6 3 0f '(t) t t
Hàm số f(t) đồng biến trên
.
Do đó
1 1
2 2 2 2 1
( ) f x f x x x
x x
2
0
1 5
2
1 1 0
x
x
(x )(x x )
( Thỏa mãn (*) )
Vậy nghiệm của phương trình đã cho là
1 5
;2 .
2
x
Bài 26: Giải phương trình:
2
2 6 1 4 5
x x x
1
Bài giải:
Điều kiện
5
4
x
Với điều kiện
thì
2
1 4 8 4 4 5 2 4 5 1
x x x x
2
2
2 2 4 5 1 2 2 4 5 1
x x x x
Trường hợp 1:
1
2 3
4 5 2 3
x
x
x x
( Thỏa mãn )
Trường hợp 2:
1
1 2
4 5 1 2
x
x
x x
( Thỏa mãn )
Vậy phương trình đã cho có nghiệm
1 2;2 3 .
x
Bài 19: Giải phương trình:
2 2 9
10
3 1 3 4 5x
x
x
1
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
46
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bài giải:
Điều kiện:
4
1
5
x
Với điều kiện
thì:
1 2 10 6 1 4 5x 9 9 3 1 3 4 5x 1 4 5x
x x x x
1 4 5x 3 9 1 9 4 5x 4x 41 0
x x
( Do
4
1;
5
x
nên
9 1 9 4 5x 4x 41 0
x
)
1 4 5x 3 0
x
1 4 5x 3 2 1. 4 5x 4 4x
x x
1 0 1
1. 4 5x 2 1 0
0
4 5x 2 1
x x
x x
x
x
Vậy phương trình đã cho có nghiêm
1;0 .
x
Bài 27: Giải phương trình:
3
3
4 2 2 2 4
2 1 2 4 2
x x x x x x x
1
Bài giải:
Điều kiện:
.x R
Phương trình tương đương
x x x x x x x x
3
3
2 2 2 4 2 4
2 1 2 2 1 2
2
Xét hàm số
f t t t
3
2
,
t
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
47
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Ta có
f t t
2
' 3 2 0
t
suy ra hàm số
f t
đồng biến trên
Phương trình
2
có dạng
f x x f x x x x x x
3 3
2 2 4 2 2 4
2 1 2 1
3
Nếu
x 0
thay vào
3
không thỏa mãn
Nếu
x 0
thì phương trình
3
x x
x x
3
1 1
2
. Đặt
x t
x
3
1
, ta có phương trình
t t t t t t
3 2
2 0 1 2 0 1
( Vì
t t t
2
2
1 7
2 0
2 4
)
Với
t 1
x x x x x
x x
2
3
1 1 1 5
1 1 1 0
2
( Thỏa mãn )
Vậy nghiệm của phương trình là
1 5
.
2
x
Bài 28: Giải phương trình:
2
4 2 2 2 4 9 16
x x x
1
Bài giải:
Điều kiện:
2 2
x
Với điều kiện
thì:
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
48
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
1
2 2 2 2 2
32 8 16 2(4 ) 9 8(4 ) 16 2(4 ) ( 8 ) 0
x x x x x x x
Đặt:
2
2(4 ) ( 0)
t x t
; PT trở thành:
2 2
4 16 ( 8 ) 0
2
x
t t x x t
4
2
x
t
So sánh với điều kiện ta loại
4
2
x
t
2
2
0 2
4 2
2(4 )
32
2 3
9
x
x
x x
x
Vậy phương trình đã cho có nghiệm
4 2
.
3
x
Bài 29: Giải phương trình:
3 2 2
5 1 1 4 25 18
x x x x
Bài giải:
Điều kiện:
1
x
3 2 2
5 1 1 4 25 18
x x x x
3 4 3 2
5 5 1 4 25 18x x x x
3 3 4 2
25 25 5 1 4 18 20
x x x x
3 3 4 2 2
25 1 5 1 4 16 16 2 4
x x x x x
2
2
3 3 2 2
5 1 5 1 2 4 2 4
x x x x
1
Hàm số
2
f t t t
đồng biến trên
0;

nên
3 2
(1) 5 1 2 4
f x f x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
49
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
3 2
5 1 2 2
x x
2 2
5 1 1 2 1 1
x x x x x x
2
Đặt:
1 0
u x
và
2
1 0
v x x
2
thành:
2
2 2
2
5 2 2 5 2 0
1
2
u
u u
v
uv u v
u
v v
v
Với
2
u
v
:
2
2
1
1 2 1
4 5 3 0
x
x x x
x x
( Vô nghiệm )
Với
1
2
u
v
:
2
2
1
5 37
2 1 1
2
5 3 0
x
x x x x
x x
.
Vậy phương trình đã cho có nghiệm
5 37
2
x
.
Bài 30: Giải phương trình:
3 2
2 2 3 2
x x x x x
1
Bài giải:
Điều kiện:
3
2
x
Với điều kiện
thì:
1
2
1 2 3 1 4 2 3 2 8 0
x x x x x
1
2
x
x
( Thỏa mãn )
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
50
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Vậy phương trình đã cho có nghiệm
1; 2 .
x
Bài 31: Giải phương trình:
2 2
7 25 19 2 35 7 2x x x x x
1
Bài giải:
Điều kiện
7
x
Phương trình tương đương
2 2
7 25 19 7 2 2 35
x x x x x
.
Bình phương 2 vế suy ra:
2
3 11 22 7 ( 2)( 5)( 7)
x x x x x
2 2
3( 5 14) 4( 5) 7 ( 5)( 5 14)
x x x x x x
Đặt
2
5 14; 5
a x x b x
.( a ,b
0) Khi đó ta có phương trình
2 2 2 2
3 4 7 3 7 4 0
3 4
a b
a b ab a ab b
a b
Với
a b
suy ra
3 2 7 ( / ); 3 2 7 ( )x t m x l
.
Với
3 4a b
suy ra
61 11137
18
x
( Thỏa mãn );
61 11137
18
x
( Loại )
Vậy phương trình đã cho có nghiệm
61 11137
3 2 7; .
18
x
Bài 32: Giải phương trình:
2
3 3 3 1 5 4
x x x x
1
Bài giải:
Điều kiện:
1
3
x
Với điều
thì
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
51
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
2
1 3 1 3 1 2 5 4 0
1 1
3 0
1 3 1 2 5 4
x x x x x x
x x
x x x x
2
0 0
x x x
hoặc
1x
.
Vậy phương trình đã cho có nghiêm
0;1 .
x
Bài 33: Giải phương trình:
3 5 3 5 4 2 7
x x x
1
Bài giải:
Điều kiện
4
5 ó :
5
x ta c
2
2
2
(3) 7 3 5 3( 5 4) 0
3 5 4
7 9 5
0
7 3 5 5 4
1 3
5 4 0
7 3 5 5 4
x x x x
x x
x x
x x x x
x x
x x x x
2
5 4 0
x x
( Vì
1 3
0
7 3 5 5 4x x x x
với mọi
x
thỏa mãn điều kiện )
1
4
x
x
( Thỏa mãn )
Vậy phương trình đã cho có nghiệm
1;4 .
x
Bài 34: Giải phương trình
3(2 2) 2 6
x x x
1
Bài giải:
Điều kiện:
2
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
52
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Với điều kiện
thì
1 2 3 6 3 2 0
x x x
8 3
2 3 0
6 3 2
x
x
x x
3
3 0
3
8
11 3 5
2 0
6 3 2 4
6 3 2
2
x
x
x
x x
x
x x
( Thỏa mãn )
Vậy phương trình đã cho có nghiệm
11 3 5
;3 .
2
x
Bài 35: Giải phương trình:
2
x 4x 14 6 x 7 2x 3x 2 0
1
Bài giải:
Điều kiện:
2
3
x
2
1 2 6 x 7 x 16 x 4 3x 2 3x 2 x 4x 4 0
2
2 9x
x 4x 4 1 0
6 x 7 x 16 4 3x 2 3x 2
2
2 6x 2 4 3x 2
x 2 0
6 x 7 x 16 4 3x 2 3x 2
2
2
2 3x 2 1
2
x 2 0
6 x 7 x 16 4 3x 2 3x 2
x 2
( Thỏa mãn )
Vậy phương trình đã cho có nghiêm
2.
x
Bài 36: Giải phương trình:
2
x 2x 16 6 x 7 2x x 0
1
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
53
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bài giải:
Điều kiện:
0
x
2 2
1 x 7 3 x x 0
x 7 3 0 x 2
x 0
x x 0
(vô lý)
PT vô nghiệm
Vậy phương trình đã cho vô nghiệm.
Bài 37: Giải phương trình:
2 2
3 2 9 3 4 2 1 1 0
x x x x x
1
Bài giải:
Điều kiện:
x R
2
2
1 2 1 2 1 3 2 ( 3 ) 2 ( 3 ) 3
x x x x
2 1 3f x f x
Xét
2
( ) 3 2
f t t t
có
'( ) 0, .f t t
f là hàm số đồng biến nên:
1
2 1 3
5
x x x
Vậy phương trình đã cho có nghiệm
1
.
5
x
Bài 38: Giải phương trình
4 2
32 16 9 9 2 1 2 0
x x x x
trên tập số thực.
Bài giải:
Điều kiện
1
2
x
, phương trình đã cho tương đương
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
54
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
4 2 2
2 2
2
32 32 16 16 7 7 9 9 2 1 0
32 1 16 1 7( 1) 9 1 2 1 0
9 2 2
32 1 ( 1) 16 1 7( 1) 0
1 2 1
x x x x x x
x x x x x x
x
x x x x x x
x
2
3 2
18
1 32 ( 1) 16 7 0
1 2 1
18
1 32 32 16 7 0 (*)
1 2 1
x x x x
x
x x x x
x
Ta có
3
2 3 2
3 2
32
32 4
8
1 32
32 8 32 32 16 7 27
2 4
16
16 8
2
18
1 2 1 1 18
1 2 1
18
32 32 16 7 9 0.
1 2 1
x
x x x x x
x
x
x
x x x
x
(*) 1x
.
Vậy phương trình có nghiệm x =1.
Bài 39 : Giải phương trình :
3 2
3
27 2 20 4 4 1
x x x x
1
Bài giải:
3
3
1 3 1 4(3 1) 1 4 1x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
55
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Xét hàm số:
tttg 4)(
3
liên tục trên R.
Ta có
043)('
2
ttg
hàm số đồng biến trên R.
Suy ra:
1192727113)1()13(
23
33
xxxxxxxgxg
3 2
2
0
27 27 8 0
27 27 8 0( )
x
x x x
x x vn
Vậy phương trình đã cho có nghiệm
0.
x
Bài 40: Giải phương trình:
2
3 3 3 1 5 4
x x x x
1
Bài giải:
Điều kiện:
1
3
x
2
3 1 3 1 2 5 4 0
x x x x x x
2
1 1
3 0
1 3 1 2 5 4
x x
x x x x
2
0
x x
( Vì
1 1
3 0
1 3 1 2 5 4x x x x
với mọi
1
3
x
)
0 1x x
( Thỏa mãn )
Vậy phương trình có nghiêm
0;1 .
x
Bài 41: Giải phương trình:
2
8 4
1 1 3
4 7
x x
x x
x x
1
Bài giải:
Điều kiện:
1
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
56
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Tiếp tục giải phương trình
Xét hàm số
Do đó hàm số
đồng biến trên
Từ
Giải phương trình
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
57
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Vậy phương trình có nghiệm
5 13
8; .
2
x
Bài 42: Giải phương trình:
2
2
2( ) 16
1
2
1 3
4 7 2 2
x
x x
x
x
x x
1
Bài giải:
Điều kiện:
1
x
2
2
4 32
1 1 1 3
4 7
x x
x x
x x
2
8 4 1 8
4 7
1 3
x x x x
x x
x
2
8
4 1
2
4 7
1 3
x
x x
x x
x
+)
8 4 ( ).x y tm
+)
2
2 1 3 4 1 4 7
pt x x x x x
2
2
1 3 1 3 2 3 . 2 3
x x x x
(3)
+) Xét hàm số
2
3 3
f t t t
với
t
có
2
' 3 1 0,f t t t
nên
đồng biến trên
.
+) Mà pt(4) có dạng:
1 2
f x f x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
58
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Do đó
2
2
3 1 2
1 4 4
x
x x
x x x
2
2
5 13
2
5 3 0
x
x
x x
(T/M)
Vậy phương trình đã cho có nghiệm
5 13
8; .
2
x
Bài 43: Giải phương trình:
3
2 3
3 5 2 2 1
x x x
1
Bài giải:
3
33 3
1 1 2 1 1 2 1
x x x x
Xét hàm số
3
( ) 2g t t t
ta thấy g(t) đồng biến trên R nên từ (**) suy ra
3 3
0
1 1
1
x
x x
x
Vậy phương trình có nghiệm
1;0 .
x
Bài 37: Giải phương trình:
2
9 3 1 2
x x
1
Bài giải:
Điều kiện:
x
2
2
2
25 3( 5)
(1) 9 4 3( 1 2)
( 1 2)
9 4
x x
x x
x
x
2
5
5 3
(2)
( 1 2)
9 4
x
x
x
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
59
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Do
2
2
5 5
3 9 1
4
9 4
x x
x x x
x
x
và
3
1 1 1 2
( 1 2)
x x
x
luôn đúng khi
x
nên
2
vô nghiệm.
Vậy phương trình đã cho có nghiệm
5.
x
Bài 44: Giải phương trình:
2 2
1 1 7 3
x x x x
1
Bài giải:
Điều kiện:
.x R
Xét hàm số:
2 2
( ) 1 1f x x x x x
Chứng minh hàm số đồng biến
Ta có nghiệm duy nhất x = 2
Vậy phương trình có nghiệm
2.
x
Bài 45: Giải phương trình:
2
3 3 1 2x 3 1 2
x x x x x
1
Bài giải:
Điều kiện:
1
x
2
3
1 3 3 1 2x 3 .
1 2
x
x x x x
x
2
3( )
3 1 2 1 2x 3 2
x TM
x x x x
2
2
2 1 2 1 2 1 2 1 2
x x x x
Xét hàm số
2
2 2
f t t t
,
0t
có
' 0f t t
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
60
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Suy ra
f t
đồng biến mà
1 1 1 1f x f x x x
2
1
3
3x 0
x
x
x
( TM )
Vậy phương trình đã cho có nghiệm
3 .
x
Bài 46: Giải phương trình:
2
4 2 22 3 8
x x x
1
Bài giải:
Điều kiện:
22
2
3
x
1
4( 2) 3( 2)
( 2)( 2)
2 2 22 3 4
x x
x x
x x
2
4 3
( 2) 0(2)
2 2 22 3 4
x
x
x x
Xét f(x) = VT(2) trên [–2; 21/3], có f’(x) > 0 nên hàm số đồng biến.
Suy ra x = –1 là nghiệm duy nhất của (2)
Vậy phương trình đã cho có nghiệm
1;2 .
x
Bài 47: Giải phương trình:
3 2 2 2 2
1 4 ( 2)( ) 3
x x x x x x x x x
1
Bài giải:
Điều kiện:
.x R
2 2 2 2 2
1 ( 1) 1 1 2 4 ( 2)( ) 0
x x x x x x x x x
2 2
2 2 2
2 2
( )
( 1) ( 2)( ) 0
1 1 2 4
x x x x
x x x x x
x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
61
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
2 2
( 1) ( 1)
( 1)( 1) ( 1)( 2) 0
1 1 2 4
x x x x
x x x x x x
x x x x
2
2 2
1 1
( 1) 1 2 0
1 1 2 4
x x x x
x x x x
2
2 2
1 1
( 1) 1 0
1 1 2 4
x x x x
x x x x
2
2 2
( 1) 0
(2)
1 1
1 0 (3)
1 1 2 4
x x
x x
x x x x
Vì
2
2
1 3
1 0;
2 4
x x x x
Nên
2
2 2
1 1
1 0;
1 1 2 4
x x x
x x x x
Suy ra phương trình (3) vô nghiệm
Giải phương trình (2):
0
( 1) 0
1
x
x x
x
( Thỏa mãn)
Vậy phương trình có nghiệm
1;0 .
x
Bài 48: Giải phương trình:
2
3 3 3 1 5 4
x x x x
1
Bài giải:
Điều kiện:
1
3
x
*
2
3 1 3 1 2 5 4 0
x x x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
62
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
1 1
3 0
1 3 1 2 5 4
x x
x x x x
2
0
0
1
x
x x
x
( Thỏa mãn )
Vậy phương trình đã cho có nghiệm
0;1 .
x
Bài 49: Giải phương trình:
3
2 3
3 5 1 8 5 0
x x x
1
Bài giải:
* Phương trình tương đương với:
3
3 2 3 3
3 3 1 5 5 1 5 1
x x x x x x
3
3
3 3
1 5 1 1 5 1
x x x x
Đặt
3
3
1 ; 1
x u x v
, phương trình trở thành:
3 3 2 2
5 5 5 0
u u v v u v u v uv u v
(do
2 2
5 0
u uv v
với mọi u, v)
*
3
3 2
1 1 3 3 0 0 1
x x x x x x
Vậy phương trình có nghiêm
1;0 .
x
Bài 50: Giải phương trình:
2 3
2 log 3 log 2 1x x x x
1
Bài giải:
Điều kiện:
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
63
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2 3 2 3
1 1
1 log 3 log 2 log 3 log 2 0 5
2 2
x x
x x x x
x x
Xét hàm số
2 3
1
log 3 log 2
2
x
g x x x
x
trên khoảng
3;

2
1 1 3
' 0 x>3
3 ln 2 2 ln 3
2
g x
x x
x
hàm số
g x
đồng biến trên
khoảng
3;

. Phương trình
5 5 5
g x g x
Vậy phương trình có nghiệm
5.
x
Bài 51: Giải phương trình:
2 2
2 11 9 2 2 1 2 2 2 1 2 11 11
x x x x x x
1
Bài giải:
2
2
2
2 11 11 0 *
1
4 2 1 2 11 11 2
x x
x x x
4 2 3 2
2 8 4 4 121 121 44 44 242x x x x x x
4 3 2 3 2
4 44 165 250 125 0 1 4 40 125 125 0
x x x x x x x x
2
1 5 4 20 25 0
x x x x
1
5
5
2
x
x
x
kết hợp điều kiện
*
ta được
1
5
x
x
Vậy phương trình có nghiệm
1;5 .
x
Bài 52: Giải phương trình
2 2 2
3 3 2 2
3 3 3 27
x x x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
64
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bài giải:
Phương trình đã cho tương đương
2 2
3 3 2
3 3
x x x x
=
2 2 2 2
2 3 2 3 3 3
3 1 3 3 1 3 1 0
x x x x x x x x
2
2 2
2
3
3 2 3
2 3
3 1 0
3 1 3 1 0
3 1 0
x x
x x x x
x x
2
3 2
0
3 1 3 0
3
x x
x
x x
x
2
2 3 2
1
3 1 2 3 0
3
x x
x
x x
x
Vậy phương trình đã cho có 4 nghiệm
0 1 3
x ; x ; x
Bài 53: Giải phương trình:
3 3
3 3 5 2 3 10 26
x x x x x
1
Bài giải:
Điều kiện:
5
1
2
x
3 2
2 2
1 3 3 3 1 5 2 3 10 24
2( )
3 2 2 2
2
2 12 12 2
3
3 3 3 1 5 2 1 5 2
3 3 3
x x x x x
x TM
x x
x x x x x
x x x
x
Phương trình (2) vô nghiệm vì với
5
1
2
x
thì
2
12 0.
x x
Vậy phương trình có nghiệm
2.
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
65
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bài 54: Giải phương trình:
2
4
2 1 2 1 1 2 3
x x x x x
1
Bài giải:
Điều kiện:
1x
.
Đặt
4
2 1a x
( 0)
a
, ta có:
4
2 1
x a
. Phương trình đã cho trở thành:
4
4
2 1 1 2
a a x x
(1)
Xét hàm số
4
( ) 2
f t t t
với
0t
Ta có
3
4
2
'( ) 1 0, 0.
2
t
f t t
t
Suy ra hàm số
( )f t
đồng biến trên
0;

.
4
(1) ( ) ( 1) 1 2 1 1f a f x a x x x
2
1
1
2 2
4 2 0
2 2
x
x
x
x x
x
.
Vậy phương trình đã cho có một nghiệm là
2 2
x
Bài 55: Giải phương trình:
3 2
3
3 5 3 3x x x x
1
Bài giải:
3
3
1 3 5 3 5 ( 1) ( 1)
x x x x
Xét hàm số
3 2
( ) , '( ) 3 1 0,
f t t t R f t t t R
. Suy ra hàm số f(t) đồng biến trên R.
(*)
3
3 5 ( 1)
f x f x
3
3 5 1x x
3 2
3 4 0
x x
1
2
x
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
66
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Vậy phương trình có nghiệm
2;1 .
x
Bài 56: Giải phương trình:
2 2
4 2 3 4
x x x x
1
Bài giải:
ĐK:
2 2
x
.
Đặt
2
2 2 2 2
4
4 4 2 4 4
2
t
t x x t x x x x
.
Phương trình trở thành
2
2
2
4
2 3 3 2 8 0
4
2
3
t
t
t t t
t
Với t = 2 ta có:
2 2
2 2
2 0 0
4 2 4 2
4 4 4 2
x x
x x x x
x x x x
(t/m)
Với
4
3
t
ta
có
2 2
4 4
4 4
3 3
x x x x
2
4
4
3
3
2 14
9 12 10 0
3
x
x
x x
x
2 14
3
x
(t/m).
Vậy pt đã cho có nghiệm x = 0; x = 2;
2 14
3
x
Bài 57: Giải phương trình:
3 3 2
3 1 19 16
x x x x x
Bài giải:
Điều kiện:
3
1 0 1
x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
67
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Phương trình đã cho tương đương với
2 3 2
3 1 1 1 1 18 1
x x x x x x x x
Đặt
2
1, 1, 0, 0
a x b x x a b
. Khi đó phương trình trở thành
2 2 2 2 2
3 1 18a ab a b b a
2 2 2
3 3 2 9a b a b b a b b a
2
3 6 0
a b a b b a
3 0
a b
, vì
2
6 0
a b b a
Suy ra
2 2
3 1 1 10 8 0 5 33
x x x x x x
, thỏa mãn điều kiện
Vậy nghiệm của phương trình là
5 33
x
Bài 58: Giải phương trình:
2 2
2 2 3
x x x x x
1
Bài giải:
2
2
2 2 2
2
2 0
2 1 2 2
x x x
x x x x x
2
2 2
2
2 2
2 0
2 2 2
x x x
x x x x x
2
2
2 0
2 6 0
x x x
x x
1 7
x
Vậy phương trình đã cho có nghiệm
1 7
x .
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
68
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bài 59: Giải phương trình:
2
4 4 2 16 2 12
x x x x
1
Bài giải:
Điều kiện:
4
x
2
1 4 4 4 4 12 0
x x x x
4 4 4
x x
Giải phương trình ta được x = 5
Vậy phương trình có nghiệm
5.
x
Bài 60: Giải phương trình:
2
3 7
2 1
x
x
x x
1
Bài giải:
ĐK: x > 0
*
Với điều kiện trên phương trình đã cho tương đương:
2
3 1 3 7
2 1 7 2 1x x x x x
x x x x
3 3 4 2 3 3 3 2 3
2 0 2 2 0
x x x x x x
x x x x x x x x x
3
2 0
3 3 2
2 0
3 2
0
x
x
x x
x x x
x
x x
2
2
2
3
4 3 0
4 3 0 1
3
1 4 0
3 4 0
x x
x x x
x
x x x
x x
.
Vậy phương trình có 2 nghiệm x = 1; x = 3.
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
69
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bài 61: Giải phương trình:
5 3
3
x x x x
1
Bài giải:
Đặt
0
t x
có hàm số
10 6 3
g t t t t
có
9 5 2
' 10 6 3 0
g t t t t
do
0t
Mà
1 3 1 1 1g t x x
Vậy phương trình có nghiệm
1.
x
Bài 62: Giải phương trình:
(2 1) 1 (2 1) 1 2x x x x x
1
Bài giải:
Điều kiện:
1 1x
2 1 1 1 1 1 0
x x x x x
.
Đặt
2 2
1 ; 0
2
1 ; 0
a x a
x a b
b x b
Phương trình trở thành
2 2
( )( 1) ( ) 0
a b a b a b
2
( )[( )( 1) 1] 0
1 5
( ) ( ) 1 0
2
a b
a b
a b a b a b
a b a b
a b
)
Với
1 1 0
a b x x x
( Thỏa mãn )
)
Với
1 5 1 5 5 5
1 1
2 2 8
a b x x x TM
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
70
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Vậy phương trình có nghiệm
5 5
0; .
8
x
Bài 63: Giải phương trình
2
2
2
16 96 208
9 log 2 3 4 6 3 5 9
12 16 45 81
x x
x x x x
x x
Bài giải:
Điều kiện
4
3
x
Ta có
2
2
2
16 96 208
9 log 2 3 4 6 3 5 9
12 16 45 81
x x
x x x x
x x
2 2
2
2
6 13 log ( 6 13)
2 3 4 3 5 9 log (2 3 4 3 5 9)(*)
x x x x
x x x x
Xét hàm số
2
1
( ) log , 0, '( ) 1 0
ln 2
f t t t t f t
t
với mọi t>0 nên
( )f t
đồng biến trên
(0; )
.
Từ (*) suy ra
2
( 6 13) (2 3 4 3 5 9)
f x x f x x
nên
2
6 13 2 3 4 3 5 9
x x x x
2
2 2
2
2
2 ( 2) 3 4 3 ( 3) 5 9 0
2( ) 3( )
( ) 0
2 3 4 3 5 9
2 3
( ) 1 0
2 3 4 3 5 9
x x x x x x
x x x x
x x
x x x x
x x
x x x x
2
( ) 0
x x
vì
2 3 4
1 0
3
2 3 4 3 5 9
x
x x x x
0; 1
x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
71
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Đối chiếu với điều kiện ban đầu suy ra phương trình có nghiệm
0; 1
x x
Bài 64: Giải phương trình:
3 1 1 1
x x x
1
Bài giải:
Điều kiện:
0 1x
*
Khi đó
3 1 1 1 3 1 1 3 (2)
x x x x x x
Ta thấy x = 1 là một nghiệm của phương trình (2)
Vói
0 1x
thì
3 1 1 3
x
còn
3 3
x x
nên (2) vô nghiệm.
Vậy phương trình đã cho có nghiệm
1.
x
Bài 65: Giải phương trình:
3 2
2 3 4 1x x x x x
1
Bài giải:
Điều kiện:
2 3
x
3 2 2
2 2 3 2
2 3 3 4 4 1 4
2 3 3
x x
x x x x x x x
x x
2
2 2 3 4
1 4
2 3 3 2 3 2
x x
x x
x x x x
2
2
2 2
2 2
2 3 3 2 3 2
x x
x x x
x x x x
2
0
2
2
2 2 0
2 3 3 2 3 2
2 0 2 1
x x x
x x x x
x x x x

Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
72
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Vậy phương trình có nghiệm
1;2 .
x
Bài 66: Giải phương trình:
2
2 2
1
2 1 3 2 4 2 3 4 4 4 4 3 2 1
4
x x x x x x x
1
Bài giải:
ĐK:
1 3
x
2 2
. Phương trình
2
2 2
2
2 1 2 1
2 1 3 2 2 1 3 2 2
2 2
x x
x x x x
Xét hàm số
2
f t t t
trên

0;
có

f ' t 2t 1 0 t 0;
nên hàm số f(t) đồng biến trên

0;
Do đó phương trình (2) trở thành :
2
2 1
2 1 3 2
2
x
f x x f
2
2
2
2 1
2 1 3 2 8 2 1 3 2 4 2 1
2
8 2 1 3 2 2 1 3 2 3
x
x x x x x
x x x x
Đặt
2 1 0
3 2 0
x a
x b
thì phương trình (3) trở thành
2
2
2 2 2 2
2 2
2 2
2 2
8 4 4
8
4 5
4
a b a b a b
a b a b
a b
a b
Từ
2 2 2 2
4 8 16 4a 2 4
a b b a b a b
2 2 2 2 4 4
4 2a 16 8 6
a b b a b a b
Đặt
0 2
ab t t
thì pt (6) trở thành
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
73
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2 4 2
16 8 16 8 2 2 4 0
t t t t t t t
0
2
1 5
1 5
t
t loai
t loai
t loai
. Vậy
1
2 1 3 2 2
2
0
3
2 1. 3 2 0
2
x
x x
t
x x
x
Vậy phương trình có nghiệm
1 3
; .
2 2
x
Bài 67: Giải phương trình:
2 2
3 2 9 3 4 2 1 1 0
x x x x x
1
Bài giải:
Điều kiện:
x R
2
2
3x 2 9 3 2 1 3 2 1 2
x x x
2
2
3 2 9 3 2 1 3 2 1 2
x x x x
Xét hàm số
2
2 2
f t t t
ta có
2
2
2
' 2 2 0
2
t
f t t
t
suy ra hàm số
đồng biến
Từ đó suy ra
1
3 2 1
5
x x x
Vậy phương trình có nghiệm
1
.
5
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
74
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bài 68: Giải phương trình:
2 2 2
2 2 1 2 1 8 8 1 0
x x x x x x x
x
Bài giải:
Đkxđ:
0 1x
2 2 2 2
2x 2x 1 2x 1 8x 8x 1 2x 1 8x 8x 1 2 1 0
x x x
2 2 2
2 2 1 5 5 1 8x 8x 1 2 1 0
x x x x x x
2 2
2 2 2
2 2 1 2 1 2 1
8x 8x 1 2x 1 8x 8x 1 2 1 0
x x x x x x x
x x x
2 2 2 2
2 1 2 2 1 2 1 8x 8x 1 2x 1 8x 8x 1 0
x x x x x x x
2
2 2
2
2 1 *
2 1 2 2 1 1 0
2 2 1 1 0 **
x x x
x x x x x x
x x x
2
1
** 2 2 1 1 0 0
2
x x x x
+) Xét:
2
1
2 2 1 0
2
f x x x x x
2
2
2
2
2 2 2
4 2 1
2 1 8 8 1
' 2.2 2 2 1 .
2
x x x
x x x
f x x x x
x x x x x x
2
2 2 1
0;
4 2
' 0 8 8 1 0
2 2 1
0;
4 2
x
f x x x
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
75
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Có:
2 2 1 1
0 0; ; 0
4 2 2
f f f
1 1
1 0 x 0;
2 2
f x
=> (**) vô nghiệm
2 2 2
4 4 1 5 5 1 0
*
1 1
2 2
x x x x x x
x x
5 5
10
x
(Thỏa mãn)
Vậy phương trình có nghiệm:
5 5
10
x
Cách 3:
Điều kiện:
0;1
x
. Phương trình đã cho tương đương với:
2 2 2
2 1 4 2 8 8 2 1 0
x x x x x x x x
2 2 2
2 2 2
2 2 2
2 2
2 1 4 2 2 1 4 2 0
2 1 4 2 2 1 0
2 1 4 2 1 0
2 1 1 4 2 0 *
x x x x x x x x x x
x x x x x x x x x
x x x x x x x x x
x x x x x x
Dễ thấy
2
2 2
1 1 1
0
2 4 2
x x x x x
2
1
1 2 4 2 4 . 1 2 0
2
x x x x x x
(điều này vô lý).
Khi đó
2
1 1
* 2 1
2
2 5
x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
76
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Vậy phương trình đã cho có nghiệm duy nhất là
1 1
2
2 5
x
Bài 69: Giải phương trình:
3 2 3 2
2 3 3 3 2 1 2 3 3 14x x x x x x x x x
Bài giải:
Điều kiện:
1
x
2 3 2
* 2 3 3 1 2 1 2 3 3 14
x x x x x x x
2 3 2
2 3 3 1 2 1 2 2 3 3 18
x x x x x x x
2 2
2 3
2 3 3 1 3 2 3 6
1 2
x
x x x x x x
x
2 2
2
3 2 3 1 2 3 6 0
1 2
x x x x x
x
2 2
3
2
2 3 1 2 3 6 0 **
1 2
x
x x x x
x
2 2
2
** 2 3 6 2 3 1
1 2
x x x x
x
Có:
1 2 2 x 1
x
2 2
2
1 2 3 6 2 3 1 1
1 2
x x x x
x
2 2 2 2
2 3 5 2 3 1 0 2 3 5 2 3 1
x x x x x x x x
4 3 2 3 2
4 12 29 30 25 4 12 4 12
x x x x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
77
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
4 3 2 2
4 8 17 26 13 0 4 13 1 0 1
x x x x x x x
Vậy phương trình có nghiệm
1
x
, x = 3
Bài 70: Giải phương trình:
2
9 3 1 2
x x
1
Bài giải:
Điều kiện:
x
Cách 1:
Đặt
2
1 , 2 1
x u u x u
thay vào (1) ta có
4 2
2 8 3 2 2
u u u
4 2 2 4 2 3 2
2 8 9 12 4 7 12 12 0 2 2 3 6 0
u u u u u u u u u u u
3 2
2 0
2 3 6 0
u
u u u
+
2 0 2 5
u u x TM
+
3 2
2 3 6 0
u u u
(4) ;
2
u
Do
2
u
nên
3 2
2 3 6 2 2 3 6 6 0
u u u u u u u
suy ra (2) vô nghiệm
Vậy phương trình có nghiệm
5.
x
Cách 2
2
2
2
3 5
25
2 9 4 3 1 2 0 3
1 2
9 4
x
x
x x
x
x
2
5
5 3
1 2
9 4
x
x
x
x
) 5
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
78
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2 2
5 3 5 5 3 3
) 5 3 1
4
1 2 2 2 1 2
9 4 9 4
x x x
x
x
x x
x x
(3) vô nghiệm.
Vậy phương trình có nghiệm
5.
x
Bài 71: Giải phương trình:
2
4 5 2 6 1x x x
1
Bài giải:
Điều kiện:
5
4
x
2
2
2
2 4 5 4 12 2 4 5 1 2 2
PT x x x x x
1
2
4 5 2 3
1 2
4 5 1 2
1 2
x
x x vn
x loai
x x
x
Vậy phương trình có nghiệm
1 2.
x
Bài 72: Giải phương trình:
2
1
1 1
2 1
2 4 8
x
x
x x
Bài giải:
Điều kiện
1
2
x
. Đặt
1 1
, ; , 0
2 4
x
u x v u v
Pt trở thành
2 2
2
2
2 2
0
0
2 2
2
0
u v
u v
u v u v
u v u v
u v
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
79
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
2
1
1
1 1
0 7 2 10
1 2 1
2 4
14 9 0
2 16
x
x
x
v u x x
x x
x x
x
( TM )
Vậy nghiệm của phương trình là:
7 2 10
x
Bài 73: Giải phương trình
3 2
3 3
3 7 7 7 12 5 6
x x x x x x x
Bài giải:
Phương trình đã cho tương đương với
3 3 2
3 3
7 3 7 7 8 12 6 1x x x x x x x x x
3
3
3 3
7 2 1 7 1x x x x x
3
2
7 1 1 4 6 0 1 1
x x x x x x x
Vậy phương trình có nghiệm
1.
x
Bài 74: Giải phương trình
7 7 17 17 24 12 17 2
x x x x x x
Bài giải:
Điều kiện
0
24
x
x
Đặt
12
12
12
t
t x
t
Phương trình trở thành:
12 5 5 5 12 5 12 17 2
f t t t t t t t
Suy ra
f t f t
, do đó f(t) là hàm số chẵn trên tập
; 12 12;D
 
nên chỉ
cần xét trên
12;

Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
80
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Ta có
2 17 2 17
' 0
2 12 5 5 5 2 12 5
t t t
f t
t t t t t t
với mọi giá trị
12;t

Suy ra f(t) đồng biến trên
12;

, nên
12 17 2
f t
có nhiều nhất một nghiệm thuộc
12;

Mà
13 12 17 2
f
, suy ra t =13 là nghiệm duy nhất của phương trình trên
12;

Do f(t) là hàm số chẵn nên t = -13 là nghiệm duy nhất thuộc
; 12
.
Vậy nghiệm của phương trình là
1; 25
x x
Bài 75: Giải phương trình:
2
2 6 5 2 1 10 0
x x x x
Bài giải:
Điều kiện
1
x
. Phương trình đã cho tương đương với
2
2
2
5 2 1 2 1 2 4 4 0 2 2 4 2 1 2 1 2 1 0
x x x x x x x x x x x
2 2 2 2 1 1 2 2 1 0 2 2 1 2 2 1 0
x x x x x x x x x x
2 2 1
2 4 1
x x
x x
Xét
2
2
2 1 2 8
8 0
x
x x x
x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
81
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Xét
2
2
1 2 4 3
4 17 15 0
x
x x x
x x
Vậy nghiệm của phương trình là x =3, x = 8
Chú ý: Có thể giải cách khác bằng cách đặt
1t x
, từ đó phương trình đã cho được biến
đổi thành
2
2 3 2 5 3 0
t t t t
Bài 76: Giải phương trình
2
3
2 11 21 3 4 4
x x x
Bài giải:
Phương trình đã cho được viết thành
2
3
2 11 21 3 4 4 2 6
x x x
2
3
2
3
3
12 3
2 11 15 3 4 4 2 3 2 5
4 4 2 4 4 4
x
x x x x x
x x
Xét phương trình
2
3
3
12
2 5
4 4 2 4 4 4
x
x x
(*)
Tam thức
2
2 11 21
x x
có
2
11 8.21 47 0
nên
2
2 11 21 0
x x x R
. Suy ra
4 4 0 1x x
.
Đặt
3
2
12
4 4, 0; f
2 4
t x t t
t t
Ta có
2
2
12 2 2
f' 0
2 4
t
t
t t
, với t > 0. Suy ra f(t) nghịch biến trên khoảng
0;

do đó
hàm số:
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
82
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
3
3
12
4 4 2 4 4 4
G x
x x
nghịch biến trên khoảng
1;

Hàm số y = 2x – 5 đồng biến trên
1;

Từ đó suy ra phương trình (*) có không quá một nghiệm trên khoảng
1;

Mặt khác G(3) = y(3). Vậy phương trình (*) có duy nhất một nghiệm x = 3 trên khoảng
1;

.
Tóm lại phương trình đã cho có nghiệm duy nhất x = 3.
Cách khác: Từ
2
2 11 21 0
x x
suy ra
4 4 0
x
Ta có
2
2
2 11 21 2 3 3 3, x R.
x x x x x
3 3
3
4 4 8 8 3 4 4 .8.8 12 4 4 3 3 4 4
x x x x x
Suy ra
2
3
2 11 21 3 4 4
x x x
, đẳng thức xảy ra khi và chỉ khi
3 0
3
4 4 8
x
x
x
Vậy nghiệm của phương trình là x = 3.
Bài 77: Giải phương trình
2
32 4 3 2
4 2 4 4 1 1
x x x x x x
Bài giải:
*) Điều kiện:
2
4 0 2 2
x x
Phương trình đã cho tương đương với
2
2 2 2
3
4 2 2 2 2
x x x x x x
(1)
Ta có
2
2 2
4 4 2 4 4
x x x x
, với mọi
2;2
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
83
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Suy ra
2
4 2
x x
, với mọi
2;2
x
(2)
Dấu đẳng thức ở (2) xảy ra khi và chỉ khi
0; 2
x x
Đặt
3
2
2
x x t
. Dễ dàng ta có được
1;2
t
, với mọi
2;2
x
Khi đó vế phải của (1) chính là
3 2
2 2, 1;2
f t t t t
Ta có
2
0
' 3 4 0
4
3
t
f t t t
t
Hơn nữa, ta lại có
4 22
1 1, 0 2, , 2 2
3 27
f f f f
Suy ra
2
f t
, với mọi
1;2
t
Do đó
2
2 2
3
2 2 2 2 2
x x x x
, Với mọi
2;2
x
(3)
Dấu đẳng thức ở (3) xảy ra khi và chỉ khi
0; 2
x x
Từ (2) và (3) ta có nghiệm của phương trình (1) là
0; 2
x x
Vậy phương trình đã cho có nghiệm
0; 2
x x
Bài 78: Giải phương trình:
2
2 9 8 2 1x x x
1
Bài giải:
Điều kiện:
1x
2
2
1 2 2 2 1
1 2 2 1 1
1 2 2 2 1
x x
x x
x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
84
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
2 9 2 2 10 4 2 0
1 2 2 2 1
2 2 2 1 0
x x
x x
x
Phương trình bậc hai
2
2 9 2 2 10 4 2 0
x x
có
2
2 2 1
nên có hai nghiệm là
1
5 2 2
2
x
và
2
2
x
. Nghiệm x
2
bị loại vì
2
2 2 2 1 0
x
Hoàn toàn tương tự ta có
5 2 2
1 2 2 2 1
2
x x x
Vậy phương trình có nghiệm
5 2 2
;2 .
2
x
Bài 79: Giải phương trình
2
2 4 2 5 1x x x x
Bài giải:
2
1 2 1 4 1 2 5 3
3 3
3 2 1
2 1 4 1
1 1
3 2 1 0
2 1 4 1
3 0
1 1
2 1 2
2 1 4 1
x x x x
x x
x x
x x
x x
x x
x
x
x x
*
3 0 3
x x
*Xét phương trình (2)
ĐK
2 4
x
5
VP
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
85
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
VT đạt giá trị lớn nhất trên đoạn [2;4] bằng
1
1
2 1
khi x=2 nên phương trình (2) vô
nghiệm
Vậy phương trình có nghiệm duy nhất x=3
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
86
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
BẤT PHƯƠNG TRÌNH
Bài 1: Giải bất phương trình:
2
2
2
2 2
1
3
3
x x
x
x
x
Bài giải:
Điều kiện
3.
x
Bất pt đã cho tương đương với
2
2
2
2 2
2 2
2
2 2
2
2
2
2
2 4
2 2
3 3
1 0 1 0
3
3 2 2
3
3
1 6
3 3
1 0
2 2
3
3
x x
x x
x x
x x
x
x x x
x
x
x x x
x x
x
x x
x
x
2
2
2
2
2
6
1 1 0
2 2
3 3
3
3
x x
x
x x
x x
x
x
2
1 0 1 1x x
(Với
3
x
thì biểu thức trong ngoặc vuông luôn dương).
Vậy tập nghiệm của bất pt là
1;1
S
Bài 2: Giải bất phương trình:
2 2
1 4 20 4 9.
x x x
Bài giải:
Bất phương trình đã cho tương đương với:
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
87
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2 2
2 2
2 2
4 16 16 4
4 9 5 6 4 20 2 0 2 0
4 9 5 6 4 20
x x
x x x x
x x
2 2
4 8 4 8
2 1 0
4 9 5 6 4 20
x x
x
x x
Từ (1) suy ra
2 2
1 4 20 4 9 0 1 x x x x
. Do đó
2 2
2 2
2 2
4 8 4 8 1 4 20 4 9
1 4 8 . 1 0
4 9 5 6 4 20
4 9 5 6 4 20
x x x x
x
x x
x x
Vậy nghiệm của bất phương trình là
2.
x
Bài 3: Giải bất phương trình
2
3
3
2 2 1
1
2 1 3
x x x
x
x
trên tập hợp số thực.
Bài giải:
- ĐK:
1, 13
x x
- Khi đó:
2 2
3
3 3
2 2 1 6
1 1 2
2 1 3 2 1 3
x x x x x
x x
x x
3
2 1 2
1 , *
2 1 3
x x
x
- Nếu
3
2 1 3 0 13
x x
(1)
thì (*)
3
2 1 2 1 1 1 1x x x x x
Do hàm
3
( )
f t t t
là hàm đồng biến trên
, mà (*):
3 2
3 3
2 1 1 2 1 1 0
f x f x x x x x x
Suy ra:
1 5 1 5
; 0;
2 2
x

DK(1)

VN
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
88
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
- Nếu
3
2 1 3 0 1 13
x x
(2)
thì (2*)
3
2 1 2 1 1 1 1x x x x x
Do hàm
3
( )
f t t t
là hàm đồng biến trên
, mà (2*):
3 3
2 3
1
1
2
1
2 1 1 2 1 1
13
2
2 1 1
x
f x f x x x
x
x x
Suy ra:
1 5
1;0 ;
2
x

DK(2)

1 5
1;0 ;13
2
x
Vậy bất phương trình có nghiêm
1 5
1;0 ;13
2
S
Bài 4: Giải bất phương trình:
2
2
5 13 57 10 3
2 9
3 19 3
x x x
x x
x x
1
Bài giải:
Điều kiện
19
3
3
4
x
x
Với điều kiện
bất phương trình
1
tương đương với:
2
3 19 3 2 3 19 3
2 9
3 19 3
x x x x
x x
x x
2
2 3 19 3 2 9x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
89
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
5 13
2 3 19 3 2
3 3
x x
x x x x
2
2
2
2 2
2
2
5 13
9 3 9 19 3
3 3
x x
x x
x x
x x
x x
2
2 1
2 0 2
5 13
9 3 9 19 3
3 3
x x
x x
x x
Vì
2 1
0
5 13
9 3 9 19 3
3 3
x x
x x
với mọi
19
3; \ 4
3
x
Do đó
2
2 2 0 2 1
x x x
( Thoả mãn )
Vậy tập nghiệm của bất phương trình là
2;1
S
.
Bài 5: Giải bất phương trình
2 2
6 1 2 1 3 9 2
x x x x x x x
1
Bài giải:
2 2
2 2
6 1 2 1 3 9 2
6 1 1 2 1 2 2 10 12
x x x x x x x
x x x x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
90
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
2
2 2
2
2
2
2
6 2
2 3
2 10 12
1 1 1 2
5 6 2 5 6
2 5 6
1 1 1 2
2 1
5 6 2 0
1 1 1 2
1 1
1
5 6 0
1 1 1 2
1;2 3;
x x x
x x
x x
x x
x x x x x
x x
x x
x
x x
x x
x
x x
x x
x

Vậy bất phương trình đã cho có nghiệm
1;2 3; .
S

Bài 6: Giải bất phương trình
2 2 2
1 1 2
1 3 5 2 1
x x x
trên tập số thực.
Bài giải:
)
Đặt t = x
2
– 2, bpt trở thành:
1 1 2
3 3 1 1t t t
ĐK: t 0 với đk trên, bpt tương
đương
1 1
( 1)( ) 2
3 3 1
t
t t
. Theo Cô-si ta có:
1 1 1
.
1 3 2 1 3
3
1 1 2 1 1 2
.
2 3 2 2 3
3
t t t t t
t t t t
t
t t
t
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
91
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
1 2 1 1 2
.
2 3 1 2 2 3 1
3 1
1 1 1 1 1 1
.
1 3 1 2 1 3 1
3 1
2 0.
t t t
t t
t
t t
t t t t
t
VT t
)
Thay ẩn x được x
2
2
( ; 2] [ 2; ) ( ; 2] [ 2; ).
x T
   
Vậy bất phương trình đã cho có nghiệm
; 2 2; .
T
 
Bài 7: Giải bất phương trình:
1 1 1
1 1
x
x
x x x
Bài giải:
ĐK: x
[-1; 0)
[1; +
)
Lúc đó:VP của (1) không âm nên (1) chỉ có nghiệm khi:
1 1 1 1
1 1 1x x x
x x x x
. Vậy (1) chỉ có nghiệm trên (1; +
).
Trên (1; +
):
1 1
1 1 1 1 1
x x
x x
x x
.
Do
2
1 1
1 0
x x
x
x x
khi x > 1 nên:
2 2
1 1 1 1
1 1 2 1 2 1 0
x x x
x x
x x x x
2 2 2
2
1 1 1
2 1 0 ( 1) 0
x x x
x x x
1 5
2
x
.
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
92
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Vậy nghiệm của bất phương trình là
1
1 5
2
x
x
Bài 8: Giải bất phương trình
2 2 2
1 1 1(1 2)
x x x x x x
Bài giải:
Bất phương trình đã cho tương đương
2 2 2 2
( 1 1 2) (1 1) 0
x x x x x x x x
2
2 2 2 2
( 1)(2 2) (1 )
0
1 1 2 1 1
x x x x x
x x x x x x x x
2
2 2 2 2
2 2
( 1)( ) 0
1 1 2 1 1
x x x
x
x x x x x x x x
( 1). 0
x A
(1) với
2
2 2 2 2
2 2
1 1 2 1 1
x x x
A
x x x x x x x x
Nếu
0
x
thì
2 2
2 2 2
2
1 1
1 2 1
2
x x x
x x x x x x
x x x
2 2 2
1 2 1 0
x x x x x x
0
A
Nếu x>0 , áp dụng bất đẳng thức AM-GM ta có:
2 2
2 2 2
2 2
2 2
1 2 3
1 2
2 2
1 1
1
2 2
x x x x
x x x x x x
x x
x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
93
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2 2 2 2
1 2 1 2 2
x x x x x x x x
2
1 0
1 1
x
A
x x
vì
2
1
1 1
x
x x
Tóm lại , với mọi
x
ta có A>0. Do đó (1) tương đương
1 0 1x x
.
Vậy tập nghiệm của bất phương trình đã cho là
(1; )
.
Chú ý : Cách 2. Phương pháp hàm số
Đặt
11
222
xxuxxu
thế vào bpt đã cho ta có
11
)11(1
2222
2222
xxxxuuuu
uuxxxxu
Xét
1)(
22
tttttf
)
tttttf 01)1()('
222
nên hàm nghịch biến trên R
Do đó
1
xxubpt
Bài 9: Giải bất phương trình:
2 2 2
3
( 2)( 2 2 5) 9 ( 2)(3 5 12) 5 7x x x x x x x
1
Bài giải:
Điều kiện xác định:
5
2
x
. Khi đó ta có
3
3 2 2 2
(1) 3 14 15 2( 2) 2 5 3( 2) 5 5 7 0x x x x x x x x
3
3 2 2 2
3 18 2( 2)( 2 5 3) 3( 2)( 5 3) 3 5 7 0x x x x x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
94
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2 2
2
2
2
3 3
2 2
2( 2)(2 4) 3( 2)( 4) 5(4 )
( 2)( 5 9) 0
2 5 3
5 3
9 3 5 7 5 7
x x x x x
x x x
x
x
x x
2
2
2
2
3 3
2 2
4( 2) 3( 2) 5( 2)
( 2) 5 9 0(*)
2 5 3
5 3
9 3 5 7 5 7
x x x
x x x
x
x
x x
Ta có với
2
2
2
2
3 3
2 2
4( 2) 4 3( 2) 3
( 2); ( 2)
3 5
2 5 3
5 3
5
5( 2) 5( 2)
2
9
9 3 5 7 5 7
x x
x x
x
x
x
x x
x x
2
2
2
2
3 3
2 2
4( 2) 3( 2) 5( 2)
5 9
2 5 3
5 3
9 3 5 7 5 7
x x x
x x
x
x
x x
2
18 57 127 5
0,
45 2
x x
x
Do đó (*)
2 0 2x x
, kết hợp với điều kiện
5
2
x
suy ra:
5
2
2
x
Vậy phương trình đã cho có nghiệm
5
;2 .
2
x
Bài 10: Giải bất phương trình
xxxxxxx 322522
22
1
Bài giải:
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
95
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Điều kiện xác định:
2
x
.
5222322)1(
22
xxxxxxxx
52216222
22
xxxxxx
1622)522(16222
222
xxxxxxxx
16222
2
xxxx
(Do
Rxxx ,0522
2
)
)2(2)1(212
2
xxxx
(2)
Đặt
)0(1,2 axbxa
, (2) trở thành
0
0)(
0
22)(
0
22
2222
22
ba
ba
ba
baba
ba
baba
Do đó ta có
2
133
013
1
)1(2
01
12
22
x
xx
x
xx
x
xx
.
Vậy bất phương trình đã cho có nghiệm
2
133
x
.
Bài 11: Giải bất phương trình
3 2
( 1) 5 8 6x x x x x
(
x
)
1
Bài giải:
Điều kiện: x
0.
(1)
3 2 2
( 6 12 8) ( 4 4) 2
x x x x x x x x
3 3 2
( ) ( 2) ( 2) ( 2)
x x x x x x
(2)
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
96
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Xét hàm số f(t) = t
3
+ t
2
+ t, có f
’
(t) = 3t
2
+ 2t + 1 > 0,
.t
Do đó hàm số y = f(t) đồng biến trên R, mặt khác (2) có dạng
2 2
f x f x x x
(3).
+) Với
0 2
x
là nghiệm của (3).
+) Với x > 2, bình phương hai vế (3) ta được
2
5 4 0 1 4
x x x
Kết hợp nghiệm ta được 2 < x
4
là nghiệm của (3).
Vậy nghiệm của (3) là
0 4
x
, cũng là nghiệm của bất phương trình (1).
Bài 12: Giải bất phương trình:
2
2 3 1 3 2 2 5 3 16
x x x x x
1
Bài giải:
Điều kiện:
1x
.
Bpt (1) tương đương:
2
2 3 1 2 3 1 20
x x x x
Đặt
2 3 1t x x
, t >0
Bpt trở thành:
2
20 0t t
5
4
t
t
. Đối chiếu đk được
.
Với
5t
, ta có:
2
2 3 1 5 2 2 5 3 3 21
x x x x x
2
2
3 21 0
2 5 3 0
3 21 0
146 429 0
x
x x
x
x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
97
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
7
3
3 7
x
x
x
Kết hợp với điều kiện
1x
suy ra
3;x

Vậy bất phương trình có nghiệm
3; .
S

Bài 13: Giải bất phương trình
2
3
3
2 2 1
1
2 1 3
x x x
x
x
trên tập hợp số thực.
Bài giải:
– ĐK:
1, 13
x x
. Khi đó:
2 2
3
3 3
2 2 1 6
1 1 2
2 1 3 2 1 3
x x x x x
x x
x x
3
2 1 2
1 , *
2 1 3
x x
x
– Nếu
3
2 1 3 0 13
x x
(1) thì (*)
3
2 1 2 1 1 1 1x x x x x
Do hàm
3
( )
f t t t
là hàm đồng biến trên
, mà (*):
3 2
3 3
2 1 1 2 1 1 0
f x f x x x x x x
Suy ra:
1 5 1 5
; 0;
2 2
x

DK(1)

VN
– Nếu
3
2 1 3 0 1 13
x x
(2)
thì (2*)
3
2 1 2 1 1 1 1x x x x x
Do hàm
3
( )
f t t t
là hàm đồng biến trên
, mà (2*):
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
98
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
3 3
2 3
1
13
1
2
2 1 1 2 1 1 1
2
2 1 1
x
f x f x x x x
x x
Suy ra:
1 5
1;0 ;
2
x

DK(2)

1 5
1;0 ;13
2
x
Vậy bất phương trình có nghiệm
1 5
1;0 ;13
2
x
Bài 15: Giải bất phương trình
3
( 2)
1
( 1)
x x
x x
Bài giải:
Điều kiện
3
3
3
( 2) 0
0
0; x 0 ( 1) 0
( 1) 0
( 1) 0
x x
x
x x x
x
x x
Do vậy
3
3
2 3 2
3 2 2
( 2)
1 ( 2) ( 1)
( 1)
2 3 4 1 2( 1) ( 1)
2 2 1 2( 1) ( 1) 0 ( 1) 1 2 ( 1) 0
x x
x x x x
x x
x x x x x x x x
x x x x x x x x x x x
2
2
1 2 ( 1) 0 ( 1) 1 0
x x x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
99
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
( 1) 1 0 ( 1) 1
x x x x
2
1 5
2
( 1) 1 1 0
1 5
2
x
x x x x
x
Kết hợp điều kiện x>0 ta được nghiệm của phương trình đã cho là
5 1
2
x
Bài 16: Giải bất phương trình:
2 2
4 7 2 10 4 8x x x x x
Bài giải:
Điều kiện:
2
x
Bất phương trình đã cho tương đương với bất phương trình
2 2
2
2 2
2
2
4 7 2 2 4 7 2 2 4
4 7 2 2 2 2 2 2 2
4 7 2 2 4 4 2 2 2 1
2 2 1 2 1 2 2 1 2 0
x x x x x x
x x x x x
x x x x x x
x x x x x x
2 2 1 1
2 2 1 2
2 2 1 3
2 2 1 4
x x
I
x x
x x
II
x x
Giải hệ (I): Từ (1) và (2) suy ra
2
2 0
2 1 2 1
x
x
x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
100
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Khi đó hệ (I) tương đương với hệ phương trình
2 0
2 2 1
x
x x
2
1
2
2
2; 1
2 2 1
x
x
x x
Giải hệ (II): Từ (3) và (4) suy ra
2
0
2 1 2 1
x
x
x x
Khi đó hệ (I) tương đương với hệ phương trình
0
2 2 1
x
x x
2
1
5 41
2
;
8
2 2 1
x
x
x x

Vậy tập nghiệm của bất pt là
5 41
2; 1 ;
8
T

Bài 17: Giải bất phương trình:
2
4 1 2 2 3 ( 1)( 2)
x x x x
1
Bài giải:
Điều kiện:
1
x
Nhận thấy x = - 1 là một nghiệm cuả bất phương trình
Xét x > -1. Khi đó bất phương trình đã cho tương đương với
3 2
4 1 2 2 2 3 3 2 12
x x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
101
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
4( 3) 4( 3)
( 3)( 2 4)
1 2 2 3 3
x x
x x x
x x
2
4 4
( 3) ( 1) 3 0
1 2 2 3 3
x x
x x
. (1)
Vì x > -1 nên
1 0
x
và
2 3 1
x
. Suy ra
4 4
3
1 2 2 3 3x x
, vì vậy
2
4 4
( 1) 3 0
1 2 2 3 3
x
x x
.
Do đó bất phương trình (1)
3 0 3
x x
Vậy nghiệm của bất phương trình là x = -1 và
x
.
Bài 18: Giải bất phương trình
2 2
3 2 2 3 1 1x x x x x
Bài giải:
Điều kiện
1
2
2
1
x
x
x
X = 1 là một nghiệm
Trường hợp 1:
1
2
x
BPT 2 1 1 2x x x
3 2 2 2 1 1 2x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
102
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
BPT 2 1 2
x x
(thỏa mãn)
Trường hợp 2:
2
x
BPT 2 2 1 1x x x
2 1 2 1x x x
2
2 3 2 2 2 3 1x x x x
2
2 2 2 3 1 0
x x x
(vô nghiệm)
Vậy tập nghiệm của BPT là;
1
; 1
2
S

Bài 19: Giải bất phương trình
2
3
3
1 1
1
2 3 1
log x
log x x
Bài giải:
Đk;
2
2
2 3 1 0
2 3 1 0
1 0
1 3
1
1 1
2 2
\0 1hay x ;
x x
x x
x
x
;

Với điều kiện trên và để ý rằng
2 2
0
3
2 3 1 1 2 3 0
2
x
x x x x ,
x
1 1 0
x x
từ đó có thể chia bài toán thành 3 trường hợp sau:
TH1: Với
2
3
1 0 0 1 1 1 0 2 3 1
x ,thi` x log ( x ) va` x x
2
3
2 3 1 0
log x x
bất phương trình đã cho vô nghiệm
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
103
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
TH2: với
1 3
0 1
2 2
x x .
thì
2 2
3 3
1 1 1 0 0 2 3 1 1 2 3 1 0
x log ( x ) va` x x log x x
bất phương trình đã cho trở thành một bất đẳng thức đúng.
TH3: với
3
3
1 1 1 0
2
x ,thi` x log x
Và
2 2
3
2 3 1 1 2 3 1 0x x log x x .
Từ đó với
3
2
x .
bất phương trình đã cho tương đương:
2
2
33
2 3 1
2 3
2
1
3
2
1
1
3
log x
x
x
x
log x x
x x
2
2
2
5 0
2 3 1 1
3
5
3
2
2
x x
x x x
x
x
x
Kêt hợp cả 3 trường hợp bât phương trình đã cho có tập nghiệm:
1 3
0 1 5
2 2
S ; ; ;

Bài 20: Giải bất phương trình:
2 2
2
4 2
3( 2) 1 3 1
1
x x x x
x x
.
Bài giải:
ĐK:
1.
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
104
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Với điều kiện đó
BPT
2 2 2
2
8 2
6( 2) 2 6 1 0
1
x x x x x
x x
2 2
2 2 2
2
4 2
3 1 1 2 5 0
1
x x x x x x
x x
Xét hàm số
4 2
( ) 5
1
f t t
t
với
0t
. Ta có
2 2
'( ) 1
( 1) 1
f t
t t
.
'( ) 0 1f t t
Bảng xét dấu
Suy ra
( ) (1), [0; )
f t f t

( ) 0, [0; )
f t t

. Dấu “=” xảy ra
1t
.
Do
2 2
2
4 2
0, [0; ) 5
1
x x x x x
x x

0, [0; )
x

.
Dấu “=” xảy ra khi
2
1 5
1
2
x x x
.
Khi đó:
2
2 2 2
2
4 2
3 1 1 2 5 0
1
x x x x x x
x x
2
2
2
2
1 0
1 0
4 2
5 0
1
x x
x x
x x
x x
1 5
2
x
.
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
105
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Tập nghiệm của bất phương trình đã cho là:
1 5
[1; ) \
2
S

.
Bài 21: Giải bất phương trình
2 3 2
5 4 1 2 4x x x x x
.
Bài giải:
Điều kiện:
3 2
1 5 0
3 4 0
1 5
x
x x x
x
Khi đó: (1)
2 2
4 2 4 5 4x x x x x
2 2
4 2 4 3 2 4x x x x x x
(2)
Trường hợp 1: với
1 5
x
thì (2)
2 2
2 4 2 4
4 3
x x x x
x x
(3)
Đặt
2
2 4
x x
t
x
( 0)
t
thì (3) trở thành:
2
4 3 0 1 3t t t
Suy ra
2
2 4
1 3
x x
x
2
2
4 0
7 4 0
x x
x x
1 17 7 65
2 2
x
Trường hợp 2: với
1 5 0
x
thì
2
5 4 0
x x
nên (2) luôn thỏa
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
106
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Vậy bất phương trình đã cho có tập nghiệm là:
1 17 7 65
S 1 5;0 ;
2 2
Bài 22: Giải bất phương trình
2 3 2
3( 1) 2 1 2( )x x x x
.
Bài giải:
*) Điều kiện:
1
2
x
.
Bất phương trình đã cho tương đương với:
2
(x 1) 2 3( 1) 2 1 0
x x x
2
( 1) 2( 1) 3( 1) 2 1 2(2 1) 0
x x x x x
( 1) 1 2 2 1 2( 1) 2 1 0
x x x x x
( 1) 1 2 2 1 0
x x x
(1)
Do
2( 1) 2 1 0
x x
, với mọi
1
2
x
.
Xét hai trường hợp sau:
+) x > 1. Khi đó (1)
1 2 1 0
x x
2
6 3 0
x x
3 2 3
3 2 3
x
x
.
Kết hợp điều kiện ta được nghiệm
3 2 3
x
.
+)
1
1
2
x
. Khi đó
(1) 1 2 2 1 0
x x
2
6 3 0
x x
3 2 3
x
3 2 3
.
Đối chiếu điều kiện ta được nghiệm
3 2 3 1x
.
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
107
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Vậy nghiệm của bất phương trình đã cho là
3 2 3 1x
và
3 2 3
x .
Bài 23: Giải bất phương trình
3
1 1 2 3 1 0
x x x
.
Bài giải:
Điều kiện:
1x
.
Đặt
1, 2a x b x
, khi đó
0, 2
a b
và
2 2
2 2
b a
.
Bất phương trình trở thành:
2
2 2
3 3
2
1 ( 3 ) 0 ( 3 ) 0
2
b a
a b a a b a
2
2
2 2 2 3 3
2
( 2 ) 4 ( 3 ) 0 1 2 4 (1 3 ) 0
a a a
b a a b a
b b b
Đặt
, 0
a
t t
b
, bất phương trình trở thành
2 2 3
(1 2 ) 4 (1 3 ) 0
t t t
.
4 3 2
104 108 40 4 1 0
t t t t
3 2
(2 1)(52 28 6 1) 0
t t t t
2
(2 1)(t(52 28 6) 1) 0
t t t
2 1 0
t
,vì
0t
và
2
52 28 6 0
t t
.
Suy ra
1 1
2 1 2 4( 1) 2 2.
2
2
x
x x x x x
x
Kết hợp điều kiện, suy ra nghiệm của bất phương trình là
1 2
x
.
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
108
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bài 24: Giải phương trình:
2
1 2 1 2 2
x x x
.
Bài giải:
ĐK:
1 1
2 2
x
.Khi đó
2
2 0
x
Bpt
2 2 4 2 2 4
2 2 1 4 4 4 2 1 4 2 4
x x x x x x
(1).
Vì
1 1
2 2
x
nên
2 2 4
2 4 0 2 4 x 0
x x
2 2 4 2
(1) 4(1 4 ) (2 4 )x x x
2 4 8 2 4 6
4 16 4 16 16 4 8x x x x x x
8 6 4 4 4 2
8 20 0 ( 8 20) 0 0
x x x x x x x
Vậy pt có nghiệm duy nhất x = 0
Bài 25: Giải bất phương trình:
2 2
1 2 3 4x x x x
Bài giải:
Điều kiện
2
2
0
0 1
1 0
3 41 3 41
2 3 4 0
8 8
x
x
x
x
x x
3 41
0
8
x
(*)
Bất phương trình đã cho tương đương với
2 2 2 2 2
1 2 (1 ) 2 3 4 3( ) (1 ) 2 ( )(1 ) 0
x x x x x x x x x x x x
2 2 2
1x x x x x x
5 34
9
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
109
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Kết hợp điều kiện (*), ta suy ra nghiệm của bất phương trình là
5 34
9
3 41
8
x
Bài 26: Giải phương trình:
2 2
2 2
3 18
1
1 1
x x x
x
x x
1
Bài giải:
Đặt
1t x
. ĐK:
0
t
và
1t
. Bất phương trình đã cho trở thành:
2 2
2 2 2
2
4
2
1 1 3 15
t t t
t
t t
2
2 4 2 3
1 15 8 2
t t t t t t
Kết hợp với ĐK ban đầu ta được:
1 1 1
0 2
0 1 2
t x
t
x
0 0
0 1 4 1 3
x x
x x
Vậy bất phương trình có tập nghiệm
1;3 \ 0
S
Bài 27: Giải bất phương trình
3 2
3
3
4 3 2 3 2 3
4 1 2
2 3 3 4 1
x x x x x
x x
x x
1
Bài giải:
ĐK:
2, 12
x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
110
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
3
3 2 2
1 2 2
2 3 3
x x
x
x
3
3 2 2
1 2
2 3 3
x x
x
TH1:
12
x
2 3
3 3
2 2 3 2 3 2 2 3
x x x x
Hàm số
3
f t t t
đồng biến trên R nên:
2 3
3
3 2 3 2 2 3 2
x x x x
3 2
2 1 0
x x
vô nghiệm vì
12
x
TH2:
2 12
x
3 3
3 3
2 2 3 2 3 2 2 4
x x x x
Hàm số
3
f t t t
đồng biến trên R nên:
2 3
3
4 2 3 2 2 3 2
x x x x
3 2 2
2 1 0 1 1 0
x x x x x
1 5 1 5
; 1 ;12
2 2
x
Đối chiếu điều kiện
2 12
x
ta có tập nghiệm của bất phương trình là:
1 5 1 5
; 1 ;12
2 2
S
Bài 28: Giải bất phương trình:
2 2
9 3 9 1 9 15
x x x
Bài giải:
Nhận xét:
2 2
1
9 1 9 15 9 3 0
9
x x x x
2 2
9 3 2 3(3 1) 9 15 4
bpt x x x
2 2
2 2
9 1 9 1
3(3 1) 0
9 3 2 9 15 4
x x
x
x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
111
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2 2
2 2
3 1 3 1
(3 1) 3 0
9 3 2 9 15 4
1 1 1
(3 1) (3 1) 3 0 3 1 0
3
9 3 2 9 15 4
x x
x
x x
x x x x
x x
Kết hợp các ĐK suy ra nghiệm của BPT là
1
3
x
là nghiệm của bpt
Bài 29: Giải bất phương trình:
4 3
3 2
2 2 1
2 2
x x x
x x
x x x
Bài giải:
ĐK:
0
x
, BPT tương đương:
3
3 3
2
2
1 1 1
1
1
1 1
1 1
x
x x x
x
x
x
x x
Xét hàm số
3
2
1
t
f t
t
trên
Ta có:
4 2
2
2
3
' 0
1
t t
f t t
t
Mà f(t) liên tục trên
nên f(t) đồng biến trên
.
(1) có dạng:
3 5
1 1 0
2
f x f x x x x
Bài 30: Giải bất phương trình
2 2
1 4x 20 4 9
x x
1
Bài giải:
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
112
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bất phương trình đã cho tương đương với:
2 2
2 2
2 2
4 16 16 4
4 9 5 6 4 20 2 0 2 0
4 9 5 6 4 20
x x
x x x x
x x
2 2
4 8 4 8
2 1 0
4 9 5 6 4 20
x x
x
x x
Từ (1) suy ra
2 2
1 4 20 4 9 0 1 x x x x
. Do đó
2 2
2 2
2 2
4 8 4 8 1 4 20 4 9
1 4 8 . 1 0
4 9 5 6 4 20
4 9 5 6 4 20
x x x x
x
x x
x x
Vậy nghiệm của bất phương trình là
2
x
Bài 32: Giải bất phương trình:
2
3
2
5 14 2
2 3 1
x x
x
x x
Bài giải:
Đkxđ:
0
x
Ta có:
2
3
2
5 14 0
2 3 1 0
x x
x x
2 2
3 3
2 2
5 14 0 2 5 14 0
0 0
2 3 1 2 3 1
x x x x
x
x x x x
0
x
quy đồng ta có:
3
3 2 2
5 14 4 6 1 x x x x x
33 2 2
5 8 4 6 1 0
x x x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
113
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
3 2
2
2
3 32 2 2
1
1 4 4 6 0
1 1
x x x
x x x
x x x x x x
2
3 32 2 2
1 1
x x x x x x A
2
2
6 1
1 2 0
x
x x
A
0 1
x
(Do
2
2
6 1
2 0 0
x
x x
A
)
Kết luận
0 1 1 x x
Vậy
0;1
x
Bài 33: Giải bất phương trình:
2
2 1
2
2
1
log log log 1 2 1 1 1
1
x
x x x
x
Giải bất phương trình
2
2 1
2
2
1
log ( ) log log (1 2 1) 1
1
x
x x x
x
Điều kiện :
2
1
0
1
0
x
x
x
x
BPT
2
2
1 2
1
1 2 1
x x
x
x
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
114
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
3 2
2
2 2 3 2
2 3 2
2 2
( 1)(1 2 1)
2
1
( 1)( 2 1) ( 1)( 2 1)
1 1
( 1)( 2 1) ( 1)
( 2 1) 0
1
( 1) 2 1 2 1
( 2 1) 0
1
2 1
0
1
x x x x
x
x
x x x x x x x x
x x
x x x x x x
x x
x
x x x x
x x
x
x x
x
2 1
1
2 1
1
1 2
1
1
2
x x
x
x x
x
x
x
Vậy
1 2
0 1
x
x
là nghiệm của bất phương trình đã cho.
Bài 34: Giải bất phương trình
2 3 2
5 4 1 2 4x x x x x
Bài giải:
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
115
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Điều kiện:
3 2
1 5
2 4 0
1 5 0
x
x x x
x
Bất phương trình đã cho tương đương với
2 2
2 4 3 4 2 4
x x x x x x
(1)
Xét hai trường hợp sau đây:
TH1: Với
1 5 0
x
khi đó
2
2 4 0
x x
và
3 0
x
. Hơn nữa hai biểu thức
2
2 4
x x
và
3x
không đồng thời bằng 0. Vì vậy
2 2
2 4 3 4 2 4
x x x x x x
Suy ra
1 5 0
x
thỏa mãn bất phương trình đã cho
TH2: Với
1 5
x khi đó
2
2 4 0
x x
. Đặt
2
2 4 0, 0
x x a x b
Bất phương trình trở thành
2 2
3 4 3 0 3a b ab a b a b b a b
2
2
2
4 0
1 17 7 65
2 4 3
2 2
7 4 0
x x
x x x x x
x x
(tmđk)
Vậy bất phương trình đã cho có nghiệm
1 17 7 65
1 5 0;
2 2
x x
Bài 35: Giải bất phương trình:
2 2
2 3 2 2
x x x x x
Bài giải:
● Điều kiện xác định:
1 3
x (1)
● Với điều kiện đó, ký hiệu (2) là bất phương trình đã cho, ta có:
2 2
2 2 2 2 1 2 3 2 2
x x x x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
116
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
1 2 2 2 1
x x x x x x
2 2 1 2 1 0
x x x x x x
(3)
Do với mọi x thỏa mãn (1), ta có
2 1 0
x x x
nên
3 2 2 1x x x
2
6 4 0
x x
3 13 3 13
x (4)
Kết hợp (1) và (4), ta được tập nghiệm của bất phương trình đã cho là:
1 3;3 13
Bài 36: Giải bất phương trình:
9 3 2 9 3
x x x
Bài giải:
Đặt
3 0
x
t
, bất phương trình trở thành
2
2 9t t t
Xét
9 0 9
t t
, khi đó bất phương trình tương đương với
2
2 0 9 1
t t t
Xét
9
t
, bất phương trình tương đương với
2 2
83
2 81 18
19
t t t t t
.
Suy ra
83
9 2
19
t
Từ (1) và (2) suy ra
83
19
t
khi đó
3
83 83
3 log
19 19
x
x
.
Vậy nghiệm của bất phương trình gồm các giá trị
3
83
log
19
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
117
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bài 37: Giải bất phương trình:
1 2 4 3
1 1
1 2 4 3
1 2 4 3
x x x
e x e x x
x x x
Bài giải:
Điều kiện
0
x
Xét hàm số
1
t
f t e t
t
với
1;t

Ta có
1
' 0
2
t
t
f t e
t t
với
1;t

. Suy ra f(t) đồng biến trên
1;t

Do đó từ bất phương trình đã cho tương đương với
1 2 4 3
x x x
1 1
2 5 2 0 2 4
2 4
x x x x
Vậy tập nghiệm của bất phương trình gồm các giá trị của x thỏa mãn
1
4
4
x
Bài 38: Giải bất phương trình
2.9 3.6
2
6 4
x x
x x
x
Bài giải:
Ta có
2.9 3.6 2.9 5.6 2.4
2 0
6 4 6 4
x x x x x
x x x x
Chia cả tử và mẫu của vế trái cho
4 0
x
, bất phương trình tương đương với
2
3 3
2. 5 2
2 2
0
3
1
2
x x
x
. Đặt
3
, 0
2
x
t t
bất phương trình trở thành
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
118
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
1
2 5 2
0
2
1
1 2
t
t t
t
t
Với
1
2
t
ta có
3 3
2 2
3 1 1
log log 2
2 2 2
x
x x
Với
1 2t
ta có
3
2
3
1 2 0 log 2
2
x
x
Vậy tập nghiệm của bất phương trình đã cho là
3 3
2 2
; log 2 0;log 2
S

Bài 39: Giải bất phương trình
2
1 1
2 1
2 3 5
x
x x
Bài giải:
Điều kiện
5
; (1; )
3
x

Xét
5
;
3
x

, vế trái bất phương trình luôn dương mà vế phải âm nên
5
;
3
x

là nghiệm bất phương trình
Xét
(1; )
x

bất phương trình
2
2 1 2 3 5
x x x
2 2 2
2
(2 1) 2 3 5 2 7 6 0
3
2
x
x x x x x
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
119
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Suy ra
3
1; [2; )
2
x

là nghiệm bất phương trình
Vậy tập nghiệm bất phương trình là
5 3
; (1; ] [2; )
3 2
 
Bài 40: Giải bất phương trình
2
2
1 3 2
1 3
x x
x x
Bài giải:
Giải bất phương trình……
Đk:
1 3
x
Đặt 1 3
t x x
2
2
4
0 3 2
2
t
t x x
, bpt trở thành:
2
3 2
2 4
1 2 4 0 2 2 2 0 2
2
t
t t t t t t
t
(t/m)
Với t > 2 ta có
2
1 3 2 3 2 0 1 3
x x x x x
Kết hợp đk ta được nghiệm bpt là:
1 3
x
Bài 41: Giải bất phương trình
5 8
2 2
2 3
2
log 2 7 log 2 7
0
3 13 4
x x x x
x x
Bài giải:
Điều kiện
2
2
2 7 0 1 2 2, 4
3 13 4 0
1 2 2
x x x x
x x
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
120
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2 2 2
2 3 2 2
3
2 2
5log 2 7 8log 2.log 2 7 log 2 7
0 5 8log 2 0
3 13 4 3 13 4
x x x x x x
Pt
x x x x
Do
5 8
3 3 3 3 3
5 8log 2 log 3 log 2 log 243 log 256 0
nên
2
2
2
log 2 7
0
3 13 4
x x
x x
2
2
2
2
2
22
2
2
2
3 13 4 0
3 13 4 0
1
log 2 7 0
2 7 0
, 4
3
3 13 4 03 13 4 0
2
2 7 0
log 2 7 0
x x
x x
x x
x x
x x
x xx x
x
x x
x x
Kết hợp với điều kiện suy ra nghiệm của bất phương trình là
1 2 2, 4
2
x x
x
THÊM DẠNG
Câu 1:
2 2
2 2 1 1.
x x x x
Lờigiải:
Điềukiện:
1.x
Bất phương trinh tương đương với:
2
3 2 0; 1
2 1 1 2 1 0 1 2 1 1 2 0
1 0 1 1;
x
x x x x x x x x x
x x S

Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
121
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Câu 2:
2 2
2 3 21 17 0.
x x x x x
Lờigiải:
Điềukiện:
17
.
21
x
Bất phương trinh tương đương:


2
2 2
2
2
2
2
2
17
0,
21
1 2 3 9
1 2
2 3 1 1 21 17 0 0
1 21 17
2 3 1
2
1 3 9
1 2 0 1 2 0 .
1
1 21 17
2 3 1
x
x x x x
x x
x x x x x
x x
x x x
x
x x
x x x x
x
x x
x x x
Kếthợpđiềukiện suy ra tậpnghiệm
17
;1 2; .
21
S

Câu 3:
3
3 2 2
2 1 2 1 2 .x x x x x x
Lờigiải:
Điềukiện:
1
.
2
x
Bất phương trinh tương đương:
3 3
2 2 2 2 2
2
2
2
2
2
3
2 2 2
3
1 1 2 1 2 0 1 2 1 2 0
1 1
1
0 1 0 1.
2 1
2 2
x x x x x x x x x x x x x
x x
x x
x x
x x
x x x x x x
Kếthợpđiềukiện suy ra tậpnghiệm
1
; \ 1 .
2
S

Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
122
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Câu 4:
2
3 2
5
1 2 4 .
4
x x
x x x
Lờigiải:
Điềukiện:
3 2
2 4 0.
x x x
Từđiềukiệnbàitoán cho ta
2
5 0
x x
vớimọi
1 5; 0 .
x
Khi đó BPT luôn đúng.
Ta xétvới
2
5 1 5 0.
x x x
Bất phương trinh tương đương:
2
2 3 2 2 3 2
4 3 3 2 2
2
2
2
2
5 4 4 2 4 5 4 16 2 4
6 15 24 16 0 7 4 4 0
7 4 0
1 17 7 65
4 0
2 2
.
4 0
1 17 7 65
2 2
7 4 0
x x x x x x x x x x
x x x x x x x x
x x
x
x x
x x
x
x x
Kếthợpđiềukiện
5 1,
x
suy ra tậpnghiệm
1 17 7 65
1 5;0 ; .
2 2
S
Câu 6:
2
7 1 .
1
x x
x
Lờigiải:
Điềukiện
1,x
bất phương trình tương đương với:
2 2 2
6 7 1 6 7 2 1 4 8 0 2.
x x x x x x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
123
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Kếthợpđiềukiện suy ra tậpnghiệm
1;2 .
S
Câu 7:
4
3 5 2 .
3
x
x x
x
Lờigiải:
Điềukiện:
5
3.
2
x
Bất phương trinh tương đương:
2 2 2
4 3 5 2 3 7 2 5 2 3
17
4 28 49 2 15 6 29 34 0 2 .
6
x x x x x x x
x x x x x x x
Kếthợpđiềukiện suy ra tậpnghiệm
17
2; .
6
S
Hếtrùi ^^
CÂU 8 :
3 2 2
2 3 3 10 11.
x x x x
Đk
10 10.
x
Xét
10 0
x
,
với
3 2 2 2
2
6
2 3 3 10 11; ' 3 4 3 0; 10;0
2 10
x
f x x x x x f x x x x
x
Suy ra
0 0 .f x f Loai
Xét
0 10.
x
(*). BPT tương đương:
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
124
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

3 2
2 2 2 2
2
2 2 2 2
2
2 2 2
0
2 2 2
1 10 3 10 0 1 1 1 1 10 3 10 0
3 10 3 10 1 1 10 3 10 0
3 10 1 3 10 1 10 0
1
3 10 0 9 10 1 0 .
1
x x x x x x x x x
x x x x x x
x x x x x
x
x x x
x
Kếthợp (*) suy ra tậpnghiệm
1; 10 .
S
CÂU 9
2
1 2 6 7 12 7 12.
x x x x x x
ĐK:
2.x
BPT tương đương

2
1 2 2 6 7 3 2 8
1 6
2 4 0
2 2 7 3
A
x x x x x x
x x
x x
x x
Với
2 6 4 2 2
2 4 2
2 2 2 7 3 0
2 2 2 2
x x x
x x
x x x A
x x
Suy ra bpt
2 0 2.x x
Kếthợpđiềukiện suy ra
2;2 .
S
CÂU 10
2 2
2 8 1 8 6 3.
x x x x x
ĐK
0.x
Bpt tương đương
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
125
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

2 2
2 2
2 2
2 1 8 1 1 1
2 8 1 3 8 3 0 0
8 1 3 8 3
2 8 1
1
1 0
8 1 3 8 3
A
x x x x x
x x x x
x x x
x x
x
x
x x x
Với
1
0.
8
x A
Với
1 1 1 1
0; 1 8 0 2 1 8 .8 1 8 2 8 1 .
8 4 16 16
x x x x x x x x
Mà
2
1 1 64 8 57 1
0.
21 16
1
8 3
8 3
64
A
x
Suy ra bpt
1 0 1.x x
Vậy
0;1 .
S
1.
2 2
16 3 3 4 1 3.
x x x x
Đk
1.x
BPT tương đương

2 2
2 2 2
3 2 2 2 2
2 2 2 2 2
16 3 3 3 4 1
8 26 12 6 1 3 4 6 16 0
2 3 2 4 2 6 36 9 16 3 16 12 7 21 0
2 9 5 3
8
3 7
3 2 4 2 6 36 9 16 3 16 12
A
x x x x
x x x x x x
x x x x x x x x x x
x x x
x x
x x x x x x x x

0
Xét
3 2 2 2
3 2 2 2 2
22 22 6 2 4 2 3 36 9 16 8
4 0
3 2 4 2 6 36 9 16 3 16 12
x x x x x x x
A
x x x x x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
126
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Suy ra bpt tương đương
3 0 0 3.
x x x
Vậy
0;3 .
S
CÂU 11
2 3 2 2
2 2 1 3 6.
x x x x x x x
ĐK
2.x
BPT tương đương
với

2 3 2 2 2
4 3 2
2
3 2 2
2
2 2 4 1 3 6 2 0
1 2 5
2 1 0.
4 1 3 6
2 2
A
x x x x x x x x
x x x x
x x
x x x x
x x
Xét
2 2
3 2 2
2
1 1 3 6
1
.
4 1 3 6
2 2
x x x x
A
x x x x
x x
Ta CM A>0 hay
2
1 3 6 0; 2.
x x x x
Xét
2
1 3 6; 2.
f x x x x x
Có
3
' 2 1 .
2 3 6
f x x
x
1
' 0 2 2 1 3 6 3 0 2 .
2
f x x x x x
Có
1 2 30 5 1
2 5; 0 0.
2 4 2
f f f x f A
Khi đó BPT
2
1
2 0 .
2
x
x x
x
Kếthợpđiềukiện suy ra
2 1; .
S
Bài 12 : Giải bất phương trình sau
3 2
2
2 5 4 2 4
3 4 4
1 2 3
x x x
x x
x
Lời giải
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
127
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Điều kiện:
2
3
, 3 3 4 0
2
x x x
Do
2
2
3 3 3
3 3 4 3. 3. 4 0
2 2 2
x x x
nên bất phương trình đã cho tương đương
2
3 2 3 2 2
3 2 2 3 2
3 4 4 2 3 1 2 3 1
2 5 4 0 2 5 4 3 4 4 2 3 1 0
2 3 1
2 2 4 3 4 4 2 3 2 3 2 3 2 2 3 2 3 2 3 2 2 3 0
x x x x
x x x x x x x
x
x x x x x x x x x x x x x x x
Đặt
2 3
a x
bất phương trình trở đã cho trở thành
3 2 3 2 2 2 2 2
2 3 2 2 0 2 2 2 0 2 2 1 0
x x a a xa x a x a x xa a x a x a x xa a
2
2
3
3
6
2
2 2 2 3
2
3
2
4 2 3
8 12 0
2
x
x
x
x a x x
x
x x
x x
Vậy bất phương trình đã cho có tập nghiệm
3
;2 6;
2
S

Bài 13 : Giải bất phương trình sau
2 2
2 1 3 2
39 12 6 17 2 6
x x x
x x x x
Lời giải
Điều kiện:
2
6 0 3 2
x x x
Bất phương trình đã cho tương đương
2 2
2 2
3 2 3 2
3 2
39 12 6 17 2 6
3 2 1
3 2 0
39 12 6 17 2 6
x x x x
x x
x x x x
x x
x x
x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
128
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Đặt
2 2 2 2
2 3 0 5 2 6 2 6 5
t x x t t x x x x t
bất phương trình
trở thành
3 2
2
2
2
1
3 2 3 2 6 12 9 0
17 5
39 6 5
3 2 3 3 3 0
t
x x x x t t t
t
t
x x t t t
Do
2
3 3 0
t t
nên bất phương trình tương đương
3 2 3 0 3 2 3 3 2 0
x x t x x x x
Trường hợp 1:
2
2
2
1
1
3 2
3 2
2
1
2
5 2 6 9
3 2 3
6 4
6 2
x x
x
x
x x
x
x x
x x
x x
x x
Trường hợp 2:
2
2
2
1
1
3 2
3 2
2
2
2
5 2 6 9
3 2 3
6 4
6 2
x x
x
x
x x
x
x x
x x
x x
x x
Kết hợp với điều kiện, vậy bất phương trình đã cho có tâp nghiệm
3; 2 1;2
S
Bài 14: Giải bất phương trình sau
2
3
1 2 2 5 2 2 3 2 6 3 3
x x x x x x
Lời giải
Điều kiện:
2
x
Bất phương trình đã cho tương đương
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
129
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2 2
3
2 2
3
2 2
3 3
1 4 2 5 2 2 3 2 6 3 3 1 2 2
3 5 2 2 3 2 6 3 3 1 2 2
3 5 2 2 3 2 6 3 3 6 2 0 3 5 2 2 7 2 3 0
x x x x x x x x
x x x x x x x
x x x x x x x x x
Trường hợp 1:
2
3 0 3
x x
Trường hợp 2:
3
5 2 2 7 2 3 0
x x
Đặt
2 2
2 0 2 2
t x t t x x t
bất phương trình đã cho trở thành
3
3
2 2 2
3
3 2 2
5 2 2 2 7 3 0 5 2 6 7 3 125 2 6 7 3
343 191 189 723 0 1 343 534 723 0 1
2 2
2 1 2 3
2 1 3
t t t t t t
t t t t t t t
x x
x x
x x
Vậy bất phương trình đã cho có tập nghiệm
2;3
S
Bài 15 : Giải bất phương trình sau
2 2 2
2 2 1 2 1 1 3
x x x x x x
Lời giải
Điều kiện:
1x
Bất phương trình đã cho tương đương
2 2 2
2 2
3 1 3 2 1 1 2 1 1 0
1 1 3 2 1 1 1 1 0 1 1 3 2 1 1 0
x x x x x x x
x x x x x x x x x
Do
1 1 0
1 1
x
x
x
nên bất phương trình đã cho tương đương
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
130
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
3 2 1 1 0
x x x
2
2
2
1 2 1 1 2 0 1 1 1 2 0
5 5
2 0
2
2
1 2 0 1 2
5 5 0
1 2
5 5
2
2
x x x x x x x x x
x
x
x
x x x x
x x
x x
x
Vậy bất phương trình đã cho có tập nghiệm
5 5 5 5
;2 ;
2 2
S

Bài 16: Giải bất phương trình sau
2
8 15 4 5 1 2 2
x x x x x
Lời giải
Điều kiện:
2
x
Do
2
2
2
4 9 9
4 5 1 2 2 0
4 5 1 2 2
x x
x x x
x x x
nên bất phương trình đã cho tương đương
2 2 2 2
2 2
8 15 4 5 1 4 2 4 1 4 1 3 4 14 7 4 4 9 2 1 0
4 9 2 4 4 9 2 1 5 1 0
x x x x x x x x x x x x x
x x x x x x
Đặt
2
4 2, 1 , 0
a x x b x a b
bất phương trình đã cho trở thành
2 2 2 2
4 5 0 5 0 4 9 2 1 4 10 3 0
5 13
4
5 13
4
a ab b a b a b a b x x x x x
x
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
131
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Kết hợp với điều kiện, vậy bất phương trình đã cho có tập nghiệm
5 13
;
4
S

Bài 17: Giải bất phương trình sau
1 2 2
1 1
2
x
x x
x x
Lời giải
Điều kiện:
0
x
Bất phương trình đã cho tương đương
2 2 2 2 2 2
2 2 2 1 1 2 1 1 0 1 1 1 0x x x x x x x x x x
x x x x x x
Do
2
1 1 0
x
x
nên bất phương trình tương đương
2
3 2
2 2 2
1 1 0 1 1 1 1 2 0 1x x x x x x x x x
x x x
Vậy bất phương trình đã cho có tập nghiệm
;1
S

Bài :
Giải bất phương trình sau
3 2
3 3 4 3 3 1 5 4
x x x x x
Lời giải
Điều kiện:
1
3
x
Bất phương trinh đã cho tương đương
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
132
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
3 2
2 2
2
2
3 3 6 1 3 1 2 5 4 0
3 2 0
1 3 1 2 5 4
1 1
3 6 0
1 3 1 2 5 4
x x x x x x x
x x x x
x x x
x x x x
x x x
x x x x
Do
1 1 1
3 6 0,
3
1 3 1 2 5 4
x x
x x x x
nên ta có
2
0 0 1x x x
Vậy bất phương trình đã cho có tập nghiệm
0;1
S
Bài 18 : Giải bất phương trình sau
2
2 2 5 2 11 7
x x x x x
Lời giải
Điều kiện:
2
5
x
Bất phương trình đã cho tương đương
2 2
2 2 2
2 2
5 2 5 2
5 2 3 11 7 5 2 0 5 2 0
5 2 3 11 7
1 5 17 5 17
5 2 1 0 5 2 0
2 2
5 2 3 11 7
x x x x
x x x x x x x x x x x
x x x x
x
x x x x x
x x x x
Vậy bất phương trình đã cho có tập nghiệm
5 17 5 17
;
2 2
S S
Bài 19 : Giải bất phương trình sau
2 2
2
6 7 6 5 2
0
3 2 10
x x x x x
x x
Lời giải
Điều kiện:
3
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
133
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Do
2
2
2
6 11
3 2 10 0
3 2 10
x x
x x
x x
nên bất phương trình đã cho tương đương
2 2 2 2 2
2 2 2 2
6 7 6 5 2 6 49 14 6 6 5 2
5 18 6 14 3 2 0 5 3 14 3 2 3 3 0
x x x x x x x x x x x x x
x x x x x x x x x x x
Đặt
2
3 , 2 , 0
a x x b x a b
bất phương trình đã cho tương đương
2 2 2
2 2
5 14 3 0 3 5 0 3 3 3 2
3 9 2 12 18 0 6 3 6 6 3 6
a ab b a b a b a b x x x
x x x x x x
Kết hợp với điều kiện, vật bất phương trình đã cho có tập nghiệm
3;6 3 6
S
Bài 20: Giải bất phương trình sau
2 1 3
1
2 2 1 1
x x
x x x x
Lời giải
Điều kiện:
0 1
x
Do
0 1
x
nên
2 2 1 1 0
x x x x
bất phương trình đã cho tương đương
2 1 3 2 2 1 1 2 1 3 1 2 1
x x x x x x x x x x x
Đặt
, 1 , 0
a x b x a b
ta có
2 2
2 2
1
2 1
a b
a b x
bất phương trình đã cho trở thành
2 2 2 2 2 2
2 2
2 2
2 2 2 2 2 3
2 2 2 2 2 2
2 2 2
1 2 3 4 4 1 2 3 4 5 2 2 2 3 2 0
a b a b a b b a b a b b
a b a b b
ab a b b ab a b b a b a a
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
134
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Mà
2
1
a
và
3
3 2 0
a a
nên
2 3
2 2 2 3 2 0
a b a a
nên dấu
" "
xảy ra khi
1
1
0
a
x
b
Vậy bất phương trình đã cho có tập nghiệm
1
S
Bài 22 : Giải bất phương trình sau
2
2
6 3 2 5 2 1
3 2 2
x x x x
x
x x x
Lời giải
Điều kiện:
2
2
0
1
3 2 5 2 0 ; 2 ; \ 0;1
2
2 5 2 0
x
x x x x
x x
 
Bất phương trình đã cho tương đương
2 2
2 2
2
6 3 2 5 2 1 6 1 3 2 5 2
1 1 0
3 2 5 2 3 2 5 2
3 2 5 2
x x x x x x x
x x
x x x x x x
x x x x
Trường hợp 1:
2 2 2 2
2
2 5 2 3 0 2 5 2 9 7 5 2 0
7
x x x x x x x x x
Trường hợp 2:
2
3 2 5 2 0
x x x
bất phương trình trở thành
2
2
2
2
0 1
3 2 5 2
0 7 5 2 0
2
7 5 2
7
x
x x x
x x x
x
x x x
Kết hợp với điều kiện, vậy bất phương trình đã cho có tập nghiệm
1 2
;2 ; 0;1
2 7
S

Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
135
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bài 23 : Giải bất phương trình sau
4 2
2 1
1
2 1 1
x
x
x x
Lời giải
Điều kiện:
x
Khi đó
2
4 2 2
3
2 1 1 2 1 1 0
2
x x x
Trường hợp 1:
1x
bất phương trình đã cho tương đương
2 4 2
1 2 1
x x x x
Ta có
2
2 2 2 2 4 2
1 1 2 1 2 1
x x x x x x x x
Dấu
" "
xảy ra khi
2 2
1 5
1 1 0
2
x x x x x
Trường hợp 2:
1x
bất phương trình đã cho tương đương
2 4 2
1 2 1
x x x x
(luôn đúng)
Vậy bất phương trình đã cho có tập nghiệm
1 5
;1
2
S

Bài 24 : Giải bất phương trình sau
3 3 3 4
3 3 3
x x
x
x x
Lời giải
Điều kiện:
1;3 \ 0
x
Trường hợp 1:
0;3
x
Ta có
4
3 3 3 0
3 3 3
x
x x
x x
nên bất phương trình đã cho tương đương
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
136
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2
2 2
2
3 3 3
4
6 2 2 3 3 3 16 3 3 3 5
4
3 3 3 5 4 4 0 2 0 2
x x
x x x x x x
x x
x x x x x x x
Trường hợp 2:
1;0
x
Ta có
4
3 3 3 0
3 3 3
x
x x
x x
nên bất phương trình đã cho tương đương
2
2
3 3 3
3 3 3 4 4
3 3 3 16
3 3 3
3 3 3
x x
x x
x x
x x x x
x x
2
6 2 2 3 3 3 16 3 3 3 5 2 0
x x x x x x x
(đúng)
Vậy bất phương trình đã cho có tập nghiệm
1;0 2
S
Bài 26: Giải bất phương trình sau
2
2 3
1
1
1
x x x
x x x x
Lời giải
Điều kiện:
0 1
x
Ta có
2 3 2
1 1 1 0, 0;1
x x x x x x x x x x x
nên bất phương trình đã cho
tương đương
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
137
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
2 2 3 2 3 2 2 3 2 2
2
2 2 2 2 2
1 1 1 1 1 1 2 1
1 2 1 0 1 0 1 1 0
1 5
2
1 5
2
x x x x x x x x x x x x x x x x x
x x x x x x x x x x
x
x l
Vậy bất phương trình đã cho có tập nghiệm
1 5
2
S
Bài 27 : Giải bất phương trình sau
2 2 3 2
3 12 5 2 1 2 10 5
x x x x x x x
Lời giải
Điều kiện:
2
x
Bất phương trình đã cho tương đương
2 2 3 2 2
2 2 3 2 2 2 2
3 2 2 3 2 2
3 2 3 2 2
3 2 2 3 2
3 12 5 2 1 3 12 5 2
3 12 5 2 1 3 12 5 2 3 12 5 2
1 3 12 5 2 1 2 3 12 5
2 1 2 1 2 3 12 5
2 10 6 2 3 2 0
x x x x x x x x x
x x x x x x x x x x x x x
x x x x x x x x x x
x x x x x x x x
x x x x x x x x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
138
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
3 2 2 2 3 2
3 2 2 3 2 2
3 2 2 3
3 3 2 2 3 2 0
3 2 3 3 2 0
3 2 4 2 0 2
x x x x x x x x x x
x x x x x x x x x x
x x x x x x x x
Vậy bất phương trình đã cho có tập nghiệm
2;S

Bài 29: Giải bất phương trình sau
3
1 3 2 3 3 1
x x x x x
Lời giải
Điều kiện:
3
2
x
Bất phương trình đã cho tương đương
2 2
1 1 3 2 3 3 3 1 1 1 3 2 3 1 3 5 2
1 2 2 3 2
1 3
2 3 1 2 3 1 0
1 1 2 3 1 1 1 2 3 1
x x x x x x x x x x x x
x x x x
x x
x x x x
x x x x
Ta có
2 3
1 3 3 1
1 3 2 2 3 1, 3 1 0
2
1 1 2 3 1 1 1 2 3 1
x
x x x
x x x x x x
x x x x
Khi đó bất phương trình trở thành
2 0 2
x x
Vậy bất phương trình đã cho có tập nghiệm
2;S

Bài29 : Giải bất phương trình sau
4 3 2 3 2
2 6 10 6 8 2 1
x x x x x x x x
Lời giải
Điều kiện:
0
x
Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
139
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bất phương trình đã cho tương đương
2 2 2 2 2 2
1 2 6 8 1 2 1 2 6 8 2 2 6 8 2x x x x x x x x x x x x x x x
Do
0
x
không thỏa mãn bất phương trình nên bất phương trình tương đương
2
4 2 2 2
2 6 1 0 2 2 1
x x x x
x
x x x
Đặt
2
t x
x
bất phương trình trở thành
2
2 2
2
1 1
2 2 1 1
2 2 1 1 0
t t
t t t
t t t
2
1 2 0 1 2 0 4
x x x x x x
x
Vậy bất phương trình đã cho có tập nghiệm
4
S
Bài 30: Giải bất phương trình sau
4 2 2 2
2
2
1 1 1
2
1
1
x x x x x
x
x
x x
Lời giải
Điều kiện:
0
x
Bất phương trình đã cho tương đương
2 2 2 2
2 2
1 1 1 1
. 1
1 1
x x x x x x x x
x x
x x
Đặt
2 2
2
1 1
, , 0
1
x x x x
a b a b
x
x
bất phương trình trở thành
2
2
2
1
1 1 1 0 1 1 1 0
x x
ab a b b a b b x
x
(đúng)
Vậy bất phương trình đã cho có tập nghiệm
0;S

Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
140
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI
Bài 31: Giải bất phương trình sau
2 2 4 2
2 2 1 1 1 3 1
x x x x
Lời giải
Điều kiện:
1 1x
Đặt
4
2 2
2 2 2
1
1 , 1
3 1 2
x ab
a x b x
x a b
bất phương trình đã cho trở thành
2 2
2 2 2 2 2 2 2 2 0
a b ab a b a b a b a b a b a b
Do
2 2 4
0 2 0 2 0 1 1 2 1 1 0
a b a b a b x x x x
Vậy bất phương trình đã cho có tập nghiệm
0
S
| 1/140
| | Tải xuống

Có thể bạn quan tâm:

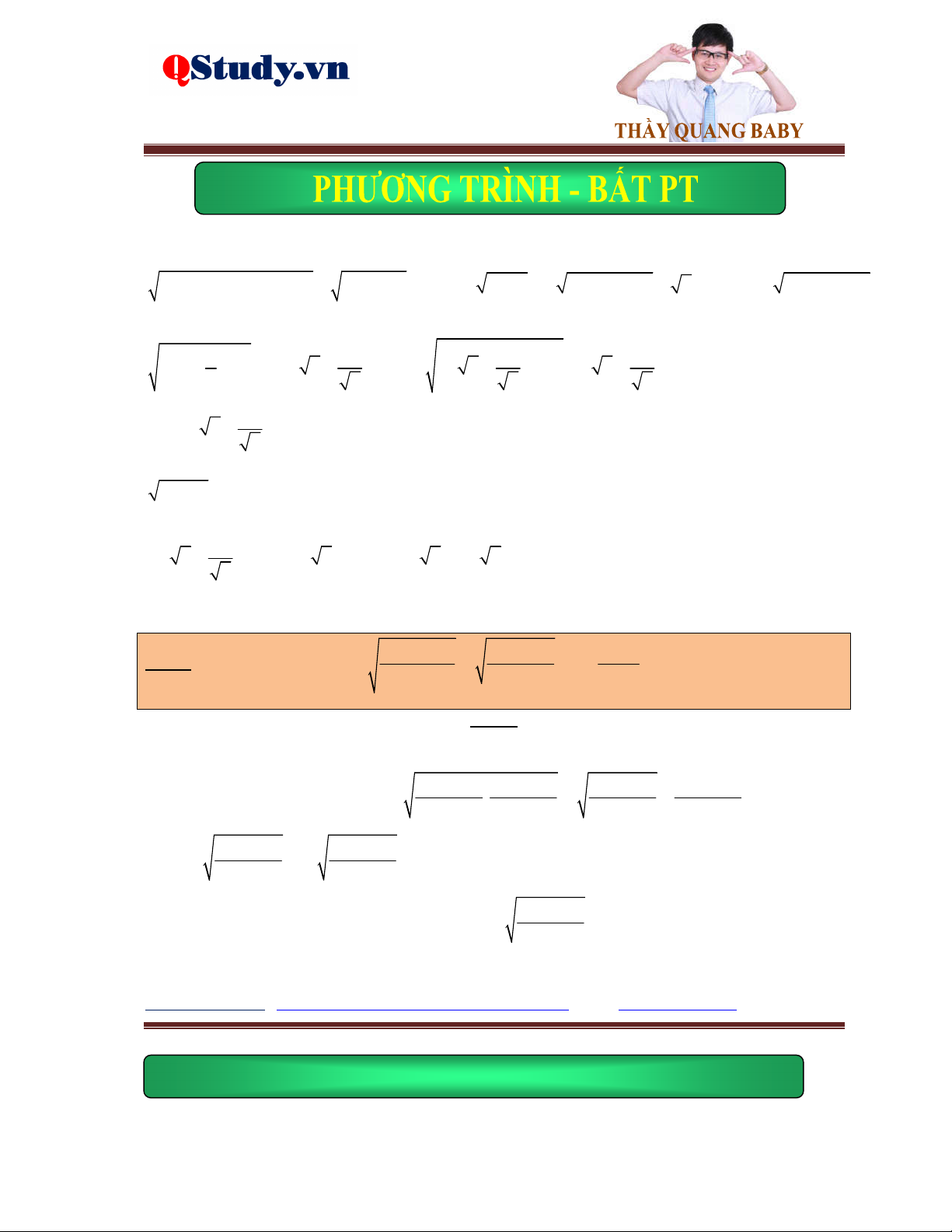
Preview text:


Tất cả vì học sinh thân yêu PHƯƠNG TRÌNH
Phương trình căn thức
Dạng 1. Phương pháp nâng lũy thừa.
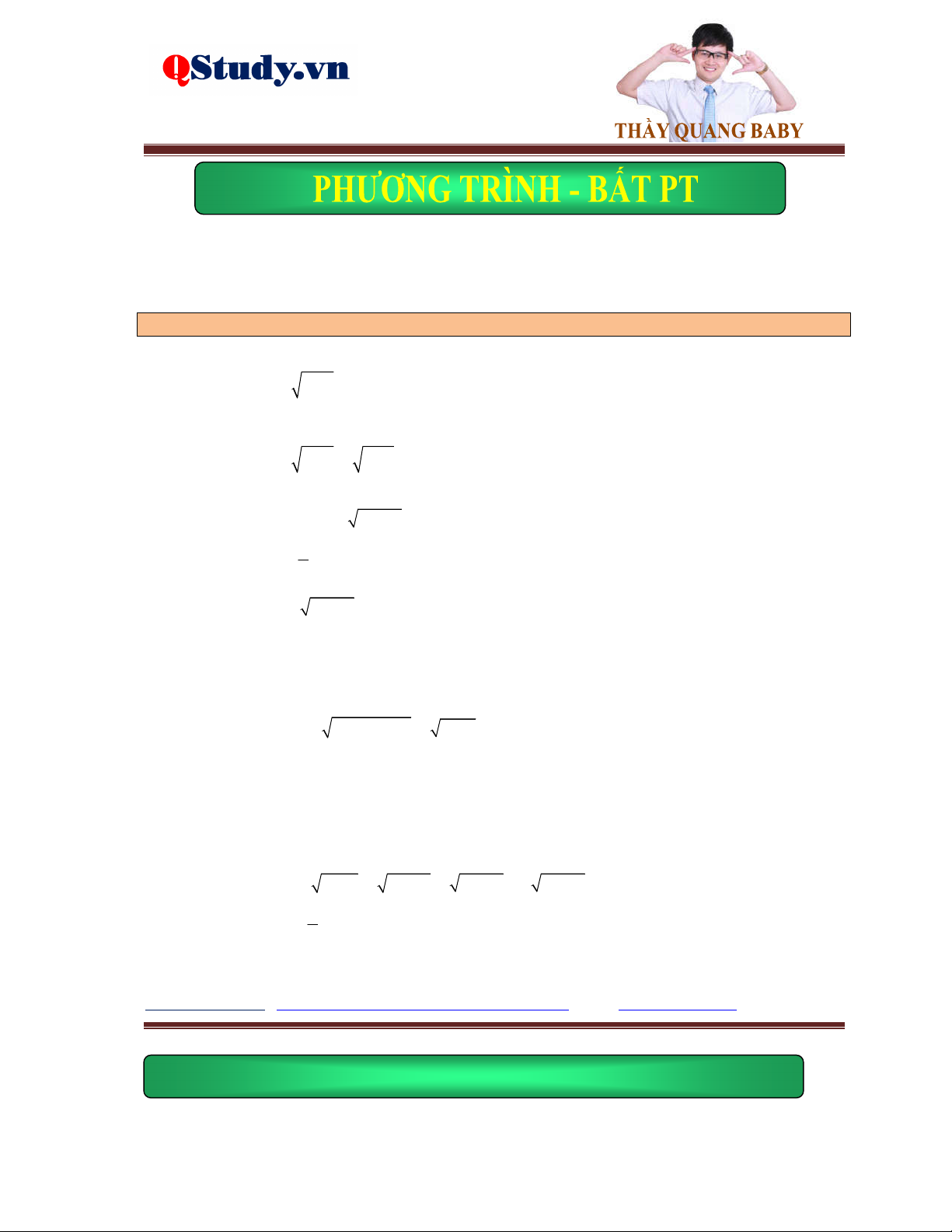
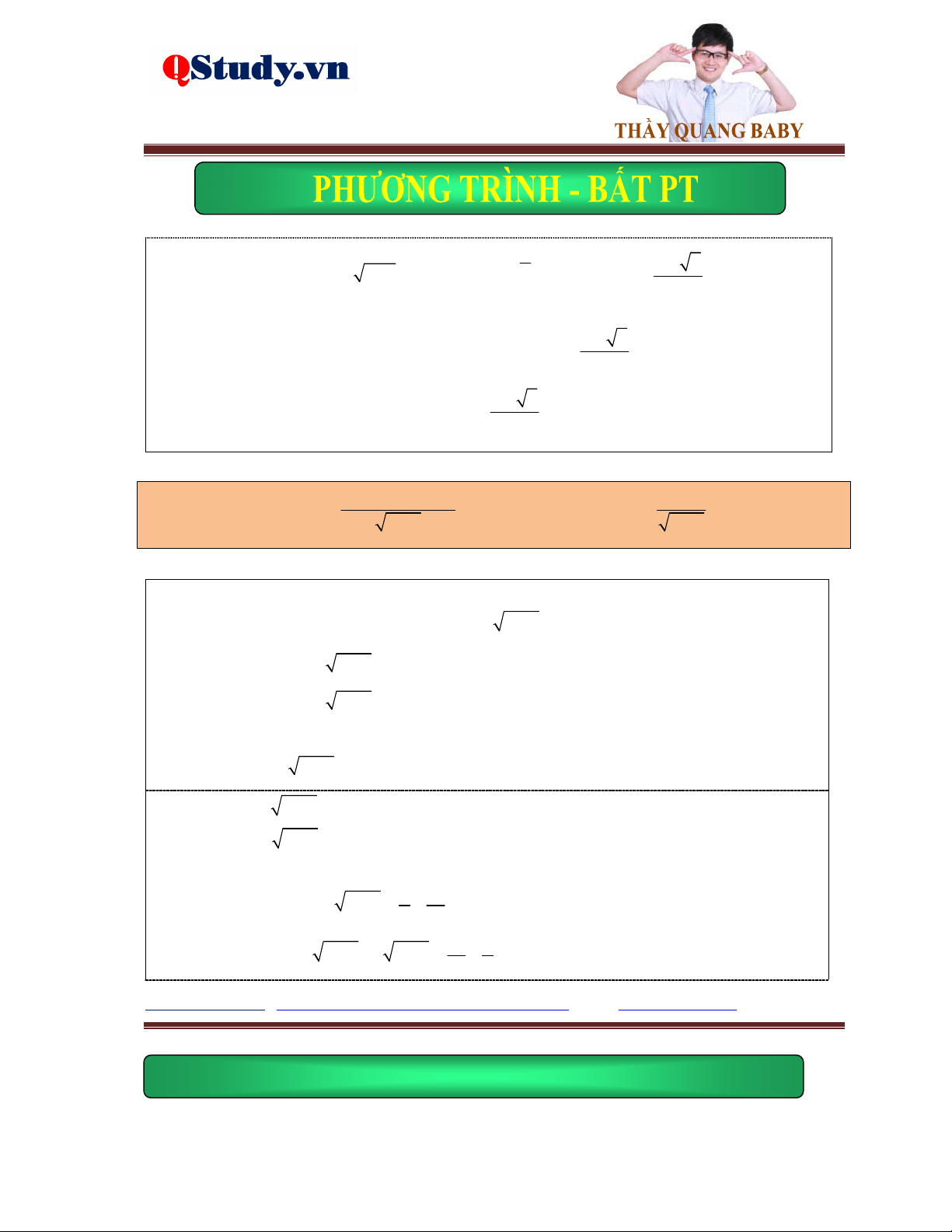
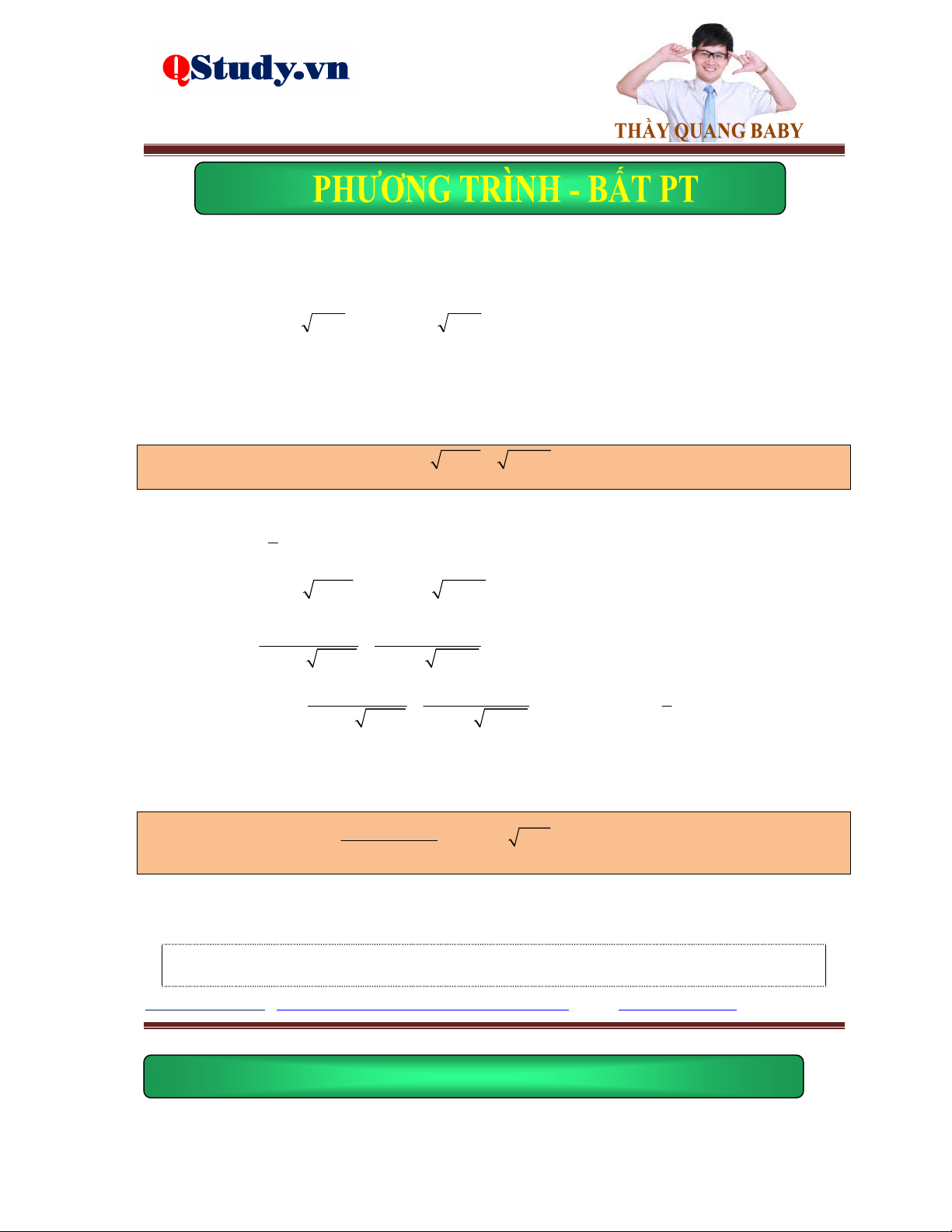
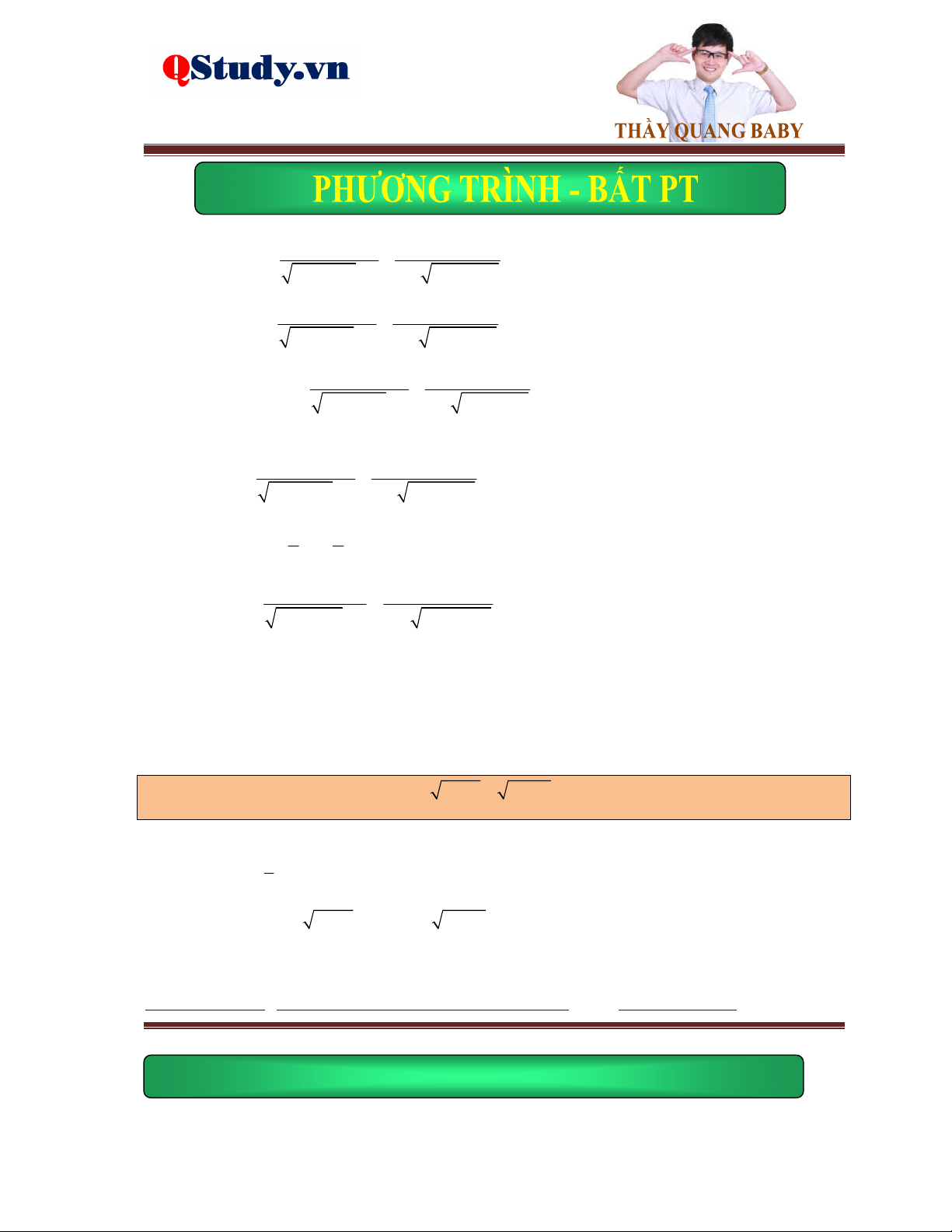
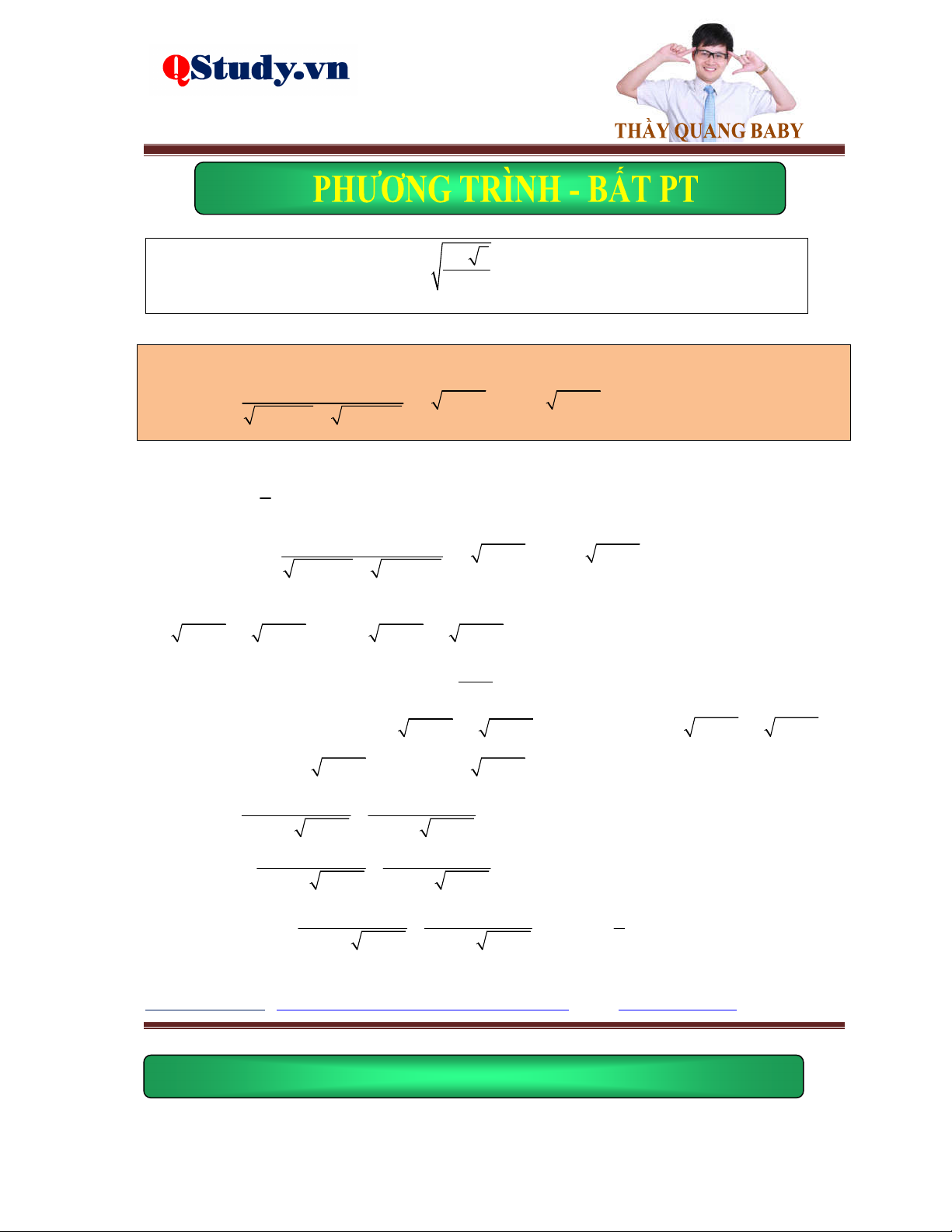
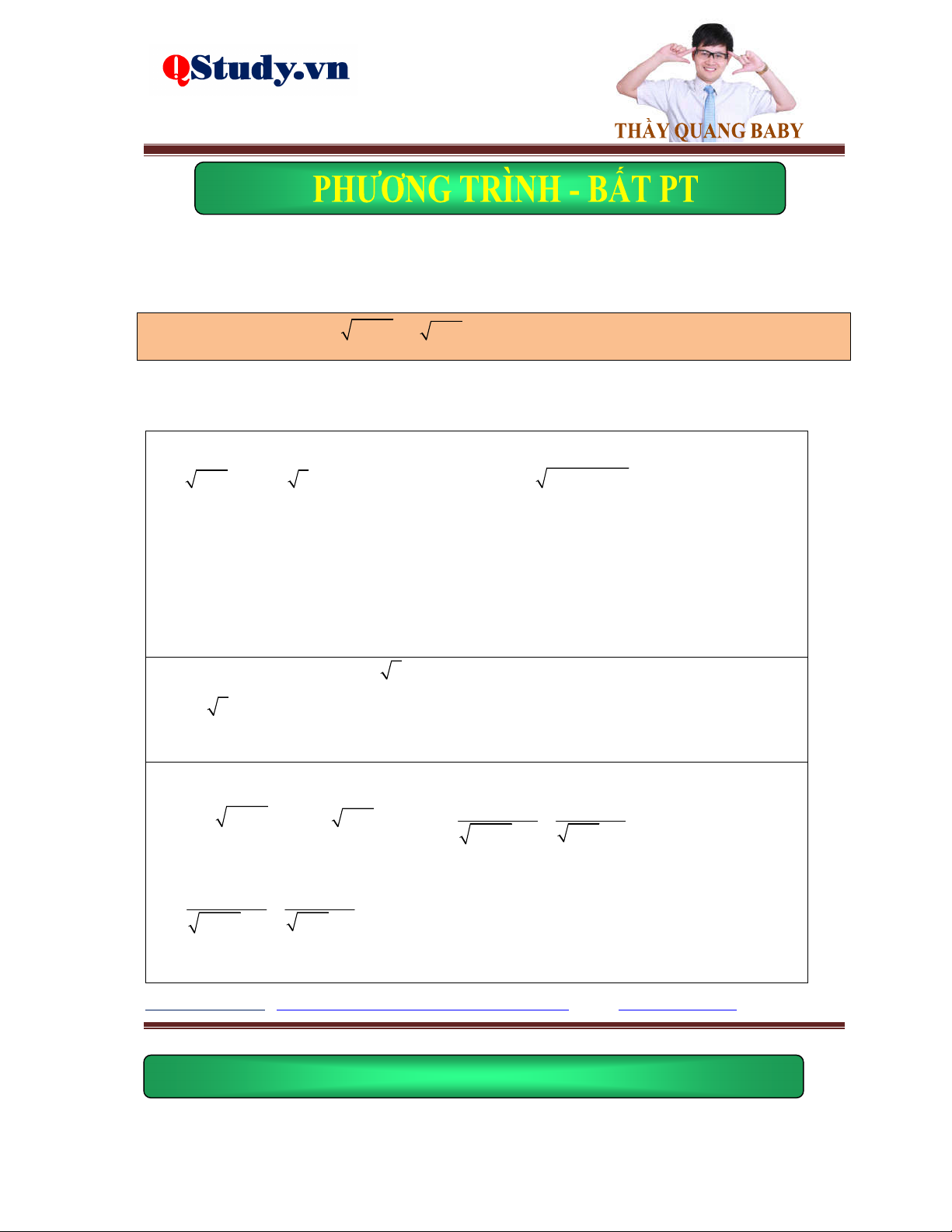
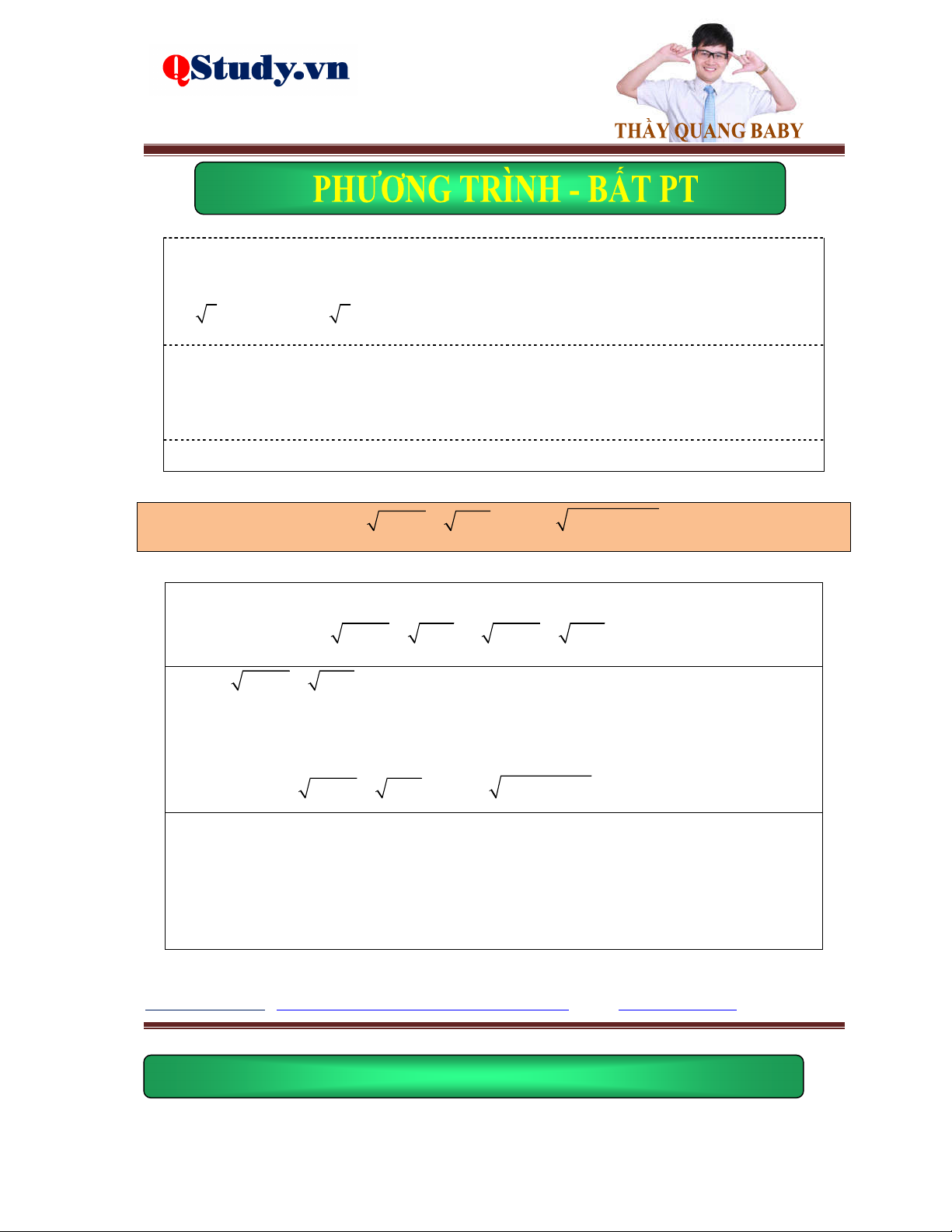
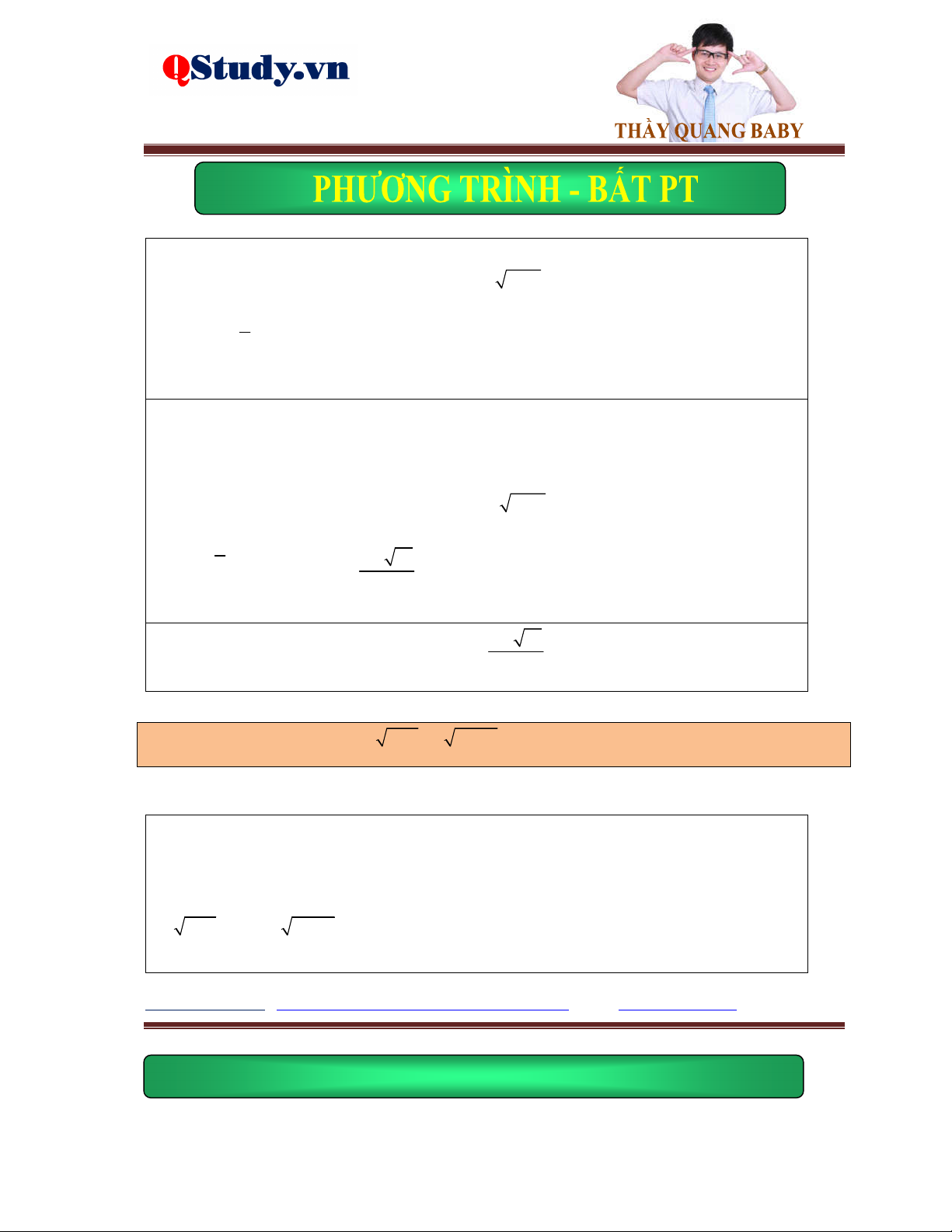
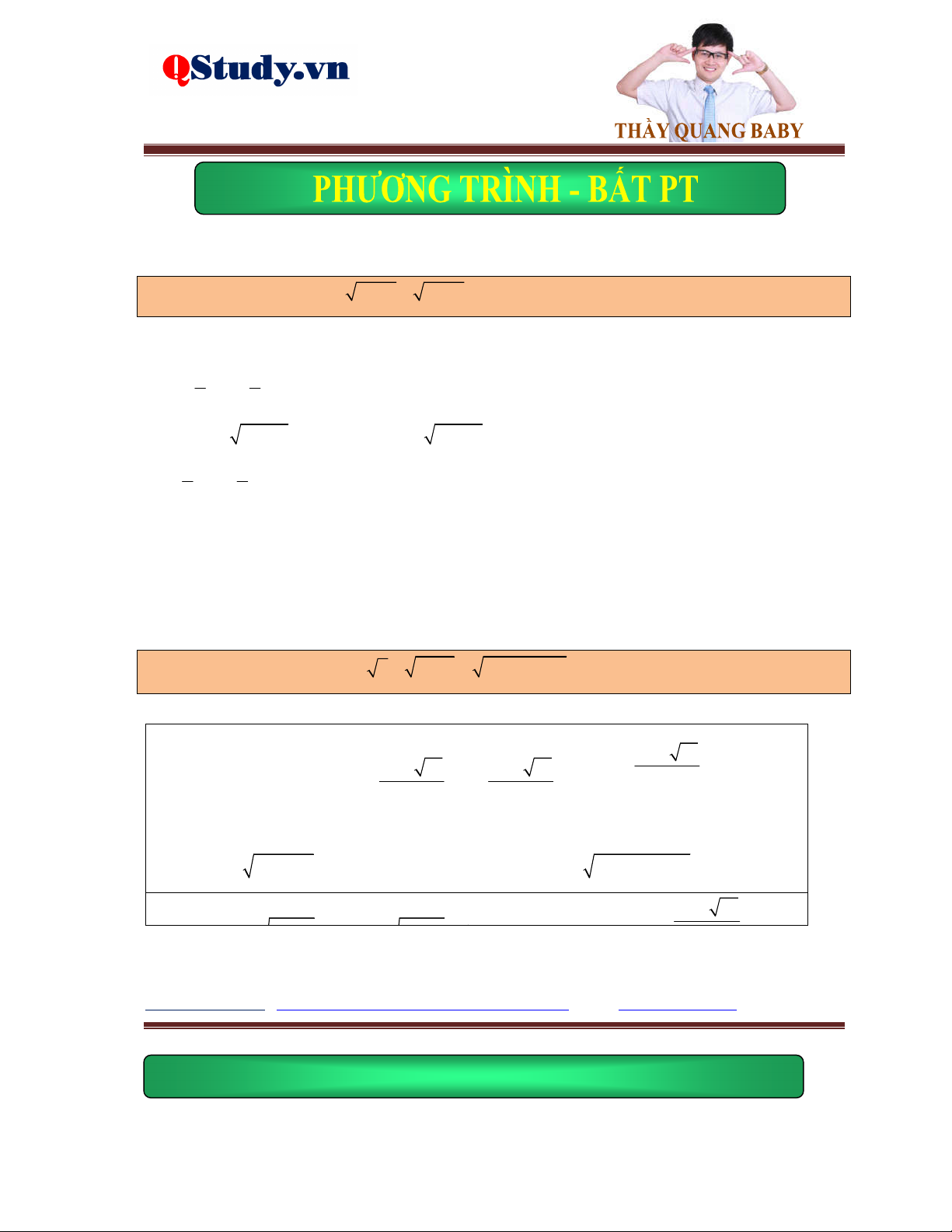
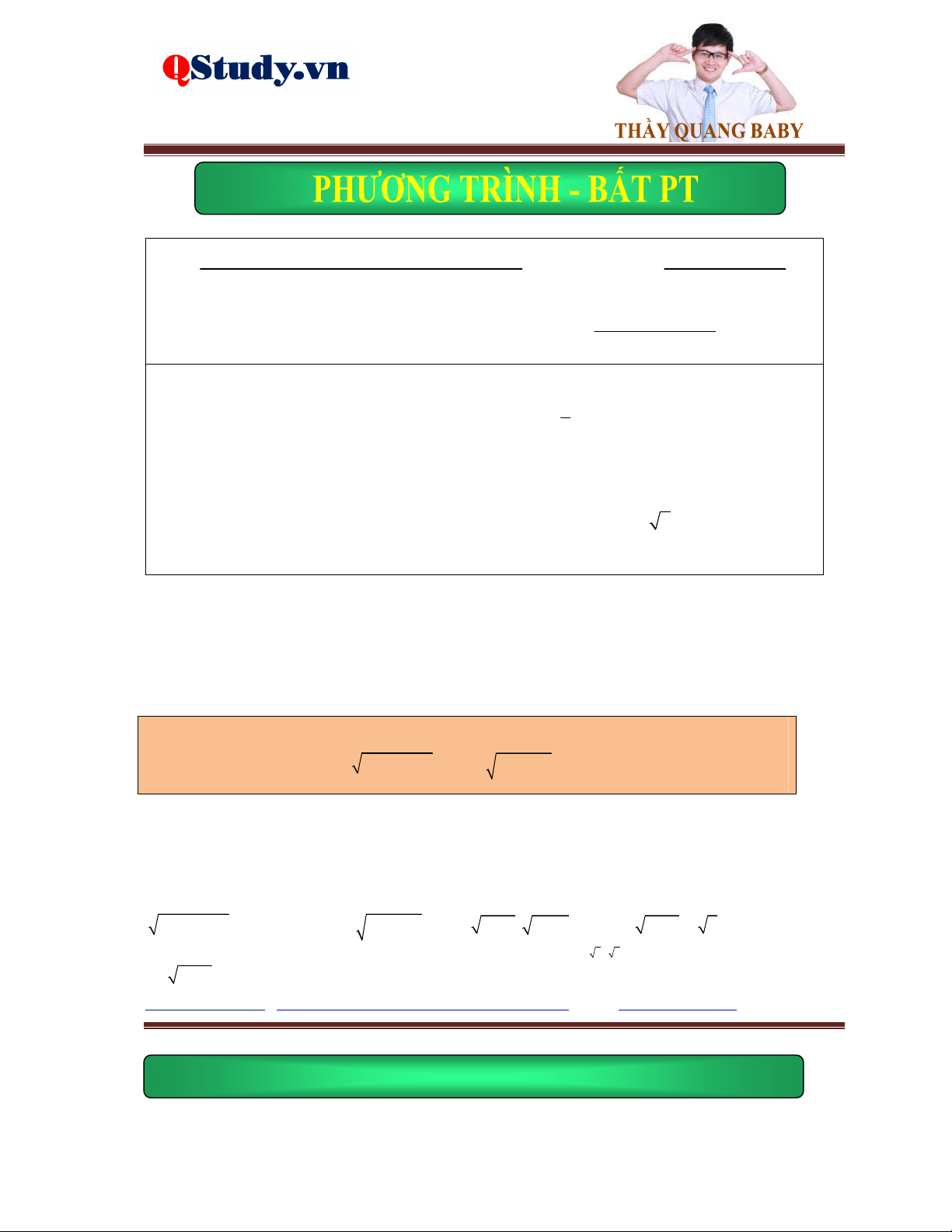
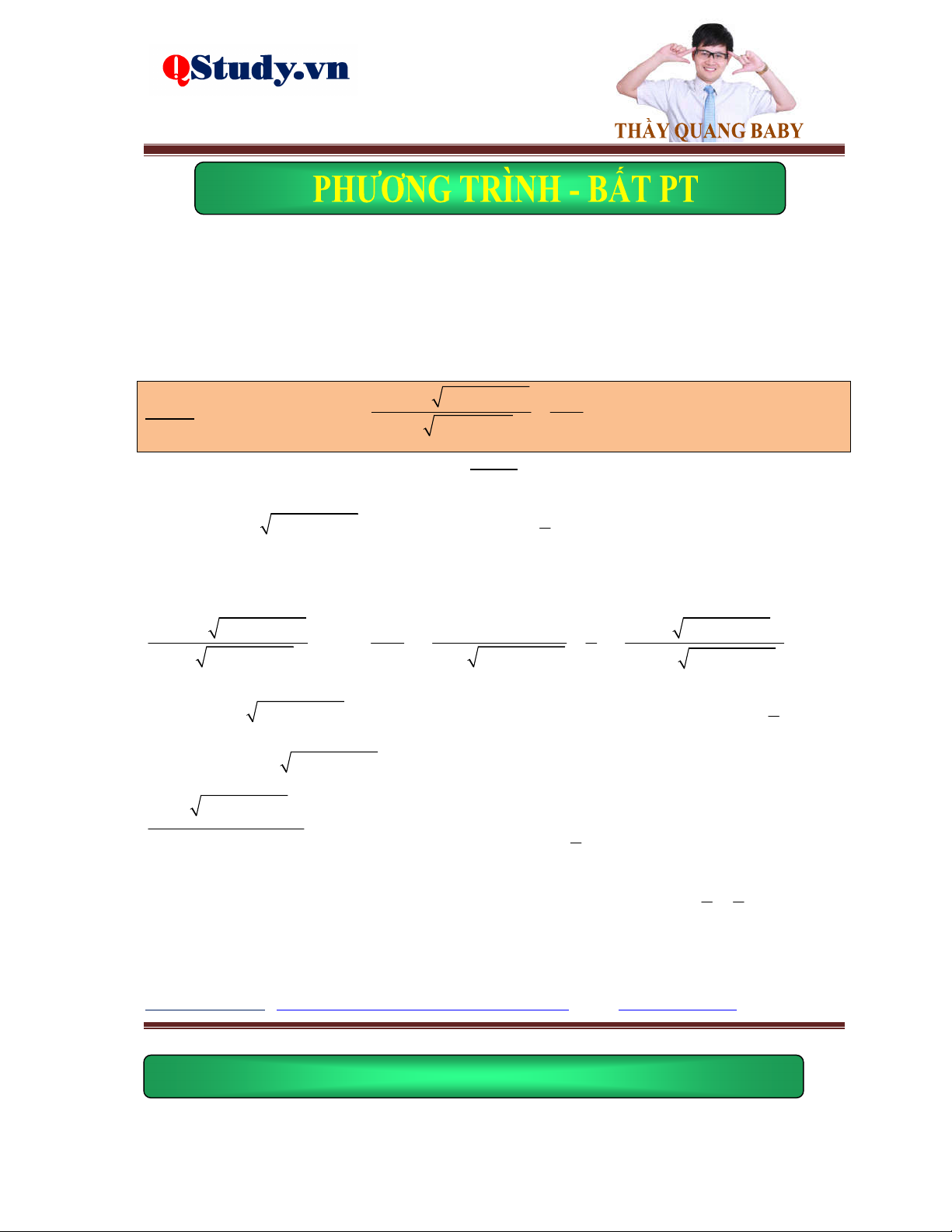
Kiến thức cơ bản: g    x  0   Phương trình f  
x gx   f   2 x   g   x 
 f x  0    Phương trình
f x  gx  gx  0 
fx gx 
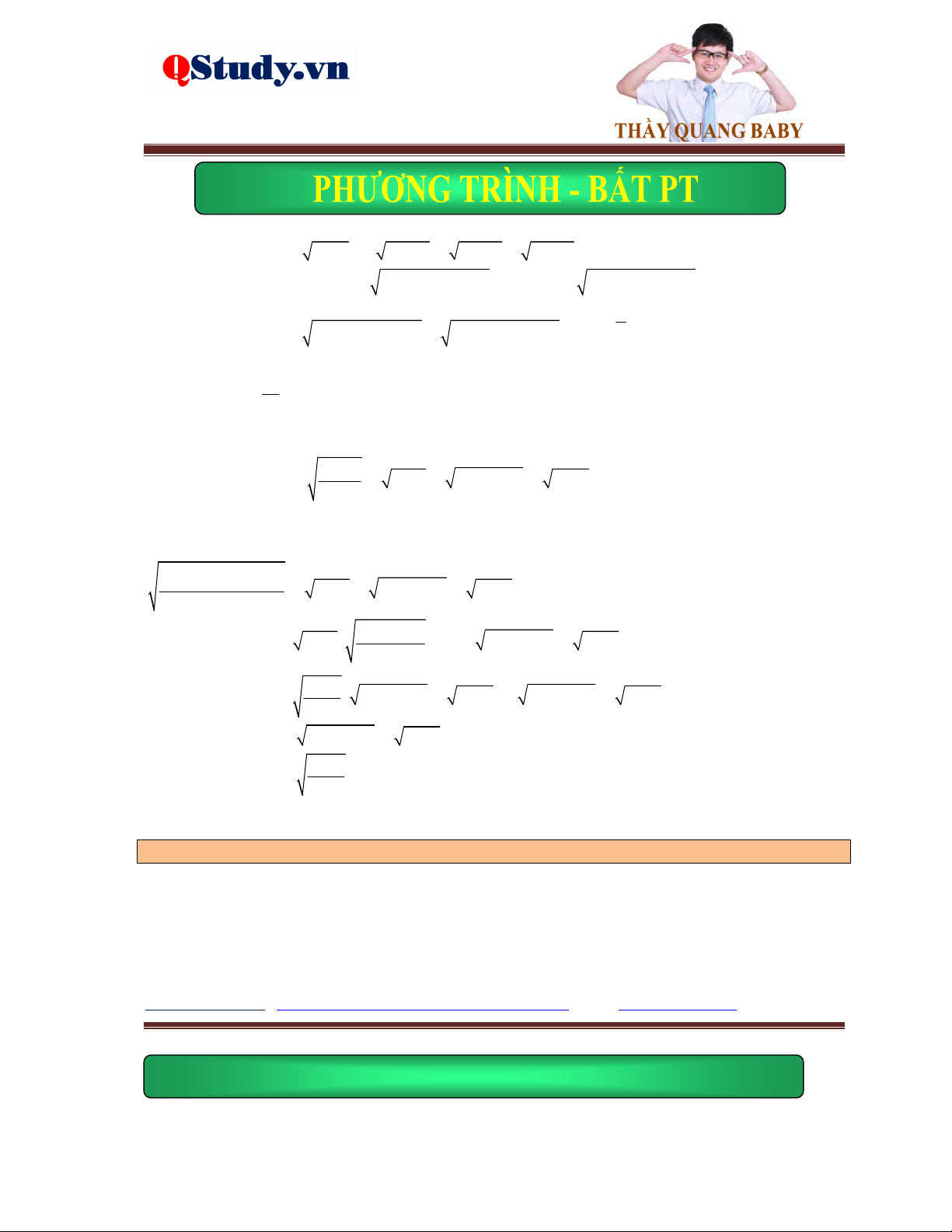
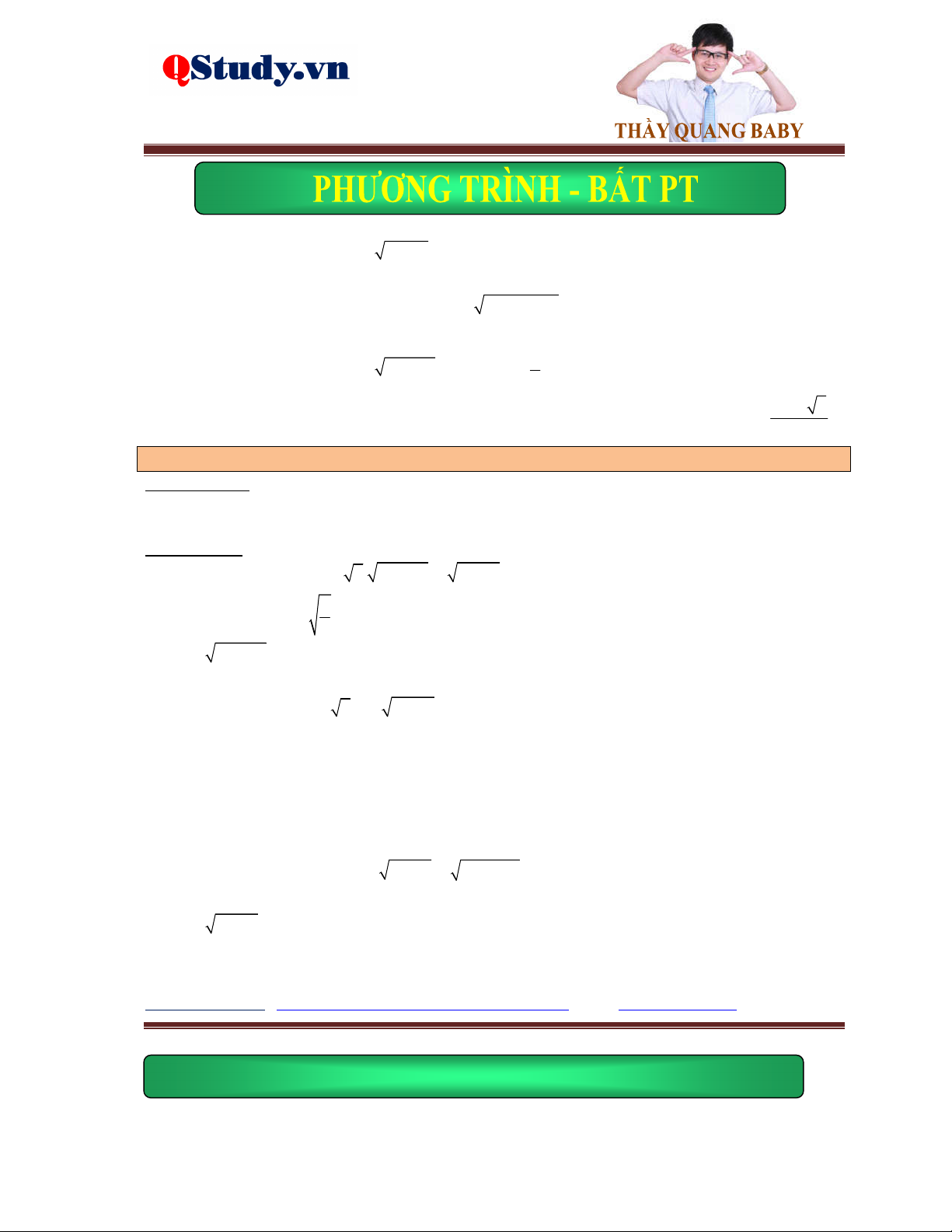
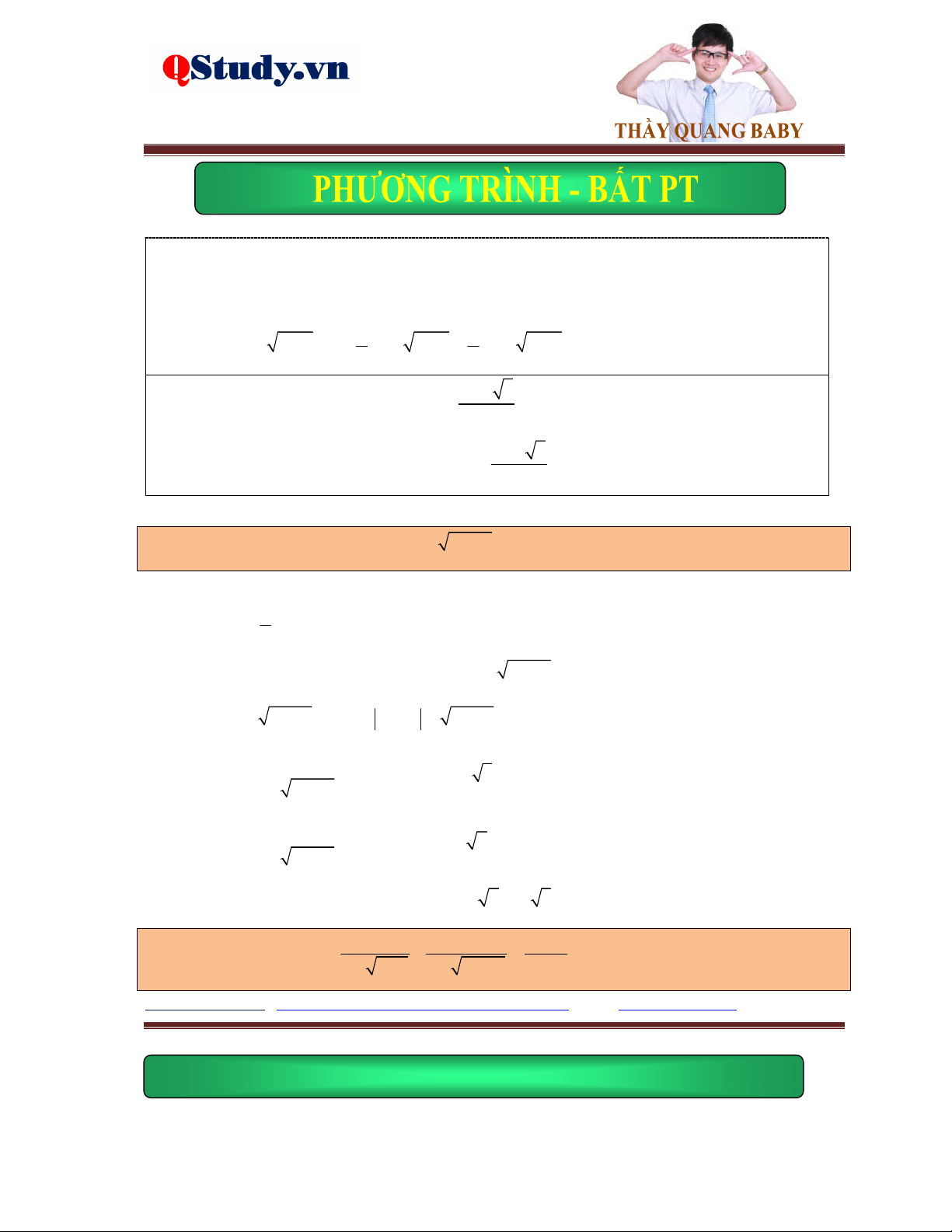
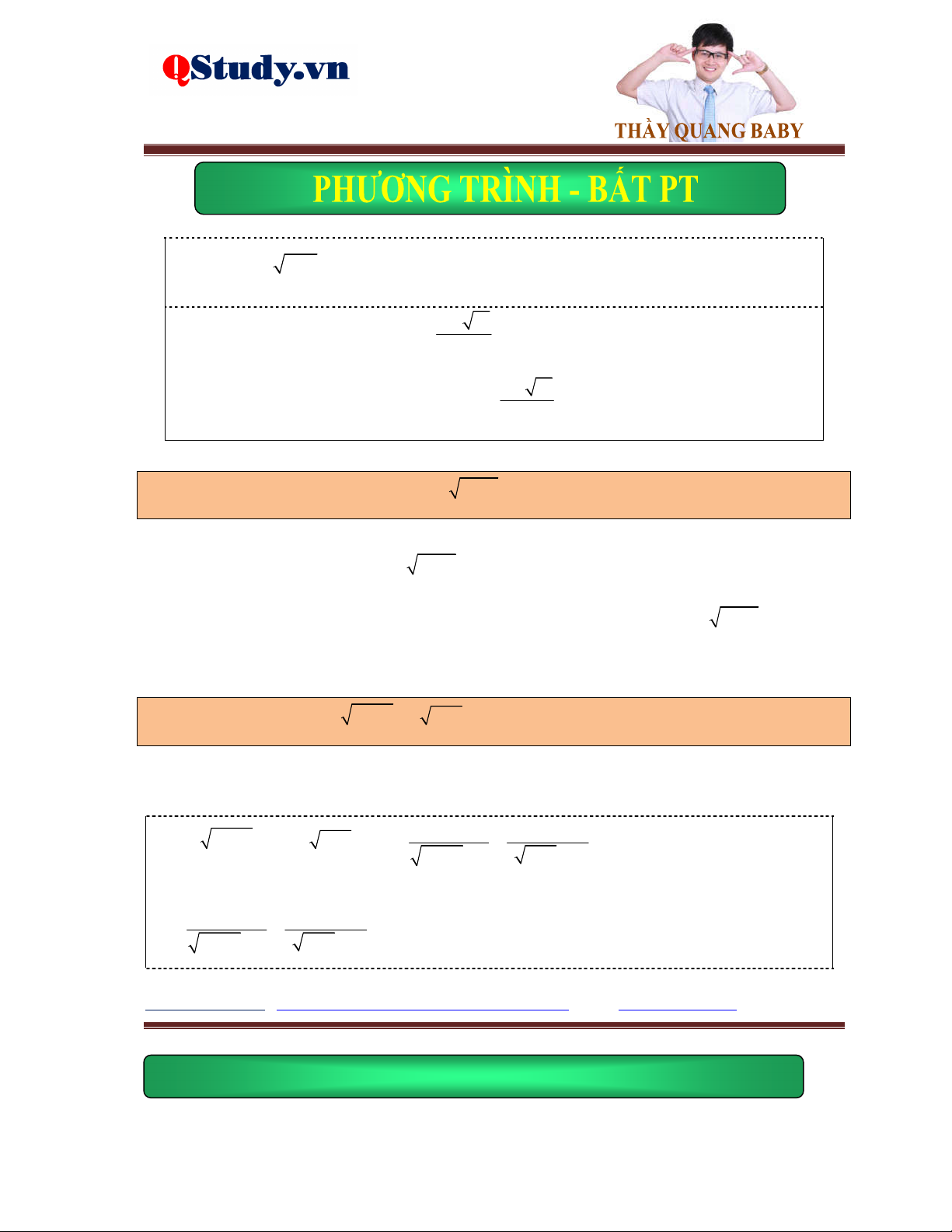
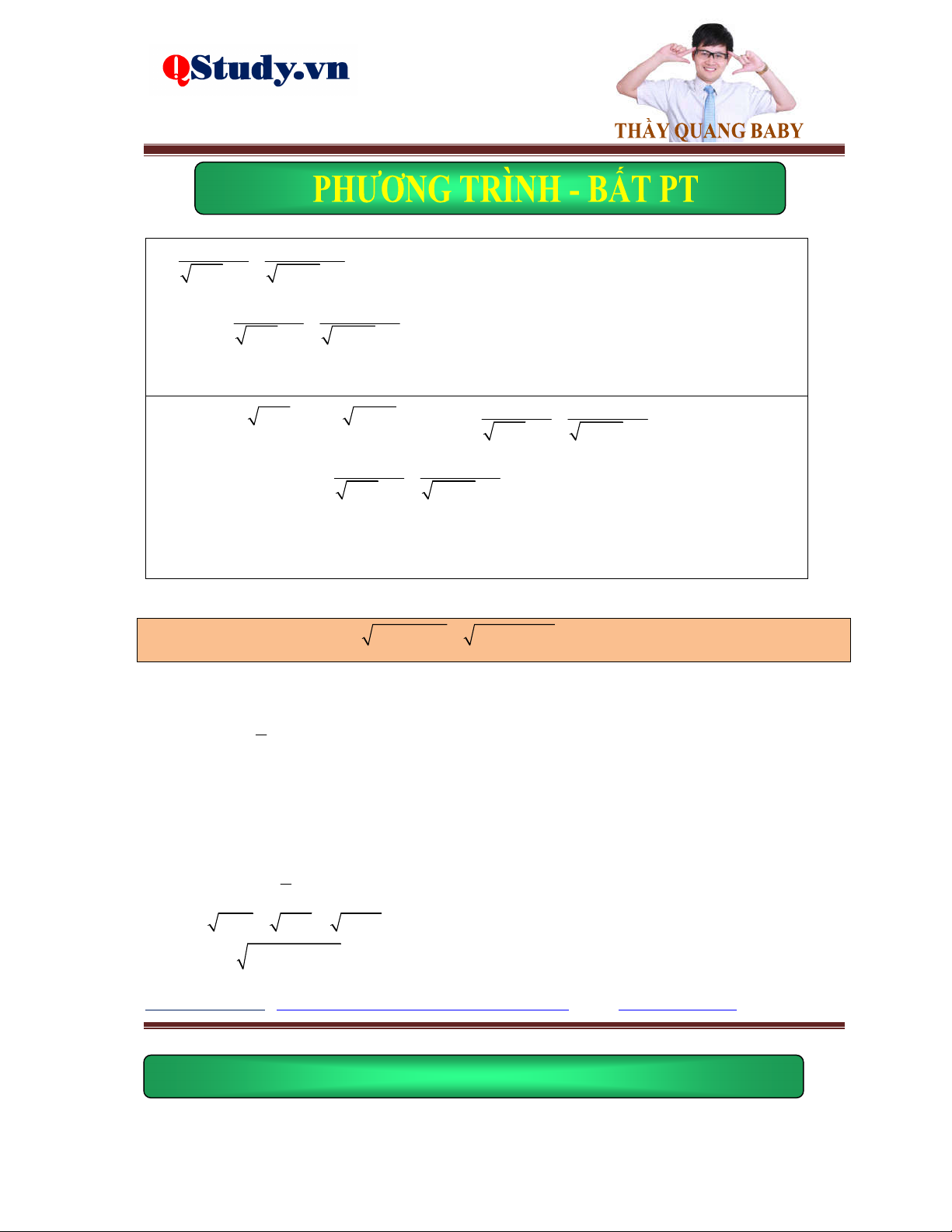
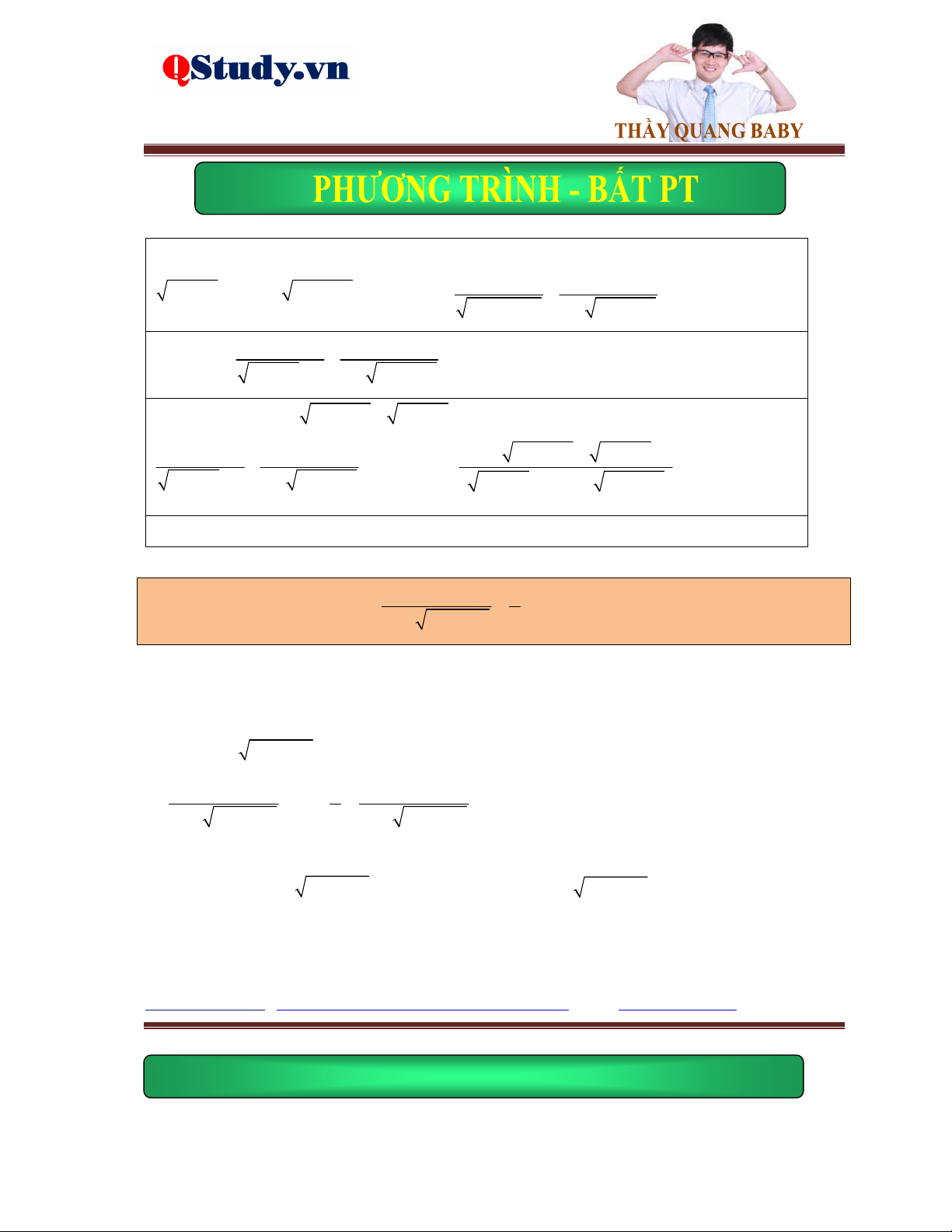
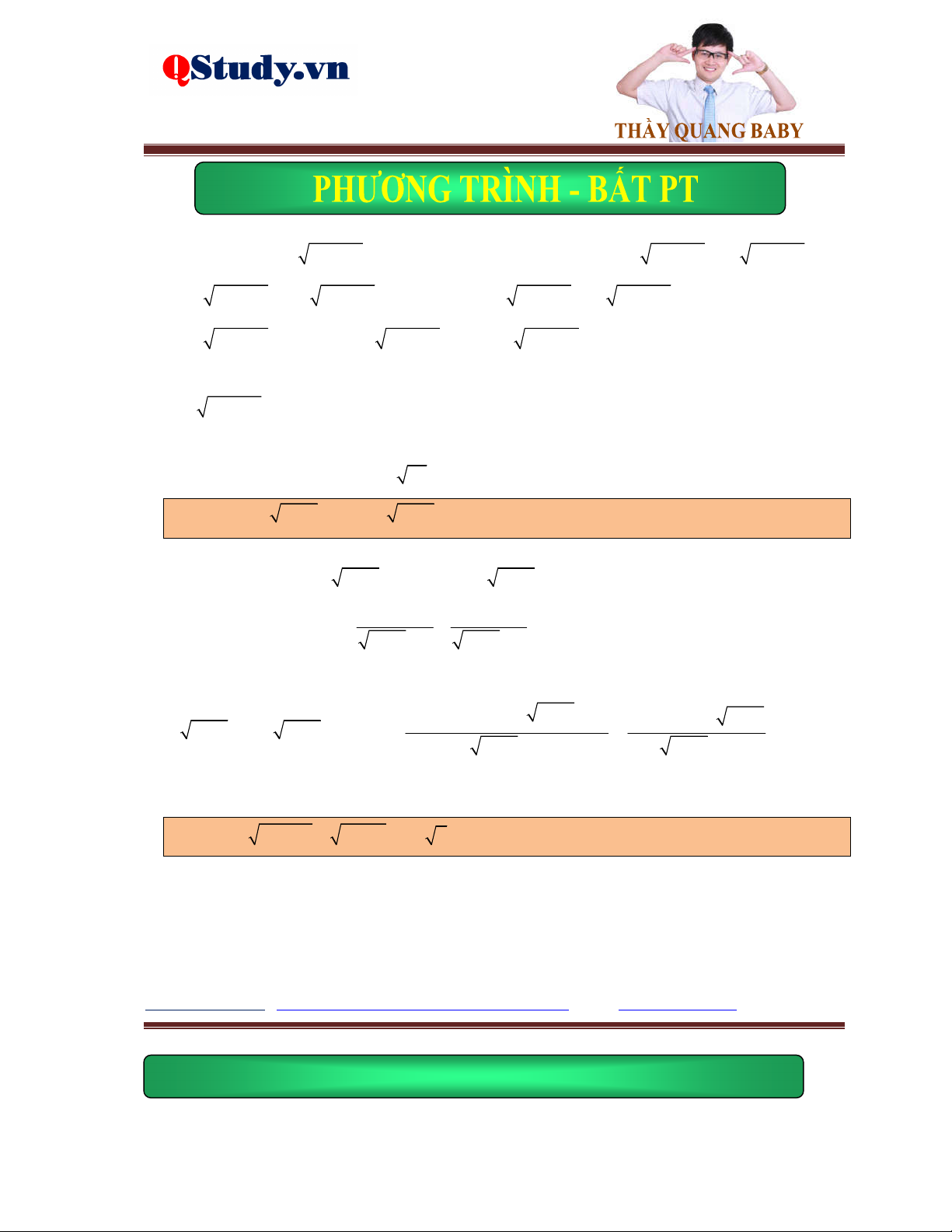
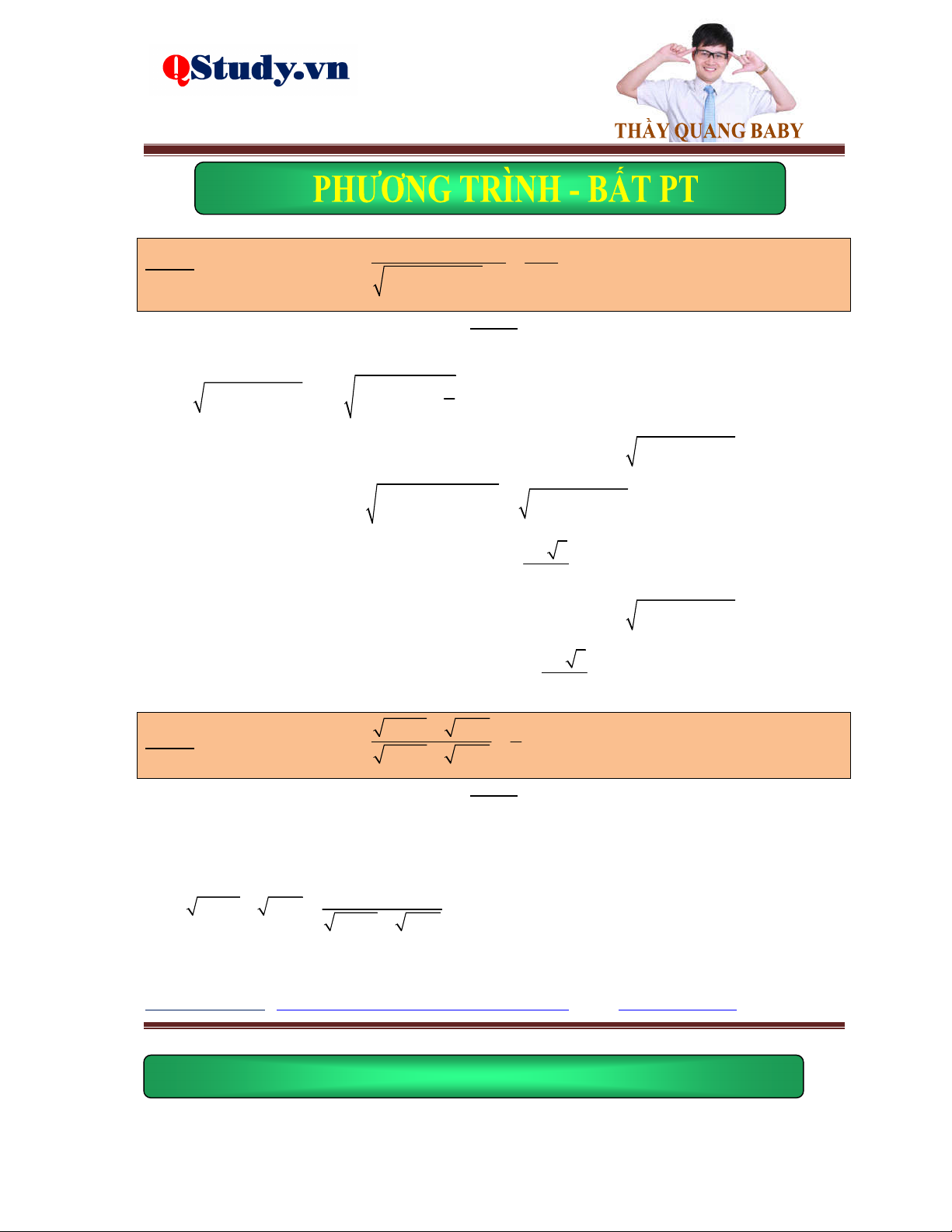
Ví dụ 1. Giải phương trình x  2x  5  4 x  . 5
Lời giải. Điều kiện: x  . Phương trình đã cho tương đương với: 2 x  4  0 x   4  
pt  2x  5  x  4     2
 x  5 x  42 2 2
 x  5  x 8x 16   x  4 x  4        x  7 2
x 10x  21  0   x     3 x  7  0 
Vậy phương trình đã cho có nghiệm duy nhất là x  7 .
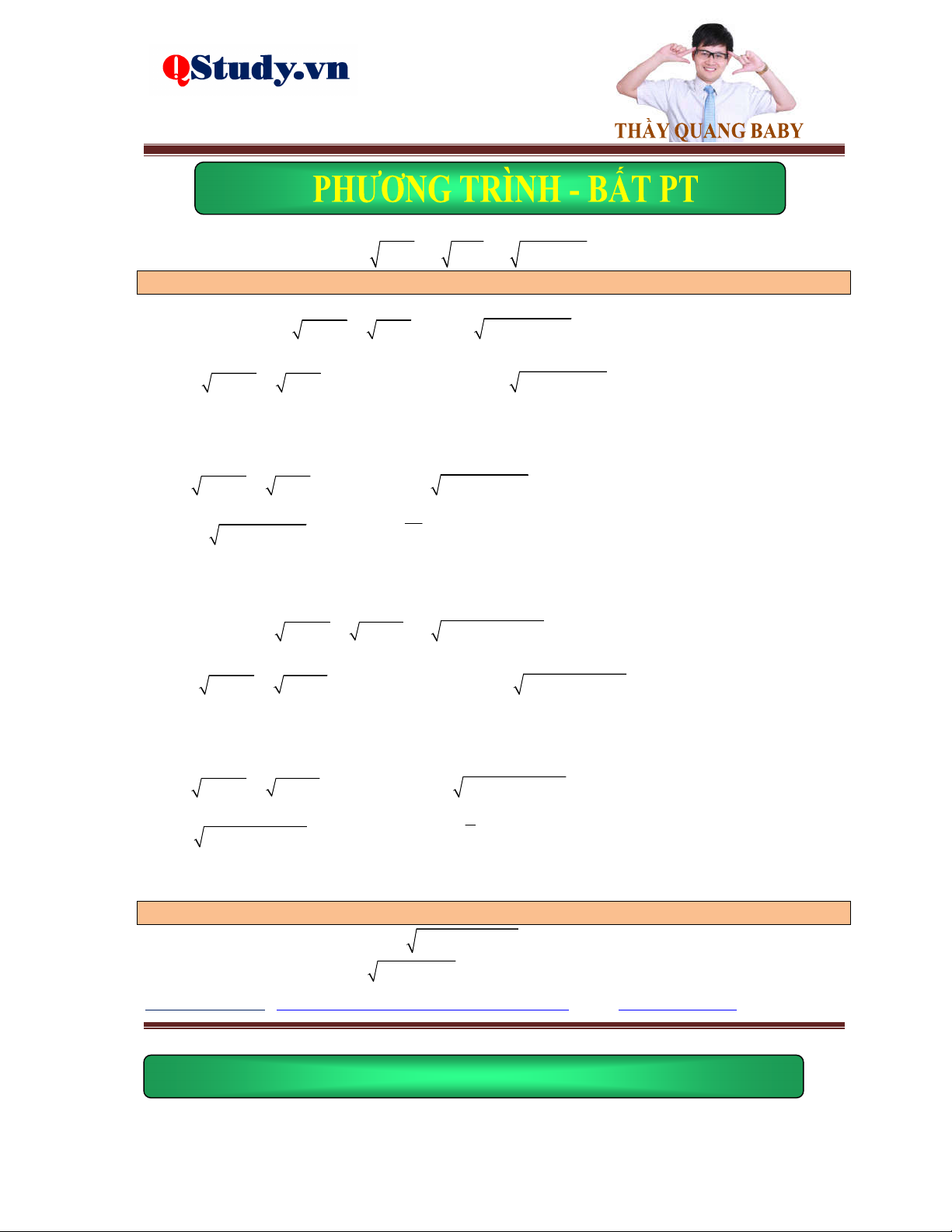
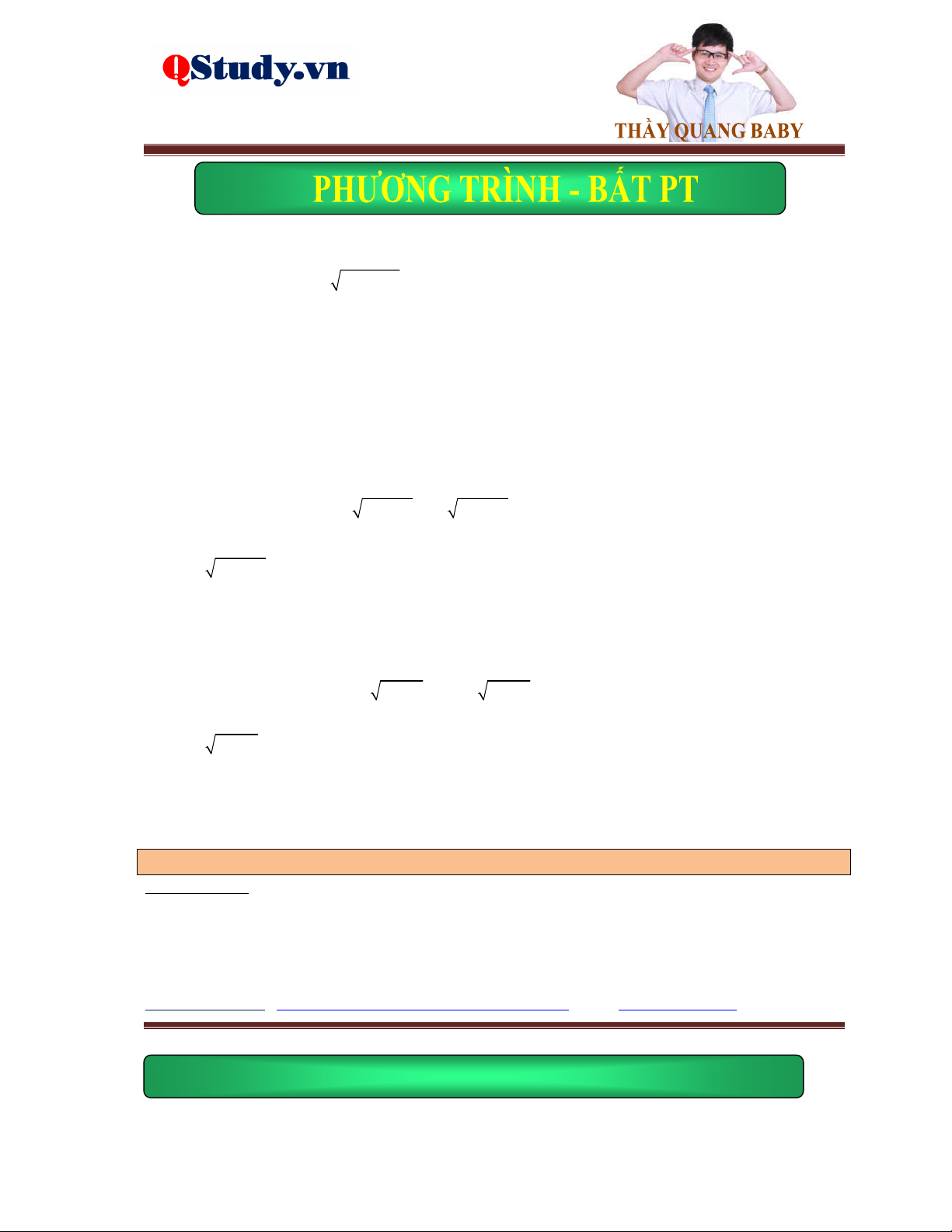
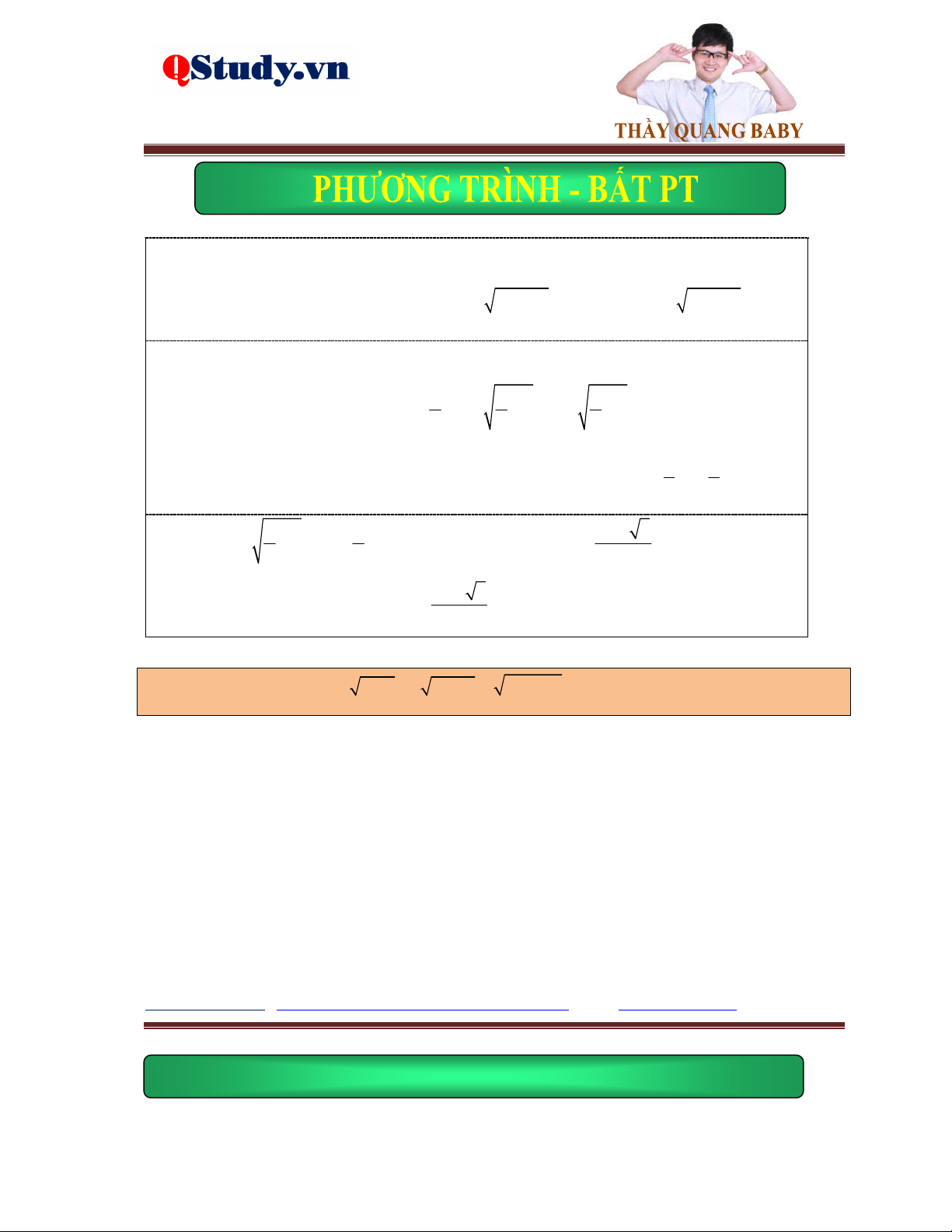
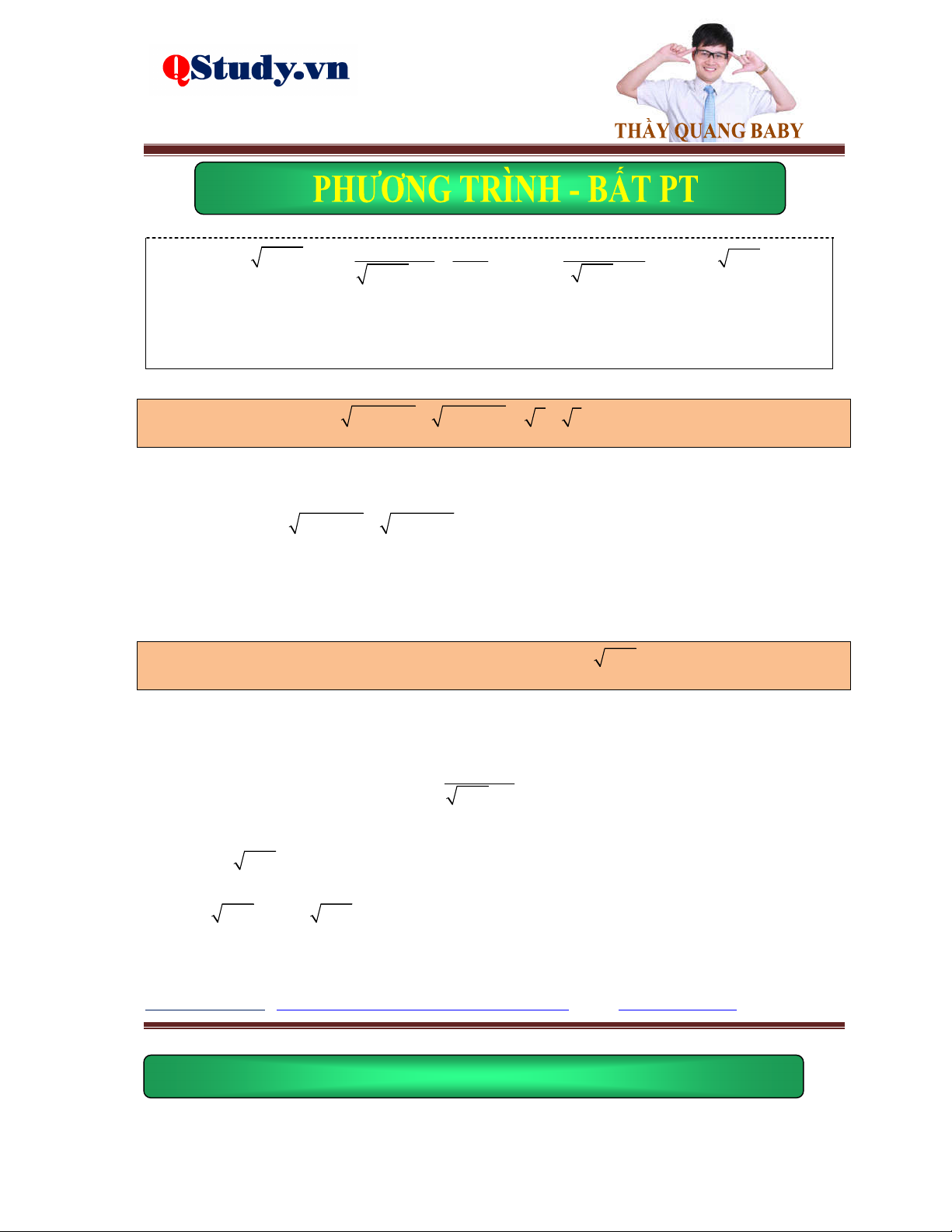
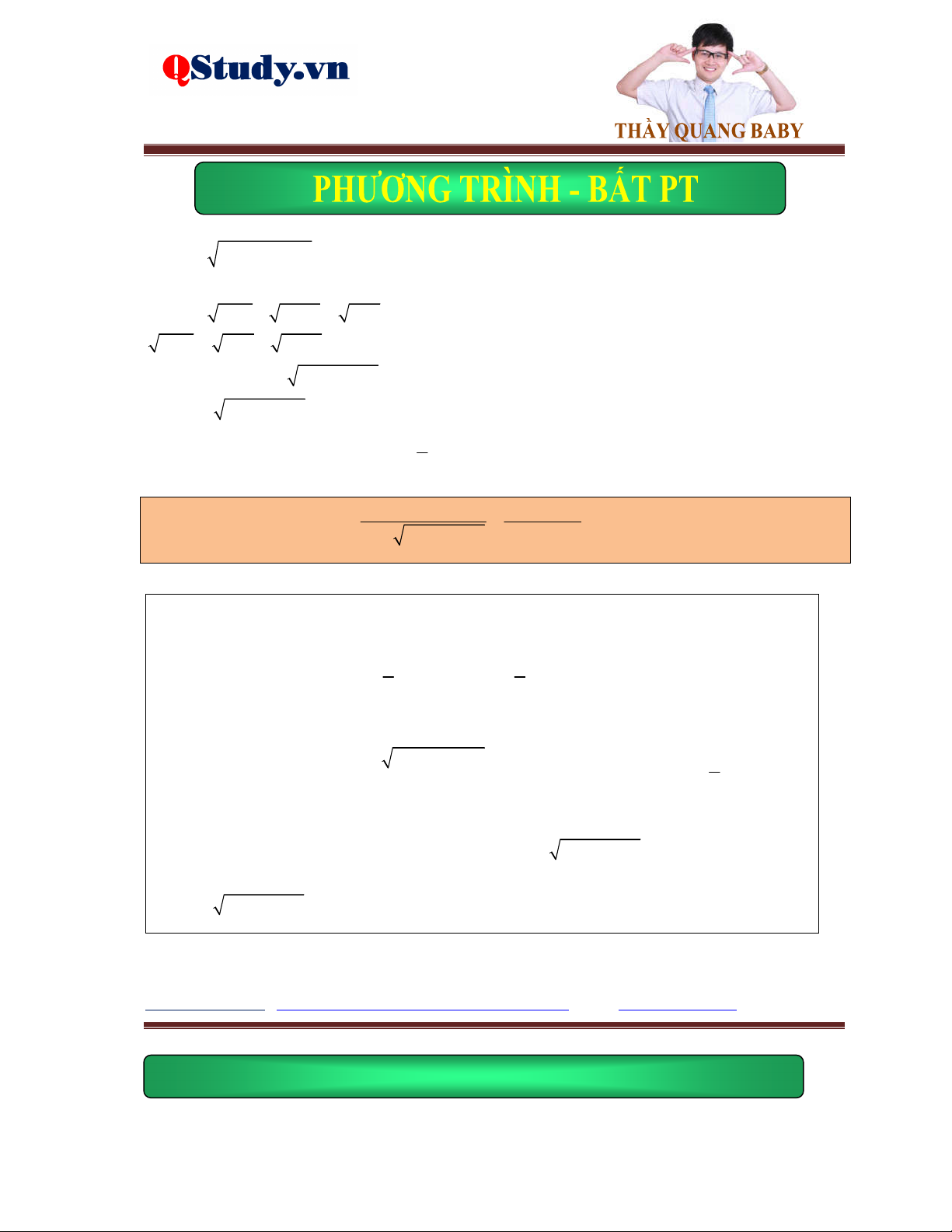
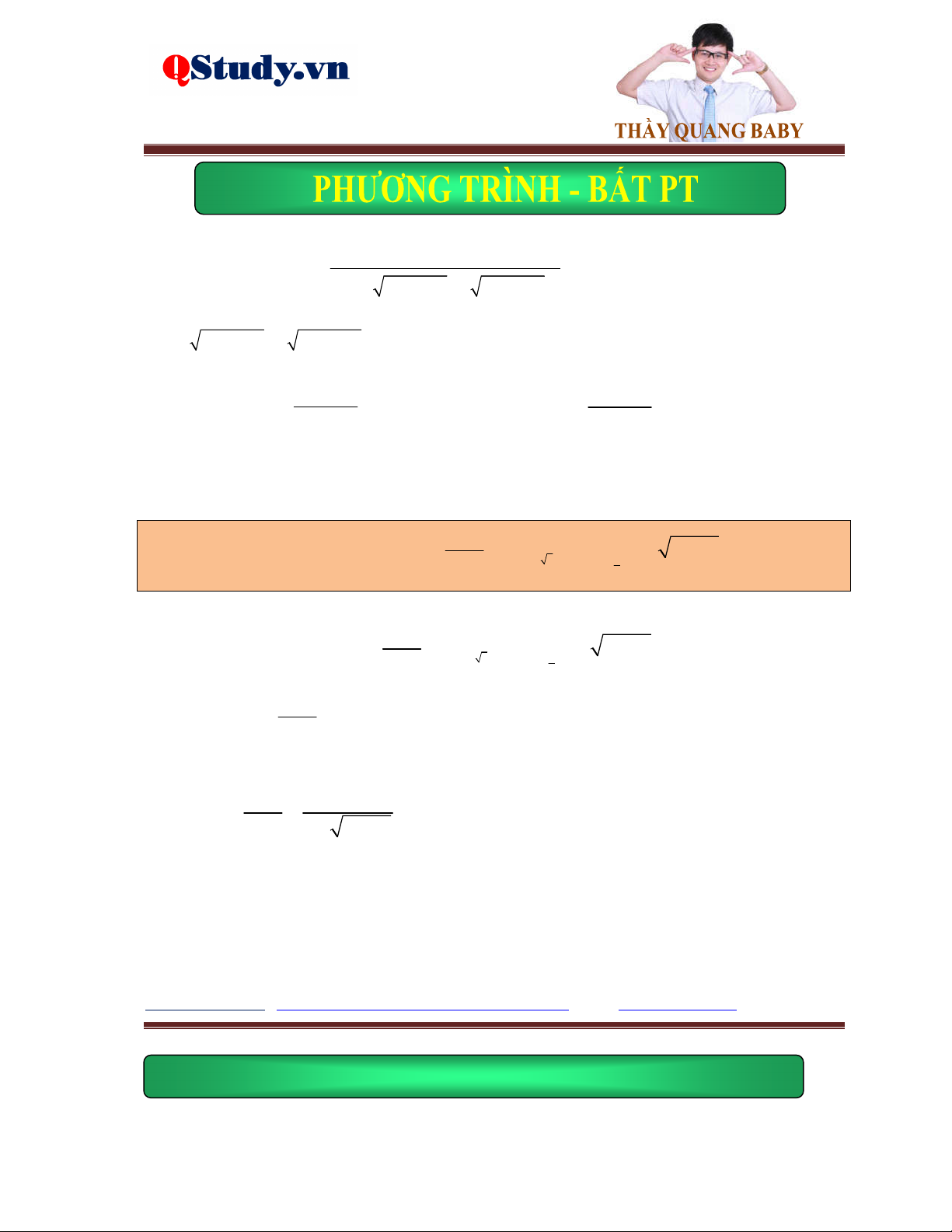
Ví dụ 2. Giải phương trình 2
x  2x  4  2  xx  .
Lời giải. Điều kiện: x  2 . Phương trình đã cho tương đương với: 2   x 2   xx  1    pt       2 2
x  2x  4  2  x x  3x  2    0 x  2   
Vậy phương trình đã cho có nghiệm là x   1  ;  2 .
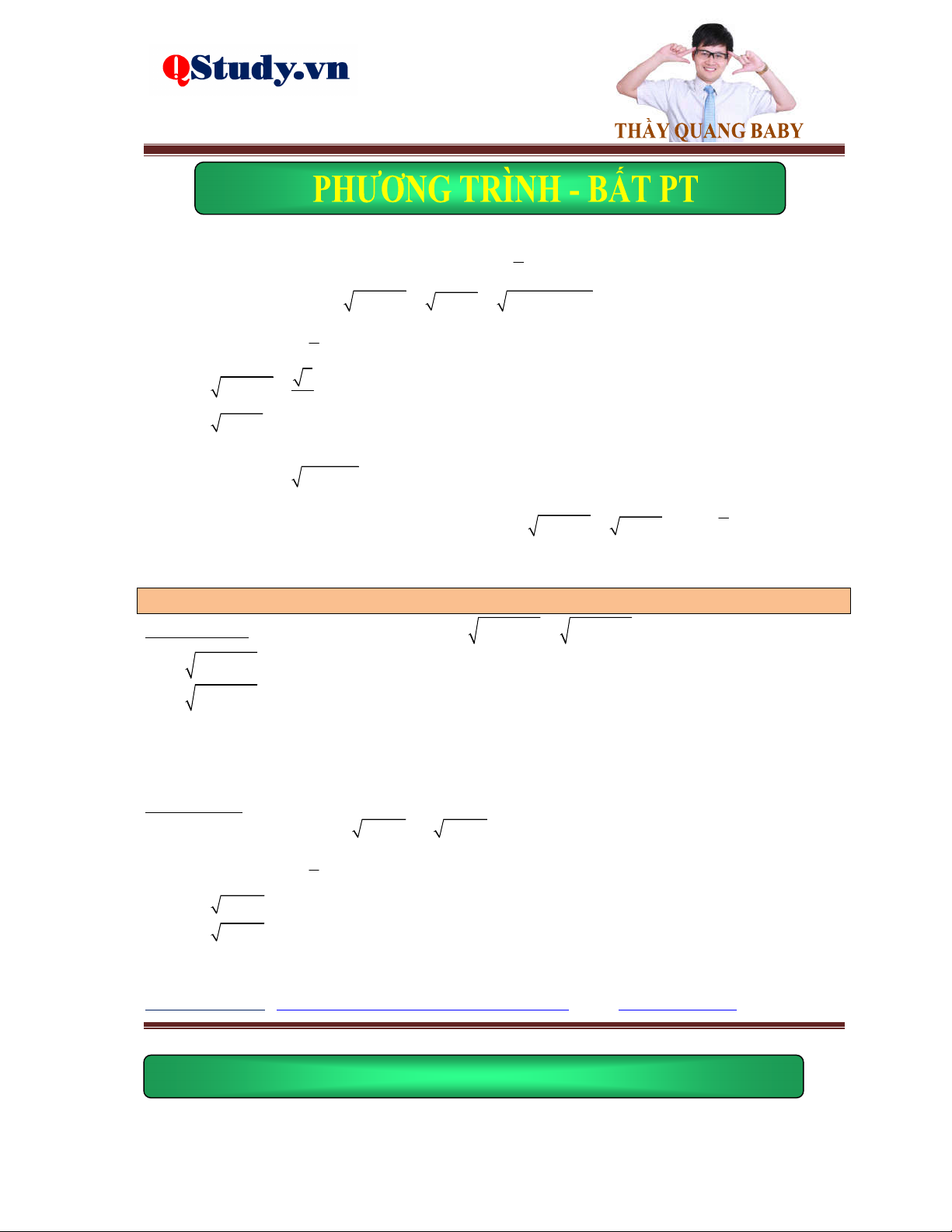
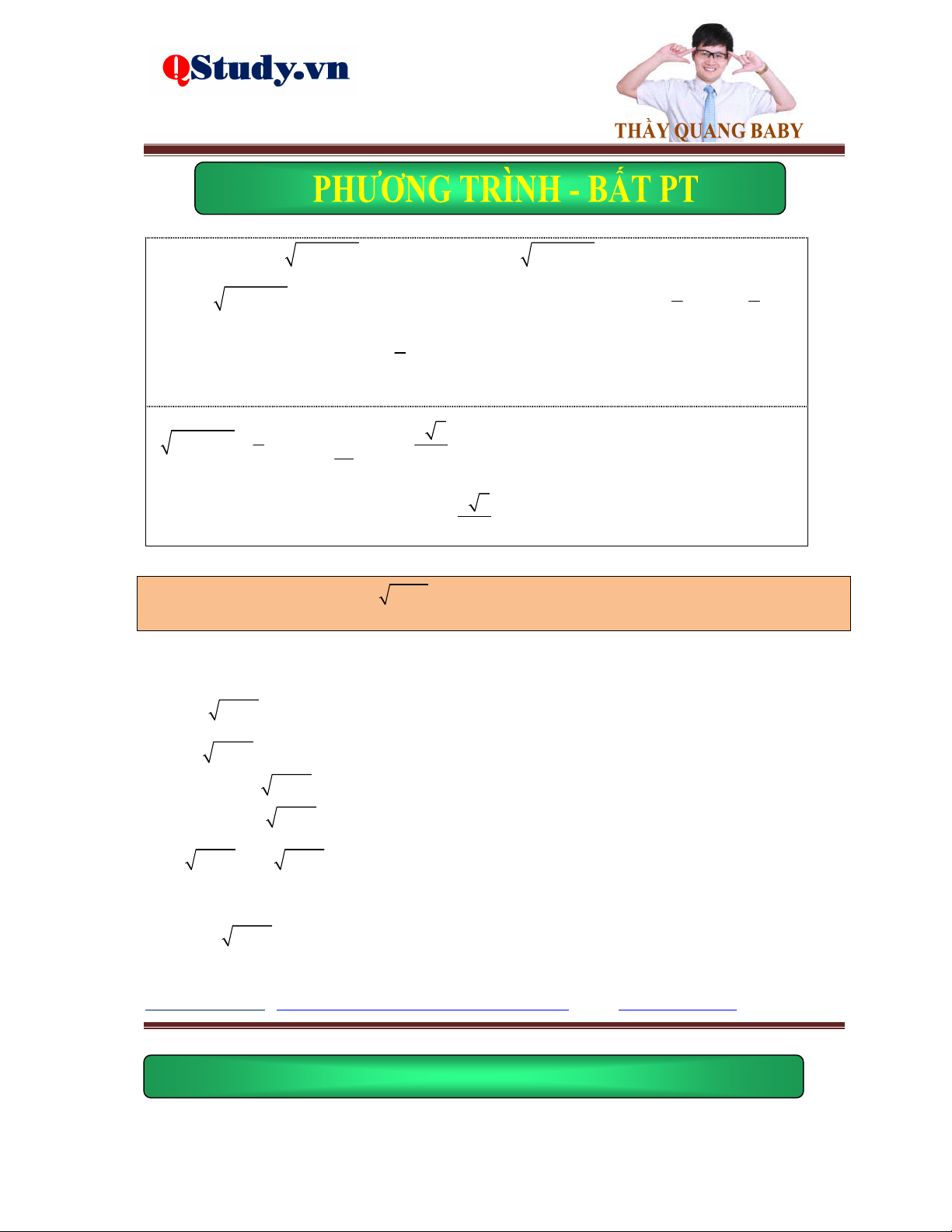
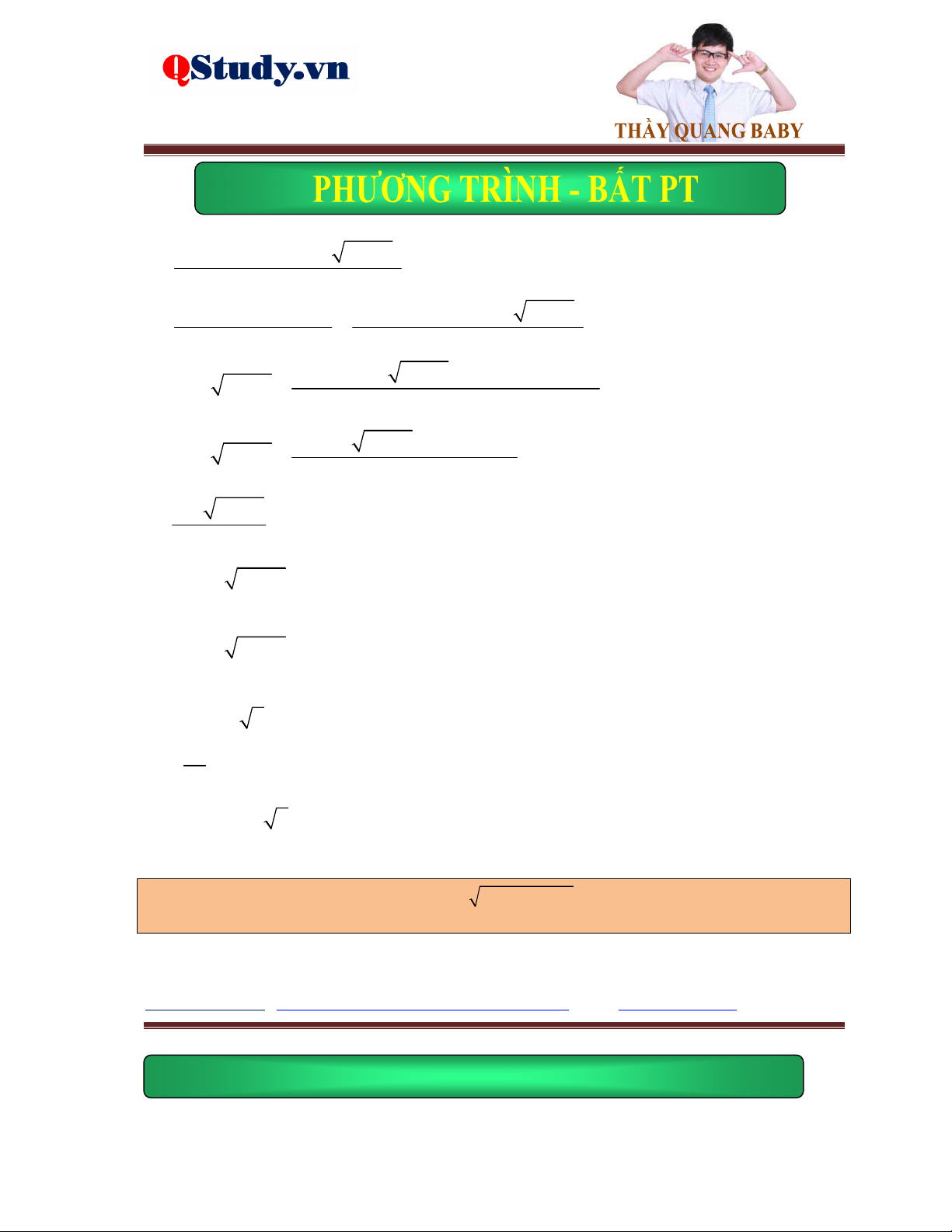
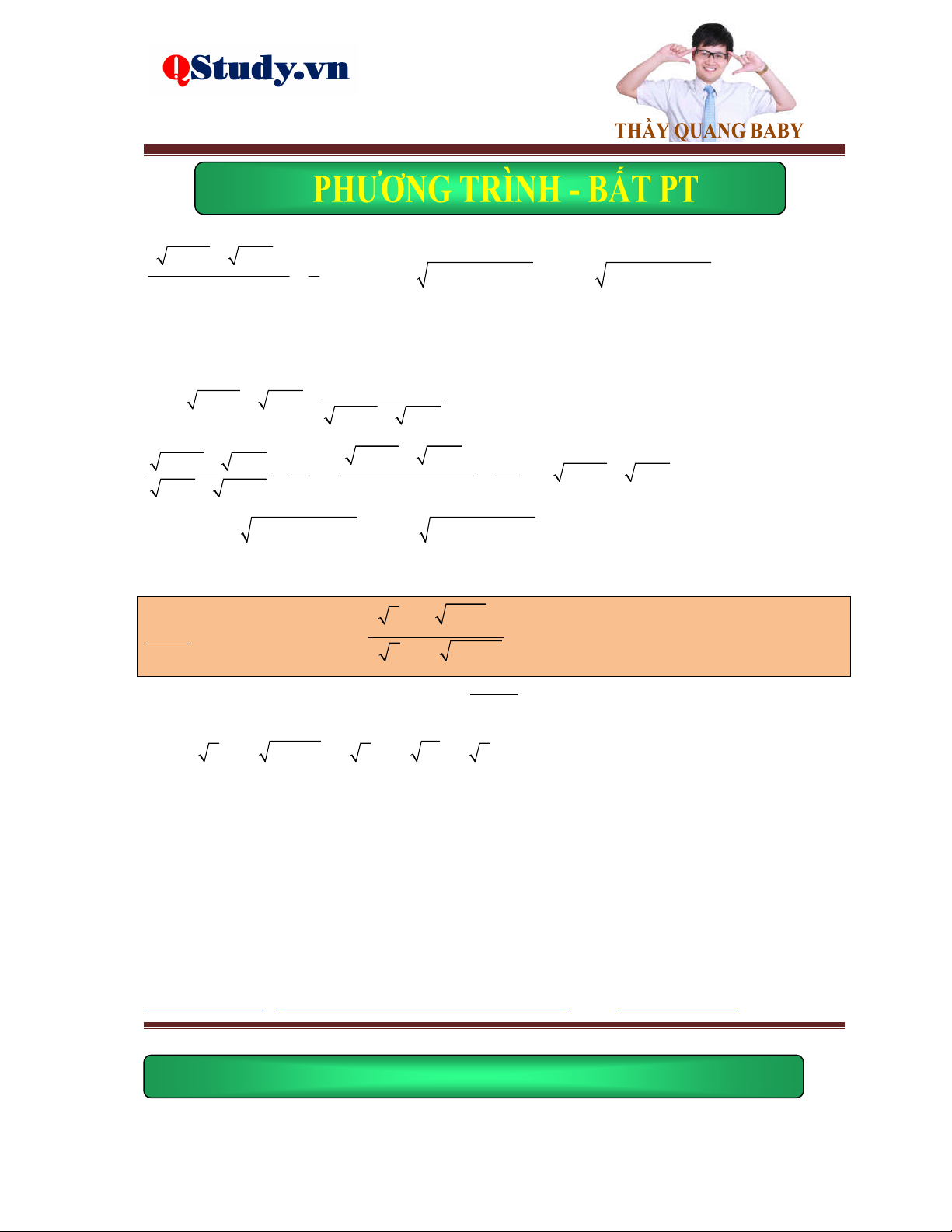
Ví dụ 3. Giải phương trình
x  7  4x  1  5x  6  2 2x  3 x   3
Lời giải. Điều kiện: x  . Nhận xét rằng x  42 
x  4x  5x  9x , chuyến vế, bình phương phương 2 trình đã cho ta được:
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 1
Tất cả vì học sinh thân yêu
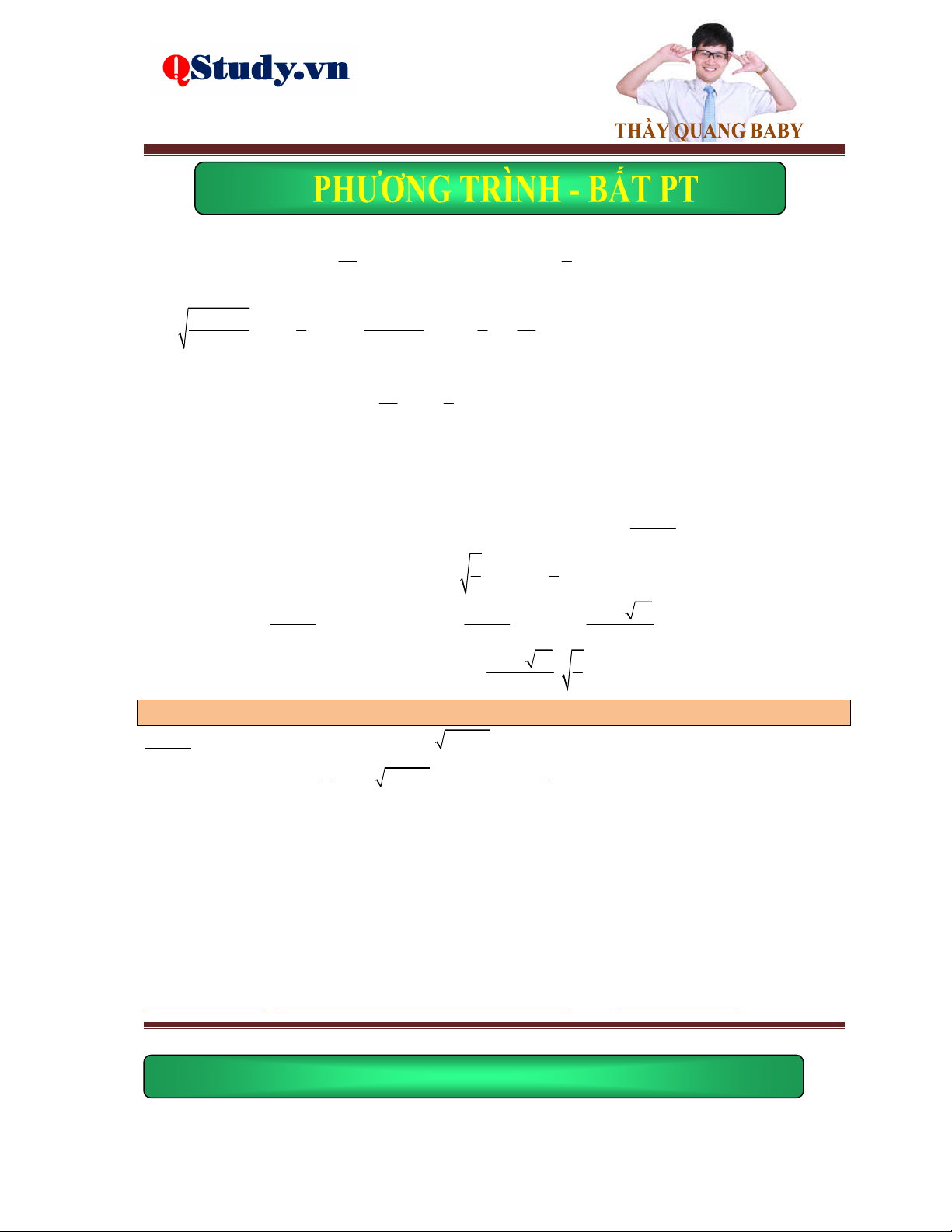
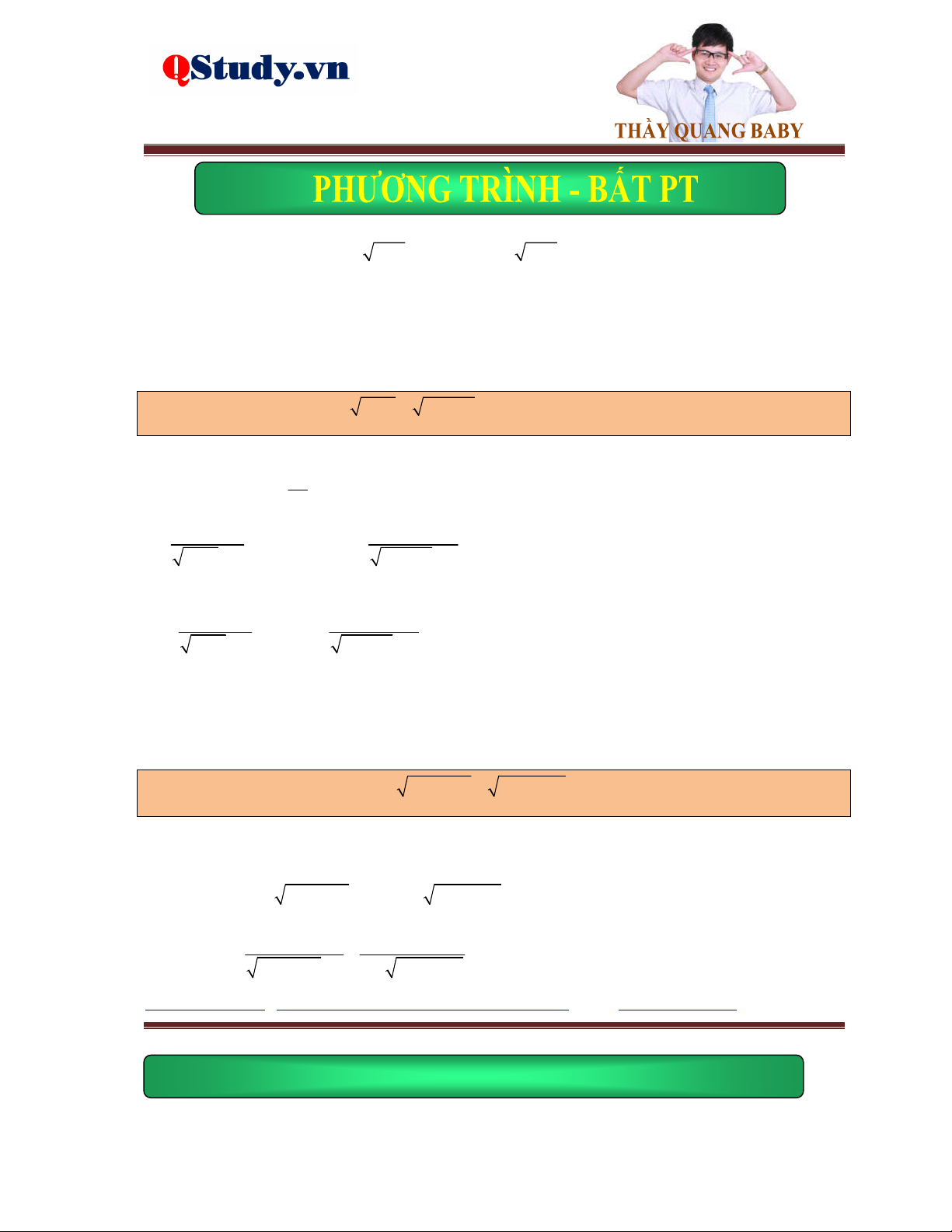
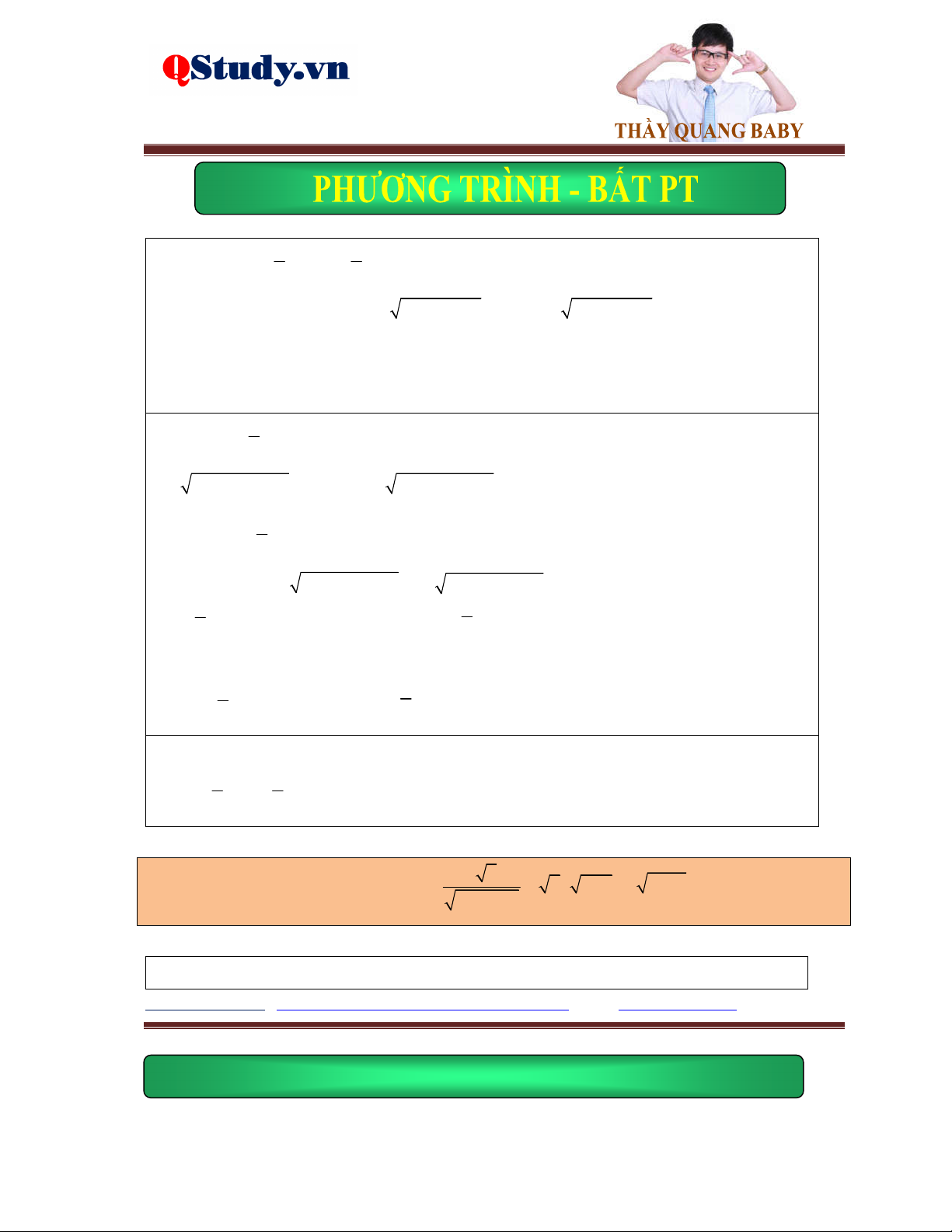
pt x  7  2 2x  3  5x  6  4x  1
 9x  5  2 x  78x  
12  9x  5  2 5x   6 4x   1  3   x   
x  78x   12  5x   6 4x   1   2   4x  13 x   2  0  13
Suy ra x  2; x
. Thử lại thấy thỏa mãn. 4
Vậy phương trình đã cho có hai nghiệm kể trên.
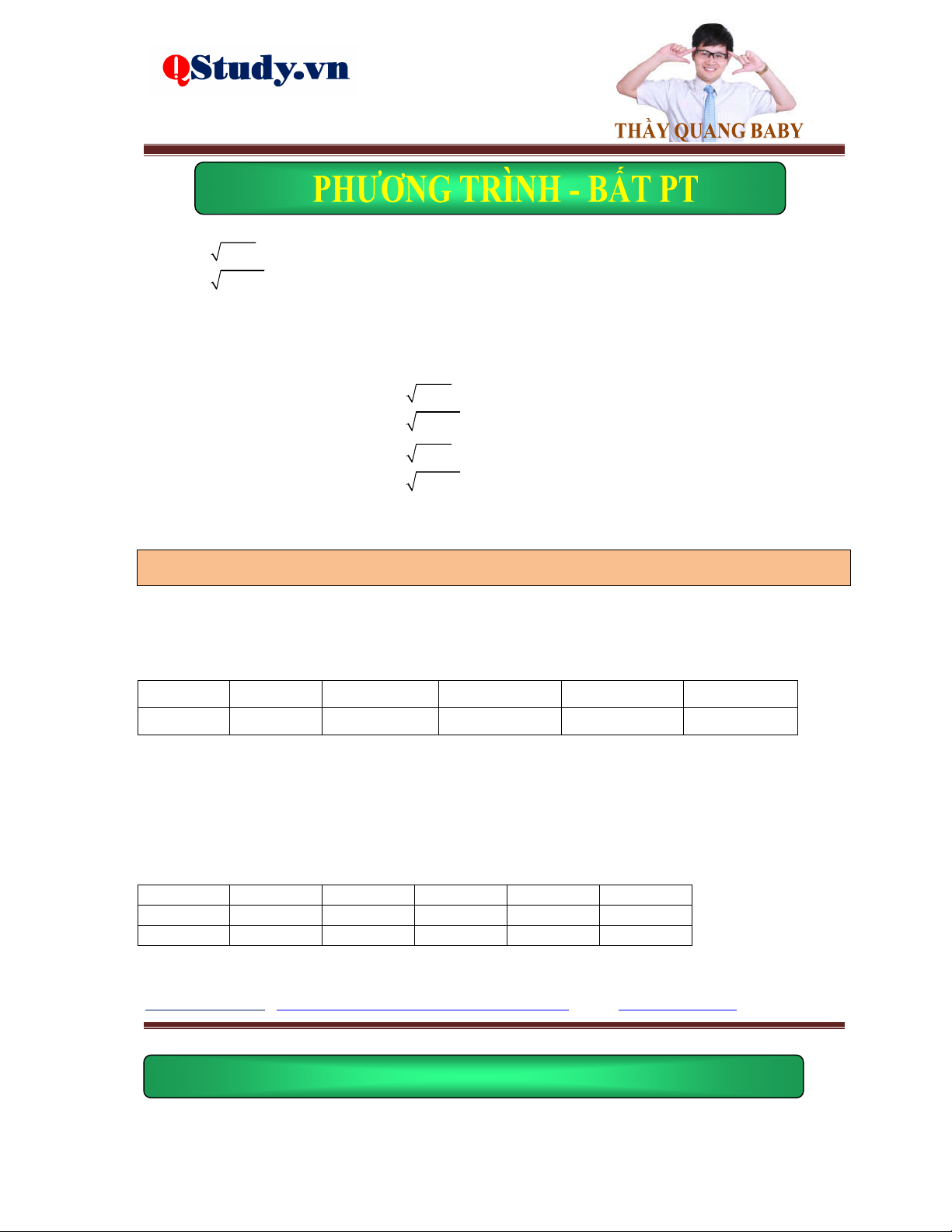
Ví dụ 4. Giải phương trình 3 x  1 2
x  1  x x  1  x  3 x   x  3
Lời giải. Điều kiện: x  1. Chú ý hằng đẳng thức 3
x   x   2 1
1 x x  
1 , nên phương trình đã cho được viết lại thành: x   1  2 x x   1 2
x  1  x x  1  x  3 x  3  2 
x x  1      2 x 1  
1  x x  1  x  3  x  3    x  1 
 2x x1 x3 2
x x  1  x  3 x  3  2
x x  1  x  3  0      1 ptvn x   1  x   3
Vậy phương trình đã cho vô nghiệm.
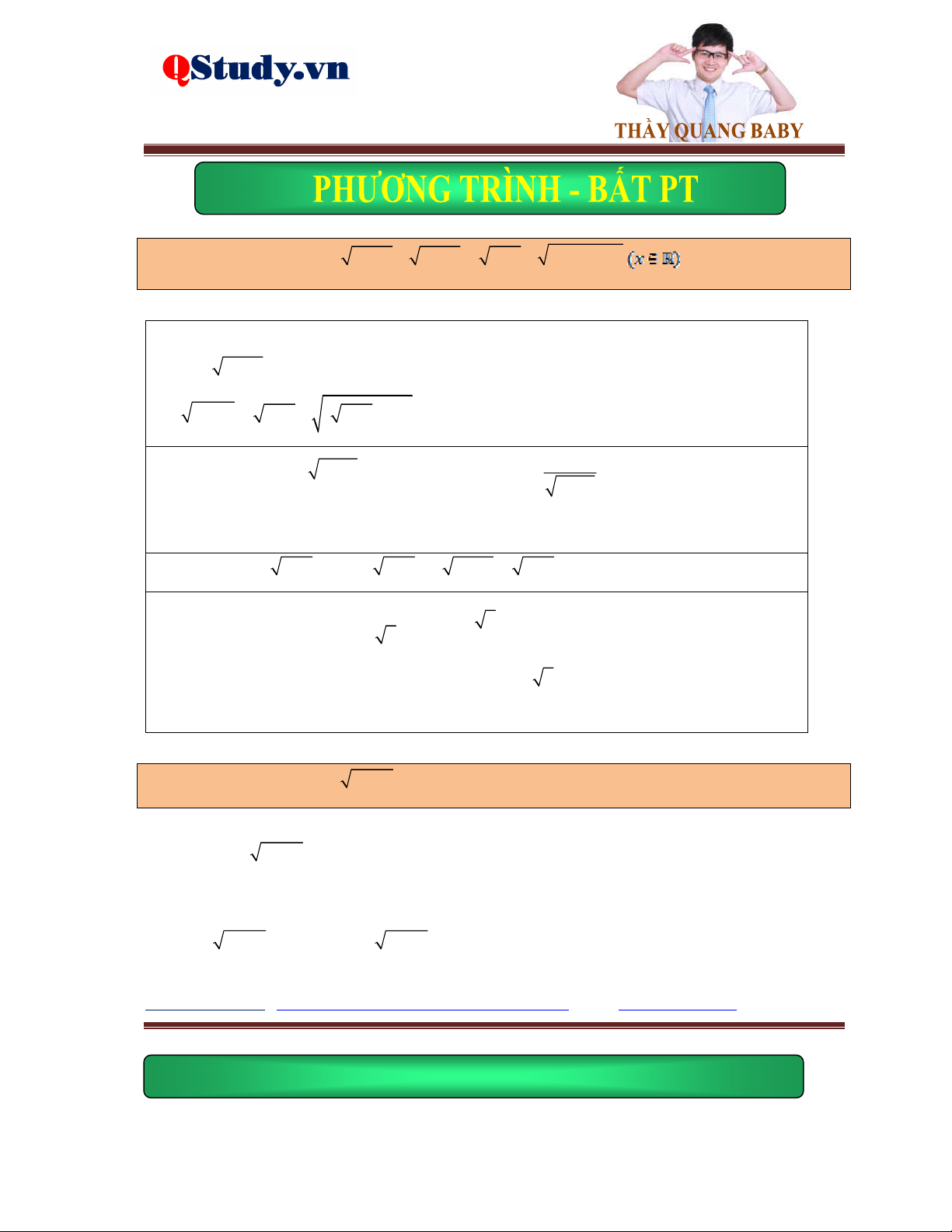
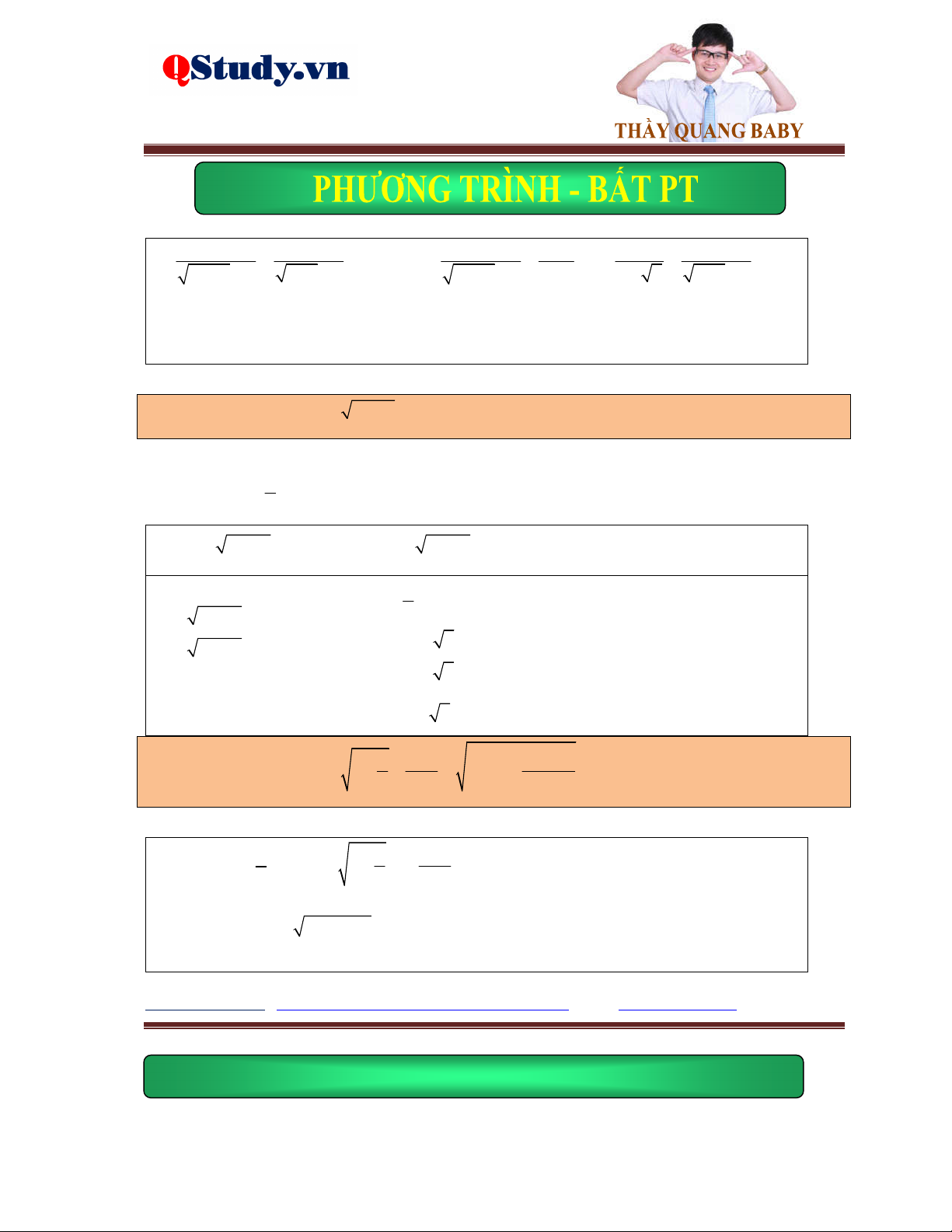
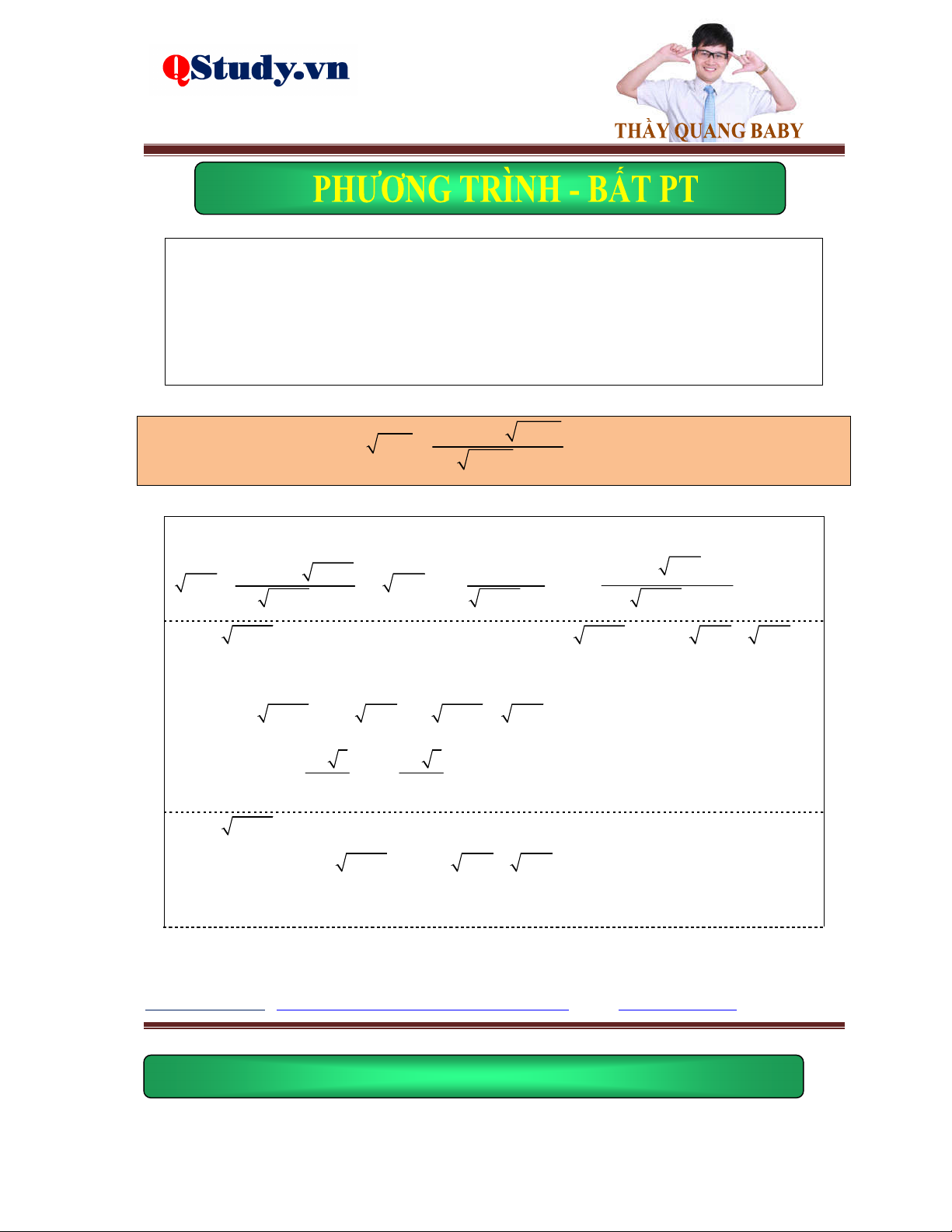
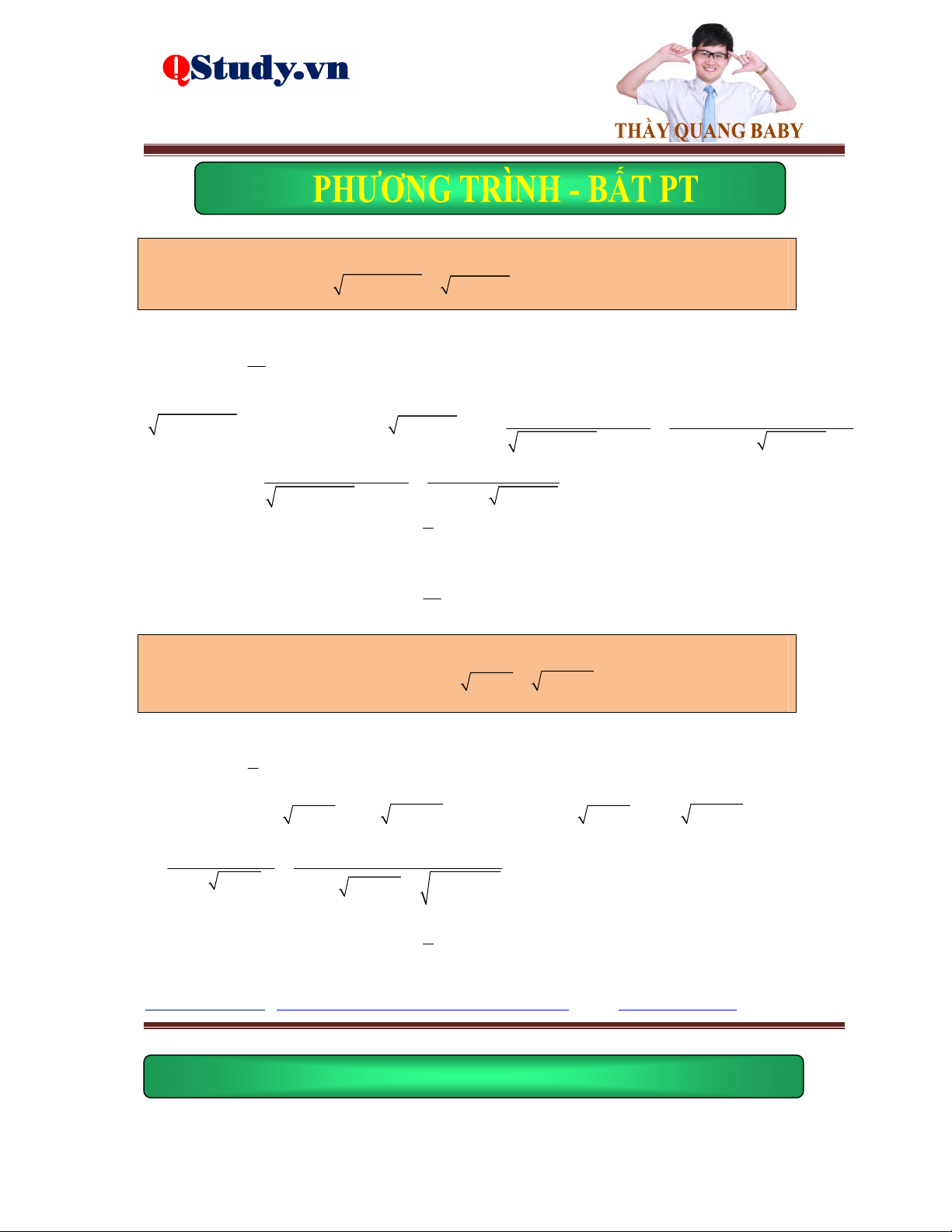
Dạng 2. Phương pháp đặt ẩn phụ hoàn toàn hoặc không hoàn toàn.
Kiến thức cơ bản:
 Đặt ẩn phụ hoàn toàn, đặt t A 
x đưa về phương trình ẩn t .
 Đặt ẩn phụ không hoàn toàn, đặt t A 
x phương trình sau khi biến đổi chứa hai ẩn t,x và xét đenta chính phương.
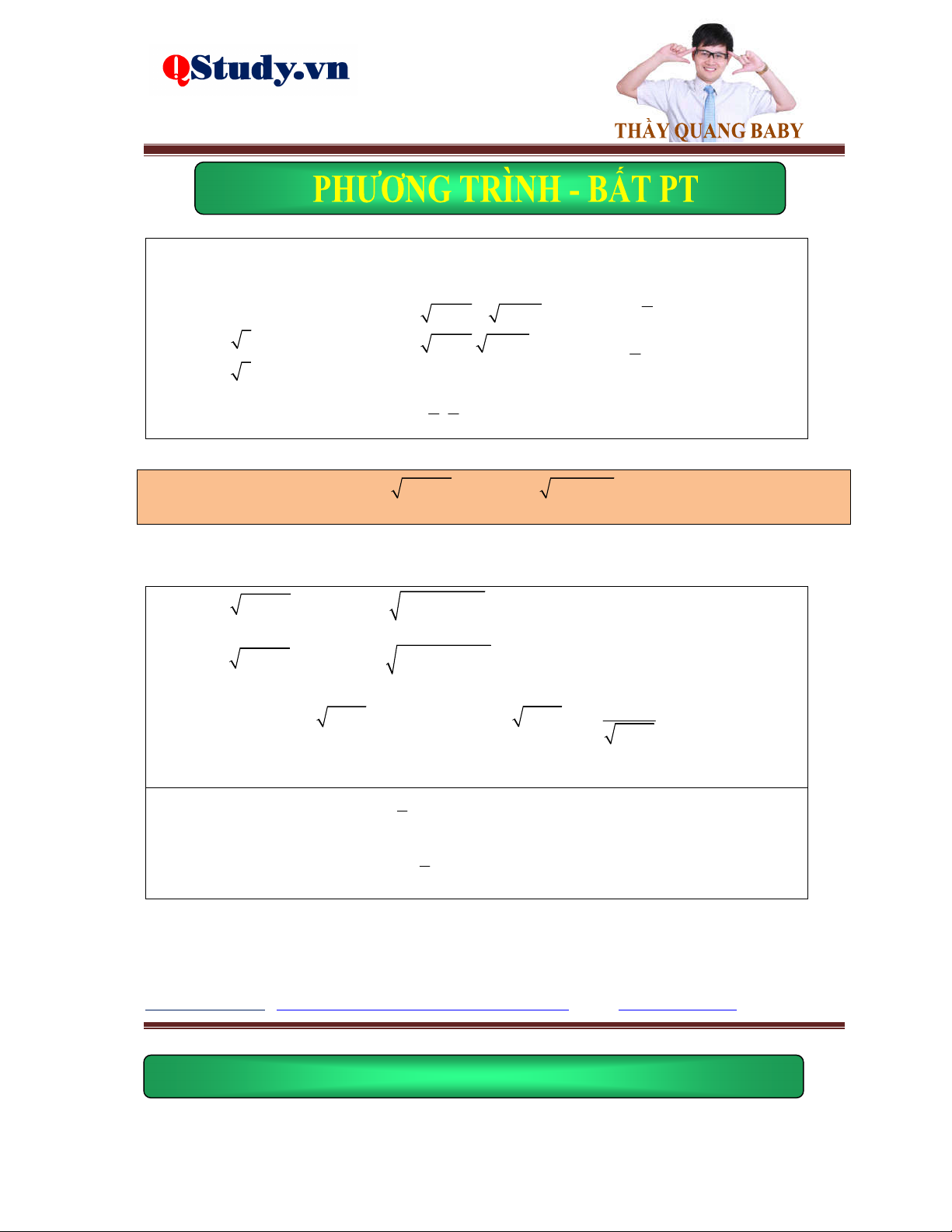
 Phương trình tổng quát dạng:
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 2
Tất cả vì học sinh thân yêu a A  x b B  x c A  x B  x dC  x D
A, Đặt ẩn phụ hoàn toàn.
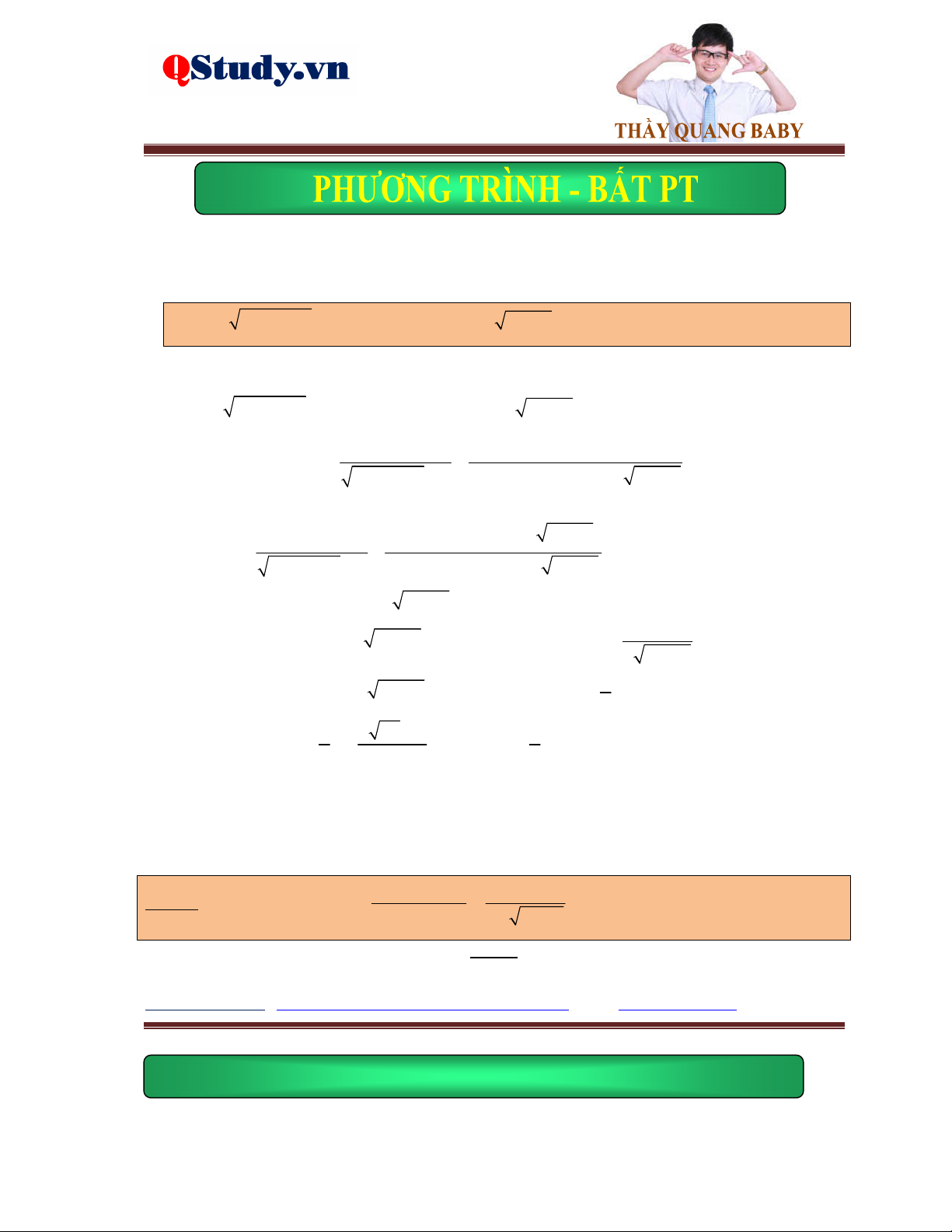
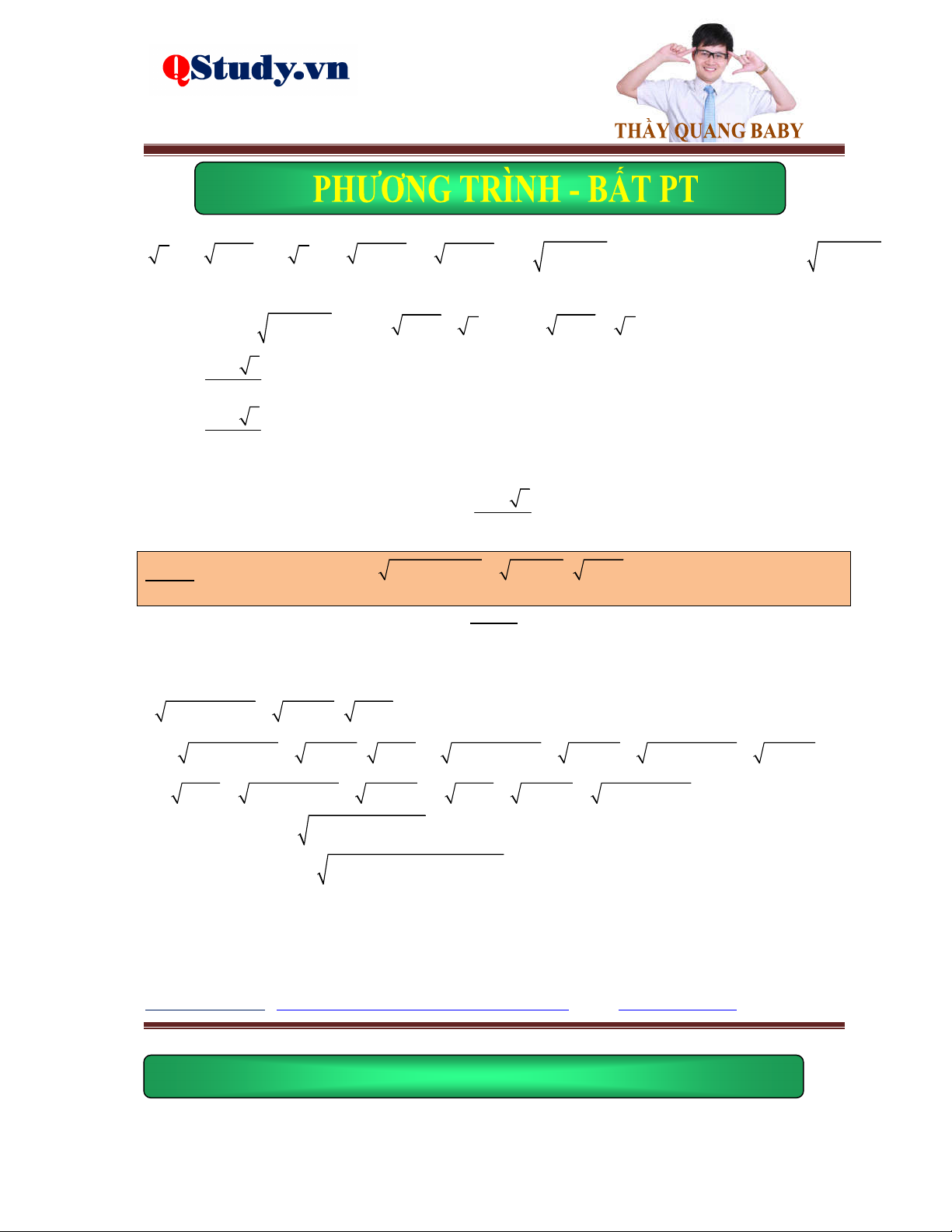
Ví dụ 1. Giải phương trình 2
2x  3  x  1  3x  2 2x  5x  3  16 x  
Lời giải. Điều kiện: x  1.
Đặt t  2x  3  x  1  0 suy ra 2 2
t  3x  4  2 2x  5x  3 . Khi đó phương trình đã cho trở thành: t   0 2 2 
t t  4  16  t t  20  0      t   t   t 5 5 4  0  Do đó 2
2x  3  x  1  5  3x  4  2 2x  5x  3  25 21   x1 2 
 2 2x  5x  3  21 3x   3  x  3  .
42x  5x   3  21 3x2 2 
Vậy phương trình đã cho có nghiệm duy nhất là x  3 .
Ví dụ 2. Giải phương trình 2
7x  7  7x  6  2 49x  7x  42  181 14xx  
Lời giải. Điều kiện: x  1.
Đặt t  7x  7  7x  6  0 suy ra 2 2
t  14x  1  2 49x  7x  42 . Khi đó phương trình đã cho trở thành: t   0 2 2 
t t  1  181  t t  182  0      t   t   t 13 13 14  0  Do đó 2
7x  7  7x  6  13  14x  1  2 49x  7x  42  169 .  6 12   x 2 
 49x  7x  42  84  7x   7  x  6 .
49x 7x 2 42  84  7 2 2 x 
Vậy phương trình đã cho có nghiệm duy nhất là x  6 .
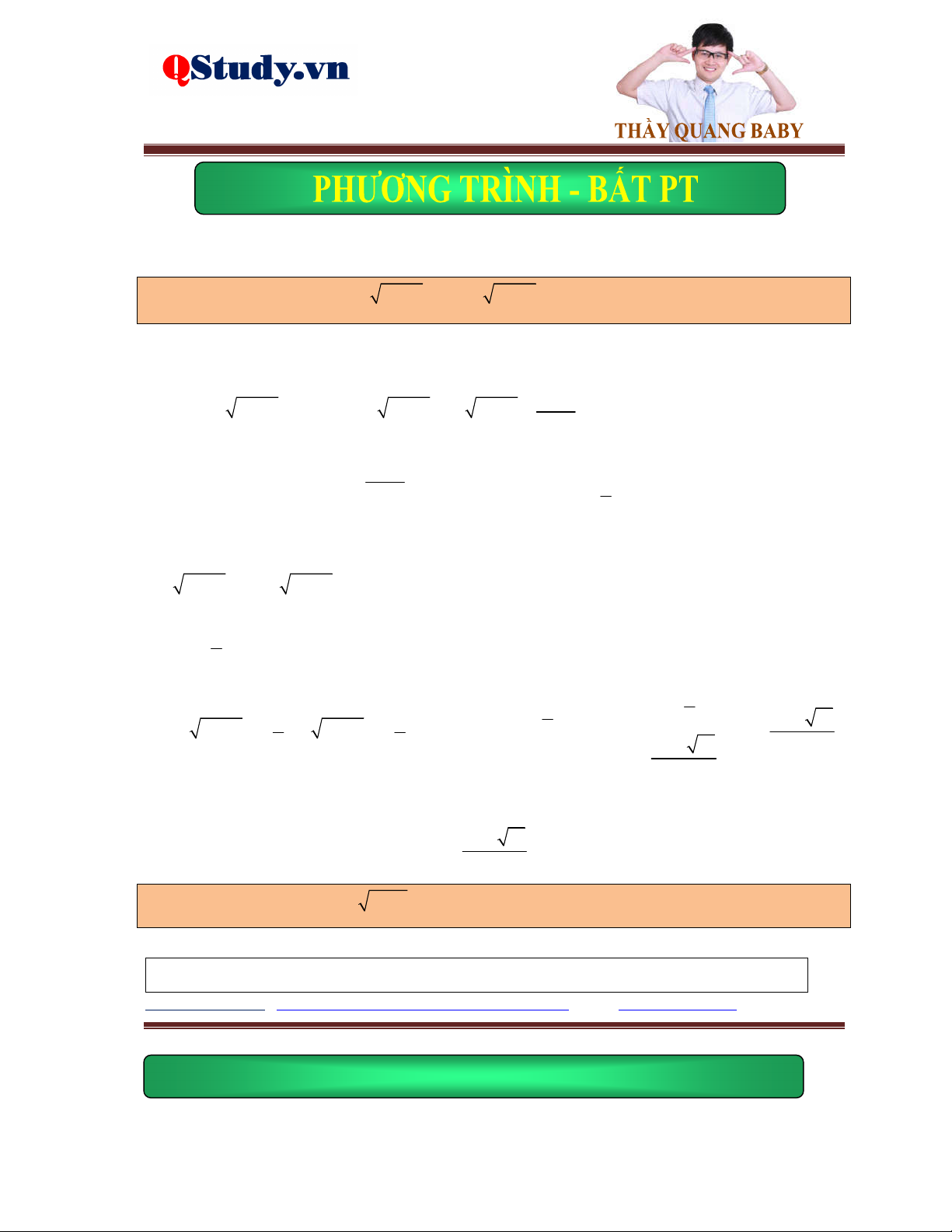
B, Đặt ẩn phụ không hoàn toàn.
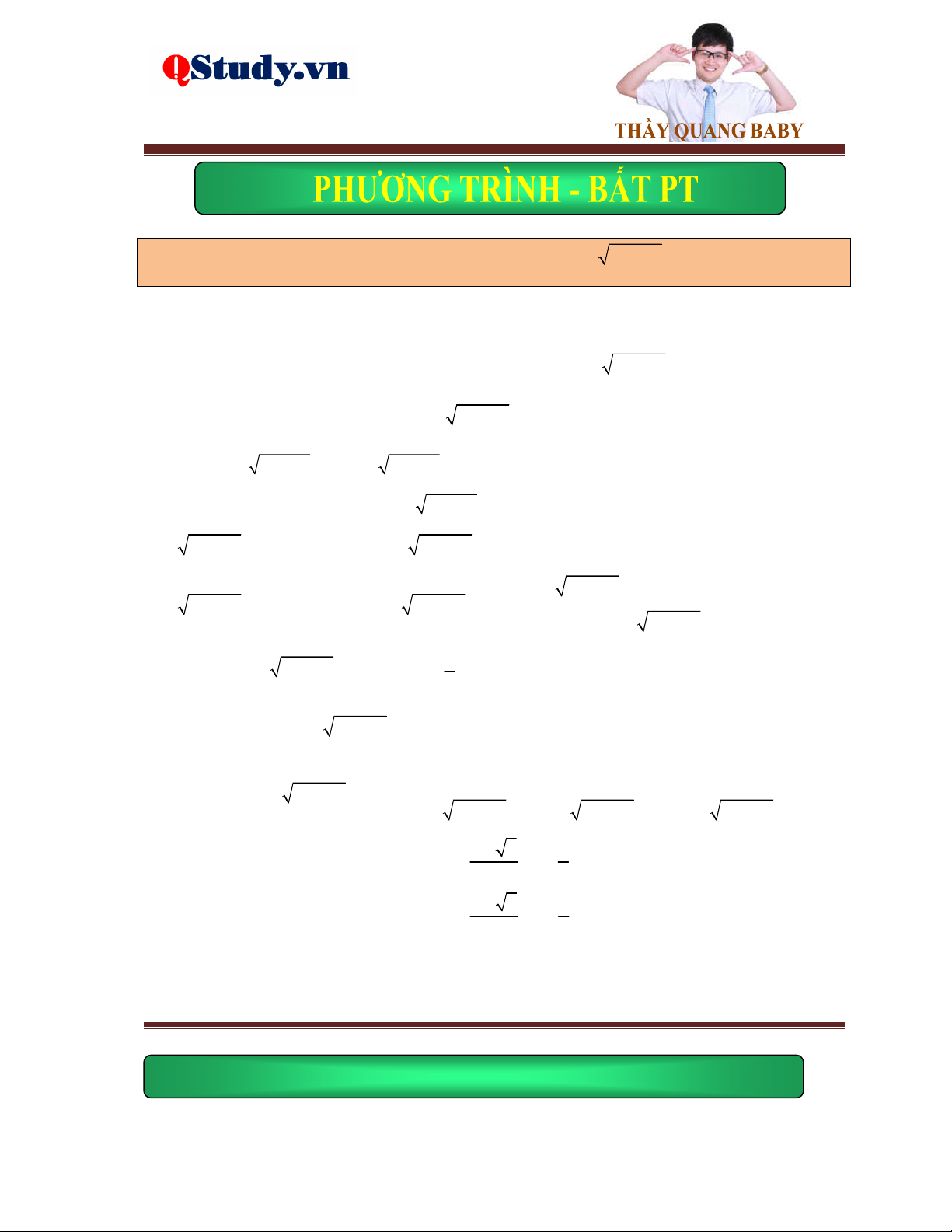
Phương trình tổng quát dạnga x b  2 2
a x b x c a x b x c . 1 1 2 2 2 3 3 3
Ví dụ 1. Giải phương trình x   2 2 1
x  2x  3  x  1 x .
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 3
Tất cả vì học sinh thân yêu
Lời giải. Điều kiện: x   .
 Bước 1. Đặt t f  
x đưa về phương trình bậc hai ẩn t . 2
 Bước 2. Tính  theo x và biểu diễn   ax  
b t gx . Đặt 2 2 2 2
t x  2x  3  x  1  2x  2  x  1  t  2x  2 , khi đó phương trình đã cho trở thành: x   2 2
1 t t  2x  2  t x  
1 t  2x  2  0    2 2
Có   x     x   2 1 4 2
2  x  6x  9  x  nên ta được:     3 
x  1  x  3 t   x 1  2   
x  2x  3  x 1 2          2 x 1 x 3
x  2x  3     2 t 2   2 2
x  2x 1 0  x  1  2
Vậy phương trình đã cho có hai nghiệm là x  1  2 .
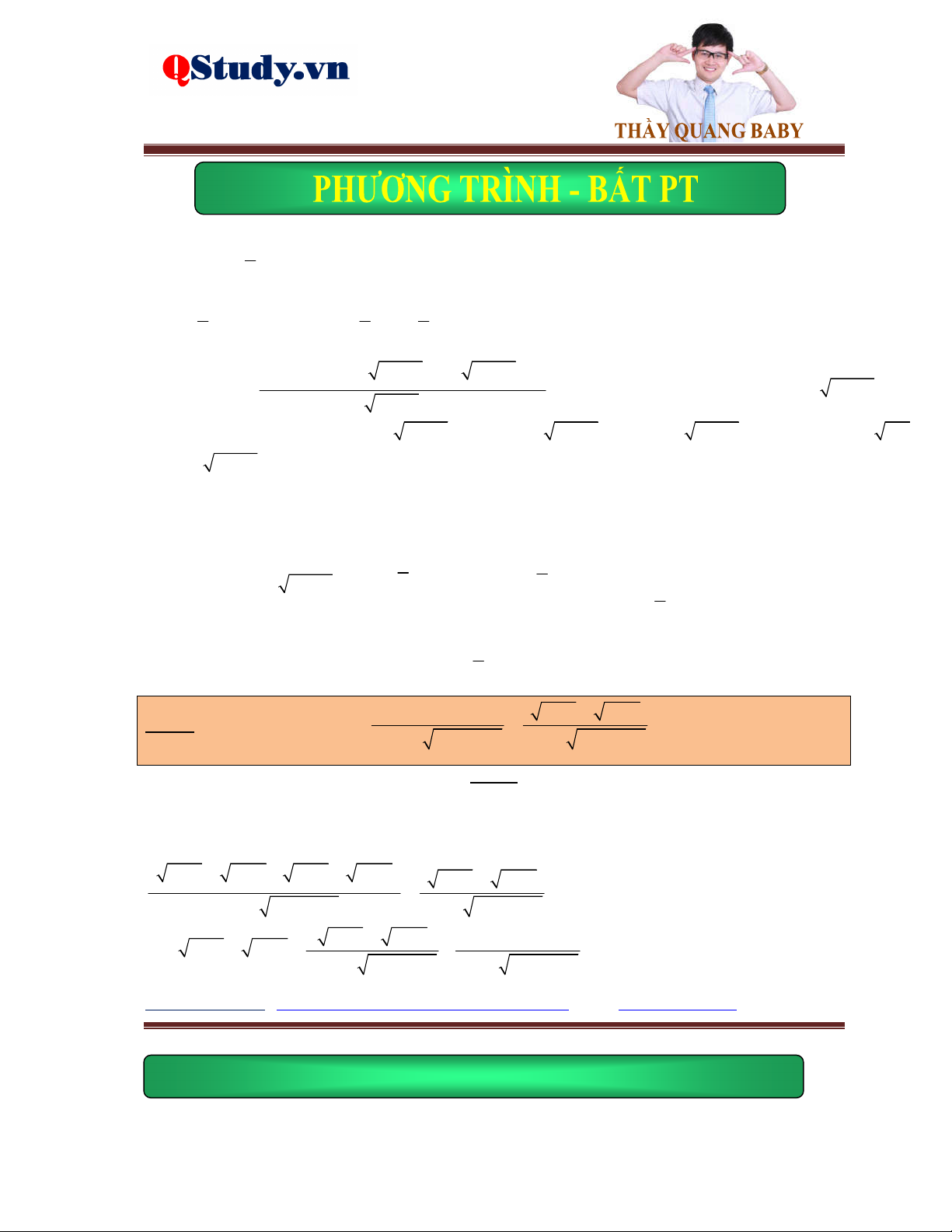
Ví dụ 2. Giải phương trình 2
x x  x   2 4 3
x x  1  1  0 x  .
Lời giải. Điều kiện: 2
x x  1 0 . Đặt 2 2 2 2 2
t x x  1  0  x x  1  t x t x  1.
Khi đó phương trình đã cho trở thành: 2
t x   x  x   2 1 4
3 t  1  0  t  x   3 t  3x  0    2 2
Ta có   x      2 3 4
3x x  6x  9  x   nên ta được:     3 0 
3  x x  3 t   3   x  1 2         x x 1 3 2             1  41 2 3 x x 3
x x 1  x       x t x  2  2    1  41
Vậy phương trình đã cho có ba nghiệm là x    1;   . 2   
Ví dụ 3. Giải phương trình  2x  x 2 3 2 1 1
1  3x  8 2x  1 x  .
Lời giải. Điều kiện: x   .
Phương trình đã cho tương đương với: 2
x x    x   2 3 3 8 3 2x  1  0
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 4
Tất cả vì học sinh thân yêu Đặt 2 2 2 2 2 2
t  2x  1  1  t  2x  1  3t  3x  3x  3 .
Khi đó phương trình đã cho trở thành: 2
t   x   2 3 8
3 t  3x x  0    2 2
Ta có    x     2 x x  2 8 3 12 3
 100x  60x  9  10x   nên     3 0 
3  8x  10x  3 xt    2    3 2x  1 6 3  x       x  0     2 3 8x 10x 3  2x  1  1     3 1 3 x t x   6
Vậy phương trình đã cho có nghiệm duy nhất là x  0 .
Ví dụ 4. Giải phương trình  x   3 3 4 1
x  1  2x  2x  1 x   .
Lời giải. Điều kiện: x  1. Đặt 3 3 2 3 2
t x  1  0  x  1  t x t  1 .
Khi đó phương trình đã cho trở thành:
 2t   x  2 2 1 4
1 t  2x  1  0  2t 4x  
1 t  2x  1  0    2 2
Ta có    x     x   2 4 1 8 2
1  16x  24x  9  4x   nên     3 0 
4x  1  4x  3       x  2 t 2x 1 3         x 1 2x 1 4        3     3 4x 1 4x 3 1  3    2 x  1  1 x   t   4  4 2   3   
Vậy phương trình đã cho có hai nghiệm là 3 x  2;   . 4   
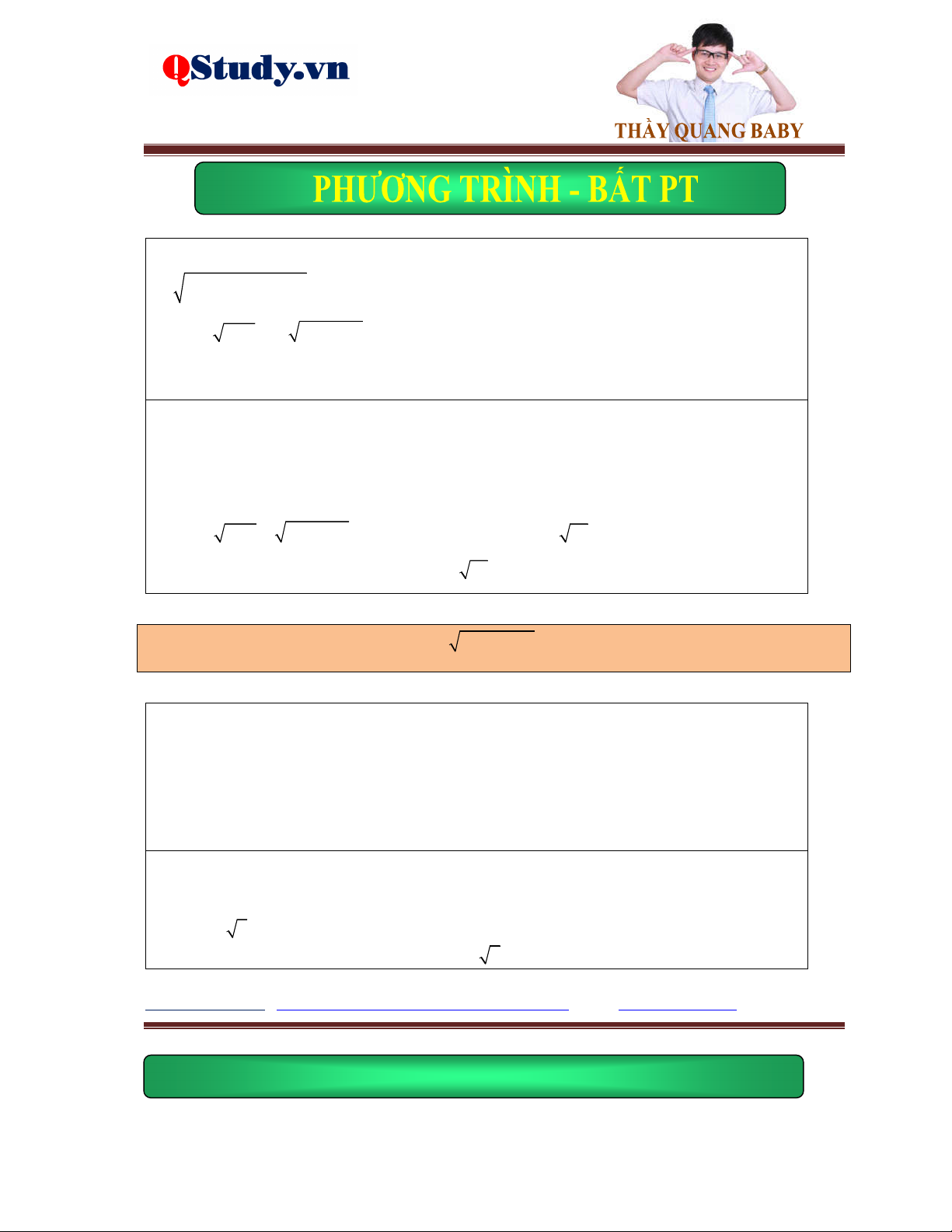
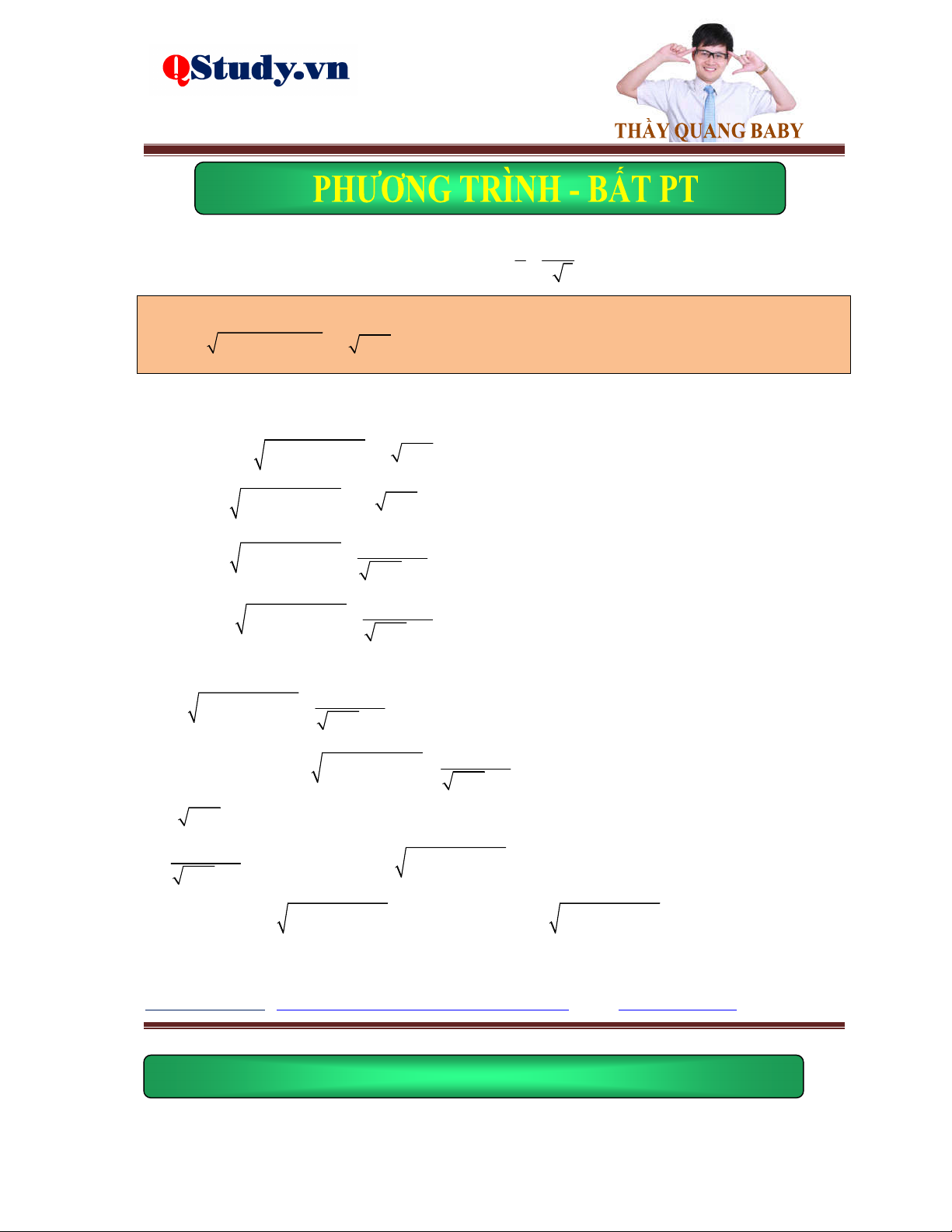
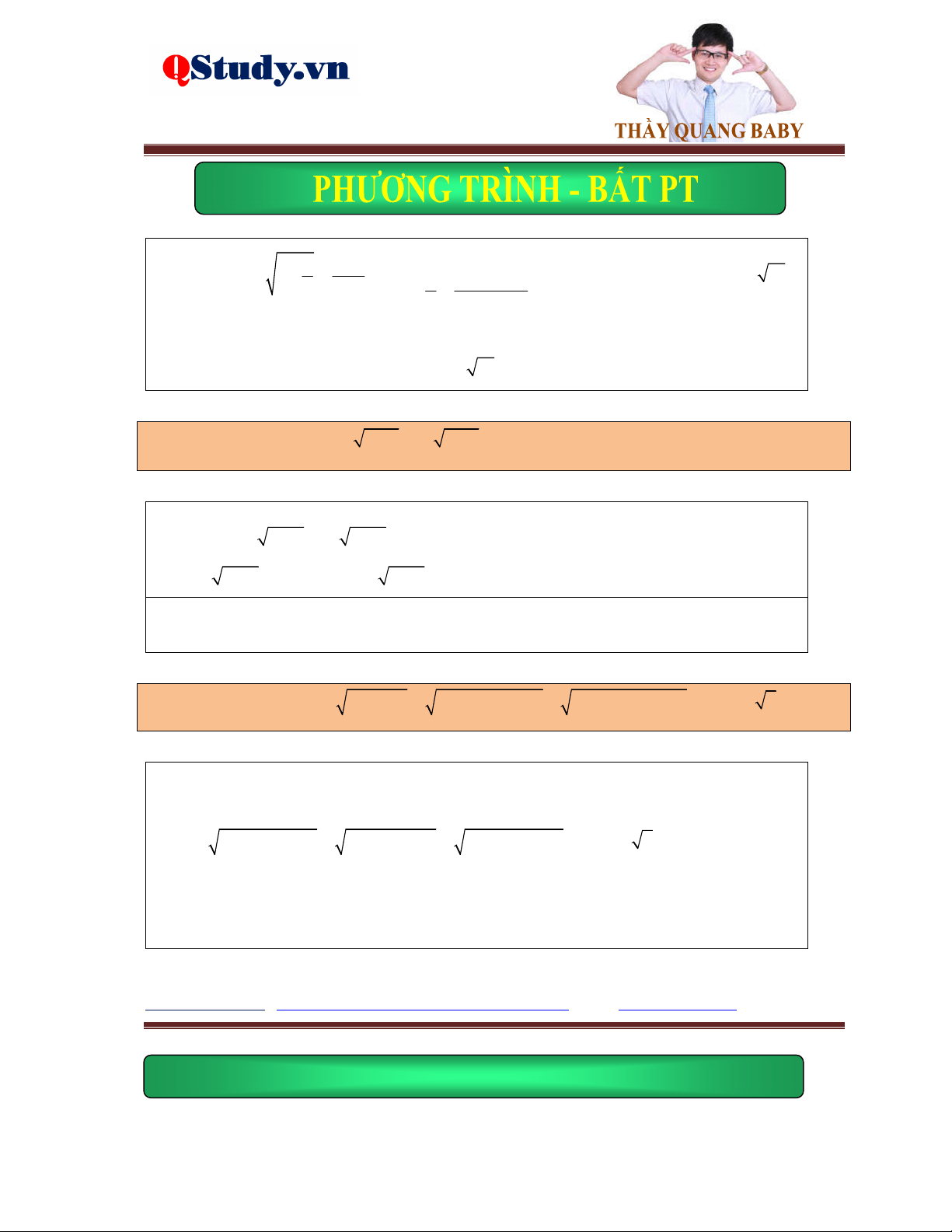
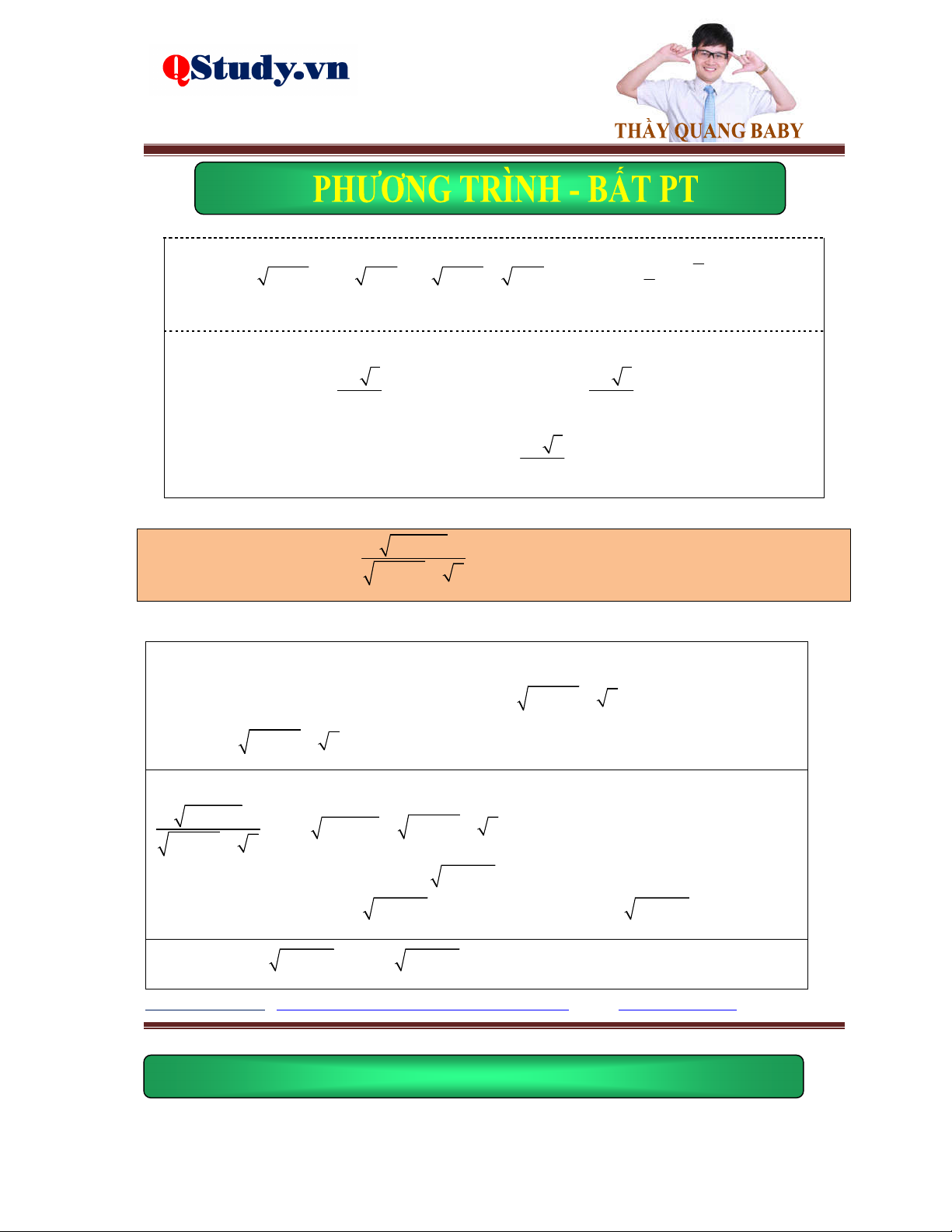
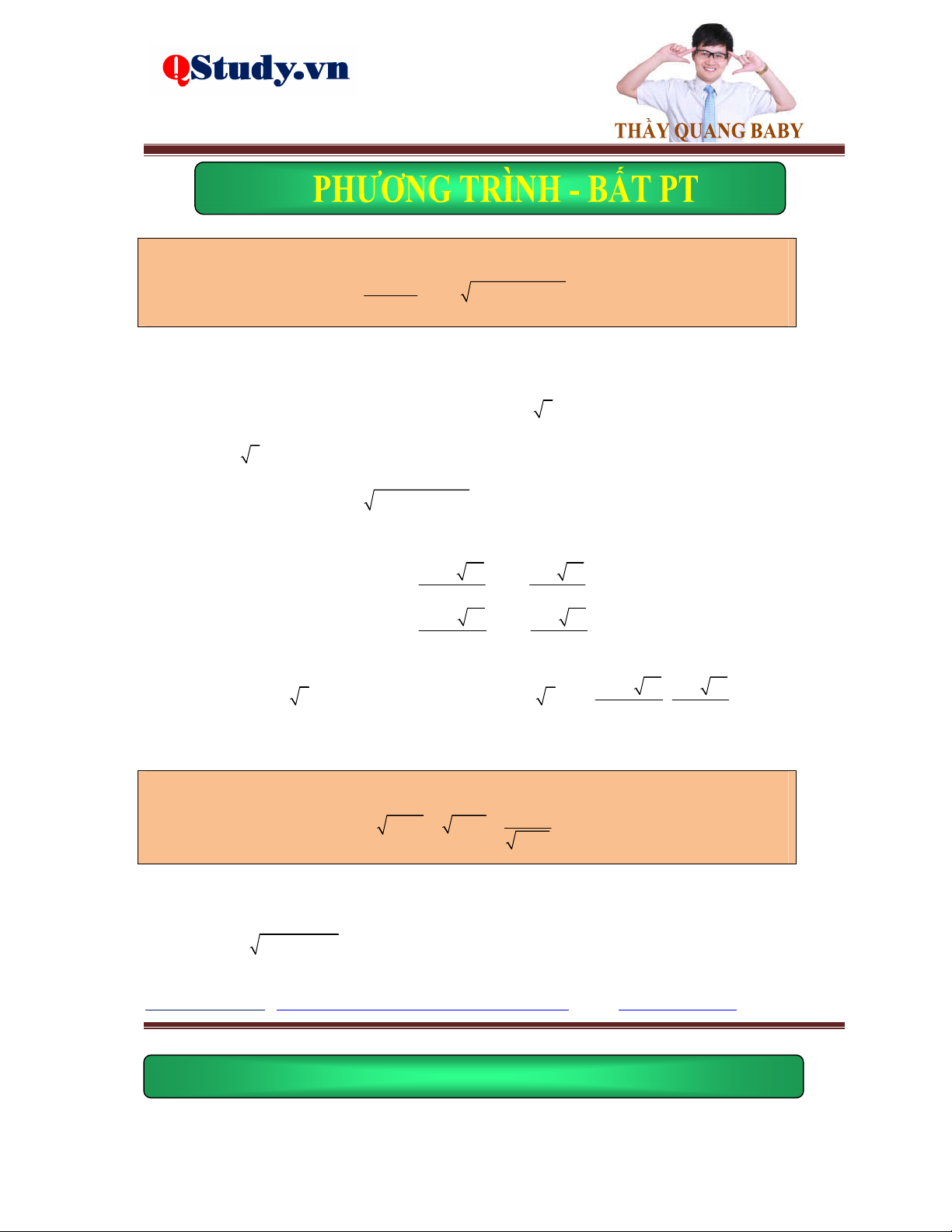
Dạng 1. Phương trình đưa về tổng các đại lượng không âm hoặc n n A B .
Dấu hiệu: Hệ số trước căn thường là những số chẵn.
1. Đưa về tổng các đại lượng không âm.
Dùng các biến đổi hoặc tách ghép hằng đẳng thức để phương trình đã cho xuất hiện các số A  0  không âm 2 2
A B D C  ...  0  B  0 C   0 
2. Biến đổi về dạng n n A B .
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 5
Tất cả vì học sinh thân yêu n nA B
Đưa phương trình về dạng 
A B n  2k  1. n  ,k      n nA BA B  Hoặc về dạng 
A B    n  2k   . n  ,k   A B  0    Bài tập ví dụ.
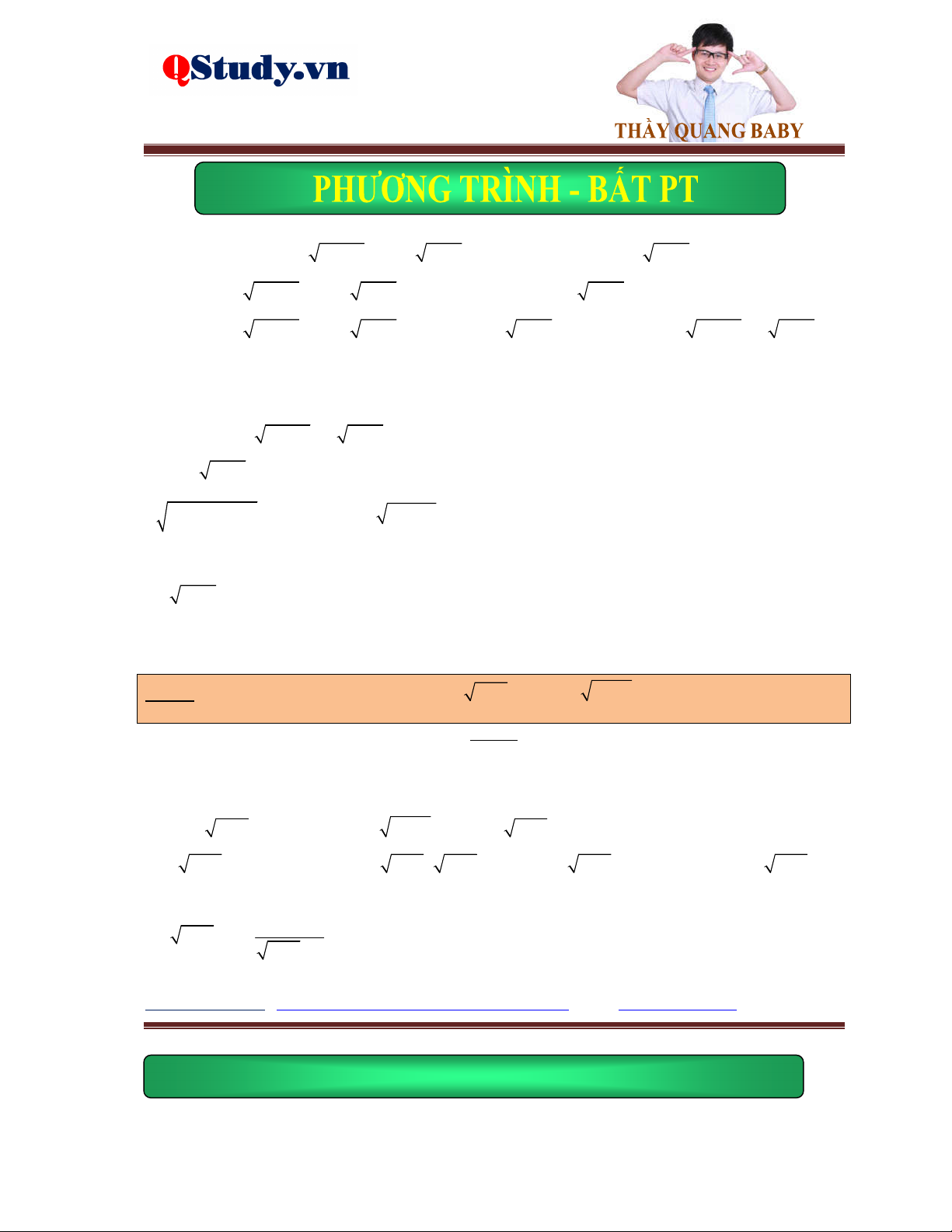
Ví dụ 1. Giải phương trình 2
4x x  3  2 2x  1  4x  3x  3 x   1
Lời giải. Điều kiện: x  . Phương trình đã cho tương đương với: 2 2
pt  4x  4x x  3  3x  3  2 2x  1  0   2
4x  4x x  3  x  32x 1 2x 1   1  0
 2x x  32  2x 1  2 1  0   2
x x  3  0  
2x x  3       x  1  2x 1 1 0      2x 1  1  
Vậy phương trình đã cho có nghiệm duy nhất là x  1 .
Ví dụ 2. Giải phương trình 2
4 6x  10  4x  14x  11 x   5
Lời giải. Điều kiện: x  . Phương trình đã cho tương đương với: 3 2
pt  6x  10  4 6x  10  4  4x  20x  25         x
 2  x  2 6x 10 2 2x 5 6 10 2 2
5   6x10 22x50   3 
 6x  10  2x  3 x  3   13     2  x   6x 10 2x 7 0   ptvn       6
 x 10 2x  2 4 3  3  13
Vậy phương trình đã cho có nghiệm là x  . 4 Bài tập vận dụng.
Vận dụng 1. Giải phương trình 2
4x  12  x  1  4x 5x 1  9  5x x 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 6
Tất cả vì học sinh thân yêu 9 1
Lời giải. Điều kiện:  x  . Phương trình đã cho tương đương với: 5 5  2
4x  5x  1 4x 5x  113  5x  4 9  5x x 1  0 2
 x  5x 1  
 2x  5x 12  9  5x  22  x 1  0   9  5x  2  x 1  x10 
Vậy phương trình đã cho có nghiệm duy nhất là x  1 .
Vận dụng 2. Giải phương trình 2
x  6 3x  1  x  9  0 x   1
Lời giải. Điều kiện: x  . Phương trình đã cho tương đương với: 3 2 2
pt x x  9  6 3x  1  x  2x  1 9  6 3x  1  3x  1       
x     x  2 2 x 1 3 3x 1 1 3 3
1  x1 3x13   x     2  3x 1 2 x  7  37      x
 3x  1  x  4 3
 x 12 2 x 2   7  37
Vậy phương trình đã cho có nghiệm duy nhất là x  . 2
Vận dụng 3. Giải phương trình 3 2
x  3x x   1
x  2  6x  4 x  2  6 x  
Lời giải. Điều kiện: x  2 . Chú ý x x x   x  3 3 2 3 3 1 1 . Và x   1
x  2  4 x  2  3x  7  x  2   1
x  2  4 x  2  3x  7
 x  3  x   x    x   3 2 3 2 3 2 1 2 1 . Khi đó ta được
pt  x  
1   x  2  3 3
1  x  1  x  2  1 x 0 
x x  2    x  2 2 x x   2 
Vậy phương trình có nghiệm duy nhất là x  2 .
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 7
Tất cả vì học sinh thân yêu
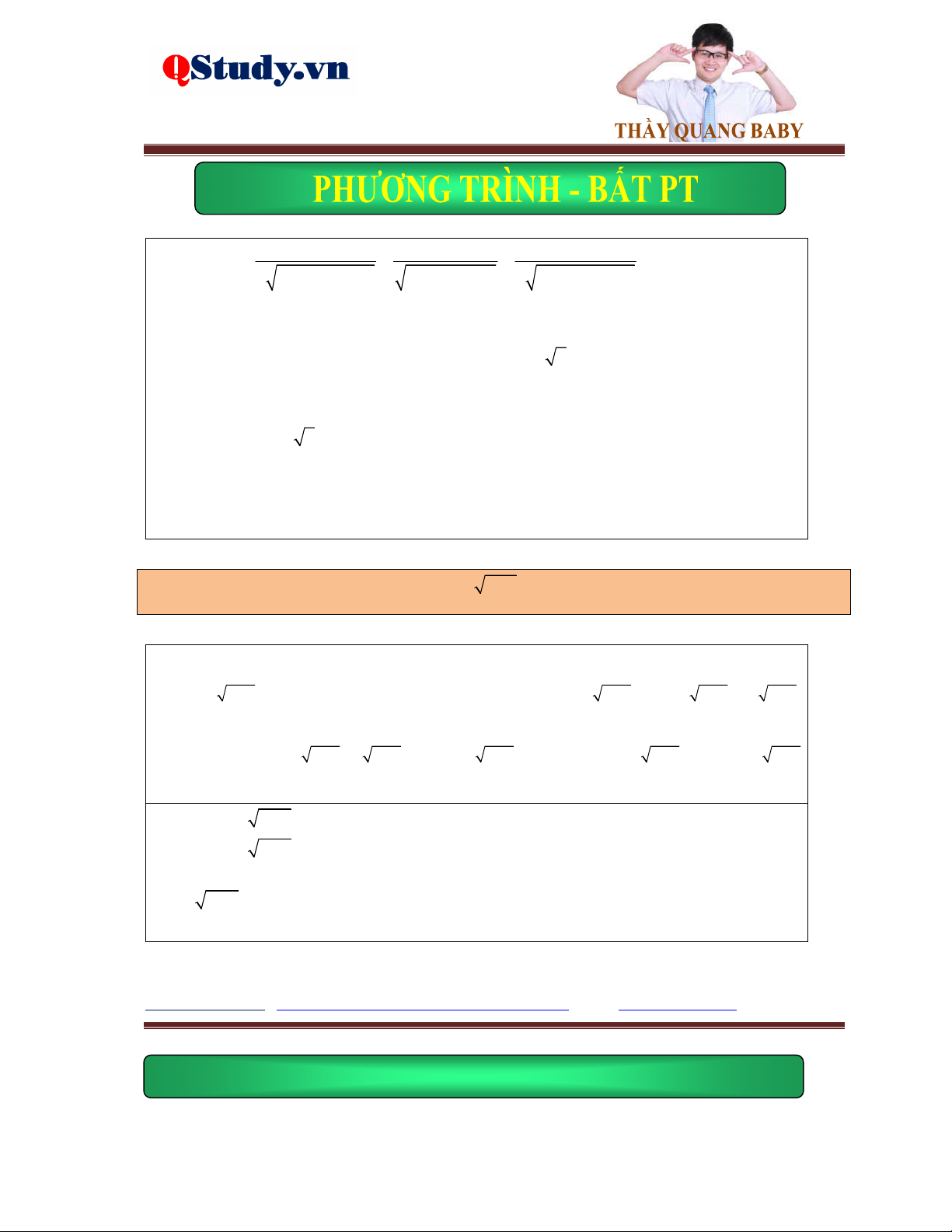
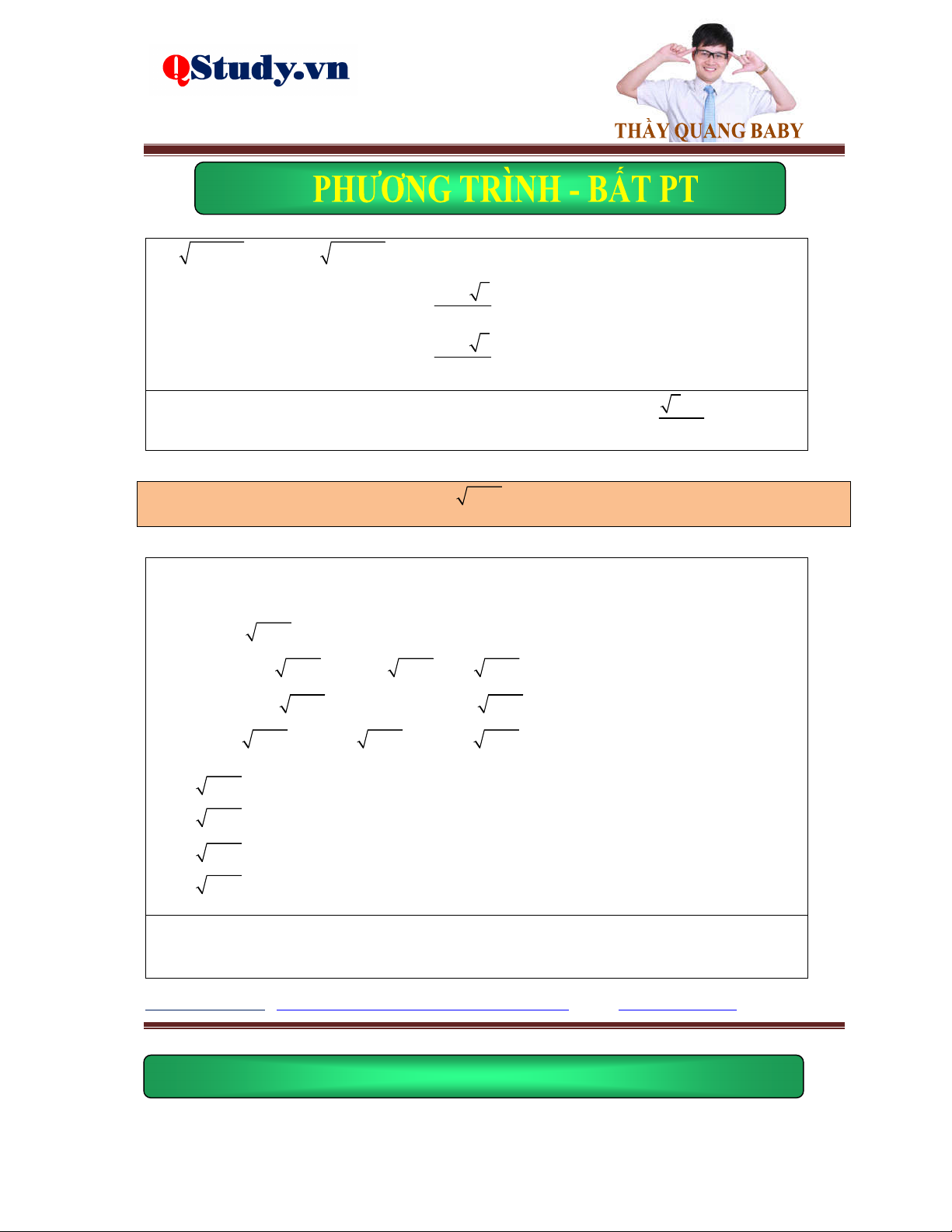
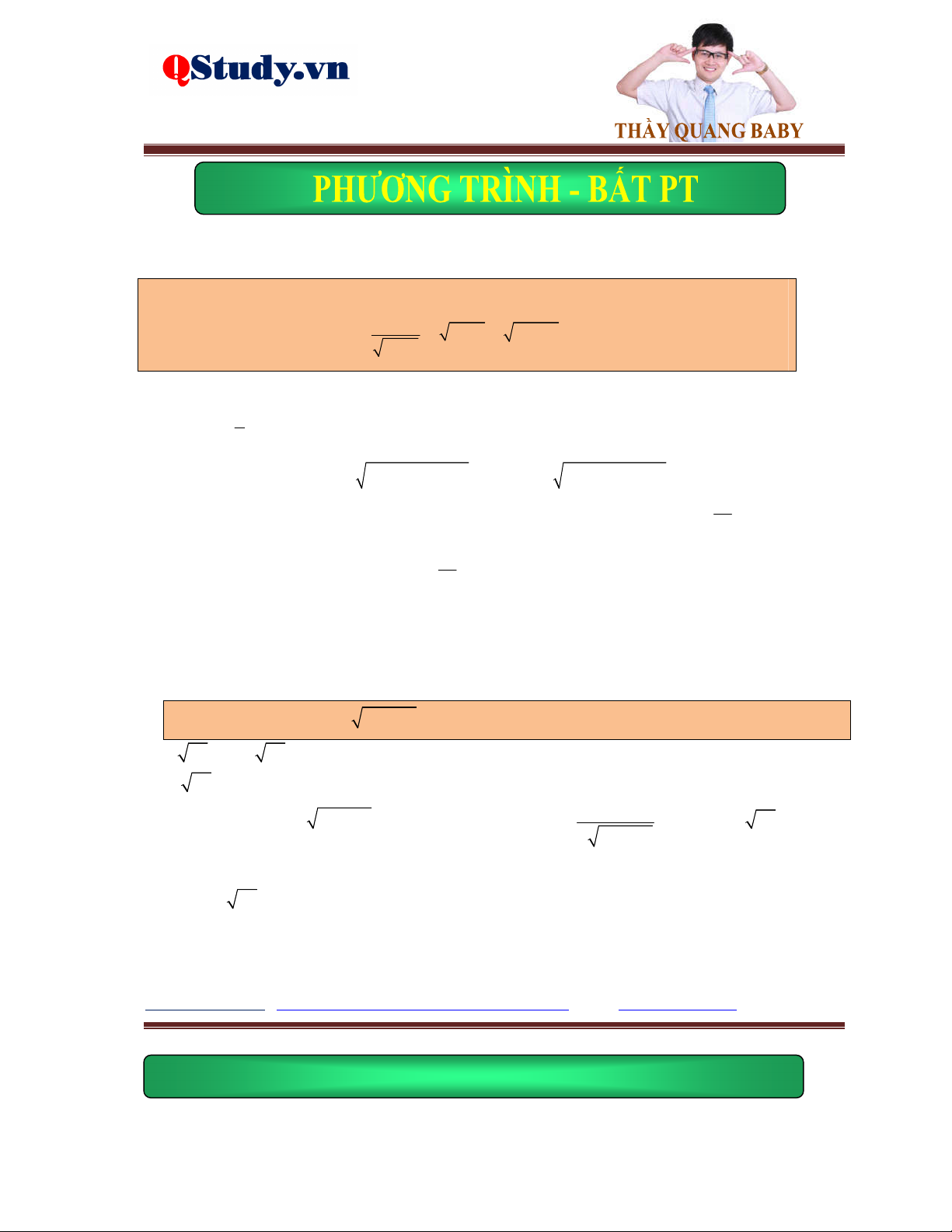
Dạng 2. Đặt ẩn phụ đưa về hệ phương trình đối xứng hai ẩn.
Ví dụ. Giải phương trình 2
x  2x  2 2x  1 x  1
Lời giải. Điều kiện: x  . Đặt y  2x  1  0 , khi đó 2 y  2x  1. 2 
x  2x  2y    x   2 2 1  2y  1
Và phương trình đã cho trở thành    2     2 y 2x 1 
y  2x   1  1   2 a   2y  1 
Với a x  1 thì hệ phương trình trên 2 2  
a y  2y  2a 2
y  2a 1         a y a y a
y  2a y  0  a ya y  
2  0  a y  20   x     1 x 1 2x 1       x  
x  1  2x 1  0   x 2 2 2 1  2x  1  
Vậy phương trình đã cho có nghiệm là x  2  2 .
Bài toán tổng quát. Giải phương trình        2 e bcax b c dx
e x
x  với d  ac   1
a  2; b  1  ; c   1 1 Chọn 2       ta được 2x 1 x 2 1 . 1  2 2
  0;   ; d  1; e  1   2 1 2 a c c  Hoặc phương trình 2
ax b x cx d x   với b ad  1        a 2 2   1 2 ac Xét hàm số 2
y x cx d có đạo hàm y'  x c  0  x   . a a 2 ac
Khi đó bằng phép đặt ax b y
, ta sẽ đưa phương trình về được dạng hệ phương trình 2 đối xứng quen thuộc. x
Ví dụ 1. Giải phương trình 2 29 12 61 3x x   x   6 36
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 8
Tất cả vì học sinh thân yêu 1
Làm nháp. f x 2 29  3x x   f ' 
x  6x  1  0  x   . 6 6
Lời giải. Điều kiện: 12x  61 0 . 12x  61 1 12x  61 1 1 Đặt  y  suy ra 2  y y  36 6 36 3 36 2 2
 12x  61 36y  12y  1  3y y x  5 29 1 Mà theo cách đặt ta có 2 2 3x x
y   3x x y  5 . 6 6  2
3x x y  5 
Do đó phương trình đã cho 2 2 
 3x  3y x y y x 2
3y y x  5  x y
 3x yx y 2x y 0  x y3x  3y   2  0   3x  2  y    3 1
 Với x y ta được 2 5
3x  5  x y  vì y   . 3 6 3x  2 x     Với y   ta được 2 3 2 1 14 3x x    5  x  . 3 3 3   1  14 5 
Vậy phương trình đã cho có các nghiệm là x   ;   . 3 3   
Dạng 3. Đặt ẩn phụ đưa về hệ phương trình đối xứng hai ẩn bằng phương pháp đồng nhất hệ số.
Ví dụ. Giải phương trình 2
4x  4x  3  2x  5 x   5 1
Lời giải. Điều kiện: x  . Đặt 2x  5  2y  1; y  . 2 2
Khi đó x    y  2 2 2 2 5 2
1  4y  4y  1  2x  5  4y  4y  4  2x .
Nên phương trình đã cho trở thành   2 2
4x  4x  3  2y  1 4x  4x  4  2y     1     2 2
4y  4y  4  2x  
4y  4y  4  2x 2  Lấy pt 
1  pt2 ta được 2 2
4x  4y  4x  4y  2y  2x
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 9
Tất cả vì học sinh thân yêu x y
 4x yx y  6x y 0  x y4x  4y  6 0   2x  3  y    2  1 y   1   17
 Với x y ta được  2  x y   .  2 4
2y y  2  0  2x  3  Với y  
ta được 2x  5  4  2x  0 2 x  2  9  37    x  . 2
 x  5 4  2x2 4    9  37 1   17 
Vậy phương trình đã cho có ba nghiệm là x   ;   . 4 4   
Phương pháp tổng quát. Đặt 2x  5  Ay B  0 với mục đích là đưa về hệ phương trình đối  f
 x,y 0  xứng hai ẩn dạng 
gx, y   0  Ta có
x   Ay B x   Ay  2 2 2 2 2 5 2 5
B A y  2ABy B  2x  5 Và 2
4x  4x  3  Ay B , khi đó ta được hệ phương trình:  2   2
4x  4x  3  Ay B
4x  4x  3  B Ay      2 2 2 2 2 2
A y  2ABy B  2x  5  
A y  2ABy B  5  2x
Để đưa về được hệ phương trình đối xứng hai ẩn, tức là hai giá trị x, y có vai trò như nhau. Nên
thế x y vào hệ phương trình trên ta có được:  2 4  A   2
4x  4x  3  B Ax 4  2AB A  2         2 2 2 2
A x  2ABx B  5  2x    3
  B B  5 B1  A2  1
Do đó ta có phép đặt 2x  5  2y  1; y  và được lời giải như trên. 2
Bài tập vận dụng.
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 10
Tất cả vì học sinh thân yêu
Vận dụng 1. Giải phương trình 2
9x  5  3x  2x  3 x  
Đáp số: phương trình vô nghiệm.
Vận dụng 2. Giải phương trình 2
x x  2004 1 16032x   1 x  
Đáp số: x  4009 . 4
Vận dụng 3. Giải phương trình 3 3 2
81x  8  x  2x x  2 x  3    3  2 6  Đáp số: x  0  ;   . 3   
Dạng 4. Đặt ẩn phụ phương trình chứa căn bậc ba đưa về hệ đối xứng. Phương pháp.
Đặt ẩn phụ bằng căn thức bậ ba. 
Biến đổi đưa về hệ phương trình đối xứng. Bài tập ví dụ.
Ví dụ 1. Giải phương trình 3 3 3 2
2. 3  2x  3  xx   3
Lời giải. Điều kiện: 3 x  . 2 Đặt 3
y  3  2x  0 suy ra 2 3 3 2
y  3  2x  2x y  3 .
Khi đó phương trình đã cho tương đương với: 3 3 2  3 2      3 2  2.y 3 x 2y  3  x 2
y x  3         3 2 3 2 3 2
2x y  3 2
 x y  3 2   
x y  3  3 3 2 2
 2x  2y y x  0  2x y 2 2
x xy y x yx y  0      y     x y 2   0 2 2
x xy y  x y  0  x y    y  1  3 2   2y y   3 
Vậy phương trình đã cho có nghiệm duy nhất là x  1 .
Ví dụ 2. Giải phương trình 3 3 2
2x  9  x  3x  13 x  
Lời giải. Điều kiện: x   . Đặt 3 3
y  9  x suy ra 3 3 x y  9 .
Khi đó phương trình đã cho tương đương với:
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 11
Tất cả vì học sinh thân yêu  3 3  3 3        3 3 x y 9 x y 9    x y  9         2
2x y  3x  13 
 2x y2 2 2 2  3x  13
x  4xy y 13   
a x y  Đặt 
nên hệ phương trình trên trở thành: b    xy       a   2 a 3  3 3 b 9
2a  6ab  18   2a  3a   2 13  a  18 a  3         2  2         2  a 2b 13 2b 13 a      b   2 2b 13 a  
x y  3  Từ đó suy ra 
 x; y   2; 1,1;  2   . xy   2 
Vậy phương trình đã cho nghiệm duy nhất là x  1,  2 .
Ví dụ 3. Giải phương trình 3 3 xx  3 3 25
x  25  x  30 x  
Hướng dẫn. Điều kiện: x   . Đặt 3 3
y  25  x suy ra 3 3
x y  25 .
Khi đó phương trình đã cho tương đương với:     
x y  25 
x y    x y2 3 3  2xy  25        
xyx y   30   xy
 x y 30 
Ví dụ 4. Giải phương trình 3 3 3 3
x  4  x  2  x 4  xx  
Hướng dẫn. Điều kiện: x   . Đặt 3 3
y  4  x suy ra 3 3 x y  4 .
Khi đó phương trình đã cho tương đương với:     
x y  4   x y
 x y2 3 3  2xy  4      
x y  2   xy  
x y  2   xy
Dạng 5. Đặt ẩn phụ đưa về phương trình đẳng cấp bậc cao.
Phương pháp. Đặt ẩn đưa phương trình vô tỷ về dạng  Đẳng cấp bậc hai 2 2
aA bAB cB  0 .  Đẳng cấp bậc ba 3 2 2 3
aA bA B cAB dB  0 .
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 12
Tất cả vì học sinh thân yêu
Xét các trường hợp để chia cả hai vế của các phương trình trên cho A hoặc B rồi đưa về ẩn A t
sau đó sử dụng lược đồ Hoocner. B Bài tập ví dụ. 3
Ví dụ 1. Giải phương trình 3 2
x  3x  2 x   6  18xx  
Lời giải. Điều kiện: x  6
 . Phương trình đã cho tương đương với:
x xx    x  3 3 3 6 2 6  0    Đặt 2
a x  6  0  x  6  a nên phương trình    trở thành: 3 2 3
x  3xa  2a  0
Nhận xét x  6 không là nghiệm của phương trình đã cho. Nên chia cả hai vế cho 3 a và đặt x t  suy ra 3
t  3t  2  0 . a
Sử dụng lược đồ Hoocner ta có 1 0 3 2 Từ đó suy ra 1 1 1 2 0 1 1 2 0 0     t 1 x a x x  6 x  3     
t t    t  2 3 3 2 0 1 t  2  0        t  2  x  2  a  
x  2 x  6  0 x  2  2 7  
Vậy phương trình đã cho có nghiệm là x  3;2  2 7 .
Ví dụ 2. Giải phương trình 3 3 3
x  1  x  2  2x  3 x  
Lời giải. Điều kiện: x   .  3 ax1  Đặt 3 3 
a b x 1  x  2  2x  3  . 3 b   x  2 
Khi đó phương trình đã cho trở thành: 3
a b a b  a b3 3 3 3 3 3 2 2 3 3 3
a b a  3a b  3ab b a b  3   x  1  0 a 0 
x  1; x  2   
 3aba    3
b  0  b  0   x  2  0    3  x      3 3 a b 0 
x  1  x  2  0  2 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 13
Tất cả vì học sinh thân yêu  3  
Vậy phương trình đã cho có các nghiệm là x  1  ;2;   .  2  
Ví dụ 3. Giải phương trình 2 2
x  2x  2x  1  3x  4x  1 x   1
Lời giải. Điều kiện: x  . 2  2 5
a x  2x  Đặt 2 2 
2  3a b  3 2
x  2x 2x   2
1  3x  8x  1  . b   2x 1  0 
Khi đó phương trình đã cho trở thành:
a b  3a b  a b2 2 2 2 2 2 2 2 2
 3a b  3a b a  2ab b  1 x  2 
 2a  2ab  0  aa b 2
 0  a b x  2x  2x 1   2  2 x  1  
Vậy phương trình đã cho vô nghiệm.
Dạng 6. Đặt ẩn phụ đưa về hệ phương trình đại số.
Phương pháp. Phương trình tổng quát dạng m   n
af x b cf  
x d k .
 af  xb u af     m
x b u acf   xm mbc cu  Đặt           cf    n
x d v
acf xn nad av cf x d v     m n
cu bc av ad . Nên phương trình đã cho trở thành: u
  v k 
 giải bằng phương pháp thế. m n cu
bc av   adBài tập ví dụ.
Ví dụ 1. Giải phương trình 3
2 3x  2  3 6  5x  8 x   6
Lời giải. Điều kiện: x  . 5  3   3
a  3x  2
a  2  3x   Đặt     5 3 a  2 3 2 6  b  . 2 b
  6  5x 0 6
 b  5x  
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 14
Tất cả vì học sinh thân yêu
2a  3b  8 
Khi đó phương trình đã cho trở thành: 5   3 a   2  3 2 6  b    8  2a    8  2a b   b      3 a  2     3    2          3 2  8 2a      b  4 3 5a 3b 8  5  a  3     8      3    3  3x  2 2  Nên suy ra   x  2  
là nghiệm duy nhất của phương trình.  6  5x  4 
Ví dụ 2. Giải phương trình 3 24  x  12  x  6 x  
Lời giải. Điều kiện: x  12 .  3  3
a  24  x
a  24  x   Đặt 3 2   
a b  36 . 2 b   12 x 0 b  12 x     a b  6 b   6  a  
Khi đó phương trình đã cho trở thành:   
a b  36   a 6  2 3 2 3 a  36  b   6  a     a;  b  0;6 , 3; 3 , 4  ;10 3 2       a
  a 12a   0  3  24  x  0   Với a; 
b  0;6 nên suy ra   x 24  .  12  x  6  3  24  x  3   Với a;  b  3;  3 nên suy ra   x  3  .  12  x  3  3  24  x  4   Với a; 
b  4;10 nên suy ra   x 88  .  12  x  10 
Vậy phương trình đã cho có nghiệm là x  3; 2  4;  88 .
Ví dụ 3. Giải phương trình 4 4
5  x  12  x  3 x 
Lời giải. Điều kiện: x  5 .
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 15
Tất cả vì học sinh thân yêu  4  4 a  5  x a   5  x   Đặt 4 4   
a b  17 . 4  4 b   12  x b  12  x  
Khi đó phương trình đã cho trở thành:   a b  3 b   3  a        4 a;  b 1;2 , 2;1 4 4     4
a b 17   a 3   a  17  4  5  x  1   Với a; 
b  1; 2 nên suy ra   x  4  . 4  12  x  2  4  5 x  2   Với a;  b  2;  1 nên suy ra   x  11   . 4  12  x  1 
Vậy phương trình đã cho có nghiệm là x  11;  4 .
Phương trình bậc cao – Kỹ thuật sử dụng lược đồ Hoocner
Lý thuyết. Xét phương trình bậc bốn 4 3 2
a x a x a x a x a  0 . 1 2 3 4 5
 Nếu a a a a a  0 , phương trình có một nghiệm là x  1 1 2 3 4 5 
Nếu có tổng hệ số chẵn bằng tổng hệ số lẻ thì phương trình có một nghiệm là x  1 .
Lược đồ Hoocner ( nhân ngang – cộng chéo ) a a a a a 1 2 3 4 5 x a A
a x a A
A x a A
A x a A A x a  0 0 1 1 1 0 2 2 2 0 3 3 3 0 4 4 4 0 5
Khi đó x là một nghiệm của phương trình đã cho, và ta phân tích phương trình ban đầu được thành 0
x x  3 2
A x A x A x A  0 . 0 1 2 3 4 
Phương trình bậc ba còn lại có nghiệm '
x và tiếp tục sử dụng lược đồ. 0
Ví dụ 1. Giải phương trình 4 3 2
2x  5x  3x  8x  4  0
Nhận xét: Tổng các hệ số của phương trình bằng 0 nên phương trình có một nghiệm là x  1 .
Lời giải. Do có một nghiệm x  1 nên tách theo lược đồ Hoocner ta có: 2 5 3  8 4 1 2 7 4 4 0 2  2 3 2  0 0
Khi đó phương trình đã cho trở thành x  x   2 1
2 2x  3x   2  0 .
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 16
Tất cả vì học sinh thân yêu  1 
Vậy phương trình đã cho có nghiệm là  x    2; ;1  .  2   
Ví dụ 2. Giải phương trình 5 4 3 2
4x  4x  21x  19x  20x  12  0 .
Nhận xét: Tổng các hệ số chẵn của phương trình bằng tổng các hệ số lẻ nên phương trình có một nghiệm là x  1  .
Lời giải. Do có một nghiệm x  1
 nên tách theo lược đồ Hoocner ta có: 4 4  21  19 20 12  1  4 8 13 32 12  0 2 4 0 13 6 0 0 1 4 2 12  0 0 0 2
Khi đó phương trình đã cho trở thành:
x  x   x  2 1 2 2
1 2x x   6  0  x  
1 x  22x   1 x   2 2x   3  0  1 3
Vậy phương trình đã cho có nghiệm là  x  2;2; ; 1  ;   .  2 2  
Ví dụ 3. Giải phương trình 4 2
x  9x  2x  15  0 .
Nhận xét: Đưa phương trình về dạng 2 f x 2
g x 0 .
Giả sử, tồn tại số thực m thỏa mãn
pt  x  2 2 2 2 2
m  2mx m  9x  2x  15  0  x  2 2
m  2m  9 2 2
x  2x  15  m  0
Xét đa thức bậc hai f  
x   m   2 2 2
9 x  2x  15  m , ta muốn đưa f  
x về dạng hằng đẳng thức bậc hai, thì trước hết '     0 . f x Ta có '    m   2 1 2
9 15  m      0 m
4 . Do đó phương trình đã cho trở thành f x
x  2 x  2 2    2
x x   2 4 1 0
5 x x   3  0 .
Lời giải. Phương trình đã cho tương đương với:
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 17
Tất cả vì học sinh thân yêu
x 8x 16x  2x  10 x 42 x  2 4 2 2 2 1  0  x  2 4 x  2 2 1  0   2 x x   5  2 x x   3  0  2
x x  5  0    1  13 1  21   x   ;   2
x x  3  0    2 2   
Vậy phương trình đã cho có các nghiệm kể trên. 2  1   36x
Ví dụ 4. Giải phương trình  2 x  4x   2 1      0   . x   x  22
Nhận xét: Đưa về phương trình          2 x a x b x c x d Ax . x  0
Lời giải. Điều kiện:  
. Phương trình đã cho tương đương với: x  2 
pt  x  4x  2x  2 1 x  22 2 3  36x  0
 x  4x  2x  3x  2 2 2 3 2  36x  0 2  2    2  x 4  
  x   3  36  0        x x     2
Đặt t x  , phương trình  
 trở thành: t  t  2 4 3  36  0 . x
Vậy phương trình đã cho có các nghiệm kể trên. 3 3
Ví dụ 5. Giải phương trình  2
x x    x    3 x   2 1 6 1
1 6x  17x   5
Nhận xét: Đưa về phương trình đẳng cấp bậc. 
Đẳng cấp bậc hai dạng 2 2 . a A  . b AB  . c B  0 .  Đẳng cấp bậc ba dạng 2 2 2 3 . a A  . b A B  . c AB  . d B  0 .
Lời giải. Giả sử tồn tại hai số m,n thỏa mãn: m  6 m  6 2  
6x  17x  5  m 2 x x  
1  nx   1     n   m  1  7 n   1    Và hằng đẳng thức 3
x   x   2 1
1 x x   1 .
A x 1  Đặt 
, khi đó phương trình đã cho trở thành: 2
B x x   1 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 18
Tất cả vì học sinh thân yêu 3 3
pt A B ABA   3 2 2 3 6 6
11B A  6A B  11AB  6B  0 A B  AB A 2  B A 3  B 0        A  2B  A   3B  x  0 
Với A B , ta được 2
x x  1  x  1   . x  2  3  13 
Với A  2B , ta được 2
x x  1  2x   1  x  . 2 
Với A  3B , ta được 2
x x  1 3x   1  x  2  6 .    3  13 
Vậy phương trình đã cho có nghiệm là x  0  ;2;2  6;   . 2    4x
Ví dụ 1: Giải phương trình sau x  3   4 x x  3 Lời giải
Điều kiện: x  0
Phương trình đã cho tương đương
x    x
x x     x   x 2 3 4 4 3 3 2  0 
x  3  2 x x  3  4x x  1
Vậy phương trình đã cho có tập nghiệm S    1
Ví dụ 2: Giải phương trình sau 2
x  4x  2  4 2x 1 Lời giải 1 Điều kiện: x  2
Phương trình đã cho tương đương
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 19
Tất cả vì học sinh thân yêu 2 2
x x    x      x    x  
x x   
x      x  2 2 2 4 2 2 1 4 2 1 4 2 1 4 2 1 2 1 2 1
  2x 1  2 * .
 2x 1  2  x 1
 2x 1  x  3
Phương trình * tương đương   
 2x 1  2  1  x
 2x 1  x  1  x  3  x  3
Với 2x  1  x  3      x  4  6 2x 1    x  32 2
x  8x  10  0  
Với 2x  1  x 1 
2x  1  x  1  0 vn
Vậy phương trình đã cho có tập nghiệm S  4  6 7 1
Ví dụ 3: Giải phương trình sau x 1   4x  2 x Lời giải
Điều kiện: x  1
Phương trình đã cho tương đương 2 2 2
8x  7x  2  x   x   2
1  x  2x x 1   x   2
1  9x  6x  1   x 1  x 2
x 1  x  3x 1
x 1  2x 1  3x  2 1
  x 1  x    
x  1  x  1  3x
x 1  1  4x  2
Với x   x   x    x   2 1 2 1 1 2 1
 4x  5x  2  0vn
Với x 1  1  4x
x 1  4x 1  0 vn
Vậy phương trình đã cho vô nghiệm 1 13  7x
Ví dụ 4: Giải phương trình sau 2
x x  2   x 2 Lời giải
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 20
Tất cả vì học sinh thân yêu
Điều kiện: x  0
Phương trình đã cho tương đương 2 2
2x x x  2  2  13x  7x   2 x x  2 2 2 2
 2x x x  2  x  9x 12x  4 2 2              x x   x2 x x 2 x 3x 2 x x 2 4x 2 2  3x  22 2     2 2  x x 2 x 2 3x      
x x  2  2  2x    1  1 x   x  Với 2
x x  2  4x  2  2    2  x  1 2
x x  2  4x  22 2 15 
x 17x  2  0   x  1  x  0 9  57 Với 2
x x  2  2  2x      x  2
x x  2   2  2x2 2
3x  9x  2  0 6     9  57  
Vậy phương trình đã cho có tập nghiệm S  1  ;  6     2x 2  x 2  
Ví dụ 5: Giải phương trình sau 3  x  2x 1 Lời giải 1 Điều kiện: x  2
Phương trình đã cho tương đương 2 2x   1
3  x  8x  4x  2x  2 2 2 1  22x   2 1 3  x   2 3  x  2
x  4x  4 2 2             x    x 2 2x 1 3 x x 2 3 x 3 x 2 1 3   x  22 2     2 2 2x 1 3 x x 2        3  x  3  x 1   x  3  x  3 Với 2
3  x  3  x      x  1 3  x   3  x2 2 x  1  
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 21
Tất cả vì học sinh thân yêu  1  1 x    x   Với 2 3  x  3  x 1  3    3  x  1  2 3   x   3  x  2 2 1 8
x  6x  2  0  
Vậy phương trình đã cho có tập nghiệm S  1;   1
Ví dụ 6: Giải phương trình sau 2
x x     x 2 2 1 2 1 x  2x 1 Lời giải Điều kiện: 2
x  2x 1  0
Phương trình đã cho tương đương 2
x  2x 1  2 1  x 2
x  2x 1  0   2 x  2x   1  2 1  x 2
x  2x  1   2 x  2x   2
1  x  2x  1 2 2              x   x x  2 x 1 x 2x 1 x 1 x 2x 1 2 1 2 1   x  2 2 1     2 2  x 1 x 2x 1 x 1        
x  2x 1  2  x   Với 2 2 2
x  2x 1  2  x  2x 1  4  x  2x  5  0  x 1 6;1 6 x  0 x  0 Với 2
x  2x  1  2x     vn 2 2 2
x  2x  1  4x
3x  2x  1  0  
Vậy phương trình đã cho có tập nghiệm S   1   6; 1   6
Ví dụ 7: Giải phương trình sau  x  2 1 x x  3  x  3 Lời giải
Điều kiện: 3  x  1
Phương trình đã cho tương đương
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 22
Tất cả vì học sinh thân yêu x  2 2
x  2x  3  x  3  2 x  2 2
x  2x  3  2x  6 2
  x  22  2 x  2 2
x  2x  3   2
x  2x  3  1   2
x  2  x  2x  3   1 2 2 x 2 x 2x 3 1       
x  2x  3  x  1     2 2
x  2  x  2x  3  1 
 x  2x  3  x  3   x  1   x  1 Với 2
x  2x  3  x  1      x  1  2 2
x  2x  3   x   2 2 1
x  2x 1  0   x  3   x  3  Với 2
x  2x  3  x  3      x  1 2
x  2x  3    x  32 2
x  4x  3  0  
Vậy phương trình đã cho có tập nghiệm S   1   2;   1
Ví dụ 8: Giải phương trình sau 4 2x 1  2 x 1  x  3 Lời giải
Điều kiện: x  1
Phương trình đã cho tương đương 2 2
x 1 1  2x 1  2  x  
1  2 x 1  1  2x  
1  4 2x 1  4   x 1   1
  2x 1  2   x 11 2 2x 1  Với x 1  1  2x  1  2  x 1  3 
2x 1  x 1  9  6 x 1  2x 1  6 x 1  x  9 x  9  x  9      x  27  6 17 36   x   1   x  92 2
x  54x  117  0  
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 23
Tất cả vì học sinh thân yêu Với x     x   x  
x    x  
x   x   2 1 1 2 2 1 1 2 1 1 3 2 2 1 2
1  1  2 2x  3x  1  3  3xx  1  x  1      x  1 4   2
2x  3x   1  9  2 1  x  2
17x 12x  5  0  
Vậy phương trình đã cho có tập nghiệm S  27  6 17  ;1 1
Ví dụ 9: Giải phương trình sau 2
1  x  1  x x  2 4 Lời giải
Điều kiện: 1  x  1
Phương trình đã cho tương đương 1 1 1 2 2 2 4
1  x  1  x  2 
x  2  2 1  x  4  x x   2 1  x  2 2  2 1  x  1  x  0 4 16 16 2      x   1  x  2 1 1 1 0 2 2 1  x  0    x  0 2 16 x  0 
Vậy phương trình đã cho có tập nghiệm S    0
Ví dụ 10: Giải phương trình sau 2 2
1  x  2x
4x 1  2x  1 Lời giải 1 Điều kiện: x  2
Phương trình đã cho tương đương
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 24
Tất cả vì học sinh thân yêu 2 4x   2 2 2
1  2 4x 1  1  2x  
1  2 2x  1  1   2 4x 1   1   2x 1   1  1 x    2 2 2 2  4x 1 
2x  1  4x  1  2x  1  4x  2x  2  0    x  1  1  x  1  ;      2 
Vậy phương trình đã cho có tập nghiệm S    1
Ví dụ 11: Giải phương trình sau 2
2x x  7  2x 2x 1  4 x  3 Lời giải 1 Điều kiện: x  2
Phương trình đã cho tương đương 2
2x x  2x 2x  1  x   x  3  4 x  3  4  0  x 2x 1 2 2x 1  
1   x  3  4 x  3  4  0
x 2x 1 1  0 2 2   2     x
x      x    2x 1 1 2 1 1 3 2  0      x  1     x   2 x 3 4 3 2  0  
Vậy phương trình đã cho có tập nghiệm S    1
Ví dụ 12: Giải phương trình sau 2
x  13x  28  4  x  4 x  3  2 2x 1 Lời giải 1 Điều kiện: x  2
Phương trình đã cho tương đương
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 25
Tất cả vì học sinh thân yêu 2
x  4 x  7  4 x  4 x  3  2x 1 2 2x 1 1  0   x  4x  7  4 x  3   2x 1   1  0 2  x  4 x  3  2  0 2 2       x  3  2
  x  4 x  3  2   2x 1   1  0      x  1    x   2 2x 1  1 2 1 1  0  
Vậy phương trình đã cho có tập nghiệm S    1
Ví dụ 13: Giải phương trình sau  x   x    x   2 2 1 3 2 2 2 1
2  x x  9x  4 Lời giải 3 Điều kiện:  x  2 2
Phương trình đã cho tương đương  x  
1 3x  2  2 x   1
3x  2   x   1  2x  
1 2  x  22x   1
2  x  2x 1  0   x  
1 3x  2  2 3x  2   1  2x  
1 2  x  2 2  x   1  0 2  x 1 3x  2 1  0 2 2        3x  2  1   x   1  3x  2   1  2x   1  2  x   1  0      x  1 2   x    x    2  x  1 2 1 2 1  0  
Vậy phương trình đã cho có tập nghiệm S    1
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 26
Tất cả vì học sinh thân yêu TUYỂN CHỌN 2016
Bài 1: Giải phương trình: 2
2x 1  4x  24x  29  0   1 Bài giải: 1
Điều kiện: x    2 Đặt 2 t
2x 1, t  0  2x t 1 2
Ta được phương trình: t   2 t     2t   4 2 1 12
1  29  0  t 14t t  42  0 t  2 t  3  loai  
 t  t   2 t t   1 29 2 3 7  0  t  loai  2  1 29 t   2 3
Với t  2  x  2 1 29 13  29 Với t   x  2 4   3 13  29  
 Vậy phương trình có nghiệm x   ; . 2 4    
Bài 2: Giải phương trình: 2
4x x  6  1 2x  5 x 1   1 Bài giải:
Điều kiện: x  1   x 1   1   x 1 2
4x x  6 1 2x x 1 2 
4x x  6  1 2x  5 x 1 3   x 1 2
4x x  6 1 2x
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 27
Tất cả vì học sinh thân yêu
x 1  0  x  1  (TM )   2
 4x x  6 1 2x x 1 2   1 x  2  7
Kết hợp (1) và (2) ta được 2 x 1  2x 1   2  x  ( Thỏa mãn ) 2 2
4x  8x  3  0    2  7  
 Vậy phương trình có nghiệm x   1  ; . 2    
Bài 3: Giải phương trình: 3 5  x  3 5x  4  2x  7   1 Bài giải: 5 Điều kiện:  x  5  4
 3 5  x  7  x  3 5x  4  x  0  2 2 3 4   5 4 5x x     x x     0
3 5  x  7  x 5x  4  x  
   x x2 1 3 4 5     0
 3 5 x 7 x 5x 4        x  2
 x  5x  4  0 ( Do  )
x  1 ( Không thỏa mãn) hoặc x  4 ( Thỏa mãn )
 Vậy phương trình có nghiêm x  4.
Bài 4: Giải phương trình: 2
3x  8x  3  4x x 1   1 Bài giải:
Điều kiện: x  1  
  x     x x  2 2 2 1 2 1
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 28
Tất cả vì học sinh thân yêu x  1  2
x  6x  3  0   x  3  2 3
2 x 1  x 1      1  ( Thỏa mãn )  5  2 13 2 x 1  1 3   xx x  3    9 2  9
x 10x  3  0   5  2 13  
 Vậy phương trình có nghiệm x   ;3  2 3. 9    
Bài 5: Giải phương trình 2
8x  10x 11  14x 18  11   1 Bài giải: 11 ĐK: x   10     2 1
4 2x x  
1   10x 11  2x  3   14x 18  2x  4  0 2 2 2x x   1 2 2 2x x 1 2 
 42x x   1    0
10x 11 2x  3
14x 18  2x  4 1 2
)2x x 1  0  x  1   x  (tmđk) 2 1 1
) f x  2    0
10x 11  2x  3
14x 18  2x  4 11  11  
Ta có: f ' x  0 x     f(x) đồng biến trên ;    10  10   11 
Từ đó f x  f   0  
nên trường hợp này vô nghiệm.  10   1 
 Vậy phương trình có nghiệm x   1  ; .  2 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 29
Tất cả vì học sinh thân yêu
Bài 6: Giải phương trình: 3 2
6 x 1  2x x  2  2x x  8   1 Bài giải: Điều kiện: x  2   Xét 3 2
2  x  1  6 x 1  2x x  2  2 3  7  2x x  8 nên (1) không có nghiệm trên  ;   1 4  x  2 x 10x  4 3   2
Xét x  1 , khi đó 6 x 1  2x x  2  2 x   1 1  1  x  2 2 2 x 10x  4 3 2 Mà 2
 2x x  8 
x  2  0. Do đó (3) xảy ra khi và chỉ khi x = 2. 2 2
 Vậy phương trình có nghiệm x  2.
Bài 7: Giải phương trình: 2 3 x 1 
x  6x  6  x   1 Bài giải: x 1  0 Điều kiện:   2
x  6x  6  0  2
 3 x 1  x x  6x  6 2 2
 9(x 1)  2x  6x  6  2x x  6x  6 2 2 2 2
 (15x 15  2x )  4x (x  6x  6)
 (x  5)(x 1)(4x  5)  0
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 30
Tất cả vì học sinh thân yêu  x  1  x  5   x  5  
. Đối chiếu điều kiện ta được 5  x   5  4 x   4  5 
 Vậy phương trình có nghiệm x   ;5.  4 
Bài 8 : Giải phương trình;  2
x   x   x   x   2 1 2 2 6 11
x  2  x   1 Bài giải: Điều kiện: x  2       2 x x   3 2 1 6 12
x  2  2x x  2x
Với x = 0 => phương trình vô nghiệm  6 12  x  2 x  2 
6 x  2  x  2 x  2
Với x  0 ta có: 1   2    1  2  2  2  2  2  x x x x x x x   x  2 Đặt  t . Ta có: x   2 2  1 6t  2 3 2 3 2
t  2  t  6t t  2  t  6t t t  2  0  t     2
6t  3t  3  0  3  x  0  9  377 2 x  0   x   TM   t
 3 x  2  2x     2 8 3 4x 9x 18 0       9  377 x  loai   8
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 31
Tất cả vì học sinh thân yêu 9  377
 Vậy phương trình có nghiệm x  . 8
Bài 9: Giải phương trình: 2
2x 1  5 x  2x  7 x  7  0   1 Bài giải: 1 Điều kiện:   x  5  2 +) Phương trình  2
2x 13 1 5 x  2x  7x  4  0 2x 8 x  4  
 (x4)(2x 1)  0 2x 1  3 1 5 xx4  0    2 1    (2x 1)  0
 2x 13 1 5  x 2 1 Dễ thấy 
 (2x 1)  0 nên x = 4 2x 1  3 1 5 x
 Vậy phương trình có nghiệm x  4.
Bài 10: Giải phương trình: 2
4 y  2 y  3 
y 1  2 y   1 Bài giải: 2
4 y  2 y  3  0 Điều kiện:  * y 1  0 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 32
Tất cả vì học sinh thân yêu 1 13 Từ  
1  y  0 kết hợp điều kiện   y  4 2 y  2 y  2 2 
4 y  2 y  3  2 y  
1   y 1   1  0   0 2
4 y  2 y  3  2 y 1 y 1 1  2 1    y  2    0 2
 4y  2y  3  2y 1 y 1 1     2 1 1 13  y  2 ( vì   0 với  y  ) 2
4 y  2 y  3  2 y 1 y 1 1 4
 Vậy phương trình đã cho có nghiệm y  2.
Bài 11: Giải phương trình: 2
4x x  6  2x  1 5 x 1   1 Bài giải: Điều kiện: x  1  
Với điều kiện  thì : x 1   1 2 
4x x  6  (1 2x)  5 x 1   x 1 2
4x x  6 1 2x
x 1  0  x  1   2
 4x x  6 1 2x x 1 (2) 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 33
Tất cả vì học sinh thân yêu  1 x  2  7 Từ  
1 ,2  2 x 1  2x 1   2  x  ( Thỏa mãn ) 2 2
4x  8x  3  0    2  7  
 Vậy phương trình đã cho có nghiệm: x   1  ; . 2    
Bài 12: Giải phương trình: 3 x  6  2 4  x x  8 Bài giải: x  6  0 ĐK: 
 6  x  4 4  x  0  2
(x  6)  9(x  6) 4  4(4  x)
(1)   x  6  3 x  6   2  2 4  x   0    0
x  6  3 x  6 2  2 4  x
(x  3)(x  6) 4(x  3)  x  6 4     0  (x  3)   0  
x  6  3 x  6 2  2 4  x
x  6  3 x  6 2  2 4  x   x  6 4 
x  3 (nhận) Do   0 x  [ 6  ; 4]   
x  6  3 x  6 2  2 4  x
 Vậy phương trình có nghiệm : x  3
Bài 13: Giải phương trình: 3 5  x  3 5x  4  2x  7 Bài giải:
3 5  x  3 5x  4  2x  7 ĐK: 4 / 5  x  5 (*)
 3 5  x  (7  x)  3( 5x  4  x)  0 2 2 4  5x  x 3( 4   5x  x )    0 3 5  x  7 (  x) 5x  4  x
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 34
Tất cả vì học sinh thân yêu  1 3  2  (4  5x  x )    0  3 5 x (7 x) 5x 4        x  2
 x  5x  4  0 ( Do (*) ) x  1   ( Thỏa mãn ) x  4 
 Vậy phương trình đã cho có nghiệm x  1;  4 .
Bài 14: Giải phương trình: 3 2
x  2  3  x x x  4x 1 Bài giải: 3 2
x  2  3  x x x  4x 1 , Đ/K 2   x  3 2
x  2 3  x  2 3 2     
  x  2  3 x   3  x x  4x  4    x   1  2 x  4
x  2  3 x 3
2  x  23  x  4      x   1  2 x  4
x  2  3 x 3 x  23 x  2 2  2
x x  2    x  2 2
x x  2
x  2  3 x 3 x  23 x  2       2 2 
x x  2 x  2   0    
x  2  3  x  3 x  23 x  2 
     0  2
x x  2  0  x  2  x  1
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 35
Tất cả vì học sinh thân yêu
 Vậy phương trình đã cho có nghiệm: x   1  ;  2 .
Bài 15: Giải phương trình: 1
2x 1  3  2x  4  2 3  4x  4x
4x  4x 32x  2 2 2 1 4 Bài giải: 1 3 ĐK:   x  . Phương 2 2 2 2 2   2 2x 1 2x 1 trình:
 2x 1 3 2x  2x 1 3 2x                 (*)  2  2   Xét hàm số   2
f t t t trên 0;  
 có f t  2t 1  0 t   0;    nên hàm số f(t)
đồng biến trên 0;   
Do đó Phương trình  tương đương với:  x   f x    x   2 2 1 2 1 3 2  f    2     x  2 2 1 
2x 1  3  2x    x  
x    x  2 8 2 1 3 2 4 2 1 2   x    x  2 8 2 1 3 2  2x   1  3  2x   ( **) 
 2x  1  a  0 Đặt  thì phương trình (**) trở thành
 3  2x b  0  2  8  2 2 2 2
 a b  a b 2 2 2 8
 a b  a b   4a b (1)    2 2 a 2 2  b  4 
a b  4 2 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 36
Tất cả vì học sinh thân yêu
Từ (1)  a b 2 2 
a b  a b 2 2 8 16 4 2  4  a b   2 2
a b ab 2 2 4 4 4 2
 16  8a b a b (***)
Đặt ab = t 0  t  2 thì pt (***) trở thành 2 4
16  8t  16  8t t t t   2
2 t  2t  4  0
t  0 ( Thỏa mãn )  t  2
 ( Loại )  t  1 5 ( Loại )  1  t  
 2x 1  3  2x  2  2 Vậy t = 0    
 2x 1. 3  2x  0 3  t   2
Chú ý: HS có thể giải theo cách khác như sau
Đặt a  2x 1  3  2x . Phương trình đã cho trở thành
a a   2
a a   4 2 2 2
4 a  8a  8a  8  0
Bài 16: Giải phương trình: x  2 
x     x   2 3 2 9 3 4 2
1 x x   1  0 Bài giải:
Phương trình đã cho tương đương với: x  
x     x     x    2 2 3 2 9 3 2 1 3 2 1  2 x x   x   x 2 2 3 2 9 3 2 1 2 2 1 3               2 t
Xét hàm số f t t  2 ( )
t  3  2 ta có 2
f '(t)  t  3  2 
 0 suy ra hàm số đồng 2 t  3
biến  f 3x  f  2  x   1 1
Từ đó suy ra 3x  2
x 1  x   . 5
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 37
Tất cả vì học sinh thân yêu 1
 Vậy phương trình đã cho có nghiệm: x   . 5
Bài 17: Giải phương trình: 2
x x 1  (2x  3) (2x  2)  x  2 . Bài giải: TXĐ D = 1;
Phương trình  x 1) x   x 1) 3 2 ( 1 (
x 1  (2x  3)  (2x  3)  2x  3 (1) Xét hàm số 3 2 2
f (t)  t t t f'(t)  3t  2t  1  f'(t)  0, t   suy ra hàm số f(t) đồng biến trên  .
Phương trình (1) có dạng
f ( x  1)  f (2x  3) . Từ hai điều trên phương trình (1) 
x 1  2x  3 x  3 / 2 x  3 / 2      x = 2 2 2
x 1  4x 12x  9
4x 13x  10  0  
 Vậy phương trình đã cho có nghiệm x    2 .
Bài 18: Giải phương trình:  2 x x
 x     x   x    3 2 5 5 10 7 3 2 6 2
2  x  2x  5x 10   1 Bài giải: Điều kiện: x  2   2
 5x  5x 10 2x  6 
Với điều kiện  thì   1   x  2      x  2 2 x  5  x  7  3 x  2  2 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 38
Tất cả vì học sinh thân yêu x  2  0 2
 5x  5x 10 2x  6    x  2 2   x  5  0    2 5x  5x 10 2x  6 2   x  7  3 x  2  2    x  5  0  x  7  3 x  2  2
) x  2  0  x  2 ( Thỏa mãn ) 2 2 5x  5x 10 2x  6 5x  5x 10 2x  6 ) 2 2   x  5  0    x  5 x  7  3 x  2  2 x  7  3 x  2  2 2 2 5x  5x 10 2x  6 5x  5x 10 2x  6     x  7  3 x  2  2 5 2   1 1   1 1 2 
 5x  5x 10     2x  6   0    x  7  3 5   x  2  2 2   1 1   0  x  7  3 5  
Với điều kiện  thì 2x  6  0 và 2
5x  5x 10  0 x   R  1 1    0   x  2  2 2
 Phương trình vô nghiệm.
 Vậy phương trình đã cho có nghiệm x    2 . 2 2  y 1  y 1  y 1 
Bài 19: Giải phương trình: 2 y .  . y  13. 1       1 7  y 7  y 7  y     Bài giải:
Điều kiện: y  7 
Với điều kiện  thì:
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 39
Tất cả vì học sinh thân yêu   2 2 2 1 2
y y  
1  y y  
1 7  y   13 y   1  7  y  4 3 2
y y  5 y  33y  36  0  y  1
  y   y   2 1 3
y  5 y 12  0   ( Thỏa mãn ) y  3 
 Vậy phương trình đã cho có nghiệm y  1;  3 .
Bài 20: Giải phương trình: 3 2
x  2  3  x x x  4x 1   1 Bài giải: Điều kiện: 2
  x  3 
Với điều kiện  thì: 2 x  2 3  x  2 3 2     
1   x  2  3  x   3  x x  4x  4    x   1  2 x  4 x  2  3  x  3
2  x  23  x   4      x  2 2 ( x x  2)
x  2  3  x  3 x  23 x  2 2
2( x x  2)    x  2 2
x x  2  0
x  2  3  x  3 x  23 x  2     2 x x  2 2  x  2      x  2  3  x  3 0
x  23  x  2  0 (vi x  2 )  x  2  2
x x  2  0  ( Thỏa mãn )   x  1
 Vậy phương trình đã cho có nghiệm x   1  ;  2 .
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 40
Tất cả vì học sinh thân yêu
x  8 x  4
Bài 21: Giải phương trình:  x 1 x 1  3   1 2    x  4x  7 Bài giải:
Điều kiện: x  1  *
x 8 x  4  x   1  x  8
Với điều kiện * thì   1   2 x  4x  7 x 1  3 x  8   x  4 x 1   2 2  
 x  4x  7 x 1  3
    x    x     x   2 2 1 3 4
1 x  4x  7  x
 x 2  x     x 2 1 3 1 3 2 3 . 2 3             (3)      
Xét hàm số f t   t   2
3 t  3 với t   có f t   t  2 ' 3 1  0 t    nên
f t  đồng biến trên  . x  2
Do đó 3  f x 1  f x  2  x 1  x  2   2
x 1  x  4x  4  x  2 5  13    x  ( Thỏa mãn ) 2
x  5x  3  0 2    5  13  
 Vậy phương trình đã cho có nghiệm x  8  ; . 2    
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 41
Tất cả vì học sinh thân yêu
Bài 22: Giải phương trình: 3
x  2  15  x 1   1 Bài giải:
Điều kiện: x  2  
Với điều kiện  thì   1 3 
x  2  3  2  15  x  0 3 
x  2  3  2  15  x  0      1 1    x  7   0   x  2  3 4  2 x 15    x 152 3 3        0 
x  7  0  x  7 ( Thỏa mãn )
 Vậy phương trình đã cho có nghiệm x  7. 2
Bài 13: Giải phương trình x x  4   x  4 x  4  2x x  4  50 . Bài giải: Điều kiện x  4   2 x
x  4   x  4  2  2x x  4  50   2 x
x  4   2x x  4  48  0
Giải phương trình  x x  4  5
Giải phương trình: x
x  4  5  x  5
 Vậy phương trình đã cho có nghiệm x  5.
Bài 23: Giải phương trình: 2
3x  8x  3  4x x 1   1
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 42
Tất cả vì học sinh thân yêu Bài giải:
Điều kiện: x  1  
Với điều kiện  thì   x  1   2
x  6x  3  0     x  3  2 3
2 x 1  x 1   
  x     x x  2 2 1 2 1 2 1     1   5  2 13
2 x 1  1 3x  x x   3    9 2  9
x 10x  3  0 
Cả 2 nghiêm đều thỏa mãn điều kiện   5  2 13  
 Vậy phương trình đã cho có nghiệm x   ;3  2 3. 9    
Bài 24: Giải phương trình: 2
4x x  6  (1 2x)  5 x 1   1 Bài giải:
Điều kiện: x  1  
Với điều kiện  thì: x 1   1   x 1 2
4x x  6 1 2x
x 1  0  x  1   2
 4x x  6 1 2x x 1 (2) 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 43
Tất cả vì học sinh thân yêu  1 x  2  7
Kết hợp (1) và (2) ta được 2 x 1  2x 1   2  x  2 2
4x  8x  3  0  2  7
Thử lại ta có: Phương trình đã cho có 2 nghiệm: x  1  ; x  2   2  7  
 Vậy phương trình đã cho có nghiệm x   1  ; . 2     5 4 3
2x  3x 14x  2 
Bài 25: Giải phương trình:   4 3 2
4x 14x  3x  2 1     1 x  2  x  2  Bài giải:
Điền kiện: x  2 (*). PT 3 2 4 3 2
 x (2x  3x 14)  (4x 14x  3x  2) x  2  2 3
x (x  2)(2x  7)  x  2  2 4 3 2
 (4x 14x  3x  2)(x  2  4) 3
x (x  2)(2x  7)  x  2  2 4 3 2
 (4x 14x  3x  2)(x  2)
x  2  0  x  2 (TM (*))   3 x (2x  7)   x  2  2 4 3 2
 4x 14x  3x  2 (1)  3 4 3 4 3 2 1
( )  x (2x  7) x  2  4x 14x  4x 14x  3x  2 3 2
 x (2x  7) x  2  3x  2
Nhận thấy x  0 không là nghiệm của phương trình  x  0. 3 2
Khi đó, PT  (2x  4  3) x  2   3 x x 2 3
 2(x  2) x  2  3 x  2   (2) 3 x x
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 44
Tất cả vì học sinh thân yêu Xét hàm số: 3
f(t)  2t  3t với t  .  Ta có: 2
f '(t)  6t  3  0 t  
 Hàm số f(t) đồng biến trên .   
Do đó ( )  f  x   1 1 2 2  f  x  2   x x  2  1  x  x    x  0 1   5    x  ( Thỏa mãn (*) ) 2 (
 x 1)(x  x 1)  0 2    1 5  
 Vậy nghiệm của phương trình đã cho là x   ; 2. 2    
Bài 26: Giải phương trình: 2
2x  6x 1  4x  5   1 Bài giải: 5
Điều kiện x    4
Với điều kiện  thì   2
1  4x  8x  4  4x  5  2 4x  5 1
  x     x   2 2 2 2 4 5 1  2x  2  4x  5 1 x  1   Trường hợp 1: 
x  2  3 ( Thỏa mãn )
 4x  5  2x  3  x  1   Trường hợp 2: 
x  1 2 ( Thỏa mãn )
 4x  5  1 2x
 Vậy phương trình đã cho có nghiệm x  1 2;2  3. 2 2 9
Bài 19: Giải phương trình:     1 3  x 1 3  4  5x x 10
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 45
Tất cả vì học sinh thân yêu Bài giải: 4
Điều kiện: 1  x   5
Với điều kiện  thì:  
1  2 x 106  x 1  4  5x   99  3 x 1  3 4  5x  x 1 4  5x 
x 1 45x 39 x 19 45x  4x   41  0  4  ( Do x  1; 
nên 9 x 1  9 4  5x  4x  41  0 ) 5    
x 1  4  5x  3  0 
x 1  4  5x  3  2 x 1. 4  5x  4  4x        x     x   x 1 0 x 1 1. 4 5x 2 1  0     x  0
 4  5x  2 x 1  
 Vậy phương trình đã cho có nghiêm x   1  ;  0 .
Bài 27: Giải phương trình: 4 2
x x   2 x x  3 3 2 4 2 1
 2  4x  2 x x   1 Bài giải: Điều kiện: x  . R 3 2 2 2 4 3
Phương trình tương đương x x    x x    x x x2  x4 2 1 2 2 1 2 2
Xét hàm số f t  t3  2t , t 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 46
Tất cả vì học sinh thân yêu
Ta có f t  t2 ' 3  2  0 t
   suy ra hàm số f t đồng biến trên  2  3 2 4  2 3
Phương trình 2 có dạng f x x    f x x
x x   x2  x4 2 1 2 1   3  
Nếu x  0 thay vào 3 không thỏa mãn 1 1 1
Nếu x  0 thì phương trình 3  x 3   2   x . Đặt 3
x t , ta có phương trình x x x 2  
t3  t    t  t2 2 0 1
t  2  0  t  1 ( Vì t2 1 7
t  2  t    0  ) 2  4   1 1 1   5 Với t  1   x  1 
x  1  x2 3
x 1  0  x  ( Thỏa mãn ) x x 2 1   5
 Vậy nghiệm của phương trình là x  . 2
Bài 28: Giải phương trình: 2
4 2  x  2 2x  4  9x 16   1 Bài giải: Điều kiện: 2
  x  2 
Với điều kiện  thì:
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 47
Tất cả vì học sinh thân yêu   1 2 2 2 2 2
 32  8x 16 2(4  x )  9x  8(4  x ) 16 2(4  x )  (x  8x)  0 x x Đặt: 2 t  2(4  x )
(t  0) ; PT trở thành: 2 2
4t 16t  (x  8x)  0  t   t    4 2 2 x
So sánh với điều kiện ta loại t    4 2 0  x  2 x  4 2 2 2(4  x )    32  x  2 2 x  3   9 4 2
 Vậy phương trình đã cho có nghiệm x  . 3
Bài 29: Giải phương trình:  3   x  2  x  2 5 1 1
4x  25x 18 Bài giải: Điều kiện: x  1    3   x  2  x  2 5 1 1
4x  25x  18 3 4 3 2
 5  5 1  x  4x  25x  18x 3 3 4 2
 25x  25  5 1  x  4x  18x  20   3 x   3   x   4 2 x x   2 25 1 5 1 4 16 16  2x  4    x 2 
x   x  2 3 3 2 2 5 1 5 1 2 4  2x  4   1 Hàm số   2
f t t t đồng biến trên 0; nên  f  3
x   f  2 (1) 5 1 2x  4
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 48
Tất cả vì học sinh thân yêu 3   x   2 5 1 2 x  2   x   2
x x     x     2 5 1 1 2 1 x x   1  2   Đặt: u x  1  0 và 2 v
x x  1  0  u 2  2  u   u    v
2 thành: 5uv  2 2 2
u v   2  5  2  0        v   v u 1    v 2 ux  1  Với  2 : 2
x  1  2 x x  1   ( Vô nghiệm ) v 2
4x  5x  3  0  u 1 x  1  5  37 Với  : 2 2 x  1 
x x  1    x  . v 2 2
x  5x  3  0 2  5  37
 Vậy phương trình đã cho có nghiệm x  . 2
Bài 30: Giải phương trình:  x   3 2 2
2x  3  x x x  2   1 Bài giải: 3
Điều kiện: x    2
Với điều kiện  thì:   2 1   x  
1  2x  3  x   1  4 
2x  3  2x  8  0 x  1    ( Thỏa mãn ) x  2 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 49
Tất cả vì học sinh thân yêu
 Vậy phương trình đã cho có nghiệm x   1  ; 2.
Bài 31: Giải phương trình: 2 2
7x  25x 19  x  2x  35  7 x  2   1 Bài giải: Điều kiện x  7
Phương trình tương đương 2 2
7x  25x 19  7 x  2  x  2x  35 . Bình phương 2 vế suy ra: 2
3x 11x  22  7 (x  2)(x  5)(x  7) 2 2
3(x  5x 14)  4(x  5)  7 (x  5)(x  5x 14) Đặt 2 a
x  5x 14;b
x  5 .( a ,b  0) Khi đó ta có phương trình a b 2 2 2 2
3a  4b  7ab  3a  7ab  4b  0   3a  4b
Với a b suy ra x  3  2 7 (t / m); x  3  2 7 (l) . 61  11137 61  11137
Với 3a  4b suy ra x  ( Thỏa mãn ); x  ( Loại ) 18 18   61 11137  
 Vậy phương trình đã cho có nghiệm x  3   2 7; . 18    
Bài 32: Giải phương trình: 2
3x x  3  3x 1  5x  4   1 Bài giải: 1
Điều kiện: x    3 Với điều  thì
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 50
Tất cả vì học sinh thân yêu   1  3 2
x x   x 1 3x 1   x  2  5x  4  0    1 1  2 x x 3   0   
x 1 3x 1
x  2  5x  4  2
x x  0  x  0 hoặc x  1 .
 Vậy phương trình đã cho có nghiêm x  0;  1 .
Bài 33: Giải phương trình: 3 5  x  3 5x  4  2x  7   1 Bài giải: 4 Điều kiện
x  5 ta ó c : 5
(3)  7  x  3 5  x  3(x  5x  4)  0
7  x2  95  x 3 2
x  5x  4    0
7  x  3 5  x x  5x  4   1 3 2 
x  5x  4   0  
 7  x  3 5  x
x  5x  4  1 3 2
x  5x  4  0 ( Vì 
 0 với mọi x thỏa mãn điều kiện )
7  x  3 5  x x  5x  4 x  1   ( Thỏa mãn ) x  4 
 Vậy phương trình đã cho có nghiệm x  1;  4 .
Bài 34: Giải phương trình 3(2 
x  2 )  2x x  6   1 Bài giải:
Điều kiện: x  2 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 51
Tất cả vì học sinh thân yêu
Với điều kiện  thì  
1  2 x  3  x  6  3 x  2  0 8 x  3  2 x  3   0
x  6  3 x  2 x  3  0  x  3  x  3    8    11 3 5 ( Thỏa mãn ) 2   0
x  6  3 x  2  4  x   
x  6  3 x  2  2 11    3 5  
 Vậy phương trình đã cho có nghiệm x   ;3. 2     2
Bài 35: Giải phương trình: x  4x  14  6 x  7  2x 3x  2  0   1 Bài giải: 2 Điều kiện: x   3                 2 1 2 6 x 7 x 16 x 4 3x 2 3x 2   x  4x  4  0       2 9x 2    x  4x  4  1  0    6 x  7  x  16 4 3x  2  3x  2          2 2 6x 2 4 3x 2 x 2     0 6 x  7  x 16 4 3x  2  3x  2    2 3x 2 1    2 2   2 x 2      0  6 x 7 x 16 4 3x 2 3x 2             x  2 ( Thỏa mãn )
 Vậy phương trình đã cho có nghiêm x  2. 2
Bài 36: Giải phương trình: x  2x  16  6 x  7  2x x  0   1
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 52
Tất cả vì học sinh thân yêu Bài giải:
Điều kiện: x  0  2 2  
1   x  7  3  x  x   0   x  7  3  0 x  2    
(vô lý)  PT vô nghiệm x  0 x  x  0  
 Vậy phương trình đã cho vô nghiệm.
Bài 37: Giải phương trình: x  2 
x     x   2 3 2 9 3 4 2
1  x x   1  0   1 Bài giải:
Điều kiện: x R
   x    x   
2      x  2 1 2 1 2 1 3 2 ( 3 ) 2  ( 3  x)  3 
f 2x   1  f  3  x
Xét f t t  2 ( )
t  3  2 có f '(t)  0, t  . 1
f là hàm số đồng biến nên: 2x  1   3x x   5 1
 Vậy phương trình đã cho có nghiệm x   . 5
Bài 38: Giải phương trình 4 2
32x  16x  9x  9 2x  1  2  0 trên tập số thực. Bài giải: 1 Điều kiện x
, phương trình đã cho tương đương 2
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 53
Tất cả vì học sinh thân yêu 4 2 2
32x  32x 16x 16x  7x  7  9  9 2x 1  0 2  32x  2 x  
1 16x x  
1  7(x 1)  9 1 2x 1  0 9 2  2x 2  
 32x x  
1 (x 1) 16x x   1  7(x 1)   0 1 2x 1  18    x   2
1 32x (x 1) 16x  7   0    1 2x 1   18    x   3 2
1 32x  32x 16x  7   0 (*)    1 2x 1  Ta có  32 3 32x   4  8  1  32 2 3 2 x   32x
 8  32x  32x  16x  7  27 2 4   16 16x   8   2 18
1  2x  1  1    18  1  2x  1 18 3 2
 32x  32x  16x  7   9  0. 1  2x  1 (*)  x  1 .
 Vậy phương trình có nghiệm x =1.
Bài 39 : Giải phương trình : 3 2 3
27x  2x  20x  4  4 1 x   1 Bài giải:
    x  3 3 1 3
1  4(3x 1)  x 1 4 x 1
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 54
Tất cả vì học sinh thân yêu Xét hàm số: g t
( )  t 3  t 4 liên tục trên R.
Ta có g'(t)  3 2
t  4  0  hàm số đồng biến trên R. Suy ra: g 3 ( x  )
1  g(3 x  1)  3x  1 3  x  1  27 3 x  27 2
x  9x  1  x  1 x  0 3 2
 27x  27x  8x  0   2
27x  27x  8  0(vn) 
 Vậy phương trình đã cho có nghiệm x  0.
Bài 40: Giải phương trình: 2
3x x  3  3x 1  5x  4   1 Bài giải: 1
Điều kiện: x    3   2
3 x x   x 1 3x 1   x  2  5x  4   0   1 1 2 
x x 3    0   
x 1 3x 1
x  2  5x  4  1 1 1 2
x x  0 ( Vì 3  
 0 với mọi x   )
x 1 3x 1
x  2  5x  4 3
x  0  x  1 ( Thỏa mãn )
 Vậy phương trình có nghiêm x  0;  1 .
x  8 x  4
Bài 41: Giải phương trình:  x 1 x 1  3   1 2    x  4x  7 Bài giải:
Điều kiện: x  1  
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 55
Tất cả vì học sinh thân yêu
Tiếp tục giải phương trình Xét hàm số Do đó hàm số đồng biến trên Từ Giải phương trình
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 56
Tất cả vì học sinh thân yêu   5  13  
 Vậy phương trình có nghiệm x  8  ; . 2     x 2
2( )  x x 16  x 1 
Bài 42: Giải phương trình: 2   x 1  3   1 2     x  4x  7  2 2  Bài giải:
Điều kiện: x  1   2 x  4x  32   1   x 1 x 1  3 2    x  4x  7  x  8
x  8 x  4  x   1  x  8     x  4 x 1 2 x  4x  7 x  1  3   2 2  
 x  4x  7 x 1  3
+) x  8  y  4 (tm).
+) pt     x    x     x   2 2 1 3 4
1 x  4x  7 2 2
x 1 3 x 1 3 x 2 3.x 2 3             (3)      
+) Xét hàm số f t   t   2
3 t  3 với t   có f t  t  2 ' 3 1  0, t   
nên f t  đồng biến trên  .
+) Mà pt(4) có dạng: f x 1  f x  2
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 57
Tất cả vì học sinh thân yêu x  2 Do đó 3 
x 1  x  2   2
x 1  x  4x  4  x  2 5  13    x  (T/M) 2
x  5x  3  0 2    5  13  
 Vậy phương trình đã cho có nghiệm x  8  ; . 2    
Bài 43: Giải phương trình: 2 3 3
3x  5x  2  2 x 1   1 Bài giải:
    x  3   x     3 x   3 3 1 1 2 1 1  2 x 1  x  0 Xét hàm số 3
g(t)  t  2t ta thấy g(t) đồng biến trên R nên từ (**) suy ra 3 3 x 1  x 1   x  1 
 Vậy phương trình có nghiệm x   1  ;  0 .
Bài 37: Giải phương trình: 2
x  9  3 x 1  2   1 Bài giải:
Điều kiện: x  3  2 x  25 3(x  5) 2 (1) 
x  9  4  3( x 1  2)   2 x  9  4 ( x 1  2) x  5   x  5 3   (2) 2
 x  9  4 ( x 1  2)
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 58
Tất cả vì học sinh thân yêu x  5 x  5 3 Do 2 x  3 
x  9  x    1 và  1  1 
x 1  x  2 2 x  4 x  9  4 ( x 1  2)
luôn đúng khi x  3 nên 2 vô nghiệm.
 Vậy phương trình đã cho có nghiệm x  5.
Bài 44: Giải phương trình: 2 2
x x 1  x x 1  7  3   1 Bài giải: Điều kiện: x  . R Xét hàm số: 2 2 f (x) 
x x 1  x x 1
Chứng minh hàm số đồng biến
Ta có nghiệm duy nhất x = 2
 Vậy phương trình có nghiệm x  2.
Bài 45: Giải phương trình:  x   x     x   2 3 3
1 x  2x  3 x 1  2   1 Bài giải: Điều kiện: x  1   x  3  
1   x  3 x  3   x   1  2 x  2x  3. x 1  2 x  3(TM )  
 x  3  x 1  2   x   1  2
x  2x  32  2    x    x  x     x 2 2 1 2 1 2 1 2 1 2                  
Xét hàm số f t   t   2
2 t  2 , t  0 có f 't  0 t   
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 59
Tất cả vì học sinh thân yêu
Suy ra f t  đồng biến mà f x 1  f x   1 
x 1  x 1 x  1    x  3 ( TM ) 2 x  3x  0 
 Vậy phương trình đã cho có nghiệm x    3 .
Bài 46: Giải phương trình: 2
4 x  2  22  3x x  8   1 Bài giải: 22
Điều kiện: 2  x    1 3 4(x  2) 3(x  2) 
 (x  2)(x  2)  x  2  2 22  3x  4 x  2   4 3   (x  2)   0(2)  x  2  2 22  3x  4
Xét f(x) = VT(2) trên [–2; 21/3], có f’(x) > 0 nên hàm số đồng biến.
Suy ra x = –1 là nghiệm duy nhất của (2)
 Vậy phương trình đã cho có nghiệm x   1  ;  2 .
Bài 47: Giải phương trình: 3 2 2 2 2
x x x x 1  x x  4  (x  2)(x x)  3   1 Bài giải: Điều kiện: x  . R   2  x x    2
x x      2
x x   2 2 1 ( 1) 1 1 2
4  (x  2)(x x)  0 2 2 x x (x x) 2 2 2
x(x 1)  
 (x  2)(x x)  0 2 2
x x 1 1
2  x x  4
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 60
Tất cả vì học sinh thân yêu x(x 1) x(x 1) 2
x(x 1)(x 1)  
x(x 1)(x  2)  0 2 2
x x 1 1 2  x x  4  1 1  2
x(x 1) x 1   x  2  0   2 2 
x x 1 1
2  x x  4   1 1  2
x(x 1) x x 1   0   2 2 
x x 1 1
2  x x  4 
x(x 1)  0 (2)   1 1 2
x x 1   0 (3) 2 2 
x x 1 1
2  x x  4 2  1  3 Vì 2
x x  1  x    0; x       2  4 1 1 Nên 2
x x  1    0; x    2 2
x x  1  1 2  x x  4
Suy ra phương trình (3) vô nghiệm x  0
Giải phương trình (2): x(x  1)  0   ( Thỏa mãn) x  1  
 Vậy phương trình có nghiệm x   1  ;  0 .
Bài 48: Giải phương trình: 2
3x x  3  3x 1  5x  4   1 Bài giải: 1
Điều kiện: x   * 3   2
3 x x   x 1 3x 1   x  2  5x  4   0
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 61
Tất cả vì học sinh thân yêu    1 1  2 x x 3    0   
x 1 3x 1
x  2  5x  4  x  0 2
x x  0   ( Thỏa mãn ) x  1 
 Vậy phương trình đã cho có nghiệm x  0;  1 .
Bài 49: Giải phương trình: 2 3 3
3x  5 x 1  8x  5  0   1 Bài giải:
* Phương trình tương đương với: 3 2 3 3 3
x  3x  3x 1 5x  5  x 1 5 x 1
  x  3   x   3 3 3 1 5
1  x 1 5 x 1 Đặt 3 3
x 1  u; x 1  v , phương trình trở thành: 3 3
u u v v  u v 2 2 5 5
u v uv  5  0  u v (do 2 2
u uv v  5  0 với mọi u, v) * 3 3 2
x 1  x 1  3x  3x  0  x  0  x  1 
 Vậy phương trình có nghiêm x   1  ;  0 .
Bài 50: Giải phương trình: x  2 log x  3  log x  2   x 1  2   3     1 Bài giải:
Điều kiện: x  3 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 62
Tất cả vì học sinh thân yêu x 1 x 1   1  log x  3  log x  2   log x  3  log x  2   0 5 2   3   2   3     x  2 x  2 x 1
Xét hàm số g x  log x  3  log x  2 
trên khoảng 3;  2   3   x 2 1 1 3 g ' x     0 x>3 
 hàm số g x đồng biến trên
x  3ln 2  x  2ln 3  x  22
khoảng 3;  . Phương trình 5  g x  g 5  x  5
 Vậy phương trình có nghiệm x  5.
Bài 51: Giải phương trình: 2 2
2x 11x  9  2 2x 1  2  2 2x 1  2x 11x 11   1 Bài giải: 2
2x 11x 11  0 *    1   2 4 2x   1   2 2x 11x   11 2    4 2 3 2
2  8x  4  4x 121x 121 44x  44x  242x 4 3 2  x x x x     x   3 2 4 44 165 250 125 0
1 4x  40x 125x 125  0
  x   x   2 1
5 4x  20x  25  0  x  1  x  1  x  5 
kết hợp điều kiện * ta được  x  5   5 x   2
 Vậy phương trình có nghiệm x  1;  5 . 2 2 2
Bài 52: Giải phương trình x 3x3 x 2 x 2 3  3
 3 x x  27
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 63
Tất cả vì học sinh thân yêu Bài giải:
Phương trình đã cho tương đương 2 2 x 3x3 x 2 2 2 2 2 3  3
x = 2x x3 x 2 x3  
x 3x   x 3 3 1 3 3 1 3 x   1  0 2   x 3x 2 
x 3x   2x2x3   3 1  0 3 1 3 1  0  2  x 2x3 3 1  0  2 x 3x 2 x  0 3
 1  x  3x  0  x  3  2 x 2 x3 2  x  1 3
 1  x  2x  3  0   x  3  
Vậy phương trình đã cho có 4 nghiệm x  0; x  1  ; x  3 
Bài 53: Giải phương trình: 3 3
3x  3  5  2x x  3x 10x  26   1 Bài giải: 5
Điều kiện: 1  x   2  
1   3x 3   3  1 52x 3 2
x 3x 10x  24 x  2(TM ) 3 x  2 2 x  2 2     x  2 2 x x 12  2  3 
x x 122 3x 3 3 1 5 2x      1 5  2x  3x 3 3 5
Phương trình (2) vô nghiệm vì với 1  x  thì 2
x x 12  0. 2
 Vậy phương trình có nghiệm x  2.
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 64
Tất cả vì học sinh thân yêu
Bài 54: Giải phương trình: 4 2
2x 1  2x 1 
x 1  x  2x  3   1 Bài giải:
Điều kiện: x  1. Đặt 4
a  2x 1 (a  0) , ta có: 4
2x a 1 . Phương trình đã cho trở thành: a a  
x    x  4 4 2 1 1  2 (1) 3 2t 4
Xét hàm số f (t)  t t  2 với t  0 Ta có f '(t)  1  0, t   0. 4 t  2
Suy ra hàm số f (t) đồng biến trên0;  . 4
(1)  f (a)  f ( x 1)  a x 1  2x 1  x 1   x  1  x  1       x  2  2 . 2
x  4x  2  0  x  2  2  
 Vậy phương trình đã cho có một nghiệm là x  2  2
Bài 55: Giải phương trình: 3 3 2
3x  5  x  3x x  3   1 Bài giải:   3 3
1  3x  5  3x  5  (x 1)  (x 1) 3 2
Xét hàm số f (t)  t t, R f '(t)  3t 1  0, t
  R . Suy ra hàm số f(t) đồng biến trên R.  x  1 3 3 3 2
(*)  f  3x  5   f (x 1)  3x  5  x 1  x  3x  4  0   x  2  
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 65
Tất cả vì học sinh thân yêu
 Vậy phương trình có nghiệm x   2   ;1 .
Bài 56: Giải phương trình: 2 2
x  4  x  2  3x 4  x   1 Bài giải: ĐK: 2   x  2 . 2 t  4 Đặt 2 2 2 2
t x  4  x t  4  2x 4  x x 4  x  . 2  t  2 2 t  4 Phương trình trở thành 2 t 2 3 3t 2t 8 0         4 2 t    3 Với t = 2 ta có:  2  x  0  x  0 2 2
x  4  x  2 
4  x  2  x    (t/m) 2 2 
4  x  4  4x x x  2   4 Với t   ta 3   4 4 x    4 4  x    3 2   14 có 2 2
x  4  x    4  x    x   3    x  3 3 2  2   14 3 9
x 12x 10  0 x      3 (t/m). 2   14
 Vậy pt đã cho có nghiệm x = 0; x = 2; x  3
Bài 57: Giải phương trình: 3 3 2
3x x 1  x x 19x 16 Bài giải: Điều kiện: 3
x 1  0  x  1
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 66
Tất cả vì học sinh thân yêu
Phương trình đã cho tương đương với
x x   2
x x     3 x     2 3 1 1 1 x x   1 18 x   1 Đặt 2 a x 1, b
x x 1, a  0,b  0 . Khi đó phương trình trở thành  2 a   2 2 2 2 3
1 ab a b b 18a 2
a b a b  b a b   2 2 3 3 2 b  9a
  a b 2 3
a b b  6a   0
 3a b  0 , vì 2
a b b  6a  0 Suy ra 2 2 3 x 1 
x x 1  x 10x  8  0  x  5  33 , thỏa mãn điều kiện
 Vậy nghiệm của phương trình là x  5  33
Bài 58: Giải phương trình: 2
x x   x   2 2
x  2x  3   1 Bài giải:  2
x x x  2  0    
x x2   x  22  x  2 1  2 x  22 2   2
x x x  2  0    
x x2   x x  22  2 x  22 2 2   2  x x  x  2  0   2
x  2x  6  0   x  1 7
 Vậy phương trình đã cho có nghiệm x  1 7 .
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 67
Tất cả vì học sinh thân yêu
Bài 59: Giải phương trình: 2
x  4  x  4  2 x 16  2x 12   1 Bài giải:
Điều kiện: x  4  2  
1   x  4  x  4   x  4  x  4  12  0 
x  4  x  4  4
Giải phương trình ta được x = 5
 Vậy phương trình có nghiệm x  5. 2 3 x  7
Bài 60: Giải phương trình: x     1 x 2 x   1 Bài giải: ĐK: x > 0 *
Với điều kiện trên phương trình đã cho tương đương: 3  1  3 7 2  x   2 1 x   x  7  2 1 x   x    xx x x 3 3 4 2 3 3  3  2  3   x   2 x    x   0  x   x   2    x   2   0 x x x x x x xx x       3 x   2  0   3   3 2  xx 2  x  0          x   x x       3 2  x    0  x x 2 2
x  4x  3  0
x  4x  3  0 x  1      . 3 
x  3x  4  0   x   1  2
x x  4  0 x  3  
 Vậy phương trình có 2 nghiệm x = 1; x = 3.
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 68
Tất cả vì học sinh thân yêu
Bài 61: Giải phương trình: 5 3
x x x x  3   1 Bài giải: Đặt t
x  0 có hàm số   10 6 3
g t t t t có g t  9 5 2 '
 10t  6t  3t  0 do t  0 Mà g   1  3  t  1 
x  1  x  1
 Vậy phương trình có nghiệm x  1.
Bài 62: Giải phương trình: (2x 1) 1  x  (2x 1) 1 x  2x   1 Bài giải: Điều kiện: 1
  x  1 
2x  1 x  1 x  
1   1 x  1 x   0 . 
a  1  x; a  0 Đặt 2 2 
 2x a b b
  1  x;b  0  Phương trình trở thành 2 2
(a b )(a b 1)  (a b)  0 a ba b (a b)[(a b)(a b 1) 1] 0            2 1  5 (a b) (a b) 1 0        a b   2
) Với a b  1  x  1  x x  0 ( Thỏa mãn ) 1 5 1 5 5  5
) Với a b
 1 x  1 x   x  TM  2 2 8
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 69
Tất cả vì học sinh thân yêu   5 5   
 Vậy phương trình có nghiệm x  0; . 8    
Bài 63: Giải phương trình 2
16x  96x  208 2 x  9  log
 2 3x  4  6x  3 5x  9 2
12x  16  45x  81 Bài giải: 4
Điều kiện x   3 2
16x  96x  208 Ta có 2 x  9  log
 2 3x  4  6x  3 5x  9 2
12x  16  45x  81 2 2
x  6x  13  log (x  6x  13) 2
 2 3x  4  3 5x  9  log (2 3x  4  3 5x  9 )(*) 2 1
Xét hàm số f (t)  t  log t,t  0, f '(t)  1 
 0 với mọi t>0 nên f (t) đồng biến trên (0; ) . 2 t ln 2 Từ (*) suy ra 2
f (x  6x  13)  f (2 3x  4  3 5x  9 ) nên 2
x  6x 13  2 3x  4  3 5x  9 2
x x  2 (x  2)  3x  4   3 (x  3)  5x  9   0     2 2 2(x x) 3(x x) 2
 (x x)    0
x  2  3x  4
x  3  5x  9  2 3 2 
 (x x) 1    0   
x  2  3x  4
x  3  5x  9  2 2 3 4
 (x x)  0 vì 1    0 x   
x  2  3x  4
x  3  5x  9 3
x  0; x  1
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 70
Tất cả vì học sinh thân yêu
Đối chiếu với điều kiện ban đầu suy ra phương trình có nghiệm x  0; x  1
Bài 64: Giải phương trình:  x  3  x  1 x   1  1   1 Bài giải:
Điều kiện: 0  x  1 *
Khi đó  x  3  x  1 x  
1  1  3 1 x  
1   x  3  x (2)
Ta thấy x = 1 là một nghiệm của phương trình (2)
Vói 0  x  1 thì 3 1 x  
1  3 còn  x  3  x   3nên (2) vô nghiệm.
 Vậy phương trình đã cho có nghiệm x  1.
Bài 65: Giải phương trình: 3 2 
x  2  3  x x x  4x 1   1 Bài giải: Điều kiện: 2   x  3 2
x  2 3  x  2 3 2     
   x  2  3 x   3  x x  4x  4    x   1  2 x  4
x  2  3 x3
2  x  23  x  4      x   1  2 x  4
x  2  3 x3 x  23 x  2 2  2
x x  2    x  2 2
x x  2
x  2  3 x 3 x  23 x  2       2 2 
x x  2 x  2   0    
x  2  3  x  3 x  23 x  2 
     0  2
x x  2  0  x  2  x  1
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 71
Tất cả vì học sinh thân yêu
 Vậy phương trình có nghiệm x   1  ;  2 .
Bài 66: Giải phương trình: 1
2x 1  3  2x  4  2 3  4x  4x
4x  4x  32x  2 2 2 1   1 4 Bài giải: 1 3 ĐK:   x  . Phương trình 2 2 2 2 2       x    x 2   x    x  2x  1 2x  1 2 1 3 2 2 1 3 2     2 2 2     Xét hàm số    2 f t t  t trên   0;  có
f 't  2t 1  0  t  0;  
 nên hàm số f(t) đồng biến trên   0;   x  
Do đó phương trình (2) trở thành : f x    x   2 2 1 2 1 3 2  f    2    2x  2 1 
2x 1  3  2x
 8 2x 1  3 2x   42x  2 1 2
 8 2x 1  3 2x   2x   1  3  2x 2  3   
 2x 1  a  0 Đặt 
thì phương trình (3) trở thành
 3  2x b  0  2 2 8 
 a b   2 2 a b  8 
 a b   2 2 a b  2 2  4a b 4    2 2 2 2 a b  4
a b  4  5 
Từ    a b 2 2  
b  a b 2 2 4 8 16 4a 2  4  a b   2 2 a b b 2 2 4 4 4 2a
 16  8a b a b 6
Đặt ab t 0  t  2 thì pt (6) trở thành
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 72
Tất cả vì học sinh thân yêu 2 4  t
t t t t   2 16 8 16 8
2 t  2t  4  0 t  0   1
t  2 loaix    
 2x 1  3  2x  2  2   . Vậy t  0    
t  1 5 loai 3 
 2x 1. 3  2x  0   x   
t  1 5 loai  2   1 3 
 Vậy phương trình có nghiệm x   ; .  2 2 
Bài 67: Giải phương trình: x  2 
x     x   2 3 2 9 3 4 2
1 x x   1  0   1 Bài giải:
Điều kiện: x R
  x     x   x   2 2 3x 2 9 3 2 1 3 2 1  2  x  
x     x     x    2 2 3 2 9 3 2 1 3 2 1  2 2 t
Xét hàm số f t   t  2t  2  2 ta có f 't 2  t  2  2   0 suy ra hàm số 2 t  2 đồng biến 1
Từ đó suy ra 3x  2
x 1  x   5 1
 Vậy phương trình có nghiệm x   . 5
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 73
Tất cả vì học sinh thân yêu
Bài 68: Giải phương trình:  2
x x   x     2 x x   2 2 2 1 2 1 8 8 1
x x  0  x   Bài giải: Đkxđ: 0  x  1   2        2        2    2 2x 2x 1 2x 1 8x 8x 1 2x 1 8x 8x 1
x x  2x   1   0   x   2
x x     2    2 2 2 1 5 5 1 8x 8x 1
x x  2x   1   0  2 2x   1  2
x x  2x   1  2
x x  2x   1    2 8x  8x   1 2x   1   2 8x  8x   1  2
x x  2x   1   0  2 x xx   x    2x x x   2   2 2 1 2 2 1 2 1 8x 8x 1 2x 1 8x 8x 1                    0   2
 x x  2x 1 *  2 x x 2x  1   22x  2 1 x x 1            0     22x   1   2
x x  1  0 **   1  
**  22x   2 1
x x 1  0 0  x     2   1 
+) Xét: f x  22x   2 1
x x 0  x     2 
4 x x  2x 1 2x 1
8x  8x 1 2    2 2 2
f ' x  2.2 x x  22x   1 .   2 2 2 2 x xx xx x  2  2  1  x   0; 4  2    f ' x 2 0 8x 8x 1 0          2  2  1  x   0; 4  2    
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 74
Tất cả vì học sinh thân yêu  2  2  1  1 
Có: f 0  0; f     ; f  0    4  2  2    1  1 
f x 1   0 x   0; => (**) vô nghiệm 2  2    2 2 2
4x  4x 1  x x 5
x  5x 1  0 5  5    *   1   1  x  (Thỏa mãn) x x    10  2  2 5  5
Vậy phương trình có nghiệm: x  10 Cách 3:
Điều kiện: x 0; 
1 . Phương trình đã cho tương đương với:
x    x   2
x x   2
x x    2 2 1 4 2 8 8 2 1 x x  0 2
 2x 1 x x  4x  2 2
x x  2x   1 4x  2 2 x x  0 2 2x 1 x x
4x 2 2x  2 1 x x  2 x x             0   2
 2x 1 x x  4x  2 2 x x  2
x 1 x x   0  2 2x 1 x x  1  4x 2 2 x x          0 *   2  1  1 1 Dễ thấy 2 2 x
 0  x x   x x     2  4 2 1
 1  2  4x 2
x x  2  4x.  1 2x x  0 (điều này vô lý). 2 1 1 Khi đó * 2
 2x 1 x x x   2 2 5
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 75
Tất cả vì học sinh thân yêu 1 1
Vậy phương trình đã cho có nghiệm duy nhất là x   2 2 5
Bài 69: Giải phương trình:  x   3 2 3 2 2 3
x  3x x  3  2 x 1  2x  3x  3x 14 x    Bài giải: Điều kiện: x  1 
    x    x   2 x   3 2 * 2 3 3
1  2 x 1  2x  3x  3x 14
  x    x   2
x     x    3 2 2 3 3 1 2
1 2  2x  3x  3x 18 2 x  3
 2 x  3  x  3 2 x     1    x  3 2
2x  3x  6 x 1  2  2 
  x  3 2  x  3   2 x   2 1 
 2x  3x  6  0   x 1  2   x  3   2
2  x  3 2 x   2 1 
 2x  3x  6  0 *  *  x 1  2 2 *  2
*  2x  3x  6  2  x  3 2 x   1  x 1  2
Có: x 1  2  2 x   1  2 2 
 1  2x  3x  6  2  x  3 2 x   1  1 x 1  2 2
x x    x   2 x   2 
x x    x   2 2 3 5 2 3 1 0 2 3 5 2 3 x   1 4 3 2 3 2
 4x 12x  29x  30x  25  4x 12x  4x 12
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 76
Tất cả vì học sinh thân yêu x x x x  
  x   x  2 4 3 2 2 4 8 17 26 13 0 4 13 1  0  x  1 
 Vậy phương trình có nghiệm x  1  , x = 3
Bài 70: Giải phương trình: 2
x  9  3 x 1  2   1 Bài giải:
Điều kiện: x  3  Cách 1: Đặt 2
x 1  u, u
2  x u 1 thay vào (1) ta có 4 2
u  2u  8  3u  2 2 4 2 2 4 2
u u   u
u   u u u
  u   3 2 2 8 9 12 4 7 12 12 0
2 u  2u  3u  6  0 u  2  0   3 2
u  2u  3u  6  0 
+ u  2  0  u  2  x  5TM  + 3 2
u  2u  3u  6  0 (4) ; u  2 Do u  2 nên 3 2
u  2u  3u  6  2u  2u  3u  6  u  6  0 suy ra (2) vô nghiệm
 Vậy phương trình có nghiệm x  5. Cách 2 2 x  25 3 x  5 2   2
x  9  4  3 x 1  2    0   3 2 x  9  4 x 1  2 x  5   x  5 3   2  x  9  4 x 1  2 ) x  5 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 77
Tất cả vì học sinh thân yêu x  5 3 x  5 x  5 3 3 )  5 x   3    1   2 2 x  9  4 x 1  2 x  4 x  9  4 2  2 x 1  2  (3) vô nghiệm.
 Vậy phương trình có nghiệm x  5.
Bài 71: Giải phương trình: 2
4x  5  2x  6x 1   1 Bài giải: 5
Điều kiện: x    4 PT x   x x    x
 2   x  2 2 2 4 5 4 12 2 4 5 1 2 2  1 x    x   x  vn 2 4 5 2 3     
x  1  2 loai
 4x  5  1  2x   x  1 2 
 Vậy phương trình có nghiệm x  1 2. 1 x 1  x  2 1
Bài 72: Giải phương trình: x    2x 1 2 4 8 Bài giải: 1 1 x 1 Điều kiện x  . Đặt u x  , v  ;u, v  0 2 2 4 u   v  0 u   v  0   Pt trở thành 2 2
u v  2u  2v     u v  2  2 2 2 u v  u v  2  0  
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 78
Tất cả vì học sinh thân yêu x  1  1 x 1  x  1  2
v u  0  x          x  7  2 10 1 x 2x 1 2 2 4 x  
x 14x  9  0    2 16 ( TM )
 Vậy nghiệm của phương trình là: x  7  2 10
Bài 73: Giải phương trình 3 x x   3 3
7 x x  7  3 2
 7x 12x  5x  6 Bài giải:
Phương trình đã cho tương đương với 3 3
x x   x x   3 7 3 7 x x  7  3 2
 8x  12x  6x  1
  x x  3   x  3 3 3 7 2 1 
x  7  x  1
x    x  3   x   2 7 1
1 x  4x  6  0  x 1  x  1 
 Vậy phương trình có nghiệm x  1  .
Bài 74: Giải phương trình x x  7   x  7 x  17   x  17 x  24  12  17 2 Bài giải: x  0 t  12 Điều kiện 
Đặt t x  12  
Phương trình trở thành: x  24   t  12  
f t   t 12t  5  t  5t  5  t 12t  5  12 17 2
Suy ra f t   f t
  , do đó f(t) là hàm số chẵn trên tập D   ;  1
 2  12;  nên chỉ
cần xét trên 12; 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 79
Tất cả vì học sinh thân yêu 2t 17 t 2t  17
Ta có f 't      0
2 t 12t  5
t  5t  5 2 t 12t  5
với mọi giá trị t 12;
Suy ra f(t) đồng biến trên 12;  , nên f t   12  17 2 có nhiều nhất một nghiệm thuộc 12;
Mà f 13  12 17 2 , suy ra t =13 là nghiệm duy nhất của phương trình trên 12; 
Do f(t) là hàm số chẵn nên t = -13 là nghiệm duy nhất thuộc  ;  12  .
 Vậy nghiệm của phương trình là x  1; x  2  5
Bài 75: Giải phương trình: 2
2x  6x  5 x  2 x 1 10  0 Bài giải: Điều kiện x  1
 . Phương trình đã cho tương đương với
  x   x    x     x x      x     x   x    x   x    x  2 2 2 5 2 1 2 1 2 4 4 0 2 2 4 2 1 2 1 2 1  0
 2 x  2  x  2  2 x  1  x  1  x  2  2 x 1  0   x  2  2 x  1 2 x  2  x  1  0        
x  2  2 x  1   2x  4  x  1  x  2
Xét 2 x  1  x  2    x  8 2 x  8x  0 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 80
Tất cả vì học sinh thân yêu x  2
Xét x  1  2x  4    x  3 2
4x 17x  15  0 
Vậy nghiệm của phương trình là x =3, x = 8
Chú ý: Có thể giải cách khác bằng cách đặt t
x  1 , từ đó phương trình đã cho được biến
đổi thành t  t   2 2
3 2t  5t  3  0
Bài 76: Giải phương trình 2 3
2x  11x  21  3 4x  4 Bài giải:
Phương trình đã cho được viết thành 2 x x    3 2 11 21 3
4x  4  2  6 12 x  3 2
 2x 11x  15  3 3 4x  4  2  
  x  32x  5  3 4x  42 3  2 4x  4  4 12
Xét phương trình 2x  5  (*) 3 4x  42 3  2 4x  4  4 Tam thức 2
2x  11x  21 có 2
  11  8.21  47  0 nên 2
2x  11x  21  0 x R . Suy ra
4x  4  0  x  1. 12 Đặt 3 t
4x  4, t  0; f t   2 t  2t  4 122t  2 Ta có f't  
 0 , với t > 0. Suy ra f(t) nghịch biến trên khoảng 0; do đó
t  2t  42 2 hàm số:
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 81
Tất cả vì học sinh thân yêu 12 G x 
nghịch biến trên khoảng 1; 3 4x  42 3  2 4x  4  4
Hàm số y = 2x – 5 đồng biến trên 1;
Từ đó suy ra phương trình (*) có không quá một nghiệm trên khoảng 1;
Mặt khác G(3) = y(3). Vậy phương trình (*) có duy nhất một nghiệm x = 3 trên khoảng 1; .
Tóm lại phương trình đã cho có nghiệm duy nhất x = 3. Cách khác: Từ 2
2x  11x  21  0 suy ra 4x  4  0 Ta có x x    x  2 2 2 11 21 2 3
x  3  x  3, x   R.
x       x   3 3 3 4 4 8 8 3 4
4 .8.8  12 4x  4  x  3  3 4x  4 x  3  0 Suy ra 2 3
2x 11x  21  3 4x  4 , đẳng thức xảy ra khi và chỉ khi   x  3 4x  4  8 
 Vậy nghiệm của phương trình là x = 3.
Bài 77: Giải phương trình 2 4 3 2
4  x  2 x  4x  4x   x  2 3 1 1 x Bài giải: *) Điều kiện: 2
4  x  0  2  x  2
Phương trình đã cho tương đương với x
x x x  x x2 2 2 2 3 4 2 2 2  2 (1) Ta có  x   x 2 2 2 4  4  2 x
4  x  4 , với mọi x  2  ; 2
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 82
Tất cả vì học sinh thân yêu Suy ra 2
x  4  x  2 , với mọi x  2  ; 2 (2)
Dấu đẳng thức ở (2) xảy ra khi và chỉ khi x  0; x  2 Đặt 3 2
x  2x t . Dễ dàng ta có được t  1
 ; 2 , với mọi x  2  ; 2
Khi đó vế phải của (1) chính là f t  3 2
t  2t  2, t  1  ; 2 t  0
Ta có f 't  2 3t 4t 0      4 t   3  4  22
Hơn nữa, ta lại có f   1  1
 , f 0  2, f  , f   2  2  3  27
Suy ra f t   2 , với mọi t  1  ; 2 Do đó x x  x x2 2 2 3 2 2 2
 2  2 , Với mọi x  2  ; 2 (3)
Dấu đẳng thức ở (3) xảy ra khi và chỉ khi x  0; x  2
Từ (2) và (3) ta có nghiệm của phương trình (1) là x  0; x  2
 Vậy phương trình đã cho có nghiệm x  0; x  2
Bài 78: Giải phương trình: 2
2x  9x  8  2 x 1   1 Bài giải:
Điều kiện: x  1   x   x  
    x     x   2 2 1 2 2 2 1 1 2 2 1 1  
x 1   2x  2 2 1 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 83
Tất cả vì học sinh thân yêu 2 2x  
9  2 2x 10  4 2  0 x 1  2x  2 2 1  
 2x  2 2 1  0  Phương trình bậc hai 2
2x  9  2 2x 10  4 2  0 có     2 2 2 1 nên có hai nghiệm là 5  2 2 x
và x  2 . Nghiệm x 2x  2 2 1  0 1 2 bị loại vì 2 2 2 5  2 2
Hoàn toàn tương tự ta có x  1   2x  2 2  1  x  2  5  2 2  
 Vậy phương trình có nghiệm x   ; 2. 2    
Bài 79: Giải phương trình 2
x  2  4  x  2x  5x 1 Bài giải:   2 1 
x  2 1  4  x 1  2x  5x  3 x  3 3  x
  x  32x   1 x  2  1 4  x  1  1 1    x  3   2x  1  0    x  2  1 4  x  1  x  3  0   1 1    2x  1 2  x  2  1 4  x  1
* x  3  0  x  3 *Xét phương trình (2) ĐK 2  x  4 VP  5
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 84
Tất cả vì học sinh thân yêu 1
VT đạt giá trị lớn nhất trên đoạn [2;4] bằng 1 
khi x=2 nên phương trình (2) vô 2  1 nghiệm
 Vậy phương trình có nghiệm duy nhất x=3
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 85
Tất cả vì học sinh thân yêu BẤT PHƯƠNG TRÌNH 2 x x  2 2
Bài 1: Giải bất phương trình: 2  x  1 2 x  3 x  3 Bài giải: Điều kiện x  3
 . Bất pt đã cho tương đương với 2 x x  2 4 2  2 x x  2 2 2 x  3 x  3 2   x  1  0   x  1  0 2 2 x  3 x  3 x x  2 2  2 x  3 x  3  2 x   1  2 x x  6  x  3 2 x  3 2   x  1  0 2 x x  2 2  2 x  3 x  3     2    x x  6  2 x   1 1  0   2   x x 2 2      x  3 2 x  3     2 x  3   x  3     2
x 1  0  1  x  1 (Với x  3
 thì biểu thức trong ngoặc vuông luôn dương).
 Vậy tập nghiệm của bất pt là S   1  ;  1
Bài 2: Giải bất phương trình: 2 2
1 4x  20  x  4x  9. Bài giải:
Bất phương trình đã cho tương đương với:
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 86
Tất cả vì học sinh thân yêu 2 2 4x 16 16  4x 2 2
4x  9  5  6  4x  20  x  2  0    x  2  0 2 2 4x  9  5 6  4x  20  4x  8 4x  8    x  2  1  0 2 2  4x  9  5 6  4x  20  Từ (1) suy ra 2 2
x 1  4x  20  4x  9  0  x  1. Do đó 2 2 4x  8 4x  8
1 4x  20  4x  9 
1  4x  8. 1  0 2 2 4x  9  5 6  4x  20  2 4x  9  5 2 6  4x  20 
 Vậy nghiệm của bất phương trình là x  2. 2 3
x x  2 2x 1
Bài 3: Giải bất phương trình x 1 
trên tập hợp số thực. 3 2x 1  3 Bài giải:
- ĐK: x  1, x  13 2 3 2
x x  2 2x 1 x x  6 - Khi đó: x 1   x 1  2  3 3 2x 1  3 2x 1  3
x  2 x 1  2  1  ,* 3 2x 1  3
- Nếu 3 2x 1  3  0  x  13 (1)
thì (*)   x   3 2
1  2x 1   x   1
x 1  x 1 Do hàm 3
f (t)  t t là hàm đồng biến trên  , mà (*):
f  3 2x 1  f x 1 3 3 2  2x 1 
x 1  x x x  0  1 5   1 5  Suy ra: x DK(1)  ;   0;      VN  2 2    
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 87
Tất cả vì học sinh thân yêu
- Nếu 3 2x 1  3  0  1   x  13 (2)
thì (2*)   x   3 2
1  2x 1   x   1 x 1  x 1 Do hàm 3
f (t)  t t là hàm đồng biến trên  , mà (2*):  1 1  x    2 
f  3 2x 1  f x 1 3  2x 1  x 1   1   x  13   2      2x  2 1   x  3 1  1 5  1 5  Suy ra: x  1  ; 0  ;  DK(2)     x  1  ; 0  ;13   2     2   1 5 
 Vậy bất phương trình có nghiêm S   1  ; 0  ;13   2   
5x  13  57  10x  2 3x
Bài 4: Giải bất phương trình:  2
x  2x  9   1
x  3  19  3x Bài giải:  19  3   x  Điều kiện  3  x  4 
Với điều kiện  bất phương trình   1 tương đương với:
x  3  19  3x 2 x  3  19  3x  2
x  2x  9
x  3  19  3x 2
 2 x  3  19  3x x  2x  9
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 88
Tất cả vì học sinh thân yêu x  5   13  x  2  2 x  3   19  3x
x x  2  3   3      2  2 x   x  2 2 x   x  2 2  
x x  2  x  5   13  x  9 x  3  9 19  3x   3   3           2 1 2 x x 2        0 2   x  5   13  x   9 x  3  9 19  3x         3   3   2 1  19 Vì 
 0 với mọi x  3; \     4  x  5   13  x  3 9 x  3  9 19  3x     3   3      Do đó    2 2
x x  2  0  2  x  1 ( Thoả mãn )
 Vậy tập nghiệm của bất phương trình là S   2  ;1   .
Bài 5: Giải bất phương trình  2
x x   x   x   2 6 1 2
x  1  3x  9x  2   1 Bài giải:  2
x x  6 x  1  x  2 2
x  1  3x  9x  2   2
x x  6 x  1  
1  x  2 x  1  2 2
 2x  10x  12
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 89
Tất cả vì học sinh thân yêu  2
x x  6x  2 x  2x  3 2  
 2x  10x  12 x  1  1 x  1  2  2
x  5x  6x  2  2
x  5x  6    2  2
x  5x  6 x  1  1 x  1  2    x  2 1  2
x  5x  6   2  0    x  1  1 x  1  2   x 1 1     1  2  2
 x  5x  6   0    x  1  1 x  1  2     x  1  ;2  3;     
 Vậy bất phương trình đã cho có nghiệm S  1; 2 3; . 1 1 2
Bài 6: Giải bất phương trình   trên tập số thực. 2 2 2 x 1 3x  5 x  2 1 Bài giải: 1 1 2
) Đặt t = x2 – 2, bpt trở thành:  
ĐK: t  0 với đk trên, bpt tương t  3 3t 1 t 1 đương 1 1 ( t 1)(  )  2 . Theo Cô-si ta có: t  3 3t 1 t t t 1 1  t t 1   .     t  3 t 1 t  3
2  t 1 t  3  1 1 2 1  1 2   .     t  3 2 t  3 2  2 t  3 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 90
Tất cả vì học sinh thân yêu t 1 2t 1  1 2t   .     3t 1 2 3t 1 2  2 3t 1 1 1 t 1 1  1 t 1   .     3t 1 t 1 3t 1
2  t 1 3t 1   VT  2 t   0.
) Thay ẩn x được x2  2  x  ( ;
  2 ] [ 2; )  T  ( ;
  2] [ 2; ).
 Vậy bất phương trình đã cho có nghiệm T   ;
  2    2;    . 1 1 x  1
Bài 7: Giải bất phương trình: x   1   1 x x x Bài giải:
ĐK: x [-1; 0)  [1; +  )
Lúc đó:VP của (1) không âm nên (1) chỉ có nghiệm khi: 1 1 1 1 x   1  x   1
x  1. Vậy (1) chỉ có nghiệm trên (1; +  ). x x x x x 1 x 1 Trên (1; +  ):   1  x 1 1   x 1   1. x x 2 x 1 x 1 Do x 1   0 khi x > 1 nên: x x 2 2 x 1 x 1 1 x 1   1  x 1  2  1  x   2 1  0 x x x x 2 2 2 x 1 x 1 x 1 2 1 5   2 1  0  ( 1)  0  x  . x x x 2
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 91
Tất cả vì học sinh thân yêu x  1 
 Vậy nghiệm của bất phương trình là  1 5 x    2
Bài 8: Giải bất phương trình 2 2 2 1 x x 1 
x x 1(1 x x  2) Bài giải:
Bất phương trình đã cho tương đương 2 2 2 2
(x x 1  x x 1 x x  2)  (1 x x 1)  0 2
(x 1)(2x x  2) x(1 x)    0 2 2 2 2
x x 1  x x 1 x x  2
1 x x 1 2 2x x  2 x  (x 1)(  )  0 2 2 2 2 x x 1 
x x 1 x x  2
1 x x 1 2 2x x  2 x
 (x 1).A  0 (1) với A   2 2 2 2
x x 1  x x 1 x x  2
1 x x 1 2 2 
x x 1  x 1 Nếu x  0 thì 2 2 2  
x x 1 x x  2  x x 1 2
x x  2  x  2 2 2 
x x 1 x x  2  x x 1  0  A  0 Nếu x>0 , áp dụng bất đẳng thức AM-GM ta có: 2 2 
x x 1 x x  2 3 2 2 2
x x 1 x x  2   x x    2 2  2 2 x x 1 1  2 2 x x 1   x    2 2
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 92
Tất cả vì học sinh thân yêu 2 2 2 2 
x x 1 x x  2  x x 1  2x x  2 x xA  1  0 vì  1 2 1 x x 1 2 1 x x 1
Tóm lại , với mọi x   ta có A>0. Do đó (1) tương đương x 1  0  x  1.
Vậy tập nghiệm của bất phương trình đã cho là (1; ) .
Chú ý : Cách 2. Phương pháp hàm số Đặt 2 u x x  1 2 2
u x x  1 thế vào bpt đã cho ta có 2 2 2
u x x x x  1  u 1 ( 2  u  1) 2 2
u u u u  1 2 2
x x x x  1 Xét f (t) 2 2
t t t t  1 ) f ' t ( )   t
(  t 2  1)2  t 2  1  0 t
 nên hàm nghịch biến trên R
Do đó bpt u x x  1
Bài 9: Giải bất phương trình: 2 2 3 2
(x  2)(x  2 2x  5) 9  (x  2)(3 x  5  x 12)  5x  7   1 Bài giải: 5
Điều kiện xác định: x   . Khi đó ta có 2 3 2 2 3 2
(1)  x  3x  14x  15  2(x  2) 2x  5  3(x  2) x  5  5x  7  0 3 2 2 3 2
x  3x x  18  2(x  2)( 2x  5  3)  3(x  2)( x  5  3)  3  5x  7  0
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 93
Tất cả vì học sinh thân yêu 2 2
2(x  2)(2x  4) 3(x  2)(x  4) 5(4 x ) 2
(x  2)(x  5x  9)     0 2x  5  3 x  5  3 2
9  3 5x  7   2 5x  72 2 3 3   2  4(x  2) 3(x  2) 5(x  2)  2
 (x  2)x  5x  9      0(*)  2x  5  3 x  5  3 2 
9  3 5x  7   2 5x  72 2 3 3     2  4(x  2) 4 3(x  2) 3 2  (x  2);  (x  2)  2 3 5  2x  5  3 x  5  3 5 Ta có với x     5(x  2) 5(x  2) 2   9 2
9  3 5x  7   2 5x  7 2 3 3  2 4(x  2) 3(x  2) 5(x  2) 2
x  5x  9     2x  5  3 x  5  3 2
9  3 5x  7   2 5x  7 2 2 3 3 2
18x  57x  127 5  0, x    45 2 5 5
Do đó (*)  x  2  0  x  2 , kết hợp với điều kiện x   suy ra:   x  2 2 2  5 
 Vậy phương trình đã cho có nghiệm x   ; 2 .  2   
Bài 10: Giải bất phương trình 2x2  x  2  5 
2  x  2  xx2  x  3  x   1 Bài giải:
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 94
Tất cả vì học sinh thân yêu
Điều kiện xác định: x  2  . ) 1 ( 
2 x  2  x 2
x x  3   x  2  x 2 2 x  2x  5
  x  2  x 2 2
x  2x  6   1  2 2 x  2x  5
  x  2  x2 2
x  2x  6   1  (2 2 x  2x  ) 5  2 2
x  2x  6   1 
x  2  x  2 2
x  2x  6 1 (Do 2x2  2x  5  , 0 x   R ) 
x  2  x 1  2(x  ) 1 2  2(x  2) (2) Đặt a
x  2, b x  (
1 a  0) , (2) trở thành a b  0 a b  0 a b  2 2 a  2 2 b    
a b  0
(a b)2  2 2 a  2 2 b (a b)2  0   x 1  0 x  1 3  13
Do đó ta có x  2  x 1      x  .
x  2  (x  ) 1 2 2
x  3x 1  0 2   3  13
 Vậy bất phương trình đã cho có nghiệm x  . 2
Bài 11: Giải bất phương trình 3 2
x (x  1)  x  5x  8x  6 ( x   )   1 Bài giải: Điều kiện: x  0. (1) 3 2 2
x x x  (x  6x 12x  8)  (x  4x  4)  2 3 3 2
 ( x )  x
x  (x  2)  (x  2)  (x  2) (2)
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 95
Tất cả vì học sinh thân yêu
Xét hàm số f(t) = t3 + t2 + t, có f’(t) = 3t2 + 2t + 1 > 0, t  .
Do đó hàm số y = f(t) đồng biến trên R, mặt khác (2) có dạng
f x   f x  2  x x  2 (3).
+) Với 0  x  2 là nghiệm của (3).
+) Với x > 2, bình phương hai vế (3) ta được 2
x  5x  4  0  1  x  4
Kết hợp nghiệm ta được 2 < x  4 là nghiệm của (3).
 Vậy nghiệm của (3) là 0  x  4 , cũng là nghiệm của bất phương trình (1).
Bài 12: Giải bất phương trình: 2 2x  3 
x 1  3x  2 2x  5x  3 16   1 Bài giải: Điều kiện: x  1  . Bpt (1) tương đương:
x   x   
x   x  2 2 3 1 2 3 1  20 Đặt t  2x  3  x  1 , t >0 t  5 Bpt trở thành: 2
t t  20  0  
. Đối chiếu đk được t  5 . t  4  
Với t  5 , ta có: 2 2x  3 
x 1  5  2 2x  5x  3  3  x  21  3  x  21  0  2
2x  5x  3  0     3  x  21  0  2
x 146x  429  0 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 96
Tất cả vì học sinh thân yêu x  7   x  3  3  x  7 
Kết hợp với điều kiện x  1
 suy ra x 3;
 Vậy bất phương trình có nghiệm S  3; . 2 3
x x  2 2x 1
Bài 13: Giải bất phương trình x 1 
trên tập hợp số thực. 3 2x 1  3 Bài giải:
– ĐK: x  1, x  13 . Khi đó: 2 3 2
x x  2 2x 1 x x  6
x  2 x 1  2 x 1   x 1  2   1  , * 3 3 2x 1  3 2x 1  3 3 2x 1  3
– Nếu 3 2x 1  3  0  x  13 (1) thì (*)   x   3 2
1  2x 1   x   1 x 1  x 1 Do hàm 3
f (t)  t t là hàm đồng biến trên  , mà (*):
f  3 2x 1  f x 1 3 3 2  2x 1 
x 1  x x x  0  1 5   1 5  Suy ra: x DK(1)  ;   0;      VN  2 2    
– Nếu 3 2x 1  3  0  1   x  13 (2)
thì (2*)   x   3 2
1  2x 1   x   1 x 1  x 1 Do hàm 3
f (t)  t t là hàm đồng biến trên  , mà (2*):
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 97
Tất cả vì học sinh thân yêu  1   x  13 1 
f  3 2x 1  f x 1 3  2x 1  x 1  1   x    2  2   2x  2 1   x  3 1  1 5  1 5  Suy ra: x  1  ; 0  ;  DK(2)     x  1  ; 0  ;13   2     2   1 5 
 Vậy bất phương trình có nghiệm x  1  ; 0  ;13   2    x(x  2)
Bài 15: Giải bất phương trình  1 3 (x  1)  x Bài giải:
x(x  2)  0 x  0  Điều kiện 3 
x  0; x  0  (x  1)  x  0 3 (x  1)  0   3 (x  1)  x  0  Do vậy x(x  2) 3  1 
x(x  2)  (x  1)  x 3 (x  1)  x 2 3 2
x  2x x  3x  4x  1  2(x  1) x(x  1) 3 2 2
x  2x  2x  1  2(x  1) x(x  1)  0  (x  1) x x  1  2 x(x  1)   0  
x x   x x  
  x x   2 2 1 2 ( 1) 0 ( 1) 1  0
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 98
Tất cả vì học sinh thân yêu
x(x  1) 1  0 
x(x  1)  1  1   5 x  2 2
x(x  1)  1  x x 1  0    1   5 x   2 5  1
Kết hợp điều kiện x>0 ta được nghiệm của phương trình đã cho là x  2
Bài 16: Giải bất phương trình:  2 x x   2 4 7
x  2  10  4x  8x Bài giải: Điều kiện: x  2 
Bất phương trình đã cho tương đương với bất phương trình  2
4x x  7 x  2  2 2
4x x  7  2  x  2  4     2
4x x  7 x  2  2  2 x  2  2 x  2  2 2 2
 4x x  7  2 x  2  4  4x x  2  2 x  2 1 2
 2x2   x  2   1
  x  2 1 2x x  2 1 2x  0
 x  2  2x 1    1   I   x  2  2  x 1 2   
 x  2  2x 1  3   II   x  2  2  x 1 4  x  2
 Giải hệ (I): Từ (1) và (2) suy ra   2   x  0 2x 1  2  x 1 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 99
Tất cả vì học sinh thân yêu 2  x  0 
Khi đó hệ (I) tương đương với hệ phương trình   x  2  2  x 1   1 2  x    2 
x 2;   1 x  2   2  x  2 1  x  2 
 Giải hệ (II): Từ (3) và (4) suy ra   x  0 2
x 1  2x 1  x  0 
Khi đó hệ (I) tương đương với hệ phương trình 
x  2  2x 1   1 x    5  41   2   x  ;    8 
x  2  2x  2 1     5  41 
 Vậy tập nghiệm của bất pt là T   2  ;   1   ;    8   
Bài 17: Giải bất phương trình: 2
4 x 1  2 2x  3  (x 1)(x  2)   1 Bài giải: Điều kiện: x  1 
Nhận thấy x = - 1 là một nghiệm cuả bất phương trình
Xét x > -1. Khi đó bất phương trình đã cho tương đương với
x     x    3 2 4 1 2 2 2
3 3  x x  2x 12
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 100
Tất cả vì học sinh thân yêu 4(x  3) 4(x  3) 2  
 (x  3)(x  2x  4) x 1  2 2x  3  3  4 4  2  (x  3) 
 (x 1)  3  0   . (1)  x 1  2 2x  3  3  4 4
Vì x > -1 nên x 1  0 và 2x  3  1. Suy ra   3 , vì vậy x 1  2 2x  3  3 4 4 2 
 (x 1)  3  0 . x 1  2 2x  3  3
Do đó bất phương trình (1)  x  3  0  x  3
 Vậy nghiệm của bất phương trình là x = -1 và x  3 .
Bài 18: Giải bất phương trình 2 2
x  3x  2  2x  3x 1  x 1 Bài giải:  1 x   2  Điều kiện x  2   x  1   X = 1 là một nghiệm 1
Trường hợp 1: x  2 BPT 
2  x  1 x  1 2x
 3  2x  2 2  x1 x  1 2x
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 101
Tất cả vì học sinh thân yêu
BPT  2  x1 x  2  (thỏa mãn)
Trường hợp 2: x  2 BPT 
x  2  2x 1  x 1 x  2 
x 1  2x 1 2
x  2  3x  2  2 2x  3x 1 2
 2x  2 2x  3x 1  0 (vô nghiệm)  1 
Vậy tập nghiệm của BPT là; S  ;      1 2    1 1
Bài 19: Giải bất phương trình  2 1 2  3 1 log x log x x 3   3 Bài giải: Đk; 2
2x  3x 1  0 2
2x  3x 1  0  1   3   hay x  1  ;   
0  1; \   x 1  0  2   2  x 1  1   x  0
Với điều kiện trên và để ý rằng 2 2
2x  3x 1  1  2x  3x  0   3 , x   2
x 1  1  x  0 từ đó có thể chia bài toán thành 3 trường hợp sau: 2
TH1: Với 1  x  0,thi`0  x 1  1  log ( x 1)  0 va` 2x  3x 1  3 2  log
2x  3x 1  0  bất phương trình đã cho vô nghiệm 3
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 102
Tất cả vì học sinh thân yêu 1 3 TH2: với 0  x  1  x . thì 2 2 2 2
x 1  1  log ( x 1)  0 va` 0 
2x  3x 1  1  log
2x  3x 1  0 3 3
 bất phương trình đã cho trở thành một bất đẳng thức đúng. 3 TH3: với x
,thi` x 1  1  log x 1  0 3   2 Và 2 2
2x  3x  1  1  log
2x  3x  1  0. 3 3 Từ đó với x
. bất phương trình đã cho tương đương: 2 log x 1 log 2x  3x  1   
2x  3x  1  x 1 3   2 2 3    3   3 x x    2   2 2
2x  3x 1   x  2 2 1
x  5x  0     3   3  x  5 x x    2   2
Kêt hợp cả 3 trường hợp bât phương trình đã cho có tập nghiệm:  1   3  S  0;  1;  5;       2   2  4 2
Bài 20: Giải bất phương trình: 2 3(x  2)   x  2
x 1  3 x 1 . 2  x x 1 Bài giải: ĐK: x  1.
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 103
Tất cả vì học sinh thân yêu Với điều kiện đó 8 2 BPT 2 2 2  6(x  2) 
 2 x x  6 x x 1  0 2 x x 1  
 3 x 1  x 2   x x  2 4 2 2 2 2 1  2 
x x  5  0  2   x x 1  4 2 2 2
Xét hàm số f (t) 
t  5 với t  0 . Ta có f '(t)  1 . t 1 (t 1) t 1 
f '(t)  0  t  1  Bảng xét dấu
Suy ra f (t)  f (1), t [0; )  f (t)  0, t
 [0; ) . Dấu “=” xảy ra  t  1. 4 2 Do 2 2
x x  0, x  [0; ) 
x x  5  0, x  [0; ) . 2 x x 1 1 5 Dấu “=” xảy ra khi 2
x x  1  x  . 2 2   4 2  Khi đó: 3 2
x 1  x    2 x x   2 1  2 
x x  5  0  2   x x 1   2 
x 1  x  0  1 5 2  
x x 1  0  x  .  2  4 2 2
x x  5  0  2  x x 1
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 104
Tất cả vì học sinh thân yêu 1    5  
Tập nghiệm của bất phương trình đã cho là: S  [1; ) \   . 2    
Bài 21: Giải bất phương trình 2 x x   3 2 5 4 1
x  2x  4x . Bài giải:
1 5  x  0 Điều kiện: 3 2
x  3x  4x  0    x  1   5  Khi đó: (1)  x  2 x x   2 4 2
4  x  5x  4  x  2 x x   2 4 2
4  3x x  2x  4 (2) 2 2 x  2x  4 x  2x  4
Trường hợp 1: với x  1 5 thì (2)  4  3  (3) x x 2 x  2x  4 Đặt t
(t  0) thì (3) trở thành: 2
t  4t  3  0  1  t  3 x 2 x  2x  4 2
x x  4  0 1 17 7  65 Suy ra 1   3     x x 2
x  7x  4  0  2 2 Trường hợp 2: với 1
  5  x  0 thì 2
x  5x  4  0 nên (2) luôn thỏa
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 105
Tất cả vì học sinh thân yêu
Vậy bất phương trình đã cho có tập nghiệm là:  1   17 7  65 
S  1 5; 0   ;     2 2   
Bài 22: Giải bất phương trình 2 3 2
3(x 1) 2x 1  2( x x ) . Bài giải: 1
*) Điều kiện: x   . 2
Bất phương trình đã cho tương đương với: 2
(x1) 2x  3(x 1) 2x 1  0 2
 (x 1) 2(x 1)  3(x 1) 2x 1  2(2x 1)  0    
 (x 1)  x 1 2 2x 1 2(x 1)  2x 1  0  (x 1) x 1 2 2x 1  0 (1)   1
Do 2(x 1)  2x 1  0 , với mọi x   . 2 Xét hai trường hợp sau:  x  3  2 3
+) x > 1. Khi đó (1)  x 1 2x 1  0 2
x  6x  3  0   . x  3  2 3 
Kết hợp điều kiện ta được nghiệm x  3  2 3 . 1 +)   x  1. Khi đó 2
(1)  x 1  2 2x 1  0 2
x  6x  3  0  3  2 3  x  3  2 3 .
Đối chiếu điều kiện ta được nghiệm 3  2 3  x  1 .
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 106
Tất cả vì học sinh thân yêu
Vậy nghiệm của bất phương trình đã cho là 3  2 3  x  1 và x  3  2 3 .
Bài 23: Giải bất phương trình  x   x x  3 1 1 2 3 1  0 . Bài giải:
Điều kiện: x  1.
Đặt a x 1,b  2x , khi đó a  0, b  2 và 2 2
b  2a  2 . Bất phương trình trở thành: 2 2 2  b  2a  3 3
1 a(b  3a)  0 
a(b  3a)  0   2   2 2  a a a 2 2 2 3 3
 (b  2a )  4a(b  3a)  0  1 2  4 (1 3 )  0  2  b b b   a Đặt t
, t  0 , bất phương trình trở thành 2 2 3
(1 2t )  4t(1 3t)  0 . b 4 3 2
 104t 108t  40t  4t 1  0 3 2
 (2t 1)(52t  28t  6t 1)  0 2
 (2t 1)(t(52t  28t  6) 1)  0
 2t 1  0 ,vì t  0 và 2
52t  28t  6  0 . x 1 1 Suy ra 
 2 x 1  2x  4(x 1)  2x x  2. 2x 2
Kết hợp điều kiện, suy ra nghiệm của bất phương trình là1  x  2 .
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 107
Tất cả vì học sinh thân yêu
Bài 24: Giải phương trình: 2
1 2x  1 2x  2  x . Bài giải: 1 1 ĐK:   x  .Khi đó 2 2  x  0 2 2 Bpt 2 2 4 2 2 4
 2  2 1 4x  4  4x x  2 1 4x  2  4x x (1). 1 1 Vì   x  nên 2 2 4
2  4x  0  2  4x  x  0 2 2 2 2 4 2
(1)  4(1 4x )  (2  4x x ) 2 4 8 2 4 6
 4 16x  4 16x x 16x  4x  8x 8 6 4 4 4 2
x  8x  20x  0  x (x  8x  20)  0  x  0
 Vậy pt có nghiệm duy nhất x = 0
Bài 25: Giải bất phương trình: 2 2
x  1 x  2  3x  4x Bài giải: x  0  0  x  1   3   41 Điều kiện 2  1 x  0   3   41 3
  41  0  x  (*) 8 2  x  2 3x 4x 0       8 8
Bất phương trình đã cho tương đương với 2 2 2 2 2
x 1 x  2 x(1 x )  2  3x  4x  3(x x)  (1 x)  2 (x x )(1 x)  0  5   34 x  2 2 2 x x x x x x 1  9
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 108
Tất cả vì học sinh thân yêu 5  34 3   41
Kết hợp điều kiện (*), ta suy ra nghiệm của bất phương trình là x  9 8 2 2 x x  3x  18
Bài 26: Giải phương trình:    1  2  x x x     2 1 1 1 Bài giải: Đặt t
x  1 . ĐK: t  0 và t  1. Bất phương trình đã cho trở thành: t  2 1 t  2 2 2 2 1  3t  15    2 4 2 t t t
t t  2 2 4 2 3 1
t t  15  t  8  t  2
Kết hợp với ĐK ban đầu ta được: t   1   x  1  1    0  t  2  0  x  1  2  x  0 x  0    0  x  1  4 1   x  3  
 Vậy bất phương trình có tập nghiệm S   1  ;3 \   0 3 2 3
x  4x  3x  2 x  3 2x  3
Bài 27: Giải bất phương trình  x  4     1 x  2    1
3 2x 3 3 x  4  1 Bài giải:
ĐK: x  2, x  12
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 109
Tất cả vì học sinh thân yêu
x  3 x  2  2
x  3 x  2  2   1  x  2  2   1  2 3 2x  3  3 3 2x  3  3 TH1: x  12 2 3
    3 x   3 2 2 3
 2x  3   x  2   x  2 3 2 3 Hàm số   3
f t t t đồng biến trên R nên:   3 3  2x  3 
x  2  2x  3   x  2 3 2
x  2x 1  0 vô nghiệm vì x  12 TH2: 2   x  12 3 3
    3 x   3 2 2 3
 2x  3   x  2   x  2 4 2 3 Hàm số   3
f t t t đồng biến trên R nên:   3 4  2x  3 
x  2  2x  3   x  2 3 2
x x     x   2 2 1 0
1 x x   1  0  1   5  1 5   x  ; 1   ;12     2 2     
Đối chiếu điều kiện 2
  x  12 ta có tập nghiệm của bất phương trình là:  1   5  1 5  S  ; 1   ;12     2 2     
Bài 28: Giải bất phương trình: 2 2
9x  3  9x 1  9x 15 Bài giải: 1 Nhận xét: 2 2
9x 1  9x 15  9x  3  0  x  9 bpt   2 x    2 9 3
2  3(3x  1)  9x  15  4 2 2 9x 1 9x  1   3(3x 1)   0 2 2 9x  3  2 9x  15  4
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 110
Tất cả vì học sinh thân yêu  3x  1 3x  1  (3x 1)   3  0   2 2  9x  3  2 9x  15  4    1 1   1
(3x 1) (3x  1)   3  
  0  3x 1  0  x  2 2 3   9x  3  2 9x  15  4   1
Kết hợp các ĐK suy ra nghiệm của BPT là x  là nghiệm của bpt 3 4 3
x  2x  2x 1
Bài 29: Giải bất phương trình: x x   3 2  
x  2x  2x Bài giải:
ĐK: x  0 , BPT tương đương: 3    1   3 1  x x x   x  3 1 x    1 2 2  
x  x    x 1 1 1  x   1 1   3 t
Xét hàm số f t   trên  2 t 1 4 2 t  3t
Ta có: f 't    0 t    t  2 2 1
Mà f(t) liên tục trên  nên f(t) đồng biến trên  . 3  5
(1) có dạng: f x   f x   1 
x x 1  0  x  2
Bài 30: Giải bất phương trình 2 2
1 4x  20  x  4x  9   1 Bài giải:
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 111
Tất cả vì học sinh thân yêu
Bất phương trình đã cho tương đương với: 2 2 4x 16 16  4x 2 2
4x  9  5  6  4x  20  x  2  0    x  2  0 2 2 4x  9  5 6  4x  20  4x  8 4x  8    x  2  1  0 2 2  4x  9  5 6  4x  20  Từ (1) suy ra 2 2
x 1  4x  20  4x  9  0  x  1. Do đó 2 2 4x  8 4x  8
1 4x  20  4x  9 
1  4x  8. 1  0 2 2 4x  9  5 6  4x  20  2 4x  9  5 2 6  4x  20 
 Vậy nghiệm của bất phương trình là x  2 2 x  5x 14 2
Bài 32: Giải bất phương trình:  3 2 2  3  1 x x x Bài giải: Đkxđ: x  0 2
x  5x 14  0  Ta có:  3 2
2  3 x x 1  0  2 2
x  5x 14  0 2
x  5x 14  0   0    0 3 2 3 2 2  3  1 x x x
2  3 x x 1
x  0 quy đồng ta có: 3 2 3 2
x  5x 14x  4  6 x x 1 3 2
x x x    3 2 5 8 4 6 x
x x 1  0
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 112
Tất cả vì học sinh thân yêu  3 2
x x x 1 2    x  
1  x  4x  4  6  0 2 2
x x x x 1   2 x x 12 3 3 2 2
x x x x    2 1 x x 12 3 3  A  6 2 x 1  6  2 x 1 2  2    x   1  x  2 
  0  x  0 1 (Do  x  2   0x  0 )  AA  
Kết luận x  0 1  x  1
 Vậy x  0  ;1  x  1 
Bài 33: Giải bất phương trình: 2 log x   log
x  log 1  2x  1  1 1 2   1 2      x 1  2 x  1 Giải bất phương trình 2 log (x  )  log
x  log (1  2x  1)  1 2 1 2 x 1 2  x  1 2 x   0 Điều kiện :  x 1 x  0  2 x  1 2x BPT 2  x   x 1 1  2x  1
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 113
Tất cả vì học sinh thân yêu 3 2
(x x x 1)(1  2x  1) 2   2x x 1 2 2 3 2
(x  1)(x  2x 1)
(x x x 1)(x  2x  1)   x 1 x 1 2 3 2
 (x 1)(x  2x 1)  (x x x 1) 
 (x  2x  1)   0 x 1   2 2
 (x 1) 2x 1  x  2x 1
 (x  2x  1)   0 x 1   x  2x  1   0 x 1 
x  2x  1  x  1 
 x  2x 1  x 1  x  1 2   1   x  1  2 x  1 2  Vậy 
là nghiệm của bất phương trình đã cho. 0  x  1 
Bài 34: Giải bất phương trình 2 x x   3 2 5 4 1 
x  2x  4x Bài giải:
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 114
Tất cả vì học sinh thân yêu x  1   5 Điều kiện: 3 2
x  2x  4x  0    1   5  x  0 
Bất phương trình đã cho tương đương với  2
x x    x x 2 2 4 3 4
x  2x  4 (1)
Xét hai trường hợp sau đây:
TH1: Với 1  5  x  0 khi đó 2
x  2x  4  0 và 3x  0 . Hơn nữa hai biểu thức 2
x  2x  4 và 3x không đồng thời bằng 0. Vì vậy  2
x x    x x 2 2 4 3 4
x  2x  4
Suy ra 1  5  x  0 thỏa mãn bất phương trình đã cho
TH2: Với x  1  5 khi đó 2
x  2x  4  0 . Đặt 2
x  2x  4  a  0, x b  0
Bất phương trình trở thành 2 2
a  3b  4ab  a ba  3b  0  b a  3b 2 
x x  4  0 1  17 7  65 2 x
x  2x  4  3 x     x  (tmđk) 2
x  7x  4  0 2 2  1   17 7  65
 Vậy bất phương trình đã cho có nghiệm 1  5  x  0;  x  2 2
Bài 35: Giải bất phương trình: 2 x x x    2 2
3 x  2x  2 Bài giải:
● Điều kiện xác định: x  1  3 (1)
● Với điều kiện đó, ký hiệu (2) là bất phương trình đã cho, ta có:   2
x x  
x x   x     2 2 2 2 2 1 2
3 x  2x  2
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 115
Tất cả vì học sinh thân yêu x x  
1  x  2  xx  2  2 x   1
  xx  2  2 x 1 xx  2  x 1  0 (3)
Do với mọi x thỏa mãn (1), ta có xx  2  x 1  0 nên
3  xx  2  2 x 1 2
x  6x  4  0
 3  13  x  3  13 (4)
Kết hợp (1) và (4), ta được tập nghiệm của bất phương trình đã cho là: 1   3;3  13  
Bài 36: Giải bất phương trình: 9x 3x 2 9 3x     Bài giải: Đặt 3x t
 0 , bất phương trình trở thành 2
t t  2  9  t
Xét 9  t  0  t  9 , khi đó bất phương trình tương đương với 2
t t  2  0  t  9   1 83
Xét t  9 , bất phương trình tương đương với 2 2
t t  2  81  18t t t  . 19 83 Suy ra  t  9 2 19 83 x 83 83
Từ (1) và (2) suy ra t  khi đó 3   x  log . 19 3 19 19 83
 Vậy nghiệm của bất phương trình gồm các giá trị x  log 3 19
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 116
Tất cả vì học sinh thân yêu
Bài 37: Giải bất phương trình:  x 1 xx  1 1 2 4 3 e  1  x   e
 2x  4 x  3  1  x 2x  4 x  3 Bài giải: Điều kiện x  0 t 1
Xét hàm số f t   e t
với t 1; t t t 1
Ta có f 't   e
 0 với t 1; . Suy ra f(t) đồng biến trên t 1; 2t t
Do đó từ bất phương trình đã cho tương đương với 1 x  2x  4 x  3 1 1
 2x  5 x  2  0   x  2   x  4 2 4 1
 Vậy tập nghiệm của bất phương trình gồm các giá trị của x thỏa mãn  x  4 4 2.9x  3.6x
Bài 38: Giải bất phương trình  2  x   6x  4x Bài giải: 2.9x  3.6x
2.9x  5.6x  2.4x Ta có  2   0 6x  4x 6x  4x
Chia cả tử và mẫu của vế trái cho 4x  0 , bất phương trình tương đương với 2 x x  3   3  2.  5  2     x  2   2   3   0 . Đặt t
,t  0 bất phương trình trở thành x    3   2  1    2 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 117
Tất cả vì học sinh thân yêu  1 2 2t  5t  2 t  0    2 t  1 1 t  2  x 1  3  1 1 Với t  ta có   x  log  x   log 2   3 3 2  2  2 2 2 2 x  3 
Với 1  t  2 ta có 1 
 2  0  x  log 2   3  2  2    
 Vậy tập nghiệm của bất phương trình đã cho là S   ;   log 2    0;log 2 3 3   2   2  1 1
Bài 39: Giải bất phương trình  2 2  1 2  3  5 x x x Bài giải:  5  Điều kiện x  ;    (1; )    3   5   Xét x   ;   
 , vế trái bất phương trình luôn dương mà vế phải âm nên  3   5  x   ;   
 là nghiệm bất phương trình  3 
 Xét x  (1; ) bất phương trình 2
 2x 1  2x  3x  5  x  2 2 2 2 (2x 1) 2x 3x 5 2x 7x 6 0            3  x   2
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 118
Tất cả vì học sinh thân yêu  3  Suy ra x  1;  [2; )  
là nghiệm bất phương trình  2   5  3
 Vậy tập nghiệm bất phương trình là  ;    (1; ]  [2; )    3  2 2
Bài 40: Giải bất phương trình 2
 1  3  2x x
x  1  3  x Bài giải:
Giải bất phương trình…… Đk: 1   x  3 2 t  4 Đặt t
x  1  3  x t  0 2
 3  2x x  , bpt trở thành: 2 2 2 t  4 3  1 
t  2t  4  0  t  2 2
t  2t  2  0  t  2 (t/m) t 2 Với t > 2 ta có 2
x  1  3  x  2  3  2x x  0  1   x  3
Kết hợp đk ta được nghiệm bpt là: 1   x  3
log  x  2x  75  log  x  2x  78 2 2 2 3
Bài 41: Giải bất phương trình  0 2 3x 13x  4 Bài giải: 2 
x  2x  7  0 
x  1 2 2, x  4 Điều kiện    2 3
x 13x  4  0  x  1 2 2 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 119
Tất cả vì học sinh thân yêu 5log  2
x  2x  7  8log 2.log  2
x  2x  7 log  2 x  2x  7 2 3 2 2  Pt   0  5  8 log 2  0 2  3  2 3x 13x  4 3x 13x  4 log  2 x  2x  7 2  Do 5 8
5  8 log 2  log 3  log 2  log 243  log 256  0 nên  0 3 3 3 3 3 2 3x 13x  4 2  2
3x 13x  4  0   3 
x 13x  4  0    2  x x   2  1 log 2 7  0 2 
x  2x  7  0  x  , x  4      3  2 2
 3x 13x  4  0 3 
 x 13x  4  0    x  2     log   2
x  2x  7  0
x  2x  7  0 2  2  
x  1 2 2, x  4
Kết hợp với điều kiện suy ra nghiệm của bất phương trình là  x  2  THÊM DẠNG Câu 1: 2 2
x x  2  x  2x   1  1. Lờigiải:
Điềukiện: x  1.
Bất phương trinh tương đương với:     2
x x  2  x   1 x   1  2x  
1  0  x  1  x  2  x   1 x  1  2   0
     3 20;x 1  
x  1  0  x 1  S  1  ;   
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 120
Tất cả vì học sinh thân yêu Câu 2: 2 2
2x x  3  21x  17  x x  0. Lờigiải: 17 Điềukiện: x
. Bất phương trinh tương đương: 21 2 x  1 x  2
x  1 x  2 x  3x  9 2
2x x  3 x   1   2 x         
1  21x  17  0    0 2 2
2x x  3  x  1
x  1  21x  17  2         
x  x   1 x 3x 9 x 1 2   0    x   1 x  2 2  0   .  2 2          x  1  2x x 3 x 1 x 1 21x 17  
 17 0, x   21 17 
Kếthợpđiềukiện suy ra tậpnghiệm S   ; 1  2;   .     21  Câu 3: 3 x x  2 x   3 2 2 1
2x  1  2x x. Lờigiải: 1
Điềukiện: x  . Bất phương trinh tương đương: 2 x 2 x   1  2 x   3 2 1
2x  1  x  2x x  0   2 x  
1 x  2x 1 3 2
x  2x x  0
x  1x 2 1 xx  2 2 1    0  x  2 1  0  x  1. x  2x  1 2 2
x x 2x x   2 3 2x x2 3  1 
Kếthợpđiềukiện suy ra tậpnghiệm  S   ; \    1 .  2  
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 121
Tất cả vì học sinh thân yêu Câu 4: 2 x  5x 3 2
 1  x  2x  4x. 4 Lờigiải: Điềukiện: 3 2
x  2x  4x  0.  
Từđiềukiệnbàitoán cho ta 2
x  5x  0 vớimọi x  1  5; 0 .   
 Khi đó BPT luôn đúng. Ta xétvới x     2 5 1
x  5x 0. Bất phương trinh tương đương:
x  5x  4  4 x  2x  4x  x  5x  2 2 3 2 2 4  16 3 2
x  2x  4x 4 3 3
x  6x 15x  24x  16  0   2
x  7x  4 2
x x  4 0  2
x  7x  4  0   1 17 7   65   2       4  0 x x x   2 2     .  2  
x x  4  0 1  17 7     65   x    2
x 7x4 0  2 2     1   17 7     65
Kếthợpđiềukiện x  5  1, suy ra tậpnghiệm S 1 5; 0 ;        .      2 2   Câu 6: 2
x  7  x  1  . x  1 Lờigiải:
Điềukiện x  1, bất phương trình tương đương với: 2 2 2
x  6x  7  x  1  x  6x  7  x  2x  1  4x  8  0  x  2.
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 122
Tất cả vì học sinh thân yêu
Kếthợpđiềukiện suy ra tậpnghiệm S  1; 2. Câu 7:
4  x  3 x  5  2x. 3  x Lờigiải: 5
Điềukiện:   x  3. Bất phương trinh tương đương: 2
4  x  3  x  5  2x3  x  7  2x  5  2x3  x 2 2 2 17
 4x  28x  49 2x x  15  6x  29x  34  0  2  x  . 6  17
Kếthợpđiềukiện suy ra tậpnghiệm S  2;  .  6    Hếtrùi ^^ 3 2 2
CÂU 8 : x  2x  3x  3 10  x  11.
Đk  10  x  10.
Xét  10  x  0 , 6x
với f x  3 x  2
2x  3x  3 10  2
x  11; f ' x  2
3x  4x  3 
 0;x   10;0 2   2 10  x
Suy ra f x  f 0  0  Loa . i
Xét 0  x  10. (*). BPT tương đương:
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 123
Tất cả vì học sinh thân yêu  3 2 x  1  2 x  10  3 10  2
x  0   x 1  x 1 x  1   x  1 10  2 x 3  10  2 x   0 2  3  10  2 x 3  10  2
x x 1  x 1 10  2 x 3  10  2 x   0
3 10 x x 12 2  2 3 10 x  x 1 2          10  x  0  
 0 x 1 2 2 2  
 3  10  x  0  9  10  x x  1  0   . x    1
Kếthợp (*) suy ra tậpnghiệm S  1; 10  .  
x   x    x   x   2 1 2 6 7
12x  7x  12. CÂU 9 ĐK: x  2.
x   x     x   x     2 1 2 2 6 7 3 x  2x  8 BPT tương đương  x  1 x  6    x  2    x  4    0  x  2  2 x  7  3 
 A Với
2x  6   x  4 x  2  2 2  x  4 x  2 x  2  x  2  2 
x  7  3  A    0 x  2  2 x  2  2
Suy ra bpt  x  2  0  x  2.
Kếthợpđiềukiện suy ra S  2;  2 . 2 2
CÂU 10 2x 8x  1 
x  8  6x x  3. ĐK x  0. Bpt tương đương
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 124
Tất cả vì học sinh thân yêu x x x x x 2x  2 1 8 1 1 1 2
8x  1  3 x  2            x  8  3  0    0 2 8x  1  2 3 x x  8  3  2x 8x 1 x  1    x  1     0 2 2
 8x  1  3 x x  8  3 
  A 1 Với x   A  0. 8  1  1 1 1 Với x  0;
 1  8x  0  2x 1  8x  .8x1  8x 
 2x 8x  1     .  8  4 16 16 1 1 64  8 57 1 Mà     A  0. 2 x  8  3 1 21 16  8  3 64
Suy ra bpt  x 1  0  x  1. Vậy S  0  ;1 . 1. 2 x   2 16
3 x  3x  4  x  1  3. Đk x  1. BPT tương đương 2 x  16  3  2
3 x  3x  4  x  1  2
8x  26x  12  6  x  1 2
x  3x  4  2 6 x  16  0  3 2 2 3 x 2x x 4 2x 6         2 x  36  2 9 x  16  2
3 x  16   x  12  7x  21x  0    29x  5 x x  3 8 
x x  3     7  0 2 2 2 2 2
3 x  2x x  4  2x  6
x  36  9 x  16
3 x  16  x  12 
   A Xét 22x  22  3 6 x  2 2x x  2 4
2x  3x  36  2 9 x  16 8 A     4  0 3 3 x  2
2x x  4  2x  2 6 x  36  2 9 x  2 16
3 x  16  x  12
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 125
Tất cả vì học sinh thân yêu
Suy ra bpt tương đương x x  3  0  0  x  3. Vậy S  0;3. 2 x x   3 x  2
x x   2 2 2
x  1 3x  6. CÂU 11 ĐK x  2. BPT tương đương 2
x x  2  2   3 x  2 x  4   2
x  1 3x  6  2
x x  2  0  4 3 2  với 1 x 2x x x 5   2 x x  2        1  0.  3 2 2 2
x x  2  2
x x  4   x 1 3x  6   
 A  2 x  1 2
x x  1  3x  6 1  Xét A   . 3 2 2 2
x x  2  2
x x  4   x  1 3x  6 Ta CM A>0 hay 2
x x  1  3x  6  0;x  2. 3
Xét f x  2
x x  1  3x  6; x  2. Có f ' x  2x 1  . 2 3x  6 1
f ' x  0  22x  1 3x  6  3  0  x  2  x  . 2  1  2 30  5  1 
Có f 2  5; f
f x  f  0  A      0.  2  4  2  x 1 2  
Khi đó BPT  x x  2  0   . x    2
Kếthợpđiềukiện suy ra S    2  1;. 3 2 2x  5x  4 2x  4
Bài 12 : Giải bất phương trình sau  2 3x  4x  4 1  2x  3 Lời giải
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 126
Tất cả vì học sinh thân yêu 3 Điều kiện: 2 x
, 3x  3x  4  0 2 2 3  3  3 Do 2 x
 3x  3x  4  3.  3.  4  0  
nên bất phương trình đã cho tương đương 2  2  2  2
3x  4x  4 2x  3  1 2x  3 1 3 2    3 2
2x  5x  4 
 0  2x  5x  4   2
3x  4x  4 2x  3   1  0 2x  3  1 3 2
 2x  2x  4x   2
3x  4x  4 3 2
2x  3  2x  3x
2x  3  22x  3 2x  3  x 2x  3  x  2 2x  3  0 Đặt a
2x  3 bất phương trình trở đã cho trở thành 3 2 3 2
x x a a xa x a
  x a 2 2
x xa a    x a    x a 2 2 2 3 2 2 0 2 2 2 0 2
2x xa a   1  0  3  3  x  6 x   x x 2a x 2 2x 3 2   2          3  2   xxx 2 2 4 2 3   
x  8x  12  0    2  3 
Vậy bất phương trình đã cho có tập nghiệm S  ; 2  6;      2  2x  1
x  3  2  x
Bài 13 : Giải bất phương trình sau  2 2
39  12 6  x x
17  2 6  x x Lời giải Điều kiện: 2
6  x x  0  3   x  2
Bất phương trình đã cho tương đương
x  3  2  x x  3  2  x
x  3  2  x  2 2
39  12 6  x x
17  2 6  x x        x    x x 3 2 x 1 3 2     0  2 2 
 39  12 6  x x
17  2 6  x x
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 127
Tất cả vì học sinh thân yêu Đặt t   x
x  t   2 2 2 2 2 3
0  t  5  2 6  x x  2 6  x x t  5 bất phương trình trở thành  
x    xt 1 3 2    
x  3  2  x
t  6t  12t  9  0 2   3 2 2 
 39  6t  5 17  t  5   
  x  3  2  x t  3 2
t  3t  3  0 Do 2
t  3t  3  0 nên bất phương trình tương đương
  x  3  2  x t  3  0   x  3  2  x  3 x  3  2  x   0 Trường hợp 1:  1  1   x  3  2  x
x  3  2  x x     x       2    2  x  1 2
x  3  2  x  3 5
  2 6  x x  9 2    2
6  x x  2
6  x x  4   Trường hợp 2:  1  1   x  3  2  x
x  3  2  x x     x       2    2  x  2 2
x  3  2  x  3 5
  2 6  x x  9 2    2
6  x x  2
6  x x  4  
Kết hợp với điều kiện, vậy bất phương trình đã cho có tâp nghiệm S   3  ; 2    1; 2
Bài 14: Giải bất phương trình sau  x   x   x   x x
    x  2 3 1 2 2 5 2 2 3 2 6 3 3 Lời giải
Điều kiện: x  2
Bất phương trình đã cho tương đương
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 128
Tất cả vì học sinh thân yêu  x 2 1 4 x 2   
5 2x  2  3x x  2  6  3x  32 3
x 1 2 x  2  
  x  32 5 2x  2  3x x  2  6  3 x  32 3
x 1 2 x  2
  x  32 5 2x  2  3x x  2  6  3x  3  6 x  2  0   x  32 3  3
5 2x  2  7 x  2  3  0
Trường hợp 1:  x  2 3  0  x  3 Trường hợp 2: 3
5 2x  2  7 x  2  3  0 Đặt t
x  t   2 2 2
0  t x  2  x t  2 bất phương trình đã cho trở thành 5 2  2 t  2 2
 2  7t  3  0  5 2t  6  7t  3  125 2 3
2t  6  7t  33 3 3 2
 343t  191t  189t  723  0  t   1  2
343t  534t  723  0  t  1 x  2 x  2  x  2  1      2  x  3 x  2  1 x  3  
Vậy bất phương trình đã cho có tập nghiệm S  2;  3
Bài 15 : Giải bất phương trình sau  2
x x   x    x   2 2 2 2 1 2 1
x 1  3  x Lời giải
Điều kiện: x  1
Bất phương trình đã cho tương đương  2 x  3 2
x  1  x  3  2x   2 1
x 1  2x   1 x 1  0   x 1   1  2
x  3  2x   1
x 1  x 1  
1  0   x 1   2
1 x  3  2x   1 x 1  0   x Do x  1  1 
 0 nên bất phương trình đã cho tương đương x  1  1
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 129
Tất cả vì học sinh thân yêu 2
x  3  2x   1 x 1  0   x   1  2x   2 1
x 1  x x  2  0   x 1  x  
1  x 1  x  2  0  5  5 2   0 x x   x  2  2 
x  1  x  2  0 
x  1  2  x       x 1   2  x2 2
x  5x  5  0    5  5   x  2  2 5  5  5  5 
Vậy bất phương trình đã cho có tập nghiệm S  ; 2  ;      2 2     
Bài 16: Giải bất phương trình sau x x   2 8 15 
4x  5x  1  2 x  2 Lời giải
Điều kiện: x  2 2 4x  9x  9 Do 2
4x  5x  1  2 x  2 
 0 nên bất phương trình đã cho tương đương 2
4x  5x  1  2 x  2 2 2
8x 15x  4x  5x  1  4  x  2  4  x   1 4x   1  x  3 2 2
 4x 14x  7  4 4x  9x  2 x 1  0   2
4x  9x  2 2
 4 4x  9x  2 x 1  5 x   1  0 Đặt 2 a
4x x  2,b
x  1a,b  0 bất phương trình đã cho trở thành 2 2
a ab b
 a ba b 2 2 4 5 0 5
 0  a b  4x  9x  2 
x 1  4x 10x  3  0  5  13 x  4   5 13 x   4
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 130
Tất cả vì học sinh thân yêu 5  13 
Kết hợp với điều kiện, vậy bất phương trình đã cho có tập nghiệm S  ;    4    1 x  2 2
Bài 17: Giải bất phương trình sau x   1  x   1 x 2 x Lời giải
Điều kiện: x  0
Bất phương trình đã cho tương đương 2 2 2 2  2   2    2x
 2   x  2 x   1  x   1   
x  2 x  1  x 1  0   x  1 1 x   x 1  0 x x x xx   x        2 Do x
 1 1  0 nên bất phương trình tương đương x 2 2 2 x
 1  x 1  0  x
 1  x  1  x
 1   x  2 3 2 1
x x  2  0  x  1 x x x
Vậy bất phương trình đã cho có tập nghiệm S   ;   1
Bài : Giải bất phương trình sau 3 2
3x  3x  4x  3  3x  1  5x  4 Lời giải 1
Điều kiện: x   3
Bất phương trinh đã cho tương đương
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 131
Tất cả vì học sinh thân yêu 3 2
3x  3x  6x   x  
1  3x 1   x  2  5x  4  0 2 2 x x x x  3 2
x x x  2    0 Do
x 1 3x 1
x  2  5x  4    1 1  2
x x 3x  6    0   
x 1 3x 1
x  2  5x  4  1 1 1 3x  6    0, x    nên ta có 2
x x  0  0  x  1
x  1  3x  1
x  2  5x  4 3
Vậy bất phương trình đã cho có tập nghiệm S  0  ;1
Bài 18 : Giải bất phương trình sau 2
2x x  2  5x  2  x 11x  7 Lời giải 2 Điều kiện: x  5
Bất phương trình đã cho tương đương 2 2 x  5x  2 x  5x  2 2 2
x  5x  2  x  3x x 11x  7  x  5x  2  0   x   2
x  5x  2  0 x  5x  2
x  3  11x  7    1 x  5  17 5  17 2
x  5x  2 2 
 1  0  x  5x  2  0   x   
x  5x  2
x  3  11x  7 2 2   5  17 5  17 
Vậy bất phương trình đã cho có tập nghiệm S S  ;   2 2   2
x x  6  7 x  6 2
x  5x  2
Bài 19 : Giải bất phương trình sau  0 x  3  2  2 x  10 Lời giải
Điều kiện: x  3
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 132
Tất cả vì học sinh thân yêu 2
x  6x 11 Do x  3  2  2 x  10 
 0 nên bất phương trình đã cho tương đương x  3  2  2 x  10 2
x x  6  7 x  6  2
x  5x  2 2
x x  6  49x  14 x  2 x x  6 2
 6x  5x  2 2
 5x 18x  6 14  2
x  3x x  2  0  5 2
x  3x 14  2
x  3x x  2  3 x  3  0 Đặt 2 a
x  3x,b
x  2 a,b  0 bất phương trình đã cho tương đương 2 2
5a 14ab  3b  0  a  3b5a b 2
 0  a  3b
x  3x  3 x  2 2
x  3x  9  x  2 2
x 12x 18  0  6  3 6  x  6  3 6
Kết hợp với điều kiện, vật bất phương trình đã cho có tập nghiệm S  3; 6  3 6    2x   1 x  3
Bài 20: Giải bất phương trình sau  1
2 x  2  x  1 x 1 x Lời giải
Điều kiện: 0  x  1
Do 0  x  1 nên 2 x  2  x  1 x 1 x  0 bất phương trình đã cho tương đương 2x   1
x  3  2 x  2  x  1 x 1 x  2x   1
x  3   x  1 x 2  1 x  2 2  a b  1 Đặt a
x, b  1  x a,b  0 ta có 
bất phương trình đã cho trở thành 2 2
2a b 1  x   2 2 a b  2 2
2a b  2  a bb  2  a b 2 2
2a b  2  b  2
 a b2 2a b  2  b  22 2 2  1 2ab 2 a  3 2
b  4b  4  1 2ab 2 a  3 2
 4b  5  b   2
2a  2  2b 3
a  3a  2  0
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 133
Tất cả vì học sinh thân yêu Mà 2 a  1 và 3
a  3a  2  0 nên  2
a    b 3 2 2 2
a  3a  2  0 nên dấu "  " xảy ra khi a  1   x  1 b  0 
Vậy bất phương trình đã cho có tập nghiệm S    1 2
6  3x  2x  5x  2 1  x
Bài 22 : Giải bất phương trình sau  2 3  2   2 x x x x Lời giải x  0    1  Điều kiện: 2 3
x  2x  5x  2  0  x   ;  2     ;  \   0;  1  2   2
2x  5x  2  0  
Bất phương trình đã cho tương đương 2 2
6  3x  2x  5x  2 1  x 6 1
3x  2x  5x  2  1  1      0 2 2 3  2  5  2 x 3  2  5  2 x x x x x x x x  2
3x  2x  5x  2  2 Trường hợp 1: 2 2 2 2
2x  5x  2  3x  0  2x  5x  2  9x  7x  5x  2  0  x   7 Trường hợp 2: 2
3x  2x  5x  2  0 bất phương trình trở thành
x x x  2 2 0  x  1 3 2 5 2 0 x  2 7x 5x 2 0        2 2 
x 7x  5x  2 x    7  1 2 
Kết hợp với điều kiện, vậy bất phương trình đã cho có tập nghiệm S   ;  2   ;    0  ;1 2 7   
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 134
Tất cả vì học sinh thân yêu x  2 1
Bài 23 : Giải bất phương trình sau   4 2 x x   x 1 2 1 1 Lời giải
Điều kiện: x  1 3
Khi đó 2  x x   1 1  2  x  2 4 2 2 1  1  0 2
Trường hợp 1: x  1 bất phương trình đã cho tương đương 2 x x    4 2 1
2 x x   1 2 Ta có 2 x x x  2 x  2 x  2 x             4 2 1 1 2 1
2 x x   1   1  5 Dấu "  " xảy ra khi 2 2
x 1  x x x 1  0  x  2
Trường hợp 2: x  1 bất phương trình đã cho tương đương 2 x x    4 2 1
2 x x   1 (luôn đúng) 1    5  
Vậy bất phương trình đã cho có tập nghiệm S    ;1    2    
3  3x  3  x 4
Bài 24 : Giải bất phương trình sau 
3  3x  3  x x Lời giải
Điều kiện: x  1  ;  3 \   0
Trường hợp 1: x  0;  3 4x
Ta có 3  3x  3  x
 0 nên bất phương trình đã cho tương đương
3  3x  3  x
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 135
Tất cả vì học sinh thân yêu
 3 3x  3 x2 4 
 6  2x  2 3  3x3  x  16  3  3x3  x  5  x 4x x
 3  3x3  x  5  x2  x  4x  4  0   x  22 2  0  x  2
Trường hợp 2: x   1  ; 0 4x
Ta có 3  3x  3  x
 0 nên bất phương trình đã cho tương đương
3  3x  3  x     3 3x  3 3 3 3 4  x x x 2 4   
  3  3x  3  x 2  16
3  x  3  3xx
3  x  3  3x x   x
  x  x  
  x  x    x   x  2 6 2 2 3 3 3 16 3 3 3 5 2  0 (đúng)
Vậy bất phương trình đã cho có tập nghiệm S  1;0   2 x  2
x  1  x
Bài 26: Giải bất phương trình sau  1 2 3 x x  1  x x Lời giải
Điều kiện: 0  x  1 Ta có 2 3 2 x x  1 
x x x x  1 
x x x  1  x  0, x  0 
;1 nên bất phương trình đã cho tương đương
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 136
Tất cả vì học sinh thân yêu x  2 x  1 x  2 3 2 3
x x 1 x x
x x  1 x  2 1 x  2 3
x x  1 x  2
1 x   2 x  2 1 x  2 2
x 1 x  2 x  2
1 x   0   2 1 x x  2 2  0  1 x
x x x 1  0  1   5 x  2   1   5 x  l  2   1   5  
Vậy bất phương trình đã cho có tập nghiệm S    2    
Bài 27 : Giải bất phương trình sau  2 2 x x   x x  3 2 3 12 5 2
x  1  2x  10x  5 Lời giải
Điều kiện: x  2
Bất phương trình đã cho tương đương  2 2
3x 12x  5  x  2x  3 x 1   2
3x 12x  5   2 x  2x   2 2
3x 12x  5  x  2x  3 x 1   2 2
3x 12x  5  x  2x  2 2
3x 12x  5  x  2x  3 2 2 3 2 2 
x 1  3x 12x  5  x  2x
x 1  x  2x  3x 12x  5 3 2
x x  2x 1 2  3 x   1  2 x  2x 2
 3x 12x  5 3 2
x  2x 10x  6  2  2
x  3x  2 3 2
x x x  0
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 137
Tất cả vì học sinh thân yêu   3 2
x x x  3 2
x  3x  2  2  2
x  3x  2 3 2
x x x  0   3 2 2
x x x
x  3x  2  3 2 2
x x x  3 x  3x  2   0 3 2 2 3 
x x x
x  3x  2  x  4x  2  0  x  2
Vậy bất phương trình đã cho có tập nghiệm S  2;  3
Bài 29: Giải bất phương trình sau  x   1
  x  3 2x  3  3x x   1 Lời giải 3 Điều kiện: x  2
Bất phương trình đã cho tương đương
x   x    x   2 x
x x   x   x      x   x    2 1 1 3 2 3 3 3 1 1 1 3 2
3 1  3x  5x  2  x   1  x  2
2  x  3 x  2   x 1 x  3   
  x  23x  
1   x  2 3x   1    0   x 1  1 2x  3  1   x 1  1 2x  3  1  Ta có x 1 x  3 3  x  1 2 x  3  
x 1  x  3  2x  2  3x  1, x    3x  1      0 x  1  1 2x  3  1 2 x 1  1 2x  3  1  
Khi đó bất phương trình trở thành x  2  0  x  2
Vậy bất phương trình đã cho có tập nghiệm S  2; 
Bài29 : Giải bất phương trình sau 4 3 2 3 x x x x  
x x   x   2 2 6 10 6 8 2 x  1 Lời giải
Điều kiện: x  0
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 138
Tất cả vì học sinh thân yêu
Bất phương trình đã cho tương đương  2 x   2
x x    x 2
x     x   2 2 2 1 2 6 8 1 2 x  1 
2x  6x  8 
x x  2 
2x  6x  8  x x  2
Do x  0 không thỏa mãn bất phương trình nên bất phương trình tương đương 2  4   2   2   2  2 x   6  1  x   0  2 x   2  x   1          x   x   x   x  2 Đặt t x
bất phương trình trở thành x t   1  t   1  2  
2t  2  t  1      t  1 2t  2   t  2 1 t    2 2 1  0  2  x   1  x
x  2  0   x  
1  x  2  0  x  4 x
Vậy bất phương trình đã cho có tập nghiệm S    4 4 2 2 2 x x  1 x x  1 x  1
Bài 30: Giải bất phương trình sau   2  x  2 x   2 1 x  1 x Lời giải
Điều kiện: x  0 2 2 2 2
x x  1 x x  1 x x  1 x x  1
Bất phương trình đã cho tương đương .    1 2 2 x  1 x x  1 x 2 2 x x  1 x x  1 Đặt a  , b
a,b  0 bất phương trình trở thành 2 x  1 x 2 x x  1
ab a  1  b  b  
1 a b   1  0  b  1 
 1   x  2 2 1  0 (đúng) x
Vậy bất phương trình đã cho có tập nghiệm S  0; 
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 139
Tất cả vì học sinh thân yêu
Bài 31: Giải bất phương trình sau  2 2 x    x  4 2 2 2 1 1
 1  x  3x  1 Lời giải
Điều kiện: 1  x  1 4 
 1  x ab Đặt 2 2
a  1  x ,b  1  x  
bất phương trình đã cho trở thành 2 2 2 3
x  1  2a b   a b 2 2 2 2
ab  2a b  2 2a b  2a ba b  2a ba b  2  0 Do 2 2 4
a b  0  2a b  0  a b  2  0  1  x  1  x  2  1  x  1  x  0
Vậy bất phương trình đã cho có tập nghiệm S    0
Facebook cá nhân : https://www.facebook.com/quang.manngoc http://qstudy. vn/
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 140