











































































































Preview text:
Tµi liÖu to¸n 11 n¨m häc 2018 1. PHƯƠNG PHÁ
P QUY NẠP TOÁN HỌC
A. TÓM TẮC LÝ THUYẾT
Nội dung phương pháp quy nạp toán học Cho
là một số nguyên dương và
là một mệnh đề có nghĩa với mọi số tự nhiên . Nếu (1) là đúng và (2) Nếu đúng, thì
cũng đúng với mọi số tự nhiên ;
thì mệnh đề P(n) đúng với mọi số tự nhiên .
Khi ta bắt gặp bài toán: Chứng minh mệnh đề
đúng với mọi số tự nhiên
ta có thể sử dụng phương pháp quy nạp như sau
Bước 1: Kiểm tra
có đúng hay không. Nếu bước này đúng thì ta chuyển qua bước hai
Bước 2: Với , giả sử đúng ta cần chứng minh cũng đúng. Kết luận: đúng với .
Lưu ý: Bước 2 gọi là bước quy nạp, mệnh đề
đúng gọi là giả thiết quy nạp.
B. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
Vấn đề 1. Dùng quy nạp để chứng minh đẳng thức. Bất đẳng thức Phương pháp .
Phương pháp: Giả sử cần chứng minh đẳng thức (hoặc ) đúng với ta
thực hiện các bước sau:
Bước 1: Tính rồi chứng minh
Bước 2: Giả sử , ta cần chứng minh .
1. caùc ví duï minh hoïa n(n + 1)
Ví dụ 1. Chứng mình với mọi số tự nhiên n ≥ 1 ta luôn có: 1 + 2 + 3 + ... + n = 2
Ví dụ 2. Chứng minh với mọi số tự nhiên n ≥ 1 ta luôn có: + + + + − = 2 1 3 5 ... 2n 1 n 1.3.5...(2n − 1) 1
Ví dụ 3. Chứng minh rằng với ∀n ≥ 1 , ta có bất đẳng thức: < 2.4.6.2n 2n + 1 n n+1 2n+ x (x + 1) x + 1 1
Ví dụ 4. Chứng minh rằng với ∀n ≥ 1,∀x > 0 ta có bất đẳng thức: ≤ . Đẳ n
ng thức xảy ra khi nào? x + 1 2
Chú ý: Trong một số trường hợp để chứng minh mệnh đề P(n) đúng với mọi số tự nhiên n ta có thể chứng minh theo cách sau
Bước 1: Ta chứng minh P(n) đúng với n = 1 và = k n 2
Bước 2: Giả sử P(n) đúng với n = k + 1, ta chứng minh P(n) đúng với n = k .
Cách chứng minh trên được gọi là quy nạp theo kiểu Cauchy (Cô si).
1i. Baøi taäp töï luaän töï luyeän
Bài 1 Chứng minh rằng với mọi số tự nhiên n ≥ 1 , ta luôn có
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 1 Tµi liÖu to¸n 11 n¨m häc 2018 2 2 2 2 n(n + 1)(2n + 1) 1 2 n 3 2n + 3
1. 1 + 2 + ... + (n − 1) + n = + + ... + = − 6 2. 2 n n 3 3 3 4 4.3
Bài 2 Chứng minh các đẳng thức sau n(n + 1)(n + 2) 1 1 1 1 n
1. 1.2 + 2.3 + ... + n(n + 1) = n 1 + + + ... + = 3 với ∀ ≥ 2. 1.5 5.9 9.13 (4n − 3)(4n + 1) 4n + 1 2 3 3 3 3 n(n + 1) 4 4 4 4 1 + 2n
3. 1 + 2 + 3 + ... + n = 1 − 1 − 1 − ... 1 − = 1 9 25 2 2 4. (2n − 1 2n 1) − 1 1 1 n 2 2 2 2 2 n(n − 1)(3n + 2) 5. + + ... + =
1.2 + 2.3 + 3.4 + ... + (n − 1).n = , ∀ n ≥ 2 1.2 2.3 n(n + 1) n + 1 6. 12 2 2 2 2n(n + 1)(2n + 1) n(n + 1)(n + 2)(n + 3) 7. 2 + 4 + ... + (2n) =
1.2.3 + 2.3.4 + ... + n(n + 1)(n + 2) = 3 8. 4 Với mọi n ∈ * . 2 2 2 2 2 n(n − 1)(3n + 2)
9. 1.2 + 2.3 + 3.4 + ... + (n − 1).n = n 2 12 với ∀ ≥ . 1 1 1 n(n + 3) 10. + + ... + = n * 1.2.3 2.3.4 n(n .
+ 1)(n + 2) 4(n + 1)(n + 2) Với mọi ∈ Bài 3
1. Chứng minh rằng với mọi số tự nhiên n ≥ 1 ta có: π
2 + 2 + 2 + . . + 2 + 2 = 2cos n (n dấu căn) +1 2 nx (n + 1)x sin sin 2 2
2. Chứng minh các đẳng thức sin x + sin 2x + . .sin nx = x k2 n 1 x với ≠ π với ≥ . sin 2
Bài 4 Chứng minh rằng với mọi n ≥ 1 ta có bất đẳng thức:
sin nx ≤ n sin x ∀x∈ Bài 5 n 1
1. Chứng minh rằng với mọi số tự nhiên n ≥ 1 , ta có : 1 + < 3 n n
2. 3 > 3n + 1 với mọi số tự nhiên n ≥ 2 ; 2.4.6.2n 3. ( n 1 1) > 2n + 1 1.3.5... 2n với mọi số tự nhiên ≥ ; −
Bài 6 Cho hàm số f xác định với mọi x ∈ và thoả mãn điều kiện : f(x + y) ≥ f(x).f(y), ∀x, y ∈ (*). Chứng minh x 2n
rằng với mọi số thực x và mọi số tự nhiên n ta có : f (x) ≥ f n 2
Bài 7 Chứng minh các bất đẳng thức sau 1 1 1 1 1 1 1 1. 1 + + + ... + < 2 − n 2 n 1 .... 2 n 2 4 9 ∀ ≥ 2. < + + + ≤ n n 2 3 n π n 3. tan α
n > n tanα với 0 < α < 2 2n 1 n 3 4(n 4. > + ∀ ≥ − 1) n+2 * n−1 * 5. 2 > 2n + 5, (∀n ∈ ) 6. 3
> n(n + 2); (∀n ∈ ,n ≥ 4) n−3 * π π 7. 2
> 3n − 1; (∀n ∈ ,n ≥ 8) 8. (n + 1)cos − n cos ≥ 1 n 1 n + 1 n với ∀ ≥ 1 3 5 2n + 1 1 1 1 1 9. . . .... < 1 ... n ;( n * ,n 2) 2 4 6 2n 10. + + + + < ∀ ∈ ≥ . + 2 3n + 4 n 2 3 2 − 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 2 Tµi liÖu to¸n 11 n¨m häc 2018 1 1 1 1 Bài 8 Cho tổng: S = + + + ... + n 1.3 3.5 5.7 (2n − 1)(2n + 1) 1. Tính S1;S2 ;S3;S4
2. Dự đoán công thức tính Sn và chứng minh bằng phương pháp qui nạp. f(x) + f(x) x + y
Bài 9 Cho hàm số f : → , n ≥ 2 là số nguyên . Chứng minh rằng nếu ≥ f ∀x,y ≥ 0 2 2 (1) thì ta có f(x ) + f(x ) + ... + f(x ) x + x + ... + x 1 2 n ≥ f 1 2 n x 0 i 1,n n , = (2). n ∀ ≥ i
Vấn đề 2. Ứng dụng phương pháp quy nạp trong số học và trong hình học
1. caùc ví duï minh hoïa n
Ví dụ 1. Cho n là số tự nhiên dương. Chứng minh rằng: a = n 16 – 15n – 1 225 n
Ví dụ 2. Chứng minh rằng với mọi số tự nhiên n ≥ 1 thì A(n) = 7 + 3n − 1 luôn chia hết cho 9
Ví dụ 3. Cho n là số tự nhiên dương. Chứng minh rằng: B = (n + 1)(n + 2)(n + 3)….(3n) n n 3
Ví dụ 4. Trong mặt mặt phẳng cho n điểm rời nhau (n > 2) tất cả không nằm trên một đường thẳng. Chứng minh rằng tất cả
các đường thẳng nối hai điểm trong các điểm đã cho tạo ra số đường thẳng khác nhau không nhỏ hơn n.
Ví dụ 5. Chứng minh rằng tổng các trong một n – giác lồi (n ≥ 3) bằng − 0 (n 2)180 .
1i. Baøi taäp töï luaän töï luyeän
Bài 1 Cho n là số nguyên dương.Chứng minh rằng: 2 n+1 2n−1
1. n(2n − 3n + 1) chia hết cho 6. 2. 11 + 12 chia hết cho 133 7 n
3. n − n chia hết cho 7
4. 13 − 1 chia hết cho 6 5 n
5. n − n chia hết cho 5 với mọi n ≥ 1
6. 16 − 15n − 1 chia hết cho 225 với mọi n ≥ 1 2n+1 7. 4.3
+ 32n − 36 chia hết cho 64 với mọi n ≥ 1 . Bài 2 n
1. Chứng minh rằng với ∀n ≥ 2 , ta luôn có a = (n + 1)(n + 2)...(n + n n) chia hết cho 2 . 2
2. Cho a, b là nghiệm của phương trình x − 27x + 14 = 0 Đặ n n
t S (n) = a + b . Chứng minh rằng với mọi số nguyên dương n thì S(n) là một số nguyên không chia hết cho 715.
3. Cho hàm số f : → thỏa f(1) = 1,f(2) = 2 và f(n + 2) = 2f(n + 1) + f(n) . 2 n
Chứng minh rằng: f (n + 1) − f(n + 2)f(n) = (−1) n 2
4. Cho pn là số nguyên tố thứ n . Chứng minh rằng: 2 > pn .
5. Chứng minh rằng mọi số tự nhiên không vượt qua n! đều có thể biểu diễn thành tổng của không quá n ước số đôi một khác nhau của n! . 2 n n Bài 3 Gọi 1
x ,x2 là hai nghiệm của phương trình : x − 6x + 1 = 0 . Đặt a = x + n 1 x2 . Chứng minh rằng : 1. a = 6a − − a − ∀ n ≥ n n 1 n 2 2 .
2. an là một số nguyên và an không chia hết cho 5 với mọi n ≥ 1 . Bài 4
1. Trong không gian cho n mặt phẳng phân biệt ( n ≥ 1 ), trong đó ba mặt phẳng luôn cắt nhau và không có bốn mặt phẳng
nào có điểm chung. Hỏi n mặt phẳng trên chia không gian thành bao nhiêu miền?
2. Cho n đường thẳng nằm trong mặt phẳng trong đó hai đường thẳng bất kì luôn cắt nhau và không có ba đường thẳng nào 2 đồ n + n + 2
ng quy. Chứng minh rằng n đường thẳng này chia mặt phẳng thành 2 miền. Bài 5
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 3 Tµi liÖu to¸n 11 n¨m häc 2018
1. Cho a, b,c,d, m là các số tự nhiên sao cho a + d , (b − 1)c , ab − a + c chia hết cho m . Chứng minh rằng x = n a.b + cn + n
d chia hết cho m với mọi số tự nhiên n .
2. Chứng minh rằng từ n + 1 số bất kì trong 2n số tự nhiên đầu tiên luôn tìm được hai số là bội của nhau.
1ii. Baøi taäp traéc nghieäm töï luyeän
Câu 1. Dùng quy nạp chứng minh mệnh đề chứa biến An 1 1 1 1
Câu 5. Cho S ... với * n . đúng vớ n
i mọi số tự nhiên n p ( p là một số tự nhiên). Ở bước 12 23 3 4 . n n 1
1 (bước cơ sở) của chứng minh quy nạp, bắt đầu với n bằng:
Mệnh đề nào sau đây đúng?
A. n 1. B. n . p C. n . p D. n . p 1 1 2 1 A. S . S . S . S . 3 B. C. D. 12 2 6 2 3 3 4
Câu 2. Dùng quy nạp chứng minh mệnh đề chứa biến An đúng vớ 1 1 1 1
i mọi số tự nhiên n p ( p là một số tự nhiên). Ở bước Câu 6. Cho S ... n n với * . 12 23 3 4 . n n 1
2 ta giả thiết mệnh đề An đúng với n k . Khẳng định nào Mệnh đề nào sau đây đúng? sau đây là đúng? n 1 n S . A. k .
p B. k . p C. k . p D. k . p A. S n B. . n n n 1
Câu 3. Khi sử dụng phương pháp quy nạp để chứng minh mệnh n 1 n 2 đề C. S . D. S .
chứa biến An đúng với mọi số tự nhiên n p ( p là một n n 2 n n 3
số tự nhiên), ta tiến hành hai bước: 1 1 1 S ... Câu 7. Cho với
Bước 1, kiểm tra mệnh đề An đúng với n . p n 13 35 2n 1 2n 1 *
n . Mệnh đề nào sau đây đúng?
Bước 2, giả thiết mệnh đề An đúng với số tự nhiên bất kỳ
n k p và phải chứng minh rằng nó cũng đúng với n 1 n A. S . S n B. . n n k 1. 2n 1 2n 1 Trogn hai bước trên: n n 2 C. S . S . n D. 3n 2 n 2n 5
A. Chỉ có bước 1 đúng. B. Chỉ có bước 2 đúng. 1 1 1
C. Cả hai bước đều đúng. D. Cả hai bước đều sai. Câu 8. Cho P 1 1 ... 1 với n 2 và n 2 2 2 2 3 n n .
Mệnh đề nào sau đây đúng?
Câu 4. Một học sinh chứng minh mệnh đề ''8n 1 chia hết cho * 7, ''
n * như sau: n 1 n 1 A. P . B. P . n 2 2n
Giả sử * đúng với n k , tức là 8k 1 chia hết cho 7. n 1 n 1 C. P . D. P . Ta có: k 1
8 1 88k
1 7 , kết hợp với giả thiết 8k 1 n 2n
chia hết cho 7 nên suy ra được k 1
8 1 chia hết cho 7. Vậy * đẳ
Câu 9. Với mọi n , hệ thức nào sau đây là sai?
ng thức * đúng với mọi * n . nn 1
Khẳng định nào sau đây là đúng?
A. 1 2 ... n 2
A. Học sinh trên chứng minh đúng. B. n 2 1 3 5 ... 2 1 n .
B. Học sinh chứng minh sai vì không có giả thiết qui nạp. n n 1 2n 1 2 2 2
C. Học sinh chứng minh sai vì không dùng giả thiết qui nạp.
C. 1 2 ... n 6
D. Học sinh không kiểm tra bước 1 (bước cơ sở) của phương pháp qui nạp.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 4 Tµi liÖu to¸n 11 n¨m häc 2018 2
2n n 1 2n 1 1 1 1 13 2 2 2
D. 2 4 6 2n . II) Với mọi * n , ta có ... . 6 n 1 n 2 2n 24
Câu 10. Xét hai mệnh đề sau: Mệnh đề nào đúng? I) Với mọi * n , số 3 2
n 3n 5n chia hết cho 3. A. Chỉ I. B. Chỉ II.
C. Không có. D. Cả I và II.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 5 Tµi liÖu to¸n 11 n¨m häc 2018
1.PHƯƠNG PHÁP QUY NẠP TOÁN HỌC
Nội dung phương pháp quy nạp toán học
Cho n0 là một số nguyên dương và P(n) là một mệnh đề có nghĩa với mọi số tự nhiên n ≥ n0 . Nếu
(1) P(n0 ) là đúng và
(2) Nếu P(k) đúng, thì P(k + 1) cũng đúng với mọi số tự nhiên k ≥ n0 ;
thì mệnh đề P(n) đúng với mọi số tự nhiên n ≥ n0 .
Khi ta bắt gặp bài toán:
Chứng minh mệnh đề P(n) đúng với mọi số tự nhiên n ≥ n0 , n ∈ 0
ta có thể sử dụng phương pháp quy nạp như sau
Bước 1: Kiểm tra P(n0) có đúng hay không. Nếu bước này đúng thì ta chuyển qua bước hai
Bước 2: Với k ≥ n0 , giả sử P(k) đúng ta cần chứng minh P(k + 1) cũng đúng.
Kết luận: P(n) đúng với ∀n ≥ n0 .
Lưu ý: Bước 2 gọi là bước quy nạp, mệnh đề P(k) đúng gọi là giả thiết quy nạp.
Vấn đề 1. Dùng quy nạp để chứng minh đẳng thức. Bất đẳng thức Phương pháp .
Phương pháp: Giả sử cần chứng minh đẳng thức P(n) = Q(n) (hoặc P(n) > Q(n) ) đúng với ∀n ≥ n , n ∈ 0 0 ta thực hiện các bước sau:
Bước 1: Tính P(n0), Q(n0) rồi chứng minh P(n ) = 0 Q(n0)
Bước 2: Giả sử P(k) = Q(k); k ∈ ,k ≥ n0 , ta cần chứng minh P(k + 1) = Q(k + 1) . Các ví dụ Ví dụ 1. n(n + 1)
Chứng mình với mọi số tự nhiên n ≥ 1 ta luôn có: 1 + 2 + 3 + ... + n = 2 Lời giải. n(n + Đặ 1)
t P(n) = 1 + 2 + 3 + ... + n : tổng n số tự nhiên đầu tiên : Q(n) = 2
Ta cần chứng minh P(n) = Q(n) ∀n ∈ ,n ≥ 1 . 1(1 + 1)
Bước 1: Với n = 1 ta có P(1) = 1, Q(1) = = 1 2
⇒ P(1) = Q(1) ⇒ (1) đúng với n = 1.
Bước 2: Giả sử P(k) = Q(k) với k ∈ ,k ≥ 1 tức là: k(k + 1) 1 + 2 + 3 + ... + k = 2 (1)
Ta cần chứng minh P(k + 1) = Q(k + 1) , tức là: (k + 1)(k + 2)
1 + 2 + 3 + ... + k + (k + 1) = 2 (2)
Thật vậy: VT(2) = (1 + 2 + 3 + . . + k) + (k + 1) k(k + 1) = + (k + 1) 2 (Do đẳng thức (1)) k (k + 1)(k + 2) = (k + 1)( + 1) = = VP(2) 2 2
Vậy đẳng thức cho đúng với mọi n ≥ 1 . Ví dụ 2.
Chứng minh với mọi số tự nhiên n ≥ 1 ta luôn có: + + + + − = 2 1 3 5 ... 2n 1 n Lời giải. • 2
Với n = 1 ta có VT = 1, VP = 1 = 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 1 Tµi liÖu to¸n 11 n¨m häc 2018
Suy ra VT = VP ⇒ đẳng thức cho đúng với n = 1 .
• Giả sử đẳng thức cho đúng với n = k với k∈ ,k ≥ 1 tức là: + + + + − = 2 1 3 5 ... 2k 1 k (1)
Ta cần chứng minh đẳng thức cho đúng với n = k + 1 , tức là: + + + + − + + = ( + )2 1 3 5 . . (2k 1) (2k 1) k 1 (2)
Thật vậy: VT(2) = (1 + 3 + 5 + . . + 2k − 1) + (2k + 1) 2
= k + (2k + 1) (Do đẳng thức (1)) 2 = (k + 1) = VP(1.2)
Vậy đẳng thức cho đúng với mọi n ≥ 1 . Ví dụ 3. 1.3.5...(2n − 1) 1
Chứng minh rằng với ∀n ≥ 1 , ta có bất đẳng thức: < 2.4.6.2n 2n + 1 Lời giải. 1 1
* Với n = 1 ta có đẳng thức cho trở thành : < ⇔ 2 > 3 2 đúng. 3
⇒ đẳng thức cho đúng với n = 1.
* Giả sử đẳng thức cho đúng với n = k ≥ 1 , tức là : 1.3.5...(2k − 1) 1 < 2.4.6...2k (1) 2k + 1
Ta phải chứng minh đẳng thức cho đúng với n = k + 1 , tức là : 1.3.5...(2k − 1)(2k + 1) 1 2.4.6....2k(2k 2) < (2) + 2k + 3 Thật vậy, ta có : 1.3.5...(2k − 1) 2k + 1 1 2k + 1 2k + 1 VT(2) = . < = 2.4.6...2k 2k + 2 2k + 1 2k + 2 2k + 2 2k + 1 1 2 Ta chứng minh: <
⇔ (2k + 1)(2k + 3) < (2k + 2) 2k + 2 2k + 3 ⇔ 3 > 1 (luôn đúng)
Vậy đẳng thức cho đúng với mọi số tự nhiên n ≥ 1 . n n+1 2n+ x (x + 1) x + 1 1
Ví dụ 4. Chứng minh rằng với ∀n ≥ 1,∀x > 0 ta có bất đẳng thức: ≤ . Đẳ n
ng thức xảy ra khi nào? x + 1 2 Lời giải. 2 3 • x(x + 1) x + 1 2 4
Với n = 1 ta cần chứng minh: ≤ ⇔ 8x(x + 1) ≤ (x + 1) x + 1 2 4 3 2 4
Tức là: x − 4x + 6x − 4x + 1 ≥ 0 ⇔ (x − 1) ≥ 0 (đúng)
Đẳng thức xảy ra khi x = 1. k k+1 2k+1 • x (x + 1) x + 1 Giả sử ≤ k , ta chứng minh x + 1 2 k+1 k+2 2k+ x (x + 1) x + 1 3 ≤ k (*) + 1 x + 1 2 Thật vậy, ta có: 2k+3 2 2k+1 2 k k+ x + 1 x + 1 x + 1 x + 1 1 x (x + 1) = ≥ 2 2 2 2 k x + 1
Nên để chứng minh (*) ta chỉ cần chứng minh
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 2 Tµi liÖu to¸n 11 n¨m häc 2018 2 k k+1 k+1 k+ x + 1 x (x + 2 1) x (x + 1) ≥ k k+ 2 x + 1 1 x + 1 x + 12 k+1 2 k+2 k Hay (x + 1) ≥ x(x + 1)(x + 1) 2 (**)
Khai triển (**) , biến đổi và rút gọn ta thu được 2k+2 2 k+ − − 1 − 2 + − 2 x (x 1) 2x (x 1) (x 1) ≥ 0 2 k+ ⇔ − 1 − 2 (x 1) (x
1) ≥ 0 BĐT này hiển nhiên đúng. Đẳng thức có ⇔ x = 1 .
Vậy bài toán được chứng minh.
Chú ý: Trong một số trường hợp để chứng minh mệnh đề P(n) đúng với mọi số tự nhiên n ta có thể chứng minh theo cách sau
Bước 1: Ta chứng minh P(n) đúng với n = 1 và = k n 2
Bước 2: Giả sử P(n) đúng với n = k + 1, ta chứng minh P(n) đúng với n = k .
Cách chứng minh trên được gọi là quy nạp theo kiểu Cauchy (Cô si).
CÁC BÀI TOÁN LUYỆN TẬP
Bài 1 Chứng minh rằng với mọi số tự nhiên n ≥ 1 , ta luôn có 2 2 2 2 n(n + 1)(2n + 1)
1. 1 + 2 + ... + (n − 1) + n = 6 1 2 n 3 2n + 3 2. + + ... + = − 2 n n 3 3 3 4 4.3
Bài 2 Chứng minh các đẳng thức sau n(n + 1)(n + 2)
1. 1.2 + 2.3 + ... + n(n + 1) = n 1 3 với ∀ ≥ 1 1 1 1 n 2. + + + ... + 1.5 5.9 9.13 (4n − 3)(4n + 1) = 4n + 1 2 3 3 3 3 n(n + 1)
3. 1 + 2 + 3 + ... + n = 2 4 4 4 4 1 + 2n 4. 1 − 1 − 1 − ... 1 − = 1 9 25 (2n − 2 1 2n 1) − 1 1 1 n 5. + + ... + = 1.2 2.3 n(n + 1) n + 1 2 2 2 2 2 n(n − 1)(3n + 2)
6. 1.2 + 2.3 + 3.4 + ... + (n − 1).n = , ∀ n ≥ 2 12 2 2 2 2n(n + 1)(2n + 1) 7. 2 + 4 + ... + (2n) = 3 n(n + 1)(n + 2)(n + 3)
8. 1.2.3 + 2.3.4 + ... + n(n + 1)(n + 2) = 4 Với mọi n ∈ * . 2 2 2 2 2 n(n − 1)(3n + 2)
9. 1.2 + 2.3 + 3.4 + ... + (n − 1).n = 12 với ∀n ≥ 2 . 1 1 1 n(n + 3) 10. + + ... + = 1.2.3 2.3.4
n(n + 1)(n + 2) 4(n + 1)(n + 2) Với mọi n ∈ * . Bài 3
1. Chứng minh rằng với mọi số tự nhiên n ≥ 1 ta có:
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 3 Tµi liÖu to¸n 11 n¨m häc 2018 π
2 + 2 + 2 + . . + 2 + 2 = 2cos n (n dấu căn) +1 2 nx (n + 1)x sin sin 2 2
2. Chứng minh các đẳng thức sin x + sin 2x + . .sin nx = x k2 n 1 x với ≠ π với ≥ . sin 2
Bài 4 Chứng minh rằng với mọi n ≥ 1 ta có bất đẳng thức:
sin nx ≤ n sin x ∀x∈ Bài 5 n 1
1. Chứng minh rằng với mọi số tự nhiên n ≥ 1 , ta có : 1 + < 3 n n
2. 3 > 3n + 1 với mọi số tự nhiên n ≥ 2 ; 2.4.6.2n 3. ( n 1 1) > 2n + 1 1.3.5... 2n
với mọi số tự nhiên ≥ ; −
Bài 6 Cho hàm số f xác định với mọi x ∈ và thoả mãn điều kiện : f(x + y) ≥ f(x).f(y), ∀x, y ∈ (*). Chứng minh x 2n
rằng với mọi số thực x và mọi số tự nhiên n ta có : f (x) ≥ f n 2
Bài 7 Chứng minh các bất đẳng thức sau 1 1 1 1 1. 1 + + + ... + < 2 − n 2 2 4 9 ∀ ≥ n n 1 1 1 2. n < 1 + + .... + ≤ 2 n 2 3 n π 3. tan α
n > n tanα với 0 < α < 4(n − 1) n 4. 2 > 2n + ∀ 1 n ≥ 3 n+2 * 5. 2 > 2n + 5, (∀n ∈ ) n−1 * 6. 3
> n(n + 2); (∀n ∈ ,n ≥ 4) n−3 * 7. 2
> 3n − 1; (∀n ∈ ,n ≥ 8) π π 8. (n + 1)cos − ncos ≥ 1 n 1 n + 1 n với ∀ ≥ 1 3 5 2n + 1 1 9. . . .... < 2 4 6 2n + 2 3n + 4 1 1 1 10. 1 + + + ... +
< n ;(∀n ∈ * ,n ≥ 2) n 2 3 . 2 − 1 1 1 1 1 Bài 8 Cho tổng: S = + + + ... + n 1.3 3.5 5.7 (2n − 1)(2n + 1) 1. Tính S1;S2 ;S3;S4
2. Dự đoán công thức tính Sn và chứng minh bằng phương pháp qui nạp. f(x) + f(x) x + y
Bài 9 Cho hàm số f : → , n ≥ 2 là số nguyên . Chứng minh rằng nếu ≥ f ∀x,y ≥ 0 2 2 (1) thì ta có f(x ) + f(x ) + ... + f(x ) x + x + ... + x 1 2 n ≥ f 1 2 n x 0 i 1,n n , = (2). n ∀ ≥ i ĐÁP ÁN Bài 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 4 Tµi liÖu to¸n 11 n¨m häc 2018
1. Bước 1: Với n = 1 ta có: 2 1(1 + 1)(2.1 + 1) VT = 1 = 1, VP = = 1 ⇒ VT = VP 6
⇒ đẳng thức cho đúng với n = 1.
Bước 2: Giả sử đẳng thức cho đúng với n = k ≥ 1 , tức là: 2 2 2 2 k(k + 1)(2k + 1) 1 + 2 + ... + (k − 1) + k = 6 (1)
Ta sẽ chứng minh đẳng thức cho đúng với n = k + 1 , tức là cần chứng minh: 2 2 2 2 2 (k + 1)(k + 1)(2k + 3)
1 + 2 + . . + (k − 1) + k + (k + 1) = 6 (2). Thật vây: do (1) 2 2 2 k(k 1)(2k 1) = 1 + 2 + ... + k + (k + 2 VT(2) 2 1) + + = + (k + 1) 6 2 + + 2 2k k (k 1)(2k + 7k + 6) = (k + 1) + k + 1 = 6 6 (k + 1)(k + 2)(2k + 3) = = VP(2) 6
⇒ (2) đúng ⇒ đẳng thức cho đúng với mọi n ≥ 1 .
2. * Với n = 1 ta có VT = 1 = VP ⇒ đẳng thức cho đúng với n = 1
* Giả sử đẳng thức cho đúng với n = k ≥ 1 , tức là: 1 2 k 3 2k + 3 + + ... + = − 2 k k 3 (1) 3 3 4 4.3
Ta sẽ chứng minh đẳng thức cho đúng với n = k + 1 , tức là cần chứng minh 1 2 k k + 1 3 2k + 5 + + ... + + = − 2 k k+1 k+1 3 (2). 3 3 3 4 4.3
Thật vậy: 3 2k+3 k+1 3 2k+5 VT(2) = − + = − = VP(2) k k+1 k+1 4 4.3 3 4 4.3
⇒ (2) đúng ⇒ đẳng thức cho đúng. Bài 2
1. 1.2 + 2.3 + ... + k(k + 1) + (k + 1)(k + 2) = k(k + 1)(k + 2) (k + 1)(k + 2)(k + 3) = + (k + 1)(k + 2) = 3 3 . 1 1 1 1 1 2. + + + ... + 1.5 5.9 9.13 (4k − 3)(4k + 1) + = (4k + 1)(4k + 5) k 1 k + 1 = + =
4k + 1 (4k + 1)(4k + 5) 4k + 5 k(k + 1)2 (k + 1)(k + 2)2 3 3. + (k + 1) = 3 3 . 4 1 + 2k (2k + 3)(2k − 1)(1 + 2k) 2k + 3 4. 1 − = − = 2 (2k + 1) 1 − 2k (2k + 2 1) (1 − 2k) −(2k + 1)
5,6,7. Bạn đọc tự làm k(k + 1)(k + 2)(k + 3) 8. + (k + 1)(k + 2)(k + 3) = 4 (k + 1)(k + 2)(k + 3)(k + 4) = 4 .
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 5 Tµi liÖu to¸n 11 n¨m häc 2018 2 k(k − 1)(3k + 2) 2 (k − 1)(3k + 2) 9. + k(k + 1) = k(k + 1) + 1 12 12 + 2
k(k 1)(3k − k − 10) (k + 1)k(k + 2)(3k + 5) = = 12 12 . k(k + 3) 1 10. + =
4(k + 1)(k + 2) (k + 1)(k + 2)(k + 3) + 2 + + 2 k(k 3) 4 (k 1) (k + 4) (k + 1)(k + 4) = = =
4(k + 1)(k + 2)(k + 3) 4(k + 1)(k + 2)(k + 3) 4(k + 2)(k + 3) . Bài 3 1. π
* Với n = 1 ⇒ VT = 2 , VP = 2 cos = 2 4
⇒ VT = VP ⇒ đẳng thức cho đúng với n = 1.
* Giả sử đẳng thức cho đúng với n = k , tức là: π
2 + 2 + 2 + . . + 2 + 2 = 2cos k (k dấu căn) (1) +1 2
Ta sẽ chứng minh đẳng thức cho đúng với n = k + 1 , tức là: π 2 + 2 + 2 + . . + 2 + 2 = 2cos k 1 k ( + dấu căn) (2). +2 2 π
Thật vậy: VT(2) = 2 + 2 + 2 + . . + 2 + 2 = 2 +
2cos k+1 2 k dau can π 2 π π = 2(1 + cos ) = 4cos = 2cos = VP(2) k+1 k+2 k+2 2 2 2
(Ở trên ta đã sử đụng công thức + = 2 a 1 cosa 2cos 2 ).
⇒ (2) đúng ⇒ đẳng thức cho đúng. x sin sin x 2
2. • Với n = 1 ta có VT = sin x, VP = = sin x n 1 x
nên đẳng thức cho đúng với = sin 2
• Giả sử đẳng thức cho đúng với n = k ≥ 1 , tức là: kx (k + 1)x sin sin + + = 2 2 sin x sin 2x . .sin kx x (1) sin 2
Ta chứng minh (4) đúng với n = k + 1 , tức là (k + 1)x (k + 2)x sin sin + + + = 2 2 sin x sin 2x . .sin(k 1)x x (2) sin 2 kx (k + 1)x sin sin 2 2 Thật vậy: VT(2) = + sin(k + 1)x x sin 2
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 6 Tµi liÖu to¸n 11 n¨m häc 2018 kx (k + 1)x x sin + + 2cos sin (k 1)x 2 2 2 = sin 2 x sin 2 (k + 1)x (k + 2)x sin sin 2 2 = = VP(2) x sin 2
Nên (2) đúng. Suy ra đẳng thức cho đúng với mọi n ≥ 1 .
Bài 4 * Với n = 1 ta có: VT = sin1 α
. = 1. sinα = VP nên đẳng thức cho đúng.
* Giả sử đẳng thức cho đúng với n = k ≥ 1 , tức là : sin kx ≤ k sin x (1)
Ta phải chứng minh đẳng thức cho đúng với n = k + 1 ,tức là : sin(k + 1 α ) ≤ (k + 1) sinα (2) Thật vậy:
sin(k + 1)α = sinkαcosα + coskαsinα
≤ sin kα . cos α + cos kα . sin α ≤ sin kα + sin α
≤ k sin α + sin α = (k + 1). sin α
Vậy đẳng thức cho đúng với n = k + 1 , nên đẳng thức cho cũng đúng với mọi số nguyên dương n . Bài 5 1 k 2 n n 1. Ta chứng minh 1 + < + + 1 ,1 ≤ k ≤
n (1) bằng phương pháp quy nạp theo k . Sau đó cho k = n ta có (7). n 2 k k 1 1 1 * Với k = 1 ⇒ VT(1) = 1 + < + + 1 = VP(1) 2 n n n ⇒ (1) đúng với k = 1 .
* Giải sử (1) đúng với k = p, 1 ≤ p ≤ n , tức là: 1 p 2 p p 1 + < + + 1 (2). n 2 n n
Ta chứng minh (1) đúng với k = p + 1 , tức là p+ 1 1 (p + 2 1) p + 1 1 + < + + 1 (3). n 2 n n p+1 p 2 1 1 1 p p 1 Thật vậy: 1 + = 1 + . 1 + < + + 1 1 + n n n 2 n n n 2 2 p p + p p + 2 1 p p + p p + 1 = + + + 1 ≤ + + + 1 3 2 2 2 n n n n n n 2 p + 2p + 1 p + 1 (p + 2 1) p + 1 < + + 1 = + + 1 2 2 ⇒ (3) đúng ⇒ đpcm. n n n n 1 n 1
Cách khác: Khi n = 1 ⇒ 2 < 3 (đúng) dễ thấy khi n > 1 ⇒ 0 ⇒ 1 + n 1 n tiến dần về ta luôn có
n tiến gần về 1.Vậy ∀ ≥ n 1 1 + < 3 n 2
2. Với n = 2 ta có: VT = 3 = 9 > VP = 3.2 + 1 = 7 nên đẳng thức cho đúng với n = 1 • k
Giả sử đẳng thức cho đúng với n = k ≥ 2 , tức là: 3 > 3k + 1 (1)
Ta chứng minh đẳng thức cho đúng với n = k + 1 , tức là :
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 7 Tµi liÖu to¸n 11 n¨m häc 2018 k+1 3 ≥ 3(k + 1) + 1 = 3k + 4 (2) k+1 k Thật vậy: 3
= 3.3 > 3(3k + 1) = 3k + 4 + (6k − 1) > 3k + 4 nên (2) đúng.
Vậy bài tóan được chứng minh. 2
3. Với n = 1 ta có: VT = = 2, VP = 3 ⇒ đẳ n 1 1 ng thức cho đúng với =
• Giả sử đẳng thức cho đúng với n = k ≥ 1 , tức là: 2.4.6.2k ( 1) > 2k + 1 1.3.5... 2k (1) −
Ta chứng minh đẳng thức cho đúng với n = k + 1 , tức là: 2.4.6.2k(2k + 2) ( 1) > 2k + 3 1.3.5... 2k − (2k + 1) (2) 2.4.6.2k(2k + 2) 2k + 2 2k + 2 Thật vậy: 1.3.5...( 2k 1. 2k − 1) > + = (2k + 1) 2k + 1 2k + 1 2k + 2 2 Nên ta chứng minh
> 2k + 3 ⇔ (2k + 2) > (2k + 1)(2k + 3) 2k + 1
⇔ 4 > 3 hiển nhiên đúng.
Vậy bài toán được chứng minh. Bài 6 x
1. Trong BĐT f(x + y) ≥ f(x).f(y) thay x và y bằng , ta đượ 2 c: 2 x x x x f f .f f (x) x + ≥ ⇒ ≥ f( ) 2 2 2 2 2
Vậy bất đẳng thức đã cho đúng với n = 1 .
Giả sử bất đẳng thức đúng với n = k ≥ 1 . Ta có 2k f (x) x ≥ f (1) k 2
Ta chứng minh bất đẳng thức đúng với n = k + 1 , tức là : 2k+1 f (x) x ≥ f k+ (2) 1 2 2 x x x x Thật vậy ta có : f = f + ≥ f k k + 1 k + 1 2 2 2 k + 1 2 k k 2 2 2 x x ⇒ f ≥ f k 2 k + 1 2 k k + 1 2 2 x x ⇒ f ≥ f k 2 k + 1 2 2k+ x 1
Do tính chất bắc cầu ta có được : f (x) ≥ f k+ 1 2
Bất đẳng thức đúng với n = k + 1 nên cũng đúng với mọi số tự nhiên n. Bài 7 1 1 1 1 1 1. 2 − + < 2 − ⇔ < k (hiển nhiên đúng) (k + 2 1) k + 1 k + 1 k
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 8 Tµi liÖu to¸n 11 n¨m häc 2018 1 2. k +
> k + 1 ⇔ k(k + 1) > k (hiển nhiên) k + 1 1 2 k +
< 2 k + 1 ⇔ 2 k(k + 1) < 2k + 1 k + 1 ⇔ + < + 2
4k(k 1) (2k 1) = 4k(k + 1) + 1 (hiển nhiên). tan α n + tanα 3. tan(n + α 1) = > (n + 1)tanα 1 − tan α n .tanα ⇔ α + α > + α − + 2 tan n tan (n 1)tan (n 1)tan α.tan α n 2 ⇔ tan α
n 1 + (n + 1)tan α > n tanα (đúng) k+1 4. 2
> 2(2k + 1) = 2k + 3 + 2k − 1 > 2k + 3 . k+3 k+2 5. 2 = 2.2
> 2(2k + 5) = 2(k + 1) + 5 + 2k + 7 > 2(k + 1) + 5 k k−1 2 6. 3 = 3.3
> 3k(k + 2) = (k + 1)(k + 2) + 2k + 3k − 2 > (k + 1)(k + 2) . k−2 k−3 7. 2 = 2.2
> 2(3k − 1) = 3k + 2 + 3k − 4 > 3k + 2
8. • Với n = 1 thì bđt hiển nhiên đúng • π π Giả sử k cos − (k − 1)cos ≥ 1 k k − 1 . Ta cần chứng minh π π π π 2 π (k + 1)cos − kcos ≥ 1 ⇔ k cos − cos ≥ 2sin k + 1 k k + 1 k 2(k + 1) (2k + 1)π π 2 π ⇔ ksin sin ≥ sin 2k(k + 1) 2k(k + 1) 2(k + 1) (1) π (2k + 1)π π (2k + 1)π π Ta có: > > > 0 ⇒ sin > sin 2 2k(k + 1) 2(k + 1) 2k(k + 1) 2(k + 1) π π
Mặt khác: sin nx ≤ n sin x ⇒ k sin ≥ sin 2k(k + 1) 2(k + 1)
Từ đó ta có được (1) luôn đúng.
Vậy bài toán được chứng minh. 1 3 5 2k + 1 2k + 3 1 2k + 3 9. . . .... . < . 2 4 6 2k + 2 2k + 4 3k + 4 2k + 4 1 2k + 3 1 Và . < 3k + 4 2k + 4 3k + 7 ⇔ + + 2 < + + 2 (3k 7)(2k 3)
(3k 4)(2k 4) ⇔ k + 1 > 0 (đúng). 1 1 10. k + < k + 1 ⇔ < 1 k+1 k+ (đúng). 2 − 1 1 2 − 1 Bài 8 1 2 3 4 1. Ta có S = ,S = ;S = ,S = 1 2 3 4 3 5 7 9 n
2. Dự đoán công thức S = n 2n + 1 .
Bài 9 • Ta chứng minh (2) đúng với = k n 2 , k ≥ 1
* Với k = 1 thì (8.2) đúng (do (1)) + * Giả sử (2) đúng với = k
n 2 , ta chứng minh (2) đúng với = k 1 n 2 x + ... + x 1 k k 2 Thật vậy: f(x ) + ...f(x ) ≥ 2 f 1 k 2 k 2
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 9 Tµi liÖu to¸n 11 n¨m häc 2018 x + ... + k x k+ + 1 k 2 1 2 f(x ) + ...f(x ) ≥ 2 f k k+ 2 + 1 1 2 k 2 x + ... + x x + ... + 1 k k x k+ 1 Do đó: k 2 k 2 + f(x ) + ...f(x ) ≥ 2 f + 2 f 1 2 1 k+1 2 k k 2 2 x + ... + x + x + ... + 1 k k x k+ + + 1 k 1 2 2 1 2 ≥ 2 f k+ 1 . 2
Do vậy (2) đúng với mọi = k n 2 .
• Giả sử (2) đúng với mọi n = k + 1 ≥ 3 , tức là f(x ) + f(x ) + ... + 1 2 f(xk+ ) x + x + ...+ 1 1 2 xk+ ≥ f 1 k + 1 k + 1 (3)
Ta chứng minh (8.2) đúng với n = k , tức là f(x ) + f(x ) + ... + f(x ) x + x + ... + x 1 2 k ≥ f 1 2 k k k (4) x + x + ... + 1 2 xk x Thật vậy: đặt xk+ = = 1 k k , áp dụng (3) ta có x x f(x ) + f(x ) + . . + f(x ) + 1 2 k f x + x + ... + k 1 2 ≥ k f k + 1 k + 1 f(x ) + f(x ) + ... + f(x ) x + x + ... + x 1 2 k 1 2 k Hay ≥ f k k .
Vậy bài toán được chứng minh.
Chú ý: Chứng minh tương tự ta cũng có bài toán sau f(x) + f(y) Nếu ≥ f( xy) x,y 0 2 ∀ ≥ (a) thì ta có f(x ) + f(x ) + . . + 1 2 f(xn) ≥ f(n 1xx2...xn ) x 0, i 1,n n với ∀ ≥ = i (b).
Vấn đề 2. Ứng dụng phương pháp quy nạp trong số học và trong hình học Các ví dụ Ví dụ 1. n
Cho n là số tự nhiên dương. Chứng minh rằng: a = n 16 – 15n – 1 225 Lời giải.
• Với n = 1 ta có: a = 0 ⇒ 1 a1 225 . • k Giả sử a = 16 − 15k − k 1 225 , ta chứng minh k+1 ak+ = 16 −15(k + 1) − 1 1 225 k k k
Thậ vậy: ak+ = 16.16 − 15k − 16 = 16 − 15k − 1 − 1 15(16 −1) k = a − k 15(16 −1) k k−1 k−2 Vì 16 − 1 = 15.(16 + 16
+ ... + 1) 15 và ak 225
Nên ta suy ra ak+1 225 . Vậy bài toán được chứng minh n
Ví dụ 2. Chứng minh rằng với mọi số tự nhiên n ≥ 1 thì A(n) = 7 + 3n − 1 luôn chia hết cho 9
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 10 Tµi liÖu to¸n 11 n¨m häc 2018 Lời giải. 1
* Với n = 1 ⇒ A(1) = 7 + 3.1 − 1 = 9 ⇒ A( 1) 9 * Giả sử A(k ) 9 ∀
k ≥ 1, ta chứng minh A(k + 1) 9 k+1 k Thật vậy: A(k + 1) = 7
+ 3(k + 1) − 1 = 7.7 + 21k − 7 − 18k + 9
⇒ A(k + 1) = 7A(k) − 9(2k − 1) A(k ) 9 Vì ⇒ A(k + 1) 9 9(2k − 1) 9
Vậy A(n) chia hết cho 9 với mọi số tự nhiên n ≥ 1 .
Ví dụ 3. Cho n là số tự nhiên dương. Chứng minh rằng: B = (n + 1)(n + 2)(n + 3)….(3n) n n 3 Lời giải. • Với n = 1, ta có : = 1 B 2.3 3
• Giả sử mệnh đề đúng với n = k, tức là :
B = (k + 1)(k + 2)(k + 3)…(3k) k k 3 Ta chứng minh : B
= (k + 2)(k + 3)(k + 4)…3( k + 1) + + k 1 k 1 3
B + = 3(k + 1)(k + 2)(k + 3)…(3k)(3k + 1)(3k + k 1 2) = 3B (3k + 1)(3k + k 2) + Mà B k k 3 nên suy ra B + k 1 k 1 3 .
Vậy bài toán được chứng minh.
Ví dụ 4. Trong mặt mặt phẳng cho n điểm rời nhau (n > 2) tất cả không nằm trên một đường thẳng. Chứng minh rằng tất cả
các đường thẳng nối hai điểm trong các điểm đã cho tạo ra số đường thẳng khác nhau không nhỏ hơn n. Lời giải.
Giả sử mệnh đề đúng với n = k ≥ 3 điểm.
Ta chứng minh nó cũng đúng cho n = k + 1 điểm.
Ta có thể chứng minh rằng tồn tại ít nhất một đường thẳng chỉ chứa có hai điểm. Ta kí hiệu đường thẳng đi qua hai điểm
An và An+1 là AnAn+1 . Nếu những điểm A1,A2,...,An nằm trên một đường thẳng thì số lượng các đường thẳng sẽ
đúng là n + 1: Gồm n đường thẳng nối An+1 với các điểm A1,A2 ,...,An và đường thẳng chúng nối chung. Nếu
A1,A2,...,An không nằm trên một đường thẳng thì theo giả thiết quy nạp có n đường thẳng khác nhau. Bây giờ ta thêm các
đường thẳng nối An+1 với các điểm A1,A2 ,...,An . Vì đường thẳng AnAn+1 không chứa một điểm nào trong
A1,A2,...,An−1 , nên đường thẳng này khác hoàn toàn với n đường thẳng tạo ra bởi A1,A2,...,An . Như vậy số đường
thẳng tạo ra cũng không nhỏ hơn n + 1. Ví dụ 5.
Chứng minh rằng tổng các trong một n – giác lồi (n ≥ 3) bằng − 0 (n 2)180 . Lời giải.
• Với n = 3 ta có tổng ba góc trong tam giác bằng 0 180
• Giả sử công thức đúng cho tất cả k-giác, với k < n , ta phải chứng minh mệnh đề cũng đúng cho n-giác. Ta có thể chia n-
giác bằng một đường chéo thành ra hai đa giác. Nếu số cạnh của một đa giác là k+1, thì số cạnh của đa giác kia là n – k + 1,
hơn nữa cả hai số này đều nhỏ hơn n. Theo giả thiết quy nạp tổng các góc của hai đa giác này lần lượt là ( − ) 0 k 1 180 và ( − − ) 0 n k 1 180 . Tổng các góc của n 0 0
-giác bằng tổng các góc của hai đa giác trên, nghĩa là (k – 1 + n − k – 1)180 = (n − 2)180 .
Suy ra mệnh đề đúng với mọi n ≥ 3 .
CÁC BÀI TOÁN LUYỆN TẬP
Bài 1 Cho n là số nguyên dương.Chứng minh rằng:
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 11 Tµi liÖu to¸n 11 n¨m häc 2018 2
1. n(2n − 3n + 1) chia hết cho 6. n+1 2n−1 2. 11 + 12 chia hết cho 133 7
3. n − n chia hết cho 7 n
4. 13 − 1 chia hết cho 6 5
5. n − n chia hết cho 5 với mọi n ≥ 1 n
6. 16 − 15n − 1 chia hết cho 225 với mọi n ≥ 1 2n+1 7. 4.3
+ 32n − 36 chia hết cho 64 với mọi n ≥ 1 . Bài 2 n
1. Chứng minh rằng với ∀n ≥ 2 , ta luôn có a = (n + 1)(n + 2)...(n + n n) chia hết cho 2 . 2
2. Cho a, b là nghiệm của phương trình x − 27x + 14 = 0 Đặ n n
t S (n) = a + b . Chứng minh rằng với mọi số nguyên dương n thì S(n) là một số nguyên không chia hết cho 715.
3. Cho hàm số f : → thỏa f(1) = 1,f(2) = 2 và f(n + 2) = 2f(n + 1) + f(n) . 2 n
Chứng minh rằng: f (n + 1) − f(n + 2)f(n) = (−1) n 2
4. Cho pn là số nguyên tố thứ n . Chứng minh rằng: 2 > pn .
5. Chứng minh rằng mọi số tự nhiên không vượt qua n! đều có thể biểu diễn thành tổng của không quá n ước số đôi một khác nhau của n! . 2 n n Bài 3 Gọi 1
x ,x2 là hai nghiệm của phương trình : x − 6x + 1 = 0 . Đặt a = x + n 1 x2 . Chứng minh rằng : 1. a = 6a − − a − ∀ n ≥ n n 1 n 2 2 .
2. an là một số nguyên và an không chia hết cho 5 với mọi n ≥ 1 . Bài 4
1. Trong không gian cho n mặt phẳng phân biệt ( n ≥ 1 ), trong đó ba mặt phẳng luôn cắt nhau và không có bốn mặt phẳng
nào có điểm chung. Hỏi n mặt phẳng trên chia không gian thành bao nhiêu miền?
2. Cho n đường thẳng nằm trong mặt phẳng trong đó hai đường thẳng bất kì luôn cắt nhau và không có ba đường thẳng nào 2 đồ n + n + 2
ng quy. Chứng minh rằng n đường thẳng này chia mặt phẳng thành 2 miền. Bài 5
1. Cho a, b,c,d, m là các số tự nhiên sao cho a + d , (b − 1)c , ab − a + c chia hết cho m . Chứng minh rằng x = n a.b + cn + n
d chia hết cho m với mọi số tự nhiên n .
2. Chứng minh rằng từ n + 1 số bất kì trong 2n số tự nhiên đầu tiên luôn tìm được hai số là bội của nhau. ĐÁP ÁN Bài 1 2 3 2
1. Đặt a = n(2n − 3n + 1) = 2n − 3n + n n 3 2 2
Ta có: an+ = 2(n + 1) − 3(n + 1) + n + 1 = a + 1 n 6n . n 1 2n 1 2. Đặt + − a = 11 + n 12 n+1 2 2n−1 2n−1 Ta có: an+ = 11.11 + 12 .12 = 11.a + 1 n 133.12 7 3. Đặt a = n − n n 7 7 k 7−k
Ta có an+ = (n + 1) − (n + 1) = 1 an+ = a + 1 n ∑C7n i=1 k 7! Mà C = ,1 ≤ k ≤ 7 7 k!(7 − k)! luôn chia hết cho 7 . n
4. Đặt a = 13 − 1 ⇒ n an+ = 13a + 1 n 12 5 5 5 3 2 5. Đặt a = n − n
n thì ta có: ak+ − a = (k + 1) − k −1 = 5k(k + 2k + 2k + 1 k 1) .
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 12 Tµi liÖu to¸n 11 n¨m häc 2018 n k+1 k
6. Đặt a = 16 − 15n − n
1 thì ta có: ak+ = 16 −15k −16 = a + 1 k 15.(16 −1) 2n+1 2k+3 2k+1 7. Đặt a = 4.3 + 32n − n 36 thì ta có: ak+ = 4.3 + 32(k + 1) − 36 = a + 32(3 + 1 k 1) Bài 2 2
1. * Với n = 2 , ta có : a = 2
(2 +1)(2 + 2) = 12 ⇒ a2 4 = 2 . + * Giả sử a k
k 2 ta chứng minh a + k 1 k 1 2 . Thật vậy:
a + = (k + 1+ 1)(k + 1+ 2). .(k + k + 1+ k 1 1)
= (k + 2)(k + 3). .(k + k + 2)
= (k + 2)(k + 3). .(k + k)(k + k + 1)(k + k + 2) 2
= (k + 1)(k + 2)(k + 3)...(k + k).2.(k + k + 1) = 2a .(k + k + 1)
k ak k k+1 k+1 Do ak 2 ⇒ 2ak 2 ⇒ ak+1 2 đpcm.
2. Ta có: S(n) = 27S(n − 1) − 14S(n − 2) rồi dùng quy nạp để chứng minh S(n) chia hết cho 751 . 3. • 2 2 1
Ta có: f(3) = 2f(2) + f(1) = 5 , nên f (2) − f(3)f(1) = 2 − 5.1 = (−1)
Suy ra đẳng thức cho đúng với n = 1.
• Giả sử đẳng thức cho đúng với n = k , tức là: 2 + − + = − k f (k 1) f(k 2)f(k) ( 1) (1)
Ta chứng minh đẳng thức cho đúng với n = k + 1 , tức là: 2 k+ + − + + = − 1 f (k 2) f(k 3)f(k 1) ( 1) (2) Ta có: 2 + − + + = 2
f (k 2) f(k 3)f(k 1) f (k + 2) − 2f(n + 2) + f(n + 1) f(k + 1) 2
= f(k + 2) f(k + 2) − 2f(k + 1) − f (k + 1) 2 k k+1
= f(k + 2)f(k) − f (k + 1) = −(−1) = (−1)
Vậy bài toán được chứng minh.
4. Trước hết ta có nhận xét: p .p . .p + 1 > 1 2 n pn+1 1 • 2 Với n = 1 ta có: 2 = 4 > p = 1 2 k k+1 • 2 2 Giả sử 2 > p ∀ k ≤ k n , ta cần chứng minh 2 > pk+1 1 2 p 2 2 2 k
Thật vậy, ta có: 2 .2 ...2 + 1 > p .p ...p + 1 > 1 2 k pk+1 k+1 1 2 k 2 −1 k+ + + + 1 2 2 ... 2 2 2 Suy ra 2 > pk+ ⇒ 2 + 1 > 1 pk+ ⇒ 2 > 1 pk+1
Vậy bài toán được chứng minh 5.
• Với n = 1 bài toán hiển nhiên đúng.
• Giả sử bài toán đúng với n = k , ta chứng minh bài toán đúng với n = k + 1
Nếu a = (k + 1)! thì bài toán hiển nhiên đúng
Ta xét a < (k + 1)! , ta có: a = (k + 1)d + r với d < k!,r < k + 1
Vì d < k! nên d = d + d + ... + 1 2 dk với d (i = i
1,k) là các ước đôi một khác nhau của k!
Khi đó: a = (k + 1)d + (k + 1)d + . . + (k + 1)d + 1 2 k r
Vì (k + 1)di ,r là các ước đôi một khác nhau của (k + 1)!
Vậy bài toán được chứng minh. Bài 3
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 13 Tµi liÖu to¸n 11 n¨m häc 2018 n−1 n−1 n−2 n−2
1. Ta có: a = (x + x )(x + x ) − x x (x + n 1 2 1 2 1 2 1 1 x ) x + x = 6 Theo đị 1 2 nh lí Viét: x x = 1 2 1 nên ta có: n−1 n−1 n−2 n− a = 6(x + x ) − (x + 2 x ) = n 1 2 1 1 6an− − 1 an−2 . 2.
* Với n = 1 ⇒ a = x + x = 6 ⇒ a ∈ 1 1 2 1
Và a1 không chia hết cho 5 * Giả sử a ∈ k
và ak không chia hết cho 5 với mọi k ≥ 1 . Ta chứng minh ak+ ∈
1 và ak+1 không chia hết cho 5. Do a + = 6a − k 1 k ak−1 Mà ak ,ak− ∈ 1 ⇒ ak+ ∈ 1 .
Mặt khác: a + = 5a + (a − a − ) = 5a + 5a − − k 1 k k k 1 k k 1 ak−2 5ak 5
Vì ak−2 không chia hết cho 5 và a không chia hết cho 5. k 1 5ak−1 5 nên suy ra + Bài 4
1. Giả sử n mặt phẳng chia không gian thành an miền 2 n + n + 2
Ta chứng minh được: an+ = a + 1 n 2 (n + 2 1)(n − n + 6)
Từ đó ta tính được: a = n 6 .
2. Gọi an là số miền do n đường thẳng trên tạo thành. Ta có: a = 1 2 .
Ta xét đường thẳng thứ n + 1 (ta gọi là d ), khi đó d cắt n đường thẳng đã cho tại n điểm và bị n đường thẳng chia
thành n + 1phần đồng thời mỗi phần thuộc một miền của an . Mặt khác với mỗi đoạn nằm trong miền của an sẽ chia miền
đó thành 2 miền, nên số miền có thêm là n + 1. Do vậy, ta có: a + = a + n + n 1 n 1 2 n n 2 Từ đây ta có: + + a = n 2 . Bài 5 1. • Với n = 0 ta có x = a + 0 d m • k Giả sử x = a.b + ck + k
d m với k ≥ 0,k∈ , ta chứng minh k+1 xk+ = a.b + c(k + 1) + 1 d m . Thật vậy: k+1 k k k xk+ − x = a.b − a.b + c = 1 k b (ab − a + c) − c.b + c k k−1 k−2
= b (ab − a + c) − c(b − 1)(b + b + ... + 1) Mà x ,ab − a + c,c(b − k 1) m ⇒ xk+1 m
Vậy bài toán được chứng minh. 2.
• Với n = 1 ta thấy bài toán hiển nhiên đúng
• Giả sử bài toán đúng với n − 1, có nghĩa là: từ n số bất kì trong 2n − 2 số tự nhiên đầu tiên luôn tìm được hai số là bội của nhau.
Ta chứng minh bài toán đúng với n , tức là: từ n + 1 số bất kì trong 2n số tự nhiên đầu tiên luôn tìm được hai số là bội của nhau.
Ta chứng minh bằng phản chứng:
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 14 Tµi liÖu to¸n 11 n¨m häc 2018
Giả sử tồn tại một tập con X có n + 1 phần tử của tập A = {1,2,...,2 }
n sao cho hai số bất kì trong X không là bội của nhau.
Ta sẽ chứng minh rằng có một tập con X' gồm n phần tử của tập {1,2,...,2n − }
2 sao cho hai phần tử bất kì của X' không là bội của nhau
Để chứng minh điều này ta xét các trường hợp sau đây
TH 1: X không chứa 2n và 2n − 1
Ta bỏ đi một phần tử bất kì của tập X ta được một tập X' gồm n phần tử và là tập con của {1,2,...,2n − } 2 mà hai phần tử
bất kì thuộc X' không là bội của nhau.
TH 2: X chứa 2n mà không chứa 2n − 1
Ta bỏ đi phần tử 2n thì ta thu được tập X' gồm n phần tử và là tập con của {1,2,...,2n − }
2 mà hai phần tử bất kì thuộc
X' không là bội của nhau.
TH 3: X chứa 2n − 1 mà không chứa 2n
Ta bỏ đi phần tử 2n − 1 thì ta thu được tập X' gồm n phần tử và là tập con của {1,2,...,2n − }
2 mà hai phần tử bất kì thuộc
X' không là bội của nhau.
TH 2: X chứa 2n và 2n − 1
Vì X không chứa hai số là bội của nhau nên X không chứa n và ước của n (Vì nếu chứa ước của n thì số đó là ước của 2n )
Bây giờ trong X , ta bỏ đi hai phần tử 2n − 1 và 2n rồi bổ sung thêm n vào thì ta thu được tập X' gồm n phần tử và là
tập con của {1,2,...,2n − }
2 mà hai phần tử bất kì thuộc X' không là bội của nhau.
Như vậy ta luôn thu được một tập con X' gồm n phần tử của tập {1,2,...,2n − }
2 mà các phần tử không là bội của nhau.
Điều này trái với giả thiết quay nạp.
Vậy bài toán được chứng minh theo nguyên lí quy nạp.
ĐÁP ÁN TRẮC NGHIỆM
Câu 1. Dùng quy nạp chứng minh mệnh đề chứa biến An đúng với mọi số tự nhiên n p ( p là một số tự nhiên). Ở bước 1
(bước cơ sở) của chứng minh quy nạp, bắt đầu với n bằng: A. n 1. B. n . p C. n . p D. n . p
Lời giải. Chọn B.
Câu 2. Dùng quy nạp chứng minh mệnh đề chứa biến An đúng với mọi số tự nhiên n p ( p là một số tự nhiên). Ở bước 2 ta
giả thiết mệnh đề An đúng với n k . Khẳng định nào sau đây là đúng? A. k . p B. k . p C. k . p D. k . p
Lời giải. Chọn B.
Câu 3. Khi sử dụng phương pháp quy nạp để chứng minh mệnh đề chứa biến An đúng với mọi số tự nhiên n p ( p là một số
tự nhiên), ta tiến hành hai bước:
Bước 1, kiểm tra mệnh đề An đúng với n . p
Bước 2, giả thiết mệnh đề An đúng với số tự nhiên bất kỳ n k p và phải chứng minh rằng nó cũng đúng với n k 1. Trogn hai bước trên:
A. Chỉ có bước 1 đúng.
B. Chỉ có bước 2 đúng.
C. Cả hai bước đều đúng.
D. Cả hai bước đều sai.
Lời giải. Chọn C.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 15 Tµi liÖu to¸n 11 n¨m häc 2018
Câu 4. Một học sinh chứng minh mệnh đề ''8n 1 chia hết cho * 7, ''
n * như sau:
Giả sử * đúng với n k , tức là 8k 1 chia hết cho 7. Ta có: k 1
8 1 88k
1 7 , kết hợp với giả thiết 8k 1 chia hết cho 7 nên suy ra được k 1
8 1 chia hết cho 7. Vậy đẳng
thức * đúng với mọi * n .
Khẳng định nào sau đây là đúng?
A. Học sinh trên chứng minh đúng.
B. Học sinh chứng minh sai vì không có giả thiết qui nạp.
C. Học sinh chứng minh sai vì không dùng giả thiết qui nạp.
D. Học sinh không kiểm tra bước 1 (bước cơ sở) của phương pháp qui nạp.
Lời giải. Chọn D. Thiếu bước 1 là kiểm tra với n 1 , khi đó ta có 1
8 1 9 không chi hết cho 7. 1 1 1 1
Câu 5. Cho S ... n n với
* . Mệnh đề nào sau đây đúng? 12 23 3 4 . n n 1 1 1 2 1 A. S . S . S . S . 3 B. C. D. 12 2 6 2 3 3 4 1 1 1
Lời giải. Nhìn vào đuôi của S n , ta đượ . n là cho 2 c . n n 1 2.2 1 23 Do đó vớ 1 1 2
i n 2 , ta có S . 2 Chọn C. 12 23 3 1 1 1 1
Câu 6. Cho S ... n n với
* . Mệnh đề nào sau đây đúng? 12 23 3 4 . n n 1 n 1 n n 1 n 2 A. S . S S . S . n B. . C. D. n n n 1 n n 2 n n 3 1 2 3
Lời giải. Cách trắc nghiệm: Ta tính được S , S , S 1 2 3
. Từ đó ta thấy quy luật là từ nhỏ hơn mẫu đúng 1 đơn vị. 2 3 4 Chọn B. 1 2 3 n
Cách tự luận. Ta có S , S , S S 1 2 3 dự đoán . 2 3 4 n n 1 1 1
Với n 1 , ta được S : đúng. 1 1.2 11 1 1 1 k
Giả sử mệnh đề đúng khi n k k 1 , tức là ... . 1.2 2.3 k k 1 k 1 1 1 1 k Ta có ... 1.2 2.3 k k 1 k 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 16 Tµi liÖu to¸n 11 n¨m häc 2018 1 1 1 1 k 1 ... 1.2 2.3 k k 1 k 1 k 2
k 1 k 1 k 2 2 1 1 1 1 k 2k 1 ... 1.2 2.3 k k 1 k
1 k 2 k 1 k 2 1 1 1 1 k 1 ...
. Suy ra mệnh đề đúng với n k 1 . 1.2 2.3 k k 1 k 1 k 2 k 2 1 1 1
Câu 7. Cho S ... n n với
* . Mệnh đề nào sau đây đúng? 13 35 2n 1 2n 1 n 1 n n n 2 A. S . S S S . n B. . C. . D. 2n 1 n 2n 1 n 3n 2 n 2n 5 1 n 1 S 1 3 6
Lời giải. Cho n 2 S . 2
Kiểm tra các đáp án chỉ cho B thỏa. Chọn B. 15 3 n
3 S 3 7 1 1 1
Câu 8. Cho P 1 1 ... 1
với n 2 và n .
Mệnh đề nào sau đây đúng? n 2 2 2 2 3 n n 1 n 1 n 1 n 1 A. P . B. P . C. P . D. P . n 2 2n n 2n 1 3 n
2 P 1 2 2 2 4
Lời giải. Vì n 2 nên ta cho . 1 1 2 n
3 P 1 . 1 3 2 2 2 3 3
Kiểm tra các đáp án chỉ cho D thỏa. Chọn D. *
Câu 9. Với mọi n , hệ thức nào sau đây là sai? nn 1
A. 1 2 ... n 2 B. n 2 1 3 5 ... 2 1 n . n n 1 2n 1 2 2 2
C. 1 2 ... n 6 2
2n n 1 2n 1 2 2 2
D. 2 4 6 2n . 6
Lời giải. Bẳng cách thử với n 1 , n 2 , n 3 là ta kết luận được. Chọn D.
Câu 10. Xét hai mệnh đề sau: I) Với mọi * n , số 3 2
n 3n 5n chia hết cho 3.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 17 Tµi liÖu to¸n 11 n¨m häc 2018 1 1 1 13 II) Với mọi * n , ta có ... . n 1 n 2 2n 24 Mệnh đề nào đúng? A. Chỉ I. B. Chỉ II. C. Không có. D. Cả I và II.
Lời giải. Chọn A.
Ta chứng minh I) đúng. Với n 1 , ta có 3 2
u 1 3.1 5.1 93 : đúng. 1
Giả sử mệnh đề đúng khi n k k 1 , tức là 3 2
u k 3k 5k3 k . Ta có u 3 2
k 3k 5k 2
3k 9k 9 u 3 k k k 2 3 3 3. k 1 Kết thúc chứng minh. 1 1 12 13
Mệnh đề II) sai vì với n 1, ta có VT : Vô lý. 11 2 24 24
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 18 Tµi liÖu to¸n 11 n¨m häc 2018 2. DÃY SỐ
A. TÓM TẮC LÝ THUYẾT
1. Dãy số là tập hợp các giá trị của hàm số
Được sắp xếp theo thứ tự tăng dần liên tiếp theo đối số tự nhiên : Ta kí hiệu bởi
và gọi là số hạng thứ n hay số hạng tổng quát của dãy số, được gọi là số
hạng đầu của dãy số.
Ta có thể viết dãy số dưới dạng khai triển hoặc dạng rút gọn .
2. Người ta thường cho dãy số theo các cách:
Cho số hạng tổng quát, tức là: cho hàm số u xác định dãy số đó
Cho bằng công thức truy hồi, tức là:
* Cho một vài số hạng đầu của dãy
* Cho hệ thức biểu thị số hạng tổng quát qua số hạng (hoặc một vài số hạng) đứng trước nó.
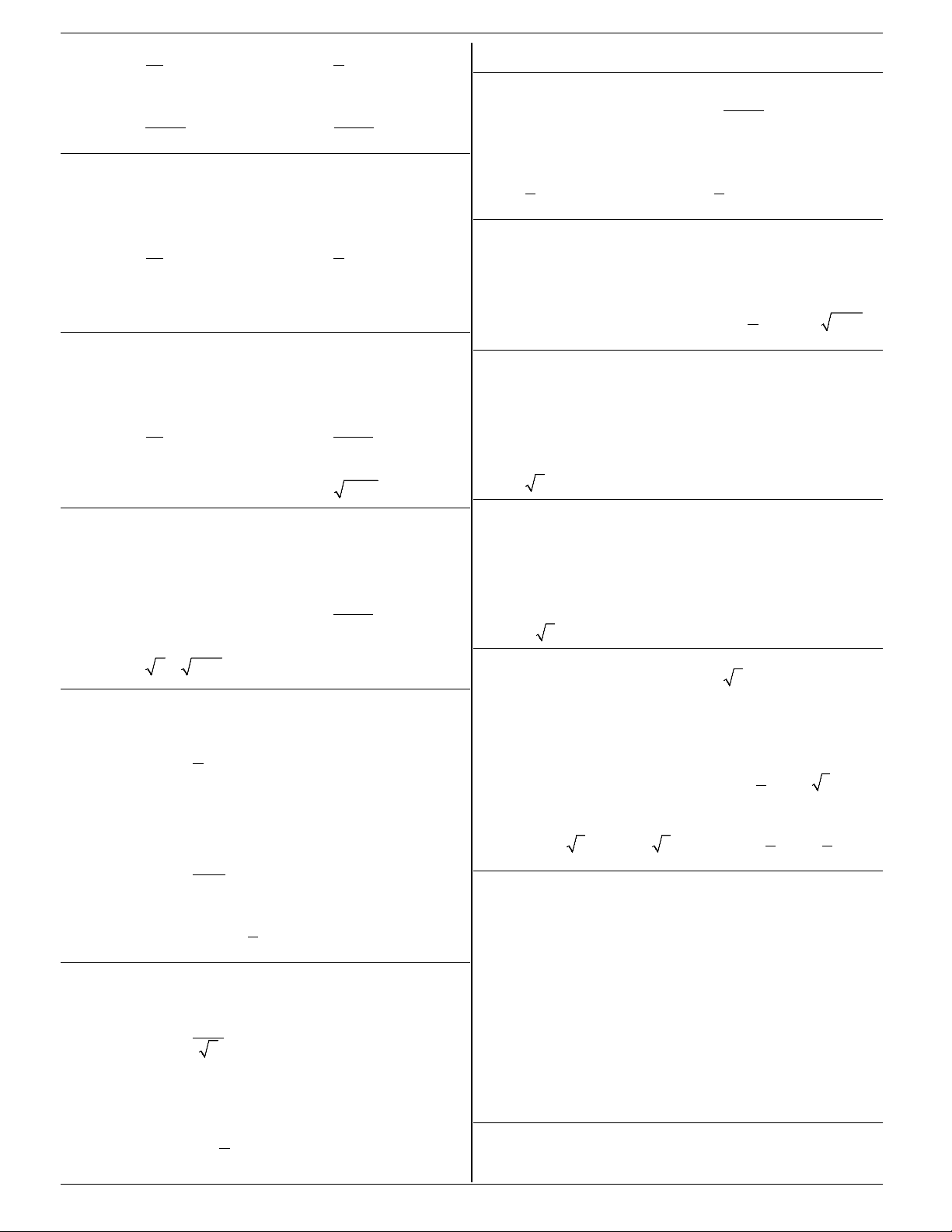
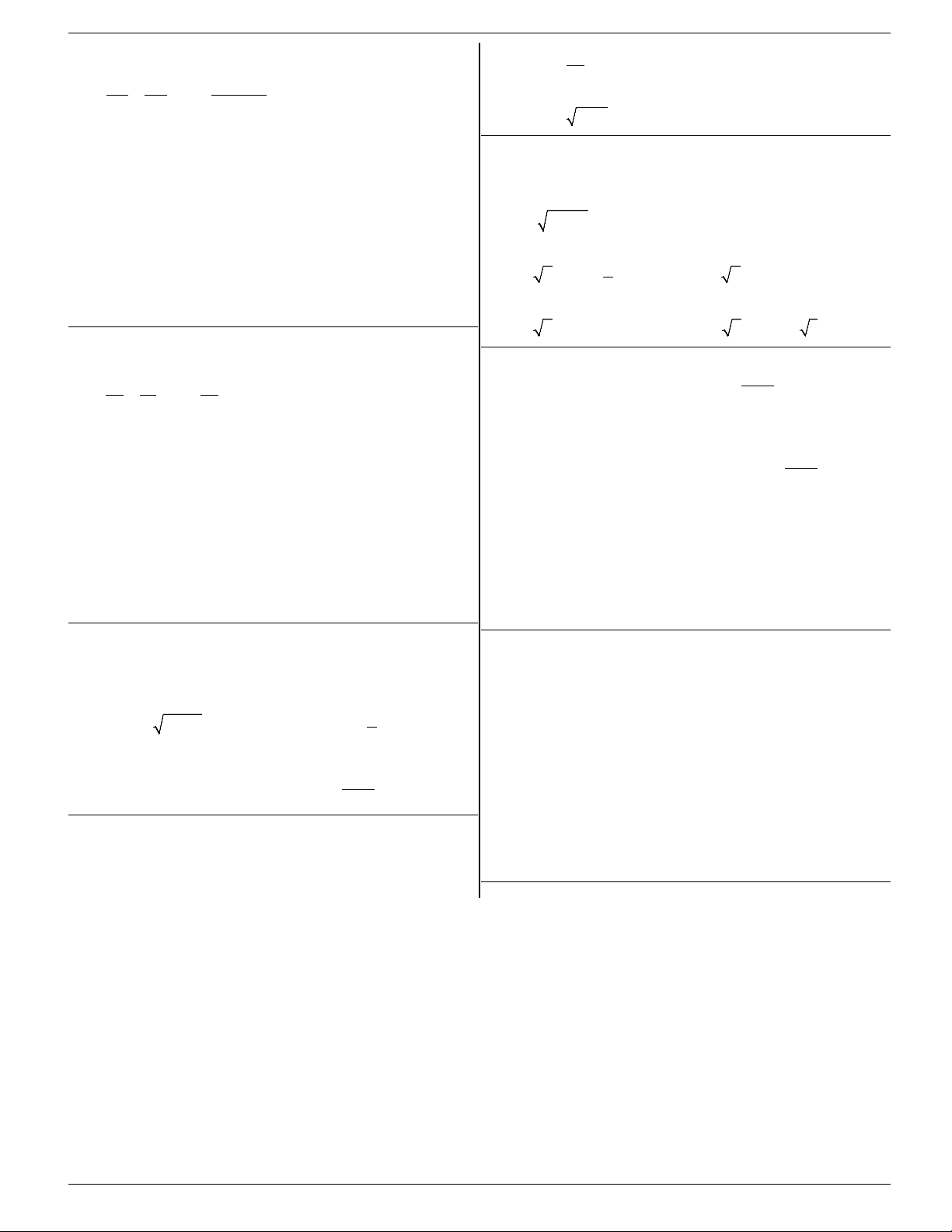
3. Dãy số tăng, dãy số giảm Dãy số gọi là dãy tăng nếu Dãy số gọi là dãy giảm nếu
4. Dãy số bị chặn Dãy số
gọi là dãy bị chặn trên nếu có một số thực sao cho . Dãy số
gọi là dãy bị chặn dưới nếu có một số thực sao cho .
Dãy số vừa bị chặn trên vừa bị chặn dưới gọi là dãy bị chặn, tức là tồn tại số thực dương sao B. CÁC D cho Ạ
NG TOÁN VÀ PH. ƯƠNG PHÁP GIẢI
Vấn đề 1. Xác định số hạng của dãy số
1. caùc ví duï minh hoïa
Ví dụ 1. Cho dãy số có 4 số hạng đầu là: −1, 3,19, 53 . Hãy tìm một quy luật của dãy số trên và viết số hạng thứ 10 của dãy
với quy luật vừa tìm. 2 n + 3n + 7
Ví dụ 2. Cho dãy số (un ) được xác định bởi u = n n + 1
1. Viết năm số hạng đầu của dãy;
2. Dãy số có bao nhiêu số hạng nhận giá trị nguyên. u = 1 1
Ví dụ 3. Cho dãy số (un ) xác định bởi: u = n 2un− + 3 ∀n ≥ 1 2 .
1. Viết năm số hạng đầu của dãy; n+1
2. Chứng minh rằng u = 2 − n 3 ; 2012
3. Số hạng thứ 2012
của dãy số có chia hết cho 7 không? u = 2 u + 2 2v
Ví dụ 4. Cho hai dãy số (u n 1 n n
n ),(vn ) được xác định như sau u = 3,v = 1 1 2 và + với n ≥ 2 . vn+ = 1 2un.vn n 2 2 2
1. Chứng minh : u − 2v = n n 1 và u − 2v = n n ( 2 −1) với ∀n≥1;
2. Tìm công thức tổng quát của hai dãy (un ) và (vn ) .
1i. Baøi taäp töï luaän töï luyeän
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 1 Tµi liÖu to¸n 11 n¨m häc 2018 2n + 1
Bài 1 Cho dãy số (un ) có số hạng tổng quát u = n n + 2 .
1. Viết năm số hạng đầu của dãy số.
2. Tìm số hạng thứ 100 và 200 167
3. Số 84 có thuộc dãy số đã cho hay không
4. Dãy số có bao nhiêu số hạng là số nguyên. u = −1,u = 1 2 3
Bài 2 Cho dãy số (an ) xác định bởi: un+ = 5u − 1 n 6un− ∀ n ≥ 1 2 .
1. Viết 7 số hạng đầu tiên của dãy n−1 n−1
2. Chứng minh rằng: u = 5.3 − n 6.2 , ∀n ≥ 1 . 2
Bài 3 Cho dãy số (un ) có số hạng tổng quát: u = 2n + n + n 4
1. Viết 6 số hạng đầu của dãy số 2. Tính u20 ,u2010
3. Dãy số đã cho có bao nhiêu số hạng là số nguyên. u = 1 2
Bài 4 Cho dãy số (un ) xác định bởi: u = n 2un− + 3n − 1, n ≥ 1 2
1. Tìm 5 số hạng đầu của dãy n
2. Chứng minh rằng u = 5.2 − 3n − 5 ∀n = n 1,2,3,...
3. Tìm số dư của u2010 khi chia cho 3 u = 2008;u = 1 2 2009
Bài 5 Cho dãy số (un ) : n ≥ 1 2un+ = u + 1 n u n+2
1. Chứng minh rằng dãy (v ) : v = u − n n n un−1 là dãy không đổi
2. Biểu thị un qua un−1 và tìm CTTQ của dãy số (un ) u = 1; u = 2 1 2
Bài 6 Cho dãy số (u 2 n ) : u n ≥ 2 n un+ = 1 un−1 u
1. Chứng minh rằng dãy (v ) : v = n n n u là dãy không đổi n−1
2. Tìm công thức tổng quát của dãy (un ) . u = 1 2
Bài 7. Cho dãy số (un ) được xác định bởi u = n 2un− + 3, n ≥ 1 2 .
1. Tìm 6 số hạng đầu của dãy; n−1
2. Chứng minh rằng u = 5.2 − n 3 với ∀n ≥ 2 ;
3. Số hạng có 3 chữ số lớn nhất của dãy là bao nhiêu?
Bài 8. Cho dãy số (un ) có 4 số hạng đầu là : u = 1,u = 1 2 3, u = 6,u = 3 4 10 .
1. Hãy tìm một quy luật của dãy số trên;
2. Tìm ba số hạng tiếp theo của dãy số theo quy luật vừa tìm trên. Bài 9 1 n n 1. Cho dãy (u ) : u = (2 + 5) + (2 − n n 5) u u 2
.Chứng minh rằng 2n là số tự nhiên chẵn và 2n+1 là số tự nhiên lẻ. n n
2. Cho dãy số (u ) : u = (4 − 2 3) + (4 + n n
2 3) . Chứng minh rằng tất cả các số hạng của dãy đều là số nguyên.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 2 Tµi liÖu to¸n 11 n¨m häc 2018 u = 1 1
3. Cho dãy số (un ) : 3
. Chứng minh rằng dãy (un ) có vô hạn các số chẵn và vô hạn các số lẻ. un+ = u ,n ≥ 1 n 1 2 2
4. Chứng minh rằng tồn tại đúng 4 dãy số nguyên dương (un ) thỏa: u = 1,u = 0 1 2 và un+ .u − 2 n un+ = 1 1.
Bài 10. (Dãy Fibonacci) Cho dãy số n
(F ) được xác định bởi F = 1,F = 1 2 1 và F = F − + n n 1 n F −2 Chứng minh rằng: n n 1 1 + 5 1 − 5 1. F = − n 5 2 2 2 2 2. F + n n F + = 1 2 F n+1 và F F + + F + F + = n n 1 n 1 n 2 2 F n+2 với mọi n ≥ 2 . k k 3. n F 5 ⇔ n 5 .
1ii. Baøi taäp traéc nghieäm töï luyeän n n n
Câu 1. Cho dãy số u u n , biết . n
Năm số hạng đầu tiên u u u . n 1
Câu 6. Cho dãy số , n biết n 2 1 . . Tìm số hạng n 3
của dãy số đó lần lượt là những số nào dưới đây? 8 8 u 2. u 2. 1 2 3 4 5 2 3 4 5 6 A. u . u . 3 B. C. D. 3 3 3 3 3
A. ; ; ; ; . B. ; ; ; ; . 2 3 4 5 6 3 4 5 6 7 u 2 1 1 2 3 4 5 2 3 4 5 6 u 1 . C. ; ; ; ; . D. ; ; ; ; .
Câu 7. Cho dãy số n xác định bởi Tìm số 2 3 4 5 6 3 4 5 6 7 u u 1 n 1 n 3 hạng u . 4 n
Câu 2. Cho dãy số un , biết u . Ba số hạng đầu tiên n 3n 1 5 2 14
của dãy số đó lần lượt là những số nào dưới đây? A. u . u 1. u . u . 4 B . C. D. 9 4 4 3 4 27 1 1 1 1 1 3 1 1 1 1 2 3 A. ; ; . B. ; ; . C. ; ; . D. ; ; . u 3 2 4 8 2 4 26 2 4 16 2 3 4 1
Câu 8. Cho dãy u u .
n xác định bởi Mệnh đề n u 2 n 1 u 1 2 1
Câu 3. Cho dãy số u n nào sau đây sai? n , biết với 0 . Ba số u u 3 n 1 n
hạng đầu tiên của dãy số đó là lần lượt là những số nào dưới 5 15 31 63 đây? A. u . B. u . C. u . D. u . 2 2 3 4 4 8 5 16
A. 1;2;5. B. 1; 4;7. C. 4;7;10. D. 1;3;7. n 1 8
Câu 9. Cho dãy số u , u n biết n . Số là số hạng 2n 1 15 2 2n 1
Câu 4. Cho dãy số u , u . u . thứ mấy của dãy số? n biết n Tìm số hạng 2 n 3 5 A. 8. B. 6. C. 5. D. 7. 1 17 7 71 A. u . u . u . u . 5 B . C. D. 4 5 12 5 4 5 39 2n 5 7
Câu 10. Cho dãy số u , u . n biết n Số là số hạng 5n 4 12 n
Câu 5. Cho dãy số u , u n thứ mấy của dãy số? n biết n 1 .2 . Mệnh đề nào sau đây sai? A. 8. B. 6. C. 9. D. 10. A. u 2. u 4. u 6. u 8. 1 B. 2 C. 3 D. 4
Câu 11. Cho dãy số u , n u u . n biết 2 . n Tìm số hạng n 1 A. u 2n.2. u 2n 1. n 1 B. n 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 3 Tµi liÖu to¸n 11 n¨m häc 2018 C. u 2 n 1 . u 2n 2. u 2 n 1 D. n 1 1
Câu 18. Cho dãy số u , . n được xác định Số hạng u 2u n 1 n
Câu 12. Cho dãy số u n u u . n , biết 3 . n Tìm số hạng 2n 1
tổng quát un của dãy số là số hạng nào dưới đây? A. 2 u 3 .3n 1. u 3n.3n . n n n 2n 1 B. 1 2n 1 A. 1 u n . u u u n B. 2 . n C. 1 2 . n D. 2. n 2n 1 C. 2 u 3 n 1. u 3 . 2n 1 D. 2n 1 1 u 1
Câu 19. Cho dãy số u , 2 . n được xác định Số
Câu 13. Cho dãy số u , n u u . n với 1 5 . n Tìm số hạng n 1 u u 2 n 1 n
hạng tổng quát un của dãy số là số hạng nào dưới đây? A. n 1 u 5 . u 5n. n 1 B. n 1 1 1 C. n 1 u 5.5 . u 5.5n . A. u 2 n
u 2 n 1 . n 1 . B. n n 1 D. 1 n 1 2 2 2n3 n 1 1 1
Câu 14. Cho dãy số u , u . u 2 . n u 2 . n n với n Tìm số hạng C. D. n 1 n 2 n 2 u . n 1 u 2 1
Câu 20. Cho dãy số u , . n được xác định 2n 1 3 n 1 2n 1 3 n 1 u u 2n 1 n 1 n A. u . u . n 1 B. n 1 n 1 n 1
Số hạng tổng quát un của dãy số là số hạng nào dưới đây? 2n3 n 2n5 n
A. u n u n n 2 2 1 . B. 2 2 . C. u . u . n n 1 D. n 2 n 1 n 2
C. u n 2 2 1 . u n n D. 2 2 1 . n 1 2 3 4
Câu 15. Dãy số có các số hạng cho bởi: 0; ; ; ; ; . có số 2 3 4 5 u 1 1
hạng tổng quát là công thức nào dưới đây?
Câu 21. Cho dãy số u , . n được xác định Số 2 u u n n 1 n n 1 n
hạng tổng quát u của dãy số là số hạng nào dưới đây? A. u . u n n B. . n n n 1
n(n 1)(2n 1) u 1 . n 1 2 n n A. n 6 C. u . u . n D. n n n 1
n(n 1)(2n 2) B. u 1 .
Câu 16. Dãy số có các số hạnh cho bởi: 1;1;1;1;1; . có số n 6
hạng tổng quát là công thức nào dưới đây?
n(n 1)(2n 1) C. u 1 . A. u 1. u n n B. 1. n 6 n n C. u u
n(n 1)(2n 2) n 1 . D. n 1 1 . D. u 1 . n 6
Câu 17. Cho dãy số có các số hạng đầu là: 2;0;2;4;6; . Số u 2
hạng tổng quát của dãy số này là công thức nào dưới đây? 1
Câu 22. Cho dãy số u , 1 . n
được xác định u 2 Số A. u 2 . n u n n 1 n B. 2. n u n
hạng tổng quát un của dãy số là số hạng nào dưới đây?
C. u 2n 1 . u n n D. 2 4. n n 1 n 1 A. u . u . n B. n n n
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 4 Tµi liÖu to¸n 11 n¨m häc 2018 n 1 n u 6 u 6 C. u . u 1 1 n D. . . . n n n 1 A. B. u 6u , n 1 u 3u , n 1 n n 1 n n 1 u 1 1 u 3 u 3
Câu 23. Cho dãy số u , . 1 n được xác định . u C. 1 . D. u n 2 1 n n 1 u 3u , n 1 u 6u , n 1 n n 1 n n 1
Số hạng tổng quát un của dãy số là số hạng nào dưới đây? a 3 1 A. u 1 . n u n
Câu 25. Cho dãy số a 1 .
n , được xác định n B. 1 . n a a , n 1 n 1 2 n n C. u u n
Mệnh đề nào sau đây sai? n 2 1 1 . D. . n 93 3
Câu 24. Cho dãy số u u 2 3n
A. a a a a a . B. a .
n có số hạng tổng quát là n 1 2 3 4 5 16 10 512 với *
n . Công thức truy hồi của dãy số đó là: 9 3 C. a a . a . n 1 n D. 2n n 2n
Vấn đề 2. Dãy số đơn điệu – Dãy số bị chặn Phương pháp:
Để xét tính đơn điệu của dãy số ta xét : * Nếu dãy tăng * Nếu dãy giảm. Khi ta có thể xét * Nếu dãy tăng * Nếu dãy giảm.
Để xét tính bị chặn của dãy số ta có thể dự đoán rồi chứng minh bằng quy nạp.
1. caùc ví duï minh hoïa u = 2 1
Ví dụ 1. Cho dãy số (un ) : u (u ) n− + 1 . Chứng minh rằng dãy
n là dãy giảm và bị chặn. u = 1 ∀n ≥ 2 n 2 u = 1,u = 1 2 2
Ví dụ 2. Cho dãy số (un ) :
. Chứng minh rằng dãy (u ) là dãy tăng và bị chặn u n n+ = u + 1 n un− ∀n ≥ 1 2
1i. Baøi taäp töï luaän töï luyeän
Bài 1 Xét tính tăng giảm của các dãy số sau 2 3n − 2n + 1 2 1. u = n u n n 1 n + 1 2. = − − n n n 3 − 1 n + (−1) 3. u = n u = n 4. 2 n 2 n
Bài 2 Xét tính tăng, giảm và bị chặn của dãy số (un ) , biết: 2n − 13 2 n + 3n + 1 1 1. u = n u = u 3n − 2 2. n n + 1 3. = n 1 + n + 2 n
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 5 Tµi liÖu to¸n 11 n¨m häc 2018 n 2 1 1 1 4. u = n u 1 ... n! 5. = + + + + n 2 2 2 . 2 3 n
Bài 3. Xét tính bị chặn của các dãy số sau 2n + 1 1. u = n u ( 1) u 3n 1 n + 2 2. = − n n 3. = − n 2 n + n + 1 n + 1 4. u = 4 − 3n − 2 n n 5. u = n u = 2 6. n − n + 1 n 2 n + 1
Bài 4. Xét tính bị chặn của các dãy số sau 1 1 1 1 1 1 1. u = + + ... + n u = + + ... + 1.3 2.4 n.(n + 2) 2. n 1.3 3.5 (2n −1)(2n +1) u = 1 1 3. un− + 2 u = 1 , n ≥ n 2 un− + 1 1
Bài 5 Xét tính tăng giảm của các dãy số sau u = u = 2 1 1 1 1. 2. 2 u + 1 3 3 n un+ = u + 1, n ≥ 1 n 1 un+ = n ≥ 1 1 4 Bài 6
1. Chứng minh rằng dãy số (un ) xác định bởi u = 2010 + 2010 + ... + n
2010 (n dấu căn). Là một dãy tăng. u = 1,u = 1 2 2
2. Cho dãy số (un ) :
. Chứng minh rằng dãy (u ) tăng và bị chặn. u = 3 3 n n un− + 1 un− ,n ≥ 2 3 an + 2
3. Cho dãy số (u ) : u = , n ≥ n n 1 2n − 1
a) Khi a = 4 , hãy tìm 5 số hạng đầu của dãy
b) Tìm a để dãy số đã cho là dãy số tăng. u = 1 2
4. Cho dãy số (un ) : u = n 3un− − 2, n = 1 2,3..
a) Viết 6 số hạng đầu của dãy n−1 b) Chứng minh u = 3 + 1, n = n 1,2,. . n−1 n
5. Cho dãy số u = −5.2 + 3 + n + n 2 , n = 1,2,...
a) Viết 5 số hạng đầu của dãy n−1 b) Chứng minh rằng: u = n 2un− + 3 − 1 n . Bài 7 n n
1. Cho dãy số (un ) : u = (1 − a) + (1 + n
a) ,trong đó a ∈(0;1) và n là số nguyên dương.
a)Viết công thức truy hồi của dãy số
b)Xét tính đơn điệu của dãy số u = 1 1
2. Cho dãy số (un ) được xác định như sau: 1 u = . n 3un− + − 2, n ≥ 1 2 2un−1
a) Viết 4 số hạng đầu của dãy và chứng minh rằng u > 0, ∀ n n
b) Chứng minh dãy (un ) là dãy tăng. u = 2011 0 3. Cho dãy số (u 2
n ) được xác định bởi : un un+ = , ∀ n = 1 1,2,... u + n 1
a) Chứng minh rằng dãy (un ) là dãy giảm
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 6 Tµi liÖu to¸n 11 n¨m häc 2018
b) Tìm phần nguyên của un với 0 ≤ n ≤ 1006 . u = 2,u = 1 2 6
4. Cho dãy số (un ) được xác định bởi: un+ = u + 2 n 2un+ , ∀ n = 1 1,2,... 2 n n
a) Gọi a, b là hai nghiệm của phương trình x − 2x − 1 = 0 . Chứng minh rằng: u = a + n b 2 n−1
b) Chứng minh rằng: un+ − 1 un+ u = (− 2 n 1) .8 .
Bài 8 Xét tính tăng giảm và bị chặn của các dãy số sau n + 1 3 1. (u ) : u = n n (u ) : u n 2n 1 n + 2 2. = + + n n u = 2 1 u = 2,u = 1 2 3 3. (un ) : u + 1 4. . n un+ = ∀ , n ≥ 2 u = u + u ∀ , n ≥ 2 1 2 n+1 n n−1 Bài 9 x = 1 0 1. Cho dãy số n− (x ) : 1 n 2n x = n x , n 2,3,... 2 ∑ = i (n − 1) i=1 Xét dãy số y = x + − n
n 1 xn . Chứng minh rằng dãy (yn ) là một tăng và bị chặn. u = 1,u = 3 0 1 2
2. Cho dãy số nguyên dương (u n ) thỏa : un+1 u . n+ = 1 + , n ≥ 2 0 un 2 n Chứng minh rằng: un+ u − 2 n un+ = 1
2 với mọi số tự nhiên n . u = 0 0
3. Cho dãy số (un ) được xác định bởi: . 2 un+ = 5u + 24u + 1, n = 1 n n 0,1,..
Chứng minh rằng dãy số (un ) là dãy số nguyên. 1 n n
4. Cho dãy số (un ) được xác định bởi: u = (2 + 5) + (2 − n 5) 2
Chứng minh rằng u2n là số tự nhiên chẵn và u2n+1 là số tự nhiên lẻ.
5. Cho hai dãy số (xn );(yn ) xác định : 2 x = x + 1 + x x = 3 n n−1 n− 1 1 và y , ∀n ≥ 2 . y = n−1 y = 1 3 n 1 + 1 + 2 yn−1
Chứng minh rằng 2 < x y < 3, ∀n ≥ n n 2 . u = 1 0
6. Cho dãy số số (un ) được xác định bởi: 1 1 . un+ = 1 u + n 2 3un 3 Chứng minh rằng: a = n 2
là một số chính phương. 3u − n 1
1ii. Baøi taäp traéc nghieäm töï luyeän
Câu 26. Cho các dãy số sau. Dãy số nào là dãy số tăng? 1 1 1 1
C. 1; 3; 5; 7; 9;
D. 1; ; ; ; ; 2 4 8 16 1 1 1 1
A. 1; 1; 1; 1; 1; 1; B . 1; ; ; ; ; 2 4 8 16
Câu 27. Trong các dãy số u u
n cho bởi số hạng tổng quát n
sau, dãy số nào là dãy số tăng?
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 7 Tµi liÖu to¸n 11 n¨m häc 2018 1 1 D. Dãy số 2
u n sin n là dãy tăng. A. u . u . n n B. 2n n n 3n 1 n 5 2n 1
Câu 33. Cho dãy số u u . u n , biết n
Dãy số n bị C. u . u . 3n 1 n D. 3n 1 n n 1
chặn trên bởi số nào dưới đây?
Câu 28. Trong các dãy số u u 1 1
n cho bởi số hạng tổng quát n A. . B. 1. C. . D. 0.
sau, dãy số nào là dãy số tăng? 3 2 2 3
Câu 34. Trong các dãy số u u
n cho bởi số hạng tổng quát A. u . u . n n B. 3n n n
sau, dãy số nào bị chặn trên? n
C. u 2n. u 2 . 1 n D. n A. 2 u n . n u u . u n n B. 2 . n C. n D. 1. n n
Câu 29. Trong các dãy số u u
n cho bởi số hạng tổng quát n
Câu 35. Cho dãy số u u n n u n , biết cos
sin . Dãy số n
sau, dãy số nào là dãy số giảm? n
bị chặn trên bởi số nào dưới đây? 1 3n 1 A. u . u . n B. 2n n n 1 A. 0. B. 1. C. 2 u n . u n C. 2.
D. Không bị chặn trên. n D. 2. n
Câu 36. Cho dãy số u u n n u n , biết sin
cos . Dãy số n
Câu 30. Trong các dãy số u u n
n cho bởi số hạng tổng quát n
bị chặn dưới bởi số nào dưới đây?
sau, dãy số nào là dãy số giảm? 2 A. 0. B. 1. n 1 A. u sin . n u . n B. n n C. 2.
D. Không bị chặn dưới. n
C. u n n 1.
u 1 . 2n 1 . n D. n
Câu 37. Cho dãy số u u n n n , biết 3 cos sin . n Dãy số un
Câu 31. Mệnh đề nào sau đây đúng?
bị chặn dưới và chặn trên lần lượt bởi các số m và M nào dưới đây? 1
A. Dãy số u 2 là dãy tăng. n n 1 A. m 2; 2 M . B. m ; 3 M 1. 2 n
B. Dãy số u
1 2n là dãy giảm. n 1 1 1
C. m 3 1; 3 M
1. D. m ; . M 2 2 n 1
C. Dãu số u là dãy giảm. n n 1 n
Câu 38. Cho dãy số u , n u n biết n 2 5 1 .5 . Mệnh đề nào 1 sau đây đúng?
D. Dãy số u 2n cos là dãy tăng. n n
A. Dãy số un bị chặn trên và không bị chặn dưới.
Câu 32. Mệnh đề nào sau đây sai?
B. Dãy số un bị chặn dưới và không bị chặn trên. 1 n
A. Dãy số u là dãy giảm. n n
C. Dãy số un bị chặn. B. Dãy số 2
u 2n 5 là dãy tăng. n
D. Dãy số un không bị chặn. n 1
C. Dãy số u 1 là dãy giảm. n n
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 8 Tµi liÖu to¸n 11 n¨m häc 2018 Câu 39. Cho dãy số u , 1 n với A. u . n u n B. 3 . n n 1 1 1 2 u ... , n 1; 2; 3 . n Mệnh đề nào 1.4 2.5 nn 3
C. u n 1. D. 2 u n . sau đây đúng? n n Câu 43. Cho dãy số
un , xác định bởi
A. Dãy số un bị chặn trên và không bị chặn dưới. u 6 1
. Mệnh đề nào sau đây đúng?
B. Dãy số u *
n bị chặn dưới và không bị chặn trên. u
6 u , n n 1 n
C. Dãy số un bị chặn. 5 A. 6 u . u n B. 6 3. 2 n
D. Dãy số un không bị chặn.
C. 6 u 2. n D. 6 u 2 3. n Câu 40. Cho dãy số u , n với 1 1 1 u u u ... , n 2; 3; 4; .
Câu 44. Cho dãy số , n với sin n . Khẳng định nào n Mệnh đề nào sau đây 2 2 2 n 1 2 3 n đúng? sau đây là đúng?
A. Dãy số u
A. Số hạng thứ n 1 của dãy là u sin .
n bị chặn trên và không bị chặn dưới. n 1 n 1
B. Dãy số un bị chặn dưới và không bị chặn trên.
B. Dãy số un là dãy số bị chặn.
C. Dãy số un bị chặn.
C. Dãy số un là một dãy số tăng.
D. Dãy số un không bị chặn.
D. Dãy số un không tăng không giảm.
Câu 41. Trong các dãy số un sau đây, dãy số nào là dãy số bị n
Câu 45. Cho dãy số u , u n với n 1 . Mệnh đề nào sau chặn? đây đúng? 1 A. 2 u n 1. u n . u n B. n
A. Dãy số n là dãy số tăng. n n
B. Dãy số un là dãy số giảm.
C. u 2n 1. u n D. . n n 1
C. Dãy số un là dãy số bị chặn.
Câu 42. Trong các dãy số u u
n cho bởi số hạng tổng quát n
D. Dãy số un là dãy số không bị chặn.
sau, dãy số nào bị chặn?
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 9 Tµi liÖu to¸n 11 n¨m häc 2018 DÃY SỐ
Vấn đề 1. Xác định số hạng của dãy số Các ví dụ
Ví dụ 1. Cho dãy số có 4 số hạng đầu là: −1,3,19,53 . Hãy tìm một quy luật của dãy số trên và viết số hạng thứ 10 của dãy
với quy luật vừa tìm. Lời giải. 3 2
Xét dãy (un ) có dạng: u = an + bn + cn + n d a + b + c + d = −1 8a + 4b + 2c + d = 3 Ta có hệ: 27a + 9b + 3c + d = 19 64a + 16b + 4c + d = 53
Giải hệ trên ta tìm được: a = 1, b = 0,c = −3,d = 1 ⇒ u = 3 n − 3n + n 1 là một quy luật . Số hạng thứ 10: u = 10 971. 2 n + 3n + 7
Ví dụ 2. Cho dãy số (un ) được xác định bởi u = n n + 1
1. Viết năm số hạng đầu của dãy;
2. Dãy số có bao nhiêu số hạng nhận giá trị nguyên. Lời giải.
1. Ta có năm số hạng đầu của dãy 2 1 + 3.1 + 7 11 u = = 17 25 47 1 u ,u ,u 7,u 1 + 1 2 , = = = = 2 3 4 5 3 4 6 5 5 2. Ta có: u = n + 2 + n , do đó u n 1 n nguyên khi và chỉ khi
là ước của 5. Điều đó xảy ra khi + 1 n n + 1 nguyên hay + n + 1 = 5 ⇔ n = 4
Vậy dãy số có duy nhất một số hạng nguyên là u = 4 7 . u = 1 1
Ví dụ 3. Cho dãy số (un ) xác định bởi: u = n 2un− + 3 ∀n ≥ 1 2 .
1. Viết năm số hạng đầu của dãy; n+1
2. Chứng minh rằng u = 2 − n 3 ; 2012
3. Số hạng thứ 2012
của dãy số có chia hết cho 7 không? Lời giải.
1. Ta có 5 số hạng đầu của dãy là: u = 1 1; u = 2u + 3 = 2 1
5 ; u = 2u + 3 = 13; u = 2u + 3 = 3 2 4 3 29 u = 2u + 3 = 5 4 61 .
2. Ta chứng minh bài toán bằng phương pháp quy nạp + 1 1 * Với n = 1 ⇒ u = 2 − 3 = 1 ⇒ 1
bài toán đúng với N = 1 k+1 k+2 * Giả sử u = 2 − k 3 , ta chứng minh uk+ = 2 − 1 3
Thật vậy, theo công thức truy hồi ta có: k+1 k+2
uk+ = 2u + 3 = 2(2 − 3) + 3 = 2 − 1 k 3 đpcm.
3. Ta xét phép chia của n cho 3 3k * n = 3k ⇒ u = 2(2 − 1) − n 1 3k k Do 2
− 1 = 8 − 1 = 7.A 7 ⇒ un không chia hết cho 7
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 1 Tµi liÖu to¸n 11 n¨m häc 2018 3k * n = 3k + 1 ⇒ u = 4(2 − 1) + 1 ⇒ n un không chia hết cho 7 3k * n = 3k + 2 ⇒ u = 8(2 − 1) + 5 ⇒ n un không chia hết cho 7 2012 Vậy số hạng thứ 2012
của dãy số không chia hết cho 7. u = 2 u + 2 2v
Ví dụ 4. Cho hai dãy số (u n 1 n n
n ),(vn ) được xác định như sau u = 3,v = 1 1 2 và + với n ≥ 2 . vn+ = 1 2un.vn n 2 2 2
1. Chứng minh : u − 2v = n n 1 và u − 2v = n n ( 2 −1) với ∀n≥1;
2. Tìm công thức tổng quát của hai dãy (un ) và (vn ) . Lời giải.
1. Ta chứng minh bài toán theo quy nạp 2 2 a) Chứng minh: u − 2v = n n 1 (1) • 2 2 2 2 Ta có u − 2v = 3 − 2.2 = 1 1 1 nên (1) đúng với n = 1 • 2 2 Giả sử u − 2v = k k 1 , khi đó ta có: 2 2 2 2 2 2 2 2 uk+ − 1 2vk+ = 1 (u + k 2vk ) − 2(2ukvk ) = (u − k 2vk ) = 1
Từ đó suy ra (1) đúng với ∀n ≥ 1 . n 2 b) Chứng minh u − 2v = n n ( 2 −1) (2) 2 2 2 Ta có: u − 2v = n n un− + 1 2vn− − 1 2 2un−1vn− = 1 (un− −1 2vn−1) 2
• Ta có: u − 2v = 3 − 2 2 = 1 1
( 2 −1) nên (2) đúng với n =1 k 2 • Giả sử u − 2v = k k ( 2 −1) , ta có: k 1 2 2 u − 2v = k 1 k 1 (u − k 2vk ) = ( 2 −1) + + +
Vậy (2) đúng với ∀n ≥ 1 . n 2
2. Theo kết quả bài trên và đề bài ta có: u + 2v = n n ( 2 +1) n n 2 2 2u = n ( 2 +1) +( 2 − 1) Do đó ta suy ra n n 2 2 2 2v = n ( 2 +1) −( 2 − 1 ) n n 2 2 1 u = n ( 2 +1) +( 2 −1) 2 Hay . n n 2 2 1 v = n ( 2 +1) −( 2 −1) 2 2
CÁC BÀI TOÁN LUYỆN TẬP 2n + 1
Bài 1 Cho dãy số (un ) có số hạng tổng quát u = n n + 2 .
1. Viết năm số hạng đầu của dãy số.
2. Tìm số hạng thứ 100 và 200 167
3. Số 84 có thuộc dãy số đã cho hay không
4. Dãy số có bao nhiêu số hạng là số nguyên.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 2 Tµi liÖu to¸n 11 n¨m häc 2018 u = −1,u = 1 2 3
Bài 2 Cho dãy số (an ) xác định bởi: un+ = 5u − 1 n 6un− ∀ n ≥ 1 2 .
1. Viết 7 số hạng đầu tiên của dãy n−1 n−1
2. Chứng minh rằng: u = 5.3 − n 6.2 , ∀n ≥ 1 . 2
Bài 3 Cho dãy số (un ) có số hạng tổng quát: u = 2n + n + n 4
1. Viết 6 số hạng đầu của dãy số 2. Tính u20 ,u2010
3. Dãy số đã cho có bao nhiêu số hạng là số nguyên. u = 1 2
Bài 4 Cho dãy số (un ) xác định bởi: u = n 2un− + 3n − 1, n ≥ 1 2
1. Tìm 5 số hạng đầu của dãy n
2. Chứng minh rằng u = 5.2 − 3n − 5 ∀n = n 1,2,3,...
3. Tìm số dư của u2010 khi chia cho 3 u = 2008;u = 1 2 2009
Bài 5 Cho dãy số (un ) : n ≥ 1 2un+ = u + 1 n u n+2
1. Chứng minh rằng dãy (v ) : v = u − n n n un−1 là dãy không đổi
2. Biểu thị un qua un−1 và tìm CTTQ của dãy số (un ) u = 1; u = 2 1 2
Bài 6 Cho dãy số (u 2 n ) : u n ≥ 2 n un+ = 1 un−1 u
1. Chứng minh rằng dãy (v ) : v = n n n u là dãy không đổi n−1
2. Tìm công thức tổng quát của dãy (un ) . u = 1 2
Bài 7. Cho dãy số (un ) được xác định bởi u = n 2un− + 3, n ≥ 1 2 .
1. Tìm 6 số hạng đầu của dãy; n−1
2. Chứng minh rằng u = 5.2 − n 3 với ∀n ≥ 2 ;
3. Số hạng có 3 chữ số lớn nhất của dãy là bao nhiêu?
Bài 8. Cho dãy số (un ) có 4 số hạng đầu là : u = 1,u = 1 2 3, u = 6,u = 3 4 10 .
1. Hãy tìm một quy luật của dãy số trên;
2. Tìm ba số hạng tiếp theo của dãy số theo quy luật vừa tìm trên. Bài 9 1 n n 1. Cho dãy (u ) : u = (2 + 5) + (2 − n n 5) u u 2
.Chứng minh rằng 2n là số tự nhiên chẵn và 2n+1 là số tự nhiên lẻ. n n
2. Cho dãy số (u ) : u = (4 − 2 3) + (4 + n n
2 3) . Chứng minh rằng tất cả các số hạng của dãy đều là số nguyên. u = 1 1
3. Cho dãy số (un ) : 3
. Chứng minh rằng dãy (un ) có vô hạn các số chẵn và vô hạn các số lẻ. un+ = u ,n ≥ 1 n 1 2 2
4. Chứng minh rằng tồn tại đúng 4 dãy số nguyên dương (un ) thỏa: u = 1,u = 0 1 2 và un+ .u − 2 n un+ = 1 1.
Bài 10. (Dãy Fibonacci) Cho dãy số n
(F ) được xác định bởi F = 1,F = 1 2 1 và F = F − + n n 1 n F −2 Chứng minh rằng:
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 3 Tµi liÖu to¸n 11 n¨m häc 2018 n n 1 1 + 5 1 − 5 1. F = − n 5 2 2 2 2 2. F + n n F + = 1 2 F n+1 và F F + + F + F + = n n 1 n 1 n 2 2 F n+2 với mọi n ≥ 2 . k k 3. n F 5 ⇔ n 5 . ĐÁP ÁN Bài 1: 5 7 3 11
1. Năm số hạng đầu của dãy là: u = 1,u = ,u = ,u = ,u = 1 2 3 4 5 4 5 2 7 . 2.100 + 1 67
2. Số hạng thứ 100: u = = 100 100 + 2 34 2.200 + 1 401 Số hạng thứ 200: u = = 200 200 + 2 202 167 2n + 1 167 3. Giả sử u = ⇒ = ⇔ 84(2n + 1) = 167(n + n 2) 84 n + 2 84 ⇔ n = 250 . 167 Vậy (u )
84 là số hạng thứ 250 của dãy số n . 2(n + 2) − 3 3 4. Ta có: u = = 2 − n n + 2 n + 2 3 ⇒ u ∈ n ⇔ ∈ ⇔ 3 n + 2 ⇔ n = 1 n + 2
Vậy dãy số có duy nhất một số hạng là số nguyên. Bài 2
1. Bốn số hạng đầu của dãy: u = 5u − 6u = 3 2 1 21 ; u = 5u − 6u = 4 3 2 87 ; u = 5u − 6u = 5 4 3 309 u = 5u − 6u = 6 5 4 1023 ; u = 5u − 6u = 7 6 5 3261.
2. Ta chứng minh bằng phương pháp quy nạp 0 0 * u = 5.3 − 6.2 = − 1 1 (đúng). k−1 k−1 * Giả sử u = 5.3 − k 6.2 , ∀k ≥ 2 .
Khi đó, theo công thức truy hồi ta có: u = 5.u − 6u = 1 k k 1 5( k−1 k− 5.3 − 1 6.2 )−6( k−2 k−2 k+ − 5.3 − 6.2 ) k−1 k−2 k−1 k−2 = 5(5.3 − 6.3 )−6(5.2 −6.2 ) k k = 5.3 − 6.2 đpcm.
Chú ý: Ta có bài toán tổng quát sau u1,u2 2 Cho dãy (un ) : b 4ac 0 a.un+ + bu + 1 n cun− = 0 ∀ n ≥ 1 2 , với − > α.x + β.x = u Khi đó: n−1 n− u = α.x + β 1 2 1 2 1 n 1 .x2 với 1
x ,x2 là hai nghiệm của phương trình ax + bx + c = 0 (*) và α,β : . α 2 .x + β 2 .x = 1 2 u2
Phương trình (*) gọi là phương trình đặc trưng của dãy. Bài 3
1. Ta có: u = 2 + 5;u = 4 + 2 2;u = 6 + 13;u = 8 + 1 2 3 4 2 5 u = 10 + 29;u = 12 + 5 6 2 10 . 2 2. Ta có: u = 40 + 20 2 101 ; u = 4020 + 2010 + 2010 4 2 2 2
3. Ta có: un nguyên ⇔ n + 4 = k ∈ ⇔ k − n = 4
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 4 Tµi liÖu to¸n 11 n¨m häc 2018
⇔ (k − n)(k + n) = 4 phương trình này vô nghiệm
Vậy không có số hạng nào của dãy nhận giá trị nguyên. Bài 4
1 Ta có: u = 2; u = 9; u = 26; u = 63; u = 1 2 3 4 5 140
2. Chứng minh bằng phương pháp quy nạp 2010 2010 3. Ta có: 5.2 ≡ 1.(−1) = 1(mod 3) Suy ra u ≡ 2010 2(mod3) . Bài 5
1. Ta có: u + − u + = u + − u ⇒ v + = v + = ... = v = n 2 n 1 n 1 n n 2 n 1 2 1
2. Ta có: u − u − = 1 ⇒ u = u − + n n 1 n n 1 1
Suy ra u = (u − u − ) + (u − − u − ) + ... + (u − u ) + n n n 1 n 1 n 2 2 1 u1
= 1 + 1 + ... + 1 + u = n − 1 + 2008 = n + 1 2007 . Bài 6 un+1 un u2 1. Ta có: = = ... = = 2 un un−1 u 1 n−1 n−1 2. Ta có u = n 2un− = ...2 u = 1 1 2 Bài 7.
1. Ta có 6 số hạng đầu của dãy là: u = 2u +3=7,u =17,u = 37,u =77,u = 2 1 3 4 5 6 157
2. Ta chứng minh bài toán bằng phương pháp quy nạp
Với n = 2 ta có: u = 5.2 − 3 = 2 7 (đúng) k−1 Giả sử u = 5.2 − k 3 , khi đó ta có: u 1 2uk 3 2( k−1 k k+ = + = 5.2 − 3) + 3 = 5.2 − 3
Vậy bài toán được chứng minh theo nguyên lí quy nạp. n−1 1003
3. Ta có u < 1000 ⇔ 2 < n 5 . 9
Mà 2 là lũy thừa lớn nhất của 2 lớn nhất có 3 chữ số nên ta có: n−1 = 9 2 2 ⇒ n = 10 .
Vậy u10 là số hạng cần tìm. Bài 8.
1. Vì dãy số cho giá trị của 4 số hạng đầu ứng với 4 giá trị tương ứng của n = 1,2,3,4 nên ta chỉ cần xác định một hàm số 3 2
theo n mà ta phải tìm 4 ẩn là được. Chẳng hạn ta xét u = an + bn + cn + n d
Theo bài ra ta có hệ phương trình : a + b + c + d = 1 a + b + c + d = 1 1 8a + 4b + 2c + d = 3 7a + 3b + c = 2 a = 0,b = c = ⇔ ⇔ 2 27a + 9b + 3c + d = 6 26a + 8b + 2c = 5 d = 0 64a + 16b + 4c + d = 10 21a + 5b + c = 3 n(n + 1) Nên u = n 2
là một dãy thỏa đề bài.
2. Ta có ba số hạng tiếp theo của dãy là: u = 15, u = 21, u = 5 6 7 28 . Bài 9 a + b = 4
1. Đặt a = 2 + 5, b = 2 − 5 ⇒ . Khi đó: ab = − 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 5 Tµi liÖu to¸n 11 n¨m häc 2018 1 n n 1 n−1 n−1 n−2 n− 2 u = (a + b ) = (a + b)(a + b ) − ab(a + n b ) 2 2 n−1 n−1 n−2 n− a + b a + 2 b = 4. + = 4un− + 1 un−2 2 2
Ta chứng minh bài toán bằng phương pháp quy nạp * u = 1 2 là số chẵn và u = 2 9 là số lẻ
* Giả sử u2k là số lẻ và u2k−1 là số chẵn. Khi đó: u + = 4u + 2k 1 2k
u2k−1 là số chẵn, u + = 4u + + 2k 2 2k 1 u2k là số lẻ Từ đó ta có đpcm.
2. Ta chứng minh được: u = 8u − − n n 1
4un−2 . Từ đây suy ra đpcm.
3. Ta chứng minh bài toán bằng phương pháp phản chứng
• Giả sử dãy (un) có hữu hạn các số chẵn, giả sử uk là số hạng lớn nhất của dãy là số chẵn. Khi đó un lẻ với ∀n ≥ k + 1. Đặ m t uk+ = 2 .p + 1
1 với m,p∈ ,p lẻ. Khi đó: m−1 3 m−1 uk+ = 3p.2 + = 3p.2 + 1 1 2 m−2 u 0 k+ = 3p.2 + 2 1 ,…, uk+ = 3p.2 + 1 = 3p + m
1 là số lẻ, suy ra vô lí.
Nên dãy (un ) chứa vô hạn số chẵn.
• Chứng minh tương tự ta cũng có dãy (un) chứa vô hạn số lẻ. u = 5 ⇒ u = 12,u = 2 3 3 13
4. Ta có: u − 4 = 1 ⇒ 2 u = 3 ⇒ u = 4,u = 2 3 3 5
a) Ta chứng minh tồn tại duy nhất dãy số nguyên dương (un ) thỏa u = 1,u = 2,u = 3,u = 2 0 1 2 3 5 và un+ .u − 2 n un+ = 1, ∀ n ≥ 1 4 (1) • Chứng minh tồn tại: v = 1,v = 0 1 2
Xét dãy (vn ) : vn+ = v + 1 n vn− , n = 1 2,3,...
Bằng quy nạp ta chứng minh được (vn ) thỏa mãn (1). 2 2 Thật vậy: vn+ .v − 2 n vn+ = 1 vn (vn+ + 1 vn ) − vn+1 2 2 = vn+1 (v − n vn+1) + v = v − n n vn−1vn+ = 1 1 • Chứng minh duy nhất.
Trước hết ta chứng minh nếu dãy (un) thỏa (1) thì (un) là dãy tăng.
Giả sử a + > a ⇒ a + − 1 ≥ n 1 n n 1 an 2 2 2 an+ ± 1 1 an+ ± 1 Từ 1 an+ a − 2 n an+ = 1⇒ 1 an+ = ≥ > 2 an+ + 1 > 1 an+1 an an+ − 1 1
Nên theo quy nạp ta có đpcm.
Giả sử tồn tại k để v ≠ k uk và v = u , ∀n < n n k . Khi đó 2 uk.uk− = 2 uk− + 1 1 Ta giả sử v < k uk , suy ra: 2 vk.vk− = 2 vk− − 1 1 ⇒ uk−2 (u − k
vk ) = 2 ⇒ 2 uk−2 điều này vô lí.
Do vậy tồn tại duy nhất dãy nguyên dương (un ) (đó chính là dãy (vn ) ) thỏa mãn (1).
b) Tương tự ta chứng minh được tồn tại dũy nhất các dãy nguyên dương thỏa: u = 1,u = 2,u = 3,u = 2 0 1 2 3 4, un+ u − 2 n un+ = 1 1 u = 1,u = 2,u = 5,u = 2 0 1 2 3 12, un+ u − 2 n un+ = 1 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 6 Tµi liÖu to¸n 11 n¨m häc 2018 u = 1,u = 2,u = 5,u = 2 0 1 2 3 13, un+ u − 2 n un+ = 1 1.
Đó là các dãy tương ứng là: u = 1,u = 2,u + = 2u + − 0 1 n 1 n 1 un u = 1,u = 2,u + = 2u + + 0 1 n 1 n 1 un u = 1,u = 2,u + = 3u + − 0 1 n 1 n 1 un .
Vậy tồn tại đúng 4 dãy số nguyên dương thỏa yêu cầu bài toán. Bài 10.
1. Trước hết ta thấy dãy n
(F ) tồn tại và duy nhất. n n 1 1 + 5 1 − 5 1 n n Xét x = − = n 5 2 2 (a −b ) 5 1 + 5 1 − 5 a + b = 1 Với a = ,b = ⇒ 2 2 ab = − 1 Ta có: x = x = 1 2 1 và 1 x + x = 1 n 2 ( n−1 n−1 n−2 n−2 n− − a − b + a − b ) 5 1 n−2 n−2 = a (a + 1) − b (b + 1) 5 1 n 2 3 + 5 n 2 3 − − − 5 = a . − b . 5 2 2 2 2 1 n 2 1 + 5 n 2 1 − − − 5 1 n n = a . − b . = 5 2 2 (a −b )=xn 5 Vậy ta có: F = x , ∀n ≥ n n 1 .
2. Ta chứng minh đồng thời hai tính chất trên theo quy nạp 2 2 2 2
Với n = 2 ta có: F + F = 1 + 2 = 5 = 2 3 5 F
Và F F + F F = 1.2 + 2.3 = 8 = 2 3 3 4 6 F 2 2 Giả sử F + k k F + = 1 2 F k+1 và F F + + F + F + = k k 1 k 1 k 2 2 F k+2 với k ≥ 2 2 2 2 2 2 2 2 Ta có: k F + + 1 k F + = 2 k F + + 1 (F + k k F +1) = k F + + F + 1 k k F + + 1 2 k F k F +1 2 2 = k F +1 ( k F + + 1 k 2F ) + (F + k k F +1)
= F + (F + + F ) + F + = F + + F + = k 1 k 2 k 2k 1 2k 2 2k 1 2k F +3 .
Và: F F + + F + F + = F (F + F − ) + F + (F + + k k 1 k 1 k 2 k k k 1 k 1 k 1 k F ) 2 2 = k F k F − + F + 1 k k F + + 1 k F +1 k F 2 2 = ( k F k F − + 1 k F k F +1) + (F + k k F +1) = F + + F + = 2k 2 2k 3 2k F +5 .
Từ đó ta có điều phải chứng minh. 3.
• Trước hết ta chứng minh: F = 5n n
5F qn với qn không chia hết cho 5 (1) 5n 5n Ta có : = − 5n 5F a b Đặ n n n n
t x = a ,y = b , như vậy ta có xy = (ab) = (−1)
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 7 Tµi liÖu to¸n 11 n¨m häc 2018 Do đó : 5F (x y) 4 2 2 2 2 4 5n x xy x y x y y ( ) = − + + + + (2) 2 2 2 2 n
Mặt khác : x + y = (x − y) + 2xy = 5F + n 2(−1) 2 4 4 2 2 2 2 2 n 2
x + y = (x + y ) − 2x y = 5F + n 2(−1) − 2 4 n 2 = 25F + n 20(−1) F + n 2 (3). 4 n 2 n 2 Từ đó, ta có:
F = 5F 25F + 20(−1) F + 2 + 5(−1) F + 2 + 5n n n n n 1 4 2 2 Hay F = 5F 5F + 5n n n n 5F (−1) + 1 = 5F q , n n trong đó: q = 4 5F + 2 n n n
5F (−1)n + 1. Rõ ràng ta thấy qn không chia hết cho 5.
• Với số tự nhiên n , ta phân tích = s n 5 t với (t,5) = 1 . Khi đó từ (1) ta có F = s n
5 tFAn trong đó An không là bội của 5.
Nếu t không là bội của 5 thì t
F không là bội của 5, do đó k ⇔ ≥ ⇔ k n F 5 s k n 5 (đpcm).
ĐÁP ÁN TRẮC NGHIỆM n
Câu 1. Cho dãy số u u n , biết . n
Năm số hạng đầu tiên của dãy số đó lần lượt là những số nào dưới đây? n 1 1 2 3 4 5 2 3 4 5 6
A. ; ; ; ; .
B. ; ; ; ; . 2 3 4 5 6 3 4 5 6 7 1 2 3 4 5 2 3 4 5 6 C. ; ; ; ; . D. ; ; ; ; . 2 3 4 5 6 3 4 5 6 7 1 2 3 4 5
Lời giải. Ta có u ; u ; u ; u ; u . Chọn A. 1 2 3 4 5 2 3 4 5 6
Nhận xét: (i) Dùng MTCT chức năng CALC để kiểm tra (tính) nhanh.
(ii) Ta thấy dãy u là dãy số âm nên loại các phương án C, D. Đáp án đúng là A hoặc B. Ta chỉ cần kiểm tra một số hạng nào đó n 1
mà cả hai đáp án khác nhau là được. Chẳng hạng kiểm tra u thì thấy u nên chọn A. 1 1 2 n
Câu 2. Cho dãy số un , biết u
. Ba số hạng đầu tiên của dãy số đó lần lượt là những số nào dưới đây? n 3n 1 1 1 1 1 1 3 1 1 1 1 2 3 A. ; ; . B. ; ; . C. ; ; . D. ; ; . 2 4 8 2 4 26 2 4 16 2 3 4
Lời giải. Dùng MTCT chức năng CALC: ta có 1 2 2 1 3 3 u ; u ; u . Chọn B. 1 2 2 3 3 2 3 1 8 4 3 1 26 u 1 1
Câu 3. Cho dãy số u n n , biết với
0 . Ba số hạng đầu tiên của dãy số đó là lần lượt là những số nào dưới đây? u u 3 n 1 n A. 1;2;5. B. 1; 4;7. C. 4;7;10. D. 1;3;7.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 8 Tµi liÖu to¸n 11 n¨m häc 2018
Lời giải. Ta có u 1; u u 3 2; u u 3 5. Chọn A. 1 2 1 3 2
Nhận xét: (i) Dùng chức năng “lặp” của MTCT để tính:
Nhập vào màn hình: X X 3.
Bấm CALC và cho X 1 (ứng với u 1) 1
Để tính u cần bấm “=” ra kết quả liên tiếp n1 lần. Ví dụ để tính u ta bấm “=” ra kết quả lần đầu tiên, bấm “=” ra kết quả n 2
thứ hai chính là u ,... 3
(ii) Vì u 1 nên loại các đáp án B, C. Còn lại các đáp án A, C; để biết đáp án nào ta chỉ cần kiểm tra u (vì u ở hai đáp án là 1 2 2
khác nhau): u u 3 2 nên chọn A. 2 1 2 2n 1
Câu 4. Cho dãy số u , u . u . n biết n Tìm số hạng 2 n 3 5 1 17 7 71 A. u . u . u . u . 5 B . C. D. 4 5 12 5 4 5 39 2 2.5 1 49 7
Lời giải. Thế trực tiếp hoặc dùng chức năng CALC: u . Chọn C. 5 2 5 3 28 4 n
Câu 5. Cho dãy số u , u n n biết n
1 .2 . Mệnh đề nào sau đây sai? A. u 2. u 4. u 6. u 8. 1 B. 2 C. 3 D. 4
Lời giải. Thay trực tiếp hoặc dùng chức năng CALC:
u 2.1 2; u 2
1 .2.2 4, u 3
1 2.3 6; u 4
1 2.4 8 . Chọn D. 1 2 3 4
Nhận xét: Dễ thấy u 0 khi n chẵn và ngược lại nên đáp án D sai. n n n
Câu 6. Cho dãy số u , u u . n biết n 2 1 . . Tìm số hạng n 3 8 8 A. u . u 2. u 2. u . 3 B. C. D. 3 3 3 3 3 3 3 2 8
Lời giải. Thay trực tiếp hoặc dùng chức năng CALC: u 1 . . Chọn D. 3 3 3 u 2 1
Câu 7. Cho dãy số u 1 . u .
n xác định bởi Tìm số hạng u u 1 4 n 1 n 3 5 2 14 A. u . u 1. u . u . 4 B . C. D. 9 4 4 3 4 27 Lời giải. Ta có 1 1 1 2 1 1 2 5 u u 1 2 1 1; u u 1 ; u
u 1 1 . Chọn A. 2 1 3 2 4 3 3 3 3 3 3 3 3 9
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 9 Tµi liÖu to¸n 11 n¨m häc 2018
Nhận xét: Có thể dùng chức năng “lặp” trong MTCT để tính nhanh. u 3 1
Câu 8. Cho dãy u u .
n xác định bởi
Mệnh đề nào sau đây sai? n u 2 n 1 2 5 15 31 63 A. u . u . u . u . 2 B. C. D. 2 3 4 4 8 5 16 u 3 7 u 7 15 1 2 u
2 2 ; u 2 2 2 3 2 2 2 2 4 4
Lời giải. Ta có Chọn A. u 15 31 u 31 63 3 4 u 2 2 ; u 2 2 . 4 5 2 8 8 2 16 16
Nhận xét: Dùng chức năng “lặp” trong MTCT để tính nhanh. n 1 8
Câu 9. Cho dãy số u , u n biết n . Số
là số hạng thứ mấy của dãy số? 2n 1 15 A. 8. B. 6. C. 5. D. 7. n 1 8
Lời giải. Ta cần tìm n sao cho u
15n 15 16n 8 n 7. Chọn D. n 2n 1 15
Nhận xét: Có thể dùng chức năng CALC để kiểm tra nhanh. 2n 5 7
Câu 10. Cho dãy số u , u . n biết n Số
là số hạng thứ mấy của dãy số? 5n 4 12 A. 8. B. 6. C. 9. D. 10.
Lời giải. Dùng chức năng “lặp” để kiểm tra đáp án. Hoặc giải cụ thể như sau: 2n 5 7 u
24n 60 35n28 11n 88 n 8. Chọn A. n 5n 4 12
Câu 11. Cho dãy số u , n u u . n biết 2 . n Tìm số hạng n 1 A. u 2n.2. u 2n 1. u 2 n 1 . u 2n 2. n 1 B. n 1 C. n 1 D. n 1
Lời giải. Thay n bằng n 1 trong công thức u ta được: n 1 u
2 2.2n . Chọn A. n n 1
Câu 12. Cho dãy số u n u u . n , biết 3 . n Tìm số hạng 2n 1 A. 2 u 3 .3n 1. u 3n.3n . 2n 1 B. 1 2n 1 2n 1 C. 2 u 3 n 1. u 3 . 2n 1 D. 2n 1 Lời giải. Ta có n n2n 1 2n 1 n n 1 u 3 u 3
3 .3 . Chọn B. n 2n 1
Câu 13. Cho dãy số u , n u u . n với 1 5 . n Tìm số hạng n 1 A. n 1 u 5 . u 5n. u 5.5n . u 5.5n . n 1 B. n 1 C. 1 n 1 D. 1 n 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 10 Tµi liÖu to¸n 11 n¨m häc 2018 n 1 nn 1 n Lời giải. 1 1 u 5 u 5
5n. Chọn B. n n 1 2n3 n 1
Câu 14. Cho dãy số u , u . u . n với n Tìm số hạng n 1 n 1 2n 1 3 n 1 2n 1 3 n 1 A. u . u . n 1 B. n 1 n 1 n 1 2n3 n 2n5 n C. u . u . n 1 D. n 2 n 1 n 2 n n n n1 n 1 1 n n n 1 2 1 3 2 3 2 5 Lời giải. u u . Chọn D. n n 1 n 1 n 1 1 n 2 1 2 3 4
Câu 15. Dãy số có các số hạng cho bởi: 0; ; ; ; ; .
có số hạng tổng quát là công thức nào dưới đây? 2 3 4 5 n 1 n n 1 2 n n A. u . u u . u . n B. . C. D. n n n 1 n n n n 1 1
Lời giải. Vì u 0 nên loại các đáp án A và B. Ta kiểm tra u ở các đáp án C, D: 1 2 2 Xét đáp án C: n 1 1 u u Chọn C. n 2 n 2 2 Xét đáp án D: n n 2 1 u u loại D. n 2 n 1 3 2 11 1 2 1 2 31 n
Nhận xét: u 0 ; u ; u ,... nên đoán 1 u . 1 2 3 1 2 2 3 3 n n
Câu 16. Dãy số có các số hạnh cho bởi: 1;1;1;1;1; .
có số hạng tổng quát là công thức nào dưới đây? n n A. u 1. u u u n B. 1. n C. n 1 . D. n 1 1 .
Lời giải. Vì dãy số đa cho không phải là dãy hằng nên loại các đáp án A và B. Ta kiểm tra u 1 ở các đáp án C, D: 1 Xét đáp án C: n u u Chọn C. n 1 1 1 Xét đáp án D: n 1 2 u u loại D. n 1 1 1 1 1
Câu 17. Cho dãy số có các số hạng đầu là: 2;0;2;4;6; .
Số hạng tổng quát của dãy số này là công thức nào dưới đây? A. u 2 . n u n
u 2 n 1 . u n n B. 2. n C. n D. 2 4. n
Lời giải. Kiểm tra u 2 ta loại các đáp án B, C. Ta kiểm tra u 0 ở các đáp án A, D: 1 2
Xét đáp án A: u 2n u 4 0 loại A. n 2
Xét đáp án D: u 2n4 2.24 0 Chọn D. n
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 11 Tµi liÖu to¸n 11 n¨m häc 2018
Nhận xét: Dãy 2; 4;6;... có công thức là *
2n n nên dãy 2;0;2;4;6; .
có được bằng cách “tịnh tiến” 2n sang trái 4 đớn
vị, tức là 2n 4. u 2 1
Câu 18. Cho dãy số u , . u n được xác định Số hạng tổng quát
của dãy số là số hạng nào dưới đây? u 2u n n 1 n A. n 1 u n . n u n u u n B. 2 . n C. 1 2 . n D. 2. n u 2 1 u 2 1
Lời giải. Từ công thức u
2u 2.2 4. 2 1 u 2u n 1 n u
2u 2.4 8 3 2 Xét đáp án A với 1 1 0 n 1
u 1 1 1 1 A loại.
Xét đáp án B, ta thấy đều thỏa mãn. Chọn B. Xét đáp án C với 1 1 2 n 1 u 2 2 4 1 C loại.
Dễ thấy đáp án D không thỏa mãn. 1 u 1
Câu 19. Cho dãy số u , 2 . u n được xác định
Số hạng tổng quát n của dãy số là số hạng nào dưới đây? u u 2 n 1 n 1 1 A. u 2 n
u 2 n 1 . n 1 . B. n 2 2 1 1 C. u 2 . n u 2 . n n D. 2 n 2 1 u 1 2 1 u 1 3
Lời giải. Từ công thức 1 2 u
u 2 2 . 2 1 2 2 u u 2 n 1 n 3 7 u
u 2 2 3 2 2 2 Xét đáp án A vớ 1 5 i n 2
u 2 2 1 2 A loại. 2 2
Xét đáp án B, ta thấy đều thỏa mãn. Chọn B. Xét đáp án C vớ 1 1 7 i n 2
u 2.2 4 2 C loại. 2 2 2 Xét đáp án D vớ 1 5 i n 1
u 2.1 1 D loại. 2 2 u 2 1
Câu 20. Cho dãy số u , . u n được xác định Số hạng tổng quát
của dãy số là số hạng nào dưới đây? u u 2n 1 n n 1 n
A. u n 2 2 1 . u n n B. 2 2 . n
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 12 Tµi liÖu to¸n 11 n¨m häc 2018
C. u n 2 2 1 . u n n D. 2 2 1 . n
Lời giải. Kiểm tra u 2 ta loại các đáp án B và C. Ta có u u 2.11 3. 1 2 1
Xét đáp án A: u 2n 2 1 u 3 Chọn A. n 2 Hoặc kiểm tra: u
u n n n n 2 2 1 2 1. n 1
Xét đáp án D: u 2n 2 1 u 1
loại D. Hoặc kiểm tra: n 2 u u n
n n n n 2 2 1 2 1 2 1. n 1 u 1 1
Câu 21. Cho dãy số u , . u n được xác định Số hạng tổng quát
của dãy số là số hạng nào dưới đây? 2 u u n n n 1 n
n(n 1)(2n 1)
n(n 1)(2n 2) A. u 1 . u 1 . n B. 6 n 6
n(n 1)(2n 1)
n(n 1)(2n 2) C. u 1 . u 1 . n D. 6 n 6
Lời giải. Kiểm tra u 1 ta loại đáp án A. Ta có 2
u u 1 2. 1 2 1 Xét đáp án B:
n(n 1)(2n 2) 2.1.6 u 1 u 1 3 2 B loại. n 2 6 6 Xét đáp án C:
n(n 1)(2n 1) 2.1.3 u u 1 u 1 2 Chọn C. n n 2 6 6 Xét đáp án D:
n(n 1)(2n 2) 2.3.2 u 1 . u 1 3 2 D loại. n 2 6 6 u 2 1
Câu 22. Cho dãy số u , 1 . u n được xác định Số hạng tổng quát
của dãy số là số hạng nào dưới đây? u 2 n n 1 u n n 1 n 1 n 1 n A. u . u . u . u n B. C. D. . n n n n n n n 1 1 3
Lời giải. Kiểm tra u 2 ta loại các đáp án A, B. Ta có u 2 . 1 2 u 2 1 Xét đáp án C: n 1 3 u u Chọn C. n 2 n 2 Xét đáp án D. n 2 u u D loại. n 2 n 1 3 u 1 1
Câu 23. Cho dãy số u , . u n được xác định Số hạng tổng quát
của dãy số là số hạng nào dưới đây? u n u n 2 1 n n 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 13 Tµi liÖu to¸n 11 n¨m häc 2018 n A. u 1 . n u n u u n n B. 1 . n C. n 2 1 1 . D. . n
Lời giải. Kiểm tra u 1 ta loại đáp án A, B và C nên chọn D. 1
Câu 24. Cho dãy số u u 2 3n n
n có số hạng tổng quát là n với
* . Công thức truy hồi của dãy số đó là: u 6 u 6 1 1 A. . B. . u 6u , n 1 u 3u , n 1 n n 1 n n 1 u 3 u 3 1 C. 1 . D. . u 3u , n 1 u 6u , n 1 n n 1 n n 1 Lời giải. Vì 1
u 2.3 6 nên ta loại các đáp án C và D. Ta có 2 u 2.3 18. 1 2 Xét đáp án A: u 6 1
u 6u 6.6 36 A loại. 2 1 u 6u , n 1 n n 1 Xét đáp án B: u 6 1
u 3u 3.6 18 chọn B. 2 1 u 3u , n 1 n n 1 a 3 1
Câu 25. Cho dãy số a , 1 . n được xác định
Mệnh đề nào sau đây sai? a a , n 1 n 1 2 n 93 3
A. a a a a a . a . 1 2 3 4 5 B. 16 10 512 9 3 C. a a . a . n 1 n D. 2n n 2n u u u u u u 3 Lời giải. Ta có 1 2 1 3 1 1 a 3; a ; a ; a ,... u
nên suy ra đáp án D sai. Chọn D. 1 2 3 2 4 3 n n 1 n 1 2 2 2 2 2 2 2 Xét đáp án A: 5 1 1 1 1 1 1 2 93
a a a a a 3 1 3. A đúng. 1 2 3 4 5 2 3 4 2 2 2 2 1 16 1 2 Xét đáp án B: 3 3 a B đúng. 10 9 2 512 Xét đáp án C. 3 3 3 3.2 9 a a C đúng. n 1 n n n 1 2 2 2n 2n
Vấn đề 2. Dãy số đơn điệu – Dãy số bị chặn Các ví dụ
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 14 Tµi liÖu to¸n 11 n¨m häc 2018 u = 2 1
Ví dụ 1. Cho dãy số (un ) : u (u ) n− + 1 . Chứng minh rằng dãy
n là dãy giảm và bị chặn. u = 1 ∀n ≥ 2 n 2 Lời giải. 1 − u − Ta có: u − u − = n 1 n n 1 2
Do đó, để chứng minh dãy (u u 1 n 1 n) giảm ta chứng minh > ∀ ≥ n Thật vậy: Với n = 1 ⇒ u = 2 > 1 1 u + 1 1+ k 1 Giả sử u > 1 ⇒ k uk+ = > = 1 1 2 2
Theo nguyên lí quy nạp ta có u > ∀ 1 n ≥ n 1
Suy ra u − u − < 0 ⇔ u < u − ∀n ≥ n n 1 n n 1 2 hay dãy (un) giảm
Theo chứng minh trên, ta có: 1 < u < u = ∀ 2 n ≥ n 1 1
Vậy dãy (un) là dãy bị chặn. u = 1,u = 1 2 2
Ví dụ 2. Cho dãy số (un ) :
. Chứng minh rằng dãy (u ) là dãy tăng và bị chặn u n n+ = u + 1 n un− ∀n ≥ 1 2 Lời giải.
Ta chứng minh dãy (un ) là dãy tăng bằng phương pháp quy nạp * Dễ thấy: u < u < 1 2 u3 . * Giả sử u − < u ∀ k ≥ k 1 k 2 , ta chứng minh u + < k 1 uk . Thật vậy:
u + = u + u − > u − + u − = k 1 k k 1 k 1 k 2 uk Vậy (un ) là dãy tăng.
Cũng bằng quy nạp ta chứng minh được u < ∀ n 4 n , hơn nữa u > n 0
Nên dãy (un ) là dãy bị chặn. CÁC BÀI TOÁN LUYỆN TẬP
Bài 1 Xét tính tăng giảm của các dãy số sau 2 3n − 2n + 1 2 1. u = n u n n 1 n + 1 2. = − − n n n 3 − 1 n + (−1) 3. u = n u = n 4. 2 n 2 n
Bài 2 Xét tính tăng, giảm và bị chặn của dãy số (un ) , biết: 2n − 13 2 n + 3n + 1 1 1. u = n u = u 3n − 2 2. n n + 1 3. = n 1 + n + 2 n n 2 1 1 1 4. u = n u 1 ... n! 5. = + + + + n 2 2 2 . 2 3 n
Bài 3. Xét tính bị chặn của các dãy số sau 2n + 1 1. u = n u ( 1) u 3n 1 n 3. = − + 2 2. = − n n n 2 n + n + 1 n + 1 4. u = 4 − 3n − 2 n n 5. u = n u = 2 6. n − n + 1 n 2 n + 1
Bài 4. Xét tính bị chặn của các dãy số sau 1 1 1 1 1 1 1. u = + + ... + n u = + + ... + 1.3 2.4 n.(n + 2) 2. n 1.3 3.5 (2n −1)(2n +1)
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 15 Tµi liÖu to¸n 11 n¨m häc 2018 u = 1 1 3. un− + 2 u = 1 , n ≥ n 2 un− + 1 1
Bài 5 Xét tính tăng giảm của các dãy số sau u = u = 2 1 1 1 1. 2. 2 u + 1 3 3 n un+ = u + 1, n ≥ 1 n 1 un+ = n ≥ 1 1 4 Bài 6
1. Chứng minh rằng dãy số (un ) xác định bởi u = 2010 + 2010 + ... + n 2010 (n dấu căn) Là một dãy tăng. u = 1,u = 1 2 2
2. Cho dãy số (un ) :
. Chứng minh rằng dãy (u ) tăng và bị chặn. u = 3 3 n n un− + 1 un− ,n ≥ 2 3 an + 2
3. Cho dãy số (u ) : u = , n ≥ n n 1 2n − 1
a) Khi a = 4 , hãy tìm 5 số hạng đầu của dãy
b) Tìm a để dãy số đã cho là dãy số tăng. u = 1 2
4. Cho dãy số (un ) : u = n 3un− − 2, n = 1 2,3..
a) Viết 6 số hạng đầu của dãy n−1 b) Chứng minh u = 3 + 1, n = n 1,2,. . n−1 n
5. Cho dãy số u = −5.2 + 3 + n + n 2 , n = 1,2,...
a) Viết 5 số hạng đầu của dãy n−1 b) Chứng minh rằng: u = n 2un− + 3 − 1 n . Bài 7 n n
1. Cho dãy số (un ) : u = (1 − a) + (1 + n
a) ,trong đó a ∈(0;1) và n là số nguyên dương.
a)Viết công thức truy hồi của dãy số
b)Xét tính đơn điệu của dãy số u = 1 1
2. Cho dãy số (un ) được xác định như sau: 1 u = . n 3un− + − 2, n ≥ 1 2 2un−1
a) Viết 4 số hạng đầu của dãy và chứng minh rằng u > 0, ∀ n n
b) Chứng minh dãy (un ) là dãy tăng. u = 2011 0 3. Cho dãy số (u 2
n ) được xác định bởi : un un+ = , ∀ n = 1 1,2,... u + n 1
a) Chứng minh rằng dãy (un ) là dãy giảm
b) Tìm phần nguyên của un với 0 ≤ n ≤ 1006 . u = 2,u = 1 2 6
4. Cho dãy số (un ) được xác định bởi: un+ = u + 2 n 2un+ , ∀ n = 1 1,2,... 2 n n
a) Gọi a, b là hai nghiệm của phương trình x − 2x − 1 = 0 . Chứng minh rằng: u = a + n b 2 n−1
b) Chứng minh rằng: un+ − 1 un+ u = (− 2 n 1) .8 .
Bài 8 Xét tính tăng giảm và bị chặn của các dãy số sau
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 16 Tµi liÖu to¸n 11 n¨m häc 2018 n + 1 3 1. (u ) : u = n n (u ) : u n 2n 1 n + 2 2. = + + n n u = 2 1 u = 2,u = 1 2 3 3. (un ) : u + 1 4. . n un u = u + u ∀ , n ≥ + = ∀ , n ≥ 2 2 1 2 n+1 n n−1 Bài 9 x = 1 0 1. Cho dãy số n− (x ) : 1 n 2n x = n x , n 2,3,... 2 ∑ = i (n − 1) i=1 Xét dãy số y = x + − n n 1
xn . Chứng minh rằng dãy (yn) là một tăng và bị chặn. u = 1,u = 3 0 1 2
2. Cho dãy số nguyên dương (u n ) thỏa : un+1 u . n+ = 1 + , n ≥ 2 0 un 2 n Chứng minh rằng: un+ u − 2 n un+ = 1
2 với mọi số tự nhiên n . u = 0 0
3. Cho dãy số (un ) được xác định bởi: . 2 un+ = 5u + 24u + 1, n = 1 n n 0,1,..
Chứng minh rằng dãy số (un ) là dãy số nguyên. 1 n n
4. Cho dãy số (un ) được xác định bởi: u = (2 + 5) + (2 − n 5) 2
Chứng minh rằng u2n là số tự nhiên chẵn và u2n+1 là số tự nhiên lẻ.
5. Cho hai dãy số (xn );(yn ) xác định : 2 x = x + 1 + x x = 3 n n−1 n− 1 1 và yn−1 , ∀n ≥ 2 . y = y = 1 3 n 1 + 1 + 2 yn−1
Chứng minh rằng 2 < x y < 3, ∀n ≥ n n 2 . u = 1 0
6. Cho dãy số số (un ) được xác định bởi: 1 1 . un+ = 1 u + n 2 3un 3 Chứng minh rằng: a = n 2
là một số chính phương. 3u − n 1 ĐÁP ÁN Bài 1 2 5n + 10n + 2 1. Ta có: un+ − u = 1 n ( (u ) 1)(n 2) > 0 n nên dãy là dãy tăng + + n 1 1 2. Ta có: un+ − u = − < 1 n 0 (n +1) + (n +1)2 −1 n + 2 n − 1 Nên dãy (un ) giảm. n 3 + 1 3. Ta có: un+ − u = 1 n un+ − u = > 0 ⇒ 1 n (u ) n dãy tăng. +1 2 n 1 2 u > 2 u1 4. Ta có: u = 0;u = ;u = ⇒ 1 2 3 ⇒ 2 9
Dãy số không tăng không giảm. u < 3 u2 Bài 2
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 17 Tµi liÖu to¸n 11 n¨m häc 2018 2n − 11 2n − 13 34 1. Ta có: un+ − u = − = > 1 n 0 n 1 3n . + 1 3n − 2 (3n + 1)(3n − 2) với mọi ≥
Suy ra u + > u ∀n ≥ 1 ⇒ n 1 n dãy (un ) là dãy tăng. 2 35 2 Mặt khác: u = − ⇒ −11 ≤ u < ∀n ≥ n 1 3 3(3n − n 2) 3
Vậy dãy (un ) là dãy bị chặn. (n + 2 1) + 3(n + 1) + 2 1 n + 3n + 1 2. Ta có: un+ − u = − 1 n n + 2 n + 1 2 + + 2 n 5n 5 n + 3n + 1 = − n + 2 n + 1 2 + + + − 2 (n 5n 5)(n 1) (n + 3n + 1)(n + 2) = (n + 1)(n + 2) 2 n + 3n + 3 = > ∀ 0 n ≥ 1 (n + 1)(n + 2) ⇒ u + > u ∀ n ≥ 1 ⇒ n 1 n
dãy (un ) là dãy số tăng. 2 n + 2n + 1 u > = n + 1 ≥ 2 ⇒ n (u ) n bị chặn dưới. + 1 dãy n 3. Ta có: u > ∀ 0 n ≥ n 1 2 2 un+ n + n + 1 n + n + 1 1 = = < ∀ 1 n ∈ * u (n + 1) + (n + 1) + 2 2 n 1 n + 3n + 3 ⇒ u + < u ∀ ≥ 1 ⇒ n 1 n
dãy (un ) là dãy số giảm.
Mặt khác: 0 < u < 1 ⇒ n
dãy (un ) là dãy bị chặn. n+1 n n+1 un+ 2 2 2 n! 2 4. Ta có: 1 = : = . = < ∀ 1 n ≥ 1 u (n + 1)! n! (n + n 1)! 2 n + n 1 Mà u > ∀ 0 n ⇒ u + < u ∀ n ≥ 1 ⇒ n n 1 n
dãy (un ) là dãy số giảm. Vì 0 < u ≤ u = ∀ 2 n ≥ 1 ⇒ n 1
dãy (un ) là dãy bị chặn. 1 5. Ta có: un+ − u = > 0 ⇒ 1 n
dãy (u ) là dãy số tăng. (n + 2 1) n 1 1 1 1 Do u < 1 + + + ... + = 2 + n 1.2 2.3 (n − 1)n n ⇒ 1 < u < ∀ 3 n ≥ 1 ⇒ n
dãy (un ) là dãy bị chặn. Bài 3
1. Ta có 0 < u < 2 ∀ n n nên dãy (un) bị chặn
2. Ta có: −1 ≤ u ≤ 1 ⇒ n (un) là dãy bị chặn
3. Ta có: u ≥ 2 ∀n ⇒ n
(un) bị chặn dưới; dãy (un) không bị chặn trên. 25 3 2 25 4. Ta có: u = − (n + ) < ⇒ n (un) (u ) 4 2 4 bị chặn trên; dãy n không bị chặn dưới.
5. Ta có: 1 < u < 2 ∀ n ⇒ n (un) bị chặn
6. Ta có: 0 < u < 2 ∀ n ⇒ n (un) bị chặn Bài 4 1 1 1 1
1. Ta có: 0 < u < + + ... + = 1 − < n 1 1.2 2.3 n.(n + 1) n + 1 Dãy (un ) bị chặn.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 18 Tµi liÖu to¸n 11 n¨m häc 2018 n 2. Ta có: u = ⇒ 0 < u < n 1 (u ) 2n bị chặn. + n 1 , dãy n
3. Bằng quy nạp ta chứng minh được 1 < u < n 2 nên dãy (un) bị chặn. Bài 5 3 3 3 3
1. Ta có: un+ = u + 1 ⇒ 1 n un+ > u = u ∀n ⇒ 1 n n dãy số tăng 2 u − 4u + n n 1 2. Ta có: un+ − u = 1 n 4
Bằng quy nạp ta chứng minh được 2 − 3 < u < ∀ n 2 n ⇒ u + − u < n 1 n 0 . Dãy (un) giảm. Bài 6 2 2 1. Ta có un+ = 2010 + 1 un ⇒ un+ − u = − 1 n un+ + 1 un+ + 1 2010 1 + 8041
Bằng quy nạp ta chứng minh được u < ∀ n n 2 Suy ra u + − u > 0 ⇒ n 1 n dãy (un ) là dãy tăng.
2. Chứng minh bằng quy nạp : 3 3 3 3 uk+ = u + 1 k uk− > 2 uk− + 1 uk− = 2 uk Ta chứng minh: 0 < u < n 3 . 3. 4n + 2 a) Với a = 4 ta có: u = n
2n − 1 . Ta có: 5 số hạng đầu của dãy là 10 14 18 22 u = 6,u = ,u = ,u = ,u = 1 2 3 4 5 3 5 7 9 .
b) Ta có dãy số (un ) tăng khi và chỉ khi: −a − 4 un+ − u = > 0, ∀ n ∈ 1 n
* ⇔ −a − 4 > 0 ⇔ a < −4 (2n . + 1)(2n − 1) 4.
a) Ta có: u = 2, u = 4, u = 10, u = 28, u = 82, u = 1 2 3 4 5 6 244
b) Chứng minh bài toán bằng phương pháp quy nạp hoặc chứng minh bằng cách sau 2 n−1 Ta có: u − 1 = n 3(un− −1) = 1
3 (un− −1) = . . = 3 (u − 2 1 1) n−1 n−1 Suy ra: u − 1 = 3 ⇒ u = 3 + n n 1 . 5.
a) Ta có: u = 1, u = 3, u = 12, u = 47, u = 1 2 3 4 5 170 n−2 n−1 b) Ta có: un− = −5.2 + 3 + n + 1 1 n n−2 n−1 n−1 Nên 2un− + 3 − n = 1
2(−5.2 + 3 + n +1) + 3 − n n−1 n = −5.2 + 3 + n + 2 = un . Bài 7 1. u = 2 1 a) Ta có: n n u n+ = u + 1 n a (1+ a) − (1− a)
b) Dãy (un ) là dãy số tăng. 2. 3 17 227 a) Ta có: u = 1,u = ,u = ,u = 1 2 3 4 2 6 34 . Ta chứng minh u > 0, ∀ n n bằng quy nạp.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 19 Tµi liÖu to¸n 11 n¨m häc 2018 1 1 Giả sử u > n 0 , khi đó: 2u + ≥ 2 2u . = n n 2 2un 2u n 1 Nên un+ = u + 1 n 2u + − n 2 > u > n 0 2u . n
b) Theo chứng minh trên ta có: u + > u , ∀ n 1 n
n nên dãy (un) là dãy tăng. 3. −un a) Ta có: un+ − u = < 0, ∀ 1 n n (u ) u là dãy giảm + n 1 nên dãy n un−1 b) Ta có: u = n un− − > 1 un− −1 > ... > u − 1 0 n un− + 1 1
Suy ra: u − > u − (n − 1) = 2012 − n 1 0 n Mặt khác:
u = (u − u − ) + (u − − u − ) + ... + (u − u ) + n n n 1 n 1 n 2 1 0 u0 u u u 0 1 n− = u − + + ... + 1 0 u + 1 u + 0 1 1 un− + 1 1 1 1 1 = u − n + 0 + + ... + u + 1 u + 0 1 1 un− + 1 1 Mà: 1 1 1 n n 0 < + + ... + < < < 1 u + 1 u + 1 u − + 1 u − + 1 2013 − 0 1 n 1 n 1 n Với mọi n = 2,1006 .
Suy ra u < u − n + 1 = 2012 − n 0 n
Do đó: 2011 − n < u < 2012 − n ⇒ u = 2011 − n n n với n = 2,1006 . 2 2011 Vì u = 0 2011 và u = = 1 2010,000497 2012
nên u = 2011 − 0, u = 2010 = 2011 − 0 1 1
Vậy u = 2011 − n, ∀ n = n 0,1006 . 4.
a) Ta chứng minh bài toán bằng quy nạp Với n = 1 ⇒ u = a + b = 1 2 n n Giả sử u = a + b ∀ , n ≤ n k Khi đó: u = 2u + u = 1 k k 1 2( k a + k b ) k−1 k−1 k+ − + a + b k k k 1 k 1 (a b)(a b ) − − = + + + a + b k+1 k+1 k−1 k−1 k−1 k−1 = a + b + ab(a + b ) + a + b k+1 k+1 k−1 k−1 k−1 k−1 = a + b − (a + b ) + a + b k+1 k+1 = a + b . b) Ta có: 2 2 un+ − 1 un+ u = 2 n un+ − 1 (2un+ + 1 un ).un 2 2 = un+1 (un+ − 1 2un ) − u = −(u − n n un+1un−1) n−1 2 n = ... = (−1) (u − 2 u3u1) = (−1) .8.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 20 Tµi liÖu to¸n 11 n¨m häc 2018 Bài 8 n + 2 n + 1 (n + 2 2) − (n + 3)(n + 1) 1. Ta có un+ − u = − = 1 n n + 3 n + 2 (n + 2)(n + 3) 1 = > 0, ∀ n (n + 2)(n + 3) . 1 Mặt khác: u = 1 − ⇒ 0 < u < 1, ∀ n n n + n 2
Vậy dãy (un ) là dãy tăng và bị chặn. 3 3
2. Ta có: un+ − u = (n + 1) + 2(n + 1) − n − 1 n 2n 2 = 3n + 3n + 3 > 0, ∀n Mặt khác: u > 1, ∀ n
n và khi n càng lớn thì un càng lớn.
Vậy dãy (un ) là dãy tăng và bị chặn dưới.
3. Trước hết bằng quy nạp ta chứng minh: 1 < u ≤ 2, ∀ n n
Điều này đúng với n = 1, giả sử 1 < u < n 2 ta có: u + 1 1 < n un+ = < 1 2 2 nên ta có đpcm. 1 − u Mà n un+ − u = < 0, ∀ 1 n n 2 .
Vậy dãy (un ) là dãy giảm và bị chặn.
4. Trước hết ta chứng minh 1 < u < 4, ∀ n n
Điều này hiển nhiên đúng với n = 1. Giả sử 1 < u < n
4 , ta có: 1 < u + = u + u − < 4 + 4 = n 1 n n 1 4
Ta chứng minh (un ) là dãy tăng Ta có: u < 1
u2 , giả sử u − < u ∀ , n ≤ n 1 n k . u < u Khi đó: k k− 1 ⇒ u + k uk− < 1 uk− + 1 uk− ⇒ 2 uk+ < u 1 k uk− < 1 u k−2
Vậy dãy (un ) là dãy tăng và bị chặn. n n− 2(n + 1) 2(n + 1 1) Bài 9 Ta có: xn+ = 1 ∑x = x + i n ∑ x i 2 2 n i=1 n i=1 2 2(n + 1) (n − 1) (n + 2 1)(n + 1) = x + x = n n . n 2n xn 2 3 n 2 Do đó: n + n + 1 y = n xn+ − x = 1 n xn 3 n
• Ta chứng minh dãy (yn) tăng. (n + 2 1) + n + 2 (n + 2 1)(n + 2 1) n + n + 1 Ta có: yn+ − y = . x − 1 n x (n + n n 3 3 3 1) n n 2 (n + 3n + 2 3)(n + 1) − 2 (n + n + 2 1)(n + 2n + 1) = x n (n + n 3 2 1) 2x = n > 0 n 1,2,. 3 , ∀ = n (n + 2 1)
• Ta chứng minh dãy (yn) bị chặn.
Trước hết ta chứng minh: x ≤ 4(n − n 1) (1) với ∀n = 2,3...
* Với n = 2 , ta có: x = 4x = 2 1 4 nên (1) đúng với n = 2
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 21 Tµi liÖu to¸n 11 n¨m häc 2018
* Giả sử (1) đúng với n , tức là: x ≤ 4(n − n 1) , ta có (n + 2 1)(n + 4 1) 4(n − 1) xn+ = x ≤ < 1 n 4n 3 3 n n
Nên (1) đúng với n + 1. Theo nguyên lí quy nạp ta suy ra (1) đúng 2 n + n + 1 4(n − 2 1)(n + n + 3 1) 4(n − 1) Ta có: y = x ≤ = < n n 4 3 3 3 n n n
Vậy bài toán được chứng minh.
2. Từ cách cho dãy số, ta thấy dãy (un ) luôn tồn tại và duy nhất. v = 1,v = 0 1 3
Xét dãy (vn ) : vn+ = 2 4vn+ − 2v , n ≥ 1 n 0 . • 2 n Ta chứng minh: vn+ .v − 2 n vn+ = 1 2 (1) 2 2 Ta có: vn+ .v − 2 n vn+ = 1 (4vn+ − 2v )v − 1 n n vn+1 2 2 = 4vn = v + (4v − v + ) + v − 1 n vn+ − 1 2vn − 2 n 1 n n 1 2vn 2 2 = vn+1.2vn− − 2v = 1 n 2(vn+1vn− − 1 vn ) n 2 n = ....... = 2 (v v − 2 0
v1 ) = 2 ⇒ (1) được chứng minh. • Ta chứng minh v > n n 2 (2) bằng quy nạp
Trước hết ta thấy dãy (vn) là dãy tăng
Với n = 1 ta thấy (2) đúng Giả sử v > n n 2 ta có: v = 2v + 2(v − v ) + + − > 2v = n 1 n 1 n n n 1 n 2 Do đó (2) đúng.
• Dựa vào các kết quả trên ta có: 2 n 2 vn+1 2 vn+ = 1 vn+ − ⇒ 2 vn+ −1 < < 2 vn+2 vn vn v n 2 2 vn+1 vn+ Hay − 1 < 1 vn+ −1 < 1 vn v n 2 2 v v Do đó: n+1 n+1 vn+ −1 = ⇔ 2 vn+ = 1+ v 2 n v n
Vì tính duy nhất nên ta có: u = v ∀ , n ≥ n n 0 .
Vậy bài toán được chứng minh. 3. Ta có u ,u ∈ 0 1 ( 2 2 2 2 un+ − 1 5un ) = 24u + 1 ⇔ n un+ − 1 10un+ u + u − 1 = 1 n n 0 (1) Ở 2 2
(1) thay n + 1 bởi n ta được: u − n 10un .un− + 1 un− −1 = 1 0 ⇔ 2 2 un− − 1 10un− .u + u − 1 = 1 n n 0 (2)
Từ (1) và (2) suy ra un+1,un−1 là hai nghiệm của phương trình 2 t − 10tu + 2 u − 1 = n n 0
Theo định lí Viet ta có: u + + u − = n 1 n 1 10un Hay u + = 10u − n 1 n un−1 Từ đó ta có: u ∈ n ∀ , n . a + b = 4
4. Đặt a = 2 + 5, b = 2 − 5 ⇒ . Khi đó: ab = − 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 22 Tµi liÖu to¸n 11 n¨m häc 2018 1 n n 1 n−1 n−1 n−2 n− 2 u = (a + b ) = (a + b)(a + b ) − ab(a + n b ) 2 2 n−1 n−1 n−2 n− a + b a + 2 b = 4. + = 4un− + 1 un−2 2 2 .
Ta chứng minh bài toán bằng phương pháp quy nạp • Với n = 1 ta có: u = 1 2 là số chẵn và u = 2 9 là số lẻ
• Giả sử u2k là số lẻ và u2k−1 là số chẵn. Khi đó: u + = 4u + 2k 1 2k u2k−1 là số chẵn u + = 4u + + 2k 2 2k 1 u2k là số lẻ Từ đó ta có đpcm. π cos + π π 1 2 π π 6 5. Ta có: x = 3 = cot ⇒ x = cot + 1 + cot = = 1 2 cot 6 6 6 π 2.6 sin 6 π
Bằng quy nạp ta chứng minh được: x = n cot n . −1 2 .6 Tương tự, ta cũng có: π y = n tan n −1 2 .3 Đặ π t α =
⇒ x = cot α ; y = tan 2α ⇒ x .y = tan 2α .cot α n n n n n n n n n n 2 .3 Đặ 2t 1 2
t t = tan α ⇒ tan 2α .cot α = . = n n n . 1 − 2 t t 1 − 2 t π π 1 2 2 Vì n ≥ 2 ⇒ 0 < α < ⇒ 0 < t < tan = ⇒ ≤ 1 − t < n 1 6 6 3 3 2 ⇒ 2 <
< 3 ⇒ 2 < x y < 3, ∀n ≥ 2 ⇒ đpcm. 1 − n n 2 t bn b ,c ∈ n n 6. Vì u ∈ n ⇒ u = n c với n (b ,c ) = n n 1 b 1 b c 2 3b + 2 c
Khi đó: n+1 = n + n = n n cn+1 2 cn 3bn 6bnc n 2 2
Bằng quy nạp ta chứng minh được (3b + n cn ,6bncn ) = 3 b = 2 3b + 2 c Suy ra n+ 1 n n cn+ = 1 2bncn 2 2
Bằng quy nạp ta chứng minh được: 3b − c = n n 3 Do đó: 3 a = = 2 n cn 2 (đpcm). 3bn −1 2 cn
ĐÁP ÁN TRẮC NGHIỆM
Câu 26. Cho các dãy số sau. Dãy số nào là dãy số tăng? 1 1 1 1
A. 1; 1; 1; 1; 1; 1; B . 1; ; ; ; ; 2 4 8 16 1 1 1 1
C. 1; 3; 5; 7; 9;
D. 1; ; ; ; ; 2 4 8 16
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 23 Tµi liÖu to¸n 11 n¨m häc 2018
Lời giải. Xét đáp án A: 1; 1; 1; 1; 1; 1; đây là dãy hằng nên không tăng không giảm. Xét đáp án B: 1 1 1 1 1; ; ; ; ;
u u u loại B. 1 2 3 2 4 8 16 Xét đáp án C: * 1; 3; 5; 7; 9;
u u , n Chọn C. n n 1 Xét đáp án D: 1 1 1 1 1; ; ; ; ;
u u u u loại D. 1 2 3 2 4 8 16 n
Câu 27. Trong các dãy số u u
n cho bởi số hạng tổng quát
sau, dãy số nào là dãy số tăng? n 1 1 n 5 2n 1 A. u . u . u . u . n B. C. D. 2n n n n 3n 1 n n 1
Lời giải. Vì 2n ; n là các dãy dương và tăng nên 1 1 ;
là các dãy giảm, do đó loại các đáp án A và B. 2n n 3 u 1 Xét đáp án C: n 5 2 u
u u loại C. n 1 2 3n 1 7 u 2 6 Xét đáp án D: 2n 1 3 1 1 u 2 u u 3 0 Chọn D. n n 1 n 1 n 1 n
n 1 n 2
Câu 28. Trong các dãy số u u
n cho bởi số hạng tổng quát
sau, dãy số nào là dãy số tăng? n 2 3 n A. u . u . n u u 2 . n B. C. 2 . D. n 3n n n n
Lời giải. Xét đáp án C: n n 1 u 2 u
u 2 2n 2n 0 Chọn C. n n 1 n
Vì 2n ; n là các dãy dương và tăng nên 1 1 ;
là các dãy giảm, do đó loại các đáp án A và B. 2n n Xét đáp án D: u u
u u loại D. n n 2 4 2 2 3 u 8 3
Câu 29. Trong các dãy số u u
n cho bởi số hạng tổng quát
sau, dãy số nào là dãy số giảm? n 1 3n 1 A. u . u . u n u n n B. C. 2 . D. 2. 2n n n 1 n n
Lời giải. Vì 2n là dãy dương và tăng nên 1 là dãy giảm Chọn A. 2n u 1 1 3n 1 Xét B: u
u u loại B. Hoặc n 5 1 2 n 1 u 2 3 3n 2 3n 1 4 u u
0 nên u là dãy tăng. n n 1 n n 2 n 1 n 1 n 2
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 24 Tµi liÖu to¸n 11 n¨m häc 2018
Xét C: u n u u n
n n loại C. n 2 2 2 1 2 1 0 n n 1 1
Xét D: u n 2 u
u n 3 n 2 0 loại D. n n 1 n
n 3 n 2
Câu 30. Trong các dãy số u u
n cho bởi số hạng tổng quát
sau, dãy số nào là dãy số giảm? n 2 n 1 A. u sin . n u . n B. n n n
C. u n n 1.
u 1 . 2n 1 . n D. n 1 1
Lời giải. A. u sin n u
u 2 cosn sin n n 1 n
có thể dương hoặc âm phụ thuộc n nên đáp án A sai. Hoặc dễ thấy sin n 2 2 có dấu thay đổi trên *
nên dãy sin n không tăng, không giảm. 2 2 n 1 1 1 1 n n 1 B. u n u u 1 0 n n 1 n
nên dãy đã cho tăng nên B sai. n n n 1 n nn 1 1
C. u n n 1 , n n u n dãy
1 0 là dãy tăng nên suy ra giảm. Chọn C. n n 1 n n
D. u 1 2n n
1 là dãy thay dấu nên không tăng không giảm. Cách trắc nghiệm.
A. u sin n n
có dấu thay đổi trên *
nên dãy này không tăng không giảm. n 1 u 2 2 n 1 1 2 n 1 B. u
u u u n , ta có 5 không giảm. n 1 2 n 2 n u n 2 2 n 1 u 1 1
C. u n n 1 u u n , ta có 1
2 nên dự đoán dãy này giảm. n
2 u 2 1 2 n
D. u 1 2n n
1 là dãy thay dấu nên không tăng không giảm. Cách CASIO. n Các dãy sin ; 1 2n n
1 có dấu thay đổi trên *
nên các dãy này không tăng không giảm nên loại các đáp án A, D.
Còn lại các đáp án B, C ta chỉ cần kiểm tra một đáp án bằng chức năng TABLE. 2 X 1
Chẳng hạn kiểm tra đáp án B, ta vào chức năng TABLE nhập F X
với thiết lập Start 1, End 10, Step 1. X
Nếu thấy cột F X các giá trị tăng thì loại B và chọn C, nếu ngược lại nếu thấy cột F X các giá trị giảm dần thị chọn B và loại C.
Câu 31. Mệnh đề nào sau đây đúng?
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 25 Tµi liÖu to¸n 11 n¨m häc 2018 1 n
A. Dãy số u 2 là dãy tăng.
B. Dãy số u
1 2n là dãy giảm. n 1 n n n 1 1
C. Dãu số u là dãy giảm.
D. Dãy số u 2n cos là dãy tăng. n n 1 n n 1 1 1
Lời giải. Xét đáp án A: u 2 u u 0 loại A. n n 1 n n n 1 n
Xét đáp án B: u n
1 2n là dãy có dấu thay đổi nên không giảm nên loại B. n 1 Xét đáp án C: n 1 2 1 1 u 1 u u 2 0 loại C. n n 1 n 1 n 1 n
n 1 n 2 Xét đáp án D: 1 1 1 u 2n cos u u 2cos cos
0 nên Chọn D. n n 1 n n n 1 n 2
Câu 32. Mệnh đề nào sau đây sai? 1 n
A. Dãy số u là dãy giảm. B. Dãy số 2
u 2n 5 là dãy tăng. n n n n 1
C. Dãy số u 1 là dãy giảm. D. Dãy số 2
u n sin n là dãy tăng. n n n 1 n 1 1 1
Lời giải. Xét A: u n u u
n n 1 0 nên dãy u là dãy giảm nên C đúng. n n n 1 n n n n 1 n Xét đáp án B: 2
u 2n 5 là dãy tăng vì 2
n là dãy tăng nên B đúng. Hoặc n u
u 2 2n 1 0 nên u là dãy tăng. n n 1 n n n n Xét đáp án C: 1 n 1 u n n n 2 2 1 u 1 0 .
là dãy tăng nên Chọn C. 1 u n n n n u n 1 n n Xét đáp án D: 2
u n sin n u u n n nên D đúng. n 2 1 sin 1 2 sin 0 n n 1 3n 1
Câu 33. Cho dãy số u u . u n , biết n
Dãy số n bị chặn trên bởi số nào dưới đây? 3n 1 1 1 A. . B. 1. C. . D. 0. 3 2 3n 1 2 5 1 1
Lời giải. Ta có u 1
1. Mặt khác: u 0 nên suy ra dãy u bị chặn trên bởi số 1. Chọn B. n n 3n 1 3n 1 2 7 2 2
Câu 34. Trong các dãy số u u
n cho bởi số hạng tổng quát
sau, dãy số nào bị chặn trên? n 1 A. 2 u n . n u u . u n n B. 2 . n C. n D. 1. n n
Lời giải. Các dãy số 2; 2n n
; n 1 là các dãy tăng đến vô hạn khi n tăng lên vô hạn nên chúng không bị chặn trên (có thể dùng
chức năng TABLE của MTCT để kiểm tra). Chọn C.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 26 Tµi liÖu to¸n 11 n¨m häc 2018 1
Nhận xét: u 1 với mọi *
n nên dãy u bị chặn trên bởi 1. n n n
Câu 35. Cho dãy số u u n n u n , biết cos sin . n
Dãy số n bị chặn trên bởi số nào dưới đây? A. 0. B. 1. C. 2.
D. Không bị chặn trên. Lời giải. Ta có MTCT u
u sin1 cos11 0 nên loại các đáp án A và B (dùng TABLE của MTCT để kiểm tra, chỉ cần 1 n 1
số hạn nào đó của dãy số lớn hơn thì dãy số đó không thể bị chặn trên bởi . )
Ta có u cos n sin n 2 sinn 2 Chọn C. n 4
Câu 36. Cho dãy số u u n n u n , biết sin cos . n
Dãy số n bị chặn dưới bởi số nào dưới đây? A. 0. B. 1. C. 2.
D. Không bị chặn dưới. Lời giải. MTCT u
u sin 5cos5 1 0
loại A và B (dùng TABLE của MTCT để kiểm tra, chỉ cần có một số hạng n 5
nào đó của dãy số nhỏ hơn thì dãy số đó không thể bị chặn dưới với số . )
Ta có u 2 sin n 2 Chọn C. n 4
Câu 37. Cho dãy số u u n n u n , biết 3 cos sin . n
Dãy số n bị chặn dưới và chặn trên lần lượt bởi các số m và M nào dưới đây? 1 A. m 2; 2 M . B. m ; 3 M 1. 2 1 1
C. m 3 1; 3 M 1. D. m ; . M 2 2 MTCT TABLE 1
Lời giải. u
u 3 1 loại C và D. n 1 2 MTCT TABLE 1
u u
loại B. Vậy Chọn A. n 4 2 3 1
Nhận xét: u 2
sin n cos n 2sinn 2 u 2. n 2 2 6 n n
Câu 38. Cho dãy số u , n u n biết n 2 5 1 .5
. Mệnh đề nào sau đây đúng?
A. Dãy số un bị chặn trên và không bị chặn dưới.
B. Dãy số un bị chặn dưới và không bị chặn trên.
C. Dãy số un bị chặn.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 27 Tµi liÖu to¸n 11 n¨m häc 2018
D. Dãy số un không bị chặn.
Lời giải. Nếu n chẵn thì 2n 1 u 5
0 tăng lên vô hạn (dương vô cùng) khi n tăng lên vô hạn nên dãy u không bị chặn trên. n n Nếu n lẻ thì 2n 1 u 5
0 giảm xuống vô hạn (âm vô cùng) khi n tăng lên vô hạn nên dãy u không bị chặn dưới. n n
Vậy dãy số đã cho không bị chặn. Chọn D. 1 1 1
Câu 39. Cho dãy số u , u ... , n 1; 2; 3 . n với n
Mệnh đề nào sau đây đúng? 1.4 2.5 nn 3
A. Dãy số un bị chặn trên và không bị chặn dưới.
B. Dãy số un bị chặn dưới và không bị chặn trên.
C. Dãy số un bị chặn.
D. Dãy số un không bị chặn. 1 1 1 1
Lời giải. Ta có u 0
u bị chặn dưới bởi 0. Mặt khác *
k nên suy ra: n n k k 3 k k 1 k k 1 1 1 1 1 1 1 1 1 1 1 1 1 u
1 1 1 n 1.2 2.3 3.4 nn 1 2 2 3 2 4 n n 1 n 1
nên dãy u bị chặn trên, do đó dãy u bị chặn. Chọn C. n n 1 1 1
Câu 40. Cho dãy số u , u ... , n 2; 3; 4; . n với n
Mệnh đề nào sau đây đúng? 2 2 2 2 3 n
A. Dãy số un bị chặn trên và không bị chặn dưới.
B. Dãy số un bị chặn dưới và không bị chặn trên.
C. Dãy số un bị chặn.
D. Dãy số un không bị chặn. 1 1 1 1
Lời giải. Ta có u 0
u bị chặn dưới bởi 0. Mặt khác *
k , k 2 nên suy ra: 2 n n k k 1 k k 1 k 1 1 1 1 1 1 1 1 1 1 1 1 u
1 1 1 n 1.2 2.3 3.4 nn 1 2 2 3 2 4 n n 1 n 1
nên dãy u bị chặn trên, do đó dãy u bị chặn. Chọn C. n n
Câu 41. Trong các dãy số un sau đây, dãy số nào là dãy số bị chặn? 1 n A. 2 u n 1. u n . n u u n B. n C. 2 1. D. . n n n n 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 28 Tµi liÖu to¸n 11 n¨m häc 2018
Lời giải. Các dãy số 2 ; ; 2n n n
dương và tăng lên vô hạn (dương vô cùng) khi n tăng lên vô hạn, nên các dãy 1 2 1; ; 2n n n
1 cũng tăng lên vô hạn (dương vô cùng), suy ra các dãy này không bị chặn trên, do đó chúng không bị chặn. n Chọn D. n 1
Nhận xét: 0 u 1 1. n n 1 n 1
Câu 42. Trong các dãy số u u
n cho bởi số hạng tổng quát n sau, dãy số nào bị chặn? 1 A. u . n u u n u n n B. 3 . C. 1. D. 2 . 2n n n n
Lời giải. Các dãy số 2; ; 3n n n
dương và tăng lên vô hạn (dương vô cùng) khi n tăng lên vô hạn nên các dãy 2; 1; 3n n n cũng
tăng lên vô hạn (dương vô cùng), suy ra các dãy này không bị chặn trên, do đó chúng không bị chặn. Chọn A. 1 1
Nhận xét: 0 u . n 2n 2 u 6 1
Câu 43. Cho dãy số u , . n xác định bởi
Mệnh đề nào sau đây đúng? * u
6 u , n n 1 n 5 A. 6 u . u n B. 6 3. 2 n
C. 6 u 2. n D. 6 u 2 3. n 5
Lời giải. Ta có u 12 3
2 nên loại các đáp án A, B, C. Chọn D. 2 2 Nhận xét: Ta có u 6 u 6 u 6 1 1 1 u 0 u 6. n n u 6 u u 0 u u n n 6 6 n 1 1 n 1 n
Ta chứng minh quy nạp u 2 3. n
u 2 3;u 2 3 u 6 u
6 2 3 6 6 2 3. 1 k k 1 k 1
Câu 44. Cho dãy số u , u n với sin n
. Khẳng định nào sau đây là đúng? n 1
A. Số hạng thứ n 1 của dãy là u sin . n 1 n 1
B. Dãy số un là dãy số bị chặn.
C. Dãy số un là một dãy số tăng.
D. Dãy số un không tăng không giảm.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 29 Tµi liÖu to¸n 11 n¨m häc 2018
Lời giải. u sin u sin sin A sai. n n 1 n 1 n 1 1 n 2 u sin
1 u 1
B đúng. Chọn B. n n 1 n u u sin sin 0 0 C, D sai. n 1 n n 2 n 1 n 2 n 1 2 n
Câu 45. Cho dãy số u , u n với n
1 . Mệnh đề nào sau đây đúng?
A. Dãy số u u
n là dãy số tăng.
B. Dãy số n là dãy số giảm.
C. Dãy số u u
n là dãy số bị chặn.
D. Dãy số n là dãy số không bị chặn. n
Lời giải. u
là dãy thay dấu nên không tăng, không giảm A, B sai. n 1 n
Tập giá trị của dãy u là 1; 1
1 u 1
C đúng. Chọn C. n 1 n
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 30 Tµi liÖu to¸n 11 n¨m häc 2018
3. CẤP SỐ CỘNG – CẤP SỐ NHÂN A. LÝ THUYẾT 1. Cấp số cộng
1.1. Định nghĩa: Dãy số (u
n) được xác định bởi
gọi là cấp số cộng; gọi là công sai.
2.1. Các tính chất:
Số hạng thứ n được cho bởi công thức: . Ba số hạng
là ba số hạng liên tiếp của cấp số cộng khi và chỉ khi .
Tổng số hạng đầu tiên
được xác định bởi công thức : . 2. Cấp số nhân
1.2. Định nghĩa: Dãy số (un) được xác định bởi
gọi là cấp số cộng; gọi là công bội.
2.2. Các tính chất:
Số hạng thứ n được cho bởi công thức: . Ba số hạng
là ba số hạng liên tiếp của cấp số cộng khi và chỉ khi .
Tổng số hạng đầu tiên
được xác định bởi công thức : .
B. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
Vấn đề 1. Xác định cấp số và xác yếu tố của cấp số Phương pháp:
• Dãy số (un) là một cấp số cộng ⇔ u + − u = n 1 n
d không phụ thuộc vào n và d là công sai. u • Dãy số (u n 1
n ) là một cấp số nhân + ⇔
= q không phụ thuộc vào n và q là công bội. u n
• Ba số a,b,c theo thứ tự đó lập thành cấp số cộng ⇔ a + c = 2b .
• Ba số a,b,c theo thứ tự đó lập thành cấp số nhân ⇔ = 2 ac b .
• Để xác định một cấp số cộng, ta cần xác định số hạng đầu và công sai. Do đó, ta thường biểu diễn giả
thiết của bài toán qua u1 và d .
• Để xác định một cấp số nhân, ta cần xác định số hạng đầu và công bội. Do đó, ta thường biểu diễn
giả thiết của bài toán qua u và q . 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 1 Tµi liÖu to¸n 11 n¨m häc 2018
1. caùc ví duï minh hoïa
Ví dụ 1. Tìm bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120 . Chú ý:
* Cách gọi các số hạng của cấp số cộng như trên giúp ta giải quyết bài toán gọn hơn.
* Nếu số hạng cấp số cộng là lẻ thì gọi công sai d = x , là chẵn thì gọi công sai d = 2x rồi viết các số hạng cấp số dưới dạng đối xứng. a + a + ... + a = 1 2 n p
* Nếu cấp số cộng (an ) thỏa: thì: 2 a + 2 a + ... + 2 a = 2 1 2 n s 2 2 1 n(n − 1) 12(ns − p ) a = p − .d 1 d = ± n . 2 và 2 n ( 2 n − 1) u − u + u = 10 2 3 5
Ví dụ 2. Cho CSC (un ) thỏa : u + u = 4 6 26
1. Xác định công sai và công thức tổng quát của cấp số;
2. Tính S = u + u + u + ... + 1 4 7 u2011. u + 3u − u = − 5 3 2 21
Ví dụ 3. Cho cấp số cộng (un ) thỏa: 3u − 2u = − 7 4 34 .
1. Tính số hạng thứ 100 của cấp số ;
2. Tính tổng 15 số hạng đầu của cấp số ;
3. Tính S = u + u + ... + 4 5 u30 . u − u + u = 2 3 5 10
Ví dụ 4. Cho cấp số cộng (un) thỏa mãn u + u = 4 6 26
1. Xác định cấp số cộng
2. Tính tổng S = u + u + …+ 5 7 u2011
Ví dụ 5. Cho một cấp số cộng (un ) có u =
1 1 và tổng 100 số hạng đầu bằng 24850 . Tính 1 1 1 S = + + ... + u u u u u u 1 2 2 3 49 50
Ví dụ 6. Cho cấp số nhân (u u
n) có các số hạng khác không, tìm 1 biết: u + u + u + u = u + u + u + u + u = 11 1 2 3 4 15 1 2 3 4 5 1. 2. 82 2 u + 2 u + 2 u + 2 u = 1 2 3 4 85 u + u = 1 5 11 2 u =
Ví dụ 7. Cho cấp số nhân (u 4 n ) thỏa: 27 . u = 3 243u8
1. Viết năm số hạng đầu của cấp số;
2. Tính tổng 10 số hạng đầu của cấp số; 2
3. Số 6561 là số hạng thứ bao nhiêu của cấp số ?
1i. Baøi taäp töï luaän töï luyeän
Bài 1 Dãy số (un ) có phải là cấp số cộng không ? Nếu phải hãy xác định số công sai ? Biết: 2 2 1. u = 2n + n 3 2. u = −3n + n 1 3. u = n + n 1 4. u = n n
Bài 2 . Dãy số (un ) có phải là cấp số nhân không ? Nếu phải hãy xác định số công bội ? Biết:
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 2 Tµi liÖu to¸n 11 n¨m häc 2018 2 1. u = n 2n 2. u = n n 4.3 3. u = n n .
Bài 3. Xét xem các dãy số sau có phải là cấp số cộng hay không? Nếu phải hãy xác định công sai. 2n + 3 n + 1 n 2 1. u = 3n + n 1 2. u = 4 − n 5n 3. u = n u = u u n 1 5 4. n n 5. = n n 6. = + 2 n
Bài 4 Xét xem các dãy số sau có phải là cấp số nhân hay không? Nếu phải hãy xác định công bội. n−1 3 n 2 − 1 1. u = n n 2 2. u = − n u 3n 1 u = u n 5 3. = − n 4. n 3 5. = 3 n . Bài 5.
1. Tam giác ABC có ba góc A, B,C theo thứ tự đó lập thành cấp số cộng và C = 5A . Xác định số đo các góc A, B,C . 3 + 3
2. Cho tam giác ABC biết ba góc tam giác lập thành cấp số cộng và sin A + sin B + sin C = 2 tính các góc của tam giác n+1
Bài 6. Cho dãy số (u 2 n ) với u = n 3
1. Chứng minh dãy số (un) là cấp số nhân
2. Tính tổng S = u + u + u + …+ 2 4 6 u 20
3. Số 19683 là số hạng thứ mấy của dãy số. Bài 7.
1. Cho cấp số nhân có 7 số hạng, số hạng thứ tư bằng 6 và số hạng thứ 7 gấp 243 lần số hạng thứ hai. Hãy tìm số hạng còn lại của CSN đó.
2. Tìm ba số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng −9 và tổng các bình phương của chúng bằng 29.
3. Cho bốn số nguyên dương, trong đó ba số đầu lập thành một cấp số cộng, ba số sau lập thành cấp số nhân. Biết tổng số
hạng đầu và cuối là 37, tổng hai số hạng giữa là 36, tìm bốn số đó. Bài 8. u − u = 7 3 8
1. Cho cấp số cộng (u u ,d n) thỏa mãn ? u .u = 2 7 75 . Tìm 1 u + u = 31 34 11
2. Cho cấp số cộng (u d 0 n) có công sai > ;
. Hãy tìm số hạng tổng quát của cấp số cộng đó. 2 u + 2 u = 31 34 101
3. Gọi S1;S2 ;S3 là tổng n1;n2 ;n3 số hạng đầu của một cấp số cộng. Chứng minh rằng: S1 ( S S n − n ) + 2 2 3 (n − 3 n1) + 3 (n − 1 n2 ) = 0 n1 n2 n 3 u + u + u + u + u = 11 1 2 3 4 5
Bài 9. Cho CSN (un ) thỏa: 82 u + u = 1 5 11
1. Tìm công bội và số hạng tổng quát của cấp số 2. Tính tổng S2011 1
3. Trên khoảng ;1 2
có bao nhiêu số hạng của cấp số. Bài 10. 1
1. Cho dãy số (x ) : x = , n = n n 1,2,3... n
. Chứng minh rằng luôn tồn tại một CSC gồm 2011 số hạng mà mỗi số hạng đều thuộc dãy số trên.
Vấn đề 2. Chứng minh tính chất của cấp số Phương pháp:
Sử dụng công thức tổng quát của cấp số, chuyển các đại lượng qua số hạng đầu và công sai, công bội.
Sử dụng tính chất của cấp số:
theo thứ tự đó lập thành CSC
theo thứ tự đó lập thành CSN
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 3 Tµi liÖu to¸n 11 n¨m häc 2018
1. caùc ví duï minh hoïa
Ví dụ 1. Chứng minh rằng các số:
1. 1, 3 , 3 không thể cùng thuộc một CSC;
2. 2,3,5 không thể cùng thuộc một CSN.
Ví dụ 2. Chứng minh rằng dãy số (un ) là:
1. CSC khi và chỉ khi u = an + n b
2. CSN khi và chỉ khi u = n n a.q .
Ví dụ 3. Chứng minh rằng : 3 2 3
1. Nếu phương trình x − ax + bx − c = 0 có ba nghiệm lập thành CSC thì 9ab = 2a + 27c 3 2 3 3
2. Nếu phương trình x − ax + bx − c = 0 có ba nghiệm lập thành CSN thì c(ca − b ) = 0
Ví dụ 4. Chứng minh rằng với mọi cách chia tập X = {1,2,3,..., }
9 thành hai tập con rời nhau luôn có một tập chứa ba số lập
thành cấp số cộng. 1
Ví dụ 5. Dãy số (xn) thỏa mãn điều kiện: xn+ − x − x < m m n m + n ∀ ∈ * m,n
. Chứng minh rằng: (xn) là một cấp số cộng.
1i. Baøi taäp töï luaän töï luyeän Bài 1 2 2
1. Cho ba số a, b,c lập thành cấp số cộng. Chứng minh rằng : a + 2bc = c + 2ab . 1 1 2
2. Cho a, b,c > 0 lập thành cấp sô cộng.Chứng minh rằng : + = . a + b b + c c + a 1 3. Cho (u u = u + u 1 k n 1
n) là cấp số cộng. Chứng minh rằng : n ( n−k n+k) 2 , ≤ ≤ − Bài 2 A B C
1. Cho tam giác ABC. Chứng minh rằng tan ;tan ; tan 2 2
2 lập thành cấp số cộng ⇔ cosA;cos B;cosC lập thành cấp số cộng. A B C
2. Cho tam giác ABC.Chứng minh rằng cot ;cot ;cot 2 2
2 lập thành cấp số cộng ⇔ sin A;sin B;sinC lập thành cấp số cộng.
Bài 3 Cho a, b,c lập thành cấp số nhân . .Chứng minh rằng : 2 2 2
1. (a + b + c)(a − b + c) = a + b + c 2 2 2 2 2
2. (a + b )(b + c ) = (ab + bc) 3 3
3. (ab + bc + ca) = abc(a + b + c) n n n n n n 2n 2n 2n *
4. (a + b + c )(a − b + c ) = a + b + c ; n ∈
Bài 4 Cho (un) là cấp số nhân .Chứng minh rằng : 2
1. a a = a .a − + , k = 1 n k n k 1 1;n 2. Sn (S − 3n S2n ) = (S − 2n Sn ) . Bài 5
1. Điều cần và đủ để ba số khác không a, b,c là ba số hạng của một CSN là tồn tại ba số nguyên khác không p, t,r sao cho p + t + r = 0 . p t r a .b .c = 1
2. Cho cấp số cộng (an) với các số hạng khác không và công sai khác không.Chứng minh rằng: 1 1 1 n − 1 + + ... + = a1a2 a2a3 an−1an a1a . n
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 4 Tµi liÖu to¸n 11 n¨m häc 2018 1 1 2 + = a1a2 a2a3 a1a3
3. Cho bốn số thực a1;a2 ;a3;a4 .Biết rằng : 1 1 1 3 + + = a1a2 a2a3 a3a4 a1a4
Chứng minh rằng : a1;a2 ;a3;a4 lập thành cấp số cộng.
4. Cho a, b,c lần lượt là ba số hạng thứ m,n,p của một cấp số cộng. Chứng minh rằng :
a.(n − p) + b.(p − m) + c.(m − n) = 0 .
5. Chứng minh rằng điều kiện cần và đủ để ba số a, b,c là ba số hạng của một CSC là tồn tại ba số nguyên khác không pa + qb + rc = 0 p,q,r thỏa: p+q +r = 0 .
6.Cho CSC (un ) thỏa S = m
Sn ( m ≠ n ). Chứng minh S + = m n 0 . 5 − 1 1+ 5
7. Chứng minh rằng nếu ba cạnh của tam giác lập thành CSN thì công bội của CSN đó nằm trong khoảng ; 2 2 . Bài 6
1. Chứng minh ba số a, b,c > 0 là 3 số hạng liên tiếp của cấp số cộng khi và chỉ khi 3 số 2 + + 2 2 + + 2 2 + + 2 a ab b ;c ca a ; b
bc c cũng là ba số hạng liên tiếp của một cấp số cộng.
2. Cho (un ) là cấp số nhân. Kí hiệu S = u + u + ... + 1 2 un ; 1 1 1 T = + + ... + ; P = u1u2...un u1 u2 u
. Hãy tính P theo S,T và n. n
Bài 7 Cho hai số tự nhiên n, k thỏa k + 3 ≤ n . k k+1 k+2
1. Chứng minh rằng tồn tại không quá hai giá trị của k sao cho Cn , Cn và Cn là ba số hạng liên tiếp của một CSC. k k+1 k+2 k+3
2. Chứng minh rằng không tồn tại k để Cn , Cn , Cn và Cn là bốn số hạng liên tiếp của một CSC. Bài 8 n n+1 k uk+ u + 1 1 un+ n + 1 1 2
1. Cho (un ) là CSC. Chứng minh rằng: ∑ = . k n 1 ∑ + k=0 C 2 2 k n k=1
2. Cho k là một số nguyên dương cho trước. Giả sử 1
s ,s2,s3,... là một dãy tăng nghặt các số nguyên dương sao cho các dãy con ss ,ss ,ss ,... và s ,s ,s
,... đều là cấp số cộng. Chứng minh rằng s ,s ,s ,... cũng là một cấp số 1 2 3 s +k s +k s +k 1 2 3 1 2 3 cộng
Vấn đề 3. Tìm điều kiện để dãy số lập thành cấp số Phương pháp:
theo thứ tự đó lập thành CSC
theo thứ tự đó lập thành CSN .
1. caùc ví duï minh hoïa
Ví dụ 1. Tìm x biết : 2
1. x + 1, x − 2,1 − 3x lập thành cấp số cộng ; 2 2
2. 1, x ,6 − x lập thành cấp số nhân. 2 2
Ví dụ 2. Cho các số 5x − y , 2x + 3y , x + 2y lập thành cấp số cộng ; các số (y + 1) ,xy + 1,(x − 1) lập thành cấp số nhân.Tính x, y
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 5 Tµi liÖu to¸n 11 n¨m häc 2018
1i. Baøi taäp töï luaän töï luyeän
Bài 1. Tìm x để các số sau lập thành cấp số cộng 3 π
1. 1;x;x 2. 1; sin − x;4sinx 6
Bài 2. Tìm x, y biết:
1. Các số x + 5y, 5x + 2y,8x + y lập thành cấp số cộng và các số ( − )2 − ( + )2
y 1 ,xy 1, x 1 lập thành cấp số nhân. 5
2. Các số x + 6y, 5x + 2y,8x + y lập thành cấp số cộng và các số x + y,y − 1,2x − 3y 3
lập thành cấp số nhân. 3
Bài 3. Xác định a, b để phương trình x + ax + b = 0 có ba nghiệm phân biệt lập thành cấp số cộng.
Bài 4 Tìm m để phương trình: 4 2
1. mx − 2 (m − 1) x + m − 1 = 0 có bốn nghiệm phân biệt lập thành cấp số cộng. 3 2
2. x − 3mx + 4mx + m − 2 = 0 có ba nghiệm lập thành cấp số nhân
Bài 5 Xác định m để: 3 2
1. Phương trình x − 3x − 9x + m = 0 có ba nghiệm phân biệt lập thành cấp số cộng. 4 2
2. Phương trình x − 2 (m + 1) x + 2m + 1 = 0 (1) có bốn nghiệm phân biệt lập thành cấp số cộng. 3 2
3. Phương trình x + 2x + (m + 1) x + 2(m + 1) = 0 có ba nghiệm lập thành cấp số nhân.
1ii. Baøi taäp traéc nghieäm
Phần 1. Câu hỏi trắc nghiệm liên quan đến cấp số cộng 1
Câu 4. Cho cấp số cộng có số hạng đầu u , 1 công sai 2
Câu 1. Trong các dãy số sau, dãy số nào là một cấp số cộng? 1
d . Năm số hạng liên tiếp đầu tiên của cấp số này là: A. 1 ;3;7;11;15;
B. 1;3;6;9;12; 2
C. 1;2;4;6;8;
D. 1;3;5;7;9; 1 1 1 1 1 A. ;0;1; ;1. B. ;0; ;0; . 2 2 2 2 2
Câu 2. Dãy số nào sau đây không phải là cấp số cộng? 1 3 5 1 1 3 ;1; ;2; . ;0; ;1; . 2 1 1 2 4 C. D. 2 2 2 2 2 2
A. ; ;0; ; ;1; ....
B. 15 2;12 2;9 2;6 2;.... 3 3 3 3 3
Câu 5. Viết ba số hạng xen giữa các số 2 và 22 để được một 4 7 9 11 1 2 3 4 3 5
cấp số cộng có năm số hạng. C. ;1; ; ; ;.... D. ; ; 3; ; ;... 5 5 5 5 3 3 3 3
A. 7; 12; 17, B.6;10;14.
C. 8; 13; 18. D. 6; 12; 18. 1 1 3
Câu 3. Cho dãy số ;0; ;1; ;..... là cấp số cộng với:
Câu 6. Cho hai số 3 và 23. Xen kẽ giữa hai số đã cho n số 2 2 2
hạng để tất cả các số đó tạo thành cấp số cộng có công sai d 2. Tìm . n 1 1
A. Số hạng đầu tiên là , công sai là . 2 2 A. n 12. B. n 13. C. n 14. D. n 15. 1 1
B. Số hạng đầu tiên là , công sai là .
Câu 7. Cho các số 4; 1; 6; x theo thứ tự lập thành một cấp số 2 2 cộng. Tìm x. 1
C. Số hạng đầu tiên là 0 , công sai là . A. x 7. B. x 10. C. x 11. D. x 12. 2
Câu 8. Biết các số 1 2 3
C ; C ; C theo thứ tự lập thành một cấp số 1 n n n
D. Số hạng đầu tiên là 0 , công sai là . n 2 cộng với 3. Tìm . n
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 6 Tµi liÖu to¸n 11 n¨m häc 2018 A. n 5. B. n 7. C. n 9. D. n 11. u 1 u 1 1 1 C. . D. . u u 1 u 2u n n 1 n n 1
Câu 9. Nếu các số 5 m; 7 2m; 17 m theo thứ tự lập thành
cấp số cộng thì m bằng bao nhiêu?
Câu 16. Trong các dãy số được cho dưới đây, dãy số nào không phải là cấp số cộng? A. m 2. B. m 3. C. m 4. D. m 5.
A. u 4n 9. u n n B. 2 19. n
Câu 10. Với giá trị nào của x và y thì các số 7; x; 11; y
theo thứ tự đó lập thành một cấp số công?
C. u 2n 21. n n D. u 2 15. n
A. x 1; y 21.
B. x 2; y 20.
Câu 17. Cho cấp số cộng u u 5 d n có 1 và 3. Số 100 là
C. x 3; y 19.
D. x 4; y 18.
số hạng thứ mấy của cấp số cộng? A. Thứ 15.
B. Thứ 20. C. Thứ 35. D. Thứ 36.
Câu 11. Cho cấp số cộng un có các số hạng đầu lần lượt là
5; 9; 13; 17; . Tìm số hạng tổng quát un của cấp số cộng.
Câu 18. Cho cấp số cộng u u 5 d n có 1 và 3. Mệnh đề nào sau đây đúng?
A. u 5n 1. u n n B. 5 1. n A. u 34. u 45. u 31. u 35. 15 B. 15 C. 13 D. 10
C. u 4n 1. u n n D. 4 1. n
Câu 19. Một cấp số cộng có 8 số hạng. Số hạng đầu là 5, số 1
Câu 12. Cho cấp số cộng u u 3 d .
hạng thứ tám là 40. Khi đó công sai d của cấp số cộng đó là bao n có 1 và Khẳng 2 nhiêu?
định nào sau đây đúng?
A. d 4.
B. d 5.
C. d 6.
D. d 7. 1 1
A. u 3 n
u 3 n 1. n 1 . B. 2 n 2
Câu 20. Cho cấp số cộng u u 4 d n có 1 và 5. Tính tổng
100 số hạng đầu tiên của cấp số cộng. 1 1
C. u 3 n u 3 n 1 . n 1 . D. n 2 4 A. S 24350. S 24350. 100 B. 100
Câu 13. Cho cấp số cộng u u 15 d u n có 3 và 2 . Tìm . n C. S 24600. S 24600. 100 D. 100 3
A. u 2n 21.
u n 12. 1 1 n B. n 2
Câu 21. Cho cấp số cộng u u d . S n có 1 và Gọi 4 4 5 3
là tổng 5 số hạng đầu tiên của cấp số cộng đã cho. Mệnh đề nào 2
C. u 3n 17. u n 4. sau đây đúng? n D. n 2 5 4 5 4
Câu 14. Trong các dãy số được cho dưới đây, dãy số nào là cấp A. S . S . S . S . 5 B. C. D. 4 5 5 5 4 5 5 số cộng? u n
A. u 7 3 . n n u
Câu 22. Số hạng tổng quát của một cấp số cộng là 3 4 n n B. 7 3 . n với *
n . Gọi Sn là tổng n số hạng đầu tiên của cấp số cộng 7 đã cho. Mệnh đề C. u . n u nào sau đây đúng? n D. 7.3 . 3n n 3n 1 73n 1
Câu 15. Trong các dãy số được cho dưới đây, dãy số nào là cấp A. S . S . n B. 2 n 2 số cộng? 2 3n 5n 2 3n 11n n C. S . D. S . A. u n u n n n 1 2 1 . B. sin . n 2 2 n
Câu 23. Xét các số nguyên dương chia hết cho 3. Tổng số 50
số nguyên dương đầu tiên đó bằng:
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 7 Tµi liÖu to¸n 11 n¨m häc 2018 A. 7650. B. 7500. C. 3900. D. 3825.
Câu 31. Cho cấp số cộng u u 12 u 18. n có 4 và 14 Tìm
số hạng đầu tiên u và công sai d của cấp số cộng đã cho.
Câu 24. Cho cấp số cộng u d S 72. 1 n có 2 và 8 Tìm số hạng đầu tiên u . 1
A. u 21; d 3.
u 20; d 3. 1 B. 1 1 1 A. u 16. u 16. u . u
. C. u 22; d 3.
D. u 21; d 3. 1 B. 1 C. 1 D. 1 1 16 1 16
Câu 32. Cho cấp số cộng u u 2001 u 1995 n có và .
Câu 25. Một cấp số cộng có số hạng đầu là 1, công sai là 4, tổng 2 5
của n số hạng đầu là 561. Khi đó số hạng thứ n của cấp số Khi đó u1001 bằng:
cộng đó là un có giá trị là bao nhiêu? A. u 4005. u 4003. 1001 B. 1001 A. u 57. u u u n B. 61. n C. 65. n D. 69. n C. u 3. D. u 1. 1001 1001
Câu 26. Một cấp số cộng có 12 số hạng. Biết rằng tổng của 12
số hạng đó bằng 144 và số hạng thứ mười hai bằng 23. Khi đó Câu 33. Cho cấp số cộng u u 1,u 8 n , biết: n n 1 . Tính
công sai d của cấp số cộng đã cho là bao nhiêu?
công sai d cảu cấp số cộng đó. A. d 2. B. d 3. C. d 4. D. d 5. A. d 9. B. d 7. C. d 7. D. d 9.
Câu 27. Tổng n số hạng đầu tiên của một cấp số cộng là Câu 34. Cho cấp số cộng u . n
Hãy chọn hệ thức đúng trong 2 3n 19n S u n với *
n . Tìm số hạng đầu tiên và công các hệ thức sau: 4 1
sai d của cấp số cộng đã cho. u u A. 10 20 u u . u u 2u . 5 10 B. 2 90 210 150 1 3
A. u 2; d .
u 4; d . 1 B. 2 1 2 u .u
C. u .u u . u . 10 30 20 D. 10 30 20 2 3 5 1
C. u ; d 2. u ; d . 1 D. 2 1 2 2
Câu 35. Cho cấp số cộng u u u 60. n thỏa mãn 2 23 Tính
Câu 28. Tổng n số hạng đầu tiên của một cấp số cộng là tổng S24 của 24 số hạng đầu tiên của cấp số cộng đã cho. 2
S n 4n u n với *
n . Tìm số hạng tổng quát n của cấp số A. S 60. S 120. S 720. 24 B. 24 C. 24 D. cộng đã cho. S 1440. 24
A. u 2n 3. u n n B. 3 2. n
Câu 36. Một cấp số cộng có 6 số hạng. Biết rằng tổng của số n 1 8
hạng đầu và số hạng cuối bằng 17; tổng của số hạng thứ hai và C. n 1 u 5.3 . u 5. . n D. n 5
số hạng thứ tư bằng 14. Tìm công sai d của câp số cộng đã cho.
Câu 29. Tính tổng S 1 2 3 4 5 ... 2n
1 2n với A. d 2. B. d 3. C. d 4. D. d 5.
n 1 và n . u u 8 A. S 0.
B. S 1. C. S . n D. S . n 7 3
Câu 37. Cho cấp số cộng u . n thỏa mãn Tìm u u 75 2 7 Câu 30. Cho cấp số cộng un thỏa mãn
công sai d của câp số cộng đã cho.
u u u u 100. 2 8 9 15
Tính tổng 16 số hạng đầu tiên của cấp 1 1 số cộng đã cho. A. d . B. d . C. d 2.
D. d 3. 2 3 A. S 100. S 200. S 300. S 400. 16 B. 16 C. 16 D. 16 u u 26 1 7
Câu 38. Cho cấp số cộng u . n thỏa mãn 2 2 u u 466 2 6
Mệnh đề nào sau đây đúng?
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 8 Tµi liÖu to¸n 11 n¨m häc 2018 u 13 2 2 2 2 2 2 2 2 2 2 2 2 u 10 u 1 u 13
b ; a ; c .
c ; a ; b .
a ; b ; c .
a ; c ; b . 1 1 1 1 A. B. C. D. A. . B. . C. . D. . d 3 d 3 d 4 d 4
Câu 47. Cho a; b; c theo thứ tự lập thành cấp số cộng. Mệnh đề u
u u 15 nào sau đây đúng? 1 3 5
Câu 39. Cho cấp số cộng u . n thỏa mãn u u 27 1 6 A. 2 2 2
a c 2ac 4b . B. 2 2
a c 2ab 2bc.
Chọn khẳng định đúng trong các khẳng định sau? C. 2 2
a c ab bc. D. 2 2
a c 2ab 2bc. u 21 u 21 u 18 u 21 1 1 1 1 A. . B. . C. . D. . d 3 d 3 d 3 d 4
Câu 48. Ba góc của một tam giác vuông tạo thành cấp số cộng.
Hai góc nhọn của tam giác có số đo (độ) là: u
u u 36
Câu 40. Cho cấp số cộng u thỏa 2 4 6
. Tìm A. 20 và 70. B. 45 và 45. n u u 54 2 3
công sai d của cấp số cộng u biết d 10. C. 20 và 45. D. 30 và 60. n ,
A B, C A B C A. d 3. B. d . 4 C. d 5. D. d 6. Câu 49. Ba góc
của tam giác tạo thành
cấp số cộng, biết góc lớn nhất gấp đôi góc bé nhất. Hiệu số đo độ u
u u 27
của góc lớn nhất với góc nhỏ nhất bằng: 1 2 3
Câu 41. Cho cấp số cộng u thỏa . Tính n 2 2 2 u
u u 275 1 2 3 A. 40. B. 45. C. 60. D. 80. u . 2
Câu 50. Một tam giác vuông có chu vi bằng 3 và độ dài các A. u 3. B. u 6. C. u 9. D. u 12. 2 2 2 2
cạnh lập thành một cấp số cộng. Độ dài các cạnh của tam giác đó là:
Câu 42. Tính tổng T 15 20 25 ... 7515. 1 3 1 5 3 5 1 7 ; 1; . ; 1; . ; 1; . ; 1; .
A. T 5651265.
B. T 5651256. A. B. C. D. 2 2 3 3 4 4 4 4
C. T 5651625.
D. T 5651526.
Câu 51. Một rạp hát có 30 dãy ghế, dãy đầu tiên có 25 ghế. Mỗi
dãy sau có hơn dãy trước 3 ghế. Hỏi rạp hát có tất cả bao nhiêu Câu 43. Tính tổng ghế? 2 2 2 2 2 2
T 1000 999 998 997 ... 2 1 . A. 1635. B. 1792. C. 2055. D. 3125.
A. T 500500.
B. T 500005.
Câu 52. Người ta trồng 3003 cây theo một hình tam giác như
C. T 505000.
D. T 500050.
sau: hàng thứ nhất trồng 1 cây, hàng thứ hai trồng 2 cây, hàng
thứ ba trồng 3 cây,...Hỏi có tất cả bao nhiêu hàng cây?
Câu 44. Cho cấp số cộng u ; u ; u ; ; u d 1 2 3 n có công sai , các
số hạng của cấp số cộng đã cho đều khác 0. Với giá trị nào của A. 73. B. 75. C. 77. D. 79. 1 1 1 1 d thì dãy số ; ; ; ; là một cấp số cộng?
Câu 53. Một chiếc đồng hồ đánh chuông, kể từ thời điểm 0 (giờ) u u u u 1 2 3 n
thì sau mỗi giờ thì số tiếng chuông được đánh đúng bằng số giờ
mà đồng hồ chỉ tại thời điểm đánh chuông. Hỏi một ngày đồng A. d 1. B. d 0. C. d 1. D. d 2.
hồ đó đánh bao nhiêu tiếng chuông?
Câu 45. Nếu a; b; c theo thứ tự lập thành cấp số cộng thì dãy A. 78. B. 156. C. 300. D. 48.
số nào sau đây lập thành cấp số cộng?
Câu 54. Trên một bàn cờ có nhiều ô vuông, người ta đặt 7 hạt dẻ 2 2 2
A. 2b ; a ; c .
B. 2b;2a;2c.
vào ô đầu tiên, sau đó đặt tiếp vào ô thứ hai số hạt nhiều hơn ô
thứ nhất là 5, tiếp tục đặt vào ô thứ ba số hạt nhiều hơn ô thứ hai
C. 2b; a; c.
D. 2b; a; c.
là 5,… và cứ thế tiếp tục đến ô thứ n . Biết rằng đặt hết số ô trên
bàn cờ người ta phải sử dụng 25450 hạt. Hỏi bàn cờ đó có bao 1 1 1 nhiêu ô vuông? Câu 46. Nếu ; ;
theo thứ tự lập thành cấp số
b c c a a b A. 98. B. 100. C. 102. D. 104.
cộng thì dãy số nào sau đây lập thành cấp số cộng?
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 9 Tµi liÖu to¸n 11 n¨m häc 2018
Câu 55. Một gia đình cần khoan một cái giếng để lấy nước. Họ Câu 7. Một cấp số nhân có hai số hạng liên tiếp là 16 và 36. Số
thuê một đội khoan giếng nước đến để khoan giếng nước. Biết hạng tiếp theo là:
giá của mét khoan đầu tiên là 80.000 đồng, kể từ mét khoan thứ
2 giá của mỗi mét khoan tăng thêm 5000 đồng so với giá của mét A. 720. B. 81. C. 64. D. 56.
khoan trước đó. Biết cần phải khoan sâu xuống 50m mới có nướ
Câu 8. Tìm x để các số 2; 8; x; 128 theo thứ tự đó lập thành
c. Vậy hỏi phải trả bao nhiêu tiền để khoan cái giếng đó? một cấp số nhân.
A. 5.2500.000 đồng. B. 10.125.000 đồng. A. x 14. B. x 32. C. x 64. D. x 68. C. 4.000.000 đồng. D. 4.245.000 đồng.
Câu 9. Với giá trị x nào dưới đấy thì các số 4; x; 9 theo
Phần 2. Câu hỏi trắc nghiệm liên quan đến cấp số nhân
thứ tự đó lập thành một cấp số nhân?
Câu 1. Trong các dãy số sau, dãy số nào là một cấp số nhân? 13 A. x 36. B. x . C. x 6. D. x 36. 2
A. 128; 64; 32; 16; 8; ... B. 2; 2; 4; 4 2; .... 1 1
Câu 10. Tìm b 0 để các số
; b; 2 theo thứ tự đó lập
C. 5; 6; 7; 8; ...
D. 15; 5; 1; ; ... 5 2
thành một cấp số nhân.
Câu 2. Trong các dãy số sau, dãy số nào không phải là một cấp A. b 1. B. b 1. C. b 2. D. b 2. số nhân? x x x
A. 2; 4; 8; 16;
B. 1; 1; 1; 1;
Câu 11. Tìm tất cả giá trị của x để ba số 2 1; ; 2 1 theo
thứ tự đó lập thành một cấp số nhân. 2 2 2 2
C. 1 ; 2 ; 3 ; 4 ; D. 3 5 7
a; a ; a ; a ; a 0. 1 1 A. x
. B. x . C. x 3. D. x 3. 3
Câu 3. Dãy số nào sau đây không phải là cấp số nhân? 3 2 3 4 x x x A. 1; 2; 4; 8; B. 3; 3 ; 3 ; 3 ;
Câu 12. Tìm x để ba số 1 ; 9 ; 33 theo thứ tự đó lập
thành một cấp số nhân. 1 1 1 1 1 1 C. 4; 2; ; ; D. ; ; ; ; x x 2 4 2 4 6 A. 1. B. 3. C. x 7.
D. x 3; x 7.
Câu 4. Dãy số 1; 2; 4; 8; 16; 32; là một cấp số nhân với:
Câu 13. Với giá trị x, y nào dưới đây thì các số hạng lần lượt là
A. Công bội là 3 và số hạng đầu tiên là 1. 2; ;
x 18; y theo thứ tự đó lập thành cấp số nhân?
B. Công bội là 2 và số hạng đầu tiên là 1. x 6 x 10 x 6 x 6
C. Công bội là 4 và số hạng đầu tiên là 2. A. . . . . B. C. D. y 54 y 26 y 54 y 54
D. Công bội là 2 và số hạng đầu tiên là 2.
Câu 14. Cho cấp số nhân có các số hạng lần lượt là
Câu 5. Cho cấp số nhân u u 2 q
x; 12; y; 192. Mệnh đề nào sau đây là đúng? n với 1 và 5. Viết
bốn số hạng đầu tiên của cấp số nhân.
A. x 1; y 144.
B. x 2; y 72.
A. 2; 10; 50; 250.
B. 2; 10; 50; 250.
C. x 3; y 48.
D. x 4; y 36.
C. 2; 10; 50; 250. D. 2; 10; 50; 250.
Câu 15. Thêm hai số thực dương x và y vào giữa hai số 5 và 1 1 1 1 1
Câu 6. Cho cấp số nhân ; ; ; ; . Hỏi số
là 320 để được bốn số 5; x; y; 320 theo thứ tự đó lập thành cấp 2 4 8 4096 4096
số nhận. Khẳng định nào sau đây là đúng?
số hạng thứ mấy trong cấp số nhân đã cho? x 25 x 20 x 15 x 30 A. 11. B. 12. C. 10. D. 13. A. . . . . B. C. D. y 125 y 80 y 45 y 90
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 10 Tµi liÖu to¸n 11 n¨m häc 2018
Câu 16. Ba số hạng đầu của một cấp số nhân là x 6; x và . y 7
A. u 7 3 . n n u u . n u n B. 7 3 . n C. n D. 7.3 . n
Tìm y , biết rằng công bội của cấp số nhân là 6. 3n 324 1296
Câu 22. Cho dãy số un là một cấp số nhân với
A. y 216. B. y . C. y
. D. y 12. 5 5 *
u 0, n . n
Dãy số nào sau đây không phải là cấp số nhân?
Câu 17. Hai số hạng đầu của của một cấp số nhân là 2x 1 và A. u ; u ; u ; ...
3u ; 3u ; 3u ; ... 1 3 5 B. 1 2 3 2
4x 1. Số hạng thứ ba của cấp số nhân là: 1 1 1
A. 2x 1.
B. 2x 1. C. ; ; ; ...
D. u 2; u 2; u 2; ... u u u 1 2 3 1 2 3 C. 3 2
8x 4x 2x 1. D. 3 2
8x 4x 2x 1.
Câu 23. Cho cấp số nhân có các số hạng lần lượt là 3; 9; 27; 81; ... u
Câu 18. Dãy số nào sau đây là cấp số nhân?
. Tìm số hạng tổng quát n của cấp số nhân đã cho. u 1 u 1 1 1 A. . B. . n n n u
u 1, n 1 u u u u
3u , n 1 A. 1 3 . B. 3 . C. 1 3 . D. n 1 n n 1 n n n n u 3 3n. n u u 2 1
Câu 24. Một cấp số nhân có 6 số hạng, số hạng đầu bằng 2 và số 1 2 C. . D. . u
2u 3, n 1
hạng thứ sáu bằng 486. Tìm công bội q của cấp số nhân đã cho. n 1 n u sin , n 1 n n 1 A. q 3. B. q 3. C. q 2. D. q 2. 3
Câu 19. Cho dãy số u u .5n. n với n Khẳng định nào sau 2 2
Câu 25. Cho cấp số nhân u u 3 q . n có 1 và Mệnh đề đây đúng? 3 nào sau đây đúng?
A. un không phải là cấp số nhân. 27 16 16 27 A. u . u . u . u . 5 B. C. D. 16 5 27 5 27 5 16 B. u q
n là cấp số nhân có công bội 5 và số hạng đầu 3 u .
Câu 26. Cho cấp số nhân u u 2 u 8 n có 1 và 2 . Mệnh đề 1 2 nào sau đây đúng? C. u q
n là cấp số nhân có công bội
5 và số hạng đầu A. S 130. B. u 256. C. S 256. D. q 4. 6 5 5 15 u . 1 2
Câu 27. Cho cấp số nhân u u 3 q n có 1 và 2 . Số 192
là số hạng thứ mấy của cấp số nhân đã cho? 5 D. u q
n là cấp số nhân có công bội và số hạng đầu 2
A. Số hạng thứ 5.
B. Số hạng thứ 6. u 3. 1
C. Số hạng thứ 7.
D. Không là số hạng của cấp số đã cho.
Câu 20. Trong các dãy số u u
n cho bởi số hạng tổng quát n
sau, dãy số nào là một cấp số nhân? 1
Câu 28. Cho cấp số nhân u u 1 q n có 1 và . Số 10 1 1 A. u . u 1. 1 n B. n2 3 n 3n
là số hạng thứ mấy của cấp số nhân đã cho? 103 10 1 1
C. u n . 2 u n .
A. Số hạng thứ 103.
B. Số hạng thứ 104. n D. 3 n 3
C. Số hạng thứ 105.
D. Không là số hạng của cấp số
Câu 21. Trong các dãy số u u đã cho.
n cho bởi số hạng tổng quát n
sau, dãy số nào là một cấp số nhân?
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 11 Tµi liÖu to¸n 11 n¨m häc 2018
Câu 29. Một cấp số nhân có công bội bằng 3 và số hạng đầu 212n 12n
bằng 5. Biết số hạng chính giữa là 32805. Hỏi cấp số nhân đã C. S . D. S 2. . 12 3
cho có bao nhiêu số hạng?
Câu 36. Một cấp số nhân có 6 số hạng với công bội bằng 2 và A. 18. B. 17. C. 16. D. 9.
tổng số các số hạng bằng 189. Tìm số hạng cuối u6 của cấp số
Câu 30. Cho cấp số nhân u u u 9. nhân đã cho. n có 81 n và n 1 Mệnh đề nào sau đây đúng? A. u 32. u 104. 6 B. 6 1 1
C. u 48. D. u 96. A. q .
B. q 9.
C. q 9.
D. q . 6 6 9 9
Câu 37. Cho cấp số nhân u u 6 q n có 1 và 2. Tổng
Câu 31. Một dãy số được xác định bởi u 4 1
và n số hạng đầu tiên của cấp số nhân đã cho bằng 2046. Tìm . n 1
u u , n 2. u n n 1 Số hạng tổng quát của dãy số đó là: 2 n A. n 9.
B. n 10.
C. n 11. D. n 12. n A. n 1 u 2 . u
Câu 38. Cho cấp số nhân un có tổng n số hạng đầu tiên là n B. n 1 2 . S 5n 1. n
Tìm số hạng thứ 4 của cấp số nhân đã cho. n 1 1 C. u u 4 . n n 1 4 2 . D. n 2 A. u 100. u 124. u 500. u 624. 4 B. 4 C. 4 D. 4
Câu 32. Cho cấp số nhân u u 3 q u n có 1 và
2. Tính Câu 39. Cho cấp số nhân n có tổng n số hạng đầu tiên là
tổng 10 số hạng đầu tiên của cấp số nhân đã cho. 3n 1 S . n
Tìm số hạng thứ 5 của cấp số nhân đã cho. n 1 3
A. S 511. S 1025. 10 B. 10 2 1 5 u . u . u 3 . u . C. S 1025. S 1023. A. 5 B. C. 5 D. 4 5 5 5 5 5 10 D. 10 3 3 3
Câu 33. Cho cấp số nhân có các số hạng lần lượt là Câu 40. Cho cấp số nhân u u 2 u 54. n có 2 và 5 Tính
1; 4; 16; 64; Gọi Sn là tổng của n số hạng đầu tiên của tổng 1000 số hạng đầu tiên của cấp số nhân đã cho.
cấp số nhân đó. Mệnh đề nào sau đây đúng? 1000 13 1000 3 1 n n 1 1 4 A. S . S . 1000 B. 4 1000 2 A. n 1 S 4 . S . n B. n 2 1000 3 1 1000 13 S . S . 4n 1 44n 1 C. 1000 D. 6 1000 6 C. S . S . n D. 3 n 3
Câu 41. Cho cấp số nhân un có tổng của hai số hạng đầu tiên
Câu 34. Cho cấp số nhân có các số hạng lần lượt là bằng 4 , tổng của ba số hạng đầu tiên bằng 13 . Tính tổng của 1 1 ; ; 1; ;
2048. Tính tổng S của tất cả các số hạng của năm số hạng đầu tiên của cấp số nhân đã cho, biết công bội của 4 2
cấp số nhân là một số dương. cấp số nhân đã cho. 181 35
A. S 2047,75.
B. S 2049,75. A. S . S 141. S 121. S . 5 B. C. D. 16 5 5 5 16
C. S 4095,75.
D. S 4096,75. 1
Câu 42. Một cấp số nhân có số hạng thứ bảy bằng , công bội 2 Câu 35. Tính tổng n 1 1 2 4 8 16 32 64 ... 2 2n S với bằng
. Hỏi số hạng đầu tiên của cấp số nhân bằng bào nhiêu? 4 n 1, n . 1 A. 4096. B. 2048. C. 1024. D. . A. S 2 . n B. 2n S . 512
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 12 Tµi liÖu to¸n 11 n¨m häc 2018
Câu 43. Cho cấp số nhân u u 6 u 486.
Câu 51. Tìm số hạng đầu u và công bội q của cấp số nhân n có 2 và 6 Tìm 1
công bội q của cấp số nhân đã cho, biết rằng u 0. u 192 3 u , 6 . n biết u 384 7 1 1 A. q 3.
B. q . C. q .
D. q 3. 3 3 u 5 u 6 u 6 u 5 1 1 1 1 A. . B. . C. . D. . q 2 q 2 q 3 q 3
Câu 44. Cho cấp số nhân u ; u ; u ; u 1. 1 2 3 với 1 Tìm công
bội q để 4u 5u 2 +
3 đạt giá trị nhỏ nhất? u u 36 4 2
Câu 52. Cho cấp số nhân u . n thỏa mãn Chọn u u 72 5 3 2 2
A. q . B. q 0. C. q .
D. q 1. khẳng định đúng? 5 5 u 4 u 6 u 9 u 9
Câu 45. Một cấp số nhân có số hạng thứ hai bằng 4 và số hạng 1 1 1 1 A. . B. . C. . D. . q 2 q 2 q 2 q 3
thứ sáu bằng 64, thì số hạng tổng quát của cấp số nhân đó có thể
tính theo công thức nào dưới đây? u 8u 20 17
Câu 53. Cho cấp số nhân u . n thỏa mãn Chọn A. n 1 u 2 . u n B. 2n n u u 272 1 5 C. n 1 u 2 . u n n D. 2 . n khẳng định đúng?
Câu 46. Cho cấp số nhân u q A. q 2. B. q 4. C. q 4. D. q 2.
n có công bội . Mệnh đề nào sau đây đúng?
Câu 54. Một cấp số nhân có năm số hạng mà hai số hạng đầu u u
tiên là các số dương, tích của số hạng đầu và số hạng thứ ba A. k 1 u u .q . k k u k 1 B. 1 1 . k 2 1
bằng 1, tích của số hạng thứ ba và số hạng cuối bằng . Tìm 16
C. u u .u .
u u k –1 q. k k 1 k2 D. k 1
số hạng đầu u1 và công bội q của cấp số nhân đã cho.
Câu 47. Cho cấp số nhân u u 0 q n có 1 và 0. Đẳng thức 1 u 2 u 2 1 nào sau đây là đúng? 1 1 u u A. 1 2 . 1 . 1 . 2 . B. C. D. 1 q q q 2 2 2 q 2 A. 3
u u .q .
u u .q . 7 4 B. 4 7 4 C. 5
u u .q . D. 6
u u .q . 7 4 7 4 u
u u 65 1 3 5
Câu 55. Cho cấp số nhân u thỏa . Tính n u u 325 1 7
Câu 48. Cho cấp số nhân u u 0 q n có 1 và 0. Với u . 1 k , m 3
đẳng thức nào dưới đây là đúng? A. u 10. B. u 15. C. u 20. D. u 25.
A. u u . k q . m u u q 3 3 3 3 m k B. . . m k C. u u . m k q . m k u u m k D. .q . m k u
u u 14 1 2 3
Câu 56. Cho cấp số nhân u thỏa . Tính n u .u .u 64 1 2 3
Câu 49. Cho một cấp số nhân có 15 số hạng. Đẳng thức nào sau đây là sai? u . 2
A. u .u u .u .
u .u u .u . A. u 4. B. u 6. C. u 8. D. u 10. 1 15 2 14 B. 1 15 5 11 2 2 2 2
C. u .u u .u .
u .u u .u . 1 15 6 9 D. 1 15 12 4
Câu 57. Cho cấp số nhân u có công bội q và thỏa n
Câu 50. Cho một cấp số nhân có n số hạng n k 55 . 1 1 1 1 1 u
u u u u 49 Đẳ 1 2 3 4 5 ng thức nào sau đây sai? u u u u u 1 2 3 4 5 . u u 35 1 3
A. u .u u .u .
u .u u .u . 1 n 2 n 1 B. 1 n 5 n4
C. u .u u .u .
u .u u .u . 1 n 55 n 55 D. 1 n k nk 1 Tính 2
P u 4q . 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 13 Tµi liÖu to¸n 11 n¨m häc 2018 A. P 24. B. P 29. C. P 34. D. P 39.
Câu 64. Gọi S 9 99 999 ... 999...9 ( n số 9 ) thì S
nhận giá trị nào sau đây?
Câu 58. Cho cấp số nhân u có công bội q và thỏa n n n u
u u 26 10 1 10 1 1 2 3 S . S 10 . A. B.
. Tìm q biết rằng q 1. 2 2 2 u
u u 364 9 9 1 2 3 10n 1 10n 1 C. S 10 . n D. S 10 . n 5 4 9 9 A. q . B. q 4. C. q . D. q 3. 4 3
Câu 65. Gọi S 111111...111...1 ( n số 1) thì S
Câu 59. Các số x 6 y, 5x 2 y, 8x y theo thứ tự đó lập nhận giá trị nào sau đây?
thành một cấp số cộng; đồng thời các số x 1, y 2, x 3y 10n 1 10n 1
theo thứ tự đó lập thành một cấp số nhân. Tính 2 2 x y . A. S . B. S 10 . 81 81 A. 2 2 x y 40. B. 2 2 x y 25. 10n 1 1 10n 1 C. S 10 . n D. S 10 n . C. 2 2
x y 100. D. 2 2 x y 10. 81 9 9
Câu 60. Ba số x; y; z theo thứ tự lập thành một cấp số nhân với 21.3b Câu 66. Biết rằng 2 10
S 1 2.3 3.3 ...11.3 a .
công bội q khác 1; đồng thời các số x; 2 y; 3z theo thứ tự lập 4
thành một cấp số cộng với công sai khác 0. Tìm giá trị của q . b
Tính P a . 4 1 1 1 A. q . B. q .
C. q . D. q 3. 3 9 3 A. P 1. B. P 2. C. P 3. D. P 4.
Câu 67. Một cấp số nhân có ba số hạng là ,
a b, c (theo thứ tự
Câu 61. Cho dãy số tăng a, b, c c theo thứ tự lập thành đó) trong đó các số hạng đều khác 0 và công bội q 0. Mệnh
cấp số nhân; đồng thời ,
a b 8, c theo thứ tự lập thành cấp số đề nào sau đây là đúng? cộng và ,
a b 8, c 64 theo thứ tự lập thành cấp số nhân. Tính
giá trị biểu thức P a b 2c. 1 1 1 1 1 1 1 1 2 A. . B. . C. . D. . 2 a bc 2 b ac 2 c ba a b c 184 92 A. P . B. P 64. C. P . D. P 32. 9 9
Câu 68. Bốn góc của một tứ giác tạo thành cấp số nhân và góc
lớn nhất gấp 27 lần góc nhỏ nhất. Tổng của góc lớn nhất và góc
Câu 62. Số hạng thứ hai, số hạng đầu và số hạng thứ ba của một bé nhất bằng:
cấp số cộng với công sai khác 0 theo thứ tự đó lập thành một cấp
số nhân với công bội q . Tìm q. A. 0 56 . B. 0 102 . C. 0 252 . D. 0 168 . 3 3
Câu 69. Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề A. q 2. B. q 2.
C. q . D. q . 2 2
mặt trên của mỗi tầng bằng nữa diện tích của mặt trên của tầng
ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện
Câu 63. Cho bố số a, b, c, d biết rằng a, ,
b c theo thứ tự đó tích của đế tháp (có diện tích là 2
12 288 m ). Tính diện tích mặt
lập thành một cấp số nhân công bội q 1 ; còn ,
b c, d theo thứ trên cùng.
tự đó lập thành cấp số cộng. Tìm q biết rằng a d 14 và A. 2 6 m . B. 2 8 m . C. 2 10 m . D. 2 12 m . b c 12.
Câu 70. Một du khách vào chuồng đua ngựa đặt cược, lần đầu 18 73 19 73 đặ A. q . B. q .
t 20000 đồng, mỗi lần sau tiền đặt gấp đôi lần tiền đặt cọc 24 24
trước. Người đó thua 9 lần liên tiếp và thắng ở lần thứ 10. Hỏi
du khác trên thắng hay thua bao nhiêu? 20 73 21 73 C. q . D. q . 24 24 A. Hòa vốn. B. Thua 20000 đồng.
C. Thắng 20000 đồng. D. Thua 40000 đồn
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 14 Tµi liÖu to¸n 11 n¨m häc 2018
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 15 Tµi liÖu to¸n 11 n¨m häc 2018
CẤP SỐ CỘNG – CẤP SỐ NHÂN
Vấn đề 1. Xác định cấp số và xác yếu tố của cấp số
Ví dụ 1. Tìm bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120 . Lời giải.
Giả sử bốn số hạng đó là a − 3x; a − x; a + x; a + 3x với công sai là d = 2x .Khi đó, ta có:
(a − 3x) + (a − x) + (a + x) + (a + 3x) = 20 ( 2 2 2 2 a −
3x) + (a − x) + (a + x) + (a + 3x) = 120 4a = 20 a = 5 ⇔ ⇔ 2 4a + 2 20x = 120 x = ± 1
Vậy bốn số cần tìm là 2, 4,6,8 . Chú ý:
* Cách gọi các số hạng của cấp số cộng như trên giúp ta giải quyết bài toán gọn hơn.
* Nếu số hạng cấp số cộng là lẻ thì gọi công sai d = x , là chẵn thì gọi công sai d = 2x rồi viết các số hạng cấp số dưới dạng đối xứng. a + a + ... + a = 1 2 n p
* Nếu cấp số cộng (an ) thỏa: thì: 2 a + 2 a + ... + 2 a = 2 1 2 n s 2 2 1 n(n − 1) 12(ns − p ) a = p − .d 1 d = ± n . 2 và 2 n ( 2 n − 1) u − u + u = 10 2 3 5
Ví dụ 2. Cho CSC (un ) thỏa : u + u = 4 6 26
1. Xác định công sai và công thức tổng quát của cấp số;
2. Tính S = u + u + u + ... + 1 4 7 u2011 . Lời giải.
Gọi d là công sai của CSC, ta có:
(u + d) − (u + 2d) + (u + 4d) = 10 u + 3d = 10 1 u = 1 1 1 1 ⇔ ⇔ 1 (u + 3d) + (u + 5d) = 1 1 26 u + 4d = 1 13 d = 3
1. Ta có công sai d = 3 và số hạng tổng quát : u = u + (n − 1)d = 3n − n 1 2 .
2. Ta có các số hạng u1,u4 ,u7 ,...,u2011 lập thành một CSC gồm 670 số hạng với công sai d' = 3d , nên ta có: 670 S = (2u + 669d') = 1 673015 2 u + 3u − u = − 5 3 2 21
Ví dụ 3. Cho cấp số cộng (un ) thỏa: 3u − 2u = − 7 4 34 .
1. Tính số hạng thứ 100 của cấp số ;
2. Tính tổng 15 số hạng đầu của cấp số ;
3. Tính S = u + u + ... + 4 5 u30 . Lời giải.
u + 4d + 3(u + 2d) − (u + d) = − 1 1 1 21
Từ giả thiết bài toán, ta có: 3(u + 6d)− 2(u + 3d) = − 1 1 34 u + 3d = −7 1 u = 2 ⇔ ⇔ 1 u + 12d = − 1 34 d = − 3 .
1. Số hạng thứ 100 của cấp số: u = u + 99d = − 100 1 295
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 1 Tµi liÖu to¸n 11 n¨m häc 2018 15
2. Tổng của 15 số hạng đầu: S = 2u + 14d = − 15 1 285 2 27
3. Ta có: S = u + u + ... + u = 2u + 26d 4 5 30 4 2 = 27 (u + 16d) = − 1 1242 .
Chú ý: Ta có thể tính S theo cách sau: 3
S = S − S = 15(2u + 29d) − (2u + 2d) = − 30 3 1 1 1242 2 . u − u + u = 2 3 5 10
Ví dụ 4. Cho cấp số cộng (un) thỏa mãn u + u = 4 6 26
1. Xác định cấp số cộng
2. Tính tổng S = u + u + …+ 5 7 u2011 Lời giải.
u + d − (u + 2d) + u + 4d = 10 1 1 1 u + 3d = 1 10 1. Ta có: ⇔ u + 3d + u + 5d = 1 1 26 u + 4d = 1 13 ⇔ u = 1,d = 1 3 ; u = u + 4d = 1 + 12 = 5 1 13 1003
2. Ta có u5 ,u7 ,...,u2011 lập thành CSC với công sai d = 6 và có 1003 số hạng nên S = (2u +1002.6) = 5 3028057 2 .
Ví dụ 5. Cho một cấp số cộng (un ) có u = 1
1 và tổng 100 số hạng đầu bằng 24850 . Tính 1 1 1 S = + + ... + u u u u u u 1 2 2 3 49 50 Lời giải.
Gọi d là công sai của cấp số đã cho 497 2u Ta có: S100 50(2u1 99d) − = + = 24850 ⇒ d = 1 = 5 99 5 5 5 ⇒ 5S = + + ... + u1u2 u2u3 u49u 50 u − u u − u u − 2 1 3 2 50 u49 = + + ... + u1u2 u2u3 u49u 50 1 1 1 1 1 1 1 1 = − + − + ... + − + − u1 u2 u2 u3 u48 u49 u49 u 50 1 1 1 1 245 = − = − = u u u u + 1 50 1 1 49d 246 49 ⇒ S = 246 .
Ví dụ 6. Cho cấp số nhân (u u
n) có các số hạng khác không, tìm 1 biết: u + u + u + u = u + u + u + u + u = 11 1 2 3 4 15 1 2 3 4 5 1. 2. 82 2 u + 2 u + 2 u + 2 u = 1 2 3 4 85 u + u = 1 5 11 Lời giải. 4 q − 1 2 3 u = u (1+ q + q + q ) = 15 15 1 1 q − 1 1. Ta có: 2 2 4 6 8 u 1 q q q 85 q 1 1 ( ) ⇔ + + + = − 2 u = 1 85 2 q − 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 2 Tµi liÖu to¸n 11 n¨m häc 2018 2 4 2 4 q = − − 45 − + 2 q 1 q 1 (q 1)(q 1) 45 ⇒ = ⇔ = ⇔ − 8 4 q 1 17 (q 1)(q 1) 17 1 q 1 − − + q = 2
Từ đó ta tìm được u = 1, u = 1 1 8 . 2 3 4 2 39 u1 (1 + q + q + q + q ) = 11 u q(1 + q + q ) = 1 11 2. Ta có: ⇔ 82 + 4 = 82 u (1 q ) u (1 + 4 1 q ) = 11 1 11 4 q + 1 82 1 ⇒ = ⇔ q = 3,q = 3 . q + 2 q + q 39 3 2 u =
Ví dụ 7. Cho cấp số nhân (u 4 n ) thỏa: 27 . u = 3 243u8
1. Viết năm số hạng đầu của cấp số;
2. Tính tổng 10 số hạng đầu của cấp số; 2
3. Số 6561 là số hạng thứ bao nhiêu của cấp số ? Lời giải.
Gọi q là công bội của cấp số. Theo giả thiết ta có: 3 2 3 2 u q = 1 u q = 1 1 27 q = 27 ⇔ ⇔ 3 2 7 5 1 u q = 243.u q q = u = 2 1 1 1 243
1. Năm số hạng đầu của cấp số là: 2 2 2 2 u = 2,u = ,u = ;u = ,u = 1 2 3 4 5 3 9 27 81 .
2. Tổng 10 số hạng đầu của cấp số 1 10 − 10 1 10 q − 1 3 1 59048 S = u = 2. = 3 1 − = 10 1 q . − 1 1 3 − 19683 1 3 2 2 n−1 8 3. Ta có: u = ⇒ u = ⇔ 3 = 6561 = 3 ⇒ n = n 9 − n n 1 3 6561 2
Vậy 6561 là số hạng thứ 9 của cấp số.
CÁC BÀI TOÁN LUYỆN TẬP
Bài 1 Dãy số (un ) có phải là cấp số cộng không ? Nếu phải hãy xác định số công sai ? Biết: 2 2 1. u = 2n + n 3 2. u = −3n + n 1 3. u = n + n 1 4. u = n n
Bài 2 . Dãy số (un ) có phải là cấp số nhân không ? Nếu phải hãy xác định số công bội ? Biết: 2 1. u = n 2n 2. u = n n 4.3 3. u = n n .
Bài 3. Xét xem các dãy số sau có phải là cấp số cộng hay không? Nếu phải hãy xác định công sai. 2n + 3 1. u = 3n + n 1 2. u = 4 − n 5n 3. u = n 5 n + 1 n 2 4. u = n u u n 1 n 5. = n n 6. = + 2 n
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 3 Tµi liÖu to¸n 11 n¨m häc 2018
Bài 4 Xét xem các dãy số sau có phải là cấp số nhân hay không? Nếu phải hãy xác định công bội. n−1 3 1. u = n n 2 2. u = − n u 3n 1 5 3. = − n n 2 − 1 4. u = n u n 3 5. = 3 n . Bài 5.
1. Tam giác ABC có ba góc A, B,C theo thứ tự đó lập thành cấp số cộng và C = 5A . Xác định số đo các góc A, B,C . 3 + 3
2. Cho tam giác ABC biết ba góc tam giác lập thành cấp số cộng và sin A + sin B + sin C = 2 tính các góc của tam giác n+1
Bài 6. Cho dãy số (u 2 n ) với u = n 3
1. Chứng minh dãy số (un) là cấp số nhân
2. Tính tổng S = u + u + u + …+ 2 4 6 u 20
3. Số 19683 là số hạng thứ mấy của dãy số. Bài 7.
1. Cho cấp số nhân có 7 số hạng, số hạng thứ tư bằng 6 và số hạng thứ 7 gấp 243 lần số hạng thứ hai. Hãy tìm số hạng còn lại của CSN đó.
2. Tìm ba số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng −9 và tổng các bình phương của chúng bằng 29.
3. Cho bốn số nguyên dương, trong đó ba số đầu lập thành một cấp số cộng, ba số sau lập thành cấp số nhân. Biết tổng số
hạng đầu và cuối là 37, tổng hai số hạng giữa là 36, tìm bốn số đó. Bài 8. u − u = 7 3 8
1. Cho cấp số cộng (u u ,d n) thỏa mãn ? u .u = 2 7 75 . Tìm 1 u + u = 31 34 11
2. Cho cấp số cộng (u d 0 n) có công sai > ;
. Hãy tìm số hạng tổng quát của cấp số cộng đó. 2 u + 2 u = 31 34 101
3. Gọi S1;S2 ;S3 là tổng n1;n2 ;n3 số hạng đầu của một cấp số cộng. Chứng minh rằng: S1 ( S S n − n ) + 2 2 3 (n − 3 n1) + 3 (n − 1 n2 ) = 0 n1 n2 n 3 u + u + u + u + u = 11 1 2 3 4 5
Bài 9. Cho CSN (un ) thỏa: 82 u + u = 1 5 11
1. Tìm công bội và số hạng tổng quát của cấp số 2. Tính tổng S2011 1
3. Trên khoảng ;1 2
có bao nhiêu số hạng của cấp số. Bài 10. 1
1. Cho dãy số (x ) : x = , n = n n 1,2,3... n
. Chứng minh rằng luôn tồn tại một CSC gồm 2011 số hạng mà mỗi số hạng đều thuộc dãy số trên. ĐÁP ÁN Bài 1
1. Ta có: u + − u = 2(n + 1) + 3 − (2n + 3) = n 1 n 2 là hằng số
Suy ra dãy (un ) là cấp số cộng với công sai d = 2 .
2. Ta có: u + − u = −3(n + 1) + 1 − (−3n + 1) = − n 1 n 3 là hằng số
Suy ra dãy (un ) là cấp số cộng với công sai d = −3 . 2 2
3. Ta có: un+ − u = (n + 1) + 1 − (n + 1) = 2n + 1 n
1 phụ thuộc vào n . Suy ra dãy (un) không phải là cấp số cộng.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 4 Tµi liÖu to¸n 11 n¨m häc 2018 2 2 −2 4. Ta có: un+ − u = − = 1 n
n + 1 n n(n + 1) phụ thuộc vào n
Vậy dãy (un ) không phải là cấp số cộng. Bài 2 . un+ n + 1 1 1. Ta có: = (u ) u
không phải là cấp số nhân. n
n phụ thuộc vào n suy ra dãy n n+1 un+ 4.3 2. Ta có: 1 = = 3 (u ) q 3 n u
không phụ thuộc vào n suy ra dãy
n là một cấp số nhân với công bội = . n 4.3 un+1 2 2 n 3. Ta có: = : = u n + 1 n n + n 1 phụ thuộc vào n .
Suy ra dãy (un ) không phải là cấp số nhân. Bài 3.
1. Ta có: u + − u = 3(n + 1) + 1 − 3n − 1 = n 1 n 3
Dãy (un ) là CSC có công sai d = 3 .
2. Ta có: u + − u = − n 1 n 5
Dãy (un ) là CSC có công sai d = −5 2 2 3. Ta có: u + − u = n 1 n (u ) d
5 . Dãy n là CSC có công sai = 5 1
4. Ta có: un+ − u = − ⇒ 1 n (u ) n(n + n 1) không là CSC
5. Tương tự ý 4 dãy (un ) không là CSC
6. Tương tự ý 4 dãy (un ) không là CSC. Bài 4 un+1 1. Ta có: = 2 ⇒ (un) q 2 u là CSN với công bội = n un+1 2. Ta có: = 3 ⇒ (un) q 3 u là CSN với công bội = n un+ 3n + 1 2 3. Ta có: = ⇒ (u ) u 3n − n n 1 không phải là CSN n+1 un+ 2 − 1 4. Ta có: 1 = ⇒ (u ) u không phải là CSN 2 − n n n 1 3 un+ (n + 1) 5. Ta có: 1 = ⇒ (un) 3 u không phải là CSN . n n Bài 5.
1. Từ giả thiết bài toán ta có hệ phương trình : A + B + C = 180 C 5A A = = 0 0 20 A + C = 2B ⇔ B = 3A ⇔ B = 0 60 . 0 C = 5A 9A = 180 C = 0 100 0 0 0
2. Ba góc của tam giác: 30 ,60 ,90 Bài 6. n+1+1 u 2 n 1 3 * 1. Ta có: + = = 3 ,∀n ∈ N ⇒ u 3 3;q 3 n u
Dãy số là cấp số nhân với = = 1 . n +1 2 3 2. Ta có u ;u ;u ;… 2 4 6
;u20 lập thành cấp số nhân số hạng đầu u = 9;q = 2 3 và có 10 số hạng nên
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 5 Tµi liÖu to¸n 11 n¨m häc 2018 1 − 10 10 3 3 − 1 9 S = u . = 9. = 10 (3 − 2 1) 1 − 3 2 2 n+1 2 9 n
3. Ta có : u = 19683 ⇔ 3 = 3 ⇔ + 1 = 9 ⇔ n = n 16 2
Vậy số 19683 là số hạng thứ 16 của cấp số. Bài 7.
1. Gọi CSN đó là (u n 1,7 . Theo đề n), = bài ta có : 3 2 u = 4 6 u .q = 1 6 u = ⇔ ⇔ 1 9 u = 243u 6 7 2 u .q = 243u .q 1 1 q = 3
Do đó các số hạng còn lại của cấp số nhân là 2 2
u = ;u = ;u = 2;u = 18;u = 54;u = 1 2 3 5 6 7 162 9 3
2. Gọi ba số hạng của CSC là a − 2x; a; a + 2x với d = 2x a = − a − 2x + a + a + 2x = − 3 9 Ta có: ⇔ 1 . (a − 2 2x) + 2 a + (a + 2 2x) = 29 x = ± 2 a + d = 37 a = 37 − d c + b = 36 c = 36 − b
3. Gọi bốn số đó là a, b,c,d ta có hệ : ⇔ a + c = 2b d = 73 − 3b 2 bd = c b(73 − 3b) = (36 − 2 b)
⇔ b = 16,c = 20,d = 25,a = 12 . Bài 8. u + 6d − u − 2d = 8 1 1 d = 2 1. Ta có: ⇔ (u + d)(u + 6d) = 1 1 75 u = 3,u = − 1 1 17 2u + 63d = 1 11 u = −89 2. 1 Ta có: ⇔ (u + 2 30d) + (u + 2 33d) = 101 d = 3 1 1
Vậy u = 3(n − 1) − 89 = 3n − n 92 . n
3. Thay công thức S = 1 1 (2u +(n − 1 1 1)d) 2 n n S = 2 3 2 (2u +(n − 2 2 1)d) S = 2u + (n − 1)d 2 ; 3 ( 3 3 ) 2
Ta có điều phải chứng minh. Bài 9.
1. Gọi q là công bội của cấp số. Khi đó ta có: 39 39 u + u + u = u (q + 2 q + 3 2 3 4 1 q ) = 11 ⇔ 11 82 82 u + u = u (1+ 4 1 5 1 q ) = 11 11 4 q + 1 82 4 3 2 Suy ra: =
⇔ 39q − 82q − 82q − 82q + 39 = 0 3 q + 2 q + q 39 ⇔ − − 2 1
(3q 1)(q 3)(13q + 16q + 13) = 0 ⇔ q = ,q = 3 3 • 1 81 81 1 q = ⇒ u = ⇒ u = 1 n . n −1 3 11 11 3
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 6 Tµi liÖu to¸n 11 n¨m häc 2018 n−1 • 1 3 q = 3 ⇒ u = ⇒ u = 1 n 11 11 . 2011 q − 1 2. Ta có: S = 2011 u1 q −1 1 243 1 • q = ⇒ S = 1 − 2011 3 22 2011 3 • 1 2011 q = 3 ⇒ S = 2011 (3 −1) 22 n−1 3 1
3. Với q = 3 ta có: u = ∈ ;1 ⇔ n = n 3 11 2
nên có một số hạng của dãy 1 1 1 Với q = u = ∈ ;1 ⇔ n = 3 3 ta có: n n− 5
nên có một số hạng của dãy. 11.3 2 Bài 10. k
1. Xét dãy số (u ) : u = , k = n k 1,2011 2011! k + 1 k 1 1 Ta có: u + = = + = u + k 1 k 2011! 2011! 2011! 2011!
Nên dãy (un ) là CSC có 2011 số hạng. Hơn nữ 1 a u = = k 1.2...( x k−1)(k+ 1.2...(k − 1)(k + 1)...2011 1)...2011 Từ đó ta có đpcm.
Vấn đề 2. Chứng minh tính chất của cấp số
Ví dụ 1. Chứng minh rằng các số:
1. 1, 3 , 3 không thể cùng thuộc một CSC;
2. 2,3,5 không thể cùng thuộc một CSN. Lời giải.
1. Giả sử 1, 3 , 3 là số hạng thứ m,n,p của một CSC (un ) . Ta có: u − 3 − 3 p un u (p − n) p − n p − n 3 = = = 1 =
vô lí vì 3 là số vô tỉ, còn 3 − 1 u − u u (n − m) n − n m 1 m n − m là số hữu tỉ.
2. Giả sử 2,3,5 là ba số hạng thứ m,n,p của CSN (vn ) có công bội q 2 u p−n m−n m m−n 5 − 2 5 (p−n)(m−n) Ta có: = = q ; = p n q = = p 3 u n 3 , suy ra 3 3 p−n m−p n− ⇒ m 2 .3 .5 = 1 vô lí.
Ví dụ 2. Chứng minh rằng dãy số (un ) là:
1. CSC khi và chỉ khi u = an + n b
2. CSN khi và chỉ khi u = n n a.q . Lời giải.
1. Giả sử (un ) là một CSC công sai d , khi đó :
u = u + (n − 1)d = dn + u − d = an + n 1 1 b .
Giả sử: u = an + b ⇒ u + − u = a ⇒ u + = u + a , ∀ n n 1 n n 1 n n
Suy ra (un ) là một CSC với công sai a .
2. Giả sử (un ) là CSN với công bội q , khi đó: u = n n u1.q un+1 Giả sử u = n n a.q , suy ra = q ⇒ un+ = q.u , ∀ 1 n n u n
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 7 Tµi liÖu to¸n 11 n¨m häc 2018
Suy ra dãy (un ) là CSN với công bội q .
Ví dụ 3. Chứng minh rằng : 3 2 3
1. Nếu phương trình x − ax + bx − c = 0 có ba nghiệm lập thành CSC thì 9ab = 2a + 27c 3 2 3 3
2. Nếu phương trình x − ax + bx − c = 0 có ba nghiệm lập thành CSN thì c(ca − b ) = 0 Lời giải.
1. Giả sử phương trình có ba nghiệm 1 x ,x2 ,x3 lập thành CSC Suy ra: x + x = 1 3 2x2 (1) 3 2
Mặt khác: x − ax + bx − c = (x − x )(x − x )(x − 1 2 x3) 3 2
= x − (x + x + x )x + (x x + x x + x x )x − 1 2 3 1 2 2 3 3 1 1 x x2x3 Suy ra x + x + x = 1 2 3 a (2) a
Từ (1) và (2), ta suy ra 3x = 2 a hay x = 2 3 a
Dẫn tới phương trình đã cho có nghiệm x = 2 3 , tức là: a 3 a 2 a 3 2a ba − a + b − c = 0 ⇔ − + − c = 0 ⇔ 9ab = 3 2a + 27c 3 3 3 27 3 Ta có đpcm.
2. Giả sử ba nghiệm 1
x ,x2 ,x3 lập thành CSN, suy ra x x = 2 1 3 x2 3 3
Theo phân tích bài trên, ta có: x x x = c ⇒ x = c ⇒ x = 1 2 3 2 2 c
Hay phương trình đã cho có nghiệm x = 3 2 c , tức là: (3 )3 2 − (3 ) + 3 − = ⇔ 3 c a c b c c 0 b c = 3 2 a c ⇔ 3 c(ca − 3 b ) = 0
Bài toán được chứng minh.
Ví dụ 4. Chứng minh rằng với mọi cách chia tập X = {1,2,3,..., }
9 thành hai tập con rời nhau luôn có một tập chứa ba số lập thành cấp số cộng. Lời giải.
Ta chứng minh bài toán bằng phương pháp phản chứng
Giả sử X được chia thành hai tập con A và B đồng thời trong A và B không có ba số nào lập thành CSC.
Xét ba CSC (1;3;5), (3;4;5), (3;5;7)
Ta thấy số 3, 5 không thể cùng nằm trong một tập hợp, vì nếu hai số này thuộc A thì 1,4,7 phải thuộc B, tuy nhiên các số 1,4,7 lại lập thành CSC.
Tương tự bằng cách xét CSC (3;5;7), (5;6;7), (5;7;9) thì ta có hai số 5,7 không thể cũng nằm trong một tập.
Vì cặp (3;5) và (5;7) hkoogn cùng thuộc một tập nên ta suy ra
(3;7) thuộc A, 5 thuộc B. Khi đó ta xét các trường hợp sau
• 4∈ A , vì 3,4∈ A ⇒ 2∉ A ⇒ 2∈ B , do 1,4,7 lập thành CSC nên 1∈ B ; 2,5,8 lập thành CSC nên 8∈ A ⇒ 9∈ B
Do đó 1,5,9∈ B lập thành CSC vô lí
• 4∈ B , do 4,5∈ B ⇒ 6∈ A mà 6,7 ∈ A ⇒ 8∈ B
5,8∈ B ⇒ 2∈A , vì 2,3∈A ⇒ 1∈ B , vì 1,5∈ B ⇒ 9∈A Do đó: 3,6,9∈ B vô lí.
Vậy bài toán được chứng minh. 1
Ví dụ 5. Dãy số (xn) thỏa mãn điều kiện: xn+ − x − x < m m n m + n ∀ ∈ * m,n
. Chứng minh rằng: (xn) là một cấp số cộng. Lời giải. Đặ 1 t a = x − n n 1 nx , khi đó ta có a = 1 0 và |am+ − a − a < | ,∀m,n ∈ n m n m + n
. Ở đây ta sẽ chứng minh a = 0,∀n ∈ n . Thật vậy, ta có:
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 8 Tµi liÖu to¸n 11 n¨m häc 2018 1 an+ − a < ,∀n ∈ 1 n lim|a a | 0 lim|a a | 0, k n hay . + 1 , nên + − = n 1 n n+ − = ∀ ∈ k n 1 Mà an+ − a − a < k n k lim|a a a | 0 n . + k nên + − − = n k n k n
Từ đây suy ra a = 0,∀k ∈ k .
Vậy ta có điều phải chứng minh. CÁC BÀI TOÁN LUYỆN TẬP Bài 1 2 2
1. Cho ba số a, b,c lập thành cấp số cộng. Chứng minh rằng : a + 2bc = c + 2ab .
2. Cho a, b,c > 0 lập thành cấp sô cộng.Chứng minh rằng : 1 1 2 + = . a + b b + c c + a
3. Cho (un) là cấp số cộng. Chứng minh rằng : 1 u = (u − + n n k un+k ) 1 k n 1 2 , ≤ ≤ − Bài 2 A B
1. Cho tam giác ABC. Chứng minh rằng tan ;tan ; 2 2 C
tan 2 lập thành cấp số cộng ⇔ cosA;cosB;cosC lập thành cấp số cộng. A B C
2. Cho tam giác ABC.Chứng minh rằng cot ;cot ;cot 2 2
2 lập thành cấp số cộng ⇔ sin A;sin B;sinC lập thành cấp số cộng.
Bài 3 Cho a, b,c lập thành cấp số nhân . .Chứng minh rằng : 2 2 2
1. (a + b + c)(a − b + c) = a + b + c 2 2 2 2 2
2. (a + b )(b + c ) = (ab + bc) 3 3
3. (ab + bc + ca) = abc(a + b + c) n n n n n n 2n 2n 2n *
4. (a + b + c )(a − b + c ) = a + b + c ; n ∈
Bài 4 Cho (un) là cấp số nhân .Chứng minh rằng : 2
1. a a = a .a − + , k = 1 n k n k 1 1;n 2. Sn (S − 3n S2n ) = (S − 2n Sn ) . Bài 5
1. Điều cần và đủ để ba số khác không a, b,c là ba số hạng của một CSN là tồn tại ba số nguyên khác không p, t,r sao cho p + t + r = 0 . p t r a .b .c = 1
2. Cho cấp số cộng (an) với các số hạng khác không và công sai khác không.Chứng minh rằng: 1 1 1 n − 1 + + ... + = a1a2 a2a3 an−1an a1a . n 1 1 2 + = a1a2 a2a3 a1a3
3. Cho bốn số thực a1;a2 ;a3;a4 .Biết rằng : 1 1 1 3 + + = a1a2 a2a3 a3a4 a1a4
Chứng minh rằng : a1;a2 ;a3;a4 lập thành cấp số cộng.
4. Cho a, b,c lần lượt là ba số hạng thứ m,n,p của một cấp số cộng. Chứng minh rằng :
a.(n − p) + b.(p − m) + c.(m − n) = 0 .
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 9 Tµi liÖu to¸n 11 n¨m häc 2018
5. Chứng minh rằng điều kiện cần và đủ để ba số a, b,c là ba số hạng của một CSC là tồn tại ba số nguyên khác không pa + qb + rc = 0 p,q,r thỏa: p+q +r = 0 .
6.Cho CSC (un ) thỏa S = m
Sn ( m ≠ n ). Chứng minh S + = m n 0 . 5 − 1 1+ 5
7. Chứng minh rằng nếu ba cạnh của tam giác lập thành CSN thì công bội của CSN đó nằm trong khoảng ; 2 2 . Bài 6
1. Chứng minh ba số a, b,c > 0 là 3 số hạng liên tiếp của cấp số cộng khi và chỉ khi 3 số 2 + + 2 2 + + 2 2 + + 2 a ab b ;c ca a ; b
bc c cũng là ba số hạng liên tiếp của một cấp số cộng.
2. Cho (un ) là cấp số nhân. Kí hiệu S = u + u + ... + 1 2 un ; 1 1 1 T = + + ... + ; P = u1u2...un u1 u2 u
. Hãy tính P theo S,T và n. n
Bài 7 Cho hai số tự nhiên n, k thỏa k + 3 ≤ n . k k+1 k+2
1. Chứng minh rằng tồn tại không quá hai giá trị của k sao cho Cn , Cn và Cn là ba số hạng liên tiếp của một CSC. k k+1 k+2 k+3
2. Chứng minh rằng không tồn tại k để Cn , Cn , Cn và Cn là bốn số hạng liên tiếp của một CSC. Bài 8 n n+1 k uk+ u + 1 1 un+ n + 1 1 2
1. Cho (un ) là CSC. Chứng minh rằng: ∑ = . k n 1 ∑ + k=0 C 2 2 k n k=1
2. Cho k là một số nguyên dương cho trước. Giả sử 1
s ,s2 ,s3,... là một dãy tăng nghặt các số nguyên dương sao cho các dãy con ss ,ss ,ss ,... và s ,s ,s
,... đều là cấp số cộng. Chứng minh rằng s ,s ,s ,... cũng là một cấp số 1 2 3 s +k s +k s +k 1 2 3 1 2 3 cộng ĐÁP ÁN Bài 1
1. Vì a, b,c lập thành cấp số cộng nên a + c = 2b . Do đó : 2 + − 2 a
2bc c − 2ab = (a − c)(a + c) − 2b(a − c)
= (a − c)(a + c − 2b) = 0 2 2 Suy ra a + 2bc = c + 2ab .
2. Gọi d là công sai của cấp số, suy ra b − a = c − b = d,c − a = 2d Do đó: 1 1 b − a c − b c − a + = + = a + b b + c d d d c − a 2 = = . d( c + a) c + a un− = u + (n − k − k 1 1)d
3. Gọi d là công sai của cấp số. Ta có: un+ = u +(n + k − k 1 1)d u u ⇒ u + u = 2u + (2n − 2) − + + − + d = 2u ⇒ u = n k n k n k n k 1 n n 2 Bài 2 A B C 1. Ta có: tan ;tan ;tan 2 2
2 lập thành cấp số cộng A + C B sin( ) sin A C B ⇔ + = ⇔ 2 2 = 2 tan tan 2tan 2 2 2 2 A C B cos cos cos 2 2 2
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 10 Tµi liÖu to¸n 11 n¨m häc 2018 2 B B A C A C ⇔ cos = sin cos + + cos − 2 2 2 2 2 2 1 + cos B 1 − cos B 1 ⇔ = + cos A + cosC 2 2 2 cosA + cosC ⇔ cos B = ⇔ cos A,cos B,cosC 2 lập thành CSC. A B B C 2. Ta có: cot − cot = cot − cot 2 2 2 2 A B − B A B C − C B cos sin cos sin cos sin cos sin ⇔ 2 2 2 2 = 2 2 2 2 A B C B sin sin sin sin 2 2 2 2 B − A B + A C − B C + B ⇔ sin cos = sin .cos 2 2 2 2
⇔ sin B − sin A = sinC − sin B ⇔ sin A + sinC = 2sin B . 2
Bài 3 Vì a, b,c lập thành cấp số nhân nên ta có b = ac . 2 2 2 2 2
1. Ta có: (a + b + c)(a − b + c) = (a + c) − b = a + 2ac + c − b 2 2 2 2 2 2 2
= a + 2b + c − b = a + b + c 2 2 2 2 2 2 2
2. Ta có: (a + b )(b + c ) = (a + ac)(ac + c ) = ac(a + c) 2 2 2 = b (a + c) = (ab + bc) . 2 3. b = ac 3 3 2 3 3
Ta có: (ab + bc + ca) = (ab + bc + b ) = b (a + b + c) = + + 3 abc(a b c) . n n 2 2n 2n 2n 2n n n 2n
4. Ta có: VT = (a + c ) − b = a + c + b + 2(a c − b ) 2n 2n 2n = a + b + c .
Bài 4 Gọi q là công bội của cấp số n−1 2 n−1 1. Ta có: a a = a .a q = 1 n 1 1 a1q k−1 n−k 2 n−1 ak.an−k+ = a .q .a .q = 1 1 1 a1.q Suy ra : a a = 1 n ak.an−k+1. n 3n 2n 2n n 2 q 1 q 1 q 1 2 q (q 1) 2. Ta có: Sn (S − 3n S2n ) − − − − = u .u − = 1 u q − 1 1 q − 1 q − 1 1 (q − 2 1) 2 2n n 2n n 2 ( q 1 q 1 q (q 1) S − S ) 2 − − − = u − u = 2 2n n u 1 q − 1 1 q − 1 1 (q − 2 1) 2 Suy ra Sn (S − 3n S2n ) = (S − 2n Sn ) . Bài 5
1. • Giải sử a, b,c là ba số hạng thứ k + 1; l + 1; m + 1 của cấp số nhân có công bội q , khi đó ta có : l−m k−l k l m a k−l b l− a a b
= u .q ; b = u .q ;c = u .q ⇒ = q ; = m l−m m−l−k+1 k−1 1 1 1 q ⇒ = ⇒ a .b .c = 1 b c b c
Đặt p = l − m;t = m − l − k + 1;r = k − 1 .
Khi đó ta có ba số p,t,r thỏa mãn yêu cầu bài toán.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 11 Tµi liÖu to¸n 11 n¨m häc 2018 p + t + r = 0 p r p r a p b r • + Giả sử ta có ⇒ a .c = b ⇒ = p t r (*) a .b .c = 1 b c
Do p + t + r = 0 nên tồn tại ít nhất một số dương và một số âm. b r r
Giải sử r > 0, t < 0 . Đặt = q ⇒ b = a.q a kết hợp với (*) ta có p r r a a.q r+ = ⇒ c = p a.q r . a.q c
Vậy ba số a, b,c là ba số hạng của cấp số nhân với a là số hạng đầu,b là số hạng thứ r + 1 ;c là số hạng thứ r + p + 1 . 1 1 1 1 2. Ta có = − akak+1 d ak a k+1 1 1 1 1 1 1 n − 1 Suy ra + + ... + = − = a1a2 a2a3 an−1an d a1 an a1a n 1 1 2 3. Ta có + =
⇔ a + a = 2a ⇒ a − a = a − a = 3 1 2 1 2 2 3 d a1a2 a2a3 a1a 3 1 1 1 3 2 1 3 + + = ⇔ + = a1a2 a2a3 a3a4 a1a4 a1a3 a3a4 a1a 4
⇔ 2a + a = 3a ⇔ 2a = 3(a + 2d) − a ⇒ a = a + 4 1 3 4 1 1 4 1 3d .
4. Ta có: b = a + (n − m)d; c = a + (p − m)d
Suy ra VT = a(n − p) + a + (n − m)d (p − m) + a + (p − m)d (m − n)
= d (n − m)(p − m) + (p − m)(m − n) = 0 .
5. • Giả sử a, b,c là ba số hạng thứ m + 1, n + 1, k + 1 của một CSC (un ) a − b d = a = u + md 1 m − n Ta có: ⇒ b = u + nd m(a − b) mb − 1 an u = a − = 1 m − n m − n
Mặt khác: c = u + kd ⇒ (m − n)c = mb − na + k(a − 1 b)
⇒ (k − n)a + (m − k)b + (n − m)c = 0 pa + qb + rc = 0
Đặt p = k − n,q = m − k,r = n − m ⇒ p+q +r = 0
• Giả sử tồn tại ba số nguyên khác không p,q,r sao cho pa + qb + rc = 0 p+ q + r = 0
Không mất tính tổng quát ta giả sử a ≥ b ≥ c và p,q,r > 0
Ta có: p = −q − r nên (−q − r)a + qb + rc = 0 ⇔ (a − b)p = (c − a)r Đặ a − b t d =
⇒ a = b + rd,c = a + pd = b + (p + r)d r
Vậy b,a,c là ba số hạng u1,ur ,up+r của một CSC. 2 2 6. Ta có S
= S ⇔ 2u (m − n) + (m − n )d − (m − n)d = m n 1 0 ⇔ 2u + (m + n − 1)d = 1 0 n + m Suy ra Sm+ = 2u + (m + n − 1)d = n 1 0 2 .
7. Giả sử a, b,c là ba cạnh tam giác theo thứ tự đó lập thành CSN với công bội q .
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 12 Tµi liÖu to¸n 11 n¨m häc 2018 2 a + aq > aq 2 q − q − 1 < 0 Ta có: ⇔ 2 aq + aq > 2 a q + q − 1 > 0 1− 5 1+ 5 q ∈ ; 2 2 5 − 1 5 + 1 ⇔ ⇔ q ∈ ; . − − − + 2 2 1 5 1 5 q ∈ −∞; ∪ ;+∞ 2 2 Bài 6 2 2 2 2 2 2
1. Ta có: a + ab + b + b + bc + c = 2(a + ca + c ) ⇔ 2 + + = 2 + + 2 2b ab bc a 2ac c ⇔ + + + 2 − + 2 b(a b c) b (a c) = 0
⇔ b(a + b + c) + (a + b + c)(b − a − c) = 0
⇔ 2b − a − c = 0 ⇔ 2b = a + c . 1 n n − 1 q − 1 1 q n 1 q − 1 2. Ta có: S = u ; T = = 1 n − q − 1 1 u1 1 u1 q (q − − 1) 1 q n(n−1) n n + 1 2+ + ... n− P S = 1 u q = n 2 1 u1 q . Suy ra: P = T Bài 7 k k+2 k+1 1. Ta có: C + C = n n 2Cn n! n! n! ⇔ + = 2
k!(n − k)! (k + 2)!(n − k − 2)! (k + 1)!(n − k − 1)!
⇔ (k + 1)(k + 2) + (n − k)(n − k − 1) = 2(k + 2)(n − k)
Đây là phương trình bậc hai ẩn k nên có nhiều nhất hai nghiệm. k k+1 k+2 k+3
2. Giả sử tồn tại k để Cn , Cn , Cn và Cn là bốn số hạng liên tiếp của một CSC. k n−k n−k n−k−1 n−k−2 n−k−3 Do C = n Cn nên suy ra: Cn ,Cn ,Cn ,Cn
cũng tạo thành bốn số hạng liên tiếp của một CSC.
Vậy ta có các bộ sau là ba số hạng liên tiếp của một CSC: k k+1 k+2 Cn ,Cn ,Cn k C k+1 k+2 k+3 n , Cn , Cn , Cn n−k−3 n−k−2 n−k−1 Cn ,Cn ,Cn n−k−2 n−k−1 n−k Cn ,Cn ,Cn
Ta chứng minh tập {k,k + 1,n − k − 3,n − k − }
2 chứa không quá hai số khác nhau. Thật vậy, giả sử k,k + 1,n − k − 3 là ba số khác nhau. Khi đó, tồ k k+1 k+2 n tại ba CSC: Cn ,Cn ,Cn k+1 k+2 k+3 Cn , Cn , Cn n−k−3 n−k−2 n−k−1 Cn ,Cn ,Cn
Điều này trái với kết quả câu 1) k = n − k − 3 k+1 n−k−2 k+2
Do k, k + 1 và k − k − 3, n − k − 2 là các số tự nhiên liên tiếp nên ta có: ⇒ C = C = C k + 1 = n − k − n n n 2 k k+1 k+2 Suy ra C = C = n n Cn (1). Xét phương trình : k k+ C = 1 n Cn (2)
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 13 Tµi liÖu to¸n 11 n¨m häc 2018 n! n! n − ⇔ = 1 ⇔ k + 1 = n − k ⇒ k =
k!(n − k)! (k + 1)!(n − k − 1)! 2
Suy ra phương trình (2) có không quá một nghiệm k , điều này dẫn tới (1) mâu thuẫn. k k+1 k+2 k+3
Vậy không tồn tại k để Cn , Cn , Cn và Cn là bốn số hạng liên tiếp của một CSC. Bài 8 u + 1 un+ = 1 uk+ + 1 un−k+1 1. Ta có , ∀ k = 0,1,2,...,n k n− C = k n Cn n n n n uk+1 uk+1 un−k+1 uk+ + 1 un−k+1 1 Nên 2 ∑ = ∑ + = ∑ = (u + 1 un+1) k k n k k ∑ − k k=0 Cn k=0 Cn Cn k=0 Cn k=0 Cn
Do đó, để chứng minh đẳng thức đã cho ta chỉ cần chứng minh n n+ 1 n + 1 k ∑ 1 2 = k n 1 ∑ + (1). k=0 C 2 k n k=1
Ta chứng minh (1) bằng quy nạp • 1 1 2 Với n = 1 ta có: VT(1) = + = 2 VP(1) = 2 + 2 = 2 0 1 và ( ) 4 1 C 1 C Nên (1) đúng với n = 1. n n+1 k n+1 n+2 k • 1 n + 1 2 1 n + 2 2 Giả sử ∑ = ∑ = k n 2 ∑ k n 1 ∑ + , ta chứng minh + (2) k=0 C 2 k C 2 k n k=1 k=0 n+1 k=1 n+1 n n 1 1 1 1 Thật vậy: ∑ = + 1 k 0 ∑ = + k 1 ∑ + k+1 k=0 Cn+1 Cn+1 k=0 Cn+1 k=0 Cn+1 k+1 (n + 1)! n + 1 k Mà Cn+ = = 1 C (k + 1)!(n − k)! k + n 1 n n n 1 1 k + 1 1 k + 1 n − k + 1 Suy ra ∑ = k 1 ∑ = k ∑ + + C n + 1 C 2(n + 1) k n−k k=0 n+1 k=0 n k=0 Cn Cn n n+1 k n+ n + 2 1 n + 2 n + 1 2 n + 1 k 2 2 = ∑ = k n 1 ∑ = n 2 ∑ + + 2(n + 1) k= C 2(n + 0 1) 2 k 2 k n k=1 k=1 n+1 n+1 k n+ 1 n + 2 2 n + 2 k 2 2 Suy ra ∑ = 1 + k n 2 ∑ = n 2 ∑ + +
dẫn tới (2) được chứng minh k=0 C 2 k 2 k n+1 k=1 k=1
2. Gọi p và q lần lượt là công sai của các cấp số cộng ss ,ss ,ss ,... và s ,s ,s ,... . Đặt a = s − p và 1 2 3 s +k s +k s +k 1 2 3 s1 b = s + − s k q . 1
Theo công thức tính số hạng tổng quát của một cấp số cộng và với số nguyên dương n ta có:
s = s + (n − 1)p = a + np, s + = s + + (n −1)q = b + s s s k s k nq. n 1 n 1 Từ dãy 1
s ,s2 ,s3,... là một dãy tăng ngặt, nên với mọi số nguyên dương n và với chú ý s + k ≤ n sn+k ta có s + k − 1 < s + ≤ s s k ss , n n n+k
từ đó ta thu được a + np + k − 1 < b + nq ≤ a + (n + 1)p,
điều này tương đương với 0 < k − 1 + b − a + n(q − p) ≤ kp,
nếu p ≠ q thì ta thấy bất đẳng thức trên mâu thuẫn khi cho n cằng lớn. Nên suy ra p = q và do đó 0 ≤ k − 1 + b − a ≤ kp (1) Đặt m = min{s + − s : n = n 1 n 1,2, } ... .
Khi đó b − a = (s + − q) − (s − p) = s + − s ≥ s k s s k s km (2) và 1 1 1 1 kp = a + (s + k)p − (a + s ) p = s − s = s sb+ − p sa+ ≥ m(b − 1 1 s a) (3) + q s k s 1 1 Ta xét hai trường hợp:
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 14 Tµi liÖu to¸n 11 n¨m häc 2018 • b − a = kp .
Khi đó, với mỗi số nguyên dương n , s + = b + np = a + (n + k)p = s k ss
, từ đây kết hợp với dãy s ,s ,s ,... là một dãy n n+k 1 2 3 tăng ngặt ta có s + = s + n k n k .
Mặt khác do s < s + < ... < s + = s + n n 1 n k n k nên s + = s + n 1 n 1 và do đó 1
s ,s2 ,s3,... là một cấp số cộng với công sai bằng 1. • b − a < kp .
Chọn số nguyên dương N sao cho s + − s = N 1 N m . Khi đó
m(a − b + p − k) = m((a + (N + 1)p) − (b + Np + k)) ≤ s + + − s + + = s − a (N 1)p b Np k s ss + s + k s + k N 1 N = (a + s + )
p − (b + (s + k)p) = (s + − s )p + a − b − N 1 N N 1 N kp = mp + a − b − kp,
do vậy: (b − a − km) + (kp − m(b − a)) ≤ 0. (4)
Từ các bất đẳng thức (2), (3) và (4) ta thu được các đẳng thức sau:
b − a = km và kp = m(b − a) .
Giả sử tồn tại số nguyên dương n sao cho s + > s + n 1 n m . Khi đó
m(m + 1) ≤ m(s + − s ) ≤ s
− s = (a + (n + 1)p) − (a + n 1 n s np) + s n 1 n m(b − a) = p = = 2 m k , vô lý.
Vì vậy điều giả sử là sai nên s + = s + n 1 n
m với mọi n ∈ hay dãy 1
s ,s2 ,s3,... là một cấp số cộng có công sai bằng m .
Vấn đề 3. Tìm điều kiện để dãy số lập thành cấp số
Ví dụ 1. Tìm x biết : 2
1. x + 1, x − 2,1 − 3x lập thành cấp số cộng ; 2 2
2. 1, x ,6 − x lập thành cấp số nhân. Lời giải. 2 2 2
1. Ta có: x + 1, x − 2,1 − 3x lập thành cấp số cộng ⇔ x + 1 + 1 − 3x = 2(x − 2) ⇔ x − 5x + 6 = 0 ⇔ x = 2 ; x = 3
Vậy x = 2, x = 3 là những giá trị cần tìm. 2 2 4 2
2. Ta có: 1, x ,6 − x lập thành cấp số nhân ⇔ x = 6 − x ⇔ x = ± 2 . 2 2
Ví dụ 2. Cho các số 5x − y , 2x + 3y , x + 2y lập thành cấp số cộng ; các số (y + 1) ,xy + 1,(x − 1) lập thành cấp số nhân.Tính x, y Lời giải.
Ta có các số 5x − y , 2x + 3y , x + 2y lập thành CSC nên suy ra 2 (2x + 3y) = 5x − y + x + 2y hay 2x = 5y (1) 2 2
Các số (y + 1) ,xy + 1,(x − 1) lập thành CSN suy ra ( + )2 = ( + )2 ( − )2 xy 1 y 1
x 1 ⇔ (4 + 2y − 2x)(4xy + 2x − 2y) = 0 (2) Thay (1) vào (2) ta đượ 2
c : (4 + 2y − 5y)(10y + 5y − 2y) = 0 4 3
⇔ y(4 − 3y)(10y + 3) = 0 ⇔ y = 0,y = ,y = − 3 10 . 10 4 3 3 Vậy (x; y) (0; 0) = ; ; ; − ;− 3 3 4 10 .
CÁC BÀI TOÁN LUYỆN TẬP
Bài 1. Tìm x để các số sau lập thành cấp số cộng 3 π
1. 1;x;x 2. 1; sin − x;4sinx 6
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 15 Tµi liÖu to¸n 11 n¨m häc 2018
Bài 2. Tìm x, y biết:
1. Các số x + 5y, 5x + 2y,8x + y lập thành cấp số cộng và các số ( − )2 − ( + )2
y 1 ,xy 1, x 1 lập thành cấp số nhân. 5
2. Các số x + 6y, 5x + 2y,8x + y lập thành cấp số cộng và các số x + y,y − 1,2x − 3y 3
lập thành cấp số nhân. 3
Bài 3. Xác định a, b để phương trình x + ax + b = 0 có ba nghiệm phân biệt lập thành cấp số cộng.
Bài 4 Tìm m để phương trình: 4 2
1. mx − 2 (m − 1) x + m − 1 = 0 có bốn nghiệm phân biệt lập thành cấp số cộng. 3 2
2. x − 3mx + 4mx + m − 2 = 0 có ba nghiệm lập thành cấp số nhân
Bài 5 Xác định m để: 3 2
1. Phương trình x − 3x − 9x + m = 0 có ba nghiệm phân biệt lập thành cấp số cộng. 4 2
2. Phương trình x − 2 (m + 1) x + 2m + 1 = 0 (1) có bốn nghiệm phân biệt lập thành cấp số cộng. 3 2
3. Phương trình x + 2x + (m + 1) x + 2(m + 1) = 0 có ba nghiệm lập thành cấp số nhân. ĐÁP ÁN Bài 2 x + 5y + 8x + y = 2(5x + 2y) 1 Ta có hệ:
giải hệ này ta tìm được (x + 2 1) (y − 2 1) = (xy − 2 1) 3 3 (x; y) = − 3;− ; 3; 2 2 .
x + 6y + 8x + y = 2(5x + 2y) 2. Ta có hệ: 5
giải hệ này ta tìm được (x + y)(2x − 3y) = (y − 2 1) 3 (x; y) ( 3; 1) 3 1 = − − ; ; 8 8 .
Bài 3 Đáp số: b = 0,a < 0 . Khi đó phương trình có ba nghiệm lập thành CSC là x = 0, x = ± −a . Bài 4. 9
1. Đáp số : m = − 16
2. Giả sử phương trình có ba nghiệm a, b,c lập thành CSN abc = 2 − m 3 Suy ra
⇒ m = 2 − b thay vào phương trình ta có 2 b = ac 4 10 b = ⇒ m = − 3
(3b − 4)(b − 2) = 0 ⇔ 3 27 b = 3 2 ⇒ m = 0
Thay ngược lại ta thấy không có giá trị nào của m thỏa yêu cầu bài toán. Bài 5:
1. Giải sử phương trình có ba nghiệm phân biệt lập thành cấp số cộng.
Khi đó: x + x = 2x ,x + x + x = 3 ⇒ x = 1 3 2 1 2 3 2 1
Thay vào phương trình ta có : m = 11 . 3 2
Với m = 11 ta có phương trình : x − 3x − 9x + 11 = 0 ⇔ (x − 1)( 2
x − 2x − 11) = 0 ⇔ x = 1− 12,x = 1,x = 1+ 1 2 3 12
Ba nghiệm này lập thành CSC.
Vậy m = 11 là giá trị cần tìm.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 16 Tµi liÖu to¸n 11 n¨m häc 2018 2
2. Đặt t = x ,t ≥ 0 . Phương trình trở 2
thành: t − 2 (m + 1) t + 2m + 1 = 0 (2)
Phương trình (1) có bốn nghiệm phân biệt khi và chỉ khi PT (2) có hai nghiệm dương phân biệt t > t > 2 1 0 . 2 ∆' > 0 (m +1) −(2m +1) > 0 1 ⇔ P > 0 ⇔ 2m + 1 > 0 ⇔ − < m ≠ 0 2 S > 0 2(m + 1) > 0
Khi đó PT(2) có bốn nghiệm là: − t ;− 2 t1 ; t1 ; t2
Bốn nghiệm này lập thành cấp số cộng khi : − t + t = −2 t 2 1 1 ⇔ t = 3 t ⇔ t = 2 1 2 9t1 − t + t = 1 2 2 t1 m 4 t + t = 1 2 2(m + 1) t1 9t1 2(m 1) = + = + Theo đị 2 nh lý viet thì : ⇒ ⇒ 9m − 32m − 16 = 0 ⇔ 4 . t t = 2m + 1 2 1 t 9t = 2m + 1 m = − 1 1 9 4
Vậy m = 4 hoặc m = − 9 là những giá trị cần tìm.
3. Giả sử phương trình có ba nghiệm phân biệt lập thành CSN,khi đó : x x = 2 x 1 3 2 m + 1 x + x + x = −2 ⇒ x = − 1 2 3 2 2 x x + x x + x x = m + 1 2 2 3 3 1 1
thay vào phương trình ta có : m = −1,m = 3,m = −4 .
Bằng cách thay từng giá trị của m vào phương trình ta thấy không có giá trị nào của m thỏa yêu cầu bài toán.
ĐÁP ÁN TRẮC NGHIỆM
PHẦN 1. CẤP SỐ CỘNG
Câu 1. Trong các dãy số sau, dãy số nào là một cấp số cộng? A. 1 ;3;7;11;15;
B. 1;3;6;9;12;
C. 1;2;4;6;8;
D. 1;3;5;7;9;
Lời giải. Ta lần lượt kiểm tra: u u u u u u ? 2 1 3 2 4 3
Xét đáp án A: 1;3;7;11;15;
u u u u u u Chọn A. 2 1 3 2 4 3
Xét đáp án B: 1;3;6;9;12;
u u 4
3 u u loại B. 2 1 3 2
Xét đáp án C: 1;2;4;6;8;
u u 3
2 u u loại C. 2 1 3 2
Xét đáp án D: 1;3;5;7;9;
u u 4
2 u u loại D. 2 1 3 2
Câu 2. Dãy số nào sau đây không phải là cấp số cộng? 2 1 1 2 4
A. ; ;0; ; ;1; ....
B. 15 2;12 2;9 2;6 2;.... 3 3 3 3 3 4 7 9 11 1 2 3 4 3 5 C. ;1; ; ; ;.... D. ; ; 3; ; ;... 5 5 5 5 3 3 3 3
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 17 Tµi liÖu to¸n 11 n¨m häc 2018
Lời giải. Chỉ cần tồn tại hai cặp số hạng liên tiếp của dãy số có hiệu khác nhau: u u u
u thì ta kết luận ngay dãy số m 1 m k 1 k
đó không phải là cấp số cộng. Xét đáp án A: 2 1 1 2 4 1 ; ;0; ; ;1; ....
u u u u u u loại A. 2 1 3 2 4 3 3 3 3 3 3 3 Xét đáp án B: 15 2;12 2;9 2; 6 2;....
3 3 u u u u u u loại B. 2 1 3 2 4 3 Xét đáp án C: 4 7 9 11 1 2 ;1; ; ; ;....
u u
u u Chọn C. 2 1 3 2 5 5 5 5 5 5 Xét đáp án D: 1 2 3 4 3 5 3 ; ; 3; ; ;...
u u u u u u loại D. 2 1 3 2 4 3 3 3 3 3 3 1 1 3
Câu 3. Cho dãy số ;0; ;1; ;..... là cấp số cộng với: 2 2 2 1 1
A. Số hạng đầu tiên là , công sai là . 2 2 1 1
B. Số hạng đầu tiên là , công sai là . 2 2 1
C. Số hạng đầu tiên là 0 , công sai là . 2 1
D. Số hạng đầu tiên là 0 , công sai là . 2
Lời giải: Nếu dãy số u là một cấp số cộng thị công sai d của nó là hiệu của một cặp số hạng liên tiếp bất kì (số hạng sau trừ n
cho số hạng trước) của dãy số đó. 1 1 1 3 u 1 2 Ta có
;0; ;1; ;..... là cấp số cộng Chọn B. 2 2 2 1 u
u d 2 1 2 1 1
Câu 4. Cho cấp số cộng có số hạng đầu u , d . 1 công sai
Năm số hạng liên tiếp đầu tiên của cấp số này là: 2 2 1 1 1 1 1 1 3 5 1 1 3
A. ;0;1; ;1. B. ;0; ;0; . C. ;1; ;2; . D. ;0; ;1; . 2 2 2 2 2 2 2 2 2 2 2 1 1 n 1
Lời giải: Ta dùng công thức tổng quát u u n 1 d n 1 1 , hoặc u
u d u để tính các số n 1 2 2 2 n 1 n n 2
hạng của một cấp số cộng.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 18 Tµi liÖu to¸n 11 n¨m häc 2018 1 u 1 2
u u d 0 2 1 1 1 1
Ta có u ; d u
u d Chọn D. 1 3 2 2 2 2
u u d 1 4 3 3 u
u d 5 4 2
Nhận xét: Dùng chức năng “lặp” của MTCT để tính: 1
Nhập: X X
(nhập X X d ). 2 1
Bấm CALC: nhập (nhập u ). 2 1
Để tính 5 số hạng đầu ta bấm dấu “=” liên tiếp để ra kết quả 4 lần nữa!
Câu 5. Viết ba số hạng xen giữa các số 2 và 22 để được một cấp số cộng có năm số hạng. A. 7; 12; 17, B. 6; 10; 14. C. 8; 13; 18. D. 6; 12; 18.
Lời giải. Giữa 2 và 22 có thêm ba số hạng nữa lập thành cấp số cộng, xem như ta có một cấp số cộng có 5 số hạng với
u 2; u 22; ta cần tìm u , u , u . 1 5 2 3 4 u
u d 7 2 1 u u 22 2 Ta có 5 1
u u 4d d 5 u
u 2d 12 Chọn A. 5 1 3 1 4 4
u u 3d 17 4 1
Câu 6. Cho hai số 3 và 23. Xen kẽ giữa hai số đã cho n số hạng để tất cả các số đó tạo thành cấp số cộng có công sai d 2. Tìm . n A. n 12. B. n 13. C. n 14. D. n 15.
Lời giải. Theo giả thiết thì ta được một cấp số cộng có n 2 số hạng với u 3, u 23. 1 n2 u u 23 3 n2 1 Khi đó u
u n 1 d n 1
13 n 12 Chọn A. n2 1 d 2
Câu 7. Cho các số 4; 1; 6; x theo thứ tự lập thành một cấp số cộng. Tìm x. A. x 7. B. x 10. C. x 11. D. x 12.
Lời giải. Vì các số 4; 1; 6; x theo thứ tự u , u , u , u lập thành cấp số cộng nên 1 2 3 4
u u u u
x 6 61 x 11 Chọn C. 4 3 3 2
Câu 8. Biết các số 1 2 3 C ; C ; C n n n
n theo thứ tự lập thành một cấp số cộng với 3. Tìm . n A. n 5. B. n 7. C. n 9. D. n 11. Lời giải. Ba số 1 2 3 C ; C ; C n n
n theo thứ tự u , u , u lập thành cấp số cộng nên 1 2 3
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 19 Tµi liÖu to¸n 11 n¨m häc 2018
n 2 n 1 n n 1 n 1 3 2
u u 2u C C 2C
n 3 n 2. 1 3 2 n n n 6 2 2 n 3n 2 n 2 2 1
n1 n 9n 14 n 7n 3 . Chọn B. 6 n 7
Nhận xét: Nếu u , u , u u u 2u . k 1 k k 1
là ba số hạng liên tiếp của một cấp số cộng thì ta có k 1 k 1 k
Câu 9. Nếu các số 5 m; 7 2m; 17 m theo thứ tự lập thành cấp số cộng thì m bằng bao nhiêu? A. m 2. B. m 3. C. m 4. D. m 5.
Lời giải. Ba số 5 m; 7 2m; 17 m theo thứ tự u , u , u lập thành cấp số cộng nên 1 2 3
u u 2u 5 m 17 m 2 7 2m m 4 Chọn C. 1 3 2
Nhận xét: Ta có thể dùng tính chất u u u u . 3 2 2 1
Câu 10. Với giá trị nào của x và y thì các số 7; x; 11; y theo thứ tự đó lập thành một cấp số công?
A. x 1; y 21. B. x 2; y 20.
C. x 3; y 19.
D. x 4; y 18.
Lời giải. Bốn số 7; x; 11; y theo thứ tự u , u , u , u lập thành cấp số cộng nên 1 2 3 4 u
u u u
y 1111 x
x y 22 x 2 4 3 3 2 Chọn B. u
u u u
y 11 x 7
x y 18 y 20 4 3 2 1
Câu 11. Cho cấp số cộng u u
n có các số hạng đầu lần lượt là 5; 9; 13; 17; . Tìm số hạng tổng quát n của cấp số cộng.
A. u 5n 1. u n u n u n n B. 5 1. n C. 4 1. n D. 4 1. n
Lời giải. Các số 5; 9; 13; 17; theo thứ tự đó lập thành cấp số cộng u nên n u 5 1 CTTQ
u u n1 d 5 4 n1 4n 1 Chọn C. n 1
d u u 4 2 1 1
Câu 12. Cho cấp số cộng u u 3 d . n có 1 và
Khẳng định nào sau đây đúng? 2 1 1
A. u 3 n
u 3 n 1. n 1 . B. 2 n 2 1 1
C. u 3 n u 3 n 1 . n 1 . D. n 2 4 u 3 1 CTTQ 1
Lời giải. Ta có
u u n1 d 3 n 1 1 Chọn C. n 1 d 2 2
Câu 13. Cho cấp số cộng u u 15 d u n có 3 và 2 . Tìm . n 3 3
A. u 2n 21.
u n 12. u n u n 4. n B. n C. 3 17. D. 2 2 n n 2
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 20 Tµi liÖu to¸n 11 n¨m häc 2018 15
u u 2d u 19 Lời giải. Ta có 3 1 1
u u n1 d 2n 21. Chọn A. n 1 d 2 d 2
Câu 14. Trong các dãy số được cho dưới đây, dãy số nào là cấp số cộng? 7
A. u 7 3 . n n u u . n u n B. 7 3 . n C. n D. 7.3 . 3n n
Lời giải. Dãy u là cấp số cộng u an b ( a,b là hằng số). Chọn A. n n
Câu 15. Trong các dãy số được cho dưới đây, dãy số nào là cấp số cộng? n A. u n u n 1 2 1 . B. sin . n n u 1 u 1 1 1 C. . D. . u u 1 u 2u n n 1 n n 1
Lời giải. Dãy u là một cấp số cộng u u
d ( d là hằng số). Chọn C. n n n 1
Câu 16. Trong các dãy số được cho dưới đây, dãy số nào không phải là cấp số cộng?
A. u 4n 9. u n u n n n B. 2 19. n C. 2 21. n D. u 2 15. n
Lời giải. Dãy số u 2n 15 không có dạng an b nên có không phải là cấp số cộng. n Chọn D.
Câu 17. Cho cấp số cộng u u 5 d n có 1 và
3. Số 100 là số hạng thứ mấy của cấp số cộng? A. Thứ 15. B. Thứ 20. C. Thứ 35. D. Thứ 36. u 5 Lời giải. 1 nu 100 n
100 u u n1 d 3n8 n 36 Chọn D. n 1 d 3
Câu 18. Cho cấp số cộng u u 5 d n có 1 và
3. Mệnh đề nào sau đây đúng? A. u 34. u 45. u 31. u 35. 15 B. 15 C. 13 D. 10 u 37 15 u 5 Lời giải. 1
u 3n8 u 31 Chọn C. n 13 d 3 u 22 10
Câu 19. Một cấp số cộng có 8 số hạng. Số hạng đầu là 5, số hạng thứ tám là 40. Khi đó công sai d của cấp số cộng đó là bao nhiêu?
A. d 4.
B. d 5.
C. d 6.
D. d 7. u 5 Lời giải. 1 d 5 Chọn B.
40 u u 7d 8 1
Câu 20. Cho cấp số cộng u u 4 d n có 1 và
5. Tính tổng 100 số hạng đầu tiên của cấp số cộng.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 21 Tµi liÖu to¸n 11 n¨m häc 2018 A. S 24350. S 24350. S 24600. S 24600. 100 B. 100 C. 100 D. 100 nn 1 100.99
Lời giải. S nu d
S 100u d 24350 Chọn B. n 1 100 1 2 2 1 1
Câu 21. Cho cấp số cộng u u d . S n có 1 và Gọi
là tổng 5 số hạng đầu tiên của cấp số cộng đã cho. Mệnh đề nào 4 4 5 sau đây đúng? 5 4 5 4 A. S . S . S . S . 5 B. C. D. 4 5 5 5 4 5 5 1 u 1 4 5.4 1 1 5 Lời giải. S 5u d 5. 10. Chọn A. 5 1 1 2 4 4 4 d 5
Câu 22. Số hạng tổng quát của một cấp số cộng là u 3n 4 S n với *
n . Gọi n là tổng n số hạng đầu tiên của cấp số cộng đã
cho. Mệnh đề nào sau đây đúng? 3n 1 73n 1 2 3n 5n 2 3n 11n A. S . S . S . S . n B. C. D. 2 n 2 n 2 n 2 u
a b
Lời giải. Câp số cộng 1
u an b . n d a u 7 nn 1 3 2 n n 2 n 1 3 11 n u 3n 4 S nu d n Chọn D. n 7 . n 1 d 3 2 2 2
Câu 23. Xét các số nguyên dương chia hết cho 3. Tổng số 50 số nguyên dương đầu tiên đó bằng: A. 7650. B. 7500. C. 3900. D. 3825.
Lời giải. Số nguyên dương chia hết cho 3 có dạng *
3n n nên chúng lập thành cấp số cộng u 3 1 50 u 3n S u u 3825 Chọn D. n 50 1 50 u 150 2 50 n nn 1 Chú ý: S u u nu d n . 1 n 1 2 2
Câu 24. Cho cấp số cộng u d S 72. u . n có 2 và 8
Tìm số hạng đầu tiên 1 1 1 A. u 16. u 16. u . u . 1 B. 1 C. 1 D. 16 1 16 d 2 Lời giải. 8.7
72 8u 28. 2 u 16 Chọn A. 1 1 72
S 8u d 8 1 2
Câu 25. Một cấp số cộng có số hạng đầu là 1, công sai là 4, tổng của n số hạng đầu là 561. Khi đó số hạng thứ n của cấp số cộng
đó là un có giá trị là bao nhiêu? A. u 57. u u u n B. 61. n C. 65. n D. 69. n
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 22 Tµi liÖu to¸n 11 n¨m häc 2018 u 1, d 4 1 2 n n Lời giải. nn 2 1 561 n
.4 2n n 561 0 n 17. 561
S nu d 2 n 1 2
u u u 16d 116.4 65 Chọn C. n 17 1
Câu 26. Một cấp số cộng có 12 số hạng. Biết rằng tổng của 12 số hạng đó bằng 144 và số hạng thứ mười hai bằng 23. Khi đó công
sai d của cấp số cộng đã cho là bao nhiêu? A. d 2. B. d 3. C. d 4. D. d 5. u 11d 23 u 1 1 1 u 23 Lời giải. 12 12 u Chọn A. S 144
u u 23 1 144 d 2 12 1 12 2 11 2 3n 19n
Câu 27. Tổng n số hạng đầu tiên của một cấp số cộng là S u n với *
n . Tìm số hạng đầu tiên và công sai d 4 1
của cấp số cộng đã cho. 1 3
A. u 2; d .
u 4; d . 1 B. 2 1 2 3 5 1
C. u ; d 2. u ; d . 1 D. 2 1 2 2 2 2 3n 19n 3 19 n n d d Lời giải. Ta có 2 2 n
n S nu d n u n n 1 1 4 4 4 2 2 2 d 3 u 4 1 2 4 . 3 Chọn B. d 19 d u 1 2 2 4
Câu 28. Tổng n số hạng đầu tiên của một cấp số cộng là 2
S n 4n u n với *
n . Tìm số hạng tổng quát n của cấp số cộng đã cho. n 1 8
A. u 2n 3. u n n u u 5. . n B. 3 2. n C. 1 5.3 . n D. n 5 d 1 d d
n n S n 2 Lời giải. Ta có 2 2 4 u n n 1 2 2 d u 4 1 2 u 5 1
u 2n 3 Chọn A. d 2 n
Câu 29. Tính tổng S 1 2 3 4 5 ... 2n
1 2n với n 1 và n . A. S 0. B. S 1. C. S . n D. S . n
Lời giải. Với mọi *
n thì 2n 1 2n 1 .
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 23 Tµi liÖu to¸n 11 n¨m häc 2018
Ta có S 1 23 45 6 2n
1 2n . Do đó ta xem S là tổng của n số hạng, mà mỗi số hạng đều bằng 1 nên S . n Chọn D.
Nhận xét: Ta có 1;3;5;; 2n 1 và 2; 4;6; ;
2n là các cấp số cộng có n số hạng nên
S 1 3 5 2n
1 2 4 6 2n
n n n n 2 n 2 1 2 1 2 2
n n . n 2 2
Câu 30. Cho cấp số cộng u
u u u u 100. n thỏa mãn 2 8 9 15
Tính tổng 16 số hạng đầu tiên của cấp số cộng đã cho. A. S 100. S 200. S 300. S 400. 16 B. 16 C. 16 D. 16
Lời giải. Ta có u u u u 100 4u 30d 100 2u 15d 50. 2 8 9 15 1 1 Khi đó 16 S u u
8 2u 15d 8.50 400 Chọn D. 16 1 16 1 2
Câu 31. Cho cấp số cộng u u 12 u 18. u n có 4 và 14
Tìm số hạng đầu tiên 1 và công sai d của cấp số cộng đã cho.
A. u 21; d 3.
u 20; d 3. 1 B. 1
C. u 22; d 3.
u 21; d 3. 1 D. 1
12 u u 3d u 21 Lời giải. 4 1 1 Chọn A. 18
u u 13d d 3 14 1
Câu 32. Cho cấp số cộng u u 2001
u 1995 . Khi đó u n có 2 và 5 1001 bằng: A. u 4005. u 4003. u 1. 1001 B. 1001 C. u 3. D. 1001 1001
2001 u u d u 2003 Lời giải. 2 1 1 u
u 1000d 3 Chọn C. 1001 1 1995
u u 4d d 2 5 1
Câu 33. Cho cấp số cộng u u 1,u 8
n , biết: n n 1
. Tính công sai d cảu cấp số cộng đó. A. d 9. B. d 7. C. d 7. D. d 9.
Lời giải. d u
u 8 1 9 Chọn D. n 1 n
Câu 34. Cho cấp số cộng u . n
Hãy chọn hệ thức đúng trong các hệ thức sau: u u A. 10 20 u u . u u 2u . 5 10 B. 2 90 210 150 u .u
C. u .u u . u . 10 30 20 D. 10 30 20 2 u u
u 9d u 29d 10 30 1 1 u 19d
Lời giải. Xét đáp án A: 1 2 2 loại A. u
u u 4d u 9d 2u 13d 5 10 1 1 2
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 24 Tµi liÖu to¸n 11 n¨m häc 2018 u
u 2u 298d 2 u 149d 90 210 2 1 Xét đáp án B: Chọn B. 2u 2 u 159d 150 1
Nhận xét: Có thể lấy một cấp số cộng cụ thể để kiểm tra, ví dụ u n * n . n
Câu 35. Cho cấp số cộng u u u 60. S n thỏa mãn 2 23
Tính tổng 24 của 24 số hạng đầu tiên của cấp số cộng đã cho. A. S 60. S 120. S 720. S 1440. 24 B. 24 C. 24 D. 24
Lời giải. u u 60 u d u 22d 60 2u 23d 60. 2 23 1 1 1 Khi đó 24 S u u
12 u u 23d 12 2u 23d 12.60 720. Chọn C. 24 1 24 1 1 1 2
Câu 36. Một cấp số cộng có 6 số hạng. Biết rằng tổng của số hạng đầu và số hạng cuối bằng 17; tổng của số hạng thứ hai và số
hạng thứ tư bằng 14. Tìm công sai d của câp số cộng đã cho.
A. d 2.
B. d 3.
C. d 4.
D. d 5. u u 17
2u 5d 17 u 16 Lời giải. 1 6 1 1 Chọn B. u u 14
2u 6d 14 d 3 2 4 1 u u 8 7 3
Câu 37. Cho cấp số cộng u . n thỏa mãn
Tìm công sai d của câp số cộng đã cho. u u 75 2 7 1 1 A. d . B. d . C. d 2.
D. d 3. 2 3 u u 8
u 6d u 2d 8 d 2 7 3 1 1 Lời giải. Chọn C. u u 75 u
d u 6d 75
u 2 u 12 75 2 7 1 1 1 1 u u 26 1 7
Câu 38. Cho cấp số cộng u . n thỏa mãn
Mệnh đề nào sau đây đúng? 2 2 u u 466 2 6 u 13 u 10 u 1 u 13 1 1 1 1 A. . B. . C. . D. . d 3 d 3 d 4 d 4 Lời giải. Ta có u u 26 2
u 6d 26 u 133d (1) 1 7 1 1 . 2 2 u u 466
u d u 5d 466
u d u 5d 466 2 2 6 1 2 1 2 1 2 1 2 Thay (1) và (2) ta đượ 2 2
c: d d 2 13 2 13 2
466 8d 338 466
d 4 u 1 1 Chọn C.
d 4 u 25 1 u
u u 15 1 3 5
Câu 39. Cho cấp số cộng u . n thỏa mãn
Chọn khẳng định đúng trong các khẳng định sau? u u 27 1 6
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 25 Tµi liÖu to¸n 11 n¨m häc 2018 u 21 u 21 u 18 u 21 1 1 1 1 A. . B. . C. . D. . d 3 d 3 d 3 d 4
u u u 15
u u 2d u 4d 15 1 3 5 1 1 1
Lời giải. Ta có u u 27
u u 5d 27 1 6 1 1
u 2d 15 u 21 1 1 . Chọn B. 2u 5d 27 d 3 1 u
u u 36
Câu 40. Cho cấp số cộng u thỏa 2 4 6
. Tìm công sai d của cấp số cộng u biết d 10. n n u u 54 2 3 A. d 3. B. d 4 . C. d 5. D. d 6. u
u u 36
u d u 3d u 5d 36 2 4 6 1 1 1
Lời giải. Ta có u u 54
u d u 2d 54 2 3 1 1 u 3d 12 1 1 . u 12 3d 2 , ta đượ Từ 1 suy ra . Thay vào c
u d u 2d 54 2 1 1 1
d d 2 12 2 12
54 d 18d 45 0 d 3 hoặc d 15 . Chọn A. u
u u 27 1 2 3
Câu 41. Cho cấp số cộng u thỏa . Tính u . n 2 2 2 2 u
u u 275 1 2 3 A. u 3. B. u 6. C. u 9. D. u 12. 2 2 2 2 u
u u 27 u
u d u 2d 27 1 2 3 1 1 1
Lời giải. Ta có 2 2 2 2 u
u u 275 1 2 3 u
u d u 2d 275 1 1 2 1 2 u d 9 1 1 . u
u d2 u 2d2 2 275 2 1 1 1 Từ
1 suy ra d 9 u 2 , ta đượ 1 . Thay vào c
u u 9u 2 2
u 29u 2 2
275 u 18u 65 0 u 13 u 5 1 1 1 1 1 1 1 1 hoặc 1 . u 13 1 u 5 Vậy hoặc 1
u u d 9 Chọn C. d 4 2 1 d 4
Câu 42. Tính tổng T 15 20 25 ... 7515.
A. T 5651265. B. T 5651256.
C. T 5651625.
D. T 5651526.
Lời giải. Ta thấy các số hạng của tổng T tạo thành một cấp số cộng với số hạng đầu u 15 d 1 và công sai 5.
Giả sử tổng trên có n số hạng thì u 7515 n
u n 1 d 7515 15 n 1 5 7515 n 1501 1 .
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 26 Tµi liÖu to¸n 11 n¨m häc 2018
2u 1500d .1501 2.15 1500.5 .1501 1 Vậy T S 5651265 Chọn A. 1501 2 2 Câu 43. Tính tổng 2 2 2 2 2 2
T 1000 999 998 997 ... 2 1 .
A. T 500500.
B. T 500005.
C. T 505000.
D. T 500050.
Lời giải. Ta có T 1.1000 9991.998 997...1.2
1 1999 1995... 3.
Ta thấy các số hạng của tổng T tạo thành một cấp số cộng với số hạng đầu u 1999 d 1 và công sai 4.
Giả sử tổng trên có n số hạng thì
u 3 u n 1 d 3 1999 n 1 4 3 n 500. n 1 u u .500 1999 3 .500 1 500 Vậy T S 500500 Chọn A. 500 2 2
Câu 44. Cho cấp số cộng u ; u ; u ; ; u d 1 2 3 n có công sai
, các số hạng của cấp số cộng đã cho đều khác 0. Với giá trị nào của 1 1 1 1 d thì dãy số ; ; ; ; là một cấp số cộng? u u u u 1 2 3 n A. d 1. B. d 0. C. d 1. D. d 2. 1 1 d u
u d u u u u Lời giải. Ta có 2 1 2 1 1 2 . u u d 1 1 d 3 2 u u u u 3 2 2 3 1 1 1 1
Theo yêu cầu bài toán thì ta phải có u u u u 2 1 3 2 d 0 d 0 1 1 d 0 Chọn B.
u u u 2 d 1 3 1 u u 1 3
Câu 45. Nếu a; b; c theo thứ tự lập thành cấp số cộng thì dãy số nào sau đây lập thành cấp số cộng? A. 2 2 2
2b ; a ; c .
B. 2b;2a;2c.
C. 2b; a; c.
D. 2b; a; c.
Lời giải. Ta có c a 2b 2c a 22b 2c2a 22b. Chọn B. 1 1 1 Câu 46. Nếu ; ;
theo thứ tự lập thành cấp số cộng thì dãy số nào sau đây lập thành cấp số cộng?
b c c a a b A. 2 2 2
b ; a ; c . B. 2 2 2
c ; a ; b . C. 2 2 2
a ; b ; c . D. 2 2 2
a ; c ; b . 2 1 1 c a
b cb a
Lời giải. Theo giả thiết ta có c a b c a b 2
2b a c
a c2 bc a 2 2
2 b ab bc ac 2 2
a c ac bc bc 2
b ab bc ac 2 2 2 2 2 2 2
a c 2b . Chọn C.
Câu 47. Cho a; b; c theo thứ tự lập thành cấp số cộng. Mệnh đề nào sau đây đúng?
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 27 Tµi liÖu to¸n 11 n¨m häc 2018 A. 2 2 2
a c 2ac 4b . B. 2 2
a c 2ab 2bc. C. 2 2
a c ab bc. D. 2 2
a c 2ab 2bc.
Lời giải. Ta có: a c b a c2 2 2 2 2 2
4b a c 2ac 4b Chọn A.
Câu 48. Ba góc của một tam giác vuông tạo thành cấp số cộng. Hai góc nhọn của tam giác có số đo (độ) là: A. 20 và 70. B. 45 và 45. C. 20 và 45. D. 30 và 60. Lời giải. Ba góc ,
A B, C của một tam giác vuông theo thứ tự đó ( A B C ) lập thánh cấp số cộng nên C 90, C A 2B .
A B C 180 3 B 180 B 60
Ta có A C 2B
AC 2B A 30 Chọn D. C 90 C 90 C 90 Câu 49. Ba góc ,
A B, C A B C của tam giác tạo thành cấp số cộng, biết góc lớn nhất gấp đôi góc bé nhất. Hiệu số đo độ
của góc lớn nhất với góc nhỏ nhất bằng: A. 40. B. 45. C. 60. D. 80. Lời giải. Ba góc ,
A B, C của một tam giác theo thứ tự đó lập thành cấp số cộng thỏa yêu cầu, thì C 2 ,
A C A 2B . Ta có 0 0 0 0
A B C 180 3 B 180 B 60 A 40 0 0 0
A C 2B
A C 2B A C 120 B 60
C A 40 . Chọn A. 0 C 2A C 2A C 2A C 80
Câu 50. Một tam giác vuông có chu vi bằng 3 và độ dài các cạnh lập thành một cấp số cộng. Độ dài các cạnh của tam giác đó là: 1 3 1 5 3 5 1 7 A. ; 1; . B. ; 1; . C. ; 1; . D. ; 1; . 2 2 3 3 4 4 4 4
Lời giải. Ba cạnh a, ,
b c a b c của một tam giác theo thứ tự đó lập thành một cấp số cộng thỏa yêu cầu thì 2 2 2 2 2 2 2 2 2
a b c
a b c
a b c
a b c 3 3 b 3 b 1 .
a c 2b
a c 2b
a 2bc 2c 3 a 4 b 5
Ta có a b c
c c c c b Chọn C. a c 2 2 2 2 2 1 2 1 4 5 0 1 . 2 4 5 c 4
Câu 51. Một rạp hát có 30 dãy ghế, dãy đầu tiên có 25 ghế. Mỗi dãy sau có hơn dãy trước 3 ghế. Hỏi rạp hát có tất cả bao nhiêu ghế? A. 1635. B. 1792. C. 2055. D. 3125.
Lời giải. Số ghế của mỗi dãy (bắt đầu từ dãy đầu tiên) theo thứ tự đó lập thành một cấp số cộng có 30 số hạng có công sai d 3 và u 25. 1 30.29
Tổng số ghế là S u u u 30u d 2055 Chọn C. 30 1 2 30 1 2
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 28 Tµi liÖu to¸n 11 n¨m häc 2018
Câu 52. Người ta trồng 3003 cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng thứ hai trồng 2 cây, hàng thứ ba
trồng 3 cây,...Hỏi có tất cả bao nhiêu hàng cây? A. 73. B. 75. C. 77. D. 79.
Lời giải. Số cây mỗi hàng (bắt đầu từ hàng thứ nhất) lập thành một cấp số cộng u có u 1, d 1. Giả sử có n hàng cây thì n 1
u u u 3003 S . 1 2 n n nn 1 Ta có 2
3003 S nu
d n n 6006 0 n 77 Chọn C. n 1 2
Câu 53. Một chiếc đồng hồ đánh chuông, kể từ thời điểm 0 (giờ) thì sau mỗi giờ thì số tiếng chuông được đánh đúng bằng số giờ
mà đồng hồ chỉ tại thời điểm đánh chuông. Hỏi một ngày đồng hồ đó đánh bao nhiêu tiếng chuông? A. 78. B. 156. C. 300. D. 48.
Lời giải. Kể từ lúc 1 (giờ) đến 24 (giời) số tiếng chuông được đánh lập thành cấp số cộng có 24 số hạng với u 1, công sai 1
d 1. Vậy số tiếng chuông được đánh trong 1 ngày là: 24 S S u u 12 1 24 300 Chọn C. 24 1 24 2
Câu 54. Trên một bàn cờ có nhiều ô vuông, người ta đặt 7 hạt dẻ vào ô đầu tiên, sau đó đặt tiếp vào ô thứ hai số hạt nhiều hơn ô
thứ nhất là 5, tiếp tục đặt vào ô thứ ba số hạt nhiều hơn ô thứ hai là 5,… và cứ thế tiếp tục đến ô thứ n . Biết rằng đặt hết số ô trên
bàn cờ người ta phải sử dụng 25450 hạt. Hỏi bàn cờ đó có bao nhiêu ô vuông? A. 98. B. 100. C. 102. D. 104.
Lời giải. Số hạt dẻ trên mỗi ô (bắt đầu từ ô thứ nhất) theo thứ tự đó lập thành cấp số cộng u có u 7, d 5. Gọi n là số ô n 1 nn 2 1 n n
trên bàn cờ thì u u u 25450 S . Ta có 25450 S nu d 7n .5 1 2 n n n 1 2 2 2
5n 9n50900 0 n 100 Chọn B.
Câu 55. Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước đến để khoan giếng nước. Biết giá
của mét khoan đầu tiên là 80.000 đồng, kể từ mét khoan thứ 2 giá của mỗi mét khoan tăng thêm 5000 đồng so với giá của mét
khoan trước đó. Biết cần phải khoan sâu xuống 50m mới có nước. Vậy hỏi phải trả bao nhiêu tiền để khoan cái giếng đó? A. 5.2500.000 đồng. B. 10.125.000 đồng.
C. 4.000.000 đồng. D. 4.245.000 đồng.
Lời giải. Giá tiền khoang mỗi mét (bắt đầu từ mét đầu tiên) lập thành cấp số cộng u có u 80 000, d 5000. Do cần khoang n 1
50 mét nên tổng số tiền cần trả là 50.49
u u u S 50u
d 50.80 000 1225.5000 10125000 Chọn B. 1 2 0 5 0 5 1 2
PHẦN 2. CẤP SỐ NHÂN
Câu 1. Trong các dãy số sau, dãy số nào là một cấp số nhân?
A. 128; 64; 32; 16; 8; ...
B. 2; 2; 4; 4 2; ....
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 29 Tµi liÖu to¸n 11 n¨m häc 2018 1
C. 5; 6; 7; 8; ...
D. 15; 5; 1; ; ... 5
Lời giải. Dãy u là cấp số nhân n u qu u u u * n 2 3 4 q u
0 , q gọi là công bội. n n 1 n u u u 1 2 3 Xét đáp án A: u 1 u u 2 3 4
128; 64; 32; 16; 8; ... Chọn A. u 2 u u 1 2 3 Xét đáp án B: u 1 u 2 3 2; 2; 4; 4 2; .... 2 loại B. u 2 u 1 2
Tương tự, ta cũng loại các đáp án C, D.
Câu 2. Trong các dãy số sau, dãy số nào không phải là một cấp số nhân?
A. 2; 4; 8; 16;
B. 1; 1; 1; 1; C. 2 2 2 2 1 ; 2 ; 3 ; 4 ; D. 3 5 7
a; a ; a ; a ; a 0. u 9 u
Lời giải. Xét đáp án C: 2 2 2 2 2 3 1 ; 2 ; 3 ; 4 ; 4 Chọn C. u 4 u 1 2
Các đáp án A, B, D đều là các cấp số nhân.
Nhận xét: Dãy u với u
0 là cấp số nhân u . n
a q , tức là các số hạng của nó đều được biểu diễn dưới dạng lũy thừa n n n
của cùng một cơ số q (công bội), các số hạng liên tiếp (kể từ số hạng thứ hai) thì số mũ của chúng cách đều nhau. Ví dụ 2; 4; 8; 16;
là cấp số nhân và u 2n. n n 1; 1; 1; 1;
là cấp số nhân và u n 1 . n 1 n 3 5 7 ; a a ; a ; a ; a 0 là cấp số nhân và 2 1 u a a n 2 . . a
Câu 3. Dãy số nào sau đây không phải là cấp số nhân? A. 1; 2; 4; 8; B. 2 3 4 3; 3 ; 3 ; 3 ; 1 1 1 1 1 1 C. 4; 2; ; ; D. ; ; ; ; 2 4 2 4 6 1
Lời giải. Các đáp án A, B, C đều là các cấp số nhân công bội lần lượt là 2;3; . 2 Xét đáp án D: 1 1 1 1 u 1 1 u 2 3 ; ; ; ; Chọn D. 2 4 6 2 u u 1 2
Câu 4. Dãy số 1; 2; 4; 8; 16; 32; là một cấp số nhân với:
A. Công bội là 3 và số hạng đầu tiên là 1.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 30 Tµi liÖu to¸n 11 n¨m häc 2018
B. Công bội là 2 và số hạng đầu tiên là 1.
C. Công bội là 4 và số hạng đầu tiên là 2.
D. Công bội là 2 và số hạng đầu tiên là 2. u 1 1
Lời giải. Cấp số nhân: 1; 2; 4; 8; 16; 32; u Chọn B. 2 q 2 u 1
Câu 5. Cho cấp số nhân u u 2 q n với 1 và
5. Viết bốn số hạng đầu tiên của cấp số nhân.
A. 2; 10; 50; 250.
B. 2; 10; 50; 250.
C. 2; 10; 50; 250.
D. 2; 10; 50; 250. u 2 1 u 2 u u q 10 Lời giải. 1 2 1 Chọn B. q 5 u u q 50 3 2
u u q 250 4 3 1 1 1 1 1
Câu 6. Cho cấp số nhân ; ; ; ; . Hỏi số
là số hạng thứ mấy trong cấp số nhân đã cho? 2 4 8 4096 4096 A. 11. B. 12. C. 10. D. 13. 1 u 1 n 1 1 1 1 1 2 1 1 1
Lời giải. Cấp số nhân: ; ; ; ; u . . 2 4 8 4096 u 1 n n 2 2 2 2 q u 2 1 1 1 1 u n 12 Chọn B. n n 12 4096 2 2
Câu 7. Một cấp số nhân có hai số hạng liên tiếp là 16 và 36. Số hạng tiếp theo là: A. 720. B. 81. C. 64. D. 56.
Lời giải. Ta có cấp số nhân u có: n u 16 u k k 9 1 q u u q 81 Chọn B. k 2 k 1 u 36 u 4 k 1 k
Câu 8. Tìm x để các số 2; 8; x; 128 theo thứ tự đó lập thành một cấp số nhân. A. x 14. B. x 32. C. x 64. D. x 68.
Lời giải. Cấp số nhân 2; 8; x; 128 theo thứ tự đó sẽ là u ; u ; u ; u , ta có 1 2 3 4 u u 2 3 8 x x 32 u u x 32 1 2 2 8
x 32 x 32 Chọn B. 2 u u 128 x x 1024 3 4 x 32 u u x 8 2 3
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 31 Tµi liÖu to¸n 11 n¨m häc 2018
Câu 9. Với giá trị x nào dưới đấy thì các số 4; x; 9 theo thứ tự đó lập thành một cấp số nhân? 13 A. x 36. B. x . C. x 6. D. x 36. 2 9 x
Lời giải. Cấp số nhân: 2 4; ; x 9
x 36 x 6 Chọn C. x 4 Nhận xét: ba số ;
a b ; c theo thứ tự đó lấp thành cấp số nhân 2 ac b . 1
Câu 10. Tìm b 0 để các số
; b; 2 theo thứ tự đó lập thành một cấp số nhân. 2 A. b 1. B. b 1. C. b 2. D. b 2.
Lời giải. Cấp số nhân b b2 1 1 ; ; 2 . 2 b 1 Chọn B. 2 2
Câu 11. Tìm tất cả giá trị của x để ba số 2x 1; x; 2x 1 theo thứ tự đó lập thành một cấp số nhân. 1 1 A. x . B. x . C. x 3. D. x 3. 3 3 1
Lời giải. Cấp số nhân 2x 1; ;
x 2x 1 2x 1 2x 2 2
1 x 3x 1 x . 3 Chọn A.
Câu 12. Tìm x để ba số 1 x; 9 x; 33 x theo thứ tự đó lập thành một cấp số nhân. A. x 1. B. x 3. C. x 7.
D. x 3; x 7.
Lời giải. Cấp số nhân x x x
x x x2 1 ; 9 ; 33 1 33 9
x 3. Chọn B.
Câu 13. Với giá trị x, y nào dưới đây thì các số hạng lần lượt là 2; ;
x 18; y theo thứ tự đó lập thành cấp số nhân? x 6 x 10 x 6 x 6 A. . . . . B. C. D. y 54 y 26 y 54 y 54 x 18 x 6 2 x
Lời giải. Cấp số nhân: 2; ;
x 18; y 324 . Vậy 18 y y 4 5 x x 18 ;
x y 6;54 hoặc ;
x y 6;54 Chọn C.
Câu 14. Cho cấp số nhân có các số hạng lần lượt là x; 12; y; 192. Mệnh đề nào sau đây là đúng?
A. x 1; y 144. B. x 2; y 72.
C. x 3; y 48.
D. x 4; y 36. 12 y 144 x 12 x x 3
Lời giải. Câp số nhân: ;
x 12; y; 192 y . Chọn C. y 192 y 48 2 y 2304 12 y
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 32 Tµi liÖu to¸n 11 n¨m häc 2018
Câu 15. Thêm hai số thực dương x và y vào giữa hai số 5 và 320 để được bốn số 5; x; y; 320 theo thứ tự đó lập thành cấp số
nhận. Khẳng định nào sau đây là đúng? x 25 x 20 x 15 x 30 A. . . . . B. C. D. y 125 y 80 y 45 y 90 u 5 1 x q 5 x 20
Lời giải. Cấp số nhân: 2 5; ; x y; 320 x . Chọn B. 2
y u u q y 80 3 1 5 3 x 3 320
u u q 4 1 25
Câu 16. Ba số hạng đầu của một cấp số nhân là x 6; x và .
y Tìm y , biết rằng công bội của cấp số nhân là 6. 324 1296
A. y 216. B. y . C. y .
D. y 12. 5 5
Lời giải. Cấp số nhân x 6; x và y có công bội q 6 nên ta có 36
u x 6, q 6 1 x 5
x u u q 6 x 6 Chọn C. 2 1 36 1296 2 y 36. y u u q 36x 3 2 5 5
Câu 17. Hai số hạng đầu của của một cấp số nhân là 2x 1 và 2
4x 1. Số hạng thứ ba của cấp số nhân là:
A. 2x 1.
B. 2x 1. C. 3 2
8x 4x 2x 1. D. 3 2
8x 4x 2x 1. 2 4x 1
Lời giải. Công bội của cấp số nhân là: q
2x 1. Vậy số hạng thứ ba của cấp số nhân là: 2x 1
2x x 3 2 4 1 2
1 8x 4x 2x 1 Chọn C.
Câu 18. Dãy số nào sau đây là cấp số nhân? u 1 u 1 1 1 A. . B. . u
u 1, n 1 u
3u , n 1 n 1 n n 1 n u u 2 1 1 2 C. . D. . u
2u 3, n 1 n 1 n u sin , n 1 n n 1
Lời giải. u là cấp số nhân u qu Chọn B. n n 1 n 3
Câu 19. Cho dãy số u u .5n. n với n
Khẳng định nào sau đây đúng? 2
A. un không phải là cấp số nhân.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 33 Tµi liÖu to¸n 11 n¨m häc 2018 3 B. u q u .
n là cấp số nhân có công bội 5 và số hạng đầu 1 2 15 C. u q u .
n là cấp số nhân có công bội 5 và số hạng đầu 1 2 5 D. u q u 3.
n là cấp số nhân có công bội và số hạng đầu 2 1 3 15
Lời giải. u .5n là cấp số nhân công bội q 5 và u Chọn C. n 2 1 2
Câu 20. Trong các dãy số u u
n cho bởi số hạng tổng quát n sau, dãy số nào là một cấp số nhân? 1 1 1 1 A. u . u 1. u n . 2 u n . n B. C. D. n2 3 n 3n n 3 n 3 n u 3 1 1 1
Lời giải. Dãy u 9.
là cấp số nhân có Chọn A. n 1 n2 3 3 q 3
Câu 21. Trong các dãy số u u
n cho bởi số hạng tổng quát n sau, dãy số nào là một cấp số nhân? 7
A. u 7 3 . n n u u . n u n B. 7 3 . n C. n D. 7.3 . 3n n u 21
Lời giải. Dãy u 7.3n là cấp số nhân có 1 Chọn D. n q 3
Câu 22. Cho dãy số u u n
n là một cấp số nhân với * 0, . n
Dãy số nào sau đây không phải là cấp số nhân?
A. u ; u ; u ; ...
3u ; 3u ; 3u ; ... 1 3 5 B. 1 2 3 1 1 1 C. ; ;
; ... D. u 2; u 2; u 2; ... u u u 1 2 3 1 2 3
Lời giải. Giả sử u là cấp số nhân công bội q, thì n
Dãy u ; u ; u ; ... 1 3 5
là cấp số nhân công bội 2 q .
Dãy 3u ; 3u ; 3u ; ... 1 2 3
là cấp số nhân công bội 2 . q 1 1 1 1 Dãy ; ;
; ... là cấp số nhân công bội . u u u 1 2 3 q
Dãy u 2; u 2; u 2; ... 1 2 3
không phải là cấp số nhân. Chọn D.
Nhận xét: Có thể lấy một cấp số nhân cụ thể để kiểm tra, ví dụ u 2n. n
Câu 23. Cho cấp số nhân có các số hạng lần lượt là 3; 9; 27; 81; ... . Tìm số hạng tổng quát un của cấp số nhân đã cho. A. n 1 u 3 . n u n u n u n B. 3 . n C. 1 3 . n D. 3 3 . n
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 34 Tµi liÖu to¸n 11 n¨m häc 2018 u 3 1
Lời giải. Câp số nhân n 1 n 1 3; 9; 27; 81; ... n 9 u u q 3.3 3 . n 1 q 3 3 Chọn B.
Câu 24. Một cấp số nhân có 6 số hạng, số hạng đầu bằng 2 và số hạng thứ sáu bằng 486. Tìm công bội q của cấp số nhân đã cho. A. q 3. B. q 3. C. q 2. D. q 2. u 2
Lời giải. Theo giải thiết ta có: 1 5 5 5
486 u u q 2q q 243 q 3. 6 1 u 486 6 Chọn A. 2
Câu 25. Cho cấp số nhân u u 3 q . n có 1 và
Mệnh đề nào sau đây đúng? 3 27 16 16 27 A. u . u . u . u . 5 B. C. D. 16 5 27 5 27 5 16 u 3 4 1 2 16 16 Lời giải. 4 2 u u q 3. 3. . Chọn B. 5 1 q 3 81 27 3
Câu 26. Cho cấp số nhân u u 2 u 8 n có 1 và 2
. Mệnh đề nào sau đây đúng? A. S 130. B. u 256. C. S 256. D. q 4. 6 5 5
u 2 1 q4 u 2 1 q 1 4 1 5 5 Lời giải. S u . 2. 410 Chọn D. 5 1 u
8 u q 2q 1 q 1 4 2 1 1 46 S 2. 1638 6 1 4
u u q 2.44 4 512. 5 1
Câu 27. Cho cấp số nhân u u 3 q n có 1 và
2 . Số 192 là số hạng thứ mấy của cấp số nhân đã cho?
A. Số hạng thứ 5.
B. Số hạng thứ 6.
C. Số hạng thứ 7.
D. Không là số hạng của cấp số đã cho. n 1 n 1 6 Lời giải. n 1 192 u u q
n Chọn C. n 3. 2 n 1 1 .2 64 6 1 .2 7. 1 1 1
Câu 28. Cho cấp số nhân u u 1 q n có 1 và . Số
là số hạng thứ mấy của cấp số nhân đã cho? 10 103 10
A. Số hạng thứ 103. B. Số hạng thứ 104.
C. Số hạng thứ 105. D. Không là số hạng của cấp số đã cho.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 35 Tµi liÖu to¸n 11 n¨m häc 2018 1 n n 1 n chan n 1 1 1 Lời giải. u u q 1.
n 104. Chọn B. 103 n 1 n 1 10 10 10 n1103
Câu 29. Một cấp số nhân có công bội bằng 3 và số hạng đầu bằng 5. Biết số hạng chính giữa là 32805. Hỏi cấp số nhân đã cho có bao nhiêu số hạng? A. 18. B. 17. C. 16. D. 9. Lời giải. n 1 n 1 n 1 8
32805 u u q 5.3 3
6561 3 n 9. Vậy u là số hạng chính giữa của cấp số nhân, nên cấp số n 1 9
nhân đã cho có 17 số hạng. Chọn B.
Câu 30. Cho cấp số nhân u u u 9. n có 81 n và n 1
Mệnh đề nào sau đây đúng? 1 1 A. q .
B. q 9.
C. q 9.
D. q . 9 9 un 9 1
Lời giải. Công bội 1 q Chọn A. u 81 9 n 1
Câu 31. Một dãy số được xác định bởi u 4
u u , n 2. u 1 và n n 1 Số hạng tổng quát của dãy số đó là: 2 n n 1 n 1 A. n 1 u 2 . u n 1 u 4 2 . u 4 . n B. n 1 2 . C. n D. n 2 u 4 u 4 n 1 1 1 n 1 Lời giải. 1 u u q 4. . 1 1 Chọn D. n 1 u u q 2 n 1 2 n 2
Câu 32. Cho cấp số nhân u u 3 q n có 1 và
2. Tính tổng 10 số hạng đầu tiên của cấp số nhân đã cho. A. S 511. S 1025. S 1025. S 1023. 10 B. 10 C. 10 D. 10 u 3 1 q 1 2 1 10 10 Lời giải. S u . 3. 1023. Chọn D. 10 1 q 2 1 q 1 2
Câu 33. Cho cấp số nhân có các số hạng lần lượt là 1; 4; 16; 64; Gọi Sn là tổng của n số hạng đầu tiên của cấp số nhân đó.
Mệnh đề nào sau đây đúng? n n 1 1 4 4n 1 44n 1 A. n 1 S 4 . S . S . S . n B. n C. D. 2 n 3 n 3 u 1 1 n q 1 4n 4n 1
Lời giải. Cấp số nhân đã cho có 1 S u . 1. . Chọn C. n 1 q 4 1 q 1 4 3 1 1
Câu 34. Cho cấp số nhân có các số hạng lần lượt là ; ; 1; ; 2048. Tính tổng S của tất cả các số hạng của cấp số nhân đã 4 2 cho.
A. S 2047,75. B. S 2049,75.
C. S 4095,75.
D. S 4096,75.
Lời giải. Cấp số nhân đã cho có
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 36 Tµi liÖu to¸n 11 n¨m häc 2018 1 u n 1 1 11 1 n 1 n2 4 2048 2 u q .2 2 n 13. 1 2 q 2
Vậy cấp số nhân đã cho có tất cả 13 số hạng. Vậy 13 13 1 q 1 1 2 S u . . 2047,75 Chọn A. 13 1 1 q 4 1 2 n 1 n
Câu 35. Tính tổng S 2 4 8 16 32 64 ... 2
2 với n 1, n . 212n 12n A. S 2 . n B. 2n S . C. S . D. S 2. . 12 3 n 1 n
Lời giải. Các số hạng 2; 4; 8; 16; 32; 64;...;2
; 2 trong tổng S gồm có n số hạng theo thứ tự đó lập thành cấp số
nhân có u 2, q 2. Vậy 1 n n 1 n q 12 12
S S u . 2. 2. Chọn D. n 1 1 q 12 3
Câu 36. Một cấp số nhân có 6 số hạng với công bội bằng 2 và tổng số các số hạng bằng 189. Tìm số hạng cuối u6 của cấp số nhân đã cho. A. u 32. u 104. u 48. u 96. 6 B. 6 C. 6 D. 6
Lời giải. Theo giả thiết: q 2 q 2 5 5 6 6 1 q 1 2
u u q 3.2 96. Chọn D. 6 1
S 189 u u . u 3 6 1 1 1 1 q 1 2
Câu 37. Cho cấp số nhân u u 6 q n có 1 và
2. Tổng n số hạng đầu tiên của cấp số nhân đã cho bằng 2046. Tìm . n A. n 9.
B. n 10.
C. n 11. D. n 12. Lời giải. Ta có n 1 n q 12 n n
2046 S u . 6.
2 2 1 2 1024 n 10. Chọn B. n 1 1 q 12
Câu 38. Cho cấp số nhân u n S
n có tổng n số hạng đầu tiên là 5 1. n
Tìm số hạng thứ 4 của cấp số nhân đã cho. A. u 100. u 124. u 500. u 624. 4 B. 4 C. 4 D. 4 q u u q u n 1 n 1 4 Lời giải. Ta có 1 1 5
1 S u . n q 1 . Khi đó n 1 1 1 1 q q 1 q 5 q 5 3 3
u u q 4.5 500 Chọn C. 4 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 37 Tµi liÖu to¸n 11 n¨m häc 2018 3n 1
Câu 39. Cho cấp số nhân u S .
n có tổng n số hạng đầu tiên là n
Tìm số hạng thứ 5 của cấp số nhân đã cho. n 1 3 2 1 5 A. u . u . u 3 . u . 5 B. C. 5 D. 4 3 5 5 3 5 5 5 3 n u 3 1 q u 2 n 1 1 3 1 1 u Lời giải. Ta có 1 3 1 S 1 n q Khi đó n n 1 1 . 1 3 3 1 q q q 3 3 2 4 u u q Chọn A. 5 1 4 3
Câu 40. Cho cấp số nhân u u 2 u 54. n có 2 và 5
Tính tổng 1000 số hạng đầu tiên của cấp số nhân đã cho. 1000 13 1000 3 1 A. S . S . 1000 B. 4 1000 2 1000 3 1 1000 13 C. S . S . 1000 D. 6 1000 6 2
2 u u q 2 1 u Lời giải. Ta có 1 3 . Khi đó 4 3 3 54
u u q u . q q 2q 5 1 1 q 3 1 q 2 1 100 100 100 3 13 S u . . Chọn D. 100 1 1 q 3 1 3 6
Câu 41. Cho cấp số nhân un có tổng của hai số hạng đầu tiên bằng 4 , tổng của ba số hạng đầu tiên bằng 13 . Tính tổng của năm
số hạng đầu tiên của cấp số nhân đã cho, biết công bội của cấp số nhân là một số dương. 181 35 A. S . S 141. S 121. S . 5 B. C. D. 16 5 5 5 16
4 S u u u 1 q 2 1 2 1 Lời giải. 2 q q q q q u Khi đó 13
S u 1q q 41 131 3 0 1. 1 2 3 1 5 5 1 q 13 S u . 1. 121 Chọn C. 5 1 1 q 13 1 1
Câu 42. Một cấp số nhân có số hạng thứ bảy bằng , công bội bằng
. Hỏi số hạng đầu tiên của cấp số nhân bằng bào nhiêu? 2 4 1 A. 4096. B. 2048. C. 1024. D. . 512 1 q 6 4 4
Lời giải. Ta có u 2048 Chọn B. 1 1 u 2 6 1
u u q 7 1 6 2 4
Câu 43. Cho cấp số nhân u u 6 u 486. u 0. n có 2 và 6
Tìm công bội q của cấp số nhân đã cho, biết rằng 3
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 38 Tµi liÖu to¸n 11 n¨m häc 2018 1 1 A. q 3.
B. q .
C. q .
D. q 3. 3 3
6 u u q 2 1 Lời giải. 4 4
q 81 3 q 3. Chọn D. 5 4 4
486 u u q u . q q 6.q 6 1 1
Câu 44. Cho cấp số nhân u ; u ; u ; u 1. 4u 5u 1 2 3 với 1
Tìm công bội q để 2 +
3 đạt giá trị nhỏ nhất? 2 2 A. q .
B. q 0. C. q .
D. q 1. 5 5 2 2 4 4 Lời giải. Ta có 2 2
4u 5u 4u q 5u q 5q 4q 5q . Vậy 2 3 1 1 5 5 5 4 2 min 4u 5u
khi q Chọn A. 2 3 5 5
Câu 45. Một cấp số nhân có số hạng thứ hai bằng 4 và số hạng thứ sáu bằng 64, thì số hạng tổng quát của cấp số nhân đó có thể
tính theo công thức nào dưới đây? A. n 1 u 2 . u n u u n n B. 2n n C. 1 2 . n D. 2 . n
4 u u q u 2 2 1 Lời giải. Ta có 1 n 1 n 1 u u q 2.2 2n. n 1 5 4 4 64
u u q u . q q 4q q 2 6 1 1 Chọn B.
Câu 46. Cho cấp số nhân u q
n có công bội . Mệnh đề nào sau đây đúng? u u A. k 1 u u .q . k k u
u u .u .
u u k –1 q. k 1 B. 1 1 . k C. D. k 1 2 k k 1 k2
Lời giải. Chọn A.
Câu 47. Cho cấp số nhân u u 0 q n có 1 và
0. Đẳng thức nào sau đây là đúng? A. 3
u u .q .
u u .q .
u u .q . 7 4 B. 4 7 4 C. 5 u u .q . D. 6 7 4 7 4 3 u u q Lời giải. 4 1 u 3 u q 3 3
.q u q Chọn A. 7 1 4 6 u u q 7 1
Câu 48. Cho cấp số nhân u u 0 q k m n có 1 và 0. Với 1
, đẳng thức nào dưới đây là đúng?
A. u u . k q . m u u q m k u u q m k u u m k B. . . m k C. . . m k D. .q . m k Lời giải. k 1 m 1 u u q u u q u q q u q Chọn C. m k 1 . m k m k k 1 1 1 k
Câu 49. Cho một cấp số nhân có 15 số hạng. Đẳng thức nào sau đây là sai?
A. u .u u .u .
u .u u .u .
u .u u .u .
u .u u .u . 1 15 2 14 B. 1 15 5 11 C. 1 15 6 9 D. 1 15 12 4 Lời giải. 14 u .u u .u .q m 1 u q n 1 . u q
u .u với m n 16. Chọn C. 1 15 1 1 1 1 m n
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 39 Tµi liÖu to¸n 11 n¨m häc 2018
Câu 50. Cho một cấp số nhân có n số hạng n k
55 . Đẳng thức nào sau đây sai?
A. u .u u .u .
u .u u .u .
u .u u .u .
u .u u .u . 1 n 2 n 1 B. 1 n 5 n4 C. 1 n 55 n 5 5 D. 1 n k nk 1 Lời giải. n 1 u u u .u q u q u q
u u với k m n 1. Chọn C. n
k 1. m 1 . 1 1 1 1 1 k m u 192 6
Câu 51. Tìm số hạng đầu u u .
1 và công bội q của cấp số nhân , n biết u 384 7 u 5 u 6 u 6 u 5 1 1 1 1 A. . B. . C. . D. . q 2 q 2 q 3 q 3 5 q 2 192 u u q 6 1 Lời giải. 192 . Chọn B. 6 384
u u q u q q 192q u 6 7 1 5 1 1 5 q u u 36 4 2
Câu 52. Cho cấp số nhân u . n thỏa mãn
Chọn khẳng định đúng? u u 72 5 3 u 4 u 6 u 9 u 9 1 1 1 1 A. . B. . C. . D. . q 2 q 2 q 2 q 3
u u u q 2 q 2 36 q 1 4 2 1 Lời giải. 36 . 2 72
u u u q 2 q 1 u q 2 q u 6 1 1 q 36q q 2 5 3 1 1 q 1 Chọn B. u 8u 20 17
Câu 53. Cho cấp số nhân u . n thỏa mãn
Chọn khẳng định đúng? u u 272 1 5 A. q 2. B. q 4. C. q 4. D. q 2. 3 19 16 q 8 u 8u u q 8u q 1 1 q 2 Lời giải. 20 17 272 . Chọn A. u u 272 u 1 q 272 u u 16 1 5 1 4 1 4 1 1 q
Câu 54. Một cấp số nhân có năm số hạng mà hai số hạng đầu tiên là các số dương, tích của số hạng đầu và số hạng thứ ba bằng 1, 1
tích của số hạng thứ ba và số hạng cuối bằng
. Tìm số hạng đầu u và công bội q của cấp số nhân đã cho. 16 1 1 u 2 u 2 1 u 1 1 u A. 1 2 . 1 . 1 . 2 . B. C. D. 1 q q q 2 2 2 q 2 u , u 0, 1 1 1 u 0 q 0 q 2 2 Lời giải. 2 2 u .u 1 . u q 1 Chọn B. 1 3 1 1 u 2 1 1 . 1 2 6 2 2 4 4 q u u u q u q q q 3 5 1 1 16 16
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 40 Tµi liÖu to¸n 11 n¨m häc 2018 u
u u 65 1 3 5
Câu 55. Cho cấp số nhân u thỏa . Tính u . n u u 325 3 1 7 A. u 10. B. u 15. C. u 20. D. u 25. 3 3 3 3 u
u u 65 u
u q u q 65 u 2 4 2 4
1q q 65 1 1 1 3 5 1 1 1
Lời giải. Ta có . 6 u u 325 u u q 325 u 6 1 7 1 q 325 2 1 1 1 6 1 q 325 Lấy 2 chia 1 , ta được 2
1 q 5 q 2 . 2 4 1q q 65 u 5 1 u 5 Vậy hoặc 1 2
u u q 5.4 20. Chọn C. q 2 3 1 q 2 u
u u 14 1 2 3
Câu 56. Cho cấp số nhân u thỏa . Tính u . n u .u .u 64 2 1 2 3 A. u 4. B. u 6. C. u 8. D. u 10. 2 2 2 2
Lời giải. Từ u .u .u 64 u .u q.u q 64 u q3 2 64 u q 4 u 4 1 2 3 1 1 1 1 1 hay 2 . u 4 u 14 u u 10 u 8 u 2 1 3 1 3 1 1
Thay vào hệ ban đầu ta được hoặc . u .4.u 64 u .u 16 u 2 u 8 1 3 1 3 3 3 u 8 1 u 2 Vậy 1 hoặc 1
u u q 4. Chọn A. q 2 1 q 2 2
Câu 57. Cho cấp số nhân u có công bội q và thỏa n 1 1 1 1 1 u
u u u u 49 1 2 3 4 5 u u u u u 1 2 3 4 5 . u u 35 1 3 Tính 2
P u 4q . 1 A. P 24. B. P 29. C. P 34. D. P 39. 1 1 1 1 1
Lời giải. Nhận xét: Nếu u , u , u , u , u , , , , 1 2 3 4
5 là một cấp số nhân với công bội q thì
cũng tạo thành cấp số u u u u u 1 2 3 4 5 1 nhân với công bội . q 1 1 5 5 q 1 1 q u . 49 . 1 1 Do đó từ giả thiết ta có q 1 u 1 . 1 1 q 2 u u q 35 2 1 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 41 Tµi liÖu to¸n 11 n¨m häc 2018 5 5 Phương trình q 1 49 q 1 2 4 2 1 u .
u q 49 u q 7 1 . 4 q 1
u q q 1 1 1 1 7 Với 2 u q 7
2 , ta đượ u 7 35 u 42 q 1 . Thay vào c 1 1 . Suy ra 2 : vô lý. 42 u 28 u 28 1 1 Với 2 u q 7
2 , ta đượ u 7 35 u 28 . Khi đó 2 1 . Thay vào c 1 1 . Vậy 1 hoặc 1 u 4q 29. Chọn B. q q 1 2 2 u
u u 26 1 2 3
Câu 58. Cho cấp số nhân u có công bội q và thỏa
. Tìm q biết rằng q 1. n 2 2 2 u
u u 364 1 2 3 5 4 A. q . B. q 4. C. q . D. q 3. 4 3 Lời giải. Ta có 2 u
u u 26 u 2
1 q q 26 2 u 2 1 q q 2 26 1 1 1 1 2 3 . 2 2 2 2 u
u u 364 u 2 4 2 2 4 1 2 3
1 q q 364 u 1 q q 364 2 1 1 Lấy 1 chia 2 , ta được
1q q 2 2 2 26 1 1 4 3 2 2
3q 7q 4q 7q 3 0 3q 7 q 4 0 . 2 4 2 1 q q 364 q q
t 1 loaïi Đặ 1 t t q
, t 2 . Phương trình trở thành 2
3t 7t 10 0 . q 10 t 3 10 1 10 1 Với t , suy ra 2 q
3q 10q 3 0 q 3 hoặc q . Vì q 1 nên q 3. Chọn D. 3 q 3 3
Câu 59. Các số x 6 y, 5x 2 y, 8x y theo thứ tự đó lập thành một cấp số cộng; đồng thời các số x 1, y 2, x 3y theo thứ
tự đó lập thành một cấp số nhân. Tính 2 2 x y . A. 2 2
x y 40. B. 2 2 x y 25. C. 2 2
x y 100. D. 2 2 x y 10.
x 6y8x y 25x 2y
Lời giải. Theo giả thiết ta có x
1 x 3y y 22 x 3y x 3y x 6 . 3 y
1 3y 3y y 22 0 y 22 y 2 Suy ra 2 2
x y 40. Chọn A.
Câu 60. Ba số x; y; z theo thứ tự lập thành một cấp số nhân với công bội q khác 1; đồng thời các số x; 2 y; 3z theo thứ tự lập
thành một cấp số cộng với công sai khác 0. Tìm giá trị của q .
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 42 Tµi liÖu to¸n 11 n¨m häc 2018 1 1 1 A. q . B. q . C. q . D. q 3. 3 9 3 2 y x ; q z xq x 0 Lời giải. 2
x 3xq 4xq x 2
3q 4q x 3z 2 2y 1 0 . 2
3q 4q 1 0
Nếu x 0 y z 0 công sai của cấp số cộng: ;
x 2 y; 3z bằng 0 (vô lí). q 1 1 Nếu 2
3q 4q 1 0 1 q q 1 . Chọn A. q 3 3
Câu 61. Cho dãy số tăng a, b, c c theo thứ tự lập thành cấp số nhân; đồng thời ,
a b 8, c theo thứ tự lập thành cấp số cộng và ,
a b 8, c 64 theo thứ tự lập thành cấp số nhân. Tính giá trị biểu thức P a b 2c. 184 92 A. P . B. P 64. C. P . D. P 32. 9 9 2 2 ac b ac b 1
Lời giải. Ta có a c 2b 8
a2b 16c 2 .
ac 64 b 2 8
ac 64a b 2 8 3
Thay (1) vào (3) ta được: 2 2
b 64a b 16b 64 4a b 4 4. c 8 a
a2b 16c 7
Kết hợp (2) với (4) ta được: 5 4a b 4 4c 60 b 7
Thay (5) vào (1) ta được: c 36 7c
8 c 4c 602 2
9c 424c 3600 0
100 c 36 c . c 9
Với c 36 a 4, b 12 P 4 12 72 64. Chọn B.
Câu 62. Số hạng thứ hai, số hạng đầu và số hạng thứ ba của một cấp số cộng với công sai khác 0 theo thứ tự đó lập thành một cấp
số nhân với công bội q . Tìm q. 3 3 A. q 2. B. q 2. C. q . D. q . 2 2
Lời giải. Giả sử ba số hạng ; a ;
b c lập thành cấp số cộng thỏa yêu cầu, khi đó ; b ;
a c theo thứ tự đó lập thành cấp số nhân công bội . q Ta có
a c 2b b 0 2
bq bq 2b . 2 2 a ; bq c bq
q q2 0
Nếu b 0 a b c 0 nên ; a ;
b c là cấp số cộng công sai d 0 (vô lí). Nếu 2
q q 2 0 q 1 hoặc q 2. Nếu q 1 a b c (vô lí), do đó q 2. Chọn B.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 43 Tµi liÖu to¸n 11 n¨m häc 2018
Câu 63. Cho bố số a, b, c, d biết rằng a, ,
b c theo thứ tự đó lập thành một cấp số nhân công bội q 1 ; còn ,
b c, d theo thứ tự
đó lập thành cấp số cộng. Tìm q biết rằng a d 14 và b c 12. 18 73 19 73 20 73 21 73 A. q . B. q . C. q . D. q . 24 24 24 24
Lời giải. Giả sử a,b, c lập thành cấp số cộng công bội .
q Khi đó theo giả thiết ta có: 2 b
aq, c aq 2
aq d 2aq 1 b d 2c
a d 14 2 a d 14 a 2
q q 12 3 b c 12
Nếu q 0 b c 0 d (vô lí)
Nếu q 1 b a
;c a b c 0 (vô lí). 12 Vậy q 0, q
1, từ (2) và (3) ta có: d 14a và a thay vào (1) ta được: 2 q q 2 3 12q 14q 14q 12 24q 3 2
12q 7q 13q 6 0 2 2 2 q q q q q q q 73 1 19 2
12q 19q 6 0 q 24 19 73
Vì q 1 nên q . Chọn B. 24
Câu 64. Gọi S 9 99 999 ... 999...9 ( n số 9 ) thì S nhận giá trị nào sau đây? 10n 1 10n 1 A. S . B. S 10 . 9 9 10n 1 10n 1 C. S 10 . n S 10 . n D. 9 9 Lời giải. Ta có 9 99 999 ... 99...9 10 1 2 10 1 ... 10n S 1 n so 9 n 1 10n 2
10 10 ...10 n 10. . n Chọn C. 110
Câu 65. Gọi S 111111... 111...1 ( n số 1) thì S nhận giá trị nào sau đây? 10n 1 10n 1 A. S . B. S 10 . 81 81 10n 1 1 10n 1 C. S 10 . n S 10 n . D. 81 9 9
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 44 Tµi liÖu to¸n 11 n¨m häc 2018 1 1 110n
Lời giải. Ta có S 9 99 999 ... 99...9 . 10.
n . Chọn D. 9 n so 9 9 110 21.3b b Câu 66. Biết rằng 2 10
S 1 2.3 3.3 ...11.3 a
. Tính P a . 4 4 A. P 1. B. P 2. C. P 3. D. P 4.
Lời giải. Từ giả thiết suy ra 2 3 11
3S 3 2.3 3.3 ...11.3 . Do đó 11 11 13 1 21.3 1 21 2 10 11 11 11
2S S 3S 133 ...3 10.3 11.3 S .3 . 13 2 2 4 4 11 1 21.3 21.3b 1 1 11 Vì S a
a , b 11 P 3. Chọn C. 4 4 4 4 4 4
Câu 67. Một cấp số nhân có ba số hạng là ,
a b, c (theo thứ tự đó) trong đó các số hạng đều khác 0 và công bội q 0. Mệnh đề nào sau đây là đúng? 1 1 1 1 1 1 1 1 2 A. . B. . C. . D. . 2 a bc 2 b ac 2 c ba a b c 1 1 Lời giải. Ta có 2 ac b Chọn B. 2 b ac
Câu 68. Bốn góc của một tứ giác tạo thành cấp số nhân và góc lớn nhất gấp 27 lần góc nhỏ nhất. Tổng của góc lớn nhất và góc bé nhất bằng: A. 0 56 . B. 0 102 . C. 0 252 . D. 0 168 .
Lời giải. Giả sử 4 góc A, B, C, D (với A B C D ) theo thứ tự đó lập thành cấp số nhân thỏa yêu cầu với công bội . q Ta có q A B C D 360 A 3 2 3
1 q q q 360 A 9
A D 252. 3 D 27 A Aq 27A 3
D Aq 243 Chọn C.
Câu 69. Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nữa diện tích của mặt trên của tầng
ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của đế tháp (có diện tích là 2
12 288 m ). Tính diện tích mặt trên cùng. A. 2 6 m . B. 2 8 m . C. 2 10 m . D. 2 12 m . 1 12 288
Lời giải. Diện tích bề mặt của mỗi tầng (kể từ 1) lập thành một cấp số nhân có công bội q và u 6 144. Khi đó 2 1 2
diện tích mặt trên cùng là 6144 10 u u q 6 Chọn A. 11 1 10 2
Câu 70. Một du khách vào chuồng đua ngựa đặt cược, lần đầu đặt 20000 đồng, mỗi lần sau tiền đặt gấp đôi lần tiền đặt cọc trước.
Người đó thua 9 lần liên tiếp và thắng ở lần thứ 10. Hỏi du khác trên thắng hay thua bao nhiêu? A. Hòa vốn. B. Thua 20000 đồng.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 45 Tµi liÖu to¸n 11 n¨m häc 2018
C. Thắng 20000 đồng. D. Thua 40000 đồng.
Lời giải. Số tiền du khác đặt trong mỗi lần (kể từ lần đầu) là một cấp số nhân có u 20 000 và công bội q 2. 1
Du khách thua trong 9 lần đầu tiên nên tổng số tiền thua là: u 9 1 p 1
S u u ... u 10220000 9 1 2 9 1 p
Số tiền mà du khách thắng trong lần thứ 10 là 9
u u . p 10240000 10 1
Ta có u S 20 000 0 nên du khách thắng 20 000. Chọn C. 10 9
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 46
Document Outline
- BÀI 1. CHỨNG MINH QUY NẠP DÃY SỐ
- BÀI 1. ĐÁP ÁN (1)
- BÀI 2. DÃY SỐ
- BÀI 2. ĐÁP ÁN
- BÀI 3. CẤP SỐ CỘNG - CẤP SỐ NHÂN
- BÀI 3. ĐÁP ÁN CẤP SỐ CỘNG - CẤP SỐ NHÂN




