Chuyên đề trắc nghiệm mặt cầu, hình cầu và khối cầu Toán 12

Tài liệu gồm 53 trang, trình bày lý thuyết trọng tâm, các dạng toán trọng tâm kèm phương pháp giải và bài tập trắc nghiệm tự luyện chuyên đề mặt cầu, hình cầu và khối cầu.Mời các bạn đón xem.

66 33 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Mặt nón, mặt trụ, mặt cầu

Môn: Toán 12

Thông tin:

53 trang 8 tháng trước

Tác giả:

Profile Lan Tường
CHỦ ĐỀ 10. MẶT CẦU - HÌNH CẦU - KHỐI CẦU
I. LÝ THUYẾT TRỌNG TÂM
1. Mặt cầu
Tập hợp các điểm trong không gian cách điểm
O
cố định một khoảng
R
không đổi gọi là mặt cầu có tâm
là
O
và bán kính bằng
R
. Kí hiệu:
(
)
{
}
;.S O R M OM R= =
2. Khối cầu
Mặt cầu
( )
;
S OR
cùng với các điểm nằm bên trong nó được gọi là một khối cầu tâm
O
, bán kính
R
. Kí
hiệu:
(
)
{ }
;.B O R M OM R= ≤
Nếu
,
OA OB
là hai bán kính của mặt cầu sao cho
,,AOB
thẳng hàng thì đoạn thẳng
AB
gọi là đường
kính của mặt cầu.
Định lí: Cho điểm cố định A, B. Tập hợp các điểm M trong không gian sao
cho
là mặt cầu đường kính AB .
•
( )
;.A S O R OA R
∈ ⇔=
•
11
OA R A<⇔
nằm trong mặt cầu.
•
22
OA R A>⇔
nằm ngoài mặt cầu.
3. Mặt cầu ngoại tiếp khối đa diện
Định nghĩa: Mặt cầu đi qua mọi đỉnh của một hình đa diện
( )
H
được gọi
là mặt cầu ngoại tiếp hình đa diện
( )
H
và khi đó
( )
H
được gọi là nội tiếp
mặt cầu đó.
Điều kiện cần và đủ để một hình chóp có mặt cầu ngoại tiếp là đáy của nó
là một đa giác nội tiếp một đường tròn.
Mọi tứ diện đều có mặt cầu ngoại tiếp.
4. Mặt cầu ngoại tiếp khối đa diện
a. Mặt cầu nội tiếp hình chóp là mặt cầu nằm bên trong hình chóp và tiếp xúc với với tất các mặt của hình
chóp.
b. Tâm mặt cầu nội tiếp hình chóp cách đều tất cả các mặt của hình chóp.
5. Vị trí tương đối giữa mặt cầu và mặt phẳng
Cho mặt cầu
( )
;S OR
và mặt phẳng
( )
P
, gọi d là khoảng cách từ O đến
( )
P
và H là hình chiếu vuông
góc của O trên
( )
P
. Khi đó
• Nếu
dR<
thì mặt phẳng (P) cắt mặt cầu
( )
;S OR
theo giao tuyến là đường tròn nằm trên mặt
phẳng
(
)
P
có tâm là H và có bán kính
22
.r Rd= −
Khi
0d =
thì mặt phẳng (P) đi qua tâm O của mặt cầu, mặt phẳng đó gọi là mặt phẳng kính; giao
tuyến của mặt phẳng kính với mặt cầu là dường tròn có tâm O và bán kính R, đường tròn đó gọi là đường
tròn lớn của mặt cầu.
• Nếu
dR=
thì mặt phẳng
( )
P
và mặt cầu
( )
;S OR
có một điểm chung duy nhất H.
Khi đó ta nói
( )
P
tiếp xúc với
( )
;S OR
tại H và
( )
P
gọi là tiếp diện của mặt cầu, H gọi là tiếp diện.
Chú ý. Cho H là một điểm thuộc mặt cầu
( )
;S OR
và mặt phẳng
( )
P
qua H . Thế thì
( )
P
tiếp xúc với
( ) ( )
;.S O R OH P⇔⊥
• Nếu
dR>
thì mặt phẳng
( )
P
và mặt cầu
( )
;S OR
không có điểm chung.
6. Vị trí tương đối giữa mặt cầu và đường thẳng
Cho mặt cầu
( )
;S OR
và đường thẳng
∆
. Gọi H là hình chiếu vuông góc của O trên
∆
và
d OH=
là
khoảng cách từ O đến
∆
. Khi đó:
• Nếu
dR<
thì
∆
cắt
( )
;S OR
tại hai điểm
,AB
và H là trung điểm của AB.
• Nếu
dR=
thì
∆
và
( )
;S OR
chỉ có một điểm chung H, trong trường hợp này
∆
được gọi là tiếp
tuyến của mặt cầu
( )
;S OR
hay
∆
tiếp xúc với
( )
;S OR
và H là tiếp điểm.
• Nếu
dR>
thì
∆
và
( )
;S OR
không có điểm chung.
7. Diện tích mặt cầu và thể tích khối cầu
Gọi R là bán kính của mặt cầu thì
• Diện tích mặt cầu:
2
4.SR
π
=
• Thể tích khối cầu:
2
4
.
3
VR
π
=
8. Một số công thức tính nhanh bán kính đường tròn ngoại tiếp
Tam giác đều cạnh
3
2
a
aR → =
Hình vuông cạnh
2
2
a
aR → =
Tam giác vuông cạnh huyền
2
b
bR → =
Hình chữ nhật đường chéo
2
d
dR
→ =
Tam giác vuông cân cạnh
2
2
a
aR → =
Định lí hàm sin:
2
sin sin sin
abc
R
ABC
= = =
Tam giác ba cạnh
,, ;
4
abc
abc R
S
→ =
với
( )( )( )
S pp a p b p c= −−−
và
.
2
abc
p
++
=
II. CÁC DẠNG TOÁN THƯỜNG GẶP VỀ MẶT CẦU
Dạng 1: Những bài toán vận dụng mức cơ bản
Ví dụ 1: Tính thể tích khối cầu có diện tích bằng diện tích xung quanh của hình lập phương cạnh a.
A.
3
6
a
π
B.
3
32
3
a
π
C.
3
a
π
D.
3
4
3
a
π
Lời giải
Diện tích xung quanh hình lập phương cạnh a là
22
44
xq mc
Sa Sa= → =
Suy ra bán kính mặt cầu là
2
22 2
44
aa
RaR R
π
π
π
= ⇔ = ⇒=
Vậy thể tích khối cầu cần tính là
3
2
44
.
3
3
a
VR
π
π
= =
Chọn D.
Ví dụ 2: Cho mặt cầu
( )
;S OR
và mặt phẳng
( )
α
. Biết khoảng cách từ O đến
( )
α
bằng
2
R
. Khi đó thiết diện
tạo bởi mặt phẳng
( )
α
với
( )
;S OR
là một đường tròn đường kính bằng
A.
.R
B.
3.R
C.
.
2
R
D.
3
.
2
R
Lời giải
Hình vẽ tham khảo
Gọi H là hình chiếu của O xuống mp
(
)
α
. Ta có
( )
( )
;
2
R
d O OH R
α
= = <
nên
( )
α
cắt
( )
;S OR
theo
đường tròn
( )
;CHr
. Bán kính đường tròn
( )
;CHr
là
22
3
.
2
R
r R OH
=−=
Suy ra dường kính của đường tròn cần tính bằng
3
.
2
R
Chọn B.
Ví dụ 3:
Cho mặt cầu
(
)
;S OR
và một điểm A thỏa mãn
2.OA R=
Qua A kẻ đường thẳng cắt
(
)
S
tại hai
điểm B, C sao cho
Khoảng cách từ O đến BC bằng
A.
.R
B.
.
2
R
C.
2.R
D.
3.R
Lời giải
Gọi H là hình chiếu của O lên BC.
Ta có
,OB OC R= =
suy ra H là trung điểm của BC nên
3
.
22
CD R
HC = =
Suy ra
22
.
2
R
OH OC HC= −=
Chọn B.
Ví dụ 4: Cho hình cầu tâm O, đường kính
' 4.
AA =
Gọi H là một điểm trên đoạn
'AA
sao cho
8
.
3
AH =
Mặt phẳng
( )
α
qua H và vuông góc với
'
AA
cắt hình cầu theo đường tròn
( )
C
. Tính diện tích của đường
tròn
( )
C
.
A.
32
.
9
π
B.
8
.
9
π
C.
8
.
3
π
D.
32
.
3
π
Lời giải
Theo giả thiết, ta có
8
.
3
AH =
Ta suy ra
2
.
3
OH AH OA= −=
Gọi
'r
là bán kính của đường tròn
(
)
C
. Ta có
2
22 22
2 32
' 2.
39
r r OH

=−=−=


Vậy diện tích cùa đường tròn
( )
C
là
2
32
'.
9
Sr
π
π
= =
Chọn A.
Ví dụ 5: Diện tích hình tròn lớn của một hình cầu là
4.
π
Một mặt phẳng
( )
α
cắt hình cầu theo một hình
tròn có diện tích là
2.
π
Khoảng cách từ tâm mặt cầu đến mặt phẳng
( )
α
bằng
A.
2
.
4
B.
1.
C.
2
.
2
D.
2.
Lời giải
Gọi khoảng cách từ tâm cầu đến mặt phẳng là d, ta có
2 22
.d Rr= −
Hình tròn lớn của hình cầu S là hình tròn tạo bởi mặt phẳng cắt hình cầu và đi qua tâm của hình cầu.
Gọi R là bán kính hình cầu thì hình tròn lớn cũng có bán kính là R .
Theo giả thiết, ta có
2
42RR
ππ
= ⇔=
và
2
22rr
ππ
= ⇔=
.
Suy ra
( )
2
22 2
2 2 2.d Rr= −= − =
Chọn D.
Ví dụ 6: Cho mặt cầu
( )
;S OR
, A là một điểm ở trên mặt cầu
( )
S
và
( )
P
là mặt phẳng đi qua A sao cho
góc giữa đường thẳng OA và mặt phẳng
( )
P
bằng
0
60 .
Diện tích của đường tròn giao tuyến bằng
A.
2
3
.
4
R
π
B.
2
.R
π
C.
2
.
4
R
π
D.
2
.
2
R
π
Lời giải
Hình vẽ tham khảo
Gọi H là hình chiếu vuông góc của O trên
( )
P
thì
• H là tâm của đường tròn giao tuyến của
( )
P
và
( )
S
.
•
(
)
( )
( )
0
; ;AH 60 .OA P OA= =
Bán kính của đường tròn giao tuyến
0
.cos 60 .
2
R
r HA OA= = =
Suy ra diện tích dường tròn giao tuyến
2
2
2
.
24
RR
r
π
ππ

= =


Chọn C.
Ví dụ 7: Cho mặt cầu
( )
;S IR
, mặt phẳng
( )
P
cắt mặt cầu
( )
S
theo giao tuyến là một đường tròn tâm O.
Hai điểm
,AB O∈
sao cho tam giác OAB đều, góc giữa hai mặt phẳng
( )
IAB
và
( )
OAB
bằng
0
60 ,
diện
tích tam giác IAB bằng
3
.
2
Bán kính R bằng
A.
3
.
2
R =
B.
2
.
2
R =
C.
13
.
2
R =
D.
5
.
2
R
=
Lời giải
Đặt
.OA OB x= =
Tam giác OAB là tam giác đều
2
3
.
4
OAB
x
S
∆
=
Mặt phẳng
( )
OAB
là hình chiếu của mặt phẳng
( )
IAB
trên mặt phẳng
( )
P
.
.cos
OAB IAB
SS
ϕ
∆∆
=
với
(
) ( )
0
; 60IAB OAB
ϕ
= =
.
2
3 33
1.
24 44
IAB
OAB
S
x
Sx
∆
∆
= = ⇒ = ⇔=
Gọi M là trung điểm của AB
0
3
60 .
2
IMO IO⇒ = ⇒=
Vậy
2
22 2
3 13
1.
22
R IA IO AO

= = + = +=


Chọn C.
Ví dụ 8: Cho mặt cầu
(
)
S
tâm
I
, bán kính
R
. Ba mặt phẳng
( ) ( ) ( )
,,PQR
qua điểm
A
không nằm trên mặt
cầu, đôi một vuông góc với nhau cắt mặt cầu
( )
S
theo thiết diện là ba hình tròn có tổng diện tích bằng
3
12 .cm
π
Biết
3 ,IA cm=
tính độ dài bán kính R của mặt cầu
( )
S
.
A.
2 3.r =
B.
5.r =
C.
3.r =
D.
2.r
=
Lời giải
Gọi
,,abc
lần lượt là khoảng cách từ I đến mặt phẳng
( ) ( ) ( )
,,PQR
.
Gọi
123
,,rrr
lần lượt là bán kính đường tròn giao tuyến của mặt cầu
( )
S
với
( ) ( ) (
)
,,PQR
.
Khi đó
( )
2 222 222 22 2 222 222
1 2 3 1 23
; ; 3 (*).R a rR b rR c r R a b c r r r=+ =+ =+⇒ =+++ ++
Mà
(
)
222 2 222
123 1 23
;.abc IASSS rrr
π
++= ++= ++
Suy ra (*)
22
123
3 3 12 15 5.
SSS
R IA R
π
++
⇔ = + =+ = ⇒=
Chọn B.
Dạng 2: Đa diện có các đỉnh cùng nhìn một đoạn nối hai đỉnh còn lại dưới góc vuông
Phương pháp giải:
Xét đa giác
12
...
n
XYA A A
có các đỉnh
12
, ,...,
n
AA A
cùng nhìn XY một góc vuông, chẳng hạn có
0
12
... 90 .A XY A XY= = =
Khi đó, mặt cầu ngoại tiếp đa diện
12
...
n
XYA A A
mặt cầu đường kính XY, tâm là
trung điểm của XY và bán kính
.
2
XY
R =
Ví dụ 1: Cho hình chóp
.S ABC
có đáy là tam giác
, 3, 2 .ABC BC a AC a= =
Cạnh bên SA vuông góc với
đáy và
.SA a=
Góc giữa đường thẳng SB và mặt phẳng
( )
ABC
bằng
0
45 .
Bán kính mặt cầu ngoại tiếp
hình chóp
.S ABC
bằng
A.
5
.
2
a
B.
3
.
2
a
C.
.
2
a
D.
2
.
2
a
Lời giải
Vì
( )
SA ABC
⊥
nên
( )
( )
0
;( ) ; 45 .SB ABC AB AB SBA= = =
Suy ra tam giác SAB vuông cân tại
.A SA AB a → = =
Ta có
( )
2
2 22 2 2
34AB BC a a a AC ABC+ = + = = ⇒∆
vuông tại B.
Do đó
AB BC⊥
mà
( )
BC SA BC SAB BC SB
⊥⇔ ⊥ ⇒ ⊥
Khi đó, hai điểm A, B cùng nhìn SC dưới một góc vuông
Vậy bán kính mặt cầu ngoại tiếp cần tính là
5
.
22
SC a
R = =
Chọn A.
Ví dụ 2: Cho hình chóp
.S ABC
có
2
SC a=
và
( )
SC ABC⊥
. Đáy ABC là tam giác vuông cân tại B có
2.AB a=
Mặt phẳng
( )
α
đi qua C và vuông góc với
(
)
,SA
α
cắt
,SA SB
lần lượt tại
,.
DE
Diện tích mặt
cầu ngoại tiếp khối đa diện ECDAB bằng
A.
2
16 .a
π
B.
2
4.a
π
C.
2
8.
a
π
D.
2
12 .a
π
Lời giải
Ta có
( )
SC AB
AB SBC CE AB
BC AB
⊥
⇒ ⇒⊥
⊥
Mà
( )
SA SA CE
α
⊥ ⇒⊥
suy ra
( )
,
CE SB
CE SAB
CE AE
⊥
⊥⇒
⊥
Do đó các điểm
,,BDE
nhìn AC dưới một góc vuông
⇒
Tâm mặt cầu ngoại tiếp khối đa diện là trung điểm AC
2
2
4.
22
AC AB
R a Sa
π
⇒ = = = → =
Chọn B.
Ví dụ 3: Cho hình chóp
.S ABCD
có đáy ABCD là hình vuông tâm
,.O BD a=
Hình chiếu vuông góc của S
trên mặt đáy
()ABCD
là trung điểm của OC. Đường thẳng SC tạo với mặt đáy một góc
0
60 .
Thể tích khối
cầu ngoại tiếp hình chóp
.S ABCD
bằng
A.
3
4
.
3
a
π
B.
3
.
3
a
π
C.
3
2
.
3
a
π
D.
3
.
6
a
π
Lời giải
Gọi H là trung điểm của
(
)
,
24
OC a
OC SH ABCD HC⇒⊥ = =
Ta có
( )
( )
0
; ; 60SC ABCD SC HC SCH= = =
Tam giác SHC vuông tại H, có
cos
2
HC a
SCH SC
SC
= ⇒=
Lại có
SH OC SOC⊥ ⇒∆
cân tại
2
a
S SO SC⇒==
Do đó
SO OA OC= =
mà
OA OB OC OD
= = =
Suy ra O là tâm mặt cầu ngoại tiếp hình chóp
.S ABCD
Vậy
3
3
4
.
22 3 6
BD a a
R VR
π
π
= = → = =
Chọn D.
Ví dụ 4: Cho hình chóp
.S ABCD
có đáy ABCD là hình vuông cạnh
2 2.
Cạnh bên
SA
vuông góc với
mặt phẳng đáy và
3.SA =
Mặt phẳng qua A và vuông góc SC với cắt các cạnh
,,SB SC SD
lần lượt tại các
điểm
, ,.MNP
Tính thể tích V của khối cầu ngoại tiếp tứ diện
..C MNP
A.
64 2
.
3
V
π
=
B.
125
.
6
V
π
=
C.
32
.
3
V
π
=
D.
108
.
3
V
π
=
Lời giải
Ta có
( )
SC AMNP SC AM⊥ ⇒⊥
mà
AM SB⊥
0
90 .AM MC AMC⇒⊥⇒ =
Tương tự
0
90APC =
Mặt khác
0
90ANC
=
nên tâm mặt cầu ngoại tiếp tứ diện
.C MNP
là trung
điểm của AC
Suy ra
3
4 32
2.
2 33
AC
R VR
ππ
= =⇒= =
Chọn C.
Ví dụ 5: Cho hình chóp
.S ABCD
có đáy ABCD là hình vuông cạnh
2 2,
cạnh bên
SA
vuông góc với mặt
phẳng đáy
( )
ABCD
. Mặt phẳng
( )
α
qua A và vuông góc với SC, cắt các cạnh
,,SB SC SD
lần lượt tại các
điểm
, ,.MNP
Tính thể tích V của khối cầu ngoại tiếp tứ diện
.,C MNP
biết khoảng cách từ A đến mặt
phẳng
( )
SBD
bằng
6
13
A.
3.
V
π
=
B.
8
.
3
V
π
=
C.
9
.
2
V
π
=
D.
4
.
3
V
π
=
Lời giải
Ta có:
BC AB
BC AM
BC SA
⊥
⇒⊥
⊥
Mặt khác:
( )
AM SC AM SBC AM MN⊥⇒⊥ ⇒⊥
Tương tự
AP PN
⊥⇒
tứ giác
AMNP
nội tiếp đường tròn
đường kính
2
MNP AMNP
AN
AN R R⇒= =
Gọi O là tâm hình vuông ABCD, dựng
6
13
AE SO AE⊥⇒=
Do đó
22 2
111
23
2
AC
AO SA
AE SA AO
==⇒=+⇒=
22
2
.
22
. 12 6 9 3
;
5 5 5 42
MPN S MPN MNP
SA AC SA SN
AN R SN R R
SC
SA AC
⇒= =⇒ = = =⇒ = + =
+
3
.
49
.
32
S MPN
VR
π
π
⇒==
Chọn C.
Dạng 3: Bài toán mặt cầu với chóp có cạnh bên vuông góc đáy
Xét khối chóp
.S ABC
có
( )
SA ABC⊥
. Tìm tâm và tính bán kính mặt cầu ngoại tiếp khối chóp
.S ABC
.
Dựng tâm. Dựng trục đường tròn ngoại tiếp d của tam
giác
ABC
, thì
//d SA
Trong mặt phẳng
( )
;SA d
, dựng đường trung trực
∆
của
SA. Tâm I của mặt cầu là giao điểm của d và
∆
.
Tính bán kính
R
của mặt cầu
Gọi O là tâm đường tròn ngoại tiếp
ABC∆
.
Gọi E là trung điểm của SA.
Xét
AOI∆
vuông tại O
Ta có
2
2222222
.
2
SA
R AI OA OI OA AE OB

==+=+ = +


với
d
OA R=
là bán kính đường tròn ngoại tiếp đáy.
Khi đó:
2
2
.
.
4
S ABC d
SA
RR= +
Tổng quát: Cho khối chóp
12
. ...
n
S AA A
có
12
.SA AA A⊥
Gọi
d
R
là bán kính đường tròn ngoại tiếp đa
giác
12
...
n
AA A A
thì bán kính mặt cầu ngoại tiếp R của khối chóp
12
. ...
n
S AA A
được tính theo công thức:
2
2
.
4
d
SA
RR= +
Ví dụ 1: Cho hình chóp
.S ABC
có đáy ABC là tam giác vuông tại
, , 3.A AB a AC a= =
Cạnh bên SA
vuông góc với đáy. Góc giữa đường thẳng SB và mặt phẳng
( )
ABC
bằng
0
60 .
Bán kính mặt cầu ngoại tiếp
hình chóp
.S ABC
bằng
A.
3
.
2
a
R =
B.
.Ra=
C.
5
.
2
a
R =
D.
7
.
2
a
R =
Lời giải
Ta có
( )
00
; 60 tan 60 . 3.SB ABC SBA SA AB a= = ⇒= =
Tam giác ABC vuông tại
222
2A AB AC BC BC a⇒ + = ⇒=
.
Hình chóp
.S ABC
có chiều cao
3;ha=
bán kính
2
day
BC
Ra= =
⇒
Bán kính mặt cầu cần tính là
( )
2
2
3
7
.
42
a
a
Ra
=+=
Chọn D.
Ví dụ 2: Cho hình chóp
.S ABC
có đáy ABC là tam giác đều có diện tích bằng
2
3.a
Cạnh bên SA vuông
góc với đáy. Diện tích tam giác SBC bằng
2
2.a
Thể tích khối cầu ngoại tiếp hình chóp
.S ABC
là
A.
57
.
6
a
R =
B.
3
.
2
a
R =
C.
5
.
2
a
R =
D.
34
.
3
a
R =
Lời giải
Đặt
2
2
3
3 2.
4
ABC
x
AB x S a x a
∆
= → = = ⇒ =
Gọi H là trung điểm của
BC AH BC⇒⊥
mà
SA BC⊥
Suy ra
(
)
2
1
.2
2
SBC
BC SAH BC SH S SH BC a
∆
⊥ ⇒⊥⇒ = =
2 22
1
.2 2 2 .
2
SH a a SH a SA SH AH a⇒ = ⇒ =⇒= − =
Hình chóp
.S ABC
có chiều cao
;
h SA a= =
bán kính
23
3
day
a
R =
⇒
Bán kính mặt cầu cần tính là
( )
2
2
23
57
.
3 46
a
aa
R = +=
Chọn A.
Ví dụ 3: Cho hình chóp
.S ABCD
có đáy ABCD là hình vuông, cạnh bên
2SA a=
và SA vuông góc với
mặt phẳng đáy, tam giác SBD là tam giác đều. Thể tích khối cầu ngoại tiếp hình chóp
.S ABCD
bằng
A.
3
4
.
3
a
B.
3
43 .
a
C.
3
6.a
D.
3
2.a
Lời giải
Đặt
2
AB x BD x= → =
và
2 2 22
2SB SA AB x a= +=+
Tam giác SBD đều
22
22
2
x xa
SB BD x a
= +
⇒ = → =
Hình chóp
.
S ABCD
có chiều cao
2;ha=
bán kính
day
Ra=
⇒
Bán kính mặt cầu cần tính là
( )
2
2
2
6
.
42
a
a
Ra=+=
Vậy thể tích khối cầu là
3
3
46
. 6.
32
a
Va
π

= =



Chọn C.
Ví dụ 4: Cho hình chóp
.S ABCD
có đáy là hình vuông, cạnh a, SA vuông góc với đáy và SC tạo với mặt
phẳng
( )
SAB
một góc
0
30 .
Diện tích mặt cầu ngoại tiếp hình chóp
.S ABCD
bằng
A.
.a
B.
3.a
C.
2.a
D.
2.a
Lời giải
Ta có
( ) (
)
(
)
( )
;;
SA BC
CB SAB SC SAB SC SB CSB
AB BC
⊥
⇒⊥ ⇒ = =
⊥
Tam giác SBC vuông tại
tan 3
BC
B CSB SB a
SB
⇒ = ⇒=
Tam giác SAB vuông tại
22
2A SA SB AB a⇒= − =
Vậy
22
2;
22 2
d
BD AB a
h SA a R= = = = =
nên
.Ra=
Chọn A.
Ví dụ 5: Cho hình chóp
.S ABC
có đáy ABC là tam giác vuông tại
0
, , 30 .A AB a ACB= =
Cạnh bên SA
vuông góc với đáy. Góc giữa đường thẳng SB và mặt phẳng
( )
ABC
bằng
0
45 .
Bán kính mặt cầu ngoại tiếp
hình chóp
.S ABC
bằng
A.
5
.
4
a
B.
5
.
2
a
C.
3
.
2
a
D.
2
.
2
a
Lời giải
Ta có
( )
( )
( )
0
;( ) ; 45 .SA ABC SB ABC SB AB SBA⊥⇒ = ==
Tam giác SAB vuông tại
A
, có
0
45
SBA SA AB a
= ⇒= =
.
Tam giác ABC vuông tại
A
, có
sin 2 .
AB
ACB AC a
AC
=⇒=
Suy ra bán kính đường tròn ngoại tiếp
ABC∆
là
.
2
ABC
AC
Ra
∆
= =
Vậy bán kính mặt cầu cần tính là
22
22
5
.
4 42
ABC
SA a a
RR a
∆
= + = +=
Chọn B.
Ví dụ 6: Cho hình chóp
.S ABCD
có đáy ABCD là hình vuông. Cạnh bên SA vuông góc với mặt phẳng đáy.
Góc giữa hai mặt phẳng
( )
SCD
và
(
)
ABCD
bằng
0
45 .
Bán kính mặt cầu ngoại tiếp khối chóp
.S ABCD
bằng
6
.
2
a
Diện tích tam giác SAB bằng
A.
2
.
2
a
B.
2
.
4
a
C.
2
.a
D.
2
2.a
Lời giải
Vì
(
) (
)
( )
(
)
( )
0
; ; 45 .CD SAD SCD ABCD SD AD SDA
⊥⇒ = ==
Tam giác SAD vuông tại A, có
0
45 .SDA SA AD x
= ⇒= =
Bán kính đường tròn ngoại tiếp ABCD là
2
.
22
ABCD
AC x
R = =
Bán kính mặt cầu là
2
2
3
.
42
ABCD
SA x
RR= +=
Mà
.
6 36
2.
2 22
S ABCD
a xa
R xa= ⇒ = ⇔=
Vậy
2
2
.
2
SAB
x
Sa
∆
= =
Chọn C.
Ví dụ 7: Cho mặt cầu
( )
S
có bán kính
3R =
đi qua điểm A cố định. Xét các điểm
,,
BCD
thuộc
( )
S
sao
cho
,,AB AC AD
đôi một vuông góc với nhau. Thể tích của khối tứ diện ABCD có giá trị lớn nhất bằng
A.
8
.
3
B.
4.
C.
4
.
3
D.
8.
Lời giải
Vì
,,,ABC D
thuộc
( ) (
)
SS⇒
ngoại tiếp tứ diện ABCD.
Tứ diện ABCD có chiều cao
;
h AD=
đáy là tam giác ABC.
Đặt
,,
AB a AC b AD c h c= = =⇒=
và
22
22
day
BC a b
R
+
= =
⇒
Bán kính mặt cầu ngoại tiếp tứ diện ABCD là
2
22 2 222
222
3 12
24 2
ab c abc
R abc

+ ++
= + = = ⇒++=



Ta có
(
)
2
222
3
4
12 3 8 .
63
ABCD
abc
a b c abc abc V= + + ≥ ⇔ ≤ → = ≤
Chọn C.
Bài toán tổng quát: Tứ diện ABCD,
,,AB AC AD
đôi một vuông góc và
,,
AB a AC b AD c= = =
thì bán
kính mặt cầu ngoại tiếp tứ diện là
222
2
abc
R
++
=
Ví dụ 8: Cho hình chóp
.S ABCD
có đáy ABCD là hình thoi cạnh
0
, 60a BAD =
và các cạnh bên
0
, 90 .SA SB SD BSD= = =
Bán kính mặt cầu ngoại tiếp tứ diện
.S ABCD
là
A.
6
.
4
a
R =
B.
6
.
2
a
R =
C.
3
.
4
a
R =
D.
2
.
4
a
R
=
Lời giải
Vì
SA SB SD
= =
và
ABD
∆
đều cạnh
.a S ABD →
là hình chóp tam giác đều.
Mặt khác
0
90 , ,BSD SB SD SA SB SD= ⇒⊥⇒
đôi một vuông góc và bằng
2
.
2
a
Áp dụng công thức giải nhanh, ta được
22 2
.
6
.
24
S ABD
SA SB SD a
RR
++
= = =
Chọn A.
Ví dụ 9: Cho ba tia
,,Ox Oy Oz
đôi một vuông góc với nhau. Gọi C là điểm cố định trên Oz, đặt
1,OC =
các điểm
,AB
thay đổi trên
,Ox Oy
sao cho
.OA OB OC+=
Giá trị bé nhất của bán kính mặt cầu ngoại
tiếp tứ diện OACB bằng
A.
min
6
.
4
R =
B.
min
6
.
3
R =
C.
min
6.R =
D.
min
6
.
2
R =
Lời giải
Đặt
,
OA a OB b= =
với
,0
ab>
suy ra
1.OA OB OC a b+ = ⇔+=
Bán kính mặt cầu ngoại tiếp tứ diện OACB (
,,OA OB OC
đôi một vuông góc) là
( )
2 2 2 22
2
22
11 1
1 1 2 22
2 22 2
OA OB OC a b
R a a aa
+ + ++
= = = + − += − +
Dễ thấy
2
22
1 33 3 23 6
1 1 ..
2 44 2 2 2 4
aa a aa R

−+= − + ≥ ⇒ −+≥ ⇒ ≥ =


Dấu bằng xảy ra khi và chỉ khi
1
.
2
ab= =
Vậy giá trị bé nhất cần tìm là
6
.
4
Chọn A.
Ví dụ 10: Cho lăng trụ đứng
. ' ' ',
ABC A B C
cạnh
, 3, ' 2AB AC a BC a AA a= = = =
. Bán kính mặt cầu
ngoại tiếp tứ diện
' 'C
AB C
bằng
A.
.Ra=
B.
5.Ra=
C.
3.Ra=
D.
2.Ra=
Lời giải
Dễ thấy tâm mặt cầu ngoại tiếp tứ diện
' 'CAB C
cũng là tâm mặt cầu ngoại tiếp khối lăng trụ
.'' 'ABC A B C
hay là tâm mặt cầu ngoại tiếp khối chóp
'. .A ABC
Sử dụng công thức tính nhanh, ta được
( )
22
2
2
'
.
44
ABC
h AA
Rr R
∆
= += +
Ta có
2 2 2 22 2
0
2
31
cos 120 .
2. . 2 2
AB AC BC a a a
BAC BAC
AB AC a
+ − +−
= = =−⇒ =
0
3
.
2.sin120
2sin
ABC
BC a
Ra
BAC
∆
⇒= = =
Khi đó
( )
2
2
'
2.
4
ABC
AA
RR a
∆
= +=
Chọn D.
Ví dụ 11: Cho hình lăng trụ đứng
.'' 'ABC A B C
có đáy ABC là tam giác vuông cân tại
,.B AB a=
Góc giữa
hai mặt phẳng
(
)
'A BC
và
( )
ABC
bằng
0
60 .
Thể tích khối cầu ngoại tiếp lăng trụ
.'' 'ABC A B C
bằng
A.
3
55
.
8
a
π
B.
3
55
.
6
a
π
C.
3
33
.
6
a
π
D.
3
33
.
8
a
π
Lời giải
Ta có
( )
'
''
AA BC
BC AA B B
AB BC
⊥
⇒⊥
⊥
và
( ) ( )
( ) ( )
' ' 'B '
' 'B
ABC AAB AB
ABC AA B AB
∩=
∩=
( ) ( )
( )
00
' ; ' ; ' 60 ' .tan 60 3A BC ABC A B AB A BA AA AB a⇒ = = =⇒= =
Tam giác ABC vuông cân tại
,B
có
2
.
22
ABC
AC a
R
∆
= =
Suy ra bán kính mặt cầu là
2
2
'5
.
42
ABC
AA a
RR
∆
= +=
Vậy thể tích khối cầu cần tính là
3
3
3
4 4 5 55
..
3 32 6
aa
VR
π
ππ

= = =



Chọn B.
Ví dụ 12: Cho hình lăng trụ đứng
.'' '
ABC A B C
có đáy ABC là tam giác vuông
,.AB BC a
= =
Biết góc
giữa hai mặt phẳng
(
)
'
ACC
và
( )
''AB C
bằng
0
60 .
Bán kính mặt cầu ngoại tiếp lăng trụ
.'' 'ABC A B C
bằng
A.
2
.
2
a
B.
.
2
a
C.
3
.
2
a
D.
3
.
3
a
Lời giải
Kẻ
( )
' '' '',BH AC H AC⊥∈
kẻ
( )
''
HK AC K AC⊥∈
.
Ta có
(
) ( )
''
' ' ''
'
B H AC
B H ACC AC B HK
HK AC
⊥
⊥ ⇒ ⇒⊥
⊥
Khi đó
(
)
( )
( )
0
' ; ' ' ; ' ' 60 .ACC AB C HK B K B KH
= = =
Tam giác
'''ABC
vuông cân tại
'' 2
'' .
22
AC a
B BH⇒= =
Tam giác
'B HK
vuông tại H, có
6
sin ' ' .
'3
BH a
BHK BK
BK
=⇒=
Tam giác
''AB C
vuông tại
',B
có
'BK
là đường cao
2 2 2 22
1 1 1 11
' 2.
' ' '' ' 2
AB a
B K AB B C AB a
⇒ = + ⇒ =⇒=
Tam giác
'AA B
vuông tại
',
A
có
(
)
2
22 2
' ' '' 2AA AB A B a a a
= − = −=
.
Vậy bán kính mặt cầu cần tìm là
2
22
2
'2 3
.
4 2 42
ABC
AA a a a
RR
∆

= + = +=



Chọn C.
Dạng 4: Bài toán về mặt cầu với hình chóp có mặt bên vuông góc với đáy
Xét khối chóp
.
S ABC
có
( ) ( )
SAB ABC⊥
. Tìm tâm và
bán kính mặt cầu ngoại tiếp khối chóp
.S ABC
.
Dựng tâm. Gọi
12
,OO
lần lượt là tâm của đường tròn
ngoại tiếp các tam giác ABC và SAB, E là trung điểm của
AB, ta có
(
) ( ) ( )
( )
11
.O E AB O E SAB do SAB ABC⊥⇒ ⊥ ⊥
( )
21
.O E AB O E ABC⊥⇒ ⊥
Qua
1
O
dựng đường thẳng
1
d
vuông góc với
( )
ABC
thì
1
d
là trục của tam giác ABC và
12
// .
d OE
Qua
2
O
dựng đường thẳng
2
d
vuông góc với
( )
SAB
thì
2
d
là trục của tam giác SAB và
21
// .d OE
Tâm I của mặt cầu là giao điểm của
1
d
và
2
d
.
Tính bán kính
R
của mặt cầu.
Tứ giác
12
EO IO
là hình chữ nhật, suy ra
222
12
.IE O E O E= +
Gọi
12
,RR
lần lượt là bán kính đường tròn ngoại tiếp tam giác ABC, SAB.
Ta có
22
2 2 22 2 2 22
11 1 2 2 2
;.
44
AB AB
O E O A EA R O E O A EA R
= −=− = −=−
Suy ra
22
2 22 2 2 2 22
12 12
.
24
AB AB
IE R R R IE EA R R
=+− ⇒= + =+−
Tổng quát: Cho khối chóp
12
. ...
n
S AA A
có
( ) ( )
12 12
... .
n
SAA AA A⊥
Đặt
1
R
là bán kính đường tròn ngoại
tiếp tam giác
12
.S AA
,
2
R
là bán kính đường tròn ngoại tiếp đáy
12
...
n
AA A
và
12
A A GT=
(gọi là giao
tuyến) thì bán kính mặt cầu ngoại tiếp
R
của khối chóp
12
. ...
n
S AA A
được tính theo công thức:
2
22
12
4
GT
R RR= +−
Ví dụ 1: Cho hình chóp
.S ABC
có
SA a=
, tam giác ABC đều, tam giác SAB vuông cân tại S và nằm trong
mặt phẳng vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp
.S ABC
bằng
A.
3
.
3
a
B.
6
.
3
a
C.
3
.
2
a
D.
6
.
2
a
Lời giải
Gọi H là trung điểm
( )
AB SH AB SH ABC⇒⊥⇒⊥
Tam giác SAB vuông cân tại
2
22
b
AB a
SR → = =
Tam giác ABC đều cạnh
36
2 2.
33
d
a
a Ra → = =
Vậy
62
;
2
;2
3
b d
a
R
a
R GT AB a= = ==
nên
6
.
3
a
R =
Chọn B.
Ví dụ 2: Cho hình chóp
.S ABCD
có đáy ABCD là hình vuông cạnh
0
, 30 ,a ASB =
tam giác SAB nằm
trong mặt phẳng vuông góc với mặt phẳng đáy. Diện tích mặt cầu ngoại tiếp hình chóp
.S ABCD
bằng
A.
2
5.a
π
B.
2
7.a
π
C.
2
9.a
π
D.
2
3.a
π
Lời giải
Tam giác SAB có
0
30 ,
2sin
b
AB
ASB AB a R a
ASB
= = → = =
ABCD là hình vuông cạnh
22
22 2
d
BD AB a
aR → = = =
Vậy
2
;
2
;
db
R
a
R Aaa GT B= = = =
nên
5
.
2
a
R =
Diện tích mặt cầu cần tính là
22
4 5.SR a
ππ
= =
Chọn A.
Ví dụ 3: Cho hình chóp
.
S ABC
có đáy ABC là tam giác cân tại C, tam giác SAB đều cạnh a. Hình chiếu
của S trên mặt phẳng
(
)
ABC
là trung điểm cạnh AB. Đường thẳng SC tạo với mặt phẳng đáy một góc
0
45 .
Bán kính mặt cầu ngoại tiếp hình chóp
.S ABC
là
A.
.
2
a
B.
3
.
2
a
C.
5
.
2
a
D.
3
.
3
a
Lời giải
Gọi H là trung điểm
( )
AB SH ABCD⇒⊥
( )
( )
( )
0
; ; 30SC ABCD SC HC SCH⇒===
Tam giác SHM vuông cân tại
,
H
có
3
2
tan
SH a
HM
SCH
= =
3
2
CH AB⇒= ⇒
Tam giác ABC đều cạnh a
Vậy
3
;
2
b d
a
R GT AB aR = = ==
nên
5
.
2
a
R =
Chọn C.
Ví dụ 4: Cho hình chóp
.S ABCD
có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác đều cạnh
2a
và
nằm trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng
( )
SBC
và
( )
ABCD
bằng
0
30 .
Bán kính
mặt cầu ngoại tiếp hình chóp
.S ABCD
bằng
A.
6
.
2
a
B.
10
.
2
a
C.
15
.
2
a
D.
21
.
2
a
Lời giải
Gọi H là trung điểm
( )
AD SH AD SH ABCD⇒⊥⇒⊥
Gọi M là trung điểm
( )
BC HM BC BC SHM⇒ ⊥⇒⊥
( ) ( )
( )
( )
0
; ; 30SHM ABCD SM HM SMH⇒===
22 22
13
BD AB AD HM AD a⇒= += +=
Vậy
13
;2
22
3;
db
BD a
R GT Aa aR
D
= = == =
nên
21
.
2
a
R =
Chọn D.
Ví dụ 5: Cho tứ diện ABCD có
, 2,AB BC BD AC a AD a
= = = = =
hai mặt phẳng
( )
ACD
và
( )
BCD
vuông góc với nhau. Diện tích mặt cầu đi qua bốn điểm
,,,ABC D
bằng
A.
2
8.
a
π
B.
2
4.a
π
C.
2
12 .a
π
D.
2
6.a
π
Lời giải
Gọi H là trung điểm
( )
CD BH CD BH ACD⇒⊥⇒⊥
Mà
BA BC BD H= = ⇒
là tâm đường tròn ngoại tiếp
ACD∆
ACD⇒∆
vuông tại
22
3A CD AC AD a⇒= + =
Tam giác BHC vuông tại
0
3
cos 120
2
HC
HC B
BC
⇒ = = ⇒=
Vậy
3;
3
2sin
;3
22
db
CD a
R
CD
Ra
B
GT CD a= = = == =
( )
( )
2
2
2
2
3
3
3 3 12 .
24
mc
a
a
Ra a S a
π

→ = + − = ⇒ =



Chọn C.
Ví dụ 6: Cho hình chóp
.S ABCD
có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân và nằm trong mặt
phẳng vuông góc với đáy. Góc giữa hai mặt phẳng
( )
SCD
và
( )
ABCD
bằng
0
45 .
Bán kính mặt cầu ngoại
tiếp hình chóp
.S ABCD
là
A.
43
.
6
a
R =
B.
41
.
6
a
R =
C.
41
.
8
a
R =
D.
43
.
8
a
R =
Lời giải
Gọi
,HM
lần lượt là trung điểm của
,.AB CD
SH AB⊥
mà
( ) ( )
( )
.SAB ABCD SH ABCD SH CD⊥ ⇒⊥ ⇒⊥
Do
HM CD⊥
suy ra
( )
CD SHM⊥
( ) ( )
0
; 45 .SCD ABCD SMH⇒==
Lại có
.. 5
4. 8
SAB SAB
SAB
SA SB AB a
SR
R
∆∆
∆
= ⇒=
và
2
.
22
ABCD
AC a
R = =
Vậy
2
22
.
41
.
48
S ABCD SAB ABCD
AB a
R RR
∆
= + −=
Chọn C.
Ví dụ 7: Cho hình chóp
.S ABCD
có đáy là tam giác đều. Tam giác SAB đều và thuộc mặt phẳng vuông
góc với đáy. Biết rằng
2 3,SC a=
diện tích mặt cầu ngoại tiếp hình chóp
.S ABCD
là
A.
40
.
3
S
π
=
B.
20
.
3
S
π
=
C.
80
.
3
S
π
=
D.
40 .S
π
=
Lời giải
Gọi H là trung điểm của AB. Khi đó
.SH AB⊥
Mặt khác
(
) ( )
.SAB ABC
⊥
Do vậy
( )
SH ABC⊥
.
Đặt
.AB x=
Ta có:
3
2
x
SH HC= =
Suy ra
6
23 22
2
x
SC a x a= = ⇒=
Ta có:
12
22
33
xa
RR= = =
Suy ra
2
22 2
12
30 40
4.
43 3
AB a
R RR S R
π
π
= + − = ⇒= =
Chọn A.
Dạng 5: Bài toán mặt cầu của hình chóp có các cạnh bên bằng nhau
Xét khối chóp
.S ABC
có
.
SA SB SC= =
Xác định tâm và tính bán kính mặt cầu ngoại tiếp khối chóp
.S ABC
(Hình chóp đều là một trường hợp đặc biệt của dạng toán này).
Dựng tâm. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC thì ta có
( )
.SO ABC⊥
Trong mặt phẳng
( )
SAO
dựng đường trung trực của SA cắt SO tại I thì I là tâm mặt cầu ngoại tiếp khối chóp
.S ABC
.
Tính bán kính
R
của mặt cầu.
Gọi E là trung điểm của AB.
Hai tam giác vuông SOA và SEI đồng dạng.
Suy ra
2
.
.
2
SO SA SE SA SA
R SI
SE SI SO SO
= ⇔= = =
Vậy
2
.
2
SA
R
SH
=
Tổng quát: Cho khối chóp
12
. ...
n
S AA A
có
12
. ...
n
S A SA SA= =
và có chiều cao
SO h=
thì bán kính mặt cầu ngoại tiếp R của khối
chóp
12
. ...
n
S AA A
được tính theo công thức:
22
.
22
R
SO h
= =

Ví dụ 1: Thể tích khối cầu ngoại tiếp hình chóp tam giác đều
.S ABC
có
,2AB a SA a= =
bằng
A.
3
45
.
75
a
π
B.
3
4 15
.
25
a
π
C.
3
43
.
25
a
π
D.
3
43
.
75
a
π
Lời giải
Gọi O là tâm đường tròn ngoại tiếp
( )
ABC SO ABC∆ → ⊥
Gọi M là trung điểm của
2 23 3
.
3 32 3
aa
BC OA AM
⇒= = =
Tam giác SAO vuông tại
22
15
3
a
O SO SA OA⇒= − =
Vậy
3
15 15 4 15
2; .
3 5 25
aa a
SA a SO R V
π
= = → = ⇒ =
Chọn B.
Mở rộng với bài toán hình chóp tam giác đều. Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng a,
với giả thiết
• Cạnh bên
SA b=
thì
2
22
3.
.
23
b
R
ba
=
−
• Cạnh bên SA hợp với đáy một góc
α
thì
3
.
3.sin 2
Ra
α
=
• Mặt bên tạo với mặt đáy một góc
β
thì
( )
2
3 4 tan
.
12 tan
Ra
β
β
+
=
• Góc
SAB
ϕ
=
thì
3.
.
4 cos .cos3
a
R
ϕϕ
=
−
• Góc
ASB
γ
=
thì
3.
.
3
4 sin .sin
22
a
R
γγ
=
Ví dụ 2: Cho hình chóp
.
S ABC
có đáy ABC là tam giác vuông cân tại
, 2.A AB a=
Các cạnh bên
.
SA SB SC= =
Góc giữa đường thẳng SA và mặt phẳng
( )
ABC
bằng
0
45 .
Bán kính mặt cầu ngoại tiếp
hình chóp
.S ABC
bằng
A.
2
.
4
a
B.
.
2
a
C.
2
.
2
a
D.
.a
Lời giải
Gọi O là trung điểm
BC O⇒
là tâm đường tròn ngoại tiếp
ABC∆
( ) ( )
(
)
( )
0
; ; 45SO ABC SA ABC SA OA SAO⇒⊥ ⇒ = = =
Tam giác ABC vuông cân tại
22A BC AB a → = =
Tam giác SAO vuông cân tại
2
BC
O SO OA a → = = =
Vậy
; 22 .SO a SA OA a R a= = = → =
Chọn D.
Ví dụ 3: Cho hình chóp đều
.S ABC
có cạnh đáy bằng 1, khoảng cách từ điểm A đến mặt phẳng
( )
SBC
bằng
6
4
. Diện tích mặt cầu ngoại tiếp tứ diện ABCD bằng
A.
25
.
12
π
B.
25
.
24
π
C.
5
.
12
π
D.
5
.
24
π
Lời giải
Gọi O là tâm tam giác
,ABC M
là trung điểm BC
( )
2 23 3 1 3
; .;
3 32 3 2 6
SO ABC OA AM OM OA
⇒⊥ = = = = =
Kẻ
( ) ( )
OH SM H SM OH SBC⊥ ∈ → ⊥
Ta có
( )
( )
66
; 3. :3
4 12
d A ABC OH OH= ⇒= =
Tam giác SMO vuông tại M có
22 2
111 3
6
SO
OH SO OM
= + ⇒=
Vậy
22
3 15 5 3
;
6 6 12
SO SA SO OA R= = + = → =
Diện tích mặt cầu cần tính là
2
25
4.
12
SR
π
π
= =
Chọn A.
Ví dụ 4: Cho ba tia
,,Sx Sy Sz
không đồng phẳng và
000
120 ; 60 ; 90 .xSy ySz zSx
= = =
Trên các tia
,,
Sx Sy Sz
lấy lần lượt các điểm
,,
ABC
sao cho
.SA SB SC a= = =
Tính bán kính
R
của mặt cầu ngoại
tiếp tứ diện
A.
.
2
a
R =
B.
.Ra=
C.
2.Ra=
D.
3.Ra
=
Lời giải
Tam giác SAB có
22
2..cos 3Ab SA SB SA SB ASB a
= +− =
Tam giác SAC vuông cân tại
22S AC SA a → = =
Suy ra
222
AC BC AB ABC
+ = → ∆
vuông tại C
Gọi O là trung điểm của
( )
AB SO ABC → ⊥
Tam giác SAO vuông tại
22
2
a
O SO SA OA⇒= − =
Vậy
2
;.
22
a SA
SO SA a R a
SO
= = → = =
Chọn B.
Ví dụ 5: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc
0
60 .
Thể tích của khối cầu ngoại tiếp khối chóp
.S ABCD
là
A.
3
4
.
3
a
π
B.
3
26
.
9
a
π
C.
3
86
.
9
a
π
D.
3
86
.
27
a
π
Lời giải
Gọi O là tâm hình vuông
( )
ABCD SO ABCD → ⊥
.
Do đó
( )
( )
0
SB; ; 60 .ABCD SB OB SBO= = =
Tam giác SBO vuông tại O, có
2
.
cos
6
.tan
2
OB
SB a
SB
SBO
a
SO
SO OB SBO
=
=

⇒

=

=
Suy ra bán kính mặt cầu cần tính là
( )
2
2
66
2 : 2. .
2 33
SB a a
Ra
SO

= = =



Vậy diện tích khối cầu cần tính là
2
3
3
4 4 686
..
3 3 3 27
aa
VR
π
ππ

= = =



Chọn D.
Ví dụ 6:
Cho hình chóp
.S ABCD
có
2,
AC a=
mặt bên
(
)
SBC
tạo với mặt đáy
( )
ABCD
một góc
0
45 .
Bán kính mặt cầu ngoại tiếp hình chóp
.S ABCD
bằng
A.
2
.
4
a
B.
.
2
a
C.
32
.
4
a
D.
.
4
a
Lời giải
Gọi M là trung điểm
( )
BC OM BC BC SMO⇒ ⊥⇒⊥
.
Do đó
( ) (
)
(
)
0
; ; 45 .SBC ABCD SM MO SMO
= = =
Vì ABCD là hình vuông có
22AC a AB a
= → =
Tam giác SMO vuông cân tại
2
2
a
O SO OM⇒= =
Tam giác SAO vuông tại
22
6
2
a
O SA SO OA⇒= + =
Vậy
6 2 32
;.
22 4
aa
SA SO R a= = → =
Chọn C.
Ví dụ 7: Cho hình chóp đều
.
S ABCD
có cạnh đáy bằng 2a, khoảng cách giữa hai đường thẳng SB và AD
bằng
3.a
Bán kính mặt cầu ngoại tiếp hình chóp
.S ABCD
bằng
A.
56
.
12
Ra=
B.
53
.
3
Ra=
C.
53
.
12
Ra=
D.
56
.
3
Ra=
Lời giải
Ta có
( )
( ) (
)
( )
// // ; ;AD BC AD SBC d SB AD d A SBC⇒ ⇒=
Gọi O là tâm hình vuông
( )
ABCD SO ABCD → ⊥
.
Gọi M là trung điểm
;BC
kẻ
( )
OH SM H SM⊥∈
( ) ( )
( )
3
; 2.
2
a
OH SBC d A SBC OH OH⇒⊥ ⇒ = ⇒=
Tam giác SMO vuông, có
22 2
111
3SO a
OH SO OM
= + ⇒=
Vậy
22
56
3; 5 .
3
SO a SA SO OA a R R a= = + = → = =
Chọn D.
Ví dụ 8: Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, tính thể tích V của
khối chóp có thể tích lớn nhất
A.
144.
V =
B.
576.V =
C.
576 2.V =
D.
Lời giải
Xét mặt cầu
( )
S
ngoại tiếp hình chóp
.S ABCD
Gọi O là tâm hình vuông
( )
ABCD SO ABCD → ⊥
Bán kính mặt cầu
(
)
S
là
2
2
18 (*)
2
SA
R SA h
h
=⇔=
Đặt
2
.
1.
..
33
S ABCD ABCD
hx
AB x V SO S
= → = =
Tam giác SAO vuông tại
2
2 2 22
2
x
O SA SO OA h
⇒=+=+
Thay vào (*), ta được
2
2 22
18 36 2
2
x
h h x hh+ = → = −
Do đó
(
)
2 23
max
2
. 36 2 12 576.
33
casio
h
V hh h h V= − = − → =
Chọn B.
Dạng 6: Hình chóp bất kì (bài toán Tổng quát – Nâng cao)
Công thức tìm nhanh bán kính mặt cầu ngoại tiếp hình chóp là
22
R xr= +
với
• r là bán kính đường tròn ngoại tiếp đa giác đáy.
•
22
:
2
SO r
xS
h
−
=
là đỉnh hình chóp, O là tâm đường tròn ngoại tiếp đa giác đáy, h là chiều cao
khối chóp.
Ví dụ 1: Cho hình chóp đều
.S ABC
có đáy ABC là tam giác đều cạnh a, cạnh bên bằng
23
.
3
a
Gọi D là
điểm đối xứng của B qua C. Bán kính của mặt cầu ngoại tiếp hình chóp
.S ABC
bằng
A.
37
.
6
a
B.
35
.
7
a
C.
36
.
7
a
D.
39
.
7
a
Lời giải
Hình vẽ tham khảo
Vì C là tâm đường tròn ngoại tiếp
ABD∆
nên
r BC a= =
Gọi H là hình chiếu của S trên mặt phẳng
( )
ABC H⇒
là tâm đường tròn ngoại tiếp
ABC∆
Tam giác SHC vuông tại H, có
22
23 3
;
33
aa
SC HC SH SC HC a
= = ⇒= − =
Vậy
rha
= =
và
23
3
a
SC
=
nên
37
.
6
a
R =
Chọn A.
Ví dụ 2: Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại A và
,D AB AD a= =
và
2.CD a=
Cạnh
bên SD vuông góc với đáy,
.SD a=
Gọi E là trung điểm của CD. Bán kính mặt cầu ngoại tiếp hình chóp
.S BCE
bằng
A.
11
.
8
a
B.
11
.
4
a
C.
11
.
6
a
D.
11
.
2
a
Lời giải
Vì E là trung điểm
DC EBC⇒∆
vuông tại E
Gọi M là trung điểm của BC
M⇒
là tâm đường tròn ngoại tiếp tam giác EBC
Xét hình chóp
.S BCE
có S là đỉnh, M là tâm đáy, chiều
cao
h SD
=
và bán kính đường tròn ngoại tiếp đáy
2
22
BC a
r = =
BCD∆
vuông cân tại
22
10
2
a
B DM BD BM⇒= + =
SDM∆
vuông tại
22
14
2
a
D SM SD DM⇒= + =
Áp dụng công thức, ta được
2
22
2
11
.
2. 2
SM r a
Rr
SD

−
= +=


Chọn D.
Ví dụ 3: Cho hình chóp
.S ABCD
có đáy ABCD là hình vuông cạnh
,a SAD
là tam giác đều và nằm trong
mặt phẳng vuông góc với mặt phẳng đáy. Gọi
,MN
lần lượt là trung điểm các cạnh
,BC CD
. Tính bán
kính
R
mặt cầu ngoại tiếp hình chóp
..S CMN
A.
37
.
6
a
R =
B.
29
.
8
a
R =
C.
53
.
12
a
R =
D.
93
.
12
a
R =
Lời giải
Gọi H là trung điểm của
AD SH AD⇒⊥
( )
.SH ABCD⇒⊥
Gọi E là trung điểm của MN, dựng
đường thẳng d qua E song song với SH, trên d lấy điểm I sao
cho
IS IC I= ⇒
là tâm mặt cầu ngoại tiếp khối chóp
..S CMN IS IC IM IN R⇒== = =
Ta có:
2
2
23
;
24 8 2
MN a a a
CE IE R SH= = ⇒= − =
22
2
2
3 15
448
a
HE CD AD

=+=


Lại có
(
)
2
22
2
22 2 2
5 3 93
.
8 2 8 12
aa a a
R HE SH IE R R R

− = − ⇔ − = − − ⇒=



Chọn D.
Ví dụ 4: Cho hình chóp
.S ABCD
có đáy ABCD là hình vuông cạnh
,2a SA a=
và vuông góc với mặt
phẳng đáy
( )
ABCD
. Gọi
,MN
lần lượt là trung điểm các cạnh
,BC CD
. Tính bán kính
R
mặt cầu ngoại
tiếp hình chóp
..S CMN
A.
3
.
4
a
R =
B.
32
.
4
a
R =
C.
33
.
4
a
R
=
D.
2
.
2
a
R =
Lời giải
Gọi E là trung điểm của MN, dựng đường thẳng d
qua E song song với SA, trên d lấy điểm I sao cho
IS IC I= ⇒
là tâm mặt cầu ngoại tiếp khối
chóp
..S CMN IS IC IM IN R⇒== = =
Ta có:
2
2
2
;2
24 8
MN a a
CE IE R SA a= = ⇒= − =
22
2
2
3 39
448
a
AE CD AD

=+=


Lại có
( )
2
22
R AE SA IE−=−
2
22
22
9 33
2.
8 84
a aa
R aR R

⇔ − = − − ⇒=



Chọn C.
Ví dụ 5:
Cho hình chóp
.S ABCD
có đáy ABCD là hình chữ nhật với
,2AB a AD a= =
. Mặt bên
( )
SAD
là
tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy
( )
ABCD
. Gọi
,MN
lần lượt là trung
điểm các cạnh
,BC CD
. Tính bán kính mặt cầu ngoại tiếp hình chóp
..S CMN
A.
23
.
3
a
R
=
B.
26
.
3
a
R =
C.
13
.
4
a
R =
D.
3
.
6
a
R =
Lời giải
Gọi H là trung điểm của
AD SH AD⇒⊥
( )
SH ABCD⇒⊥
. Gọi E là trung điểm của MN, dựng
đường thẳng d qua E song song với SH, trên d lấy điểm I
sao cho
IS IC I= ⇒
là tâm mặt cầu ngoại tiếp khối
chóp
..S CMN IS IC IM IN R⇒== = =
Ta có:
2
2
55
;3
2 4 16
MN a a
CE IE R SH a= = ⇒= − =
22
2
2
3 1 13
4 4 16
a
HE CD AD

=+=


Lại có
( )
2
22
R HE SH IE
−=−
2
22
22
13 5 2 3
3.
16 16 3
a aa
R aR R

⇔ − = − − ⇒=



Chọn A.
Ví dụ 6: Cho hình chóp
.S ABC
có đáy ABC là tam giác đều cạnh
,a
hình chiếu vuông góc của S lên mặt
phẳng
( )
ABC
là điểm đối xứng của C qua AB và mặt bên
(
)
SAB
tạo với đáy góc
0
60 .
Tính bán kính R mặt
cầu ngoại tiếp hình chóp đã cho.
A.
91
.
12
a
R =
B.
217
.
12
a
R =
C.
91
.
15
a
R =
D.
273
.
12
a
R =
Lời giải
Gọi H là đối xứng của C qua
.AB CH AB⇒⊥
O là trung điểm của
CH
0
3
; 60
2
a
OH CO SOH
⇒== =
Suy ra
0
3
tan 60
2
a
SH OH= =
Gọi E là trọng tâm tam giác ABC, dựng đường thẳng d
qua E song song với SH, trên d lấy điểm I sao cho
IS IC I= ⇒
là tâm mặt cầu ngoại tiếp khối
chóp
.S CMN
.IS IC IM IN R⇒= = = =
có:
3
2
2 3 23
;2
33 3 3
CO a a a
CE IE R HE CE= = ⇒= − = =
Lại có
( )
2
22
R HE SH IE−=−
2
22
22
4 3 217
.
3 2 3 12
aa a a
R RR

⇔ − = − − ⇒=



Chọn B.
Dạng 7: Bài toán mặt cầu của một số tứ diện đặc biệt
Mẫu 1: Cho tứ diện ABCD có
,,AB CD a AC BD b AD BC c= = = = = =
(tứ diện gần đều)
Bán kính mặt cầu ngoại tiếp tứ diện là:
222
.
8
abc
R
++
=
Chứng minh: Gọi
,,M NO
lần lượt là trung điểm của
;AB CD
và
MN
Ta có:
(
)
ACD BDC c c c DM CM
∆ =∆ −− ⇒ =
Khi đó
,MN CD⊥
tương tự
MN AB
⊥
suy ra O là tâm mặt
cầu ngoại tiếp tứ diện.
Ta có:
22
222 2 2
44
MN a
R OA OB OM AM===+=+
Xét
CMN
∆
có:
2222
2 22
2 44
bc a a
MN CM CN
+
= − = −−
222 222 2 222
2
.
2 848
bca bca a abc
R
+− +− ++
= ⇒= +=
Vậy
222
.
8
abc
R
++
=
Ví dụ 1: Cho tứ diện ABCD có
3,2,22.AB CD AC BD AD BC= = = = = =
Diện tích mặt cầu ngoại tiếp
tứ diện ABCD là
A.
21
.
2
S
π
=
B.
19
.
2
S
π
=
C.
9.S
π
=
D.
4.S
π
=
Lời giải
Áp dụng công thức nhanh ta có:
( )
2
22
222
2
3 2 22
21 21
4.
8 88 2
abc
R SR
π
π
++
++
= = = ⇒= =
Chọn A.
Ví dụ 2: Cho tứ diện ABCD có
,.
AB CD a AC BD AD BC b= = = = = =
Bán kính của mặt cầu ngoại tiếp tứ
diện ABCD là
A.
22
2
.
8
ab
R
+
=
B.
22
2
.
8
ab
R
+
=
C.
22
2
.
2
ab
R
+
=
D.
22
2
.
2
ab
R
+
=
Lời giải
Áp dụng công thức nhanh ta có:
222 2 2
2
.
88
abc a b
RR
++ +
= = =
Chọn A.
Ví dụ 3: Cho tứ diện ABCD có
2, 1.AB CD AC BD AD BC= = = = = =
Thể tích mặt cầu ngoại tiếp tứ diện
ABCD là
A.
9
.
8
V
π
=
B.
92
.
8
V
π
=
C.
2
.
3
V
π
=
D.
92
.
8
V
π
=
Lời giải
Áp dụng công thức nhanh ta có:
222 222
3
122 3 4 92
.
8 8 38
22
abc
R VR
π
π
++ ++
= = = ⇒= =
Chọn D.
Ví dụ 1: Cho tứ diện ABCD có
3, 5, 6.AB CD AC BD AD BC= = = = = =
Thể tích khối cầu ngoại tiếp tứ
diện ABCD thuộc khoảng nào dưới đây?
A.
( )
100;102 .
B.
( )
95;98 .
C.
( )
106;109 .
D.
( )
103;107 .
Lời giải
Bán kính mặt cầu ngoại tiếp tứ diện ABCD là
222
35
.
82
AB AC AD
R
++
= =
Vậy thể tích khối cầu ngoại tiếp tứ diện ABCD là
3
3
4 4 35 35 35
..
3 32 6
VR
π
ππ

= = =



Chọn C.
Ví dụ 5: Cho tứ diện ABCD có
, , 2 3.AB CD x AC BD y AD BC= = = = = =
Bán kính khối cầu ngoại tiếp
tứ diện ABCD bằng
2.
Giá trị lớn nhất của
xy
bằng
A. 2. B. 4. C.
2 2.
D.
2.
Lời giải
Bán kính mặt cầu ngoại tiếp tứ diện ABCD là
222
.
8
AB AC AD
R
++
=
Khi đó
( )
2
22
22
23
24
8
xy
xy
++
= ⇔+=
mà
22
4
2.
22
xy
xy
+
≤==
Dấu bằng xảy ra khi và chỉ khi
2.xy= =
Vậy
{ }
max
2.xy =
Chọn A.
Mẫu 2: Cho tứ diện ABCD có
;; .AB x CD y AD BC AC BD z= = = = = =
Tính bán kính mặt cầu
ngoại tiếp tứ diện ABCD.
Gọi
,MN
lần lượt là trung điểm của AB và CD ta có:
DAC DBC AN BN∆ =∆ ⇒=
suy ra
NM
là trung trực của AB,
tương tự MN là trung trực của DC
Khi đó
I MN∈
sao cho
ID IA=
Lại có
2
2 22
4
y
AN AD DN z= −=−
22
2 22
44
yx
MN AN AM z⇒ = − = −−
Mặt khác
2 22 2
MN IM IN R AM R DN= += − + −
2 2 22
222
4 4 44
x y yz
RR z⇒ −+ − = −−
Vậy bán kính mặt cầu ngoại tiếp tứ diện ABCD là nghiệm của phương trình:
2 2 22
222
.
4 4 44
x y yz
RR z−+ −= −−
Ví dụ 1: Cho tứ diện ABCD có
2; 4,AB a CD a
= =
các cạnh còn lại đều bằng
3.a
Tính bán kính mặt cầu
ngoại tiếp tứ diện ABCD.
A.
2.a
B.
65
.
4
a
C.
71
.
4
a
D.
5
.
2
a
Lời giải
Ta có:
22 2 2 2 2
4 95 2Ra R a a a a−+ − = − =
(
)
22 22 22 2 2222
2 4 44 4 4Ra aRa Ra aaRaRa⇔ −= − − ⇒−= − − +−
22
65
4.
44
aa
Ra R⇔ − =⇔=
Chọn B.
Ví dụ 2: Cho tứ diện ABCD có
4; 6,AB a CD a= =
các cạnh còn lại đều bằng
22.a
Tính diện tích mặt cầu
ngoại tiếp tứ diện ABCD.
A.
85
.
9
S
π
=
B.
340
.
3
S
π
=
C.
340
.
9
S
π
=
D.
340
.
27
S
π
=
Lời giải
Ta có:
22 22 2 2
4 9 22 13 3Ra Ra a a a−+ −= − =
(
)
22 22 22 2 2222
4 3 9 496 9 9
Ra aRa Ra aaRaRa⇔ − = − − ⇒− = − − +−
22 2
4 85 340
9 4.
64 9
aa
Ra R S R
π
π
⇔ − = ⇔= ⇒= =
Chọn C.
Ví dụ 3: Cho tứ diện ABCD có
2; 8,AB a CD a= =
các cạnh còn lại đều bằng
26.a
Tính bán kính mặt cầu
ngoại tiếp tứ diện ABCD.
A.
4.a
B.
14.a
C.
10.a
D.
9
.
2
a
Lời giải
Ta có:
22 2 2 2 2
9 26 10 4Ra R a a a a−+ − = − =
(
)
22 22 22 2 2222
4 9 16 8 9 9Ra aRa Ra aaRaRa⇔ −= − − ⇒ −= − − +−
22
9 10.R a a Ra
⇔ − =⇔=
Chọn C.
Ví dụ 4: Cho tứ diện ABCD có
4 ; 10 ,AB a CD a= =
các cạnh còn lại đều bằng
78.a
Tính diện tích mặt
cầu ngoại tiếp tứ diện ABCD.
A.
2
30 .Sa
π
=
B.
2
29 .Sa
π
=
C.
2
116
.
3
a
S
π
=
D.
2
116 .Sa
π
=
Lời giải
Ta có:
22 2 2 2 2
4 25 78 29 7Ra R a a a a−+ − = − =
(
)
22 22 22 2 2222
4 7 25 4 49 14 25 25RaaRaRa aaRaRa⇔ − = − − ⇒− = − − +−
( )
22 2 2
25 2 29 4 116 .
C
R a a Ra S R a
ππ
⇔ − = ⇔= ⇒ = =
Chọn D.
Ví dụ 5: Cho tứ diện ABCD có
2; 8,
AB a CD a= =
các cạnh còn lại đều bằng
.
x
Tìm x biết bán kính mặt
cầu ngoại tiếp tứ diện bằng
17a
.
A.
42.xa=
B.
6.xa=
C.
38.xa=
D.
33.xa=
Lời giải
Ta có:
22 2 2 2 2
16 17Ra R a x a−+ − = −
Với
22 2 2
17 17 4 5 42 42.Ra x a aa a x a xa= ⇒ − = += ⇒ = ⇒=
Chọn A.
BÀI TẬP TỰ LUYỆN
Câu 1: Cho hình chóp
.S ABC
có đáy ABC là tam giác vuông tại B và
( )
.SA ABC⊥
Điểm nào sau đây là
tâm của mặt cầu qua các điểm
,,, ?S ABC
A. Trung điểm của AC. B. Trung điểm của AB.
C. Trung điểm của BC. D. Trung điểm của SC.
Câu 2: Cho hình chóp
.S ABC
có đáy ABC là tam giác vuông tại B và
( )
.SA ABC⊥
Gọi I và J lần lượt là
hình chiếu vuông góc của A trên SB và SC. Điểm nào sau đây là tâm của mặt cầu qua năm điểm
, , ,, ?ABCI J
A. Trung điểm của AC. B. Trung điểm của BC.
C. Trung điểm của IJ. D. Trọng tâm của
.ABC∆
Câu 3: Cho hình chóp
.S ABCD
có đáy ABCD là hình vuông và
( )
.SA ABCD⊥
Gọi
,,IJK
lần lượt là hình
chiếu vuông góc của A trên
,,.
SB SC SD
Điểm nào sau đây là tâm của mặt cầu qua bảy điểm
, , , ,, , ?ABCDI J K
A. Tâm của ABCD. B. Trung điểm của SB.
C. Trung điểm của SC. D. Trung điểm của SD.
Câu 4: Cho tứ diện ABCD với tam giác BCD vuông tại
,, 3B BC a BD= =
và
2.AB AC AD a= = =
Điểm nào sau đây là tâm của mặt cầu ngoại tiếp tứ diện ABCD?
A. Trung điểm của BC. B. Trung điểm của CD.
C. Trung điểm của BD. D. Trọng tâm của
.BCD∆
Câu 5: Cho hình chóp
.S ABC
có đáy ABC là tam giác đều, SA vuông góc với mặt phẳng
( )
ABC
. Gọi H là
hình chiếu của A lên đường thẳng SB. Điểm nào sau đây là tâm của mặt cầu ngoại tiếp khối chóp
.?A BCH
A. Trọng tâm của
.ABC∆
B. Trọng tâm của
.ABCH∆
C. Trọng tâm của
.
ACH∆
D. Trọng tâm của
.ABH∆
Câu 6: Cho tứ diện ABCD có O là trung điểm đoạn thẳng nối trung điểm của hai cạnh đối diện. Tập hợp các
điểm M trong không gian thỏa mãn hệ thức
( )
0MA MB MC MD a a+++ = >
   
là
A. Mặt cầu tâm O bán kính
.
4
a
r
=
B. Mặt cầu tâm O bán kính
.
2
a
r
=
C. Mặt cầu tâm O bán kính
.ra=
D. Mặt cầu tâm O bán kính
.
3
a
r =
Câu 7: Cho tứ diện DABC, đáy ABC là tam giác vuông tại
,B DA
vuông góc với mặt đáy. Biết
3, 4, 5.AB a BC a AD a= = =
Bán kính mặt cầu ngoại tiếp hình chóp DABC có bán kính bằng
A.
52
.
2
a
B.
52
.
3
a
C.
53
.
3
a
D.
53
.
3
a
Câu 8: Cho hình chóp tam giác
.S ABC
có các cạnh
,,SA SB SC
vuông góc với nhau từng đôi một và
,,.SA a SB b SC c= = =
Mặt cầu ngoại tiếp hình chóp có bán kính là:
A.
222
1
.
2
abc++
B.
222
1
.
3
abc++
C.
222
3
.
2
abc++
D.
222
2
.
3
abc++
Câu 9: Cho hình chóp tam giác
.S ABC
có các cạnh
,,SA SB SC
vuông góc với nhau từng đôi một và
2, 4.SA SB a SC a= = =
Mặt cầu ngoại tiếp hình chóp có bán kính tính theo a là:
A.
6
.
2
a
B.
3.
a
C.
6
.
3
a
D.
6a
.
Câu 10: Cho hình chóp tam giác
.
S ABC
, đáy là tam giác vuông tại
, 3, 4,A AB AC SA= =
vuông góc với
đáy,
2 14.SA =
Thể tích V của khối cầu ngoại tiếp hình chóp
.S ABC
là
A.
169
.
6
V
π
=
B.
2197
.
8
V
π
=
C.
729
.
6
V
π
=
D.
13
.
8
V
π
=
Câu 11: Cho tứ diện ABCD cạnh a, đường cao AH, O là trung điểm AH. Tính bán kính R của mặt cầu ngoại
tiếp tứ diện OCBD.
A.
3
.
2
a
R =
B.
6
.
4
a
R =
C.
2
.
3
a
R =
D.
6
.
3
a
R =
Câu 12: Cho hình chóp tam giác
.S ABC
có đáy là tam giác vuông cân tại
,
B AB a
=
, các cạnh bên đều bằng
a. Bán kính của mặt cầu ngoại tiếp hình chóp bằng
A.
2
.
4
a
B.
2
.
2
a
C.
2
.
6
a
D.
3
.
4
a
Câu 13: Cho tứ diện đều ABCD cạnh a. Mặt cầu nội tiếp tứ diện này có bán kính theo a là:
A.
6
.
12
a
B.
6
.
9
a
C.
6
.
6
a
D.
6
.
8
a
Câu 14: Cho tứ diện đều ABCD cạnh a. Mặt cầu ngoại tiếp tứ diện này có bán kính theo a là:
A.
2
3
.
2
a
π
B.
2
3
.
4
a
π
C.
2
5
.
4
a
π
D.
2
.a
Câu 15: Cho tứ diện đều ABCD cạnh a. Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng
A.
3
6
.
8
a
π
B.
3
6
.
6
a
π
C.
3
6
.
4
a
π
D.
3
36
.
8
a
π
Câu 16: Cho tứ diện đều ABCD cạnh a. Biết mặt cầu ngoại tiếp tứ diện có bán kính bằng 1. Tính giá trị của
a.
A.
2
.
3
a =
B.
6
.
3
a =
C.
26
.
3
a
=
D.
3
.
3
a =
Câu 17: Cho hình chóp
.S ABC
có đáy ABC là tam giác đều cạnh
3a
, cạnh bên
2SC a=
, và SC vuông góc
với đáy. Tính diện tích của mặt cầu ngoại tiếp hình chóp
.S ABC
A.
2
16 .a
π
B.
2
36 .
a
π
C.
2
24 .
a
π
D.
2
8
.
3
a
π
Câu 18: Cho hình chóp
.S ABC
có đáy là tam giác ABC vuông tại
,,B AB a=
góc BAC bằng
0
60 ,
chiều cao
2.SA a=
Tính thể tích V của khối cầu ngoại tiếp hình chóp.
A.
3
6.Va
π
=
B.
3
46
.
3
a
V
π
=
C.
3
26
.
3
a
V
π
=
D.
3
6.Va
π
=
Câu 19: Cho khối chóp
.S ABCD
có SC vuông góc với
( )
,,ABCD SA SB SD ABD= =
là tam giác cân tại A
có
, 3,
AB a BD a= =
góc giữa SA và
( )
ABCD
bằng
0
45 .
Tính bán kính R của mặt cầu ngoại tiếp hình
chóp
.S ABCD
.
A.
73
.
12
a
R =
B.
23
.
3
a
R
=
C.
.Ra=
D.
5
.
2
a
R =
Câu 20: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng a, các cạnh bên bằng b. Tính theo
,ab
bán
kính mặt cầu ngoại tiếp hình chóp
.S ABCD
là:
A.
2
2
2
.
2
2
b
a
b −
B.
2
2
2
.
2
2
a
b
a −
C.
2
2
2
.
2
3
b
a
b −
D.
2
2
2
.
2
3
a
b
a −
Câu 21: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng a và góc giữa mặt bên và mặt phẳng đáy
bằng
0
45 .
Diện tích của mặt cầu ngoại tiếp hình chóp
.S ABCD
là:
A.
2
9
.
4
a
π
B.
2
4
.
3
a
π
C.
2
3
.
4
a
π
D.
2
2
.
3
a
π
Câu 22: Cho hình chóp tứ giác đều
.S ABCD
có đáy hợp với cạnh bên một góc
0
45 .
Bán kính mặt cầu ngoại
tiếp hình chóp
.S ABCD
bằng
2.
Thể tích khối chóp là
A.
4
.
3
B.
22
.
3
C.
4 2.
D.
42
.
3
Câu 23: Thể tích khối cầu ngoại tiếp khối chóp tứ giác đều có tất cả các cạnh bằng a là
A.
3
8
.
3
a
π
B.
3
2
.
3
a
π
C.
3
2.a
π
D.
3
42
.
3
a
π
Câu 24: Cho hình chóp tứ giác đều
.S ABCD
có tất cả các cạnh bằng a. Mặt cầu ngoại tiếp hình chóp này có
diện tích tính theo a là
A.
2
.a
π
B.
2
2.a
π
C.
2
3.a
π
D.
2
4.a
π
Câu 25: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
32,
a
cạnh bên bằng
5.a
Tính bán kính R
của mặt cầu ngoại tiếp hình chóp
.S ABCD
.
A.
3.Ra=
B.
2.Ra
=
C.
25
.
8
a
R =
D.
2.Ra=
Câu 26: Cho hình chóp
.
S ABCD
có đáy ABCD là hình vuông cạnh bằng a. Cạnh bên SA vuông góc với mặt
phẳng
( )
ABC
và
2.
SA a=
Tính thể tích của mặt cầu ngoại tiếp hình chóp
.S ABCD
.
A.
3
6.
a
π
B.
3
.
6
a
π
C.
3
46
.
3
a
π
D.
3
3
.
46
a
π
Câu 27: Cho hình chóp
.S ABCD
có đáy ABCD là hình vuông cạnh bằng a. Cạnh bên SA vuông góc với mặt
phẳng
( )
ABC
và
3.
SA a
=
Diện tích của mặt cầu ngoại tiếp hình chóp
.S ABCD
là
A.
2
5.a
π
B.
2
3
.
6
a
π
C.
2
4
.
3
a
π
D.
2
4
.
5
a
π
Câu 28: Cho hình chóp
.S ABCD
có đáy ABCD là tứ giác có
2 , 2,AB a BC AC a AD a= = = =
và
3.BD a=
Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích của mặt cầu ngoại
tiếp hình chóp
.S ABCD
.
A.
3
.
32
a
π
B.
3
3
.
32
a
π
C.
3
32 3
.
27
a
π
D.
3
32
.
9
a
π
Câu 29: Cho hình chóp
.S ABCD
có đáy ABCD là hình vuông cạnh bằng a. Cạnh bên SA vuông góc với mặt
phẳng
(
)
ABC
và
6.SA a=
Diện tích của mặt cầu ngoại tiếp hình chóp
.
S ABCD
là
A.
2
8.
Sa
π
=
B.
2
2.Sa=
C.
2
2.Sa=
D.
2
2.Sa
π
=
Câu 30: Cho hình chóp
.S ABC
có đáy ABC là tam giác vuông tại B với
3AB BC a= =
và
0
90 .SAB SCB= =
Khoảng cách từ điểm A đến mặt phẳng
( )
SBC
bằng
2.a
Tính thể tích của mặt cầu
ngoại tiếp hình chóp
.
S ABC
.
A.
3
16
.
3
a
V
π
=
B.
3
8.Va
π
=
C.
3
43 .
Va
π
=
D.
3
33 .Va
π
=
Câu 31: Cho hình chóp
.S ABCD
có đáy ABCD là hình chữ nhật và
3, 4.AB a BC a= =
Cạnh bên SA vuông
góc với mặt phẳng
( )
ABC
và
12 .SA a
=
Tính bán kính R của mặt cầu ngoại tiếp hình chóp
.S ABCD
.
A.
5
.
2
a
R =
B.
17
.
2
a
R =
C.
13
.
2
a
R =
D.
6.Ra=
Câu 32: Cho hình chóp
.S ABCD
có đáy ABCD là hình vuông cạnh
2 2,
cạnh bên SA vuông góc với mặt
phẳng đáy và
3.SA =
Mặt phẳng
( )
α
đi qua A và vuông góc với SC cắt các cạnh
;;SB SC SD
lần lượt tại các
điểm
,,MNP
. Tính thể tích V của khối cầu ngoại tiếp tứ diện CMNP
A.
64 2
.
3
V
π
=
B.
125
.
6
V
π
=
C.
32
.
3
V
π
=
D.
108
.
3
V
π
=
Câu 33: Cho tứ diện ABCD có
4, 6AB a CD a
= =
và các cạnh còn lại đều bằng
22.a
Tính bán kính mặt
cầu ngoại tiếp tứ diện ABCD.
A.
3.Ra=
B.
85
.
3
a
R =
C.
79
.
3
a
R =
D.
5
.
2
a
R =
Câu 34: Cho hình chóp
.
S ABCD
có SA vuông góc với đáy và
6.SA a=
Đáy ABCD là hình thang vuông tại
, , 2 2 2.A B AD AB BC a
= = =
Gọi E là trung điểm AD. Tính bán kính R của mặt cầu ngoại tiếp hình chóp
SECD.
A.
6.Ra=
B.
30
.
3
a
R =
C.
2
.
2
a
R =
D.
114
.
6
a
R =
Câu 35: Cho hình chóp
.S ABC
có đáy ABC là tam giác đều cạnh a, mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp hình chóp đã cho.
A.
3
43
.
27
a
π
B.
3
5
.
3
a
π
C.
3
5 15
.
54
a
π
D.
3
5 15
.
18
a
π
Câu 36: Cho hình chóp
.S ABC
có đáy ABC là tam giác vuông cân tại
,.
A AB AC a
= =
Mặt bên SAB là tam
giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối cầu ngoại tiếp hình chóp
.S ABC
.
A.
3
.
3
a
V
π
=
B.
3
7 21
.
54
a
V
π
=
C.
3
21
.
54
a
V
π
=
D.
3
.
54
a
V
π
=
Câu 37: Cho hình chóp tam giác đều
0
. , , 90 .
S ABC SA a ASB= =
Tính theo a bán kính mặt cầu ngoại tiếp
hình chóp
.
S ABC
.
A.
3
.
3
a
R =
B.
3
.
2
a
R =
C.
23
.
3
a
R =
D.
3.
Ra
=
Câu 38: Cho hình chóp
.S ABCD
có đáy ABCD là hình vuông cạnh
2.a
Mặt bên SAB là tam giác vuông cân
tại S và nằm trong mặt phẳng vuông góc với đáy. Tính bán kính r của mặt cầu ngoại tiếp hình chóp
.
S ABCD
.
A.
2
.
2
a
r =
B.
3
.
2
a
r =
C.
.ra=
D.
2.ra=
Câu 39: Cho hình chóp
.S ABCD
có
( )
,SA ABCD⊥
đáy ABCD là hình chữ nhật,
, 2,AB a AD a= =
góc
giữa đường thẳng SC và đáy bằng
0
45 .
Tính theo a thể tích của khối cầu ngoại tiếp hình chóp
.S ABCD
.
A.
3
6.Va
π
=
B.
3
10
.
3
a
V
π
=
C.
3
5
.
6
a
V
π
=
D.
3
5 10
.
3
a
V
π
=
Câu 40: Cho tứ diện SABC có tam giác ABC vuông tại
, , 3, 2B AB a BC a SA a= = =
và
2, 5.SB a SC a= =
Tính bán kính mặt cầu ngoại tiếp tứ diện
..S ABC
A.
259
.
7
a
R =
B.
259
.
4
a
R =
C.
259
.
2
a
R =
D.
37
.
14
a
R =
Câu 41: Cho khối chóp
.S ABCD
có đáy ABCD là hình vuông cạnh
,3a SA a
=
và SA vuông góc với đáy.
Gọi
,MN
lần lượt là trung điểm của
,CD BC
và K là giao điểm của AM và DN. Tính bán kính R của mặt
cầu ngoại tiếp khối chóp
..S ABNK
A.
17
.
4
a
R =
B.
32
.
4
a
R =
C.
17
.
2
a
R =
D.
15
.
4
a
R =
Câu 42: Cho khối chóp
.
S ABCD
có ABCD là hình chữ nhật tâm
, 2 , 2 3,O AB a BC a= =
góc hợp giữa hai
đường thẳng SB và mặt phẳng
(
)
ABCD
bằng
0
60 .
Hình chiếu vuông góc của đỉnh S xuống mặt phẳng
( )
ABCD
trùng với trọng tâm H của tam giác ABC. Tính bán kính R của mặt cầu ngoại tiếp khối chóp
.
S ABCD
.
A.
2 21
.
9
a
R =
B.
23
.
3
a
R
=
C.
4 21
.
9
a
R =
D.
43
.
3
a
R =
Câu 43: Cho hình chóp
.S ABCD
có đáy là hình thang vuông với đường cao
( )
, 2,AB BC a AD a SA ABCD= = = ⊥
và
2.SA a=
Gọi E là trung điểm của AD. Kẻ
EK SD⊥
tại K. Bán
kính mặt cầu đi qua sáu điểm
,,,,,S ABCEK
bằng
A.
.a
B.
3
.
2
a
C.
1
.
2
a
D.
6
.
2
a
Câu 44: Cho hình chóp
.S ABCD
có đáy ABCD là hình vuông cạnh a và
2,SA a SA=
vuông góc với
( )
,ABCD
kẻ AH vuông góc với SB và AK vuông góc với SD. Mặt phẳng
( )
AHK
cắt SC tại E. Tính thể tích
khối cầu ngoại tiếp khối ABCDEHK
A.
3
2
.
3
a
π
B.
3
42
.
3
a
π
C.
3
82
.
3
a
π
D.
3
2
.
6
a
π
Câu 45: Cho hình chóp
.
S ABCD
có cạnh
1, 2AB AC= =
và góc
.BAC
α
=
Cạnh SA vuông góc với mặt
phẳng
( )
ABC
. Điểm
1
B
và
1
C
lần lượt là hình chiếu vuông góc của
A
trên
SB
và
SC
. Tính bán kính R
của mặt cầu đi qua các điểm
11
,,, ,ABCC B
A.
5 4cos
.
3 sin
R
α
α
−
=
B.
2 5 4cos
.
3 sin
R
α
α
−
=
C.
5 4cos
.
2 sin
R
α
α
−
=
D.
5 4cos
.
2sin
R
α
α
−
=
Câu 46: Cho hình lập phương
. ' ' ' '.ABCD A B C D
Gọi
123
,,
RRR
lần lượt là bán kính của mặt cầu ngoại tiếp
khối lập phương, mặt cầu nội tiếp khối lập phương và mặt cầu tiếp xúc với tất cả các cạnh của hình lập
phương. Đẳng thức nào sau đây là đúng về
123
,,RRR
A.
2
12 3
..RR R=
B.
22 2
12 3
..RR R=
C.
2
23 1
..RR R=
D.
22 2
23 1
.RRR+=
Câu 47: Các kí hiệu
123
,,RRR
lần lượt là bán kính của mặt cầu ngoại tiếp, nội tiếp và tiếp xúc với tất cả các
cạnh của hình lập phương. Tìm khẳng định đúng?
A.
123
.
RRR
>>
B.
231
.
RRR
>>
C.
132
.RRR>>
D.
312
.
RRR
>>
Câu 48: Cho hình lăng trụ đều
.'' 'ABC A B C
có mặt phẳng
( )
'A BC
tạo với đáy
( )
ABC
một góc
0
30 .
Tam
giác
'A BC
có diện tích bằng 18. Tính diện tích S mặt cầu ngoại tiếp khối lăng trụ trên.
A.
57 .S
π
=
B.
57
.
4
S
π
=
C.
57
.
2
S
π
=
D.
57
.
3
S
π
=
Câu 49: Cho hình chóp
.S ABCD
có đáy ABCD là hình chữ nhật,
, 2,AB a AD a= =
tam giác SAB đều và
nằm trong mặt phẳng vuông góc với đáy. Gọi
,MN
lần lượt là trung điểm của các cạnh
,.
AD DC
Tính bán
kính R của mặt cầu ngoại tiếp hình chóp
.DMNS
.
A.
39
.
6
a
R =
B.
31
.
4
a
R =
C.
102
.
6
a
R
=
D.
39
.
13
a
R
=
Câu 50: Cho tứ diện
.S ABC
có đáy ABC là tam giác vuông tại A với
3, 4.AB a AC a= =
Hình chiếu H của S
trùng với tâm đường tròn nội tiếp tam giác ABC. Biết
2,SA a=
bán kính mặt cầu ngoại tiếp hình chóp
.S ABC
là
A.
118
.
4
a
R =
B.
118
.
2
a
R =
C.
118
.
8
a
R =
D.
118.Ra
=
Câu 51: Cho tứ diện ABCD có
( )
2, 2 .AB AC BC AD BD a CD b a b
= = = = = = >
Xác định bán kính R của
mặt cầu ngoại tiếp tứ diện ABCD
A.
22
22
4
.
3
ab
Rb
ab
−
=
−
B.
22
22
3
.
4
ab
Ra
ab
−
=
−
C.
22
22
4
.
3
ab
Ra
ab
−
=
−
D.
22
22
3
.
4
ab
Rb
ab
−
=
−
Câu 52: Cho tứ diện ABCD có
8, 6, 4.AB AD BC AC BD CD
= = = = = =
Tínhh bán kính R của mặt cầu
ngoại tiếp tứ diện ABCD
A.
187
.
10
R =
B.
5.
R =
C.
177
.
10
R =
D.
65
.
2
R =
LỜI GIẢI BÀI TẬP TỰ LUYỆN
Câu 1: Gọi P là tâm đường tròn ngoại tiếp
.ABC∆
Trục đường tròn ngoại tiếp
ABC∆
cắt SC tại O.
Ta có
.
OA OB OC
OA OB OC OS
OC OS
= =
⇒== =
=
Vậy O là tâm mặt cầu qua các điểm
,,,.S ABC
Chọn D.
Câu 2: Gọi O là trung điểm của AC.
Ta có
AB BC OA OC OB
AJ JC OA OC OJ
⊥⇒= =
=⇒= =
Từ
( )
.
BC AB
BC SAB BC AI
BC SA
⊥
⇒⊥ ⇔⊥
⊥
Mà
(
)
AI SB AI SBC AI IC
⊥⇒⊥ ⇒⊥
.OA OC OI OA OB OC OI OJ
⇒==⇒== ==
Vậy O là tâm mặt cầu cần tìm. Chọn A.
Câu 3: Gọi O là tâm của hình vuông ABCD.
Ta có
( )
.
BC AB
BC SAB BC AI
BC SA
⊥
⇒⊥ ⇒⊥
⊥
( )
.AI SB AI SBC AI IC OA OC OI⊥⇒⊥ ⇒⊥⇒= =
Tương tự
.OA OC OK= =
Mà
AJ SC OA OC OJ⊥⇒= =
OA OB OC OD OI OJ OK O⇒== = ===⇒
là tâm mặt
cầu cần tìm. Chọn A.
Câu 4: Ta có
AB AC AD= =
, kẻ
( )
AO BCD O⊥⇒
là tâm đường
tròn ngoại tiếp tam giác BCD.
Ta có
2 22
2 2 22
4
4
AD AC a
CD BD BC a
+=
=+=
222
.AD AC CD AD AC OA OC OD⇒ + = ⇒ ⊥⇒= =
Vậy
OB OC OD OA O
= = = ⇒
là tâm mặt cầu cần tìm. Chọn
B.
Câu 5: Ta có
.AH HB
⊥
Trục đường tròn ngoại tiếp tam giác ABH đi qua trung điểm của
AB và vuông với
( )
.
ABH
Trục đường tròn ngoại tiếp tam giác ABC đi qua tâm O của tam
giác đều ABC và vuông góc với
( )
.
ABC
Hai đường thẳng này cắt nhau tại chính O.
Ta có:
.
OA OB OH
OA OB OC OH
OA OB OC
= =
⇒== =
= =
Vậy O là tâm mặt cầu cần tìm. Chọn A.
Câu 6: Gọi
,EF
lần lượt là trung điểm của
,.BD AC
MA MB MC MD
+++
   
(
)
(
)
( )
( )
( )
( )
4 224
4.
4
OA OM OB OM OC OM OD OM
OA OC OB OD OM OF OE OM
a
OM a OM
=−+−+−+−
=+++− = + −
⇒ =⇒=
       
       

Chọn A.
Câu 7: Gọi O là trung điểm của CD.
Ta có
1
.
2
OA OB OC OD R CD= = = = =
Cạnh
2 2 222
52CD AD AC AD AB BC a= + = ++ =
5 2.Ra=
Chọn A.
Câu 8: Ta có
( )
.
SA SB
SA SBC
SA SC
⊥
⇒⊥
⊥
Kí hiệu các điểm như hình vẽ với OP là trục đường tròn ngoại tiếp
tam giác SBC và OK là trung trực của SA thì O là tâm mặt cầu.
Ta có
22
.R OS OP SP= = +
22
11
;
22 2 2
SA a
OP SK SP BC b c= = = = = +
222
1
.
2
R abc= ++
Chọn A.
Câu 9: Ta có
( )
.
SA SB
SA SBC
SA SC
⊥
⇒⊥
⊥
Kí hiệu các điểm như hình vẽ với OP là trục đường tròn ngoại tiếp
tam giác SBC và OK là trung trực của SA thì O là tâm mặt cầu.
Ta có
22
.R OS OP SP= = +
22
11
;5
2 22
SA
OP SK a SP BC SB SC a=== = = +=
6.
Ra=
Chọn D.
Câu 10: Kí hiệu các điểm như hình vẽ với OP là trục đường tròn ngoại
tiếp tam giác ABC và OK là trung trực của SA thì O là tâm mặt cầu.
Ta có
22
.
R OA OP AP= = +
22
11 5
14; 3 4
2 22 2
SA
OP AK AP BC= = = = = +=
3
9 4 243
.
23 2
R VR
ππ
⇒=⇒= =
Chọn C.
Câu 11: Kí hiệu các điểm như hình vẽ với OP là trung trực của AC thì
O là tâm mặt cầu
22
22
2
2
AC AC
R OA
AH
AD DH
⇒= = =
−
6
;.
4
33
AB a a
AC AD a DH R= = = = ⇒=
Chọn B.
Câu 12: Ta có
,SA SB SC a= = =
kẻ
( )
SH ABC H⊥⇒
là tâm
đường tròn ngoại tiếp tam giác ABC.
Tam giác ABC vuông cân tại B nên H là trung điểm của AC.
Gọi O là tâm đường tròn ngoại tiếp tam giác SAC thì O là tâm mặt cầu, ta có
.R SO=
.. 1 .
.
42 2
SAC
SA SC AC SA SC
S SH AC SO
SO SH
= = ⇒=
22
;SA SC a SH SA AH= = = −
11
2
22
22
aa
AH AC AB SH= = =⇒=
2
.
2
a
R SO⇒= =
Chọn B.
Câu 13: Ta có
( )
3
.
12
.
3 12
S ABCD ABC ABD ACD BCD
a
V rS S S S= +++ =
2
36
.
4 12
ABC ABD ACD BCD
aa
SSSS r= = = = ⇒=
Chọn A.
Câu 14: Kí hiệu như hình vẽ với
( )
,AH BCD OP⊥
là trung trực của
AC thì O là tâm mặt cầu
Ta có
22
22
2
2
AC AC
R OA
AH
AD DH
= = =
−
;
33
AB a
AC AD a DH= = = =
22
63
4.
42
a
R SR a
ππ
⇒= ⇒= =
Chọn A.
Câu 15: Kí hiệu như hình vẽ với
( )
,AH BCD OP⊥
là trung trực của
AC thì O là tâm mặt cầu
Ta có
22
22
2
2
AC AC
R OA
AH
AD DH
= = =
−
;
33
AB a
AC AD a DH= = = =
33
64 6
.
4 38
a
R VR a
ππ
⇒= ⇒= =
Chọn A.
Câu 16: Kí hiệu như hình vẽ với
( )
,AH BCD OP⊥
là trung trực của
AC thì O là tâm mặt cầu
Ta có
22
22
2
2
AC AC
R OA
AH
AD DH
= = =
−
;
33
AB a
AC AD a DH= = = =
6 26
1.
43
a
Ra⇒= ⇒=
Chọn C.
Câu 17: Bán kính đường tròn ngoại tiếp tam giác ABC là
33
3
3
a
ra= =
Ta có
2
2 22 2 2
3 2 4 16 .
2
SC
R r a a aS R a
ππ

= + = + = ⇒= =


Chọn A.
Câu 18: Ta có
22
tan 3 2
BC
BAC BC AB a AC AB BC a
AB
=⇒== ⇒= + =
Bán kính đường tròn ngoại tiếp tam giác ABC là
2
AC
ra
= =
Ta có
2
2 33
64
6.
2 23
SA a
R r V Ra
ππ

= + = ⇒= =


Chọn A.
Câu 19: Ta có
( )
SC ABCD⊥
và
SA SB SC C= = ⇒
là tâm đường tròn ngoại tiếp tam giác ABD
Gọi M là trung điểm của BD. Ta có
2
22
13
.
22 4
ABD
aa
AM AB BM S AM BD= − =⇒= =
Mà
2
.. .. ..3
44
3
4.
4
ABD ABD
ABD
AB BD AD AB BD AD a a a
S R a AC BC CD a
RS
a
= ⇒ = = =⇒===
Ta có
{ }
()SA ABCD A∩=
và
0
( ) (,( ))(, ) 45SA ABCD SA ABCD SA AC SAC⊥⇒ = ==
Ta có
2
2
5
tan tan .
22
ABD
SC SC a
SAC SC AC SAC a R R
AC


= ⇒ = =⇒= + =





Chọn D.
Câu 20: Chiều cao của hình chóp là
2
2
22
2
22
aa
hb b

=−=−



Bán kính mặt cầu là
22
2
2
.
2
2
2
bb
R
h
a
b
= =
−
Chọn A.
Câu 21:
2
02
23
tan 45
2 22
2
ha a a
h SA h
a

= ⇒= ⇒ = + =



Bán kính mặt cầu là
22
2
39
4.
24 4
SA a a
R SR
h
π
π
= = ⇒= =
Chọn A.
Câu 22: Giả sử hình chóp có cạnh bên là a, chiều cao
2
2
2 22
2
a
hR a h
h
⇒= = ⇒ =
Mặt khác ta có
0
sin 45 2.
h
ah
a
=⇒=
Do đó suy ra
2, 2ha= =
Ta có
22
.
2 1 42
22 4 . .
2 33
ABCD S ABCD ABCD
AB
a h AB S V h S
= −= ⇒ =⇒ =⇒ = =
Chọn D.
Câu 23: Chiều cao của hình chóp là
2
2
22
22
aa
ha

=−=



23
3
24 2
.
23 3
2
2
2
aa a
R VR
a
π
π
⇒= = ⇒= =
Chọn B.
Câu 24: Chiều cao của hình chóp là
2
2
22
22
aa
ha

=−=



2
22
2
4 2.
2
2
2
2
aa
R SR a
a
ππ
⇒= = ⇒= =
Chọn B.
Câu 25: Chiều cao của hình chóp là
( )
2
2
3 2. 2
54
2
a
ha a

=−=



( )
2
5
25
.
2.4 8
a
a
R
a
⇒= =
Chọn C.
Câu 26: Bán kính đường tròn đáy là
2
22
d
AC a
R
= =
Do
( )
SA ABC⊥
nên bán kính mặt cầu ngoại tiếp hình chóp là
2
2
6
.
42
d
SA a
RR= +=
Thể tích của mặt cầu ngoại tiếp hình chóp
.S ABCD
là:
33
4
6.
3
V Ra
ππ
= =
Chọn A.
Câu 27: Bán kính đường tròn đáy là
2
22
d
AC a
R = =
Do
( )
SA ABC⊥
nên bán kính mặt cầu ngoại tiếp hình chóp là
2
2
5
.
42
d
SA a
RR= +=
Diện tích của mặt cầu ngoại tiếp hình chóp
.S ABCD
là:
23
4 5.
SR a
ππ
= =
Chọn A.
Câu 28: Ta có
2 2 22
2 2 22
4
4
AD BD
AD BD AB a
AC BC
AC BC AB a
⊥
+==
⇒

⊥
+==
,
CD
⇒
cùng nhìn AB dưới một góc vuông nên tứ giác ABCD
nội tiếp đường tròn bán kính
1
.
2
ABCD
AB
RR a
= = =
Lại có
SAB∆
đều nên:
2
323
33
SAB
AB a
RR= = =
Do
( ) ( )
SAB ABC⊥
nên
2
22
. 12
2
.
4
3
S ABCD
AB a
R RR
= +− =
Thể tích của mặt cầu ngoại tiếp hình chóp
.S ABCD
là:
( )
3
3
4 32 3
.
3 27
C
a
VR
π
π
= =
Chọn C.
Câu 29: Bán kính đường tròn đáy là
2
22
d
AC a
R = =
Do
( )
SA ABC⊥
nên bán kính mặt cầu ngoại tiếp hình chóp là
2
2
2.
4
d
SA
R Ra= +=
Diện tích của mặt cầu ngoại tiếp hình chóp
.S ABCD
là:
23
4 8.SR a
ππ
= =
Chọn A.
Câu 30: Gọi H là chân đường cao hạ từ S xuống mặt phẳng
( )
ABC
Ta có
( )
SA AB
AB SHA AB HA
AB SH
⊥
⇒⊥ ⇒⊥
⊥
Tương tự ra có:
BC HC ABCH⊥⇒
là hình vuông.
Do
( )
// //AH BC AH SBC⇒
( )
( )
( )
( )
;;d A SBC d H SBC
⇒=
Dựng
HK SC
⊥
do
( )
BC HK HK SBC⊥⇒⊥
Do đó
(
)
( )
;2
d A SBC HK a= =
Mặt khác
22 2
11 1
6SH a
SH HC HK
+ = ⇒=
Ta có:
2
2
..
4
S ABCD S HABC d
SH
RR R= = +
(do tứ giác HABC nội tiếp)
Trong đó
( )
33
.
26 4
3 43 .
22 2 3
d S ABC
C
AC AB a
R R aV R a
ππ
== = ⇒ = ⇒= =
Chọn C.
Câu 31: Bán kính đường tròn đáy là
22
5
.
2 22
d
AC AB BC a
R
+
= = =
Do
( )
SA ABC⊥
nên bán kính mặt cầu ngoại tiếp hình chóp là:
2
2
13
.
42
d
SA
RR
= +=
Chọn C.
Câu 32: Ta có
SC AM⊥
mặt khác
AM SB⊥
do đó
.AM MC⊥
Như
vậy
0
90AMC =
Tương tự
0
90 .APC =
Lại có
0
90ANC =
vậy tâm mặt cầu ngoại tiếp tứ
diện
.C MNP
là trung điểm của AC.
Suy ra
3
4 32
2.
2 33
AC
R VR
ππ
= =⇒= =
Chọn C.
Câu 33: Đặt
;;AB x CD y AD BC AC BD z
= = = = = =
Gọi
,MN
lần lượt là trung điểm của AB và CD ta có:
DAC DBC AN BN∆ =∆ ⇒=
suy ra NM là trung trực
của AB, tương tự MN là trung trực của DC
Khi đó
I MN∈
sao cho
ID IA
=
Lại có
2
2 22
4
y
AN AD DN z= −=−
22
2 22
44
yx
MN AN AM z⇒ = − = −−
Mặt khác
2 22 2
MN IM IN R AM R DN
= += − + −
2 2 22
222
,
4 4 44
x y yx
RR z⇒ −+ − = −−
giải phương trình
tìm R.
Áp dụng:
22 22 2 2
4 9 22 13 3
Ra Ra a a a−+ −= − =
(
)
22 22 22 2 2222
4 3 9 496 9 9Ra aRa Ra aaRaRa
⇔ − = − − ⇒− = − − +−
22
2 85
9.
33
aa
Ra R⇔ − = ⇔=
Chọn B.
Câu 34: Ta có
( ) ( ) ( )
.SA ECD SED ECD⊥ ⇒⊥
Đặt
12
,
SED CED
RR R R= =
Ta có:
ECD∆
vuông tại E và
,ED a CE a= =
Do đó
22
2
2
.
22
CE ED a
R
+
= =
Lại có:
22
6
sin
10
SA SA
SDA
SD
SA AD
= = =
+
Suy ra
22
1
105
.
6
6
2sin
2.
10
SE SA AE
R
SDE
+
= = =
Do đó
2
22
. 12
114
.
46
S ECD
ED a
R RR= +− =
Chọn D.
Câu 35: Gọi
1
R
và
2
R
lần lượt là bán kính đường tròn ngoại tiếp tam giác đều
( )
SAB
và
( )
ABC
ta có:
( ) ( )
12
3
,.
3
a
R R AB SAB ABC= = = ∩
Do
(
)
( )
SAB ABC⊥
nên
2
22
. 12
15
.
46
S ABC
AB a
R RR= +− =
Thể tích khối cầu ngoại tiếp hình chóp đã cho là:
( )
3
3
4 5 15
.
3 54
C
a
VR
π
π
= =
Chọn C.
Câu 36: Đặt
( ) ( )
12
;,
ABC SAB
R R R R AB SAB ABC= = = ∩
Tam giác ABC vuông cân tại A nên
22
1
2
.
22 2
BC AB AC a
R
+
= = =
Tam giác SAB là tam giác đều nên
2
22
. 12
21
.
46
S ABC
AB a
R RR= +− =
Thể tích khối cầu ngoại tiếp hình chóp đã cho là:
( )
3
3
4 7 21
.
3 54
C
a
VR
π
π
= =
Chọn B.
Câu 37: Do
.S ABC
là hình chóp tam giác đều nên
.SA SB SC a
= = =
Ta có:
0 22
90 2.
ASB AB SA SB a=⇒= + =
Gọi M là trung điểm của BC và H là trọng tâm tam giác AB
Khi đó
( )
36
,
22
AB a
SH ABC AM⊥==
22
26 3
.
33 3
aa
AH AM SH SA AH⇒ = = ⇒= − =
Bán kính đường tròn ngoại tiếp hình chóp
.S ABC
là:
2
.
3
.
22
S ABC
SA a
R
SH
= =
Chọn B.
Câu 38: Đặt
(
) ( )
12
;,
ABCD SAB
R R R R AB SAB ABC= = = ∩
Tam giác ABDC là hình vuông cạnh bằng 2a nên
1
22
2.
22
AC a
Ra= = =
Tam giác SAB vuông cân tại S nên
2
.
2
AB
Ra= =
Do
( ) ( )
SAB ABC⊥
nên
2
22
. 12
2.
4
S ABC
AB
rR R R a
= = +− =
Chọn D.
Câu 39: Do
(
) ( )
(
)
0
; 45 .SA ABCD SC ABCD SCA⊥⇒ ==
Ta có:
22 0
5 tan 45 5.
AC AB AD a SA AC a= + = ⇒= =
Lại có:
5
.
22
d ABCD
AC a
RR= = =
Do
( )
2
2
10
.
42
d
SA a
SA ABCD R R⊥ ⇒= + =
Thể tích khối cầu ngoại tiếp hình chóp
.S ABCD
là:
3
3
4 5 10
.
33
a
VR
π
π
= =
Chọn D.
Câu 40: Gọi H là trung điểm của AB.
Do
.SA SB SH AB=⇒⊥
Ta có:
2 2 22
5
SB BC SC a SB BC
+ = = ⇒⊥
Mặt khác:
( )
AB BC BC SAB BC SH⊥⇒⊥ ⇒⊥
Suy ra
( )
,SH ABC⊥
đặt
1
.
2
ABC
AC
RR a
= = =
Đặt
2
2
.. .. .
4 2. . 2
SAB
SAB
SA SB AB SA SB AB SA SB a
RR
S SH AB SH SH
= = = = =
Trong đó
22
2
72
.
2
7
aa
SH SB HB R= − = ⇒=
Suy ra
2
22
. 12
259
.
4 14
S ABC
AB a
R RR= +− =
Chọn B.
Câu 41: Vì ABNK là tứ giác nội tiếp
0
90AKN⇒=
Do đó tâm đường tròn ngoại tiếp tứ giác ABKN là trung điểm AN
Suy ra:
2
2
22
2
5
22 24
ABNK
a
a
AN AB BN a
R

+

+

= = = =
Vậy bán kính mặt cầu ngoại tiếp khối chop S.ABNK là:
( )
2
2
2
2
3
5 17
.
4 4 44
ABNK ABNK
a
SA a a
RR

= += + =



Chọn A.
Câu 42: Công thức tìm nhanh bán kính mặt cầu ngoại tiếp hình chóp là
22
R xr= +
với
• r là bán kính đường tròn ngoại tiếp đa giác đáy.
•
22
:
2
SO r
xS
h
−
=
là đỉnh hình chóp, O là tâm đường tròn ngoại tiếp đa giác đáy, h là chiều cao khối
chóp.
Ta có
(
) (
)
(
)
0
; ; 60
SH ABCD SB ABCD SB BH SBH⊥⇒ = ==
Tam giác ABC vuông tại
22
2
22
AC AB BC
B BO a
+
⇒= = =
Do đó
24 2
;
3 3 33
a BO a
BH BO HO= = = =
Vậy
0 22
4 3 2 13
.tan 60
33
aa
SH BH SO SH OH= = ⇒= + =
Bán kính đường tròn ngoại tiếp ABCD là
2
2
AC
ra= =
Áp dụng công thức, ta được
2
22
2
4 21
.
2. 9
SO r a
Rr
SH

−
= +=


Chọn C.
Câu 43: Vì E là trung điểm
AD ABCE⇒
là hình vuông
CE AD⇒⊥
mà
( )
SA CE CE SAD CE SE⊥⇒⊥ ⇒⊥
Ta có
AB BC⊥
mà
( )
SA BC BC SAB SB BC⊥ ⇒ ⊥ ⇒⊥
Lại có
EK SD⊥
mà
( )
EC SD SD CKE CK SK⊥⇒⊥ ⇒ ⊥
Gọi I là trung điểm
SC IS IA IB IC IE IK⇒=== ==
Do đó I là tâm mặt cầu đi qua sáu điểm
,,,,,S ABCE K
Vậy bán kính cần tìm là
22
.
22
SC SA AC
Ra
+
= = =
Chọn A.
Câu 44: Dễ thấy
,BD
nhìn dưới AC một góc
0
90
Ta có
AD CD⊥
mà
( )
SA CD CD SAD CD AK⊥⇒⊥ ⇒⊥
Lại có
AK SD⊥
mà
( )
0
90AK SCD AK KC AKC⇒⊥ ⇒⊥⇒ =
Chứng minh tương tự, ta được
0
90AHC =
AC⇒
là đường kính mặt cầu ngoại tiếp khối chóp ABCDEHK
Vậy
3
3
24 2
.
22 3 3
AC a a
R VR
π
π
= = → = =
Chọn A.
Câu 45: Áp dụng định lý Cosin, ta có
22
2. . .cos 5 4cosBC AB AC AB AC BAC
α
= +− =−
Suy ra bán kính đường tròn ngoại tiếp
ABC∆
là
5 4cos
2sin
2.sin
ABC
BC
R
BAC
α
α
∆
−
= =
(định lý Sin)
Gọi O là tâm đường tròn ngoại tiếp
ABC∆
Gọi M là trung điểm
AB OM AB
⇒⊥
mà
SA OM⊥
Suy ra
( )
OM SAB⊥
mà M là tâm đường tròn ngoại tiếp
1
ABB∆
Do đó
1
.OA OB OB= =
Chứng minh tương tự, ta được
1
OA OC OC= =
Vậy O là tâm mặt cầu ngoại tiếp đi qua các điểm
11
5 4cos
,,, , .
2sin
ABC
ABCC B R R
α
α
∆
−
⇒= =
Chọn D.
Câu 46: Chọn độ dài cạnh lập phương
.'' 'ABCD A B C D
là 1
Gọi I là tâm hình lập phương
.'' 'ABCD A B C D
(tham khảo hình vẽ dưới đây)
• Bán kính mặt cầu ngoại tiếp hình lập phương là
1
'3
22
AC
R AI= = =
• Bán kính mặt cầu nội tiếp hình lập phương là
2
1
22
AB
R = =
• Bán kính mặt cầu nội tiếp tiếp xúc với tất cả các cạnh là
( )
3
; '' 1R d I C D IM= = =


Vậy
22 2
123
.
RRR+=
Chọn B.
Câu 47: Chọn độ dài cạnh lập phương
.'' 'ABCD A B C D
là 1
Gọi I là tâm hình lập phương
.'' 'ABCD A B C D
(tham khảo hình vẽ dưới đây)
• Bán kính mặt cầu ngoại tiếp hình lập phương là
1
'3
22
AC
R AI
= = =
• Bán kính mặt cầu nội tiếp hình lập phương là
2
1
22
AB
R = =
• Bán kính mặt cầu nội tiếp tiếp xúc với tất cả các cạnh là
( )
3
; '' 1R d I C D IM= = =


Vậy
31 2
.RRR>>
Chọn D.
Câu 48: Gọi M là trung điểm
( )
'
'
AM BC
BC BC AA M
AA BC
⊥
⇒ ⇒⊥
⊥
Do đó
( ) ( )
( )
0
' ; ' ; ' 60A BC ABC A M AM A MA= = =
Đặt
3 33
':
2 22
cos '
x AM x
AB x AM A M x
A MA
=→= ⇒ = = =
Suy ra
2
2
'
1
. ' . 18 36 6
22
A BC
x
S A M BC x x
∆
= = = → = ⇔ =
Khi đó bán kính đường tròn ngoại tiếp
ABC∆
là
3
23
3
ABC
x
R
∆
= =
Vậy bán kính mặt cầu cần tính là
( )
22
2
2
' 3 57
23 .
4 42
ABC
AA
RR
∆
= + = +=
Chọn B.
Câu 49: Ta có
22
5.AC AB BC a= +=
Gọi H là trung điểm của
AB SH AB⇒⊥
(
)
.SH ABCD⇒⊥
Gọi E là trung điểm của MN, dựng
đường thẳng d qua E song song với SH, trên d lấy điểm I
sao cho
IS ID I= ⇒
là tâm mặt cầu ngoại tiếp khối chóp
..S DMN IS ID IM IN R⇒= = = =
Ta có
DMN∆
vuông tại
5
244
MN AC a
D DE⇒= = =
2
22 2
53
,.
16 2
aa
IE R DE R SH→= − = − =
Mặt khác:
22
2
2
3 1 37
4 4 16
a
HE AD AB

=+=


Lại có:
(
)
2
22
2
22 2 2
37 3 5
16 2 16
aa a
R HE SH IE R R

− = − ⇔− = − −



CACL 4 đáp án vào biểu thức
2
22
37 3 5 102
.
16 2 16 6
X XX

− − − − ⇒=



Chọn C.
Câu 50:
Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Theo công thức tính diện tích tam giác ta có:
1
.
2
2
ABC
AB AC
S
r
AB BC CA
p
= =
++
trong đó
22
5BC AB AC a= +=
. Suy ra
2
6
.
6
a
ra
a
= =
Tam giác ABC vuông tại
,A AP AE
=
suy ra tam giác APE vuông cân tại
A ⇒
tam giác AEH vuông cân tại
.E AE HE a
⇒==
Ta có:
22 2 2
2 2.AH AE HE a SH SA AH a= + = ⇒= − =
Ta có:
2
22
5
3.
22 4
BC a a
EC AC AE a CF MF CF HM HF=−==⇒ = − =⇒ + =
Mặt khác
( )
2
2
22 2 2 2 2 2 2
25
2
4
a
IC IS MI MC SK IK IM a IM HM=⇔ + = +⇔ + = ± +
(Dấu cộng khi
,SI
cùng phía với mặt phẳng
( )
ABC
và dấu trừ khi
,SI
khác phía với mặt phẳng
( )
ABC
)
( )
22
2
2
25 5
2
44
aa
IM a IM⇔+ = ± +
Giải phương trình trên
22
3 2 118
.
44
aa
IM R IC IM MC⇒ = ⇒= = + =
Chọn A.
Câu 51: Đặt
;AB x CD y AD BC AC BD z= = = = = = =
Ta có:
2 2 22
222
4 4 44
x y yx
RR z−+ −= −−
(
)
(
)
22 22 2 22
22 22 22
22 22 22 22 22
4 22 4
22 22 22 22
22
4 22 2 2
2
22 22
4
3
3 23
44
23
3
44
.
33
Ra Rb a ab
Ra ab Rb
Ra ab abRb Rb
a ab b
ab abRb Rb
ab
a ab a b
R Ra
ab ab
⇒ −+ −= − +
⇔ −= −− −
⇔ −= −− − −+ −
−+
⇔ −= − −⇔ −=
−
−−
⇔ = ⇔=
−−
Chọn C.
Câu 52: Gọi
,IK
lần lượt là trung điểm của AB và CD.
Ta có:
(
)
.DAB CBA c c c IC ID IK CD
∆ =∆ −− ⇒ = ⇒ =
Tương tự
( )
.ACD BDC c c c KB KA KI AB∆ =∆ −− ⇒ = ⇒ =
Do đó KI là đường trung trực của AB và CD.
Gọi O là tâm mặt cầu ngoại tiếp tứ diện ABCD thì
.O IK∈
Ta có:
2 2 22
4 2 4.AK AC CK IK AK AI= − = ⇒= − =
Mặt khác
22
16 4 4OI R R= − + −=
2 2 2 22
16 4 4 16 16 8 4 4R R R RR⇔ − =− −⇒ − = − −+ −
2
7 65
4.
22
RR⇔ −=⇒ =
Chọn D.
| 1/53
| | Tải xuống

Có thể bạn quan tâm:

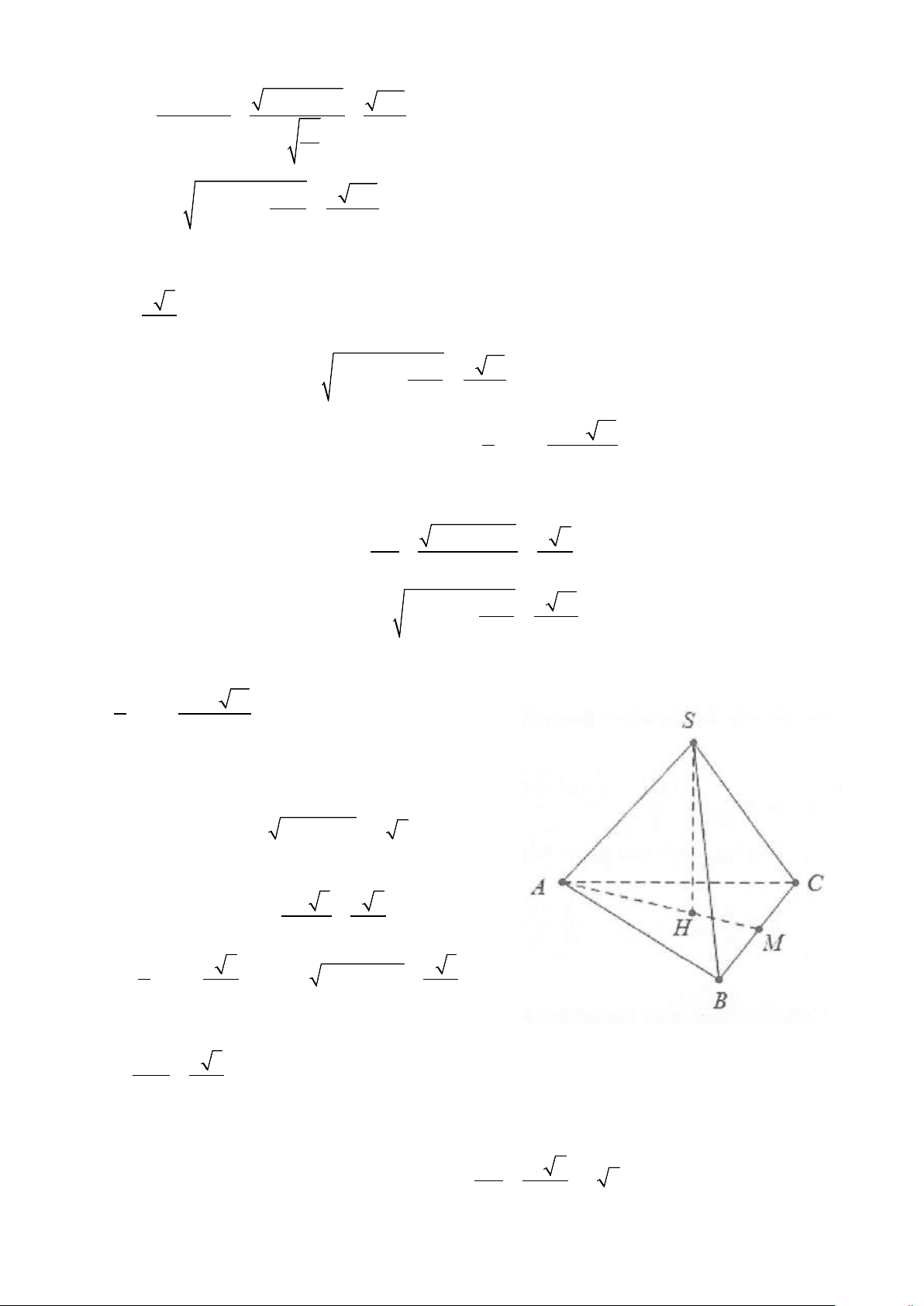
Preview text:

CHỦ ĐỀ 10. MẶT CẦU - HÌNH CẦU - KHỐI CẦU
I. LÝ THUYẾT TRỌNG TÂM 1. Mặt cầu
Tập hợp các điểm trong không gian cách điểm O cố định một khoảng R không đổi gọi là mặt cầu có tâm
là O và bán kính bằng R . Kí hiệu: S ( ; O R) = {M OM = } R . 2. Khối cầu Mặt cầu S ( ;
O R) cùng với các điểm nằm bên trong nó được gọi là một khối cầu tâm O , bán kính R . Kí hiệu: B( ;
O R) = {M OM ≤ } R . Nếu ,
OA OB là hai bán kính của mặt cầu sao cho ,AO,B thẳng hàng thì đoạn thẳng AB gọi là đường kính của mặt cầu.
Định lí: Cho điểm cố định A, B. Tập hợp các điểm M trong không gian sao cho  0
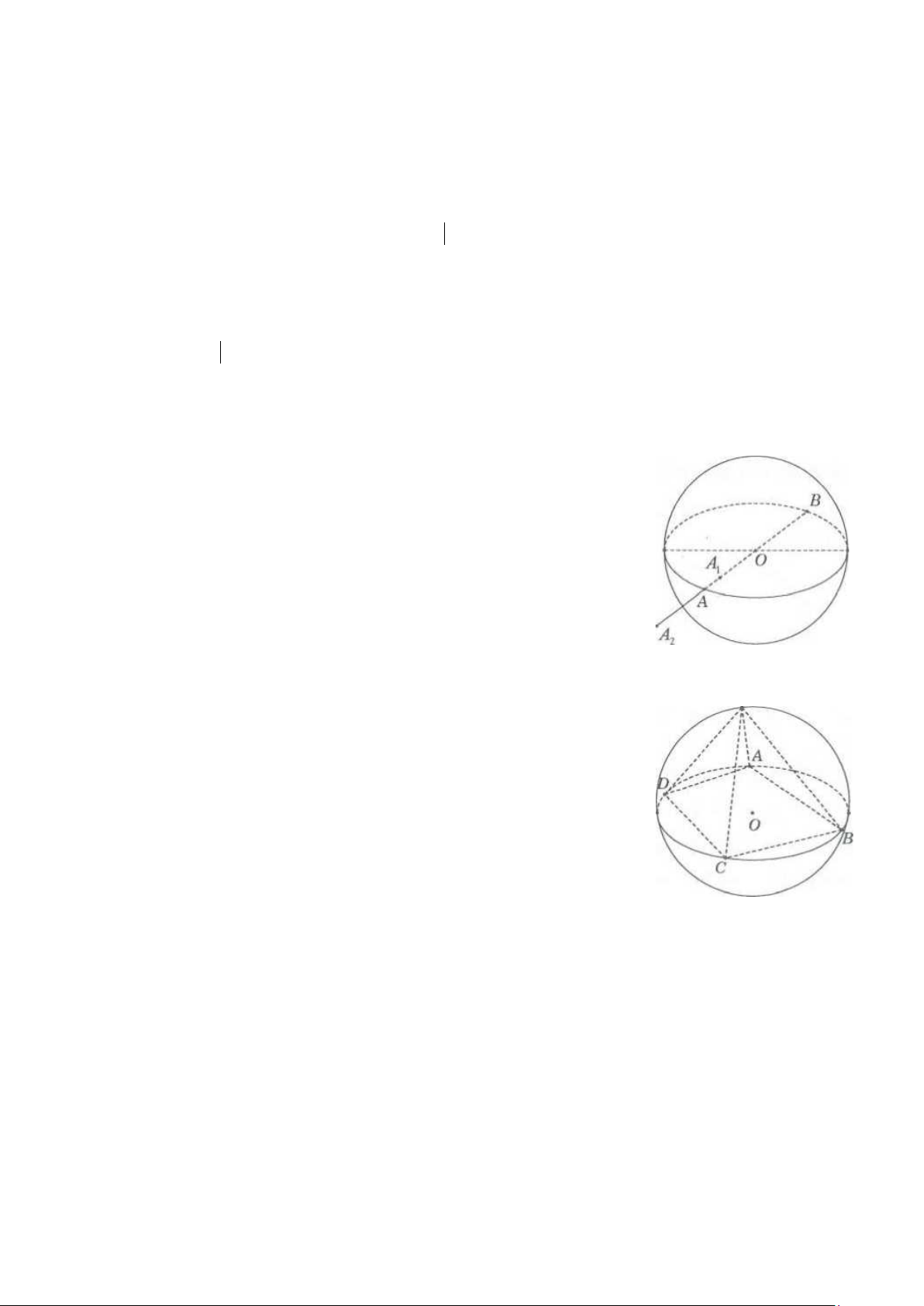
AMB = 90 là mặt cầu đường kính AB . • A∈ S ( ; O R) ⇔ OA = . R
• OA < R ⇔ A 1
1 nằm trong mặt cầu.
• OA > R ⇔ A 2
2 nằm ngoài mặt cầu.
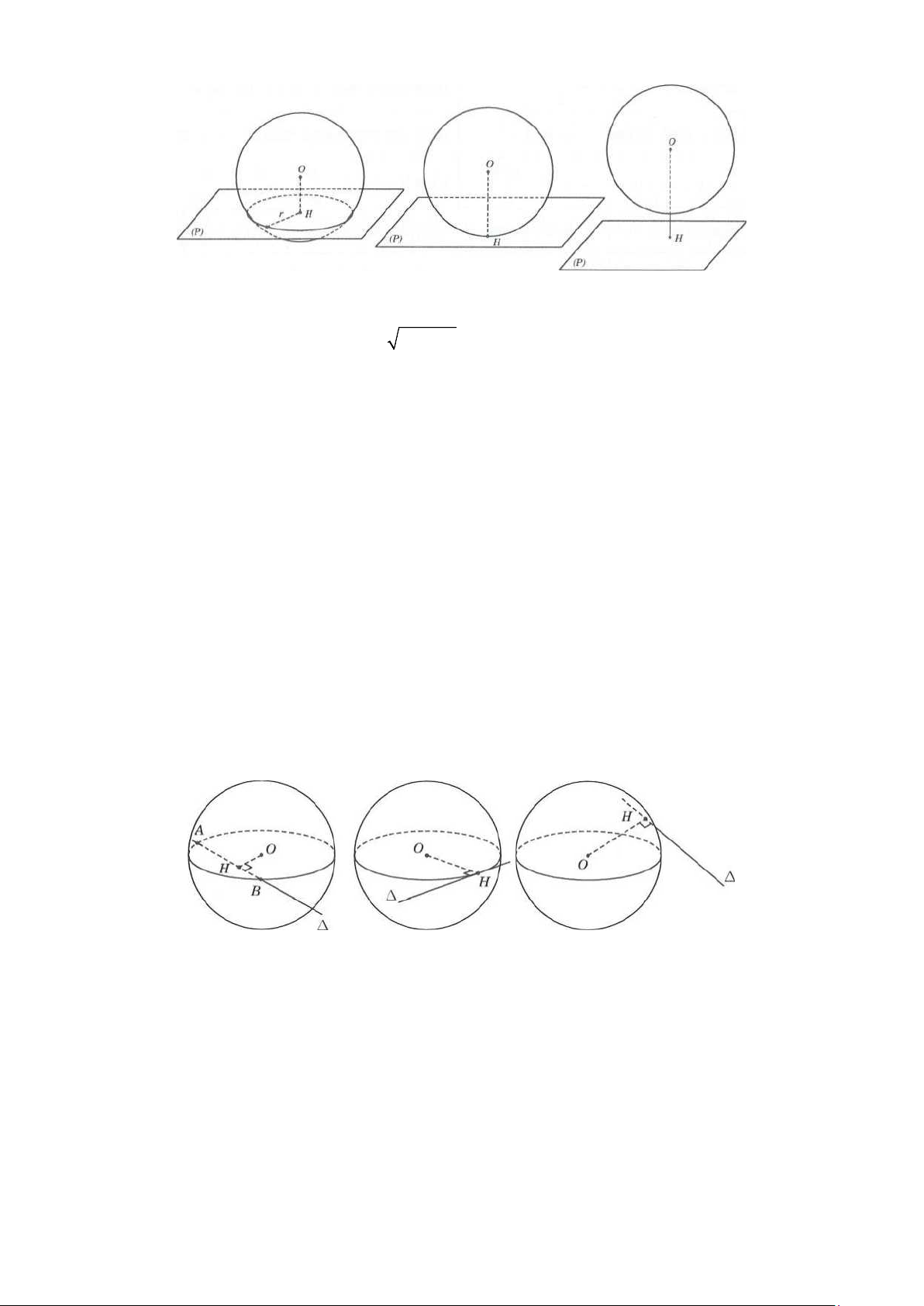
3. Mặt cầu ngoại tiếp khối đa diện
Định nghĩa: Mặt cầu đi qua mọi đỉnh của một hình đa diện (H ) được gọi
là mặt cầu ngoại tiếp hình đa diện (H ) và khi đó (H ) được gọi là nội tiếp mặt cầu đó.
Điều kiện cần và đủ để một hình chóp có mặt cầu ngoại tiếp là đáy của nó
là một đa giác nội tiếp một đường tròn.
Mọi tứ diện đều có mặt cầu ngoại tiếp.
4. Mặt cầu ngoại tiếp khối đa diện
a. Mặt cầu nội tiếp hình chóp là mặt cầu nằm bên trong hình chóp và tiếp xúc với với tất các mặt của hình chóp.
b. Tâm mặt cầu nội tiếp hình chóp cách đều tất cả các mặt của hình chóp.
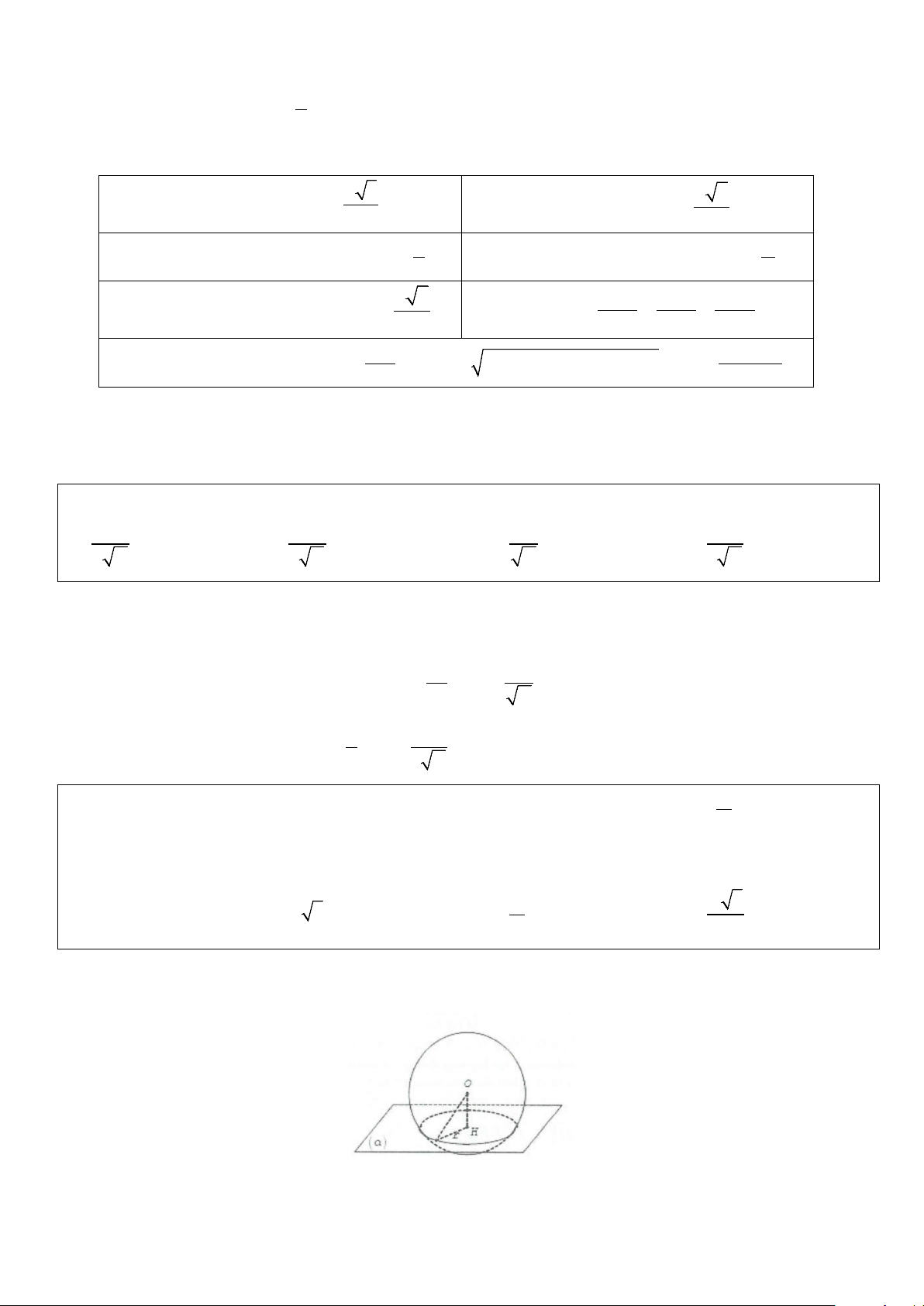
5. Vị trí tương đối giữa mặt cầu và mặt phẳng
Cho mặt cầu S ( ;
O R) và mặt phẳng (P) , gọi d là khoảng cách từ O đến (P) và H là hình chiếu vuông
góc của O trên (P) . Khi đó
• Nếu d < R thì mặt phẳng (P) cắt mặt cầu S ( ;
O R) theo giao tuyến là đường tròn nằm trên mặt
phẳng (P) có tâm là H và có bán kính 2 2
r = R − d .
Khi d = 0 thì mặt phẳng (P) đi qua tâm O của mặt cầu, mặt phẳng đó gọi là mặt phẳng kính; giao
tuyến của mặt phẳng kính với mặt cầu là dường tròn có tâm O và bán kính R, đường tròn đó gọi là đường
tròn lớn của mặt cầu.
• Nếu d = R thì mặt phẳng (P) và mặt cầu S ( ;
O R) có một điểm chung duy nhất H.
Khi đó ta nói (P) tiếp xúc với S ( ;
O R) tại H và (P) gọi là tiếp diện của mặt cầu, H gọi là tiếp diện.
Chú ý. Cho H là một điểm thuộc mặt cầu S ( ;
O R) và mặt phẳng (P) qua H . Thế thì (P) tiếp xúc với S ( ;
O R) ⇔ OH ⊥ (P).
• Nếu d > R thì mặt phẳng (P) và mặt cầu S ( ;
O R) không có điểm chung.
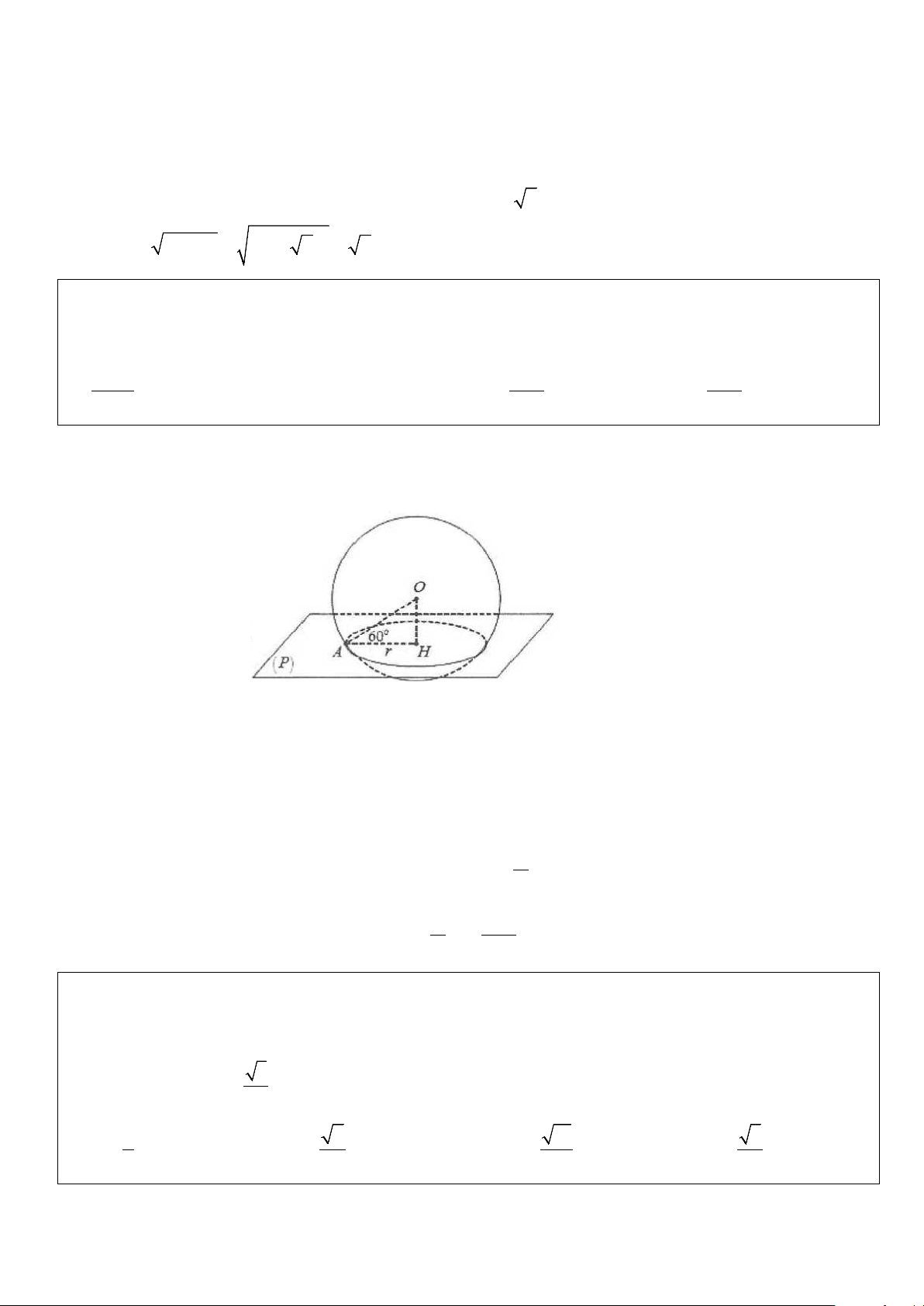
6. Vị trí tương đối giữa mặt cầu và đường thẳng
Cho mặt cầu S ( ;
O R) và đường thẳng ∆ . Gọi H là hình chiếu vuông góc của O trên ∆ và d = OH là
khoảng cách từ O đến ∆ . Khi đó:
• Nếu d < R thì ∆ cắt S ( ;
O R) tại hai điểm ,
A B và H là trung điểm của AB.
• Nếu d = R thì ∆ và S ( ;
O R) chỉ có một điểm chung H, trong trường hợp này ∆ được gọi là tiếp
tuyến của mặt cầu S ( ;
O R) hay ∆ tiếp xúc với S ( ;
O R) và H là tiếp điểm.
• Nếu d > R thì ∆ và S ( ;
O R) không có điểm chung.
7. Diện tích mặt cầu và thể tích khối cầu
Gọi R là bán kính của mặt cầu thì • Diện tích mặt cầu: 2 S = 4π R . • Thể tích khối cầu: 4 2 V = π R . 3
8. Một số công thức tính nhanh bán kính đường tròn ngoại tiếp a 3 a  → R = Hình vuông cạnh a 2 a  → R = Tam giác đều cạnh 2 2
Tam giác vuông cạnh huyền b b  → R =
Hình chữ nhật đường chéo d d  → R = 2 2 a 2 a  → R = Định lí hàm sin: a b c = = = 2R Tam giác vuông cân cạnh 2
sin A sin B sin C Tam giác ba cạnh , , abc a b c  → R =
; với S = p( p − a)( p − b)( p − c) và a b c p + + = . 4S 2
II. CÁC DẠNG TOÁN THƯỜNG GẶP VỀ MẶT CẦU
Dạng 1: Những bài toán vận dụng mức cơ bản
Ví dụ 1: Tính thể tích khối cầu có diện tích bằng diện tích xung quanh của hình lập phương cạnh a. 3 3 3 3 A. a B. 32a C. a D. 4a 6 π 3 π π 3 π Lời giải
Diện tích xung quanh hình lập phương cạnh a là 2 2 S = a  → S = a xq 4 mc 4 2
Suy ra bán kính mặt cầu là 2 2 2 4π = 4 a a R a ⇔ R = ⇒ R = π π 3
Vậy thể tích khối cầu cần tính là 4 2 4a V = π R = . Chọn D. 3 3 π
Ví dụ 2: Cho mặt cầu S ( ;
O R) và mặt phẳng(α ) . Biết khoảng cách từ O đến (α ) bằng R . Khi đó thiết diện 2
tạo bởi mặt phẳng (α ) với S ( ;
O R) là một đường tròn đường kính bằng A. . R B. R 3. C. R . D. R 3 . 2 2 Lời giải Hình vẽ tham khảo
Gọi H là hình chiếu của O xuống mp(α ) . Ta có ( ;(α )) R d O
= OH = < R nên (α ) cắt S ( ; O R) theo 2
đường tròn C (H;r). Bán kính đường tròn C (H;r) là 2 2 R 3
r = R − OH = . 2
Suy ra dường kính của đường tròn cần tính bằng R 3 . Chọn B. 2
Ví dụ 3: Cho mặt cầu S ( ;
O R) và một điểm A thỏa mãn OA = 2 .
R Qua A kẻ đường thẳng cắt (S ) tại hai
điểm B, C sao cho BC = R 3. Khoảng cách từ O đến BC bằng A. . R B. R . C. R 2. D. R 3. 2 Lời giải
Gọi H là hình chiếu của O lên BC. CD R 3 HC = = .
Ta có OB = OC = R, suy ra H là trung điểm của BC nên 2 2 2 2 R
OH = OC − HC = . Suy ra 2 Chọn B.
Ví dụ 4: Cho hình cầu tâm O, đường kính AA' = 4. Gọi H là một điểm trên đoạn AA' sao cho 8 AH = . 3
Mặt phẳng (α ) qua H và vuông góc với AA'cắt hình cầu theo đường tròn (C). Tính diện tích của đường tròn (C). A. 32π π π π . B. 8 . C. 8 . D. 32 . 9 9 3 3 Lời giải Theo giả thiết, ta có 8 AH = . Ta suy ra 2
OH = AH − OA = . 3 3 2
Gọi r ' là bán kính của đường tròn (C). Ta có 2 2 2 2  2  32
r ' = r − OH = 2 − =   .  3  9
Vậy diện tích cùa đường tròn(C) là 2 32π S = π r ' = . Chọn A. 9
Ví dụ 5: Diện tích hình tròn lớn của một hình cầu là 4π. Một mặt phẳng (α ) cắt hình cầu theo một hình
tròn có diện tích là 2π. Khoảng cách từ tâm mặt cầu đến mặt phẳng (α ) bằng A. 2 . B. 1. C. 2 . D. 2. 4 2 Lời giải
Gọi khoảng cách từ tâm cầu đến mặt phẳng là d, ta có 2 2 2
d = R − r .
Hình tròn lớn của hình cầu S là hình tròn tạo bởi mặt phẳng cắt hình cầu và đi qua tâm của hình cầu.
Gọi R là bán kính hình cầu thì hình tròn lớn cũng có bán kính là R .
Theo giả thiết, ta có 2
π R = 4π ⇔ R = 2 và 2
π r = 2π ⇔ r = 2 .
Suy ra d = R − r = − ( )2 2 2 2 2 2 = 2. Chọn D.
Ví dụ 6: Cho mặt cầu S ( ;
O R) , A là một điểm ở trên mặt cầu (S ) và (P) là mặt phẳng đi qua A sao cho
góc giữa đường thẳng OA và mặt phẳng (P) bằng 0
60 . Diện tích của đường tròn giao tuyến bằng 2 2 2 A. 3π R π π . B. 2 π R . C. R . D. R . 4 4 2 Lời giải Hình vẽ tham khảo
Gọi H là hình chiếu vuông góc của O trên (P) thì
• H là tâm của đường tròn giao tuyến của (P) và (S ) . ( ; OA P )  = ( ; OA AH)  0 • ( ) = 60 .
Bán kính của đường tròn giao tuyến 0 = = .cos60 R r HA OA = . 2 2 2 π
Suy ra diện tích dường tròn giao tuyến 2 R R π r π   = =   . Chọn C.  2  4
Ví dụ 7: Cho mặt cầu S (I; R) , mặt phẳng (P) cắt mặt cầu(S ) theo giao tuyến là một đường tròn tâm O. Hai điểm ,
A B ∈O sao cho tam giác OAB đều, góc giữa hai mặt phẳng (IAB) và (OAB) bằng 0 60 , diện
tích tam giác IAB bằng 3 . Bán kính R bằng 2 A. 3 R = . B. 2 R = . C. 13 R = . D. 5 R = . 2 2 2 2 Lời giải
Đặt OA = OB = .x Tam giác OAB là tam giác đều 2 x 3 S =
Mặt phẳng (OAB) là hình chiếu của mặt phẳng (IAB) trên mặt phẳng (P) . OA ∆ B . 4 S =
với ϕ = (IAB) (OAB)  0 ; = 60 . ∆ S ϕ OAB I ∆ AB .cos 2 S∆ x IAB 3 3 3 S = = ⇒ = ⇔ = ∆ x OAB 1. 2 4 4 4 ⇒  0 3
IMO = 60 ⇒ IO = .
Gọi M là trung điểm của AB 2 2 2 2 3 2 13 R IA IO AO   = = + = +1 =   . Vậy  2  2 Chọn C.
Ví dụ 8: Cho mặt cầu (S ) tâm I, bán kính R. Ba mặt phẳng (P),(Q),(R) qua điểm A không nằm trên mặt
cầu, đôi một vuông góc với nhau cắt mặt cầu (S ) theo thiết diện là ba hình tròn có tổng diện tích bằng 3 12π .
cm Biết IA = 3 ,
cm tính độ dài bán kính R của mặt cầu (S ). A. r = 2 3. B. r = 5. C. r = 3. D. r = 2. Lời giải
Gọi a,b,c lần lượt là khoảng cách từ I đến mặt phẳng (P),(Q),(R).
Gọi r ,r ,r lần lượt là bán kính đường tròn giao tuyến của mặt cầu (S ) với (P),(Q),(R). 1 2 3 Khi đó 2 2 2 2 2 2 2 2 2 2 2 2 2
R = a + r ; R = b + r ; R = c + r ⇒ 3R = a + b + c + ( 2 2 2
r + r + r (*). 1 2 3 1 2 3 ) Mà 2 2 2 2
a + b + c = IA ;S + S + S = π ( 2 2 2
r + r + r . 1 2 3 1 2 3 ) Suy ra (*) 2 2 S + S + S 1 2 3 ⇔ 3R = IA +
= 3+12 =15 ⇒ R = 5. Chọn B. π
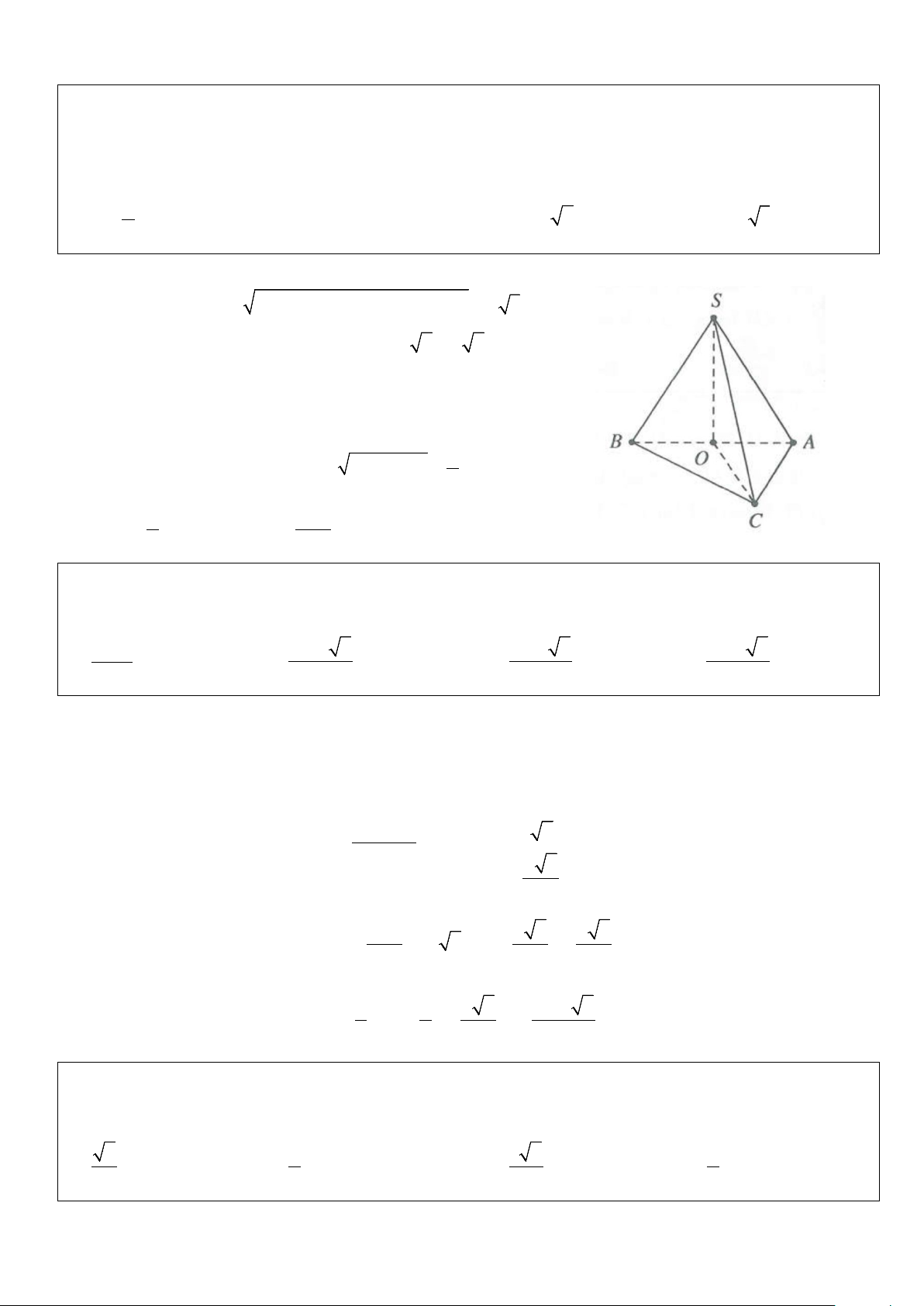
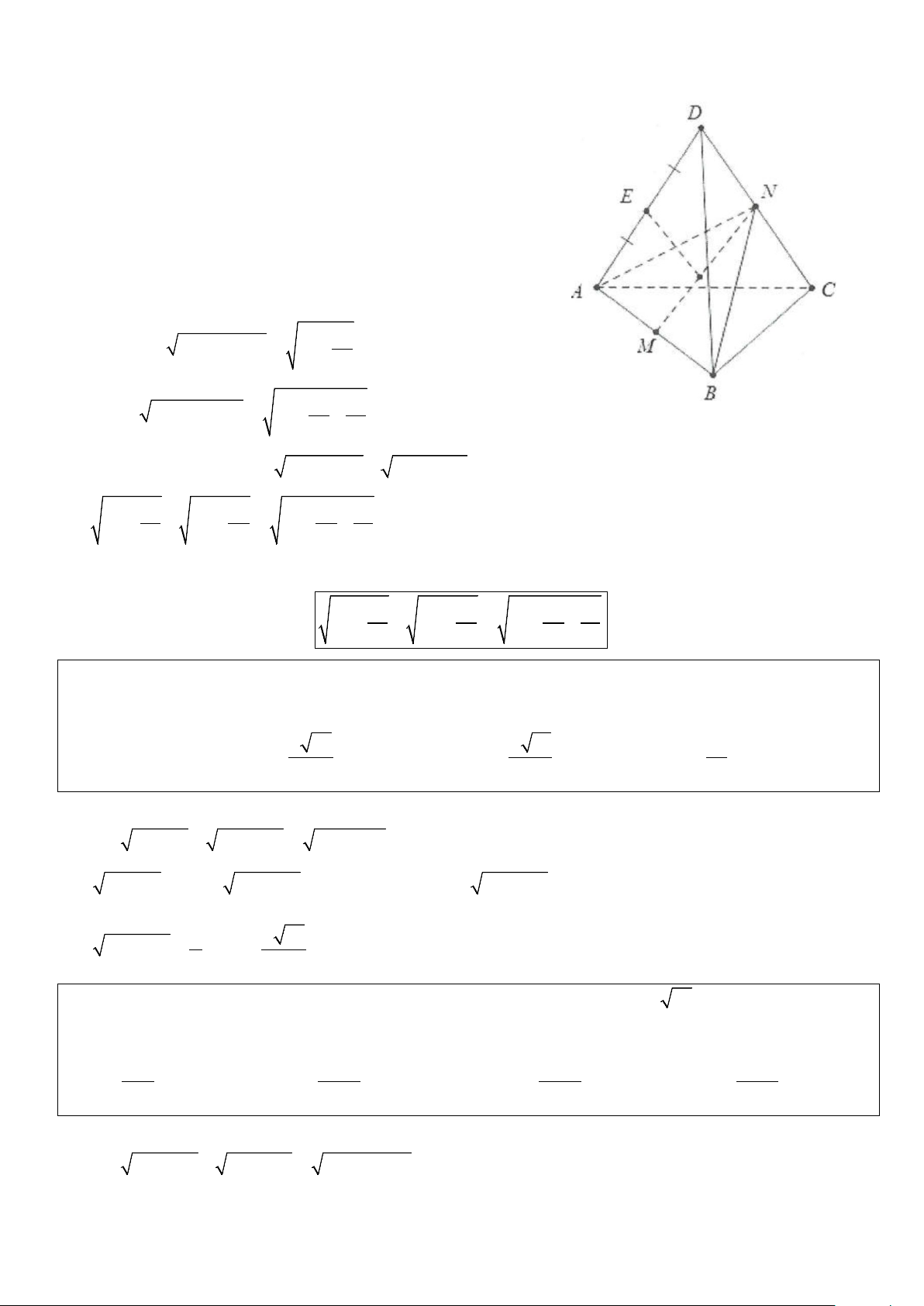
Dạng 2: Đa diện có các đỉnh cùng nhìn một đoạn nối hai đỉnh còn lại dưới góc vuông Phương pháp giải:
Xét đa giác XYA A ...A có các đỉnh A , A ,..., A cùng nhìn XY một góc vuông, chẳng hạn có 1 2 n 1 2 n  =  0
A XY A XY = ... = 90 . Khi đó, mặt cầu ngoại tiếp đa diện XYA A ...A mặt cầu đường kính XY, tâm là 1 2 1 2 n
trung điểm của XY và bán kính XY R = . 2
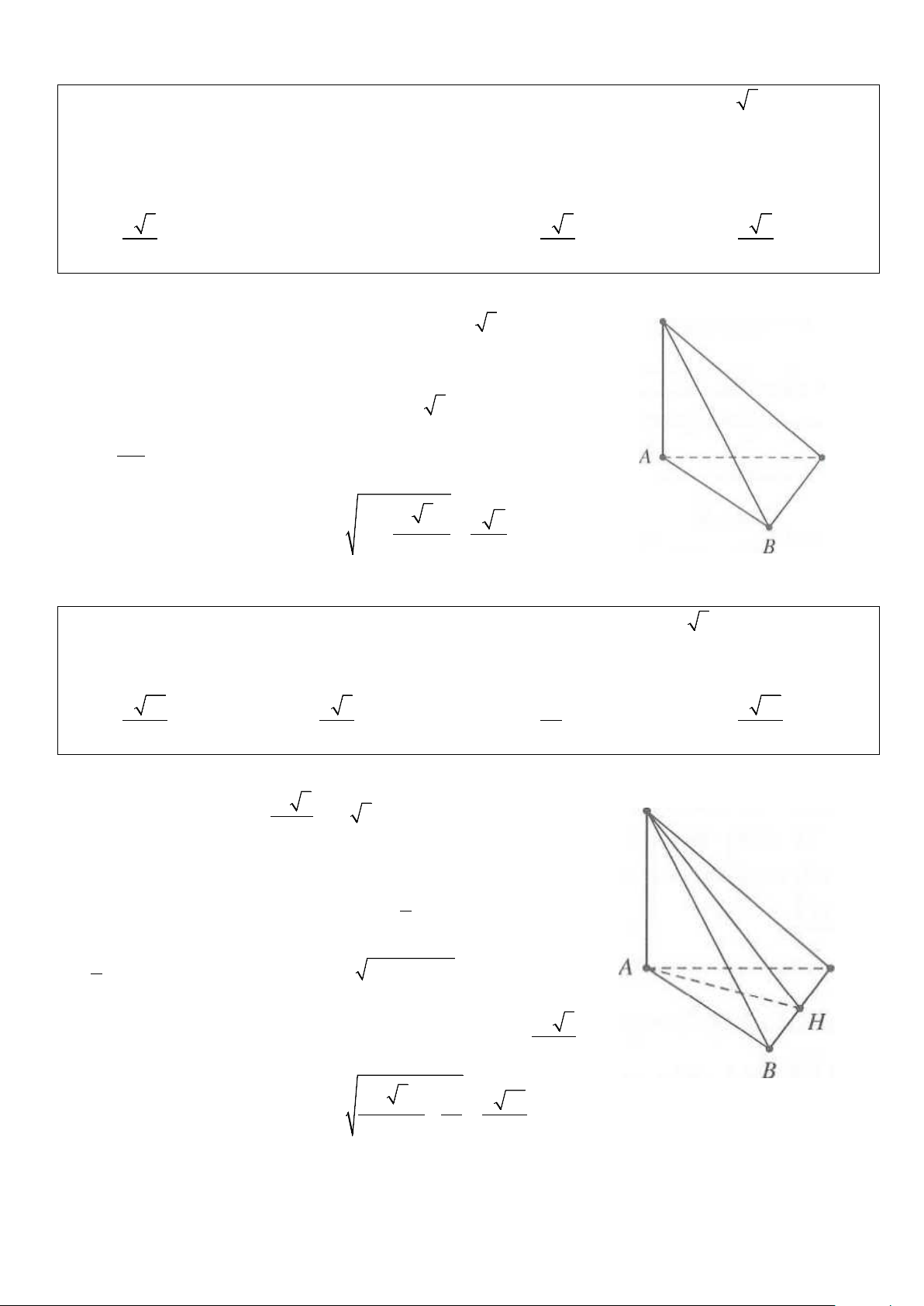
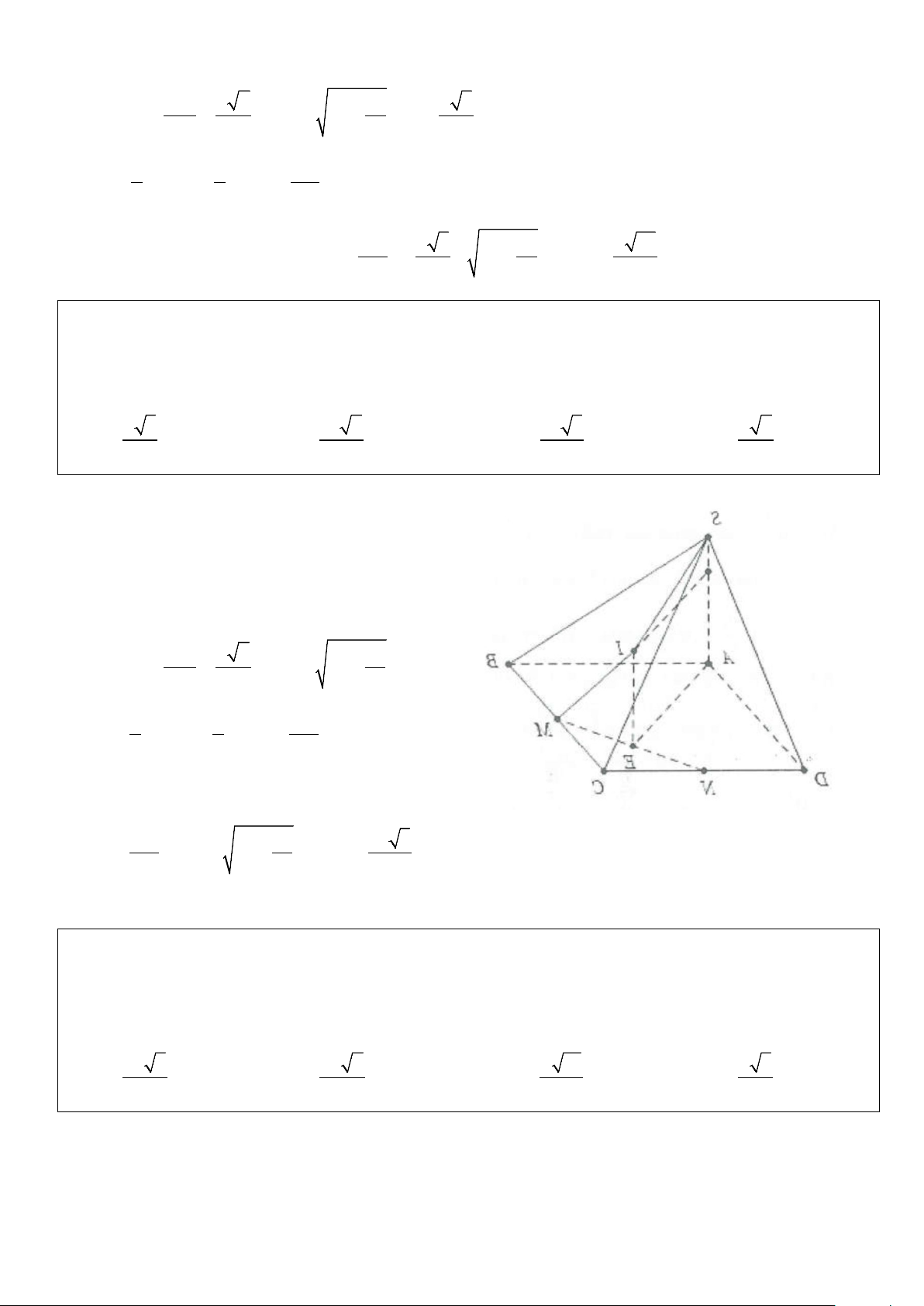
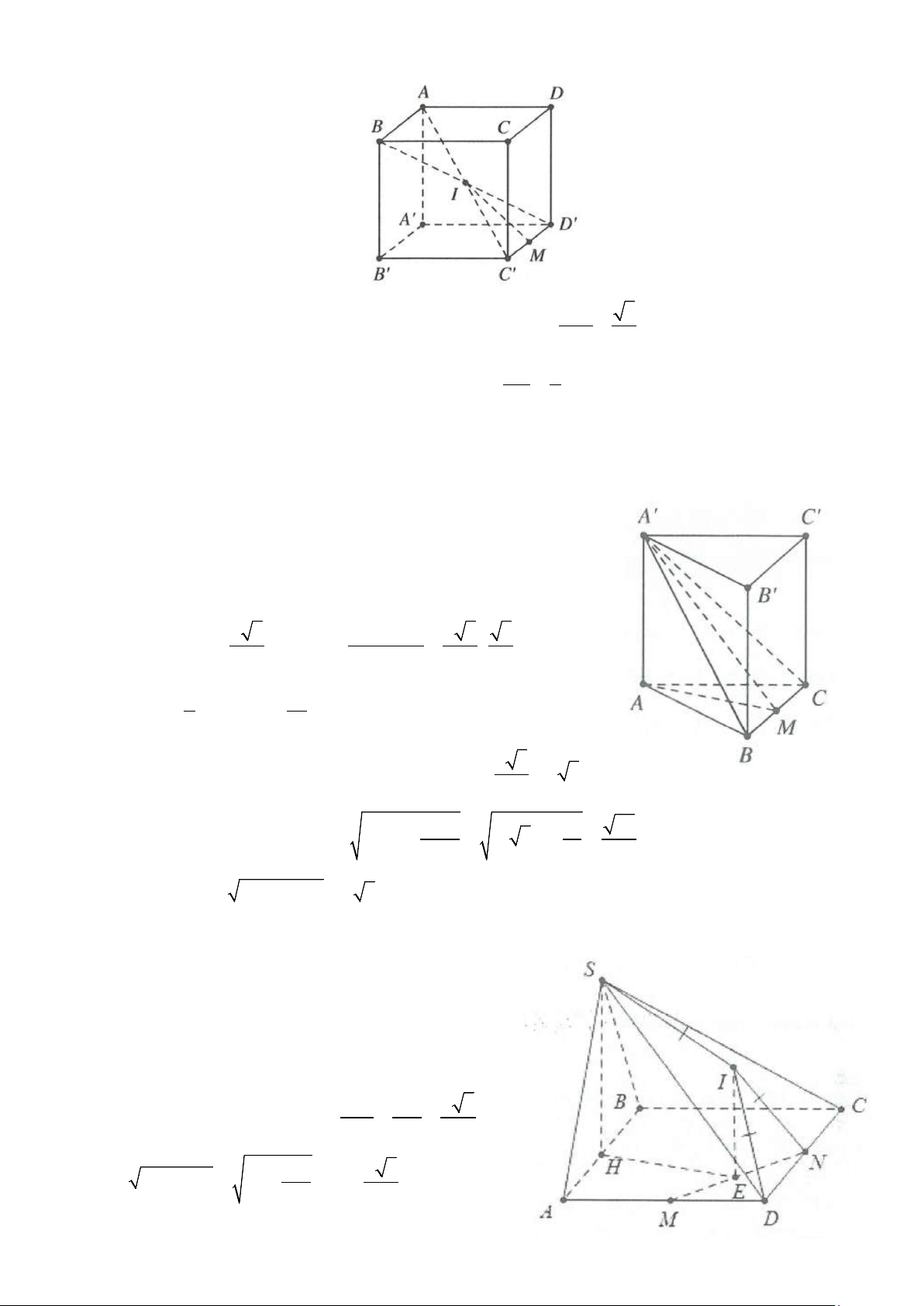
Ví dụ 1: Cho hình chóp S.ABC có đáy là tam giác ABC, BC = a 3, AC = 2 .
a Cạnh bên SA vuông góc với đáy và SA = .
a Góc giữa đường thẳng SB và mặt phẳng ( ABC) bằng 0
45 . Bán kính mặt cầu ngoại tiếp
hình chóp S.ABC bằng A. a 5 . B. a 3 . C. a . D. a 2 . 2 2 2 2 Lời giải
Vì SA ⊥ ( ABC) nên  (SB ABC )=  (AB AB)=  0 ;( ) ; SBA = 45 .
Suy ra tam giác SAB vuông cân tại A  → SA = AB = . a
Ta có AB + BC = a + (a )2 2 2 2 2 2
3 = 4a = AC ⇒ A
∆ BC vuông tại B.
Do đó AB ⊥ BC mà BC ⊥ SA ⇔ BC ⊥ (SAB) ⇒ BC ⊥ SB
Khi đó, hai điểm A, B cùng nhìn SC dưới một góc vuông
Vậy bán kính mặt cầu ngoại tiếp cần tính là SC a 5 R = = . 2 2 Chọn A.
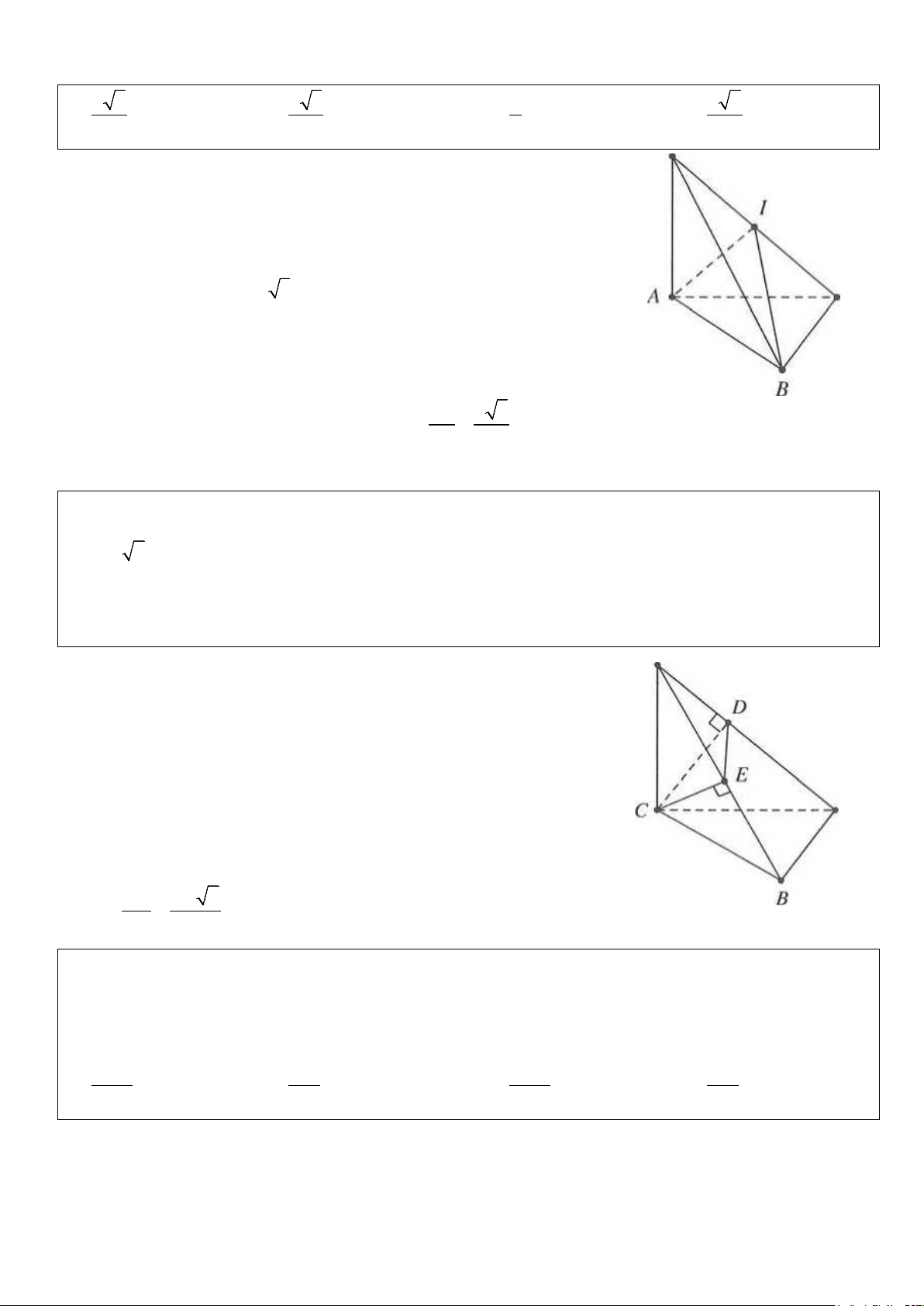
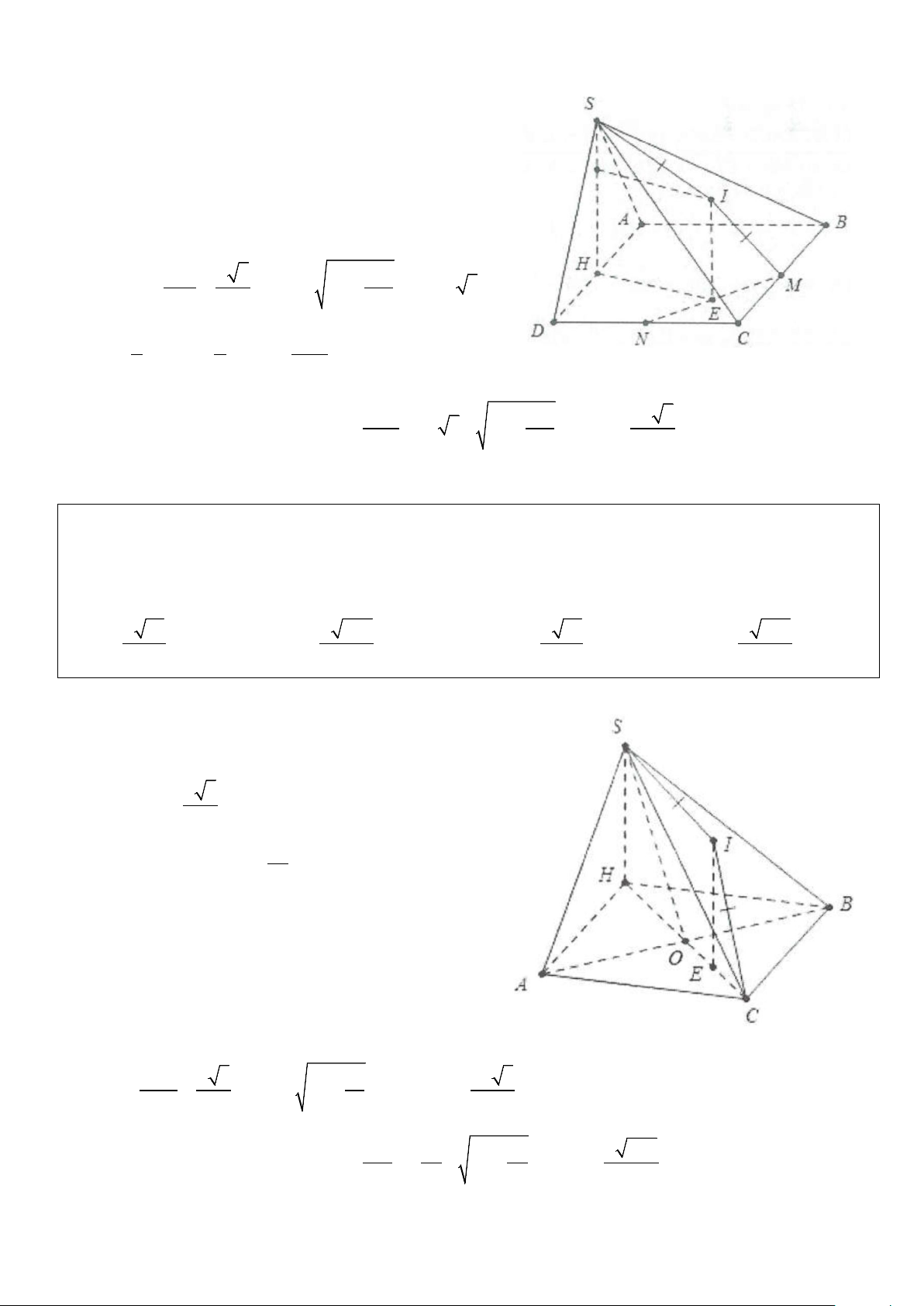
Ví dụ 2: Cho hình chóp S.ABC có SC = 2a và SC ⊥ ( ABC) . Đáy ABC là tam giác vuông cân tại B có
AB = a 2. Mặt phẳng (α ) đi qua C và vuông góc với , SA (α ) cắt ,
SA SB lần lượt tại D,E. Diện tích mặt
cầu ngoại tiếp khối đa diện ECDAB bằng A. 2 16π a . B. 2 4π a . C. 2 8π a . D. 2 12π a . Lời giảiSC ⊥ AB Ta có 
⇒ AB(SBC) ⇒ CE ⊥ AB BC ⊥ ABCE ⊥ SB
Mà SA ⊥ (α ) ⇒ SA ⊥ CE suy ra CE ⊥ (SAB) ⇒  , CE ⊥ AE
Do đó các điểm B, D, E nhìn AC dưới một góc vuông
⇒ Tâm mặt cầu ngoại tiếp khối đa diện là trung điểm AC AC AB 2 2 ⇒ R = = = a  → S = 4π a . 2 2 Chọn B.
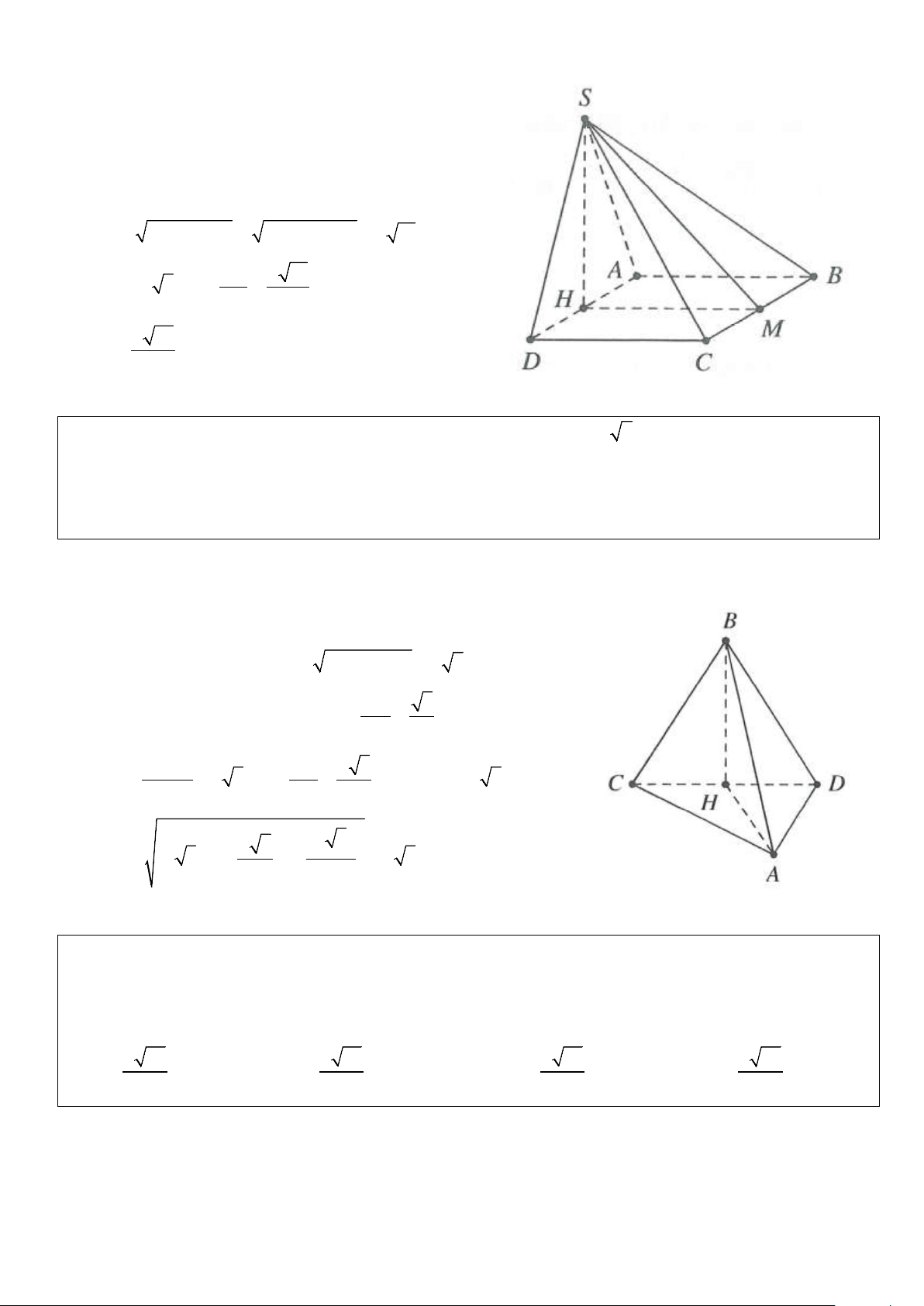
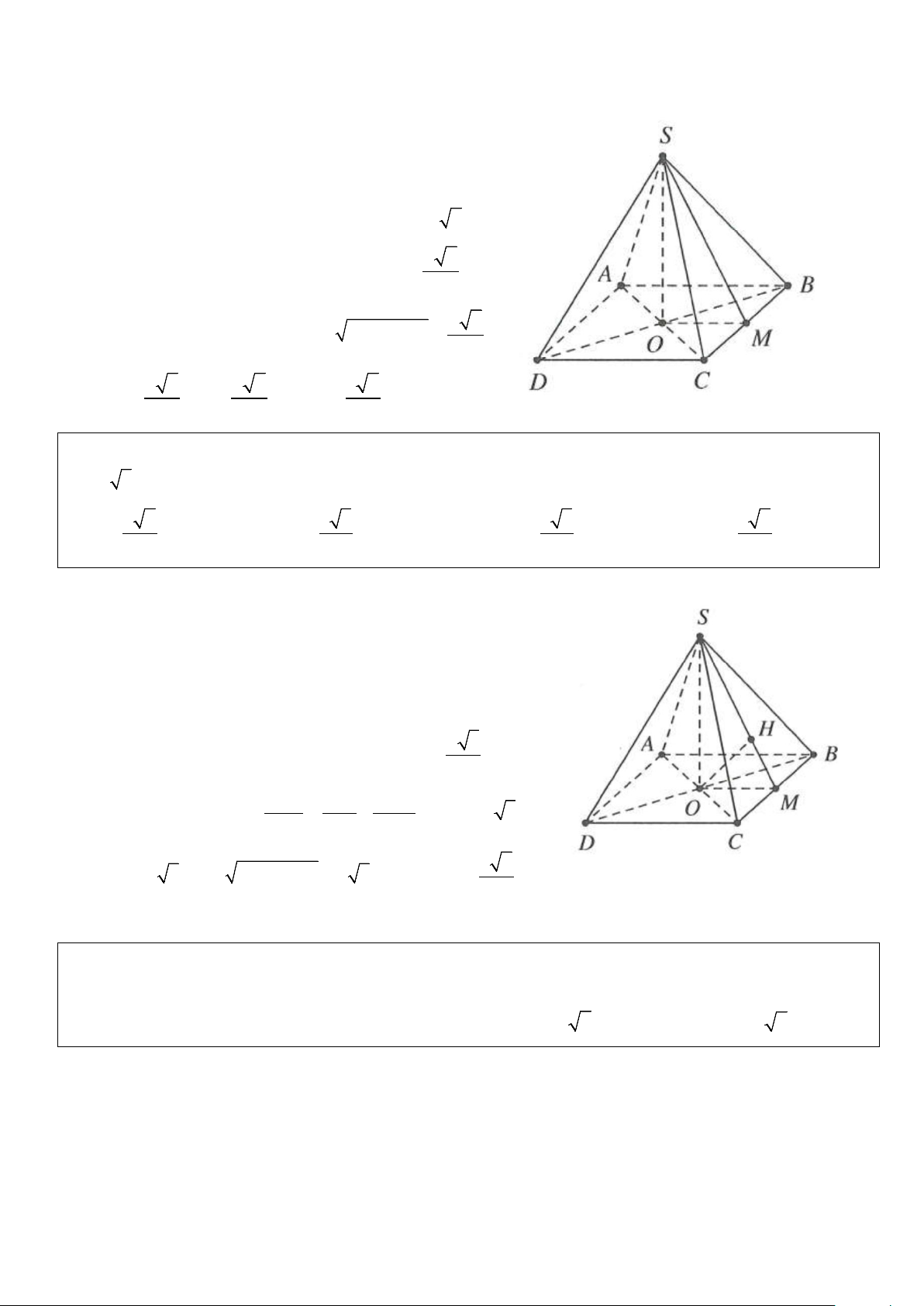
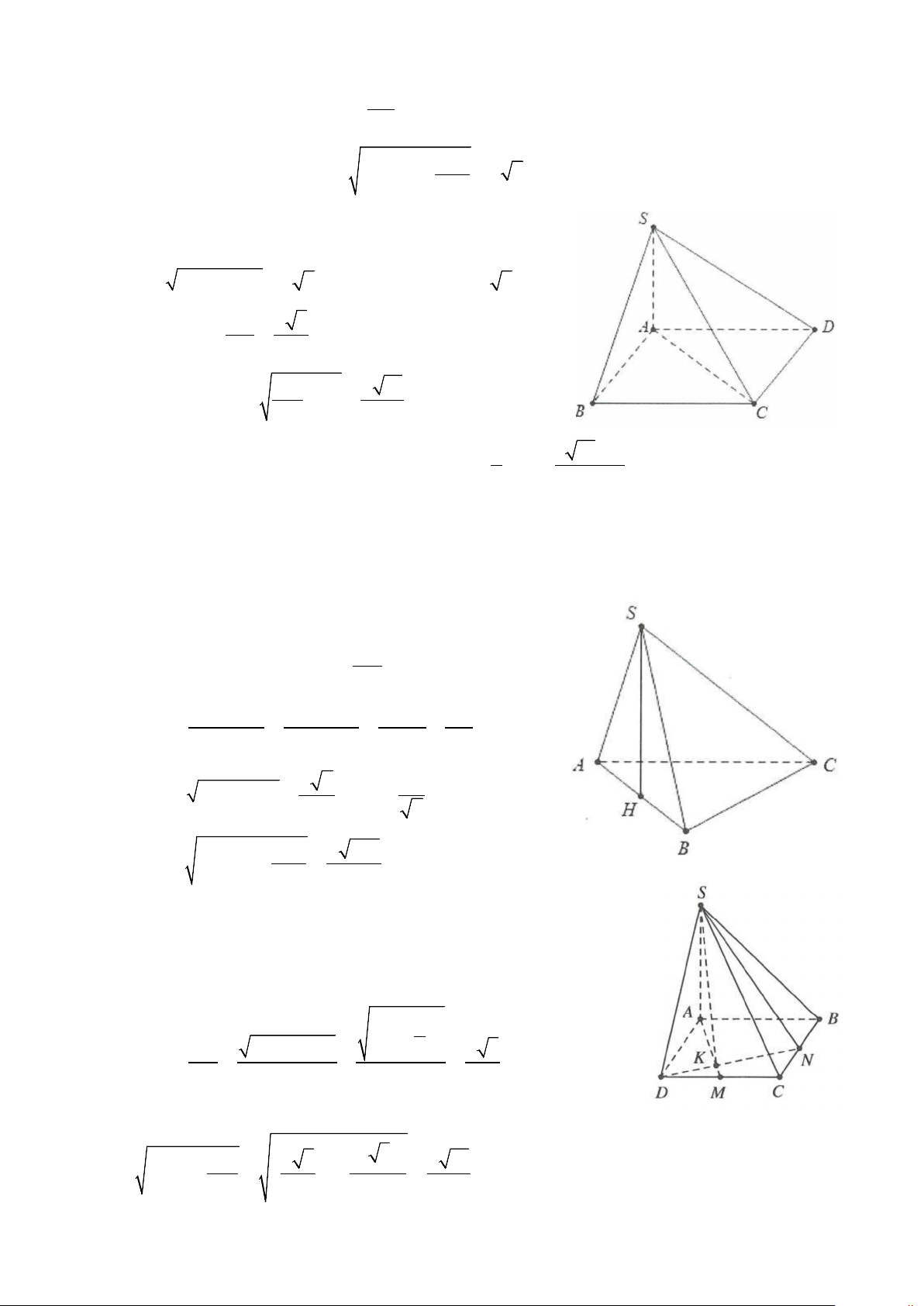
Ví dụ 3: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, BD = .
a Hình chiếu vuông góc của S
trên mặt đáy (ABCD) là trung điểm của OC. Đường thẳng SC tạo với mặt đáy một góc 0 60 . Thể tích khối
cầu ngoại tiếp hình chóp S.ABCD bằng 3 3 3 3 A. 4π a π π π . B. a . C. 2 a . D. a . 3 3 3 6 Lời giải
Gọi H là trung điểm của ⇒ ⊥ ( ), OC a OC SH ABCD HC = = 2 4
Ta có SC ( ABCD)  =  (SC HC)=  0 ; ; SCH = 60
Tam giác SHC vuông tại H, có  cos HC a SCH = ⇒ SC = SC 2
Lại có SH ⊥ OC ⇒ S ∆ OC cân tại a
S ⇒ SO = SC = 2
Do đó SO = OA = OC mà OA = OB = OC = OD
Suy ra O là tâm mặt cầu ngoại tiếp hình chóp S.ABCD 3 Vậy BD a 4 3 π a R = =  →V = π R = . Chọn D. 2 2 3 6
Ví dụ 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 2. Cạnh bên SA vuông góc với
mặt phẳng đáy và SA = 3. Mặt phẳng qua A và vuông góc SC với cắt các cạnh SB, SC, SD lần lượt tại các điểm M , N, .
P Tính thể tích V của khối cầu ngoại tiếp tứ diện C.MN . P A. 64 2π V π π π = . B. 125 V = . C. 32 V = . D. 108 V = . 3 6 3 3 Lời giải
Ta có SC ⊥ ( AMNP) ⇒ SC ⊥ AM mà AM ⊥ SB ⇒ ⊥ ⇒  0 AM MC
AMC = 90 . Tương tự  0 APC = 90 Mặt khác  0
ANC = 90 nên tâm mặt cầu ngoại tiếp tứ diện C.MNP là trung điểm của AC Suy ra AC 4 3 32 R =
= 2 ⇒ V = π R = π. Chọn C. 2 3 3
Ví dụ 5: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 2, cạnh bên SA vuông góc với mặt
phẳng đáy ( ABCD) . Mặt phẳng (α ) qua A và vuông góc với SC, cắt các cạnh SB, SC, SD lần lượt tại các điểm M , N, .
P Tính thể tích V của khối cầu ngoại tiếp tứ diện C.MNP, biết khoảng cách từ A đến mặt phẳng (SBD) bằng 6 13 A. V π π π = 3π. B. 8 V = . C. 9 V = . D. 4 V = . 3 2 3 Lời giảiBC ⊥ AB Ta có:  ⇒ BC ⊥ AM BC ⊥ SA
Mặt khác: AM ⊥ SC ⇒ AM ⊥ (SBC) ⇒ AM ⊥ MN
Tương tự AP ⊥ PN ⇒ tứ giác AMNP nội tiếp đường tròn đường kính AN AN ⇒ R = R = MNP AMNP 2
Gọi O là tâm hình vuông ABCD, dựng 6
AE ⊥ SO ⇒ AE = 13 Do đó AC 1 1 1 AO = = 2 ⇒ = + ⇒ SA = 3 2 2 2 2 AE SA AO 2 2 . SA AC 12 6 SA 9 2 SN 3 ⇒ AN = = ⇒ R = SN = = ⇒ R = R + = MPN ; S. 2 2 SA + AC 5 5 SC 5 MPN MNP 4 2 4 3 9π ⇒ V = π R = Chọn C. S MPN . . 3 2
Dạng 3: Bài toán mặt cầu với chóp có cạnh bên vuông góc đáy
Xét khối chóp S.ABC có SA ⊥ ( ABC) . Tìm tâm và tính bán kính mặt cầu ngoại tiếp khối chóp S.ABC .
Dựng tâm. Dựng trục đường tròn ngoại tiếp d của tam
giác ABC , thì d / /SA Trong mặt phẳng ( ;
SA d ) , dựng đường trung trực ∆ của
SA. Tâm I của mặt cầu là giao điểm của d và ∆ .
Tính bán kính R của mặt cầu
Gọi O là tâm đường tròn ngoại tiếp A ∆ BC .
Gọi E là trung điểm của SA. Xét A
∆ OI vuông tại O 2 2 2 2 2 2 2 2 SA R AI OA OI OA AE OB   = = + = + = +   . Ta có  2 
với OA = Rd là bán kính đường tròn ngoại tiếp đáy. 2 SA 2 R = + R S ABC d . Khi đó: . 4
S.A A ...A SA ⊥ AA A . R
Tổng quát: Cho khối chóp 1 2 n có
1 2 Gọi d là bán kính đường tròn ngoại tiếp đa giác AA A ...A
S.A A ...A 1 2
n thì bán kính mặt cầu ngoại tiếp R của khối chóp 1 2
n được tính theo công thức: 2 SA 2 R = + R . 4 d
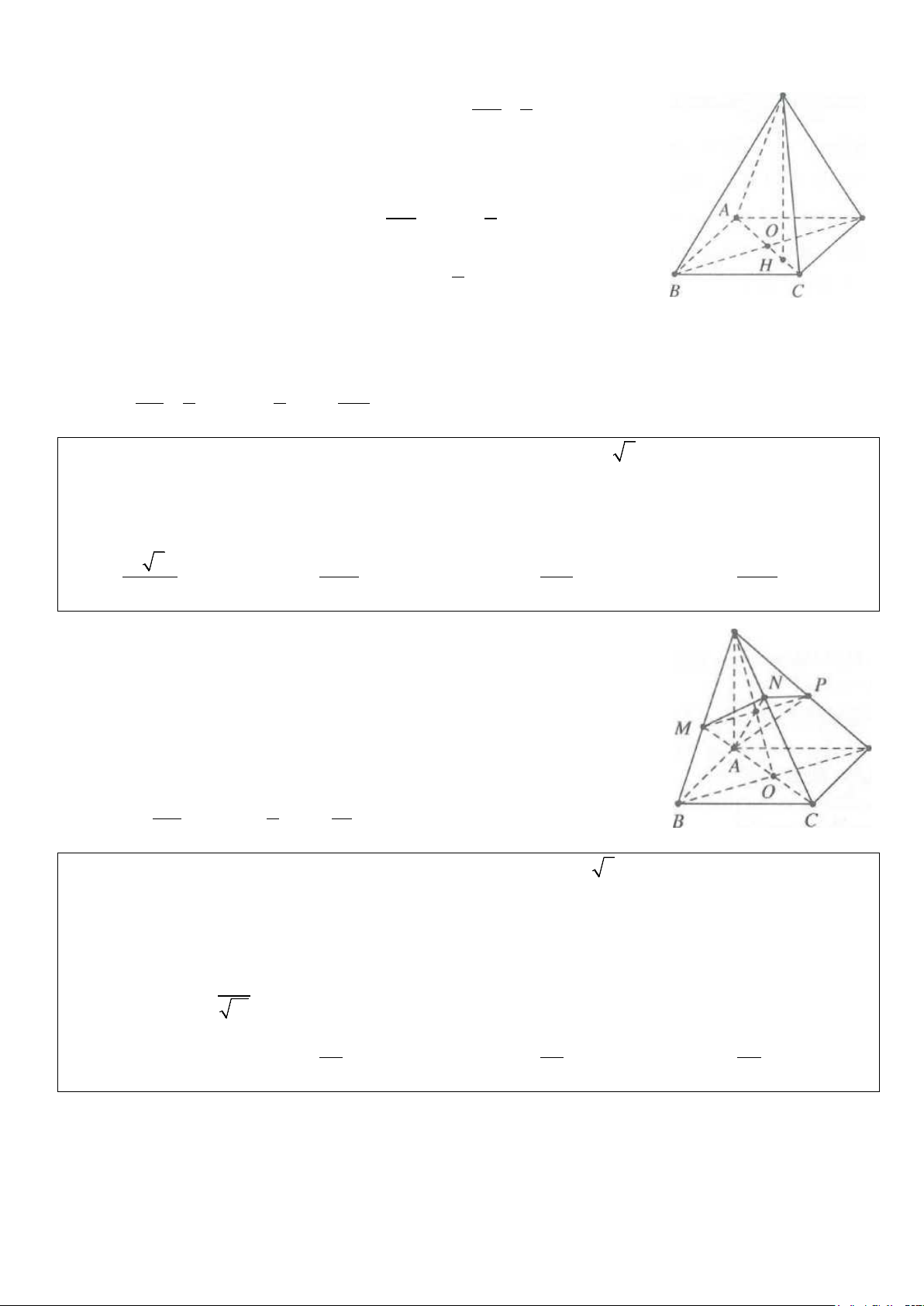
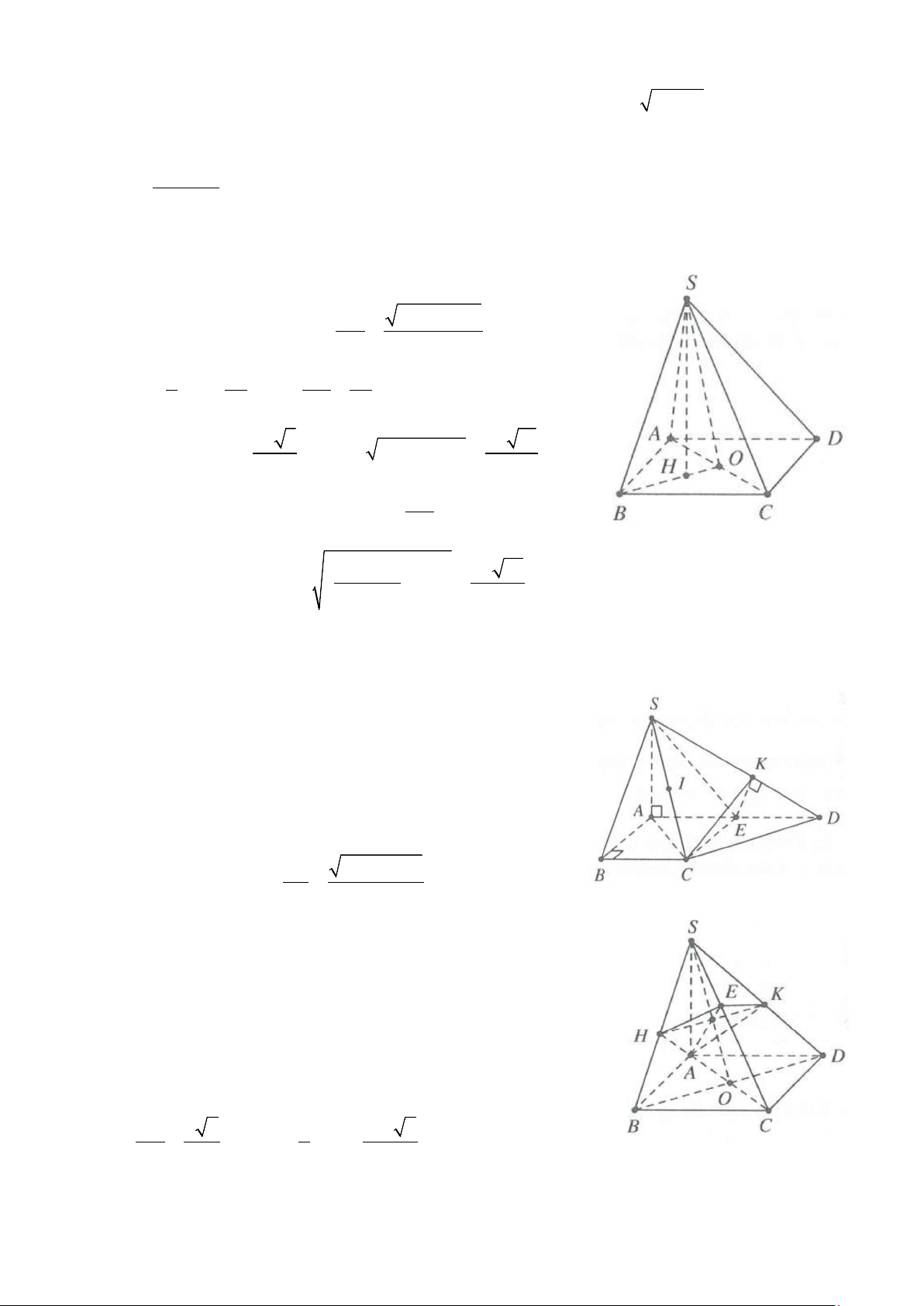
Ví dụ 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại , A AB = a,
AC = a 3. Cạnh bên SA
vuông góc với đáy. Góc giữa đường thẳng SB và mặt phẳng ( ABC) bằng 0
60 . Bán kính mặt cầu ngoại tiếp
hình chóp S.ABC bằng A. a 3 R = . B. R = . a C. a 5 R = . D. a 7 R = . 2 2 2 Lời giải
 Ta có SB ( ABC)  =  0 0 ;
SBA = 60 ⇒ SA = tan 60 .AB = a 3.
Tam giác ABC vuông tại 2 2 2
A ⇒ AB + AC = BC ⇒ BC = 2a .
Hình chóp S.ABC có chiều cao h = a 3; bán kính BC R = = a day 2 (a 3)2 2 a 7 R = a + = .
⇒ Bán kính mặt cầu cần tính là 4 2 Chọn D.
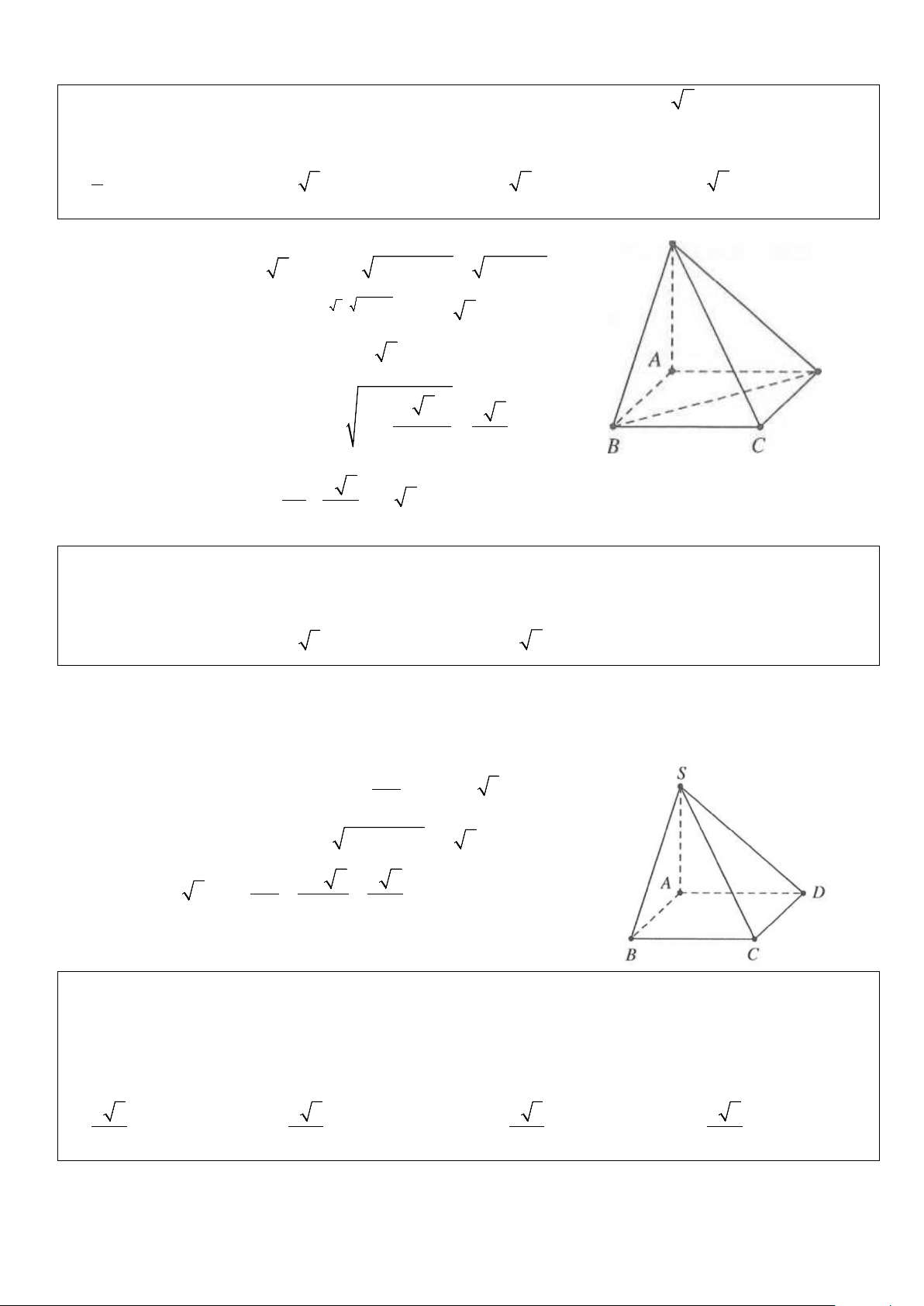
Ví dụ 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều có diện tích bằng 2
a 3. Cạnh bên SA vuông
góc với đáy. Diện tích tam giác SBC bằng 2
2a . Thể tích khối cầu ngoại tiếp hình chóp S.ABC là A. a 57 R = . B. a 3 R = . C. 5a R a = . D. 34 R = . 6 2 2 3 Lời giải 2 x 3  Đặt 2 AB = x  → S = = ⇒ = ∆ a x a ABC 3 2 . 4
Gọi H là trung điểm của BC ⇒ AH ⊥ BC mà SA ⊥ BC BC ⊥ (SAH ) 1 2
⇒ BC ⊥ SH ⇒ S = = ∆ SH BC a SBC . 2 Suy ra 2 1 2 2 2
⇒ SH.2a = 2a ⇒ SH = 2a ⇒ SA = SH − AH = . a 2 a
 Hình chóp S.ABC có chiều cao h = SA = ; a bán kính 2 3 R = day 3 (2a 3)2 2a a 57 R = + = .
⇒ Bán kính mặt cầu cần tính là 3 4 6 Chọn A.
Ví dụ 3: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA = 2a và SA vuông góc với
mặt phẳng đáy, tam giác SBD là tam giác đều. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD bằng A. 4 3 a . B. 3 4 3a . C. 3 6a . D. 3 2a . 3 Lời giải
 Đặt AB = x 
→ BD = x 2 và 2 2 2 2
SB = SA + AB = x + 2a 2 2 Tam giác SBD đều
x 2= x +2a
⇒ SB = BD → x = a 2
 Hình chóp S.ABCD có chiều cao h = a 2; bán kính R = a day (a 2)2 2 a 6 R = a + = .
⇒ Bán kính mặt cầu cần tính là 4 2 3 4π  a 6  3 V = .  = 6a .  
Vậy thể tích khối cầu là 3 2   Chọn C.
Ví dụ 4: Cho hình chóp S.ABCD có đáy là hình vuông, cạnh a, SA vuông góc với đáy và SC tạo với mặt
phẳng (SAB) một góc 0
30 . Diện tích mặt cầu ngoại tiếp hình chóp S.ABCD bằng A. . a B. a 3. C. a 2. D. 2 . a Lời giảiSA ⊥ BC Ta có 
⇒ CB ⊥ (SAB) ⇒ SC (SAB)  ( )=  (SC SB)=  ; ; CSB AB ⊥ BC
Tam giác SBC vuông tại ⇒  tan BC B CSB = ⇒ SB = a 3 SB
Tam giác SAB vuông tại 2 2
A ⇒ SA = SB − AB = a 2 Vậy BD AB 2 a 2
h = SA = a 2; R = = = nên R = . a d 2 2 2 Chọn A. =  0
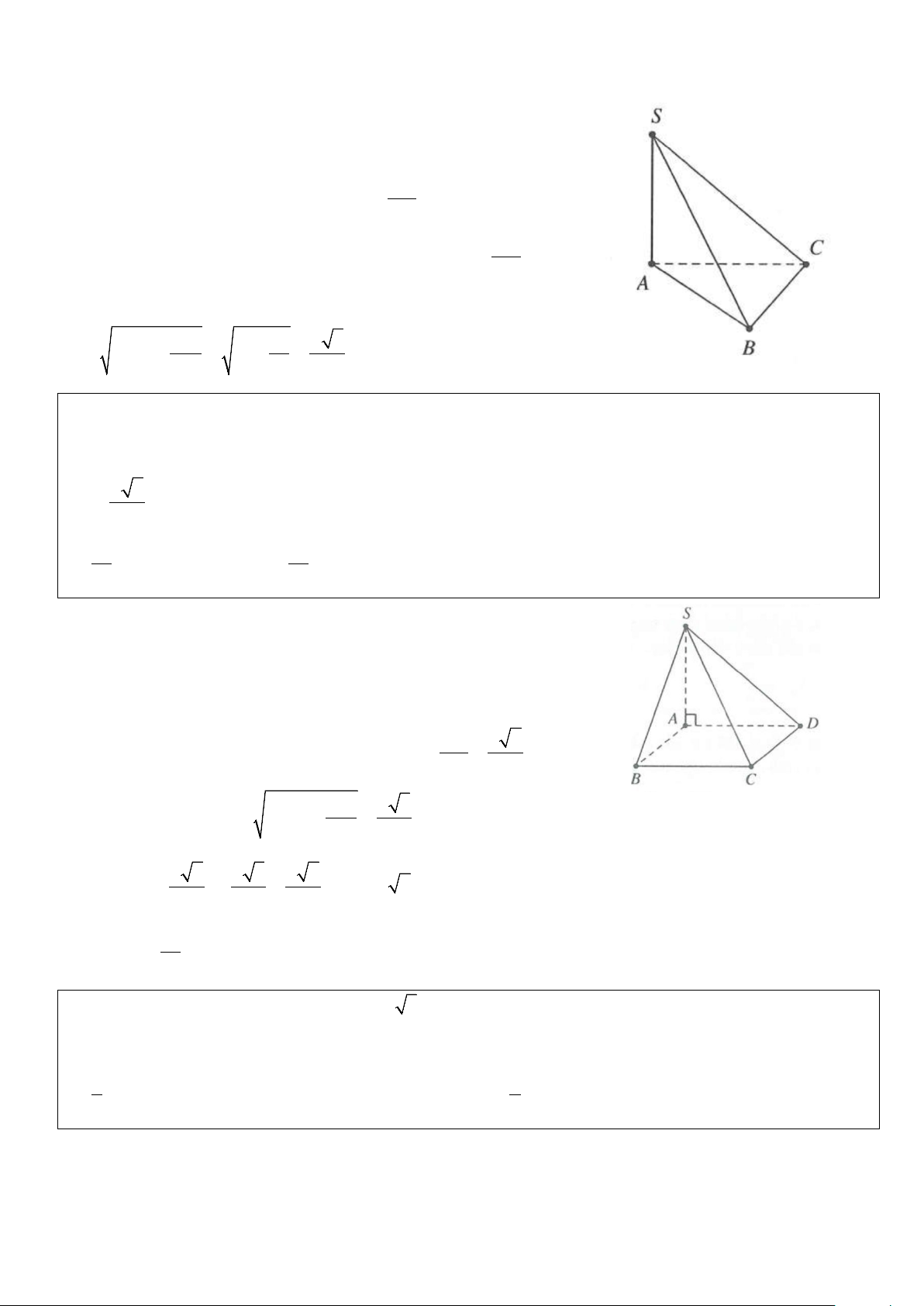
Ví dụ 5: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại ,
A AB a, ACB = 30 . Cạnh bên SA
vuông góc với đáy. Góc giữa đường thẳng SB và mặt phẳng ( ABC) bằng 0
45 . Bán kính mặt cầu ngoại tiếp
hình chóp S.ABC bằng A. a 5 . B. a 5 . C. a 3 . D. a 2 . 4 2 2 2 Lời giải
Ta có SA ⊥ ( ABC) ⇒  (SB ABC )=  (SB AB)=  0 ;( ) ; SBA = 45 .
Tam giác SAB vuông tại A , có  0
SBA = 45 ⇒ SA = AB = a .
Tam giác ABC vuông tại A , có  sin AB ACB = ⇒ AC = 2 . a AC
Suy ra bán kính đường tròn ngoại tiếp A ∆ BC là AC R = = ∆ a ABC . 2
Vậy bán kính mặt cầu cần tính là 2 2 2 SA 2 a a 5 R = R + = + = ∆ a ABC . 4 4 2 Chọn B.
Ví dụ 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Cạnh bên SA vuông góc với mặt phẳng đáy.
Góc giữa hai mặt phẳng (SCD) và ( ABCD) bằng 0
45 . Bán kính mặt cầu ngoại tiếp khối chóp S.ABCD
bằng a 6 . Diện tích tam giác SAB bằng 2 2 2 A. a . B. a . C. 2 a . D. 2 2a . 2 4 Lời giải
Vì CD ⊥ (SAD) ⇒ (SCD) ( ABCD)  ( )=  (SD AD)=  0 ; ; SDA = 45 .
Tam giác SAD vuông tại A, có  0
SDA = 45 ⇒ SA = AD = . x
Bán kính đường tròn ngoại tiếp ABCD là AC x 2 R = = ABCD . 2 2 2 2 SA x 3 R = R + = ABCD . Bán kính mặt cầu là 4 2 a 6 x 3 a 6 R = ⇒ = ⇔ x = a S ABCD 2. Mà . 2 2 2 2 x 2 S = = ∆ a SAB . Vậy 2 Chọn C.
Ví dụ 7: Cho mặt cầu (S ) có bán kính R = 3 đi qua điểm A cố định. Xét các điểm B,C, D thuộc (S ) sao
cho AB, AC, AD đôi một vuông góc với nhau. Thể tích của khối tứ diện ABCD có giá trị lớn nhất bằng A. 8. B. 4. C. 4 . D. 8. 3 3 Lời giải Vì ,
A B,C, D thuộc (S ) ⇒ (S ) ngoại tiếp tứ diện ABCD.
Tứ diện ABCD có chiều cao h = A ;
D đáy là tam giác ABC. 2 2
Đặt AB = a, AC = b, AD = c ⇒ h = c và BC a b R + = = day 2 2
⇒ Bán kính mặt cầu ngoại tiếp tứ diện ABCD là 2  2 2  2 2 2 2 a + b c a + b + c 2 2 2 R =   + =
= 3 ⇒ a + b + c =12  2  4 2   Ta có 2 2 2 abc 4 3
12 = a + b + c ≥ 3 (abc)2 ⇔ abc ≤ 8  →V = ≤ Chọn C. ABCD . 6 3
Bài toán tổng quát: Tứ diện ABCD, AB, AC, AD đôi một vuông góc và AB = a, AC = b, AD = c thì bán 2 2 2
kính mặt cầu ngoại tiếp tứ diện là a b c R + + = 2  0
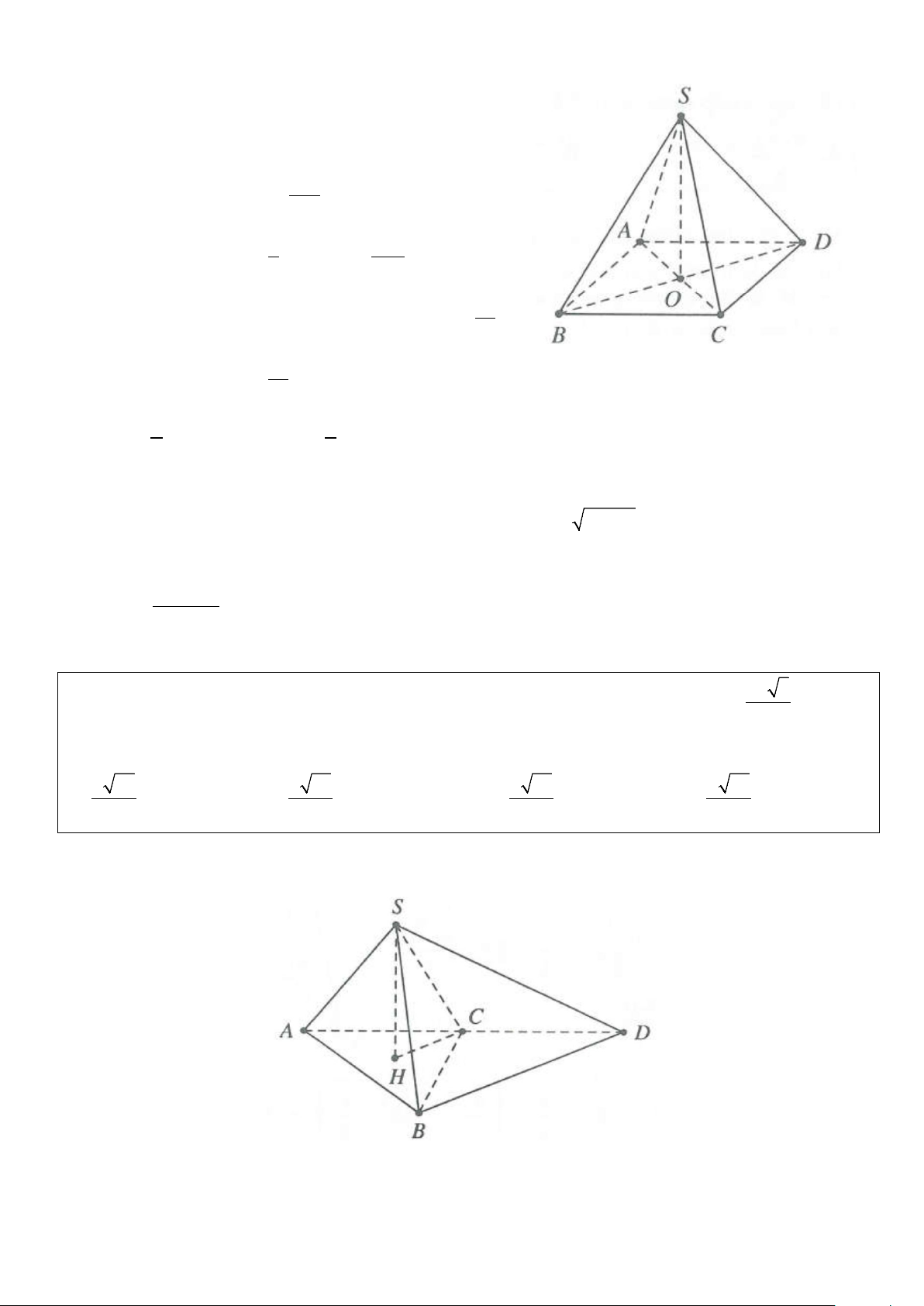
Ví dụ 8: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, BAD = 60 và các cạnh bên = =  0
SA SB SD, BSD = 90 . Bán kính mặt cầu ngoại tiếp tứ diện S.ABCD là A. 6a R = . B. 6a R = . C. 3a R = . D. 2a R = . 4 2 4 4 Lời giải
Vì SA = SB = SD và A
∆ BD đều cạnh a 
→ S.ABD là hình chóp tam giác đều. Mặt khác  0
BSD = 90 ⇒ SB ⊥ SD ⇒ ,
SA SB, SD đôi một vuông góc và bằng a 2 . 2 2 2 2
Áp dụng công thức giải nhanh, ta được
SA + SB + SD a 6 R = = R = Chọn A. S ABD . . 2 4
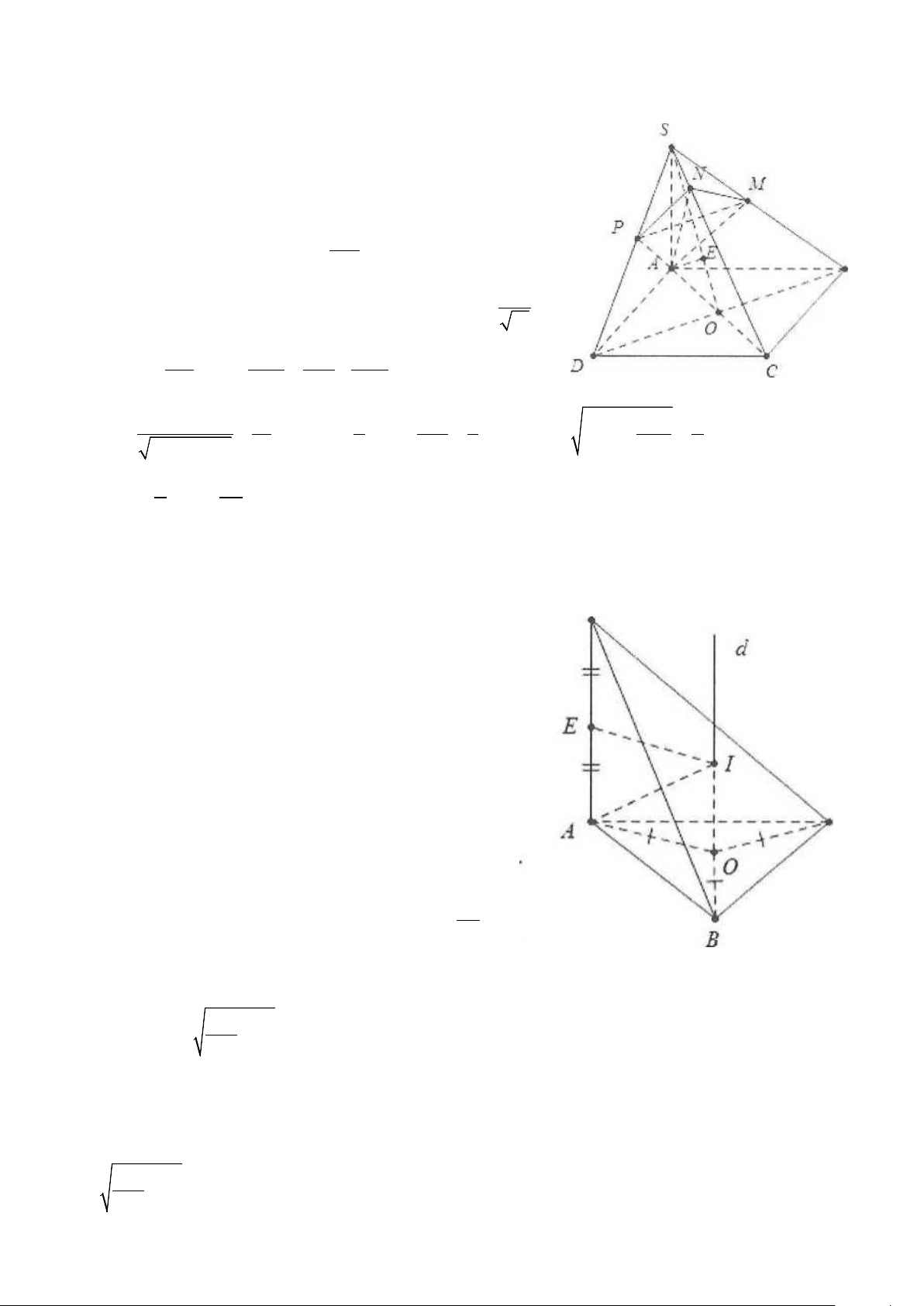
Ví dụ 9: Cho ba tia Ox,Oy,Oz đôi một vuông góc với nhau. Gọi C là điểm cố định trên Oz, đặt OC =1, các điểm ,
A B thay đổi trên Ox,Oy sao cho OA + OB = OC. Giá trị bé nhất của bán kính mặt cầu ngoại
tiếp tứ diện OACB bằng A. 6 R = . B. 6 R = . C. R = 6. D. 6 R = . min 4 min 3 min min 2 Lời giải
Đặt OA = a,OB = b với a,b > 0 suy ra OA + OB = OC ⇔ a + b =1.
Bán kính mặt cầu ngoại tiếp tứ diện OACB ( ,
OA OB,OC đôi một vuông góc) là 2 2 2 2 2
OA + OB + OC a + b +1 1 2 R = = = a + (1− a)2 1 2 +1 = 2a − 2a + 2 2 2 2 2 2 Dễ thấy 2  1  3 3 2 3 2 3 6
a − a +1 = a −
+ ≥ ⇒ a − a +1 ≥ ⇒ R ≥ . =   .  2  4 4 2 2 2 4
Dấu bằng xảy ra khi và chỉ khi 1
a = b = . Vậy giá trị bé nhất cần tìm là 6 . Chọn A. 2 4
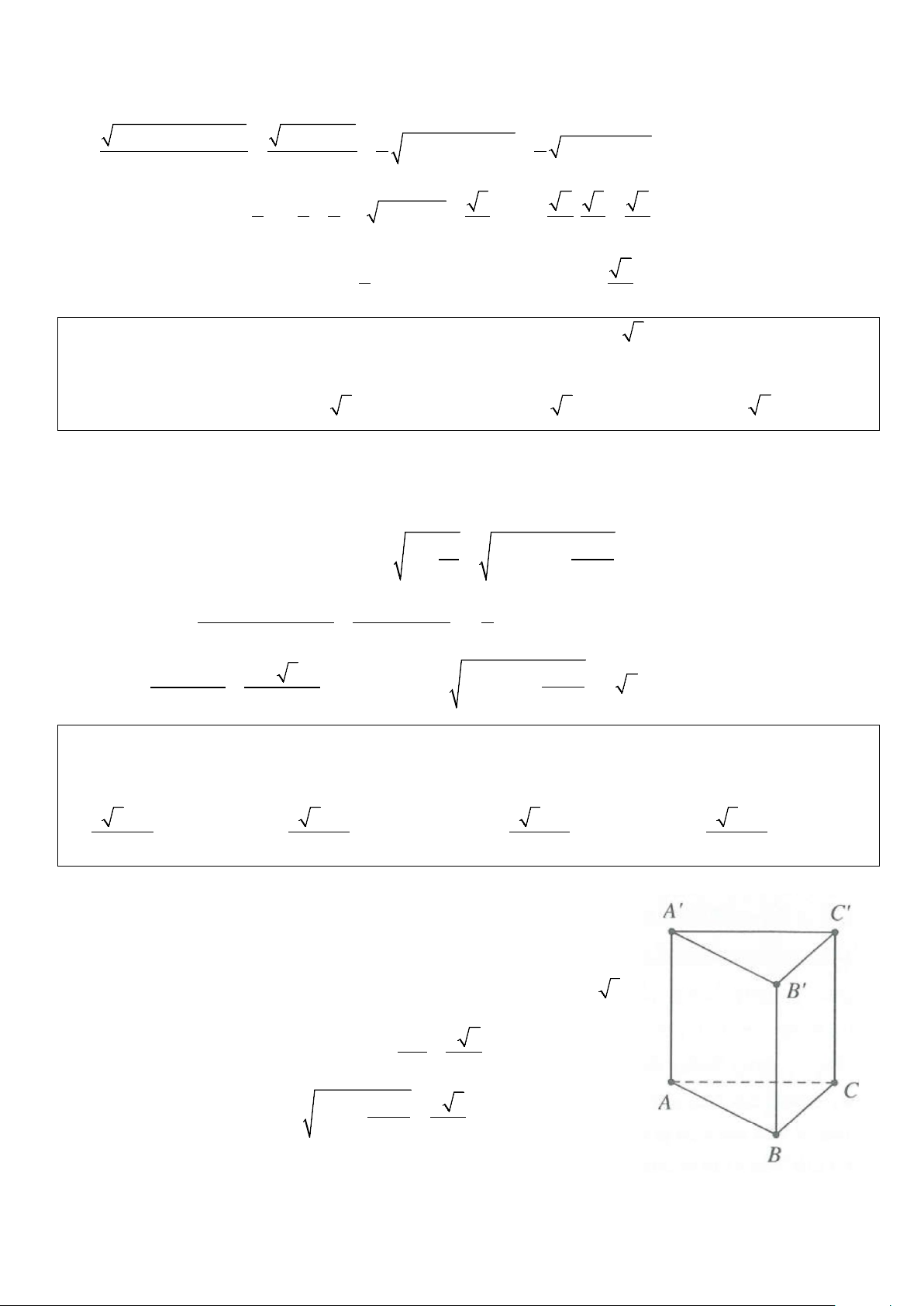
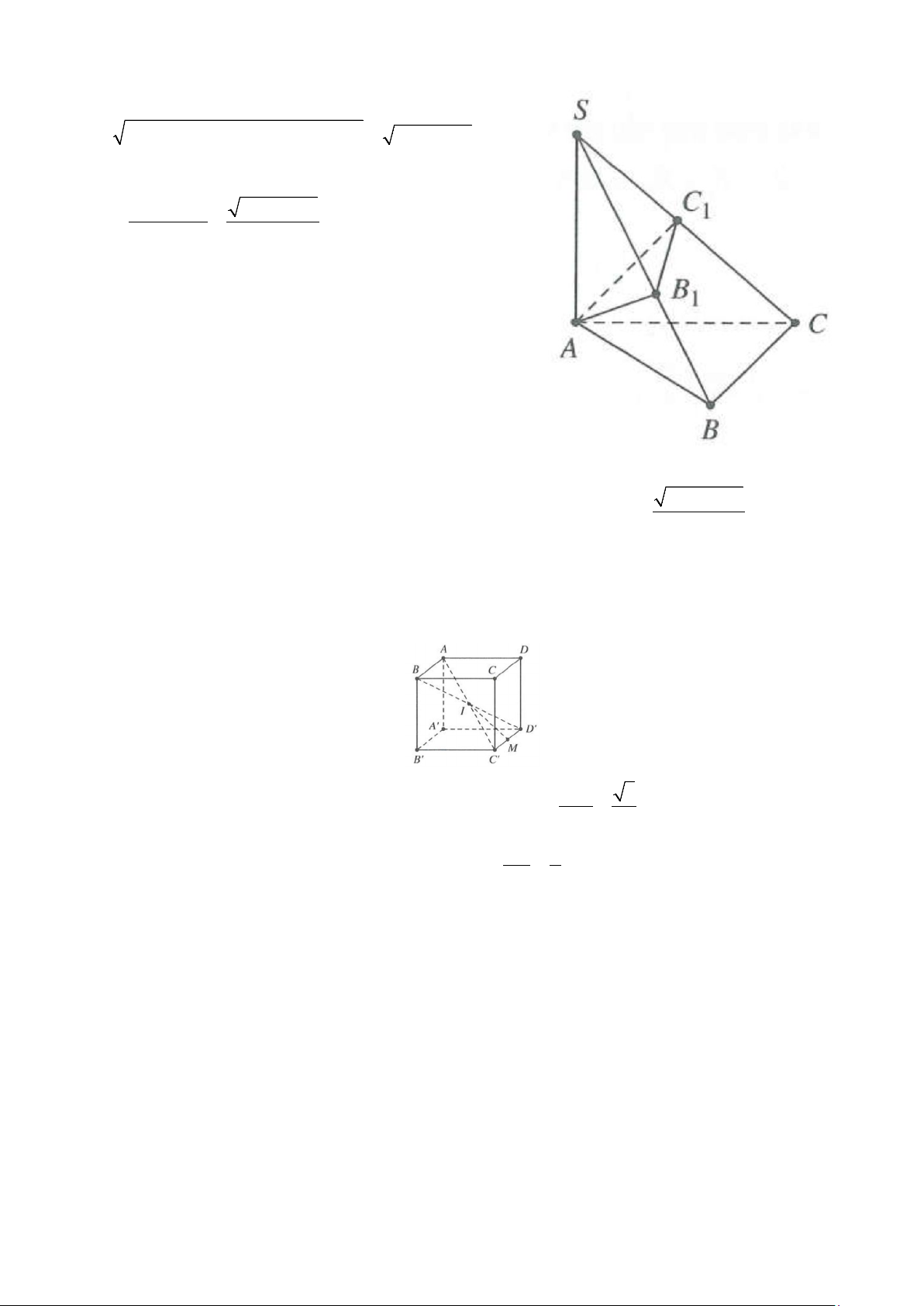
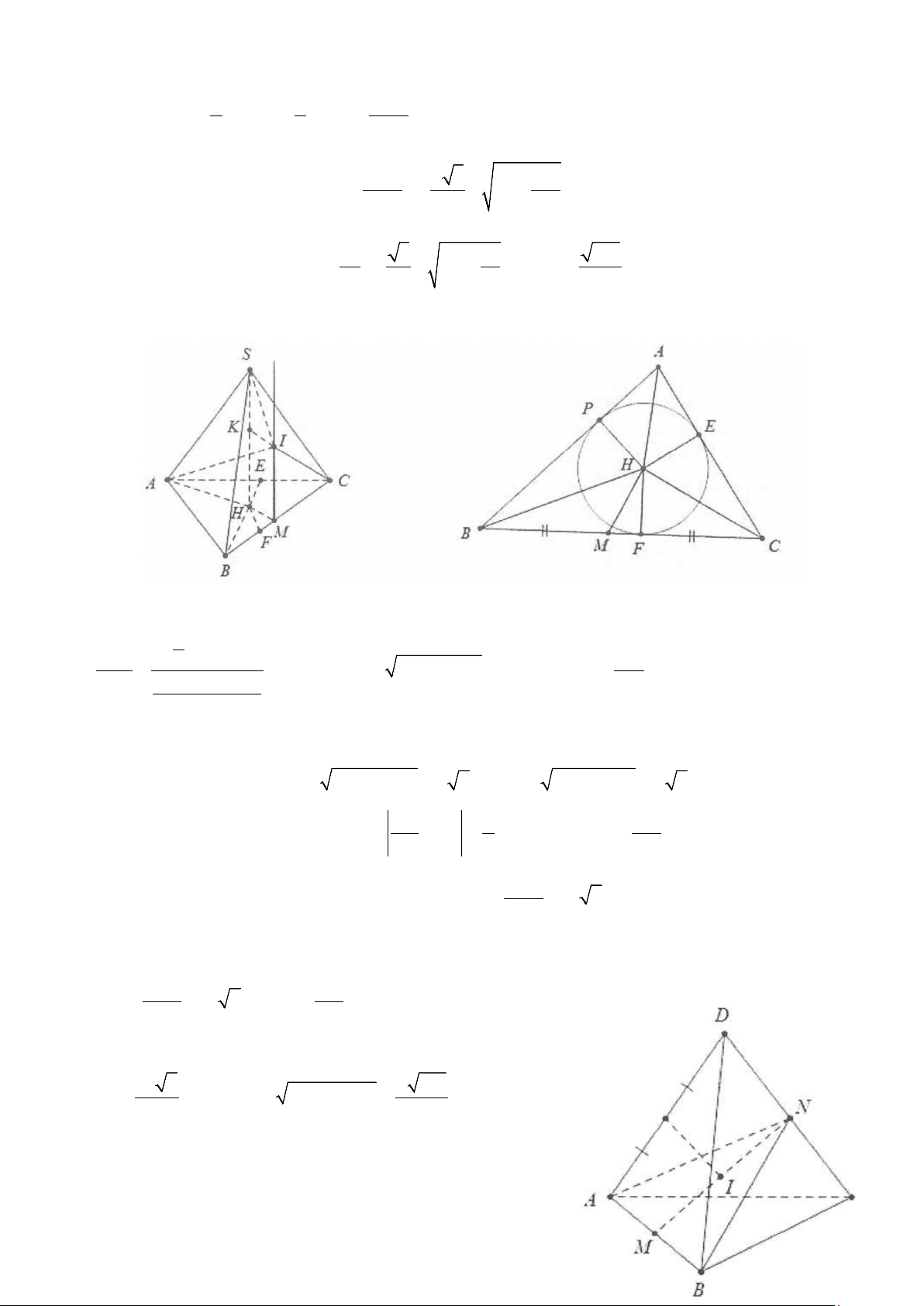
Ví dụ 10: Cho lăng trụ đứng ABC.A'B 'C ', cạnh AB = AC = a, BC = a 3, AA' = 2a . Bán kính mặt cầu
ngoại tiếp tứ diện AB 'C 'C bằng A. R = . a
B. R = a 5.
C. R = a 3.
D. R = a 2. Lời giải
Dễ thấy tâm mặt cầu ngoại tiếp tứ diện AB 'C 'C cũng là tâm mặt cầu ngoại tiếp khối lăng trụ
ABC.A'B 'C ' hay là tâm mặt cầu ngoại tiếp khối chóp A'.ABC. 2 2
Sử dụng công thức tính nhanh, ta được 2 h = + = ( A A R r R + ABC ∆ )2 ' . 4 4 2 2 2 2 2 2 Ta có
AB + AC − BC
a + a − 3a 1 = = = − ⇒  0 cos BAC BAC =120 . 2 2.A . B AC 2a 2 BC a 3 2 ⇒ R = = = Khi đó = ( A A R R + = Chọn D. ∆ a ABC )2 ' 2. ∆ a ABC  . 0 2sin BAC 2.sin120 4
Ví dụ 11: Cho hình lăng trụ đứng ABC.A'B 'C ' có đáy ABC là tam giác vuông cân tại B, AB = . a Góc giữa
hai mặt phẳng ( A'BC) và ( ABC) bằng 0
60 . Thể tích khối cầu ngoại tiếp lăng trụ ABC.A'B 'C ' bằng 3 3 3 3 A. 5 5π a π π π . B. 5 5 a . C. 3 3 a . D. 3 3 a . 8 6 6 8 Lời giảiAA' ⊥ BC
( A'BC) ∩( AA'B'B) = A'B Ta có 
⇒ BC ⊥ ( AA'B 'B) và   AB ⊥ BC (  ABC
)∩( AA'B'B) = AB
⇒ ( A BC) ( ABC)  =  (A B AB)=  0 0 ' ; ' ;
A'BA = 60 ⇒ AA' = A . B tan 60 = a 3
Tam giác ABC vuông cân tại B, có AC a 2 R = = ABC ∆ . 2 2 2
Suy ra bán kính mặt cầu là 2 A' A a 5 R = R + = . ABC ∆ 4 2 3 3  
Vậy thể tích khối cầu cần tính là 4 3 4 a 5 5 5π = π = π. a V R   = . Chọn B. 3 3  2  6  
Ví dụ 12: Cho hình lăng trụ đứng ABC.A'B 'C ' có đáy ABC là tam giác vuông, AB = BC = . a Biết góc
giữa hai mặt phẳng ( ACC ') và ( AB'C ') bằng 0
60 . Bán kính mặt cầu ngoại tiếp lăng trụ ABC.A'B 'C ' bằng A. a 2 . B. a . C. a 3 . D. a 3 . 2 2 2 3 Lời giải
Kẻ B 'H ⊥ A'C '(H ∈ A'C '), kẻ HK ⊥ AC '(K ∈ AC ') .
B ' H ⊥ AC '
Ta có B 'H ⊥ ( ACC ') ⇒ 
⇒ AC ' ⊥ (B 'HK )  HK ⊥ AC '
Khi đó ( ACC ) ( AB C )  = (HK B K)  =  0 ' ; ' ' ; ' B ' KH = 60 .
Tam giác A'B 'C ' vuông cân tại A'C ' a 2
B ' ⇒ B 'H = = . 2 2 Tam giác BH a
B ' HK vuông tại H, có  6 sin B 'HK = ⇒ B ' K = . B 'K 3
Tam giác AB 'C ' vuông tại B ', có B 'K là đường cao 1 1 1 1 1 ⇒ = + ⇒ = ⇒ AB ' = a 2. 2 2 2 2 2 B ' K AB ' B 'C ' AB ' 2a
Tam giác AA'B vuông tại A', có AA = AB − A B = (a )2 2 2 2 ' ' ' ' 2 − a = a . 2 2 2  
Vậy bán kính mặt cầu cần tìm là 2 AA' a 2 a a 3 R = R + =   + = . Chọn C. ABC ∆ 4  2  4 2  
Dạng 4: Bài toán về mặt cầu với hình chóp có mặt bên vuông góc với đáy
Xét khối chóp S.ABC có (SAB) ⊥ ( ABC) . Tìm tâm và
bán kính mặt cầu ngoại tiếp khối chóp S.ABC .
Dựng tâm. Gọi O ,O lần lượt là tâm của đường tròn 1 2
ngoại tiếp các tam giác ABC và SAB, E là trung điểm của AB, ta có
O E ⊥ AB ⇒ O E ⊥ SAB do . SAB ⊥ ABC 1 1 ( )( ( ) ( ))
O E ⊥ AB ⇒ O E ⊥ ABC . 2 1 ( )
Qua O dựng đường thẳng d vuông góc với ( ABC) thì d là trục của tam giác ABC và d / /O E. 1 1 1 1 2
Qua O dựng đường thẳng d vuông góc với (SAB) thì d là trục của tam giác SAB và d / /O E. 2 2 2 2 1
Tâm I của mặt cầu là giao điểm của d và d . 1 2
Tính bán kính R của mặt cầu.
Tứ giác EO IO là hình chữ nhật, suy ra 2 2 2
IE = O E + O E . 1 2 1 2
Gọi R , R lần lượt là bán kính đường tròn ngoại tiếp tam giác ABC, SAB. 1 2 2 2 Ta có 2 2 2 2 AB 2 2 2 2 = − = − ; AB O E O A EA R
O E = O A − EA = R − . 1 1 1 2 2 2 4 4 2 2 Suy ra 2 2 2 AB 2 2 2 2 2 AB
IE = R + R −
⇒ R = IE + EA = R + R − . 1 2 1 2 2 4
Tổng quát: Cho khối chóp S.A A ...A có (SA A ⊥ A A ...A Đặt R là bán kính đường tròn ngoại n . 1 2 ) ( 1 2 ) 1 2 n 1
tiếp tam giác S.A A , R là bán kính đường tròn ngoại tiếp đáy A A ...A và A A = GT (gọi là giao 1 2 2 1 2 n 1 2
tuyến) thì bán kính mặt cầu ngoại tiếp R của khối chóp S.A A ...A được tính theo công thức: 1 2 n 2 2 2 GT
R = R + R − 1 2 4
Ví dụ 1: Cho hình chóp S.ABC có SA = a , tam giác ABC đều, tam giác SAB vuông cân tại S và nằm trong
mặt phẳng vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng A. a 3 . B. a 6 . C. a 3 . D. a 6 . 3 3 2 2 Lời giải
Gọi H là trung điểm AB ⇒ SH ⊥ AB ⇒ SH ⊥ ( ABC)
Tam giác SAB vuông cân tại AB a 2 S  → R = = b 2 2
Tam giác ABC đều cạnh 3 a 6 a 2  → R = a = d 2. 3 3 Vậy a 2 6 R a = R =
GT = AB = a nên a 6 R = . b ; d ; 2 2 3 3 Chọn B.
Ví dụ 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh  0
a, ASB = 30 , tam giác SAB nằm
trong mặt phẳng vuông góc với mặt phẳng đáy. Diện tích mặt cầu ngoại tiếp hình chóp S.ABCD bằng A. 2 5π a . B. 2 7π a . C. 2 9π a . D. 2 3π a . Lời giải Tam giác SAB có  0 = 30 , AB ASB AB = a  → R = = a b  2sin ASB
ABCD là hình vuông cạnh BD AB 2 a 2 a  → R = = = d 2 2 2 Vậy 2 R a = a R =
GT = AB = a nên a 5 R = . b ; d ; 2 2 2 2
S = 4π R = 5π a .
Diện tích mặt cầu cần tính là Chọn A.
Ví dụ 3: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại C, tam giác SAB đều cạnh a. Hình chiếu
của S trên mặt phẳng ( ABC) là trung điểm cạnh AB. Đường thẳng SC tạo với mặt phẳng đáy một góc 0 45 .
Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là A. a . B. a 3 . C. a 5 . D. a 3 . 2 2 2 3 Lời giải
Gọi H là trung điểm AB ⇒ SH ⊥ ( ABCD) ⇒ (SC ( ABCD))  = (SC HC)  =  0 ; ; SCH = 30
Tam giác SHM vuông cân tại H, có SH a 3 HM =  = tan SCH 2 3 ⇒ CH =
AB ⇒ Tam giác ABC đều cạnh a 2 Vậy a 3 R = R =
GT = AB = a nên a 5 R = . Chọn C. b d ; 2 2
Ví dụ 4: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác đều cạnh 2a và
nằm trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng (SBC) và ( ABCD) bằng 0 30 . Bán kính
mặt cầu ngoại tiếp hình chóp S.ABCD bằng A. a 6 . B. a 10 . C. a 15 . D. a 21 . 2 2 2 2 Lời giải
Gọi H là trung điểm AD ⇒ SH ⊥ AD ⇒ SH ⊥ ( ABCD)
Gọi M là trung điểm BC ⇒ HM ⊥ BC ⇒ BC ⊥ (SHM )
⇒ ((SHM ) ( ABCD))  = (SM HM )  =  0 ; ; SMH = 30 2 2 2 2
⇒ BD = AB + AD = HM + AD = a 13 Vậy BD a 13 R = a R = =
GT = AD = a b 3; d ; 2 2 2 nên a 21 R = . 2 Chọn D.
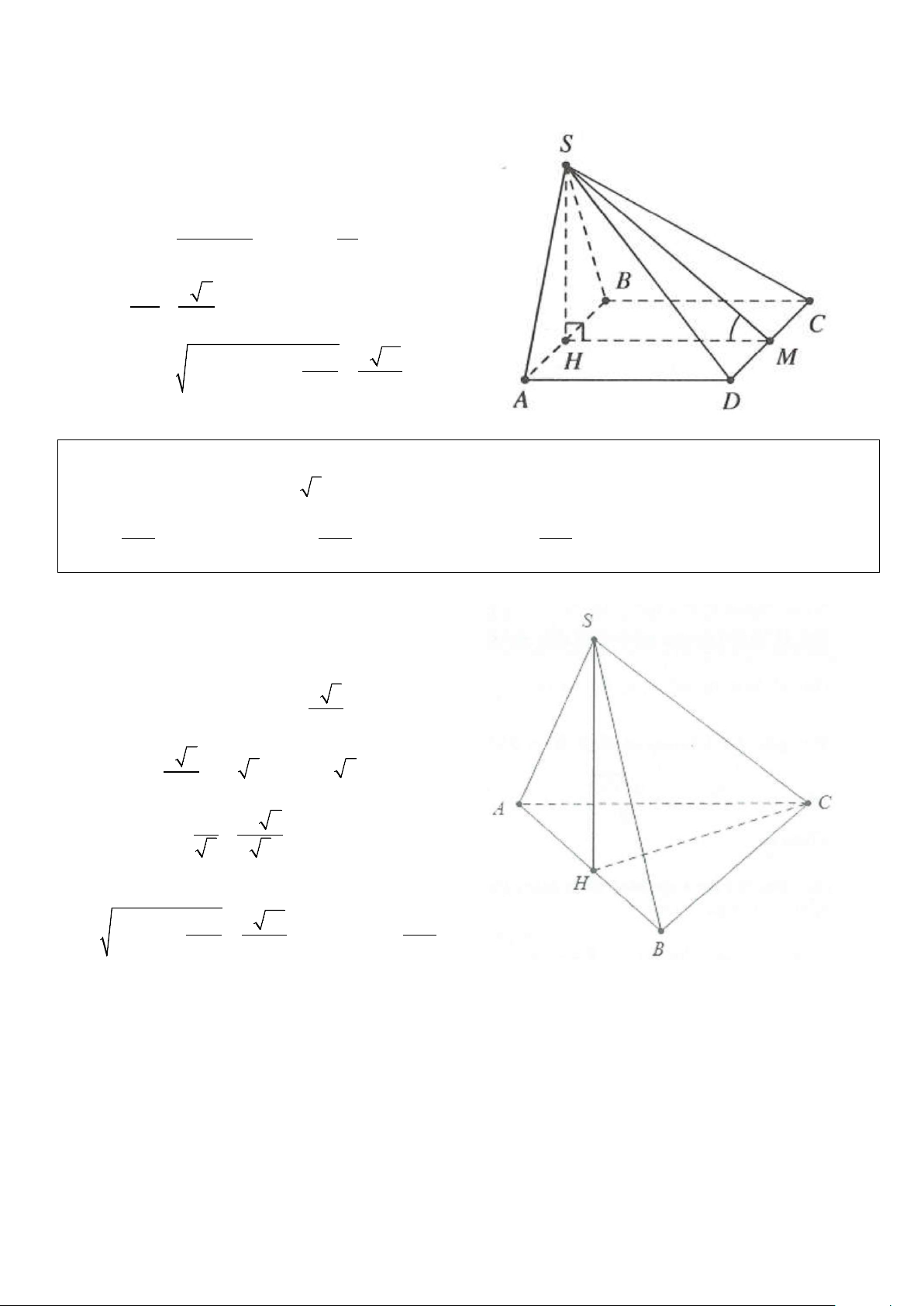
Ví dụ 5: Cho tứ diện ABCD có AB = BC = BD = AC = a, AD = a 2, hai mặt phẳng ( ACD) và
(BCD) vuông góc với nhau. Diện tích mặt cầu đi qua bốn điểm ,
A B,C, D bằng A. 2 8π a . B. 2 4π a . C. 2 12π a . D. 2 6π a . Lời giải
Gọi H là trung điểm CD ⇒ BH ⊥ CD ⇒ BH ⊥ ( ACD)
Mà BA = BC = BD ⇒ H là tâm đường tròn ngoại tiếp A ∆ CD ⇒ A ∆ CD vuông tại 2 2
A ⇒ CD = AC + AD = a 3
Tam giác BHC vuông tại HC 3 ⇒ = = ⇒  0 H cosC B =120 BC 2 Vậy CD CD a R = = a R = =
GT = CD = a b 3; 3 d ; 3 2sin B 2 2    → R = ( a a 3) a ( 3 3 )2 2 2 2 +   −
= a 3 ⇒ S =12π a .  2  4 mc   Chọn C.
Ví dụ 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân và nằm trong mặt
phẳng vuông góc với đáy. Góc giữa hai mặt phẳng (SCD) và ( ABCD) bằng 0
45 . Bán kính mặt cầu ngoại
tiếp hình chóp S.ABCD là A. a 43 R = . B. a 41 R = . C. a 41 R = . D. a 43 R = . 6 6 8 8 Lời giải
Gọi H, M lần lượt là trung điểm của AB,C . D
SH ⊥ AB mà (SAB) ⊥ ( ABCD) ⇒ SH ⊥ ( ABCD) ⇒ SH ⊥ C . D
Do HM ⊥ CD suy ra CD ⊥ (SHM )
⇒ (SCD) ( ABCD)  =  0 ; SMH = 45 . Lại có . SA . SB AB 5a S = ⇒ = và ∆ R SAB 4. S ∆ AB R S∆AB 8 AC a 2 R = = ABCD . 2 2 2 Vậy 2 2 AB a 41 R = R + − = ∆ R S ABCD SAB ABCD . . 4 8 Chọn C.
Ví dụ 7: Cho hình chóp S.ABCD có đáy là tam giác đều. Tam giác SAB đều và thuộc mặt phẳng vuông
góc với đáy. Biết rằng SC = 2a 3, diện tích mặt cầu ngoại tiếp hình chóp S.ABCD là A. 40π π π S = . B. 20 S = . C. 80 S = . D. S = 40π. 3 3 3 Lời giải
Gọi H là trung điểm của AB. Khi đó SH ⊥ A . B
Mặt khác (SAB) ⊥ ( ABC). Do vậy SH ⊥ ( ABC) .
Đặt AB = .x Ta có: x 3 SH = HC = 2 Suy ra x 6 SC =
= 2a 3 ⇒ x = 2a 2 2 Ta có: x 2a 2 R = R = = 1 2 3 3 Suy ra 2 2 2 AB a 30 2 40π
R = R + R − = ⇒ S = 4π R = . 1 2 4 3 3 Chọn A.
Dạng 5: Bài toán mặt cầu của hình chóp có các cạnh bên bằng nhau
Xét khối chóp S.ABC có SA = SB = SC. Xác định tâm và tính bán kính mặt cầu ngoại tiếp khối chóp
S.ABC (Hình chóp đều là một trường hợp đặc biệt của dạng toán này).
Dựng tâm. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC thì ta có SO ⊥ ( ABC). Trong mặt phẳng
(SAO) dựng đường trung trực của SA cắt SO tại I thì I là tâm mặt cầu ngoại tiếp khối chóp S.ABC .
Tính bán kính R của mặt cầu.
Gọi E là trung điểm của AB.
Hai tam giác vuông SOA và SEI đồng dạng. 2 Suy ra SO SA SE.SA SA = ⇔ R = SI = = . SE SI SO 2SO 2 Vậy SA R = . 2SH
Tổng quát: Cho khối chóp S.A A ...A có S.A = SA ...SA = 1 2 n 1 2 n
và có chiều cao SO = h thì bán kính mặt cầu ngoại tiếp R của khối 2 2
chóp S.A A ...A được tính theo công thức: R =  =  . 1 2 n 2SO 2h
Ví dụ 1: Thể tích khối cầu ngoại tiếp hình chóp tam giác đều S.ABC có AB = a, SA = a 2 bằng 3 3 3 3 A. 4 5π a π π π . B. 4 15 a . C. 4 3 a . D. 4 3 a . 75 25 25 75 Lời giải
Gọi O là tâm đường tròn ngoại tiếp A ∆ BC 
→ SO ⊥ ( ABC)
Gọi M là trung điểm của 2 2 a 3 a 3
BC ⇒ OA = AM = . = 3 3 2 3
Tam giác SAO vuông tại 2 2 a 15
O ⇒ SO = SA − OA = 3 3 Vậy a 15 a 15 4 15π = 2; a SA a SO =  → R = ⇒ V = . 3 5 25 Chọn B.
Mở rộng với bài toán hình chóp tam giác đều. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, với giả thiết 2 3.
• Cạnh bên SA = b thì b R = . 2 2 2 3b − a
• Cạnh bên SA hợp với đáy một góc α thì 3 R = . a 3.sin 2α ( 2 3 4 + tan β )
• Mặt bên tạo với mặt đáy một góc β thì R = . a 12 tan β • Góc SAB = ϕ thì 3.a R = . 4 −cosϕ.cos3ϕ • Góc ASB = γ thì 3.a R = . γ 3 4 sin .sin γ 2 2
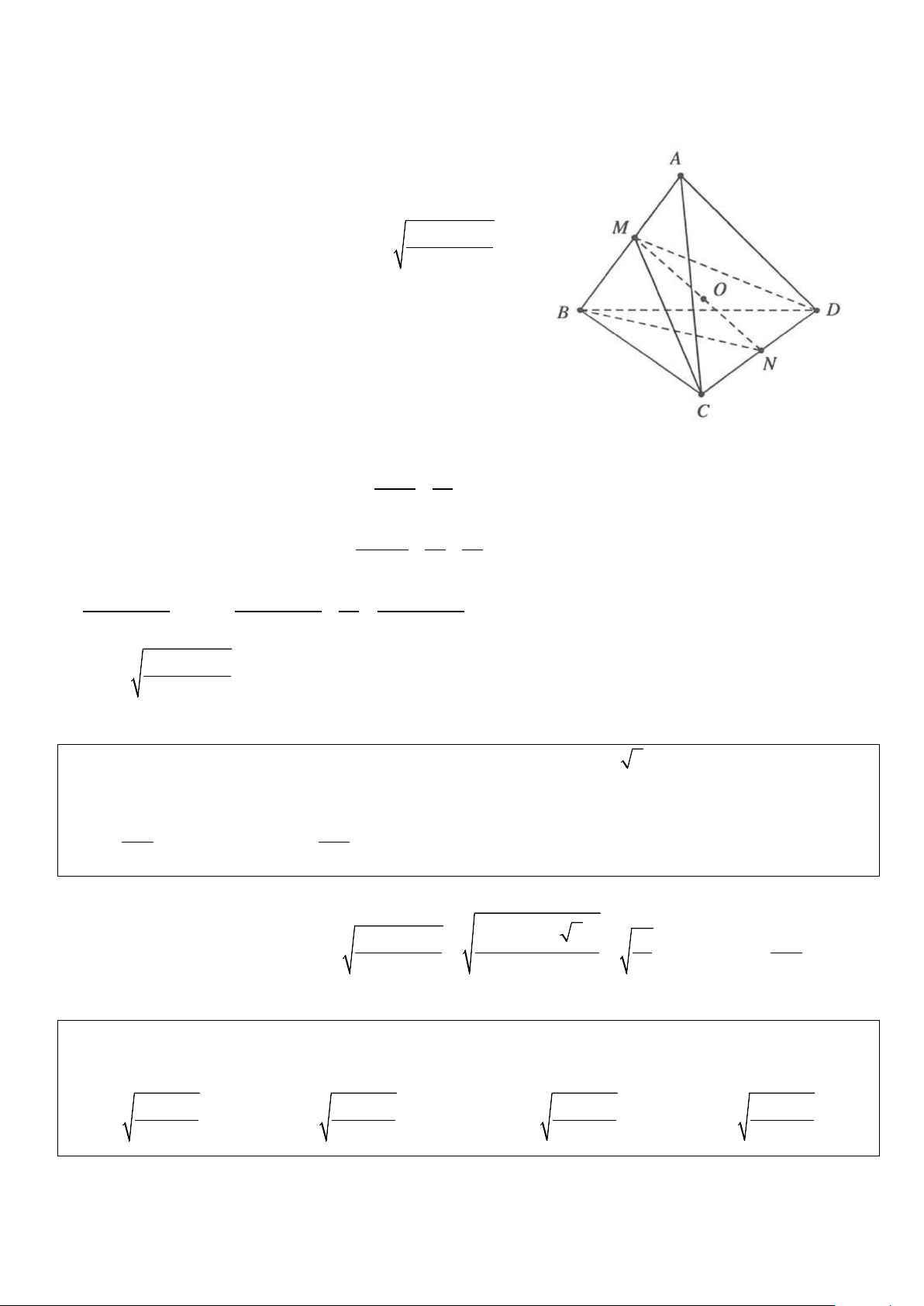
Ví dụ 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại ,
A AB = a 2. Các cạnh bên
SA = SB = SC. Góc giữa đường thẳng SA và mặt phẳng ( ABC) bằng 0
45 . Bán kính mặt cầu ngoại tiếp
hình chóp S.ABC bằng A. a 2 . B. a . C. a 2 . D. . a 4 2 2 Lời giải
Gọi O là trung điểm BC ⇒ O là tâm đường tròn ngoại tiếp A ∆ BC
⇒ SO ⊥ ( ABC) ⇒ SA ( ABC)  ( )=(SA OA)  =  0 ; ; SAO = 45
Tam giác ABC vuông cân tại A 
→ BC = AB 2 = 2a
Tam giác SAO vuông cân tại BC O  → SO = OA = = a 2 Vậy SO = ;
a SA = OA 2 = a 2  → R = . a Chọn D.
Ví dụ 3: Cho hình chóp đều S.ABC có cạnh đáy bằng 1, khoảng cách từ điểm A đến mặt phẳng (SBC)
bằng 6 . Diện tích mặt cầu ngoại tiếp tứ diện ABCD bằng 4 A. 25π π π π . B. 25 . C. 5 . D. 5 . 12 24 12 24 Lời giải
Gọi O là tâm tam giác ABC, M là trung điểm BC
⇒ SO ⊥ ( ABC) 2 2 3 3 1 3 ;OA = AM = . = ;OM = OA = 3 3 2 3 2 6
Kẻ OH ⊥ SM (H ∈ SM )  →OH ⊥ (SBC)
Ta có d ( A ( ABC)) 6 6 ; = 3.OH ⇒ OH = :3 = 4 12
Tam giác SMO vuông tại M có 1 1 1 3 = + ⇒ SO = 2 2 2 OH SO OM 6 Vậy 3 2 2 15 5 3 SO =
;SA = SO + OA =  → R = 6 6 12
Diện tích mặt cầu cần tính là 2 25π S = 4π R = . Chọn A. 12
Ví dụ 4: Cho ba tia Sx, Sy, Sz không đồng phẳng và  0 =  0 =  0
xSy 120 ; ySz 60 ; zSx = 90 . Trên các tia
Sx, Sy, Sz lấy lần lượt các điểm ,
A B,C sao cho SA = SB = SC = .
a Tính bán kính R của mặt cầu ngoại tiếp tứ diện A. a R = . B. R = . a
C. R = a 2.
D. R = a 3. 2 Lời giải Tam giác SAB có 2 2 = + −  Ab SA SB 2 . SA .
SB cos ASB = a 3
Tam giác SAC vuông cân tại S 
→ AC = SA 2 = a 2 Suy ra 2 2 2
AC + BC = AB  → A
∆ BC vuông tại C
Gọi O là trung điểm của AB 
→ SO ⊥ ( ABC)
Tam giác SAO vuông tại 2 2 a
O ⇒ SO = SA − OA = 2 2 Vậy a = ; SA SO SA = a  → R = = . a Chọn B. 2 2SO
Ví dụ 5: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc 0 60 .
Thể tích của khối cầu ngoại tiếp khối chóp S.ABCD là 3 3 3 3 A. 4π a π π π . B. 2 a 6 . C. 8 a 6 . D. 8 a 6 . 3 9 9 27 Lời giải
Gọi O là tâm hình vuông ABCD 
→ SO ⊥ ( ABCD) . Do đó ( ABCD)  = (SB OB)  =  0 SB; ; SBO = 60 .  OBSB = a 2 SB = 
Tam giác SBO vuông tại O, có   cos SBO  ⇒  . a 6   =  .tan SO SO OB SBO =  2 2  
Suy ra bán kính mặt cầu cần tính là SB R = = (a )2 a 6 a 6 2 :2.  = . 2SO  3  3   2 3  
Vậy diện tích khối cầu cần tính là 4 3 4 a 6 8π a 6
V = π R = π.  = . Chọn D. 3 3  3  27  
Ví dụ 6: Cho hình chóp S.ABCD có AC = 2a, mặt bên (SBC) tạo với mặt đáy ( ABCD) một góc 0 45 .
Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD bằng A. 2 . a B. a . C. 3 2 . a D. a . 4 2 4 4 Lời giải
Gọi M là trung điểm BC ⇒ OM ⊥ BC ⇒ BC ⊥ (SMO) .
Do đó (SBC) ( ABCD)  = (SM MO)  =  0 ; ; SMO = 45 .
Vì ABCD là hình vuông có AC = 2a  → AB = a 2
Tam giác SMO vuông cân tại a 2
O ⇒ SO = OM = 2
Tam giác SAO vuông tại 2 2 a 6
O ⇒ SA = SO + OA = 2 Vậy a 6 a 2 3 2 SA = ;SO =  → R = . a Chọn C. 2 2 4
Ví dụ 7: Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a, khoảng cách giữa hai đường thẳng SB và AD bằng 3 .
a Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD bằng A. 5 6 R = . a B. 5 3 R = . a C. 5 3 R = . a D. 5 6 R = . a 12 3 12 3 Lời giải
Ta có AD / /BC ⇒ AD / / (SBC) ⇒ d (S ; B AD) = d ( ; A (SBC))
Gọi O là tâm hình vuông ABCD 
→ SO ⊥ ( ABCD) .
Gọi M là trung điểm BC; kẻ OH ⊥ SM (H ∈ SM )
⇒ OH ⊥ (SBC) ⇒ d ( A (SBC)) a 3 ; = 2.OH ⇒ OH = 2
Tam giác SMO vuông, có 1 1 1 = + ⇒ SO = a 3 2 2 2 OH SO OM Vậy 2 2 5 6
SO = a 3;SA = SO + OA = a 5  → R = R = . a 3 Chọn D.
Ví dụ 8: Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, tính thể tích V của
khối chóp có thể tích lớn nhất A. V =144. B. V = 576. C. V = 576 2. D. V =144 6. Lời giải
Xét mặt cầu (S ) ngoại tiếp hình chóp S.ABCD
Gọi O là tâm hình vuông ABCD 
→ SO ⊥ ( ABCD) 2
Bán kính mặt cầu (S ) là SA 2 R = ⇔ SA =18h (*) 2h 2 Đặt 1 . h x AB = x  →V = SO S = S ABCD . . . 3 ABCD 3 2
Tam giác SAO vuông tại 2 2 2 2 x
O ⇒ SA = SO + OA = h + 2 2
Thay vào (*), ta được 2 x 2 2 h + = 18h 
→ x = 36h − 2h 2 Do đó h V = .( 2 36h − 2h ) 2 2 3 = 12 casio
h − h  →V = 576. Chọn B. max 3 3
Dạng 6: Hình chóp bất kì (bài toán Tổng quát – Nâng cao)
Công thức tìm nhanh bán kính mặt cầu ngoại tiếp hình chóp là 2 2
R = x + r với
• r là bán kính đường tròn ngoại tiếp đa giác đáy. 2 2 • SO − r x =
: S là đỉnh hình chóp, O là tâm đường tròn ngoại tiếp đa giác đáy, h là chiều cao 2h khối chóp.
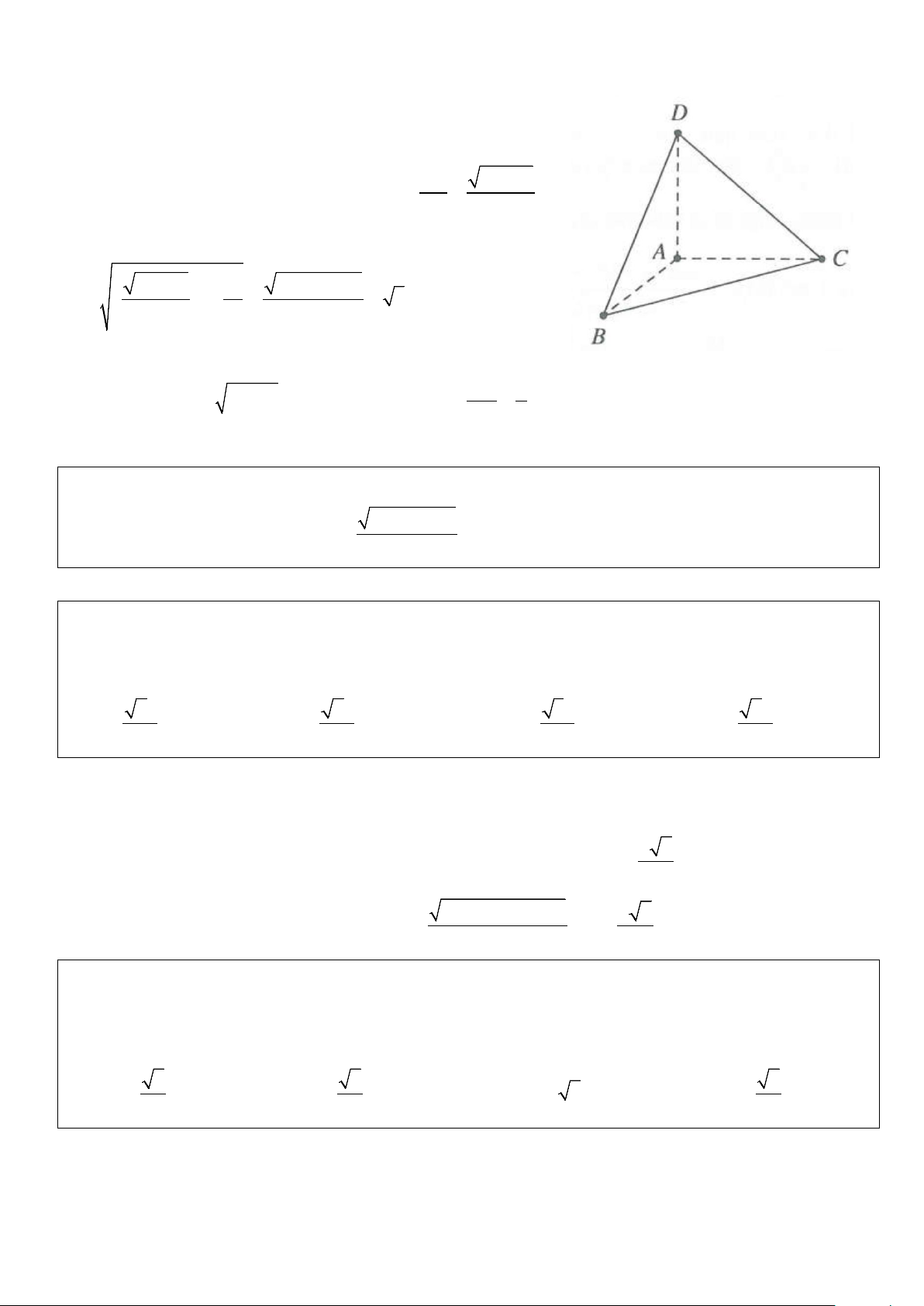
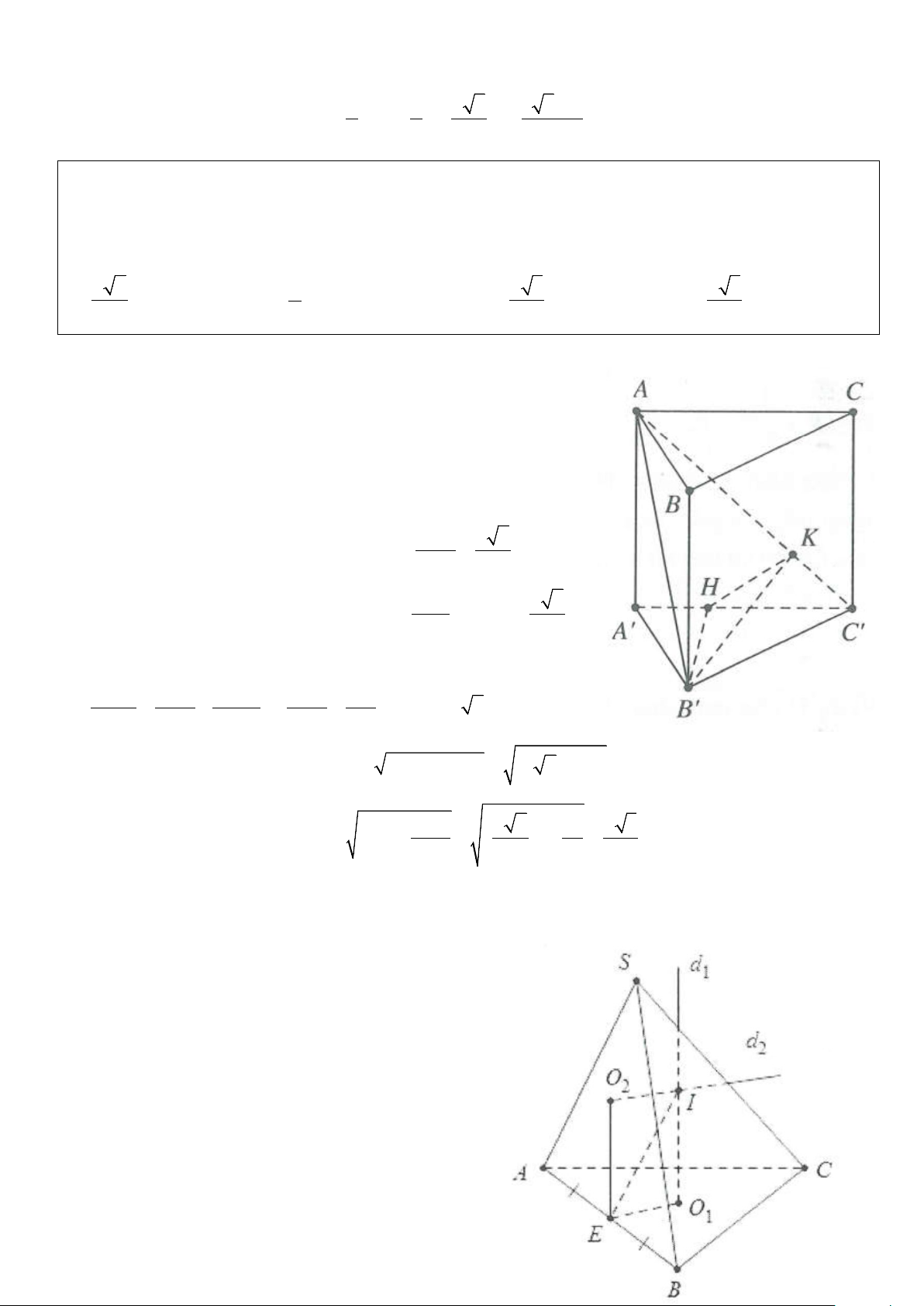
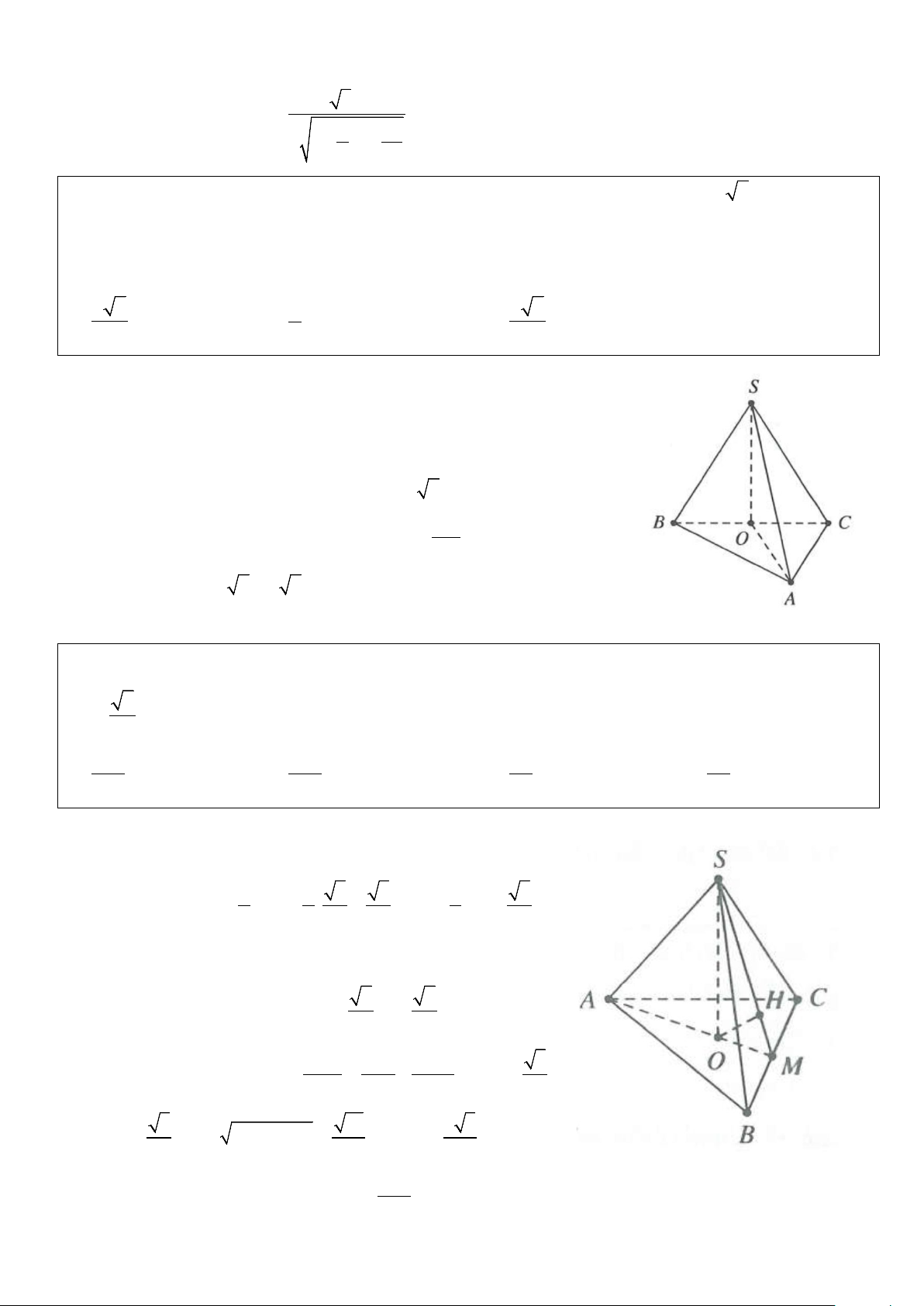
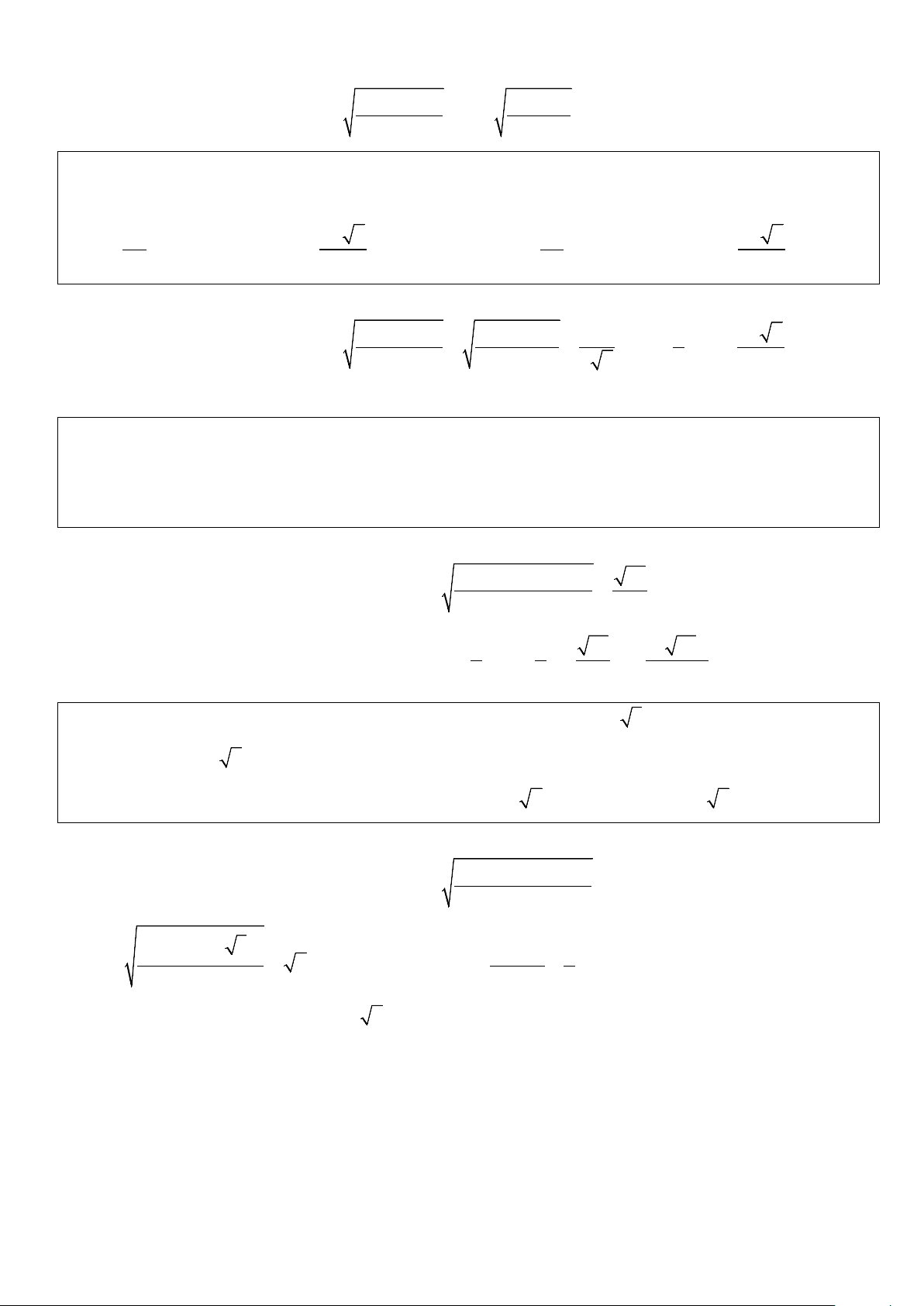
Ví dụ 1: Cho hình chóp đều S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên bằng 2a 3 . Gọi D là 3
điểm đối xứng của B qua C. Bán kính của mặt cầu ngoại tiếp hình chóp S.ABC bằng A. a 37 . B. a 35 . C. a 36 . D. a 39 . 6 7 7 7 Lời giải Hình vẽ tham khảo
Vì C là tâm đường tròn ngoại tiếp A
∆ BD nên r = BC = a
Gọi H là hình chiếu của S trên mặt phẳng ( ABC) ⇒ H là tâm đường tròn ngoại tiếp A ∆ BC
Tam giác SHC vuông tại H, có 2a 3 a 3 2 2 SC = ; HC =
⇒ SH = SC − HC = a 3 3
Vậy r = h = a và 2a 3 SC = nên a 37 R = . Chọn A. 3 6
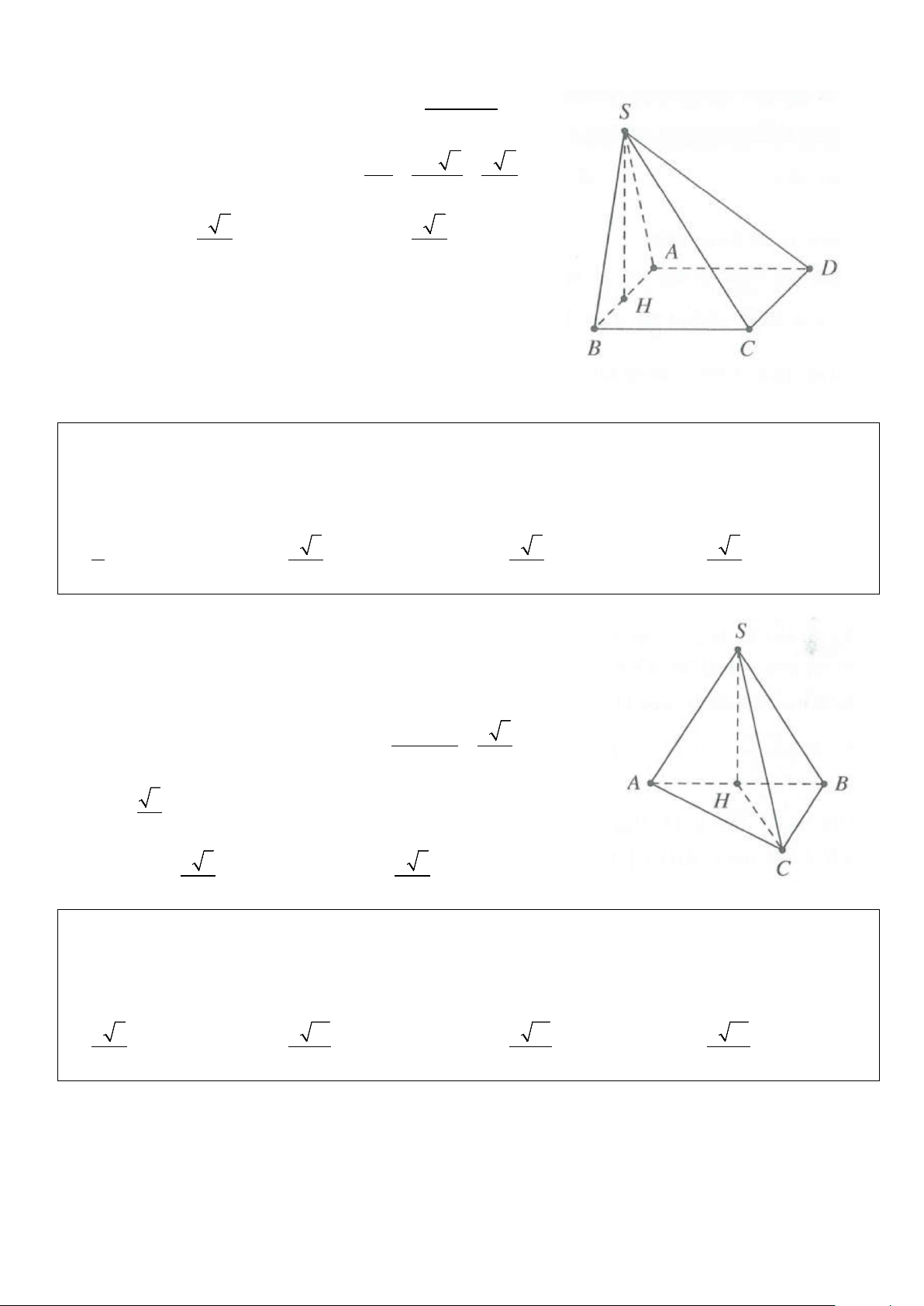
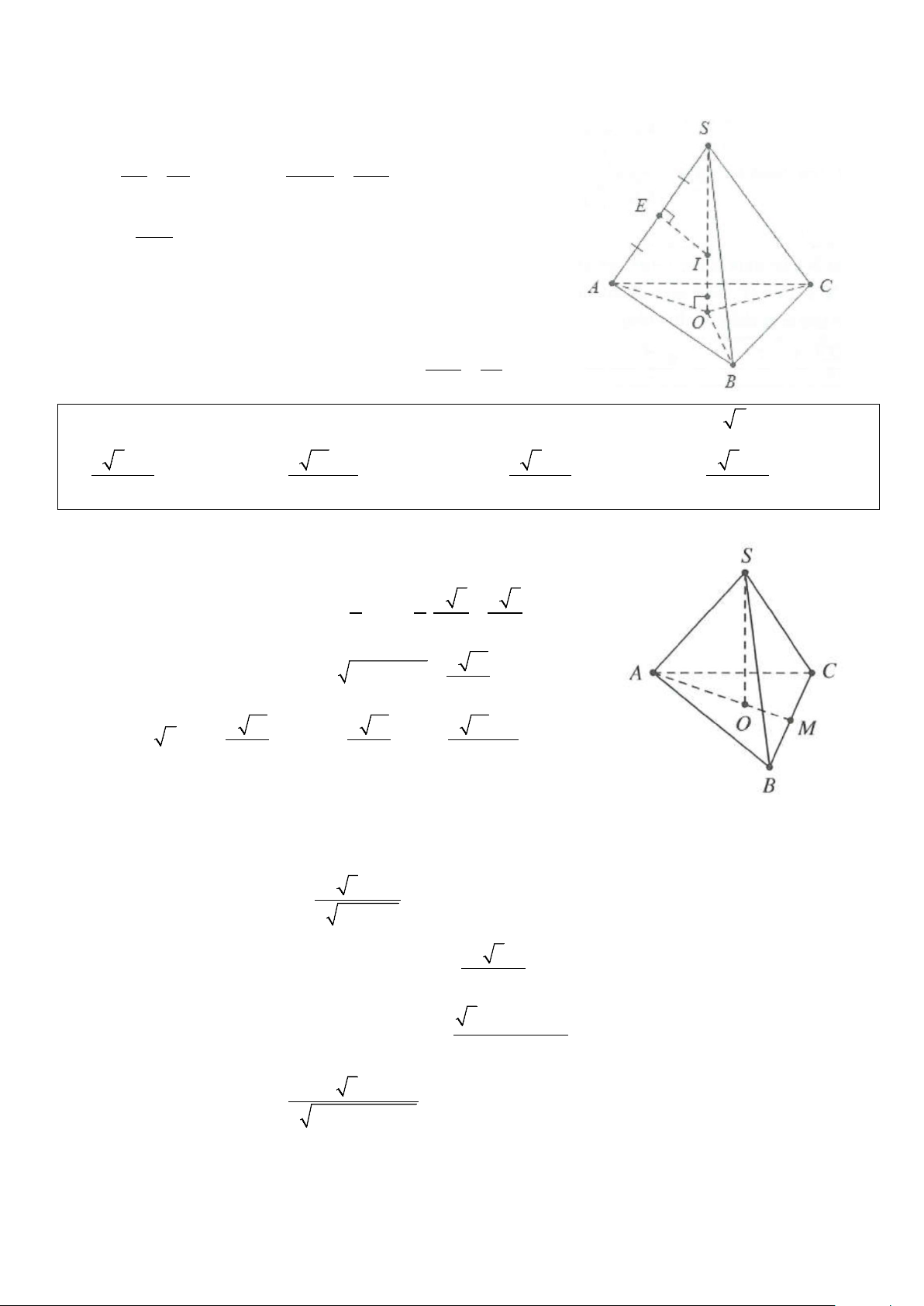
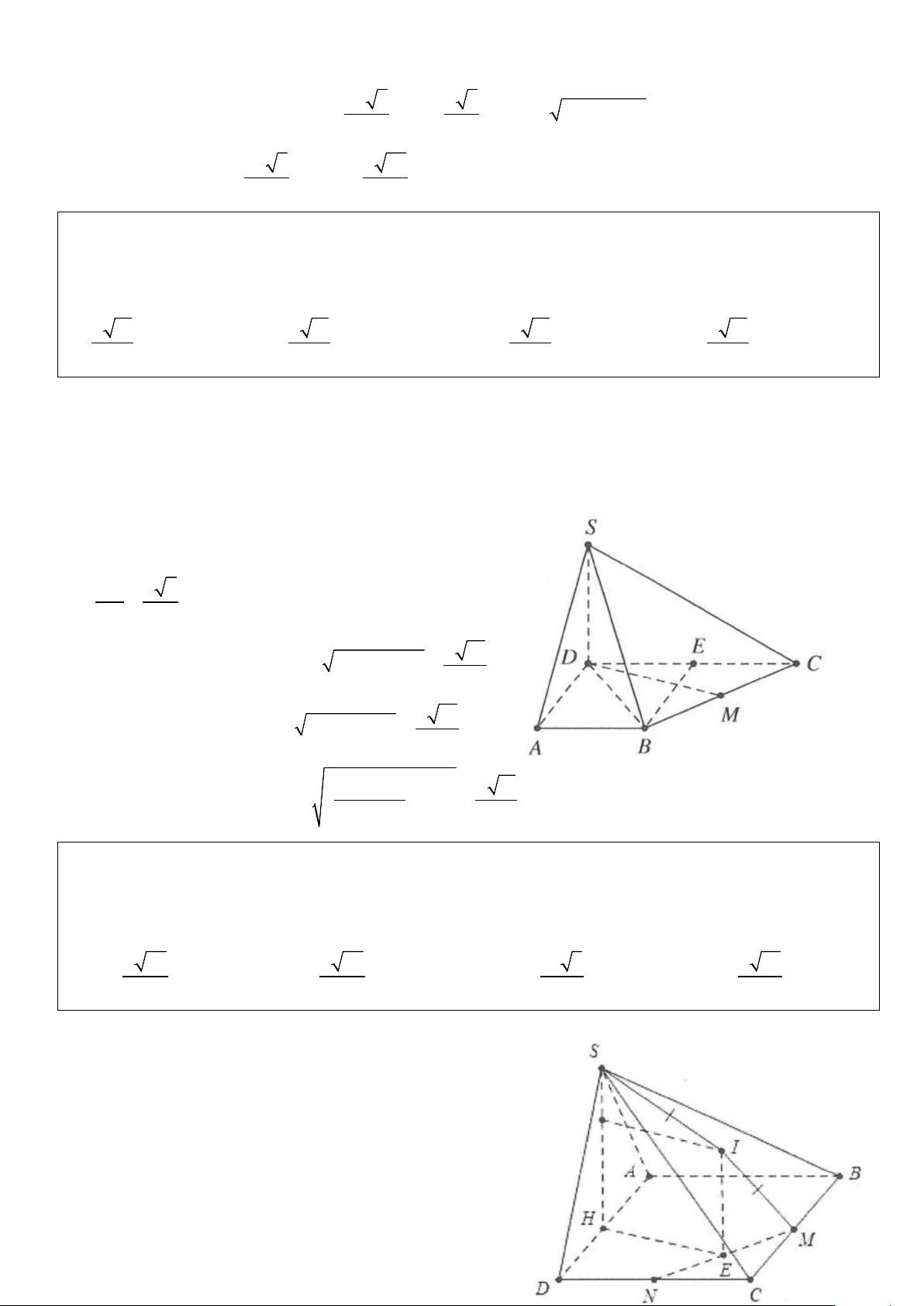
Ví dụ 2: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D, AB = AD = a và CD = 2 . a Cạnh
bên SD vuông góc với đáy, SD = .
a Gọi E là trung điểm của CD. Bán kính mặt cầu ngoại tiếp hình chóp S.BCE bằng A. a 11 . B. a 11 . C. a 11 . D. a 11 . 8 4 6 2 Lời giải
Vì E là trung điểm DC ⇒ E
∆ BC vuông tại E
Gọi M là trung điểm của BC
⇒ M là tâm đường tròn ngoại tiếp tam giác EBC
Xét hình chóp S.BCE có S là đỉnh, M là tâm đáy, chiều
cao h = SD và bán kính đường tròn ngoại tiếp đáy BC a 2 r = = 2 2 B
∆ CD vuông cân tại 2 2 a 10
B ⇒ DM = BD + BM = 2 S ∆ DM vuông tại 2 2 a 14
D ⇒ SM = SD + DM = 2 2 2 2  − 
Áp dụng công thức, ta được SM r 2 a 11 R =   + r = . Chọn D.  2.SD  2
Ví dụ 3: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAD là tam giác đều và nằm trong
mặt phẳng vuông góc với mặt phẳng đáy. Gọi M , N lần lượt là trung điểm các cạnh BC,CD . Tính bán
kính R mặt cầu ngoại tiếp hình chóp S.CMN. A. a 37 R = . B. a 29 R = . C. 5a 3 R = . D. a 93 R = . 6 8 12 12 Lời giải
Gọi H là trung điểm của AD ⇒ SH ⊥ AD
⇒ SH ⊥ ( ABCD). Gọi E là trung điểm của MN, dựng
đường thẳng d qua E song song với SH, trên d lấy điểm I sao
cho IS = IC ⇒ I là tâm mặt cầu ngoại tiếp khối chóp
S.CMN ⇒ IS = IC = IM = IN = . R 2 Ta có: MN a 2 2 a a 3 CE = = ⇒ IE = R − ;SH = 2 4 8 2 2 2 2 2  3   1  5a HE = CD +   AD =  4 4      8 2 2  2  Lại có 2 2
R − HE = (SH − IE)2 2 5a a 3 2 a a 93 ⇔ R − =  − R −  ⇒ R = . Chọn D. 8  2 8  12  
Ví dụ 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = 2a và vuông góc với mặt
phẳng đáy ( ABCD) . Gọi M , N lần lượt là trung điểm các cạnh BC,CD . Tính bán kính R mặt cầu ngoại
tiếp hình chóp S.CMN. A. a 3 R = . B. 3a 2 R = . C. 3a 3 R = . D. a 2 R = . 4 4 4 2 Lời giải
Gọi E là trung điểm của MN, dựng đường thẳng d
qua E song song với SA, trên d lấy điểm I sao cho
IS = IC ⇒ I là tâm mặt cầu ngoại tiếp khối
chóp S.CMN ⇒ IS = IC = IM = IN = . R 2 Ta có: MN a 2 2 a CE = = ⇒ IE = R − ;SA = 2a 2 4 8 2 2 2 2  3   3  9a AE = CD +   AD =  4 4      8 Lại có 2 2
R − AE = (SA − IE)2 2 2  2  2 9a 2 a 3a 3 ⇔ R −
=  2a − R −  ⇒ R = . 8  8  4   Chọn C.
Ví dụ 5: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2a . Mặt bên (SAD) là
tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy ( ABCD) . Gọi M , N lần lượt là trung
điểm các cạnh BC,CD . Tính bán kính mặt cầu ngoại tiếp hình chóp S.CMN. A. 2a 3 R = . B. 2a 6 R = . C. a 13 R = . D. a 3 R = . 3 3 4 6 Lời giải
Gọi H là trung điểm của AD ⇒ SH ⊥ AD
⇒ SH ⊥ ( ABCD) . Gọi E là trung điểm của MN, dựng
đường thẳng d qua E song song với SH, trên d lấy điểm I
sao cho IS = IC ⇒ I là tâm mặt cầu ngoại tiếp khối
chóp S.CMN ⇒ IS = IC = IM = IN = . R 2 Ta có: MN a 5 2 5a CE = = ⇒ IE = R − ;SH = a 3 2 4 16 2 2 2 2  3   1  13a HE = CD +   AD =  4 4      16 2 2  2  Lại có 2 2
R − HE = (SH − IE)2 2 13a 2 5a 2a 3 ⇔ R −
=  a 3 − R −  ⇒ R = . 16  16  3   Chọn A.
Ví dụ 6: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của S lên mặt
phẳng ( ABC) là điểm đối xứng của C qua AB và mặt bên (SAB) tạo với đáy góc 0
60 . Tính bán kính R mặt
cầu ngoại tiếp hình chóp đã cho. A. a 91 R = . B. a 217 R = . C. a 91 R = . D. a 273 R = . 12 12 15 12 Lời giải
Gọi H là đối xứng của C qua AB ⇒ CH ⊥ A . B
O là trung điểm của CH a 3 ⇒ = =  0 OH CO ;SOH = 60 2 Suy ra 0 3 = tan 60 a SH OH = 2
Gọi E là trọng tâm tam giác ABC, dựng đường thẳng d
qua E song song với SH, trên d lấy điểm I sao cho
IS = IC ⇒ I là tâm mặt cầu ngoại tiếp khối chóp S.CMN
⇒ IS = IC = IM = IN = . R 3 có: 2CO a 3 2 a 2a 3 CE = =
⇒ IE = R − ; HE = 2CE = 3 3 3 3 2 2  2  Lại có 2 2
R − HE = (SH − IE)2 2 4a 3a 2 a a 217 ⇔ R − =  − R −  ⇒ R = . 3  2 3  12   Chọn B.
Dạng 7: Bài toán mặt cầu của một số tứ diện đặc biệt Mẫu 1: Cho tứ diện ABCD có
AB = CD = a, AC = BD = ,
b AD = BC = c (tứ diện gần đều) 2 2 2
Bán kính mặt cầu ngoại tiếp tứ diện là: a b c R + + = . 8
Chứng minh: Gọi M , N,O lần lượt là trung điểm của A ; B CD và MN Ta có: A ∆ CD = B
∆ DC (c − c − c) ⇒ DM = CM
Khi đó MN ⊥ CD, tương tự MN ⊥ AB suy ra O là tâm mặt
cầu ngoại tiếp tứ diện. 2 2 Ta có: 2 2 2 2 2 MN a
R = OA = OB = OM + AM = + 4 4 2 2 2 2 Xét C ∆ MN có: 2 2 2 b c a a MN CM CN + = − = − − 2 4 4 2 2 2 2 2 2 2 2 2 2
b + c − a 2
b + c − a a a + b + c = ⇒ R = + = . 2 8 4 8 2 2 2 Vậy a b c R + + = . 8
Ví dụ 1: Cho tứ diện ABCD có AB = CD = 3, AC = BD = 2, AD = BC = 2 2. Diện tích mặt cầu ngoại tiếp tứ diện ABCD là A. 21π π S = . B. 19 S = . C. S = 9π. D. S = 4π. 2 2 Lời giải 3 + 2 a b c + + + (2 2)2 2 2 2 2 2
Áp dụng công thức nhanh ta có: 21 2 21π R = = = ⇒ S = 4π R = . 8 8 8 2 Chọn A.
Ví dụ 2: Cho tứ diện ABCD có AB = CD = a, AC = BD = AD = BC = .
b Bán kính của mặt cầu ngoại tiếp tứ diện ABCD là 2 2 2 2 2 2 2 2 A. a 2b R + = . B. 2a b R + = . C. a 2b R + = . D. 2a b R + = . 8 8 2 2 Lời giải 2 2 2 2 2
Áp dụng công thức nhanh ta có: a + b + c a + 2b R = = R = . Chọn A. 8 8
Ví dụ 3: Cho tứ diện ABCD có AB = CD = AC = BD = 2, AD = BC =1. Thể tích mặt cầu ngoại tiếp tứ diện ABCD là A. 9π π π π V = . B. 9 2 V = . C. 2 V = . D. 9 2 V = . 8 8 3 8 Lời giải 2 2 2 2 2 2 + + + + π
Áp dụng công thức nhanh ta có: a b c 1 2 2 3 4 3 9 2 R = = = ⇒ V = π R = . 8 8 2 2 3 8 Chọn D.
Ví dụ 1: Cho tứ diện ABCD có AB = CD = 3, AC = BD = 5, AD = BC = 6. Thể tích khối cầu ngoại tiếp tứ
diện ABCD thuộc khoảng nào dưới đây? A. (100;102). B. (95;98). C. (106;109). D. (103;107). Lời giải 2 2 2
Bán kính mặt cầu ngoại tiếp tứ diện ABCD là AB AC AD 35 R + + = = . 8 2 3  
Vậy thể tích khối cầu ngoại tiếp tứ diện π ABCD là 4 3 4 35 35 35
V = π R = π.  = . Chọn C. 3 3  2  6  
Ví dụ 5: Cho tứ diện ABCD có AB = CD = x, AC = BD = y, AD = BC = 2 3. Bán kính khối cầu ngoại tiếp
tứ diện ABCD bằng 2. Giá trị lớn nhất của xy bằng A. 2. B. 4. C. 2 2. D. 2. Lời giải 2 2 2
Bán kính mặt cầu ngoại tiếp tứ diện ABCD là AB AC AD R + + = . 8 x + y + (2 3)2 2 2 2 2 Khi đó 2 2
= 2 ⇔ x + y = 4 mà x y 4 xy + ≤ = = 2. 8 2 2
Dấu bằng xảy ra khi và chỉ khi x = y = 2. Vậy {x } y = 2. Chọn A. max  Mẫu 2: Cho tứ diện ABCD có AB = ;
x CD = y; AD = BC = AC = BD = z. Tính bán kính mặt cầu
ngoại tiếp tứ diện ABCD.
Gọi M , N lần lượt là trung điểm của AB và CD ta có: D ∆ AC = D
∆ BC ⇒ AN = BN suy ra NM là trung trực của AB,
tương tự MN là trung trực của DC
Khi đó I ∈ MN sao cho ID = IA 2 Lại có 2 2 2 y
AN = AD − DN = z − 4 2 2 2 2 2 y x
⇒ MN = AN − AM = z − − 4 4 Mặt khác 2 2 2 2
MN = IM + IN = R − AM + R − DN 2 2 2 2 2 x 2 y 2 y z ⇒ R − + R − = z − − 4 4 4 4
Vậy bán kính mặt cầu ngoại tiếp tứ diện ABCD là nghiệm của phương trình: 2 2 2 2 2 x 2 y 2 y z R − + R − = z − − . 4 4 4 4
Ví dụ 1: Cho tứ diện ABCD có AB = 2a;CD = 4a, các cạnh còn lại đều bằng 3 .
a Tính bán kính mặt cầu
ngoại tiếp tứ diện ABCD. A. 2 . a B. a 65 . C. a 71 . D. 5a . 4 4 2 Lời giải Ta có: 2 2 2 2 2 2
R − a + R − 4a = 9a − 5a = 2a 2 2 ⇔ R − a = ( 2 2
a − R − a ) 2 2 2 2 2 2 2 2 4
⇒ R − a = 4a − 4a R − 4a + R − 4a 2 2 a a 65
⇔ R − 4a = ⇔ R = . Chọn B. 4 4
Ví dụ 2: Cho tứ diện ABCD có AB = 4a;CD = 6a, các cạnh còn lại đều bằng a 22. Tính diện tích mặt cầu
ngoại tiếp tứ diện ABCD. A. 85π π π π S = . B. 340 S = . C. 340 S = . D. 340 S = . 9 3 9 27 Lời giải Ta có: 2 2 2 2 2 2
R − 4a + R − 9a = 22a −13a = 3a 2 2 ⇔ R − a = ( 2 2
a − R − a ) 2 2 2 2 2 2 2 4 3 9
⇒ R − 4a = 9a − 6a R − 9a + R − 9a 2 2 4a a 85 2 340π ⇔ R − 9a = ⇔ R = ⇒ S = 4π R = . Chọn C. 6 4 9
Ví dụ 3: Cho tứ diện ABCD có AB = 2a;CD = 8a, các cạnh còn lại đều bằng a 26. Tính bán kính mặt cầu
ngoại tiếp tứ diện ABCD. A. 4 . a B. a 14. C. a 10. D. 9a . 2 Lời giải Ta có: 2 2 2 2 2 2
R − a + R − 9a = 26a −10a = 4a 2 2 ⇔ R − a = ( 2 2
a − R − a ) 2 2 2 2 2 2 2 4 9
⇒ R − a =16a −8a R − 9a + R − 9a 2 2
⇔ R − 9a = a ⇔ R = a 10. Chọn C.
Ví dụ 4: Cho tứ diện ABCD có AB = 4 ;
a CD =10a, các cạnh còn lại đều bằng a 78. Tính diện tích mặt
cầu ngoại tiếp tứ diện ABCD. 2 A. 2 π S = 30π a . B. 2 S = 29π a . C. 116 a S = . D. 2 S =116π a . 3 Lời giải Ta có: 2 2 2 2 2 2
R − 4a + R − 25a = 78a − 29a = 7a 2 2 ⇔ R − a = ( 2 2
a − R − a ) 2 2 2 2 2 2 2 4 7 25
⇒ R − 4a = 49a −14a R − 25a + R − 25a 2 2 2 2
⇔ R − 25a = 2a ⇔ R = a 29 ⇒ S( ) = 4π R =116πa . Chọn D. C
Ví dụ 5: Cho tứ diện ABCD có AB = 2a;CD = 8a, các cạnh còn lại đều bằng .x Tìm x biết bán kính mặt
cầu ngoại tiếp tứ diện bằng a 17 .
A. x = a 42. B. x = 6 . a
C. x = a 38.
D. x = a 33. Lời giải Ta có: 2 2 2 2 2 2
R − a + R −16a = x −17a Với 2 2 2 2
R = a 17 ⇒ x −17a = 4a + a = 5a ⇒ x = 42a ⇒ x = a 42. Chọn A.
BÀI TẬP TỰ LUYỆN
Câu 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và SA ⊥ ( ABC). Điểm nào sau đây là
tâm của mặt cầu qua các điểm S, , A B,C ?
A. Trung điểm của AC.
B. Trung điểm của AB.
C. Trung điểm của BC.
D. Trung điểm của SC.
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và SA ⊥ ( ABC). Gọi I và J lần lượt là
hình chiếu vuông góc của A trên SB và SC. Điểm nào sau đây là tâm của mặt cầu qua năm điểm ,
A B,C, I, J ?
A. Trung điểm của AC.
B. Trung điểm của BC.
C. Trung điểm của IJ.
D. Trọng tâm của A ∆ BC.
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA ⊥ ( ABCD). Gọi I, J, K lần lượt là hình
chiếu vuông góc của A trên SB, SC, .
SD Điểm nào sau đây là tâm của mặt cầu qua bảy điểm ,
A B,C, D, I, J, K ?
A. Tâm của ABCD.
B. Trung điểm của SB.
C. Trung điểm của SC.
D. Trung điểm của SD.
Câu 4: Cho tứ diện ABCD với tam giác BCD vuông tại B, BC = a, BD = 3 và AB = AC = AD = a 2.
Điểm nào sau đây là tâm của mặt cầu ngoại tiếp tứ diện ABCD?
A. Trung điểm của BC.
B. Trung điểm của CD.
C. Trung điểm của BD.
D. Trọng tâm của B ∆ C . D
Câu 5: Cho hình chóp S.ABC có đáy ABC là tam giác đều, SA vuông góc với mặt phẳng ( ABC). Gọi H là
hình chiếu của A lên đường thẳng SB. Điểm nào sau đây là tâm của mặt cầu ngoại tiếp khối chóp . A BCH ?
A. Trọng tâm của A ∆ BC.
B. Trọng tâm của A ∆ BCH.
C. Trọng tâm của A ∆ CH.
D. Trọng tâm của A ∆ BH.
Câu 6: Cho tứ diện ABCD có O là trung điểm đoạn thẳng nối trung điểm của hai cạnh đối diện. Tập hợp các
   
điểm M trong không gian thỏa mãn hệ thức MA + MB + MC + MD = a(a > 0) là
A. Mặt cầu tâm O bán kính a r = .
B. Mặt cầu tâm O bán kính a r = . 4 2
C. Mặt cầu tâm O bán kính r = . a
D. Mặt cầu tâm O bán kính a r = . 3
Câu 7: Cho tứ diện DABC, đáy ABC là tam giác vuông tại B, DA vuông góc với mặt đáy. Biết
AB = 3a, BC = 4a, AD = 5 .
a Bán kính mặt cầu ngoại tiếp hình chóp DABC có bán kính bằng A. 5a 2 . B. 5a 2 . C. 5a 3 . D. 5a 3 . 2 3 3 3
Câu 8: Cho hình chóp tam giác S.ABC có các cạnh ,
SA SB, SC vuông góc với nhau từng đôi một và
SA = a, SB = , b SC = .
c Mặt cầu ngoại tiếp hình chóp có bán kính là: A. 1 2 2 2
a + b + c . B. 1 2 2 2
a + b + c . C. 3 2 2 2
a + b + c . D. 2 2 2 2
a + b + c . 2 3 2 3
Câu 9: Cho hình chóp tam giác S.ABC có các cạnh ,
SA SB, SC vuông góc với nhau từng đôi một và
SA = SB = 2a, SC = 4 .
a Mặt cầu ngoại tiếp hình chóp có bán kính tính theo a là: A. a 6 . B. a 3. C. a 6 . D. a 6 . 2 3
Câu 10: Cho hình chóp tam giác S.ABC , đáy là tam giác vuông tại ,
A AB = 3, AC = 4, SA vuông góc với
đáy, SA = 2 14. Thể tích V của khối cầu ngoại tiếp hình chóp S.ABC là A. 169π π π π V = . B. 2197 V = . C. 729 V = . D. 13 V = . 6 8 6 8
Câu 11: Cho tứ diện ABCD cạnh a, đường cao AH, O là trung điểm AH. Tính bán kính R của mặt cầu ngoại
tiếp tứ diện OCBD. A. a 3 R = . B. a 6 R = . C. a 2 R = . D. a 6 R = . 2 4 3 3
Câu 12: Cho hình chóp tam giác S.ABC có đáy là tam giác vuông cân tại B, AB = a , các cạnh bên đều bằng
a. Bán kính của mặt cầu ngoại tiếp hình chóp bằng A. a 2 . B. a 2 . C. a 2 . D. a 3 . 4 2 6 4
Câu 13: Cho tứ diện đều ABCD cạnh a. Mặt cầu nội tiếp tứ diện này có bán kính theo a là: A. a 6 . B. a 6 . C. a 6 . D. a 6 . 12 9 6 8
Câu 14: Cho tứ diện đều ABCD cạnh a. Mặt cầu ngoại tiếp tứ diện này có bán kính theo a là: 2 2 2 A. 3π a π π . B. 3 a . C. 5 a . D. 2 a . 2 4 4
Câu 15: Cho tứ diện đều ABCD cạnh a. Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng 3 3 3 3 A. π a 6 π π π . B. a 6 . C. a 6 . D. 3 a 6 . 8 6 4 8
Câu 16: Cho tứ diện đều ABCD cạnh a. Biết mặt cầu ngoại tiếp tứ diện có bán kính bằng 1. Tính giá trị của a. A. 2 a = . B. 6 a = . C. 2 6 a = . D. 3 a = . 3 3 3 3
Câu 17: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 3a , cạnh bên SC = 2a , và SC vuông góc
với đáy. Tính diện tích của mặt cầu ngoại tiếp hình chóp S.ABC 2 A. 2 π 16π a . B. 2 36π a . C. 2 24π a . D. 8 a . 3
Câu 18: Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B, AB = a, góc BAC bằng 0 60 , chiều cao
SA = a 2. Tính thể tích V của khối cầu ngoại tiếp hình chóp. 3 3 A. 3 π π V = a π 6. B. 4 a 6 V = . C. 2 a 6 V = . D. 3 V = π a 6. 3 3
Câu 19: Cho khối chóp S.ABCD có SC vuông góc với ( ABCD),SA = SB = SD, ABD là tam giác cân tại A
có AB = a, BD = a 3, góc giữa SA và ( ABCD) bằng 0
45 . Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD . A. 7a 3 R = . B. 2a 3 R = . C. R = . a D. a 5 R = . 12 3 2
Câu 20: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, các cạnh bên bằng b. Tính theo a,b bán
kính mặt cầu ngoại tiếp hình chóp S.ABCD là: 2 2 2 2 A. b . B. a . C. b . D. a . 2 2 2 2 2 2 a b − 2 2 b a − 2 2 a b − 2 2 b a − 2 2 3 3
Câu 21: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa mặt bên và mặt phẳng đáy bằng 0
45 . Diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD là: 2 2 2 2 A. 9π a π π π . B. 4 a . C. 3 a . D. 2 a . 4 3 4 3
Câu 22: Cho hình chóp tứ giác đều S.ABCD có đáy hợp với cạnh bên một góc 0
45 . Bán kính mặt cầu ngoại
tiếp hình chóp S.ABCD bằng 2. Thể tích khối chóp là A. 4 . B. 2 2 . C. 4 2. D. 4 2 . 3 3 3
Câu 23: Thể tích khối cầu ngoại tiếp khối chóp tứ giác đều có tất cả các cạnh bằng a là 3 3 3 A. 8π a π π . B. 2 a . C. 3 2π a . D. 4 2 a . 3 3 3
Câu 24: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Mặt cầu ngoại tiếp hình chóp này có
diện tích tính theo a là A. 2 π a . B. 2 2π a . C. 2 3π a . D. 2 4π a .
Câu 25: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 3 2a, cạnh bên bằng 5 .
a Tính bán kính R
của mặt cầu ngoại tiếp hình chóp S.ABCD . A. R = 3 . a B. R = 2 . a C. 25a R = . D. R = 2 . a 8
Câu 26: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Cạnh bên SA vuông góc với mặt
phẳng ( ABC) và SA = 2 .
a Tính thể tích của mặt cầu ngoại tiếp hình chóp S.ABCD . 3 3 A. 3 π π π a 6. B. a . C. 4 6 3 π a . D. 3 a . 6 3 4 6
Câu 27: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Cạnh bên SA vuông góc với mặt
phẳng ( ABC) và SA = a 3. Diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD là 2 2 2 A. 2 π π π 5π a . B. a 3 . C. 4 a . D. 4 a . 6 3 5
Câu 28: Cho hình chóp S.ABCD có đáy ABCD là tứ giác có AB = 2a, BC = AC = a 2, AD = a và
BD = a 3. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích của mặt cầu ngoại
tiếp hình chóp S.ABCD . 3 3 3 3 A. π a π π π . B. a 3 . C. 32 3 a . D. 32 a . 32 32 27 9
Câu 29: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Cạnh bên SA vuông góc với mặt
phẳng ( ABC) và SA = a 6. Diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD là A. 2 S = 8π a . B. 2 S = 2a . C. 2 S = 2a . D. 2 S = 2π a .
Câu 30: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B với AB = BC = a 3 và  =  0
SAB SCB = 90 . Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng a 2. Tính thể tích của mặt cầu
ngoại tiếp hình chóp S.ABC . 3 A. 16π a V = . B. 3 V = 8π a . C. 3 V = 4 3π a . D. 3 V = 3 3π a . 3
Câu 31: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và AB = 3a, BC = 4 .
a Cạnh bên SA vuông
góc với mặt phẳng ( ABC) và SA =12 .
a Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD . A. 5a R = . B. 17a R = . C. 13a R = . D. R = 6 . a 2 2 2
Câu 32: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 2, cạnh bên SA vuông góc với mặt
phẳng đáy và SA = 3. Mặt phẳng (α ) đi qua A và vuông góc với SC cắt các cạnh ;
SB SC;SD lần lượt tại các
điểm M , N, P . Tính thể tích V của khối cầu ngoại tiếp tứ diện CMNP A. 64 2π π π π V = . B. 125 V = . C. 32 V = . D. 108 V = . 3 6 3 3
Câu 33: Cho tứ diện ABCD có AB = 4a,CD = 6a và các cạnh còn lại đều bằng a 22. Tính bán kính mặt
cầu ngoại tiếp tứ diện ABCD. A. R = 3 . a B. a 85 R = . C. a 79 R = . D. 5a R = . 3 3 2
Câu 34: Cho hình chóp S.ABCD có SA vuông góc với đáy và SA = a 6. Đáy ABCD là hình thang vuông tại ,
A B, AD = 2AB = 2BC = 2 .
a Gọi E là trung điểm AD. Tính bán kính R của mặt cầu ngoại tiếp hình chóp SECD.
A. R = a 6. B. a 30 R = . C. a 2 R = . D. a 114 R = . 3 2 6
Câu 35: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp hình chóp đã cho. 3 3 3 3 A. π 4π a 3 π π . B. 5 a . C. 5 a 15 . D. 5 a 15 . 27 3 54 18
Câu 36: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại , A AB = AC = .
a Mặt bên SAB là tam
giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối cầu ngoại tiếp hình chóp S.ABC . 3 3 3 3 A. π a π π π V = . B. 7 a 21 V = . C. a 21 V = . D. a V = . 3 54 54 54
Câu 37: Cho hình chóp tam giác đều =  0
S.ABC, SA a, ASB = 90 . Tính theo a bán kính mặt cầu ngoại tiếp
hình chóp S.ABC . A. a 3 R = . B. a 3 R = . C. 2a 3 R = .
D. R = a 3. 3 2 3
Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 .
a Mặt bên SAB là tam giác vuông cân
tại S và nằm trong mặt phẳng vuông góc với đáy. Tính bán kính r của mặt cầu ngoại tiếp hình chóp S.ABCD . A. a 2 r = . B. 3a r = . C. r = . a
D. r = a 2. 2 2
Câu 39: Cho hình chóp S.ABCD có SA ⊥ ( ABCD), đáy ABCD là hình chữ nhật, AB = a, AD = 2a, góc
giữa đường thẳng SC và đáy bằng 0
45 . Tính theo a thể tích của khối cầu ngoại tiếp hình chóp S.ABCD . 3 3 3 A. 3 π π π V = π a 6. B. 10 a V = . C. 5 a V = . D. 5 10 a V = . 3 6 3
Câu 40: Cho tứ diện SABC có tam giác ABC vuông tại B, AB = a, BC = a 3, SA = a 2 và
SB = a 2, SC = a 5. Tính bán kính mặt cầu ngoại tiếp tứ diện S.ABC. A. a 259 R = . B. a 259 R = . C. a 259 R = . D. a 37 R = . 7 4 2 14
Câu 41: Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = a 3 và SA vuông góc với đáy.
Gọi M , N lần lượt là trung điểm của CD, BC và K là giao điểm của AM và DN. Tính bán kính R của mặt
cầu ngoại tiếp khối chóp S.ABNK. A. a 17 R = . B. 3a 2 R = . C. a 17 R = . D. a 15 R = . 4 4 2 4
Câu 42: Cho khối chóp S.ABCD có ABCD là hình chữ nhật tâm O, AB = 2a, BC = 2a 3, góc hợp giữa hai
đường thẳng SB và mặt phẳng ( ABCD) bằng 0
60 . Hình chiếu vuông góc của đỉnh S xuống mặt phẳng
( ABCD) trùng với trọng tâm H của tam giác ABC. Tính bán kính R của mặt cầu ngoại tiếp khối chóp S.ABCD . A. 2a 21 R = . B. 2a 3 R = . C. 4a 21 R = . D. 4a 3 R = . 9 3 9 3
Câu 43: Cho hình chóp S.ABCD có đáy là hình thang vuông với đường cao
AB = BC = a, AD = 2a, SA ⊥ ( ABCD) và SA = a 2. Gọi E là trung điểm của AD. Kẻ EK ⊥ SD tại K. Bán
kính mặt cầu đi qua sáu điểm S, ,
A B,C, E, K bằng A. . a B. 3 . a C. 1 . a D. 6 . a 2 2 2
Câu 44: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và SA = 2a, SA vuông góc với
( ABCD), kẻ AH vuông góc với SB và AK vuông góc với SD. Mặt phẳng ( AHK ) cắt SC tại E. Tính thể tích
khối cầu ngoại tiếp khối ABCDEHK 3 3 3 3 A. π a 2 π π π . B. 4 a 2 . C. 8 a 2 . D. a 2 . 3 3 3 6
Câu 45: Cho hình chóp S.ABCD có cạnh AB =1, AC = 2 và góc 
BAC = α. Cạnh SA vuông góc với mặt
phẳng ( ABC). Điểm B và C lần lượt là hình chiếu vuông góc của A trên SB và SC . Tính bán kính R 1 1
của mặt cầu đi qua các điểm ,
A B,C,C , B 1 1 A. 5 − 4cosα − α − α − α R = . B. 2 5 4cos R = . C. 5 4cos R = . D. 5 4cos R = . 3 sinα 3 sinα 2 sinα 2sinα
Câu 46: Cho hình lập phương ABC .
D A' B 'C ' D '. Gọi R , R , R lần lượt là bán kính của mặt cầu ngoại tiếp 1 2 3
khối lập phương, mặt cầu nội tiếp khối lập phương và mặt cầu tiếp xúc với tất cả các cạnh của hình lập
phương. Đẳng thức nào sau đây là đúng về R , R , R 1 2 3 A. 2
R .R = R . B. 2 2 2
R .R = R . C. 2
R .R = R . D. 2 2 2
R + R = R . 1 2 3 1 2 3 2 3 1 2 3 1
Câu 47: Các kí hiệu R , R , R lần lượt là bán kính của mặt cầu ngoại tiếp, nội tiếp và tiếp xúc với tất cả các 1 2 3
cạnh của hình lập phương. Tìm khẳng định đúng?
A. R > R > R .
B. R > R > R .
C. R > R > R .
D. R > R > R . 1 2 3 2 3 1 1 3 2 3 1 2
Câu 48: Cho hình lăng trụ đều ABC.A'B 'C 'có mặt phẳng ( A'BC) tạo với đáy ( ABC) một góc 0 30 . Tam
giác A'BC có diện tích bằng 18. Tính diện tích S mặt cầu ngoại tiếp khối lăng trụ trên. A. π π π S = 57π. B. 57 S = . C. 57 S = . D. 57 S = . 4 2 3
Câu 49: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, tam giác SAB đều và
nằm trong mặt phẳng vuông góc với đáy. Gọi M , N lần lượt là trung điểm của các cạnh AD, DC. Tính bán
kính R của mặt cầu ngoại tiếp hình chóp S.DMN . A. a 39 R = . B. a 31 R = . C. a 102 R = . D. a 39 R = . 6 4 6 13
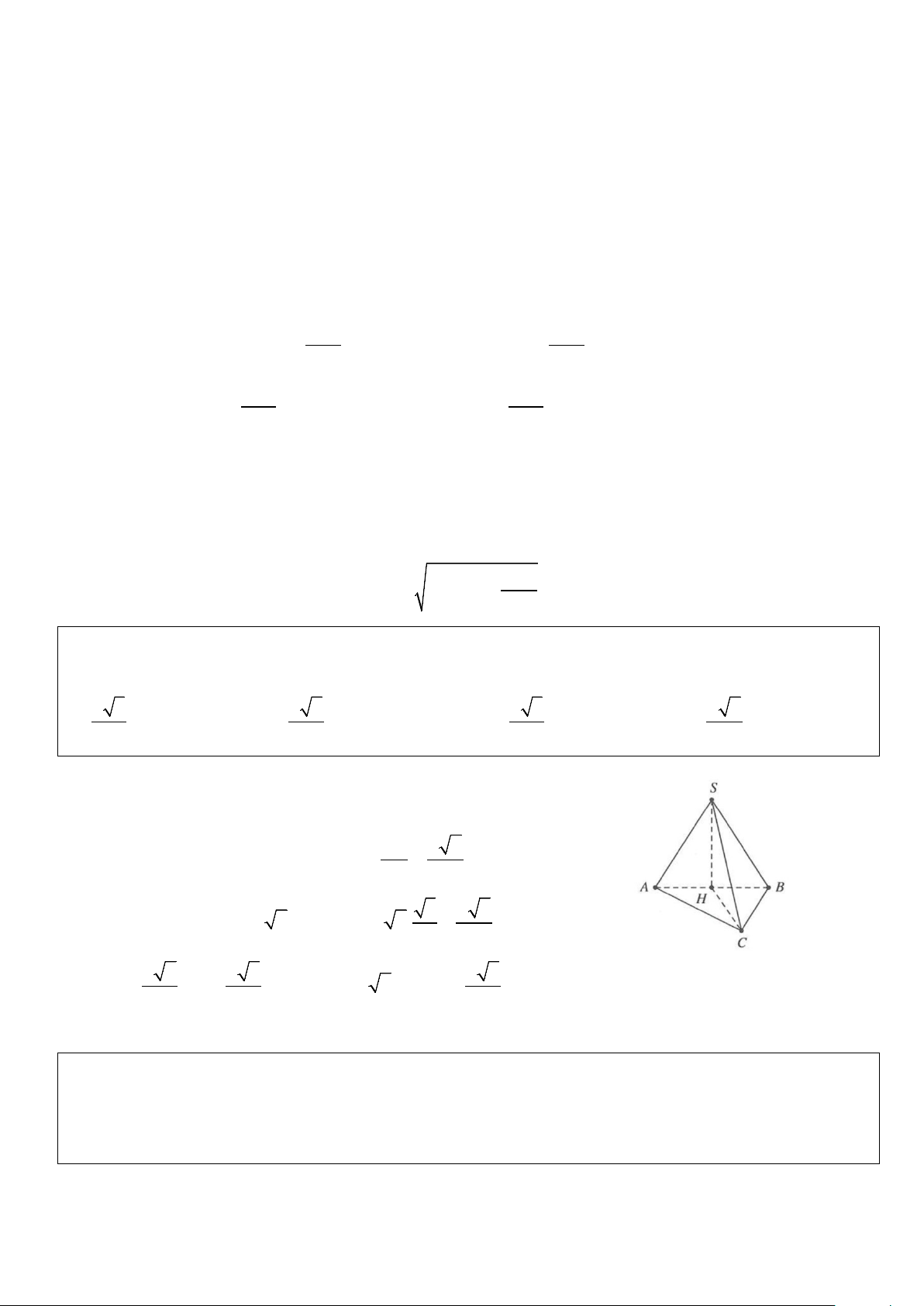
Câu 50: Cho tứ diện S.ABC có đáy ABC là tam giác vuông tại A với AB = 3a, AC = 4 .
a Hình chiếu H của S
trùng với tâm đường tròn nội tiếp tam giác ABC. Biết SA = 2a, bán kính mặt cầu ngoại tiếp hình chóp S.ABC là A. a 118 R = . B. a 118 R = . C. a 118 R = .
D. R = a 118. 4 2 8
Câu 51: Cho tứ diện ABCD có AB = AC = BC = AD = BD = 2a,CD = 2b(a > b). Xác định bán kính R của
mặt cầu ngoại tiếp tứ diện ABCD 2 2 2 2 2 2 2 2 A. 4a − b R − − − = b . B. 3a b R = a . C. 4a b R = a . D. 3a b R = b . 2 2 3a − b 2 2 4a − b 2 2 3a − b 2 2 4a − b
Câu 52: Cho tứ diện ABCD có AB = AD = BC = 8, AC = BD = 6,CD = 4. Tínhh bán kính R của mặt cầu
ngoại tiếp tứ diện ABCD A. 187 R = . B. R = 5. C. 177 R = . D. 65 R = . 10 10 2
LỜI GIẢI BÀI TẬP TỰ LUYỆN
Câu 1: Gọi P là tâm đường tròn ngoại tiếp A ∆ BC.
Trục đường tròn ngoại tiếp A
∆ BC cắt SC tại O. OA  = OB = OC Ta có 
⇒ OA = OB = OC = OS. OC  = OS
Vậy O là tâm mặt cầu qua các điểm S, , A B,C. Chọn D.
Câu 2: Gọi O là trung điểm của AC.
AB ⊥ BC ⇒ OA = OC = OB Ta có 
AJ = JC ⇒ OA = OC = OJBC ⊥ AB Từ 
⇒ BC ⊥ (SAB) ⇔ BC ⊥ AI.  BC ⊥ SA
Mà AI ⊥ SB ⇒ AI ⊥ (SBC) ⇒ AI ⊥ IC
⇒ OA = OC = OI ⇒ OA = OB = OC = OI = OJ.
Vậy O là tâm mặt cầu cần tìm. Chọn A.
Câu 3: Gọi O là tâm của hình vuông ABCD. BC ⊥ AB Ta có 
⇒ BC ⊥ (SAB) ⇒ BC ⊥ AI.  BC ⊥ SA
AI ⊥ SB ⇒ AI ⊥ (SBC) ⇒ AI ⊥ IC ⇒ OA = OC = OI.
Tương tự OA = OC = OK.
Mà AJ ⊥ SC ⇒ OA = OC = OJ
⇒ OA = OB = OC = OD = OI = OJ = OK ⇒ O là tâm mặt
cầu cần tìm. Chọn A.
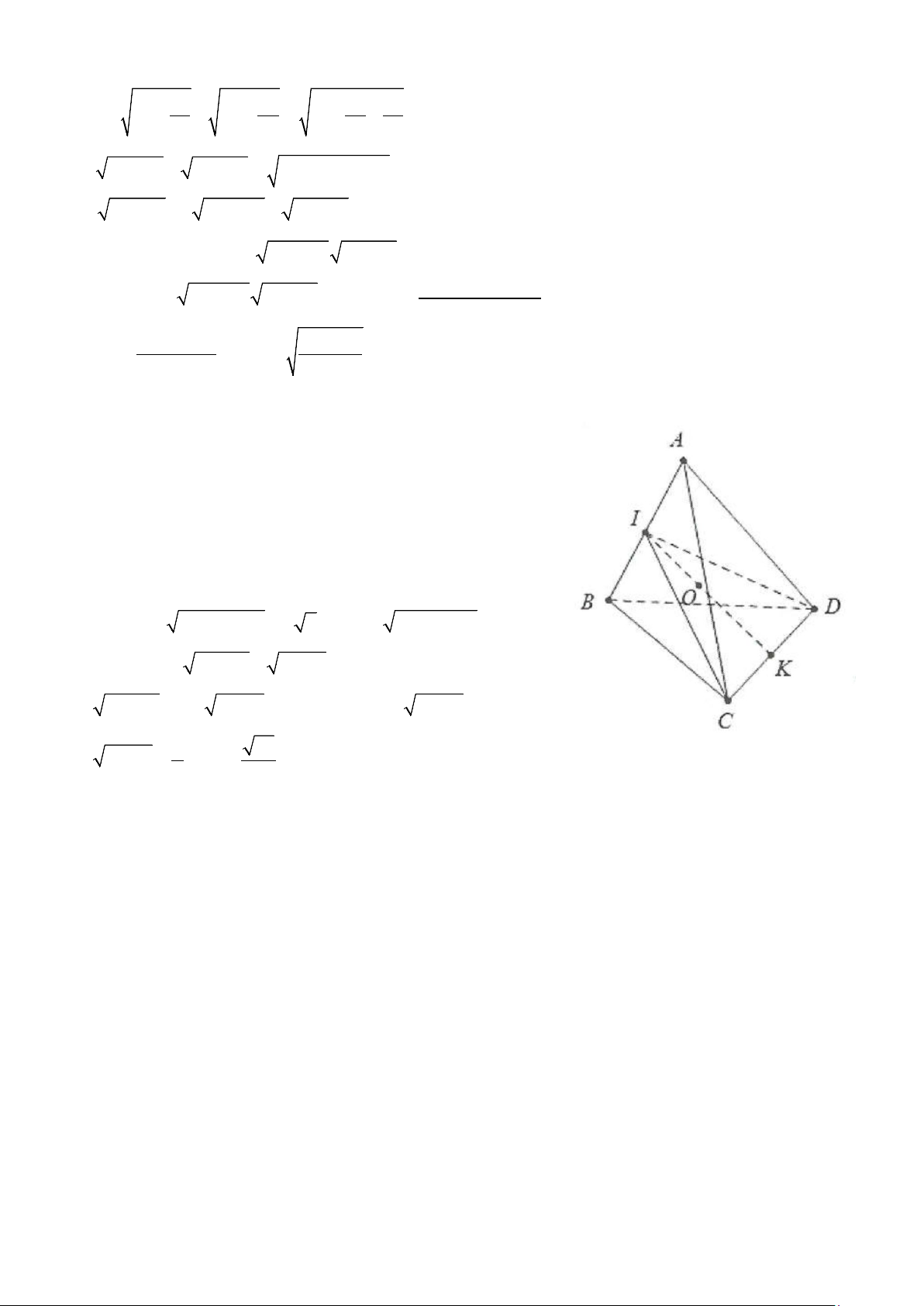
Câu 4: Ta có AB = AC = AD , kẻ AO ⊥ (BCD) ⇒ O là tâm đường
tròn ngoại tiếp tam giác BCD. 2 2 2  + = Ta có AD AC 4a  2 2 2 2 C
D = BD + BC = 4a 2 2 2
⇒ AD + AC = CD ⇒ AD ⊥ AC ⇒ OA = OC = O . D
Vậy OB = OC = OD = OA ⇒ O là tâm mặt cầu cần tìm. Chọn B.
Câu 5: Ta có AH ⊥ . HB
Trục đường tròn ngoại tiếp tam giác ABH đi qua trung điểm của
AB và vuông với ( ABH ).
Trục đường tròn ngoại tiếp tam giác ABC đi qua tâm O của tam
giác đều ABC và vuông góc với ( ABC).
Hai đường thẳng này cắt nhau tại chính O.
OA = OB = OH Ta có: 
⇒ OA = OB = OC = OH. OA  = OB = OC
Vậy O là tâm mặt cầu cần tìm. Chọn A.
Câu 6: Gọi E, F lần lượt là trung điểm của BD, AC.
   
MA + MB + MC + MD        
= (OA−OM )+(OB −OM ) +(OC −OM ) +(OD −OM )        
= (OA+OC)+(OB +OD)− 4OM = 2OF + 2OE − 4OM  ⇒ 4 a
OM = a ⇒ OM = . 4 Chọn A.
Câu 7: Gọi O là trung điểm của CD. Ta có 1
OA = OB = OC = OD = R = C . D 2 Cạnh 2 2 2 2 2
CD = AD + AC = AD + AB + BC = 5a 2
R = 5a 2. Chọn A. SA ⊥ SB Câu 8: Ta có 
⇒ SA ⊥ (SBC). SA ⊥ SC
Kí hiệu các điểm như hình vẽ với OP là trục đường tròn ngoại tiếp
tam giác SBC và OK là trung trực của SA thì O là tâm mặt cầu. Ta có 2 2
R = OS = OP + SP . SA a 1 1 2 2 OP = SK = = ;SP = BC = b + c 2 2 2 2 1 2 2 2 R =
a + b + c . Chọn A. 2 SA ⊥ SB Câu 9: Ta có 
⇒ SA ⊥ (SBC). SA ⊥ SC
Kí hiệu các điểm như hình vẽ với OP là trục đường tròn ngoại tiếp
tam giác SBC và OK là trung trực của SA thì O là tâm mặt cầu. Ta có 2 2
R = OS = OP + SP . SA 1 1 2 2 OP = SK = = ; a SP = BC =
SB + SC = a 5 2 2 2
R = a 6. Chọn D.
Câu 10: Kí hiệu các điểm như hình vẽ với OP là trục đường tròn ngoại
tiếp tam giác ABC và OK là trung trực của SA thì O là tâm mặt cầu. Ta có 2 2
R = OA = OP + AP . SA 1 1 2 2 5 OP = AK = = 14; AP = BC = 3 + 4 = 2 2 2 2 9 4 3 243
⇒ R = ⇒ V = π R = π. Chọn C. 2 3 2
Câu 11: Kí hiệu các điểm như hình vẽ với OP là trung trực của AC thì 2 2 O là tâm mặt cầu AC AC ⇒ R = OA = = 2 2
2AH 2 AD − DH AB a a 6 AC = AD = ; a DH = = ⇒ R = . Chọn B. 3 3 4
Câu 12: Ta có SA = SB = SC = a, kẻ SH ⊥ ( ABC) ⇒ H là tâm
đường tròn ngoại tiếp tam giác ABC.
Tam giác ABC vuông cân tại B nên H là trung điểm của AC.
Gọi O là tâm đường tròn ngoại tiếp tam giác SAC thì O là tâm mặt cầu, ta có R = . SO . SA SC.AC 1 . SA SC S = = SH AC ⇒ SO = SAC . 4SO 2 2SH 2 2
SA = SC = a;SH = SA − AH 1 1 = = 2 a a AH AC AB = ⇒ SH = 2 2 2 2 a 2 ⇒ R = SO = . Chọn B. 2 3 Câu 13: Ta có 1 a 2 V = r S + S + S + S = S ABCD ABC ABD ACD BCD . . ( ) 3 12 2 a 3 a 6 S = S = S = S = ⇒ r = Chọn A. ABC ABD ACD BCD . 4 12
Câu 14: Kí hiệu như hình vẽ với AH ⊥ (BCD),OP là trung trực của
AC thì O là tâm mặt cầu 2 2 Ta có AC AC R = OA = = 2 2
2AH 2 AD − DH = = ; AB a AC AD a DH = = 3 3 a 6 2 3 2 ⇒ R =
⇒ S = 4π R = π a . Chọn A. 4 2
Câu 15: Kí hiệu như hình vẽ với AH ⊥ (BCD),OP là trung trực của
AC thì O là tâm mặt cầu 2 2 Ta có AC AC R = OA = = 2 2
2AH 2 AD − DH = = ; AB a AC AD a DH = = 3 3 a 6 4 3 6 3 ⇒ R = ⇒ V = π R =
π a . Chọn A. 4 3 8
Câu 16: Kí hiệu như hình vẽ với AH ⊥ (BCD),OP là trung trực của
AC thì O là tâm mặt cầu 2 2 Ta có AC AC R = OA = = 2 2
2AH 2 AD − DH = = ; AB a AC AD a DH = = 3 3 a 6 2 6 ⇒ R = 1⇒ a = . Chọn C. 4 3
Câu 17: Bán kính đường tròn ngoại tiếp tam giác ABC là 3a 3 r = = a 3 3 2 Ta có  SC  2 2 2 2 2 R =
+ r = a + 3a = 2a ⇒ S = 4π R =  
16π a . Chọn A.  2  Câu 18: Ta có  BC 2 2 tan BAC =
⇒ BC = AB = a 3 ⇒ AC = AB + BC = 2a AB
Bán kính đường tròn ngoại tiếp tam giác ABC là AC r = = a 2 2 Ta có  SA  2 a 6 4 3 3 R = + r = ⇒ V = π R =  
a π 6. Chọn A.  2  2 3
Câu 19: Ta có SC ⊥ ( ABCD) và SA = SB = SC ⇒ C là tâm đường tròn ngoại tiếp tam giác ABD 2
Gọi M là trung điểm của BD. Ta có 2 2 a 1 a 3
AM = AB − BM = ⇒ S = AM BD = ABD . 2 2 4 Mà A . B B . D AD A . B B . D AD . a . a a 3 S = ⇒ R = =
= a ⇒ AC = BC = CD = a ABD ABD 2 4R 4SABD a 3 4. 4
Ta có SA∩ (ABCD) = { } A và ⊥ ⇒  =  =  0 SA (ABCD) (S ,
A (ABCD)) (S , A AC) SAC = 45 2   Ta có  SC = ⇒ =   SC  2 a 5 tan SAC
SC AC tan SAC = a ⇒ R =  +   R  = Chọn D. ABD . AC  2    2   2 2  
Câu 20: Chiều cao của hình chóp là 2 a 2 2 a h = b −   = b −  2  2   2 2 Bán kính mặt cầu là b b R = = . Chọn A. 2 2h 2 2 a b − 2 2   Câu 21: 0 h a a 2 2 a 3
tan 45 = ⇒ h = ⇒ SA =   + h = a 2  2  2   2 2 2 Bán kính mặt cầu là SA 3a 2 9π = = ⇒ = 4 a R S π R = . Chọn A. 2h 4 4 2
Câu 22: Giả sử hình chóp có cạnh bên là a, chiều cao a 2 h ⇒ R =
= 2 ⇒ a = 2 2h 2h Mặt khác ta có 0 sin 45 h
= ⇒ a = h 2. Do đó suy ra h = 2,a = 2 a Ta có AB 2 2 2 1 4 2
= a − h = 2 ⇒ AB = 2 ⇒ S = ⇒ V = h S = Chọn D. ABCD 4 S ABCD . ABCD . . 2 3 3 2  
Câu 23: Chiều cao của hình chóp là 2 a 2 a 2 h = a −   =  2  2   2 3 a a 2 4 3 2π a ⇒ R = = ⇒ V = π R = . Chọn B. a 2 2 3 3 2 2 2  
Câu 24: Chiều cao của hình chóp là 2 a 2 a 2 h = a −   =  2  2   2 a a 2 2 2 ⇒ R = =
⇒ S = 4π R = 2π a . Chọn B. a 2 2 2 2 2   ( a)2 5
Câu 25: Chiều cao của hình chóp là h = ( a)2 3 2 . a 2 5 − 25a   = 4a  ⇒ R = = . Chọn C. 2    2.4a 8
Câu 26: Bán kính đường tròn đáy là AC a 2 R = = d 2 2 2
Do SA ⊥ ( ABC) nên bán kính mặt cầu ngoại tiếp hình chóp là SA 2 a 6 R = + R = d . 4 2
Thể tích của mặt cầu ngoại tiếp hình chóp S.ABCD là: 4 3 3
V = π R = π a 6. Chọn A. 3
Câu 27: Bán kính đường tròn đáy là AC a 2 R = = d 2 2 2
Do SA ⊥ ( ABC) nên bán kính mặt cầu ngoại tiếp hình chóp là SA 2 a 5 R = + R = d . 4 2
Diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD là: 2 3
S = 4π R = 5π a . Chọn A. 2 2 2 2
AD + BD = AB = aAD ⊥ BD Câu 28: Ta có 4  ⇒ 2 2 2 2 
AC + BC = AB = 4aAC ⊥ BC
⇒ C, D cùng nhìn AB dưới một góc vuông nên tứ giác ABCD
nội tiếp đường tròn bán kính AB R = R = = a ABCD . 1 2 Lại có S ∆ AB đều nên: AB 3 2a 3 R = = = R SAB 2 3 3 2
Do (SAB) ⊥ ( ABC) nên 2 2 AB 2a R = R + R − = S ABCD . . 1 2 4 3 3
Thể tích của mặt cầu ngoại tiếp hình chóp π S.ABCD là: 4 3 32 3 a ( V = π R = Chọn C. C) . 3 27
Câu 29: Bán kính đường tròn đáy là AC a 2 R = = d 2 2 2
Do SA ⊥ ( ABC) nên bán kính mặt cầu ngoại tiếp hình chóp là SA 2 R = + R = 2 . a 4 d
Diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD là: 2 3
S = 4π R = 8π a . Chọn A.
Câu 30: Gọi H là chân đường cao hạ từ S xuống mặt phẳng ( ABC)  SA ⊥ AB Ta có 
⇒ AB ⊥ (SHA) ⇒ AB ⊥ HAAB ⊥ SH
Tương tự ra có: BC ⊥ HC ⇒ ABCH là hình vuông.
Do AH / /BC ⇒ AH / / (SBC) ⇒ d ( ;
A (SBC)) = d (H;(SBC))
Dựng HK ⊥ SC do BC ⊥ HK ⇒ HK ⊥ (SBC) Do đó d ( ;
A (SBC)) = HK = a 2 Mặt khác 1 1 1 + = ⇒ SH = a 6 2 2 2 SH HC HK 2 Ta có: SH 2 R = R =
+ R (do tứ giác HABC nội tiếp) S.ABCD S.HABC 4 d Trong đó AC AB 2 a 6 4 3 3 R = = = ⇒ R = a ⇒ V = π R = π a Chọn C. d S ABC 3 4 3 . . (C) 2 2 2 3 2 2
Câu 31: Bán kính đường tròn đáy là AC AB BC 5a R + = = = d . 2 2 2 2
Do SA ⊥ ( ABC) nên bán kính mặt cầu ngoại tiếp hình chóp là: SA 2 13 R = + R = Chọn C. d . 4 2
Câu 32: Ta có SC ⊥ AM mặt khác AM ⊥ SB do đó AM ⊥ MC. Như vậy  0 AMC = 90 Tương tự  0
APC = 90 . Lại có  0
ANC = 90 vậy tâm mặt cầu ngoại tiếp tứ
diện C.MNP là trung điểm của AC. Suy ra AC 4 3 32 R =
= 2 ⇒ V = π R = π. Chọn C. 2 3 3
Câu 33: Đặt AB = ;
x CD = y; AD = BC = AC = BD = z
Gọi M , N lần lượt là trung điểm của AB và CD ta có: D ∆ AC = D
∆ BC ⇒ AN = BN suy ra NM là trung trực
của AB, tương tự MN là trung trực của DC
Khi đó I ∈ MN sao cho ID = IA 2 Lại có 2 2 2 y
AN = AD − DN = z − 4 2 2 2 2 2 y x
⇒ MN = AN − AM = z − − 4 4 Mặt khác 2 2 2 2
MN = IM + IN = R − AM + R − DN 2 2 2 2 2 x 2 y 2 y x ⇒ R − + R − = z − − , giải phương trình 4 4 4 4 tìm R. Áp dụng: 2 2 2 2 2 2
R − 4a + R − 9a = 22a −13a = 3a 2 2 ⇔ R − a = ( 2 2
a − R − a ) 2 2 2 2 2 2 2 4 3 9
⇒ R − 4a = 9a − 6a R − 9a + R − 9a 2 2 2a a 85 ⇔ R − 9a = ⇔ R = . Chọn B. 3 3
Câu 34: Ta có SA ⊥ (ECD) ⇒ (SED) ⊥ (ECD). Đặt R = R R = R SED , 1 2 CED Ta có: E
∆ CD vuông tại E và ED = a,CE = a 2 2 Do đó CE ED a 2 R + = = . 2 2 2 Lại có:  SA SA 6 sin SDA = = = 2 2 SD SA + AD 10 2 2 Suy ra SE SA + AE 105 R = = = . 1  2sin SDE 6 6 2. 10 2 Do đó 2 2 ED a 114 R = R + R − = Chọn D. S ECD . . 1 2 4 6
Câu 35: Gọi R và R lần lượt là bán kính đường tròn ngoại tiếp tam giác đều (SAB) và ( ABC) ta có: 1 2 a 3 R = R =
, AB = SAB ∩ ABC . 1 2 ( ) ( ) 3 2
Do (SAB) ⊥ ( ABC) nên 2 2 AB a 15 R = R + R − = S ABC . . 1 2 4 6 3
Thể tích khối cầu ngoại tiếp hình chóp đã cho là: 4 3 5π a 15 ( V = π R = Chọn C. C) . 3 54
Câu 36: Đặt R = R R = R
AB = SAB ∩ ABC ABC ; SAB , 1 2 ( ) ( ) 2 2
Tam giác ABC vuông cân tại A nên BC AB AC a 2 R + = = = . 1 2 2 2 2
Tam giác SAB là tam giác đều nên 2 2 AB a 21 R = R + R − = S ABC . . 1 2 4 6
Thể tích khối cầu ngoại tiếp hình chóp đã cho là: 3 4 3 7π a 21 ( V = π R = Chọn B. C) . 3 54
Câu 37: Do S.ABC là hình chóp tam giác đều nên
SA = SB = SC = . a Ta có:  0 2 2
ASB = 90 ⇒ AB = SA + SB = a 2.
Gọi M là trung điểm của BC và H là trọng tâm tam giác AB
Khi đó SH ⊥ ( ABC) AB 3 a 6 , AM = = 2 2 2 a 6 2 2 a 3 ⇒ AH = AM =
⇒ SH = SA − AH = . 3 3 3
Bán kính đường tròn ngoại tiếp hình chóp S.ABC là: 2 SA a 3 R = = Chọn B. S ABC . . 2SH 2
Câu 38: Đặt R = R R = R
AB = SAB ∩ ABC ABCD ; SAB , 1 2 ( ) ( )
Tam giác ABDC là hình vuông cạnh bằng 2a nên AC 2a 2 R = = = a 2. 1 2 2
Tam giác SAB vuông cân tại S nên AB R = = . a 2 2 2
Do (SAB) ⊥ ( ABC) nên 2 2 AB r = R = R + R − = a Chọn D. S ABC 2. . 1 2 4
Câu 39: Do SA ⊥ ( ABCD) ⇒ SC ( ABCD)  ( )=  0 ; SCA = 45 . Ta có: 2 2 0
AC = AB + AD = a 5 ⇒ SA = AC tan 45 = a 5. Lại có: AC a 5 R = R = = d ABCD . 2 2 2
Do SA ⊥ ( ABCD) SA 2 a 10 ⇒ R = + R = d . 4 2 3
Thể tích khối cầu ngoại tiếp hình chóp π S.ABCD là: 4 3 5 10 a V = π R = . Chọn D. 3 3
Câu 40: Gọi H là trung điểm của AB.
Do SA = SB ⇒ SH ⊥ A . B Ta có: 2 2 2 2
SB + BC = SC = 5a ⇒ SB ⊥ BC
Mặt khác: AB ⊥ BC ⇒ BC ⊥ (SAB) ⇒ BC ⊥ SH
Suy ra SH ⊥ ( ABC), đặt AC R = R = = a ABC . 1 2 2 Đặt . SA . SB AB . SA . SB AB . SA SB a R = R = = = = 2 SAB 4S SH AB SH SH SAB 2. . 2 Trong đó 2 2 a 7 2a
SH = SB − HB = ⇒ R = . 2 2 7 2 Suy ra 2 2 AB a 259 R = R + R − = Chọn B. S ABC . . 1 2 4 14
Câu 41: Vì ABNK là tứ giác nội tiếp ⇒  0 AKN = 90
Do đó tâm đường tròn ngoại tiếp tứ giác ABKN là trung điểm AN 2 2  a a  + 2 2   Suy ra: AN AB + BN  2  a 5 R = = = = ABNK 2 2 2 4
Vậy bán kính mặt cầu ngoại tiếp khối chop S.ABNK là:   a 3 2 SA a 5 ( )2 2 2 a 17 R = R + =   + = Chọn A. ABNK ABNK . 4  4  4 4  
Câu 42: Công thức tìm nhanh bán kính mặt cầu ngoại tiếp hình chóp là 2 2
R = x + r với
• r là bán kính đường tròn ngoại tiếp đa giác đáy. 2 2 − • SO r x =
: S là đỉnh hình chóp, O là tâm đường tròn ngoại tiếp đa giác đáy, h là chiều cao khối 2h chóp.
Ta có SH ⊥ ( ABCD) ⇒ SB ( ABCD)  = (SB BH )  =  0 ; ; SBH = 60 2 2
Tam giác ABC vuông tại AC AB + BC B ⇒ BO = = = 2a 2 2 Do đó 2 4a BO 2 = = ; a BH BO HO = = 3 3 3 3 Vậy 0 4a 3 2 2 2a 13 SH = BH.tan 60 =
⇒ SO = SH + OH = 3 3
Bán kính đường tròn ngoại tiếp ABCD là AC r = = 2a 2 2 2 2  − 
Áp dụng công thức, ta được SO r 2 4a 21 R =   + r = . Chọn C.  2.SH  9
Câu 43: Vì E là trung điểm AD ⇒ ABCE là hình vuông
⇒ CE ⊥ AD mà SA ⊥ CE ⇒ CE ⊥ (SAD) ⇒ CE ⊥ SE
Ta có AB ⊥ BC mà SA ⊥ BC ⇒ BC ⊥ (SAB) ⇒ SB ⊥ BC
Lại có EK ⊥ SD mà EC ⊥ SD ⇒ SD ⊥ (CKE) ⇒ CK ⊥ SK
Gọi I là trung điểm SC ⇒ IS = IA = IB = IC = IE = IK
Do đó I là tâm mặt cầu đi qua sáu điểm S, ,
A B,C, E, K 2 2
Vậy bán kính cần tìm là SC SA + AC R = = = . a Chọn A. 2 2
Câu 44: Dễ thấy B, D nhìn dưới AC một góc 0 90
Ta có AD ⊥ CD mà SA ⊥ CD ⇒ CD ⊥ (SAD) ⇒ CD ⊥ AK
Lại có AK ⊥ SD mà ⇒ AK ⊥ (SCD) ⇒ ⊥ ⇒  0 AK KC AKC = 90
Chứng minh tương tự, ta được  0 AHC = 90
⇒ AC là đường kính mặt cầu ngoại tiếp khối chóp ABCDEHK 3 Vậy AC a 2 4 3 π a 2 R = =  →V = π R = . Chọn A. 2 2 3 3
Câu 45: Áp dụng định lý Cosin, ta có 2 2 = + −  BC AB AC 2.A .
B AC.cos BAC = 5 − 4cosα
Suy ra bán kính đường tròn ngoại tiếp A ∆ BC là BC 5 − 4cosα R = = (định lý Sin) ABC ∆  2.sin BAC 2sinα
Gọi O là tâm đường tròn ngoại tiếp A ∆ BC
Gọi M là trung điểm AB ⇒ OM ⊥ AB mà SA ⊥ OM
Suy ra OM ⊥ (SAB) mà M là tâm đường tròn ngoại tiếp A ∆ BB 1
Do đó OA = OB = OB . Chứng minh tương tự, ta được 1
OA = OC = OC 1 Vậy − α
O là tâm mặt cầu ngoại tiếp đi qua các điểm 5 4cos ,
A B,C,C , B ⇒ R = R = ABC ∆ . 1 1 2sinα Chọn D.
Câu 46: Chọn độ dài cạnh lập phương ABC .
D A'B 'C 'D là 1
Gọi I là tâm hình lập phương ABC .
D A' B 'C ' D (tham khảo hình vẽ dưới đây)
• Bán kính mặt cầu ngoại tiếp hình lập phương là AC ' 3 R = AI = = 1 2 2
• Bán kính mặt cầu nội tiếp hình lập phương là AB 1 R = = 2 2 2
• Bán kính mặt cầu nội tiếp tiếp xúc với tất cả các cạnh là R = d I; C 'D '  = IM =1 3  ( ) Vậy 2 2 2
R + R = R . Chọn B. 1 2 3
Câu 47: Chọn độ dài cạnh lập phương ABC .
D A'B 'C 'D là 1
Gọi I là tâm hình lập phương ABC .
D A' B 'C ' D (tham khảo hình vẽ dưới đây)
• Bán kính mặt cầu ngoại tiếp hình lập phương là AC ' 3 R = AI = = 1 2 2
• Bán kính mặt cầu nội tiếp hình lập phương là AB 1 R = = 2 2 2
• Bán kính mặt cầu nội tiếp tiếp xúc với tất cả các cạnh là R = d I; C 'D '  = IM =1 3  ( )
Vậy R > R > R . Chọn D. 3 1 2 AM ⊥ BC
Câu 48: Gọi M là trung điểm BC ⇒ 
⇒ BC ⊥ ( AA'M )  AA' ⊥ BC
Do đó ( A BC) ( ABC)  = (A M AM )  =  0 ' ; ' ; A'MA = 60 Đặt x 3 AM x 3 3
AB = x → AM = ⇒ A'M =  = : = x 2 cos A'MA 2 2 2 Suy ra 1 x 2 S = = =  → = ⇔ = ∆ A M BC x x A BC . ' . 18 36 6 ' 2 2
Khi đó bán kính đường tròn ngoại tiếp A ∆ BC là x 3 R = = ABC ∆ 2 3 3 2 2 2
Vậy bán kính mặt cầu cần tính là 2 AA' R = R + = + = Chọn B. ABC ∆ ( ) 3 57 2 3 . 4 4 2 Câu 49: Ta có 2 2
AC = AB + BC = a 5.
Gọi H là trung điểm của AB ⇒ SH ⊥ AB
⇒ SH ⊥ ( ABCD). Gọi E là trung điểm của MN, dựng
đường thẳng d qua E song song với SH, trên d lấy điểm I
sao cho IS = ID ⇒ I là tâm mặt cầu ngoại tiếp khối chóp
S.DMN ⇒ IS = ID = IM = IN = . R Ta có D ∆ MN vuông tại MN AC a 5 D ⇒ DE = = = 2 4 4 2 2 2 2 5a a 3
→ IE = R − DE = R − , SH = . 16 2 2 2 2 Mặt khác: 2  3   1  37a HE = AD +   AB =  4 4      16 2 2  2  Lại có: 2 2 − = ( − )2 2 37a a 3 2 5a R HE SH IE ⇔ R − =  − R −  16  2 16    2  
CACL 4 đáp án vào biểu thức 2 37 3 2 5 102 X − −  − X −  ⇒ X = . Chọn C. 16  2 16  6   Câu 50:
Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Theo công thức tính diện tích tam giác ta có: 1 A .BAC S 2 6a ABC 2 r = = trong đó 2 2
BC = AB + AC = 5a . Suy ra r = = . a p
AB + BC + CA 6a 2
Tam giác ABC vuông tại ,
A AP = AE suy ra tam giác APE vuông cân tại A ⇒ tam giác AEH vuông cân tại
E ⇒ AE = HE = . a Ta có: 2 2 2 2
AH = AE + HE = a 2 ⇒ SH = SA − AH = a 2. 2 Ta có: BC a 2 2 5 = − = 3 a EC AC AE
a = CF ⇒ MF =
− CF = ⇒ HM + HF = . 2 2 4 2 Mặt khác 25a
IC = IS ⇔ MI + MC = SK + IK ⇔ IM + = (a 2 ± IM )2 2 2 2 2 2 2 2 2 + HM 4
(Dấu cộng khi S, I cùng phía với mặt phẳng ( ABC) và dấu trừ khi S, I khác phía với mặt phẳng ( ABC)) 2 a ⇔ + = ( ± ) 2 2 2 25 5 2 a IM a IM + 4 4 Giải phương trình trên 3a 2 2 2 a 118 ⇒ IM =
⇒ R = IC = IM + MC = . Chọn A. 4 4
Câu 51: Đặt AB = ;
x CD = y = AD = BC = AC = BD = z 2 2 2 2 Ta có: 2 x 2 y 2 y x R − + R − = z − − 4 4 4 4 2 2 2 2 2
⇒ R − a + R − b = 4a − ( 2 2 a + b ) 2 2 ⇔ R − a = ( 2 2 2 2
3a − b − R − b ) 2 2 2 2 2 2 2 2 2 2
⇔ R − a = 3a − b − 2 3a − b R − b + R − b 4 2 2 4 2 2 2 2 2 2 2 2 4a − 4 ⇔ 2 − = 3 a b + b a b
a − b R − b ⇔ R − b = 2 2 3a − b 4 2 2 2 2 2 4a − a b 4a − b ⇔ R = ⇔ R = a . 2 2 2 2 3a − b 3a − b Chọn C.
Câu 52: Gọi I, K lần lượt là trung điểm của AB và CD. Ta có: D ∆ AB = C
∆ BA(c − c − c) ⇒ IC = ID ⇒ IK = C . D Tương tự A ∆ CD = B
∆ DC (c − c − c) ⇒ KB = KA ⇒ KI = A . B
Do đó KI là đường trung trực của AB và CD.
Gọi O là tâm mặt cầu ngoại tiếp tứ diện ABCD thì O ∈ IK. Ta có: 2 2 2 2
AK = AC − CK = 4 2 ⇒ IK = AK − AI = 4. Mặt khác 2 2
OI = R −16 + R − 4 = 4 2 2 2 2 2
⇔ R −16 = 4 − R − 4 ⇒ R −16 =16 −8 R − 4 + R − 4 2 7 65
⇔ R − 4 = ⇒ R = . Chọn D. 2 2
Document Outline

  • ITMTTL~1
  • IIBITP~1
  • IIILIG~1