Chuyên đề trắc nghiệm mặt nón, hình nón và khối nón Toán 12

Tài liệu gồm 51 trang, trình bày lý thuyết trọng tâm, các dạng toán trọng tâm kèm phương pháp giải và bài tập trắc nghiệm tự luyện chuyên đề mặt nón, hình nón và khối nón.Mời các bạn đón xem.

78 39 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Mặt nón, mặt trụ, mặt cầu

Môn: Toán 12

Thông tin:

51 trang 7 tháng trước

Tác giả:

Profile Lan Tường
CHỦ ĐỀ 12: MẶT NÓN - HÌNH NÓN - KHỐI NÓN
A. LÝ THUYẾT TRỌNG TÂM
I. ĐỊNH NGHĨA MẶT NÓN
Cho đường thẳng ∆. Xét một đường thẳng d cắt ∆ tại S tạo thành một góc α với
2
0
π
α
<
<
. Mặt tròn xoay
sinh bởi đường thẳng d như thế khi quay quanh ∆ gọi là mặt nón tròn xoay (hay đơn giản hơn là mặt nón)
∆ gọi là trục của mặt nón
D gọi là đường sinh của mặt nón
S gọi là đỉnh của mặt nón
Góc 2α gọi là góc ở đỉnh của mặt nón (hình vẽ bên)
II. HÌNH NÓN VÀ KHỐI NÓN
Cho mặt nón (N) với trục ∆ , đỉnh S, góc ở đỉnh 2α
Gọi (P) là mặt phẳng vuông góc với A tại điểm I khác S. Mặt phẳng (P) cắt mặt nón theo một đường tròn
(C) có tâm I. Lại gọi (P’) là mặt phẳng vuông góc với A tại S.
Khi đó: Phần của mặt nón (N) giới hạn bởi hai mặt phẳng (P) và (P’) cùng với hình tròn xác định bởi (C)
được gọi là hình nón:
S gọi là đỉnh của hình nón
Đường tròn (C) gọi là đường tròn đáy của hình nón
Với mỗi điểm M nằm trên đường tròn (C), đoạn thẳng SM gọi là đường sinh của hình nón
Đoạn thẳng SI gọi là trục của hình nón (đó chính là khoảng cách từ đỉnh S đến mặt đáy)
Một hình nón chia không gian thành hai phần: phần bên trong và phần bên ngoài của nó. Hình nón
cùng với phần bên trong của nó gọi là khối nón
III. KHÁI NIỆM VỀ DIỆN TÍCH HÌNH NÓN VÀ THỂ TÍCH KHỐI NÓN
Một hình chóp gọi là nội tiếp hình nón nếu:
- Đáy của hình chóp là đa giác nội tiếp đáy của hình nón
- Đỉnh của hình chóp là đỉnh của hình nón
1. Định nghĩa.
Diện tích xung quanh của hình nón là giới hạn của diện tích xung quanh của một hình chóp đều nội tiếp
hình nón đó khi số cạnh đáy tăng lên vô hạn
Thể tích của khối nón là giới hạn của thể tích khối chóp đều nội tiếp khối nón đó khi số cạnh tăng lên vô
hạn
2. Diện tích xung quanh, diện tích toàn phần của hình nón
Diện tích xung quanh:
RlS
xq
π
=
Diện tích toàn phần:
2
RRlSSS
đxqtp
ππ
+=+=
Trong đó , R, l lần lượt là bán kính đáy và đường sinh của hình nón
3. Thể tích của khối nón
Thể tích của khối nón có bán kính đáy R và chiều cao h là
h
RV
2
3
1
π
=
4. Mối liên hệ giữa chiều cao, đường sinh và bán kính đáy
Tam giác SAO vuông tại A, có
22
2
OASOSA +=
Do đó
22 2
lhR= +
(tham khảo hình vẽ bên)
IV. VỊ TRÍ TƯƠNG ĐỐI CỦA HÌNH NÓN VỚI MỘT MẶT PHẲNG QUA ĐỈNH CỦA NÓ
Cho một hình nón (N) và một mặt phẳng (P) đi qua đỉnh S của hình nón.
Có ba vị trí tương đối giữa (P) và (N)
(P) và (N) có một điểm chung duy nhất
(P) và (N) có chung một đường sinh duy nhất. Khi đó (P) tiếp xúc với (N) và (P) gọi là tiếp diện của
(N)
(P) và (N) có chung hai đường sinh (Hình 1). Nếu (P) chứa trục của hình nón thì thiết diện của (P) và
hình nón gọi là thiết diện qua trục (Hình 2)
Thiết diện qua trục của hình nón là tam giác cân có cạnh bên SA = l, cạnh đáy AB = 2R
B. CÁC DẠNG TOÁN TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. Bài toán liên quan đến công thức diện tích, thể tích
Ví dụ 1: Diện tích xung quanh hình nón có bán kính đáy R = 3, chiều cao h = 4 bằng
A. 12
π
B.
C.
π
15
D.
π
9
Lời giải
Độ dài đường sinh
543
2222
=+=+= hRl
Vậy diện tích xung quanh hình nón là
ππ
15== RlS
xq
. Chọn C
Ví dụ 2: Cho hình nón (N) có bán kính đáy bằng 4, diện tích xung quanh bằng 20
π
. Thể tích khối nón đã
cho bằng
A.
π
4
B.
C.
π
20
D.
π
16
Lời giải
Theo giả thiết, ta có
=
=
⇔
=
=
⇔
=
=
5
4
20
4
20
4
l
R
Rl
R
S
R
xq
ππ
π
Lại có:
345
2222222
=−=−=→+= RlhRhl
Vậy thể tích khối nón (N) là
( )
π
π
π
163.4.
33
1
22
=== hRV
N
Chọn D
Ví dụ 3: Cho hình nón (N) có diện tích xung quanh bằng
π
2
, diện tích toàn phần bằng
π
3
. Thể tích khối
nón đã cho bằng
A.
π
3
3
B.
π
6
3
C.
π
6
6
D.
π
2
3
Lời giải
Diện tích xung quanh hình nón là
22 =↔== RlRlS
xq
ππ
Diện tích toàn phần hình nón là
33
22
=+↔=+= RRlRRlS
tp
πππ
Do đó
3
2
1
2
1
3
2
22
2
2
=−=
→
=
=
⇔
=
=
⇔
=+
=
R
lh
l
R
Rl
R
RRl
Rl
Vậy thể tích khối nón (N) là
( )
π
π
π
3
3
3.1.
33
1
22
=== hRV
N
Chọn A
Ví dụ 4: Cho hình nón (N) có góc ở đỉnh bằng 60°, độ dài đường sinh bằng 4. Thể tích khối nón đã cho
bằng
A.
3
34
π
B.
3
38
π
C.
π
32
D.
2
3
π
Lời giải
Vì góc ở đỉnh của hình nón bằng 60°
242 =⇒== RRl
Ta có
3224
2222222
=−=−=⇒=+ RlhlRh
Vậy thể tích khối nón đã cho là
3
3
8
32
.2
.
3
1
3
1
2
2
π
ππ
=
==
h
RV
.
Chọn B.
Ví dụ 5: Trong không gian, cho tam giác AC vuông tại A, AB = a và AC = a
3
. Độ dài đường sinh l của
hình nón nhận được khi quay tam giác ABC xung quanh trục AB bằng
A.
al =
B.
2
al
=
C.
3al =
D.
a
l
2=
Lời giải
Kỹ năng vẽ hình: Tam giác quay quanh cạnh nào thì cạnh đó là trục, động thời chính là chiều cao của
hình nón
Quay tam giác ABC xung quanh trục AB, ta được hình nón có chiều cao h = AB = a, bán kính đáy
3a
AC
R =
=
(hình vẽ bên)
Do đó, độ dài đường sinh là
a
Rh
l
2
2
2
=
+
=
.
Chọn D.
Ví dụ 6: Trong không gian, cho tam giác ABC vuông tại A, góc ABC = 60°, BC = 4a. Thể tích khối nón
nhận được khi quay tam giác ABC xung quanh trục AC bằng
A.
3
34
3
a
π
B.
3
38
3
a
π
C.
9
38
3
a
π
D.
9
34
3
a
π
Lời giải
Tam giác ABC vuông tại A, có
3
2
ˆ
sin
aAC
BC
AC
C
BA
=
⇒=
Và
( )
( )
aaaACBCAB 2324
2
2
22
=−=−=
Quay tam giác ABC xung quanh trục AC, ta được hình nón có chiều cao
32aAC
h ==
, bán kính đáy
a
ABR
2
==
(hình vẽ bên)
Vậy thể tích khối nón cần tìm là
3
38
3
1
3
2
a
hRV
π
π
==
Chọn B
Ví dụ 7: Trong không gian, cho tam giác ABC đều cạnh 2a. Gọi H là trung điểm của BC. Thể tích của khối
nón nhận được khi quay tam giác ABC xung quanh trục AH bằng
A.
9
3
3
a
π
B.
2
3
3
a
π
C.
3
3
3
a
π
D.
6
3
3
a
π
Lời giải
Quay tam giác ABC quanh trục AH, ta được hình nón có chiều cao
3a
AHh ==
, bán kính đáy
BC
R BH a
2
= = =
(hình vẽ bên)
Vậy thể tích khối nón cần tính là
3
3
3
1
3
2
a
hRV
π
π
==
Chọn C
Ví dụ 8: Trong không gian, cho tam giác ABC vuông tại A, AB = 3a, BC = 5a. Thể tích khối tròn xoay
nhận được khi quay tam giác ABC xung quanh trục BC bằng
A.
5
36
3
a
π
B.
25
48
3
a
π
C.
5
16
3
a
π
D.
5
48
3
a
π
Lời giải
Gọi H là hình chiếu vuông góc của A trên BC
Tam giác ABC vuông tại A, có
aABBCAC 4
22
=−=
Suy ra
( ) ( )
5
12
4
1
3
1111
22
222
a
AH
aa
ACABAH
=⇒+=+=
Quay tam giác ABC quanh trục BC, ta được hai hình nón có chiều cao lần lượt là
CHhBHh
==
21
,
và
bán kính đáy R = AH (hình vẽ bên)
Vậy thể tích khối tròn xoay cần tính là
12
VVV= +
( )
3
22 2 2
1 2 12
1 1 1 1 48 a
R h R h R h h .AH .BC
33 3 3 5
π
=π +π =π + =π =
Chọn D.
Ví dụ 9: Trong không gian, cho hình thang ABCD vuông tại A và D, AB = AD = a, CD = 2a. Thể tích khối
tròn xoay nhận được khi quay hình thang ABCD xung quanh trục AD bằng
A.
3
7
3
a
π
B.
3
5
3
a
π
C.
3
4
3
a
π
D.
3
8
3
a
π
Lời giải
Quay hình thang ABCD quanh trục AD, ta được khối nón cụt có hai bán kính đáy lần lượt là
CDR
ABR =
=
21
,
và chiều cao h = AD
Công thức tính thể tích nón cụt
( )
22
1 2 12
1
V hRRRR
3
=π ++
được phát triển từ công thức thể tích tổng
quát của khối có hai đáy song song
Vậy thể tích cần tính là
(
)
[ ]
3
7
2
.2
.
3
1
3
2
2
a
a
aa
a
aV
π
π
=+
+=
Chọn A.
Ví dụ 10: Trong không gian, cho hình thang ABCD có AB//CD và AB = AD = BC =a, CD = 2a. Thể tích
khối tròn xoay nhận được khi quay hình thang ABCD xung quanh trục AB bằng
A.
3
5
3
a
π
B.
3
a
π
C.
4
5
3
a
π
D.
2
5
3
a
π
Lời giải
Thể tích khối tròn xoay khi quay hình thang ABCD quanh trục AB ta được khối tròn xoay có thể tích V
tạo bởi hai khối:
Khối trụ tròn xoay có chiều cao h = CD = MN =2a và bán kính đường tròn đáy
2
3
22
a
NADADNR =−=
=
( như hình vẽ bên ).
Thể tích khối trụ trên trừ đi thể tích 2.V
2
của hai khối nón có chiều cao
2
2
a
h =
và bán kính đường
tròn đáy
2
3a
DNR ==
.
Vậy thể tích khối tròn xoay cần tính là
22
3
12
3a 2 a 3a 5
V V 2.V .2a. . . . a
4 3 24 4
= − =π −π =π
Chọn C
Ví dụ 11: Người thợ gia công của một cơ sở chất lượng cao X cắt một miêng tôn hình tròn với bán kính 60
cm thành ba miếng hình quạt bằng nhau. Sau đó người thợ ấy quấn và hàn ba miệng tôn đó để được ba cái
phễu hình nón. Thể tích của mỗi cái phễu bằng
A.
3
2
8
π
lít B.
3
216
π
lít C.
3
21600
π
lít D.
3
232
π
lít
Lời giải
Khi quấn hình quạt để tạo thành một hình nón, ta được
Đường sinh hình nón bằng bán kính hình quạt
cmRl 60==
Chu vi đáy hình nón bằng độ dài cung hình quạt
2060.2.
3
1
2 =⇒== rrC
ππ
Do đó, chiều cao của hình nón là
cmrlh 2402060
22
22
=−=−=
Vậy thể tích của mỗi cái phễu là
3
216
3
21600
240.20.
3
1
3
1
222
ππ
ππ
==== cmhrV
lít.
Chọn B.
Ví dụ 12: Có một miếng tôn hình tam giác đều ABC cạnh 3 dm (như hình vẽ).
Gọi K là trung điểm của BC. Người ta dùng compa có tâm là A và bán kính AK vạch ra cung tròn MN (M,
N theo thứ tự thuộc cạnh AB và AC) rồi cắt miếng tôn theo cung tròn đó. Lấy phần hình quạt người ta gò
sao cho cạnh AM và AN' trùng nhau thành một cái phếu hình nón không đáy với đỉnh A. Tính thể tích V
của cái phễu.
A.
3
64
.141
dmV
π
=
B.
3
64
.105
dmV
π
=
C.
3
32
.33
dmV
π
=
D.
3
64
3
dmV
π
=
Lời giải
Độ dài đường sinh của phễu là
2
33
=== AKAMl
N
Độ dài cung MN là
( )
60 1 3 3 3
.2 .AK . dm
360 3 2 2
π
= π=π =
Bán kính đáy của phễu là
3
r
24
= =
π
suy ra
( )
2 22 2 3
N
1 1 105
V r h r . r dm
3 3 64
π
=π =π −=
Chọn B.
Ví dụ 13: Từ miếng tôn hình vuông cạnh bằng 4 dm, người ta cắt ra hình quạt tâm A bán kính AB = AD =
4 dm (xem hình) để cuộn lại thành một chiếc phễu hình nón (khi đó AB trùng với AD). Chiều cao của chiếc
phễu có số đo gần đúng (làm tròn đến 3 chữ số thập phân) là
A. 3,872 dm B. 3,874 dm C. 3,871 dm D. 3,873 dm
Lời giải
Chu vi của đáy hình nón có độ dài bằng cung BD.
Độ dài cung BDlà:
( )
π
π
24
.2.
4
1
=
=l
. Suy ra bán kính đường tròn đáy hình nón là :
1
2
2
==
π
π
r
Độ dài đường sinh của hình nón là
22
4dm h r 3,873dm= ⇒= − =

.
Chọn D.
Ví dụ 14: Từ một tấm kim loại dẻo hình quạt (như hình vẽ) có bán kính R= 13 và chu vi hình quạ
t là
π
12=P
, người ta gò tấm kim loại đó thành những chiếc phễu hình nón theo hai cách:
Cách 1: Gò tấm kim loại ban đầu thành mặt xung quanh của một cái phễu.
Cách 2: Chia đôi tấm kim loại thành hai phần bằng nhau rồi gò thành mặt xung quanh của hai cái phễu.
Gọi V
1
là thể tích của cái phễu ở cách 1, V
2
là tổng thể tích của hai cái phễu ở cách 2. Tính tỉ số
2
1
V
V
A.
160
133
2
1
=
V
V
B.
160
1332
2
1
=
V
V
C.
133
1602
2
1
=
V
V
D.
2
5
2
1
=
V
V
Lời giải
Theo cách 1 ta có: Độ dài đường sinh của hình nón là:
13=
, chu vi đáy
6
2
12
=
=
π
π
r
Khi đó thể tích của chiếc phễu là:
22 2
1
1
V r h 12 133
3
=π −=π
Theo cách 2 ta có: Độ dài đường sinh của hình nón là:
13=
, chu vi đáy mỗi phễu là:
3
2
6
=⇒= r
r
r
π
π
Khi đó tổng thể tích của hai chiếc phễu là:
22 2
2
2
V r h 24 10
3
=π −=π
Quy ra
160
133
2
102
133
2
1
==
V
V
Chọn D.
Ví dụ 15: Một cái phễu có dạng hình nón. Người ta đổ một lượng nước vào phễu sao cho chiều cao của
lượng nước trong phễu bằng
3
1
chiều cao của phễu. Hỏi nêu bịt kín miệng phễu rồi lộn ngược phễu lên thì
chiều cao nước xấp xỉ bằng bao nhiêu? Biết rằng chiều cao của phễu là 15 cm
A. 0,5 cm B. 0,3 cm C. 0,188 cm D. 0,216 cm
Lời giải
Gọi bán kính đáy của phễu là R, chiều cao của phễu là h = l5 em
Vì chiều cao nước trong phễu ban đầu bằng
h
3
1
Suy ra bán kính đáy hình nón tạo bởi lượng nước là
R
3
1
Thể tích phễu và thể tích nước lần lượt là
2
2
1
22
27
5
3
.
3
3
1
,
5
3
1
R
h
R
V
RhRV
ππ
ππ
=
==
=
Do đó, thể tích phần khối nón không chứa nước là
27
26
27
130
27
5
5
2
2
22
12
=⇒=
−=−=
V
V
RRRVVV
πππ
Gọi h’ và r lần lượt là chiều cao và bán kính đáy của khối nón không chứa nước
3
3
3
3
3
2
265'
27
26
15
'''
=
→===⇒= h
h
h
h
V
V
R
r
h
h
Vậy chiều cao cần tính là
cmhhh
o
188,026515'
3
=−=−=
Chọn C.
Ví dụ 16: Bạn Hùng có một tấm bìa hình tròn như vẽ bên dưới, Hùng muốn biến hình tròn đó thành một cái
phễu hình nón. Khi đó bạn Hùng phải cắt bỏ hình quạt tròn AOB rồi dán hai bán kính OA và OB lại với
nhau (diện tích chỗ dán nhỏ không đáng kể). Gọi x là góc ở tâm hình quạt dùng làm phễu. Tìm x để thể tích
phễu lớn nhất?
A.
3
32
π
B.
3
6
2
π
C.
2
3
π
D.
6
3
π
Lời giải
Gọi R, h lần lượt là bán kính đáy, chiều cao của hình nón
Thể tích khối nón là
22
2
2
.
33
1
Rl
RhRV
−
==
π
π
Ta có:
( ) ( )
27
4
27
2
2
.
4.
2
.
2
.4
6
3
22
22
22
22
224
l
Rl
RR
R
l
RR
RlR =
−++
≤
−=−
Do đó
( )
27
32
9
32
27
4
.
336
222
l
V
ll
RlR
π
≤⇒=≤−
Dấu bằng xảy ra khi
2
6
2
3
2
22
22
2
R
l
RlRl
R
=⇔=
⇔−=
(1)
Hình nón nhận được là có đường sinh l = OA, chu vi đáy là độ dài cung AB
Vì
x AOB= ⇒
độ dài cung
l
R
xlxR
lxxOAAB
π
π
2
2
=⇒=⇒=×=
(2)
Từ (1), (2) suy ra
3
62
6
2
.
2.
2
π
π
π
==
=
l
R
x
.
Chọn B.
Ví dụ 17: Cho nửa đường tròn đường kính AB = 2R, kí hiệu A là đường thắng vuông góc với AB tại B.
Trên nửa đường tròn lấy điểm E di động, tiếp tuyến của nửa đường tròn tại E và cắt tia đối của tia AB tại D
và cắt ∆ tại C (như hình vẽ dưới). Khi quay tam giác BCD quanh trục AB ta được khối tròn xoay có thể tích
nhỏ nhất là ?
A.
27
8
3
R
π
B.
9
38
3
R
π
C.
3
8
3
R
π
D.
9
8
3
R
π
Lời giải
Đặt
( )
oo
BOC 45 ;90 tan 1=α⇒α∈ ⇒ α>
, chú ý công thức tan sau
α
α
α
2
tan1
tan2
2tan
−
=
Tam giác OBC vuông tại B, có
BC
tan BOC BC R.tan
BO
= ⇒= α
Ta có
( )
( )
oo
BCD 2 90 BD BC.tan 180 2 BC.tan 2= −α ⇒ = − α =− α
.
Khi quay tam giác BCD quanh trục AB ta được khối tròn xoay có thể tích là
3
8
1tan
tan
..
3
2
2tan..
3
..
33
1
3
2
4
3222
R
RBCBDBChrV
π
α
απ
α
ππ
π
≥
−
=−=−=
Vì
( ) ( ) (
)
oo
90;45;02tan
1tan4
tan
2
224
∈
∀≥−⇔−≥
αααα
. Vậy
3
8
3
min
R
V
π
=
Chọn C.
Dạng 2. Bài toán về thiết diện qua đỉnh nón
Ví dụ 1: Cắt hình nón bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác có cạnh huyền bằng
6a
. Thể tích V của khối nón đã cho bằng
A.
4
6
3
a
V
π
=
B.
3
6
3
a
V
π
=
C.
6
6
3
a
V
π
=
D.
2
6
3
a
V
π
=
Lời giải
Thiệt diện qua trục hình nón là tam giác cân SAB có cạnh bên SA = l, cạnh đáy AB = 2R
Theo bài ra, ta có
242
22222
RlRlABSBSA =⇔=⇔=+
Mặt khác
6
62 aR
aRAB
=⇒==
suy ra
32.
2
6
a
a
l ==
Do đó
4
6
3
1
2
6
3
222
a
hRV
a
Rlh
π
π
==→=−=
Chọn A.
Ví dụ 2: Thiết diện qua trục của hình nón (N) là tam giác vuông cân và có diện tích bằng a
2
. Diện tích xung
quanh của hình nón đã cho bằng
A.
2
2 aS
xq
π
=
B.
2
2
aS
xq
π
=
C.
2
4 aS
xq
π
=
D.
2
22 aS
xq
π
=
Lời giải
Thiết diện qua trục hình nón là tam giác cân SAB có cạnh bên SA = l, cạnh đáy AB =2R
Theo bài ra, tam giác SAB vuông
2
22
2
22
ala
lSA
S
SB
SA
SAB
=⇒===
⇒⊥
⇒
∆
Do đó
a
l
RRl ==⇒=
2
2
. Vậy diện tích cần tìm là
2
2 a
RlS
xq
ππ
==
. Chọn B.
Ví dụ 3: Cho hình nón đỉnh S, đáy là hình tròn tâm O, thiết diện qua trục là tam giác đều cạnh a. Thể tích
của khối nón đã cho là
A.
8
3
3
a
π
B.
6
3
3
a
π
C.
24
3
3
a
π
D.
12
3
3
a
π
Lời giải
Theo bài ra, tam giác SAB đều cạnh a
a
ABSBSA ===
⇒
Do đó, chiều cao
2
3a
SO
=
, bán kính đáy
22
aAB
R ==
Vậy thể tích cần tính là
24
3
2
3
.
2
.
33
1
3
2
2
aaa
hR
V
ππ
π
=
==
Chọn C
Ví dụ 4: Cho hình nón (N) có bán kính đáy bằng 9 cm, góc giữa đường sinh và mặt đáy là 30
o
. Diện tích
thiết diện qua trục của hình nón (N) bằng
A.
2
39 cm
B.
2
318 cm
C.
2
36 cm
D.
2
327 cm
Lời giải
Theo bài ra, tacó
18
2 == RAB
và
o
SAO 30=
Tam giác SAO vuông tại O, có
o
SO OA.tan SAO 9.tan 30 3 3= = =
Thiết diện qua trục hình nón là tam giác cân SAB
Suy ra diện tích cần tính là
2
32718.33.
2
1
.
2
1
cmABSOS
SAB
===
∆
Chọn D
Ví dụ 5: Thiết diện qua trục của hình nón (N) là tam giác có chu vi bằng 10 cm, diện tích bằng
2
5
2 cm
.
Tính thể tích khối nón (N), biết rằng bán kính là số nguyên dương.
A.
2
3
52
cm
π
B.
2
3
54
cm
π
C.
2
3
58
cm
π
D.
2
52 cm
π
Lời giải
Theo bài ra, ta có
=−
−=
⇔
=
=+
⇔
=
=+
52.
5
52.
5
522.
2
1
1022
22
RlR
Rl
Rh
Rl
Rh
Rl
Do đó
( )
[ ]
( )
2020251051025205.
232
222
=⇒=+−⇔=−⇔=−− RRRR
RRRR
Suy ra
5=h
Vậy thể tích cần tính là
322
3
54
5.2.
3
1
3
1
cmhRV
π
ππ
===
. Chọn B
Ví dụ 6: Hình nón (N) có đỉnh S, tâm đường tròn đáy là O, góc ở đỉnh bằng 120
o
. Một mặt phẳng qua S cắt
hình nón (N) theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách giữa hai đường thẳng AB và
SO bằng 3. Tính diện tích xung quanh
xq
S
của hình nón (N)
A.
π
318=
xq
S
B.
π
39=
xq
S
C.
π
336=
xq
S
D.
π
327=
xq
S
Lời giải
Vì góc ở đỉnh bằng
ROASAlR
o
3
32
3
32
32120 ==⇒=⇒
Gọi H là trung điểm của AB
ABOH
⊥
⇒
mà
OHSO ⊥
Suy ra OH là đoạn vuông góc chung của AB và SO => OH =3
Tam giác OAH vuông tại H, có
9
222
−=−
= ROHOAAH
Tam giác SAB vuông tại S, có
22
2
AB
SB
SA =
+
( )
6
3
336
3
4
9
4
3
3
2
.2
22
2
=
⇒
=⇒
−=−
⇔−
=
⇔ l
RRR
R
Vậy diện tích xung quanh cần tính là
ππ
318== RlS
xq
.
Chọn A.
Ví dụ 7: Cho hình nón đỉnh S có đáy là hình tròn tâm O, bán kính R. Dựng hai đường sinh SA và SB, biết
AB chắn trên đường tròn đáy một cung có số đo bằng 60°, khoảng cách từ tâm O đến mặt phẳng (SAB)
bằng
2
R
. Đường cao h của hình nón bằng
A.
2R
B.
4
6
R
C.
2
3R
D.
3R
Lời giải
Theo giả thiết, ta có tam giác OAB đều cạnh R
Gọi E là trung điểm AB, suy ra
ABOE
⊥
và
2
3R
OE =
Gọi h là hình chiếu của O trên SE
SEOH ⊥⇒
Ta có
( )
OHABSEOAB
SOAB
OEAB
⊥⇒⊥⇒
⊥
⊥
Từ đó suy ra
( )
SAB
OH ⊥
nên
( )( )
2
;
R
OH
SABOd ==
Tam giác SEO vuông tại O, có
4
6
3
81
11
2222
R
SO
ROEOHSO
=⇒=−=
Chọn B
Ví dụ 8: Cho hình nón đỉnh S có đáy là hình tròn tâm O. Dựng hai đường sinh SA và SB, biết tam giác
SAB vuông và có diện tích bằng
2
4a
. Góc tạo bởi giữa trục SO và mặt phẳng (SAB) bằng 30
o
. Đường cao
h của hình nón bằng
A.
2a
B.
4
6a
C.
2
3a
D.
3a
Lời giải
Theo giả thiết, ta có tam giác SAB vuông cân tại S
Gọi E là trung điểm AB, suy ra
⊥
⊥
ABOE
ABSE
và
ABSE
2
1
=
Ta có
a
ABa
AB
ABaSE
ABS
SAB
4
4
2
1
.
2
1
4
.
2
1
22
=
⇒=
⇔
==
∆
Gọi H là hình chiếu của O trên SE =>
SEOH ⊥
Lại có
( )
OHABSEOAB
SOAB
OEAB
⊥⇒⊥⇒
⊥
⊥
Từ đó suy ra
( ) ( )
( )
o
OH SAB SO; SAB OSH 30⊥⇒ ==
Tam giác SEO vuông tại O, có
SO SE.cosOSE a 3= =
.
Chọn D.
Ví dụ 9: Cho hình nón đỉnh S, đường cao SO. Gọi A, B là hai điểm thuộc đường tròn đáy của hình nón sao
cho khoảng cách từ O đến AB bằng a và
oo
SAO 30 ,SAB 60= =
. Độ dài đường sinh l của hình nón bằng
A.
al =
B.
3al
=
C.
2al =
D.
al 2=
Lời giải
Gọi I là trung điểm AB, suy ra
ABSIABOI ⊥⊥ ,
và OI = a
Tam giác SAO vuông tại O, có
SA 3
OA SA.cosSAO
2
= =
Tam giác SAI vuông tại I, có
SA
IA SAcosSAB
2
= =
Tam giác OIA vuông tại I, có
2
22
IA
OIOA +
=
22
4
1
4
3
2222
2
aSAaSASAaSA =⇒=⇔+=⇔
Vậy độ dài đường sinh cần tìm là
2al =
. Chọn C.
Ví dụ 10: Một hình nón có bán kính đáy R, góc ở đỉnh là 60°. Một thiết diện qua đỉnh nón chắn trên đáy
một cung có số đo 90°. Diện tích của thiết diện là
A.
2
7
2
R
B.
2
3
2
R
C.
2
3
2
R
D.
2
6
2
R
Lời giải
Vì góc ở đỉnh là 60
o
nên thiết diện qua trục SAC là tam giác đều cạnh 2R
⇒
Đường cao của hình nón là
3R
SI =
Tam giác SA là thiết diện qua đỉnh, chắn trên đáy cung AB có số đo bằng 90° nên IAB là tam giác vuông
cân tại I
2RAB =⇒
Gọi M là trung điểm của AB thì
⊥
⊥
ABSM
ABIM
và
2
2
R
IM =
Tam giác SMI vuông tại I, có
2
14
22
R
IMSISM =+=
Vậy diện tích cần tính là
2
7
.
2
1
2
R
SMABS
SAB
==
∆
. Chọn A.
Dạng 3. Hình nón nội — ngoại tiếp khối chóp đều
Mô hình Hình vẽ tham khảo (3D) Tính chất
Hình nón nội tiếp hình chóp tam
giác đều
Chiều cao SO là chiề
u cao
của hình chóp
Bán kính đáy OE là bán kính
đường tròn nội tiếp tam giác
đáy
Đường sinh
SEl =
Hình nón ngoại tiếp hình chóp
tam giác đều
Chiều cao SO là chiề
u cao
của hình chóp
Bán kính đáy OA là bán kính
đường tròn ngoại tiếp tam
giác đáy
Đường sinh
SAl =
Hình nón nội tiếp hình chóp tứ
giác đều
Chiều cao SO là chiề
u cao
của hình chóp
Bán kính đáy OM (với M là
trung điểm AB) là bán kính
đường tròn nội tiế
p hình
vuông đáy
Đường sinh
SMl
=
Hình nón ngoại tiếp hình chóp tứ
giác đều
Chiều cao SO là chiề
u cao
của hình chóp
Bán kính đáy OA là bán kính
đường tròn ngoại tiế
p hình
vuông đáy
Đường sinh
SA
l =
Ví dụ 1: Thể tích khối nón ngoại tiếp tứ diện đều cạnh a là
A.
9
3
3
a
π
B.
27
3
3
a
π
C.
27
6
3
a
π
D.
9
6
3
a
π
Lời giải
Gọi O là tâm đường tròn ngoại tiếp ∆BCD
( )
BCDAO ⊥⇒
Dễ thấy, bán kính đường tròn ngoại tiếp ∆BCD là
3
3a
OB
=
Suy ra bán kính đáy hình nón là
3
3a
R =
Tam giác ABO vuông tại O, có
3
6
22
a
OBABAO =−=
Do đó, chiều cao của hình nón là
3
6a
AOh ==
Vậy thể tích cần tính là
27
6
3
6
.
3
3
.
3
1
3
1
3
2
2
aa
a
hR
V
π
ππ
=
=
=
Chọn C
Ví dụ 2: Diện tích xung quanh của hình nón ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a và cạnh
bên bằng 4a là
A.
2
22 a
π
B.
2
2 a
π
C.
2
4
a
π
D.
2
2
a
π
Lời giải
Theo bài ra, ta có bán kính đáy
2
2
a
R =
; đường sinh
al 4
=
(xem mô hình ở lý thuyết)
Vậy diện tích xung quanh cần tính là
2
2
24.
2
2
. a
a
a
RlS
xq
πππ
=
==
. Chọn A.
Ví dụ 3: Cho hình chóp tam giác đều S.ABC có SA = AB = a. Thể tích khối nón đỉnh S và có đường tròn
đáy nội tiếp tam giác ABC bằng
A.
27
3
3
a
π
B.
27
6
3
a
π
C.
108
6
3
a
π
D.
108
3
3
a
π
Lời giải
Gọi O là tâm đường tròn ngoại tiếp ∆ABC
( )
ABCSO ⊥⇒
Bán kính đáy hình nón là
6
3a
OMrR
ABC
===
∆
Tam giác SAO vuông tại O, có
3
6
22
a
OASASO =−=
Vậy thể tích khối nón cần tính là
108
6
3
6
.
6
3
.
33
1
3
2
2
a
a
a
h
RV
ππ
π
=
==
Chọn C.
Ví dụ 4: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Tam giác SAB có diện tích bằng
2
2
a
.
Thể tích khối nón có đỉnh S và đường tròn đáy nội tiếp tứ giác ABCD bằng
A.
6
7
3
a
π
B.
8
7
3
a
π
C.
4
7
3
a
π
D.
2
7
3
a
π
Lời giải
Gọi M là trung điểm AB
AB
SMS
ABSM
SAB
.
2
1
=⇒
⊥
⇒
∆
Mà
a
aaSMaABaS
SAB
4:2.2;2
22
==→==
∆
Bán kính đáy hình nón
22
aAB
OMR ===
Tam giác SMO vuông tại M, có
2
73
22
a
OM
SMSO =−
=
Vậy thể tích khối nón cần tính là
8
773
.
2
.
33
1
3
2
2
aaa
hRV
ππ
π
=
==
Chọn B.
Ví dụ 5: Cho hình nón (N) có bán kính đáy bằng a và diện tích xung quanh
2
2 aS
xq
π
=
. Tính thể tích V của
khối chóp tứ giác đều S.ABCD có đáy ABCD nội tiếp đáy hình nón và đỉnh S trùng với đỉnh của hình nón
(N)?
A.
3
3
3
a
B.
3
2
3
a
C.
2
3
3
a
D.
3
32
3
a
Lời giải
Gọi O là tâm hình vuông ABCD
⇒
O là tâm đường tròn ngoại tiếp hình vuông ABCD
Theo bài ra, đáy hình nón là đường tròn ngoại tiếp ABCD
2
2
2
aABa
ACa
AC
OAR
R
ABCD
=
⇒=⇒
==
==
⇒
Diện tích xung quanh hình nón là
a
la
RlS
xq
2
2
2
=
⇒=
=
π
π
Hình nón (N) có đường sinh
aSA
l 2
==
Tam giác SAO vuông tại O, có
3
22
aOASASO =−=
Vậy thể tích khối chóp S.ABCD là
( )
3
32
2.
3
3
.
3
1
3
2
.
a
a
a
SSOV
ABCDABCDS
===
Chọn D
Ví dụ 6: Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a, góc tạo bởi hai mặt phẳng (SAB) và
(ABC) bằng 60
o
. Diện tích xung quanh của hình nón đỉnh S và có đường tròn đáy ngoại tiếp tam giác ABC
bằng
A.
6
7
2
a
π
B.
3
7
2
a
π
C.
2
3
2
a
π
D.
6
3
2
a
π
Lời giải
Gọi O là tâm đường tròn ngoại tiếp
( )
ABCSOABC ⊥⇒∆
Bán kính đáy hình nón là
3
3a
OA
RR
ABC
==
=
∆
Gọi M là trung điểm AB
( )
SMOAB
SOAB
OMAB
⊥⇒
⊥
⊥
⇒
Do đó
(
)
( )
(
)
(
)
o
OM
SOM
SMABC
SAB 60
ˆ
;
; =
=
=
Tam giác SMO vuông tại O, có
3
3
ˆ
cos
a
SM
SM
OM
O
M
S =
⇒=
Tam giác SBM vuông tại M, có
6
21
2
2
a
BM
SMSB
=+
=
Vậy hình nón có đường sinh
6
7
6
21
2
a
RlS
a
l
sq
π
π
==
→=
Chọn A.
Ví dụ 7: Cho hình chóp tam giác đều S.ABC có cạnh AB = BC = 10a, AC = 12a, góc tạo bởi hai mặt phẳng
(SAB) và (ABC) bằng 45
o
. Thể tích khối nón đỉnh S và có đường tròn đáy nội tiếp tam giác ABC bằng
A.
3
3
a
π
B.
3
9
a
π
C.
3
27 a
π
D.
3
12 a
π
Lời giải
Gọi O là tâm đường tròn nội tiếp ∆ABC
( )
ABCSO ⊥
Kẻ
OMABOM ⇒⊥
là bán kính đường tròn nội tiếp ∆ABC
Diện tích ∆ABC là
(
)
(
)
(
)
2
48
ac
p
bp
a
pp
S
ABC
=
−
−−
=
∆
Suy ra bán kính đường tròn nội tiếp
a
p
S
rABC
ABC
3==⇒∆
∆
Ta có
(
) (
)
( )
(
)
o
AB SMO SAB ; ABC SMO 45⊥⇒ ==
Tam giác SMO vuông tại O, có
arOM
SO
ABC
3===
∆
Vậy thể tích khôi nón cần tính là
( )
3
2
2
93.3.
33
1
aa
ahRV
π
π
π
==
=
Chọn B.
Ví dụ 8: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a, khoảng cách từ tâm O của đường tròn
ngoại tiếp tam giác ABC đến một mặt bên là
2
a
. Thể tích của khối nón ngoại tiếp hình chóp S.ABC bằng
A.
3
4
3
a
π
B.
27
4
3
a
π
C.
9
4
3
a
π
D.
3
2
3
a
π
Lời giải
Gọi M là trung điểm BC
( )
SAMBCAMBC ⊥⇒⊥⇒
Kẻ
SM
OH ⊥
mà
( )
ABCOHOHBC ⊥⇒⊥
Tacó
3
3
2
.
2
3
.
3
1
2
3
.
3
1
3
1 a
a
ABAMOM =
=
==
Tam giác SMO vuông tại O, có
aSO
OMSOOH
=⇒+=
222
1
11
Bán kính đường tròn ngoại tiếp
ABC∆
là
3
3
2a
R
ABC
=
∆
Vậy thể tích khối nón cần tính là
9
4
3
32
.
33
1
3
2
2
aaa
hRV
ππ
π
=
==
Chọn C
Dạng 4. Hình nón nội - ngoại tiếp hình trụ, hình cầu
Hình nón ngoại tiếp hình cầu
Lý thuyết: Xét mặt cắt qua trục, ta đưa về bài toán tam giác ngoại tiếp đường tròn
Bài toán: Gọi R, r, h lần lượt là bán kính mặt cầu, bán kính đáy và chiều cao hình nón
SIhIBrOIR ===⇒ ,,
Ta có
22
~
rh
Rh
r
R
SB
SO
IB
OE
SIBSEO
+
−
=⇒=⇒∆
∆
Vậy mối liên hệ cần tìm là
22
rh
R
r rh
=
++
Hình nón nội tiếp hình cầu
Lý thuyết: Xét mặt cắt qua trục, ta đưa về bài toán tam giác nội tiếp đường tròn
Bài toán: Gọi R, r, h lần lượt là bán kính mặt cầu, bán kính đáy và chiều cao hình nón
Ta có
222
Rrx =+
mà
( )
22
2
RrRhRhx =+−⇒−=
Vậy mối liên hệ cần tìm là
22 2
h r hr
R
2h 2 2h
+
= = +
Hình nón ngoại tiếp hình trụ
Lý thuyết: Xét mặt cắt qua trục, ta đưa về bài toán tam giác ngoại tiếp hình chữ nhật, cụ thể là tam giác
SAB (thiết diện qua trục hình nón) và hình chữ nhật MNPO (thiết diện qua trục hình trụ)
Bài toán: Gọi R, h, R’, H’ lần lượt là bán kính đáy và chiều cao hình nón; bán kính đáy và chiều cao hình
trụ
=
=
=
=
⇒
OIh
INR
SIh
IAR '
;
Ta có
R
RR
h
h
AI
AN
SI
MN
ASI
AMN
''
~
−
=⇒=⇒∆∆
Vậy mối liên hệ cần tìm là
h' R R'
hR
−
=
Ví dụ 1: Cho hình cầu bán kính bằng 5 cm, cắt hình cầu này bằng một mặt phẳng sao cho thiết diện tạo
thành là một đường tròn đường kính 4 cm. Tính thể tích khối nón có đáy là thiết diện vừa tạo và đỉnh là tâm
của hình cầu đã cho.
A.
3
18,19 cm≈
B.
3
20,19
cm≈
C.
3
21,19 cm≈
D.
3
19,19 cm≈
Lời giải
Theo bài ra, ta có R = 5 cm, r = 2 cm
Chiều cao của khối nón là
cmrRh 21
22
=−=
Vậy thể tích khối nón là
32
20,19
3
214
3
1
cmhrV ≈==
π
π
.
Chọn B.
Ví dụ 2: Cho mặt cầu (S) tâm O, bán kính R (không đổi). Mặt phẳng (P) cách O một khoảng bằng x, (x< R)
và cắt (S) theo giao tuyến là đường tròn (C) có tâm H. Gọi T là giao điểm của tia HO với (S). Thể tích của
khối nón có đỉnh T và đáy là hình tròn (C) bằng
A.
( )
( )
6
22
hRxR +−
π
B.
( )
( )
22
2R x Rhπ− +
C.
( )
( )
3
22
hRxR +−
π
D.
( )
( )
22
R x Rhπ− +
Lời giải
Bán kính đáy hình nón là
22
xRr −=
Chiều cao hình nón là
hROHOTh +=+=
Vậy thể tích khối nón là
( )
( )
33
1
22
2
hRxR
hrV
+−
==
π
π
Chọn C.
Ví dụ 3: Cho hình nón (N) có bán kính đáy bằng 6, chiều cao bằng 8. Biết rằng có một mặt cầu tiếp xúc với
tất cả các đường sinh của hình nón, đồng thời tiếp xúc với mặt đáy của hình nón. Tìm bán kính của mặt cầu
đó
A. 4 B. 2 C. 6 D. 3
Lời giải
Bài toán: Hình nón ngoại tiếp hình cầu
2 2 22
rh 6.8
R3
r rh 6 68
⇒= = =
++ ++
Chọn D.
Ví dụ 4: Cho khối cầu tâm O, bán kính R =2. Mặt phẳng (P) cách O một khoảng x cắt khối cầu theo một
hình tròn (C). Một khối nón (N) có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón (N) có thể tích
lớn nhất, khi đó giá trị của x bằng
A.
3
2
=x
B.
3
3
=
x
C.
3
1
=x
D.
2
3
=x
Lời giải
Bài toán: Hình nón nội tiếp hình cầu.
Ta có
22
2
xR
r −
=
, với r là bán kính đáy hình nón
Chiều cao hình nón là
Rxh +=
. Thể tích khối nón là
( )
( )
2 22
11
V rh R x .x R
33
=π=π − +
Lại có
( )( )( )
(
)
81
32
27
22
.
6
.
.22.
6
3
3
R
xRxRxR
x
RxRxRV
ππ
π
=
++++−
≤+
+−=
Dấu bằng xảy ra khi và chỉ khi
3
2
3
2
2
==
⇔+=
−
R
xx
Rx
R
Chọn A.
Ví dụ 5: Cho hình nón tròn xoay (N) có đỉnh là S, có đáy là đường tròn tâm O bán kính R. Đường cao SO =
h. Tính chiều cao x của hình trụ có thể tích lớn nhất nội tiếp hình nón đã cho ?
A.
3
h
x =
B.
3
3
h
x =
C.
6
h
x =
D.
6
3
h
x
=
Lời giải
Bài toán: Hình nón ngoại tiếp hình trụ
R
RR
h
h ''
−
=⇒
Với R’, h’ lần lượt là bán kính đáy, chiều cao hình trụ
(
)
'. RR
R
h
x −=⇒
Thể tích khối trụ là
( )
[ ]
)'
.('.'..''
222
RRR
R
h
RR
R
h
RxRV −=−==
π
ππ
Ta có:
(
)
3
3
2
R' R'
R R'
R' R' 4R
22
R ' . R R ' 4. . .(R R ') 4.
2 2 27 27

+ +−


−= −≤ =
Suy ra
27
4
27
4
.
23
hRR
R
h
V
ππ
=≤
. Dấu = xảy ra khi
33
2
''
2
' h
xRRRR
R
=⇒=⇒−=
.
Chọn A.
BÀI TẬP TỰ LUYỆN
Câu 1: Một khối nón tròn xoay có chiều cao h = 4, bán kính đáy r = 5. Tính thể tích của khối nón
A.
3
100
π
B.
π
15
C.
π
41
D.
3
25
π
Câu 2: Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón (N). Diện tích xung
quanh của (N) là
A.
RhS
xq
π
=
B.
RlS
xq
π
2=
C.
hRS
xq
2
π
=
D.
RlS
xq
π
=
Câu 3: Cho khối nón (N) có bán kính đáy bằng 3 và thể tích bằng
π
12
. Tính diện tích xung quanh của hình
nón
A.
π
15=
xq
S
B.
π
24=
xq
S
C.
π
16=
xq
S
D.
π
18=
xq
S
Câu 4: Cho hình nón có bán kính đáy bằng 3 và chiều cao bằng 4. Tính diện tích xung quanh của hình nón
đó
A.
π
60=
xq
S
B.
π
15=
xq
S
C.
π
20=
xq
S
D.
π
25=
xq
S
Câu 5: Một hình nón có bán kính đáy bằng 5a, độ dài đường sinh bằng 13a. Tính độ dài đường cao của hình
nón
A.
6
7a
h =
B.
ah 12=
C.
ah 17=
D.
ah
8
=
Câu 6: Một hình nón có bán kính đáy bằng 1 cm, chiều cao bằng 2 cm. Khi đó góc ở đỉnh của hình nón là
ϕ
2
thỏa mãn
A.
5
5
2
sin
=
ϕ
B.
5
5
tan
=
ϕ
C.
5
52
cos =
ϕ
D.
5
5
cot =
ϕ
Câu 7: Cho hình nón có bán kính đáy là 6a, chiều cao là 8a. Tính diện tích xung quanh của hình nón
A.
2
20
a
π
B.
2
60 a
π
C.
2
50 a
π
D.
2
40 a
π
Câu 8: Một hình nón có đường sinh bằng 3a và bán kính đường tròn đáy bằng 2a. Tính diện tích xung quanh
của hình nón đó.
A.
2
3
54
aS
xq
π
=
B.
2
3 aS
xq
π
=
C.
2
12 aS
xq
π
=
D.
2
6 aS
xq
π
=
Câu 9: Cho khối nón có chiều cao bằng 8 cm và độ dài đường sinh bằng 10 cm. Tính thể tích V của khối
nón đó
A.
3
124 cmV
π
=
B.
3
140 cmV
π
=
C.
3
128 cmV
π
=
D.
3
96 cmV
π
=
Câu 10: Một hình nón có bán kính đáy r = 3a, chiều cao h = 4a. Kí hiệu góc ở đỉnh của hình nón là
α
2
.
Trong các mệnh đề sau, mệnh đề nào đúng?
A.
5
4
sin
=
α
B.
5
4
cos =
α
C.
5
4
tan =
α
D.
5
4
cot =
α
Câu 11: Cho hình nón có diện tích xung quanh bằng
2
3 a
π
và bán kính đáy bằng a. Tính độ dài đường sinh l
của hình nón đã cho
A.
2
5
a
l
=
B.
al
2
2=
C.
2
3a
l =
D.
al 3=
Câu 12: Cho một khối nón có bán kính đáy bằng 3 và thể tích bằng
π
12
. Tính diện tích xung quanh
xq
S
của
hình nón
A.
π
15=
xq
S
B.
π
45
=
xq
S
C.
π
30=
xq
S
D.
π
60=
xq
S
Câu 13: Khối nón (N) có bán kính đường tròn đáy bằng 10 và diện tích xung quanh bằng
π
120
. Tính chiều
cao của khối nón (N)
A.
112
B.
3
11
C.
2
11
D.
11
Câu 14: Cho tam giác ABC vuông tại C, BC = a, AC = b. Tính thể tích khối tròn xoay tạo thành khi quay
tam giác ABC quanh AC.
A.
3
2
ba
π
B.
b
a
2
π
C.
3
3
ba
π
D.
b
a
3
π
Câu 15: Trong không gian, cho tam giác ABC vuông tại A với AC = 3a, AB = 4a. Tính theo a diện tích
xung quanh S của hình nón khi quay tam giác ABC quanh trục AC.
A.
π
2
30aS =
B.
π
2
40aS =
C.
π
2
20aS =
D.
π
2
15aS =
Câu 16: Cho tam giác ABC đều cạnh 2a, đường cao AH. Tính thể tích của khối nón tròn xoay tạo thành khi
quay hình tam giác ABC quanh AH.
A.
3
3
a
π
B.
3
3
3
a
π
C.
6
3
3
a
π
D.
4
3
3
a
π
Câu 17: Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Tính thể tích vật tròn xoay thu được khi quay tam
giác ABC quanh cạnh AC.
A.
π
10
B.
π
11
C.
π
12
D.
π
13
Câu 18: Cho tam giác ABC vuông tại A có
o
ABC 30=
quay quanh cạnh góc vuông
aAC =
tạo thành hình
nón tròn xoay có diện tích xung quanh bằng
A.
32
2
a
π
B.
34
2
a
π
C.
3
2
a
π
D.
2
2 a
π
Câu 19: Trong không gian cho tam giác vuông IOM vuông tại I, góc
o
IOM 30=
và cạnh IM = a. Khi quay
tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OIM tạo thành một hình nón tròn xoay. Tính
thể tích V của khối nón tròn xoay tương ứng.
A.
3
3
3
a
V
=
B.
3
3
3
a
V
π
=
C.
3
3
aV
π
=
D.
6
3
3
a
V
π
=
Câu 20: Cho tam giác ABC vuông tại A, có AB = 10,
o
ABC 60=
. Tính diện tích xung quanh S
xq
của hình
nón tạo thành khi quay tam giác ABC quanh đường thắng chứa cạnh AC.
A.
π
31000=
xq
S
B.
π
3100
=
xq
S
C.
π
3200
=
xq
S
D.
π
200=
xq
S
Câu 21: Cho tam giác ABC vuông cân tại A và có AB = 3cm. Cho tam giác ABC quay quanh trục AB ta
nhận được khối tròn xoay (T). Tính thể tích của (T)
A.
( )
3
18 cm
π
B.
( )
3
9 cm
π
C.
(
)
3
27 cm
π
D.
( )
3
3 cm
π
Câu 22: Gọi S là diện tích hình nón tròn xoay được sinh ra bởi đoạn thắng AC’ của hình lập phương
ABCD.A’B’C’D’ có cạnh b khi quay quanh trục CC’. Diện tích xung quanh S là
A.
2
b
π
B.
2
2
b
π
C.
3
2
b
π
D.
6
2
b
π
Câu 23: Cho hình nón có bán kính đường tròn đáy là 6 cm và diện tích hình tròn đáy bằng diện tích xung
quanh của hình nón. Tính thể tích V của khối nón đã cho
A.
( )
3
48 cm
V
π
=
B.
( )
3
64 cmV
π
=
C.
( )
3
96 cmV
π
=
D.
( )
3
288 cmV
=
Câu 24: Một khối nón có thể tích bằng
3
25
cm
π
, nếu giữ nguyên chiều cao và tăng bán kính đáy khối nón đó
lên 2 lần thì thể tích của khối nón mới bằng
A.
3
100
cm
π
B.
3
150 cm
π
C.
3
200 cm
π
D.
3
50
cm
π
Câu 25: Cho hình nón đỉnh S, đáy là hình tròn tâm O, góc ở đỉnh bằng 150
o
. Trên đường tròn đáy lấy điểm
A cố định. Có bao nhiêu vị trí của điểm M trên đường tròn đáy của hình nón để diện tích tam giác SMA đạt
giá trị lớn nhất?
A. 2 B. 1 C. 4 D. 3
Câu 26: Cho hình thang ABCD (AB//CD) vuông tại A có AB = 8, CD = 5 và BC = 5. Tính thể tích V của
hình tròn xoay tạo thành khi quay đường gấp khúc ADC quanh trục AB.
A.
3
128
π
=V
B.
π
128=V
C.
3
256
π
=V
D.
π
96=V
Câu 27: Cho tam giác ABC cân tại A, biết cạnh AB = a và
o
BAC 120=
. Tính thể tích khối tròn xoay sinh ra
khi quay tam giác ABC quanh cạnh AC.
A.
4
3
3
a
V
π
=
B.
8
3
a
V
π
=
C.
8
3
3
a
V
π
=
D.
4
3
a
V
π
=
Câu 28: Cho hình nón đỉnh S và đường tròn đáy có tâm O. Điểm A thuộc đường tròn đáy. Tính số đo góc
O
AS
ˆ
, biết tỉ số giữa diện tích xung quanh và diện tích đáy của hình nón là
3
2
A. 120
o
B. 45
o
C. 30
o
D. 60
o
Câu 29: Cho tam giác ABC có AB, BC, CA lần lượt bằng 3, 5, 7. Tính thể tích của khối tròn xoay sinh ra do
hình tam giác ABC quay quanh đường thẳng AB.
A.
π
50
B.
4
75
π
C.
8
275
π
D.
8
125
π
Câu 30: Cho tam giác AC có AB = 3a, BC = 5a, CA = 7a. Tính thể tích khối tròn xoay sinh ra khi cho hình
tam giác ABC quay quanh đường thẳng AB.
A.
3
76
3
π
a
B.
π
3
16a
C.
4
75
3
π
a
D.
π
3
20a
Câu 31: Cho hình nón đỉnh S, xét hình chóp S.ABC có đáy ABC là tam giác ngoại tiếp đường tròn đáy của
hình nón và có AB = BC = 10a,AC = 12a, góc giữa hai mặt phẳng (SAB) và (ABC) bằng 45
o
. Tính thể tích
của khối nón đã cho.
A.
3
9 a
π
B.
3
12 a
π
C.
3
27 a
π
D.
3
3 a
π
Câu 32: Cho S.ABCD là hình chóp tứ giác đều, cạnh đáy bằng a, cạnh bên hợp với đáy góc 45
o
. Hình tròn
xoay đỉnh S, đáy là đường tròn nội tiếp hình vuông ABCD. Tính diện tích xung quanh của hình nón tròn
xoay đó.
A.
2
2 a
S
xq
π
=
B.
2
aS
xq
π
=
C.
2
2
a
S
xq
π
=
D.
4
2
a
S
xq
π
=
Câu 33: Cho hình chóp tam giác đều có đáy bằng a và đường cao bằng 6a. Tính thể tích khối nón nội tiếp
hình chóp đó?
A.
9
3
a
π
B.
6
3
a
π
C.
3
3
a
π
D.
4
3
a
π
Câu 34: Cho hình chóp tam giác đều S.ABC có các cạnh bên bằng a, góc giữa mặt bên và mặt phẳng đáy
bằng α với
5tan =
α
. Tính thể tích V của khối nón có đỉnh S và có đường tròn đáy là đường tròn nội tiếp
tam giác ABC.
A.
81
5
3
a
V
π
=
B.
27
5
3
a
V
π
=
C.
9
5
3
a
V
π
=
D.
81
5
3
a
V
π
=
Câu 35: Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Một khối nón có đỉnh là tâm của hình vuông
ABCD và đáy là hình tròn nội tiếp hình vuông A’B'C'D'. Tính diện tích toàn phần của khối nón đó.
A.
4
3
a
S
tp
π
=
B.
4
5
2
a
S
tp
π
=
C.
(
)
1
52
4
2
+
=
a
S
tp
π
D.
( )
15
4
2
+=
a
S
tp
π
Câu 36: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Gọi M, N lần lượt là trung điểm của SB,
SC ; mặt phẳng (AMN) vuông góc với (SBC). Tính diện tích xung quanh của hình nón nội tiếp hình chóp đã
cho.
A.
12
6
2
a
π
B.
6
6
2
a
π
C.
4
5
2
a
π
D.
4
2
a
π
Câu 37: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với mặt đáy góc 60
o
. Hình
nón có đỉnh S, đáy là đường tròn nội tiếp tứ giác ABCD có diện tích xung quanh là
A.
4
2
a
S
π
=
B.
4
14
2
a
S
π
=
C.
4
7
2
a
S
π
=
D.
2
2
a
S
π
=
Câu 38: Cho tam giác ABC vuông tại A có
o
ABC 30=
và cạnh góc vuông AC = 2a. Quay tam giác quanh
cạnh AC tạo thành hình nón tròn xoay có diện tích xung quanh bằng
A.
2
2
a
π
B.
3
3
4
2
a
π
C.
38
2
a
π
D.
316
2
a
π
Câu 39: Cho tam giác ABC có
A : B : C 3: 2 :1, AB 10cm= =
. Tính độ dài đường sinh l của hình nón, nhận
được khi quay tam giác ABC xung quanh trục AB
A. 20 cm B.
cm310
C. 30 cm D. 10 cm
Câu 40: An có một tờ giấy hình tròn tâm O, bán kính là 12 cm. Trên đường tròn, An lấy một cung AB có số
đo là
3
2
π
, sau đó cắt hình tròn dọc theo hai đoạn OA và OB. An dán mép OA và OB lại với nhau để được
hai hình nón đỉnh O. Tính tỉ số thể tích của khối nón nhỏ so với khối nón lớn (xem phần dán giấy không
đáng kể).
A.
8
1
B.
4
1
C.
10
10
D.
5
10
Câu 41: Người thợ gia công của một cơ sở chất lượng cao X cắt một miếng tôn hình tròn với bán kính 60cm
thành ba miền hình quạt bằng nhau. Sau đó người thợ ấy quấn và hàn ba miếng tôn đó để được ba cái phễu
hình nón. Hỏi thể tích V của mỗi cái phễu đó bằng bao nhiêu?
A.
lítV
3
216000
=
B.
lítV
3
2
16
π
=
C.
lítV
3
216000
π
=
D.
lít
V
3
2
160
π
=
Câu 42: Cắt bỏ hình quạt tròn AOB từ một mảnh các tông hình tròn bán kính R rồi dán hai bán kính OA và
OB của hình quạt tròn lại với nhau để được một cái phễu có dạng của một hình nón. Gọi x là góc ở tâm của
hình quạt tròn dùng làm phễu,
π
20 << x
. Tìm giá trị lớn nhất của thể tích khối nón.
A.
3
27
34
R
π
B.
3
27
2
R
π
C.
3
9
32
R
π
D.
3
27
3
2
R
π
Câu 43: Từ một miếng sắt tây hình tròn bán kính R, ta cắt đi một hình quạt và cuộn phần còn lại thành một
cái phễu hình nón. Số đo cung của hình quạt bị cắt đi phải là bao nhiêu độ (làm tròn đến đơn vị độ) để hình
nón có dung tích lớn nhất?
A. 65
o
B. 90
o
C. 45
o
D. 60
o
Câu 44: Bình có một tấm bìa hình tròn như hình vẽ. Bạn ấy muốn biến hình tròn đó thành một hình cái phễu
hình nón. Khi đó Bình phải cắt bỏ hình quạt tròn AOB rồi dán hai bán kính OA và OB lại với nhau. Gọi x là
góc ở tâm hình quạt tròn dùng làm cái phễu. Tìm x để thể tích cái phễu lớn nhất.
A.
( )
3
626
π
−
B.
3
π
C.
3
62
π
D.
( )
3
626
π
+
Câu 45: Cho nửa đường tròn đường kính AB = 2R và điểm C thay đổi trên nửa đường tròn đó. Đặt
CAB
= α
và gọi H là hình chiếu vuông góc của C lên AB. Tìm
α
tan
sao cho thể tích khối tròn xoay tạo
thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất.
A.
1tan =
α
B.
2
1
tan =
α
C.
3
3
tan
=
α
D.
3tan =
α
Câu 46: Cho ba hình tam giác đều cạnh bằng a chồng lên nhau như hình vẽ bên (cạnh đáy của tam giác trên
đi qua các trung điểm hai cạnh bên của tam giác dưới). Tính theo α thể tích của khối tròn xoay tạo thành khi
quay chúng xung quanh đường thẳng d
.
A.
96
311
3
a
π
B.
8
311
3
a
π
C.
8
3
3
a
π
D.
96
313
3
a
π
Câu 47: Cho khối nón có bán kính 3a. Cắt khối nón đã cho bởi một mặt phẳng vuông góc với trục và bỏ
phần trên của khối nón ( phần chứa đỉnh của khối nón ). Biết thiết diện là hình tròn có bán kính bằng a và độ
dài phần đường sinh còn lại bằng
10
29a
Tính thể tích V phần còn lại của khối nón theo a.
A.
3
3
a
V
π
=
B.
27
6
3
a
V
π
=
C.
10
29
3
a
V
π
=
D.
10
91
3
a
V
π
=
Câu 48: Một hình nón (N) có bán kính đáy R, đường cao SO. Gọi (P) là mặt phẳng vuông góc với SO tại
sao cho
SOSI
3
1
=
, Một mặt phẳng (Q) qua trục hình nón (N) cắt phần khối nón nằm giữa và đáy hình nón
theo thiết diện là hình thang cân ABCD có hai đường vuông góc nhau hình vẽ. Thể tích phần hình nón (N)
nằm giữa mặt phẳng (P) và mặt phẳng chứa đáy hình nón (N) là
A.
81
76
3
R
π
B.
81
52
3
R
π
C.
81
64
3
R
π
D.
81
40
3
R
π
LỜI GIẢI BÀI TẬP TỰ LUYỆN
Câu 1:
ππ
3
100
3
1
2
=
= h
rV
. Chọn A
Câu 2:
RlS
xq
π
=
. Chọn D
Câu 3: Ta có
ππ
π
ππ
154
3
1
12
3
22
2
=
+=
=
⇒=⇒
=
=
=
r
h
rrl
Sh
hrV
r
xq
. Chọn A
Câu 4:
22
xq
S rl h r 15=π=π + = π
. Chọn B
Câu 5: Ta có
a
rlh
12
22
=−=
. Chọn B
Câu 6: Ta có
22
SO h 2
cos cos ASO
SA
5
hr
φ= = = =
+
Chọn C
Câu 7:
22 2
xq
S rl h r 60 a .=π=π + = π
Chọn B
Câu 8:
2
xq
S rl 6 a=π=π
. Chọn D
Câu 9:
( )
3222
96
3
1
3
1
cmhhlhrV
πππ
=−==
. Chọn D
Câu 10: Ta có
5
4
coscos
22
=
+
===
rh
h
SA
SO
ASO
ϕ
Chọn B
Câu 11: Ta có
al
a
r
a
rlS
xq
3
3
2
=⇒
=
==
π
π
. Chọn D
Câu 12:
22
xq
2
r3
h 4 S rl r h r 15
1
V rh
3
=
⇒ =⇒ =π=π + = π
= π
. Chọn A
Câu 13:
22
22
xq
r 10
h 100 12 h 2 11
S rl h r 120
=
⇒ + = ⇒=
=π=π + = π
Chọn A
Câu 14:
3
2
ba
V
π
=
. Chọn A
Câu 15:
2
22
205
4,3 arl
S
ar
h
larah
xq
π
π
=
=
⇒=
+=
⇒==
Chọn C
Câu 16:
3
3
3
1
,3
2
32
3
2
a
hrVara
a
h
π
π
==⇒===
Chọn B
Câu 17:
ππ
12
3
1
3
,4
2
==
⇒=
= h
r
Vr
h
Chọn C
Câu 18:
22
AC AC
tan ABC AB a 3 BC AB AC 2a
AB
tan ABC
= ⇒= = ⇒= + =
Ta có
322,3,
2
arlSalarah
xq
ππ
==⇒===
Chọn A
Câu 19:
22
IM IM
tan IOM IO a 3 OM IM IO 2a
IO
tan IOM
= ⇒= = ⇒ = + =
Ta có
3
3
3
1
,
,3
3
2
a
h
rVara
h
π
π
=
=⇒==
Chọn B
Câu 20:
22
AC
tan ABC AC AB tan ABC 10 3 BC AB AC 20
AB
= ⇒= = ⇒= + =
Ta có
ππ
20020,10,310 ==⇒=== rlSlrh
xq
Chọn D
Câu 21:
π
π
9
3
1
3,3
2
==⇒== hr
Vhr
Chọn B
Câu 22:
63
,
22,'
,3
'
2
b
rlS
b
lb
rbACbCC
b
AC
xq
π
π
=
=⇒
=
=⇒===
Chọn D
Câu 23:
32
22
2
96
3
1
8
10
5
3
6
cm
hr
Vr
l
h
l
rlr
cm
r
ππ
ππ
=
=⇒
=−
=
⇒
=
⇒
=
=
Chọn C
Câu 24:
( )
ππ
π
π
100
2
3
1
'
25
3
1
2
2
=
=⇒
=
= h
rV
h
rV
Chọn A
Câu 25: Kẻ
AM
SH
⊥
HM
HA
SMSA
=
⇒=
AMOHOMOA ⊥⇒=
22
..
2
1
2
22
lAHSH
AHSHAMSHS
SAM
=
+
≤
==
Dấu “=” xảy ra
o
ASM 90=⇔
Có 2 điểm M thỏa mãn bài toán (đối xứng nhau qua AB)
Chọn A
Câu 26: Ta có
( )
4
2
2
=−−= CDABBCAD
( )
πππ
96.
3
1
..
22
=−+=⇒
CDABADCDADV
Chọn D
Câu 27:
3120cos..2
22
a
ACABACABBC
o
=−+=
. Kẻ
ACBH
⊥
22
3
22
BH a 3 3a
sin ACB BH BCsin ACB CH BC BH
BC 2 2
11 a
V .CH.BH .AH.BH
33 4
=⇒= = ⇒= − =
π
=π −π =
Chọn D
Câu 28:
o
2
2 rl l SA OA 3
cos SAO SAO 30
r r OA SA 2
3
π
===⇒ ==⇒=
π
Chọn C
Câu 29: Kẻ
AB
CH ⊥
. Ta có
222
AB AC BC 11
cos BAC
2AB.AC 14
+−
= =
Mà
AH 11 5
cos BAC AH AC cos BAC BH AH AB
AC 2 2
= ⇒ = =⇒=−=
Ta có
4
75
.
3
1
.
3
1
2
35
2222
π
ππ
=−=⇒=−= BHCHAHCHVAHACCH
Chọn B
Câu 30: Kẻ
ABCH ⊥
. Ta có
222
AB AC BC 11
cos BAC
2AB.AC 14
+−
= =
Mà
2
5
2
11
ˆ
cos
ˆ
cos
a
ABAHBH
a
CABACAH
AC
AH
CAB =−=⇒
==⇒=
Ta có
4
75
.
3
1
.
3
1
2
35
3
2
2
22
a
BHCHAH
CHV
a
AHAC
CH
π
ππ
=−
=⇒=
−=
Chọn C
Câu 31: Diện tích tam giác ABC là
( )( )( )
2
48a
ACpBCpABppS
ABC
=−−−=
∆
Bán kính đường tròn nội tiếp
ABC∆
là
a
a
a
p
S
rrpS
ABC
3
16
48
.
2
===⇒=
∆
Gọi H là hình chiếu của I trên AB
( ) ( ) (
)
( )
o
AB SIH SAB ; ABC SHI 45⇒⊥ ⇒ = =
Tam giác SIH vuông cân tại I có
aIHSI 3==
. Vậy
(
)
32
9
3
1
ahrV
N
ππ
==
Chọn A
Câu 32: Bán kính đường tròn nội tiếp hình vuông ABCD là
2
a
r =
Gọi O là tâm hình vuông ABCD
( ) ( )
( )
( )
SO ABC SA; ABCD SA;OA SAO⇒⊥ ⇒ = =
Tam giác SAO vuông tại O, có
2
2
45
ˆ
a
OASOOAS
o
==⇒=
Vậy diện tích xung quanh của hình nón là
2
.
2
..
.
2
a
a
a
SA
OA
RlS
xq
π
π
ππ
=
==
=
Chọn C
Câu 33: Bán kính đường tròn nội tiếp tam giác đều cạnh a là
6
3a
r =
Thể tích khối nón cần tính là
6
6.
6
3
.
33
1
3
2
2
a
a
a
hrV
ππ
π
=
==
Chọn B
Câu 34: Gọi H là tâm của tam giác ABC
( )
ABCSH ⊥⇒
Gọi M là trung điểm của BC
( )
SAMBCBCAM ⊥
⇒⊥⇒
Khi đó
( ) ( )
( )
SH
SBC ; ABC SMA tan SMA
HM
=⇒=
Đặt
6
3x
HMxAB =⇒=
và
4
2
222
x
aBMSBSM −=−=
3
2
4
3
12
5
3
5
12
:
3
2
2
23
2
22
2
a
x
x
a
x
x
a
xx
a
=
⇔
=⇔
=
−
⇔
=
−
⇒
Vậy
81
5
3
5
.
3
.
3
3
1
3
2
2
a
aa
hRV
ππ
π
=
==
. Chọn A
Câu 35: Bán kính đáy của khối nón là
2
a
r =
và chiều cao của khối nón là
ah =
Độ dài đường sinh của khối nón là
2
5
2
2
222
aa
arhl =
+=+=
Vậy diện tích toàn phần cần tính là
(
)
15
2
4
2
2
+
=+
=
a
rl
hr
S
tp
π
ππ
Chọn C
Câu 36: Gọi I, K lần lượt là trung điểm của MN, BC
Và H là tâm đường tròn ngoại tiếp ∆ABC
( )
ABCSH ⊥⇒
Vì ∆AMN cân
MN
AI ⊥⇒
và ∆SMN cân
MN
SI ⊥
⇒
Suy ra
( ) ( )
( )
o
AMN ; SBC SIA 90 SAK= = ⇒∆
cân tại A
2
2
2
3
2
2
a
HK
SH
SK
a
AKSA
=
+
=
⇒
==
⇒
Bán kính đường tròn nội tiếp ∆ABC là
6
3a
HKr ==
Vậy thể tích khối nón cần tính là
12
6
3
1
2
2
a
h
rV
π
π
==
Chọn A
Câu 37: Bán kính đáy (hình vuông ABCD) của khối nón là
2
a
r =
Gọi O là tâm hình vuông ABCD
( )
ABCDSO ⊥⇒
( )
( )
( )
o
SA; ABCD SA;OA SAO 60⇒===
Gọi M là trung điểm của AB
ABOM ⊥⇒
SM⇒
là đường sinh của khối nón
Tam giác SMO vuông tại O, có
2
7
22
a
OMSOSM =+=
Vậy diện tích xung quanh là
4
7
2
7
.
2
.
2
aaa
rlS
xq
π
ππ
===
Chọn C
Câu 38: Tam giác ABC vuông tại A, có
o
AC AC 2a
tan ABC AB 2a 3
AB tan 30
tan ABC
=⇒= = =
Suy ra
(
)
( )
aaaAC
ABBC
4232
2
2
22
=+=
+=
Quay tam giác ABC xung quanh trục AC, ta được hình nón có chiều cao
,4== ACh
bán kính đáy
3== AB
R
(hình vẽ bên)
Vậy diện tích xung quanh hình nón là
3
8
2
aRl
S
xq
π
π
=
=
Chọn C
Câu 39: Ta có
o
CBA 180
ˆ
ˆ
ˆ
=++
mà
=
=
=
⇒=
o
o
o
C
B
A
CBA
30
ˆ
60
ˆ
90
ˆ
1:2:3
ˆ
:
ˆ
:
ˆ
Do đó tam giác ABC vuông tại A
=
=
⇒
20
310
BC
AC
Quay tam giác ABC xung quanh trục AB, ta được hình nón có chiều cao
10== ABh
, bán kính đáy
310=
= ACR
(hình vẽ bên)
Vậy độ dài đường sinh cần tính là
cmBC
l 20
==
Chọn A
Câu 40: Khối nón có độ dài đường sinh
R 12cm= =
Hình nón nhỏ có đường sinh
12=
và bán kính đáy
cm
R
r 4
2
3
2
.
1
==
π
π
Hình nón nhỏ có đường sinh
12=
và bán kính đáy
cm
R
r 8
2
3
2
2.
2
=
−
=
π
π
π
Tỷ số thể tích của khối nón nhỏ so với khối nón lớn là
222
11
1
222
2
22
r. r
V
10
V 10
r. r
−
= =
−
Chọn C
Câu 41: Ba hình quạt, mỗi hình quạt có độ dài cung là:
dmRL
π
π
ϕ
46.
3
2
. ===
Độ dài cung là chu vi đáy của hình nón
dmrrCL 22 =⇒==⇒
π
Chiều cao của hình nón là:
22
h r 4 2dm
= −=
Thể tích của mỗi phễu là
líthrV
2
216
24.2.
33
1
22
ππ
π
===
Chọn B
Câu 42: Phễu chính là khối nón có độ dài đường sinh l = R. Chuẩn hóa R = 1
Gọi h, r lần lượt là chiều cao và bán kính đáy của khối nón
h
rV
2
3
1
π
=⇒
Ta có
222222
1..
33
1
3
1
rrrlrhrV −=−==
π
ππ
Mà
( )
( )
27
32
39
2
1.
327
4
27
1
22
.41.
2
.
2
.41
2
3
2
22
2
22
24
πππ
=≤−=⇒=
−++
≤−=− rrV
r
rr
r
rr
rr
Dấu “=” xảy ra khi và chỉ khi
3
6
3
2
1
2
22
2
=⇔=⇔
−= rr
r
r
Độ dài cung tròn AB là
xRxL == .
chính bằng chu vi đường tròn đáy của khối nón
Khi đó
3
62
22
π
ππ
==⇒=
== rxrCx
L
Chọn D
Câu 43: Xét hình nón được tạo thành, có độ dài đường sinh bằng
Rl
n
=
.
Gọi α (rad) là số đo cung của hình quạt còn lại, khi đó độ dài cung còn lại là
RL
α
=
.
Và L chính là chu vi đường tròn đáy của hình nón
π
α
απ
2
2
R
rRLr
nn
=
⇔==⇒
.
Vậy thể tích khối nón là
2222222
.
3
1
.
3
1
..
3
1
xRxrlrhrV
nnnnn
−=−==
πππ
với
n
rx =
Ta có
( )
( )
3
9
2
33
2
27
.4.
2
.
2
.4
3
max
3
222
6
22
22
2
24
R
V
R
xRx
R
xR
x
x
xRx
π
=⇒≤−⇒≤−=−
Dấu đẳng thức xảy ra khi và chỉ khi
o
n
R
rRxR
x
294
3
8
2
.
.
2
3
2
3
2
2
2222
2
≈=⇔
==⇔−=
πα
π
α
Vậy số đo cung bị cắt là: 3
ooo
66294360 =−
.
Chọn A.
Câu 44: Phễu chính là khối nón có độ dài đường sinh
Rl =
. Chuẩn hóa R = 1.
Gọi h, r lần lượt là chiều cao và bán kính đáy của khối nón
hr
V
2
3
1
π
=
⇒
Ta có
22222
2
1..
33
1
3
1
rrrl
rhrV −=−=
=
π
π
π
Mà
( )
( )
27
3
2
39
2
1.
3
27
4
27
1
2
2
.
41.
2
.
2
.4
1
2
3
2
2
2
2
22
2
4
π
ππ
=≤
−=
⇒=
−
+
+
≤−=
− r
rV
r
rr
r
r
r
rr
Dấu “=” xảy ra khi và chỉ khi
3
6
3
2
1
2
22
2
=⇔=⇔−= rrr
r
Độ dài cung tròn AB là
xRxL == .
chính bằng chu vi đường tròn đáy của khối nón
Khi đó
3
62
22
π
ππ
==⇒=== rxrCxL
Chọn C
Câu 45: Đặt
rCHh
AH ==
;
lần lượt là đường cao và bán kính đáy của hình nón khi quay tam giác ACH
quanh trục AB.
Ta có:
hrV
2
3
1
π
=
. Mặt khác HB = 2R - h
HBHACH .
2
=⇒
(hệ thức lượng)
Suy ra
( )
( ) (
)
[ ]
max
2
max
2
2
2
3
1
2 h
hR
VhR
hV
hR
hr −
⇔⇒
−=⇒
−=
π
Cách 1: Xét hàm số
( ) ( ) ( )
Rh
hhRhf 202
2
<<−=
Cách 2:
( ) ( )
2
3
2
27
2
3
22
2
4
1
2
.
2
.2
4
1
2 R
hh
hR
hh
hRhhR =
++−
≤−=−
Dấu “=” xảy ra
3
22
3
4
4
3
2
2
R
AHrRhhR
h
h
R ==⇒=⇒=⇔=
−⇔
2
1
tan ===⇔
h
r
AH
CH
α
Chọn B
Câu 46: Nếu ba tam giác không trùng lên nhau thì thể tích khối tròn xoay là thể tích của 3 khối nón có chiều
cao
2
3
1
a
h =
và bán kính đáy
8
3
3
1
.3
2
3
1
2
111
a
hrV
a
r
π
π
=
=
⇒=
Thể tích phần bị trồng lên nhau là hai khối nón có chiều cao
4
3
1
a
h =
và bán kính
đáy
96
3
3
1
.2
4
3
1
2
12
1
a
hrV
a
r
π
π
=
=⇒
=
Thể tích cần tìm là:
96
311
3
21
a
VVV
π
=−=
Chọn A
Câu 47: Dựng hình như hình vẽ bên trong đó:
aOAaN
O 3;' =
=
và
10
29a
MA =
Ta có:
'2'
3
1''
SOOO
OA
MO
SO
SO
=⇒=
=
Mặt khác
( )
2
2
'' MOOAOOMA −+
=
2
6
;
20
21
'
10
21
'4'
10
29
22
2
==⇒=⇒+=
⇔ SOaSOaOOaOO
Thể tích V phần còn lại của khối nón là:
( )
322
10
91
'.'.
3
1
aSOMOSOOAV
πππ
=−=
Chọn D.
Câu 48: Ta có:
33
1 R
IA
OD
IA
SO
SI
=
⇒==
, gọi
KABBDACK ∆⇒∩=
vuông cân tại K
32
RAB
KI ==⇒
Tương tự ta có:
3
4
R
KOKI
OIRKO
=
+
=⇒=
.
Mặt khác
RSI
OI
SO
R
SISI
OI
SOSI
2
;
3
2
2
3
1
=+
=
=⇒
=
⇒=
Thể tích phần hình nón (N) nằm giữa mặt phẳng (P) và mặt phẳng chứa đáy hình nón (N) là:
( )
81
52
..
3
1
3
22
R
SIIASOODV
π
π
=−=
Chọn B.
| 1/51
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHỦ ĐỀ 12: MẶT NÓN - HÌNH NÓN - KHỐI NÓN
A. LÝ THUYẾT TRỌNG TÂM
I. ĐỊNH NGHĨA MẶT NÓN
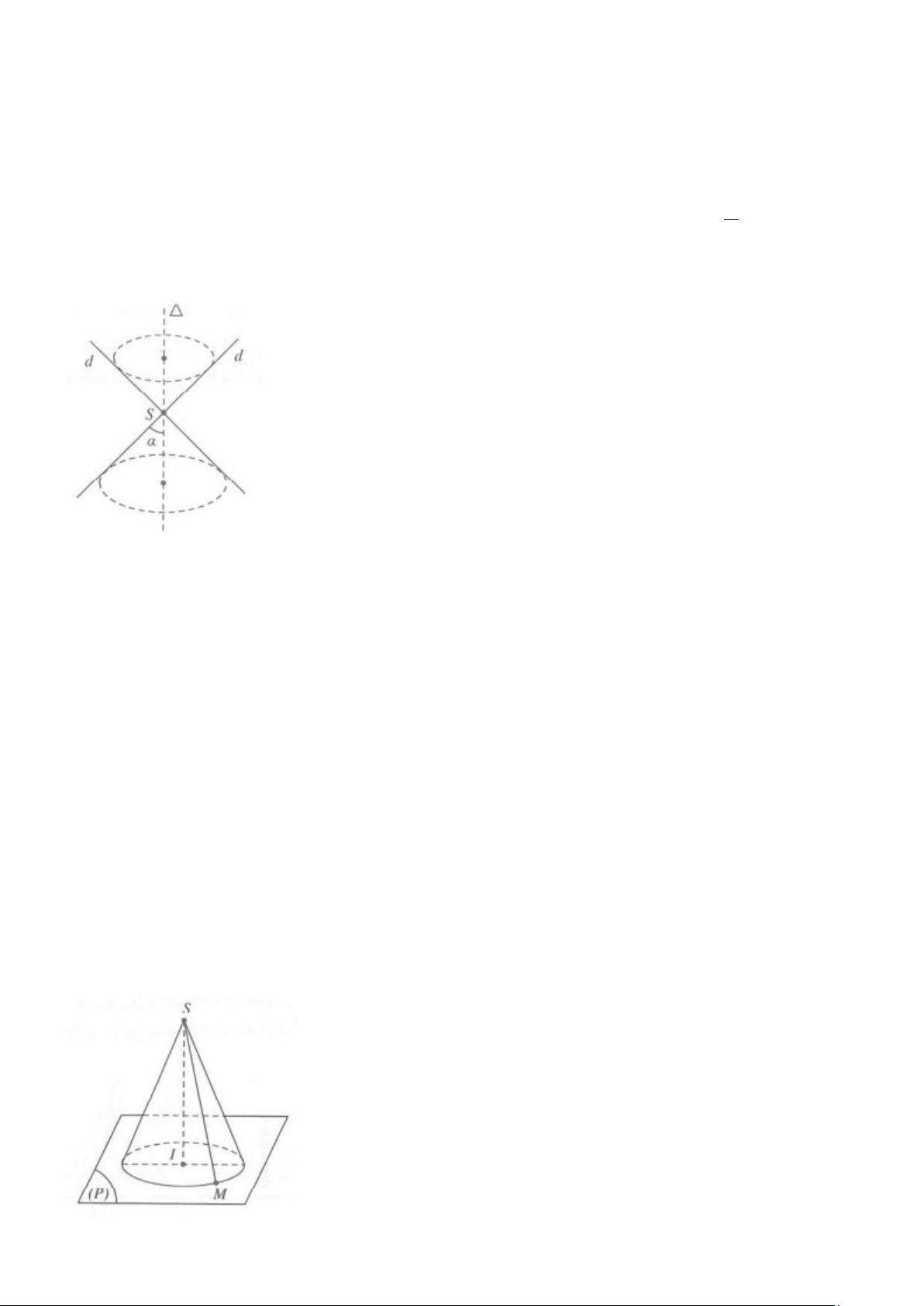
Cho đường thẳng ∆. Xét một đường thẳng d cắt ∆ tại S tạo thành một góc α với π
0 < α < . Mặt tròn xoay 2
sinh bởi đường thẳng d như thế khi quay quanh ∆ gọi là mặt nón tròn xoay (hay đơn giản hơn là mặt nón)
 ∆ gọi là trục của mặt nón
 D gọi là đường sinh của mặt nón
 S gọi là đỉnh của mặt nón
 Góc 2α gọi là góc ở đỉnh của mặt nón (hình vẽ bên)
II. HÌNH NÓN VÀ KHỐI NÓN
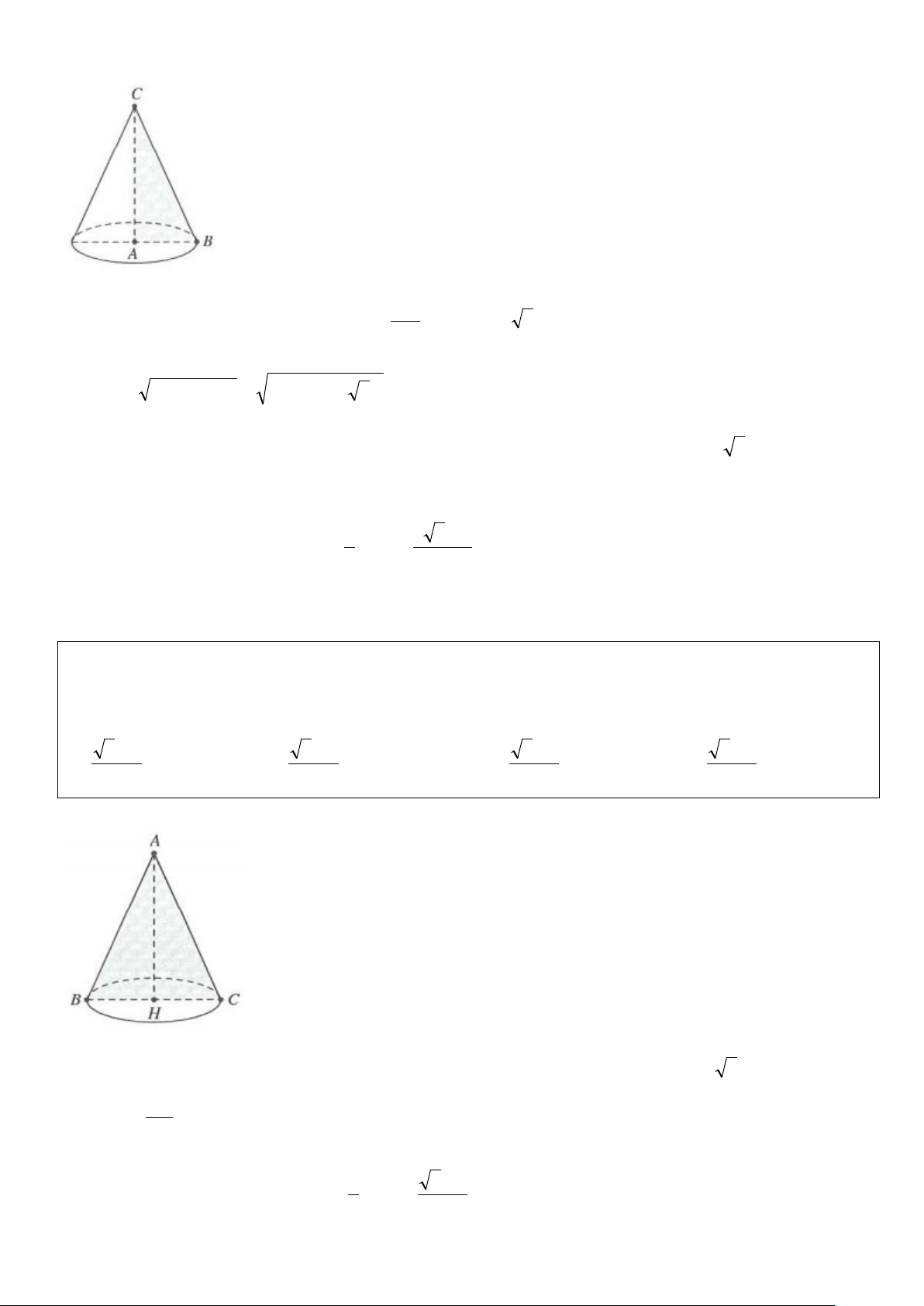
Cho mặt nón (N) với trục ∆ , đỉnh S, góc ở đỉnh 2α
Gọi (P) là mặt phẳng vuông góc với A tại điểm I khác S. Mặt phẳng (P) cắt mặt nón theo một đường tròn
(C) có tâm I. Lại gọi (P’) là mặt phẳng vuông góc với A tại S.
Khi đó: Phần của mặt nón (N) giới hạn bởi hai mặt phẳng (P) và (P’) cùng với hình tròn xác định bởi (C)
được gọi là hình nón:
 S gọi là đỉnh của hình nón
 Đường tròn (C) gọi là đường tròn đáy của hình nón
 Với mỗi điểm M nằm trên đường tròn (C), đoạn thẳng SM gọi là đường sinh của hình nón
 Đoạn thẳng SI gọi là trục của hình nón (đó chính là khoảng cách từ đỉnh S đến mặt đáy)
 Một hình nón chia không gian thành hai phần: phần bên trong và phần bên ngoài của nó. Hình nón
cùng với phần bên trong của nó gọi là khối nón
III. KHÁI NIỆM VỀ DIỆN TÍCH HÌNH NÓN VÀ THỂ TÍCH KHỐI NÓN
Một hình chóp gọi là nội tiếp hình nón nếu:
- Đáy của hình chóp là đa giác nội tiếp đáy của hình nón
- Đỉnh của hình chóp là đỉnh của hình nón 1. Định nghĩa.
Diện tích xung quanh của hình nón là giới hạn của diện tích xung quanh của một hình chóp đều nội tiếp
hình nón đó khi số cạnh đáy tăng lên vô hạn
Thể tích của khối nón là giới hạn của thể tích khối chóp đều nội tiếp khối nón đó khi số cạnh tăng lên vô hạn
2. Diện tích xung quanh, diện tích toàn phần của hình nón
Diện tích xung quanh: S = π xq Rl Diện tích toàn phần: 2 S = + = π +π tp Sxq Sđ Rl R
Trong đó , R, l lần lượt là bán kính đáy và đường sinh của hình nón
3. Thể tích của khối nón
Thể tích của khối nón có bán kính đáy R và chiều cao h là V 1 = R2 π h 3
4. Mối liên hệ giữa chiều cao, đường sinh và bán kính đáy
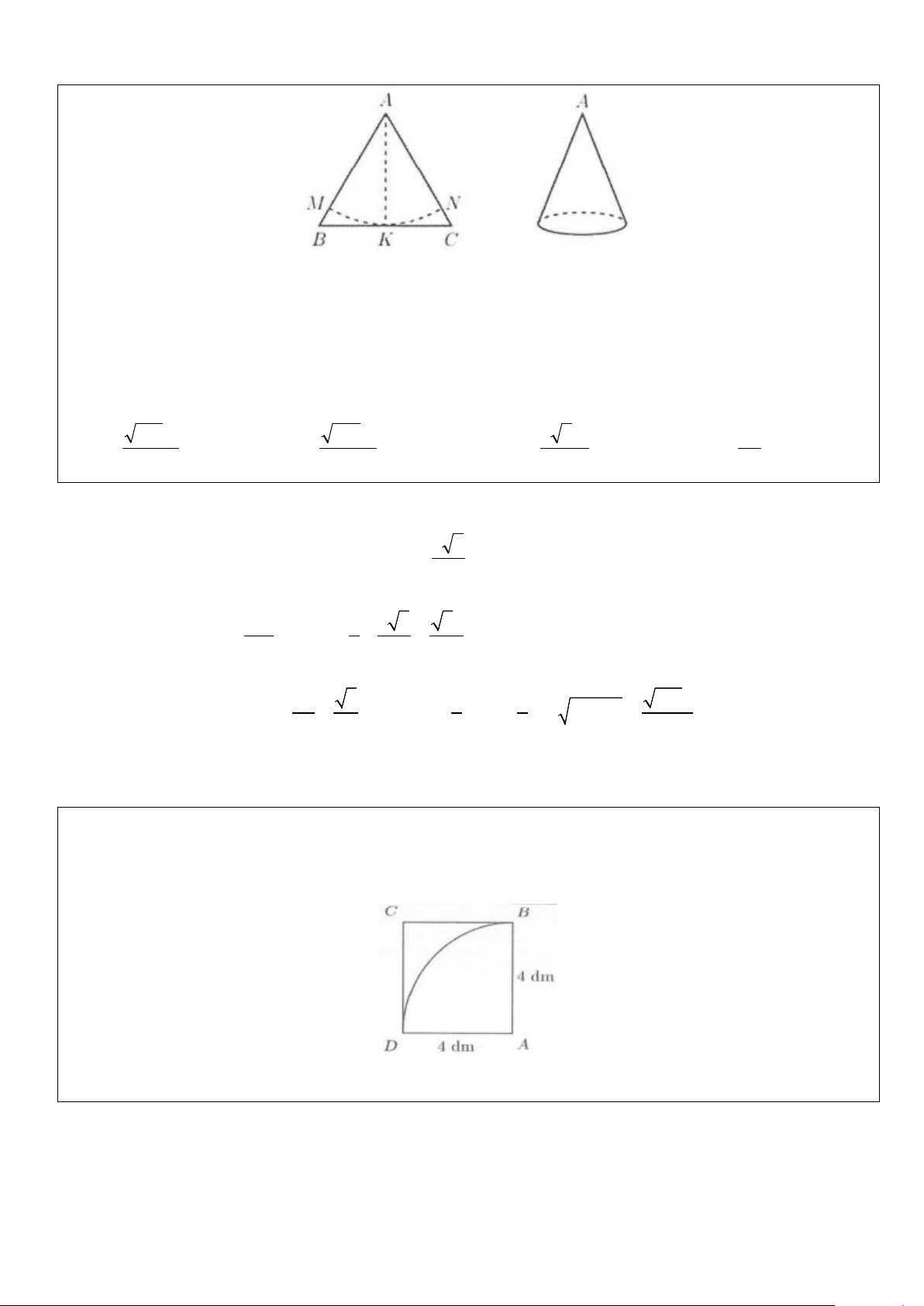
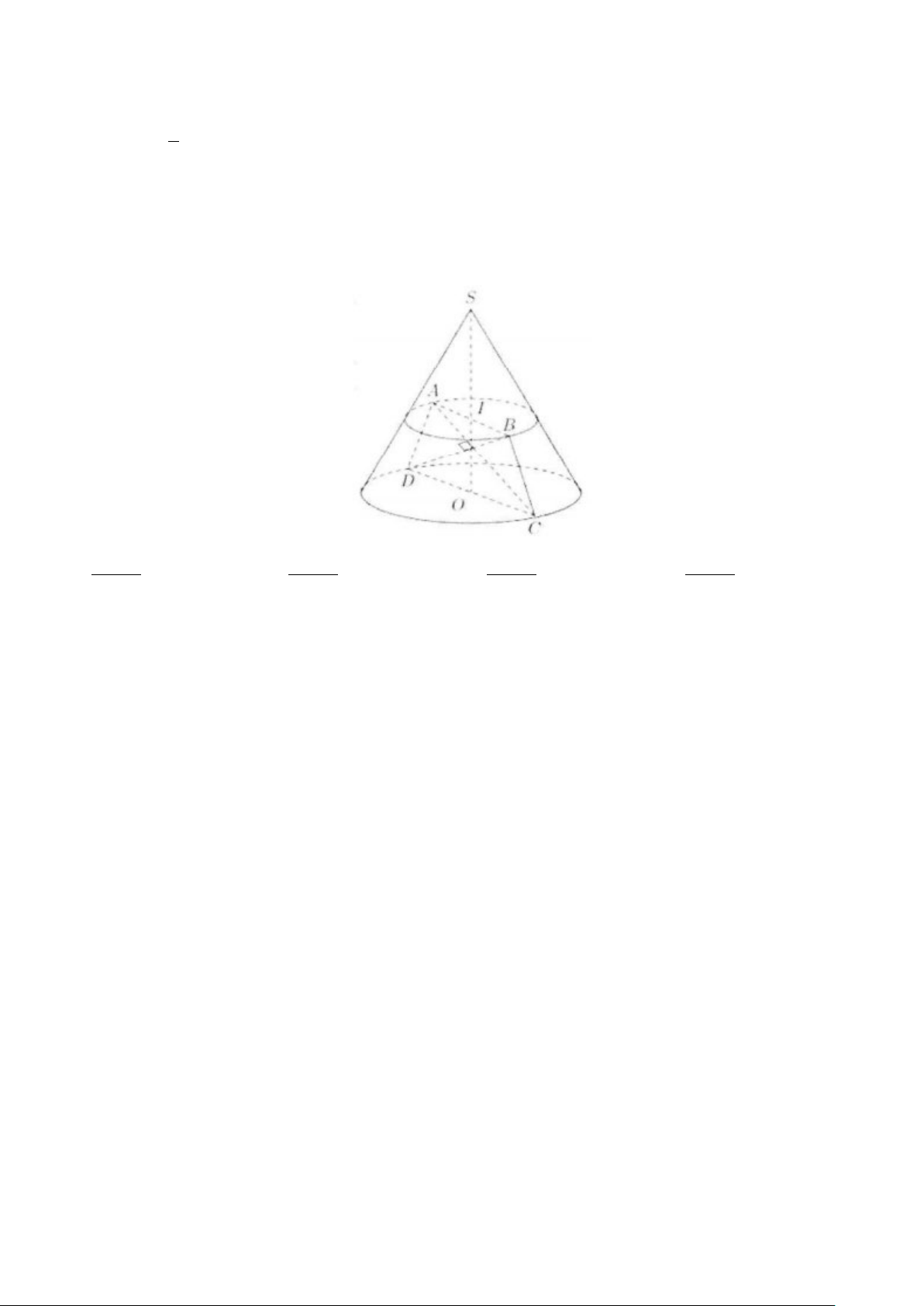
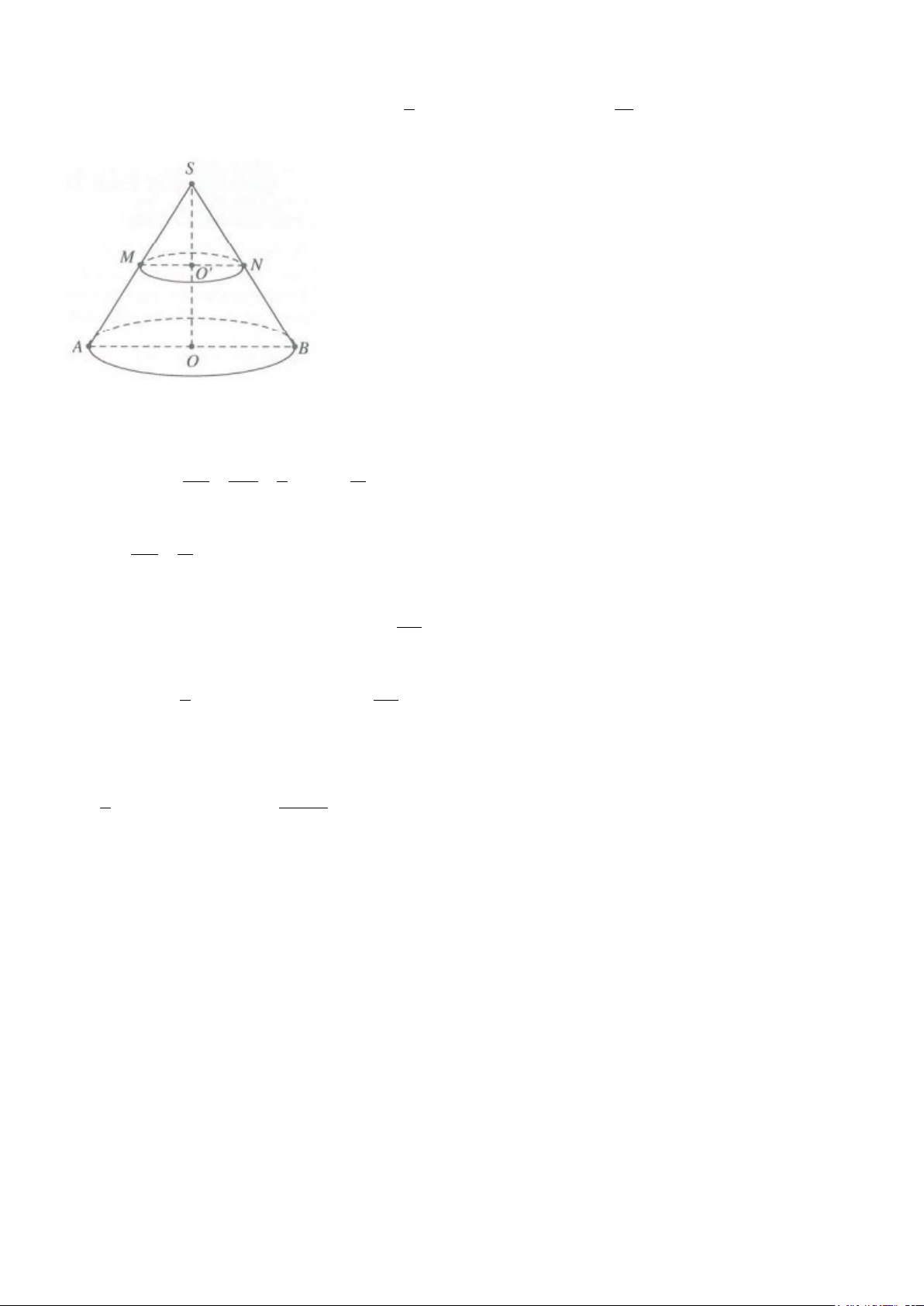
Tam giác SAO vuông tại A, có 2 2 2
SA = SO + OA Do đó 2 2 2
l = h + R (tham khảo hình vẽ bên)
IV. VỊ TRÍ TƯƠNG ĐỐI CỦA HÌNH NÓN VỚI MỘT MẶT PHẲNG QUA ĐỈNH CỦA NÓ
Cho một hình nón (N) và một mặt phẳng (P) đi qua đỉnh S của hình nón.
Có ba vị trí tương đối giữa (P) và (N)
 (P) và (N) có một điểm chung duy nhất
 (P) và (N) có chung một đường sinh duy nhất. Khi đó (P) tiếp xúc với (N) và (P) gọi là tiếp diện của (N)
 (P) và (N) có chung hai đường sinh (Hình 1). Nếu (P) chứa trục của hình nón thì thiết diện của (P) và
hình nón gọi là thiết diện qua trục (Hình 2)
 Thiết diện qua trục của hình nón là tam giác cân có cạnh bên SA = l, cạnh đáy AB = 2R
B. CÁC DẠNG TOÁN TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. Bài toán liên quan đến công thức diện tích, thể tích
Ví dụ 1: Diện tích xung quanh hình nón có bán kính đáy R = 3, chiều cao h = 4 bằng A. 12π B. π 6 C. π 15 D. π 9 Lời giải Độ dài đường sinh 2 2
l = R + h = 32 + 42 = 5
Vậy diện tích xung quanh hình nón là S = π . Chọn C xq Rl = π 15
Ví dụ 2: Cho hình nón (N) có bán kính đáy bằng 4, diện tích xung quanh bằng 20π . Thể tích khối nón đã cho bằng A. π 4 B. π 8 C. π 20 D. π 16 Lời giảiR = 4 R = 4 R = 4 Theo giả thiết, ta có  ⇔  ⇔  S = π xq 20  R π l = 20π l = 5 Lại có: 2 2 2 2 2
l = h + R → h = l − R = 52 − 42 = 3
Vậy thể tích khối nón (N) là 1 2 π 2 ( V N ) = πR h = 4 . 3 . = π 16 3 3 Chọn D
Ví dụ 3: Cho hình nón (N) có diện tích xung quanh bằng π
2 , diện tích toàn phần bằng π 3 . Thể tích khối nón đã cho bằng A. 3 π B. 3 π C. 6 π D. 3 π 3 6 6 2 Lời giải
Diện tích xung quanh hình nón là S = π π xq
Rl = 2 ↔ Rl = 2
Diện tích toàn phần hình nón là 2 S = π π π tp Rl + R = 3 2 ↔ Rl + R = 3 Rl = 2 2 R =1 R =1 Do đó 2 2  ⇔  ⇔ 
→ h = l − R = 3 2 Rl + R = 3 Rl = 2 l = 2
Vậy thể tích khối nón (N) là 1 2 π 2 3 ( V N ) = πR h = 1 . . 3 = π 3 3 3 Chọn A
Ví dụ 4: Cho hình nón (N) có góc ở đỉnh bằng 60°, độ dài đường sinh bằng 4. Thể tích khối nón đã cho bằng A. 4 3π B. 8 3π C. 2 π 3 D. 3π 3 3 2 Lời giải
Vì góc ở đỉnh của hình nón bằng 60° l = 2R = 4 ⇒ R = 2 Ta có 2 2 2 2 2
h + R = l ⇒ h = l − R = 42 − 22 = 2 3
Vậy thể tích khối nón đã cho là 1 2 1 2 8 3π V = πR h = π 2 . 2 . 3 = . 3 3 3 Chọn B.
Ví dụ 5: Trong không gian, cho tam giác AC vuông tại A, AB = a và AC = a 3 . Độ dài đường sinh l của
hình nón nhận được khi quay tam giác ABC xung quanh trục AB bằng
A. l = a
B. l = a 2
C. l = a 3
D. l = 2a Lời giải
Kỹ năng vẽ hình: Tam giác quay quanh cạnh nào thì cạnh đó là trục, động thời chính là chiều cao của hình nón
Quay tam giác ABC xung quanh trục AB, ta được hình nón có chiều cao h = AB = a, bán kính đáy
R = AC = a 3 (hình vẽ bên)
Do đó, độ dài đường sinh là l = h2 + R2 = 2a . Chọn D.
Ví dụ 6: Trong không gian, cho tam giác ABC vuông tại A, góc ABC = 60°, BC = 4a. Thể tích khối nón
nhận được khi quay tam giác ABC xung quanh trục AC bằng 3 3 3 3 A. 4 3 a π B. 8 3 a π C. 8 3 a π D. 4 3 a π 3 3 9 9 Lời giải
Tam giác ABC vuông tại A, có sin ˆ AC C B A = ⇒ AC = 2a 3 BC
Và AB = BC2 − AC2 = (4a) − (2a 3)2 2 = 2a
Quay tam giác ABC xung quanh trục AC, ta được hình nón có chiều cao h = AC = 2a 3 , bán kính đáy
R = AB = 2a (hình vẽ bên) 3
Vậy thể tích khối nón cần tìm là 1 2 8 3 a π V = R π h = 3 3 Chọn B
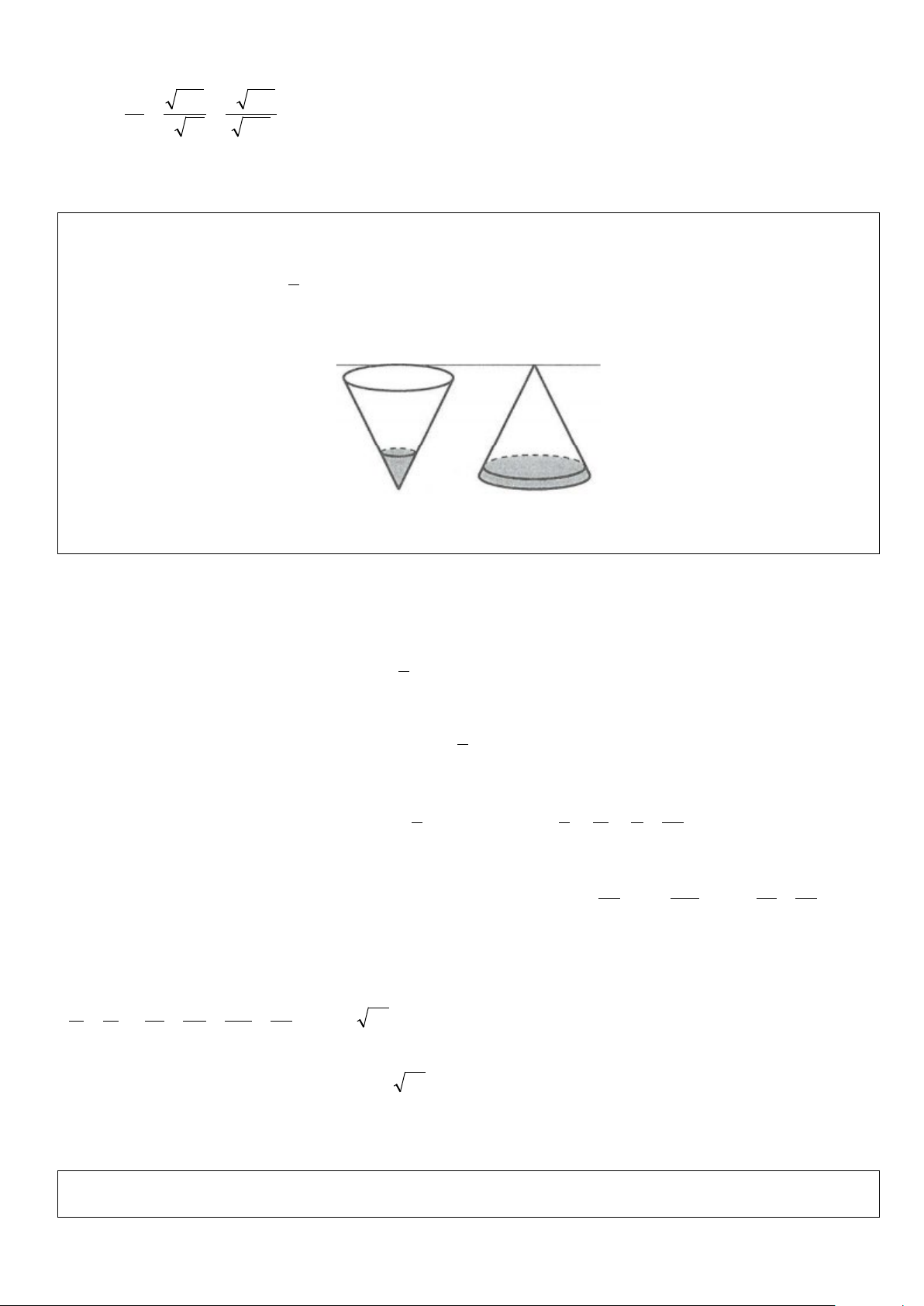
Ví dụ 7: Trong không gian, cho tam giác ABC đều cạnh 2a. Gọi H là trung điểm của BC. Thể tích của khối
nón nhận được khi quay tam giác ABC xung quanh trục AH bằng A. 3 3 a π B. 3 3 a π C. 3 3 a π D. 3 3 a π 9 2 3 6 Lời giải
Quay tam giác ABC quanh trục AH, ta được hình nón có chiều cao h = AH = a 3 , bán kính đáy BC R = BH = = a (hình vẽ bên) 2 3
Vậy thể tích khối nón cần tính là 1 2 3 a π V = R π h = 3 3 Chọn C
Ví dụ 8: Trong không gian, cho tam giác ABC vuông tại A, AB = 3a, BC = 5a. Thể tích khối tròn xoay
nhận được khi quay tam giác ABC xung quanh trục BC bằng A. 36 3 a π B. 48 3 a π C. 16 3 a π D. 48 3 a π 5 25 5 5 Lời giải
Gọi H là hình chiếu vuông góc của A trên BC
Tam giác ABC vuông tại A, có AC = BC2 − AB2 = 4a Suy ra 1 1 1 1 1 12a = + = + ⇒ AH = 2 2 2 AH AB AC (3a)2 (4a)2 5
Quay tam giác ABC quanh trục BC, ta được hai hình nón có chiều cao lần lượt là h = , và 1 BH h = 2 CH
bán kính đáy R = AH (hình vẽ bên)
Vậy thể tích khối tròn xoay cần tính là V = V + V 1 2 3 1 2 1 2 1 2 ( ) 1 2 48 a R h R h R h h .AH .BC π = π + π = π + = π = 1 2 1 2 3 3 3 3 5 Chọn D.
Ví dụ 9: Trong không gian, cho hình thang ABCD vuông tại A và D, AB = AD = a, CD = 2a. Thể tích khối
tròn xoay nhận được khi quay hình thang ABCD xung quanh trục AD bằng A. 7 3 a π B. 5 3 a π C. 4 3 a π D. 8 3 a π 3 3 3 3 Lời giải
Quay hình thang ABCD quanh trục AD, ta được khối nón cụt có hai bán kính đáy lần lượt là R = , và chiều cao h = AD 1 AB R = 2 CD 1
Công thức tính thể tích nón cụt V = h π ( 2 2 R + R + R R 1 2 1 2 ) 3
được phát triển từ công thức thể tích tổng
quát của khối có hai đáy song song 3
Vậy thể tích cần tính là 1 π V = a π [. 2
a + (2a)2 + a ] 7 2 . a a = 3 3 Chọn A.
Ví dụ 10: Trong không gian, cho hình thang ABCD có AB//CD và AB = AD = BC =a, CD = 2a. Thể tích
khối tròn xoay nhận được khi quay hình thang ABCD xung quanh trục AB bằng A. 5 3 a π B. 3 a π C. 5 3 a π D. 5 3 a π 3 4 2 Lời giải
Thể tích khối tròn xoay khi quay hình thang ABCD quanh trục AB ta được khối tròn xoay có thể tích V tạo bởi hai khối:
 Khối trụ tròn xoay có chiều cao h = CD = MN =2a và bán kính đường tròn đáy 2 2 a 3
R = DN = DA − NA = ( như hình vẽ bên ). 2 a
 Thể tích khối trụ trên trừ đi thể tích 2.V2 của hai khối nón có chiều cao h = và bán kính đường 2 2 tròn đáy a 3 R = DN = . 2 2 2
Vậy thể tích khối tròn xoay cần tính là 3a 2 a 3a 5 3 V = V − 2.V = .2a π . − . . π . = a π 1 2 4 3 2 4 4 Chọn C
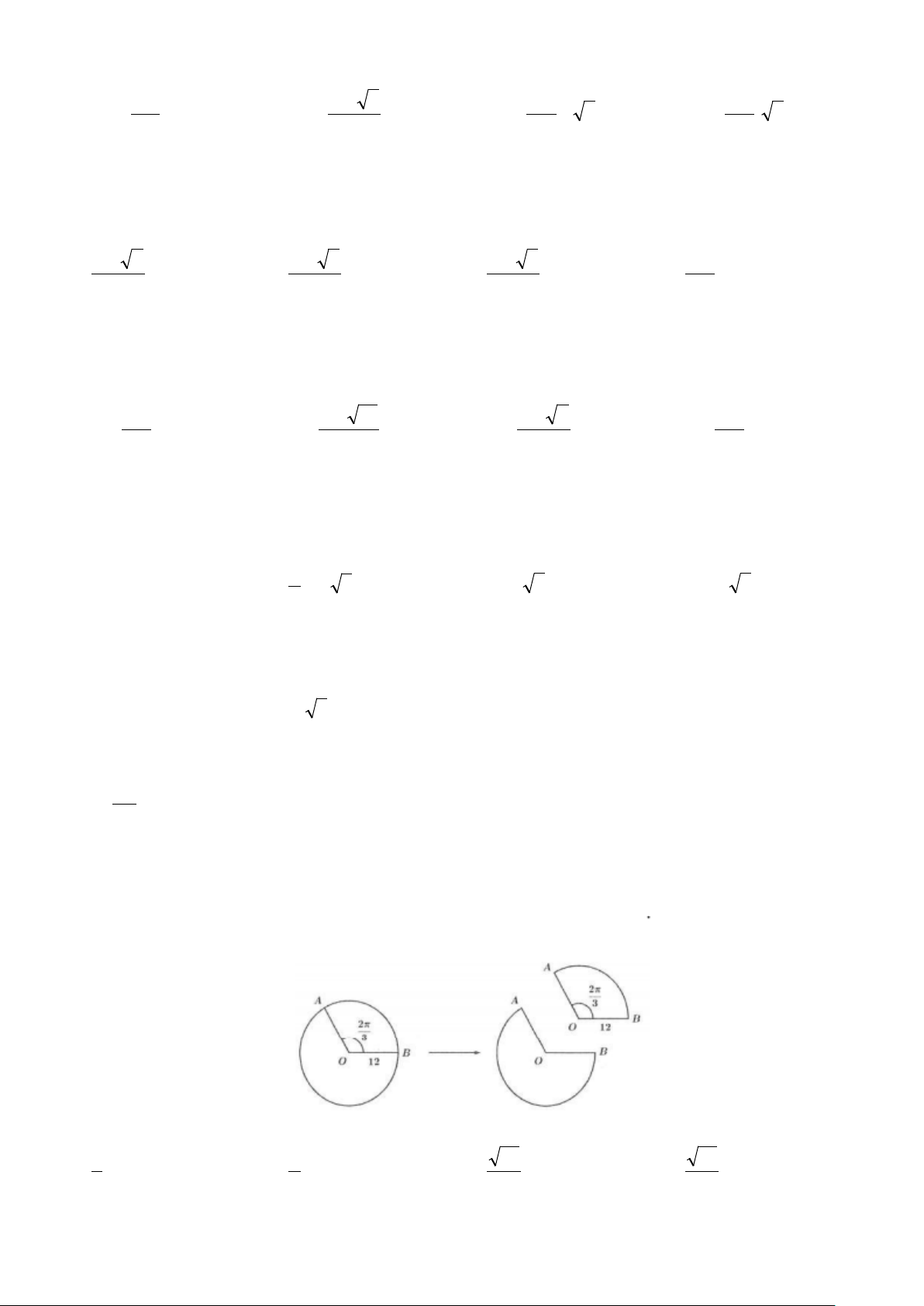
Ví dụ 11: Người thợ gia công của một cơ sở chất lượng cao X cắt một miêng tôn hình tròn với bán kính 60
cm thành ba miếng hình quạt bằng nhau. Sau đó người thợ ấy quấn và hàn ba miệng tôn đó để được ba cái
phễu hình nón. Thể tích của mỗi cái phễu bằng A. 8 2π lít B. 16 2π lít C. 1600 2π lít D. 32 2π lít 3 3 3 3 Lời giải
Khi quấn hình quạt để tạo thành một hình nón, ta được
 Đường sinh hình nón bằng bán kính hình quạt l = R = 60cm 1
 Chu vi đáy hình nón bằng độ dài cung hình quạt C = 2 r π = 2 . π 60 . ⇒ r = 20 3
Do đó, chiều cao của hình nón là h = l2 − r2 = 602 − 202 = 40 2cm
Vậy thể tích của mỗi cái phễu là 1 2 1 2 1600 2π 2 16 2π
V = πr h = π 20 . 40 . 2 = cm = lít. 3 3 3 3 Chọn B.
Ví dụ 12: Có một miếng tôn hình tam giác đều ABC cạnh 3 dm (như hình vẽ).
Gọi K là trung điểm của BC. Người ta dùng compa có tâm là A và bán kính AK vạch ra cung tròn MN (M,
N theo thứ tự thuộc cạnh AB và AC) rồi cắt miếng tôn theo cung tròn đó. Lấy phần hình quạt người ta gò
sao cho cạnh AM và AN' trùng nhau thành một cái phếu hình nón không đáy với đỉnh A. Tính thể tích V của cái phễu. A. 14 . 1π 3 π π π V = dm B. 105. 3 V = dm C. 3 3. 3 V = dm D. 3 3 V = dm 64 64 32 64 Lời giải
Độ dài đường sinh của phễu là 3 3 l = N AM = AK = 2 Độ dài cung MN là 60 1 3 3 3  .2 .AK . π = π = π = (dm) 360 3 2 2
Bán kính đáy của phễu là  3 r π = = suy ra 1 2 1 2 2 2 105 V = r π h = r π .  − r = ( 3 dm N ) 2π 4 3 3 64 Chọn B.
Ví dụ 13: Từ miếng tôn hình vuông cạnh bằng 4 dm, người ta cắt ra hình quạt tâm A bán kính AB = AD =
4 dm (xem hình) để cuộn lại thành một chiếc phễu hình nón (khi đó AB trùng với AD). Chiều cao của chiếc
phễu có số đo gần đúng (làm tròn đến 3 chữ số thập phân) là A. 3,872 dm B. 3,874 dm C. 3,871 dm D. 3,873 dm Lời giải
Chu vi của đáy hình nón có độ dài bằng cung BD. Độ dài cung BDlà: 1 π l = (. π 2 .4) = π
2 . Suy ra bán kính đường tròn đáy hình nón là : 2 r = = 1 4 2π
Độ dài đường sinh của hình nón là 2 2
 = 4dm ⇒ h =  − r = 3,873dm . Chọn D.
Ví dụ 14: Từ một tấm kim loại dẻo hình quạt (như hình vẽ) có bán kính R= 13 và chu vi hình quạt là P = π
12 , người ta gò tấm kim loại đó thành những chiếc phễu hình nón theo hai cách:
Cách 1: Gò tấm kim loại ban đầu thành mặt xung quanh của một cái phễu.
Cách 2: Chia đôi tấm kim loại thành hai phần bằng nhau rồi gò thành mặt xung quanh của hai cái phễu. Gọi V V
1 là thể tích của cái phễu ở cách 1, V2 là tổng thể tích của hai cái phễu ở cách 2. Tính tỉ số 1 V2 A. V V V V1 5 1 2 160 1 2 133 1 133 = B. = C. = D. = V V V V2 2 2 160 2 160 2 133 Lời giải
Theo cách 1 ta có: Độ dài đường sinh của hình nón là: 12π
 =13, chu vi đáy r = = 6 2π
Khi đó thể tích của chiếc phễu là: 1 2 2 2 V = r π  − h =12π 133 1 3
Theo cách 2 ta có: Độ dài đường sinh của hình nón là: 6π
 =13, chu vi đáy mỗi phễu là: r = ⇒ r = 3 2 r π
Khi đó tổng thể tích của hai chiếc phễu là: 2 2 2 2 V = r π  − h = 24π 10 2 3 Quy ra V1 133 2 133 = = V2 2 10 160 Chọn D.
Ví dụ 15: Một cái phễu có dạng hình nón. Người ta đổ một lượng nước vào phễu sao cho chiều cao của
lượng nước trong phễu bằng 1 chiều cao của phễu. Hỏi nêu bịt kín miệng phễu rồi lộn ngược phễu lên thì 3
chiều cao nước xấp xỉ bằng bao nhiêu? Biết rằng chiều cao của phễu là 15 cm A. 0,5 cm B. 0,3 cm C. 0,188 cm D. 0,216 cm Lời giải
Gọi bán kính đáy của phễu là R, chiều cao của phễu là h = l5 em
Vì chiều cao nước trong phễu ban đầu bằng 1 h 3
Suy ra bán kính đáy hình nón tạo bởi lượng nước là 1 R 3 2
Thể tích phễu và thể tích nước lần lượt là 1 2 2 1  R h 5 2 V = R π h = 5 R π ,V = π   . = R π 1 3 3  3  3 27
Do đó, thể tích phần khối nón không chứa nước là 2 5 2 130 2 V 26
V = V −V = R π − R π = R π ⇒ = 2 1 5 2 27 27 V 27
Gọi h’ và r lần lượt là chiều cao và bán kính đáy của khối nón không chứa nước 3 3 h' r V h' h' 26 2 3 = ⇒ = = = → h'= 5 26 3 3 h R V h 15 27
Vậy chiều cao cần tính là h = − '=15 − 53 26 = 18 , 0 8 o h h cm Chọn C.
Ví dụ 16: Bạn Hùng có một tấm bìa hình tròn như vẽ bên dưới, Hùng muốn biến hình tròn đó thành một cái
phễu hình nón. Khi đó bạn Hùng phải cắt bỏ hình quạt tròn AOB rồi dán hai bán kính OA và OB lại với
nhau (diện tích chỗ dán nhỏ không đáng kể). Gọi x là góc ở tâm hình quạt dùng làm phễu. Tìm x để thể tích phễu lớn nhất? A. 2 3π B. 2 6π C. 3π D. 3π 3 3 2 6 Lời giải
Gọi R, h lần lượt là bán kính đáy, chiều cao của hình nón Thể tích khối nón là 1 2 π 2 2 2 V = R
π h = R . l − R 3 3 3 2 2  R R  2 2 + + l − R 2 2   4 2 2 R R 2 2  2 2 6
Ta có: R (l − R )= 4. . (.l − R )  4 ≤ . 4 l = 2 2 27 27 6 3 3 π Do đó 2 R (. 2 2 l − R ) 4l 2 3l 2 3 l ≤ = ⇒ V ≤ 27 9 27 2
Dấu bằng xảy ra khi R 2 2 2 3 2 R 6
= l − R ⇔ l = R ⇔ l = (1) 2 2 2
Hình nón nhận được là có đường sinh l = OA, chu vi đáy là độ dài cung AB Vì π =  x AOB ⇒ độ dài cung 2 R
AB = OA× x = lx ⇒ 2 R π = lx ⇒ x = (2) l Từ (1), (2) suy ra R 2 2 6π x = 2π. = 2π. = . l 6 3 Chọn B.
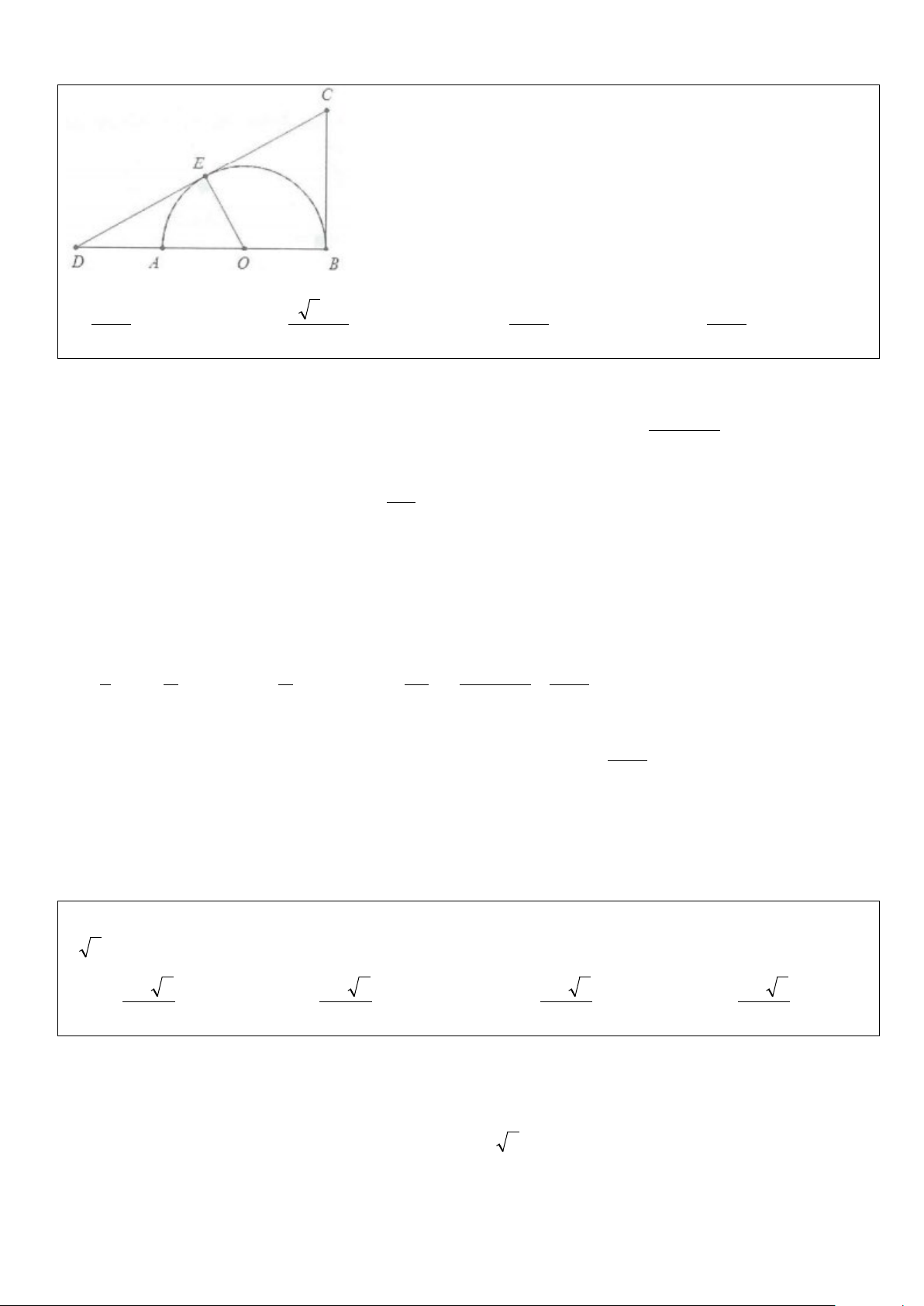
Ví dụ 17: Cho nửa đường tròn đường kính AB = 2R, kí hiệu A là đường thắng vuông góc với AB tại B.
Trên nửa đường tròn lấy điểm E di động, tiếp tuyến của nửa đường tròn tại E và cắt tia đối của tia AB tại D
và cắt ∆ tại C (như hình vẽ dưới). Khi quay tam giác BCD quanh trục AB ta được khối tròn xoay có thể tích nhỏ nhất là ? 3 A. 8 3 R π B. 8 3 R π C. 8 3 R π D. 8 3 R π 27 9 3 9 Lời giải Đặt  = α ⇒ α ∈( o o BOC
45 ;90 ) ⇒ tan α >1, chú ý công thức tan sau 2 tanα tan α 2 = 2 1− tan α
Tam giác OBC vuông tại B, có  BC tan BOC = ⇒ BC = R.tan α BO Ta có  = ( o − α) ⇒ = ( o BCD 2 90
BD BC.tan 180 − 2α) = −BC.tan 2α .
Khi quay tam giác BCD quanh trục AB ta được khối tròn xoay có thể tích là 1 2 π 2 π 2 2π tan4 3 α 8 3 π V = r
π h − .BC .BD = − .BC .tan 2α = . . R R ≥ 3 3 3 3 tan2 α −1 3 Vì π tan4 α ≥ 4(tan2 α − ) 1 ⇔ (tan α − 2)2 2 ≥ ; 0 ∀α ∈( o o 45 90 ; ). Vậy 8 3 R V = min 3 Chọn C.
Dạng 2. Bài toán về thiết diện qua đỉnh nón
Ví dụ 1: Cắt hình nón bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác có cạnh huyền bằng
a 6 . Thể tích V của khối nón đã cho bằng 3 3 3 3 A. a π 6 π π π V = B. a 6 V = C. a 6 V = D. a 6 V = 4 3 6 2 Lời giải
Thiệt diện qua trục hình nón là tam giác cân SAB có cạnh bên SA = l, cạnh đáy AB = 2R Theo bài ra, ta có 2 2 2
SA + SB = AB ⇔ 2 2 l = 4 2
R ⇔ l = R 2
Mặt khác AB = 2R = a 6 ⇒ R = a 6 suy ra a 6 l = . 2 = a 3 2 3 Do đó 2 2 a 6 1 2 a π 6
h = l − R = →V = R π h = 2 3 4 Chọn A.
Ví dụ 2: Thiết diện qua trục của hình nón (N) là tam giác vuông cân và có diện tích bằng a2. Diện tích xung
quanh của hình nón đã cho bằng A. 2 S = π B. 2 S = π C. 2 S = π D. 2 S = π xq 2 2 a xq 4 a xq 2 a xq 2 a Lời giải
Thiết diện qua trục hình nón là tam giác cân SAB có cạnh bên SA = l, cạnh đáy AB =2R 2 2
Theo bài ra, tam giác SAB vuông SA l 2
⇒ SA ⊥ SB ⇒ S = = = ⇒ = SA ∆ B a l a 2 2 2 Do đó l
l = R 2 ⇒ R =
= a . Vậy diện tích cần tìm là 2 S = π = π . Chọn B. xq Rl 2 a 2
Ví dụ 3: Cho hình nón đỉnh S, đáy là hình tròn tâm O, thiết diện qua trục là tam giác đều cạnh a. Thể tích
của khối nón đã cho là 3 3 3 3 A. a π 3 B. a π 3 C. a π 3 D. a π 3 8 6 24 12 Lời giải
Theo bài ra, tam giác SAB đều cạnh a ⇒ SA = SB = AB = a Do đó, chiều cao a 3 SO = , bán kính đáy AB a R = = 2 2 2 2 3
Vậy thể tích cần tính là 1 2 π  a a 3 a π 3 V = R π h = .  . = 3 3  2  2 24 Chọn C
Ví dụ 4: Cho hình nón (N) có bán kính đáy bằng 9 cm, góc giữa đường sinh và mặt đáy là 30o. Diện tích
thiết diện qua trục của hình nón (N) bằng A. 2 9 3cm B. 2 18 3cm C. 2 6 3cm D. 2 27 3cm Lời giải
Theo bài ra, tacó AB = 2R =18 và  o SAO = 30
Tam giác SAO vuông tại O, có =  o SO OA.tanSAO = 9.tan 30 = 3 3
Thiết diện qua trục hình nón là tam giác cân SAB
Suy ra diện tích cần tính là 1 1 2 S = = = SA ∆ B . SO AB 3 . 3.18 27 3cm 2 2 Chọn D
Ví dụ 5: Thiết diện qua trục của hình nón (N) là tam giác có chu vi bằng 10 cm, diện tích bằng 2 2 5cm .
Tính thể tích khối nón (N), biết rằng bán kính là số nguyên dương. A. 2 5π 2 π π cm B. 4 5 2 cm C. 8 5 2 cm D. 2 2 5 c π m 3 3 3 Lời giải 2l + 2R =10  l + R = 5 l = 5 − R Theo bài ra, ta có  1 ⇔  ⇔   h 2 . R = 2 5  . h R = 2 5  . 2 R l − 2 R = 2 5 2 Do đó 2 R . ([5 2 − R ) 2 − R ]= 20 2
⇔ R (25 −10R) = 5 ⇔ 10 3 R − 25 2
R + 20 = 0 ⇒ R = 2 Suy ra π
h = 5 Vậy thể tích cần tính là 1 2 1 2 4 5 3 V = R π h = π.2 . 5 =
cm . Chọn B 3 3 3
Ví dụ 6: Hình nón (N) có đỉnh S, tâm đường tròn đáy là O, góc ở đỉnh bằng 120o. Một mặt phẳng qua S cắt
hình nón (N) theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách giữa hai đường thẳng AB và
SO bằng 3. Tính diện tích xung quanh S của hình nón (N) xq A. S = B. S = C. S = D. S = xq 27 π 3 xq 36 π 3 xq 9 π 3 xq 18 π 3 Lời giải Vì góc ở đỉnh bằng o
120 ⇒ 2R = l 3 ⇒ SA 2 3 = OA 2 3 = R 3 3
Gọi H là trung điểm của AB⇒ OH ⊥ AB mà SO ⊥ OH
Suy ra OH là đoạn vuông góc chung của AB và SO => OH =3
Tam giác OAH vuông tại H, có 2 2 2
AH = OA − OH = R − 9
Tam giác SAB vuông tại S, có 2 2 2
SA + SB = AB  2 3 2 ⇔ . 2 R = 4( 2 R − ) 4 9 2 ⇔ − R = 36
− ⇒ R = 3 3 ⇒ l = 6   3   3
Vậy diện tích xung quanh cần tính là S = π . xq Rl =18 π 3 Chọn A.
Ví dụ 7: Cho hình nón đỉnh S có đáy là hình tròn tâm O, bán kính R. Dựng hai đường sinh SA và SB, biết
AB chắn trên đường tròn đáy một cung có số đo bằng 60°, khoảng cách từ tâm O đến mặt phẳng (SAB)
bằng R . Đường cao h của hình nón bằng 2 A. R 2 B. R 6 C. R 3 D. R 3 4 2 Lời giải
Theo giả thiết, ta có tam giác OAB đều cạnh R
Gọi E là trung điểm AB, suy ra OE ⊥ AB và R 3 OE = 2
Gọi h là hình chiếu của O trên SE ⇒ OH ⊥ SE AB ⊥ OE Ta có 
⇒ AB ⊥ (SEO)⇒ AB ⊥ OH AB ⊥ SO
Từ đó suy ra OH ⊥ (SAB) nên d( ; O (SAB) R = OH = 2
Tam giác SEO vuông tại O, có 1 1 1 8 R 6 = − = ⇒ SO = 2 2 2 SO OH OE 3 2 R 4 Chọn B
Ví dụ 8: Cho hình nón đỉnh S có đáy là hình tròn tâm O. Dựng hai đường sinh SA và SB, biết tam giác
SAB vuông và có diện tích bằng 2
4a . Góc tạo bởi giữa trục SO và mặt phẳng (SAB) bằng 30o. Đường cao h của hình nón bằng A. a 2 B. a 6 C. a 3 D. a 3 4 2 Lời giải
Theo giả thiết, ta có tam giác SAB vuông cân tại S SE ⊥ AB
Gọi E là trung điểm AB, suy ra 1  và SE = AB OE ⊥ AB 2 Ta có S 1 2 1 1 = ∆ . = 4 ⇔ . = 4 2 ⇒ = 4 SAB AB SE a AB AB a AB a 2 2 2
Gọi H là hình chiếu của O trên SE => OH ⊥ SE AB ⊥ OE Lại có 
⇒ AB ⊥ (SEO)⇒ AB ⊥ OH AB ⊥ SO Từ đó suy ra ⊥ ( ) ⇒ ( ( ))  =  o OH SAB SO; SAB OSH = 30
Tam giác SEO vuông tại O, có =  SO SE.cosOSE = a 3 . Chọn D.
Ví dụ 9: Cho hình nón đỉnh S, đường cao SO. Gọi A, B là hai điểm thuộc đường tròn đáy của hình nón sao
cho khoảng cách từ O đến AB bằng a và  o =  o
SAO 30 ,SAB = 60 . Độ dài đường sinh l của hình nón bằng
A. l = a
B. l = a 3
C. l = a 2
D. l = 2a Lời giải
Gọi I là trung điểm AB, suy ra OI ⊥ AB, SI ⊥ AB và OI = a
Tam giác SAO vuông tại O, có =  SA 3 OA SA.cosSAO = 2
Tam giác SAI vuông tại I, có =  SA IA SA cosSAB = 2
Tam giác OIA vuông tại I, có 2 2 2
OA = OI + IA 3 2 2 1 2 2
⇔ SA = a + SA ⇔ SA = 2 2
a ⇒ SA = a 2 4 4
Vậy độ dài đường sinh cần tìm là l = a 2 . Chọn C.
Ví dụ 10: Một hình nón có bán kính đáy R, góc ở đỉnh là 60°. Một thiết diện qua đỉnh nón chắn trên đáy
một cung có số đo 90°. Diện tích của thiết diện là 2 2 2 A. R 7 B. R 3 C. 3 2 R D. R 6 2 2 2 2 Lời giải
Vì góc ở đỉnh là 60o nên thiết diện qua trục SAC là tam giác đều cạnh 2R ⇒ Đường cao của hình nón là SI = R 3
Tam giác SA là thiết diện qua đỉnh, chắn trên đáy cung AB có số đo bằng 90° nên IAB là tam giác vuông
cân tại I ⇒ AB = R 2 IM ⊥ AB
Gọi M là trung điểm của AB thì R 2  và IM = SM ⊥ AB 2
Tam giác SMI vuông tại I, có 2 2 R 14
SM = SI + IM = 2
Vậy diện tích cần tính là 1 2 R 7 S = = . Chọn A. SA ∆ B A . B SM 2 2
Dạng 3. Hình nón nội — ngoại tiếp khối chóp đều Mô hình
Hình vẽ tham khảo (3D) Tính chất
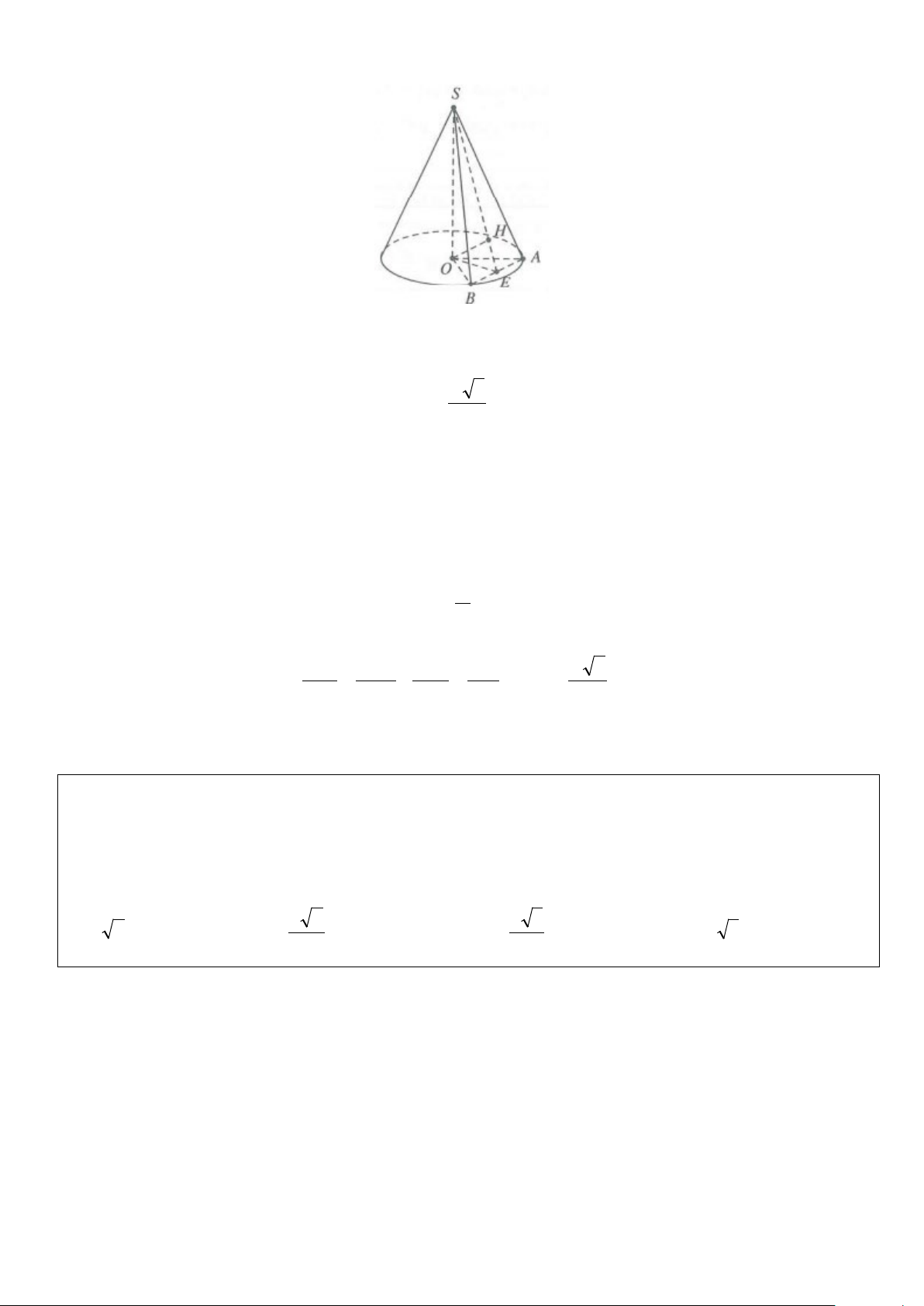
Hình nón nội tiếp hình chóp tam
 Chiều cao SO là chiều cao giác đều của hình chóp
 Bán kính đáy OE là bán kính
đường tròn nội tiếp tam giác đáy
 Đường sinh l = SE
Hình nón ngoại tiếp hình chóp
 Chiều cao SO là chiều cao tam giác đều của hình chóp
 Bán kính đáy OA là bán kính
đường tròn ngoại tiếp tam giác đáy
 Đường sinh l = SA
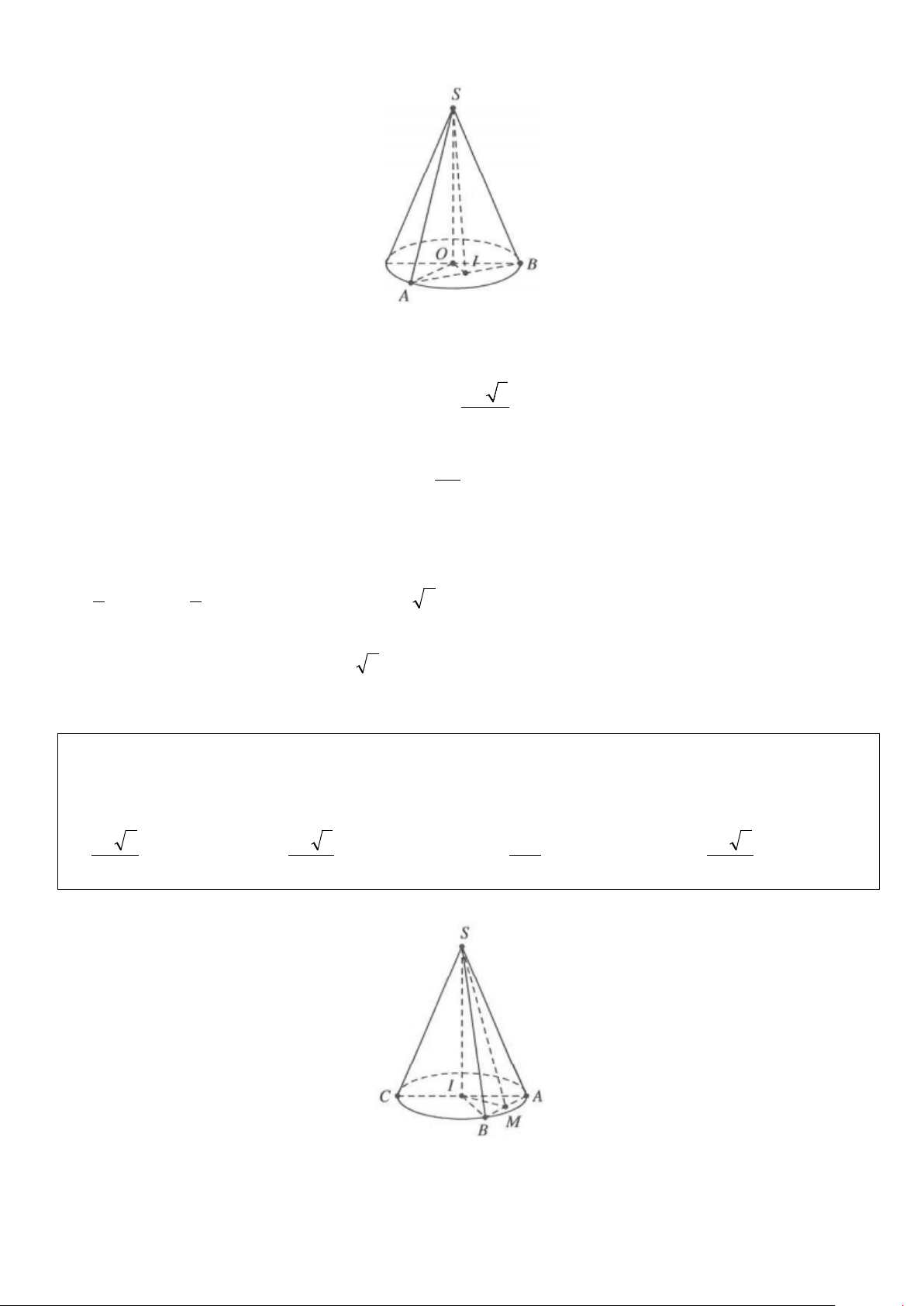
Hình nón nội tiếp hình chóp tứ
 Chiều cao SO là chiều cao giác đều của hình chóp
 Bán kính đáy OM (với M là
trung điểm AB) là bán kính
đường tròn nội tiếp hình vuông đáy
 Đường sinh l = SM
Hình nón ngoại tiếp hình chóp tứ
 Chiều cao SO là chiều cao giác đều của hình chóp
 Bán kính đáy OA là bán kính
đường tròn ngoại tiếp hình vuông đáy
 Đường sinh l = SA
Ví dụ 1: Thể tích khối nón ngoại tiếp tứ diện đều cạnh a là A. 3 3 a π B. 3 3 a π C. 6 3 a π D. 6 3 a π 9 27 27 9 Lời giải
Gọi O là tâm đường tròn ngoại tiếp ∆BCD ⇒ AO ⊥ (BCD)
Dễ thấy, bán kính đường tròn ngoại tiếp ∆BCD là a 3 OB = 3
Suy ra bán kính đáy hình nón là a 3 R = 3
Tam giác ABO vuông tại O, có 2 2 a 6
AO = AB − OB = 3
Do đó, chiều cao của hình nón là a 6 h = AO = 3 2 3  
Vậy thể tích cần tính là 1 2 1 a 3 a 6 6π V = R π h = π. . a = 3 3  3  3 27 Chọn C
Ví dụ 2: Diện tích xung quanh của hình nón ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng 4a là A. 2 2 2 a π B. 2 2 a π C. 2 4 a π D. 2 2 a π Lời giải
Theo bài ra, ta có bán kính đáy a 2 R =
; đường sinh l = 4a (xem mô hình ở lý thuyết) 2
Vậy diện tích xung quanh cần tính là a 2 2 S = π = π = π . Chọn A. xq Rl . .4a 2 2 a 2
Ví dụ 3: Cho hình chóp tam giác đều S.ABC có SA = AB = a. Thể tích khối nón đỉnh S và có đường tròn
đáy nội tiếp tam giác ABC bằng A. 3 3 a π B. 6 3 a π C. 6 3 a π D. 3 3 a π 27 27 108 108 Lời giải
Gọi O là tâm đường tròn ngoại tiếp ∆ABC ⇒ SO ⊥ (ABC)
Bán kính đáy hình nón là a 3 R = r = = ABC ∆ OM 6
Tam giác SAO vuông tại O, có 2 2 a 6
SO = SA − OA = 3 2 3  
Vậy thể tích khối nón cần tính là 1 2 π a 3 a 6 6π V = R π h = . . a = 3 3  6  3 108 Chọn C.
Ví dụ 4: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Tam giác SAB có diện tích bằng 2 2a .
Thể tích khối nón có đỉnh S và đường tròn đáy nội tiếp tứ giác ABCD bằng 3 3 3 3 A. a π 7 B. a π 7 C. a π 7 D. a π 7 6 8 4 2 Lời giải
Gọi M là trung điểm AB ⇒ SM ⊥ AB ⇒ S 1 = ∆ . SAB SM AB 2 Mà S = ∆ 2 2; = → = 2 . 2 2 : = 4 SAB a AB a SM a a a Bán kính đáy hình nón AB a R = OM = = 2 2
Tam giác SMO vuông tại M, có 2 2 3 7a
SO = SM − OM = 2 2 3 π   π
Vậy thể tích khối nón cần tính là 1 2 a 3 7a a 7 V = R π h = .  . = 3 3  2  8 Chọn B.
Ví dụ 5: Cho hình nón (N) có bán kính đáy bằng a và diện tích xung quanh 2
S = π . Tính thể tích V của xq 2 a
khối chóp tứ giác đều S.ABCD có đáy ABCD nội tiếp đáy hình nón và đỉnh S trùng với đỉnh của hình nón (N)? 3 A. 3 3 a B. 2 3 a C. 3 3 a D. 2 3a 3 3 2 3 Lời giải
Gọi O là tâm hình vuông ABCD ⇒ O là tâm đường tròn ngoại tiếp hình vuông ABCD
Theo bài ra, đáy hình nón là đường tròn ngoại tiếp ABCD AC ⇒ R = R = = = ⇒ = ⇒ = ABCD OA a AC 2a AB a 2 2
Diện tích xung quanh hình nón là S = π = 2 2 π ⇒ = 2 xq Rl a l a
Hình nón (N) có đường sinh l = SA = 2a
Tam giác SAO vuông tại O, có 2 2
SO = SA − OA = a 3 3
Vậy thể tích khối chóp S.ABCD là 1 a 3 a V = = = S ABCD SO SABCD a . . (. 2)2 2 3 3 3 3 Chọn D
Ví dụ 6: Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a, góc tạo bởi hai mặt phẳng (SAB) và
(ABC) bằng 60o. Diện tích xung quanh của hình nón đỉnh S và có đường tròn đáy ngoại tiếp tam giác ABC bằng A. 7 2 a π B. 7 2 a π C. 3 2 a π D. 3 2 a π 6 3 2 6 Lời giải
Gọi O là tâm đường tròn ngoại tiếp A
∆ BC ⇒ SO ⊥ (ABC)
Bán kính đáy hình nón là a 3 R = R = = ABC ∆ OA 3 AB ⊥ OM
Gọi M là trung điểm AB ⇒ 
⇒ AB ⊥ (SMO) AB ⊥ SO
Do đó (SAB);(ABC) = (SM ;OM ) o = S ˆO M = 60
Tam giác SMO vuông tại O, có OM a 3 cos S ˆO M = ⇒ SM = SM 3
Tam giác SBM vuông tại M, có 2 2 a 21
SB = SM + BM = 6 2
Vậy hình nón có đường sinh a 21 7 a π l = → S = π = sq Rl 6 6 Chọn A.
Ví dụ 7: Cho hình chóp tam giác đều S.ABC có cạnh AB = BC = 10a, AC = 12a, góc tạo bởi hai mặt phẳng
(SAB) và (ABC) bằng 45o. Thể tích khối nón đỉnh S và có đường tròn đáy nội tiếp tam giác ABC bằng A. 3 3 a π B. 3 9 a π C. 3 27 a π D. 3 12 a π Lời giải
Gọi O là tâm đường tròn nội tiếp ∆ABC SO ⊥ (ABC)
Kẻ OM ⊥ AB ⇒ OM là bán kính đường tròn nội tiếp ∆ABC
Diện tích ∆ABC là S = − − − = ABC ∆
p(p a)(p b)(p c) 2 48a
Suy ra bán kính đường tròn nội tiếp S A ∆ BC ⇒ r = = ∆ 3 ABC a p Ta có ⊥ ( ) ⇒ (( ) ( )) =  o AB SMO SAB ; ABC SMO = 45
Tam giác SMO vuông tại O, có SO = OM = r = ∆ 3 ABC a
Vậy thể tích khôi nón cần tính là 1 2 π V = R π h = (.3a)2 3 3 . a = 9 a π 3 3 Chọn B.
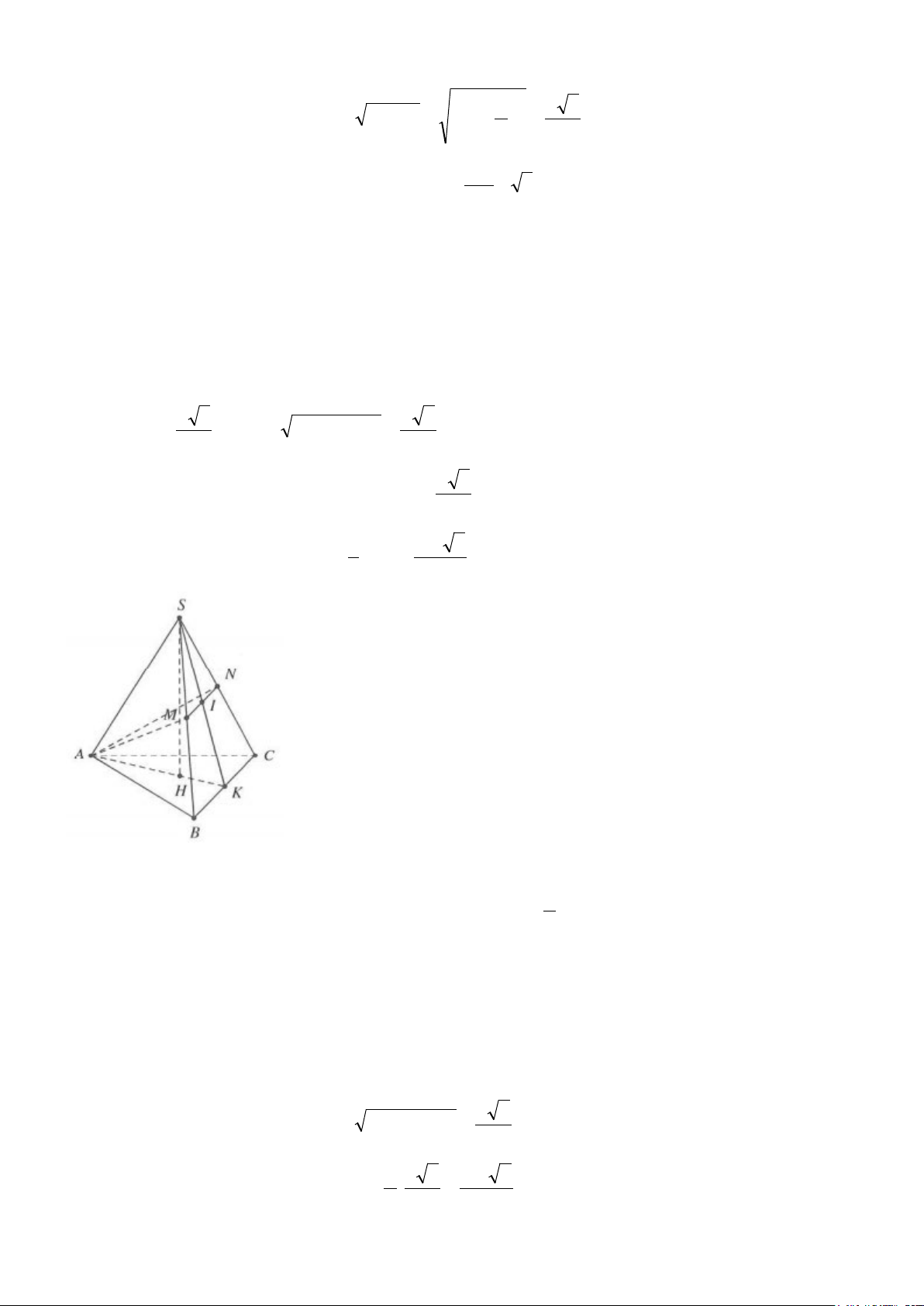
Ví dụ 8: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a, khoảng cách từ tâm O của đường tròn
ngoại tiếp tam giác ABC đến một mặt bên là a . Thể tích của khối nón ngoại tiếp hình chóp S.ABC bằng 2 A. 4 3 a π B. 4 3 a π C. 4 3 a π D. 2 3 a π 3 27 9 3 Lời giải
Gọi M là trung điểm BC ⇒ BC ⊥ AM ⇒ BC ⊥ (SAM )
Kẻ OH ⊥ SM mà BC ⊥ OH ⇒ OH ⊥ (ABC) Tacó 1 1 3 1 3 a 3 OM = AM = . AB = . 2 . a = 3 3 2 3 2 3
Tam giác SMO vuông tại O, có 1 = 1 + 1 ⇒ SO = a
OH 2 SO2 OM 2
Bán kính đường tròn ngoại tiếp A ∆ BC là 2a 3 R = ABC ∆ 3 2 3  
Vậy thể tích khối nón cần tính là 1 2 a π 2a 3 4π V = R π h = . a = 3 3  3  9 Chọn C
Dạng 4. Hình nón nội - ngoại tiếp hình trụ, hình cầu
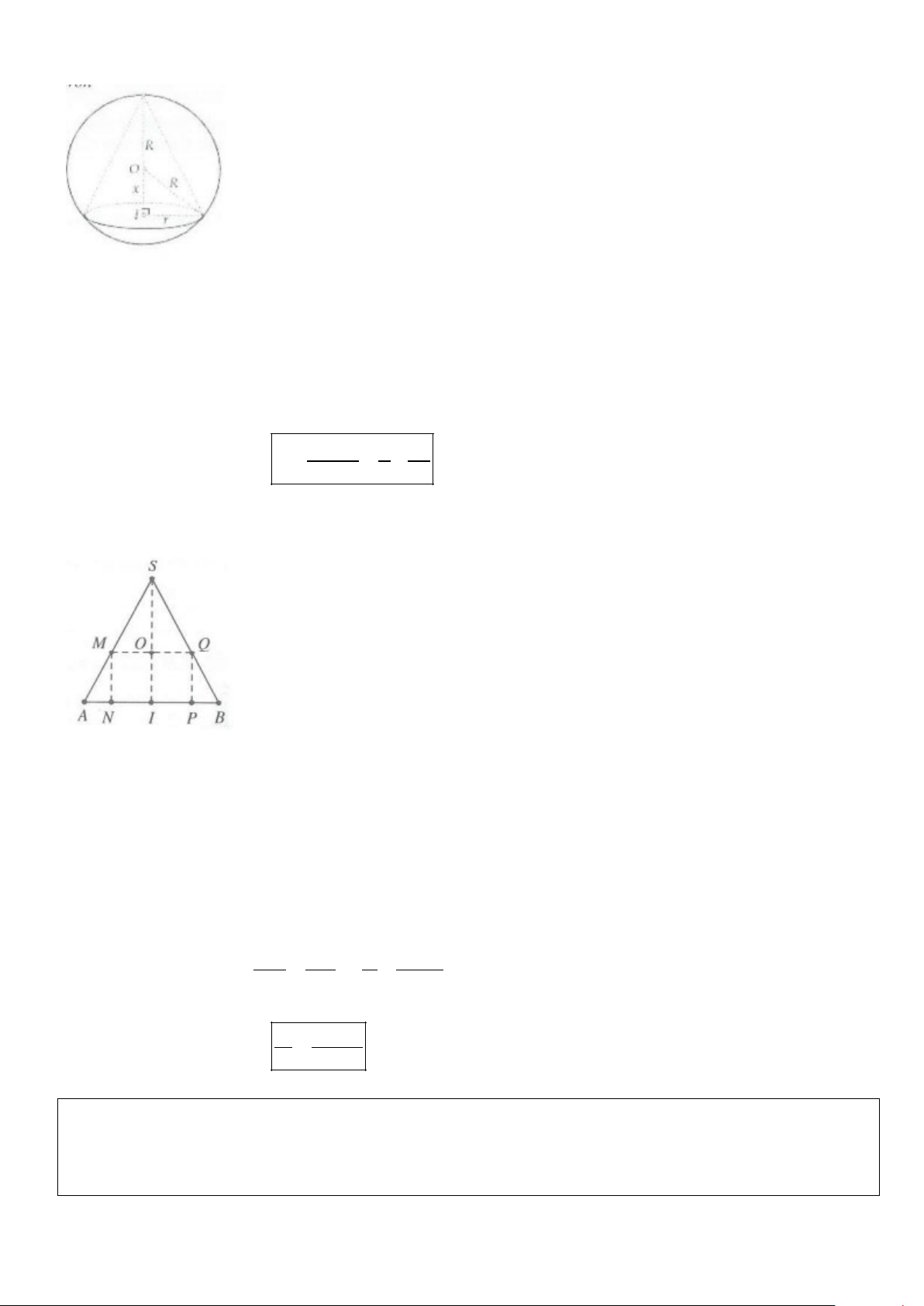
Hình nón ngoại tiếp hình cầu
Lý thuyết: Xét mặt cắt qua trục, ta đưa về bài toán tam giác ngoại tiếp đường tròn
Bài toán: Gọi R, r, h lần lượt là bán kính mặt cầu, bán kính đáy và chiều cao hình nón
⇒ R = OI,r = IB,h = SI Ta có S ∆ EO ~ OE SO R h − R SIB ∆ ⇒ = ⇒ = 2 2 IB SB r h + r rh
Vậy mối liên hệ cần tìm là R = 2 2 r + r + h
Hình nón nội tiếp hình cầu
Lý thuyết: Xét mặt cắt qua trục, ta đưa về bài toán tam giác nội tiếp đường tròn
Bài toán: Gọi R, r, h lần lượt là bán kính mặt cầu, bán kính đáy và chiều cao hình nón Ta có 2 2 2
x + r = R mà x = h − R ⇒ (h − R)2 2 2 + r = R 2 2 2 h + r h r
Vậy mối liên hệ cần tìm là R = = + 2h 2 2h
Hình nón ngoại tiếp hình trụ
Lý thuyết: Xét mặt cắt qua trục, ta đưa về bài toán tam giác ngoại tiếp hình chữ nhật, cụ thể là tam giác
SAB (thiết diện qua trục hình nón) và hình chữ nhật MNPO (thiết diện qua trục hình trụ)
Bài toán: Gọi R, h, R’, H’ lần lượt là bán kính đáy và chiều cao hình nón; bán kính đáy và chiều cao hình
R = IA R'= IN trụ ⇒  ;
h = SI h = OI Ta có MN AN
h' R − R AMN ∆ ~ A ∆ SI ' ⇒ = ⇒ = SI AI h R h ' R − R '
Vậy mối liên hệ cần tìm là = h R
Ví dụ 1: Cho hình cầu bán kính bằng 5 cm, cắt hình cầu này bằng một mặt phẳng sao cho thiết diện tạo
thành là một đường tròn đường kính 4 cm. Tính thể tích khối nón có đáy là thiết diện vừa tạo và đỉnh là tâm của hình cầu đã cho. A. 3 ≈ 18 , 19 cm B. 3 ≈ , 19 20cm C. 3 ≈ , 19 21cm D. 3 ≈ 19 , 19 cm Lời giải
Theo bài ra, ta có R = 5 cm, r = 2 cm
Chiều cao của khối nón là h = R2 − r2 = c 21 m
Vậy thể tích khối nón là 1 2 4 21π 3 V = r π h = ≈ , 19 20cm . 3 3 Chọn B.
Ví dụ 2: Cho mặt cầu (S) tâm O, bán kính R (không đổi). Mặt phẳng (P) cách O một khoảng bằng x, (x< R)
và cắt (S) theo giao tuyến là đường tròn (C) có tâm H. Gọi T là giao điểm của tia HO với (S). Thể tích của
khối nón có đỉnh T và đáy là hình tròn (C) bằng π ( 2 2
R − x )(R + h) π ( 2 2
R − x )(R + h) A. B. π( 2 2 2 R − x )(R + h) C. D. π( 2 2 R − x )(R + h) 6 3 Lời giải
Bán kính đáy hình nón là 2 2
r = R − x
Chiều cao hình nón là h = OT + OH = R + h 1 2 π ( 2 2
R − x )(R + h)
Vậy thể tích khối nón là V = r π h = 3 3 Chọn C.
Ví dụ 3: Cho hình nón (N) có bán kính đáy bằng 6, chiều cao bằng 8. Biết rằng có một mặt cầu tiếp xúc với
tất cả các đường sinh của hình nón, đồng thời tiếp xúc với mặt đáy của hình nón. Tìm bán kính của mặt cầu đó A. 4 B. 2 C. 6 D. 3 Lời giải
Bài toán: Hình nón ngoại tiếp hình cầu rh 6.8 ⇒ R = = = 3 2 2 2 2 r + r + h 6 + 6 + 8 Chọn D.
Ví dụ 4: Cho khối cầu tâm O, bán kính R =2. Mặt phẳng (P) cách O một khoảng x cắt khối cầu theo một
hình tròn (C). Một khối nón (N) có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón (N) có thể tích
lớn nhất, khi đó giá trị của x bằng A. 2 x = B. 3 x = C. 1 x = D. 3 x = 3 3 3 2 Lời giải
Bài toán: Hình nón nội tiếp hình cầu. Ta có 2 2 2
r = R − x , với r là bán kính đáy hình nón
Chiều cao hình nón là h = x + R . Thể tích khối nón là 1 2 1 V = r π h = π( 2 2 R − x ).(x + R) 3 3 3 3 Lại có π π − + + + + π
V = (.2R − 2x)(.R + x)(.R + x)
(2R 2x R x R x) 32 ≤ . R = 6 6 27 81
Dấu bằng xảy ra khi và chỉ khi R 2
2R − 2x = R + x ⇔ x = = 3 3 Chọn A.
Ví dụ 5: Cho hình nón tròn xoay (N) có đỉnh là S, có đáy là đường tròn tâm O bán kính R. Đường cao SO =
h. Tính chiều cao x của hình trụ có thể tích lớn nhất nội tiếp hình nón đã cho ? A. h x = B. h 3 x = C. h x = D. h 3 x = 3 3 6 6 Lời giải
Bài toán: Hình nón ngoại tiếp hình trụ
h' R − R' ⇒ = h R
Với R’, h’ lần lượt là bán kính đáy, chiều cao hình trụ h ⇒ x = (.R − R') R Thể tích khối trụ là π V = R
π '2 x = π '2. h R (.R − ') h R =
[.R'2.(R−R')] R R 3  R ' R ' R R' + + −   3 Ta có: 2 R ' .(R − R ') R ' R '  2 2  4R = 4. . .(R − R ') ≤ 4. = 2 2 27 27 3 2 Suy ra h π 4R 4π V ≤ . R h =
. Dấu = xảy ra khi R' 2
= R − R'⇒ R' h = R ⇒ x = . R 27 27 2 3 3 Chọn A.
BÀI TẬP TỰ LUYỆN
Câu 1: Một khối nón tròn xoay có chiều cao h = 4, bán kính đáy r = 5. Tính thể tích của khối nón A. 100π B. π 15 C. π 41 D. 25π 3 3
Câu 2: Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón (N). Diện tích xung quanh của (N) là A. S = π B. S = π 2 C. S 2 = π D. S = π xq Rl xq R h xq Rl xq Rh
Câu 3: Cho khối nón (N) có bán kính đáy bằng 3 và thể tích bằng π
12 . Tính diện tích xung quanh của hình nón A. S = π B. S = π C. S = π D. S = π xq 18 xq 16 xq 24 xq 15
Câu 4: Cho hình nón có bán kính đáy bằng 3 và chiều cao bằng 4. Tính diện tích xung quanh của hình nón đó A. S = π B. S = π C. S = π D. S = π xq 25 xq 20 xq 15 xq 60
Câu 5: Một hình nón có bán kính đáy bằng 5a, độ dài đường sinh bằng 13a. Tính độ dài đường cao của hình nón
A. h = 7a 6
B. h =12a
C. h =17a D. h = a 8
Câu 6: Một hình nón có bán kính đáy bằng 1 cm, chiều cao bằng 2 cm. Khi đó góc ở đỉnh của hình nón là ϕ 2 thỏa mãn A. 2 5 sinϕ = B. 5 tanϕ = C. 2 5 cosϕ = D. 5 cotϕ = 5 5 5 5
Câu 7: Cho hình nón có bán kính đáy là 6a, chiều cao là 8a. Tính diện tích xung quanh của hình nón A. 2 20 a π B. 2 60 a π C. 2 50 a π D. 2 40 a π
Câu 8: Một hình nón có đường sinh bằng 3a và bán kính đường tròn đáy bằng 2a. Tính diện tích xung quanh của hình nón đó. A. 4 5 2 S = π B. 2 S = π C. 2 S = π D. 2 S = π xq 6 a xq 12 a xq 3 a xq a 3
Câu 9: Cho khối nón có chiều cao bằng 8 cm và độ dài đường sinh bằng 10 cm. Tính thể tích V của khối nón đó A. 3 V =124 c π m B. 3 V =140 c π m C. 3 V =128 c π m D. 3 V = 96 c π m
Câu 10: Một hình nón có bán kính đáy r = 3a, chiều cao h = 4a. Kí hiệu góc ở đỉnh của hình nón là α 2 .
Trong các mệnh đề sau, mệnh đề nào đúng? A. 4 sinα = B. 4 cosα = C. 4 tanα = D. 4 cotα = 5 5 5 5
Câu 11: Cho hình nón có diện tích xung quanh bằng 2 3 a
π và bán kính đáy bằng a. Tính độ dài đường sinh l của hình nón đã cho A. a 5 l =
B. l = 2 2a C. 3a l = D. l = a 3 2 2
Câu 12: Cho một khối nón có bán kính đáy bằng 3 và thể tích bằng π
12 . Tính diện tích xung quanh S của xq hình nón A. S = π B. S = π C. S = π D. S = π xq 60 xq 30 xq 45 xq 15
Câu 13: Khối nón (N) có bán kính đường tròn đáy bằng 10 và diện tích xung quanh bằng 12 π 0 . Tính chiều cao của khối nón (N) A. 2 11 B. 11 C. 11 D. 11 3 2
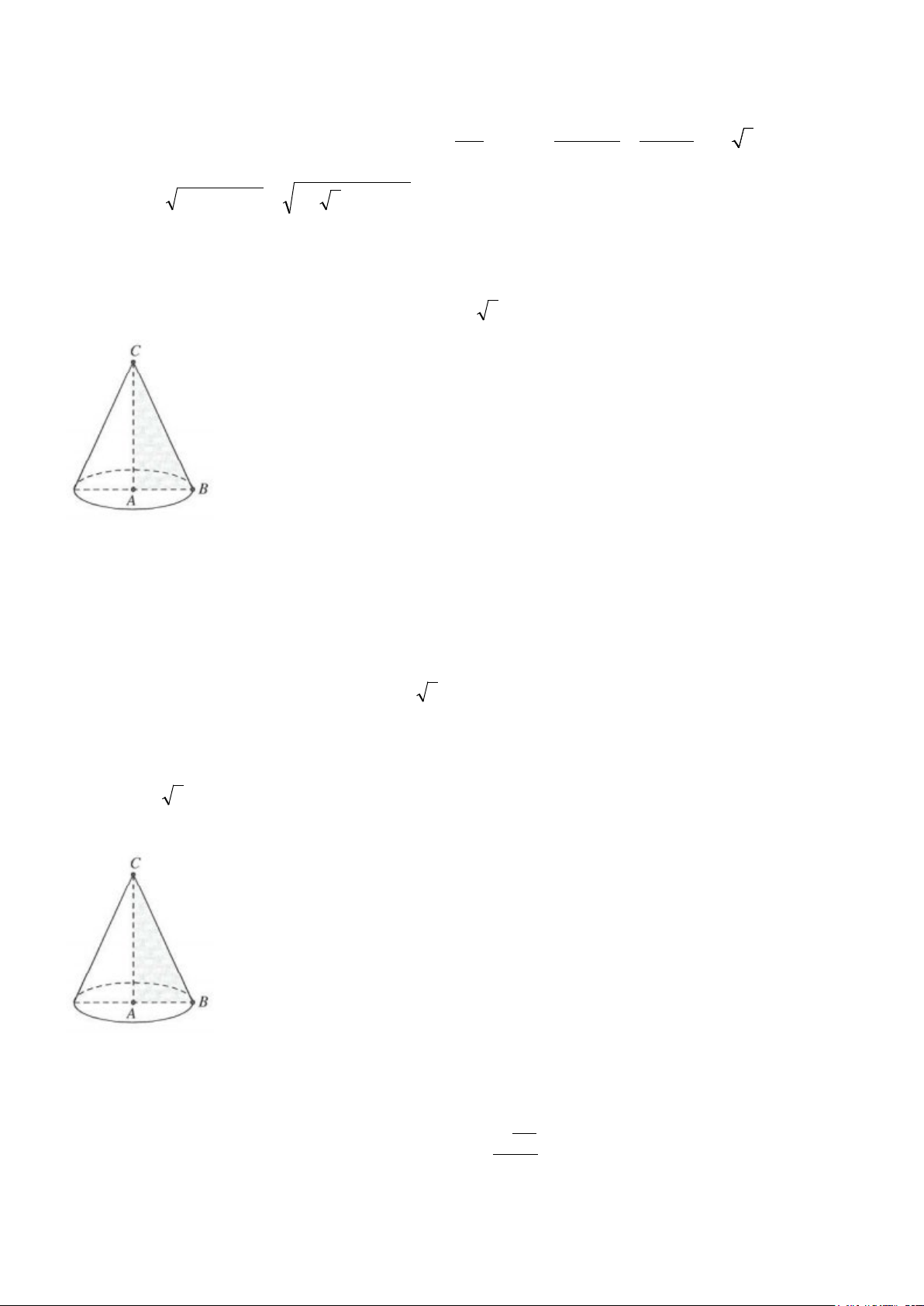
Câu 14: Cho tam giác ABC vuông tại C, BC = a, AC = b. Tính thể tích khối tròn xoay tạo thành khi quay tam giác ABC quanh AC. 2 3 A. a π b B. a2 π b C. a π b D. a b 3 π 3 3
Câu 15: Trong không gian, cho tam giác ABC vuông tại A với AC = 3a, AB = 4a. Tính theo a diện tích
xung quanh S của hình nón khi quay tam giác ABC quanh trục AC. A. S = π 2 30a B. S = π 2 40a C. S = π 2 20a D. S = π 2 15a
Câu 16: Cho tam giác ABC đều cạnh 2a, đường cao AH. Tính thể tích của khối nón tròn xoay tạo thành khi
quay hình tam giác ABC quanh AH. 3 3 3 A. 3 a π 3 B. a π 3 C. a π 3 D. a π 3 3 6 4
Câu 17: Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Tính thể tích vật tròn xoay thu được khi quay tam giác ABC quanh cạnh AC. A. π 10 B. π 11 C. π 12 D. π 13
Câu 18: Cho tam giác ABC vuông tại A có  o
ABC = 30 quay quanh cạnh góc vuông AC = a tạo thành hình
nón tròn xoay có diện tích xung quanh bằng A. 2 2 a π 3 B. 4 2 a π 3 C. 2 a π 3 D. 2 2 a π
Câu 19: Trong không gian cho tam giác vuông IOM vuông tại I, góc  o
IOM = 30 và cạnh IM = a. Khi quay
tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OIM tạo thành một hình nón tròn xoay. Tính
thể tích V của khối nón tròn xoay tương ứng. 3 3 3 A. a 3 π π V = B. a 3 V = C. 3 V = a π 3 D. a 3 V = 3 3 6
Câu 20: Cho tam giác ABC vuông tại A, có AB = 10,  o
ABC = 60 . Tính diện tích xung quanh Sxq của hình
nón tạo thành khi quay tam giác ABC quanh đường thắng chứa cạnh AC. A. S = B. S = C. S = D. S = xq 20 π 0 xq 200 π 3 xq 100 π 3 xq 1000 π 3
Câu 21: Cho tam giác ABC vuông cân tại A và có AB = 3cm. Cho tam giác ABC quay quanh trục AB ta
nhận được khối tròn xoay (T). Tính thể tích của (T) A. π ( 3 18 cm ) B. π ( 3 9 cm ) C. π ( 3 27 cm ) D. π ( 3 3 cm )
Câu 22: Gọi S là diện tích hình nón tròn xoay được sinh ra bởi đoạn thắng AC’ của hình lập phương
ABCD.A’B’C’D’ có cạnh b khi quay quanh trục CC’. Diện tích xung quanh S là A. 2 b π B. 2 b π 2 C. 2 b π 3 D. 2 b π 6
Câu 23: Cho hình nón có bán kính đường tròn đáy là 6 cm và diện tích hình tròn đáy bằng diện tích xung
quanh của hình nón. Tính thể tích V của khối nón đã cho A. V = π ( 3 48 cm ) B. V = π ( 3 64 cm ) C. V = π ( 3 96 cm ) D. V = ( 3 288 cm )
Câu 24: Một khối nón có thể tích bằng 3 25 c
π m , nếu giữ nguyên chiều cao và tăng bán kính đáy khối nón đó
lên 2 lần thì thể tích của khối nón mới bằng A. 3 100 c π m B. 3 150 c π m C. 3 200 c π m D. 3 50 c π m
Câu 25: Cho hình nón đỉnh S, đáy là hình tròn tâm O, góc ở đỉnh bằng 150o. Trên đường tròn đáy lấy điểm
A cố định. Có bao nhiêu vị trí của điểm M trên đường tròn đáy của hình nón để diện tích tam giác SMA đạt giá trị lớn nhất? A. 2 B. 1 C. 4 D. 3
Câu 26: Cho hình thang ABCD (AB//CD) vuông tại A có AB = 8, CD = 5 và BC = 5. Tính thể tích V của
hình tròn xoay tạo thành khi quay đường gấp khúc ADC quanh trục AB. A. 128π V = B. V =12 π 8 C. 256π V = D. V = π 96 3 3
Câu 27: Cho tam giác ABC cân tại A, biết cạnh AB = a và  o
BAC =120 . Tính thể tích khối tròn xoay sinh ra
khi quay tam giác ABC quanh cạnh AC. 3 3 3 A. a π 3 π π π V = B. a V = C. 3 3 a V = D. a V = 4 8 8 4
Câu 28: Cho hình nón đỉnh S và đường tròn đáy có tâm O. Điểm A thuộc đường tròn đáy. Tính số đo góc S ˆO
A , biết tỉ số giữa diện tích xung quanh và diện tích đáy của hình nón là 2 3 A. 120o B. 45o C. 30o D. 60o
Câu 29: Cho tam giác ABC có AB, BC, CA lần lượt bằng 3, 5, 7. Tính thể tích của khối tròn xoay sinh ra do
hình tam giác ABC quay quanh đường thẳng AB. A. π 50 B. 75π C. 275π D. 125π 4 8 8
Câu 30: Cho tam giác AC có AB = 3a, BC = 5a, CA = 7a. Tính thể tích khối tròn xoay sinh ra khi cho hình
tam giác ABC quay quanh đường thẳng AB. A. 76 3 a π B. π 3 16a C. 75 3 a π D. π 3 20a 3 4
Câu 31: Cho hình nón đỉnh S, xét hình chóp S.ABC có đáy ABC là tam giác ngoại tiếp đường tròn đáy của
hình nón và có AB = BC = 10a,AC = 12a, góc giữa hai mặt phẳng (SAB) và (ABC) bằng 45o. Tính thể tích của khối nón đã cho. A. 3 9 a π B. 3 12 a π C. 3 27 a π D. 3 3 a π
Câu 32: Cho S.ABCD là hình chóp tứ giác đều, cạnh đáy bằng a, cạnh bên hợp với đáy góc 45o. Hình tròn
xoay đỉnh S, đáy là đường tròn nội tiếp hình vuông ABCD. Tính diện tích xung quanh của hình nón tròn xoay đó. 2 2 A. 2 π π S = π B. 2 S = π C. a S = D. a S = xq a xq 2 a xq 2 xq 4
Câu 33: Cho hình chóp tam giác đều có đáy bằng a và đường cao bằng 6a. Tính thể tích khối nón nội tiếp hình chóp đó? 3 3 3 3 A. a π B. a π C. a π D. a π 9 6 3 4
Câu 34: Cho hình chóp tam giác đều S.ABC có các cạnh bên bằng a, góc giữa mặt bên và mặt phẳng đáy
bằng α với tanα = 5 . Tính thể tích V của khối nón có đỉnh S và có đường tròn đáy là đường tròn nội tiếp tam giác ABC. 3 3 3 A. a π 5 π π π V = B. a 5 V = C. a 5 V = D. 5 3 a V = 81 27 9 81
Câu 35: Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Một khối nón có đỉnh là tâm của hình vuông
ABCD và đáy là hình tròn nội tiếp hình vuông A’B'C'D'. Tính diện tích toàn phần của khối nón đó. 3 2 2 2 A. a π π π π S = B. a 5 S = C. = a S D. = a S tp ( 5 + )1 tp (2 5 + )1 tp 4 tp 4 4 4
Câu 36: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Gọi M, N lần lượt là trung điểm của SB,
SC ; mặt phẳng (AMN) vuông góc với (SBC). Tính diện tích xung quanh của hình nón nội tiếp hình chóp đã cho. 2 2 2 2 A. a π 6 B. a π 6 C. a π 5 D. a π 12 6 4 4
Câu 37: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với mặt đáy góc 60o. Hình
nón có đỉnh S, đáy là đường tròn nội tiếp tứ giác ABCD có diện tích xung quanh là 2 2 2 2 A. a π π π π S = B. a 14 S = C. a 7 S = D. a S = 4 4 4 2
Câu 38: Cho tam giác ABC vuông tại A có  o
ABC = 30 và cạnh góc vuông AC = 2a. Quay tam giác quanh
cạnh AC tạo thành hình nón tròn xoay có diện tích xung quanh bằng A. 2 2 a π B. 4 2 a π 3 C. 8 2 a π 3 D. 16 2 a π 3 3
Câu 39: Cho tam giác ABC có   
A : B: C = 3: 2 :1,AB =10cm . Tính độ dài đường sinh l của hình nón, nhận
được khi quay tam giác ABC xung quanh trục AB A. 20 cm B. 10 c 3 m C. 30 cm D. 10 cm
Câu 40: An có một tờ giấy hình tròn tâm O, bán kính là 12 cm. Trên đường tròn, An lấy một cung AB có số
đo là 2π , sau đó cắt hình tròn dọc theo hai đoạn OA và OB. An dán mép OA và OB lại với nhau để được 3
hai hình nón đỉnh O. Tính tỉ số thể tích của khối nón nhỏ so với khối nón lớn (xem phần dán giấy không đáng kể). A. 1 B. 1 C. 10 D. 10 8 4 10 5
Câu 41: Người thợ gia công của một cơ sở chất lượng cao X cắt một miếng tôn hình tròn với bán kính 60cm
thành ba miền hình quạt bằng nhau. Sau đó người thợ ấy quấn và hàn ba miếng tôn đó để được ba cái phễu
hình nón. Hỏi thể tích V của mỗi cái phễu đó bằng bao nhiêu? A. π π π V 16000 2 = lít B. V 16 2 = lít C. V 16000 2 = lít D. V 160 2 = lít 3 3 3 3
Câu 42: Cắt bỏ hình quạt tròn AOB từ một mảnh các tông hình tròn bán kính R rồi dán hai bán kính OA và
OB của hình quạt tròn lại với nhau để được một cái phễu có dạng của một hình nón. Gọi x là góc ở tâm của
hình quạt tròn dùng làm phễu, 0 < x < π
2 . Tìm giá trị lớn nhất của thể tích khối nón. A. 4 3 3 R π B. 2 3 R π C. 2 3 3 R π D. 2 3 3 R π 27 27 9 27
Câu 43: Từ một miếng sắt tây hình tròn bán kính R, ta cắt đi một hình quạt và cuộn phần còn lại thành một
cái phễu hình nón. Số đo cung của hình quạt bị cắt đi phải là bao nhiêu độ (làm tròn đến đơn vị độ) để hình
nón có dung tích lớn nhất? A. 65o B. 90o C. 45o D. 60o
Câu 44: Bình có một tấm bìa hình tròn như hình vẽ. Bạn ấy muốn biến hình tròn đó thành một hình cái phễu
hình nón. Khi đó Bình phải cắt bỏ hình quạt tròn AOB rồi dán hai bán kính OA và OB lại với nhau. Gọi x là
góc ở tâm hình quạt tròn dùng làm cái phễu. Tìm x để thể tích cái phễu lớn nhất. (6−2 6) (6+2 6) A. π B. π C. 2 6π D. π 3 3 3 3
Câu 45: Cho nửa đường tròn đường kính AB = 2R và điểm C thay đổi trên nửa đường tròn đó. Đặt 
CAB = α và gọi H là hình chiếu vuông góc của C lên AB. Tìm tanα sao cho thể tích khối tròn xoay tạo
thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất. A. tanα =1 B. 1 tanα = C. 3 tanα = D. tanα = 3 2 3
Câu 46: Cho ba hình tam giác đều cạnh bằng a chồng lên nhau như hình vẽ bên (cạnh đáy của tam giác trên
đi qua các trung điểm hai cạnh bên của tam giác dưới). Tính theo α thể tích của khối tròn xoay tạo thành khi
quay chúng xung quanh đường thẳng d . 3 3 3 A. 11 3 a π B. 11 3 a π C. 3 3 a π D. 13 3 a π 96 8 8 96
Câu 47: Cho khối nón có bán kính 3a. Cắt khối nón đã cho bởi một mặt phẳng vuông góc với trục và bỏ
phần trên của khối nón ( phần chứa đỉnh của khối nón ). Biết thiết diện là hình tròn có bán kính bằng a và độ
dài phần đường sinh còn lại bằng 29a Tính thể tích V phần còn lại của khối nón theo a. 10 3 3 A. a π π π π V = B. a 6 V = C. 29 3 a V = D. 91 3 a V = 3 27 10 10
Câu 48: Một hình nón (N) có bán kính đáy R, đường cao SO. Gọi (P) là mặt phẳng vuông góc với SO tại sao cho SI 1
= SO , Một mặt phẳng (Q) qua trục hình nón (N) cắt phần khối nón nằm giữa và đáy hình nón 3
theo thiết diện là hình thang cân ABCD có hai đường vuông góc nhau hình vẽ. Thể tích phần hình nón (N)
nằm giữa mặt phẳng (P) và mặt phẳng chứa đáy hình nón (N) là A. 76 3 R π B. 52 3 R π C. 64 3 R π D. 40 3 R π 81 81 81 81
LỜI GIẢI BÀI TẬP TỰ LUYỆN Câu 1: 1 V = π 2 100 r h = π . Chọn A 3 3
Câu 2: S = π . Chọn D xq Rlr = 3 Câu 3: Ta có  1
⇒ h = 4 ⇒ S = π . Chọn A xq rl = π 2 2 r h + r = π 15 V = π  12 = π 2 r h  3 Câu 4: 2 2 S = rl
π = π h + r =15π . Chọn B xq
Câu 5: Ta có h = l2 − r2 =12a . Chọn B Câu 6: Ta có φ =  SO h 2 cos cos ASO = = = 2 2 SA h + r 5 Chọn C Câu 7: 2 2 2 S = rl π = π h + r = 60 a π . Chọn B xq Câu 8: 2 S = rl π = 6 a π . Chọn D xq Câu 9: 1 2 1 V = r π h = π ( 2 2 l − h ) 3 h = 96 c π m . Chọn D 3 3 Câu 10: Ta có SO h 4 cosϕ = cos ASO = = = 2 2 SA h + r 5 Chọn B S = π = 3 2 π xq rl a Câu 11: Ta có  ⇒ l = a 3 . Chọn D r = a r = 3 Câu 12:  2 2  1 ⇒ h = 4 ⇒ S = rl π = r
π h + r =15π. Chọn A 2 xq V = r π  h  3 r =10 Câu 13:  2 2  ⇒ h +100 =12 ⇒ h = 2 11 2 2 S  = r π l = π h + r =120π  xq Chọn A 2 Câu 14: a π b V = . Chọn A 3 Câu 15: 2 2 2
h = 3a,r = 4a ⇒ l = h + r = 5a ⇒ S = π = π xq rl 20 a Chọn C 3 Câu 16: 2a 3 1 2 a π 3 h =
= a 3,r = a ⇒ V = r π h = 2 3 3 Chọn B Câu 17: 1 h = ,
4 r = 3 ⇒ V = π 2 r h = π 12 3 Chọn C AC AC Câu 18:  2 2 tan ABC = ⇒ AB =
 = a 3 ⇒ BC = AB + AC = 2a AB tan ABC
Ta có h = a,r = a 3,l = 2a ⇒ S = π = π xq rl 2 2 a 3 Chọn A IM IM Câu 19:  2 2 tan IOM = ⇒ IO =
 = a 3 ⇒ OM = IM + IO = 2a IO tan IOM 3 Ta có 1 2 a π 3
h = a 3,r = a,⇒ V = r π h = 3 3 Chọn B Câu 20:  AC = ⇒ =  2 2 tan ABC
AC ABtan ABC =10 3 ⇒ BC = AB + AC = 20 AB
Ta có h =10 3,r = ,
10 l = 20 ⇒ S = π xq rl = 20 π 0 Chọn D Câu 21: 1 r = ,
3 h = 3 ⇒ V = π 2 r h = π 9 3 Chọn B
Câu 22: AC'= b 3,CC'= ,
b AC = b 2 ⇒ r = b 2,l = b 3 2 ⇒ S = π = π xq rl b 6 Chọn D r = 6cm Câu 23:  2 2 1 2 3  3
⇒ l =10 ⇒ h = l − r = 8 ⇒ V = r π h = 96 c π m 2  r π = rl π 3  5 Chọn C Câu 24: 1 V = π 2 r h = π 1
25 ⇒ V '= π (2r)2h =10 π 0 3 3 Chọn A
Câu 25: Kẻ SH ⊥ AM
SA = SM ⇒ HA = HM
OA = OM ⇒ OH ⊥ AM 1 2 2 2 S + = = ≤ = SAM SH.AM SH. SH AH l AH 2 2 2 Dấu “=” xảy ra o ⇔ ASM = 90
Có 2 điểm M thỏa mãn bài toán (đối xứng nhau qua AB) Chọn A Câu 26: Ta có 2
AD = BC − (AB − CD)2 = 4 ⇒ V = π 2 1 .AD .CD + π 2
AD (.AB − CD) = π 96 3 Chọn D Câu 27: 2 2
BC = AB + AC − 2A .
B AC.cos120o = a 3 . Kẻ BH ⊥ AC  BH = ⇒ =  a 3 2 2 3a sin ACB BH BCsin ACB = ⇒ CH = BC − BH = BC 2 2 3 1 2 1 2 a V .CH.BH .AH.BH π = π − π = 3 3 4 Chọn D Câu 28: 2 rl π l SA = = = ⇒  OA 3 = = ⇒  o cosSAO SAO = 30 2 3 r π r OA SA 2 Chọn C Câu 29: Kẻ + −
CH ⊥ AB . Ta có  2 2 2 AB AC BC 11 cos BAC = = 2AB.AC 14 Mà  AH = ⇒ =  11 5 cos BAC AH ACcos BAC = ⇒ BH = AH − AB = AC 2 2 Ta có 2 2 5 3 1 2 1 2 75π
CH = AC − AH =
⇒ V = πCH .AH − πCH .BH = 2 3 3 4 Chọn B Câu 30: Kẻ + −
CH ⊥ AB . Ta có  2 2 2 AB AC BC 11 cos BAC = = 2AB.AC 14 Mà AH 11a 5 ˆ = ⇒ = ˆ cos C A B AH AC cos a C A B =
⇒ BH = AH − AB = AC 2 2 3 Ta có 2 2 5 3a 1 2 1 2 75π
CH = AC − AH = ⇒ V = CH π .AH − CH π . a BH = 2 3 3 4 Chọn C
Câu 31: Diện tích tam giác ABC là S = − − − = ABC ∆
p(p AB)(p BC)(p AC) 2 48a 2
Bán kính đường tròn nội tiếp A ∆ BC là S∆ 48 ABC a
S = p r. ⇒ r = = = a 3 p 16a
Gọi H là hình chiếu của I trên AB ⇒ ⊥ ( ) ⇒ (( ) ( ))  =  o AB SIH SAB ; ABC SHI = 45
Tam giác SIH vuông cân tại I có SI = IH = a 3 . Vậy 1 2 3 ( V = π = π N ) r h 9 a 3 Chọn A
Câu 32: Bán kính đường tròn nội tiếp hình vuông ABCD là a r = 2
Gọi O là tâm hình vuông ABCD ⇒ ⊥ ( ) ⇒ ( ( ))  = ( )  =  SO ABC SA; ABCD SA;OA SAO
Tam giác SAO vuông tại O, có o a 2 ˆO A S
= 45 ⇒ SO = OA = 2 2 π
Vậy diện tích xung quanh của hình nón là S = π = π = π = xq Rl . . OA . a SA . a a 2 2 Chọn C
Câu 33: Bán kính đường tròn nội tiếp tam giác đều cạnh a là a 3 r = 6 2 3  
Thể tích khối nón cần tính là 1 2 π a 3 π V = r π h = . 6 . a a = 3 3  6  6 Chọn B
Câu 34: Gọi H là tâm của tam giác ABC ⇒ SH ⊥ (ABC)
Gọi M là trung điểm của BC⇒ AM ⊥ BC ⇒ BC ⊥ (SAM ) Khi đó (( ) ( ))  =  ⇒  SH SBC ; ABC SMA tanSMA = HM 2 Đặt x 3
AB = x ⇒ HM = và 2 2 2 x
SM = SB − BM = a − 6 4 2 2 3   2 x x 2 x 5 2 x 3 2 2 x 2 ⇒ a − : = 5 a ⇔ a − = ⇔ a = ⇔ x =   3  12 3 12 4 3 2 3 Vậy 1 2 π  a a 5 a π 5 V = R π h = .  . = . Chọn A 3 3  3  3 81
Câu 35: Bán kính đáy của khối nón là a
r = và chiều cao của khối nón là h = a 2 2
Độ dài đường sinh của khối nón là 2 2 2  a a 5
l = h + r = a +   =  2  2 2
Vậy diện tích toàn phần cần tính là 2 π S = π π tp r h + = a rl (2 5 + )1 4 Chọn C
Câu 36: Gọi I, K lần lượt là trung điểm của MN, BC
Và H là tâm đường tròn ngoại tiếp ∆ABC ⇒ SH ⊥ (ABC)
Vì ∆AMN cân ⇒ AI ⊥ MN và ∆SMN cân ⇒ SI ⊥ MN Suy ra (( ) ( ))  =  o AMN ; SBC SIA = 90 ⇒ SA ∆ K cân tại A a 3 2 2 a 2 ⇒ SA = AK =
⇒ SK = SH + HK = 2 2
Bán kính đường tròn nội tiếp ∆ABC là a 3 r = HK = 6
Vậy thể tích khối nón cần tính là 1 2 2 a π 6 V = r π h = 3 12 Chọn A
Câu 37: Bán kính đáy (hình vuông ABCD) của khối nón là a r = 2
Gọi O là tâm hình vuông ABCD ⇒ SO ⊥ (ABCD) ⇒ ( ( ))  = ( )  =  o SA; ABCD SA;OA SAO = 60
Gọi M là trung điểm của AB ⇒ OM ⊥ AB
⇒ SM là đường sinh của khối nón
Tam giác SMO vuông tại O, có 2 2 a 7
SM = SO + OM = 2 2
Vậy diện tích xung quanh là a a 7 a π 7 S = π = π = xq rl . . 2 2 4 Chọn C AC AC 2a
Câu 38: Tam giác ABC vuông tại A, có  tan ABC = ⇒ AB = = = AB  2a 3 o tan ABC tan 30
Suy ra BC = AB2 + AC = (2a 3)2 2 + (2a)2 = 4a
Quay tam giác ABC xung quanh trục AC, ta được hình nón có chiều cao h = AC = , 4 bán kính đáy
R = AB = 3(hình vẽ bên)
Vậy diện tích xung quanh hình nón là S = π = π xq Rl 8 2 a 3 Chọn C Aˆ = o 90 Câu 39: Ta có o
Aˆ + Bˆ + Cˆ =180 mà 
Aˆ: Bˆ Cˆ
: = 3: 2 :1⇒ Bˆ = o 60   o ˆ C = 30 
Do đó tam giác ABC vuông tại A AC = ⇒ 10 3  BC = 20
Quay tam giác ABC xung quanh trục AB, ta được hình nón có chiều cao h = AB =10 , bán kính đáy
R = AC =10 3 (hình vẽ bên)
Vậy độ dài đường sinh cần tính là l = BC = c 20 m Chọn A
Câu 40: Khối nón có độ dài đường sinh  = R =12cm π R 2 .
Hình nón nhỏ có đường sinh  =12 và bán kính đáy r 3 = = 1 c 4 m 2π π R  2 . 2   π − 
Hình nón nhỏ có đường sinh  3
 =12 và bán kính đáy r  = = 2 c 8 m 2π 2 2 2 V r .  − r
Tỷ số thể tích của khối nón nhỏ so với khối nón lớn là 10 1 1 1 = = 2 2 2 V r .  − r 10 2 2 2 Chọn C
Câu 41: Ba hình quạt, mỗi hình quạt có độ dài cung là: π L = ϕ R 2 . = 6 . = 4 dm π 3
Độ dài cung là chu vi đáy của hình nón ⇒ L = C = 2 r π ⇒ r = 2dm
Chiều cao của hình nón là: 2 2 h =  − r = 4 2dm
Thể tích của mỗi phễu là π V 1 = r2 π π h 2 16 2 = .2 .4 2 = lít 3 3 2 Chọn B
Câu 42: Phễu chính là khối nón có độ dài đường sinh l = R. Chuẩn hóa R = 1
Gọi h, r lần lượt là chiều cao và bán kính đáy của khối nón ⇒ V 1 = r2 π h 3 Ta có 1 2 1 2 2 2 π 2 2 V = r π h = r π
l − r = .r . 1− r 3 3 3 3 2 2  r r  + +1 2 − r 2 2   4 2 r r 2  2 2 Mà r (  π π π 1− r )= . 4 . (.1−r ) 4 2 2 2 3 ≤ . 4 =
⇒ V = r. 1− r ≤ = 2 2 27 27 3 9 3 27 2
Dấu “=” xảy ra khi và chỉ khi r 2 2 2 6
= 1− r ⇔ r = ⇔ r = 2 3 3
Độ dài cung tròn AB là L = x R
. = x chính bằng chu vi đường tròn đáy của khối nón Khi đó 2π 6
L = x = C = 2πr ⇒ x = 2πr = 3 Chọn D
Câu 43: Xét hình nón được tạo thành, có độ dài đường sinh bằng l = . n R
Gọi α (rad) là số đo cung của hình quạt còn lại, khi đó độ dài cung còn lại là L = αR .
Và L chính là chu vi đường tròn đáy của hình nón α ⇒ π 2 r = = ⇔ = . n L α R R rn π 2
Vậy thể tích khối nón là 1 2 1 2 2 2 1 2 2 2 V = π.r = π − = π − với x = r n .hn rn . ln rn .x R x 3 3 3 n 2 2 6 3 3 Ta có 4 π x ( 2 2 R − )= . 4 x x . x (. 2 2 R − x ) R 2 2 2 2R 2 ≤ . 4 R
⇒ x R − x ≤ ⇒ V = 2 2 27 3 3 max 9 3 2 2
Dấu đẳng thức xảy ra khi và chỉ khi x 2 2 2 3 2 3 α R .  8 o
= R − x ⇔ R = r = .  ⇔ α = π ≈ 294 n 2 2 2  2π  3
Vậy số đo cung bị cắt là: 3 o o o 360 − 294 = 66 . Chọn A.
Câu 44: Phễu chính là khối nón có độ dài đường sinh l = R . Chuẩn hóa R = 1.
Gọi h, r lần lượt là chiều cao và bán kính đáy của khối nón ⇒ V 1 = r2 π h 3 Ta có 1 2 1 2 2 2 π 2 2 V = r π h = r π
l − r = .r . 1− r 3 3 3 3 2 2  r r  + +1 2 − r 2 2   4 2 r r 2  2 2 Mà r (  π π π 1− r )= . 4 . (.1−r ) 4 2 2 2 3 ≤ 4. =
⇒ V = r. 1− r ≤ = 2 2 27 27 3 9 3 27 2
Dấu “=” xảy ra khi và chỉ khi r 2 2 2 6
= 1− r ⇔ r = ⇔ r = 2 3 3
Độ dài cung tròn AB là L = x R
. = x chính bằng chu vi đường tròn đáy của khối nón Khi đó 2π 6
L = x = C = 2πr ⇒ x = 2πr = 3 Chọn C
Câu 45: Đặt AH = h;CH = r lần lượt là đường cao và bán kính đáy của hình nón khi quay tam giác ACH quanh trục AB. Ta có: V 1 = r2
π h . Mặt khác HB = 2R - h ⇒ CH 2 = HA HB . (hệ thức lượng) 3 Suy ra 2
r = h( R − h) 1 2 ⇒ V = h
π (2R − h)⇒ V ⇔ ([2R − h) 2 h max ]max 3
Cách 1: Xét hàm số f (h) = (2R − h)h2(0 < h < 2R) 3   2 h h R − h  + + 
Cách 2: ( R − h) 2 1 2
h = (2R − h) h h 1 ≤  2 2 2 2 . .  = R 4 2 2 4 3 27     Dấu “=” xảy ra h 3 4 2 2 ⇔ 2 R
R − h = ⇔ R = h ⇒ h = R ⇒ r = AH = 2 4 3 3 CH r 1 ⇔ tanα = = = AH h 2 Chọn B
Câu 46: Nếu ba tam giác không trùng lên nhau thì thể tích khối tròn xoay là thể tích của 3 khối nón có chiều 3 cao a 3   π h = và bán kính đáy a 1 2 a 3
r = ⇒ V =  r π h  = 1 1 . 3 1 2 2  3 1 1  8
Thể tích phần bị trồng lên nhau là hai khối nón có chiều cao a 3 h = và bán kính 1 4 3 đáy a  1 2  a π 3
r = ⇒ V =  r π h  = 1 2 . 2 4  3 1 1  96 3 Thể tích cần tìm là: 11 3 a π
V = V −V = 1 2 96 Chọn A
Câu 47: Dựng hình như hình vẽ bên trong đó:
O' N = a;OA = a 3 và 29a MA = 10
Ta có: SO' O'M 1 = = ⇒ OO'= 2SO' SO OA 3 Mặt khác 2
MA = OO' +(OA − O'M )2  29 2  2 2 21 21 6 ⇔   = OO' 4 + a ⇒ OO'= a ⇒ SO'= ; a SO =  10  10 20 2
Thể tích V phần còn lại của khối nón là: 1 V = ( 2 2 OA π .SO − O π 'M .SO') 91 3 = a π 3 10 Chọn D.
Câu 48: Ta có: SI IA 1 R =
= ⇒ IA = , gọi K = AC ∩ BD ⇒ K
∆ AB vuông cân tại K SO OD 3 3 AB R ⇒ KI = = 2 3 Tương tự ta có: 4R
KO = R ⇒ OI = KI + KO = . 3 Mặt khác 1 2R
SI = SO ⇒ OI = 2SI ⇒ SI =
;SO = OI + SI = 2R 3 3
Thể tích phần hình nón (N) nằm giữa mặt phẳng (P) và mặt phẳng chứa đáy hình nón (N) là: 1 π V = π ( 3 2 OD . 2 SO − IA ) 52 . R SI = 3 81 Chọn B.
Document Outline

  • ITMTTL~1
  • IIBITP~1
  • IIILIG~1