



































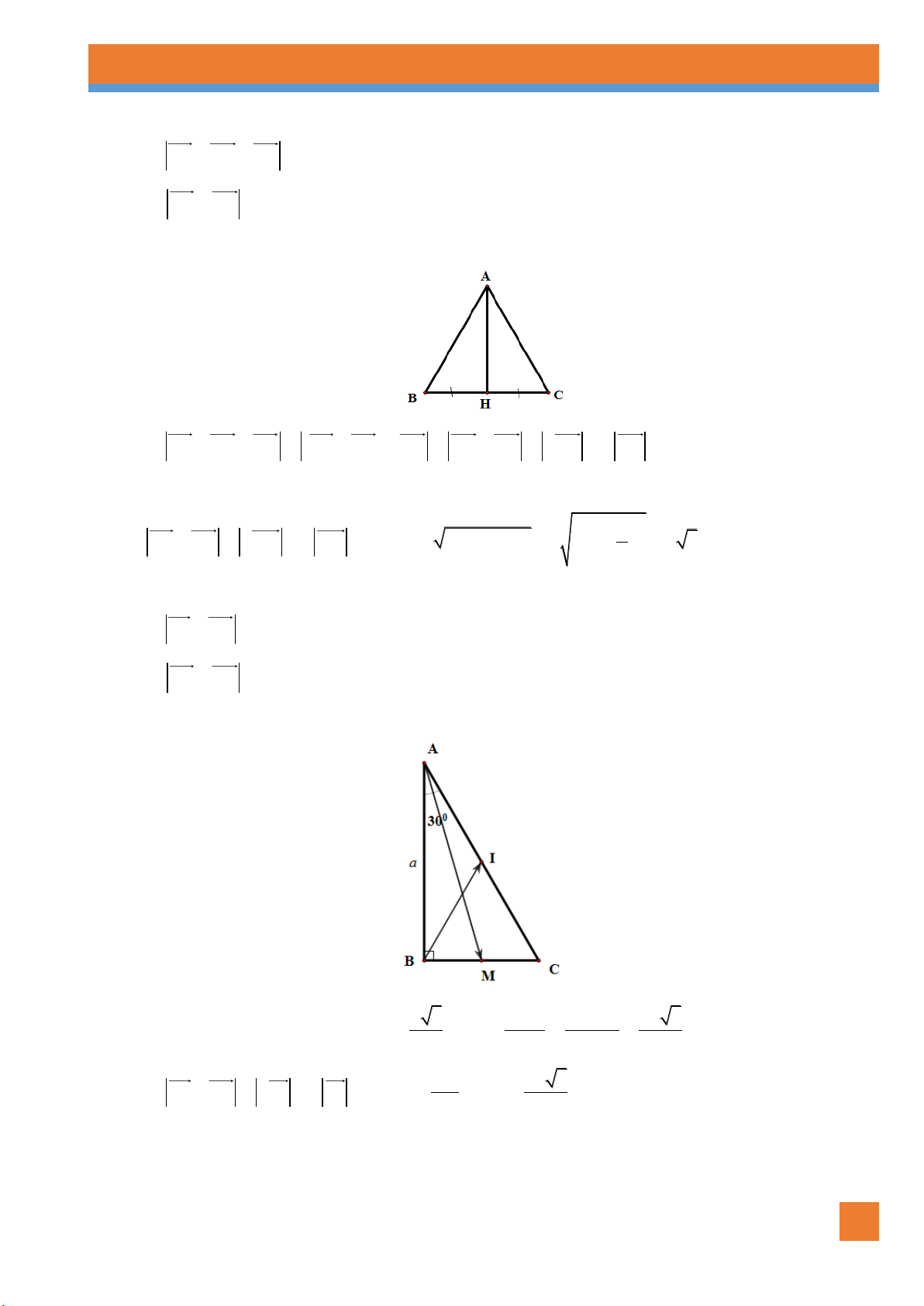

































































Preview text:
CĐ: VECTO TLDH CHUYÊN ĐỀ VECTO (CHƯƠNG 1 LỚP 10)
BÀI 1. CÁC ĐỊNH NGHĨA ........................................................................................................................................ 2
A. KIẾN THỨC SÁCH GIÁO KHOA CẦN CẦN NẮM .................................................................................... 2
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP ....................................................................................... 2 Ban thực hiện Tên giáo viên Đơn vị công tác GV Soạn
Cô Phạm Thị Thu Ngà
Trường THPT chuyên Lương Văn Chánh (Phú Yên) GV phản biện
Thầy Trần Chí Trung
Trường THPT Trần Đại Nghĩa (TP Hồ Chí Minh) TT Tổ soạn Cô Phạm Thị Hoài
Trường THCS Nguyễn Hiền (Nha Trang) TT Tổ phản biện
Thầy Nguyễn Văn Vũ Trường THPT YaLy (Gia Lai) Người triển khai Thầy Phạm Lê Duy
Trường THPT Chu Văn An (An Giang)
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 1 CĐ: VECTO TLDH
BÀI 1. CÁC ĐỊNH NGHĨA
A. KIẾN THỨC SÁCH GIÁO KHOA CẦN CẦN NẮM
1. Định nghĩa vectơ:
Vectơ là đoạn thẳng có hướng, nghĩa là trong hai điểm mút của đoạn thẳng đã chỉ rõ điểm nào là
điểm đầu, điểm nào là điểm cuối.
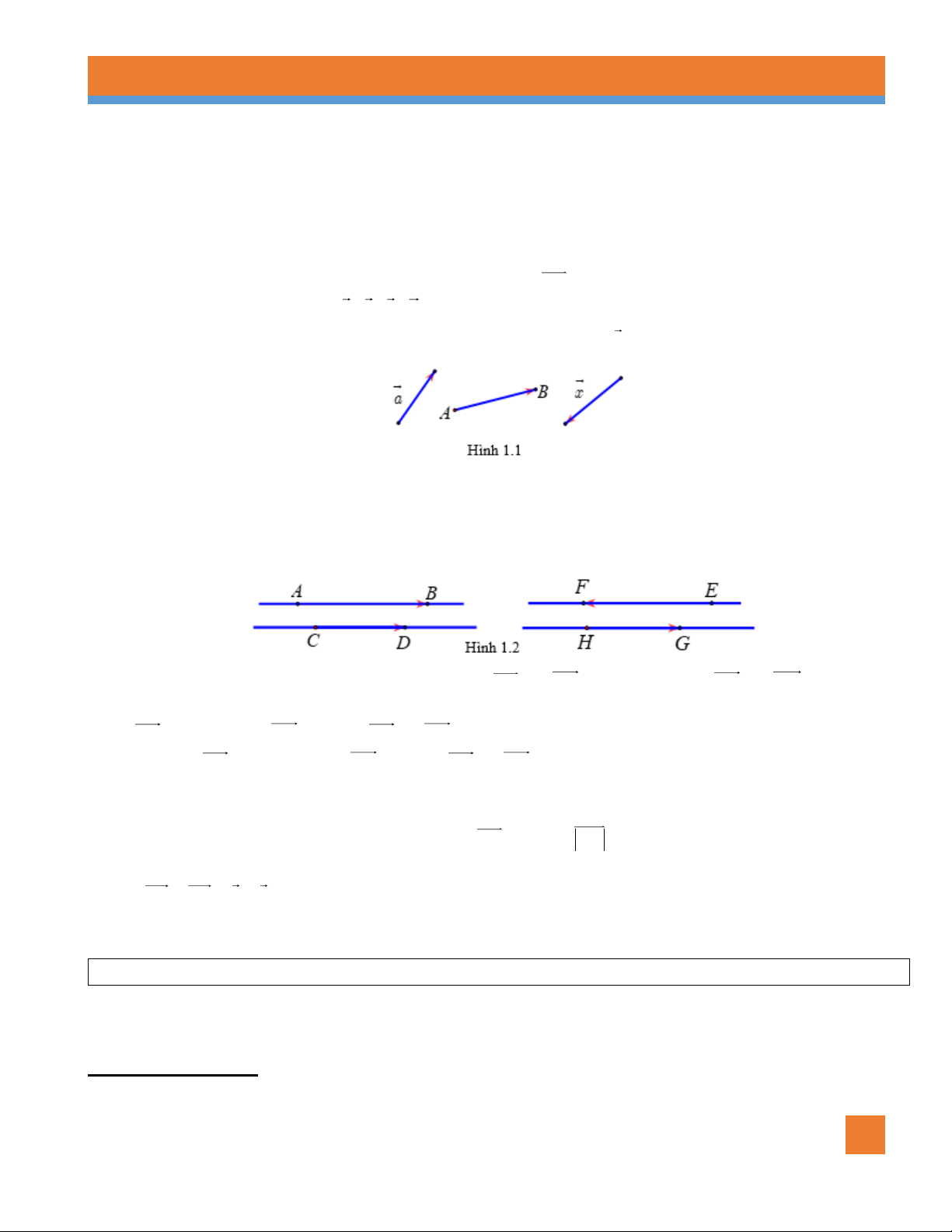
Vectơ có điểm đầu là A , điểm cuối là B ta kí hiệu : AB
Vectơ còn được kí hiệu là: a, ,
b x, y,...
Vectơ – không là vectơ có điểm đầu trùng điểm cuối. Kí hiệu là 0
2. Hai vectơ cùng phương, cùng hướng.
- Đường thẳng đi qua điểm đầu và điểm cuối của vectơ gọi là giá của vectơ
- Hai vectơ có giá song song hoặc trùng nhau gọi là hai vectơ cùng phương
- Hai vectơ cùng phương thì hoặc cùng hướng hoặc ngược hướng.
Ví dụ: Ở hình vẽ trên trên (hình 2) thì hai vectơ AB và CD cùng hướng còn EF và HG ngược hướng.
AB cùng hướng CD kí hiệu: AB CD
AB ngược hướng CD kí hiệu: AB CD
Đặc biệt: vectơ – không cùng hướng với mọi véc tơ.
3. Hai vectơ bằng nhau
- Độ dài đoạn thẳng AB gọi là độ dài véc tơ AB , kí hiệu AB .
- Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài.
- AA BB = 0 , | 0 |= 0.
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Xác định một vectơ; phương, hướng của vectơ; độ dài của vectơ
+ Xác định một vectơ và xác định sự cùng phương, cùng hướng của hai vectơ theo định nghĩa
+ Dựa vào các tình chất hình học của các hình đã cho biết để tính độ dài của một vect
PHẦN 1: CÁC VÍ DỤ
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 2 CĐ: VECTO TLDH
Ví dụ 1. Cho tam giác ABC có bao nhiêu vec tơ khác vec tơ- không có điểm đầu và điểm cuối là các đỉnh của tam giác. Lời giải
Hai điểm phân biệt, giả sử ,
A B tạo thành hai vec tơ khác vec tơ- không là AB và BA . Vì vậy từ 3 đỉnh ,
A B,C của tam giác ta có 3 cặp điểm phân biệt nên có 6 vec tơ khác vec tơ – không được tạo thành.
Ví dụ 2. Cho 3 điểm ,
A B,C phân biệt và thẳng hàng. Trong trường hợp nào hai vec tơ AB, AC cùng
hướng. Trong trường hợp nào hai vec tơ AB, AC ngược hướng. Lời giải
Hai vec tơ AB, AC cùng hướng khi và chỉ khi A nằm ngoài đoạn BC . Ngược lại hai vec tơ
AB, AC ngược hướng khi và chỉ khi A nằm trong đoạn BC .
Ví dụ 3. Cho vec tơ AB và điểm C . Hãy dựng điểm D sao cho AB CD . Chứng minh rằng điểm D như thế là duy nhất. Lời giải
Điểm D thoả mãn điều kiện đề bài là duy nhất. Thật vậy: Giả sử có điểm D' sao cho AB CD '
thì CD CD ', khi đó C, ,
D D ' thẳng hàng, D và D ' ở cùng một phía đối với C và CD CD ' nên D D'
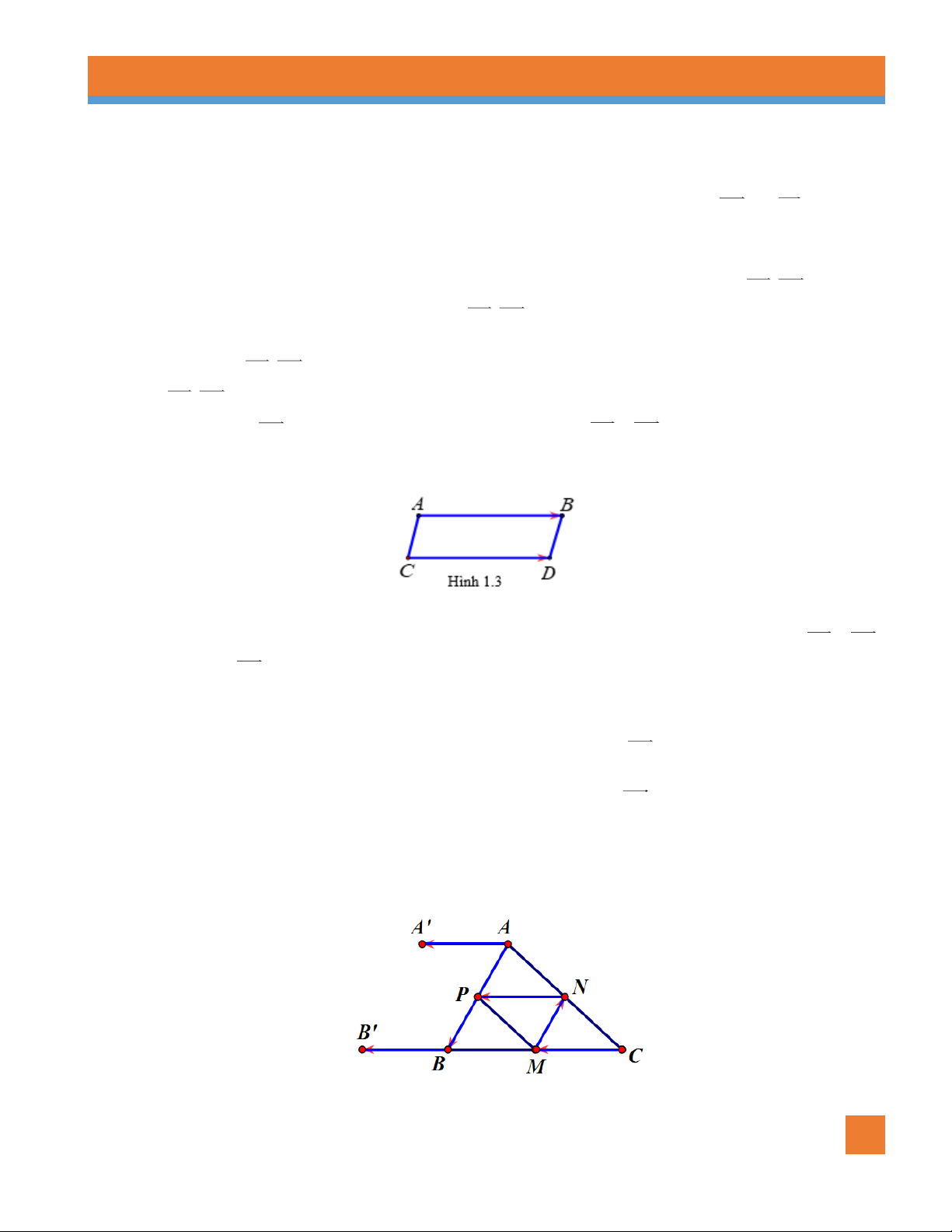
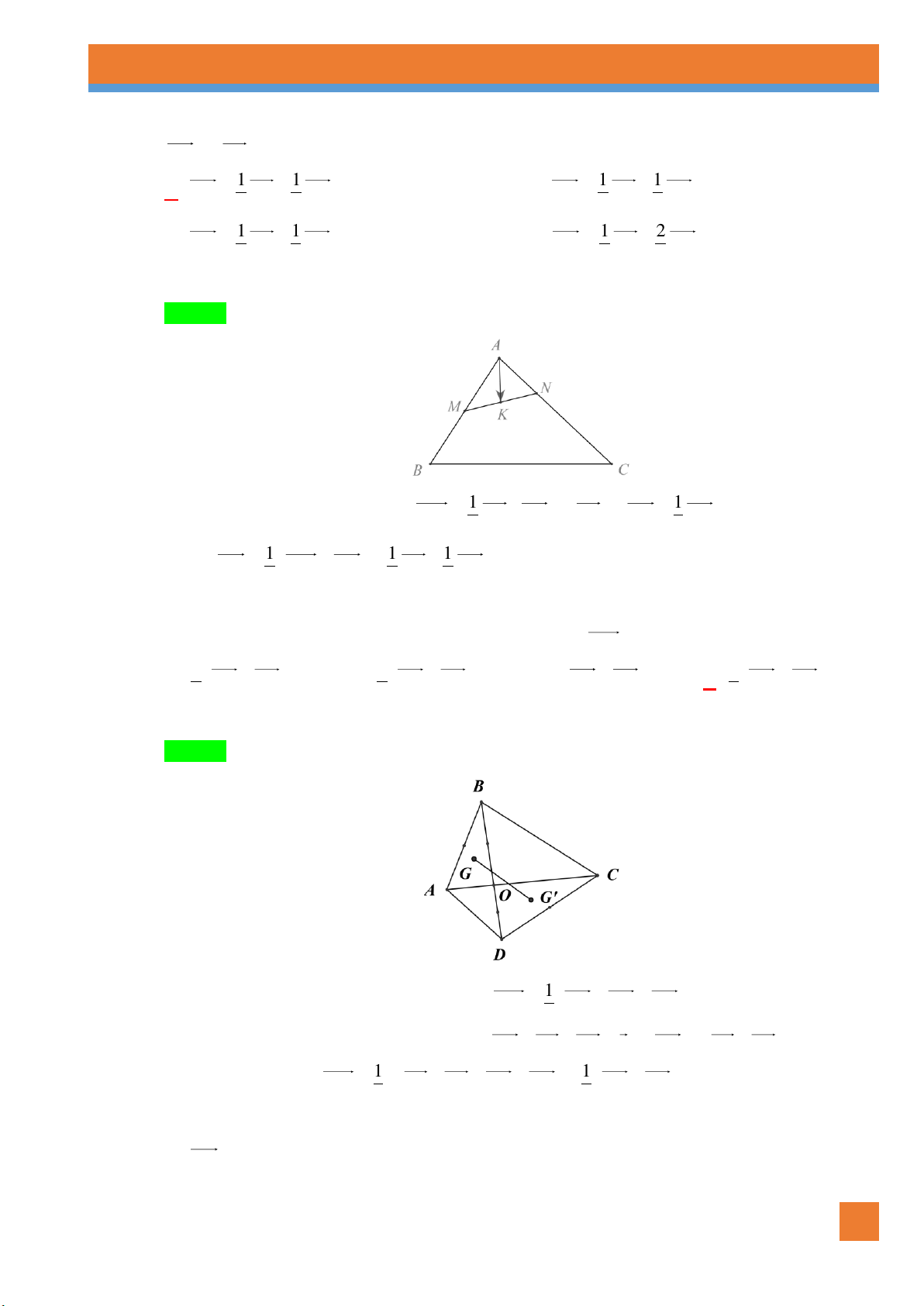
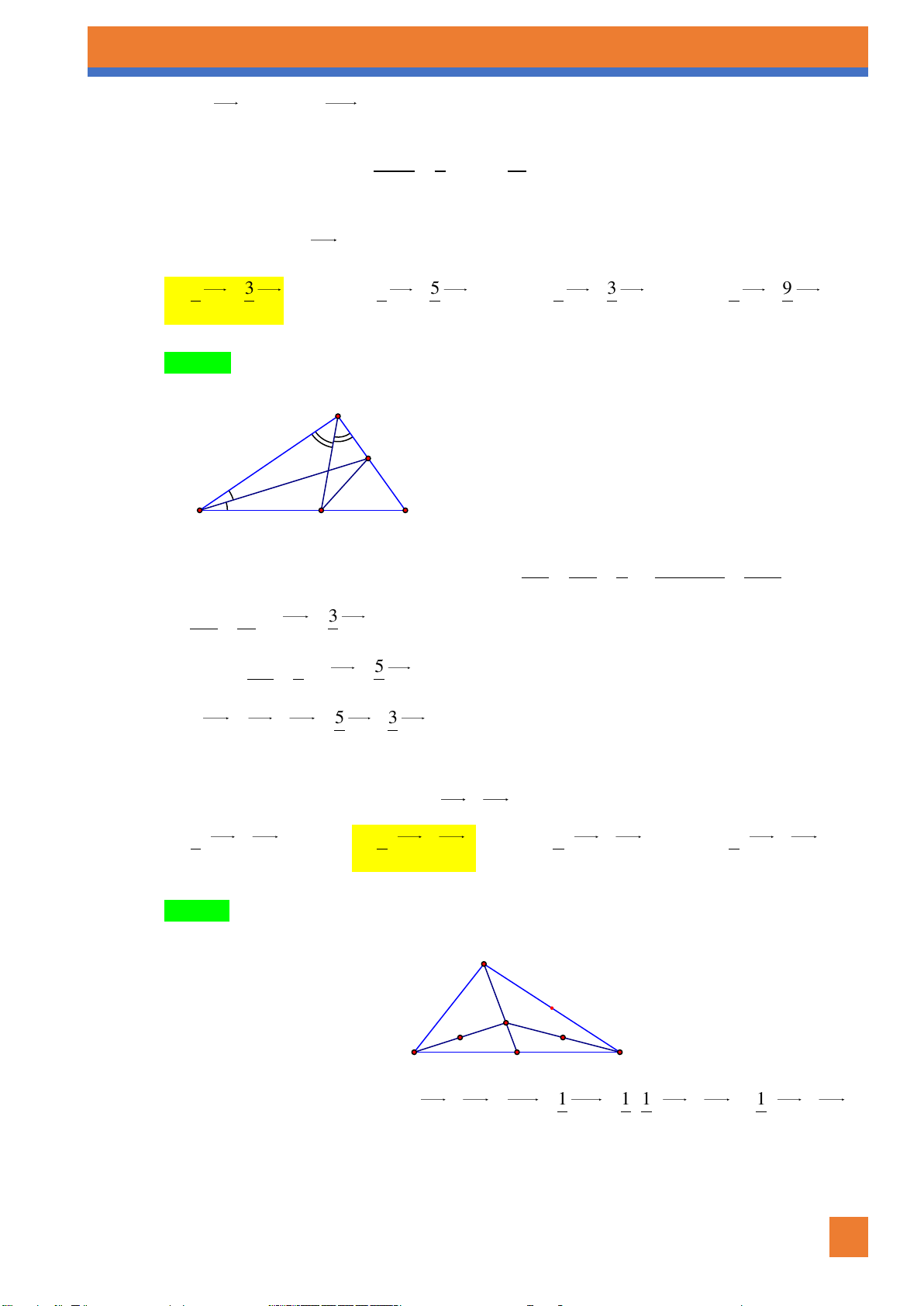
Ví dụ 4. Cho tam giác ABC , gọi M, N, P lần lượt là trung điểm của BC,C , A AB . a.
Có bao nhiêu vec tơ khác vec tơ- không cùng hướng với AB có điểm đầu, điểm cuối lấy trong các điểm đã cho.
b. Có bao nhiêu vectơ khác vectơ - không cùng hướng với AB có điểm đầu và điểm cuối lấy trong các điểm đã cho. Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 3 CĐ: VECTO TLDH a.
Các vec tơ khác vec tơ- không cùng hướng với AB là AB, PB, NM .
b. Các vectơ khác vectơ - không cùng hướng với AB là AP, PB, NM .
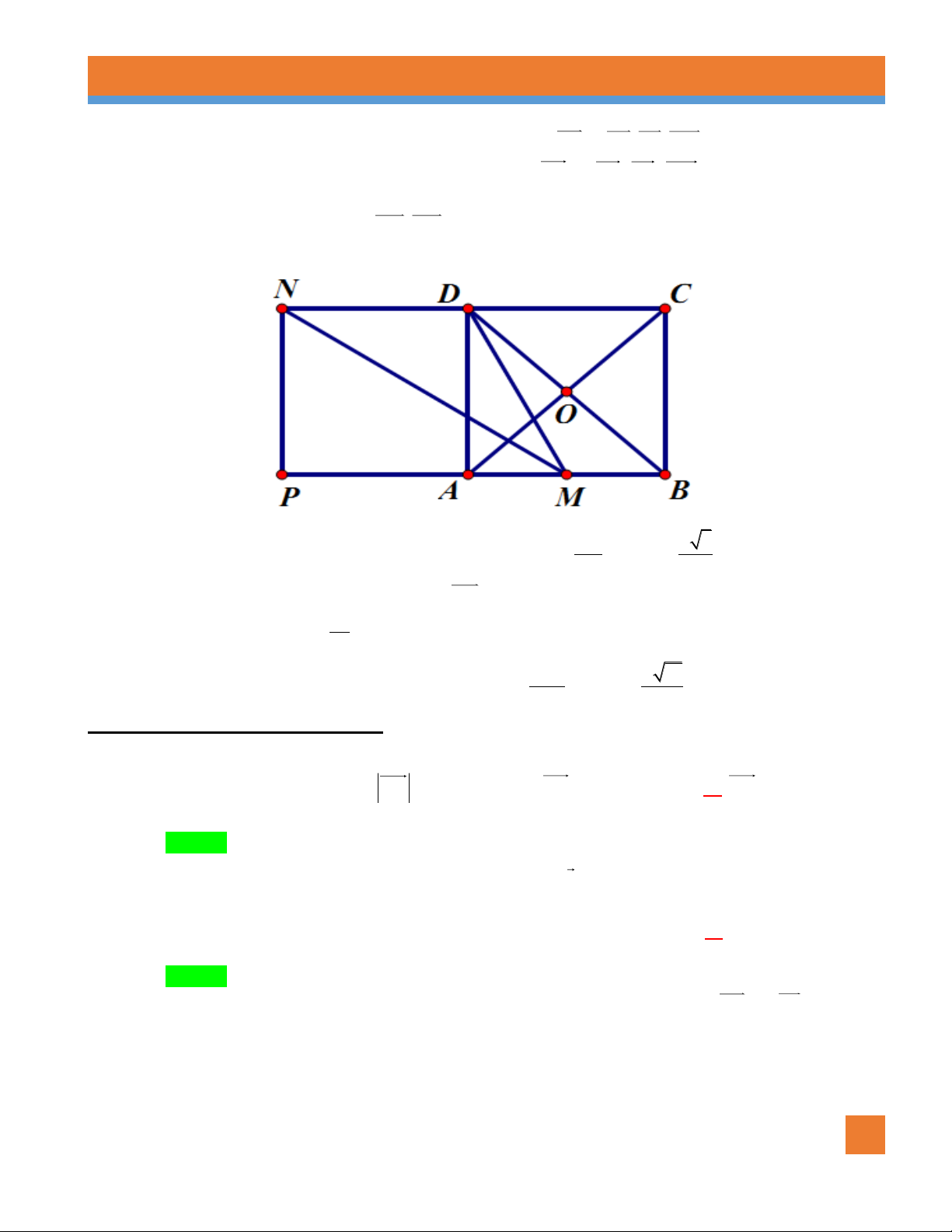
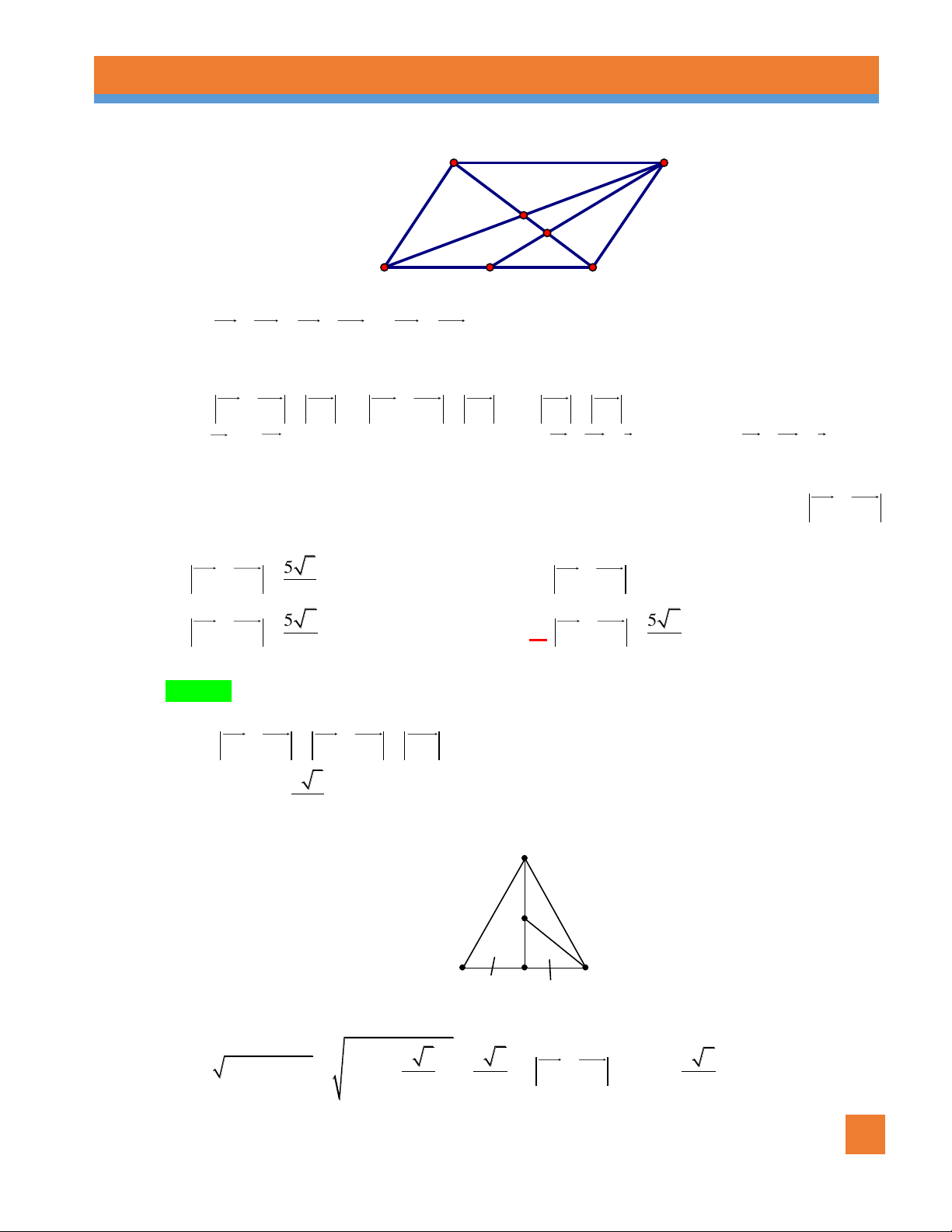
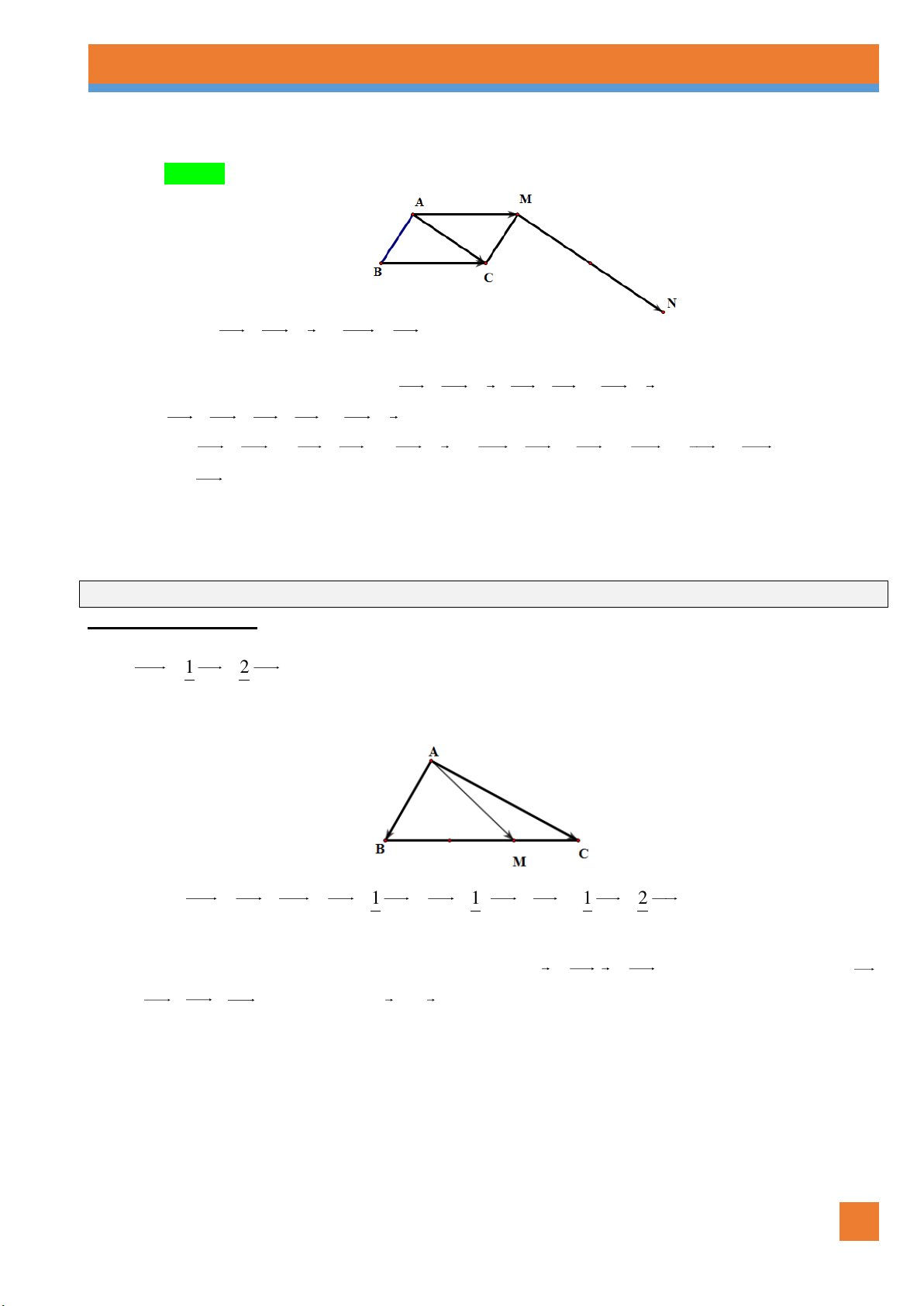
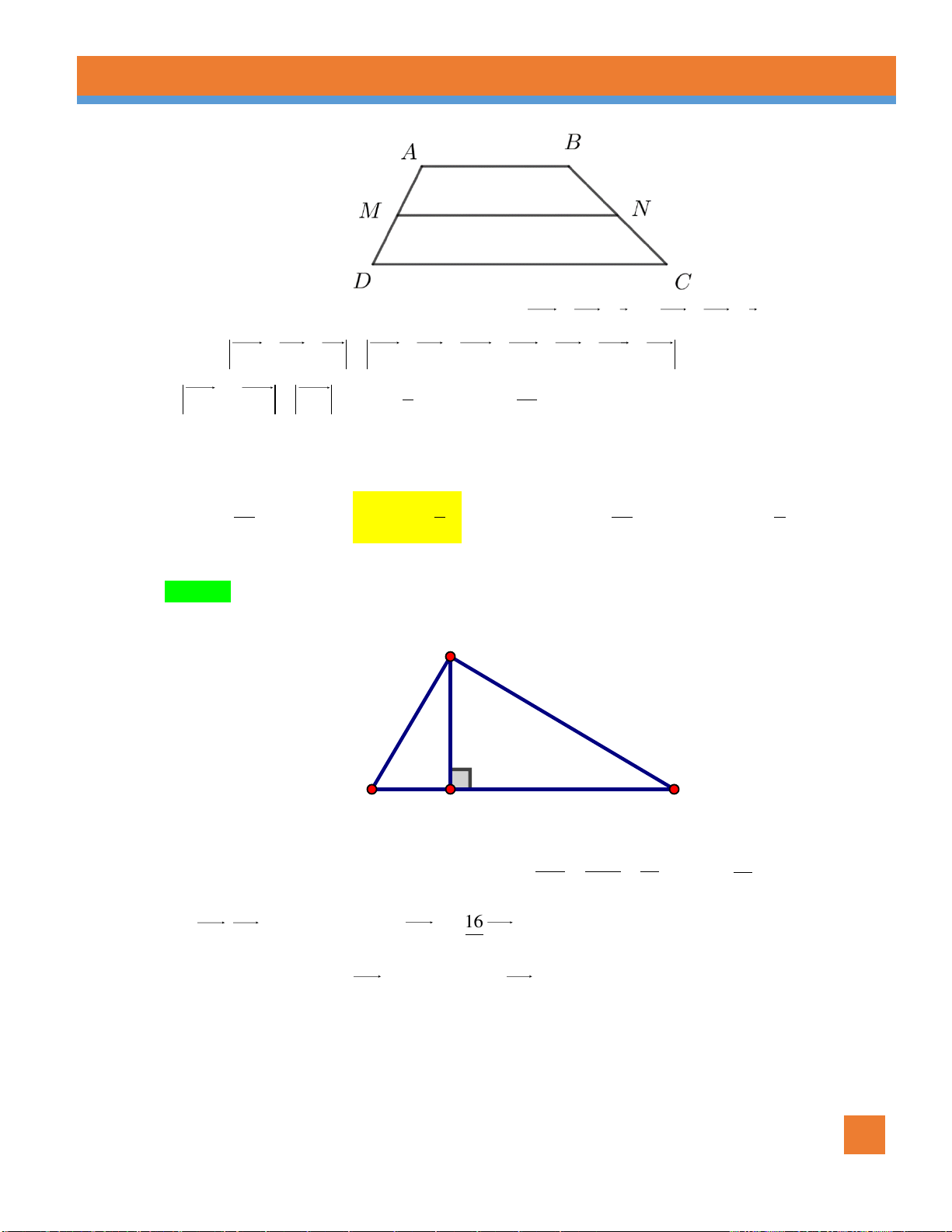
Ví dụ 5. Cho hình vuông ABCD tâm O cạnh a . Gọi M là trung điểm AB , N là điểm đối xứng với C
qua D .Hãy tính độ dài của MD, MN . Lời giải 2 Xét tam giác vuông 5a a 5 MAD ta có: 2 2 2
MD AD AM MD . 4 2
Qua N kẻ đường thẳng song song với AD cắt AB tại P . Khi đó tứ giác ADNP là hình vuông và 3a
PM PA AM . 2 2 Xét tam giác 13a a 13 NPM ta có: 2 2 2
MN PM PN MN . 4 2
PHẦN 2 : CÂU HỎI TRẮC NGHIỆM
Câu 1. [0H1-1.1-1] Vectơ có điểm đầu là D , điểm cuối là E được kí hiệu là: A. . DE B. DE . C. . ED D. DE. Lời giải Chọn D
Câu 2. [0H1-1.1-1] Cho tứ giác ABC .
D Số các vectơ khác 0 có điểm đầu và cuối là đỉnh của tứ giác bằng: A. 4 B. 6 C. 8 D. 12. Lời giải Chọn D
Hai điểm phân biệt, giả sử ,
A B tạo thành hai vec tơ khác vec tơ- không là AB và BA . Vì vậy từ 4 đỉnh ,
A B,C, D của tam giác ta có 6 cặp điểm phân biệt nên có 12 vec tơ khác vec
tơ – không được tạo thành.
Câu 3. [0H1-1.2-1] Mệnh đề nào sau đây đúng
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 4 CĐ: VECTO TLDH
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ. Lời giải Chọn A Là vectơ 0
Câu 4. [0H1-1.2-1] Cho ba điểm , A ,
B C phân biệt. Khi đó:
A. Điều kiện cần và đủ để , A ,
B C thẳng hàng là AB cùng phương với AC.
B. Điều kiện đủ để , A ,
B C thẳng hàng là với mọi M , MA cùng phương với . AB
C. Điều kiện cần để , A ,
B C thẳng hàng là với mọi M , MA cùng phương với . AB
D. Điều kiện cần để , A ,
B C thẳng hàng là AB AC. Lời giải Chọn A
Câu 5. [0H1-1.2-1] Gọi M , N lần lượt là trung điểm của các cạnh A ,
B AC của tam giác đều ABC .
Hỏi cặp vectơ nào sau đây cùng hướng?
A. MN và CB. B. AB và . MB C. MA và . MB D. AN và . CA Lời giải Chọn A
Câu 6. [0H1-1.2-1] Cho hình bình hành ABCD . Mệnh đề nào sau đây đúng?
A. Hai vectơ AB; BC cùng phương. B. Hai vectơ ; AB CD cùng phương. C. Hai vectơ ; AB CD cùng hướng.
D. Hai vectơ A ;
B DC ngược hướng. Lời giải Chọn B
Câu 7. [0H1-1.3-1] Cho AB ≠ 0 và một điểm C, có bao nhiêu điểm D thỏa mãn: AB CD A. 0. B. 1. C. 2. D. Vô số. Lời giải Chọn D
Tập hợp điểm D là đường tròn tâm C , bán kính bằng AB
Câu 8. [0H1-1.2-1] Xét các mệnh đề sau
(I): Véc tơ – không là véc tơ có độ dài bằng 0 .
(II): Véc tơ – không là véc tơ có nhiều phương. A. Chỉ (I) đúng. B. Chỉ (II) đúng.
C. (I) và (II) đúng. D. (I) và (II) sai. Lời giải Chọn C
Câu 9. [0H1-1.3-1] Cho tam giác đều ABC cạnh a , mệnh đề nào sau đây đúng?
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 5 CĐ: VECTO TLDH
A. AC BC .
B. AC a .
C. AB AC .
D. AB a . Lời giải Chọn D
Câu 10. [0H1-1.3-1] Cho tam giác đều ABC cạnh a , mệnh đề nào sau đây sai?
A. AB BC .
B. AC BC .
C. AB BC .
D. AC, BC không cùng phương. Lời giải Chọn A
Câu 11. [0H1-1.3-1] Gọi C là trung điểm của đoạn thẳng AB. Hãy chọn khẳng định đúng trong các khẳng định sau :
A. CA CB .
B. AB vaø AC cùng phương .
C. AB vaø CB ngược hướng .
D. AB CB Lời giải Chọn B
Câu 12. [0H1-1.3-1] Cho M là một điểm thuộc đoạn thẳng AB sao cho AB = 3AM. Hãy tìm khẳng định sai? A. MB 2 MA . B. MA 2 MB . C. BA 1 3 AM . D. AM BM . 2 Lời giải Chọn D
Câu 13. [0H1-1.3-1] Cho hình bình hành ABCD . Khẳng định nào sau đây đúng?
A. AD = BC .
B. AB = AC .
C. AC = DB .
D. AB = CD . Lời giải Chọn A
Câu 14. [0H1-1.2-1] Cho hình bình hành ABCD tâm O . Các véctơ ngược hướng với OB là:
A. BD, OD
DB, OD, BO DB, DO
BD, OD, BO . B. . C. . D. Lời giải Chọn D
Câu 15. [0H1-1.2-1] Cho hình bình hành ABCD . Mệnh đề nào sau đây đúng?
A. Hai vectơ AB; BC cùng phương. B. Hai vectơ ; AB CD cùng phương. C. Hai vectơ ; AB CD cùng hướng.
D. Hai vectơ A ;
B DC ngược hướng. Lời giải Chọn B
Câu 16. [0H1-1.3-1] Cho hình chữ nhật ABCD có AB 3, AD 4. Khẳng định nào sau đây đúng ?
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 6 CĐ: VECTO TLDH A. AC BD . B. CD BC . C. AC AB .
D. BD 7 . Lời giải Chọn A
Câu 17. [0H1-1.3-1] Cho hình chữ nhật ABCD tâm I , AB 3, BC 4 . Khi đó BI là: 5 7 A.7. B. . C.5. . D. . 2 2 Lời giải Chọn B
Câu 18. [0H1-1.2-1] Mệnh đề nào sau đây đúng?
A. Hai vectơ cùng phương thì chúng cùng hướng.
B. Hai vectơ cùng phương thì giá của chúng song song hoặc trùng nhau.
C. Hai vectơ có giá vuông góc thì cùng phương.
D. Hai vectơ ngược hướng với 1 vectơ thứ ba thì cùng phương. Lời giải Chọn B
Câu 19. [0H1-1.3-1] Cho tam giác đều ABC với đường cao AH . Đẳng thức nào sau đây đúng? 3
A. HB HC .
B. AC 2 HC . C. AH HC .
D. AB AC . 2 Lời giải Chọn B
Câu 20. [0H1-1.3-1] Cho tam giác đều ABC cạnh a , mệnh đề nào sau đây đúng? 3
A. AC BC .
B. AC a .
C. AB AC .
D. AH a . 2 Lời giải Chọn D
Dạng 2: Chứng minh hai vectơ bằng nhau
+ Để chứng minh hai vectơ bằng nhau ta chứng minh chúng có cùng độ dài và cùng hướng hoặc dựa
vào nhận xét nếu tứ giác ABCD là hình bình hành thì AB DC hoặc AD BC . PHẦN 1: CÁC VÍ DỤ
Ví dụ 6. Cho hình bình hành ABCD tâm O . Từ 5 điểm , A , B C, ,
D O . Tìm các vec tơ bằng vec tơ AB OB . Lời giải
AB DC, OB DO
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 7 CĐ: VECTO TLDH
Ví dụ 7. Cho hình bình hành ABCD. Chứng minh rằng nếu AB DC thì AD BC . Lời giải
Ta có: AB DC khi và chỉ khi tứ giác ABCD là hình bình hành. Suy ra AD BC .
Ví dụ 8. Cho hình thang ABCD có hai đáy là A ,
B CD với AB 2CD . Từ C vẽ CI DA . Chứng minh:
a. DI CB .
b. AI IB DC . Lời giải
a. Ta có : CI DA suy ra AICD là hình bình hành. Suy ra AD IC .
Ta có : DC AI , AB 2CD do đó 1 AI
AB suy ra I là trung điểm AB . 2 DC IB Ta có :
BCDI là hình bình hành suy ra DI CB DC//IB
b. I là trung điểm AB AI IB và BCDI là hình bình hành IB DC AI IB DC
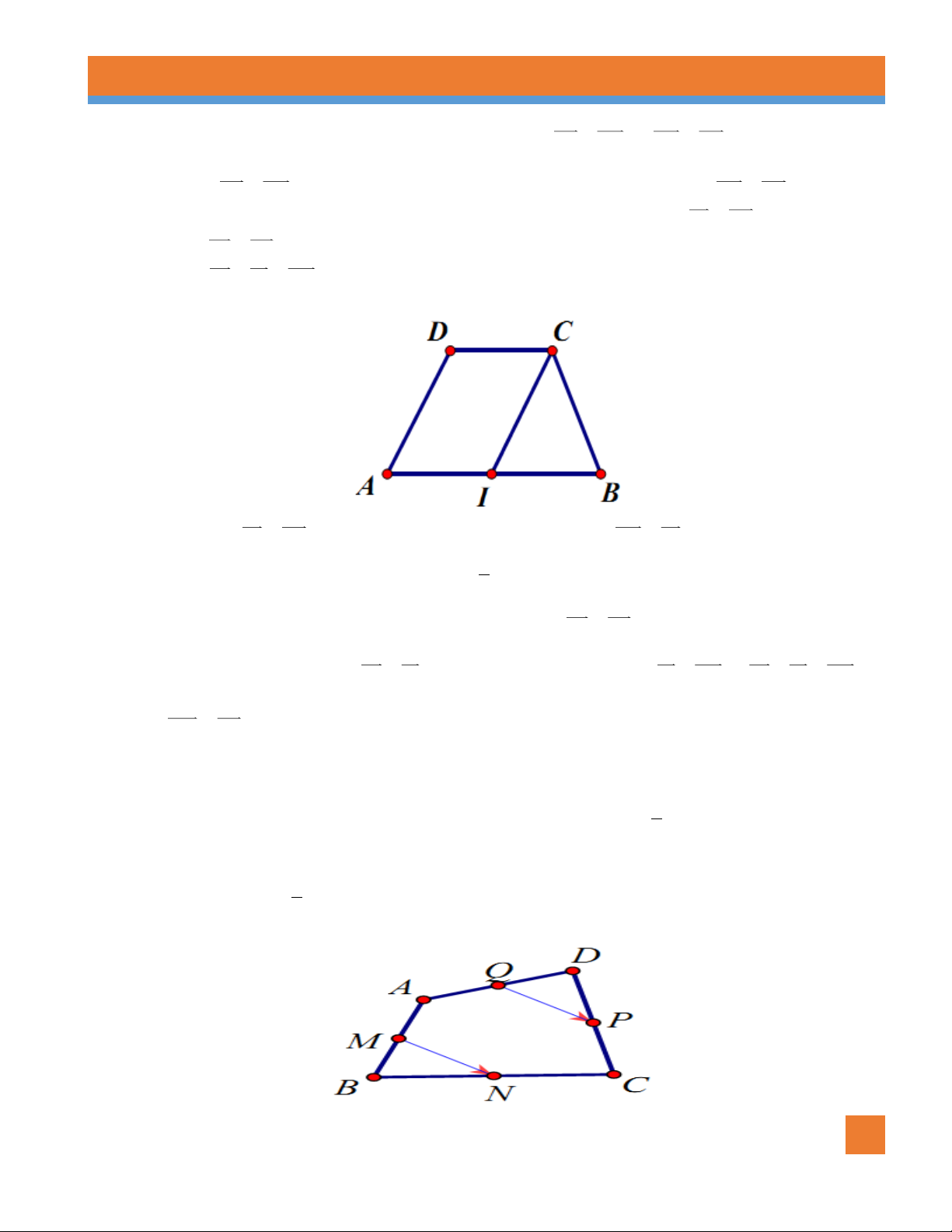
Ví dụ 9. Cho tứ giác ABCD. Gọi M , N, ,
P Q lần lượt là trung điểm A , B BC,C , D DA . Chứng minh MN QP Lời giải MN //AC
Ta có MN là đường trung bình của tam giác ABC suy ra 1 1 . MN AC 2 Q P//AC Tương tự 1 2 QB AC 2
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 8 CĐ: VECTO TLDH Từ
1 &2 suy ra tứ giác MNQP là hình bình hành nên MN QP .
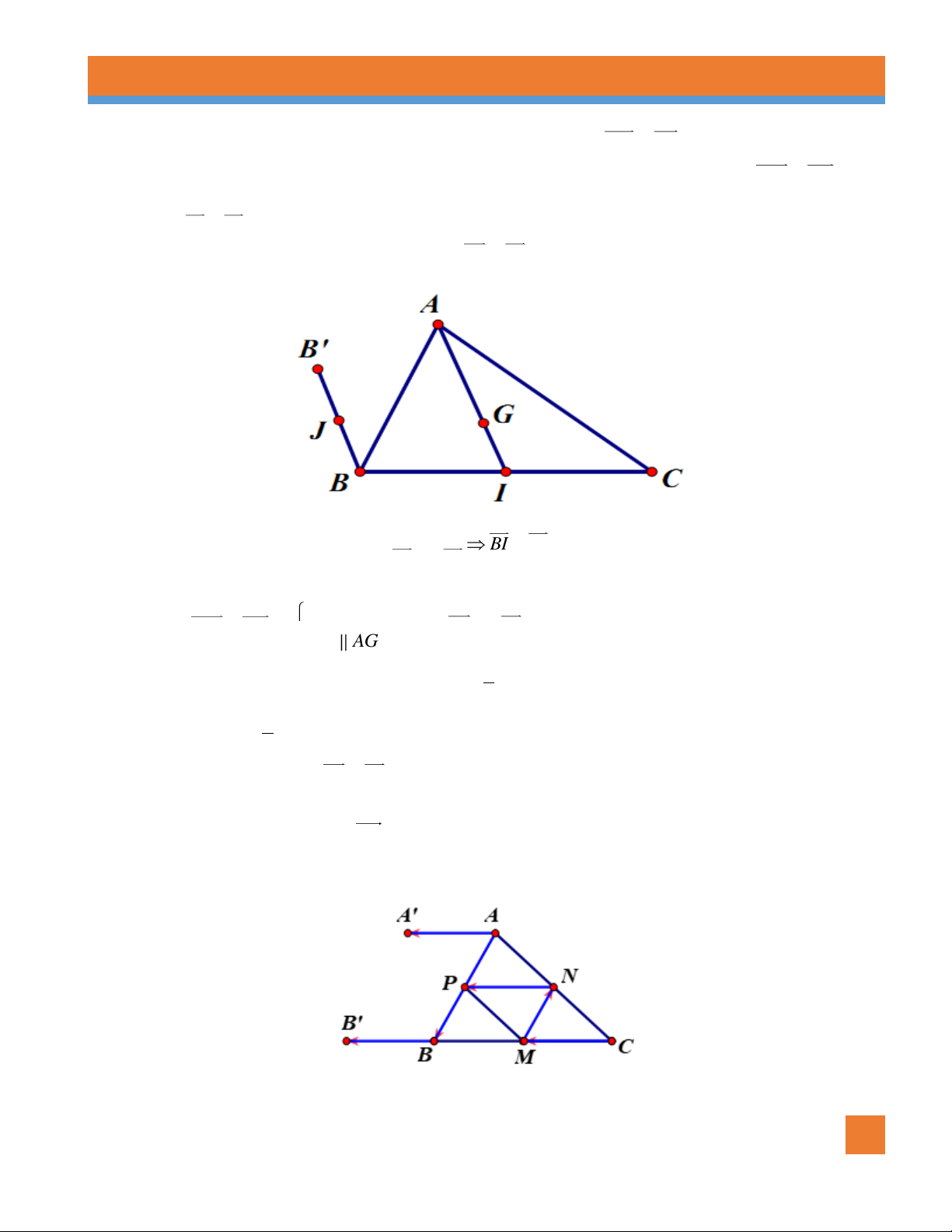
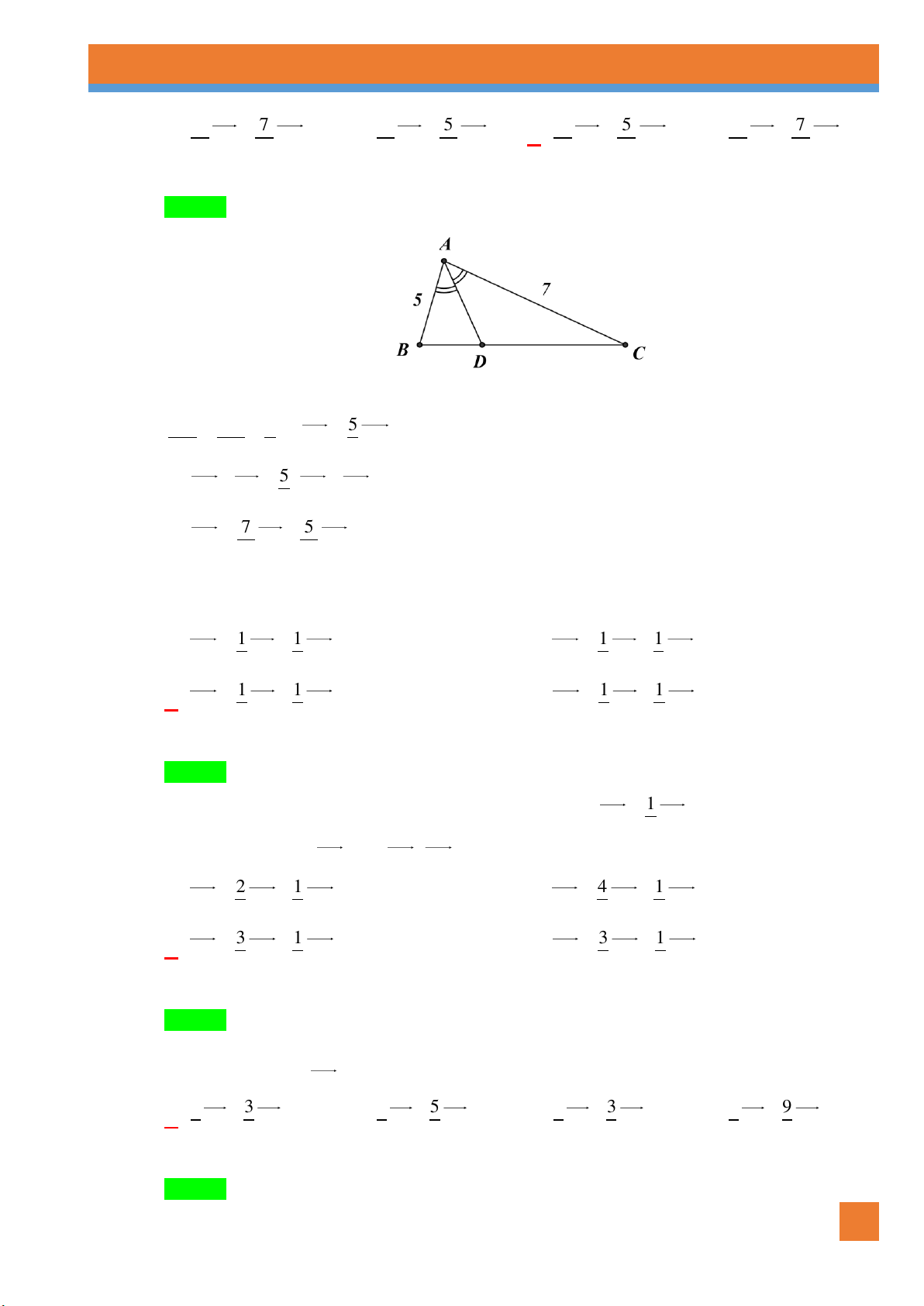
Ví dụ 10. Cho tam giác ABC có trọng tâm G . Gọi I là trung điểm BC , dựng điểm B ': B ' B AG . Chứng minh: a. BI IC .
b. Gọi J là trung điểm BB ',chứng minh BJ IG . Lời giải BI CI
a.Vì I là trung điểm BC nên BI IC BI IC
B'B AG
Vì B ' B AG
. Do đó BJ IG 1 . B'B AG
Vì G là trọng tâm.tam giác 1 ABC IG
AG , J là trung điểm 2 1 BB ' BJ
BB ' BJ IG 2 2 Từ
1 &2 suy ra BJ IG .
Ví dụ 11. Cho tam giác ABC . Gọi M, N, P lần lượt là trung điểm của BC,C , A AB .
Vẽ các vectơ bằng vectơ NP mà có điểm đầu , A B . Lời giải
Trên tia CB lấy điểm B ' sao cho BB' NP
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 9 CĐ: VECTO TLDH
Khi đó ta có BB ' là vectơ có điểm đầu là B và bằng vectơ NP .(Ta cũng có thể dựng hình bình hành PNBB' )
Qua A dựng đường thẳng song song với đường thẳng NP . Trên đường thẳng đó lấy điểm A'
sao cho AA ' cùng hướng với NP và AA' NP .(Ta cũng có thể dựng hình bình hành PNAA' )
Khi đó ta có AA' là vectơ có điểm đầu là A và bằng vectơ NP .
PHẦN 2 : CÂU HỎI TRẮC NGHIỆM
Câu 21. [0H1-1.3-1] Cho lục giác đều ABCDEF tâm O . Số các vectơ bằng OC có điểm đầu và cuối
là đỉnh của lục giác là: A. 4 B. 2 C. 7 D. 9. Lời giải Chọn B
Đó là AB, ED .
Câu 22. [0H1-1.3-1] Khẳng định nào sau đây đúng ?
A. Hai vectơ a và b được gọi là bằng nhau nếu chúng cùng hướng và cùng độ dài.
B. Hai vectơ a và b được gọi là bằng nhau nếu chúng cùng phương và cùng độ dài.
C. Hai vectơ AB và CD được gọi là bằng nhau khi và chỉ khi tứ giác ABCD là hình bình hành
D. Hai vectơ a và b được gọi là bằng nhau nếu cùng độ dài. Lời giải Chọn A
Câu 23. [0H1-1.3-1] Cho tam giác đều ABC cạnh a , mệnh đề nào sau đây sai?
A. AB BC .
B. AC BC .
C. AB BC .
D. AC, BC không cùng phương. Lời giải Chọn A
Câu 24. [0H1-1.3-1] Cho hình bình hành ABCD . Khẳng định nào sau đây đúng?
A. AD = BC .
B. AB = AC .
C. AC = DB .
D. AB = CD . Lời giải Chọn A
Câu 25. [0H1-1.3-1] Cho hình bình hành ABCDcó tâm O. Vectơ OB bằng với vectơ nào sau đây ? A. DO B. OD C. CO D. OC . Lời giải Chọn A
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 10 CĐ: VECTO TLDH
Câu 26. [0H1-1.3-1] Gọi O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD. Đẳng
thức nào sau đây là đẳng thức sai?
A. OB DO
B. AB DC
C. OA OC
D. CB DA Lời giải Chọn C
Câu 27. [0H1-1.3-1] Cho AB CD .Tìm khẳng định sai trong các khẳng định sau
A. AB cùng hướng . CD
B. AB cùng phương . CD
C. AB CD .
D. ABCD là hình bình hành. Lời giải Chọn D
Phải suy ra ABDC là hình bình hành.
Câu 28. [0H1-1.3-1] Gọi M , N lần lượt là trung điểm của các cạnh A ,
B AC của tam giác đều ABC .
Đẳng thức nào sau đây đúng?
A. MA M . B
B. AB AC.
C. MN BC.
D. BC 2 MN . Lời giải Chọn D A M N B C
Ta có MN là đường trung bình của tam giác ABC .
Do đó BC 2MN
BC 2 MN .
Câu 29. [0H1-1.3-1] Cho tứ giác ABCD. Điều kiện nào là điều kiện cần và đủ để AB CD ?
A. ABCD là hình bình hành.
B. ABDC là hình bình hành.
C. AD và BC có cùng trung điểm.
D. AB C . D Lời giải Chọn B Ta có: A B AB CD
AB CD
ABDC là hình bình hành. AB CD
Mặt khác, ABDC là hình bình hành D C AB CD AB CD . AB CD
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 11 CĐ: VECTO TLDH
Do đó, điều kiện cần và đủ để AB CD là ABDC là hình bình hành.
Câu 30. [0H1-1.3-1] Cho lục giác đều ABCDEF có tâm O . Đẳng thức nào sau đây là sai?
A. AB E . D
B. AB AF .
C. OD BC.
D. OB O . E Lời giải Chọn D C B D A O E F
Hai vectơ này ngược hướng.
Câu 31. [0H1-1.3-1] Cho hình bình hành ABCD tâm O . Gọi P,Q, R lần lượt là trung điểm A ,
B BC, AD . Lấy 8 điểm trên làm điểm gốc hoặc điểm ngọn các vectơ. Tìm mệnh đề sai :
A. Có 2 vectơ bằng PQ
B. Có 4 vectơ bằng AR
C. Có 3 vectơ bằng BO
D. Có 5 vectơ bằng OP Lời giải Chọn C
Câu 32. [0H1-1.3-1] Cho hai điểm phân biệt A và B . Điều kiện để điểm I là trung điểm của đoạn thẳng AB là:
A. IA BI .
B. AI BI .
C. IA IB .
D. IA IB . Lời giải Chọn A IA BI .
Câu 33. [0H1-1.3-1] Cho hình chữ nhật ABCD. Khẳng định nào sau đây là đúng ? A. AB DC . B. AC DB . C. AD CB . D. AB AD . Lời giải Chọn A AB DC Vì : AB DC . AB DC
Câu 34. [0H1-1.3-1] Cho lục giác đều ABCDEF có tâm O . Đẳng thức nào
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 12 CĐ: VECTO TLDH sau đây là sai?
A. AB E . D
B. AB AF .
C. OD BC.
D. OB O . E Lời giải Chọn D C B D A O E F
Câu 35. [0H1-1.3-1] Cho hình thoi ABCD có tâm I . Hãy cho biết số khẳng định đúng trong các khẳng định sau ? a) AB BC b) AB DC c) IA IO d) IB IA e) AB BC
f) 2 IA BD A. 3. B. 4. C. 5. D. 6. Lời giải Chọn A
Câu 36. [0H1-1.3-1] Cho AB 0 và một điểm C , có bao nhiêu điểm D thỏa mãn AB C . D A. 1. B. 2. C. 0. D. Vô số. Lời giải Chọn A
Câu 37. [0H1-1.3-1] Cho AB khác 0 và cho điểm C . Có bao nhiêu điểm D thỏa AB CD . A. Vô số. B. 1 điểm. C. 2 điểm.
D. không có điểm nào. Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 13 CĐ: VECTO TLDH Chọn A
Ta có AB CD AB CD . Suy ra tập hợp các điểm D thỏa yêu cầu bài toán là đường tròn tâm C bán kính . AB
Có vô số điểm D thỏa AB CD .
Câu 38. [0H1-1.3-1] Cho AB 0 và một điểm C , có bao nhiêu điểm D thỏa mãn AB C . D A. 1. B. 2. C. 0. D. Vô số. Lời giải Chọn A.
Câu 39. [0H1-1.3-1] Cho tứ giác ABCD. Điều kiện nào là điều kiện cần và đủ để AB CD ?
A. ABCD là hình bình hành.
B. ABDC là hình bình hành.
C. AD và BC có cùng trung điểm.
D. AB C . D Lời giải Chọn B Ta có: AB CD
AB CD
ABDC là hình bình hành. AB CD AB CD
Mặt khác, ABDC là hình bình hành AB CD . AB CD
Do đó, điều kiện cần và đủ để AB CD là ABDC là hình bình hành.
Câu 40. [0H1-1.3-1] Cho hình bình hành ABCD tâm O . Gọi P,Q, R lần lượt là trung điểm A ,
B BC, AD . Lấy 8 điểm trên làm điểm gốc hoặc điểm ngọn các vectơ. Tìm mệnh đề sai :
A. Có 2 vectơ bằng PQ
B. Có 4 vectơ bằng AR
C. Có 3 vectơ bằng BO
D. Có 5 vectơ bằng OP Lời giải Chọn C
Câu 41. [0H1-1.1-1] Véctơ là một đoạn thẳng: A. Có hướng.
B. Có hướng dương, hướng âm.
C. Có hai đầu mút.
D. Thỏa cả ba tính chất trên. Lời giải Chọn A
Câu 42. [0H1-1.2-1] Hai véc tơ có cùng độ dài và ngược hướng gọi là:
A. Hai véc tơ bằng nhau.
B. Hai véc tơ đối nhau.
C. Hai véc tơ cùng hướng.
D. Hai véc tơ cùng phương. Lời giải Chọn B
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 14 CĐ: VECTO TLDH
Theo định nghĩa hai véc tơ đối nhau.
Câu 43. [0H1-1.3-1] Hai véctơ bằng nhau khi hai véctơ đó có:
A. Cùng hướng và có độ dài bằng nhau.
B. Song song và có độ dài bằng nhau.
C. Cùng phương và có độ dài bằng nhau.
D. Thỏa mãn cả ba tính chất trên. Lời giải Chọn A
Theo định nghĩa hai véctơ bằng nhau.
Câu 44. [0H1-1.2-1] Điền từ thích hợp vào dấu (...) để được mệnh đề đúng. Hai véc tơ ngược hướng thì ... A. Bằng nhau. B. Cùng phương. C. Cùng độ dài.
D. Cùng điểm đầu. Lời giải Chọn B
Câu 45. [0H1-1.2-1] Cho 3 điểm phân biệt A , B , C . Khi đó khẳng định nào sau đây đúng nhất ?
A. A , B , C thẳng hàng khi và chỉ khi AB và AC cùng phương.
B. A , B , C thẳng hàng khi và chỉ khi AB và BC cùng phương.
C. A , B , C thẳng hàng khi và chỉ khi AC và BC cùng phương.
D. Cả A, B, C đều đúng. Lời giải Chọn D Cả 3 ý đều đúng.
Câu 46. [0H1-1.2-1] Mệnh đề nào sau đây đúng ?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất 2 vectơ cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ. Lời giải Chọn A
Ta có vectơ 0 cùng phương với mọi vectơ.
Câu 47. [0H1-1.3-1] Phát biểu nào sau đây đúng?
A. Hai vectơ không bằng nhau thì độ dài của chúng không bằng nhau.
B. Hai vectơ không bằng nhau thì chúng không cùng phương.
C. Hai vectơ bằng nhau thì có giá trùng nhau hoặc song song nhau.
D. Hai vectơ có độ dài không bằng nhau thì không cùng hướng. Lời giải Chọn C
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 15 CĐ: VECTO TLDH
A. sai do hai vectơ không bằng nhau thì có thể hai vecto ngược hướng nhưng độ dài vẫn bằng nhau.
B. sai do một trong hai vectơ là vectơ không.
C. đúng do hai vectơ bằng nhau thì hai vectơ cùng hướng.
Câu 48. [0H1-1.2-1] Khẳng định nào sau đây đúng ?
A. Hai vectơ cùng phương với 1 vectơ thứ ba thì cùng phương.
B. Hai vectơ cùng phương với 1 vectơ thứ ba khác 0 thì cùng phương.
C. Vectơ–không là vectơ không có giá.
D. Điều kiện đủ để 2 vectơ bằng nhau là chúng có độ dài bằng nhau. Lời giải Chọn B
Hai vectơ cùng phương với 1 vectơ thứ ba khác 0 thì cùng phương.
Câu 49. [0H1-1.2-1] Cho hai vectơ không cùng phương a và b . Khẳng định nào sau đây đúng ?
A. Không có vectơ nào cùng phương với cả hai vectơ a và b .
B. Có vô số vectơ cùng phương với cả hai vectơ a và b .
C. Có một vectơ cùng phương với cả hai vectơ a và b , đó là vectơ 0 .
D. Cả A, B, C đều sai. Lời giải Chọn C
Vì vectơ 0 cùng phương với mọi vectơ. Nên có một vectơ cùng phương với cả hai vectơ a và b , đó là vectơ 0 .
Câu 50. [0H1-1.3-1] Cho vectơ a . Mệnh đề nào sau đây đúng ?
A. Có vô số vectơ u mà u a .
B. Có duy nhất một u mà u a .
C. Có duy nhất một u mà u a .
D. Không có vectơ u nào mà u a . Lời giải Chọn A
Cho vectơ a , có vô số vectơ u cùng hướng và cùng độ dài với vectơ a . Nên có vô số vectơ u mà u a .
Câu 51. [0H1-1.3-1] Chọn khẳng định đúng.
A. Hai véc tơ cùng phương thì bằng nhau.
B. Hai véc tơ ngược hướng thì có độ dài không bằng nhau.
C. Hai véc tơ cùng phương và cùng độ dài thì bằng nhau.
D. Hai véc tơ cùng hướng và cùng độ dài thì bằng nhau. Lời giải Chọn D
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 16 CĐ: VECTO TLDH
Hai véc tơ cùng hướng và cùng độ dài thì bằng nhau.
Câu 52. [0H1-1.3-1] Cho hình bình hành ABCD. Trong các khẳng định sau hãy tìm khẳng định sai
A. AD CB .
B. AD CB .
C. AB DC .
D. AB CD . Lời giải Chọn A
Ta có ABCD là hình bình hành. Suy ra AD BC .
Câu 53. [0H1-1.1-1] Chọn khẳng định đúng.
A. Véc tơ là một đường thẳng có hướng.
B. Véc tơ là một đoạn thẳng.
C. Véc tơ là một đoạn thẳng có hướng.
D. Véc tơ là một đoạn thẳng không phân biệt điểm đầu và điểm cuối. Lời giải Chọn C
Véc tơ là một đoạn thẳng có hướng.
Câu 54. [0H1-1.1-1] Cho vectơ có điểm đầu và điểm cuối trùng nhau. Hãy chọn câu sai
A. Được gọi là vectơ suy biến.
B. Được gọi là vectơ có phương tùy ý.
C. Được gọi là vectơ không, kí hiệu là 0 .
D. Là vectơ có độ dài không xác định. Lời giải Chọn C
Vectơ không có độ dài bằng 0 .
Câu 55. [0H1-1.3-1] Cho hình vuông ABCD, khẳng định nào sau đây đúng:
A. AC BD .
B. AB BC .
C. AB CD .
D. AB và AC cùng hướng. Lời giải Chọn B
Ta có ABCD là hình vuông. Suy ra AB BC .
Câu 56. [0H1-1.2-1] Cho ba điểm ,
A B,C phân biệt. Điều kiện cần và đủ để ba điểm ,
A B,C thẳng hàng là:
A. AB, AC cùng phương.
B. AB, AC cùng hướng.
C. AB BC .
D. AB, CB ngược hướng. Lời giải Chọn A
Câu 57. [0H1-1.2-1] Cho ba điểm ,
A B,C phân biệt thẳng hàng.Khi nào thì hai vectơ AB và AC cùng hướng ?
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 17 CĐ: VECTO TLDH
A. A nằm trong đoạn BC
B. AB CA
C. A nằm ngoài đoạn BC
D. AB AC Lời giải Chọn C
A nằm ngoài đoạn BC
Câu 58. [0H1-1.1-1] Cho bốn điểm ,
A B,C, D phân biệt.Nếu AB BC thì có khẳng định nào sau đây đúng
A. B là trung điểm của AC .
B. B nằm ngoài đoạn AC .
C. ABCD là hình bình hành.
D. ABCD là hình vuông. Lời giải: Chọn A
Câu 59. [0H1-1.3-1] Gọi C là trung điểm của đoạn AB . Hãy chọn khẳng định đúng trong các khẳng định sau :
A. CA CB .
B. AB và AC cùng hướng.
C. AB và CB ngược hướng.
D. AB CB . Lời giải Chọn B
Ta có C là trung điểm của đoạn AB và AC cùng hướng.
Câu 60. [0H1-1.3-1] Gọi O là giao điểm của hai đường chéo hình chữ nhật ABCD. Mệnh đề nào sau đây đúng?
A. OA O . C
B. OB và OD cùng hướng.
C. AC và BD cùng hướng.
D. AC BD . Lời giải Chọn D
Câu 61. [0H1-1.3-2] Cho hình bình hành ABGE . Đẳng thức nào sau đây đúng.
A. BA EG . B. AG BE .
C. GA BE .
D. BA GE . Lời giải Chọn D
Hình bình hành ABGE BA GE .
Câu 62. [0H1-1.3-2] Cho tam giác đều ABC . Mệnh đề nào sau đây sai ?
A. AB BC .
B. AC BC .
C. AB BC .
D. AC không cùng phương BC . Lời giải Chọn A
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 18 CĐ: VECTO TLDH
Ta có tam giác đều ABC AB, BC không cùng hướng AB BC .
Câu 63. [0H1-1.2-2] Chọn khẳng định đúng
A. Hai vec tơ cùng phương thì cùng hướng.
B. Hai véc tơ cùng hướng thì cùng phương.
C. Hai véc tơ cùng phương thì có giá song song nhau.
D. Hai vec tơ cùng hướng thì có giá song song nhau. Lời giải Chọn B
Hai véc tơ cùng hướng thì cùng phương.
Câu 64. [0H1-1.2-2] Cho 3 điểm A , B , C không thẳng hàng, M là điểm bất kỳ. Mệnh đề nào sau đây đúng ? A. M
,MA MB . B. M
,MA MB MC . C. M
,MA MB MC . D. M
,MA MB . Lời giải Chọn C
Ta có 3 điểm A , B , C không thẳng hàng, M là điểm bất kỳ. Suy ra M ,
A MB, MC không cùng phương M
,MA MB MC .
Câu 65. [0H1-1.1-2] Cho hai điểm phân biệt ,
A B . Số vectơ ( khác 0 ) có điểm đầu và điểm cuối lấy từ các điểm , A B là: A. 2 . B. 6 . C. 13 . D. 12 . Lời giải Chọn A
Số vectơ ( khác 0 ) là AB ; BA .
Câu 66. Gọi C là trung điểm của đoạn AB . Hãy chọn khẳng định đúng trong các khẳng định sau :
A. CA CB .
B. AB và AC cùng hướng.
C. AB và CB ngược hướng.
D. AB CB . Lời giải Chọn B
Ta có C là trung điểm của đoạn AB và AC cùng hướng.
Câu 67. [0H1-1.2-2] Cho ba điểm A , B , C phân biệt. Khi đó :
A. Điều kiện cần và đủ để A , B , C thẳng hàng là AC cùng phương với AB .
B. Điều kiện đủ để A , B , C thẳng hàng là CA cùng phương với AB .
C. Điều kiện cần để A , B , C thẳng hàng là CA cùng phương với AB .
D. Điều kiện cần và đủ để A , B , C thẳng hàng là AB AC .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 19 CĐ: VECTO TLDH Lời giải Chọn A
Điều kiện cần và đủ để A , B , C thẳng hàng là AC cùng phương với AB .
Các vectơ đó là: AB, AC, AD, ,
BA BC, BD, C ,
A CB, CD, D , A DB, DC .
Câu 68. [0H1-1.3-2] Cho đoạn thẳng AB , I là trung điểm của AB . Khi đó:
A. BI AI .
B. BI cùng hướng AB .
C. BI 2 IA .
D. BI IA . Lời giải Chọn D
BI IA vì I là trung điểm của AB .
Câu 69. [0H1-1.3-2] Cho tam giác đều ABC . Mệnh đề nào sau đây là sai?
A. AC BC .
B. AB BC .
C. AB BC .
D. AC không cùng phương BC . Lời giải Chọn B
B. sai do hai vectơ không cùng phương.
Câu 70. [0H1-1.2-2] Cho hình bình hành ABCD. Các vectơ là vectơ đối của vectơ AD là
A. AD, BC .
B. BD, AC . C. D , A CB .
D. AB, CB . Lời giải Chọn C
Vectơ đối của vectơ AD là D , A CB .
Câu 71. [0H1-1.3-2] Cho lục giác đều ABCDEF tâm O . Ba vectơ bằng vecto BA là:
A. OF , DE,OC . B. C ,
A OF , DE .
C. OF , DE,CO .
D. OF , ED, OC . Lời giải Chọn C
Ba vectơ bằng vecto BA là OF, DE,CO .
Câu 72. [0H1-1.3-2] Cho tứ giác ABCD. Nếu AB DC thì ABCD là hình gì? Tìm đáp án sai. A. Hình bình hành. B. Hình vuông. C. Hình chữ nhật. D. Hình thang. Lời giải Chọn D
Câu 73. [0H1-1.3-2] Cho lục giác ABCDEF , tâm O . Khẳng định nào sau đây đúng nhất?
A. AB ED .
B. AB OC .
C. AB FO .
D. Cả A,B,C đều đúng. Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 20 CĐ: VECTO TLDH Chọn D
Ta có ABCDEF là lục giác, tâm O . Suy ra AB ED , AB OC , AB FO .
Câu 74. [0H1-1.3-2] Chọn câu sai :
A. Mỗi vectơ đều có một độ dài, đó là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
B. Độ dài của vectơ a được kí hiệu là a .
C. 0 0, PQ PQ .
D. AB AB BA . Lời giải Chọn C
Vì PQ PQ .
Câu 75. [0H1-1.3-2] Cho khẳng định sau
(1). 4 điểm A , B , C , D là 4 đỉnh của hình bình hành thì AB CD .
(2). 4 điểm A , B , C , D là 4 đỉnh của hình bình hành thì AD CB .
(3). Nếu AB CD thì 4 điểm ,
A B,C, D là 4 đỉnh của hình bình hành.
(4). Nếu AD CB thì 4 điểm A , B , C , D theo thứ tự đó là 4 đỉnh của hình bình hành.
Hỏi có bao nhiêu khẳng định sai? A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn B
Nếu AD CB thì 4 điểm A , D , B , C theo thứ tự đó là 4 đỉnh của hình bình hành.
Câu 76. [0H1-1.3-2] Cho đoạn thẳng AB , I là trung điểm của AB . Khi đó:
A. BI AI .
B. BI cùng hướng AB .
C. BI 2 IA .
D. BI IA . Lời giải Chọn D
BI IA vì I là trung điểm của AB .
Câu 77. [0H1-1.3-2] Cho tam giác đều ABC . Mệnh đề nào sau đây là sai?
A. AC BC .
B. AB BC .
C. AB BC .
D. AC không cùng phương BC . Lời giải Chọn B
B. sai do hai vectơ không cùng phương.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 21 CĐ: VECTO TLDH
Câu 78. [0H1-1.3-2] Cho bốn điểm ,
A B,C, D phân biệt.Nếu AB BC thì có khẳng định nào sau đây đúng
A. B là trung điểm của AC .
B. B nằm ngoài đoạn AC .
C. ABCD là hình bình hành.
D. ABCD là hình vuông. Lời giải: Chọn A
Câu 79. [0H1-1.2-2] Cho ba điểm ,
A B,C phân biệt thẳng hàng.Khi nào thì hai vectơ AB và AC cùng hướng ?
A. A nằm trong đoạn BC
B. AB CA
C. A nằm ngoài đoạn BC
D. AB AC Lời giải Chọn C
A nằm ngoài đoạn BC
Câu 80. [0H1-1.3-2] Cho tứ giác ABCD. Gọi M , N, ,
P Q lần lượt là trung điểm của A , B BC,C , D DA .
Trong các khẳng định sau, hãy tìm khẳng định sai?
A. MN QP .
B. MQ NP .
C. PQ MN .
D. MN AC . Lời giải Chọn D A M Q B D N P C Ta có 1 1
MN là đường trung bình của tam giác ABC . Suy ra MN AC hay MN AC 2 2
Câu 81. [0H1-1.1-3] Số vectơ ( khác 0 ) có điểm đầu và điểm cuối lấy từ 7 điểm phân biệt cho trước là A. 42 . B. 3 . C. 9 . D. 27 . Lời giải Chọn A
Số vectơ ( khác 0 ) có điểm đầu và điểm cuối lấy từ 7 điểm phân biệt cho trước là 7.6 42
Câu 82. [0H1-1.1-3] Cho lục giác ABCDEF . Có bao nhiêu vectơ khác vectơ-không có điểm đầu và
điểm cuối là đỉnh của lục giác.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 22 CĐ: VECTO TLDH A. 20 B. 12 C. 30 D. 16 Lời giải Chọn C
Hai điểm phân biệt, chẳng hạn ,
A B ta xác định được hai vectơ khác vectơ-không là AB, BA .
Một vectơ khác vectơ -không được xác định bởi 2 điểm phân biệt. Do đó có 30 cách chọn 2
điểm trong 4 điểm của tứ giác (có tính thứ tự các điểm) nên có thể lập được 30 vectơ.
Câu 83. [0H1-1.1-3] Cho tứ giác ABCD. Gọi M , N, ,
P Q lần lượt là trung điểm của A , B BC,C , D DA .
Trong các khẳng định sau, hãy tìm khẳng định sai?
A. MN QP .
B. MQ NP .
C. PQ MN .
D. MN AC . Lời giải Chọn D Ta có 1 1
MN là đường trung bình của tam giác ABC . Suy ra MN AC hay MN AC 2 2
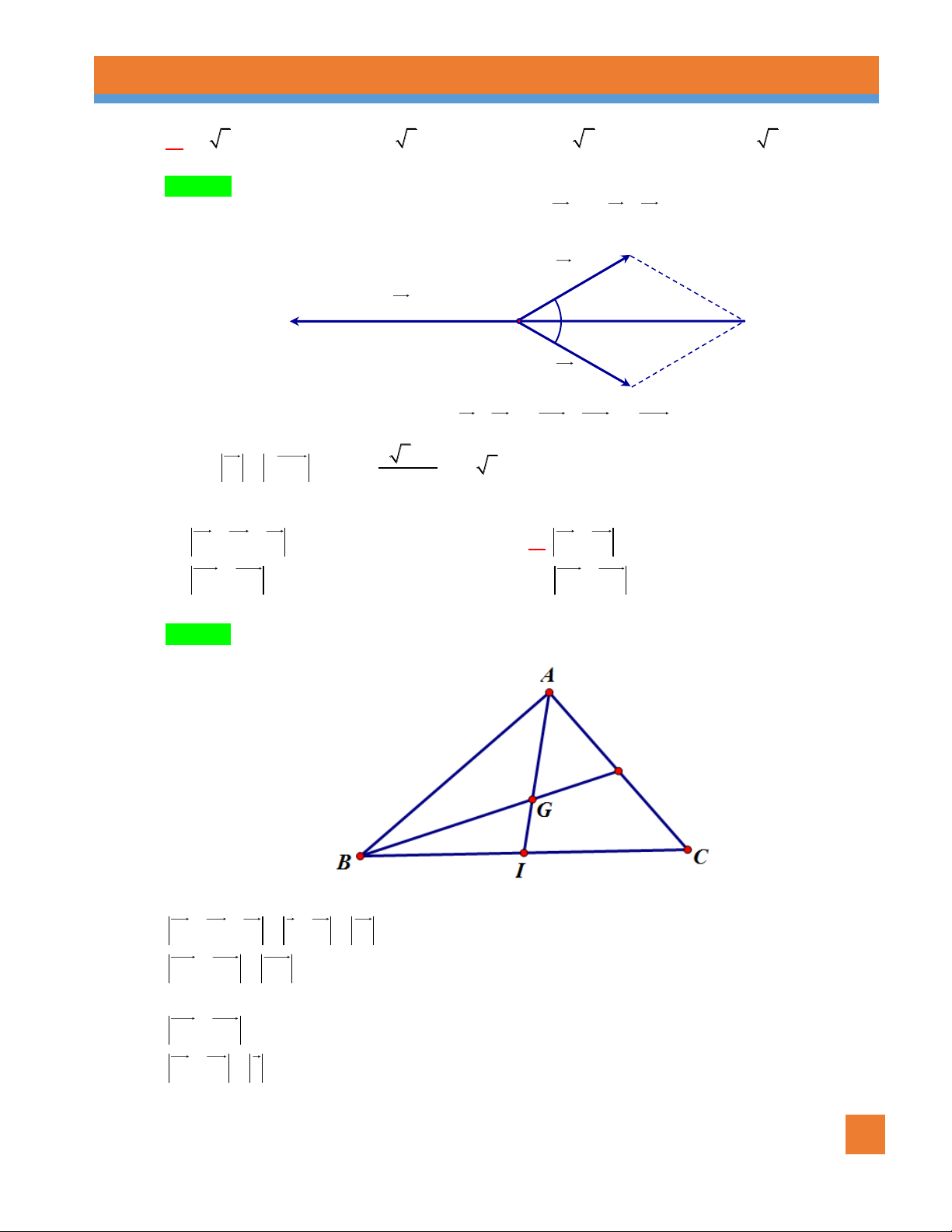
Câu 84. [0H1-1.1-3] Cho tam giác ABC đều cạnh a và G là trọng tâm. Gọi I là trung điểm của AG .
Độ dài của vectơ BI là 21 21 3 3 A. a . B. a . C. a . D. a . 6 3 6 2 Lời giải Chọn A
Ta có AB AB a
Gọi M là trung điểm của BC 2 Ta có 2 2 2 2 2 a a 3 AG AG AM AB BM 2 a 3 3 3 4 3 2 2 a a a 21 2 2 BI BI BM MI 4 3 6
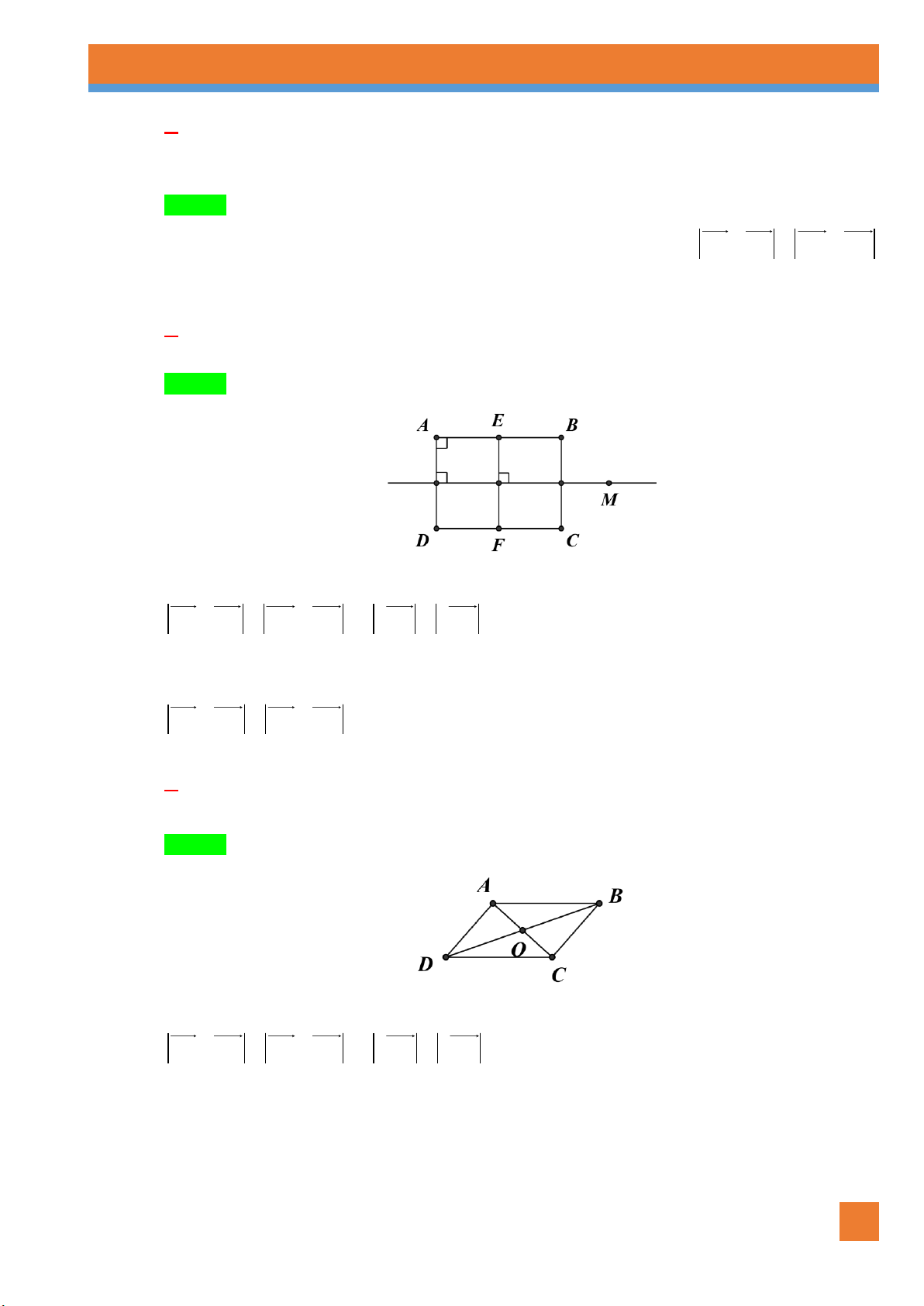
Câu 85. [0H1-1.1-3] Cho hình bình hành ABCD. Trên các đoạn thẳng DC, AB theo thứ tự lấy các điểm
M , N sao cho DM BN . Gọi P là giao điểm của AM , DB và Q là giao điểm của CN, DB . Khẳng định nào đúng?
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 23 CĐ: VECTO TLDH A. DP QB . B. MQ NP . C. PQ MN . D. MN AC . Lời giải Chọn A
Ta có DM BN AN MC , mặt khác AN song song với MC do đó tứ giác ANCM là hình
bình hành. Suy ra AM NC . Xét tam giác D MP và B
NQ ta có DM NB (giả thiết), PDM QBN (so le trong)
Mặt khác DMP APB (đối đỉnh) và APQ NQB (hai góc đồng vị) suy ra DMP BNQ . Do đó D MP B
NQ (c.g.c) suy ra DB QB .
Dễ thấy DB, QB cùng hướng vì vậy DB QB .
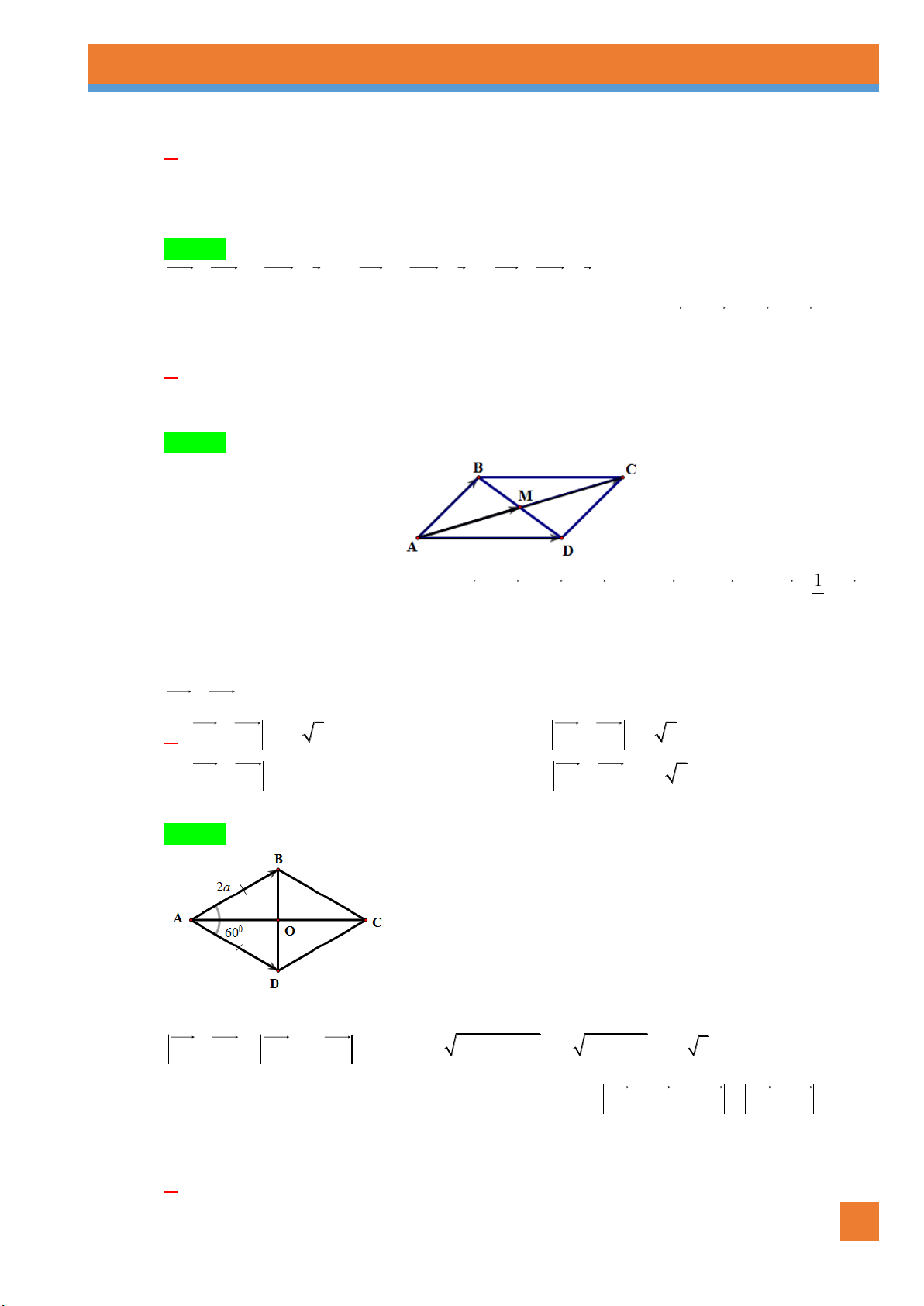
Câu 86. [0H1-1.3-3] Cho hình thoi ABCD cạnh a và BAD 60 . Đẳng thức nào sau đây đúng? A. AB . AD B. BD . a
C. BD AC.
D. BC D . A Lời giải Chọn B B A C D
Từ giả thiết suy ra tam giác ABD đều cạnh a nên BD a BD . a
Câu 87. [0H1-1.3-3] Cho hình bình hành ABCD. Gọi M , N lần lượt là trung điểm của DC, AB ; P là
giao điểm của AM , DB và Q là giao điểm của CN, DB .Khẳng định nào sau đây là đúng nhất.
A. DM NB
B. DP PQ QB
C. Cả A, B đều đúng D. Cả A, B đều sai Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 24 CĐ: VECTO TLDH Chọn C A N B Q P D M C
Ta có tứ giác DMBN là hình bình hành vì 1 DM NB
AB, DM / / NB . Suy ra DM NB . 2
Xét tam giác CDQ có M là trung điểm của DC và MP / /QC do đó P là trung điểm của
DQ . Tương tự xét tam giác ABP suy ra được Q là trung điểm của PB
Vì vậy DP PQ QB từ đó suy ra DP PQ QB .
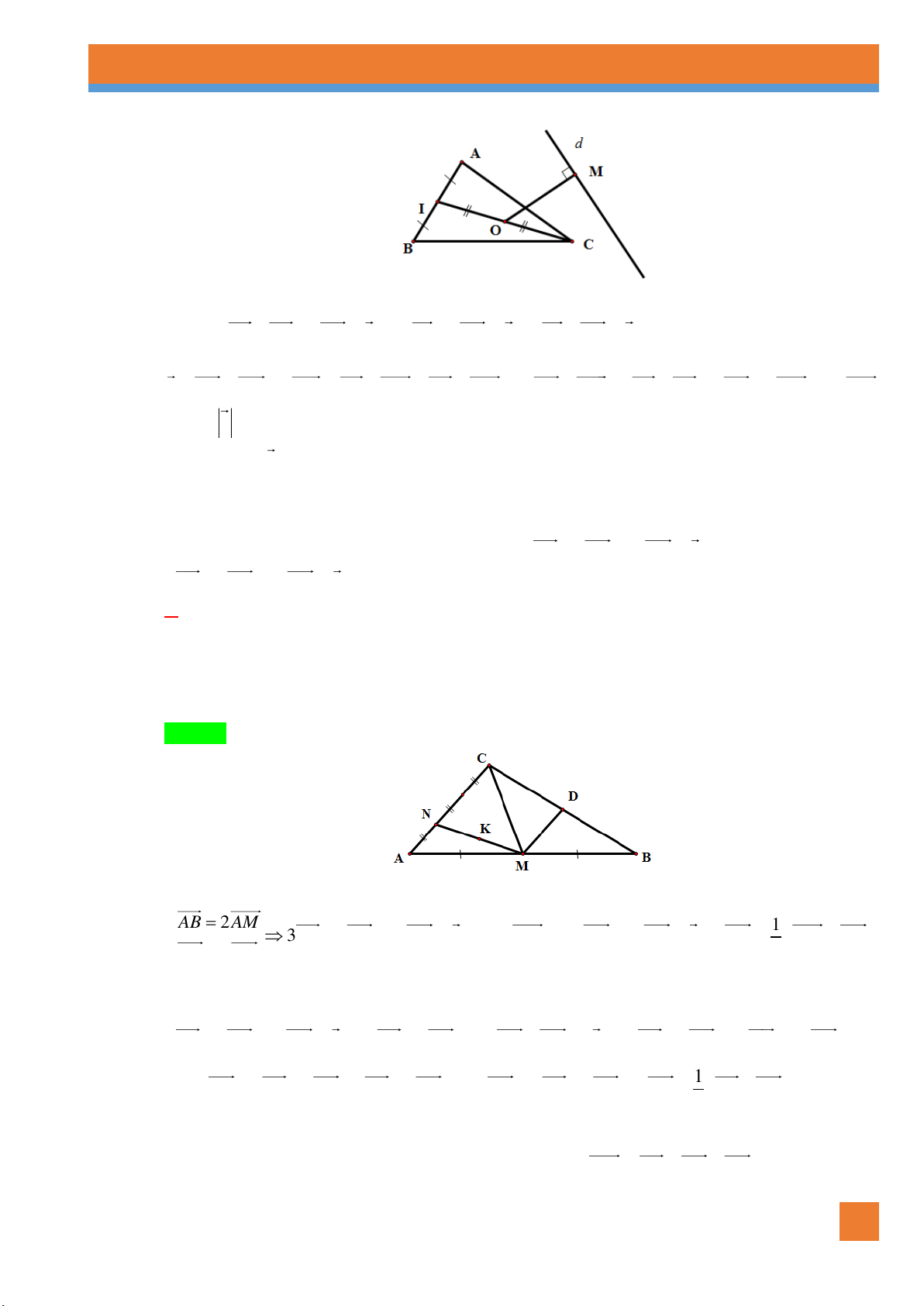
Câu 88. [0H1-1.3-3] Cho hình thang ABCD có hai đáy là AB và CD với AB 2CD . Từ C vẽ
CI DA . Khẳng định nào sau đây là đúng nhất?
A. AD IC
B. DI CB
C. Cả A, B đều đúng D. A đúng, B sai Lời giải Chọn C
Ta có CI DA suy ra AICD là hình bình hành AD IC D C
Ta có DC AI mà AB 2CD do đó 1 AI
AB I là trung 2 điểm AB
Ta có DC IB và DC / /IB tứ giác BCDI là hình bình hành A I B
Suy ra DI CB
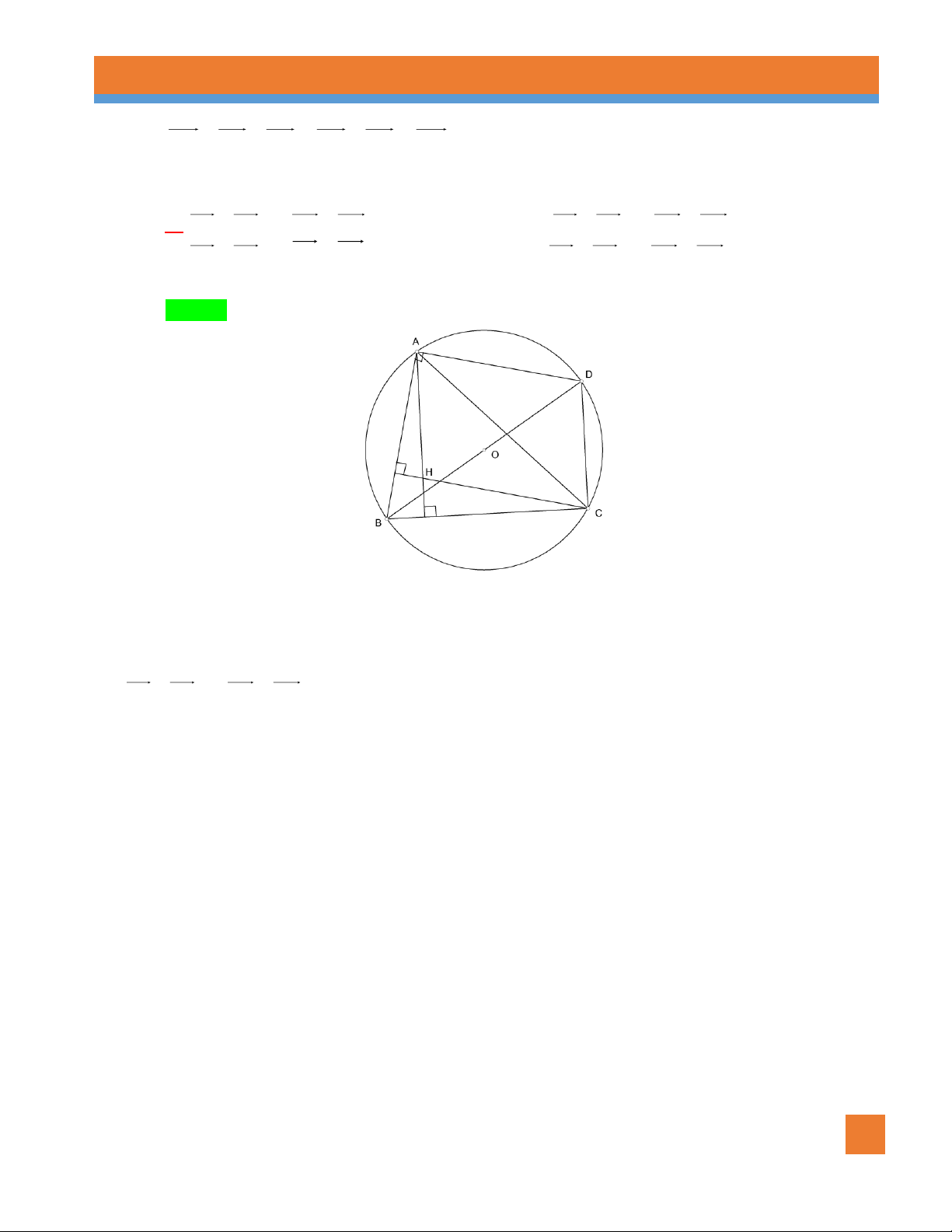
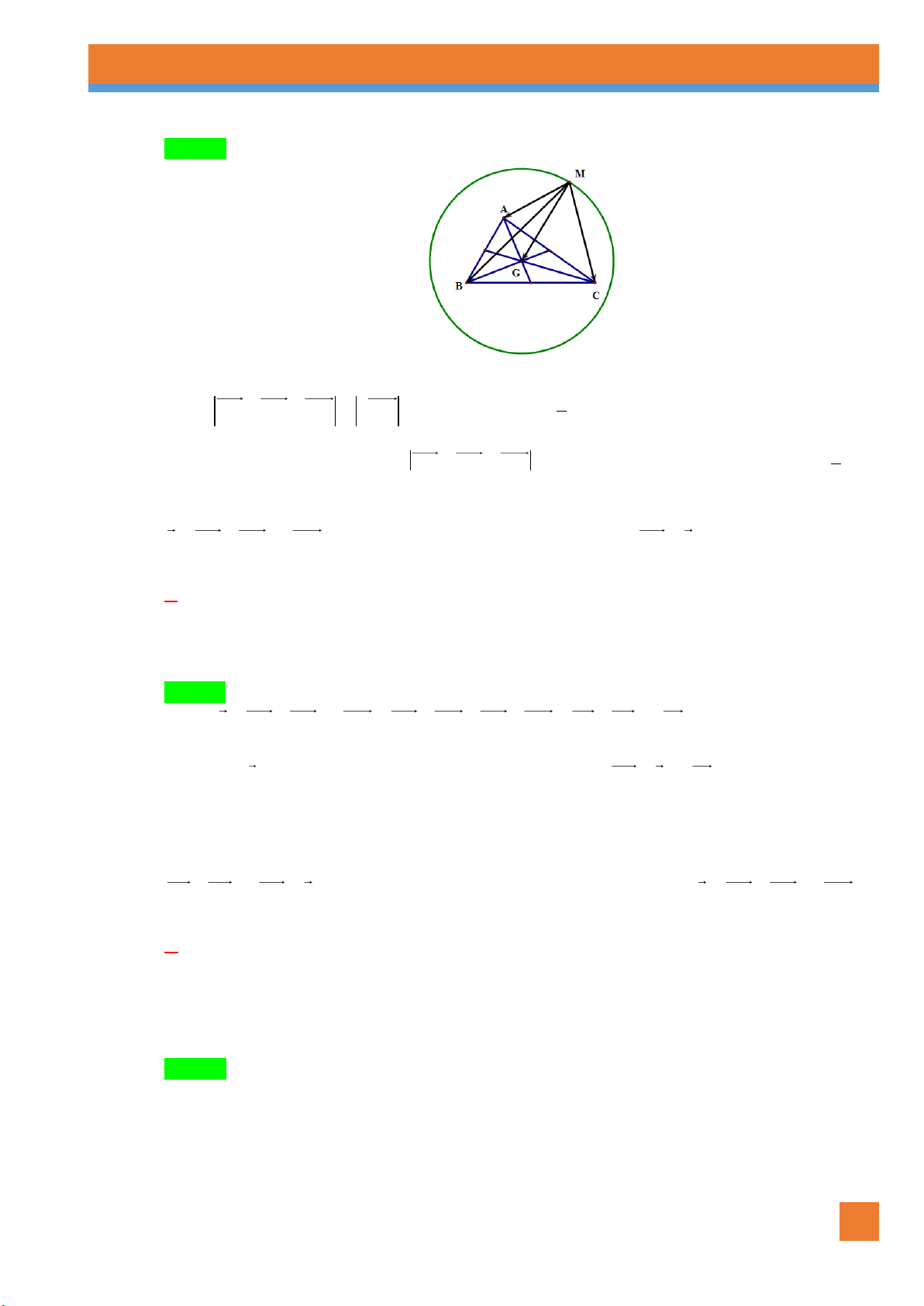
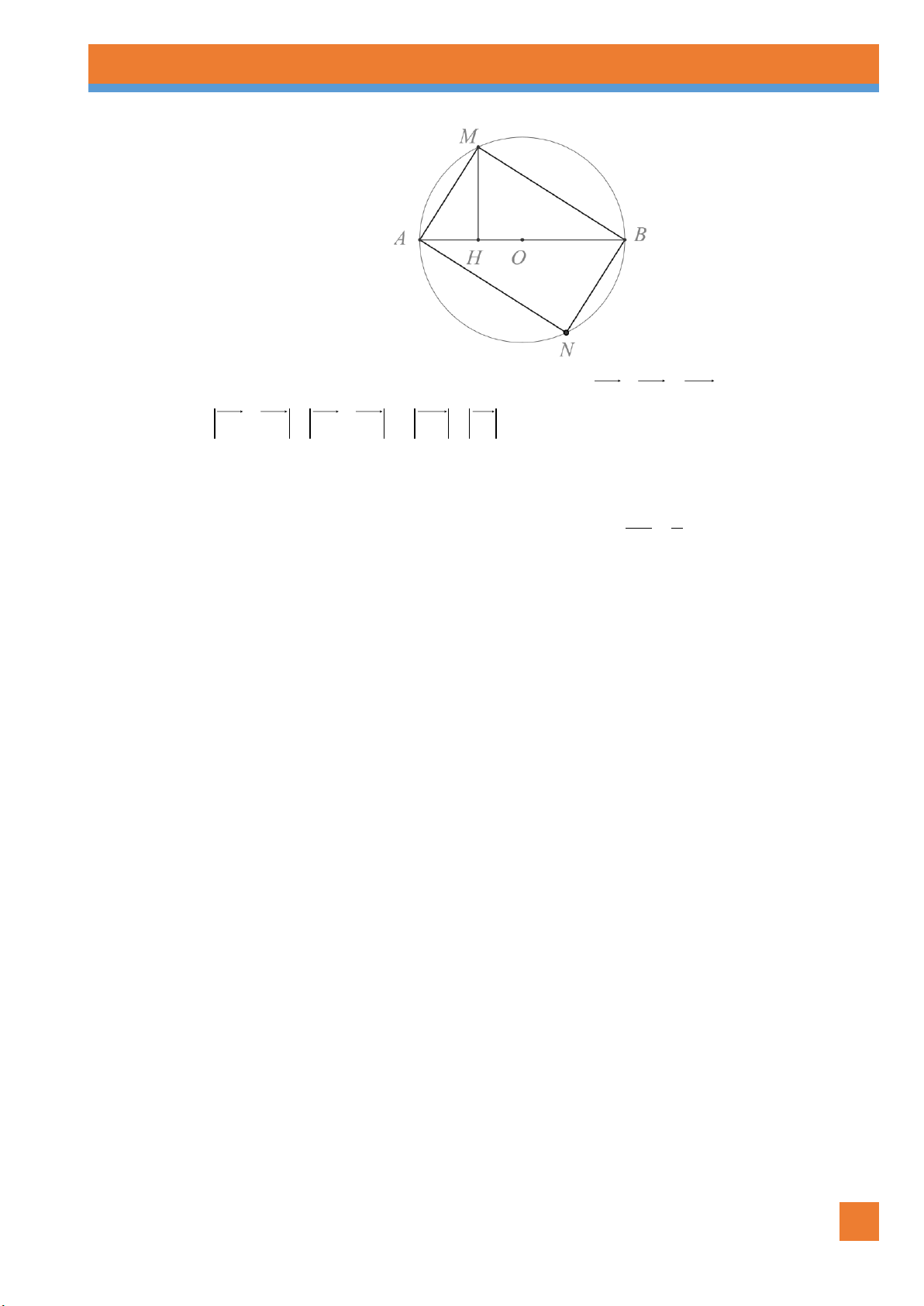
Câu 89. [0H1-1.3-3] Cho tam giác ABC có trực tâm H. Gọi D là điểm đối xứng với B qua tâm O của
đường tròn ngoại tiếp tam giác ABC . Khẳng định nào sau đây là đúng?
A. HA CD và AD CH .
B. HA CD và AD HC .
C. HA CD và AC CH .
D. HA CD và AD HC và OB OD . Lời giải Chọn B A D H O B C
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 25 CĐ: VECTO TLDH
Ta có AH BC và DC BC (do góc DCB chắn nửa đường tròn). Suy ra AH DC.
Tương tự ta cũng có CH A . D
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 26 VECTƠ TLDH CHUYÊN ĐỀ VECTƠ
(CHƯƠNG I – HÌNH HỌC LỚP 10)
BÀI 2. TỔNG VÀ HIỆU CỦA HAI VECTƠ ............................................................................................2
A. KIẾN THỨC SÁCH GIÁO KHOA CẦN NẮM ...............................................................................2
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP ........................................................................3
Dạng 1: Các bài toán liên quan đến tổng các vectơ ...........................................................................3
Dạng 2: Vectơ đối, hiệu của hai vectơ .................................................................................................9
Dạng 3:Chứng minh đẳng thức vectơ ...............................................................................................16
Dạng 4: Các bài toán xác định điểm thỏa đẳng thức vec tơ ...........................................................24
Dạng 5: Các bài toán tính độ dài của vec tơ .....................................................................................30 Ban thực hiện Tên giáo viên Đơn vị công tác GV Soạn
Thầy Trần Chí Trung
Trường THPT Trần Đại Nghĩa (TP Hồ Chí Minh) GV phản biện
Thầy Bùi Văn Huấn
Trường PT DTNT Hòa Bình (Hòa Bình) TT Tổ soạn Cô Phạm Thị Hoài
Trường THCS Nguyễn Hiền (Nha Trang) TT Tổ phản biện
Thầy Nguyễn Văn Vũ Trường THPT YaLy (Gia Lai) Người triển khai Thầy Phạm Lê Duy
Trường THPT Chu Văn An (An Giang)
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 1 VECTƠ TLDH
BÀI 2. TỔNG VÀ HIỆU CỦA HAI VECTƠ
A. KIẾN THỨC SÁCH GIÁO KHOA CẦN NẮM
I. TỔNG CỦA HAI VECTƠ
1. Định nghĩa tổng của hai vectơ
Cho hai vectơ a và b . Lấy một điểm A nào đó rồi xác định các điểm B và C sao cho AB a ,
BC b . Khi đó vectơ AC được gọi là tổng của hai vectơ a và b . Kí hiệu
AC a b .
Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ. 2. Các tính chất Tính chất giao hoán:
a b b a ; Tính chất kết hợp:
a bc a b c;
Tính chất của vectơ-không: a 0 a .
Chú ý: Do tính chất kết hợp, các vectơ a b c và a b c bằng nhau, bởi vậy, chúng có
thể được viết một cách đơn giản là a b c , và gọi là tổng của ba vectơ a, b, c . Tương tự, ta
cũng có định nghĩa cho tổng của nn ,n 4 vectơ.
3. Các qui tắc cần nhớ
Qui tắc ba điểm: Với ba điểm bất kì A , B , C , ta có AB BC AC .
Qui tắc hình bình hành: Nếu ABCD là hình bình hành thì ta có AB AD AC .
4. Kết quả quan trọng
Điểm M là trung điểm của đoạn thẳng AB khi và chỉ chi MA MB 0;
Điểm G là trọng tâm tam giác ABC khi và chỉ khi GA GB GC 0.
II. HIỆU CỦA HAI VECTƠ
1. Vectơ đối của một vectơ
Nếu tổng của hai vectơ a và b là vectơ-không, thì ta nói a là vectơ đối của b , hoặc b là vectơ đối của a .
Vectơ đối của vectơ a là vectơ ngược hướng với vectơ a và có cùng độ dài với vectơ a .
Đặc biệt, vectơ đối của vectơ 0 là vectơ 0 .
2. Định nghĩa hiệu của hai vectơ
Hiệu của hai vectơ a và b , kí hiệu a b , là tổng của vectơ a và vectơ đố
i của vectơ b , tức là
a b a b .
Phép lấy hiệu của hai vectơ gọi là phép trừ vectơ.
3. Qui tắc cần nhớ
Với ba điểm bất kì A , B , C , ta có BC AC AB .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 2 VECTƠ TLDH
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Các bài toán liên quan đến tổng các vectơ
PHẦN 1: CÁC VÍ DỤ
Ví dụ 1. Cho hình bình hành ABCD, xác định các vectơ CB CD , AC DA . Lời giải
CB CD CA và AC DA DA AC DC .
Ví dụ 2. Cho tam giác ABC , xác định các vectơ AB CA BC , AB AC . Lời giải
AB CA BC AB BC CA AC CA AA 0
Gọi D là điểm sao cho ABCD là hình bình hành. Khi đó
AB AC AD .
Ví dụ 3. Cho lục giác đều ABCDEF tâm O, xác định các vectơ AB OD , AB AE OD . Lời giải
AB OD AB BC AC
AB AE OD AO OD AD .
Ví dụ 4. Cho n điểm A , A , A ,..., A , xác định vectơ 1 2 3 n A A A A
A A ... A A A A . n 1 n n2 n 1 n 3 n2 2 3 1 2 Lời giải A A A A
A A ... A A A A n 1 n n2 n 1 n3 n2 2 3 1 2
A A A A ... A A A A A A 1 2 2 3 n3 n2 n2 n 1 n 1 n
Do đó A A A A A A ... A A A A A A . n 1 n n2 n 1 n 3 n2 2 3 1 2 1 n
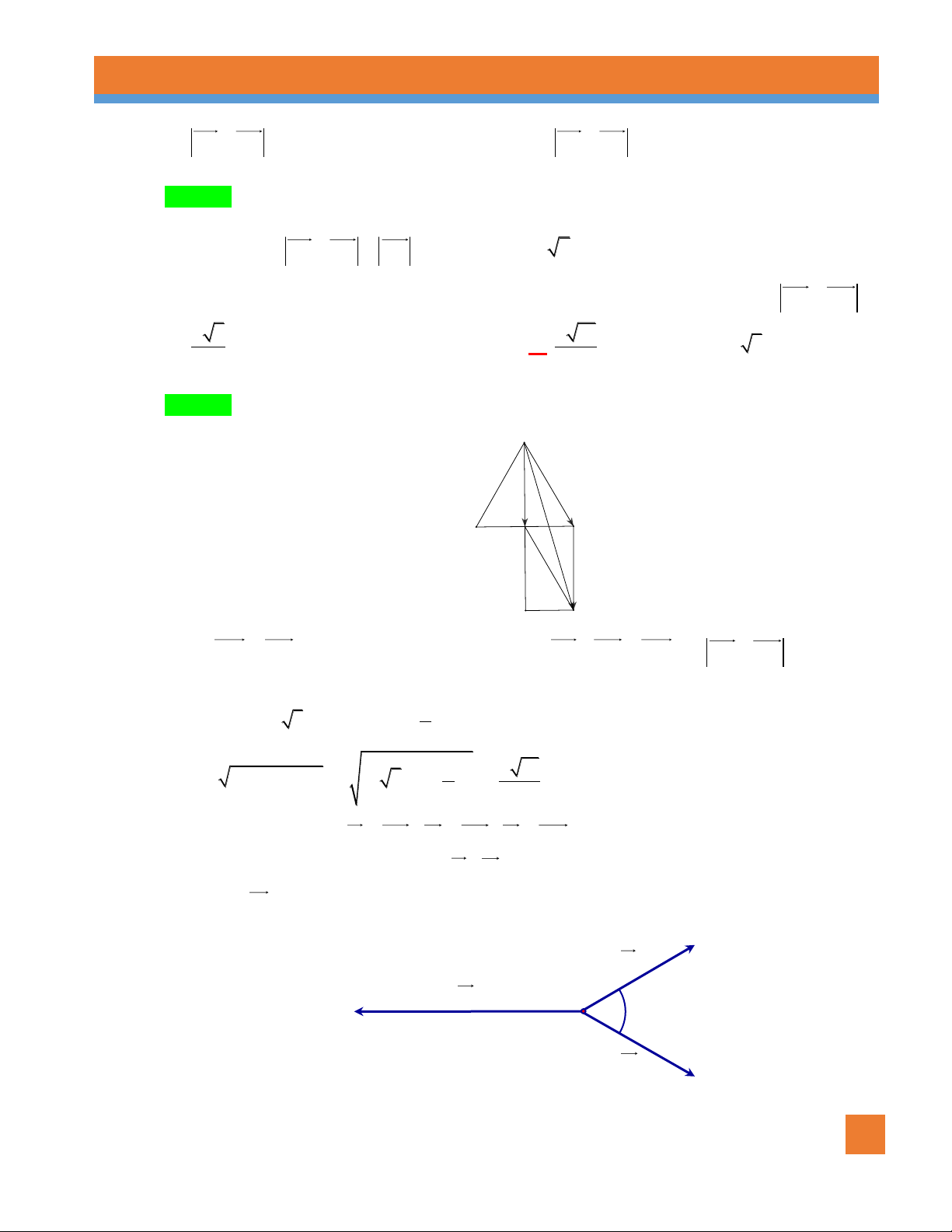
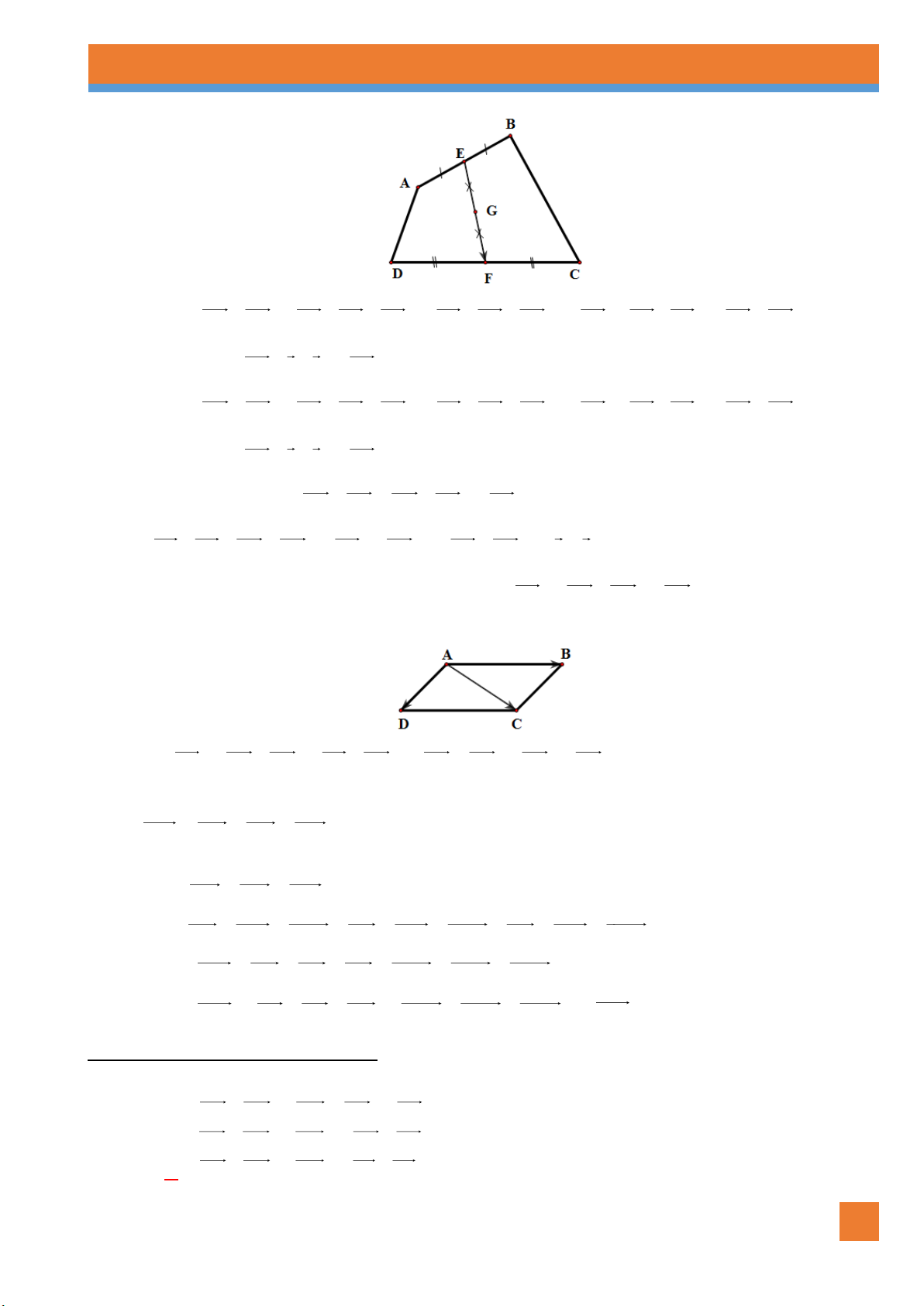
Ví dụ 5. Cho tam giác ABC . Bên ngoài của tam giác vẽ các hình bình hành ABIJ , BCPQ ,CARS . Chứng
minh rằng RJ IQ PS 0 . Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 3 VECTƠ TLDH
RJ RA AJ , IQ IB BQ , PS PC CS .
RJ IQ PS RA AJ IB BQ PC CS
RACSAJ IBBQ PC
SC CSBI IBCP PC
SS BB CC 0
Vậy RJ IQ PS 0 .
PHẦN 2: CÂU HỎI TRẮC NGHIỆM
Câu 1. [0H1-2.1-1] Cho ba vectơ a , b và c khác vectơ-không. Trong các khẳng định sau, khẳng định nào sai?
A. a b b a .
B. a b c a b c .
C. a 0 a .
D. 0 a 0 . Lời giải Chọn D 0 a a .
Câu 2. [0H1-2.1-1] Cho hình bình hành ABCD. Vectơ tổng CB CD bằng A. CA . B. BD . C. AC . D. DB . Lời giải Chọn A
CB CD CA .
Câu 3. [0H1-2.1-1] Cho ba điểm phân biệt ,
A B,C . Trong các khẳng định sau, khẳng định nào sai?
A. AB BC AC .
B. AC CB AB .
C. CA BC BA .
D. CB AC BA . Lời giải Chọn D
CB AC AB .
Câu 4. [0H1-2.1-2] Cho bốn điểm phân biệt ,
A B,C, D . Vectơ tổng AB CD BC DA bằng A. 0 . B. AC . C. BD . D. BA . Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 4 VECTƠ TLDH Chọn A
AB CD BC DA AB BC CD DA AA 0 .
Câu 5. [0H1-2.1-2] Cho tam giác ABC . Gọi M, N, P lần lượt là trung điểm của AB, BC,CA . Vectơ tổng
MP NP bằng A. BP . B. MN . C. CP . D. PA . Lời giải Chọn A
MP NP BM MP BP .
Câu 6. [0H1-2.1-2] Cho hình bình hành ABCD và gọi I là giao điểm của hai đường chéo. Trong các
khẳng định sau, khẳng định nào đúng?
A. IA DC IB .
B. AB AD BD .
C. IA BC IB .
D. AB IA BI . Lời giải Chọn A
IA DC IA AB IB .
Câu 7. [0H1-2.1-2] Cho hình bình hành ABCD và gọi I là giao điểm của hai đường chéo. Trong các
khẳng định sau, khẳng định nào sai?
A. IA DC IB .
B. DA DC BI DI .
C. ID AB IC .
D. AB AD CI IA . Lời giải Chọn D
AB AD CI AC CI AI .
Câu 8. [0H1-2.1-2] Cho các điểm phân biệt M , N, , P ,
Q R . Xác định vectơ tổng
MN PQ RP NP QR . A. MP . B. MN . C. MQ . D. MR . Lời giải Chọn A
MN PQ RP NP QR MN NP PQ QR RP MP .
Câu 9. [0H1-2.1-2] Cho hình bình hành ABCD. Trong các khẳng định sau, khẳng định nào sai?
A. AB BD BC .
B. AB AD AC .
C. AC CD CB .
D. DC DA DB . Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 5 VECTƠ TLDH Chọn C
AC CD AD BC .
Câu 10. [0H1-2.1-2] Cho tam giác ABC và M, N, P lần lượt là trung điểm của BC,C , A AB . Trong các
khẳng định sau, khẳng định nào sai?
A. AB BC CA 0 .
B. AP BM CN 0 .
C. MN NP PM 0.
D. PB MC MP . Lời giải Chọn D
PB MC PB BM PM .
Câu 11. [0H1-2.1-1] Cho lục giác đều ABCDEF có tâm O . Trong các khẳng định sau, khẳng định nào sai? .
A. OA OC OE 0 .
B. OA OC OB EB .
C. AB CD EF 0 .
D. BC EF AD . . Lời giải Chọn D
BC EF 0 .
Câu 12. [0H1-2.1-2] Cho hình vuông ABCD, tâm O. Trong các khẳng định sau, khẳng định nào đúng?
A. BC AB CA .
B. OC AO CA .
C. BA DA CA .
D. DC BC CA . Lời giải Chọn A
BA DA CD DA CA .
Câu 13. [0H1-2.1-2] Cho lục giác đều ABCDEF có tâm O . Trong các khẳng định sau, khẳng định nào sai? .
A. OA OB OC OD OE OF 0 .
B. OA AB BO 0 .
C. OA FE 0 .
D. OA ED FA 0 . Lời giải Chọn D
OA ED OA AB FA .
Câu 14. [0H1-2.1-3] Cho tam giác ABC có trọng tâm G . Gọi M là trung điểm BC , G là điểm đối 1
xứng của G qua M . Vectơ tổng G B G C bằng 1 1 A. GA . B. BC . C. G A . D. G M . 1 1 Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 6 VECTƠ TLDH Chọn A
G B G C G G GA . 1 1 1
Câu 15. [0H1-2.1-3] Xét tam giác ABC có trọng tâm G và tâm đường tròn ngoại tiếp O thỏa mãn
OA OB OC 0 . Hỏi trong các khẳng định sau, có bao nhiêu khẳng định đúng? 1) OG 0 ;
2) Tam giác ABC là tam giác vuông cân;
3) Tam giác ABC là tam giác đều;
4) Tam giác ABC là tam giác cân. A. 3 . B. 1. C. 2 . D. 4 . Lời giải Chọn A
OA OB OC OG OG OG 0 O G . Do đó tam giác ABC là tam giác đều.
Câu 16. [0H1-2.1-3] Xét tam giác ABC có trọng tâm H và tâm đường tròn ngoại tiếp O thỏa mãn
HA HB HC 0 . Hỏi trong các khẳng định sau, có bao nhiêu khẳng định đúng? 1) HG 0 ;
2) Tam giác ABC là tam giác vuông cân; 3) OG 0 ;
4) Tam giác ABC là tam giác cân. A. 3 . B. 1. C. 2 . D. 4 . Lời giải Chọn A
HA HB HC HG HG HG 0 H G . Do đó tam giác ABC là tam giác đều.
Câu 17. [0H1-2.1-3] Xét tam giác ABC nội tiếp có O là tâm đường tròn ngoại tiếp, H là trực tâm. Gọi
D là điểm đối xứng của A qua O . Hỏi trong các khẳng định sau, có bao nhiêu khẳng định đúng?
1) HB HC HD ;
2) DA DB DC HA ;
3) HA HB HC HH , với H là điểm đối xứng của H qua O ; 1 1
4) Nếu HA HB HC 0 thì tam giác ABC là tam giác đều. A. 3 . B. 1. C. 2 . D. 4 . Lời giải Chọn A
HB HC HD HA HB HC HH . 1
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 7 VECTƠ TLDH
Nếu HA HB HC 0 thì HH 0 , suy ra H O . 1
Câu 18. [0H1-2.1-2] Cho 5 điểm phân biệt M , N , P , Q , R . Mệnh đề nào sau đây đúng?
A. MN PQ RN NP QR MP .
B. MN PQ RN NP QR PR .
C. MN PQ RN NP QR MR .
D. MN PQ RN NP QR MN . Lời giải Chọn D
MN PQ RN NP QR MN .
Câu 19. [0H1-2.1-2] Cho hình bình hành ABCD, tâm O . Vectơ tổng BA DA AC bằng A. 0 . B. BD . C. OC . D. OA . Lời giải Chọn A
BA DA AC CD DA AC CC 0 .
Câu 20. [0H1-2.1-4] Cho n điểm phân biệt trên mặt phẳng. Bạn An kí hiệu chúng là A , A ,..., A . Bạn 1 2 n
Bình kí hiệu chúng là B , B ,..., B
A B ). Vectơ tổng A B A B ... A B bằng 1 2 n ( 1 n 1 1 2 2 n n A. 0 . B. A A . C. B B . D. A B . 1 n 1 n 1 n Lời giải Chọn A
Lấy điểm O bất kì. Khi đó
A B A B ... A B A O A O ... A O OB OB ... OB 1 1 2 2 n n 1 2 n 1 2 n
Vì B , B ,..., B A , A ,..., A nên 1 2 n 1 2 n
OB OB ... OB OA OA ... OA 1 2 n 1 2 n
Do đó A B A B ... A B AO OA A O OA ... A O OA 0 . 1 1 2 2 n n 1 1 2 2 n n
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 8 VECTƠ TLDH
Dạng 2: Vectơ đối, hiệu của hai vectơ PHẦN 1: CÁC VÍ DỤ
Ví dụ 1. Cho tam giác ABC . Gọi M, N, P lần lượt là trung điểm của BC, C ,
A AB . Chứng minh rằng: a) AP AN AC BM 0 b) OA OB OC OM ON
OP với O là điểm bất kì. Lời giải A N P B C M
a) Vì tứ giác APMN là hình bình hành nên theo quy tắc hình bình hành ta có AP AN AM
, kết hợp với quy tắc trừ AP AN AC BM AM AC BM CM BM Mà CM BM
0 do M là trung điểm của BC . Vậy AP AN AC BM 0 .
b) Theo quy tắc ba điểm ta có OA OB OC OP PA OM MB ON NC OM ON OP PA MB NC OM ON OP BM CN AP BM CN AP 0 suy ra OA OB OC OM ON OP .
Ví dụ 2. Cho hai hình bình hành ABCD và AB 'C 'D ' có chung đỉnh A. Chứng minh rằng B 'B CC ' D 'D 0 Lời giải
Theo quy tắc trừ và quy tắc hình bình hành ta có B 'B CC ' D 'D AB AB ' AC ' AC AD AD ' AB AD AC AB ' AD ' AC 0 .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 9 VECTƠ TLDH
Ví dụ 3. Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm của AB, AC, BC.
a) Tìm AM AN;MN N ;
C MN PN; BP CP .
b) Phân tích AM theo hai vectơ MN;MP . Lời giải
a) AM AN = NM
MN NC = MN MP = PN (Vì NC MP )
MN PN = MN NP = MP
BP CP = BP PC = BC
b) AM NP MP MN .
Ví dụ 4. Cho 5 điểm A, B, C, D, E. Chứng minh rằng: AC DE DC CE CB AB Lời giải
Ta có DC C ;
D CE EC nên
VT = AC DE DC CE CB = AC DE CD EC CB
= AC CD DE EC CB AB =VP đpcm.
Ví dụ 5. Cho n điểm phân biệt trên mặt phẳng. Bạn An kí hiệu chúng là A , A ,..., A . Bạn Bình kí hiệu 1 2 n
chúng là B , B ,..., B
A B ). Chứng minh rằng 1 2 n ( 1 n
A B A B ... A B 0. 1 1 2 2 n n Lời giải
Lấy điểm O bất kì. Khi đó
A B A B ... A B OB OB ... OB
OA OA ... OA 1 1 2 2 n n 1 2 n 1 2 n
Vì B , B ,..., B A , A ,..., A nên 1 2 n 1 2 n
OB OB ... OB OA OA ... OA 1 2 n 1 2 n
Do đó A B A B ... A B 0. 1 1 2 2 n n
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 10 VECTƠ TLDH
PHẦN 2: CÂU HỎI TRẮC NGHIỆM
Câu 1. [0H1-2.3-1] Cho a và b
là các vectơ khác 0 với a là vectơ đối của b . Khẳng định nào sau đây sai?
A. Hai vectơ a, b cùng phương.
B. Hai vectơ a, b ngược hướng.
C. Hai vectơ a, b cùng độ dài.
D. Hai vectơ a, b chung điểm đầu. Lời giải Chọn D Ta có a
b . Do đó, a và b cùng phương, cùng độ dài và ngược hướng nhau..
Câu 2. [0H1-2.3-1] Gọi O là tâm hình bình hành ABCD . Đẳng thức nào sau đây sai? A. OA OB C . D . B. OB OC OD O . A . C. AB AD D . B . D. BC BA DC D . A . Lời giải Chọn B A B O D C Xét các đáp án:
Đáp án A. Ta có OA OB BA CD . Vậy A đúng.
Đáp án B. Ta có OB OC CB AD . Vậy B sai. OD OA AD
Đáp án C. Ta có AB AD D . B Vậy C đúng.
Đáp án D. Ta có BC BA AC . Vậy D đúng DC DA AC
Câu 3. [0H1-2.3-1] Gọi O là tâm hình vuông ABCD . Tính OB OC . A. BC . B. DA . C. OD OA . D. AB . Lời giải Chọn B OB OC CB DA .
Câu 4. [0H1-2.3-1] Cho O là tâm hình bình hành ABCD . Hỏi vectơ AO DO bằng vectơ nào? A. BA . B. BC . C. DC . D. AC . Lời giải Chọn B
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 11 VECTƠ TLDH A B O D C AO DO OD OA AD BC .
Câu 5. [0H1-2.3-1] Chọn khẳng định sai:
A. Nếu I là trung điểm đoạn AB thì IA IB 0 .
B. Nếu I là trung điểm đoạn AB thì AI BI AB .
C. Nếu I là trung điểm đoạn AB thì AI IB 0 .
D. Nếu I là trung điểm đoạn AB thì IA BI 0 . Lời giải Chọn A
IA IB BA 0.
Câu 6. [0H1-2.3-1] Cho 4 điểm bất kỳ , A ,
B C, D . Đẳng thức nào sau đây là đúng:
A. OA CA CO .
B. BC AC AB 0 .
C. BA OB OA .
D. OA OB BA . Lời giải Chọn B
BC AC AB AB BC AC AC AC 0 .
Câu 7. [0H1-2.3-1] Cho các điểm phân biệt , A ,
B C, D . Đẳng thức nào sau đây đúng ?
A. AB CD BC DA .
B. AC BD CB AD .
C. AC DB CB DA .
D. AB AD DC BC . Lời giải Chọn D
Ta có: AB AD DB, DC BC DC CB DB .
Vậy: AB AD DC BC .
Câu 8. [0H1-2.3-1] Chỉ ra vectơ tổng MN QP RN PN QR trong các vectơ sau A. MR . B. MQ . C. MP . D. MN . Lời giải Chọn D
MN NP PQ QR RN MN .
Câu 9. [0H1-2.3-2] Cho hình bình hành ABCDvà điểm M tùy ý. Đẳng thức nào sau đây đúng ?
A. MA MB MC MD .
B. MA MD MC MB .
C. AM MB CM MD .
D. MA MC MB MD .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 12 VECTƠ TLDH Lời giải Chọn D
Ta có: MA MC MB MD
MA MC MB MD 0
MA MB MC MD 0
BA DC 0.(đúng).
Câu 10. [0H1-2.3-1] Cho tam giác ABC có M , N, D lần lượt là trung điểm của AB, AC, BC . Khi đó,
các vectơ đối của vectơ DN là:
A. AM , MB, ND . B. M ,
A MB, ND .
C. MB, AM .
D. AM , BM , ND . Lời giải Chọn A .
Nhìn hình ta thấy vectơ đối của vectơ DN là: AM , MB, ND .
Câu 11. [0H1-2.3-1] Cho các điểm phân biệt , A ,
B C . Đẳng thức nào sau đây đúng?
A. AB BC AC .
B. AB CB CA .
C. AB BC CA .
D. AB CA CB . Lời giải Chọn D
OA BO BA CD .
Câu 12. [0H1-2.3-1] Cho hình bình hành ABCD tâm O . Khi đó CB CA bằng
A. OC OB . B. AB .
C. OC DO . D. CD . Lời giải Chọn B
AB CB CA (qui tắc 3 điểm).
Câu 13. [0H1-2.3-2] Cho bốn điểm ,
A B, C, D phân biệt. Khi đó vectơ u AD CD CB DB là: A. u 0 .
B. u AD .
C. u CD .
D. u AC . Lời giải Chọn D
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 13 VECTƠ TLDH
u AD CD CB DB AD DC CB BD AC CD AD .
Câu 14. [0H1-2.3-2] Cho bốn điểm ,
A B, C, D phân biệt. Khi đó vectơ u AD CD CB AB bằng:
A. u AD . B. u 0 .
C. u CD .
D. u AC . Lời giải Chọn B
u AD CD CB AB AD AB CB CD BD DB 0 .
Câu 15. [0H1-2.3-2] Cho 4 điểm , A ,
B C, D . Đẳng thức nào sau đây đúng?
A. AB DC AC DB .
B. AB CD AD BC .
C. AB DC AD CB . D. AB CD DA CB . Lời giải Chọn C
AB DC AD DB CD AD CB .
Câu 16. [0H1-2.3-1] Cho Cho hình bình hành ABCD tâmO . Đẳng thức nào sau đây đúng ?
A. AO BO CO DO 0 .
B. AO BO CO DO 0 .
C. AO OB CO OD 0 .
D. OA OB CO DO 0 . Lời giải Chọn B
Ta có: AO BO CO DO AO CO BO DO 0 .
Do AO, CO đối nhau, BO, DO đối nhau.
Câu 17. [0H1-2.3-3] Cho Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào dưới đây là đẳng thức sai?
A. OA OC EO 0 .
B. BC EF AD .
C. OA OB EB OC .
D. AB CD EF 0 . Lời giải Chọn D
Ta có: AB CD EF AB BO OA AO OA 2AO 0 .
Câu 18. [0H1-2.3-1] Cho hình bình hành ABCD. Đẳng thức nào sau đây đúng?
A. BA BC DC CB .
B. BA BC DC BC .
C. BA BC DC AD .
D. BA BC DC CA .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 14 VECTƠ TLDH Lời giải Chọn A
BA BC DC CA DC DC CA DA CB .
Câu 19. [0H1-2.3-2] Cho 4 điểm A, B, C, D. Đẳng thức nào sau đây đúng?
A. AB CD AD CB .
B. AB CD AD BC .
C. AB CD AC BD .
D. AB CD DA BC . Lời giải Chọn A
AB CD AD CB AB AD CB CD DB DB .
Câu 20. [0H1-2.3-3] Cho ABC, vẽ bên ngoài tam giác các hình bình hành ABEF, ACPQ, BCMN. Xét các mệnh đề :
(I ) NE FQ MP
(II ) EF QP MN
III AP BF CN AQ EB MC Mệnh đề đúng là :
A. Chỉ I .
B. Chỉ III .
C. I và (II ) .
D. Chỉ (II ) . Lời giải Chọn A
NE FQ MP .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 15 VECTƠ TLDH
Dạng 3:Chứng minh đẳng thức vectơ PHẦN 1: CÁC VÍ DỤ
Ví dụ 1. Cho năm điểm , A , B C, ,
D E . Chứng minh rằng a) AB CD EA CB ED b) AC CD EC AE DB CB Lời giải
a) Biến đổi vế trái ta có VT AC CB CD ED DA CB ED AC CD DA CB ED AD DA CB ED VP .
b) Đẳng thức tương đương với AC AE CD CB EC DB 0 EC BD EC DB 0 BD DB 0 (đúng).
Ví dụ 2. Cho hình bình hành ABCD tâm O . M là một điểm bất kì trong mặt phẳng. Chứng minh rằng a) BA DA AC 0 b) OA OB OC OD 0 c) MA MC MB MD . Lời giải A B O D C a) Ta có BA DA AC AB AD AC AB AD AC
Theo quy tắc hình bình hành ta có AB AD AC suy ra BA DA AC AC AC 0
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 16 VECTƠ TLDH
b) Vì ABCD là hình bình hành nên ta có: OA CO OA OC OA AO 0 Tương tự: OB OD 0 OA OB OC OD 0 .
c) Cách 1: Vì ABCD là hình bình hành nên AB DC BA DC BA AB 0 MA MC MB BA MD DC MB MD BA DC MB MD
Cách 2: Đẳng thức tương đương với MA MB MD MC BA
CD (đúng do ABCD là hình bình hành).
Ví dụ 3. Cho tam giác ABC . Gọi M, N, P lần lượt là trung điểm của BC, C ,
A AB . Chứng minh rằng: BM CN AP 0. Lời giải A N P B C M
Vì PN, MN là đường trung bình của tam giác ABC nên
PN / /BM , MN / / BP suy ra tứ giác BMNP là hình bình hành BM PN
N là trung điểm của AC CN NA
Do đó theo quy tắc ba điểm ta có BM CN AP PN NA AP PA AP 0.
Ví dụ 4. Cho hai hình bình hành ABCD và AB 'C 'D ' có chung đỉnh A. Chứng minh rằng B 'B CC ' D 'D 0 Lời giải
Theo quy tắc trừ và quy tắc hình bình hành ta có B 'B CC ' D 'D AB AB ' AC ' AC AD AD ' AB AD AC AB ' AD ' AC 0 .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 17 VECTƠ TLDH
Ví dụ 5. Cho hình bình hành ABCD . Dựng AM BA, MN D , A NP DC, PQ BC . Chứng minh rằng: AQ 0 . Lời giải
Theo quy tắc ba điểm ta có AQ AM MN NP PQ BA DA DC BC Mặt khác BA BC B , D DA DC DB suy ra AQ BD DB 0 .
PHẦN 2: CÂU HỎI TRẮC NGHIỆM
Câu 1. [0H1-2.2-1]Cho 5 điểm phân biệt M , N, , P ,
Q R . Mệnh đề nào sau đây đúng?
A. MN PQ RN NP QR MP .
B. MN PQ RN NP QR PR .
C. MN PQ RN NP QR MR .
D. MN PQ RN NP QR MN . Lời giải Chọn D.
Ta có MN PQ RN NP QR MN NP PQ QR RN MN .
Câu 2. [0H1-2.2-1]Cho hình bình hành ABCD, đẳng thức véctơ nào sau đây đúng?
A. CD CB CA .
B. AB AC AD .
C. BA BD BC .
D. CD AD AC . Lời giải Chọn A.
Đẳng thức véctơ CD CB CA đúng theo quy tắc cộng hình bình hành.
Câu 3. [0H1-2.2-1]Cho hình bình hành ABCD có tâm O . Khẳng định nào sau đây là đúng:
A. AB AC DA.
B. AO AC BO .
C. AO BO CD .
D. AO BO BD . Lời giải Chọn A. B C O A D
Ta có AB AC CB . Do ABCD là hình bình hành nên CB DA nên AB AC DA.
Câu 4. [0H1-2.2-1]Cho 4 điểm bất kì A , B , C , O . Đẳng thức nào sau đây đúng?
A. OA OB BA .
B. OA CA CO .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 18 VECTƠ TLDH
C. AB AC BC .
D. AB OB OA . Lời giải Chọn B
OA OB BA OA OB BA BA BA nên A sai
OA CA CO OA CA C
O OA AC C
O OC C O nên B đúng.
Câu 5. [0H1-2.2-1] Cho 3 điểm phân biệt ,
A B,C . Đẳng thức nào sau đây đúng?
A. AB BC CA .
B. AB CB AC .
C. AB BC AC .
D. AB CA BC . Lời giải Chọn B
AB AC CB CB AC .
Câu 6. [0H1-2.2-1] Cho hình bình hành ABCD tâm O . Khi đó OA BO bằng
A. OC OB . B. AB .
C. OC DO . D. CD . Lời giải Chọn D
OA BO BA CD .
Câu 7. [0H1-2.2-1] Cho 6 điểm , A , B C, ,
D E, F . Đẳng thức nào sau đây đúng?
A. AB CD FA BC EF DE 0 .
B. AB CD FA BC EF DE AF .
C. AB CD FA BC EF DE AE .
D. AB CD FA BC EF DE AD . Lời giải Chọn A
AB CD FA BC EF DE .
AB BC CD DE EF FA
AC CE EA 0
Câu 8. [0H1-2.2-1] Cho hình bình hành ABCD, gọi M, N lần lượt là trung điểm của đoạn BC và AD. Tính
tổng NC MC . A. AC. . B. NM . . C. . CA . D. MN. . Lời giải Chọn A
NC MC NC AN AN NC AC.
Câu 9. [0H1-2.2-2] Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào dưới đây là đẳng thức sai?
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 19 VECTƠ TLDH
A. OA OC OE 0 .
B. BC FE AD .
C. OA OB OC EB .
D. AB CD FE 0 . Lời giải Chọn D
AB CD FE AB BO FE AO OD AD 0 .
Câu 10. [0H1-2.2-2] Cho 6 điểm , A , B C, ,
D E, F . Tổng véc tơ : AB CD EF bằng
A. AF CE DB .
B. AE CB DF .
C. AD CF EB .
D. AE BC DF . Lời giải Chọn C
AB CD EF AD DB CF FD EB BF AD CF EB .
Câu 11. [0H1-2.2-2] Cho các điểm phân biệt , A , B C, ,
D E, F . Đẳng thức nào sau đây sai ?
A. AB CD EF AF ED BC .
B. AB CD EF AF ED CB .
C. AE BF DC DF BE AC .
D. AC BD EF AD BF EC . Lời giải Chọn A
Ta có: AB CD EF AF ED BC
AB AF CD BC EF ED 0
FB DF CD CB 0
DB CD CB 0
CB CB 0 (vô lý)..
Câu 12. [0H1-2.2-1] Cho các điểm phân biệt , A ,
B C, D . Đẳng thức nào sau đây đúng?
A. AC BD BC DA .
B. AC BD CB DA .
C. AC BD CB AD .
D. AC BD BC AD . Lời giải Chọn D
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 20 VECTƠ TLDH
AC BD AD DC BC CD AD BC .
Câu 13. [0H1-2.2-1] Cho hình bình hành ABCD với I là giao điểm của hai đường chéo. Khẳng định nào
sau đây là khẳng định sai?
A. IA IC 0 .
B. AB AD AC .
C. AB DC .
D. AC BD . Lời giải Chọn D
ABCD là hình bình hành với I là giao điểm của hai đường chéo nên I là trung điểm của AC
và BD nên ta có: IA IC 0 ; AB AD AC ; AB DC
Câu 14. [0H1-2.2-1] Cho tam giác .
ABC Khẳng định nào sau đây đúng?
A. AB AC BC .
B. CA BA CB .
C. AA BB AB .
D. AB CA CB . Lời giải Chọn D
Ta có AB CA CA AB CB B đúng.
Câu 15. [0H1-2.2-1] Cho hình bình hành ABCD tâm O . Tìm khẳng định sai trong các khẳng định sau:
A. AB AD AC .
B. AB AD DB .
C. OA OB AD .
D. OA OB CB . Lời giải Chọn C
Gọi M là trung điểm AB , ta có: OA OB 2OM DA .
Câu 16. [0H1-2.2-2] Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào dưới đây là đẳng thức sai?
A. OA OC OE 0 .
B. BC FE AD .
C. OA OB OC EB .
D. AB CD FE 0 . Lời giải Chọn D
AB CD EF 0 .
Câu 17. [0H1-2.2-3] Cho tam giác ABC , trung tuyến AM . Trên cạnh AC lấy điểm E và F sao cho
AE EF FC , BE cắt AM tại N . Chọn mệnh đề đúng:
A. NA NM 0 .
B. NA NB NC 0 .
C. NB NE 0 .
D. NE NF EF . Lời giải Chọn A
Trong tam giác BCE có MF là đường trung bình nên MF / /BE MF / /NE
N là trung điểm của AM nên NA NM 0.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 21 VECTƠ TLDH
Câu 18. [0H1-2.2-3] Cho tam giác ABC . Gọi ,
D E, F lần lượt là trung điểm của các cạnh BC,C , A AB . Hệ thức nào là đúng ?
A. AD BE CF AF CE BD .
B. AD BE CF AB AC BC .
C. AD BE CF AE AB CD .
D. AD BE CF BA BC AC . Lời giải A F E B D C Chọn A
Ta có AD BE CF AF FD BD DE CE EF
AF CE BD FD DE EF AF CE BD FF AF CE BD 0 AF CE BD .
Câu 19. [0H1-2.2-3] Cho hình lục giác đều ABCDEF , tâm O . Đẳng thức nào sau đây đúng?
A. AF FE AB AD .
B. AB BC CD BA AF FE
C. AB BC CD DE EF FA 6 AB .
D. AB AF DE DC 0 . Lời giải Chọn A
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 22 VECTƠ TLDH
AF FE AB AE AB AD .
Câu 20. [0H1-2.2-4] Cho tam giác ABC có trực tâm H , D là điểm đối xứng với B qua tâm O của
đường tròn ngoại tiếp tam giác ABC . Khẳng định nào sau đây là đúng?
A. HA CD và AD CH .
B. HA CD và AD HC .
C. HA CD và AC HD .
D. HA CD và AD HC . Lời giải Chọn A
Ta có : Vì D đối xứng với B qua O nên D thuộc đường tròn O
AD / /DH (cùng vuông góc với AB )
AH / /CD (cùng vuông góc với BC )
Suy ra ADHC là hình bình hành
Vậy HA CD và AD CH .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 23 VECTƠ TLDH
Dạng 4: Các bài toán xác định điểm thỏa đẳng thức vec tơ
PHẦN 1: CÁC VÍ DỤ
Ví dụ 1. Cho ABC
, tìm M thỏa MA MB MC O . Lời giải
MA MB MC O BA MC CM BA .
Suy ra M là điểm cuối của vec tơ có điểm đầu là C sao cho CM BA .
Ví dụ 2. Cho ABC
, tìm M thỏa MA MC AB MB . Lời giải
MA MC AB MB MA AB MC MB MB MC MB CM O
Suy ra M trùng C . Ví dụ 3. ABC
, tìm điểm M thỏa MA BC BM AB BA . Lời giải
MA BC BM AB BA MA MC BA AB MA MC O
Suy ra M là trung điểm AC . Ví dụ 4. ABC
, tìm điểm M thỏa MC MB BM MA CM CB . Lời giải
MC MB BM MA CM CB BC BA BM BC BM AB CM BA .
Suy ra M là điểm thỏa ABCM là hình bình hành.
Ví dụ 5. Cho tứ giác ABCD, tìm điểm M thỏa MA MB AC MD CD . Lời giải
MA MB AC MD CD
BA AC MD CD
BC MD CD
MD DC CB DM BD .
Vậy M là điểm đối xứng với B qua D .
PHẦN 2: CÂU HỎI TRẮC NGHIỆM
Câu 1. [0H1-2.3-1] Cho đoạn thẳng AB , M là điểm thỏa MA BA O . Mệnh đề nào sau đây đúng?
A. M là trung điểm AB .
B. M trùng A .
C. M trùng B .
D. A là trung điểm MB . Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 24 VECTƠ TLDH Chọn D
MA BA O AM AB O A là trung điểm MB .
Câu 2. [0H1-2.3-1] Cho 2 điểm phân biệt A , B . Tìm điểm I thỏa IA BI . Mệnh đề nào sau đây đúng?
A. I là trung điểm AB .
B. I thuộc đường trung trực của AB .
C. Không có điểm I .
D. Có vô số điểm I . Lời giải Chọn A
IA BI IA IB O I là trung điểm AB .
Câu 3. [0H1-2.3-2] Cho ABC
, B . Tìm điểm I để IA và CB cùng phương. Mệnh đề nào sau đây đúng?
A. I là trung điểm AB .
B. I thuộc đường trung trực của AB .
C. Không có điểm I .
D. Có vô số điểm I . Lời giải Chọn D
IA và CB cùng phương nên AI // CB . Suy ra có vô số điểm I .
Câu 4. [0H1-2.3-1] Cho 2 điểm phân biệt A , B . Tìm điểm M thỏa MA MB O . Mệnh đề nào sau đây đúng?
A. M là trung điểm AB .
B. M thuộc đường trung trực của AB .
C. Không có điểm M .
D. Có vô số điểm M . Lời giải Chọn C
MA MB O BA O (vô lý).
Câu 5. [0H1-2.3-1] Cho đoạn thẳng AB , M là điểm thỏa MB MA O . Mệnh đề nào sau đây đúng?
A. M là trung điểm AB .
B. M trùng A .
C. M trùng B .
D. A là trung điểm MB . Lời giải Chọn A
MB MA O suy ra M là trung điểm AB .
Câu 6. [0H1-2.3-1] Cho tam giác ABC , M là điểm thỏa MA MB MC O . Mệnh đề nào sau đây đúng?
A. M là trung điểm AB .
B. M là trọng tâm ABC .
C. M trùng B .
D. A là trung điểm MB . Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 25 VECTƠ TLDH Chọn B
MA MB MC O nên M là trọng tâm ABC .
Câu 7. [0H1-2.3-2] Cho tứ giác ABCD, M là điểm thỏa AM DC AB BD . Mệnh đề nào sau đây đúng?
A. M trùng D .
B. M trùng A .
C. M trùng B .
D. M trùng C . Lời giải Chọn D
AM DC AB BD DC AD AD DC AC .
Câu 8. [0H1-2.3-2] Cho ABCDlà hình bình hành, M là điểm thỏa AM AB AD . Mệnh đề nào sau đây đúng?
A. M trùng D .
B. M trùng A .
C. M trùng B .
D. M trùng C . Lời giải Chọn D
AM AB AD AC .
Câu 9. [0H1-2.3-2] Cho ABCDlà hình bình hành tâm O , M là điểm thỏa AM OC . Mệnh đề nào sau đây đúng?
A. M trùng O .
B. M trùng A .
C. M trùng B .
D. M trùng C . Lời giải Chọn A
AM OC suy ra AM AO ( O là trung điểm AC ) nên M trùng O .
Câu 10. [0H1-2.3-1] Cho ABCDlà hình bình hành tâm O , M là điểm thỏa AM BC . Mệnh đề nào sau đây đúng?
A. M trùng D .
B. M trùng A .
C. M trùng B .
D. M trùng C . Lời giải Chọn A
AM BC AD , suy ra M trùng D .
Câu 11. [0H1-2.3-2] Cho ABCDlà hình bình hành tâm O , M là điểm thỏa AM AB DC . Mệnh đề nào sau đây đúng?
A. M trùng O .
B. M trùng A .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 26 VECTƠ TLDH
C. M trùng B .
D. M trùng C . Lời giải Chọn B
AM DC AB O .
Câu 12. [0H1-2.3-2] Cho tứ giác PQRN có O là giao điểm 2 đường chéo, M là điểm thỏa
MN PQ RN NP QR ON . Mệnh đề nào sau đây đúng ?
A. M trùng P .
B. M trùng Q .
C. M trùng O .
D. M trùng R . Lời giải Chọn C
ON MN PQ RN NP QR NM NO .
Câu 13. [0H1-2.3-2] Cho ABC
, tìm điểm M thỏa MB MC CM CA . Mệnh đề nào sau đây đúng ?
A. M là trung điểm AB .
B. M là trung điểm BC .
C. M là trung điểm CA .
D. M là trọng tâm ABC . Lời giải Chọn D
MB MC CM CA MB MC AM MA MB MC O
Suy ra M là trọng tâm ABC .
Câu 14. [0H1-2.3-2] Cho D
EF , tìm M thỏa MD ME MF O . Mệnh đề nào sau đây đúng ?
A. MF ED .
B. FM ED .
C. EM DF .
D. FM DE . Lời giải Chọn B
MD ME MF O ED MF O FM ED .
Suy ra M là điểm cuối của vec tơ có điểm đầu là F sao cho FM ED .
Câu 15. [0H1-2.3-2] Cho D
EF , M là điểm thỏa MD ME MF O . Mệnh đề nào sau đây đúng?
A. EM ED EF .
B. FD EM .
C. MD MF EM . D. FM DE . Lời giải Chọn A
MD ME MF O ED MF O FM ED .
Suy ra DEFM là hình bình hành. Do đó EM ED EF .
Câu 16. [0H1-2.3-1] Cho ABC
có O là trung điểm BC , tìm M thỏa MA MC AB MB . Mệnh đề nào sau đây đúng?
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 27 VECTƠ TLDH
A. M trùng A .
B. M trùng B .
C. M trùng O .
D. M trùng C . Lời giải Chọn D
MA MC AB MB MA AB MC MB MB MC MB CM O
Suy ra M trùng C .
Câu 17. [0H1-2.3-3] Cho ABC
, tìm điểm M thỏa MA BC BM AB BA . Mệnh đề nào sau đây đúng?
A. M là trung điểm AB .
B. M là trung điểm BC .
C. M là trung điểm CA .
D. M là trọng tâm ABC . Lời giải Chọn C
MA BC BM AB BA MA MC BA AB MA MC O
Suy ra M là trung điểm AC .
Câu 18. [0H1-2.3-3] Cho ABC
, điểm M thỏa MC MB BM MA CM CB . Mệnh đề nào sau đây đúng?
A. M trùng A .
B. M trùng B .
C. ACMB là hình bình hành.
D. BA BC BM . Lời giải Chọn D
MC MB BM MA CM CB BC BA BM BC BM AB CM BA
Suy ra M là điểm thỏa ABCM là hình bình hành. Nên BA BC BM .
Câu 19. [0H1-2.3-3] Cho ABC
, D là trung điểm AB , E là trung điểm BC , điểm M thỏa
MA BC BM AB BA . Mệnh đề nào sau đây đúng ?
A. BD CM .
B. AM ED .
C. M là trung điểm BC .
D. EM BD . Lời giải Chọn D
MA BC BM AB BA MA MC BA AB MA MC O
Suy ra M là trung điểm AC . Suy ra BEMD là hình bình hành nên EM BD .
Câu 20. [0H1-2.3-3] Cho tứ giác ABCD, điểm M thỏa MA MB AC MD CD . Mệnh đề nào sau đây đúng ?
A. M là trung điểm AB .
B. M là trung điểm BC .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 28 VECTƠ TLDH
C. D là trung điểm BM .
D. M là trung điểm DC . Lời giải Chọn D
MA MB AC MD CD
BA AC MD CD
BC MD CD
MD DC CB DM BD .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 29 VECTƠ TLDH
Dạng 5: Các bài toán tính độ dài của vec tơ
PHẦN 1: CÁC VÍ DỤ
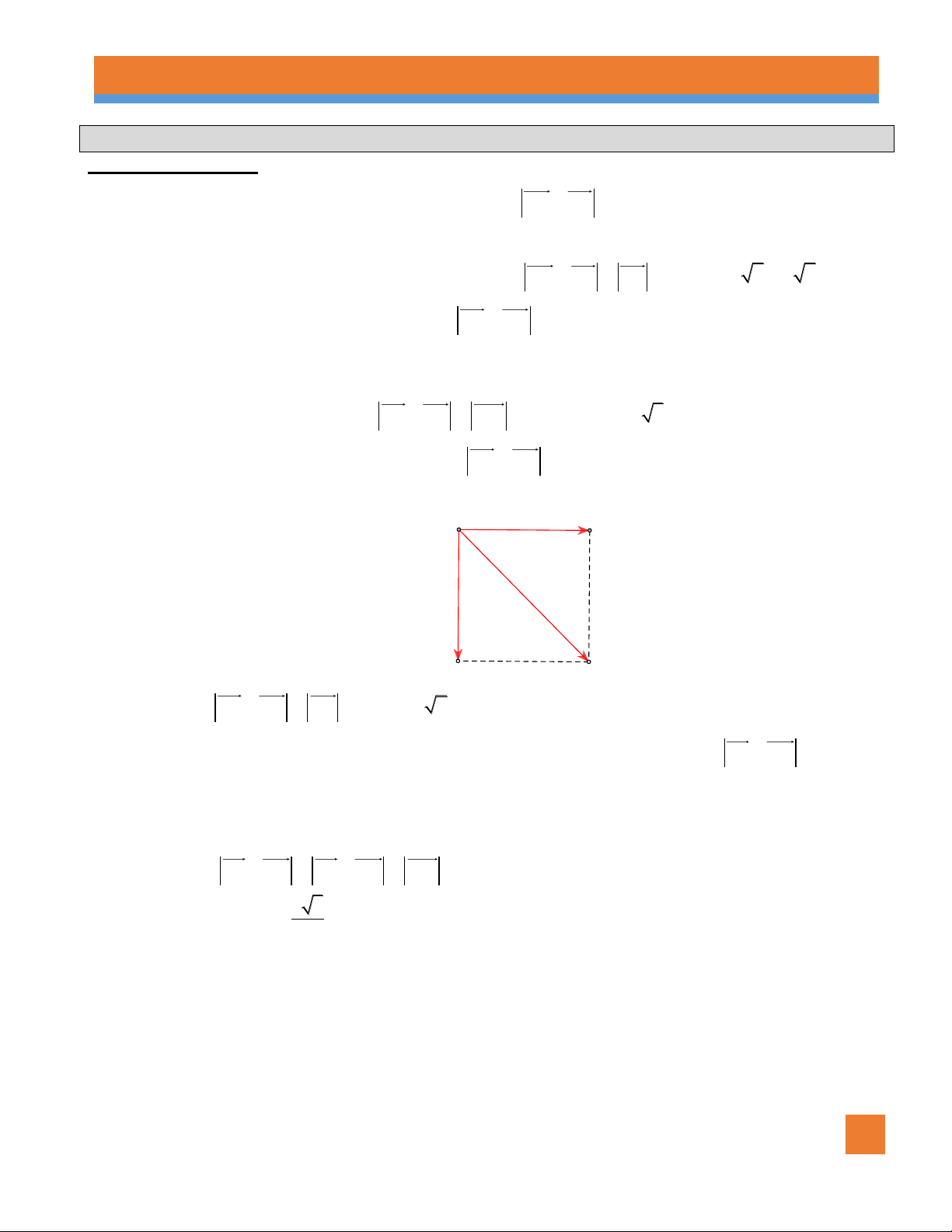
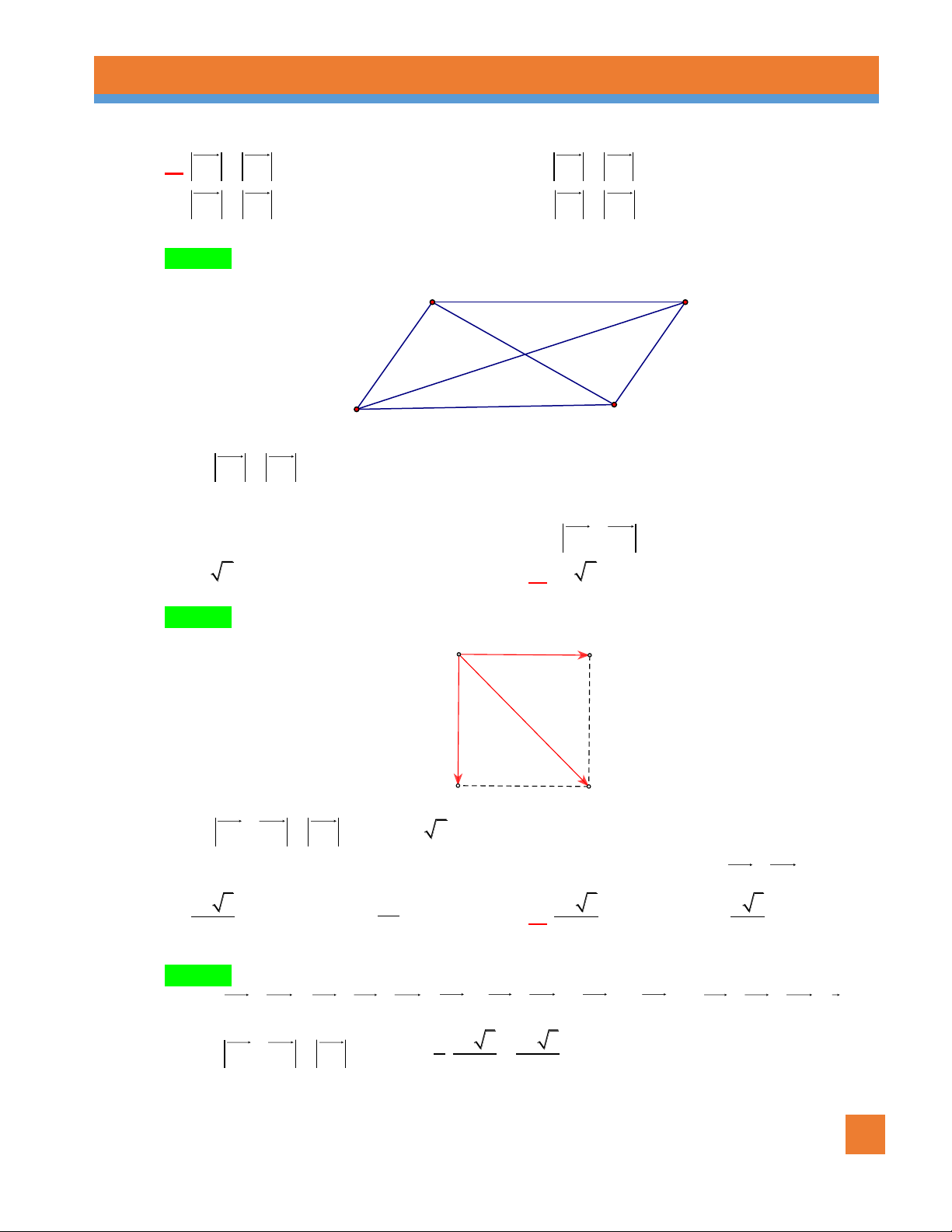
Ví dụ 1. Cho hình vuông ABCD có cạnh bằng a . Tính AD AB . Lời giải
Theo quy tắc đường chéo hình bình hành, ta có AD AB AC AC AB 2 a 2 .
Ví dụ 2. Cho tam giác ABC đều cạnh a . Tính AB AC . Lời giải
Gọi M là điểm sao cho ABMC là hình bình hành. Ta có AB AC nên ABMC là hình thoi. Gọi
O là tâm hình thoi ABMC . AB AC AM AM 2AO a 3 .
Ví dụ 3. Cho hình vuông ABCD cạnh 2a . Tính AB AD . Lời giải A B D C
Ta có AB AD AC AC 2a 2 .
Ví dụ 4. Cho tam giác ABC đều có cạnh AB 5, H là trung điểm của BC . Tính CA HC . Lời giải
Gọi M là điểm sao cho CHMA là hình bình hành.
Ta có: CA HC CA CH CM CM 2CE ( E là tâm cúa hình bình hành CHMA). Ta lại có: 5 3 AH ( ABC
đều, AH là đường cao). 2
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 30 VECTƠ TLDH A E B C H
Trong tam giác HEC vuông tại H , có: 2 5 3 5 7 2 2 2 5 7
EC CH HE 2.5
CA HC 2CE . 4 4 2
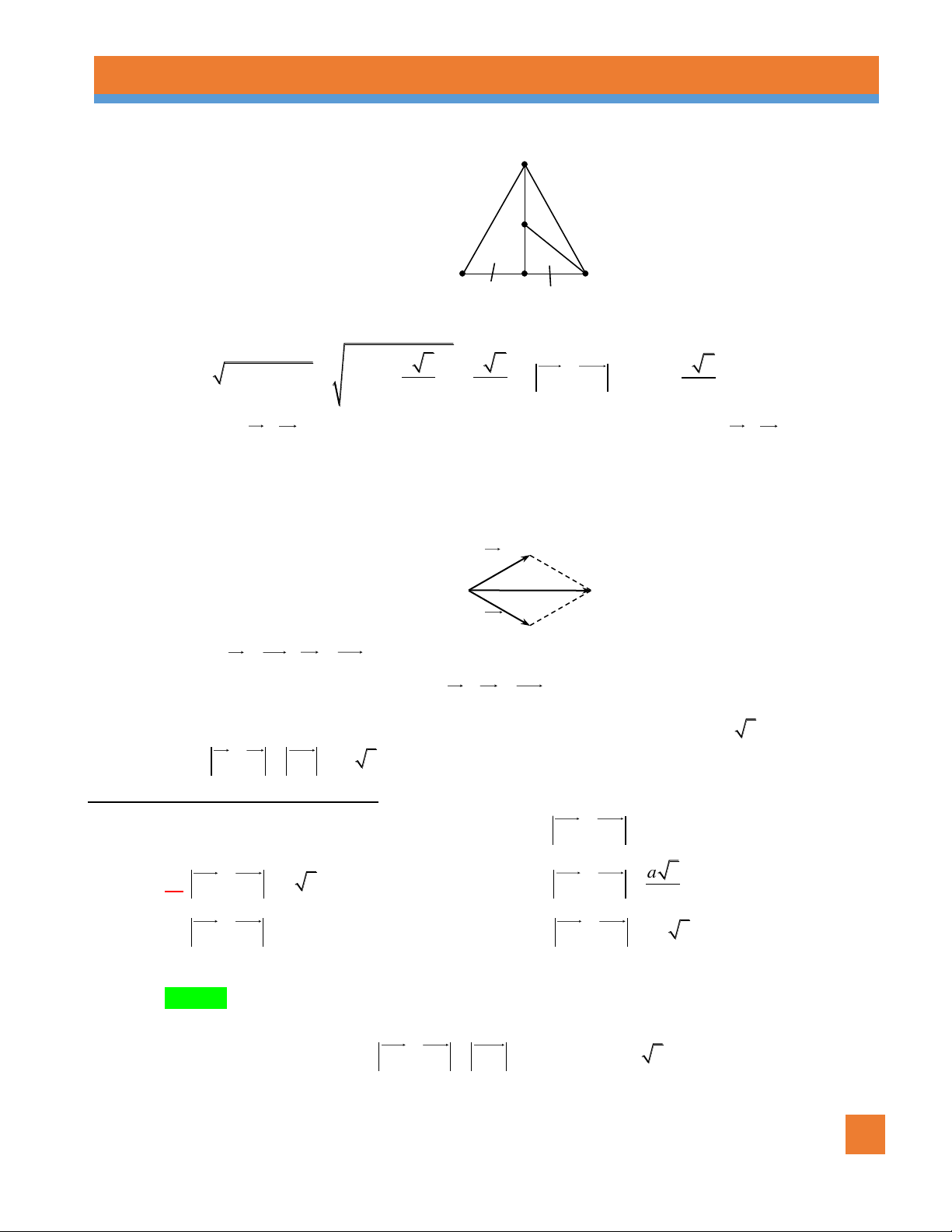
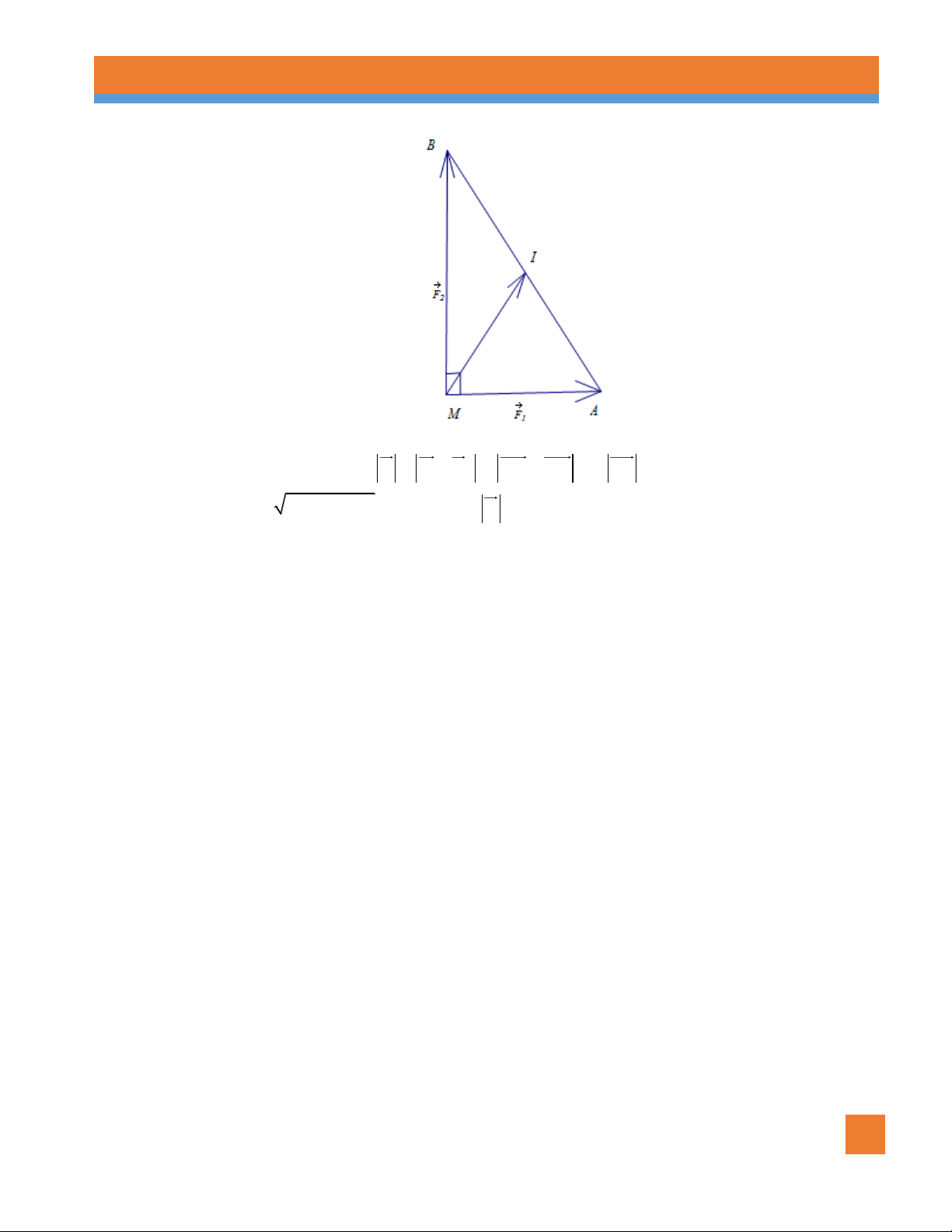
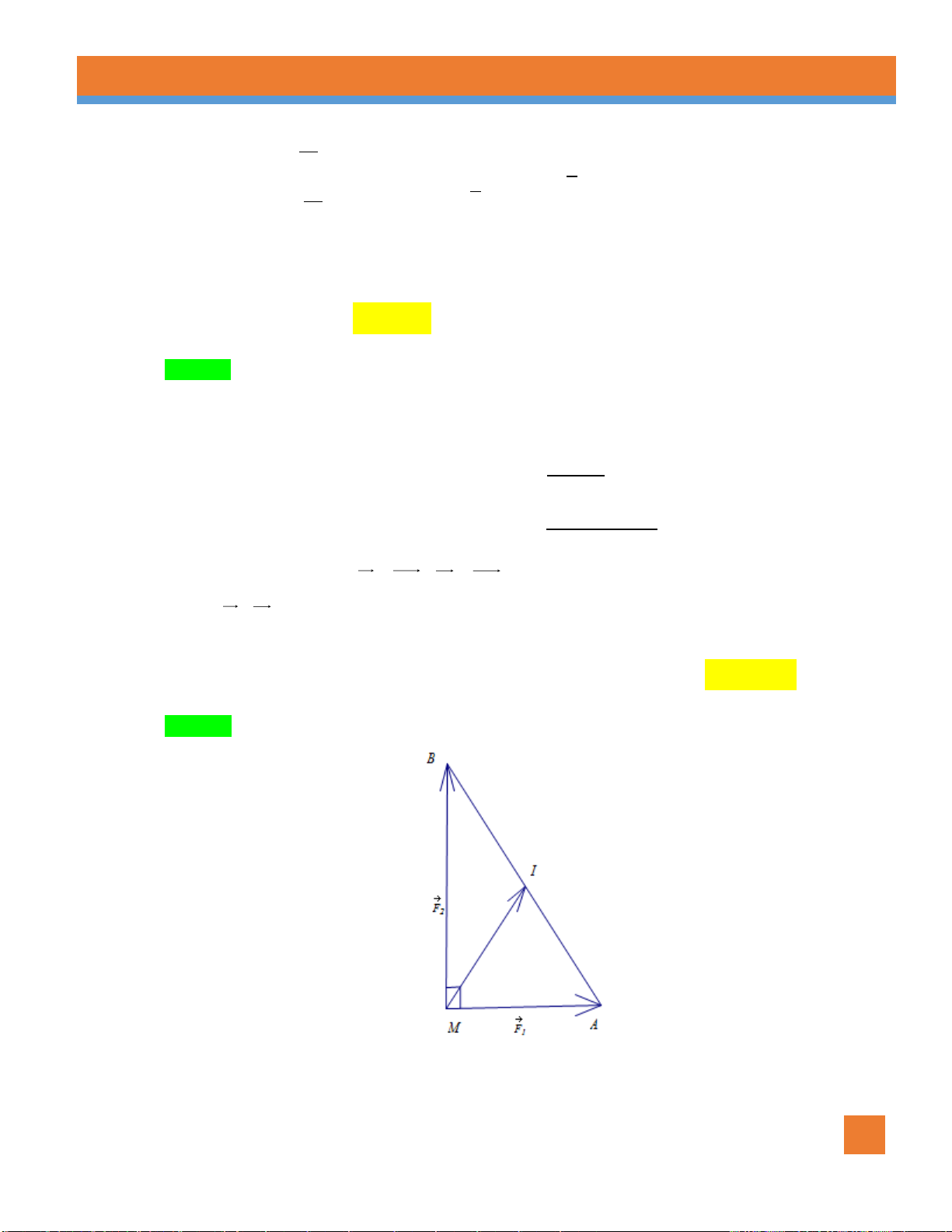
Ví dụ 5. Có hai lực F , F cùng tác động vào một vật đứng tại điểm O , biết hai lực F , F đều có cường 1 2 1 2
độ là 50 N và chúng hợp với nhau một góc 60. Hỏi vật đó phải chịu một lực tổng hợp có
cường độ bằng bao nhiêu? Lời giải A F1 O C F2 B
Giả sử F OA, F OB . 1 2
Theo quy tắc hình bình hành, suy ra F F OC , như hình vẽ. 1 2
Ta có AOB 60 , OA OB 50 , nên tam giác OAB đều, suy ra OC 50 3 .
Vậy F F OC 50 3 N . 1 2
PHẦN 2: CÂU HỎI TRẮC NGHIỆM
Câu 1. [0H1-2.5-2] Cho tam giác ABC đều cạnh a . Tính AB AC . a 3
A. AB AC a 3 .
B. AB AC . M trùng A . 2
C. AB AC 2a .
D. AB AC 2a 3 . Lời giải Chọn A
Gọi M là điểm sao cho ABMC là hình bình hành. Ta có AB AC nên ABMC là hình thoi. Gọi
O là tâm hình thoi ABMC . AB AC AM AM 2AO a 3 .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 31 VECTƠ TLDH
Câu 2. [0H1-2.5-1] Cho hình vuông ABCD có cạnh bằng a . Độ dài AD AB bằng a 2 a 3 A. 2a B. . C. . D. a 2 . 2 2 Lời giải Chọn D.
Theo quy tắc đường chéo hình bình hành, ta có
AD AB AC AC AB 2 a 2 .
Câu 3. [0H1-2.5-1] Cho tam giác đều ABC cạnh a , mệnh đề nào sau đây đúng?
A. AC BC .
B. AC a .
C. AB AC .
D. AB a . Lời giải Chọn D.
AB AB a .
Câu 4. [0H1-2.5-2] Cho AB khác 0 và cho điểm C .Có bao nhiêu điểm D thỏa AB CD ? A. Vô số. B. 1 điểm. C. 2 điểm.
D. Không có điểm nào. Lời giải Chọn A.
Ta có AB CD AB CD .
Suy ra tập hợp các điểm D là đường tròn tâm C bán kính AB . Câu 5.
[0H1-2.5-1] Chọn mệnh đề sai trong các mệnh đề sau đây:
A. 0 cùng hướng với mọi vectơ.
B. 0 cùng phương với mọi vectơ. C. AA 0 . D. AB 0 . Lời giải Chọn D.
Mệnh đề AB 0 là mệnh đề sai, vì khi A B thì AB 0 .
Câu 6. [0H1-2.5-3] Cho hình bình hành ABCD tâm I ; G là trọng tâm tam giác BCD. Đẳng thức nào sau đây sai?
A. BA DA BA DC .
B. AB AC AD 3AG .
C. BA BC DA DC .
D. IA IB IC ID 0 . Lời giải Chọn A.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 32 VECTƠ TLDH A D I G B M C
Ta có BA DA BA DC DA DC (vôlý) A sai.
G là trọng tâm tam giác BCD; A là một điểm nằm ngoài tam giác BCD đẳng thức ở đáp án B đúng.
Ta có BA BC BD và DA DC DB . Mà DB BD đáp án C đúng.
Ta có IA và IC đối nhau, có độ dài bằng nhau IA IC 0 ; tương tự IB ID 0 đáp án D là đúng.
Câu 7. [0H1-2.5-3] Cho tam giác ABC đều có cạnh AB 5, H là trung điểm của BC . Tính CA HC . 5 3
A. CA HC .
B. CA HC 5 . 2 5 7 5 7
C. CA HC .
D. CA HC . 4 2 Lời giải Chọn D.
Gọi M là điểm sao cho CHMA là hình bình hành.
Ta có: CA HC CA CH CM CM 2CE ( E là tâm cúa hình bình hành CHMA). Ta lại có: 5 3 AH ( ABC
đều, AH là đường cao). 2 A E B C H
Trong tam giác HEC vuông tại H , có: 2 5 3 5 7 2 2 2 5 7
EC CH HE 2.5
CA HC 2CE . 4 4 2
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 33 VECTƠ TLDH
Câu 8. [0H1-2.5-1] Gọi O là giao điểm của hai đường chéo hình bình hành ABCD. Đẳng thức nào sau đây sai?
A. BA CD .
B. AB CD .
C. OA OC .
D. AO OC . Lời giải Chọn C.
Ta có O là trung điểm của AC nên OA O C .
Câu 9. [0H1-2.5-4] Có hai lực F , F cùng tác động vào một vật đứng tại điểm O , biết hai lực F , F 1 2 1 2
đều có cường độ là 50 N và chúng hợp với nhau một góc 60. Hỏi vật đó phải chịu một lực
tổng hợp có cường độ bằng bao nhiêu? A. 100 N . B. 50 3 N . C. 100 3 N . D. Đáp án khác. Lời giải Chọn B. A F1 O C F2 B
Giả sử F OA, F OB . 1 2
Theo quy tắc hình bình hành, suy ra F F OC , như hình vẽ. 1 2
Ta có AOB 60 , OA OB 50 , nên tam giác OAB đều, suy ra OC 50 3 .
Vậy F F OC 50 3 N . 1 2
Câu 10. [0H1-2.5-2] Cho tứ giác ABCD có AB DC và AB BC . Khẳng định nào sau đây sai?
A. AD BC .
B. ABCD là hình thoi.
C. CD BC .
D. ABCD là hình thang cân. Lời giải Chọn D.
Tứ giác ABCD có AB DC ABCD là hình bình hành
1 , nên AD BC .
Mà AB BC 2 . Từ
1 và 2 ta có ABCD là hình thoi nên CD BC .
Câu 11. [0H1-2.5-2] Cho tam giác ABC vuông cân tại A có AB a . Tính AB AC . a 2
A. AB AC a 2 .
B. AB AC . 2
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 34 VECTƠ TLDH
C. AB AC 2a .
D. AB AC a . Lời giải Chọn A.
Gọi D là điểm thỏa ABDC là hình bình hành. Tam giác ABC vuông cân tại A suy ra ABDC
là hình vuông. AB AC AD 2AM BC a 2 .
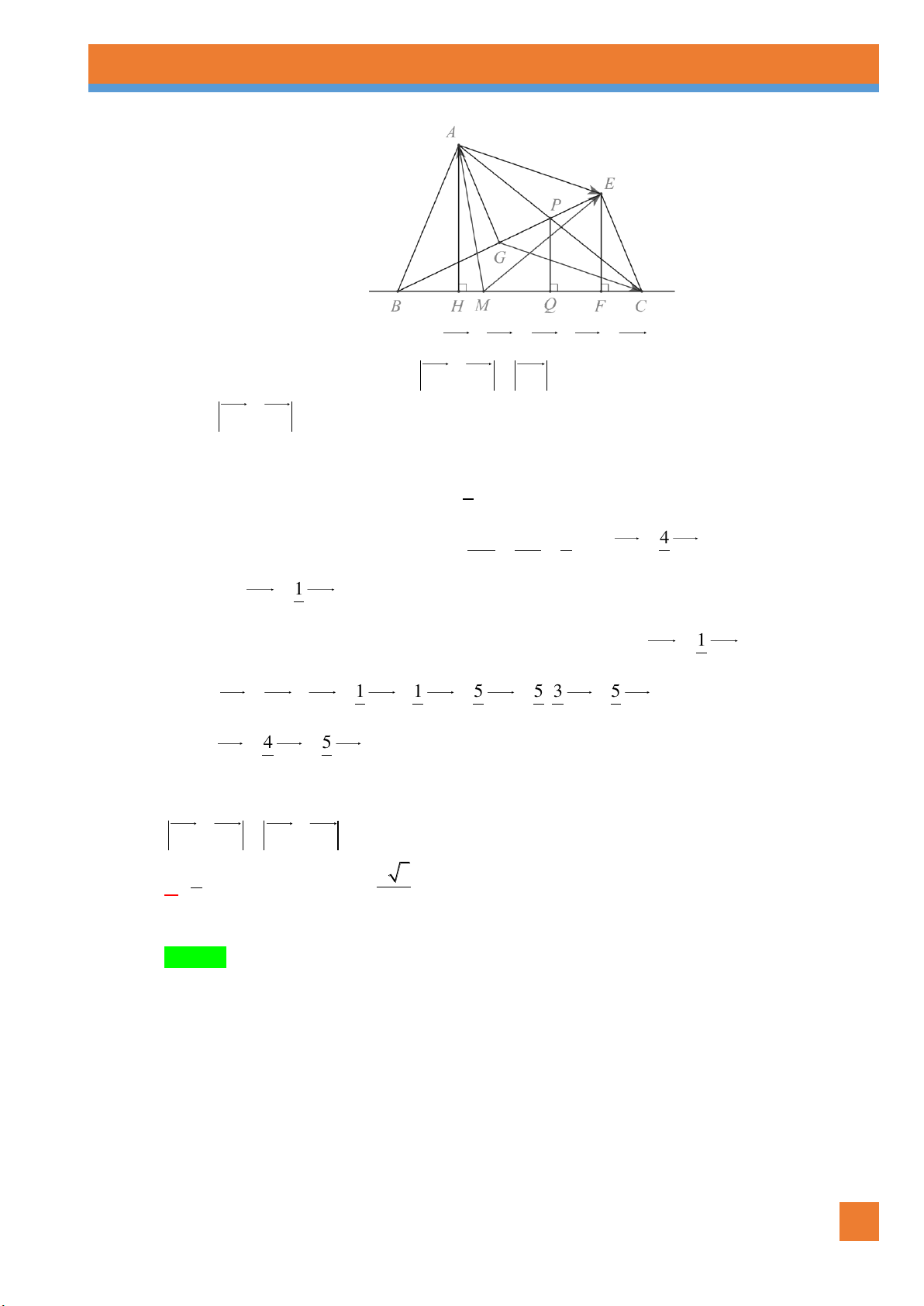
Câu 12. [0H1-2.5-3] Cho tam giác ABC đều cạnh a , có AH là đường trung tuyến. Tính AC AH . a 3 a 13 A. . B. 2a . C. . D. a 3 . 2 2 Lời giải Chọn C. A C B H K M
Dựng CM AH AHMC là hình bình hành AC AH AM AC AH AM .
Gọi K đối xứng với A qua BC A
KM vuông tại K . a
AK 2 AH a 3 ; KM CH . 2 a 2 2 a 13 AM
AK KM a 2 2 3 . 2 2
Câu 13. [0H1-2.5-4] Cho ba lực F MA , F MB , F MC cùng tác động vào một vật tại điểm M và 1 2 3
vật đứng yên. Cho biết cường độ của F , F đều bằng 25N và góc AMB 60 . Khi đó cường 1 2
độ lực của F là 3 A F1 F3 60 C M F2 B
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 35 VECTƠ TLDH A. 25 3 N . B. 50 3 N . C. 50 2 N . D. 100 3 N . Lời giải Chọn A.
Vật đứng yên nên ba lực đã cho cân bằng. Ta được F F F . 3 1 2 A F1 F3 C M N F2 B
Dựng hình bình hành AMBN . Ta có F F MA MB MN . 1 2 2 3MA
Suy ra F MN MN 25 3 . 3 2
Câu 14. [0H1-2.5-3] Cho tam giác ABC có G là trọng tâm, I là trung điểm BC . Tìm khẳng định sai.
A. IB IC IA IA .
B. IB IC BC .
C. AB AC 2AI .
D. AB AC 3GA . Lời giải Chọn B.
IB IC IA 0 IA IA IA (Do I là trung điểm BC ) nên khẳng định ở A đúng.
AB AC AD AD 2AI (Gọi D là điểm thỏa ABDC là hình bình hành, I là trung điểm
BC ) nên khẳng định ở C đúng.
AB AC 2AI 3GA (Do G là trọng tâm tam giác ABC ) nên khẳng định ở D đúng.
IB IC 0 0 (Do I là trung điểm BC ) nên khẳng định ở B sai.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 36 VECTƠ TLDH
Câu 15. [0H1-2.5-1] Cho hình bình hành ABCD. Đẳng thức nào sau đây sai?
A. AC BD .
B. BC DA .
C. AD BC .
D. AB CD . Lời giải Chọn A. B C D A
Ta có AC BD là đẳng thức sai vì độ dài hai đường chéo của hình bình hành không bằng nhau.
Câu 16. [0H1-2.5-2] Cho hình vuông ABCD cạnh 2a . Tính AB AD . A. 4a 2 . B. 4a . C. 2a 2 . D. 2a . Lời giải Chọn C. A B D C
Ta có AB AD AC AC 2a 2 .
Câu 17. [0H1-2.5-3] Cho tam giác ABC đều, cạnh 2a , trọng tâm G . Độ dài vectơ AB GC là 2a 3 2a 4a 3 a 3 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn C.
Ta có : AB GC GB GA GC GB GA GC GB G
B vì GAGB GC 0. Khi đó 2 2a 3 4a 3
AB GC GE 2GB 2. .
( E đối xứng với G qua M ). 3 2 3
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 37 VECTƠ TLDH
Câu 18. [0H1-2.5-3] Tam giác ABC thỏa mãn: AB AC AB AC thì tam giác ABC là
A. Tam giác vuông A .
B. Tam giác vuông C .
C. Tam giác vuông B .
D. Tam giác cân tại C . Lời giải Chọn A.
Gọi E là trung điểm BC , M là điểm thỏa ABCM là hình bình hành. Ta có 1
AB AC AB AC AM CB AE
BC . Trung tuyến kẻ từ A bằng một nửa cạnh 2
BC nên tam giác ABC vuông tại A .
Câu 19. [0H1-2.5-2] Cho tam giác đều ABC cạnh 2a có G là trọng tâm. Khi đó AB GC là a 3 2a 3 4a 3 2a A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn C. A G B C M N
Gọi M là trung điểm BC , dựng điểm N sao cho BN AG . Ta có a a
: AB GC GB GA GC GB GA GC 2 2 3 4 3
2GB 2.GB 2. . 3 2 3
( E đối xứng với B qua G ).
Câu 20. [0H1-2.5-4] Cho hai lực F MA, F MB cùng tác động vào một vật tại điểm M cường độ hai 1 2
lực F , F lần lượt là 300N và 400N . AMB 90 . Tìm cường độ của lực tổng hợp tác động 1 2 vào vật. A. 0 N . B. 700N . C. 100N . D. 500N . Lời giải Chọn D.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 38 VECTƠ TLDH
Cường độ lực tổng hợp của F F F 2 MA MB 2 MI
AB ( I là trung điểm của AB 1 ). Ta có 2 2 AB
MA MB 500 suy ra F 500 N .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 39 CHUYÊN ĐỀ: VECTƠ TLDH CHUYÊN ĐỀ VECTƠ (CHƯƠNG 1 LỚP 10)
BÀI 3. TÍCH CỦA VECTƠ VỚI MỘT SỐ .............................................................................................................. 2
A. KIẾN THỨC SÁCH GIÁO KHOA CẦN CẦN NẮM ................................................................................... 2
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP ...................................................................................... 2
Dạng 1: Xác định vectơ ka ............................................................................................................................... 2
Dạng 2: Hai vectơ cùng phương, ba điểm thẳng hàng .................................................................................. 10
Dạng 3: Biểu thị một vectơ theo hai vectơ không cùng phương ................................................................... 12
Dạng 4: Đẳng thức vectơ chứa tích của vectơ với một số.............................................................................. 18 Ban thực hiện Tên giáo viên Đơn vị công tác GV Soạn
Thầy Bùi Văn Huấn
Trường PT DTNT Hòa Bình (Hòa Bình) GV phản biện
Thầy Nguyễn Đình Hải
Lớp học TH Class Ngã Tư Sở (Hà Nội) TT Tổ soạn Cô Phạm Thị Hoài
Trường THCS Nguyễn Hiền (Nha Trang) TT Tổ phản biện
Thầy Nguyễn Văn Vũ Trường THPT YaLy (Gia Lai) Người triển khai Thầy Phạm Lê Duy
Trường THPT Chu Văn An (An Giang)
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 1 CHUYÊN ĐỀ: VECTƠ TLDH
BÀI 3. TÍCH CỦA VECTƠ VỚI MỘT SỐ
A. KIẾN THỨC SÁCH GIÁO KHOA CẦN CẦN NẮM I. ĐỊNH NGHĨA
Cho vectơ a và số k . Tích của vectơ a và số k là một vectơ, kí hiệu là ka , được xác định như sau:
ka cùng hướng với a nếu k 0 , ka ngược hướng với a nếu k 0 .
ka k . a . II. TÍNH CHẤT
1. Với hai vectơ a và b bất kì, với mọi số k và l , ta có:
k a b ka kb
(k l)a ka la ;
k la (kl)a ;
0.a 0 , k.0 0.
1.a a , 1 .a a .
ka 0 k 0 hoặc a 0.
2. Tính chất trung điểm của đoạn thẳng và trọng tâm của tam giác
Hệ thức trung điểm đoạn thẳng:
M là trung điểm của đoạn thẳng AB MA MB 0 OA OB 2OM (O tuỳ ý).
Hệ thức trọng tâm tam giác:
G là trọng tâm ABC
GA GB GC 0 OA OB OC 3OG (O tuỳ ý).
III. ĐIỀU KIỆN ĐỂ HAI VECTƠ CÙNG PHƯƠNG, BA ĐIỂM THẲNG HÀNG
1. Điều kiện để hai vectơ cùng phương
a và b a 0 cùng phương k
: b ka .
2. Điều kiện để ba điểm thẳng hàng Ba điểm phân biệt , A ,
B C thẳng hàng k
0: AB k AC .
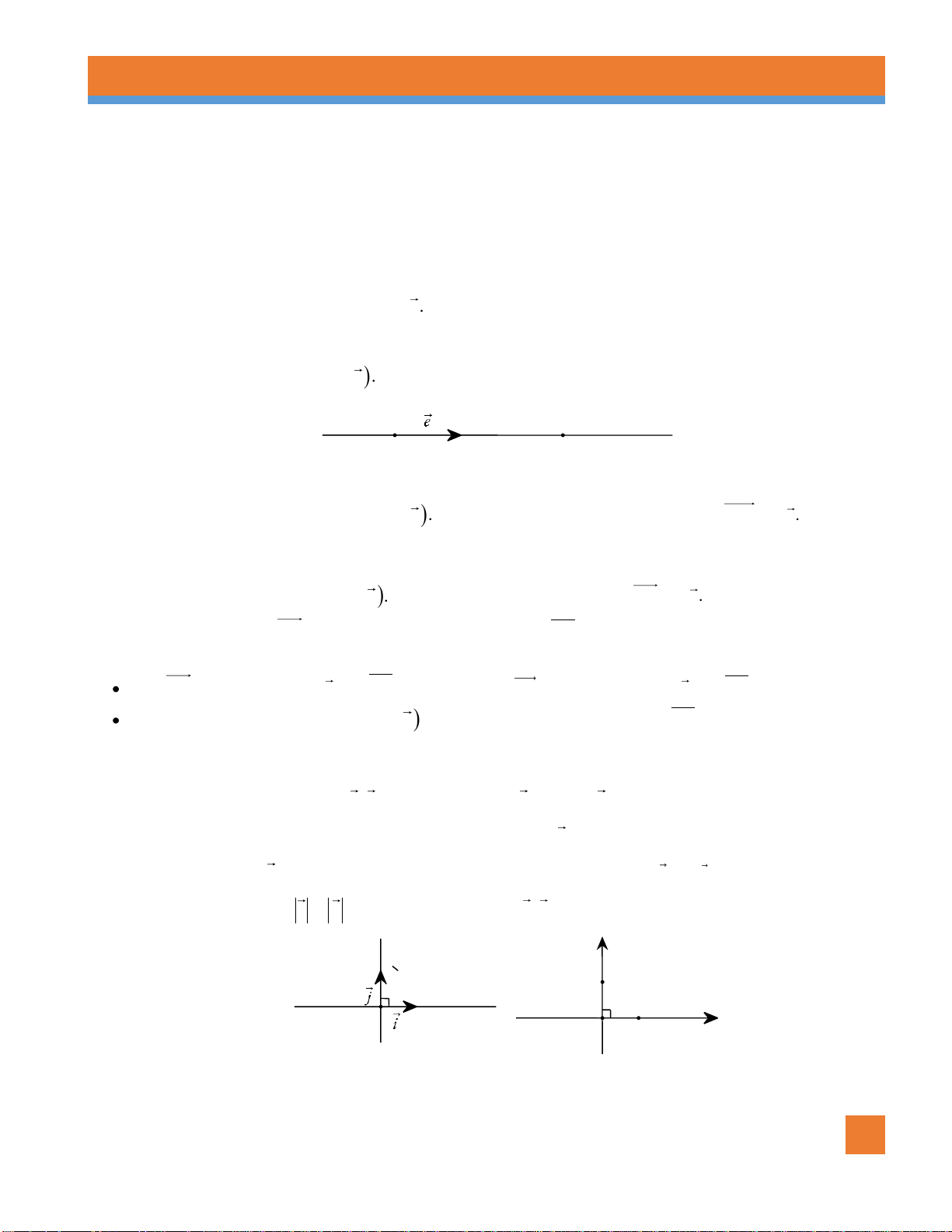
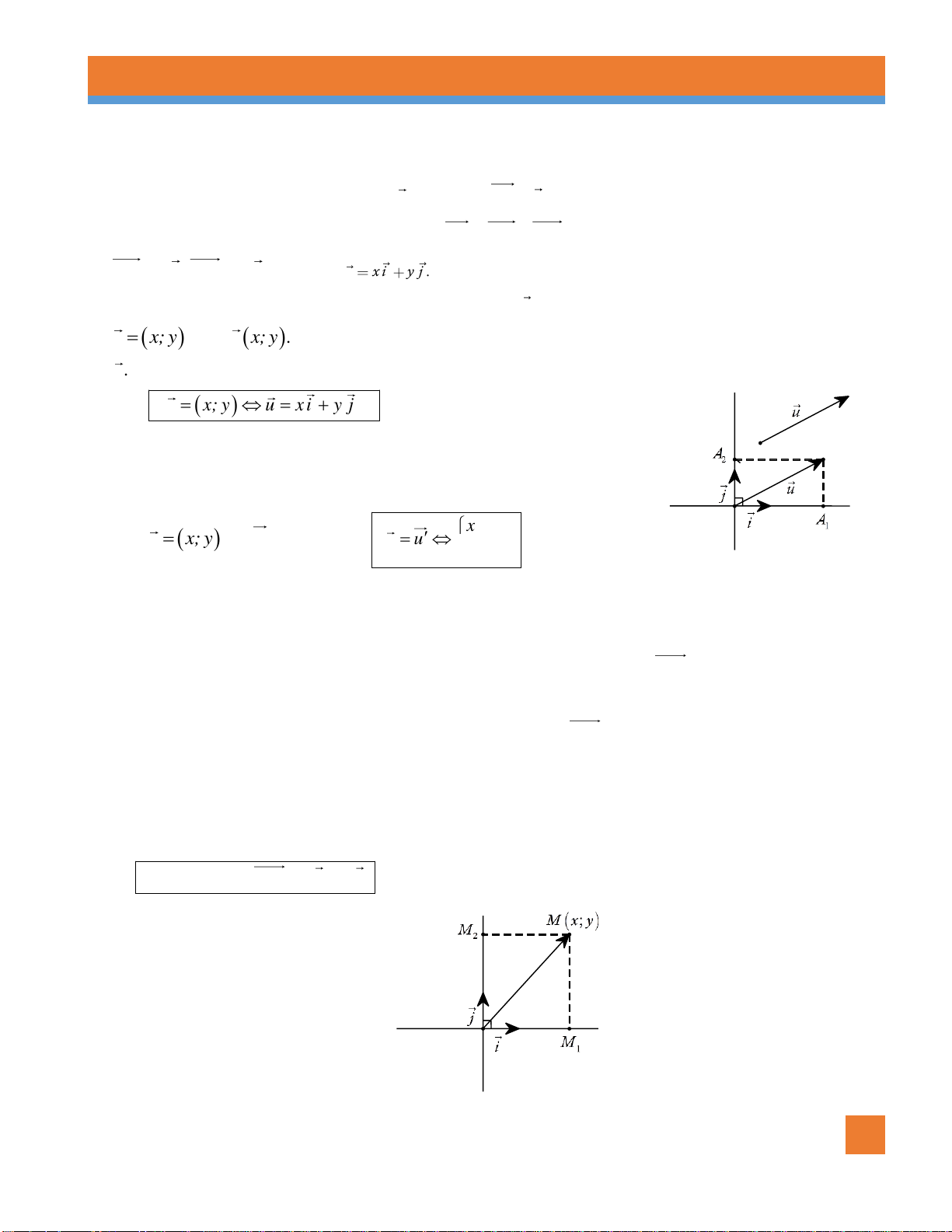
IV. BIỂU THỊ MỘT VECTƠ THEO HAI VECTƠ KHÔNG CÙNG PHƯƠNG
Cho hai vectơ không cùng phương a và b . Khi đó mọi vectơ x đều phân tích được một cách duy nhất
theo hai vectơ a và b , nghĩa là có duy nhất cặp số m và n sao cho x ma nb .
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Xác định vectơ ka
{Dựa vào định nghĩa và các tính chất của tích vectơ với một số }
PHẦN 1: CÁC VÍ DỤ
Ví dụ 1. Cho a AB và điểm O . Xác định hai điểm M và N sao cho: OM 3a; ON 4a Lời giải
Vẽ d đi qua O và song song với giá của a (nếu O thuộc giá của a thì d là giá của a )
Trên d lấy điểm M sao cho OM 3 a , OM và a cùng hướng khi đó OM 3a .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 2 CHUYÊN ĐỀ: VECTƠ TLDH
Trên d lấy điểm N sao cho ON 4 a , ON và a ngược hướng nên ON 4 a . Ví dụ 1
2. Cho đoạn thẳng AB và M là một điểm nằm trên đoạn AB sao cho AM
AB . Tìm k trong 5 các đẳng thức sau: a) AM k AB
b) MA k MB c) MA k AB Lời giải A M B | AM | AM 1 1 a) AM k AB | k |
, vì AM AB k . | AB | AB 5 5 1 b) k . 4 1 c) k . 5
Ví dụ 3. Cho hai điểm phân biệt ,
A B . Xác định điểm M biết 2MA 3MB 0 Lời giải Ta có:
2MA 3MB 0 2MA 3(MA AB) 0 MA 3AB 0 AM 3AB
AM , AB cùng hướng và AM 3AB .
Ví dụ 4. Cho tam giác ABC .
a) Tìm điểm K sao cho KA 2KB CB
b) Tìm điểm M sao cho MA MB 2MC 0 Lời giải
a) Ta có: KA 2KB CB KA 2KB KB KC KA KB KC 0
K là trọng tâm của tam giác ABC .
b) Gọi I là trung điểm của AB . Ta có: MA MB 2MC 0 2MI 2MC 0 MI MC 0
M là trung điểm của IC .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 3 CHUYÊN ĐỀ: VECTƠ TLDH
Ví dụ 5. Cho tam giác đều ABC cạnh a . Tính
a) AB AC BC b) AB AC Lời giải
a) AB AC BC ( AB BC) AC AC AC 2AC 2 AC 2AC 2a .
b) Gọi H là trung điểm của BC . Ta có: 2 a 2 2 2
AB AC 2AH 2 AH 2AH 2 AB BH 2 a a 3 2
Ví dụ 6. Cho ABC vuông tại B có 0
A 30 , AB a . Gọi I là trung điểm của AC . Hãy tính: a) BA BC b) AB AC Lời giải Ta có: a 3 AB a 2a 3 0
BC AB tan A a tan 30 , AC 3 0 cos A cos 30 3 AC 2a 3
a) BA BC 2BI 2 BI 2BI 2. AC . 2 3
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 4 CHUYÊN ĐỀ: VECTƠ TLDH 2 a 3 a 39 b) 2 2 2
AB AC 2AM 2 AM 2AM 2 AB BM 2 a . 6 3
PHẦN 2: CÂU HỎI TRẮC NGHIỆM
Câu 1. [0H1-3.1-1] Khẳng định nào sai?
A. 1.a a
B. k a và a cùng hướng khi k 0
C. k a và a cùng hướng khi k 0
D. Hai vectơ a và b 0 cùng phương khi có một số k để a kb Lời giải Chọn C
(Dựa vào định nghĩa tích của một số với một vectơ)
Câu 2. [0H1-3.3-2] Trên đường thẳng MN lấy điểm P sao cho MN 3
MP . Điểm P được xác định
đúng trong hình vẽ nào sau đây: A. Hình 3 B. Hình 4 C. Hình 1 D. Hình 2 Lời giải Chọn A MN 3
MP MN ngược hướng với MP và MN 3 MP .
Câu 3. [0H1-3.1-1] Cho ba điểm phân biệt ,
A B,C . Nếu AB 3
AC thì đẳng thức nào dưới đây đúng? A. BC 4 AC B. BC 2 AC
C. BC 2AC
D. BC 4AC Lời giải Chọn D
Câu 4. [0H1-3.1-1] Cho tam giác ABC . Gọi I là trung điểm của BC .Khẳng định nào sau đây đúng A. BI IC B. 3BI 2IC C. BI 2IC D. 2BI IC Lời giải Chọn A
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 5 CHUYÊN ĐỀ: VECTƠ TLDH
Vì I là trung điểm của BC nên BI CI và BI cùng hướng với IC do đó hai vectơ BI , IC bằng nhau hay BI IC .
Câu 5. [0H1-3.1-2] Cho tam giác ABC . Gọi M và N lần lượt là trung điểm của AB và AC . Trong
các mệnh đề sau, tìm mệnh đề sai? 1
A. AB 2AM
B. AC 2CN C. BC 2 NM D. CN AC 2 Lời giải Chọn B
Câu 6. [0H1-3.1-1] Cho a 0 và điểm O . Gọi M , N lần lượt là hai điểm thỏa mãn OM 3a và ON 4 a. Khi đó:
A. MN 7a B. MN 5 a C. MN 7 a D. MN 5 a Lời giải Chọn C
Ta có: MN ON OM 4
a 3a 7 a .
Câu 7. [0H1-3.1-1] Tìm giá trị của m sao cho a mb , biết rằng a,b ngược hướng và a 5, b 15 1 1 A. m 3 B. m C. m D. m 3 3 3 Lời giải Chọn B a 5 1
Do a, b ngược hướng nên m . b 15 3
Câu 8. [0H1-3.1-2] Cho tam giác ABC đều có cạnh bằng 2a . Độ dài của AB AC bằng: a 3 A. 2a B. a 3 C. 2a 3 D. 2 Lời giải Chọn C a
Gọi H là trung điểm của BC . Khi đó: 2 3
AB AC 2.AH 2.AH 2. 2a 3 . 2
Câu 9. [0H1-3.3-2] Cho tam giác ABC . Gọi I là trung điểm của AB . Tìm điểm M thỏa mãn hệ thức
MA MB 2MC 0 .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 6 CHUYÊN ĐỀ: VECTƠ TLDH
A. M là trung điểm của BC
B. M là trung điểm của IC
C. M là trung điểm của IA
D. M là điểm trên cạnh IC sao cho IM 2MC Lời giải Chọn B
MA MB 2MC 0 2MI 2MC 0 MI MC 0 M là trung điểm của IC .
Câu 10. [0H1-3.3-2] Cho hình bình hành ABCD, điểm M thõa mãn 4AM AB AD AC . Khi đó điểm M là:
A. Trung điểm của AC B. Điểm C
C. Trung điểm của AB
D. Trung điểm của AD Lời giải Chọn A 1
Theo quy tắc hình bình hành, ta có: 4AM AB AD AC 4AM 2.AC AM .AC 2
M là trung điểm của AC .
Câu 11. [0H1-3.1-2] Cho hình thoi ABCD tâm O , cạnh 2a . Góc 0
BAD 60 . Tính độ dài vectơ
AB AD .
A. AB AD 2a 3
B. AB AD a 3
C. AB AD 3a
D. AB AD 3a 3 Lời giải Chọn A
Tam giác ABD cân tại A và có góc 0
BAD 60 nên ABD đều 2 2 2 2
AB AD AC 2AO 2.AO 2. AB BO 2. 4a a 2a 3
Câu 12. [0H1-3.1-3] Cho tam giác ABC có điểm O thỏa mãn: OA OB 2OC OA OB . Khẳng
định nào sau đây là đúng?
A. Tam giác ABC đều
B. Tam giác ABC cân tại C
C. Tam giác ABC vuông tại C
D. Tam giác ABC cân tại B
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 7 CHUYÊN ĐỀ: VECTƠ TLDH Lời giải Chọn C
Gọi I là trung điểm của AB . Ta có:
OA OB 2OC OA OB OA OC OB OC BA CA CB AB 1
2.CI AB 2CI AB CI AB Tam giác ABC vuông tại C . 2
Câu 13. [0H1-3.1-3] Cho tam giác OAB vuông cân tạ O với OA OB a . Độ dài của véc tơ 21 5 u OA OB là: 4 2 a 140 a 321 a 520 a 541 A. B. C. D. 4 4 4 4 Lời giải Chọn D 21 5
Dựng điểm M , N sao cho: OM O , A ON OB . Khi đó: 4 2 2 2 21a 5a a 541 2 2
u OM ON NM MN OM ON . 4 2 4
Câu 14. [0H1-3.1-3] Cho ngũ giác ABCDE . Gọi M , N, ,
P Q lần lượt là trung điểm các cạnh A , B BC,C ,
D DE . Gọi I và J lần lượt là trung điểm các đoạn MP và NQ . Khẳng định nào sau đây đúng? 1 1 1 1 A. IJ AE B. IJ AE C. IJ AE D. IJ AE 2 3 4 5 Lời giải Chọn C
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 8 CHUYÊN ĐỀ: VECTƠ TLDH
Ta có: 2IJ IQ IN IM MQ IP PN MQ PN
MQ MA AE EQ 1 1
2MQ AE BD MQ AE BD, PN BD 2 MQ MB BD DQ 2 1 1 1 1 Suy ra: 2IJ
AEBD BD AE IJ AE. 2 2 2 4 Câu 15. 1
[0H1-3.1-2] Cho đoạn thẳng AB . Gọi M là một điểm trên AB sao cho AM AB . Khẳng 4
định nào sau đây sai? 1 1 3 A. MA MB . B. AM AB . C. BM BA . D. MB 3 MA . 3 4 4 1
Câu 16. [0H1-3.1-2] Cho đoạn thẳng AB và M là một điểm trên đoạn AB sao cho MA AB . Trong 5
các khẳng định sau, khẳng định nào sai ? 1 1 4 A. AM AB B. MA MB C. MB 4 MA D. MB AB 5 4 5 Lời giải Chọn D 4
Ta thấy MB và AB cùng hướng nên MB AB là sai. 5
Câu 17. [0H1-3.1-3] Cho tam giác ABC . Gọi M là trung điểm của BC và N là trung điểm AM .
Đường thẳng BN cắt AC tại P . Khi đó AC xCP thì giá trị của x là: 4 2 3 5 A. B. C. D. 3 3 2 3 Lời giải Chọn C
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 9 CHUYÊN ĐỀ: VECTƠ TLDH
Kẻ MK / /BP (K AC) . Do M là trung điểm của BC nên suy ra K là trung điểm của CP
Vì MK / /BP MK / /NP mà N là trung điểm của AM nên suy ra P là trung điểm của AK 3 3
Do đó: AP PK KC . Vậy AC CP x . 2 2
Dạng 2: Hai vectơ cùng phương, ba điểm thẳng hàng
{Điều kiện hai vectơ cùng phương, điều kiện ba điểm thẳng hàng } PHẦN 1: CÁC VÍ DỤ
Ví dụ 1. Cho tam giác ABC có trung tuyến AM . Gọi I là trung điểm AM và K là trung điểm AC sao 1 AK
AC . Chứng minh ba điểm ,
B I, K thẳng hàng. 3 Lời giải 1
Ta có 2BI BA BM BA BC 4BI 2BA BC 1 2 1
Ta có BK BA AK BA 1 2 1 AC BA (BC ) BA BA BC 3 3 3 3
3BK 2BA BC 2 4 Từ
1 và 2 3BK 4BI BK BI ,
B I , K thẳng hàng. 3
Ví dụ 2. Cho tam giác ABC . Hai điểm M , N được xác định bởi hệ thức:
BC MA 0 , AB NA 3AC 0 . Chứng minh MN / /AC. Lời giải
Ta có BC MA AB NA 3AC 0 hay AC MN 3AC 0 MN 2AC .
Vậy MN, AC cùng phương.
Theo giả thiết BC AM . Mà ,
A B,C không thẳng hàng nên bốn điểm ,
A B,C, M là bốn đỉnh
của hình bình hành M không thuộc AC .
Vậy MN / / AC .
PHẦN 2: CÂU HỎI TRẮC NGHIỆM
Câu 1. [0H1-3.5-1] Cho ba điểm ,
A B,C phân biệt. Điều kiện cần và đủ để ba điểm thẳng hàng là:
A. AB AC B. k
0 : AB k.AC C. AC AB BC
D. MA MB 3MC, điểm M
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 10 CHUYÊN ĐỀ: VECTƠ TLDH Lời giải Chọn B
Câu 2. [0H1-3.5-2] Cho ABC
. Đặt a BC,b AC . Các cặp vectơ nào sau đây cùng phương?
A. 2a b, a 2b
B. a 2b, 2a b
C. 5a b, 10
a 2b D. a b, a b Lời giải Chọn C Ta có: 10
a 2b 2.(
5a b) 5a b và 10
a 2b cùng phương.
Câu 3. [0H1-3.1-1] Cho hai vectơ a và b không cùng phương. Hai vectơ nào sau đây cùng phương? 1 A. 3
a b và 1 a 6b B.
a b và 2a b 2 2 1 1 C. a b và 1 a b D.
a b và a 2b 2 2 2 Lời giải Chọn C
Câu 4. [0H1-3.1-1] Cho hai vectơ a và b không cùng phương. Hai vectơ nào sau đây là cùng phương? 3
A. u 2a 3b và 1 v a 3b B. u a 3b và 3
v 2a b 2 5 5 2 3 C. u
a 3b và v 2a 9b
D. u 2a b và 1 1 v a b 3 2 3 4 Lời giải Chọn D
Câu 5. [0H1-3.1-2] Biết rằng hai vec tơ a và b không cùng phương nhưng hai vec tơ 3a 2b và
(x 1)a 4b cùng phương. Khi đó giá trị của x là: A. 7 B. 7 C. 5 D. 6 Lời giải Chọn A x 1 4
Điều kiện để hai vec tơ 3a 2b và (x 1)a 4b cùng phương là: x 7 3 2 .
Câu 6. [0H1-3.1-2] Biết rằng hai vec tơ a và b không cùng phương nhưng hai vec tơ 2a 3b và
a x
1 b cùng phương. Khi đó giá trị của x là: 1 3 1 3 A. B. C. D. 2 2 2 2 Lời giải Chọn C
Câu 7. [0H1-3.5-3] Cho tam giác ABC . Hai điểm M , N được xác định bởi các hệ thức BC MA 0 ,
AB NA 3AC 0 . Trong các khẳng định sau, khẳng định nào đúng?
A. MN AC
B. MN / / AC
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 11 CHUYÊN ĐỀ: VECTƠ TLDH
C. M nằm trên đường thẳng AC
D. Hai đường thẳng MN và AC trùng nhau Lời giải Chọn B
Ta có: BC MA 0 AM BC M là điểm thứ tư của hình bình hành ABCM nên M AC (1)
Cộng vế theo vế hai đẳng thức BC MA 0 , AB NA 3AC 0 , ta được:
BC MA AB NA 3AC 0
(MA AN) (AB BC) 3AC 0 MN AC 3AC MN 2AC MN cùng phương với AC (2)
Từ (1) và (2) suy ra MN / / AC .
Dạng 3: Biểu thị một vectơ theo hai vectơ không cùng phương PHẦN 1: CÁC VÍ DỤ
Ví dụ 1. Cho tam giác ABC . Gọi M là một điểm trên cạnh BC sao cho MB 2MC . Chứng minh rằng: 1 2 AM AB AC . 3 3 Lời giải 1 1 1 2
Ta có: AM AC CM AC BC AC (AC AB) AB AC (đpcm). 3 3 3 3
Ví dụ 2. Cho ABC
có trọng tâm G . Cho các điểm ,
D E, F lần lượt là trung điểm của các cạnh BC, C ,
A AB và I là giao điểm của AD và EF . Đặt u AE, v AF . Hãy phân tích các vectơ AI
, AG , DE , DC theo hai vectơ u và v . Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 12 CHUYÊN ĐỀ: VECTƠ TLDH
Ta có: AEDF là hình bình hành AD AE AF Ta có 1 1 1 AI AD ( AE AF) (u v) 2 2 2 2 2 2 AG AD
( AE AF ) (u v) 3 3 3
DE FA AF 0.u (1)v
DC FE AE AF u v
Ví dụ 3. Cho AK và BM là hai trung tuyến của tam giác ABC , trọng tâm G . Hãy phân tích các
vectơ AB , BC , CA theo hai vectơ u AK , v BM Lời giải C M K G A B 2 2
* AB AG GB AK BM 3 3
* BC BK BG GK 2 1 1 4 2 2
2. BM AK AK BM 3 3 3 3 1
* CA AC (
AK KC) ( AK BC) 2
PHẦN 2: CÂU HỎI TRẮC NGHIỆM
Câu 1. [0H1-3.4-2] Trên đường thẳng chứa cạnh BC của tam giác ABC lấy một điểm M sao cho
MB 3MC . Khi đó đẳng thức nào sau đây đúng? 1 3 A. AM AB AC
B. AM 2AB AC 2 2
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 13 CHUYÊN ĐỀ: VECTƠ TLDH 1
C. AM AB AC D. AM ( AB AC) 2 Lời giải Chọn A
Gọi I là trung điểm của BC . Khi đó C là trung điểm của MI . Ta có: 1 1 3
AM AI 2AC AM AI 2AC ( AB AC) 2AC AB AC . 2 2 2
Câu 2. [0H1-3.4-3] Cho tam giác ABC biết AB 8, AC 9, BC 11. Gọi M là trung điểm BC và N
là điểm trên đoạn AC sao cho AN x (0 x 9) . Hệ thức nào sau đây đúng? 1 x 1 x 1 1 A. MN AC AB B. MN CA BA 2 9 2 9 2 2 x 1 1 x 1 1 C. MN AC AB D. MN AC AB 9 2 2 9 2 2 Lời giải Chọn D Ta có: x 1 x 1 1
MN AN AM AC ( AB AC) AC AB . 9 2 9 2 2
Câu 3. [0H1-3.4-3] Cho tam giác ABC . Gọi G là trọng tâm và H là điểm đối xứng với B qua G .
Trong các khẳng định sau, khẳng định nào đúng? 2 1 1 1 A. AH AC AB B. AH AC AB 3 3 3 3 2 1 2 1 C. AH AC AB D. AH AB AC 3 3 3 3 Lời giải Chọn A
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 14 CHUYÊN ĐỀ: VECTƠ TLDH
Gọi M , I lần lượt là trung điểm của BC và AC .
Ta thấy AHCG là hình bình hành nên 2 2 1
AH AG AC AH
AM AC AH . AB AC AC 3 3 2 1
AH AC AB AC 2 1
AH AC AB . 3 3 3
Câu 4. [0H1-3.4-2] Cho tam giác ABC có trọng tâm G . Gọi các điểm ,
D E, F lần lượt là trung điểm
của các cạnh BC,CA và AB . Trong các khẳng định sau, khẳng định nào đúng? 1 1 1 1 3 3 2 2 A. AG AE
AF B. AG AE
AF C. AG AE
AF D. AG AE AF 2 2 3 3 2 2 3 3 Lời giải Chọn D 2 2 1 1 2 2
Ta có: AG AD . AB AC 2AF 2AE AE AF . 3 3 2 3 3 3 Câu 2 5.
[0H1-3.4-2] Cho tam giác ABC . Gọi D là điểm sao cho BD
BC và I là trung điểm của 3
cạnh AD , M là điểm thỏa mãn 2 AM
AC. Vectơ BI được phân tích theo hai vectơ BA và 5
BC . Hãy chọn khẳng định đúng trong các khẳng định sau? 1 1 1 1 A. BI BA BC . B. BI BA BC . 2 3 2 2 1 3 1 1 C. BI BA BC . D. BI BA BC . 2 4 4 6 Lời giải Chọn A
Ta có: I là trung điểm của cạnh AD nên 1 BI
BABD 1 2 1 1 BA BC BA BC 2 2 3 2 3
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 15 CHUYÊN ĐỀ: VECTƠ TLDH
Câu 6. [0H1-3.4-2] Cho tam giác ABC . Gọi M là trung điểm của AB , N là điểm thuộc AC sao cho
CN 2NA . K là trung điểm của MN . Mệnh đề nào sau đây là đúng? 1 1 1 1 A. AK AB AC. B. AK AB AC. 4 6 2 3 1 1 1 2 C. AK AB AC. D. AK AB AC. 4 3 2 3 Lời giải Chọn A Ta có 1
M là trung điểm AB nên 1 AM
AB ; CN 2NA AN AC . 2 3 Do đó 1 AK
AM AN 1 1 AB AC. 2 4 6
Câu 7. [0H1-3.4-3] Cho tứ giác ABCD, O là giao điểm của hai đường chéo AC và BD. Gọi G theo
thứ tự là trọng tâm của tam giác OAB và OCD . Khi đó GG bằng: 1 2 1
A. AC BD .
B. AC BD .
C. 3 AC BD .
D. AC BD . 2 3 3 Lời giải Chọn D Vì 1
G là trọng tâm của tam giác OCD nên GG GO GC GD . (1) 3
Vì G là trọng tâm của tam giác OAB nên: GO GA GB 0 GO GA GB (2) 1 1
Từ (1) và (2) suy ra: GG
GAGBGCGD ACBD. 3 3
Câu 8. [0H1-3.4-2] Cho tam giác ABC với phân giác trong AD . Biết AB 5, BC 6 , CA 7 . Khi đó AD bằng:
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 16 CHUYÊN ĐỀ: VECTƠ TLDH 5 7 7 5 7 5 5 7 A. AB AC . B. AB AC . C. AB AC . D. AB AC . 12 12 12 12 12 12 12 12 Lời giải Chọn C
Vì AD là phân giác trong của tam giác ABC nên: BD AB 5 5
BD DC DC AC 7 7 5
AD AB AC AD 7 7 5 AD AB AC . 12 12
Câu 9. [0H1-3.4-2] Cho tam giác ABC . Gọi M là trung điểm của AB và N là một điểm trên cạnh
AC sao cho NC 2NA. Gọi K là trung điểm của MN . Khi đó: 1 1 1 1 A. AK AB AC B. AK AB AC 6 4 4 6 1 1 1 1 C. AK AB AC D. AK AB AC 4 6 6 4 Lời giải Chọn C Câu 1
10. [0H1-3.4-2] Cho tam giác ABC , N là điểm xác định bởi CN
BC , G là trọng tâm tam giác 2
ABC . Hệ thức tính AC theo AG, AN là: 2 1 4 1 A. AC AG AN B. AC AG AN 3 2 3 2 3 1 3 1 C. AC AG AN D. AC AG AN 4 2 4 2 Lời giải Chọn C
Câu 11. [0H1-3.4-3] Cho AD và BE là hai phân giác trong của tam giác ABC . Biết AB 4 , BC 5
và CA 6. Khi đó DE bằng: 5 3 3 5 9 3 3 9
A. CA CB .
B. CA CB .
C. CA CB .
D. CA CB . 9 5 5 9 5 5 5 5 Lời giải Chọn A
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 17 CHUYÊN ĐỀ: VECTƠ TLDH CD AC CD
AD là phân giác trong của tam giác ABC nên 6 6 DB AB 4 CD DB 6 4 CD 6 3 CD CB . CB 10 5 Tương tự CE 5 5 :
CE CA. CA 9 9 5 3
Vậy DE CE CD CA CB . 9 5
Dạng 4: Đẳng thức vectơ chứa tích của vectơ với một số PHẦN 1: CÁC VÍ DỤ
Ví dụ 1. Cho tứ giác ABCD. Gọi I, J lần lượt là trung điểm của AC và BD. Chứng minh rằng:
AB CD 2IJ . Lời giải
IJ IA AB BJ Ta có:
2IJ (IA IC) (AB CD) (BJ DJ )
IJ IC CD DJ
2IJ 0 AB CD 0 AB CD .
Ví dụ 2. Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB và CD .
a) Chứng minh rằng: AC BD AD BC 2EF
b) Gọi G là trung điểm của EF . Chứng minh rằng GA GB GC GD 0 Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 18 CHUYÊN ĐỀ: VECTƠ TLDH a)
AC BD AE EF FC BE EF FD 2EF AE BE FC FD
2EF 0 0 2EF 1
AD BC AE EF FD BE EF FC 2EF AE BE FD FC
2EF 0 0 2EF 2 Từ
1 và 2 suy ra: AC BD AD BC 2EF
b) GA GB GC GD 2GE 2GF 2GE GF 20 0 .
Ví dụ 3. Cho hình bình hành ABCD. Chứng minh rằng: AB 2AC AD 3AC Lời giải
VT AB 2AC AD AB AD 2AC AC 2AC 3AC VP.
Ví dụ 4. Chứng minh rằng nếu G và G lần lượt là trọng tâm tam giác ABC và A B C thì
3GG AA BB CC . Lời giải
VP AA' BB ' CC '
AG GG ' G ' A' BG GG ' G ' B ' CG GG ' G 'C '
3GG ' AG BG CG G ' A' G ' B ' G 'C '
3GG' (GA GB GC) G' A' G' B' G'C ' 3GG ' = VP.
PHẦN 2: CÂU HỎI TRẮC NGHIỆM
Câu 1. [0H1-3.2-2] Cho tam giác ABC và một điểm M tùy ý. Hãy chọn hệ thức đúng:
A. 2MA MB 3MC AC 2BC
B. 2MA MB 3MC 2AC BC
C. 2MA MB 3MC 2CA CB
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 19 CHUYÊN ĐỀ: VECTƠ TLDH
D. 2MA MB 3MC 2CB CA Lời giải Chọn C
Câu 2. [0H1-3.2-3] Cho tam giác ABC với H, ,
O G lần lượt là trực tâm, tâm đường tròn ngoại tiếp,
trọng tâm của tam giác. Hệ thức đúng là: 3 1 A. OH OG
B. OH 3OG C. OG GH D. 2GO 3 OH 2 2 Lời giải Chọn B
Câu 3. [0H1-3.2-2] Ba trung tuyến AM , BN, CP của tam giác ABC đồng quy tại G . Hỏi vectơ
AM BN CP bằng vectơ nào? 3 1 A.
GAGBCG B. 3MG NGGP C. ABBC AC D. 0 2 2 Lời giải Chọn D Ta có: 3 3 3 3
AM BN CP AG BG CG
AGBGCG0. 2 2 2 2
Câu 4. [0H1-3.2-2] Cho hình chữ nhật ABCD, I và K lần lượt là trung điểm của BC, CD . Hệ thức nào sau đây đúng?
A. AI AK 2 AC
B. AI AK AB AD 3
C. AI AK IK
D. AI AK AC 2 Lời giải Chọn D
Câu 5. [0H1-3.2-3] Cho tam giác đều ABC tâm O . Điểm M là điểm bất kỳ trong tam giác. Hình chiếu
của M xuống ba cạnh của tam giác lần lượt là ,
D E, F . Hệ thức giữa các vectơ
MD, ME, MF , MO là: 1 2
A. MD ME MF MO
B. MD ME MF MO 2 3 3 3
C. MD ME MF MO
D. MD ME MF MO 4 2
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 20 CHUYÊN ĐỀ: VECTƠ TLDH
Câu 6. [0H1-3.2-2] Cho tứ giác ABCD. Gọi M , N là trung điểm AB và DC . Lấy các điểm P, Q lần
lượt thuộc các đường thẳng AD và BC sao cho PA 2
PD , QB 2QC . Khẳng định nào sau đây đúng? 1 A. MN
AD BC .
B. MN MP MQ . 2 1 1
C. MN AD BC . D. MN
MD MC NB N A. 2 4
Câu 7. [0H1-3.2-1] Cho I là trung điểm của đoạn thẳng AB . Với điểm M bất kỳ, ta luôn có: 1
A. MA MB MI
B. MA MB 2MI
C. MA MB 3MI
D. MA MB MI 2 Lời giải Chọn B
Áp dụng tính chất trung điểm của đoạn thẳng: Với điểm M bất kỳ, ta luôn có MA MB 2MI
Câu 8. [0H1-3.2-1] Cho G là trọng tâm của tam giác ABC . Với mọi điểm M , ta luôn có:
A. MA MB MC MG
B. MA MB MC 2MG
C. MA MB MC 3MG
D. MA MB MC 4MG Lời giải Chọn C
Áp dụng tính chất trọng tâm của tam giác: Với mọi điểm M , ta luôn có
MA MB MC 3MG .
Câu 9. [0H1-3.2-2] Cho ABC
có G là trọng tâm, I là trung điểm BC . Đẳng thức nào đúng? 1
A. GA 2GI
B. IG IA
C. GB GC 2GI
D. GB GC GA 3 Lời giải
Áp dụng tính chất trung điểm của đoạn thẳng, ta có: GB GC 2GI .
Câu 10. [0H1-3.2-2] Cho hình bình hành ABCD. Đẳng thức nào đúng?
A. AC BD 2BC
B. AC BC AB
C. AC BD 2CD
D. AC AD CD Lời giải Chọn A
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 21 CHUYÊN ĐỀ: VECTƠ TLDH
Ta có: AC BD AB BC BC CD 2BC (AB CD) 2BC .
Câu 11. [0H1-3.2-2] Cho G là trọng tâm của tam giác ABC . Trong các mệnh đề sau, tìm mệnh đề đúng? 2
A. AB AC AG
B. BA BC 3BG
C. CA CB CG
D. AB AC BC 0 3 Lời giải Chọn B 3
Gọi M là trung điểm của AC . Khi đó: BA BC 2BM 2. BG 3BG . 2
Câu 12. [0H1-3.2-2] Cho hình vuông ABCD có tâm là O . Trong các mệnh đề sau, tìm mệnh đề sai? 1 1
A. AB AD 2AO
B. AD DO CA C. OA OB CB
D. AC DB 4AB 2 2 Lời giải Chọn D
AC DB AB BC DC CB AB DC 2AB .
Câu 13. [0H1-3.2-2] Cho tứ giác ABCD. Gọi M , N lần lượt là trung điểm của AB và CD . Khi đó
AC BD bằng: A. MN B. 2MN C. 3MN D. 2MN Lời giải Chọn B
MN MA AC CN Ta có:
2MN AC BD .
MN MB BD DN
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 22 CHUYÊN ĐỀ: VECTƠ TLDH
Câu 14. [0H1-3.2-2] Cho hình bình hành ABCD tâm O và điểm M bất kì. Khẳng định nào sau đây đúng?
A. MA MB MC MD MO
B. MA MB MC MD 2MO
C. MA MB MC MD 3MO
D. MA MB MC MD 4MO Lời giải Chọn D
Ta có: MA MB MC MD (MA MC) (MB MD) 2MO 2MO 4MO
Câu 15. [0H1-3.2-3] Cho tam giác ABC nội tiếp trong đường tròn tâm O . Gọi H là trực tâm của tam
giác. Trong các khẳng định sau, khẳng định nào đúng?
A. OH 4OG
B. OH 3OG
C. OH 2OG
D. 3OH OG Lời giải Chọn B
Gọi D là điểm đối xứng với A qua O . Ta có: HA HD 2HO (1)
Vì HBDC là hình bình hành nên HD HB HC (2) Từ (1), (2) suy ra:
HA HB HC 2HO (HO O )
A (HO OB) (HO OC) 2HO
3HO (OA OB OC) 2HO OA OB OC HO 3OG OH .
Câu 16. [0H1-3.2-3] Cho tứ giác ABCD. Gọi G là trọng tâm của tam giác ABD, I là điểm trên GC
sao cho IC 3IG . Với mọi điểm M ta luôn có MA MB MC MD bằng: A. 2MI B. 3MI C. 4MI D. 5MI Lời giải Chọn C
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 23 CHUYÊN ĐỀ: VECTƠ TLDH
Ta có: 3IG IC .
Do G là trọng tâm của tam giác ABD nên
IA IB ID 3IG IA IB ID IC IA IB IC ID 0 Khi đó:
MA MB MC MD MI IA MI IB MI IC MI ID
4MI (IA IB IC ID) 4MI 0 4MI
Câu 17. [0H1-3.2-4] Cho tam giác đều ABC có tâm O . Gọi I là một điểm tùy ý bên trong tam giác a
ABC . Hạ ID, IE, IF tương ứng vuông góc với BC,C ,
A AB . Giả sử ID IE IF IO (với b
a là phân số tối giản). Khi đó ab bằng: b A. 5 B. 4 C. 6 D. 7 Lời giải Chọn A
Qua điểm I dựng các đoạn MQ / / A ,
B PS / / BC, NR / /CA.
Vì ABC là tam giác đều nên các tam giác IMN, IP ,
Q IRS cũng là tam giác đều. Suy ra ,
D E, F lần lượt là trung điểm của MN, P , Q RS . 1 1 1
Khi đó: ID IE IF IM IN IP IQ IR IS 2 2 2 1
IQ IRIM ISIN IP 1
IAIBIC 2 2 1 3
.3IO IO a 3,b 2. Do đó: a b 5. 2 2
Câu 18. [0H1-3.6-3] Cho tam giác ABC , có bao nhiêu điểm M thoả mãn: MA MB MC 1 A. 0 B. 1 C. 2 D. vô số
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 24 CHUYÊN ĐỀ: VECTƠ TLDH Lời giải Chọn D
Gọi G là trọng tâm của tam giác ABC 1
Ta có MA MB MC 3MG 3MG 1 MG 3 1
Tập hợp các điểm M thỏa mãn MA MB MC 1 là đường tròn tâm G bán kính R . 3
Câu 19. [0H1-3.3-3] Cho tam giác ABC và một điểm M tùy ý. Chứng minh rằng vectơ
v MA MB 2MC . Hãy xác định vị trí của điểm D sao cho CD v .
A. D là điểm thứ tư của hình bình hành ABCD
B. D là điểm thứ tư của hình bình hành ACBD
C. D là trọng tâm của tam giác ABC
D. D là trực tâm của tam giác ABC Lời giải Chọn B
Ta có: v MA MB 2MC MA MC MB MC CA CB 2CI (Với I là trung điểm của AB )
Vậy vectơ v không phụ thuộc vào vị trú điểm M . Khi đó: CD v 2CI I là trung điểm của CD
Vậy D D là điểm thứ tư của hình bình hành ACBD .
Câu 20. [0H1-3.7-4] Cho tam giác ABC và đường thẳng d . Gọi O là điểm thỏa mãn hệ thức
OA OB 2OC 0 . Tìm điểm M trên đường thẳng d sao cho vectơ v MA MB 2MC có độ dài nhỏ nhất.
A. Điểm M là hình chiếu vuông góc của O trên d
B. Điểm M là hình chiếu vuông góc của A trên d
C. Điểm M là hình chiếu vuông góc của B trên d
D. Điểm M là giao điểm của AB và d Lời giải Chọn A
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 25 CHUYÊN ĐỀ: VECTƠ TLDH
Gọi I là trung điểm của AB .
Khi đó: OA OB 2OC 0 2OI 2OC 0 OI OC 0 O là trung điểm của IC Ta có:
v MA MB 2MC OA OM OB OM 2(OC OM ) OA OB 2OC 4OM 4OM
Do đó v 4OM .
Độ dài vectơ v nhỏ nhất khi và chỉ khi 4OM nhỏ nhất hay M là hình chiếu vuong góc của O trên d .
Câu 21. [0H1-3.3-3] Cho tam giác ABC . Gọi M là trung điểm của AB và N thuộc cạnh AC sao cho
NC 2NA. Hãy xác định điểm K thỏa mãn: 3AB 2AC 12AK 0 và điểm D thỏa mãn:
3AB 4AC 12KD 0 .
A. K là trung điểm của MN và D là trung điểm của BC
B. K là trung điểm của BC và D là trung điểm của MN
C. K là trung điểm của MN và D là trung điểm của AB
D. K là trung điểm của MN và D là trung điểm của AC Lời giải Chọn A Ta có: AB 2AM 1
3AB 2AC 12AK 0 3.2AM 2.3AN 12AK 0 AK AM AN 2 AC 3AN
Suy ra K là trung điểm của MN Ta có:
3AB 4AC 12KD 0 3AB 4AC 12 AD AK 0 3AB 4AC 12AK 12AD 1
12AD 3AB 4AC 3AB 2AC 12AD 6AB 6AC AD AB AC 2
Suy ra D là trung điểm của BC .
Câu 22. [0H1-3.3-2] Cho hình bình hành ABCD, điểm M thỏa 4AM AB AC AD . Khi đó điểm M là:
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 26 CHUYÊN ĐỀ: VECTƠ TLDH A. trung điểm AC B. điểm C C. trung điểm AB D. trung điểm AD Lời giải Chọn A
Câu 23. [0H1-3.6-2] Cho hình chữ nhật ABCD. Tập hợp các điểm M thỏa mãn MA MB MC MD là:
A. Đường tròn đường kính AB .
B. Đường tròn đường kính BC .
C. Đường trung trực của cạnh AD .
D. Đường trung trực của cạnh AB . Lời giải Chọn C
Gọi E, F lần lượt là trung điểm của AB và DC .
MA MB MC MD 2ME 2MF ME MF
Do đó M thuộc đường trung trực của đoạn EF hay M thuộc đường trung trực của cạnh AD .
Câu 24. [0H1-3.6-2] Cho hình bình hành ABCD. Tập hợp các điểm M thỏa mãn
MA MC MB MD là:
A. Một đường thẳng.
B. Một đường tròn.
C. Toàn bộ mặt phẳng ABCD . D. Tập rỗng. Lời giải Chọn C
Gọi O là tâm của hình bình hành ABCD . Ta có:
MA MC MB MD 2MO 2MO
MO MO (đúng với mọi M )
Vậy tập hợp các điểm M là toàn bộ mặt phẳng ABCD .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 27 CHUYÊN ĐỀ: VECTƠ TLDH
Câu 25. [0H1-3.6-2] Cho tam giác ABC và điểm M thỏa 2 MA MB MC 3 MB MC . Tập hợp M là:
A. Một đường tròn
B. Một đường thẳng
C. Một đoạn thẳng
D. Nửa đường thẳng Lời giải Chọn B
Câu 26. [0H1-3.6-2] Cho tam giác ABC. Có bao nhiêu điểm M thỏa MA MB MC 3 A. 1 B. 2 C. 3 D. Vô số Lời giải Chọn D
Câu 27. [0H1-3.6-3] Cho tam giác ABC và điểm M thỏa 3MA 2MB MC MB MA . Tập hợp M là:
A. Một đoạn thẳng
B. Một đường tròn
C. Nửa đường tròn
D. Một đường thẳng Lời giải Chọn B
Câu 28. [0H1-3.2-2] Cho năm điểm , A , B C, ,
D E . Khẳng định nào đúng?
A. AC CD EC 2 AE DB CB
B. AC CD EC 3 AE DB CB C. AE DB CB AC CD EC 4
D. AC CD EC AE DB CB Lời giải Chọn D
AC CD EC AE DB CB AC AE CD CB EC DB 0
EC BD EC DB 0
BD DB 0 (đúng) ĐPCM.
Câu 29. [0H1-3.7-4] Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho 1 BH
HC . Điểm M di động nằm trên BC sao cho BM xBC . Tìm x sao cho độ dài của 3
vectơ MA GC đạt giá trị nhỏ nhất. 4 5 6 5 A. . B. . C. . D. . 5 6 5 4 Lời giải Chọn B
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 28 CHUYÊN ĐỀ: VECTƠ TLDH
Dựng hình bình hành AGCE . Ta có MA GC MA AE ME .
Kẻ EF BC F BC . Khi đó MA GC ME ME EF .
Do đó MA GC nhỏ nhất khi M F .
Gọi P là trung điểm AC , Q là hình chiếu vuông góc của P lên BC Q BC .
Khi đó P là trung điểm GE nên 3 BP BE . 4 Ta có BQ BP 4
BPQ và BEF đồng dạng nên 3
hay BF BQ . BF BE 4 3 Mặt khác, 1 BH HC . 3 1
PQ là đường trung bình AHC nên Q là trung điểm HC hay HQ HC . 2 1 1 5 5 3 5
Suy ra BQ BH HQ HC HC HC . BC BC. 3 2 6 6 4 8 Do đó 4 5 BF BQ BC . 3 6
Câu 30. [0H1-3.7-3] Cho đoạn thẳng AB có độ dài bằng a. Một điểm M di động sao cho
MA MB MA MB . Gọi H là hình chiếu của M lên AB . Tính độ dài lớn nhất của MH ? a a 3 A. . B. . C. a. D. 2 . a 2 2 Lời giải Chọn A
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 29 CHUYÊN ĐỀ: VECTƠ TLDH
Gọi N là đỉnh thứ 4 của hình bình hành MANB . Khi đó MA MB MN .
Ta có MA MB MA MB MN BA hay MN AB.
Suy ra MANB là hình chữ nhật nên 90o AMB .
Do đó M nằm trên đường tròn tâm O đường kính AB . AB a
MH lớn nhất khi H trùng với tâm O hay max MH MO . 2 2
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 30 CHUYÊN ĐỀ : VECTO TLDH CHUYÊN ĐỀ VÉCTƠ (CHƯƠNG 1 LỚP 10)
BÀI 4. HỆ TRỤC TỌA ĐỘ ........................................................................................................................................ 2
A. KIẾN THỨC SÁCH GIÁO KHOA CẦN CẦN NẮM .................................................................................... 2
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP ....................................................................................... 4
Dạng 1: Tìm tọa độ của một điểm; tọa độ vectơ; độ dài đại số của vectơ và chứng minh hệ thức liên quan trên
trục O;i ............................................................................................................................................................. 4
Dạng 2: Tìm tọa độ điểm, tọa độ vectơ trên mặt phẳng Oxy ......................................................................... 7
Dạng 3: Xác định tọa độ điểm, vectơ liên quan đến biểu thức dạng u v, u v, k u ................................ 11
Dạng 4: Xác định tọa độ các điểm của một hình ............................................................................................ 16
Dạng 5: Bài toán liên quan đến sự cùng phương của hai vectơ. Phân tích một vectơ qua hai vectơ không
cùng phương ....................................................................................................................................................... 26 Ban thực hiện Tên giáo viên Đơn vị công tác GV Soạn
Thầy Nguyễn Đình Hải
Lớp học TH Class Ngã Tư Sở (Hà Nội) GV phản biện
Thầy Phạm Phú Quốc
Trường THPT Nguyễn Tri Phương (Lâm Đồng) TT Tổ soạn Cô Phạm Thị Hoài
Trường THCS Nguyễn Hiền (Nha Trang) TT Tổ phản biện
Thầy Nguyễn Văn Vũ Trường THPT YaLy (Gia Lai) Người triển khai Thầy Phạm Lê Duy
Trường THPT Chu Văn An (An Giang)
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 1 CHUYÊN ĐỀ : VECTO TLDH
BÀI 4. HỆ TRỤC TỌA ĐỘ
A. KIẾN THỨC SÁCH GIÁO KHOA CẦN CẦN NẮM
I. TRỤC VÀ ĐỘ DÀI ĐẠI SỐ TRÊN TRỤC 1. Trục tọa độ Định nghĩa
Trục tọa độ (hay gọi tắt là trục) là một đường thẳng trên đó đã xác định một điểm O gọi là
điểm gốc và một vectơ đơn vị e .
Điểm O gọi là gốc tọa độ.
Hướng của vecto đơn vị là hướng của trục.
Ta kí hiệu trục đó là O;e. O M
2. Tọa độ của một điểm
Cho M là một điểm tùy ý trên trục O;e . Khi đó có duy nhất một số k sao cho OM k e.
Ta gọi số k đó là tọa độ của điểm M đối với trục đã cho. 3. Tọa độ vecto
Cho hai điểm A và B trên trục O;e . Khi đó có duy nhất số a sao cho AB a e. Ta gọi số a là
độ dài đại số của vectơ AB đối với trục đã cho và kí hiệu a AB. Nhận xét.
Nếu AB cùng hướng với e thì AB AB, còn nếu AB ngược hướng với e thì AB AB.
Nếu hai điểm A và B trên trục O;e có tọa độ lần lượt là a và b thì AB b a. II. HỆ TỌA ĐỘ 1. Hệ tọa độ
Định nghĩa. Hệ trục tọa độ O;i , j gồm hai trục O;i và O; j vuông góc với nhau.
Điểm gốc O chung của hai trục gọi là gốc tọa độ. Trục O;i được gọi là trục hoành và kí
hiệu là Ox, trục O; j được gọi là trục tung và kí hiệu là .
Oy Các vectơ i và j là các vectơ
đơn vị trên Ox và Oy và i j 1. Hệ trục tọa độ O;i , j còn được kí hiệu là Oxy. y 1 x O O 1
Mặt phẳng mà trên đó đã cho một hệ trục tọa độ Oxy còn được gọi là mặt phẳng tọa độ Oxy
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 2 CHUYÊN ĐỀ : VECTO TLDH
Hay gọi tắt là mặt phẳng Oxy. 2. Tọa độ vecto
Trong mặt phẳng Oxy cho một vectơ u tùy ý. Vẽ OA u và gọi A , A lần lượt là hình chiếu 1 2
của vuông góc của A lên Ox và Oy. Ta có OA OA OA và cặp số duy nhất x; y để 1 2
OA x i , OA y j. Như vậy u x i y j . 1 2
Cặp số x; y duy nhất đó được gọi là tọa độ của vectơ u đối với hệ tọa độ Oxy và viết
u x; y hoặc u x; y. Số thứ nhất x gọi là hoành độ, số thứ hai y gọi là tung độ của vectơ u . Như vậy
u x; y u x i y j
Nhận xét. Từ định nghĩa tọa độ của vectơ, ta thấy hai A
Vectơ bằng nhau khi và chỉ khi chúng có hoành độ bằng
nhau và tung độ bằng nhau. O x x
Nếu u x; y và u x ;
y thì u u . y y
Như vậy, mỗi vectơ được hoàn toàn xác định khi biết tọa độ của nó.
3. Tọa độ của một điểm
Trong mặt phẳng tọa độ Oxy cho một điểm M tùy ý. Tọa độ của vectơ OM đối với hệ trục
Oxy được gọi là tọa độ của điểm M đối với hệ trục đó.
Như vậy, cặp số x; y là tọa độ của điểm M khi và chỉ khi OM x; y. Khi đó ta viết
M x; y hoặc M x; y. Số x được gọi là hoành độ, còn số y được gọi là tung độ của
điểm M. Hoành độ của điểm M còn được kí hiệu là x , tung độ của điểm M còn được kí M hiệu là y . M
M x; y OM x i y j O
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 3 CHUYÊN ĐỀ : VECTO TLDH
Chú ý rằng, nếu MM Ox, MM Oy thì x OM , y OM . 1 2 1 2
4. Liên hệ giữa tọa độ của điểm và tọa độ của vectơ trong mặt phẳng
Cho hai điểm Ax ; y và B x ; y . Ta có A A B B AB x x ; y y . B A B A
III. BIỂU THỨC TỌA ĐỘ CỦA PHÉP TOÁN VECTO Đinh lý: Cho u ( ; x y) ; u '
(x '; y ') và số thực k . Khi đó ta có : x x ' 1) u u ' y y ' 2) u v (x x '; y y ') 3) k.u (k ; x ky) x ' kx
4) u ' cùng phương u ( u
0 ) khi và chỉ khi có số k sao cho y ' ky 5) Cho (
A x ; y ), B(x ; y ) thì AB x x ; y y A A B B B A B A
IV. TỌA ĐỘ TRUNG ĐIỂM CỦA ĐOẠN THẲNG - TỌA ĐỘ TRỌNG TÂM CỦA TAM GIÁC
1. Tọa độ trung điểm của đoạn thẳng
Cho đoạn thẳng AB có A x ; y , B x ; y . Ta dễ dàng chứng minh được tọa độ trung điểm A A B B
I x ; y của đoạn thẳng AB là I I x x y y A B A B x , y . I 2 I 2
2. Tọa độ trọng tâm của tam giác
Cho tam giác ABC có Ax ; y , B x ; y , C x ; y . Khi đó tọa độ của trọng tâm A A
B B C C
G x ; y của tam giác ABC được tính theo công thức G G
x x x
y y y A B C A B C x , y . G 3 G 3
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Tìm tọa độ của một điểm; tọa độ vectơ; độ dài đại số của vectơ và chứng minh hệ thức liên quan
trên trục O;i
PHẦN 1: CÁC VÍ DỤ
Ví dụ 1: Trên trục tọa độ O;i cho 2 điểm A,B có tọa độ lần lượt là 2 1
; . Tìm tọa độ của vecto AB .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 4 CHUYÊN ĐỀ : VECTO TLDH Lời giải
Ta có: AB 1 2 3 AB 3i.
Ví dụ 2: Trên trục tọa độ O;i cho 2 điểm A,B có tọa độ lần lượt3 và 5
. Tọa độ trung điểm I của AB là. Lời giải ( )
Tọa độ điểm I là: 3 5 x 1 . I 2
Ví dụ 3: Trên trục O;i cho 3 điểm A,B,C có tọa độ lần lượt là a;b;c. Tìm điểm I sao cho IA IB IC 0 . Lời giải
Gọi điểm I có tọa độ là x .
IA a x IA ( a x )i;
IB b x IB ( b x )i;
IC c x IC ( c x )i;
IA IB IC 0 ( a b c 3x )i 0
a b c
a b c 3x 0 x . 3
Ví dụ 4: Trên trục O;i , cho ba điểm A,B,C lần lượt có tọa độ là 5
;2;4. Tìm tọa độ điểm M thỏa
mãn 2MA 4MB 3MC 0 . Lời giải
Gọi điểm M có tọa độ là x . MA 5
x MA ( 5 x )i;
MB 2 x MB ( 2 x )i;
MC 4 x MC ( 4 x )i;
2MA 4MB 3MC 0 1
0 2xi 84xi 123xi 0 10
10 9x 0 x . 9
Ví dụ 5. Trên trục tọa độ ; O i cho 4 điểm , A , B C, D bất kỳ. Chứng minh A . B CD AC.DB A . D BC 0 . Lời giải
Nhận thấy tọa độ điểm M 1; 1
;0 thỏa mãn phương trình đường thẳng d .
Cách 1: Giả sử tọa độ các điểm , A ,
B C, D lần lượt là , a , b , c d .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 5 CHUYÊN ĐỀ : VECTO TLDH Ta có A . B CD b a d c bd ac bc ad AC.DB c a b d bc ad cd ab A . D BC d a c b cd ab ac bd
Cộng vế với vế lại ta được A . B CD AC.DB A . D BC 0 Cách 2: A . B CD AC.DB A . D BC A . B AD AC A . C AB AD A . D AC AB A . B AD A . B AC .AC.AB AC.AD A . D AC A . D AB 0 .
PHẦN 2: CÂU HỎI TRẮC NGHIỆM
Câu 1: [0H1-5.2-1] Trên trục tọa độ ; O e , các điểm ,
A B và C có tọa độ lần lượt là 1 ;2 và 3 . Tìm
giá trị của AB 2AC . A. 11. B. 1. C. 7 . D. 11 . Lời giải Chọn A. AB 2
1 3, AC 3
1 4 AB 2AC 3 2.4 11 .
Câu 2. [0H1-4.1-2] Cho trục tọa độ ,
O e . Khẳng định nào sau đây luôn đúng?
A. AB AB .
B. AB A . B e .
C. Điểm M có tọa độ là a đối với trục tọa độ ,
O e thì OM a .
D. AB AB . Lời giải Chọn C.
Theo lý thuyết sách giáo khoa thì C đúng.
Câu 3. Trên trục O;i , cho ba điểm A,B lần lượt có tọa độ là 2; 6. Tìm tọa độ điểm I sao cho IA 3 IB . A. 4 . B. 4 . C. 5. D. 10 .
Câu 4. Trên trục O;i , cho ba điểm M ,N lần lượt có tọa độ là 2
;3 . Độ dài đại số của MN là: A. 5 . B. 5 . C. 1. D. 1 .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 6 CHUYÊN ĐỀ : VECTO TLDH
Dạng 2: Tìm tọa độ điểm, tọa độ vectơ trên mặt phẳng Oxy
PHẦN 1: CÁC VÍ DỤ
Ví dụ 1. Trong mặt phẳng tọa độ Oxy . Cho điểm M x; y . Tìm tọa độ của các điểm M1 đối xứng với M qua trục hoành? Lời giải M
1 đối xứng với M qua trục hoành suy ra M x; y . 1
Ví dụ 2. Trong không gian Oxy , cho hai điểm A1;2 , B 2 ;
3 . Tìm tọa độ của vectơ AB ? Lời giải Ta có AB 2 1;3 2 3 ; 1 .
Ví dụ 3. Vectơ a 4
;0 được phân tích theo hai vectơ đơn vị ;i j như thế nào? Lời giải Ta có: a 4 ;0 a 4
i 0 j 4 i .
Ví dụ 4. Trong hệ trục tọa độ Oxy , cho hình vuông ABCD tâm I và có A(1;3) . Biết điểm B thuộc trục
Ox và BC cùng hướng với i . Tìm tọa độ các vectơ AC ? Lời giải
Từ giả thiết ta xác định được hình vuông trên mặt y
phẳng tọa độ Oxy như hình vẽ bên. A D
Vì điểm A(1;3 ) suy ra AB 3, OB 1
Do đó B1;0, C4;0, D4; 3 O
Vậy AC 3; 3 .
Ví dụ 5. Trong mặt phẳng tọa độ Oxy . Cho hình thoi ABCD O B C x cạnh a và 0
BAD 60 . Biết A trùng với gốc tọa độ O ;
C thuộc trục Ox và x 0, y 0 . Tìm tọa độ các đỉnh B và C của hình thoi ABCD . B B Lời giải
Từ giả thiết ta xác định được hình thoi trên mặt phẳng tọa độ y Oxy B a
Gọi I là tâm hình thoi ta có 0
BI AB sin BAI a sin 30 2 C 2 a a 3 A I x 2 2 2 AI
AB BI a 4 2 D
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 7 CHUYÊN ĐỀ : VECTO TLDH a 3 a a 3 a
Suy ra A0;0 , B
; , C a 3;0, D ; . 2 2 2 2
PHẦN 2: CÂU HỎI TRẮC NGHIỆM
Câu 1: [0H1-5.3-1] Trong mặt phẳng tọa độ Oxy , tọa độ i là
A. i 0; 0 .
B. i 0; 1 .
C. i 1; 0 .
D. i 1; 1 . Lời giải Chọn C.
Câu 2. [0H1-5.3-1] Trong hệ tọa độ Oxy, cho A5; 2 , B10; 8 Tìm tọa độ của vectơ AB?
A. 15; 10 . B. 2; 4 . C. 5; 6 .
D. 50; 16. Lời giải Chọn C
Ta có AB 5; 6.
Câu 3. [0H1-5.3-1]Trong mặt phẳng Oxy cho A 5; 2
,B 10;
8 . Tọa độ vectơ AB là:
A. AB15;10 .
B. AB 2;4 .
C. AB 5;10 .
D. AB50;16 . Lời giải Chọn C A 5; 2
,B 10;8 AB 5;10 .
Câu 4: [0H1-5.3-1] Trong mặt phẳng toạ độ Oxy cho hai điểm A1;4 và B3;5. Khi đó: A. AB 2 ; 1 .
B. BA 1;2 .
C. AB 2; 1 .
D. AB 4;9 . Lời giải. Chọn C.
Ta có : AB 2; 1 .
Câu 5: [0H1-5.3-1] Trong mặt phẳng tọa độ Oxy cho A5;
3 , B7;8 . Tìm tọa độ của véctơ AB A. 15;10. B. 2;5 . C. 2;6 . D. 2 ; 5 . Lời giải. Chọn B.
Ta có : AB 2;5 .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 8 CHUYÊN ĐỀ : VECTO TLDH
Câu 6. [0H1-5.3-2] Trong hệ tọa độ Oxy, cho tam giác ABC có B9; 7, C11;
1 . Gọi M , N lần
lượt là trung điểm của AB, AC. Tìm tọa độ vectơ MN ?
A. 2; 8 .
B. 1; 4 .
C. 10; 6 . D. 5; 3 . Lời giải Chọn B A N M C B 1 1
Ta có MN BC 2; 8 1; 4 . 2 2
Câu 7. [0H1-5.3-2] Trong hệ tọa độ Oxy, cho hình vuông ABCD có gốc O làm tâm hình vuông và các
cạnh của nó song song với các trục tọa độ. Khẳng định nào đúng?
A. OA OB A . B
B. OA OB, DC cùng hướng.
C. x x , y y .
D. x x , y y . A C A C B C B C Lời giải Chọn A
Ta có OA OB CO OB CB A .
B (do OA CO ).
Câu 8. [0H1-5.3-2] Trong hệ tọa độ Oxy, cho M 3; 4 Gọi M , M lần lượt là hình chiếu vuông góc 1 2
của M trên O , x O .
y Khẳng định nào đúng? A. OM 3.
B. OM 4. 1 2
C. OM OM 3 ; 4 .
D. OM OM 3; 4 . 1 2 1 2 Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 9 CHUYÊN ĐỀ : VECTO TLDH Chọn D
Ta có M 3; 0 , M 0; 4 2 1 A. Sai vì OM 3. 1 B. Sai vì OM 4. 2
C. Sai vì OM OM M M 3; 4 . 1 2 2 1
Câu 10. [0H1-5.3-2] Trong hệ tọa độ Oxy, cho hình bình hành OABC, C O .
x Khẳng định nào sau đây đúng?
A. AB có tung độ khác 0. B. ,
A B có tung độ khác nhau.
C. C có hoành độ khác 0.
D. x x x 0. A C B Lời giải Chọn C
Ta có OABC là hình bình hành AB OC x ; 0 . C
Câu 11. Trong hệ trục tọa độ O,i, j , cho tam giác đều ABC cạnh a , biết O là trung điểm BC , i cùng
hướng với OC , j cùng hướng OA . Tìm tọa độ của các đỉnh của tam giác ABC .Gọi x , x , x A B C
lần lượt là hoành độ các điểm A , B , C . Giá trị của biểu thức x x x bằng: A B C a a 3 a A. 0 . B. . C. . D. . 2 2 2 Lời giải Chọn A a 3 a a Ta có A ; 0 , B ;0 , C ; 0
x x x 2 2 2 suy ra 0 . A B C
Câu 12. Trong hệ trục tọa độ O,i, j , cho tam giác đều ABC cạnh a , biết O là trung điểm BC , i cùng
hướng với OC , j cùng hướng OA . Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC . a 3 a 3 a 3 a 3
A. G 0; .
B. G 0; . C. G ;0 . D. G ;0 . 6 4 6 4 Lời giải Chọn A a 3
Tâm đường tròn ngoại tiếp tam giác đều trùng với trọng tâm G 0; 6
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 10 CHUYÊN ĐỀ : VECTO TLDH
Câu 13. Trong hệ trục tọa độ O,i, j , cho hình thoi ABCD tâm O có AC 8, BD 6 . Biết OC và i
cùng hướng, OB và j cùng hướng. Tính tọa độ trọng tâm tam giác ABC 1 3 A. G 0; 1 . B. G 1 ;0. C. ; 0 . D. 0; . 2 2 Lời giải Chọn A Ta có A ; 4 0 , C ; 4 0 , B ; 0 3 , D ; 0 3 G ; 0 1 .
Dạng 3: Xác định tọa độ điểm, vectơ liên quan đến biểu thức dạng u v, u v, k u
{các bài toán tìm tâm I, bán kính R, xác định xem một phương trình có phải là phương trình mặt cầu hay
không, tìm điều kiện (có chứa tham số m) để một phương trình là phương trình mặt cầu, các bài toán về
họ mặt cầu, bài toán quỹ tích….}
PHẦN 1: CÁC VÍ DỤ
Ví dụ 1. Trong không gian Oxy , cho hai vectơ a1;
3 , b 3; 4. Tìm tọa độ vectơ a b ? Lời giải
Ta có a b 13;3 4 2 ;7.
Ví dụ 2. Cho a ;
x 2,b 5 ; 1 , c ;
x 7 . Tìm x để Vec tơ c 2a 3b . Lời giải
Ta có x 2.x 3. 5 x 15.
Ví dụ 3. Cho hai điểm A1;0 và B0; 2
.Tọa độ điểm D sao cho AD 3 AB là: Lời giải x 1 3 x 4 D 0 1 Ta có D D4;6. y 0 3 y 6 D 2 0 D
Ví dụ 4. Trong mặt phẳng Oxy , cho các điểm A1;
3 , B4;0. Tọa độ điểm M thỏa 3AM AB 0 là Lời giải 3
x x M 1 4 1 0 0
Ta có: 3AM AB 0 M M 0;4. 3
y 3 y M 0 3 0 4 M
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 11 CHUYÊN ĐỀ : VECTO TLDH
Ví dụ 5. Trong mặt phẳng Oxy , cho các điểm A 3 ;
3 , B1;4,C 2;
5 . Tọa độ điểm M thỏa mãn
2MA BC 4CM là: Lời giải 1 x 2 3 x x M 2 1 4 2 M M Ta có: 6 1 5
2MA BC 4CM M . 2 3 y y M 5 4 4 5 M ; 5 6 6 y M 6
PHẦN 2: CÂU HỎI TRẮC NGHIỆM
Câu 1. [0H1-5.3-1] Cho a 1
; 2 , b 5; 7 Tìm tọa độ của a . b
A. 6; 9
B. 4; 5 C. 6 ; 9 D. 5 ; 14 . Lời giải Chọn C
Ta có a b 1 5; 2 7 6 ; 9.
Câu 2. [0H1-5.3-1] Cho a 3; 4, b 1
; 2 Tìm tọa độ của a . b A. 4 ; 6
B. 2; 2
C. 4; 6 D. 3 ; 8 Lời giải Chọn B
Ta có a b 3
1 ; 4 2 2; 2 .
Câu 3. [0H1-5.3-1] Trong hệ trục tọa độ ; O ;
i j tọa độ i j là: A. 0; 1 . B. (1; 1) C. ( 1 ; 1) D. (1; 1) Lời giải Chọn D
Ta có i 1; 0, j 0;
1 i j 1; 1
Câu 4. [0H1-5.3-1]Trong mặt phẳng Oxy cho a 1 ; 3 , b 5; 7
. Tọa độ vectơ 3a 2b là: A. 6; 1 9 . B. 13; 2 9. C. 6 ;10. D. 1 3;2 3 . Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 12 CHUYÊN ĐỀ : VECTO TLDH Chọn D a 1 ;3 3 a 3 ;9 3a 2b 1 3;23 . b 5; 7 2b 10; 1 4
Câu 5: [0H1-5.3-1] Trong mặt phẳng tọa độ Oxy , cho a 1; 2,b 3;4 . Tọa độ c 4a b là A. c 1 ; 4.
B. c 4; 1 .
C. c 1; 4 . D. c 1 ; 4 . Lời giải Chọn C.
Ta có: c 4a 2b 41;2 3;4 1;4.
Câu 6: [0H1-5.3-1] Trong mặt phẳng tọa độ Oxy , cho a 2; 1 ,b 3; 2
và c 2a 3b . Tọa độ của vectơ c là A. 13; 4. B. 13; 4 . C. 1 3; 4 . D. 1 3; 4. Lời giải Chọn A.
Ta có: c 2a 3b 22; 1 33; 2 13; 4 .
Câu 7: [0H1-5.3-1] Cho a2;7 , b 3
;5 . Tọa độ của véctơ a b là. A. 5;2 . B. 1 ;2 . C. 5 ; 2 . D. 5; 2 . Lời giải. Chọn A.
Ta có: a b 2;7 3 ;5 5;2. a3; 4 b 1 ;2
Câu 8: [0H1-5.3-1] Cho ,
. Tọa độ của véctơ a 2b là A. 4 ;6 . B. 4; 6 . C. 1;0 . D. 0; 1 . Lời giải. Chọn C. a 3; 4 b 1
;2 2b 2 ;4
a 2b 1;0.
Câu 9: [0H1-5.3-1] Trong hệ trục ,
O i, j , tọa độ của i j là A. 0; 1 . B. 1; 1 . C. 1; 1 . D. 1 ; 1 . Lời giải.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 13 CHUYÊN ĐỀ : VECTO TLDH Chọn C. i 1;0 Ta có :
i j 1; . j 1 0;1 a 1;2 b 3;4
Câu 10: [0H1-5.3-1] Cho và
với c 4a b thì tọa độ của c là: A. c 1 ;4.
B. c 4; 1 .
C. c 1;4. D. c 1 ; 4. Lời giải. Chọn C.
Ta có: c 4a 2b 41;2 3;4 1;4.
Câu 11: [0H1-5.3-1] Cho a 1; 5, b 2 ;
1 . Tính c 3a 2b .
A. c 7; 1 3 .
B. c 1; 17. C. c 1 ; 17.
D. c 1; 16 . Lời giải Chọn B a 1; 5 3 a 3; 15 Ta có
c 3a 2b 1 ; 17. b 2 ; 1 2b 4 ; 2
Câu 12: [0H1-5.3-1] Cho a 2i 3 j và b i 2 j . Tìm tọa độ của c a b .
A. c 1 ; 1 .
B. c 3 ;5 . C. c 3 ; 5 .
D. c 2 ; 7 . Lời giải Chọn B
c a b 2i 3 j i
2 j 3i 5 j c 3 ; 5 .
Câu 13: [0H1-5.3-1] Cho hai vectơ a 1; 4 ; b 6 ;1
5 . Tìm tọa độ vectơ u biết u a b A. 7;19 . B. –7;19 . C. 7; –19 . D. –7; –19 . Lời giải Chọn B
Ta có u a b u b a 7 ;19 .
Câu 14: [0H1-5.3-1] Tìm tọa độ vectơ u biết u b 0 , b 2; – 3 . A. 2; – 3 . B. –2; – 3 . C. –2; 3 . D. 2; 3 . Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 14 CHUYÊN ĐỀ : VECTO TLDH Chọn C
Ta có u b 0 u b 2 ; 3 .
Câu 15. [0H1-5.3-2] Trong hệ tọa độ Oxy, cho A2; 5, B1; 1 , C 3;
3 . Tìm tọa độ đỉểm E sao cho
AE 3AB 2AC A. 3; 3 . B. 3 ; 3 . C. 3 ; 3 . D. 2 ; 3 . Lời giải Chọn C Gọi E ;
x y .
Ta có AE 3AB 2AC AE AB 2 AB AC BE 2CB x y x 1 4 x 3 1; 1 2 2; 2 y 1 4 y 3 Vậy E 3 ; 3.
Câu 16. [0H1-5.3-2] Cho a 2; 4 , b 5 ;
3 . Tìm tọa độ của u 2a b
A. u 7; 7 .
B. u 9; 1 1
C. u 9; 5 . D. u 1 ; 5. Lời giải Chọn B
Ta có u 22; 4 5 ; 3 9; 1 1 .
Câu 17: [0H1-5.3-2] Cho 3 điểm A–4;0, B–5; 0 , C 3;
0 . Tìm điểm M trên trục Ox sao cho
MA MB MC 0 . A. –2;0 . B. 2;0 . C. –4;0 .
D. –5;0 . Lời giải Chọn A
Ta có M Ox nên M ;0
x . Do MA MB MC 0 nên 4 5 3 x 2 . 3
Câu 18: [0H1-5.3-2] Trong hệ trục O,i, j cho 2 vectơ a 3 ; 2 , b i 5 j . Mệnh đề nào sau đây sai ?
A. a 3i 2 j . B. b 1 ; 5 .
C. a b 2 ; 7 .
D. a b 2 ; 3 . Lời giải Chọn D
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 15 CHUYÊN ĐỀ : VECTO TLDH
a 3 ; 2, b 1
; 5 a b 4 ; 3 .
Câu 19: [0H1-5.3-2] Cho u 2i 3 j , v 5i j . Gọi X;Y là tọa độ của w 2u 3v thì tích XY bằng: A. 57 . B. 57 . C. 63 . D. 63 . Lời giải Chọn A
w 2u 3v 22i 3 j 3 5
i j 19i 3j . X 19, Y 3 XY 5 7.
Dạng 4: Xác định tọa độ các điểm của một hình
PHẦN 1: CÁC VÍ DỤ
Ví dụ 1. Trong hệ tọa độ Oxy,cho tam giác ABC có A3;
5 , B1;2 , C 5;2. Tìm tọa độ trọng tâm G
của tam giác ABC ? Lời giải 3 1 5 x 3 G Ta có 3
G 3;3. 5 2 2 y 3 G 3
Ví dụ 2. Trong hệ tọa độ Oxy,cho tam giác ABC có A 2
;2, B3;
5 và trọng tâm là gốc tọa độ
O0;0. Tìm tọa độ đỉnh C ? Lời giải
Gọi C x; y . 2 3 x 0 x 1 Vì 3
O là trọng tâm tam giác ABC nên . 2 5 y y 7 0 3
Ví dụ 3. Cho M 2;0, N 2;2, P 1 ;
3 lần lượt là trung điểm các cạnh BC,C , A AB của ABC . Tọa độ B là: Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 16 CHUYÊN ĐỀ : VECTO TLDH A P N B M C
x x x x
x 2 2 ( 1 ) x 1
Ta có: BPNM là hình bình hành nên B N P M B B .
y y y y y 2 0 3 y 1 B N P M B B
Ví dụ 4. Trong mặt phẳng tọa độ Oxy , cho tam giác MNP có M 1; 1 , N 5;
3 và P thuộc trục Oy ,
trọng tâm G của tam giác nằm trên trục Ox .Toạ độ của điểm P là Lời giải
Ta có: P thuộc trục Oy P0; y, G nằm trên trục Ox G ;0 x 1 5 0 x x 2 3
G là trọng tâm tam giác MNP nên ta có: ( 1 ) ( 3 ) y y 4 0 3 Vậy P0;4 .
Ví dụ 5. Cho tam giác ABC với AB 5 và AC 1. Tính toạ độ điểm D là của chân đường phân giác
trong góc A , biết B( 7; 2 ),C(1;4 ). Lời giải A B C D DB AB
Theo tính chất đường phân giác:
5 DB 5DC DB 5 DC. DC AC
Gọi D x; y DB 7 x; 2 y;DC 1 x;4 y . 7 x 5 1 x x 2 Suy ra: . 2 y 5
4 y y 3 Vậy D2; 3 .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 17 CHUYÊN ĐỀ : VECTO TLDH
Ví dụ 6. Trong mặt phẳng tọa độ Oxy cho A3; 1 , B 1
;2 và I 1;
1 . Xác định tọa độ các điểm C ,
D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC . Tìm tọa tâm O
của hình bình hành ABCD . Lời giải
Vì I là trọng tâm tam giác ABC nên
x x x A B C x
x 3x x x 1 I 3 C I A B
y y y A B C y
y 3y y y 4 I 2 C I A B Suy ra C 1; 4
Tứ giác ABCD là hình bình hành suy ra 1 3 1 x x 5 D D
AB DC D( 5; 7 ) 2 1 4 y y 7 D D
Điểm O của hình bình hành ABCD suy ra O là trung điểm AC do đó x x y y 5 5 A C x 2 A C , y
O 2; O 2 O 2 2 2
PHẦN 2: CÂU HỎI TRẮC NGHIỆM
Câu 1: [0H1-5.3-1] Cho A4; 0 , B2; –
3 , C9; 6 . Tọa độ trọng tâm G của tam giác ABC là: A. 3; 5 . B. 5; 1 . C. 15; 9 . D. 9; 15 . Lời giải Chọn B
Trọng tâm G của tam giác ABC có toạ độ thoả mãn:
x x x 4 2 9 A B C x x G G x 5 3 3 G G 5; 1 .
y y y 3 6 y 1 A B C G y y G 3 G 3
Câu 2. [0H1-5.3-1] Trong hệ tọa độ Oxy, cho tam giác ABC có A3; 5, B1; 2, C 5; 2 . Tìm tọa
độ trọng tâm G của tam giác ABC? A. 3 ; 4. B. 4; 0 .
C. 2; 3 . D. 3; 3 . Lời giải Chọn D
3 1 5 5 2 2
Ta có tọa độ G ; 3; 3 . 3 3
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 18 CHUYÊN ĐỀ : VECTO TLDH
Câu 3. [0H1-5.3-1] Trong hệ tọa độ Oxy, cho A2;
3 , B 4; 7 . Tìm tọa độ trung điểm I của đoạn thẳng AB A. 6; 4 .
B. 2; 10 . C. 3; 2 . D. 8; 2 1 . Lời giải Chọn C 2 4 3 7 Ta có I ; 3; 2 . 2 2
Câu 4. [0H1-5.3-1]Trong mặt phẳng Oxy cho tam giác ABC có A 3;
5 , B 1;2,C 5;2 . Trọng
tâm G của tam giác ABC có tọa độ là: A. 3 ;4. B. 4;0 . C. 2;3. D. 3;3 . Lời giải Chọn D
Ta có Gx ; y là trọng tâm tam giác ABC nên: G G
x x x 3 1 5 A B C x 3 G 3 3 G 3;3 .
y y y 5 2 2 A B C y 3 G 3 3
Câu 5: [0H1-5.3-1] Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có tọa độ ba đỉnh lần lượt là A2;
3 , B5; 4 , C 1 ;
1 . Tọa độ trọng tâm G của tam giác có tọa độ là: A. 3; 3 . B. 2; 2 . C. 1; 1 . D. 4; 4 . Lời giải Chọn B.
x x x A B C x G Để 3
G là trọng tâm tam giác ABC G2;2 .
y y y A B C y G 3
Câu 6: [0H1-5.3-1] Cho tam giác ABC có tọa độ ba đỉnh lần lượt là A2;
3 , B5;4 , C 2;2 . Tọa độ
trọng tâm G của tam giác có tọa độ là A. 3;3 B. 2;2 C. 1; 1 D. 4;4 . Lời giải. Chọn A.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 19 CHUYÊN ĐỀ : VECTO TLDH
x x x 3x Ta có : A B C G G3; 3 .
y y y 3y A B C G
B3;2 C 5;4
Câu 7: [0H1-5.3-1] Cho hai điểm ,
. Toạ độ trung điểm M của BC là
A. M –8; 3 . B. M 4; 3 .
C. M 2;2 .
D. M 2; –2 . Lời giải. Chọn B. x x C B x M Ta có 2 : M 4; 3 . y y C B y M 2 A5; 2
B0; C 5 ; Câu 8: 3 1
[0H1-5.3-1] Trong mặt phẳng toạ độ Oxy Oxy, cho ba điểm , , . Khi đó trọng tâm ABC là: A. G0;1 1 . B. G1; 1 .
C. G 10;0 .
D. G 0;0 . Lời giải. Chọn D.
x x x 3x Ta có : A B C G
G0;0.
y y y 3y A B C G
Câu 9: [0H1-5.3-1] Trong mặt phẳng tọa độ Oxy cho A2;
3 , B4;7 . Tọa độ trung điểm I của đoạn thẳng AB là: A. I 6;4
B. I 2;10 .
C. I 3;2 .
D. I 8; 2 1 . Lời giải. Chọn C. x x A B x I Ta có 2 : I 3;2 . y y A B y I 2
A3;5 B1;2 C 2;0
Câu 10: [0H1-5.3-1] Trong mặt phẳng tọa độ Oxy cho , và
. Tìm tọa độ trọng tâm
G của tam giác ABC 7 7
A. G 3,7 . B. G 6; 3 . C. G 3, D. G 2; . 3 3
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 20 CHUYÊN ĐỀ : VECTO TLDH Lời giải. Chọn D.
x x x 3x 7
Để G là trọng tâm tam giác ABC A B C G G 2; .
y y y 3y 3 A B C G
Câu 11: [0H1-5.3-1] Trong mặt phẳng tọa độ Oxy cho A3;5, B1;2. Tìm tọa độ trung điểm I của đoạn thẳng AB . 7 7 A. I 4;7. B. I 2 ; 3 . C. I 2; . D. I 2; . 2 2 Lời giải. Chọn C. x x A B x I 7 Ta có 2 : I 2; . y y 2 A B y I 2 1
Câu 12: [0H1-5.3-1] Cho tam giác ABC với A 3 ;6 ; B9; 1 0 và G ;0
là trọng tâm. Tọa độ C 3 là :
A. C 5; 4 .
B. C 5;4 . C. C 5 ;4. D. C 5 ; 4. Lời giải. Chọn C.
x x x 3x
x 3x x x C G A B Ta có : A B C G C 5 ;4 .
y y y 3y
y 3y y y C G A B A B C G
Câu 13. [0H1-5.3-1] Trong mặt phẳng Oxy cho A4;2, B1;
5 . Tìm trọng tâm G của tam giác OAB . 5 5 5 1 A. G ; 1 . B. G ; 2 . C. G 1; 3 . D. G ; . 3 3 3 3 Lời giải Chọn A
x x x 0 4 1 5 O A B x G 3 3 3 5 G ; 0 .
y y y 0 2 5 3 O A B y 1 G 3 3
Câu 14. [0H1-5.3-2] Trong hệ tọa độ Oxy, cho tam giác ABC có A 2
; 2, B3; 5 và trọng tâm là gốc
O . Tìm tọa độ đỉnh C ?
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 21 CHUYÊN ĐỀ : VECTO TLDH A. 1 ; 7 .
B. 2; 2. C. 3 ; 5 . D. 1; 7 . Lời giải Chọn A
2 3 x 0 x 1 3 Gọi C ;
x y . Ta có O là trọng tâm 2 5 y y 7 0 3 Vậy C 1 ; 7.
Câu 15. [0H1-5.3-2] Trong hệ tọa độ Oxy, cho tam giác ABC có A6; 1 , B 3 ; 5 và trọng tâm G 1 ;
1 . Tìm tọa độ đỉnh C ?
A. 6; 3 . B. 6 ; 3 . C. 6 ; 3 . D. 3 ; 6. Lời giải Chọn C 6 3 x 1 x 6 Gọi C ;
x y . Ta có G là trọng tâm 3 1 5 y y 3 1 3 Vậy C 6 ; 3.
Câu 16. [0H1-5.3-2] Trong hệ tọa độ Oxy, cho tam giác ABC có M 2;
3 , N 0; 4, P 1 ; 6 lần lượt
là trung điểm của các cạnh BC,C ,
A AB . Tìm tọa độ đỉnh A ? A. 1; 5. B. 3 ; 1 . C. 2 ; 7 .
D. 1; 10 . Lời giải Chọn B
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 22 CHUYÊN ĐỀ : VECTO TLDH A N P C M B Gọi A ;
x y . Ta có PA MN x 1; y 6 2 ; 7 . x 1 2 x 3 . Vậy A 3 ; 1 .. y 6 7 y 1
Câu 17. [0H1-5.3-2] Trong hệ tọa độ Oxy, cho ba điểm A1;
1 , B3; 2, C 6; 5 . Tìm tọa độ điểm D
để ABCD là hình bình hành. A. 4; 3 . B. 3; 4 . C. 4; 4 . D. 8; 6 . Lời giải Chọn C Gọi D ;
x y, ABCD là hình bình hành AD BC x 1; y 1 3; 3 . x 1 3 x 4 y 1 3 y 4
Vậy D4; 4 .
Câu 18. [0H1-5.3-2] Trong hệ tọa độ Oxy, cho ba điểm A2; 1 , B0; 3 , C 3;
1 . Tìm tọa độ điểm
D để ABCD là hình bình hành. A. 5; 5 .
B. 5; 2 .
C. 5; 4 . D. 1 ; 4 . Lời giải Chọn A
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 23 CHUYÊN ĐỀ : VECTO TLDH A B D C Gọi D ;
x y, ABCD là hình bình hành AD BC x 2; y 1 3; 4 x 2 3 x 5 y 1 4 y 5
Vậy D 5; 5 .
Câu 19. [0H1-5.3-2]Trong mặt phẳng Oxy cho 3 điểm A 1 ;
3 , B 2;0,C 6;2 . Tìm tọa độ D
sao cho ABCD là hình bình hành. A. 9; 1 . B. 3;5 . C. 5;3 . D. 1 ;9. Lời giải Chọn B
ABCD là hình bình hành khi AB DC .
Ta có AB 3; 3 , DC 6 ;
x 2 y, D ; x y . 6 x 3 x 3
Nên AB DC D3;5. 2 y 3 y 5
A1; B 1 ;2 C0; Câu 20: 1 1
[0H1-5.3-2] Cho hình bình hành ABCD . Biết , ,
. Tọa độ điểm D là: A. 2;0 . B. 2 ;0 C. 2 ;2 . D. 2; 2 Lời giải. Chọn A. Gọi D ,
x y là điểm cần tìm Ta có : AB 2 ; 1 , DC ;1 x y x 2
Để ABCD là hình bình hành AB DC D2;0 . 1 y 1
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 24 CHUYÊN ĐỀ : VECTO TLDH
Câu 21: [0H1-5.3-2] Cho tam giác. ABC . Gọi M , N , P lần lượt là trung điểm BC ,CA , AB . Biết A1; 3 , B 3 ;
3 , C 8;0 . Giá trị của x x x bằng: M N P A. 2 . B. 3 . C. 1. D. 6 . Lời giải. Chọn D. Ta có 5
: M là trung điểm BC x M 2 9
N là trung điểm AC x N 2
P là trung điểm AB x 1 P 5 9
x x x 1 6 M N P 2 2 A 2
;0 B0; C4;4 Câu 22: 1
[0H1-5.3-2] Cho hình bình hành ABCD có ; ,
. Toạ độ đỉnh D là: A. D2; 3 . B. D6; 3 . C. D6;5 D. D2;5. Lời giải. Chọn D. Gọi D ,
x y là điểm cần tìm
Ta có : AB 2; 1 , DC 4 ; x 4 y 4 x 2
Để ABCD là hình bình hành AB DC D2;5 . 4 y 1 A 5 ;6 B 4 ; C 4; Câu 23: 1 3
[0H1-5.3-2] Cho tam giác ABC với , và
. Tìm D để ABCD là hình bình hành:
A. D3;10 . B. D3; 1 0. C. D 3 ;10. D. D 3 ; 1 0. Lời giải. Chọn A. Gọi D ,
x y là điểm cần tìm Ta có : AB 1; 7
, DC 4 ; x 3 y 4 x 1
Để ABCD là hình bình hành AB DC D3;10 . 3 y 7
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 25 CHUYÊN ĐỀ : VECTO TLDH
Dạng 5: Bài toán liên quan đến sự cùng phương của hai vectơ. Phân tích một vectơ qua hai vectơ không cùng phương
PHẦN 1: CÁC VÍ DỤ
Ví dụ 1. Cho A1;2, B 2
;6 . Tìm tạo độ điểm M trên trục Oy sao cho ba điểm , A , B M thẳng hàng. Lời giải
Ta có: M trên trục Oy M 0; y Ba điểm , A ,
B M thẳng hàng khi AB cùng phương với AM Ta có AB 3 ;4, AM 1
; y 2. Do đó, AB cùng phương với 1 y 2 AM y 10 M 0;10 . 3 . Vậy 4
Ví dụ 2. Cho các vectơ a 4; 2 ,b 1 ;
1 , c 2;5 . Phân tích vectơ b theo hai vectơ a và c . Lời giải 1 m 1
4m 2n 8 1 1
Giả sử b ma nc
. Vậy b a c . 1 2 m 5n 1 8 4 n 4
Ví dụ 3. Trong mặt phẳng Oxy , cho Am1;
1 , B2;2 2m,C m 3;
3 . Tìm giá trị m để , A B,C là ba điểm thẳng hàng? Lời giải
Ta có: AB 3 ;
m 3 2m, AC 4;4 Ba điểm ,
A B,C thẳng hàng khi và chỉ khi AB cùng phương với AC 3 m 3 2m m 0 . 4 4
Ví dụ 4. Trong mặt phẳng tọa độ Oxy , cho ba điểm A( 6;3), B( 3
;6 ), C(1; 2
) . Xác định điểm E trên
trục hoành sao cho ba điểm A, B, E thẳng hàng. Lời giải
Vì E thuộc đoạn BC và BE E 2 C suy ra BE E 2 C
Gọi E x; y khi đó BE x 3; y 6 , EC 1 x; 2 y 1 x
x 3 21 x Do đó 3 y 6 2 2 y 2 y 3
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 26 CHUYÊN ĐỀ : VECTO TLDH 1 2 Vậy E ; . 3 3
Ví dụ 5. Trong mặt phẳng tọa độ Oxy cho 4 điểm A0; 1 , B1;
3 , C 2;7 và D ; 0 3 . Tìm giao điểm
của 2 đường thẳng AC và BD . Lời giải
Gọi I x; y là giao điểm AC và BD suy ra AI ; AC cùng phương và BI ; BD cùng phương Mặt khác x y 1
AI ( x ; y 1 ), AC ( 2 ;6 ) suy ra
6x 2y 2 (1) 2 6
BI ( x 1; y 3 ), BD ( 1;0 ) suy ra y 3 thế vào (1) ta có 2 x 3 2 Vậy I ;3 là điểm cần tìm. 3
PHẦN 2: CÂU HỎI TRẮC NGHIỆM
Câu 1: [0H1-5.4-1] Cho a 2i 3 j , b m j i . Nếu a, b cùng phương thì: 2 3 A. m 6 .
B. m 6. C. m . D. m . 3 2 Lời giải Chọn D m a 2 ;
3 và b 1 ; m cùng phương 1 3 m 2 3 . 2
Câu 2: [0H1-5.4-1] Hai vectơ nào có toạ độ sau đây là cùng phương?
A. 1; 0 và 0; 1 . B. 2; 1 và 2; –
1 . C. –1;0 và 1;0 .
D. 3; –2 và 6; 4 . Lời giải Chọn C
Ta có: i 1;0 và i 1 ;0 cùng phương.
Câu 3. [0H1-5.4-2] Trong hệ tọa độ Oxy, cho tam giác ABC có A1; 1 , B 2 ; 2, C 7 ; 7.
Khẳng định nào sau đây đúng?
A. G 2; 2 là trọng tâm tam giác . ABC
B. B ở giữa hai điểm A và C.
C. A ở giữa hai điểm B và C.
D. AB, AC cùng hướng. Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 27 CHUYÊN ĐỀ : VECTO TLDH Chọn C Ta có AB 3 ;
3 , AC 6; 6 và AC 2 AB
Vậy A ở giữa hai điểm B và C.
Câu 4. [0H1-5.4-2] Trong hệ tọa độ Oxy, cho A 1 ; 5 , B5; 5 , C 1 ; 1
1 . Khẳng định nào sau đây đúng? A. ,
A B, C thẳng hàng.
B. AB, AC cùng phương.
C. AB, AC không cùng phương.
D. AB, AC cùng hướng. Lời giải Chọn C
Ta có AB 6; 0 , AC 0; 6 AB, AC không cùng phương.
Câu 5. [0H1-5.4-2] Trong hệ tọa độ Oxy, cho bốn điểm A3; 2, B7; 1 , C 0; 1 , D 8 ; 5.
Khẳng định nào sau đây đúng?
A. AB, CD là hai vectơ đối nhau.
B. AB, CD ngược hướng.
C. AB, CD cùng hướng. D. , A ,
B C, D thẳng hàng. Lời giải Chọn B
Ta có AB 4; 3, CD 8 ; 6 2
AB AB, CD ngược hướng.
Câu 6. [0H1-5.4-2] Cho u 3; 2, v 1; 6. Chọn khẳng định đúng?
A. u v và a 4 ; 4 ngược hướng.
B. u, v cùng phương.
C. u v và c k.a . h b cùng hướng.
D. 2u v, v cùng phương. Lời giải Chọn C
Ta có u v 4; 4 và u v 2; 8 4 4 Xét tỉ số
u v và a 4
; 4 không cùng phương. Loại A 4 4
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 28 CHUYÊN ĐỀ : VECTO TLDH Xét tỉ 3 2 số
u, v không cùng phương. Loại B 1 6 Xét tỉ 2 8 số
3 0 u v và b 6; 24 cùng hướng. 6 2 4
Câu 7. [0H1-5.4-2] Khẳng định nào sau đây là đúng? A. a 5 ; 0, b 4 ; 0 cùng hướng.
B. c 7;
3 là vectơ đối của d ; 7 3 .
C. u 4; 2, v 8; 3 cùng phương.
D. a 6; 3 , b 2; 1 ngược hướng. Lời giải Chọn A Ta có a 5 5 5 ; 0 4
; 0 b a, b cùng hướng. 4 4
Câu 8: [0H1-5.4-2] Các điểm và các vectơ sau đây cho trong hệ trục O ;i, j (giả thiết , m , n p , q là
những số thực khác 0 ). Mệnh đề nào sau đây sai ?
A. a m ; 0 a // i .
B. b 0 ; n b // j .
C. Điểm An ; p x O
x n 0.
D. A0 ; p, Bq ; p thì AB // x O x . Lời giải Chọn C
An ; p x O
x p 0 .
Câu 9: [0H1-5.4-2] Hai vectơ nào sau đây không cùng phương:
A. a 3 ; 5 và 6 10 b ; .
B. c và 4c . 7 7
C. i 1 ; 0 và 5 m ; 0 .
D. m 3 ; 0 và n 0 ; 3 . 2 Lời giải Chọn D
m 3 ; 0 và n 0 ; 3 . Ta có: a b a b 3 3 0 3 0 1 2 2 1
Vậy m và n không cùng phương.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 29 CHUYÊN ĐỀ : VECTO TLDH
Câu 10: [0H1-5.4-2] Cho u 2x 1;
3 , v 1 ; x 2. Có hai giá trị x , x 1
2 của x để u cùng phương
với v . Tính x .x . 1 2 5 5 5 5 A. . B. . C. . D. . 3 3 2 3 Lời giải Chọn C x
u, v cùng phương 2 1 3 x ) 1 x (với 2 2 5
x x 2 2 1
2 3 2x 3x 5 0. Vậy x .x . 1 2 2
Câu 11: [0H1-5.4-2] Trong mặt phẳng Oxy , cho ba vectơ a (1;2),b ( 3 ;1),c ( 4 ;2) . Biết
u 3a 2b 4c . Chọn khẳng định đúng.
A. u cùng phương với i .
B. u không cùng phương với i .
C. u cùng phương với j .
D. u vuông góc với i . Lời giải Chọn B x 3.1 2.( 3 ) 4.( 4 ) 1 9 Gọi u ( ; x y) . Ta có u ( 1 9;16).
y 3.2 2.1 4.2 16
A2;5 B1;7 C 1;5 D0;9
Câu 11: [0H1-5.5-2] Cho bốn điểm , , ,
. Ba điểm nào sau đây thẳng hàng: A. , A B, C . B. , A C, D .
C. B, C, D . D. , A B, D . Lời giải. Chọn D. Ta có: AB 1 ;2, AC 1 ;0, AD 2
;4 AD 2AB ,
A B, D thẳng hàng.
Câu 12. [0H1-5.5-2] Trong hệ tọa độ Oxy, cho 4 điểm A3;0, B4; 3 ,C 8; 1 , D 2 ; 1 . Ba điểm nào
trong bốn điểm đã cho thẳng hàng ?
A. B, C, D . B. , A , B C . C. , A , B D . D. ,
A C, D . Lời giải Chọn D
Ta có AC 5; 1 ; AD 5 ;
1 AC AD . Vậy ba điểm ,
A C, D thẳng hàng.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 30 CHUYÊN ĐỀ : VECTO TLDH
Câu 13. [0H1-5.5-2] Trong mặt phẳng Oxy cho A 2 ; m m ,B2 ;
m m. Với giá trị nào của m thì
đường thẳng AB đi qua O ? A. m 3 . B. m 5 . C. m . .
D. Không có m . Lời giải Chọn C Ta có OA 2 ;
m m , OB 2 ;
m m . Đường thẳng AB đi qua O khi OA , OB cùng phương
Mặt khác ta thấy OA 2 ;
m m 2 ; m m O B , m
nên AB đi qua O , m .
Câu 14. [0H1-5.5-2] Cho 2 điểm A 2 ; 3 , B4;
7 . Tìm điểm M y O
y thẳng hàng với A và B . 4 1 1 A. M ; 0 . B. M ; 0 .
C. M 1;0 . D. M ; 0 . 3 3 3 Lời giải Chọn B M y O
y M 0; m . AM 2; m
3 ; AB 6; 10 . Để 2 m 3 1
A , B , M thẳng hàng thì
3m 3 10 m . 6 10 3
Câu 15. [0H1-5.5-2] Ba điểm nào sau đây không thẳng hàng ? A. M 2 ;4, N 2 ;7, P 2 ;2. B. M 2
;4, N 5;4, P7;4. C. M 3; 5 , N 2 ;5,P 2 ;7. D. M 5; 5 , N 7; 7 ,P 2 ;2. Lời giải Chọn C C. MN 5 ; 0,MP 5
; 2 MN , MP không cùng phương
M , N , P không thẳng hàng.
Câu 16: [0H1-5.5-2] Cho ba điểm A2 ; 4 , B6 ; 0 ,Cm ; 4 . Định m để ,
A B, C thẳng hàng ?
A. m 10 . B. m 6 .
C. m 2 . D. m 10 . Lời giải Chọn A
AB 4 ; 4 ; AC m 2 ; 8. m 2 8 , A ,
B C thẳng hàng AB, AC cùng phương m 10 . 4 4
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 31 CHUYÊN ĐỀ : VECTO TLDH
Câu 17: [0H1-5.5-2] Cho A0 ; 2 , B 3 ;
1 . Tìm tọa độ giao điểm M của AB với trục x O x . 1 A. M 2 ; 0.
B. M 2 ; 0 . C. M ; 0 .
D. M 0 ; 2 . 2 Lời giải Chọn A
M x ; 0 x O
x AM x ; 2 ; AB 3 ; 3 . x ,
A B, M thẳng hàng AB, AM cùng phương 2 x 2 3 . 3 Vậy, M 2 ; 0.
Câu 18: [0H1-5.5-2] Cho bốn điểm ( A 1; 1 ), ( B 2;4), ( C 2 ; 7 ), (3
D ;3) . Ba điểm nào trong bốn điểm đã cho thẳng hàng? A. , A B, C . B. , A B, D .
C. B,C, D . D. , A C, D . Lời giải Chọn D 3
AB (1;5), AC ( 3 ; 6
), AD (2;4) AC AD ,
A C, D thẳng hàng. 2
Câu 19: [0H1-5.5-2] Cho hai điểm M –2;2, N 1;
1 . Tìm tọa độ điểm P trên Ox sao cho 3 điểm
M, N, P thẳng hàng.
A. P 0;4 .
B. P 0; –4 .
C. P –4;0 .
D. P 4;0 . Lời giải Chọn D
Do P Ox nên P ;0
x , mà MP x 2; 2
;MN 3; 1 x
Do M, N, P thẳng hàng nên 2 2 x 4 3 1 .
Câu 20: [0H1-5.7-2] Cho 3 vectơ a 5;
3 ; b 4;2 ; c 2;0 . Hãy phân tích vectơ c theo 2 vectơ a và b .
A. c 2a 3b . B. c 2 a 3b .
C. c a b .
D. c a 2b . Lời giải Chọn B 5
m 4n 2 m 2
Giả sử c ma nb , ta có: .
3m 2n 0 n 3
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 32 CHUYÊN ĐỀ : VECTO TLDH
Câu 21. [0H1-5.4-3] Trong hệ tọa độ Oxy, cho bốn điểm A2; 1 , B 2; 1 , C 2 ; 3 , D 2 ; 1 . Xét ba mệnh đề:
I ABCD là hình thoi.
II ABCD là hình bình hành.
III AC cắt BD tại M 0; 1. Chọn khẳng định đúng
A. Chỉ I đúng.
B. Chỉ II đúng.
C. Chỉ II và III đúng.
D. Cả ba đều đúng. Lời giải Chọn C Ta có 0; 2,
0; 2 ABDC AB DC
ABCD là hình bình hành.
Trung điểm AC là 0;
1 III đúng. AC 4
; 4, BD 4 ; 0 A .
C BD 16 0 AC, BD không vuông góc nhau.
Câu 22. [0H1-5.3-3] Trong hệ tọa độ Oxy , cho hai điểm A2;
3 , B3; 4 . Tìm tọa độ điểm M trên trục hoành sao cho , A , B M thẳng hàng. 5 1 17
A. M 1; 0.
B. M 4; 0 . C. M ; . D. M ; 0 . 3 3 7 Lời giải Chọn D
Điểm M Ox M ; m 0 .
Ta có AB 1; 7 và AM m 2; 3 . m 2 3 17 Để , A , B M thẳng hàng m . 1 7 7
Câu 23. Trong mặt phẳng tọa độ Oxy , cho ba điểm A( 6;3), B( 3
;6 ), C(1; 2
) . Xác định điểm E trên
cạnh BC sao cho BE 2EC . 1 2 1 2 2 1 2 1
A. E ; .
B. E ; . C. E ; .
D. E ; . 3 3 3 3 3 3 3 3 Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 33 CHUYÊN ĐỀ : VECTO TLDH Chọn A
Vì E thuộc đoạn BC và BE E 2 C suy ra BE E 2 C
Gọi E x; y khi đó BE x 3; y 6 , EC 1 x; 2 y 1 x
x 3 21 x Do đó 3 y 6 2 2 y 2 y 3 1 2 Vậy E ; . 3 3 Câu 1 2
24. Trong mặt phẳng tọa độ Oxy , cho ba điểm A( 6;3 ), B ; , C(1; 2
), D(15;0 ) . Xác định 3 3
giao điểm I hai đường thẳng BD và AC . 7 1 7 1 7 1 7 1 A. I ; . B. I ; .
C. I ; . D. I ; . 2 2 2 2 2 2 2 2 Lời giải Chọn D
Gọi I x; y là giao điểm của BD và AC . 3 x 15 Do đó 3y DI x ; y 46 2 15 ,DB ; cùng phương suy ra
x 23y 15 0 (1) 3 3 4 6 2 x y
AI x 6; y 3 , AC 5 ; 5 cùng phương suy ra 6 3
x y 3 0 5 5 (2) Từ (1) và (2) suy ra 7 x và 1 y 2 2
Vậy giao điểm hai đường thẳng BD và AC là 7 1 I ; . 2 2
Câu 25. Cho ba điểm A( 1 ; 1 ), B(0 1
; ), C( 3;0 ). Xác định tọa độ điểm D biết D thuộc đoạn thẳng BC
và 2BD 5DC . 15 2 15 2 2 15 15 2 A. ; . B. ; . C. ; . D. ; . 7 7 7 7 7 7 7 7 Lời giải Chọn A
Ta có 2BD 5DC, BDx ; y
1 ,DC 3 x ;y D D D D
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 34 CHUYÊN ĐỀ : VECTO TLDH 15 x
2x 5 x D 3 D D Do đó 7 15 2 D ; . 2
y y D 1 5 D 2 7 7 y D 7
Câu 26. Cho tam giác ABC có A( 3;4 ), B( 2 1 ; ), C( 1 ; 2
) . Tìm điểm M trên đường thẳng BC sao cho S 3S . ABC ABM A. M 0 1
; , M 3;2 . B. M 1;0 , M 3;2 . C. M 1;0 , M
2;3 . D. M 0 1 ; , M 2;3 . 1 2 1 2 1 2 1 2 Lời giải Chọn B Ta có S 3S
BC 3BM BC 3 BM ABC ABM
Gọi M x; y BM x 2; y 1 ; BC 3 ; 3 3 3x 2 x 1 3
3x 2 x 3 Suy ra hoặc 3 3
y 1 y 0 3 3 y 1 y 2
Vậy có hai điểm thỏa mãn M 1;0 , M 3;2 . 1 2
Câu 27. Cho hình bình hành ABCD có A ; 2 3 và tâm I ; 1 1 . Biết điểm K ; 1 2 nằm trên đường
thẳng AB và điểm D có hoành độ gấp đôi tung độ. Tìm các đỉnh B,D của hình bình hành.
A. B2; 1 , D0; 1 .
B. B0; 1 ; D( 4; 1
).. C. B0; 1 ; D2;
1 ,. D. B2;
1 , D4; 1 . Lời giải Chọn C
Ta có I là trung điểm AC nên C 4; 1
Gọi D2a;a B2 2a;2 a AK 1;
1 , AB 4 2a; 1 a 4 2a 1 a
Vì AK , AB cùng phương nên
a 1 D2; 1 , B 0; 1 1 1 .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 35 CHUYÊN ĐỀ: VECTO TLDH CHUYÊN ĐỀ VÉCTƠ (CHƯƠNG 1 LỚP 10) Ban thực hiện Tên giáo viên Đơn vị công tác GV Soạn
Thầy Phạm Phú Quốc
Trường THPT Nguyễn Tri Phương (Lâm Đồng) GV phản biện
Thầy Nguyễn Thanh Tâm Trung tâm BDVH_LTĐH Số 1 Tây Ninh (Tây Ninh) TT Tổ soạn Cô Phạm Thị Hoài
Trường THCS Nguyễn Hiền (Nha Trang) TT Tổ phản biện
Thầy Nguyễn Văn Vũ Trường THPT YaLy (Gia Lai) Người triển khai Thầy Phạm Lê Duy
Trường THPT Chu Văn An (An Giang)
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 1 CHUYÊN ĐỀ: VECTO TLDH
BÀI 5. ÔN TẬP CHƯƠNG 1
Câu 1: [0H1-1.1-1] Véctơ có điểm đầu là A , điểm cuối là B được kí hiệu là A. AB . B. AB . C. BA . D. AB .
Câu 2: [0H1-5.3-1] Trong mặt phẳng tọa độ Oxy , cho hai điểm A 4
; 0 và B0; 3 . Xác định tọa độ
của vectơ u 2 AB . A. u 8 ; 6 .
B. u 8; 6 . C. u 4 ; 3.
D. u 4; 3 .
Câu 3: [0H1-5.3-1] Trong mặt phẳng tọa độ Oxy , cho A3; 1 , B 1
;2 và I 1; 1 . Tìm tọa độ điểm
C để I là trọng tâm tam giác ABC .
A. C 1; 4 .
B. C 1;0 .
C. C 1;4 .
D. C 9; 4 .
Câu 4: [0H1-1.1-1] Xét các mệnh đề sau
(I): Véc tơ – không là véc tơ có độ dài bằng 0 .
(II): Véc tơ – không là véc tơ có nhiều phương. A. Chỉ (I) đúng. B. Chỉ (II) đúng.
C. (I) và (II) đúng. D. (I) và (II) sai.
Câu 5: [0H1-2.6-1] Cho hình vuông ABCD có cạnh bằng a . Độ dài AD AB bằng a 2 a 3 A. 2a B. . C. . D. a 2 . 2 2
Câu 6: [0H1-3.2-1] Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A2; 5 và B4; 1 . Tọa độ
trung điểm I của đoạn thẳng AB là A. I 1; 3 . B. I 1 ; 3 .
C. I 3;2 . D. I 3; 2 .
Câu 7: [0H1-3.3-1] Cho tam giác ABC với A 2 ; 3 , B4;
1 , trọng tâm của tam giác là G 2; 1 .
Tọa độ đỉnh C là A. 6; 4 . B. 6; 3 . C. 4; 5. D. 2; 1 .
Câu 8: [0H1-3.1-1] Cho các điểm A , B , C , D và số thực k . Mệnh đề nào sau đây đúng?
A. AB k CD AB kCD .
B. AB kCD AB kCD .
C. AB kCD AB k CD .
D. AB kCD AB kCD .
Câu 9: [0H1-5.3-1] Trong mặt phẳng với hệ tọa độ Oxy cho các điểm A1;2 , B3; 1 , C 0; 1 . Tọa
độ của véctơ u 2AB BC là
A. u 2;2 . B. u 4 ; 1 .
C. u 1; 4 . D. u 1 ;4.
Câu 10: [0H1-1.1-1] Mệnh đề nào sau đây sai?
A. G là trọng tâm ABC
thì GA GB GC 0 .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 2 CHUYÊN ĐỀ: VECTO TLDH
B. Ba điểm A , B , C bất kì thì AC AB BC .
C. I là trung điểm AB thì MI MA MB với mọi điểm M .
D. ABCD là hình bình hành thì AC AB AD .
Câu 11: [0H1-1.1-1] Cho ABC
có trọng tâm G . Khẳng định nào sau đây đúng?
A. AG AB AC .
B. AG 2 AB AC . 1 2
C. AG AB AC . D. AG
AB AC . 3 3
Câu 12: [0H1-5.3-1] Cho hai điểm A 3 ; 1 và B1;
3 . Tọa độ của vectơ AB là A. 2 ; 2. B. 1 ; 1 . C. 4; 4 . D. 4 ; 4 .
Câu 13: [0H1-5.3-1] Trong hệ tọa độ Oxy, cho a 3; 4 , b 1
;2 . Tìm tọa độ của a b .
A. a b 4; 6 .
B. a b 2; 2 .
C. a b 4 ;6.
D. a b 3 ; 8 .
Câu 14: [0H1-2.5-1] Cho 5 điểm phân biệt M , N , P , Q , R . Mệnh đề nào sau đây đúng?
A. MN PQ RN NP QR MP .
B. MN PQ RN NP QR PR .
C. MN PQ RN NP QR MR .
D. MN PQ RN NP QR MN .
Câu 15: [0H1-2.4-1] Cho hình bình hành ABCD, đẳng thức véctơ nào sau đây đúng?
A. CD CB CA .
B. AB AC AD .
C. BA BD BC .
D. CD AD AC .
Câu 16: [0H1-1.1-2] Cho 4 điểm A , B , C , D . Gọi I , J lần lượt là trung điểm của AB và CD ; O là
trung điểm của IJ . Mệnh đề nào sau đây sai? 1 A. IJ ADBC.
B. AB CD AD CB . 2 1 C. IJ AC BD.
D. OA OB OC OD 0 . 2
Câu 17: [0H1-1.1-2] Cho hình bình hành ABCD tâm I ; G là trọng tâm tam giác BCD. Đẳng thức nào sau đây sai?
A. BA DA BA DC .
B. AB AC AD 3AG .
C. BA BC DA DC .
D. IA IB IC ID 0 .
Câu 18: [0H1-1.5-2] Cho tam giác ABC đều có cạnh AB 5, H là trung điểm của BC . Tính CA HC . 5 3 5 7 5 7
A. CA HC .
B. CA HC 5 .
C. CA HC
. D. CA HC . 2 4 2
Câu 19: [0H1-1.6-2] Gọi O là giao điểm của hai đường chéo hình bình hành ABCD. Đẳng thức nào sau đây sai?
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 3 CHUYÊN ĐỀ: VECTO TLDH
A. BA CD .
B. AB CD .
C. OA OC .
D. AO OC .
Câu 20: [0H1-3.5-2] Cho tam giác ABC và điểm I thỏa mãn IA 2
IB . Biểu diễn IC theo các vectơ AB , AC . 2 2 A. IC 2
AB AC . B. IC 2AB AC . C. IC AB AC . D. IC AB AC . 3 3
Câu 21: [0H1-1.5-2] Cho tam giác OAB vuông cân tại O , cạnh OA 4. Tính 2OA OB .
A. 2OA OB 4 . B. Đáp án khác.
C. 2OA OB 12 .
D. 2OA OB 4 5 .
Câu 22: [0H1-2.4-2] Có hai lực F , F cùng tác động vào một vật đứng tại điểm O , biết hai lực F , F 1 2 1 2
đều có cường độ là 50 N và chúng hợp với nhau một góc 60. Hỏi vật đó phải chịu một lực
tổng hợp có cường độ bằng bao nhiêu? A. 100 N . B. 50 3 N . C. 100 3 N . D. Đáp án khác.
Câu 23: [0H1-5.3-2] Trong hệ trục tọa độ ; O ;
i j cho hai véc tơ a 2i 4 j ; b 5i 3 j . Tọa độ của
vectơ u 2a b là
A. u 9; 5 . B. u 1 ; 5 .
C. u 7; 7 .
D. u 9; 1 1 .
Câu 24: [0H1-1.1-2] Cho 4 điểm A , B , C , D . Khẳng định nào sau đây sai?
A. Điều kiện cần và đủ để NA MA là N M .
B. Điều kiện cần và đủ để AB CD là tứ giác ABDC là hình bình hành.
C. Điều kiện cần và đủ để AB 0 là A B .
D. Điều kiện cần và đủ để AB và CD là hai vectơ đối nhau là AB CD 0 .
Câu 25: [0H1-5.3-2] Trong mặt phẳng tọa độ Oxy cho hai điểm A 2 ;
2 ; B5; 4 . Tìm tọa độ trọng tâm G của O AB . 7 7 2 3 A. G ;1 . B. G ; .
C. G1; 2 . D. G ; 3 2 3 3 2
Câu 26: [0H1-5.3-2] Trong mặt phẳng tọa độ Oxy , cho điểm M 1;
3 . Khẳng định nào sau đây sai?
A. Hình chiếu vuông góc của M trên trục hoành là H 1;0 .
B. Điểm đối xứng với M qua gốc tọa độ là P3; 1 .
C. Điểm đối xứng với M qua trục hoành là N 1; 3 .
D. Hình chiếu vuông góc của M trên trục tung là K 0; 3 .
Câu 27: [0H1-1.1-2] Cho tứ giác ABCD có AB DC và AB BC . Khẳng định nào sau đây sai?
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 4 CHUYÊN ĐỀ: VECTO TLDH
A. AD BC .
B. ABCD là hình thoi.
C. CD BC .
D. ABCD là hình thang cân.
Câu 28: [0H1-5.3-2] Trong mặt phẳng toạ độ Oxy , cho ba điểm A 2
;5 , B2;2 , C10; 5 . Tìm
điểm E m
;1 sao cho tứ giác ABCE là hình thang có một đáy là CE . A. E 2 ; 1 . B. E 0; 1 . C. E 2; 1 . D. E 1 ; 1 .
Câu 29: [0H1-2.7-2] Cho hình vuông ABCD tâm O cạnh a . Biết rằng tập hợp các điểm M thỏa mãn 2 2 2 2 2
2MA MB 2MC MD 9a là một đường tròn. Bán kính của đường tròn đó là
A. R 2a .
B. R 3a .
C. R a .
D. R a 2 .
Câu 30: [0H1-3.5-2] Cho hình chữ nhật ABCD tâm O . Gọi M , N lần lượt là trung điểm của OA và
CD . Biết MN . a AB .
b AD . Tính a b . 1 3 1
A. a b 1.
B. a b .
C. a b .
D. a b . 2 4 4
Câu 31: [0H1-3.5-2] Cho tam giác ABC . Gọi I , J là hai điểm xác định bởi IA 2IB , 3JA 2JC 0 . Hệ thức nào đúng? 5 5 2 2 A. IJ AC 2AB . B. IJ
AB 2AC . C. IJ
AB 2AC . D. IJ AC 2AB . 2 2 5 5
Câu 32: [0H1-3.6-2] Cho tam giác ABC . Vị trí của điểm M sao cho MA MB MC 0 là
A. M trùng C .
B. M là đỉnh thứ tư của hình bình hành CBAM .
C. M trùng B .
D. M là đỉnh thứ tư của hình bình hành CABM .
Câu 33: [0H1-3.5-2] Cho ba lực F MA , F MB , F MC cùng tác động vào một vật tại điểm M 1 2 3
và vật đứng yên. Cho biết cường độ của F , F đều bằng 25N và góc AMB 60 . Khi đó cường 1 2
độ lực của F là 3 A F1 F3 60 C M F2 B A. 25 3 N . B. 50 3 N . C. 50 2 N . D. 100 3 N .
Câu 34: [0H1-3.5-2] Cho tam giác ABC . Gọi M là điểm trên cạnh BC sao cho MB 2MC . Khi đó: 1 2 2 1 A. AM AB AC . B. AM AB AC . 3 3 3 3
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 5 CHUYÊN ĐỀ: VECTO TLDH 2 3
C. AM AB AC . D. AM AB AC . 5 5
Câu 35: [0H1-5.3-2] Trong mặt phẳng tọa độ Oxy , cho hình bình hành ABCD có A2; 3 và tâm I 1 ;
1 . Biết điểm M 4; 9 nằm trên đường thẳng AD và điểm D có tung độ gấp đôi hoành
độ. Tìm các đỉnh còn lại của hình bình hành?
A. Tọa độ các đỉnh C 4 ; 1 , B 5
; 4, D3; 6 .
B. Tọa độ các đỉnh C 4 ; 1 , B 4
; 2 , D2; 4.
C. Tọa độ các đỉnh C 4 ; 1 , B 1 ; 4, D 1 ; 2.
D. Tọa độ các đỉnh C 4; 1 , B 5
; 4, D3; 6 .
Câu 36: [0H1-5.7-3] Cho tứ giác ABCD trên cạnh AB , CD lần lượt lấy các điểm M , N sao cho
3AM 2AB và 3DN 2DC . Tính vectơ MN theo hai vectơ AD , BC . 1 2 1 1 A. MN AD BC . B. MN AD BC . 3 3 3 3 1 2 2 1 C. MN AD BC . D. MN AD BC . 3 3 3 3
Câu 37: [0H1-5.5-4] Cho ABC
. Gọi M , N là các điểm thỏa mãn: MA MB 0 , 2NA 3NC 0 và
BC k BP . Tìm k để ba điểm M , N , P thẳng hàng. 1 2 3 A. k . B. k 3. C. k . D. k . 3 3 5 Câu 38: 1
[0H1-5.8-3] Cho hai véc tơ a và b thỏa mãn các điều kiện a
b 1, a 2b 15 . Đặt 2
u a b và v 2ka b , k
. Tìm tất cả các giá trị của k sao cho u,v 60 3 5 3 5 17 17 A. k 4 . B. k 4 . C. k 5 . D. k 5 . 2 2 2 2
Câu 39: [0H1-5.7-3] Cho tứ giác ABCD, trên cạnh AB , CD lấy lần lượt các điểm M , N sao cho
3 AM 2 AB và 3 DN 2 DC . Tính vectơ MN theo hai vectơ AD , BC . 1 1 1 2 A. MN AD BC . B. MN AD BC . 3 3 3 3 1 2 2 1 C. MN AD BC . D. MN AD BC . 3 3 3 3
Câu 40: [0H1-5.8-3] Trong hệ tọa độ Oxy , cho hai điểm A2; 3 , B3; 4
. Tìm tọa độ điểm M trên
trục hoành sao cho chu vi tam giác AMB nhỏ nhất.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 6 CHUYÊN ĐỀ: VECTO TLDH 18 17 A. M ; 0 .
B. M 4;0 .
C. M 3;0 . D. M ; 0 . 7 7
Câu 41: [0H1-5.8-3] Cho M 1
;2 , N 3;2 , P4;
1 . Tìm E trên Ox sao cho EM EN EP nhỏ nhất.
A. E 4;0 .
B. E 3;0 .
C. E 1;0 .
D. E 2;0 .
Câu 42: [0H1-2.0-3] Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC 12 . Tổng hai véctơ
GB GC có độ dài bằng bao nhiêu? A. 2 . B. 4 . C. 8 . D. 2 3 .
Câu 43: [0H1-3.7-3] Cho tam giác ABC . Tập hợp những điểm M sao cho: MA 2MB 6 MA MB là
A. M nằm trên đường tròn tâm I , bán kính R 2AB với I nằm trên cạnh AB sao cho IA 2IB .
B. M nằm trên đường trung trực của BC .
C. M nằm trên đường tròn tâm I , bán kính R 2AC với I nằm trên cạnh AB sao cho IA 2IB .
D. M nằm trên đường thẳng qua trung điểm AB và song song với BC .
Câu 44: [0H1-3.5-3] Cho tam giác ABC . Gọi M là điểm được xác định: 4BM 3BC 0 . Khi đó vectơ AM bằng 1 1 1 2 1 3
A. AB AC . B. AB AC . C. AB AC . D. AB AC . 2 3 3 3 4 4
Câu 45: [0H1-1.5-3] Cho tam giác ABC đều, cạnh 2a , trọng tâm G . Độ dài vectơ AB GC là 2a 3 2a 4a 3 a 3 A. . B. . C. . D. . 3 3 3 3
Câu 46: [0H1-1.5-3] Tam giác ABC thỏa mãn: AB AC AB AC thì tam giác ABC là
A. Tam giác vuông A .
B. Tam giác vuông C .
C. Tam giác vuông B .
D. Tam giác cân tại C .
Câu 47: [0H1-1.5-3] Cho tam giác đều ABC cạnh 2a có G là trọng tâm. Khi đó AB GC là a 3 2a 3 4a 3 2a A. . B. . C. . D. . 3 3 3 3
Câu 48: [0H1-5.0-3] Trong mặt phẳng tọa độ Oxy , tọa độ điểm N trên cạnh BC của tam giác ABC có A1; 2 , B2; 3 , C 1 ; 2 sao cho S 3S là ABN ANC
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 7 CHUYÊN ĐỀ: VECTO TLDH 1 3 1 3 1 1 1 1 A. ; . B. ; . C. ; . D. ; . 4 4 4 4 3 3 3 3
Câu 49: [0H1-1.5-3] Cho hình thang ABCD có đáy AB a , CD 2a . Gọi M , N lần lượt là trung
điểm AD và BC . Tính độ dài của véctơ MN BD CA. 5a 7a 3a a A. . B. . C. . D. . 2 2 2 2
Câu 50: [0H1-5.3-3] Trên mặt phẳng tọa độ Oxy , cho ABC
vuông tại A có B1;
3 và C 1;2 . Tìm
tọa độ điểm H là chân đường cao kẻ từ đỉnh A của ABC
, biết AB 3 , AC 4 . 24 6 24 6 A. H 1; . B. H 1; . C. H 1; . D. H 1; . 5 5 5 5
Câu 51: [0H1-5.3-3] Trong mặt phẳng Oxy , cho tam giác MNP có M 1; 1 , N 5; 3 và P là điểm
thuộc trục Oy , trọng tâm G của tam giác MNP nằm trên trục Ox . Tọa độ điểm P là A. 2; 4 . B. 0; 4 . C. 0; 2 . D. 2; 0 .
Câu 52: [0H1-3.5-3] Cho hai lực F MA, F MB cùng tác động vào một vật tại điểm M cường độ 1 2
hai lực F , F lần lượt là 300N và 400N . AMB 90 . Tìm cường độ của lực tổng hợp tác 1 2 động vào vật. A. 0 N . B. 700N . C. 100N . D. 500N .
Câu 53: [0H1-3.0-3] Cho tam giác ABC , M và N là hai điểm thỏa mãn: BM BC 2AB ,
CN x AC BC . Xác định x để A , M , N thẳng hàng. 1 1 A. 3. B. . C. 2. D. . 3 2 Câu 54: [0H1-3.7-4] Cho ABC . Tìm tập hợp các điểm M sao cho:
MA 3MB 2MC 2MA MB MC .
A. Tập hợp các điểm M là một đường tròn.
B. Tập hợp của các điểm M là một đường thẳng.
C. Tập hợp các điểm M là tập rỗng.
D. Tập hợp các điểm M chỉ là một điểm trùng với A .
Câu 55: [0H1-3.0-4] Tam giác ABC là tam giác nhọn có AA là đường cao. Khi đó véctơ
u tan B A B
tanC A C là
A. u BC . B. u 0 .
C. u AB .
D. u AC .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 8 CHUYÊN ĐỀ: VECTO TLDH Hướng dẫn giải:
Câu 1: [0H1-1.1-1] Véctơ có điểm đầu là A , điểm cuối là B được kí hiệu là A. AB . B. AB . C. BA . D. AB . Lời giải Chọn D.
Câu 2: [0H1-5.3-1] Trong mặt phẳng tọa độ Oxy , cho hai điểm A 4
; 0 và B0; 3 . Xác định tọa độ
của vectơ u 2 AB . A. u 8 ; 6 .
B. u 8; 6 . C. u 4 ; 3.
D. u 4; 3 . Lời giải Chọn B.
AB 4; 3 u 2AB 8; 6 .
Câu 3: [0H1-5.3-1] Trong mặt phẳng tọa độ Oxy , cho A3; 1 , B 1
;2 và I 1; 1 . Tìm tọa độ điểm
C để I là trọng tâm tam giác ABC .
A. C 1; 4 .
B. C 1;0 .
C. C 1;4 .
D. C 9; 4 . Lời giải Chọn A.
x x x A B C x I Điể 3
m I là trọng tâm tam giác ABC
y y y A B C y I 3
x 3x x x
x 3 3 C 1 1 C I A B .
y 3y y y y 3 C 1 2 4 C I A B
Vậy điểm C 1; 4 .
Câu 4: [0H1-1.1-1] Xét các mệnh đề sau
(I): Véc tơ – không là véc tơ có độ dài bằng 0 .
(II): Véc tơ – không là véc tơ có nhiều phương. A. Chỉ (I) đúng. B. Chỉ (II) đúng.
C. (I) và (II) đúng. D. (I) và (II) sai. Lời giải Chọn C.
Véc tơ – không là véc tơ có điểm đầu, điểm cuối trùng nhau nên có độ dài bằng 0 .
Véc tơ – không cùng phương với mọi véc tơ.
Câu 5: [0H1-2.6-1] Cho hình vuông ABCD có cạnh bằng a . Độ dài AD AB bằng a 2 a 3 A. 2a B. . C. . D. a 2 . 2 2
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 9 CHUYÊN ĐỀ: VECTO TLDH Lời giải Chọn D.
Theo quy tắc đường chéo hình bình hành, ta có AD AB AC AC AB 2 a 2 .
Câu 6: [0H1-3.2-1] Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A2; 5 và B4; 1 . Tọa độ
trung điểm I của đoạn thẳng AB là A. I 1; 3 . B. I 1 ; 3 .
C. I 3;2 . D. I 3; 2 . Lời giải Chọn D. x x A B x I 2 x 3
Tọa độ trung điểm I của đoạn thẳng AB : I I 3; 2 . y y y 2 A B y I I 2
Câu 7: [0H1-3.3-1] Cho tam giác ABC với A 2 ; 3 , B4;
1 , trọng tâm của tam giác là G 2; 1 .
Tọa độ đỉnh C là A. 6; 4 . B. 6; 3 . C. 4; 5. D. 2; 1 . Lời giải Chọn C.
x x x A B C x G
Do G là trọng tâm tam giác ABC nên 3
y y y A B C y G 3
x 3x x x x 4 C G A B C .
y 3y y y y 5 C G A B C
Vậy C 4; 5 .
Câu 8: [0H1-3.1-1] Cho các điểm A , B , C , D và số thực k . Mệnh đề nào sau đây đúng?
A. AB k CD AB kCD .
B. AB kCD AB kCD .
C. AB kCD AB k CD .
D. AB kCD AB kCD . Lời giải Chọn C.
Theo định nghĩa phép nhân véc tơ với một số.
Câu 9: [0H1-5.3-1] Trong mặt phẳng với hệ tọa độ Oxy cho các điểm A1;2 , B3; 1 , C 0; 1 . Tọa
độ của véctơ u 2AB BC là
A. u 2;2 . B. u 4 ; 1 .
C. u 1; 4 . D. u 1 ;4. Lời giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 10 CHUYÊN ĐỀ: VECTO TLDH Chọn C.
Ta có AB 2;
3 2AB 4; 6 , BC 3 ;2 .
Nên u 2AB BC 1; 4 .
Câu 10: [0H1-1.1-1] Mệnh đề nào sau đây sai?
A. G là trọng tâm ABC
thì GA GB GC 0 .
B. Ba điểm A , B , C bất kì thì AC AB BC .
C. I là trung điểm AB thì MI MA MB với mọi điểm M .
D. ABCD là hình bình hành thì AC AB AD . Lời giải Chọn C.
Với mọi điểm M , ta dựng hình bình hành AMBC .
Khi đó, theo quy tắc hình bình hành: MA MB MC 2MI .
Câu 11: [0H1-1.1-1] Cho ABC
có trọng tâm G . Khẳng định nào sau đây đúng?
A. AG AB AC .
B. AG 2 AB AC . 1 2
C. AG AB AC . D. AG
AB AC . 3 3 Lời giải Chọn C. 2 1 1
Gọi M là trung điểm BC , ta có: 2 AG AM
. AB AC AB AC . 3 3 2 3
Câu 12: [0H1-5.3-1] Cho hai điểm A 3 ; 1 và B1;
3 . Tọa độ của vectơ AB là A. 2 ; 2. B. 1 ; 1 . C. 4; 4 . D. 4 ; 4 . Lời giải Chọn C.
AB 1 3 ; 3 1 4; 4 .
Câu 13: [0H1-5.3-1] Trong hệ tọa độ Oxy, cho a 3; 4 , b 1
;2 . Tìm tọa độ của a b .
A. a b 4; 6 .
B. a b 2; 2 .
C. a b 4 ;6.
D. a b 3 ; 8 . Lời giải Chọn B.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 11 CHUYÊN ĐỀ: VECTO TLDH
a b 3 1 ; 4 2 2; 2 .
Câu 14: [0H1-2.5-1] Cho 5 điểm phân biệt M , N , P , Q , R . Mệnh đề nào sau đây đúng?
A. MN PQ RN NP QR MP .
B. MN PQ RN NP QR PR .
C. MN PQ RN NP QR MR .
D. MN PQ RN NP QR MN . Lời giải Chọn D.
Ta có MN PQ RN NP QR MN NP PQ QR RN MN .
Câu 15: [0H1-2.4-1] Cho hình bình hành ABCD, đẳng thức véctơ nào sau đây đúng?
A. CD CB CA .
B. AB AC AD .
C. BA BD BC .
D. CD AD AC .
Câu 16: [0H1-1.1-2] Cho 4 điểm A , B , C , D . Gọi I , J lần lượt là trung điểm của AB và CD ; O là
trung điểm của IJ . Mệnh đề nào sau đây sai? 1 A. IJ ADBC.
B. AB CD AD CB . 2 1 C. IJ AC BD.
D. OA OB OC OD 0 . 2 Lời giải Chọn A. Ta có 1 IJ
IA ACCJ IBBDDJ 1
AC BD suy ra C. đúng. 2 2
AB CD AD DB CD AD CB suy ra B. đúng.
OA OB OC OD 2OI OJ 0 suy ra D. đúng.
Câu 17: [0H1-1.1-2] Cho hình bình hành ABCD tâm I ; G là trọng tâm tam giác BCD. Đẳng thức nào sau đây sai?
A. BA DA BA DC .
B. AB AC AD 3AG .
C. BA BC DA DC .
D. IA IB IC ID 0 . Lời giải Chọn A. A D I G B M C
Ta có BA DA BA DC DA DC (vôlý) A sai.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 12 CHUYÊN ĐỀ: VECTO TLDH
G là trọng tâm tam giác BCD; A là một điểm nằm ngoài tam giác BCD đẳng thức ở đáp án B đúng.
Ta có BA BC BD và DA DC DB . Mà DB BD đáp án C đúng.
Ta có IA và IC đối nhau, có độ dài bằng nhau IA IC 0 ; tương tự IB ID 0 đáp án D là đúng.
Câu 18: [0H1-1.5-2] Cho tam giác ABC đều có cạnh AB 5, H là trung điểm của BC . Tính CA HC . 5 3 5 7 5 7
A. CA HC .
B. CA HC 5 .
C. CA HC
. D. CA HC . 2 4 2 Lời giải Chọn D.
Ta có: CA HC CA CH 2CE 2CE (với E là trung điểm của AH ). Ta lại có: 5 3 AH ( ABC
đều, AH là đường cao). 2 A E B C H
Trong tam giác HEC vuông tại H , có: 2 5 3 5 7 5 7 2 2 2
EC CH HE 2.5
CA HC 2CE . 4 4 2
Câu 19: [0H1-1.6-2] Gọi O là giao điểm của hai đường chéo hình bình hành ABCD. Đẳng thức nào sau đây sai?
A. BA CD .
B. AB CD .
C. OA OC .
D. AO OC . Lời giải Chọn C.
Ta có O là trung điểm của AC nên OA O C .
Câu 20: [0H1-3.5-2] Cho tam giác ABC và điểm I thỏa mãn IA 2
IB . Biểu diễn IC theo các vectơ AB , AC . 2 2 A. IC 2
AB AC . B. IC 2AB AC . C. IC AB AC . D. IC AB AC . 3 3
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 13 CHUYÊN ĐỀ: VECTO TLDH Lời giải Chọn C. Ta có IA 2 2
IB IA AB . 3 2
Vậy IC IA AC AB AC . 3
Câu 21: [0H1-1.5-2] Cho tam giác OAB vuông cân tại O , cạnh OA 4. Tính 2OA OB .
A. 2OA OB 4 . B. Đáp án khác.
C. 2OA OB 12 .
D. 2OA OB 4 5 . Lời giải Chọn D.
Dựng OC 2OA 2OA OB OC OB BC 2 2 2 2
BC OC OB 8 4 4 5 .
Câu 22: [0H1-2.4-2] Có hai lực F , F cùng tác động vào một vật đứng tại điểm O , biết hai lực F , F 1 2 1 2
đều có cường độ là 50 N và chúng hợp với nhau một góc 60. Hỏi vật đó phải chịu một lực
tổng hợp có cường độ bằng bao nhiêu? A. 100 N . B. 50 3 N . C. 100 3 N . D. Đáp án khác. Lời giải Chọn B. A F1 O C F2 B
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 14 CHUYÊN ĐỀ: VECTO TLDH
Giả sử F OA, F OB . 1 2
Theo quy tắc hình bình hành, suy ra F F OC , như hình vẽ. 1 2
Ta có AOB 60 , OA OB 50 , nên tam giác OAB đều, suy ra OC 50 3 .
Vậy F F OC 50 3 N . 1 2
Câu 23: [0H1-5.3-2] Trong hệ trục tọa độ ; O ;
i j cho hai véc tơ a 2i 4 j ; b 5i 3 j . Tọa độ của
vectơ u 2a b là
A. u 9; 5 . B. u 1 ; 5 .
C. u 7; 7 .
D. u 9; 1 1 . Lời giải Chọn D.
Ta có a 2; 4 và b 5 ;
3 u 2a b 9; 1 1 .
Câu 24: [0H1-1.1-2] Cho 4 điểm A , B , C , D . Khẳng định nào sau đây sai?
A. Điều kiện cần và đủ để NA MA là N M .
B. Điều kiện cần và đủ để AB CD là tứ giác ABDC là hình bình hành.
C. Điều kiện cần và đủ để AB 0 là A B .
D. Điều kiện cần và đủ để AB và CD là hai vectơ đối nhau là AB CD 0 . Lời giải Chọn B.
Xét 4 điểm A , B , C , D thẳng hàng và AB CD nhưng ABDC không là hình bình hành.
Câu 25: [0H1-5.3-2] Trong mặt phẳng tọa độ Oxy cho hai điểm A 2 ;
2 ; B5; 4 . Tìm tọa độ trọng tâm G của O AB . 7 7 2 3 A. G ;1 . B. G ; .
C. G1; 2 . D. G ; 3 2 3 3 2 Lời giải Chọn C.
x x x 2 5 A B O x 1 G 3 3
Tọa độ trọng tâm G của tam giác OAB là .
y y y 2 4 A B O y 2 G 3 3 Vậy G1; 2 .
Câu 26: [0H1-5.3-2] Trong mặt phẳng tọa độ Oxy , cho điểm M 1;
3 . Khẳng định nào sau đây sai?
A. Hình chiếu vuông góc của M trên trục hoành là H 1;0 .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 15 CHUYÊN ĐỀ: VECTO TLDH
B. Điểm đối xứng với M qua gốc tọa độ là P3; 1 .
C. Điểm đối xứng với M qua trục hoành là N 1; 3 .
D. Hình chiếu vuông góc của M trên trục tung là K 0; 3 . Lời giải Chọn B.
Trong mặt phẳng tọa độ Oxy
+ Hình chiếu vuông góc của M trên trục hoành là H 1;0 . Đáp án A đúng.
+ Điểm đối xứng với M qua gốc tọa độ là P 1 ; 3 . Đáp án B sai.
+ Điểm đối xứng với M qua trục hoành là N 1; 3 . Đáp án C đúng.
+ Hình chiếu vuông góc của M trên trục tung là K 0; 3 . Đáp án D đúng.
Câu 27: [0H1-1.1-2] Cho tứ giác ABCD có AB DC và AB BC . Khẳng định nào sau đây sai?
A. AD BC .
B. ABCD là hình thoi.
C. CD BC .
D. ABCD là hình thang cân. Lời giải Chọn D.
Tứ giác ABCD có AB DC ABCD là hình bình hành
1 , nên AD BC .
Mà AB BC 2 . Từ
1 và 2 ta có ABCD là hình thoi nên CD BC .
Câu 28: [0H1-5.3-2] Trong mặt phẳng toạ độ Oxy , cho ba điểm A 2
;5 , B2;2 , C10; 5 . Tìm
điểm E m
;1 sao cho tứ giác ABCE là hình thang có một đáy là CE . A. E 2 ; 1 . B. E 0; 1 . C. E 2; 1 . D. E 1 ; 1 . Lời giải Chọn C. Ta có BA 4 ; 3 , BC 8; 7
BA , BC không cùng phương nên A , B , C không thẳng
hàng, CE m10;6 . Để ABCE là hình thang có một đáy là CE thì CE cùng chiều với BA m 10 6
0 m . Vậy E 2; 1 . 4 2 3
Câu 29: [0H1-2.7-2] Cho hình vuông ABCD tâm O cạnh a . Biết rằng tập hợp các điểm M thỏa mãn 2 2 2 2 2
2MA MB 2MC MD 9a là một đường tròn. Bán kính của đường tròn đó là
A. R 2a .
B. R 3a .
C. R a .
D. R a 2 . Lời giải Chọn C.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 16 CHUYÊN ĐỀ: VECTO TLDH 2 2 2 2 2
2MA MB 2MC MD 9a
MO OA2 MO OB2 MO OC2 MO OD2 2 2 2 9a 2 2 2 2 2
6MO 2OA OB 2OC OD 2MO2OA 2OC OB OD 2 9a 0 2 2 2 6MO 3
a 9a MO a .
Vậy tập hợp các điểm M là đường tròn tâm O bán kính R a .
Câu 30: [0H1-3.5-2] Cho hình chữ nhật ABCD tâm O . Gọi M , N lần lượt là trung điểm của OA và
CD . Biết MN . a AB .
b AD . Tính a b . 1 3 1
A. a b 1.
B. a b .
C. a b .
D. a b . 2 4 4 Lời giải Chọn A. A B M O D C N 1 1 1
MN MO ON AC AD ABBC 1 1
AD AB AD 1 1 3
AD AB AD . 4 2 4 2 4 2 4 4 1 3 a ; b
. Vậy a b 1. 4 4 Câu 31:
[0H1-3.5-2] Cho tam giác ABC . Gọi I , J là hai điểm xác định bởi IA 2IB ,
3JA 2JC 0 . Hệ thức nào đúng? 5 5 2 2 A. IJ AC 2AB . B. IJ
AB 2AC . C. IJ
AB 2AC . D. IJ AC 2AB . 2 2 5 5 Lời giải Chọn D.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 17 CHUYÊN ĐỀ: VECTO TLDH J A C B I Ta có: 2 2
IJ IA AJ 2
AB AC AC 2AB . 5 5
Gọi M là trung điểm AB , ta có: OA OB 2OM DA .
Câu 32: [0H1-3.6-2] Cho tam giác ABC . Vị trí của điểm M sao cho MA MB MC 0 là
A. M trùng C .
B. M là đỉnh thứ tư của hình bình hành CBAM .
C. M trùng B .
D. M là đỉnh thứ tư của hình bình hành CABM . Lời giải Chọn D. A D B C
MA MB MC 0 BA MC 0 CM BA .
Vậy M thỏa mãn CBAM là hình bình hành.
Câu 33: [0H1-3.5-2] Cho ba lực F MA , F MB , F MC cùng tác động vào một vật tại điểm M 1 2 3
và vật đứng yên. Cho biết cường độ của F , F đều bằng 25N và góc AMB 60 . Khi đó cường 1 2
độ lực của F là 3 A F1 F3 60 C M F2 B A. 25 3 N . B. 50 3 N . C. 50 2 N . D. 100 3 N . Lời giải Chọn A.
Vật đứng yên nên ba lực đã cho cân bằng. Ta được F F F . 3 1 2
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 18 CHUYÊN ĐỀ: VECTO TLDH A F1 F3 C M N F2 B
Dựng hình bình hành AMBN . Ta có F F MA MB MN . 1 2 2 3MA
Suy ra F MN MN 25 3 . 3 2
Câu 34: [0H1-3.5-2] Cho tam giác ABC . Gọi M là điểm trên cạnh BC sao cho MB 2MC . Khi đó: 1 2 2 1 A. AM AB AC . B. AM AB AC . 3 3 3 3 2 3
C. AM AB AC . D. AM AB AC . 5 5 Lời giải Chọn A. A B M C Cách 1: 2 2 1 2
Ta có AM AB BM AB BC AB
AC AB AB AC . 3 3 3 3
Cách 2: Ta có MB 2MC MB 2
MC (vì MB và MC ngược hướng)
AB AM AC AM 1 2 2
AM AB AC . 3 3
Câu 35: [0H1-5.3-2] Trong mặt phẳng tọa độ Oxy , cho hình bình hành ABCD có A2; 3 và tâm I 1 ;
1 . Biết điểm M 4; 9 nằm trên đường thẳng AD và điểm D có tung độ gấp đôi hoành
độ. Tìm các đỉnh còn lại của hình bình hành?
A. Tọa độ các đỉnh C 4 ; 1 , B 5
; 4, D3; 6 .
B. Tọa độ các đỉnh C 4 ; 1 , B 4
; 2 , D2; 4.
C. Tọa độ các đỉnh C 4 ; 1 , B 1 ; 4, D 1 ; 2.
D. Tọa độ các đỉnh C 4; 1 , B 5
; 4, D3; 6 . Lời giải Chọn A.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 19 CHUYÊN ĐỀ: VECTO TLDH
Ta có I là trung điểm của AC C 4 ; 1 .
Điểm D có tung độ gấp đôi hoành độ Dx ;2x . D D
Lại có AM 2; 6 , AD x 2; 2x 3 . D D
Mà A , M , D thẳng hàng 6x 2 22x
3 x 3 D3; 6 . D D D
I là trung điểm BD B 5 ; 4 .
Câu 36: [0H1-5.7-3] Cho tứ giác ABCD trên cạnh AB , CD lần lượt lấy các điểm M , N sao cho
3AM 2AB và 3DN 2DC . Tính vectơ MN theo hai vectơ AD , BC . 1 2 1 1 A. MN AD BC . B. MN AD BC . 3 3 3 3 1 2 2 1 C. MN AD BC . D. MN AD BC . 3 3 3 3 Lời giải Chọn C. D N E A M K I P M N F B Q C
Ta chứng minh bài toán sau: 1
Gọi E , F lần lượt là trung điểm của MN , PQ thì ta có: EF MQNP. 2 1 1 1
Thật vậy, ta có: EF
EPEQ EN NPEM MQ MQ NP 2 2 2
Gọi I , K lần lượt là trung điểm của AM và DN . Khi đó áp dụ 1 1 1
ng kết quả của bài toán trên ta có: MN
BCIK BC
ADMN 2 2 2
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 20 CHUYÊN ĐỀ: VECTO TLDH 1 2
MN AD BC . 3 3
Câu 37: [0H1-5.5-4] Cho ABC
. Gọi M , N là các điểm thỏa mãn: MA MB 0 , 2NA 3NC 0 và
BC k BP . Tìm k để ba điểm M , N , P thẳng hàng. 1 2 3 A. k . B. k 3. C. k . D. k . 3 3 5 Lời giải Chọn A. Cách 1: Tự luận: Ta có 3 1
MN AN AM AC AB 1 5 2 2
NP NC CP
AC BP BC 5 A 2 1 AC 1 BC 5 k M N 2 1 AC 1
AC AB 5 k B C P 1 2 1 AC 1 AB k 5 k
Để ba điểm M , N , P thẳng hàng thì m
: NP mMN 1 3 1 3m m AC 1 AB AC AB k 5 k 5 2 1 3 3m m 4 Điề k 5 5 u kiện: . 1 1 m k 1 3 k 2 1 Vậy k . 3
Cách 2: Trắc nghiệm: Ta có MA
MA MB 0 MA MB 1 MB PB
BC k BP PB 1 k PC 1 k PC 3 NA 3
2NA 3NC 0 2NA NC 2 NC 2
Theo định lí Mêlêxauýt ba điểm M , N , P thẳng hàng khi
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 21 CHUYÊN ĐỀ: VECTO TLDH MA PB NC
1 k 3 1 1 . 1 . 1 k . MB PC NA 2 3 1 Vậy k . 3 Câu 38: 1
[0H1-5.8-3] Cho hai véc tơ a và b thỏa mãn các điều kiện a
b 1, a 2b 15 . Đặt 2
u a b và v 2ka b , k
. Tìm tất cả các giá trị của k sao cho u,v 60 3 5 3 5 17 17 A. k 4 . B. k 4 . C. k 5 . D. k 5 . 2 2 2 2 Lời giải Chọn A. 2 2
a 2b 15 a 4 b 4ab 15 2ab 1 .
uv a b ka b 2 2
k a b k 2k 1 2 2 2
1 ab 2k 4 . 2 2 2 2 2
u v 2 a b 2ka b 2 a b ab 2 2
4k a b 4kab ab 2 5 2
4k 4 4k ab 2
6 4k 4 2k u v 2
6 4k 4 2k . 2k 1 2k 4 uv 1
u, v 60 cos60 2 2
6 4k 4 2k 6k 9 u v 2 6 2
4k 4 2k 3 k 3 k 2
6 4k 4 2k 6k 9 2 2 6 2
4k 2 k 6k 9 2 1
2k 96k 57 0 3 k 2 3 5 k 4 . 3 5 2 k 4 2
Câu 39: [0H1-5.7-3]Cho tứ giác ABCD, trên cạnh AB , CD lấy lần lượt các điểm M , N sao cho
3 AM 2 AB và 3 DN 2 DC . Tính vectơ MN theo hai vectơ AD , BC . 1 1 1 2 A. MN AD BC . B. MN AD BC . 3 3 3 3 1 2 2 1 C. MN AD BC . D. MN AD BC . 3 3 3 3 Lời giải Chọn C.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 22 CHUYÊN ĐỀ: VECTO TLDH
Ta có MN MA AD 2 2 DN BA AD DC 3 3 2
BC CA 2
AD DA 2 2
AC BC AD 1 2 AD AD BC . 3 3 3 3 3 3
Câu 40: [0H1-5.8-3] Trong hệ tọa độ Oxy , cho hai điểm A2; 3 , B3; 4
. Tìm tọa độ điểm M trên
trục hoành sao cho chu vi tam giác AMB nhỏ nhất. 18 17 A. M ; 0 .
B. M 4;0 .
C. M 3;0 . D. M ; 0 . 7 7 Lời giải Chọn D.
Cách 1: Do M trên trục hoành M ;0
x , AB 1; 1 AB 2 .
AM x 2;
3 , BM x 3;4 Ta có chu vi tam giác 2 2 AMB : P x 2 x 2 2 2 3 3 4 ABM 2 2 x 2 x2 2 2 2 2 3 3
4 2 x 2 3 x 3 4 x 2 3 17 P
6 2 . Dấu bằng xảy ra khi x 17 M ; 0 . ABM 3 x 4 7 7
Cách 2: Lấy đối xứng A qua Ox ta được A2;
3 . Ta có MA MB MA MB A B .
Dấu bằng xảy ra khi M trùng với giao điểm của A B với Ox .
Câu 41: [0H1-5.8-3] Cho M 1
;2 , N 3;2 , P4;
1 . Tìm E trên Ox sao cho EM EN EP nhỏ nhất.
A. E 4;0 .
B. E 3;0 .
C. E 1;0 .
D. E 2;0 . Lời giải Chọn D.
Do E Ox E ;0 a . Ta có: EM 1 ;
a 2 ; EN 3 ;
a 2 ; EP 4 ; a 1
Suy ra EM EN EP 6 3 ; a 1 .
Do đó: EM EN EP a2 2 6 3 1 a2 6 3 1 1 .
Giá trị nhỏ nhất của EM EN EP bằng 1. Dấu “ ”
xảy ra khi và chỉ khi 63a 0 a 2 . Vậy E 2;0 .
Câu 42: [0H1-2.0-3] Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC 12 . Tổng hai véctơ
GB GC có độ dài bằng bao nhiêu?
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 23 CHUYÊN ĐỀ: VECTO TLDH A. 2 . B. 4 . C. 8 . D. 2 3 . Lời giải Chọn B.
Gọi M là trung điểm của BC . M cũng là tâm của đường tròn ngoại tiếp tam giác vuông ABC tại A .
Ta có: GB GC 2GM .
Mà G là trọng tâm tam giác vuông ABC nên 1 GM AM 3
Do đó: GB GC 2 2GM AM . 3
Suy ra GB GC 2 2 GM 2 AM 2 1 AM 2 1 . BC . .12 4 . 3 3 3 2 3 2
Câu 43: [0H1-3.7-3] Cho tam giác ABC . Tập hợp những điểm M sao cho: MA 2MB 6 MA MB là
A. M nằm trên đường tròn tâm I , bán kính R 2AB với I nằm trên cạnh AB sao cho IA 2IB .
B. M nằm trên đường trung trực của BC .
C. M nằm trên đường tròn tâm I , bán kính R 2AC với I nằm trên cạnh AB sao cho IA 2IB .
D. M nằm trên đường thẳng qua trung điểm AB và song song với BC . Lời giải Chọn A.
Gọi I là điểm trên cạnh AB sao cho 3BI BA , ta có:
MA 2MB MB BA 2MB 3MB BA 3MB 3BI 3MI .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 24 CHUYÊN ĐỀ: VECTO TLDH
MA MB BA .
MA 2MB 6 MA MB 3MI 6 BA MI 2AB .
Vậy M nằm trên đường tròn tâm I , bán kính R 2AB với I nằm trên cạnh AB sao cho IA 2IB.
Câu 44: [0H1-3.5-3] Cho tam giác ABC . Gọi M là điểm được xác định: 4BM 3BC 0 . Khi đó vectơ AM bằng 1 1 1 2 1 3
A. AB AC . B. AB AC . C. AB AC . D. AB AC . 2 3 3 3 4 4 Lời giải Chọn D.
Ta có: 4BM 3BC 0 4 AM AB 3 AC AB 0
4AM 4AB 3AC 3AB 1 3 0 AM AB AC . 4 4
Câu 45: [0H1-3.5-3]Cho tam giác ABC đều, cạnh 2a , trọng tâm G . Độ dài vectơ AB GC là 2a 3 2a 4a 3 a 3 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn C.
Ta có : AB GC GB GA GC GB GA GC GB G
B vì GAGB GC 0. Khi đó 2 2a 3 4a 3
AB GC 2GB 2GB 2. . . 3 2 3
Câu 46: [0H1-1.5-3] Tam giác ABC thỏa mãn: AB AC AB AC thì tam giác ABC là
A. Tam giác vuông A .
B. Tam giác vuông C .
C. Tam giác vuông B .
D. Tam giác cân tại C . Lời giải Chọn A.
Gọi M là trung điểm BC . Ta có 1
AB AC AB AC 2AM CB AM BC . Trung 2
tuyến kẻ từ A bằng một nửa cạnh BC nên tam giác ABC vuông tại A .
Câu 47: [0H1-1.5-3] Cho tam giác đều ABC cạnh 2a có G là trọng tâm. Khi đó AB GC là a 3 2a 3 4a 3 2a A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn C.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 25 CHUYÊN ĐỀ: VECTO TLDH A G B C M N
Gọi M là trung điểm BC , dựng điểm N sao cho BN AG . Ta có a a
: AB GC GB GA GC GB GA GC 2 2 3 4 3
2GB 2.GB 2. . 3 2 3
Câu 48: [0H1-5.0-3]Trong mặt phẳng tọa độ Oxy , tọa độ điểm N trên cạnh BC của tam giác ABC có A1; 2 , B2; 3 , C 1 ; 2 sao cho S 3S là ABN ANC 1 3 1 3 1 1 1 1 A. ; . B. ; . C. ; . D. ; . 4 4 4 4 3 3 3 3 Lời giải Chọn B.
Gọi H là chân đường cao kẻ từ A của tam giác ABC . Theo đề 1 3 ta có: S 3S AH.BN
AH.CN BN 3CN ABN ACN 2 2 A BN 3
CN BN 3
BN BC 4BN 3BC * .
Ta có BN x 2; y 3 ; BC 3 ; 5 . N N 1 B H N C 4 2 x x N 3 3 N Do đó 4 1 3 * . Vậy N ; . 4 y 3 4 4 N 3 5 3 y N 4
Câu 49: [0H1-1.5-3] Cho hình thang ABCD có đáy AB a , CD 2a . Gọi M , N lần lượt là trung điểm
AD và BC . Tính độ dài của véctơ MN BD CA . 5a 7a 3a a A. . B. . C. . D. . 2 2 2 2 Lời giải Chọn C.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 26 CHUYÊN ĐỀ: VECTO TLDH
Ta có M , N là trung điểm của AD và BC nên MD MA 0 và BN CN 0 .
Khi đó: MN BD CA MN BN NM MD CN NM MA 1
NM NM NM AB CD 3a MN 2 . 2 2
Câu 50: [0H1-5.3-3] Trên mặt phẳng tọa độ Oxy , cho ABC
vuông tại A có B1;
3 và C 1;2 . Tìm
tọa độ điểm H là chân đường cao kẻ từ đỉnh A của ABC
, biết AB 3 , AC 4 . 24 6 24 6 A. H 1; . B. H 1; . C. H 1; . D. H 1; . 5 5 5 5 Lời giải Chọn B. A B C H 2 Ta có 2 CH AC 16
AB BH.BC và 2
AC CH.CB . Do đó: 16 HC .HB . 2 BH AB 9 9
Mà HC, HB ngược hướng nên 16 HC HB . 9 Khi đó, gọi H ;
x y thì HC 1 x;2 y , HB 1 x; 3 y .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 27 CHUYÊN ĐỀ: VECTO TLDH 16 1 x 1 x x 1 9 6 Suy ra: 6 H 1; . 16 y 5 2 y 3 y 5 9
Câu 51: [0H1-5.3-3] Trong mặt phẳng Oxy , cho tam giác MNP có M 1; 1 , N 5; 3 và P là điểm
thuộc trục Oy , trọng tâm G của tam giác MNP nằm trên trục Ox . Tọa độ điểm P là A. 2; 4 . B. 0; 4 . C. 0; 2 . D. 2; 0 . Lời giải Chọn B.
P Oy P0; y .
G Ox G ; x 0 . 1 5 0 x x 2 Điể 3
m G là trọng tâm của tam giác MNP . 1 3 y y 4 0 3
Câu 52: [0H1-3.5-3] Cho hai lực F MA, F MB cùng tác động vào một vật tại điểm M cường độ 1 2
hai lực F , F lần lượt là 300N và 400N . AMB 90 . Tìm cường độ của lực tổng hợp tác 1 2 động vào vật. A. 0 N . B. 700N . C. 100N . D. 500N . Lời giải Chọn D.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 28 CHUYÊN ĐỀ: VECTO TLDH
Cường độ lực tổng hợp của F F F 2 MA MB 2 MI
AB ( I là trung điểm của AB 1 ). Ta có 2 2 AB
MA MB 500 suy ra F 500 N .
Câu 53: [0H1-3.0-3] Cho tam giác ABC , M và N là hai điểm thỏa mãn: BM BC 2AB ,
CN x AC BC . Xác định x để A , M , N thẳng hàng. 1 1 A. 3. B. . C. 2. D. . 3 2 Lời giải Chọn D. Ta có
BM BC 2 AB AM BC AB AM AC 2BC
CN x AC BC. CA AN x AC BC AN x 1 AC BC Để ,
A M , N thẳng hàng thì k
0 sao cho AM k AN 1 k
x 1 k 2 Hay x
1 AC BC k AC 2BC 1 2k 1 x 2 Câu 54: [0H1-3.7-4] Cho ABC . Tìm tập hợp các điểm M sao cho:
MA 3MB 2MC 2MA MB MC .
A. Tập hợp các điểm M là một đường tròn.
B. Tập hợp của các điểm M là một đường thẳng.
C. Tập hợp các điểm M là tập rỗng.
D. Tập hợp các điểm M chỉ là một điểm trùng với A . Lời giải Chọn A. A A N C
Gọi I là điểm thỏa mãn IA 3IB 2IC 0 .
MA 3MB 2MC 2MA MB MC 2MI IA 3IB 2IC BA CA 1 .
Gọi N là trung điểm BC . Ta được:
1 2 MI 2 AN IM AN .
I , A , N cố định nên tập hợp các điểm M là đường tròn tâm I , bán kính AN .
Câu 55: [0H1-3.0-4] Tam giác ABC là tam giác nhọn có AA là đường cao.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 29 CHUYÊN ĐỀ: VECTO TLDH
Khi đó véctơ u tan B A B
tanC A C là
A. u BC . B. u 0 .
C. u AB .
D. u AC . Lời giải Chọn B. A B A C AA AA
u tan B A B
tanC A C u A B A C BA CA . AA Ta thấy hai vecto AB BA và AA A C CA
ngược hướng và độ dài mỗi vecto bằng AA nên chúng
là hai vecto đối nhau. Vậy u 0 .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 30 CHUYÊN ĐỀ: VECTƠ TLDH Ban thực hiện Tên giáo viên Đơn vị công tác GV Soạn
Thầy Nguyễn Thanh Tâm TT BDVH_LTĐH Số 1 Tây Ninh (Tây Ninh) GV phản biện
Cô Phạm Thị Thu Ngà
Trường THPT chuyên Lương Văn Chánh (Phú Yên) TT Tổ soạn Cô Phạm Thị Hoài
Trường THCS Nguyễn Hiền (Nha Trang) TT Tổ phản biện
Thầy Nguyễn Văn Vũ Trường THPT YaLy (Gia Lai) Người triển khai Thầy Phạm Lê Duy
Trường THPT Chu Văn An (An Giang) Chương I: VÉCTƠ
KIỂM TRA 1 TIẾT CHƯƠNG 1 BÀI KIỂM TRA SỐ 1 I. MỤC TIÊU: Kiến thức:
Ôn tập toàn bộ kiến thức trong chương I. Kĩ năng:
Chứng minh được đẳng thức véctơ.
Tìm được điểm thoả mãn các điều kiện cho trước.
Phân tích được một véctơ qua các véctơ cho trước.
Sử dụng tốt các tính chất trung điểm và trọng tâm Thái độ:
Rèn luyện tính cẩn thận, chính xác. II. CHUẨN BỊ:
Giáo viên: Giáo án. Đề kiểm tra.
Học sinh: Ôn tập toàn bộ kiến thức chương 1. III. MA TRẬN ĐỀ:
MA TRẬN ĐỀ KIỂM TRA Tổng Mức độ Vận dụng Vận dụng Biết Hiểu Số Số Chủ đề thấp cao câu điểm Các định nghĩa 2 1 3 0,8 0,4 1,2 Tổng và hiêu hai 2 2 1 5 vectơ 0,8 0,8 0,4 2,0 Tích vectơ với 2 1 1 1 5 một số 0,8 0,4 0,4 0,4 2,0 Hệ trục tọa độ 3 4 3 2 12 1,2 2,0 1,2 0,8 4,8 Tổng Số câu 9 8 5 3 25 Số điểm 3,6 3,2 2,0 1,2 10,0 MÔ TẢ MA TRẬN Kiến thức Câu Mô tả
NB: Mệnh đề đúng (sai) về khái niệm mối quan hệ giữa hai véctơ cùng Các định nghĩa 1
phương, cùng hướng, đối nhau, bằng nhau
NB: Nhận biết được các véc tơ cùng phương, cùng hướng, bằng nhau Các định nghĩa 2 trong hình.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 1 CHUYÊN ĐỀ: VECTƠ TLDH Tổng và hiêu hai
NB: Tính đúng sai của quy tắc 3 điểm đối với phép cộng, trừ hai véctơ, vectơ 3 quy tắc hình bình hành. Tổng và hiêu hai
NB: Độ dài của véctơ là tổng ( hiệu) hai vectơ cho trước ( xác định vectơ 4
véctơ tổng,hiệu bằng quy tắc ba điểm) Tích vectơ với một 5
NB: Khái niệm tích một số với véctơ. số Tích vectơ với một 6
NB: Hệ thức véc tơ đối với trọng tâm tam giác. số
Hệ trục tọa độ 7
NB: Các công thức liên quan tới tọa độ của vecto và các phép toán
Hệ trục tọa độ 8
NB: Xác định tọa độ của vectơ v biết….
Hệ trục tọa độ 9
NB: Tìm tọa độ vectơ AB biết……….
TH: Cho AB 0 và một điểm C , có bao nhiêu điểm D thỏa mãn: Các định nghĩa 10
AB CD …… Tổng và hiêu hai vectơ 11
TH: Áp dụng quy tắc cộng trừ vào bái toán vectơ Tổng và hiêu hai vectơ 12
TH: Bài toán liên quan tới các đẳng thức vectơ Tích vectơ với một
TH: Hệ thức véc tơ đối với trung điểm đoạn thẳng hoặc trọng tân tam 13 số
giác áp dụng trong rút gọn hệ thức véc tơ.
Hệ trục tọa độ 14
TH: Tìm tọa độ trung điểm hoặc trọng tâm tam giác
Hệ trục tọa độ 15
TH: Tìm điều kiện để hai vectơ cùng phương hoặc bằng nhau
Hệ trục tọa độ 16
TH: Các phép toán liên quan tới tổng hiêu vecto
TH: Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có B ,C
Hệ trục tọa độ 17
và N, M lần lượt là trung điểm của AB và AC . Tọa độ của vectơ MN . Tổng và hiêu hai vectơ 18
VDT: Bài toán thực tế liên quan tới tổng hiệu 2 vecto Tích vectơ với một 19
VDT: Bài toán tính độ dài tổ hợp vectơ số
Hệ trục tọa độ 20
VDT: Các phép toán liên quan tới các phép toán vectơ
Hệ trục tọa độ 21
VDT: Tìm tọa độ điểm thỏa mãn 1 đẳng thức vectơ,.
VDT: Trong mặt phẳng tọa độ Oxy , tọa độ A , B .Tìm tọa độ
Hệ trục tọa độ 22
C Ox sao cho ,
A B, C thẳng hàng Tích vectơ với một
VDC: Tìm điểm M thỏa mãn đẳng thức vectơ cho trước hoặc bài toán 23 số
liên quan tới phân tích vectơ
Hệ trục tọa độ 24
VDC: Bài toán liên quan tới tọa độ đỉnh, trong tâm tam giác
Hệ trục tọa độ
VDC: Trong mặt phẳng tọa độ Oxy cho a ,b ,c .Biết 25 c . m a .
n b .Tính m n ….
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 2 CHUYÊN ĐỀ: VECTƠ TLDH SỞ GD VÀ ĐT ABC
ĐỀ KIỂM TRA 1 TIẾT – NĂM HỌC 2018 2019 TRƯỜNG THPT ….
Môn: TOÁN – Hình học 10, CHƯƠNG I, Đề 1
Thời gian làm bài: 45 phút Điểm:
Họ và tên: …………………………………….
Lớp: ……………………………………………
Chọn đáp án đúng nhất.
Câu 1. [0H1-1.1-1] Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ.
Câu 2. [0H1-1.4-1] Cho lục giác đều ABCDEF tâm O . Số các vectơ khác vectơ không, cùng phương
với OC có điểm đầu và điểm cuối là các đỉnh của lục giác là: A. 4 . B. 6 . C. 7 . D. 9 .
Câu 3. [0H1-2.2-1] Cho ba điểm phân biệt A, B, C . Đẳng thức nào sau đây đúng?
A. CA BA BC .
B. AB AC BC .
C. AB CA CB .
D. AB BC CA .
Câu 4. [0H1-2.5-1] Cho tam giác ABC đều cạnh a . Khi đó AB AC bằng: a 3
A. AB AC a 3 .
B. AB AC . 2
C. AB AC 2a .
D. Một đáp án khác.
Câu 5. [0H1-3.0-1] Cho số thực k và vectơ a 0. Chọn khẳng định sai?
A. Vectơ k a cùng phương với a với mọi số thực k .
B. Vectơ k a cùng hướng với a nếu k 0, ngược hướng với a nếu k 0 và có độ dài bằng k . a .
C. Vectơ k a cùng hướng với a nếu k 0, ngược hướng với a nếu k 0 và có độ dài bằng k. a .
D. Điều kiện cần và đủ để hai vectơ a và b b 0 cùng phương là có một số k để a k b. .
Câu 6. [0H1-3.3-1] Cho ABC
có G là trọng tâm tam giác.Trong các biểu thức sau, đâu là biểu thức đúng?
A. AG GB GC 0 . B. AG BG GC 0 .
C. AG BG GC 0 . D. MA MB MC 3MG với điểm M tùy ý.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 3 CHUYÊN ĐỀ: VECTƠ TLDH
Câu 7. [0H1-5.7-1] Cho u 3
;2;v 2; 3 .Khi đó w 3
;15 được biểu diễn là
A. w 3u 2v .
B. w u 2v .
C. w 3u 3v .
D. w 3u 2v .
Câu 8. [0H1-5.3-1] Cho u 3 ;2, 7; 3 .Biết
u 2v ,tọa độ v là 1 1 5 1 1 A. 5; . B. 5; . C. ; . D. 5; . 2 2 2 2 2 Câu 9. 1
[0H1-5.3-1] Cho A 4; và 7 B 2;
.Tọa độ AB là 2 6 10 2 1 5 A. 2; . B. 6; . C. 3; . D. 1; . 3 3 3 3
Câu 10. [0H1-3.6-2] Cho hình bình hành ABCD với E là trung điểm của BC ; F là điểm thuộc đường
thẳng AC sao cho AB EF .Có bao nhiêu điểm F thỏa mãn điều kiện đã cho A. 0 . B. 1. C. 2 . D. 3 .
Câu 11. [0H1-2.2-2] Cho 5 điểm M , N, , P ,
Q R . Vectơ tổng MN PQ RN NP QR bằng: A. MP . B. PR . C. MR . D. MN .
Câu 12. [0H1-2.5-2] Cho 4 điểm ,
A B, C, D , Ta có đẳng thức sau:
A. AB CD AC BD . B. AB CD AC BD .
C. AB CD DA BA . D. AB AC BD DC . Câu 13. 1
[0H1-3.5-2] Cho tam giác ABC , E là điểm trên cạnh BC sao cho BE
BC . Hãy chọn đẳng 4 thức đúng: 3 1
A. AE 3AB 4AC . B. AE AB AC . 4 4 1 1 1 1 C. AE AB
AC . D. AE AB AC . 3 5 4 4
Câu 14. [0H1-5.3-2] Trong mặt phẳng tọa độ Oxy , cho tam giác ABC , biết A5; 2 ,B0; 3 ,C 5 ;
1 . Trọng tâm G của tam giác ABC có tọa độ: A. 0;0 . B. 10;0 . C. 1; 1 . D. 0;1 1 .
Câu 15. [0H1-3.5-2] Cho hai vectơ a và b không cùng phương. Hai vectơ nào sau đây là cùng phương: 1 3 3
A. u 2a 3b và v a 3b . B. u
a 3b và v 2a b . 2 5 5
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 4 CHUYÊN ĐỀ: VECTƠ TLDH 2 3 1 1 C. u
a 3b và v 2a 9b .
D. u 2a
b và v a b . 3 2 3 4
Câu 16. [0H1-2.2-2] Cho tam giác ABC , gọi I, J, K lần lượt là trung điểm của các cạnh BC,C , A A . B
Xét các mệnh đề sau: (I) AB BC AC 0, (II)KB JC AI, (III) AK BI CJ 0 . Mệnh đề sai là A. Chỉ (I) .
B. (II) và (III). . C. Chỉ (II) .
D. (I) và (III). .
Câu 17. [0H1-5.3-2] Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có B1; 3 ,C 13; 5 và N, M
lần lượt là trung điểm của A ,
B AC . Tìm tọa độ của vectơ MN .
A. MN 6; 1 .
B. MN 7;4 .
C. MN 12;2 .
D. MN 14;8 .
Câu 18. [0H1-3.5-3] Cho hai lực F , F có điểm đặt tại O , có cường độ bằng nhau và tạo với nhau một 1 2 góc 0
120 . Biết cường độ lực tổng hợp của hai lực đó là 100(N) . Tính cường độ của lực F . 1
A. F 100(N) .
B. F 100 3(N) .
C. F 50(N) .
D. F 50 3(N) . 1 1 1 1
Câu 19. [0H1-2.6-3] Cho tam giác đều ABC cạnh AB 4 . Tính AB AC .
A. AB AC 4 3 .
B. AB AC 2 3 . C. AB AC 6 3 . D. AB AC 3 3. .
Câu 20. [0H1-2.2-3] Cho 4 điểm A, B, C, D phân biệt. Tổng AB CD AD CB bằng A. 0 . B. AD . C. BD . D. 2BD .
Câu 21. [0H1-5.3-3] Cho hai điểm M 1 ; 6 và N 6 ;
3 . Tìm điểm P mà PM 2PN .
A. P11 ; 0 .
B. P 6 ; 5 .
C. P2 ; 4 . D. P0 ; 1 1 .
Câu 22. [0H1-5.6-3] Cho hai điểm M –2;2 , N 1;
1 . Tìm tọa độ điểm P trên Ox sao cho 3 điểm
M , N, P thẳng hàng. A. P0;4 .
B. P 0; –4 .
C. P –4;0 . D. P4;0 .
Câu 23. [0H1-3.5-4] (Quy) Cho tam giác ABC với phân giác trong AD . Biết AB 5, BC 6 , CA 7
. Khi đó AD bằng: 5 7 7 5 7 5 5 7 A. AB AC . B. AB AC . C. AB AC . D. AB AC . 12 12 12 12 12 12 12 12
Câu 24. [0H1-3.8-4] Cho ABC có A0; 2
, B4;0 , C1;
1 và G là trọng tâm. Nếu M là điểm trên
đường thẳng d có phương trình y 2 sao cho MA MB MC bé nhất thì tọa độ của vectơ MG là:
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 5 CHUYÊN ĐỀ: VECTƠ TLDH 5 7 5 7 7 7 A. ; . B. ; . C. 0; . D. 0; . 3 3 3 3 3 3
Câu 25. [0H1-5.3-4] Trong mặt phẳng tọa độ Oxy , cho ba vectơ a 1;3 , b 1;2 , c 3; 1 . Biết
a xb yc . Tính A xy x . y A. A 5 . B. A 6 . C. A 3 . D. A 1. --------HẾT---------
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 6 CHUYÊN ĐỀ: VECTƠ TLDH ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 A B C A C D C A B C 11 12 13 14 15 16 17 18 19 20 D A B A D A A A A A 21 22 23 24 25 A D C D D ĐÁP ÁN CHI TIẾT.
Câu 1. [0H1-1.1-1] Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ. Lời giải Chọn A.
Vì Vectơ không cùng phương với mọi vectơ.
Câu 2. [0H1-1.3-1] Cho lục giác đều ABCDEF tâm O . Số các vectơ khác vectơ không, cùng phương
với OC có điểm đầu và điểm cuối là các đỉnh của lục giác là: A. 4 . B. 6 . C. 7 . D. 9 Lời giải Chọn B. C B D A O E F
Đó là các vectơ: AB, B ,
A DE, ED, FC, CF .
Câu 3. [0H1-2.2-1] Cho ba điểm phân biệt , A ,
B C . Đẳng thức nào sau đây đúng?
A. CA BA BC .
B. AB AC BC .
C. AB CA CB .
D. AB BC CA Lời giải Chọn C Xét các đáp án: Đáp án.
A. Ta có CA BA CA AB CB BC . Vậy A sai.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 7 CHUYÊN ĐỀ: VECTƠ TLDH Đáp án.
B. Ta có AB AC AD BC (với D là điểm thỏa mãn ABDC là
hình bình hành). Vậy B sai. Đáp án.
C. Ta có AB CA CA AB CB . Vậy C đúng.
Câu 4. [0H1-2.6-1] Cho tam giác ABC đều cạnh a . Khi đó AB AC bằng: a 3
A. AB AC a 3 .
B. AB AC . 2
C. AB AC 2a .
D. Một đáp án khác. Lời giải Chọn A.
Gọi H là trung điểm của BC AH BC A BC 3 a 3 Suy ra AH 2 2 a Ta lại có 3
AB AC 2 AH 2. a 3 . 2 B H C
Câu 5. [0H1-3.0-1] Cho số thực k và vectơ a 0. Chọn khẳng định sai?
A. Vectơ k a cùng phương với a với mọi số thực k .
B. Vectơ k a cùng hướng với a nếu k 0, ngược hướng với a nếu k 0 và có độ dài bằng k . a .
C. Vectơ k a cùng hướng với a nếu k 0, ngược hướng với a nếu k 0 và có độ dài bằng k. a .
D. Điều kiện cần và đủ để hai vectơ a và b b 0 cùng phương là có một số k để a k b. Lời giải Chọn C.
Câu 6. [0H1-3.3-1] Cho ABC
có G là trọng tâm tam giác.Trong các biểu thức sau,đâu là biểu thức đúng?
A. AG GB GC 0 . B. AG BG GC 0 .
C. AG BG GC 0 . D. MA MB MC 3MG với điểm M tùy ý. Lời giải Chọn D.
Câu 7. [0H1-5.3-1] Cho u 3
;2,v 2; 3 . Khi đó w 3
;15 được biểu diễn là
A. w 3u 2v .
B. w u 2v .
C. w 3u 3v .
D. w 3u 2v . Lời giải Chọn C.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 8 CHUYÊN ĐỀ: VECTƠ TLDH x . a x bx 3 3 a 2b a 3
Giả sử a, b là cặp số thỏa mãn u v
au bv . y . a y by
15 2a 3b b 3 u v
Câu 8. [0H1-5.3-1] Cho u 3 ;2, 7; 3 .Biết
u 2v ,tọa độ v là 1 1 5 1 1 A. 5; . B. 5; . C. ; . D. 5; . 2 2 2 2 2 Lời giải Chọn A. a 5
x x 2x 7 3 2a
Giả sử v a,b thỏa mãn u 2 u v v 1 .
y y 2 y 3 2 2b b u v 2 Câu 9. 1
[0H1-5.3-1] Cho A 4; và 7 B 2;
.Tọa độ AB là 2 6 10 2 1 5 A. 2; . B. 6; . C. 3; . D. 1; . 3 3 3 3 Lời giải Chọn B. Theo định nghĩa vectơ, 2 AB 6; . 3
Câu 10. [0H1-1.5-2] Cho hình bình hành ABCD với E là trung điểm của BC ; F là điểm thuộc đường
thẳng AC sao cho AB EF .Có bao nhiêu điểm F thỏa mãn điều kiện đã cho A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn C. H A D F1 F2 B E C
dựng EH / / AB . Đường tròn E, EH cắt AC tại hai điểm F , F . 1 2
Câu 11. [0H1-2.2-2] Cho 5 điểm M , N, , P ,
Q R . Vectơ tổng MN PQ RN NP QR bằng: A. MP . B. PR . C. MR . D. MN . Lời giải Chọn D.
Sử dụng quy tắc cộng:
MN PQ RN NP QR MN NP PQ QR RN MP PR RN MR RN MN .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 9 CHUYÊN ĐỀ: VECTƠ TLDH
Câu 12. [0H1-2.3-2] Cho 4 điểm ,
A B, C, D . Ta có đẳng thức sau:
A. AB CD AC BD .
B. AB CD AC BD .
C. AB CD DA BA .
D. AB AC BD DC . Lời giải Chọn A. Câu 13. 1
[0H1-3.5-2] Cho tam giác ABC , E là điểm trên cạnh BC sao cho BE
BC . Hãy chọn đẳng 4 thức đúng:
A. AE 3AB 4AC . 3 1 B. AE AB AC . 4 4 1 1 1 1 C. AE AB AC . D. AE AB AC . 3 5 4 4 Lời giải Chọn B.
Vì khi phân tích AE hAB k AC thì hai số h, k không thể lớn hơn 1, không có số âm và không thể bằng nhau.
Câu 14. [0H1-5.3-2] Trong mặt phẳng tọa độ Oxy , cho tam giác ABC , biết A5; 2 ,B0; 3 ,C 5 ;
1 . Trọng tâm G của tam giác ABC có tọa độ: A. 0;0 . B. 10;0 . C. 1; 1 . D. 0;1 1 . Lời giải Chọn A.
Sử dụng công thức tính tọa độ trọng tâm G khi biết tọa độ ba đỉnh , A B, C .
x x x A B C x G 3 .
y y y A B C y G 3
Câu 15. [0H1-3.5-2] Cho hai vectơ a và b không cùng phương. Hai vectơ nào sau đây là cùng phương: 1 3 3
A. u 2a 3b và v a 3b . B. u
a 3b và v 2a b . 2 5 5 2 3 1 1 C. u
a 3b và v 2a 9b .
D. u 2a
b và v a b 3 2 3 4 Lời giải Chọn D:
Cách 1: Sử dụng kiến thức nếu u kv thì u và v cùng phương. Cách 2: x y x y Cho u ;
x y ; v x ; y . Lập tỉ số ;
x y , nếu x
y thì u và v cùng phương.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 10 CHUYÊN ĐỀ: VECTƠ TLDH
Chú ý: Xét tỉ số dấu trước để loại phương án.
Câu 16. [0H1-2.2-2] Cho tam giác ABC , gọi I, J, K lần lượt là trung điểm của các cạnh BC,C , A A . B
Xét các mệnh đề sau: (I) AB BC AC 0, (II)KB JC AI, (III) AK BI CJ 0 . Mệnh đề sai là A. Chỉ (I) .
B. (II) và (III). . C. Chỉ (II) .
D. (I) và (III). Lời giải Chọn A:
Sử định nghĩa phép cộng vectơ
Phân tích phương án nhiễu:
B,C, D: Học sinh nhầm lẫn tính chất vectơ.
Câu 17. [0H1-2.2-2] Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có B1; 3 ,C 13; 5 và N, M
lần lượt là trung điểm của A ,
B AC . Tìm tọa độ của vectơ MN
A. MN 6; 1 .
B. MN 7;4 .
C. MN 12;2 .
D. MN 14;8 . Lời giải Chọn A: 1 Sử dụng MN BC. 2
Phân tích phương án nhiễu:
B,C, D: Học sinh nhầm lẫn công thức tính tọa độ của vectơ.
Câu 18. [0H1-3.5-3] Cho hai lực F , F có điểm đặt tại O , có cường độ bằng nhau và tạo với nhau một 1 2 góc 0
120 . Biết cường độ lực tổng hợp của hai lực đó là 100(N) . Tính cường độ của lực F . 1
A. F 100(N) . 1
B. F 100 3(N) . 1
C. F 50(N) . 1
D. F 50 3(N) 1 Lời giải Chọn A:
Sử dụng các tính chất của hình thoi, tam giác đều.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 11 CHUYÊN ĐỀ: VECTƠ TLDH
Phân tích phương án nhiễu:
B,C, D: Học sinh nhầm lẫn tính chất.
Câu 19. [0H1-2.6-3] Cho tam giác đều ABC cạnh AB 4 . Tính AB AC .
A. AB AC 4 3 .
B. AB AC 2 3 .
C. AB AC 6 3 .
D. AB AC 3 3. Lời giải Chọn A:
Sử dụng các tính chất của hình thoi, tam giác đều.
Phân tích phương án nhiễu:
B,C, D: Học sinh nhầm lẫn tính chất.
Câu 20. [0H1-2.2-3] Cho 4 điểm A, B, C, D phân biệt. Tổng AB CD AD CB bằng A. 0 . B. AD . C. BD . D. 2BD . Lời giải Chọn A:
Sử dụng các tính chất của phép cộng trừ vectơ.
Phân tích phương án nhiễu:
B,C, D: Học sinh nhầm lẫn tính chất.
Câu 21. [0H1-5.3-3]Cho hai điểm M 1 ; 6 và N 6 ;
3 . Tìm điểm P mà PM 2PN .
A. P11 ; 0 .
B. P 6 ; 5 .
C. P 2 ; 4 . D. P0 ; 1 1 . Lời giải Chọn A. 1 2.6 x 11 P 1 2
PM 2PN P 11 ; 0 . 6 2.3 y 0 P 1 2
Câu 22. [0H1-2.7-3] Cho hai điểm M –2;2 , N 1;
1 . Tìm tọa độ điểm P trên Ox sao cho 3 điểm
M , N, P thẳng hàng. A. P0;4 .
B. P 0; –4 .
C. P –4;0 . D. P4;0 . Hướng dẫn giải:
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 12 CHUYÊN ĐỀ: VECTƠ TLDH Chọn D
Do P Ox nên P ;0
x , mà MP x 2; 2
;MN 3; 1 x
Do M , N, P thẳng hàng nên 2 2 x 4 . 3 1
Câu 23. [0H1-3.5-4] Cho tam giác ABC với phân giác trong AD . Biết AB 5, BC 6 , CA 7 . Khi
đó AD bằng: 5 7 7 5 7 5 5 7 A. AB AC . B. AB AC . C. AB AC . D. AB AC . 12 12 12 12 12 12 12 12 Hướng dẫn giải Chọn C. A 7 5 B D C
Vì AD là phân giác trong của tam giác ABC nên: BD AB 5 5
BD DC DC AC 7 7 5
AD AB AC AD 7 7 5 AD AB AC . 12 12
Câu 24. [0H1-5.3-4]Cho ABC có A0; 2
, B4;0 , C1;
1 và G là trọng tâm. Nếu M là điểm trên
đường thẳng d có phương trình y 2 sao cho MA MB MC bé nhất thì tọa độ của vectơ MG là: 5 7 5 7 7 7 A. ; . B. ; . C. 0; . D. 0; . 3 3 3 3 3 3 Lời giải Chọn D.
Vì G là trọng tâm tam giác ABC
nên MA MB MC 3MG MA MB MC 3 MG
bé nhất MG bé nhất M là chân đường vuông góc kẻ từ G đến d . Khi đó 5 7 x x M ; 2 MG 0; . M G 3 3
Câu 25. [0H1-5.3-4] Trong mặt phẳng tọa độ Oxy , cho ba vectơ a 1;3 , b 1;2 , c 3; 1 .
Biết a xb yc . Tính A xy x . y A. A 5 . B. A 6 . C. A 3 . D. A 1 . Hướng dẫn giải
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 13 CHUYÊN ĐỀ: VECTƠ TLDH Chọn D. x 3y 1 x 2
Ta có a xb yc
. Do đó A xy x y 1. 2
x y 3 y 1
----------------------HẾT-------------------
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 14 CHUYÊN ĐỀ: VECTƠ TLDH
Chương I: VÉCTƠ HỆ TRỤC TỌA ĐỘ TRONG MẶT PHẲNG
KIỂM TRA 1 TIẾT CHƯƠNG 1 I. MỤC TIÊU: 1. Kiến thức:
Ôn tập toàn bộ kiến thức trong chương I. 2. Kĩ năng:
Biết được khái niệm vectơ, giá của vectơ, hai vectơ cùng phương, hai vectơ cùng hướng, độ dài vectơ.
Vận dụng tính độ dài vectơ.
Hiểu và vận dụng được các quy tắc: Quy tắc ba điểm, quy tắc hình bình hành, quy tắc trừ để giải toán.
Tích của một số với một vectơ:
Biết biểu diễn một vectơ thông qua một vectơ cho trước.
Biết phân tích một vectơ thông qua hai vectơ cùng phương.
Biết được các khái niệm trục tọa độ, hệ trục tọa độ.
Biết được tọa độ của điểm, của vectơ trên trục và trong hệ trục tọa độ.
Biết và vận dụng được công thức tính tọa độ trung điểm của đoạn thẳng, tọa độ trọng tâm tam giác. 3. Thái độ:
Rèn luyện tính cẩn thận, chính xác. II. CHUẨN BỊ:
1. Giáo viên: Giáo án. Đề kiểm tra.
2. Học sinh: Ôn tập toàn bộ kiến thức chương 1. III. MA TRẬN ĐỀ:
MA TRẬN NHẬN THỨC Tầm quan Trọng số Tổng điểm theo trọng (Mức độ Tổng thang điểm 10
Chủ đề hoặc mạch kiến thức, kĩ (Mức cơ bản nhận thức điểm năng trọng tâm của của Chuẩn KTKN) KTKN) 1. Định nghĩa vectơ: 15 3 50 1.0 2. Tổng của hai véctơ 20 4 60 2.0 3. Tổng của hai véctơ 20 4 60 2.0
4. Tích của một số với một vectơ: 15 2 30 1.0 5. Hệ trục tọa độ: 30 5 80 4.0 100% 280 10
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 15 CHUYÊN ĐỀ: VECTƠ TLDH
MA TRẬN ĐỀ KIỂM TRA Tổng Mức độ Vận dụng Vận dụng Biết Hiểu Số Số Chủ đề thấp cao câu điểm Định nghĩa 2 1 3 Véctơ 0,8 0,4 1,2 Cộng hai vectơ 1 3 4 0,4 1,2 1,6 Hiệu hai vectơ 1 1 1 1 4 0,4 0,4 0,4 0,4 1,6 Nhân một số với 1 2 1 1 2 6 vectơ 0,8 0,4 0,4 0,8 2,4 Hệ trục tọa độ 3 2 3 8 1,2 0,8 1,2 3,2 Tổng Số câu 9 8 5 3 25 Số điểm 3,6 3,4 2,0 1,2 10,0 MÔ TẢ MA TRẬN Kiến thức Câu Mô tả ĐN-VT 1
Nhận biết: Định nghĩa hai vectơ cùng phương. ĐN-VT 2
Nhận biết: Hai vectơ bằng nhau. Cộng VT 3
Nhận biết: quy tắc 3 điểm. Hiệu-VT 4
Nhận biết: quy tắc hiệu. Nhân –VT 5
Nhận biết: Cho tam giác ABC có trọng tâm G. Chọn đáp án đúng. Nhân-VT 6
Nhận biết: Dựa vào tính chất phép nhân một số với 1 vectơ.
Hệ trục tọa độ 7
Nhận biết: Tọa độ của điểm M theo hai vectơ đơn vị.
Hệ trục tọa độ 8
Nhận biết: Tọa độ tổng hai vectơ.
Hệ trục tọa độ 9
Nhận biết: Công thức tính tọa độ vectơ AB . ĐN-VT 10
Thông hiểu: Tìm số vectơ bằng vectơ cho trước. Nhân-VT 11
Thông hiểu: Tìm số vectơ bằng vectơ cho trước. Cộng –VT 12
Thông hiểu: Cho 4 điểm bất kỳ.Chọn đáp án đúng khi tìm tổng các vectơ 13
Thông hiểu: Chọn đáp án sai trong quy tắc 3 điểm,quy tắc hiệu hai véc Hiệu-VT tơ. Cộng –VT 14
Thông hiểu: Cho hình vuông.Tính độ dài của tổng 2 vectơ. Cộng-VT 15
Thông hiểu: Cho tam giác.Xác định vị trí điểm.
Hệ trục tọa độ 16
Thông hiểu: Tọa độ trọng tâm của tam giác. 17
Thông hiểu: Cho trước tọa độ hai vectơ. Tìm tọa độ của vectơ biểu diễn
Hệ trục tọa độ theo hai vectơ cho trước. Hiệu -VT 18
Vận dụng thấp: Tính độ dài một vectơ.
Hệ trục tọa độ 19
Vận dụng thấp: Tìm tọa độ 1 điểm qua phép: tổng, hiệu, tích (vận dụng
các quy tắc,các tính chất của hai véc tơ). Nhân-VT 20
Vận dụng thấp: Cho tam giác đều.Tính độ dài một vectơ (sử dụng t/c
trung điểm đoạn thẳng).
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 16 CHUYÊN ĐỀ: VECTƠ TLDH
Hệ trục tọa độ 21
Vận dụng thấp: Tìm toạ độ đỉnh thứ tư của hình bình hành.
Hệ trục tọa độ 22
Vận dụng thấp: Tìm tọa độ điểm, thỏa điều kiện ba điểm thẳng hàng. Nhân-VT 23
Vận dụng cao:Biểu thị một vectơ theo hai vectơ không cùng phương. Nhân-VT 24
Vận dụng cao: Biểu thị một vectơ theo hai vectơ không cùng phương. Cộng-Trừ-Nhân 25
Vận dụng cao:Xác định tập hợp điểm M thỏa điều kiện bài toán. SỞ GD VÀ ĐT ABC
ĐỀ KIỂM TRA 1 TIẾT – NĂM HỌC 2018-2019 TRƯỜNG THPT ….
Môn: TOÁN – Hình học, CHƯƠNG I, Đề 2
Thời gian làm bài: 45 phút Điểm:
Họ và tên: …………………………………….
Lớp: ……………………………………………
Chọn đáp án đúng nhất.
Câu 1. [0H1-1.1-1] Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ.
Câu 2. [0H1-1.6-1] Hai vectơ được gọi là bằng nhau khi và chỉ khi
A. Giá của chúng trùng nhau và độ dài của chúng bằng nhau.
B. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành.
C. Chúng trùng với một trong các cặp cạnh đối của một tam giác đều.
D. Chúng cùng hướng và độ dài của chúng bằng nhau.
Câu 3. [0H1-2.2-1] Khẳng định nào sau đây đúng?
A. AB AC BC .
B. MP NM NP .
C. CA BA CB .
D. AA BB AB .
Câu 4. [0H1-2.2-2] Gọi O là tâm hình bình hành ABCD. Đẳng thức nào sau đây sai?
A. OA OB CD .
B. OB OC OD OA .
C. AB AD DB .
D. BC BA DC DA .
Câu 5. [0H1-3.3-2] Cho ABC
có trung tuyến AM và trọng tâm G . Khẳng định nào sau đây đúng: 1
A. AM AB AC .
B. MG MA MB MC . 3 2
C. AM 3MG . D. AG
AB AC. 3
Câu 6. [0H1-3.3-2] Cho ABC
có trung tuyến AM và trọng tâm G . Khẳng định nào sau đây đúng:
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 17 CHUYÊN ĐỀ: VECTƠ TLDH 1
A. AM AB AC .
B. MG MA MB MC . 3 2
C. AM 3MG . D. AG
AB AC. 3
Câu 7. [0H1-5.2-1] Trong hệ trục tọa độ ; O ;
i j tọa độ i j là: A. 0; 1 . B. (1; 1 ) . C. ( 1 ;1) . D. (1;1) .
Câu 8. [0H1-5.3-1] Cho a 3; 4 , b 1
;2. Tìm tọa độ của a . b A. 4 ;6 . B. 2; 2 . C. 4; 6 . D. 3 ; 8 .
Câu 9. [0H1-5.3-1] Trong mặt phẳng tọa độ Oxy, cho A 5
;2, B10;8. Tìm tọa độ của vectơ . AB A. 5;10 . B. 15;6 . C. 5;6. D. 5 0;16.
Câu 10. [0H1-5.4-2] Cho tứ giác ABCD. Điều kiện nào là điều kiện cần và đủ để AB CD ?
A. ABCD là hình bình hành.
B. ABDC là hình bình hành.
C. AD và BC có cùng trung điểm.
D. AB C . D .
Câu 11. [0H1-1.6-2] Gọi M , N lần lượt là trung điểm của các cạnh A ,
B AC của tam giác đều ABC .
Đẳng thức nào sau đây đúng?
A. MA MB .
B. AB AC .
C. MN BC .
D. BC 2 MN .
Câu 12. [0H1-2.3-2] Cho bốn điểm , A ,
B C, D . Mệnh đề nào sau đây đúng?
A. AB CD AD CB .
B. AB BC CD DA .
C. AB BC CD DA .
D. AB AD CD CB .
Câu 13. [0H1-2.3-2] Cho tam giác ABC vuông cân đỉnh A , đường cao AH . Khẳng định nào sau đây sai?
A. AH HB AH HC .
B. AH AB AC AH .
C. BC BA HC HA .
D. AH AB AH .
Câu 14. [0H1-2.5-2] Cho hình vuông ABCD cạnh a , tâm O . Tính OA CB 2 a 2 a 2 A. . B. 1 a . C. a . D. . 2 2 2
Câu 15. [0H1-2.7-2] Cho tam giác ABC và điểm M thỏa mãn điều kiện MA MB MC 0 . Mệnh
đề nào sau đây sai?
A. MABC là hình bình hành.
B. AM AB AC .
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 18 CHUYÊN ĐỀ: VECTƠ TLDH
C. BA BC BM .
D. MA BC..
Câu 16. [0H1-5.3-2] Trong hệ tọa độ Oxy, cho tam giác ABC có A6; 1 , B 3 ;5 và trọng tâm G 1 ;
1 . Tìm tọa độ đỉnh C ? A. 6; 3 . B. 6 ; 3 . C. 6 ; 3 . D. 3 ;6 .
Câu 17. [0H1-5.3-2] Trong mặt phẳng tọa độ Oxy , cho hai vectơ a 1;
1 , b 0;2 . Xác định tọa
độ của vectơ x sao cho x b 2a . A. x 2 ;0 . B. x 2 ;4 . C. x 1 ; 1 . D. x 1 ;3.
Câu 18. [0H1-2.6-2] Cho tam giác ABC đều cạnh a , H là trung điểm của BC . Tính CA HC . a 3a 2 3a a 7
A. CA HC .
B. CA HC .
C. CA HC
. D. CA HC . 2 2 3 2
Câu 19. [0H1-3.6-2] Trong mặt phẳng tọa độ Oxy , cho ba điểm A1;
1 , B2;0 , C 3;5 . Tìm tọa
độ điểm D sao cho AB 2AC 3AD 0 . 8 A. D 2; . B. D3; 3 . C. D6;6 . D. D3; 2 . 3
Câu 20. [0H1-3.4-2] Cho tam giác ABC đều cạnh 2a . Khi đó độ dài vectơ AB AC bằng: A. 2a . B. 2a 3 . C. 4a . D. a 3 .
Câu 21. [0H1-3.7-2] Trong hệ tọa độ Oxy, cho ba điểm A1;
1 , B3;2, C 6;
5 . Tìm tọa độ điểm D
để ABCD là hình bình hành. A. 4;3. B. 3; 4. C. 4;4 . D. 8;6.
Câu 22. [0H1-3.7-3] Trong hệ tọa độ Oxy , cho hai điểm A2;
3 , B3;4. Tìm tọa độ điểm M trên trục hoành sao cho , A , B M thẳng hàng. 5 1 17
A. M 1;0 .
B. M 4;0 . C. M ; . D. M ; 0 . 3 3 7
Câu 23. [0H1-3.5-3] Cho AD và BE là hai phân giác trong của tam giác ABC . Biết AB 4 , BC 5
và CA 6. Khi đó DE bằng: 5 3 3 5 9 3 3 9
A. CA CB .
B. CA CB .
C. CA CB .
D. CA CB . 9 5 5 9 5 5 5 5
Câu 24. [0H1-2.4-3] Cho tam giác ABC , AM là trung tuyến, G là trọng tâm. Gọi E, F theo thứ tự là
trung điểm của BG và CG . Khi đó GE GF bằng:
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 19 CHUYÊN ĐỀ: VECTƠ TLDH 1 1 2 5
A. AB AC .
B. AB AC .
C. AB AC .
D. AB AC . 3 6 3 6
Câu 25. [0H1-3.7-4] Cho tam giác đều ABC cạnh a. Biết rằng tập hợp các điểm M thỏa mãn đẳng
thức 2MA 3MB 4MC MB MA là đường tròn cố định có bán kính .
R Tính bán kính R theo a. a a a a A. r . . B. r . . C. r . . D. r . 3 9 2 6
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 20 CHUYÊN ĐỀ: VECTƠ TLDH ĐÁP ÁN 1.A 2.D 3.B 4.D 5.B 6.B 7.D 8.B 9.B 10.B 11.D 12.A 13.B 14.D 15.D 16.C 17.B 18.D 19.A 20.B 21.C 22.D 23.A 24.B 25.B ĐÁP ÁN CHI TIẾT.
Câu 1. [0H1-1.1-1] Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ. Lời giải. Chọn A.
Vì Vectơ không cùng phương với mọi vectơ.
Câu 2. [0H1-1.6-1] Hai vectơ được gọi là bằng nhau khi và chỉ khi
A. Giá của chúng trùng nhau và độ dài của chúng bằng nhau.
B. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành.
C. Chúng trùng với một trong các cặp cạnh đối của một tam giác đều.
D. Chúng cùng hướng và độ dài của chúng bằng nhau. Lời giải. Chọn D.
Câu 3. [0H1-2.2-1] Khẳng định nào sau đây đúng?
A. AB AC BC .
B. MP NM NP .
C. CA BA CB .
D. AA BB A . B Lời giải. Chọn B. Xét các đáp án: Đáp án.
A. Ta có AB AC AD BC (với D là điểm thỏa mãn ABDC là
hình bình hành). Vậy A sai. Đáp án.
B. Ta có MP NM NM MP NP . Vậy B đúng. Đáp án.
C. Ta có CA BA AC AB AD CB (với D là điểm thỏa
mãn ABDC là hình bình hành). Vậy C sai. Đáp án.
D. Ta có AA BB 0 0 0 AB . Vậy D sai.
Câu 4. [0H1-2.2-2] Gọi O là tâm hình bình hành ABCD. Đẳng thức nào sau đây sai?
A. OA OB CD .
B. OB OC OD OA .
C. AB AD DB .
D. BC BA DC D . A Lời giải.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 21 CHUYÊN ĐỀ: VECTƠ TLDH Chọn D. Xét các đáp án: D Đáp án.
A. Ta có OA OB BA CD . Vậy A A B đúng. O OB
OC CB AD Đáp án. B. Ta có . Vậy B D C OD OA AD sai. Đáp án.
C. Ta có AB AD D . B Vậy C đúng.
BC BA AC Đáp án. D. Ta có . Vậy D đúng.
DC DA AC
Câu 5. [0H1-3.3-2] Cho ABC
có trung tuyến AM và trọng tâm G . Khẳng định nào sau đây đúng: 1
A. AM AB AC .
B. MG MA MB MC . 3 2
C. AM 3MG . D. AG AB AC. 3 Lời giải. Chọn B. A G B M C .
Ta có: Nếu G là trọng tâm của ABC
và M là điểm tùy ý thì 1
MA MB MC 3MG MG
MAMBMC 3
Phân tích phương án nhiễu:
Phương án A: Sai do HS dùng sai M là trung điểm của cạnh BC 1 AM AB AC. 2
Phương án C: Sai do HS dùng sai AM và MG là 2 vectơ ngược chiều AM 3 MG
Phương án D: Sai do HS dùng sai M là trung điểm của cạnh BC 2 2 1 AG AM AB AC 1 .
AB AC. 3 3 2 3
Câu 6. [0H1-3.3-2] Cho ABC
có trung tuyến AM và trọng tâm G . Khẳng định nào sau đây đúng: 1
A. AM AB AC .
B. MG MA MB MC . 3
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 22 CHUYÊN ĐỀ: VECTƠ TLDH 2
C. AM 3MG . D. AG AB AC. 3 Lời giải. Chọn B. A G B M C .
Ta có: Nếu G là trọng tâm của ABC
và M là điểm tùy ý thì 1
MA MB MC 3MG MG
MAMBMC 3
Phân tích phương án nhiễu:
Phương án A: Sai do HS dùng sai M là trung điểm của cạnh BC 1 AM AB AC. 2
Phương án C: Sai do HS dùng sai AM và MG là 2 vectơ ngược chiều AM 3 MG
Phương án D: Sai do HS dùng sai M là trung điểm của cạnh BC 2 2 1 AG AM AB AC 1 .
AB AC. 3 3 2 3
Câu 7. [0H1-5.2-1] Trong hệ trục tọa độ ; O ;
i j tọa độ i j là: A. 0; 1 . B. (1; 1 ) . C. ( 1 ;1) . D. (1;1) . Lời giải. Chọn D.
Ta có i 1;0, j 0; 1
i j 1; 1 . .
Câu 8. [0H1-5.3-1] Cho a 3; 4 , b 1
;2. Tìm tọa độ của a . b A. 4 ;6 . B. 2; 2 . C. 4; 6 . D. 3 ; 8 . Lời giải. Chọn B.
Ta có a b 3 1 ; 4 2 2; 2 ..
Câu 9. [0H1-5.3-1] Trong mặt phẳng tọa độ Oxy, cho A 5
;2, B10;8. Tìm tọa độ của vectơ . AB A. 5;10 . B. 15;6 . C. 5;6. D. 5 0;16. Lời giải.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 23 CHUYÊN ĐỀ: VECTƠ TLDH Chọn B.
Ta có: AB x x ; y y 105;8 2 15;6 B A B A
Phân tích phương án nhiễu:
Phương án A: Sai do cộng tọa độ với nhau.
Phương án C: Sai do dùng công thức tọa độ của vectơ, không đổi dấu.
Phương án D: Sai do nhầm lẫn một phần công thức tích vô hướng.
Câu 10. [0H1-5.4-2] Cho tứ giác ABCD. Điều kiện nào là điều kiện cần và đủ để AB CD ?
A. ABCD là hình bình hành.
B. ABDC là hình bình hành.
C. AD và BC có cùng trung điểm.
D. AB C . D Lời giải. Chọn B. Ta có: AB CD
AB CD
ABDC là hình bình hành. AB CD AB CD
Mặt khác, ABDC là hình bình hành AB CD . AB CD
Do đó, điều kiện cần và đủ để AB CD là ABDC là hình bình hành.
Câu 11. [0H1-1.6-2] Gọi M , N lần lượt là trung điểm của các cạnh A ,
B AC của tam giác đều ABC .
Đẳng thức nào sau đây đúng?
A. MA MB .
B. AB AC .
C. MN BC .
D. BC 2 MN . Lời giải. Chọn D. A M N B C
Ta có MN là đường trung bình của tam giác ABC .
Do đó BC 2MN
BC 2 MN . .
Câu 12. [0H1-2.3-2] Cho bốn điểm , A ,
B C, D . Mệnh đề nào sau đây đúng?
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 24 CHUYÊN ĐỀ: VECTƠ TLDH
A. AB CD AD CB .
B. AB BC CD DA .
C. AB BC CD D . A .
D. AB AD CD C . B Lời giải. Chọn A.
Ta có AB CD AD DB CB BD AD CB .
Câu 13. [0H1-2.3-2] Cho tam giác ABC vuông cân đỉnh A , đường cao AH . Khẳng định nào sau đây sai?
A. AH HB AH HC .
B. AH AB AC AH .
C. BC BA HC HA .
D. AH AB AH . Lời giải. Chọn B. Do ABC
cân tại A , AH là đường cao nên H là trung điểm BC . Xét các đáp án: A
AH HB AB a Đáp án A. Ta có
AH HC AC a B H C
AH HB AH HC .
AH AB BH Đáp án B. Ta có .
AH AC CH BH
Đáp án C. Ta có BC BA HC HA AC.
Đáp án D. Ta có AB AH HB AH . (do ABC
vuông cân tại A ).
Câu 14. [0H1-2.5-2] Cho hình vuông ABCD cạnh a , tâm O . Tính OA CB 2 a 2 a 2 A. . B. 1 a . C. a . D. . 2 2 2 Lời giải. Chọn D. A B O D C
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 25 CHUYÊN ĐỀ: VECTƠ TLDH
Ta có: hình vuông ABCD cạnh a , tâm O nên đường chéo BD a 2 BD a Mặt khác: 2
OA CB OA AD OD OD . 2 2
Phân tích phương án nhiễu:
Phương án A: Sai do HS tính 2 2 2 2 4 2
BD BA AD a a a a . 2 BD a
OA CB OA AD OD OD . 2 2
Phương án B: Sai do HS tính a 2 2 OA CB a 1 a . 2 2
Phương án C: Sai do HS tính BD BA AD a a 2a . BD 2a
OA CB OA AD OD OD a . 2 2
Câu 15. [0H1-2.7-2] Cho tam giác ABC và điểm M thỏa mãn điều kiện MA MB MC 0 . Mệnh
đề nào sau đây sai?
A. MABC là hình bình hành.
B. AM AB AC .
C. BA BC BM .
D. MA BC. Lời giải. Chọn A. Ta có A M
MA MB MC 0 BA MC 0 MC AB B C
MABC là hình bình hành. .
Câu 16. [0H1-5.3-2] Trong hệ tọa độ Oxy, cho tam giác ABC có A6; 1 , B 3 ;5 và trọng tâm G 1 ;
1 . Tìm tọa độ đỉnh C ? A. 6; 3 . B. 6 ; 3 . C. 6 ; 3 . D. 3 ;6 . Lời giải. Chọn C. 6 3 x 1 x 6 Gọi C ;
x y . Ta có G là trọng tâm 3 1 5 y y 3 1 3
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 26 CHUYÊN ĐỀ: VECTƠ TLDH Vậy C 6 ; 3 .
Câu 17. [0H1-5.3-2] Trong mặt phẳng tọa độ Oxy , cho hai vectơ a 1;
1 , b 0;2 . Xác định tọa
độ của vectơ x sao cho x b 2a . A. x 2 ;0.. B. x 2 ;4.. C. x 1 ; 1 . . D. x 1 ; 3 . Lời giải Chọn B.
Ta có x b 2a 2 ;4.
Một lỗi học sinh hay vấp là thay vì 2 2
4 lại bỏ mất 1 dấu trừ thành 2 2 0 nên chọn
A; hoặc thực hiện phép tính 2a chỉ nhân 2 vào hoành độ hoặc tung độ nên có thể chọn C,. D.
Câu 18. Cho tam giác ABC đều cạnh a , H là trung điểm của BC . Tính CA HC . a 3a 2 3a a 7
A. CA HC .
B. CA HC .
C. CA HC
. D. CA HC . 2 2 3 2 Lời giải. Chọn D.
Gọi D là điểm thỏa mãn tứ giác ACHD là hình bình hành. D A
AHBD là hình chữ nhật.
CA HC CA CH CD C . D 2 Ta có: 3a a 7 2 2 2 2 2 CD BD BC AH BC a . 4 2 B H C
Câu 19. [0H1-3.6-2] Trong mặt phẳng tọa độ Oxy , cho ba điểm A1;
1 , B2;0 , C 3;5 . Tìm tọa
độ điểm D sao cho AB 2AC 3AD 0 . 8 A. D 2; . B. D3; 3 . C. D6;6 . D. D3; 2 . 3 Lời giải Chọn A. Gọi D ; x y. Ta có AB 1;
1 , AC 2;6 , AD x 1; y 1 . x x 2 1 2.2 3 1 0
Khi đó AB 2AC 3AD 0 1 2.6 3 y 8 . 1 0 y 3
Học sinh dễ sai khi tính toán tọa độ vectơ AB, AC, AD dẫn đến các kết quả sai.
Câu 20. [0H1-3.4-2] Cho tam giác ABC đều cạnh 2a . Khi đó độ dài vectơ AB AC bằng:
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 27 CHUYÊN ĐỀ: VECTƠ TLDH A. 2a . B. 2a 3 . C. 4a . D. a 3 . Lời giải Chọn B.
Vẽ hình bình hành ABCD và gọi M là trung điểm . BC Ta có 2 2 2 2
AB AC AD 2AM 2 AB BM 2 (2a) a 2a 3 A 2a B M C D .
Câu 21. [0H1-3.7-2] Trong hệ tọa độ Oxy, cho ba điểm A1;
1 , B3;2, C 6;
5 . Tìm tọa độ điểm D
để ABCD là hình bình hành. A. 4;3. B. 3; 4. C. 4;4 . D. 8;6. Lời giải. Chọn C. Gọi D ;
x y, ABCD là hình bình hành
AD BC
x 1; y 1 3; 3 x 1 3 x 4 y 1 3 y 4
Vậy D4;4 .
Câu 22. [0H1-3.7-3] Trong hệ tọa độ Oxy , cho hai điểm A2;
3 , B3;4. Tìm tọa độ điểm M trên trục hoành sao cho , A , B M thẳng hàng. 5 1 17
A. M 1;0 .
B. M 4;0 . C. M ; . D. M ; 0 . 3 3 7 Lời giải. Chọn D.
Điểm M Ox M ; m 0.
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 28 CHUYÊN ĐỀ: VECTƠ TLDH
Ta có AB 1;7 và AM m 2; 3 . Để m , A , B M thẳng hàng 2 3 17 m .. 1 7 7
Câu 23. [0H1-3.5-3] Cho AD và BE là hai phân giác trong của tam giác ABC . Biết AB 4 , BC 5
và CA 6. Khi đó DE bằng: 5 3 3 5 9 3 3 9
A. CA CB .
B. CA CB .
C. CA CB .
D. CA CB . 9 5 5 9 5 5 5 5 Lời giải Chọn A. A E B D C CD AC CD
AD là phân giác trong của tam giác ABC nên 6 6 DB AB 4 CD DB 6 4 CD 6 3 CD CB . CB 10 5 Tương tự CE 5 5 :
CE CA. CA 9 9 5 3
Vậy DE CE CD CA CB . 9 5
Câu 24. [0H1-2.4-3] Cho tam giác ABC , AM là trung tuyến, G là trọng tâm. Gọi E, F theo thứ tự là
trung điểm của BG và CG . Khi đó GE GF bằng: 1 1 2 5
A. AB AC .
B. AB AC .
C. AB AC .
D. AB AC . 3 6 3 6 Lời giải Chọn B. A G E F B C Vì 1 1 1 1
GEMF là hình bình hành nên GE GF GM AM
AB AC AB AC . 3 3 2 6
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 29 CHUYÊN ĐỀ: VECTƠ TLDH
Câu 25. [0H1-3.7-4] Cho tam giác đều ABC cạnh a. Biết rằng tập hợp các điểm M thỏa mãn đẳng
thức 2MA 3MB 4MC MB MA là đường tròn cố định có bán kính .
R Tính bán kính R theo a. a a a a A. r . B. r . C. r . D. r . 3 9 2 6 Lời giải. Chọn B.
Gọi G là trọng tâm của tam giác . ABC
Ta có 2MA 3MB 4MC 2MI IA3MI IB 4MI IC.
Chọn điểm I sao cho 2IA 3IB 4IC 0 3IA IB IC IC IA 0.
Mà G là trọng tâm của tam giác ABC IA IB IC 3 I . G
Khi đó 9 IG IC IA 0 9 IG AI IC 0 9 IG CA .
Do đó 2MA 3MB 4MC MB MA 9MI 2IA 3IB 4IC AB 9MI A . B
Vì I là điểm cố định thỏa mãn
nên tập hợp các điểm M cần tìm là đường tròn tâm I , bán kính AB a r . 9 9
NHÓM SOẠN CHUYÊN ĐỀ KHỐI 10 30
Document Outline
- 0H1-1
- 0H1-2
- 0H1-3
- 0H1-4
- 0H1-5
- 0H1-6_KT