CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG
BÀI 5: TỪ VUÔNG GÓC ĐẾN SONG SONG Mục tiêu  Kiến thức
+ Phát biểu được quan hệ giữa tính vuông góc với tính song song.
+ Phát biểu được tính chất của ba đường thẳng song song.  Kĩ năng
+ Vận dụng được các tính chất để chứng minh bài toán. Trang 1 I. LÍ THUYẾT TRỌNG TÂM
Quan hệ giữa tính vuông góc với tính song song
Hai đường thẳng phân biệt cùng vuông góc với một
đường thẳng thứ ba thì chúng song song với nhau.
Một đường thẳng vuông góc với một trong hai
đường thẳng song song thì nó cũng vuông góc với đường thẳng kia. a  c   a//b . b   c a//b   c  b . c  a
Ba đường thẳng song song
Hai đường thẳng phân biệt cùng song song với
đường thẳng thứ ba thì chúng song song với nhau. a//c   a//b b  //c II. CÁC DẠNG BÀI TẬP
Dạng 1: Chứng minh hai đường thẳng vuông góc, hai đường thẳng song song Phương pháp giải
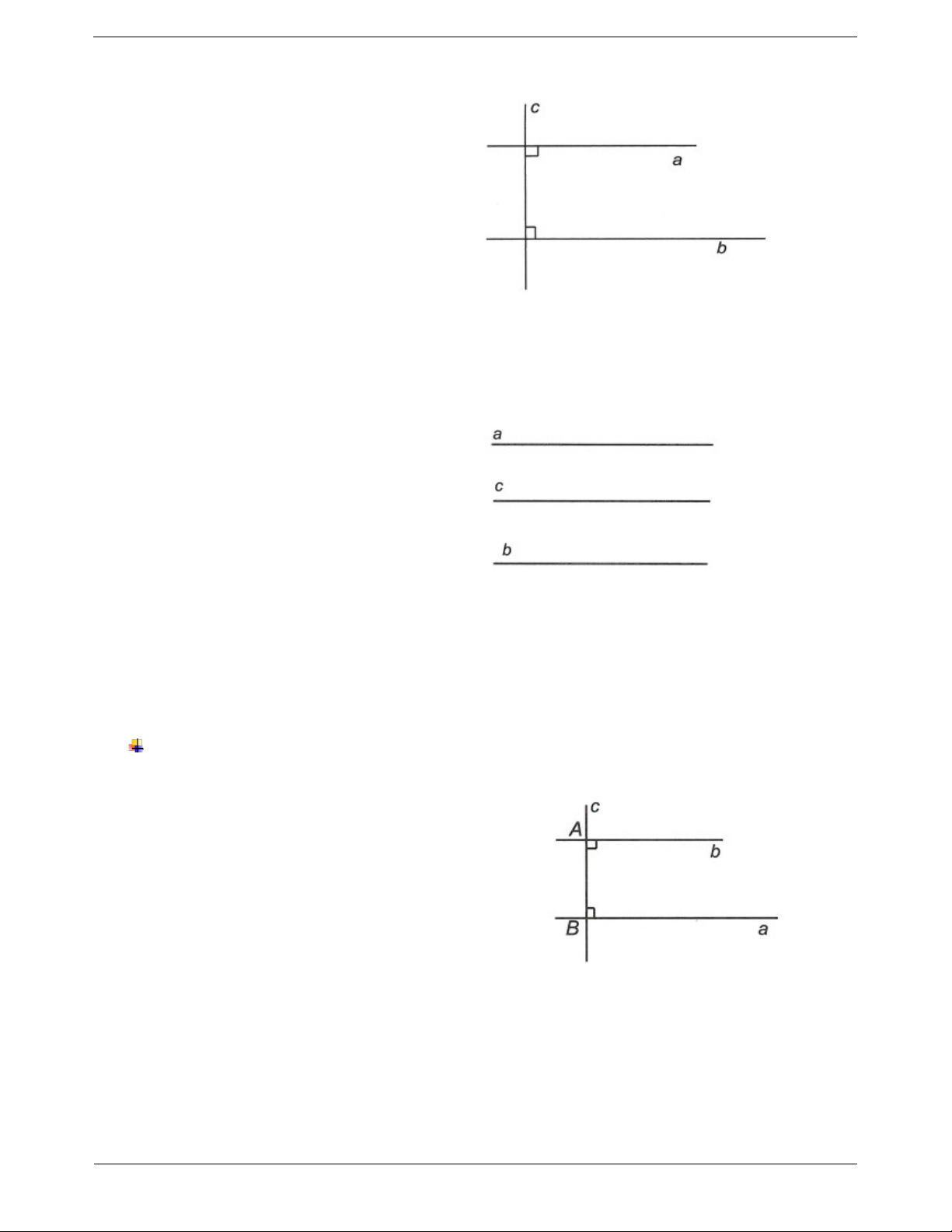
Chứng minh hai đường thẳng song song: Ví dụ 1: Cho hình vẽ:
Ngoài sử dụng các dấu hiệu (hai góc so le trong
bằng nhau, hai góc đồng vị bằng nhau, hai góc
trong cùng phía bù nhau....), ta có thể dựa vào dấu
hiệu: hai đường thẳng cùng vuông góc hoặc song
song với một đường thẳng thứ ba.
Chứng minh hai đường thẳng vuông góc ta có thể dựa vào: Chứng minh a//b .
• Định nghĩa hai đường vuông góc: Hai đường Hướng dẫn giải
thẳng vuông góc là hai đường thẳng cắt nhau và Vì hai đường thẳng a và b cùng vuông góc với
trong các góc tạo thành có một góc vuông. đường c nên a//b .
• Một đường thẳng vuông góc với một trong hai Ví dụ 2: Cho hình vẽ: Trang 2
đường thẳng song song thì nó cũng vuông góc với một đường thẳng kia.
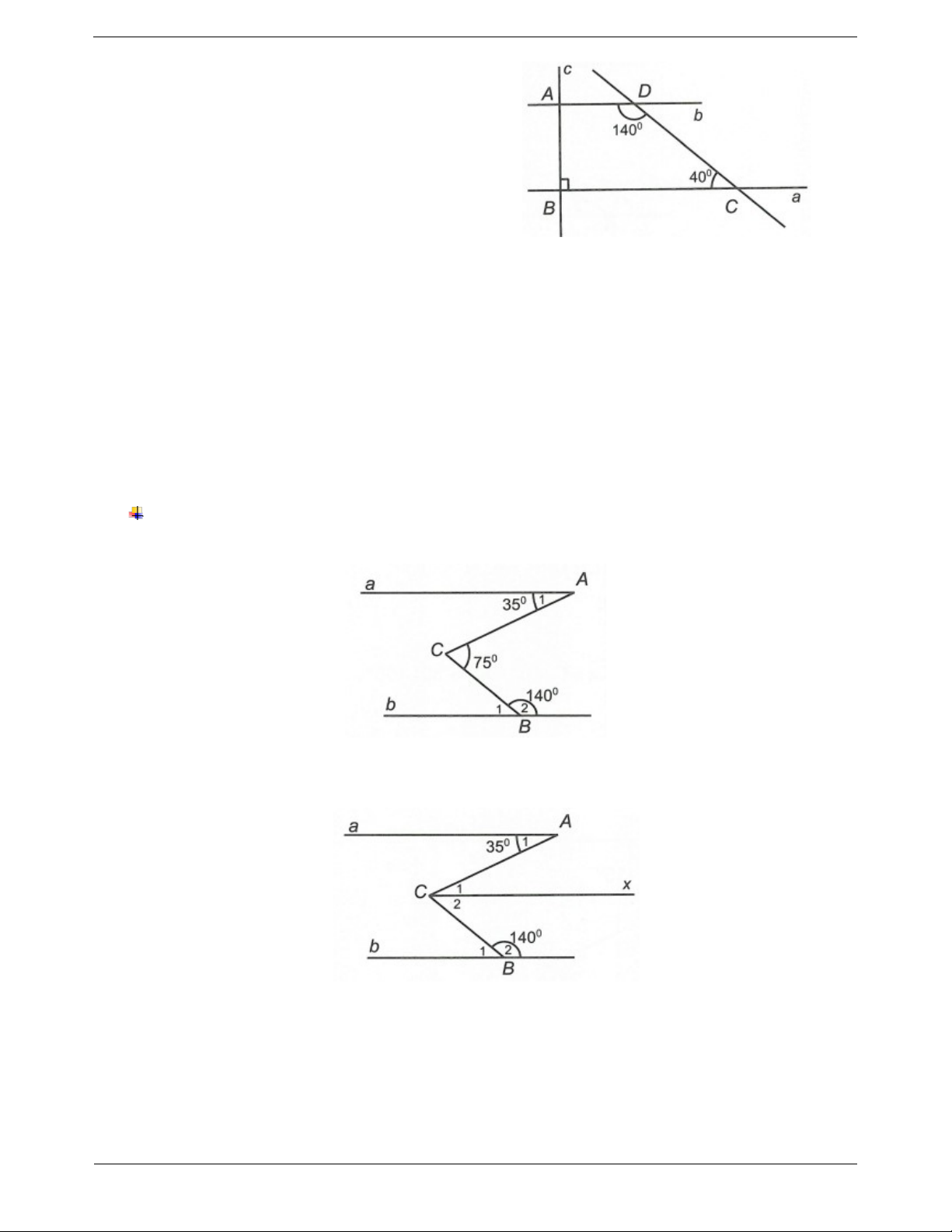
• Hai tia phân giác của hai góc kề bù thì vuông góc với nhau. Chứng minh b  c . Hướng dẫn giải Ta có  ADC  
BCD  140  40  180 .
Suy ra b//a (hai góc trong cùng phía bù nhau).
Ta có B  90 suy ra c  a .
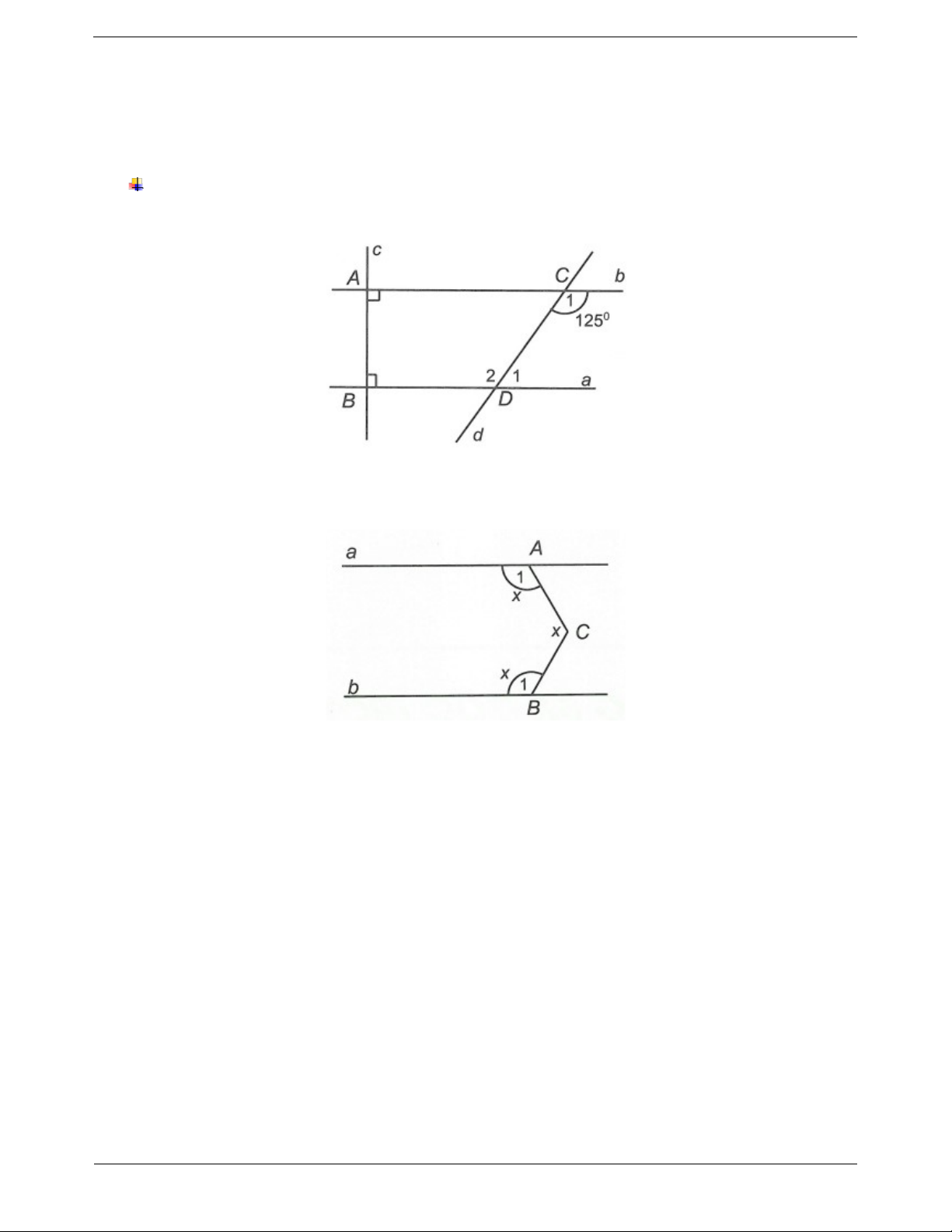
Mà b//a nên c  b (quan hệ giữa tính vuông góc và tính song song). Ví dụ mẫu Ví dụ 1. Cho hình vẽ:
Chứng minh hai đường thẳng a và b song song với nhau. Hướng dẫn giải Ta có  B  
B  180 (hai góc kề bù). 1 2 Mà  B  140 nên  B  180  
B  180 140  40 . 2 1 2 Vẽ tia Cx trong góc  ACB sao cho Cx//a   A  
C  35 (hai góc so le trong bằng nhau). 1 1 Trang 3 Mặt khác  ACB   C   C   C   ACB  
C  75  35  40 . 1 2 2 1 Do đó  B  
C  40 suy ra Cx//b (hai góc so le trong bằng nhau). 1 2
Vậy a//b (hai đường thẳng cùng song song với đường thẳng thứ ba). Ví dụ 2. Cho hình vẽ: Biết 
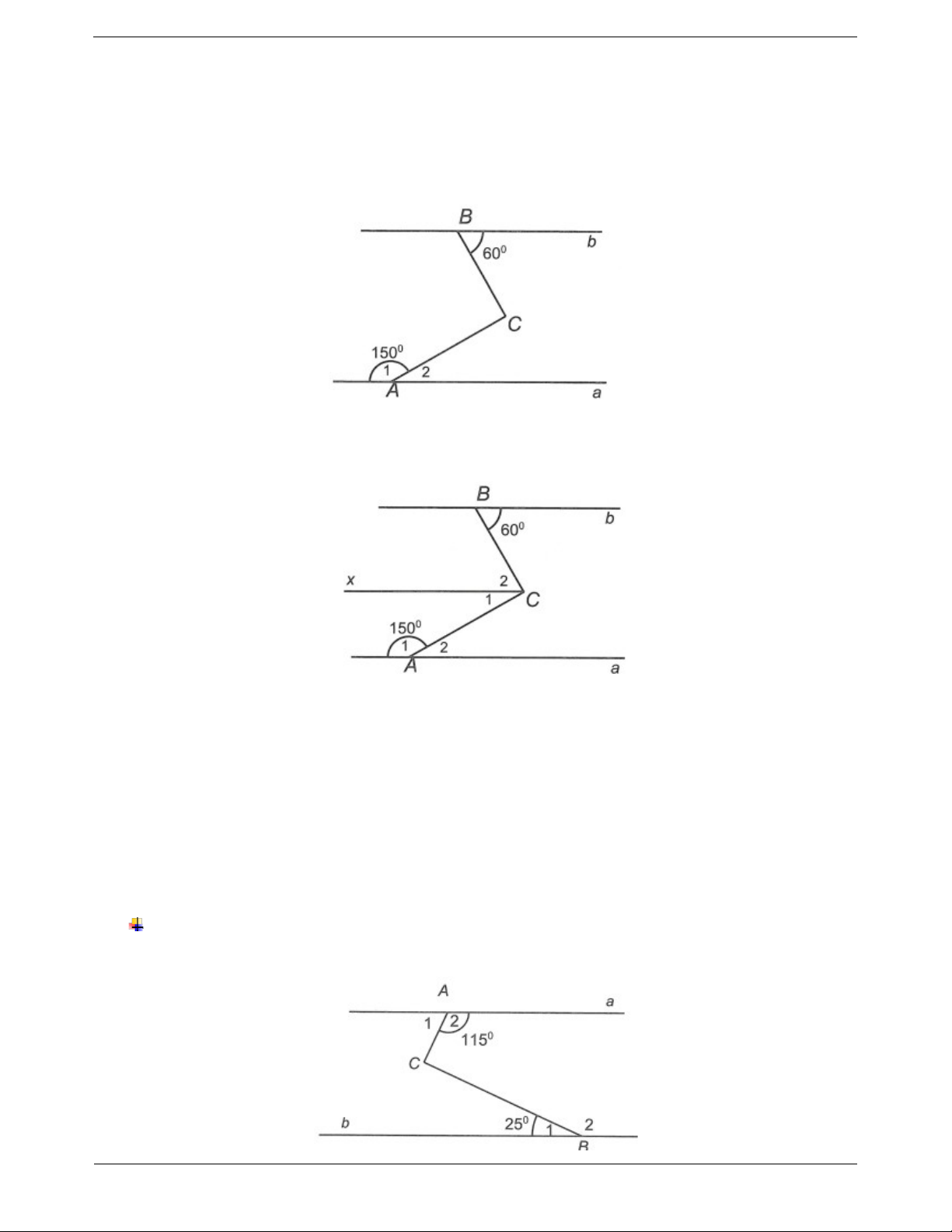
A  150 , B  60 và a//b . Chứng minh rằng AC  BC . 1 Hướng dẫn giải Ta có  A  
A  180 (hai góc kề bù)   A  180  
A  180 150  30 . 1 2 2 1
Từ C kẻ đường thẳng Cx//a//b (Cx nằm trong  ACB ). Ta có Cx//b nên 
C  B  60 (hai góc so le trong); 2 Cx//a nên  C  
A  30 (hai góc so le trong). 1 2
Mà tia Cx nằm giữa CA và CB nên  ACB   ACx   BCx   C  
C  60  30  90 . 1 2 Vậy AC  BC .
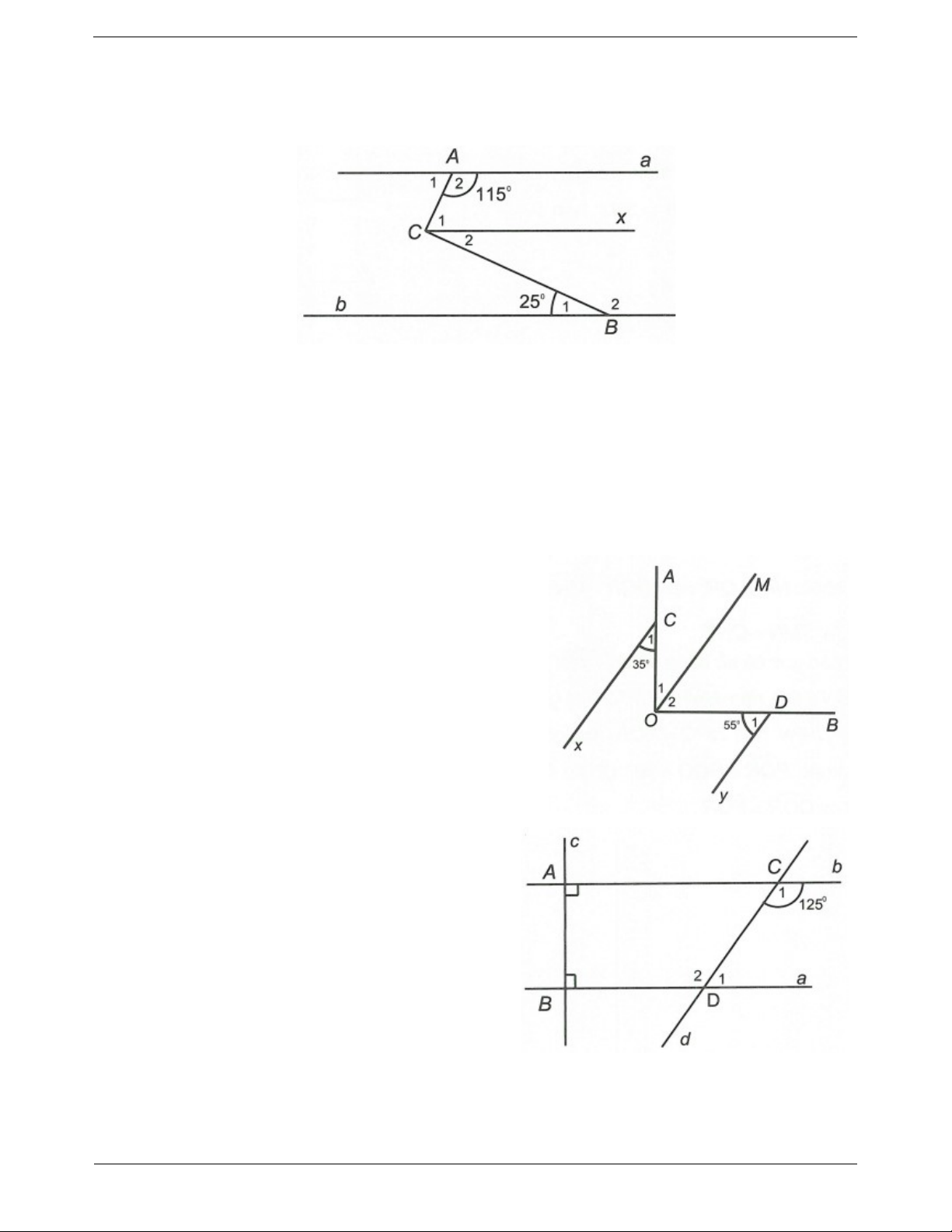
Bài tập tự luyện dạng 1 Câu 1: Cho hình vẽ: Trang 4 Biết a//b ,  A  115 , 
B  25 . Chứng minh AC  BC . 2 1 Câu 2: Cho góc 
AOB . Trên OA, OB lần lượt lấy C và D. Vẽ ngoài góc 
AOB hai tia Cx và tia Dy sao cho Cx//Dy . Biết  OCx  35 , 
ODy  55 (như hình vẽ dưới). Chứng minh OA  OB . Dạng 2: Tính góc Phương pháp giải Ví dụ 1: Cho hình vẽ: Biết 
C  135 . Xác định số đo của các góc  D . 1 Hướng dẫn giải
Bước 1. Chứng minh hai đường thẳng vuông góc Ta có c  a , c  b (giả thiết) suy ra a//b (vì cùng hoặc song song. vuông góc với c).
Bước 2. Sử dụng tính chất các cặp góc đối đỉnh, Do đó C  D 180(hai góc trong cùng phía).
các góc kề bù nhau, các góc tạo bởi một đường 1 1
thẳng cắt hai đường thẳng song song... để tính góc. Suy ra  D  180  
C  180 135  45 . 1 1 Vậy  D  45 . 1 Ví dụ mẫu Ví dụ 1. Cho hình vẽ:
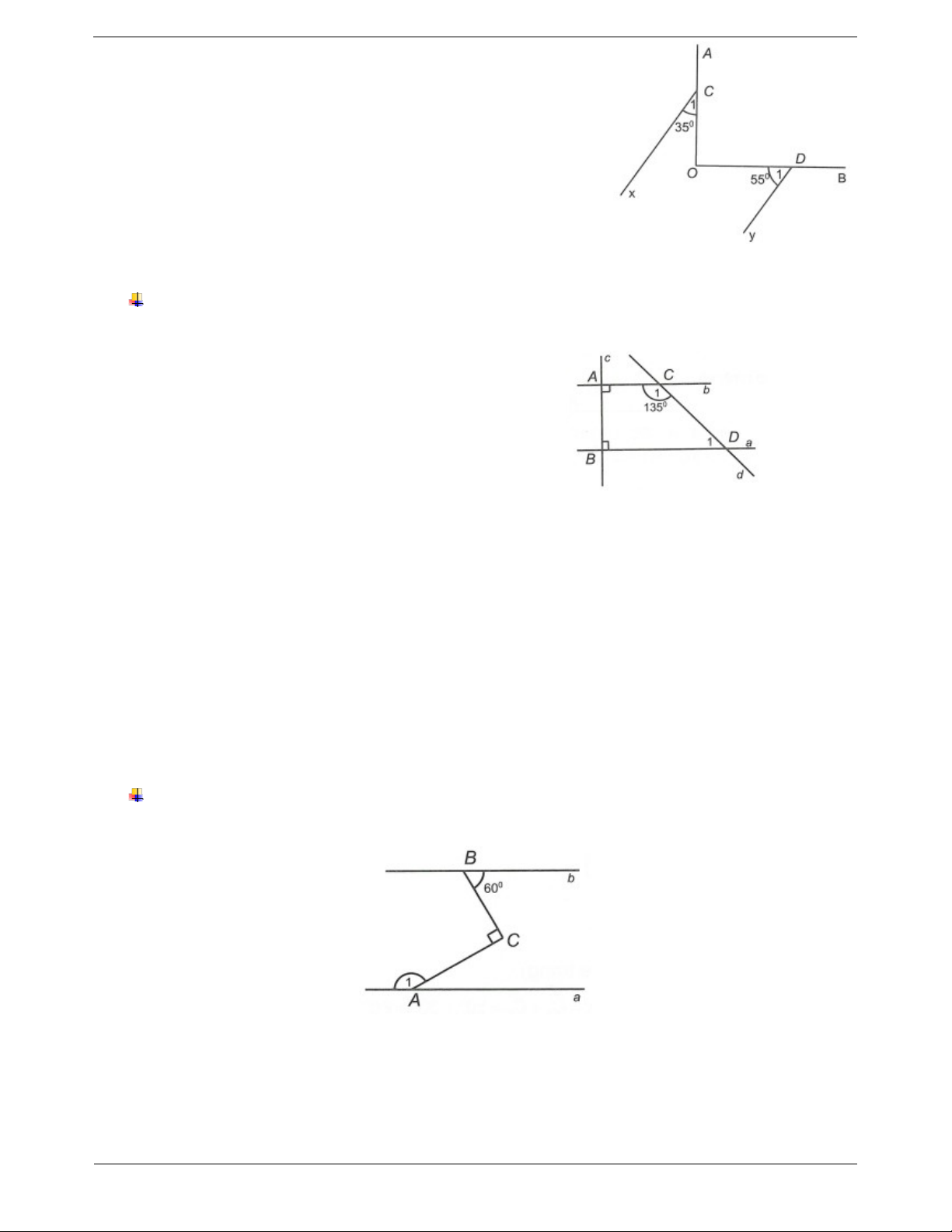
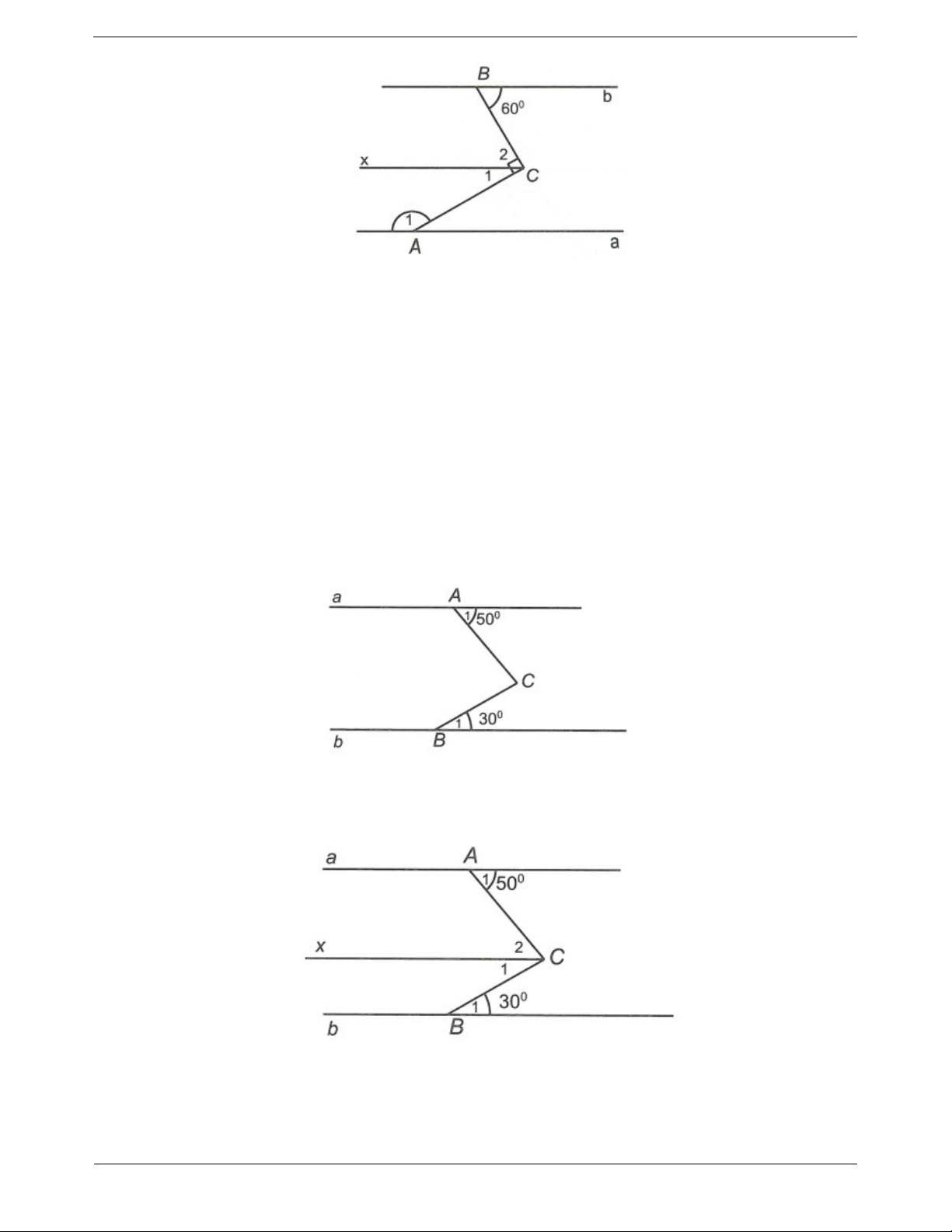
Biết a//b và B  60 . Xác định số đo của góc  A . 1 Hướng dẫn giải Trang 5 Trong góc 
ACB vẽ tia Cx//a , khi đó Cx//b (vì a//b ). Suy ra  C  
B  60 (hai góc so le trong). 2
Vì tia Cx nằm giữa tia CA và tia CB nên  ACB   C   C . 1 2 Suy ra  C   ACB  
C  90  60  30 . 1 2 Ta có Cx//a nên  C  
A  180 (hai góc trong cùng phía) 1 1   A  180  
C  180  30  150. 1 1 Vậy  A  150 . 1 Ví dụ 2. Cho hình vẽ: Biết a//b và  A  50 , 
B  30 . Tính số đo góc  ACB . 1 1 Hướng dẫn giải
Từ C kẻ đường thẳng Cx//a (Cx nằm trong  ACB ) Mà a//b nên Cx//b . Suy ra  BCx   C  
B  30 (hai góc so le trong) 1 1 Trang 6 Lại có Cx//a nên  ACx   C  
A  50 (hai góc so le trong) 2 1
Mà tia Cx nằm giữa CA và CB nên  ACB   ACx   BCx   C  
C  50  30  80 . 2 1
Bài tập tự luyện dạng 2 Câu 1: Cho hình vẽ: Biết 
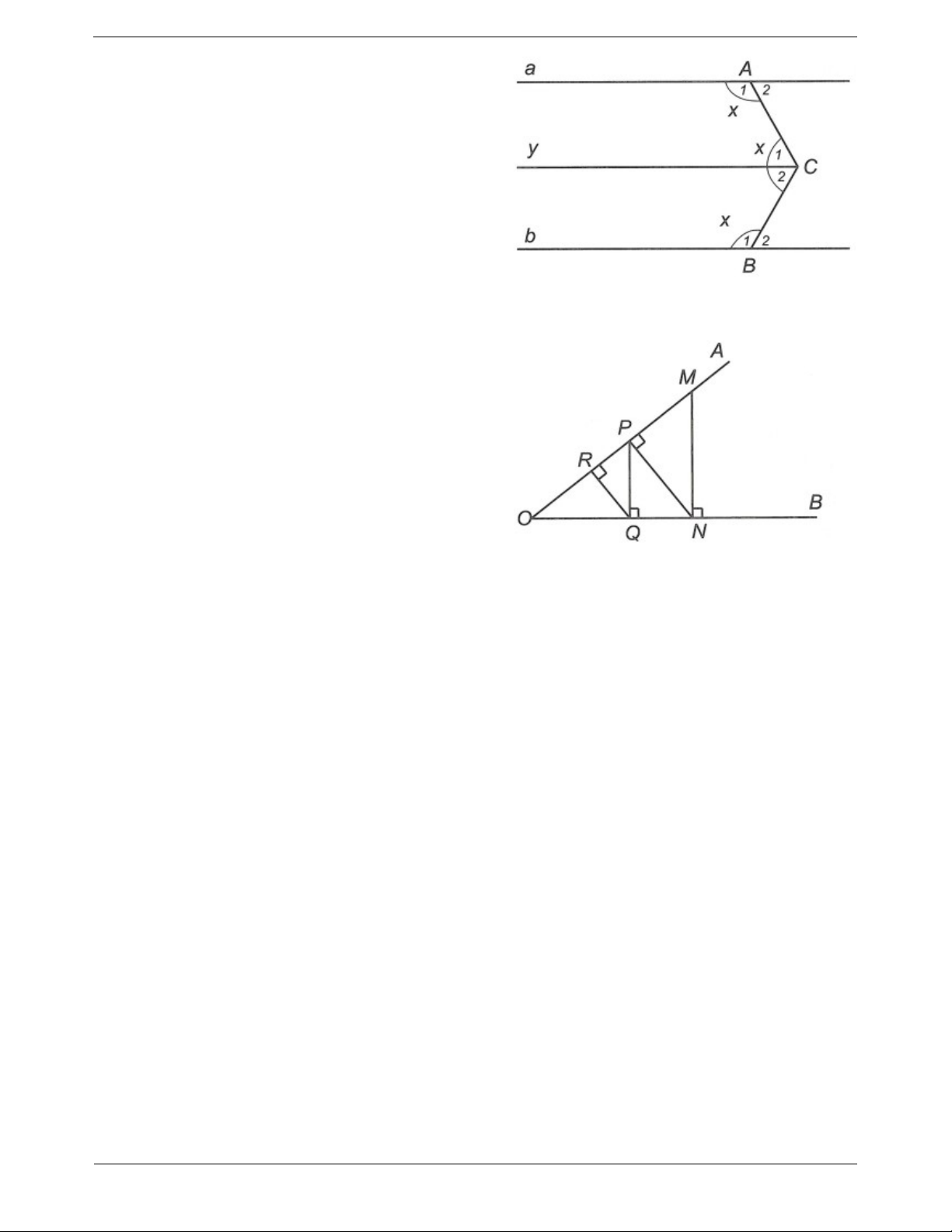
C  125 , c  a , c  b . Tính  D và  D . 1 1 2 Câu 2: Cho hình vẽ: Biết a//b ,  A   B   C . Tìm x. 1 1 Câu 3: Cho góc nhọn 
AOB . Từ M trên tia OA vẽ MN vuông góc với OB  N OB , từ N vẽ NP vuông
góc với OA P OA , từ P vẽ PQ vuông góc với OB Q OB , từ Q vẽ QR  OAR OA .
a) Chứng minh MN //PQ và NP//QR .
b) Xác định các góc có số đo bằng số đo góc 
PMN , các góc có số đo bằng số đo  MNP biết  QOR   RQO  90 . Trang 7 ĐÁP ÁN
Dạng 1. Chứng minh hai đường thẳng vuông góc, song song Câu 1.
Từ C kẻ đường thẳng Cx//a  Cx//b (Cx nằm trong  ACB ). Vì Cx//b nên  BCx   C  
B  25 (hai góc so le trong). 2 1 Cx//a nên  ACx  
A  180 (hai góc trong cùng phía). 2 Mà  A  115 nên  ACx  180   A  
ACx  180 115  65 . 2 2
Mặt khác tia Cx nằm giữa CA và CB nên  ACB   ACx   BCx   C  
C  25  65  90 . 2 1 Vậy CA  CB . Câu 2. Trong góc 
AOB dựng tia OM //Cx  OM //Dy . Vì OM //Cx nên  C   O (hai góc so le trong), 1 1 OM //Dy nên  D   O (hai góc so le trong). 1 2 Mặt khác  C  35 ,  D  55 nên 1 1  AOB   O   O   C  
D  35  55  90 . 1 2 1 1 Vậy OA  OB . Dạng 2. Tính góc Câu 1.
Ta có c  a , c  b (giả thiết) suy a//b (vì cùng vuông góc với c). Vì a//b nên  C  
D  125 (hai góc so le trong), 1 2  D  
C  180 (hai góc trong cùng phía). 1 1 Suy ra  D  180  
C  180 125  55 . 1 1 Vậy  D  55 ,  D  125 . 1 2 Câu 2.
Từ C kẻ tia Cy//a  Cy//b (Cy nằm trong  ACB ). Trang 8 Vì Cy//a nên  C   A (hai góc so le trong), 1 2 Cy//b nên  C   B (hai góc so le trong). 2 2 Mà  A   A   B  
B  180 180  360 nên 1 2 1 2  A   C   B   C  360 . 1 1 1 2 Mặt khác  A   B   C   C  x nên 1 1 2 1  A   C   B  
C  3x  360  x  120 . 1 1 1 2 Cây 3.
a) MN  OB , PQ  OB (giả thiết) suy ra MN //PQ
NP  OA , QR  OA (giả thiết) suy ra QR//PN b) Vì MN //PQ nên  PMN   RPQ (hai góc đồng vị); Lại có NP//QR nên  PQR   QPN (hai góc so le trong).  Q  PR   QPN  90 Mả    RPQ    hay    OQR OQR RQP  90  OQR   PMN Mặt khác NP//QR nên  OQR   QNP (hai góc đồng vị). Suy ra  PMN   QNP .
Vậy các góc có số bằng số đo  PMN là  QNP ,  QPR ,  OQR . Vì MN //PQ nên  MNP  
NPQ (hai góc so le trong bằng nhau); QR//PN nên  NPQ  
PQR (hai góc so le trong bằng nhau). Mặt khác  PQR  
RQO  90 ( PQ  OB ) và  QOR  
RQO  90 (giả thiết). Suy ra  QOR   PQR .
Vậy các góc có số đo bằng góc  MNP là  NPQ ,  PQR ,  QOR . Trang 9