Chuyên đề và bộ đề ôn thi học kỳ 1 Toán 10 năm học 2018 – 2019 – Lê Văn Đoàn

Nhằm hỗ trợ các em học sinh lớp 10 trong quá trình ôn thi HK1 Toán 10, VietJack giới thiệu đến các em tài liệu chuyên đề và bộ đề ôn thi học kỳ 1 Toán 10 năm học 2018 – 2019 do thầy Lê Văn Đoàn biên soạn và giảng dạy, tài liệu gồm 84 trang trình bày kiến thức và bài tập 7 chuyên đề Toán 10 giai đoạn học kỳ 1 và 13 đề thi HK1 Toán 10 của các trường THPT năm học 2017 – 2018.

113 57 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

N¨m häc 2018 – 2019

M«n To¸n – Líp 10

Trung taâm Hoaøng Gia

56 Phoá Chôï – P. Taân Thaønh – Q. Taân Phuù

MỤC LỤC

Trang

Chuyên đề 1. Parabol & một số vấn đề liên quan ..................................................................... 1

Chuyên đề 2. Giải và biện luận phương trình bậc nhất ........................................................... 5

Chuyên đề 3. Bài toán chứa tham số trong phương trình bậc hai .......................................... 7

Chuyên đề 4. Phương trình quy về phương trình bậc hai ....................................................... 13

Chuyên đề 5. Bất đẳng thức và GTLN, GTNN ......................................................................... 23

Chuyên đề 6. Hệ trục tọa độ ........................................................................................................ 29

Chuyên đề 7. Tích vô hướng và hệ thức lượng ......................................................................... 42

Đề số 01. THPT Bình Hưng Hòa (2017 – 2018) .................................................................. 49

Đề số 02. THPT Trần Phú (2017 – 2018) .............................................................................. 51

Đề số 03. THPT Lê Trọng Tấn (2017 – 2018) ....................................................................... 53

Đề số 04. THPT Bình Tân (2017 – 2018) ............................................................................... 56

Đề số 05. THPT Nguyễn Hữu Cảnh (2017 – 2018) ............................................................ 58

Đề số 06. THPT Trần Quang Khải (2017 – 2018) ................................................................ 61

Đề số 07. THPT Nguyễn Thượng Hiền (2017 – 2018) ....................................................... 63

Đề số 08. THPT Hàn Thuyên (2017 – 2018) ........................................................................ 66

Đề số 09. THPT Nguyễn Chí Thanh (2017 – 2018) ............................................................ 69

Đề số 10. THPT Tây Thạnh (2017 – 2018) ............................................................................ 72

Đề số 11. THPT Chuyên Lê Hồng Phong (2017 – 2018) .................................................... 74

Đề số 12. THPT Nguyễn Thị Minh Khai (2017 – 2018) ..................................................... 77

Đề số 13. THPT Bùi Thị Xuân (2017 – 2018) ....................................................................... 79

Chóc c¸c trß rÌn luyÖn tèt vµ ®¹t kÕt qu¶ cao trong kú thi s¾p ®Õn !

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 1 -

Chuyªn ®Ò 1. Parabol & mét sè bµi to¸n liªn quan

 Cần nhớ: Parabol

( ) :

P y ax bx c

  

có đỉnh ;

2 4

a a

 









 











 

và trục đối xứng

 

(hoành độ đỉnh). Khi

0 :



đồ thị có dạng



và

0 :



đồ thị có dạng



1. Tìm parabol

( ) : 4 ,

P y ax x c

  

biết

rằng

( )

đi qua

(1; 2)



và

(2;3).

2. Tìm parabol

( ): 2,

P y ax bx

  

biết rằng

( )

đi qua

(1;5), ( 2;8).

A B



............................................................................

.................................................................................

3. Tìm parabol

( ) : 3,

P y ax bx

  

biết

( )

đi qua điểm

(3;0)

và có trục đối

xứng là



4. Tìm parabol

( ) : 4 ,

P y ax x c

  

biết

( )

có hoành độ đỉnh bằng



và đi qua

điểm

( 2;1).



............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 2 -

5. Tìm parabol

( ) : ,

P y ax bx c

  

biết

( )

đi qua

(1;0), (2;8), (0; 6).

A B C



6. Tìm parabol

( ) : ,

P y ax bx c

  

biết

( )

đi qua điểm

(0;5)

và có đỉnh

(3; 4).



............................................................................

.................................................................................

7. Tìm parabol

( ) :

P y ax bx c

  

khi biết

bảng biến thiên:







8. Tìm parabol

( ) :

P y ax bx c

  

khi biết

bảng biến thiên:







............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 3 -

9. Tìm parabol

( ) :

P y ax bx c

  

khi biết

đồ thị của nó là

10. Tìm parabol

( ) :

P y ax bx c

  

khi biết đồ

thị của nó là

............................................................................

.................................................................................

11. Vẽ parabol

( ) : 2 2.

P y x x

  

Dựa

vào đồ thị biện luận nghiệm phương

trình:

2 4 3 0.

x x m

   

12. Vẽ parabol

( ) : 4 5.

P y x x

   

Dựa

vào

đồ thị biện luận nghiệm phương trình:

4 5 0.

x x m

   

............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 4 -

13. Vẽ parabol

( ) : 4 3.

P y x x

   

Tìm

để phương trình

4 0

x x m

  

có

nghiệm thỏa

1 2

0 2 .

x x

  

14. Vẽ parabol

( ) : 4 5.

P y x x

   

Dựa

vào đồ thị biện luận nghiệm phương trình:

4 5 0.

x x m

   

............................................................................

.................................................................................

15. Vẽ parabol

( ) : 2 .

P y x x

 

Suy ra đồ

thị hàm số

( ) : 2 .

P y x x



 

16. Vẽ

( ) : 6 5.

P y x x

   

Hãy biên luận

nghiệm

6 4

x x m

  

trên

( 1; 4].



............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 5 -

Chuyªn ®Ò 2. Ph¬ng tr×nh bËc nhÊt

1. Giải và biện luận:

( 1) 9 3.

m mx x

  

2. Giải và biện luận:

2 4 .

m x m x

  

Giải. Phương trình

9 3

m x m x

   

9 3

m x x m

   

( 9) 3

m x m

   

( )





Với

9 0 3.

m m

    

Khi



thì

( )



trở thành

0 6,



suy ra phương trình vô nghiệm.

Khi

 

thì

( )



trở thành

0 0





phương trình nghiệm đúng

 





Với

9 0 3

m m

    

3 1

( )



    



Kết luận:

3 :



Phương trình vô nghiệm.

3 :

 

Phương trình nghiệm đúng

 



3 :

 

Phương trình có nghiệm

 



.................................................................................

3. Giải và biện luận:

( 2 8) 4 .

m m x m

   

4. Giải và biện luận:

(4 2) 1 2 .

m x m x

   

............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 6 -

5. Tìm

để phương trình có nghiệm:

3 2 5 3

1 1

x m x m

x x

  

   

 

6. Tìm

để phương trình có nghiệm:

2 1 1

2 1

1 1

mx m

x x

 

   

 

Giải. Điều kiện:

1 0 1.

x x

    

Quy đồng và bỏ mẫu, phương trình đã cho

3 1 2 5 3

x m x x m

      

2 6 2

x m

  

3 1.

x m

  

Vì

 

nên phương trình có nghiệm

khi

3 1 1

x m m

       

.................................................................................

7. Tìm tham số

để phương trình sau có

nghiệm nguyên:

( 2) 1.

m x m

  

8. Tìm tham số

để phương trình sau có

nghiệm nguyên:

( 3) .

m x x m

  

Giải. Với

2 0 2

m m

   

thì phương

trình

1 ( 2) 3

2 2

m m

  

  

 

  



Vì





nên

3 ( 2)





2 3 5

2 3 1

2 1 3

2 1 1

m m

 

  

 

    

 

 

 

  

 

   

 

 

.................................................................................

9. Tìm tham số

để phương trình

2 2

( ) 2 1

m m x x m

   

vô nghiệm.

10. Tìm tham số

để phương trình

2 2

4 2

m x x m m

   

có nghiệm.

............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 7 -

Chuyªn ®Ò 3. Bµi to¸n chøa tham sè trong ph¬ng tr×nh bËc hai

1. Cho phương trình

2 2

(2 3) 4 0.

x m x m

    

Tìm tham số

để phương trình:

a) Có một nghiệm



Tìm nghiệm còn

lại.

b) Có

nghiệm pb

1 2

x x

thỏa

2 2

1 2

17.

x x

 

Lời giải.

Thế

 

vào phương trình, ta được:

2 2

( 7) 7(2 3) 4 0

m m

     

14 24 0

m m



 



     



 







Với

 

thì phương trình trở thành:

7 0 0

x x x

   

hoặc

 



Với

 

thì phương trình trở thành

27 140 0 7 20.

x x x x

        

Kết luận:

Với

 

thì nghiệm còn lại là



Với

 

thì nghiệm còn lại là

20.



Lời giải. Phương trình có

nghiệm phân biệt

khi:

2 2

L1 0 :

3) 4( 4)

m m











 

 

 

 





 



 

12 25 0

m m     

( )



Theo Viét:

1 2

2 3

S x x m

     

và

1 2

P x x m

   

Theo đề:

2 2 2

1 2

17 2 17

x x S P

    

2 2

(2 3) 2( 4) 17

m m

    

2 12 0 0

m m m

    

hoặc



So với

( ),



giá trị cần tìm là



2. Cho phương trình

2 2

(2 3) 4 0.

x m x m

    

Tìm tham số

để phương trình:

a) Có

nghiệm



Tìm nghiệm còn lại.

b) Có

nghiệm pb

1 2

x x

thỏa

2 2

1 2

17.

x x

 

............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 8 -

3. Cho phương trình

2 2

2 3 0.

x mx m m

   

Tìm tham số

để phương trình:

a) Có nghiệm kép. Tính nghiệm kép đó.

b) Có

nghiệm pb

1 2

x x

thỏa

2 2

1 2

x x

 

............................................................................

.................................................................................

4. Cho phương trình

( 1) 3 1 0.

m x x

   

Tìm tham số

để phương trình:

a) Có 1 nghiệm bằng

Tìm nghiệm còn lại.

b) Có

nghiệm pb

1 2

x x

thỏa

1 2

1 .

x x

 

............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 9 -

5. Cho phương trình

(2 3) 2(2 3) 1 2 0.

m x m x m

     

Tìm

để phương trình:

a) Có 1 nghiệm bằng



Tìm nghiệm còn

lại của phương trình.

b) Có

nghiệm phân biệt

1 2

x x

thỏa mãn

1 2 1 2

(5 1)(5 1) 13 1.

x x x x

   

............................................................................

.................................................................................

6. Cho phương trình

4 1 0.

x x m

   

Tìm tham số

để phương trình:

a) Có hai nghiệm trái dấu ?

Có hai nghiệm dương phân biệt.

b) Có

nghiệm phân biệt

1 2

x x

thỏa mãn

1 2 1 2

6 2 .

x x x x

 

............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 10 -

7. Cho phương trình

2( 3) 6 0.

mx m x m

    

Tìm tham số

để phương trình:

a) Có

nghiệm phân biệt thỏa

1 2

1 1

x x

 

b) Có hai nghiệm trái dấu và có giá trị tuyệt

đối bằng nhau.

............................................................................

.................................................................................

8. Cho phương trình

2 1 0.

mx x

  

Tìm tham số

để phương trình:

a) Có hai nghiệm trái dấu ? Có hai nghiệm

phân biệt cùng dương ? Có hai nghiệm

đối nhau ?

b) Có hai nghiệm là độ dài của hai cạnh góc

vuông trong một tam giác vuông có độ dài

cạnh huyền bằng

............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 11 -

9. Cho phương trình

( 5) 0.

x m x m

   

Tìm tham số

để phương trình:

a) Chứng minh phương trình luôn có hai

nghiệm phân biệt. Tìm

để phương

trình có hai nghiệm dương phân biệt ?

b) Có hai nghiệm phân biệt

1 2

x x

thỏa mãn

điều kiện

1 2

2 5.

x x

 

............................................................................

.................................................................................

10. Cho phương trình

2 2

(2 2) 4 0.

x m x m

    

Tìm tham số

để phương trình:

a) Có nghiệm ? Có hai nghiệm pb dương ?

b) Có hai nghiệm pb

1 2

x x

thỏa

1 2

2 .

x x



............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 12 -

11. Cho phương trình

( 2) ( 1) 4 0.

x x m x

 

    

 

 

Tìm tham số

để phương trình:

a) Có ba nghiệm phân biệt ? b) Có hai nghiệm ?

............................................................................

.................................................................................

12. Cho phương trình

3 2

2 2 1 0.

x mx mx

   

Tìm tham số

để phương trình:

a) Có ba nghiệm phân biệt ? b) Có hai nghiệm ?

............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 13 -

Chuyªn ®Ò 4. Ph¬ng tr×nh quy vÒ ph¬ng tr×nh bËc hai

1. Giải:

2 2 2

4(2 3 1)(2 4 1) 3 .

x x x x x

    

2. Giải:

( 1)( 2)( 6)( 12) 6 .

x x x x x

    

............................................................................

.................................................................................

3. Giải:

2 2

2 13

2 5 3 2 3

x x

x x x x

 

   

4. Giải:

2 2

4 5 10

2 3 4 3

x x

x x x x

  

   

............................................................................

.................................................................................

5. Giải:

2 2

2 3 5 3 3

4 3 6 3

x x x x

   

  

   

6. Giải:

2 2

2 15 3

4 15 6 15

x x x

x x x x

 

 

   

............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 14 -

7. Giải:

4 1 2 4.

x x x

   

8. Giải:

3 5 2 3.

x x x

   

Lời giải. Áp dụng

A B













 









 











Điều kiện:

2 4 0.

x x

  

Phương trình

4 1 2 4

4 1 ( 2 4)

x x x



   







    





2 3 0

3 2 3

6 3 0

3 2 3

x x



 







  



 



  

  







  





Thế các nghiệm vào điều kiện, các nghiệm

thỏa mãn là



và

3 2 3.

  

.................................................................................

9. Giải:

2 4 2.

x x x

   

10. Giải:

2 2

2 2 7 9.

x x x x

    

............................................................................

.................................................................................

11. Giải:

4 2 2.

x x x

   

12. Giải:

2 3 1 1 2 .

x x x

   

............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 15 -

13. Giải:

2 2

3 2 6 .

x x x

  

14. Giải:

3 4 2 .

x x

  

Lời giải. Áp dụng

A B







 



 





thì

2 2

3 2 6

x x x



  



   



  





4 2 6 0

2 2 6 0 : VN

x x



 



   



  



  







.................................................................................

15. Giải:

2 2

5 3 2 1 .

x x x

   

16. Giải:

2 2

2 2 2 .

x x x x   

............................................................................

.................................................................................

17. Giải:

6 9 2 1 .

x x x   

18. Giải:

4 12 9 3 2 .

x x x   

Lời giải. Áp dụng

A B A B

  

thì phương trình

6 9 2 1

x x x

   

2 2

6 9 (2 1)

x x x

    

2 2

6 9 4 4 1

x x x x

     

3 10 8 0 4,

x x x x

        

.................................................................................

19. Giải:

2 3 2 1 .

x x

  

20. Giải:

3 9 1 2 .

x x x   

............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 16 -

21. Giải:

( 3). 1 4

x x x

  

( )



22. Giải:

( 1). 3 4( 2).

x x x

   



TH1

: N

ếu

1 0 1.

x x

   

( )



trở thành

( 3)( 1) 4

x x x

  

2 3 0 1, 3.

x x x x

       

So với



nhận nghiệm





TH2: Nếu

1 0 1.

x x

   

( )



trở thành

( 3)(1 ) 4

x x x

  

6 3 0 3 2 3.

x x x

       

So với



nhận nghiệm

3 2 3.

  

Kết luận: Tập nghiệm

{ 3 2 3;3}.

  

.................................................................................

23. Giải:

4 2 2 1

2 1.

4 3

x x x

  

 



24. Giải:

1 1 2 1

x x

 

  



...........................................................................

............................................................................

.................................................................................

25. Giải:

2 1 2

2 1.

2 2 1

x x

 

 

 

(ẩn phụ) 26. Giải:

1 1

10 2x x

    

(ẩn phụ)

...........................................................................

............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 17 -

27. Giải:

3 2 3.

x x x

   

28. Giải:

6 4 3 4 0.

x x x

    

Lời giải.

0 (hay 0)

B A

A B





 



 











Phương trình

3 0

3 2 3

x x x





 









   





4 1 0

2 3

x x













 

 

 

 

  

 

 









2 3

  

là nghiệm cần tìm.

.................................................................................

29. Giải:

1 2 2 5.

x x

  

30. Giải:

3 1 8 11.

x x x

   

............................................................................

.................................................................................

31. Giải:

1 3 .

x x x

   

32. Giải:

5 21 8 2.

x x x

   

Lời giải. Áp dụng

A B









 











Phương trình

2 2

3 0

1 (3 )

x x x





 









   





2 2

1 9 6

x x x x















 

 

 

 

    



 









 

là nghiệm cần tìm.

.................................................................................

33. Giải:

2 3 2 1 1 3 .

x x x

   

34. Giải:

2 12 18 1 2.

x x x

   

............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 18 -

35. Giải:

2 2

5 4 5 5 28 0.

x x x x

     

36. Giải:

2 2

5 2 7 2 3.

x x x x

    

Lời giải. Đặt

t x x

 

thì phương trình trở

thành

4 5 28 0

t t

   

4 0

5 28 4

25( 28) ( 4)

t t





 



    





  





17 684 0

t t





 







 







   

 



 

  

 







 











Với

36 5 36 .

t x x







    



 





 Cách khác: Đặt

2 2

5 28 0 .

t x x t

    

.............................................................................

37. Giải:

2 2

3 3 3 9 7 1 0.

x x x x

     

38. Giải:

2 2

2 6 12 7 0.

x x x x

    

.................................................................................

.............................................................................

39. Giải:

( 3)(1 ) 5 2 7.

x x x x

     

40.

4 3 2

( 2)( 3) 2 2 2.

x x x x x

      

.................................................................................

.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 19 -

41. Giải:

2 1 2 3.

x x

   

42. Giải:

4 2 6 1.

x x

   

Lời giải. Điều kiện

2 1 0

3 0





 



 





 





Phương trình

2 1 2 3

x x

    

2 2

( 2 1) (2 3)

x x

    

2 1 4 4 3 3

x x x

      

4 3 .

16( 3)

x x















    









 











So với điều kiện và thử lại, suy ra

{4;12}.



 Cần nhớ: Dạng tổng quát

A B C

 

Điều kiện



Chuyển vế sao cho hai vế dương

và bình phương, giải phương trình hệ quả.

.............................................................................

43. Giải:

1 4 1 2.

x x x

    

44. Giải:

3 4 4 2 .

x x x

   

.................................................................................

.............................................................................

45. Giải:

4 1 1 2 .

x x x

    

46. Giải:

2 3 1 1 2 2 1.

x x x

    

.................................................................................

.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 20 -

47. Giải:

( 3) 5 4 2 6.

x x x x

    

48. Giải:

2 2

( 3) 4 9.

x x x

   

Lời giải. Điều kiện

5 4 0

x x

  

( )



( 3) 5 4 2( 3) 0

x x x x

      

( 3) 5 4 2( 3) 0

x x x x

      

( 3)( 5 4 2) 0

x x x

     

3 0

5 4 4

5 4 2

x x



 





 



  





0, 5

x x











 





Thế các nghiệm vào điều

kiện

( ),



nghiệm cần tìm là

0, 5.

x x

 

.............................................................................

49. Giải:

( 1) 2 3 4 3.

x x x x

    

50. Giải:

(2 1) 1 2 7 3.

x x x x

     

.................................................................................

.............................................................................

51.

2 2 2 2 1.

x x x x

      

52.

3 2 1 2 4 3.

x x x x x x

      

Lời giải. Điều kiện

2 0

1 0





 



 





 





( 2)( 1) 2 2 ( 1 2)

x x x x

       

2.( 1 2) ( 1 2) 0

x x x

       

( 1 2).( 2 1) 0

x x

     

1 2 1 4

2 1

x x



   



   



 



 





So với điều kiện, nghiệm cần tìm là



.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 21 -

53.

3 6 3 (3 )(6 ).

x x x x

      

54.

2 2 2 4 2 2.

x x x x

      

.................................................................................

.............................................................................

55. Giải:

2 2

2 9 2 1 4.

x x x x x

      

56. Giải:

2 2

15 3 2 8.

x x x

    

.................................................................................

.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 22 -

57. Giải hệ:

2 2

2 7 0

2 2 4 0

x y

y x x y





  









    





58. Giải hệ:

2 2

6 2 0

8 0

x y x y

x y





   









  





.................................................................................

.............................................................................

59. Giải hệ:

2 2

x y xy

x y x y





  









   





60. Giải hệ:

2 2

x y xy

x y y x





  









 





.................................................................................

.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 23 -

Chuyªn ®Ò 5. BÊt ®¼ng thøc – Gi¸ trÞ lín nhÊt & gi¸ trÞ nhá nhÊt

1. Chứng minh rằng với mọi





ta luôn

có

4 3 0.

x x

  

2. Chứng minh rằng với mọi

, ,

a b c





thì

2 2

4 2 2 .

a b ab a b

    

Giải. Thêm bớt để đưa về hằng đẳng thức, tức

4 2 2 2 2

4 3 ( ) 2 1 2( 2 1)

x x x x x x

 

       

 

 

2 2 2

( 1) 2( 1) 0, .

x x x

      



Dấu

" "



xảy ra khi

1 0





 



 





 





 Nhận xét: Đối với bài toán

 



ta nên

sử dụng hằng đẳng thức để đưa về dạng:

2 2 2

0 :

A B C

  

luôn đúng và dấu

" "



xảy ra khi

A B C

  

.............................................................................

3. Chứng minh rằng với mọi

x y





thì ta

luôn có

2 2

3 3 3 0.

x y xy x y

     

4. Chứng minh rằng với mọi

, ,

a b c





thì có

2 2 2

12 4( ).

a b c a b c

     

.................................................................................

.............................................................................

5. Chứng minh rằng

0, 0

a b

 

ta luôn có

3 3 2 2

a b a b ab

  

6. Chứng minh rằng

0, 0

a b

 

ta luôn

có

4 4 3 3

a b a b ab

  

.................................................................................

.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 24 -

7. Chứng minh rằng với mọi

, , 0

a b c



luôn có

2 2 2

a b c ab bc ca

    

8. Chứng minh với mọi

, , 0

a b c



thì

( ).

ab bc ca abc a b c

    

ải

Áp d

ụng BĐT Cauchy

Ta có:

Cauchy

2 2 2 2

Cauchy

2 2 2 2

Cauchy

2 2 2 2

2 2

a b a b ab

b c b c bc

c a c a ac





  



  





  





2 2 2

2( ) 2( )

a b c ab bc ca



     

2 2 2

a b c ab bc ca

    

(đpcm).

Dấu

" "



xảy ra khi

a b c

  

 Nhận xét: Nhận dạng











Tæng Tæng

Tæng H»ng sè



Cauchy xoay vòng, rồi cộng lại.

.............................................................................

9. Chứng minh rằng với mọi

, , 0

a b c



thì

1 1 1

a b c

bc ca ab a b c

     

10. Chứng minh rằng với mọi

, , 0

a b c



thì

3 3 3

a b c

ab bc ca

b c a

    

.................................................................................

.............................................................................

11. Chứng minh rằng với mọi

a b





thì ta

luôn có

2 2

4 9 5 4( 3 ).

a b a b

   

(Lưu ý:

x x x

 

12. Chứng minh rằng với

0 , ,

a b c

 



thì

2 2 2

a c b a b c

b c a

c b a

     

.................................................................................

.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 25 -

13. Chứng minh rằng với mọi

, , 0

a b c



có

( )( )( ) 8 .

a b b c c a abc

   

14. Chứng minh rằng

, , 0

a b c



ta luôn

có

2 2 2

( 2)( 2)( 2) 16 2 .

a b c abc

   

Lời giải. Áp dụng bất đẳng thức Cauchy

Ta có:

Cauchy

a b ab

b c bc

c a ca





 



 





 





và nhân vế theo vế

nhân

2 2 2

( )( )( ) 8 8 .

a b b c c a a b c abc

     

Dấu

" "



xảy ra khi

a b c

  

 Nhận xét: Dạng











TÝch TÝch

TÝch H»ng sè



Cauchy trong dấu

( )

  

và nhân lại.

.............................................................................

15. Chứng minh rằng với mọi

, , 0

a b c



có

( )( )( ) 8 .

a b b c c a abc

   

16. Chứng minh rằng

, , 0

a b c



ta luôn

có

2 2 2

( )( ) 9 .

a b c a b c abc

    

.................................................................................

.............................................................................

17. Chứng minh rằng với mọi

0, 0

a b

 

có

1 1

( 2). 4.

1 1

a b

 







   











 

 

18. Chứng minh rằng

, , 0

a b c



ta có:

1 1 1 9

( )

a b c

a b b c c a

 







     











  

 

HD:

2 ( 1) ( 1).

a b a b

     

.................................................................................

HD:

2( ) ( ) ( ) ( ).

a b c a b b c c a

       

.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 26 -

19. Với



hãy tìm giá trị nhỏ nhất của

hàm số

3 1

y x



  



20. Với



hãy tìm giá trị nhỏ nhất của

hàm số

2 1

y x



  



Giải. Ta có:

3( 1) 4

9( 1) 9

y x

 

   





9( 1) 12

y x

    





Cauchy

2. 9( 1) 12 24.

y x

     





Giá trị nhỏ nhất của hàm số là

24.

Dấu

" "



khi

4 5

9( 1)

1 3

x x

    



.............................................................................

21. Với



hãy tìm giá trị nhỏ nhất của

hàm số

y x

   



22. Với

 

hãy tìm giá trị nhỏ nhất

của hàm số

x x

 

 



.................................................................................

.............................................................................

23. Với



hãy tìm giá trị nhỏ nhất của

hàm số

x x

 

 



24. Với



hãy tìm giá trị nhỏ nhất của

hàm số

(2 5)(5 14)

x x

 

 

.................................................................................

.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 27 -

25. Với



hãy tìm giá trị nhỏ nhất của

hàm số

3y x

  

26. Với



hãy tìm giá trị nhỏ nhất của

hàm số

100

5y x

  

Giải. Sử dụng

2 2

n mx mx n

y mx

x x

    

3 3 4

2 2

x x

  

Cauchy

3 3 4

3. 3 9.

2 2

x x

 

Suy ra giá trị nhỏ nhất của

là

3 9.

Dấu

" "



xảy ra khi

3 4 2

   

.............................................................................

27. Với



hãy tìm giá trị nhỏ nhất của

hàm số

5y x

  

28. Với



hãy tìm giá trị nhỏ nhất của

hàm số

2y x

  

HD:

3 3

3 3 3

n mx mx mx n

y mx

x x

      

.................................................................................

HD:

2 2

n n n

y mx mx

x x x

     

.............................................................................

29. Với



hãy tìm giá trị nhỏ nhất của

hàm số

4y x

  

30. Với



hãy tìm giá trị nhỏ nhất của

hàm số

8y x

  

.................................................................................

.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 28 -

31. Với

0; ,

 

 



 

 

hãy tìm giá trị lớn nhất của

hàm số

(5 2 ).

y x x

 

32. Với

0; ,

 

 



 

 

hãy tìm giá trị lớn nhất

của biểu thức

4 (9 5 ).

y x x

 

Giải. Áp dụng

( )

a b

a b ab ab



   

Ta có:



(5 2 ) (2 ).(5 2 )

y x x x x

    



Cauchy

1 [(2 ) (5 2 )] 25

2 4 8

x x

 

    

Suy ra giá trị nhỏ nhất của hàm số bằng



Dấu

" "



xảy ra khi

2 5 2

x x x

    

.............................................................................

33. Với

0 3

 

và

0 4,

 

tìm giá trị

lớn nhất của

(3 )(4 )(2 3 ).

P x y x y

   

34. Với mọi

[ 2;2],

 

hãy tìm giá trị lớn

nhất của hàm số

. 4 .

y x x

 

.................................................................................

.............................................................................

35. Tìm giá trị lớn nhất và giá trị nhỏ nhất của

hàm số

2 6 .

y x x

   

36. Tìm giá trị lớn nhất và giá trị nhỏ nhất

của hàm số

1 5 .

y x x

   

Lời giải. Tập xác định

[2;6].



Vì

 

4 2 ( 2)(6 ) 4.

y x x

    

2 min 2

y y

   

khi



hoặc



Ta lại có

4 2 ( 2).(6 )

a b

y x x

   

 

4 ( 2) (6 ) 8 2 2.

y x x y

        

max 2 2

 

khi

2 6 4.

x x x

    

Kết luận:

min 2



và

max 2 2.



.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 29 -

37. Một công ty đang lập cải tiến sản phẩm và

xác định rằng tổng chi phí dành cho việc

cải tiến là

( ) 2 4 , ( 6)

C x x x

   



trong đó

là số sản phẩm được cải tiến.

Tìm số sản phẩm mà công ty cần cải tiến

để tổng chi phí là thấp nhất ?

38. Độ giảm huyết áp của bệnh nhân đư

ợc

cho bởi công thức

( ) 0,025 (30 ),

G x x x

 

trong đó

(mg)

là liều lư

ợng thuốc

được tiêm cho b

ệnh nhân. Tính liều

lượng thuốc cần tiêm cho b

ệnh nhân để

huyết áp giảm nhiều nhất và tính đ

ộ

giảm đó ?

.................................................................................

.............................................................................

39. Hình chữ nhật có chu vi không đổi là

8m.

Tìm diện tích lớn nhất

max

của hình chữ

nhật đó.

40. Cho tam giác vuông có t

ổng một cạnh

góc vuông và cạnh huyền bằng

Tìm

độ dài ba c

ạnh của tam giác sao cho diện

tích của tam giác lớn nhất.

.................................................................................

.............................................................................

41. Tìm

max

là giá trị lớn nhất của thể tích các khối hộp chữ nhật có đường chéo bằng

3 2cm

và diện tích toàn phần bằng

18cm .

.................................................................................

.............................................................................

3 2

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 30 -

Chuyªn ®Ò 6. HÖ trôc täa ®é Oxy

1. Trong mặt phẳng tọa độ

Oxy

cho ba điểm

(1;2), (3;5), ( 2; 3).

A B C

 

a) Chứng minh

, ,

A B C

tạo thành một tam giác. Tìm trọng tâm

của tam giác

ABC

Tính

cosin góc

và cho biết góc

là góc nhọn hay tù ?

Chứng minh

, ,

A B C

tạo thành một tam giác:

Ta có:

(2; 3)

2 3

3 5

( 3; 5)





 







 





 

  











không cùng phương



Suy ra

, ,

A B C

tạo thành một tam giác.

Tìm tọa độ trọng tâm

của tam giác

ABC

Ta có

là trọng tâm tam giác

ABC

1 3 ( 2) 2

2 3

3 3 3

;

2 5 ( 3) 3 3 4

3 3 4

A B C

x x x

y y y





 

  



  



 











 











 

 

  

 



  





Tính cosin góc

Ta có

(3;5), (5;8)

CA CB

 

 

2 2 2 2

. 3.5 5.8 55

. . .cos cos

3026

3 5 . 5 8

CACB

CACB CA CB C C

CA CB



     

 

 

   

 

Vì

cos 0

 

góc

là góc nhọn.

b) Tìm giao điểm

của trục hoành với

(tìm tọa điểm

trên trục hoành sao cho

, ,

E A C

thẳng hàng).

c) Tìm giao điểm

của trục tung với

(Tìm tọa điểm

trên trục tung sao cho

, ,

F B C

thẳng hàng).

Vì

E Ox



nên gọi

( ;0)

E x

và

E AC



nên

, ,

E A C

thẳng hàng.

Ta có:

( 1; 2).

AE x  



Để

, ,

E A C

thẳng hàng thì



cùng

phương với

AC AE k AC

 

  

2 1

3 5 5



     

 

Kết luận:

 



















 

thỏa yêu cầu bài toán.

Vì

F Oy



nên gọi

(0; )

F y

và

F BC



nên

, ,

F B C

thẳng hàng.

Ta có:

( 3; 5).

BF y  



Để

, ,

F B C

thẳng hàng thì



cùng

phương với



BF k CB

 

 

3 1

5 8 5



     

Kết luận:

 

















 

thỏa yêu cầu bài toán.

 Cần nhớ:



cùng phương



cùng phương

a k b

  



 

Hoµnh Tung

Tích vô hướng

. . .cos( , ).

a b a b a b



  

Diện tích

( )( )( ).

S p p a p b p c

   

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 31 -

2. Trong mặt phẳng tọa độ

Oxy

cho ba điểm

( 2; 3), ( 2; 4), (5;1).

A B C

  

a) Chứng minh

, ,

A B C

tạo thành một tam giác. Tìm trọng tâm

của tam giác

ABC

Tính

cosin góc

và cho biết góc

là góc nhọn hay tù ? Tìm chu vi và diện tích của tam giác.

..................................................................................................................................................................

b) Tìm giao điểm của trục hoành với

c) Tìm giao điểm của trục tung với

..............................................................................

................................................................................

d) Tìm tọa độ điểm

thuộc trục hoành sao cho

, ,

A E G

thẳng hàng.

..................................................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 32 -

3. Trong mặt phẳng tọa độ

Oxy

cho ba điểm

(10;1), ( 7; 2), (1;3).

A B C

 

a) Chứng minh

, ,

A B C

tạo thành một tam giác. Tìm trọng tâm

của tam giác

ABC

Tính

cosin góc

và cho biết góc

là góc nhọn hay tù ? Tìm chu vi và diện tích của tam giác.

..................................................................................................................................................................

b) Tìm giao điểm của trục hoành với

c) Tìm giao điểm của trục tung với

..............................................................................

...............................................................................

d) Tìm tọa độ điểm

thuộc trục tung sao cho

, ,

A E G

thẳng hàng.

..................................................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 33 -

4. Trong mặt phẳng tọa độ

Oxy

cho hai điểm

(3;2), (1; 1).

A B



a) Tìm tọa độ điểm

thuộc trục hoành và

thuộc trục tung sao cho tam giác

AMN

nhận

là trọng tâm.

b) Hãy tìm tọa độ điểm

thuộc đường thẳng

: 2 4 3 0

d x y

  

để ba điểm

, ,

A B E

thẳng hàng.

Giải. Gọi

( ;0)

M x Ox



và

(0; ) .

N y Oy



Để tam giác

AMN

nhận

là trọng tâm,

nghĩa là

là trọng tâm

AMN



3 0

3 3

2 0

3 3

A M N M

A M N N

x x x x

y y y y

 

 

   

 

 

 



 

 

   

 

  

 

 

(0;0), (0; 5).

M N









  





 





Kết luận:

(0;0)

(0; 5)















Giải. Vì

: 2 4 3 0

E d x y

   

3 1

2 4 3 0

4 2

E E E E

x y y x

      

3 1

;

4 2

E E

E x x

 







  











 

Có

1 5

( 2; 3), 3;

2 4

E E

AB AE x x

 







      











 

 

Để

, ,

A B E

thẳng hàng thì



cùng phương

với



2 3

3 5 1

4 2

 

 

 



13 7 13 7

;

4 8 4 8

E E

x y E

 









      











 

5. Trong mặt phẳng tọa độ

Oxy

cho hai điểm

(1; 2), (2; 1).

A B

 

a) Tìm tọa độ điểm

thuộc trục hoành và

thuộc trục tung sao cho tam giác

AMN

nhận

là trọng tâm.

b) Hãy tìm tọa độ điểm

thuộc đường thẳng

: 2 1 0

d x y

  

để ba điểm

, ,

A B E

thẳng hàng.

..............................................................................

................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 34 -

6. Trong mặt phẳng tọa độ

Oxy

cho hai điểm

(5;1), ( 3; 2).

A B

 

a) Tìm tọa độ điểm

thuộc trục hoành và

thuộc trục tung sao cho tam giác

BMN

nhận

là trọng tâm.

b) Hãy tìm tọa độ điểm

thuộc đường thẳng

: 3 0

d x y

  

sao cho ba điểm

, ,

A B E

thẳng hàng.

..............................................................................

...............................................................................

7. Trong mặt phẳng tọa độ

Oxy

cho hai điểm

(1;4), ( 2;2).

A B



a) Tìm tọa độ điểm

thuộc trục hoành và

thuộc trục tung sao cho tam giác

BMN

nhận

là trọng tâm.

b) Hãy tìm tọa độ điểm

thuộc đường thẳng

: 4 2 5 0

d x y

  

để ba điểm

, ,

A B E

thẳng hàng.

..............................................................................

...............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 35 -

8. Trong mặt phẳng tọa độ

Oxy

cho tam giác

ABC

với

(2;3), (0;2), (4; 1).

A B C



a) Hãy tính chu vi và diện tích của tam giác

ABC

b) Tìm tọa độ tâm

và bán kính đường tròn

ngoại tiếp tam giác

ABC

2 2

( 2; 1) 2 1 5.

AB AB

      





2 2

(2; 4) 2 4 2 5.

AC AC

     





2 2

(4; 3) 4 3 5.

BC BC

     





Nhận thấy

2 2 2

AB AC BC

 

nên theo

Pitago đảo thì tam giác

ABC

vuông tại

Chu vi

ABC



ABC

C AB AC BC

  

5 2 5 5 3 5 5.

    

Diện tích tam giác

ABC

1 1

. 5.2 5 5.

2 2

ABC

S AB AC

  

Vì tam giác

ABC

vuông tại

nên tâm

đường tròn ngoại tiếp tam giác

ABC

nằm tại

trung điểm cạnh huyền

 

0 4

2 2

2 1

2 2 2

B C

x x

y y









  



 











  











  



 



   





là bán kính đường tròn ngoại tiếp tam giác

ABC

2 2

R IA IB IC

      

Kết luận: Tâm

 

















 

và bán kính

 

c) Tìm tọa độ điểm

là điểm đối xứng của

qua

b) Hãy tìm tọa độ

là giao điểm của hai

đường chéo trong hình bình hành

ABCD

Ta có

là điểm đối xứng của

qua



là trung điểm

nên

2 2

3 2

2 2 2

A J J

A J J J

x x x

y y y y

 

 

 

 

 



 





 



 

 

  

  

   

  



 

 

 

Kết luận:

(2; 2).



Vì

là giao điểm của hai đường chéo trong

ABCD

nên

là trung điểm của

2 4

2 2

(3;1).

3 1

2 2

A C

x x

y y









  















  





Kết luận:

(3;1).

9. Trong mặt phẳng tọa độ

Oxy

cho tam giác

ABC

với

(1; 1), (5; 3), (2;0).

A B C

 

a) Hãy tính chu vi và diện tích của tam giác

ABC

b) Tìm tọa độ tâm

và bán kính đường tròn

ngoại tiếp tam giác

ABC

..............................................................................

................................................................................

c) Tìm tọa độ điểm

là điểm đối xứng của

qua

b) Hãy tìm tọa độ

là giao điểm của hai

đường chéo trong hình bình hành

ABCD

..............................................................................

................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 36 -

10. Trong mặt phẳng tọa độ

Oxy

cho tam giác

ABC

với

(1; 1), (5;1), (3;5).

A B C



a) Hãy tính chu vi và diện tích của tam giác

ABC

b) Tìm tọa độ tâm

và bán kính đường tròn

ngoại tiếp tam giác

ABC

..............................................................................

...............................................................................

c) Tìm tọa độ điểm

là điểm đối xứng của

qua

b) Hãy tìm tọa độ

là giao điểm của hai

đường chéo trong hình bình hành

ABDC

..............................................................................

...............................................................................

11. Trong mặt phẳng tọa độ

Oxy

cho tam giác

ABC

với

(4;1), (1;4), (2; 1).

A B C



a) Hãy tính chu vi và diện tích của tam giác

ABC

b) Tìm tọa độ tâm

và bán kính đường tròn

ngoại tiếp tam giác

ABC

..............................................................................

...............................................................................

c) Tìm tọa độ điểm

là điểm đối xứng của

qua

b) Hãy tìm tọa độ

là giao điểm của hai

đường chéo trong hình bình hành

ABCD

..............................................................................

...............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 37 -

12. Trong mặt phẳng tọa độ

Oxy

cho hai điểm

(3;2), (1; 1).

A B



a) Tìm tọa độ điểm

thuộc trục hoành sao

cho tam giác

ABM

vuông tại

b) Tìm tọa độ điểm

thuộc trục tung sao cho

tam giác

ABN

vuông tại

Giải. Vì

M Ox



nên gọi

( ;0).

M x

Ta có:

( 3; 2)

( 1;1)

AM x

BM x





  









 









Để tam giác

ABM

vuông tại

thì

. 0

AM BM AM BM

  

   

( 3)( 1) 2 0

M M

x x

    

4 1 0

M M

x x

   

2 3



 







 



Do đó:

(2 3;0)



hoặc

(2 3;0).



Giải. Vì

N Oy



nên gọi

(0; ).

N y

Ta có:

( 3; 2)

( 2; 3)

AN y





  









  







Để tam giác

ABN

vuông tại

thì

. 0

AN AB AN AB

  

   

( 3).( 2) ( 2).( 3) 0

      

6 3 6 0

   

 

Vậy

(0; 4)

là điểm thỏa yêu cầu bài toán.

13. Trong mặt phẳng tọa độ

Oxy

cho hai điểm

(1; 3), (2;5).

A B



a) Tìm tọa độ điểm

thuộc trục hoành sao

cho tam giác

ABM

vuông tại

b) Tìm tọa độ điểm

thuộc trục tung sao cho

tam giác

ABN

vuông tại

..............................................................................

................................................................................

14. Trong mặt phẳng tọa độ

Oxy

cho hai điểm

(1; 1), (3; 2)

A B

 

và

là gốc tọa độ.

a) Tìm tọa độ điểm

thuộc trục hoành sao

cho tam giác

OBM

vuông tại

b) Tìm tọa độ điểm

thuộc trục tung sao cho

tam giác

ABN

vuông tại

..............................................................................

................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 38 -

15. Trong mặt phẳng tọa độ

Oxy

cho tam giác

ABC

với

(1;3), (2; 1), (2; 3).

A B C

 

a) Hãy tìm tọa độ trực tâm

của tam giác

ABC

b) Gọi

là hình chiếu vuông góc của

lên

cạnh

Tìm tọa độ của

Giải. Gọi

( ; )

H H

H x y

là trực tâm

ABC



Ta có:

. 0

AH BC AH BC

BH AC









 





 

 





 







 

( )



Có

( 1; 3)

H H

AH x y

  



và

(0; 2)

 



( 2; 1)

H H

BH x y

  



và

(1; 6).

 



2( 3) 0 3

( ) .

2 6( 1) 0 26

H H

H H H

y y

x y x

 

 

   

 

  

 

 

    

 

 

Suy ra

(3;26).

Kết luận:

(3;26)

thỏa yêu cầu bài toán.

Giải. Gọi

( ; )

K K

K x y

là hình chiếu vuông góc

của

lên cạnh

CK AB

 

và

, ,

K A B

thẳng hàng.

Ta có

( 2; 3), (1; 4)

K K

CK x y AB

    

 

Vì

. 0

CK AB CK AB

  

 

2 4( 3) 0 4 14

K K K K

x y x y

       

Mà

( 1; 3)

K K

AK x y

  



và

AB AK



 

nên

3 4





 

4 14 1

3 4

 

 

 

49 434

17 17

K K

y x   

434 49

;

17 17

 







  











 

16. Trong mặt phẳng tọa độ

Oxy

cho tam giác

ABC

với

(3;8), (7; 2), (1;1).

A B C



a) Hãy tìm tọa độ trực tâm

của tam giác

ABC

b) Gọi

là hình chiếu vuông góc của

lên

cạnh

. Tìm tọa độ điểm

..............................................................................

...............................................................................

17. Trong mặt phẳng tọa độ

Oxy

cho tam giác

ABC

với

(2; 4), (5;0), (3;2).

A B C



a) Hãy tìm tọa độ trực tâm

của tam giác

ABC

b) Gọi

là trung điểm

Tìm tọa độ điểm

sao cho

là trực tâm tam giác

AEC

..............................................................................

...............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 39 -

18. Trong mặt phẳng tọa độ

Oxy

cho tam giác

ABC

với

(3;8), (7; 2), (1;1).

A B C



a) Tìm tâm và bán kính đường tròn ngoại

tiếp tam giác

ABC

b) Tìm tọa độ điểm

: 2 4 0

N d x y

   

để

tam giác

ABN

cân tại

Giải. Gọi

( ; )

I I

I x y

là tâm đường tròn ngoại

tiếp

ABC R IA IB IC

    

2 2

( 3) ( 8)

( 7) ( 2)

( 1) ( 1)

I I

AI x y

BI x y

CI x y

   

   

   



Ta có:

2 2

IA IB IA IB

IA IC





 





 

 



 







2 2 2 2

( 3) ( 8) ( 7) ( 2)

( 3) ( 8) ( 1) ( 1)

I I I I

x y x y





      







      





6 16 73 14 4 53

6 16 73 2 2 2

I I I I

x y x y





      









      





Suy ra

x  và

 



Tâm

95 27

;

16 8

 

















 

và

7685

R IA

  

Giải. Gọi

( ;2 4) : 2 4 0.

N a a d x y

    

Vì

ABN



cân tại

nên

AN AB



................................................................................

19. Trong mặt phẳng tọa độ

Oxy

cho tam giác

ABC

với

( 2; 3), ( 2; 4), (5;1).

A B C

  

a) Tìm tâm và bán kính đường tròn ngoại

tiếp tam giác

ABC

b) Tìm tọa độ điểm

: 3 10 0

N d x y

   

để tam giác

ABN

cân tại

..............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 40 -

20. Trong mặt phẳng tọa độ

Oxy

cho tam giác

ABC

với

(2;3), (3;2), (4; 1).

A B C



a) Tìm tọa độ điểm

sao cho

ABCD

là

hình bình hành.

b) Tìm tọa độ điểm

thuộc trục hoành sao

cho

ABCI

là hình thang nhận

là đáy.

Giải. Gọi

( ; )

D D

D x y

là đỉnh thứ tư của hình

bình hành

ABCD

AB DC

 

 

( )



Ta có

(1; 1)

(4 ; 1 )

D D

DC x y





 







   







1 4 3

( ) (3;0).

1 1 0

D D

x x

y y

 

 

  

 

   

 

 

    

 

 

Giải. Vì

I Ox



nên gọi

( ; 0).

I x

Ta có

( 4;1).

CI x 



Để

ABCI

là hình thang nhận

là đáy thì







1 1

4 1



   



Vậy

(3; 0)

thỏa mãn yêu cầu bài toán.

c) Tìm tọa độ điểm

là chân đường phân giác trong của góc

trong tam giác

ABC

Giải. Gọi

( ; )

J J

J x y

là chân đường phân giác trong của



BJ AB AB

BJ JC

CJ AC AC

    

 

Ta có:

(1; 1) 2

1 1

2 2

(2; 2) 2 2

AB AB

BJ JC

AC AC





   



    





   







 



Mà

( 3; 2)

1 1 1 1

(4 ; 1 ) 2 ;

2 2 2 2

J J

J J J J

BJ x y

CJ x y CJ x y





  



 











        















 







 

3 2

1 1

2 2

J J

x x

y y





  









   









 













 











 

 









thỏa mãn yêu cầu bài toán.

21. Trong mặt phẳng tọa độ

Oxy

cho tam giác

ABC

với

(1; 1), (5; 3), (2;0).

A B C

 

a) Tìm tọa độ điểm

sao cho

ABCD

là

hình bình hành.

b) Tìm tọa độ điểm

thuộc trục hoành sao

cho

ABCI

là hình thang nhận

là đáy.

..............................................................................

.............................................................................

c) Tìm tọa độ điểm

là chân đường phân giác trong của góc

trong tam giác

ABC

...................................................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 41 -

22. Trong mặt phẳng tọa độ

Oxy

cho tam giác

ABC

với

( 1; 4), (1;2), ( 8; 5).

A B C

   

a) Tìm tọa độ điểm

sao cho

ABCD

là

hình bình hành.

b) Tìm tọa độ điểm

thuộc trục hoành sao

cho

BACI

là hình thang nhận

là đáy.

..............................................................................

c) Tìm tọa độ điểm

là chân đường phân giác trong của góc

trong tam giác

ABC

...................................................................................................................................................................

23. Trong mặt phẳng tọa độ

Oxy

cho tam giác

ABC

với

(10;5), (3;2), (6; 5).

A B C



a) Tìm tọa độ điểm

sao cho

ABCD

là

hình bình hành.

b) Tìm tọa độ điểm

thuộc trục hoành sao

cho

ABCI

là hình thang nhận

là đáy.

..............................................................................

c) Tìm tọa độ điểm

là chân đường phân giác trong của góc

trong tam giác

ABC

...................................................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 42 -

Chuyªn ®Ò 7. TÝch v« híng & HÖ thøc lîng

1. Cho tam giác

ABC

đều cạnh

tâm

Hãy tính:

AB AC

 

. .

AB BC

 

Ta có

. . cos( , )

AB AC AB AC AB AC



     

. .cos 60 . .

2 2

AB AC a a

    

Ta có:

. .

AB BC BA BC

 

   

. cos( , )

BA BC BA BC

 

   

. .cos 60 . .

2 2

BA BC a a

       

( )( ).

OB OC AB AC

 

   

( 2 )( 3 ).

AB AC AB BC

 

   

..............................................................................

.............................................................................

2. Cho hình thang

ABCD

có đáy lớn

3 ,

BC a



đáy nhỏ

AD a



đường cao

2 .

AB a



( )( ).

OB OC AB AC

 

   

c) Gọi

là trung điểm

Tính



(

;

AI B

..............................................................................

.............................................................................

Cần nhớ:

. . .cos( , )

a b a b a b



  

Bình phương vô hướng:

a a



 

( ) 2 .

a b a a b b

    

  

và

( )( ).

a b a b a b

   

  

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 43 -

3. Cho tam giác

ABC

có

6, 19

AB BC

 

và

15.



Tính bán kính đường tròn

ngoại tiếp, nội tiếp của tam giác

ABC

4. Cho tam giác

ABC

có

2, 4

AB BC

 

và

2 7.



Tính bán kính đường tròn

ngoại tiếp, nội tiếp của tam giác

ABC

Lời giải. Nửa chu vi

19 15 6

20.

 

 

Diện tích

( )( )( )

S p p a p b p c

   

20(20 19)(20 15)(20 6) 10 14.

    

Bán kính đường tròn ngoại tiếp

ABC



19.15.6 171 14

4 4 56

4.10 14

abc abc

S R

R S

     

Bán kính đường tròn nội tiếp

ABC



10 14 14

20 2

S pr r

     

.............................................................................

5. Cho tam giác

ABC

có

10, 16

AB AC

 

và

14.



Tính bán kính đường tròn

ngoại tiếp, nội tiếp, của tam giác

ABC

6. Cho tam giác

ABC

có

5, 7

AB AC

 

và

10.



Tính bán kính đường tr

òn

ngoại tiếp, nội tiếp, của tam giác

ABC

.................................................................................

.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 44 -

7. Cho tam giác

ABC

có

6, 8

AB AC

 

và



60 .

BAC

 

Tính

, ,

h R r

với

R r

lần lượt là bán kính đường tròn ngoại tiếp,

nội tiếp tam giác

ABC

8. Cho tam giác

ABC

có

6, 10

AB AC

 

và



120 .

BAC

 

Tính

, ,

h R r

với

R r

lần lượt là bán kính đường tròn ngoại

tiếp, nội tiếp tam giác

ABC

Lời giải. Theo định lý hàm cos, ta có:

2 2 2

2 cos

a b c bc A

  

64 36 2.8.6.cos60 49 7.

     

Diện tích tam giác

ABC

1 1

sin .8.6.sin 60 10 3.

2 2

ABC

S bc A



   

Đường cao xuất phát từ đỉnh

1 2 2.10 3 20 3

2 7 7

ABC a a

S a h h

     

Áp dụng định lý hàm sin, suy ra bán kính

đường tròn ngọa tiếp tam giác

ABC

7 7 3

sin 2.sin 60 3

R R

    



Nửa chu vi

7 8 6 21

2 2 2

a b c

   

   

Bán kính đường tròn nội tiếp

ABC

2.10 3 20 3

21 21

ABC

S pr r



     

.............................................................................

9. Cho tam giác

ABC

có

13, 14

AB AC

 

và

15.



Tính diện tích tam giác

, sin ,

ABC A

độ dài đường trung tuyến kẻ

từ

của tam giác

ABC

10. Cho tam giác

ABC

có

5, 7

AB AC

 

và



Tính diện tích tam giác

, sin ,

ABC A

độ dài đường trung tuyến

kẻ từ

của tam giác

ABC

.................................................................................

.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 45 -

11. Cho

ABC



có

2 , 3

AB a AC a

 

và



60 .

BAC

 

Gọi

là trung điểm

a) Tính cạnh

trung tuyến

và bán

kính đường tròn ngoại tiếp

ABC



.................................................................................

b) Gọi

là điểm trên cạnh

sao cho

5 7 0.

NA NC

 

  

CM:

AM BN



.............................................................................

12. Cho hình bình hành

ABCD

có



5 , 8 , 60 .

AB a AD a BAD

   

a) Tính các tích vô hướng:

. , . .

AB AD AC AD

   

.................................................................................

b) Tính độ dài đoạn

và bán kính đường

tròn ngoại tiếp tam giác

ABC

.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 46 -

13. Cho tam giác

ABC

có

10cm, 16cm, 14cm.

AB AC BC

  

a) Hãy tính số đo góc



BAC

, tính diện tích tam

giác

ABC

tính bán kính đường tròn ngoại

tiếp

và tính bán kính đường tròn nội tiếp

của tam giác

ABC

.................................................................................

b) Gọi

là trung điểm

và

là trọng

tâm tam giác

ABC

Tính độ dài

và

tích vô hướng

. .

AG BC

 

.............................................................................

14. Cho hình thang vuông

ABCD

vuông tại

và

với

3 ,

BC a AD a

 

và

2 .

AB a



Tính:

. ; . ; . .

AB CD BC BD AC BD

     

.................................................................................

.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 47 -

15. Cho tam giác

ABC

có



, 2, 135 .

AB a AC a BAC

   

Gọi

là điểm thỏa mãn:

3 .

AM AC



 

a) Tính

AB AC

 

và

. .

BABM

 

.................................................................................

b) Tính độ dài

và cosin của góc



ABM

.............................................................................

16. Cho tam giác

ABC



có



6, 5, 60 .

AB AC BAC

   

Gọi

thỏa mãn đẳng thức

véctơ:

2 0.

IB IC

 

  

a) Chứng minh:

2 3 .

AB AC AI

 

  

.................................................................................

b) Tính

AB AC

 

và độ dài đoạn thẳng

.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 48 -

17. Cho tam giác

ABC

có

5, 8, 60 .

AB AC A

   

a) Tính độ dài cạnh

của tam giác.

.................................................................................

b) Gọi

là trung điểm

Tính

. .

AK BC

 

.............................................................................

18. Cho tam giác

ABC

a) Gọi

M D

lần lượt là trung điểm

, .

BC AM

Chứng minh:

2 0.

DB DC DA

  

   

.................................................................................

b) Biết

2, 3

AB AC

 

và



120 .

BAC

 

Tính

AB AC

 

và bán kính đường tròn

ngoại tiếp tam giác

ABC

.............................................................................

19. Cho tam giác

ABC

có



5, 8, 120 .

AB AC BAC

   

a) Tính

AB AC

 

và độ dài

.................................................................................

là trọng tâm

ABC



Tính

. .

AG BC

 

.............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 49 -

ĐỀ SỐ 01 – THPT BÌNH HƯNG HÒA (2017 – 2018)

Câu 1. (4,0 điểm) Giải các phương trình sau:

2 6 2 3.

x x x

   

2 2

3 4 5 4 9.

x x x x

    

............................................................................

.................................................................................

2 1 6

4 2 4( 2)

x x

 

  

 

3 1 ( 1).

x x x x   

............................................................................

.................................................................................

Câu 2. (1,0 điểm) Tìm tất cả các giá trị của tham số

để phương trình

2 2 0

x x m

   

có hai nghiệm dương phân biệt.

..................................................................................................................................................................

Câu 3. (1,0 điểm) Tìm tham số

để phương trình

2 2

2( 1) 3 0

x m x m

    

có hai

nghiệm phân biệt

1 2

x x

thỏa mãn

2 2

1 2

x x

 

..................................................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 50 -

Câu 4. (1,0 điểm) Chứng minh rằng

1 1 1

a b c

bc ac ab a b c

    

với mọi

, , 0.

a b c



..................................................................................................................................................................

Câu 5. (3,0 điểm) Trong mặt phẳng

Oxy

cho ba điểm

( 1;3), ( 4; 5)

A B

  

và

(1; 2).



a) Chứng tỏ

, ,

A B C

là ba đỉnh của tam

giác và tìm trọng tâm

của

ABC



............................................................................

b) Tìm tọa độ điểm

để

ABC

là hình bình

hành. Tìm tọa độ trực tâm H của

ABC



.................................................................................

c) Tìm tọa độ điểm

thuộc trục hoành sao cho 2

MA MC



 

đạt giá trị nhỏ nhất.

..................................................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 51 -

ĐỀ SỐ 02 – THPT TRẦN PHÚ (2017 – 2018)

Câu 1. (1,0 điểm) Cho ba tập hợp:

( 4;4), [4;6], (0; 8).

A B C

   

Tìm

( ) .

A B C

 

..................................................................................................................................................................

Đáp số:

( ) (0;6].

A B C

  

..............................................................................................................

Câu 2. (1,0 điểm) Tìm tập xác định của hàm số: 1

y x

   



..................................................................................................................................................................

Đáp số:

[ 1; ) \ {2}.

  

..............................................................................................................

Câu 3. (1,0 điểm) Cho đường thẳng

: 1

d y x

 

và parabol

( ) : 2 .

P y x x

 

Gọi

là đỉnh

của

( )

và

là điểm trên

sao cho

 

Tìm tọa độ điểm

..................................................................................................................................................................

Đáp số:

1 1

;

2 2

 







 











 

..............................................................................................................................

Câu 4. (1,0 điểm) Cho phương trình

2( 1) 2( 2) 0 (1).

x m x m

    

Chứng minh rằng

phương trình

(1)

luôn có hai nghiệm phân biệt

1 2

x x

và tìm tham số

để biểu thức

1 2 1 2

( ) 8 1

A x x x x

   

đạt giá trị nhỏ nhất.

..................................................................................................................................................................

Đáp số:

đạt giá trị nhỏ nhất bằng

khi



..........................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 52 -

Câu 5. (1,0 điểm) Giải phương trình

( 1)( 4 1 1) 0.

x x

   

..................................................................................................................................................................

Đáp số:



.......................................................................................................................................

Câu 6. (1,0 điểm) Giải phương trình

2 2

3 4 5 4 1 0.

x x x x

     

..................................................................................................................................................................

Đáp số:



.......................................................................................................................................

Câu 7. (1,0 điểm) Tìm giá trị nhỏ nhất của hàm số:

( )

2 2

f x

 



khi



..................................................................................................................................................................

Đáp số: Giá trị nhỏ nhất của

( )

f x

bằng

tại



......................................................................

Câu 8. (1,0 điểm) Cho tam giác

ABC

có

2, 2 3,

AB AC

 

góc

30 .

 

Tính độ dài

cạnh

bán kính đường tròn ngoại tiếp và diện tích tam giác

ABC

..................................................................................................................................................................

Đáp số:

2, 2, 3.

BC R S

  

.....................................................................................................

Câu 9. (1,0 điểm) Cho tam giác

ABC

Gọi

là điểm trên cạnh

sao cho

2 .

MB MC



Hãy phân tích



theo

, .

AB AC

 

..................................................................................................................................................................

Đáp số:

1 2

3 3

AM AB AC

 

  

............................................................................................................

Câu 10. (1,0 điểm) Cho tam giác

ABC

với

( 1;1), (1;2), (3; 4).

A B C

 

Gọi

là trung điểm

BC K

là điểm trên đường thẳng

sao cho

BK AM



Tìm tọa độ điểm

..................................................................................................................................................................

Đáp số:

3 1

;

11 11

 







 











 

...........................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 53 -

ĐỀ SỐ 03 – THPT LÊ TRỌNG TẤN (2017 – 2018)

Câu 1. (1,0 điểm) Xét tính chẵn lẻ của hàm số

4 2

x x

  

 

..................................................................................................................................................................

Đáp số: Hàm số lẻ..................................................................................................................................

Câu 2. (1,0 điểm) Khảo sát sự biến thiên và vẽ đồ thị của hàm số

4 3.

y x x

   

..................................................................................................................................................................

Câu 3. (1,0 điểm) Xác định parabol

( ) : ,

P y ax bx c

  

biết

( )

đi qua

(1; 3)

và có tọa

độ đỉnh là

1 3

;

2 4

 







 











 

..................................................................................................................................................................

Đáp số:

( ) : 1.

P y x x

  

.............................................................................................................

Câu 4. (2,0 điểm) Giải các phương trình sau:

5 1 .

x x

  

6 3 3.

x x x

   

............................................................................

Đáp số:



.................................................

.................................................................................

Đáp số:

{5;6}.



...............................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 54 -

2 (6 )(4 ) 12.

x x x x    

3 1 8 1.

x x

   

............................................................................

Đáp số:

{ 2; 4}.

 

.......................................

.................................................................................

Đáp số:

{8}.



..................................................

Câu 5. (1,0 điểm) Cho phương trình:

2( 1) 3 0

mx m x m

    

(

tham số). Xác định

để phương trình có

nghiệm phân biệt

1 2

x x

thỏa mãn

1 2

1 1 1

x x

  

..................................................................................................................................................................

Đáp số:

  

...............................................................................................................................

Câu 6. (1,0 điểm) Cho tam giác

ABC

có



3, 4, 120 .

AB BC ABC

   

a) Tính tích vô hướng

. .

BA BC

 

............................................................................

Đáp số:

. 6.

BA BC

 

 

...................................

b) Tính độ dài cạnh

.................................................................................

Đáp số:

37.



.............................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 55 -

Câu 7. (3,0 điểm) Trong mặt phẳng

Oxy

cho

ABC



có

( 2; 0), (5; 3)

A B



và

(3; 2).



a) Chứng minh

ABC



vuông cân. b) Tìm điểm

sao cho

là trung điểm

............................................................................

Đáp số: Tam giác vuông cân tại

.................................................................................

Đáp số:

( 9; 3).

 

...............................................

c) Tìm tọa độ điểm

M N

sao cho

M N

chia đoạn

thành

đoạn bằng nhau.

d) Tìm tọa độ điểm

sao cho

ABC

là hình

bình hành.

............................................................................

Đáp số:

 

















 

và

 



















 

.................................................................................

Đáp số:

( 4; 5).

 

..............................................

e) Tìm tâm đường tròn ngoại tiếp

và trực tâm

của tam giác

ABC

..................................................................................................................................................................

Đáp số:

3 3

;

2 2

 



















 

....................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 56 -

ĐỀ SỐ 04 – THPT BÌNH TÂN (2017 – 2018)

Câu 1. (1,0 điểm) Xác định parabol

( ) : 2,

P y ax bx

  

biết

( )

đi qua hai điểm

(4; 6)

và

( 1; 4).

 

..................................................................................................................................................................

Đáp số:

( ) : 5 2.

P y x x

   

.........................................................................................................

Câu 2. (1,0 điểm) Tìm tham số

để phương trình

2 2

2 2 1 0

x mx m m

    

có hai

nghiệm phân biệt dương.

..................................................................................................................................................................

Đáp số:

 

.....................................................................................................................................

Câu 3. (1,0 điểm) Tìm tham số

để phương trình

2 2

(2 1) 2 0

x m x m

    

có hai

nghiệm thỏa mãn

1 2 1 2

3 . 5( ) 7 0.

x x x x

   

..................................................................................................................................................................

Đáp số:



......................................................................................................................................

Câu 4. (1,0 điểm) Giải phương trình

1 3 2 2 .

x x

  

..................................................................................................................................................................

Đáp số:

; 1.

x x

 

.........................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 57 -

Câu 5. (1,0 điểm) Giải hệ phương trình

2 2

x y





 







 





..................................................................................................................................................................

Đáp số:

( ; ) {( 4; 5),(5;4)}.

S x y

   

..............................................................................................

Câu 6. (1,0 điểm) Cho hai số

, 4.

a b



Chứng minh rằng

4 4

a b b a

    

..................................................................................................................................................................

Đáp số: Dấu

" "



xảy ra khi và chỉ khi

a b

 

........................................................................

Câu 7. (1,0 điểm) Cho bốn điểm

, , , .

A B C D

Chứng minh rằng

AB CD CA DB

  

   

..................................................................................................................................................................

Câu 8. (1,0 điểm) Trong mặt phẳng

Oxy

cho ba điểm

( 4;1), (2; 4), ( 1; 5).

A B C

  

Tìm tọa

độ điểm

biết

2 3 .

DA BD CB

 

  

..................................................................................................................................................................

Đáp số:

(17;34).

.................................................................................................................................

Câu 9. (1,0 điểm) Tìm tọa độ trực tâm

của

MNP



với

(1;2), ( 2; 1), (3;1).

M N P

 

..................................................................................................................................................................

Câu 10. (1,0 điểm) Cho

ABC



có trực tâm

và

là trung điểm của

Chứng minh

rằng:

4 . .

MH MA BC



 

..................................................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 58 -

ĐỀ SỐ 05 – THPT NGUYỄN HỮU CẢNH (2017 – 2018)

Câu 1. (1,0 điểm) Khảo sát sự biến thiên và vẽ đồ thị hàm số

2 1.

y x x

  

..................................................................................................................................................................

Câu 2. (1,0 điểm) Giải và biện luận phương trình

( 1) 1.

m x m x

  

..................................................................................................................................................................

Câu 3. (3,0 điểm) Giải các phương trình sau:

1 2

x x



  

 

5 4 4.

x x x

   

............................................................................

Đáp số:

{0;5}.



..........................................

.................................................................................

Đáp số:

{0;6}.



...............................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 59 -

1 1

4 2 6 0.

x x

    

2 6 10 5( 2) 1 0.

x x x x

     

............................................................................

Đáp số:

{ 0,5; 1}.

  

................................

.................................................................................

Đáp số:

{3;8}.



...............................................

Câu 4. (1,0 điểm) Cho phương trình

2 2

(2 1) 3 2 0

x m x m m

     

với

là tham số.

Định

để phương trình có hai nghiệm phân biệt

1 2

x x

thỏa

1 2

1 1 3

x x

   

..................................................................................................................................................................

Đáp số:



......................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 60 -

Câu 5. (1,0 điểm) Giải hệ phương trình

2 5

3 0

x y

x y x





 







   





..................................................................................................................................................................

Đáp số:

( ; ) {(1;3);(2;1)}.

x y



Câu 6. (2,0 điểm) Trong hệ trục tọa độ

Oxy

cho

ABC



có

(2;3), (4;1), ( 1; 2).

A B C

 

a) Tìm điểm

thỏa

2 3 .

AD AC BC

 

  

b) CM:

ABC



và tính diện tích

ABC



............................................................................

Đáp số:

(8;5).

...............................................

.................................................................................

Đáp số:



......................................................

Câu 7. (1,0 điểm) Cho tam giác đều

ABC

cạnh

Trên hai cạnh

AB AC

lần lượt lấy hai

điểm

M N

sao cho

1 1

, .

3 5

AM AB AN AC

 

Chứng minh:

BN CM



..................................................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 61 -

ĐỀ SỐ 06 – THPT TRẦN QUANG KHẢI (2017 – 2018)

Câu 1. (4,0 điểm) Giải các phương trình sau:

5 9 2 1.

x x x

   

3 3 3 2.

x x x

   

............................................................................

Đáp số:

{1;2}.



..........................................

.................................................................................

Đáp số:

{1}.



...................................................

2 2

4 4 4 4 9 0.

x x x x

     

1 1 4 3 .

x x x

   

............................................................................

Đáp số:

 

 

  

 

 

 

....................................

.................................................................................

Đáp số:

 

 

 

 

 

 

.................................................

Câu 2. (2,0 điểm) Cho phương trình

2 3 2 0.

x mx m

   

a) Tìm tham số

để phương trình có hai nghiệm trái dấu .........................................................

..................................................................................................................................................................

Đáp số:

 

.....................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 62 -

b) Tìm

để phương trình có hai nghiệm phân biệt

1 2

x x

thỏa mãn

2 2

1 2 1 2

4 .

x x x x

   

..................................................................................................................................................................

Đáp số:



......................................................................................................................................

Câu 3. (1,0 điểm) Với

0, 0,

a b

 

chứng minh bất đẳng thức

1 1 4

a b a b

  



..................................................................................................................................................................

Câu 4. (3,0 điểm) Trong mặt phẳng

Oxy

cho tam giác

ABC

với

(1;2), ( 2;6), (9;8).

A B C



a) Chứng minh rằng tam giác

ABC

vuông

tại

b) Tìm

là trung điểm của

và tính độ

dài trung tuyến

của tam giác

ABC

............................................................................

.................................................................................

Đáp số:

(5;5), 5 2.

M BM



.............................

c) Gọi

là điểm trên cạnh

sao cho

3 .

BN NC



 

Tính diện tích tam giác

ABN

..................................................................................................................................................................

Đáp số:

3 75

4 4

ABN ABC

S S

 

  

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 63 -

ĐỀ SỐ 07 – THPT NGUYỄN THƯỢNG HIỀN (2017 – 2018)

Câu 1. (1,0 điểm) Xác định parabol

( ) : ,

P y ax bx c

  

biết rằng nó đi qua gốc tọa độ

và có đỉnh

(1; 4).



..................................................................................................................................................................

Đáp số:

( ) : 4 8 .

P y x x

 

................................................................................................................

Câu 2. (2,0 điểm) Cho phương trình

3 2 2 0.

x x m

   

Tìm

để phương trình có hai

nghiệm phân biệt

1 2

x x

thỏa mãn

2 2

1 2 1 2

4( ) 17 . .

x x x x

 

..................................................................................................................................................................

Đáp số:

 

hoặc

 

.........................................................................................................

Câu 3. (2,0 điểm) Giải các phương trình sau:

2 2

2 5 2 3.

x x x x

    

2 7 343.

x x x

   

............................................................................

Đáp số:

{1}.



..............................................

.................................................................................

Đáp số:

{7}.



..................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 64 -

Câu 4. (1,0 điểm) Tìm giá trị nhỏ nhất của hàm số

2 1

 



với



..................................................................................................................................................................

Đáp số: Giá trị nhỏ nhất của

bằng

khi



.........................................................................

Câu 5. (2,0 điểm) Trong mặt phẳng tọa độ

Oxy

cho

ABC



với

(0;4), ( 6;1), ( 2;8).

A B C

 

a) Chứng minh tam giác

ABC

tam giác vuông. Tìm tọa độ tâm và tính bán kính đường tròn

ngoại tiếp tam giác

ABC

..............................................................................................................

..................................................................................................................................................................

Đáp số: Tam giác

ABC

vuông tại

nên tâm

 



















 

là trung điểm

và

 

.....

b) Tìm tọa độ điểm

thuộc

sao cho tam giác

MAB

vuông tại

..................................................................................................................................................................

Đáp số:

( 3 5;0)

M   hoặc

( 3 5;0).

M   ...............................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 65 -

Câu 6. (2,0 điểm) Cho tam giác

ABC

có

2, 2 7

AB AC

 

và



a) Tính góc

bán kính đường tròn ngoại tiếp tam giác

ABC

và diện tích tam giác

ABC

..................................................................................................................................................................

Đáp số:



2 21

B 120 , ,

R  

2 3.

ABC

S  ..................................................................................

b) Tính độ dài đường phân giác trong của góc

của tam giác

ABC

..................................................................................................................................................................

Đáp số:

 

.................................................................................................................................

c) Tìm tập hợp các điểm

thỏa

( 2 ).( ) 0.

MA MB AB AC

  

   

..................................................................................................................................................................

Đáp số:

MI CB



 



Tập hợp các điểm

là đường thẳng đi qua

và vuông góc với

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 66 -

ĐỀ SỐ 08 – THPT HÀN THUYÊN (2017 – 2018)

Câu 1. (0,75 điểm) Tìm tập xác định của hàm số

1 3

2 8

x x

  

 

 

..................................................................................................................................................................

Đáp số:

[ 1; ) \ {2}.

  

..............................................................................................................

Câu 2. (1,0 điểm) Tìm parabol

( ) : 2,

P y ax bx

  

biết parabol có đỉnh

(2; 2).



..................................................................................................................................................................

Đáp số:

( ) : 4 2.

P x x

 

....................................................................................................................

Câu 3. (2,5 điểm) Giải các phương trình sau:

2 3

5 3 .



 



 







 













 

............................................................................

Đáp số:

{1}.



.............................................

.................................................................................

Đáp số:

{7}.



..................................................

3 5 3 2 .

x x

   

2 2

2 3 11 3 4 .

x x x x

    

............................................................................

Đáp số:

 

 

 

 

 

 

........................................

.................................................................................

Đáp số:

{2; 1 3}.

  

..................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 67 -

Câu 4. (0,75 điểm) Giải và biện luận phương trình:

( 2) 7 (6 )( ) 2.

m x m m x m

     

..................................................................................................................................................................

Đáp số:

3 :

 

PTVN,

2 :



PT có nghiệm tùy ý,

3, 2 :

m m x



    



Câu 5. (0,75 điểm) Giải hệ phương trình

4 5

8 15

x y x y





 



 







 



 





..................................................................................................................................................................

Đáp số:

( ; ) {(3; 2)}.

x y

 

....................................................................................................................

Câu 6. (1,5 điểm) Trong mặt phẳng

Oxy

cho

ABC



có

( 1;1), (3;5), (2; 3).

A B C

 

a) Tìm

để

ABCD

là hình bình hành. b) Tìm tọa độ trực tâm

của tam giác

ABC

............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 68 -

............................................................................

Đáp số:

( 2; 7).

 

.........................................

.................................................................................

Đáp số:

15 8

;

7 7

 







 











 

...........................................

Câu 7. (2,5 điểm) Cho hình chữ nhật

ABCD

tâm

có cạnh bằng

3 , 2 .

AD a AB a

 

Lấy

điểm

trên cạnh

sao cho

AM AD



a) Chứng minh rằng

OA OB OC OD

   

    

...........................................................................

..................................................................................................................................................................

b) Tính tích vô hướng:

. .

AB AC

 

.........................................................................................................

..................................................................................................................................................................

Đáp số:

. 4 .

AB AC a



 

........................................................................................................................

c) Gọi

là trung điểm của

Tính góc giữa hai véctơ



và



......................................

..................................................................................................................................................................

Đáp số:

( ; ) 90 .

BM AI

 

 

.....................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 69 -

ĐỀ SỐ 09 – THPT NGUYỄN CHÍ THANH (2017 – 2018)

Câu 1. (1,0 điểm) Xét tính chẵn lẻ của hàm số

2018 2018

( )

x x

y f x

  

  



..................................................................................................................................................................

Câu 2. (1,0 điểm) Xác định parabol

( ) : ,

P y ax bx c

  

biết

( )

có trục đối xứng



và đi qua các điểm

(4;2), (1; 1).

A B



..................................................................................................................................................................

Câu 3. (1,0 điểm) Giải phương trình

2 6 1 2 .

x x x

   

..................................................................................................................................................................

Câu 4. (1,0 điểm) Giải hệ phương trình

2 2

8 0

6 2 0

x y

x y x y





  







   





..................................................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 70 -

Câu 5. (1,0 điểm) Tính tuổi của cha hiện nay, biết rằng trước đây hai năm thì tuổi cha gấp bảy

lần tuổi con và sau ba năm nữa thì tuổi cha chỉ còn gấp bốn lần tuổi con.

..................................................................................................................................................................

Câu 6. (1,0 điểm) Chứng minh

( 1) ( 1) 1 ; , 0.

a b b a a b ab a b

        

..................................................................................................................................................................

Câu 7. (2,0 điểm) Cho tam giác

ABC

có



5, 8, 60 .

AB AC BAC

   

a) Tìm độ dài cạnh

và bán kính đường

tròn ngoại tiếp tam giác

ABC

b) Tính diện tích tam giác

ABC

và bán kính

đường tròn nội tiếp tam giác

ABC

............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 71 -

Câu 8. (1,0 điểm) Trong mặt phẳng tọa độ

Oxy

cho hai điểm

(1; 3), (4;2).

A B

Chứng minh

tam giác

OAB

vuông cân và tính diện tích tam giác

OAB

..................................................................................................................................................................

Câu 9. (1,0 điểm) Trong mặt phẳng tọa độ

Oxy

cho tam giác

ABC

biết

( 2;3), (4;1)

A B



và

(0; 3).



Tìm tọa độ điểm



là hình chiếu vuông góc của

lên

..................................................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 72 -

ĐỀ SỐ 10 – THPT TÂY THẠNH (2017 – 2018)

Câu 1. (1,0 điểm) Tìm tọa độ giao điểm của đường thẳng : 2d y x  và

( ) : 2 2 2.

P y x x  

..................................................................................................................................................................

Đáp số: (1; 2), ( 1;2).A B  ..................................................................................................................

Câu 2. (1,0 điểm) Lập bảng biến thiên và vẽ đồ thị của hàm số

2 4 1.y x x   

............................................................................................

Đồ thị của parabol:

..................................................................

Câu 3. (1,0 điểm) Cho parabol

( ) : , ( 0)P y ax bx c a    có đồ thị như hình vẽ bên dưới.

Hãy trình bày cách tìm , , a b c và suy ra tổng

3 .a b c 

............................................................................................................

Đáp số: 1, 2, 1a b c     và

3 0.a b c  

.......................................................................

Câu 4. (1,0 điểm) Giải phương trình

2 2 .x x x   

..................................................................................................................................................................

Đáp số: 2.x   ....................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 73 -

Câu 5. (1,0 điểm) Giải phương trình

4 2

( 1) 3( 2 ) 3 0.

x x x

    

..................................................................................................................................................................

Đáp số:

1, 1 3, 1 3.

x x x

       

.................................................................................

Câu 6. (1,0 điểm) Tìm tất cả các giá trị của tham số

để phương trình

2 2

( 1) 1 0

x m x

   

có hai nghiệm phân biệt sao cho

2 2

1 2

x x

 

..................................................................................................................................................................

Đáp số:

1, 1.

m m

  

.....................................................................................................................

Câu 7. (1,0 điểm) Tìm tham số

để phương trình

( 1) (2 1) 0

m x m x m

    

có nghiệm

..................................................................................................................................................................

Đáp số:



...........................................................................................................................................

Câu 8. (1,5 điểm) Cho tam giác

ABC

và điểm

trên cạnh

sao cho

2 0,

MA MB

 

  

là trọng tâm tam giác

ACM

a) Chứng minh:

3 2 .

CM CA CB

 

  

b) Phân tích



theo hai véctơ

, .

GA GC

 

............................................................................

.................................................................................

Đáp số:

5 3 .

GB GA GC

  

  

.............................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 74 -

Câu 9. (1,5 điểm) Trong mặt phẳng tọa độ

Oxy

cho

ABC



có

(0;2), (0; 3), (2; 1).

A B C

 

a) Tìm tọa độ

thỏa

GA GB GC

  

   

b) Tìm tọa độ điểm

D Ox



để

ABCD

là hình

thang với hai đáy là

, .

AB CD

............................................................................

Đáp số:

2 2

;

3 3

 







 











 

.........................................

.................................................................................

Đáp số:

(2;0).

....................................................

ĐỀ SỐ 11 – THPT CHUYÊN LÊ HỒNG PHONG (2017 – 2018)

Câu 1. (1,0 điểm) Giải phương trình:

2 3 1 1.

x x x

   

..................................................................................................................................................................

Câu 2. (1,0 điểm) Giải hệ phương trình:

2 2

3 1

x y xy





   







  





..................................................................................................................................................................

Câu 3. (1,0 điểm) Tìm parabol

( ) : , ( 0),

P y ax bx c a

   

biết rằng

( )

có đỉnh

(2;1)

và đi qua điểm

(3;2).

..................................................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 75 -

Câu 4. (1,0 điểm) Cho phương trình

( 3)( 2 4) 0 (1) (

x x mx m m

    

là tham số). Định

để phương trình

(1)

có ba nghiệm phân biệt, trong đó có hai nghiệm dương và một

nghiệm âm.

..................................................................................................................................................................

Câu 5. (1,0 điểm) Tìm các giá trị nguyên âm của

để hệ phương trình

2 1

mx y m

x my m





  







 





có nghiệm duy nhất

( ; )

x y

sao cho

x y

là các số nguyên.

..................................................................................................................................................................

Câu 6. (1,0 điểm) Định

để bất phương trình

( 2 3) 2 1 0

m m x m

    

vô nghiệm.

..................................................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 76 -

Câu 7. (1,0 điểm) Trong mặt phẳng tọa độ

Oxy

cho tam giác

ABC

với

(1;2), (3;5)

A B

và

(4;7).

Tìm tọa độ trực tâm

của tam giác

ABC

..................................................................................................................................................................

Câu 8. (1,0 điểm) Cho tam giác

ABC

có

7, 8, 13.

AB BC BC

  

Tính

. .

AB AC

 

..................................................................................................................................................................

Câu 9. (1,5 điểm) Cho tam giác

ABC

có

2, 3

AB AC

 

và



120 .

BAC

 

Tính độ dài

diện tích tam giác

ABC

bán kính đường tròn ngoại tiếp và độ dài đường phân

giác trong

của tam giác

ABC

..................................................................................................................................................................

Câu 10. (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức

1 2

( )

f x

x x

 



với

0 1.

 

..................................................................................................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 77 -

ĐỀ SỐ 12 – THPT NGUYỄN THỊ MINH KHAI (2017 – 2018)

Câu 1. (3,0 điểm) Giải các phương trình và hệ phương trình sau:

1 5 3 2 .

x x x

   

...................................................................................................................

..................................................................................................................................................................

Đáp số:

 

....................................................................................................................................

2 3

3 5 1 4 4 3 .

x x x x x

      

..................................................................................................................................................................

Đáp số:



.......................................................................................................................................

2 2

x y xy

x y





  









 





..................................................................................................................................................................

Đáp số:

( ; ) {(2;1);(1;2)}.

x y



..............................................................................................................

Câu 2. (2,0 điểm) Tìm tham số

sao cho:

a) Phương trình

2 2

4 2

m x x m m

  

có

nghiệm tủy ý.

b) Phương trình

2 4 0

x mx

  

có hai

nghiệm

1 2

x x

thỏa mãn

1 2

2 2.

x x 

............................................................................

Đáp số:



................................................

.................................................................................

Đáp số:

 

...............................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 78 -

Câu 3. (1,0 điểm) Tìm giá trị lớn nhất của hàm số

y x x

 

với

0 1.

 

..................................................................................................................................................................

Câu 4. (2,0 điểm) Cho tam giác

ABC

có

là trung điểm của

Gọi

I J

là các điểm thỏa

mãn

AI AC



 

và

2 .

JB JC



 

a) Chứng minh rằng: ba điểm

, ,

K I J

thẳng hàng.

b) Tìm tập hợp các điểm

thỏa mãn:

2 3 2 .

MA MB MC MB MC

   

    

............................................................................

Đáp số:

KJ IK

 

 

, ,

K I J

thẳng hàng

.................................................................................

Đáp số: Đường tròn tâm

bán kính

Câu 5. (2,0 điểm) Trong mặt phẳng

Oxy

cho

( 2;2), (1; 0), (3; 3).

A B C

 

a) Tìm tọa độ trực tâm

của tam giác

ABC

b) Tìm

D Oy



để

ABCD

là hình thang với

đáy lớn là

............................................................................

Đáp số:

(13;12).

.................................................................................

Đáp số: Không có điểm

thỏa giả thiết.

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 79 -

ĐỀ SỐ 13 – THPT BÙI THỊ XUÂN (2017 – 2018)

Câu 1. (3,0 điểm) Cho phương trình

( 1) 2( 4) 1 0.

m x m x m

     

a) Tìm

để phương trình trên có nghiệm. .....................................................................................

..................................................................................................................................................................

Đáp số:

  

...............................................................................................................................

b) Tìm

để phương trình có hai nghiệm

1 2

x x

trái dấu sao cho

 

..........................

..................................................................................................................................................................

Đáp số:

 

.....................................................................................................................................

c) Tìm tất cả giá trị nguyên âm của tham số

để phương trình có hai nghiệm

1 2

x x

đều là

các số nguyên. ...................................................................................................................................

..................................................................................................................................................................

Đáp số:

 

và thử lại. ................................................................................................................

Câu 2. (3,0 điểm)

a) Giải và biện luận phương trình

( 2) 24 16 2

m x x m

   

theo tham số

.....................

..................................................................................................................................................................

Đáp số:

2( 3)

4 , 4 , 4

m 4

m S m S m S

 

 



 

            

 

 



 

 



¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 80 -

b) Định

để hệ phương trình

2 2

( 1) 1

mx y m

m x y m





  







   





vô nghiệm..........................................

..................................................................................................................................................................

Đáp số:



......................................................................................................................................

c) Giải hệ phương trình:

2 2

( 2) 6( 2) 4 20

( 3) 2 (2 1)

x x y y

x y





    







   





..........................................................

..................................................................................................................................................................

Đáp số:

4, 1.

x y

   

....................................................................................................................

Câu 3. (2,0 điểm) Trong mặt phẳng tọa độ

Oxy

cho tam giác

ABC

( 2; 4), ( 3; 1),

A B

   

(1; 1)



và

là trọng tâm tam giác

ABC

a) Tìm

thỏa

3 .

AM AG BC

 

  

b) Tìm tâm đường tròn ngoại tiếp

ABC



............................................................................

.................................................................................

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 81 -

............................................................................

Đáp số:

(4;2).

.................................................................................

Đáp số:

( 1; 2).

 

Câu 4. (2,0 điểm) Cho tam giác

ABC

có

3, 5

AB AC

 

và



60 .

BAC

 

Gọi

là trung

điểm của

và

là điểm trên cạnh

sao cho

4 .

AC AE



 

a) Tính

và bán kính nội tiếp

AMC



b) Tính tích vô hướng

. .

BE AC

 

............................................................................

Đáp số:

CM  và

15 3

AMC

 

.................................................................................

Đáp số:

BE AC

  

 

¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019

Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 82 -

MỤC LỤC

Trang

Chuyên đề 1. Parabol & một số vấn đề liên quan ..................................................................... 1

Chuyên đề 2. Giải và biện luận phương trình bậc nhất ........................................................... 5

Chuyên đề 3. Bài toán chứa tham số trong phương trình bậc hai .......................................... 7

Chuyên đề 4. Phương trình quy về phương trình bậc hai ....................................................... 13

Chuyên đề 5. Bất đẳng thức và GTLN, GTNN .......................................................................... 23

Chuyên đề 6. Hệ trục tọa độ ......................................................................................................... 29

Chuyên đề 7. Tích vô hướng và hệ thức lượng ......................................................................... 42

Đề số 01. THPT Bình Hưng Hòa (2017 – 2018) ................................................................... 49

Đề số 02. THPT Trần Phú (2017 – 2018) .............................................................................. 51

Đề số 03. THPT Lê Trọng Tấn (2017 – 2018) ....................................................................... 53

Đề số 04. THPT Bình Tân (2017 – 2018) ............................................................................... 56

Đề số 05. THPT Nguyễn Hữu Cảnh (2017 – 2018) ............................................................. 58

Đề số 06. THPT Trần Quang Khải (2017 – 2018) ................................................................ 61

Đề số 07. THPT Nguyễn Thượng Hiền (2017 – 2018) ........................................................ 63

Đề số 08. THPT Hàn Thuyên (2017 – 2018) ......................................................................... 66

Đề số 09. THPT Nguyễn Chí Thanh (2017 – 2018) ............................................................. 69

Đề số 10. THPT Tây Thạnh (2017 – 2018) ............................................................................ 72

Đề số 11. THPT Chuyên Lê Hồng Phong (2017 – 2018) .................................................... 74

Đề số 12. THPT Nguyễn Thị Minh Khai (2017 – 2018) ...................................................... 77

Đề số 13. THPT Bùi Thị Xuân (2017 – 2018) ........................................................................ 79

Chóc c¸c trß rÌn luyÖn tèt vµ ®¹t kÕt qu¶ cao trong kú thi s¾p ®Õn !

Bấm Tải xuống để xem toàn bộ.

| 1/84

| | Tải xuống

Preview text:

Trung taâm Hoaøng Gia
56 Phoá Chôï – P. Taân Thaønh – Q. Taân Phuù M«n To¸n – Líp 10 N¨m häc 2018 – 2019 MỤC LỤC Trang
Chuyên đề 1. Parabol & một số vấn đề liên quan ..................................................................... 1
Chuyên đề 2. Giải và biện luận phương trình bậc nhất ........................................................... 5
Chuyên đề 3. Bài toán chứa tham số trong phương trình bậc hai .......................................... 7
Chuyên đề 4. Phương trình quy về phương trình bậc hai ....................................................... 13
Chuyên đề 5. Bất đẳng thức và GTLN, GTNN ......................................................................... 23
Chuyên đề 6. Hệ trục tọa độ ........................................................................................................ 29
Chuyên đề 7. Tích vô hướng và hệ thức lượng ......................................................................... 42
Đề số 01. THPT Bình Hưng Hòa (2017 – 2018) .................................................................. 49
Đề số 02. THPT Trần Phú (2017 – 2018) .............................................................................. 51
Đề số 03. THPT Lê Trọng Tấn (2017 – 2018) ....................................................................... 53
Đề số 04. THPT Bình Tân (2017 – 2018) ............................................................................... 56
Đề số 05. THPT Nguyễn Hữu Cảnh (2017 – 2018) ............................................................ 58
Đề số 06. THPT Trần Quang Khải (2017 – 2018) ................................................................ 61
Đề số 07. THPT Nguyễn Thượng Hiền (2017 – 2018) ....................................................... 63
Đề số 08. THPT Hàn Thuyên (2017 – 2018) ........................................................................ 66
Đề số 09. THPT Nguyễn Chí Thanh (2017 – 2018) ............................................................ 69
Đề số 10. THPT Tây Thạnh (2017 – 2018) ............................................................................ 72
Đề số 11. THPT Chuyên Lê Hồng Phong (2017 – 2018) .................................................... 74
Đề số 12. THPT Nguyễn Thị Minh Khai (2017 – 2018) ..................................................... 77
Đề số 13. THPT Bùi Thị Xuân (2017 – 2018) ....................................................................... 79
Chóc c¸c trß rÌn luyÖn tèt vµ ®¹t kÕt qu¶ cao trong kú thi s¾p ®Õn !
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Chuyªn ®Ò 1. Parabol & mét sè bµi to¸n liªn quan  b     b
 Cần nhớ: Parabol 2
(P) : y  ax bx  c có đỉnh I   ;   x    và trục đối xứng  2a 4a  2a
(hoành độ đỉnh). Khi a  0 : đồ thị có dạng  và a  0 : đồ thị có dạng .  1. Tìm parabol 2
(P) : y  ax  4x  , c biết 2. Tìm parabol 2 ( )
P : y ax bx 2, biết rằng rằng (P) đi qua ( A 1; 2  ) và B(2;3). (P) đi qua ( A 1;5), ( B 2  ;8).
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. 3. Tìm parabol 2
(P) : y  ax bx  3, biết 4. Tìm parabol 2
(P) : y  ax  4x  c, biết (P) đi qua điểm (
A 3;0) và có trục đối
(P) có hoành độ đỉnh bằng 3 và đi qua xứng là x  1. điểm ( A 2  ;1).
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 1 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 5. Tìm parabol 2
(P) : y  ax bx  ,
c biết 6. Tìm parabol 2
(P) : y  ax bx  , c biết (P) (P) đi qua ( A 1;0), ( B 2;8), C(0; 6  ). đi qua điểm (
A 0;5) và có đỉnh I(3; 4  ).
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. 7. Tìm parabol 2 ( )
P : y ax bx c khi biết 8. Tìm parabol 2 ( )
P : y ax bx c khi biết bảng biến thiên: bảng biến thiên: x  0 2  x  1 3      y y 3 4  1  0
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 2 -
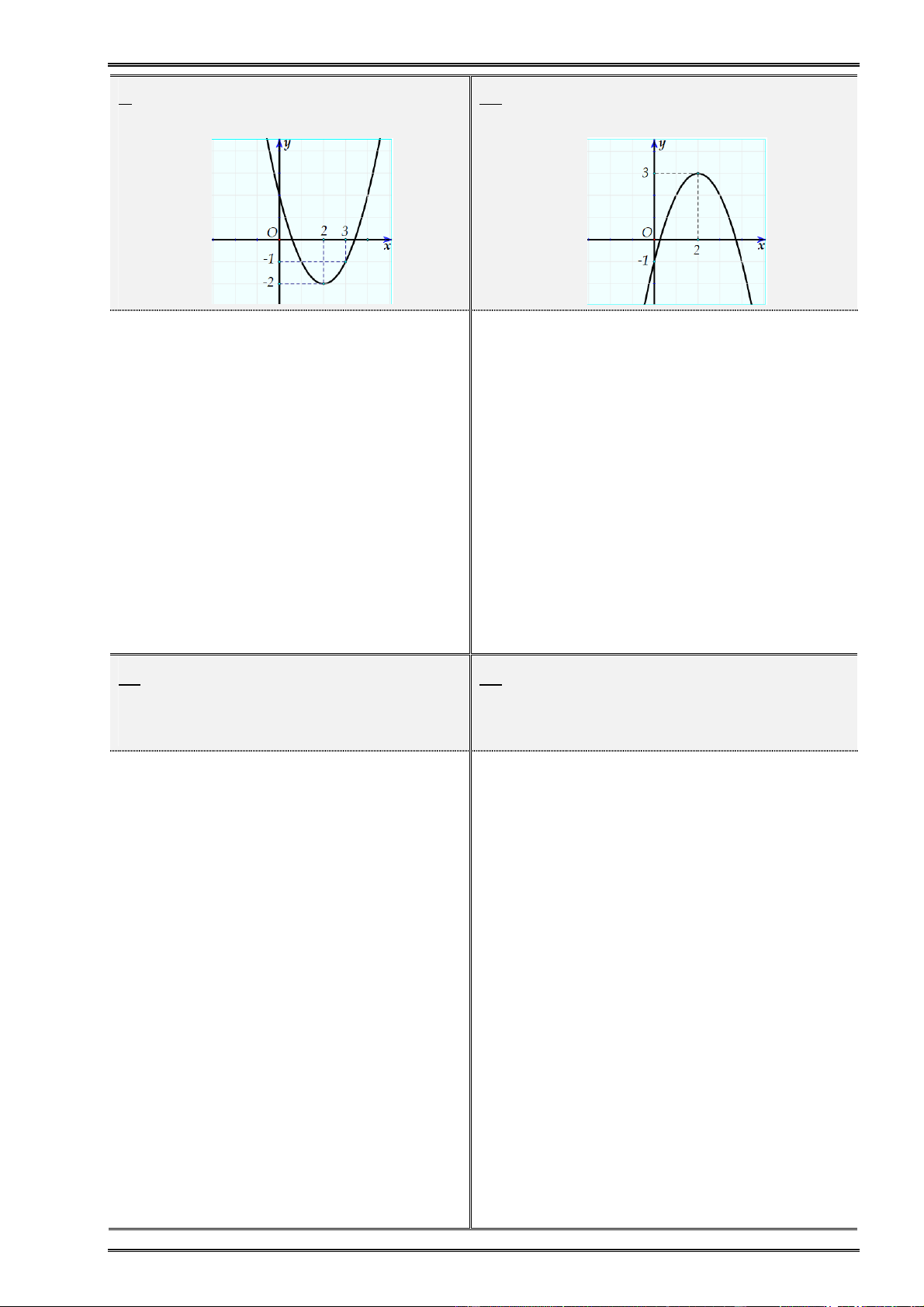
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 9. Tìm parabol 2 ( )
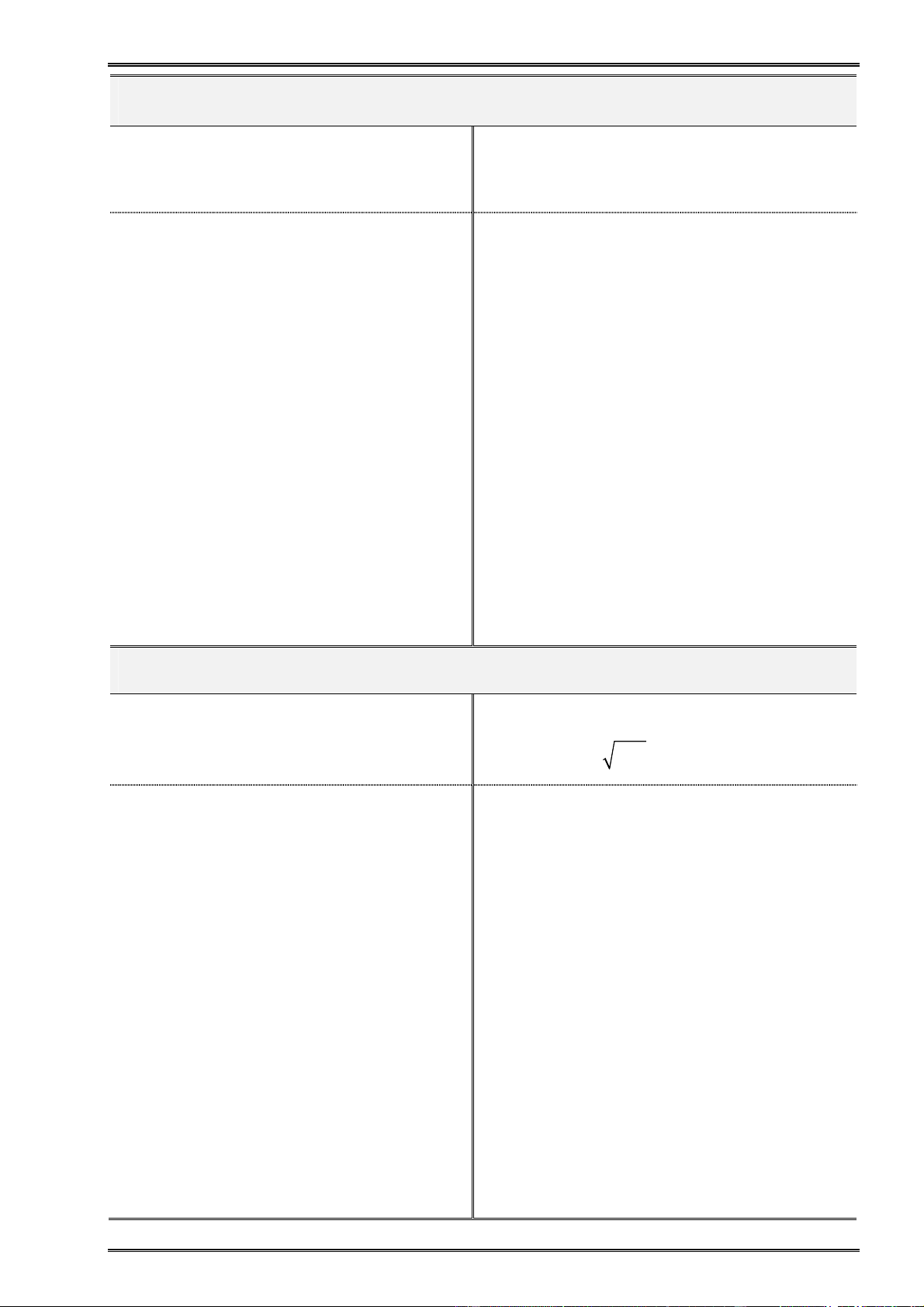
P : y ax bx c khi biết 10. Tìm parabol 2 ( )
P : y ax bx c khi biết đồ đồ thị của nó là thị của nó là
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. 11. Vẽ parabol 2
(P) : y  x  2x  2. Dựa 12. Vẽ parabol 2
(P) : y  x
  4x  5. Dựa vào
vào đồ thị biện luận nghiệm phương
đồ thị biện luận nghiệm phương trình: trình: 2
2x  4x  m  3  0. 2
x  4x  5  m  0.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 3 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 13. Vẽ parabol 2
(P) : y  x
  4x  3. Tìm 14. Vẽ parabol 2
(P) : y  x
  4x  5. Dựa
m để phương trình 2
x  4x  m  0 có
vào đồ thị biện luận nghiệm phương trình:
2 nghiệm thỏa 0  x  2  x . 2
x  4x  5  m  0. 1 2
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. 15. Vẽ parabol 2
(P) : y  x  2x. Suy ra đồ 16. Vẽ 2
(P) : y  x
  6x  5. Hãy biên luận thị hàm số 2 (P )
 : y  x  2x . nghiệm 2
x  6 x  4  m trên (1; 4].
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 4 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Chuyªn ®Ò 2. Ph¬ng tr×nh bËc nhÊt
1. Giải và biện luận: (
m mx 1)  9x  3. 2. Giải và biện luận: 2
m x  2  m  4x.
Giải. Phương trình 2
 m x  m  9x  3
................................................................................. 2
 m x  9x  m  3
................................................................................. 2
 (m  9)x  m  3
................................................................................. ( ) 
.................................................................................  Với 2
m  9  0  m  3  .
................................................................................. Khi m  3 thì ( )
 trở thành 0x  6,
suy ra phương trình vô nghiệm.
................................................................................. Khi m  3  thì ( )
 trở thành 0x  0
.................................................................................
 phương trình nghiệm đúng x  .
 .................................................................................  Với 2
m  9  0  m  3 
................................................................................. m  3 1
................................................................................. ( )   x    2 m  9 m  3
................................................................................. Kết luận:
.................................................................................
m  3 :Phương trình vô nghiệm.
................................................................................. m  3
 :Phương trình nghiệm đúng x   .
 ................................................................................. 1
................................................................................. m  3
 :Phương trình có nghiệm x  m 3 
.................................................................................
3. Giải và biện luận: 2
(m 2m8)x  4 .
m 4. Giải và biện luận: 2
(4m 2)x  1 2m x.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 5 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
5. Tìm m để phương trình có nghiệm:
6. Tìm m để phương trình có nghiệm: 3x  m 2x  5m  3 2mx  1 m  1  x  1    2 x  1   x  1 x  1 x  1 x  1
Giải. Điều kiện: x  1  0  x  1  .
.................................................................................
Quy đồng và bỏ mẫu, phương trình đã cho .................................................................................
 3x  m  x  1  2x  5m  3
.................................................................................
 2x  6m  2
.................................................................................
 x  3m  1.
.................................................................................
Vì x  1 nên phương trình có nghiệm
................................................................................. 2
khi x  3m  1  1  m   
................................................................................. 3
7. Tìm tham số m để phương trình sau có 8. Tìm tham số m để phương trình sau có
nghiệm nguyên: (m  2)x  m  1. nghiệm nguyên: (
m x  3)  x  . m
Giải. Với m  2  0  m  2 thì phương ................................................................................. m  1 (m  2)  3 trình  x  
................................................................................. m  2 m  2
................................................................................. 3  x  1 
................................................................................. m  2
.................................................................................
Vì x   nên 3(m  2)
................................................................................. m  2 3    m  5   m  2 3     m  1
.................................................................................     . m  2 1    m  3  
................................................................................. m   2 1     m  1  
.................................................................................
9. Tìm tham số m để phương trình
10. Tìm tham số m để phương trình 2 2
(m  m)x  2x  m 1 vô nghiệm. 2 2
m x  4x  m  m  2 có nghiệm.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 6 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Chuyªn ®Ò 3. Bµi to¸n chøa tham sè trong ph¬ng tr×nh bËc hai
1. Cho phương trình 2 2
x  (2m  3)x  m  4  0. Tìm tham số m để phương trình:
a) Có một nghiệm 7. Tìm nghiệm còn
b) Có 2 nghiệm pb x , x thỏa 2 2 x  x  17. 1 2 1 2 lại. Lời giải.
Lời giải. Phương trình có 2 nghiệm phân biệt   Thế x  7
 vào phương trình, ta được: a  0 1   0 : L   Đ khi:    2 2 ( 7
 )  7(2m  3)  m  4  0 2 2   0 (
 2m  3)  4(m 4) 0      m   2 12 2 m 14m 24 0       
 12m  25  0  m  ( )  m   12  25 b  Với m  2
 thì phương trình trở thành: Theo Viét: S  x  x    2m  3 và 1 2 a 2
x  7x  0  x  0 hoặc x  7  . c 2 P  x x   m  4.  Với m  1
 2 thì phương trình trở thành 1 2 a 2
x  27x  140  0  x  7   x  2  0. 2 2 2
Theo đề: x  x  17  S  2P  17 1 2 Kết luận: 2 2
 (2m  3)  2(m  4)  17 Với m  2
 thì nghiệm còn lại là x  0. 2
 2m 12m  0  m  0 hoặc m  6. Với m  1
 2 thì nghiệm còn lại là x  2  0. So với ( )
 , giá trị cần tìm là m  0.
2. Cho phương trình 2 2
x  (2m  3)x  m  4  0. Tìm tham số m để phương trình:
a) Có 1 nghiệm 7. Tìm nghiệm còn lại.
b) Có 2 nghiệm pb x , x thỏa 2 2 x  x  17. 1 2 1 2
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 7 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
3. Cho phương trình 2 2
x  2mx  m  3m  0. Tìm tham số m để phương trình:
a) Có nghiệm kép. Tính nghiệm kép đó.
b) Có 2 nghiệm pb x , x thỏa 2 2 x  x  8. 1 2 1 2
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. 4. Cho phương trình 2
(m 1)x  3x 1  0. Tìm tham số m để phương trình:
a) Có 1 nghiệm bằng 3. Tìm nghiệm còn lại. b) Có 2 nghiệm pb x , x thỏa x  1  x . 1 2 1 2
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 8 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 5. Cho phương trình 2
(2m  3)x  2(2m  3)x  1  2m  0. Tìm m để phương trình: a) Có 1 nghiệm bằng 1
 . Tìm nghiệm còn b) Có 2 nghiệm phân biệt x , x thỏa mãn 1 2 lại của phương trình.
(5x  1)(5x  1)  13x x  1. 1 2 1 2
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
6. Cho phương trình 2
x  4x  m  1  0. Tìm tham số m để phương trình:
a) Có hai nghiệm trái dấu ?
b) Có 2 nghiệm phân biệt x , x thỏa mãn 1 2
Có hai nghiệm dương phân biệt.
x x  6  2 x x . 1 2 1 2
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 9 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 7. Cho phương trình 2
mx  2(m  3)x  m  6  0. Tìm tham số m để phương trình: 1 1
b) Có hai nghiệm trái dấu và có giá trị tuyệt
a) Có 2 nghiệm phân biệt thỏa   1  . x x đối bằng nhau. 1 2
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. 8. Cho phương trình 2
mx  2x  1  0. Tìm tham số m để phương trình:
a) Có hai nghiệm trái dấu ? Có hai nghiệm b) Có hai nghiệm là độ dài của hai cạnh góc
phân biệt cùng dương ? Có hai nghiệm
vuông trong một tam giác vuông có độ dài đối nhau ? cạnh huyền bằng 2.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 10 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
9. Cho phương trình 2
x (m  5)x  m  0. Tìm tham số m để phương trình:
a) Chứng minh phương trình luôn có hai b) Có hai nghiệm phân biệt x , x thỏa mãn 1 2
nghiệm phân biệt. Tìm m để phương
điều kiện x  2x  5. 1 2
trình có hai nghiệm dương phân biệt ?
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
10. Cho phương trình 2 2
x (2m  2)x  m  4  0. Tìm tham số m để phương trình:
a) Có nghiệm ? Có hai nghiệm pb dương ?
b) Có hai nghiệm pb x , x thỏa x  2x . 1 2 1 2
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 11 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
11. Cho phương trình  2 (x 2) x (m 1)x 4      0.  
Tìm tham số m để phương trình:
a) Có ba nghiệm phân biệt ? b) Có hai nghiệm ?
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................
12. Cho phương trình 3 2
x  2mx  2mx  1  0. Tìm tham số m để phương trình:
a) Có ba nghiệm phân biệt ? b) Có hai nghiệm ?
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 12 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Chuyªn ®Ò 4. Ph¬ng tr×nh quy vÒ ph¬ng tr×nh bËc hai 1. Giải: 2 2 2
4(2x 3x 1)(2x  4x 1)  3x . 2. Giải: 2
(x 1)(x  2)(x  6)(x  12)  6x .
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. 2x 13x 4x 5x 10 3. Giải:   6. 4. Giải:    2 2 2x  5x  3 2x  x  3 2 2 x  2x  3 x  4x  3 9
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. 2 2 x  2x  3 x  5x  3 3 2 x  2x  15 3x 5. Giải:    6. Giải:   2 2 x  4x  3 x  6x  3 4 2 2 x  4x  15 x  6x  15
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 13 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 7. Giải: 2
4x  1  x  2x  4. 8. Giải: 2
3x  5  2x  x  3. B   0 
................................................................................. 
Lời giải. Áp dụng A  B   A   B  
.................................................................................  A   B   
................................................................................. Điều kiện: 2
x  2x  4  0.
.................................................................................  2
4x  1  x  2x  4 
................................................................................. Phương trình   2 4x  1  (
 x  2x  4) 
................................................................................. x  1  
................................................................................. 2 
x  2x  3  0 x  3  
.................................................................................    .  2
x  6x  3  0 x  3   2 3  
................................................................................. x  3   2 3 
.................................................................................
Thế các nghiệm vào điều kiện, các nghiệm .................................................................................
thỏa mãn là x  3 và x  3   2 3.
................................................................................. 9. Giải: 2
x  2  x  4x  2. 10. Giải: 2 2
x  2x  2  x  7x  9.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. 11. Giải: 2
x  4x  2  x  2. 12. Giải: 2
2x  3x  1  1  2x.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 14 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 13. Giải: 2 2
3x  2x  6  x .
14. Giải: 3x  4  x  2 . A  B
.................................................................................
Lời giải. Áp dụng A B     thì A  B  
................................................................................. 
.................................................................................  2 2
3x  2x  6  x 2 2 3x 2x 6 x      
................................................................................. 2 2
3x  2x  x  6 
.................................................................................   2 x  1
4x  2x  6  0  
.................................................................................      2 3
2x  2x  6  0 : VN   x 
................................................................................. o   2 15. Giải: 2 2
5x  3x  2  x  1 . 16. Giải: 2 2
x  2x  2x  x  2 .
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. 17. Giải: 2
x  6x  9  2x 1 . 18. Giải: 2
4x 12x  9  3x  2 .
.................................................................................
Lời giải. Áp dụng 2
A  B  A  B
................................................................................. thì phương trình 2
x  6x  9  2x  1
................................................................................. 2 2
 x  6x  9  (2x  1)
................................................................................. 2 2
 x  6x  9  4x  4x  1
................................................................................. 2 2
 3x  10x  8  0  x  4, x   
................................................................................. 3
.................................................................................
19. Giải: 2 3  2x  x  1 . 20. Giải: 2
3x  9x  1  x  2 .
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 15 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
21. Giải: (x  3). x  1  4x ( ) 
22. Giải: (x  1). x  3  4(x  2).
 TH1: Nếu x 1  0  x  1.
................................................................................. ( )
 trở thành (x  3)(x  1)  4x 2
 x  2x  3  0  x  1  , x  3.
.................................................................................
So với x  1, nhận nghiệm x  3.
.................................................................................
 TH2: Nếu x 1  0  x  1.
................................................................................. ( )
 trở thành (x  3)(1  x)  4x
................................................................................. 2
 x  6x  3  0  x  3  2 3.
.................................................................................
So với x  1 nhận nghiệm x  3
  2 3. .................................................................................
Kết luận: Tập nghiệm S  { 3   2 3;3}. 2
4x  2x  2x  1 x 1 1 2x 1 23. Giải:  2x  1. 24. Giải:    4x  3 2 x x  1 x  x
........................................................................... .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. 2x  1 x  2 1 1 25. Giải:  2
 1. (ẩn phụ) 26. Giải: 2 x   10  2 x   (ẩn phụ) x  2 2x  1 2 x x
........................................................................... .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 16 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 27. Giải: 2
x  3x  2  x  3. 28. Giải: 2
6x  4x  3  x  4  0. B
  0 (hay A  0) 
.................................................................................
Lời giải. A  B   . A   B 
................................................................................. x   3  0 
................................................................................. Phương trình   2 x
  3x  2  x  3 
................................................................................. x   3 x   3  
.................................................................................     2 x   4x  1  0 x   2  3  
.................................................................................
 x  2  3 là nghiệm cần tìm.
.................................................................................
29. Giải: x  1  2 2x  5. 30. Giải: 2
3 x  1  x  8x  11.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. 31. Giải: 2
x  x  1  3  x. 32. Giải: 2
5x  21x  8  x  2. B   0 
.................................................................................
Lời giải. Áp dụng A  B   . 2 A   B 
................................................................................. 3   x  0 
................................................................................. Phương trình   2 2 x
  x  1  (3  x) 
.................................................................................  x   3 x   3 
.................................................................................       2 2 8 x
  x  1  9  6x  x  x 
.................................................................................      7
................................................................................. 8
 x  là nghiệm cần tìm. 7
................................................................................. 33. Giải: 2
2 3x  2x  1  1  3x. 34. Giải: 2
2x  12x  18x  1  2.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 17 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 35. Giải: 2 2
x  5x  4  5 x  5x  28  0. 36. Giải: 2 2
5 x  2x  7  x  2x  3. Lời giải. Đặt 2
t  x  5x thì phương trình trở .............................................................................
thành t  4  5 t  28  0
............................................................................. t   4  0 5 t 28 t 4       
............................................................................. 2 25
 (t  28)  (t  4) 
............................................................................. t   4
............................................................................. t   4     
  t  36  t  36 2
t  17t  684  0   
.............................................................................     t  19  
.............................................................................
............................................................................. x  4  Với 2
t  36  x  5x  36  . 
............................................................................. x  9 
.............................................................................
 Cách khác: Đặt 2 2
t  x  5x 28  0 t . 37. Giải: 2 2
x  3x  3 3x  9x  7  1  0. 38. Giải: 2 2
2x  x  6x  12x  7  0.
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. ............................................................................. 39. Giải: 2
(x  3)(1  x)  5
 x  2x  7. 40. 4 3 2
(x 2)(x  3)  x  2x x 2  2.
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 18 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
41. Giải: 2x  1  2  x  3.
42. Giải: x  4  2x  6  1. 2  x  1  0 
Lời giải. Điều kiện   x  3.
............................................................................. x   3  0 
.............................................................................
Phương trình  2x  1  2  x  3
............................................................................. 2 2
 ( 2x  1)  (2  x  3)
.............................................................................
 2x  1  4  4 x  3  x  3
............................................................................. x   0 x  4
............................................................................. 4 x 3 x         . 2
16(x  3)  x   x  12    
.............................................................................
So với điều kiện và thử lại, suy ra S  {4;12}. .............................................................................
 Cần nhớ: Dạng tổng quát A  B  C . .............................................................................
Điều kiện  Chuyển vế sao cho hai vế dương .............................................................................
và bình phương, giải phương trình hệ quả.
43. Giải: x  1  4x  1  x  2.
44. Giải: 3x  4  x  4  2 x .
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
45. Giải: x  4  1  x  1  2x .
46. Giải: 2 3x  1  x  1  2 2x  1.
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 19 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 47. Giải: 2
(x  3) x  5x  4  2x  6. 48. Giải: 2 2
(x  3) x  4  x  9.
Lời giải. Điều kiện 2
x  5x  4  0 ( ) 
............................................................................. PT 2
 (x  3) x  5x  4  2(x  3)  0
............................................................................. 2
 (x  3) x  5x  4  2(x  3)  0
.............................................................................
............................................................................. 2
 (x  3)( x  5x  4  2)  0
............................................................................. x   3  0 x   3     
............................................................................. 2  2
 x  5x  4  2
x  5x  4  4   
............................................................................. x  3   .
............................................................................. 
Thế các nghiệm vào điều x  0, x  5 
............................................................................. kiện ( )
 , nghiệm cần tìm là x  0, x  5.
............................................................................. 49. Giải: 2
(x  1) 2x  3  x  4x  3. 50. Giải: 2
(2x  1) x  1  2x  7x  3.
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. ............................................................................. 51. 2
x  x  2  2 x  2  2  x  1. 52. 2
x 3 2x x 1  2x  x  4x 3. x   2  0 
.............................................................................
Lời giải. Điều kiện   x  2. x   1  0 
.............................................................................
.............................................................................
PT  (x 2)(x  1)  2 x  2  ( x  1  2)
.............................................................................
 x  2.( x  1  2)( x  1  2)  0
.............................................................................
 ( x  1 2).( x  2 1)  0
.............................................................................  x 1 2    x  1  4  
.............................................................................     x  3.   x  2  1 x  2  1   
.............................................................................
So với điều kiện, nghiệm cần tìm là x  3.
.............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 20 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 53.
3 x  6x  3  (3 x)(6 x). 54. 2
x 2  x 2  2 x 4 2x 2.
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. ............................................................................. 55. Giải: 2 2
2x x 9  2x x 1  x  4. 56. Giải: 2 2
x  15  3x  2  x  8.
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 21 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 2
 x  y  7  0   2 2  x 
 y  6x  2y  0  57. Giải hệ:     2 2 58. Giải hệ: y
  x  2x  2y  4  0        x y 8 0 
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. ............................................................................. x
  y  xy  5   x
  y  xy  3  59. Giải hệ:     2 2 60. Giải hệ: x 
 y  x  y  8 2 2       x y y x 2 
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 22 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Chuyªn ®Ò 5. BÊt ®¼ng thøc – Gi¸ trÞ lín nhÊt & gi¸ trÞ nhá nhÊt
1. Chứng minh rằng với mọi x  ,
 ta luôn 2. Chứng minh rằng với mọi a, , b c   có 4
x  4x  3  0. thì 2 2
a  b  4  ab  2a  2 . b
Giải. Thêm bớt để đưa về hằng đẳng thức, tức ............................................................................. 4 2 2 2 2 x 4x 3 (x ) 2x 1    
  2(x 2x 1) 
.............................................................................  
............................................................................. 2 2 2
 (x 1)  2(x  1)  0, x   . 
.............................................................................  2 x  1  0  Dấu "  " xảy ra khi   x  1.
............................................................................. x  1  0 
.............................................................................
 Nhận xét: Đối với bài toán x  ,  ta nên
.............................................................................
sử dụng hằng đẳng thức để đưa về dạng:
............................................................................. 2 2 2
A  B C  0 : luôn đúng và dấu "  "
.............................................................................
xảy ra khi A  B  C  0.
3. Chứng minh rằng với mọi x, y   thì ta 4. Chứng minh rằng với mọi a, , b c   luôn có 2 2
x  y  xy  3x  3y  3  0. thì có 2 2 2
a  b  c  12  4(a  b  c).
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
5. Chứng minh rằng a  0, b  0 ta luôn có 6. Chứng minh rằng a  0, b  0 ta luôn 3 3 2 2
a  b  a b  ab . có 4 4 3 3
a  b  a b  ab .
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 23 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
7. Chứng minh rằng với mọi a, ,
b c  0 ta 8. Chứng minh với mọi a, , b c  0 thì luôn có 2 2 2
a  b  c  ab  bc  ca.
ab bc ca  abc( a  b  c).
Giải. Áp dụng BĐT Cauchy 
............................................................................. Cauchy  2 2 2 2 a   b
 2 a b  2ab 
.............................................................................  Cauchy  Ta có: 2 2 2 2 b   c
 2 b c  2bc
.............................................................................   Cauchy  2 2 2 2
............................................................................. c
 a  2 c a  2ac 
.............................................................................  2 2 2
 2(a  b  c )  2(ab  bc  ca)
............................................................................. 2 2 2
a  b  c  ab  bc  ca (đpcm).
.............................................................................
Dấu "  " xảy ra khi a  b  c  0.
............................................................................. Tæng  Tæng
 Nhận xét: Nhận dạng 
............................................................................. Tæng   H»ng sè
............................................................................. 2 P 
 Cauchy xoay vòng, rồi cộng lại.
9. Chứng minh rằng với mọi a, ,
b c  0 thì 10. Chứng minh rằng với mọi a, , b c  0 a b c 1 1 1 3 3 3       a b c  
 ab bc  ca. bc ca ab a b c thì b c a
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
11. Chứng minh rằng với mọi a, b   thì ta 12. Chứng minh rằng với 0  a, , b c   luôn có 2 2
4a  9b  5  4(a  3b). 2 2 2 a c b a b c thì       2 2 2 c b a b c a (Lưu ý: 2
x  x  x).
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 24 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
13. Chứng minh rằng với mọi a, ,
b c  0 ta 14. Chứng minh rằng a, ,
b c  0 ta luôn
có (a  b)(b  c)(c  a)  8ab . c có 2 2 2
(a  2)(b  2)(c  2)  16 2ab . c
Lời giải. Áp dụng bất đẳng thức Cauchy
.............................................................................  Cauchy
a b  2 ab
.............................................................................  Cauchy 
............................................................................. Ta có: b
  c  2 bc  và nhân vế theo vế  Cauchy 
............................................................................. c
 a  2 ca 
............................................................................. nhân
............................................................................. 2 2 2
 (a  b)(b  c)(c  a)  8 a b c  8abc.
.............................................................................
Dấu "  " xảy ra khi a  b  c  0. 
............................................................................. TÝch  TÝch
 Nhận xét: Dạng 
............................................................................. TÝch   H»ng sè 2
............................................................................. P 
 Cauchy trong dấu (  ) và nhân lại.
15. Chứng minh rằng với mọi a, ,
b c  0 ta 16. Chứng minh rằng a, ,
b c  0 ta luôn
có (a  b)(b  c)(c  a)  8ab . c có 2 2 2
(a  b  c)(a  b  c )  9ab . c
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
17. Chứng minh rằng với mọi a  0, b  0 ta 18. Chứng minh rằng a, ,
b c  0 ta có:  1 1     1 1 1    9
có (a  b  2).    4. 
(a  b  c)       a  1 b  1
a b b c c a 2
HD: a  b  2  (a  1)  (b  1).
HD: 2(a b  ) c  (a  ) b (b  ) c (c  ) a .
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 25 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
19. Với x  1, hãy tìm giá trị nhỏ nhất của 20. Với x  1, hãy tìm giá trị nhỏ nhất của 3x  1 2x  1
hàm số y  9x  
hàm số y  3x   x  1 x  1 3(x  1)  4
.............................................................................
Giải. Ta có: y  9(x  1)  9  x  1
............................................................................. 4
 y  9(x  1)   12
.............................................................................   x  1 a
............................................................................. b Cauchy
............................................................................. 4
 y  2. 9(x 1)  12  24. x  1
.............................................................................
 Giá trị nhỏ nhất của hàm số là 24.
............................................................................. 4 5
.............................................................................
Dấu "  " khi 9(x  1)   x   x  1 3
.............................................................................
21. Với x  1, hãy tìm giá trị nhỏ nhất của 22. Với x  1, hãy tìm giá trị nhỏ nhất 4 2 x  x  4
hàm số y  x  1   của hàm số y   x  3 x  1
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
23. Với x  2, hãy tìm giá trị nhỏ nhất của 24. Với x  0, hãy tìm giá trị nhỏ nhất của 2 x  x  9
(2x  5)(5x  14) hàm số y   hàm số y   x  2 x
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 26 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
25. Với x  0, hãy tìm giá trị nhỏ nhất của 26. Với x  0, hãy tìm giá trị nhỏ nhất của 4 100
hàm số y  3x  
hàm số y  5x   2 x 2 x n mx mx n
.............................................................................
Giải. Sử dụng y  mx     2 2 x 2 2 x
............................................................................. 3x 3x 4 Cauchy 3x 3x 4
............................................................................. y    3 3  3.  3 9. 2 2 2 x 2 2 2 x
.............................................................................
Suy ra giá trị nhỏ nhất của y là 3 3 9.
............................................................................. 3x 4 2
............................................................................. Dấu "  " xảy ra khi   x   2 3 2 x 3
.............................................................................
27. Với x  0, hãy tìm giá trị nhỏ nhất của 28. Với x  0, hãy tìm giá trị nhỏ nhất của 15 4
hàm số y  5x   hàm số 2
y  2x   3 x x n mx mx mx n n n n
HD: y  mx       HD: 2 2 y  mx   mx    3 3 x 3 3 3 x x 2x 2x
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
29. Với x  0, hãy tìm giá trị nhỏ nhất của 30. Với x  0, hãy tìm giá trị nhỏ nhất của 16 16 hàm số 2 y  4x   hàm số 3 y  8x   x x
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 27 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019  5  9
31. Với x  0;  ,    
hãy tìm giá trị lớn nhất của 32. Với x
0; , hãy tìm giá trị lớn nhất 2     5  
hàm số y  x(5  2x ).
của biểu thức y  4x(9  5x). 2 (a  b)
.............................................................................
Giải. Áp dụng a  b  2 ab  ab  4
............................................................................. 1
Ta có: y  x(5  2x)    (2x).(5  2x)
............................................................................. 2  a b
............................................................................. Cauchy 2
1 [(2x)  (5  2x)] 25  y     2 4 8
............................................................................. 25
.............................................................................
Suy ra giá trị nhỏ nhất của hàm số bằng  8
............................................................................. 5
Dấu "  " xảy ra khi 2x  5  2x  x  
............................................................................. 4
33. Với 0  x  3 và 0  y  4, tìm giá trị 34. Với mọi x  [ 2
 ;2], hãy tìm giá trị lớn
lớn nhất của P  (3  x)(4  y)(2x  3y). nhất của hàm số 2
y  x . 4  x .
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
35. Tìm giá trị lớn nhất và giá trị nhỏ nhất của 36. Tìm giá trị lớn nhất và giá trị nhỏ nhất
hàm số y  x  2  6  x .
của hàm số y  x  1  5  x .
Lời giải. Tập xác định D  [2;6].
............................................................................. Vì y  0  2
y  4  2 (x  2)(6  x)  4.
.............................................................................
 y  2  miny  2 khi x  2 hoặc x  6. .............................................................................
............................................................................. Ta lại có 2
y  4  2 (x  2).(6  x)
 
............................................................................. a b 2 
.............................................................................
y  4  (x  2)  (6  x)  8  y  2 2.
.............................................................................
 max y  2 2 khi x  2  6  x  x  4.
.............................................................................
Kết luận: miny  2 và max y  2 2.
.............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 28 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
37. Một công ty đang lập cải tiến sản phẩm và 38. Độ giảm huyết áp của bệnh nhân được
xác định rằng tổng chi phí dành cho việc cho bởi công thức 2 (
G x)  0,025x (30 x), 2 x
cải tiến là C(x)  2x  4  , (x  6) trong đó
(mg) là liều lượng thuốc x  6
được tiêm cho bệnh nhân. Tính liều
trong đó x là số sản phẩm được cải tiến.
lượng thuốc cần tiêm cho bệnh nhân để
Tìm số sản phẩm mà công ty cần cải tiến
huyết áp giảm nhiều nhất và tính độ
để tổng chi phí là thấp nhất ? giảm đó ?
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
39. Hình chữ nhật có chu vi không đổi là 8m. 40. Cho tam giác vuông có tổng một cạnh
Tìm diện tích lớn nhất S của hình chữ
góc vuông và cạnh huyền bằng 2. Tìm max
độ dài ba cạnh của tam giác sao cho diện nhật đó.
tích của tam giác lớn nhất.
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. ............................................................................. 41. Tìm V
là giá trị lớn nhất của thể tích các khối hộp chữ nhật có đường chéo bằng max
3 2cm và diện tích toàn phần bằng 2 18cm .
.............................................................................
............................................................................. c 3 2
............................................................................. a b
.............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 29 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Chuyªn ®Ò 6. HÖ trôc täa ®é Oxy
1. Trong mặt phẳng tọa độ Oxy, cho ba điểm (
A 1;2), B(3;5), C (2;3). a) Chứng minh ,
A B, C tạo thành một tam giác. Tìm trọng tâm G của tam giác ABC . Tính
cosin góc C và cho biết góc C là góc nhọn hay tù ? Chứng minh ,
A B, C tạo thành một tam giác:  A  B  (2;3) 2 3    Ta có:   
 AB không cùng phương AC A
 C  (3;5) 3 5  Suy ra ,
A B, C tạo thành một tam giác.
Tìm tọa độ trọng tâm G của tam giác ABC : 
x  x  x 1  3  (2) 2  A B C x        G 2 3   
Ta có G là trọng tâm tam giác ABC 3 3 3   G  ;  
y  y  y 2  5  (3) 3   3 4 A B C y     G  3 3 4  
Tính cosin góc C : Ta có CA  (3; 5), CB  (5; 8)       C . ACB 3.5  5.8 55 C .
ACB  CA . CB .cosC  cosC       2 2 2 2 CA . CB 3  5 . 5  8 3026
Vì cosC  0  góc C là góc nhọn.
b) Tìm giao điểm E của trục hoành với AC . c) Tìm giao điểm F của trục tung với BC .
(tìm tọa điểm E trên trục hoành sao cho
(Tìm tọa điểm F trên trục tung sao cho E, ,
A C thẳng hàng).
F, B, C thẳng hàng).
Vì E  Ox nên gọi E(x ; 0) và E  AC nên Vì F  Oy nên gọi F(0;y ) và F  BC nên E F E, ,
A C thẳng hàng.
F, B, C thẳng hàng.  
Ta có: AE  (x  1;2).
Ta có: BF  (3;y  5). E F   Để E, ,
A C thẳng hàng thì AE cùng Để F, B, C thẳng hàng thì BF cùng      
phương với AC  AE  k.AC
phương với CB  BF  k.CB x  1 2 1 3 y  5 1 E    x    F     y   3 5 E 5 5 8 F 5  1     1  
Kết luận: E   ;0  F 0;  
thỏa yêu cầu bài toán. Kết luận:
thỏa yêu cầu bài toán.  5   5     Hoµnh Tung
 Cần nhớ: a cùng phương b cùng phương  a  k.b    Hoµnh Tung      
Tích vô hướng a.b  a . b . cos(a,b ). Diện tích S  (
p p  a)(p b)(p c).
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 30 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
2. Trong mặt phẳng tọa độ Oxy, cho ba điểm (
A 2;3), B(2; 4), C(5;1). a) Chứng minh ,
A B, C tạo thành một tam giác. Tìm trọng tâm G của tam giác ABC . Tính
cosin góc A và cho biết góc A là góc nhọn hay tù ? Tìm chu vi và diện tích của tam giác.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
b) Tìm giao điểm của trục hoành với AC .
c) Tìm giao điểm của trục tung với BC .
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
d) Tìm tọa độ điểm E thuộc trục hoành sao cho ,
A E, G thẳng hàng.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 31 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
3. Trong mặt phẳng tọa độ Oxy, cho ba điểm (
A 10;1), B(7;2), C (1;3). a) Chứng minh ,
A B, C tạo thành một tam giác. Tìm trọng tâm G của tam giác ABC . Tính
cosin góc B và cho biết góc B là góc nhọn hay tù ? Tìm chu vi và diện tích của tam giác.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
b) Tìm giao điểm của trục hoành với AC .
c) Tìm giao điểm của trục tung với BC .
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
d) Tìm tọa độ điểm E thuộc trục tung sao cho ,
A E, G thẳng hàng.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 32 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
4. Trong mặt phẳng tọa độ Oxy, cho hai điểm (
A 3;2), B(1;1).
a) Tìm tọa độ điểm M thuộc trục hoành và b) Hãy tìm tọa độ điểm E thuộc đường thẳng
N thuộc trục tung sao cho tam giác
d : 2x  4y  3  0 để ba điểm , A B, E
AMN nhận B là trọng tâm. thẳng hàng.
Giải. Vì E  d : 2x  4y  3  0
Giải. Gọi M(x ; 0)  Ox và N (0;y )  Oy. M N 3 1
 2x  4y  3  0  y   x
Để tam giác AMN nhận B là trọng tâm, E E E 4 2 E
nghĩa là B là trọng tâm AMN :  3 1   E x
 ;  x     
x  x  x  3  x  0 E E     4 2  A M N x   1  M    B  3  3        1 5   
y  y  y  2  0  y AB  ( 2
 ;3), AE  x   3; x    Có   A M N y  E E     1 N   2 4 B  3    3  Để ,
A B, E thẳng hàng thì AB cùng phương x   0   M  
 M(0; 0), N(0;5). 2  3  y   5 với AE    N  x  3 5 1 E  x 4 2 E M  (0;0)  Kết luận:  . 13 7 13 7  N  (0;5)     x 
 y    E  ;   E 4 E 8  4 8 
5. Trong mặt phẳng tọa độ Oxy, cho hai điểm (
A 1;2), B(2;1).
a) Tìm tọa độ điểm M thuộc trục hoành và b) Hãy tìm tọa độ điểm E thuộc đường thẳng
N thuộc trục tung sao cho tam giác
d : 2x  y  1  0 để ba điểm , A B, E
AMN nhận B là trọng tâm. thẳng hàng.
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 33 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
6. Trong mặt phẳng tọa độ Oxy, cho hai điểm (
A 5;1), B(3;2).
a) Tìm tọa độ điểm M thuộc trục hoành và b) Hãy tìm tọa độ điểm E thuộc đường thẳng
N thuộc trục tung sao cho tam giác
d : x  y  3  0 sao cho ba điểm , A B, E
BMN nhận A là trọng tâm. thẳng hàng.
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
7. Trong mặt phẳng tọa độ Oxy, cho hai điểm (
A 1; 4), B(2;2).
a) Tìm tọa độ điểm M thuộc trục hoành và b) Hãy tìm tọa độ điểm E thuộc đường thẳng
N thuộc trục tung sao cho tam giác
d : 4x  2y  5  0 để ba điểm , A B, E
BMN nhận A là trọng tâm. thẳng hàng.
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 34 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
8. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với (
A 2;3), B(0;2), C(4;1).
a) Hãy tính chu vi và diện tích của tam giác b) Tìm tọa độ tâm I và bán kính đường tròn ABC .
ngoại tiếp tam giác ABC . 
Vì tam giác ABC vuông tại A nên tâm I 2 2
 AB  (2;1)  AB  2  1  5. 
đường tròn ngoại tiếp tam giác ABC nằm tại 2 2
 AC  (2;4)  AC  2  4  2 5. trung điểm cạnh huyền BC.   2 2 
 BC  (4;3)  BC  4  3  5. x  x 0  4  B C x     2 I   1  2 2         Nhận thấy 2 2 2
AB  AC  BC nên theo   y  y    I 2; 2 1   1  2 
Pitago đảo thì tam giác ABC vuông tại . A B C y      I  2 2 2
Chu vi ABC : C
 AB  AC  BC ABC
R là bán kính đường tròn ngoại tiếp tam giác
 5  2 5  5  3 5  5. BC 5
ABC  R  IA  IB  IC   
Diện tích tam giác ABC : 2 2   1 1 1   5 S  AB.AC  5.2 5  5. I 2  ;  R   Kết luận: Tâm   và bán kính ABC 2 2  2 2
c) Tìm tọa độ điểm J là điểm đối xứng của b) Hãy tìm tọa độ K là giao điểm của hai A qua I.
đường chéo trong hình bình hành ABCD.
Ta có J là điểm đối xứng của A qua I  I Vì K là giao điểm của hai đường chéo trong
là trung điểm AJ nên
ABCD nên K là trung điểm của AC.  x  x  2  x    x  x 2  4 A J x   2  J     A C  x     3 I   x   2 2  2  J  K       2 2   K(3;1).  y  y 1 3  y y   2   y  y 3  1 A J  J  J y       A C y     1 I  2   2 2 K  2 2
Kết luận: J (2;2).
Kết luận: K(3;1).
9. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với (
A 1;1), B(5;3), C (2;0).
a) Hãy tính chu vi và diện tích của tam giác b) Tìm tọa độ tâm I và bán kính đường tròn ABC .
ngoại tiếp tam giác ABC .
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
c) Tìm tọa độ điểm J là điểm đối xứng của b) Hãy tìm tọa độ K là giao điểm của hai A qua I.
đường chéo trong hình bình hành ABCD.
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 35 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
10. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với (
A 1;1), B(5;1), C (3;5).
a) Hãy tính chu vi và diện tích của tam giác b) Tìm tọa độ tâm I và bán kính đường tròn ABC .
ngoại tiếp tam giác ABC .
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
c) Tìm tọa độ điểm J là điểm đối xứng của b) Hãy tìm tọa độ H là giao điểm của hai C qua B.
đường chéo trong hình bình hành ABDC .
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
11. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với (
A 4;1), B(1;4), C (2;1).
a) Hãy tính chu vi và diện tích của tam giác b) Tìm tọa độ tâm I và bán kính đường tròn ABC .
ngoại tiếp tam giác ABC .
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
c) Tìm tọa độ điểm J là điểm đối xứng của b) Hãy tìm tọa độ F là giao điểm của hai A qua B.
đường chéo trong hình bình hành ABCD.
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 36 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
12. Trong mặt phẳng tọa độ Oxy, cho hai điểm (
A 3;2), B(1;1).
a) Tìm tọa độ điểm M thuộc trục hoành sao b) Tìm tọa độ điểm N thuộc trục tung sao cho
cho tam giác ABM vuông tại M .
tam giác ABN vuông tại . A
Giải. Vì M  Ox nên gọi M(x ; 0).
Giải. Vì N  Oy nên gọi N(0;y ). M N   A
 M  (x  3;2)   A
 N  (3;y  2)  Ta có: M   Ta có: N   B
 M  (x 1;1) A
 B  (2;3) M  
Để tam giác ABM vuông tại M thì
Để tam giác ABN vuông tại A thì        
AM  BM  AM.BM  0
AN  AB  AN.AB  0
 (x  3)(x  1)  2  0  ( 3  ).( 2  )  (y  2).( 3  )  0 M M N x  2  3
 6  3y  6  0 N 2  
x  4x  1  0 M   M M x  2  3  y  4. M  N N
Do đó: M (2  3; 0) hoặc M(2  3; 0).
Vậy (0; 4) là điểm thỏa yêu cầu bài toán.
13. Trong mặt phẳng tọa độ Oxy, cho hai điểm (
A 1;3), B(2;5).
a) Tìm tọa độ điểm M thuộc trục hoành sao b) Tìm tọa độ điểm N thuộc trục tung sao cho
cho tam giác ABM vuông tại M .
tam giác ABN vuông tại . A
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
14. Trong mặt phẳng tọa độ Oxy, cho hai điểm (
A 1;1), B(3;2) và O là gốc tọa độ.
a) Tìm tọa độ điểm M thuộc trục hoành sao b) Tìm tọa độ điểm N thuộc trục tung sao cho
cho tam giác OBM vuông tại B.
tam giác ABN vuông tại . A
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
.............................................................................. ................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 37 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
15. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với (
A 1; 3), B(2;1), C(2;3).
a) Hãy tìm tọa độ trực tâm H của tam giác b) Gọi K là hình chiếu vuông góc của C lên ABC .
cạnh AB. Tìm tọa độ của K.
Giải. Gọi H(x ;y ) là trực tâm ABC .
Giải. Gọi K(x ;y ) là hình chiếu vuông góc H H K K  
của C lên cạnh AB. A  H  BC A
 H.BC  0    CK  AB K A B Ta có: 
   ( )  và , , thẳng hàng. B  H  AC    B    H.AC  0 
Ta có CK  (x  2;y  3), AB  (1;4)   K K  
Có AH  (x  1;y  3) và BC  (0;2)
Vì CK  AB  CK.AB  0 H H  
 x  2  4(y  3)  0  x  4y  14
BH  (x  2;y  1) K K K K và AC  (1;6).    H H
AK  x  y    Mà ( 1; 3) và AB AK nên 2(y  3)  0 y   3 K K ( )  H  H      . x  1 1 4y  14  1 1 x 
 2  6(y  1)  0 x   26  K  K   H H   H  y  3 4  y  3 4  K K Suy ra H (3;26). 49 434 434 49 y    x   K  ;   
Kết luận: H (3;26) thỏa yêu cầu bài toán. K 17 K 17  17 17 
16. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với (
A 3;8), B(7;2), C (1;1).
a) Hãy tìm tọa độ trực tâm H của tam giác b) Gọi K là hình chiếu vuông góc của A lên ABC .
cạnh BC . Tìm tọa độ điểm K.
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
17. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với (
A 2;4), B(5;0), C (3;2).
a) Hãy tìm tọa độ trực tâm H của tam giác b) Gọi E là trung điểm HC . Tìm tọa độ điểm ABC .
D sao cho O là trực tâm tam giác AEC.
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
.............................................................................. ...............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 38 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
18. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với (
A 3;8), B(7;2), C (1;1).
a) Tìm tâm và bán kính đường tròn ngoại b) Tìm tọa độ điểm N  d : 2x  y  4  0 để tiếp tam giác ABC .
tam giác ABN cân tại . A
Giải. Gọi I(x ;y ) là tâm đường tròn ngoại N a a   d x  y   I I Giải. Gọi ( ;2 4) : 2 4 0. tiếp A
 BC  R  IA  IB  IC.
Vì ABN cân tại A nên AN  AB. 2 2
 AI  (x  3)  (y  8) I I
................................................................................ 2 2
 BI  (x  7)  (y  2) I I
................................................................................ 2 2
 CI  (x  1)  (y  1) I I
................................................................................   2 2 I  A  IB I  A  IB  
................................................................................ Ta có:    2 2 I  A  IC I  A  IC  
................................................................................  2 2 2 2 (
 x  3)  (y  8)  (x  7)  (y  2) 
................................................................................ I I I I  2 2 2 2 (
 x  3)  (y  8)  (x 1)  (y 1) 
................................................................................ I I I I 
6x 16y  73  14x  4y  53
................................................................................  I I I I  
6x  16y  73  2x  2y  2 
................................................................................ I I I I  95 27
................................................................................ Suy ra x  và y   I 16 I 8
................................................................................ 95 27 7685
................................................................................    Tâm I  ;   R  IA    và 16 8  16
................................................................................
19. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với (
A 2;3), B(2; 4), C(5;1).
a) Tìm tâm và bán kính đường tròn ngoại b) Tìm tọa độ điểm N  d : x  3y  10  0 tiếp tam giác ABC .
để tam giác ABN cân tại N .
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 39 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
20. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với (
A 2;3), B(3;2), C(4;1).
a) Tìm tọa độ điểm D sao cho ABCD là b) Tìm tọa độ điểm I thuộc trục hoành sao hình bình hành.
cho ABCI là hình thang nhận AB là đáy.
Giải. Gọi D(x ;y ) là đỉnh thứ tư của hình D D
Giải. Vì I  Ox nên gọi I(x ; 0).   I 
bình hành ABCD  AB  DC ( ) 
Ta có CI  (x  4;1).  I A  B  (1;1)  Ta có  .
Để ABCI là hình thang nhận AB là đáy thì D
 C  (4  x ;1y )   1 1 D D  AB  CI    x  3. 1   4  x x   3 x  4 1 I I ( )  D  D       D(3;0).  1  1  y y   0 I 
Vậy (3; 0) thỏa mãn yêu cầu bài toán. D   D 
c) Tìm tọa độ điểm J là chân đường phân giác trong của góc A trong tam giác ABC .    BJ AB AB
Giải. Gọi J(x ;y ) là chân đường phân giác trong của A    BJ   JC. J J CJ AC AC  A
 B  (1;1)  AB  2 AB 1  1   Ta có:   
 BJ  JC. A
 C  (2;2)  AC  2 2 AC 2 2    B
 J  (x  3;y 2)  1  J J  x   3  2  x  J J  Mà  1   1 1 1  2   C
 J  (4  x ;1y )  CJ  2
  x ;  y   1 1 J J   2  y   2    y   2 J 2 2 J   J  2 2 J  10 x    10    J     3  J  ;1  
thỏa mãn yêu cầu bài toán.   3  y   1   J 
21. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với (
A 1;1), B(5;3), C (2;0).
a) Tìm tọa độ điểm D sao cho ABCD là b) Tìm tọa độ điểm I thuộc trục hoành sao hình bình hành.
cho ABCI là hình thang nhận AB là đáy.
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
c) Tìm tọa độ điểm J là chân đường phân giác trong của góc A trong tam giác ABC .
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 40 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
22. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với (
A 1;4), B(1;2), C (8;5).
a) Tìm tọa độ điểm D sao cho ABCD là b) Tìm tọa độ điểm I thuộc trục hoành sao hình bình hành.
cho BACI là hình thang nhận AB là đáy.
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
c) Tìm tọa độ điểm J là chân đường phân giác trong của góc A trong tam giác ABC .
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
23. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với (
A 10;5), B(3;2), C (6;5).
a) Tìm tọa độ điểm D sao cho ABCD là b) Tìm tọa độ điểm I thuộc trục hoành sao hình bình hành.
cho ABCI là hình thang nhận AB là đáy.
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
.............................................................................. ..............................................................................
c) Tìm tọa độ điểm J là chân đường phân giác trong của góc A trong tam giác ABC .
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 41 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Chuyªn ®Ò 7. TÝch v« híng & HÖ thøc lîng
1. Cho tam giác ABC đều cạnh a, tâm O. Hãy tính: A      
Cần nhớ: a.b  a . b . cos(a,b )   2 Bình phương vô hướng: 2 a  a O    2   2  2  2      2
 (a b )  a  2a.b  b và a  b  (a b )(a  b ). B E C     a) AB.AC b) AB.BC .          
Ta có: AB.BC  B  . A BC
Ta có AB.AC  AB . AC cos(A , B AC )    
  BA . BC cos(B , A BC ) 2 1 a
 AB.AC.cos 60  a.a.   2 1 a 2 2   .
BA BC.cos 60  a  .a.    2 2        
b) (OB  OC )(AB  AC ).
c) (AB  2AC )(AB  3BC ).
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
2. Cho hình thang ABCD có đáy lớn BC  3a, đáy nhỏ AD  a, đường cao AB  2a.     
b) (OB  OC )(AB  AC ).
c) Gọi I là trung điểm CD. Tính (AI ;BD).
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
.............................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 42 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
3. Cho tam giác ABC có AB  6, BC  19 4. Cho tam giác ABC có AB  2, BC  4
và AC  15. Tính bán kính đường tròn
và CA  2 7. Tính bán kính đường tròn
ngoại tiếp, nội tiếp của tam giác ABC .
ngoại tiếp, nội tiếp của tam giác ABC . 19  15  6
.............................................................................
Lời giải. Nửa chu vi p   20. 2
............................................................................. Diện tích S  (
p p  a)(p b)(p  c)
.............................................................................
 20(20  19)(20  15)(20  6)  10 14.
.............................................................................
Bán kính đường tròn ngoại tiếp ABC :
.............................................................................
............................................................................. abc abc 19.15.6 171 14 S   R     4R 4S 56 4.10 14
.............................................................................
.............................................................................
Bán kính đường tròn nội tiếp ABC :
............................................................................. S 10 14 14
S  pr  r     p 20 2
.............................................................................
5. Cho tam giác ABC có AB  10, AC  16 6. Cho tam giác ABC có AB  5, AC  7
và BC  14. Tính bán kính đường tròn
và BC  10. Tính bán kính đường tròn
ngoại tiếp, nội tiếp, của tam giác ABC .
ngoại tiếp, nội tiếp, của tam giác ABC .
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 43 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
7. Cho tam giác ABC có AB  6, AC  8 8. Cho tam giác ABC có AB  6,AC  10  
và BAC  60. Tính h , , R r với , R r
và BAC  120. Tính h , , R r với , R r a a
lần lượt là bán kính đường tròn ngoại tiếp,
lần lượt là bán kính đường tròn ngoại
nội tiếp tam giác ABC .
tiếp, nội tiếp tam giác ABC .
Lời giải. Theo định lý hàm cos, ta có:
............................................................................. 2 2 2
a  b  c  2bc cos A
............................................................................. 0
 64  36  2.8.6.cos 60  49  a  7.
.............................................................................
Diện tích tam giác ABC :
............................................................................. 1 1
............................................................................. S
 bc sin A  .8.6.sin 60  10 3. A  BC 2 2
.............................................................................
Đường cao xuất phát từ đỉnh A :
............................................................................. 1 2S 2.10 3 20 3
............................................................................. S
 a.h  h     ABC 2 a a a 7 7
.............................................................................
Áp dụng định lý hàm sin, suy ra bán kính .............................................................................
đường tròn ngọa tiếp tam giác ABC :
............................................................................. a 7 7 3  2R  R   
............................................................................. sin A 2.sin 60 3
.............................................................................
a  b  c 7  8  6 21 Nửa chu vi p   
 ............................................................................. 2 2 2
.............................................................................
Bán kính đường tròn nội tiếp ABC :
............................................................................. S 2.10 3 20 3 A  BC S  pr  r   
 ............................................................................. A  BC p 21 21
9. Cho tam giác ABC có AB  13, AC  14 10. Cho tam giác ABC có AB  5,AC  7
và BC  15. Tính diện tích tam giác
và BC  8. Tính diện tích tam giác ABC, sin ,
A độ dài đường trung tuyến kẻ ABC, sin ,
A độ dài đường trung tuyến
từ C của tam giác ABC .
kẻ từ A của tam giác ABC .
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 44 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 
11. Cho ABC có AB  2 ,
a AC  3a và BAC  60. Gọi M là trung điểm BC.
a) Tính cạnh BC, trung tuyến AM và bán b) Gọi N là điểm trên cạnh AC sao cho   
kính đường tròn ngoại tiếp ABC .
5NA  7NC  0. CM: AM  BN .
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. ............................................................................. 
12. Cho hình bình hành ABCD có AB  5a, AD  8a, BAD  60.
   
a) Tính các tích vô hướng: AB.AD, AC.AD.
b) Tính độ dài đoạn BD và bán kính đường
tròn ngoại tiếp tam giác ABC . B C
.............................................................................
............................................................................. 60o
............................................................................. A D
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 45 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
13. Cho tam giác ABC có AB  10cm, AC  16cm, BC  14cm. 
a) Hãy tính số đo góc BAC , tính diện tích tam b) Gọi M là trung điểm BC và G là trọng
giác ABC, tính bán kính đường tròn ngoại
tâm tam giác ABC . Tính độ dài AM và  
tiếp R và tính bán kính đường tròn nội tiếp
tích vô hướng AG.BC.
r của tam giác ABC .
............................................................................. B
.............................................................................
.............................................................................
............................................................................. A C
.............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
.................................................................................
14. Cho hình thang vuông ABCD vuông tại A và B với BC  3 ,
a AD  a và AB  2a.
     
Tính: AB.CD; BC .BD; AC .BD. A D
.............................................................................
.............................................................................
............................................................................. B C
.............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 46 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 
15. Cho tam giác ABC có AB  a, AC  a 2, BAC  135. Gọi M là điểm thỏa mãn:   3AM  AC.      a) Tính . AB AC và . BABM.
b) Tính độ dài BM và cosin của góc ABM.
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. ............................................................................. 
16. Cho tam giác ABC có AB  6, AC  5, BAC  60. Gọi I thỏa mãn đẳng thức   
véctơ: IB  2IC  0.     
a) Chứng minh: AB  2AC  3AI . b) Tính .
AB AC và độ dài đoạn thẳng AI.
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 47 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
17. Cho tam giác ABC có AB  5, AC  8, A  60 .   
a) Tính độ dài cạnh BC của tam giác.
b) Gọi K là trung điểm BC . Tính AK .BC .
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
18. Cho tam giác ABC .
a) Gọi M, D lần lượt là trung điểm BC, AM.     
b) Biết AB  2, AC  3 và BAC  120.  
Chứng minh: DB  DC  2DA  0.
Tính AB.AC và bán kính đường tròn ABC
................................................................................. ngoại tiếp tam giác .
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. ............................................................................. 
19. Cho tam giác ABC có AB  5, AC  8, BAC  120.    
a) Tính AB.AC và độ dài BC .
b) G là trọng tâm ABC . Tính AG.BC .
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
................................................................................. .............................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 48 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
ĐỀ SỐ 01 – THPT BÌNH HƯNG HÒA (2017 – 2018)
Câu 1. (4,0 điểm) Giải các phương trình sau: a) 2
x  2x  6  2x  3. b) 2 2
3 x  4x  5  x  4x  9.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. x  2 1 x  6 27 c)        4 x  2 4(x  2) d) 2 x 3x x 1 (x 1). 4
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Câu 2. (1,0 điểm) Tìm tất cả các giá trị của tham số m để phương trình 2
x  2x  m  2  0
có hai nghiệm dương phân biệt.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Câu 3. (1,0 điểm) Tìm tham số m để phương trình 2 2
x  2(m  1)x  m  3  0 có hai
nghiệm phân biệt x , x thỏa mãn 2 2 x  x  4. 1 2 1 2
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 49 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 a b c 1 1 1
Câu 4. (1,0 điểm) Chứng minh rằng  
   với mọi a, , b c  0. bc ac ab a b c
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Câu 5. (3,0 điểm) Trong mặt phẳng Oxy, cho ba điểm (
A 1; 3), B(4;5) và C (1;2). a) Chứng tỏ ,
A B, C là ba đỉnh của tam b) Tìm tọa độ điểm D để ABCD là hình bình
giác và tìm trọng tâm G của A  BC.
hành. Tìm tọa độ trực tâm H của A  BC.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................  
c) Tìm tọa độ điểm M thuộc trục hoành sao cho 2MA  MC đạt giá trị nhỏ nhất.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 50 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
ĐỀ SỐ 02 – THPT TRẦN PHÚ (2017 – 2018)
Câu 1. (1,0 điểm) Cho ba tập hợp: A  (4; 4), B  [4; 6], C  (0; 8). Tìm (A  B)  C .
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: (A  B)  C  (0;6]. .............................................................................................................. x
Câu 2. (1,0 điểm) Tìm tập xác định của hàm số: y  x  1   x  2
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: D  [1;  )
 \ {2}. ..............................................................................................................
Câu 3. (1,0 điểm) Cho đường thẳng d : y  x  1 và parabol 2
(P) : y  x  2x. Gọi I là đỉnh 1
của (P ) và M là điểm trên d sao cho MI 
 Tìm tọa độ điểm M . 2
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 1 1  
Đáp số: M  ;   
.............................................................................................................................. 2 2
Câu 4. (1,0 điểm) Cho phương trình 2
x  2(m  1)x  2(m  2)  0 (1). Chứng minh rằng
phương trình (1) luôn có hai nghiệm phân biệt x , x và tìm tham số m để biểu thức 1 2 2
A  (x  x )  8x x  1 đạt giá trị nhỏ nhất. 1 2 1 2
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: A đạt giá trị nhỏ nhất bằng 1 khi m  3. ..........................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 51 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Câu 5. (1,0 điểm) Giải phương trình (x  1)( 4x  1  1)  0.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: x  0. .......................................................................................................................................
Câu 6. (1,0 điểm) Giải phương trình 2 x  x  2 3 4
5  x  4x  1  0.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: x  2. ....................................................................................................................................... x 8
Câu 7. (1,0 điểm) Tìm giá trị nhỏ nhất của hàm số: f (x)   khi x  2. 2 x  2
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: Giá trị nhỏ nhất của f (x ) bằng 5 tại x  6. ......................................................................
Câu 8. (1,0 điểm) Cho tam giác ABC có AB  2 , AC  2 3, góc A  30. Tính độ dài
cạnh BC , bán kính đường tròn ngoại tiếp và diện tích tam giác ABC .
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: BC  2, R  2, S  3. .....................................................................................................
Câu 9. (1,0 điểm) Cho tam giác ABC . Gọi M là điểm trên cạnh BC sao cho MB  2MC .   
Hãy phân tích AM theo AB , AC .
..................................................................................................................................................................
..................................................................................................................................................................  1  2 
Đáp số: AM 
AB  AC. ............................................................................................................ 3 3
Câu 10. (1,0 điểm) Cho tam giác ABC với (
A 1;1), B(1;2), C (3;4). Gọi M là trung điểm
BC, K là điểm trên đường thẳng AC sao cho BK  AM. Tìm tọa độ điểm K.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................  3 1   
Đáp số: K   ;   
...........................................................................................................................  11 11
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 52 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
ĐỀ SỐ 03 – THPT LÊ TRỌNG TẤN (2017 – 2018) 4 2 x   x  1
Câu 1. (1,0 điểm) Xét tính chẵn lẻ của hàm số y   x
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: Hàm số lẻ..................................................................................................................................
Câu 2. (1,0 điểm) Khảo sát sự biến thiên và vẽ đồ thị của hàm số 2 y  x   4x  3.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Câu 3. (1,0 điểm) Xác định parabol 2
(P) : y  ax  bx  ,
c biết (P ) đi qua ( A 1; 3) và có tọa  1 3   độ đỉnh là I   ;     2 4
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. Đáp số: 2
(P) : y  x  x  1. .............................................................................................................
Câu 4. (2,0 điểm) Giải các phương trình sau:
a) 5  x  1  x. b) 2
x  6x  3  x  3.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Đáp số: x  8. ................................................. Đáp số: S  {5;6}. ...............................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 53 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 c) 2
x  2x  (6  x)(4  x)  12.
d) 3x  1  8  x  1.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Đáp số: S  {2; 4}........................................ Đáp số: S  {8}. ..................................................
Câu 5. (1,0 điểm) Cho phương trình: 2
mx  2(m  1)x  m  3  0 (m tham số). Xác định 1 1 1
m để phương trình có 2 nghiệm phân biệt x , x thỏa mãn    1 2 x x 6 1 2
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 9
Đáp số: m  
 ............................................................................................................................... 11 
Câu 6. (1,0 điểm) Cho tam giác ABC có AB  3, BC  4, ABC  120.  
a) Tính tích vô hướng B . A BC.
b) Tính độ dài cạnh AC.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................   Đáp số: B .
A BC  6. ................................... Đáp số: AC  37. .............................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 54 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Câu 7. (3,0 điểm) Trong mặt phẳng Oxy, cho AB  C có ( A 2; 0), B
(5; 3) và C (3;2).
a) Chứng minh ABC vuông cân.
b) Tìm điểm E sao cho A là trung điểm BE.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Đáp số: Tam giác vuông cân tại C .
Đáp số: E(9;3). ...............................................
c) Tìm tọa độ điểm M , N sao cho M , N d) Tìm tọa độ điểm D sao cho ABCD là hình
chia đoạn AB thành 3 đoạn bằng nhau. bình hành.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. 1    8   
.................................................................................
Đáp số: M  ;1  N  ;2  và 3  3 
Đáp số: D(4;5). ..............................................
e) Tìm tâm đường tròn ngoại tiếp I và trực tâm H của tam giác ABC .
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 3 3  
Đáp số: I  ;   
.................................................................................................................................... 2 2
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 55 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
ĐỀ SỐ 04 – THPT BÌNH TÂN (2017 – 2018)
Câu 1. (1,0 điểm) Xác định parabol 2
(P) : y  ax  bx  2, biết (P ) đi qua hai điểm (4 A ; 6) và B(1;4).
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. Đáp số: 2
(P) : y  x
  5x  2. .........................................................................................................
Câu 2. (1,0 điểm) Tìm tham số m để phương trình 2 2
x  2mx  m  2m  1  0 có hai
nghiệm phân biệt dương.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 1
Đáp số: m 
 ..................................................................................................................................... 2
Câu 3. (1,0 điểm) Tìm tham số m để phương trình 2 2
x  (2m  1)x  m  2  0 có hai
nghiệm thỏa mãn 3x .x  5(x  x )  7  0. 1 2 1 2
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: m  2. ......................................................................................................................................
Câu 4. (1,0 điểm) Giải phương trình 1  3x  2  2x.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 3
Đáp số: x 
; x  1. ......................................................................................................................... 4
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 56 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019  2 2 x   y  41 
Câu 5. (1,0 điểm) Giải hệ phương trình  . x   y  1 
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: S  (x;y)  {(4;5),(5; 4)}. .............................................................................................. ab
Câu 6. (1,0 điểm) Cho hai số a, b  4. Chứng minh rằng a b  4  b a  4   2
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: Dấu "  " xảy ra khi và chỉ khi a  b  8. ........................................................................    
Câu 7. (1,0 điểm) Cho bốn điểm ,
A B, C, D. Chứng minh rằng AB CD CA  DB.
..................................................................................................................................................................
..................................................................................................................................................................
Câu 8. (1,0 điểm) Trong mặt phẳng Oxy, cho ba điểm (
A 4;1), B(2; 4), C (1;5). Tìm tọa   
độ điểm D biết DA  2BD  3CB.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: D(17; 34). .................................................................................................................................
Câu 9. (1,0 điểm) Tìm tọa độ trực tâm H của M
 NP với M (1;2), N(2;1), P(3;1).
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Câu 10. (1,0 điểm) Cho ABC có trực tâm H và M là trung điểm của BC . Chứng minh   rằng: 2
4MH.MA  BC .
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 57 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
ĐỀ SỐ 05 – THPT NGUYỄN HỮU CẢNH (2017 – 2018)
Câu 1. (1,0 điểm) Khảo sát sự biến thiên và vẽ đồ thị hàm số 2
y  x  2x  1.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Câu 2. (1,0 điểm) Giải và biện luận phương trình 2
m x  m(x  1)  1.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Câu 3. (3,0 điểm) Giải các phương trình sau: x  1 x a)  1   b) 2
x  5x  4  x  4. x  1 x  2
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Đáp số: S  {0;5}. .......................................... Đáp số: S  {0;6}. ...............................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 58 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 1 1 c) 2 4x   2x   6  0.       2 x x x x x x d) 2 2 6 10 5( 2) 1 0.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Đáp số: S  { 0  ,5; 1
 }. ................................ Đáp số: S  {3;8}. ...............................................
Câu 4. (1,0 điểm) Cho phương trình 2 2
x  (2m  1)x  m  3m  2  0 với m là tham số. 1 1 3
Định m để phương trình có hai nghiệm phân biệt x , x thỏa     1 2 x x 4 1 2
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: m  1. ......................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 59 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 2
 x  y  5 
Câu 5. (1,0 điểm) Giải hệ phương trình  . 2 x 
 y  x  3  0 
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: (x;y)  {(1;3);(2;1)}.
Câu 6. (2,0 điểm) Trong hệ trục tọa độ Ox , y cho A  BC có ( A 2;3), ( B 4;1), C( 1  ; 2  ).   
a) Tìm điểm D thỏa 2AD  AC  3BC . b) CM: A
 BC và tính diện tích A  BC.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. Đáp số: (
D 8;5). ............................................... Đáp số: S  8. ......................................................
Câu 7. (1,0 điểm) Cho tam giác đều ABC, cạnh a. Trên hai cạnh A ,
B AC lần lượt lấy hai 1 1
điểm M, N sao cho AM  A ,
B AN  AC. Chứng minh: BN  CM. 3 5
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 60 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
ĐỀ SỐ 06 – THPT TRẦN QUANG KHẢI (2017 – 2018)
Câu 1. (4,0 điểm) Giải các phương trình sau: a) 2
x  5x  9  2x  1. b) 2
x  3x  3  3x  2.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Đáp số: S  {1;2}. .......................................... Đáp số: S  {1}. ................................................... c) 2 2
4x  x  4 4x  x  4  9  0. d) 2
x  1  1  4x  3x .
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................  5    1  
Đáp số: S    ;1  S     
.................................... Đáp số:
................................................. 4    2  
Câu 2. (2,0 điểm) Cho phương trình 2
x  2mx  3m  2  0.
a) Tìm tham số m để phương trình có hai nghiệm trái dấu .........................................................
..................................................................................................................................................................
.................................................................................................................................................................. 2
Đáp số: m 
 ..................................................................................................................................... 3
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 61 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
b) Tìm m để phương trình có hai nghiệm phân biệt x , x thỏa mãn 2 2
x  x  4  x  x . 1 2 1 2 1 2
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: m  0. ...................................................................................................................................... 1 1 4
Câu 3. (1,0 điểm) Với a  0, b  0, chứng minh bất đẳng thức    a b a  b
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Câu 4. (3,0 điểm) Trong mặt phẳng Ox ,
y cho tam giác ABC với ( A 1;2), ( B 2  ;6), C(9;8).
a) Chứng minh rằng tam giác ABC vuông b) Tìm M là trung điểm của AC và tính độ tại . A
dài trung tuyến BM của tam giác ABC .
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ Đáp số: M(5;5), BM  5 2. .............................  
c) Gọi N là điểm trên cạnh BC sao cho BN  3NC . Tính diện tích tam giác ABN .
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 3 75 Đáp số: S  S   A  BN 4 A  BC 4
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 62 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
ĐỀ SỐ 07 – THPT NGUYỄN THƯỢNG HIỀN (2017 – 2018)
Câu 1. (1,0 điểm) Xác định parabol 2
(P) : y  ax  bx  ,
c biết rằng nó đi qua gốc tọa độ O và có đỉnh I(1; 4  ).
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. Đáp số: 2
(P) : y  4x  8x. ................................................................................................................
Câu 2. (2,0 điểm) Cho phương trình 2
x  3x  2m  2  0. Tìm m để phương trình có hai
nghiệm phân biệt x , x thỏa mãn 2 2
4(x  x )  17 x .x . 1 2 1 2 1 2
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 43
Đáp số: m  1 hoặc m 
 ......................................................................................................... 25
Câu 3. (2,0 điểm) Giải các phương trình sau: a) 2 2
x  2x  5  x  2x  3. b) 3
2x  7  x  x  343.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Đáp số: S  {1}. .............................................. Đáp số: S  {7}. ..................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 63 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 x 8
Câu 4. (1,0 điểm) Tìm giá trị nhỏ nhất của hàm số y   với x  1. 2 x 1
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 9
Đáp số: Giá trị nhỏ nhất của y bằng khi x  5. ......................................................................... 2
Câu 5. (2,0 điểm) Trong mặt phẳng tọa độ Ox , y cho A  BC với ( A 0;4), ( B 6  ;1), C( 2  ;8).
a) Chứng minh tam giác ABC tam giác vuông. Tìm tọa độ tâm và tính bán kính đường tròn
ngoại tiếp tam giác ABC . ..............................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................  9   65
Đáp số: Tam giác ABC vuông tại A nên tâm I   4;   R   
là trung điểm BC và .....  2 2
b) Tìm tọa độ điểm M thuộc Ox sao cho tam giác MAB vuông tại M .
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: M (3  5; 0) hoặc M (3  5; 0). ............................................................................... 1 2
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 64 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Câu 6. (2,0 điểm) Cho tam giác ABC có AB  2, AC  2 7 và BC  4. a) Tính góc ,
B bán kính đường tròn ngoại tiếp tam giác ABC và diện tích tam giác ABC . .
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................  2 21 Đáp số: B  120 ,  R  , S
 2 3. .................................................................................. 3 ABC
b) Tính độ dài đường phân giác trong của góc B của tam giác ABC .
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 4
Đáp số: BD 
 ................................................................................................................................. 3    
c) Tìm tập hợp các điểm M thỏa (MA  2MB).(AB  AC )  0.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................  
Đáp số: MI  CB  Tập hợp các điểm M là đường thẳng đi qua I và vuông góc với CB.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 65 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
ĐỀ SỐ 08 – THPT HÀN THUYÊN (2017 – 2018)
x  1  x  3
Câu 1. (0,75 điểm) Tìm tập xác định của hàm số y   2 x  2x  8
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. Đáp số: D  [ 1  ; )
 \ {2}. ..............................................................................................................
Câu 2. (1,0 điểm) Tìm parabol 2
(P) : y  ax  bx  2, biết parabol có đỉnh I(2; 2  ).
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. Đáp số: 2
(P) : x  4x  2. ....................................................................................................................
Câu 3. (2,5 điểm) Giải các phương trình sau: 2x  3 2 2  x  a)  5  3x. 2 x       8. x  1 b)   x  1
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Đáp số: S  {1}. ............................................. Đáp số: S  {7}. ..................................................
c) x  3  5  3 2  x . d) 2 2
2 x  3x  11  3x  4  x .
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. 4   
.................................................................................
Đáp số: S   ;2  
........................................ 3   
Đáp số: S  {2; 1
  3}. ..................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 66 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Câu 4. (0,75 điểm) Giải và biện luận phương trình: 2
m (x  2)  7m  (6  m)(x  m)  2.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. m  1
Đáp số: m  3 : PTVN, m  2 : PT có nghiệm tùy ý, m  3, m  2 : x   m  3  4 5    3
 x  y x y
Câu 5. (0,75 điểm) Giải hệ phương trình  .  8 15    11 x  y x  y 
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: (x;y)  {(3; 2
 )}. ....................................................................................................................
Câu 6. (1,5 điểm) Trong mặt phẳng Ox , y cho A  BC có ( A 1
 ;1), B(3;5), C(2; 3  ).
a) Tìm D để ABCD là hình bình hành.
b) Tìm tọa độ trực tâm H của tam giác ABC .
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 67 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................  15 8  
Đáp số: H   ;     
 ........................................... Đáp số: D( 2  ; 7
 ). .........................................  7 7
Câu 7. (2,5 điểm) Cho hình chữ nhật ABCD tâm ,
O có cạnh bằng AD  3 ,
a AB  2a. Lấy 1
điểm M trên cạnh AD sao cho AM  AD. 3     
a) Chứng minh rằng OA  OB  OC  OD  0. ...........................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................  
b) Tính tích vô hướng: AB.AC. .........................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................   Đáp số: 2
AB.AC  4a . ........................................................................................................................  
c) Gọi I là trung điểm của MC. Tính góc giữa hai véctơ BM và AI. ......................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................  
Đáp số: (BM;AI )  90 .
 .....................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 68 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
ĐỀ SỐ 09 – THPT NGUYỄN CHÍ THANH (2017 – 2018)
x  2018  x  2018
Câu 1. (1,0 điểm) Xét tính chẵn lẻ của hàm số y  f (x)   2 x  9
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Câu 2. (1,0 điểm) Xác định parabol 2
(P) : y  ax  bx  ,
c biết (P) có trục đối xứng x  2 và đi qua các điểm ( A 4;2), B(1; 1  ).
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Câu 3. (1,0 điểm) Giải phương trình 2
x  2x  6  1  2x.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. x
  y  8  0 
Câu 4. (1,0 điểm) Giải hệ phương trình  . 2 2 x 
 y  6x  2y  0 
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 69 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Câu 5. (1,0 điểm) Tính tuổi của cha hiện nay, biết rằng trước đây hai năm thì tuổi cha gấp bảy
lần tuổi con và sau ba năm nữa thì tuổi cha chỉ còn gấp bốn lần tuổi con.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Câu 6. (1,0 điểm) Chứng minh (a  1) b  (b  1) a  1  a  b  a ; b  , a b  0.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 
Câu 7. (2,0 điểm) Cho tam giác ABC có AB  5, AC  8, BAC  60.
a) Tìm độ dài cạnh BC và bán kính đường b) Tính diện tích tam giác ABC và bán kính
tròn ngoại tiếp tam giác ABC .
đường tròn nội tiếp tam giác ABC .
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 70 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Câu 8. (1,0 điểm) Trong mặt phẳng tọa độ Ox , y cho hai điểm (
A 1; 3), B(4;2). Chứng minh
tam giác OAB vuông cân và tính diện tích tam giác OAB.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Câu 9. (1,0 điểm) Trong mặt phẳng tọa độ Ox ,
y cho tam giác ABC biết ( A 2  ; 3), B(4;1) và C(0; 3
 ). Tìm tọa độ điểm A là hình chiếu vuông góc của A lên BC.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 71 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
ĐỀ SỐ 10 – THPT TÂY THẠNH (2017 – 2018)
Câu 1. (1,0 điểm) Tìm tọa độ giao điểm của đường thẳng d : y  2  x và 2 ( )
P : y  2x 2x 2.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. Đáp số: ( A 1; 2  ),B( 1
 ;2). ..................................................................................................................
Câu 2. (1,0 điểm) Lập bảng biến thiên và vẽ đồ thị của hàm số 2
y  2x  4x  1.
............................................................................................ Đồ thị của parabol:
............................................................................................ ..................................................................
............................................................................................ ..................................................................
............................................................................................ ..................................................................
............................................................................................ ..................................................................
............................................................................................ ..................................................................
............................................................................................ ..................................................................
............................................................................................ ..................................................................
Câu 3. (1,0 điểm) Cho parabol 2
(P) : y  ax  bx  ,
c (a  0) có đồ thị như hình vẽ bên dưới.
Hãy trình bày cách tìm a, ,
b c và suy ra tổng 3a  b  c.
............................................................................................................
............................................................................................................
............................................................................................................
............................................................................................................
............................................................................................................
............................................................................................................
............................................................................................................
Đáp số: a  1, b  2  , c  1
 và 3a  b  c  0. .......................................................................
Câu 4. (1,0 điểm) Giải phương trình 2
2x  x  2  x  .
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: x  2. ....................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 72 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Câu 5. (1,0 điểm) Giải phương trình 4 2
(x  1)  3(x  2x)  3  0.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: x  1  , x  1   3, x  1
  3. .................................................................................
Câu 6. (1,0 điểm) Tìm tất cả các giá trị của tham số m để phương trình 2 2
x  (m  1)x  1  0
có hai nghiệm phân biệt sao cho 2 2 x  x  0. 1 2
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: m  1
 , m  1. .....................................................................................................................
Câu 7. (1,0 điểm) Tìm tham số m để phương trình 2
(m  1)x  (2m  1)x  m  0 có nghiệm
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: m. ...........................................................................................................................................   
Câu 8. (1,5 điểm) Cho tam giác ABC và điểm M trên cạnh AB sao cho 2MA  MB  0,
G là trọng tâm tam giác ACM.      
a) Chứng minh: 3CM  2CA  CB.
b) Phân tích GB theo hai véctơ G , A GC.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................   
............................................................................ Đáp số: GB  5GA  3GC. .............................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 73 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Câu 9. (1,5 điểm) Trong mặt phẳng tọa độ Ox , y cho A  BC có ( A 0;2), B(0; 3  ), C(2; 1  ).    
b) Tìm tọa độ điểm D  Ox để ABCD là hình
a) Tìm tọa độ G thỏa GA GB GC  0.
thang với hai đáy là A , B CD.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ ................................................................................. 2 2  
.................................................................................
Đáp số: G  ;   
......................................... 3 3
Đáp số: D(2; 0). ....................................................
ĐỀ SỐ 11 – THPT CHUYÊN LÊ HỒNG PHONG (2017 – 2018)
Câu 1. (1,0 điểm) Giải phương trình: 2
2x  3x  1  x  1.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................  2 2 x 
 y  3xy  1 
Câu 2. (1,0 điểm) Giải hệ phương trình:  . x
  y  xy  1 
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Câu 3. (1,0 điểm) Tìm parabol 2
(P) : y  ax  bx  ,
c (a  0), biết rằng (P) có đỉnh I(2;1) và đi qua điểm ( A 3;2).
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 74 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Câu 4. (1,0 điểm) Cho phương trình 2
(x  3)(x  2mx  m  4)  0 (1) (m là tham số). Định
m để phương trình (1) có ba nghiệm phân biệt, trong đó có hai nghiệm dương và một nghiệm âm.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. m
 x  y  2m  1 
Câu 5. (1,0 điểm) Tìm các giá trị nguyên âm của m để hệ phương trình  x
  my  3m 
có nghiệm duy nhất (x;y) sao cho x, y là các số nguyên.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Câu 6. (1,0 điểm) Định m để bất phương trình 2
(m  2m  3)x  2m  1  0 vô nghiệm.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 75 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Câu 7. (1,0 điểm) Trong mặt phẳng tọa độ Ox ,
y cho tam giác ABC với (
A 1;2), B(3;5) và
C(4;7). Tìm tọa độ trực tâm H của tam giác ABC.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................  
Câu 8. (1,0 điểm) Cho tam giác ABC có AB  7, BC  8, BC  13. Tính AB.AC.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 
Câu 9. (1,5 điểm) Cho tam giác ABC có AB  2, AC  3 và BAC  120. Tính độ dài
BC, diện tích tam giác ABC, bán kính đường tròn ngoại tiếp và độ dài đường phân
giác trong AD của tam giác ABC .
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 1 2
Câu 10. (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức f (x)   với 0  x  1. x 1  x
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 76 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
ĐỀ SỐ 12 – THPT NGUYỄN THỊ MINH KHAI (2017 – 2018)
Câu 1. (3,0 điểm) Giải các phương trình và hệ phương trình sau: a) 2
1  5  3x  x  2x. ...................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: x  1. .................................................................................................................................... b) 2 3
3x  5  x  1  4  4x  x  3x.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: x  3. ....................................................................................................................................... x
  y  xy  5  c)   2 2 x   y  5 
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: (x;y)  {(2;1);(1;2)}. ..............................................................................................................
Câu 2. (2,0 điểm) Tìm tham số m sao cho: a) Phương trình 2 2
m x  4x  2m  m có b) Phương trình 2
x  2mx  4  0 có hai nghiệm tủy ý.
nghiệm x , x thỏa mãn x  x  2 2. 1 2 1 2
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Đáp số: m  2. ................................................ Đáp số: m   6. ...............................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 77 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
Câu 3. (1,0 điểm) Tìm giá trị lớn nhất của hàm số 2
y  x 1  x với 0  x  1.
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Câu 4. (2,0 điểm) Cho tam giác ABC có K là trung điểm của BC . Gọi I, J là các điểm thỏa  1    mãn AI 
AC và 2JB  JC. 3
a) Chứng minh rằng: ba điểm K, I, J
b) Tìm tập hợp các điểm M thỏa mãn:      thẳng hàng.
2MA  3MB  2MC  MB  MC .
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................   1
Đáp số: KJ  3IK  K, I, J thẳng hàng Đáp số: Đường tròn tâm ,
L bán kính BC. 3
Câu 5. (2,0 điểm) Trong mặt phẳng Ox , y cho ( A 2
 ;2), B(1; 0), C(3; 3  ).
a) Tìm tọa độ trực tâm H của tam giác b) Tìm D  Oy để ABCD là hình thang với ABC. đáy lớn là BC .
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Đáp số: H (13;12).
Đáp số: Không có điểm D thỏa giả thiết.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 78 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
ĐỀ SỐ 13 – THPT BÙI THỊ XUÂN (2017 – 2018)
Câu 1. (3,0 điểm) Cho phương trình 2
(m  1)x  2(m  4)x  m  1  0.
a) Tìm m để phương trình trên có nghiệm. .....................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 17
Đáp số: m  
 ............................................................................................................................... 8 2
b) Tìm m để phương trình có hai nghiệm x , x trái dấu sao cho x 
 .......................... 1 2 1 x2
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 1
Đáp số: m 
 ..................................................................................................................................... 3
c) Tìm tất cả giá trị nguyên âm của tham số m để phương trình có hai nghiệm x , x đều là 1 2
các số nguyên. ...................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: m  1 và thử lại. ................................................................................................................ Câu 2. (3,0 điểm)
a) Giải và biện luận phương trình 2
m (x  2)  24  16x  2m theo tham số m. .....................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 2(m  3)  
Đáp số: m  4  S  ,
 m  4  S  ,
 m  4  S      m 4   
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 79 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 m
 x  2y  m  2 
b) Định m để hệ phương trình  2 2
vô nghiệm.......................................... (
 m 1) x  y  m  1 
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: m  2. ......................................................................................................................................  2 2 (
 x  2)  6(x  2)y  4y  20 
c) Giải hệ phương trình: 
. .......................................................... 2 2 (
 x  3)  2 (2y  1) 
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
Đáp số: x  4  , y  1
 . ....................................................................................................................
Câu 3. (2,0 điểm) Trong mặt phẳng tọa độ Ox ,
y cho tam giác ABC ó ( A 2  ;4), B( 3  ; 1  ), C(1; 1
 ) và G là trọng tâm tam giác ABC.   
a) Tìm M thỏa AM  3AG  BC.
b) Tìm tâm đường tròn ngoại tiếp A  BC.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 80 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
Đáp số: M(4;2). Đáp số: I( 1  ; 2  ). 
Câu 4. (2,0 điểm) Cho tam giác ABC có AB  3, AC  5 và BAC  60. Gọi M là trung  
điểm của AB và E là điểm trên cạnh AC sao cho AC  4AE.  
a) Tính CM và bán kính nội tiếp AMC. b) Tính tích vô hướng BE.AC.
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................
............................................................................ .................................................................................   79 15 3 5
Đáp số: CM  và S  
Đáp số: BE.AC    2 AMC 8 4
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 81 -
¤n tËp thi häc k× 1 líp 10 n¨m häc 2018 – 2019 MỤC LỤC Trang
Chuyên đề 1. Parabol & một số vấn đề liên quan ..................................................................... 1
Chuyên đề 2. Giải và biện luận phương trình bậc nhất ........................................................... 5
Chuyên đề 3. Bài toán chứa tham số trong phương trình bậc hai .......................................... 7
Chuyên đề 4. Phương trình quy về phương trình bậc hai ....................................................... 13
Chuyên đề 5. Bất đẳng thức và GTLN, GTNN .......................................................................... 23
Chuyên đề 6. Hệ trục tọa độ ......................................................................................................... 29
Chuyên đề 7. Tích vô hướng và hệ thức lượng ......................................................................... 42
Đề số 01. THPT Bình Hưng Hòa (2017 – 2018) ................................................................... 49
Đề số 02. THPT Trần Phú (2017 – 2018) .............................................................................. 51
Đề số 03. THPT Lê Trọng Tấn (2017 – 2018) ....................................................................... 53
Đề số 04. THPT Bình Tân (2017 – 2018) ............................................................................... 56
Đề số 05. THPT Nguyễn Hữu Cảnh (2017 – 2018) ............................................................. 58
Đề số 06. THPT Trần Quang Khải (2017 – 2018) ................................................................ 61
Đề số 07. THPT Nguyễn Thượng Hiền (2017 – 2018) ........................................................ 63
Đề số 08. THPT Hàn Thuyên (2017 – 2018) ......................................................................... 66
Đề số 09. THPT Nguyễn Chí Thanh (2017 – 2018) ............................................................. 69
Đề số 10. THPT Tây Thạnh (2017 – 2018) ............................................................................ 72
Đề số 11. THPT Chuyên Lê Hồng Phong (2017 – 2018) .................................................... 74
Đề số 12. THPT Nguyễn Thị Minh Khai (2017 – 2018) ...................................................... 77
Đề số 13. THPT Bùi Thị Xuân (2017 – 2018) ........................................................................ 79
Chóc c¸c trß rÌn luyÖn tèt vµ ®¹t kÕt qu¶ cao trong kú thi s¾p ®Õn !
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 Trang - 82 -

Chuyên đề và bộ đề ôn thi học kỳ 1 Toán 10 năm học 2018 – 2019 – Lê Văn Đoàn

Thông tin :

Tài liệu liên quan:

Chuyên đề một số phương pháp đếm trong các bài toán tổ hợp

Các dạng toán vectơ Toán 10 thường gặp

Các dạng toán mệnh đề và tập hợp Toán 10 thường gặp

Đề cương giữa học kỳ 1 Toán 10 năm 2024 – 2025 trường THPT Hoàng Văn Thụ – Hà Nội

Đề cương giữa học kỳ 1 Toán 10 năm 2024 – 2025 trường THPT Xuân Đỉnh – Hà Nội