








































































































































































Preview text:
LÊ MINH TÂM t Chương 01
. CÁC ĐỊNH NGHĨA.
. TỔNG HIỆU HAI VÉCTƠ.
. TÍCH CỦA VÉCTƠ VỚI MỘT SỐ.
. HỆ TRỤC TỌA ĐỘ.
TÀI LIỆU LƯU HÀNH NỘI BỘ Chương 01. LÊ MINH TÂM
※※※MỤC LỤC※※※
BÀI 01. CÁC ĐỊNH NGHĨA ............................................................................................................... 4
I. KHÁI NIỆM VECTƠ. ................................................................................................................................ 4
1.1. Định nghĩa: ........................................................................................................................................... 4
1.2. Kí hiệu: ................................................................................................................................................... 4
II. VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG. ..................................................................................... 4
2.1. Giá của vectơ: ........................................................................................................................................ 4
2.2.Vectơ cùng phương, vectơ cùng hướng: ........................................................................................... 4
III. HAI VECTƠ BẰNG NHAU. ................................................................................................................. 5
3.1. Độ dài vectơ: ......................................................................................................................................... 5
3.2. Định nghĩa: ........................................................................................................................................... 5
IV. VECTƠ KHÔNG. .................................................................................................................................... 6
V. CÁC DẠNG TOÁN. ................................................................................................................................. 6
Dạng 01. XÁC ĐỊNH MỘT VÉCTƠ, SỰ CÙNG PHƯƠNG VÀ HƯỚNG CỦA HAI
VÉCTƠ. ......................................................................................................................................................... 6
Dạng 02. CHỨNG MINH HAI VÉCTƠ BẰNG NHAU ................................................................. 9
BÀI 02. TỔNG HIỆU HAI VECTƠ ............................................................................................. 16
I. TỔNG CỦA HAI VECTƠ ....................................................................................................................... 16
1.1. Định nghĩa: ......................................................................................................................................... 16
1.2. Tính chất: ............................................................................................................................................. 16
1.3. Quy tắc hình bình hành: .................................................................................................................. 16
II. HIỆU CỦA HAI VECTƠ. ....................................................................................................................... 18
2.1. Định nghĩa: ......................................................................................................................................... 18
2.2. Quy tắc về hiệu vectơ: ....................................................................................................................... 18
II. CÁC DẠNG TOÁN ................................................................................................................................ 20
Dạng 01. CHỨNG MINH ĐẲNG THỨC VECTƠ. ....................................................................... 20
Dạng 02. TÌM MÔĐUN (ĐỘ DÀI) VÉCTƠ. .................................................................................. 38
BÀI 03. TÍCH CỦA MỘT VECTƠ VỚI MỘT SỐ .............................................................. 46
I. ĐỊNH NGHĨA. .......................................................................................................................................... 46
II. TÍNH CHẤT. ............................................................................................................................................ 47
III. TRUNG ĐIỂM CỦA ĐOẠN THẲNG VÀ TRỌNG TÂM CỦA TAM GIÁC. .......................... 47 Trang 2 Chương 01. LÊ MINH TÂM
IV. ĐIỀU KIỆN ĐỂ HAI VECTO CÙNG PHƯƠNG. ........................................................................... 48
V. PHÂN TÍCH MỘT VEC TƠ THEO HAI VECTO KHÔNG CÙNG PHƯƠNG. ........................ 48
VI. CÁC DẠNG TOÁN ............................................................................................................................... 49
Dạng 01. BIỄU DIỄN VÉCTƠ. .......................................................................................................... 49
Dạng 02. CHỨNG MINH BA ĐIỂM THẲNG HÀNG, HAI ĐIỂM TRÙNG NHAU, HAI
ĐƯỜNG THẲNG SONG SONG, BA ĐƯỜNG THẲNG ĐỒNG QUY. ...................................... 54
Dạng 03. TẬP HỢP ĐIỂM THỎA MÃN ĐẲNG THỨC VECTƠ. ............................................. 63
BÀI 04. HỆ TRỤC TỌA ĐỘ ........................................................................................................... 70
I. TRỤC TỌA ĐỘ. ........................................................................................................................................ 70
1.1. Định nghĩa .......................................................................................................................................... 70
1.2. Tọa độ của vectơ và của điểm trên trục ......................................................................................... 70
1.3. Độ dài đại số của vectơ trên trục: .................................................................................................... 70
II. HỆ TRỤC TỌA ĐỘ. ................................................................................................................................ 71
2.1. Định nghĩa .......................................................................................................................................... 71
2.2. Tọa độ điểm, tọa độ vectơ ................................................................................................................ 71
2.3. Tọa độ trung điểm của đoạn thẳng. Tọa độ trọng tâm tam giác ............................................... 71
2.4. Biểu thức tọa độ của các phép toán vectơ. ..................................................................................... 72
III. TỔNG KẾT. ............................................................................................................................................ 74
IV. CÁC DẠNG TOÁN ............................................................................................................................... 75
Dạng 01. TÌM TỌA ĐỘ CỦA MỘT ĐIỂM; VECTƠ ; ĐỘ DÀI CỦA VECTƠ VÀ CHỨNG
MINH HỆ THỨC. ..................................................................................................................................... 75
Dạng 02. TÌM TỌA ĐỘ CỦA MỘT ĐIỂM; VECTƠ TRÊN MẶT PHẲNG Oxy. ................... 77
Dạng 03. VÉCTƠ CÙNG PHƯƠNG & ỨNG DỤNG. ................................................................. 96
V. BÀI TẬP NÂNG CAO .......................................................................................................................... 112
BÀI 05. TỔNG ÔN TẬP CHƯƠNG ......................................................................................... 123
I. BÀI TẬP TỰ LUẬN. ............................................................................................................................... 123
II. BÀI TẬP TRẮC NGHIỆM. .................................................................................................................. 162 Trang 3 Chương 01. LÊ MINH TÂM BÀI 1 CÁC ĐỊNH NGHĨA
I. KHÁI NIỆM VECTƠ.
※ Cho đoạn thẳng AB . Nếu chọn điểm A làm điểm đầu, điểm B làm điểm cuối thì đoạn
thẳng AB có hướng từ A đến B . Khi đó ta nói AB là một đoạn thẳng có hướng. 1.1. Định nghĩa:
Vectơ là một đoạn thẳng có hướng. 1.2. Kí hiệu:
Vectơ có điểm đầu A và điểm cuối B được kí hiệu là AB , đọc là "vectơ AB ".
Vectơ còn được kí hiệu là a,b,x, y, khi không cần chỉ rõ điểm đầu và điểm cuối của nó. Ví dụ 1 Cho tam giác
. Hãy kể tên các vectơ có điểm đầu và cuối là các đỉnh ? Lời giải
Các vectơ có điểm đầu và cuối là các đỉnh A, , B C là: A ,
B BA, AC,CA,C ,
B BC, AA, B , B CC
II. VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG. 2.1. Giá của vectơ:
※ Đường thẳng đi qua điểm đầu và điểm cuối của 1 vectơ được gọi là giá của vectơ đó.
2.2.Vectơ cùng phương, vectơ cùng hướng:
※ Hai vectơ được là cùng phương nếu giá của chúng song song hoặc trùng nhau.
※ Hai vectơ cùng phương thì chúng chỉ có thể cùng hướng hoặc ngược hướng. Ví dụ 2
Hãy liệt kê các vectơ cùng phương, cùng hướng, ngược hướng trong hình vẽ sau: Trang 4 Chương 01. LÊ MINH TÂM Lời giải
Các vectơ cùng phương: AB,CD và EF
Các vecto ngược hướng: AB và CD ; CD và EF
Các vectơ cùng hướng: AB và EF Nhận xét
Ba điểm phân biệt A, ,
B C thẳng hàng khi và chỉ khi hai vectơ AB và BC cùng phương.
III. HAI VECTƠ BẰNG NHAU. 3.1. Độ dài vectơ:
※ Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
Kí hiệu là AB , như vậy AB AB .
※ Vectơ có độ dài bằng 1 gọi là vectơ đơn vị. 3.2. Định nghĩa:
※ Hai vectơ a và b được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài.
Kí hiệu a b . Ví dụ 2 Cho hình bình hành tâm
. Hãy liệt kê các vectơ bằng nhau trên hình bình hành đó. Lời giải
Các vectơ bằng nhau trên hình bình hành đó là:
AB DC; BA C ; D BC A ;
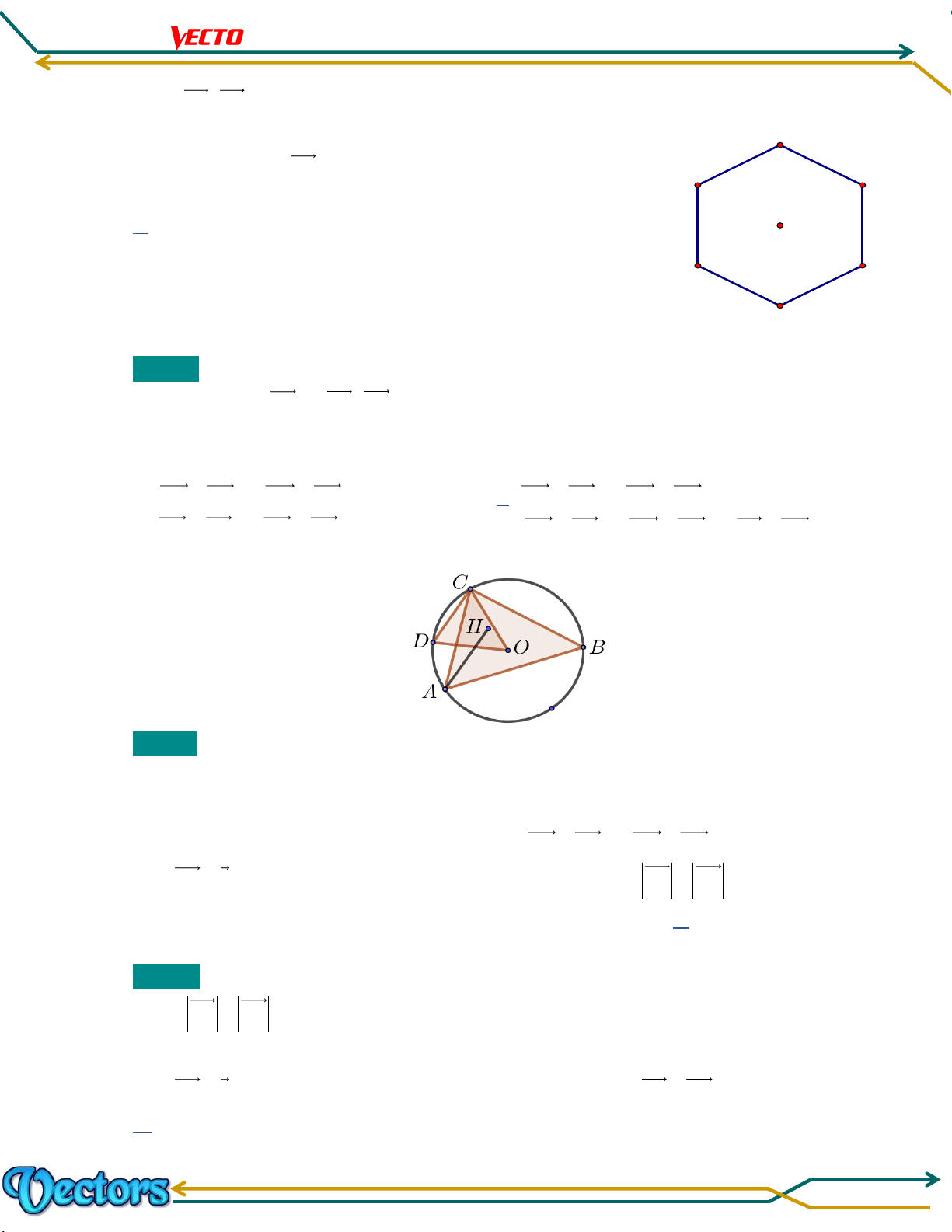
D CB DA ; AO OC;CO O ; A BO O ; D DO OB . Ví dụ 3 Cho lục giác đều có tâm
. Tìm các vectơ bằng vectơ . Trang 5 Chương 01. LÊ MINH TÂM Lời giải
Các vectơ bằng vectơ BA là: C ; O OF; DE .
★ Chú ý: Khi cho trước vectơ a và điểm O , thì ta luôn tìm được một điểm A duy nhất sao cho OA a . IV. VECTƠ KHÔNG.
※ Vectơ-không là vectơ đặc biệt có điểm đầu và điểm cuối đều cùng một điểm, ta kí hiệu là 0 .
※ Ta quy ước vectơ-không cùng phương, cùng hướng với mọi vectơ.
※ Như vậy 0 AA BB ... và MN 0 M N . V. CÁC DẠNG TOÁN.
Dạng 01. XÁC ĐỊNH MỘT VÉCTƠ, SỰ CÙNG PHƯƠNG VÀ HƯỚNG CỦA HAI VÉCTƠ.
Phương pháp giải
Để xác định véctơ ta cần biết điểm đầu và điểm cuối của véctơ hoặc biết độ dài và hướng của chúng.
Chẳng hạn với hai điểm A, B phân biệt, ta có hai véctơ khác véctơ-không là AB và BA .
Véctơ a là véctơ-không khi và chỉ khi a 0 hoặc a AA với A là điểm bất kì. Bài 01.
Cho 5 điểm phân biệt. Có bao nhiêu véctơ khác véctơ-không có điểm đầu và điểm cuối là các điểm đã cho. Lời giải
★ Xét các điểm A,B,C,D,E phân biệt.
Các véctơ khác véctơ-không có điểm đầu và điểm cuối là các điểm trên là:
AB, AC, AD, AE, BA, BC, BD, BE , CA,CB,CD,CE , DA, DB, DC, DE , EA, EB, EC, ED .
Vậy có 20 véctơ khác véctơ-không có điểm đầu và điểm cuối là các điểm đã cho. Bài 02.
Hãy tính số các véctơ (khác) mà các điểm đầu và điểm cuối được lấy từ các điểm phân biệt đã cho
trong các trường hợp sau đây: ⓵ Hai điểm. ⓶ Ba điểm. ⓷ Bốn điểm. Lời giải ⓵ Hai điểm. Trang 6 Chương 01. LÊ MINH TÂM
Xét hai điểm A,B phân biệt. Ta có AB,BA .
Vậy có 2 véctơ khác véctơ-không có điểm đầu và điểm cuối là các điểm đã cho. ⓶ Ba điểm.
Xét các điểm A,B,C phân biệt.
Các véctơ khác véctơ-không có điểm đầu và điểm cuối là các điểm trên là:
AB, AC , BA, BC ,CA,CB .
Vậy có 6 véctơ khác véctơ-không có điểm đầu và điểm cuối là các điểm đã cho. ⓷ Bốn điểm.
Xét các điểm A,B,C,D phân biệt.
Các véctơ khác véctơ-không có điểm đầu và điểm cuối là các điểm trên là:
AB, AC, AD , BA, BC, BD ,CA,CB,CD , DA, DB, DC .
Vậy có 12 véctơ khác véctơ-không có điểm đầu và điểm cuối là các điểm đã cho. Bài 03.
Cho hình bình hành. Hãy chỉ ra các vectơ khác nhau và khác vectơ – không, có điểm đầu và điểm
cuối một trong bốn điểm của hình hành. Trong các vectơ trên hãy chỉ ra:
⓵ Các cặp vectơ cùng phương.
⓶ Các cặp vectơ cùng phương nhưng ngược hướng. Lời giải
Giả sử hình bình hành là ABCD . Có 12 vectơ khác nhau và khác vectơ – không, có điểm
đầu và điểm cuối một trong bốn điểm của hình hành là
AB , AC , AD , BA , BC , BD , CA , CB , CD , DA , DB , DC
⓵ Các cặp vectơ cùng phương.
AB , BA , CD , DC .
AD , DA , BC , CB . AC , CA . BD , DB .
⓶ Các cặp vectơ cùng phương nhưng ngược hướng.
AB và BA ; AB và CD , BA và DC , AD và DA , AD và CB , DA và BC , AC và CA . BD và DB . Trang 7 Chương 01. LÊ MINH TÂM Bài 04.
Xác định vị trí tương đối của ba điểm phân biệt A , B , C trong các trường hợp sau:
⓵ AB và AC cùng hướng, AB AC .
⓶ AB và AC ngược hướng.
⓷ AB và AC cùng hướng và AB AC . Lời giải
⓵ AB và AC cùng hướng, AB AC .
AB và AC cùng hướng điểm A nằm ngoài đoạn BC .
Do AB AC nên điểm C là điểm giữa của hai điểm A và B .
⓶ AB và AC ngược hướng.
AB và AC ngược hướng nên điểm A là điểm giữa hai điểm B và C .
⓷ AB và AC cùng hướng và AB AC .
AB và AC cùng hướng và AB AC nên điểm B là điểm giữa của hai điểm A và C . Bài 05.
Cho hai vectơ không cùng phương u và v . Có hay không có một vectơ cùng phương với hai vectơ đó? Lời giải
Có, chọn vectơ đó là vectơ 0 , vectơ 0 cùng phương với mọi vectơ. Bài 06.
Cho ba vectơ cùng phương u , v , w . Chứng tỏ rằng có ít nhất hai vectơ trong ba vectơ đó cùng hướng. Lời giải
Chú ý rằng hai vectơ cùng phương chỉ có thể cùng hướng hoặc ngược hướng.
Giả sử u và v không cùng hướng.
Khi đó vì w cùng phương với u nên w cùng hướng hoặc ngược hướng với u .
Nếu w cùng hướng với u thì bài toán được chứng minh.
Nếu w ngược hướng với u thì v , w cùng ngược hướng với u nên hai vectơ v , w cùng hướng nhau. Trang 8 Chương 01. LÊ MINH TÂM Bài 07.
Các khẳng định sau đúng hay sai?
⓵ Hai vecto cùng phương với một vecto thứ ba thì cùng phương.
⓶ Hai vecto cùng phương với một vecto thứ ba khác 0 thì cùng phương.
⓷ Hai vecto cùng hướng với một vecto thứ ba thì cùng hướng.
⓸ Hai vecto cùng hướng với một vecto thứ ba khác 0 thì cùng hướng.
⓹ Hai vecto ngược hướng với một vecto khác 0 thì cùng hướng.
⓺ Điều kiện cần và đủ để hai vecto bằng nhau là chúng có độ dài bằng nhau. Lời giải
⓵ Hai vecto cùng phương với một vecto thứ ba thì cùng phương.
Khẳng định sai trong trường hợp vecto thứ ba là vecto 0 .
⓶ Hai vecto cùng phương với một vecto thứ ba khác 0 thì cùng phương. Khẳng định đúng.
⓷ Hai vecto cùng hướng với một vecto thứ ba thì cùng hướng.
Khẳng định sai trong trường hợp vecto thứ ba là vecto 0 .
⓸ Hai vecto cùng hướng với một vecto thứ ba khác 0 thì cùng hướng. Khẳng định đúng.
⓹ Hai vecto ngược hướng với một vecto khác 0 thì cùng hướng. Khẳng định đúng.
⓺ Điều kiện cần và đủ để hai vecto bằng nhau là chúng có độ dài bằng nhau.
Khẳng định sai. Vì: điều kiện cần và đủ để hai vecto bằng nhau là chúng có độ dài bằng nhau và cùng hướng.
Dạng 02. CHỨNG MINH HAI VECTƠ BẰNG NHAU.
Phương pháp giải
Để chứng minh hai véctơ bằng nhau ta có thể dùng một trong ba cách sau: Cách 01 a
b và a ; b cùng hướng a b . Cách 02
Tứ giác ABCD là hình bình hành AB DC và BC AD . Cách 03
Nếu a b ; b c thì a c . Bài 01. Trang 9 Chương 01. LÊ MINH TÂM
Cho tam giác ABC có D , E , F lần lượt là trung điểm của BC ,CA , AB . Chứng minh EF CD . Lời giải
Ta có: D ,E,F lần lượt là trung điểm của BC ,CA, AB . 1
EF là đường trung bình ABC và EF BC 1 . 2 1
Lại có D là trung điểm BC CD CB 2 . 2
Dễ thấy EF cùng hướng CD 3 Từ
1 ; 2 ; 3 EF CD . Bài 02.
Cho hình bình hành ABCD . Hai điểm M và N lần lượt là trung điểm của BC và AD . Điểm I là
giao điểm của AM và BN , K là giao điểm của DM và CN . Chứng minh AM NC , DK NI Lời giải
Chứng minh AM NC . Ta có: 1
+ M trung điểm BC MC BC . 2 1
+ N trung điểm AD AN AD . 2
Mà AD BC AN MC
Tứ giác AMCN là hình bình hành AM NC .
Chứng minh DK NI . AN//MB 1
Ta có: AN MB ABMN là hình bình hành I là trung điểm NB NI NB 1 . 2 MN//AB DN//MC 1
Ta có: DN MC CDNM là hình bình hành K là trung điểm MD DK DM 2 . 2 MN//DC BN//MD
Dễ thấy BNDM là hình bình hành do
nên ND BM 3. BN MD Từ
1 ; 2 ;3 DK NI . Bài 03.
Cho tam giác ABC có H là trực tâm và O là tâm đường tròn ngoại tiếp. Gọi B là điểm đối xứng của
B qua O . Chứng minh AH B C . Lời giải Trang 10 Chương 01. LÊ MINH TÂM
Ta có B là điểm đối xứng của B qua O
Nên BB là một đường kính của đường tròn ngoại tiếp tam giác ABC . 1
Ta có: OC BB nên tam giác CBB vuông tại C . 2 B C BC Ta có: B C //AH 1. AH BC 1
Tương tự:OA BB nên tam giác ABB vuông tại 2 A . B A AB Ta có: B A //CH 2. CH AB Từ
1 và 2 ta có tứ giác AHCBlà hình bình hành. Suy ra AH B C (đpcm). Bài 04.
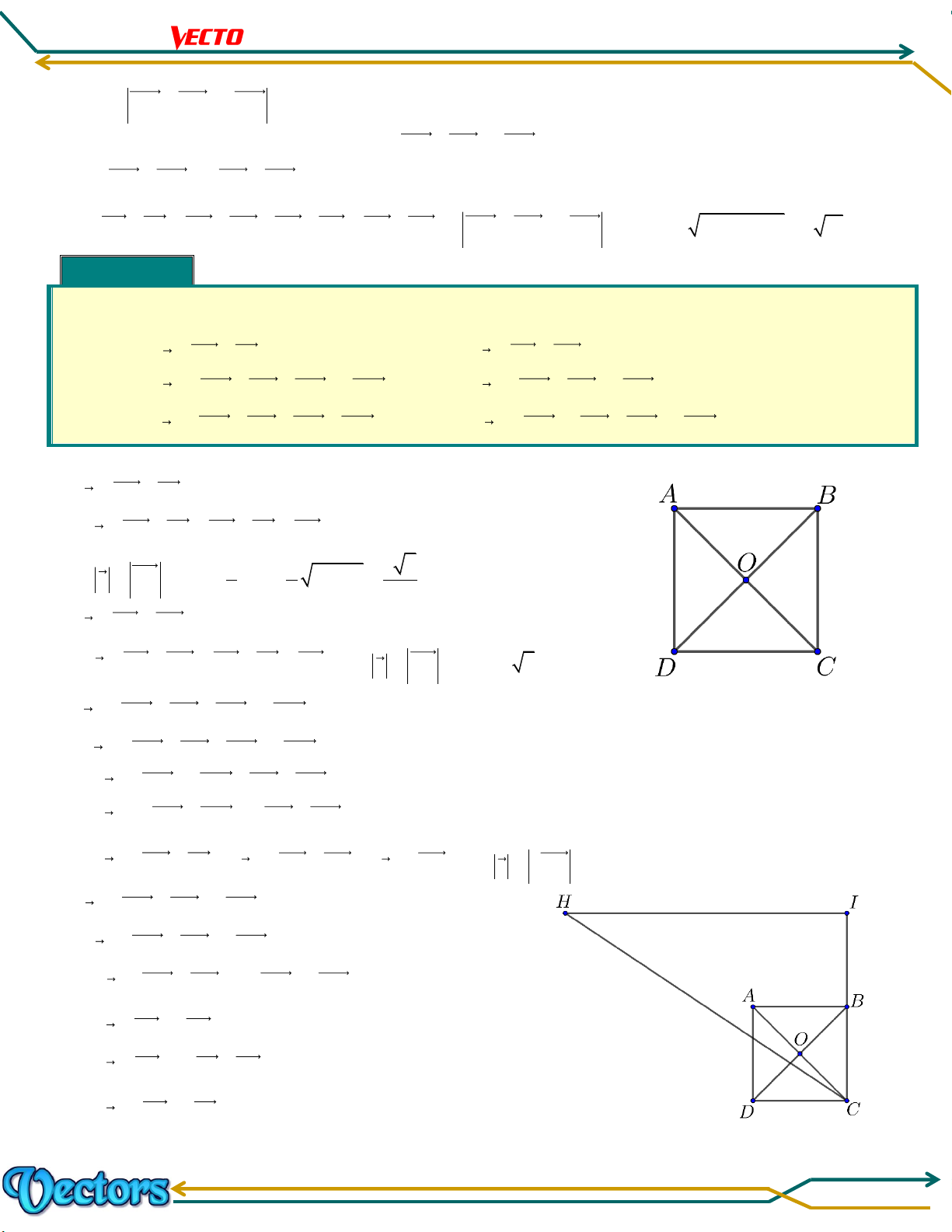
Cho hình vuông ABCD tâm O . Liệt kê tất cả các véctơ bằng nhau (khác 0 ) nhận đỉnh hoặc tâm của
hình vuông là điểm đầu và điểm cuối. Lời giải
Ta có các cặp véctơ sau:
AB DC ; BA CD ; AD BC ;
DA CB ; AO OC ;
OA CO ; OB DO ; BO OD . Bài 05.
Cho tứ giác ABCD . Gọi M , N , P ,Q lần lượt là trung điểm của các cạnh A , B BC,C , D DA . Chứng
minh NP MQ và PQ NM . Lời giải 1 NP BD Ta có: 2 MP MQ . 1 MQ BD 2 1 PQ CA Ta có: 2 PQ NM . 1 NM CA 2 Trang 11 Chương 01. LÊ MINH TÂM Bài 06.
Cho hình bình hành ABCD . Dựng AM BA , MN DA, NP DC, PQ BC . Chứng minh AQ 0 . Lời giải DC AB
Ta có: ABCD là hình bình hành nên .
BC DA
Ta có: AQ AM MN NP PQ .
BA DA DC BC AB DC DA BC AB AB DA DA 0 . Bài 07.
Cho tam giác ABC nội tiếp đường tròn tâm O . Gọi H là trực tâm của tam giác ABC . Tia AO cắt
đường tròn tâm O tại D . Chứng minh HB CD . Lời giải
Vì H là trực tâm của tam giác ABC (giả thiết) Nên HB AC (1)
Vì tia AO cắt đường tròn tâm O tại D (giả thiết)
Nên AD là đường kính của đường tròn tâm O
ACD 90 (góc nội tiếp chắn nửa đường tròn) CD AC (2)
Từ (1) và (2) HB // CD
Chứng minh tương tự BD// HC
Do đó tứ giác BDCH là hình bình hành (dấu hiệu nhận biết)
Khi đó ta có: HB cùng chiều với CD và HB CD
Vậy HB CD (theo định nghĩa). Trang 12 Chương 01. LÊ MINH TÂM Bài 08.
Tứ giác ABCD là hình gì nếu có AB DC và AB BC . Lời giải
Vì AB DC AB DC và AB cùng phương với AB DC DC AB // DC
Nên tứ giác ABCD là hình bình hành (1)
Vì AB BC AB BC (2)
Nên ABCD là hình thoi. Bài 09.
Cho a b 0 . So sánh độ dài, phương và hướng của hai véc tơ a và b . Lời giải
Ta có: a b 0 a b 0 a và b là hai véc tơ đối nhau.
Do đó, hai véc tơ a và b cùng phương, ngược chiều và cùng độ dài. Bài 10.
Cho hai véc tơ a và b là hai véc tơ khác véc tơ không. Khi nào đẳng thức sau xảy ra?
⓵ a b a b
⓶ a b a b Lời giải
⓵ a b a b 2 2 2
Ta có: a b a b 2 2 2
a b 2.ab a b 2.ab .
Và a b 2 2 2
a b 2. a . b . 2
Do đó a b a b a b a b 2 ab a . b , mà a.b a . b .cosa ;b .
cosa ;b 1 a ;b 0 0 .
a và b là hai véc tơ cùng chiều.
⓶ a b a b
a b a b a b b a a b b a b b .
hay a b b a b b .
Áp dụng phần ⓵ ta suy ra a b và b là hai véc tơ cùng chiều.
Hay a b và b là hai véc tơ ngược chiều. Trang 13 Chương 01. LÊ MINH TÂM Bài 11.
Cho tam giác ABC . Vẽ D đối xứng với A qua B , E đối xứng với B qua C và F đối xứng với C
qua A . Gọi G là giao điểm của trung tuyến AM của tam giác ABC với trung tuyến DN của tam
giác DEF . Gọi I và K lần lượt là trung điểm GA và GD. Chứng minh rằng:
⓵ AB NM .
⓶ MK NI
Lời giải
⓵ AB NM .
Ta có A,N lần lượt là trung điểm của FC,FE 1 1
AN CE BC (Vì C là trung điểm của BE ). 2 2 1
Mà BM BC suy ra AN BM 2
tứ giác ANMB là hình bình hành NM AB (đpcm).
⓶ MK NI
Ta có I,K lần lượt là trung điểm của GA và GD 1
IK AD AB NM 2
Tứ giác INMK là hình bình hành nên MK NI (đpcm). Bài 12.
Cho tam giác ABC và M là một điểm không thuộc các cạnh của tam giác. Gọi D,E,F lần lượt là
trung điểm của AB , BC ,CA . Vẽ điểm P đối xứng với M qua D , điểm Q đối xứng với P qua E ,
điểm N đối xứng với Q qua F . Chứng minh rằng MA AN . Lời giải Ta có :
D là trung điểm AB và M đối xứng P qua
D D là trung điểm MP .
Nên AMBP là hình bình hành MA BP 1 .
E là trung điểm BC và P đối xứng Q qua E E là trung điểm PQ .
Nên BPCQ là hình bình hành BP QC 2 .
F là trung điểm AC và Q đối xứng N qua F F là trung điểm NQ .
Nên QCNA là hình bình hành QC AN 3 . Từ
1 ; 2 và 3 AN QC BP MA MA AN . Trang 14 Chương 01. LÊ MINH TÂM Bài 13.
Cho tam giác ABC và tam giác AEF có cùng trọng tâm G . Chứng minh: BE FC . Lời giải
Ta có G là trọng tâm ABC GA GB GC 0 1 .
Và G là trọng tâm AEF GA GE GF 0 2 . Từ 1 và 2 :
GAGBGC GAGEGF GBGC GEGF GC GF GE GB FC BE
------------------HẾT------------------ Trang 15 Chương 01. LÊ MINH TÂM BÀI 2
TỔNG HIỆU HAI VÉCTƠ I. TỔNG CỦA HAI VECTƠ 1.1. Định nghĩa:
※ Cho hai vectơ a và b .
Lấy một điểm A tùy ý, vẽ AB a , BC b .
Vectơ AC được gọi là tổng của hai a ; b .
Kí hiệu a b .
Vậy AC a b .
Quy tắc ba điểm
Với ba điểm A,B,C ta luôn có AC AB BC . Ví dụ 1 Cho bốn điểm tính tổng các vectơ sau Lời giải
Theo quy tắc 3 điểm ta có AD DC CB AC CB AB . 1.2. Tính chất:
※ Với a,b,c tùy ý, ta có:
⓵ Tính chất giao hoán a b b a .
⓶ Tính chất kết hợp a b c a b c
⓷ Tính chất của vectơ không a 0 0 a a
1.3. Quy tắc hình bình hành:
※ Tứ giác A,B,C,D là hình bình hành, ta có AC AB AD Trang 16 Chương 01. LÊ MINH TÂM Ví dụ 2 Cho hình bình hành với là trung điểm của
. Tìm tổng của hai vectơ ⓵ và ⓶ và Lời giải
⓵ NC và MC
Ta có NC MC CN CM C A AC
Do tứ giác AMCN là hình bình hành nên
CN CM CA .
⓶ AM và CD
Ta có AM CD NC CD ND
Do tứ giác AMCN là hình bình hành nên AM NC . ★ Chú ý
⓵ Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi IA IB 0
⓶ ĐiểmG là trọng tâm của ABC khi và chỉ khi GA GBGC 0 Ví dụ 3 Cho tam giác . Gọi là trung điểm của . Chứng minh rằng ⓵ . ⓶ , với là điểm bất kì. Lời giải
⓵ BM CN AP 0 .
Ta có BM PN ,CN MP , AP NM
BM CN AP N
P MP NM 0 .
⓶ OAOBOC OM ON OP,
Theo câu ⓵ ta có BM CN AP 0
BOOMCOONAOOP 0
OM ON OP AO BOCO
OM ON OP OAOBOC. Trang 17 Chương 01. LÊ MINH TÂM
II. HIỆU CỦA HAI VECTƠ. 2.1. Định nghĩa:
※ Vectơ đối của vecto a , kí hiệu là a , là vectơ cùng phương nhưng ngược hướng với vecto a .
※ Cho hai vecto a và b . Ta gọi hiệu của hai vectơ a và b là vecto a (b) , kí hiệu a b . Ví dụ 4 Cho có
lần lượt là trung điểm của
. Hãy tìm các vectơ đối nhau
trong hình vẽ bên dưới. Lời giải
Các cặp vecto đối nhau là:
AB và BA ; AC và CA ; BC và CB ; AF và FA ; AF và BF ; AF và DE ; AE và EA ; AE và DF ;….
2.2. Quy tắc về hiệu vectơ:
※ Với 3 điểm O, A,B tùy ý ta luôn có: AB OBOA. Ví dụ 5 Cho . Các điểm
và lần lượt là trung điểm các cạnh và
⓵ Tìm các hiệu sau và . ⓶ Phân tích vectơ theo hai vecto và .
Lời giải
⓵ Tìm AM AN; MN NC và MN PN .
AM AN NM ;
MN NC MN CN MN NA MA(Vì CN NA ).
Ta có: MN PN MN NP MP . Trang 18 Chương 01. LÊ MINH TÂM
⓶ Phân tích vectơ AM theo vecto MN và MP .
Ta có: AM NP MP MN Ví dụ 6 Cho bốn điểm bất kỳ và
. Hãy chứng minh đẳng thức
Lời giải
Ta có: AB CD AD CB
ABCD DA BC 0
ABCA BC 0
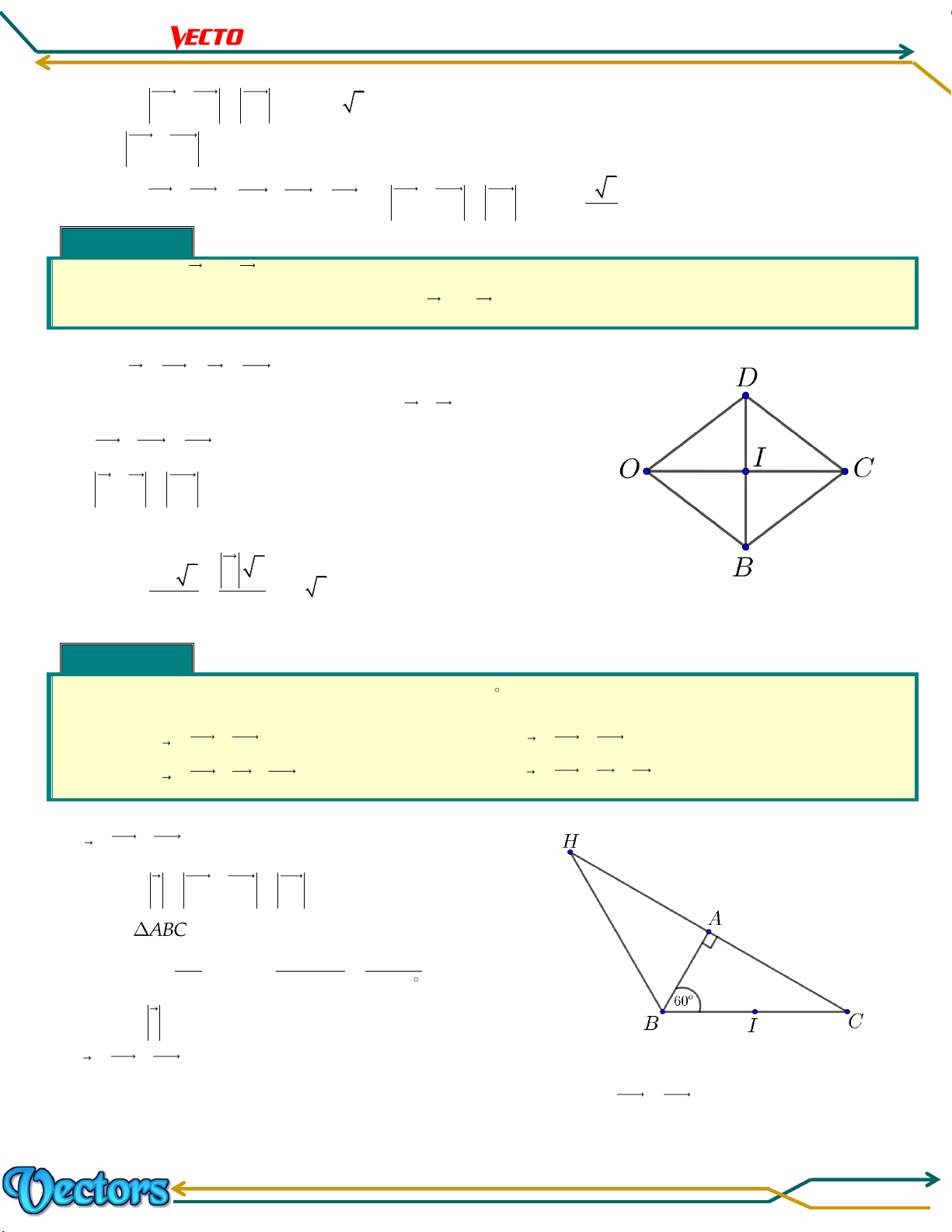
AB BC CA 0 AC CA 0 AA 0(Đúng). Ví dụ 6 Cho hình vuông
có cạnh bằng với tâm là . Tính ⓵ Độ dài vectơ . ⓶ .
Lời giải
⓵ Độ dài vectơ OACB .
Có OA CB AC a 2
CO BC CO BOOC BO . 2 2
⓶ AB DC .
Dựng vecto BA DC .
Có AB DC AB BA AA 2AB 2a . Trang 19 Chương 01. LÊ MINH TÂM II. CÁC DẠNG TOÁN
Dạng 01. CHỨNG MINH ĐẲNG THỨC VECTƠ.
Phương pháp giải
Sử dụng quy tắc ba điểm, quy tắc hình bình hành, hệ thức trung điểm, trọng tâm kết hợp với
các tính chất phép cộng, phép trừ, phép nhân để biến đổi tương đương cho biểu thức cần chứng
minh. Khi đó ta có hướng sau:
Biến đổi một vế thành một vế còn lại. Khi đó nếu xuất phát từ vế phức
Hướng 01 tạp, ta cần thực hiện việc đơn giản biểu thức. Còn nếu xuất phát từ vế
đơn giản, ta cần thực hiện phép phân tích vectơ.
Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn
đúng (chẳng hạn: hệ thức trung điểm, trọng tâm,…). Hoặc ngược lại,
Hướng 02 biến đổi một đẳng thức vectơ là luôn đúng thành đẳng thức vectơ cần chứng minh. Bài 01.
Cho 5 điểm A , B ,C , D , E . Chứng minh rằng:
⓵ ABCD EA CB ED .
⓶ CD EA CA ED . Lời giải
⓵ ABCD EA CB ED .
⓶ CD EA CA ED .
ABCBCDEA ED 0
CDCA ED EA
AD AD (ĐPCM).
AB BC CD DA 0 AA 0(ĐPCM). Bài 02.
Cho cho tứ giác lồi ABCD . Gọi E, F lần lượt là trung điểm của AB ,CD và G là trung điểm EF . Chứng minh rằng:
⓵ AC BD AD BC 2EF .
⓶ GA GBGC GD 0 . Lời giải
⓵ AC BD AD BC 2EF .
★ AC BD 2EF 1 .
E là trung điểm AB 2OE OAOB với O tùy ý.
F là trung điểm CD 2OF OC OD với O tùy ý.
1 OC OA OD OB 2OF 2OE
OC OA OD OB OC ODOAOB Trang 20 Chương 01. LÊ MINH TÂM
OC OC OD OD OB OB OA OA 0 ĐPCM. 0 0 0 0
★ AD BC 2EF 2 .
Do E là trung điểm AB nên 2OE OA OB với O là một điểm tùy ý.
Do F là trung điểm CD nên 2OF OC OD với O là một điểm tùy ý.
2 OD OA OC OB 2OF 2OE
OD OA OC OB OC ODOAOB
OC OC OD OD OB OB OA OA 0 ĐPCM. 0 0 0 0
⓶ GA GB GC GD 0 3 .
Do E là trung điểm AB nên 2OE OA OB với O là một điểm tùy ý.
Do F là trung điểm CD nên 2OF OC OD với O là một điểm tùy ý.
3 2GEGBGBGC 2GF GC 0
2GE 2GF 0 2GE GF 0 ĐPCM. 0 Bài 03.
Cho hình bình hành ABCD . Hai điểm M và N lần lượt là trung điểm của BC và AD . Tìm tổng của
hai vectơ NC và MC ; AM và CD ; AD và NC . Lời giải
Vì MC AN , nên: NC MC AN NC AC .
Vì AM NC , nên: AM CD NC CD ND .
Gọi I là trung điểm NC .
Vì NC AM, AD 2AN ,
Nên AD NC AN AN AM AN AC 2AI . Bài 04.
Cho tứ giác ABCD . Gọi hai điểm M và N theo thứ tự là trung điểm của các đoạn AD , BC . ⓵ 1 1
Chứng minh rằng MN AB DC AC DB. 2 2
⓶ Gọi I là trung điểm của MN . Chứng minh rằng: IA IB IC ID 0 . Lời giải Trang 21 Chương 01. LÊ MINH TÂM ⓵ 1 1
Chứng minh rằng MN AB DC AC DB. 2 2 ★ 1
Chứng minh MN AB DC. 2
Vì M là trung điểm của AD nên MA MD 0
Vì N là trung điểm của BC nên BN CN 0
Áp dụng quy tắc ba điểm, ta có:
MN MA AB BN
MN MD DC CN
2MN MA MD ABCDBN CN 0 ABCD0 ABCD. 1
MN AB DC (ĐPCM). 2 ★ 1 1
Chứng minh AB DC AC DB . 2 2
AB AC CB
ABCD AC DBCB BC AC DB (ĐPCM).
DC DB BC 1 1
Vậy: MN AB DC AC DB (ĐPCM). 2 2
⓶ Gọi I là trung điểm của MN. Chứng minh rằng: IA IB IC ID 0 .
IA ID 2IM
Theo hệ thức trung điểm, ta có:
IB ID 2IN
IA ID IB ID 2IM IN 2 0. 0 (Vì I là trung điểm MN). Bài 05.
Cho lục giác đều ABCDEF tâm O . Chứng minh: OA OB OC OD OE OF 0 . Lời giải
Vì O là tâm của hình lục giác đều ABCDEF
Nên OA và OD ; OB và OE ; OC và OF là các cặp
vectơ đối nhau nên ta có:
OAOBOC ODOEOF 0
OAODOBOEOC OF 0 0 0 (đpcm). Trang 22 Chương 01. LÊ MINH TÂM Bài 06.
Cho ngũ giác đều ABCDE tâm O .
⓵ Chứng minh rằng: hai vectơ OA OB và OC OE đều cùng phương với OD .
⓶ Chứng minh hai vectơ AB và EC cùng phương.
⓷ Chứng minh: OA OBOC OD OE 0 . Lời giải
⓵ Chứng minh rằng: hai vectơ OA OB và OC OE đều cùng phương với OD .
Gọi d là đường thẳng chứa OD
Thì d là một trục đối xứng của ngũ giác đều. Ta có:
OA OB OM , trong đó M là đỉnh của hình thoi
OAMB và M d .
Tương tự OC OE ON , trong đó N là đỉnh của
hình thoi OENC và Nd .
Do đó hai vectơ OA OB và OC OE đều có giá là đường thẳng d
Nên hai vectơ OA OB và OC OE cùng phương
với nhau và cùng phương với véctơ OD .
⓶ Chứng minh hai vectơ AB và EC cùng phương. EC d
Ta có: OAMB và OENC là các hình thoi nên ta có: AB // EC . AB d
Do đó hai vectơ AB và EC cùng phương.
⓷ Chứng minh: OAOBOC ODOE 0.
Theo câu ⓵ ta có:
v OA OB OC OD OE OA OB OC OEOD OM ON OD
Nên v có giá là đường thẳng d .
Mặt khác: v OBOCOD OAOE thì v có giá là đường thẳng OE.
Vì v có 2 giá khác nhau nên v 0 .
Vậy OAOBOC OD OE 0 (đpcm). Trang 23 Chương 01. LÊ MINH TÂM Bài 07.
Cho tam giác ABC , gọi M là trung điểm BC và I là trung điểm của AM .
⓵ Chứng minh rằng: 2IA IB IC 0 .
⓶ Với O là điểm bất kì, chứng minh rằng: 2OA OBOC 4OI . Lời giải
⓵ Chứng minh rằng: 2IA IB IC 0 .
Ta có: 2IA IB IC
2IA 2IM ( IB IC 2IM do M là trung điểm BC )
2IA IM
0 ( IA IM 0 do I là trung điểm của AM ) (đpcm).
⓶ Với O là điểm bất kì, chứng minh rằng: 2OAOBOC 4OI .
Ta có: 2IA IB IC 0
2IO 2OA IOOB IOOC 0
4IO 2OAOBOC 0
2OAOBOC 4 IO
2OAOBOC 4OI (đpcm). Bài 08.
Cho tứ giác ABCD . Gọi E, F,G, H lần lượt là trung điểm A ,
B BC,CD, DA và M là điểm tùy ý. Chứng minh rằng:
⓵ AF BG CH DE 0 .
⓶ MA MB MC MD ME MF MG MH .
⓷ AB AC AD 4AI với I là trung điểm FH . Lời giải
⓵ AF BGCH DE 0 .
Ta có: AF BG CH DE 1
AB AC 1
BC BD 1
CDCA 1
DA DB 2 2 2 2 1
AB AC BC BDCDCA DA DB 2 1
AB BC CD DA AC CA BD DB 0 2 (đpcm).
⓶ MA MB MC MD ME MF MG MH . Trang 24 Chương 01. LÊ MINH TÂM
Ta có: MA MB MC MD ME MF MG MH
ME MF MG MH MA MB MC MD 0
MF MA MG MB MH MC ME MD 0
AF BG CH DE 0 (đpcm).
⓷ AB AC AD 4AI với I là trung điểm FH .
Ta có: AB AC AD
2AF AD ( AB AC 2AF do F là trung điểm BC )
2AF 2AH ( AD 2AH do H là trung điểm AD )
2AF AH 4AI ( AF AH 2AI do I là trung điểm FH ) (đpcm). Bài 09.
Cho hình bình hành ABCD tâm O , M là một điểm bất kì. Chứng minh rằng:
⓵ OA OBOC OD 0.
⓶ DA DB DC 0.
⓷ DO AO A . B
⓸ MA MC MB MD 2M . O Lời giải
⓵ OAOBOC OD 0.
Ta có: O là trung điểm của AC và BD
Nên OA OC 0 và OB OD 0.
Vậy: OAOBOC OD 0.
⓶ DA DB DC 0.
Ta có: DA DB DC BA DC 0 (vì ABCD là hình bình hành nên BA và DC đối nhau)
Vậy: DA DB DC 0.
⓷ DO AO A . B
Ta có: O là trung điểm của BD nên DO O . B
Do đó: DO AO OB AO AO OB A . B
Vậy: DO AO A . B
⓸ MA MC MB MD 2M . O
Ta có: O là trung điểm của AC và BD nên OA OC 0 và OB OD 0.
MA MC MO OA MO OC 2MO Do đó:
MB MD MO OB MO OD 2MO
Vậy: MA MC MB MD 2M . O Trang 25 Chương 01. LÊ MINH TÂM Bài 10.
Cho hình bình hành ABCD tâm O và E là trung điểm của AD . Chứng minh rằng:
⓵ OA OBOC OD 0.
⓶ EA EB 2EC 3A . B
⓷ EB 2EA 4ED E . C Lời giải
⓵ OAOBOC OD 0.
Ta có: O là trung điểm của AC và BD
Nên OA OC 0 và OB OD 0.
Vậy: OAOBOC OD 0.
⓶ EA EB 2EC 3A . B
Ta có: EA EB 2EC EA EA AB 2EA AB BC
4EA 2BC 3AB 2DA 2BC 3AB
2DA BC3AB 3AB (vì DA và BC đối nhau nên DA BC 0 )
Vậy: EA EB 2EC 3A . B
⓷ EB 2EA 4ED E . C
Vì E là trung điểm của AD nên EA ED 0
Ta có: EB 2EA 4ED EC CB 2EA ED 2ED
EC CB 2ED EC CB AD EC (vì CB và AD đối nhau nên CB AD 0 ).
Vậy: EB 2EA 4ED E . C Bài 11.
Cho hình bình hành ABCD . Gọi M là trung điểm của CD . Lấy N trên đoạn BM sao cho BN 2MN . Chứng minh rằng:
⓵ 3AB 4CD CM ND M . N
⓶ AC 2.AB BD . ⓷ 4 2
AN AB B . D 3 3 Lời giải
⓵ 3AB 4CD CM ND M . N
3.AB 4.CD 3.AB 3.CD CD
3.ABCDCD CD
CM ND MN CM MN ND CD .
Vậy 3.AB 4.CD CM ND M . N Trang 26 Chương 01. LÊ MINH TÂM
⓶ AC 2.AB BD .
Ta có 2.AB BD AB BD AB AD AB AC . ⓷ 4 2
AN AB B . D 3 3
Ta có AN AB BN 2 AB BM 3 2 1
AB . BD BC 3 2 1 1 1 1 1 1
AB BD BC AB BD AD AB BD AB BD 4 2 AB BD . 3 3 3 3 3 3 3 3 Bài 12.
Cho hình bình hành ABCD có M là trung điểm BC và G là trọng tâm tam giác ACD . Chứng minh rằng: ⓵ 1
AM AB A . D ⓶ 2 1
MG AB A . D 2 3 6 Lời giải ⓵ 1
AM AB A . D 2 Ta có 1
AM AB AC 1
AB AB AD 1 AB A . D 2 2 2 ⓶ 2 1
MG AB A . D 3 6
Ta có MG MA AG 2
AM AI (với I là trung điểm DC) 3 1
AB AC 2 1
. AD AC 2 3 2 1
AB AB AD 2 1
. AD AB AD 2 1
AB A . D 2 3 2 3 6 Bài 13.
Cho tam giác ABC có D, M lần lượt là trung điểm của BC và AB , điểm N thuộc cạnh AC sao cho NC 2N .
A Gọi K là trung điểm của .
MN Chứng ming rằng: ⓵ 1 1 AK
AB AC. ⓶ 1 1 KD
AB AC. 4 6 4 3 Lời giải Trang 27 Chương 01. LÊ MINH TÂM ⓵ 1 1 AK
AB AC. 4 6 1 1
Theo giả thiết ta có: AM A ; B AN AC. 2 3
Vì K là trung điểm của MN 1 1 1 1 Nên AK AM AN
AB AC (đpcm). 2 2 4 6 ⓶ 1 1 KD
AB AC. 4 3 1 1
Vì D là trung điểm của BC nên AD AB AC. 2 2 1 1 1 1 1 1
Ta có: KD AD AK AB AC AB AC AB AC (đpcm). 2 2 4 6 4 3 Bài 14.
Cho tam giác ABC , trên hai cạnh AB, AC lần lượt lấy các điểm D, E sao cho AD 2D ; B CE 3E . A
Gọi M là trung điểm của DE và I là trung điểm của .
BC Chứng ming rằng: ⓵ 1 1
AM AB AC. ⓶ 1 3 MI
AB AC. 3 8 6 8 Lời giải ⓵ 1 1
AM AB AC. 3 8 2 1
Theo giả thiết ta có: AD A ; B AE AC. 3 4
Vì M là trung điểm của DE 1 1 1 1 Nên AM
AD AE AB AC (đpcm). 2 2 3 8 ⓶ 1 3 MI AB AC. 6 8 1 1
Vì I là trung điểm của BC nên AI AB AC 2 2 1 1 1 1 1 3
Ta có: MI AI AM AB AC AB AC AB AC (đpcm). 2 2 3 8 6 8 Bài 15.
Cho tam giác ABC với I , J , K lần lượt là trung điểm của các cạnh AB , BC , CA . Gọi D thuộc đoạn 2
BC sao cho DB BC và M là trung điểm của AD . 3
⓵ Chứng minh AK CJ BI 0 .
⓶ Chứng minh 6BM 2AC 5AB . Lời giải Trang 28 Chương 01. LÊ MINH TÂM
⓵ Chứng minh AK CJ BI 0.
Ta có VT AK CJ BI 1 1 1 1
AC CB BA AC CB BA 0 VP . 2 2 2 2
⓶ Chứng minh 6BM 2AC 5AB .
Do M là trung điểm của AD nên ta có 1
BM BA BD 1 2 BA BC 2 2 3 1 1 1 1
AB BC AB AC AB 1 5
AC AB
6BM 2AC 5AB . 2 3 2 3 3 6 Bài 16.
Cho tam giác ABC có G là trọng tâm, I là trung điểm của BC và H là điểm đối xứng của C qua G . Chứng minh. ⓵ 2 1 1 1 5 AH
AB AC .
⓶ HB AB AC.
⓷ IH AB AC . 3 3 3 6 6 Lời giải ⓵ 2 1 AH
AB AC . 3 3
Do G là trung điểm của HC nên ta có 1
AG AH AC 2
AH 2AG AC . 2
AH 2. AI AC 3 2 1
AH 2. . AB AC 2 1 AC AH AB AC . 3 2 3 3 ⓶ 1
HB AB AC. 3 2 1 1
Ta có VT HB AB AH AB
AB AC AB AC VP . 3 3 3 ⓷ 1 5
IH AB AC . 6 6 1 1 1 1 5
Ta có : VT IH IB BH BC HB AC AB AB AC AB AC VP . 2 2 3 6 6 Bài 17.
Cho tứ giác OABC . Gọi M, N lần lượt là trung điểm của OB,OC . Chứng minh ⓵ 1 1 1
AM OB OA ⓶ 1
BN OC OB
⓷ MN OC OB . 2 2 2 2 Lời giải Trang 29 Chương 01. LÊ MINH TÂM ⓵ 1
AM OB OA 2
Ta có AM OM OA , mà M là trung điểm của OB 1 1
Nên OM OB do đó AM OB OA (đpcm). 2 2 ⓶ 1
BN OC OB 2 1
Ta có BN ON OB OC OB (đpcm). 2 ⓷ 1 1
MN OC OB . 2 2 1 1
Ta có MN ON OM OC OB (đpcm). 2 2 Bài 18.
Cho tam giác ABC , gọi G, H,O lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác
ABC . Gọi D là điểm đối xứng của A qua O và M là trung điểm của BC . Chứng minh:
⓵ HB HC HD
⓶ HA HB HC 2HO
⓷ HA HB HC 2OA.
⓸ OA OB OC OH
⓹ OH 3OG
⓺ AH 2OM . Lời giải
⓵ HB HC HD
Xét tứ giác BHCD có BH//CD (vì cùng vuông góc với AC )
CH//BD (vì cùng vuông góc với AB )
Nên BHCD là hình bình hành.
Áp dụng quy tắc hình bình ta có HB HC HD (đpcm).
⓶ HA HB HC 2HO
Ta có VT HA HB HC
HA HB HC HA HD
HOOAHOOD
2HO OAOD 2HO VP (do O là trung điểm của AD OA OD 0) (đpcm).
⓷ HA HB HC 2OA.
Ta có VT HA HB HC HA HB HC HA HD DA 2OA VP (đpcm). Trang 30 Chương 01. LÊ MINH TÂM
⓸ OA OB OC OH
Ta có VT OA OB OC
OH HAOH HBOH HC
3OH HA HB HC
3OH 2HO OH 2OH HO OH 0 OH VP (đpcm).
⓹ OH 3OG
Theo ⓸ ta có OA OB OC OH , mà G là trọng tâm của ABC
Nên OA OBOC 3OG nên ta suy ra OH 3OG (đpcm).
⓺ AH 2OM .
Ta có BHCD là hình bình hành (cmt) và M là trung điểm của BC
Nên suy ra M cũng là trung điểm của HD .
Xét DHA có MD MH và OM OA 1
OM là đường trung bình OM HA 2
Hay HA 2OM và HA,OM cùng hướng AH 2OM (đpcm). Bài 19.
Cho tam giác ABC . Gọi M, N, P lần lượt là trung điểm của AB, BC, .
CA Gọi G là trọng tâm của tam giác AB . C Chứng minh rằng:
⓵ AC 2AM BN. ⓶ AM BN CP 0.
⓷ AM BN AP BM M . C Lời giải
⓵ AC 2AM BN.
Xét VP 2AM BN 2MB BN 2MN AC VT (đpcm).
⓶ AM BN CP 0. AC
Xét VT AM BN CP
CP (câu ⓵) 2
PC CP 0 VP (đpcm).
⓷ AM BN AP BM M . C
Xét AM BN AP BM MC Trang 31 Chương 01. LÊ MINH TÂM
AM BM BN AP CM CA CB
0 BN AP
BN AP PA NB 0 AM BN AP BM MC . 2 Bài 20.
Cho tam giác ABC . Dựng bên ngoài tam giác các hình bình hành ABIF, BCPQ, CAR . S Chứng minh
rằng: RF IQ PS 0. Lời giải
Ta có: RF RA AF
IQ IB BQ
PS PC CS
RF IQ PS RA AF IB BQ PC CS
RACSAF IBBQ PC 0 0 0 0 (đpcm). Bài 21.
Cho tứ giác ABCD . Dựng bên ngoài tứ giác các hình bình hành ABEF , BCGH ,CDIJ , DAKL . Chứng minh rằng:
⓵ KF EH GJ IL 0 .
⓶ EL HI FK GJ . Lời giải
⓵ KF EH GJ IL 0 .
Ta có VT KF EH GJ IL
KA AF EB BH GC CJ ID DL
Theo tính chất hình bình hành:
VT KA DL AF EB BH GC CJ ID 0
⓶ EL HI FK GJ .
VT EL HI EF FK KL HG GJ JI
FK GJ EF KL HG JI
FK GJ BA AD BC CD FK GJ BA AD DC CB FK GJ BB FK GJ (đpcm). Trang 32 Chương 01. LÊ MINH TÂM Bài 22.
Cho hình bình hành ABCD . Trên đường chéo lấy các điểm BD lấy G và H sao cho DG GH HB
. Gọi M, N là giao điểm của AH , BC và AG , DC . Chứng minh:
⓵ AB AD AG AH .
⓶ 2AM 2AN 3AC . Lời giải
⓵ AB AD AG AH .
Theo giả thiết ta có HB G D
VT AB AD
AH HB AG GD
AH AG HBGD AH AG (đpcm).
⓶ 2AM 2AN 3AC . HM BH 1 3 3
Do BM / / AD nên
AM AH AM AH . AH HD 2 2 2 3
Chứng minh tương tự ta có AN AG . 2
Từ đó 2AM 2AN 3AG AH 3AB AD 3AC (đpcm). Bài 23.
Chứng minh rằng các tam giác ABC, A B C
có cùng trọng tâm khi và chỉ khi AA BB CC 0 . Lời giải
Giả sử các tam giác ABC,A B C
có cùng trọng tâm G . Ta chứng minh AA BB CC 0 .
Thật vậy, ta có: AA BB CC
AG GABG GBCG GC AG BGCGGAGBGC 0.
(Do G là trọng tâm của hai tam giác ABC, A B C ).
Giả sử AA BBCC 0 . Ta chỉ ra các tam giác ABC,A B C
có cùng trọng tâm.
Thật vậy, gọi G,G lần lượt là trọng tâm của các tam giác ABC, A B C .
Ta có: AA BB CC 0
AGGGG A
BGGGG BCGGGG C 0
AG BG CGG A G B G C
3GG 0
3GG 0 GG 0 G G .
Vậy hai tam giác ABC, A B C
có cùng trọng tâm. Trang 33 Chương 01. LÊ MINH TÂM Bài 24.
Cho tam giác ABC . Gọi A là điểm đối xứng của A qua B , B là điểm đối xứng của B qua C , C
là điểm đối xứng của C qua A . Chứng minh rằng hai tam giác ABC, A B C
có cùng trọng tâm. Lời giải
Theo bài 23, để chứng minh hai tam giác ABC, A B C
có cùng trọng tâm ta chỉ ra
AA BB CC 0 . Thật vậy ta có
AA BB CC
2AB 2BC 2CA
2AB BC CA 2AC CA 2AA 2 0. 0.
Vậy hai tam giác ABC, A B C
có cùng trọng tâm. Bài 25.
Cho tam giác ABC và I , J, K xác định bởi: 2IB 3IC 0, 2JC 3JA 0 và 2KA 3KB 0. Chứng minh
hai tam giác ABC và IJK có cùng trọng tâm. Lời giải
Gọi G là trọng tâm của tam giác ABC , ta có: GA GBGC 0 . Theo đề:
2IB 3IC 0 2IG 2GB 3IG 3GC 0 5IG 2GB 3GC 0 1 Tương tự:
2JC 3JA 0 5JG 2GC 3GA 0 2
2KA 3KB 0 5KG 2GA 3GB 0 3
123 5IG JGKGGAGBGC 0 IG JGKG 0 GI GJ GK 0.
Do đó, G cũng là trọng tâm của tam giác IJK. Ta được đpcm. Bài 26. Cho tứ giác ABC .
D Các điểm M, N , P,Q lần lượt là trung điểm của AB, BC,CD, D . A Chứng minh
hai tam giác ANP và CMQ có cùng trọng tâm. Lời giải
Gọi G là trọng tâm của tam giác ANP , ta có:
GA GN GP 0
GM MA GC CN GQ QP 0 GM GC GQ MACN QP 0 . Trang 34 Chương 01. LÊ MINH TÂM 1 1
Ta thấy: MA CN QP BA CB AC CA AC 0. 2 2
Do đó: GM GC GQ 0.
Nên G cũng là trọng tâm của tam giác CMQ . Ta được đpcm. Bài 27. Cho tam giác AB .
C Gọi M, N, P là những điểm được xác định bởi: MB 3MC, NC 3NA, PA 3P .
B Chứng minh rằng:
⓵ 2OM 3OC OB, O bất kỳ. ⓶ A BC và M
NP có cùng trọng tâm. Lời giải
⓵ 2OM 3OC OB, O bất kỳ.
Theo giả thiết: MB 3MC
OB OM 3OC OM 3OM OM 3OC OB 2OM 3OC OB, O bất kỳ. ⓶ A BC và M
NP có cùng trọng tâm.
Gọi G là trọng tâm A
BC , khi đó ta có OA OB OC 3OG, O bất kỳ.
Tương tự câu a) ta có: MB 3MC 2OM 3OC OB;
NC 3NA 2ON 3OA OC ;
PA 3PB 2OP 3OB O . A
Cộng theo vế ta có: 2OM ON OP 2OAOBOC 6OG, O bất kỳ.
Do đó OM ON OP 3OG, O bất kỳ.
Vậy tam giác MNP cũng nhận điểm G làm trọng tâm. (đpcm). Bài 28.
Cho tam giác ABC cân tại A và điểm M bất kì nằm trong tam giác. Đường thẳng qua M song song
với BC cắt AB, AC lần lượt tại D, E . Dựng MK vuông góc với BC tại K và gọi I là trung điểm
BC . Chứng minh 2MK MD ME 2MI . Lời giải
Qua M kẻ đường thẳng song song với AB cắt AC
và BC lần lượt tại P,Q ;
Kẻ đường thẳng song song với AC cắt BA,BC lần
lượt tại R,S . A
BC cân tại A nên M
QS cân tại M
K là trung điểm QS MQ MS 2MK (1) Trang 35 Chương 01. LÊ MINH TÂM
Theo cách dựng đường thẳng song song thì các tứ giác
MQBD và MSCE là hình bình hành nên ta có
MQ MD M ;
B MS ME MC (2)
Từ (1) và (2) ta có 2MK MD ME MQ MS MD ME MQ MDMS MD
2MK MD ME MB MC 2MI (ĐPCM) Bài 29.
Cho tam giác ABC đều tâm O và điểm M bất kì nằm bên trong tam giác. Gọi D, E, F lần lượt là 3
hình chiếu của M lên các cạnh BC, AC, AB . Chứng minh MD ME MF MO . 2 Lời giải
Qua M kẻ đường thẳng song song với AB cắt AC và
BC lượt tại I , J ;
Kẻ đường thẳng song song với AC cắt BA, BC lần lượt tại K, L ;
Kẻ đường thẳng song song với BC cắt AB, AC lần lượt tại P,Q .
Theo cách dựng, các tứ giác MPBJ , MLCQ , MIAK là hình bình hành
Nên: MJ MP MB ; ML MQ MC ; MI MK MA . A
BC đều nên M
JL; MQI; MKP cũng đều. Do đó ;
E F; D lần lượt là trung điểm của IQ; PK; JL . 1 1 1
Ta có: MD ME MF MJ ML MI MQ MK MP 2 2 2 1
MD ME MF MJMP
MLMQMKMP 2 1 3 MD ME MF MB MC MA
MD ME MF MO 2 2 3
Vậy MD ME MF MO . 2 Bài 30. CA m
Cho đoạn thẳng AB . Trên đoạn AB lấy điểm C sao cho
và S là điểm bất kỳ. Chứng minh CB n n n rằng: SC SA SB . m n m n Lời giải Trang 36 Chương 01. LÊ MINH TÂM CA m AC m Từ giả thiết: CB n
AC CB mn m AC AC CB m n m m AC AC CB AC AB . m n m n m
Từ SC SA SBSA m n m m SC SA SB . m n m n Bài 31. 2 2 2 2
Cho hình chữ nhật ABCD tâm O và S là điểm bất kỳ. Chứng minh rằng: SA SC SB SD . Lời giải 2 2 2 2
Ta có SA SC SB SD 1
SOOA2 SOOC2 SOOB2 SOOD2 A B 2 2 2 2
A SO 2.S .
O OA OA SO 2.S . O OC OC Lại có 2 2 2 2
B SO 2.S .
O OB OB SO 2.S . O OD OD 2 2 2. .
SO OA OA 2. . SO OC OC 2 2 2. .
SO OB OB 2. . SO OD OD
Mặt khác tứ giác ABCD hình chữ nhật tâm O có
OA OB OC 2 2 2 2
OD OA OB OC OD . 1 . SO OA . SO OC . SO OB .
SO OD SOOA OC SOOBOD OA OC 0
Lại có O là trung điểm của AC, BD . Khi đó OB OD 0
1 SO0 SO0(luôn đúng với điểmS là điểm bất kỳ) (điều phải chứng minh) Trang 37 Chương 01. LÊ MINH TÂM
Dạng 02. TÌM MÔĐUN (ĐỘ DÀI) VÉCTƠ.
Phương pháp giải
Để tính a b c d ta thực hiện theo hai bước sau:
Bước 1: Biến đổi và rút gọn biểu thức véctơ a b c d v dựa vào qui tắc Chasles, tính chất
trung điểm, hình bình hành, trọng tâm,… sao cho v đơn giản nhất.
Bước 2: Tính môđun (độ dài) của v dựa vào tính chất hình học đã cho. Bài 01.
Chứng minh các khẳng định sau:
⓵ Nếu a và b cùng hướng thì a b a b .
⓶ Nếu a và b ngược hướng và b a thì a b b a .
⓷ a b a b . Khi nào xảy ra dấu đẳng thức. Lời giải
Giả sử: a AB và b BC thì a b AB BC AC .
⓵ Nếu a và b cùng hướng thì a b a b .
Nếu a và b cùng hướng thì 3 điểm A, B ,C cùng thuộc một đường thẳng và B nằm giữa A ,C .
Do đó a b AB BC AC AB BC a b .
Vậy a b a b .
⓶ Nếu a và b ngược hướng và b a thì a b b a .
Nếu a và b ngược hướng và b a thì ba điểm A, B ,C cùng thuộc một đường thẳng và
A nằm giữa B ,C .
Do đó a b AB BC AC BC AB b a . Trang 38 Chương 01. LÊ MINH TÂM
Vậy a b b a .
⓷ a b a b . Khi nào xảy ra dấu đẳng thức.
Từ chứng minh ở câu ⓵ và ⓶:
Nếu a và b cùng phương thì a b a b hoặc a b a b .
Nếu a và b không cùng phương thì A,B,C không thẳng hàng.
Xét ABC có hệ thức AC AB BC . Do đó a b a b .
Như vậy, trong mọi trường hợp ta có: a b a b , đẳng thức xảy ra khi a và b cùng hướng. Bài 02.
Cho tam giác ABC vuông tại A , có AB 3cm, AC 4cm . Gọi I là trung điểm BC . Xác định và
tính độ dài các véctơ:
⓵ u BA BC .
⓶ v 2IA CA . Lời giải
⓵ u BA BC .
Gọi K là trung điểm AC khi đó 2BK BA BC với B là điểm bất kỳ.
Nên u BA BC 2BK 2 BK . 2 2
Xét ABK vuông tại 2 2
A : BK AK AB 2 3 13 .
Vậy u 2 BK 2 13 .
⓶ v 2IA CA .
Theo giả thiết: I là trung điểm BC khi đó 2AI AB AC với A là điểm bất kỳ.
v 2IA CA AB AC CA ABAC CA AB . 0
Khi đó: v AB AB 3 . Bài 03.
Cho tam giác ABC đều cạnh a , gọi G là trọng tâm tam giác ABC và H là trung điểm của BC . Tính theo a
⓵ AB AC
⓶ AB AC
⓷ GB GC ⓸ GA GC
⓹ AH BC Trang 39 Chương 01. LÊ MINH TÂM Lời giải
⓵ AB AC
AB AC AE AE với ABEC là hình bình hành. a 3
Do ABC đều nên AH . 2 a 3
AE 2AH 2. a 3
AB AC a 3 . 2
⓶ AB AC CB CB a
⓷ GB GC
Ta có G là trọng tâm ABC GAGBGC 0 2 2 a 3 a 3
GB GC G
A GA AH . . 3 3 2 3
⓸ GA GC
GA GC CA CA a . ⓹ AH BC
AH BC BC CF BF BF với CF AH ( ACFH là hình bình hành) 2 a 3 a 7 Có 2 2 2
BF BC CF a
(Vì BCF vuông tại C ). 2 2 Bài 04.
Cho tam giác ABC vuông cân tại A , AB a ,. Tính theo a :
⓵ AB AC
⓶ AB AC
⓷ AB 2AC Lời giải
Ta có BC AB 2 a 2
⓵ AB AC
AB AC CB CB a 2 .
⓶ AB AC
AB AC AE AE BC a 2 , với ABEC là hình vuông. Trang 40 Chương 01. LÊ MINH TÂM
⓷ AB 2AC
AB 2AC AB AC AC AE AC AF AF ,
với AEFC là hình bình hành.
Do ABF vuông tại B và BF BE EF BE AC 2a Nên ta có
AF AB BF a a2 2 2 2 2 a 5 .
Vậy AB 2AC a 5 . Bài 05.
Cho hình chữ nhật ABCD có AB 3 , BC 4 . Gọi M , N lần lượt là trung điểm của BC và CD .
Tính AB AC AD và AM AN . Lời giải
★ Tính AB AC AD
Ta có: AB AD AC AB AC AD AC AC
AB AC AD AC AC AC AC 2AC .
Xét ABC vuông tại A : 2 2 2 2
AC AB BC AC 25 AC 5
Vậy AB AC AD 2AC 10
★ Tính AM AN
Ta có: AM AN AB BM AD DN AB ADBM DN AC ON OM AC OC AC 15
Vậy AM AN AC OC AC
( AC ,OC là hai vec tơ cùng hướng) 2 2 Bài 06.
Cho hình chữ nhật ABCD tâm O và có AB 4 , AD 3 . Gọi M là điểm tùy ý. Hãy tính: AC BD và
MA MB 2MC . Lời giải
★ Tính AC BD
Ta có: AC BD AB BC BC CD BC BC
(Do AB và CD là hai véc tơ đối)
AC BD 2BC 6 Trang 41 Chương 01. LÊ MINH TÂM
★ Tính MA MB 2MC
Gọi N là trung điểm của AB , ta có: MA MB 2MC
MA MCMB MC
CACB CN NACN NB CN CN 2 2
MA MB 2MC 2CN 2 CB BN 2 13 Bài 07.
Cho hình vuông ABCD cạnh a , tâm O , lấy điểm M tùy ý. Chứng minh rằng các vectơ sau không
đổi và tính độ dài của chúng.
⓵ u OA CB.
⓶ v CD DA .
⓷ x 2MA MB MC 2MD.
⓸ y 3MA MB 2MC .
⓹ z 3MA MB MC MD .
⓺ w 4MA 3MB MC 2MD Lời giải
⓵ u OACB.
u OA CB CO CB BO . (Không đổi do B,O cố định) 1 1 a 2 2 2
u BO BO BD a a 2 2 2
⓶ v CD DA .
v CD DA CD CB BD
v BD BD a 2 .
⓷ x 2MA MB MC 2MD.
x 2MA MB MC 2MD
x 2MA 2MD MB MC
x 2MA MDMB MC
x 2DACB x 2DA DA x 3DA
x 3DA 3DA 3a
⓸ y 3MA MB 2MC .
y 3MA MB 2MC
y MA MB2MA2MC
y BA 2CA
y BA 2CB BA
y 3BA 2CB Trang 42 Chương 01. LÊ MINH TÂM
Gọi I, H là các điểm sao cho CI 2CB,IH 3BA từ đó ta có 2 2 2 2
y 3BA 2CB IH CI CH
y CH CH CI IH 4a 9a a 13
⓹ z 3MA MB MC MD .
z 3MA MB MC MD
z MA MBMA MCMA MD
z BACA DA
z AB ADCA
z AC CA
z 2CA
z 2CA 2CA 2a 2
⓺ w 4MA3MB MC 2MD
w 3MA MBMC MDMA MD
w 3BA DC DA
w 3BA DB
w 2BA DB BA
w 2BA DA
Gọi F là điểm sao cho AF 2BA từ đó ta có; 2 2 2 2
w 2BA DA AF DA DF
w DF DF DA AF a 4a a 5 Bài 08.
Cho hình thoi ABCD có BAD 60 và cạnh là a . Gọi O là giao điểm của hai đường chéo AC và
BD . Tính theo a : AB AD , BA BC , OB DC . Lời giải
★ Tính AB AD :
AB AD AC AB AD AC AC 2AO . a 3
Do BAD 60 nên tam giác ABD đều OA 2
AC a 3 .
Vậy AB AD a 3 .
★ Tính BA BC : Trang 43 Chương 01. LÊ MINH TÂM
Ta có BA BC CA CA a 3 .
★ Tính OB DC : a
Ta có OB DC DO DC CO OB DC 3 CO OC . 2 Bài 09.
Cho hai lực F và F có điểm đặt O và tạo với nhau một góc 60 . Tìm cường độ tổng hợp lực của 1 2
hai lực ấy biết rằng cường độ của hai lực F và F đều là 100N . 1 2 Lời giải
Đặt F OB , F OD . 1 2
Dựng hình bình hành OBCD. Khi đó F F 1 2
OBOD OC .
F F OC OC 2OI . 1 2
Do BOD 60 và OB OD nên tam giác OBD đều. F 3 1 OB 3 OI 50 3N . 2 2 Bài 10.
Cho tam giác ABC vuông tại A , có góc ABC 60 , cạnh AB a . Gọi I là trung điểm của BC . Tính
độ dài của các vectơ sau:
⓵ a AB AC
⓶ b AB AC
⓷ c AB IC AC
⓸ d BA BI IC Lời giải
⓵ a AB AC
Ta có a AB AC CB CB .
Xét ABC vuông tại A : AB AB a cos ABC BC 2a . BC cos ABC cos 60
Vậy a 2a .
⓶ b AB AC
Trên tia đối của tia AC lấy điểm H sao cho HA AC . Khi đó HA AC . Trang 44 Chương 01. LÊ MINH TÂM
Ta có b AB AC AB HA HA AB HB HB .
Xét tam giác HBC có: BA là đường cao
BA là đường trung tuyến (do AH AC )
HBC cân tại B BH BC 2a.
Vậy b 2a .
⓷ c AB IC AC
Ta có c AB IC AC AB IC CA AB IA IA AB IB IB . BC 2a
Do I là trung điểm của BC nên IB a . 2 2
Vậy c a .
⓸ d BA BI IC
Ta có d BA BI IC IA IC CA CA. AC
Xét tam giác ABC vuông tại A : tan ABC AC A . B tan ABC .
a tan 60 a 3 . AB
Vậy d a 3 .
--------------------HẾT -------------------- Trang 45 Chương 01. LÊ MINH TÂM BÀI 3
TÍCH CỦA MỘT VÉCTƠ VỚI MỘT SỐ I. ĐỊNH NGHĨA.
※ Cho số k 0 và một véc tơ a 0 . Tích của véc tơ a với k là một véc tơ, kí hiệu ka , cùng
hướng với a nếu k 0 , ngược hướng với a nếu k 0và có độ dài bằng k . a .
※ Quy ước: 0.a 0;0.k 0 . Ví dụ 1 Cho và điểm . Xác định hai điểm sao cho . Lời giải
Ta có: OM 3a;ON 4
a nên OM,a cùng hướng và OM 3AB; ON,a ngược hướng và ON 4AB. Ví dụ 2 Cho đoạn thẳng và điểm nằm trên đoạn thẳng sao cho . Tìm trong các đẳng thức sau: ⓵ . ⓶ . ⓷ .
Lời giải
⓵ AM kAB . 1 1 1
Vì AM và AB cùng hướng và AM AB nên AM AB k . 5 5 5
⓶ MA kMB . 1 1 1
Vì MA và MB ngược hướng và MA MB nên MA MB k . 4 4 4 Trang 46 Chương 01. LÊ MINH TÂM
⓷ MA kAB . 1 1 1
Vì MA và AB ngược hướng và MA AB nên MA AB k . 5 5 5 II. TÍNH CHẤT.
※ Với hai véc tơ a,b bất kì và hai số thực số k,h ta có
⓵ k a b ka kb
⓶ h ka ha ka
⓷ hka hka
⓸ 1a a; 1 a a Ví dụ 3
⓵ Chứng minh véc tơ đối của là .
⓶ Tìm véc tơ đối của và .
Lời giải
⓵ Chứng minh véc tơ đối của 5a là 5 a .
Véc tơ đối của 5a là 1 5 . a 5 a .
⓶ Tìm véc tơ đối của 2a 3b và a 2b .
Véc tơ đối của 2a 3b là
1 2a 3b 2 a 3b .
Véc tơ đối của a 2b là
1 a 2b a 2b .
III. TRUNG ĐIỂM CỦA ĐOẠN THẲNG VÀ TRỌNG TÂM CỦA TAM GIÁC.
I là trung điểm của AB IA IB 0 và M , MA MB 2MI Nếu thì ta có
G là trọng tâm của ABC
GA GB GC 0
MA MB MC 3MG Ví dụ 4 Cho tam giác có là trung điểm của , là trung điểm của . Chứng minh rằng
Lời giải
Ta có: M là trung điểm của BC
Nên DB DC 2DM . Do đó:
2DA DB DC 2DA 2DM 2DA DM 2 0 . 0 . Trang 47 Chương 01. LÊ MINH TÂM
IV. ĐIỀU KIỆN ĐỂ HAI VECTO CÙNG PHƯƠNG.
※ Điều kiện cần và đủ để hai véc tơ a,b (b 0 ) là có một số thực k để a kb .
Nhận xét: Ba điểm phân biệt A,B,C thẳng hàng khi và chỉ khi có một số thực k 0 để AB k AC . Ví dụ 5 Cho tam giác có hai điểm và xác định bởi , . Chứng minh rằng .
Lời giải
Ta có: BC MA 0
BC AM AM AC AB 1
AB NA 3AC 0 AB AN 3AC 0 AN 3AC AB2 . Từ
1 ,2 AN AM 3AC AB AC AB
MN 2AC . Mà M , A,C không thẳng hàng nên MN//AC .
V. PHÂN TÍCH MỘT VEC TƠ THEO HAI VECTO KHÔNG CÙNG PHƯƠNG.
※ Cho hai véc tơ a,b không cùng phương.
Khi đó mọi vec tơ x đều phân tích được một cách
duy nhất theo hai véc tơ a,b , nghĩa là có duy nhất
cặp số h,k thực duy nhất sao cho x ha kb . Ví dụ 6 Cho tam giác có điểm nằm trên cạnh sao cho . Hãy phân tích theo hai vec tơ .
Lời giải
Ta có: AM AB BM 2
AM AB BC 3 2
AM AB AC AB 3 1 2 1 2
AM AB AC
AM u v . 3 3 3 3 Trang 48 Chương 01. LÊ MINH TÂM Ví dụ 7 Cho tam giác có trung tuyến . Gọi là trung điểm và thuộc cạnh sao cho . Chứng minh thẳng hàng.
Lời giải
Ta có: BI AI AB 1
BI AM AB 2 1
BI AB AC 3 1
AB AB AC 1 . 4 4 4 1
Ta có: BK AK AB AB AC 2 . 3 Từ , 3 1 2 BI
BK hay B, I , K thẳng hàng. 4 VI. CÁC DẠNG TOÁN
Dạng 01. BIỄU DIỄN VÉCTƠ.
Phương pháp giải
ba biểm A, B,C thẳng hàng
AB kAC, với số k xác định.
ABCD là hình bình hành
AC AB AD. Nếu thì
I là trung điểm của AB IA IB 0 và MA MB 2 M , MI ta có
G là trọng tâm của ABC
GA GB GC 0
MA MB MC 3MG Bài 01.
Cho tam giác ABC có trung tuyến AM, M là trung điểm của .
BC Hãy biểu diễn vectơ AM theo 2
vectơ AB và AC. Lời giải 1 1
Cách 1: Vì M là trung điểm của BC nên AB AC 2AM AM AB AC. 2 2
Cách 2: Do M là trung điểm của BC nên BM CM 0. Trang 49 Chương 01. LÊ MINH TÂM
Áp dụng quy tắc 3 điểm, ta có: AM AB BM 1
Lại có: AM AC CM 2
Cộng vế với vế của 1 ,2 ta được:
2AM AB AC BM CM 1 1
2AM AB AC 0 AM AB A . C 2 2
Cách 3: Xét hình bình hành ABDC có M là trung điểm của BC nên M cũng là trung điểm của
AD AD 2AM 1 ( )
Áp dụng quy tắc hình bình hành: AB AC AD 2 Từ 1 1
1 2 AB AC 2AM AM AB AC. 2 2 Bài 02.
Gọi G là trọng tâm của tam giác ABC . Hãy biểu diễn các vectơ AB, BC,GC,CA theo
a GA; b G . B Lời giải
Ta có: AB GBGA b a .
Vì G là trọng tâm của tam giác ABC
Nên GA GB GC 0 GC G
AGB a b .
Ta có: BC BG GC b a b a 2b .
Ta có: CA GA GC a a b 2a b Bài 03.
Cho tam giác ABC có M trên cạnh BC thỏa mãn MB 2MC . Hãy phân tích véc tơ AM theo hai
véc tơ u AB và v AC Lời giải
Ta có AM AB BM 2 2
AM AB BC AB AC AB 1 2 AB AC 3 3 3 3 . 1 2
Vậy AM u v . 3 3 Trang 50 Chương 01. LÊ MINH TÂM Bài 04.
Điểm M gọi là chia đoạn thẳng AB theo tỉ số k 1 nếu MA kMB . OA kOB
Chứng minh rằng với mọi điểm O ta có OM 1 k Lời giải
Từ giả thiết MA kMB , với k 1 OA kOB
Ta có: OA OM k OB OM 1 kOM OA OB OM 1 . k Bài 05.
Cho tam giác ABC . Gọi M là trung điểm của AB và N là một điểm trên cạnh AC sao cho
NA 2NC . Gọi K là trung điểm MN . Phân tích vectơ AK theo AB và AC . Lời giải
Ta có: M,K lần lượt là trung điểm của AB, MN . 1 Nên AM
AB và 2AK AM AN . 2 2
Mặt khác: NAC và NA 2NC AN AC . 3 1
AK AM AN 2 1 1 2 1 1 AK AB AC AB AC . 2 2 3 4 3 Bài 06.
Cho tam giác ABC có trọng tâm G . Cho các điểm D , E , F lần lượt là trung điểm của BC ,CA AB
và I là giao điểm của AD và EF . Đặt u AE , v AF . Hãy phân tích các vectơ AI , AG , DE , DC
theo hai vectơ u , v . Lời giải
Ta có : E , F lần lượt là trung điểm của CA, AB
EF là đường trung bình của ABC IE AI IF EF// BC CD AD BD 1
IF IE 2AI AF AE AI u v . 2
G là trọng tâm ABC
D , E , F lần lượt là trung điểm của BC ,CA AB . Trang 51 Chương 01. LÊ MINH TÂM 2 1
AG AD AB AC 1
AF AE 2 2 2
u v 3 3 3 3 1
DE là đường trung bình ABC DE
AB AF DE AF v . 2
EF là đường trung bình ABC EF CD DC FE AE AF u v . Bài 07.
Cho tam giác vuông cân OAB với OA OB a . 11 3
Dựng và tính độ dài các véctơ 3OA 4OB; OA OB . 4 7 Lời giải
Vẽ điểm C ,D sao cho OC 3OA và OD 4OB ,
Vẽ hình bình hành CODE thì :
3OA 4OB OC OD OE 3OA 4OB OE
OE OD ED a2 a2 2 2 3 4 5a . 11 OH OA
Vẽ điểm H ,K sao cho: 4 3 O K OB 7 2 2 11 3 11 3 11 3 6073
OA OB OH OK KH . 2 2
OA OB KH OH OK a a a 4 7 4 7 4 7 28 Bài 08.
Cho tam giác ABC có G là trọng tâm.
⓵ Hãy phân tích véctơ AG theo hai véctơ AB, AC .
⓶ Gọi E,F là hai điểm xác định bởi các điều kiện: EA 2EB,3FA 2FC 0 . Hãy phân tích
EF theo hai véctơ AB , AC .
Lời giải
⓵ Hãy phân tích véctơ AG theo hai véctơ AB, AC .
AG BC M M là trung điểm BC
AB AC 2AM.
Mà G là trọng tâm ABC 2 3
AG AM AM AG . 3 2 Trang 52 Chương 01. LÊ MINH TÂM 3
AB AC 2AM 2. AG 1 1
3AG AG AB AC . 2 3 3
⓶ Hãy phân tích EF theo hai véctơ AB, AC .
Ta có: EF EA AF .
Theo gt: EA 2EB EA 2AB . 2
Từ 3FA 2FC 0 AF 2
AC EF EA AF 2AB AC . 5 5 Bài 09.
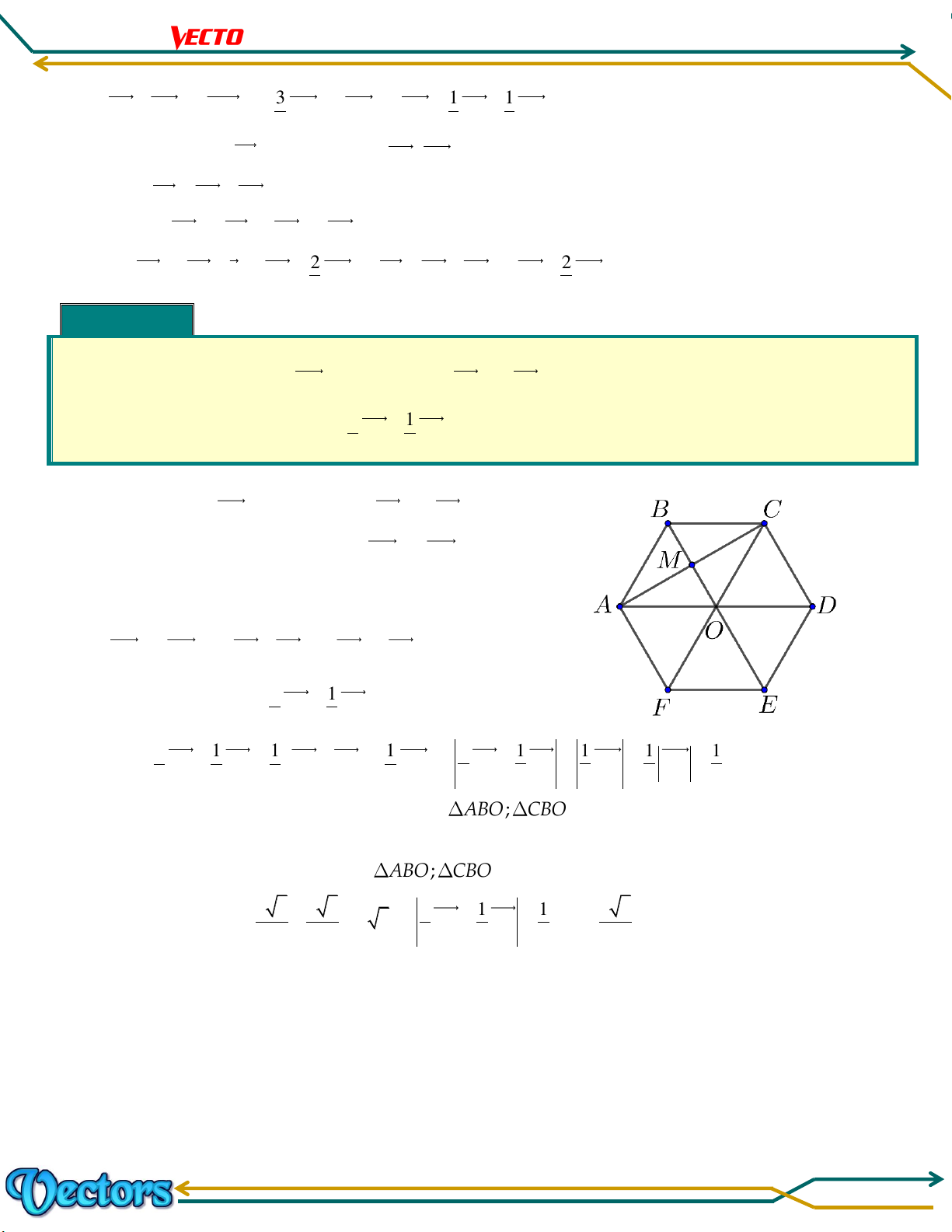
Cho lục giác đều ABCDEF tâm O cạnh a :
⓵ Phân tích véctơ AD theo hai véctơ AB và AF . ⓶ 1 1
Tính độ dài của véctơ AB BC theo a . 2 2 Lời giải
⓵ Phân tích véctơ AD theo hai véctơ AB và AF .
Ta có: O là trung điểm AD nên AD 2AO . AB//FO Lại có:
ABOF là hình bình hành AF//BO
AD 2AO 2AB AF 2AB 2AF . ⓶ 1 1
Tính độ dài của véctơ AB BC theo a . 2 2 1 1 1 1
Ta có: AB BC AB BC 1 1 1 1 1 AC AB BC AC AC AC . 2 2 2 2 2 2 2 2 2
Theo đề bài: ABCDEF là lục giác đều nên ABO; CBO là tam giác đều cạnh a .
Gọi M là trung điểm BO
AM; MC lần lượt là đường cao ABO; CBO và AC AM MC a 3 a 3 1 1 1 a 3
AC AM MC
a 3 AB BC AC . 2 2 2 2 2 2 Trang 53 Chương 01. LÊ MINH TÂM
Dạng 02. CHỨNG MINH BA ĐIỂM THẲNG HÀNG, HAI ĐIỂM TRÙNG
NHAU, HAI ĐƯỜNG THẲNG SONG SONG, BA ĐƯỜNG THẲNG ĐỒNG QUY.
Phương pháp giải
⓵ Ba điểm phân biệt A,B,C thẳng hàng AB và AC cùng phương AB k.AC .
⓶ Để chứng minh hai điểm M ,N trùng nhau ta chứng minh chúng thỏa mãn đẳng thức
OM ON với O là một điểm nào đó hoặc MN 0 .
⓷ Nếu AB CD và hai đường thẳng AB và CD phân biệt thì A // B CD . Bài 01.
Cho tam giác ABC có trung tuyến AM . Gọi I là trung điểm của AM và K là điểm trên cạnh AC 1
sao cho AK AC . Chứng minh rằng ba điểm B, I, K thẳng hàng. 3 Lời giải 1
Ta có BI BA BM (Do BI là đường trung tuyến 2 ABM ) 1 1 BA
BC (Do M là trung điểm của cạnh BC ) 2 2 1 1 BA BC 2 4 1
BK KA 1
BK KC 3 1 1
BK KA KC 2 4 4 2 4 1 1 1
Mà AK AC nên KC 2KA KC 2
KA KC 2KA 0 KC KA 0 . 3 4 2 3 3
Do đó BI BK 0 BK . Vậy ba điểm B, I, K thẳng hàng. 4 4 Bài 02.
Cho tam giác ABC . Hai điểm M, N được xác định bởi hệ thức BC MA 0 , AB NA 3AC 0 .
Chứng minh rằng MN // AC . Lời giải
Ta có BC MA 0 MA BC nên MA // BC .
Do đó M AC 1 .
Ta có AB NA 3AC 0 Trang 54 Chương 01. LÊ MINH TÂM
AB NM MA3AC 0
AB NM MA3AC 0
NM AB MA3AC NM AB BC 3AC AC 3AC 2 AC 2 . Từ
1 ,2 ta có MN // AC . Bài 03.
Cho 4 điểm O, A, B,C sao cho OA 2OB 3OC 0 . Chứng tỏ rằng A, B,C thẳng hàng. Lời giải
Ta có: OA 2OB3OC 0
OA 2OA AB3OA AC 0 3
OA 2OA 2AB 3OA 3AC 0 2AB 3AC AB AC Vậy: A,B,C thẳng hàng. 2 Bài 04.
Cho hình bình hành ABCD trên BC lấy điểm H , trên BD lấy điểm K sao cho 1 1
BH BC, BK BD . Chứng minh A,K, H thẳng hàng. 5 6 Lời giải 1 1 1 BH BC
AH AB BC
AH AB BC 5 5 5 Ta có: 1 1 1 BK BD AK AB BD
AK AB BD 6 6 6 1 1 1 1 5 1 5 1
Mà: AK AB BD AB BC CD AB BC AB AB BC AB BC 6 6 6 6 6 6 6 5 5
Khi đó: AK AH Vậy A,K,H thẳng hàng. 6 Bài 05. 1
Cho ABC với I , J,K lần lượt được xác định bởi IB 2IC ; JC JA ; KA KB . 2
⓵ Tính IJ ;IK theo AB; AC .
⓶ Chứng minh ba điểm I , J,K thẳng hàng. Lời giải Trang 55 Chương 01. LÊ MINH TÂM
⓵ Tính IJ ;IK theo AB; AC .
Ta có: IJ IC CJ 1
IJ BC AC BA AC 1 4
AC AB AC . 3 3 3
IK IB BK 1
IK BC AB BA AC 1 3 2 2
AB AB 2AC . 2 2 2
⓶ Chứng minh ba điểm I , J,K thẳng hàng. 4 4
IJ AB AC
IJ AB AC 3 3 Theo câu ⓵: 3
IK IJ Vậy I , J,K thẳng hàng. 3 3 2 2
IK AB 2AC
IK AB AC 2 2 4 Bài 06.
Cho ABC . Trên các đường thẳng BC, AC, AB lần lượt lấy các điểm M, N, P sao cho
MB 3MC ; NA 3CN ; PA PB 0 .
⓵ Tính PM; PN theo AB; AC .
⓶ Chứng minh ba điểm M,N,P thẳng hàng. Lời giải
⓵ Tính PM; PN theo AB; AC .
Ta có: PA PB 0 P là trung điểm AB .
PM PB BM 1 3 1 3
PM AB BC AB AC AB 3
AB AC . 2 2 2 2 2 1 3 1 3
PN PA AN
BA AC AB AC . 2 4 2 4
⓶ Chứng minh ba điểm M,N,P thẳng hàng. 3 3
PM AB AC
PM AB AC 2 1 Theo câu a: 2 PN PM . 1 3 1 3 2
PN AB AC PN
AB AC 2 4 2 2
Vậy N, M,P thẳng hàng. Bài 07. Trang 56 Chương 01. LÊ MINH TÂM 1
Cho hình bình hành ABCD . Trên các tia AD, AB lần lượt lấy các điểm F, E sao cho AD AF, 2 1 AB AE . Chứng minh: 2
⓵ Ba điểm F,C,E thẳng hàng.
⓶ Các tứ giác BDCE,BDFC là hình bình hành. Lời giải
⓵ Ba điểm F,C,E thẳng hàng.
Ta có D là trung điểm của AF ,
B là trung điểm của AE .
Ta có CE CB BE DA AB FD DC FC
Nên ba điểm F,C,E thẳng hàng.
⓶ Các tứ giác BDCE,BDFC là hình bình hành. BE / /DC Ta có
BDCE là hình bình hành. BE DC DF / /BC
BDFC là hình bình hành. DF BC
Vậy các tứ giác BDCE,BDFC là hình bình hành Bài 08.
Cho tam giác ABC . Hai điểm I , J được xác định bởi IA 3IC 0, JA 2JB 3JC 0 . Chứng minh ba
điểm I, J, B thẳng hàng. Lời giải
IA 3IC 0 Ta có
JA 2JB 3JC 0 IA 3IC 0 IA 3IC 0
JI IB JI IC
JI IB IA IC 6JI 2IB 0 IB 3JI JI IA 2 3 0 6 2 3 0
Vậy I, J, B thẳng hàng. Bài 09.
Cho ABC . Hai điểm M, N lần lượt xác định bởi 3MA 4MB 0 , NB3NC 0 . Chứng minh 3
điểm M, N,G thẳng hàng, với G là trọng tâm ABC . Lời giải Trang 57 Chương 01. LÊ MINH TÂM
Ta có: 3MA 4MB 0 3MA MB MB 0
3.3MG MC MB 0
9MG 3MC MB 0
9MG 3MN NCMN NB 0
MG MN NB NC 2 9 2 3
0 9MG 2MN 0 0 MG MN 9
Vậy M, N,G thẳng hàng. Bài 10.
Cho ABC . Về phía ngoài ABC vẽ các hình bình hành ABIJ , BCPQ , AR C S. Chứng minh các
tam giác RIP , JQS có cùng trọng tâm. Lời giải
Cách 1. Gọi G , G' lần lượt là trọng tâm RIP , JQS .
Ta có RS IJ PQ
RG GG' G'S IG GG' G' J PG GG' G'Q
3GG' ( vì RG IG PG 0 , G'S G' J G'Q 0 )
RS IJ PQ 3GG '
Mà RS AC; IJ BA; PQ CB
AC BACB 3GG'
BC CB 3GG' 3GG' 0 Vậy các tam giác RIP , JQS có cùng trọng tâm.
Cách 2. Gọi G , G' lần lượt là trọng tâm RIP , JQS .
Ta có: 3GG' GJ GQ GS (vì G' là trọng tâm JQS ).
GI IJGP PQGR RS
GI GP GRIJ PQ RS 0
BACB AC 0 G G'
Vậy các tam giác RIP , JQS có cùng trọng tâm. Bài 11. AA BB CC
Trên các cạnh AB, BC,CA của A
BC lấy các điểm A,B,C sao cho . Chứng minh AB BC AC A BC và A B C
có chung trọng tâm. Lời giải Trang 58 Chương 01. LÊ MINH TÂM
Gọi G,G lần lượt là trọng tâm của A BC và A B C .
Khi đó GA GBGC 0 và G A G B G C 0 . AA kAB AA BB CC Ta đặt:
k 0 BB kBC . AB BC AC CC kCA
Do G là trọng tâm của các A
BC nên GAGBGC 0
GGG A A A
GGG B B BGGG CC C 0
3GG G A G B G C
AA BBCC 0 3GG 0
k AB BC CA 0
3GG k 0
. 0 3GG 0 G G
Vậy các tam giác A BC và A B C
có chung trọng tâm. Bài 12.
Cho tam giác ABC và một điểm M tùy ý. Gọi A, B,C lần lượt là các điểm đối xứng của M qua
các trung điểm K, I , J của các cạnh BC,CA, AB .
⓵ Chứng minh ba đường thẳng AA,BB,CC đồng quy tại một điểm N .
⓶ Chứng minh rằng khi M di động đường thẳng MN luôn đi qua trọng tâm G của A BC . Lời giải
⓵ Chứng minh ba đường thẳng AA,BB,CC đồng quy tại N .
Gọi O, P,Q lần lượt là trung điểm của AA,BB,CC Ta có: 1
MO MA MA 1
MA MB MC 2 2 1
MP MB MB 1
MA MB MC 2 2 1
MQ MA MC 1
MA MB MC 2 2
(Do các tứ giác MBA C , MAB C , MAC B
là các hình bình hành ).
MO MP MQ O P Q .
Do đó ba đường thẳng AA,BB,CC đồng quy tại trung điểm N O P Q của mỗi đường..
⓶ Chứng minh rằng khi M di động đường thẳng MN luôn đi qua trọng tâm G của A BC . Trang 59 Chương 01. LÊ MINH TÂM
Vì G là trọng tâm của A BC 1
Nên ta có MG MA MB MC. 3 1
Mặt khác MN MA MB MC (cmt). 2 2
MG MN . 3
Do đó 3 điểm M, N,G thẳng hàng.
Vậy khi M di động đường thẳng MN luôn đi qua
trọng tâm G của A BC . Bài 13. 1
Cho tam giác ABC có trọng tâm .
G Các điểm M, N thỏa mãn 3MA 4MB 0; CN BC. Chứng 2
ming đường thẳng MN đi qua trọng tâm G của tam giác AB . C Lời giải
Theo giả thiết ta có:
3MA 4MB 0 3MG GA 4MG GB 0 7MG 3GA GB GB 0 1 .
Vì G là trọng tâm của tam giác ABC nên GA GB GC 0 GA GB GC , 2
Thay (2) vào (1) ta được: 7MG 3GC GB 0 7MG 3GC G . B 1 1
Lại có CN BC GN GC GC GB 2GN 3GC GB 2GN 7M . G 2 2
Vậy ba điểm M, N, G thẳng hàng (đpcm). Bài 14. Cho tam giác AB .
C Gọi I là trung điểm của .
BC Hai điểm D, E thỏa mãn BD DE E . C Chứng minh rằng:
⓵ AB AC AD A . E
⓶ Tính AS AB AD AC AE theo AI. Suy ra ba điểm A, I, S thẳng hàng. Lời giải
⓵ AB AC AD A . E
Theo giả thiết ta có I là trung điểm của BC và
Hai điểm D, E thỏa mãn BD DE EC
Nên I cũng là trung điểm của . DE
Do vậy AB AC AD AE 2AI (đpcm).
⓶ Tính AS AB AD AC AE theo AI. Suy ra ba điểm A, I, S thẳng hàng. Trang 60 Chương 01. LÊ MINH TÂM
Ta có: AS AB AD AC AE AB ACAD AE 2AI 2AI 4AI.
Vì AS 4AI nên ba điểm A, I, S thẳng hàng. Bài 15.
Cho tam giác ABC . Các điểm M , N được xác định bởi BM BC 2AB , CN xAC BC .
⓵ Xác định x để A , M , N thẳng hàng. ⓶ IM
Xác định x để đường thẳng MN đi qua trung điểm I của BC . Tính . IN Lời giải
⓵ Xác định x để A , M , N thẳng hàng.
BM BC 2AB AB BM BC BA AM 2BC AC Ta có:
CN xAC BC AN AC xAC BC AN BC x 1 AC
Khi đó A , M , N thẳng hàng khi và chỉ khi tồn tại k sao cho AN kAM 1 k 1 2k
BC x
1 AC 2kBC k AC 2 . x 1 k 1 x 2 1
Vậy x thì A , M , N thẳng hàng. 2 ⓶ IM
Xác định x để đường thẳng MN đi qua trung điểm I của BC . Tính . IN
MN AN AM x 2 AC 3BC Ta có: 1 5
MI AI AM AC CI AC 2BC 2AC BC 2BC 2AC BC 2 2
Khi đó đường thẳng MN đi qua trung điểm I của BC thì M , N , I thẳng hàng 6
2l x 2 l l
tồn tại l sao cho MN lMI x 5 5
2 AC 3BC 2lAC BC 5l . 2 3 2 2 x 5 2 Vậy x
thì đường thẳng MN đi qua trung điểm I của BC . 5 Bài 16.
Cho ba điểm cố định A , B , C và ba số thực a , b , c sao cho a b c 0.
⓵ Chứng minh rằng có một và chỉ một điểm điểm G thỏa mãn aGAbGBcGC 0.
⓶ Chứng minh ba điểm G , M , P thẳng hàng. Trang 61 Chương 01. LÊ MINH TÂM Lời giải
⓵ Chứng minh rằng có một và chỉ một điểm điểm G thỏa mãn aGAbGBcGC 0.
Ta lấy một điểm O nào đó thì:
aGA bGB cGC 0
aOAOGbOBOGcOC OG 0
a b c 1 OG . a OA . b OB . c OC OG
.aOA .bOBc.OC
a b c
Vậy G hoàn toàn xác định và duy nhất.
⓶ Chứng minh ba điểm G , M , P thẳng hàng. 1
Với điểm M ta có MG
aMAbMBcMC.
a b c 1
Mặt khác MP aMA bMB cMC MG MP .
a b c
Vậy ba điểm G , M , P thẳng hàng. Bài 17.
Cho tam giác ABC . Các điểm M, N thỏa mãn MN 2MA 3MB MC .
⓵ Tìm I thỏa mãn 2IA3IB IC 0 .
⓶ Chứng minh đường thẳng MN luôn đi qua một điểm cố định. Lời giải
⓵ Tìm I thỏa mãn 2IA3IB IC 0 .
Ta có 2IA 3IB IC 0
2IA IBIB IC 0 IH BK
Với H, P,K lần lượt là trung điểm của A , B BC, BP .
Vậy I là đỉnh hình bình hành BKHI .
⓶ Chứng minh đường thẳng MN luôn đi qua một điểm cố định.
Ta có MN 2MI IA3MI IBMI IC 4MI 2IA3IBIC 4MI .
Vậy MN luôn qua I cố định. Bài 18.
Cho tam giác ABC . Các điểm M, N thỏa mãn MN 2MA MB MC .
⓵ Tìm I thỏa mãn 2IA IB IC 0 .
⓶ Chứng minh đường thẳng MN luôn đi qua một điểm cố định.
⓷ Gọi P là trung điểm của BN . Chứng minh đường thẳng MP luôn đi qua một điểm cố định. Trang 62 Chương 01. LÊ MINH TÂM Lời giải
⓵ Tìm I thỏa mãn 2IA IB IC 0 .
Ta có 2IA IB IC 0 2IA CB IA CH .
Với H là trung điểm của BC .
Vậy I là đỉnh hình bình hành CHAI .
⓶ Chứng minh đường thẳng MN luôn đi qua một điểm cố định.
Ta có MN 2MA MB MC
2MI IAMI IBMI IC 2MI 2IA IB IC 2MI
Vậy MN luôn qua I cố định.
⓷ Chứng minh đường thẳng MP luôn đi qua một điểm cố định.
Do P là trung điểm của BN nên 2MP MB MN 2MA MC 3MK 2KA KC 3MK .
Với K thuộc cạnh AC và CK 2KA .
Vậy MP luôn qua K cố định.
Dạng 03. TẬP HỢP ĐIỂM THỎA MÃN ĐẲNG THỨC VECTƠ.
Phương pháp giải
Để tìm tập hợp điểm M thỏa mãn một đẳng thức véctơ, ta biến đổi đẳng thức véc tơ
đó về các tập hợp điểm cơ bản đã biết. Chẳng hạn:
Tập hợp các điểm cách đều hai đầu mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
Tập hợp các điểm các đều một điểm cố định một khoảng không đổi là đường tròn có
tâm là điểm cố định và bán kính là khoảng không đổi. Bài 01.
Cho tam giác ABC . Tìm tập hợp điểm M trong mỗi trường hợp sau:
⓵ MA MB.
⓶ MA MB MC 0 . Lời giải
⓵ MA MB.
Ta có MA MB MA MB 0 BA 0 .
Vì A và B là hai điểm phân biệt nên không tồn tại điểm M .
⓶ MA MB MC 0 . Trang 63 Chương 01. LÊ MINH TÂM
Gọi G là điểm thoản mãn GA GBGC 0 (hay G là trọng tâm tam giác ABC ).
Khi đó MA MB MC 0 3MG GAGBGC 0 3MG 0 MG 0 M G .
Vậy tập hợp điểm M là trọng tâm tam giác ABC . Bài 02.
Cho tam giác 𝐴𝐵𝐶. Tìm tập hợp điểm 𝑀 trong mỗi trường hợp sau:
⓵ MA MB MA MB .
⓶ MA MB MC MA 2MB .
⓷ 2MA MB MA 2MB . Lời giải
⓵ MA MB MA MB .
MA MB MA MB MA MB BA MA MB AB (1). AB
Gọi I là trung điểm AB , khi đó 1
( ) 2MI IA IB AB 2MI AB MI . 2 AB
Vậy tập hợp điểm M là đường tròn tâm I , bán kính R . 2
⓶ MA MB MC MA 2MB .
Gọi G là trọng tâm ABC , và I là điểm thỏa mãn IA 2IB 0 .
Biểu thức * 3MG 3MI 3MG 3MI MG MI .
Vậy tập hợp điểm M là đường trung trực của đoạn GI .
⓷ 2MA MB MA 2MB .
Gọi I và J lần lượt là các điểm thỏa mãn: 2IA IB 0, JA 2JB 0 .
Biểu thức * 3MI 3MJ 3MJ 3MJ MI MJ .
Vậy tập hợp điểm M là đường trung trực của đoạn IJ . Bài 03.
Cho tam giác ABC . Tìm tập hợp điểm M sao cho: ⓵ 3
MA MB MC MB MC 2
⓶ 2MA MB 4MB MC
⓷ 4MA MB MC 2MA MB MC Trang 64 Chương 01. LÊ MINH TÂM Lời giải ⓵ 3
MA MB MC MB MC 2
Gọi G là trọng tâm ABC , I là trung điểm của BC . 3 3
Ta có: MA MB MC
MB MC 3MG
2MI MG MI MG MI . 2 2
Vậy, tập hợp điểm M là đường trung trực của đoạn GI .
⓶ 2MA MB 4MB MC
Gọi P,Q là hai điểm thỏa mãn: 2PA PB 0 , 4QB QC 0 .
Ta có: 2MA MB 4MB MC 3MP 3MQ MP MQ MP MQ
Vậy, tập hợp điểm M là đường trung trực của đoạn PQ .
⓷ 4MA MB MC 2MA MB MC
Gọi G là trọng tâm ABC , K là trung điểm của AG .
Ta có: 4MA MB MC 2MA MB MC GA
3MA MG 3MA MG 6MK 3GA MK . 2 GA
Vậy, tập hợp điểm M là đường tròn tâm K bán kính R 2 Bài 04. Cho tam giác ABC .
⓵ Xác định điểm I sao cho: 3IA2IB IC 0 .
⓶ Chứng minh rằng đường thẳng nối hai điểm M,N xác định bởi: MN 3MA2MB MC
luôn đi qua một điểm cố định.
⓷ Tìm tập hợp điểm H sao cho: 3HA 2HB HC HA HB .
⓸ Tìm tập hợp điểm K sao cho: 2 KA KB KC 3 KB KC . Lời giải
⓵ Xác định điểm I sao cho: 3IA2IB IC 0 .
Gọi E là trung điểm của AC .
Ta có: 3IA 2IB IC 0 2IA IBIA IC 0 2BA 2IE 0 IE AB
Vậy I là đỉnh của hình bình hành ABEI . Trang 65 Chương 01. LÊ MINH TÂM
⓶ Chứng minh rằng đường thẳng nối hai điểm M,N xác định bởi: MN 3MA2MB MC luôn đi
qua một điểm cố định.
Ta có: MN 3MA 2MB MC MN 2MI M,N,I thẳng hàng.
Do đó đường thẳng nối hai điểm M,N luôn đi qua điểm I cố định.
⓷ Tìm tập hợp điểm H sao cho: 3HA 2HB HC HA HB . AB
Ta có: 3HA 2HB HC HA HB 2HI BA HI . 2 AB
Vậy tập hợp điểm H là đường tròn tâm I bán kính R . 2
⓸ Tìm tập hợp điểm K sao cho: 2 KA KB KC 3 KB KC .
Gọi G là trọng tâm ABC , F là trung điểm của BC .
Ta có: 2 KA KB KC 3 KB KC 6 KG 6 KF KG KF .
Vậy, tập hợp điểm K là đường trung trực của đoạn GF . Bài 05. Cho tam giác ABC .
⓵ Xác định điểm I sao cho IA 3IB 2IC 0 .
⓶ Xác định điểm D sao cho 3DB 2DC 0 .
⓷ Chứng minh rằng ba điểm A,I,Dthẳng hàng.
⓸ Tìm tập hợp các điểm M sao cho MA 3MB 2MC 2MA MB MC Lời giải
⓵ Xác định điểm I sao cho IA 3IB 2IC 0 .
IA 3IB 2IC 0 IA IB 2IB 2IC 0 .
2IE 2IB IC 0 , với E là trung điểm của AB.
2IE 2CB 0 IE C
B IE BC .
Vậy điểm I thoả mãn IECB là hình bình hành.
⓶ Xác định điểm D sao cho 3DB 2DC 0 .
3DB 2DC 0 DB 2DB 2DC 0 .
DB 2DB DC 0 DB 2CB 0 DB 2
CB DB 2BC . Trang 66 Chương 01. LÊ MINH TÂM
Vậy điểm D thẳng hàng với B,C và D thuộc tia đối của tia BC thoả mãn DB 2BC (như hình vẽ) .
⓷ Chứng minh rằng ba điểm A,I,Dthẳng hàng.
Có IE BC và DB 2BC (Theo câu ⓵, ⓶)
nên DB 2IE DI IA AB 2IA AE
DI IA AB 2IA 2AE DI AB 2IA IA AB .
DI IA . Vậy ba điểm A,I,Dthẳng hàng.
⓸ Tìm tập hợp các điểm M sao cho MA 3MB 2MC 2MA MB MC
MA 3MB 2MC 2MA MB MC
MI 3MI 2MI IA 3IB 2IC 2MA MB MC
MI 3MI 2MI 0 2MA 2MJ 2MI 2JA IM AJ , với J là trung điểm của BC .
Vậy tập hợp điểm M là đường tròn tâm I (xác định ở phần a), bán kính R AJ , với J là trung điểm của BC . Bài 06.
Cho điểm O cố định và hai vectơ u ; v cố định. Với mỗi số m ta xác định được điểm M sao cho
OM mu 1 m v . Tìm tập hợp điểm M khi m thay đổi. Lời giải
Từ O dựng OA u ; OB v thì A,B cố định.
OM mOA 1 mOB
OM mOA OB OB OM OB mOA OB BM mBA .
Từ đó suy ra A,B, M thẳng hàng. Vậy tập hợp điểm M chính là đường thẳng AB . Bài 07. Trang 67 Chương 01. LÊ MINH TÂM
Cho ABC và ba vectơ cố định u ; v ; w . Với mỗi số thực t , ta lấy các điểm A, B, C sao cho AA tu
, BB tv , CC tw . Tìm quỹ tích trọng tâm G của A B C
khi t thay đổi. Lời giải
Gọi G là trọng tâm ABC GAGBGC 0 , khi đó:
3GG GA GB GC
GA AAGB BBGC CC
GA GB GC AA BBCC AA BBCC t.u t.v t.w t u v w 0 1 Đặt
u v w thì vectơ cố định và GG t. . 3
Trường hợp 1: Nếu 0 thì các điểm G trùng với điểm G .
Trường hợp 2: Nếu 0 thì quỹ tích các điểm G là đường thẳng đi qua G và song song với giá của vectơ . Bài 08.
Cho tứ giác ABCD . Với mỗi số k tùy ý, lấy các điểm M, N sao cho AM k AB , DN kDC . Tìm tập
hợp các trung điểm I của đoạn thẳng MN khi k thay đổi. Lời giải
Gọi O, O lần lượt là trung điểm của AD và BC . Khi đó: 1
OO OBOC 1
OA ABOD DC 1
AB DC 2 2 2
Vì O và I lần lượt là trung điểm AD và MN 1 k
Nên OI AM DN AB DC kOO 2 2
Do đó: khi k thay đổi, tập hợp các điểm I là đường thẳng OO . Bài 09★.
Cho năm điểm trong đó không có ba điểm nào thẳng hàng . Gọi
là tam giác có ba đỉnh lấy trong
năm điểm đó, hai điểm còn lại xác định một đoạn thẳng t . Chứng minh rằng với cách chọn khác
nhau, đường thẳng đi qua trọng tâm tam giác
và trung điểm đoạn thẳng t luôn đi qua một điểm cố định . Lời giải
Giả sử năm điểm trong đó không có ba điểm nào thẳng hàng là A,B,C ,D,E .
Gọi G là điểm thỏa mãn : GA GBGC GD GE 0.
1 G là điểm cố định .
Gọi G là trọng tâm của qua ba đỉnh A,B,C GAGBGC 3GG. 2 Trang 68 Chương 01. LÊ MINH TÂM
M là trung điểm của hai đỉnh còn lại D , E GD GE 2GM . 3 Từ
1 , 2 và 3 3GG 2GM 0 G ,G , M thẳng hàng .
Suy ra điều phải chứng minh . Bài 10★.
Cho tam giác ABC , I là trung điểm của đoạn thẳng AB . Một đường thẳng d thay đổi luôn đi qua
I , lần lượt cắt hai đường thẳng CA,CB tại A', B' . Chứng minh rằng giao điểm M của AB' và A' B
nằm trên một đường thẳng cố định. Lời giải
Đặt CB mCB' , MB' nMA
Xét tam giác ABB' với ba đường đồng quy là AC , MB
và B' I ( đồng quy tại A' ).
Vì IA IB nên theo định lí Xê- va, ta có mn 1 hay mn 1.
Từ MB' nMA ta suy ra mMB' mnMA MA .
Vậy ta có CB mCB' và MA mMB' , điều này chứng tỏ rằng CM // AB .
Vậy điểm M luôn nằm trên đường thẳng cố định đi qua C và song song với AB .
--------------------HẾT-------------------- Trang 69 Chương 01. LÊ MINH TÂM BÀI 4
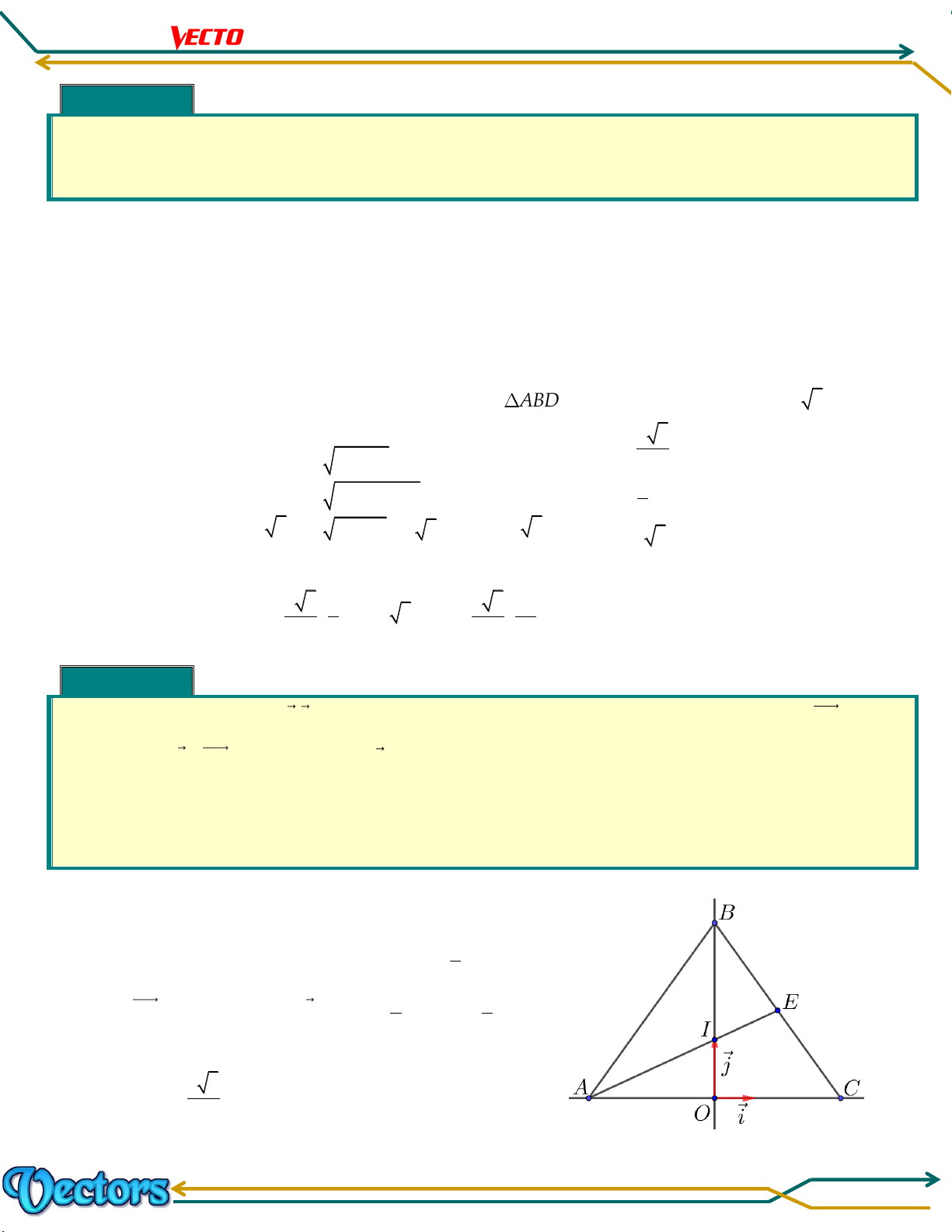
HỆ TRỤC TỌA ĐỘ I. TRỤC TỌA ĐỘ. 1.1. Định nghĩa
※ Trục tọa độ (Trục hay trục số) là một đường thẳng trên đó đã xác định một điểm gốc O
và một vectơ đơn vị i (tức là i 1).
※ Điểm O được gọi là gốc tọa độ, vectơ i được gọi là vectơ đơn vị của trục tọa độ.
※ Kí hiệu O;i hoặc đơn giản là Ox .
1.2. Tọa độ của vectơ và của điểm trên trục
※ Cho vectơ u nằm trên trục O; i khi đó số a được gọi là tọa độ của vectơ u trên trục
O;i khi và chỉ khi u .ai
※ Cho điểm M nằm trên trục O; i khi đó số m được gọi là tọa độ của điểm M trên trục
O;i khi và chỉ khi OM mi .
Như vậy tọa điểm M là tọa độ vectơ OM .
1.3. Độ dài đại số của vectơ trên trục:
※ Cho hai điểm A,B nằm trên trục Ox thì tọa độ của vectơ AB kí hiệu là AB và gọi là độ
dài đại số của vectơ AB trên trục Ox .
Vậy: AB A . B i . ※ Tính chất:
⓵ AB BA.
⓶ AB CD AB CD ⓷ A
,B,C O;i:AB BC AC . Ví dụ 1 Trên trục cho các điểm
lần lượt có tọa độ
. Tính độ dài đại số của các vectơ ; suy ra hai vectơ ; ngược hướng. Lời giải Trang 70 Chương 01. LÊ MINH TÂM Lời giải
AB 3; BC 5. 3
AB BC suy ra hai vectơ AB ; BC ngược hướng. 5
II. HỆ TRỤC TỌA ĐỘ. 2.1. Định nghĩa
※ Hệ trục tọa độ gồm hai trục vuông góc Ox và Oy với hai
vectơ đơn vị lần lượt là i ; j . Điểm O là gốc tọa độ, Ox gọi là
trục hoành và Oy gọi là trục tung.
★ Kí hiệu: Oxy hay O; i ; j .
2.2. Tọa độ điểm, tọa độ vectơ
※ Trong hệ trục tọa độ O; i ; j , cặp số ;xy gọi là tọa độ của vectơ u x;y u .
x i y.j .
★ Kí hiệu: u x; y hay ux; y .
※ Trong hệ trục tọa độ O; i ; j , tọa độ của vectơ OM gọi là tọa độ của điểm M.
★ Kí hiệu: M ;
x y hay M x; y .
2.3. Tọa độ trung điểm của đoạn thẳng. Tọa độ trọng tâm tam giác x x A B x M ※
M là trung điểm của đoạn 2 AB . y y A B y M 2
x x x A B C x G
※ G là trọng tâm tam giác ABC 3 .
y y y A B C y G 3 Ví dụ 2
Trong mặt phẳng tọa độ , cho .
⓵ Tìm tọa độ trung điểm của đoạn thẳng .
⓶ Tìm tọa độ trọng tâm tam giác .
Lời giải Trang 71 Chương 01. LÊ MINH TÂM ⓵ 2 3 1 2 1 3
I là trung điểm của đoạn thẳng AC I ; I ; . 2 2 2 2 ⓶
2 1 3 1 2 2 2 1
G là trọng tâm tam giác ABC G ; G ; . 3 3 3 3
2.4. Biểu thức tọa độ của các phép toán vectơ. ⓵ x x
u u . y y
⓶ u u x x ; y y.
⓷ ku kx; ky. x kx
⓸ Véctơ u cùng phương với vectơ u u 0 khi và chỉ khi tồn tại số k sao cho . y ky
⓹ Cho hai điểm Ax ,y ,Bx ; y thì AB x x ; y y . B A B A A A B B Ví dụ 3
Trong mặt phẳng tọa độ , cho
⓵ Tìm tọa độ các vectơ .
⓶ Phân tích vectơ theo hai vectơ ; .
Lời giải
⓵ Tìm tọa độ các vectơ a,b,c,m 3a 2b .
a 2i ,b 3
j ,c 3i 4j a 2;0,b 0; 3 ,c 3; 4 . 3 a 6;0
m 3a 2b 6;6 2 b 0;6
⓶ Phân tích vectơ c theo hai vectơ a ; b .
Giả sử c ma nb ma 2 ; m 0 nb 0; 3 n 3 m 2m 3 3 4 2
c ma nb
c a b . 3 n 4 4 2 3 n 3 Trang 72 Chương 01. LÊ MINH TÂM Ví dụ 4
Trong mặt phẳng tọa độ , cho 3 điểm .
⓵ Chứng minh 3 điểm tạo thành tam giác.
⓶ Tìm tọa độ điểm sao cho là hình bình hành.
Lời giải
⓵ Chứng minh 3 điểm A,B,C tạo thành tam giác.
Ta có AB 4; 4 , AC 5; 1 . 4 4
AB và AC không cùng phương hay ba điểm A,B,C tạo thành 1 tam giác. 5 1
⓶ Tìm tọa độ điểm D sao cho ABCD là hình bình hành. x 1 4 3 x 0
ABCD là hình bình hành khi và chỉ khi D D
AD BC y 2 1 2 y 5 D D D0; 5. Ví dụ 5 Cho tam giác , có hai điểm , điểm ở trên trục và trọng tâm trên trục . Tìm toạ độ và .
Lời giải
Đặt C 0; y ,G ; x 0 .
x x x A B C x x 4 G x 4 Ta có: 3 8 y
C4;0 ,G0;8 .
y y y y 8 A B C 0 y G 3 3 Ví dụ 6
Tìm toạ độ điểm của hình thang , có 2 đáy là , và với , , .
Lời giải x 0
Đặt Dx; y , khi đó: BC 2AD 2; 4 2x 1; y 2 D0;8 . y 8 Trang 73 Chương 01. LÊ MINH TÂM III. TỔNG KẾT.
Là một đường thẳng trên đó đã xác định một điểm gốc O và một vectơ đơn vị i .
Kí hiệu O; i .
Tọa độ của vectơ u trên trục O; i là a u .ai .
Tọa độ của điểm trên trục: Số k gọi là tọa độ của điểm O; i Ộ
M đối với trục Đ A
OM ki .
Độ dài đại số của vectơ trên trục: AB a AB . a i . C TỌ Chú ý Ụ
⓵ Nếu AB cùng hướng với i thì AB AB . TR
⓶ Nếu AB ngược hướng với i thì AB AB .
⓷ Nếu hai điểm A,B trên trục O; i có tọa độ lần lượt là a,b thì AB ba .
⓸ Hệ thức Charles: Với A,B,C tùy ý trên trục, ta có AB BC AC .
⓹ Hai vectơ AB và CD bằng nhau AB CD .
Hệ gồm hai trục tọa độ O; i , O; j vuông góc với nhau.Điểm O là gốc tọa độ.
Trục O; i gọi là trục hoành, kí hiệu Ox .
Trục O; j gọi là trục tung, kí hiệu Oy .
Hệ trục tọa độ O,i, j còn được kí hiệu là Oxy .
Mặt phẳng tọa độ Oxy gọi tắt là mặt phẳng Oxy . Ộ Đ
Tọa độ của vectơ đối với hệ trục tọa độ: u x; y u . x i y.j . ỌA
Tọa độ của điểm đối với hệ trục tọa độ: M x; y OM .
x i y.j .( x : hoành độ, y : C T tung độ). Ụ
Tính chất: Cho a x; y,b x'; y',k , Ax ; y ,Bx ; y ,Cx ; y . A A B B C C TR x x HỆ ⓵ ' a b . y y '
⓶ a b x x'; y y' . ⓷
x x x
y y y
Tọa độ trọng tâm G của tam giác ABC : A B C x ; A B C y . G 3 G 3
⓸ M chia đoạn AB theo tỉ số k MA kMB . ⓹ x x y y
Ba điểm A, B,C thẳng hàng B A B A . x x y y C A C A Trang 74 Chương 01. LÊ MINH TÂM IV. CÁC DẠNG TOÁN
Dạng 01. TÌM TỌA ĐỘ CỦA MỘT ĐIỂM; VECTƠ ; ĐỘ DÀI CỦA VECTƠ VÀ CHỨNG MINH HỆ THỨC.
Phương pháp giải
Sử dụng các kiến thức cơ bản sau :
Điểm M có tọa độ là a OM a i
Vectơ AB có độ dài đại số là m AB AB m i
Nếu a, b lần lượt là tọa độ của A, B thì AB b a ※ Tính chất:
⓵ AB BA.
⓶ AB CD AB CD ⓷ A
,B,C O;i:AB BC AC . Bài 01.
Trên trục tọa độ O;i cho 3 điểm A, B,C có tọa độ lần lượt là 2 ;1; 4 .
⓵ Tính tọa độ các vectơ A ; B BC; CA
⓶ Chứng minh B là trung điểm của AC . Lời giải
⓵ Tính tọa độ các vectơ A ; B BC; CA
Tọa độ vectơ AB là AB 1 2 3
Tọa độ vectơ BC là BC 4 1 3
Tọa độ vectơ CA là CA 2 4 6
⓶ Chứng minh B là trung điểm của AC .
Ta có AB BC 3 AB BC
3 điểm A, B, C thẳng hàng và AB BC B là trung điểm của AC . Bài 02.
Trên trục tọa độ 0;i cho bốn điểm A,B,C,D bất kỳ. Chứng minh A .
B CD AC. DB AD.BC 0 Lời giải
Gọi tọa độ của A,B,C,D lần lượt là a,b,c,d . Khi đó: Trang 75 Chương 01. LÊ MINH TÂM AB b ; a AC c ;
a AD d a
CD d c; DB b ; d BC c . b A .
B CD AC . DB AD.BC b ad c c ab d d ac b
bd bc ad ac cb cd ab ad dc db ac ab 0. Bài 03.
Trên trục tọa độ 0;i cho hai điểm A,B có tọa độ lần lượt là a,b.
⓵ Tìm tọa độ điểm M sao cho MA kMB, k 1 .
⓶ Tìm tọa độ trung điểm I của AB .
⓷Tìm tọa độ điểm N sao cho 2NA 5NB . Lời giải
⓵ Tìm tọa độ điểm M sao cho MA kMB, k 1 .
Gọi tọa độ điểm M là x .
MA a x a kb Khi đó:
MA kMB a x k b x x , k 1 . 1 k MB b x a kb
Vậy tọa độ điểm M là , k 1 1 . k
⓶ Tìm tọa độ trung điểm I của AB.
Gọi tọa độ điểm I là y . I là trung điểm của AB khi và chỉ khi IA IB .
IA a y a b Ta có:
IA IB a y b y y 2
IB b y a b
Vậy tọa độ điểm I là . 2
⓷Tìm tọa độ điểm N sao cho 2NA 5NB .
Gọi tọa độ điểm N là x .
NA a x a b Khi đó:
NA NB a x b x 2 5 2 5 2 5 x . 7
NB b x 2a 5 b
Vậy tọa độ điểm N là . 7 Trang 76 Chương 01. LÊ MINH TÂM Bài 04.
Trên trục O;i , cho 3 điểm A, ,
B C có tọa độ lần lượt là a, b, c . Tìm điểm I sao cho IA IB IC 0 Lời giải
Gọi điểm I có tọa độ là x .
IA a x i IA a x
Ta có: IB b x IB b x i
IC c x
IC c x i a b c
Khi đó: IA IB IC 0 a b c 3x i 0
a b c 3x 0 x . 3 Bài 05.
Trên trục O;i , cho 4 điểm A, B, C, D có tọa độ lần lượt là a, b, c, d và thỏa mãn hệ thức DA CA
2ab cd a bc d . Chứng minh rằng: . DB CB Lời giải
Ta có: DA a d ; DB b d ; CA a c ; CB b c .
Theo đề bài: 2ab cd a bc d
2ab 2cd ac adbc bd
abac cdbd bc cd adab
abc dc b cb d ad b a d a c b c a d b d a c b d b c DA CA Vậy . DB CB
Dạng 02. TÌM TỌA ĐỘ CỦA MỘT ĐIỂM; VECTƠ TRÊN MẶT PHẲNG Oxy.
Phương pháp giải
Ta cần nhớ các kết quả sau:
AB x x ;y y B A B A
Với hai điểm Ax , y ,Bx ; y , ta có: . A A B B
AB AB x x y y B A 2 B A2
a x .i y .j 1 1 a x ;y 1 1 x x Với hai vectơ , ta có: 1 2
a b . b x ;y y y 2 2 1 2 . m a . n b
mx nx ;my ny 1 2 1 2 Trang 77 Chương 01. LÊ MINH TÂM Bài 06.
Viết tọa độ của các vectơ sau: ⓵ 1
a 2i 3j ,b i 5j ,c 3i ,d 2 j 3 ⓶ 1 3
a i 3j ,b i j ,c i j ,d 4
j ,e 3i 2 2 Lời giải ⓵ 1
a 2i 3j ,b i 5j ,c 3i ,d 2 j 3 1
a 2;3 ,b
; 5 , c 3; 0 ,d 0; 2 . 3 ⓶ 1 3
a i 3j ,b i j ,c i j ,d 4
j ,e 3i 2 2 1 3 a 1; 3 ,b ;1 ,c 1 ; ,d 0; 4 ,e 3;0 2 2 Bài 07. 1
Cho a 2; 0 ,b 1 ; , c 4; 6 2
⓵ Tìm tọa độ của vectơ d 2a 3b 5c .
⓶ Tìm hai số m,n sao cho: ma b nc 0. Lời giải
⓵ Tìm tọa độ của vectơ d 2a 3b 5c .
x 2.2 3. 1 5 4 . x 27 63
Gọi d x; y, ta có: 1 d ; . y 2 0 . 3. 5. 6 27 63 y 2 2 2
⓶ Tìm hai số m,n sao cho: ma b nc 0. 1
2m 1 4n 0 m 3
Ta có: ma b nc 0 1 6 n 0 1 2 n 12 1 1
Vậy m ;n . 3 12 Bài 08.
Cho a 1; 2 ,b 1
; 4,c 0;4 . Tìm tọa độ và độ dài của các vectơ u,v biết:
⓵ u 2a 4b c 5j .
⓶ v a b 3c 2i . Trang 78 Chương 01. LÊ MINH TÂM Lời giải
⓵ u 2a 4b c 5j .
Ta có j 0; 1 . x 2 1 . 4. 1 0 5 0 . x 6
Gọi u x; y, ta có: u 6;13 y 2 2 . 4 4 . 4 5 1 . y 13
Độ dài của vectơ u là: 2 2
u 6 13 205 .
⓶ v a b 3c 2i .
Ta có i 1;0 . x 11 3 0 . 2 1 . x 2
Gọi v x; y, ta có: v 2; 6 y 2 4 3 4 . 2 0 . y 6
Độ dài của vectơ v là: v 2 2 2 6 2 10 . Bài 09.
Biểu diễn véctơ c theo các véctơ a,b biết
⓵ a 2;
1 , b 3; 4 và c 4 ;7.
⓶ a 1; 1 ,b 2; 3 và c 1 ;3. ⓷ a 4 ;3,b 2 ;
1 và c 0;5 .
⓸ a 4; 2 ,b 5;3 và c 2;0.
⓹ a 2; 2
,b 1;4 và c 5;0 .
⓺ a 1;3 ,b 1;
1 và c 4;3 . Lời giải
⓵ a 2;
1 , b 3; 4 và c 4 ;7. 4 x 2 . . y 3
2x 3y 4 x 1
Giả sử c xa yb
c a 2b . 7 . x ( 1 ) y 4 .
x 4y 7 y 2
⓶ a 1; 1 ,b 2; 3 và c 1 ;3. 3 x 1 x 1 . y 2 .
x 2y 1 3 4 Giả sử 5
c xa yb
c a b . 3 x 1 . .( y 3 )
x 3y 3 4 5 5 y 5 ⓷ a 4 ;3,b 2 ;
1 và c 0;5 . 0 .x( 4 ) . y 2 4
x 2y 0 x 1
Giả sử c xa yb
c a 2b . 5 x 3 . . y ( 1 ) 3
x y 5 y 2
⓸ a 4;2,b 5;3 và c 2;0. Trang 79 Chương 01. LÊ MINH TÂM 2 x 4 . y 5 .
4x 5y 2 x 3
Giả sử c xa yb
c 3a 2b . 0 x 2 . y 3 . 2x 3y 0 y 2
⓹ a 2; 2
,b 1;4 và c 5;0 . 5 x 2 . y 1 .
2x y 5 x 2
Giả sử c xa yb
c 2a b . 0 . x ( 2 ) y 4 . 2
x 4y 0 y 1
⓺ a 1;3,b 1;
1 và c 4;3 . 1 x 4 x 1 . y 1 . x y 4 1 9 Giả sử 2
c xa yb
c a b . 3 x 3 . y 1 . 3
x y 3 9 2 2 y 2 Bài 10. Cho u (2; 5
), v (3; 4), w ( 5 ;7) .
⓵ Tìm tọa độ của véctơ a u 3v 5w .
⓶ Tìm tọa độ của véctơ x sao cho u 2v 3w x 0 .
⓷ Tìm 𝑚 biết rằng c 6;m cùng phương với w . Lời giải
⓵ Tìm tọa độ của véctơ a u 3v 5w . x 23 3 . 5. 5 36
Giả sử a x; y a 36; 8 2 . y 5 3 4 . 5 7 . 2 8
⓶ Tìm tọa độ của véctơ x sao cho u 2v 3w x 0 . 2 2 3 . 3. 5 x 0 x 23
Giả sử a x; y a 23 ;18. 5 2 4 . 3 7 . y 0 y 18
⓷ Tìm 𝑚 biết rằng c 6;m cùng phương với w . 6 m 42
c 6;m cùng phương với w m 5 . 7 5 Bài 11.
Cho a (2;1),b (3; 4),c ( 7 ; 2) .
⓵ Tìm tọa độ của véctơ u 3a 2b 4c .
⓶ Tìm tọa độ của véctơ x sao cho x a b c .
⓷ Tìm các số 𝑘, 𝑙 để c ka lb . Lời giải
⓵ Tìm tọa độ của véctơ u 3a 2b 4c . Trang 80 Chương 01. LÊ MINH TÂM x 3 2 . 2 3 . 4. 7 40
Giả sử u x; y u 40; 3 . y 3 1 . 2 4 . 4 2 . 3
⓶ Tìm tọa độ của véctơ x sao cho x a b c .
x 2 3 7 x 8
Giả sử x x; y x 8; 1 . y 1 4 2 y 1
⓷ Tìm các số 𝑘, 𝑙 để c ka lb . 34 k 7 k 2 . l 3 .
2k 3l 7 34 11 Ta có 5 c a b . 2 k 1 . l 4 .
k 4l 2 11 5 5 l 5 Bài 12.
Trong mặt phẳng tọa độ Oxy, cho điểm ( M ;
x y). Tìm tọa độ của các điểm
⓵ M đối xứng với M qua trục hoành. 1
⓶ M đối xứng với M qua trục tung. 2
⓷ M đối xứng với M qua gốc tọa độ. 3 Lời giải
⓵ M đối xứng với M qua trục hoành M x; y . 1 1
⓶ M đối xứng với M qua trục tung
M x; y . 2 2
⓷ M đối xứng với M qua gốc tọa độ M ; x y . 3 3 Bài 13.
Trong hệ trục tọa độ O;i, j, cho hình vuông ABCD tâm I và có A1;3. Biết điểm B thuộc trục
O;ivà BC cùng hướng với i. Tìm tọa độ các vectơ AB,BC,A .C Lời giải
BC cùng hướng với i mà AB BC B là hình chiếu của A trên trục O;i B1;0.
BC cùng hướng với i C thuộc trục O;i. Gọi Cc,0;c 0.
Ta có BC c 1;0 , AB 0; 3 2 c (t ) m BC AB
c 1 0 0 3 2 4 2 2
c 1 3 c 2 (l)
Vậy AB 0; 3 ,BC 3;0 , AC 3; 3. Trang 81 Chương 01. LÊ MINH TÂM Bài 14.
Trong mặt phẳng tọa độ Oxy, cho hình thoi ABCD cạnh a và góc BAD bằng 60o. Biết A trùng với
gốc tọa độ O,C thuộc trục Ox và x 0, y 0. Tìm tọa độ các đỉnh của hình thoi ABC . D B B Lời giải
Ta có A trùng với gốc tọa độ O A0;0. Gọi (
B x, y) (x, y 0) (
D x, y) (vì B và D đối xứng với nhau qua AC hay qua trục hoành).
Vì C thuộc trục Ox nên gọi C(z,0) (z 0).
Hình thoi ABCD có góc BAD bằng 60o ABD đều AB BD a AC a 3. a 3 x 2 2 2 2 2 x y a 2 AB a x y a a Ta có 2 2 BD a 0 ( 2
y) a 2y a y
(vì x, y 0, z 0) 2 2 2 AC a 3
z 0 a 3 z a 3 z a 3 a 3 a a 3 a
Vậy A0; 0 , B , ,C
a 3,0,D , . 2 2 2 2 Bài 15.
Trong hệ trục tọa độ O,i, j, cho tam giác ABC đều cạnh a , biết O là trung điểm BC , OC cùng
hướng với i , OA cùng hướng với j .
⓵ Tính tọa độ các đỉnh của tam giác ABC .
⓶ Tìm tọa độ trung điểm E của AC .
⓷ Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC . Lời giải
⓵ Tính tọa độ các đỉnh của tam giác ABC . a
Ta có O là trung điểm BC nên OB OC . 2 a a
Mà OC cùng hướng với i nên C ; 0 , B ; 0 . 2 2
Tam giác đều ABC cạnh a , O là trung điểm BC a 3 Nên OA . 2 Trang 82 Chương 01. LÊ MINH TÂM a 3
Mà OA cùng hướng với j nên A0; . 2
⓶ Tìm tọa độ trung điểm E của AC . a a 3
E là trung điểm của AC nên tọa độ của điểm E ; . 4 4
⓷ Tìm tọa độ tâm đường tròn ngoại tiếp ABC .
Gọi I x ; y là tâm đường tròn ngoại tiếp ABC . I I
Do tam giác ABC đều nên I chính là trọng tâm của ABC . 1 x 0 . x 0 1 I I 3
OI OA a 3 . 3 1 a 3 y y . I I 6 3 2 a 3
Vậy tọa độ tâm đường tròn ngoại tiếp tam giác ABC là I 0; . 6 Bài 16.
Trong hệ trục tọa độ O,i, j, cho hình thoi ABCD tâm O có AC 8, BD 6. Biết OC và i cùng
hướng , OB và j cùng hướng.
⓵ Tính tọa độ các đỉnh của hình thoi.
⓶ Tìm tọa độ trung điểm I của BC và trọng tâm ABC . Lời giải
⓵ Tính tọa độ các đỉnh của hình thoi.
Hình thoi ABCD tâm O , AC 8, BD 6
OA OC 4,OB OD 3.
OC và i cùng hướng C4;0, A 4 ;0 .
OB và j cùng hướng B0;3,D0; 3 .
⓶ Tìm tọa độ trung điểm I của BC và trọng tâm ABC 3
I là trung điểm của BC tọa độ I 2 ; . 2
Gọi Gx ; y là trọng tâm tam giác ABC G G
x x x A B C x G x 0 3 G
Vậy trọng tâm tam giác ABC là G0; 1 .
y y y y 1 A B C G y G 3 Trang 83 Chương 01. LÊ MINH TÂM Bài 17.
Cho hình bình hành ABCD có AD 4 và chiều cao tương ứng với cạnh AD bằng 3 , 0 BAD 60 .
Chọn hệ trục tọa độ A,i, j sao cho i và AD cùng hướng , y 0 . Tìm tọa độ các vectơ AB, BC , B CD và AC . Lời giải
A là gốc tọa độ nên A0;0 .
AD 4, i và AD cùng hướng nên D4;0
Gọi BH là đường cao tương ứng với cạnh
AD, H AD
ABH vuông tại H và có 0
BAH 60 , BH 3 BH 3 AB 2 3 , 0 sin BAH sin 60 BH 3 AH 3 . 0 tan BAH tan 60
Do y 0 nên B 3,3 . B x 3 4 x 4 3
ABCD hình bình hành nên C C
BC AD C 4 3;3 y 3 0 y 3 C C
Vậy AB 3;3,BC 4;0,CD 3; 3
,AC 4 3;3 . Bài 18.
Cho lục giác đều ABCDEF . Chọn hệ trục tọa độ O; i ; j trong đó O là tâm lục giác đều, i cùng
hướng OD , j cùng hướng EC . Tìm tọa độ các đỉnh lục giác đều biết cạnh của lục giác là 6 Lời giải Ta có ( O 0; 0; 0) .
i cùng hướng OD OD 6i D6;0 . OA O
D 6i A6;0 2 2 2 E
OC :EC OE OC 2O . E O . C cosEOC 2 2 6 6 2 6 . 6 . .co 1
s 20 108 EC 6 3
Gọi I là trung điểm của BC 1
OI EC 3 3 OI 3 3 j I 0;3 3 2 Trang 84 Chương 01. LÊ MINH TÂM 1 x 0 6 . x 3 1
Gọi C x; y 2
IC OD C 3;3 3 2 1 y 3 3 y 3 3 0 . 2
Do I là trung điểm của BC B 3 ;3 3
Do O là trung điểm của BE E3; 3 3
Do O là trung điểm của CF F 3;3 3 Vậy A 6
;0 , B3;3 3 , C3;3 3 ,D6;0, E3; 3 3, F 3 ; 3 3 Bài 19.
Trong mặt phẳng Oxy cho hai điểm A 1 ; 1 , B1;3 .
⓵ Tìm tọa độ điểm M sao cho BM 3;0
⓶ Tìm tọa độ điểm N sao cho NA 1; 1
Lời giải
⓵ Tìm tọa độ điểm M sao cho BM 3;0 Gọi ( M x; y ) . x 1 3 x 4
BM x 1; y 3 3;0 M 4;3 . y 3 0 y 3
⓶ Tìm tọa độ điểm N sao cho NA 1; 1
Gọi N(x; y) . 1 x 1 x 2 NA 1
x;1 y 1; 1 N 2 ;0 . 1 y 1 y 0 Bài 20.
Trong mặt phẳng Oxy cho hai điểm A 4 ;0,B0; 3 ,C 2; 1 .
⓵ Tìm tọa độ điểm u 2AB AC
⓶ Tìm tọa độ điểm M sao cho MA 2MB3MC 0
Lời giải
⓵ Tìm tọa độ điểm u 2AB AC AB 4;3 Ta có
u 2AB AC 2;5 u 2;5. AC 6; 1 Trang 85 Chương 01. LÊ MINH TÂM
⓶ Tìm tọa độ điểm M sao cho MA 2MB3MC 0
MA 4 x ; y
Gọi M x; y
MB x;3 y .
MC 2 x ;1 y
MA 2MB 3MC 4 x 2x 6 3x; y 6 2y 3 3y 6x 10; 6y 9 5 x 6 x 10 0 5 3 3
MA 2MB 3MC 0 M ; 6 y 9 0 3 3 2 y 2 Bài 24.
Trong mặt phẳng Oxy , cho ba điểm A3; 4 , B2; 1 , C 1 ; 2 .
⓵ Tìm tọa độ trung điểm của cạnh BC và tọa độ trọng tâm của ABC .
⓶ Tìm tọa độ điểm D sao cho ABCD là hình bình hành.
Lời giải
⓵ Tìm tọa độ trung điểm của cạnh BC và tọa độ trọng tâm của ABC .
※ Gọi M là trung điểm của cạnh BC . x x 2 1 1 B C x x x M M M 1 1
Tọa độ điểm M : 2 2 2 M ; . y y 1 2 1 2 2 B C y y y M 2 M 2 M 2
※ Gọi G là trọng tâm của ABC .
x x x 3 2 1 A B C x x 4 G G x 4
Tọa độ điểm G : 3 3 G 3 G ;1 .
y y y 4 1 2 3 A B C y y y 1 G G G 3 3
⓶ Tìm tọa độ điểm Dsao cho ABCDlà hình bình hành.
Ta có AB 1; 3 . 1 x 1 x 0
ABCD là hình bình hành D D
DC AB D0; 1 . 2 y 3 y 1 D D Trang 86 Chương 01. LÊ MINH TÂM Bài 25.
Trong mặt phẳng Oxy , cho hai điểm A3; 5 , B1;0 .
⓵ Tìm tọa độ trung điểm của cạnh BC và tọa độ trọng tâm của ABC .
⓶ Tìm tọa độ điểm D sao cho ABCD là hình bình hành.
Lời giải
⓵ Tìm tọa độ điểm C sao cho OC 3 AB. Ta có ( AB 2 ;5) . Vì OC 3
AB và tọa độ OC cũng là tọa độ điểm C nên x 3 .( 2 ) x 6 C C C 6; 1 5 . y 3 5 . y 1 5 C C
⓶ Tìm tọa độ điểm D đối xứng A qua C .
D đối xứng A qua C C là trung điểm AD.
2x x x
x 2x x x 2 6 . 3 x 9 C A D D C A D D D9; 2 5 .
2y y y
y 2y y y 2.( 1 5) 5 y 2 5 C A D D C A D D Bài 26.
Trong mặt phẳng Oxy , cho hình bình hành ABCD có ( A 1 ; 2 ) , ( B 3; 2) , C( 4
;1) . Tìm tọa độ đỉnh D .
Lời giải
Ta có AB 4; 4 . 4 x 4 x 8
ABCD là hình bình hành D D
DC AB D 8 ; 3 . 1 y 4 y 3 D D Bài 27.
Trong mặt phẳng Oxy , cho hai điểm A1; 1 , B4;3 .
⓵ Tìm tọa độ trung điểm của AB .
⓶ Tìm điểm M chia đoạn thẳng theo tỉ số k 2 .
⓷ Tìm điểm C sao cho AB OC .
Lời giải
⓵ Tìm tọa độ trung điểm của AB. x x 5 A B x I 5 2 2
I là trung điểm của AB I ;1 . y y 2 A B y 1 I 2 Trang 87 Chương 01. LÊ MINH TÂM
⓶ Tìm điểm M chia đoạn thẳng theo tỉ số k 2 .
Gọi Mx; y . MA 1 x; 1 y , MB 4 x;3 y . 1
x 24 x x 7
M chia đoạn thẳng theo tỉ số k 2 MA 2MB M ; . 1 y 2 3 y 7 7 y 7
⓷ Tìm điểm C sao cho AB OC .
Gọi C x ; y . AB 3; 4 ,OC x ; y C C C C 3 x Ta có: C
AB OC C 3;4. 4 y C Bài 28.
Trong mặt phẳng Oxy , cho hai điểm A1; 2
,B0;4,C3;2
⓵ Tìm tọa độ các vectơ AB, AC,BC .
⓶ Tìm tọa độ điểm M sao cho CM 2AB3AC .
⓷ Tìm tọa độ điểm N sao cho AN 2BN 4CN 0 .
Lời giải
⓵ Tìm tọa độ các vectơ AB, AC,BC .
AB 1; 6 . AC 2; 4. BC 3; 2 .
⓶ Tìm tọa độ điểm M sao cho CM 2AB3AC . Gọi M ;
a b. CM a 3; b 2 .
a 3 2. 1 3 2 . a 5
Ta có: CM 2AB 3AC M 5 ; 2 . b 2 2 6 . 3 4 . b 2
⓷ Tìm tọa độ điểm N sao cho AN 2BN 4CN 0 .
Gọi N x; y. AN x 1; y 2 . BN x; y 4 . CN x 3; y 2 .
x 1 2.x 4.x 3 0 x 11
Ta có: AN 2BN 4CN 0 N ; y 2 2.
y 44.y 2 11 2 0 y 2 Bài 29.
Trong mặt phẳng Oxy , cho hai điểm A1; 2
,B2;3,C 1 ; 2 .
⓵ Tìm tọa độ điểm D đối xứng của A qua C .
⓶ Tìm tọa độ điểm E là đỉnh thứ tư của hình bình hành có 3 đỉnh là A,B,C .
⓷ Tìm tọa độ trọng tâm của tam giác ABC .
Lời giải Trang 88 Chương 01. LÊ MINH TÂM
⓵ Tìm tọa độ điểm D đối xứng của A qua C .
D đối xứng của A qua C x x A D x C x 2x x 3
C là trung điểm của 2 AD D C A D 3 ; 2 . y y
y 2y y 2 A D D C A y C 2
⓶ Tìm tọa độ điểm E là đỉnh thứ tư của hình bình hành có 3 đỉnh là A,B,C . Gọi E ; x y .
E là đỉnh thứ tư của hình bình hành có 3 đỉnh là A, B,C . x 1 1 2 x 2
Trường hợp 1: ABCE là hình bình hành CE BA E 2 ; 7 . y 2 2 3 y 7 x 1 2 1 x 0
Trường hợp 2: ABCE là hình bình hành CE AB E0;3 . y 2 3 2 y 3 x 1 2 1 x 4
Trường hợp 3: ACBE là hình bình hành AE CB E4;3. y 2 3 2 y 3 Vậy E 2 ; 7
,E 0;3 hoặc E 4;3 . 3 1 2
⓷ Tìm tọa độ trọng tâm của tam giác ABC .
x x x 2 A B C x x G G 2 1
Trọng tâm G của tam giác ABC 3 3 G ; .
y y y 1 3 3 A B C y y G 3 G 3 Bài 30.
Cho mặt phẳng Oxyz , cho ba điểm A 2 ; 1 ; B3; 2 ;C0;3 .
⓵ Tìm tọa độ của u AB 3BC 2CA .
⓶ Chứng minh A,B,C là ba đỉnh của một tam giác, tìm trọng tâm G của ABC .
⓷ Tìm tọa độ điểm D sao cho CD 2AB3BC .
⓸ Tìm điểm E sao cho tứ giác ABCE là hình bình hành. Tìm tâm của hình bình hành đó.
Lời giải
⓵ Tìm tọa độ của u AB 3BC 2CA .
Ta có: AB 5; 3; BC 3;5;CA 2; 2,
Khi đó: u AB 3BC 2CA 0;16 .
⓶ Chứng minh A,B,C là ba đỉnh của một tam giác, tìm trọng tâm G của ABC . Trang 89 Chương 01. LÊ MINH TÂM
Ta có: AB 5; 3; AC 2; 2 , 5 3 Mà:
AB kAC , 2 2
Vậy A,B,C là ba đỉnh của một tam giác 1 2
Trọng tâm G của ABC là: G ; . 3 3
⓷ Tìm tọa độ điểm D sao cho CD 2AB3BC .
Ta có: CD 2AB3BC
x x 2 x x x x x D C
B A 3 C B 0 2 D 3 2 30 3 x 1 D D ; .
y y 2 y y y y y y D C
B A 3 C B 3 2 D 2 1 33 2 1 12 12 D
Gọi I là tâm của hình bình hành khi đó I là trung điểm của AC I 1 ; 2.
⓸ Tìm điểm E sao cho tứ giác ABCE là hình bình hành. Tìm tâm của hình bình hành đó.
Tứ giác ABCE là hình bình hành
x x x x 0 x 3 2 x 5 C E B A E E
EC AB E 5 ;6 .
y y y y 3 y 2 1 y 6 C E B A E E Bài 31.
Cho mặt phẳng Oxyz , cho điểm A3;0; B 3
;0 . Xác định tọa độ điểm C,D sao cho.
⓵ CA 3CB 0 .
⓶ DA3DB 0 .
Lời giải
⓵ CA3CB 0.
x x x x x x A C B C C C 3 3 0 3 3 3 0 x 3
CA 3CB 0 C C ; .
y y 3 y y y y A C B C 0 0 3 C 0 C 2 0 0 2 y 0 C
⓶ DA3DB 0 .
x x 3 x x x x A D B D 0 3 3 D 3 D 0 x 6
DA 3DB 0 D C ; .
y y 3 y y y y y A D B D 0 0 3 D 0 D 6 0 0 0 D Bài 32.
Cho mặt phẳng Oxyz , cho điểm A3; 4; B 1 ; 2; I 4;
1 . Xác định tọa độ điểm C, D sao cho tứ giác
ABCD là hình bình hành và I là trung điểm của CD . Tìm tọa độ tâm O của hình bình hành ABCD .
Lời giải
Gọi tọa độ hai điểm C ;
a b ,Dc;d . Trang 90 Chương 01. LÊ MINH TÂM
Tứ giác ABCD và I là trung điểm của CD 1
3 a c a c 4 a 2 AB DC
2 4 b d
b d 2 b 0 .
c 4 a 4 0 c a 8 c 6 ID IC 0
d1b1 0 db 2 d 2
Vậy C 2;0,D6;2 . Bài 33.
Trong mặt phẳng Oxy , cho A3; 1 ; B1; 3
. Đỉnh C nằm trên Oy và trọng tâm G nằm trên trục
hoành. Tìm tọa độ điểm C .
Lời giải
C Oy C 0;c ; GOx Gg;0
Do G là trọng tâm tam giác ABC nên ta có
x x x A B C x G y 3 3 y y y C G A B c 3 0 . 1 3
2 C0;2
y y y
x 3x x x A B C C G A B y G 3 Bài 34.
Trong mặt phẳng Oxy cho tam giác ABC có M; N; P lần lượt là trung điểm của BC; AC; AB .Biết M 1; 1 ; N 2 ; 3 ; P2;
1 . Tìm tạo độ các đỉnh của tam giác ABC .
Lời giải
Gọi Ba;b
x 2x x 2 a M 1;
1 là trung điểm của BC nên ta có C M B
y 2y y 2 b C M B
NP 4; 2;CB 2a 2; 2b 2
N; P là trung điểm của AC; AB nên NP là đường trung bình của tam giác ABC 2a 2 8 a 5
Do vậy 2NP CB 8;4 2a 2;2b 2 B5; 3 ;C 3 1 2 b 2 4 b 3
x 2x x 1 N 2 ; 3
là trung điểm của AC nên A N C A 1 ; 5
y 2y y 5 A N C Bài 35.
Trong mặt phẳng Oxy , cho tam giác ABC có A3; 4 ; B 1 ; 2;C4;
1 . A' là điểm đối xứng của A
qua B . B' là điểm đối xứng của B qua C . C' là điểm đối xứng của C qua A .
⓵ Tìm tọa độ các điểm A'; B';C' .
⓶ Chứng minh các tam giác ABC và A'B'C' có cùng trọng tâm. Trang 91 Chương 01. LÊ MINH TÂM
Lời giải
⓵ Tìm tọa độ các điểm A';B';C' . 7
A3; 4 ; B 1 ; 2;C4;
1 Tọa độ trọng tâm G của tam giác ABC là G 2 ; 3 Ta có B 1
; 2 là trung điểm của AA' với A3;4 nên A' 5 ;0 C 4;
1 là trung điểm của BB' với B 1 ; 2 nên B'9;0
A3; 4 là trung điểm của CC' với C 4; 1 nên C '2; 7
⓶ Chứng minh các tam giác ABC và A'B'C'có cùng trọng tâm. 7
Trọng tâm G' của tam giác A' B'C' là G ' 2 ; 3
Do vậy Trọng tâm hai tam giác A' B'C' và tam giác ABC trùng nhau. Bài 36.
Trong mặt phẳng Oxy , cho ba điểm A 3 ;6, B1; 2 , C6;3 .
⓵ Tìm tọa độ điểm D để ABCD là hình bình hành và tìm tọa độ trọng tâm G của ABC
⓶ Tìm tọa độ điểm E thỏa biểu thức véc tơ CE 2AB3AC .
⓷ Tìm tọa độ điểm F thỏa biểu thức véc tơ AF 2BF 4CF 0 .
⓸ Tìm điểm K thỏa biểu thức véc tơ 4KA 3BK CK 0 .
⓹ Tìm tâm I và bán kính của đường tròn ngoại tiếp ABC .
⓺ Tìm các điểm A , A , A sao cho ABC nhận các điểm đó làm trung điểm các cạnh 1 2 3
⓻ Tìm các điểm M , N , P sao cho MNP nhận các điểm A , B , C làm trung điểm các cạnh.
⓼ Tìm hai điểm chia đoạn AC làm ba phần bằng nhau.
⓽ Tìm diện tích ABC và diện tích hình tròn ngoại tiếp ABC .
Lời giải
⓵ Tìm tọa độ điểm D để ABCD là hình bình hành và tìm tọa độ trọng tâm G của ABC
AB 4; 8, DC 6 x ;3 y D D 6 x 4
ABCD là hình bình hành AB DC D D2;1 1 3 y 8 D
Gọi Gx ; y G G 3 1 6 x G 4 7
G là trọng tâm ABC 3 G ; 6 2 3 3 3 y G 3 Trang 92 Chương 01. LÊ MINH TÂM
⓶ Tìm tọa độ điểm E thỏa biểu thức véc tơ CE 2AB3AC .
Gọi Ex ; y E E
AB 4; 8, AC 9; 3 , CE x 6; y 3 E E x 6 2 4 . 3 9 .
CE 2AB3AC E E ; y 3 2. E 8 3. 3 13 4
⓷ Tìm tọa độ điểm F thỏa biểu thức véc tơ AF 2BF 4CF 0.
Gọi F x ; y AF x 3; y 6 , BF x 1; y 2 ,CF x 6; y 3 F F F F F F F F
x 3 2 x x F F 1 4 6 F 0
AF 2BF 4CF 0 F ;
y 6 2 y y F 2 F 4 2 F 25 6 0
⓸ Tìm điểm K thỏa biểu thức véc tơ 4KA 3BK CK 0 .
Gọi Kx ; y KA 3 x ;6 y , BK x 1; y 2 ,CF x 6; y 3 K K K K K K K K 4 3
x x x K 3 K 1 6 K 0 5 5
4KA 3BK CK 0 K ; 4
6 y y y k 3 2 K 3 K 0 2 2
⓹ Tìm tâm I và bán kính của đường tròn ngoại tiếp ABC .
Gọi I x ; y IA 3 x ;6 y , IB 1 x ; 2 y , IC 6 x ;3 y I I I I I I I I 2 2 IA IB
Để I là tâm đường tròn ngoại tiếp ABC 2 2 IA IC 3 x y x y I 2
6 I 2 1 I 2 2 I 2 3 x y x y I 2
6 I 2 6 I 2 3 I 2 8
x 16y 40 I I I 1;3 18
x 6y 0 I I
R IA 2 2 3 1 6 3 5
⓺ Tìm các điểm A , A , A sao cho ABC nhận các điểm đó làm trung điểm các cạnh 1 2 3 3 1 x A 1 Gọi A x ; y là trung điểm cạnh 2 AB A 1 ; 2 1 1 A A 1 1 6 2 y A1 2 5 1 3 9
Tương tự A , A lần lượt là trung điểm BC , AC A ; , A ; 2 3 2 2 2 3 2 2
⓻ Tìm các điểm M, N , P sao cho MNP nhận các điểm A , B , C làm trung điểm các cạnh. Trang 93 Chương 01. LÊ MINH TÂM
Gọi Mx ; y , Nx ; y , Px ; y P P N N M M
Giả sử A , B , C lần lượt là trung điểm MN , NP , PM
x x 2.
y y 2. M N 6 M N 3
Khi đó: x x 2 1 .
và y y 2. M2;1 1 , N 8 ; 1 , P 10; 5 N P 2 N P x x 2 6 . y y 2.3 P M P M
⓼ Tìm hai điểm chia đoạn AC làm ba phần bằng nhau. 1
Gọi Q x ; y , Rx ; y thuộc đoạn AC sao cho AQ QR RC AC R R Q Q 3
Có AQ x 3; y 6 ; RC 6 x ;3 y ; AC 9; 3 R R Q Q 1 1
Vì AQ AC và RC AC 3 3 1 1 x 3 .9 6 x .9 Q R Nên 3 và 3
Q0;5 và R3;4 1 1 y 6 . 3 y . R 3 Q 3 3 3
⓽ Tìm diện tích ABC và diện tích hình tròn ngoại tiếp ABC . Gọi T 3 ; 2 , U6; 2 , V 6;6
TU AV 9, AT VU 8, VC 3, CU 5, BU 5,TB 4 1 27 1 25 1 S 9.8 72 ,S 9 3 . , S 5 . 5 . , S 8 4 . 16 ATUV AVC 2 2 BCU 2 2 ABT 2 27 25 S 72 16 30(đvdt) ABC 2 2
Diện tích hình tròn ngoại tiếp ABC là 2 2 .R 5 . 25 Bài 37.
Trong mặt phẳng Oxy , tìm điểm M sao cho 2 2
x y nhỏ nhất khi biết tọa độ có dạng M M
⓵ M1 2t;13t
⓶ M1 2t;1t
Lời giải
⓵ M1 2t;13t Ta có 2 2 x y M M 2 5 25 1 5 1 1
t2 t2 1 2 1 3 2
13t 10t 2 2
13 t 2. .t 13 t 13 169 13 13 13 13 1 Vậy 2 2
x y đạt giá trị nhỏ nhất bằng M M 13 Trang 94 Chương 01. LÊ MINH TÂM
⓶ M12t;1t 2 2 2 1 9 9 Ta có 2 2
x y 1 2t 1 t 2
5t 2t 2 5 t M M 5 5 5 9 Vậy 2 2
x y đạt giá trị nhỏ nhất bằng . M M 5 Bài 38.
Trong mặt phẳng Oxy , cho hai điểm A4; 4, B0;
1 . Tìm điểm C trên Oy sao cho trung trực của
đoạn AC đi qua B
Lời giải
Gọi C 0;c
Có AB 4; 3 , BC 0;c 1
Để trung trực của đoạn AC đi qua B AB BC
2 2 c 6 c 2 2 4 3 0 1
Vậy C 0;6 hoặc C0; 4 thì thỏa ycbt. c 4
y 6 M36;6 M y 3 N N 9;3 Với . y 2 M4; 2 M y 1 N N 1; 1 Bài 39.
Trong mặt phẳng Oxy , cho ABC có A 1 ; 1 , B5;
3 , đỉnh C nằm trên trục tung Oy và trọng
tâm G của tam giác thuộc trục hoành Ox . Tìm tọa điểm C và tính diện tích ABC .
Lời giải C Oy C 0; yC Ta có: . G Ox G x ;0 G
Gọi M là trung điểm AB M 2; 2 CM 2; 2 y CG x C , 2 ; 2 G
Với G là trọng tâm ABC 3 2 x 2 y G 5 3 C 2 10
CM CG
10 C 0 ; 5 và G ; 0 . 2 3 x 3 2 y . 2 G C 3 2 AB 6;2 1 1 Từ đó ta có: S AB; AC 6 4 . 1 2 . 11 ABC . AC 1;4 2 2 Trang 95 Chương 01. LÊ MINH TÂM Bài 40.
Trong mặt phẳng Oxy , tìm hai điểm M N P 2 ,
: y x . Biết rằng IM 4IN và I 0; 2
Lời giải
IM x ; y 2 IM y y M M 2 ; 2 2 M M
Ta có M , N P
: y x . IN x ;y 2
IN y y N N 2 ; 2 N N 2 2 2 2 y 4y y 4y Lại có: IM 4 M N M N IN
y 2 4y 8
y 2 4y 8 M N M N y 2y y 2y y 2y y 6 M N M N M N M
y 2 4y 8 2
y 2 4y 8 2 y 6 y 3 M N N N N N . y 2 y y 2 y y 2 y y 2 M N M N M N M y 2 4y 8
2y 2 4y 8 6y 6 y 1 M N N N N N
Dạng 03. VÉCTƠ CÙNG PHƯƠNG & ỨNG DỤNG.
Phương pháp giải
Ta cần nhớ các kết quả sau: cho u x; y;v x; y. x kx
⓵ Véctơ v cùng phương với vectơ u u 0 . y ky x y
⓶ Nếu xy 0 ta có u cùng phương v . x y
⓷ Để phân tích c c ;c qua hai véctơ u x; y;v x; y không cùng phương, ta giả sử 1 2
mx nx c m c . m u .
n v . Khi đó ta quy về giải hệ phương trình 1 .
my ny c n 2
⓸ Với 3 điểm Ax ; y ; Bx ; y ;Cx ; y . A A B B C C x x x x
Để A, B ,C thẳng hàng thì B A C A AB AC . y y y y B A C A
⓹ Với ABC bất kì thì CACB AB. Dấu “=” xảy ra A,B,C thẳng hàng.
⓺ Bất đẳng thức véctơ
u v u v u v Dấu “=” xảy ra u , v cùng phương và hướng.
u v w u v w Dấu “=” xảy ra u , v , w cùng phương và hướng. 2 2
Lưu ý: a x y 2 2 ;
a x y và AB AB x x y y . B A B A
Nắm vững công thức tính diện tích , các bất đẳng thức cơ bản (cauchy, B.C.S).
Để chứng minh ba điểm là ba đỉnh , ta chứng minh ba điểm đó không thẳng hàng. Trang 96 Chương 01. LÊ MINH TÂM Bài 41.
Cho a 1; 2, b 3
; 0 , c 1 ;3
⓵ Chứng minh hai vectơ a ; b không cùng phương.
⓶ Phân tích vectơ c qua a ; b . Lời giải
⓵ Chứng minh hai vectơ a ; b không cùng phương. k. 1 1 3 k
Giả sử a kb
3 (Vô lý) a kb . Suy ra a ; b không cùng phương. 2 k 0 . 2 0
⓶ Phân tích vectơ c qua a ; b . 5 n
m 3n 1 3 5
Giả sử ta có: c ma nb khi đó ta có 6
c a b . 2 m 3 3 2 6 m 2 Bài 42. Cho u 2
m m 2; 4 và v ;
m 2 . Tìm m để hai vecto u , v cùng phương. Lời giải
Ta có : u , v cùng phương khi và chỉ khi tồn tại k sao cho m 1 2 2 2
m m 2 km
m m 2 2m
m m 2 0 m 2 . 4 k 2 . k 2 k 2 k 2 m 1 Vậy
thỏa yêu cầu bài toán. m 2 Bài 43.
Trong mặt phẳng tọa độ Oxy , cho ba điểm A6;3, B 3 ;6 , C1; 2 .
⓵ Chứng minh A , B , C là ba đỉnh một tam giác.
⓶ Xác định điểm D trên trục hoành sao cho ba điểm A , B , D thẳng hàng.
⓷ Xác định điểm E trên cạnh BC sao cho BE 2EC .
⓸ Xác định giao điểm hai đường thẳng DE và AC . Lời giải
⓵ Chứng minh A , B , C là ba đỉnh một tam giác.
Ta có AB 9;3 ; AC 5; 5 . Trang 97 Chương 01. LÊ MINH TÂM 9 3 Vì
nên AB và AC không cùng phương 5 5
A , B , C không thẳng hàng hay A , B , C là ba đỉnh một tam giác.
⓶ Xác định điểm D trên trục hoành sao cho ba điểm A , B , D thẳng hàng. Gọi D ;
x 0 trên trục hoành, AD x 6,3 . 9 k.x 6 9
1x 6 x 15
Khi đó A , B , D thẳng hàng AB kAD . 3 k 3 k 1 k 1
Vậy D15;0 thỏa mãn YCBT.
⓷ Xác định điểm E trên cạnh BC sao cho BE 2EC .
Gọi E x; y trên cạnh BC sao cho BE 2EC .
Ta có: BE x 3; y 6 ; EC 1 x; 2 y 1 x 3 21 x x Mà BE 3
2EC nên BE 2EC . y 6 2 2 y 2 y 3 1 2 Vậy E ; thỏa mãn YCBT. 3 3
⓸ Xác định giao điểm hai đường thẳng DE và AC .
Gọi Mx; y là giao điểm của DE và AC , 46 2
Ta có MD 15 x; y ; DE ; . 3 3 x 15 y
Mà D , M , E thẳng hàng nên:
x 23y 15 . 46 2 3 3 6 x 3 y
MA 6 x;3 y ; AC 5; 5 , mà A , M , C thẳng hàng:
x y 3. 5 5 7 x
2x 23y 15
Khi đó tọa độ điểm M là nghiệm của hệ phương trình 2 . x y 3 1 y 2 7 1
Vậy M ; là giao điểm của DE và AC . 2 2 Trang 98 Chương 01. LÊ MINH TÂM Bài 44.
Trong mặt phẳng tọa độ Oxy cho 4 điểm A1; 1 , B2;
1 , C 4;3 , D16;3 . Hãy phân tích véc tơ AD
theo hai véc tơ AB và AC . Lời giải
Ta có: AB 2 1; 1
1 AB 1; 2 .
AC 4 1;3
1 AC 3; 2 .
AD 16 1;3
1 AD 15; 2 .
m1 n3 15 m 3
Giả sử AD mAB nAC . m 2 n2 2 n 4
Vậy AD 3AB 4AC . Bài 45.
Trong mặt phẳng tọa độ Oxy cho 4 điểm A0;
1 , B2; 0 ,C 1 ; 2 , D6; 4
. Hãy phân tích véc tơ
AD theo hai véc tơ AB và AC . Lời giải
Ta có: AB 2 0;0
1 AB 2; 1 .
AC 1 0; 2
1 AC 1; 1 .
AD 6 0; 4
1 AD 6; 5 .
m2 n 1 6 m 1
Giả sử AD mAB nAC . m
1n1 5 n 4
Vậy AD AB 4AC . Bài 46.
Trong mặt phẳng tọa độ Oxy cho 4 điểm A1; 2
, B0;3 ,C 3 ; 4, D 1 ;8 .
⓵ Chứng minh AB và AC không cùng phương.
⓶ Hãy phân tích véc tơ CD theo hai véc tơ AB và AC . Lời giải
⓵ Chứng minh AB và AC không cùng phương.
Ta có: AB 01;3 2
AB 1 ;5 . AC 3 1; 4 2
AC 4 ;6. Trang 99 Chương 01. LÊ MINH TÂM 1 5 Suy ra
. Vậy AB và AC không cùng phương. 4 6
⓶ Hãy phân tích véc tơ CD theo hai véc tơ AB và AC .
CD 1 3;8 4 CD 2; 4 . m 1 n 4 2 m 2
Giả sử CD mAB nAC .
m5 n6 4 n 1
Vậy CD 2AB AC . Bài 47.
Trong mặt phẳng tọa độ Oxy cho bốn điểm A0;
1 , B1;3 ,C 2; 7 và D0;3. Tìm giao điểm của hai
đường thẳng AC và . BD Lời giải
Ta có: AC 2;6 , BD 1;0.
Gọi Mx; y là giao điểm của AC và . BD
Khi đó: A, M,C thẳng hàng và B, M,D thẳng hàng. x 2k
Vì A, M,C thẳng hàng nên AM, AC cùng phương k
0 : AM kAC 1 y 1 6k x 1 n
Vì B, M,D thẳng hàng nên BM, BD cùng phương n
0 : BM nBD 2 y 3 1 k 2 Từ (1)(2) suy ra: 3 M ;3. 1 3 n 3 Bài 48.
Trong mặt phẳng Oxy, cho tam giác ABC có A3; 4 ,B2; 1 ,C 1 ; 2
. Tìm điểm M trên đường
thẳng BC sao cho S 3S . ABC ABM Lời giải
Gọi Mx; y là điểm cần tìm. Khi đó: BC 3; 3 ,BM x 2; y 1 . 1 1 Ta có: S . . h BC,S . . h BM. ABC 2 ABM 2 S BC
Theo bài ra ta có: ABC 3
3 BC 3BM. S BM ABM Trang 100 Chương 01. LÊ MINH TÂM 3 3
x2 x 1
Trường hợp 1: Nếu M nằm trong đoạn BC thì BC 3BM M ; . 3 3 y 1 0 1 y 0 3 3
x2 x 3
Trường hợp 2: Nếu M nằm ngoài đoạn BC thì BC 3BM M ; . 3 3 y 3 2 1 y 2
Vậy có hai điểm M1;0,M3;2 thỏa mãn điều kiện bài toán. Bài 49.
Trong mặt phẳng Oxy, cho ba điểm A 1 ; 1 , B0; 1 ,C 3; 0.
⓵ Chứng minh ba điểm A,B,C tạo thành một tam giác.
⓶ Xác định tọa độ điểm D thuộc đoạn thẳng BC và 2BD 5D . C
⓷ Xác định tọa độ giao điểm của AD và BG trong đó G là trọng tâm tam giác AB . C Lời giải
⓵ Chứng minh ba điểm A,B,C tạo thành một tam giác.
Ta có: AB 1; 2 , AC 4; 1 . 1 1 4k k
Giả sử A, B,C thẳng hàng. Khi đó k
0 : AB kAC 4 (vô lí) 2 k k 2
Suy ra A,B,C không thẳng hàng nên A,B,C tạo thành một tam giác.
⓶ Xác định tọa độ điểm D thuộc đoạn thẳng BC và 2BD 5D . C
Ta có: BC 3; 1 .
Gọi Dx; y là điểm thuộc đoạn thẳng BC thỏa mãn 2BD 5D . C BD 5 BD 5 BD 5
Ta có: 2BD 5DC . CD 2 BD CD 5 2 BC 7 15 x 5 15 2
Mà D thuộc đoạn thẳng BC nên 7 BD BC D ; . 7 2 7 7 y 7
⓷ Xác định tọa độ giao điểm của AD và BG trong đó G là trọng tâm tam giác AB . C x x x y y y 2
Có G là trọng tâm tam giác ABC nên A B C G ; A B
C G ;0. 3 3 3 22 9 2 Ta có: AD ; , BG ; 1 . 7 7 3
Gọi Mx; y là giao điểm của AD,B . M
Khi đó: ba điểm A, M,D thẳng hàng và ba điểm ,
B M,G thẳng hàng. Trang 101 Chương 01. LÊ MINH TÂM 22 x 1 k
Vì A, M,D thẳng hàng nên AM, AD cùng phương 7
AM kAD 1. 9 y 1 k 7 2 x n Vì ,
B M,G thẳng hàng nên BM, BG cùng phương n
0 : BM nBG 3 2 y 1 n 7 k 5 1 Từ (1)(2) suy ra: 12 M ; . 5 6 4 n 4 5 1 Vậy M ; là điểm cần tìm. 6 4 Bài 50.
Trong mặt phẳng Oxy, tìm trên trục hoành điểm P sao cho tổng khoảng cách từ P tới hai điểm A và B nhỏ nhất ⓵ A1;
1 và B2; 4 .
⓶ A1; 2 và B3; 4. Lời giải
Theo giả thiết P Ox Px ;0 P ⓵ A1;
1 và B2; 4 . Ta có: A1;
1 và B2; 4 khác phía với trục hoành.
Gọi P AB Ox , khi đó A ; B ; P thẳng hàng AB cùng phương với AP 0 0 0 1 5 6 6
x P ;0. 0 0 x 1 1 5 5 0
Ta có PA PB AB , vậy PA PB nhỏ nhất A; B; P thẳng hàng P P . 0
⓶ A1;2 và B3;4.
Ta có: A1; 2 và B3; 4 cùng phía với trục hoành.
Gọi A là điểm đối xứng với A qua trục hoành
A1; 2 và PA PA .
Ta có PA PB PA PB A B . x 1 0 2 5
Dấu bằng xảy ra A P cùng phương với P A B x . 3 1 4 2 P 3 Trang 102 Chương 01. LÊ MINH TÂM Bài 51.
Trong mặt phẳng Oxy, cho hình bình hành ABCD có A 2
;3 và tâm I 1;
1 . Biết điểm K 1 ; 2 nằm
trên đường thẳng AB và điểm D có hoành độ gấp đôi tung độ. Tìm các đỉnh còn lại của hình bình hành. Lời giải Ta có I 1;
1 là tâm hình bình hành nên I 1;
1 là trung điểm AC C 4; 1 .
Gọi Dx; y, theo giả thiết điểm D có hoành độ gấp đôi tung độ D2y; y.
Lại có I 1;
1 là trung điểm BD B2 2y ; 2 y. AK 1;
1 và AB 4 2y ; 1 y . 4 2y 1 y B0; 1
Vì K AB nên AK cùng phương AB y 1 . 1 1 D 2; 1 Bài 52. 1
Trong mặt phẳng Oxy, cho a
i 5j ; b ki 4j . Tìm giá trị của k để hai véctơ a ; b cùng phương. 2 Lời giải 1 1
a i 5j a ; 5 Theo giả thiết 2 2 . b ki 4j b k;4 1 5 2
Để hai véctơ a ; b cùng phương 2 k k 4 . 5 Bài 53.
Trong mặt phẳng Oxy cho a 2
x 1; 3x 2 ,b 2;
1 và điểm A0; 1 .
⓵ Tìm x để véc tơ a cùng phương với véc tơ b .
⓶ Tìm tọa độ điểm M để véc tơ AM cùng phương với véc tơ b và có độ dài bằng 5 . Lời giải
⓵ Tìm x để véc tơ a cùng phương với véc tơ b . 2 x 1 x 1 3x 2
Ta có a cùng phương với b 2
x 1 23x 2 2
x 6x 5 0 2 1 x 5
Vậy với x 1; x 5 thì véc tơ a cùng phương với véc tơ b .
⓶ Tìm tọa độ điểm M để véc tơ AM cùng phương với véc tơ b và có độ dài bằng 5 . Trang 103 Chương 01. LÊ MINH TÂM m n 1 Gọi M ;
m n , ta có AM m; n
1 cùng phương với b
m 2n 1 (1). 2 1
AM 5 m n 2 2 1 5 (2) 2 2
Thay (1) vào (2) ta có 4n 1 n 1 5 n 2 1 1 2
n 2n 0
n 0 m 2 M 2;0 .
n 2 m 2 M 2;2 Vậy M 2
;0 hoặc M2;2 thì AM cùng phương với b và có độ dài bằng 5 . Bài 54.
Trong mặt phẳng Oxy , cho ba điểm A ; x 3 , B 4
; 2,C3;5. Tìm x để A,B,C thẳng hàng. Lời giải
Ta có BA x 4;
1 , BC 7; 3 . x 4 1 7 5
A, B,C thẳng hàng BA và BC cùng phương b
x 4 x . 7 3 3 3 5 Vậy với x
thì ba điểm A, B,C thẳng hàng. 3 Bài 55.
Trong mặt phẳng Oxy , cho ba điểm A1; 1 , B 2 ;
1 ,C m 1; 2m 3 . Tìm m để ba điểm A, B,C thẳng hàng. Lời giải
Ta có AB 3;0 , AC m; 2m 2 .
Ba điểm A,B,C thẳng hàng khi và chỉ khi AB và AC cùng phương, khi và chỉ khi tồn tại m k. 1 3 k
một số thực k sao cho AC k AB 3 . 2
m 2 k 0 . m 1 Vậy với m 1
thì ba điểm A,B,C thẳng hàng. Bài 56. 1 1
Trong mặt phẳng Oxy , cho bốn điểm ( A 1 ;5),B 2; ,C(3; 1
), D ;3 . Chứng minh rằng: 2 3
⓵ D nằm trên đường thẳng AB .
⓶ B thuộc đoạn AC . Lời giải
⓵ D nằm trên đường thẳng AB . Trang 104 Chương 01. LÊ MINH TÂM 4 5 5 Ta có AD ; 2 , BD ; 3 3 2 4 2 Thấy 3
AD,BD cùng phương 5 5 3 2
D, A,B thẳng hàng hay D nằm trên đường thẳng AB .
⓶ B thuộc đoạn AC . 9 3 Ta có BA 3 ; , BC 1 ; 2 2 9 3 Ta có BA 3 ; 3 1; 3
BC BA, BC ngược hướng hay B thuộc đoạn AC . 2 2 Bài 57.
Trong mặt phẳng Oxy , cho ba điểm ( A 3 ; 4),B1; 1 ,C 9 ( ; 5 ) . Chứng minh rằng:
⓵ Chứng minh A,B,C thẳng hàng.
⓶ Tìm tọa độ D sao cho A là trung điểm BD .
⓷ Tìm tọa độ E trên trục Ox sao cho A,B,E thẳng hàng. Lời giải
⓵ Chứng minh A,B,C thẳng hàng.
Ta có AB 4; 3 , AC 12; 9 4 3
Véctơ AB, AC có
. Suy ra AB, AC cùng phương A, B,C thẳng hàng . 12 9
⓶ Tìm tọa độ D sao cho A là trung điểm BD . Gọi ( D x; y) 1 x 3 x 7
A là trung điểm BD 2 . Vậy ( D 7; 7) . 1 y y 7 4 2
⓷ Tìm tọa độ E trên trục Ox sao cho A,B,E thẳng hàng. Gọi (
E x; 0) Ox . Ta có AB 4; 3 , AE x 3; 4 7 x 3 4 7
A, B, E thẳng hàng AB, AE cùng phương
x . Vậy E ;0 . 4 3 3 3 Trang 105 Chương 01. LÊ MINH TÂM Bài 58.
Trong mặt phẳng Oxy , cho ba điểm ( A 1 ; 4),B 3 ; 2 , ( C 4 ; 2 ). Chứng minh rằng:
⓵ Chứng minh A,B,C là ba đỉnh một tam giác.
⓶ Tìm tọa độ D sao cho ABCD là hình bình hành. ⓷ Tìm tọa độ (
E x; 6) sao cho A, B, E thẳng hàng. Lời giải
⓵ Chứng minh A,B,C là ba đỉnh một tam giác.
Ta có AB 2; 6 , AC 3; 6 2 6
Véctơ AB, AC có
. Suy ra AB, AC không cùng phương A, B,C không thẳng 3 6
hàng suy ra A, B,C là ba đỉnh một tam giác.
⓶ Tìm tọa độ D sao cho ABCD là hình bình hành. Gọi (
D x; y), ta có AB 2; 6 , DC 4 x; 2 y 2 4 x x 2
ABCD là hình bình hành AB DC . Vậy ( D 2; 4) . 6 2 y y 4 ⓷ Tìm tọa độ (
E x; 6) sao cho A, B, E thẳng hàng.
Ta có AB 2; 6 , AE x 1; 2 x 1 2 1
A, B, E thẳng hàng AB, AE cùng phương x . 2 6 3 Bài 59.
Trong mặt phẳng Oxy , cho ba điểm A0; 4 ; B3; 2 , D3;0 .
⓵ Chứng minh rằng ba điểm A, B , C thẳng hàng, biết rằng C 6
3t ;8 2t, t .
⓶ Chứng minh rằng ba điểm A, B , D không thẳng hàng. Từ đó tính chu vi của ABC . Lời giải
⓵ Chứng minh rằng ba điểm A, B , C thẳng hàng, biết rằng C 6
3t ;8 2t, t .
Ta có AB 3; 2 và AC 6 3t; 4 2t .
Do đó AC 2 t AB nên ba điểm A, B , C thẳng hàng.
⓶ Chứng minh rằng ba điểm A, B , D không thẳng hàng. Từ đó tính chu vi của ABC .
Ta có AB 3; 2 và AD 3; 4 nên A, B , D không thẳng hàng. 2 2 2 2
AB x x y y
3 0 2 4 13 B A B A Trang 106 Chương 01. LÊ MINH TÂM 2 2
AD 3 0 0 4 5 2 2
BD 3 3 0 2 2
Vậy chu vi của tam giác ABC : C 7 13 . ABC Bài 60.
Trong mặt phẳng Oxy , cho hai điểm A2; 1 ; B6;
1 . Tìm điểm P khác B sao cho A, B , P thẳng hàng và PA 2 5 . Lời giải
Giả sử Px; y , ta có AP x 2; y
1 và AB 4; 2 x 2 y 1
Để A, B , P thẳng hàng thì x 2 2
y 2 x 2 y 4 1 4 2 2 2
Vì PA 2 5 x 2 y 1 20 2
Giải hệ tạo bởi hai phương trinh 1 và 2 x 6 x 2 y 4
x 2y 4 x 2 y 4 y 1 y 1 . 2 y 2 2 2 y 2 1 20 5
y 10y 15 0 x 2 y 3 y 3
Vì P khác B nên điểm phải tìm là P 2 ;3 . Bài 61.
Trong mặt phẳng Oxy , cho hai điểm A 1
; 4 ; B3;4. Tìm điểm P khác B sao cho A, B , P thẳng hàng và PA 3 5 . Lời giải
Giả sử Px; y , ta có AP x 1; y 4 và AB 4;8 x 1 y 4
Để A, B , P thẳng hàng thì
y 2x 2 1 4 8 2 2
Vì PA 3 5 x
1 y 4 45 2
Giải hệ tạo bởi hai phương trình 1 và 2 x 2 x 2 y 2x 2
y 2x 2 y 2 x 4 . x 2 2
1 2x 22 45 5
x 10x 40 0 x 4
y 2x 2 y 10
Vậy có hai điểm thỏa mãn đầu bài P 2; 2 ; P 4 ; 10 . 2 1 Trang 107 Chương 01. LÊ MINH TÂM Bài 62.
Trong mặt phẳng tọa độ Oxy , cho ba điểm A1; 1 , B3;
3 , C 2; 0 . Tính diện tích tam giác ABC .
Hãy tìm tất cả các điểm M trên trục Ox sao cho góc AMB nhỏ nhất. Lời giải
Ta có AB2; 2 , AC 1; 1 . AB AC 2 1 . 2. 1 0
Vậy tam giác ABC vuông tại A 1 1 S .A .
B AC . 2 2 . 1 (đvdt). ABC 2 2 2 2 1 2 2 2
Gọi M Ox Mx ;0 . Góc AMB nhỏ nhất 0
AMB 0 A, M,B thẳng hàng M x x y y x 1 1
AM cùng phương với AB M A M A M
x 0 M O. x x y y 3 1 3 1 M B A B A Bài 63.
Trong mặt phẳng tọa độ Oxy , cho ba điểm A1; 3 , B3; 1 , C 2; 4 .
⓵ Tính diện tích tam giác ABC .
⓶ Tìm tất cả các điểm MOx sao cho góc AMB nhỏ nhất. Lời giải
⓵ Tính diện tích tam giác ABC . Ta có AB2; 2 , AC 1; 1 .
AB AC 2.1 2.1 0
Vậy tam giác ABC vuông tại A 1 1 S .A . B AC . 2 (đvdt). ABC 22 2 2 2 . 1 1 2 2 2
⓶ Tìm tất cả các điểm MOx sao cho góc AMB nhỏ nhất.
Gọi M Ox Mx ;0 . Góc AMB nhỏ nhất M 0
AMB 0 A, M,B thẳng hàng x x y y x 1 3
AM cùng phương với AB M A M A M
x 4 M . M 4;0 x x y y 3 1 1 3 B A B A Bài 64.
Trong mặt phẳng tọa độ Oxy , tìm trên trục hoành Ox một điểm P sao cho tổng các khoảng cách từ
điểm P đến các điểm A và B là nhỏ nhất ( hay PA PB ). Biết rằng: min ⓵ A1; 1 , B2; 4 .
⓶ A1;2, B3;4. Lời giải ⓵ A1; 1 , B2; 4 . Trang 108 Chương 01. LÊ MINH TÂM
Dễ thấy A , B nằm hai phía đối với trục hoành. Gọi POx Px ;0 P
Ta có PA PB AB . Dấu '' '' xảy ra khi A,P,B thẳng hàng và PA cùng phương với x x y y x 1 p 1 6 6 AB P A P A
x P ;0. x x y y 2 1 4 1 P 5 5 B A B A
⓶ A1;2, B3;4.
Dễ thấy A , B nằm cùng một phía đối với trục hoành. Gọi POx Px ;0 P
Gọi A là điểm đối xứng của A qua Ox A1; 2 A B 2 10
Khi đó PA PA ; P Ox
PA PB PA PB A B
PA PB 2 10 1 .
1 xảy ra dấu '' '' khi P,A,B thẳng hàng P A BOx A B, A P cùng phương. Mà A B 2;6 x 1 p 2 5 5
x P ;0 . P A P x 1;2 2 6 3 3 P Bài 65.
Trong mặt phẳng Oxy, tìm trên đường thẳng d : x y 0 điểm M sao cho tổng các khoảng cách từ
M đến các điểm A và B là nhỏ nhất trong các trường hợp sau ⓵ A1; 1 , B 2 ; 4 . ⓶ A1; 1 , B3; 2 . Lời giải ⓵ A1; 1 , B 2 ; 4 .
Ta có PA,d.PB,d x y x y 2. 6 0. A A B B
Suy ra hai điểm A và B nằm khác phía so với đường thẳng . d 2 2
Ta có MA MB AB 2 1 4 1
34 (Bất đẳng thức tam giác).
Dấu “=” xảy ra A,B, M thẳng hàng hay M thuộc đường thẳng . AB
Đường thẳng AB đi qua A1; 1 và B 2 ; 4
nên có phương trình AB: 5x 3y 2 0.
Mặt khác, vì M thuộc đường thẳng d nên tọa độ điểm M thỏa mãn hệ 5
x 3y 2 0 1 1 M ; . x y 0 4 4 ⓶ A1; 1 , B3; 2 .
Ta có PA,d.PB,d x y x y 2 1 . 0. A A B B
Suy ra hai điểm A và B nằm cùng phía so với đường thẳng . d
Gọi A là điểm đối xứng của A qua . d Trang 109 Chương 01. LÊ MINH TÂM 1 .x 1 1 y 1 0
Khi đó tọa độ điểm Ax; y thỏa mãn hệ x 1 A y 1; 1 1 . 0 2 2 2 2
Ta có MA MB MA MB A B 3 1 2 1
17 (Bất đẳng thức tam giác).
Dấu “=” xảy ra A, M,B thẳng hàng hay M thuộc đường thẳng A . B
Đường thẳng A B đi qua A 1 ; 1 và B3; 2
nên có phương trình A B
: x 4y 5 0.
x 4y 5 0 5 5
Mặt khác, vì M thuộc đường thẳng d nên M thỏa M ; . x y 0 3 3 Bài 66.
Trong mặt phẳng Oxy, cho điểm M 4;
1 và hai điểm A ;
a 0 , B0; b với a,b 0 sao cho A, B, M
thẳng hàng. Xác định tọa độ điểm A, B sao cho
⓵ Diện tích tam giác OAB là nhỏ nhất S min . OAB
⓶ OAOB nhỏ nhất. ⓷ 1 1 nhỏ nhất. 2 2 OA OB Lời giải x y
Đường thẳng đi qua hai điểm A ;
a 0 và B0;b có dạng AB : 1. a b 4 1
Vì A, B, M thẳng hàng nên 1 (*). a b
⓵ Diện tích tam giác OAB là nhỏ nhất S min . OAB 1 1 Ta có S O . A OB a . b O AB 2 2 4 1 4
Theo bất đẳng thức Cauchy cho hai số thực dương, ta có (*) 1 ab 16. a b ab 1 Suy ra S 1 . 6 8. O AB 2 4 1 a 8
Dấu “=” xảy ra khi và chỉ khi a b
. Vậy A8;0 ,B0; 2. 4 1 b 2 1 a b
⓶ OAOB nhỏ nhất. 4b 4b 4 (*) a
OA OB a b b
b 1 5 9 (BĐT Cauchy). b 1 b 1 b 1 Trang 110 Chương 01. LÊ MINH TÂM 4b a a 6
Dấu “=” xảy ra khi và chỉ khi b 1
. Vậy A6;0 ,B0;3. 4 b 3 b 1 b 1 ⓷ 1 1 nhỏ nhất. 2 2 OA OB 1 1 4 1 1 1 1 1 1 1 Ta có 4 1 2 2 2 1 hay . 2 2 2 2 a
b a b a b 17 2 2 OA OB 17 4 1 17 a 17
Dấu “=” xảy ra khi và chỉ khi b a 4 . Vậy A ; 0 , B0;17. 4 1 4 1 b 17 a b Bài 67.
Trong mặt phẳng Oxy, cho điểm M 2;
1 và hai điểm A ;
a 0 , B0; b với a,b 0 sao cho A, B, M
thẳng hàng. Xác định tọa độ điểm A, B sao cho
⓵ Diện tích tam giác OAB là nhỏ nhất S min . OAB
⓶ OAOB nhỏ nhất. ⓷ 1 1 nhỏ nhất. 2 2 OA OB Lời giải x y
Đường thẳng đi qua hai điểm A ;
a 0 và B0;b có dạng AB : 1. a b 2 1
Vì A, B, M thẳng hàng nên 1 (*). a b
⓵ Diện tích tam giác OAB là nhỏ nhất S min . OAB 1 1 Ta có S O . A OB a . b O AB 2 2 2 1 2 2
Theo bất đẳng thức Cauchy cho hai số thực dương, ta có (*) 1 ab 8. a b ab 1 Suy ra S 8 . 4. O AB 2 2 1 a 4
Dấu “=” xảy ra khi và chỉ khi a b
. Vậy A4;0 ,B0; 2. 2 1 b 2 1 a b
⓶ OAOB nhỏ nhất. Trang 111 Chương 01. LÊ MINH TÂM 2b 2b 2 (*) a
OA OB a b b
b 1 3 2 2 3(BĐT Cauchy). b 1 b 1 b 1 2b a a 2 2
Dấu “=” xảy ra khi và chỉ khi b 1
. Vậy A 2 2;0,B0;1 2 . 2 b 1 2 b 1 b 1 ⓷ 1 1 nhỏ nhất. 2 2 OA OB 1 1 2 1 1 1 1 1 1 1 Ta có 2 1 2 2 2 1 hay . 2 2 2 2 a
b a b a b 5 2 2 OA OB 5 2 1 5 a 5
Dấu “=” xảy ra khi và chỉ khi b a
2 . Vậy A ; 0 , B0; 5. 2 1 2 1 b 5 a b
V. BÀI TẬP NÂNG CAO Bài 68.
Với a, b là các hằng số thỏa mãn điều kiện a 0,b 0 , tìm giá trị nhỏ nhất của hàm số: 2 2 2 2
y x 2ax 2a x 2bx 2b Lời giải
Gọi A, B là hai điểm có tọa độ : Ax a,a; Bx b,b
OA x a,a OA x a2 2 2 2
a x 2ax 2a Do đó: .
OB x b,b OB x b2 2 2 2
b x 2bx 2b 2 2 2 2
OA OB x 2ax 2a x 2bx 2b 2 2 2 2
x 2ax 2a x 2bx 2b nhỏ nhất khi O, A,B thẳng hàng tức: x a a
bx a ax b bx ab ax ab bx ax x 0 x b b Khi đó 2 2
y 2a 2b 2 a 2 b 2 b a . Bài 69.
Tìm giá trị nhỏ nhất của hàm số sau 2 2
y x x 1 x x 1 Lời giải 2 2 1 3 1 3 Ta có: 2 2
y x x 1 x x 1 x x 2 4 2 4 Trang 112 Chương 01. LÊ MINH TÂM 1 3 1 3
Gọi A, B là hai điểm có tọa độ: A x ,
; B x , 2 2 2 2 2 1 3 1 3 2
OA x ,
OA x x x 1 2 2 2 4 Do đó : 2 1 3 1 3 2
OB x ,
OB x x x 1 2 2 2 4 2 2
OA OB x x 1 x x 1 2 2
y x x 1 x x 1 nhỏ nhất khi O, A,B thẳng hàng tức: 1 3 1 x x 1 1 2 2 2 1
x x x 0 1 1 3 2 2 x x 2 2 2 Khi đó y 2. Bài 70.
Tìm giá trị nhỏ nhất của hàm số 2 2
y x 4x 8 x 2x 2 Lời giải 2 2 Ta có: 2 2
y x 4x 8 x 2x 2 y x 2 4 x 1 1 .
Gọi Ax2;2 ; Bx1; 1 .
OA x 2; 2OA x 22 2
4 x 4x 8 Do đó :
OB x 1;
1 OB x 2 2
1 1 x 2x 2 2 2
OA OB x 4x 8 x 2x 2 2 2
x 4x 8 x 2x 2 nhỏ nhất khi O , A,B x 1 x 2 2 thẳng hàng tức là x 4 . x 1 1
Khi đó: y 3 10 . Bài 71. với a,b
tìm giá trị nhỏ nhất của hàm số 2 2 2 2
y x 2ax 2a x 2bx 2b Lời giải 2 2 Ta có: 2 2 2 2
y x 2ax 2a x 2bx 2b 2 2 y x a a y b b . Trang 113 Chương 01. LÊ MINH TÂM
Gọi Ax a,a; Bx b,b
OA x a,a OA x a2 2 2 2
a x 2ax 2a Do đó :
OB x b,b OB x b2 2 2 2
b x 2bx 2b 2 2 2 2
OA OB x 2ax 2a x 2bx 2b 2 2 2 2
x 2ax 2a x 2bx 2b nhỏ nhất khi O, A,B thẳng hàng tức: x a a
bx a ax b bx ab ax ab bx ax x 0 x b b Khi đó 2 2
y 2a 2b 2 a 2 b 2 a b . Bài 72.
Tìm giá trị nhỏ nhất của biểu thức 2 2 2 2
P x y 2x 4y 5 x y 6x 4y 13 Lời giải Ta có: 2 2 2 2
P x y 2x 4y 5 x y 6x 4y 13
P x 2 y 2 x 2 y 2 1 2 3 2 . 2 2 Ta chứng minh: 2 2 2 2
a b c d a c b d 2 2 2 2 2 2 2 2 2 2 2 2
a b c d 2 a b . c d a b c d 2ac 2bd 2 2 2 2 a b
c d ac bd 2 2 2 2 2 2 2 2 2 a c a d b d b c ac bd 2 2 2 2 2 2 2 2 2 2 2 2
a c a d b d b c a c b d 2abcd
a d b c abcd a d abcd b c ad bc2 2 2 2 2 2 2 2 2 2 2 0 0 luôn đúng. 2 2 Từ đó ta có: 2 2 2 2
a b c d a c b d .
P x 2 y 2 x 2 y 2 1 2 3 2
x x2 y y2 1 3 2 2 16 4 P 4 , min Dấu “=” xảy ra x
1 2 y y 23 x y 23 x x
1 0 y 2 ; 1 x 3 . Trang 114 Chương 01. LÊ MINH TÂM Bài 73.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 2 y cos 2cos 2 cos 6cos 13 Lời giải 2 2
Ta có y 1 cos 1 3 cos 4 . u 1 cos ; 1 u 1cos 2 1 Xét 2 véctơ: . v 3 cos ; 2
v 3 cos 2 4
u v ; 2 2
4 3 u v 4 3 5 . 2 2
Lại có: u v u v 1 cos 1 3 cos 4 5 y 5 , min
Dấu “=” xảy ra u cùng phương v k
0 : u kv
cos k cos 1 cos 1 3 3 . 1 2 k 1 k 2 Bài 74.
Trong mặt phẳng , cho Oxy ba điểm A0;6 ,B2;5 , M2t 2;t . Tìm tọa độ điểm M sao cho:
⓵ MA MB
⓶ MA MB min max Lời giải
⓵ MA MB min
Theo bất đẳng thức Min – kow – ski:
MA MB t 2 t 2 t 2 t 2 t 2 t 2 ( t) t2 2 2 2 6 2 4 5 2 2 6 4 2 5
( t t) t t2 2 2 2 2 2 4 2 6 5 2 1 5 MA MB 2t 2 t 6 2 5
12t 14t 24 0 min 4 2t 5 t
Phương trình vô nghiệm không tồn tại t, hay không tồn tại M thỏa mãn yêu cầu bài toán.
⓶ MA MB max
Ta thấy Md : x 2y 2 0 Ta có: (0 2 6 . 2)(2 2 5
. 2) 60 0 . Suy ra A , B cùng phía so với d .
Phương trình đường thẳng AB : x 2y 12 0 Trang 115 Chương 01. LÊ MINH TÂM
Ta có: MA MB AB . Dấu “=” xảy ra M , A , B thẳng hàng M12;0
Vậy điểm M12;0 Bài 75.
Trong mặt phẳng Oxy, A1; 2 ,B2;5 , M2t 2;t . Tìm tọa độ điểm M sao cho :
⓵ MA MB
⓶ MA MB min max
⓷ MA MB ⓸ MA MB max min Lời giải
⓵ MA MB min
Ta có: Md,d : x 2y 2 0 . Nhận thấy A , B cùng phía so với d .
Lấy A đối xứng với A qua d AA d u n 2; AA : 2x y 4 0 . d AA 1
Gọi I là trung điểm AA I AAd I 2;0 A3; 2 .
MA MB MA MB A B . 8 1 MA MB
khi M, A', B thẳng hàng . Suy ra M ; . min 3 3
⓶ MA MB max
MA MB 2MI , I là trung điểm của AB.
Do đó: MA MB 2MI , max max
Không tồn tại điểm M như thế
⓷ MA MB max 2 2 2 MA MB
t t 2
t t 2 2 2 1 2 4 5
5t 5 5t 10t 25 t t 2 2 2 2 5 1 5 1 4
5 t 1 (t 1) 4 .
Xét các điểm A 0;1 ,B 1; 2 , M t;0 . 1 1 1
Khi đó: MA MB 5 M A M B . Do đó MA MB M A M B . 1 1 1 1 1 1 1 1 max max
Vì M chạy trên trục hoành và A ; B nằm về một phía của Ox 1 1 1 Nên M A M B
M A B Ox. 1 1 1 1 1 1 1 max u
A B 1;1 n
1; 1 A B : x y 1 0 A B 1 1 A B 1 1 1 1 1 1
M A B Ox M 1 ;0 t 1 M0; 1 . 1 1 1 1 Trang 116 Chương 01. LÊ MINH TÂM
⓸ MA MB min
Ta có MA MB 0 , dấu “=” xảy ra khi và chỉ khi MA MB
M thuộc đường trung trực của AB . Bài 76. 2 2 2 2
Cho a,b,c
. Chứng minh a c b a c b 2 2
2 a b . Lời giải
Gọi u a c;b,v a c;b.
Theo bất đẳng thức u v u v 2 2 2 2 2 2
Suy ra a c b a c b a c a c b b 2 2
2 a b (đpcm). Bài 77.
Cho a,b,c . Chứng minh 2 2 2 2
a 4b 6a 9 a 4b 2a 12b 10 5. Lời giải 2 2 2 2
Bất đẳng thức cần chứng minh a 3 2b 1 a 3 2b 5
Gọi u a 3;2b,v 1 ; a 3 2b.
Theo bất đẳng thức u v u v
a 2 b2 a2 b2 a a2 b b2 2 2 3 2 1 3 2 3 1 2 3 2 4 3 5
(điều phải chứng minh). Bài 78.
Cho a ,b ,c . Chứng minh: 2 2 2 2 2 2
a ab b a ac c b bc c Lời giải 2 2 b 3 b 3 2 2
u a ; b u a
b a ab b 2 2 2 2 Xét . 2 2 c 3 c 3 2 2
v a ;
c v a
c a ac c 2 2 2 2 b c 3
Và u v ; bc 2 2 Trang 117 Chương 01. LÊ MINH TÂM 2 2 b c 3 u v bc 2 2 b 2bc c 3 2 2
b 2bc c 2 2
b bc c . 2 2 4 4 Lại có: 2 2 2 2 2 2
u v u v a ab b a ac c b bc c ĐPCM. Bài 79.
Cho a ,b ,c . Chứng minh: 2 2 2 cos .
a cos b sin a b 2 2 2 4 4sin .
a sin b sin a b 2 Lời giải u
2cos .acosb;sinab Xét v
2sin .asinb;sinab u
2cos .acosb2 sinab2 2 2 2 4cos .
a cos b sin a b .
v 2sin .asinb2 sinab2 2 2 2 4sin .
a sin b sin a b
Và u v 2cos .acosb sin .asin b; 2sina b 2cosa b; 2sin a b
u v cosab2 sinab2 2 2 2
4cos a b 2
4sin a b 2
4cos a b 2
sin a b 2 . 1 Lại có: 2 2 2
u v u v cos .
a cos b sin a b 2 2 2 4 4sin .
a sin b sin a b 2 ĐPCM. Bài 80. 2 2
x xy y 3
Cho ba số dương x, y, z thỏa mãn điều kiện
. Chứng minh: xy yz zx 8. 2 2
y yz z 16 Lời giải Ta có: .
u v u . v .cosu,v u . v
1 . Đẳng thức xảy ra khi u và v cùng hướng. x x 3 3z z
Xét u y ; và v ; y . 2 2 2 2 Suy ra: z 3 x x 3 z 3 zx xz 3 . u v y y zy xy zy xy zx 2 2 2 2 2 2 2 2 2 Trang 118 Chương 01. LÊ MINH TÂM 2 2 x x 3 2 2 u y
x xy y 3 3 2 2 2 2 z 3 z 2 2 v y
z zy y 4 4 2 2 3
Thế (2), (3), (4) vào (1) ta được:
zy xy zx 4. 3 zyxyzx8 (ĐPCM). 2 Bài 81. Tìm GTNN của biểu thức 2 2
P x x 1 x x 1 , x . Lời giải 2 Ta có .
u v u . v .cosu,v u . v và u 2 u . 2 2 2
Nên u v u 2. . u v v 2 2
u 2. u v v 2
u v u v 2 u v u v 1 .
Đẳng thức xảy ra khi u và v cùng hướng. 1 3 1 3
Xét u x ;
và v x; 2 2 2 2
Ta có: u v 1 ; 3 u v 2 2 . 2 2 2 2 1 3 1 3 2 u x
x x 1 3 và 2 v x
x x 1 4 2 2 2 2
Thế (2), (3), (4) vào (1) ta được 2 2
x x 1 x x 1 2 hay P 2 . 1 3 x
Vậy GTNN của P bằng 2 khi u và v cùng hướng 2 2 x 0 . 1 3 x 2 2 Bài 82.
Cho x, y, z
là các số dương và x 3y 5z 3. Chứng minh: 4 4 2
3xy 625z 4 15yz x 4 5zx 81y 4 45 5xy . z Lời giải
Bất đẳng thức đã cho tương đương với 4 4 2
3xy 625z 4 15yz x 4 5zx 81y 4 45 5xyz Trang 119 Chương 01. LÊ MINH TÂM 2 2 2 3xy 5 . z 5z2 2 2 15 yzx x 5 z 3 x y 3y2 2 2 45xyz 5 5z x 3 y 2 2 2 5z2 2 2 x 3y2 2 2 3 5 5z x 3 y 2 2 2 2 2 2
Xét các vectơ u 5 z;
,v x; ,w 3y;
u v w x 3y 5z; . 5z x 3 y x 3y 5z
Ta có: u v w u v w 2 2 2 2 z2 2 x2 2 y2 2
x y z2 1 1 1 5 3 3 5 4. 5z x 3 y
x 3y 5z
Ta có x y z 1 1 1 1 1 1 9 3 5 9 .
x 3y 5z x 3y 5z
x 3y 5z 2 2 2 1 1 1 2 9
Khi đó x 3y 5z 4.
x 3y 5z 4. **
x 3y 5z
x 3y 5z 2 2 9
Mà x 3y 5z 2 9 . 18 1 ;
x 3y 5z 2 9 243 243 3.
27 2 (vì x 3y 5z 3). 2 2
x 3y 5z
x y z 3 3 5
Cộng theo vế các bất đẳng thức (1) và (2) ta được 2
x y z2 9 3 5 4.
18 27 45 * * *.
x 3y 5z 2 2 2 2 2 2 2 2
Từ , , ta suy ra 5z 2 x
3y 3 5(đúng) 5z x 3 y
Vậy có điều phải chứng minh. Bài 83.
Cho x, y . Chứng minh: 2 2 2 2
x 4 x 2x y 1 y 6y 10 5. Lời giải
Xét các vectơ u ;
x 2; v 1 ;
x y; w 1
;3 y u v w 0;5.
Khi đó ta luôn có: u v w u v w x
x2 y y2 2 2 2 2 2 2 2 1 3 1 0 5 5 Trang 120 Chương 01. LÊ MINH TÂM 2 2 2 2
x 4 x 2x y 1 y 6y 10 5
Ta có điều phải chứng minh. Bài 84. 1
x y1 xy 1
Cho x, y . Chứng minh: . 2 2 1 x 2 1 y 2 Lời giải Đặt u 2
x; x ; v 2 2 1 1 y ; 2y. 2
Ta có u x 2 x 2 2 2 1 1 x . Tương tự 2 v 1 y . Và 2 2
u v 2x 2xy 2y 2x y 2x y1 xy.
Ta lại có uv u v x y xy
2x y1 xy 1 1 1 2 1 x 2 1 y 2 2 1 x 2 1 y 2 Ta có đpcm.
Dấu " " xảy ra khi và chỉ khi u ; v cùng phương. Bài 85.
x, y,z 0 1 1 1 Nếu thì 2 2 2 x y z 82.
x y z 1 2 2 2 x y z Lời giải 1 1 1 Đặt u
x; 2 ; v y; 2 ; z z; 2 . x y z 2 1 1 Ta có 2 u x 2 x . 2 x x 1 1 Tương tự 2 2 v y ; z z . 2 2 y z 1 1 1
Và u v z x y z;3 2 x y z
Do x y z 1 1 1 1 1 1 9
9 x y z x y z x y z 1 1 1
Mà x y z 1 nên 9. x y z Trang 121 Chương 01. LÊ MINH TÂM
Ta lại có u v z u v z 1 1 1 x y z 9 1 3 22 2 2 2 2 82. 2 2 2 x y z Ta có đpcm. 1
Dấu " " xảy ra khi và chỉ khi u, v, z cùng hướng hay x y z . 3
--------------------HẾT-------------------- Trang 122 Chương 01. LÊ MINH TÂM BÀI 5
TỔNG ÔN TẬP CHƯƠNG
I. BÀI TẬP TỰ LUẬN. Bài 01.
Cho 4 điểm A , B , C , D . Rút gọn các tổng sau: AB BC CD , BA CB DC AD . Lời giải
Ta có AB BC CD AB BCCD AC CD AD.
Ta có: BA CB DC AD BA AD DC CB BD DB BB 0. Bài 02. Cho A
BC đều cạnh a trực tâm H . Tính độ dài các vec tơ AB , AB BC , AB BC CA , HA , AB AC . Lời giải
Ta có AB AB a .
AB BC AC AC a .
AB BC CA AC CA AA 0 0 . 2 2 a 3 a 3 HA AH AM . . 3 3 2 3
Dựng hình bình hành ABDC , khi đó theo quy tắc hình bình hành thì a AB AC 3
AD AB AC AD 2.AM 2.
a 3 . 2 Bài 03.
Cho hình vuông ABCD cạnh a tâm O . Tính độ dài các vec tơ AB AD , AB AD , AB AC ,
AB AD AC . Lời giải Trang 123 Chương 01. LÊ MINH TÂM
Ta có AB AD DB AB AD DB BD a 2 .
AB AD AC AB AD AC AC a 2 .
Dựng hình bình hành ABEC , khi đó AB AC AE 2 a a 5 2 2 2
AB AC AE 2. AB MB 2. a 2. a 5 2 2
AB AD AC AC AC 2 AC 2.AC 2a 2. Bài 04.
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Chứng minh
⓵ AC BA AD , AB AD AC .
⓶ Nếu AB AD CB CD thì ABCD là hình chữ nhật. Lời giải
⓵ AC BA AD , AB AD AC .
Ta có: VT AC BA BA AC BC.
Do đó: AC BA AD BC AD.
Do ABCD là hình bình hành nên BC AD .
Vậy suy ra điều phải chứng minh.
Theo quy tắc hình bình hành:
AB AD AC AB AD AC AC (đpcm).
⓶ Nếu AB AD CB CD thì ABCD là hình chữ nhật.
Nếu AB AD CB CD thì ABCD là hình chữ nhật.
Ta có AB AD CB CD AC DB AC BD.
Do đó ABCD là hình bình hành có hai đường chéo bằng nhau nên ABCD là hình chữ nhật. Bài 05.
Cho hai véc tơ a ; b . Trong trường hợp nào thì đẳng thức sau đây là đúng a b a b . Lời giải 2 2 2 2
Ta có a b a b a b a b a b a b 2 2 2 2
a 2a.b b a 2a.b b a.b 0 a b .
Vậy đẳng thức a b a b đúng khi a b . Trang 124 Chương 01. LÊ MINH TÂM Bài 06.
Cho hình bình hành ABCD gọi ;
E F; M và N lần lượt là trung điểm các cạnh A ;
B BC;CD và DA .
⓵ Chứng tỏ rằng 3 véctơ EF, AC, MN cùng phương và EF NM
⓶ Từ đó suy ra tứ giác EFMN là hình bình hành? Lời giải
⓵ Chứng tỏ rằng EF, AC,MN cùng phương và EF NM
Ta suy ra được FE//AC//MN nên EF, AC, MN cùng phương 1
EF MN AC 2
⓶ Từ đó suy ra tứ giác EFMN là hình bình hành?
Kết hợp với câu ⓵ suy ra EF NM .
EFMN là hình bình hành. Bài 07.
Cho hai hình bình hành ABCD và ABEF . Dựng EH và FG bằng AD . Chứng minh CDGH là hình bình hành Lời giải
Ta có : EH FG AD
Nên tứ giác EFGH là hình bình hành G
H // FE // AB // DC Suy ra :
GH FE AB DC
Hay tứ giác CDGH là hình bình hành. Bài 08.
Cho tam giác ABC có trung tuyến AM . Trên cạnh AC lấy điểm E và F sao cho AE EF FC ;
BE cắt AM tại N . Chứng minh NA MN . Lời giải
FM / /BE vì FM là đường trung bình của tam giác CEB .
Ta có EA EF .
Vậy EN là đường trung bình của tam giác AFM .
Suy ra N là trung điểm của AM .
Vậy NA MN . Trang 125 Chương 01. LÊ MINH TÂM Bài 09.
Cho hình bình hành ABCD . Hai điểm M và N lần lượt là trung điểm của BC và AD . Điểm I là
giao điểm của AM và BN , K là giao điểm của DM và CN . Chứng minh DK IB . Lời giải
Theo giả thiết M và N là trung điểm BC và AD 1 1 Nên AN
AD, BM BC . 2 2
Mà AD BC do ABCD là hình bình hành.
Suy ra ANMB là hình bình hành.
Ta có I là giao điểm của hai đường chéo AM và BN của hình bình hành ANMB Nên I là
trung điểm của BN .
Tương tự, ta cũng chứng minh được K là trung điểm của DM .
Từ đó dễ dàng chứng minh được DKIB là hình bình hành suy ra DK IB . Bài 10.
Cho tam giác ABC .
⓵ Xác định véc-tơ a AB BC .
⓶ Xác định véc-tơ b AB AC .
⓷ Xác định véc-tơ c AB AC . Lời giải Ta có:
⓵ Xác định véc-tơ a AB BC .
a AB BC AC
⓶ Xác định véc-tơ b AB AC .
b AB AC CB
⓷ Xác định véc-tơ c AB AC .
c AB AC AD ( ABDC là hình bình hành). Bài 11.
Cho hình bình hành ABCD , tâm O . Hãy xác định các vec-tơ sau đây.
⓵ x AB AD .
⓶ y AO CD.
⓷ z CD AC .
⓸ t OA BD . Lời giải Trang 126 Chương 01. LÊ MINH TÂM Ta có:
⓵ x AB AD .
x AB AD AC .
⓶ y AO CD.
y AO CD OC CD OD .
⓷ z CD AC .
z CD AC CD CA CE ( dựng hình bình hành CDEA ).
⓸ t OA BD .
t OA BD OA DB OAOF OH ( trong đó dựng OF DB và hình bình hành OFHA ). Bài 12.
Cho tam giác ABC đều, G là trọng tâm và M là trung điểm cạnh BC . Hãy xác định các vec-tơ sau đây:
⓵ GB GC .
⓶ AG CB.
⓷ AB MC .
⓸ AB GB GC . Lời giải
⓵ GB GC .
GB GC GK ( dựng hình bình hành GBKC ).
⓶ AG CB.
AG CB BF CB CF ( dựng BF AG ).
⓷ AB MC .
AB MC AB BM AM .
⓸ AB GB GC .
AB GB GC AB GK AB BF AF . Bài 12.
Cho đoạn thẳng AB có trung điểm là I . Gọi M là một điểm tùy ý không nằm trên đường thẳng
AB . Lấy trên tia MI một điểm N sao cho IN MI . Hãy xác định các vec-tơ
⓵ MA MB MI .
⓶ AM NI . Lời giải Trang 127 Chương 01. LÊ MINH TÂM
⓵ MA MB MI .
MA MB MI MN MI IN .
⓶ AM NI .
AM NI NI NB NK ( INBK là hình bình hành). Bài 13.
Cho hình bình hành ABCD có tâm O . Xác định các véc-tơ đối của véc- tơ sau đây:
⓵ OA,DO .
⓶ AC,DA . Lời giải
⓵ OA,DO O
A AO OC,DO OD BO
⓶ AC,DA .
AC CA,DA AD BC . Bài 14.
Cho hình bình hành ABCD có tâm O . Xác định các véc- tơ sau đây:
⓵ OAOBOC OD
⓷ AC BD BA DA
⓶ OA BO CO DO
⓸ OA CB OC AD Lời giải
⓵ OAOBOC OD
Do hình bình hành ABCD có tâm O OA OB OC OD 0
⓶ OA BO CO DO
OA BO CO DO CO OA BO DO CA
⓷ AC BD BA DA
AC BD BA DA BA AC BD DA AC BA BC
⓸ OA CB OC AD
OA OC CB AD 0 . Bài 15.
Cho tam giác ABC . Tìm véc- tơ x trong trường hợp: Trang 128 Chương 01. LÊ MINH TÂM
⓵ x BC AC BA.
⓶ AC x CB AB. Lời giải
⓵ x BC AC BA x AC CB BA x AB BA 0
⓶ AC x CB AB x CACB BA BA BA BE , với AE BA . Bài 16.
Cho tam giác ABC . Gọi M, N, P lần lượt là trung điểm BC, AC, AB . Xác định các véc-tơ sau đây:
⓵ PB MC NA .
⓶ BA PACM. Lời giải
⓵ PB MC NA AP PN NA 0
⓶ BA PACM BA NP PA BA NA ND( dựng thêm điểm D sao cho AD BA ). Bài 17.
Cho tam giác ABC . Gọi M là trung điểm AC và N là điểm đối xứng của B qua M . Xác định các véc- tơ sau đây:
⓵ AB AN .
⓶ BA CN .
⓷ AB MC MN .
⓸ BA BC MN . Lời giải
Ta có, tứ giác BANC là hình bình hành .
⓵ AB AN AC ( tính chất hình bình hành BANC )
⓶ BA CN BE ( dựng AE CN )
⓷ AB MC MN AB AM MN AB AN AC
⓸ BA BC MN BN NM BM. Bài 18.
Cho hình lục giác ABCDEF . Gọi M, N, P,Q, R,S lần lượt là trung điểm AB, BC,CD, DE, EF, FA . Xác
định các véc-tơ sau đây:
⓵ AD BECF AE BF CD.
⓶ MQ RN PS . Lời giải
⓵ AD BECF AE BF CD ED FE DF 0 .
⓶ MQ RN PS BD FB DF 0 . Bài 19. Trang 129 Chương 01. LÊ MINH TÂM 1 1 1
Cho tam giác ABC . Gọi D, E, F lần lượt nằm trên cạnh BD BC,CE CA,AF AB . Xác định các 3 3 3 véc-tơ sau đây:
⓵ AF BDCE.
⓶ AF BDCE. Lời giải
⓵ AF BDCE.
Lấy thêm các điểm P,Q về phía ngoài cạnh AB, AC sao cho CE AP,QA AF .
Theo đó, tam giác APQ đồng dạng tam giác ACB
Nên ta có PQ BD . Khi đó, AF BD CE QA PQ AP 0
⓶ AF BDCE.
AD BE CF AE BF CD CB AF AC BDCE AFBACB AC 0 Bài 20.
Cho tam giác ABC , trên cạnh ABC lấy M sao cho BM 3CM , trên đoạn AM lấy N sao cho
2AN 5MN . G là trọng tâm tam giác ABC .
⓵ Phân tích các véc-tơ AM; BN qua các véc-tơ A ; B AC
⓶ Phân tích các véc-tơGC; MN qua các véc-tơ GA và GB Lời giải
⓵ Phân tích các véc-tơ AM; BN qua các véc-tơ A ; B AC 3 5
Theo giả thiết BM BC và AN AM 4 7 Suy ra: 3 3 1 3
AM AB BM AB BC AB AC AB AB AC 4 4 4 4 5
BN BA AN AB 5 1 3 23 15 AM AB AB AC AB AC . 7 7 4 4 28 28
⓶ Phân tích các véc-tơ GC; MN qua các véc-tơ GA và GB
Vì G là trọng tâm tam giác ABC nên GA GB GC 0 . Suy ra GC G A GB . 2 2 1 3
Ta có MN AM AB AC 7 7 4 4 1 GBGA 3 GCGA 1 GBGA 3
GAGBGA 1 1 GA GB. 14 14 14 14 2 7 Trang 130 Chương 01. LÊ MINH TÂM Bài 21.
Cho ABC . Đặt a AB , b AC . ⓵ 1
Hãy dựng các điểm M , N thỏa mãn AM AB , CN 2BC . 3
⓶ Hãy phân tích CM , AN , MN theo các vec tơ a , b . Lời giải ⓵ 1
Dựng các điểm M , N thỏa mãn AM AB , CN 2BC . 3 1 1
Vì AM AB nên M thuộc cạnh AB và AM AB . 3 3
Vì CN 2BC nên N thuộc tia BC và CN 2BC .
⓶ Phân tích CM , AN , MN theo các vec tơ a , b . 1 1
Ta có CM CA AM AC AB a b . 3 3
Và AN AB BN AB 3BC AB 3AC AB 2 a 3b . 1 7
Tương tự MN MA AN a 2a 3b a 3b . 3 3 Bài 22.
Cho ABC có trung tuyến AM , M là trung điểm của BC . Hãy biểu diễn AM theo AB , AC . Lời giải 1
M là trung điểm của BC nên AM AB AC . 2 Bài 23.
Cho hình bình hành ABCD có E là trung điểm của CD . Hãy biểu diễn AE theo u AD , v AB . Lời giải
Do hình bình hành ABCD nên AC AB AD .
Do E là trung điểm của CD nên AC AD 2AE . 1 1
Từ đó suy ra AB 2AD 2AE AE AD AB u v . 2 2 Bài 24.
Gọi G là trọng tâm của ABC . Hãy biểu diễn AB , GC , BC , CA theo a GA , b GB . Lời giải Trang 131 Chương 01. LÊ MINH TÂM
Ta có AB GB GA b a .
Vì GA GBGC 0 GC G
AGB a b .
Ta có BC GC GB a
bb a 2b.
Và CA GA GC a a b 2a b . Bài 25.
Cho ABC . Điểm M trên cạnh BC sao cho MB 2MC . Hãy phân tích AM theo hai vec tơ u AB , v AC . Lời giải 2 2 1 2
Ta có AM AB BM AB BC AB AC AB AB AC . 3 3 3 3 Bài 26.
Cho ABC . Điểm M trung điểm AB và N là một điểm trên cạnh AC sao cho NA 2NC . Gọi K là
trung điểm MN . Phân tích vec tơ AK theo các vec tơ AB và AC . Lời giải 1 1 1 2 1 1
Ta có AK AM AN AB AC AB AC . 2 2 2 3 4 3 Bài 27.
Cho tam giác OAB. Gọi M, N lần lượt là trung điểm của cạnh OA, OB . Tìm các số m,n của mỗi
đẳng thức OM mOA nOB , MN mOA nOB , MB mOA nOB . Lời giải 1 1 1
Ta có OM OA OA 0.OB , nên m , n 0 . 2 2 2 1 1 1 1
Và MN ON OM OA OB, nên m , n . 2 2 2 2 1 1
Ta có MB OB OM OA 1.OB , nên m , n 1. 2 2 Bài 28.
Một đường thẳng cắt cạnh DA, DC và đường chéo DB của hình bình hành ABCD lần lượt tại các
điểm E, F và M . Biết rằng DE mDA , DF nDC ,
m n 0 . Hãy biểu diễn DM qua DB và m,n. Lời giải
Đặt DM xDB , EM yFM thì DM xDA xDC .
Do đó EM DM DE xDA xDC mDA x m DA xDC . Trang 132 Chương 01. LÊ MINH TÂM
Và FM DM DF xDA x n DC .
Ta có EM yFM x m DA xDC xyDA y x n DC .
x m xy
Do DA và DC không cùng phương nên . x y
xn xy yn m mn mn
Giải hệ trên ta được y và x DM DB . n m n m n Bài 29.
Điểm M được gọi là điểm chia đoạn thẳng AB theo tỉ số k 1 nếu MA kMB . Chứng minh rằng OA kOB
với mọi điểm O thì OM 1 . k Lời giải
Ta có MA kMB OA OM k OBOM 1 kOM OA kOB . OA kOB
Vì k 1 nên OM 1 . k Bài 30. 1
Gọi I là trung điểm của đoạn AB . Chứng minh với điểm O bất kỳ ta có OI OA OB. 2 Lời giải OI
OA AI 1 Ta có
2OI OA OB AI BI OAOB OI OAOB. 2
OI OB BI Bài 31.
Cho đoạn AB và điểm I sao cho 2IA 3IB 0 .
⓵ Tìm số k mà AI kAB. ⓶ 2 3
Chứng minh với mọi điểm M thì có MI MA MB . 5 5 Lời giải
⓵ Tìm số k mà AI kAB.
IA IB IA AB AI 3 3 2 3 0 2 3
0 AI AB k . 5 5 ⓶ 2 3
Chứng minh với mọi điểm M thì có MI MA MB . 5 5
IA IB MA MI MB MI 2 3 2 3 0 2 3
0 2MA 3MB 5MI 0 MI MA MB . 5 5 Trang 133 Chương 01. LÊ MINH TÂM Bài 32.
Cho tam giác ABC . Gọi H là điểm đối xứng với B qua G với G là trọng tâm tam giác ABC . Chứng minh rằng ⓵ 2 1 1 1 AH
AC AB và CH AB AC . 3 3 3 3 ⓶ 1 5 MH
AC AB , với M là trung điểm của BC . 6 6 Lời giải ⓵ 2 1 1 1 AH
AC AB và CH AB AC . 3 3 3 3 2
AH AG AB ACAB 2 1 2
AB AC AB Ta có 3 3 3 . 1 1 CH
AH AC AB AC 3 3 ⓶ 1 5 MH
AC AB , với M là trung điểm của BC . 6 6 1 1 5
Ta có MH AH ABCH AC AB. 2 6 6 Bài 33.
Cho tam giác ABC có trọng tậm G. Chứng minh
⓵ Với mọi điểm M thì MA MB MC 3MG .
⓶ Nếu MA MB MC 0 thì M là trọng tâm G . Lời giải
⓵ Với mọi điểm M thì MA MB MC 3MG .
Ta có MA MB MC
MG GAMG GBMG GC 3MG GAGBGC 3MG0 3MG
⓶ Nếu MA MB MC 0 thì M là trọng tâm G .
Áp dụng câu ⓵ ta có MA MB MC 0 3MG 0 MG 0 M G Bài 34.
Cho tam giác ABC có ba trung tuyến AM ; BN ;CP . Chứng minh AM BN CP 0 . Lời giải Cách 1
Vì M, N, P là trung điểm 3 cạnh nên AM BN CP Trang 134 Chương 01. LÊ MINH TÂM 1 1 1 1 AB AC 1
BC BA 1
CACB AB BA AC CA BC CB 0 2 2 2 2 2 2 Cách 2 3
Gọi G là trọng tâm tam giác ABC thì AM BN CP GA GBGC 0 2 Bài 35.
Cho tứ giác ABCD . Gọi I , J lần lượt là trung điểm của AB và CD,O là trung điểm của IJ . Chứng minh rằng
⓵ AC BD 2IJ .
⓶ OAOBOC OD 0.
⓷ MA MB MC MD 4MO với M là điểm bất kỳ. Lời giải
⓵ AC BD 2IJ .
Theo quy tắc ba điểm ta có AC AI IC AI IJ JC
Tương tự BD BI IJ JD
Mà I, J lần lượt là trung điểm của AB và CD nên AI BI 0 , JC JD 0 .
Vậy AC BD AI BIJC JD 2IJ 2IJ (đpcm).
⓶ OAOBOC OD 0.
Theo hệ thức trung điểm ta có OA OB 2OI , OC OD 2OJ .
Mặt khác O là trung điểm IJ nên OI OJ 0 .
Suy ra OA OB OC OD 2OI OJ 0 (đpcm).
⓷ MA MB MC MD 4MO với M là điểm bất kỳ.
Theo câu ⓶ ta có OAOBOC OD 0
Do đó với mọi điểm M thì OAOBOC OD 0
OM MAOM MBOM MCOM MD 0
MA MB MC MD 4MO (đpcm). Bài 36.
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Chứng minh
⓵ Với điểm M bất kì ta có MA MB MC MD 4MO
⓶ Chứng minh AB 2AC AD 3AC Trang 135 Chương 01. LÊ MINH TÂM Lời giải
⓵ Với điểm M bất kì ta có MA MB MC MD 4MO
MA MC 2MO
Vì O là trung điểm của AC ; BD nên
MB MD 2MO
Vậy MA MB MC MD 4MO
⓶ Chứng minh AB 2AC AD 3AC
Vì ABCD là hình bình hành nên AB AD AC
Do đó AB 2AC AD AC AD 2AC AC 2AC 3AC Bài 37.
Chứng minh rằng nếu hai hình bình hành ABCD và A B C D có cùng tâm thì
AA BB CC DD 0 . Lời giải
Gọi O là tâm của hình bình hành. Ta có:
AA BB CC DD OAOA OBOB OCOC ODOD
OAOCOBODOAOCOBOD 0 Bài 38.
Cho hình bình hành ABCD và M là điểm tùy ý. Chứng minh:
MA MB MD MC Lời giải
Ta có: MA MB BA, MD MC CD . Mà tứ giác ABCD là hình bình hành nên BA CD
Do đó ta có điều phải chứng minh. Bài 39.
Cho hình bình hành ABCD . Chứng minh rằng với điểm M bất kì ta luôn có
MA MC MB MD Lời giải
Ta có: MA MC MB MD MA MBMC MD 0 BA DC 0 .
(Luôn đúng do tứ giác ABCD là hình bình hành)
Do đó ta có điều phải chứng minh. Bài 40. Trang 136 Chương 01. LÊ MINH TÂM
Cho tam giác ABC . Gọi M, N, P lần lượt là trung điểm của các cạnh BC,CA, AB . Chứng minh rằng
với điểm O bất kì ta luôn có
OA OB OC OM ON OP Lời giải
Ta có: OA OBOC OM ON OP
OAOMOBONOC OP 0
MA NB PC 0 AM BN CP 0
AM AC CM
Mặt khác BN BA AN CP CB BP
AM BN CP AC CB BACM BP AN CM BP AN BP MN Lại có
AM BN CP CM MN NC 0 AN NC
Do đó ta có điều phải chứng minh. Bài 41.
Cho hình bình hành ABCD và A B C D
. Chứng minh rằng : B B
CC D D 0 Lời giải B B
AB AB Ta có CC
AC AC B B
CC D D
AB AD ACAB AD AC 0 D D AD AD Bài 42.
Cho hình bình hành ABCD . Gọi E và F lần lượt là trung điểm của hai cạnh AB và CD . Nối AF và
CE , hai đường thẳng này cắt đường chéo BD lần lượt tại M và N . Chứng minh rằng:
DM MN NB . Lời giải
Gọi I là giao điểm của AC và BD
Dễ thấy I là trung điểm của MN
Dễ thấy M là trọng tâm của A
DC DM 2MI
N là trọng tâm của A
BC BN 2NI DM MN NB DM MN NB . Bài 43. Trang 137 Chương 01. LÊ MINH TÂM
Cho ngũ giác đều ABCDE tâm O . Chứng minh rằng OAOBOC ODOE 0 . Lời giải
Các điểm B,E đối xứng với nhau qua OA OB OE có giá là đường thẳng OA.
Các điểm D,C đối xứng với nhau qua OA OC O D có giá là đường thẳng OA.
u OAOBOC ODOE có giá là đường thẳng OA
Tương tự các vectơ OAOC,OD OE có giá là đường thẳng OB .
Vectơ u OAOBOC ODOE có gi á là đường thẳng OB.
Do OA và OB có giá không trùng nhau u 0 Bài 44.
Cho hình chữ nhật ABCD tâm O , AB 2a , AD a , M là trung điểm CD .
⓵ Chứng minh AB AD CB CD .
⓶Tính BD OM . Lời giải
⓵ Chứng minh AB AD CB CD .
AB AD DB Ta có
AB AD CB CD . C
B CD DB
⓶Tính BD OM .
Dựng điểm E sao cho OEMD là hình bình hành. Khi đó
BD OM BD DE BE . 2 2 9a 25a a Ta có 2 2 2 2
BE AB AE 4a 5
BD OM BE BE 4 4 2 Bài 45.
Cho hình bình hành ABCD , I là trung điểm BC . Tìm điểm M thoả mãn: BC MD BI CA Lời giải
Ta có sự tương đương sau:
BC MD BI CA BC CA MD BI
BA MD BI BA BI MD 0 IA DM .
Vậy M là điểm sao cho MDIA là hình bình hành. Trang 138 Chương 01. LÊ MINH TÂM Bài 46.
Cho tam giác ABC . Về phía ngoài tam giác vẽ các hình bình hành ABCD, BCPQ, CARS . Chứng minh rằng
RJ IQ PS 0. Lời giải Ta có
RJ IQ PS
RA AJ IB BQ PC CS
RACSAJ IBBQ PC 0.
Vậy ta có điều phải chứng minh. Bài 47.
Cho tam giác ABC . Gọi A , A , A lần lượt là trung điểm các cạnh BC,CA, AB . Chứng minh 1 2 3
AA BB CC 0 . 1 1 1 Lời giải Ta có
AA BB CC AC C A BA A B CB B C 1 1 1
1 1 1 1 1 1 1 1 1
AC A B BA BC CB C A 000 0. 1 1 1 1 1 1 1 1 1 Bài 48.
Cho ABC . Gọi A là điểm đối xứng với B qua A , gọi B là điểm đối xứng với C qua B , gọi C là
điểm đối xứng với A qua C . Chứng minh rằng với một điểm O bất kì ta có
OA OB OC OA OB OC Lời giải
Ta có: OAOBOC OA A A
OB B B
OCC C
OAOBOC A A B B C C
OAOBOC AB BC CA
OAOBOC 0 OAOBOC Trang 139 Chương 01. LÊ MINH TÂM Bài 49.
Cho bảy điểm A, ,
B C, D, ,
E F, H . Chứng minh:
AB CD EF HA CB ED HF Lời giải Ta có:
AB CD EF HA CB ED HF
AB CDCBEF EDHA HF
AB BD DF FA AB BF FA AF FA 0
Vậy ABCD EF HA CB ED HF . Bài 50. 1 1 2
Cho tam giác ABC . Điểm I trên cạnh AC sao cho CI CA , J là điểm mà BJ AC AB . 4 2 3 ⓵ 3 Chứng minh BI AC AB.
⓶ Chứng minh B,I, J thẳng hàng 4
Lời giải ⓵ 3 Chứng minh BI AC AB 4 3
BI BA AI AB AC 4
⓶ Chứng minh B,I, J thẳng hàng 2 1 2 2 3 BI AB
AC AB AC 3 3 4 3 2 2
Vậy BJ BI . Suy ra ba điểm B, I, J thẳng hàng 3 Bài 52.
Cho tam giác ABC có trung tuyến AM . Gọi I là trung điểm của AM và K là điểm trên cạnh AC sao cho 1
AK AC. Chứng minh ba điểm B, I,K thẳng hàng. 3
Lời giải
Đặt u B ;
A v BC , ta có: 1 1
BK BA AK u AC u BC BA 1
u v u 2 1 u v 3 3 3 3 2 1 1 1 1 1
Và BI BA BM
u v u v 2 2 2 2 2 Trang 140 Chương 01. LÊ MINH TÂM 4
Do đó 3BK 4BI nên BK
BI Vậy ba điểm B, I,K thẳng hàng. 3 Bài 54. Cho tam giác AB .
C Hai điểm M, N được xác định bởi các hệ thức BC MA 0, AB NA 3AC 0. Chứng minh MN // A . C
Lời giải
Ta có: BC MA AB NA3AC 0 0 0
hay AB BC MA AN 3AC 0 AC MN 3AC 0 MN 2AC
Do đó MN cùng phương với AC.
Mà M không thuộc đường thẳng AC nên MN // A . C Bài 55. Cho tam giác AB . C
⓵ Chứng minh rằng tồn tại duy nhất một điểm I thoả 2IA3IB4IC 0.
⓶ Tìm quỹ tích điểm thoả mãn 2MA 3MB 4MC MB MA .
Lời giải
⓵ Chứng minh rằng tồn tại duy nhất một điểm I thoả 2IA3IB4IC 0.
Ta có 2IA3IB 4IC 0
IA IA AB IA AC 3AB 4AC 2 3 4
0 9IA 3AB 4AC 0 IA 9
Suy ra I tồn tại và duy nhất.
⓶ Tìm quỹ tích điểm thoả mãn 2MA 3MB 4MC MB MA .
Với I là điểm được xác định ở câu ⓵, ta có
2MA 3MB 4MC 9MI 2IA 3IB 4IC 9MI AB
Và MB MA AB nên 2MA 3MB 4MC MB MA 9MI AB MI . 9 AB
Vậy quỹ tích của M là đường tròn tâm I bán kính . 9 Bài 56. Cho AB .
C Tập hợp điểm M trong các trường hợp sau:
⓵ 2MA 3MB 3MB 2MC . Trang 141 Chương 01. LÊ MINH TÂM
⓶ 4MA MB MC 2MA MB MC
Lời giải
⓵ 2MA 3MB 3MB 2MC .
Gọi K là điểm thoả 2KA 3KB 0, L là điểm thoả mãn 3LB 2LC 0.
Ta có: 2MA 3MB 3MB 2MC MK ML .
Tập hợp điểm M là đường trung trực của đoạn . KL
⓶ 4MA MB MC 2MA MB MC
Với I là trung điểm . BC
Gọi J là điểm thoả 4JA JB JC 0. Ta có:
4MA MB MC 2MA MB MC 6MJ 2MA 1
2MI 6MJ 2IA MJ I . A 3 1
Tập hợp điểm M là đường tròn tâm J bán kính R I . A 3 Bài 57. Cho tam giác AB .
C Tìm tập hợp các điểm M trong mỗi trường hợp sau:
⓵ MA MB
⓶ MA MB MC 0.
⓷ MA MB MA MC .
Lời giải
⓵ MA MB
Ta có: MA MB MA MB 0 B A trái với giả thiết.
Vậy không có điểm M thoả mãn.
⓶ MA MB MC 0.
Ta có MA MB MC 0 M là trọng tâm tam giác AB . C
⓷ MA MB MA MC .
Gọi I , J lần lượt là trung điểm của AB, AC ta được: MA MB 2MI; MA MC 2MJ
Nên MA MB MA MC MI MJ MI MJ
Như vậy M cách đều 2 điểm cố định I , J Trang 142 Chương 01. LÊ MINH TÂM
Nên tập hợp các điểm M thoả điều kiện bài toán là đường trung trực của IJ. Bài 58.
Cho hai lực F , F đều có cường độ là 40 N , có điểm đặt tại O và hợp với nhau một góc 60 . Tính 1 2
cường độ lực tổng hợp của hai lực này. Lời giải
Theo quy tắc hình bình hành thì F F OR . 1 2
Mà OF OF 40 N 1 2
Nên OF RF là hình thoi có góc FOF 60 và hai đường 1 2 1 2
chéo RO, F F vuông góc với nhau tại trung điểm H . 1 2 3 Ta có OH 40
20 3 (OH là đường cao của tam 2
giác đều cạnh bằng 40 )
Vậy cường độ lực tổng hợp của hai lực đã cho là F F OR 40 3 N . 1 2 Bài 59.
Cho hai lực F , F lầ lượt có cường độ là 30 N và 40 N , có điểm đặt tại O và vuông góc với nhau. Tính 1 2
cường độ lực tổng hợp của chúng. Lời giải
Do hai lực F ,F có cùng điểm đặt O 1 2
Nên tổng hợp lực F F là đường chéo OR của hình bình 1 2 hành OF RF . 1 2
Do hai lực F ,F vuông góc với nhau 1 2
Nên hình bình hành OF RF trở thành hình chữ nhật. 1 2
Vậy F F OR . 1 2
Ta có OF 30,OF 40 . 1 2 Như vậy 2 2
OR F F 40 30 50 . 1 2
Do đó cường độ lực tổng hợp OR là 2 2
F F 40 30 50 N . 1 2 Bài 60. 1 3
Viết tọa độ của các vectơ sau: a 2i 3j ; b i 5j ; c 3i ; d i j ; e 4 j 3 2
Lời giải
a 2i 3j a 2; 3. Trang 143 Chương 01. LÊ MINH TÂM 1 1
b i 5j b ; 5 . 3 3
c 3i c 3; 0. 3 3 d i j d 1 ; . 2 2 e 4
j e 0; 4 . Bài 61.
Viết dưới dạng u xi yj khi biết tọa độ của vectơ u 2; 3;u 1
; 4; u 2;0; u 0; 1
Lời giải
u 2; 3 u 2i 3j
u 1; 4 u i 4j
u 2;0 u 2i u 0;
1 u j Bài 62.
Cho a 1; 2 ,b 0;3 . Tìm tọa độ của các vectơ sau:
⓵ x a b ; y a b ⓶ 1
u 3a 2b ; v 2a b ; w 4a b 2
Lời giải
⓵ x a b ; y a b
x a b 1 0; 2 3 1; 1
y a b 1 0; 2 3 1; 5 ⓶ 1
u 3a 2b ; v 2a b ; w 4a b 2
u 3a 2b 3 1 . 2.0; 3. 2 2 3 . 3; 12 .
v 2a b 2.1 0; 2.2 3 2; 1 . 1 1 1 19
w 4a b 4 1 . 0 . ; 4. 2 3 . 4 ; . 2 2 2 2 Trang 144 Chương 01. LÊ MINH TÂM Bài 63. 1
Cho a 2; 0 ,b 1
; ,c 4; 6 . 2
⓵ Tìm tọa độ của d 2a 3b 5c . ⓶ Tìm ,
m n sao cho: ma b nc 0
⓷ Biểu diễn vectơ c theo a ;b .
Lời giải
⓵ Tìm tọa độ của d 2a 3b 5c . 1 3 6 d 2 2 . 3. 1 5 4 . ; 2 0 . 3. 5. 6 20 ; . 2 2 ⓶ Tìm ,
m n sao cho: ma b nc 0 1 . m 2 1 . n 4 0 m
ma b nc 0 3 1 . . m 0 . n 6 0 1 2 n 12
⓷ Biểu diễn vectơ c theo a ;b . .
m 2 n 1 4 m 4
Giả sử c ma nb
c 4a 12 1 b .
m 0 n 6 n 12 2 Bài 64.
Cho 4 điểm A1; 1 , B2;
1 , C 4;3 , D16;3 . Hãy biểu diễn AD theo các vectơ AB, AC .
Lời giải
Ta có AB 1; 2 , AC 3; 2 , AD 15; 2 . m 1 . n 3 . 15 m 3
Giả sử AD mAB nAC . m 2 n 2 . 2 n 4
Vậy AD 3AB 4AC . Bài 65.
Chứng minh ba điểm A 1 ;
1 , B1;3 ,C 2 ;0 thẳng hàng.
Lời giải
Ta có AB 2; 2 , AC 1;
1 AB 2AC .
AB và AC cùng phương hay ba điểm A,B,C thẳng hàng. Trang 145 Chương 01. LÊ MINH TÂM Bài 66.
Tìm m để 2 vectơ a 2 ; m 3 m 1 và b 4 ; 8 cùng phương.
Lời giải 2 m 3 m 1
a và b cùng phương khi và chỉ khi
4 m 3 m 1 m 1 4 8 . Bài 67.
Tìm m để 3 điểm A1;
1 , B3; 2 ,C m 4; 2m 1 thẳng hàng.
Lời giải AB 2;
1 , AC m 3; 2m .
Yêu cầu bài toán tương đương k : AC kABk 0 . 3 m m 3 2k 5
m 3; 2m k 2; 1 . 2m k 6 k 5 3 6
Vậy m thì AC AB hay 3 điểm A,B,C thẳng hàng. 5 5 Bài 68.
Cho hai điểm A3; 5 ,B1;0.
⓵ Tìm toạ độ điểm C thoả mãn OC 3 AB.
⓶ Tìm điểm D đối xứng với A qua C .
⓷ Tìm điểm M trên trục Ox , sao cho A,B,M thẳng hàng.
⓸ Tìm điểm N trên Oy sao cho ABNO là hình thang có cạnh đáy AO
Lời giải
⓵ Tìm toạ độ điểm C thoả mãn OC 3 AB.
Gọi C x; y
Ta có: OC x; y , AB 2;5 x 6 Khi đó: OC 3
AB x; y 32;5 C 6;15 . y 15
⓶ Tìm điểm D đối xứng với A qua C .
Gọi Dx; y Trang 146 Chương 01. LÊ MINH TÂM
Ta có: AD x 3; y 5 , AC 3; 10 x 9
Khi đó: AD 2AC x 3; y 5 23; 1 0 D9; 2 5 y 25
⓷ Tìm điểm M trên trục Ox , sao cho A,B,M thẳng hàng.
Vì MOx nên M x;0
x 3 .k 2 k 1
Để A,B, M thẳng hàng thì k k 0
: AM kAB M 1;0 5 k 5 . x 1
⓸ Tìm điểm N trên Oy sao cho ABNO là hình thang có cạnh đáy AO
Vì N Oy nên N 0; y ,
Để ABNO là hình thang có cạnh đáy AO 1 k tm 1 k. 3 5 Thì 3 k
k 0 : BN k.AO N 0 ; . y k 5 . 5 3 y 3 Bài 69. Cho ba điểm A1; 2
,B0;4,C3;2.
⓵ Tìm toạ độ điểm M thoả mãn CM 2AB3AC .
⓶ Tìm toạ độ điểm N thoả mãn AN 2BN 4CN 0 .
Lời giải
⓵ Tìm toạ độ điểm M thoả mãn CM 2AB3AC .
Đặt Mx; y
Ta có CM 2AB3AC x 5
x 3; y 2 2 1 ;632;4 M 5 ; 2 y 2
⓶ Tìm toạ độ điểm N thoả mãn AN 2BN 4CN 0 .
Đặt N x; y, từ AN 2BN 4CN 0 x 1
Suy ra: x 1; y 2 2 ;
x y 4 4x 3; y 2 0;0 N 1 ; 2 y 2 Bài 70. Cho ba điểm A1; 2
,B2;3,C 1 ; 2 .
⓵ Chứng minh ba điểm A,B,C không thẳng hàng . Trang 147 Chương 01. LÊ MINH TÂM
⓶ Tìm toạ độ điểm E , sao cho ABEC là hình bình hành.
⓷ Tìm toạ độ trọng tâm G của tam giác ABC .
Lời giải
⓵ Chứng minh ba điểm A,B,C không thẳng hàng .
AB 1;5 , AC 2; 0 .
Ta có: AB , AC không cùng phương nên A, B,C không thẳng hàng .
⓶ Tìm toạ độ điểm E , sao cho ABEC là hình bình hành. Đặt E ; x y .
Do A, B,C không thẳng hàng
Nên ABEC là hình bình hành khi AB EC x 2 1;5 1 ; x 2 y E 2 ; 7 y 7
⓷ Tìm toạ độ trọng tâm G của tam giác ABC . 1 2 1 2 3 2 2 1
Vì G là trọng tâm của tam giác ABC nên G ; hay G ; . 3 3 3 3 Bài 71. Cho A 4 ;
1 , B2; 4 ,C2; 2 .
⓵ Tìm điểm D sao cho C là trọng tâm tam giác ABD .
⓶ Tìm điểm E sao cho ABCE là hình bình hành.
Lời giải
⓵ Tìm điểm D sao cho C là trọng tâm tam giác ABD . 4 2 x 2 Giả sử 3
Dx; y . Điểm C là trọng tâm tam giác ABD . 1 4 y 2 3
Suy ra x 8, y 1
1 nên D8;1 1 .
⓶ Tìm điểm E sao cho ABCE là hình bình hành. Gọi E ;
x y . Ta có EC 2 x; 2 y . 2 x 6 x 4
Tứ giác ABCE là hình bình hành khi và chỉ khi AB E C . 2 y 3 y 5 Vậy E 4 ; 5 Trang 148 Chương 01. LÊ MINH TÂM Bài 72.
Cho tam giác ABC . Các điểm M1;
1 , N 2;3 ,P0; 4 lần lượt là trung điểm các cạnh BC,CA, AB .
Tính tọa độ các đỉnh của tam giác.
Lời giải
Ta có: PANM là hình bình hành nên PA N M x 1 x 1 Suy ra A A y 4 2 y 2 A A x 1 x 3
Tương tự ta tính được: B và C y 6 y 8 B C
Vậy tọa độ các đỉnh của tam giác là: A1; 2,B 1 ; 6 ,C3;8 Bài 73.
Cho ba điểm A2;5 ,B1; 1 ,C3; 3 .
⓵ Tìm tọa độ điểm D sao cho AD 3AB2AC .
⓶ Tìm tọa độ điểm E sao cho ABCE là hình bình hành. Tìm tọa độ tâm hình bình hành ấy.
Lời giải
⓵ Tìm tọa độ điểm D sao cho AD 3AB2AC .
Gọi Dx; y . Khi đó AB 1; 4 , AC 1; 2 ;
x 2 3 1 2 1 . x 3
AD 3AB 2AC . y 5 3
42.2 y 3 Vậy D 3 ; 3 .
⓶ Tìm tọa độ điểm E sao cho ABCE là hình bình hành. Tìm tọa độ tâm hình bình hành ấy.
Gọi Ex; y . x 2 2 x 4
Từ ABCE là hình bình hành suy ra AE B C . Vậy E4;7 . y 5 2 y 7 5
Tâm I của hình bình hành cũng là trung điểm của AC nên I ; 4 . 2 Bài 74. Trang 149 Chương 01. LÊ MINH TÂM
Cho hai điểm phân biệt Ax ; y ,Bx ; y . Ta nói điểm M chia đoạn thẳng A B theo tỉ số k nếu A A B B x kx A B x M
MA kMB k 1 . Chứng minh rằng 1 k . y ky A B y M 1 k
Lời giải x kx x x x k x x A M B M A B M Ta có 1 k
MA kMB k .
y y k y y y ky A M B M 1 A B y M 1 k x x A B x M Khi k 1 thì 2
. M là trung điểm của A B . y y A B y M 2 Bài 75. Cho ba điểm A 1 ; 1 , B1;3 ,C 2 ;0 .
⓵ Chứng minh rằng ba điểm A, , B C thẳng hàng.
⓶ Tìm các tỉ số mà điểm A chia đoạn thẳng BC , điểm B chia đoạn thẳng AC , điểm C chia đoạn thẳng AB .
Lời giải
⓵ Chứng minh rằng ba điểm A, , B C thẳng hàng.
Gọi AB 2; 2 , AC 1; 1
Nên AB 2AC .
Vậy hai véctơ AB, AC cùng phương, do đó A, , B C thẳng hàng.
⓶ Tìm các tỉ số mà điểm A chia đoạn thẳng BC , điểm B chia đoạn thẳng AC , điểm C chia đoạn thẳng AB
Vì AB 2AC nên A chia đoạn thẳng BC theo tỉ số 2 . 2
Vì BA 2; 2 , BC 3; 3 nên BA BC . 3 2
Vậy B chia đoạn thẳng AC theo tỉ số . 3 1
Vì CA 1;
1 ,CB 3;3 nên CA CB . 3 1
Vậy C chia đoạn thẳng AB theo tỉ số . 3 Trang 150 Chương 01. LÊ MINH TÂM Bài 76.
Trên mặt phẳng Oxy , cho tam giác ABC biết A0; 2 ,B1; 1 ,C 1
; 2 . Các điểm C, A,B lần lượt 1
chia đoạn thẳng AB , BC , CA theo các tỉ số 1 , , 2 . 2
⓵ Tìm tọa độ của A,B,C .
⓶ Chứng minh rằng ba điểm A,B,C thẳng hàng.
Lời giải
⓵ Tìm tọa độ của A,B,C . 0 1 1 2 1 3
Tọa độ của C : x ; y . C 2 2 C 2 2 1 1 1 1 1 2 Tọa độ của 2 2 A : x 3 ; y 4 . A 1 A 1 1 1 2 2 1 2 0 . 1 2 2 2 . 2
Tọa độ của B : x ; y B 1 2 3 B 1 . 2 3
⓶ Chứng minh rằng ba điểm A,B,C thẳng hàng. 1 1 2 3 5 5
Ta có: C ' B' ; ; 3 2 3 2 6 6 1 3 5 5
Và C ' A' 3 ; 4 ; 2 2 2 2
Vậy C ' A' 3C ' B' nên A; B;C thẳng hàng. Bài 77.
⓵ Cho A1;
1 , B3; 2 và C m 4; 2m
1 . Tìm m để ba điểm A; B;C thẳng hàng.
⓶ Cho A3;4, B2;5 . Tìm x để điểm C 7
; x thuộc đường thẳng AB.
Lời giải
⓵ Cho A1;
1 , B3; 2 và C m 4; 2m
1 . Tìm m để ba điểm A; B;C thẳng hàng. AB 2;
1 , AC m 3; 2m m 3 2 m
A; B;C thẳng hàng m 1 2 1
⓶ Cho A3;4, B2;5 . Tìm x để điểm C 7
; x thuộc đường thẳng AB.
C thuộc đường thẳng AB khi: ba điểm A; B;C thẳng hàng. Trang 151 Chương 01. LÊ MINH TÂM
Ta có: AB 1;
1 , AC 10; x 4 AC k.AB x 4 10 x 14 Bài 78. Cho ba điểm A 3 ; 4,B1; 1 ,C5;5 .
⓵ Chứng minh rằng ba điểm A, ,
B C không thẳng hàng.
⓶ Tìm D sao cho A là trung điểm của BD .
Lời giải
⓵ Chứng minh rằng ba điểm A, ,
B C không thẳng hàng.
AB 4; 3 , AC 4; 4
Suy ra AB kAC . Vậy ba điểm A; B;C không thẳng hàng.
⓶ Tìm D sao cho A là trung điểm của BD . x 1
Gọi Dx; y . Điểm A là trung điểm của BD khi và chỉ khi 3 x 7 2 7 Vậy D ; 0 . 3 Bài 79.
Cho tam giác ABC có A 1 ; 1 , B5; 3
, đỉnh C nằm trên trục Oy và trọng tâm G nằm trên trục Ox.
Tìm tọa độ điểm C.
Lời giải 1 5 0 g 4 g
Ta có: G g; Ox; C ;c 3 0 0 Oy 3 1 3 c 0 c 2 3 4
Vậy G ; 0 , C(0; 2) 3 Bài 80.
Cho bốn điểm A 2 ; 3
B3;7 C0;3 D 4 ; 5
;. Chứng minh rằng hai đường thẳng ABvà CD song song với nhau.
Lời giải
Ta có AB 5;10 ; CD 4; 8 . 4 Lại có CD =
AB nên hai đường thẳng AB và CD song song hoặc trùng nhau. 5 5 10
Ta có AC 2; 6 và AB không cùng phương vì 2 6 Trang 152 Chương 01. LÊ MINH TÂM
Vậy AB và CD song song. Bài 81.
Cho hình thoi ABCD tâm O có AC 8, BD 6 Chọn hệ tọa độ O;i;j sao cho i và j cùng hướng
với OB và OC .
⓵ Tính tọa độ các đỉnh của hình thoi.
⓶ Tìm tọa độ trung điểm I của BC và trọng tâm G của tam giác ABC .
⓷ Tìm tọa độ điểm đối xứng Icủa I qua tâm O . Chứng minh ;
A I; D thẳng hàng.
⓸ Tìm tọa độ của véc-tơ AC ; BD ; BC .
Lời giải
⓵ Tính tọa độ các đỉnh của hình thoi.
Ta có OA OC 4, OB OD 3nên A 4
;0 ,C4;0 B0;3 D0; 3 .
⓶ Tìm tọa độ trung điểm I của BC và trọng tâm G của tam giác ABC .
x x y y
x x x y y y B C I ; B C và A B C G ; A B
C nên I 2;3, G0; 1 . 2 2 3 3
⓷ Tìm tọa độ điểm đối xứng Icủa I qua tâm O . Chứng minh ;
A I; D thẳng hàng. 2 2 I 2
; ; AI 2;
; AD 4; 3 . 3 3
Vậy AD =2 AI ' . Suy ra ba điểm '
A, I , D thằng hang.
⓸ Tìm tọa độ của véc-tơ AC ; BD ; BC
AC 8;0; BD 0; 6
,BC 4;3 . Bài 82.
Cho lục giác đều ABCDEF . Chọn hệ tọa độ O;i;j trong đó O là tâm của lục giác đều, hai véc-tơ i
và j cùng hướng OD và EC . Tính tọa độ các đỉnh của lục giác biết độ dài cạnh lục giác bằng 6.
Lời giải 6 3
Tam giác OCD đều cạnh bên là 6 nên OH 3 và CH 3 3 2
Dựa vào tính chất đối xứng thì có 6 đỉnh A 6
;0; D6;0; B 3
;3 3;C3;3 3;F 3 ; 3 3;E3; 3 3. Bài 83. Trang 153 Chương 01. LÊ MINH TÂM
Cho bốn điểm A; B;C ; D . Gọi I và J lần lượt là trung điểm của AB và CD .
⓵ Chứng minh rằng AC BD c a d b ;c a d b 1 1 1 1 2 2 2 2
⓶ Gọi G là trung điểm của IJ. Chứng minh rằng GAGBGC GD 0.
⓷ Gọi P;Q là trung điểm các đoạn thẳng AC và BD , M và N là trung điểm các đoạn
thẳng AD và BC. Chứng minh rằng ba đoạn thẳng IJ , MN , PQ có chung trung điểm.
Lời giải
Ta dùng phương pháp tọa độ: đặt tọa độ của A; B;C; D lần lượt là:a ;a , b ;b , c ;c , d ;d 1 2 1 2 1 2 1 2 thì:
a b a b c d c d 1 1 2 2 1 1 2 2 I ; , J ; 2 2 2 2
⓵ Chứng minh rằng AC BD c a d b ;c a d b 1 1 1 1 2 2 2 2
Ta có AC BD c a d b c a d b ; 1 1 1 1; 2 2 2 2
AD BC d a c b d a c b ; 1 1 1 1; 2 2 2 2 c d
a b c d a b 1 1 1 1 2 2 2 2 2IJ 2 ;
c d a b ;c d a b . 1 1 1 1 2 2 2 2 2 2 2 2
So sánh các tọa độ bằng nhau thì có đpcm.
⓶ Gọi G là trung điểm của IJ. Chứng minh rằng GAGBGC GD 0.
Chứng minh tương tự thì GAGBGC GD 0.
⓷ Chứng minh rằng ba đoạn thẳng IJ , MN , PQ có chung trung điểm.
Ba trung điểm của cả ba đoạn thẳng IJ , MN , PQ đều có tọa độ
a b c d a b c d 1 1 1 1 2 2 2 2 ;
nên chúng có cùng trung điểm. 4 4 Bài 84.
Trong mặt phẳng tọa độ Oxy, cho ba điểm A6, 3 , B 3 ,6,C1, 2 .
⓵ Chứng minh A;B;C là ba đỉnh một tam giác;
⓶ Xác định điểm D trên trục hoành sao cho ba điểm A; B; D thẳng hàng;
⓷ Xác định điểm E trên cạnh BC sao cho BE 2EC .
⓸ Xác định giao điểm hai đường thẳng DE và AC .
Lời giải
⓵ Chứng minh A;B;C là ba đỉnh một tam giác; Trang 154 Chương 01. LÊ MINH TÂM Ta có AB 9 ;3, AC 5 ;5. 9 3 Vì 5 5
suy ra AB và AC không cùng phương.
Hay A; B;C là ba đỉnh một tam giác.
⓶ Xác định điểm D trên trục hoành sao cho ba điểm A; B; D thẳng hàng;
D trên trục hoành D ; x 0
Ba điểm A; B; D thẳng hàng suy ra AB và AD cùng phương.
Mặt khác AD x 6; 3 x 6 3 Do đó x 9 15 3 Vậy D15;0.
⓷ Xác định điểm E trên cạnh BC sao cho BE 2EC .
Vì E thuộc đoạn BC và BE = 2EC suy ra BE 2EC Gọi E ;
x y khi đó BE x 3; y 6 , EC 1 x; 2 y . 1 3 2 1 x x x 1 2 Do đó 3 E ; y 6 2 2 y 2 3 3 y 3
⓸ Xác định giao điểm hai đường thẳng DE và AC .
Gọi I x; y là giao điểm của DE và AC
Do đó DI x ; y 46 2 15 , DE ; cùng phương 3 3
3x 15 3y Suy ra
x 23y 15 0. 4 1 6 2 x 6 y 3
AI x 6; y 3 , AC 5; 5 cùng phương suy ra
x y 3 0 2 5 5 7 1 Từ
1 và 2 suy ra x và y 2 2 7 1
Vậy giao điểm hai đường thẳng DE và AC là I ; . 2 2 Bài 85.
Cho tam giác ABC có A3; 4 , B2; 1 , C 1 ; 2
Tìm điểm M trên đường thẳng BC sao cho S 3S . ABC ABM Trang 155 Chương 01. LÊ MINH TÂM
Lời giải Ta có S 3S
BC 3BM BC 3MB ABC ABM
Gọi Mx; y BM = x 2; y 1 ; BC = 3 ; 3 3 3
x2 x 1 3 3
x2 x 3 Suy ra hoặc 3 3
y 1 y 0 3 3
y 1 y 2
Vậy có hai điểm thỏa mãn M 1;0 , M 3;2 . 2 1 Bài 86.
Trong hệ tọa độ Oxy, cho ba điểm A2; 4 , B1;0 , C 2
;8 . Biết đỉểm Mx; y thỏa mãn
MA MB 2MC 0 . Khi đó ta có giá trị của 3 2 5x y là ?
Lời giải
MA 2 x;4 y
Ta có MB 6 x; y
MC 2 x;8 y 2MC 4 2x;16 2y
MA MB 2MC 4 4x;20 4y 4 4x 1 x 1
Từ: MA MB 2MC 0 . Vậy 3 2
5x y 30 . 20 4 y 5 y 5 Bài 87.
Trong hệ tọa độ Oxy, cho ba điểm A2;0 , B1;3 . Tìm tọa điểm M thuộc trục tung sao cho biểu
thức P MA 2MB đạt giá trị nhỏ nhất.
Lời giải
Gọi I x; y là điểm thỏa mãn : IA 2IB 0 .
IA 2 x; y Ta có :
IA 2IB 4 3x; 6 3y . IB
1 x;3 y 2IB 22x;62y 4 4 3x 0 x 4
Từ : IA 2IB 0
3 . Vậy M ; 2 . 6 3 y 0 3 y 2
Khi đó P MA 2MB MI IA 2MI 2IB 3 MI 3MI.
Để P nhỏ nhất MI nhỏ nhất. Mà M thuộc trục tung nên MI nhỏ nhất khi M là hình
chiếu vuông góc của I lên trục tung M 0; 2. Bài 88. Trang 156 Chương 01. LÊ MINH TÂM
Trong hệ tọa độ Oxy, cho ba điểm A1;0 , B0;3 và C 3 ; 5
. Tọa độ điểm M thuộc trục hoành
sao cho biểu thức P 2MA 3MB 2MC đạt giá trị nhỏ nhất là:
Lời giải
Ta có 2MA 3MB 2MC 2MI IA3MI IB 2MI IC
MI 2IA3IB 2IC
Chọn điểm I sao cho 2IA 3IB 2IC 0. *
21 x30 x 2 3 x 0 x 4
Gọi I x; y, từ * ta có I ; . 2
0 y 32 y 2 5 y 4 16 0 y 16
Khi đó P 2MA 3MB 2MC MI MI.
Để P nhỏ nhất MI nhỏ nhất. Mà M thuộc trục hoành nên MI nhỏ nhất khi M là
hình chiếu vuông góc của I lên trục hoành M 4 ;0. Bài 89.
Cho ba điểm A1;0 ,B0;3 ,C 3
; 5. Tìm điểm M thuộc trục Ox mà T 2MA 3MB 2MC bé nhất.
Lời giải
Gọi I(x, y) là điểm thỏa mãn:
x x x x 4 2 1 3 2 3 0
2IA 3IB 2IC 0
y y y 19 2 3 3 2 5 0 y 3
Ta có:T 2MA 3MB 2MC
2MI IA3MI IB 2MI IC MI 2IA3IB 2IC MI MI
Vì I cố định và M thuộc Ox nên T bé nhất khi M là hình chiếu I lên Ox . Vậy M4;0 . Bài 90.
Cho tam giác ABC cho điểm M thỏa MA MB 2MC 0 . Chứng minh M là trung điểm IC với I là trung điểm AB .
Lời giải
Ta có MA MB 2MC 0
2MI 2MC 0 (gọi I là trung điểm AB)
2MI MC 0 Trang 157 Chương 01. LÊ MINH TÂM
4MJ 0 (gọi J là trung điểm IC ).
MJ 0 M J .
Vậy M là trung điểm IC với I là trung điểm AB . Bài 91.
Cho tam giác ABC vuông cân tại A có BC a 2 . Tính độ dài của vectơ BC BA ?
Lời giải
Dựng điểm D sao cho tứ giác ABCD là hình bình hành.
Ta có: BC BA BD BC BA BD 2BO (O là
giao điểm của AC và BD ).
Từ giả thiết tam giác ABC vuông cân tại A có BC a 2
suy ra AB AC a. a 5 Do đó 2 2
BO AB AO . 2
Vậy BC BA 2BO a 5 . Bài 92.
Cho tam giác ABC cân tại A có AB AC 2a và BAC 120 . Tính AB AC ?
Lời giải
Dựng điểm D sao cho tứ giác ABDC là hình bình hành.
Khi đó AB AC AD AB AC AD .
Hình bình hành ABDC có AB AC và BAC 120
Nên ABDC là hình thoi và DAC 60 .
Suy ra tam giác ADC là tam giác đều. Do đó
AD AC 2a .
Vậy AB AC 2a . Bài 93.
Cho tam giác ABC đều cạnh a , M là trung điểm của BC . Tính CA MC ?
Lời giải Trang 158 Chương 01. LÊ MINH TÂM
Ta có: CA MC CA CM .
Dựng điểm E sao cho tứ giác CAEM là hình bình hành.
Khi đó CA MC CA CM CE .
Từ đó ta có CA MC CE 2CO (O là giao điểm của AM và CE ).
Do tam giác ABC đều cạnh a , M là trung điểm của BC a 3
nên AM BC và AM . 2 2 2
a 3 a a 7 a 7 Suy ra 2 2
CO OM CM
Vậy CA MC 4 2 4 2 Bài 94.
Cho tam giác ABC thỏa mãn điều kiện CA CB CA CB . Chứng minh ABC vuông tại C .
Lời giải
Dựng hình bình hành ACBD . Ta có:
CA CB CD CD; CA CB BA AB .
CA CB CA CB CD AB .
Vậy tứ giác ACBD là hình chữ nhật, tức là tam giác
ABC vuông tại C . Bài 95.
Cho tam giác ABC và một điểm M tùy ý. Chứng minh rằng vectơ v MA MB 2MC . Hãy xác
định vị trí của điểm D sao cho CD v .
Lời giải
Ta có: v MA MB 2MC MA MC MB MC CA CB 2CI (Với I là trung điểm của AB )
Vậy vectơ v không phụ thuộc vào vị trí điểm M .
Khi đó: CD v 2CI I là trung điểm của CD
Vậy D là điểm thứ tư của hình bình hành ACBD . Bài 96. Trang 159 Chương 01. LÊ MINH TÂM
Cho hai lực F và F có điểm đặt O và tạo với nhau góc 60. Tìm cường độ lực tổng hợp của hai 1 2
lực ấy biết rằng cường độ của hai lực F và F đều là 100 N ? 1 2
Lời giải
Ta có: F F F OD . 1 2
F OD 100 3 .
Vậy cường độ lực tổng hợp là 100 3 N . Bài 97.
Cho đa giác đều A A ...A n 1 2 n với n và
3 có tâm O . Chứng minh rằng
u OA OA OA 0 1 2 n
Lời giải
Ta xét hai trường hợp
Trường hợp 1: n là số chẵn n 2k với k ,k 2 .
Khi đó các cặp điểm A và A
i k đối xứng với nhau qua O i k với 1, i O
A OA 0 1 k 1 O
A OA 0 2 k2 u 0 ...
OA OA 0 k 2k
Trường hợp 2: n là số lẻ n 2k 1 với k ,k 1.
Khi đó các cặp điểm A và A
i , k đối xứng với nhau qua OA i 2k3 với 2 1 i 1
Giá của vectơ OA OA
là đường thẳng OA . i 2k3i 1
Giá của vectơ u là đường thẳng OA . 1
Tương tự, giá của các vectơ OA OA , OA OA
là đường thẳng OA . 1 3 2 4 2
Giá của vectơ u là đường thẳng OA . 2
u có giá là đường thẳng OA và đường thẳng OA u 0. 1 2 Bài 98.
Cho n véctơ a ,a ,,a . Dựng OA a , A A a ,, A A a . Chứng minh rằng điều kiện cần và 1 2 n 1 1 1 2 2 n 1 n n
đủ để đường gấp khúc OA A ...A khép kín là a a a 0 . 1 2 n 1 2 n
Lời giải Trang 160 Chương 01. LÊ MINH TÂM
Dựng OA a , A A a ,, A A a . Khi đó a a a OA . 1 1 1 2 2 n 1 n n 1 2 n n
Như vậy đường gấp khúc OA A ...A khép kín khi và chỉ khi O trùng với A . 1 2 n n Bài 99.
Cho 2018 điểm trên mặt phẳng. Bạn Quỳnh kí hiệu chúng là A , A ,, A
. Bạn Vân kí hiệu chúng 1 2 2018 là B , B , ,
B . Chứng minh rằng: 1 2 2018
A B A B A B 0 1 1 2 2 2018 2018
Lời giải
Lấy một điểm O nào đó.
Ta có A B A B A B 1 1 2 2 2018 2018
OB OA OB OA OB OA 1 1 2 2 2018 2018
OB OB OB
OA OA OA . 1 2 2018 1 2 2018
Vì 2018 điểm B ,B , ,
B cũng là 2018 điểm A , A ,, A nhưng được kí hiệu một 1 2 2018 1 2 2018 cách khác, do đó
OB OB OB
OA OA OA 1 2 2018 1 2 2018
Suy ra A B A B A B 0 1 1 2 2 2018 2018 Bài 100.
Cho đa giác đều A , A ,, A ( n lẻ, n 2 ) nội tiếp đường tròn tâm O . Chứng minh rằng 1 2 n
OA OA OA 0 1 2 n
Lời giải
Gọi d là đường thẳng đi qua O và điểm A . 1 1
Xét các đỉnh của đa giác đã cho mà không nằm trên d . 1
Chúng có thể phân tích thành những cặp đỉnh A , A đối xứng nhau qua đường thẳng d i j 1
(chẳng hạn cặp A , A A , A ,... 2 n 1 , cặp 3 n ). 2
Khi đó tổng OA OA là một vectơ nằm trên đường thẳng d . i j 1
Từ đó suy ra OA OA OA cũng là một vectơ có giá nằm trên đường thẳng d . 1 2 n 2
Vì hai đường thẳng d ,d không trùng nhau nên OA OA OA có hai phương 1 2 1 2 n
khác nhau, hay OA OA OA 0 . 1 2 n Trang 161 Chương 01. LÊ MINH TÂM
II. BÀI TẬP TRẮC NGHIỆM. Câu 1.
Véc tơ có điểm đầu là D và điểm cuối là E được ký hiệu là: A. DE . B. DE . C. ED . D. DE . Lời giải Chọn D Câu 2.
Cho tam giác ABC có bao nhiêu véc tơ khác véc tơ không có điểm cầu và điểm cuối là các đỉnh của tứ giác A. 2 . B. 6 . C. 4 . D. 9 . Lời giải Chọn B
Đó là các véc tơ AB, BA, BC,CB,CA, AC . Câu 3.
Cho tứ giác ABCD . Có bao nhiêu véc tơ khác véc tơ không có điểm đầu và điểm cuối là các đỉnh của tứ giác A. 4 . B. 6 . C. 8 . D. 12 . Lời giải Chọn D
Xét các véc tơ có điểm A là điểm đầu thì có các véc tơ thỏa mãn là: AB, AC, AD .
Vậy có ba véc tơ thỏa mãn. Tương tự các điểm còn lại ; B C; D . Câu 4.
Mệnh đề nào sau đây đúng
A. Có duy nhất một véc tơ cùng phương với mọi véc tơ.
B. Có ít nhất hai véc tơ cùng phương với mọi véc tơ.
C. Có vô số véc tơ cùng phương với mọi véc tơ.
D. Không có véc tơ nào cùng phương với mọi véc tơ. Lời giải Chọn A
Véc tơ không cùng phương với mọi véc tơ. Câu 5. Cho ba điểm ; A ;
B C phân biệt. Khi đó
A. Điều kiện cần và đủ để A; B;C thẳng hàng là AB cùng phương với AC .
B. Điều kiện đủ để A; B;C thẳng hàng là với mọi M , MA cùng phương với AB .
C. Điều kiện cần để A; B;C thẳng hàng là với mọi M , MA cùng phương với AB .
D. Điều kiện cần để A; B;C thẳng hàng là AB AC . Lời giải Chọn A Trang 162 Chương 01. LÊ MINH TÂM Câu 6.
Gọi M; N lần lượt là trung điểm các cạnh A ;
B AC của tam giác đều ABC . Hỏi cặp véc tơ nào sau đây cùng hướng
A. MN và CB .
B. AB và MB .
C. MA và MB .
D. AN và CA . Lời giải Chọn B Câu 7.
Cho lục giác đều ABCDEF tâm O . Số các véc tơ khác véc tơ không, cùng phương với OC có
điểm đầu và điểm cuối là các đỉnh của lục giác là: A. 4 . B. 6 . C. 7 . D. 9 . Lời giải Chọn A
Các véc tơ cùng phương với OC là: AB, BA, DE, ED, FC,CF . Câu 8.
Với DE (khác véc tơ không) thì độ dài đoạn ED được gọi là
A. Phương của ED . B. Hướng của ED . C. Giá của ED .
D. Độ dài của ED . Lời giải Chọn D Câu 9.
Mệnh đề nào sau đây sai? A. AA 0 .
B. 0 cùng hướng với mọi véc-tơ. C. AB 0 .
D. 0 cùng phương với mọi véc-tơ. Lời giải Chọn C
Vì có thể xảy ra trường hợp AB 0 A B .
Câu 10. Hai véc tơ được gọi là bằng nhau khi và chỉ khi
A. Giá của chúng trùng nhau và độ dài của chúng bằng nhau.
B. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành.
C. Chúng trùng với một trong các cặp cạnh đối của một tam giác đều.
D. Chúng cùng hướng và độ dài của chúng bằng nhau. Lời giải Chọn D
Câu 11. Cho bốn điểm phân biệt A, B, C, D . Điều kiện nào trong các đáp án sau đây là điều kiện cần
và đủ để AB CD
A. ABCD là hình bình hành.
B. ABDC là hình bình hành.
C. AC BD .
D. AB CD. Lời giải Chọn B Trang 163 Chương 01. LÊ MINH TÂM AB / /CD
Ta có AB CD
suy ra ABDC là hình bình hành. AB CD AB / /CD
Mặt khác ABDC là hình bình hành AB CD . AB CD
Do đó điều kiện cần và đủ để AB CD là ABDC là hình bình hành.
Câu 12. Cho bốn điểm phân biệt A, B, C, D thỏa mãn AB CD . Khẳng định nào sau đây sai?
A. AB cùng hướng với CD .
B. AB cùng phương với CD .
C. AB CD .
D. ABCD là hình bình hành. Lời giải Chọn D
Ta có bốn điểm phân biệt A, B, C, D thỏa mãn AB CD suy ra ABCD là hình bình hành
(nếu A, B, C, D không thẳng hàng) hoặc bốn điểm A, B, C, D thẳng hàng.
Câu 13. Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD . Đẳng thức nào sau đây sai?
A. AB DC .
B. OB DO .
C. OA OC .
D. CB DA . Lời giải Chọn C
Ta có OA, OC ngược hướng nên chúng không bằng nhau.
Câu 14. Cho tứ giác ABCD . Gọi M, N, P, Q lần lượt là trung điểm của A ,
B BC, CD, DA . Khẳng định nào sau đây sai?
A. MN QP
B. MN QP .
C. MQ NP .
D. MN AC . Lời giải Chọn D MN||PQ 1 Ta có
(do cùng song song và bằng AC ). Do đó MNPQ là hình bình hành . MN PQ 2
Câu 15. Cho hình vuông ABCD . Khẳng định nào sau đây đúng?
A. AC BD .
B. AB CD .
C. AB BC .
D. Hai véc-tơ AB, AC cùng hướng. Lời giải Chọn C
Vì AB BC nên AB BC .
Câu 16. Gọi O là giao điểm của hai đường chéo hình chữ nhật ABCD . Mệnh đề nào dưới đây đúng? Trang 164 Chương 01. LÊ MINH TÂM
A. OA OC .
B. OB và OD cùng hướng.
C. AC và BD cùng hướng.
D. AC BD . Lời giải Chọn D
Vì AC BD nên AC BD .
Câu 17. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC của tam giác đều ABC . Đẳng thức nào sau đây đúng?
A. MA MB .
B. AB AC .
C. MN BC .
D. BC 2 MN . Lời giải Chọn D
Ta có MN là đường trung bình của tam giác ABC .Do đó BC 2MN suy ra BC 2 MN .
Câu 18. Cho giác đều ABC đều cạnh a . Gọi M là trung điểm của BC . Khẳng định nào sau đây đúng? a 3 a 3
A. MB MC . B. AM .
C. AM a . D. AM . 2 2 Lời giải Chọn D a 3
Ta có AM là đường trung tuyến của tam giác đều cạnh a suy ra AM AM . 2
Câu 19. Cho hình thoi ABCD cạnh a và 0
BAD 60 . Đẳng thức nào sau đây đúng?
A. AB AD .
B. BD a .
C. BD AC .
D. BC DA . Lời giải Chọn B
Từ giả thiết ta suy ra tam giác ABD đều cạnh a nên BD a suy ra BD a .
Câu 20. Cho lục giác đều ABCDEF có tâm O . B
Đẳng thức nào sau đây sai? A C
A. AB ED . O
B. AB AF . D C. F OD BC .
D. OB OE . E Lời giải Chọn D Trang 165 Chương 01. LÊ MINH TÂM
Ta có OB, OE ngược hướng nên chúng không bằng nhau.
Câu 21. Cho lục giác đều ABCDEF có tâm O . B
Số các véc tơ bằng OC có điểm đầu và điểm cuối là các đỉnh A C của lục giác là O A. 2 . B. 3 . F D C. 4 . D. 6 . E Lời giải Chọn A
Các véc tơ bằng OC là AB, ED .
Câu 22. Cho tam giác ABC có trực tâm H . Gọi D là điểm đối xứng với B qua tâm O của đường tròn
ngoại tiếp tam giác ABC . Khẳng định nào sau đây đúng?
A. HA CD à v AD CH .
B. HA CD à v AD HC .
C. HA CD và AC CH .
D. HA CD à v AD HC v à OB OD Lời giải Chọn B
Ta có AH BC và DC BC ( do góc DCB chắn nữa đường tròn)
Suy ra AH / /DC , Tương tự ta cũng có CH / / AD
Suy ra tứ giác ADCH là hình bình hành. Do đó HA CD à v AD HC .
Câu 23. Cho AB 0 và một điểm C . Có bao nhiêu điểm D thỏa mãn AB CD ? A. 0 . B. 1. C. 2 . D. Vô số Lời giải Chọn D
Ta có AB CD AB CD . Suy ra tập hợp các điểm D thỏa mãn yêu cầu bài toán là
đường tròn tâm C bán kính AB .
Câu 24. Cho AB 0 và một điểm C . Có bao nhiêu điểm D thỏa mãn AB CD A. 0 . B. 1. C. 2 . D. Vô số Trang 166 Chương 01. LÊ MINH TÂM Lời giải ChọnA.
Câu 25. Cho hình vuông ABCD . Khẳng định nào sau đây đúng?
A. AB BC .
B. AB CD .
C. AC BD .
D. AD CB Lời giải Chọn D
ABCD là hình vuông AD BC C B | A | D | C | B .
Câu 26. Cho tứ giác ABCD . Có bao nhiêu véc – tơ ( khác 0 ) có điểm đầu và điểm cuối là các đỉnh của tứ giác A. 8 . B. 12 . C. 6 . D. 4 Lời giải Chọn B
Do tứ giác ABCD có tất cả 4 cạnh ( A ,
B BC, CD, AD ) và hai đường chéo ( AC, BD ) nên số
véc – tơ thỏa mãn yêu cầu bài toán là AB, BA, BC,CB,CD, DC, DA, AD, AC,CA, BD, DB.
Câu 27. Cho tam giác ABC đều có cạnh bằng 1, trọng tâm G . Độ dài véc – tơ AG bằng 3 3 3 3 A. . B. . C. . D. 6 2 3 4 Lời giải Chọn C
Tam giác ABC đều có cạnh bằng 1 nên độ dài đường trung tuyến xuất phát từ A là 3 m a 2 2 3
Do đó AG m . 3 a 3
Câu 28. Cho lục giác đều ABCDEF có tâm O . Đẳng thức nào sau đây sai?
A. OA OC OE 0.
B. OA OC OB EB .
C. AB CD EF O.
D. BC EF AD . Lời giải Chọn D Ta có Trang 167 Chương 01. LÊ MINH TÂM
OA OC OE OB OE O đúng.
OA OC OB OB OB 2OB EB đúng.
AB CD EF AB BO OA AO OA AA 0 đúng.
Câu 29. Cho lục giác đều ABCDEF có tâm O . Đẳng thức nào sau đây sai?
A. OA OB OC OD 0 .
B. AC AB AD .
C. BA BC DA DC .
D. AB CD AB CB . Lời giải Chọn D Ta có
OA OB OC OD OA OC OB OD 0
AB AD AC (quy tắc hình bình hành)
BA BC BD BD
DA DC DB BD
Do AB CD AB CB CD CB sai.
Câu 30. Cho hình bình hành ABCD . Gọi G là trọng tâm của ABC . A B G D C
Mệnh đề nào sau đây đúng?
A. GA GC GD BD .
B. GA GC GD CD .
C. GA GC GD O .
D. GA GC GD DC . Lời giải Chọn A
Vì G là trọng tâm của tam giác ABC nên GA GB GC O GA GC G B.
Do GA GC GD G
BGD GDGB BD
Câu 31. Cho ba điểm A, B,C không thẳng hàng, mệnh đề nào sau đây là mệnh đề đúng ? A. M
, MA MB . B. M
, MA MB MC . C. M
, MA MC . D. M
,MA MB MC Lời giải Trang 168 Chương 01. LÊ MINH TÂM Chọn D
Với mọi điểm M ta luôn có: MA MB MC .
Câu 32. Cho tam giác đều ABC cạnh a . Tìm mệnh đề đúng.
A. AB AC a .
B. AB AC a 3 . a 3
C. AB AC .
D. AB AC 2a 2 Lời giải Chọn D
AB AC AB AC 2a .
Câu 33. Cho tam giác ABC vuông cân tại A có AB AC a . Độ dài của véc-tơ 3AB 4AC là bao nhiêu ? A. 5a . B. 7a . C. a . D. 12a . Lời giải Chọn A
Ta gọi AB' 3AB ; AC' 4AC .
AB AC AB AC C B
AB AC C B
AB2 AC2 3 4 3 4 5a .
Câu 34. Cho tam giác ABC . Gọi M, N, P lần lượt là trung điểm các cạnh AB, AC, BC . Véc-tơ PM
không cùng hướng với các véc-tơ nào dưới đây ? A. CN . B. CA . C. AC . D. NA . Lời giải Chọn C
Véc-tơ PM cùng hướng với véc-tơ CA , do đó nó ngược hướng với AC . Trang 169 Chương 01. LÊ MINH TÂM
Câu 35. Khẳng định nào dưới đây sai?
A. Hai véc-tơ ( khác 0 ) cùng hướng thì chúng cùng phương.
B. Hai véc-tơ ( khác 0 ) có giá song song thì chúng cùng phương.
C. Hai véc-tơ ( khác 0 ) cùng phương thì chúng cùng hướng.
D. Hai véc-tơ ( khác 0 ) ngược hướng thì cùng phương. Lời giải Chọn C
Các khẳng định A, B, D đúng. Khẳng định C sai vì :Hai véc-tơ ( khác 0 ) cùng phương thì
chưa chắc cùng hướng, chúng có thể ngược hướng.
Câu 36. Hai véc tơ có cùng độ dài và ngược hướng gọi là :
A.Hai véc tơ cùng hướng .
B. Hai véc tơ cùng phương.
C. Hai véc tơ đối nhau .
D. Hai véc tơ bằng nhau Lời giải Chọn C
Hai véc tơ đối nhau là hai vec tơ có cùng độ dài và ngược hướng. Do đó chọn đáp án C.
Câu 37. Cho ba điểm M, N, P thẳng hàng trong đó điểm N nằm giữa M và P . Khi đó các cặp véc
tơ nào sau đây cùng hướng
A. MP và PN .
B. MN và PN .
C. NM và NP .
D. MN và MP . Lời giải Chọn D
Nhìn vào hình vẽ ta thấy MN và MP cùng hướng.
Câu 38. Chọn mệnh đề sai trong các mệnh đề sau đây.
A.Véc tơ 0 cùng hướng với mọi vec tơ.
B. Véc tơ 0 cùng phương với mọi vecto. C. AA 0 . D. AB 0 . Lời giải Chọn D
Mệnh đề AB 0 là mệnh đề sai, vì khi A B thì AB 0 .
Câu 39. Cho tam giác ABC . Số các vec-to khác vec-tơ 0 nhận các đỉnh của tam giác làm điểm đầu và điểm cuối là A. 5 . B. 6 . C. 3 . D. 4 . Lời giải Chọn B Trang 170 Chương 01. LÊ MINH TÂM
Ứng với đỉnh A ta có 2 vec-tơ có điểm đầu là A và điểm cuôi là B,C . Vậy tam giác có 3 đỉnh
nên có 6 vec-tơ có điểm đầu và điểm cuối là các đỉnh của tam giác.
Câu 40. Cho hinh bình hành ABCD . Trong các khẳng định sau hãy tìm khẳng định sai?
A. AB DC .
B. AD CB .
C. AD CB .
D. AB CD . Lời giải Chọn C
Tư hình vẽ, ta thấy vì ABCD là hình bình hành nên AB DC AD CB AB CD AD BC
Câu 41. Cho ba điếm M, N, P thẳng hàng, N nằm giữa M và P . Khi đó cặp vec-tơ nào sau đây cùng hướng?
A. MN và PN .
B. MN và MP .
C. MP và PN .
D. NM và NP . Lời giải Chọn B
Từ hình vẽ ta thấy MN và MP cùng hướng.
Câu 42. Cho tam giác đều ABC cạnh bằng 2a. Đẳng thức nào sau đây đúng?
A. AB AC .
B. AB 2a .
C. AB 2a .
D. AB AB . Lời giải Chọn C
Do tam giác ABC đều cạnh 2a nên AB AB 2a
Câu 43. Cho lục giác đều ABCDEEF tâmO . Số các véc-tơ khác 0 cùng phương Với OC có điểm đầu
và điểm cuối là các đỉnh của lục giác bằng A. 6 . B. 4 . C. 8 . D. 7 . Lời giải Chọn A Trang 171 Chương 01. LÊ MINH TÂM
Số các véc-to khác 0 cùng phương với OC có điểm đầu và điểm cuối là các đỉnh của lục giác
là AB, BA, FC, CF, ED, DE .
Câu 44. Cho hai véc-tơ a,b đều khác 0 . Tìm khẳng định đúng trong các khẳng định sau:
A.Hai véc-tơ a,b cùng phương với một vec-tơ thứ 3 khác 0 thì cùng phương.
B. Hai véc-tơ a,b ngược hướng với một vec-tơ thứ 3 khác 0 thì ngược hướng.
C. Hai véc-tơ a,b ngược hướng với một vec-tơ thứ 3 khác 0 thì không cùng phương.
D. Hai véc-tơ a,b cùng phương thì cùng hướng. Lời giải Chọn A
+Hai véc-tơ a,b ngược hướng với một vec-tơ thứ 3 khác 0 thì ngược hướng nhau. Sai , phải
cùng hướng nhau mới đúng.
+Hai véc-tơ a,b ngược hướng với một vec-tơ thứ 3 khác 0 thì không cùng phương. Sai, hai vec-tơ cùng phương nhau.
+Hai véc-tơ a,b cùng phương thì cùng hướng. Sai, cùng phương thì có thể cùng hướng hoặc ngược hướng.
Câu 45. Cho tứ giác ABCD có AB DC và AB AD thì tứ giác ABCD là hình gì? A. Hình thoi. B. Hình chữ nhật.
C. Hình bình hành. D. Hình vuông. Lời giải Chọn A
Vì AB DC nên ABCD là hình bình hành. Mặt khác AB AD nên ABCD là hình thoi.
Câu 46. Cho tam giác AB .
C Gọi M, N, P là các điểm được xác định bởi MC 3MB , NA 2NB và
AP k AC. . Ba điểm M, N, P thẳng hàng khi và chỉ khi Trang 172 Chương 01. LÊ MINH TÂM 2 3 3 2 A. k . B. k . C. k . D. k . 5 5 5 5 Lời giải Chọn A 1 3 1
Ta có MB BC , MC BC , NB AB , PC 1 k AC . 2 2 3 1 1
MN MB NB BC AB 2 3 Do đó: 3
MP MC PC BC k 1 1 AC k BC k 1AB 2 2 1 k k 1
Để M, N, P thẳng hàng thì 2 2k 1 3 k 3 2 k . 1 1 5 2 3 Chọn đáp án A
Câu 47. Cho hình bình hành ABCD . Gọi M là trung điểm cạnh AB , P là điểm trên cạnh AD thỏa
mãn PD 3PA . Điểm N trên cạnh AC thỏa mãn tỉ lệ nào sau đây để ba điểm M, N, P thẳng hàng? 1 5
A. 4NC 3A . C
B. NC 4A . N C. AN AC.
D. AC NC. 4 3 Lời giải Chọn B
M, N, P thẳng hàng khi và chỉ khi AN k AM 1 k AP với k 0.
Ta lại có: AC AB AD AC AB AD AN AM AP AN AM AP AB AD AC AC Từ đó ta có : 5 . AM AP AN AN
Vậy NC 4A . N
Câu 48. Cho tam giác ABC có E, F lần lượt là trung điểm của AB , BC . Gọi M là điểm thỏa mãn
MA MB MB MC . Tập hợp tất cả điểm M là
A. Đường cao kẻ từ B của tam giác ABC . B. Đường trung trực của EF .
C. Đường EF .
D. Đường trung trực của AC . Lời giải Chọn B
Gọi E, F lần lượt là trung điểm của AB , BC , ta có
MA MB MB MC 2ME 2M . F
Tập hợp điểm M là đường trung trực của EF . Trang 173 Chương 01. LÊ MINH TÂM Chọn đáp án B. Câu 49.
Cho đoạn thẳng AB . Tập hợp tất cả điểm M thỏa mãn MA MB MA MB là
A. Đường trung trực của đoạn thẳng AB .
B. Đường tròn đường kính AB
C. Trung điểm của đoạn thẳng AB .
D. Là điểm M thỏa mãn tam giác MABlà tam giác đều. Lời giải Chọn B
Gọi I là trung điểm của đoạn thẳng AB , Ta có MA MB MA MB 2MI BA AB MI
. Vậy quỹ tích M là đường tròn đường kính AB . 2 Chọn đáp án B.
Câu 50. Cho hình vuông ABCD cố định và I là giao điểm hai đường chéo của nó.Gọi điểm M là
điểm thay đổi thỏa mãn MA MB MC MD 3MA MB MC MD . Tập hợp tất cả điểm M là
A. Một đường thẳng qua A .
B. Một đường thẳng qua I .
C. Đường tròn tâm A .
D. Đường tròn tâm I . Lời giải Chọn D
MAMBMCMD 3MAMBMCMD
2MI 2MI 3MA MA AB MA AC MA AD
4MI AB AD AC AC
4MI 2AC MI 2 AC
Vậy tập hợp tất cả điểm M là đường tròn tâm I , bán kính R . 2 Chọn đáp án D.
Câu 51. Cho tam giác ABC và điểm M thỏa mãn 3MA 2MB MC MA MB . Tập hợp điểm M là
A. một đoạn thẳng.
B. một đường tròn.
C. nửa đường tròn.
D. một đường thẳng. Lời giải Chọn B Trang 174 Chương 01. LÊ MINH TÂM Vì 3 2 1 0 I
sao cho 3IA 2IB IC 0 . Khi đó ta có:
3MA 2MB MC 3MI IA 2MI IB MI IC 2MI . 1
Vậy 3MA 2MB MC MA MB 2 MI BA MI
AB . Do đó quỹ tích điểm M 2 là đường tròn.
Câu 52. Cho tam giác ABC tìm tập hợp điểm M sao cho MA 3MB 2MC 2MA MB MC .
A. Tập hợp các điểm M là một đường tròn.
B. Tập hợp các điểm M là một đường thẳng.
C. Tập hợp các điểm M là một tập rỗng.
D. Tập hợp các điểm M chỉ là một điểm trùng với A . Lời giải Chọn A
Gọi I là điểm thỏa mãn IA 3IB 2IC 0 . Khi đó ta có:
MA 3MB 2MC 2MA MB MC
MI IA 3MI IB 2MI IC MA MB MA MC
2MI IA 3IB 2IC BA CA
2MI 2JA ( với J là trung điểm BC )
MI JA ( hằng số)
Vậy tập hợp điểm M là đường tròn tâm I bán kính JA .
Câu 53. Cho hình chữ nhật ABCD tâm I và đường thẳng d cố định. Gọi M là một điểm thay đổi
trên d . Khi u MA 2MB MC có độ dài nhỏ nhất thì :
A. M là hình chiếu vuông góc của I lên d .
B. M là hình chiếu vuông góc của trung điểm đoạn IB lên d .
C. M là hình chiếu vuông góc của trung điểm đoạn ID lên d .
D. M trùng với I . Lời giải Chọn B Ta có:
u MA 2MB MC MG GA 2MG GB MG GC 4MG GA 2GBGC .
Chọn điểm G thỏa mãn GA 2GB GC 0 ta được u 4MG .
Để độ dài MG nhỏ nhất thì M trùng với hình chiếu vuông góc của G trên d . Ta sẽ xác
định vị trí của G . Trang 175 Chương 01. LÊ MINH TÂM
Ta có : GA 2GB GC 0 2GI 2GB 0 G là trung điểm IB .
Câu 54. Cho tam giác ABC đều cạnh bằng a . Độ dài véc-tơ AB BC và AB BC lần lượt là
A. a và a 3 .
B. đều bằng a .
C. a và 2a .
D. a và a 2 . Lời giải Chọn A
Gọi I là trung điểm của AC . a 3
Ta có AB BC AC a và AB BC AB CB 2IB 2. a 3 . 2
Suy ra MC , MI ngược hướng nhau, đồng nhau MC 2MI MC 100 3 .
Câu 55. Cho tam giác ABC đều cạnh bằng a , trọng tâm G . Tính theo a độ dài véc-tơ
v GA GB GC 2a 3 a 3 3a A. . B. 2a . C. . D. . 3 2 2 Lời giải Chọn A
Vì GA GBGC 0 nên v GA GB GC 2GC 2 2 a 3 2a 3
v 2GC 2. CI 2. .
, với I là trung điểm AB . 3 3 2 3
Câu 56. Cho tam giác đều ABC cạnh a . Trong các mệnh đề sau, mệnh đề nào đúng? a 3
A. AB CA a 3 .
B. AB CA
. C. AB CA a .
D. AB CA 0 . 2 Lời giải Chọn A Trang 176 Chương 01. LÊ MINH TÂM
Gọi I là trung điểm BC . Ta có: AB CA AB AC 2AI 2AI a 3 .
Câu 57. Cho hai lực F F 100 N , có điểm đặt tại O và tạo với nhau góc 120 . Cường độ lực tổng 1 2
hợp của hai lực ấy bằng bao nhiêu? A. 100 N. B. 100 5 N . C. 200 N . D. 50 3 N . Lời giải Chọn A 1
Ta có: AOM 60 nên OM O .
A cos 60 100. 50 . 2
Ta có: F F OD OD 2OM 100 N . 1 2
Câu 58. Cho tam giác ABC có đường trung tuyến AM và trọng tâm G . Khẳng định nào sau đây đúng? 1
A. AM AB AC .
B. MG MA MB MC. 3 2
C. AM 3MG .
D. AG AB AC . 3 Lời giải Chọn B
Vì M là trung điểm của BC nên ta có MB MC 0 . Trang 177 Chương 01. LÊ MINH TÂM 1
Vì G là trọng tâm tam giác ABC nên MG MA . 3 1
Từ đó, ta suy ra MG MA MB MC. 3
Câu 59. Cho hình bình hành ABCD , M là trung điểm AB , DM cắt AC tại I . Mệnh đề nào sau đây là đúng? 2 1 1 3 A. AI AC .
B. AI AC . C. AI AC . D. AI AC . 3 3 4 4 Lời giải Chọn B Đường thẳng A //
B CD cắt hai cạnh CI, DI của tam giác CDI lần lượt tại A, M . Áp dụng AM AI MI 1 định lí Thales ta có: . CD IC ID 2 AI 1 1 1 Từ đó ta có:
. Vậy AI AC . AI IC 1 2 3 3
Câu 60. Cho tam giác đều ABC cạnh a . Gọi G là trọng tâm của tam giác ABC . Mệnh đề nào sau đây là sai? a 3
A. AB AC a .
B. AB AC . 2 a 3
C. GA GB GC 0 .
D. GB GC . 3 Lời giải Chọn B Ta có: Trang 178 Chương 01. LÊ MINH TÂM
+) AB AC CB CB a . a 3
+) AB AC 2AM 2AM 2. a 3 . 2
+) GA GB GC 0 GA GB GC 0 . 2 2 a 3 a 3
+) GB GC 2GM 2GM AM . . 3 3 2 3
Câu 61. Cho hình chữ nhật ABCD tâm O . Gọi M, N lần lượt là trung điểm của OA và CD . Biết MN . a AB .
b AD. Tính a b . 1 3 1
A. a b 1.
B. a b .
C. a b .
D. a b . 2 4 4 Lời giải Chọn A 1 1 1 1
Ta có: MN MO ON
AC AD AB BC AD. 4 2 4 2 1 1 1 3
Suy ra: MN AB AD AD AB AD . 4 2 4 4 1 3
Khi đó: a ; b
. Vậy a b 1. 4 4
Câu 62. Cho tam giác ABC . Gọi M, N lần lượt là trung điểm của các cạnh AB, AC . Hỏi vectơ MN
bằng vectơ nào dưới đây? 1 1 1 1 1
A. AM AN .
B. AB AC .
C. AC AB . D. CB . 2 2 2 2 2 Lời giải Chọn C Trang 179 Chương 01. LÊ MINH TÂM 1 1 1 1
Ta có: MN BC AC AB AC AB. 2 2 2 2 Câu 63. Cho A
BC có trung tuyến AM . Hãy phân tích AM theo hai vec- tơ AB và AC . AB AC AB AC AB AC BC AC A. AM . B. AM AM . D. AM . 2 . C. 2 2 2 Lời giải Chọn A AB AC
Do AM là đường trung tuyến, suy ra AB AC 2AM AM . 2
Câu 64. Cho tam giác ABC . Tìm điểm M thỏa mãn đẳng thức MA MB MC 0
A. M là đỉnh thứ tư của hình bình hành ABCM .
B. M là trọng tâm tam giác ABC .
C. M là trung điểm của AB .
D. M là đỉnh thứ tư của hình bình hành CAMB. Lời giải Chọn A
MA MB MC 0 BA MC 0 BA CM .
Vậy M là đỉnh thứ tư của hình bình hành ABCM .
Câu 65. Cho hình bình hành ABCD , điểm M thỏa mãn 4AM AB AC AD . Khi đó điểm M là
A. Trung điểm AC . B. Điểm C .
C. Trung điểm AB D. Trung điểm AD Lời giải Chọn A Trang 180 Chương 01. LÊ MINH TÂM AC
AB AC AD 2AC 4AM AM . 2
Vậy M là trung điểm AC .
Câu 66. Gọi G là trọng tâm A
BC . Đặt GA a,GB b . Tìm các giá trị thực m,n để BC . m a . n b .
A. m 1,n 2 . B. m 1 ,n 2 . C. m 2 ,n 1 .
D. m 2,n 1. Lời giải Chọn B
Vì G là trọng tâm tam giác A
BC nên GAGBGC 0 GC G
BGA a b . m 1
BC GC GB a b b a 2.b . n 2
Câu 67. Cho hình bình hành ABCD , M là trung điểm AB , DM cắt AC tại I . Khẳng định nào sau đây đúng? 2 1 1 3 A. AI AC .
B. AI AC . C. AI AC . D. AI AC . 3 3 4 4 Lời giải Chọn B IA AM 1 1 Theo Ta-lét ta có
AI AC . IC CD 2 3 1
AI, AC cùng hướng nên AI AC . 3
Câu 68. Cho tứ giác ABCD . Gọi M, N lần lượt là trung điểm của AD, BC . Hãy tìm m,n sao cho
MN mAB nDC ? 1 1 1 1 1 1 1 1
A. m ,n .
B. m ,n .
C. m ,n .
D. m ,n . 2 2 2 2 2 2 2 2 Lời giải Chọn A 1 1
Ta có MN MB MC MA AB MD DC . 2 2 1 1
Do M là trung điểm của AD nên MA MD 0 . Suy ra MN AB DC 2 2
Câu 69. Cho tam giác ABC . Gọi D là điểm xác định bởi hệ thức AD BC . Biết
BD mAB nAC m,n . Tính tổng T m n Trang 181 Chương 01. LÊ MINH TÂM A. T 3 . B. T 1 . C. T 3. D. T 1. Lời giải Chọn B
Từ giả thiết suy ra tứ giác ABCD là hình bình hành.
Ta có BD BA BC AB AC AB 2 AB AC Suy ra m 2
,n 1T 2 1 1 .
Câu 70. Cho tam giác ABC . Gọi M là điểm trên cạnh BC sao cho MB 2MC . Khẳng định nào dưới đây đúng? 1 2 2 1
A. AM AB AC . B. AM AB AC . 3 5 3 3 2 3
C. AM AB AC . D. AM AB AC . 5 5 Lời giải Chọn A 2 2 1 2
Ta có AM AB BM AB BC AB AC AB AB AC . 3 3 3 3
Câu 71. Cho hình bình hành ABCD trên cạnh AB,CD lần lượt lấy hai điểm M, N sao cho
3AM AB, 2NC CD . Gọi G là trọng tâm tam giác BMN . Đặt AG mAB nAD . Hãy tính
T m n ? 5 2 7 11 A. T . B. T . C. T . D. T . 6 3 8 12 Lời giải Chọn D Trang 182 Chương 01. LÊ MINH TÂM 1
Ta có AG AB AM AN. 3 1 AM AB 1 1 1 7 1 Mà 4
AG AB AB AD AB AB AD 1 3 4 2 12 3
AN AD DN AD AB 2 7 1 7 1 11 Vậy m ,n T . 12 3 12 3 12
Câu 72. Cho tam giác ABC và I thỏa mãn IA 3IB . Phân tích CI theo CA,CB ? 1
A. CI CA 3CB.
B. CI CA 3CB . 2 1
C. CI 3CBCA.
D. CI C A 3CB . 2 Lời giải Chọn C
Ta có CI CA AI CA 3IB CA 3IC CB CA 3CI 3CB 1
CI CA CB 1 3
3CBCA. 2 2
Câu 73. Cho tứ giác ABCD trên cạnh AB,CD lầ lượt lấy các điểm M, N sao cho 3AM 2AB và
3DN 2DC . Biểu diễn véc tơ MN theo hai véc tơ AD, BC ? 1 2 1 1
A. MN AD BC .
B. MN AD BC . 3 3 3 3 1 2 2 1
C. MN AD BC . D. MN AD BC . 3 3 3 3 Trang 183 Chương 01. LÊ MINH TÂM Lời giải Chọn C
Ta chứng minh bài toán sau: 1
Nếu E, F lần lượt là trung điểm của MN , PQ thì EF MQ NP. 2 1 1 1
Thật vậy, ta có EF EP EQ EN NP EM MQ MQ NP . 2 2 2
Gọi I, K lần lượt là trung điểm của AM, DN .
Khi đó, áp dụng kết quả bài toán trên ta có: 1
MN BC IK 1 1
BC AD MN 1 2
MN AD BC . 2 2 2 3 3
Câu 74. Cho tam giác ABC có AK, BM là hai đường trung tuyến. Đặt AK a, BM b . Hãy biểu thị
BC theo a,b . 2 4 2 4
A. BC a b .
B. BC a b . 3 3 3 3 2 4 1 4
C. BC a b .
D. BC a b . 3 3 3 3 Lời giải Chọn A 2 2
Ta có AB AG GB a b . (1) 3 3 4 2
AB AC 2AK AC 2a AB a b . (2) 3 3 2 4
Từ (1) và (2) BC a b . 3 3
Câu 75. Cho tam giác ABC và điểm D thoả mãn AD mAB nAC . Điều kiện cần và đủ để điểm D
thuộc đường thẳng BC là 1
A. mn 1.
B. m n .
C. m n 1.
D. m n 1. 2 Lời giải Chọn C Từ giả thiết ta có: Trang 184 Chương 01. LÊ MINH TÂM
BD BA mBA nBC BA
BD 1 mnBA nBC.
Điểm D thuộc đường thẳng BC khi và chỉ khi tồn tại số k sao cho BD kBC .
Thay vào đẳng thức ở trên ta được: kBC 1 m n BA nBC k n BC 1 m n . BA
Tứ đó suy ra k n 1 mn 0. Vây m n 1.
Câu 76. Cho tam giác ABC . Gọi M là trung điểm của AB và N là một điểm trên cạnh AC sao cho
NC 2NA,K là trung điểm của MN . Khi đó 1 1 1 1 A. AK AB AC . B. AK AB AC . 6 4 4 6 1 1 1 1 C. AK AB AC . D. AK AB AC . 4 6 6 4 Lời giải Chọn C 1 1 1 1 Ta có: AK AM AN
AB AC . 2 2 4 6 1
Câu 77. Cho tam giác ABC , N là điểm xác định bởi CN BC,G là trọng tâm của tam giác ABC . 2
Hệ thức tính AC theo AG và AN là 2 1 4 1 A. AC AG AN . B. AC AG AN . 3 2 3 2 3 1 3 1 C. AC AG AN . D. AC AG AN . 4 2 4 2 Lời giải Chọn C 1 1 1 3
Ta có: AN AC CN AC BC AC AC AB AB AC 2 2 2 2 1
AG AC 3 3 3
AC AG 2AC . 2 2 2 3 1 Do đó: AC
AG AN . 4 2
Câu 78. Cho tam giác ABC có G là trọng tâm tam giác. Lấy các điểm P, Q sao cho
PA 2PB,3QA 2QC 0 . Biểu diễn véc-tơ AG theo các véc-tơ AP, AQ . 1 5 5 1
A. AG AP AQ . B. AG AP AQ . 3 6 6 6 1 5 1 1 C. AG AP AQ . D. AG AP AQ . 6 6 2 3 Lời giải Chọn C Ta có
AP 2BP 2(AP A )
B AP 2AB . Trang 185 Chương 01. LÊ MINH TÂM 2
3AQ 2QC 2(AC A ) Q AQ AC . 5 1 1 1 5
Do đó AG AB AC AP AQ . 3 3 6 6
Câu 79. Cho tam giác ABC . Gọi I là điểm trên cạnh BC sao cho 2CI 3BI và J thuộc BC kéo dài
sao cho 5JB 2JC . Gọi G là trọng tâm tam giác ABC . Biễu diễn véc-tơ AG theo các véc-tơ AI , AJ . 35 1 35 1 A. AG AI AJ . B. AG AI AJ 48 16 48 16 25 3 25 3 C. AG AI AJ D. AG AI AJ 16 16 16 16 Lời giải Chọn B 3 2 5 3 AI AB AC AB AI AJ Ta có 5 5 8 8 . 5 2 25 9 AJ AB AC AC AI AJ 3 5 16 16 1 35 1
Do đó AG (AB AC) AI AJ . 3 48 16
Câu 80. Cho tam giác ABC . Gọi G là trọng tâm tam giác và H là điểm đối xứng của B qua G . Gọi
M là trung điểm BC . Biểu diễn véc-tơ MH theo các véc-tơ AB, AC . 5 1 1 5
A. MH AB AC .
B. MH AB AC 6 6 6 6 5 1 1 5
C. MH AB AC
D. MH AB AC 6 6 6 6 Lời giải Chọn C 2 1
AH AC AG AC AB Ta có 3 3 . 2
BH 2BG (AC 2AB) 3 1 1 1 1 5 1
Do đó MH HM HB HC BH (AC AH) AB AC . 2 2 2 2 6 6
Câu 81. Cho tam giác ABC . Gọi M là trung điểm của AB và N là một điểm trên cạnh AC sao cho
NC 2NA. Gọi K là điểm trên cạnh MN sao cho KN 3KM. Kết quả nào dưới đây đúng? 3 1 3 1
A. AK AB AC
B. AK AB AC 8 12 8 12 3 1 3 1
C. AK AB AC
D. AK AB AC 8 12 8 12 Lời giải Chọn C Trang 186 Chương 01. LÊ MINH TÂM 1 1
Ta có AK AM MK AB MN 2 4 1 1 1 1 1 3 1
AB (AN AM) AB
AC AB AB AC . 2 4 2 12 8 8 12
Câu 82. Cho hình bình hành ABCD . Gọi I là điểm xác định bởi BI kBC (với k 1). Tìm hê thức
liên hệ giữa AI, AB, AC .
A. AI (k 1)AB k AC . B. AI 1
( k)AB k AC .
C. AI (k 1)AB k AC .
D. AI (k 1)AB k AC . Lời giải Chọn B
AI AB BI AB kBC AB k(AC A ) B 1
( k)AB k AC . 1
Câu 83. Cho tam giác ABC, N là điểm xác định bởi CN
BC . Gọi G là trọng tâm tam giác ABC . 2
Hệ thức tính AC theo AG và AN là 2 1 4 1 A. AC AG AN B. AC AG AN 3 2 3 2 3 1 3 1 C. AC AG AN D. AC AG AN . 4 2 4 2 Lời giải Chọn C
Gọi M là trung điểm của BC . 3
Vì G là trọng tâm tam giác ABC AM AG . 2 1 1 3 1 3 1
Ta có: AC (AM AN) AG AN AG AN . 2 2 2 2 4 2
Câu 84. Cho ABC , gọi D là trung điểm cạnh AC,K là trọng tâm BCD . Khẳng định nào sau đây đúng?
A. 3KB 2KC AK
B. 2KB 3KC AK 1 1 1 1
C. KB KC AK
D. KB KC AK 3 2 2 3 Lời giải Trang 187 Chương 01. LÊ MINH TÂM Chọn B
Vì K là trọng tâm BCD nên ta có KB KC KD 0 .
KB KC KA AD 0
AK KB KC AD 1
AK KB KC AC 2 1
AK KB KC (KC K ) A 2
AK 2KB3KC .
Câu 85. Cho tam giác ABC . Gọi M, N, P là các điểm được xác định bởi MC 3MB, NA 2 NB và
AP k AC . Ba điểm M, N, P thẳng hàng khi và chỉ khi 2 3 3 2 A. k . B. k . C. k . D. k . 5 5 5 5 Lời giải Chọn A 1 3 1
Ta có MB BC, MC BC, NB AB, PC 1 ( k)AC 2 2 3 1 1
MN MB NB BC AB 2 3 Do đó 3 1
MP MC PC
BC (k 1)AC k BC (k 1)AB 2 2 1 k k 1 2
Để M, N, P thẳng hàng thì 2 2k 1 3
k 3 k . 1 1 5 2 3
Câu 86. Mệnh đề nào sau đây đúng?
A. Hai vectơ u 2;
1 và v 1; 2 đối nhau.
B. Hai vectơ u 2;
1 và v 2; 1 đối nhau.
C. Hai vectơ u 2; 1 và v 2; 1 đối nhau. Trang 188 Chương 01. LÊ MINH TÂM
D. Hai vectơ u 2; 1 và v 2 ; 1 đối nhau. Lời giải Chọn D
Ta có: u 2; 1 2;
1 v u và v đối nhau.
Câu 87. Cho hình chữ nhật ABCD có AB 3, BC 4 . Độ dài của vec tơ AC là: A. 9. B. 5. C. 6. D. 7. Lời giải Chọn B Ta có: 2 2 2 2
AC AC AB BC 3 4 5 .
Câu 88. Cho hai điểm A1;0 và B0; 2
. Tọa độ trung điểm của đoạn thẳng AB là: 1 1 1 A. ; 1 . B. 1 ; . C. ; 2 . D. 1; 1 . 2 2 2 Lời giải Chọn A
x x y y 1 0 0 ( 2 ) 1
Ta có: Trung điểm của đoạn thẳng AB là: A B I ; A B ; ; 1 . 2 2 2 2 2
Câu 89. Cho các vectơ u u ;u , v v ; v . Điều kiện để vectơ u v là 1 2 1 2 u u u v u v u v A. 1 2 . B. 1 1 . C. 1 1 . D. 1 2 . v v u v u v u v 1 2 2 2 2 2 2 1 Lời giải Chọn C u v Ta có: 1 1 u v . u v 2 2
Câu 90. Vectơ a 4; 0 được phân tích theo hai vectơ đơn vị như thế nào? A. a 4 i j .
B. a i 4j . C. a 4 j .
D. a 4i . Lời giải Chọn D
Ta có: a 4; 0 a 4i 0j 4i .
Câu 91. Cho hai điểm A1;0 và B0; 2
. Vec tơ đối của vectơ AB có tọa độ là: A. 1 ; 2. B. 1 ; 2 . C. 1; 2 . D. 1; 2 . Lời giải Chọn C Trang 189 Chương 01. LÊ MINH TÂM
Ta có vectơ đối của AB là BA 1 0; 0 2 1; 2 .
Câu 92. Tam giác ABC có C 2 ; 4
, trọng tâm G0;4, trung điểm cạnh BC là M2;0 . Tọa độ A và B là:
A. A4;12 ,B4;6 . B. A 4 ; 1 2,B6;4. C. A 4 ;12,B6;4. D. A4; 1 2,B 6 ; 4. Lời giải Chọn C x ( 2 ) 2 B x 6 Ta có: M 2
2; 0 là trung điểm BC nên B B6;4 y (4) y 4 0 B B 2 x 6 ( 2 ) 0 A x 4 3
G 0; 4là trọng tâm tam giác ABC nên A A 4 ;12 . y 4 ( 4 ) y 12 4 A A 3
Câu 93. Trong mặt phẳng tọa độ Oxy cho bốn điểm A3; 2 , B7; 1 , C 0; 1 , D 8 ; 5 . Khẳng định
nào sau đây là đúng?
A. AB,CD đối nhau.
B. AB,CD cùng phương nhưng ngược hướng.
C. AB,CD cùng phương cùng hướng.
D. A, B, C, D thẳng hàng. Lời giải Chọn B
Ta có: AB 4;3 ,CD 8; 6 CD 2AB .
Câu 94. Trong mặt phẳng Oxy , cho A 2 ;0, B5; 4 , C 5 ;
1 . Tọa độ điểm D để tứ giác BCAD là hình bình hành là: A. D 8 ; 5 . B. D8;5. C. D 8 ;5 . D. D8; 5 . Lời giải Chọn D 5 5 2 x x 8
Ta có: tứ giác BCAD là hình bình hành khi D D
BC DA 1 4 0 y y 5 D D
Câu 95. Cho 4 điểm A1; 2
,B0;3,C 3 ; 4,D 1
;8 . Ba điểm nào trong 4 điểm đã cho là thẳng hàng?
A. A, B,C .
B. B,C, D .
C. A, B, D .
D. A,C, D . Lời giải Chọn C Trang 190 Chương 01. LÊ MINH TÂM
Ta có: AD 2;10 , AB1;5 AD 2AB 3 điểm A, B,D thẳng hàng.
Câu 96. Cho tam giác ABC có trọng tâm là gốc tọa độ O , hai đỉnh A và B có tọa độ là A 2 ; 2 ;
B3;5 . Tọa độ của đỉnh C là: A. 1; 7. B. 1 ; 7 . C. 3 ; 5 . D. 2; 2 . Lời giải Chọn B
x x x 2 3 x A B C x 0 C O x 1 Ta có: 3 3 C .
y y y 2 5 y y 7 A B C y 0 C C O 3 3
Câu 97. Trong hệ tọa độ Oxy, cho hai điểm A3; 2 , B 1
;3 . Biết đỉểm I ;
a b là diểm thỏa IA IB 0.
Khi đó ta có giá trị của tổng a b là 1 3 A. . B. 2. C. . D. 1 . 2 2 Lời giải Chọn C a 1 1 3
Do IA IB 0 I là trung điểm của AB I 1 ;
a b . 1 2 b 2 2
Câu 98. Trong hệ tọa độ Oxy, cho ba điểm A1; 2 , B 1 ;5, C4; 3
. Biết đỉểm H ;
a b là diểm thỏa
HA HB HC 0. Khi đó ta có giá trị của tích ab là 4 2 A. . B. 0. C. . D. 1. 3 3 Lời giải Chọn B
Ta có: AB 2; 7 , AC 3;
1 nên AB, AC không cùng phương ABC được thành lập. 4 a 4
Do HA HB HC 3
0 H là trọng tâm của tam giác ABC H ; 0 ab 0 . 3 0 b 2
Câu 99. Trong hệ tọa độ Oxy, cho hai điểm A1; 2 , B 2 ;
3 . Tọa độ đỉểm I sao cho IA 2IB 0 là 8 2 A. I 1 ; . B. I 1 ; .
C. I 1; 2. D. I 2; 2 . 3 5 Lời giải Trang 191 Chương 01. LÊ MINH TÂM Chọn A
IA 1 x;2 y
Gọi I x; y . Ta có IB 2
x;3 y 2IB 4
2x;6 2y
IA 2IB 3 3x;83y. x 1 3 3x 0 8
Từ: IA 2IB 0 8 . Vậy I 1 ; . 8 3 y 0 y 3 3
Câu 100. Trong hệ tọa độ Oxy, cho hai điểm A2; 2 , B4;
3 . Biết đỉểm I ;
a b thỏa mãn 3IA 2IB . Khi đó ta có giá trị của 2 2
a b là: A. 4. B. 9. C. 25. D. 20. Lời giải Chọn A
IA 2a;2 b 3
IA 63a;63b Ta có IB
4a;3b 2IB
82a;62b
6 3a 8 2a a 2
Từ: 3IA 2IB . Vậy 2 2 a b 4 . 6 3 b 6 2b b 0
Câu 101. Trong hệ tọa độ Oxy, cho ba điểm A3; 1 , B 3
;7, C2;5 . Biết đỉểm Mx; y thỏa mãn
MA 2MB . Khi đó ta có tọa độ của u MC AB là: A. 6; 3 . B. 6 ;3. C. 3; 6 . D. 3 ;6. Lời giải Chọn D
MA 3 x;1 y Ta có MB 3
x;7 y 2
MB 6 2x; 1 4 2y 3
x 6 2x x 1 Từ: MA 2 MB . Vậy M 1 ;5. 1 y 1 4 2y y 5 MC 3;0 Ta có:
u MC AB 3;6 . AB 6 ;6
Câu 102. Trong hệ tọa độ Oxy, cho ba điểm A0; 2 , B1; 1 , C 3
;7. Biết đỉểm Mx; y thỏa mãn
MA 2MB MC 0 . Khẳng định đúng là: A. x 0. B. y 0.
C. x y 0.
D. x y 0. Lời giải Chọn C Trang 192 Chương 01. LÊ MINH TÂM
MA x;2 y
Ta có MB 1 x;1 y 2MB 2 2x; 2 2y MC 3
x;7 y
MA 2MB MC 5 2x;3 2y 5 x 5 2x 0 Từ: 2
MA 2MB 2MC 0
. Vậy x y 1. 2 3 y 0 3 y 2
Câu 103. Trong hệ tọa độ Oxy, cho ba điểm A1;0 , B0;3 , biết rằng điểm M thuộc trục hoành và
biểu thức P MA MB đạt giá trị nhỏ nhất. Khi đó ta có khẳng định đúng là: A. x 3.
B. 0 x 1. C. x 0.
D. 1 x 2. M M M M Lời giải Chọn B 1 3
Gọi I là trung điểm của AB ta có : MA MB 2MI và I ; . 2 2
Khi đó P MA MB 2 MI 2MI.
Để P nhỏ nhất MI nhỏ nhất. Mà M thuộc trục hoành nên MI nhỏ nhất khi M là hình 1
chiếu vuông góc của I lên trục hoành M ; 0. 2
Câu 104. Trong hệ tọa độ Oxy, cho ba điểm A1;
1 , B4;3 , Tọa điểm M thuộc trục hoành sao cho biểu
thức P 3MA 2MB đạt giá trị nhỏ nhất là:
A. M 2; 0. B. M 5 ;0. C. M 7 ;0. D. M 3 ;0. Lời giải Chọn B
Gọi I x; y là điểm thỏa mãn : 3IA 2IB 0 .
IA 1 x;1 y 3IA 33x;33y Ta có : IB
4 x;3 y 2
IB 8 2x;6 2y
3IA 2IB 5 x;3 y . 5 x 0 x 5
Từ : 3IA 2IB 0 . Vậy M 5 ; 3 . 3 y 0 y 3 Trang 193 Chương 01. LÊ MINH TÂM
Khi đó P 3MA 2MB 3MI 3IA 2MI 2IB MI MI.
Để P nhỏ nhất MI nhỏ nhất. Mà M thuộc trục hoành nên MI nhỏ nhất khi M là hình
chiếu vuông góc của I lên trục hoành M 5 ;0.
Câu 105. Trong hệ tọa độ Oxy, cho ba điểm A2;0 , B3; 1 và C 7
;5. Tọa độ điểm M thuộc trục hoành
sao cho biểu thức P MA MB MC đạt giá trị nhỏ nhất là: 5 1 2 1
A. M ; 0. B. M ; 0. C. M ; 0. D. M ; 0. 3 2 3 3 Lời giải Chọn C 2
Gọi G là trọng tâm của tam giác ABC ta có : GA GB GC 0 và G ; 2 3
Khi đó P MA MB MC 3MG GA GB GC 3 MI 3MI.
Để P nhỏ nhất MI nhỏ nhất. Mà M thuộc trục hoành nên MI nhỏ nhất khi M là hình 2
chiếu vuông góc của I lên trục hoành M ; 0. 3
Câu 106. Trong hệ tọa độ Oxy, cho ba điểm A 1
;0, B2;3 và C 5
; 4. Tọa độ điểm M thuộc trục hoành
sao cho biểu thức P 2MA 4MB 3MC đạt giá trị nhỏ nhất là: A. M 5 ;0. B. M 8;0.
C. M 7; 0. D. M 6 ;0. Lời giải Chọn C
Ta có 2MA 4MB 3MC 2MI IA 4MI IB3MI IC
3MI 2IA4IB3IC
Chọn điểm I sao cho 2IA 4IB 3IC 0. * 2 1
x 42 x 3 5 x 0 x 7
Gọi I x; y , từ * ta có: I ; . 2
0 y 43 y 34 y 7 0 0 y 0
Khi đó P 2MA 4MB 3MC 3 MI 3MI.
Để P nhỏ nhất MI nhỏ nhất. Mà M thuộc trục hoành nên MI nhỏ nhất khi M là hình
chiếu vuông góc của I lên trục hoành M 7;0.
Câu 107. Cho tam giác ABC với A 5 ;6 , B 4 ;
1 và điểm C 4;3 . Tìm tọa độ điểm D sao cho ABCD là hình bình hành Trang 194 Chương 01. LÊ MINH TÂM A. D 3;10 B. D 3; 1 0 . C. D 3 ;10 . D. D 3 ; 1 0 . Lời giải Chọn A A B D C Gọi D ,
x y là điểm cần tìm Ta có : AB 1; 7
, DC 4 ; x 3 y 4 x 1
Để ABCD là hình bình B2;0 A 1
;3hành AB DC D3;10 . 3 y 7
Câu 108. Trong mặt phẳng Oxy cho ba điểm , và điểm C 6; 2 . Tìm tọa độ điểm D sao cho ABCD là hình bình hành A. 9; 1 B. 3;5 . C. 5;3 . D. 1 ;9 . Lời giải Chọn B Ta có AB 3; 3
, DC 6 ;
x 2 y , D ; x y . 6 x 3 x 3
ABCD là hình bình hành M, N, P ABC khi AB DC D 3;5 . 2 y 3 y 5
Câu 109. Cho tam giác . Gọi lầ lượt là trung điểm của các cạnh BC,CA, AB . Biết A1;3 , B 3
;3 , C 8;0 .
Giá trị của x x x M N P bằng A. 2 B. 3 . C. 1 . D. 6 . Lời giải Chọn D 5
Ta có : M là trung điểm BC x M 2 9
N là trung điểm AC x N 2
P là trung điểm AB x 1 P 5 9
x x x 1 6 M N P 2 2
Câu 110. Trong mặt phẳng Oxy , cho tam giác ABC có B9; 7, C 11;
1 . Gọi M , N lần lượt là trung
điểm của AB, AC. Tìm tọa độ của véc tơ MN A. 2; 8 B. 1; 4 . C. 10; 6 . D. 5; 3 . Trang 195 Chương 01. LÊ MINH TÂM Lời giải Chọn B 1 1 Ta có MN BC
2; 8 1; 4. 2 2
Câu 111. Trong mặt phẳng Oxy , cho tam giác ABC có M 2; 3, N 0; 4, P 1
; 6 lần lượt là trung điểm của BC,C ,
A AB . Tìm tọa độ đỉnh A A. 1; 5 B. 3 ; 1 . C. 2 ; 7 . D. 1; 10 . Lời giải Chọn C A N P C M B Gọi A ;
x y . Ta có PA MN x 1; y 6 2 ; 7 . x 1 2 x 3 . Vậy A 3 ; 1 . y 6 7 y 1
Câu 112. Trong mặt phẳng Oxy , cho tam giác ABC có A6; 1 , B 3
; 5 và trọng tâm G 1 ; 1 . Tìm tọa độ đỉnh C A. 6; 3 B. 6 ; 3 . C. 6 ; 3 . D. 3 ; 6. Lời giải Chọn C 6 3 x 1 x 6 Gọi C ;
x y . Ta có 3 G C 6 ; 3 là trọng tâm . 1 5 y y 3 1 3
Câu 113. Trong mặt phẳng Oxy , cho tam giác ABC có A 2
; 2, B3; 5 và trọng tâm là gốc O . Tìm tọa độ đỉnh C A. 1 ; 7 B. 2; 2 . C. 3 ; 5 . D. 1; 7 . Lời giải Chọn A 2 3 x 0 x 1 3 Gọi C ;
x y . Ta có O là trọng tâm Vậy C 1 ; 7 2 5 y y 7 0 3 Trang 196 Chương 01. LÊ MINH TÂM
Câu 114. Trong mặt phẳng Oxy , cho bốn điểm A1; 1 ,, B2;
1 , C 4; 3 và D3; 5 . Khẳng định nào sau đây đúng? 5
A. Tứ giác ABCD là hình bình hành B. G 2;
là trọng tâm tam giác BC . D 3
C. AB C . D
D. AC, AD cùng phương. Lời giải Chọn A
Ta có AB 1; 2, DC 1; 2 Tứ giác ABCD là hình bình hành.
Câu 115. Trong mặt phẳng Oxy ,cho hai điểm A1; 2, B 2
; 3 . Tìm tọa độ điểm I sao cho IA 2IB 0 . 2 8 A. 1; 2 B. 1; . C. 1; . D. 2; 2 . 5 3 Lời giải Chọn C Gọi I ;
x y . Ta có IA 2IB 0 1 ;
x 2 y 2 2 ;
x 3 y 0; 0 x 1 1
x 4 2x 0 8 8 Vậy I 1; .
2 y 6 2y 0 y 3 3
Câu 116. Trong mặt phẳng Oxy ,cho hai điểm A2; 3, B 3; 4 . Tìm tọa độ điểm M trên trục hoành sao cho ,
A B, M thẳng hàng. 5 1 17 A. M 1; 0
B. M 4; 0 . C. M ; . D. M ; 0 . 3 3 7 Lời giải Chọn D
Điểm M Ox M ;
m 0 . Ta có AB 1; 7 và AM m 2; 3 . m 2 3 17 Để ,
A B, M thẳng hàng m 17 . Vậy M ; 0 . 1 7 7 7
Câu 117. Trong mặt phẳng Oxy ,cho tam giác ABC có A3; 5 , B 1; 2 , C 5; 2 . Tìm tọa độ trọng tâm G của tam giác ABC A. 3 ; 4 B. 4; 0 . C. 2; 3 . D. 3; 3 . Lời giải Chọn D
3 1 5 5 2 2
Ta có tọa độ G ; 3; 3 . 3 3 Trang 197 Chương 01. LÊ MINH TÂM
Câu 118. Trong mặt phẳng Oxy, cho các điểm A4; 2 ,B 2 ;
1 ,C 0;3 , M 3 ;7 . Giả sử AM .
x AB y.AC x, y . Khi đó x y bằng 12 12 A. . B. 5 . C. . D. 5 . 5 5 Lời giải Chọn A
AM 7;5 , AB6; 1 , AC 4; 1 . Giả sử AM .
x AB y.AC x, y . 13 x
6x 4y 7 Hệ phương trình 10 . x y 5 37 y 10
Câu 119. Trong mặt phẳng Oxy ;cho các véc tơ a 2;
1 ; b 0; 4 và c 3;
3 . Gọi m và n là hai số thực
sao cho c ma nb . Tính giá trị biểu thức 2 2
P m n . 225 100 97 193 A. P . B. P . C. P . D. P . 64 81 64 64 Lời giải Chọn A
Ta có ma nb 2 ;
m m 4n . 3 m 2m 3 Khi đó 2
c ma nb .
m 4n 3 9 n 8 225 Vậy 2 2
P m n . 64
Câu 120. Cho a 2; 1 , b 3
; 4 , c 4
; 9 . Hai số thực m , n thỏa ma nb c . Tính 2 2 m n ? A. 5 . B. 3 . C. 4 . D. 1. Lời giải Chọn A
2m 3n 4 m 1
Ta có: ma nb c .
m 4n 9 n 2
Câu 121. Với hai véc tơ không cùng phương a và b . Xét hai véc tơ u 2a 3b và v a x
1 b . Tìm x để
u và v cùng phương. 3 1 1 3 A. x . B. x . C. x . D. x . 2 2 2 2 Trang 198 Chương 01. LÊ MINH TÂM Lời giải Chọn B
Do hai véc tơ a và b không cùng phương nên điều kiện để hai véc tơ u 2a 3b và k 2 2 k 1 .
v a x
1 b cùng phương là: u kv . k x 1 3 1 x 2
Câu 122. Trong mặt phẳng Oxy cho tam giác ABC có A2; 1 , B 1
; 2,C3;0 . Tứ giác ABCE là hình bình
hành khi tọa độ E là cặp số nào sau đây? A. 6; 1 B. 0; 1 C. 1; 6 D. 6; 1 Lời giải Chọn A A B E C Gọi E ; x y . x x
Tứ giác ABCE là hình bình hành AE 2 4 6 BC y 1 2 y 1 Vậy E6; 1 .
Câu 123. Trong mặt phẳng với hệ tọa độ Oxy , cho véctơ a 3; 2 , b 1
( ; 4). Tọa độ của véctơ v a b ? A. v ( 2 ; 6). B. v ( 4 ; 2) . C. v ( 2 ;6) .
D. u (4; 2) . Lời giải Chọn C
Ta có v a b ( 3 1;2 4) ( 2 ;6).
Câu 124. Trong mặt phẳng với hệ tọa độ Oxy , cho véctơ a 2; 4 , b ( 5
;3). Tọa độ của véctơ u 2a b
A. u 7; 7 .
B. u 9; 1 1 .
C. u 9;5 . D. u 1 ;5 . Lời giải Chọn B
Ta có u 2a b 2 2 . 5; 2.( 4
) 3 9;1 1 .
Câu 125. Trong mặt phẳng với hệ tọa độ Oxy , cho các véctơ a ;
m 3 , b 2
;n, u 4;3, ( , m n ).
Tính giá trị của S 2m n , biết rằng véctơ u a 3b . A. 18. B. 10. C. 8 . D. 22 . Trang 199 Chương 01. LÊ MINH TÂM Lời giải Chọn A m m
Ta có u a b ; m ; n 6 4 10 3 4 3 6 3 3 3 3n 3 n 2
Câu 126. Trong mặt phẳng Oxy, cho các điểm A1; 2 ,B 3
;5,C0;4,D 3 ; 5 . Giả sử AD . m AB .
n AC m,n . Tính giá trị của S . m n? A. 24 . B. 5 . C. 11. D. 24 . Lời giải Chọn D
AD 4; 7 , AB4;3 , AC 1 ; 2 . Giả sử AD . m AB .
n AC m,n (*) 4
m n 4 m 3
Thay tọa độ vào(*) ta có hệ phương trình 3m 2n 7 n 8
Câu 127. Trong mặt phẳng Oxy , cho các véc tơ a 4;13 ; b 0;
1 và c 2; 5 . Mệnh đề nào dưới đây là đúng ?
A. a 2b 3c .
B. a 3b 2c .
C. a 3b 2c .
D. a 2b 3c . Lời giải Chọn B
0m 2n 4
Giả sử có cặp số thực (m, )
n thỏa mãn a mb nc . Thay tọa độ ta có
m 5n 13 n 2
a 3b 2 . c m 3
Câu 128. Cho tam giác ABC . Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC . Đẳng thức nào
dưới đây là đúng ?
A. AP AM AN .
B. AP AB AC . 1 1 C. AP AM AN .
D. AP AM AN . 2 2 Lời giải Chọn D
Theo giả thiết ta có tứ giác AMPN là hình bình hành nên AP AM AN. Trang 200 Chương 01. LÊ MINH TÂM A M N B C P
Câu 129. Cho tam giác ABC . Gọi I là trung điểm của các cạnh BC , G là trọng tâm của tam giác ABC . Đẳng
thức nào dưới đây là đúng ? 1 1
A. GI GB GC .
B. GI GB GC . 2 2 1 1
C. GI GB GC .
D. GI GB GC . 2 2 Lời giải Chọn C 1 1
Theo tính chất trung điểm của đoạn thẳng ta có 2GI GB GC GI GB GC. 2 2 A G B C I
Câu 130. Cho tam giác ABC có tọa độ các đỉnh A 3 ; 1 , B2; 2
,C0;4 . Gọi M là điểm thỏa mãn hệ thức
MA MB MC . Tọa độ của điểm M là ? A. (5;1). B. (5; 1) . C. ( 5 ;1). D. ( 5 ;1) . Lời giải Chọn C MA ( 3
x;1 y) Gọi tọa độ điểm ( M ;
x y) . Ta có: MB (2 x; 2 y)
MC (x;4 y) 2 2x 3 x x 5
Theo giả thiết MA MB MC suy ra . 2 2 y 1 y y 1 A M B C Trang 201 Chương 01. LÊ MINH TÂM
Câu 131. Cho hình bình hành ABCD tâm O . Khi đó OA BO bằng
A. OC OB . B. AB .
C. OC DO . D. CD . Lời giải Chọn D A D B C
Ta có OA BO BO OA BA CD .
Câu 132. Cho tam giác ABC là tam giác đều, O là tâm đường tròn ngoại tiếp tam giác ABC . Mệnh
đề nào là đúng trong các mệnh đề sau?
A. OA OB OC .
B. OA OC OB .
C. OA OB OC .
D. OA OB CO . Lời giải Chọn D
Do tam giác ABC là tam giác đều nên O cũng là trọng tâm của tam giác ABC . Do vậy, ta
có OA OB OC 0 OA OB CO .
Câu 133. Cho tứ giác ABCD . Xét các khẳng định sau
(I) AB BC CD DA 0 .
(II) AB BD CD CA .
(III) AB AD CB CD .
(IV) AC AB DB DC .
Số khẳng định đúng là A. 0 . B. 1. C. 2 . D. 4 . Lời giải Chọn C
Ta có AB BC CD DA AC CA 0 . Khẳng định (I) đúng.
AB BD CD AD DC AC . Suy ra (II) sai.
AB AD DB và CB CD DB . Suy ra (III) đúng.
AC AB BC và DB DC CB . Suy ra (IV) sai.
Câu 134. Cho tam giác đều ABC cạnh a , trọng tâm G . Tính theo a độ dài của v GA GB GC . 2a 3 a 3 3a A. . B. 2a . C. . D. . 3 2 2 Lời giải Chọn A Trang 202 Chương 01. LÊ MINH TÂM A H G B C
Do G là trọng tâm của tam giác ABC nên GA GB GC 0 GA GB G C . 2 a 3 2a 3
Suy ra v GA GB GC 2GC . Vậy v 2 GC 2 . 3 2 3
Câu 135. Cho hình vuông ABCD cạnh a , tâm O . Tính theo a độ dài của véc-tơ u AB OD BC . B C O A D a 2 3a 2 A. . B. . C. a 2 . D. a . 2 2 Lời giải Chọn A
Ta có u AB OD BC AB BO AD AO AD DO . a 2
Suy ra u DO . 2
Câu 136. Cho tam giác ABC . Gọi D, ,
E F,G, H, I theo thứ tự là trung điểm các cạnh AB, BC,CA , DF ,
DE , EF . Véc-tơ u BE GH AI FE bằng véc-tơ nào sau đây? A D G F H I B C E A. DA . B. FC . C. CE . D. AB . Lời giải Chọn A
u BE GH AI FE BE HG IA FE BE EI IA FE BA AD BD DA .
Câu 137. Cho ABCD là hình bình hành. O là giao điểm hai đường chéo. Xét các khẳng định sau đây
I. CO OB BA .
II. AB BC DB .
III. DA DB OD OC . Trang 203 Chương 01. LÊ MINH TÂM
IV. DA DB DC 0 .
Các khẳng định đúng là A. Chỉ (I). B. (I) và (III). C. (II) và (III).
D. (I), (III) và (IV). Lời giải Chọn D A B O D C
CO OB CO BO BO OA BA . Suy ra (I) đúng.
AB BC AC . Suy ra (II) sai.
DA DB BA , OD OC CD và BA CD . Suy ra (III) đúng.
DA DB DC BA DC BA AB 0 . Suy ra (IV) đúng.
Câu 138. Cho tam giác ABC . Gọi I, J,K lần lượt là trung điểm của các cạnh BC,CA, AB . Tìm mệnh
đề sai trong các mệnh đề dưới đây
I. AB BC AC 0 .
II. KB JC AI .
III. AK BI CJ 0 . A. Chỉ (I). B. (II) và (III). C. Chỉ (II). D. (I) và (III). Lời giải Chọn A A K J B C I
AB BC AC 2AC . Suy ra (I) sai.
KB JC AK AJ AI (quy tắc hình bình hành). Suy ra (II) đúng.
AK BI CJ KB BI CJ KI CJ 0 . Suy ra (III) đúng.
Câu 139. Cho bốn điểm A, B,C, D phân biệt, đặt u AB DC BC AD . Khi đó u bằng véctơ nào sau đây? A. u 0 .
B. u BD .
C. u AC .
D. u 2DC . Lời giải Chọn A
Ta có: u AB DC BC AD AB BCAD DC AC AC 0 .
Câu 140. Cho tam giác ABC . Gọi M, N, P lần lượt là trung điểm các cạnh AB, AC, BC . Hỏi MP NP bằng véctơ nào? Trang 204 Chương 01. LÊ MINH TÂM A. AM B. PB . C. AP . D. MN . Lời giải Chọn C A M N B C P
Theo đề bài M, N, P lần lượt là trung điểm các cạnh AB, AC, BC nên MP AN
MP NP AN NP AP .
Câu 141. Cho 4 điểm bất kỳ A,B,C,O . Đẳng thức nào sau đây là đúng?
A. OA CA CO.
B. BC AC AB 0 . C. BA OB OA .
D. OA OB BA . Lời giải Chọn B
Ta có: BC AC AB BC (AC AB) BC BC 0 .
Câu 142. Gọi O là tâm của hình vuông ABCD . Vectơ nào trong các vectơ dưới đây bằng CA ?
A. BC AB . B. O A OC .
C. BA DA .
D. DC CB . Lời giải Chọn C A D O B C
Vì ABCD là hình vuông nên ta có: BA CD BA DA CD DA CA .
Câu 143. Cho hình bình hành ABCD tâm O , đặt u OB OA . Khi đó u bằng
A. OB OC . B. BA .
C. OC OD . D. CD . Lời giải Chọn C A D O B C
Vì ABCD là hình bình hành tâm O nên OB DO O ;
D OA CO O C .
Khi đó u OB OA O D O
C OC OD . Trang 205 Chương 01. LÊ MINH TÂM
Câu 144. Gọi O là tâm hình bình hành ABCD . Đẳng thức nào sau đây sai?
A. OA OB CD.
B. OB OC OD O . A
C. AB AD D . B
D. BC BA DC D . A Lời giải Chọn B A D O B C
Xét đáp án A. Ta có OA OB BA CD . Vậy A đúng. O
BOC CB AD Xét đáp án B. Ta có . Vậy B sai. O
D OA AD
Xét đáp án C. Ta có AB AD D . B Vậy C đúng.
BC BA AC Xét đáp án D. Ta có . Vậy D đúng.
DC DA AC
Câu 145. Cho hình vuông ABCD có cạnh bằng a . Khi đó AB AD bằng: a 2 A. a 2 . B. . C. 2a . D. a . 2 Lời giải Chọn A A a D a B C
Vì ABCD là hình vuông nên ta có AB AD AC và 2 2
AC AB AD a 2 .
Suy ra: AB AD AC AC a 2 .
Câu 146. Cho hình vuông ABCD cạnh a . Tính AB AC AD ? A. 2a 2 . B. 3a . C. a 2 . D. 2a . Lời giải Chọn A Trang 206 Chương 01. LÊ MINH TÂM A a D a B C
Vì ABCD là hình vuông nên ta có: AB AD AC
AB AC AD AB AD AC 2AC 2AC 2a 2 .
Câu 147. Cho hình vuông ABCD có cạnh bằng a . Khi đó AB AC bằng: a 5 a 3 a 3 A. . B. . C. . D. a 5 . 2 2 3 Lời giải Chọn D A a D a B C M
Gọi M là trung điểm BC . 2 a Ta có: 2 2 2
AB AC 2AM 2AM 2 AB BM 2 a a 5 . 2 Câu 148. Cho A
BC vuông tại A và AB 3 , AC 4 . Véctơ CB AB có độ dài bằng A. 13 . B. 2 13 . C. 2 3 . D. 3 . Lời giải Chọn B B 3 A C M
Gọi M là trung điểm AC .
Ta có : CB AB = BC BA BC BA 2 BM 2MB. Suy ra: 2 2 2 2
CB AB 2MB 2BM 2 AB AM 2 3 2 2 13 .
Câu 149. Cho hình chữ nhật ABCD biết AB 4a và AD 3a thì độ dài AB AD bằng Trang 207 Chương 01. LÊ MINH TÂM A. 7a . B. 6a .
C. 2a 3 . D. 5a . Lời giải Chọn D A 3a B 4a D C 2 2
Ta có: AB AD AC AC 4a 3a 5a .
Câu 150. Cho tam giác đều ABC cạnh a . Độ dài của AB AC là a 3 A. a 3 . B. . C. a 6 . D. 2a 3 . 3 Lời giải Chọn A A a a B C M AB 3 a 3
Gọi M là trung điểm của BC , ta có: AB AC 2AM và AM . 2 2
Suy ra AB AC 2AM 2AM a 3 .
--------------------HẾT-------------------- Trang 208




