Cơ học lượng tử| Bài giảng môn Vật lý đại cương 3 | Trường Đại học Bách Khoa Hà Nội
Cơ học lượng tử | Bài giảng môn Vật lý đại cương 3 | Trường Đại học Bách Khoa Hà Nội. Tài liệu gồm 33 trang giúp bạn tham khảo ôn tập đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem.
Preview text:
Chương 7 CƠ HỌC LƯỢNG TỬ
7.1. Lưỡng tính sóng - hạt của hạt vi mô
7.2. Hàm sóng trong cơ học lượng tử, ý nghĩa, điều kiện
7.3. Phương trình Schrodinger
7.4. Ứng dụng phương trình Schrodinger
7.1. Lưỡng tính sóng - hạt của hạt vi mô
1. Lưỡng tính sóng - hạt của ánh sáng Ánh sáng Sóng Hạt Giao thoa, nhiễu
Bức xạ nhiệt, hiện tượng quang xạ, phân cực,…
điện, tán xạ Compton,… Thuyết photon của Einstein Ánh sáng cấu tạo
bởi các hạt photon
7.1. Lưỡng tính sóng - hạt của hạt vi mô
1. Lưỡng tính sóng - hạt của ánh sáng Ánh sáng cấu tạo
bởi các hạt photon 𝒉𝒄 𝒉
Năng lượng E = h =
Động lượng p =
Tính chất sóng (, ) và hạt (E, p) có liên quan
Hàm sóng của ánh sáng đơn sắc được biểu thị qua E, p
7.1. Lưỡng tính sóng - hạt của hạt vi mô
1. Lưỡng tính sóng - hạt của ánh sáng
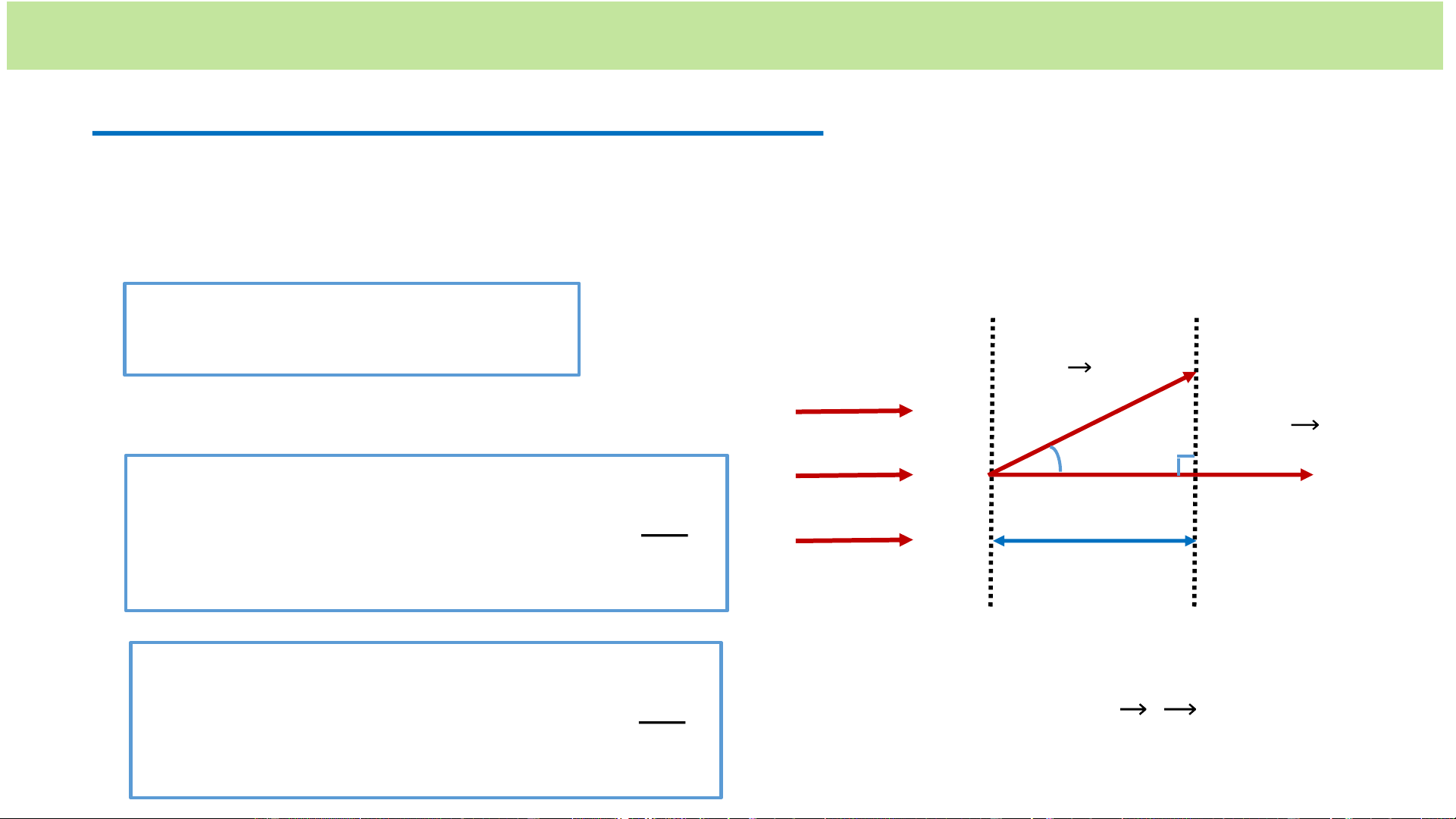
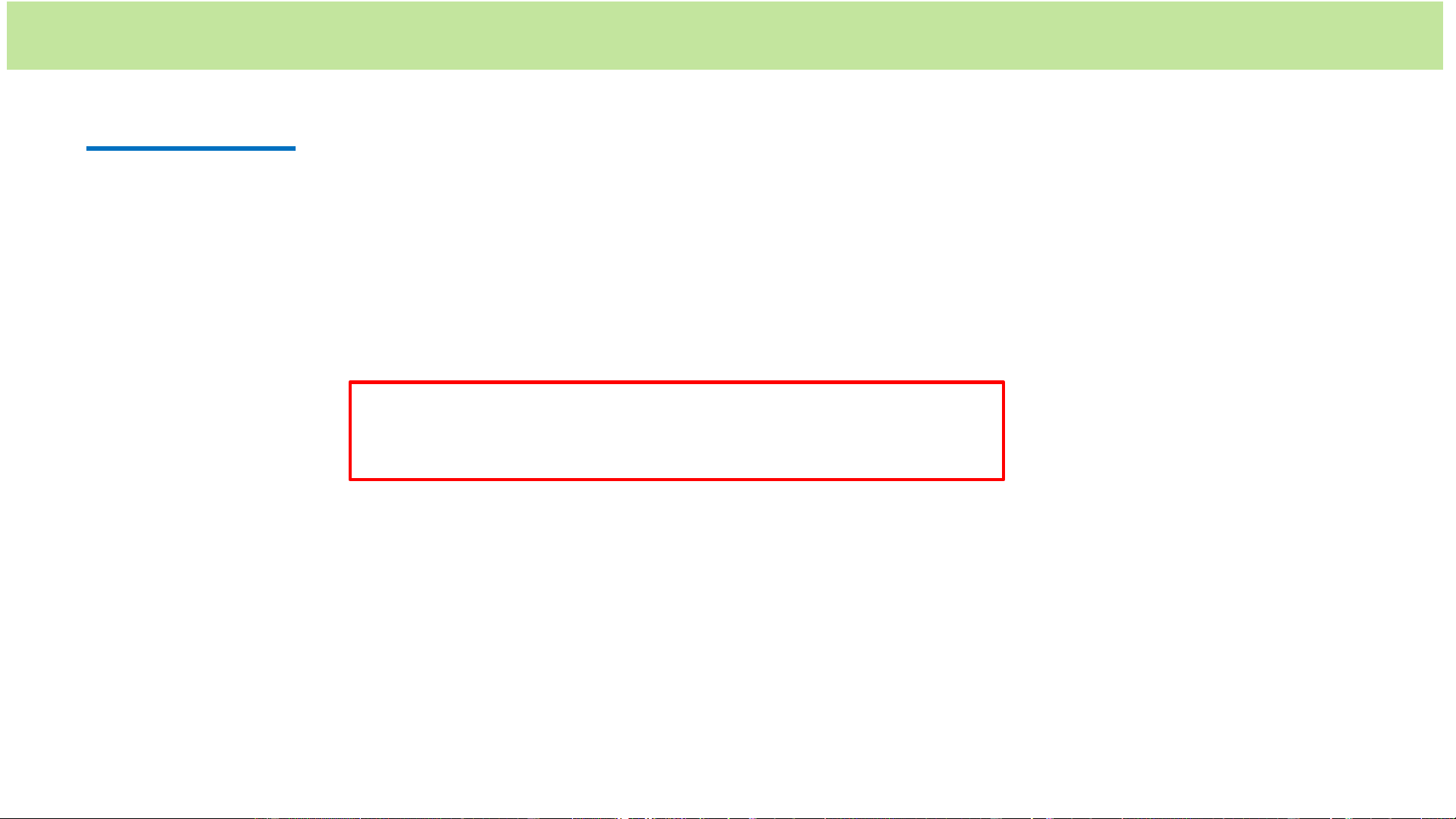
* Hàm sóng phẳng của ánh sáng đơn sắc • Hàm sóng tại O
a cos(2 t ) 0 M 𝒓 • Hàm sóng tại M M’ O α 𝒏 d
a cos 2 (t ) M c d d
a cos 2 (t ) M
Mà d = rcosα = 𝒓. 𝒏
7.1. Lưỡng tính sóng - hạt của hạt vi mô
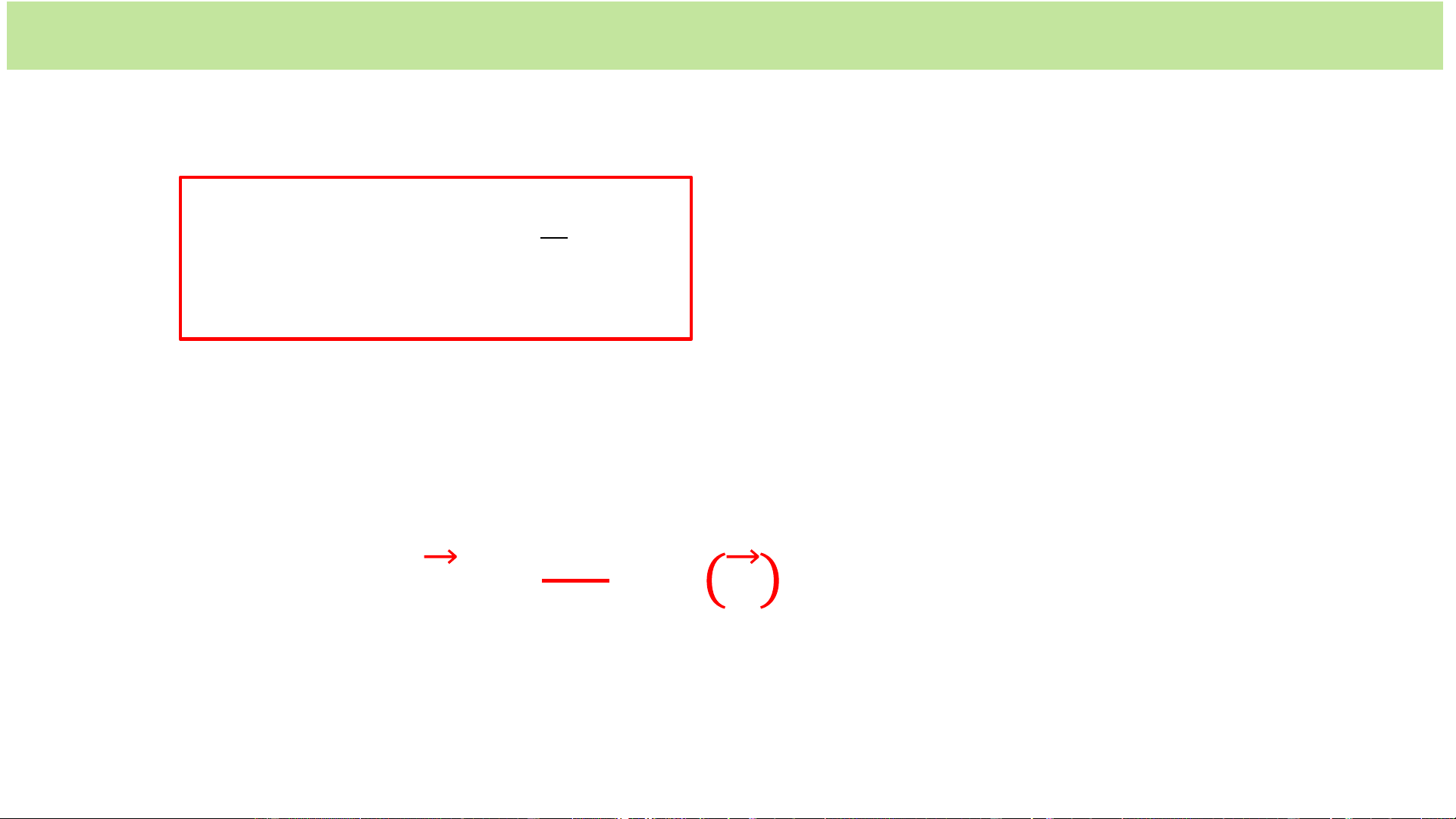
Hàm sóng phẳng của ánh sáng đơn sắc r . n
a cos 2 (t ) M
• Biểu diễn hàm sóng dưới dạng phức r .n 2i(t ) ae
i( tk .r ) Với 𝟐 𝒌 = ae
𝒏: Véc tơ sóng
7.1. Lưỡng tính sóng - hạt của hạt vi mô
Hàm sóng (biểu diễn qua năng lượng và động lượng của photon) i
(Et p.r ) ae Với 𝒉
ħ = 𝟐 = 1,05. 𝟏𝟎−𝟑𝟒Js: Hằng số Planck rút gọn 𝒉 𝒑 = ħ. 𝒌 = 𝒏
7.1. Lưỡng tính sóng - hạt của hạt vi mô
2. Giả thuyết De Broglie
Một vi hạt tự do có năng lượng xác định, động lượng xác định
tương ứng với một sóng phẳng đơn sắc xác định.
• Năng lượng của vi hạt liên hệ với tần số dao động của sóng
tương ứng theo hệ thức:
𝑬 = 𝒉 hay 𝑬 = ħ
• Động lượng của vi hạt liên hệ với bước sóng của sóng tương ứng theo hệ thức:
𝒑 = 𝒉/ hay 𝒑 = ħ𝒌
Thực nghiệm xác nhận tính chất sóng của hạt vi mô
7.1. Lưỡng tính sóng - hạt của hạt vi mô
3. Hệ thức bất định Heisenberg
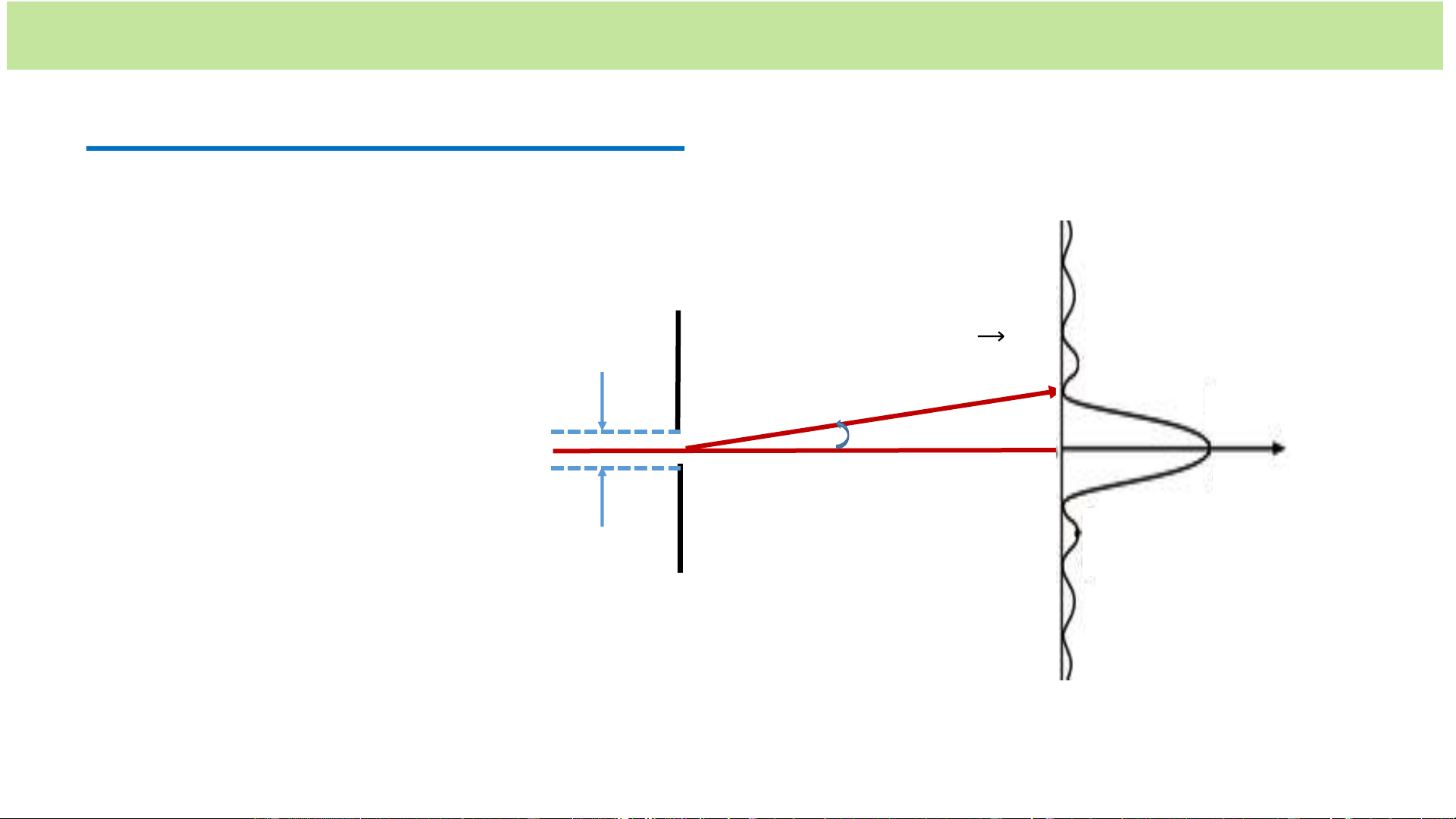
Nhiễu xạ của chùm vi hạt qua một khe hẹp E + Chùm electron qua
khe hẹp bị nhiễu xạ 𝒑 A theo mọi phương. b Trên màn E: phân
bố các electron giống B phân bố cường độ sáng trong nhiễu xạ của chùm ánh sáng
đơn sắc qua khe hẹp.
7.1. Lưỡng tính sóng - hạt của hạt vi mô
3. Hệ thức bất định Heisenberg
* Sau khi qua khe, vị trí, động lượng 𝒑 của hạt thay đổi
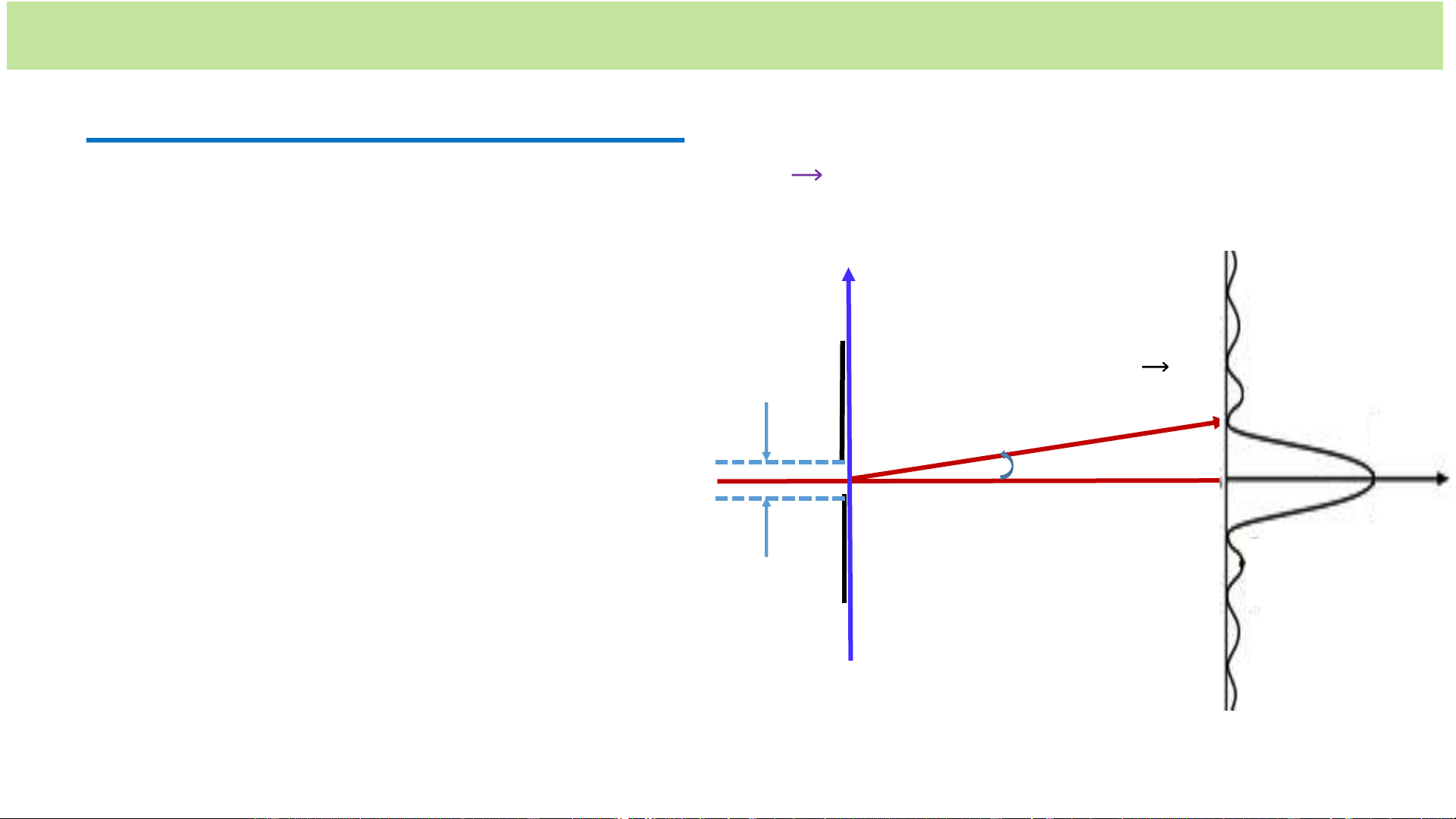
+ Xét hạt theo phương x E x
Tọa độ của hạt trong khe 0 x b 𝒑 A
Độ bất định của vị trí b
x b B
+ Hình chiếu của động lượng của hạt lên ox 0 𝒑 𝒙 psin
7.1. Lưỡng tính sóng - hạt của hạt vi mô
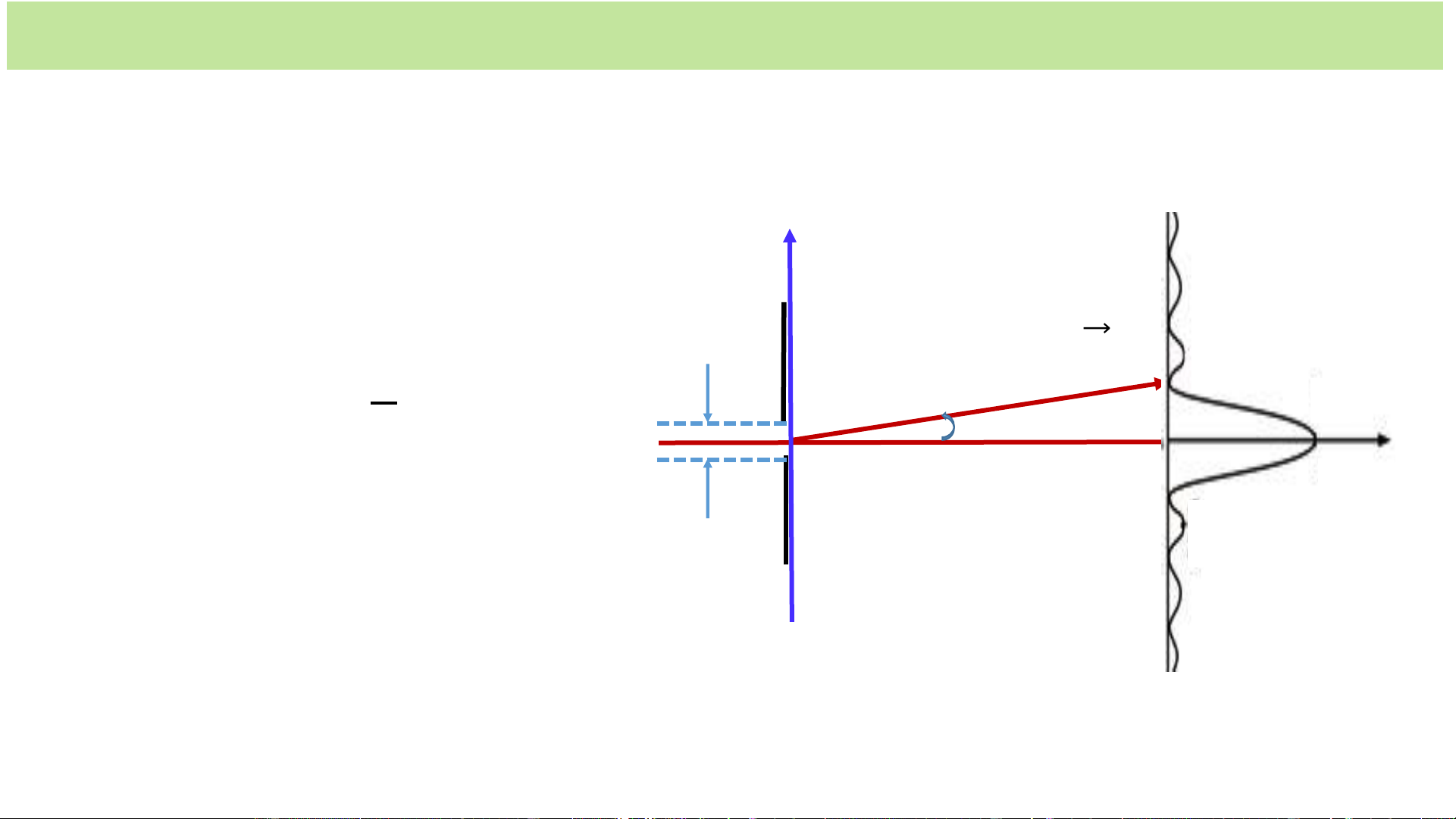
+ Vì các hạt rơi chủ yếu vào cực đại giữa nên: 0 𝒑 𝒙 psin𝟏 E x 𝒑 𝒙 𝒑𝒔𝒊𝒏𝟏 𝒑 A
Mà 𝒔𝒊𝒏𝟏 = 𝒃 1 b
x.𝒑 𝒙 𝒑 B với 𝒑 = 𝒉/
x.𝒑 𝒙 𝒉
Tương tự ta có: y.𝒑 𝒚
𝒉; z.𝒑𝒛 𝒉
7.1. Lưỡng tính sóng - hạt của hạt vi mô
Hệ thức bất định x.𝒑 𝒙 𝒉 x.𝒑 𝒙 ħ y.𝒑 𝒚 𝒉 hay y.𝒑 𝒚 ħ z.𝒑 𝒛 𝒉 z.𝒑 𝒛 ħ
(Hệ thức bất định giữa tọa độ và động lượng)
Tọa độ và động lượng của vi hạt không được xác định đồng
thời. Tọa độ của hạt càng xác định thì động lượng của hạt
càng bất định và ngược lại.
Trong thế giới vi mô không có khái niệm quỹ đạo.
7.1. Lưỡng tính sóng - hạt của hạt vi mô
Hệ thức bất định đối với năng lượng:
E.𝒕 𝒉 hay
E.𝒕 ħ
Nếu năng lượng của một hệ ở một trạng thái nào đó càng xác
định thì thời gian tồn tại ở trạng thái đó càng dài.
Ngược lại nếu năng lượng của một hệ ở một trạng thái nào đó
càng bất định thì thời gian tồn tại ở trạng thái đó càng ngắn.
Trạng thái có năng lượng bất định: Trạng thái không bền.
Trạng thái có năng lượng xác định: Trạng thái bền.
7.2. Hàm sóng trong cơ học lượng tử, ý nghĩa, điều kiện 1. Hàm sóng
* Hàm sóng: Dùng để mô tả trạng thái của vi hạt.
+ Vi hạt tự do: Trạng thái của hạt được mô tả bởi một hàm sóng
tương tự như sóng phẳng ánh sáng đơn sắc (sóng De Broglie) i
(Et p.r )
i( t k .r ) e e 0 0 ( 𝟐
𝟎 là biên độ của hàm sóng, 𝟎 = 𝟐 = ∗
∗ là liên hợp phức của )
7.2. Hàm sóng trong cơ học lượng tử, ý nghĩa, điều kiện 1. Hàm sóng
+ Vi hạt chuyển động trong trường thế: Hàm sóng của hạt là
một hàm phức tạp của tọa độ và thời gian
(r , t) (x, y, z, t)
7.2. Hàm sóng trong cơ học lượng tử, ý nghĩa, điều kiện
2. Ý nghĩa thống kê hàm sóng
+ Bình phương biên độ sóng (𝟐𝟎 = 𝟐) tại M đặc trưng cho
khả năng tìm thấy hạt trong một đơn vị thể tích bao quanh M
𝟐: Mật độ xác suất - Xác suất tìm thấy hạt trong một đơn
vị thể tích bao quanh M.
Xác suất tìm thấy hạt trong thể tích V: 𝟐𝒅𝑽 𝑽
7.2. Hàm sóng trong cơ học lượng tử, ý nghĩa, điều kiện
2. Ý nghĩa thống kê hàm sóng
Xác suất tìm thấy hạt trong toàn bộ không gian: +
𝟐𝒅𝑽 = 1 : Điều kiện chuẩn hóa hàm sóng −
Hàm sóng có ý nghĩa thống kê
3. Điều kiện của hàm sóng
• Hàm sóng phải giới nội
• Hàm sóng phải đơn trị
• Hàm sóng phải liên tục
7.3. Phương trình Schrodinger
* Vi hạt chuyển động trong trường thế U(𝒓), hàm sóng có dạng: 𝒊
𝒓, 𝒕 = 𝒆− 𝑬𝒕 ħ . 𝒓
Trong đó E là năng lượng của vi hạt, 𝒓 𝐥à phần phụ thuộc tọa
độ 𝒓 của hàm sóng.
+ 𝒓 là nghiệm của phương trình: 𝟐𝒎 (𝒓) +
(𝑬 − 𝑼(𝒓)) 𝒓 = 0 ħ𝟐
(Phương trình Schrodinger)
7.3. Phương trình Schrodinger 𝟐 𝟐 𝟐 Với = + + : toán tử Laplace 𝒙𝟐 𝒚𝟐 𝒛𝟐
Phương trình Schrodinger: Phương trình cơ bản của cơ học lượng tử
* Vi hạt chuyển động tự do hàm sóng có dạng hàm sóng phẳng
đơn sắc (sóng De Broglie) i i i
(Et p.r ) Et ( p.r )
(r , t) e
e ( e ) 0 0
7.3. Phương trình Schrodinger Với i ( p.r )
(r ) e 0
là nghiệm của phương trình Schrodinger: 𝟐𝒎 (𝒓) + 𝑬 𝒓 = 0 ħ𝟐
7.4. Ứng dụng phương trình Schrodinger U
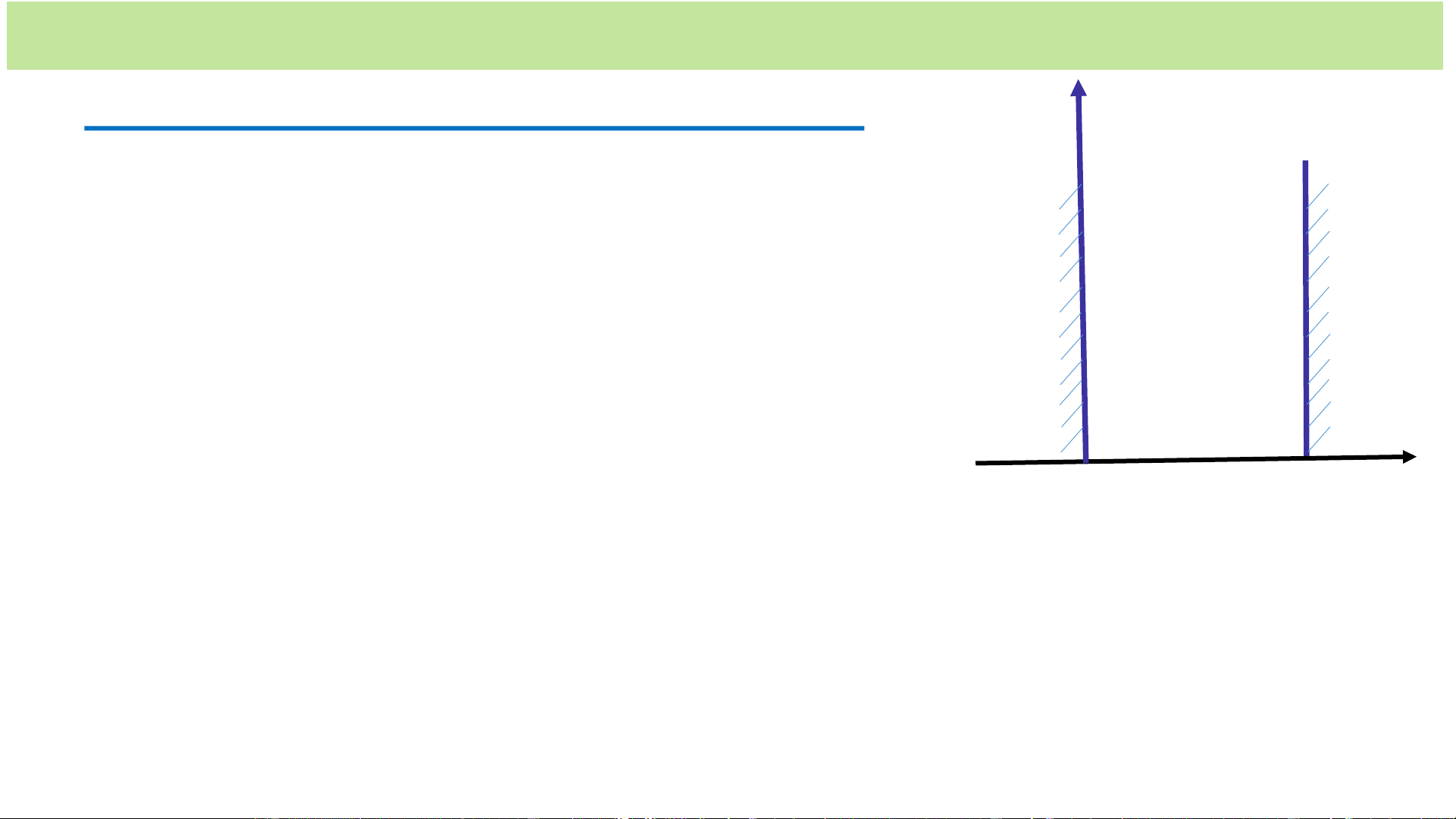
1. Vi hạt trong giếng thế năng một chiều
• Xét chuyển động của hạt theo phương x,
trong miền mà thế năng U có dạng:
𝟎 𝐤𝐡𝐢 𝟎 < 𝒙 < 𝒂
𝑼 = ቊ khi 𝒙 𝟎 𝒗à 𝒙 𝒂
(Vi hạt bị “giam” trong giếng thế năng một
chiều có thành cao vô hạn) 0 a x
+ Nhận xét: Hạt chỉ có thể chuyển động tự do trong giếng và không
thể vượt ra ngoài giếng.
Xác suất tìm hạt ở ngoài giếng bằng 0.
Hàm sóng ở ngoài giếng bằng 0.