Công Thức Cuối Kỳ Môn Giải Tích 1 - HCMUT-CNCP

HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG
TRƯỜNG ĐẠI HỌC QUỐC GIA HỒ CHÍ MINH
TRƯỜNG BÁCH KHOA HỒ CHÍNH MINH
HCMUT-CNCP & CÔNG THỨC CUỐI KÌ
MÔN GIẢI TÍCH 1 HK231
Biên soạn: Nguyễn Quốc Vương
Chủ sở hữu:……………
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 1 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG Mục Lục
1.Nguyên hàm (tích phân bất định) và tích phân xác định. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.1 Phương pháp đổi biến. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3
1.2 Phương pháp đổi biến ( đặt ẩn phụ ). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3
1.3 Một số tìm nguyên hàm hay gặp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4
1.4 Nguyên hàm hàm hữu tỉ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.Đạo hàm của tích phân. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
3.Ứng dụng của nguyên hàm, tích phân trong hình học. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
3.1 Trường hợp diện tích miền D được giới hạn bởi �(�) và trục hoàng. . . . . . . . . . . . . . . . . . . . . . . . . 5
3.2 Trường hợp diện tích miền D được giới hạn bởi �(�) và trục tung. . . . . . . . . . . . . . . . . . . . . . . . . . . 5
3.3 Trường hợp diện tích miền D được giới hạn bởi �(�) và �(�). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
3.4 Tính chiều dài sợ dây. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
a/ Phương trình f(x) là y = f(x). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
b/ Phương trình f(x) là phương trình tham số như sau. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
3.5 Tính thể tích hình tròn xoay. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
a/Thể tích vật thể khi quay miền D hoặc hàm �(�) quanh 0x. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
b/Thể tích vật thể khi quay miền D hoặc hàm �(�) quang oy. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
c/Thể tích của vật thể tạo bởi khi quay hình thang cong quanh trục Oy. . . . . . . . . . . . . . . . . . . . . . . . 8
3.6 Diện tích xung quanh của vật thể tròn xoay. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
a/ Phương trình f(x). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
b/ Phương trình f(x) là phương trình tham số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .8
4. Ứng dụng của nguyên hàm, tích phân trong các bài toán khác. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .8
4.1 Bài toán tính công lực F. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
4.2 Bài toán tính quãng đường. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
5. Định lý giá trị trung bình. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
6. Tổng Reiman. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
6.1 Định nghĩa. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
a, Tổng Riemann trái. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
b, Tổng Riemann phải. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10
c, Tổng Riemann trung tâm với phân hoạch là 2.dx. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10
6.2 Các dạng toán hay gặp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
a/ Dạng ước tính tích phân. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
b/ Dạng cho bảng giá trị. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 2 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG
c/ Dạng cho hình vẽ (ước tích diện tích, thể tích). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11
7. Tích phân suy rộng. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
7.1 Tích phân suy rộng loại 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
7.2 Tích phân suy rộng loại 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 8
Phương pháp giải phương trình vi phân cấp 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
a, Phương trình vi phân tách biến. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
b, Phương trình vi phân tuyến tính. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
c, Phương trình đẳng cấp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
d, Phương trình vi phân Bernoully. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
e, Dạng phương trình vi phân đưa về tách biến. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
9 Ứng dụng phương trình vi phân cấp 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14
9.1 Dạng toán 1: Bài toán hỗn hợp hòa tan. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
9.2 Dạng toán 2: Bài toán dẫn về phương trình vi phân. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
9.3 Dạng toán 3: Cho sẵn phương trình. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
9.4 Dạng toán 4: Bài toán tăng trưởng. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
10 Phương pháp giải phương trình vi phân cấp 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .16
11 Hệ phương trình vi phân tuyến tính cấp 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 �. Lý Thuyết
Các lớp ôn tập cuối kì giá siêu hạt dẻ cho K23:
 Lớp ôn tập cuối kì Giải Tích 1 là 175k
 Lớp ôn tập cuối kì Vật Lý 1 là XXX
 Lớp ôn tập cuối kì Đại Số Tuyến Tính là 150k
 Lớp ôn tập cuối kì Hóa Đại Cương 150k
1. Nguyên hàm (tích phân bất định) và tích phân xác định
1.1 Phương pháp đổi biến
u(x).v '(x)dx  u(x).v(x) u '(x).v(x)dx
1.2 Phương pháp đổi biến ( đặt ẩn phụ ) Tìm nguyên hàm ∫ �(�)��
Đặt t  u(x) biến đổi
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 3 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG Ta đạo hàm 2 vế:
�� = �′(�)�� → �� = �� Thay vào �(�), ta được: �′(�)
∫ �(�)�� = ∫ �(�)��
1.3 Một số tìm nguyên hàm hay gặp 1/ dx 
 arctan x  C 1 x2 2 /
dx  1 arctan x  C
 a2  x2 a a
3 /  dx  arcsin x C 1 x2
4 /  dx  arcsin x C a2  x2 a dx 5 /
 ln x  x2  k   C x2  k a2 x
6 /  a2  x2dx  x  arcsin  C a2  x2 2 2 a
7 /  x2  kdx  x x2  k  k ln x x2  k C 2 2
8/ cosh x dx  sinh xC
9 / sinh x dx  cosh x C 10/
dx  tanh xC  cosh2x 11/
dx  coth xC sinh2 x
12/ dx ln(| xa|)C x  a
1.4 Nguyên hàm hàm hữu tỉ
Cách làm: Tìm các hệ số A,B,C,… g(x)  dx  A   B . . Z dx
(x  a)(x  b). . (x  z)
(x  a) (x  b) (x  Z) Skill casio:g(x) g(x)
A= (x b). . (x  z) tại x =a; B= (xa)(xc). . (x z) tại x = b; ……… Dạng toán
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 4 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG ( ) 1 2 ∫ ( = ∫ + + ��
� − �)2(� − �)(� − �)
(� − �) (� − �)2 + (� − �) (� − �)  �2 = �(�) Tại x = a (�−�)(�−�) ( )  �1 = ( )′ Tại x = a (�−�)(�−�)  � = �(�) Tại x = b (�−�)2(�−�)  � = �(�) Tại x = c (�−�)2(�−�)
2. Đạo hàm của tích phân ℎ(�) �(�) = ∫
�(�)�� => �′(�) = ℎ′(�). �(ℎ(�)) + �′(�). �(�(�)) ( )
3. Ứng dụng của nguyên hàm, tích phân trong hình học
3.1 Trường hợp diện tích miền D được giới hạn bởi �(�) và trục hoàng � = ∫ |�(�)|��
3.2 Trường hợp diện tích miền D được giới hạn bởi �(�) và trục tung � = ∫ |�(�)|��
3.3 Trường hợp diện tích miền D được giới hạn bởi �(�) và �(�)
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 5 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG
Có 2 phương pháp giải như sau: b S 
f (x)  g(x) |dx x |a d S  y
 | f (y) g(y)|dy c
3.4 Tính chiều dài sợ dây
a/ Phương trình f(x) là y = f(x)
Có 2 phương pháp giải như sau: b x  L 
1 ( f '(x))2dx a d L 
1 ( f '(y))2dy y c
Khối lượng sợ dây khi biết mật độ khối lượng là p(x) b
L   1 f '(x)2 p(x)dx a
b/ Phương trình f(x) là phương trình tham số như sau
x  x(t) ,a  t  b 
y  y(t) b
L   x'(t)2  y'(t)2dt a
Khối lượng sợ dây khi biết mật độ khối lượng là p(x) b
L   1 f '(x)2 p(x)dx a
3.5 Tính thể tích hình tròn xoay
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 6 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG
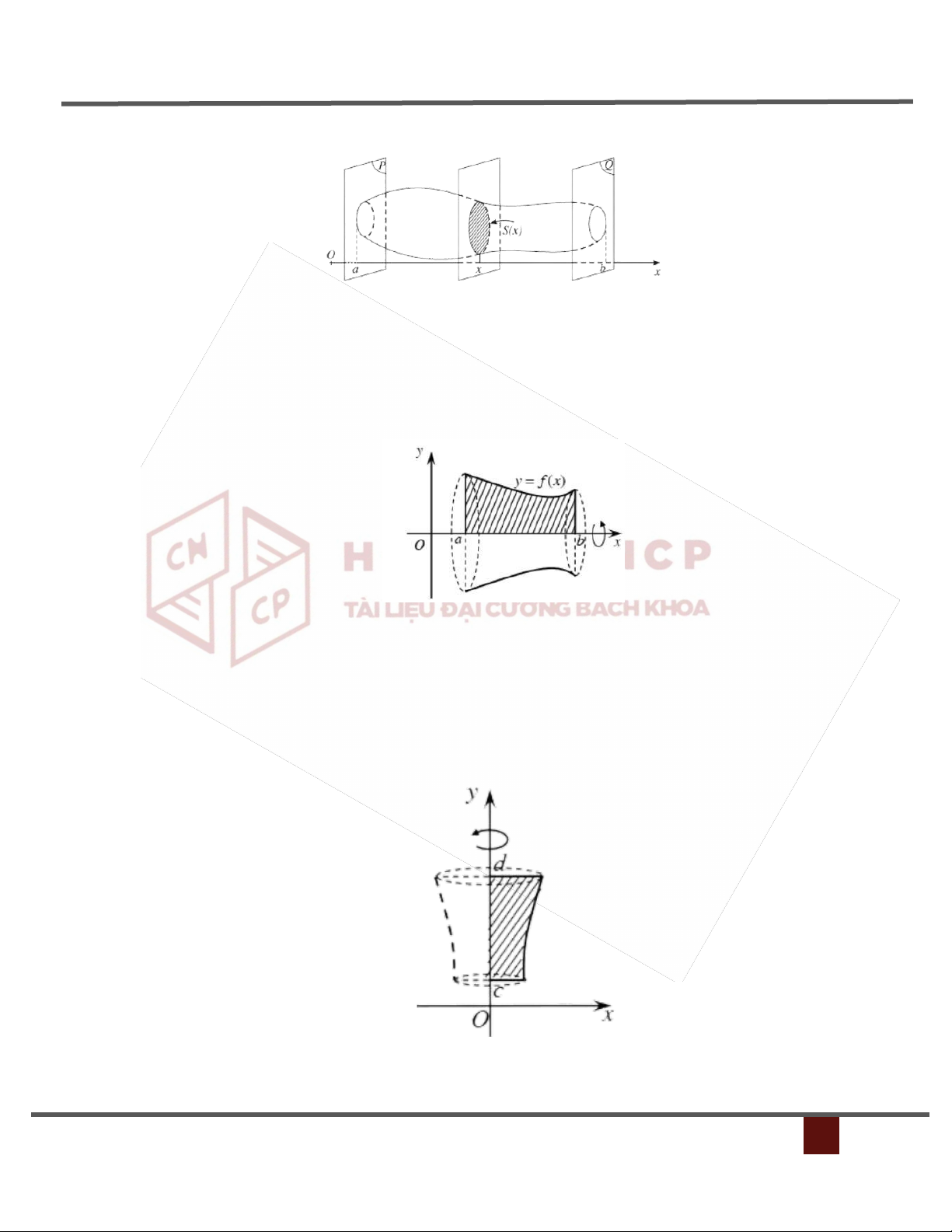
Nguồn gốc từ một công thức cấp 3: b
V   S(x)dx a
a/Thể tích vật thể khi quay miền D hoặc hàm �(�) quanh 0x b V f 2(x)dx ox   a
b/Thể tích vật thể khi quay miền D hoặc hàm �(�) quang oy b V f 2 (y)dy oy   a
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 7 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG
c/Thể tích của vật thể tạo bởi khi quay hình thang cong quanh trục Oy b
Voy  2 | xf (x) | dx a
3.6 Diện tích xung quanh của vật thể tròn xoay a/ Phương trình f(x)
y  f (x),a  x  b
Khi xoay f(x) quanh trục ox ta được 1 vật thể thì diện tích xung quanh vật thể đó là b S 
f (x) 1 f '(x)2 dx vx 2 a
Khi xoay f(x) quanh trục oy ta được 1 vật thể thì diện tích xung quanh vật thể đó là (� ≤ � ≤ �) d S
f (y) 1 f '(y)2 dy vy  2 c
b/ Phương trình f(x) là phương trình tham số
x  x(t) ,a  t  b
y  y(t)
Khi xoay f(x) quanh trục ox ta được 1 vật thể thì diện tích xung quanh vật thể đó là b S
y(t) x '(t)2  y '(t)2 dt vx  2 a
4. Ứng dụng của nguyên hàm, tích phân trong các bài toán khác
4.1 Bài toán tính công lực F
Công để di chuyển một vật từ vị trí a sang vi trí b được tính như sau:
∫ �(�)��: Với �(�) là lực tác động �
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 8 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG
4.2 Bài toán tính quãng đường
Cho 1 chất điểm với hàm vận tốc �(�). Quãng đường từ � = � đến � = � chất điểm đi được là: ∫ |�(�)|��
Lưu ý: Nếu hỏi từ � = � đến � = � chất điểm cách vị trí ban đầu là bao nhiêu thì dung công thức ∫ �(�)��
Một số bài toán khác sẽ gặp khi chúng ta vào các buổi ôn tập cuối kì K23
5. Định lý giá trị trung bình
Nếu khả tích trên [a,b], giá trị trung bình của f trên [a, b] được định nghĩa là: 1 ∫ �(�)�� � − �
Nếu f liên tục trên [a,b], khi đó tồn tại c [a,b] sao cho 1 ( ) = ∫ �(�)�� � − � 6. Tổng Reiman 6.1 Định nghĩa
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 9 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG b
Ước tính  f (x)dx bằng tổng Riemann với phân hoạch là dx a a, Tổng Riemann trái b
 f (x)dx  f (a).dx f (x1).dx f (x2)dx. . f (x5)dx a b, Tổng Riemann phải b
 f (x)dx  f (x1).dx  f (x2)dx . . f (x5)dx  f (b)dx a
c, Tổng Riemann trung tâm với phân hoạch là 2.dx b
 f (x)dx  f (x1).2.dx f (x3).2dx  f (x5).2.dx a
6.2 Các dạng toán hay gặp
a/ Dạng ước tính tích phân
Ước tính giá trị của ∫� �(�)dx với phân hoạch n đoạn Bài giải
Ta có khoảng phân hoạch: ∆� = �−�  Dùng Reiman trái
∫� �(�)dx≈ ∆�. �(�) + ∆� ∗ �(� + ∆�) + ⋯ + ∆� ∗ �(� + (� − 1) ∗ ∆�) ≈ ∑�=�−1
=0 ∆� ∗ �(� + ∆� ∗ �) (Dùng để casio)  Dùng Reiman phải
∫� �(�)dx≈ ∆�. �(� + ∆�) + ∆� ∗ �(� + 2. ∆�) + ⋯ + ∆� ∗ �(�) ≈ ∑�=�
=1∆� ∗ �(� + ∆� ∗ �) (Dùng để casio)
 Dùng Reiman trung tâm với khoảng phân hoạch 2. ∆�
∫� �(�)dx≈ 2∆�. �(� + ∆�) + ∆� ∗ �(� + 3∆�) + ⋯ + ∆� ∗ �(� − ∆�) ≈ ∑�=�/2
=1 ∆� ∗ �(� + ∆� ∗ (2� − 1)) (Dùng để casio)
b/ Dạng cho bảng giá trị 1 2 3 4 5 6 7 ( ) a b c d e f k
Mỗi giá trị của x các đều nhau ∆�
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 10 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG
Dùng tổng Riemann để ước tính ∫�7 �(�)�� 1 Với phân hoạch ∆�
 Tổng Riemann trái: ∫�7 �(�)�� = ∆��(�1) + ∆��(�2)+. . +∆��(�6) 1
 Tổng Riemann phải: ∫�7 �(�)�� = ∆��(�2) + ∆��(�3)+. . +∆��(�7) 1 Với phân hoạch 2∆�
 Tổng Riemann trung tâm: ∫�7 �(�)�� = 2∆��(�2) + 2∆��(�4) + ∆��(�6) 1
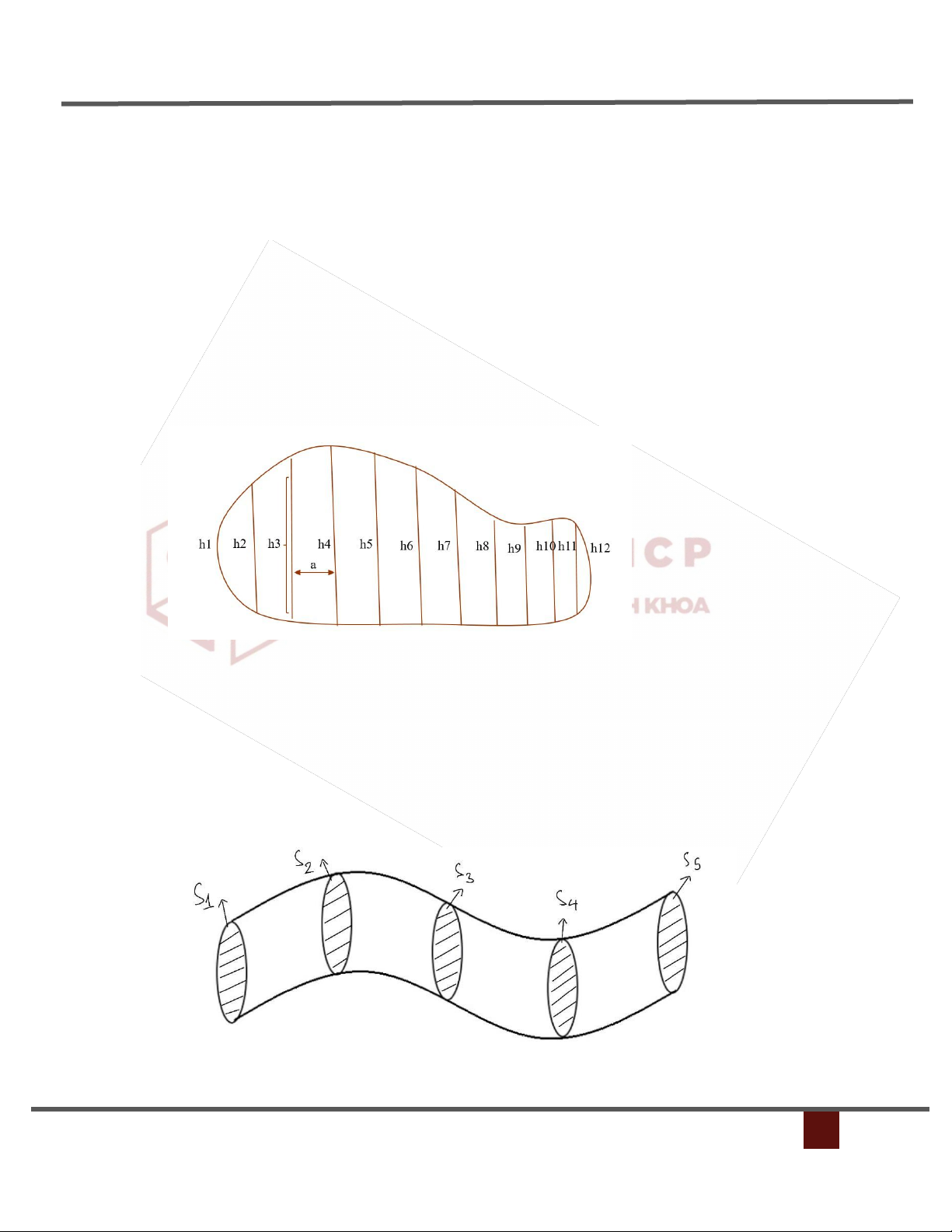
c/ Dạng cho hình vẽ (ước tích diện tích, thể tích)
a/Ước diện tích một mặt phẳng bằng tổng Riemann Với phân hoạch là a
 Dùng tổng Riemann trái: ���á� = �(ℎ1 + ℎ2 + ℎ3 + ⋯ + ℎ11)
 Dùng tổng Riemann phải: ���á� = �(ℎ2 + ℎ3 + ℎ4 + ⋯ + ℎ12) Với phân hoạch là 2a
 Dùng tổng Riemann trung tâm:
������ �â� = 2�(ℎ2 + ℎ4 + ℎ6 + ⋯ + ℎ11)
b/Ước tính thể tích vật thể bằng tổng Riemann
 Dùng tổng Riemann trái: ���á� = �(�1 + �2 + �3 + ⋯ + �4)
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 11 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG
 Dùng tổng Riemann phải: ���á� = �(�2 + �3 + �4 + ⋯ + �5)
 Dùng tổng Riemann trung tâm: (Với phân hoạch là 2a)
������ �â� = 2�(�2 + �4) 7. Tích phân suy rộng 7.1
Tích phân suy rộng loại 1
a,Nhận biết tích phân suy rộng loại 1
Tích phân có 1 cận là  hoặc cả 2 cận là  thì đó là tích phân suy rộng loại 1
b, Cách giải tích phân suy rộng loại 1
Giải sử F(x) là nguyên hàm của f(x). Ta có:
 f (x)dx  F(x) | lim F(x)  F(a)  a x a 7.2
Tích phân suy rộng loại 2
a, Nhận biết tích phân suy rộng loại 2
Tích phân có chứa điểm không xác định của của hàm f(x) Ví dụ: 5
  ln(x) dx là tích phân suy rộng loại 2 vì cận chứa điểm x = 0 05 x 1  ex
là tích phân suy rộng loại 2 vì cận chứa điểm x = 0, x = -1  dx x(x 1) 2
b, Cách giải tích phân suy rộng loại 2
Với a,b là điểm không xác định của hàm số b a  
f (x)dx  F(x) |b  lim F(x)  lim F(x) xb xa a
Lưu ý: Một tích phân có thể vừa là loại 1 vừa là loại 2
8 Phương pháp giải phương trình vi phân cấp 1
8.1, Phương trình vi phân tách biến
Là phương trình vi phân có thể đưa về dạng sau:
f (x)dx  g( y)dy
Phương pháp giải bằng cách nguyên hàm 2 vế:
 f (x)dx   g(y)dy
8.2, Phương trình vi phân tuyến tính
Là phương trình vi phân có thể đưa về dạng sau:
y ' p(x)y  q(x) dy
Đối với dạng này thì nên ghi y' chứ không nên ghi dx làm rối mắt
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 12 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG Cách giải:
Bước 1: Tìm K(x)=  p(x)dx sau đó nhân hai vế PTVP cho ek(x) .Ta được:
y 'ek(x)  p(x).ek(x).y  q(x)
 ( y.ek(x))'  q(x) Bước 2: Nguyên hàm 2 vế
(y.ek(x))'dx  q(x)ek(x)dx
 y   q(x)ek(x)dx
q(x)ek(x)dx  y  ek(x)
Đi thi thì có thể chứng minh lại từ đầu hoặc nhớ công thức cuối cùng
8.3, Phương trình đẳng cấp
Là phương trình vi phân có thể đưa về dạng sau: y y '  f ( ) x Cách giải:
Đặt u  y  y  ux  y '  u'x  u x Thay y’ vào phương trình
u'x  u  f (u)  u'  1
f (u)  u x
Bài toán trở về phương trình vi phân tách biến
 du   1 dx
f (u)  u x
8.4, Phương trình vi phân Bernoully
Là phương trình vi phân có thể đưa về dạng sau:
y'  p(x)y  f (x).y
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 13 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG Cách giải Chia hai vế cho y
y'  p(x) 1  y y1 f (x) 1 1 ' y' Đặt z(x)   y
 z (x)  (1). y1 y
Ta thế z(x) phương trình vi phân ta sẽ được phương trình tiếp tuyến
(xem cách giải phương trình tuyến tính ở trên)
8.5, Dạng phương trình vi phân đưa về tách biến
�′ = �(�� + �� + �) (*)
Đặt � = �� + �� + � => �′ = � + ��′ => �′ = �′−�. Thế vào (*)
�′ − � = ( ) <=> ( )+ =
9 Ứng dụng phương trình vi phân cấp 1
9.1 Dạng toán 1: Bài toán hỗn hợp hòa tan
Một thùng nước chức V0 lít nước tinh khiết. Người ta bơm vào lượng muối có nồng độ a
kg/lít với tốc độ M lít/phút, hỗn hợp được bơm ra với tốc độ N lít/phút . Thành lập PTVP
để tìm hàm lượng muốn có trong bể sau t phút. Bài giải
Giả sử y(t) là lượng muối còn trong bể sau t phút
Suy ra y’(t) là vận tốc thay đổi lượng muối sau t (phút)
Ta có theo ý nghĩa đạo hàm cấp 1
y’(t) = vận tốc muối bơm vào tại t – vận tốc lượng muối bơm ra tại t Mà :
 Vận tốc muối bơm vào tại t là a. M (kg/phút)
 Thể tích thùng nước sau t phút là Vo + M. t − N. t (lít)
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 14 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG
 Nồng độ muối trong thùng sau t phút là y(t) (kg/lít) V0+M.t−N.t
Vận tốc lượng muối bơm ra tại t là y(t) . N (kg/phút) V0+M.t−N.t Vậy y′(t) = a. M − y(t) . N V0+M.t−N.t
9.2 Dạng toán 2: Bài toán dẫn về phương trình vi phân Khi phát biếu:
 A tỉ lệ thuận với B hoặc A tỉ lệ với B thì ta có phương trình � = ��
 A tỉ lệ nghịch với B thì ta có phương trình � = �
 A tỉ lệ (thuận) với B và C thì ta có phương trình � = ���
Ví dụ: Vận tốc nguội lạnh của một vật trong không khí tỷ lệ với hiệu giữa nhiệt độ của
vật và nhiệt độ không khí. Tìm quy luật giảm nhiệt của vật nếu nhiệt độ của không khí là
100C, nhiệt độ ban đầu của vật là 500C, sau 20 phút nhiệt độ của vật còn 300C
Gọi �(�) là nhiệu độ của vật thể tại thời điểm t
�′(�) = �(�(�) − 10)
9.3 Dạng toán 3: Cho sẵn phương trình
Ví dụ 6(đề cuối kì K22):: Cường độ dòng điện trong mạch có cuộn cảm với từ dung L
(Henry), điện trở R (Ohm), hiệu điện thế U (volt) thỏa mãn phương trình
L dI  RI  U dt
Có thể học thuộc luôn nghiệm của PTVP này là:
�(�) = �. �− � +�
9.4 Dạng toán 4: Bài toán tăng trưởng
Mô hình gia tăng dân số tự nhiên (đơn loài):
P′(t) = kP(t) (P là dân số, k là hằng số) => P(t) = Poekt
Mô hình gia tăng dân số trong môi trường hạn chế (Logistic) (đơn loài) P(t) P′(t) = kP(t)(1 − ) L
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 15 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG
(L là số cá thể tối đa sinh sống ở khu vực đang xét.) LCekt L
P = L + Cekt hoặc P = 1 + Ce−kt 10
Phương pháp giải phương trình vi phân cấp 2
Giải phương trình vi phân cấp 2 sau
ay '  by ' c  f (x) Bước 1: Tìm ���
Giải phương trình thuần nhất
ay '  by ' c  0 Phương trình đặc trưng
ak2  bk  c  0
Ta tìm ra 2 nghiệm của phương trình đặc trưng là k1,k2 Nếu -
k1,k2 là nghiệm thực và k1#k2 vậy nghiệm thuần nhất
ytn  C1e  C2e k1x k 2x -
k1,k2 là nghiệm thực và k1 k2 vậy nghiệm thuần nhất
y  C1xekx  C2ekx tn -
Nghiệm là số phức có dạng   i vậy nghiệm thuần nhất là
y  C1ex cos( x)  C2ex sin( x) tn Bước 2: Tìm ��
Trường hợp 1: Phương trình
Trường hợp 2: Phương trình đặc trưng ở bước
đặc trưng ở bước 1 là số thực
1 là nghiệm số phức k     1 , k2 i
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 16 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG Đưa
Đưa f (x) về dạng exP(x)
f (x) về dạng
e 'x (P (x)cos( ' x)  P (x)sin( ' x)) n m
Vậy y  exxsQ(x) r Vậy Với
y  e 'xxs (Q (x)cos( ' x)  Q (x)sin( ' x)) r m n
- S=0 nếu  khác k1,k2 Với
- S=1 nếu   k1 hoặc -
S=0 nếu  '  'i khác k1,k2   k2 -
S=1 nếu  '  'i giống k1,k2
- S=2 nếu   k1 k2 Với Với Q
Q(x) là đa thức cùng bậc
m (x),Qn (x) là đa thức cùng bậc với bậc với
đa thức lớn nhất trong 2 đa thức P P(x)
n (x) , Pm (x) -
Q(x) bậc 0 có dạng A -
Q(x) bậc 1 có dạng Ax  B -
Q(x) bậc 2 có dạng
Ax2  Bx  C
Kết luận: ��� = ��� + ��
Lưu ý: Nếu f (x)  0 thì suy ra �� = ��� = ���
11 Hệ phương trình vi phân tuyến tính cấp 1
Giải hệ phương trình vi phân sau
�′(�) = �1� + �1� + �1(�) (∗)
{�′(�) = �2 + 2� + �2(�) (∗∗) Phương pháp thế
Step1: Rút y từ phương trình (*) � = �′(�)−�1�−�1(�) (***)
Step2: Đạo hàm 2 vế theo biến t phương trình (***) �′′(�) − � �′ = 1�′ − �′1(�)
Qua hai step 1, 2 ta có được � và �′ thế vào (**) ta sẽ tìm được phương trình vi phân cấp 2 của �(�)
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 17 HCMUT CNCP GIẢI TÍCH 1 NGUYỄN QUỐC VƯƠNG
Step 3: Áp dụng giải phường trinh vi phân cấp 2 đã bài trước để tìm �(�), từ đó thế
�(�) và (***) tìm được �(�) ��. Bài tập
(sẽ được học khi đăng kí học lớp giải tích 1 cuối kì)
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 18
Document Outline

• Mục Lục
• u' 1