Công thức thống kê - XSTK: Hướng dẫn và Quy tắc Kiểm định môn Xác suất thống kê| Đại học Duy Tân

14:42, 11/01/2026
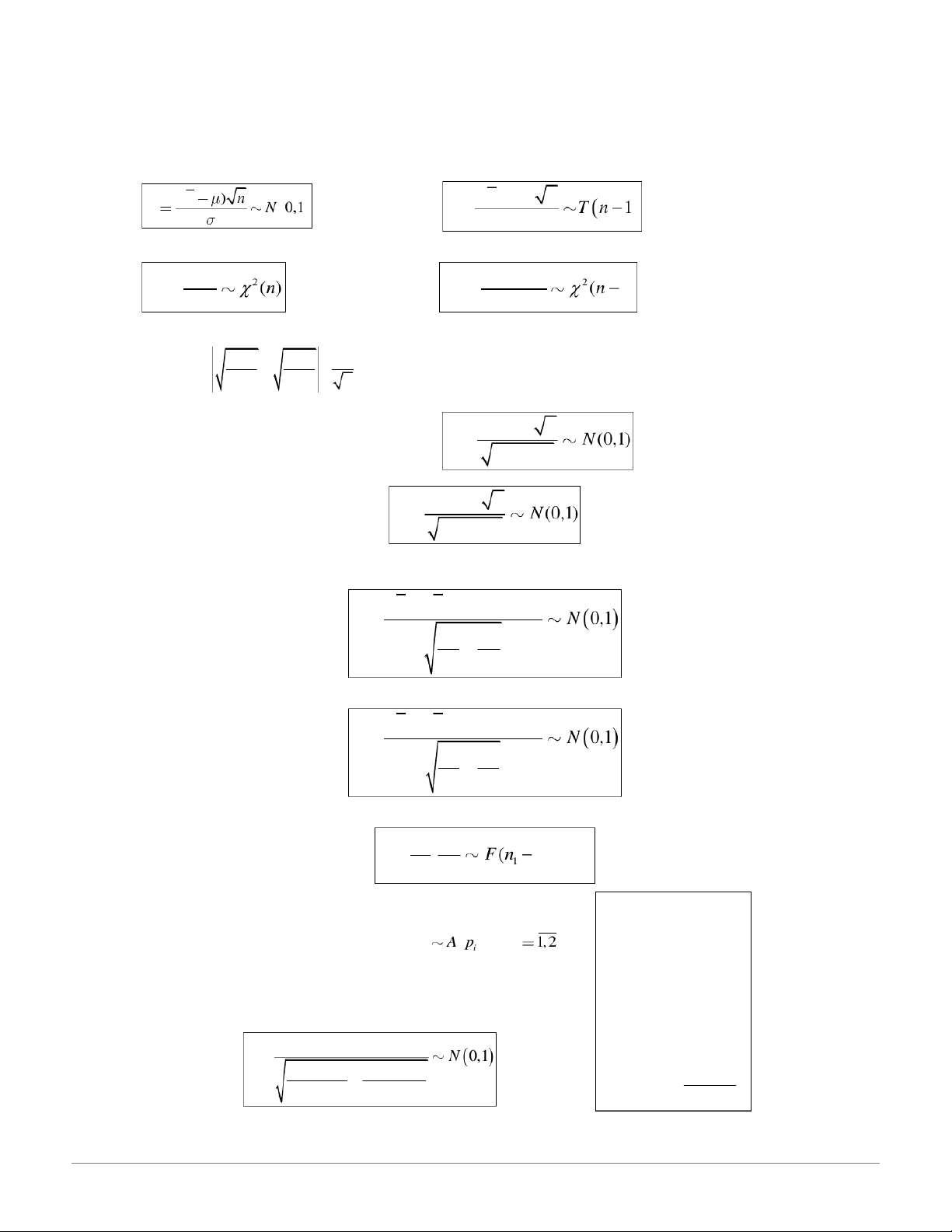
Công thức thống kê - XSTK: Hướng dẫn và Quy tắc Kiểm định - Studocu ( ( ) X   n  X T 1) U 2)  S 2 nS ( 1) 1)  n  S  *2   2 3) 2  4) 2  2 p 1 p 1 0,3 5) Nếu n>5 và 1     p p n ( ) f  p n U  Hoặc nếu n  30 thì (1 ) p p
6) Cũng với mẫu trên, nếu n100, ( ) f  p n U  (1 ) f f   7) Từ hai tổng thể X  
1, X2 lập hai mẫu ngẫu nhiên độc lập kích thước n1, n2 và chứng minh được:
X  X   U  1 2 1 2  2  2 1 n 2 n 1 2  
8) Cũng với hai mẫu trên, n   1>30, n2>30 thì
X  X   U  1 2 1 2 S S 2  2 1 n 2 n 1 2
9) Cũng với hai mẫu trên, S . 1, 1) F  2 2 n  1 S 2 2 2 2 2 1 Chú ý:
10) Trong hai tổng thể có:    X i P X  x   
Từ hai tổng thể đó lập hai mẫu ngẫu nhiên độc lập kích tihước n1, n2: W t  u   , ,. ., X  X X f  df30:   df   1 11 12 1 1 W u u  X ,  X ,. ., n X  1 f     1  2 21 22 2 2  n
f  f  p  p t t 2      Nếu n U  df df 1>30, n2>30 thì 1 p (1 2p ) 1 p (1 2p ) 1   1  ff 1 n 1 2 n 2    1, 2 df df   12, 1 1 2 df df  14:42, 11/01/2026
Công thức thống kê - XSTK: Hướng dẫn và Quy tắc Kiểm định - Studocu
BÀI OÁN S Y DIỄN ỐNG KÊ
Suy diễn X của X N(,2)
Suy diễn K về phương sai mẫu S2 2 2 p   σσ  u X    2 1  n n  2 2 1   1   u   2 1    p S χ   χ  1 α   n n  1α 1 α 2 n  n 1  1   2 2 u X u
 σσ 21nn 2 2 1   /2 /2 1        p S χ   χ  1 α    n n 1α/2 α/2 n  n 1  1 22 1 hoặc   p X  u  σχ n 1 α /2 1   2   p S n     n   1α  1    p X   u 1 22 1   2 σχ  n 1 α  n  p S n    α   1  
p X   u 1   n 
Suy diễn K về tần suất mẫu f P p(1-p) p(1-p) Suy diễn: p  - u u 1  α  2 1 α 2 α  n n X X , f  f , S1 1 2 1 2 2 P p(1-p) p(1-p) S 2 p  - u u 1  α αα  2 2  n n  p(1-p) u 1 hoặc α P f p      α2  n  p(1-p) P f p   u 1 α α   n  p(1-p) P f p   u  1 α α   n
Ước lượng μ của X N(,2) 2 đã biết 2 chưa biết    P X u S S  ( 1n)n  ( 1) /2  X  u  /2 1    P X 
t /2   X  t /2 1     n n  n n    P X S  u  1  n P X t   ( 1) 1     n   n     P X S  u  1  n P X t   ( 1) 1     n   n 
Kích thước mẫu n để II0 hay 0:
Kích thước mẫu n để II0 hay 0: 222 4 222 
- Trước hết điều tra một mẫu kích thước m2 n u  hoặc n u 2 2  
- Kích thước mẫu n cần điều tra được tính 0 I  0 22 4 22 mS S n t   hay m n t   2  (  1) 2  ( 1 )2 2  0 I  0
 Điều tra thêm (n-m) quan sát 14:42, 11/01/2026
Công thức thống kê - XSTK: Hướng dẫn và Quy tắc Kiểm định - Studocu
Ước lượng p của X A(p) n≥100 n<100  f (f1 ) f f (1 ) 1 P f  u p  f   u     /2 /2 P p   p p     n n  1 2 1  Trong đó: f (1f ) 1 P p  f  u     n 2 2 2nf u
f (1 f) u  f (1 f ) 1 α/2 α/ 2 p ,2p( ) n u P p  f   u 1 2 2     α/2  n
Kích thước mẫu n để II0 hay 0: 4f (1 f  ) 22 f f (1 ) n u  hoặc 22 n u  2 I  2   0 0
Ước lượng 2 của X N(,2) μ đã biết μ chưa biết *2 *2  n.S n.S 2 2  2 (n-1).S (n-1).S p  σ   1 α  2  p  σ   1 α  2( ) 2( ) χχ n n  2( 1) 2( 1) χχ n n α 2 1 α   2 α 2 1 α   2 *2  n.S 2  (n-1).S 2 p 2 σ   1 α  p σ   1 α   2( ) χ χ 2 n ( 1) n   1α  1α 2 *2 p n.S  2 (n-1).S 2 p σ    1 α  σ  1 α   χ 2 n ( 1) 2( ) χ  n  α α
Kiểm định giả thuyết về μ của X N(,2)
MBB đối với H0 khi 2 đã biết
MBB đối với H0 khi 2 chưa biết H :  0 0     (    X n X n μ μ) ; | | 0 ; | | 0 n W  T  T T  H :  W  U   U  u ( 1) 1 0 α α/2 α α/2 σ   S   H :  0 0  X n   (      X n μ μ) ;n 0; 0 W  T   T T    H :  W  U   U u  ( 1) 1 0 αα αα σ   S   H :  0 0     (    X n X n μ μ) ;n 0; 0 W  T  T T  H :  W  U   U  u ( 1) 1 0 αα αα σ   S  
Kiểm định so sánh hai tham số μ1, μ2 của X1 N( ,112), X 2N(2,22)
MBB đối với H0 khi 2 đã biết
MBB đối với H0 khi 2 chưa biết n1, n2 đủ lớn H :  0 1 2    H :    1 1 2  X X  X X 1 2 W  U   ; | U |u 1 2 W  U   ; | U |u α α/2 2 2  α α/2 σσ 2 2  S S 1 2  1 2   n n   n n 1 2  1 2 14:42, 11/01/2026
Công thức thống kê - XSTK: Hướng dẫn và Quy tắc Kiểm định - Studocu H :  0 1 2    H :    1 1 2  X X  X X 1 2 W  U   ; U u  1 2 W  U   ; U u  αα 2 2 αα  σσ 2 2 S S 1 2  1 2   n n   n n 1 2  1 2 H :  0 1 2    H :    1 1 2  X X  X X 1 2 W  U   ; U  u 1 2 W  U   ; U  u αα 2 2 αα  σσ 2 2  S S 1 2  1 2   n n   n n 1 2  1 2
Kiểm định G về 2 và so sánh hai tham số 12, 22
MBB đối với H0 khi  chưa biết
MBB đối với H0 khi 1, 2 chưa biết 2 2 H   : 2 2( 1) 21 n 2 2 H   : 21α/2 1 2  S F F    ( n 1, n 1) 0 0 α/2   ( 1 n )S χχ  2  0 1 2  1 W F ; F( 1 F , n 1) 2 2 W  χ; n    H :   n 2 2  H : α2 1 0 α22 2( 1) σ   1 1 2  S  0χχ α/2  2 α/2 1 2 2 2 H   : 2  ( 1 n ) 2 2 H   : 2  0 0 S S  2 2 2( 1) W 0 1 2 1    χ  ; χ  χ n  W  F  ; F  F n( 1  , n 1  ) 2 2   H : α 2 1 α 2 2 H : α 2 1 α 1 2 S 1 0  σ  0 1 1 2  2 2 2 H   2 2 2   2 0 0:  ( 1 n )S H :  S  2 2 2( 1) W 0 1 2 1   χ  ; χ  χ n  W  F  ; F  F (n 1  , n 1  ) 2 2 H  αα 2 2 2   α α 1 2 2 1 0:  σ H : S 0 1 1 2  2
Kiểm định G về P và so sánh hai tham số P1, P 2 MBB đối với H0 MBB đối với H0 H : p p  H :  0 0  p p    ( f p )n; 01 2 0      H : W U U u H :  1 0 p p α α/2 p p  p (1 p )  1 1 2 0 0  f f 1 2 W  U   ; U  u α α/2  1  1 f (1 ) f  n n     1 2 H :  H :  0 0 p p  P P    ( f p )n; 01 2 0  H : W  U   U u  H :  1 0 p p αα P P  p (1 p ) 1 1 2  0 0  f f 1 2 W  U   ; U u   αα  1  1 f (1 ) f  n n     1 2 H :  H :  0 0 p p  P P    ( f p )n; 01 2 0      H : W U U u H :  1 0 p p αα P P  p (1 p ) 1 1 2  0 0  f f 1 2 W  U   ; U  u αα  1  1 f (1 ) f  n n     1 2 14:42, 11/01/2026
Công thức thống kê - XSTK: Hướng dẫn và Quy tắc Kiểm định - Studocu 14:42, 11/01/2026
Công thức thống kê - XSTK: Hướng dẫn và Quy tắc Kiểm định - Studocu