




Preview text:
Công thức tính chu vi, diện tích hình tròn chính xác nhất
1. Thế nào là đường tròn, thế nào là hình tròn?
Nhiều người thường nhầm lẫn giữa đường tròn và hình tròn, nhưng thực tế trong hình học phẳng đường
tròn và hình tròn là hai khái niệm không hề giống nhau. Cụ thể:
- Hình tròn là tập hợp tất cả những điểm nằm bên trong và bên trên đường tròn, hay nói cách khác, hình
tròn là tập hợp tất cả các điểm cách tâm một khoảng nhỏ hơn hoặc bằng bán kính. Trong khi đó, đường tròn
là quỹ tích của tất cả các điểm nằm trên một mặt phẳng và cách đều một điểm cho trước (tâm đường tròn)
một khoảng cách bằng bán kính đường tròn.
- Đường tròn không có diện tích như hình tròn
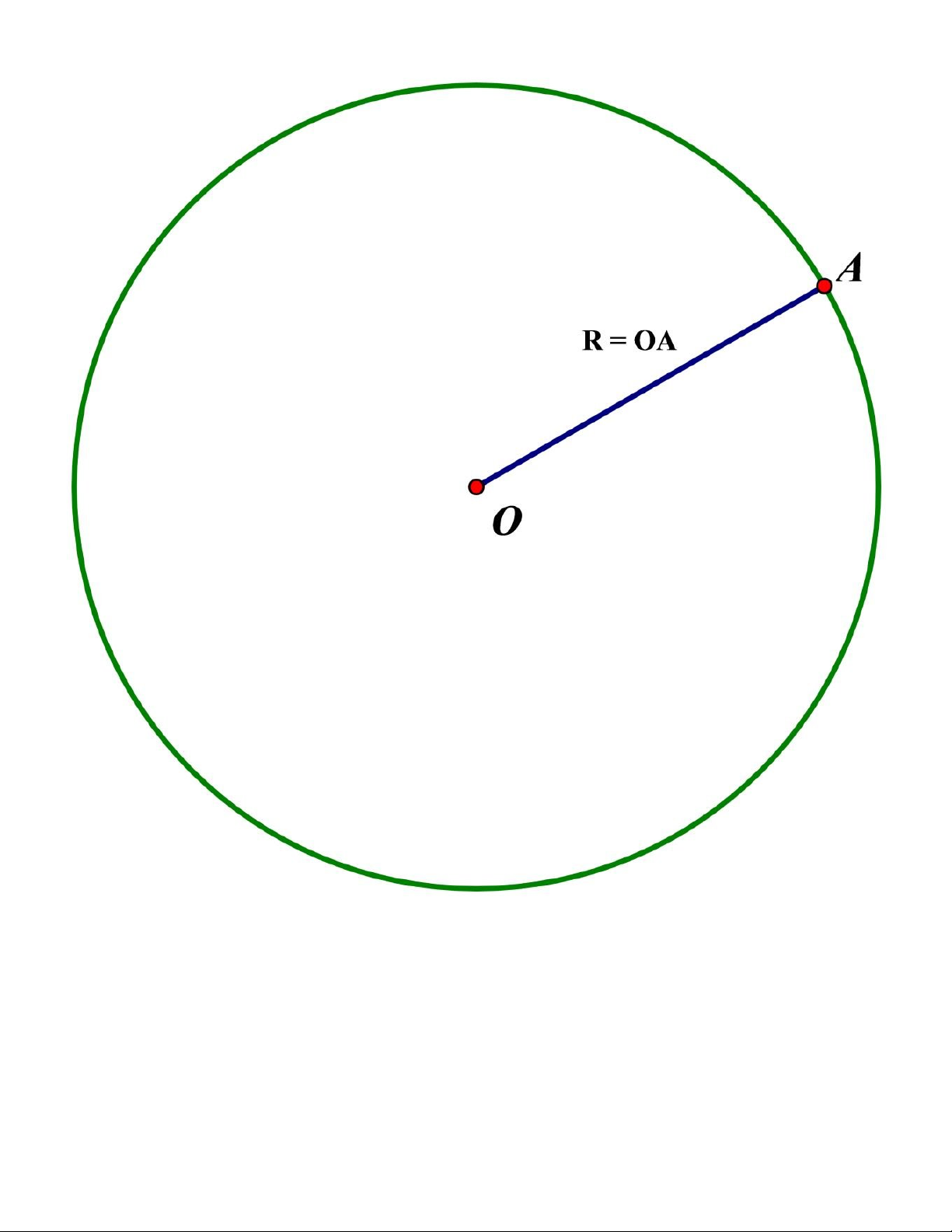
Đường tròn tâm O, bán kính R là hình bao gồm tất cả các điểm cách tâm O một khoảng bằng bán kính R.
Bất kỳ điểm nào nằm trên đường tròn và nối trực tiếp với tâm O đều được gọi là bán kính.
1.1. Có 3 vị trí tương đối của một điểm bất kỳ nào đó với đường tròn
- Nếu điểm A nằm trong đường tròn tâm O, bán kính R thì OA < R
- Nếu điểm A nằm trên đường tròn tâm O, bán kính R thì OA = R
- Nếu điểm A nằm ngoài đường tròn tâm O, bán kính R thì OA > R
1.2. Các tính chất của đường tròn
- Các đường tròn bằng nhau thì sẽ có chu vi bằng nhau
- Bán kính của đường tròn luôn bằng nhau
- Đường kính là đoạn thẳng dài nhất trong hình tròn
- Góc ở tâm của đường tròn bằng 360 độ
- Chu vi của mỗi đường tròn khác nhau, tỉ lệ với độ dài của bán kính
- Hai điểm tiếp tuyến vẽ cùng trên 1 đường tròn từ 1 điểm nằm bên ngoài thì có chiều dài bằng nhau.
1.3. Các tính chất của hình tròn
- Đường kính là trường hợp đặc thù của dây cung đi qua tâm đường tròn và nó cũng là đoạn thằng dài nhất
đi qua hình tròn và chia hình tròn thành hai nửa bằng nhau
- Độ dài đường kính của một đường tròn dài gấp 2 lần bán kính của đường tròn đó. Bán kính của hình tròn
là khoảng cách từ tâm của đường tròn tới đường tròn đó.
2. Công thức tính chu vi hình tròn
Chu vi hình tròn là là đường biên giới hạn của hình tròn. Chu vi hình tròn tính bằng công thức sau:
C = d x = 2 x r x Trong đó: C là chu vi hình tròn; d là đường kính; r là bán kính
Lưu ý: Thông thường ta lấy = 3,14 do đó đôi khi ta bắt gặp công thức tính chu vi hình tròn như sau:
C = d x 3,14 = 2 x r x 3,14
3. Công thức tính diện tích hình tròn
Diện tích hình tròn được tính theo công thức sau:
S = r x r x = (d/2)^2 x Trong đó: S là diện tích hình tròn; d là đường kính; r là bán kính
hoặc: S = C^2 / 4 Trong đó: S là diện tích hình tròn; C là chu vi hình tròn
4. Một số bài tập áp dụng công thức tính chu vi, diện tích hình tròn
4.1. Bài tập ví dụ
Bài tập 1: Sân trường hình thang có trung bình cộng hai đáy là 40 m, chiều cao 30 m. Giữa sân, người ta
xây một bồn hoa hình tròn có chu vi 12,56 m. Tính diện tích còn lại của sân trường? Lời giải:
Diện tích sân trường đó là: 40 x 30 = 1200 (m2)
Diện tích bồn hoa là: 12,56^2 : 4 = 123,9 (m2)
Diện tích còn lại của sân trường là: 1200 - 123,9 = 1076,1 (m2)
Bài tập 2: Một sân vận động có hình dáng và kích thước như hình dưới. Hãy tính: a) Chu vi sân vận động
b) Diện tích sân vận động Lời giải:
Sân vận động được tạo bởi 1 hình chữ nhật có chiều dài 120m, chiều rộng 80m và 2 nửa hình tròn có đường kính 80m
a) Chu vi sân vận động = Chu vi 2 nửa hình tròn + Chiều dài hình chữ nhật x 2 = 80 x : 2 x 2 + 120 x 2 = 491,33 (m)
b) Diện tích sân vận động = Diện tích 2 nửa hình tròn + Diện tích hình chữ nhật = 40 x 40 x + 120 x 80 = 14 626,53 (m2)
Bài tập 3: Tính diện tích hình tròn ở hình dưới đây biết rằng hình vuông ABCD có BD = 24 cm. Lời giải:
Gọi độ dài cạnh hình vuông ABCD là a. Ta có: a^2 + a^2 = 24^2 => a^2 = 288 => a = 16,97 cm
Bán kính hình tròn có độ dài bằng 1/2 độ dài cạnh hình vuông ABCD => r = a/2 = 8,485 cm
Diện tích của hình tròn ở hình trên là: S = r x r x = 8,485 x 8,485 x = 226,18 cm2
Bài tập 4: Một tấm bảng chỉ đường hình tròn có đường kính 50 cm.
a) Diện tích tấm bảng chỉ đường bằng bao nhiêu mét vuông?
b) Người ta sơn hai mặt tấm bảng đó, mỗi mét vuông hết 7000 đồng. Hỏi sơn tấm bảng đó tốn hết bao nhiêu tiền? Lời giải:
a) Bán kính tấm bảng chỉ đường đó là: 50 : 2 = 25 (cm) Đổi 25 cm = 0,25 m
Diện tích tấm bảng chỉ đường đó là: S = 0,25 x 0,25 x = 0,196 (m2)
b) Sơn tấm bảng đó hết số tiền là: 0,196 x 7000 = 1372 đồng
Bài tập 5: Miệng giếng nước là một hình tròn có bán kính 0,7 m. Người ta xây thành giếng rộng 0,3m bao
quanh miệng giếng. Tính diện tích của thành giếng đó. Lời giải:
Diện tích của hình tròn bé (miệng giếng) là: 0,7 x 0,7 x 3,14 = 1,5386 (cm2)
Bán kính của hình tròn lớn là: 0,7 + 0,3 = 1 (m)
Diện tích của hình tròn lớn là: 1 x 1 x 3,14 = 3,14 (cm2)
Diện tích của thành giếng là: 3,14 - 1,5386 = 1,6014 (m2)
4.2. Một số bài tập tự luyện
Bài tập 1: Tính chu vi và diện tích hình tròn có:
a) r = 5 cm; r = 0,8 cm; r = 4/5 dm
b) d = 5,2m; d = 1,2m; d = 3/5 dm
Bài tập 2: Một cái nong hình tròn có chu vi đo được là 376,8 cm. Tính diện tích cái nong theo đơn vị mét vuông?
Bài tập 3: Sân trường bạn Hoa có hình chữ nhật, kích thước như sau: Chiều dài 45 m và chiều dài hơn
chiều rộng 6,5m. Chính giữa sân có 1 bồn hoa hình tròn đường kính 3,2 m. Tính diện tích còn lại của sân trường?
Bài tập 4: Trong sân trường, người ta trồng hai bồn hoa hình tròn. Bồn trồng hoa cúc có đường kính 40 dm.
Bồn trồng hoa hồng có chu vi 9,42 m. Hỏi bồn hoa nào có diện tích lớn hơn và lớn hơn bao nhiêu dm? Bài tập 5:
a) Một mặt bàn ăn hình tròn có chu vi là 4,082 m. Tính bán kính của mặt bàn đó.
b) Một biển báo giao thông có dạng hình tròn và có chu vi là 1,57 m. Tính đường kính của hình tròn đó.
Bài tập 6: Một bánh xe ô tô có bán kính bằng 0,25 m. Hỏi:
a) Đường kính của bánh xe dài bao nhiêu mét?
b) Chu vi của bánh xe bằng bao nhiêu mét?
Bài tập 7: Một hình tròn có chu vi bằng 254,24 dm. Hỏi đường kính và bán kính của hình tròn đó bằng bao nhiêu dm?
Bài tập 8: Một hình tròn có bán kính bằng số đo cạnh của một hình vuông có chu vi bằng 25 cm. Tính chu vi của hình tròn đó?
Bài tập 9: Cho hình tròn tâm O, đường kính AB = 8 cm.
a) Tính chu vi hình tròn tâm O, đường kính AB; hình tròn tâm M, đường kính OA và hình tròn tâm N, đường kính OB
b) So sánh tổng chu vi của hình tròn tâm M và hình tròn tâm N với chu vi hình tròn tâm O.
Bài tập 10: Tính bán kính hình tròn có chu vi C = 16,328 dm; C = 8,792 cm.




