














Preview text:
Greedy Traveling Saleman (GTS1)
Thuật toán Greedy Traveling Saleman (GTS1):là một phương pháp tiếp
cận đơn giản cho bài toán người đi du lịch tham lam (Traveling Salesman
Problem - TSP). TSP là một bài toán tối ưu hóa trong đó người bán hàng
cần tìm một hành trình ngắn nhất để thăm qua tất cả các thành phố (điểm
du lịch) và quay trở về thành phố xuất phát ban đầu.
Trong Greedy Traveling Salesman (GTS1), thuật toán bắt đầu từ một
thành phố ngẫu nhiên và sau đó luôn chọn thành phố gần nhất chưa được
thăm làm thành phố tiếp theo trong hành trình. Thuật toán tiếp tục lặp lại
quá trình này cho đến khi tất cả các thành phố đã được thăm qua và hành trình hoàn thành.
Mặc dù GTS1 đơn giản và dễ triển khai, nó không đảm bảo tìm ra lời giải
tối ưu cho bài toán người đi du lịch. Thuật toán này thường dẫn đến một
lời giải gần tối ưu, nhưng không chắc chắn là tối ưu. Để tìm lời giải tối ưu
cho TSP, cần sử dụng các phương pháp tìm kiếm khác như thuật toán tìm
kiếm quay lui, thuật toán di truyền, hoặc thuật toán lập lịch động như Dynamic Programming.
Greedy Traveling Saleman (GTS2)
Thuật toán Greedy Traveling Saleman (GTS2): là một bài toán tối ưu hóa
trong đó người bán hàng cần tìm một hành trình ngắn nhất để thăm qua
tất cả các thành phố và quay trở về thành phố xuất phát ban đầu. Trong
thuật toán tham lam (greedy algorithm), người bán hàng chọn thành phố
tiếp theo dựa trên một quy tắc đơn giản, thường là chọn thành phố gần
nhất chưa được thăm.Nó là phiên bản hoàn chỉnh hơn của GTS1. Thuật toán A*:
Thuật toán A* (hay còn được gọi là A-star) là một thuật toán tìm kiếm
đường đi trong đồ thị hoặc lưới đường. Đặc biệt, A* được sử dụng rộng
rãi trong lĩnh vực trò chơi để tìm kiếm đường đi từ điểm xuất phát đến
mục tiêu. Thuật toán này kết hợp cả yếu tố của thuật toán tìm kiếm theo
chiều rộng (BFS) và thuật toán tìm kiếm theo chiều sâu (DFS).
A* sử dụng một hàm chi phí ước tính (heuristic) để ước lượng chi phí còn
lại từ một điểm bất kỳ đến đích, cùng với chi phí đã đi qua từ điểm xuất
phát. Thuật toán lựa chọn nút tiếp theo để khám phá dựa trên một ước
tính tổng chi phí từ điểm đang xét thông qua điểm đó đến mục tiêu. Điều
này giúp A* tìm kiếm theo hướng tiếp cận tốt nhất đến mục tiêu và
thường dẫn đến hành trình tối ưu.
Hướng Dẫn sử dụng chương trình:
Greedy Traveling Saleman (GTS1):
Trong ví dụ này tôi chọn bài toán người bán hàng với ma trận 6x6 để mô
tả. Ta có thể thay đổi chi phí giữa các thành phố (trọng số) để có thể cho
ra kết quả khác. Nhưng tuyệt đối không được thay đổi giá trị trên đường
chéo chính. Điều này có thể làm thay đổi và mắc sai số đối với bài toán.
Khi chạy chương trình,chương trình sẽ hiển thị thông báo "Starting City:
" và yêu cầu bạn nhập một số nguyên đại diện cho thành phố xuất phát,
thành phố được nhập phải có rang buộc nhất định (0< p <=6).
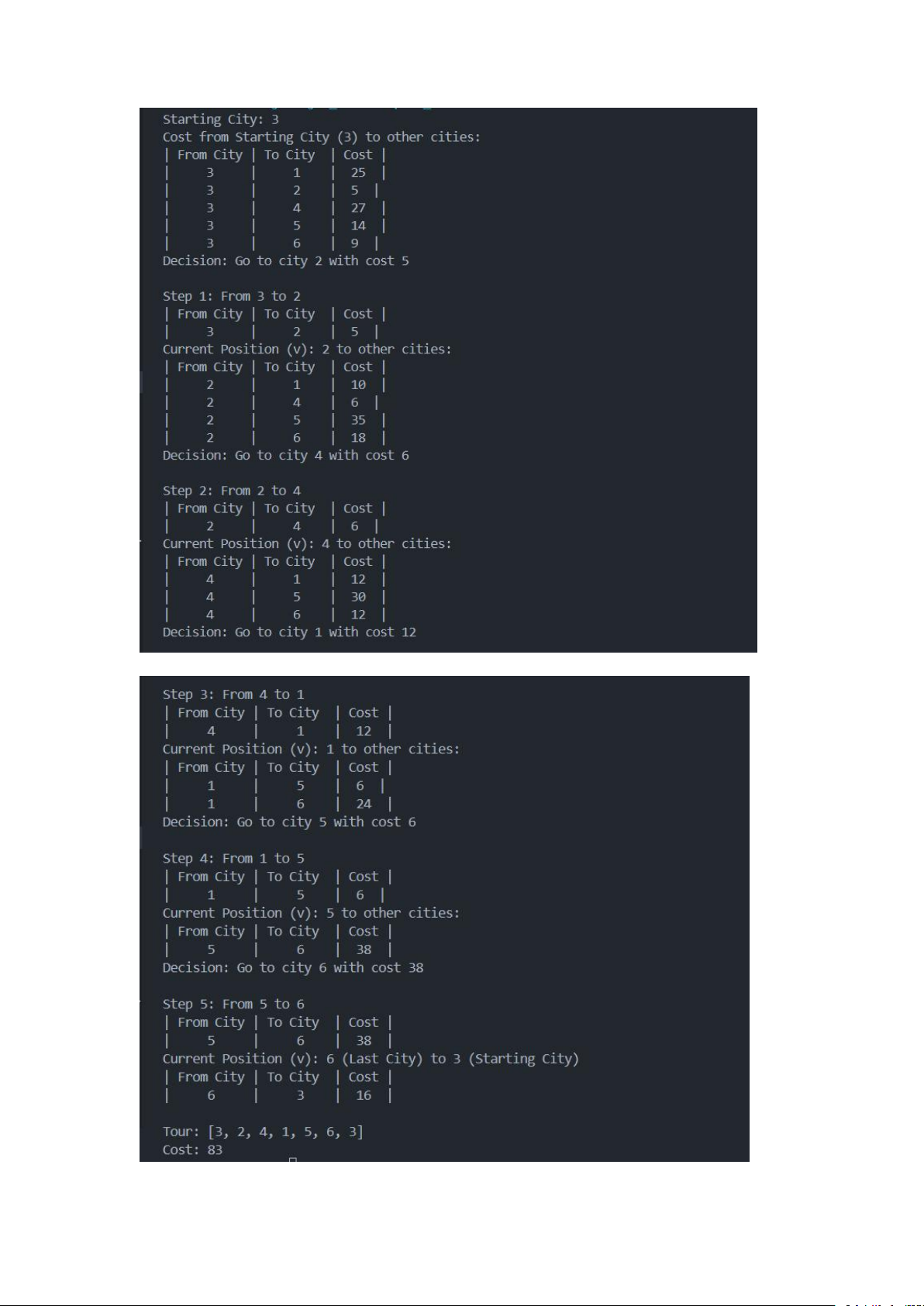
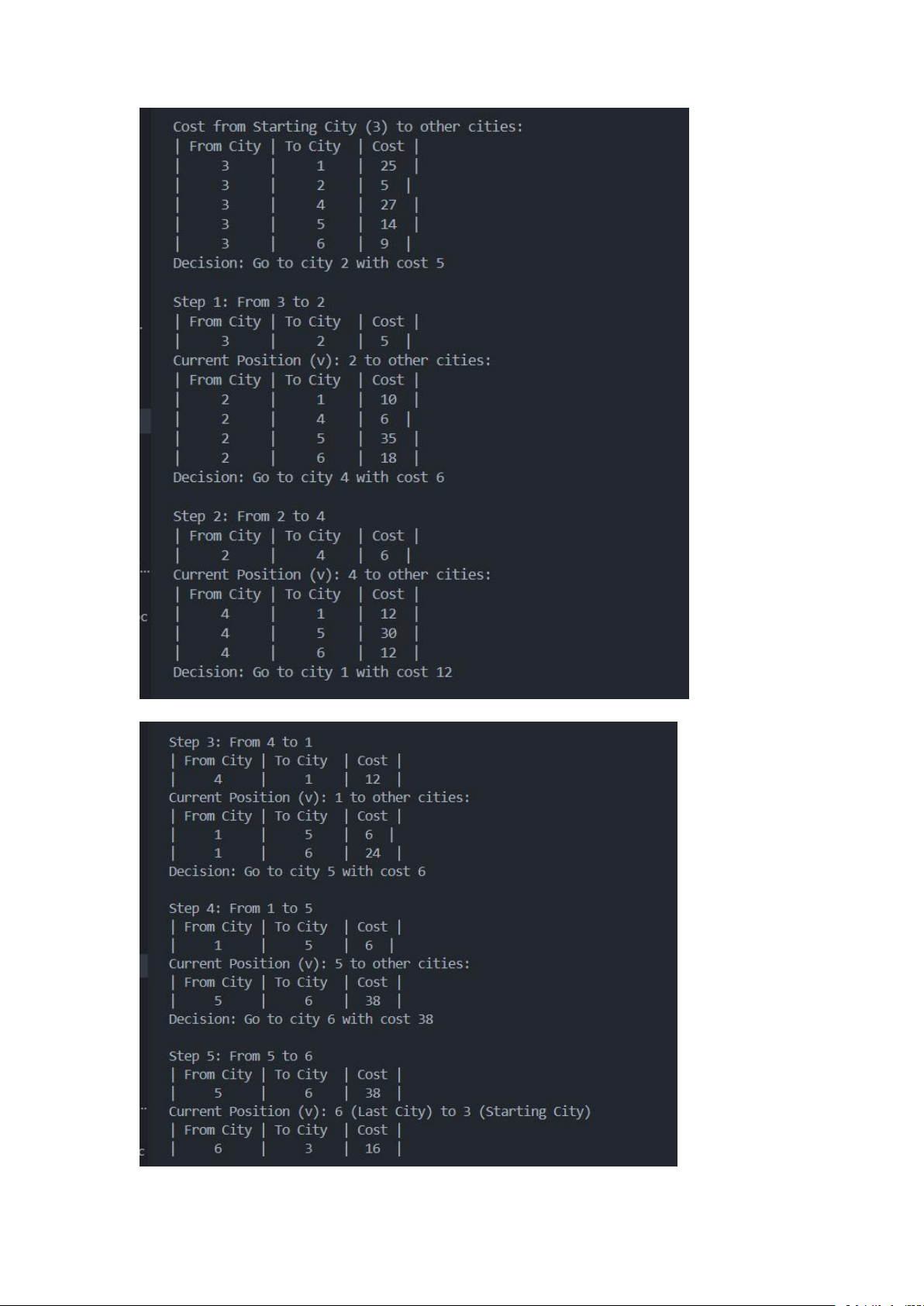
Kết quả cho ra từng bước (step), bước này sẽ bao gồm bước di chuyển từ
thành giữa các thành phố (từ thành phố này qua thành phố khác), thành
phố hiện tại đang đứng, chi phi từ thành phố đang đứng đến các thành
phố chưa đi và cuối cùng là quyết định đến với thành phố có chi phi thấp
nhát. Sau tất cả các bước trên thì sẽ quay về thành phố ban đầu (starting
city). Cuối cùng là sẽ tổng hợp lại Tour với chi phí từ khi bắt đầu đến kết
thúc và chi phí cho chuyến đi.
Trong ví dụ này, sau khi chạy chương trình, tôi đã nhập số 3 làm thành
phố xuất phát. Sau đó, chương trình tính toán hành trình và in ra từng
bước di chuyển và chi phí tương ứng. Cuối cùng, nó in ra hành trình [3, 2,
4, 1, 5,6, 3] và chi phí tổng cộng là 83.
Bạn có thể thay đổi số thành phố xuất phát và thử lại để xem các kết quả khác nhau.
Greedy Traveling Saleman (GTS2):
Trong ví dụ này tiếp tục là bài toán người bán hang với ma trận 6x6 để
mô tả. Ta có thể thay đổi chi phí giữa các thành phố (trọng số) để có thể
cho ra kết quả khác. Nhưng tuyệt đối không được thay đổi giá trị trên
đường chéo chính. Điều này có thể làm thay đổi và mắc sai số đối với bài toán.
Khi chạy chương trình lúc này sẽ cho ra thông báo “How many times do
you want to run GTS1:”. Điều này đúng với bài toán người bán hang để
tìm ra chi phí tối ưu nhất giữa các thành phố đã được chọn để bắt đầu.
Vậy nền lặp lại thuật toán GTS1 n lần (0 < n <= 6) để tìm ra chi phí thấp nhất.
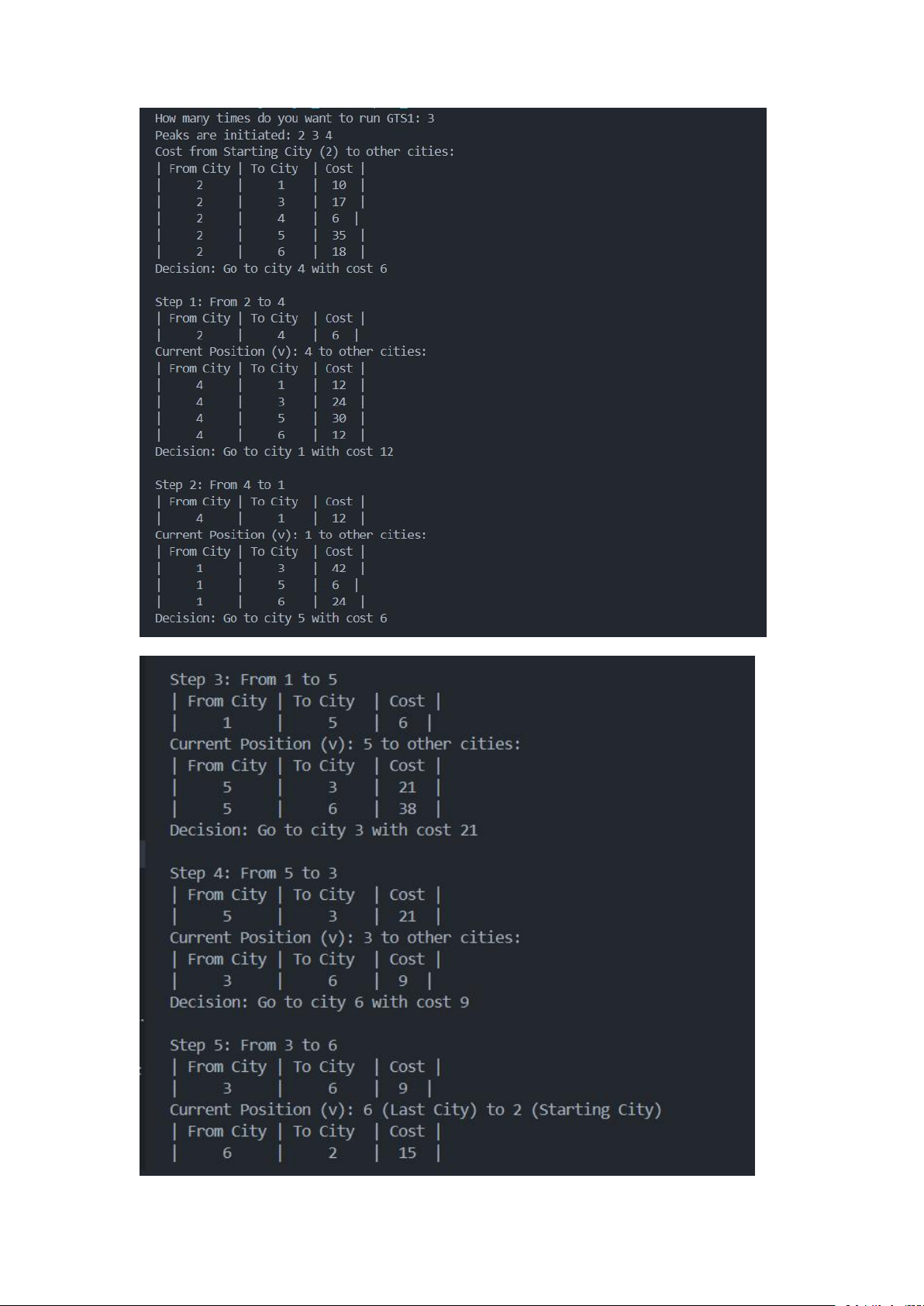
Kết quả cho ra từng bước (step) của mỗi thành phố, bước này sẽ bao gồm
bước di chuyển từ thành giữa các thành phố (từ thành phố này qua thành
phố khác), thành phố hiện tại đang đứng, chi phi từ thành phố đang đứng
đến các thành phố chưa đi và cuối cùng là quyết định đến với thành phố
có chi phi thấp nhất. Sau tất cả các bước trên thì sẽ quay về thành phố ban
đầu (starting city). Cuối cùng là sẽ tổng hợp lại Tour với chi phí thấp nhất
từ khi bắt đầu đến kết thúc và chi phí cho chuyến đi đó.
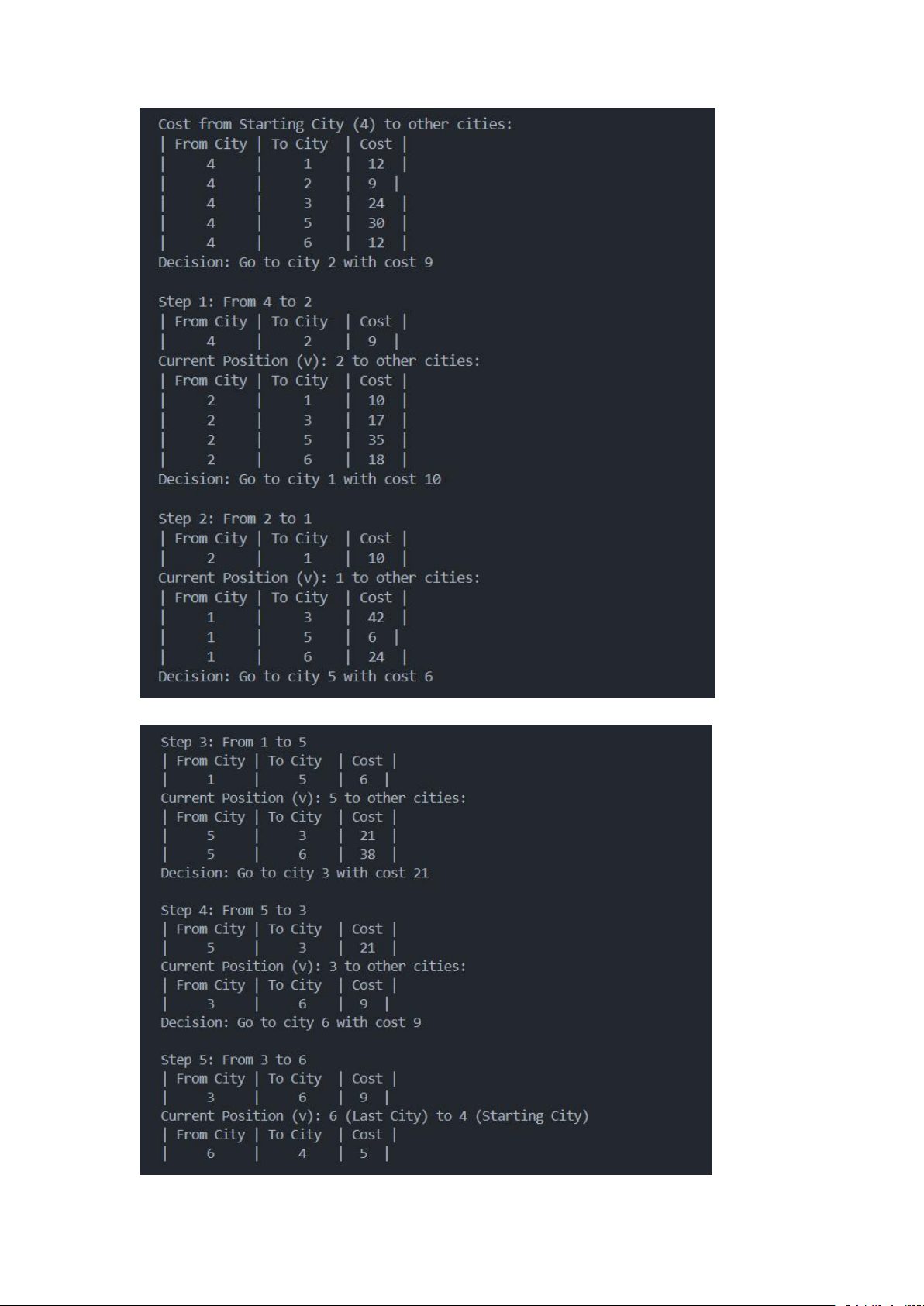
Ở đây, khi chương trình chạy tôi đã nhập số lần lặp lại cho GTS 1 là 3 lần
và bắt đầu lần lượt ở các đỉnh 2, 3, 4. Chương trình sẽ chạy từng bước
từng bước tới thành phố cuối cùng của từng đỉnh và tính toán chi phí cho
từng hành trình lần lượt là 69, 83, 60 đó. Cuối cùng là sẽ cho ra ra hành
trình có chi phí thấp nhất [4, 2, 1, 5, 3, 6, 4]. Thuật toán A*:
- Trong ví dụ này, tôi chọn bài Puzzle để làm cho ví dụ A* . Về phần
cấu trúc dữ liệu, trước khi đi sâu vào thuật toán, chúng ta cần xác
định các cấu trúc dữ liệu sẽ được sử dụng:
+ PuzzleState: Lớp này đại diện cho một trạng thái của bài toán Puzzle.
Mỗi trạng thái được biểu diễn bằng một ma trận 3 x 3.
+ AStarNode: Lớp này đại diện cho một nút trong thuật toán A*. Mỗi nút
bao gồm trạng thái Puzzle, nút cha, và các chỉ số chi phí g, h, f.
- Hàm Heuristic: hàm heuristic được sử dụng để ước lượng chi phí
từ một trạng thái đến trạng thái mục tiêu. Trong trường hợp của bài
toán Puzzle, hàm heuristic được tính bằng cách đếm số ô không
đúng vị trí so với trạng thái mục tiêu. - Xây dựng và triển khai
+ Đầu tiên, chúng ta cần xây dựng các lớp PuzzleState và AStarNode để
biểu diễn trạng thái và nút trong thuật toán. Sau đó, chúng ta cần triển
khai hàm heuristic, các phương thức tạo ra trạng thái kề và hàm tìm
đường đi trong lớp AStarAlgorithm.
+ Cuối cùng, chúng ta sử dụng lớp Main để khởi tạo trạng thái ban đầu và
mục tiêu của bài toán Puzzle, và gọi phương thức findPath từ lớp
AStarAlgorithm để tìm đường đi giữa hai trạng thái này. Kết quả sẽ được in ra màn hình.
- Đây là những gì code chương trình chạy và sẽ hiển thị khi làm bài
ví dụ 8 puzzle cho bài A* này: Initial State: 2 8 3 1 6 4 7 _ 5 OPEN: 2 8 3 1 _ 4 7 6 5 costG=1, costH=3, costF=4 2 8 3 1 6 4 _ 7 5 costG=1, costH=5, costF=6 2 8 3 1 6 4 7 5 _ costG=1, costH=5, costF=6 CLOSED: 2 8 3 1 6 4 7 _ 5 costG=0, costH=4, costF=0 Initial State: 2 8 3 1 6 4 7 _ 5 OPEN: 2 _ 3 1 8 4 7 6 5 costG=2, costH=3, costF=5 2 8 3 _ 1 4 7 6 5 costG=2, costH=3, costF=5 2 8 3 1 6 4 7 5 _ costG=1, costH=5, costF=6 2 8 3 1 6 4 _ 7 5 costG=1, costH=5, costF=6 2 8 3 1 4 _ 7 6 5 costG=2, costH=4, costF=6 CLOSED: 2 8 3 1 6 4 7 _ 5 costG=0, costH=4, costF=0 2 8 3 1 _ 4 7 6 5 costG=1, costH=3, costF=4 Initial State: 2 8 3 1 6 4 7 _ 5 OPEN: 2 8 3 _ 1 4 7 6 5 costG=2, costH=3, costF=5 _ 2 3 1 8 4 7 6 5 costG=3, costH=2, costF=5 2 8 3 1 6 4 7 5 _ costG=1, costH=5, costF=6 2 8 3 1 6 4 _ 7 5 costG=1, costH=5, costF=6 2 8 3 1 4 _ 7 6 5 costG=2, costH=4, costF=6 2 3 _ 1 8 4 7 6 5 costG=3, costH=4, costF=7 CLOSED: 2 8 3 1 6 4 7 _ 5 costG=0, costH=4, costF=0 2 8 3 1 _ 4 7 6 5 costG=1, costH=3, costF=4 2 _ 3 1 8 4 7 6 5 costG=2, costH=3, costF=5 Initial State: 2 8 3 1 6 4 7 _ 5 OPEN: _ 2 3 1 8 4 7 6 5 costG=3, costH=2, costF=5 2 8 3 1 6 4 _ 7 5 costG=1, costH=5, costF=6 2 8 3 1 6 4 7 5 _ costG=1, costH=5, costF=6 2 3 _ 1 8 4 7 6 5 costG=3, costH=4, costF=7 2 8 3 1 4 _ 7 6 5 costG=2, costH=4, costF=6 _ 8 3 2 1 4 7 6 5 costG=3, costH=3, costF=6 2 8 3 7 1 4 _ 6 5 costG=3, costH=4, costF=7 CLOSED: 2 8 3 1 6 4 7 _ 5 costG=0, costH=4, costF=0 2 8 3 1 _ 4 7 6 5 costG=1, costH=3, costF=4 2 _ 3 1 8 4 7 6 5 costG=2, costH=3, costF=5 2 8 3 _ 1 4 7 6 5 costG=2, costH=3, costF=5 Initial State: 2 8 3 1 6 4 7 _ 5 OPEN: 1 2 3 _ 8 4 7 6 5 costG=4, costH=1, costF=5 2 8 3 1 4 _ 7 6 5 costG=2, costH=4, costF=6 2 8 3 1 6 4 _ 7 5 costG=1, costH=5, costF=6 2 3 _ 1 8 4 7 6 5 costG=3, costH=4, costF=7 2 8 3 7 1 4 _ 6 5 costG=3, costH=4, costF=7 _ 8 3 2 1 4 7 6 5 costG=3, costH=3, costF=6 2 8 3 1 6 4 7 5 _ costG=1, costH=5, costF=6 CLOSED: 2 8 3 1 6 4 7 _ 5 costG=0, costH=4, costF=0 2 8 3 1 _ 4 7 6 5 costG=1, costH=3, costF=4 2 _ 3 1 8 4 7 6 5 costG=2, costH=3, costF=5 2 8 3 _ 1 4 7 6 5 costG=2, costH=3, costF=5 _ 2 3 1 8 4 7 6 5 costG=3, costH=2, costF=5 Initial State: 2 8 3 1 6 4 7 _ 5 OPEN: 1 2 3 8 _ 4 7 6 5 costG=5, costH=0, costF=5 2 8 3 1 6 4 7 5 _ costG=1, costH=5, costF=6 2 8 3 1 6 4 _ 7 5 costG=1, costH=5, costF=6 2 8 3 1 4 _ 7 6 5 costG=2, costH=4, costF=6 2 8 3 7 1 4 _ 6 5 costG=3, costH=4, costF=7 _ 8 3 2 1 4 7 6 5 costG=3, costH=3, costF=6 1 2 3 7 8 4 _ 6 5 costG=5, costH=2, costF=7 2 3 _ 1 8 4 7 6 5 costG=3, costH=4, costF=7 CLOSED: 2 8 3 1 6 4 7 _ 5 costG=0, costH=4, costF=0 2 8 3 1 _ 4 7 6 5 costG=1, costH=3, costF=4 2 _ 3 1 8 4 7 6 5 costG=2, costH=3, costF=5 2 8 3 _ 1 4



