Dạng toán xác định góc giữa đường thẳng và mặt phẳng Toán 11

Tài liệu gồm 30 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, hướng dẫn phương pháp giải dạng toán xác định góc giữa đường thẳng và mặt phẳng trong chương trình môn Toán 11 (chuyên đề góc và khoảng cách trong không gian).

125 63 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 7: Quan hệ vuông góc trong không gian (KNTT)

Môn: Toán 11

Thông tin:

30 trang 9 tháng trước

Tác giả:

Profile Kim Oanh
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Dạng toán: XÁC ĐỊNH GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
I. PHƯƠNG PHÁP
Trong không gian, cho đường thẳng
d
và mặt phẳng
.P
Để xác định góc giữa đường thẳng
d
và mặt phẳng
P
, thông thường ta thực hiện theo các
bước sau:
Bước 1: Chiếu vuông góc đường thẳng
d
lên mặt phẳng
P
ta được đường thẳng
'.d
Bước 2: Xác định
; ; .d P d P SIH

P
d'
d
I
S
II. BÀI TẬP TRẮC NGHIỆM
Câu 1: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
.a
Biết
SA
vuông góc với mặt phẳng
ABC
và
3.SA a
Góc giữa đường thẳng
SB
và mặt phẳng
ABC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 2: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
2.a
Biết
SA
vuông góc với mặt
phẳng
ABC
và
2 2.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
SAB
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 3: Cho hình chóp
.S ABC
có
.AB a
Biết
SA
vuông góc với mặt phẳng
ABC
và
3.SA a
Góc
giữa đường thẳng
SB
và mặt phẳng
ABC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 4: Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
,.B AB a
Biết
SA
vuông góc với mặt
phẳng
ABC
và
2.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 5: Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
,.B AB a
Biết
SA
vuông góc với mặt
phẳng
ABC
và
2.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
SAB
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 6: Cho hình chóp
.S ABCD
có đáy là hình vuông có cạnh bằng
.a
Biết
SA
vuông góc với mặt
phẳng
ABCD
và
3.SA a
Góc giữa đường thẳng
SB
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 7: Cho hình chóp
.S ABCD
có đáy là hình vuông có cạnh bằng
.a
Biết
SA
vuông góc với mặt
phẳng
ABCD
và
6.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 8: Cho hình chóp
.S ABCD
có đáy là hình vuông có cạnh bằng
.a
Biết
SA
vuông góc với mặt
phẳng
ABCD
và
2.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
SAB
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 9: Cho hình chóp
.S ABCD
có đáy là hình vuông có cạnh bằng
.a
Biết
SA
vuông góc với mặt
phẳng
ABCD
và
.SA a
Góc giữa đường thẳng
SB
và mặt phẳng
SAC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 10: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật có
2.BC a
Biết
SA
vuông góc với mặt
phẳng
ABCD
và
2 3.SA a
Góc giữa đường thẳng
SD
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 11: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
, 2 .AB a BC a
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
15
.
3
a
SA
Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 12: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
, 2 .AB a BC a
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
3
.
3
a
SA
Góc giữa đường thẳng
SC
và mặt phẳng
SAB
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 13: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
, 2 .AB a BC a
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
15
.
15
a
SA
Góc giữa đường thẳng
SB
và mặt phẳng
SAC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 14: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
,AB
với
2 2 2 .AD AB BC a
Biết
SA
vuông góc với mặt phẳng
ABCD
và
6.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 15: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
,AB
với
2 2 2 .AD AB BC a
Biết
SA
vuông góc với mặt phẳng
ABCD
và
2.SA a
Góc giữa đường thẳng
SD
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 16: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
,AB
với
2 2 2 .AD AB BC a
Biết
SA
vuông góc với mặt phẳng
ABCD
và
2.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
SAB
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 17: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
,AB
với
2 2 2 .AD AB BC a
Biết
SA
vuông góc với mặt phẳng
ABCD
và
.SA a
Góc giữa đường thẳng
SB
và mặt phẳng
SAC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 18: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
,AB
với
2 2 2 .AD AB BC a
Biết
SA
vuông góc với mặt phẳng
ABCD
và
2.SA a
Góc giữa đường thẳng
SD
và mặt phẳng
SAC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 19: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
a
với
60 .BAD 
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 20: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
a
với
60 .BAD 
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
.SA a
Gọi
là góc giữa đường thẳng
SC
và mặt phẳng
.SAB
Khẳng định nào dưới đây đúng?
A.
3
sin .
4
B.
3
sin .
8
C.
2
sin .
4
D.
3
sin .
4
Câu 21: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
a
với
60 .BAD 
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
3.SA a
Gọi
là góc giữa đường thẳng
SB
và mặt phẳng
.SAC
Khẳng định nào dưới đây đúng?
A.
3
sin .
4
B.
3
sin .
8
C.
2
sin .
4
D.
1
sin .
4
Câu 22: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
a
với
120 .BAD 
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 23: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
a
với
120 .BAD 
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
2.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
SAB
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 24: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
a
với
120 .BAD 
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
2.SA a
Góc giữa đường thẳng
SB
và mặt phẳng
SAC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 25: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
a
với
120 .BAD 
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
.
2
a
SA
Góc giữa đường thẳng
SA
và mặt phẳng
SBD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 26: Cho hình lăng trụ đứng
.ABC A B C
có đáy là tam giác đều cạnh
, 3.a AA a
Góc giữa
đường thẳng
AB
và mặt phẳng
ABC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 27: Cho hình lăng trụ đứng
.ABC A B C
có đáy là tam giác đều cạnh
, 2.a AA a
Góc giữa
đường thẳng
AC
và mặt phẳng
ABB A

bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 28: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
, 2.B AB AA a

Góc giữa đường thẳng
AB
và mặt phẳng
ABC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 29: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
, , 2.B AB a AA a

Góc giữa đường thẳng
AC
và mặt phẳng
ABB A

bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 30: Cho hình hộp chữ nhật
.ABCD A B C D
có
, 3.AB AD a AA a
Góc giữa đường thẳng
AB
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 31: Cho hình hộp chữ nhật
.ABCD A B C D
có
; 2 , 5.AB a AD a AA a
Góc giữa đường thẳng
AC
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 32: Cho hình hộp chữ nhật
.ABCD A B C D
có
; 6.AB AA a AD a
Góc giữa đường thẳng
AC
và mặt phẳng
ABB A

bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 33: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
.a
Mặt bên
SAB
là tam giác vuông
cân tại
S
và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng
SC
và mặt
phẳng
ABC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 34: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
.a
Mặt bên
SAB
là tam giác vuông
cân tại
S
và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng
SC
và mặt
phẳng
SAB
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 35: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh bằng
.a
Mặt bên
SAB
là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng
SB
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Câu 36: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh bằng
.a
Mặt bên
SAB
là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Gọi
là góc giữa đường thẳng
SC
và mặt phẳng
.ABCD
Khẳng định nào dưới đây đúng?
A.
5
tan .
15
B.
15
tan .
15
C.
5
tan .
5
D.
15
tan .
5
Câu 37: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
2.a
Biết hình chiếu vuông góc của
đỉnh
S
trên mặt phẳng
ABC
là trung điểm
H
của
AB
. Góc giữa đường thẳng
SC
và mặt
phẳng
ABC
bằng
60 .
Tính
.SH
A.
2.SH a
B.
3.SH a
C.
3.SH a
D.
.SH a
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 38: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
3 , 2 .a SB a
Biết hình chiếu vuông
góc của đỉnh
S
trên mặt phẳng
ABC
là điểm
H
trên cạnh
AB
sao cho
2.AH HB
Gọi
là
góc giữa đường thẳng
SC
và mặt phẳng
.ABC
Khẳng định nào dưới đây đúng?
A.
21
tan .
21
B.
15
tan .
15
C.
21
tan .
7
D.
15
tan .
5
Câu 39: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh bằng
3 , 2 .a SB a
Biết hình chiếu vuông
góc của đỉnh
S
trên mặt phẳng
ABCD
là điểm
H
trên cạnh
AB
sao cho
2.AH HB
Gọi
là góc giữa đường thẳng
SC
và mặt phẳng
.ABCD
Khẳng định nào dưới đây đúng?
A.
21
tan .
21
B.
10
tan .
10
C.
21
tan .
7
D.
30
tan .
10
Câu 40: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh bằng
3 , 2 .a SB a
Biết hình chiếu vuông
góc của đỉnh
S
trên mặt phẳng
ABCD
là điểm
H
trên cạnh
AB
sao cho
2.AH HB
Gọi
là góc giữa đường thẳng
SD
và mặt phẳng
.ABCD
Khẳng định nào dưới đây đúng?
A.
21
tan .
21
B.
39
tan .
13
C.
21
tan .
7
D.
15
tan .
5
III. LỜI GIẢI CHI TIẾT
Câu 1: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
.a
Biết
SA
vuông góc với mặt phẳng
ABC
và
3.SA a
Góc giữa đường thẳng
SB
và mặt phẳng
ABC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
S
A
B
C
Ta có:
SA ABC AB 
là hình chiếu vuông góc của
SB
trên mặt phẳng
.ABC
Suy ra:
; ; .SB ABC SB AB SBA
Xét tam giác
SAB
vuông tại
:tan 3 60 .
SA
A SBA SBA
AB

Vậy
; 60 .SB ABC 
Câu 2: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
2.a
Biết
SA
vuông góc với mặt
phẳng
ABC
và
2 2.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
SAB
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Lời giải:
H
C
B
A
S
Dựng
,.
CH AB
CH AB H AB CH SAB
CH SA
 
Ta có:
CH SAB SH 
là hình chiếu vuông góc của
SC
trên mặt phẳng
.SAB
Suy ra:
; ; .SC SAB SC SH HSC
Ta có:
22
23
3; 2 3 .
2
a
HC a SC SA AC a
Xét tam giác
SCH
vuông tại
1
:sin 30 .
2
HC
H HSC HSC
SC

Vậy
; 30 .SC SAB 
Câu 3: Cho hình chóp
.S ABC
có
.AB a
Biết
SA
vuông góc với mặt phẳng
ABC
và
3.SA a
Góc
giữa đường thẳng
SB
và mặt phẳng
ABC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
C
B
A
S
Ta có:
SA ABC AB 
là hình chiếu vuông góc của
SB
trên mặt phẳng
.ABC
Suy ra:
; ; .SB ABC SB BA SBA
Xét tam giác
SAB
vuông tại
:tan 3 60 .
SA
A SBA SBA
AB

Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Vậy
; 60 .SB ABC 
Câu 4: Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
,.B AB a
Biết
SA
vuông góc với mặt
phẳng
ABC
và
2.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
S
A
B
C
Ta có:
SA ABC AC 
là hình chiếu vuông góc của
SC
trên mặt phẳng
.ABC
Suy ra:
; ; .SC ABC SC AC SCA
Xét tam giác
SAC
vuông tại
:tan 1 45 .
SA
A SCA SCA
AC

Vậy
; 45 .SC ABC 
Câu 5: Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
,.B AB a
Biết
SA
vuông góc với mặt
phẳng
ABC
và
2.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
SAB
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
S
A
B
C
Ta có:
BC AB
BC SAB SB
BC SA
 
là hình chiếu vuông góc của
SC
trên mặt phẳng
.SAB
Suy ra:
; ; .SC SAB SC SB BSC
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Ta có:
22
3.SB SA AB a
Xét tam giác
SBC
vuông tại
3
:tan 30 .
3
BC
B BSC BSC
SB

Vậy
; 30 .SC SAB 
Câu 6: Cho hình chóp
.S ABCD
có đáy là hình vuông có cạnh bằng
.a
Biết
SA
vuông góc với mặt
phẳng
ABCD
và
3.SA a
Góc giữa đường thẳng
SB
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
S
A
B
C
D
Ta có:
SA ABCD AB 
là hình chiếu vuông góc của
SB
trên mặt phẳng
.ABCD
Suy ra:
; ; .SB ABCD SB BA SBA
Xét tam giác
SAB
vuông tại
:tan 3 60 .
SA
A SBA SBA
AB

Vậy
; 60 .SB ABCD 
Câu 7: Cho hình chóp
.S ABCD
có đáy là hình vuông có cạnh bằng
.a
Biết
SA
vuông góc với mặt
phẳng
ABCD
và
6.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
D
C
B
A
S
Ta có:
SA ABCD AC 
là hình chiếu vuông góc của
SC
trên mặt phẳng
.ABCD
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Suy ra:
; ; .SC ABCD SC AC SCA
Xét tam giác
SAC
vuông tại
:tan 3 60 .
SA
A SCA SCA
AC

Vậy
; 60 .SC ABCD 
Câu 8: Cho hình chóp
.S ABCD
có đáy là hình vuông có cạnh bằng
.a
Biết
SA
vuông góc với mặt
phẳng
ABCD
và
2.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
SAB
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
D
C
B
A
S
Ta có:
BC AB
BC SAB SB
BC SA
 
là hình chiếu vuông góc của
SC
trên mặt phẳng
.SAB
Suy ra:
; ; .SC SAB SC SB BSC
Ta có:
22
3.SB SA AB a
Xét tam giác
SBC
vuông tại
3
:tan 30 .
3
BC
B BSC BSC
SB

Vậy
; 30 .SC SAB 
Câu 9: Cho hình chóp
.S ABCD
có đáy là hình vuông có cạnh bằng
.a
Biết
SA
vuông góc với mặt
phẳng
ABCD
và
.SA a
Góc giữa đường thẳng
SB
và mặt phẳng
SAC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
O
S
A
B
C
D
Gọi
O
là tâm hình vuông
.ABCD
Ta có:
BO AC
BO SAC SO
BO SA
 
là hình chiếu vuông góc của
SB
trên mặt phẳng
.SAC
Suy ra:
; ; .SB SAC SB SO BSO
Ta có:
22
2.SB SA AB a
Xét tam giác
SBO
vuông tại
1
:sin 30 .
2
BO
O BSO BSO
SB

Vậy
; 30 .SB SAC 
Câu 10: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật có
2.BC a
Biết
SA
vuông góc với mặt
phẳng
ABCD
và
2 3.SA a
Góc giữa đường thẳng
SD
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
D
C
B
A
S
Ta có:
SA ABCD AD 
là hình chiếu vuông góc của
SD
trên mặt phẳng
.ABCD
Suy ra:
; ; .SD ABCD SD AD SDA
Xét tam giác
SAD
vuông tại
:tan 3 60 .
SA
A SDA SDA
AD

Vậy
; 60 .SD ABCD 
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 11: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
, 2 .AB a BC a
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
15
.
3
a
SA
Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
D
C
B
A
S
Ta có:
SA ABCD AC 
là hình chiếu vuông góc của
SC
trên mặt phẳng
.ABCD
Suy ra:
; ; .SC ABCD SC AC SCA
Xét tam giác
SAC
vuông tại
3
:tan 30 .
3
SA
A SCA SCA
AC

Vậy
; 30 .SC ABCD 
Câu 12: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
, 2 .AB a BC a
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
3
.
3
a
SA
Góc giữa đường thẳng
SC
và mặt phẳng
SAB
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
D
C
B
A
S
Ta có:
BC AB
BC SAB SB
BC SA
 
là hình chiếu vuông góc của
SC
trên mặt phẳng
.SAB
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Suy ra:
; ; .SC SAB SC SB BSC
Ta có:
22
23
.
3
a
SB SA AB
Xét tam giác
SBC
vuông tại
:tan 3 60 .
BC
B BSC BSC
SB
Vậy
; 60 .SC SAB 
Câu 13: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
, 2 .AB a BC a
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
15
.
15
a
SA
Góc giữa đường thẳng
SB
và mặt phẳng
SAC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
H
S
A
B
C
D
Dựng
,.BH AC H AC
Ta có:
BH AC
BH SAC SH
BH SA
 
là hình chiếu vuông góc của
SB
trên mặt phẳng
.SAC
Suy ra:
; ; .SB SAC SB SH BSH
Ta có:
22
2 2 2
4 15 1 1 1 2 5
;.
15 5
aa
SB SA AB BH
BH BA BC

Xét tam giác
SBH
vuông tại
3
:sin 60 .
2
BH
H BSH BSH
SB

Vậy
; 60 .SB SAC 
Câu 14: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
,AB
với
2 2 2 .AD AB BC a
Biết
SA
vuông góc với mặt phẳng
ABCD
và
6.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
C
B
A
S
D
Ta có:
SA ABCD AC 
là hình chiếu vuông góc của
SC
trên mặt phẳng
.ABCD
Suy ra:
; ; .SC ABCD SC AC SCA
Ta có:
22
2.AC AB BC a
Xét tam giác
SAC
vuông tại
:tan 3 60 .
SA
A SCA SCA
AC

Vậy
; 60 .SC ABCD 
Câu 15: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
,AB
với
2 2 2 .AD AB BC a
Biết
SA
vuông góc với mặt phẳng
ABCD
và
2.SA a
Góc giữa đường thẳng
SD
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
D
S
A
B
C
Ta có:
SA ABCD AD 
là hình chiếu vuông góc của
SD
trên mặt phẳng
.ABCD
Suy ra:
; ; .SD ABCD SD AD SDA
Xét tam giác
SAD
vuông tại
:tan 1 45 .
SA
A SDA SDA
AD

Vậy
; 45 .SD ABCD 
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 16: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
,AB
với
2 2 2 .AD AB BC a
Biết
SA
vuông góc với mặt phẳng
ABCD
và
2.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
SAB
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
C
B
A
S
D
Ta có:
BC AB
BC SAB SB
BC SA
 
là hình chiếu vuông góc của
SC
trên mặt phẳng
.SAB
Suy ra:
; ; .SC SAB SC SB BSC
Ta có:
22
3.SB SA AB a
Xét tam giác
SBC
vuông tại
3
:tan 30 .
3
BC
B BSC BSC
SB

Vậy
; 30 .SC SAB 
Câu 17: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
,AB
với
2 2 2 .AD AB BC a
Biết
SA
vuông góc với mặt phẳng
ABCD
và
.SA a
Góc giữa đường thẳng
SB
và mặt phẳng
SAC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
I
O
D
S
A
B
C
Gọi
I
là trung điểm
AD ABCI
là hình vuông.
Gọi
O
là tâm hình vuông
.ABCI
Ta có:
BO AC
BO SAC SO
BO SA
 
là hình chiếu vuông góc của
SB
trên mặt phẳng
.SAC
Suy ra:
; ; .SB SAC SB SO BSO
Ta có:
22
2.SB SA AB a
Xét tam giác
SBO
vuông tại
1
:sin 30 .
2
BO
O BSO BSO
SB

Vậy
; 30 .SB SAC 
Câu 18: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
,AB
với
2 2 2 .AD AB BC a
Biết
SA
vuông góc với mặt phẳng
ABCD
và
2.SA a
Góc giữa đường thẳng
SD
và mặt phẳng
SAC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
D
S
A
B
C
Gọi
I
là trung điểm
90 .AD IA ID IC ACD 
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Ta có:
CD AC
CD SAC SC
CD SA

là hình chiếu vuông góc của
SD
trên mặt phẳng
.SAC
Suy ra:
; ; .SD SAC SD SC DSC
Ta có:
22
2 2 .SD SA AD a
Xét tam giác
SCD
vuông tại
1
:sin 30 .
2
CD
C CSD CSD
SD

Vậy
; 30 .SD SAC 
Câu 19: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
a
với
60 .BAD 
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
O
a
a
A
B
C
D
S
A
B
C
D
Do
ABCD
là hình thoi cạnh
a
với
60BAD 
nên
,ABD BCD
là các tam giác đều cạnh
.a
Ta có:
SA ABCD AC 
là hình chiếu vuông góc của
SC
trên mặt phẳng
.ABCD
Suy ra:
; ; .SC ABCD SC AC SCA
Ta có:
3
2 2. 3.
2
a
AC AO a
Xét tam giác
SAC
vuông tại
3
:tan 30 .
3
SA
A SCA SCA
AC

Vậy
; 30 .SC ABCD 
Câu 20: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
a
với
60 .BAD 
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
.SA a
Gọi
là góc giữa đường thẳng
SC
và mặt phẳng
.SAB
Khẳng định nào dưới đây đúng?
A.
3
sin .
4
B.
3
sin .
8
C.
2
sin .
4
D.
3
sin .
4
Lời giải:
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
H
K
K
H
D
C
B
A
S
D
C
B
A
a
a
O
Do
ABCD
là hình thoi cạnh
a
với
60BAD 
nên
,ABD BCD
là các tam giác đều cạnh
.a
Dựng
3
, ; , .
2
a
CK AB K AB DH AB H AB CK DH 
Ta có:
CK AB
CK SAB SK
CK SA
 
là hình chiếu vuông góc của
SC
trên mặt phẳng
.SAB
Suy ra:
; ; .SC SAB SC SK KSC
Ta có:
2
2 2 2
2 2 .SC SA AC SA AO a
Xét tam giác
SKC
vuông tại
33
:sin sin .
44
CK
K KSC
SC

Câu 21: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
a
với
60 .BAD 
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
3.SA a
Gọi
là góc giữa đường thẳng
SB
và mặt phẳng
.SAC
Khẳng định nào dưới đây đúng?
A.
3
sin .
4
B.
3
sin .
8
C.
2
sin .
4
D.
1
sin .
4
Lời giải:
O
D
C
B
A
S
D
C
B
A
a
a
O
Do
ABCD
là hình thoi cạnh
a
với
60BAD 
nên
,ABD BCD
là các tam giác đều cạnh
.a
Gọi
O
là tâm hình thoi
.ABCD
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Ta có:
BO AC
BO SAC SO
BO SA
 
là hình chiếu vuông góc của
SB
trên mặt phẳng
.SAC
Suy ra:
; ; .SB SAC SB SO BSO
Ta có:
22
1
2 ; .
22
a
SB SA AB a BO BD
Xét tam giác
SBO
vuông tại
11
:sin sin .
44
BO
O BSO
SB
Câu 22: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
a
với
120 .BAD 
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
O
a
a
A
B
C
D
S
A
B
C
D
Do
ABCD
là hình thoi cạnh
a
với
120BAD 
nên
,ABC ACD
là các tam giác đều cạnh
.a
Ta có:
SA ABCD AC 
là hình chiếu vuông góc của
SC
trên mặt phẳng
.ABCD
Suy ra:
; ; .SC ABCD SC AC SCA
Xét tam giác
SAC
vuông tại
:tan 1 45 .
SA
A SCA SCA
AC

Vậy
; 45 .SC ABCD 
Câu 23: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
a
với
120 .BAD 
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
2.SA a
Góc giữa đường thẳng
SC
và mặt phẳng
SAB
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
H
D
C
B
A
S
D
C
B
A
H
a
O
Do
ABCD
là hình thoi cạnh
a
với
120BAD 
nên
,ABC ACD
là các tam giác đều cạnh
.a
Dựng
,.
CH AB
CH AB H AB CH SAB
CH SA
 
Ta có:
CH SAB SH 
là hình chiếu vuông góc của
SC
trên mặt phẳng
.SAB
Suy ra:
; ; .SC SAB SC SH HSC
Ta có:
22
3
; 3 .
2
a
HC SC SA AC a
Xét tam giác
SCH
vuông tại
1
:sin 30 .
2
HC
H HSC HSC
SC

Vậy
; 30 .SC SAB 
Câu 24: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
a
với
120 .BAD 
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
2.SA a
Góc giữa đường thẳng
SB
và mặt phẳng
SAC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
O
a
a
A
B
C
D
S
A
B
C
D
O
Do
ABCD
là hình thoi cạnh
a
với
120BAD 
nên
,ABC ACD
là các tam giác đều cạnh
.a
Gọi
O
là tâm hình thoi
.ABCD
Ta có:
BO AC
BO SAC SO
BO SA
 
là hình chiếu vuông góc của
SB
trên mặt phẳng
.SAC
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Suy ra:
; ; .SB SAC SB SO BSO
Ta có:
22
3
3; .
2
a
SB SA AB a BO
Xét tam giác
SBO
vuông tại
1
:sin 30 .
2
BO
O BSO BSO
SB

Vậy
; 30 .SB SAC 
Câu 25: Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
a
với
120 .BAD 
Biết
SA
vuông góc với
mặt phẳng
ABCD
và
.
2
a
SA
Góc giữa đường thẳng
SA
và mặt phẳng
SBD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
O
D
C
B
A
S
D
C
B
A
a
a
O
Do
ABCD
là hình thoi cạnh
a
với
120BAD 
nên
,ABC ACD
là các tam giác đều cạnh
.a
Gọi
O
là tâm hình thoi
.ABCD
Dựng
AH SO
AH SO AH SBD SH SO
AH BD
  
là hình chiếu vuông góc của
SA
trên mặt phẳng
.SBD
Suy ra:
; ; .SA SBD SA SO ASO
Xét tam giác
SAO
vuông tại
:tan 1 45 .
AO
A ASO ASO
SA

Vậy
; 45 .SA SBD 
Câu 26: Cho hình lăng trụ đứng
.ABC A B C
có đáy là tam giác đều cạnh
, 3.a AA a
Góc giữa
đường thẳng
AB
và mặt phẳng
ABC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
C
B
A
B'
C'
A'
Do
AA ABC AB

là hình chiếu vuông góc của
AB
trên mặt phẳng
.ABC
Suy ra:
; ; .A B ABC A B AB A BA

Xét tam giác
A BA
vuông tại
: tan 3 60 .
AA
A A BA A BA
AB


Vậy
; 60 .A B ABC

Câu 27: Cho hình lăng trụ đứng
.ABC A B C
có đáy là tam giác đều cạnh
, 2.a AA a
Góc giữa
đường thẳng
AC
và mặt phẳng
ABB A

bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
H
A'
C'
B'
A
B
C
Dựng
.
CH AB
CH AB CH ABB A
CH AA

 
Vậy
AH
là hình chiếu vuông góc của
AC
trên mặt phẳng
.ABB A

Suy ra:
; ; .A C ABB A A C A H HA C

Ta có:
22
3
3; .
2
a
A C A A AC a HC

Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Xét tam giác
A HC
vuông tại
1
: sin 30 .
2
HC
H HA C HA C
AC


Vậy
; 30 .A C ABB A

Câu 28: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
, 2.B AB AA a

Góc giữa đường thẳng
AB
và mặt phẳng
ABC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
C
B
A
B'
C'
A'
Do
AA ABC AB

là hình chiếu vuông góc của
AB
trên mặt phẳng
.ABC
Suy ra:
; ; .A B ABC A B AB A BA

Xét tam giác
A BA
vuông tại
: tan 1 45 .
AA
A A BA A BA
AB


Vậy
; 45 .A B ABC

Câu 29: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
, , 2.B AB a AA a

Góc giữa đường thẳng
AC
và mặt phẳng
ABB A

bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
A'
C'
B'
A
B
C
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Ta có:
.
CB AB
CB ABB A
CB AA


Vậy
AB
là hình chiếu vuông góc của
AC
trên mặt phẳng
.ABB A

Suy ra:
; ; .A C ABB A A C A B BA C

Ta có:
22
2 ; .A C A A AC a BC a

Ta có:

22
2 ; .A C A A AC a BC a
Xét tam giác
A BC
vuông tại


1
: sin 30 .
2
BC
B BA C BA C
AC
Vậy
; 30 .A C ABB A

Câu 30: Cho hình hộp chữ nhật
.ABCD A B C D
có
, 3.AB AD a AA a
Góc giữa đường thẳng
AB
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
D'
A'
B'
C'
D
A
B
C
Do
AA ABCD AB

là hình chiếu vuông góc của
AB
trên mặt phẳng
.ABCD
Suy ra:
; ; .A B ABCD A B AB A BA

Xét tam giác
A BA
vuông tại
: tan 3 60 .
AA
A A BA A BA
AB


Vậy
; 60 .A B ABCD

Câu 31: Cho hình hộp chữ nhật
.ABCD A B C D
có
; 2 , 5.AB a AD a AA a
Góc giữa đường thẳng
AC
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
C
B
A
D
C'
B'
A'
D'
Do
AA ABCD AC

là hình chiếu vuông góc của
AC
trên mặt phẳng
.ABCD
Suy ra:
; ; .A C ABCD A C AC A CA

Ta có:
22
5.AC AB BC a
Xét tam giác
A CA
vuông tại
: tan 1 45 .
AA
A A CA A CA
AC


Vậy
; 45 .A C ABCD

Câu 32: Cho hình hộp chữ nhật
.ABCD A B C D
có
; 6.AB AA a AD a
Góc giữa đường thẳng
AC
và mặt phẳng
ABB A

bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
C
B
A
D
C'
B'
A'
D'
Ta có:
.
CB AB
CB ABB A
CB AA


Vậy
AB
là hình chiếu vuông góc của
AC
trên mặt phẳng
.ABB A

Suy ra:
; ; .A C ABB A A C A B BA C

Xét tam giác
A BC
vuông tại
: tan 3 60 .
BC
B BA C BA C
AB


Vậy
; 60 .A C ABB A

Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 33: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
.a
Mặt bên
SAB
là tam giác vuông
cân tại
S
và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng
SC
và mặt
phẳng
ABC
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
H
S
A
B
C
Gọi
H
là trung điểm
.AB SH AB
Ta có:
.
SH AB
SH ABC
SAB ABC

Suy ra:
HC
là hình chiếu vuông góc của
SC
trên mặt phẳng
.ABC
Suy ra:
; ; .SC ABC SC HC SCH
Xét tam giác
SHC
vuông tại
3
: tan 30 .
3
SH
H SCH SCH
HC

Vậy
; 30 .SC ABC 
Câu 34: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
.a
Mặt bên
SAB
là tam giác vuông
cân tại
S
và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng
SC
và mặt
phẳng
SAB
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
C
B
A
S
H
Gọi
H
là trung điểm
.AB HC AB
Ta có:
.
HC AB
HC SAB
SAB ABC

Suy ra:
SH
là hình chiếu vuông góc của
SC
trên mặt phẳng
.SAB
Suy ra:
; ; .SC SAB SC SH CSH
Ta có:
3
;
22
aa
HC SH
Xét tam giác
SHC
vuông tại
: tan 3 60 .
HC
H CSH CSH
HS

Vậy
; 60 .SC SAB 
Câu 35: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh bằng
.a
Mặt bên
SAB
là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng
SB
và mặt phẳng
ABCD
bằng
A.
30 .
B.
45 .
C.
90 .
D.
60 .
Lời giải:
D
S
A
B
C
H
Gọi
H
là trung điểm
.AB SH AB
Ta có:
.
SH AB
SH ABCD
SAB ABCD

Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Suy ra:
HB
là hình chiếu vuông góc của
SB
trên mặt phẳng
.ABCD
Ta có:
3
;
2
a
HC SB a
Suy ra:
; ; 60 .SB ABCD SB HB SBH
Câu 36: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh bằng
.a
Mặt bên
SAB
là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Gọi
là góc giữa đường thẳng
SC
và mặt phẳng
.ABCD
Khẳng định nào dưới đây đúng?
A.
5
tan .
15
B.
15
tan .
15
C.
5
tan .
5
D.
15
tan .
5
Lời giải:
H
C
B
A
S
D
Gọi
H
là trung điểm
.AB SH AB
Ta có:
.
SH AB
SH ABCD
SAB ABCD

Suy ra:
HC
là hình chiếu vuông góc của
SC
trên mặt phẳng
.ABCD
Suy ra:
; ; .SC ABCD SC HC SCH
Ta có:
22
35
;.
22
aa
SH HC HB BC
Xét tam giác
SHC
vuông tại
15
: tan .
5
H SCH
Câu 37: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
2.a
Biết hình chiếu vuông góc của
đỉnh
S
trên mặt phẳng
ABC
là trung điểm
H
của
AB
. Góc giữa đường thẳng
SC
và mặt
phẳng
ABC
bằng
60 .
Tính
.SH
A.
2.SH a
B.
3.SH a
C.
3.SH a
D.
.SH a
Lời giải:
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
H
S
A
B
C
Theo giả thiết:
.SH ABC
Suy ra:
HC
là hình chiếu vuông góc của
SC
trên mặt phẳng
.ABC
Suy ra:
; ; .SC ABC SC HC SCH
Xét tam giác
SHC
vuông tại
23
: tan .tan . 3 3 .
2
a
SH
H SCH SH HC SCH a
HC

Câu 38: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
3 , 2 .a SB a
Biết hình chiếu vuông
góc của đỉnh
S
trên mặt phẳng
ABC
là điểm
H
trên cạnh
AB
sao cho
2.AH HB
Gọi
là
góc giữa đường thẳng
SC
và mặt phẳng
.ABC
Khẳng định nào dưới đây đúng?
A.
21
tan .
21
B.
15
tan .
15
C.
21
tan .
7
D.
15
tan .
5
Lời giải:
C
B
A
S
H
Theo giả thiết:
.SH ABC
Suy ra:
HC
là hình chiếu vuông góc của
SC
trên mặt phẳng
.ABC
Suy ra:
; ; .SC ABC SC HC SCH
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Ta có:
2 2 2 2 2 2
3; 2 . .cos 7 7.SH SB HB a HC BH BC BH BC HBC a HC a 
Xét tam giác
SHC
vuông tại
21
: tan .
7
SH
H SCH
HC

Câu 39: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh bằng
3 , 2 .a SB a
Biết hình chiếu vuông
góc của đỉnh
S
trên mặt phẳng
ABCD
là điểm
H
trên cạnh
AB
sao cho
2.AH HB
Gọi
là góc giữa đường thẳng
SC
và mặt phẳng
.ABCD
Khẳng định nào dưới đây đúng?
A.
21
tan .
21
B.
10
tan .
10
C.
21
tan .
7
D.
30
tan .
10
Lời giải:
D
S
A
B
C
H
Theo giả thiết:
.SH ABCD
Suy ra:
HC
là hình chiếu vuông góc của
SC
trên mặt phẳng
.ABCD
Suy ra:
; ; .SC ABCD SC HC SCH
Ta có:
2 2 2 2
3; 10.SH SB HB a HC BH BC a
Xét tam giác
SHC
vuông tại
30
: tan .
10
SH
H SCH
HC

Câu 40: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh bằng
3 , 2 .a SB a
Biết hình chiếu vuông
góc của đỉnh
S
trên mặt phẳng
ABCD
là điểm
H
trên cạnh
AB
sao cho
2.AH HB
Gọi
là góc giữa đường thẳng
SD
và mặt phẳng
.ABCD
Khẳng định nào dưới đây đúng?
A.
21
tan .
21
B.
39
tan .
13
C.
21
tan .
7
D.
15
tan .
5
Lời giải:
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
H
C
B
A
S
D
Theo giả thiết:
.SH ABCD
Suy ra:
HD
là hình chiếu vuông góc của
SD
trên mặt phẳng
.ABCD
Suy ra:
; ; .SD ABCD SD HD SDH
Ta có:
2 2 2 2
3; 13.SH SB HB a HD AH BD a
Xét tam giác
SHC
vuông tại
39
: tan .
13
SH
H SDH
HD

__________________________HẾT__________________________
Huế, 09h40’ Ngày 30 tháng 12 năm 2023
| 1/30
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 Dạng toán:
XÁC ĐỊNH GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG I. PHƯƠNG PHÁP
Trong không gian, cho đường thẳng d và mặt phẳng P.
Để xác định góc giữa đường thẳng d và mặt phẳng P , thông thường ta thực hiện theo các bước sau:
Bước 1: Chiếu vuông góc đường thẳng d lên mặt phẳng P ta được đường thẳng d'.
Bước 2: Xác định d ;P  d;P  SIH. S I d' H P d
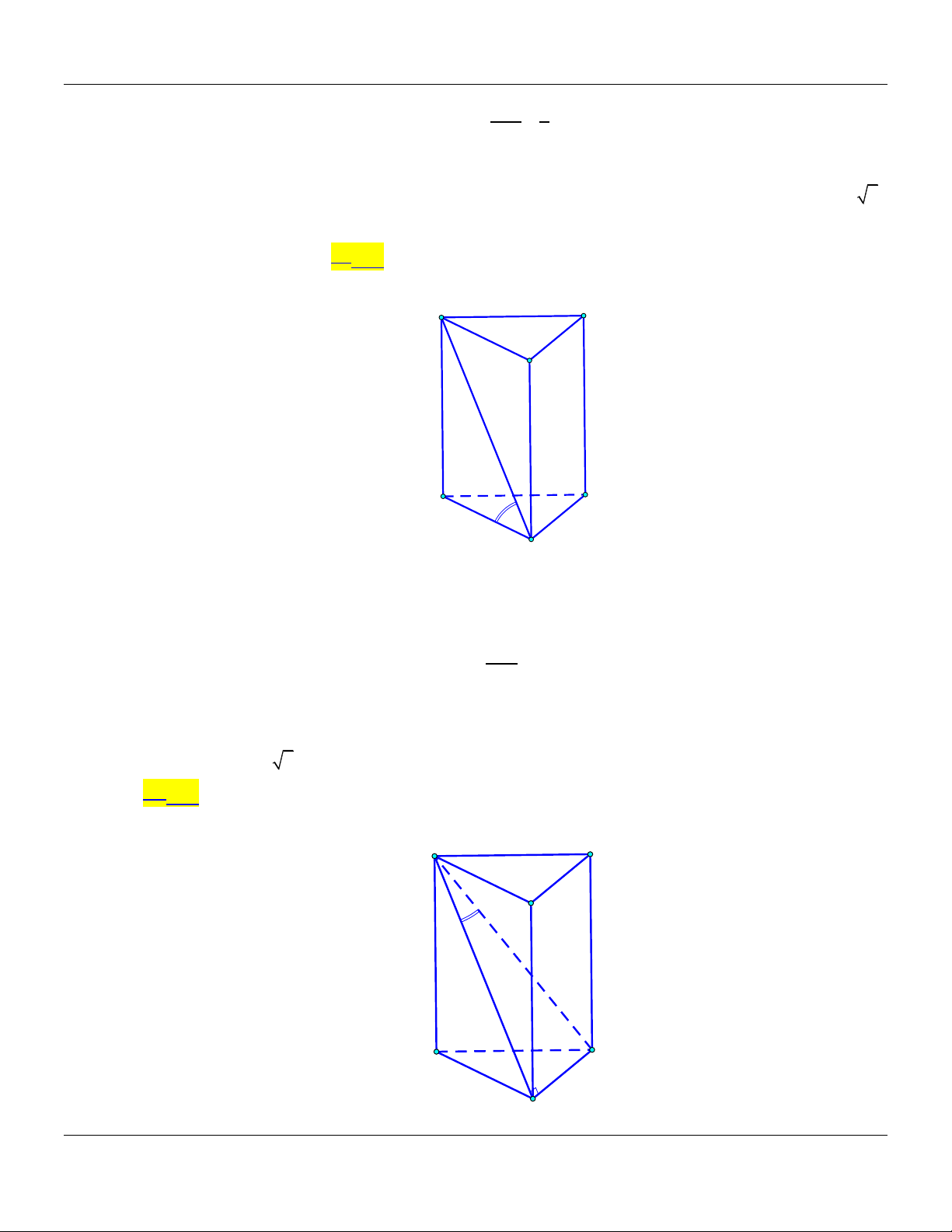
II. BÀI TẬP TRẮC NGHIỆM Câu 1: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh bằng .
a Biết SA vuông góc với mặt phẳng
ABC và SA a 3. Góc giữa đường thẳng SB và mặt phẳng ABC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Câu 2: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh bằng 2 .
a Biết SA vuông góc với mặt
phẳng  ABC và SA  2a 2. Góc giữa đường thẳng SC và mặt phẳng SAB bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Câu 3: Cho hình chóp .
S ABC có AB  .
a Biết SA vuông góc với mặt phẳng  ABC và SA a 3. Góc
giữa đường thẳng SB và mặt phẳng  ABC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Câu 4: Cho hình chóp .
S ABC có đáy là tam giác vuông cân tại B, AB  .
a Biết SA vuông góc với mặt
phẳng  ABC và SA a 2. Góc giữa đường thẳng SC và mặt phẳng  ABC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Câu 5: Cho hình chóp .
S ABC có đáy là tam giác vuông cân tại B, AB  .
a Biết SA vuông góc với mặt
phẳng  ABC và SA a 2. Góc giữa đường thẳng SC và mặt phẳng SAB bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Câu 6: Cho hình chóp .
S ABCD có đáy là hình vuông có cạnh bằng .
a Biết SA vuông góc với mặt
phẳng  ABCD và SA a 3. Góc giữa đường thẳng SB và mặt phẳng  ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Câu 7: Cho hình chóp .
S ABCD có đáy là hình vuông có cạnh bằng .
a Biết SA vuông góc với mặt
phẳng  ABCD và SA a 6. Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
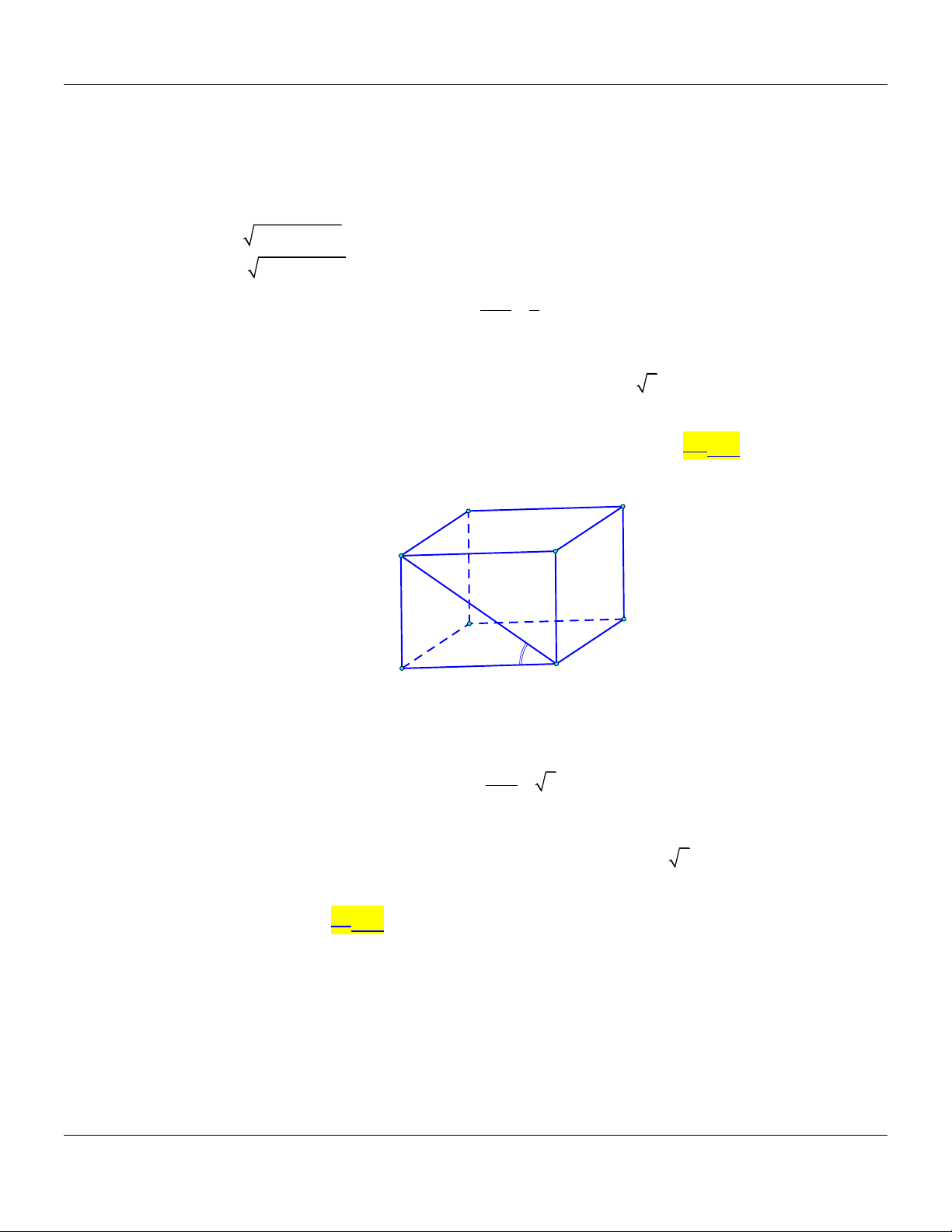
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 Câu 8: Cho hình chóp .
S ABCD có đáy là hình vuông có cạnh bằng .
a Biết SA vuông góc với mặt
phẳng  ABCD và SA a 2. Góc giữa đường thẳng SC và mặt phẳng SAB bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Câu 9: Cho hình chóp .
S ABCD có đáy là hình vuông có cạnh bằng .
a Biết SA vuông góc với mặt
phẳng  ABCD và SA  .
a Góc giữa đường thẳng SB và mặt phẳng SAC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 10: Cho hình chóp .
S ABCD có đáy là hình chữ nhật có BC  2 .
a Biết SA vuông góc với mặt
phẳng  ABCD và SA  2a 3. Góc giữa đường thẳng SD và mặt phẳng  ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 11: Cho hình chóp .
S ABCD có đáy là hình chữ nhật với AB a, BC  2 .
a Biết SA vuông góc với a 15
mặt phẳng  ABCD và SA
. Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng 3 A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 12: Cho hình chóp .
S ABCD có đáy là hình chữ nhật với AB a, BC  2 .
a Biết SA vuông góc với a 3
mặt phẳng  ABCD và SA
. Góc giữa đường thẳng SC và mặt phẳng SAB bằng 3 A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 13: Cho hình chóp .
S ABCD có đáy là hình chữ nhật với AB a, BC  2 .
a Biết SA vuông góc với a 15
mặt phẳng  ABCD và SA
. Góc giữa đường thẳng SB và mặt phẳng SAC bằng 15 A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 14: Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A, B với AD  2AB  2BC  2 . a Biết
SA vuông góc với mặt phẳng  ABCD và SA a 6. Góc giữa đường thẳng SC và mặt phẳng ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 15: Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A, B với AD  2AB  2BC  2 . a Biết
SA vuông góc với mặt phẳng  ABCD và SA  2 .
a Góc giữa đường thẳng SD và mặt phẳng ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 16: Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A, B với AD  2AB  2BC  2 . a Biết
SA vuông góc với mặt phẳng  ABCD và SA a 2. Góc giữa đường thẳng SC và mặt phẳng SAB bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 17: Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A, B với AD  2AB  2BC  2 . a Biết
SA vuông góc với mặt phẳng  ABCD và SA  .
a Góc giữa đường thẳng SB và mặt phẳng SAC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Câu 18: Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A, B với AD  2AB  2BC  2 . a Biết
SA vuông góc với mặt phẳng  ABCD và SA  2 .
a Góc giữa đường thẳng SD và mặt phẳng SAC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 19: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a với BAD  60 .
 Biết SA vuông góc với
mặt phẳng  ABCD và SA  .
a Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 20: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a với BAD  60 .
 Biết SA vuông góc với
mặt phẳng  ABCD và SA  .
a Gọi  là góc giữa đường thẳng SC và mặt phẳng SAB.
Khẳng định nào dưới đây đúng? 3 3 2 3 A. sin  . B. sin  . C. sin  .
D. sin  . 4 8 4 4
Câu 21: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a với BAD  60 .
 Biết SA vuông góc với
mặt phẳng  ABCD và SA a 3. Gọi  là góc giữa đường thẳng SB và mặt phẳng SAC.
Khẳng định nào dưới đây đúng? 3 3 2 1 A. sin  . B. sin  . C. sin  .
D. sin  . 4 8 4 4
Câu 22: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a với BAD  120 .
 Biết SA vuông góc với
mặt phẳng  ABCD và SA  .
a Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 23: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a với BAD  120 .
 Biết SA vuông góc với
mặt phẳng  ABCD và SA a 2. Góc giữa đường thẳng SC và mặt phẳng SAB bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 24: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a với BAD  120 .
 Biết SA vuông góc với
mặt phẳng  ABCD và SA a 2. Góc giữa đường thẳng SB và mặt phẳng SAC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 25: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a với BAD  120 .
 Biết SA vuông góc với a
mặt phẳng  ABCD và SA  . Góc giữa đường thẳng SA và mặt phẳng SBD bằng 2 A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 26: Cho hình lăng trụ đứng ABC.A BC
  có đáy là tam giác đều cạnh a, AA  a 3. Góc giữa đường thẳng A B
 và mặt phẳng ABC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 27: Cho hình lăng trụ đứng ABC.A BC
  có đáy là tam giác đều cạnh a, AA  a 2. Góc giữa đường thẳng A C
 và mặt phẳng ABB A   bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Câu 28: Cho hình lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại B, AB AA  a 2.
Góc giữa đường thẳng A B
 và mặt phẳng ABC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 29: Cho hình lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại
B, AB a, AA  a 2. Góc giữa đường thẳng A C
 và mặt phẳng ABB A   bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
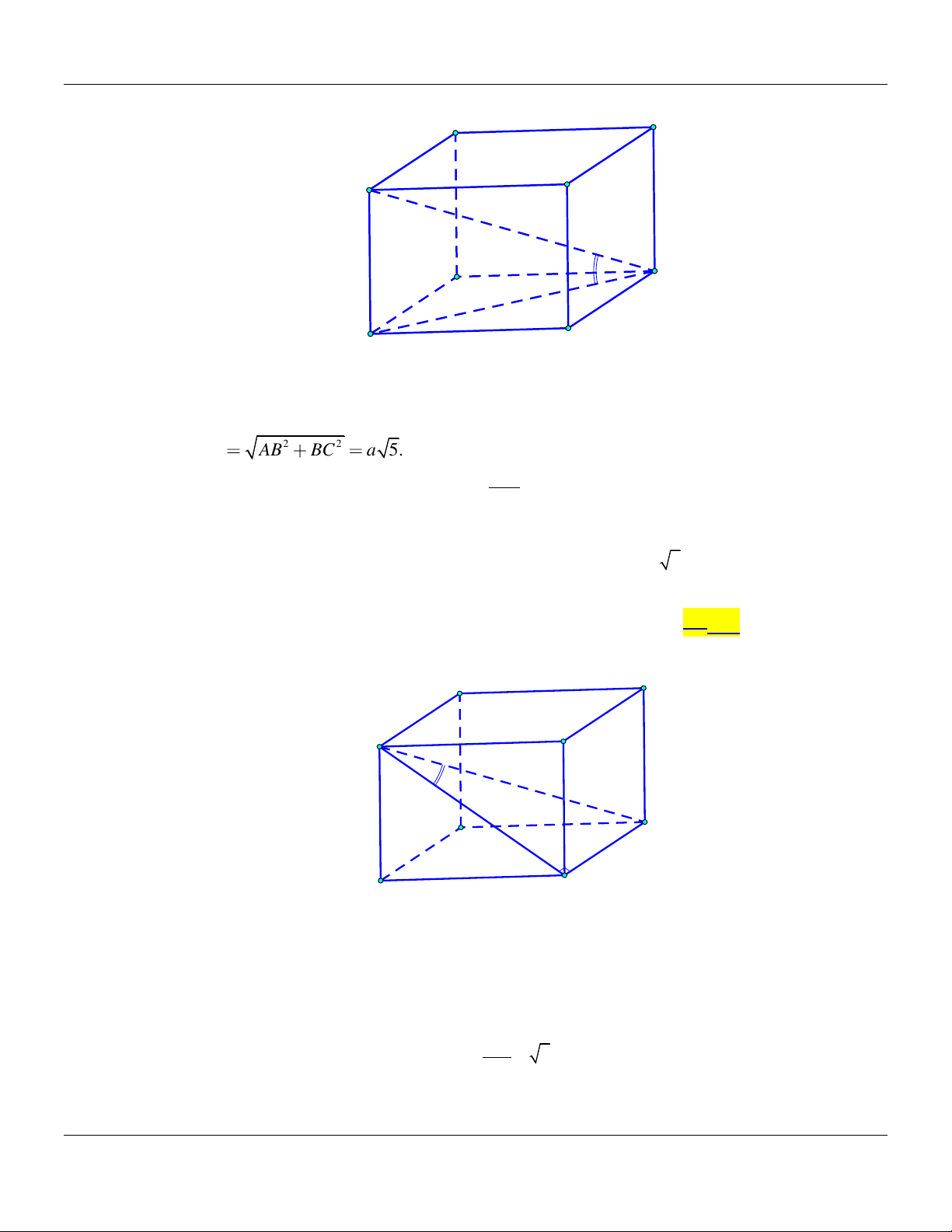
Câu 30: Cho hình hộp chữ nhật A .
BCD ABC D
  có AB AD a, AA  a 3. Góc giữa đường thẳng A B
và mặt phẳng  ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 31: Cho hình hộp chữ nhật A . BCD A BCD
  có AB a; AD  2a, AA  a 5. Góc giữa đường thẳng A C
 và mặt phẳng ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 32: Cho hình hộp chữ nhật A .
BCD ABC D
  có AB AA  a; AD a 6. Góc giữa đường thẳng A C
 và mặt phẳng ABB A   bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 33: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh bằng .
a Mặt bên SAB là tam giác vuông
cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt
phẳng  ABC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 34: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh bằng .
a Mặt bên SAB là tam giác vuông
cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt
phẳng SAB bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 35: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng .
a Mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SB và mặt phẳng  ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Câu 36: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng .
a Mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Gọi  là góc giữa đường thẳng SC và mặt phẳng
ABCD. Khẳng định nào dưới đây đúng? 5 15 5 15 A. tan  . B. tan  . C. tan  . D. tan  . 15 15 5 5
Câu 37: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh bằng 2 .
a Biết hình chiếu vuông góc của
đỉnh S trên mặt phẳng  ABC là trung điểm H của AB . Góc giữa đường thẳng SC và mặt
phẳng  ABC bằng 60 .  Tính SH. A. SH  2 . a B. SH  3 . a C. SH  3 . a D. SH  . a
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
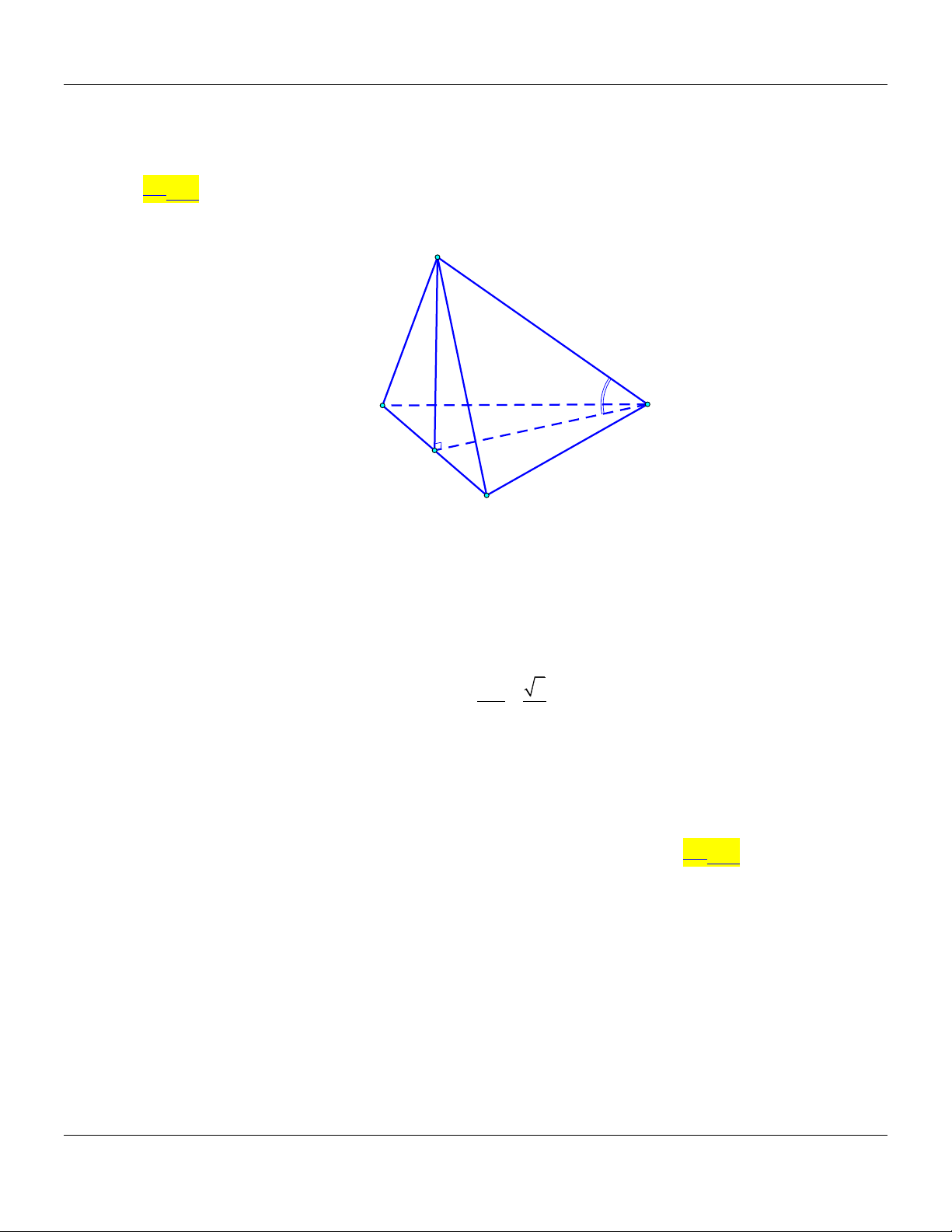
Câu 38: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh bằng 3a,SB  2 .
a Biết hình chiếu vuông
góc của đỉnh S trên mặt phẳng  ABC là điểm H trên cạnh AB sao cho AH  2H . B Gọi  là
góc giữa đường thẳng SC và mặt phẳng  ABC. Khẳng định nào dưới đây đúng? 21 15 21 15 A. tan  . B. tan  . C. tan  . D. tan  . 21 15 7 5
Câu 39: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng 3a,SB  2 .
a Biết hình chiếu vuông
góc của đỉnh S trên mặt phẳng  ABCD là điểm H trên cạnh AB sao cho AH  2H . B Gọi 
là góc giữa đường thẳng SC và mặt phẳng  ABCD. Khẳng định nào dưới đây đúng? 21 10 21 30 A. tan  . B. tan  . C. tan  . D. tan  . 21 10 7 10
Câu 40: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng 3a,SB  2 .
a Biết hình chiếu vuông
góc của đỉnh S trên mặt phẳng  ABCD là điểm H trên cạnh AB sao cho AH  2H . B Gọi 
là góc giữa đường thẳng SD và mặt phẳng  ABCD. Khẳng định nào dưới đây đúng? 21 39 21 15 A. tan  . B. tan  . C. tan  . D. tan  . 21 13 7 5
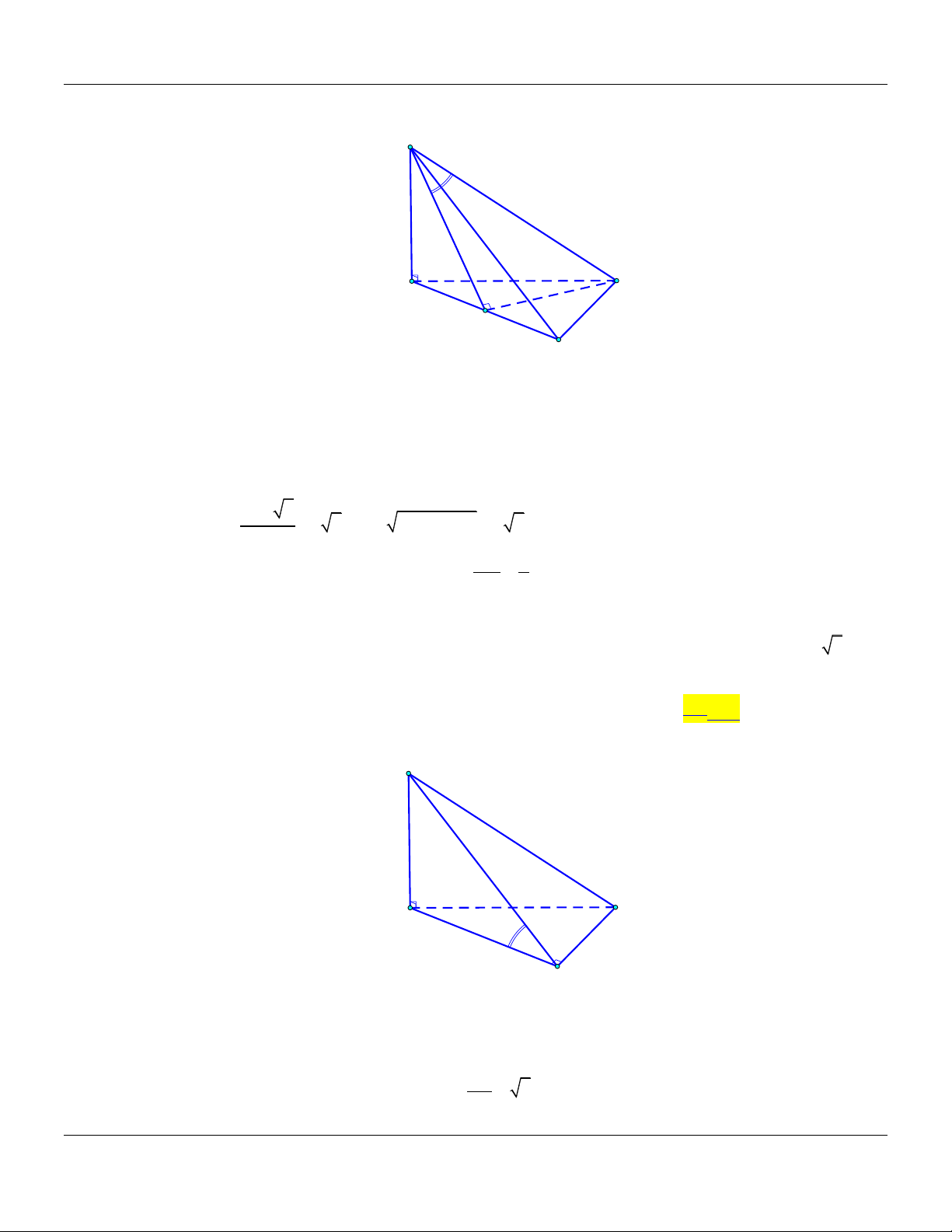
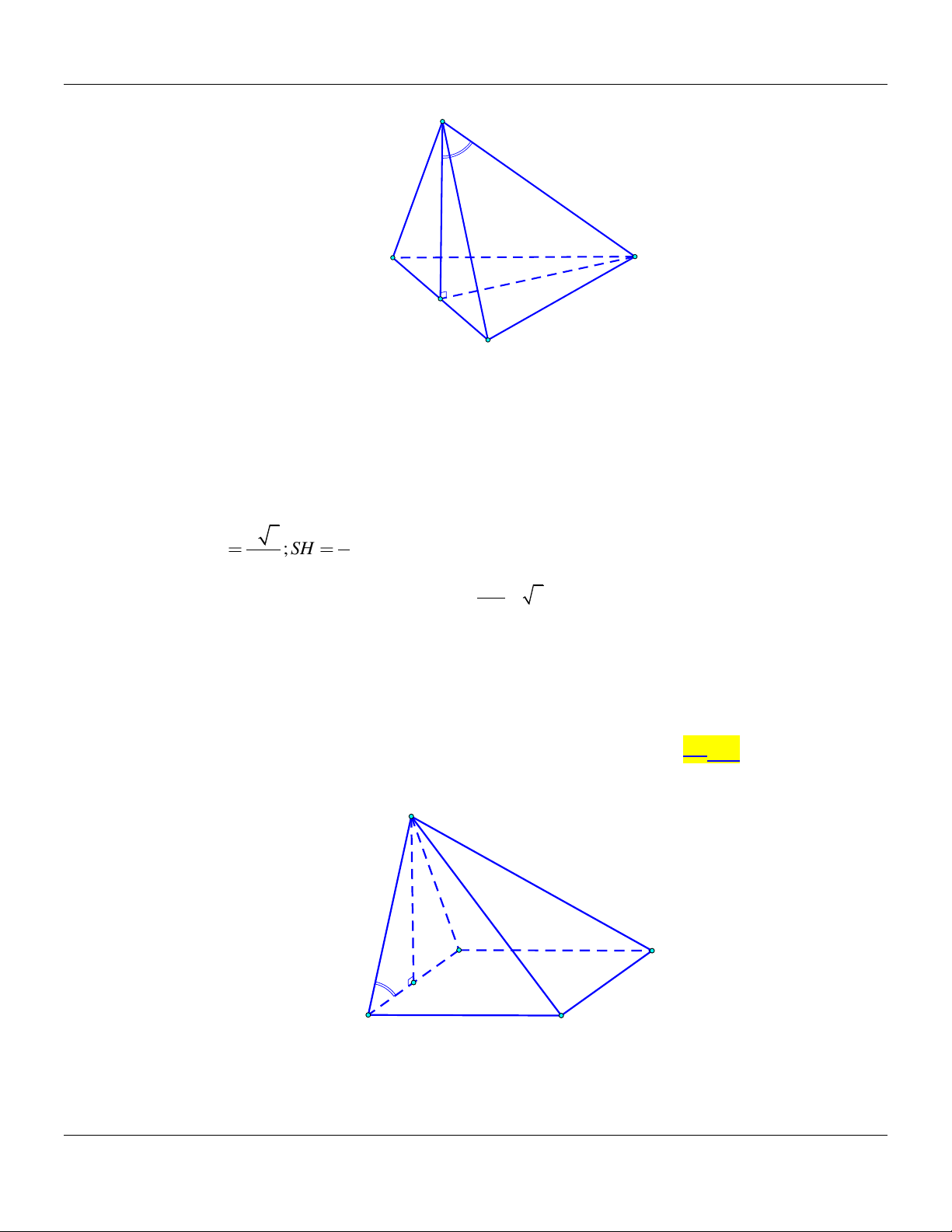
III. LỜI GIẢI CHI TIẾT Câu 1: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh bằng .
a Biết SA vuông góc với mặt phẳng
ABC và SA a 3. Góc giữa đường thẳng SB và mặt phẳng ABC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S C A B
Ta có: SA   ABC 
AB là hình chiếu vuông góc của SB trên mặt phẳng ABC. Suy ra:  ;
SB ABC   ;
SB AB  SB . A SA
Xét tam giác SAB vuông tại A :tanSBA   3  SBA  60 .  AB Vậy  ;
SB ABC  60 .  Câu 2: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh bằng 2 .
a Biết SA vuông góc với mặt
phẳng  ABC và SA  2a 2. Góc giữa đường thẳng SC và mặt phẳng SAB bằng A. 30 .  B. 45 .  C. 90 .  D. 60 . 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 Lời giải: S C A H B CH AB
Dựng CH AB,H AB   
CH  SAB. CH   SA
Ta có: CH  SAB 
SH là hình chiếu vuông góc của SC trên mặt phẳng SAB.
Suy ra: SC;SAB  SC;SH  HSC. 2a 3 Ta có: 2 2 HC
a 3;SC SA AC  2 3 . a 2 HC 1
Xét tam giác SCH vuông tại H :sin HSC    HSC  30 .  SC 2
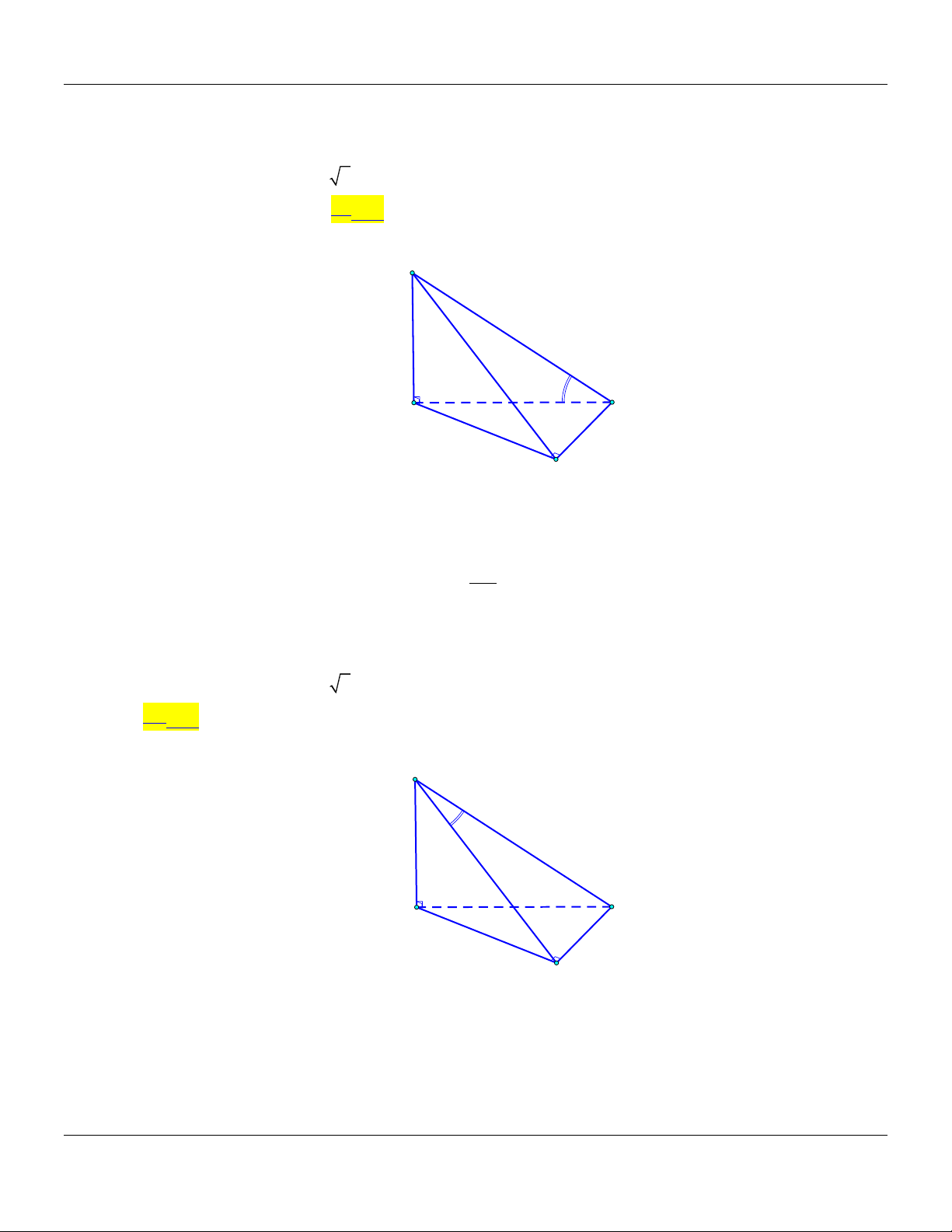
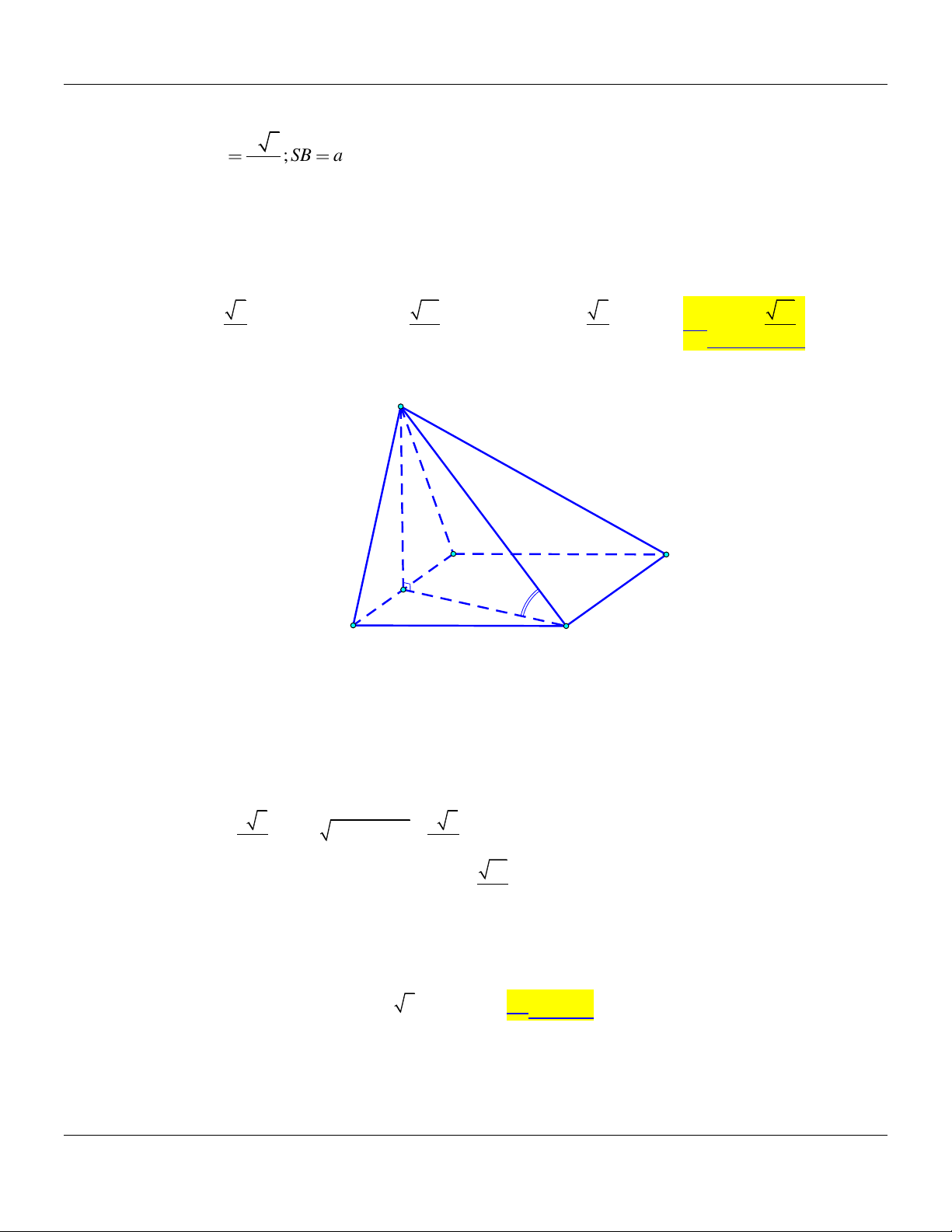
Vậy SC;SAB  30 . Câu 3: Cho hình chóp .
S ABC có AB  .
a Biết SA vuông góc với mặt phẳng  ABC và SA a 3. Góc
giữa đường thẳng SB và mặt phẳng  ABC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S C A B
Ta có: SA   ABC 
AB là hình chiếu vuông góc của SB trên mặt phẳng ABC. Suy ra:  ;
SB ABC   ;
SB BA  SB . A SA
Xét tam giác SAB vuông tại A :tanSBA   3  SBA  60 .  AB
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 Vậy  ;
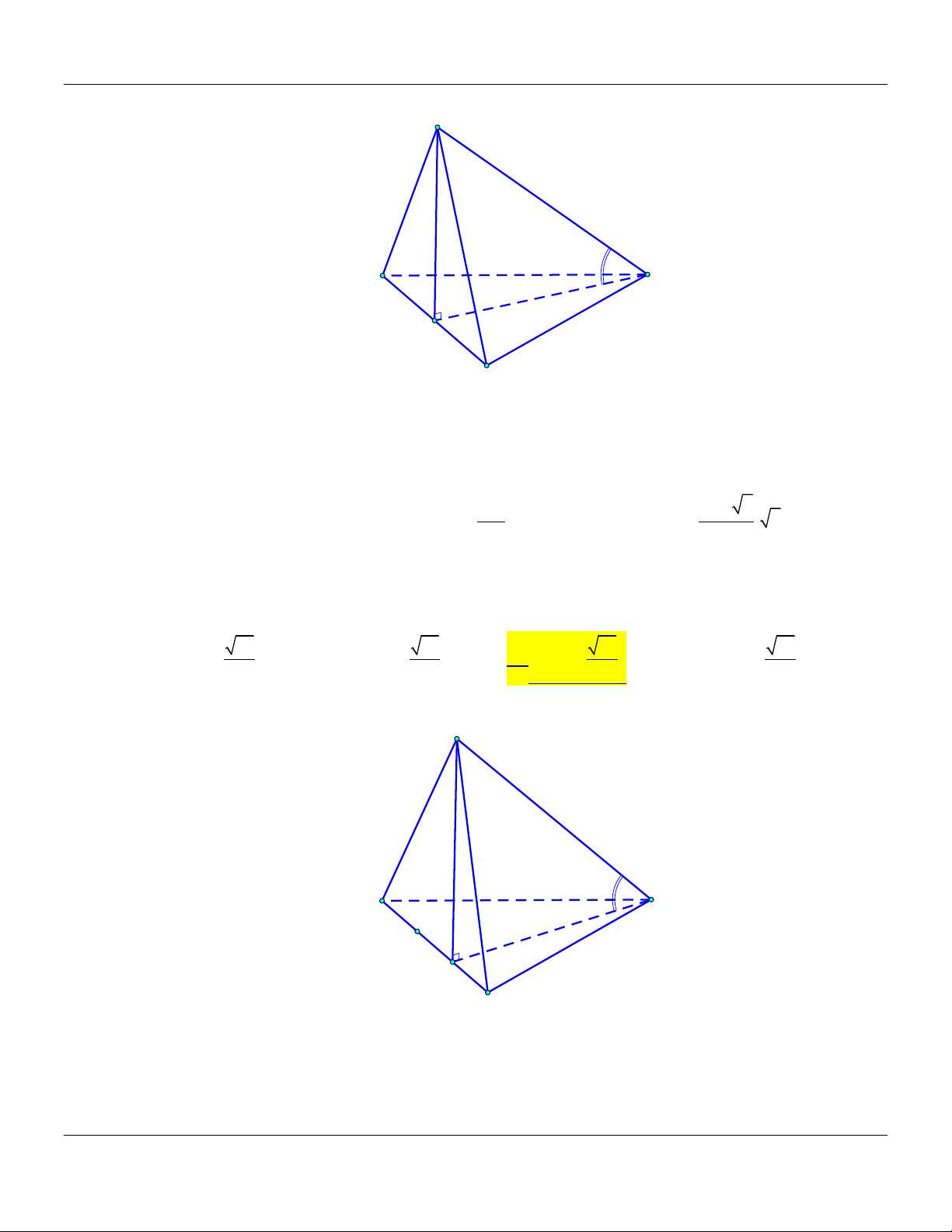
SB ABC  60 .  Câu 4: Cho hình chóp .
S ABC có đáy là tam giác vuông cân tại B, AB  .
a Biết SA vuông góc với mặt
phẳng  ABC và SA a 2. Góc giữa đường thẳng SC và mặt phẳng  ABC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S C A B
Ta có: SA   ABC 
AC là hình chiếu vuông góc của SC trên mặt phẳng ABC.
Suy ra: SC;ABC  SC; AC  SC . A SA
Xét tam giác SAC vuông tại A :tanSCA   1 SCA  45 .  AC
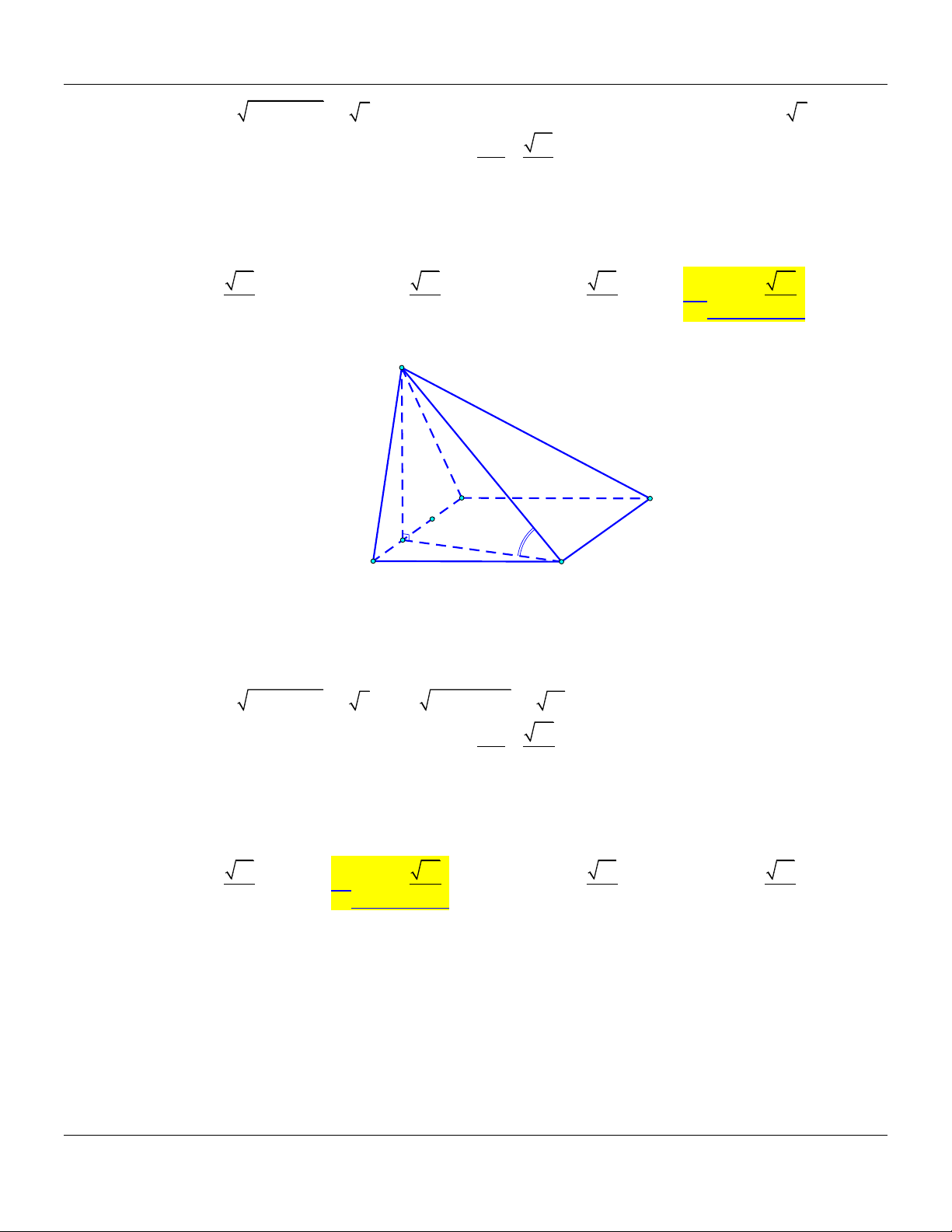
Vậy SC;ABC  45 . Câu 5: Cho hình chóp .
S ABC có đáy là tam giác vuông cân tại B, AB  .
a Biết SA vuông góc với mặt
phẳng  ABC và SA a 2. Góc giữa đường thẳng SC và mặt phẳng SAB bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S C A B BC AB Ta có:  
BC  SAB SB là hình chiếu vuông góc của SC trên mặt phẳng BC   SASAB.
Suy ra: SC;SAB  SC;SB  BSC.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 Ta có: 2 2
SB SA AB  3 . a BC 3
Xét tam giác SBC vuông tại B :tan BSC    BSC  30 .  SB 3
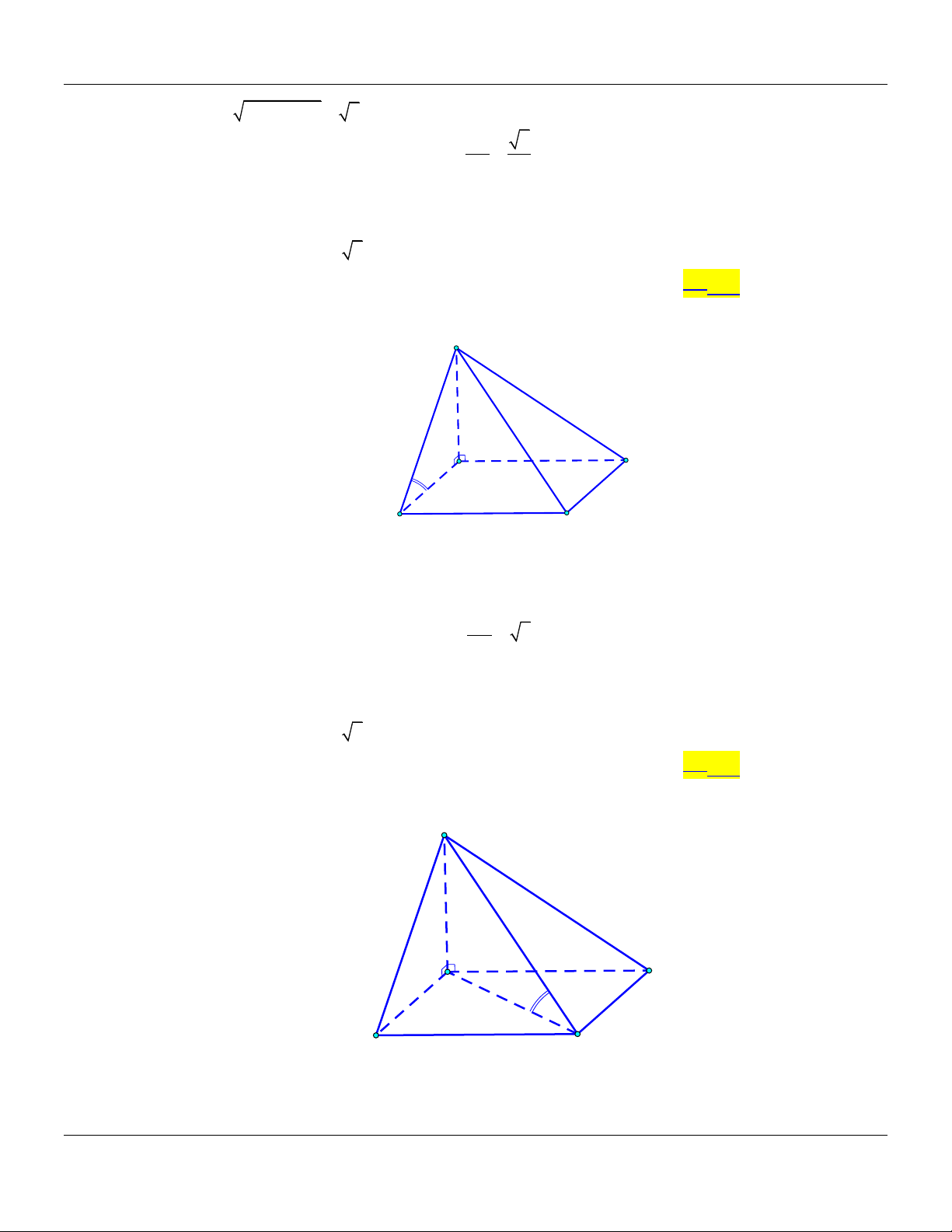
Vậy SC;SAB  30 . Câu 6: Cho hình chóp .
S ABCD có đáy là hình vuông có cạnh bằng .
a Biết SA vuông góc với mặt
phẳng  ABCD và SA a 3. Góc giữa đường thẳng SB và mặt phẳng  ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S A D B C
Ta có: SA   ABCD 
AB là hình chiếu vuông góc của SB trên mặt phẳng ABCD. Suy ra:  ;
SB ABCD   ;
SB BA  SB . A SA
Xét tam giác SAB vuông tại A :tanSBA   3  SBA  60 .  AB Vậy  ;
SB ABCD  60 .  Câu 7: Cho hình chóp .
S ABCD có đáy là hình vuông có cạnh bằng .
a Biết SA vuông góc với mặt
phẳng  ABCD và SA a 6. Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S A D B C
Ta có: SA   ABCD 
AC là hình chiếu vuông góc của SC trên mặt phẳng ABCD.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Suy ra: SC;ABCD  SC; AC  SC . A SA
Xét tam giác SAC vuông tại A :tanSCA   3  SCA  60 .  AC
Vậy SC;ABCD  60 . Câu 8: Cho hình chóp .
S ABCD có đáy là hình vuông có cạnh bằng .
a Biết SA vuông góc với mặt
phẳng  ABCD và SA a 2. Góc giữa đường thẳng SC và mặt phẳng SAB bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S A D B C BC AB Ta có:  
BC  SAB SB là hình chiếu vuông góc của SC trên mặt phẳng BC   SASAB.
Suy ra: SC;SAB  SC;SB  BSC. Ta có: 2 2
SB SA AB  3 . a BC 3
Xét tam giác SBC vuông tại B :tan BSC    BSC  30 .  SB 3
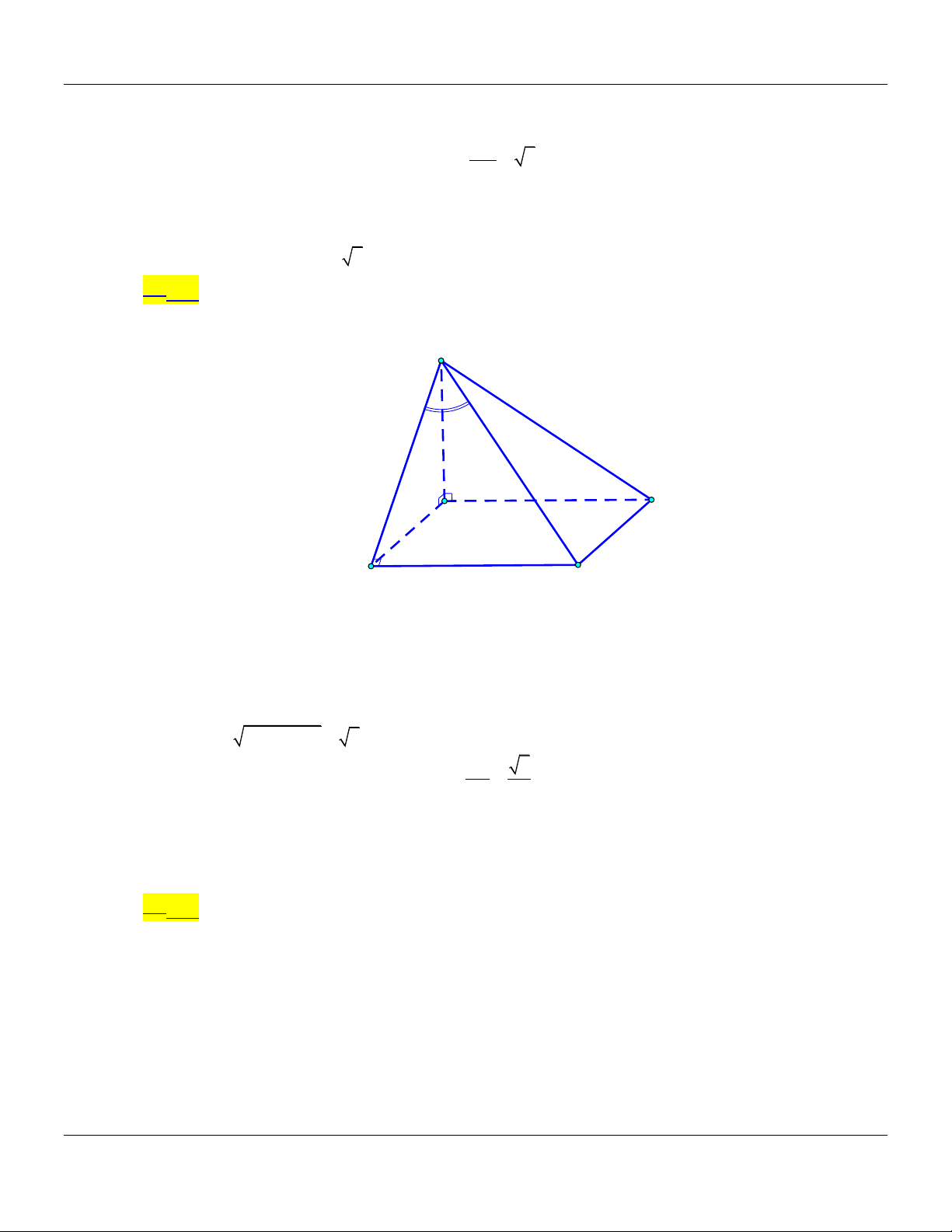
Vậy SC;SAB  30 . Câu 9: Cho hình chóp .
S ABCD có đáy là hình vuông có cạnh bằng .
a Biết SA vuông góc với mặt
phẳng  ABCD và SA  .
a Góc giữa đường thẳng SB và mặt phẳng SAC  bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 S A D O B C
Gọi O là tâm hình vuông ABCD. BO AC Ta có:  
BO  SAC SO là hình chiếu vuông góc của SB trên mặt phẳng BO   SASAC. Suy ra:  ;
SB SAC   ; SB SO  B . SO Ta có: 2 2
SB SA AB  2 . a BO 1
Xét tam giác SBO vuông tại O :sin BSO    BSO  30 .  SB 2 Vậy  ;
SB SAC  30 . 
Câu 10: Cho hình chóp .
S ABCD có đáy là hình chữ nhật có BC  2 .
a Biết SA vuông góc với mặt
phẳng  ABCD và SA  2a 3. Góc giữa đường thẳng SD và mặt phẳng  ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S A D B C
Ta có: SA   ABCD 
AD là hình chiếu vuông góc của SD trên mặt phẳng ABCD.
Suy ra: SD;ABCD  SD; AD  SD . A SA
Xét tam giác SAD vuông tại A :tanSDA   3  SDA  60 .  AD
Vậy SD;ABCD  60 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Câu 11: Cho hình chóp .
S ABCD có đáy là hình chữ nhật với AB a, BC  2 .
a Biết SA vuông góc với a 15
mặt phẳng  ABCD và SA
. Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng 3 A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S A D B C
Ta có: SA   ABCD 
AC là hình chiếu vuông góc của SC trên mặt phẳng ABCD.
Suy ra: SC;ABCD  SC; AC  SC . A SA 3
Xét tam giác SAC vuông tại A :tanSCA    SCA  30 .  AC 3
Vậy SC;ABCD  30 .
Câu 12: Cho hình chóp .
S ABCD có đáy là hình chữ nhật với AB a, BC  2 .
a Biết SA vuông góc với a 3
mặt phẳng  ABCD và SA
. Góc giữa đường thẳng SC và mặt phẳng SAB bằng 3 A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S A D B C BC AB Ta có:  
BC  SAB SB là hình chiếu vuông góc của SC trên mặt phẳng BC   SASAB.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Suy ra: SC;SAB  SC;SB  BSC. 2 3a Ta có: SB  2 SA  2 AB  . 3 BC
Xét tam giác SBC vuông tại B :tan BSC   3  BSC  60 .  SB
Vậy SC;SAB  60 .
Câu 13: Cho hình chóp .
S ABCD có đáy là hình chữ nhật với AB a, BC  2 .
a Biết SA vuông góc với a 15
mặt phẳng  ABCD và SA
. Góc giữa đường thẳng SB và mặt phẳng SAC bằng 15 A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S A D H B C
Dựng BH AC,H AC. BH AC Ta có:  
BH  SAC SH là hình chiếu vuông góc của SB trên mặt phẳng BH   SASAC. Suy ra:  ;
SB SAC   ;
SB SH   BSH. 4 15a 1 1 1 2 5a Ta có: 2 2
SB SA AB  ;    BH  . 2 2 2 15 BH BA BC 5 BH 3
Xét tam giác SBH vuông tại H :sin BSH    BSH  60 .  SB 2 Vậy  ;
SB SAC  60 . 
Câu 14: Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A, B với AD  2AB  2BC  2 . a Biết
SA vuông góc với mặt phẳng  ABCD và SA a 6. Góc giữa đường thẳng SC và mặt phẳng ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 S A D B C
Ta có: SA   ABCD 
AC là hình chiếu vuông góc của SC trên mặt phẳng ABCD.
Suy ra: SC;ABCD  SC; AC  SC . A Ta có: 2 2
AC AB BC a 2. SA
Xét tam giác SAC vuông tại A :tanSCA   3  SCA  60 .  AC
Vậy SC;ABCD  60 .
Câu 15: Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A, B với AD  2AB  2BC  2 . a Biết
SA vuông góc với mặt phẳng  ABCD và SA  2 .
a Góc giữa đường thẳng SD và mặt phẳng ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S A D B C
Ta có: SA   ABCD 
AD là hình chiếu vuông góc của SD trên mặt phẳng ABCD.
Suy ra: SD;ABCD  SD; AD  SD . A SA
Xét tam giác SAD vuông tại A :tanSDA   1 SDA  45 .  AD
Vậy SD;ABCD  45 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Câu 16: Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A, B với AD  2AB  2BC  2 . a Biết
SA vuông góc với mặt phẳng  ABCD và SA a 2. Góc giữa đường thẳng SC và mặt phẳng SAB bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S A D B C BC AB Ta có:  
BC  SAB SB là hình chiếu vuông góc của SC trên mặt phẳng BC   SASAB.
Suy ra: SC;SAB  SC;SB  BSC. Ta có: 2 2
SB SA AB  3 . a BC 3
Xét tam giác SBC vuông tại B :tan BSC    BSC  30 .  SB 3
Vậy SC;SAB  30 .
Câu 17: Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A, B với AD  2AB  2BC  2 . a Biết
SA vuông góc với mặt phẳng  ABCD và SA  .
a Góc giữa đường thẳng SB và mặt phẳng SAC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 S A I D O B C
Gọi I là trung điểm AD 
ABCI là hình vuông.
Gọi O là tâm hình vuông ABCI. BO AC Ta có:  
BO  SAC SO là hình chiếu vuông góc của SB trên mặt phẳng BO   SASAC. Suy ra:  ;
SB SAC   ; SB SO  B . SO Ta có: 2 2
SB SA AB  2 . a BO 1
Xét tam giác SBO vuông tại O :sin BSO    BSO  30 .  SB 2 Vậy  ;
SB SAC  30 . 
Câu 18: Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A, B với AD  2AB  2BC  2 . a Biết
SA vuông góc với mặt phẳng  ABCD và SA  2 .
a Góc giữa đường thẳng SD và mặt phẳng SAC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S A D B C
Gọi I là trung điểm AD 
IA ID IC   ACD  90 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 CD AC Ta có:  
CD  SAC SC là hình chiếu vuông góc của SD trên mặt phẳng CD   SASAC.
Suy ra: SD;SAC  SD;SC  DSC. Ta có: 2 2
SD SA AD  2 2 . a CD 1
Xét tam giác SCD vuông tại C :sinCSD    CSD  30 . SD 2
Vậy SD;SAC  30 .
Câu 19: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a với BAD  60 .
 Biết SA vuông góc với
mặt phẳng  ABCD và SA  .
a Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S A a a B O A D D B C C
Do ABCD là hình thoi cạnh a với BAD  60 nên ABD  , BC
D là các tam giác đều cạnh . a
Ta có: SA   ABCD 
AC là hình chiếu vuông góc của SC trên mặt phẳng ABCD.
Suy ra: SC;ABCD  SC; AC  SC . A a 3
Ta có: AC  2AO  2.  a 3. 2 SA 3
Xét tam giác SAC vuông tại A :tanSCA    SCA  30 .  AC 3
Vậy SC;ABCD  30 .
Câu 20: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a với BAD  60 .
 Biết SA vuông góc với
mặt phẳng  ABCD và SA  .
a Gọi  là góc giữa đường thẳng SC và mặt phẳng SAB.
Khẳng định nào dưới đây đúng? 3 3 2 3 A. sin  . B. sin  . C. sin  .
D. sin  . 4 8 4 4 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 S A a a H B O A D D H K B C K C
Do ABCD là hình thoi cạnh a với BAD  60 nên ABD  , BC
D là các tam giác đều cạnh . a a 3
Dựng CK AB,K A ;
B DH AB,H AB  CK DH  . 2 CK AB Ta có:  
CK  SAB SK là hình chiếu vuông góc của SC trên mặt phẳng CK   SASAB.
Suy ra: SC;SAB  SC;SK  KSC  .
Ta có: SC SA AC SA   AO2 2 2 2 2  2 . a CK 3 3
Xét tam giác SKC vuông tại K :sin KSC    sin  . SC 4 4
Câu 21: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a với BAD  60 .
 Biết SA vuông góc với
mặt phẳng  ABCD và SA a 3. Gọi  là góc giữa đường thẳng SB và mặt phẳng SAC.
Khẳng định nào dưới đây đúng? 3 3 2 1 A. sin  . B. sin  . C. sin  .
D. sin  . 4 8 4 4 Lời giải: S A a a B O A D D O B C C
Do ABCD là hình thoi cạnh a với BAD  60 nên ABD  , BC
D là các tam giác đều cạnh . a
Gọi O là tâm hình thoi ABCD.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 BO AC Ta có:  
BO  SAC SO là hình chiếu vuông góc của SB trên mặt phẳng BO   SASAC. Suy ra:  ;
SB SAC   ; SB SO  B . SO a Ta có: 2 2 1
SB SA AB  2a; BO BD  . 2 2 BO 1 1
Xét tam giác SBO vuông tại O :sin BSO    sin  . SB 4 4
Câu 22: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a với BAD  120 .
 Biết SA vuông góc với
mặt phẳng  ABCD và SA  .
a Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S A a A D B D O a B C C
Do ABCD là hình thoi cạnh a với BAD  120 nên ABC  , AC
D là các tam giác đều cạnh . a
Ta có: SA   ABCD 
AC là hình chiếu vuông góc của SC trên mặt phẳng ABCD.
Suy ra: SC;ABCD  SC; AC  SC . A SA
Xét tam giác SAC vuông tại A :tanSCA   1 SCA  45 .  AC
Vậy SC;ABCD  45 .
Câu 23: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a với BAD  120 .
 Biết SA vuông góc với
mặt phẳng  ABCD và SA a 2. Góc giữa đường thẳng SC và mặt phẳng SAB bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 S A H A D B D O a H B C C
Do ABCD là hình thoi cạnh a với BAD  120 nên ABC  , AC
D là các tam giác đều cạnh . a CH AB
Dựng CH AB,H AB   
CH  SAB. CH   SA
Ta có: CH  SAB 
SH là hình chiếu vuông góc của SC trên mặt phẳng SAB.
Suy ra: SC;SAB  SC;SH  HSC. a 3 Ta có: 2 2 HC
;SC SA AC  3 . a 2 HC 1
Xét tam giác SCH vuông tại H :sin HSC    HSC  30 .  SC 2
Vậy SC;SAB  30 .
Câu 24: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a với BAD  120 .
 Biết SA vuông góc với
mặt phẳng  ABCD và SA a 2. Góc giữa đường thẳng SB và mặt phẳng SAC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S A a A D B D O a O B C C
Do ABCD là hình thoi cạnh a với BAD  120 nên ABC  , AC
D là các tam giác đều cạnh . a
Gọi O là tâm hình thoi ABCD. BO AC Ta có:  
BO  SAC SO là hình chiếu vuông góc của SB trên mặt phẳng BO   SASAC.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 Suy ra:  ;
SB SAC   ; SB SO  B . SO a Ta có: 2 2 3
SB SA AB a 3; BO  . 2 BO 1
Xét tam giác SBO vuông tại O :sin BSO    BSO  30 .  SB 2 Vậy  ;
SB SAC  30 . 
Câu 25: Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a với BAD  120 .
 Biết SA vuông góc với a
mặt phẳng  ABCD và SA  . Góc giữa đường thẳng SA và mặt phẳng SBD bằng 2 A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S A a A D B D O a O B C C
Do ABCD là hình thoi cạnh a với BAD  120 nên ABC  , AC
D là các tam giác đều cạnh . a
Gọi O là tâm hình thoi ABCD. AH SO
Dựng AH SO   
AH  SBD SH SO là hình chiếu vuông góc của AH   BD
SA trên mặt phẳng SBD.
Suy ra: SA;SBD  SA;SO  A . SO AO
Xét tam giác SAO vuông tại A :tan ASO   1  ASO  45 .  SA
Vậy SA;SBD  45 .
Câu 26: Cho hình lăng trụ đứng ABC.A BC
  có đáy là tam giác đều cạnh a, AA  a 3. Góc giữa đường thẳng A B
 và mặt phẳng ABC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 C' A' B' C A B
Do AA   ABC 
AB là hình chiếu vuông góc của A B
 trên mặt phẳng ABC. Suy ra: A ;
B ABC   A ; B AB  A B  . A A A  Xét tam giác A B
A vuông tại A : tan A BA   3   A BA  60 . AB Vậy A B
 ;ABC  60 .
Câu 27: Cho hình lăng trụ đứng ABC.A BC
  có đáy là tam giác đều cạnh a, AA  a 2. Góc giữa đường thẳng A C
 và mặt phẳng ABB A   bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: A' C' B' A C H B CH AB
Dựng CH AB   
CH  ABB A  . CH   AA Vậy A H
 là hình chiếu vuông góc của A C
 trên mặt phẳng ABB A  . Suy ra: A C  ;ABB A
   A C  ; A H    HA C  . a Ta có: 2 2 3 A C   A A
AC a 3; HC  . 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 HC 1 Xét tam giác A H
C vuông tại H : sin HA C     HA C   30 . A C  2 Vậy A C  ;ABB A    30 .
Câu 28: Cho hình lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại B, AB AA  a 2.
Góc giữa đường thẳng A B
 và mặt phẳng ABC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: C' A' B' C A B
Do AA   ABC 
AB là hình chiếu vuông góc của A B
 trên mặt phẳng ABC. Suy ra: A ;
B ABC   A ; B AB  A B  . A A A  Xét tam giác A B
A vuông tại A : tan A BA   1  A BA  45 . AB Vậy A B
 ;ABC  45 .
Câu 29: Cho hình lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại
B, AB a, AA  a 2. Góc giữa đường thẳng A C
 và mặt phẳng ABB A   bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: A' C' B' A C B
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 CB AB Ta có:  
CB  ABB A  . CB   AA Vậy A B
 là hình chiếu vuông góc của A C
 trên mặt phẳng ABB A  . Suy ra: A C  ;ABB A
   A C  ; A B    BA C  . Ta có: 2 2 A C   A A
AC  2a; BC  . a Ta có:  A C A 2 A  2
AC  2a; BC  . a BC 1
Xét tam giác ABC vuông tại B : sin B A C    B A C  3   0 . A C 2 Vậy A C  ;ABB A    30 .
Câu 30: Cho hình hộp chữ nhật A .
BCD ABC D
  có AB AD a, AA  a 3. Góc giữa đường thẳng A B
và mặt phẳng  ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: D' C' A' B' D C A B
Do AA   ABCD 
AB là hình chiếu vuông góc của A B
 trên mặt phẳng ABCD. Suy ra: A ;
B ABCD  A B
 ; AB  A B  . A A A  Xét tam giác A B
A vuông tại A : tan A BA   3   A BA  60 . AB Vậy  A B
 ;ABCD  60 .
Câu 31: Cho hình hộp chữ nhật A . BCD A BCD
  có AB a; AD  2a, AA  a 5. Góc giữa đường thẳng A C
 và mặt phẳng ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 C' D' B' A' D C A B
Do AA   ABCD 
AC là hình chiếu vuông góc của A C
 trên mặt phẳng ABCD. Suy ra:  A C
 ;ABCD  A C
 ; AC  A . CA Ta có: 2 2 AC AB BC a 5. A A  Xét tam giác A C
A vuông tại A : tan A CA   1  A CA  45 . AC Vậy A C
 ;ABCD  45 .
Câu 32: Cho hình hộp chữ nhật A .
BCD ABC D
  có AB AA  a; AD a 6. Góc giữa đường thẳng A C
 và mặt phẳng ABB A   bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: C' D' B' A' D C A B CB AB Ta có:  
CB  ABB A  . CB   AA Vậy A B
 là hình chiếu vuông góc của A C
 trên mặt phẳng ABB A  . Suy ra: A C  ;ABB A
   A C  ; A B    BA C  . BC Xét tam giác A B
C vuông tại B : tan BA C    3  BA C   60 . A B  Vậy A C  ;ABB A    60 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Câu 33: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh bằng .
a Mặt bên SAB là tam giác vuông
cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt
phẳng  ABC bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S C A H B
Gọi H là trung điểm AB  SH  . AB SH    AB Ta có:     SAB   ABCSHABC.
Suy ra: HC là hình chiếu vuông góc của SC trên mặt phẳng  ABC.
Suy ra: SC;ABC  SC; HC  SCH. SH 3
Xét tam giác SHC vuông tại H : tanSCH    SCH  30 .  HC 3
Vậy SC;ABC  30 .
Câu 34: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh bằng .
a Mặt bên SAB là tam giác vuông
cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt
phẳng SAB bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 S C A H B
Gọi H là trung điểm AB  HC  . AB HC   AB Ta có:     SAB   ABCHCSAB.
Suy ra: SH là hình chiếu vuông góc của SC trên mặt phẳng SAB.
Suy ra: SC;SAB  SC;SH  CSH. a 3 a Ta có: HC ; SH 2 2 HC
Xét tam giác SHC vuông tại H : tanCSH   3  CSH  60 .  HS
Vậy SC;SAB  60 .
Câu 35: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng .
a Mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SB và mặt phẳng  ABCD bằng A. 30 .  B. 45 .  C. 90 .  D. 60 .  Lời giải: S A D H B C
Gọi H là trung điểm AB  SH  . AB SH   AB Ta có:     SAB   ABCDSHABCD.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11
Suy ra: HB là hình chiếu vuông góc của SB trên mặt phẳng  ABCD. a 3 Ta có: HC ; SB a 2 Suy ra:  ;
SB ABCD   ;
SB HB  SBH  60 . 
Câu 36: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng .
a Mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Gọi  là góc giữa đường thẳng SC và mặt phẳng
ABCD. Khẳng định nào dưới đây đúng? 5 15 5 15 A. tan  . B. tan  . C. tan  . D. tan  . 15 15 5 5 Lời giải: S A D H B C
Gọi H là trung điểm AB  SH  . AB SH   AB Ta có:     SAB   ABCDSHABCD.
Suy ra: HC là hình chiếu vuông góc của SC trên mặt phẳng  ABCD.
Suy ra: SC;ABCD  SC; HC  SCH. a 3 a 5 Ta có: 2 2 SH
; HC HB BC  . 2 2 15
Xét tam giác SHC vuông tại H : tanSCH  . 5
Câu 37: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh bằng 2 .
a Biết hình chiếu vuông góc của
đỉnh S trên mặt phẳng  ABC là trung điểm H của AB . Góc giữa đường thẳng SC và mặt
phẳng  ABC bằng 60 .  Tính SH. A. SH  2 . a B. SH  3 . a C. SH  3 . a D. SH  . a Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 S C A H B
Theo giả thiết: SH   ABC.
Suy ra: HC là hình chiếu vuông góc của SC trên mặt phẳng  ABC.
Suy ra: SC;ABC  SC; HC  SCH. SH 2a 3
Xét tam giác SHC vuông tại H : tanSCH  
SH HC.tanSCH  . 3  3 . a HC 2
Câu 38: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh bằng 3a,SB  2 .
a Biết hình chiếu vuông
góc của đỉnh S trên mặt phẳng  ABC là điểm H trên cạnh AB sao cho AH  2H . B Gọi  là
góc giữa đường thẳng SC và mặt phẳng  ABC. Khẳng định nào dưới đây đúng? 21 15 21 15 A. tan  . B. tan  . C. tan  . D. tan  . 21 15 7 5 Lời giải: S C A H B
Theo giả thiết: SH   ABC.
Suy ra: HC là hình chiếu vuông góc của SC trên mặt phẳng  ABC.
Suy ra: SC;ABC  SC; HC  SCH  .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 Ta có: 2 2 2 2 2 2
SH SB HB a 3; HC BH BC  2BH.BC.cos HBC  7a  HC a 7. SH 21
Xét tam giác SHC vuông tại H : tanSCH   . HC 7
Câu 39: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng 3a,SB  2 .
a Biết hình chiếu vuông
góc của đỉnh S trên mặt phẳng  ABCD là điểm H trên cạnh AB sao cho AH  2H . B Gọi 
là góc giữa đường thẳng SC và mặt phẳng  ABCD. Khẳng định nào dưới đây đúng? 21 10 21 30 A. tan  . B. tan  . C. tan  . D. tan  . 21 10 7 10 Lời giải: S A D H B C
Theo giả thiết: SH   ABCD.
Suy ra: HC là hình chiếu vuông góc của SC trên mặt phẳng  ABCD.
Suy ra: SC;ABCD  SC; HC  SCH  . Ta có: 2 2 2 2
SH SB HB a 3; HC BH BC a 10. SH 30
Xét tam giác SHC vuông tại H : tanSCH   . HC 10
Câu 40: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng 3a,SB  2 .
a Biết hình chiếu vuông
góc của đỉnh S trên mặt phẳng  ABCD là điểm H trên cạnh AB sao cho AH  2H . B Gọi 
là góc giữa đường thẳng SD và mặt phẳng  ABCD. Khẳng định nào dưới đây đúng? 21 39 21 15 A. tan  . B. tan  . C. tan  . D. tan  . 21 13 7 5 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN Toán 11 S A D H B C
Theo giả thiết: SH   ABCD.
Suy ra: HD là hình chiếu vuông góc của SD trên mặt phẳng  ABCD.
Suy ra: SD;ABCD  SD; HD  SDH  . Ta có: 2 2 2 2
SH SB HB a 3; HD AH BD a 13. SH 39
Xét tam giác SHC vuông tại H : tanSDH   . HD 13
__________________________HẾT__________________________
Huế, 09h40’ Ngày 30 tháng 12 năm 2023
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115