91 trang 10 lượt tải

Đáp án cho mạch điện, lý thuyết và thực hành | Lí thuyết mạch điện | Trường Đại học Bách khoa Hà Nội

19

Tài liệu được sưu tầm và soạn thảo dưới dạng file PDF với mục đích hỗ trợ học tập và tham khảo. Nội dung tài liệu được trình bày rõ ràng, dễ tiếp cận, phù hợp cho việc ôn tập và củng cố kiến thức trong quá trình học đại học. Đây sẽ là nguồn tư liệu hữu ích giúp các bạn sinh viên chuẩn bị tốt hơn cho các buổi học, đồng thời mở rộng thêm hiểu biết về môn học. Hy vọng tài liệu này sẽ mang lại nhiều giá trị và hỗ trợ các bạn trong hành trình học tập. Mời bạn đọc cùng tham khảo!

Môn: Lý thuyết mạch điện 1 32 tài liệu

Trường: Đại học Bách Khoa Hà Nội 5.4 K tài liệu

Tác giả:

Profile

Mai Nguyệt

1 tuần trước
Tải xuống
Báo cáo
Danh sách Quiz
Tải xuống
/91
LÝ THUY T M CH II Ế Ạ
BÀI T P T NG H P Ậ Ổ Ợ
Bài1:TínhcôngsutphátcangunEvàcôngsuttiêuthca3ñintr.Bit(N–s
th t ca sinh viên)
220 0
=
ɺ
∡
;
1
20
R
=
;
2
40
R
=
;
15
C
Z j
= −
;
*(15 0,1 )
L
Z j N
= +
; ñin tr phi tuyn
x
R
có ñ,c tính cho theo tr/ hiu dng
3
(20 ) 0,5
x x x
U N I I
= + ⋅ + ⋅
ɺ ɺ ɺ
Bài2:Tínhdòng
2
( )
i t
quañintrt3i
t
R
bit
( ) 220 (10 0,1 )sin( )
e t N t
= + +
(v5i
N–sthtcasinhviên),
10
t
R
=
,m7nghaic8athu9ntrcó
2 100
0,5 3
=
A ,
cu:ndâyphituyncóñ,ctínht<cth=i
3
5 0,7
i i
ψ
= +
.
Bài3:M:tñư=ngdâydàikhôngtiêutáncó
0
48
L mH km
=
và
9
0
3.10
C F km
−
=
.
CuEiñư=ngdâycólGpm:tt3i
2
1000
R
=
ñưHcb3ovbit
(
)
2
4
C N mH
= +
.
Xác ñ/nh ñin áp khúc x7 vào t3i và ñin áp ph3n x7 khi có m:t sóng
( ) 1000. ( )
u t t kV
=
1
ñánht5icuEiñư=ngdây.Bit3nhLaplace
1000
( ( ))L u t
p
=
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Bi4:Chom¹ch®iÖnnh−h×nhvÏ.TÝnhc«ngsuÊtph¸tcñanguån
1
E
ɺ
vc«ngsuÊttiªu
thôcña®iÖntrë
1
R
v
2
R
.BiÕt
1
20 0 ;
E V
=
ɺ
∡
1
20 ;
R
=
2
10 ;
R
=
10;
C
Z j
= −
cuén
d©yphituyÕncã®ÆctÝnhcñagi¸trÞhiÖudôngcho
theob¶ngsau
U
ɺ
0 3,2 5 8 12
I
ɺ
0 0,25 0,5
0,75 1
Bi5:Chom¹ch®iÖnnh−h×nhvÏ.BiÕt
(
)
1
40 sin 3 ;
e t V
= +
1
10 ;
R
=
2
12 ;
R
=
0,1 ;
L H
=
tô
®iÖnphituyÕn
x
C
cã®ÆctÝnh
3 5 3
10 10
q u u
− −
= + .TÝnh
dßngquatô
x
C
.
Bi 6: Cho ®−êng d©y truyÒn ti kh«ng tiªu t¸n nh− h×nh vÏ. BiÕt ®−êng d©y cã
250
c
Z
=
,vËntèctruyÒnsãng
250.000 /
v km s
=
,chiÒudi
200
l km
=
.Cuèi®−êng
d©ycãl¾pti
2
250
R
=
cïngvíihaiphÇntöb¶ovÖ
2
0,8
L H
=
v
2
0,1
C mF
=
.BiÕt
t¹ithêi®iÓm
0
t
=
cãmétsãng®¸nhtíi®Çu®−êngd©yvíi
250
( ) 750 ( )
t
toi
u t e t kV
1
−
= .
HIytÝnh®iÖn¸ptrªnti
2
( )
R
u t
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Bài7:
Chom7chñinnhưhìnhvO.
Bit
1
15 ;
E V
=
2
( ) 0,1sin(5 );
e t t
=
1
12 ;
R
=
2
18
R
=
;
10 ;
C mF
=
1,6 100
0,01 1,25
=
A ;
ñintrphituyn
x
R
cóñ,ctínhVônRAmpe:
3
15 0,6
u i i
= +
.Tínhñináp
( )
x
R
u t
trênñintrphituyn.
Bài8:
Cho m7ch ñin như hình vO. Bit ngun dòng
m:t chiUu
2 ;
J A
=
1
10 ;
R
=
2
15 ;
R
=
3
25 ;
R
=
4
30 ;
R
=
0,1
C mF
=
;cu:ndâyphi
tuyn có ñ,c tính WebeRAmpe:
3 3
2 0,75
ai bi i i
Ψ = + = +
. S8 dng phương
phápcácbưcsaiphânliêntip,tínhdòngñin
( )
L
i t
cho
0, ,2 , ,4
t h h h
=
…
bitt7i
0
t
=
tañóng
khóaK.Bư5csaiphân
10
h ms
=
.
Bài9:
Cho ñư=ng dây truyUn t3i có các thông sE ñ,c trưng sau:
0
0,12 / ;
R km
=
3
0
1,5.10 / ;
L H km
−
=
6
0
0,45.10 / ;
G S km
−
=
8
0
10 / ;
C F km
−
=
chiUu dài
200
l km
=
,
t9n sE trong m7ch
50
f Hz
=
. Y cuEi ñư=ng dây ta có t3i bao gm m:t t ñin
6
2
5 10
C F
−
= ⋅
vàm:tñintr
2
500
R
=
.
a) Tính ñin áp
1
U
ɺ
c9n cp ñ9u ñư=ng dây ñZ có ñin áp trên t3i là
2
220 0
U kV
=
ɺ
∡
.Tínhcôngsuttiêutántrênñư=ngdâykhiñó.
b) V5i ngunñinápñ9u ñư=ngdây
1
U
ɺ
câu(a),tínhcông sut tiêu tántrên
ñư=ngdâykhitacós[cEñ<tt3ikh\im7chvàkhicós[cEngGnm7ch(ch]p
m7ch)cuEiñư=ngdây.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Câu10.Chom7chñinnhưhình1.
Trongñó:
1
8
R
=
;
1
2 ; 97
j A E V
= =
Ph9nt8phituynR
2
vàR cóñ,ctính
3
giEngnhauvàñưHcchonhưb3ng1.Ph9n
t8phituynR
4
cóñ,ctínhchonhưb3ng
2.Tìmcôngsutcangun
1
E
(
1
E
P
)?
1
R
1
E
Hình1
2
R
3
R
4
R
j
B/ng1
i(A) 0 0,5
1,0
1,5
2,0
2,5
3,0
u(V) 0 7 20 30 35 40 42
B/ng2
i(A) 0 0,5 1,0 1,5 2,0 2,5 3,0
u(V) 0 5 15 25 30 35 37
Câu11:
Chom7chñinnhưhình2.Trongñó:
1
35
R
=
;
1
65 ;
E V
=
(
)
3 2 sin 100 ( )
j t A
= +
M7nghaic8athu9ntrcómatr]nb:sEZnhư
sau:
( )
11 12
21 22
15 5
5 10
z z
Z
z z
−
= =
−
ð,ctínhcacu:ndâyphituynvàtñinphi
tuynl9nlưHtnhưsau:
1
i
1
R
1
E
2
i
1
u
2
u
j
(i)
Ψ
q(u)
[
]
Z
Hình2
3 3
( ) 0,1 0,05 ;
i ai bi i i
Ψ = + = +
3 4 7 3
( ) 10 1,09.10
q u u u u u
− −
= α + β = +
Tìmdòngñinquangun
1
E
.
Câu12:
ChohthEngñư=ngdâydàikhôngtiêutánnhư
hình3.v5icácthôngsEcacácñư=ngdâycho
nhưsau:
ðư5ng1:
3
1
10 / ;
L H m
−
=
9
1
6,25.10 / ;
C F m
−
=
1
100
l km
=
.ðư5ng2:
3
2
0,15.10 / ;
L H m
−
=
10
2
6.10 / ;
C F m
−
=
2
500
l km
=
.
C
2 2
L ,C
1 1
L ,C
L
1
l
2
l
DC
Hình3
U 675KV
=
Giiañư=ngdây1và2ñưHcnEiv5im:tñinc3mt]ptrung
0.45
L H
=
,cuEiñư=ngdây2
nEiv5itñint]ptrung
6
3.10
C F
−
= vàm:tñ:ngcơñincótjngtr
dc
1000
Z
=
.
a) T7it=0,cóm:tsóngáphìnhchinh]tv5ibiênñ:U=675KVñ]pt5icuEiñư=ng
dây1.Tínhñinápkhúcx7vàoñ:ngcơ.
b) T7i
4
2.10
t s
−
= ,tínhñináptrênñ:ngcơ
vàñinápph3nx7trên
nht?
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Câu13.Chom7chñinnhưhìnhvOsE1.
E
j
1
R
2
R
3
R
4
R
3
L
3
C
CácthôngsEcam7ch:
50
E V
=
(m:tchiUu);
(
)
0,1 2 sin 100
j t
= (A);
1
20
R
=
;
2
5
R
=
;
3
25
R
=
;
3
0,5
L H
=
;
4
3
4.10
C F
−
= ;
4
R
phi
tuyncóñ,ctínhchodư5id7ngb3ngsEliu
sau:
I(A) 0 0,25
0,5
1 1,5
2 2,5
U(V)
0 14 25 33
40 43
50
Yêuc9u:
R TìmbiZuth<ct<cth=icadòngñin
quaR
4
?
R TìmtjngtrZ canhánh3ñZcông
3
sutphátlênnól5nnht?
Hình1
Câu14.Chom7chñinnhưhìnhvOsE2.
4
R
3
R
2
R
L
J
1
R
C
E
1
2
K
(
)
i t
CácthôngsEcam7ch:
1
J A
=
(m:tchiUu);
50
E V
=
(m:t
chiUu);
1
10
R
=
;
2
30
R
=
;
3
10
R
=
;
4
20
R
=
;
4
2.10
C F
−
=
;cu:ndâyphi
tuyncóñ,ctính
3 3
( ) 2 3,25
i ai bi i i
Ψ = + = +
;
Tínhdòngñinquáñ:quacu:n
dâyphituynLkhichuyZnkhóaKtn1
sang2bongphươngphápcácbư5csai
phânliêntip?(BitkhiK1m7chñã
xác l]p; chqn bư5c sai phân h = 1ms;
tính5bư5csaiphânñ9utiên)
Hình2
Câu 15. Cho ñư=ng dây dài có các thông sE cơ b3n như sau:
(
)
0
0 /
R km
=
;
(
)
0
0 /
G S km
=
;
(
)
3
0
4.10 /
L H km
−
=
;
(
)
7
0
4.10 /
C F km
−
=
; chiUu dài ñư=ng dây
500
l km
=
,cuEidâynEiv5it3i
2
200 20
Z j
= +
.TínhiuñintruyUntrênñư=ngdâycó
t9nsEdaoñ:ng
50
f Hz
=
.
1.TínhhsEtruyUnsóng,tjngtrsóng,v]ntEctruyUnsóngvàhsEph3nx7cuEi
ñư=ngdâycañư=ngdâydàinêutrên?
2.TínhphânbEdòngvàápt7iñiZmgiiadâyvàñ9uñư=ngdâykhit7icuEiñư=ng
dâycóñináp
0
2
120 0
U kV
=
ɺ
∡
?
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Câu16
Xétm7chñinhình1,E
1
=E
2
=12V;
ñ,ctínhcañintrphituynchob3ng
1;ñ,ctínht<cth=icacu:ndâythu9n
c3mchob3ng2;R
1
=4s; =60s;R
3
C
=0,39tF.
B/ng1:
( )
U V
0 6 9 10,2
12
( )
I A
0 0,5 0,9
1,4 3
Hình1
B/ng2:
( )
Wb
Ψ
R1,5 R1 1 1,5
( )
I A
R2 R1 1 2
a)Tínhdòngxácl]pcaR
1
khikhoáKv/tríA.
b)T7ith=iñiZmt=0,khoáchuyZnsangv/tríB.Tínhdòngbanñ9u
(0)
L
i .BitñiZm
làmviccacu:ndâyphituynchvdaoñ:ngtrongm:tño7ntuyntính.Xácñ/nhñin
c3mtuyntínhtươngñươngcacu:ndâytrongquátrìnhquáñ:này.
Câu17
Xétm7chñinhình2,
)314sin(2100)( tte = V;quan
hgiiadòngñinhiudng&ñináphiudngca
ñintrphituynchohình5;L=0,05H; ( )=q u au–
bu
3
;u
C
(R0)=0;a=10 ;
–5
b=0,5.10 .
–9
B/ng1:
( )
U V
0 50 65 80 100
( )
I A
0 0,5 1 3 4
Hình2
a)Tínhdòngxácl]pca khikhoáv/tríA.L
b)T7ith=iñiZmt=0,khoáchuyZnsangv/tríB.Tính3giátr/ñ9utiêncañinápquá
ñ:catbongphươngphápsaiphân,chqnh=0,002s.
Câu18
Tronghình3,cácñư=ngdâydàiñUukhôngtiêután.ChúngcócácthôngsEsau:L
1
=
10
–6
H/m;C
1
=2,7.10 F/m; =100km; =2.10 H/m; =1,6.10 F/m;
–11
l
1
L
2
–6
C
2
–11
l
2
=60km;
L
3
=1,2.10 H/m; =2,2.10 F/m; =110km; =0,9.10 H/m;
–6
C
3
–11
l
3
L
4
–6
C
4
=3.10 F/m;
–11
l
4
=75km; =150s; =10 F; =200s; =0,02H; =R
B
C
B
–11
R
C
L
D
R
F
440s.
a)Tínhtjngtrsóngcacácñư=ngdây.
b)T7ith=iñiZmt
0
=0cóm:tsóngchinh]tdàivôh7nU
A
=500kVbGtñ9uxut
pháttnA&ch7ydqcñư=ngdây1,
b1–Tínhdòngñinkhúcx7&ñinápkhúcx7t7iñiZmB.
b2–Tínhñinápkhúcx7ñiZmFt7ith=iñiZmt
1
=0,3ms.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Hình3
Hình2
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Bi19:
Chom¹ch®iÖnnh−h×nhvÏ.TÝnhc«ngsuÊtph¸tcñanguån
1
E
ɺ
vc«ngsuÊt
tiªuthôcña®iÖntrë
1
R
v
2
R
.BiÕt
1
20 0 ;
E V
=
ɺ
∡
5;
ω
=
1
20 ;
R
=
2
10 ;
R
=
10;
C
Z j
= −
cuénd©yphituyÕncã®ÆctÝnhcñagi¸trÞ
hiÖudôngchotheobngsau
Ψ
ɺ
0 0,6 0,9
1,4 2
I
ɺ
0 0,25 0,5
0,75 1
Bi20:Chom¹ch®iÖnnh−h×nhvÏ.BiÕt
(
)
1
50 2sin 5 ;
e t V
= +
1
10 ;
R
=
2
15 ;
R
=
0,1 ;
L H
=
tô
®iÖnphituyÕn
x
C
cã®ÆctÝnh
3 5 3
10 10
q u u
− −
= + .TÝnh
c«ngsuÊttiªuthôtrªn
1
R
v
2
R
.
Bi21:Cho®−êngd©ytruyÒntikh«ngtiªut¸nnh−h×nhvÏ.BiÕt®−êngd©ycã
400
c
Z
=
,®iÖndungriªngdäc®−êngd©yl
8
0
10 /
C F km
−
= ,chiÒudi
250
l km
=
.
Cuèi®−êngd©ycãl¾pti
2
150
R
=
cïngvíihaiphÇntöbovÖ
2
0,6
L H
=
v
2
0,1
C mF
=
.BiÕtt¹ithêi®iÓm
0
t
=
cãmétsãng®¸nhtíi®Çu®−êngd©yvíi
200
( ) 500 ( )
t
toi
u t e t kV
−
= 1 .HIytÝnh®iÖn¸ptrªnti
2
( )
R
u t
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Bài22:(4ñim)
Chom7chñinnhưhình1.Bit =25s;R
1
ñintrphituyn cóñ,ctínhphituynR
2
nhưhình2; =80 F.TínhdòngñinquaC 8
R
2
trong2trư=nghHpsau:
a) =75V(m:tchiUu).e
b)
( )
75 5 2 sin 314 V
e t
= + .
Hình1
Hình2
Bài23:(2ñim)
M:tñư=ngdâytruyUnt3iñincócácthôngsEsau:
0
0,1 / ;
R km
=
4
0
9.10 / ;
L H km
−
=
8
0
1,5.10 / ;
C F km
−
=
6
0
0,5.10 / ;
G S km
−
=
250 .
l km
=
a)TínhhsEtruyUnsóngvàtjngtrsóngcañư=ngdây.
b)Tìmb:sE cam7nghaic8atươngñươngcañư=ngdây.A
Bài24:(3ñim)
M:tñư=ngdâydàikhôngtiêutáncótjngtrsóng
1200
C
Z
=
.CuEi ñư=ngdâynàycót3it]p
trunggmñintr
400
R
=
nEitipv5im:tcu:ndâyphituyncóñ,ctính(trongño7nlàmvic)
0,002 0,260
( ) 95,61 105,00
i i
i e e
−
Ψ = − . T7i th=i ñiZm
0
t
=
có m:t sóng chi nh]t
(
)
100. ( )
t
U t kV
= 1
truyUntnñ9uñư=ngdâyñnt5icuEiñư=ngdây.TnmôhìnhPetersenvàbongphươngphápcác
bư5csaiphânliêntiptính3ñiZmr=ir7cñ9utiêncadòngñinquáñ:trêncu:ndây.Chqnbư5c
tính
0,5
h ms
=
.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Bài25:(3,5ñim)
Chom7chñinnhưhình1.NgunápE=80V,R
1
=10s,
R
3
=30s,C=5mF.Cu:ndâyphituyncóñ,ctính:
ψ(i)=3iR0,5i .ð,ctínhcañintrphituynR cho
3
2
trênb3ngsau.
a)KhikhóaKñóng,m7chtr7ngtháixácl]p.Tính
dòngquacu:ndâyvàñináptrêntñin.
b)T7ith=iñiZmt=0,khoáKm,hãytìmñináptrênt
ñinu
c
theophươngphápsaiphânliêntipv5ibư5csai
phânh=2ms,tínhgiátr/3bư5ctínhñ9utiên.
Hình1
ð,ctínhñintrR
2
:
U(V)
0 40 60 80
I(A) 0 0,55
0,8 1,7
Bài26:(3,5ñim)
Chom7chñinnhưhình2.Bit:
( ) 3 0, 2 2 sin100
j t t
= + A,
1
100 ;
R
=
2
50 ;
R
=
5
2.10 .
C F
−
= Cu:ndâyphituyncó
ñ,ctính
3
( ) 4 0, 25
i i i
Ψ = − .
TínhdòngquaR
1
vàcôngsutphátcangun.
Hình2
Bài27:(2ñim)
Chomôhìnhhaiñư=ngdâydàighépnEitipnhưtrênhình
3.ðư=ngdây1có
1
300 ,
C
Z
=
ñư=ngdây2có
2
60 .
C
Z
=
Kho3ngcáchño7nAB
100 ,
AB
l km
=
t
3
10 .
C F
−
= T7i
0
t
=
cóm:tsóngáphìnhchinh]t
(
)
1500. ( )
t
U t kV
= 1 truyUntn
ñư=ngdây1t5i.
a)Tínhñinápkhúcx7t7iñiZmA?
b)Tínhñinápt7iBbitsóngtruyUntnAñnBv5iv]n
tEc2.10
5
km/s.
Hình3
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Bài28:(3ñim)
Chom7chñinnhưhình1.Ngundòngm:tchiUu
1
1
J A
=
,ngunáp
2
( ) 10 2 sin100
e t t
= V;
1
100 ;
R
=
2
50 ;
R
=
4
10 .
C F
−
= ðintrphituyncóñ,ctínhphi
tuynchobib3ngsau:
U(V)
0 7 20 30 35 40
I(A) 0 0,5 1 1,5 2 2,5
Cu:ndâyphituyncóñ,ctính
(
)
3
2 3,25
i i i
Ψ = + .Tìm
biZuth<ct<cth=icacácdòngñinquacácph9nt8phi
tuyn?
Hình1
Bài29:(2,5ñim)
Chom7chñinnhưhình2.Bit:
1
( ) 100 2 sin1000
e t t
= V;
2
50
E V
=
(m:tchiUu);
1
100 ;
R
=
2
30 ;
R
=
5
2 10 .
C F
−
= ⋅
Cu:nc3mphituyncóñ,ctính
(
)
3
2 3,15
i i i
Ψ = + .
Tìmbongphươngphápsaiphânliêntip3giátr/ñ9utiên
cadòngñinquáñ:trêncu:nc3mphituynkhikhóaK
chuyZntn1sang2.(BitkhiK1m7chñãxácl]p;chqn
bư5csaiphânh=1ms)
Hình2
Bài30:(3,5ñim)
Tronghình3,2ñư=ngdâydàiñUukhôngtiêután.ðư=ng
dây1:
1
0,8 /
L H km
=
;
6
1
5 10 / .
C F km
−
= ⋅ ðư=ngdây2(ño7n
AB):
2
0,05 /
L H km
=
;
6
2
0,05 10 / ;
C F km
−
= ⋅
800 .
AB
l km
=
Các
ph9nt8t]ptrung
6
0,5 10 ;
C F
−
= ⋅
0,5 ;
L H
=
500 .
t
R
=
T7it
=0,cóm:tsóngáphìnhchinh]t
(
)
(
)
500.
t
U t kV
= 1 truyUn
tnñư=ngdây1t5i.
a)Tínhñinápkhúcx7t7iñiZmA?
b)Tínhdòngvàápkhúcx7trênt3iR
t
?
Hình3
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Bài31:
Chom7chñinnhưhình1.Bitngun1chiUu
3
15 ;
E V
=
4
( ) 0,5sin(10 );
e t t
=
3
10 ;
R
=
5
20
R
=
;
4
10 ;
C mF
=
m7nghaic8athu9ntr
cómatr]nñ,ctrưngchotheocácdòngRápnhư
hìnhvOlà
1,25 0,5
0,25 0,9
A
=
;cu:ndâyphituyn
x
L
cóñ,ctínhWebeRAmper:
3
2 0,4
i i
ψ
= +
.
Tínhñináp
5
( )
R
u t
trênñintr
5
R
.
Hình1
Bài32:
Chom7chñinnhưhình2.Bitngunápm:tchiUu
1
15 ;
E V
=
2
1 ;
E V
=
1
5 ;
R
=
2
20 ;
R
=
3
5 ;
R
=
cu:ndâyphituyncóñ,ctínhWebeR
Amper:
3
0,5 0,1
i i
Ψ = +
;tñinphituyncóñ,c
tínhCulombRVolt:
3
0,2 0,001
q u u
= + .Tínhñináp
trêntphituyn
( )
Cx
u t
cho
0
t
≥
bit
Hình2
t7i
0
t
=
tañóngkhóa .Trư5ckhiñóngkhóam7chñãtr7ngtháixácl]p.K
Bài33:
Cho ñư=ng dây truyUn t3i có các thông sE ñ,c
trưngsau:
0
0,1 / ;
R km
=
3
0
1,5.10 / ;
L H km
−
=
0
0 / ;
G S km
=
8
0
10 / ;
C F km
−
=
chiUu dài
150
l km
=
, t9n sE trong m7ch
50
f Hz
=
. Y
cuEiñư=ngdâytacót3iñintr
2
200
R
=
mGc
song song v5i t ñin b3o v
2
0,1
C mF
=
. Bit
ñinápñ9uñư=ngdâylà
1
220 0
U kV
=
ɺ
∡
.
Hình3
a)TínhñinápcuEiñư=ngdây
2
U
ɺ
vàcôngsuttiêutántrênñư=ngdâykhiñó.
b)Khib\t3iR
2
vàC
2
cuEiñư=ngdây(hm7chcuEiñư=ngdây)thìv5i
1
220 0
U kV
=
ɺ
∡
dòng
ñ9uvào
1
I
ɺ
sOlàbaonhiêu?
CuuDuongThanCong.com https://fb.com/tailieudientucntt
ây có m t s b n th c m c t i sao khi ph c hóa m ch n thì giá trỞ đ ộ ố ạ ắ ắ ạ ứ ạ điệ ị ồ của ngu n xoay
chiều không chia cho 2, lí do là vì: áp s c n tìm d i d ng hàm th√ đ ố ầ ở ướ ạ ờ ứi gian, nên khi ph c hóa
nếu chia 2 thì khi tính ra dòng n thì ph√ điệ ải nhân 2 tr l i, vi√ ở ạ ệ ểc này có th gây ra sai s .ố
Do ó tùy vào tr ng h p hay câu h i c a bài toán mà vi c ph c hóa có th là cđ ườ ợ ỏ ủ ệ ứ ể ần thiết hay không.
Ví d nh hàm th i gian cho biên d i d ng 2*A*sin(w*t) thì nên chia ụ ư ờ độ ướ ạ √ √ ợ ẹ2 để đư c số đ p hơn.
Các bài t p v ng dây dài c n chú ý v g c th i gian t=0 lúc sóng ánh vàoậ ề đườ ầ ề ố ờ đ
để hiệ ỉ ờu ch nh th i gian các thông số đề yêu cầu

Tài liệu khác của Đại học Bách Khoa Hà Nội

Preview text:


LÝ THUYẾT MẠCH II
BÀI TẬP TỔNG HỢP
Bài1:TínhcôngsutphátcangunEvàcôngsuttiêuthca3ñintr.Bit(N–s
th t ca sinh viên) E = 220 0 ɺ ∡
; R = 20; R = 40 ; Z = − 1 j 5; 1 2 C
Z = j * (15 + 0,1N ) ; ñin tr phi tuyn R  có ñ,c tính cho theo tr/ hiu dng L x 3
Uɺ = (20 + N ) ⋅ Iɺ +0,5 ⋅ Iɺ  x x x  
Bài2:Tínhdòng i (t) quañintrt3i R bit e(t) = 220 +(10 + 0,1N )sin(t) (v5i 2 t  2 100
N–sthtcasinhviên), R =10,m7nghaic8athu9ntrcó A =   , t 0  ,5 3   
cu:ndâyphituyncóñ,ctínht3 ψ = 5i + 0,7 i .   
Bài3:M:tñư=ngdâydàikhôngtiêutáncó L = 48mH km và − 9 C =3.10 F km. 0 0
CuEiñư=ngdâycólGpm:tt3i R =1000 ñưHcb3ovbit C = 4 + N mH . 2 ( ) 2
Xác ñ/nh ñin áp khúc x7 vào t3i và ñin áp ph3n x7 khi có m:t sóng 1000 ( u ) t =1000. (
1 )tkV ñánht5icuEiñư=ngdây.Bit3nhLaplaceL(u(t)) =  p  CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Bi4:Chom¹ch®iÖnnh−h×nhvÏ.TÝnhc«ngsuÊtph¸tcñanguånEɺ vc«ngsuÊttiªu 1
thôcña®iÖntrë R v R .BiÕt E = 20 0 ɺ ∡ V ; R = 20 ;
  R = 10; Z = − 1 j 0; cuén 1 2 1 1 2 C
d©yphituyÕncã®ÆctÝnhcñagi¸trÞhiÖudôngcho theob¶ngsau Uɺ  0 3,2 5 8 12 Iɺ  0 0,25 0,5 0,75 1  
Bi5:Chom¹ch®iÖnnh−h×nhvÏ.BiÕt e = 40 + sin 3t V ; R =10 ;
  R = 12;L = 0,1H ; tô 1 ( ) 1 2
®iÖnphituyÕn C cã®ÆctÝnh −3 −5 3 q= 10 u+ 10 u .TÝnh x dßngquatôCx .
Bi 6: Cho ®−êng d©y truyÒn t¶i kh«ng tiªu t¸n nh− h×nh vÏ. BiÕt ®−êng d©y cã
Z = 250 ,vËntèctruyÒnsãng v = 250.000km/ s ,chiÒudi l = 200km .Cuèi®−êng c
d©ycãl¾pt¶i R = 250 cïngvíihaiphÇntöb¶ovÖ L = 0,8H v C = 0,1mF .BiÕt 2 2 2
t¹ithêi ®iÓm t = 0 cã métsãng®¸nhtíi®Çu®−êngd©yvíi 2 − 50 u ( ) t = 750 t e 1 t kV . toi ( )
HIytÝnh®iÖn¸ptrªnt¶iu t  R ( ) 2     CuuDuongThanCong.com
https://fb.com/tailieudientucntt  Bài7:
Chom7chñinnhưhìnhvO. Bit E = 15V ; 1 e (t) = 0,1sin(5t);  2 R = 12 ;   R =18; 1 2  1,6 100  C = 10mF ; A =   ; 0,  01 1,25  
ñintrphituyn R cóñ,ctínhVônRAmpe: 3
u =15i + 0,6i .Tínhñináp u (t) x x R
trênñintrphituyn.  Bài8:
Cho m7ch ñin như hình vO. Bit ngun dòng m:t chiUu J = 2 ; A  R 1 = 0 ; R =15 ; 1   2   R = 25 ; R = 30 ; C= mF;cu:ndâyphi 3     0,1 4 tuyn có ñ,c tính  WebeRAmpe: 3 3
Ψ = ai+ bi = 2i+ 0,75i . S8 dng phương
phápcácbưcsaiphânliêntip,tínhdòngñin  i (t )cho t = 0, , h 2 , h ,
… 4hbitt7i t = 0 tañóng L
khóaK.Bư5csaiphân h = 10ms.  Bài9:
Cho ñư=ng dây truyUn t3i có các thông sE ñ,c trưng sau: R = 0,12 /km;  0 − 3 L 1 = ,5.10 H /km; 6 G 0,45.10− = S / k ; m   −8 C =10 F / k ;
m  chiUu dài l = 200km, 0 0 0
t9n sE trong m7ch f = 50Hz . Y cuEi ñư=ng dây ta có t3i bao gm m:t t ñin − 6 C =5 1
⋅ 0 F vàm:tñintr R 5 = 00 2 2 .
a) Tính ñin áp Uɺ  c9n cp  ñ9u ñư=ng dây ñZ có ñin áp trên t3i là 1 U = 220 0 k  ɺ ∡
V .Tínhcôngsuttiêutántrênñư=ngdâykhiñó. 2
b) V5ingunñinápñ9uñư=ngdây Uɺ câu(a),tínhcông suttiêu tántrên 1
ñư=ngdâykhitacós[cEñm7ch)cuEiñư=ngdây.  CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Câu10.Chom7chñinnhưhình1. R 2
Trongñó:R = 8 ; j = 2A;E = 97V  1 1
Ph9nt8phituynR2vàR3cóñ,ctính R 1 R
giEngnhauvàñưHcchonhưb3ng1.Ph9n 3 R j 4
t8phituynR4cóñ,ctínhchonhưb3ng E1
2.Tìmcôngsutcangun E (P )? 1 E1 Hình1  B/ng1 B/ng2 i(A) 0
0,5 1,0 1,5 2,0 2,5 3,0 i(A) 0 0,5 1,0 1,5 2,0 2,5 3,0 u(V) 0 7 20 30 35 40 42  u(V) 0 5 15 25 30 35 37   Câu11:
Chom7chñinnhưhình2.Trongñó:R = 35 ; ( Ψ i) 1 i i 1 2
E = 65V;  j = 3 + 2 sin (100t) ( ) A  1 R
M7nghaic8athu9ntrcómatr]nb:sEZnhư 1 q(u) [Z] u sau: u j 1 2 z z  15 − 5  E1 11 12 Z = = (     ) z z   5 −  10 21 22 
ð,ctínhcacu:ndâyphituynvàtñinphi Hình2 
tuynl9nlưHtnhưsau: 3 3
Ψ(i ) = ai +bi = 0,1i + 0,05i ; 3 −4 −7 3
q(u) = αu + βu = 10 u + 1,09.10 u 
Tìmdòngñinquangun E .  1  Câu12:
ChohthEngñư=ngdâydàikhôngtiêutánnhư U 6 = 75KV
hình3.v5icácthôngsEcacácñư=ngdâycho l l 1 2 DC nhưsau: L ,C L L ,C 1 1 2 2 ðư5ng1: 3 − =  −9 =  1 L 10 H /m; 1 C 6, 25.10 F / m; C l = 100km .ðư5ng2: − 3 L = 0,15.10 H /m ; 1 2 Hình3  −10 C = 6.10 F / ; m l = 500km . 2 2
Giiañư=ngdây1và2ñưHcnEiv5im:tñinc3mt]ptrung L = 0.45H ,cuEiñư=ngdây2
nEiv5itñint]ptrung −6
C = 3.10 F vàm:tñ:ngcơñincótjngtr Z =1000. dc
a) T7it=0,cóm:tsóngáphìnhchinh]tv5ibiênñ:U=675KVñ]pt5icuEiñư=ng
dây1.Tínhñinápkhúcx7vàoñ:ngcơ. b) T7i 4 t 2.10 − =
s ,tínhñináptrênñ:ngcơvàñinápph3nx7trên nht? CuuDuongThanCong.com
https://fb.com/tailieudientucntt 
Câu13.Chom7chñinnhưhìnhvOsE1. 
CácthôngsEcam7ch:E = 50V (m:tchiUu); R1 R R 2 3
j = 0,1 2 sin(100t )(A); R = 20 ; R = 5 ; 1 2 − L3 R = 25 ;L = 0,5H ; 4 C =4.10 F ; R phi 3 3 3 4 E j
tuyncóñ,ctínhchodư5id7ngb3ngsEliu R C 4 3 sau:   I(A) 0
0,25 0,5 1 1,5 2 2,5 Hình1 U(V)  0 14 25 33 40 43 50 Yêuc9u:
R TìmbiZuthquaR4?
R TìmtjngtrZ3canhánh3ñZcông
sutphátlênnól5nnht? 
Câu14.Chom7chñinnhưhìnhvOsE2.
CácthôngsEcam7ch: K R 1 3 R4 2
J = 1A (m:tchiUu);E = 50V (m:t
chiUu); R =10; R =30;R = 10 ; 1 2 3 R2 R = 20; 4 C 2.10− = F ;cu:ndâyphi 4 C i (t ) E
tuyncóñ,ctính J R1 3 3 L
Ψ(i) = ai + bi = 2i + 3,25i ;  
Tính dòng ñin quá ñ: qua cu:n Hình2
dâyphituynLkhichuyZnkhóaKtn1
sang 2bongphươngpháp cácbư5csai
phânliêntip?(BitkhiK1m7chñã
xác l]p; chqn bư5c sai phân h = 1ms;
tính5bư5csaiphânñ9utiên) 
Câu 15. Cho ñư=ng dây dài có các thông sE cơ b3n như sau:R = 0  / km ; 0 ( ) G = 0 S / km ; −3 L = 4.10 H /km ; 7 C 4.10− =
F / km ; chiUu dài ñư=ng dây 0 ( ) 0 ( ) 0 ( )
l = 500km,cuEidâynEiv5it3iZ = 200 + j20 .TínhiuñintruyUntrênñư=ngdâycó 2
t9nsEdaoñ:ngf = 50Hz .
1.TínhhsEtruyUnsóng,tjngtrsóng,v]ntEctruyUnsóngvàhsEph3nx7cuEi
ñư=ngdâycañư=ngdâydàinêutrên?
2.TínhphânbEdòngvàápt7iñiZmgiiadâyvàñ9uñư=ngdâykhit7icuEiñư=ng
dâycóñináp ɺ 0 U =120∡0 kV ? 2  CuuDuongThanCong.com
https://fb.com/tailieudientucntt  Câu16
Xétm7chñinhình1,E1=E2=12V;
ñ,ctínhcañintrphituynchob3ng
1;ñ,ctínhtc3mchob3ng2;R1=4s;R3=60s;C =0,39tF.    Hình1 B/ng1: B/ng2: U (V )  0 6 9 10,2 12 Ψ(W ) b  R1,5 R1 1 1,5 I (A )  0 0,5 0,9 1,4 3  I( ) A  R2 R1 1 2 
a)Tínhdòngxácl]pcaR1khikhoáKv/tríA.
b)T7ith=iñiZmt=0,khoáchuyZnsangv/tríB.Tínhdòngbanñ9u i (0) .BitñiZm L
làmviccacu:ndâyphituynchvdaoñ:ngtrongm:tño7ntuyntính.Xácñ/nhñin
c3mtuyntínhtươngñươngcacu:ndâytrongquátrìnhquáñ:này.  Câu17
Xétm7chñinhình2,e(t) = 100 2 sin(314t) V;quan
hgiiadòngñinhiudng&ñináphiudngca
ñintrphituynchohình5;L=0,05H;q(u)=au– bu3;u –5 –9 C(R0)=0;a=10 ;b=0,5.10 . B/ng1: Hình2 U (V )  0 50 65 80 100 I (A )  0 0,5 1 3 4 
a)Tínhdòngxácl]pcaLkhikhoáv/tríA.
b)T7ith=iñiZmt=0,khoáchuyZnsangv/tríB.Tính3giátr/ñ9utiêncañinápquá
ñ:catbongphươngphápsaiphân,chqnh=0,002s.  Câu18
Tronghình3,cácñư=ngdâydàiñUukhôngtiêután.ChúngcócácthôngsEsau:L1= 10–6H/m;C –11 –6 –11 1=2,7.10
F/m;l1=100km;L2=2.10 H/m;C2=1,6.10 F/m;l2 =60km;L –6 –11 –6 3=1,2.10 H/m;C3=2,2.10
F/m;l3=110km;L4=0,9.10 H/m;C4 =3.10–11F/m;l –11
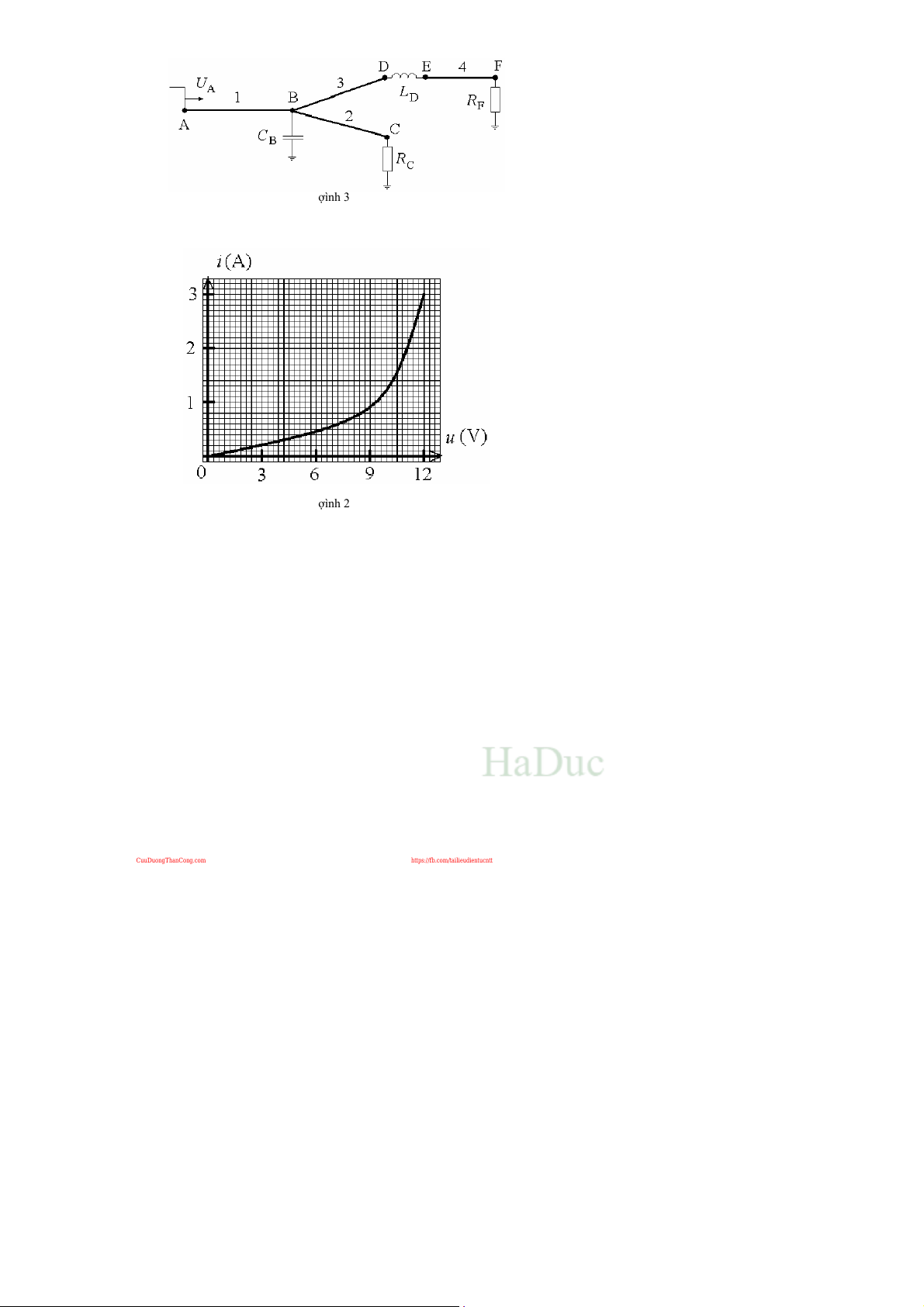
4=75km;RB=150s;CB=10
F;RC=200s;LD=0,02H;RF= 440s.
a)Tínhtjngtrsóngcacácñư=ngdây.
b)T7ith=iñiZmt0=0cóm:tsóngchinh]tdàivôh7nUA=500kVbGtñ9uxut
pháttnA&ch7ydqcñư=ngdây1,
b1–Tínhdòngñinkhúcx7&ñinápkhúcx7t7iñiZmB.
b2–Tínhñinápkhúcx7ñiZmFt7ith=iñiZmt1=0,3ms. CuuDuongThanCong.com
https://fb.com/tailieudientucntt  Hình3      Hình2  CuuDuongThanCong.com
https://fb.com/tailieudientucntt 
Bi19:Chom¹ch®iÖnnh−h×nhvÏ.TÝnhc«ngsuÊtph¸tcñanguånEɺ vc«ngsuÊt 1
tiªuthôcña®iÖntrë R vR .BiÕtE = 20 0 V  ɺ ∡
;  ω = 5;  R = 20; R = 10; 1 2 1 1 2 Z = − 1 j 0; C
cuénd©yphituyÕncã®ÆctÝnhcñagi¸trÞ
hiÖudôngchotheob¶ngsau Ψɺ  0 0,6 0,9 1,4 2 Iɺ  0 0,25 0,5 0,75 1  
Bi20:Chom¹ch®iÖnnh−h×nhvÏ.BiÕt
e = 50 + 2sin 5t V ; R =10 ;   R =15 ;   L = 0,1H; tô 1 ( ) 1 2 ®iÖnphituyÕn C q − u − = + u .TÝnh x cã®ÆctÝnh 3 5 3 10 10
c«ngsuÊttiªuthôtrªn R R 1 v 2 .
Bi21:Cho®−êngd©ytruyÒnt¶ikh«ngtiªut¸nnh−h×nhvÏ.BiÕt®−êngd©ycã
Z = 400 ,®iÖndungriªngdäc®−êngd©yl − 8
C = 10 F/ km,chiÒudil = 250km . c 0
Cuèi®−êngd©ycãl¾pt¶i R = 150 cïngvíihaiphÇntöb¶ovÖL = 0,6H v 2 2
C = 0,1mF .BiÕtt¹ithêi®iÓmt = 0cãmétsãng®¸nhtíi®Çu®−êngd©yvíi 2 2 − 00 u ( ) t = 500 t e ( 1 )
t kV .HIytÝnh®iÖn¸ptrªnt¶iu (t ) toi R2     CuuDuongThanCong.com
https://fb.com/tailieudientucntt 
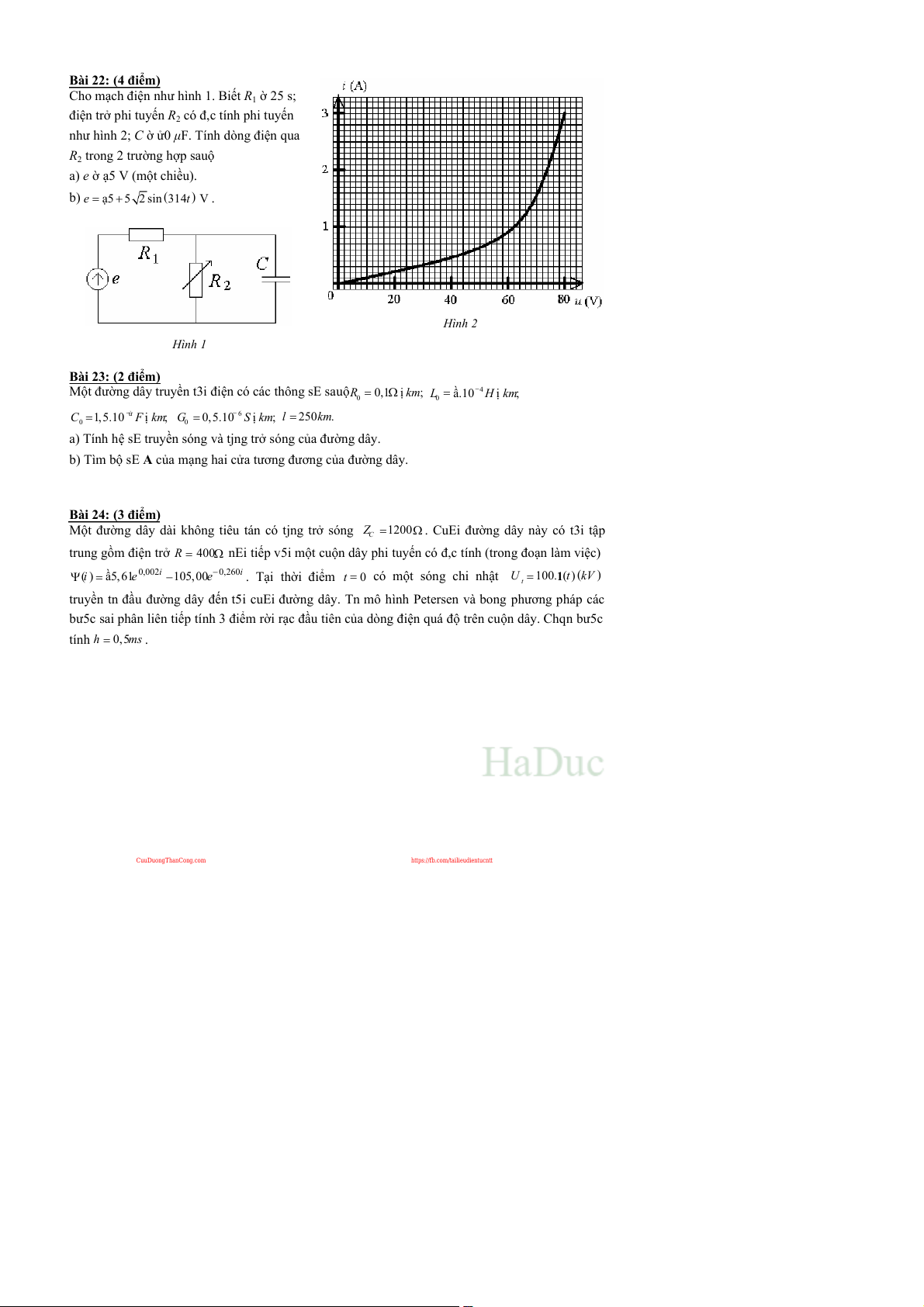
Bài22:(4ñim)
Chom7chñinnhưhình1.BitR1=25s;
ñintrphituynR2cóñ,ctínhphituyn
nhưhình2;C=808F.Tínhdòngñinqua
R2trong2trư=nghHpsau:
a)e=75V(m:tchiUu).
b)e = 75 + 5 2 sin (314t ) V .     Hình2 Hình1 
Bài23:(2ñim)
M:tñư=ngdâytruyUnt3iñincócácthôngsEsau:R = 0,1 / k ; m  −4 L = 9.10 H / k ; m  0 0 8 C 1,5.10 − = F / k ; m  − 6 G = 0,5.10 S / k ; m l = 250k . m  0 0
a)TínhhsEtruyUnsóngvàtjngtrsóngcañư=ngdây.
b)Tìmb:sEAcam7nghaic8atươngñươngcañư=ngdây.  
Bài24:(3ñim)
M:t ñư=ng dây dài không tiêu tán có tjng tr sóng Z =1200 . CuEi ñư=ng dây này có t3i t]p C
trunggmñintrR = 400 nEitipv5im:tcu:ndâyphituyncóñ,ctính(trongño7nlàmvic) 0,002i 0,260 ( ) 95, 61 105,00 i i e e− Ψ = −
. T7i th=i ñiZm t = 0 có m:t sóng chi nh]t U = 100.1(t ) (kV )  t
truyUntnñ9uñư=ngdâyñnt5icuEiñư=ngdây.TnmôhìnhPetersenvàbongphươngphápcác
bư5csaiphânliêntiptính3ñiZmr=ir7cñ9utiêncadòngñinquáñ:trêncu:ndây.Chqnbư5c tínhh = 0,5ms .  CuuDuongThanCong.com
https://fb.com/tailieudientucntt 
Bài25:(3,5ñim)
Chom7chñinnhưhình1.NgunápE=80V,R1=10s,
R3=30s,C=5mF.Cu:ndâyphituyncóñ,ctính:
ψ(i)=3iR0,5i3.ð,ctínhcañintrphituynR2cho trênb3ngsau.
a)KhikhóaKñóng,m7chtr7ngtháixácl]p.Tính 
dòngquacu:ndâyvàñináptrêntñin. Hình1 
b)T7ith=iñiZmt=0,khoáKm,hãytìmñináptrênt ð,ctínhñintrR2:
ñinuctheophươngphápsaiphânliêntipv5ibư5csai U(V)  0 40 60 80
phânh=2ms,tínhgiátr/3bư5ctínhñ9utiên. I(A) 0 0,55 0,8 1,7   
Bài26:(3,5ñim)
Chom7chñinnhưhình2.Bit:j(t) = 3 + 0, 2 2 sin100t A, R = 100; R = 50;  −5
C = 2.10 F. Cu:ndâyphituyncó 1 2 ñ,ctính 3 Ψ(i) = 4i −0, 25i .
TínhdòngquaR1vàcôngsutphátcangun.  Hình2 
Bài27:(2ñim)
Chomôhìnhhaiñư=ngdâydàighépnEitipnhưtrênhình
3.ðư=ngdây1cóZ =
 ñư=ngdây2cóZ =   C 60 . C 300 , 1 2
Kho3ngcáchño7nABl = km t −3 C 10 = F. T7it = 0  AB 100 ,
cóm:tsóngáphìnhchinh]t U = 1 t kV truyUntn t 1500. ( )( ) ñư=ngdây1t5i. 
a)Tínhñinápkhúcx7t7iñiZmA?  Hình3
b)Tínhñinápt7iB bitsóngtruyUntnAñnBv5iv]n tEc2.105km/s. CuuDuongThanCong.com
https://fb.com/tailieudientucntt 
Bài28:(3ñim) 
Chom7chñinnhưhình1.Ngundòngm:tchiUu
J =1A ,ngunápe t = t V; R = 100 ;  1 2 ( ) 10 2 sin100 1 R = 50 ;   − 4
C = 10 F.ðintrphituyncóñ,ctínhphi 2
tuynchobib3ngsau: U(V)  0 7 20 30 35 40 I(A) 0 0,5 1 1,5 2 2,5 
Cu:ndâyphituyncóñ,ctính Ψ (i) 3 = 2i + 3, 25i .Tìm
Hình1 biZuthtuyn? 
Bài29:(2,5ñim)
Chom7chñinnhưhình2.Bit: = V; 1 e ( ) t 100 2 sin1000t
E = 50V (m:tchiUu); R = 100; R = 30 ;   −5 C = 2⋅10 F.  2 1 2
Cu:nc3mphituyncóñ,ctính Ψ(i ) 3 = 2i + 3,15i .
Tìmbongphươngphápsaiphânliêntip3giátr/ñ9utiên
cadòngñinquáñ:trêncu:nc3mphituynkhikhóaK  Hình2
chuyZntn1sang2.(BitkhiK1m7chñãxácl]p;chqn
bư5csaiphânh=1ms) 
Bài30:(3,5ñim)
Tronghình3,2ñư=ngdâydàiñUukhôngtiêután.ðư=ng dây1:L = 0,8H /km ; 6 C 5 10− = ⋅ F / k .
m ðư=ngdây2(ño7n 1 1 AB):L = 0,05 H / km ; −6 C = 0,05 1 ⋅ 0 F / k ; m l =800km.Các 2 2 AB ph9nt8t]ptrung 6 C 0,5 10− = ⋅
F ;  L = 0,5H ; R = 500.T7it t
=0,cóm:tsóngáphìnhchinh]t U = 500.1(t) (kV )truyUn  t 
tnñư=ngdây1t5i. Hình3
a)Tínhñinápkhúcx7t7iñiZmA?
b)Tínhdòngvàápkhúcx7trênt3iRt?  CuuDuongThanCong.com
https://fb.com/tailieudientucntt  Bài31:
Chom7chñinnhưhình1.Bitngun1chiUu
E = 15V ; e (t) = 0,5sin(10t); R =10 ; 3     4 3 R = 20 C =10mF; 5 ;
m7nghaic8athu9ntr 4
cómatr]nñ,ctrưngchotheocácdòngRápnhư 1  ,25 0,5 hìnhvOlà A = 
 ;cu:ndâyphituyn 0  ,25 0,9    
L cóñ,ctínhWebeRAmper: 3 ψ = 2i + 0,4i . Hình1 x
Tínhñináp u (t)trênñintr R . R5 5  Bài32:
Chom7chñinnhưhình2.Bitngunápm:tchiUu E = 15V; E = 1V; R = 5 ;  R = 20 ;   1 2 1 2
R = 5; cu:ndâyphituyncóñ,ctínhWebeR 3 Amper: 3
Ψ = 0,5i + 0,1i ;tñinphituyncóñ,c tínhCulombRVolt: 3
q = 0,2u + 0,001u .Tínhñináp 
trêntphituyn u (t ) chot ≥ 0bit Hình2 Cx
t7i t = 0tañóngkhóaK.Trư5ckhiñóngkhóam7chñãtr7ngtháixácl]p.  Bài33: 
Cho ñư=ng dây truyUn t3i có các thông sE ñ,c
trưngsau:R = 0,1/ k ; m  −3 L = 1,5.10 H /km; 0 0 G = 0S / k ; m  − 8
C =10 F /km;  chiUu dài 0 0
l =150km , t9n sE trong m7ch f = 50Hz . Y
cuEiñư=ngdâytacót3iñintrR = 200 mGc 2 
song song v5i t ñin b3o v C = 0,1mF . Bit 2 Hình3
ñinápñ9uñư=ngdâylàU = 220 0 ɺ ∡ kV . 1
a)TínhñinápcuEiñư=ngdâyUɺ vàcôngsuttiêutántrênñư=ngdâykhiñó. 2 b)Khib\t3iR  ɺ
2và C2 cuEiñư=ng dây(h m7ch cuEiñư=ngdây) thìv5i U = 220 0 ∡ kV dòng 1
ñ9uvào Iɺ sOlàbaonhiêu? 1  CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Ở đây có một số bạn thắc mắc tại sao khi phức hóa mạch điện thì giá trị của nguồn xoay
chiều không chia cho 2, lí do là vì: √
đáp số cần tìm ở dưới dạng hàm thời gian, nên khi phức hóa
nếu chia 2 thì khi tính ra dòng √
điện thì phải nhân√2 trở lại, việc này có thể gây ra sai số.
Do đó tùy vào trường hợp hay câu hỏi của bài toán mà việc phức hóa có thể là cần thiết hay không.
Ví dụ như hàm thời gian cho biên độ dưới dạng 2*A*sin(w*t) thì nên chia √
√2 để được số đẹp hơn.
Các bài tập về đường dây dài cần chú ý về gốc thời gian t=0 lúc sóng đánh vào
để hiệu chỉnh thời gian các thông số đề yêu cầu

Tài liệu liên quan: