Đáp án đề số 3 - Đề thi thử kì thi tốt nghiệp THPT quốc gia 2025 môn Toán lớp 12

ĐỀ SỐ
ĐÁP ÁN - ĐỀ THI THỬ KÌ THI TỐT 03
NGHIỆP THPT QUỐC GIA 2025
Môn: Toán; khối: 12
Thời gian làm bài: 90 phút
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN Câu 1.
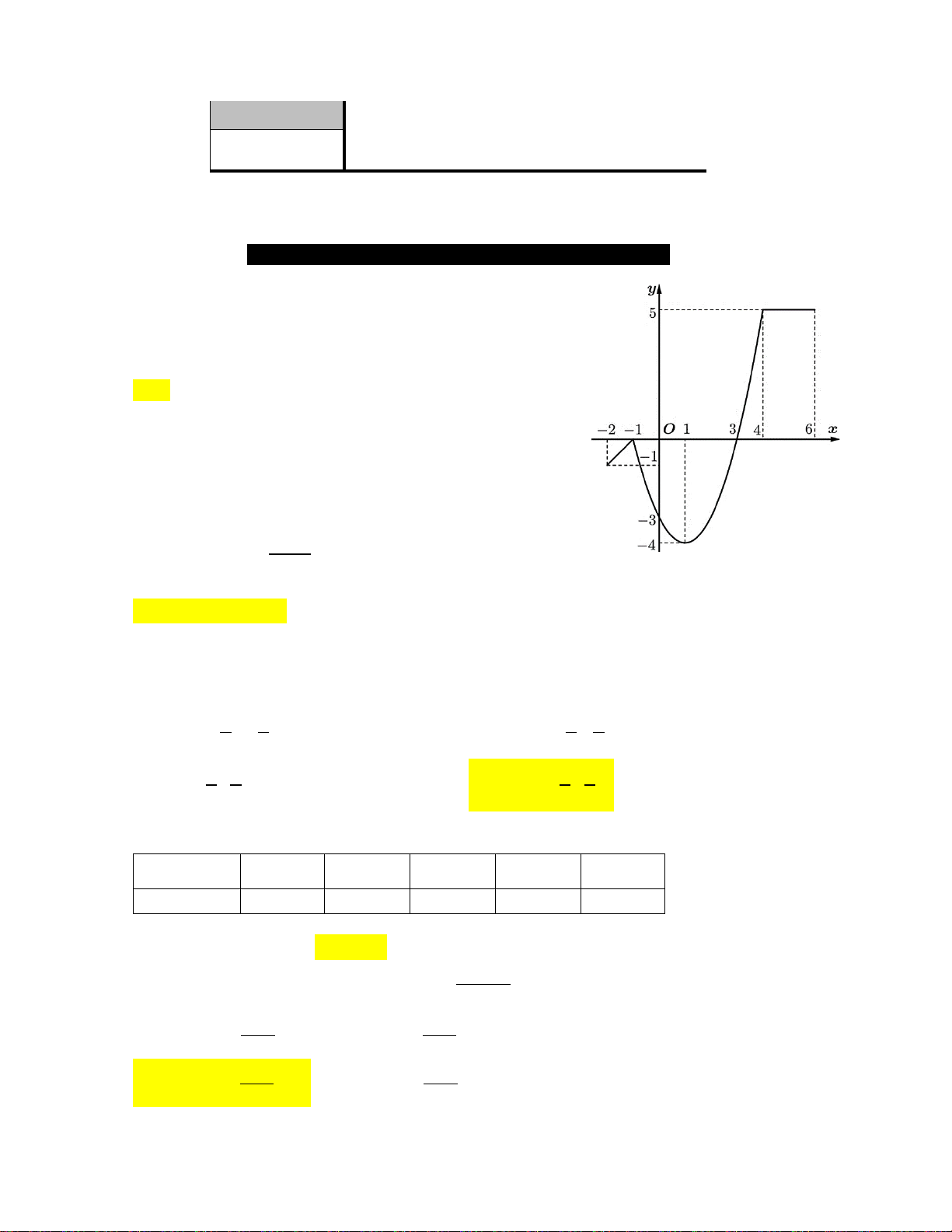
Cho hàm số y  f  x liên tục trên đoạn 2; 6 và có đồ thị như hình vẽ bên dưới.
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số
đã cho trên đoạn 2; 6 . Giá trị của M  m bằng A. 9 . B. 8  . C. 9  . D. 8 . 1 3x Câu 2.
Đồ thị hàm số y 
có các đường tiệm cận đứng và tiệm x  2
cận ngang lần lượt là:
A. x  2 và y  3 .
B. x  2 và y  1.
C. x  2 và y  3 .
D. x  2 và y  1. Câu 3.
Trong không gian Oxyz , cho ba điểm A1; 1; 
1 , B 5; 1; 2 , C 3; 2;  4 Tìm tọa độ điểm M uuur uuur uuuur r
thỏa mãn MA  2MB  MC  0 .  3 9   3 9 
A. M 4;  ;    . B. M 4  ;  ;   .  2 2   2 2   3 9   3 9  C. M 4; ;   . D. M 4;  ;   .  2 2   2 2  Câu 4.
World cup 2022 diễn ra tại Qatar có tất cả 64 trận đấu, người ta thống kê lại số phút bù giờ (hiệp 2)
của 64 trận đấu này theo bảng dưới đây: Nhóm 5; 7 7; 9
9; 1 1 11; 13 13; 15 Số trận đấu 7 16 21 12 8
Độ lệch chuẩn của mẫu số liệu ghép nhóm gần nhất với giá trị nào sau đây? A. 2, 233 . B. 2, 344 . C. 2, 455 . D. 2,133 . 3x 1 Câu 5.
Họ tất cả các nguyên hàm của hàm số f (x) 
trên khoảng (1;  ) là 2 (x 1) 1 2
A. 3ln(x 1) 
 C . B. 3ln(x 1)   C . x 1 x 1 2 1
C. 3ln(x 1) 
 C . D. 3ln(x 1)   C . x 1 x 1 1 3 3 Câu 6. Cho
f (x) dx  1  
; f (x) dx  5  . Tính f (x) dx  . 0 0 1 A. 1. B. 4 . C. 5 . D. 6 . Câu 7.
Cho hình lập phương có thể tích bằng 8 . Diện tích toàn phần của hình lập phương là A. 36 . B. 48 . C. 16 . D. 24 . Câu 8. Hàm số 2
y  x ln x đạt cực trị tại điểm 1 1 A. x  e .
B. x  0 ; x  . C. x  0 . D. x  . e e Câu 9.
Trong không gian Oxyz , một véctơ pháp tuyến của mặt phẳng Oyz  là r r r r
A. i  1; 0; 0 .
B. n  0; 1;  1 .
C. j  0; 1; 0 .
D. k  0; 0;  1 . x  3 y  2 z  2
Câu 10. Trong không gian Oxyz , cho đường thẳng d :  
và hai điểm A5; 3;   1 , 1 1  2
B 3; 1;  2 . Tọa độ điểm C thuộc d sao cho tam giác ABC vuông tại B là A. 4; 1; 0 . B. 3; 2;  2 . C. 2; 3;  4 .
D. 5; 0; 2 . 13x  2  25
Câu 11. Tập nghiệm S của bất phương trình    là  5  4 1   1 
A. S  ;  1 . B. S  ;     . C. S  ;  .
D. S  1;   .   3   3
Câu 12. Phương trình tiếp tuyến của đồ thị hàm số y  f  x   x  2 2
1 tại điểm M 2; 9 là
A. y  6x  3 .
B. y  8x  7 .
C. y  24x  39 .
D. y  6x  21 .
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI   
Câu 13. Cho hàm số f  x  tan x    .  4 
Xét tính đúng sai các mệnh đề sau: Đúng Sai 3 
a) Tập xác định của hàm số y  f  x là ¡ \ 
 k2 | k ¢  .    4 
b) Hàm số y  f  x tuần hoàn với chu kỳ 2 .   
c) Phương trình f  x  0 có nghiệm x 
 k , k ¢ .   4 
d) Phương trình f  x  cot
có bốn nghiệm thuộc  2   ; 2  .   5
Hướng dẫn giải a) Mệnh đề sai.   3
Hàm số xác định  x 
  k , k ¢  x 
 k , k ¢ . 4 2 4 3 
Do đó tập xác định hàm số là D  ¡ \ 
 k | k ¢ .  4  b) Mệnh đề sai.   
Xét hàm số f  x  tan x    ;  4       
Với mọi x  D thì x    D và f  x     tan x     tan x   f     x  4   4    
Do vậy hàm số f  x  tan x  
 tuần hoàn với chu kỳ T   .  4 
c) Mệnh đề đúng.     
Ta có: f  x  0  tan x   0  
 x   k , k ¢  x   k , k ¢ .  4  4 4
d) Mệnh đề đúng.        
Ta có: f  x  cot  tan x   tan      5  4   2 5     11
 x     k , k ¢  x 
 k , k ¢ . 4 2 5 20 11 Vì x  2   ; 2  nên 2   
 k  2 , k ¢ 20 51 29 51 29    k  , k  ¢    k 
, k  ¢  k  2  ; 1; 0;  1 . 20 20 20 20  29 9
Do đó phương trình f  x  cot
có bốn nghiệm thuộc  2
  ; 2  là: x   ; x   ; 5 20 20 11 31 x  ; x  . 20 20
Câu 14. Mộ bộ bài tú lơ khơ có 52 lá được chia như sau:
 Người thứ nhất rút 2 lá.
 Người thứ hai rút 2 lá từ 50 lá còn lại.
Bổ túc kiến tức cờ bạc: Một bộ bài tú lơ khơ có 26 lá bài đỏ và 26 lá bài
đen; cả bộ bài có 4 lá Át (2 đỏ và 2 đen).
Xét tính đúng sai các mệnh đề sau: Đúng Sai 31
a) Xác suất để người thứ nhất rút được ít nhất 1 lá Át bằng   221
b) Xác suất để người thứ hai rút được đúng 1 lá Át, biết người thứ nhất không rút 181  Át nào bằng .  1225 26
c) Xác suất để người thứ hai rút được đúng 1 lá đỏ bằng .   51
d) Xác suất người thứ nhất đã rút được 1 lá đen và 1 lá đỏ, biết người thứ hai rút 24   được 1 lá đỏ bằng . 49
Hướng dẫn giải
a) Mệnh đề sai. 2 C 188
Xác suất để người thứ nhất không rút được lá Át nào là 48  . 2 C 221 52 188 33
Xác suất để người thứ nhất rút được ít nhất 1 lá Át là 1  . 221 221 b) Mệnh đề sai.
Người thứ nhất không rút được lá Át nào nên trong 50 lá còn lại vẫn còn 4 lá Át (cụ thể là còn 4 lá Át và 46 lá khác). 1 1 C  C 184
Xác suất để người thứ hai rút được đúng 1 lá Át là 4 46  . 2 C 1225 50 c) Mệnh đề đúng.
Gọi các biến cố B: “Người thứ hai rút được ít nhất 1 lá đỏ” và biến cố A: “Người thứ nhất rút được 1 lá đen và 1 lá đỏ”. C 24  26 26  26 25  25 C 26  24 26
Ta có: P  B 2 2 26 26        . 2 2 2 2 2 2 C C C C C C 51 52 50 52 50 52 50 d) Mệnh đề sai. 26  26 25 25  2 2 P AB C C 25
Ta có: P  A | B   52 50    . P  B 26 49 51
Câu 15. Trên cánh đồng vắng, với một hệ trục tọa độ Oxyz thích hợp
sao cho mặt đất là mặt phẳng Oxy, tia Oz hướng lên trời, đơn vị
trên mỗi trục là mét, một con chim rời khỏi tổ của mình ở vị trí  r
0; 8; 4, 5 và bay đi với vectơ chỉ hướng u  2;  4;  1 , vận
tốc trung bình của chim khoảng 3 21 m/s. Cùng lúc đó, có một
viên đá được bắn đi từ vị trí 40;  2; 1,5 với vectơ chỉ r
hướng là v   36
 ; 2; 5 , vận tốc viên đá là 5 53 m/s.
Xét tính đúng sai các mệnh đề sau: Đúng Sai x y  8 z  4,5
a) Phương trình đường bay của chim là   .   2 4  1
b) Nếu không có gì thay đổi, viên đá sẽ đi qua vị trí 4; 0; 6,5  
c) Mặt phẳng chứa đường bay của chim và viên đạn có phương trình  
11x  23y  70z  499  0 .
d) Kể từ lúc bay ra khỏi tổ thì khoảng cách ngắn nhất giữa chim và viên đá bằng bao nhiêu?  
Hướng dẫn giải
a) Mệnh đề đúng. x y  8 z  4, 5
Phương trình đường bay của chim là d :   . 1 2 4  1
b) Mệnh đề đúng. x  40 y  2 z 1,5
Phương trình đường bay của viên đạn là d :   . 2 3  6 2 5 4  40 0  2 6,5 1,5
Thay tọa độ 4; 0; 6,5 vào phương trình d ta được:   (đúng). 2 3  6 2 5
Do vậy đường bay viên đạn sẽ qua 4; 0; 6,5 .
c) Mệnh đề đúng. x  2t  2t  40 8  4t  2 4, 5  t 1, 5
Phương trình tham số d :  y  8  4t ; thay vào d :    t  2 . 1 2  3  6 2 5 z  4, 5  t 
Do đó hai đường thẳng d , d cắt nhau tại M 4; 0; 6,5 . 1 2 r r r
Mặt phẳng (P) chứa d , d có vectơ pháp tuyến u , v   2  2; 46; 1  40  2  11; 23; 70  2  n . 1 2
Phương trình (P) là 11 x  4  23 y  0  70 z  6,5  0 hay 11x  23y  70z  499  0 .
d) Mệnh đề đúng. r 1 r  2 4  1 
Vectơ vận tốc của chim là a  r u 3 21  ; ; 3 21    6; 12; 3. u  21 21 21  r 1 r  3  6 2 1 
Vectơ vận tốc viên đá là b  r v 5 53  ; ; 5 53     3  6; 2; 5 . v  5 53 5 53 53 
Tọa độ của chim và viên đá tại thời điểm t lần lượt là: M 6t ; 8 12t ; 4,5  3t  , uuuur
N 40  36t ;  2  2t ; 1,5  5t  ; suy ra MN  40  42t ; 10 14t ;  3  2t  và MN  
 t2   t  2   t  2 40 42 14 10 2 3 .
Giá trị MN bé nhất là MN
 3,36 m ; khi đó t  0,93 giây. min
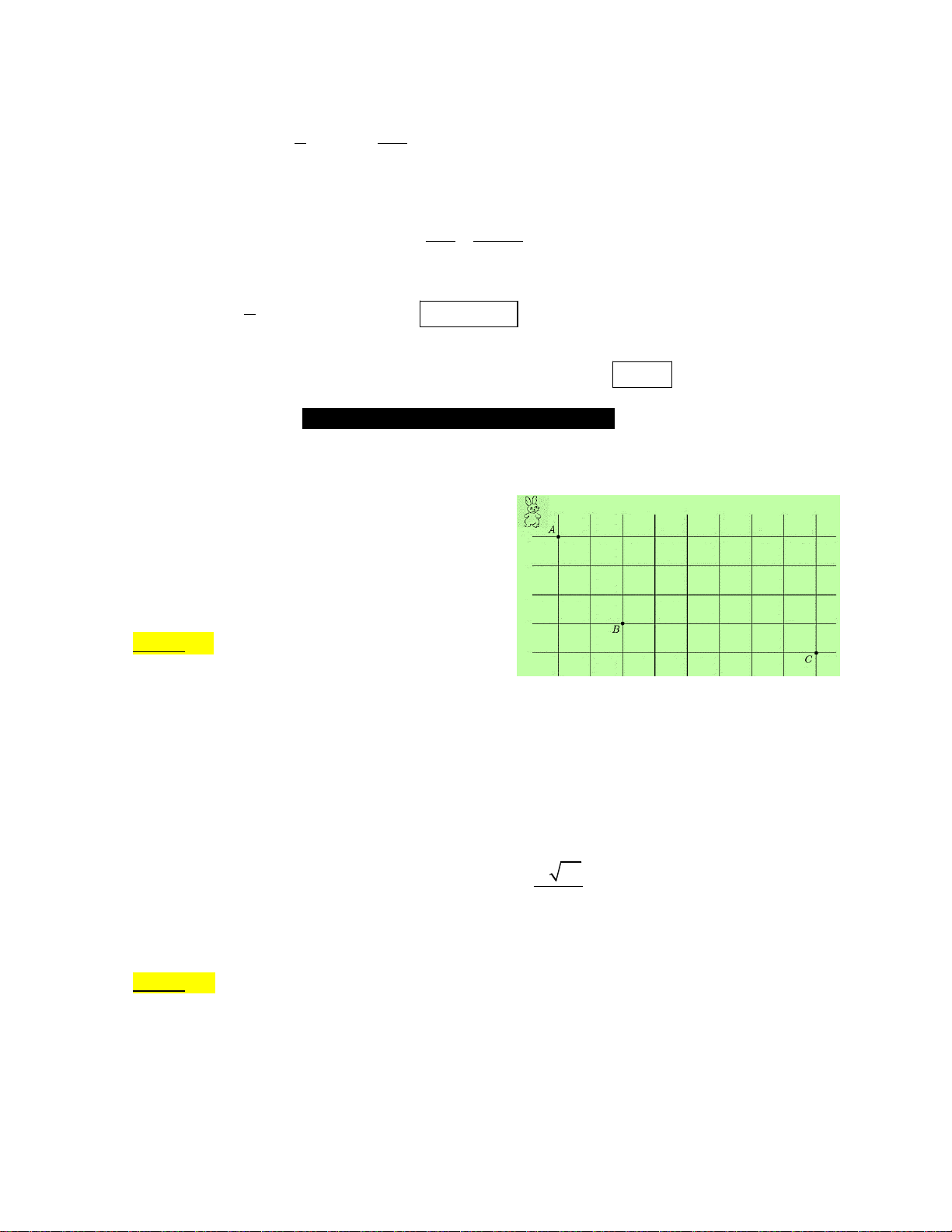
Câu 16. Chậu nước có chiều cao 2 m; thiết diện qua trục cho ta hình ảnh hai parabol
đối xứng nhau qua trục chậu nước, hai đỉnh parabol này cách nhau 1 m. Hai
đường tròn đáy và miệng chậu nước đều có bán kính 1 m. Mực nước ban
đầu trong chậu cao 0,2 m.
Dựng một hệ trục tọa độ Oxy sao cho gốc tọa độ trùng với tâm của đường
tròn đáy, tia Ox đi qua tâm của miệng chậu nước. Gọi parabol (P) là một
đường sinh của chậu nước.
Xét tính đúng sai các mệnh đề sau: Đúng Sai
a)  P qua các điểm 0; 0, 1; 0,5, 2;  1 .   14
b) Thể tích chậu nước bằng 3  m .   15
c) Thể tích nước trong chậu bằng 3
0, 53 m (làm tròn đến hàng phần trăm).  
d) Bỏ một viên bi có bán kính 0,1 m vào chậu; chiều cao nước tăng thêm  
bằng 0,2 cm (làm tròn đến hàng phần chục của cm).
Hướng dẫn giải
Dựng hệ trục tọa độ Oxy theo yêu cầu đề bài, không làm mất tính tổng quát, ta cho mặt cầu tiếp xúc
đáy chậu tại tâm của đáy chậu. Gọi hàm số bậc hai là  P 2
: y  ax  bx  c a  0 . a) Mệnh đề sai.
P qua các điểm 0; 1, 1; 0,5, 2; 1.
b) Mệnh đề đúng.
Từ câu a) ta có hệ phương trình  1 a  c 1  2  
a  b  c  0,5  b   1 hay  
4a  2b  c  1 c  1    P 1 2 : y  x  x 1 . 2 2 2  1  14 Thể tích chậu là 2 3 V   x  x 1 dx   m   .  2  15 0 c) Mệnh đề sai. 0,2 2  1  7 732
Thể tích nước ban đầu trong chậu là 2 3 V   x  x 1 dx    0,52 m  . 0    2  46875 0
d) Mệnh đề đúng. 4  Thể tích viên bi là 3 V   0,1  . 1 3 750
Vì nước ban đầu có chiều cao 0,2 m mà bi có bán kính 0,1 m nên bi sẽ chìm trong nước.  7 732
Tổng thể tích bi và nước là V  V V  
  0,52239 (lưu vào A). 2 0 1 750 46875 h 2 1 Ta có 2 V     x  x 1
dx  A  h  0, 202 m  (lưu vào B). 2    2  0
Chiều cao tăng thêm của mực nước là h
  h  0, 2  0,00199 m  0, 2 cm .
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
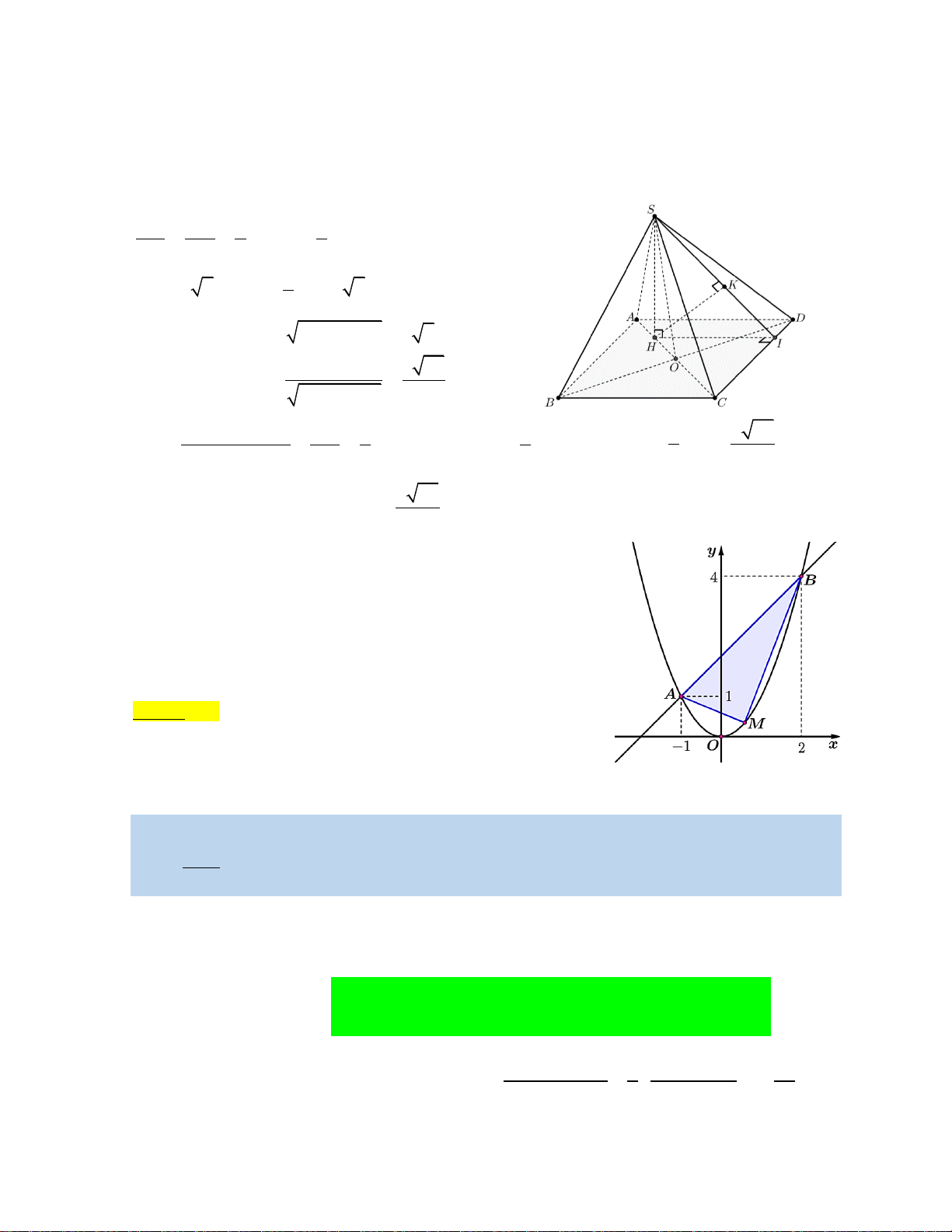
Câu 17. Trên hình vẽ là lưới các ô vuông có cạnh 1 đơn vị. Một con thỏ từ vị trí A cần đến vị trí B để tìm thức
ăn, sau đó đến vị trí C để uống nước, và cuối cùng lại trở về vị trí A ban đầu. Biết rằng mỗi lần nhảy là
thỏ di chuyển được qua một cạnh của hình vuông
đơn vị; khi đi từ A đến B rồi từ B đến C thì thỏ chỉ có
hai hướng: xuống hoặc sang phải; khi đi từ C về A thì
thỏ đi đúng con đường đã chọn khi đi từ A đến C.
Hỏi thỏ có bao nhiêu cách đi như thế?
Trả lời:  Đáp số: 70
Hướng dẫn giải
Khi đi từ A đến B có 2 lần sang phải và 3 lần xuống dưới nên có tổng cộng là 2 3
C  C  10 cách. 5 3
Khi đi từ B đến C có 6 lần sang phải và 1 lần xuống dưới nên có tổng cộng là 6 1
C  C  7 cách. 7 1
Khi đi từ C đến A thỏ chỉ có 1 cách đi (đó cũng là con đường lúc đi từ A đến C).
Vậy số cách đi của thỏ là 10  7 1  70 (cách).
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh bằng 4a . Cạnh bên SA  2a .
Hình chiếu vuông góc của đỉnh S trên mặt phẳng  ABCD là trung điểm H của đoạn AO . m 22
Khoảng cách giữa các đường thẳng SD và AB bằng
a (trong đó m , n nguyên tố cùng n nhau). Tính giá trị 2 2 m  n .
Trả lời:  Đáp số: 137
Hướng dẫn giải
Ta có AB// SCD  d  AB , SD  d  AB , SCD  d  A, SCD.
Gọi I là hình chiếu của H trên CD và K là hình chiếu của H trên SI . C  D  HI  Ta có: 
 CD  SHI   CD  HK ; mà SI  HK nên CD  SH  do SH   ABCD
HK  SCD  d H , SCD  HK . Vì
HI //AD (cùng vuông góc với CD) nên HI CH 3   3
 HI  AD  3a; AD CA 4 4 1
AC  4 2a ; AH  AC  2a . 4 Xét S V HA có: 2 2 SH 
SA  AH  a 2 . HI  SH 3 22 Xét SHI V có: HK   a . 2 2  11 SH HI
d  A, SCD AC 4 4 Ta có:      4 4 22  HK  . a d 
d  A, SCD 
d H , SCD H , SCD   HC 3 3 3 11 4 22 m  4
Vậy d  AB , SD  d  A, SCD  2 2 a  
 m  n 1 7 3 . 11 n 11 Câu 19. Cho parabol 2
(P) : y  x và hai điểm (
A 1; 1) , B(2; 4) thuộc (P).
Biết M là điểm trên cung AB của (P) sao cho diện tích tam giác
MAB lớn nhất; khi đó tính diện tích phần nằm trong tam giác
cong AMB và nằm ngoài tam giác AMB, làm tròn đến hàng phần trăm.
Trả lời:  Đáp số: 1,13
Hướng dẫn giải
Nhận xét: Trong bài giải này, chúng ta sử dụng một dẫn xuất từ BĐT AM-GM như sau: 2  a  b  ab  
 với mọi a , b không âm; dấu đẳng thức xảy ra khi và chỉ khi a  b .  2  Gọi 2
M (a ; a )  (P) , ( 1
  a  2 ); phương trình đường thẳng AM : y  (a 1)x  a .
Phương trình đường thẳng BM : y  (a  2)x  2a ; phương trình đường thẳng AB : y  x  2 . a 2
Diện tích tam giác MAB là: S   x  2  (a 1)x  adx  
x2(a2)x2adx  1  a a 2 2          3(2 a)(a 1) 3 2 a a 1  27
2x  ax  2  adx  x  ax  2a  2dx      . 2 2  2  8 1  a 27  
Giá trị lớn nhất của diện tích MAB là S 
; khi đó 2  a  a  1 1  a  1 1  M ; . max   8 2  2 4  2 27
Diện tích cần tính là S   2
x  2  x dx    1,13 8 1 
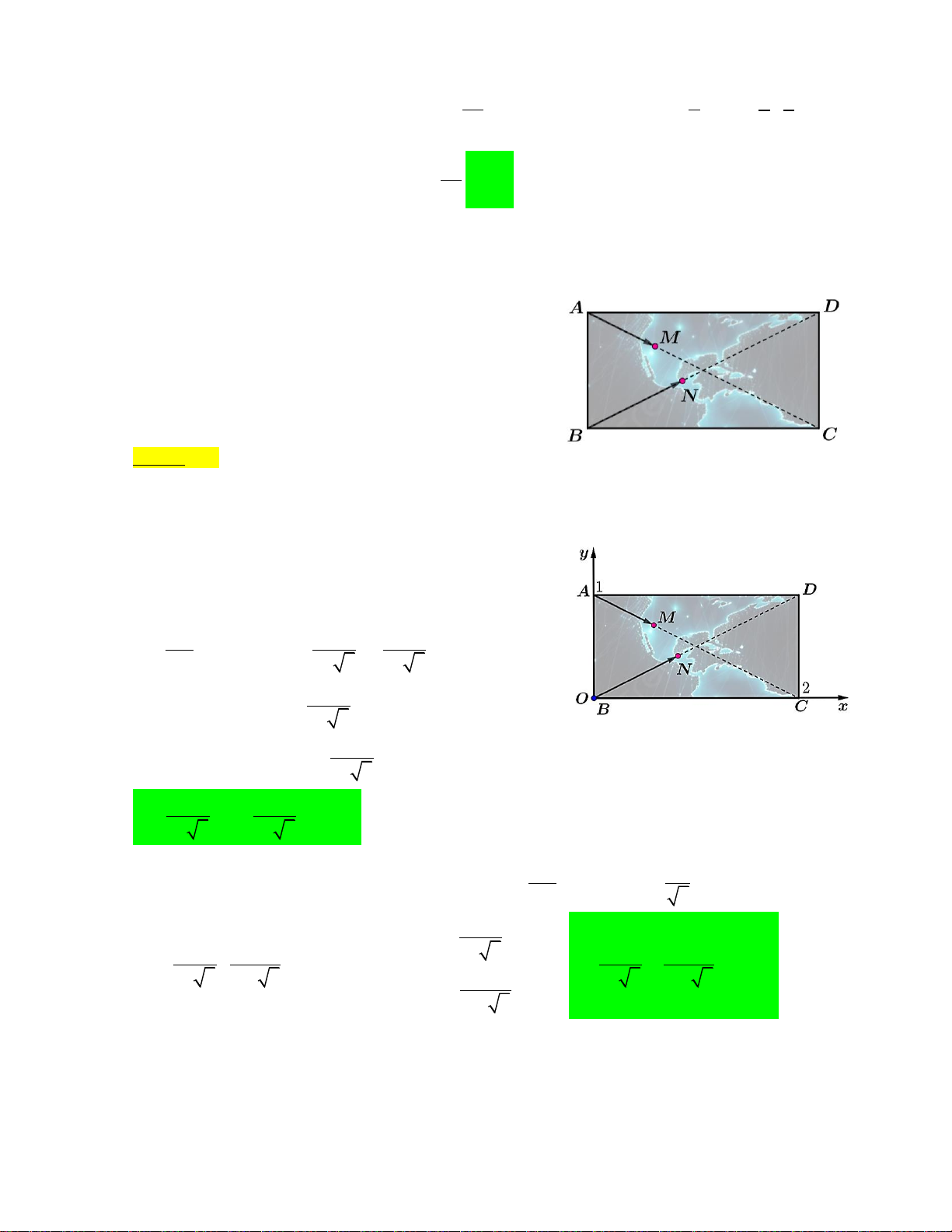
Câu 20. Trên một banner quảng cáo du lịch có bề mặt hình chữ nhật, người ta gắn hai đèn led chạy dọc theo
các đường chéo AC và BD, khi bật nguồn thì chúng bắt đầu cùng lúc.
Đèn led thứ nhất có điểm chạy là M: chạy từ A đến C với tốc độ 2 cm/s.
Đèn led thứ hai có điểm chạy là N: chạy từ B đến D với tốc độ 3 cm/s.
Tính khoảng cách ngắn nhất của MN và làm tròn đến hàng
phần trăm theo đơn vị mét biết ABCD là hình chữ nhật có
hai cạnh lần lượt là 1 m và 2 m.
Trả lời:  Đáp số: 0,37
Hướng dẫn giải
Dựng hệ trục tọa độ Oxy như hình vẽ với B trùng với gốc tọa độ O; tia Ox trùng tia BC, tia Oy trùng tia
BA; đơn vị trên mỗi trục là mét.
Ta có: B 0; 0, A0; 
1 , C 2; 0, D 2;  1 . uuur
Do đó AC  2;  
1 ; vectơ vận tốc đèn led thứ nhất là 1 uuur r  1 1  u   AC 0,02  ;    ; phương trình AC  25 5 50 5   1 x  t  25 5
chuyển động AC là    1  y 1 t  50 5  1 1  M t ; 1 t  AC   .  25 5 50 5  uuur 1 uuur r 1 Ta có BD  2; 
1 , vectơ vận tốc đèn led thứ hai là v   BD0,03  2;  1  0, 03 ; hay BD 5  3 x  t  r  3 3   50 5  3 3  v  ; 
phương trình BD:    N t ; t  BD   .  50 5 100 5  3   50 5 100 5  y  t  100 5 2 2  1   1  2 29 Ta có MN  t  t 1   
 ; giá trị nhỏ nhất MN   0,37 m ; khi đó  min 50 5   20 5  29 t  38, 55 giây.
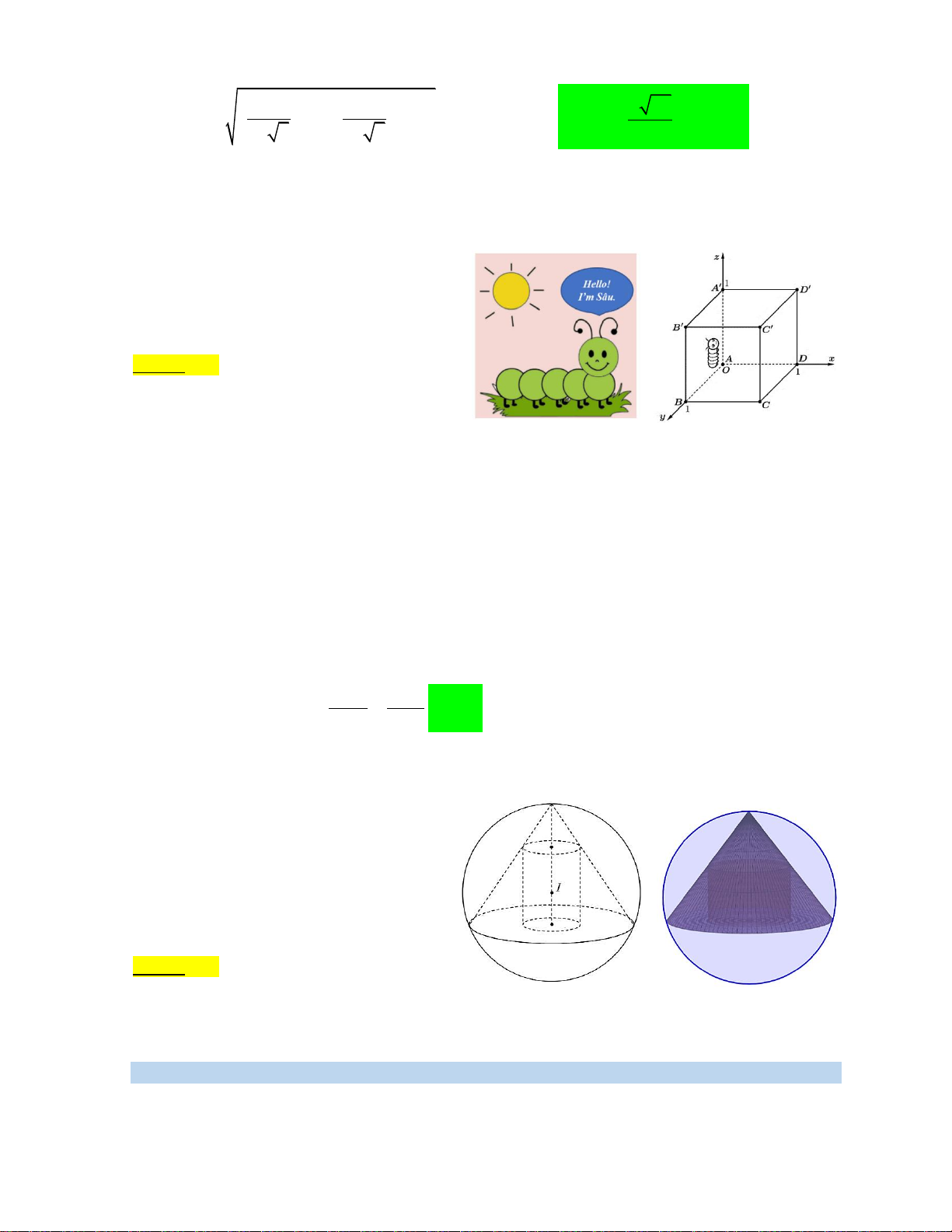
Câu 21. Một bé sâu đang ở đỉnh A trên một hình lập phương ABC . D AB C  D
  . Mỗi lần di chuyển, bé sâu bò
theo cạnh của hình lập phương và đi đến đỉnh kề với đỉnh bé đang đứng. Tính xác suất sao cho sau 9
lần di chuyển, bé sâu đứng tại đỉnh C của
hình lập phương đó (làm tròn kết quả đến hàng phần trăm).
Trả lời:  Đáp số: 0,25
Hướng dẫn giải
Mỗi lần di chuyển, con sâu có 3 phương án đi nên số phần tử của không gian mẫu là 9 3 .
Xét hệ trục tọa độ Oxyz như hình vẽ với gốc tọa độ là A0; 0; 0  O , điểm C1; 1;  1 .
Mỗi lần di chuyển, tọa độ vị trí con sâu đang đứng thay đổi đúng một trong ba thành phần x hoặc y
hoặc z ; và thay đổi từ 0 thành 1 hoặc từ 1 thành 0.
Vì tọa độ ban đầu là 0; 0; 0 và tọa độ kết thúc là 1; 1; 
1 nên số lần thay đổi ở mỗi thành phần
là số lẻ và tổng số lần thay đổi bằng 9.
Số lần thay đổi ở các thành phần x ; y ; z có thể là: 1; 1; 7 ; 1; 3; 5 ; 3; 3; 3 và các hoán vị của
nó. Do đó, số đường đi là: 1 1 1 3 3 3
3C C  3!C C  C C  4920 . 9 8 9 8 9 6 4920 1640
Vậy xác suất cần tìm là P    0, 25 . 9 3 6561
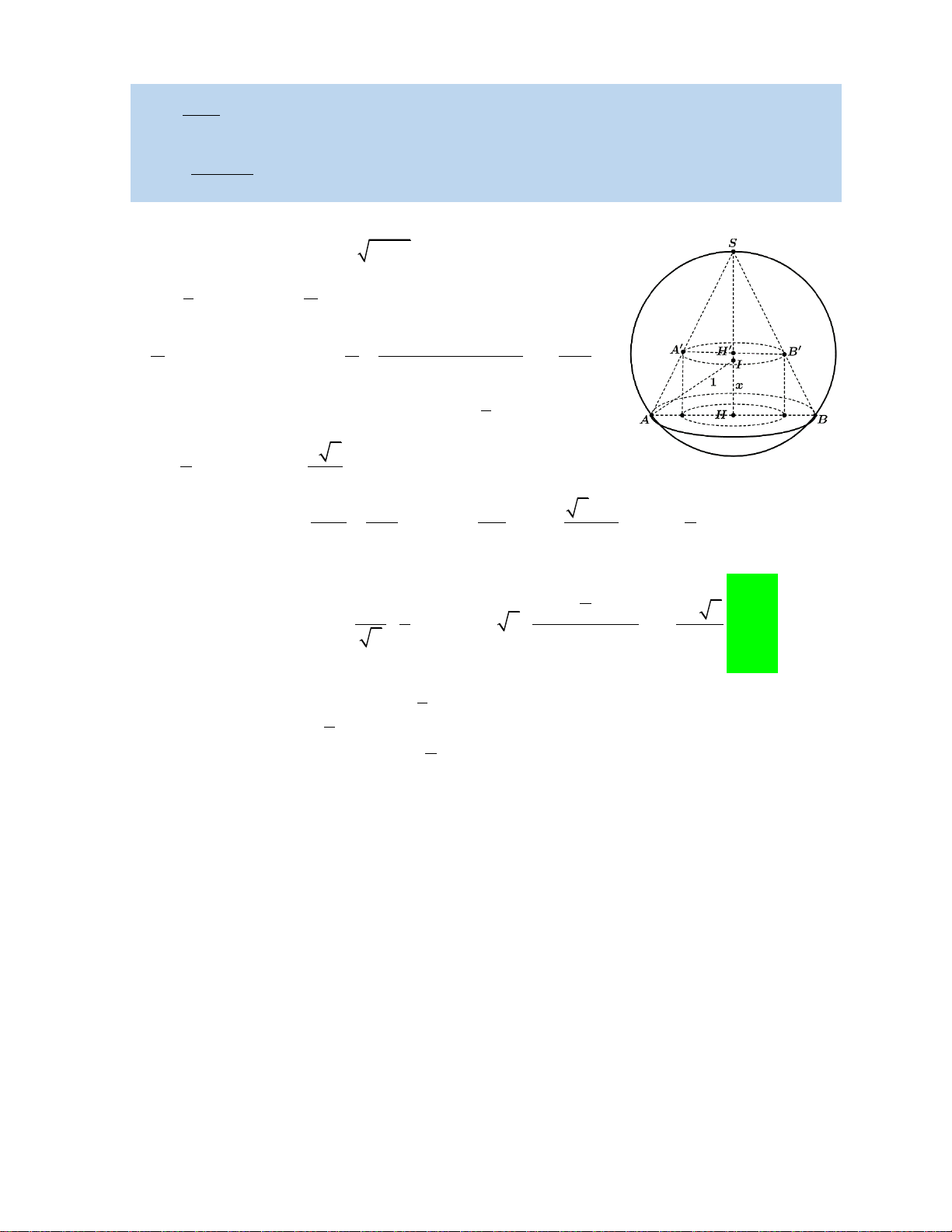
Câu 22. Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2x  2 y  2z  2  0 . Gọi  N  là hình
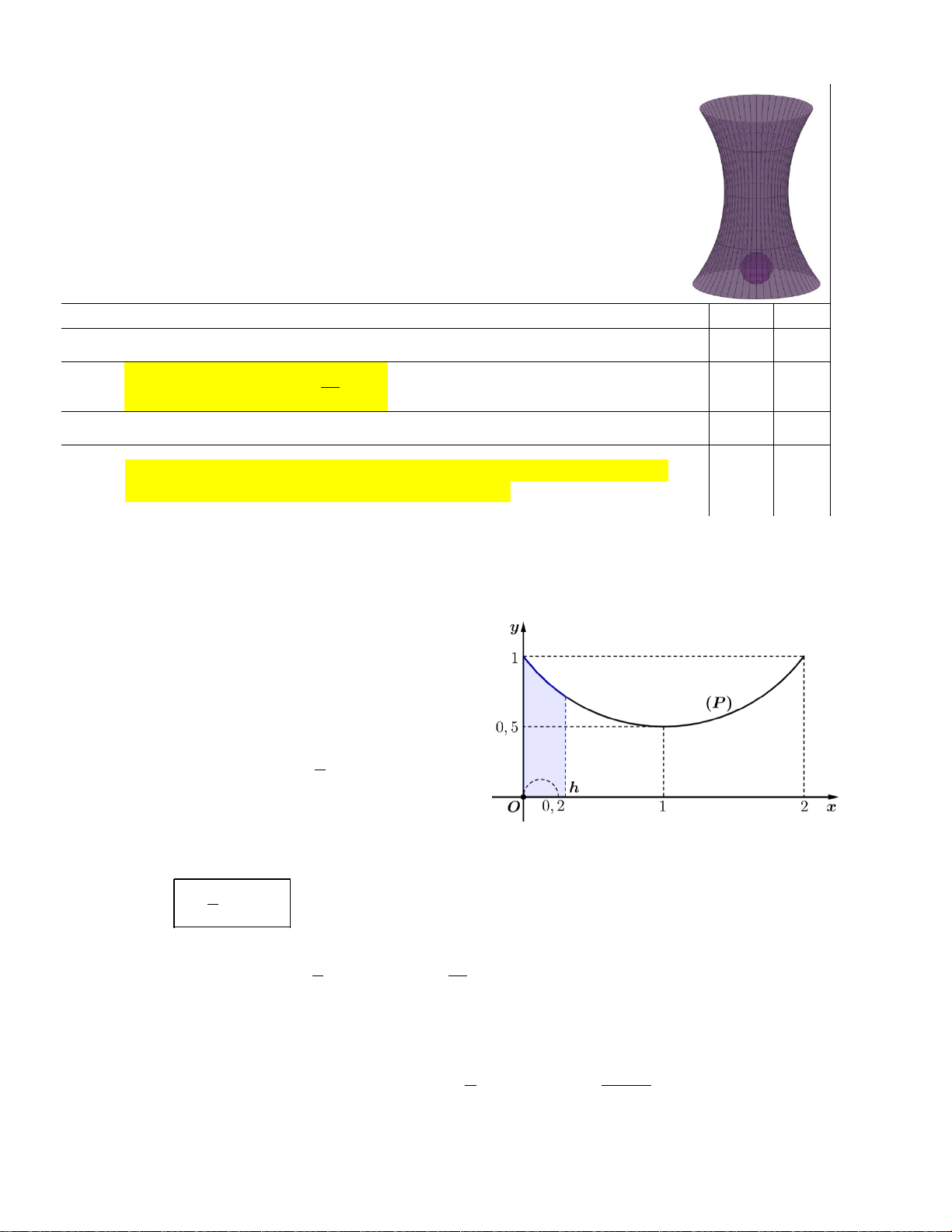
nón có thể tích lớn nhất nội tiếp trong mặt
cầu S  và T  là hình
trụ có diện tích xung quanh lớn nhất S max
nội tiếp bên trong hình nón (như hình vẽ).
Tìm diện giá trị S đó và làm tròn đến max hàng phần trăm.
Trả lời:  Đáp số: 1,97
Hướng dẫn giải
Nhận xét: Trong bài giải này, chúng ta sử dụng một dẫn xuất từ BĐT AM-GM như sau: 2  a  b  ab  
 với mọi a , b không âm; dấu đẳng thức xảy ra khi và chỉ khi a  b .  2  3
 a  b  c  abc  
 với mọi a , b, c không âm; dấu đẳng thức xảy ra khi và chỉ khi a  b  c .  3 
Mặt cầu S  tâm I 1; 1; 
1 , bán kính R  1 .
Đặt IH  x   2
0; 1  AH  1 x , thể tích khối nón là 1  2 V
   HA  SH   x  x N  2 1 1    3 3  3            1 x 1 x 2 2x 32
1 x1 x2  2x      . 6 6  3  81 1  V
đạt giá trị lớn nhất khi 1 x  2  2x  x  ; N  3 4 2 2 SH 
 HA  HB  . 3 3 H B   SH HB 2SH  4
Theo định lí Ta-lét ta có:   H B     SH  ; HH    SH . HB SH SH 2 3
Diện tích xung quanh của trụ là 2  4  SH    SH SH   4    4 2 3 S    H B
  HH     SH         1,97 . xq T  2 2 2 2  3  2 9      1 H I  2  3
Dấu bằng xảy ra khi SH    
, khi đó I là trung điểm HH  . 3 2 HH   3
_________________HẾT_________________