Đáp án đề số 9 - Đề thi thử kì thi tốt nghiệp THPT quốc gia 2025 môn Toán lớp 12

ĐỀ SỐ
ĐÁP ÁN - ĐỀ THI THỬ KÌ THI TỐT 09
NGHIỆP THPT QUỐC GIA 2025
Môn: Toán; khối: 12
Thời gian làm bài: 90 phút
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN Câu 1.
Nghiệm của phương trình log 2x 1  2 là: 3   9 7 A. x  3 . B. x  5 . C. x  . D. x  . 2 2 Câu 2.
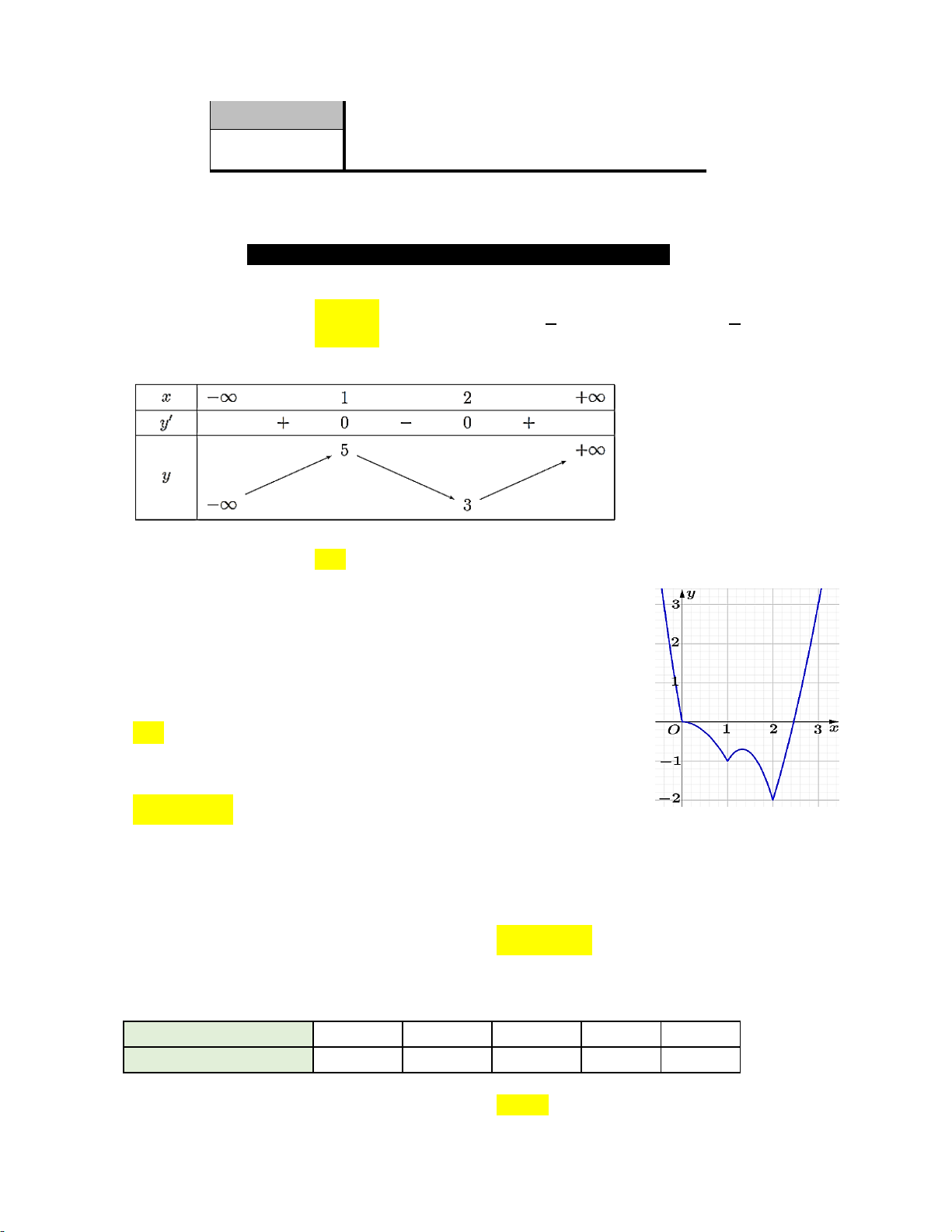
Cho hàm số y  f  x có bảng biến thiên như hình vẽ.
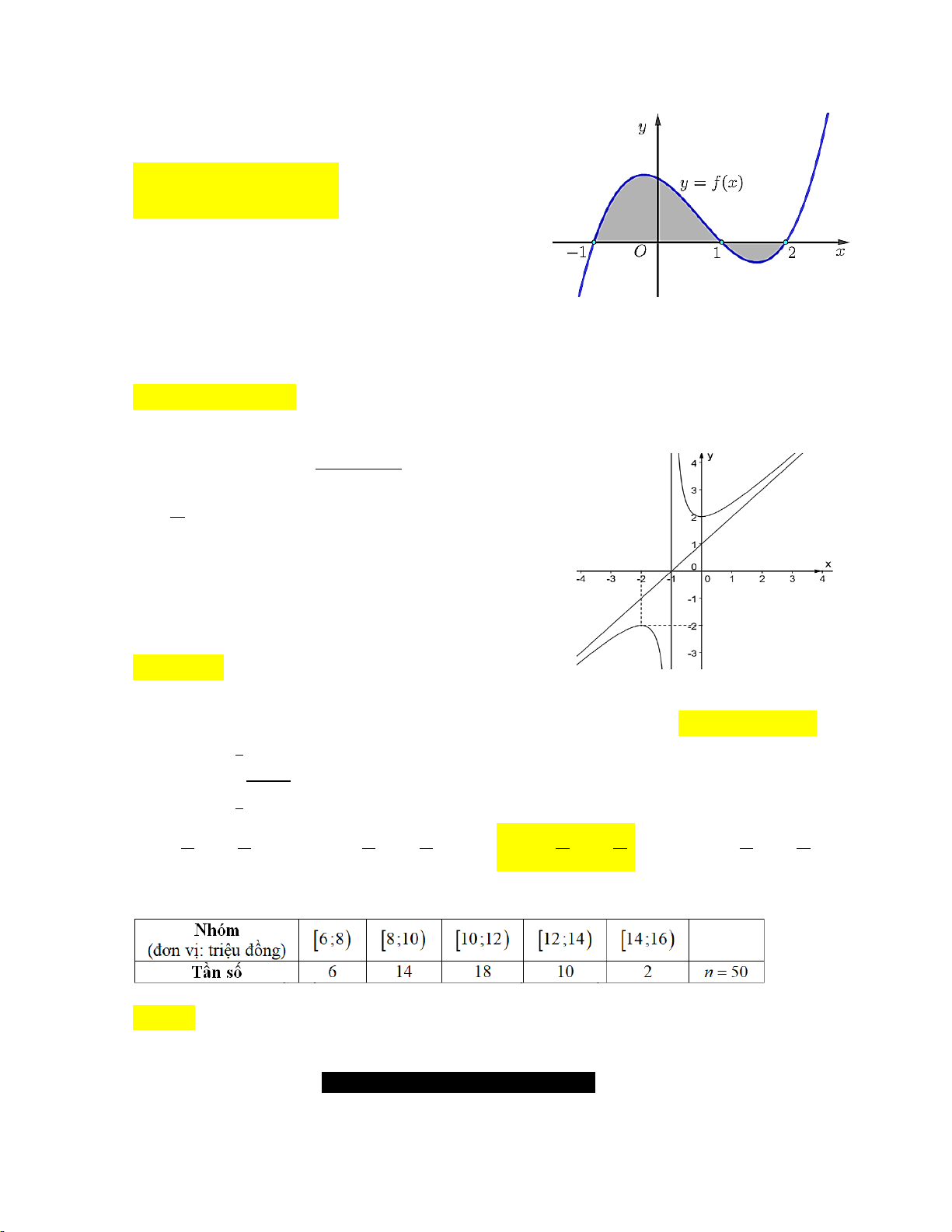
Giá trị cực tiểu của hàm số đã cho bằng A. 2. B. 3. C. 1. D. 5. Câu 3.
Cho hàm số f  x liên tục trên đoạn 0; 
3 và có đồ thị như hình vẽ
bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên 0; 
3 . Giá trị của M  m bằng? A. 5 . B. 3 . C. 2 . D.1. uuuur r r r Câu 4.
Trong không gian Oxyz , cho OM  6 j  4i  3k . Toạ độ của điểm M là A. 4;6;  3 . B.  6  ; 4;3 . C.  4  ;6;3 .
D. 6; 4;  3 . uuur uuur Câu 5.
Trong không gian, cho tứ diện ABCD . Ta có AB  CD bằng uuur uuur uuur uuur
A. AD  BC .
B. DA  CB . uuur uuur uuur uuur
C. DA  BC .
D. AD  CB . Câu 6.
Dũng là học sinh rất giỏi chơi rubik, bạn có thể giải nhiều loại khối rubik khác nhau. Trong một lần tập
luyện giải khối rubik 3 × 3, bạn Dũng đã tự thống kê lại thời gian giải rubik trong 25 lần giải liên tiếp ở bảng sau: Thời gian giải rubik [8; 10) [10; 12) [12; 14) [14; 16) [16; 18) Số lần 4 6 8 4 3
Độ lệch chuẩn của mẫu số liệu ghép nhóm có giá trị gần nhất với giá trị nào dưới đây? A. 5,98. B. 6. C. 2,44. D. 2,5. Câu 7.
Gọi S là diện tích miền hình phẳng tô đậm trong hình vẽ bên dưới. Công thức tính S là 2 A. S  f (x)dx  . 1  1 2 B. S 
f (x)dx  f (x)dx   . 1  1 1 2
C. S   f (x)dx  f (x)dx   . 1  1 2 D. S  f (x)dx  . 1  r Câu 8.
Trong không gian Oxyz , mặt phẳng   đi qua điểm A 1;
 2; 4 và nhận vectơ n  1;  2; 3
làm vectơ pháp tuyến có phương trình là
A. x  2 y  3z  7  0 .
B. x  2 y  4z  7  0 .
C. x  2 y  4z  7  0 . D. x  2 y  3z  7  0 . ax bx c Câu 9. Cho hàm số y f  x 2    
(với a  0, m  0 mx  n
và  n không là nghiệm của 2
ax  bx  c  0 ) có đồ thị m như hình vẽ.
Tiệm cận xiên của đồ thị hàm số đã cho là A. x  2 .
B. y  x  2 .
C. y  x 1.
D. y  x 1.
Câu 10. Nguyên hàm của hàm số f  x  4x  sin x là A. 2
x  cos x  C. B. 2
2x  cos x  C . C. 2
x  cos x  C . D. 2
2x  cos x  C .  3 d
Câu 11. Tích phân   x I bằng 2  sin x 4         A. cot  cot . B. cot  cot . C.  cot  cot . D.  cot  cot . 3 4 3 4 3 4 3 4
Câu 12. Mẫu số liệu ghép nhóm thống kê mức lương của một công ty (đơn vị: triệu đồng) được cho trong bảng dưới đây.
Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm (làm tròn đến hàng phần trăm). A. 3, 02 . B. 3,15 . C. 3, 34 . D. 2, 96 .
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Câu 13. Số giờ có ánh sáng mặt trời của thành phố A ở vĩ độ o 40 Bắc trong ngày
thứ t của một năm không nhuận được cho bởi hàm số:  d t     3sin t 80 12  
với t  ¥ và 0  t  365 . 182 
Xét tính đúng sai các mệnh đề sau: Đúng Sai
a) Ngày thứ 80 trong năm thì thành phố có đúng 10 giờ nhận ánh sáng mặt trời.      
b) Đạo hàm của hàm số đã cho là dt  3  cos (t  80)   .   182 182 
c) Nghiệm của phương trình d t   0 trên đoạn 1; 17  1 là t  171.  
d) Ngày thứ 160 có số giờ ánh sáng lớn nhất trong năm.  
Hướng dẫn giải
a) Mệnh đề sai.
Với t  80  d (t)  3sin 0 12  12 .
Vậy ngày thứ 80 thì thành phố có 12 giờ nhận ánh sáng mặt trời.
b) Mệnh đề đúng.    
Ta có: dt  3  cos (t  80)   . 182 182 
c) Mệnh đề đúng.     dt  3  0  cos (t  80)  0  (t  80) 
 k , k ¢ 182 182 182 2
 t  80  91182k , k ¢  t  171182k , k  ¢ .
Với t 1; 17 
1 thì phương trình d t   0 có nghiệm duy nhất thỏa mãn là t  171.
d) Mệnh đề sai.   
Ta có: d t   3sin
t 80 12  3112 15   . 182      
Dấu đẳng thức xảy ra khi và chỉ khi sin t 80 1
t 80   k2 , k    ¢ 182  182 2
 t  80  91 364k, k ¢  t 171 364k, k ¢ .
Vì 0  t  171 nên phương trình t  171 364k, k  ¢ chỉ cho một nghiệm t  171.
Câu 14. Có hai chất điểm đang chuyển động thì xảy ra va chạm. Biết rằng
sau khi va chạm hai chất điểm di chuyển về hai hướng ngược
nhau, một chất điểm di chuyển tiếp với vận tốc v t  6  3t 1  
m / s , chất điểm còn lại di chuyển với vận tốc v t 12  4t 2  
m / s trước khi cả hai dừng lại, t là thời gian tính bằng giây.
Xét tính đúng sai các mệnh đề sau: Đúng Sai
a) Quãng đường chất điểm thứ nhất di chuyển được sau va chạm được biểu 3t  
diễn bởi hàm số s t  2  6t   C (mét). 1 1 2
b) Quãng đường chất điểm thứ hai di chuyển sau khi va chạm được biểu  
diễn bởi hàm số s t  2
 12t  2t  C (mét). 2 2
c) Quãng đường chất điểm thứ nhất di chuyển được kể từ khi va chạm đến  
khi dừng lại là 18 m .
d) Khoảng cách hai chất điểm sau khi đã dừng hẳn 23 m .  
Hướng dẫn giải
a) Mệnh đề đúng. 3t
Ta có s t   v
 tdt  63t 2 dt  6t   C (mét). 1 1 1 2
b) Mệnh đề đúng.
Ta có s t   v
 tdt  124t 2 dt  2
1 t  2t  C (mét). 2 2 2
c) Mệnh đề sai.
Thời gian để chất điểm thứ nhất dừng lại sau va chạm là 6  3t  0  t  2 (giây). 2 2 2  3t 
Chất điểm này di chuyển được đoạn đường S  6  3t dt   6t    6 (mét). 1    2  0 0
d) Mệnh đề sai.
Thời gian để chất điểm thứ hai dừng lại sau va chạm là 12  4t  0  t  3 (giây). 3
Chất điểm này di chuyển được đoạn đường S  12  4t dt 
 12t  2t  3 2  18 (mét). 2   0 0
Khoảng cách hai xe khi đã dừng hẳn là: S  S  S  6 18  24 (mét). 1 2
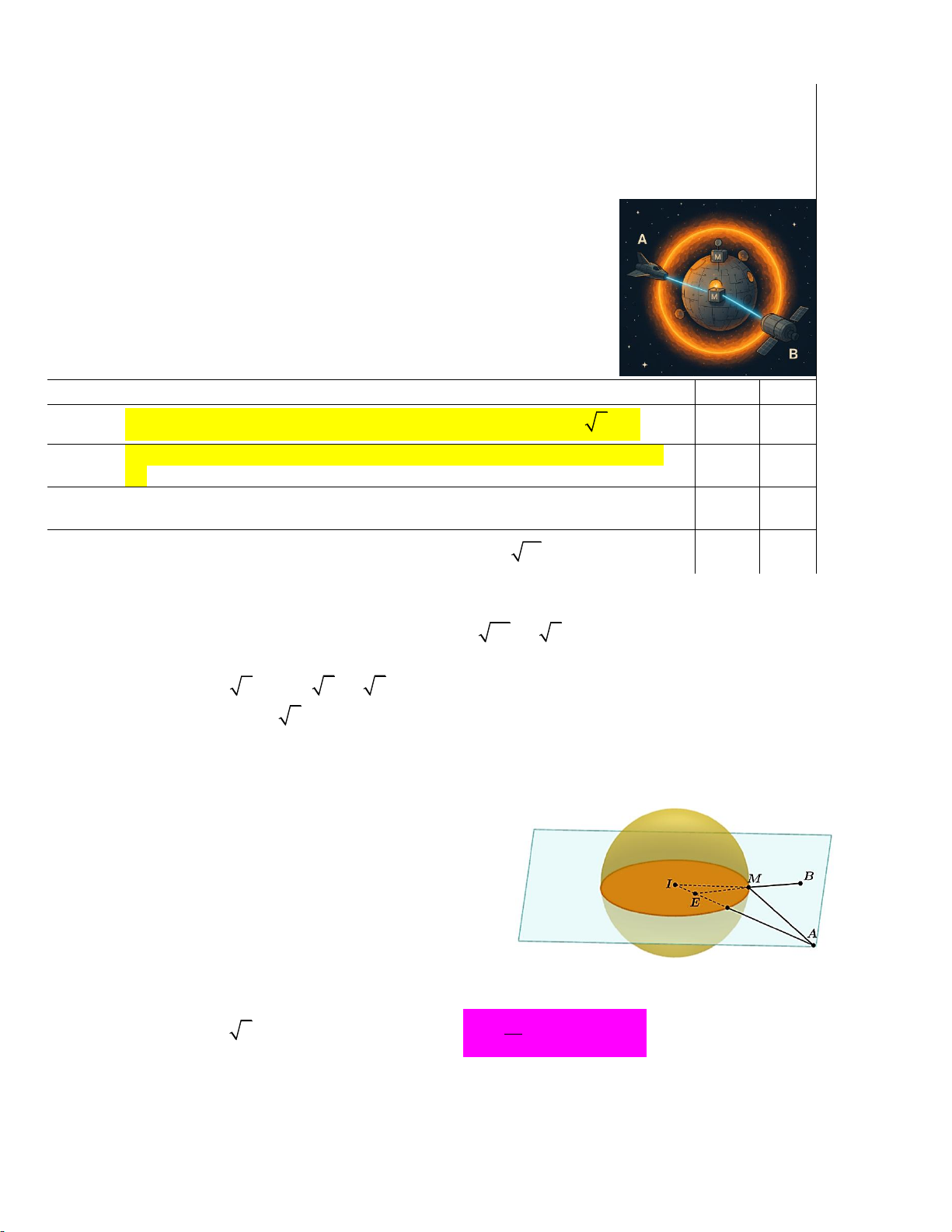
Câu 15. Trong một hệ thống giám sát không gian 3D, gốc tọa độ O 0; 0; 0 là trung tâm điều khiển
chính. Các đơn vị trên mỗi trục Ox , Oy , Oz được tính bằng kilômét (km).
Một trạm không gian hình cầu (S) có phương trình 2 2 2
(x 1)  ( y  2)  (z 1)  72 . Trạm này có
một hệ thống phòng thủ hoạt động theo cơ chế phát ra một trường năng lượng bảo vệ các thiết
bị nằm trên bề mặt của nó. Hai tàu vũ trụ A và B đang di chuyển
trong không gian, có vị trí đang khảo sát lần lượt là A1; 16; 17
và B 7;  6;   1 .
Một thiết bị đặc biệt M có thể di chuyển tự do trên bề mặt trạm
không gian (S). Để duy trì kết nối ổn định với hai tàu vũ trụ A và B,
thiết bị M phải tối ưu hóa một chỉ số kết nối tổng thể T được định
nghĩa bởi công thức T  MA  3MB , trong đó MA và MB là
khoảng cách từ thiết bị M đến tàu A và tàu B (tính bằng km).
Xét tính đúng sai các mệnh đề sau: Đúng Sai
a) Tâm và bán kính của trạm không gian (S) là I 1; 2;  
1 , R  6 2 km.  
b) Hai tàu vũ trụ A và B đều đang nằm ngoài vùng bảo vệ của trạm không gian   (S).
c) Đường bay thẳng của tàu vũ trụ A đến tàu vũ trụ B có cắt qua vùng bảo vệ của  
trạm không gian (S).
d) Chỉ số kết nối tổng thể T đạt giá trị nhỏ nhất bằng 5 19 km.  
Hướng dẫn giải
a) Mệnh đề đúng.
Mặt cầu (S) có tâm I 1; 2;  
1 và bán kính R  72  6 2 km .
b) Mệnh đề đúng.
Ta có IA  18 2 km ; 18 2  6 2  R nên tàu vũ trụ A nằm ngoài trạm không gian (S);
IB  10 km ; 10  6 2  R nên tàu vũ trụ B cũng nằm ngoài trạm không gian (S). c) Mệnh đề sai. uuur
Đường bay AB có vectơ chỉ phương AB  6; 10; 18 . x  1 6t 
Phương trình tham số của AB :  y  16 10t .
z 17 18t 
Thay phương trình của AB vào (S): 2 2 2 (6t)  ( 1
 6 10t  2)  (17 18t 1)  72. Thu gọn ta được: 2
115t  252t 144  0. Phương trình này vô nghiệm.
Vậy đường bay A đến B không cắt qua vùng bảo vệ của trạm không gian (S). d) Mệnh đề sai. uur 1 uur
Ta có IA  18 2  3R ; chọn điểm E thỏa mãn IE 
IA  E 1; 0; 1 . 2   3 I$ chung  M E 1
Hai tam giác IEM, IMA đồng dạng vì   IE IM 1 ; suy ra
  MA 3M E .    MA 3  IM IA 3
Ta có: T  MA  3MB  3M E  3M B  3ME  M B  3EB  6 19 km.
Vậy T đạt giá trị bé nhất bằng 6 19 km; khi đó E, M, B thẳng hàng theo thứ tự đó.
Câu 16. Một cửa hàng có ba loại hộp quà: Hộp A, Hộp B, và Hộp C, với số lượng ban đầu lần lượt là 20, 30,
và 50 hộp. Mỗi hộp quà chứa một số lượng ngẫu nhiên các phiếu giảm giá có mệnh giá khác nhau,
được phân phối như sau:
 Hộp A: Có 5 phiếu giảm giá 10% và 5 phiếu giảm giá 20%.
 Hộp B: Có 4 phiếu giảm giá 10%, 3 phiếu giảm giá 20% và 3 phiếu giảm giá 30%.
 Hộp C: Có 3 phiếu giảm giá 10%, 3 phiếu giảm giá 20% và 4 phiếu giảm giá 30%.
Một khách hàng ngẫu nhiên chọn một hộp quà. Sau đó,
họ ngẫu nhiên rút hai phiếu giảm giá từ hộp đã chọn.
Xét tính đúng sai các mệnh đề sau: Đúng Sai
a) Xác suất để khách hàng chọn được hộp quà loại A là 0,2.   1
b) Xác suất để rút được 2 phiếu 20% nếu biết hộp B đã được chọn là .   15 22
c) Xác suất để cả hai phiếu rút được đều có mệnh giá 20% bằng .   225
d) Biết rằng cả hai phiếu rút được đều có mệnh giá 20%, xác suất rằng khách 9  
hàng đó đã chọn hộp quà loại B là . 44
Hướng dẫn giải Gọi các biến cố:
H : “Khách hàng chọn hộp A”; H : “Khách hàng chọn hộp B”; H :“Khách hàng chọn hộp C”; A B C
D : “Rút được 2 phiếu giảm giá 20%”. 20
Tổng số hộp quà: 20  30  50  100 hộp.
a) Mệnh đề đúng. So h á oä p A 20
Xác suất để khách hàng chọn được hộp quà loại A: PH 0,2 . A     Toå ng soáh ä op 100
b) Mệnh đề đúng.
Ta cần tính xác suất có điều kiện P  D ∣ H . 20 B 
Trong hộp B có 10 phiếu (4 phiếu 10%, 3 phiếu 20%, 3 phiếu 30%).
Số cách chọn 2 phiếu bất kỳ từ 10 phiếu là: 2 C  45 . 10 3 1
Số cách chọn 2 phiếu 20% từ 3 phiếu 20% là: 2
C  3 . Do đó P  D ∣ H   . 20 B  3 45 15
c) Mệnh đề đúng. C 2 C 1
Từ hộp A, ta có P  D ∣ H 
 . Từ hộp B, ta có PD ∣ H   . 20 B  2 3 A  2 5 20 2 C 9 2 C 15 10 10 C 1
Từ hộp C, ta có P  D ∣ H   . C  2 3 20 2 C 15 10
Áp dụng công thức xác suất toàn phần, ta có: P  D
 P D ∣ H  P H  P D ∣ H  P H  P D ∣ H  P H 20 
 20 A  A
 20 B   B 
 20 C   C  2 1 1  0,2  0,3 0,5  22 . 9 15 15 225
d) Mệnh đề đúng.
Xác suất để khách hàng chọn hộp B biết cả hai phiếu rút được đều có mệnh giá 20%: 1 0,3 ∣ 0, 02 0, 02  225 4, 5 P  P D H P H B B 15 H ∣ D       9 . B 20   20    P  D 22 22 22 22 44 20  225 225
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Câu 17. Một món quà lưu niệm được làm từ thủy tinh và có dạng hình chóp cụt
tứ giác đều. Món quà thủy tinh nằm bên trong một hộp quà đẹp, nó có
chiều cao bằng cạnh đáy nhỏ và bằng 3 cm, cạnh đáy lớn bằng 6 cm. Tìm
thể tích món quà thủy tinh đó theo đơn vị cm khối.
Trả lời:  Đáp số: 63
Hướng dẫn giải
Thể tích khối chóp cụt đều (khối thủy tinh): 1 V 
h S  S  S.S ; trong đó: 3 2 2 2 2
h  3cm, S  6  36 cm , S  3  9 cm . 1
Do vậy: V  .3.36  9  36.9 3  63cm . 3
Câu 18. Một xưởng may áo thun thủ công đã nghiên cứu thị trường để đưa ra các hàm số sau:
 Hàm chi phí tổng C q : q 
Tổng chi phí (nghìn đồng) để sản xuất q áo thun là C q 200 1000  , q  0. q 10
 Hàm doanh thu tổng R q :
Tổng doanh thu (nghìn đồng) khi bán q áo thun là R q 2  0  ,05q  500 . q
Xưởng may sẽ thu được bao nhiêu lợi nhuận tăng thêm (hay lợi
nhuận cận biên) nếu sản xuất và bán chiếc áo thun thứ 101 (số
lượng áo tăng từ 100 đến 101)? Kết quả được làm tròn đến hàng
đơn vị của nghìn đồng.
Trả lời:  Đáp số: 490
Hướng dẫn giải
Tổng lợi nhuận của công ty khi sản xuất và bán được q chiếc áo thun:   200q 1000
q  R q  C q   2 0
 ,05q  500q . q 10 1000
Hàm lợi nhuận cận biên là:  q  Rq  Cq  0  ,1q  500  . 2 (q 10)
Lợi nhuận cận biên cần tính là  100  490 (nghìn đồng).  Lưu ý:
 Hàm lợi nhuận cận biên được tìm khi lấy đạo hàm của hàm tổng lợi nhuận theo số lượng sản phẩm.
 Tìm lợi nhuận cận biên khi làm ra sản phẩm thứ n 1 (tức là mức lợi nhuận thu được khi số
lượng sản phẩm tăng từ 100 đến 101 đơn vị), ta thay q  n vào hàm lợi nhuận cân biên để tính toán.
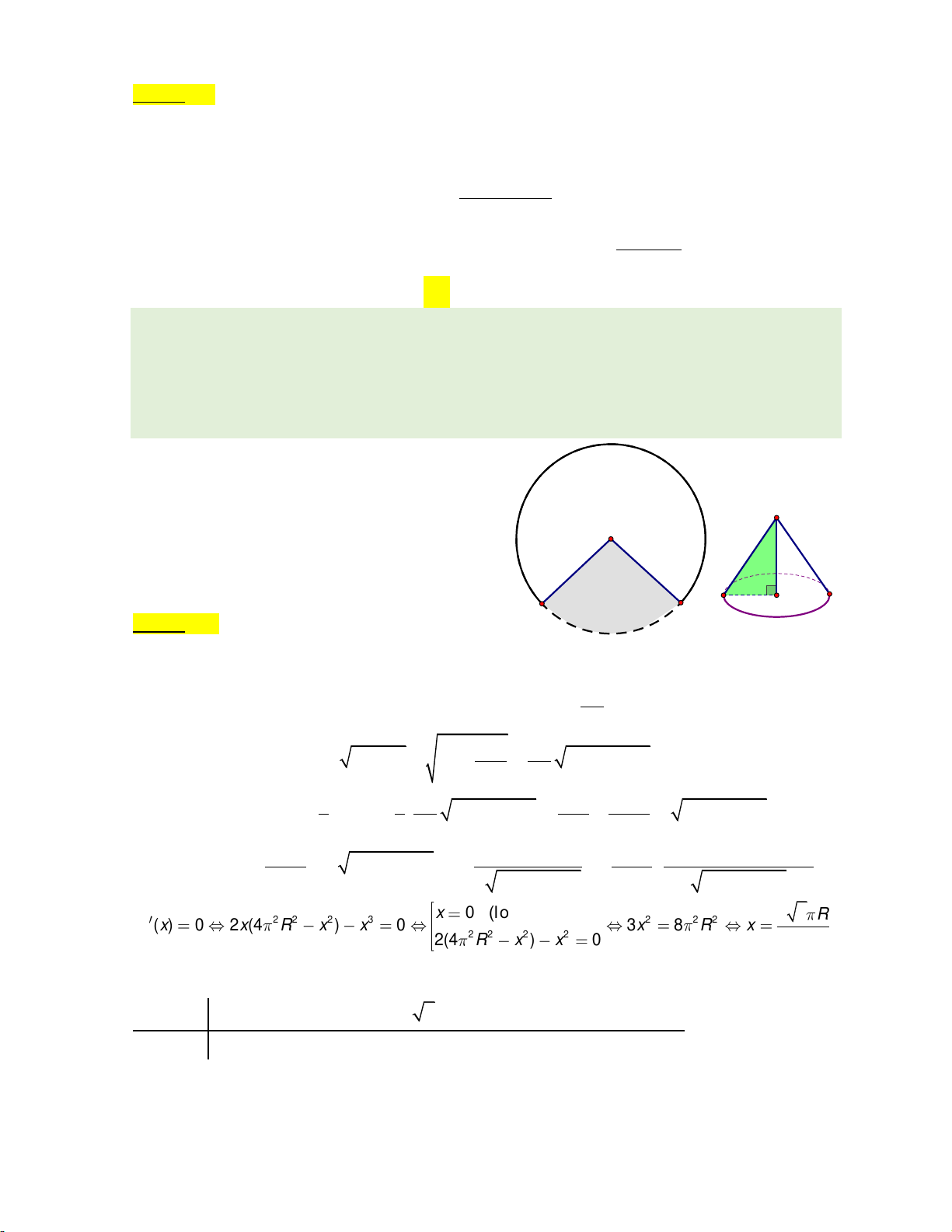
Câu 19. Với một đĩa phẳng hình tròn bằng thép bán kính R,
phải làm một cái phễu bằng cách cắt đi một hình
quạt của đĩa này và gấp phần còn lại thành một hình x
nón. Gọi độ dài cung tròn của hình quạt còn lại là x. O
Khi thể tích khối nón tạo thành nhận giá trị lớn nhất O
thì x  mR với m là số thực, tìm m và làm tròn đến R h hàng R
Trả lời:  r Đáp số: 5,13 x
Hướng dẫn giải x
Đáy hình nón tạo thành là đường tròn có chu vi 2 r  x  r  (với x  0 ). 2 2 x 1
Theo định lí Pitago, ta có 2 2 2 2 2 2 h  R  r  R   4 R  x . 2 4 2 2 1 1 1 x 1 Thể tích khối nón: 2 2 2 2 2 2 2 2 V (x)  . h  .r  .
4 R  x . .  x 4 R  x . 2 2 3 3 2 4 24 2 2 2 3 1  2  x  1
2x(4 R  x )  x  Đạo hàm: 2 2 2 2 V (  x) 
 2x 4 R  x  x .    . 2 2 2 2 2 2 2 2 24    24 2 4 R x    4 R  x  x 0 (loaïi) 2 6 R 2 2 2 3 2 2 2 V ( ) x 0 2x(4 R x ) x 0 3x 8 R x . 2 2 2 2 2(4 R x ) x 0 3 Bảng biến thiên: x 0 2. R  V (  x)  0  V max V (x) 2 6 R 2 6
Ta nhận thấy thể tích khối nón đạt giá trị lớn nhất khi x   mR  m   5,13 . 3 3
Câu 20. Bác Ba Khía có một mảnh đất hình vuông ABCD cạnh 40 m.
Mảnh đất của bác rất phù hợp để trồng hoa màu vì bên
trong có một ao nước tự nhiên được giới hạn bởi các
đường cong  L , L và ba cạnh của hình vuông (xem 1   2
hình vẽ). Biết rằng đường cong  L là một nhánh của 1 
parabol nhận điểm E (trung điểm AB) làm đỉnh và đi qua
điểm F với F  AD và 4 AF  AD . Đường cong  L là 2 
tập hợp tất cả điểm M sao cho khoảng cách từ M đến tâm I
bằng với khoảng cách từ M đến cạnh AB. Tính diện tích còn
lại của mảnh đất mà bác Ba Khía có thể trồng hoa màu và
làm tròn đến hàng đơn vị của mét vuông.
Trả lời:  Đáp số: 1200
Hướng dẫn giải
Dựng hệ trục tọa độ Oxy như hình vẽ, đơn vị trên mỗi trục là 10 m.
L có đỉnh E 0; 2 và qua F 1; 0 nên parabol 1  tương ứng là 2 y  2
 x  2 x  0, y  0 .
Gọi M  x; y là tập hợp các điểm tạo nên  L , ta có: 2 
MI  d M AB   x  2   y  2 , 2 2  x 2 2 2
 x  4x  4  y  4y  4  x 1 2 2  4
 x  4y  8  y  0  x  y  y  2 . 4
Diện tích tam giác cong AEF trên thực tế là 1 2 400 S  10  2 2
 x  2 dx   2 m . 1  3 0 Diện tích hình phẳng giới hạn bởi
L với ba cạnh AD, DC, CB là 2  4  1  2 2 2 3200 S  40 10
y  y  2 dy   2 m . 2    4  3 0
Tổng diện tích mà bác Ba Khía có thể trồng trên mảnh đất hình vuông là S  S  2 1200 m . 1 2
Câu 21. Trong hệ thống định vị và truyền thông vệ tinh của một công ty công nghệ, gốc tọa độ O 0; 0; 0
là trung tâm điều khiển chính trên mặt đất. Các đơn vị trên mỗi trục được tính bằng kilômét (km).
Một vệ tinh trung tâm có vùng ảnh hưởng hình cầu để đảm bảo việc thu phát tín hiệu, vùng ảnh
hưởng này được mô tả bởi phương trình S  2 2 2
: (x  5)  ( y  3)  (z  7)  72 .
Công ty muốn lắp đặt một trạm phát sóng cục bộ tại điểm A0; 8; 2 để truyền dữ liệu đến vệ
tinh trung tâm. Tuy nhiên, để đảm bảo an toàn thông tin và hiệu quả tín hiệu, trạm phát sóng
này phải hoạt động trên một mặt phẳng P có vectơ pháp
tuyến rn  1; m; n và tiếp xúc với vùng ảnh hưởng của vệ
tinh trung tâm S  .
Ngoài ra, họ có một cơ sở dữ liệu quan trọng đặt tại vị trí
B 9;  7; 23 . Để giảm thiểu rủi ro bị tấn công mạng từ bên
ngoài, công ty muốn đặt mặt phẳng P sao cho khoảng
cách từ cơ sở dữ liệu B đến mặt phẳng P là lớn nhất. Tìm
giá trị lớn nhất đó theo đơn vị km (làm tròn đến hàng phần chục).
Trả lời:  Đáp số: 25,5
Hướng dẫn giải
Mặt cầu S  có tâm I (5;  3; 7) và bán kính R  6 2 . r
Mặt phẳng  P qua A0; 8; 2 và nhận n  1; m; n làm véc tơ pháp tuyến nên có phương trình
x  my  nz  8m  2n  0 . 5n 11m  5
Mặt phẳng  P tiếp xúc với S   d I , P  R   6 2 . 2 2 1 m  n 21n 15m  9
5n 11m  5  4m 16n  4
Ta có: d B , P   . 2 2 2 2 1 m  n 1 m  n
Áp dụng cả hai bất đẳng thức tam giác và Cauchy Schwarz, ta có: 2 2 2 2 2
5n 11m  5  4m 16n  4       4  ( 1
 ) 1 (n  m 1)
5n 11m 5 4 4n m 1     6 2  4 18 2. 2 2 1 m  n 2 2 2 2 1 m  n 1 m  n n m 1    m  1 
Dấu bằng xảy ra khi  4 1  1   .     n  m  
 n  m   n 4 5 11 5 4 1  0
Vậy khoảng cách lớn nhất từ B đến (P) là 18 2  25,5 km .
Câu 22. Một cái túi chứa bốn con xúc xắc đặc biệt gồm có:
 2 con xúc xắc loại A: Là xúc xắc 6 mặt cân đối thông thường .
 1 con xúc xắc loại B: Chỉ có các mặt 1, 2, 3 xuất hiện với xác suất bằng nhau
 1 con xúc xắc loại C: Có 4 mặt mang số 1 và 2 mặt mang số 5.
Biết rằng tổng số chấm của ba lần tung là một số nguyên
tố bé hơn 10, hãy tính xác suất để con xúc xắc được chọn
là loại B. (Làm tròn kết quả đến hàng phần trăm).
Trả lời:  Đáp số: 0,34
Hướng dẫn giải
Gọi X , X , X lần lượt là biến cố chọn được xúc xắc loại A, B, C. A B C 2 1 1 1 Ta có: P  X   P X  P X  . A  ,  B  ,  C  4 2 4 4
Gọi E : “Tổng 3 lần tung là một số nguyên tố bé hơn 10”. Các số nguyên tố đó là: 3, 5, 7. P E  X P E∣ X P X B  B   B 
Ta cần tính P  X ∣ E   . B    P  E P  E 
Tính P  E∣ X
(xúc xắc có đủ 6 mặt). A 
 Các bộ có tổng 3 là: (1, 1, 1) có 1 cách.
 Các bộ có tổng 5 là: (1, 1, 3) có 3 cách; (1, 2, 2) có 3 cách. Tổng là có 6 cách.
 Các bộ có tổng 7: (1, 1, 5) có 3 cách; (1, 2, 4)  có 6 cách; (1, 3, 3) có 3 cách;
(2, 2, 3) có 3 cách. Tổng là có 15 cách. 1 6 15 22 11
Do vậy P  E∣ X    . A  3 6 216 108
Tính P  E∣ X
(xúc xắc chỉ có mặt 1, 2, 3): B 
 Các bộ có tổng 3: (1, 1, 1) có 1 cách.
 Các bộ có tổng 5: (1, 1, 3) có 3 cách; (1, 2, 2) có 3 cách. Tổng là có 6 cách.
 Các bộ có tổng 7: (1, 3, 3) có 3 cách; (2, 2, 3) có 3 cách. Tổng có 6 cách. 1 6  6 13
Do vậy P  E∣ X   . B  3 3 27
Tính P  E∣ X
(xúc xắc có 4 mặt 1 và 2 mặt 5): C  3    2 8
Các bộ có tổng 3: (1, 1, 1) Xác suất:    .  3  27 2    2 1 12
Các bộ có tổng 7: (1, 1, 5) có 3 cách Xác suất: 3     .  3  3 27 20
Do đó: P  E∣ X    . C  8 12 27 27 27
Ta có: P  E   P  E∣ X
 P X  P E∣ X  P X  P E∣ X  P X A   A  B   B   C   C  P  E 11 1 13 1 20 1        77 . 108 2 27 4 27 4 216 13 1  P E  X P E∣ X P X 26 B  B   B 
Khi đó: P  X ∣ E   27 4    0,34 B    P  E P  E  77 77 216
_________________HẾT_________________