









































Preview text:
ĐỀ 1 : Ngày 17/4/2018 Câu 1:
a. Gọi A = “ Người ó nhập úng mã pin ”. P(A)= A10 720
b. Gọi H1= “ Bò mắc bệnh iên”
H2= “Bò không mắc bệnh iên” H1,
H2 là nhóm biến cố ầy ủ P(H1) = 1,3 = 1,3. 10−5 , P(H2) = 1 - = 0,999987 100 000
A= “Con bò phản ứng dương tính với xét nghiệm”.
P(A/H1) = 0,7 → 𝑃(𝐴/H1) = 0,3.
P(A/H2) = 0,1 → 𝑃(𝐴/𝐻2) = 0,9.
Áp dụng công thức xác suất ầy ủ ta có :
P(A) = P(H1).P(A/H1)+P(H2).P(A/H2 ) = 1,3. 10−5 .0,7 + 0,999987.0,1 = 0,1000078
Xác suất ể con bò bị bệnh iên nếu nó dương tính với xét nghiệm là ( H1 ) .P ( A/H1 ) 1,3.10 −5 .0 7 , = ≈0,0001 P(H1/A) = P P(A) 0,1000078 Câu 2: a. Ta có: ( 2𝑥 − 𝑘) 𝑑𝑥 =1 Mà ( 2𝑥 − 𝑘) 𝑑𝑥 = ( 2𝑥 − 𝑘) 𝑑𝑥 + ( 2𝑥 − 𝑘) 𝑑𝑥 + ( 2𝑥 − 𝑘) 𝑑𝑥 = ( 2𝑥 − 𝑘) 𝑑𝑥 = 2.𝑥2 │2 - kx│12
= 4 - 1- k = 3 - k =1→ 𝑘 = 2
Với k =2 ta có hàm mật ộ xác suất là: p(x) = 2x – 2 với x ∈ (1,2)
b. Nhu cầu nước ngọt Cocacola trung bình hằng tuần tại cửa hàng này là : − 2𝑥) 𝑑𝑥
= 2. 𝑥33 │12- 2. 𝑥22 │12 .7 − 3 = 1,6667.
Vậy nhu cầu nước ngọt Cocacola trung bình tại cửa hàng này là 1,6667 nghìn lít Câu 3:
X: = Chỉ số IQ của học sinh tốt nghiệp THPT X ~ N (98; 122) Ta có: n= 600
Y: = Học sinh sẽ ạt trong ợt tuyển chọn . P{𝑋 ≥ 105}= 0.5- 𝜙0( = 0,27983
E(Y) = n. P{𝑋 ≥ 105}= 600.0,27983= 167,898 (học sinh)
Vậy trung bình có 167. 898 học sinh ạt trong ợt tuyển chọn Câu 4:
X: = Doanh thu ở cửa hàng. ( ơn vị: trăm triệu ồng/ tuần) X ~
N (𝜇 ; δ2) μ ≔ Doanh thu trung bình (Đơn vị: trăm nghìn
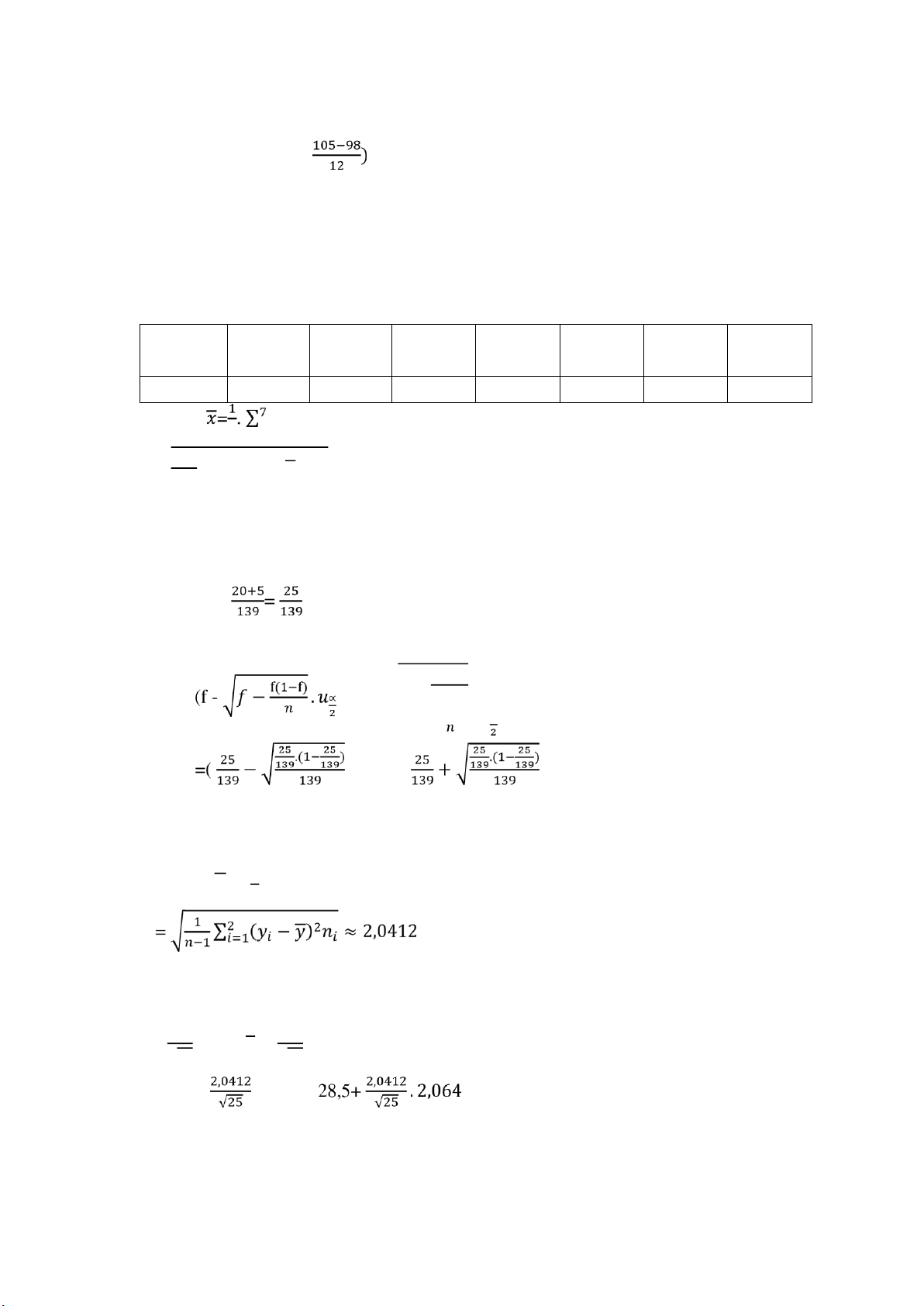
ồng/ tuần ) Bảng phân phối thực nghiệm Doanh 2,5 7,5 12,5 17,5 22,5 27,5 32,5 thu Số tuần 9 23 27 30 25 20 5 n = 139, 𝑛
𝑖=1 𝑥𝑖 𝑛𝑖 ≈ 16,7806 1 √ ∑ 7 𝑖=1( s= 𝑥 𝑖 − 𝑥 ) 2 𝑛−1 𝑛𝑖 = 7,9300
a. Gọi p là tỷ lệ những tuần hiệu quả ở cửa hàng.
f là tỷ lệ những tuần hiệu quả ở cửa hàng trong mẫu . n = 139, f =
Với ộ tin cậy 0,9 →1-∝ = 0,9 →∝ = 0,1
Khoảng tin cậy ối xứng của P là
; 𝑓 + √𝑓 + f(1−f) . 𝑢∝ ) . 1,645 ; . 1,645 ) = (0,1263; 0,2334)
b. Gọi Y : = Doanh thu trong một tuần hiệu quả ở cửa hàng. μ1:
Doanh thu trung bình trong một tuần hiệu quả tại cửa hàng. 1
𝑛𝑌 = 25 , 𝑌 = ∑ 2 𝑛𝑖=1 𝑥𝑖 𝑛𝑖 ≈ 28,5 𝑆𝑌
1-∝ = 0,95 →∝ = 0,05 → 𝑡0,02524 =2,064
Khoảng tin cậy ối xứng của 𝑛𝑦 là y .t y n−1 ; y + .t n−1 ( y- ∝/2 ∝/2 S S √ n y √ n y ) = (28,5 - . 2,064 ; ) = (27,6574 ; 29,3426)
c. Do n = 139 >30 và 1-∝ = 0,95 →∝= 0,05 ; 𝑢0,05= 1,645
Khoảng tin cậy tối a của 𝑆
Vậy với ộ tin cậy 95% doanh thu trung bình trong một tuần ở cửa hàng A không vượt quá
17,8870 trăm triệu ồng/ tuần.
d.Gọi 𝑛0 là kích thước mẫu tối thiểu cần lấy ể ước lượng doanh thu trung bình có ộ chính
xác là 100 triệu và ộ tin cậy là 0.98.
Với 1−∝= 0,98 → ∝= 0,02
Ta có: Sai số của ước lượng về doanh thu trung bình là 𝑆 .𝑢 𝛼 𝜀0 = 0 √ 𝑛 0 2
với 𝑠0 ≈ 𝑠 = 7,93, 𝑢0,01 = 2,3263 , 𝜀 = 1 → 𝑛0= 341 (tuần)
Vậy cần theo dõi thêm 202 tuần nữa e. Kiểm ịnh giả thiết 𝐻0: "𝜇 = 20" 𝐻1: "𝜇 < 20" TCKĐ: T= = - 4,7864
MBB với →∝= 0,05 : 𝑛∝= (-∞; −𝑈∝) =(-∞; −1,645)
Nhận thấy 𝑇𝑞𝑠 ∈ 𝑊∝ → 𝐵á𝑐 𝐵ỏ 𝐻0 , 𝑐ℎấ𝑝 𝑛ℎậ𝑛 𝐻1
Vậy với mức ý nghĩa 5% có thể cho rằng việc thay ổi này làm tăng doanh thu trung bình trong tuần ở cửa hàng.
ĐỀ 2: Ngày 21/06/2018 Ca 1 Câu 1:
Gọi H1 = “ Nhẫn lấy từ két 2 sang két 1 là nhẫn bạc ”
H2= “ Nhẫn lấy từ két 2 sang két 1 là nhẫn vàng ”
A = “ Nhẫn lấy ra từ két thứ 1 là nhẫn vàng ”
B = “ Lấy ược nhẫn bạc từ két thứ nhất mà không phải từ két 2 chuyển sang ”
a) Theo công thức xác suất ầy ủ ta có:
P(A)=P(H1).P(A/H1)+P(H2).P(A/H2)= . + . = b) Ta có:
P(B)=P(H1).P(B/H1)+P(H2).P(B/H2)= . + . =
Xác suất cần tìm là P(B|𝐴 ) = P(BAP(A̅̅ )) = P(AP(B) )= 4041 Câu 2:
Gọi 𝑥𝑜:= lượng tiền trong cây ATM (0 ≤ 𝑥0 ≤ 1) ( ơn vị: trăm triệu ồng) Để
cây ATM hết tiền thì X ≥ 𝑥0 Ta có: P{X≥ 𝑥𝑜} = 0,05 𝑑𝑥 = 𝑥0 = 0.4507
Vậy lượng tiền trong cây ATM là 45.07 triệu ồng Câu 3:
X : = Thời gia i từ nhà ến cơ quan của luật sư ( ơn vị : phút). X~N(24; 3.82)
Nếu cơ quan mở cửa vào lúc 9:00 sáng và người luật sư rời khỏi nhà lúc 8:40 hàng ngày
thì xác suất anh ta i muộn là : P{X>20}=1-P{X
Số ngày anh ấy i muộn chiếm gần 85,31%. Câu 4:
Gọi X : = Thu nhập hàng năm của mỗi hộ gia ình ( ơn vị: triệu ồng/năm)
X~N(𝜇;𝜎2) μ := mức thu nhập trung bình của mỗi hộ gia ình
ở huyện A. Bảng phân phối thực nghiệm Xi(triệu ồng/năm) 190 205 215 225 235 Số hộ 5 15 25 25 30 n =100
𝑛𝑖=1 𝑥𝑖𝑛𝑖 =220.75 s = =12.6406
a. Với ộ tin cậy 98% => 1- 𝛼 = 0.98 => 𝛼 = 0.02 .
Khoảng tin cậy ối xứng của μ là : (x − s; x + s(217.8094;223.6906).
Vậy ước lượng mức thu nhập trung bình hàng năm của mỗi hộ gia ình ở huyện A với ộ
tin cậy 98% là (217.8094; 223.6906)
b. Gọi 𝑛0 là kích thước mẫu tối thiểu cần lấy. ε= u Vì n ≥ 30 ta có √ 𝑛 s
0 2 α với 𝑠0 ≈ 𝑠 =12.6406, 𝜀 =2.2 𝑛0= 126.8242 ≈ 127
Vậy với ộ tin 95% , phải iều tra thêm ít nhất 27 hộ nữa ể ộ chính xác là 2,2 .
c. Gọi N’ là số hộ gia ình có thu nhập cao hàng năm ở huyện A.
p là tỷ lệ hộ gia ình có thu nhập cao ở huyện A.
f là tỷ lệ hộ gia ình có thu nhập cao ở mẫu . p = N′ 1000 f = = 0.55
Với ộ tin cậy 98% => 1-𝛼 = 0.98 => 𝛼 = 0.02
Ta có nf > 10 , n(1-f) > 10 nên khoảng tin cậy của p là : ; 𝑓 + ) 𝑁′ 434.3 < N’ < 665.7
Vậy hộ gia ình có thu nhập cao hàng năm ở huyện A nằm trong khoảng ( 434.3; 665.7)
d. Gọi 𝜀 là độ chính xác trong ước lượng tỷ lê số hộ gia đình có thu nhập cao. 𝜀 = => 1 − 𝛼 = 0.9296
Vậy ộ tin cậy cần tìm là 92.96% e. Kiểm ịnh giả thiết: H0: “ 𝜇=215 ” H1: "𝜇<215 ” Tiêu chuẩn kiểm ịnh T=
Với ∝= 0.05 => 𝑢0.05 = 1.645 miền bác bỏ 𝑙à 𝑊∝ = (−∞; −1.645) Nhận
thấy Tqs ∉ 𝑊∝. Tạm chấp nhận H0,bác bỏ H1.
Vậy với mức ý nghĩa 5% ,không thể cho rằng thu nhập ở huyện B cao hơn huyện A.
ĐỀ 3: Ngày thi 21/06/2018 ca 2
Câu 1: Gọi H1= “ Người có thu nhập tốt”
H2 = “Người có thu nhập không tốt”. P(H1)=0.45; P(H2)=0.55
H1;H2 là nhóm có ầy ủ các biến cố .
A:= “ Người ó thích tiết kiệm”.
𝐴 := “Người ó không thích tiết kiệm”.
P(A/H1)=0.55 =>P(𝐴 /H1) = 0.45
P(A/H2)=0.25=> P(𝐴 /𝐻2) = 0.75
a. Xác suất ể người ó ở vùng A không thích tiết kiệm là
P(𝐴 ) = 𝑃(𝐻1) ∗ 𝑃(𝐴 /𝐻1) + 𝑃(𝐻2) ∗ 𝑃(𝐴 /𝐻2)=0.45*0.45+0.55*0.75 = 0.615
Vậy tỷ lệ ể người ó ở vùng A không thích tiết kiệm là 61.5%
b. Xác suất ể người ấy có thu nhập tốt nếu không thích gửi tiết kiệm là P(H1/𝐴 ) =
𝑃(𝐻1)𝑃(𝐴.𝑃(𝐴 ) /𝐻1) = 0.45∗0.450.615 = 0.3293 Câu 2:
X: = Số tiền mà công ty hàng không có thể phải bồi thường cho mỗi khách do mất
hành lý ( ơn vị: triệu ồng)
Bảng phân phối xác suất của X là X 0 1 P 0.995 0.005 E(X)=0.005 triệu ồng
Vậy nên tăng giá mỗi vé thêm 5000 ồng Câu 3:
X: = Tỉ giá của USD với VNĐ trong ngày . X~N(15000;5002) P{14500) − 𝜙0 ( ) = 𝜙0(3) − 𝜙0(−1) = 0.84
Y:= Số ngày có tỉ giá nằm trong khoảng từ 14500 ồng ến 16500 ồng. Y~B(7;0.84)
P(Y=4)=𝐶74 ∗ 0.8440.163 = 0.0714
Câu 4: Bảng phân phối thực nghiệm Xi 12 14 16 18 20 22 24 Số phiên 5 17 23 33 25 16 2 7 1 𝑥 = ∑ 𝑋𝑖 = 17,8512 𝑛 𝑖=1 1 √ s = ∑ 7 2𝑛 𝑖=1( 𝑥 𝑖 = 2.8421 𝑛−1 𝑖 − 𝑥 ) n = 121
a. Gọi μ là giá bán trung bình (Đơn vị: nghìn ồng).
Với ộ tin cậy 95% =>1-∝= 0.95 => ∝= 0.05
Khoảng tin cậy ối xứng của μ là : (𝑥 −
𝑠 𝑢𝛼; 𝑥 + 𝑠 𝑢𝛼)=(17.3448;18.3576) 22
Vậy khoảng tin cậy ối xứng của doanh thu trung bình khi bán 50000 cổ phiếu A trên thị
trường là (867240;917880) nghìn ồng b. No là kích thước mẫu tối thiều cần lấy.
Ta có sai số ước lượng về giá bán trung bình là: 𝑆 .𝑢 𝛼 𝜀0 = 0 √ 𝑛 0 2
với 𝑠0 ≈ 𝑠 = 2.8421, 𝑢0,01 = 2,3263 , 𝜀 = 0.5 No=175
Vậy cần phải iều tra thêm 54 phiên nữa.
c. Gọi p là tỉ lệ cổ phiếu A có giá trên 17 ( ơn vị: nghìn ồng)
f là tỉ lệ cổ phiếu A có giá trên 17 trong mẫu . f = Với ộ tin cậy 95% :
1-𝑎 = 0.95 => 𝑎 = 0.05 => 𝑢0.05 = 1.645.
Khoảng tin cậy tối thiếu của p là
Vậy với ộ tin cậy 95% tỉ lệ cổ phiếu A có giá trị bán trên 17 nghìn ồng không nhỏ hơn 17 nghìn ồng là 55,58% 𝜒
d. Với độ tin cậy 90% => 1-𝑎 = 0.9 => 𝑎/2 = 0.05 => { 𝜒
(𝑛−1)𝑆2 (𝑛−1)𝑆2 khoảng
tin cậy của phương sai giá bán một cổ phiếu A: 𝜒 𝜒 0,05 0,95
Khoảng tin cậy cụ thể là :
e. Gọi 𝜎2là phương sai của giá bán cổ phiếu A hiện nay.
Cần k cặp giá trị 𝜎2 = 11; 𝐻1: 𝜎2 < 11
Giá trị quan sát của TCKĐ là :𝑇𝑞𝑠
= (𝑛−1)𝑆2 ≈ 120𝑥8,0775 ≈ 88,118
Với mức ý nghĩa 5%, miền bác bỏ giả thuyết là 𝑊𝑎
Do 𝑇𝑞𝑠 ∈ 𝑊𝑎 nên bác bỏ H0, hay có cơ sở cho rằng ộ phân tán của giá bán cổ phiếu giảm xuống.
ĐỀ 4: Ngày 03/07/2018 Câu 1:
Gọi H1 = “ sản phẩm của xí nghiệp I”
H2 = “ sản phẩm của xí nghiệp II”
H3 = “ sản phẩm của xí nghiệp III”
P(H1)=0.3; P(H2)=0.4; P(H3)=0.3
H1; H2; H3 tạo thành nhóm có ầy ủ biến cố.
A = “ sản phẩm là phế phẩm”
𝐴 = “ sản phẩm là chính phẩm”
P(A/H1)=0.1 => P(𝐴 /𝐻1) = 0.9 ;
P(A/H2)=0.05=> P(𝐴 /𝐻2) = 0.95; P(A/H3)=0.15=> P(𝐴 /𝐻3) = 0.85
a. Xác suất ể chính phẩm ở trong kho ó là:
P(A)=P(H1)*P(A/H1)+P(H2)*P(A/H2)+P(H3)*P(A/H3)=0.3*0.9+0.4*0.95+0.3*0.85=0. 905
Vậy tỉ lệ chính phẩm trong kho là 90.5%
b. Gọi X: = số sản phẩm là phế phẩm trong 3 sản phẩm lấy ra trong kho. Với P(A)=1-P(𝐴 )=0.095 X~B(3;0.095)
Xác suất ể trong số sản phẩm ã lấy có ít nhất 1 phế phẩm :
P{X≥ 1} = 1 − 𝑃{𝑋 < 1} = 1 − 𝑃{𝑋 = 0} = 1 − 𝐶300.09500.9053 = 0.2588 Câu 2:
Gọi X: = số khách trên mỗi chuyến xe a
là giá vé xe buýt ( ơn vị: nghìn ồng ).
Y: = Lợi nhuận của mỗi chuyến ( ơn vị: nghìn ồng )
Ta có : Y= a*X - 200 và E(X)=∑𝑖 𝑥𝑖𝑝𝑖 =29.5
Theo giả thiết E(Y) = E(a*X-200)=a*E(X)-200=a*29.5-200=100=>a=10.1695
Vậy muốn thu ược lãi bình quân cho mỗi chuyến xe là 100 nghìn ồng cty này phả quy ịnh
giá vé 10.1695 nghìn ồng. Câu 3
X: = doanh thu hàng tháng của cửa hàng ( ơn vị: triệu) X~N(8,1.22)
μ′ là doanh thu trung bình cần phải phấn đấu (đơn vị ∶ triệu) P{X => 9 − 𝜇′ ′ = 10.54 = −1.2816 => 𝜇 1.2
Vậy ể ạt doanh thu tối thiểu 9 triệu là 90% cần phấn ấu ạt doanh thu trung bình là 10.54 triệu.
Câu 4: Gọi X: = giá óng cửa của 1 loại cổ phiếu ( ơn vị: nghìn ồng)
μ ≔ giá cổ phiếu trung bình ( đơ𝑛 𝑣ị ∶ 𝑛𝑔ℎì𝑛 đồ𝑛𝑔) Bảng phân phối thực nghiệm Xi (Nghìn 27 30 32 34 37 ồng) Ngày 4 10 15 8 3 n=40 ;
𝑛𝑘𝑖=1 𝑥𝑖𝑛𝑖=31.795 ; s=
a.Với ộ tin cậy 95% => 1-
Khoảng tin cậy của 𝜇 là 𝑠 𝑠 ; 𝑥 + =(30.9983; 32.5517)
Vậy với ộ tin cậy 95% thì ước lượng giá cổ phiếu Trung bình bằng khoảng tin cậy là (30.9983; 32.5517)
b.Gọi 𝜎 là ộ lệch chuẩn về giá óng cửa của loại cổ phiếu này ( ơn vị: nghìn ồng)
Với mức ý nghĩa 5% =>∝= 0.05 Kiểm ịnh 𝐻0: "𝜎 = 5" 𝐻1: "𝜎 ≠ 5"
(𝑛 − 1)𝑠2 39 ∗ 6.2815 𝑇𝑖ê𝑢 𝑐ℎ𝑢ẩ𝑛
𝑘𝑖ể𝑚 đị𝑛ℎ: 𝜒2 = 𝜎02 = = 9.7992
Với 𝛼 = 0.05. 𝑡𝑎 𝑐ó miền bác bỏ: 𝑤𝑎
Nhận thấy 𝜒𝑞𝑠2 ∈ 𝑊𝑎. 𝑛ê𝑛 𝑏á𝑐 𝑏ỏ 𝐻0 ; 𝑐ℎấ𝑝 𝑛ℎậ𝑛 𝐻1
Vậy không thể cho rằng mức ộ biến ộng của giá cổ phiếu này là 5000 ồng Câu 5:
Gọi p là tỷ lệ khách hàng thích sản phẩm này; f là
tỷ lệ khách hàng thích sản phẩm này trong mẫu; f= = 0.3
a. Với ộ tin 90% => 1-∝= 0.9 => 𝑎 = 0.1. 𝑓 ( 1− 𝑓 ) √
Khoảng tin cậy bên trái của p là (0; 𝑓 + 𝑛 ∗ 𝑢𝑎
Ta có 𝑢0.1 = 1.2316 => 𝑝 ∈ (0; 0.3339)
Vậy với ộ tin cậy 90%, tỷ lệ khách hàng thích loại sản phẩm ó không vượt quá 0.3339
b.Gọi ε độ chính xác trong ước lượng tỷ lệ khách hàng thích sản phẩm
𝜀 = √𝑓(1−𝑓)𝑛 𝑢𝛼/2với
𝑉ậ𝑦 độ 𝑡𝑖𝑛 𝑐ậ𝑦 đạ𝑡 đượ𝑐 𝑙à 90.06%.
c. Gọi n0 là số phiếu thăm dò cần được tiến hành điều tra 𝑓(1−𝑓) 𝑈𝑎/2 2 𝜀 = √ 𝑛0
𝑢𝛼/2 => 𝑛0=f (1-f).( 𝜀)
Với 𝜀 = 0.03. độ 𝑡𝑖𝑛 𝑐ậ𝑦 95% => 1 − 𝑎 = 0.95 => 𝑎 = 0.05. 𝑢0.025 = 1.96 => 𝑛0=897 (phiếu thăm dò)
Vậy cần phải iều tra thêm 597 phiếu thăm dò nữa. ĐỀ 5: Câu 1: Gọi:
H1 = “ 1 người dân trong vùng thuộc loại “ít rủi rỏ”
H2 = “1 người dân trong vùng thuộc loại “rủi rot rung bình” H3
= “1 người dân trong vùng thuộc loại “rủi ro cao” H1,H3,H3 tạo thành hệ ầy ủ .
A = “1 người dân trong vùng gặp rủi ro trong 1 năm “
𝐴 = " 1 người dân trong vùng không gặp rủi ro trong 1 năm ”
=> P(A/H1) = 0,05; P(A/H2) = 0,15; P(A/H3) = 0,3
P(H1) = 0,2; P(H2) = 0,5; P(H3) = 0,3
1. Theo công thức xác suất ầy ủ
P(A)= P(H1).P(A/H1)+P(H2).P(A/H2)+P(H3).P(A/H3)
= 0,2.0,05+0,5.0,15+0,3.0,3=0,175
Vậy tỷ lệ dân gặp rủi ro trong 1 năm là 17,5%
2. Nếu một người không gặp rủi ro trong năm, thì xác suất người ó thuộc loại ít rủi ro là: P(𝐻1/𝐴 )=
𝑃(𝐻1)𝑃(𝐴.𝑃(𝐴 ) /𝐻1) = 𝑃(𝐻11−).𝑃(𝐴𝑃(𝐴 /𝐻1)) = 0,2.(1−0,05)1−0,175 = 0,2303 Câu 2:
Gọi 𝑥𝑜:= lượng tiền trong cây ATM (0 < 𝑥0 < 1) ( ơn vị: trăm triệu ồng)
Để cây ATM hết tiền thì X ≥ 𝑥0
Ta có: P{X≥ 𝑥𝑜} = 0,05 =P{𝑥0 ≤ 𝑋 < 1} 𝑑𝑥 = 𝑥0 = 0.4507
Vậy lượng tiền trong cây ATM là 45.07 triệu ồng Câu 3:
a. Gọi X1: = lãi suất cổ phiếu trên thị trường A, X1~N (19,36)
X2: = lãi suất cổ phiếu trên thị trường B, X2 ~ N (22, 100)
P{X1≥ 10}=1- P{X1< 10} = 0,5 + Φ0(1,5) = 0,5 + 0.4332 = 0,9332
P{X2≥ 10}=1- P{X2< 10} = 0,5 + Φ0(1,2) = 0,8849
Vì P{X1≥ 10}> P{X2≥ 10} nên ầu tư vào cổ phiếu ở thị trường A b. Gọi:
t: tỷ lệ ầu tư vào cổ phiếu trên thị trường A 1-t:
tỷ lệ ầu tư vào cổ phiếu trên thị trường B
Do X1, X2 là các biến ộc lập nên D(t.X1+ (1-t)X2) ạt giá trị nhỏ nhất khi
𝑡2. 𝐷(𝑋1) + (1 − 𝑡)2𝐷(𝑋2) = 𝑡2. 36 + (1 − 𝑡)2. 100 𝑚𝑖𝑛 136t2 - 200t +100 min T min= 25/34≈ 0.74
Vậy ể phương sai nhỏ nhất nên ầu tư theo tỷ lệ 0.74 vào cổ phiếu A. Câu 4:
1.Gọi X: = doanh thu do bán sữa của quầy A (Đơn vị: triệu ồng/ ngày)
μ ≔ doanh thu trung bình quầy hàng A ( ơn vị: triệu ồng/ ngày) σ
≔ độ lệch chuẩn quầy hàng A( ơn vị: triệu ồng) X~N(𝜇; 𝜎2)
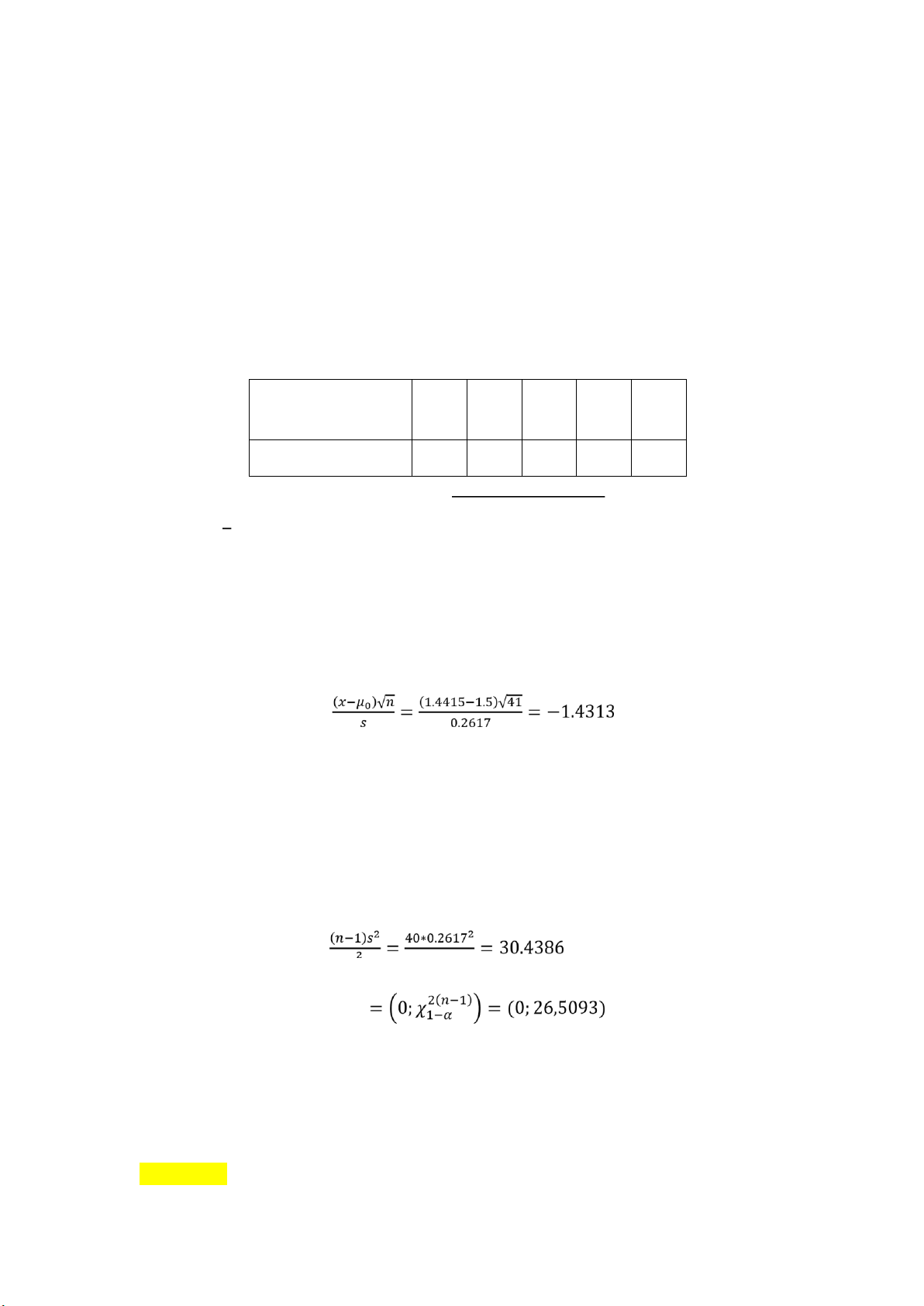
a.Bảng phân phối thực nghiệm: Doanh thu 1,1 1,3 1,5 1,7 1,9 ( Triệu ồng/ ngày) Số ngày 8 13 8 7 5
N=41; 𝑥 = 𝑛1 ∑5𝑖=1 𝑥𝑖𝑛𝑖 = 1.4415; 𝑠 = √𝑛−11 ∑5𝑖=1(𝑥𝑖 − 𝑥 )2𝑛𝑖 = 0.2617
a.Ước tính doanh thu trung bình trong 1 tuần của quầy A là: 7.𝑥 =10.0905
(𝑡𝑟𝑖ệ𝑢 đồ𝑛𝑔/𝑛𝑔à𝑦)2
b. Kiểm ịnh giả thuyết: 𝐻0: "𝜇 = 1.5" 𝐻1: "𝜇 < 1.5"
Tiêu chuẩn kiểm ịnh : T=
Miền bác bỏ với 𝛼 = 0.05: 𝑤𝛼 = (−∞; −𝑡𝛼𝑛−1) = (−∞; −1.6839)
Nhận thấy 𝑡𝑞𝑠 ∉ 𝑤𝛼 nên bác bỏ 𝐻1 𝑡ạ𝑚 𝑐ℎấ𝑝 𝑛ℎậ𝑛 𝐻0
Vậy với mức ý nghĩa 5% không thể cho rằng doanh thu trung bình mỗi ngày của quầy B cao hơn quầy A
c. Kiểm ịnh giả thuyết: 𝐻0: " 𝜎 = 0.3" 𝐻1: "𝜎 < 0.3" Tiêu chuẩn kiểm ịnh: T= 2 𝜎0 0.3
Miền bác bỏ với 𝛼 = 0.05: 𝑤𝛼
Nhận thấy 𝑡𝑞𝑠 ∉ 𝑤𝛼 nên bác bỏ 𝐻1 𝑡ạ𝑚 𝑐ℎấ𝑝 𝑛ℎậ𝑛 𝐻0
Vậy với mức ý nghĩa 5% không thể cho rằng mức ộ rủi ro trong bán sữa ở quầy A nhỏ hơn quầy B
2. Gọi N’là số người dùng thẻ tín dụng ở quận T
P là tỉ lệ những người dùng thẻ A trong những người dùng thẻ P =5000/N’ N=400; f= 270/400
Với ộ tin cậy 95% ta có ( f- 𝑢𝛼/2. < 𝑓 + 𝑢𝛼/2. √𝑓(1−𝑓) ) 𝑁′ => 6936< N’<7947
b. M là số dân của T p là tỉ lệ số người dùng thẻ A ở trong quận T p=5000/M n’=900; f=270/900 với 𝛾 = 95% 𝑡𝑎 𝑐ó √𝑓 ( 1− 𝑓 ) 5000 √𝑓 ( 1−𝑓 ) 𝑢 𝛼 . < < 𝑓 ′ + 𝑢 𝛼 . f’- 2 √ 𝑛 ′ 𝑀 2 √ 𝑛 ′ 0.3∗0.7 5000 0.3∗0.7 √ < <0.3+1.96 √ =>0.3 − 1.96 900 𝑀 900
=> 0.2701< 5000/M <0.3299 =>15157< M <18511
ĐỀ 6: Ngày 5/1/2019 Ca 2 Câu 1
a) 𝐻1:= “Sản phẩm bị mất là tốt”
𝐻2:= “Sản phẩm bị mất là xấu” 𝑃(𝐻1) = = 0,8 𝑃(𝐻2) = = 0,2 100
A:= “Lấy ược sản phẩm tốt”
𝑃(𝐴) = 𝑃(𝐻1). 𝑃(𝐴 𝐻⁄ 1) + 𝑃(𝐻2). 𝑃(𝐴 𝐻⁄ 2) = 0,8. + 0,2. = 0,8
Vậy xác suất ể lấy ược sản phẩm tốt là: 0,8 b) 𝑃(𝐻2⁄ )𝐴 =
𝑃(𝐻2)𝑃.𝑃(𝐴(𝐴 𝐻) ⁄ 2) = = 0,2020
Vậy xác suất ể lấy ược sản phẩm tốt khi sản phẩm mất là sản phẩm xấu là 0,2020 Câu 2:
X:= Số cây không ạt tiêu chuẩn trong 10 cây X~H(60;7;10)
Trung bình số cây không ạt tiêu chuẩn: E(X) = n.p = 10. = = 1,1667
Vậy số cây trung bình ạt tiêu chuẩn là 1,1667
Câu 3: X:= Số khách có nhu cầu thuê xe X~𝑃(2)
Y:= SỐ ô tô cửa hàng cho thuê
Y(Ω) = {0; 1; 2; 3; 4} P(Y=0)=P(X=0)= 𝑒−2×20 P(Y=1)=P(X=1)= 𝑒 −2×21 0.2707 P(Y=2)=P(X=2)= 𝑒 −2×22 0.2707 P(Y=3)=P(X=3)= 𝑒 −2×23 0.1804
P(Y=4)=P(X≥ 4) = 1 − 𝑃(𝑋 < 4)= 0.1429 Câu 4:
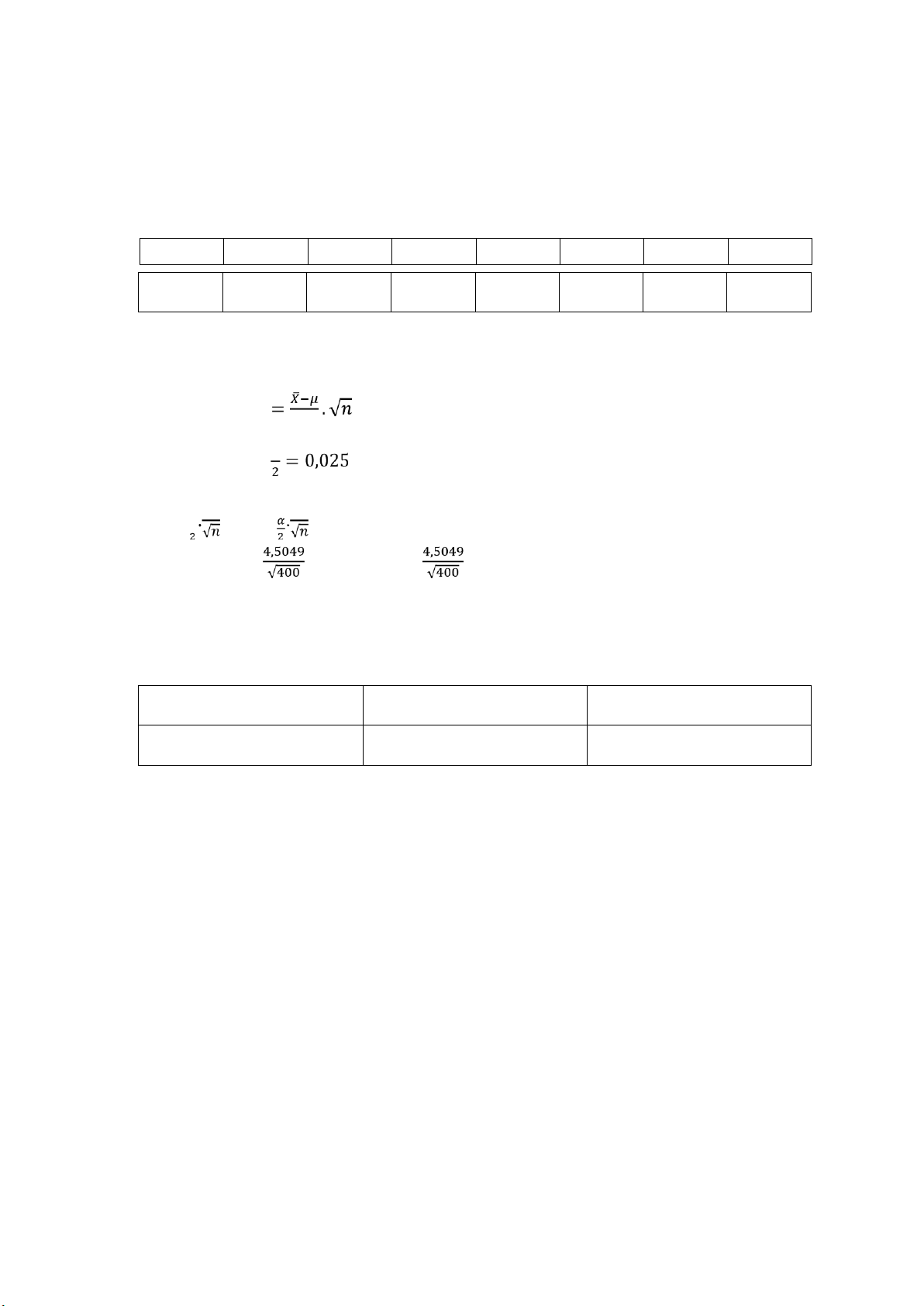
X:= Thời gian tự học trong một tuần của 1 sinh viên (giờ/tuần) X~QLBK với n=400>30 Bảng tần số: X 0 2 5 8 11 14 18 N 30 65 125 85 50 25 20 𝑋 = 6,7375 s = 4,5049 a)
Tìm KTCĐX cho 𝜇 = 𝐸(𝑋) Chọn thống kê: G~𝑁(0; 12) 𝑠 Với 𝛾 = 0,95 → 𝛼 → 𝑢0,025 = 1,96
KTCĐX cho 𝜇 = 𝐸(𝑋) 𝑙à: (𝑋 - 𝑢𝛼 𝑆 ,𝑋 + 𝑢 𝑆 ) =(6,7375 – 1,96. ; 6,7375 + 1,96. ) =(6,2960; 7,1789)
Vậy khoảng tin cậy ối xứng của số giờ tự học trong tuần trung bìn
chính quy trường này là: (6,2960; 7,1789) b) Y:= Số sinh viên
chăm học Bảng phân phối thực nghiệm: h của một sinh viên Y 14 18 N 25 20 𝑌 = 15,7778 𝑠 = 2,0101
A:= “Khảo sát ược sinh viên chăm học” 𝑓 = 𝑓(𝐴) = = 0,1125 p = p(A)
Tìm khoảng tin cậy ối xứng cho p: Chọn thống kê (𝑓 − 𝑝) 𝐺 =
𝑣ớ𝑖 𝑛𝑓 = 400.0,1125 = 45 > 10 √𝑓 ∗ (1 − 𝑓)
𝑛. (1 − 𝑓) = 400. (1 − 0,1125) = 355 > 10
Với 𝛾 = 0,95 → 𝛼2 = 0,025 → 𝑢0,025 = 1,96 KTCĐX cho p là: √𝑓. (1 − 𝑓) (𝑓 − 𝑢 ; 𝑓 + 𝑢 ; 0,1125 ) =(0,0815; 0,1435)
Vậy với ộ tin cậy 95%, khoảng tin cậy ối xứng của tỉ lệ sinh viên chăm học trong
trường này là: (0,0815; 0,1435) c) Xây dựng cặp giả thuyết: 𝐻0: 𝜇 = 𝜇0 = 16 𝐻
Chọn tiêu chuẩn kiểm ịnh: 𝑋 − 𝜇 𝐻0 đú𝑛𝑔 = . √ 𝑛 G⇔ 𝑁(0, 12) 𝑠 Miền bác bỏ 𝐻 : 𝑊𝛼 =( =(- 1,96) 𝐺𝑞𝑠 𝛼
→ 𝐵á𝑐 𝑏ỏ 𝐻 , 𝑐ℎấ𝑝 𝑛ℎậ𝑛 𝐻0
Vậy chấp nhận ý kiến số giờ tự học một sinh viên chăm học là 16 giờ/tuần với mức ý nghĩa 5%. Câu 5:
Chọn ược sản phẩm loại A” 𝑓 = 𝑓(𝐴) = = 0,825 p = p(𝐴) 𝑝0 = = 0,9
Xác ịnh cặp giả thuyết: 𝐻 : 𝑝 = 𝑝 𝐻
Chọn tiêu chuẩn kiểm ịnh: (𝑓 − 𝑝0) 𝐺 =
𝑉ớ𝑖 𝑛. 𝑝0 = 400.0,9 = 360 > 5
𝑛. (1 − 𝑝0) = 400.0,1 = 40 > 5 Miền bác bỏ 𝐻0: 𝑊𝛼 Gqs
→ Bác bỏ H , chấp nhận H .
Vậy với mức ý nghĩa 5%, nếu cho rằng số sản phẩm loại A của lô hàng là 4500 thì không thể chấp nhận ược.
b) Gọi là sai số khi ước lượng số sản phẩm loại A Ta có: Mà 𝜀 = 𝑢2 √ 𝑛 𝛼
Vậy muốn ước lượng sản phẩm loại A của lô hàng ạt ộ chính xác là 150 sản phẩm thì ộ
tin cậy ạt ược là 88,56%.
ĐỀ 7: NGÀY 6/7/2019 Câu 1:
a) A:= “Người ó thắng cổ phiếu TBS”
B:= “Người ó thắng cổ phiếu SCB”
C:= “Người ó thắng ít nhất 1 trong 2 loại cổ phiếu” P(C) =
P(A∪ 𝐵) = 𝑃(𝐴) + 𝑃(𝐵) − 𝑃(𝐴𝐵) = 0,6 + 0,5 − 0,45 = 0,65
Vậy xác suất ể người ó thắng ít nhất một trong hai loại cổ phiếu là: 0,65 b) P(𝐴 /𝐵 ) = 𝑃(𝐵 ) = 𝑃(𝐵 ) = 1−0,5 = 0,7
Vậy xác suất ể người ó thất bại ở cổ phiếu TBS biết người ấy ã thất bại ở cổ phiếu SCB là 0,7. Câu 2:
Gọi x là số tiền giá vé tăng thêm (nghìn ồng)
X:= Số tiền ền bù khi mất hành lí (nghìn ồng) X(Ω) = {0; 600}
𝑝1 = 𝑝(𝑋 = 0) = 1 − 0,005 = 0,995
𝑝2 = 𝑝(𝑋 = 600) = 0,005
=> x = E(X) = 0.0,995+ 600.0,005 = 3 (nghìn ồng) Vậy
nên tăng thêm mỗi giá vé 3000 ồng. Câu 3:
X:= Số cây không cho giao dịch trong 1 giờ X~𝐵(10; 0,08)
Số cây không cho giao dịch có khả năng cao nhất là:
Mod(X) = [(n+1).p] = [0,88] = 0
Vậy có 0 cây không giao dịch có khả năng cao nhất trong một giờ ở phường này. Câu 4:
X:= Nhu cầu về loại hàng H của một gia ình trong một tháng (Kg/tháng)
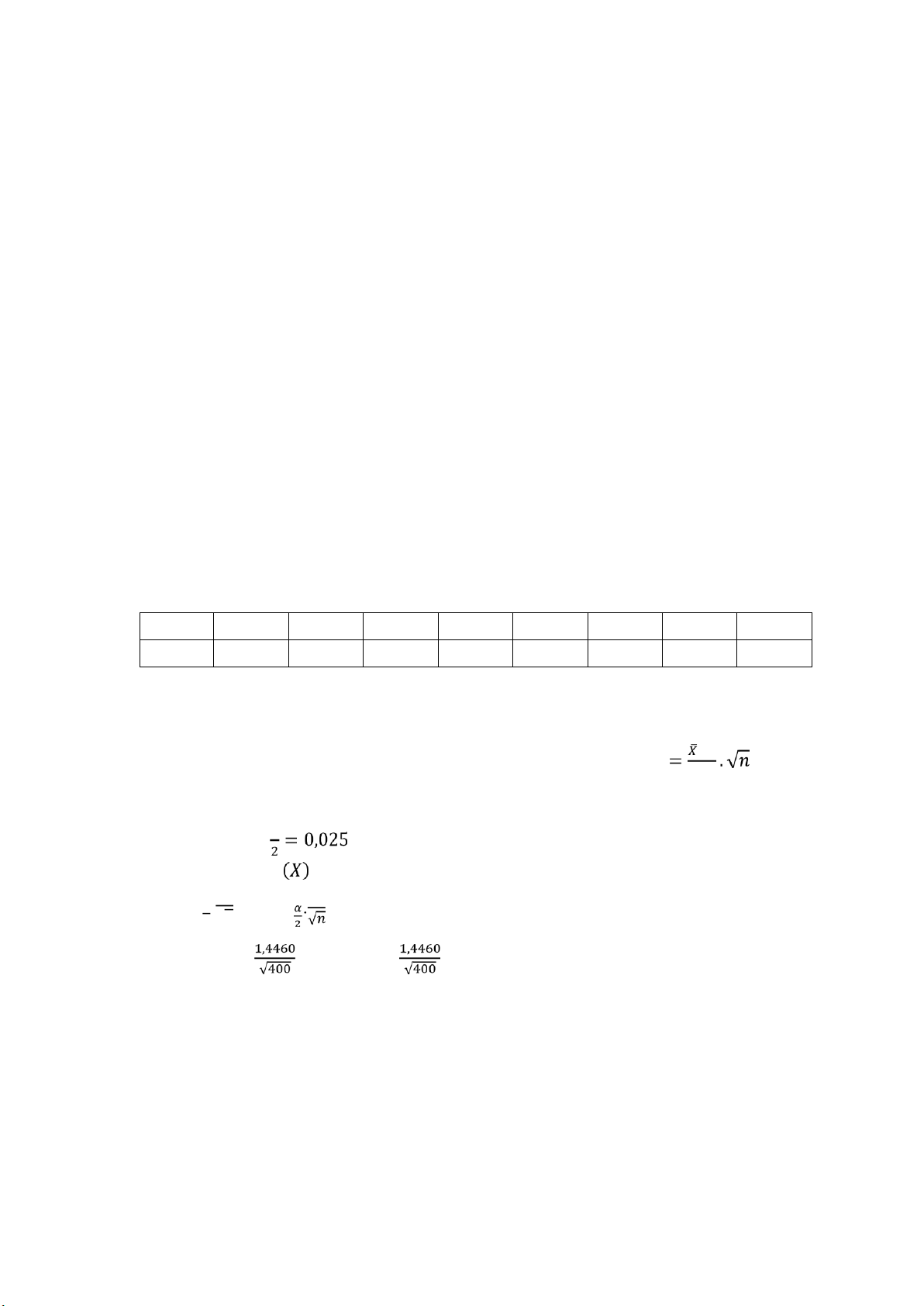
X~𝑄𝐿𝐵𝐾 𝑣ớ𝑖 𝑛 = 400 > 30 Bảng tần số: X 0,5 1,5 2,5 3,5 4,5 5,5 6,5 7,5 N 10 35 86 132 78 31 18 10 𝑋 = 3,62 S = 1,4460
a) Tìm khoảng tin cậy ối xứng cho 𝜇 = 𝐸(𝑋): Chọn thống kê: G −𝜇 ~ 𝑁(0; 12) 𝑠 Với 𝛾 = 0,95 → 𝛼 → 𝑢0,025 = 1,96 KTCĐX cho 𝜇 = 𝐸 𝑙à: 𝛼 . (𝑋 - 𝑢 √ 𝑛𝑆 2 , 𝑋 + 𝑢 𝑆 ) = (3,62 – 1,96. ; 3,62 + 1,96. ) = (3,4783; 3,7617)
=> KTCĐX cho của nhu cầu trung bình về hàng H ở toàn khu vực K trong một năm là:
(3,4783.12.4000 ; 3,7617.12.4000) = (166958,4; 180561,6) kg
Vậy với ộ tin cậy 95%, khoảng tin cậy ối xứng của nhu cầu trung bình về hàng H ở toàn
khu vực A trong một năm là (166958,4; 180561,6) kg
b) Gọi 𝜀 là ộ chính xác khi ước lượng nhu cầu về hàng H ở toàn khu vực K trong một tháng (Kg/tháng) 𝜀 = = 0,1 Ta có: 𝑠 𝜀 = 𝑢 0,1 = 𝑢 => 𝑛 = => 𝑛 =
=> Cần khảo sát thêm 804 – 400 = 404 hộ gia ình
Vậy nếu ta muốn ạt ộ tin cậy 95% và ộ chính xác là 4,8 tấn thì cần khảo sát thêm 404 hộ gia ình ở khu vực K. c) 𝜇0 = = 4
Xây dựng cặp giả thuyết: 𝐻 : 𝜇 = 𝜇 𝐻
Chọn tiêu chuẩn kiểm ịnh: 𝑋 − 𝜇0 𝐻0 đú𝑛𝑔 𝐺 = . √ 𝑛 ⇔ 𝑁 𝑠 Miền bác bỏ : 𝑊 𝐺𝑞𝑠
=> Bác bỏ 𝐻0, 𝑐ℎấ𝑝 𝑛ℎậ𝑛 𝐻1.
Vậy với mức ý nghĩa 5%, vậy không nên tin tài liệu này. Câu 5:
(𝑡𝑟𝑖ệ𝑢đồ𝑛𝑔/𝑛ă𝑚)
𝑋~𝑄𝐿𝐵𝐾 𝑣ớ𝑖 𝑛 = 100 > 30 Bảng phân phối thực nghiệm: X 28 36 44 52 60 68 76 n 8 12 20 25 20 10 5
a) Số người có thu nhập cao (thu nhập trên 56 triệu ồng/năm) là:
20 + 10 + 5 = 35(𝑛𝑔ườ𝑖)
A:= “Khảo sát ược nhân viên có thu nhập cao” 𝑓 = 𝑓(𝐴) = = 0,35
Gọi N là tổng số người có thu nhập cao trong công ty A 𝑁 𝑝 = 𝑝(𝐴) = 3000
Tìm khoảng tin cậy ối xứng cho p: Chọn thống kê: 𝐺 = 𝑓−𝑝 √𝑓 ( 1− 𝑓 ) 𝑣ớ𝑖 𝑛𝑓 𝑛. 𝛼 𝛾 = 0,98
Khoảng tin cậy ối xứng cho p: √ ( 1− 𝑓 ) √ ( 1− 𝑓 ) 𝑓 𝑓 𝛼 . 𝛼 . ) (𝑓 − 2 √ 𝑛 2 √ 𝑛 𝑢; 𝑓 + 𝑢 ; 0,35 0,2390; 0,4610 𝑁 ⇒ 0,2390
=> 717Vậy số nhân viên có thu nhập cao của công ty A nằm trong khoảng (717; 1383) b)
Xây dựng cặp giả thuyết 𝐻0: 𝑝 = 𝑝0 = 0,2 𝐻1: 𝑝 > 0,2
Chọn tiêu chuẩn kiểm ịnh: 𝐻 đú𝑛𝑔 𝑓−𝑝 0 . √ 𝑛
𝐺 = √𝑝 0 . ( 1− 𝑝 0 ) ⇔ 𝑁(0; 12)
𝑉ớ𝑖 𝑛. 𝑝0 = 100.0,2 = 20 > 5
𝑛. (1 − 𝑝0) = 100.0,8 = 80 > 5
𝛼 = 0,05 ⇒ 𝑢0,05 = 1,6449 Miền bác bỏ 𝐻0:
𝑊𝛼 = (𝑢𝛼; +∞) = (𝑢0,05; +∞) = (1,6449; +∞) 𝐺𝑞𝑠 . 𝛼 √0,2(1 − 0,2)
⇒ 𝐵á𝑐 𝑏ỏ 𝐻0, 𝑐ℎấ𝑝 𝑛ℎậ𝑛 𝐻1.
Vậy với mức ý nghĩa 5%, không thể kết luận tỷ lệ nhân viên có thu nhập cao của công ty A là 20%.
Đề 8: Ngày thi 20/06/2019 Câu 1:
𝐴𝑖:= “Khách hàng gửi tiết kiệm ến năm thứ i" 𝑖 = 1,3 𝑝(𝐴1) = 0,7 p(𝐴2) = 0,3 p(𝐴3) = 0,1 0 ,3
a) 𝑝(𝐴2/𝐴1) = 𝑝(𝑝𝐴(1𝐴.𝐴1)2) = 𝑝𝑝((𝐴𝐴 )) = = 0,4286 0 ,7 21
Vậy nếu khách hàng ã gửi tiền tới 1 năm thì xác suất ể người ó tiếp tục gửi tiền tới 2 năm là 0,4286. 0 ,1
b) 𝑝(𝐴3/𝐴1) = 𝑝(𝑝𝐴(1𝐴.𝐴1)3) = 𝑝𝑝((𝐴𝐴 )) = = 0,1429 0 ,7 31
Vậy nếu khách hàng ã gửi tiền tới 1 năm thì xác suất ể người ó gửi tiền thêm 2 năm nữa là 0,1429. Câu 2:
Vì F(X) liên tục trên R tại x=5 nên ta có: 𝑘 lim(1 − 𝑥2) = 𝐹(5) 𝑥→5 𝑘 <=> 1 − 52 = 0 => 𝑘 = 25 Câu 3:
X:= Doanh thu hàng tháng của một cửa hàng (triệu ồng) 𝐸(𝑋) = 𝜇 = 8 𝜎 = 1,2 𝑋~𝑁(8; 1,22) 𝑝
Vậy xác suất ể cửa hàng có doanh thu trên 10,4 triệu ồng/tháng là 0,0228. Câu 4:
X:= Mức dùng nhiên liệu ể sản xuất ra một ơn vị sản phẩm ở nhà máy M (g/sản phẩm)
𝑋~𝑄𝐿𝐵𝐾với 𝑛 = 50 > 30
Bảng phân phối thực nghiệm: X 28 29 30 31 32 n 3 11 17 11 8 𝑋 = 30,2 𝑠 = 1,1429
a) Tìm khoảng tin cậy ối xứng cho 𝜇 = 𝐸(𝑋): Chọn thống kê: G ~𝑁(0; 12) 𝑠
Với 𝛾 = 0,98 → 𝛼2 = 0,01 → 𝑢0,01 = 2,3263
Khoảng tin cậy ối xứng cho 𝜇 = 𝐸(𝑋) 𝑙à: (𝑋 - 𝑢𝛼 𝑆 , 𝑋 + 𝑢 . 𝑆 ) 2 ; 30,2 + 2,3263. ) =(29,8240; 30,5760)
=> Số tiền mua nguyên liệu cho từng quý là:
(29,8240.600.50000; 30,5760.600.50000) = (893220000; 917280000)
Vậy với ộ tin cậy 98%, số tiền ể mua nhiên liệu trong từng quý của xí nghiệp A nằm trong
khoảng (893220000; 917280000) ồng.
b) Xây dựng cặp giả thuyết: 𝐻0: 𝜇 = 𝜇0 = 31 𝐻1: 𝜇 < 31 Chọn tiêu chuẩn kiểm ịnh: 𝑋 − 𝜇 𝐻0 đú𝑛𝑔 2) = . √ 𝑛 G 𝑁(0, 1 𝑠 𝛼 = 0,05 Miền bác bỏ 𝐻 : 𝑊𝛼 = ( = (- ) 𝐺𝑞𝑠 𝑊𝛼
→ 𝐵á𝑐 𝑏ỏ 𝐻0, 𝑐ℎấ𝑝 𝑛ℎậ𝑛 𝐻1
Vậy với mức ý nghĩa 5%, công nghệ mới này có làm giảm mức dùng nhiên liệu. c) Gọi
là sai số khi ước lượng mức dùng nhiên liệu (g/sản phẩm) 𝜀 = = 0,3333 𝛼
𝛾 = 0,99 ⇒ = 0,005 ⇒ 𝑢0,005 = 2,5758 2 Ta có: 𝜀 = 𝑢 𝑆 0,3333 = 𝑛 = 78,01356 => n = 79
Vậy muốn ước lượng trung bình số tiền ể mua nhiên liệu trong từng quý của toàn nhà máy
M ạt ộ tin cậy 99% và ộ chính xác là 10 triệu ồng thì cần mẫu có kích thước là 78 sản phẩm.
d) Số sản phẩm có mức dùng nhiên liệu trên 30g/sản phẩm là: 11+8=19 (sản phẩm)
A:= “Theo dõi ược sản phẩm dùng nhiên liệu trên 30g/sản phẩm” 𝑓 = 𝑓(𝐴) = = 0,38 p = p(A)
Tìm khoảng tin cậy ối xứng cho p: Chọn thống kê 𝐺 =
𝑣ớ𝑖 𝑛𝑓 = 50.0,38 = 19 > 10
𝑛. (1 − 𝑓) = 50. (1 − 0,38) = 31 > 10
Với 𝛾 = 0,95 → 𝛼2 = 0,025 → 𝑢0,025 = 1,96 KTCĐX cho p là: √𝑓. (1 − 𝑓) √𝑓. (1 − 𝑓) (𝑓 − 𝑢 ; 𝑓 + 𝑢 = (0,38 – 1,96. ; 0,38 + 1,96. = (0,2455; 0,5145)
Vậy với ộ tin cậy 95%, tỉ lệ sản phẩm có mức dùng nhiên liệu trên 30g/sản phẩm nằm
trong khoảng (0,2455; 0,5145)
e) Theo tiêu chuẩn không chệch, phương sai của mức tiêu dùng nguyên liệu cho một đơn vị sản phẩm là: 𝑠2 ≈ 1.3062
Đề 9: Ngày 8/7/2019 Ca Câu 1:
A:= “Phòng có hệ thống ống nước hỏng” 𝐻
Khách hàng ặt phòng tại Metropole" 𝐻
“Khách hàng ặt phòng tại Sheraton” 𝐻
Khách hàng ặt phòng tại Lake View” P(𝐻 P(𝐻 P(𝐻3) = 0,3 Có: 𝐻 𝐻 →
𝑙à 𝑛ℎó𝑚 đầ𝑦 đủ 𝑐á𝑐 𝑏𝑖ế𝑛 𝑐ố
a) Áp dụng công thức xác suất ầy ủ:
P(A) = P(𝐻1). P(𝐴 𝐻⁄ 1) + P(𝐻2). P(𝐴 𝐻⁄2) + P(𝐻3).P(𝐴 𝐻⁄ 3)
= 0,2.0,02 + 0,5.0,01 + 0,3.0,04 = 0,021
Vậy xác suất ể khách hàng sẽ gặp phải phòng có hệ thống ống nước hỏng là: 0,021 b) P(𝐻 ⁄𝐴) = 𝑃
Vậy xác suất ể một khách hàng sẽ ở khách sạn Lake View và biết rằng người ó gặp
phải phòng có hệ thống ống nước hỏng là 0,5714 Câu 2: Ta có: Có 𝑝(𝑥 > 2) => (𝑥 > 2)
Vậy xác suất ể thiết bị này sử dụng ược ít nhất 2 năm là 0,0183. Cách 2:
Ta có: 𝑷(𝑿 ≥ 𝟐) = ∫𝟐+∞ 𝟐. 𝒆−𝟐𝒙𝒅𝒙 = 𝐥𝐢𝐦𝒃→+∞ ∫𝟐𝒃. 𝒆−𝟐𝒙𝒅𝒙 = 𝐥𝐢𝐦 − 𝒆𝒃→+∞ −𝟐𝒙|𝑏2 = 𝑒−4 = 0.0183 Câu 3:
X:= Số máy ếm tiền hỏng trong 1 ngày của 1 chi nhánh
Do p(A)=0,1 trong cả 10 phép thử này nên 𝑋~𝐵(10; 0,1)
Vậy luật phân phối xác suất của số máy ếm tiền hỏng trong 1 ngày của 1 chi nhánh là:
𝑋~𝐵(10; 0,1) Câu 4:
X:= Tỷ lệ khoáng chất trong một chai nước (%)
𝑋~𝑄𝐿𝐵𝐾 𝑣ớ𝑖 𝑛 =100 > 30
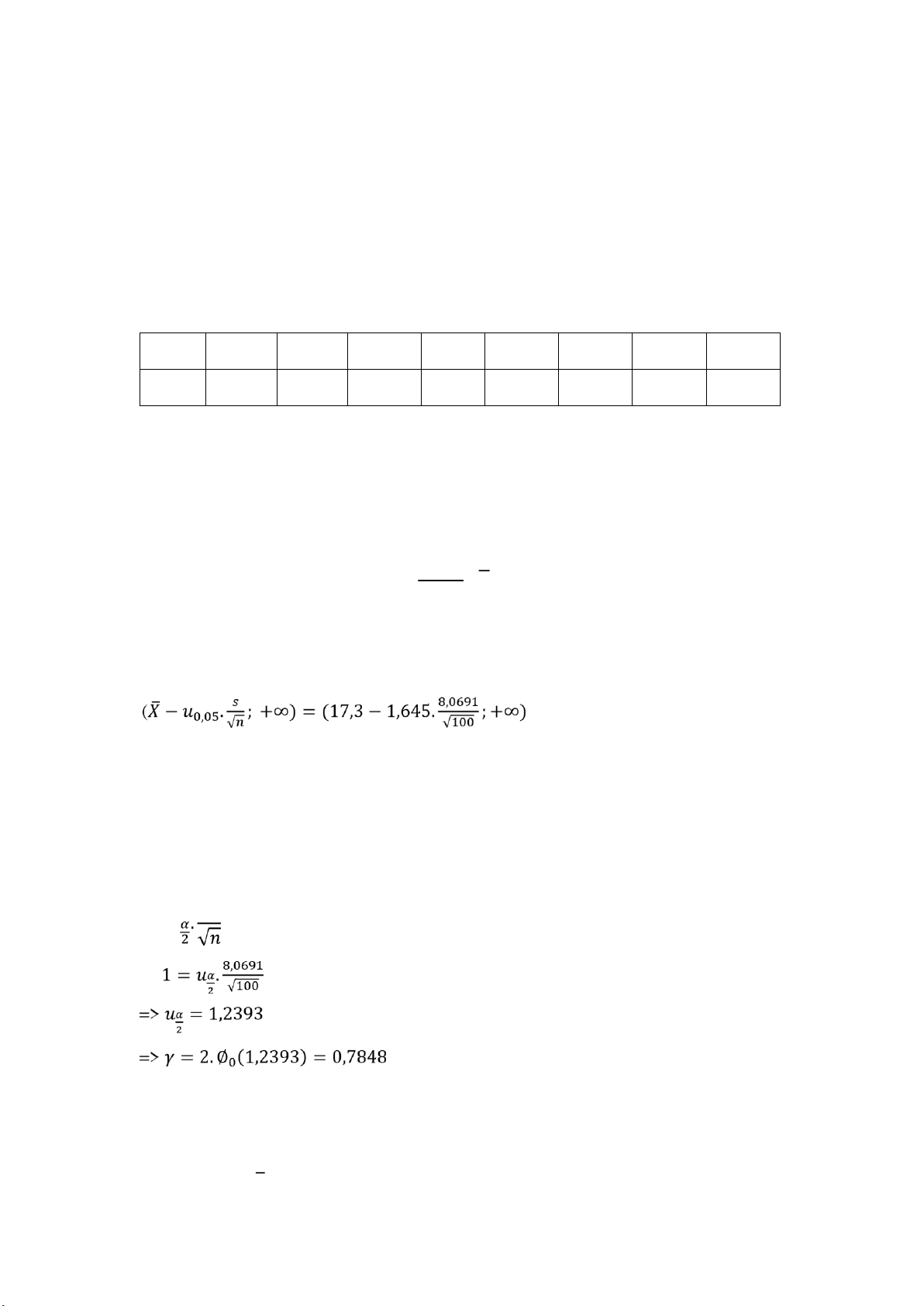
Bảng phân phối thực nghiệm X 2,5 7,5 12,5 17,5 22,5 27,5 32,5 37,5 n 7 12 20 25 18 12 5 1 𝑋 = 17,3 S = 8,0691
a) Tìm khoảng tin cậy bên phải cho 𝜇 = 𝐸(𝑋): Chọn thống kê:
𝐺 = 𝑋 − 𝜇 √𝑛~𝑁(0; 12) 𝑠
𝛾 = 0,95 ⇒ 𝛼 = 0,05 ⇒ 𝑢0,05 = 1,645
Khoảng tin cậy bên phải cho 𝜇: = (15,9726; +∞)
Vậy với ộ tin cậy 95%, trung bình tỷ lệ khoáng chất trong mỗi chai nước A không bé hơn 15,9726%.
b) Gọi 𝜀 là ộ chính xác khi ước lượng tỷ lệ khoáng chất của mỗi chai nước A (%) 𝑠 𝜀 = 𝑢
Vậy với ộ chính xác 1% thì ộ tin cậy là 78,48%.
c) 𝛾 = 0,96 ⇒ 𝛼 2 = 0,02 ⇒ 𝑢0,02 = 2,0538 𝜀 = 1,2 Ta có: 𝑠 𝜀 = 𝑢 𝑛 = (𝑢 . 𝑠 𝜀 2 𝑛 = (2,0538. ) => 𝑛 = 190,7 => 𝑛 = 191
=> Số chai nước phải xét nghiệm thêm là 191-100=91 (chai)
Vậy muốn ộ tin cậy 96% vầ ộ chính xác là 1,2% thì phải xét nghiệm thêm 91 chai nước nữa.
d) Số chai nước không ạt yêu cầu (có tỷ lệ khoáng chất nhỏ hơn 10%) là: 7+12=19 (Chai)
A:= “Xét nghiệm ược chai không ạt yêu cầu” 𝑓 = 𝑓(𝐴) = = 0,19
Gọi N là số chai không ặt yêu cầu trong 5000 chai. 𝑁 𝑝 = 𝑝(𝐴) = 5000 Chọn thống kê ( 𝑓−𝑝 ) ∗ √ 𝑛
𝐺 = với 𝑛𝑓 = 100.0,19 = 19 > 10 √𝑓∗ ( 1−𝑓)
𝑛. (1 − 𝑓) = 100. (1 − 0,19) = 81 > 10
Với 𝛾 = 0,95 → 𝛼2 = 0,025 → 𝑢0,025 = 1,96 Khoảng
tin cậy ối xứng cho p là: √ ( 1− 𝑓 ) √ ( 1− 𝑓 ) 𝑓. 𝑓. 𝛼 . 𝛼 . ) (𝑓 − 2 2 𝑢; 𝑓 + 𝑢 √ 𝑛 √ 𝑛 ; 0,19 = (0,1131; 0,2669) 0,1131 < 𝑁 < 0,2669 5000 565,5 < N < 1334,5
Vậy với ộ tin cậy 95% số chai nước không ạt yêu cầu trong kho nằm trong khoảng (565,4;1334,5)
e) B:= “Xét nghiệm ược chai ạt yêu cầu”
𝑓 = 𝑓(𝐵) = 1 − 𝑓(𝐴) = 1 − 0,19 = 0,81 𝑝 = 𝑝(𝐵)
Xây dựng cặp giả thuyết: 𝐻0: 𝑝 = 𝑝0 = 0,8 𝐻1: 𝑝 > 0,8
Chọn tiêu chuẩn kiểm ịnh: 𝐻 đú𝑛𝑔 𝑓−𝑝 0 𝐺 . √ 𝑛 √𝑝 =⇔ 𝑁(0; 12) 0 . ( 1− 𝑝 0 )
𝑉ớ𝑖 𝑛. 𝑝0 = 100.0,8 = 80 > 5
𝑛. (1 − 𝑝0) = 100. (1 − 0,8) = 20 > 5 𝛼 = 0,05 ⇒ 𝑢 Miền bác bỏ 𝐻 : 𝑊𝛼 0 ,81 −0 ,8 = 𝐺𝑞𝑠 √ 0 ,8(1−0, 8) . 𝛼
⇒ 𝐶ℎấ𝑝 𝑛ℎậ𝑛 𝐻0, 𝑏á𝑐 𝑏ỏ 𝐻1.
Vậy với mức ý nghĩa 5% tỷ lệ chai nước A ạt yêu cầu trong kho không trên 80%.
Đề 10: Ngày 8/7/2019 Ca 2 Câu 1:
A:= “Giá xăng dầu trong nước tăng”
𝐻1:= “ Giá dầu thô trên thế giới tăng”
𝐻2 ≔ "Giá dầu thô trên thế giới không tăng" P(𝐻1)=0,45 p(𝐻2)=0,55
a) P(𝐴 .𝐻2) = 𝑃(𝐻2). 𝑃(𝐴 ⁄𝐻2)
= 𝑃(𝐻2). (1 − 𝑃(𝐴/𝐻2)
= 0,55. (1 − 0,07) = 0,5115
Vậy xác suất trong tháng tới giá dầu thô trên thế giới và giá xăng dầu trong nước ều không tăng là 0,5115 b) Có 𝐻1. 𝐻2 = ∅ 𝐻1 ∪ 𝐻2 = Ω
→ {𝐻1; 𝐻2} 𝑙à 𝑛ℎó𝑚 đầ𝑦 đủ 𝑐á𝑐 𝑏𝑖ế𝑛 𝑐ố Áp
dụng công thức xác suất ầy ủ:
P(A) = P(𝐻1). 𝑃(𝐴 𝐻⁄2) + 𝑃(𝐻2). 𝑃(𝐴 𝐻⁄2) = 0,45.0,85 + 0,55.0,07 = 0,421 P(𝐻1⁄𝐴) =
𝑃(𝐻1)𝑃.𝑃(𝐴(𝐴 𝐻) ⁄ 1) = 0,38250,421 ≈ 0,9086
Vậy xác suất ể trong tháng tới giá dầu thô trên thới giới tăng, nếu giá xăng dầu trong nước tăng là 0,9086. Câu 2:
X:= Số tiền ền bù cho khách bị mất hành lý (Nghìn ồng) X(Ω) = {0; 500; 3000}
𝑝1 = 𝑝(𝑋 = 0) = 1 − 0,005 = 0,995 𝑝2 = 𝑝(𝑋 = 500) = . 0,005 = 3. 10−3 𝑝3 = 𝑝(𝑋 = 3000) = . 0,005 = 2. 10−3
Số tiền phải ền bù trung bình cho khách bị mất hành lý cũng chính là số tiền phải tăng giá vé là:
E(X) = 𝑖 = 13𝑥𝑖𝑝𝑖 = 0.0.995 + 500.3. 10−3 + 3000.2. 10−3
= 7,5 (𝑛𝑔ℎì𝑛 đồ𝑛𝑔)
Vậy ể bù vừa ủ cho số tiền phải trả do ền bù thì hãng hàng không phải tăng mỗi vé 7500 ồng. Câu 3:
X:= Số tiền bị hủy trong một ngày ở Ngân hàng Nhà nước (Triệu ồng) X~𝑃(10)
Y:= Số tiền phát hành trong một ngày ở Ngân hàng Nhà nước (Triệu ồng)
Y~𝑃(11) P[P(X=10).P(Y=10)] = 𝑒−10. 10 10 . 𝑒−11. 11 10 = 0,0149 10! 10!
Vậy xác suất ể số tiền bị hủy và phát hành trong một ngày nào ó ều là 10 triệu ồng là 0,0149 Câu 4:
X:= Khối lượng của một sản phẩm ở xí nghiệp A (g)
X=~𝑄𝐿𝐵𝐾 𝑣ớ𝑖 𝑛 = 100 > 30 Bảng phân phối thực nghiệm X 825 875 925 975 1025 1075 1125 n 5 10 20 30 15 10 10 𝑋 = 980 𝑠 = 79,2961
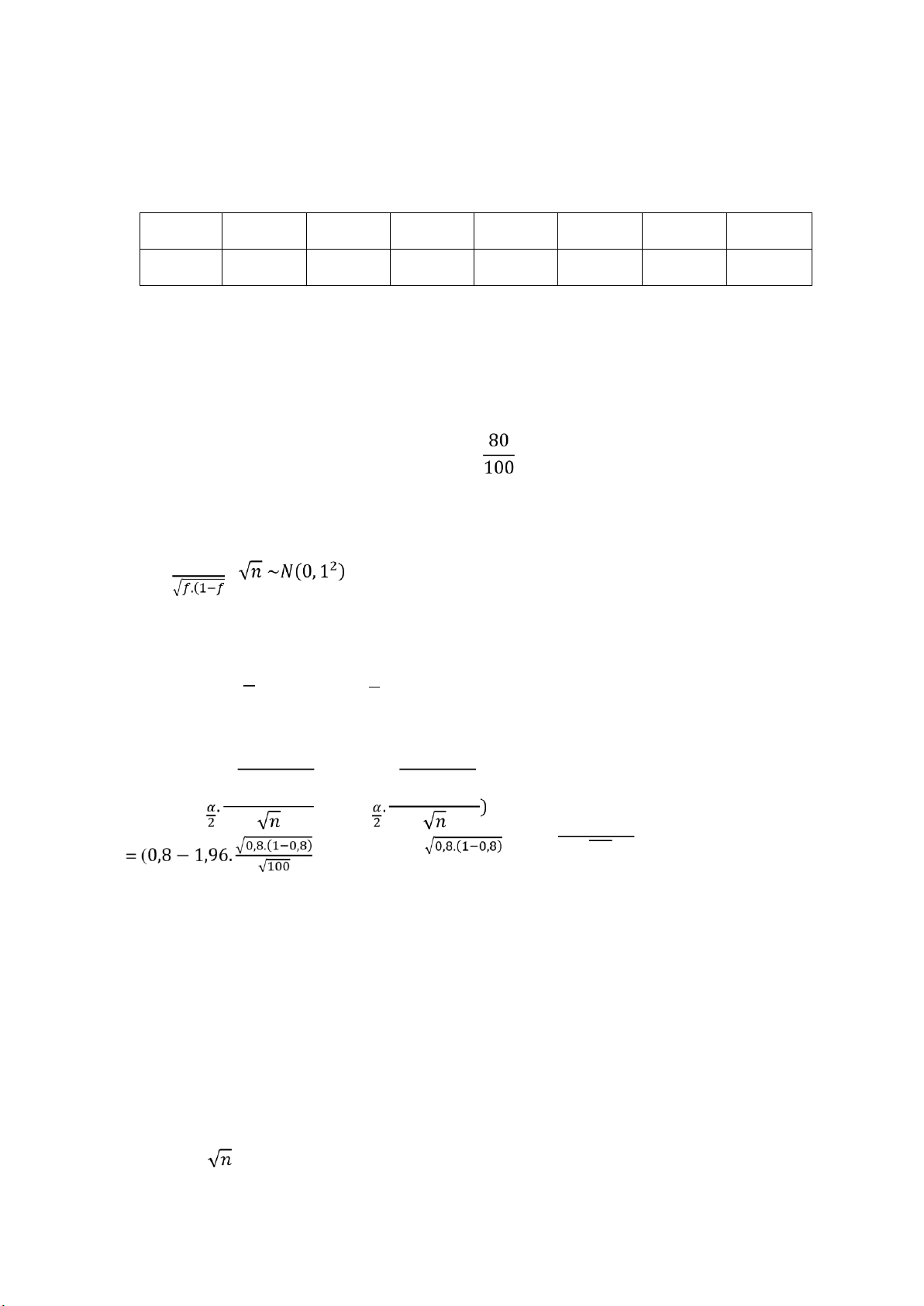
a) 𝐴 ≔ ”𝑆ả𝑛 𝑝ℎẩ𝑚 𝑘ℎô𝑛𝑔 đạ𝑡 𝑙𝑜ạ𝑖 1” 𝑓 = 𝑓(𝐴) = = 0,8 𝑝 = 𝑝(𝐴) Chọn thống kê: 𝑓−𝑝 𝐺 = . 𝑣ì 𝑛𝑓 > 10 𝑛. (1 − 𝑓) > 10 𝛼
𝛾 = 95% => = 0,025 => 𝑢𝛼 = 1,96 2 2
Khoảng tin cậy ối xứng cho p: √𝑓. (1 − 𝑓) √𝑓. (1 − 𝑓) (𝑓 − 𝑢 ; 𝑓 + 𝑢 √ 100 ; 0,8 + 1,96. ) = (0,7216; 0,8784)
Vậy với ộ tin cậy 95%, khoảng tin cậy ối xứng cho tỉ lệ sản phẩm không ạt loại 1 là: (0,7216; 0,8784)
b) Xác ịnh cặp giả thuyết: 𝐻0: 𝜇 = 𝜇0 = 1000 𝐻1: 𝜇 < 1000
Chọn tiêu chuẩn kiểm ịnh: 𝐻0 đú𝑛𝑔 − µ 0
G = 𝑋 𝑆 . ↔ Ɲ(0; 12) vì n = 53 > 30 Miền bác bỏ 𝐻 : 𝑊𝛼 𝐺𝑞𝑠 𝛼
=> Bác bỏ 𝐻0, chấp nhận 𝐻1
Vậy với mức ý nghĩa 5%, có thể cho rằng cải tiến này làm tăng khối lượng trung bình của sản phẩm. c)
Khối lượng của sản phẩm loại 1 ở xí nghiệp A (g) Y~𝑁(𝜇; 𝜎2)
Bảng phân phối thực nghiệm Y 1075 1125 n 10 10 𝑌 =1100 𝑠 = 25,6495 Chọn thống kê: G = − µ 0 𝑌 𝑆 . ~ 𝑇(𝑛−1) 𝛼 (19)
𝛾 = 0,95 => 2 = 0,025 => 𝑡0,025 = 2,093
Khoảng tin cậy ối xứng cho 𝜇 = 𝐸(𝑌): ) ; 1100 ) = (1087,9958; 1112,0042)
Vậy với ộ tin cậy 95%, khoảng tin cậy ối xứng của khối lượng trung bình của sản phẩm
loại 1 thuộc khoảng (1087,9958; 1112,0042)
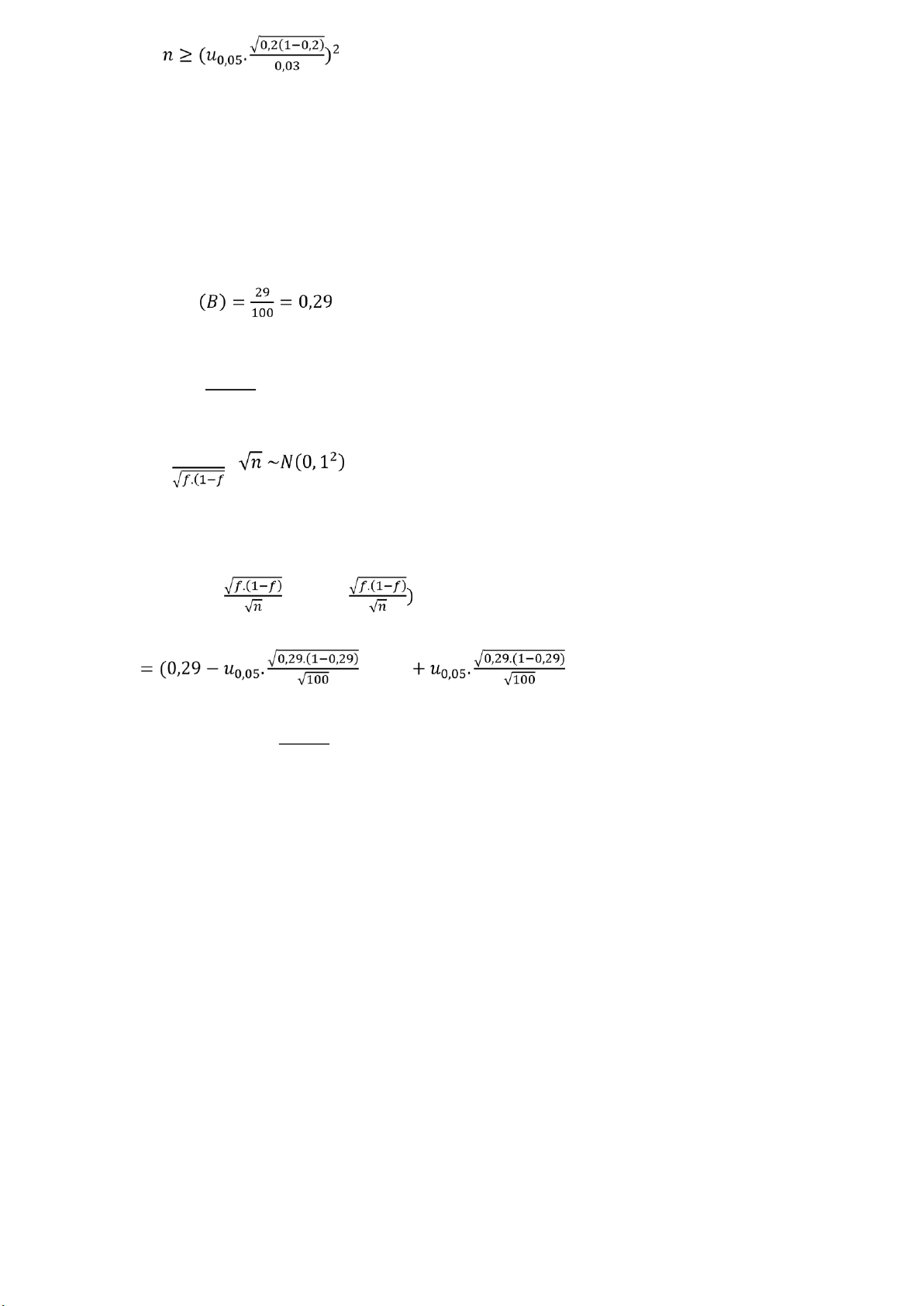
d) Gọi 𝜀 là sai số cho ước lượng tỉ lệ sản phẩm loại 1 √𝑓. ( 1− 𝑓 ) 𝜀≥𝑢 𝛼 . 2 √ 𝑛 𝑛 ≥ 481,0711 => 𝑛 = 482
Vậy với ộ tin cậy 90% và ộ chính xác là 0,03 thì cần iều tra thêm số sản phẩm là: 482 − 100 = 382
e) 𝐵 ≔ ”𝐿ấ𝑦 đượ𝑐 𝑠ả𝑛 𝑝ℎẩ𝑚 𝑐ủ𝑎 𝑥í 𝑛𝑔ℎ𝑖ệ𝑝 𝐵” 𝑓
Gọi N là số sản phẩm của xí nghiệp A 𝑝(𝐵) = 1000 1000+𝑁 Chọn thống kê: 𝑓−𝑝 𝐺 = . 𝑣ì 𝑛𝑓 > 10
𝑛. (1 − 𝑓) > 10 Khoảng tin cậy ối xứng cho p: (𝑓 − 𝑢𝛼. ; 𝑓 + 𝑢𝛼. 22 ; 0,29 ) = (0,2154; 0,3646) 0,2154 < 1000 < 0,3646 1000+𝑁
1742,73182 < N < 3642,5255
Vậy với ộ tin cậy 90%, số sản phẩm của xí nghiệp A trong kho thuộc khoảng (1743; 3642)
Đề 11: Ca thi 2 ngày 7/1/2020 Câu 1:
A := “ Sản phẩm ưa ra thị trường là chính phẩm”
H1:= “ lấy ược chính phẩm”
H2 := “ lấy ược phế phẩm” P(H1)= 0.7; P(H2) = 0.3
⟹ {𝐻1; 𝐻2} nhóm ầy ủ biến cố a) ADCT xác suất ầy ủ:
P(A) = P(H1)*P(A/H1)+P(H2)*P(A/H2)
= 0.7*0.9 + 0.3*(1-0.95) = 0.645
( 𝐻2 ) ∗𝑃 ( 𝐴/𝐻2 ) 0.3∗ ( 1−0.95 ) b) P(H2/A) = 𝑃 = =0.0233 𝑃(𝐴) 0.645
Câu 2: Gọi m là mức thu nhập cần tìm (triệu ồng) (𝑚 ≥ 2) 𝑃(𝑋 > 𝑚) = 0.5 ⟺ 𝐹(𝑚) = 0.5 ⟺ 1 − 𝑚2 ⟺ 𝑚 = 2.8284
Vậy mức thu nhập cần tìm là 2.8284 triệu ồng. Câu 3:
X := tuổi thọ của một loại thiết bị iện ( giờ) 𝑋~𝒩(1500; 1502) Gọi
t là thời gian quy ịnh bảo hành cần tìm( t>0) (giờ) 𝑡 − 1500 𝑃 𝑡 − 1500
⟺ ∅0(𝑡−1500150 ) = −∅0(2.3263)
⟺ 𝑡 = 1151.055(𝑔𝑖ờ) Câu 4:
X := Nhu cầu nước sạch trong mùa Đông 2017 của 1 hộ gia ình ở phường A(𝑚3/𝑛𝑔à𝑦) 𝑋~𝒩(𝜇; 𝜎2) Ta
có bảng phân phối thực nghiệm: X 1.1 1.2 1.3 1.4 1.5 N 3 10 14 10 3 𝑥 =
𝑥𝑖𝑛𝑖 = 1.3(𝑚3/𝑛𝑔à𝑦) 𝑛 𝑠 = (𝑚3/𝑛𝑔à𝑦)
a) Nhu câu trung bình về nước sạch mỗi tuần của các hộ ở phường A là:
400*7*𝑥 =3640(𝑚3/𝑛𝑔à𝑦) 2(39)
b) Có 𝛾 = 0.95 ⟶ 𝛼2 = 0.025 ⟶ {𝜒𝜒0.9750.0252(39) == 23.654358.1201
Khoảng tin cậy ối xứng cho phương sai về nhu cầu nước sạch hàng ngày của mỗi hộ gia ình ở
phường A mùa Đông 2017 là:
(𝑛 − 1) ∗ 𝑠2 (𝑛 − 1) ∗ 𝑠2 ( 2(𝑛−1) ; 2(𝑛−1) ) 𝜒 𝜒 0.025 0.975 ⟺ ( ⟺ (0.0076; 0.0186)
c) Gọi 𝜇 𝑙à 𝑛ℎ𝑢 𝑐ầ𝑢 𝑠ử 𝑑ụ𝑛𝑔 𝑛ướ𝑐𝑐 𝑡𝑟𝑢𝑛𝑔 𝑏ì𝑛ℎ 𝑐ủ𝑎 𝑚ỗ𝑖 ℎộ 𝑡𝑟𝑜𝑛𝑔 𝑚ù𝑎 Đô𝑛𝑔 2017(𝑚3/𝑛𝑔à𝑦)
𝜇0𝑙à 𝑛ℎ𝑢 𝑐ầ𝑢 𝑠ử 𝑑ụ𝑛𝑔 𝑛ướ𝑐 𝑡𝑟𝑢𝑛𝑔 𝑏ì𝑛ℎ 𝑐ủ𝑎 𝑚ỗ𝑖 ℎộ trong mùa Thu 2017 (𝑚3/𝑛𝑔à𝑦)
𝐾𝑖ể𝑚 đị𝑛ℎ 𝑔𝑖ả 𝑡ℎ𝑢𝑦ế𝑡: {𝐻0: 𝜇 = 𝜇0 = 1.5 𝐻1: 𝜇 < 𝜇0 = 1.5 𝑥
Tiêu chuẩn kiểm ịnh: 𝑇 = −𝜇 √ 𝑛 𝑠 ⇒ 𝑇𝑞𝑠
𝑀𝑖ề𝑛 𝑏á𝑐 𝑏ỏ:
𝜔𝛼 = (−∞; −𝑢𝛼) = (−∞; −𝑢0.05 = −1.645)
Vì Tqs∈ 𝜔𝛼 nên chấp nhận H1; Bác bỏ H0
Vậy có thể cho rằng nhu cầu nước sạch trung bình của mỗi hộ trong mùa Đong nhỏ hơn trong mùa Thu.
d) Gọi 𝜎2𝑙à 𝑝ℎươ𝑛𝑔 𝑠𝑎𝑖 𝑣ề 𝑛ℎ𝑢 𝑐ầ𝑢 𝑛ướ𝑐 𝑠ạ𝑐ℎ ℎà𝑛𝑔 𝑛𝑔à𝑦 𝑡𝑟𝑜𝑛𝑔 𝑚ù𝑎 Đô𝑛𝑔 2017
𝜎02 𝑙à 𝑝ℎươ𝑛𝑔 𝑠𝑎𝑖 về nhu cầu nước sạch hàng ngày trong mùa Thu 2017 Kiểm ịnh giả thuyết:
{𝐻𝐻0:: 𝜎 𝜎22 <= 𝜎𝜎0022 = (0.11)= (0.11)22 1 Tiêu chuẩn kiểm ịnh: T= (𝑛−12)∗𝑠2 ⟹ 𝑇𝑞𝑠 = 𝜎 Miền bác bỏ:
𝜔𝛼 = (0; 𝜒1−2(𝑛−1)𝛼)=(0; 25.6954)
Vì Tqs ∉ 𝜔𝛼 ⟶ 𝐶ℎấ𝑝 𝑛ℎậ𝑛 𝐻𝑜; 𝐵á𝑐 𝑏ỏ 𝐻1
Vậy với mức ý nghĩa 5%, không thể cho rằng nhu cầu sử dụng nước hàng ngày của mỗi hộ
ịa phương A trong mùa Đông ổn ịnh hơn mùa Thu năm 2017. Câu 5:
Gọi p là tỷ lệ người Hà Nội i nghỉ mát f là tỷ
lệ người Hà Nội i nghỉ mát trong mẫu f= = 0.375 𝑛𝑓 > 10 Điều kiện: { 𝑛(1 − 𝑓) > 10
Có 𝛾 = 0.95 → 𝛼 = 0.05 → 𝑢𝛼 = 1.645
Khoảng tin cậy tối a cho p là: 𝒇(𝟏 − 𝒇)
(𝟎; 𝒇 + √ ∗ 𝒖𝜶) 𝒏 ĐỀ 12
Câu 1: < nhân tổng quát + xs iều kiện>
Ai:= “ thí sinh vượt qua vòng thứ I” (i= 1; 2;3)
Ta có: P(A1)= 0.8; P(A2/A1)= 0.7; P(A3/A1A2)= 0.5
a) +Áp dụng công thức nhân tổng quát:
+Xác suất ể thí sinh vượt qua cả 3 vòng thi là:
P(A1.A2.A3)= P(A1).P(A2/A1).P(A3/A1A2) = 0.8*0.78*0.5= 0.28
Vậy xác suất ể thí sinh vượt qua cả 3 vòng thi là: 0.28
b) C:= “ thí sinh bị loại”
Xác suất thí sinh bị loại là: P(C)= 1- P(A1.A2.A3)= 1-0.28=0.72
P(A1. 𝐴2 /𝐶) = 𝑃(𝐴1.𝐴2 .𝐶)=𝑃(𝐴1.𝐴2) 𝑃(𝐶) 𝑃(𝐶) 0.8∗(1−0.7)
= 𝑃(𝐴1).𝑃(𝐴2 /𝐴1) = 0.72 𝑃(𝐶) = 0.3333
Vậy xác suất thí sinh bị loại ở vòng 2 biết rằng thí sinh ó bị loại là 0.3333 Câu 2:
X:= Số tiền lãi thu ược từ thương vụ (triệu ồng) X= {- 800; 150}
Gọi p là xác suất thắng lợi
→1-p là xác suất thất bại
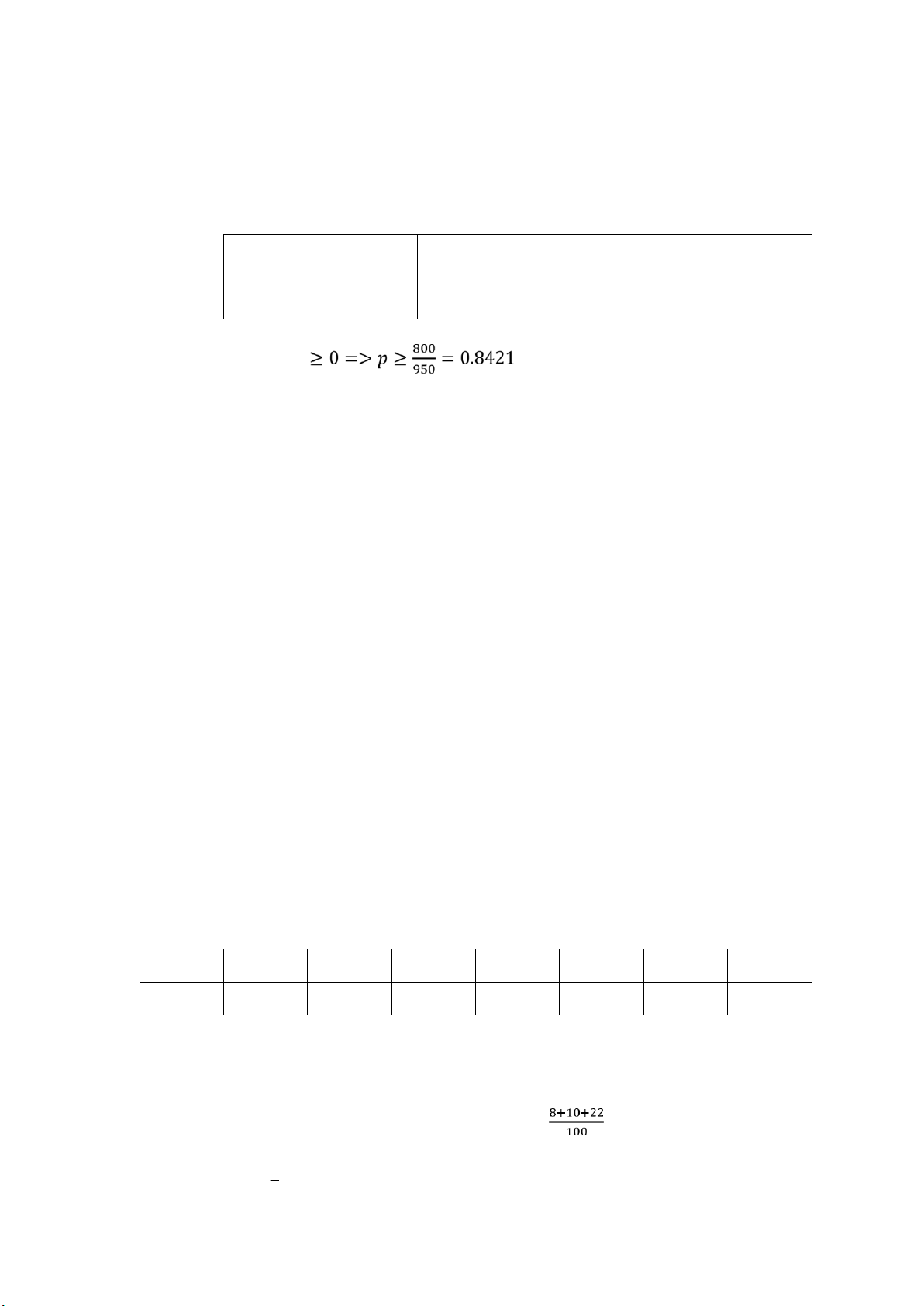
BẢNG PHÂN PHỐI XÁC SUẤT: X -800 150 P 1-p p
E(X)=-800*(1-p)+ 150p= 950p-800 E(X)>=0 950p-800
Vậy xác suất thắng của thương vụ tối thiểu là 0.8421. Câu 3:
X:= Lãi suất ầu tư vào cổ phiếu A (%) X~𝑁(19; 62)
Y:= Lãi suất ầu tư vào cổ phiếu B (%) Y~𝑁(22; 102)
Gọi a là tỷ lệ ầu tư vào A
→ (1- a) là tỷ lệ ầu tư vào B
Gọi Z là lợi nhuận khi ầu tư vào cả A và B
Z= a.X+(1-a).Y => E(Z)= a.E(X)+(1-a).E(Y)
V(Z)= V(a.X+ (1-a).Y) = 𝑎2𝑉(𝑋) + (1 − 𝑎)2. 𝑉(𝑌) = 36𝑎2 + 100𝑎2 − 200𝑎 + 100 =136𝑎2 − 200𝑎 + 100
Để rủi ro nhỏ nhất V(Z) min {136𝑎2 − 200𝑎 + 100}min a= 25/34=0.7353=> 1- a=0.2647
Vậy nên ầu tư vào A 73.53% và ầu tư vào B 26.47% Câu 4:
X:= khối lượng óng gói của 1 loại ường (g) X~𝑁(𝜇; 𝜎2)
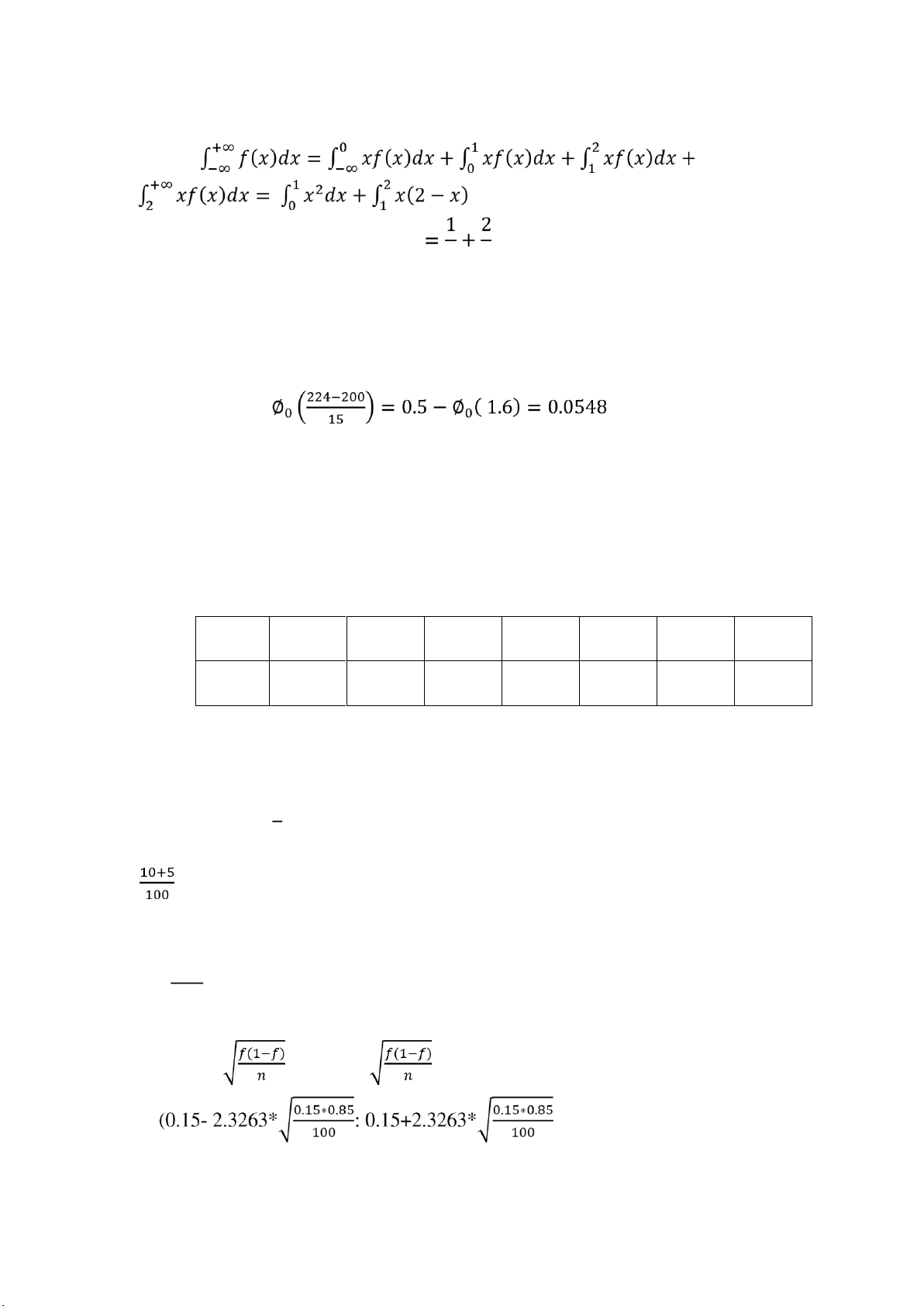
Bảng phân phối thực nghiệm: X 495 497 498 500 502 503 504 n 8 10 22 34 14 8 4 N= 100 𝑋 = 499.54; 𝑆 = 2.3545
a) Gọi f là tần số xuất hiện gói ường bị óng thiếu trong kho f= = 0.4
Ước lượng số gói ường bị óng thiếu trong kho là: 10000*f=4000( gói)
b) Với 𝛾 = 0.95 => 𝛼 2 = 0.025 => 𝑢0.025 = 1.96
Khoảng tin cậy ối xứng cho khối lượng trung bình của gói ường là:
Vậy với ội tin cậy 95%, khoảng tin cậy ối xứng cho khối lượng trung bình mỗi gói ườg là ( 499.0785; 500,0015) (g)
c) Gọi 𝜀 𝑙à độ 𝑐ℎí𝑛ℎ 𝑥á𝑐 𝑘ℎ𝑖 ướ𝑐 𝑙ượ𝑛𝑔 𝑡𝑟𝑢𝑛𝑔 𝑏ì𝑛ℎ ADCT: 𝜀 = 𝑢𝛼/2
Lại có: 𝜀1 = 0.9𝜀 => 𝜀1 = 0.4154 Mà 𝜀1 = 𝑢𝛼/2
√𝑆𝑛1 => n1= 123,417 => n1= 124
Vậy kích thước mẫu cần tìm là 124 gói 𝛼 𝜒2(99) = 128.422
d) Có 𝛾 = 0.95 ⟶ 2 = 0.025 ⟶ {𝜒0.9750.0252(99) = 73.3611
Khoảng tin cậy ối xứng cho phương sai là:
(𝑛 − 1) ∗ 𝑠2 (𝑛 − 1) ∗ 𝑠2 ( 2(𝑛−1) ; 2(𝑛−1) ) 𝜒 𝜒 ⟺ ( ⟺ (4.2736; 7.4811)
e) Kiểm ịnh giả thuyết: {𝐻𝑜: 𝜇 = 𝜇0 = 500 𝐻1: 𝜇 < 𝜇0 = 500 Tiêu chuẩn kiểm ịnh: 𝑋 − 𝜇 499.54 − 500 𝑇 = √𝑛 => 𝑡𝑞𝑠 = √100 = −1.9537 𝑆 2.3545
Miền bác bỏ: 𝜔𝛼 = (−∞; −𝑢𝛼) = (−∞; −1.645)
Vì tqs∈ 𝜔𝛼 => 𝐵á𝑐 𝑏ỏ 𝐻0,𝐶ℎấ𝑝 𝑛ℎậ𝑛 𝐻1 Vậy
có thể cho rằng nhận ịnh trên là úng. Đề 13: Câu 1:
A:= “ dân cư gặp rủi ro trong 1 năm”
H1:= “ dân cư ít rủi ro trong 1 năm”
H2:= “ dân cư rủi rot rung bình trong 1 năm”
H3:= “ dân cư rủi ro cao trong 1 năm”
P(H1)= 0.2; P(H2)= 0.5: P(H3)= 0.3
{H1; H2; H3} nhóm ầy ủ các biến cố a)
Áp dụng công thức xác suất ầy ủ:
P(A) = P(H1).P(A/H1)+P(H2).P(A/H2)+P(H3).P(A/H3) = 0.2*0.04+0.5*0.12+0.3*0.32 = 0.164
b) Áp dụng công thức bayes: )=
𝑃(𝐻1𝑃)(.𝑃(𝐴 ) 𝐻1 𝐴 ) 0.2∗ P(H1/𝐴 Câu 2:
X:= số máy không cho giao dịch
Ai:= “ máy thứ i không cho giao dịch” (i= 1,2,3) X(Ω) = {0; 1; 2; 3}
P(X=0)=P( 𝐴1𝐴2𝐴3 )= 0.98*0.97*0.95=0.9031
P(X=1)= P( 𝐴1𝐴2 𝐴3 + 𝐴1𝐴3 𝐴2 + 𝐴2𝐴3 𝐴1) = 0.98 ∗ 0.97 ∗ 0.05 + 0.98 ∗ 0.95 ∗
0.03 + 0.97 ∗ 0.95 ∗ 0.02 = 0.0939
P(X=2) = P( 𝐴1 𝐴2𝐴3 + 𝐴2 𝐴1𝐴3 +
𝐴3 A1A2)=0.98*0.03*0.05+0.02*0.97*0.05+0.02*0.03*0.95=0.003
P(X=3) = P(A1A2A3)= 0.02*0.03*0.05=0.00003 Mod[X]= 0 vì P(X=0) max
Vậy số máy không cho giao dịch tin chắc nhất là 0. Câu 3:
X:= Thời gian hoạt ộng tốt của 1 loại máy tính X~𝑁(4300; 2502)
Thời gian bảo hành là 360*10= 3600 ( giờ) P(X =0.256%
Vậy tỷ lệ máy bảo hành là 0.256% Câu 4:
X:= Thu nhập của 1 người làm việc ở công ty Bảng phân phối thực nghiệm: X 28 34 36 40 48 52 n 20 50 130 100 60 30 𝑋 = 39.45 S=6.0902
a) Gọi f là tần số xuất hiện người có thu nhập thấp f= 20/400=0.05
iều kiện: nf> 10; n(1-f)>10 ( thỏa mãn) với 𝛾
= 0.95 => 𝛼2 = 0.025 => 𝑢0.025=1.96
Khoảng tin cậy ối xứng cho tỷ lệ người có thu nhập thấp là: (𝑓 − 𝑢 ; 𝑓 + 𝑢 ) (0.0286; 0.0713)
b) Gọi 𝜇0𝑙à 𝑚ứ𝑐 𝑡ℎ𝑢 𝑛ℎậ𝑝 𝑏ì𝑛ℎ 𝑞𝑢â𝑛 𝑡ℎ𝑒𝑜 𝑏á𝑜 𝑐á𝑜 (triệu ồng/năm) 𝜇0 = 3 ∗ 12 = 36(𝑡𝑟đ/𝑛ă𝑚)
𝜇 𝑙à 𝑚ứ𝑐 𝑡ℎ𝑢 𝑛ℎậ𝑝 𝑏ì𝑛ℎ 𝑞𝑢â𝑛 𝑡ℎ𝑒𝑜 𝑡ℎự𝑐 𝑡ế (𝑡𝑟đ/𝑛ă𝑚 ) Kiểm ịnh giả thuyết: {𝐻0: 𝜇 = 𝜇0 = 36 𝐻1: 𝜇 > 𝜇0 = 36
Miền bác bỏ: 𝑊𝛼 = ( 𝑢𝛼;
+∞) = (𝑢0.05; +∞) = (1.645; +∞) Tiêu chuẩn kiểm ịnh: T= => Tqs= = 11.3296 𝑆
Vì 𝑇𝑞𝑠 ∈ 𝑊𝛼 => 𝐵á𝑐 𝑏ỏ 𝐻𝑜; 𝑐ℎấ𝑝 𝑛ℎậ𝑛 𝐻1 Vậy
không thể tin báo cáo này của công ty.
c) Gọi 𝜀 𝑙à độ 𝑐ℎí𝑛ℎ 𝑥á𝑐 𝑘ℎ𝑖 ướ𝑐 𝑙ượ𝑛𝑔 𝑡ℎ𝑢 𝑛ℎậ𝑝 𝑡𝑟𝑢𝑛𝑔 𝑏ì𝑛ℎ Áp dụng công thức: 𝑆 6.0902 𝛼 0.5 = 𝑢 𝛼
=> 𝑢 𝛼 =1.64 => =0.0503 => 𝛼=0.1006 2 √ 𝑛 2 √ 400 2 2 𝛼 𝛾=1−𝛼=1−0.1006 =0.8994 = 𝜀 = 𝑢 89.94%
Vậy ộ tin cậy cần tìm là 89.94%. Câu 5:
a) f là tần số xuất hiện sản phẩm loại I trong mẫu f= 350/400= 0.875
po là tỷ lệ sản phẩm loại I theo báo cáo po=3700/4000=0.925 Kiểm ịnh giả thuyết:
Điều kiện: n.po≥ 5; 𝑛(1 − 𝑝0) ≥ 5 Tiêu chuẩn kiểm ịnh: 𝑓−𝑝𝑜 T= 𝑛 = √ > Tqs = = - 3.796 √𝑝0(1−𝑝0) Miền bác bỏ:
=( -∞; −1.96) ∪ (1.96; +∞)
Vì Tqs∈ 𝑊𝛼 => 𝐵á𝑐 𝑏ỏ 𝐻𝑜; 𝑐ℎấ𝑝 𝑛ℎậ𝑛 𝐻1 Vậy
không thể chấp nhận số lượng trên.
b) Gọi 𝜀 𝑙à độ 𝑐ℎí𝑛ℎ 𝑥á𝑐 𝑘ℎ𝑖 ướ𝑐 𝑙ượ𝑛𝑔 𝑡ỷ 𝑙ệ 𝑠ả𝑛
𝑝ℎẩ𝑚 𝑙𝑜ạ𝑖 𝐼 Ta có: 𝑓(1 − 𝑓) 𝜀 = 𝑢𝛼/2√ 𝑛 Có: 0.035 = 1.96* => n1= 343( sản phẩm)
Vậy cần iều tra mẫu 343 sản phẩm. Đề 14: Câu 1:
A:= “ Khách hàng thích iPad”
H1:= “ Khách hàng thích iPhone”
H2:= “ khách hàng không thích iphone” P(H1) = 0.7; P(H2)= 0.3
a) P(H1.A)= P(H1).P(A/H1)= 0.7*0.8= 0.56
b) P(A) = P(H1)*P(A/H1) + P(H2).P(A/H2) = 0.7*0.8+0.3*0.4= 0.68 P(H1/𝐴 )= Câu 2:
X:= số tiền lãi khi bán 1 bảo hiểm ( triệu ồng) X(Ω) = {−9.9; 0.1} P(X = 0.1) = 0.995 P(X=-9.9) =1-0.995=0.005
E(X)= ∑ 𝑋𝑖. 𝑃𝑖 = 0.1 ∗ 0.995 + (−9.9) ∗ 0.005 = 0.05(𝑡𝑟𝑖ệ𝑢 đồ𝑛𝑔) = 50000( đồ𝑛𝑔)
Vậy số tiền lãi trung bình thu ược từ mỗi hợp ồng bảo hiểm là 50.000 ồng Câu 3:
X:= Số tờ tiền giả trong 4 tờ tiền lấy ra X~ 𝐻(20; 5; 4)
Số tờ tiền giả trung bình trong 4 tờ tiền là: E(X)= 𝑀 = 1 𝑁
Vậy số tiền phạ trung bình là: 1*2*50.000= 100.000( ồng) Câu 4:
X:= Thu nhập của nhân viên ở ngân hàng A( triệu ồng/ năm) 𝑋~𝑁(𝜇; 𝜎2)
Ta có bảng phân phối thực nghiệm: X 184 190 194 198 202 206 214 N 10 14 26 28 12 8 2 Ta có: n= 100 𝑋 =195.88 S= 6.3869
a) Có 𝛾 = 0,95 => 𝛼 = 0.05 => 𝑢0.05 = 1.645
Khoảng tin cậy tối a cho thu nhập trung bình hàng năm là:
b) Gọi f là tần số xuất hiện nhân viên có thu nhập cao f= = 0.22
Gọi 𝜀 𝑙à độ 𝑐ℎí𝑛ℎ 𝑥á𝑐 𝑐ủ𝑎 ướ𝑐 𝑙ượ𝑛𝑔 𝑡ỉ 𝑙ệ 𝑓(1 − 𝑓) √ 𝜀 = 𝑢𝛼/2 𝑛 = 0.0681
Vậy ộ chính xác cần tìm là 0.0681
c) Gọi po là tỷ lệ nhân viên có thu nhập cao năm trước
po=0,2 P là tỷ lệ nhân viên có thu nhập cao năm nay Kiểm ịnh giả thuyết: 𝐻𝑜: 𝑝 = 𝑝0 = 0.2 Điều kiện: n.po Tiêu chuẩn kiểm ịnh: T= => Tqs = = 0.5 𝑝0(1−𝑝0) Miền bác bỏ: 𝑊𝛼
=( -∞; −1.96) ∪ (1.96; +∞)
Vì Tqs∉ 𝑊𝛼 => 𝐵á𝑐 𝑏ỏ 𝐻1; 𝑐ℎấ𝑝 𝑛ℎậ𝑛 𝐻0 Vậy
không thể cho rằng tỉ lệ năm nay khác năm trước Câu 5:
X:= Doanh thu hàng tháng của mỗi hộ gia ình ( triệu ồng/ tháng) 𝑋~𝑁(𝜇; 𝜎2) Bảng phân phối thực nghiệm: X 20 22 24 26 28 n 10 21 32 25 12 Ta có: n= 100 𝑋 = 24.26 S= 2.3213
a) Ước lượng không chệch của doanh thu trung bình là: 𝑋 = 24.26( 𝑡𝑟đ/ 𝑛ă𝑚)
b) Có 𝛾 = 0.95 => 𝛼2 = 0.025 => {𝜒𝜒0.9750.02522(99)(99) == 73.3611128.422
Khoảng tin cậy ối xứng cho phương sai là: ) ( 𝜒𝜒 Đề 15: Câu 1:
A:= “ ôi giày i kiểm tra là phế phẩm”
H1:= “ ôi giày sản xuất ở ca sáng” H2:=
“ ôi giày sản xuất ở ca chiều”
H3:= “ ôi giày sản xuất ở ca tối”
P(H1)= 0.55; P(H2)= 0.4; P(H3)= 0.05
=> {𝐻1; 𝐻2; 𝐻3} 𝑛ℎó𝑚 đầ𝑦 đủ 𝑏𝑖ế𝑛 𝑐ố
𝑎) 𝑃(𝐴) = P(H1).P(A/H1)+P(H2).P(A/H2)+P(H3)*P(A/H3)
= 0.55 ∗ 0.04 + 0.4 ∗ 0.05 + 0.05 ∗ 0.06 = 0.045 𝑃(𝐻1). 𝑃(𝐴/𝐻1) 0.55 ∗ 0.04 𝑏) 𝑃(𝐻1/𝐴) = == 0.4889 𝑃(𝐴) 0.045 𝑃(𝐻2/𝐴) 𝑃(𝐴) 0.045 𝑃(𝐻3). 𝑃(𝐴/𝐻3) 0.05 ∗ 0.06 𝑃(𝐻3/𝐴) = == 0.0667 𝑃(𝐴) 0.045
Vì P(H1/A) > P(H2/A) > P(H3/A)
Nhận ịnh ó là sai Câu 2:
X:= thời gian 1 gia ình sử dụng máy hút bụi trong 1 năm ( vi: 100 giờ) Số
giờ sử dụng trung bình là: E(X)= 𝑑𝑥 = 1 3 3
Vậy thời gian hoạt ộng trung bình của máy hút là 100 giờ Câu 3:
X:= Lượng nước ngọt trong 1 lần rót ( ml) X~𝑁(200; 152) P(X>224) = 0.5-
Y:= số lần rót bị tràn trong 1000 lần Y~𝐵(1000; 0.0548)
E(Y)= np= 1000*0.0548= 54,8 ( lần) Câu 4:
X:= Thu nhập của mỗi nhân viên ở công ty A ( tr / năm) Bảng phân phối thực nghiệm: X 110 130 150 175 195 220 280 n 8 12 20 25 20 10 5 Ta có: n=100 𝑋 = 173.15 S= 39.3935
a) Có 𝛾 = 0.98 => 𝛼2 = 0.01 => 𝑢𝛼/2 = 𝑢0.01 = 2.3263
Gọi f là tần số xuất hiện người có thu nhập cao f= = 0.15
iều kiện : nf >10; n(1-f) > 10
Gọi N là số người có thu nhập cao của công ty P= 𝑁 2000
Khoảng tin cậy ối xứng cho tỷ lệ là: (𝑓 − 𝑢𝛼/2 ; 𝑓 + 𝑢𝛼/2 ) ) ( 0.0669 ; 0.2331)
Ta có: 0.0669 < p< 0.2331 0.0669 < 𝑁 <0.2331
133.8< N< 466.2 134 ≤ 𝑁 ≤ 446
b) gọi 𝜇0𝑙à 𝑡ℎ𝑢 𝑛ℎậ𝑝 𝑡𝑟𝑢𝑛𝑔 𝑏ì𝑛ℎ 𝑡ℎ𝑒𝑜 𝑏á𝑜 𝑐á𝑜 ( tr /năm) 𝜇0 = 13 ∗ 12 = 156
𝜇 𝑙à 𝑡ℎ𝑢 𝑛ℎậ𝑝 𝑡𝑟𝑢𝑛𝑔 𝑏ì𝑛ℎ 𝑡ℎ𝑒𝑜 𝑡ℎư𝑐 𝑡ế ( tr / năm)
𝐾𝑖ể𝑚 đị𝑛ℎ 𝑔𝑖ả 𝑡ℎ𝑢𝑦ế𝑡: Tiêu chuẩn kiểm ịnh: 𝑋 − 𝜇 𝑇 = √ 𝑛 => Tqs= 𝑆 Miền bác bỏ: 𝑊𝛼
=( -∞; −1.96) ∪ (1.96; +∞)
Vì 𝑇𝑞𝑠 ∈ 𝑊𝛼 => 𝑏á𝑐 𝑏ỏ 𝐻𝑜; 𝑐ℎấ𝑝 𝑛ℎậ𝑛 𝐻1 Vậy
không thể chấp nhận báo cáo trên.
c) Gọi 𝜀 𝑙à độ 𝑐ℎí𝑛ℎ 𝑥á𝑐 𝑘ℎ𝑖 ướ𝑐 𝑙ượ𝑛𝑔 𝑡ℎ𝑢 𝑛ℎậ𝑝 𝑡𝑟𝑢𝑛𝑔 𝑏ì𝑛ℎ Ta có: 𝜀 = 𝑢𝛼/2 𝑆 => 𝑢𝛼/2 Có: 𝑢0.0639= 1.5231 => 𝛼 => 𝛾 = 0.8722 = 87.22%
𝐶â𝑢 5: 𝑋 ≔ 𝑙ã𝑖 𝑥𝑢ấ𝑡 𝑐ổ 𝑝ℎ𝑖ế𝑢 𝑐ủ𝑎 𝑚ộ𝑡 𝑐ô𝑛𝑔 𝑡𝑦 ( đơ𝑛 𝑣ị: %)
X~𝑁( 𝜇; 𝜎2) Ta có: n= 10 𝑋 = 15.4 𝑆 = 4.5018 2(9)
a) Với 𝛾 = 0.95 => 𝛼 2 = 0.025 => {𝜒0.025𝜒0.9752(9)== 2.719.02
Khoảng tin cậy ối xứng của phương sai: ) 𝜒𝜒
b) Gọi 𝜎02 𝑙à đô 𝑝ℎâ𝑛 𝑡á𝑛 𝑐ủ𝑎 𝑙𝑎𝑖𝑥 𝑠𝑢ấ𝑡 𝑐ổ 𝑝ℎ𝑖ế𝑢 𝑡ℎ𝑒𝑜 𝑏á𝑜 𝑐á𝑜 𝜎02 = 20 Kiểm ịnh giả thuyết:
𝐻𝑜: 𝜎2 = 𝜎02 = 20 {𝐻1: 𝜎 > 𝜎2 = 20 0 Tiêu chuẩn kiểm ịnh: 2 (𝑛 − 1)𝑆2 2 9 ∗ 4.50182 = =9.1197 𝜒 𝜎 2 => 𝜒 𝑞𝑠 = 20 Miền bác bỏ: 𝑊𝛼
Vì 𝜒𝑞𝑠2 ∉ 𝑊𝛼 => 𝑏á𝑐 𝑏ỏ 𝐻1; 𝑐ℎấ𝑝 𝑛ℎậ𝑛 𝐻𝑜
Vậy không thể cho rằng ộ phân tán của lãi suất vượt quá 20. Đề 16 Câu 1:
A:= “ giá cước vận tải giảm”
H1:= “ giá xăng dầu tăng “
H2: = “ giá xăng dầu giảm” P(H1)= 0.8 ; P(H2)= 0.2 P(A/H1)= 0.01; P(A/H2)= 0.45
{H1; H2} nhóm ầy ủ biến cố a) ADCT xs ầy ủ:
P(A)= P(H1).P(A/H1)+P(h2).P(A/H2)= 0.8*0.01+ 0.2*0.45=0.098 Vậy
xs ể giá cước vận tải giảm là 0.098
b) P(H1/𝐴 = 𝑃(𝐻1𝑃)(.𝑃(𝐴 ) 𝐻1𝐴 ) = 0.81−0.098∗(1−0.01) = 0.878 Vậy…. Câu 2:
X:= lơi nhuận thu ược khi nhập về 120 lit bia ( nghìn ồng)
- Khi nhu cầu là 80 lít thì số tiền lãi là:X1= 80*3-40*2= 160 ( nghìn ồng) với p1= 0.15
- Khi nhu cầu là 100 thì số tiền lãi là: X2= 100*3-20*2= 260 ( nghìn ồng) vơi p2= 0.2 -
Khi nhu cầu là 120 trở lên thì số tiền lãi là: X3= 120*3= 360( nghìn ồng) với p= 1- (0.15+0.2)= 0.65
Bảng phân phối xác suất: X 160 260 360 P 0.15 0.2 0.65 E(X)= 310 ( nghìn ồng)
Y:= lợi nhuận thu ược khi nhập 140 lít bia ( nghìn ồng)
- Khi nhu cầu là 80 thì Y1= 80*3-60*2=120 vói p= 0.15
- Khi nhu cầu là 100 thì Y2= 100*3-40*2=220 vơi p= 0.2
- Khi nhu cầu là 120 thì Y3= 120*3-20*2=320 với p= 0.3
- Khi nhu cầu từ 140 trở lên thì Y4= 420 với p= 0.35
BẢNG PHÂN PHỐI XÁC SUẤT x 120 220 320 420 P 0.15 0.2 0.3 0.35 E(Y)= 305 ( nghìn ồng)
Vì E(X)>E(Y) nên cửa hàng không nên nhập thêm.
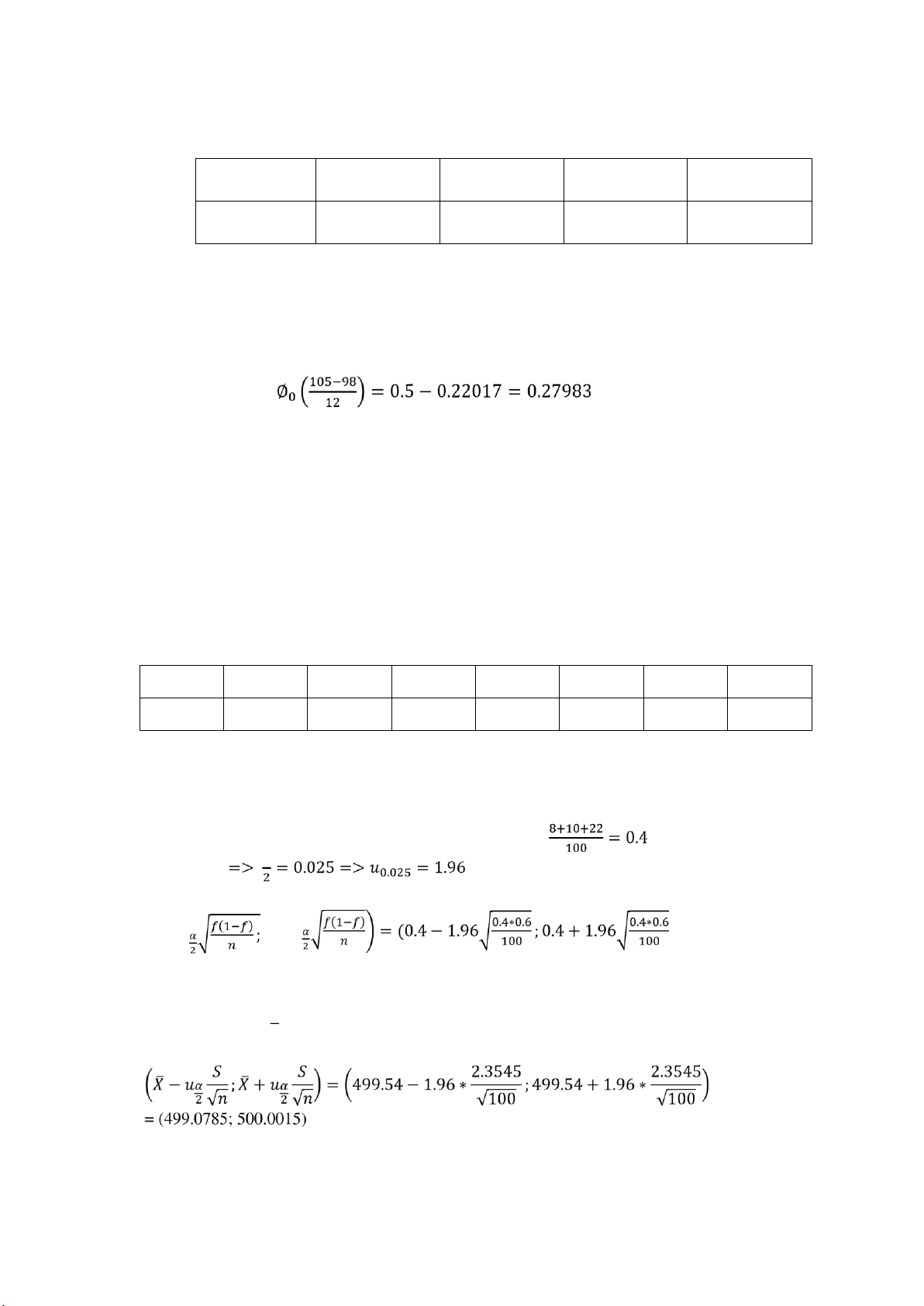
Câu 3: X:= chỉ số IQ của một học sinh tốt nghiệp THPT X~𝑁(98; 122) P(X>= 105)= 0.5-
Y:= Số sinh viên ạt trong ợt tuyển chọn Y~𝐵(600; 0.27983)
E(Y)=600*0.27983=167.898 (học sinh)
Vậy trung bình có 167.898 học sinh ạt trong ợt tuyển chọn. Câu 4:
X:= khối lượng óng gói của 1 loại ường (g) X~𝑁(𝜇; 𝜎2)
Bảng phân phối thực nghiệm: X 495 497 498 500 502 503 504 n 8 10 22 34 14 8 4 N= 100 𝑋 = 499.54; 𝑆 = 2.3545
a) Gọi f là tần số xuất hiện gói ường bị óng thiếu trong kho f= Có 𝛾 = 0.95 𝛼
Khoảng tin cậy ối xứng cho tỷ lệ số gói ường bị óng thiếu trong kho là: (𝑓 − 𝑢 𝑓 + 𝑢 ) = (0.304;0.496)
Vậy ước lượng số gói ường bị óng thiếu tỏng kho là ( 3040; 4960) gói
b) Với 𝛾 = 0.95 => 𝛼 2 = 0.025 => 𝑢0.025 = 1.96
Khoảng tin cậy ối xứng cho khối lượng trung bình của gói ường là:
Vậy với ội tin cậy 95%, khoảng tin cậy ối xứng cho khối lượng trung bình mỗi gói ườg là ( 499.0785; 500,0015) (g)
c) Gọi 𝜀 𝑙à độ 𝑐ℎí𝑛ℎ 𝑥á𝑐 𝑘ℎ𝑖 ướ𝑐 𝑙ượ𝑛𝑔 𝑡𝑟𝑢𝑛𝑔 𝑏ì𝑛ℎ ADCT: 𝜀 = 𝑢𝛼/2
Lại có: 𝜀1 = 0.9𝜀 => 𝜀1 = 0.4154 Mà 𝜀1 = 𝑢𝛼/2
√𝑆𝑛1 => n1= 123,417 => n1= 124
Vậy kích thước mẫu cần tìm là 124 gói 𝛼 𝜒2(99) = 128.422
d) Có 𝛾 = 0.95 ⟶ 2 = 0.025 ⟶ {𝜒0.9750.0252(99) = 73.3611
Khoảng tin cậy ối xứng cho phương sai là:
(𝑛 − 1) ∗ 𝑠2 (𝑛 − 1) ∗ 𝑠2 ( 2(𝑛−1) ; 2(𝑛−1) ) 𝜒 𝜒 ⟺ ( ⟺ (4.2736; 7.4811)
e) Kiểm ịnh giả thuyết: {𝐻𝑜: 𝜇 = 𝜇0 = 500 𝐻1: 𝜇 < 𝜇0 = 500 Tiêu chuẩn kiểm ịnh: 𝑋 − 𝜇 499.54 − 500 𝑇 = √𝑛 => 𝑡𝑞𝑠 = √100 = −1.9537 𝑆 2.3545
Miền bác bỏ: 𝜔𝛼 = (−∞; −𝑢𝛼) = (−∞; −1.645)
Vì tqs∈ 𝜔𝛼 => 𝐵á𝑐 𝑏ỏ 𝐻0,𝐶ℎấ𝑝 𝑛ℎậ𝑛 𝐻1 Vậy
có thể cho rằng nhận ịnh trên là úng. ĐỀ 17 Câu 1:
A:= “ Lượng tiền gửi của dân cư tăng” H1:=
“ Lãi suất huy ộng vốn tăng”
H2:= “ Lãi suất huy ộng vốn không tăng”
P(H1)=0.4; P(H2)= 0.6; P(A/H1)=0.9; P(A/H2)=0.65
{H1; H2} nhóm ầy ủ biến cố a) ADCT XS đầy đủ:
P(A)= P(H1).P(A/H1)+P(h2).P(A/H2)=0.4*0.9+0.6*0.65=0.75=75% b) ADCT bayes: P(H2/𝐴 ) = 𝑃 (𝐻2).(1−𝑃(𝐴/𝐻2) 0.6∗(1−0.65) Câu 2:
X:= Lượng tiền rút tỏng 1 tuần tại 1 cây ATM (tỷ ồng) 𝑑𝑥 = 0.00032 Câu
3: X:= Số khách có nhu cầu thuê xe X~𝑃(2)
Y:= SỐ ô tô cửa hàng cho thuê
Y(Ω) = {0; 1; 2; 3; 4} P(Y=0)=P(X=0)=𝑒 −2×20 P(Y=1)=P(X=1)= 𝑒 −2×21 0.2707 P(Y=2)=P(X=2)= 𝑒 −2×22 0.2707 P(Y=3)=P(X=3)= 𝑒 −2×23 0.1804
P(Y=4)=P(X≥ 4) = 1 − 𝑃(𝑋 < 4)= 0.1429 Câu 4:
Bảng phân phối thực nghiệm Xi 12 14 16 18 20 22 24 Số phiên 5 17 23 33 25 16 2 7 1 𝑥 = ∑ 𝑋𝑖 = 17,8512 𝑛 𝑖=1 1 s =√ 2 𝑛𝑖 = ∑ 7 ( 2.8421 n = 121 𝑖=1 𝑥 𝑛−1 𝑖 − 𝑥 )
e. Gọi μ là giá bán trung bình (Đơn vị: nghìn ồng).
Với ộ tin cậy 95% =>1-∝= 0.95 => ∝= 0.05
Khoảng tin cậy ối xứng của μ là : (𝑥 −
𝑠 𝑢𝛼; 𝑥 + 𝑠 𝑢𝛼)=(17.3448;18.3576) 22
Vậy khoảng tin cậy ối xứng của doanh thu trung bình khi bán mỗi cổ phiếu A trên thị
trường là (17.3448;18.3576) nghìn ồng
f. No là kích thước mẫu tối thiều cần lấy.
Ta có sai số ước lượng về giá bán trung bình là: 𝑆 .𝑢 𝛼 𝜀0 = 0 √ 𝑛 0 2
với 𝑠0 ≈ 𝑠 = 2.8421, 𝑢0,01 = 2,3263 , 𝜀 = 0.5 No=175
Vậy cần phải iều tra thêm 54 phiên nữa.
g. Gọi p là tỉ lệ cổ phiếu A có giá trên 17 ( ơn vị: nghìn ồng)
f là tỉ lệ cổ phiếu A có giá trên 17 trong mẫu . f = Với ộ tin cậy 95% :
1-𝑎 = 0.95 => 𝑎 = 0.05. 𝑢0.05 = 1.645.
Khoảng tin cậy tối thiếu của p là
Vậy với ộ tin cậy 95% tỉ lệ cổ phiếu A có giá trị bán trên 17 nghìn ồng không nhỏ hơn 17 nghìn ồng là 55,58% 2(120)
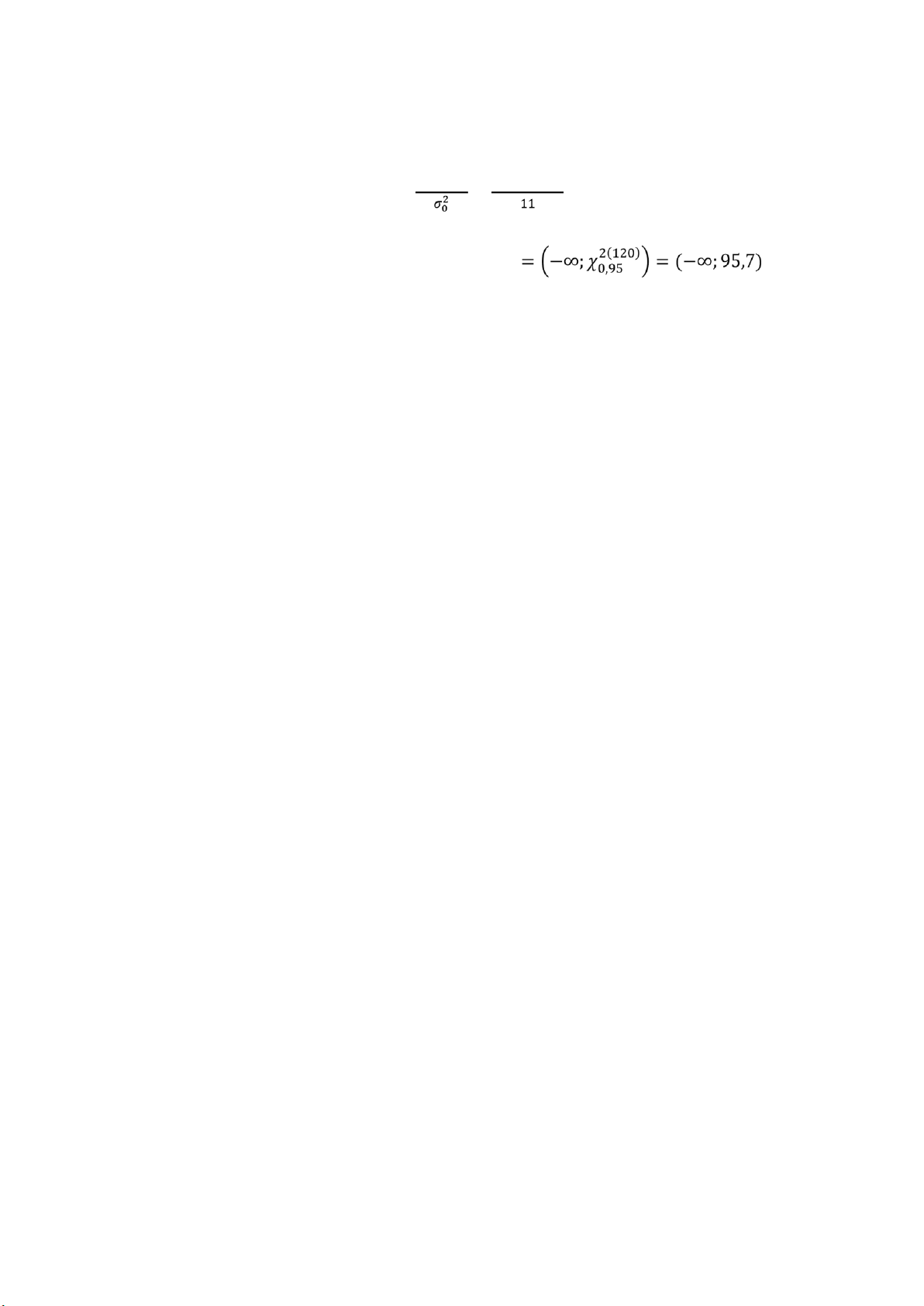
d. 𝛾 = 0.9 => 𝛼2 = 0.05 => {𝜒𝜒0,0052,(95120)==146.5795.7
khoảng tin cậy của phương sai giá bán một cổ phiếu A: 𝜒0,05 𝜒0,95
Khoảng tin cậy cụ thể là :
e. Gọi 𝜎2là phương sai của giá bán cổ phiếu A hiện nay.
Cần k cặp giá trị 𝜎2 = 11; 𝐻1: 𝜎2 < 11
Giá trị quan sát của TCKĐ là :𝑇𝑞𝑠
= (𝑛−1)𝑆2 ≈ 120𝑥8,0775 ≈ 88,118
Với mức ý nghĩa 5%, miền bác bỏ giả thuyết là 𝑊𝑎
Do 𝑇𝑞𝑠 ∈ 𝑊𝑎 nên bác bỏ H0, hay có cơ sở cho rằng ộ phân tán của giá bán cổ phiếu giảm
xuống. Đề 18 Câu 1:
A:= “ lấy ra ược 2 thẻ MB”
H1:= “ Lấy ược thẻ của BIDV từ hộp 1”
H2:= “ Lấy ược thẻ MB từ hộp 1” P(H1)= 10/12; P(H2)= 2/12
P(A/H1)=𝐶𝐶232 ;P(A/H2)=𝐶𝐶16242 16
{H1; H2} nhóm đầy đủ các biến cố a) ADCT XS đầy đủ:
P(A)= P(H1).P(A/H1)+P(h2).P(A/H2) = 0.0292 ADCT bayes: 𝑃(𝐻1).𝑃(𝐴/𝐻1) P(H1/𝐴) = =12∗𝐶216 = 0.7135 𝑃(𝐴) 0.0292 Câu 2:
X:= Số tiền lãi thu ược từ thương vụ (triệu ồng) X= {-700; 1500}
Gọi p là xác suất thắng lợi
→1-p là xác suất thất bại
BẢNG PHÂN PHỐI XÁC SUẤT: X -700 1500 P 1-p p
E(X)=-700*(1-p)+ 1500p= 2200p-700 E(X)>=0 2200p-700
Vậy xác suất thắng của thương vụ tối thiểu là 0.3182. Câu 3:
X:= Lãi suất ầu tư vào cổ phiếu A (%) X~𝑁(19; 62)
Y:= Lãi suất ầu tư vào cổ phiếu B (%) Y~𝑁(22; 102)
Gọi a là tỷ lệ ầu tư vào A
→ (1- a) là tỷ lệ ầu tư vào B
Gọi Z là lợi nhuận khi ầu tư vào cả A và B
Z= a.X+(1-a).Y => E(Z)= a.E(X)+(1-a).E(Y)
V(Z)= V(a.X+ (1-a).Y) = 𝑎2𝑉(𝑋) + (1 − 𝑎)2. 𝑉(𝑌) = 36𝑎2 + 100𝑎2 − 200𝑎 + 100 =136𝑎2 − 200𝑎 + 100
Để rủi ro nhỏ nhất V(Z) min {136𝑎2 − 200𝑎 + 100}min a= 25/34=0.7353=> 1- a=0.2647
Vậy nên ầu tư vào A 73.53% và ầu tư vào B 26.47%
Câu 4: Gọi X: = giá óng cửa của 1 loại cổ phiếu ( ơn vị: nghìn ồng)
μ ≔ giá cổ phiếu trung bình ( đơ𝑛 𝑣ị ∶ 𝑛𝑔ℎì𝑛 đồ𝑛𝑔) Bảng phân phối thực nghiệm Xi (Nghìn 27 30 32 34 37 ồng) Ngày 4 10 15 8 3 n=40 ;
𝑛𝑘𝑖=1 𝑥𝑖𝑛𝑖=31.795 ; s=
a.Với ộ tin cậy 95% => 1-
Khoảng tin cậy của 𝜇 là 𝑠 𝑠 ; 𝑥 + =(30.9983; 32.5517)
Vậy với ộ tin cậy 95% thì ước lượng giá cổ phiếu Trung bình bằng khoảng tin cậy là (30.9983; 32.5517)
b.Gọi 𝜎 là ộ lệch chuẩn về giá óng cửa của loại cổ phiếu này ( ơn vị: nghìn ồng)
Với mức ý nghĩa 5% =>∝= 0.05 Kiểm ịnh 𝐻0: "𝜎 = 5" 𝐻1: "𝜎 ≠ 5"
(𝑛 − 1)𝑠2 39 ∗ 6.2815 𝑇𝑖ê𝑢 𝑐ℎ𝑢ẩ𝑛
𝑘𝑖ể𝑚 đị𝑛ℎ: 𝜒2 = 𝜎02 = = 9.7992
Với 𝛼 = 0.05. 𝑡𝑎 𝑐ó miền bác bỏ: 𝑤𝑎
Nhận thấy 𝜒𝑞𝑠2 ∈ 𝑊𝑎. 𝑛ê𝑛 𝑏á𝑐 𝑏ỏ 𝐻0 ; 𝑐ℎấ𝑝 𝑛ℎậ𝑛 𝐻1
Vậy không thể cho rằng mức ộ biến ộng của giá cổ phiếu này là 5000 ồng Câu 5:
Gọi p là tỷ lệ khách hàng thích sản phẩm này; f là
tỷ lệ khách hàng thích sản phẩm này trong mẫu; f= = 0.3
a. Với ộ tin 90% => 1-∝= 0.9 => 𝑎 = 0.1. 𝑓 ( 1− 𝑓 ) √
Khoảng tin cậy bên trái của p là (0; 𝑓 + 𝑛 ∗ 𝑢𝑎
Ta có 𝑢0.1 = 1.2316 => 𝑝 ∈ (0; 0.3339)
Vậy với ộ tin cậy 90%, tỷ lệ khách hàng thích loại sản phẩm ó không vượt quá 0.3339 b.Gọi
ε độ chính xác trong ước lượng tỷ lệ khách hàng thích sản phẩm
𝜀 = √𝑓(1−𝑓)𝑛 𝑢𝛼/2với
𝑉ậ𝑦 độ 𝑡𝑖𝑛 𝑐ậ𝑦 đạ𝑡 đượ𝑐 𝑙à 90.06%.
c. Gọi n0 là số phiếu thăm dò cần được tiến hành điều tra 𝑓(1−𝑓) 𝑈𝑎/2 2 𝜀 = √ 𝑛0
𝑢𝛼/2 => 𝑛0=f (1-f).( 𝜀)
Với 𝜀 = 0.03. độ 𝑡𝑖𝑛 𝑐ậ𝑦 95% => 1 − 𝑎 = 0.95 => 𝑎 = 0.05. 𝑢0.025 = 1.96 => 𝑛0=897 (phiếu thăm dò)
Vậy cần phải iều tra thêm 597 phiếu thăm dò nữa.




