Đáp án tham khảo 40 câu hỏi ôn tập Thống kê xã hội học kỳ 1 2022 2023
Đáp án tham khảo 40 câu hỏi ôn tập Thống kê xã hội học kỳ 1 2022 2023với những kiến thức và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống.
Preview text:
Nhóm học tập RAM(K70, K71, K72 – HNUE ) Tham gia làm:
+ Đại diện Khoa Toán tin RAM Nguyễn Thế Huy Hoàng
+ Thành viên RAM Lê Quý Phong – Khoa Toán tin – HNUE
+ Thành viên RAM Nguyễn Hồng Sơn – Khoa Toán tin – HNU E
+ Thành viên RAM Đỗ Thanh Tùng – Khoa Toán tin – HNU E 1
Nhóm học tập RAM(K70, K71, K72 – HNUE )
Câu 1: Xác suất để lấy được bóng trắng là: 4 2 10 = 5
Câu 2: Để số chấm mặt trên của xác suất lớn hơn 4 thì số chấm là 5 hoặc 6.
Xác suất để số chấm mặt trên của xúc xắc lớn hơn 4 là: 2 1 6 = 3
Câu 3 Áp dụng công thức Bernoulli: B
Câu 4: P[Z<25]=P[Z=10]+P[Z=15]+P[Z=20]=0,15+0,15+0,1=0,4
Câu 5: E[X]= 1.0,1+3.0,3+4.0,1+6.0,3+10.0,2=5,2
Câu 6: Var[X]=E[𝑋2]-𝐸[𝑋]2= 3064,75
Bấm máy tính: Mode 3 ->1 -> Nhập bảng -> AC ->Shift 1-> Chọn dữ liệu cần xuất
Câu 8: Điểm trung bình là:
𝑇ổ𝑛𝑔 đ𝑖ể𝑚 =
𝑇ổ𝑛𝑔 𝑠ố ℎọ𝑐 𝑠𝑖𝑛ℎ 1.2 + 0 2.1 + 0 3.2 + 5 4.3 + 0 5.6 + 0 6.20+7.2 + 0 8.8+9.5+1 . 0 2 = 4.62 200 2
Nhóm học tập RAM(K70, K71, K72 – HNUE ) 𝑇ổ𝑛𝑔 đ𝑖ể𝑚
Câu 9: Trung bình mẫu là:= =
𝑇ổ𝑛𝑔 𝑠ố ℎọ𝑐 𝑠𝑖𝑛ℎ 2,7.5+2,9.1 + 0 3,1.1 + 2 3,3.4+3,5.9 = 3,11 40
Câu 10: Phương sai mẫu là: Bấm máy tính D
Bấm máy tính: Mode 3 ->1 -> Nhập bảng -> AC ->Shift 1-> Chọn dữ liệu cần xuất (phương sai là sx) Câu 11:
Chiều cao trung bình cây (m) 6,75 7,25 7,75 8,25 8,75 9,25 Số cây 2 4 10 11 5 3
Bấm máy độ lệch mẫu là: 𝑠 = 0,6427
Câu 12: Sắp xếp theo thứ tự ta có:
0 0 0 … 0 0 1 1 … 1 2 2 … 2 3 3 3 4 4 5 5
(19 số 0) - (8 số 1) – (6 số 2) – (3 số 3) – (2 số 4) – (2 số 577) Trung vị mẫu là 1 ( 𝑥 = 1 2 20 + 𝑥21) = 1+1 2
Câu 13: Học sinh nghỉ 0 buổi nhiều nhất thì mode = 0 2+3
Câu 14: Tỷ lệ cam loại II là: = 5% 2+3+1 + 5 2 + 6 28+6+8+8+4 3
Nhóm học tập RAM(K70, K71, K72 – HNUE ) Câu 15: Khối 6 7 8 9 Số học sinh 9 7 5 4
Tỷ lệ học sinh khối 9 tham gia clb: 4 = 16% 9+7+5+4
Câu 16: Số học sinh trung bình là 20%. 500=100 (học sinh) Câu 17:
A sai vì nếu kích thước mẫu tăng gấp đôi thì độ dài khoảng ước lượng giảm √𝟐 lần.
B sai vì với cùng một bộ số liệu thì khoảng ước lượng có độ tin cậy cao sẽ dài hơn
khoảng ước lượng có độ tin cậy cao hơn. C Đúng
D Sai vì độ dài của khoảng ước lượng không phụ thuộc vào trung bình mẫu. Câu 18: Chọn B
Câu 19: Trên cùng một mẫu thì khoảng rộng hơn sẽ có độ tin cậy cao hơn nên chọn A
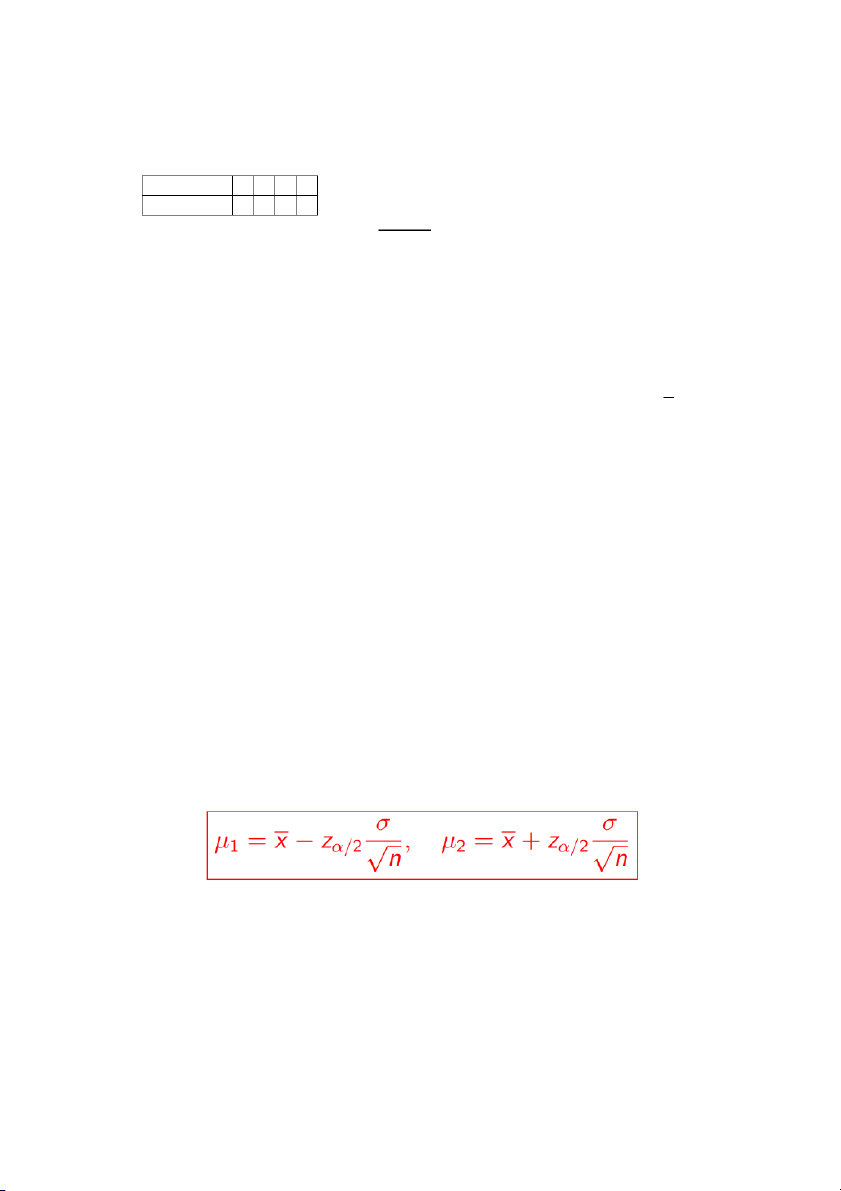
Câu 20: vì biết σ .Áp dụng công thức 4
Nhóm học tập RAM(K70, K71, K72 – HNUE ) 0,5 0,5
𝑢1 = 8 − 1,96 5 = 7,804 𝑢2 = 8+1,96 5 = 8,196 Câu 21: + Với cùng một mẫu s nhất ((p1,p2) ngắn nhấ 𝑚𝑎 𝑚
(theo bảng phân phối stude => độ t .=> đáp án: A 𝑚𝑎 𝑚𝑖 Câu 22: + Dễ thấy: n=1 có độ lệch nên ta sử dụng công thức KƯL cho
i của quần thể đã biết: α): ượng với cùng độ t á trị trung bình với ƯL có độ dài lớn ) lớn nhất) khi: 𝑚𝑎 => đáp án: B 𝑚 C + =60
ng), n=100(sinh viên), 1 – α= 0,95 => α= 0,05 => α/2= + Dễ thấy: n=100 (
>30) lại có độ lệch mẫu s nên ta sử dụng công thức KƯL cho trun của mẫu cỡ lớn : 5 NUE ) = 60 – 1,96= 58,04 = 60 + 1,96= 61,96 10 đáp án: C = = 100 0 đáp án C C +
(kg), 1 – α= 0,95 => α= 0,05 => α/2= 9
+ Áp dụng công thức xác định cỡ mẫu cho bài toán tìm khoảng ước lượng cho giá
trị trung bình với 𝜇 đã Biết: 𝑧 2 1,96.1 2 𝑛 ≈ ቀ 𝛼 2Τ⋅𝜎 𝜀 ቁ = ( 0,8 ) = 6,0025 đáp án C Câu 26: 6 N K72 – HNUE ) +
1 – α= 0,95 => α= 0,05 => α/2= 9 + Áp dụng cô
ng ước lượng cho tỷ lẹ bằng phươn 2 643 đáp án B Câu 27: + quy tắc quyết định: Quyết định H0 đúng H1 đúng Bác bỏ giả thuyết H0 Sai lầm loại 1 Quyết định đúng
Chấp nhận giả thuyết H0 Quyết định đúng Sai lầm loại 2
Trong bài toán kiểm định giả thuyết h0 với đối quyết H1 ta mắc sai lầm
loại 2 khi chấp nhận giả thuyết h0 khi h1 đúng nói cách khác chấp nhận
giả thuyết h0 khi h0 sai. => đáp án Câu 28:
+ Trong bài toán kiểm định giả thuyết h0 với đối quyết H1, mức ý nghĩa ∝ là xác
suất mắc sai lầm loại 1 ( bác bỏ giả thuyết h0 khi h0 đúng ) => đáp án A Câu 29:
=10 là mẫu cỡ nhỏ (n<30) nên ta áp dụng công thúc kieemrr định giả
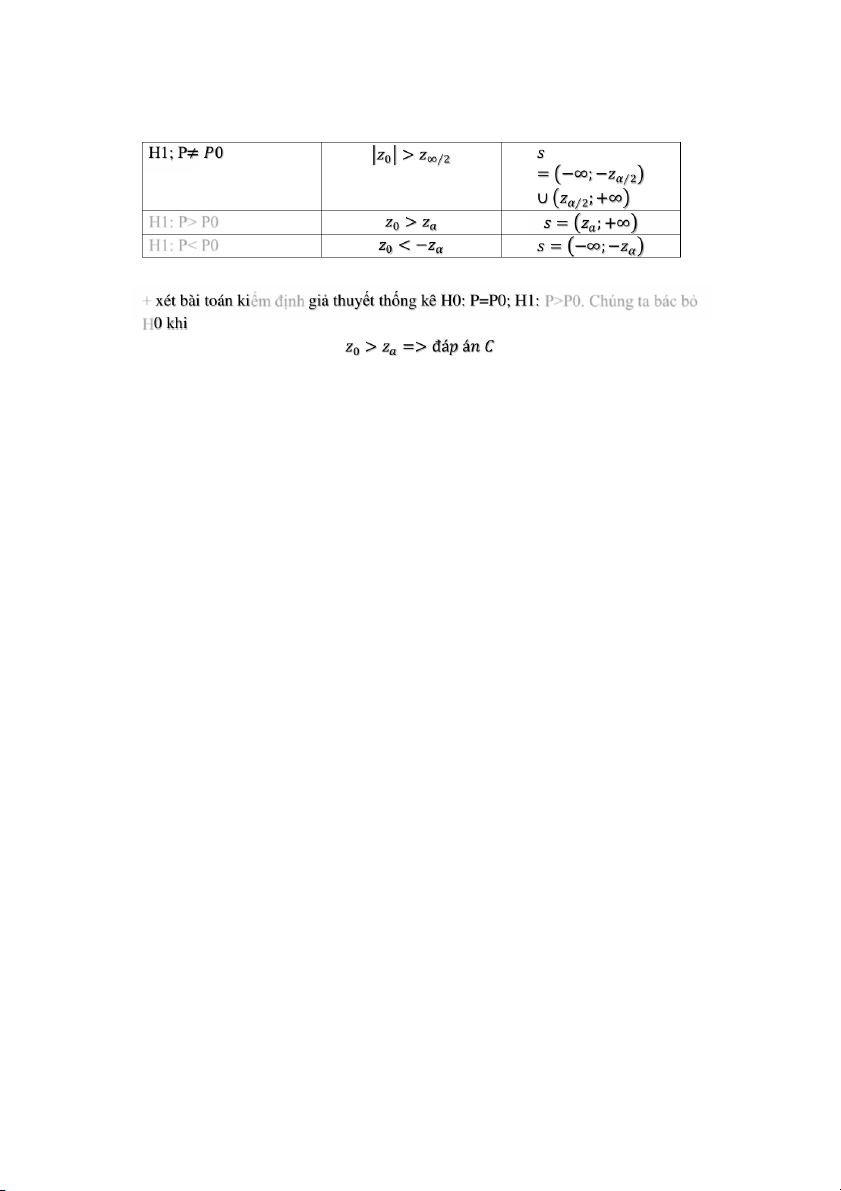
ê cho giá trị trung bình với mẫu cỡ nhỏ: => đáp án B Câu 30: Đối thuyết Tiêu chuẩn bác bỏ H 0 Miền tiêu chuẩn S 7
Nhóm học tập RAM(K70, K71, K72 – HNUE ) H1: P> P0 H1: P< P0 + ểm định P>P0. Chúng ta bác bỏ H 8
Nhóm học tập RAM(K70, K71, K72 – HNUE )
Nhóm học tập RAM(K70, K71, K72 – HNUE )
Nhóm học tập RAM(K70, K71, K72 – HNUE )