103 trang 67 lượt tải

Đáp án và lời giải chi tiết đề chính thức tốt nghiệp THPT 2022 môn Toán

134

Giới thiệu đến quý thầy, cô giáo và các em học sinh bảng đáp án và lời giải chi tiết đề thi chính thức kỳ thi tốt nghiệp Trung học Phổ thông năm 2022 môn Toán các mã đề 101 – 102 – 103 – 104; đáp án và lời giải

Chủ đề: Đề thi THPTQG môn Toán năm 2022 75 tài liệu

Môn: Toán 2.2 K tài liệu

Tác giả:

Profile

Nguyễn Vân

1 năm trước
Danh sách Quiz
/103
Trang 1/22 - WordToan
BỘ GD&ĐT
DIỄN ĐÀN GIÁO VIÊN TOÁN
MÃ ĐỀ 101
ĐỀ THI TN THPT NĂM HỌC 2021 – 2022
MÔN THI: TOÁN
Thời gian: 90 phút (Không kể thời gian phát đề)
Câu 1. Nếu
2
0
d 4f x x
thì
2
0
1
2 d
2
f x x
bằng
A.
6
. B.
8
. C.
4
. D.
2
.
Câu 2. Cho khối lăng trụ có diện tích đáy là
2
3a
và chiều cao
2 .a
Thể tích khối lăng trụ đã cho bằng
A.
3
a
. B.
3
6a
. C.
3
3a
. D.
3
2a
.
Câu 3. Nếu
5
1
d 3f x x
thì
1
5
df x x
bằng
A.
5
. B.
6
. C.
4
. D.
3
.
Câu 4. Cho
d cos .f x x x C
Khẳng định nào dưới đây đúng?
A.
sin .f x x
B.
cos .f x x
C.
sin .f x x
D.
cos .f x x
Câu 5. Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
1; .
B.
0;1 .
C.
1;0 .
D.
0; .
Câu 6. Trong không gian
,Oxyz
cho mặt cầu
2 2
2
: 2 1 6.S x y z
Đường kính của
S
bằng:
A.
6.R
B.
12.
C.
2 6.R
D.
3.
Câu 7. Trong không gian
Oxyz
, cho điểm
1;2; 3A
. Hình chiếu vuông góc của
A
lên mặt phẳng
Oxy
có tọa độ là
A.
0;2; 3
. B.
1;0; 3
. C.
1;2;0
. D.
1;0;0
.
Câu 8. Cho khối chóp
.S ABC
có chiều cao bằng
3
, đáy
ABC
có diện tích bằng
10
. Thể tích khối chóp
.S ABC
bằng
A.
2
. B.
15
. C.
10
. D.
30
.
Câu 9. Cho cấp số nhân
n
u
với
1
1u
và
2
2u
. Công bội của cấp số nhân đã cho là:
A.
1
2
q
. B.
2q
. C.
2q
. D.
1
2
q
.
Câu 10. Cho hình trụ có chiều cao
1h
và bán kính
2r
. Diện tích xung quanh của hình trụ đã cho bằng
A.
4
. B.
2
. C.
3
. D.
6
.
Câu 11. Tiệm cận ngang của đồ thì hàm số
2 1
2 4
x
y
x
là đường thẳng có phương trình:
A.
2x
. B.
1x
. C.
1y
. D.
2y
.
Câu 12. Tập nghiệm của bất phương trình
5
log 1 2x
là
A.
9;
. B.
25;
. C.
31;
. D.
24;
.
Câu 13. Hàm số nào dưới đây có bảng biến thiên như sau?
Trang 2/22 – Diễn đàn giáo viên Toán
A.
4 2
2y x x . B.
3
3y x x . C.
4 2
2y x x . D.
3
3y x x .
Câu 14. Môđun của số phức
3 4z i
bằng
A.
25
. B. 7 . C.
5
. D.
7
.
Câu 15. Cho hàm số
4 2
f x ax bx c
có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình
1f x
là
A.
1
. B.
2
. C.
4
. D.
3
.
Câu 16. Tập xác định của hàm số
3
log 4y x
là
A.
5;
. B.
; 
. C.
4; 
. D.
;4
.
Câu 17. Với
a
là số thực dương tùy ý,
4log a
bằng
A.
2log a
. B.
2loga
. C.
4log a
. D.
8log a
.
Câu 18. Số các tổ hợp chập
3
của
12
phần tử là
A.
1320
. B.
36
. C.
220
. D.
1728
.
Câu 19. Cho hàm số
( )y f x
có bảng biến thiên như sau:
Điểm cực tiểu của hàm số đã cho là:
A.
2x
. B.
2x
. C.
1x
. D.
1x
.
Câu 20. Trong không gian
Oxyz
, phương trình của mặt phẳng
( )Oyz
là:
A.
0z
. B.
0x
. C.
0 x y z
. D.
0y
.
Câu 21. Nghiệm của phương trình
2 1 2
3 3
x x
là:
A.
1
3
x
. B.
0x
. C.
1 x
. D.
1x
.
Câu 22. Cho hàm số
4 2
y ax bx c có đồ thị như đường cong trong hình bên.
Trang 3/22 - WordToan
Số điểm cực trị của hàm số đã cho là:
A. 2. B. 3. C. 1. D. 0.
Câu 23. Trong không gian
Oxyz
, cho đường thẳng
2
: 1 2
1 3
x t
d y t
x t
. Vec-tơ nào dưới đây là một véc-tơ chỉ
phương của
d
?
A.
1
2;1; 1u
. B.
2
1;2;3u
. C.
3
1; 2;3u
. D.
4
2;1;1u
.
Câu 24. Cho tam giác
OIM
vuông tại
I
có
3OI
và
4IM
. Khi quay tam giác
OIM
quanh cạnh góc
vuông
OI
thì đường gấp khúc
OMI
tạo thành hình nón có độ dài đường sinh bằng
A.
7
. B.
3
. C.
5
. D.
4
.
Câu 25. Trên mặt phẳng tọa độ, điểm biểu diễn số phức
2 7z i
có tọa độ là
A.
2;7
. B.
2;7
. C.
2; 7
. D.
7;2
.
Câu 26. Cho hai số phức
1
2 3z i và
2
1 .z i Số phức
1 2
z z bằng
A.
5 .i
B.
3 2 .i
C.
1 4 .i
D.
3 4 .i
Câu 27. Cho hàm số
2 .
x
f x e x
Khẳng định nào dưới đây đúng?
A.
2
d .
x
f x x e x C
B.
d .
x
f x x e C
C.
2
d .
x
f x x e x C
D.
2
d 2 .
x
f x x e x C
Câu 28. Đạo hàm của hàm số
3
y x
là
A.
4
y x
. B.
2
1
2
y x
. C.
4
1
3
y x
. D.
4
3y x
.
Câu 29. Trong không gian
Oxyz
, cho ba điểm
1;2; 1A
,
3;0;1B
và
2; 2; 2C
. Đường thẳng đi qua
A
và vuông góc với mặt phẳng
ABC
có phương trình là
A.
1 2 1
1 2 3
x y z
. B.
1 2 1
1 2 1
x y z
.
C.
1 2 1
1 2 1
x y z
. D.
1 2 1
1 2 1
x y z
.
Câu 30. Giá trị lớn nhất của hàm số
3 2
3 9 10 f x x x x
trên đoạn
2;2
bằng
A.
12
. B.
10
. C.
15
. D.
1
.
Câu 31. Có bao nhiêu giá trị nguyên thuộc tập xác định của hàm số
log 6 2
y x x
?
Trang 4/22 – Diễn đàn giáo viên Toán
A.
7
. B.
8
. C.
9
. D. Vô số.
Câu 32. Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
6 0 z z
. Khi đó
1 2 1 2
z z z z
bằng:
A.
7
. B.
5
. C.
7
. D.
5
.
Câu 33. Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
B
,
2AC
,
3AB
và
1
AA
(tham khảo hình bên).
Góc giữa hai mặt phẳng
ABC
và
ABC
bằng
A.
0
30
. B.
0
45
. C.
0
90
. D.
0
60
.
Câu 34. Cho hình hộp chữ nhật
.ABCD A B C D
có
AB a
,
2BC a
và
3AA a
(tham khảo hình bên).
Khoảng cách giữa hai đường thẳng
BD
và
A C
bằng
A.
a
. B.
2a
. C.
2a
. D.
3a
.
Câu 36. Hàm số nào dưới đây đồng biến trên
?
A.
4 2
y x x
. B.
3
y x x
. C.
1
2
x
y
x
. D.
3
y x x
.
Câu 37. Trong không gian
Oxyz
, cho điểm
0; 3;2A
và mặt phẳng
: 2 3 5 0P x y z
. Mặt phẳng đi
qua
A
và song song với
P
có phương trình là
A.
2 3 9 0x y x
. B.
2 3 3 0x y x
. C.
2 3 3 0x y x
. D.
2 3 9 0x y x
.
Câu 35. Cho hàm số
2
1
1
cos 2
f x
x
. Khẳng định nào dưới đây đúng?
A.
d tan 2f x x x x C
. B.
1
d cot 2
2
f x x x x C
.
C.
1
d tan 2
2
f x x x x C
. D.
1
d tan 2
2
f x x x x C
.
Câu 38. Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn
40;60
. Xác suất để chọn được số
có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
A.
4
7
B.
2
5
C.
3
5
D.
3
7
Câu 39. Có bao nhiêu số nguyên dương
a
sao cho ứng với mỗi
a
có đúng ba số nguyên
b
thỏa mãn
3 3 .2 18 0
b b
a
?
A.
72
B.
73
C.
71
D.
74
Câu 40. Cho hàm số
4 2
( ) ( 1) 2 1f x m x mx
với
m
là tham số thực. Nếu
[0;3]
min ( ) (2)f x f
thì
[0;3]
max ( )f x
bằng
Trang 5/22 - WordToan
A.
13
3
. B.
4
. C.
14
3
. D.
1
.
Câu 41. Biết
( )F x
và
( )G x
là hai nguyên hàm của hàm số
( )f x
trên
và
3
0
( ) (3) (0) ( 0)f x dx F G a a
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
( ), ( ), 0y F x y G x x
và
3x
. Khi
15S
thì
a
bằng:
A.
15
. B.
12
. C.
18
. D.
5
.
Câu 42. Trong không gian
Oxyz
, cho điểm
1;2; 2A
. Gọi
P
là mặt phẳng chứa trục
Ox
sao cho
khoảng cách từ
A
đến
P
lớn nhất. Phương trình của
P
là
A.
2 0y z
. B.
2 0y z
. C.
0y z
. D.
0y z
.
Câu 43. Cho hình nón có góc ở đỉnh là
0
120
và chiều cao bằng 4. Gọi
S
là mặt cầu đi qua đỉnh và chứa
đường tròn đáy của hình nón đã cho. Tính diện tích của
S
bằng:
A.
64
. B.
256
. C.
192
. D.
96
.
Câu 44. Xét tất cả các số thực
x
,
y
sao cho
2
2
5
4 log
40
25
x a
y
a
với mọi số thực dương
a
. Giá trị lớn nhất
của biểu thức
2 2
3P x y x y
bằng
A.
125
2
. B.
80
. C.
60
. D.
20
.
Câu 45. Cho các số phức
1
z ,
2
z ,
3
z thỏa mãn
1 2 3
2 2z z z
và
1 2 3 1 2
8 3z z z z z
. Gọi
A
,
B
,
C
lần lượt là các điểm biểu diễn của
1
z ,
2
z ,
3
z trên mặt phẳng tọa độ. Diện tích tam giác
ABC
bằng
A.
55
32
. B.
55
16
. C.
55
44
. D.
55
8
.
Câu 46. Cho khối lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
,
2AB a
. Góc
giữa đường thẳng BC
và mặt phẳng
ACC A
bằng
30
. Thể tích của khối lăng trụ đã cho bằng
A.
3
3a
. B.
3
a
. C.
3
12 2a
. D.
3
4 2a
.
Câu 47. Cho hàm số
y f x
. Biết rằng hàm số
lng x f x
có bảng biến thiên như sau:
Diện tích hình phẳng giới hạn bởi các đường
y f x
và
y g x
thuộc khoảng nào dưới đây?
A.
5;6
. B.
4;5
. C.
2;3
. D.
3;4
.
Câu 48. Có bao nhiêu số phức
z
thỏa mãn
2
2z z z
và
2
( 4)( 4 ) 4 ?z z i z i
A.
3.
B.
1.
C.
2.
D.
4.
Câu 49. Trong không gian
Oxyz
, cho mặt cầu
S
tâm
1;3;9I
bán kính bằng
3
. Gọi
M
,
N
là hai điểm
lần lượt thuộc hai trục
Ox
,
Oz
sao cho đường thẳng
MN
tiếp xúc với
S
, đồng thời mặt cầu
Trang 6/22 – Diễn đàn giáo viên Toán
ngoại tiếp tứ diện
OIMN
có bán kính bằng
13
2
. Gọi
A
là tiếp điểm của
MN
và
S
, giá trị
AM AN
bằng
A.
39
. B.
12 3
. C.
18
. D.
28 3
.
Câu 50. Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 2
2 64
y x mx x
có đúng ba
điểm cực trị
A.
5
. B.
6
. C.
12
. D.
11
.
------------- Hết -------------
Trang 7/22 - WordToan
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A B D C B C C C B A C D D C B C B C D B A B C C C
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
B A D D C A B B D C D D D B B D D B C B D D D B C
LỜI GIẢI CHI TIẾT
Câu 1. Nếu
2
0
d 4f x x
thì
2
0
1
2 d
2
f x x
bằng
A.
6
. B.
8
. C.
4
. D.
2
.
Lời giải
Chọn A
Ta có:
2 2 2
0 0 0
1 1
2 d d 2d 2 4 6
2 2
f x x f x x x
.
Câu 2. Cho khối lăng trụ có diện tích đáy là
2
3a
và chiều cao
2 .a
Thể tích khối lăng trụ đã cho bằng
A.
3
a
. B.
3
6a
. C.
3
3a
. D.
3
2a
.
Lời giải
Chọn B
Ta có:
2 3
.. 3 2 6V h a a aB
.
Câu 3. Nếu
5
1
d 3f x x
thì
1
5
df x x
bằng
A.
5
. B.
6
. C.
4
. D.
3
.
Lời giải
Chọn A
Ta có:
1 5
5 1
d d 3 3f x x f x x
.
Câu 4. Cho
d cos .f x x x C
Khẳng định nào dưới đây đúng?
A.
sin .f x x
B.
cos .f x x
C.
sin .f x x
D.
cos .f x x
Lời giải
Chọn C
Áp dụng công thức
sin d cos .x x x C
Suy ra
sin .f x x
Câu 5. Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
1; .
B.
0;1 .
C.
1;0 .
D.
0; .
Lời giải
Chọn B
Câu 6. Trong không gian
,Oxyz
cho mặt cầu
2 2
2
: 2 1 6.S x y z
Đường kính của
S
bằng:
A.
6.R
B.
12.
C.
2 6.R
D.
3.
Trang 8/22 – Diễn đàn giáo viên Toán
Lời giải
Chọn C
Ta có bán kính mặt cầu
6.
R
suy ra đường kính mặt cầu bằng
2 2 6.
R
Câu 7. Trong không gian
Oxyz
, cho điểm
1;2; 3
A
. Hình chiếu vuông góc của
A
lên mặt phẳng
Oxy
có tọa độ là
A.
0;2; 3
. B.
1;0; 3
. C.
1;2;0
. D.
1;0;0
.
Lời giải
Chọn C
Do điểm
1;2; 3
A
nên hình chiếu vuông góc của
A
lên mặt phẳng
Oxy
có tọa độ là
1;2;0
.
Câu 8. Cho khối chóp .
S ABC
có chiều cao bằng
3
, đáy
ABC
có diện tích bằng
10
. Thể tích khối chóp
.
S ABC
bằng
A.
2
. B.
15
. C.
10
. D.
30
.
Lời giải
Chọn C
Thể tích khối chóp .
S ABC
là
1 1
. .10.3 10
3 3
V B h
.
Câu 9. Cho cấp số nhân
n
u
với
1
1
u
và
2
2
u
. Công bội của cấp số nhân đã cho là:
A.
1
2
q
. B.
2
q
. C.
2
q
. D.
1
2
q
.
Lời giải
Chọn B
Ta có
2
2 1
1
. 2
u
u u q q
u
.
Câu 10. Cho hình trụ có chiều cao
1
h
và bán kính
2
r
. Diện tích xung quanh của hình trụ đã cho bằng
A.
4
. B.
2
. C.
3
. D.
6
.
Lời giải
Chọn A
Ta có
2 4
xq
S rh
.
Câu 11. Tiệm cận ngang của đồ thì hàm số
2 1
2 4
x
y
x
là đường thẳng có phương trình:
A.
2
x
. B.
1
x
. C.
1
y
. D.
2
y
.
Lời giải
Chọn C
Ta có
2 1
lim 1
2 4
x
x
x

suy ra tiệm cận ngang của đồ là đường thẳng
1
y
.
Câu 12. Tập nghiệm của bất phương trình
5
log 1 2
x
là
A.
9;

. B.
25;

. C.
31;

. D.
24;
.
Lời giải
Chọn D
Đkxđ:
1
x
5 5 5
log 1 2 log 1 log 25 1 25 24
x x x x
Câu 13. Hàm số nào dưới đây có bảng biến thiên như sau?
Trang 9/22 - WordToan
A.
4 2
2y x x . B.
3
3y x x . C.
4 2
2y x x . D.
3
3y x x .
Lời giải
Chọn D
Từ BBT ta nhận thấy hàm số có hai điểm cực trị và đồng biến trên khoảng
1; .
Do đó hàm số
là hàm đa thức bậc ba có hệ số
0.a
Câu 14. Môđun của số phức
3 4z i
bằng
A.
25
. B. 7 . C.
5
. D.
7
.
Lời giải
Chọn C
Ta có
2 2
3 4 25 5z
Câu 15. Cho hàm số
4 2
f x ax bx c
có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình
1f x
là
A.
1
. B.
2
. C.
4
. D.
3
.
Lời giải
Chọn B
Đường thẳng
d
có phương trình
1y
cắt đồ thị hàm số
y f x
tại
2
điểm phân biệt.
Suy ra phương trình
1f x
có
2
nghiệm thực phân biệt.
Câu 16. Tập xác định của hàm số
3
log 4y x
là
A.
5;
. B.
; 
. C.
4; 
. D.
;4
.
Lời giải
Chọn C
Trang 10/22 – Diễn đàn giáo viên Toán
Điều kiện:
4 0 4x x
.
Tập xác định:
4;D 
.
Câu 17. Với
a
là số thực dương tùy ý,
4log a
bằng
A.
2log a
. B.
2loga
. C.
4log a
. D.
8log a
.
Lời giải
Chọn B
Với
0a
, ta có
1
2
1
4log 4log 4. log 2log
2
a a a a
.
Câu 18. Số các tổ hợp chập
3
của
12
phần tử là
A.
1320
. B.
36
. C.
220
. D.
1728
.
Lời giải
Chọn C
Số các tổ hợp chập
3
của
12
phần tử là
3
12
C 220
.
Câu 19. Cho hàm số
( )y f x
có bảng biến thiên như sau:
Điểm cực tiểu của hàm số đã cho là:
A.
2x
. B.
2x
. C.
1x
. D.
1x
.
Lời giải
Chọn D
Từ bảng biến thiên ta suy ra: điểm cực tiểu của hàm số đã cho là
1x
.
Câu 20. Trong không gian
Oxyz
, phương trình của mặt phẳng
( )Oyz
là:
A.
0z
. B.
0x
. C.
0 x y z
. D.
0y
.
Lời giải
Chọn B
Phương trình của mặt phẳng
( )Oyz
là:
0x
.
Câu 21. Nghiệm của phương trình
2 1 2
3 3
x x
là:
A.
1
3
x
. B.
0x
. C.
1 x
. D.
1x
.
Lời giải
Chọn A
2 1 2
1
3 3 2 1 2 3 1
3
x x
x x x x
.
Câu 22. Cho hàm số
4 2
y ax bx c
có đồ thị như đường cong trong hình bên.
Trang 11/22 - WordToan
Số điểm cực trị của hàm số đã cho là:
A. 2. B. 3. C. 1. D. 0.
Lời giải
Chọn B
Dựa vào hình dáng của đồ thị. Ta thấy hàm số đã cho có 3 cực trị.
Câu 23. Trong không gian
Oxyz
, cho đường thẳng
2
: 1 2
1 3
x t
d y t
x t
. Vec-tơ nào dưới đây là một véc-tơ chỉ
phương của
d
?
A.
1
2;1; 1u
. B.
2
1;2;3u
. C.
3
1; 2;3u
. D.
4
2;1;1u
.
Lời giải
Chọn C
Theo định nghĩa phương trình đưởng thẳng. Ta có
3
1; 2;3u
là một véc-tơ chỉ phương của
d
.
Câu 24. Cho tam giác
OIM
vuông tại
I
có
3OI
và
4IM
. Khi quay tam giác
OIM
quanh cạnh góc
vuông
OI
thì đường gấp khúc
OMI
tạo thành hình nón có độ dài đường sinh bằng
A.
7
. B.
3
. C.
5
. D.
4
.
Lời giải
Chọn C
Ta có chiều cao hình nón
3h OI
, bán kính đáy
4r IM
thì độ dài đường sinh là:
2 2 2 2
3 4 5l OM IM OI
.
Câu 25. Trên mặt phẳng tọa độ, điểm biểu diễn số phức
2 7z i
có tọa độ là
A.
2;7
. B.
2;7
. C.
2; 7
. D.
7;2
.
Lời giải
Chọn C
Điểm biểu diễn số phức
2 7z i
trên mặt phẳng tọa độ có tọa độ là
2; 7
.
Câu 26. Cho hai số phức
1
2 3z i và
2
1 .z i Số phức
1 2
z z bằng
A.
5 .i
B.
3 2 .i
C.
1 4 .i
D.
3 4 .i
Lời giải
Chọn B
r
h
l
M
O
I
Trang 12/22 – Diễn đàn giáo viên Toán
Vì
1
2 3
z i
và
2
1
z i
nên
1 2
2 3 1 3 2 .
z z i i i
Câu 27. Cho hàm số
2 .
x
f x e x
Khẳng định nào dưới đây đúng?
A.
2
d .
x
f x x e x C
B.
d .
x
f x x e C
C.
2
d .
x
f x x e x C
D.
2
d 2 .
x
f x x e x C
Lời giải
Chọn A
Ta có:
2
d 2 d .
x x
f x x e x x e x C
Câu 28. Đạo hàm của hàm số
3
y x
là
A.
4
y x
. B.
2
1
2
y x
. C.
4
1
3
y x
. D.
4
y x
.
Lời giải
Chọn B
Ta có:
3 1 4
3 3
y x x
.
Câu 29. Trong không gian
Oxyz
, cho ba điểm
1;2; 1
A
,
3;0;1
B
và
2; 2; 2
C
. Đường thẳng đi qua
A
và vuông góc với mặt phẳng
ABC
có phương trình là
A.
1 2 1
1 2 3
x y z
. B.
1 2 1
1 2 1
x y z
.
C.
1 2 1
1 2 1
x y z
. D.
1 2 1
1 2 1
x y z
.
Lời giải
Chọn B
Ta có:
2; 2;2
AB
;
1;0; 1
AC
.
Đường thẳng đi qua
A
và vuông góc với mặt phẳng
ABC
có véc-tơ chỉ phương là
; 2;4;2 1;2;1
AB AC

nên có phương trình:
1 2 1
1 2 1
x y z
.
Câu 30. Giá trị lớn nhất của hàm số
3 2
3 9 10
f x x x x trên đoạn
2;2
bằng
A.
12
. B.
10
. C.
15
. D.
1
.
Lời giải
Chọn C
Xét hàm số
3 2
3 9 10
f x x x x
trên đoạn
2;2
2
3 6 9
f x x x
.
2
0 3 6 9 0
f x x x
1 2;2
3 2;2
x
x
.
Ta có:
2 8; 1 15; 2 12
f f f
.
Vậy giá trị lớn nhất của hàm số
3 2
3 9 10
f x x x x
trên đoạn
2;2
bằng 15.
Câu 31. Có bao nhiêu giá trị nguyên thuộc tập xác định của hàm số
log 6 2
y x x
?
A.
7
. B.
8
. C.
9
. D. Vô số.
Lời giải
Chọn A
Trang 13/22 - WordToan
Điều kiện xác định
2
6 2 0 4 12 0 2 6 x x x x x
.
Vậy có tất cả 7 giá trị nguyên thuộc tập xác định của hàm số
log 6 2
y x x
.
Câu 32. Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
6 0 z z
. Khi đó
1 2 1 2
z z z z
bằng:
A.
7
. B.
5
. C.
7
. D.
5
.
Lời giải
Chọn B
Vì phương trình
2
6 0 z z
có hai nghiệm
1
z
và
2
z
. Theo định lí Vi-et, ta có:
1 2
1 2
1
6
z z
z z
. Do
đó:
1 2 1 2
1 6 5 z z z z
.
Câu 33. Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
B
,
2AC
,
3AB
và
1
AA
(tham khảo hình bên).
Góc giữa hai mặt phẳng
ABC
và
ABC
bằng
A.
0
30
. B.
0
45
. C.
0
90
. D.
0
60
.
Lời giải
Chọn B
Tam giác
ABC
vuông tại
B
nên
2 2
1BC AC AB
.
Ta có:
,
,
ABC ABC AB
BC tai B ABC Do BCAB BC AA B B
AB BCBC tai B ABC
Suy ra góc giữa hai mặt phẳng
ABC
và
ABC
là góc
C BC
.
Xét
C BC
vuông tại
C
ta có:
tan 1
CC AA
BC
C B
BC
C
0
45C BC
.
Vậy góc giữa hai mặt phẳng
ABC
và
ABC
là
0
45
.
Câu 34. Cho hình hộp chữ nhật
.ABCD A B C D
có
AB a
,
2BC a
và
3AA a
(tham khảo hình bên).
Khoảng cách giữa hai đường thẳng
BD
và
A C
bằng
A.
a
. B.
2a
. C.
2a
. D.
3a
.
Lời giải
Chọn D
Trang 14/22 – Diễn đàn giáo viên Toán
A C A B C D
,
// , , , 3BD A B C D d BD A C d BD A B C D d B A B C D BB a
.
Câu 35. Cho hàm số
2
1
1
cos 2
f x
x
. Khẳng định nào dưới đây đúng?
A.
d tan 2f x x x x C
. B.
1
d cot 2
2
f x x x x C
.
C.
1
d tan 2
2
f x x x x C
. D.
1
d tan 2
2
f x x x x C
.
Lời giải
Chọn C
2 2
d 2
1 1 1
d 1 d d tan 2
cos 2 2 cos 2 2
x
f x x x x x x C
x x
.
Câu 36. Hàm số nào dưới đây đồng biến trên
?
A.
4 2
y x x
. B.
3
y x x
. C.
1
2
x
y
x
. D.
3
y x x
.
Lời giải
Chọn D
Ta có:
3 2
3 1 0y x x y x x
.
Câu 37. Trong không gian
Oxyz
, cho điểm
0; 3;2A
và mặt phẳng
: 2 3 5 0P x y z
. Mặt phẳng đi
qua
A
và song song với
P
có phương trình là
A.
2 3 9 0x y x
. B.
2 3 3 0x y x
. C.
2 3 3 0x y x
. D.
2 3 9 0x y x
.
Lời giải
Chọn D
Mặt phẳng đi qua
A
và song song với
P
có phương trình là
2 3 3 2 0x y z
2 3 9 0x y z
.
Câu 38. Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn
40;60
. Xác suất để chọn được số
có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
A.
4
7
B.
2
5
C.
3
5
D.
3
7
Lời giải
Chọn D
Từ 40 đến 60 ta có 21 số nên
21n
Các số thỏa mãn đề bài:
45; 46; 47;48;49;56;57;58;59
Có 9 số.
Xác suất để chọn được số thoản mãn đề bài:
9 3
21 7
P
Câu 39. Có bao nhiêu số nguyên dương
a
sao cho ứng với mỗi
a
có đúng ba số nguyên
b
thỏa mãn
3 3 .2 18 0
b b
a
?
A.
72
B.
73
C.
71
D.
74
Lời giải
Chọn B
Trang 15/22 - WordToan
TH1:
2
2
1
3 3
3 3 0
18
1 log
18
18
log
2
.2 18 0
b
b
b
b
b
b
b
a
a
a
a
Để có đúng ba số nguyên
b
thì
2
18 18 9 9
4 log 5 16 32
16 8
a
a a
.
Trường hợp này có
1
giá trị
1
a
nguyên thỏa mãn.
TH2:
2
2
1
3 3
3 3 0
18
log 1
18
18
log
2
.2 18 0
b
b
b
b
b
b
b
a
a
a
a
Để có đúng ba số nguyên
b
thì
2
18 1 18 1
3 log 2 72 144
8 4
a
a a
.
Trường hợp này có
144 72 72
giá trị
a
nguyên thỏa mãn.
Vậy số giá trị nguyên của
a
là:
72 1 73
.
Câu 40. Cho hàm số
4 2
( ) ( 1) 2 1
f x m x mx
với
m
là tham số thực. Nếu
[0;3]
min ( ) (2)
f x f
thì
[0;3]
max ( )
f x
bằng
A.
13
3
. B.
4
. C.
14
3
. D.
1
.
Lời giải
Chọn B
Ta có:
3 2
'( ) 4( 1) 4 4 (( 1) )
f x m x mx x m x m
2
0
'( ) 0
1
x
f x
m
x
m
(
1
m
không thỏa yêu cầu bài toán)
Vì
[0;3]
min ( ) (2)
f x f
2
x
là nghiệm của
'( ) 0
f x
4
4 4 4
1 3
m
m m m
m
4 2
1 8
( ) 1
3 3
f x x x
81 72 3 12
(0) 1, (3) 4
3 3 3 3
f f
Vậy
[0;3]
max ( ) 4
f x
Câu 41. Biết
( )
F x
và
( )
G x
là hai nguyên hàm của hàm số
( )
f x
trên
và
3
0
( ) (3) (0) ( 0)
f x dx F G a a
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
( ), ( ), 0
y F x y G x x
và
3
x
. Khi
15
S
thì
a
bằng:
A.
15
. B.
12
. C.
18
. D.
5
.
Lời giải
Chọn D
Ta có:
( ), ( )
F x G x
là nguyên hàm của
( ) ( ) ( )
f x F x G x C
Trang 16/22 – Diễn đàn giáo viên Toán
3 3 3
0 0 0
( ) ( ) 3 15 5 5S F x G x dx C dx Cdx C C C
3
0
( ) (3) (0) (3) ( (0) ) (3) (0) (3) (0)f x dx F F F G C F G C F G a
5a C
(do
0a
)
Câu 42. Trong không gian
Oxyz
, cho điểm
1;2; 2A
. Gọi
P
là mặt phẳng chứa trục
Ox
sao cho
khoảng cách từ
A
đến
P
lớn nhất. Phương trình của
P
là
A.
2 0y z
. B.
2 0y z
. C.
0y z
. D.
0y z
.
Lời giải
Chọn D
Gọi
H
,
K
lần lượt là hình chiếu của
A
lên mặt phẳng
P
và trục
Ox
.
Ta có:
;d A P AH AK
.
Suy ra khoảng cách từ
A
đến
P
lớn nhất khi
H K
, hay mặt phẳng
P
nhận véc-tơ
AK
làm
véc-tơ pháp tuyến.
K
là hình chiếu của
A
trên trục
Ox
suy ra:
1;0;0K
,
0; 2;2AK
.
Mặt phẳng
P
đi qua
K
có phương trình:
2 0 2 0 0y z
0y z
.
Câu 43. Cho hình nón có góc ở đỉnh là
0
120
và chiều cao bằng 4. Gọi
S
là mặt cầu đi qua đỉnh và chứa
đường tròn đáy của hình nón đã cho. Tính diện tích của
S
bằng:
A.
64
. B.
256
. C.
192
. D.
96
.
Lời giải
Chọn B
Ta có
4SH
Trang 17/22 - WordToan
0
2 2. .tan 2.4.tan 60 8 3AB AH SH ASH
Có
OS
là bán kính mặt cầu cũng là bán kính đường tròn ngoại tiếp
SAB
Suy ra:
0
8 3
2 8
sin 2.sin120
AB
OS OS
ASB
Vậy diện tích mặt cầu:
2
4 .8 256S
Câu 44. Xét tất cả các số thực
x
,
y
sao cho
2
2
5
4 log
40
25
x a
y
a
với mọi số thực dương
a
. Giá trị lớn nhất
của biểu thức
2 2
3P x y x y
bằng
A.
125
2
. B.
80
. C.
60
. D.
20
.
Lời giải
Chọn C
Ta có
2
2
5
4 log
40
25
x a
y
a
2
2
5
4 log
40
5 5
log log 25
x a
y
a
2
5 5
4 2log log 2 40x a a y
2 2
5 5
log 2 log 40 0a x a y
*
Coi
*
là bất phương trình bậc hai ẩn
5
log a
Để
*
đúng với mọi số thực dương
a
thì
0
2 2
40 0x y
2 2
40 0x y
1
.
Ta có biểu thức
1
là hình tròn
1
C
tâm
0;0O
, bán kính
1
2 10R
.
Mặt khác
2 2
3P x y x y
2 2
3 0x y x y P là phương trình đường tròn
2
C
tâm
1 3
;
2 2
I
, bán kính
2
1
10 4
2
R P
.
Để tồn tại điểm chung của đường tròn
2
C
với hình tròn
1
C
thì
2 1
R R OI
1 1
10 4 2 10 10
2 2
P
10 4 5 10P
60P
.
Vậy
max
60P .
Câu 45. Cho các số phức
1
z ,
2
z ,
3
z thỏa mãn
1 2 3
2 2z z z
và
1 2 3 1 2
8 3z z z z z
. Gọi
A
,
B
,
C
lần lượt là các điểm biểu diễn của
1
z ,
2
z ,
3
z trên mặt phẳng tọa độ. Diện tích tam giác
ABC
bằng
A.
55
32
. B.
55
16
. C.
55
44
. D.
55
8
.
Trang 18/22 – Diễn đàn giáo viên Toán
Lời giải
Chọn B
Ta có:
1 2
2z z
2OA OB
;
3
1z
1OC
.
+)
1 2 3 1 2
8 3z z z z z
1 2
1 2
3
8 3
z z
z z
z
1 2
1 2
3
8 3
z z
z z
z
1 2
3
2
z z
.
Gọi
H
là trung điểm của
AB
, biểu diễn số phức
1 2
2
z z
, ta có:
1 2
3
2 4
z z
OH
+)
2 2 2 2
1 2 1 2 1 2
2z z z z z z
1 2
55
2
z z
55
2
AB
.
+)
1 2 3 1 2
8 3z z z z z
1 3 2 3 1 2 1 3 2 3 1 2
3
8 8 3
8
z z z z z z z z z z z z
Đặt
3
2
8
a
, suy ra:
1 3 2 3 1 2
2z z z z az z
1 3 2 1 3 2
z z az az z z
1 3 2 1 3 2
z z az az z z
2 2
3 2 1 3
z az az z
2 3 2 3 1 3 1 3
z z z z z z z z b
2 2 2
2
3 1 3 1 1 3 1 3
5AC z z z z z z z z b .
2 2 2
2
3 2 3 2 2 3 2 3
5BC z z z z z z z z b .
Suy ra:
2 2
AC BC AC BC
hay tam giác
ABC
cân tại
C
.
3 1
1
4 4
CH OC OH
Vậy
1 1 55 1 55
. . .
2 2 2 4 16
ABC
S AB CH
.
Câu 46. Cho khối lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
,
2AB a
. Góc
giữa đường thẳng BC
và mặt phẳng
ACC A
bằng
30
. Thể tích của khối lăng trụ đã cho bằng
A.
3
3a
. B.
3
a
. C.
3
12 2a
. D.
3
4 2a
.
Lời giải
Chọn D
Trang 19/22 - WordToan
Ta có:
AB AC
AB ACC A AB AC
AB AA
.
Vậy góc giữa đường thẳng BC
và mặt phẳng
ACC A
là góc
BC A
.
Trong tam giác vuông BC A
ta có
30 ; 2 .cot 2 . 3BC A AB a AC AB BC A a
.
Trong tam giác vuông ACC
ta có
2 2
2 2 .CC AC AC a
Vậy thể tích khối lăng trụ đã cho là:
2 2 3
1 1
. 2 2 . .4 4 2 .
2 2
V CC AB a a a
Câu 47. Cho hàm số
y f x
. Biết rằng hàm số
lng x f x
có bảng biến thiên như sau:
Diện tích hình phẳng giới hạn bởi các đường
y f x
và
y g x
thuộc khoảng nào dưới đây?
A.
5;6
. B.
4;5
. C.
2;3
. D.
3;4
.
Lời giải
Chọn D
Ta có
g x
f x e .
Từ bảng biến thiên suy ra:
ln 2
ln 2 2
g x
g x e e .
+)
g x
f x g x e
.
Phương trình hoành độ giao điểm của
f x
và
g x
:
0f x g x
0
g x
g x e g x
1 0
g x
g x e
0g x
1
2
3
x x
x x
x x
.
Trang 20/22 – Diễn đàn giáo viên Toán
Mặt khác từ bảng biến thiên ta cũng có:
0
g x
,
1 2
;
x x x
;
0
g x
,
2 3
;
x x x
.
Suy ra:
3
1
d
x
x
S f x g x x
3
1
d
x
g x
x
g x e g x x
3
1
1 d
x
g x
x
g x e x
3
2
1 2
1 d 1 d
xx
g x g x
x x
g x e x g x e x
32
1 2
1 d 1 d
xx
g x g x
x x
e g x e g x
2 3
1 2
x x
g x g x
x x
e g x e g x
2 1 3 2
2 1 3 2
g x g x g x g x
e g x e g x e g x e g x
2 1 3
2 1 3
2 2
g x g x g x
e e e g x g x g x
43 43
2.6 2 2ln 6 ln ln 2
8 8
37 43
ln 3,416
8 144
.
Câu 48. Có bao nhiêu số phức
z
thỏa mãn
2
2
z z z
và
2
( 4)( 4 ) 4 ?
z z i z i
A.
3.
B.
1.
C.
2.
D.
4.
Lời giải
Chọn D
Ta có
2
4 ( 4)( 4 ) ( 4)( 4 ) 4 4 4 4 .
z i z z i z z i z z i z z i
Suy ra
4 0
z i
hoặc
4 4 .
z i z
Nếu
4 0
z i
thì
4
z i
:
2
2
4 16
2 2 8 16
z i
z z i
thỏa mãn.
Nếu
4 4
z i z
thì đặt
z x yi
với
,x y
ta được
2 2 2 2
2
2 2
0 2 2
( 4) ( 4)
0 2 2.
2 4
4
x y
y y y
x y x y
x x x
y y
x y y
Vậy có
4
số phức thỏa mãn là
0
,
2 2
i
,
2 2
i
,
4
i
.
Câu 49. Trong không gian
Oxyz
, cho mặt cầu
S
tâm
1;3;9
I
bán kính bằng
3
. Gọi
M
,
N
là hai điểm
lần lượt thuộc hai trục
Ox
,
Oz
sao cho đường thẳng
MN
tiếp xúc với
S
, đồng thời mặt cầu
ngoại tiếp tứ diện
OIMN
có bán kính bằng
13
2
. Gọi
A
là tiếp điểm của
MN
và
S
, giá trị
AM AN
bằng
A.
39
. B.
12 3
. C.
18
. D.
28 3
.
Lời giải
Chọn B
Ta có
1;3;9
I và
3
R
. Suy ra
d , 3
I OMN
.
Vậy mặt cầu
S
tiếp xúc
OMN
tại
1;0;9
A
.
Gọi tọa độ
;0;0
M m
và
0;0;
N n
.
Ta có
1;0; 9
AM m
;
1;0; 9
AN n
.
Trang 21/22 - WordToan
Do
, ,
A M N
thẳng hàng nên
1 9 9 1
m n
.
Do
IA OMN
và
H
là trung điểm
MN
thì
H
là tâm đường tròn ngoại tiếp
OMN
.
Suy ra
K
là tâm mặt cầu ngoại tiếp
IOMN
KH IMN
bán kính đường tròn ngoại tiếp
IMN
bằng
13
2
(đường tròn lớn)
2 2
1 . .
. . . 39 1 90 9 10 39 2
13
2
4.
2
IM IN MN
IH MN IM IN m n .
Từ (1) và (2) suy ra
2 2
1 9 9
1 90 9 10 39
m n
m n
.
Đặt
2
2
1
9
u m
v n
, ta có hệ phương trình
2 2
81
81
90 10 1521
1 90 9 10 39
81 27
90 10 540 3
uv
uv
u vm n
uv u
v u v
Vậy
. 81 1 12 3
AM AN u v
.
Câu 50. Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 2
2 64
y x mx x
có đúng ba
điểm cực trị
A.
5
. B.
6
. C.
12
. D.
11
.
Lời giải
Chọn C
Xét hàm số
4 2
2 64
y x mx x
.
Ta có:
3
4 4 64
y x mx
.
*
Phương trình hoành độ giao điểm:
4 2
3
0
2 64 0
2 64 0 1
x
x mx x
x mx
Phương trình
1
luôn có một nghiệm
0
x
nên đồ thị hàm số
4 2
2 64
y x mx x
cắt
Ox
ít nhất
hai điểm và
4 2
lim 2 64
x
x mx x


.
Suy ra để hàm số
4 2
2 64
y x mx x
có
3
điểm cực trị thì hàm số
4 2
2 64
y x mx x
có đúng
một điểm cực trị
phương trình
*
có đúng một nghiệm đơn
2
16
m x
x
có đúng một nghiệm đơn.
Xét hàm số:
2
16
f x x
x
,
2
16
2f x x
x
.
2
16
0 2 0 2
f x x x
x
.
Bảng biến thiên:
Trang 22/22 – Diễn đàn giáo viên Toán
Từ bảng biến thiên suy ra
12m
.
Suy ra:
*
1;2;3;...;11;12
12
m
m
m
.
Vậy có
12
giá trị nguyên dương của tham số
m
để hàm số
4 2
2 64y x mx x
có đúng ba điểm
cực trị .
------------ Hết -------------
NHÓM WORD
&
BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 1
ĐỀ THI TN THPT MÔN TOÁN NĂM 2022
Mã đề 102
Môn: TOÁN – LỚP 12
Thời gian: 90 phút (Không kể thời gian phát đề)
TRAO ĐỔI & CHIA SẺ
KIẾN THỨC
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan
Câu 1. Cho hàm số
2
x
f x e x
. Khẳng định nào dưới đây đúng?
A.
2
2
x
f x dx e x C
. B.
2x
f x dx e x C
.
C.
x
f x dx e C
. D.
2x
f x dx e x C
.
Câu 2. Đạo hàm của hàm số
3
y x
là
A.
4
y x
. B.
4
3y x
. C.
4
1
3
y x
. D.
2
1
2
y x
.
Câu 3. Hàm số nào dưới đây có bảng biến thiên như sau?
A.
3
3y x x . B.
3
3y x x .
C.
4 2
2y x x . D.
4 2
2y x x .
Câu 4. Trong không gian
Oxyz
, phương trình mặt phẳng
Oyz
là
A.
0x
. B.
0x y z
. C.
0z
. D.
0y
.
Câu 5. Tiệm cận ngang của đồ thị hàm số
2 1
2 4
x
y
x
là đường thẳng có phương trình
A.
2 y
. B.
2 x
. C.
1x
. D.
1y
.
Câu 6. Cho hàm số
( )y f x
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
0;
. B.
1;
. C.
1;0
. D.
0;1
.
NĂM HỌC: 2021-2022 NHÓM WORD & BIÊN SOẠN TOÁN THPT
Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 7. Cho hàm số
y f x
có bảng biến thiên như sau
Điểm cực tiểu của hàm số đã cho là
A.
2
x
. B.
1
x
. C.
1
x
. D.
2
x
.
Câu 8. Trên mặt phẳng tọa độ, điểm biểu diễn số phức
2 7
z i
có tọa độ là
A.
2;7
. B.
2; 7
. C.
2;7
. D.
7;2
.
Câu 9. Cho cấp số nhân
n
u
với
1
1
u
và
2
2.
u
Công bội của cấp số nhân đã cho là
A.
1
2
. B.
2
. C.
2
. D.
1
2
.
Câu 10. Cho 2 số phức
1
2 3
z i
và
2
1 .
z i
Số phức
1 2
z z
bằng
A.
3 4 .
i
B.
1 4 .
i
C.
5 .
z i
D.
3 2 .
i
Câu 11. Với
a
là số thực dương tùy ý,
4log
a
bằng
A.
4 log
a
. B.
8log
a
. C.
2log
a
. D.
2 log
a
.
Câu 12. Cho
d cos
f x x x C
. Khẳng định nào dưới đây đúng?
A.
sin
f x x
. B.
cos
f x x
. C.
sin
f x x
. D.
cos
f x x
.
Câu 13. Cho hình trụ có chiều cao
1
h
và bán kính đáy
2
r
. Diện tích xung quanh của hình trụ đã cho
bằng
A.
3
. B.
4
. C.
2
. D.
6
.
Câu 14. Cho khối chóp .
S ABC
có chiều cao bằng
3
, đáy
ABC
có diện tích bằng
10
. Thể tích khối chóp
.
S ABC
bằng
A.
15
. B.
10
. C.
2
. D.
30
.
Câu 15. Mô đun của số phức
3 4
z i
bằng
A.
7
B.
5
. C.
7
. D.
25
.
Câu 16. Nghiệm của phương trình
2 1 2
3 3
x x
là
A.
1
3
x
. B.
0
x . C.
1
x . D.
1
x
.
Câu 17. Cho hàm số
4 2
f x ax bx c
có đồ thị là đường cong trong hình vẽ sau
Số nghiệm thực của phương trình
1
f x
là
A.
4
. B.
3
. C.
2
. D.
1
.
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 3
Câu 18. Tập nghiệm của bất phương trình
5
log 1 2
x
là
A.
24;
. B.
9;
. C.
25;
. D.
31;
.
Câu 19. Nếu
2
0
d 4
f x x
thì
2
0
1
2 d
2
f x x
bằng
A.
2
. B.
6
. C.
4
. D.
8
.
Câu 20. Tập xác định của hàm số
3
log 4
y x
là.
A.
;4

. B.
4;

. C.
5;

. D.
;
 
.
Câu 21. Cho hàm số
4 2
y ax bx c
có đồ thị như đường cong trong hình bên.
Số điểm cực trị của hàm số đã cho là
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 22. Số các tổ hợp chập 3 của 12 phần tử là
A.
1728
. B.
220
. C.
1320
. D.
36
.
Câu 23. Trong không gian
Oxyz
, cho điểm
1;2; 3
A
. Hình chiếu vuông góc của
A
lên mặt phẳng
Oxy
có tọa độ là
A.
1;0; 3
. B.
1;0;0
. C.
1;2;0
. D.
0;2; 3
.
Câu 24. Trong không gian
Oxyz
, cho mặt cầu
2 2
2
: 2 1 6
S x y z
. Đường kính của
S
bằng
A.
3
. B.
6
. C.
2 6
. D.
12
.
Câu 25. Cho tam giác
OIM
vuông tại
I
có
3
OI
và
4
IM
. Khi quay tam giác
OIM
quanh cạnh góc
vuông
OI
thì đường gấp khúc
OMI
tạo thành hình nón có độ dài đường sinh bằng
A.
4
. B.
3
. C.
5
. D.
7
.
Câu 26. Cho khối lăng trụ có diện tích đáy
2
3
a
và chiều cao
2
a
. Thể tích khối lăng trụ đã cho bằng
A.
3
3
a
. B.
3
6
a
. C.
3
2
a
. D.
3
a
.
Câu 27. Trong không gian
,
Oxyz
cho đường thẳng
2
: 1 2
1 3
x t
d y t
z t
. Vectơ nào dưới đây là một véctơ chỉ
phương của
d
?
A.
4
2;1;1
u
. B.
1
2;1; 1
u
.
C.
3
1; 2; 3
u
. D.
3
1; 2; 3
u
.
Câu 28. Nếu
5
1
d 3
f x x
thì
1
5
d
f x x
bằng
A.
3
. B.
4
. C.
6
. D.
5
.
Câu 29. Cho hình hộp chữ nhật
. ' ' ' '
ABCD A B C D
có
AB a
,
2
BC a
và
' 3
AA a
(tham khảo hình
bên). Khoảng cách giữa hai đường thẳng
BD
và
' '
A C
bằng
NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT
Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA
A.
2a
. B.
2a
. C.
3a
. D.
a
.
Câu 30. Hàm số nào dưới đây đồng biến trên
?
A.
4 2
y x x
. B.
3
y x x . C.
1
2
x
y
x
. D.
3
y x x
.
Câu 31. Giá trị trị lớn nhất của hàm số
3 2
3 9 10f x x x x
trên đoạn
2;2
bằng
A.
15
. B.
10
. C.
1
. D.
12
.
Câu 32. Trong không gian
Oxyz
, cho ba điểm
1;2; 1A
,
3;0;1B
và
2;2; 2C
. Đường thẳng đi qua
A
và vuông góc với mặt phẳng
ABC
có phương trình là
A.
1 2 1
1 2 1
x y z
. B.
1 2 1
1 2 3
x y z
.
C.
1 2 1
1 2 1
x y z
. D.
1 2 1
1 2 1
x y z
.
Câu 33. Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn
40;60
. Xác suất để chọn được
số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
A.
2
5
. B.
4
7
. C.
3
7
. D.
3
5
.
Câu 34. Trong không gian
Oxyz
, cho ba điểm
1;2; 1A
,
3;0;1B
,
2;2; 2C
. Đường thẳng đi qua
A
và vuông góc với mặt phẳng
ABC
có phương trình là:
A.
1 2 1
1 2 1
x y z
. B.
1 2 1
1 2 3
x y z
.
C.
1 2 1
1 2 1
x y z
. D.
1 2 1
1 2 1
x y z
.
Câu 35. Gọi
1 2
,z z là hai nghiệm phức của phương trình
2
6 0z z
. Khi đó
1 2 1 2
.z z z z bằng
A.
5
. B.
7
. C.
7
. D.
5
.
Câu 36. Cho hàm số
2
1
1
cos 2
f x
x
. Khẳng định nào dưới đay đúng?
A.
1
d cos 2
2
f x x x x C
. B.
d tan 2f x x x x C
.
C.
1
d tan 2
2
f x x x x C
. D.
1
d tan 2
2
f x x x x C
.
Câu 37. Có bao nhiêu số nguyên thuộc tập xác định của hàm số
log 6 2y x x
?
A.
7
. B.
8
. C. Vô số. D.
9
.
Câu 38. Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông tại
B
,
2, 3AC AB
và
1AA
(tham khảo hình bên dưới).
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 5
Góc giữa hai mặt phẳng
ABC
và
ABC
bằng
A.
90
. B.
60
. C.
30
. D.
45
.
Câu 39. Cho hàm số
4 2
( ) 2( 1)
f x mx m x
với
m
là tham số thực. Nếu
[0;2]
min ( ) (1)
f x f
thì
[0;2]
max ( )
f x
bằng
A.
2
. B.
1
. C.
4
. D.
0
.
Câu 40. Có bao nhiêu số nguyên dương
a
sao cho ứng với mỗi
a
có đúng hai số nguyên
b
thỏa mãn
5 1 .2 5 0
b b
a
?
A.
20
. B.
21
. C.
22
. D.
19
.
Câu 41. Biết
F x
và
G x
là hai nguyên hàm của hàm số
f x
trên
và
5
0
d 5 0 , 0
f x x F G a a
. Gọi
S
là diện tích hình phẳng giới hạn bỡi các đường
y F x
,
y G x
,
0
x
và
5
x
. Khi
20
S
thì
a
bằng?
A.
4
. B.
15
. C.
25
. D.
20
.
Câu 42. Cho khối lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
,
AB a
. Góc
giữa đường thẳng
BC
và mặt phẳng
ACC A
bằng
30
. Thể tích của khối lăng trụ đã cho
bằng
A.
3
1
8
a
. B.
3
3
8
a
. C.
3
3 2
2
a
. D.
3
2
2
a
.
Câu 43. Cho hình nón có góc ở đỉnh bằng
120
và chiều cao bằng
1
. Gọi
S
là mặt cầu đi qua đỉnh và
chứa đường tròn đáy của hình nón đã cho. Diện tích của
S
bằng
A.
. B.
. C.
4
. D.
48
Câu 44. Xét các số thực
,
x y
sao cho
2
2
7
4 log
9
49
x a
y
a
với mọi số thực dương
a
. Giá trị lớn nhất của biểu
thức
2 2
4 3
P x y x y
bằng:
A.
121
4
. B.
39
4
. C.
24
. D.
39
.
Câu 45. Cho các số phức
1 2 3
, ,
z z z
thỏa mãn
1 2 3
2 2
z z z
và
1 2 3 1 2
3 4
z z z z z
. Gọi
, ,
A B C
lần lượt là các điểm biểu diễn của
1 2 3
, ,
z z z
trên mặt phẳng tọa độ. Diện tích tam giác
ABC
bằng
A.
7
4
. B.
3 7
4
. C.
7
2
. D.
3 7
2
.
Câu 46. Có bao nhiêu số phức
z
thỏa mãn
2
z z z
và
2
2 2 2 ?
z z i z i
A.
4
. B.
2
. C.
3
. D.
1
.
NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT
Trang 6 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 47. Trong không gian
Oxyz
, cho điểm
2;1; 1A
. Gọi
P
là mặt phẳng chứa trục
Oy
sao cho
khoảng cách từ
A
đến
P
là lớn nhất. Phương trình của
P
là:
A.
2 0x z
. B.
2 0x z
. C.
0x z
. D.
0x z
.
Câu 48. Cho hàm số bậc bốn
y f x
. Biết rằng hàm số
lng x f x
có bảng biến thiên như sau:
Diện tích hình phẳng giới hạn bởi các đường
y f x
và
y g x
thuộc khoảng nào dưới
đây?
A.
38;39
. B.
25;26
. C.
28;29
. D.
35;36
.
Câu 49. Trong không gian
Oxyz
, cho mặt cầu
S
tâm
4;1;2I
bán kính bằng
2
. Gọi
M
;
N
là hai
điểm lần lượt thuộc hai trục
Ox
;
Oy
sao cho đường thẳng
MN
tiếp xúc với
S
, đồng thời mặt
cầu ngoại tiếp tứ diện
OIMN
có bán kính bằng
7
2
. Gọi
A
là tiếp điểm của
MN
và
S
, giá trị
.AM AN
bằng
A.
6 2
. B.
14
. C.
8
. D.
9 2
.
Câu 50. Có bao nhiêu giá trị nguyên âm của tham số
a
để hàm số
4 2
2 8y x ax x
có đúng ba điểm
cực trị?
A.
2
. B.
6
. C.
5
. D.
3
.
NHÓM WORD
&
BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 7
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
B B
A
D
D
B
B
B
D
C
C
B
B
B
A
C
A
B
B
D
B C
C
C
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
B
C
A
C
B
A
C
B
C
D
D
A
D
C
B
A
D
A
C
A
A
A
D
A
D
Câu 1. Cho hàm số
2
x
f x e x
. Khẳng định nào dưới đây đúng?
A.
2
2
x
f x dx e x C
. B.
2x
f x dx e x C
.
C.
x
f x dx e C
. D.
2x
f x dx e x C
.
Lời giải
GVSB: Trần Thành Thống/ ; GVPB1: Bùi Hà; GVPB2:
Chọn D
Ta có
2x
f x dx e x C
.
Câu 2. Đạo hàm của hàm số
3
y x
là
A.
4
y x
. B.
4
3y x
. C.
4
1
3
y x
. D.
2
1
2
y x
.
Lời giải
GVSB: Trần Thành Thống; GVPB1: Bùi Hà; GVPB2:
Chọn B
Ta có
4
3y x
.
Câu 3. Hàm số nào dưới đây có bảng biến thiên như sau?
A.
3
3y x x . B.
3
3y x x . C.
4 2
2y x x . D.
4 2
2y x x .
Lời giải
GVSB: Trần Quang Nam; GVPB1: Bùi Hà; GVPB2:
Chọn B
Từ đồ thị ta có đây là đồ thị hàm số bậc
3
với hệ số
0a
.
Câu 4. Trong không gian
Oxyz
, phương trình mặt phẳng
Oyz
là
A.
0x
. B.
0x y z
. C.
0z
. D.
0y
.
Lời giải
GVSB: Trần Quang Nam; GVPB1: Bùi Hà; GVPB2:
Chọn A
Ta có một véc tơ pháp tuyến của mặt phẳng
Oyz
là:
1; 0 ; 0 .n
Mặt phẳng đi qua gốc tọa độ
0 ; 0 ; 0 .O
Phương trình mặt phẳng
Oyz
là:
1 0 0 0 0 0 0x y z
hay
0x
.
NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT
Trang 8 TÀI LIỆU ÔN THI THPT QUỐC GIA
Ta chọn đáp án#A.
Câu 5. Tiệm cận ngang của đồ thị hàm số
2 1
2 4
x
y
x
là đường thẳng có phương trình
A.
2 y
. B.
2 x
. C.
1x
. D.
1y
.
Lời giải
GVSB: Vũ Dự; GVPB1: Bùi Hà; GVPB2: Kim Dung
Chọn D
Ta có
2 1
lim lim 1
2 4
 
x x
x
y
x
và
2 1
lim lim 1
2 4
 
x x
x
y
x
.
Vậy đồ thị hàm số có tiệm cận ngang là đường thẳng có phương trình
1y
.
Câu 6. Cho hàm số
( )y f x
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
0;
. B.
1;
. C.
1;0
. D.
0;1
.
Lời giải
GVSB: Vũ Dự; GVPB1: Bùi Hà; GVPB2: Kim Dung
Chọn D
Câu 7. Cho hàm số
y f x
có bảng biến thiên như sau
Điểm cực tiểu của hàm số đã cho là
A.
2x
. B.
1x
. C.
1x
. D.
2x
.
Lời giải
GVSB: Nguyễn Thị Nhung; GVPB1:...; GVPB2:…
Chọn B
Từ bảng biến thiên suy ra điểm cực tiểu của hàm số đã cho là
1x
.
Câu 8. Trên mặt phẳng tọa độ, điểm biểu diễn số phức
2 7z i
có tọa độ là
A.
2;7
. B.
2; 7
. C.
2;7
. D.
7;2
.
Lời giải
GVSB: Nguyễn Thị Nhung; GVPB1:...; GVPB2:…
Chọn B
Điểm biểu diễn số phức
2 7z i
có tọa độ là
2; 7
Câu 9. Cho cấp số nhân
n
u
với
1
1u và
2
2.u Công bội của cấp số nhân đã cho là
A.
1
2
. B.
2
. C.
2
. D.
1
2
.
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 9
Lời giải
GVSB: Lê Mẫn ; GVPB1: Tuyet Trinh; GVPB2: Thuy Nguyen
Chọn B
Công bội của cấp số nhân là
2
1
2
2.
1
u
q
u
Câu 10. Cho 2 số phức
1
2 3
z i
và
2
1 .
z i
Số phức
1 2
z z
bằng
A.
3 4 .
i
B.
1 4 .
i
C.
5 .
z i
D.
3 2 .
i
Lời giải
GVSB: Lê Mẫn ; GVPB1: Tuyet Trinh; GVPB2: Thuy Nguyen
Chọn D
Ta có:
1 2
2 3 1 3 2 .
z z i i i
Câu 11. Với
a
là số thực dương tùy ý,
4log
a
bằng
A.
4log
a
. B.
8log
a
. C.
2log
a
. D.
2log
a
.
Lời giải
GVSB: Thảo Nguyễn; GVPB1: Tuyet Trinh; GVPB2: Kim Dung
Chọn C
Ta có:
1
2
4log 4log 2log
a a a
.
Câu 12. Cho
d cos
f x x x C
. Khẳng định nào dưới đây đúng?
A.
sin
f x x
. B.
cos
f x x
. C.
sin
f x x
. D.
cos
f x x
.
Lời giải
GVSB: Dương Quá; GVPB1: Tuyet Trinh; GVPB2: Kim Dung
Chọn C
Ta có:
cos sin
f x x C x
.
Câu 13. Cho hình trụ có chiều cao
1
h
và bán kính đáy
2
r
. Diện tích xung quanh của hình trụ đã cho
bằng
A.
3
. B.
4
. C.
2
. D.
6
.
Lời giải
GVSB:Nguyễn Thị Thu ; GVPB1:Thuy Nguyen ; GVPB2:
Chọn B
Diện tích xung quanh
2 4
xq
S rl
.
Câu 14. Cho khối chóp .
S ABC
có chiều cao bằng
3
, đáy
ABC
có diện tích bằng
10
. Thể tích khối chóp
.
S ABC
bằng
A.
15
. B.
10
. C.
2
. D.
30
.
Lời giải
GVSB:Nguyễn Thị Thu ; GVPB1:Thuy Nguyen ; GVPB2:
Chọn B
.
1 1
3.10 10
3 3
S ABC
V hB
.
Câu 15. Mô đun của số phức
3 4
z i
bằng
A.
7
B.
5
. C.
7
. D.
25
.
Lời giải
GVSB: Chau Nguyen Minh; GVPB1:Thuy Nguyen ; GVPB2:
Chọn B
NĂM HỌC: 2021-2022 NHÓM WORD & BIÊN SOẠN TOÁN THPT
Trang 10 TÀI LIỆU ÔN THI THPT QUỐC GIA
Ta có
2 2
3 4 5.
z
Câu 16. Nghiệm của phương trình
2 1 2
3 3
x x
là
A.
1
3
x
. B.
0
x . C.
1
x . D.
1
x
.
Lời giải
GVSB: Chau Nguyen Minh; GVPB1:Thuy Nguyen ; GVPB2:
Chọn A
Ta có
2 1 2
3 3
2 1 2
3 1
1
3
x x
x x
x
x
Câu 17. Cho hàm số
4 2
f x ax bx c
có đồ thị là đường cong trong hình vẽ sau
Số nghiệm thực của phương trình
1
f x
là
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
GVSB: Lưu Anh Bảo; GVPB1:Thuy Nguyen ; GVPB2:
Chọn C
Số nghiệm thực của phương trình
1
f x
bằng với số giao điểm của đường thẳng
: 1
d y
và đồ thị
C
của hàm số
y f x
. Dựa vào hình vẽ, ta thấy
d
và
C
cắt nhau tại hai điểm
phân biệt nên phương trình đã cho có hai nghiệm thực phân biệt.
Câu 18. Tập nghiệm của bất phương trình
5
log 1 2
x
là
A.
24;
. B.
9;
. C.
25;
. D.
31;
.
Lời giải
GVSB: Lưu Anh Bảo; GVPB1:Thuy Nguyen ; GVPB2:
Chọn A
Ta có
5
log 1 2
x
2
1 5
x
24
x
.
Vậy tập hợp nghiệm của bất phương trình là
24;S
.
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 11
Câu 19. Nếu
2
0
d 4
f x x
thì
2
0
1
2 d
2
f x x
bằng
A.
2
. B.
6
. C.
4
. D.
8
.
Lời giải
GVSB: Hồng Hà Nguyễn ; GVPB1: Vu Khien; GVPB2:
Chọn B
2 2 2
0 0 0
1 1
2 d d 2d 2 4 6
2 2
f x x f x x x
.
Câu 20. Tập xác định của hàm số
3
log 4
y x
là.
A.
;4

. B.
4;

. C.
5;

. D.
;
 
.
Lời giải
GVSB: Hồng Hà Nguyễn ; GVPB1: Vu Khien; GVPB2:
Chọn B
ĐKXĐ
4 0 4
x x
.
Vậy tập xác định của hàm số
3
log 4
y x
là
4;

.
Câu 21. Cho hàm số
4 2
y ax bx c
có đồ thị như đường cong trong hình bên.
Số điểm cực trị của hàm số đã cho là
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
GVSB: Tuoi Nguyenthihong; GVPB1:Vũ Khiên; GVPB2:
Chọn D
Dựa vào đố thị hàm số suy ra hàm số có 3 điểm cực trị.
Câu 22. Số các tổ hợp chập 3 của 12 phần tử là
A.
1728
. B.
220
. C.
1320
. D.
36
.
Lời giải
GVSB: Tuoi Nguyenthihong; GVPB1:Vũ Khiên; GVPB2:
Chọn B
Số các tổ hợp chập 3 của 12 phần tử là
3
12
220
C
.
Câu 23. Trong không gian
Oxyz
, cho điểm
1;2; 3
A
. Hình chiếu vuông góc của
A
lên mặt phẳng
Oxy
có tọa độ là
A.
1;0; 3
. B.
1;0;0
. C.
1;2;0
. D.
0;2; 3
.
Lời giải
GVSB: Đức Huy; GVPB1: Vũ Khiên; GVPB2: Kim Dung
Chọn C
Hình chiếu vuông góc của
1;2; 3
A
lên mặt phẳng
Oxy
có tọa độ là
1;2;0
.
Câu 24. Trong không gian
Oxyz
, cho mặt cầu
2 2
2
: 2 1 6
S x y z
. Đường kính của
S
bằng
A.
3
. B.
6
. C.
2 6
. D.
12
.
NĂM HỌC: 2021-2022 NHÓM WORD & BIÊN SOẠN TOÁN THPT
Trang 12 TÀI LIỆU ÔN THI THPT QUỐC GIA
Lời giải
GVSB: Đức Huy; GVPB1: Vũ Khiên; GVPB2: Kim Dung
Chọn C
Đường kính của
S
bằng
2 2 6
R
.
Câu 25. Cho tam giác
OIM
vuông tại
I
có
3
OI
và
4
IM
. Khi quay tam giác
OIM
quanh cạnh góc
vuông
OI
thì đường gấp khúc
OMI
tạo thành hình nón có độ dài đường sinh bằng
A.
4
. B.
3
. C.
5
. D.
7
.
Lời giải
GVSB: Nguyễn Anh Tuấn; GVPB1: Linh Nguyen; GVPB2:
Chọn C
Ta có chiều cao hình nón
3
h OI
, bán kính đáy
4
r IM
thì độ dài đường sinh
2 2 2 2
3 4 5
l OM IM OI
.
Câu 26. Cho khối lăng trụ có diện tích đáy
2
3
a
và chiều cao
2
a
. Thể tích khối lăng trụ đã cho bằng
A.
3
3
a
. B.
3
6
a
. C.
3
2
a
. D.
3
a
.
Lời giải
GVSB: Nguyễn Anh Tuấn; GVPB1: Linh Nguyen; GVPB2:
Chọn B
Ta có thể tích khối lăng trụ bằng
2 3
. 3 .2 6
V B h a a a
.
Câu 27. Trong không gian
,
Oxyz
cho đường thẳng
2
: 1 2
1 3
x t
d y t
z t
. Vectơ nào dưới đây là một véctơ chỉ
phương của
d
?
A.
4
2;1;1
u
. B.
1
2;1; 1
u
. C.
3
1; 2; 3
u
. D.
3
1; 2; 3
u
.
Lời giải
GVSB: Dương Chiến; GVPB1: Linh Nguyen; GVPB2:
Chọn C
Một véctơ chỉ phương của đường thẳng
d
là
3
1; 2; 3
u
.
Câu 28. Nếu
5
1
d 3
f x x
thì
1
5
d
f x x
bằng
A.
3
. B.
4
. C.
6
. D.
5
.
Lời giải
GVSB: Dương Chiến; GVPB1: Linh Nguyen; GVPB2:
Chọn A
1 5
5 1
d d 3
f x x f x x
.
Câu 29. Cho hình hộp chữ nhật
. ' ' ' '
ABCD A B C D
có
AB a
,
2
BC a
và
' 3
AA a
(tham khảo hình
bên). Khoảng cách giữa hai đường thẳng
BD
và
' '
A C
bằng
r
h
l
M
O
I
NHÓM WORD
&
BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 13
A.
2a
. B.
2a
. C.
3a
. D.
a
.
Lời giải
GVSB: Tai Pham Anh; GVPB:Hồ Đức Bân; GVPB2: Nguyễn Thị Nhung
Chọn C
, ' ' , ' ' ' ' , ' ' ' ' ' 3d BD A C d BD A B C D d B A B C D BB a
.
Câu 30. Hàm số nào dưới đây đồng biến trên
?
A.
4 2
y x x
. B.
3
y x x . C.
1
2
x
y
x
. D.
3
y x x
.
Lời giải
GVSB: Tai Pham Anh; GVPB: Hồ Đức Bân; GVPB2: Nguyễn Thị Nhung
Chọn B
Hàm số
3
y x x
2
' 3 1 0,y x x
. Do đó hàm số đồng biến trên
.
Câu 31. Giá trị trị lớn nhất của hàm số
3 2
3 9 10f x x x x
trên đoạn
2;2
bằng
A.
15
. B.
10
. C.
1
. D.
12
.
Lời giải
GVSB: Nguyễn Đức Tài; GVPB1: Hồ Đức Bân; GVPB2: Kim Dung
Chọn A
Ta có
2
3 6 9f x x x
.
0f x
1
3
x
x
lo¹ i
Do đó
2 8f
,
1 15f
,
2 12f
.
Vậy
2;2
max 1 15f x f
.
Câu 32. Trong không gian
Oxyz
, cho ba điểm
1;2; 1A
,
3;0;1B
và
2;2; 2C
. Đường thẳng đi qua
A
và vuông góc với mặt phẳng
ABC
có phương trình là
A.
1 2 1
1 2 1
x y z
. B.
1 2 1
1 2 3
x y z
.
C.
1 2 1
1 2 1
x y z
. D.
1 2 1
1 2 1
x y z
.
Lời giải
GVSB: Nguyễn Đức Tài; GVPB1: Hồ Đức Bân; GVPB2: Kim Dung
Chọn C
Gọi
là đường thẳng cần tìm.
Ta có
; 2;4;2AB AC
NĂM HỌC: 2021-2022 NHÓM WORD & BIÊN SOẠN TOÁN THPT
Trang 14 TÀI LIỆU ÔN THI THPT QUỐC GIA
Đường thẳng
đi qua
1;2; 1
A
và có VTCP
1;2;1
u n
có phương trình
1 2 1
1 2 1
x y z
.
Câu 33. Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn
40;60
. Xác suất để chọn được
số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
A.
2
5
. B.
4
7
. C.
3
7
. D.
3
5
.
Lời giải
GVSB: Hoàng Văn Quảng; GVPB1: Cham Tran ; GVPB2:
Chọn B
Số cách chọn 1 số thuộc đoạn
40;60
có
21
cách chọn.
Số có chữ số hàng đơn vị lớn hơn chữ số hàng chục:
Đoạn
40;49
gồm
45;46;...49
có 5 số.
Đoạn
50;59
gồm
56;57;...59
có 4 số.
Đoạn
60;69
gồm
67;68;69
có 3 số.
Vậy có
3 4 5 12
số.
Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục là
12 4
21 7
P
.
Câu 34. Trong không gian
Oxyz
, cho ba điểm
1;2; 1
A
,
3;0;1
B
,
2;2; 2
C
. Đường thẳng đi qua
A
và vuông góc với mặt phẳng
ABC
có phương trình là:
A.
1 2 1
1 2 1
x y z
. B.
1 2 1
1 2 3
x y z
.
C.
1 2 1
1 2 1
x y z
. D.
1 2 1
1 2 1
x y z
.
Lời giải
GVSB: Hoàng Văn Quảng; GVPB1: Cham Tran; GVPB2:
Chọn C
2; 2;2
AB
,
1;0; 1
AC
.
, 2;4;2 2 1;2;1
AB AC
Vì đường thẳng cần tìm vuông góc với mặt phẳng
ABC
nên đường thẳng cần tìm có véctơ chỉ
phương là
1;2;1
u
và đi qua
1;2; 1
A
. Suy ra phương trình đường thẳng cần tìm là:
1 2 1
1 2 1
x y z
.
Câu 35. Gọi
1 2
,
z z
là hai nghiệm phức của phương trình
2
6 0
z z
. Khi đó
1 2 1 2
.
z z z z
bằng
A.
5
. B.
7
. C.
7
. D.
5
.
Lời giải
GVSB: Trần Thị Vân; GVPB1: Cham Tran; GVPB2:
Chọn D
1 2 1 2 1 2 1 2
1 6
. . 5
1 1
z z z z z z z z
(áp dụng định lý Vi-et).
Câu 36. Cho hàm số
2
1
1
cos 2
f x
x
. Khẳng định nào dưới đay đúng?
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 15
A.
1
d cos 2
2
f x x x x C
. B.
d tan 2
f x x x x C
.
C.
1
d tan 2
2
f x x x x C
. D.
1
d tan 2
2
f x x x x C
.
Lời giải
GVSB: Trần Thị Vân; GVPB1: Bích Vân Bùi Thị; GVPB2: Minh Bùi
Chọn D
2
1 1
d 1 d tan 2
cos 2 2
f x x x x x C
x
.
Câu 37. Có bao nhiêu số nguyên thuộc tập xác định của hàm số
log 6 2
y x x
?
A.
7
. B.
8
. C. Vô số. D.
9
.
Lời giải
GVSB:Phương Lan; GVPB1:Bích Vân Bùi Thị; GVPB2:
Chọn A
ĐKXĐ:
6 2 0 2 6
x x x
.
Mà
1;0;1;2;3;4;5
x x
Vậy có 7 số nguyên thuộc tập xác định của hàm số
log 6 2
y x x
.
Câu 38. Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
B
,
2, 3
AC AB
và
1
AA
(tham khảo hình bên dưới).
Góc giữa hai mặt phẳng
ABC
và
ABC
bằng
A.
90
. B.
60
. C.
30
. D.
45
.
Lời giải
GVSB: Lê Huỳnh Cùng; GVPB1: Minh Bùi; GVPB2:
Chọn D
NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT
Trang 16 TÀI LIỆU ÔN THI THPT QUỐC GIA
Ta có
AB CC CC ABC
AB BC
AB C CB
AB C B
.
C AB ABC AB
C B AB
CB AB
; ;C AB ABC C B BC C BC
.
ABC
vuông tại
B
nên
2
2 2 2
2 3 1BC AC AB
.
Trong tam giác vuông C BC
,
1
tan 1
1
C C
C BC
BC
.
Do đó
45C BC
. Vậy
; 45C AB ABC
.
Câu 39. Cho hàm số
4 2
( ) 2( 1)f x mx m x với
m
là tham số thực. Nếu
[0;2]
min ( ) (1)f x f
thì
[0;2]
max ( )f x
bằng
A.
2
. B.
1
. C.
4
. D.
0
.
GVSB: Đào Văn Tiến/ Văn Thắng Đình; GVPB1:…; GVPB2:…
Lời giải
Chọn C
3
( ) 4 4( 1)f x mx m x
.
Do
f x
là hàm đa thức và
[0;2]
1
min ( ) (1) 1 0 4 4 1 0
2
f x f f m m m
.
Thay
1
2
m
vào hàm số ban đầu ta được
4 2 4 2 3
1 1 1
2 1 2 2 2 1 1
2 2 2
y x x x x y x x x x x
.
Ta có BBT:
Vậy với
1
2
m
, thì
[0;2]
min ( ) (1)f x f TM
.
Dựa vào BBT ta có
[0;2]
max ( ) (2) 4f x f
.
Câu 40. Có bao nhiêu số nguyên dương
a
sao cho ứng với mỗi
a
có đúng hai số nguyên
b
thỏa mãn
5 1 .2 5 0
b b
a
?
A.
20
. B.
21
. C.
22
. D.
19
.
Lời giải
GVSB: Tô Lê Diễm Hằng/ Đinh Văn Thư ; GVPB1:…; GVPB2:Doãn Hoàng Anh
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 17
Chọn B
2
0
5 1 0
5 1 .2 5 0
5
log
.2 5 0
b
b b
b
b
a
b
a
a
.
TH1:
2
5
log 0
5
0
a
a
a
.
Vì hàm số
1
x
y a a
là hàm đồng biến nên
2
5
5 1 .2 5 0 log 0
b b
a b
a
.
Yêu cầu của bài toán suy ra
*
2
40
5 1 5 1
3 log 2 21,22,....40
20
8 4
a
a
a
a
a a
.
TH1:
2
5
log 0
0 5
0
a
a
a
Vì hàm số
1
x
y a a
là hàm đồng biến nên
2
5
5 1 .2 5 0 0 log
b b
a b
a
.
Yêu cầu của bài toán suy ra
*
2
5
5 5
4
2 log 3 4 8 1
5
8
a
a
a
a a
a
.
Vậy có 21 số nguyên
a
thỏa mãn yêu cầu của bài toán.
Câu 41. Biết
F x
và
G x
là hai nguyên hàm của hàm số
f x
trên
và
5
0
d 5 0 , 0
f x x F G a a
. Gọi
S
là diện tích hình phẳng giới hạn bỡi các đường
y F x
,
y G x
,
0
x
và
5
x
. Khi
20
S
thì
a
bằng?
A.
4
. B.
15
. C.
25
. D.
20
.
Lời giải
GVSB: Nguyễn Anh Tuấn/ Nguyễn Thị Nhung; GVPB1:…; GVPB2:Doãn Hoàng Anh
Chọn A
Đặt
G x F x C
(
C
là hằng số).
5
0
d 5 0 5 0 5 0
f x x F F F G C F G C
Suy ra
C a
.
5 5 5
0 0 0
d d d 5
S F x G x x a x a x a
.
Theo giả thiết
5 20 4
a a
Câu 42. Cho khối lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
,
AB a
. Góc
giữa đường thẳng
BC
và mặt phẳng
ACC A
bằng
30
. Thể tích của khối lăng trụ đã cho
bằng
A.
3
1
8
a
. B.
3
3
8
a
. C.
3
3 2
2
a
. D.
3
2
2
a
.
NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT
Trang 18 TÀI LIỆU ÔN THI THPT QUỐC GIA
Lời giải
GVSB: Lại Thị Quỳnh/ Dương Thùy; GVPB1: Doãn Hoàng Anh; GVPB2:...
Chọn D
Diện tích đáy:
2
1
.
2 2
ABC
a
S AB AC .
Ta có:
, 30
AB AC
AB ACC A BC ACC A BC A
AB AA
.
Khi đó
2
2 2 2
.cot 30 3 3 2AC AB a AA AC A C a a a
.
Vậy, thể tích khối lăng trụ đã cho là:
2
3
2
. . 2 .
2 2
ABC
a
V S AA a a
.
Câu 43. Cho hình nón có góc ở đỉnh bằng
120
và chiều cao bằng
1
. Gọi
S
là mặt cầu đi qua đỉnh và
chứa đường tròn đáy của hình nón đã cho. Diện tích của
S
bằng
A.
16
. B.
12
. C.
4
. D.
48
Lời giải
GVSB: Đỗ Ngọc Nam/ Phạm Quốc Toàn; GVPB1: Doãn Hoàng Anh; GVPB2: Minhhai Bui
Chọn A
Xét tam giác vuông
SMO
có
tan tan 60 3
1
OM OM
MSO OM
OS
Kẻ đường kính
SS
của mặt cầu ngoại tiếp hình nón.
Tam giác
SMS
vuông tại
M
có
MO SS
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 19
2
2
. 3 1. 3
MO OS OS OS OS
Vậy bán kính mặt cầu ngoại tiếp hình nón là
1 3
2
2 2
OS OS
R
Diện tích
S
là
2 2
4 4 .2 16
S R
.
Câu 44. Xét các số thực
,
x y
sao cho
2
2
7
4 log
9
49
x a
y
a
với mọi số thực dương
a
. Giá trị lớn nhất của biểu
thức
2 2
4 3
P x y x y
bằng:
A.
121
4
. B.
39
4
. C.
24
. D.
39
.
GVSB: Nguyễn Thị Kim Cúc/ Quy Tín; GVPB: Nguyễn Duy Nam
Lời giải
Chọn C
Ta có
2
2
7
4 log
9
49
x a
y
a
2
2
7
4 log
9
7 7
log 49 log
x a
y
a
.
2 2
7 7 7
9 log 49 4 log log
y x a a
2
7 7
2 9 2 2 log log
y x a a
.
1
Đặt
7
log
t a
, khi
0
a
thì
t
,
1
trở thành
2 2
2 . 9 0
t x t y
.
2
1
đúng với mọi
0
a
2
đúng với mọi
t
2 2
9 0
x y
2 2
9
x y
.
Xét
2 2
2 2
4 3 16 9 4 3 225 4 3 15
x y x y x y x y
Suy ra
2 2
4 3 9 15 24
P x y x y
, đẳng thức xảy ra khi
2 2
12 9
;
5 5
4 3
12 9
;
9
5 5
x y
x y
x y
x y
.
Vậy GTLN của
P
bằng
24
.
Câu 45. Cho các số phức
1 2 3
, ,
z z z
thỏa mãn
1 2 3
2 2
z z z
và
1 2 3 1 2
3 4
z z z z z
. Gọi
, ,
A B C
lần lượt là các điểm biểu diễn của
1 2 3
, ,
z z z
trên mặt phẳng tọa độ. Diện tích tam giác
ABC
bằng
A.
7
4
. B.
3 7
4
. C.
7
2
. D.
3 7
2
.
GVSB: Trần Nhung/ Lê Trần Bảo An; GVPB1: Tô Lan ; GVPB2: Thanh bui
Lời giải
Chọn A
Ta có
1 2 3 1 2 1 2 3 1 2 1 2 3 1 2
3 4 3 4 3 4
z z z z z z z z z z z z z z z
1 2
3
z z
.
NĂM HỌC: 2021-2022 NHÓM WORD & BIÊN SOẠN TOÁN THPT
Trang 20 TÀI LIỆU ÔN THI THPT QUỐC GIA
Lấy
D
đối xứng với
B
qua
O
, suy ra
D
biểu diễn
2
z
.
Ta có
1 2
3 3
z z AD
.
ABD
có trung tuyến
1
2
AO BD
nên
ABD
vuông tại
A
2 2
7
AB BD AD .
+
1 2 3 1 2
3 4
z z z z z
1 2 3 2 3
3 4 4
z z z z z
1 2 3 2 3
3 4 4
z z z z z
2 3
3 4 4
z z
3 4 4
OB OC
 
2 2
9 16 24 . .cos 16
OB OC OB OC BOC
3
cos
4
BOC
.
Áp dụng định lí cosin cho
BOC
ta có:
2 2
3
2 . .cos 4 1 4. 2
4
BC OB OC OB OC BOC
.
Tương tự ta tính được
2
AC
.
Vậy
7
4
ABC
S
.
Câu 46. Có bao nhiêu số phức
z
thỏa mãn
2
z z z
và
2
2 2 2 ?
z z i z i
A.
4
. B.
2
. C.
3
. D.
1
.
Lời giải
GVSB: Phạm Văn Bình; GVPB1: Tô Lan ; GVPB2: Thanh bui
Chọn A
Gọi
z a bi
với ;a b
Ta có:
2 2 2
2 *
z z z a b b
Mặt khác
2
2 2 2 **
z z i z i
Vì
2 2
z i z i
nên
2 2
z i z i
.
Nên từ (**)
2 0 2
2 2
z i z i
z z i
.
Với
2 0 2
z i z i
( thoả mãn
*
NHÓM WORD
&
BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 21
Với
2 2
2 2
2 2 2 2z z i a b a b a b
thay vào (*) ta được:
2 2 2
0
0 0
2 1
1 1
1
1 1
z
b a
b b b b b z i
b a
z i
b a
.
Vậy có tất cả 4 số phức thỏa mãn yêu cầu bài toán.
Câu 47. Trong không gian
Oxyz
, cho điểm
2;1; 1A
. Gọi
P
là mặt phẳng chứa trục
Oy
sao cho
khoảng cách từ
A
đến
P
là lớn nhất. Phương trình của
P
là:
A.
2 0x z
. B.
2 0x z
. C.
0x z
. D.
0x z
.
Lời giải
GVSB: Hải Quan/ Hoàng Diệp Phạm; GVPB1: Thanh bui ; GVPB2:
Chọn A
Gọi
H
là hình chiếu vuông góc của điểm
A
lên mặt phẳng
P
,
A
là hình chiếu vuông góc
của điểm
A
lên trục
Oy
suy ra
0;1;0A
. Khi đó khoảng cách từ
A
đến
P
là đoạn thẳng
'AH AA
. Độ dài đoạn thẳng
AH
dài nhất khi
H
và
A
trùng nhau. Khi đó mặt phẳng
P
nhận
2;0; 1A A
làm véc tơ pháp tuyến. Suy ra phương trình mặt phẳng
P
đi qua
0;1;0A
có VTPT:
2;0; 1A A
là:
2 0 0 1 1 0 0 2 0x y z x z
.
Câu 48. Cho hàm số bậc bốn
y f x
. Biết rằng hàm số
lng x f x
có bảng biến thiên như sau:
Diện tích hình phẳng giới hạn bởi các đường
y f x
và
y g x
thuộc khoảng nào dưới
đây?
A.
38;39
. B.
25;26
. C.
28;29
. D.
35;36
.
GVSB: Phí Mạnh Tiến; GVPB1:… ; GVPB2:…
Lời giải
Chọn D
+ Ta có:
f x
g x
f x
.
+ Từ bảng biến thiên ta thấy
0g x
,
x
suy ra
e 1
g x
f x ,
x
.
NĂM HỌC: 2021-2022 NHÓM WORD & BIÊN SOẠN TOÁN THPT
Trang 22 TÀI LIỆU ÔN THI THPT QUỐC GIA
+ Phương trình
f x g x
. . 1 0
g x f x g x g x f x
0
g x
1
2
3
x x
x x
x x
.
+ Diện tích hình phẳng giới hạn bởi các đường
y f x
và
y g x
là
3 32
1 1 2
d d d
x x
x
x x x
f x f x
S f x g x x f x x f x x
f x f x
42 37
10 42
1 1
1 d 1 d
t f x
t t
t t
35,438
35;36
.
Câu 49. Trong không gian
Oxyz
, cho mặt cầu
S
tâm
4;1;2
I
bán kính bằng
2
. Gọi
M
;
N
là hai
điểm lần lượt thuộc hai trục
Ox
;
Oy
sao cho đường thẳng
MN
tiếp xúc với
S
, đồng thời mặt
cầu ngoại tiếp tứ diện
OIMN
có bán kính bằng
7
2
. Gọi
A
là tiếp điểm của
MN
và
S
, giá trị
.
AM AN
bằng
A.
6 2
. B.
14
. C.
8
. D.
9 2
.
Lời giải
GVSB: Minh Phạm/ Bùi Thanh Sơn; GVPB1: ; GVPB2:
Chọn A
Cách 1:
Ta có :
,( ) 2
d I Oxy
nên mặt cầu
S
tiếp xúc với mặt phẳng
Oxy
tại điểm
4;1;0
A , đồng
thời đường thẳng
MN
tiếp xúc với
S
cũng tại điểm
4;1;0
A
do
MN Oxy
Gọi
;0;0
M m
;
0; ;0
N n
,
, 0
m n
Do
A MN
nên
AM k AN
4 4
1 1
m k
k n
4
4 1 4 , 1 0
1
n
m n m n
n
.
Phương trình mặt phẳng trung trực đoạn
21
:4 2 0
2
OI x y z
Phương trình mặt phẳng trung trực đoạn
:
2
m
OM x
Phương trình mặt phẳng trung trực đoạn
:
2
n
ON y
Do đó tâm mặt cầu ngoại tiếp tứ diện
OIMN
là
2
6 21
; ;
2 2 4 4
m n n n
J
n
Theo giả thuyết cầu ngoại tiếp tứ diện
OIMN
có bán kính bằng
7
2
nên
7
2
OJ
2
49
4
OJ
2
2
2 2
2 2
6 21
4 49
4 4
1 16 1
n n
n n
n n
4 3 2
4 10 28 49 0
n n n n
1 2 2
n
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 23
Vì
0
n
nên chọn
1 2 2
n , suy ra
4 2
m
Khi đó
. 6 2
AM AN .
Cách 2:
Dễ thấy mặt cầu
S
tiếp xúc với mặt phẳng
Oxy
tại điểm
4;1;0
A
, đồng thời đường thẳng
MN
tiếp xúc với
S
cũng tại điểm
1;4;0
A
do
MN Oxy
Gọi
;0;0
M a
;
0; ;0
N b
.
Do
A MN
nên
AM k AN
4 4
1 1
a k
k b
1 4
1
b a
.
Gọi
J
là trung điểm
MN
; ;0
2 2
a b
J
và
4;1;2
I
thuộc đường thẳng
vuông góc với
Oxy
tại điểm
J
. Phương trình
là
2
2
a
x
b
y
z t
Tâm của mặt cầu ngoại tiếp tứ diện
OIMN
là điểm
; ;
2 2
a b
K t
.
Theo giả thiết ta có hệ:
1 4
1
7
2
7
2
b a
OK
IK
2 2
2
2 2
2
1 4
1
49
4 4 4
49
4 1 2
2 2 4
b a
a b
t
a b
t
2 2
2
4
1
4 4 21 0
49
4 4 4
b
a
b
a b t
a b
t
2
2 2
2
4
1
6 21
4 1
49
4 4 4
b
a
b
b b
t
b
a b
t
2
2
2 2
2 2
6 21
4 49
4 4
1 16 1
b b
b b
b b
2 2
2
1 16
4 64 1 5 196
1 1
b b
b b
2
2
2 2
128 64 1 256
4 64 5 32 5 . 196
1 1
1 1
b b b
b b
b b
2
2
320 1
5 10 25 32 5 4 . 132
1
1
b b b
b
b
2
2
64
1 16
1
b
b
2
2
1 8 0
b
2
1 8
b
1 2 2
1 2 2
b
b
Với
1 2 2
b ta được
4 2
a
. 6 2
AM AN .
Với
1 2 2
b ta được
4 2
a
. 6 2
AM AN .
NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT
Trang 24 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 50. Có bao nhiêu giá trị nguyên âm của tham số
a
để hàm số
4 2
2 8y x ax x
có đúng ba điểm
cực trị?
A.
2
. B.
6
. C.
5
. D.
3
.
Lời giải
GVSB: Bùi Thanh Sơn/
Kieu Hung
; GVPB1: Lê Văn Tùng ; GVPB2:
Chọn D
Xét hàm số
4 2
2 8f x x ax x
trên
.
3
4 4 8f x x ax
.
0f x
3
4 4 8 0x ax
2
2
a x
x
(Do
0x
không thỏa mãn nên
0x
).
Xét hàm số
2
2
g x x
x
trên
\ 0
.
2
2
2g x x
x
.
0f x
2
2
2 0x
x
1x
.
Bảng biến thiên của hàm số
g x
:
Dễ thấy phương trình
0f x
có ít nhất hai nghiệm phân biệt, trong đó có ít nhất một nghiệm
đơn
0x
nên yêu cầu bài toán Hàm số
f x
có đúng một điểm cực trị Phương trình
a g x
có một nghiệm đơn duy nhất
3a
.
Do
a
nguyên âm nên
3; 2; 1a
.
Vậy có
3
giá trị nguyên âm của tham số
a
thỏa mãn yêu cầu bài toán.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 1.
BỘ GIÁO DỤC VÀ ĐÀO TẠO
(Đề thi gồm 07 trang)
KỲ THI TỐT NGHIỆP TRUNG HOC PHỔ
THÔNG NĂM 2022
Bài thi: TOÁN
Ngày thi: 07/7/2022
Thời gian làm bài: 90 phút
(không kể thời gian chép đề)
ĐỀ BÀI
Câu 1. Hàm số nào dưới đây có bảng biến thiên như sau
A.
3
3y x x . B.
3
3y x x . C.
2
2y x x . D.
2
2y x x .
Câu 2. Nếu
3
0
d 6
f x x
thì
3
0
1
2 d
3
f x x
bằng?
A.
8
. B.
5
. C.
9
. D.
6
.
Câu 3. Phần ảo của số phức
2 1z i i
bằng
A.
3
. B.
1
. C.
1
. D.
3
.
Câu 4. Khẳng định nào dưới đây đúng?
A.
d
x x
e x xe C
. B.
1
d
x x
e x e C
. C.
1
d
x x
e x e C
. D.
d
x x
e x e C
.
Câu 5. Cho hàm số
4 2
y ax bx c có đồ thị là đường cong trong hình dưới. Giá trị cực tiểu của hàm số
đã cho bằng
A.
1
. B.
4
. C.
1
. D.
3
.
Câu 6. Cho
5 2
3 , 3 a b
và
6
3c mệnh đề nào dưới đây đúng
A.
a c b
. B.
a b c
. C.
b a c
. D.
c a b
.
x
y
4
3
-1
O 1
Mã đề thi 103
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 2.
Câu 7. Nếu
2
1
d 2
f x x
và
5
2
d 5
f x x
thì
1
5
d
f x x
bằng
A
7
. B.
3
. C.
4
. D.
7
.
Câu 8. Cho hàm số
y f x
có bảng biến thiên như sau
Số giao điểm của đồ thị hàm số đã cho và đường thẳng
1y
là
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 9. Từ các chữ số
1,2,3,4,5
lập được bao nhiêu số tự nhiên gồm năm chữ số đôi một khác nhau?
A.
120
. B.
5
. C.
3 1 2 5
. D.
1
.
Câu 10. Cho khối nón có diện tích đáy bằng
2
3a
và chiều cao
2 a
. Thể tích của khối nón đã cho bằng?
A.
3
3a
. B.
3
6a
. C.
3
2a
. D.
3
2
3
a
.
Câu 11. Số nghiệm thực của phương trình
2
1
2 4
x
là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 12. Với
a
là số thực dương tùy ý,
log 100a
bằng
A.
1 log a
. B.
2 log a
. C.
2 log a
. D.
1 log a
.
Câu 13. Cho khối chóp
.S ABC
có chiều cao bằng 5 , đáy
A B C
có diện tích bằng
6
. Thể tích khối chóp
.S ABC
bằng
A.
11
. B.
10
. C.
15
. D.
3 0
.
Câu 14. Hàm số
cotF x x
là một nguyên hàm của hàm số nào dưới đây trên khoảng
0;
2
A.
2
2
1
sin
f x
x
. B.
1
2
1
cos
f x
x
.
C.
4
2
1
cos
f x
x
. D.
3
2
1
sin
f x
x
.
Câu 15. Cho hàm số bậc ba
y f x
có đồ thị là đường cong hình bên.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 3.
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ
A.
1; 1
. B.
3;1
. C.
1;3
. D.
1; 1
.
Câu 16. Số phức nào dưới đây có phần ảo bằng phần ảo của số phức
w 1 4i
A.
2
3 4 z i . B.
1
5 4 z i . C.
3
1 5 z i . D.
4
1 4 z i .
Câu 17. Cho cấp số nhân
n
u
với
1
3u
và công bội
2q
. Số hạng tổng quát
2
n
u n
bằng
A.
1
3.2
n
. B.
2
3.2
n
. C.
3.2
n
. D.
1
3.2
n
.
Câu 18. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 1 3 4S x y z
. Tâm của
S
có tọa độ là
A.
4; 2; 6
. B.
4; 2; 6
. C.
2; 1;3
. D.
2;1; 3
.
Câu 19. Cho khối chóp và khối lăng trụ có diện tích đáy, chiều cao tương ứng bằng nhau và có thể tích lần
lượt là
1 2
,V V
. Tỉ số
1
2
V
V
bằng
A.
2
3
. B.
3
. C.
3
2
. D.
1
3
.
Câu 20. Trong không gian
Oxyz
, cho đường thẳng
2 1 1
:
1 2 3
x y z
d
. Điểm nào dưới đây thuộc
d
?
A.
2;1;1Q
. B.
1; 2;3M
. C.
2;1; 1P
. D.
1; 2; 3N
.
Câu 21. Trong không gian
Oxyz
, phương trình của mặt phẳng
Oxy
là:
A.
0z
. B.
0x
. C.
0y
. D.
0 x y
.
Câu 22. Cho điểm M nằm ngoài mặt cầu
;S O R
. Khẳng định nào dưới đây đúng?
A.
OM R
. B.
OM R
. C.
OM R
. D.
OM R
.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 4.
Câu 23. Trên mặt phẳng tọa độ, điểm biểu diễn số phức
2 7 z i
có tọa độ là
A.
2; 7
. B.
2; 7
. C.
7; 2
. D.
2; 7
.
Câu 24. Nghiệm của phương trình
1
2
log 2 1 0 x
là
A.
3
4
x
. B.
1x
. C.
1
2
x
. D.
2
3
x
.
Câu 25. Tập xác định của hàm số
2
log 1 y x
là
A.
2;
. B.
;
. C.
1;
. D.
;1
.
Câu 26. Cho hàm số
y f x
có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình:
A.
1x
. B.
1y
. C.
2y
. D.
2x
.
Câu 27. Trong không gian
Oxyz
. Cho hai vectơ
1; 4;0u
và
1; 2;1v
. Vectơ
3u v
có tọa độ là
A.
2; 6; 3
. B.
4; 8; 4
. C.
2; 10; 3
. D.
2; 10; 3
.
Câu 28. Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
0; 3
. B.
0;
. C.
1; 0
. D.
; 1
.
Câu 29. Cho hàm số
4 2
( )f x ax bx c
có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị
nguyên thuộc đoạn
2; 5
của tham số
m
để phương trình
( )f x m
có đúng 2 nghiệm thực phân
biệt?
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 5.
A.
1
. B
6
. C.
7
. D.
5
.
Câu 30. Cho hàm số
2
( ) 1
x
f x e
. Khẳng định nào dưới đây là đúng?
A.
1
( ) .
2
x
f x dx x e C
B
2
( ) 2 .
x
f x dx x e C
C.
2
1
( ) .
2
x
f x dx x e C
D.
2
( ) .
x
f x dx x e C
Câu 31. Gọi
1
z và
2
z là hai nghiệm phức của phương trình
2
2 5 0z z
. Khi đó
2 2
1 2
z z
bằng
A.
6
. B.
8i
. C.
8i
. D.
6
.
Câu 32. Cho hình lập phương
. ' ' ' 'ABC D A B C D
(tham khảo hình bên). Giá trị
sin của góc giữa đường thẳng
'AC
và mặt phẳng
ABCD
bằng
A.
3
3
. B.
6
3
.
C.
3
2
. D.
2
2
.
Câu 33. Trong không gian
Oxyz
, cho điểm
1; 2; 3A
. Phương trình của mặt cầu
tâm
A
và tiếp xúc với mặt phẳng
2 2 3 0 x y x
là
A.
2 2 2
1 2 3 2 x y z
. B.
2 2 2
1 2 3 2 x y z
.
C.
2 2 2
1 2 3 4 x y z
. D.
2 2 2
1 2 3 4 x y z
.
Câu 34. Với
,a b
là các số thực dương tùy ý và
1a
,
1
3
1
log
a
b
bằng
C'
B'
D'
A'
C
D
A
B
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 6.
A. 3log
a
b. B. log
a
b . C. 3log
a
b . D.
1
log
3
a
b
.
Câu 35. Cho hình lập phương
. ' ' ' 'ABC D A B C D
có cạnh bằng 3 (tham
khảo hình bên). Khoảng cách từ
B
đến mặt phẳng
' 'ACC A
bằng
A.
3 2
2
. B.
3
2
.
C.
3 2
. D.
3
.
Câu 36. Cho hàm số
y f x
có đạo hàm
1f x x
với mọi
x
. Hàm số đã cho nghịch biến trên
khoảng nào dưới đây?
A.
1;
. B.
1;
. C.
; 1
. D.
;1
.
Câu 37. Trong không gian
Oxyz
, cho điểm
2 ; 2;1M
và mặt phẳng
: 2 3 1 0P x y z
. Đường thẳng
đi qua
M
và vuông với
P
có phương trình là:
A.
2 2
2 3
1
x t
y t
z t
. B.
2 2
2 3
1
x t
y t
z t
. C.
2 2
2 3
1
x t
y t
z t
. D.
2 2
3 2
1
x t
y t
z t
.
Câu 38. Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn
30 ; 50
. Xác suất để chọn được số
có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
A.
11
21
. B.
8
21
. C.
13
21
. D.
10
21
.
Câu 39. Biết
;F x G x
là hai nguyên hàm của hàm số
f x
trên
và
4
0
4 0 0f x dx F G a a
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
; ; 0; 4.y F x y G x x x
Khi
8S
thì
a
bằng
A.
8
B.
4
C.
12
D.
2
Câu 40. Cho hàm số
4 2
2 4 1f x ax a x
với
a
là tham số thực. Nếu
0;2
max 1f x f
thì
0;2
min f x
bằng
A.
17
B.
16
C.
1
D.
3
H
D'
C'
A'
B'
D
A
B
C
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 7.
Câu 41. Có bao nhiêu số nguyên dương
a
sao cho ứng với mỗi
a
có đúng hai số nguyên
b
thỏa mãn
4 1 .3 10 0
b b
a
?
A.
182
. B.
179
. C.
180
. D.
181
.
Câu 42. Cho hình nón có góc ở đỉnh bằng
0
120
và chiều cao bằng 3. Gọi
S
là mặt cầu đi qua đỉnh và chứa
đường tròn đáy của hình nón đã cho. Diện tích của
S
bằng
A.
144
. B.
108
. C.
48
. D.
96
.
Câu 43. Cho hàm số bậc bốn
y f x
. Biết rằng hàm số
lng x f x
có bảng biến thiên
Diện tích hình phẳng giới hạn bởi các đường
y f x
và
y g x
thuộc khoảng nào dưới
đây?
A.
33;35
. B.
37;40
. C.
29;32
. D.
24;26
.
Câu 44. Xét tất cả số thực
,x y
sao cho
3
2
3
6 log
5
27
x a
y
a
với mọi số thực dương
a
. Giá trị nhỏ nhất của
biểu thức
2 2
4 8P x y x y bằng
A.
15
. B.
25
. C.
5
. D.
20
.
Lời giải
Câu 45. Cho các số phức
1 2 3
, ,z z z thỏa mãn
1 2 3
2 2 2z z z
và
1 2 3 1 2
3z z z z z
. Gọi
, ,A B C
lần
lượt là các điểm biểu diễn của
1 2 3
, ,z z z trên mặt phẳng tọa độ. Diện tích tam giác
A B C
bằng
A.
5 7
8
. B.
5 7
16
. C.
5 7
24
. D.
5 7
32
.
Câu 46. Trong không gian
Oxyz
, cho điểm
1; 2; 2A
. Gọi
P
là mặt phẳng chứa trục
Ox
sao cho khoảng
cách từ
A
đến
P
lớn nhất. Phương trình của
P
là:
A.
2 0y z
. B.
2 0y z
. C.
0y z
. D.
0y z
.
Câu 47. Có bao nhiêu số phức
z
thỏa mãn
2
z z z
và
2
2 2 2z z i z i
?
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 48. Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có đáy
A B C
là tam giác vuông cân tại
A
, cạnh bên
2A A a
, góc giữa hai mặt phẳng
A BC
và
ABC
bằng
30
. Thể tích của khối lăng trụ đã cho bằng
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 8.
A.
3
24a
. B.
3
8
3
a
. C.
3
8a
. D.
3
8
9
a
.
Câu 49. Có bao nhiêu giá trị nguyên âm của tham số
a
để hàm số
4 2
8y x ax x
có đúng 3 điểm cực
trị?
A.
5
. B.
6
. C.
11
. D.
10
.
Câu 50. Trong không gian
Oxyz
cho mặt cầu
S
tâm
9;3;1I
bán kính bằng 3. Gọi
,M N
là hai điểm lần
lượt thuộc 2 trục
,Ox Oz
sao cho đường thẳng
M N
tiếp xúc với
S
, đồng thời mặt cầu ngoại tiếp
tứ diện
O IM N
có bán kính bằng
13
2
. Gọi
A
là tiếp điểm của
M N
và
S
, giá trị
.AM AN
bằng
A.
12 3
. B.
18
. C.
28 3
. D.
39
.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 9.
BẢNG ĐÁP ÁN
LỜI GIẢI CHI TIẾT
Câu 1. Hàm số nào dưới đây có bảng biến thiên như sau
A
3
3y x x
. B.
3
3y x x
. C.
2
2y x x
. D.
2
2y x x
.
Lời giải
Chọn B
Dựa vào bảng biến thiên ta nhận thấy:
Đây là hàm
3 2
0y ax bx cx d a
.
lim 0
x
y a

.
Do đó hàm số thỏa mãn là
3
3y x x
.
Câu 2. Nếu
3
0
d 6
f x x
thì
3
0
1
2 d
3
f x x
bằng?
A.
8
. B.
5
. C.
9
. D.
6
.
Lời giải
Chọn A
Ta có
3 3 3
0 0 0
1 1 1
2 d 2 6 6 8
3 3 3
f x x f x dx dx
.
Câu 3. Phần ảo của số phức
2 1z i i
bằng
A
3
. B.
1
. C.
1
. D.
3
.
Lời giải
Chọn B
Ta có
2 1 3z i i i
. Vậy phần ảo là
1
.
Câu 4. Khẳng định nào dưới đây đúng?
A
d
x x
e x xe C
. B.
1
d
x x
e x e C
. C.
1
d
x x
e x e C
. D.
d
x x
e x e C
.
1.B 2.A 3.B 4.D 5.D 6.C 7.B 8.D 9.A 10.C 11.B 12.B 13.B 14.D 15.D
16.B 17.A 18.C 19.D 20.C 21.A 22.B 23.B 24.B 25.C 26.D 27.D 28.C 29.C 30.C
31.D 32.A 33.D 34.A 35.A 36.C 37.B 38.A 39.A 40.B 41.D 42.A 43.A 44.A 45.B
46.D 47.D 48.A 49.B 50.A
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 10.
Lời giải
Chọn D
Ta có
d
x x
e x e C
.
Câu 5. Cho hàm số
4 2
y ax bx c
có đồ thị là đường cong trong hình dưới. Giá trị cực tiểu của hàm số
đã cho bằng
A
1
. B.
4
. C.
1
. D.
3
.
Lời giải
Chọn D
Dựa vào đồ thị hàm số ta thấy giá trị cực tiểu bằng
3
.
Câu 6. Cho
5 2
3 , 3 a b
và
6
3c mệnh đề nào dưới đây đúng
A
a c b
. B.
a b c
. C.
b a c
. D.
c a b
.
Lời giải
Chọn C
Ta có
5 2 4 6
3 , 3 3 , 3a b c
và
4 5 6
3 1
b a c
.
Câu 7. Nếu
2
1
d 2
f x x
và
5
2
d 5
f x x
thì
1
5
d
f x x
bằng
A
7
. B.
3
. C.
4
. D.
7
.
Lời giải
Chọn B
Ta có
5 2 5
1 1 2
d d d 2 5 3f x x f x x f x x
.
Câu 8. Cho hàm số
y f x
có bảng biến thiên như sau
x
y
4
3
-1
O 1
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 11.
Số giao điểm của đồ thị hàm số đã cho và đường thẳng
1y
là
A
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn D
Dựa vào bảng biến thiên ta thấy đường thẳng
1y
cắt đồ thị hàm số tại 3 điểm.
Câu 9. Từ các chữ số
1,2,3,4,5
lập được bao nhiêu số tự nhiên gồm năm chữ số đôi một khác nhau?
A.
120
. B.
5
. C.
3 1 2 5
. D.
1
.
Lời giải
Chọn A
Số các số tự nhiên gồm năm chữ số khác nhau lập từ các số
1,2,3,4,5
là
5! 120
.
Câu 10. Cho khối nón có diện tích đáy bằng
2
3a
và chiều cao
2 a
. Thể tích của khối nón đã cho bằng?
A.
3
3a
. B.
3
6a
. C.
3
2a
. D.
3
2
3
a
.
Lời giải
Chọn C
Thể tích của khối nón đã cho bằng
2 3
1
.3 .2 2
3
V a a a
.
Câu 11. Số nghiệm thực của phương trình
2
1
2 4
x
là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn B
2
1 2 2 2
1
2 2 1 2 1
1
x
x
x x
x
Câu 12. Với
a
là số thực dương tùy ý,
log 100a
bằng
A.
1 log a
. B.
2 log a
. C.
2 log a
. D.
1 log a
.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 12.
Lời giải
Chọn B
log 100 log 100 log 2 loga a a
Câu 13. Cho khối chóp
.S ABC
có chiều cao bằng 5 , đáy
A B C
có diện tích bằng
6
. Thể tích khối chóp
.S ABC
bằng
A.
11
. B.
10
. C.
15
. D.
3 0
.
Lời giải
Chọn B
.
1 1
. . .6.5 10
3 3
S ABC
V S h
Câu 14. Hàm số
cotF x x
là một nguyên hàm của hàm số nào dưới đây trên khoảng
0;
2
A.
2
2
1
sin
f x
x
. B.
1
2
1
cos
f x
x
.
C.
4
2
1
cos
f x
x
. D.
3
2
1
sin
f x
x
.
Lời giải
Chọn D
Có
2
1
cot
sin
dx x C
x
suy ra
cotF x x
trên khoảng
0;
2
là một nguyên hàm của hàm
số
3
2
1
sin
f x
x
.
Câu 15. Cho hàm số bậc ba
y f x
có đồ thị là đường cong hình bên.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 13.
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ
A.
1; 1
. B.
3;1
. C.
1;3
. D.
1; 1
.
Lời giải
Chọn D
Dựa vào đồ thị, điểm cực tiểu của đồ thị hàm số đã cho là
1; 1
Câu 16. Số phức nào dưới đây có phần ảo bằng phần ảo của số phức
w 1 4i
A.
2
3 4 z i . B.
1
5 4 z i . C.
3
1 5 z i . D.
4
1 4 z i .
Lời giải
Chọn B
Cả hai số phức
w 1 4 i
và
1
5 4 z i đều có phần ảo bằng
4
nên ta chọn B.
Câu 17. Cho cấp số nhân
n
u
với
1
3u
và công bội
2q
. Số hạng tổng quát
2
n
u n
bằng
A.
1
3.2
n
. B.
2
3.2
n
. C.
3.2
n
. D.
1
3.2
n
.
Lời giải
Chọn A
Cấp số nhân
n
u
với
1
3u
và công bội
2q
có số hạng tổng quát
1
3.2
n
n
u
.
Câu 18. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 1 3 4S x y z
. Tâm của
S
có tọa độ là
A.
4; 2; 6
. B.
4; 2; 6
. C.
2; 1;3
. D.
2;1; 3
.
Lời giải
Chọn C
Mặt cầu
2 2 2
: 2 1 3 4S x y z
có tâm là
2; 1;3
.
Câu 19. Cho khối chóp và khối lăng trụ có diện tích đáy, chiều cao tương ứng bằng nhau và có thể tích lần
lượt là
1 2
,V V
. Tỉ số
1
2
V
V
bằng
A.
2
3
. B.
3
. C.
3
2
. D.
1
3
.
Lời giải
Chọn D
Gọi diện tích đáy và chiều cao tương ứng của khối chóp và khối lăng trụ là
B
và
h
.
Ta có
1
1
2
2
1
1
3
3
V Bh
V
V
V Bh
.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 14.
Câu 20. Trong không gian
Oxyz
, cho đường thẳng
2 1 1
:
1 2 3
x y z
d
. Điểm nào dưới đây thuộc
d
?
A.
2;1;1Q
. B.
1; 2;3M
. C.
2;1; 1P
. D.
1; 2; 3N
.
Lời giải
Chọn C
Cho
2 0 2
1 0 1
1 0 1
x x
y y
z z
vậy
2;1; 1 P d
.
Câu 21. Trong không gian
Oxyz
, phương trình của mặt phẳng
Oxy
là:
A.
0z
. B.
0x
. C.
0y
. D.
0 x y
.
Lời giải
Chọn A
Câu 22. Cho điểm M nằm ngoài mặt cầu
;S O R
. Khẳng định nào dưới đây đúng?
A.
OM R
. B.
OM R
. C.
OM R
. D.
OM R
.
Lời giải
Chọn B
Câu 23. Trên mặt phẳng tọa độ, điểm biểu diễn số phức
2 7 z i
có tọa độ là
A.
2; 7
. B.
2; 7
. C.
7; 2
. D.
2; 7
.
Lời giải
Chọn B
Câu 24. Nghiệm của phương trình
1
2
log 2 1 0 x
là
A.
3
4
x
. B.
1x
. C.
1
2
x
. D.
2
3
x
.
Lời giải
Chọn B
1
2
log 2 1 0 2 1 1 1x x x
.
Vậy nghiệm của phương trình là
1x
.
Câu 25. Tập xác định của hàm số
2
log 1 y x
là
A.
2;
. B.
;
. C.
1;
. D.
;1
.
Lời giải
Chọn C
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 15.
Hàm số xác định khi
1 0 1x x
.
Tập xác định của hàm số là
1;D
.
Câu 26. Cho hàm số
y f x
có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình:
A.
1x
. B.
1y
. C.
2y
. D.
2x
.
Lời giải
Chọn D
Ta thấy:
2
lim
x
f x


và
2
lim
x
f x


.
Vậy tiệm cận đứng của hàm số đã cho là
2x
.
Câu 27. Trong không gian
Oxyz
. Cho hai vectơ
1; 4;0u
và
1; 2;1v
. Vectơ
3u v
có tọa độ là
A.
2; 6; 3
. B.
4; 8; 4
. C.
2; 10; 3
. D.
2; 10; 3
.
Lời giải
Chọn D
Ta có:
1; 4;0u
3 3; 6;3v
Vậy:
3 2; 10;3u v
Câu 28. Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
0; 3
. B.
0;
. C.
1; 0
. D.
; 1
.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 16.
Lời giải
Chọn C
Câu 29. Cho hàm số
4 2
( )f x ax bx c có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị
nguyên thuộc đoạn
2; 5
của tham số
m
để phương trình
( )f x m
có đúng 2 nghiệm thực phân
biệt?
A.
1
. B
6
. C.
7
. D.
5
.
Lời giải
Chọn C
Dựa vào đồ thị ta thấy phương trình
( )f x m
có đúng hai nghiệm thực phân biệt khi
2m
Hoặc
1m
. Vậy
2; 0;1; 2;3;4;5m
. Vậy có 7 giá trị
m
thĩa mãn.
Câu 30. Cho hàm số
2
( ) 1
x
f x e
. Khẳng định nào dưới đây là đúng?
A.
1
( ) .
2
x
f x dx x e C
B
2
( ) 2 .
x
f x dx x e C
C.
2
1
( ) .
2
x
f x dx x e C
D.
2
( ) .
x
f x dx x e C
Lời giải
Chọn C
Ta có
2 2
1
(1 ) .
2
x x
e dx x e C
Câu 31. Gọi
1
z và
2
z là hai nghiệm phức của phương trình
2
2 5 0z z
. Khi đó
2 2
1 2
z z
bằng
A.
6
. B.
8i
. C.
8i
. D.
6
.
Lời giải
Chọn D
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 17.
Phương trình
2
2 5 0z z
có nghiệm là
1
1 2z i và
2
1 2z i nên ta có:
2 2
2 2
1 2
1 2 1 2 6z z i i
.
Câu 32. Cho hình lập phương
. ' ' ' 'ABC D A B C D
(tham khảo hình bên). Giá trị
sin của góc giữa đường thẳng
'AC
và mặt phẳng
ABCD
bằng
A.
3
3
. B.
6
3
.
C.
3
2
. D.
2
2
.
Lời giải
Chọn A
Ta có
' 2AC CC
2 2
' ' ' 3 AC AC CC CC
Ta có
'; '; ' AC ABCD AC AC CAC
' ' 3
sin '
' 3
' 3
CC CC
CAC
AC
CC
.
Câu 33. Trong không gian
Oxyz
, cho điểm
1; 2; 3A
. Phương trình của mặt cầu tâm
A
và tiếp xúc với mặt
phẳng
2 2 3 0 x y x
là
A.
2 2 2
1 2 3 2 x y z
. B.
2 2 2
1 2 3 2 x y z
.
C.
2 2 2
1 2 3 4 x y z
. D.
2 2 2
1 2 3 4 x y z
.
Lời giải
Chọn D
Bán kính mặt cầu
2
2
1 2.2 2.3 3
6
2
3
1 2 2
R
Do đó phương trình của mặt cầu
2 2 2
2
1 2 3 2 4x y z
Câu 34. Với
,a b
là các số thực dương tùy ý và
1a
,
1
3
1
log
a
b
bằng
A. 3log
a
b. B. log
a
b . C. 3log
a
b . D.
1
log
3
a
b
.
Lời giải
C'
B'
D'
A'
C
D
A
B
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 18.
Chọn A
3
1
3
1
log log 3log
a a
a
b b
b
Câu 35. Cho hình lập phương
. ' ' ' 'ABC D A B C D
có cạnh bằng 3 (tham
khảo hình bên). Khoảng cách từ
B
đến mặt phẳng
' 'ACC A
bằng
A.
3 2
2
. B.
3
2
.
C.
3 2
. D.
3
.
Lời giải
Chọn A
Gọi
H
là trung điểm của
A C
.
Vì
. ' ' ' 'ABC D A B C D
là hình lập phương nên
' 'BH ACC A
1
; ' '
2
B ACC A BH AC
Mà
ABC D
là hình vuông cạnh 3 nên
3 2AC
3 2
; ' '
2
B ACC A
Câu 36. Cho hàm số
y f x
có đạo hàm
1f x x
với mọi
x
. Hàm số đã cho nghịch biến trên
khoảng nào dưới đây?
A.
1;
. B.
1;
. C.
; 1
. D.
;1
.
Lời giải
Chọn C
Ta có:
0 1 0 1f x x x
.
Bảng xét dấu:
Vậy hàm số đã cho nghịch biến trên khoảng
; 1
.
Câu 37. Trong không gian
Oxyz
, cho điểm
2 ; 2;1M
và mặt phẳng
: 2 3 1 0P x y z
. Đường thẳng
đi qua
M
và vuông góc với
P
có phương trình là:
H
D'
C'
A'
B'
D
A
B
C
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 19.
A.
2 2
2 3
1
x t
y t
z t
. B.
2 2
2 3
1
x t
y t
z t
. C.
2 2
2 3
1
x t
y t
z t
. D.
2 2
3 2
1
x t
y t
z t
.
Lời giải
Chọn B
Gọi
d
là đường thẳng đi qua
M
và vuông góc với
P
.
Do
d
vuông góc với
P
nên
d
có một vectơ chỉ phương là
2 ; 3; 1u
.
Vậy phương trình của đường thẳng
d
là:
2 2
2 3
1
x t
y t
z t
.
Câu 38. Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn
30 ; 50
. Xác suất để chọn được số
có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
A.
11
21
. B.
8
21
. C.
13
21
. D.
10
21
.
Lời giải
Chọn A
Số phần tử của không gian mẫu là
21n
.
Gọi
A
là biến cố:
"
chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục
"
.
Khi đó
34 ; 35;36 ;37 ;38; 39 ; 45; 46 ;47 ; 48 ; 49 11A n A
.
Vậy
11
21
n A
P A
n
.
Câu 39. Biết
;F x G x
là hai nguyên hàm của hàm số
f x
trên
và
4
0
4 0 0f x dx F G a a
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
; ; 0; 4.y F x y G x x x
Khi
8S
thì
a
bằng
A.
8
B.
4
C.
12
D.
2
Lời giải
Chọn D
Đặt
F x G x c
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 20.
4
0
4
0
2 2
4 0
4 0 4 0
0 0
2
S F x G x dx F x G x hay c
f x dx F G a
F F F G a
G c G a
a c
a
Mà
0 2a a
Câu 40. Cho hàm số
4 2
2 4 1f x ax a x
với
a
là tham số thực. Nếu
0;2
max 1f x f
thì
0;2
min f x
bằng
A.
17
B.
16
C.
1
D.
3
Lời giải
Chọn A
Từ giả thiết ta có
1 0f
4 4 4 0a a
2a
và
4 2
2 4 1f x x x
Ta có
0 1f
,
1 1f
,
2 17f
Vậy
0;2
min (2) 17f x f
Câu 41. Có bao nhiêu số nguyên dương
a
sao cho ứng với mỗi
a
có đúng hai số nguyên
b
thỏa mãn
4 1 .3 10 0
b b
a
?
A.
182
. B.
179
. C.
180
. D.
181
.
Lời giải
Chọn D
Theo đề bài
; 1a a
và
b
.
Trường hợp 1:
3
0
4 1 0
10
log
3 10 0
b
b
b
b
a
a
Vì có đúng hai số nguyên
b
thỏa mãn nên
2; 1b
.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 21.
Do đó
3
10
2 log 3 270 90a
a
nên
91;92;...; 270a
. Có 180 giá trị của
a
thoả mãn
trường hợp 1.
Trường hợp 2:
3
0
4 1 0
10
log
3 10 0
b
b
b
b
a
a
Vì có đúng hai số nguyên
b
thỏa mãn nên
1; 2b
.
Do đó
3
10 10 10
3 log 2
9 27
a
a
nên
1a
. Có 1 giá trị của
a
thoả mãn trường hợp 2.
Vậy có
180 1 181
giá trị của
a
thoả mãn yêu cầu bài toán.
Câu 42. Cho hình nón có góc ở đỉnh bằng
0
120
và chiều cao bằng 3. Gọi
S
là mặt cầu đi qua đỉnh và chứa
đường tròn đáy của hình nón đã cho. Diện tích của
S
bằng
A.
144
. B.
108
. C.
48
. D.
96
.
Lời giải
Chọn A
Gọi H là tâm đáy, AB là đường kính của đáy hình nón và
SC
là đường kính của mặt cầu
S
. Khi
đó
3SH
và
0
60ASC .
0
6
cos 60
SH
SA
(đvdd)
2 2
. 6 3. 12SA SH SC SC SC
Bán kính của mặt cầu
S
là
6R
nên diện tích của
S
là
2
4 .6 144S
(đvdt).
Câu 43. Cho hàm số bậc bốn
y f x
. Biết rằng hàm số
lng x f x
có bảng biến thiên
Diện tích hình phẳng giới hạn bởi các đường
y f x
và
y g x
thuộc khoảng nào dưới đây?
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 22.
A.
33;35
. B.
37;40
. C.
29;32
. D.
24;26
.
Lời giải
Chọn A
Từ bảng biến thiên hàm số
lng x f x
ta có
ln ln 3, 3,f x x f x x
.
Ta có
f x
g x
f x
.
Từ bảng biến thiên ta có đồ thị hàm số
y g x
có 3 điểm cực trị là
1 2 3
;ln 30 , ; ln 35 , ; ln 3A x B x C x
nên
1 2 3
0f x f x f x
và
1 2 3
30, 35, 3f x f x f x
.
Do
y f x
là hàm số bậc 3 nên phương trình
0f x
chỉ có 3 nghiệm
1 2 3
, ,x x x .
Xét phương trình hoành độ giao điểm của
f x
và
g x
ta có
1
2
3
0
1 VN
x x
f x
f x
f x g x f x x x
f x
f x
x x
.
Diện tích hình phẳng giới hạn bởi các đường
y f x
và
y g x
là:
3 3 3
1 1 1
1
d d . 1 d
x x x
x x x
f x
S g x f x x f x x f x x
f x f x
3
2
1 2
1 1
. 1 d . 1 d
xx
x x
f x x f x x
f x f x
+ Tính
2 2
1 1
1
1 1
. 1 d . 1 d
x x
x x
I f x x f x x
f x f x
(do
1 2
0, ;f x x x x
)
Đặt
d dt f x t f x x
.
Đổi cận:
1 1
30x x t f x
.
2 2
35x x t f x
.
Suy ra
35
35
1
30
30
1 6
1 d ln 35 ln 35 30 ln 30 5 ln
7
I t t t
t
.
+ Tính
3 3
2 2
2
1 1
. 1 d . 1 d
x x
x x
I f x x f x x
f x f x
(do
2 3
0, ;f x x x x
).
Đặt
d dt f x t f x x
.
Đổi cận:
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 23.
2 2
35x x t f x
.
3 3
3x x t f x
.
Suy ra
3
3
2
35
35
1 35
1 d ln 3 ln 3 35 ln 35 32 ln
3
I t t t
t
.
Vậy
6 35 18
5 ln 32 ln 37 ln 34,39 33;35
7 3 245
S
.
Câu 44. Xét tất cả số thực
,x y
sao cho
3
2
3
6 log
5
27
x a
y
a
với mọi số thực dương
a
. Giá trị nhỏ nhất của
biểu thức
2 2
4 8P x y x y bằng
A.
15
. B.
25
. C.
5
. D.
20
.
Lời giải
Chọn A
Giả sử
,x y
thỏa
3
2
3
6 log
5
27
x a
y
a
với mọi số thực dương
a
.
Ta có
2 2 2 2
4 8 4 8 0P x y x y x y x y P
Suy ra điểm
;M x y
thuộc đường tròn tâm
2; 4I
và bán kính
2
2
1
2 4 20R P P
.
3
2
3
6 log
5 2 3 2
3 3 3 3
27 5 .3 6 log log 5 .3 6 3log log
x a
y
a y x a a y x a a
Đặt
3
log ,t a t
.
Suy ra
2 2 2
5 .3 6 3 3 6 15 3 0y x t t t xt y
Theo đề bài ta có
3
2
3
6 log
5
27
x a
y
a
đúng với mọi số thực dương
a
nên
2 2
3 6 15 3 0t xt y
đúng với mọi
t
.
Do đó
2 2 2 2
2
2
3 0
9 9 45 0 5
3 3 15 3 0
x y x y
x y
.
Suy ra tập hợp các điểm
;M x y
là hình tròn tâm
0; 0O
và bán kính
2
5R
.
Vậy để tồn tại cặp
;x y
thì đường tròn
1
;I R
và hình tròn
; 5O phải có điểm chung
Do đó
2
2
1
5 2 4 20 5 5 20 15IO R P P P
.
Vậy giá trị nhỏ nhất của
P
là
1 5
Câu 45. Cho các số phức
1 2 3
, ,z z z thỏa mãn
1 2 3
2 2 2z z z
và
1 2 3 1 2
3z z z z z
. Gọi
, ,A B C
lần
lượt là các điểm biểu diễn của
1 2 3
, ,z z z trên mặt phẳng tọa độ. Diện tích tam giác
A B C
bằng
A.
5 7
8
. B.
5 7
16
. C.
5 7
24
. D.
5 7
32
.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 24.
Lời giải
Chọn B
Không mất tính tổng quát, giả sử
3
2z .
Khi đó
1 2 3 1 2
3z z z z z
trở thành
1 2 1 2
2 3z z z z
1 2
1 1 3
2z z
.
Đặt
1
1
,x yi x y
z
2
1 3
2
x yi
z
.
Ta có
3
2z và
1 2 3
2 2 2z z z
nên
1 2
1z z
1 2
1 1
1
z z
.
Suy ra
2 2
2
2
1
3
1
2
x y
x y
3
4
7
4
7
4
x
y
y
3 3
2 4
7
4
7
4
x
y
y
Do đó
1 1
3 7 3 7
;
4 4 4 4
z i z i
.
Nên tọa độ các điểm là
3 7 3 7
; ; ; ; 2;0
4 4 4 4
A B C
.
Diện tích tam giác
A B C
là
1 1 7 3 5 7
. ; .2. . 2
2 2 4 4 16
ABC
S AB d C AB
.
Câu 46. Trong không gian
Oxyz
, cho điểm
1; 2; 2A
. Gọi
P
là mặt phẳng chứa trục
Ox
sao cho khoảng
cách từ
A
đến
P
lớn nhất. Phương trình của
P
là:
A.
2 0y z
. B.
2 0y z
. C.
0y z
. D.
0y z
.
Lời giải
Chọn D
Gọi hình chiếu vuông góc của điểm
1; 2; 2A
lên trục
Ox
là
1; 0; 0M
.
Khoảng cách từ
A
đến
P
lớn nhất nên mặt phẳng
P
có vecto pháp tuyến là
0;2;2MA
.
Phương trình mặt phẳng
P
đi qua điểm
1; 0; 0M
và có vecto pháp tuyến là
0;2;2MA
nên
0. 1 2 0 2 0 0x y z
0y z
.
Câu 47. Có bao nhiêu số phức
z
thỏa mãn
2
z z z
và
2
2 2 2z z i z i
?
A.
2
. B.
3
. C.
1
. D.
4
.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 25.
Lời giải
Chọn D
2
2 2 2 2 2 2 2z z i z i z z i z i z i
2 2 2z i z z i
Trường hợp 1.
2 0 2 2z i z i z i
Trường hợp 2.
2 2 0 2 2 0z z i z z i
Đặt
z x y i
ta có
2 2z x y i
và
2 2z i x y i
.
Khi đó
2 2
2 2
2 2 2 2z z i x y x y
2 2 2 2
4 4 4 4x x y x y y
4 4x y x y
Lại có
2 2 2 2
2 2 2 2 1 0z z z x y y y y y y
0y
hoặc
1y
.
Do đó ta có các số
0;1 ; 1 ; 2z i i i
thỏa mãn.
Vậy có
4
số phức thỏa mãn yêu cầu bài toán.
Câu 48. Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có đáy
A B C
là tam giác vuông cân tại
A
, cạnh bên
2A A a
, góc giữa hai mặt phẳng
A BC
và
ABC
bằng
30
. Thể tích của khối lăng trụ đã cho bằng
A.
3
24a
. B.
3
8
3
a
. C.
3
8a
. D.
3
8
9
a
.
Lời giải
Chọn A
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 26.
Kẻ
A H BC
, ta có
AA ABC
nên
'AA B C
.
AH B C
và
'A A BC
suy ra
BC AA H A H BC
.
Suy ra góc giữa
A BC
và
ABC
là
30A HA A HA
.
Δ 'A AH
vuông tại
A
có
2 2
tan tan 30 2 3.
tan 30
AA a a
A HA AH a
AH AH
ΔAB C
vuông cân tại
A
nên 2 4 3BC AH a .
2
1 1
2 3 4 3 12 .
2 2
ABC
S AH BC a a a
Vậy thể tích của khối lăng trụ đứng
. ' ' 'ABC A B C
là
Câu 49. Có bao nhiêu giá trị nguyên âm của tham số
a
để hàm số
4 2
8y x ax x
có đúng 3 điểm cực
trị?
A.
5
. B.
6
. C.
11
. D.
10
.
Lời giải
Chọn B
Xét
4 2
8g x x ax x
3
4 2 8g x x ax
Xét
3
3 2
2 4 4
0 4 2 8 0 2
x
g x x ax a x h x
x x
(do
0x
không là nghiệm)
3
3 2
0
0
8 8
8 0
x
g x
x
x ax a x k x
x x
H
B'
C'
A'
A
C
B
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 27.
2
4
4 0 1h x x x
x
.
3
2
8
2 0 4k x x x
x
.
Để hàm số
y g x
có đúng 3 cực trị
6 6a a
.
Mà
a
là số nguyên âm nên
6; 5; 4; 3; 2; 1a
.
Câu 50. Trong không gian
Oxyz
cho mặt cầu
S
tâm
9;3;1I
bán kính bằng 3. Gọi
,M N
là hai điểm lần
lượt thuộc 2 trục
,Ox Oz
sao cho đường thẳng
M N
tiếp xúc với
S
, đồng thời mặt cầu ngoại tiếp
tứ diện
O IM N
có bán kính bằng
13
2
. Gọi
A
là tiếp điểm của
M N
và
S
, giá trị
.AM AN
bằng
A.
12 3
. B.
18
. C.
28 3
. D.
39
.
Lời giải
Chọn A
9;3;1 3I d I Oxz R S
tiếp xúc với
Oxz
.
Gọi
;0; 0M a Ox
0; 0;N b Oz
M N
tiếp xúc với
S
tại
A
nên
A
là hình chiếu của
I
lên
Oxz
.
Suy ra
9; 0;1A
.
Gọi
K
là trung điểm
;0;
2 2
a b
MN K
.
Gọi
H
là tâm mặt cầu ngoại tiếp tứ diện
13
2
OIMN OH HK MN
.
Gọi
T
là trung điểm
OM
OM KT
OM KHT OM HK HK OMN
OM HT
Mà
//IA OMN HK IA
.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 28.
Ta có
0;3;0AI
; 0;
2 2
H H H
a b
KH x y z
.
AI
cùng phương
KH
nên
2
0
2
H
H
H
a
x
y c c
b
z
; ;
2 2
a b
H c
2 2
2
13 169
1
2 4 4 4
a b
OH c
2 2
2
13 169
9 3 1 2
2 2 2 4
a b
HI OH c
Từ
1
và
2
suy ra
2 2
2 2
2
2
9 3 1
4 4 2 2
a b a b
c c
9 6 91 3a b c
9;0; 1
9;0; 1
AM a
AN b


, ,A M N
thẳng hàng
9 1
9 1
a
b
2 1 9
9 9 9
9 0
1
9
1
a b
ab a b
ab a b
a b ab
b
a
b
Từ
9
3 9. 6 91
1
b
b c
b
2 2 2
2
81
6 91
1
80 80 11 91
6 91 6 91
1 1 1
11 91
6 1
b
b c
b
b b b b b b
c c
b b b
b b
c
b
Ta có
2 2 2
4 169a c b
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 29.
2
2
2
2
2 2
2 4 2 3 2 2
9 11 91
4 169
1 6 1
9.81 121 8281 22 182 2002 9 1 169.9. 1
b b b
b
b b
b b b b b b b b b
2 4 2 3 2 4 3 2 2
4 3 2
729 121 8281 22 182 2002 9 18 9 1521 3042 1521
10 40 480 1040 6760 0
9 1 3 3
1 3 3 9 3
3 3
9 1 3 3
1 3 3 9 3
3 3
b b b b b b b b b b b
b b b b
b a
b a
+ Trường hợp 1:
9 3; 1 3 3 3;0; 1 2a b AM AM

.
9;0;3 3 108AN AN
.
. 2. 108 12 3AM AN .
+ Trường hợp 2:
9 3; 1 3 3 3;0; 1 2a b AM AM
.
9;0; 3 3 108AN AN
.
. 2. 108 12 3AM AN
.
HẾT
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM
Trang: 30.
LỜI GIẢI ĐƯỢC THỰC HIỆN BỞI
Tập Thể Giáo Viên Nhóm Toán “Tiểu Học – THCS – THPT VIỆT NAM”
Tạ Thị Huyền Trang Nguyễn Trí Chính Phạm Thụ
Trần Hùng Quân Le Hoop Việt Dũng
Lê Hường Nguyễn Đông Ngonnguyen Quocman
Phạm Thái Ly Trần Lệnh Ánh Võ Tự Lực
Tran Tran Do Lan Anh Nguyen Lê Cảnh Hoài
Người Dạy Toán Phạm Thu Hà Kien Cao
Vũ Đình Thắng Duy Dang Đường Ngọc Lan
Lê Minh Đức Ngọc Diệp Nguyễn Huy Hoàng
Phạm Hoài Phạm Hồng Nhung Thế Long
Thống Trần Hoàng Điệp Phạm Xu Ka
Trần Tuấn Tú
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 1
KỲ THI TN THPT QUỐC GIA
NĂM HỌC 2021 – 2022
Môn: TOÁN – Mã đề: 104
HỌC HỎI - CHIA SẺ KIẾN THỨC Thời gian: 90 phút (không kể thời gian phát đề)
LINK NHÓM: https://www.facebook.com/groups/1916660125164699
Câu 1. Số phức nào dưới đây có phần ảo bằng phần ảo của số phức
1 4w i
?
A.
1
5 4z i . B.
4
1 4z i . C.
3
1 5z i . D.
2
3 4z i .
Câu 2. Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới.
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là
A.
1;3
. B.
3;1
. C.
1; 1
. D.
1; 1
.
Câu 3. Phần ảo của số phức
2 1z i i
bằng
A.
3
. B.
1
. C.
3
. D.
1
.
Câu 4. Nếu
2
1
d 2f x x
và
5
2
d 5f x x
thì
5
1
df x x
bằng
A.
7
. B.
3
. C.
7
. D.
4
.
Câu 5. Cho khối chóp
.S ABC
có chiều cao bằng
5,
đáy
ABC
có diện tích bằng
6.
Thể tích khối chóp
.S ABC
bằng
A.
30
. B.
10
. C.
15
. D.
11
.
Câu 6. Cho khối chóp và khối lăng trụ có diện tích đáy, chiều cao tương ứng bằng nhau và có thể tích
lần lượt là
1 2
,V V . Tỉ số
1
2
V
V
bằng
A.
2
3
. B.
3
2
. C.
3
. D.
1
3
.
Câu 7. Với
a
là số thực dương tuỳ ý,
log 100a
bằng
A.
2 log a
. B.
2 log a
. C.
1 log a
. D.
1 log a
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 8. Hàm số nào dưới đây có bảng biến thiên như sau?
A.
3
3y x x . B.
2
2y x x . C.
3
3y x x . D.
2
2y x x .
Câu 9. Số nghiệm thực của phương trình
2
1
2 4
x
là
A.
1
. B.
2
. C.
0
. D.
3
.
Câu 10. Trong không gian
0xyz
, phương trình của mặt phẳng
Oxy
là
A.
0y
. B.
0x
.
C.
0x y
. D.
0z
.
Câu 11. Hàm số
cotF x x
là một nguyên hàm của hàm số nào dưới đây trên khoảng
0;
2
?
A.
2
2
1
sin
f x
x
. B.
1
2
1
cos
f x
x
. C.
3
2
1
sin
f x
x
. D.
4
2
1
cos
f x
x
.
Câu 12. Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
; 1
. B.
0;3
. C.
0;
. D.
1;0
.
Câu 13. Trong không gian
Oxyz
, cho đường thẳng
2 1 1
:
1 2 3
x y z
d
. Điểm nào dưới đây thuộc
d
?
A.
2;1; 1P
. B.
1;2;3M
. C.
2;1;1Q
. D.
1; 2;3N
.
Câu 14. Trên mặt phẳng tọa độ, điểm biểu diễn số phức
2 7z i
có tọa độ là
A.
2; 7
. B.
2; 7
. C.
7;2
. D.
2;7
.
Câu 15: Cho điểm
M
nằm ngoài mặt cầu
; .S O R
Khẳng định nào dưới đây đúng?
A.
.OM R
B.
.OM R
C.
.OM R
D.
.OM R
Câu 16: Khẳng định nào sau đây đúng?
A.
e d e
x x
x C
. B.
e d e
x x
x x C
. C.
1
e d e
x x
x C
. D.
1
e d e
x x
x C
.
Câu 17. Trong không gian
Oxyz
, cho hai vectơ
1; 4;0u
và
1; 2;1v
. Vectơ
3u v
có tọa độ
là
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 3
A.
2; 10;3
. B.
2; 6;3
. C.
4; 8;4
. D.
2; 10; 3
.
Câu 18. Cho cấp số nhân
n
u
1
3u và công bội
2q
. Số hạng tổng quát
2
n
u n
bằng
A.
3.2
n
. B.
2
3.2
n
. C.
1
3.2
n
. D.
1
3.2
n
.
Câu 19. Cho
5
3a
,
2
3b
và
6
3c
. Mệnh đề nào dưới đây đúng?
A.
a b c
. B.
a c b
. C.
c a b
. D.
b a c
.
Câu 20. Cho khối nón có diện tích đáy
2
3a
và chiều cao
2a
. Thể tích của khối nón đã cho là
A.
3
3a
. B.
3
6a
. C.
3
2a
. D.
3
2
3
a
.
Câu 21. Nếu
3
0
d 6f x x
thì
3
0
1
2 d
3
f x x
bằng
A.
6
. B.
5
. C.
9
. D.
8
.
Câu 22. Tập xác định của hàm số
2
log 1y x
là
A.
2;
. B.
;
. C.
;1
. D.
1;
.
Câu 23. Cho hàm số
4 2
y ax bx c có đồ thị là đường cong trong hình bên. Giá trị cực tiểu của hàm
số đã cho bằng
A.
3
. B.
4
. C.
1
. D.
1
.
Câu 24. Nghiệm của phương trình
1
2
log 2 1 0x
là
A.
1x
. B.
3
4
x
. C.
2
3
x
. D.
1
2
x
.
Câu 25. Cho hàm số
y f x
có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị đã cho là đường thẳng có phương trình:
A.
1y
. B.
2y
. C.
2x
. D.
1x
.
O
x
y
4
3
1
1
- ∞
+ ∞
- 1
- 1
-
-
+ ∞
- 2
- ∞
f
x
( )
f '
x
( )
x
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 26. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 1 3 4S x y z
. Tâm của
S
có tọa
độ là
A.
2;1; 3
. B.
4;2; 6
. C.
4; 2;6
. D.
2; 1;3
.
Câu 27. Từ các chữ số 1, 2, 3, 4, 5 lập được bao nhiêu số tự nhiên có năm chữ số đôi một khác nhau?
A.
3125
. B.
1
. C.
120
. D.
5
.
Câu 28. Cho hàm số
y f x
có bảng biến thiên như sau:
Số giao điểm của đồ thị hàm số đã cho và đường thẳng
1y
là
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 29. Cho hình lập phương
.ABCD A B C D
(tham khảo hình vẽ bên dưới).
Giá trị sin của góc giữa đường thẳng
AC
và mặt phẳng
( )ABCD
bằng
A.
3
3
. B.
2
2
. C.
3
2
. D.
6
3
.
Câu 30. Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn
30;50
. Xác suất để chọn được
số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
A.
11
21
. B.
13
21
. C.
10
21
. D.
8
21
.
Câu 31. Với
,a b
là các số thực dương tùy ý và
1a
,
1
3
1
log
a
b
bằng
A. log
a
b . B. 3log
a
b . C.
1
log
3
a
b
. D. 3log
a
b .
Câu 32. Cho hàm số
2
1 e
x
f x
. Khẳng định nào dưới đây đúng?
A.
1
d e
2
x
f x x x C
. B.
2
d 2e
x
f x x x C
.
C.
2
d e
x
f x x x C
. D.
2
1
d e
2
x
f x x x C
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 5
Câu 33. Gọi
1 2
,z z là hai nghiệm phức của phương trình
2
2z 5 0z
. Khi đó
2 2
1 2
z z
bằng
A.
6
. B.
8i
. C.
8i
. D.
6
.
Câu 34. Cho hàm số
y f x
có đạo hàm
1f x x
với mọi x
. Hàm số đã cho nghịch biến trên
khoảng nào dưới đây?
A.
; 1
. B.
;1
. C.
1; 
. D.
1;
.
Câu 35. Trong không gian
Oxyz
, cho điểm
1;2;3A
. Phương trình của mặt cầu tâm
A
và tiếp xúc với
mặt phẳng
2 2 3 0x y z
là
A.
2 2 2
1 2 3 2x y z
. B.
2 2 2
1 2 3 2x y z
.
C.
2 2 2
1 2 3 4x y z
. D.
2 2 2
1 2 3 4x y z
.
Câu 36. Cho hàm số
4 2
( )f x ax bx c
có đồ thị là đường cong trong hình bên dưới.
Có bao nhiêu giá trị nguyên thuộc đoạn
2;5
của tham số
m
để phương trình
( )f x m
có
đúng 2 nghiệm thực phân biệt?
A.
7.
B.
6.
C.
5.
D.
1.
Câu 37. Trong không gian
Oxyz
, cho điểm
2; 2;1M
và mặt phẳng . Đường thẳng đi qua
M
và vuông
góc với mặt phẳng
P
có phương trình là
A.
2 2
2 3
1
x t
y
t
z t
. B.
2 2
2 3
1
x t
y t
z t
. C.
2 2
2 3
1
x t
y t
z t
. D.
2 2
3 2
1
x t
y t
z t
.
Câu
38. Cho hình lập phươn
: 2 3 1 0P x y z
g
.ABCD A B C D
có cạnh bằng
3
(tham khảo hình
bên dưới).
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Trang 6 TÀI LIỆU ÔN THI THPT QUỐC GIA
Khoảng cách từ
B
đến mặt phẳng
ACC A
bằng
A.
3
. B.
3 2
. C.
3 2
2
. D.
3
2
.
Câu 39. Có bao nhiêu số nguyên dương
a
sao cho với mỗi
a
có đúng hai số nguyên
b
thỏa mãn
3 3 .2 16 0
b b
a
A. 34 . B. 32. C. 31. D. 33.
Câu 40. Cho hàm số
4 2
3 2 1
f x a x ax
với
a
là tham số thực. Nếu
0; 3
2
max f x f thì
0; 3
min
f x
bằng
A.
9
. B.
4
. C.
1
. D.
8
.
Câu 41. Biết
F x
và
G x
là hai nguyên hàm của hàm số
f x
trên
và
2
0
d 2 0 0
f x x F G a a
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
y F x
,
y G x
,
0
x
và
2
x
, Khi
6
S
thì
a
bằng
A.
4
. B.
6
. C.
3
. D.
8
.
Câu 42. Cho các số phức
1 2 3
, ,
z z z
thỏa mãn
1 2 3
2 2 2
z z z
và
1 2 3 1 2
2
z z z z z
. Gọi
, ,
A B C
lần
lượt là các điểm biểu diễn của
1 2 3
, ,
z z z
trên mặt phẳng tọa độ. Diện tích tam giác
ABC
bằng
A.
3 3
4
. B.
3
8
. C.
3 3
8
. D.
3
4
.
Câu 43. Cho khối lăng trụ đứng .
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
, cạnh bên
2
AA a
, góc giữa hai mặt phẳng
A BC
và
ABC
bằng
60
. Thể tích của khối lăng trụ đã
cho bằng
A.
3
8
9
a
. B.
3
8
a
. C.
3
8
3
a
. D.
3
24
a
.
Câu 44. Cho hình nón có góc ở đỉnh bằng
120
và chiều cao bằng
2
. Gọi
S
là mặt cầu đi qua đỉnh và
chứa đường tròn đáy của hình nón đã cho. Diện tích của
S
bằng
A.
16
3
. B.
64
3
. C.
64
. D.
48
.
Câu 45: Xét tất cả các số thực
x
,
y
sao cho
3
2
2
6 log9
8
x a
y
a
với mọi số thực dương
a
. Giá trị nhỏ nhất
của biểu thức
2 2
6 8
P x y x y
bằng
A.
21
. B.
6
. C.
25
. D.
39
.
Câu 46. Cho hàm số bậc bốn
y f x
. Biết rằng hàm số
ln
g x f x
có bảng biến thiên như sau
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 7
Diện tích hình phẳng giới hạn bởi các đường
y f x
và
y g x
thuộc khoảng nào dưới
đây?
A.
7;8
. B.
6;7
. C.
8;9
. D.
10;11
.
Câu 47. Trong không gian
Oxyz
, cho điểm
2;1;1A
. Gọi
P
là mặt phẳng chứa trục
Oy
sao cho
khoảng cách từ
A đến
P
lớn nhất. Phương trình của
P
là
A.
0x z
. B.
0x z
. C.
2 0x z
. D.
2 0x z
.
Câu 48. Có bao nhiêu số phức
z
thỏa
2
2z z z và
2
4 4 4z z i z i
.
A.
4
. B.
2
. C.
1
D.
3
.
Câu 49. Có bao nhiêu số nguyên dương của tham số
m
để hàm số
4 2
64y x mx x
có đúng 3 điểm
cực trị ?
A.
23
. B.
12
. C.
24
. D.
11
.
Câu 50. Trong không gian
Oxyz
, cho mặt cầu
S
tâm
1;4;2I
, bán kính bằng 2. Gọi
,M N
là hai điểm
lần lượt thuộc hai trục
,Ox Oy
sao cho đường thẳng
MN
tiếp xúc với
S
, đồng thời mặt cầu
ngoại tiếp tứ diện
OIMN
có bán kính bằng
7
2
. Gọi
A
là tiếp điểm của
MN
và
S
, giá trị
.AM AN
bằng
A.
9 2
. B.
14
. C.
6 2
. D.
8
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Trang 8 TÀI LIỆU ÔN THI THPT QUỐC GIA
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT
BẢNG ĐÁP ÁN
1.A 2.C 3.B 4.B 5.B 6.D 7.B 8.C 9.B 10.D
11.C 12.D 13.A 14.D 15.C 16.A 17.A 18.D 19.D 20.C
21.D 22.D 23.A 24.A 25.C 26.D 27.C 28.C 29.A 30.A
31.D 32.D 33.D 34.A 35.D 36.A 37.C 38.C 39.D 40.D
41.C 42.A 43.C 44.C 45.A 46.A 47.C 48.A 49.C 50.C
LỜI GIẢI CHI TIẾT
Câu 1. Số phức nào dưới đây có phần ảo bằng phần ảo của số phức
1 4w i
?
A.
1
5 4z i . B.
4
1 4z i . C.
3
1 5z i . D.
2
3 4z i .
Lời giải
GVSB: Vân Anh Đào Nguyễn; GVPB1: Nguyen Ly; GVPB2: Bùi Kim Thoa
Chọn A
Số phức
1 4w i
có phần ảo bằng
4
.
Trong các số phức đã cho, số phức
1
5 4z i cũng có phần ảo bằng
4
.
Câu 2. Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới.
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là
A.
1;3
. B.
3;1
. C.
1; 1
. D.
1; 1
.
Lời giải
GVSB: Vân Anh Đào Nguyễn; GVPB1: Nguyen Ly; GVPB2: Bùi Kim Thoa
Chọn C
Từ đồ thị hàm số bậc ba
y f x
, ta có điểm cực tiểu của đồ thị hàm số có tọa độ là
1; 1
.
Câu 3. Phần ảo của số phức
2 1z i i
bằng
A.
3
. B.
1
. C.
3
. D.
1
.
Lời giải
GVSB: Nguyễn Bình; GVPB1: Bông Thối; GVPB2: Bùi Kim Thoa
Chọn B
Ta có:
2 1 3z i i i
.
Vậy phần ảo của số phức
z
bằng
1
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 9
Câu 4. Nếu
2
1
d 2
f x x
và
5
2
d 5
f x x
thì
5
1
d
f x x
bằng
A.
7
. B.
3
. C.
7
. D.
4
.
Lời giải
GVSB: Nguyễn Bình; GVPB1: Bông Thối; GVPB2: Bùi Kim Thoa
Chọn B
Ta có:
5 2 5
1 1 2
d d d 2 5 3
f x x f x x f x x
.
Câu 5. Cho khối chóp .
S ABC
có chiều cao bằng
5,
đáy
ABC
có diện tích bằng
6.
Thể tích khối chóp
.
S ABC
bằng
A.
30
. B.
10
. C.
15
. D.
11
.
Lời giải
GVSB: Vũ Ngọc Thành; GVPB1: Suol Nguyen; GVPB2: Thuỳ Dung
Chọn B
Thể tích khối chóp .
S ABC
là
.
1
.5.6 10
3
S ABC
V
.
Câu 6. Cho khối chóp và khối lăng trụ có diện tích đáy, chiều cao tương ứng bằng nhau và có thể tích
lần lượt là
1 2
,
V V
. Tỉ số
1
2
V
V
bằng
A.
2
3
. B.
3
2
. C.
3
. D.
1
3
.
Lời giải
GVSB: Vũ Ngọc Thành; GVPB1: Suol Nguyen; GVPB2: Thuỳ Dung
Chọn D
Gọi đường cao, diện tích đáy lần lượt là
,
h B
.
Khi đó áp dụng công thức thể tích khối chóp, khối lăng trụ ta được
1
1
.
3
V B h
và
2
.
V B h
.
Suy ra:
1
2
1
.
1
3
. 3
B h
V
V B h
.
Câu 7. Với
a
là số thực dương tuỳ ý,
log 100
a
bằng
A.
2 log
a
. B.
2 log
a
. C.
1 log
a
. D.
1 log
a
.
Lời giải
GVSB: Võ Thành Tài; GVPB1: Phạm Trung Khuê; GVPB2: Thuỳ Dung
Chọn B
Với
0
a
, ta có
2
log 100 log100 log log10 log 2 log
a a a a
.
Câu 8. Hàm số nào dưới đây có bảng biến thiên như sau?
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Trang 10 TÀI LIỆU ÔN THI THPT QUỐC GIA
A.
3
3y x x . B.
2
2y x x . C.
3
3y x x . D.
2
2y x x .
Lời giải
GVSB: Võ Thành Tài; GVPB1: Phạm Trung Khuê; GVPB2: Thuỳ Dung
Chọn C
Dựa vào bảng biến thiên trên, ta nhận thấy đây là hàm số bậc ba có dạng
3 2
y ax bx cx d
với
0a
.
Mà
3 2
lim
x
ax bx cx d


0a
.
Do đó có duy nhất hàm số
3
3y x x thoả mãn.
Câu 9. Số nghiệm thực của phương trình
2
1
2 4
x
là
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải
GVSB: Trần Hương Trà; GVPB1: Trần Hương Trà; GVPB2: Đỗ Ngọc Đức
Chọn B
Ta có
2
1 2 2
2 4 1 2 1 1.
x
x x x
Câu 10. Trong không gian
Oxyz , phương trình của mặt phẳng
Oxy
là
A.
0y
. B.
0x
.
C.
0x y
. D.
0z
.
Lời giải
GVSB: Trần Hương Trà; GVPB1: Trần Hương Trà; GVPB2:Đỗ Ngọc Đức
Chọn D
Phương trình của mặt phẳng
Oxy
là
0z
.
Câu 11. Hàm số
cotF x x
là một nguyên hàm của hàm số nào dưới đây trên khoảng
0;
2
?
A.
2
2
1
sin
f x
x
. B.
1
2
1
cos
f x
x
. C.
3
2
1
sin
f x
x
. D.
4
2
1
cos
f x
x
.
Lời giải
GVSB: Vu Ngoc Anh; GVPB1: ThienMinh Nguyễn; GVPB2: Đỗ Ngọc Đức
Chọn C
Ta có:
2
1
d cot
sin
x x C
x
.
Câu 12. Cho hàm số
y f x
có bảng biến thiên như sau:
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 11
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
; 1
. B.
0;3
. C.
0;
. D.
1;0
.
Lời giải
GVSB: Vu Ngoc Anh; GVPB1: ThienMinh Nguyễn; GVPB2: Đỗ Ngọc Đức
Chọn D
Ta có đồ thị tăng trên khoảng
1;0
, nên đó là đáp án đúng.
Câu 13. Trong không gian
Oxyz
, cho đường thẳng
2 1 1
:
1 2 3
x y z
d
. Điểm nào dưới đây thuộc
d
?
A.
2;1; 1P
. B.
1;2;3M
. C.
2;1;1Q
. D.
1; 2;3N
.
Lời giải
GVSB: Phạm Quang Linh; GVPB1:Phan Huy; GVPB2: Tuan Pham;
Chọn A
Thay tọa độ điểm
2;1; 1P
vào phương trình đường thẳng
d
ta có :
2 2 1 1 1 1 0 0 0
0
1 2 3 1 2 3
(thỏa mãn).
Thay tọa độ điểm
1;2;3M
vào phương trình đường thẳng
d
ta có :
1 2 2 1 3 1 1 1 4
1 2 3 1 2 3
(vô lí).
Thay tọa độ điểm
2;1;1Q
vào phương trình đường thẳng
d
ta có :
2 2 1 1 1 1 0 0 2
1 2 3 1 2 3
(vô lí).
Thay tọa độ điểm
1; 2;3N
vào phương trình đường thẳng
d
ta có :
1 2 2 1 3 1 1 3 4
1 2 3 1 2 3
(vô lí).
Vậy điểm
2;1; 1P
thuộc đường thẳng
d
.
Câu 14. Trên mặt phẳng tọa độ, điểm biểu diễn số phức
2 7z i
có tọa độ là
A.
2; 7
. B.
2; 7
. C.
7;2
. D.
2;7
.
Lời giải
GVSB: Phạm Quang Linh; GVPB1:Phan Huy; GVPB2: Tuan Pham;
Chọn D
Trên mặt phẳng tọa độ, điểm biểu diễn số phức
2 7z i
có tọa độ là
2;7
.
Câu 15: Cho điểm
M
nằm ngoài mặt cầu
; .S O R
Khẳng định nào dưới đây đúng?
A.
.OM R
B.
.OM R
C.
.OM R
D.
.OM R
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Trang 12 TÀI LIỆU ÔN THI THPT QUỐC GIA
Lời giải
GVSB: Minh Hiếu; GVPB2: Tuan Pham;
Chọn C
M
nằm ngoài mặt cầu
;
S O R
OM R
.
Câu 16: Khẳng định nào sau đây đúng?
A. e d e
x x
x C
. B. e d e
x x
x x C
. C.
1
e d e
x x
x C
. D.
1
e d e
x x
x C
.
Lời giải
GVSB: Minh Hiếu; GVPB2: Tuan Pham;
Chọn A
e d e
x x
x C
.
Câu 17. Trong không gian
Oxyz
, cho hai vectơ
1; 4;0
u
và
1; 2;1
v
. Vectơ
3
u v
có tọa độ
là
A.
2; 10;3
. B.
2; 6;3
. C.
4; 8;4
. D.
2; 10; 3
.
Lời giải
GVSB: Nguyễn Đức Tài; GVPB1: Nguyễn Minh Luận; GVPB2:
Chọn A
Ta có
3 3; 6;3
v
.
Do đó
3 2; 10;3
u v
.
Câu 18. Cho cấp số nhân
n
u
1
3
u
và công bội
2
q
. Số hạng tổng quát
2
n
u n
bằng
A.
3.2
n
. B.
2
3.2
n
. C.
1
3.2
n
. D.
1
3.2
n
.
Lời giải
GVSB: Nguyễn Đức Tài; GVPB1: Nguyễn Minh Luận; GVPB2:
Chọn D
Ta có
1 1
1
. 3.2
n n
n
u u q
.
Câu 19. Cho
5
3
a ,
2
3
b
và
6
3
c . Mệnh đề nào dưới đây đúng?
A.
a b c
. B.
a c b
. C.
c a b
. D.
b a c
.
Lời giải
GVSB: Nguyễn Minh Luận; GVPB1: Nguyễn Thắng; GVPB2:
Chọn D
Ta có
2 5 6
mà cơ số
3 1
nên
2 5 6
3 3 3
hay
b a c
.
Câu 20. Cho khối nón có diện tích đáy
2
3
a
và chiều cao
2
a
. Thể tích của khối nón đã cho là
A.
3
3
a
. B.
3
6
a
. C.
3
2
a
. D.
3
2
3
a
.
Lời giải
GVSB: nguyễn Minh Luận ; GVPB1: Ngguyễn Thắng; GVPB2:
Chọn C
Thể tích của khối nón đã cho là
2 3
1 1
. . .3 .2 2 .
3 3
V B h a a a
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 13
Câu 21. Nếu
3
0
d 6f x x
thì
3
0
1
2 d
3
f x x
bằng
A.
6
. B.
5
. C.
9
. D.
8
.
Lời giải
GVSB: Hoàng Dương; GVPB1: Hoàng Dương; GVPB2: Hoàng Dương
Chọn D
Ta có
3 3 3
0 0 0
1 1
2 d d 2d 2 6 8
3 3
f x x f x x x
.
Câu 22. Tập xác định của hàm số
2
log 1y x
là
A.
2;
. B.
;
. C.
;1
. D.
1;
.
Lời giải
GVSB: Hoàng Dương; GVPB1: Hoàng Dương; GVPB2: Hoàng Dương
Chọn D
Điều kiện:
1 0 1x x
.
Vậy tập xác định của hàm số đã cho là
1;D
.
Câu 23. Cho hàm số
4 2
y ax bx c có đồ thị là đường cong trong hình bên. Giá trị cực tiểu của hàm
số đã cho bằng
A.
3
. B.
4
. C.
1
. D.
1
.
Lời giải
GVSB: Nguyễn Loan; GVPB1: Nguyễn Loan; GVPB2: Hoàng Dương
Chọn A
Dựa vào đồ thị hàm số đã cho ta dễ dàng thấy giá trị cực tiểu của hàm số đã cho bằng
3
.
Câu 24. Nghiệm của phương trình
1
2
log 2 1 0x
là
A.
1x
. B.
3
4
x
. C.
2
3
x
. D.
1
2
x
.
Lời giải
GVSB: Nguyễn Loan; GVPB1: Nguyễn Loan; GVPB2: Hoàng Dương
Chọn A
Có
1
2
1
2 1 1
log 2 1 0 1
1
2 1 0
2
x
x
x x
x
x
.
V
ậy nghiệm phương trình đã cho là
1x
.
Câu 25. Cho hàm số
y f x
có bảng biến thiên như sau:
O
x
y
4
3
1
1
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Trang 14 TÀI LIỆU ÔN THI THPT QUỐC GIA
Tiệm cận đứng của đồ thị đã cho là đường thẳng có phương trình:
A.
1y
. B.
2y
. C.
2x
. D.
1x
.
Lời giải
GVSB: Kim Anh; GVPB1: Kim Anh; GVPB2: Nguyễn Ngọc Minh Châu
Chọn C
Từ bảng biến thiên ta có
2
lim
x
f x

và
2
lim
x
f x

, suy ra đồ thị hàm số đã cho có
tiệm cận đứng là đường thẳng
2x
.
Câu 26. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 1 3 4S x y z
. Tâm của
S
có tọa
độ là
A.
2;1; 3
. B.
4;2; 6
. C.
4; 2;6
. D.
2; 1;3
.
Lời giải
GVSB: Kim Anh; GVPB1: Kim Anh; GVPB2: Nguyễn Ngọc Minh Châu
Chọn D
Mặt cầu
2 2 2
: 2 1 3 4S x y z
có tâm
2; 1;3I
.
Câu 27. Từ các chữ số 1, 2, 3, 4, 5 lập được bao nhiêu số tự nhiên có năm chữ số đôi một khác nhau?
A.
3125
. B.
1
. C.
120
. D.
5
.
Lời giải
GVSB: Nguyễn Thị Kiên; GVPB1: Trần Đại Nghĩa; GVPB2: Nguyễn Ngọc Minh Châu
Chọn C
Số các số tự nhiên có năm chữ số đôi một khác nhau được lập từ các chữ số 1, 2, 3, 4, 5 là hoán
vị của 5 phẩn tử nên có
5! 120
(số).
Câu 28. Cho hàm số
y f x
có bảng biến thiên như sau:
Số giao điểm của đồ thị hàm số đã cho và đường thẳng
1y
là
A.
2
. B.
1
. C.
3
. D.
0
.
Lời giải
GVSB: Nguyễn Thị Kiên; GVPB1: Trần Đại Nghĩa; GVPB2: Nguyễn Ngọc Minh Châu
Chọn C
- ∞
+ ∞
- 1
- 1
-
-
+ ∞
- 2
- ∞
f
x
( )
f '
x
( )
x
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 15
Ta vẽ đường thẳng
1y
Đường thẳng
1y
cắt đồ thị hàm số tại 3 giao điểm.
Câu 29. Cho hình lập phương
.ABCD A B C D
( tham khảo hình vẽ bên dưới).
Giá trị sin của góc giữa đường thẳng
AC
và mặt phẳng
( )ABCD
bằng
A.
3
3
. B.
2
2
. C.
3
2
. D.
6
3
.
Lời giải
GVSB: Thành đặng; GVPB1: Hoang Ha
Chọn A
Hình chiếu của đường thẳng
'AC
lên mặt phẳng
( )ABCD
là đường thẳng AC suy ra góc giữa
đường thẳng
AC
và mặt phẳng
( )ABCD
, suy ra
, ,CA ACBCD CA CA CAC
.
Gọi cạnh hình lập phương bằng 1, suy ra
2AC
.
Xét tam giác vuông
CAC
vuông tại C ta có:
2
2 2
2 1 3AC CC AC
.
Suy ra:
3
sin ,( ) sin
3
CC
CA ABCD CAC
AC
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Trang 16 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 30. Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn
30;50
. Xác suất để chọn được
số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
A.
11
21
. B.
13
21
. C.
10
21
. D.
8
21
.
Lời giải
GVSB: Thành Đặng; GVPB1: Hoang Ha
Chọn A
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn
30;50
, nên ta có số phần tử của
không gian mẫu:
50 30 1 21
n
.
Gọi
A
“Biến cố để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục”.
TH1: Chữ số hàng chục là 3, có 6 cách chọn số tự nhiên có chữ số hàng đơn vị lớn hơn chữ số
hàng chục { 34, 35, 36, 37, 38, 39}.
TH2: Chữ số hàng chục là 4, có 5 cách chọn số tự nhiên có chữ số hàng đơn vị lớn hơn chữ số
hàng chục { 45, 46, 47, 48, 49}.
Suy ra
6 5 11
n A
.
Xác suất của biến cố
A
:
11
21
P A
.
Câu 31. Với
,
a b
là các số thực dương tùy ý và
1
a
,
1
3
1
log
a
b
bằng
A.
log
a
b
. B.
3log
a
b
. C.
1
log
3
a
b
. D.
3log
a
b
.
Lời giải
GVSB: Nguyễn Linh Trang; GVPB1: Nguyễn Thị Hường; GVPB2: Minh Văn Nguyễn
Chọn D
Ta có:
1
3
1
3
1
log log 3log
a
a
a
b b
b
.
Câu 32. Cho hàm số
2
1 e
x
f x . Khẳng định nào dưới đây đúng?
A.
1
d e
2
x
f x x x C
. B.
2
d 2e
x
f x x x C
.
C.
2
d e
x
f x x x C
. D.
2
1
d e
2
x
f x x x C
.
Lời giải
GVSB: Nguyễn Linh Trang; GVPB1: Nguyễn Thị Hường; GVPB2: Minh Văn Nguyễn
Chọn D
Ta có:
2 2
1
d 1 e d e
2
x x
f x x x x C
.
Câu 33. Gọi
1 2
,
z z
là hai nghiệm phức của phương trình
2
2z 5 0
z
. Khi đó
2 2
1 2
z z
bằng
A.
6
. B.
8
i
. C.
8
i
. D.
6
.
Lời giải
GVSB: Vân Vũ; GVPB2: Bùi Văn Huấn
Chọn D
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 17
Vì
1 2
,z z là hai nghiệm của phương trình
2
2z 5 0z
nên ta có:
1 2
1 2
2
. 5
b
z z
a
c
z z
a
.
Ta có:
2
2 2 2
1 2 1 2 1 2
2. . 2 2.5 6z z z z z z
.
Câu 34. Cho hàm số
y f x
có đạo hàm
1f x x
với mọi
x
. Hàm số đã cho nghịch biến trên
khoảng nào dưới đây?
A.
; 1
. B.
;1
. C.
1; 
. D.
1;
.
Lời giải
GVSB:Vân Vũ; GVPB2: Bùi Văn Huấn
Chọn A
Ta có :
0 1 0 1f x x x
.
Vậy hàm số
y f x
nghịch biến trên khoảng
; 1
.
Câu 35. Trong không gian
Oxyz
, cho điểm
1;2;3A
. Phương trình của mặt cầu tâm
A
và tiếp xúc với
mặt phẳng
2 2 3 0x y z là
A.
2 2 2
1 2 3 2x y z
. B.
2 2 2
1 2 3 2x y z
.
C.
2 2 2
1 2 3 4x y z
. D.
2 2 2
1 2 3 4x y z
.
Lời giải
GVSB: Lê Minh; GVPB1:Dương Ju-i; GVPB2: Bùi Văn Huấn
Chọn D
Mặt cầu tâm
A
tiếp xúc với mặt phẳng đã cho có bán kính
1 2.2 2.3 3
2
1 4 4
R
Vậy phương trình mặt cầu cần tìm là:
2 2 2
1 2 3 4x y z
.
Câu 36. Cho hàm số
4 2
( )f x ax bx c có đồ thị là đường cong trong hình bên dưới.
Có bao nhiêu giá trị nguyên thuộc đoạn
2;5
của tham số
m
để phương trình
( )f x m
có
đúng 2 nghiệm thực phân biệt?
A.
7.
B.
6.
C.
5.
D.
1.
Lời giải
GVSB: Trần Ba; GVPB1: Dương Ju-i; GVPB2: Bùi Văn Huấn
Chọn A
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Trang 18 TÀI LIỆU ÔN THI THPT QUỐC GIA
Ta có yêu cầu bài toán tương đương với
2
.
1
m
m
Do
2;5m
và
m
nguyên nên có 7 giá trị
m
cần tìm là
2,0,1,2,3,4,5.
Câu 37. Trong không gian
Oxyz
, cho điểm
2; 2;1M
và mặt phẳng
: 2 3 1 0P x y z
. Đường
thẳng đi qua
M
và vuông góc với mặt phẳng
P
có phương trình là
A.
2 2
2
3
1
x t
y t
z t
. B
.
2 2
2
3
1
x t
y t
z t
. C
.
2 2
2
3
1
x t
y t
z t
. D
.
2 2
3
2
1
x t
y t
z t
.
Lời giải
GVSB: Trần Thông; GVPB1: Thanh Huyền; GVPB2: Bùi Thanh Sơn
Chọn C
Đường thẳng vuông góc với mặt phẳng
P
có véc tơ chỉ phương là
( )
2; 3; 1
P
u n

.
Đường thẳng đi qua
M
và vuông góc với mặt phẳng
P
có phương trình là
2 2
2
3
1
x t
y t
z t
.
C
âu 38. Cho hình lập phương
.ABCD A B C D
có cạnh bằng
3
(tham khảo hình bên dưới).
Khoảng cách từ
B
đến mặt phẳng
ACC A
bằng
A.
3
. B.
3 2
. C.
3 2
2
. D.
3
2
.
Lời giải
GVSB: Trần Bảo Nghĩa; GVPB1: Thanh Huyền; GVPB2: Bùi Thanh Sơn
Chọn C
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 19
Gọi
O
là tâm hình vuông
ABCD
.
Do
ABCD
là hình vuông nên
BD AC
tại
O
.
Do
.ABCD A B C D
là hình lập phương nên
AA ABCD AA BD
.
BO ACC A
tại
O
2
2
;
1 3
2
Bd B AC O BDC A
.
Câu 39. Có bao nhiêu số nguyên dương
a
sao cho với mỗi
a
có đúng hai số nguyên
b
thỏa mãn
3 3 .2 16 0
b b
a
A. 34 . B. 32. C. 31. D. 33.
Lời giải
GVSB: Đoàn Văn Định; GVPB1: Trịnh Đềm; GVPB2: …
Chọn D
TH1:
1 3 3 2 16 0
b b
a
.
Nếu
1b
hoặc
4b
không thỏa mãn bpt và
2; 3b
thỏa mãn.
Vậy
1a thỏa mãn.
TH2:
1
2 3 3 2.2 16 0 3 3 2 16 0
b b b b
a
.
Nếu
1b
hoặc
3b
không thỏa mãn bpt và
2b
thỏa mãn.
Vậy
2a
không thỏa mãn.
TH3:
3 3 3 3.2 16 0
b b
a
.
Nếu
1b
hoặc
3b
không thỏa mãn bpt và
2b
thỏa mãn.
Vậy
3a
không thỏa mãn.
TH4:
3a
.
Ta cần tìm
a
để bpt
3 3 .2 16 0
b b
a
có 2 nghiệm
b
.
Nếu
3 3 3 .2 16 24. 3.8 16 0
b b
b a
không thỏa mãn bpt.
Nếu
2 3 3 .2 16 6 4.4 16 0
b b
b a
không thỏa mãn bpt.
Nếu
1b
không thỏa mãn.
Nếu
1 3 3 0
b
b
. BPT tương đương
.2 16 0
b
a
.
Hay
16
2
b
a
có hai nghiệm
b
suy ra
33 64a
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Trang 20 TÀI LIỆU ÔN THI THPT QUỐC GIA
Kết hợp lại suy ra có tất cả 33 số nguyên dương
a
thỏa mãn.
Cách 2:
Xét
3 3 .2 16 0
b b
a
. Do
*
a
nên
2
1
16
log
b
b
a
.
TH1:
2
16
log 1 8
a
a
.
BPT có đúng 2 nghiệm nguyên
2
16
3 log 4 1 2 1
b a a
a
(thỏa mãn).
TH2:
2
16
log 1 8
a
a
.
BPT có đúng 2 nghiệm nguyên
2
16
2 log 14 32 64
b a
a
có 32 giá trị
a
.
Vậy có 33 giá trị của
a
thỏa mãn.
Câu 40. Cho hàm số
4 2
3 2 1
f x a x ax
với
a
là tham số thực. Nếu
0; 3
2
max f x f thì
0; 3
min
f x
bằng
A.
9
. B.
4
. C.
1
. D.
8
.
Lời giải
GVSB: Đoàn Văn Định; GVPB1: Trịnh Đềm…; GVPB2: …
Chọn D
Xét hàm
4 2 3
3 2 1 4 3 4
f x a x ax f x a x ax
.
Hàm số đạt GTLN tại
2
x
và liên tục trên đoạn
0;3
.
2 0 32 3 8 0 4
f a a a
.
Với
4
a
ta có
4 2
8 1
f x x x
với
0;3
x .
3
4 16
f x x x
.
Cho
0
0 2
2
x TM
f x x TM
x L
.
Khi đó
0 1
f
,
2 17
f
,
3 8
f
.
Suy ra
0;3
max 2 17
f x f
(thỏa mãn giả thiết).
Vậy
0;3
min 3 8
f x f
.
Câu 41. Biết
F x
và
G x
là hai nguyên hàm của hàm số
f x
trên
và
2
0
d 2 0 0
f x x F G a a
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
y F x
,
y G x
,
0
x
và
2
x
, Khi
6
S
thì
a
bằng
A.
4
. B.
6
. C.
3
. D.
8
.
Lời giải
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 21
GVSB: Công Phan Đình; GVPB1: …; GVPB2: …
Chọn C
F x
và
G x
là hai nguyên hàm của hàm số
f x
trên
nên ta có
:
x F x G x C
(với
C
là hằng số).
Do đó
0 0
F G C
(1).
Lại có
2
0
d 2 0
f x x F F
2 0 2 0 0 0
F G a F F F G a
(2).
Từ (1) và (2) suy ra
C a
.
Khi đó
F x G x a
, x
F x G x a
, x
.
Diện tích hình phẳng giới hạn bởi các đường
y F x
,
y G x
,
0
x
và
2
x
là
2 2
0 0
.d .d 2 6 3
S F x G x x a x a a
.
Câu 42. Cho các số phức
1 2 3
, ,
z z z
thỏa mãn
1 2 3
2 2 2
z z z
và
1 2 3 1 2
2
z z z z z
. Gọi
, ,
A B C
lần
lượt là các điểm biểu diễn của
1 2 3
, ,
z z z
trên mặt phẳng tọa độ. Diện tích tam giác
ABC
bằng
A.
3 3
4
. B.
3
8
. C.
3 3
8
. D.
3
4
.
Lời giải
GVSB: Hoàng Đức Hùng; GVPB1: Vũ Thơm; GVPB2: Nguyễn Thị Thùy Nương.
Chọn A
- Từ giả thiết ta được
1 2
1
z z
và
3
2
z
.
- Theo giả thiết
1 2 3 1 2 1 2 3 1 2 1 2
2 2 1
z z z z z z z z z z z z
.
- Từ đẳng thức
2 2 2 2
1 2 1 2 1 2 1 2
2 3 3.
z z z z z z z z AB
- Theo giả thiết
1 2 3 1 2 1 2 3 1 3 2
2 2
z z z z z z z z z z z
1 2 3 1 3 2
2
z z z z z z
1 3
3 3.
z z AC
- Theo giả thiết
1 2 3 1 2 3 2 1 1 3 2
2
z z z z z z z z z z z
3 2 1 1 3 2
z z z z z z
3 2
3 3.
z z BC
Suy ra tam giác
ABC
đều cạnh
3
. Suy ra
3 3
4
ABC
S
.
Câu 43. Cho khối lăng trụ đứng .
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
, cạnh bên
2
AA a
, góc giữa hai mặt phẳng
A BC
và
ABC
bằng
60
. Thể tích của khối lăng trụ đã
cho bằng
A.
3
8
9
a
. B.
3
8
a
. C.
3
8
3
a
. D.
3
24
a
.
Lời giải
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Trang 22 TÀI LIỆU ÔN THI THPT QUỐC GIA
GVSB: Phan Thị Thúy Hà; GVPB1: Tuyet Trinh; GVPB2: Nguyễn Thị Hồng Gấm
Chọn C
Gọi
I
là trung điểm của
BC
.
Ta có: +
ABC
là tam giác vuông cân tại
A
nên
AI BC
+
.ABC A B C
là khối lăng trụ đứng nên
AA BC
suy ra
BC AA I BC A I
.
Do đó, góc giữa hai mặt phẳng
A BC
và
ABC
bằng góc giữa
A I
và
AI
, mà tam giác
AA I
vuông tại
A
nên ta có
AIA
là góc nhọn. Suy ra góc giữa hai mặt phẳng
A BC
và
ABC
bằng
60AIA
.
Trong tam giác vuông
AA I
, ta có
2
tan 60
3
AA a
AI
.
ABC
là tam giác vuông cân tại
A
nên
4
2
3
a
BC AI ,
2 6
3
2
BC a
AB AC .
Vậy thể tích khối lăng trụ đã cho là
2
3
1 1 2 6 8
. . . .2 .
2 2 3 3
ABC
a a
V AA S AA AB AC a
.
Câu 44. Cho hình nón có góc ở đỉnh bằng
120
và chiều cao bằng
2
. Gọi
S
là mặt cầu đi qua đỉnh và
chứa đường tròn đáy của hình nón đã cho. Diện tích của
S
bằng
A.
16
3
. B.
64
3
. C.
64
. D.
48
.
Lời giải
GVSB: …; GVPB1: …; GVPB2: Lê Duy
Chọn C
Gọi hình nón đỉnh
A
, đường kính đáy hình nón là
BC
.
Gọi
I
là tâm mặt cầu
S
.
I
C'
B'
A
C
B
A'
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 23
Ta có
ABC
cân tại
A
có
120BAC và
AI BC
tại
O
nên
60BAI suy ra
IAB
đều.
Tam giác
IAB
đều và
OB IA
tại
O
suy ra
OB
là đường trung tuyến của
IAB
.
Mà
2OA
suy ra
2 4AI OA
.
Vậy diện tích mặt cầu
S
là:
2
4 64S AI
.
Câu 45: Xét tất cả các số thực
x
,
y
sao cho
3
2
2
6 log9
8
x ay
a
với mọi số thực dương
a
. Giá trị nhỏ nhất
của biểu thức
2 2
6 8P x y x y bằng
A.
21
. B.
6
. C.
25
. D.
39
.
Lời giải
GVSB: Tu Duy; GVPB: Thien Pro
Chọn A
Ta có:
3
2
2
6 log
9
8
x a
y
a
,
0a
2
2 2
3 9 6 3log logy x a a
,
0a
2 2
2 2
log 2 log 9 0a x a y
,
0a
2 2
9 0x y
.
Gọi
;M x y
thuộc hình tròn
C
tâm
O
, bán kính
3R
.
Gọi
3;4A
, ta có:
5OA R
. Do đó
A
nằm ngoài hình tròn
C
.
Khi đó:
2 2 2
2
3 4 25 25 25 21P x y MA OA R
.
Vậy
min 21P
khi
, ,O M A
theo thứ tự thẳng hàng.
Câu 46. Cho hàm số bậc bốn
y f x
. Biết rằng hàm số
lng x f x
có bảng biến thiên như sau
O
B
I
C
A
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Trang 24 TÀI LIỆU ÔN THI THPT QUỐC GIA
Diện tích hình phẳng giới hạn bởi các đường
y f x
và
y g x
thuộc khoảng nào dưới
đây?
A.
7;8
. B.
6;7
. C.
8;9
. D.
10;11
.
Lời giải
GVSB:; GVPB1: Hoàng Ngọc Hùng; GVPB2: Nam Bui
Chọn A
Từ BBT của
g x
ta có
ln ln 4 4;f x f x x R
.
Ta có
f x
g x
f x
.
Xét phương trình
0 (*)
1 (**)
f x
f x g x
f x
Do
4;f x x R
suy ra phương trình
(**)
vô nghiệm.
Từ đó suy ra
1
2
3
0 0
x x
f x g x x x
x x
.
M
ặt khác
1
. 1f x g x f x
f x
.
Ta có bảng xét dấu
Vậy
3 3
2
1 1 2
d d d
x x
x
x x x
S f x g x x f x g x x f x g x x
32
1 2
xx
x x
f x g x f x g x
2 1 3 2 1 3
2 2ln ln lnf x f x f x f x f x f x
199 199
2 12 4 2ln ln12 ln 4 7,704 7;8
16 16
.
Câu 47. Trong không gian
Oxyz
, cho điểm
2;1;1A
. Gọi
P
là mặt phẳng chứa trục
Oy
sao cho
khoảng cách từ
A
đến
P
lớn nhất. Phương trình của
P
là
A.
0x z . B. 0x z . C. 2 0x z . D. 2 0x z .
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 25
Lời giải
GVSB: …; GVPB1: …; GVPB2: Vũ Hồng Toàn
Chọn C
Gọi
H
và
K
lần lượt là hình chiếu của
A
trên
P
và trục
Oy
.
Ta có
,d A P AH AK
. Do đó khoảng cách từ
A
đến
P
lớn nhất khi
0;1;0H K
.
Khi đó
P
đi qua
0;1;0K
và có một vectơ pháp tuyến là
2;0; 1 2;0;1AK
nên có
phương trình là
2 0x z
.
Câu 48. Có bao nhiêu số phức
z
thỏa
2
2z z z và
2
4 4 4z z i z i
.
A.
4
. B.
2
. C.
1
D.
3
.
Lời giải
GVSB: Tran Phuc; GVPB1: Tran Phuc; GVPB2: Ngô Trí Thụ
Chọn A
Gọi
z a bi
,
,a b
.
Ta có :
2 2 2
2 4z z z a b b (1).
2 2
4 4 4 4 . 4 4z z i z i z z i z i
2 2 2
2 2 2
4 . 4 4a b a b a b
2 2 2
2 2 2
4 . 4 4 0a b a b a b
.
+ TH-1:
2
2
0
4 0
4
a
a b
b
thỏa (1) .
Vậy
4z i
.
+ TH-2:
2 2
2 2
4 4 0a b a b a b
.
Thay vào ta được (1) :
2
2 4 0 0 2b b b b
.
Với
0
0 0 0
0
b
b b z
a
.
Với
2 2
2 2 2 2 2 2
2 2
b b
b b z i z i
a a
.
Kết luận: có 4 số phức
z
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Trang 26 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 49. Có bao nhiêu số nguyên dương của tham số
m
để hàm số
4 2
64y x mx x
có đúng 3 điểm
cực trị ?
A.
23
. B.
12
. C.
24
. D.
11
.
Lời giải
GVSB: Lê Năng; GVPB1: …; GVPB2: Nguyễn Ninh
Chọn C
Xét hàm số
4 2
64g x x mx x
;
3
4 2 64g x x mx
; có
lim
x
f x


.
3
0
0
64 0
x
g x
x mx
0g x
có ít nhất 2 nghiệm phân biệt.
Do đó hàm số
y g x
có đúng 3 điểm cực trị hàm số
y g x
có đúng 1 cực trị
g x
đổi dấu đúng 1 lần (*).
Nhận xét nếu
0 0 64 0x g
g x
không có cực trị (hay
0x
không thỏa mãn).
Nên
2
32
0 2g x m x
x
. Đặt
2
32
2h x x
x
.
Có
3
2 2
4 8
32
4
x
h x x
x x
;
0 2h x x
.
Bảng biến thiên
Từ bảng biến thiên suy ra
* 24m
.
Kết hợp với điều kiện
m
nguyên dương suy ra
1;2;3;...;24m
.
Câu 50. Trong không gian
Oxyz
, cho mặt cầu
S
tâm
1;4;2I
, bán kính bằng 2. Gọi
,M N
là hai điểm
lần lượt thuộc hai trục
,Ox Oy
sao cho đường thẳng
MN
tiếp xúc với
S
, đồng thời mặt cầu
ngoại tiếp tứ diện
OIMN
có bán kính bằng
7
2
. Gọi
A
là tiếp điểm của
MN
và
S
, giá trị
.AM AN
bằng
A.
9 2
. B.
14
. C.
6 2
. D.
8
.
Lời giải
GVSB: Tuấn Anh; GVPB1: Anh Tuấn; GVPB2: Anh Tuấn
Chọn C
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 27
Gọi
;0;0 , 0; ;0M a Ox N b Oy
.
Ta có
; 2d I Oxy R
nên
S
tiếp xúc với mặt phẳng
Oxy
tại điểm
1;4;0A
và
MN
cũng đi qua
A
.
Lại có
1; 4;0 , 1; 4;0AM a AN b
và 3 điểm
, ,A M N
thẳng hàng nên ta được:
1 4
1 4 4 1
1 4
a
a b
b
.
Tứ diện
OIMN
có
IA OMN
và
OMN
vuông tại
O
nên nếu gọi
J
là tâm mặt cầu ngoại
tiếp tứ diện
OIMN
thì
J IMN
.
Suy ra bán kính mặt cầu ngoại tiếp tứ diện
OIMN
bằng bán kính đường tròn ngoại tiếp
IMN
.
Ta có
. .
4
IMN
IM IN MN
S
r
(với
7
2
r
bán kính đường tròn ngoại tiếp
IMN
).
1 . .
. . 7 . 14
7
2
4.
2
IM IN MN
IA MN IM IN IA IM IN
2 2
1 20 4 5 196 2a b
.
Đặt
1
4
m a
n b
.
Từ (1|) và (2) ta có hệ
2 2
2
2
4
3
4
16
20 5 196
20 5 196 4
n
mn
m
m n
m
m
.
T
ừ (4) ta được:
2 2 2
20 16 5 196m m m
4 2 2
5 80 320 0 8m m m
2 2 2
2 2 2
m n
m n
.
Suy ra
1 2 2, 4 2
1 2 2, 4 2
a b
a b
. Vậy
. 6 2AM AN
.

Tài liệu khác của Toán

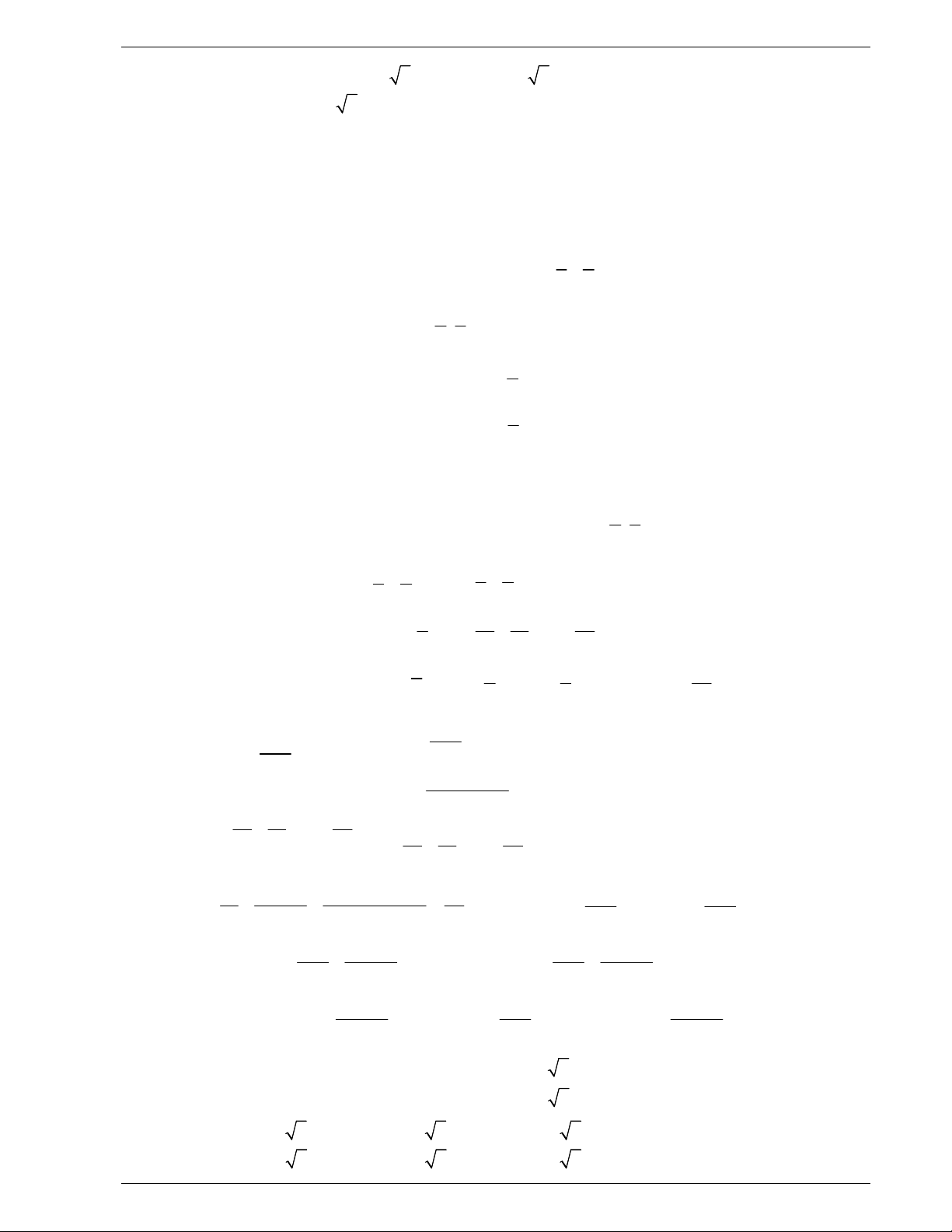
Preview text:

BỘ GD&ĐT
ĐỀ THI TN THPT NĂM HỌC 2021 – 2022 MÔN THI: TOÁN
DIỄN ĐÀN GIÁO VIÊN TOÁN
Thời gian: 90 phút (Không kể thời gian phát đề) MÃ ĐỀ 101 2 2 1  Câu 1. Nếu f  xdx  4 thì f  x  2 dx  bằng 2  0 0  A. 6 . B. 8 . C. 4 . D. 2 .
Câu 2. Cho khối lăng trụ có diện tích đáy là 2 3a và chiều cao 2 .
a Thể tích khối lăng trụ đã cho bằng A. 3 a . B. 3 6a . C. 3 3a . D. 3 2a . 5 1 Câu 3. Nếu f  xdx  3 thì f  xdx bằng 1  5 A. 5 . B. 6 . C. 4 . D. 3 . Câu 4. Cho f
 xdx  cos x C.Khẳng định nào dưới đây đúng? A. f x  sin . x B. f x  cos . x C. f  x  sin . x D. f  x  cos . x
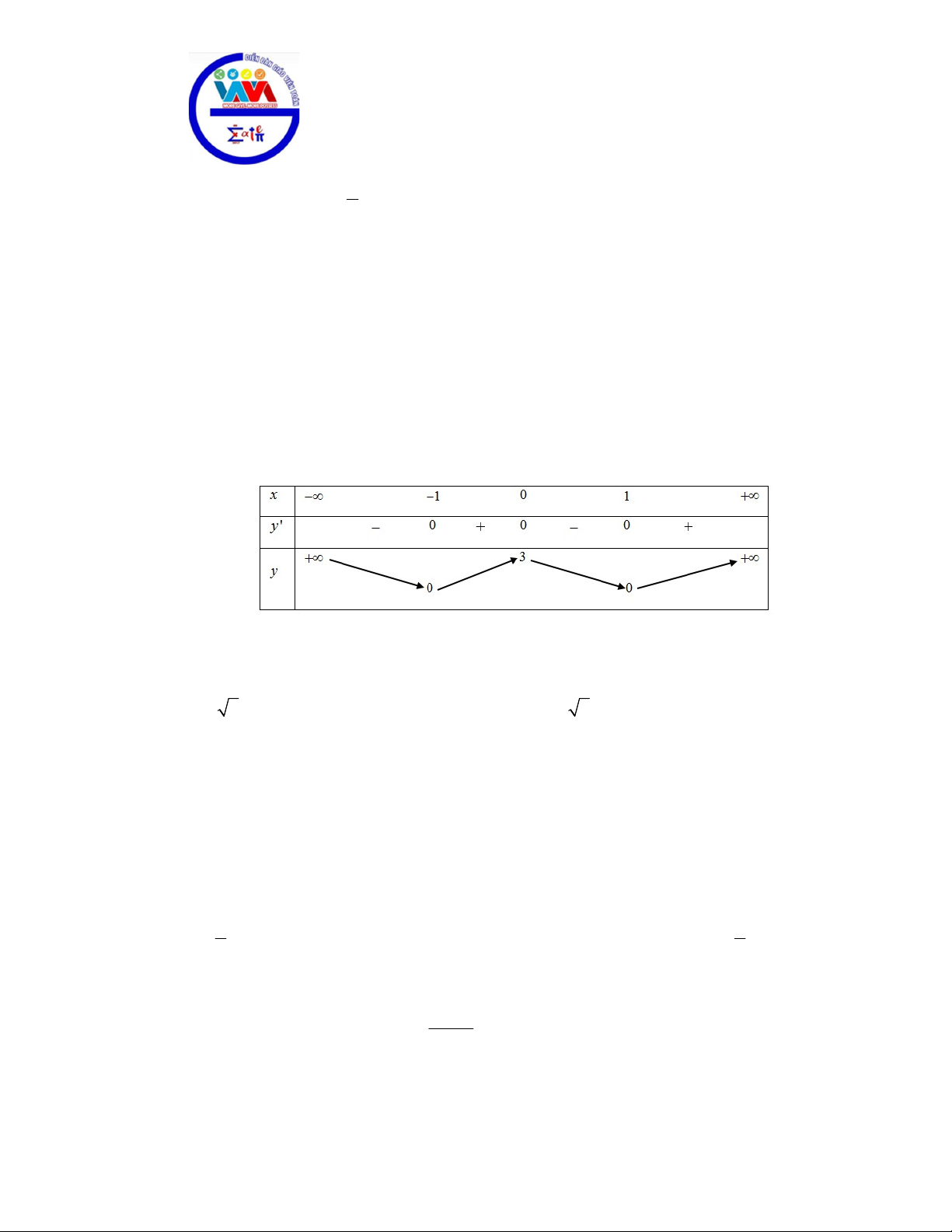
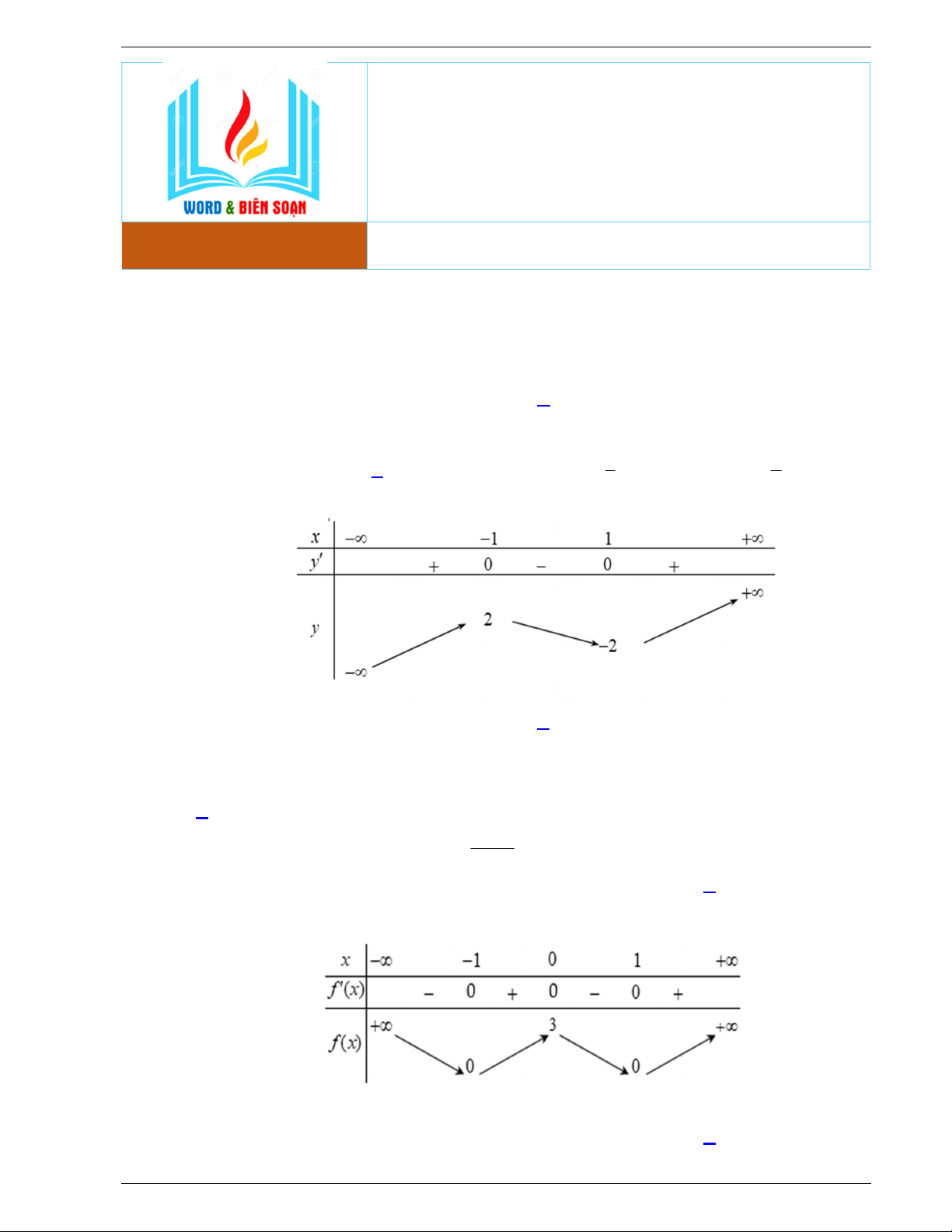
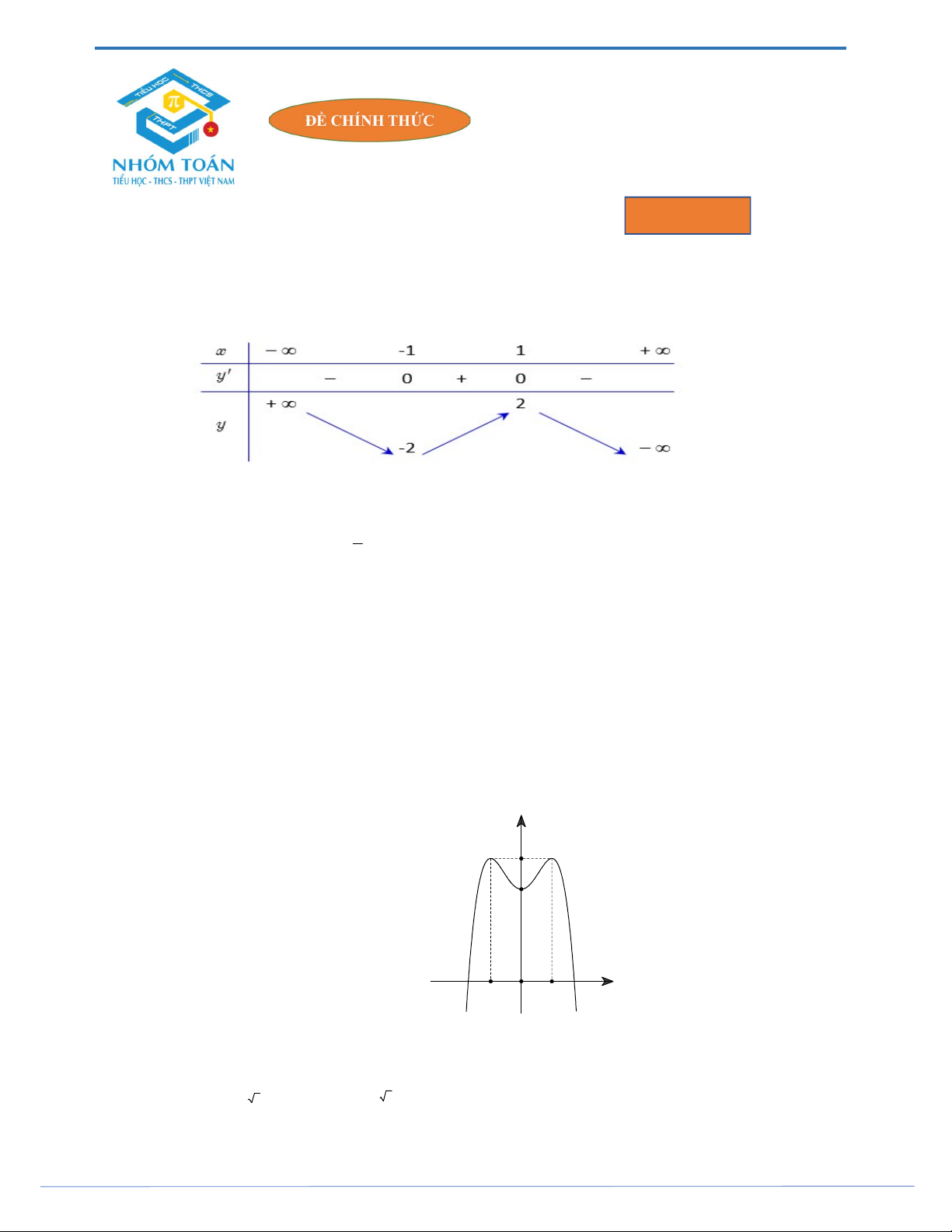
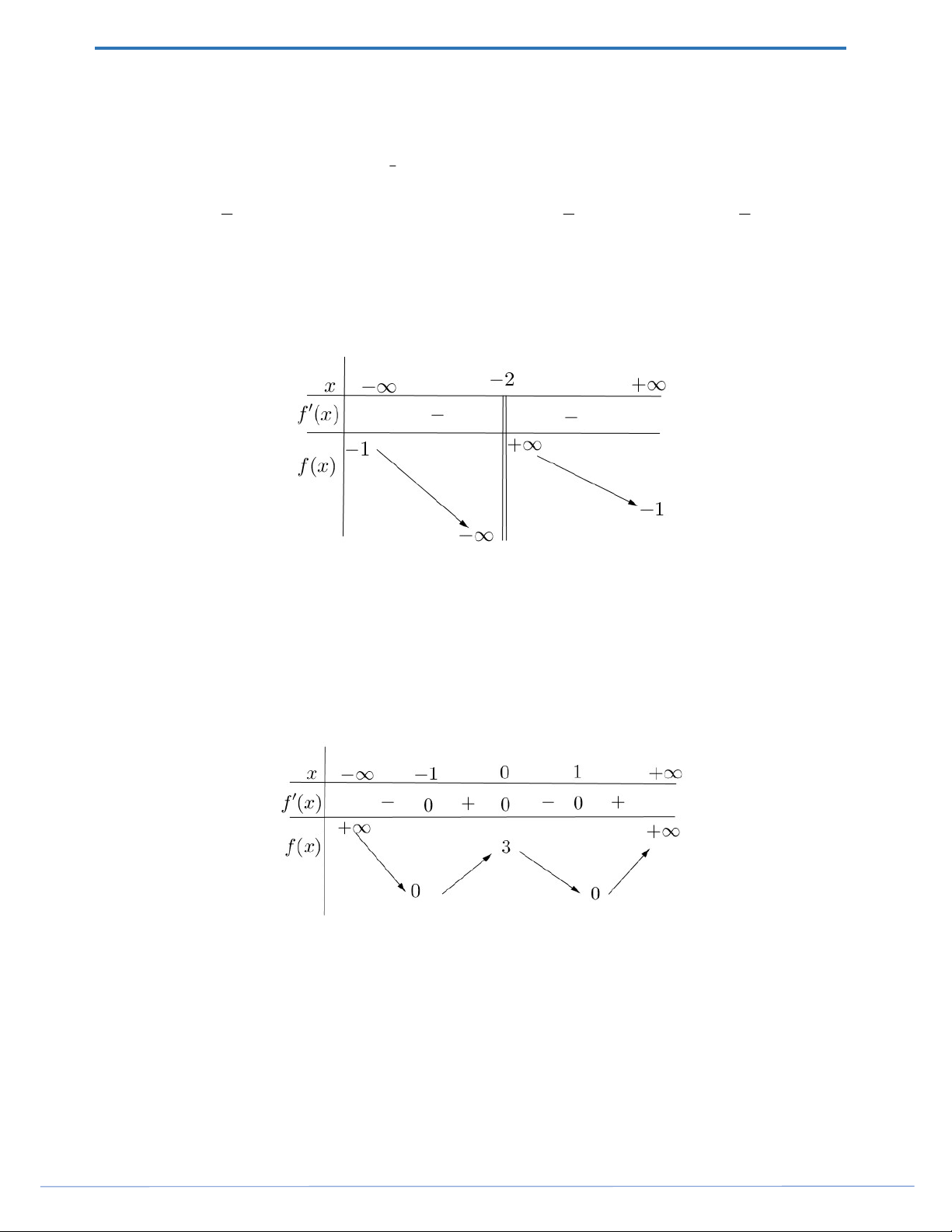
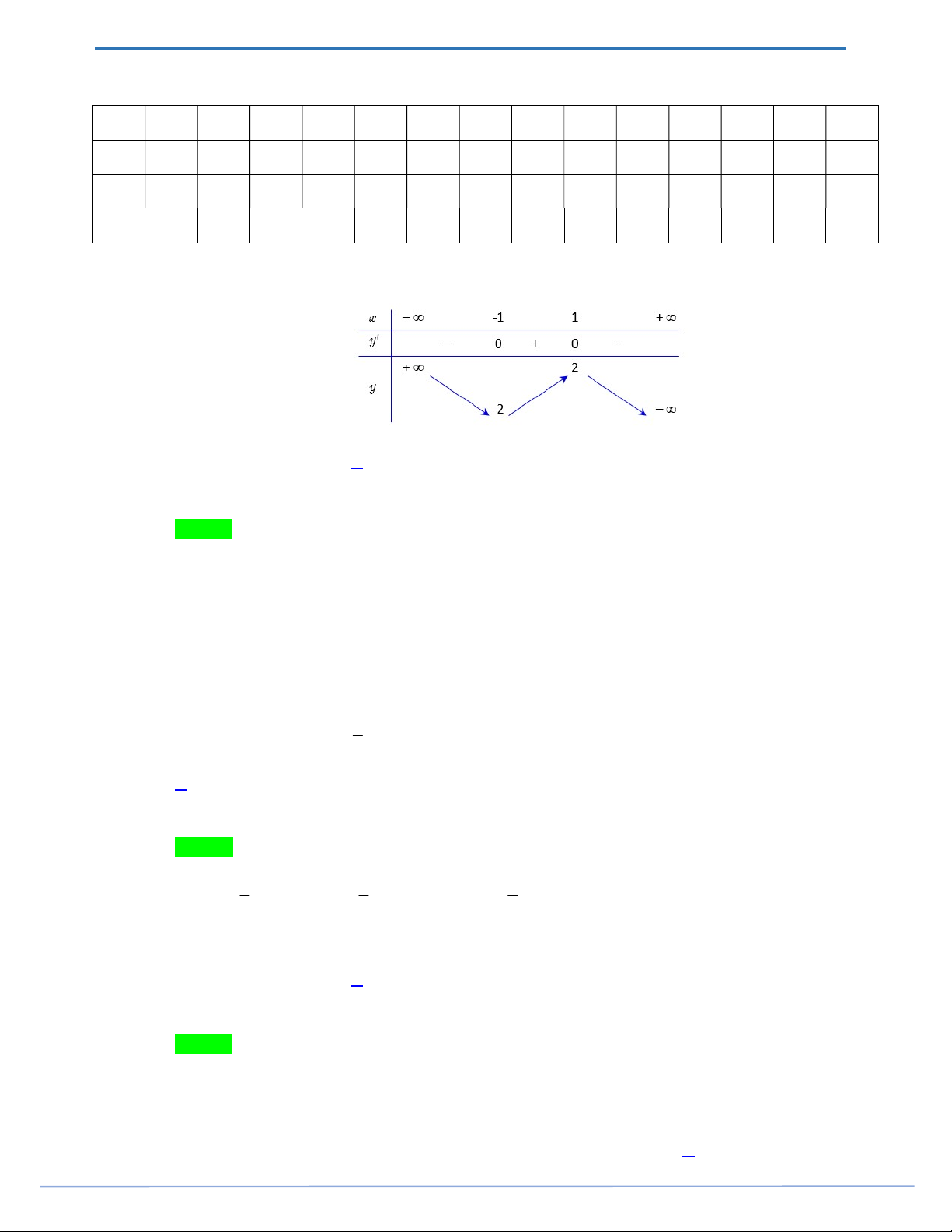
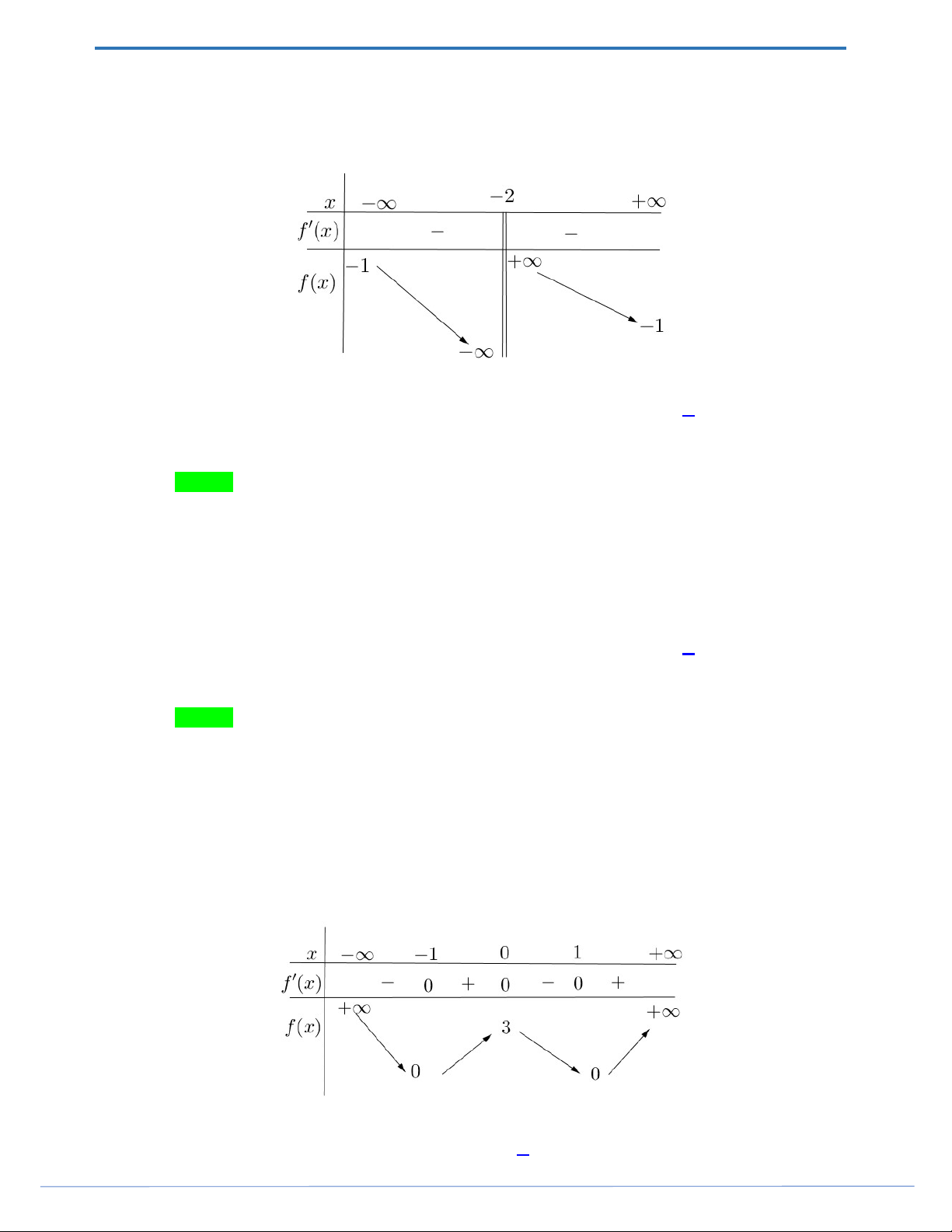
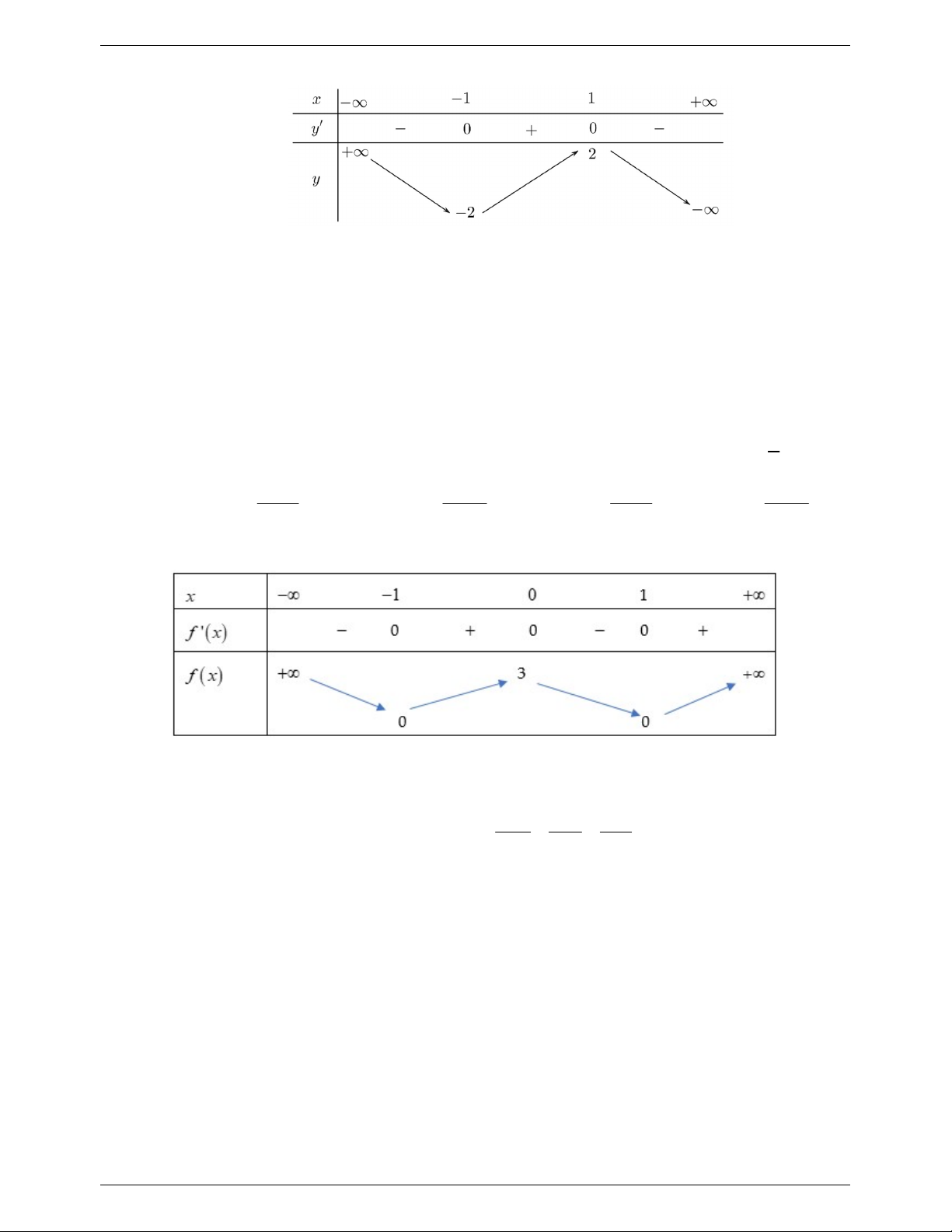
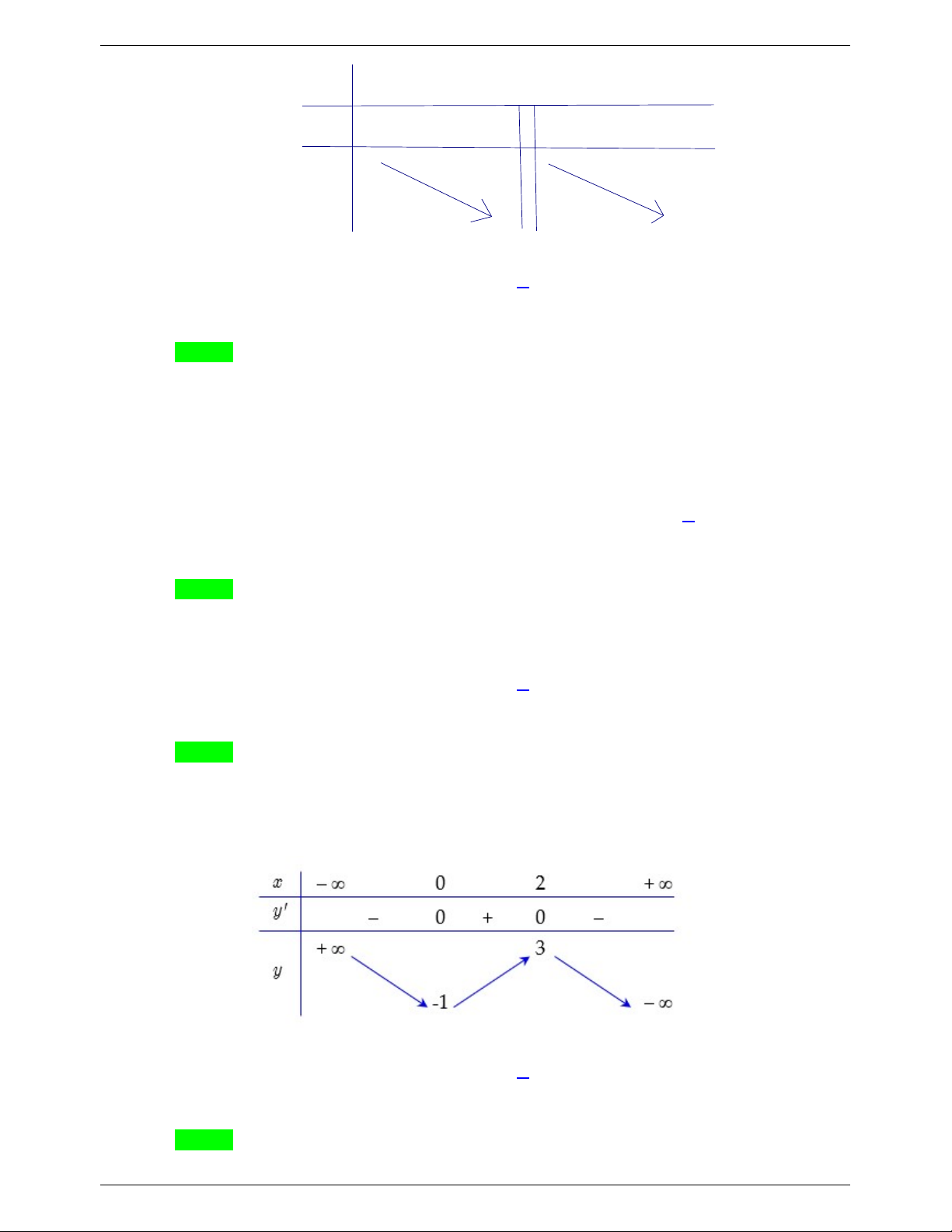
Câu 5. Cho hàm số y  f  x có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 1; . B. 0;  1 . C. 1;0. D. 0; .
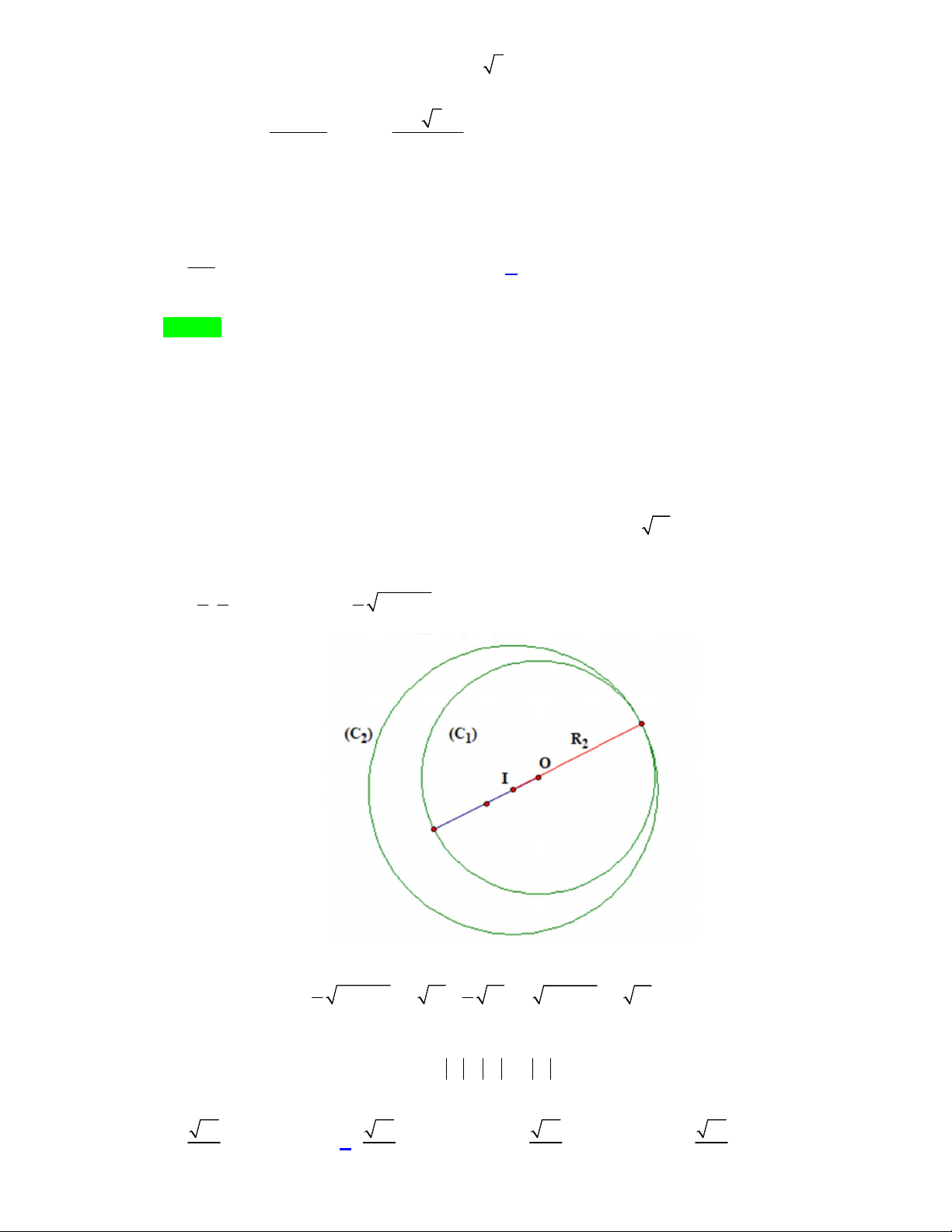
Câu 6. Trong không gian Oxyz, cho mặt cầu S  x   y  2   z  2 2 : 2
1  6. Đường kính của S  bằng: A. R  6. B. 12. C. R  2 6. D. 3.
Câu 7. Trong không gian Oxyz , cho điểm A1;2;  3 . Hình chiếu vuông góc của A lên mặt phẳng Oxy có tọa độ là A. 0;2; 3 . B. 1;0; 3 . C. 1;2;0 . D. 1;0;0 .
Câu 8. Cho khối chóp S.ABC có chiều cao bằng 3 , đáy ABC có diện tích bằng 10 . Thể tích khối chóp S.ABC bằng A. 2 . B. 15 . C. 10 . D. 30 .
Câu 9. Cho cấp số nhân u
với u  1 và u  2 . Công bội của cấp số nhân đã cho là: n  1 2 1 1 A. q  . B. q  2 . C. q  2  . D. q   . 2 2
Câu 10. Cho hình trụ có chiều cao h  1 và bán kính r  2 . Diện tích xung quanh của hình trụ đã cho bằng A. 4 . B. 2 . C. 3 . D. 6 . 2x 1
Câu 11. Tiệm cận ngang của đồ thì hàm số y 
là đường thẳng có phương trình: 2x  4 A. x  2 . B. x  1 . C. y  1. D. y  2 .
Câu 12. Tập nghiệm của bất phương trình log x 1  2 là 5   A. 9; . B. 25; . C. 31; . D. 24; .
Câu 13. Hàm số nào dưới đây có bảng biến thiên như sau? Trang 1/22 - WordToan A. 4 2 y  x  2x . B. 3 y  x  3x . C. 4 2 y  x  2x . D. 3 y  x  3x .
Câu 14. Môđun của số phức z  3  4i bằng A. 25 . B. 7 . C. 5 . D. 7 . Câu 15. Cho hàm số   4 2
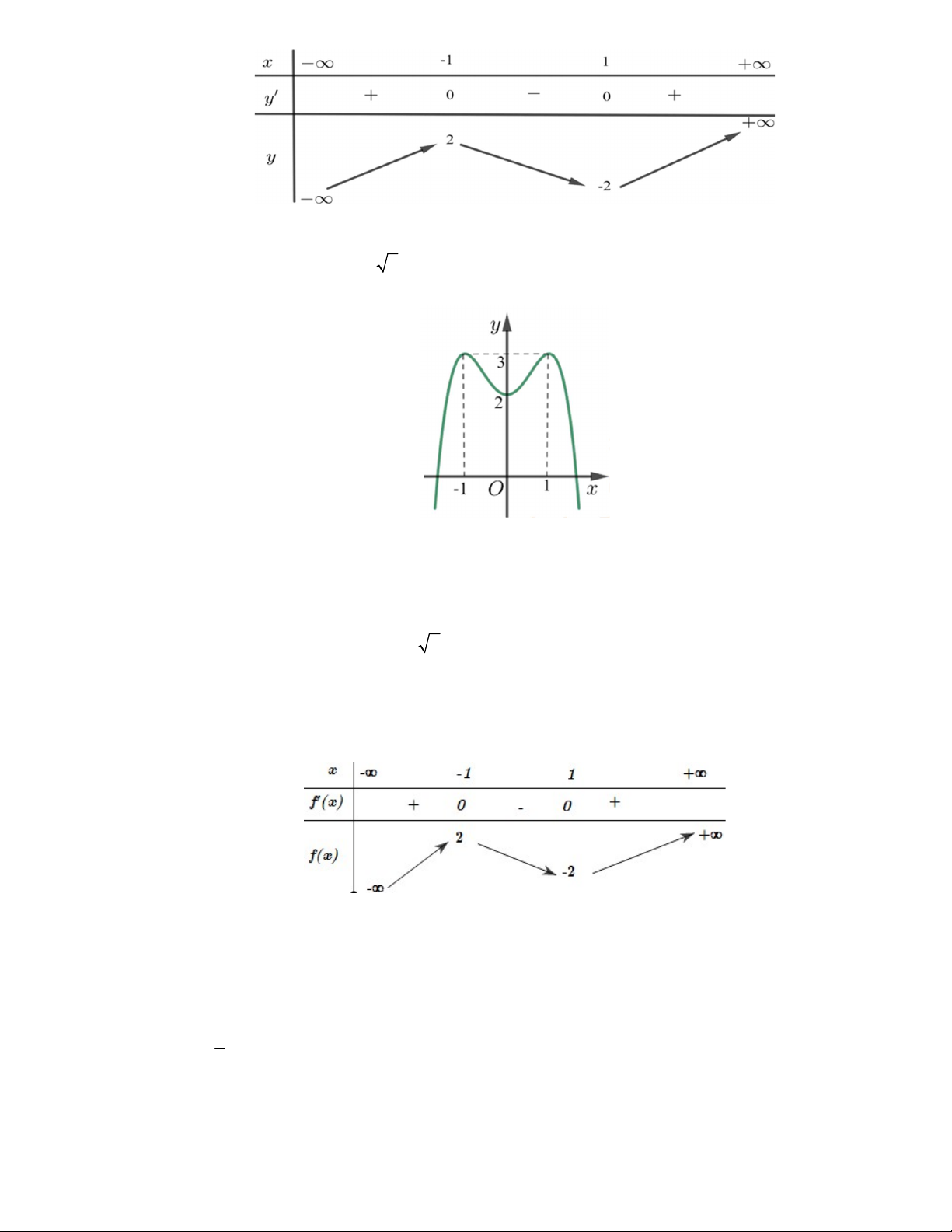
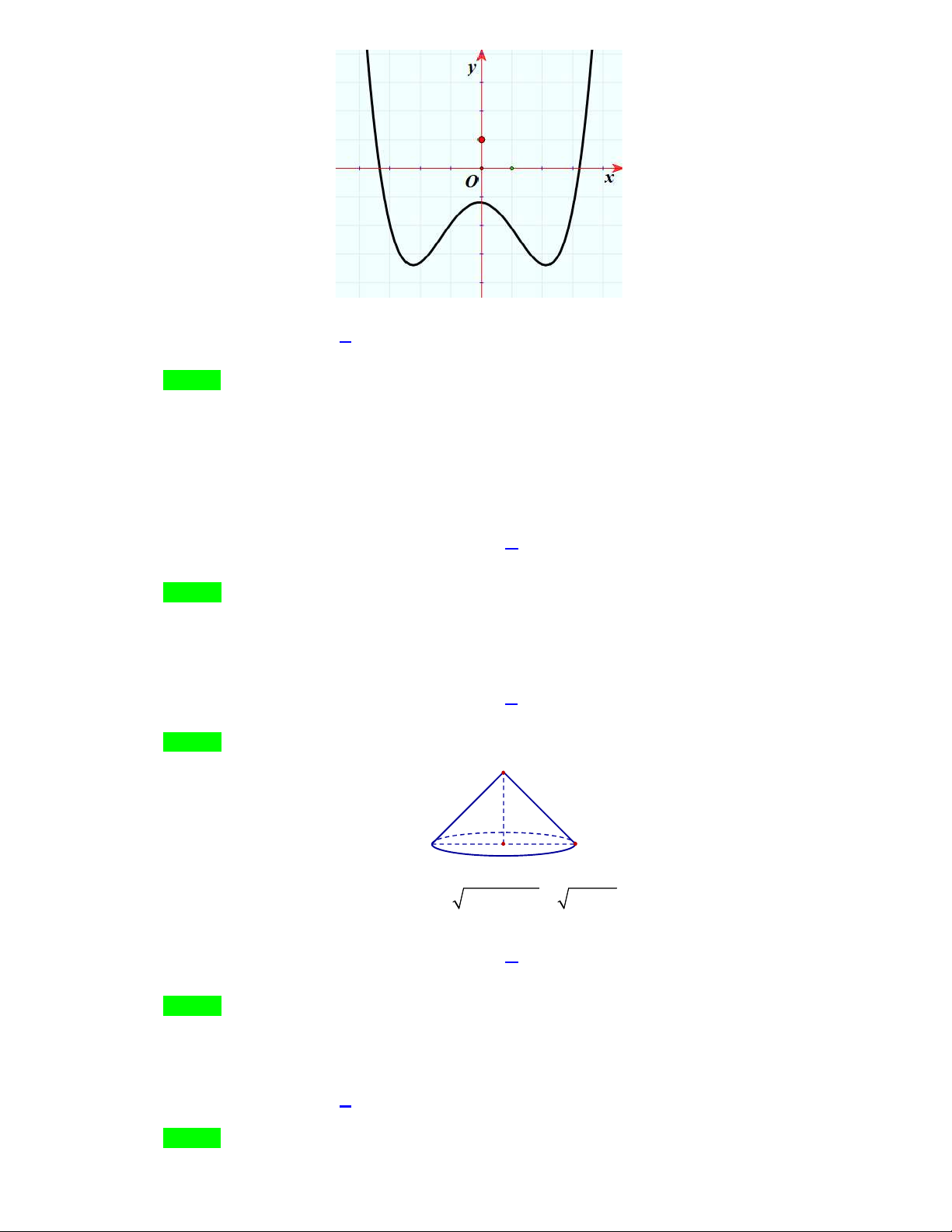
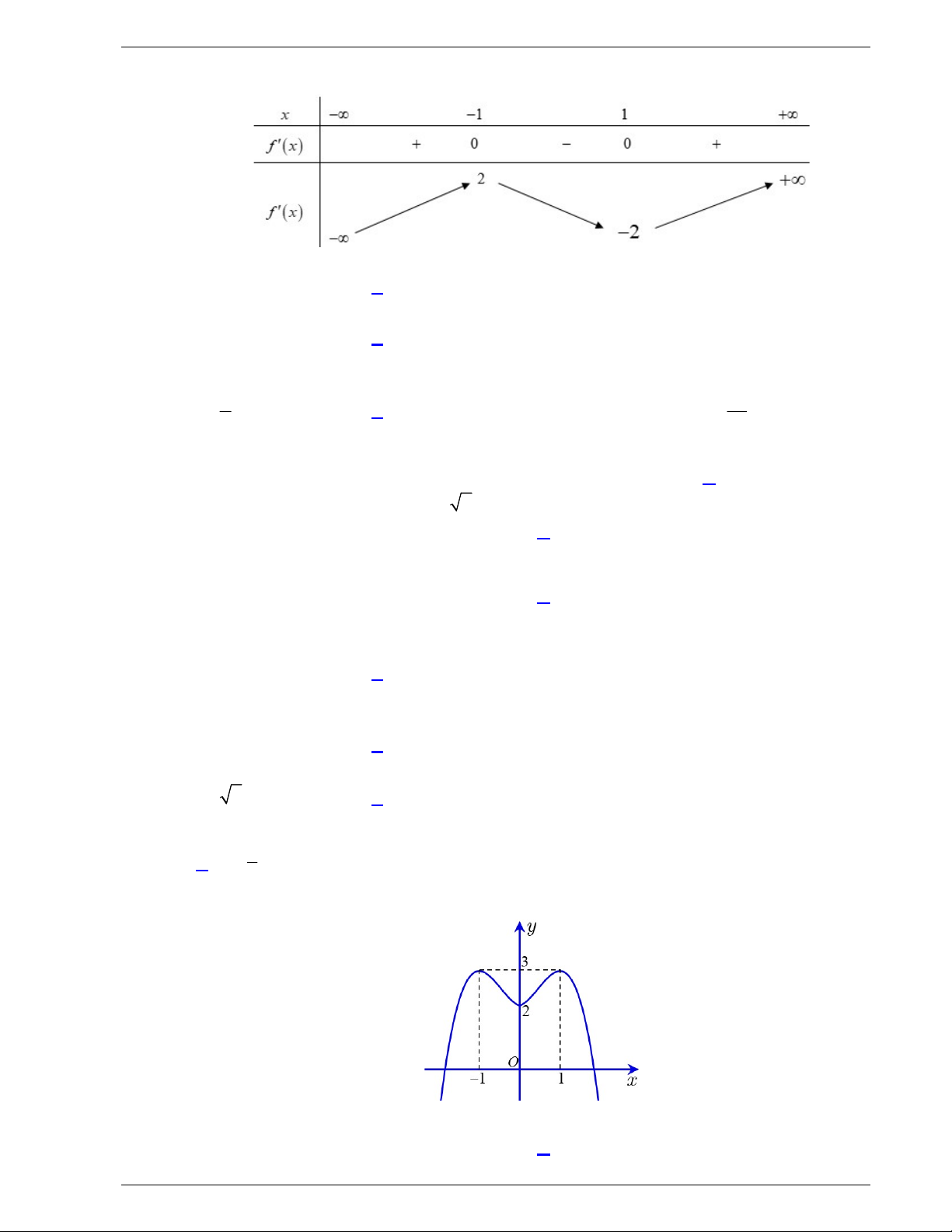
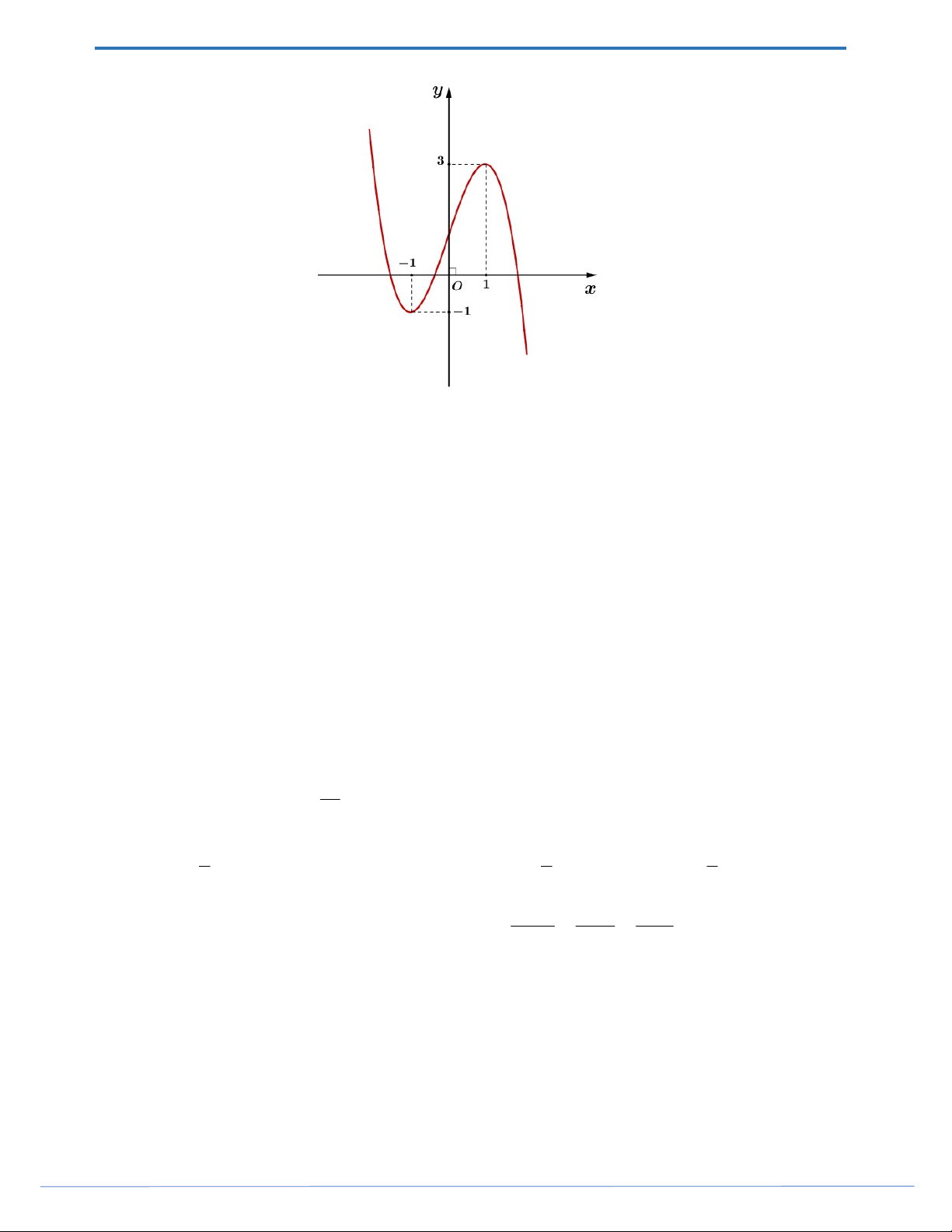
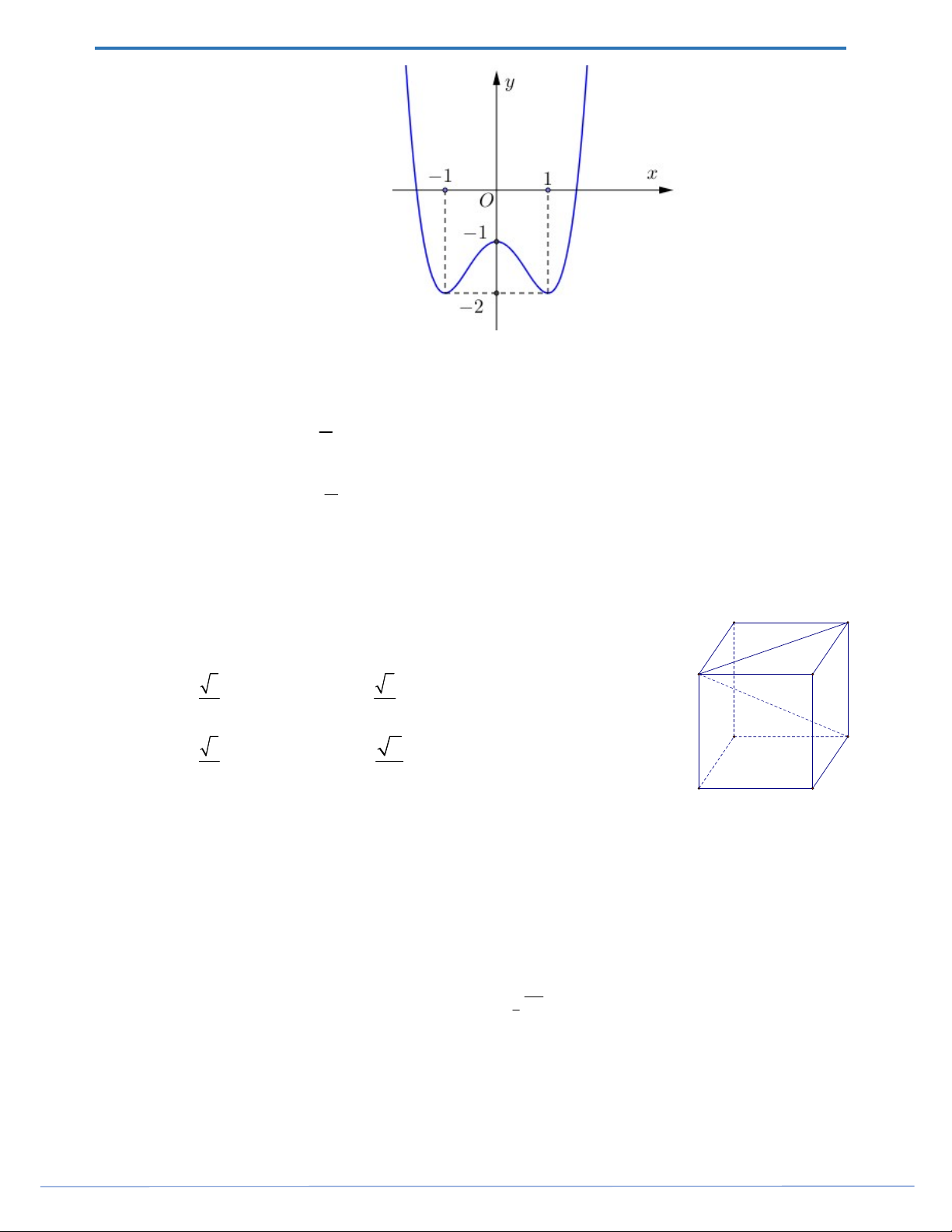
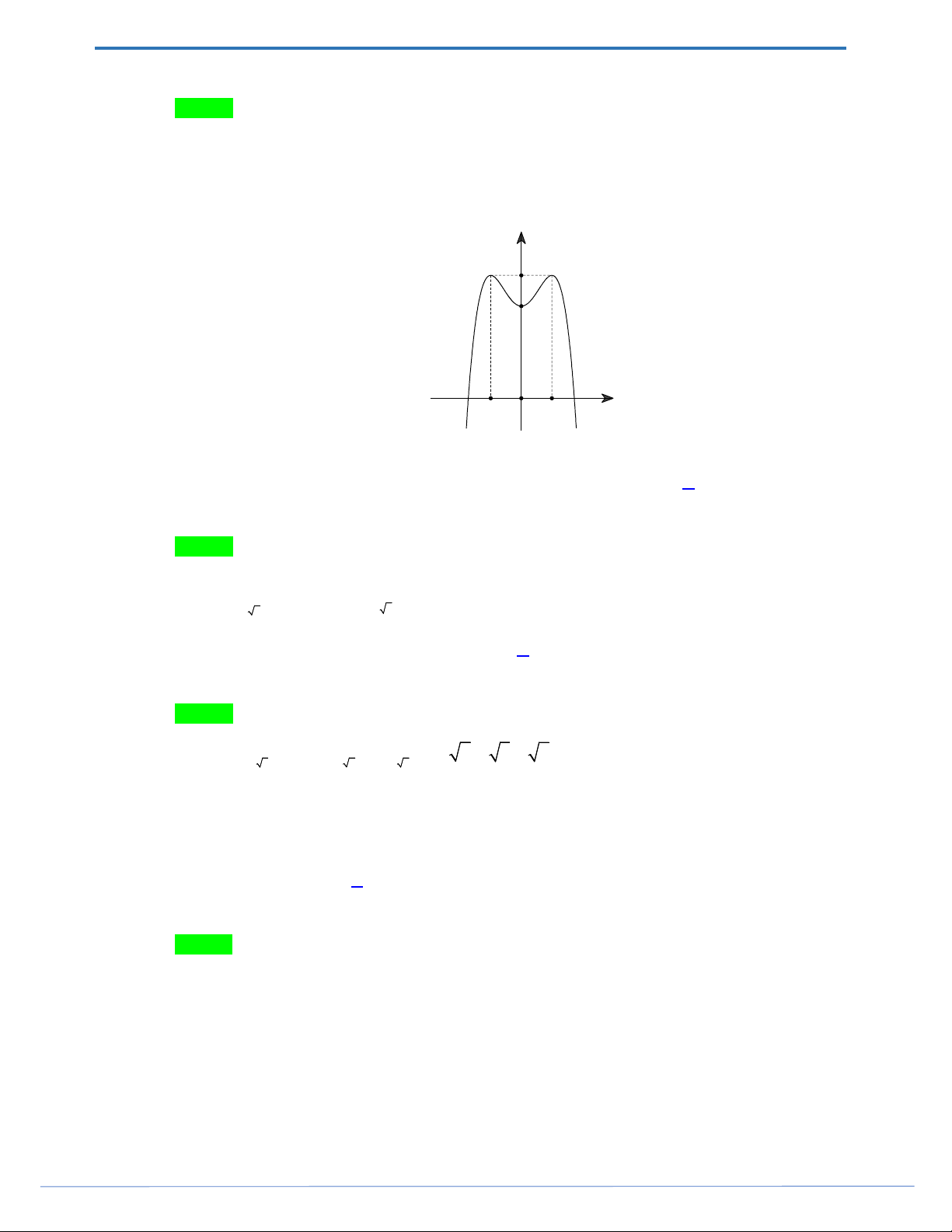
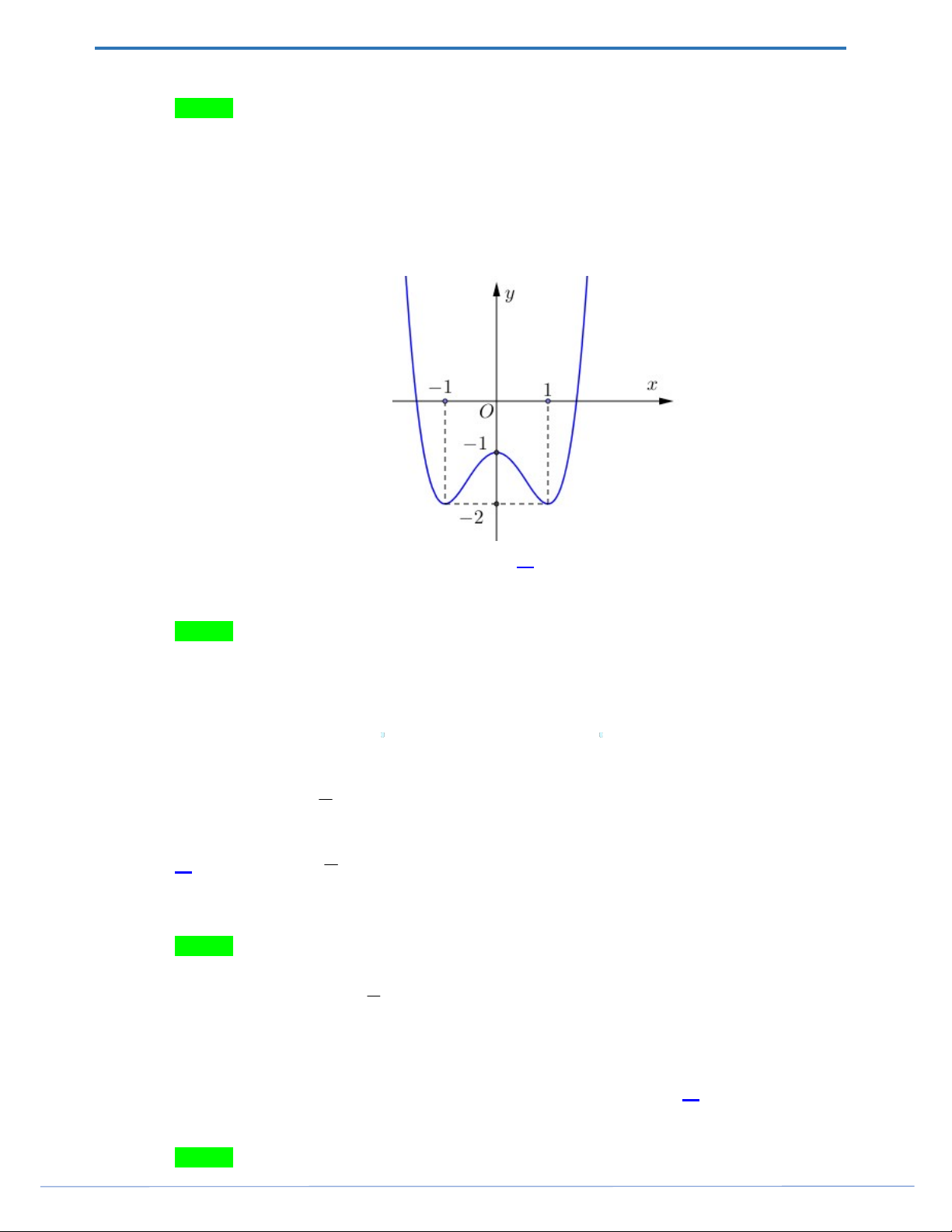
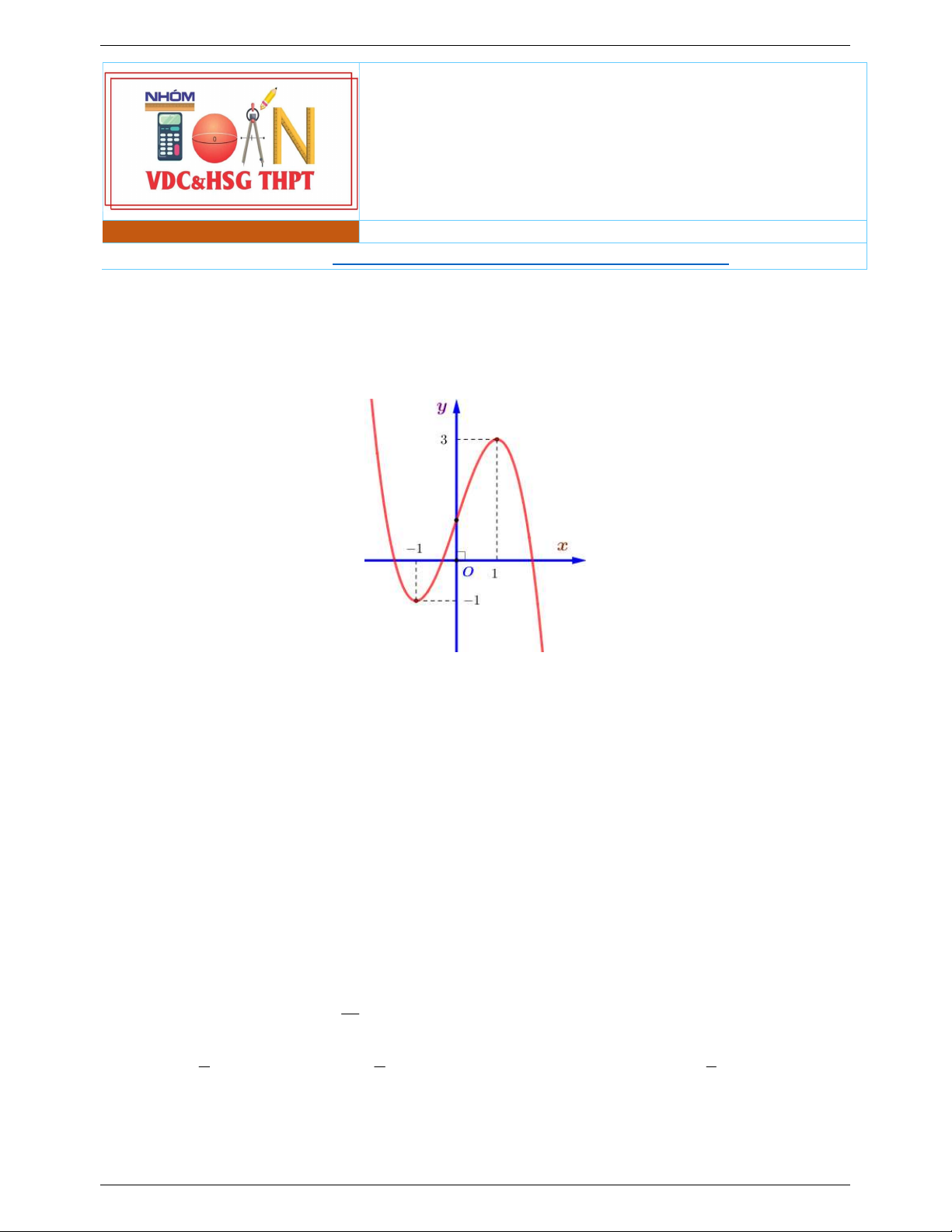
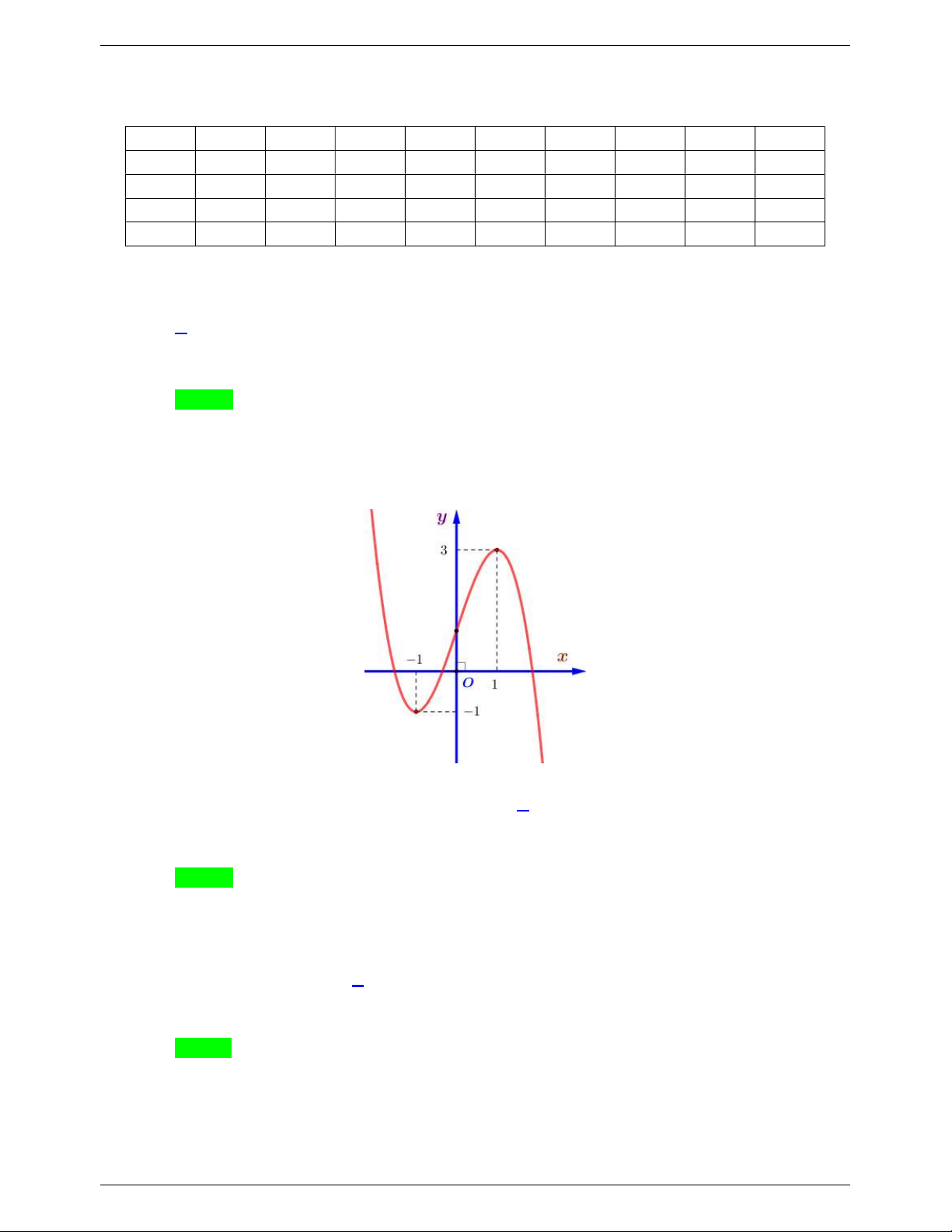
f x  ax  bx  c có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình f  x  1 là A. 1. B. 2 . C. 4 . D. 3 .
Câu 16. Tập xác định của hàm số y  log x  4 là 3   A. 5; . B.  ;   . C. 4; . D.  ;  4 .
Câu 17. Với a là số thực dương tùy ý, 4log a bằng A. 2  log a . B. 2 log a . C. 4  log a . D. 8log a .
Câu 18. Số các tổ hợp chập 3 của 12 phần tử là A. 1320 . B. 36 . C. 220 . D. 1728 .
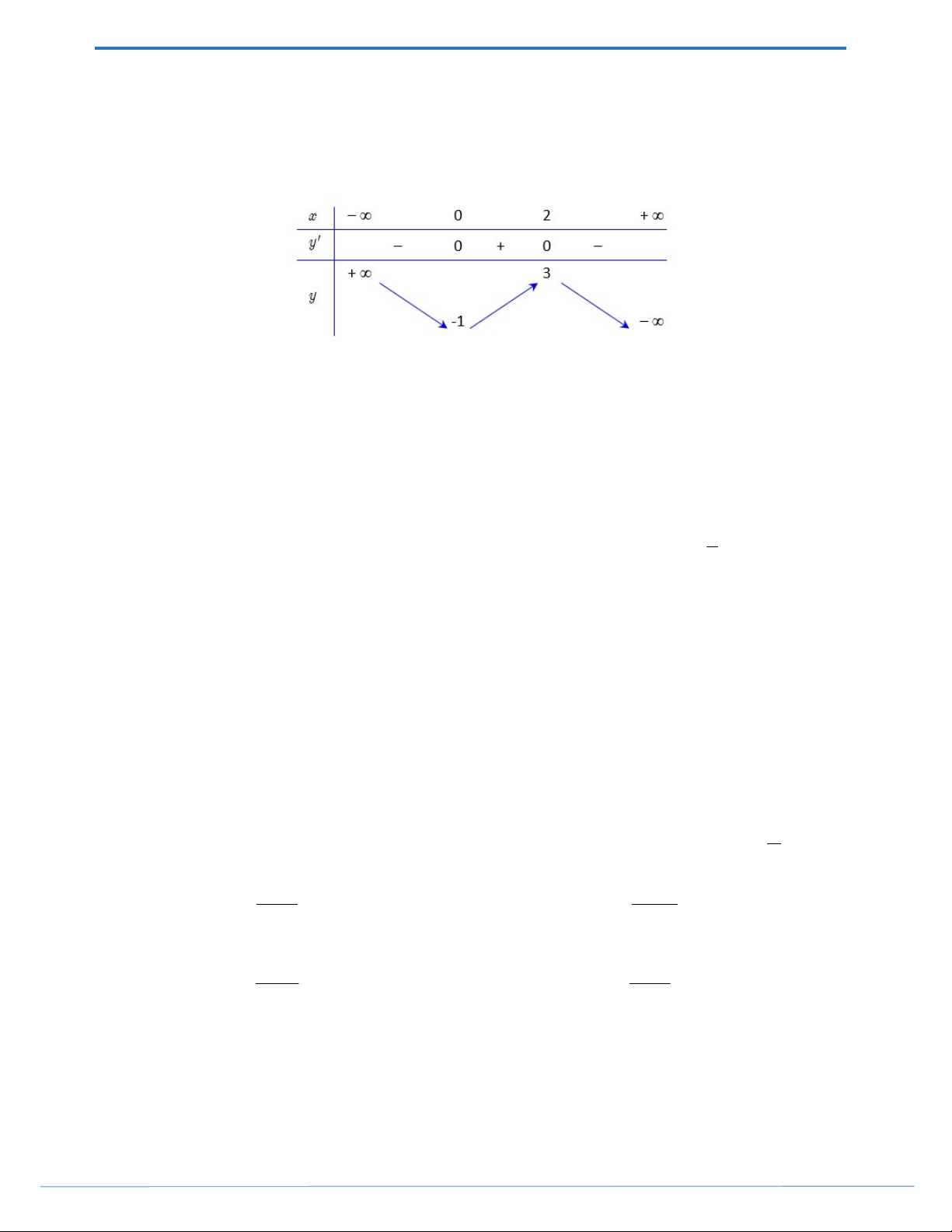
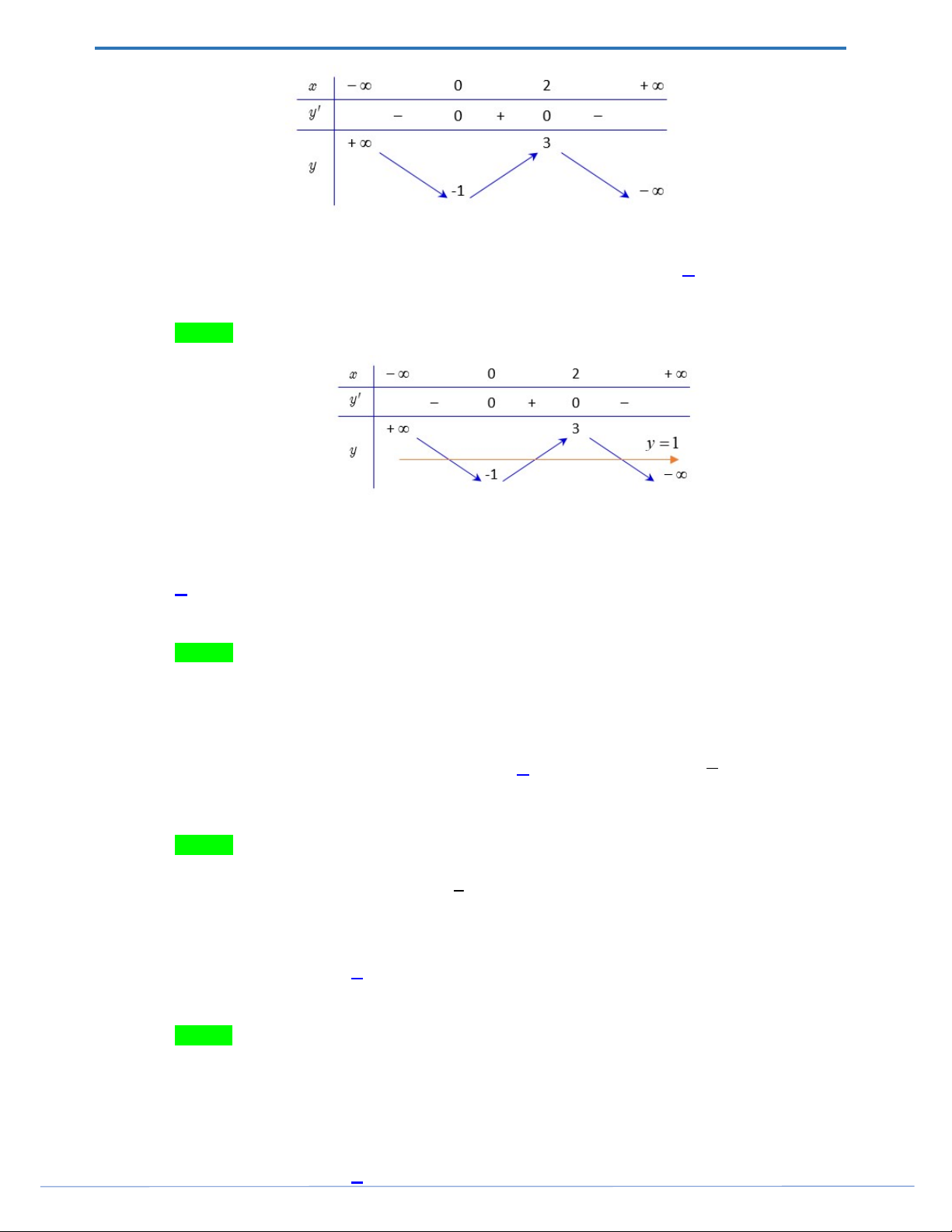
Câu 19. Cho hàm số y  f (x) có bảng biến thiên như sau:
Điểm cực tiểu của hàm số đã cho là: A. x  2  . B. x  2 . C. x  1  . D. x 1.
Câu 20. Trong không gian Oxyz , phương trình của mặt phẳng (Oyz) là: A. z  0 . B. x  0 . C. x  y  z  0 . D. y  0 .
Câu 21. Nghiệm của phương trình 2x 1  2 3  3 x là: 1 A. x  . B. x  0 . C. x  1  . D. x  1. 3 Câu 22. Cho hàm số 4 2
y  ax  bx  c có đồ thị như đường cong trong hình bên.
Trang 2/22 – Diễn đàn giáo viên Toán
Số điểm cực trị của hàm số đã cho là: A. 2. B. 3. C. 1. D. 0. x  2  t 
Câu 23. Trong không gian Oxyz , cho đường thẳng d : y 1 2t . Vec-tơ nào dưới đây là một véc-tơ chỉ x  1   3t  phương của d ?     A. u  2;1; 1 . B. u  1; 2;3 . C. u  1; 2;3 . D. u  2;1;1 . 4   3   2   1  
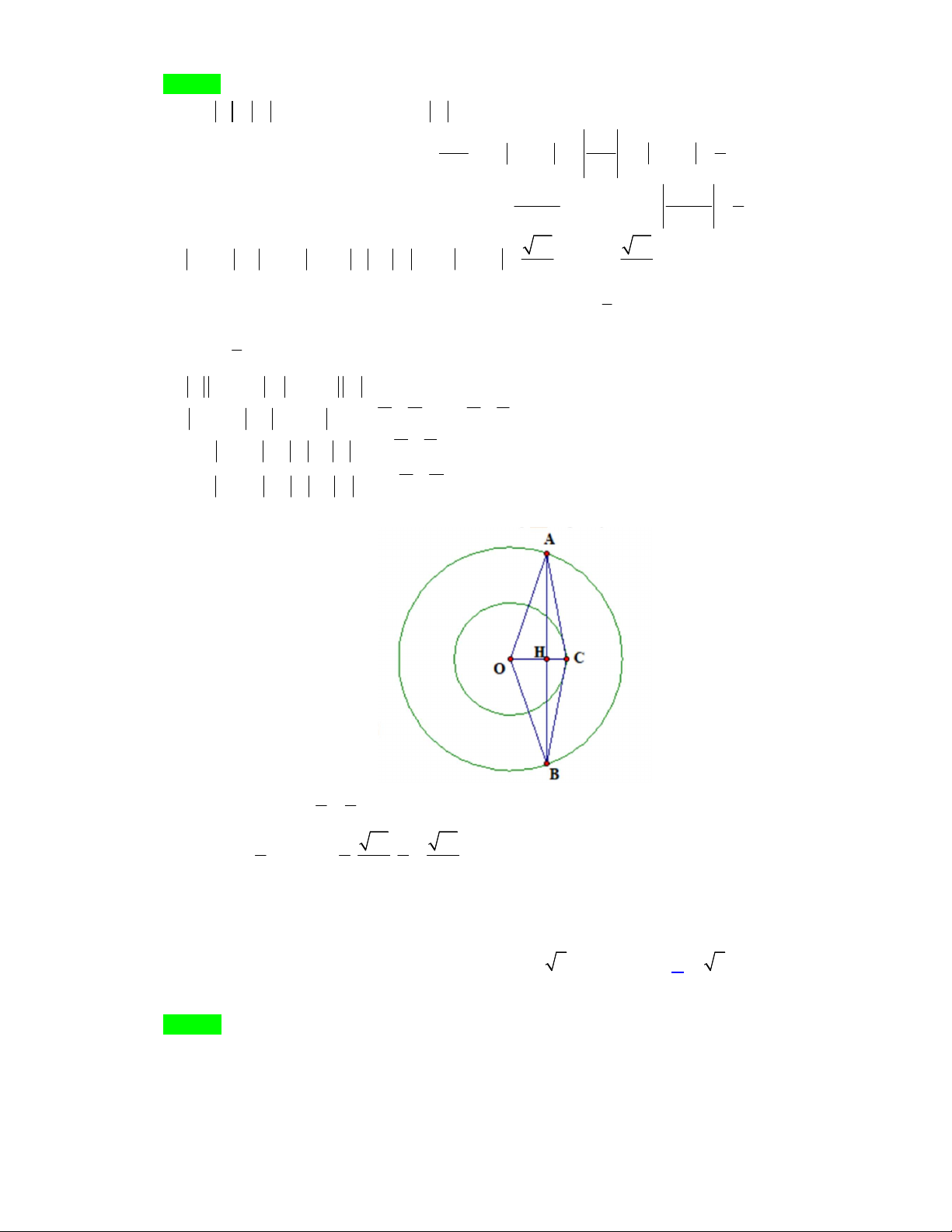
Câu 24. Cho tam giác OIM vuông tại I có OI  3 và IM  4 . Khi quay tam giác OIM quanh cạnh góc
vuông OI thì đường gấp khúc OMI tạo thành hình nón có độ dài đường sinh bằng A. 7 . B. 3 . C. 5 . D. 4 .
Câu 25. Trên mặt phẳng tọa độ, điểm biểu diễn số phức z  2  7i có tọa độ là A. 2;7 . B.  2  ;7 . C. 2; 7   . D.  7  ;2 .
Câu 26. Cho hai số phức z  2  3i và z  1 .i Số phức z  z bằng 1 2 1 2 A. 5  .i B. 3  2 .i C. 1 4 .i D. 3  4i.
Câu 27. Cho hàm số    x f x e  2 .
x Khẳng định nào dưới đây đúng? A.  f x x 2 dx  e  x  C. B.   d  x f x x e  C. C.  f x x 2 dx  e  x  C. D.  f x x 2 dx  e  2x  C.
Câu 28. Đạo hàm của hàm số 3 y x  là 1 1 A. 4 y x    . B. 2 y x    . C. 4 y x    . D. 4 y 3x    . 2 3
Câu 29. Trong không gian Oxyz , cho ba điểm A1;2;  1 , B 3;0;  1 và C 2;2; 2
  . Đường thẳng đi qua A
và vuông góc với mặt phẳng  ABC  có phương trình là x 1 y  2 z 1 x 1 y  2 z 1 A.   . B.   . 1 2 3 1 2 1 x 1 y  2 z 1 x 1 y  2 z 1 C.   . D.   . 1 2 1 1 2 1
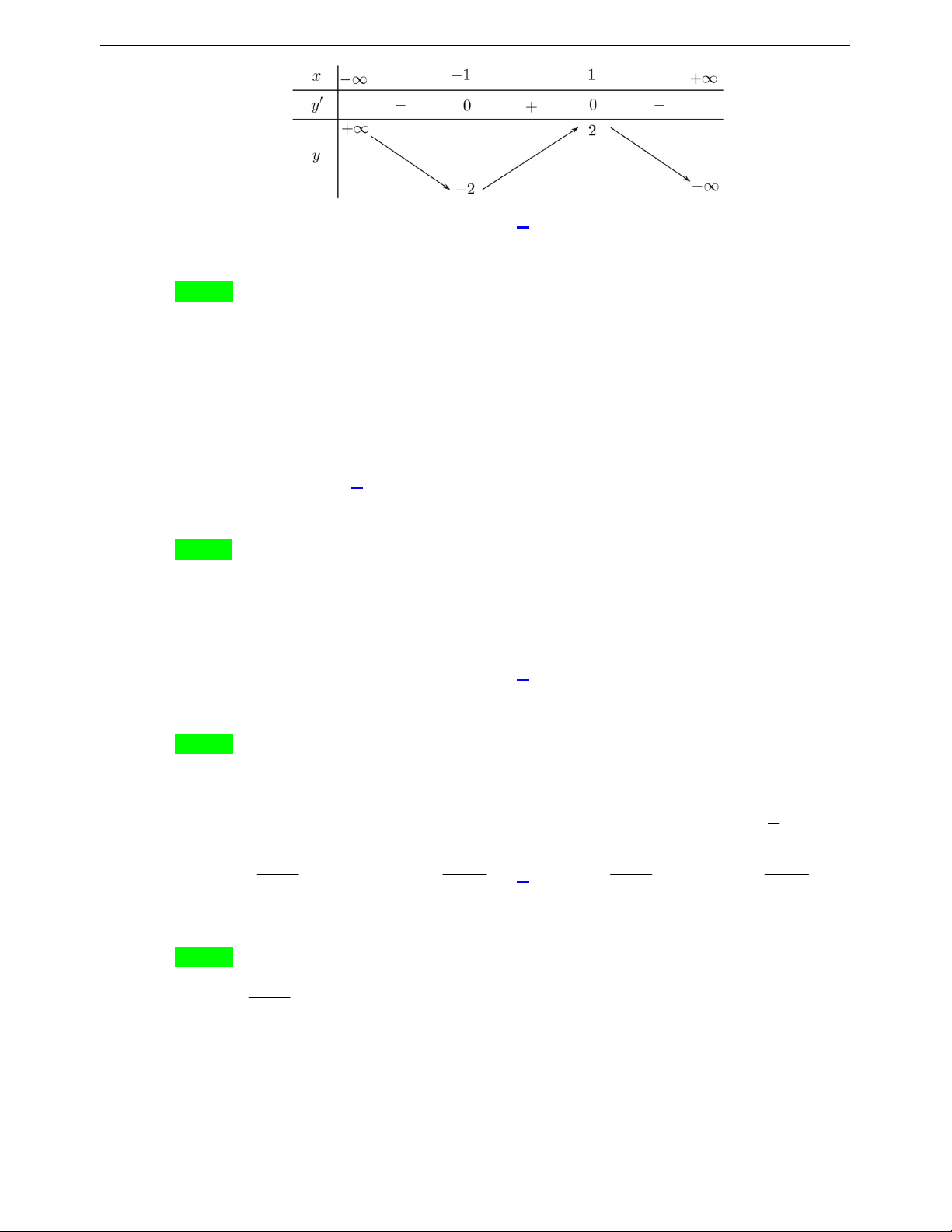
Câu 30. Giá trị lớn nhất của hàm số f  x 3 2
 x  3x  9x 10 trên đoạn  2  ;2 bằng A. 12 . B. 10. C. 15. D. 1  .
Câu 31. Có bao nhiêu giá trị nguyên thuộc tập xác định của hàm số y  log 6  x x  2   ? Trang 3/22 - WordToan A. 7 . B. 8 . C. 9 . D. Vô số.
Câu 32. Gọi z và z là hai nghiệm phức của phương trình 2
z  z  6  0 . Khi đó z  z  z z bằng: 1 2 1 2 1 2 A. 7 . B. 5 . C. 7 . D. 5 .
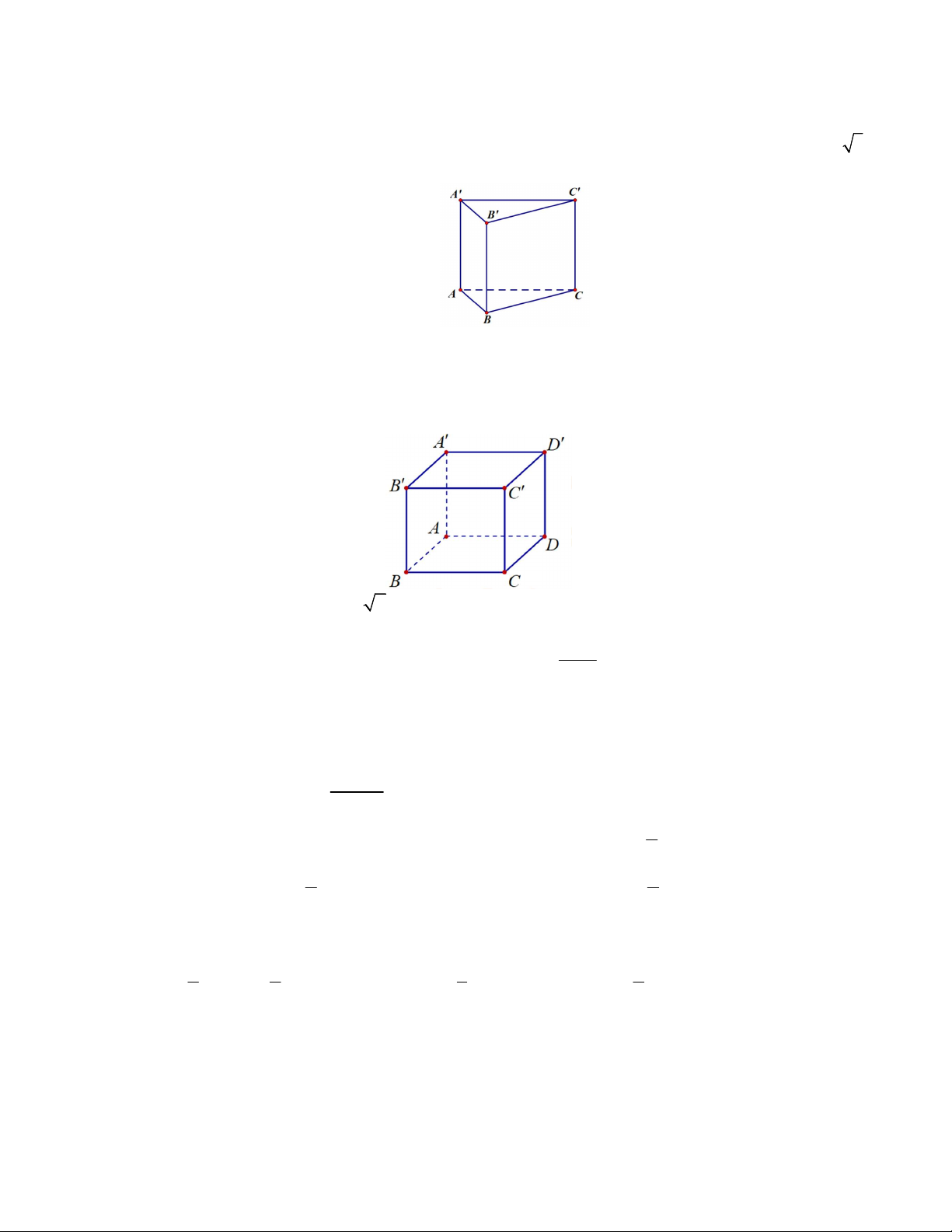
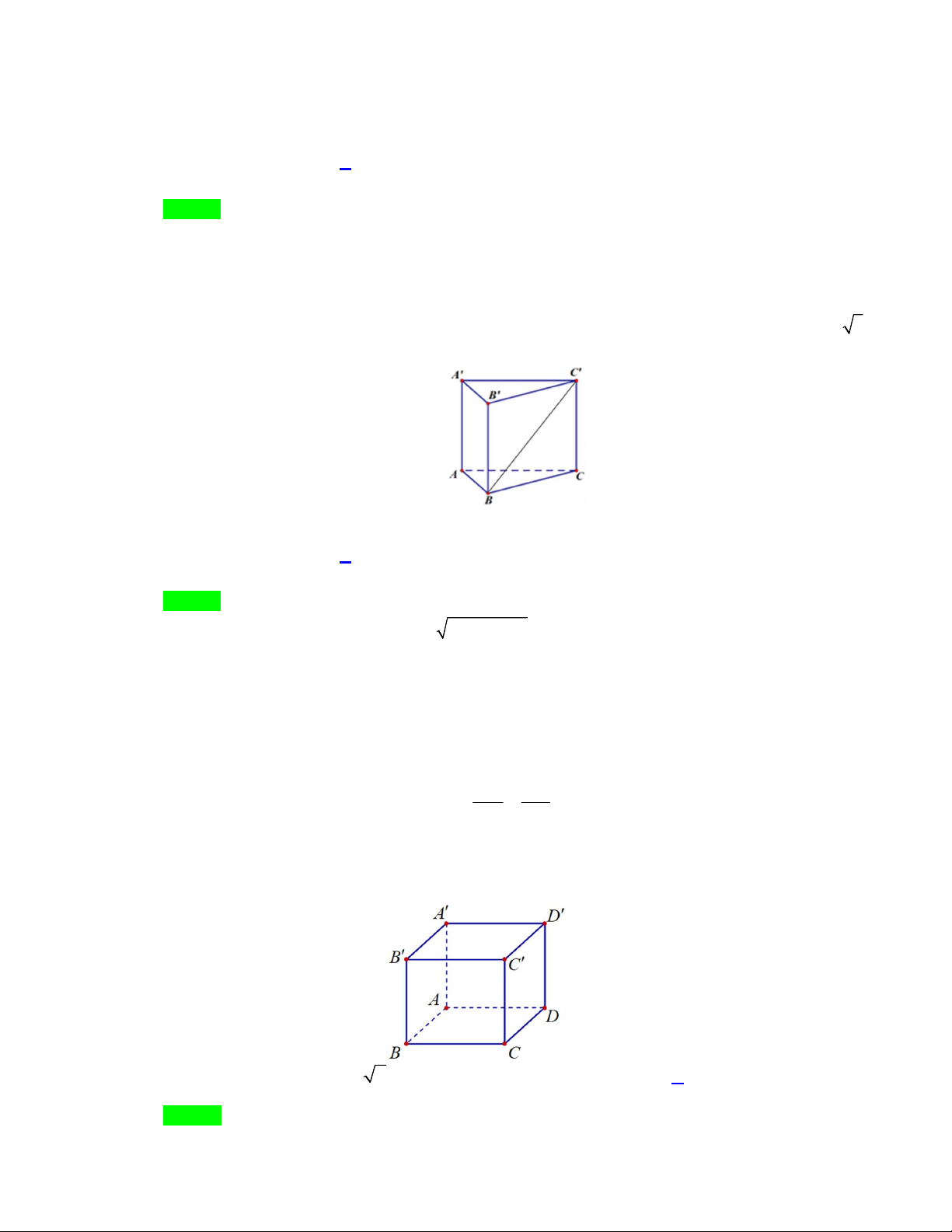
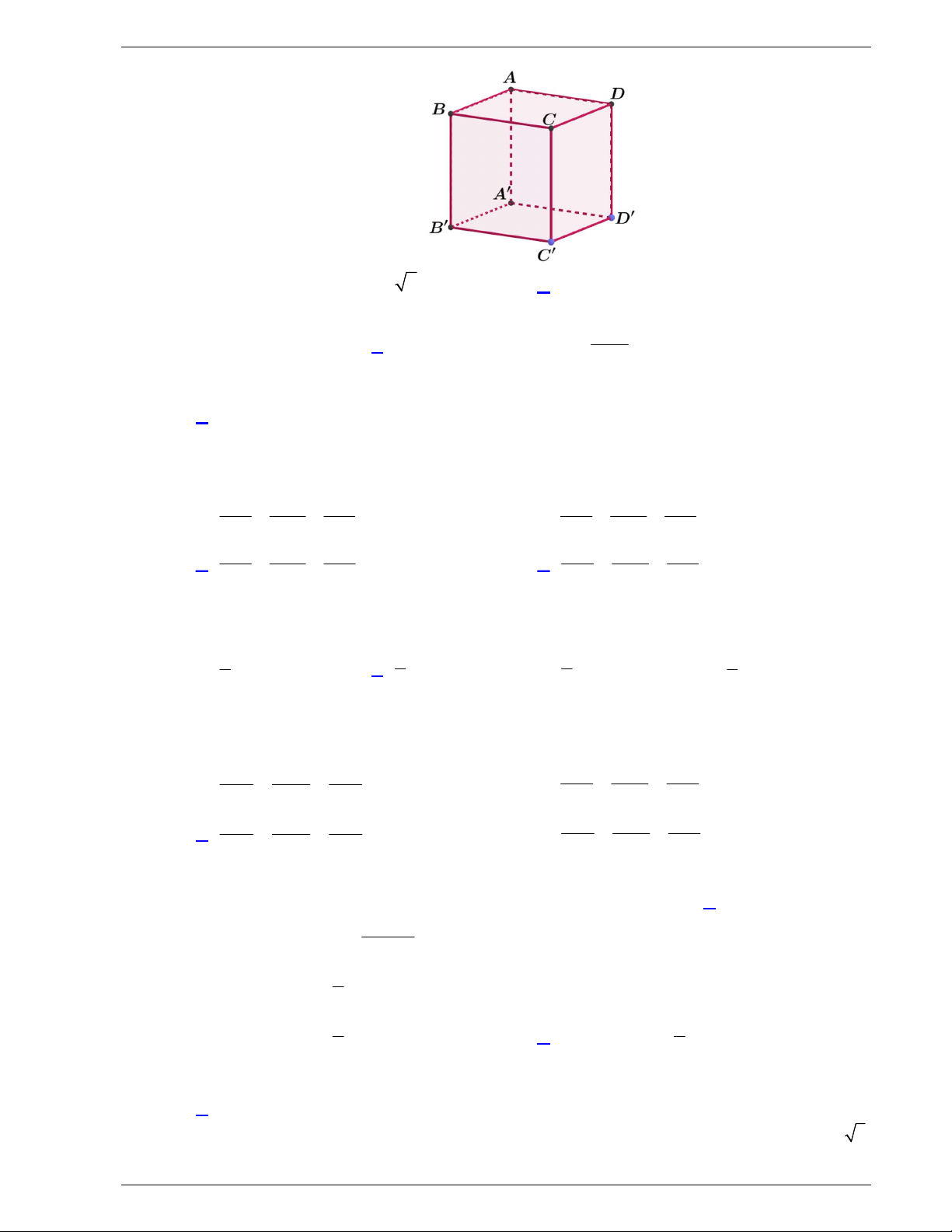
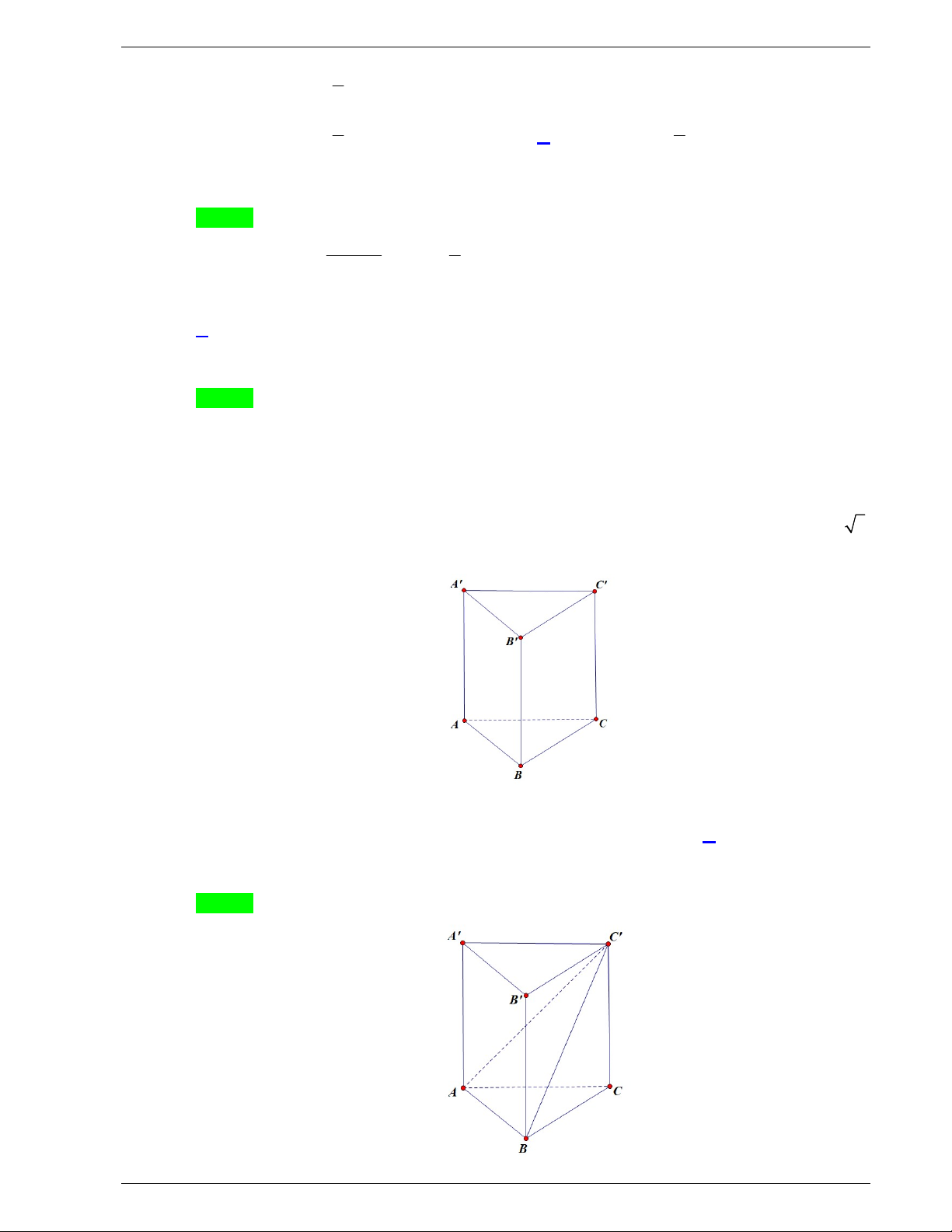
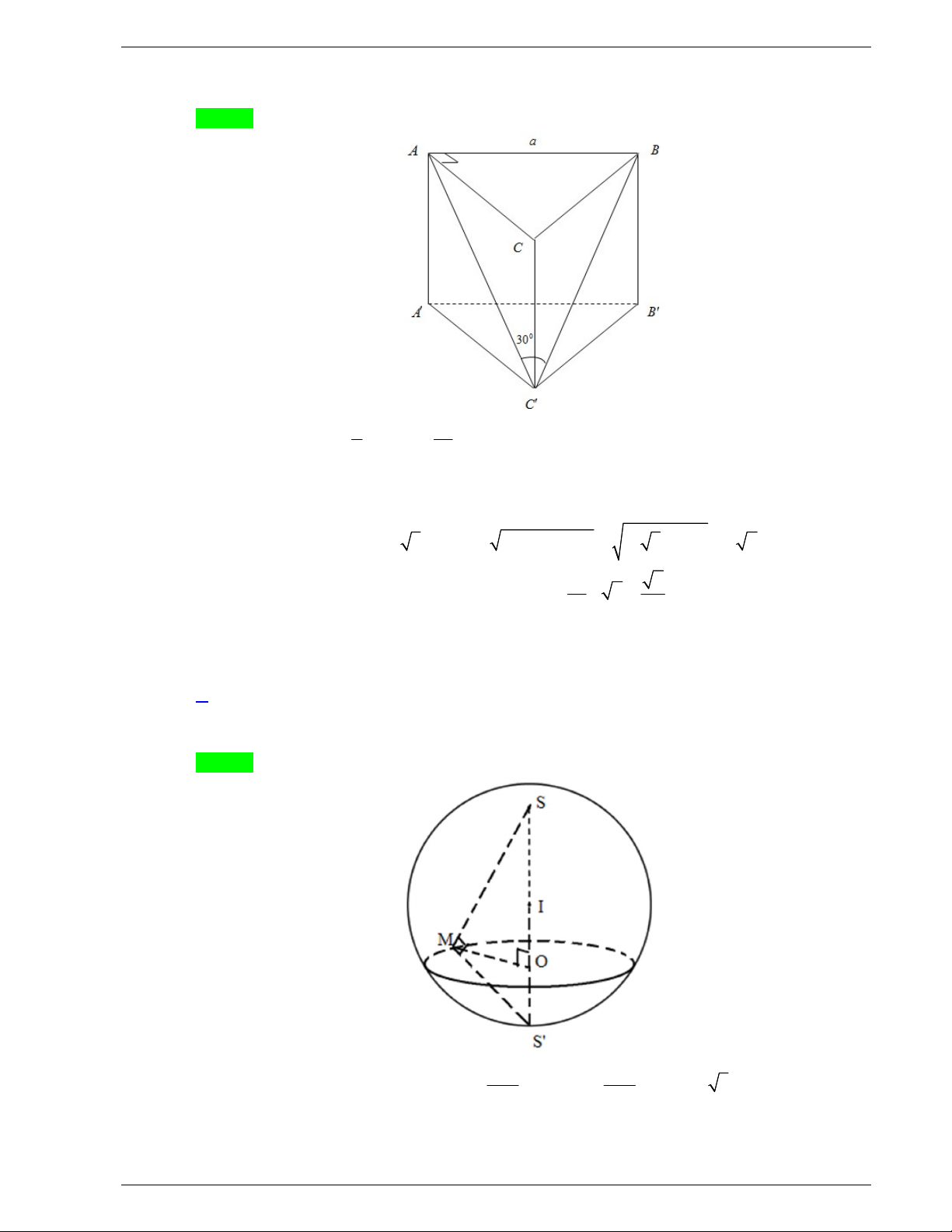
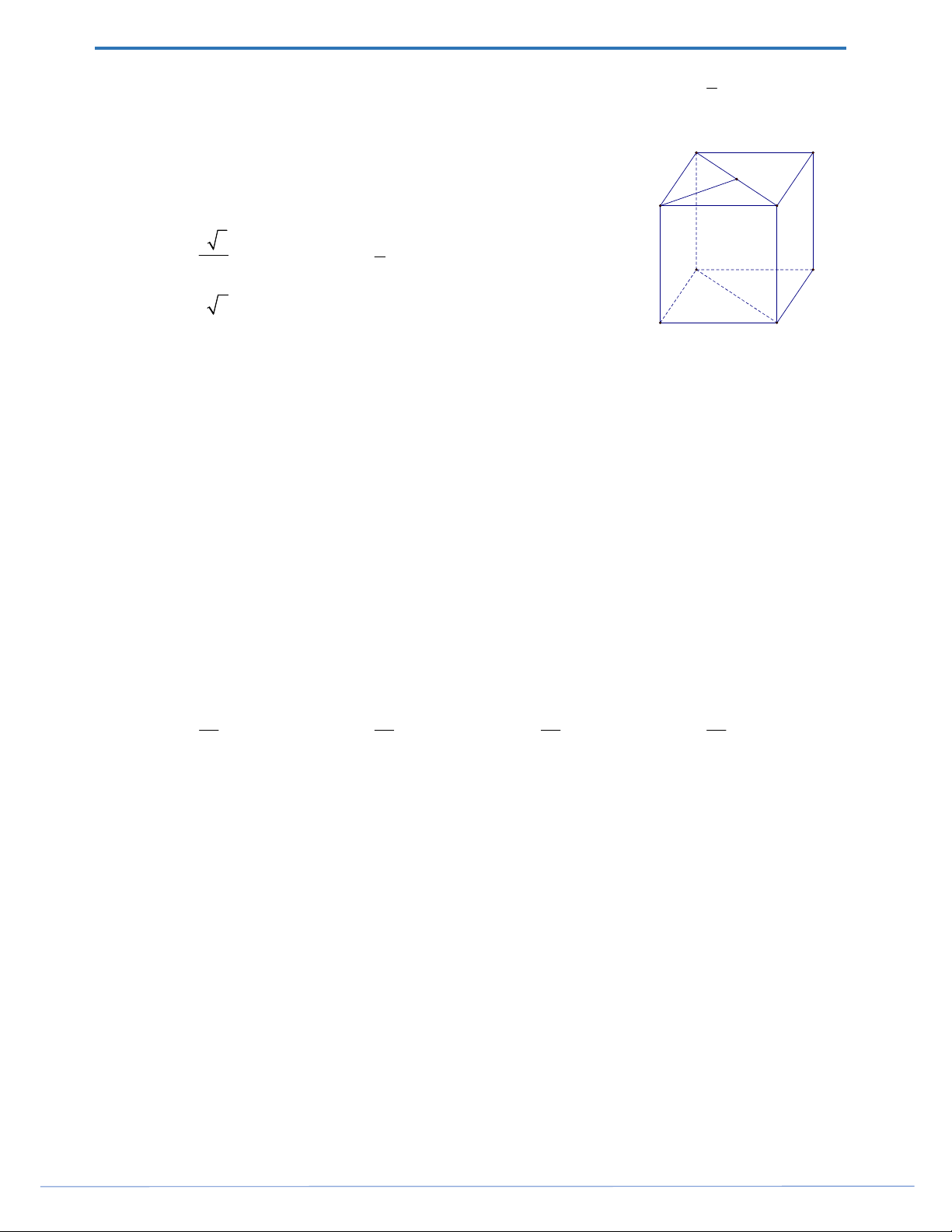
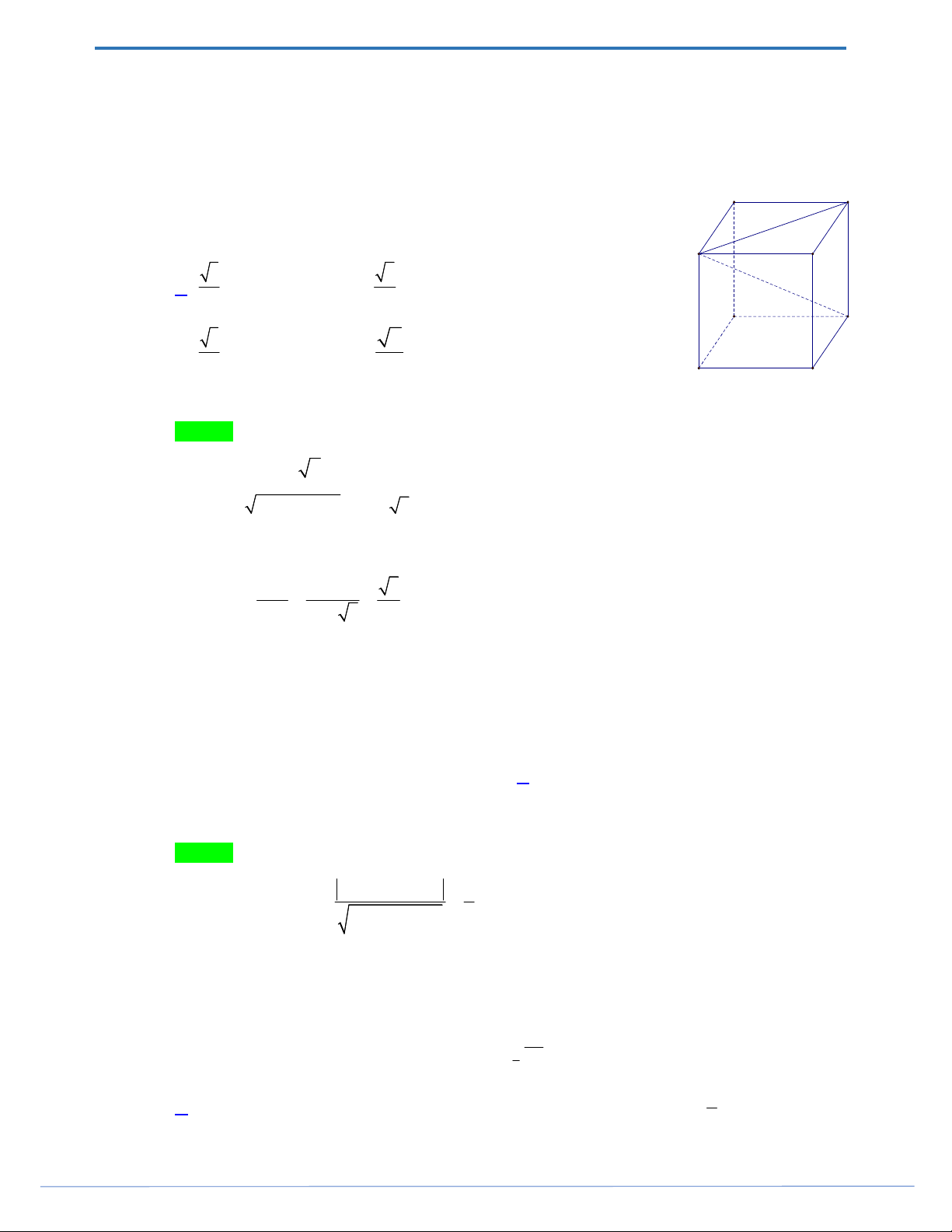
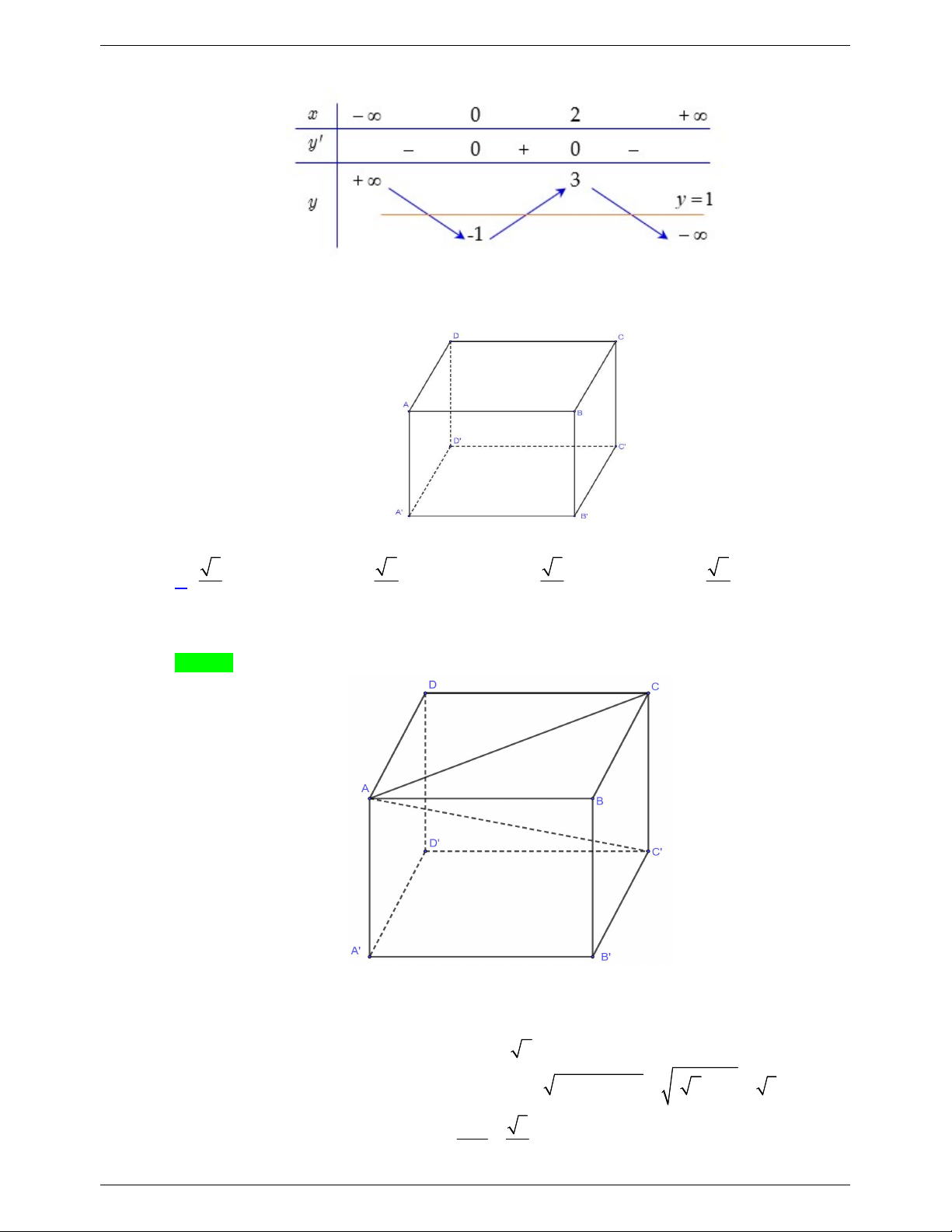
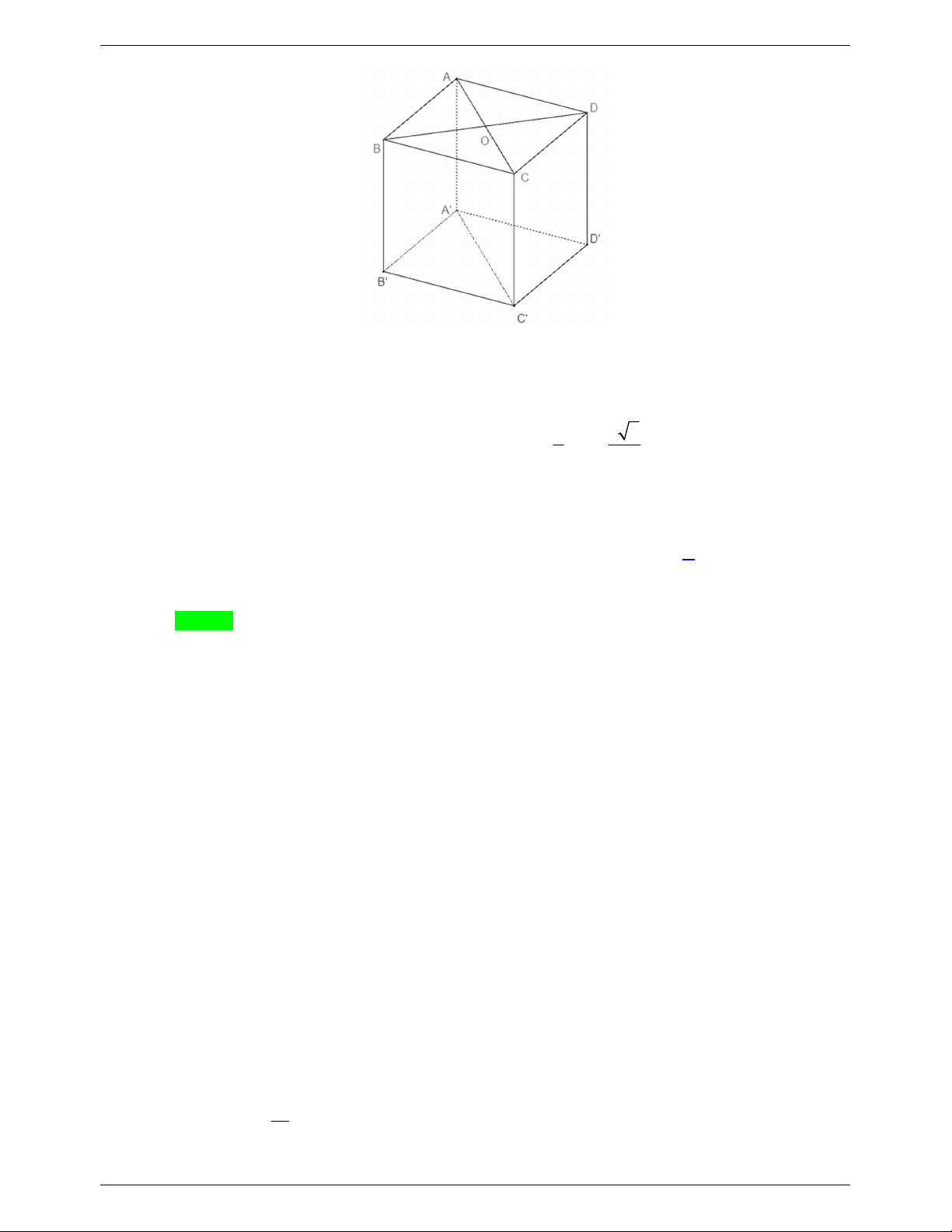
Câu 33. Cho hình lăng trụ đứng ABC. 
A BCcó đáy ABC là tam giác vuông tại B , AC  2 , AB  3 và A 
A  1 (tham khảo hình bên).
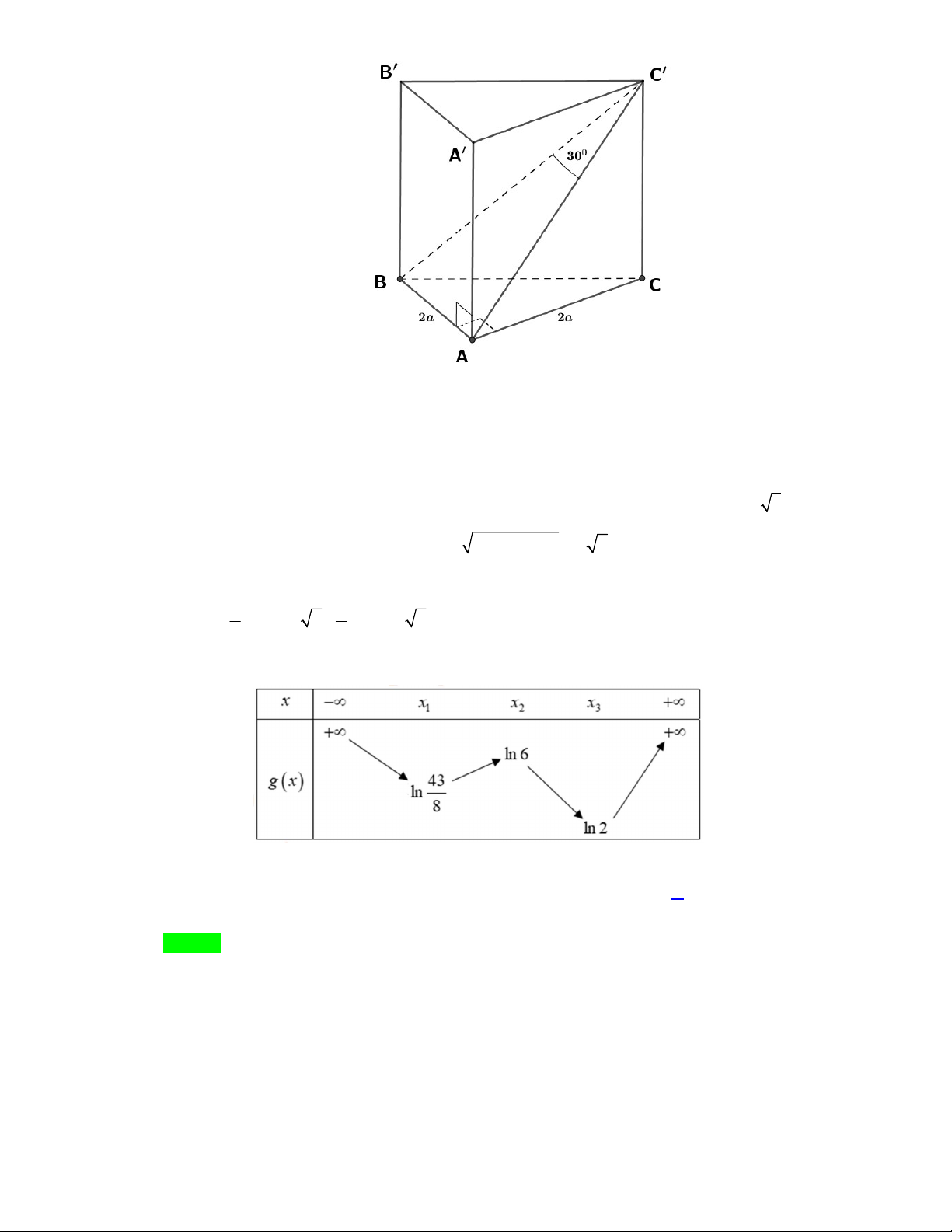
Góc giữa hai mặt phẳng  ABC và  ABC bằng A. 0 30 . B. 0 45 . C. 0 90 . D. 0 60 .
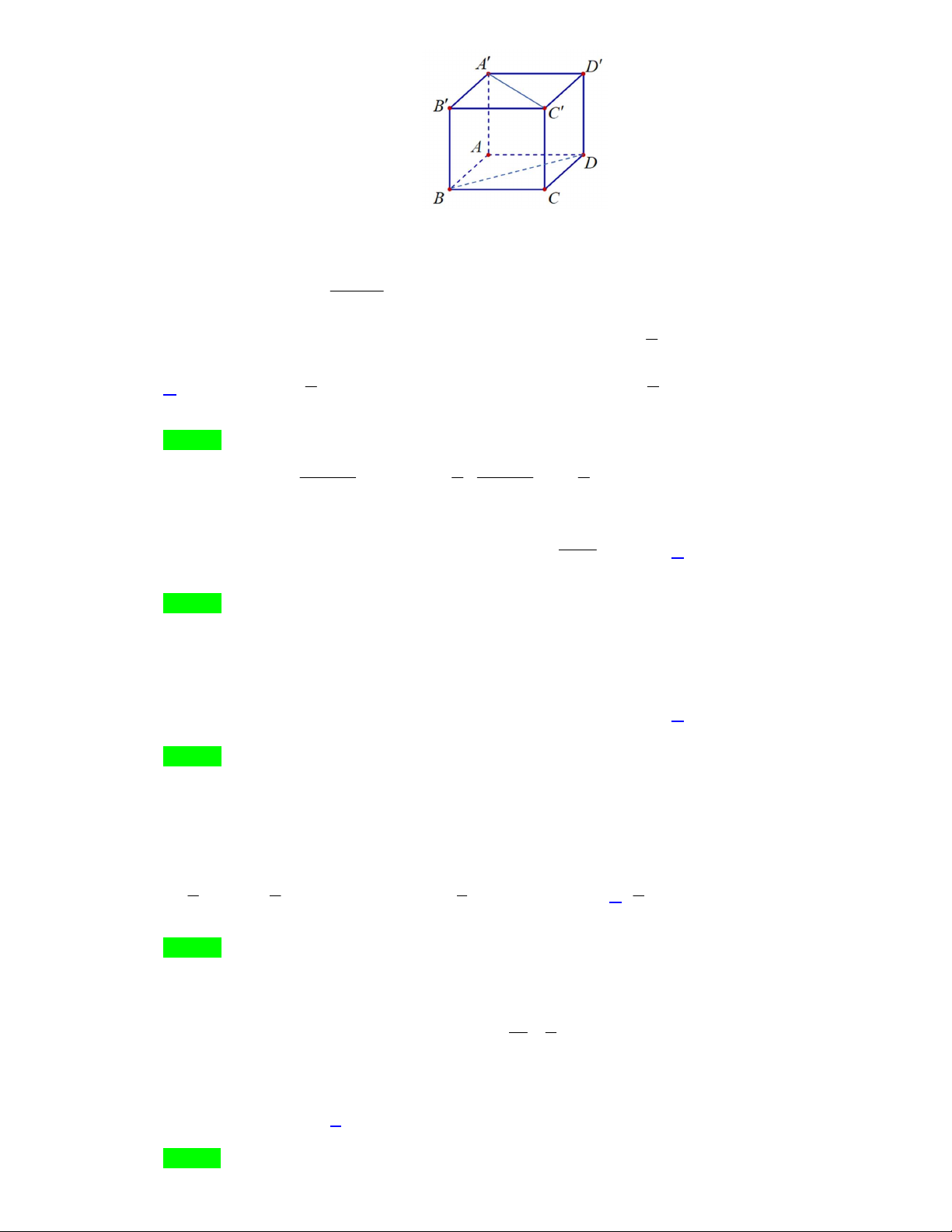
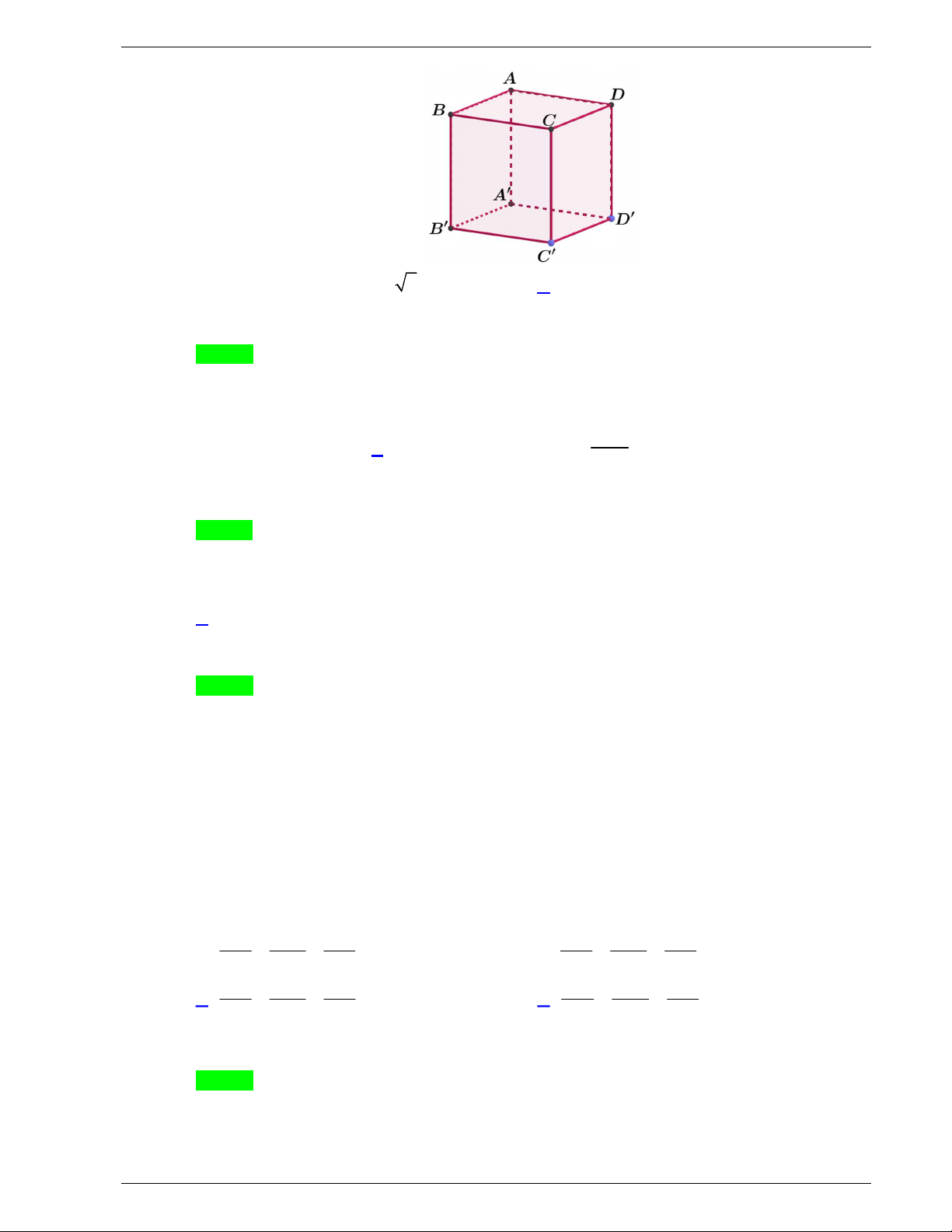
Câu 34. Cho hình hộp chữ nhật ABC . D A B  C  D
  có AB  a , BC  2a và AA  3a (tham khảo hình bên).
Khoảng cách giữa hai đường thẳng BD và AC bằng A. a . B. 2a . C. 2a. D. 3a .
Câu 36. Hàm số nào dưới đây đồng biến trên  ? x 1 A. 4 2 y  x  x . B. 3 y  x  x . C. y  . D. 3 y  x  x . x  2
Câu 37. Trong không gian Oxyz , cho điểm A0;3;2 và mặt phẳng P : 2x  y  3z  5  0 . Mặt phẳng đi
qua A và song song với P có phương trình là
A. 2x  y  3x  9  0 . B. 2x  y  3x  3  0 . C. 2x  y  3x  3  0 . D. 2x  y  3x  9  0 . 1
Câu 35. Cho hàm số f  x  1
. Khẳng định nào dưới đây đúng? 2 cos 2x A. f
 x dx  x  tan 2x C . B. f  x 1 dx  x  cot 2x  C . 2 C. f  x 1 dx  x  tan 2x  C . D. f  x 1 dx  x  tan 2x  C . 2 2
Câu 38. Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn 40;60. Xác suất để chọn được số
có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng 4 2 3 3 A. B. C. D. 7 5 5 7
Câu 39. Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng ba số nguyên b thỏa mãn 3b 3 .2b a 18  0 ? A. 72 B. 73 C. 71 D. 74 Câu 40. Cho hàm số 4 2
f (x)  (m 1)x  2mx 1 với m là tham số thực. Nếu min f (x)  f (2) thì [0;3] max f (x) bằng [0;3]
Trang 4/22 – Diễn đàn giáo viên Toán 13 14 A.  . B. 4 . C.  . D. 1. 3 3 Câu 41. Biết
F(x) và G(x) là hai nguyên hàm của hàm số f (x) trên  và 3
f (x)dx  F(3)  G(0)  a (a  0) 
. Gọi S là diện tích hình phẳng giới hạn bởi các đường 0
y  F(x), y  G(x), x  0 và x  3 . Khi S  15 thì a bằng: A. 15 . B. 12 . C. 18 . D. 5 .
Câu 42. Trong không gian Oxyz , cho điểm A1;2;2 . Gọi P là mặt phẳng chứa trục Ox sao cho
khoảng cách từ A đến P lớn nhất. Phương trình của P là A. 2 y  z  0 . B. 2 y  z  0 . C. y  z  0 . D. y  z  0 .
Câu 43. Cho hình nón có góc ở đỉnh là 0
120 và chiều cao bằng 4. Gọi S  là mặt cầu đi qua đỉnh và chứa
đường tròn đáy của hình nón đã cho. Tính diện tích của S  bằng: A. 64 . B. 256 . C. 192 . D. 96 .
Câu 44. Xét tất cả các số thực x , y sao cho 2 2 4 x log5 a 40 25 y a   
với mọi số thực dương a . Giá trị lớn nhất của biểu thức 2 2
P  x  y  x  3y bằng 125 A. . B. 80 . C. 60 . D. 20 . 2
Câu 45. Cho các số phức z , z , z thỏa mãn z  z  2 z  2 và 8 z  z z  3z z . Gọi A , B , C 1 2  1 2 3 1 2 3 3 1 2
lần lượt là các điểm biểu diễn của z , z , z trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng 1 2 3 55 55 55 55 A. . B. . C. . D. . 32 16 44 8
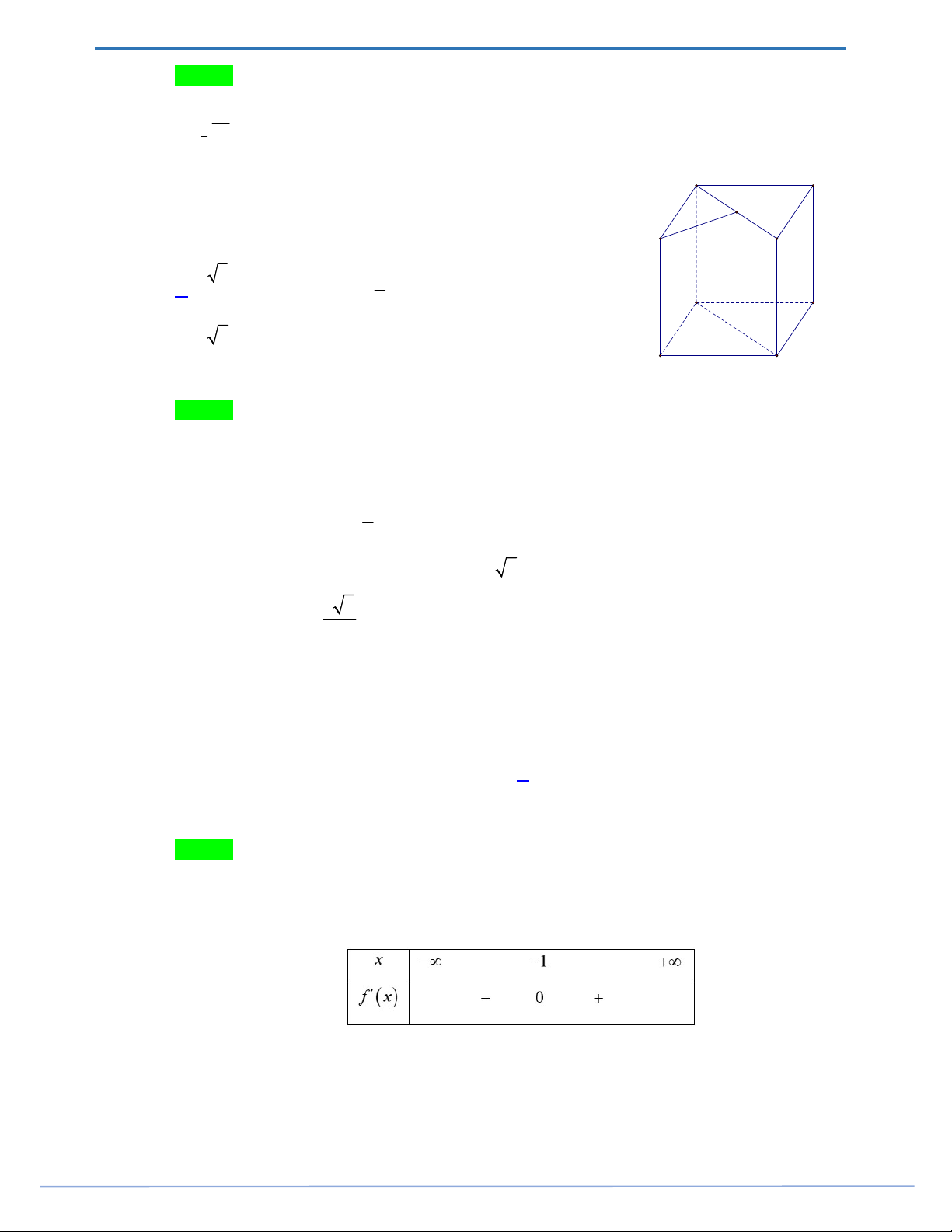
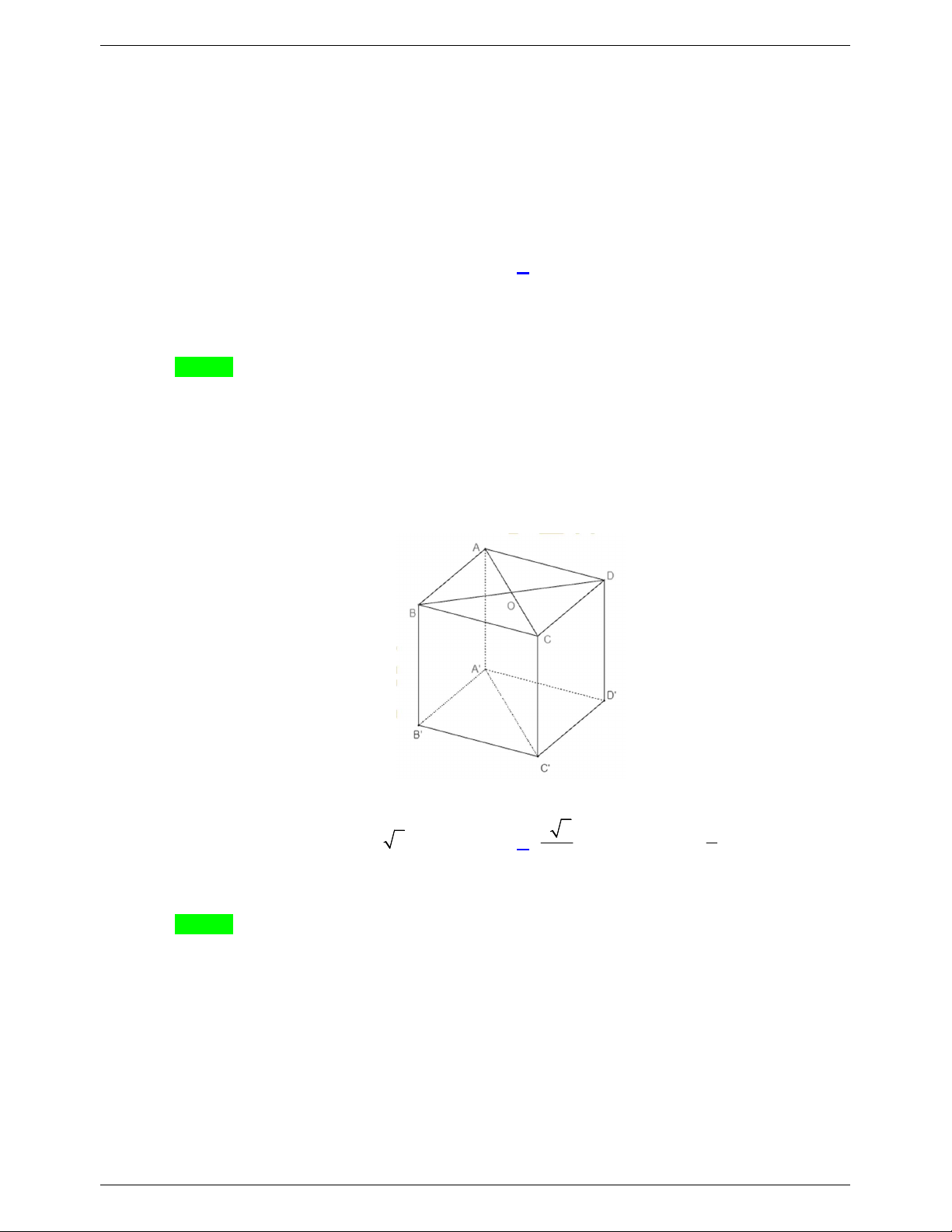
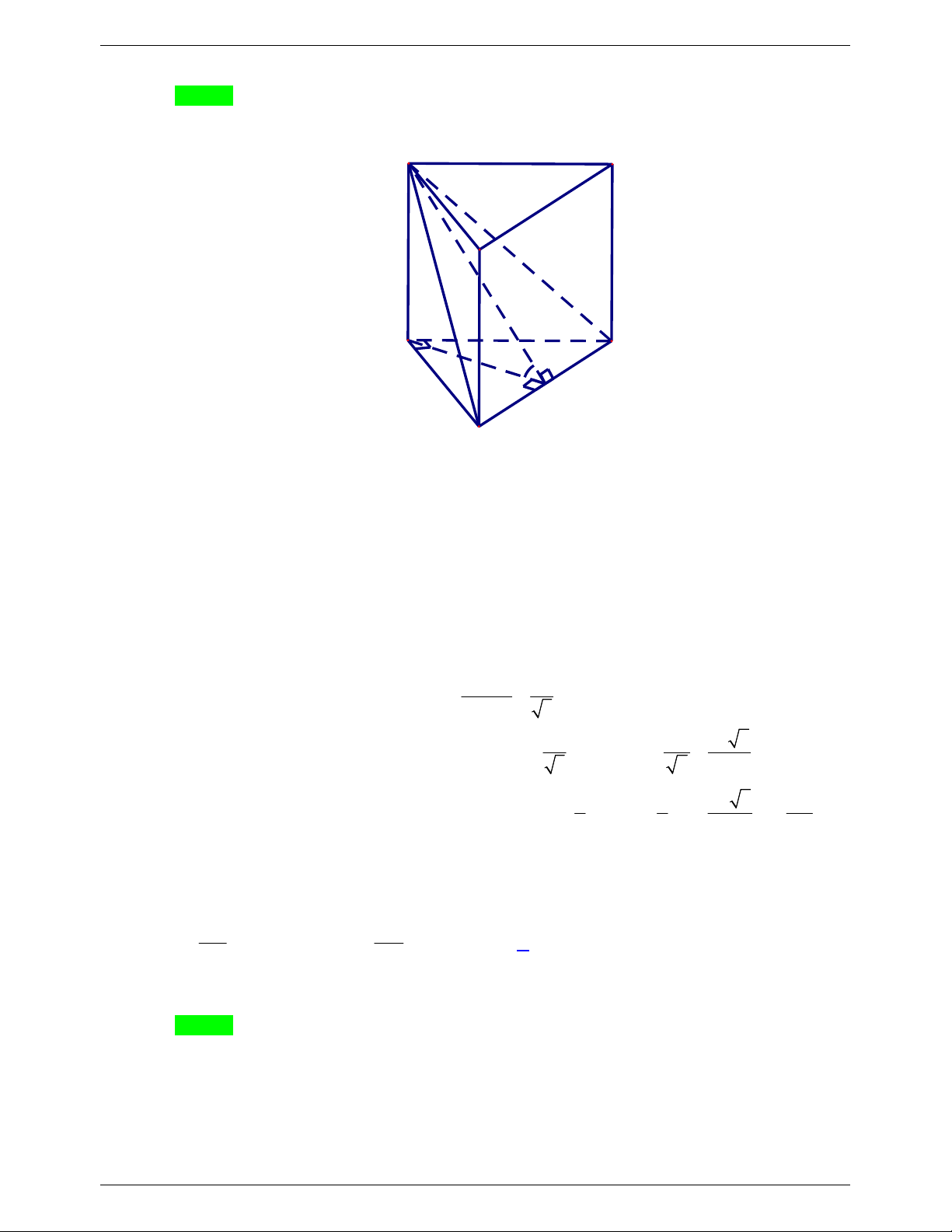
Câu 46. Cho khối lăng trụ đứng ABC.A B  C
  có đáy ABC là tam giác vuông cân tại A , AB  2a . Góc
giữa đường thẳng BC và mặt phẳng  ACC A
  bằng 30 . Thể tích của khối lăng trụ đã cho bằng A. 3 3a . B. 3 a . C. 3 12 2a . D. 3 4 2a .
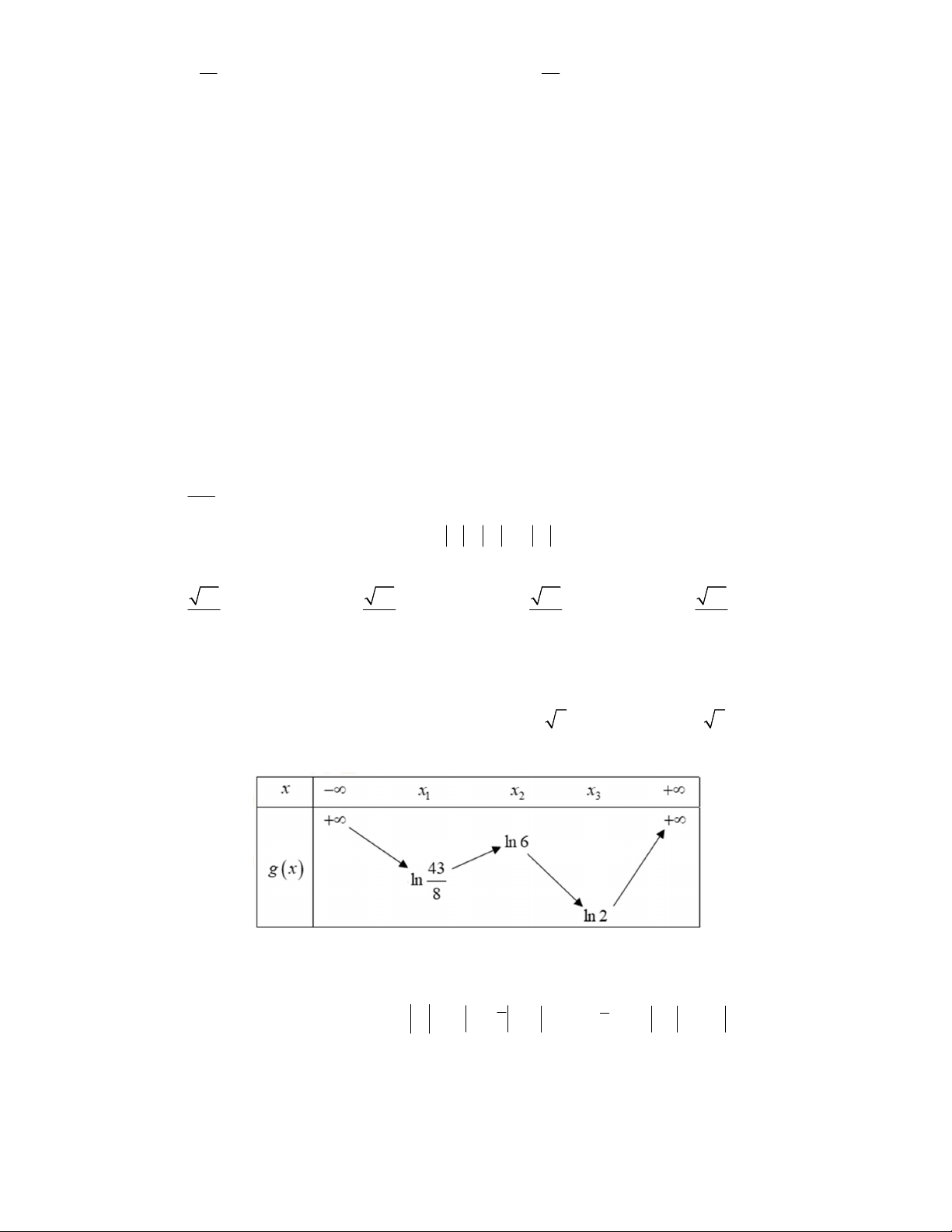
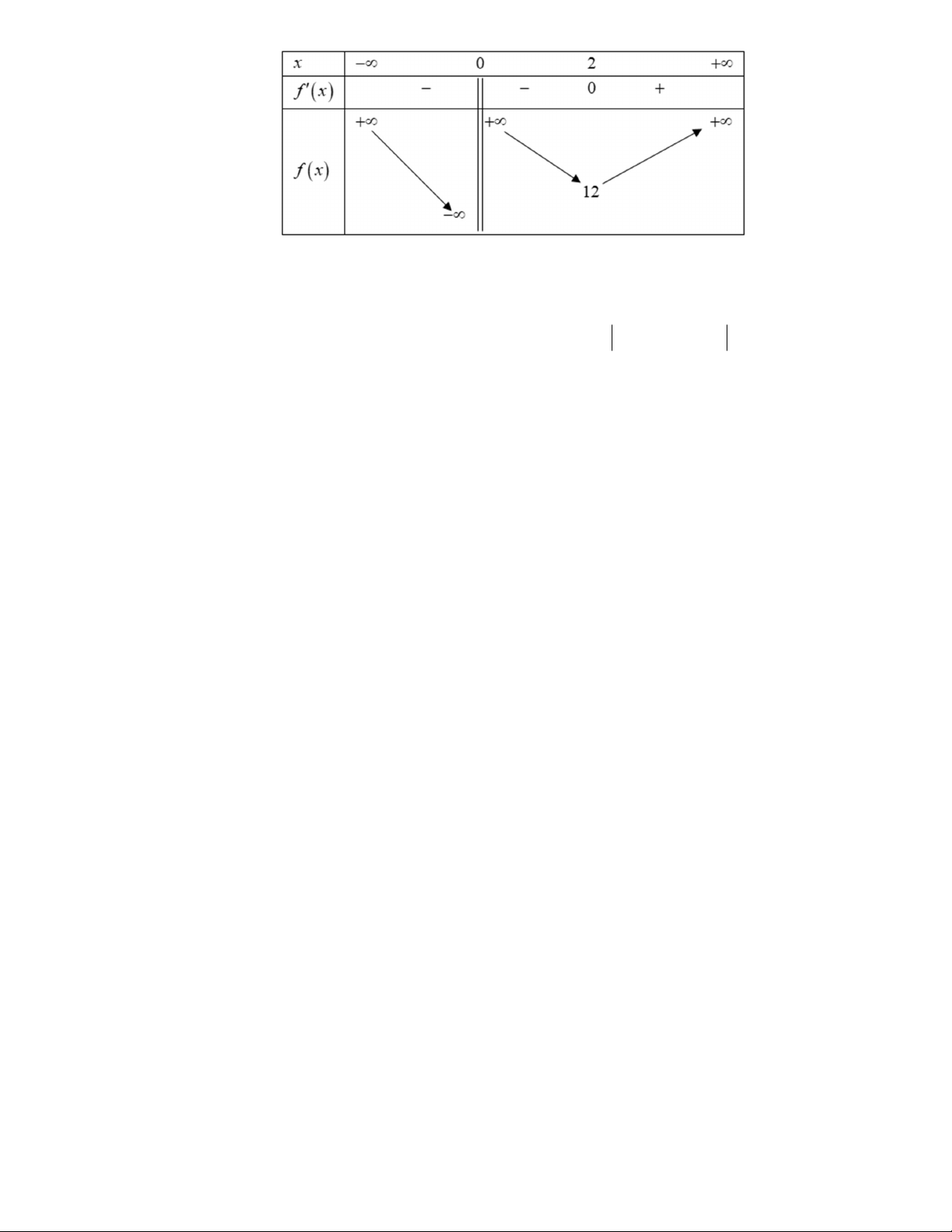
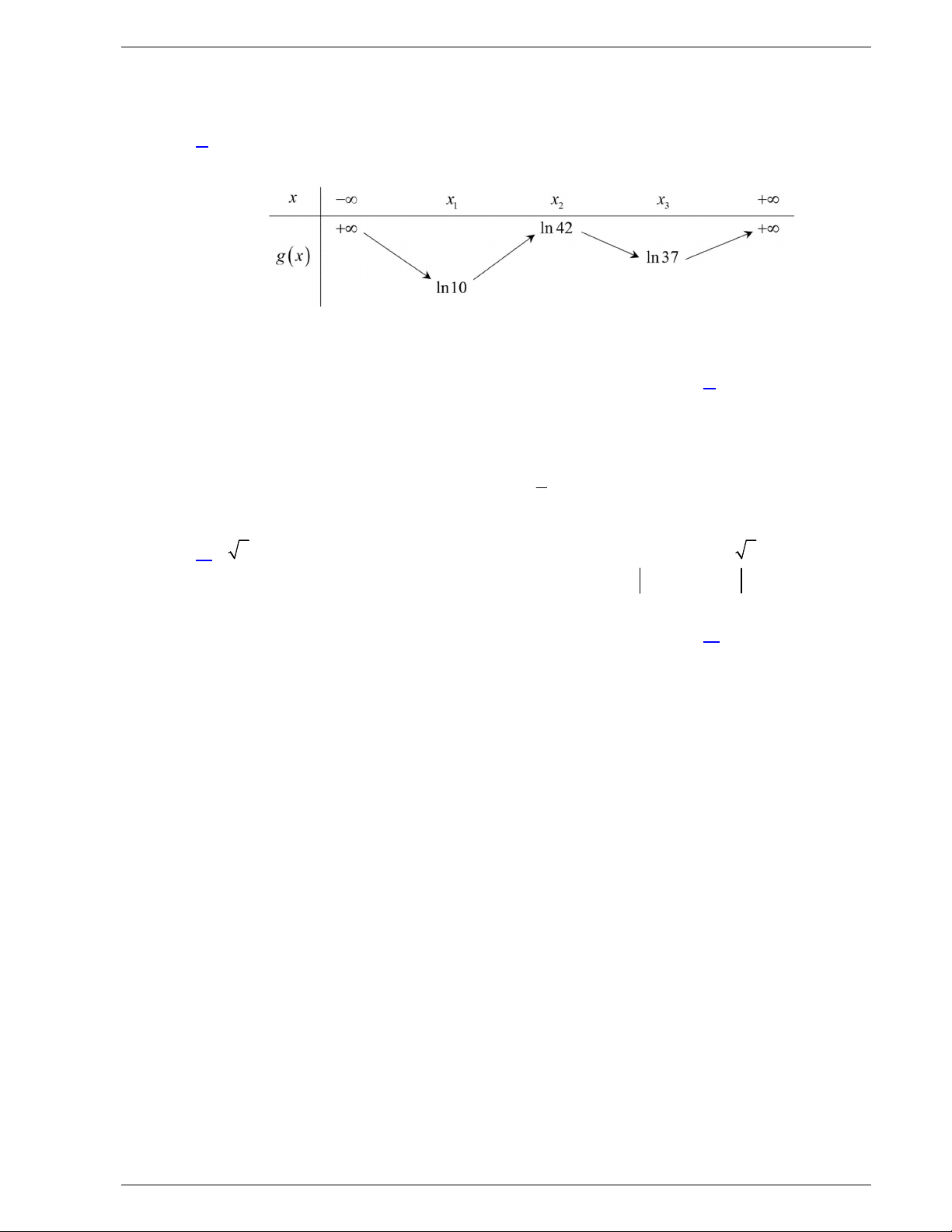
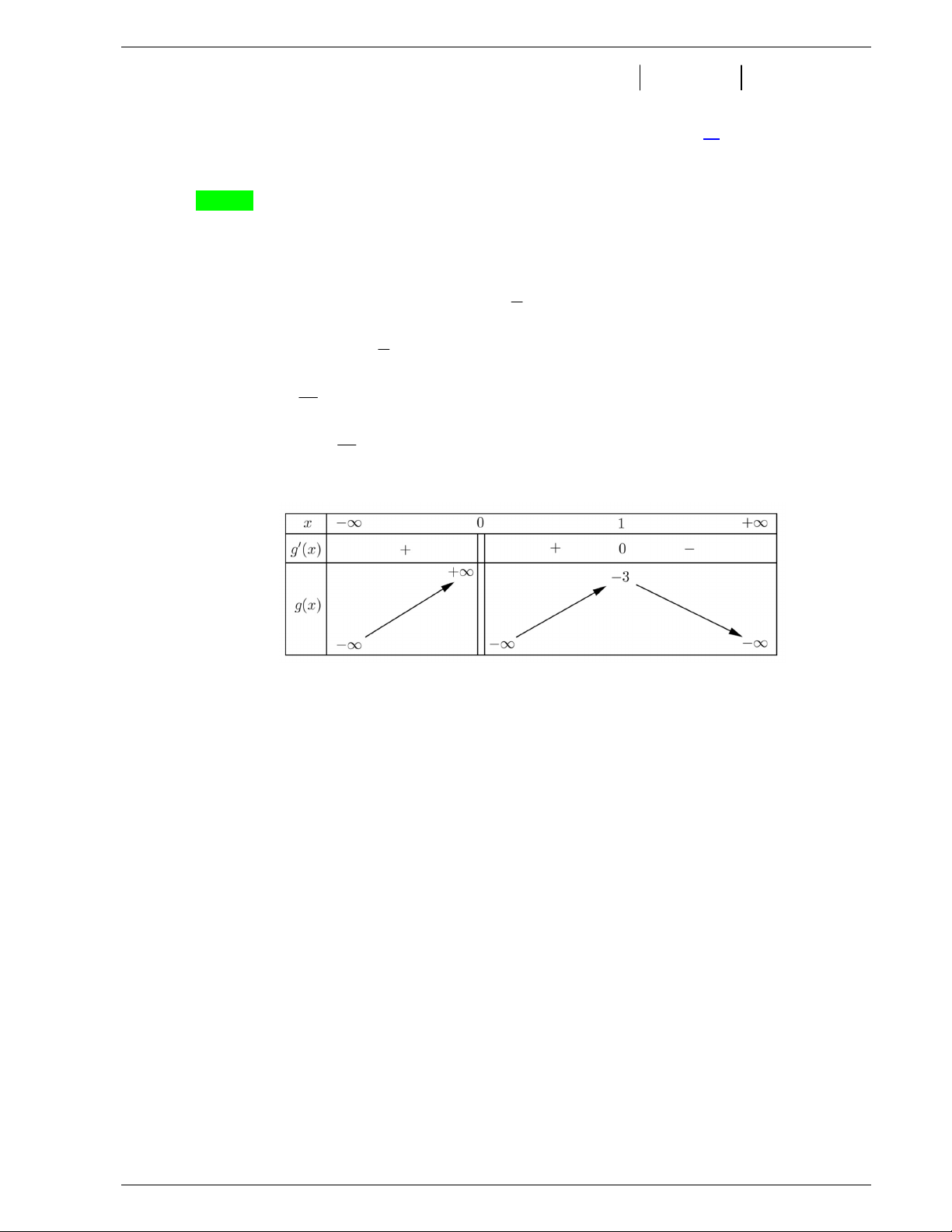
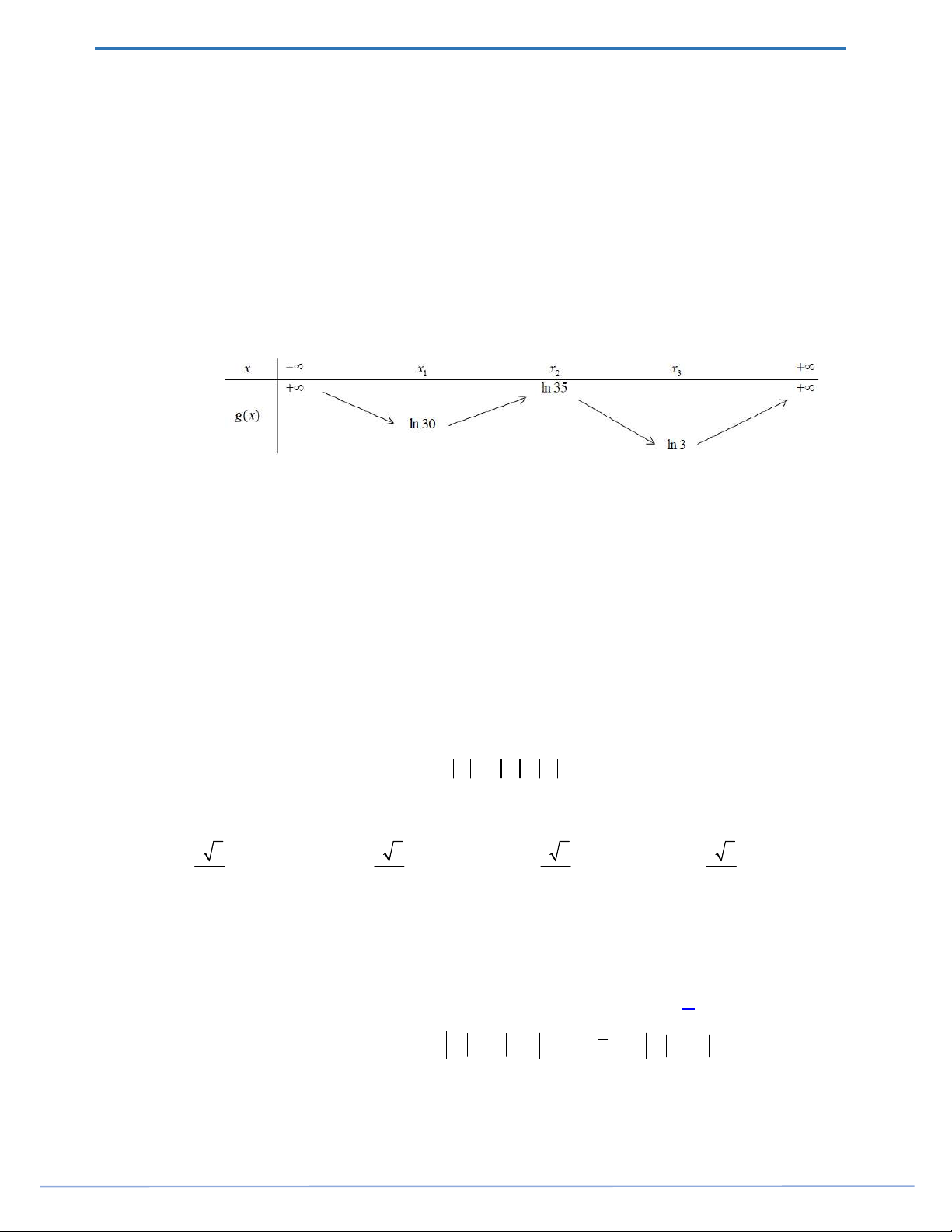
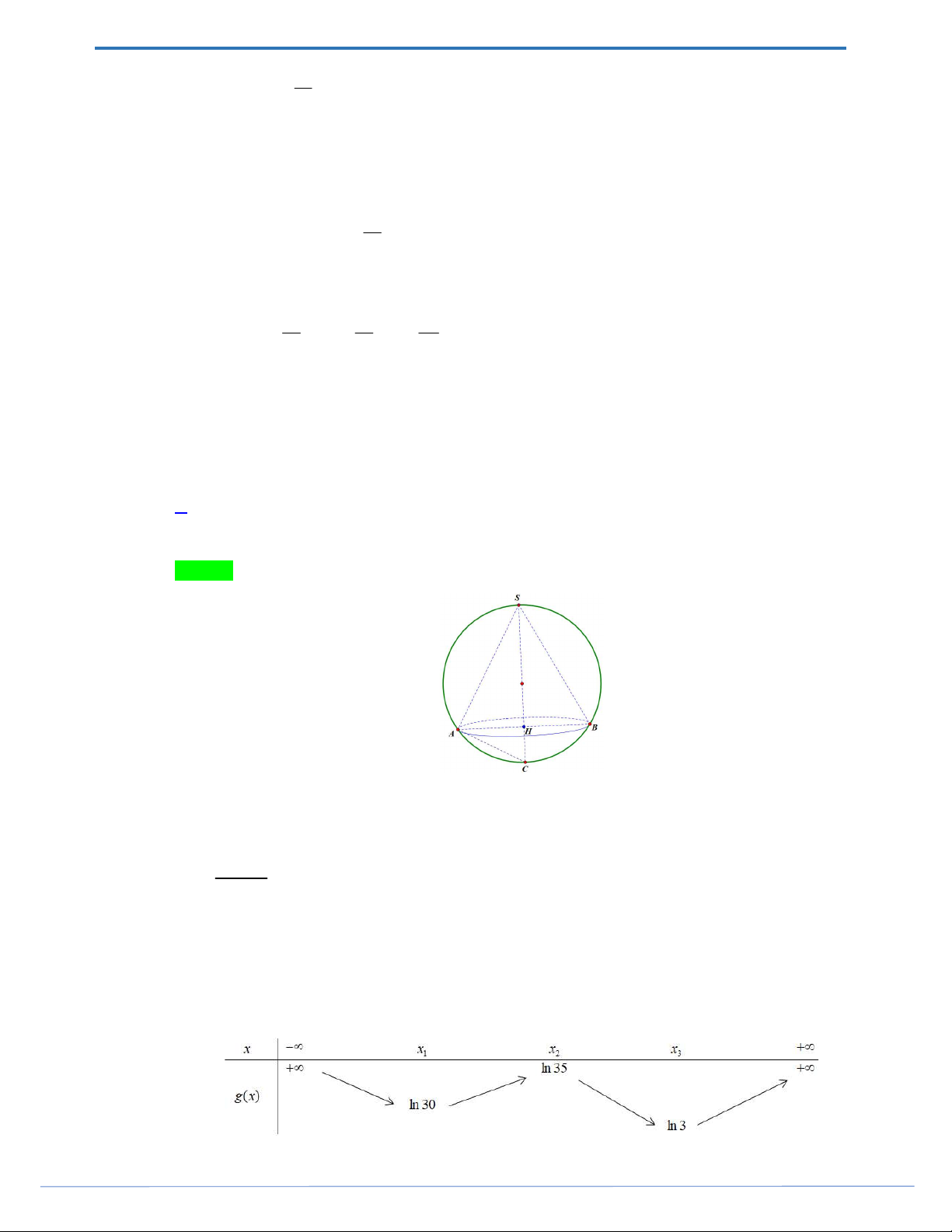
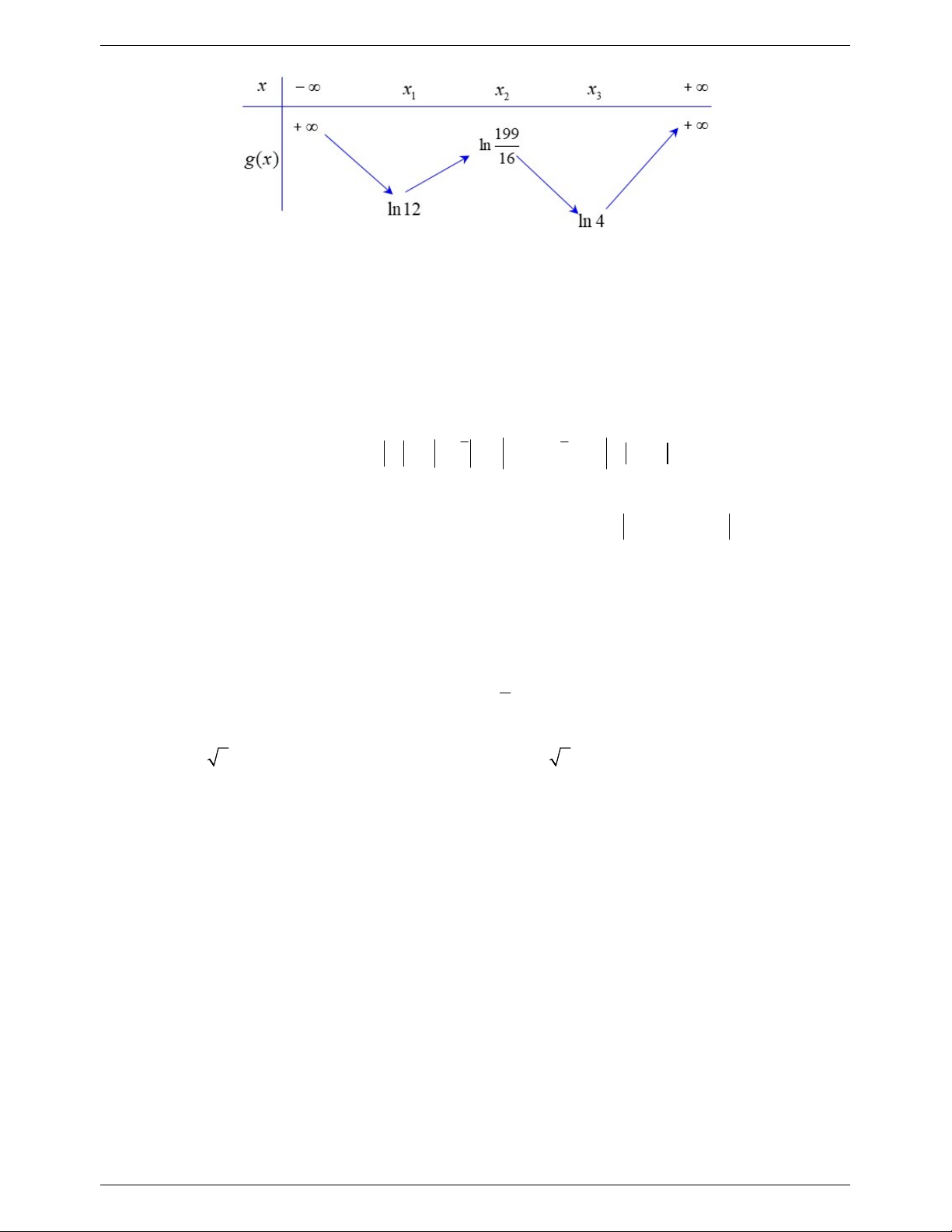
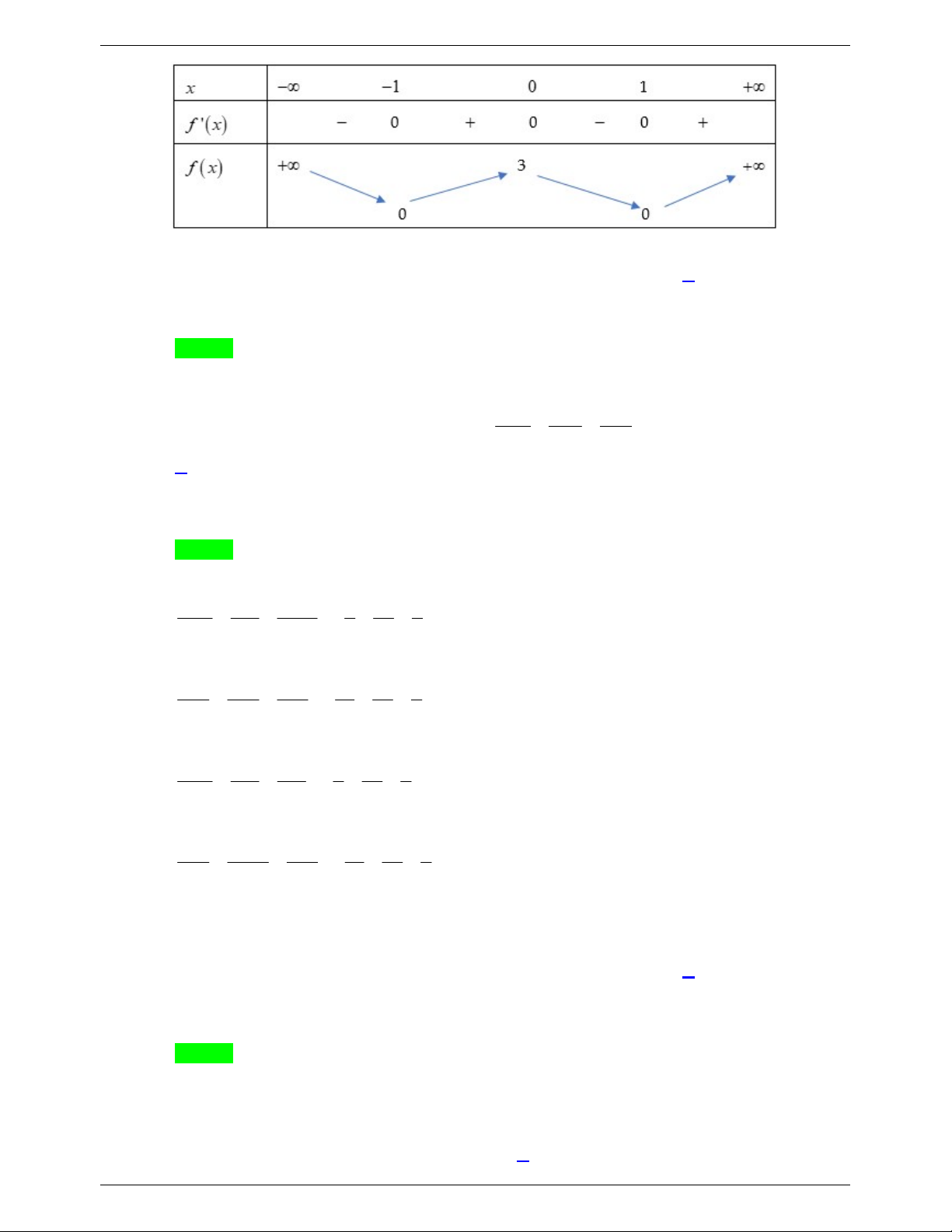
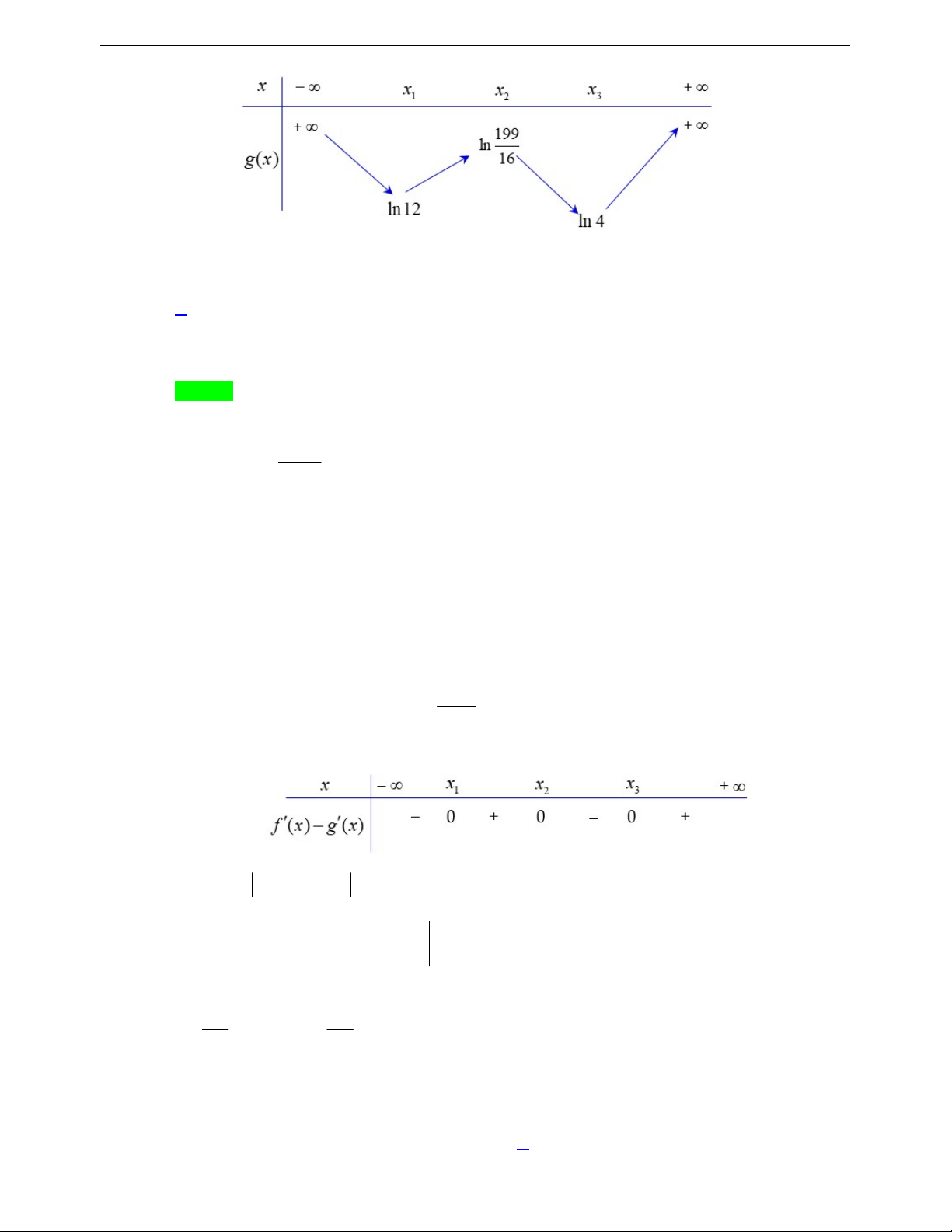
Câu 47. Cho hàm số y  f  x . Biết rằng hàm số g  x  ln f  x có bảng biến thiên như sau:
Diện tích hình phẳng giới hạn bởi các đường y  f x và y  g x thuộc khoảng nào dưới đây? A. 5;6 . B. 4;5 . C. 2;3. D. 3;4 . 2
Câu 48. Có bao nhiêu số phức z thỏa mãn 2
z  2 z  z và (z  4)(z  4i)  z  4i ? A. 3. B. 1. C. 2. D. 4.
Câu 49. Trong không gian Oxyz , cho mặt cầu S  tâm I 1;3;9 bán kính bằng 3. Gọi M , N là hai điểm
lần lượt thuộc hai trục Ox , Oz sao cho đường thẳng MN tiếp xúc với S  , đồng thời mặt cầu Trang 5/22 - WordToan 13
ngoại tiếp tứ diện OIMN có bán kính bằng
. Gọi A là tiếp điểm của MN và S  , giá trị 2 AM.AN bằng A. 39. B. 12 3 . C. 18 . D. 28 3 .
Câu 50. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 4 2
y  x  2mx  64x có đúng ba điểm cực trị A. 5 . B. 6 . C. 12 . D. 11.
------------- Hết -------------
Trang 6/22 – Diễn đàn giáo viên Toán BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A B D C B C C C B A C D D C B C B C D B A B C C C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B A D D C A B B D C D D D B B D D B C B D D D B C LỜI GIẢI CHI TIẾT 2 2 1  Câu 1. Nếu f  xdx  4 thì f  x  2 dx  bằng 2    0 0 A. 6 . B. 8 . C. 4 . D. 2 . Lời giải Chọn A 2 2 2 1  1 Ta có: f  x 2 dx  f
 xdx  2dx  2  4  6   . 2    2 0 0 0
Câu 2. Cho khối lăng trụ có diện tích đáy là 2 3a và chiều cao 2 .
a Thể tích khối lăng trụ đã cho bằng A. 3 a . B. 3 6a . C. 3 3a . D. 3 2a . Lời giải Chọn B Ta có: 2 3 V  . B h  3a .2a  6a . 5 1 Câu 3. Nếu f  xdx  3 thì f  xdx bằng 1  5 A. 5 . B. 6 . C. 4 . D. 3 . Lời giải Chọn A 1 5 Ta có: f  xdx   f  xdx   3    3. 5 1  Câu 4. Cho f
 xdx  cos x C.Khẳng định nào dưới đây đúng? A. f x  sin . x B. f x  cos . x C. f  x  sin . x D. f  x  cos . x Lời giải Chọn C
Áp dụng công thức sin x dx   cos x  C.  Suy ra f  x  sin . x
Câu 5. Cho hàm số y  f  x có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 1; . B. 0;  1 . C. 1;0. D. 0; . Lời giải Chọn B
Câu 6. Trong không gian Oxyz, cho mặt cầu S  x   y  2   z  2 2 : 2
1  6. Đường kính của S  bằng: A. R  6. B. 12. C. R  2 6. D. 3. Trang 7/22 - WordToan Lời giải Chọn C
Ta có bán kính mặt cầu R  6. suy ra đường kính mặt cầu bằng 2R  2 6.
Câu 7. Trong không gian Oxyz , cho điểm A1;2; 3 . Hình chiếu vuông góc của A lên mặt phẳng Oxy có tọa độ là A. 0;2;  3 . B. 1;0; 3 . C. 1; 2;0 . D. 1;0;0 . Lời giải Chọn C
Do điểm A1;2; 3 nên hình chiếu vuông góc của A lên mặt phẳng Oxy có tọa độ là 1; 2;0 .
Câu 8. Cho khối chóp S.ABC có chiều cao bằng 3, đáy ABC có diện tích bằng 10 . Thể tích khối chóp S.ABC bằng A. 2 . B. 15. C. 10. D. 30. Lời giải Chọn C 1 1
Thể tích khối chóp S.ABC là V  . B h  .10.3  10 . 3 3
Câu 9. Cho cấp số nhân u
với u  1 và u  2 . Công bội của cấp số nhân đã cho là: n  1 2 1 1 A. q  . B. q  2 . C. q  2  . D. q   . 2 2 Lời giải Chọn B u Ta có 2 u  u .q  q   2 . 2 1 u1
Câu 10. Cho hình trụ có chiều cao h  1 và bán kính r  2 . Diện tích xung quanh của hình trụ đã cho bằng
A. 4 . B. 2 . C. 3 . D. 6 . Lời giải Chọn A
Ta có S  2 rh  4 . xq 2x 1
Câu 11. Tiệm cận ngang của đồ thì hàm số y 
là đường thẳng có phương trình: 2x  4 A. x  2 . B. x  1. C. y  1. D. y  2 . Lời giải Chọn C 2x 1 Ta có lim
1 suy ra tiệm cận ngang của đồ là đường thẳng y 1. x 2x  4
Câu 12. Tập nghiệm của bất phương trình log x 1  2 là 5   A. 9; . B. 25;. C. 31; . D. 24; . Lời giải Chọn D Đkxđ: x  1
log x 1  2  log x 1  log 25  x 1  25  x  24 5   5   5
Câu 13. Hàm số nào dưới đây có bảng biến thiên như sau?
Trang 8/22 – Diễn đàn giáo viên Toán A. 4 2 y  x  2x . B. 3 y  x  3x . C. 4 2 y  x  2x . D. 3 y  x  3x . Lời giải Chọn D
Từ BBT ta nhận thấy hàm số có hai điểm cực trị và đồng biến trên khoảng 1;. Do đó hàm số
là hàm đa thức bậc ba có hệ số a  0.
Câu 14. Môđun của số phức z  3  4i bằng A. 25 . B. 7 . C. 5 . D. 7 . Lời giải Chọn C Ta có 2 2 z  3  4  25  5 Câu 15. Cho hàm số   4 2
f x  ax  bx  c có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình f  x  1 là A. 1. B. 2 . C. 4 . D. 3 . Lời giải Chọn B
Đường thẳng d  có phương trình y  1 cắt đồ thị hàm số y  f  x tại 2 điểm phân biệt.
Suy ra phương trình f  x  1 có 2 nghiệm thực phân biệt.
Câu 16. Tập xác định của hàm số y  log x  4 là 3   A. 5; . B.  ;   . C. 4; . D.  ;  4 . Lời giải Chọn C Trang 9/22 - WordToan
Điều kiện: x  4  0  x  4 .
Tập xác định: D  4;  .
Câu 17. Với a là số thực dương tùy ý, 4log a bằng A. 2  log a . B. 2 log a . C. 4  log a . D. 8log a . Lời giải Chọn B 1   1 Với a  0 , ta có 2
4log a  4log  a   4. log a  2log a . 2  
Câu 18. Số các tổ hợp chập 3 của 12 phần tử là A. 1320 . B. 36 . C. 220 . D. 1728 . Lời giải Chọn C
Số các tổ hợp chập 3 của 12 phần tử là 3 C  220 . 12
Câu 19. Cho hàm số y  f (x) có bảng biến thiên như sau:
Điểm cực tiểu của hàm số đã cho là: A. x  2  . B. x  2 . C. x  1  . D. x 1. Lời giải Chọn D
Từ bảng biến thiên ta suy ra: điểm cực tiểu của hàm số đã cho là x 1.
Câu 20. Trong không gian Oxyz , phương trình của mặt phẳng (Oyz) là: A. z  0 . B. x  0 . C. x  y  z  0 . D. y  0 . Lời giải Chọn B
Phương trình của mặt phẳng (Oyz) là: x  0 .
Câu 21. Nghiệm của phương trình 2x 1  2 3  3 x là: 1 A. x  . B. x  0 . C. x  1  . D. x  1. 3 Lời giải Chọn A 2 x 1  2x 1 3  3
 2x 1  2  x  3x 1  x  . 3 Câu 22. Cho hàm số 4 2
y  ax  bx  c có đồ thị như đường cong trong hình bên.
Trang 10/22 – Diễn đàn giáo viên Toán
Số điểm cực trị của hàm số đã cho là: A. 2. B. 3. C. 1. D. 0. Lời giải Chọn B
Dựa vào hình dáng của đồ thị. Ta thấy hàm số đã cho có 3 cực trị. x  2  t 
Câu 23. Trong không gian Oxyz , cho đường thẳng d : y 1 2t . Vec-tơ nào dưới đây là một véc-tơ chỉ x  1   3t  phương của d ?     A. u  2;1; 1 . B. u  1; 2;3 . C. u  1; 2;3 . D. u  2;1;1 . 4   3   2   1   Lời giải Chọn C 
Theo định nghĩa phương trình đưởng thẳng. Ta có u  1; 2;3 là một véc-tơ chỉ phương của d . 3  
Câu 24. Cho tam giác OIM vuông tại I có OI  3 và IM  4 . Khi quay tam giác OIM quanh cạnh góc
vuông OI thì đường gấp khúc OMI tạo thành hình nón có độ dài đường sinh bằng A. 7 . B. 3 . C. 5 . D. 4 . Lời giải Chọn C O l h I r M
Ta có chiều cao hình nón h  OI  3 , bán kính đáy r  IM  4 thì độ dài đường sinh là: 2 2 2 2
l  OM  IM  OI  3  4  5 .
Câu 25. Trên mặt phẳng tọa độ, điểm biểu diễn số phức z  2  7i có tọa độ là A. 2;7 . B.  2  ;7 . C. 2; 7   . D.  7  ;2 . Lời giải Chọn C
Điểm biểu diễn số phức z  2  7i trên mặt phẳng tọa độ có tọa độ là 2;7 .
Câu 26. Cho hai số phức z  2  3i và z  1 .i Số phức z  z bằng 1 2 1 2 A. 5  .i B. 3  2 .i C. 1 4 .i D. 3  4i. Lời giải Chọn B Trang 11/22 - WordToan
Vì z  2  3i và z  1 i nên z  z  2  3i  1 i  3  2 .i 1 2     1 2
Câu 27. Cho hàm số    x f x e  2 .
x Khẳng định nào dưới đây đúng? A.  f x x 2 dx  e  x  C. B.   d  x f x x e  C. C.  f x x 2 dx  e  x  C. D.  f x x 2 dx  e  2x  C. Lời giải Chọn A
Ta có:  f x x   xe  x x 2 d 2 dx  e  x  C.
Câu 28. Đạo hàm của hàm số 3 y x  là 1 1 A. 4 y x    . B. 2 y x    . C. 4 y x    . D. 4 y 3x    . 2 3 Lời giải Chọn B Ta có: 3 1  4 y  3x  3x .
Câu 29. Trong không gian Oxyz , cho ba điểm A1;2;  1 , B 3;0; 
1 và C 2;2;2 . Đường thẳng đi qua A
và vuông góc với mặt phẳng  ABC  có phương trình là x 1 y  2 z 1 x 1 y  2 z 1 A.   . B.   . 1 2 3 1 2 1 x 1 y  2 z 1 x 1 y  2 z 1 C.   . D.   . 1 2 1 1 2 1 Lời giải Chọn B  Ta có: AB 2; 2  ;2; AC 1;0;  1 .
Đường thẳng đi qua A và vuông góc với mặt phẳng  ABC  có véc-tơ chỉ phương là    x 1 y  2 z 1 A ;
B AC   2;4;2  1;2;  1   nên có phương trình:   . 1 2 1
Câu 30. Giá trị lớn nhất của hàm số f  x 3 2
 x  3x  9x 10 trên đoạn  2  ;2 bằng A. 12 . B. 10. C. 15. D. 1  . Lời giải Chọn C Xét hàm số f  x 3 2
 x  3x  9x 10 trên đoạn  2  ;2  f x 2  3x  6x  9. x  1   2  ;2 f  x 2
 0  3x  6x  9  0   . x  3    2  ;2 Ta có: f  2    8; f   1  15; f 2  1  2 .
Vậy giá trị lớn nhất của hàm số f  x 3 2
 x  3x  9x 10 trên đoạn  2  ;2 bằng 15.
Câu 31. Có bao nhiêu giá trị nguyên thuộc tập xác định của hàm số y  log 6  x x  2   ? A. 7 . B. 8 . C. 9 . D. Vô số. Lời giải Chọn A
Trang 12/22 – Diễn đàn giáo viên Toán
Điều kiện xác định   x x   2 6
2  0  x  4x 12  0  2   x  6 .
Vậy có tất cả 7 giá trị nguyên thuộc tập xác định của hàm số y  log 6  x x  2   .
Câu 32. Gọi z và z là hai nghiệm phức của phương trình 2
z  z  6  0 . Khi đó z  z  z z bằng: 1 2 1 2 1 2 A. 7 . B. 5 . C. 7 . D. 5 . Lời giải Chọn B z  z  1 Vì phương trình 2
z  z  6  0 có hai nghiệm z và z . Theo định lí Vi-et, ta có: 1 2 . Do 1 2 z z  6  1 2
đó: z  z  z z  1 6  5 . 1 2 1 2
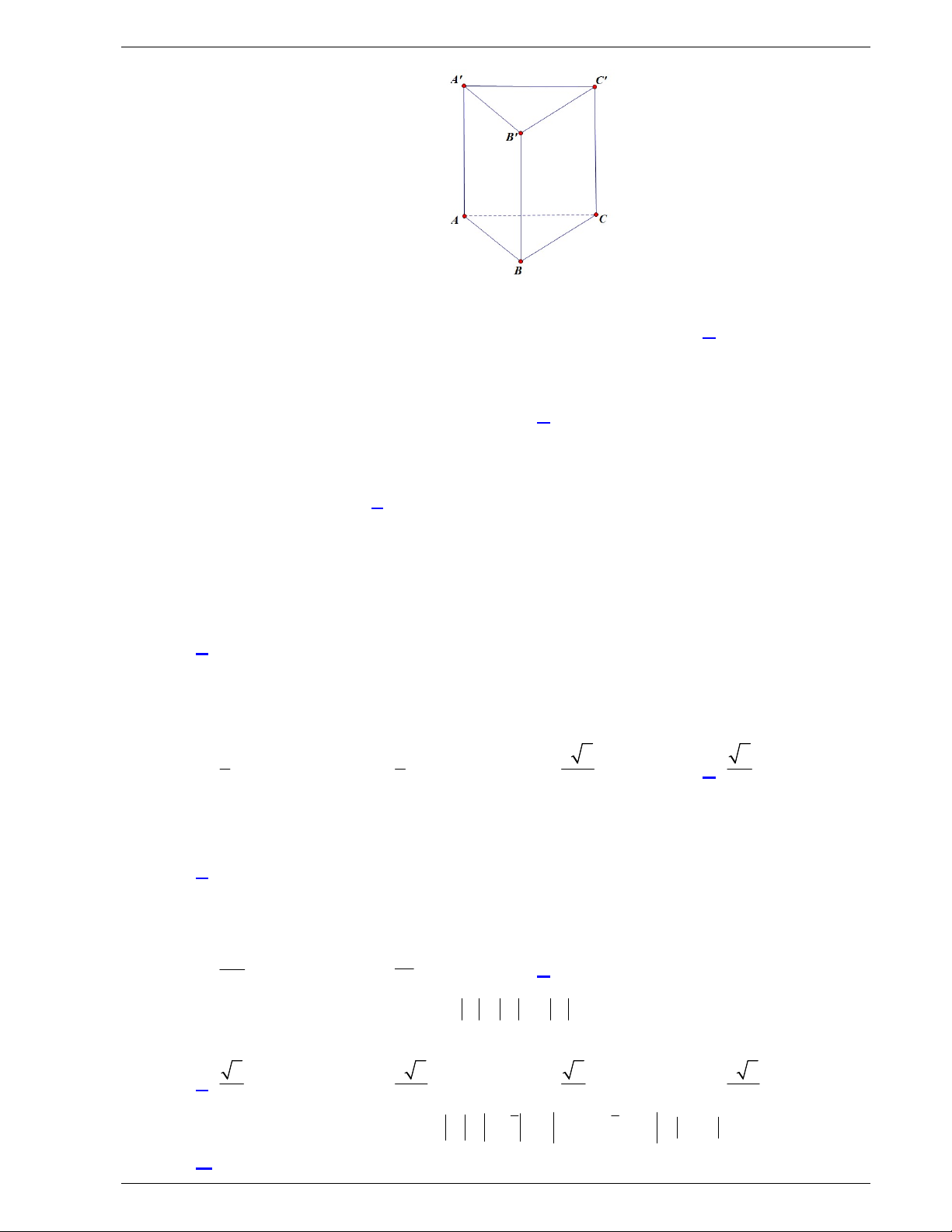
Câu 33. Cho hình lăng trụ đứng ABC. 
A BCcó đáy ABC là tam giác vuông tại B , AC  2 , AB  3 và A 
A  1 (tham khảo hình bên).
Góc giữa hai mặt phẳng  ABC và  ABC bằng A. 0 30 . B. 0 45 . C. 0 90 . D. 0 60 . Lời giải Chọn B
Tam giác ABC vuông tại B nên 2 2 BC  AC  AB  1.
ABCABC  AB 
Ta có: AB  BC tai B, BC   ABC Do BC   AA B  B   
AB  BC tai B, BC   ABC
Suy ra góc giữa hai mặt phẳng  ABC và  ABC là góc  C BC  . CC AA Xét C B
 C vuông tại C ta có: tan  C B  C    1   0 C BC   45 . BC BC
Vậy góc giữa hai mặt phẳng  ABC và  ABC là 0 45 .
Câu 34. Cho hình hộp chữ nhật ABC . D A B  C  D
  có AB  a , BC  2a và AA  3a (tham khảo hình bên).
Khoảng cách giữa hai đường thẳng BD và AC bằng A. a . B. 2a . C. 2a. D. 3a . Lời giải Chọn D Trang 13/22 - WordToan A C     AB C  D  , BD//  A B  C  D    d B , D A C    d BD, A B  C  D
   d B, A B  C  D
   BB  3a . 1
Câu 35. Cho hàm số f  x  1
. Khẳng định nào dưới đây đúng? 2 cos 2x A. f
 x dx  x  tan 2x C . B. f  x 1 dx  x  cot 2x  C . 2 C. f  x 1 dx  x  tan 2x  C . D. f  x 1 dx  x  tan 2x  C . 2 2 Lời giải Chọn C   f  x 1 1 d 2x 1 dx  1 dx  dx   x  tan 2x  C    . 2  2  cos 2x  2 cos 2x 2
Câu 36. Hàm số nào dưới đây đồng biến trên  ? x 1 A. 4 2 y  x  x . B. 3 y  x  x . C. y  . D. 3 y  x  x . x  2 Lời giải Chọn D Ta có: 3 2
y  x  x  y  3x 1  0 x    .
Câu 37. Trong không gian Oxyz , cho điểm A0;3;2 và mặt phẳng P : 2x  y  3z  5  0 . Mặt phẳng đi
qua A và song song với P có phương trình là
A. 2x  y  3x  9  0 . B. 2x  y  3x  3  0 . C. 2x  y  3x  3  0 . D. 2x  y  3x  9  0 . Lời giải Chọn D
Mặt phẳng đi qua A và song song với P có phương trình là
2x   y  3  3z  2  0  2x  y  3z 9  0 .
Câu 38. Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn 40;60. Xác suất để chọn được số
có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng 4 2 3 3 A. B. C. D. 7 5 5 7 Lời giải Chọn D
Từ 40 đến 60 ta có 21 số nên n   21
Các số thỏa mãn đề bài: 45; 46; 47;48; 49;56;57;58;59  Có 9 số. 9 3
Xác suất để chọn được số thoản mãn đề bài: P   21 7
Câu 39. Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng ba số nguyên b thỏa mãn 3b 3 .2b a 18  0 ? A. 72 B. 73 C. 71 D. 74 Lời giải Chọn B
Trang 14/22 – Diễn đàn giáo viên Toán 3b   b   b 3 1 3   3  0   18  TH1:          b    b b 18 18 1 log2  .2 a 18  0 2  b  log      a 2   a   a  18  18 9 9
Để có đúng ba số nguyên b thì 4  log  5  16   32   a  . 2    a  a 16 8
Trường hợp này có 1 giá trị a  1 nguyên thỏa mãn. 3b   b   b 3 1 3   3  0   18  TH2:          b    b b 18 18 log 1 2  .2 a 18  0 2  b  log      a 2   a   a  18  1 18 1
Để có đúng ba số nguyên b thì 3  log  2     72  a 144 . 2    a  8 a 4
Trường hợp này có 144  72  72 giá trị a nguyên thỏa mãn.
Vậy số giá trị nguyên của a là: 72 1  73. Câu 40. Cho hàm số 4 2
f (x)  (m 1)x  2mx 1 với m là tham số thực. Nếu min f (x)  f (2) thì [0;3] max f (x) bằng [0;3] 13 14 A.  . B. 4 . C.  . D. 1. 3 3 Lời giải Chọn B Ta có: 3 2
f '(x)  4(m 1)x  4mx  4x((m 1)x  m) x  0 f '(x) 0   
m ( m  1 không thỏa yêu cầu bài toán) 2 x   m 1
Vì min f (x)  f (2)  x  2 là nghiệm của f '(x)  0 [0;3] m 4 
 4  m  4m  4  m  m 1 3 1 8 4 2  f (x)  x  x 1 3 3 81 72 3 12 f (0)  1, f (3)      4 3 3 3 3 Vậy max f (x)  4 [0;3] Câu 41. Biết
F(x) và G(x) là hai nguyên hàm của hàm số f (x) trên  và 3
f (x)dx  F (3)  G(0)  a (a  0) 
. Gọi S là diện tích hình phẳng giới hạn bởi các đường 0
y  F(x), y  G(x), x  0 và x  3 . Khi S  15 thì a bằng: A. 15 . B. 12 . C. 18 . D. 5 . Lời giải Chọn D Ta có:
F(x),G(x) là nguyên hàm của f (x) F(x)  G(x)  C Trang 15/22 - WordToan 3 3 3
 S  F(x)  G(x) dx  C dx  Cdx  3C 15  C  5  C  5     0 0 0 3
f (x)dx  F(3)  F(0)  F(3)  (G(0)  C)  F(3)  G(0)  C  F(3)  G(0)  a 0  a  C   5 (do a  0 )
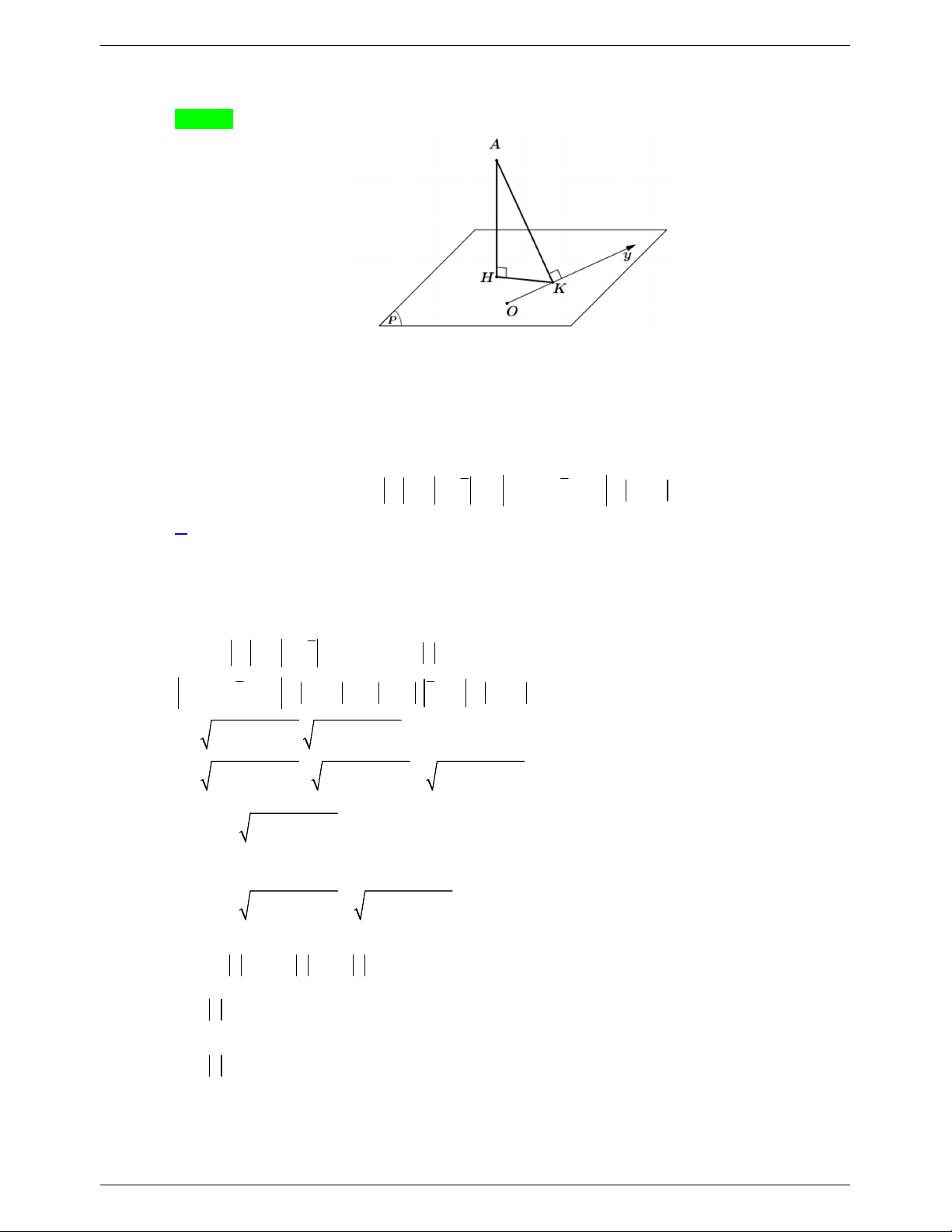
Câu 42. Trong không gian Oxyz , cho điểm A1;2;2 . Gọi P là mặt phẳng chứa trục Ox sao cho
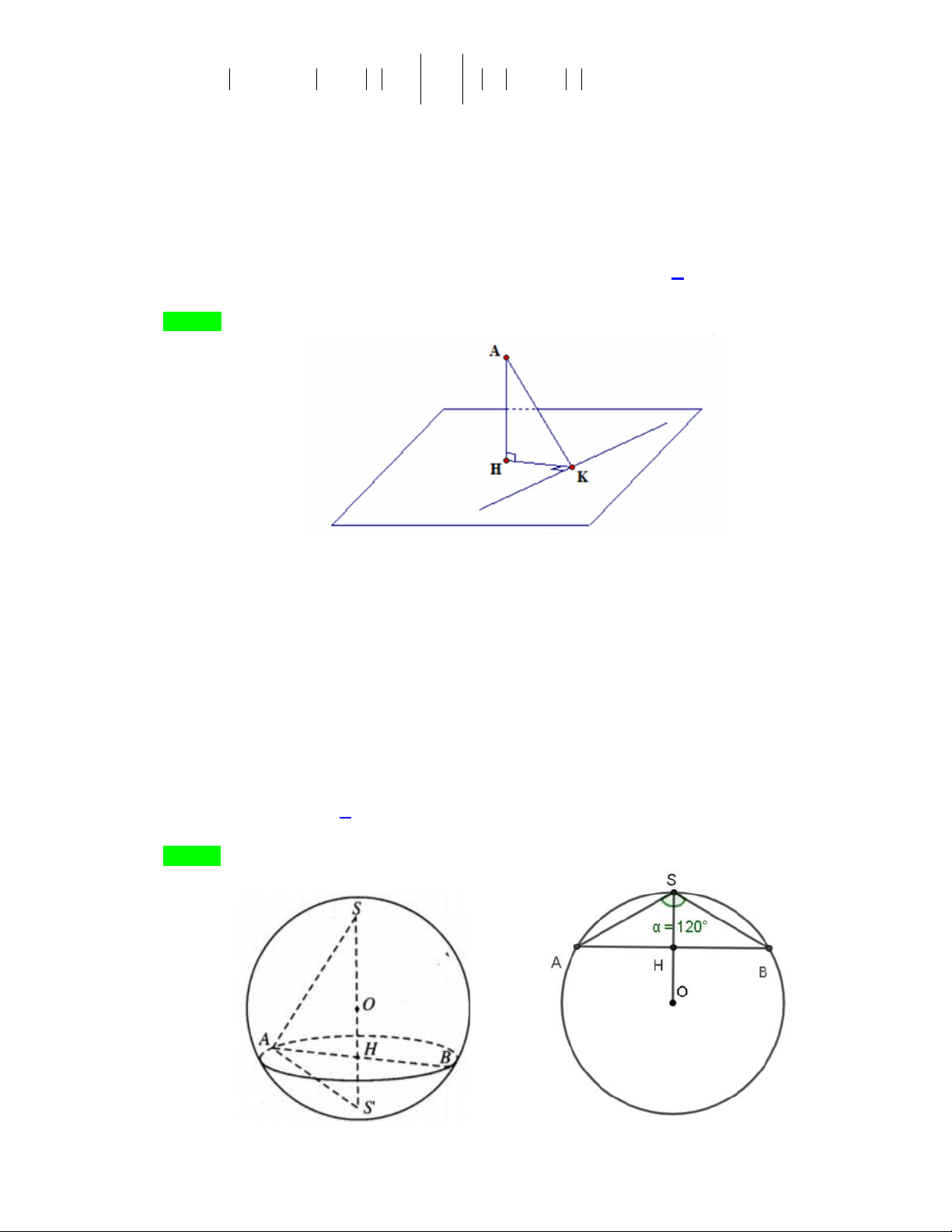
khoảng cách từ A đến P lớn nhất. Phương trình của P là A. 2 y  z  0 . B. 2 y  z  0 . C. y  z  0 . D. y  z  0 . Lời giải Chọn D
Gọi H , K lần lượt là hình chiếu của A lên mặt phẳng P và trục Ox . Ta có: d  ; A P  AH  AK . 
Suy ra khoảng cách từ A đến P lớn nhất khi H  K , hay mặt phẳng P nhận véc-tơ AK làm véc-tơ pháp tuyến. 
K là hình chiếu của A trên trục Ox suy ra: K 1;0;0 , AK 0; 2  ;2 .
Mặt phẳng P đi qua K có phương trình: 2 y  0  2z  0  0  y  z  0.
Câu 43. Cho hình nón có góc ở đỉnh là 0
120 và chiều cao bằng 4. Gọi S  là mặt cầu đi qua đỉnh và chứa
đường tròn đáy của hình nón đã cho. Tính diện tích của S  bằng: A. 64 . B. 256 . C. 192 . D. 96 . Lời giải Chọn B Ta có SH  4
Trang 16/22 – Diễn đàn giáo viên Toán AB  AH  SH  0 2 2.
.tan ASH  2.4.tan 60  8 3
Có OS là bán kính mặt cầu cũng là bán kính đường tròn ngoại tiếp SAB AB 8 3 Suy ra: 2OS   OS   8 0 sin ASB 2.sin120
Vậy diện tích mặt cầu: 2 S  4.8  256
Câu 44. Xét tất cả các số thực x , y sao cho 2 2 4 x log5 a 40 25 y a   
với mọi số thực dương a . Giá trị lớn nhất của biểu thức 2 2
P  x  y  x  3y bằng 125 A. . B. 80 . C. 60 . D. 20 . 2 Lời giải Chọn C Ta có 2 2 4 x log5 a 40 25 y a    2 2 4 x log5 a 40 log log 25 y a    
 4x  2log alog a  2 2 40  y 5 5  5 5 2 2
 log a  2x log a  40  y  0 * 5 5
Coi * là bất phương trình bậc hai ẩn log a 5
Để * đúng với mọi số thực dương a thì   0 2  x   2 40  y   0 2 2  x  y  40  0  1 . Ta có biểu thức  
1 là hình tròn C tâm O 0;0 , bán kính R  2 10 . 1  1 Mặt khác 2 2 P  x  y  x  3y 2 2
 x  y  x  3y  P  0 là phương trình đường tròn C tâm 2   1 3  1 I  ;   , bán kính R  10  4P .  2 2  2 2
Để tồn tại điểm chung của đường tròn C với hình tròn C thì 1  2  R  R  1 1 OI  10  4P  2 10 
10  10  4P  5 10  P  60 . 2 1 2 2 Vậy P  60 . max
Câu 45. Cho các số phức z , z , z thỏa mãn z  z  2 z  2 và 8 z  z z  3z z . Gọi A , B , C 1 2  1 2 3 1 2 3 3 1 2
lần lượt là các điểm biểu diễn của z , z , z trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng 1 2 3 55 55 55 55 A. . B. . C. . D. . 32 16 44 8 Trang 17/22 - WordToan Lời giải Chọn B
Ta có: z  z  2  OA  OB  2 ; z  1  OC  1. 1 2 3 z z z z 3
+) 8 z  z z  3z z  8 z  z  3 1 2  8 z  z  3  z  z  . 1 2  1 2 1 2  3 1 2 z 1 2 z 1 2 2 3 3 z  z z  z 3
Gọi H là trung điểm của AB , biểu diễn số phức 1 2 , ta có: 1 2 OH   2 2 4 55 +) 2 2 z  z  z  z  2 2 2 z  z  z  z  55  AB  . 1 2 1 2 1 2  1 2 2 2 3
+) 8 z  z z  3z z  8z z  8z z  3z z  z z  z z  z z 1 2  3 1 2 1 3 2 3 1 2 1 3 2 3 1 2 8 3
Đặt 2a  , suy ra: z z  z z  2az z  z z  az  az  z z 1  3 2   1 3 8 1 3 2 3 1 2 2  z z  az  az  z z 1 3 2 1 3 2 2 2
 z  az  az  z  z z  z z  z z  z z  b 3 2 1 3 2 3 2 3 1 3 1 3 2 2 2 2 AC  z  z
 z  z  z z  z z  5  b . 3 1 3 1  1 3 1 3 2 2 2 2 BC  z  z
 z  z  z z  z z  5  b . 3 2 3 2  2 3 2 3 Suy ra: 2 2
AC  BC  AC  BC hay tam giác ABC cân tại C . 3 1 CH  OC  OH  1  4 4 1 1 55 1 55 Vậy S  . AB CH  . .  . A  BC 2 2 2 4 16
Câu 46. Cho khối lăng trụ đứng ABC.A B  C
  có đáy ABC là tam giác vuông cân tại A , AB  2a . Góc
giữa đường thẳng BC và mặt phẳng  ACC A
  bằng 30 . Thể tích của khối lăng trụ đã cho bằng A. 3 3a . B. 3 a . C. 3 12 2a . D. 3 4 2a . Lời giải Chọn D
Trang 18/22 – Diễn đàn giáo viên Toán AB  AC Ta có:   AB   ACC A    AB  AC . AB  AA
Vậy góc giữa đường thẳng BC và mặt phẳng  ACC A   là góc  BC A  . Trong tam giác vuông BC A  ta có         BC A 30 ; AB 2a AC  . AB cot BC A   2 . a 3 .
Trong tam giác vuông ACC ta có 2 2
CC  AC  AC  2 2 . a
Vậy thể tích khối lăng trụ đã cho là: 1 1 2 2 3 V  CC . AB  2 2 . a .4a  4 2a . 2 2
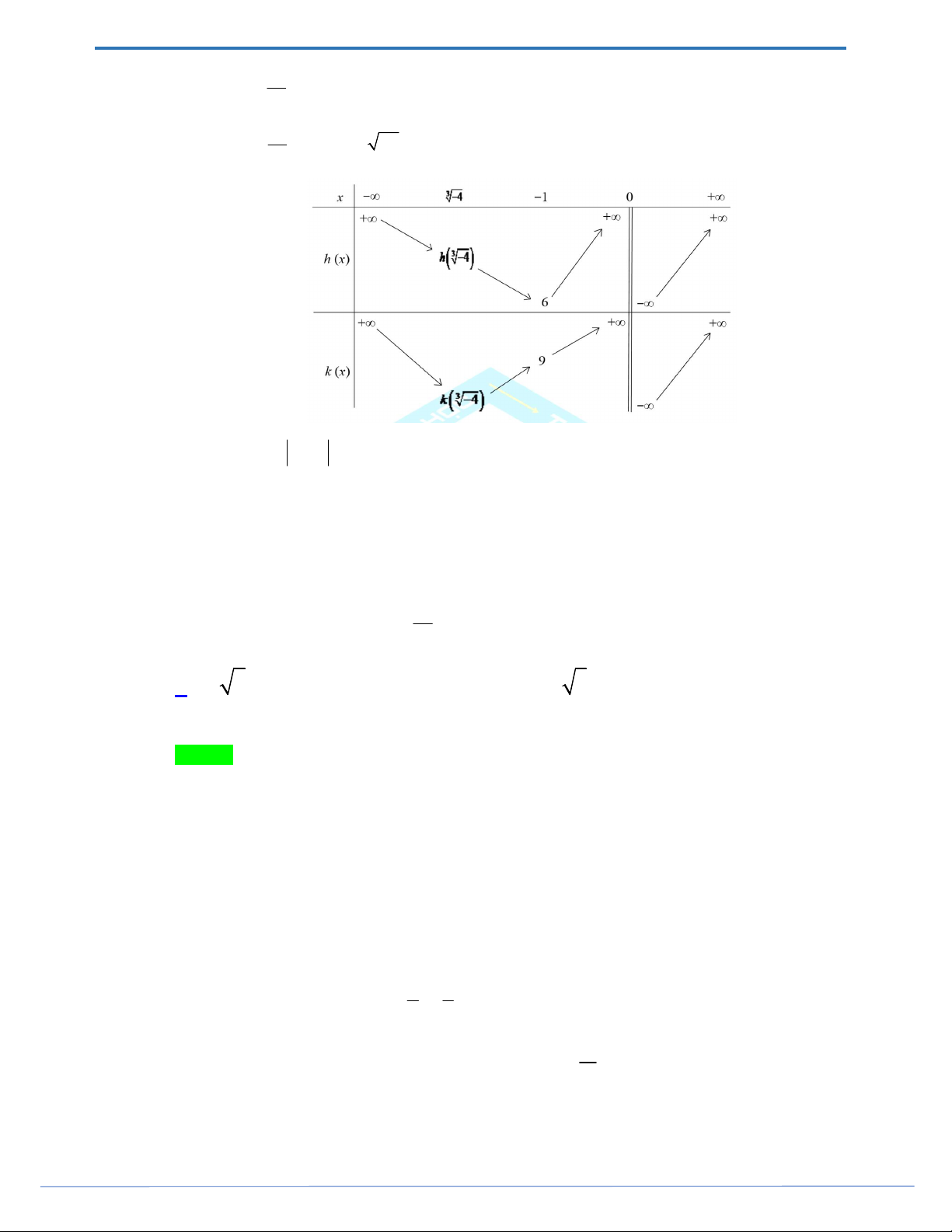
Câu 47. Cho hàm số y  f  x . Biết rằng hàm số g  x  ln f  x có bảng biến thiên như sau:
Diện tích hình phẳng giới hạn bởi các đường y  f x và y  g x thuộc khoảng nào dưới đây? A. 5;6. B. 4;5 . C. 2;3. D. 3;4 . Lời giải Chọn D Ta có f  x gx  e .
Từ bảng biến thiên suy ra: g  x gx ln 2  ln 2  e  e  2 .
+) f  x  g x gx e .
Phương trình hoành độ giao điểm của f  x và g x : x  x1
f  x  g x  0  g x gx e
 g x  0  gx gx
e  10  gx  0   x  x . 2  x  x  3 Trang 19/22 - WordToan
Mặt khác từ bảng biến thiên ta cũng có: g x  0, x
 x ; x ; gx  0, x  x ; x . 2 3  1 2  Suy ra: 3 x 3 x 3 x S  f 
 x gx dx  g  x gx e
 gx dx  gx gx e   1 dx 1 x 1 x 1 x 2 x x  gx gx e   3 1 dx  g x gx e    1dx 1 x 2 x 2 x x gx
 e  1dg x 3 gx  e    1dgx 1 x x2 2 x 3 x gx  e  g x g x  e  g x 1 x 2 x gx2      g x g x g x e g x  e  g x   e  g x  e  g x  2   1  1  3  3  2  2     g 2 x  g 1 x  g 3 x   2e  e  e  2g  x  g x  g x 2   1  3 43 43  2.6   2  2ln 6  ln  37 43 ln 2   ln  3,416 . 8 8 8 144
Câu 48. Có bao nhiêu số phức z thỏa mãn 2 z  2 z  z và 2
(z  4)(z  4i)  z  4i ? A. 3. B. 1. C. 2. D. 4. Lời giải Chọn D Ta có 2
z  4i  (z  4)(z  4i)  (z  4)(z  4i)  z  4 z  4i  z  4 z  4i .
Suy ra z  4i  0 hoặc z  4i  z  4 . 2 2  z  4i 16
Nếu z  4i  0 thì z  4i :  thỏa mãn.
2 z  z  2 8i  16 
Nếu z  4i  z  4 thì đặt z  x  yi với x, y   ta được 2 2 2 2
 x  (y  4)  (x  4)  x   y y   y  0  y  2  y  2          2  2 2 x  y  4 y 2 y  4 y x  0 x  2  x  2.     
Vậy có 4 số phức thỏa mãn là 0 , 2  2i , 2   2i , 4i .
Câu 49. Trong không gian Oxyz , cho mặt cầu S  tâm I 1;3;9 bán kính bằng 3. Gọi M , N là hai điểm
lần lượt thuộc hai trục Ox , Oz sao cho đường thẳng MN tiếp xúc với S  , đồng thời mặt cầu 13
ngoại tiếp tứ diện OIMN có bán kính bằng
. Gọi A là tiếp điểm của MN và S  , giá trị 2 AM .AN bằng A. 39. B. 12 3 . C. 18 . D. 28 3 . Lời giải Chọn B
Ta có I 1;3;9 và R  3. Suy ra dI,OMN   3 .
Vậy mặt cầu S  tiếp xúc OMN  tại A1;0;9 . Gọi tọa độ M  ; m 0;0 và N 0;0;n .  
Ta có AM  m 1;0; 9 ; AN   1  ;0;n  9 .
Trang 20/22 – Diễn đàn giáo viên Toán Do ,
A M , N thẳng hàng nên m   1 n  9  9   1 .
Do IA  OMN  và H là trung điểm MN thì H là tâm đường tròn ngoại tiếp OMN .
Suy ra K là tâm mặt cầu ngoại tiếp IOMN  KH  IMN  13
bán kính đường tròn ngoại tiếp IMN bằng (đường tròn lớn) 2 1 IM .IN.MN .IH.MN   IM.IN  39  m   n    . 2 13
 21 90 92 10 39 2 4. 2   m   1 n  9  9  Từ (1) và (2) suy ra  .  m  2 1  90   n92 1039 u   m   2 1 Đặt  , ta có hệ phương trình v   n 92 uv   81  uv  81     m  2 1  90 
 n92 1039 u90v10 1521 uv   81 u   27     90  v 10u  540 v  3
Vậy AM .AN  u  81 v 1  12 3 .
Câu 50. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 4 2
y  x  2mx  64x có đúng ba điểm cực trị A. 5 . B. 6 . C. 12 . D. 11. Lời giải Chọn C Xét hàm số 4 2 y  x  2mx  64x . Ta có: 3 y  4x  4mx  64 . * x  0
Phương trình hoành độ giao điểm: 4 2
x  2mx  64x  0   3 x  2mx  64  0    1 Phương trình  
1 luôn có một nghiệm x  0 nên đồ thị hàm số 4 2
y  x  2mx  64x cắt Ox ít nhất hai điểm và  4 2
lim x  2mx  64x   . x Suy ra để hàm số 4 2
y  x  2mx  64x có 3 điểm cực trị thì hàm số 4 2
y  x  2mx  64x có đúng
một điểm cực trị  phương trình * có đúng một nghiệm đơn 16 2 m  x 
có đúng một nghiệm đơn. x 16 16 Xét hàm số: f  x 2  x  , f  x  2x  . x 2 x f  x 16  0  2x   0  x  2 . 2 x Bảng biến thiên: Trang 21/22 - WordToan
Từ bảng biến thiên suy ra m  12 . * m Suy ra:    m 1;2;3;...;11;  12 . m  12 
Vậy có 12 giá trị nguyên dương của tham số m để hàm số 4 2
y  x  2mx  64x có đúng ba điểm cực trị .
------------ Hết -------------
Trang 22/22 – Diễn đàn giáo viên Toán
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
ĐỀ THI TN THPT MÔN TOÁN NĂM 2022 Mã đề 102 Môn: TOÁN – LỚP 12
Thời gian: 90 phút (Không kể thời gian phát đề) TRAO ĐỔI & CHIA SẺ LINK NHÓM: KIẾN THỨC
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan Câu 1. Cho hàm số   x
f x  e  2x . Khẳng định nào dưới đây đúng? A. f  x x 2 dx  e  2x  C . B. f  x x 2 dx  e  x  C . C.    x f x dx  e  C . D. f  x x 2 dx  e  x  C .
Câu 2. Đạo hàm của hàm số 3 y x  là 1 1 A. 4 y x    . B. 4 y 3x    . C. 4 y x    . D. 2 y x    . 3 2
Câu 3. Hàm số nào dưới đây có bảng biến thiên như sau? A. 3 y  x  3x . B. 3 y  x  3x . C. 4 2 y  x  2x . D. 4 2 y  x  2x .
Câu 4. Trong không gian Oxyz , phương trình mặt phẳng Oyz là A. x  0 . B. x  y  z  0 . C. z  0 . D. y  0 . 2x 1
Câu 5. Tiệm cận ngang của đồ thị hàm số y 
là đường thẳng có phương trình 2x  4 A. y  2 . B. x  2  . C. x  1. D. y  1.
Câu 6. Cho hàm số y  f (x) có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 0; . B. 1; . C.  1  ;0 . D. 0;  1 .
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 1 NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT
Câu 7. Cho hàm số y  f  x có bảng biến thiên như sau
Điểm cực tiểu của hàm số đã cho là A. x  2  . B. x  1. C. x  1  . D. x  2 .
Câu 8. Trên mặt phẳng tọa độ, điểm biểu diễn số phức z  2  7i có tọa độ là A. 2;7 . B. 2; 7 . C.  2  ;7 . D.  7  ;2.
Câu 9. Cho cấp số nhân u với u  1 và u  2. Công bội của cấp số nhân đã cho là n  1 2 1 1 A. . B. 2 . C. 2 . D. . 2 2
Câu 10. Cho 2 số phức z  2  3i và z  1 .i Số phức z  z 1 2 1 2 bằng A. 3 4 .i B. 1 4 .i C. z  5  .i D. 3 2 .i
Câu 11. Với a là số thực dương tùy ý, 4 log a bằng A. 4 log a . B. 8log a . C. 2 log a . D. 2 log a . Câu 12. Cho f
 xdx  cos x C . Khẳng định nào dưới đây đúng? A. f x  sin x . B. f x  cos x . C. f  x  sin x . D. f  x  cos x .
Câu 13. Cho hình trụ có chiều cao h  1 và bán kính đáy r  2 . Diện tích xung quanh của hình trụ đã cho bằng A. 3 . B. 4 . C. 2 . D. 6 .
Câu 14. Cho khối chóp S.ABC có chiều cao bằng 3 , đáy ABC có diện tích bằng 10. Thể tích khối chóp S.ABC bằng A. 15 . B. 10. C. 2 . D. 30 .
Câu 15. Mô đun của số phức z  3  4i bằng A. 7 B. 5 . C. 7 . D. 25 .
Câu 16. Nghiệm của phương trình 2x 1  2 3 3   x là 1 A. x  . B. x  0 . C. x  1 . D. x  1. 3 Câu 17. Cho hàm số   4 2
f x  ax  bx  c có đồ thị là đường cong trong hình vẽ sau
Số nghiệm thực của phương trình f  x 1 là A. 4 . B. 3 . C. 2 . D. 1. Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
Câu 18. Tập nghiệm của bất phương trình log x 1  2 là 5   A. 24;   . B. 9;  . C. 25;  . D. 31;   . 2 2 1  Câu 19. Nếu f  xdx  4 thì f  x 2 dx  bằng 2    0 0 A. 2 . B. 6 . C. 4 . D. 8 .
Câu 20. Tập xác định của hàm số y  log x  4 là. 3   A. ; 4 . B. 4; . C. 5; . D.  ;   . Câu 21. Cho hàm số 4 2
y  ax  bx  c có đồ thị như đường cong trong hình bên.
Số điểm cực trị của hàm số đã cho là A. 1. B. 0 . C. 2 . D. 3 .
Câu 22. Số các tổ hợp chập 3 của 12 phần tử là A. 1728 . B. 220 . C. 1320 . D. 36.
Câu 23. Trong không gian Oxyz , cho điểm A1;2;3 . Hình chiếu vuông góc của A lên mặt phẳng Oxy có tọa độ là A. 1;0; 3 . B. 1;0;0 . C. 1;2;0 . D. 0;2; 3 .
Câu 24. Trong không gian Oxyz , cho mặt cầu S  x   y  2   z  2 2 : 2
1  6 . Đường kính của S  bằng A. 3 . B. 6 . C. 2 6 . D. 12 .
Câu 25. Cho tam giác OIM vuông tại I có OI  3 và IM  4 . Khi quay tam giác OIM quanh cạnh góc
vuông OI thì đường gấp khúc OMI tạo thành hình nón có độ dài đường sinh bằng A. 4 . B. 3 . C. 5 . D. 7 .
Câu 26. Cho khối lăng trụ có diện tích đáy 2
3a và chiều cao 2a . Thể tích khối lăng trụ đã cho bằng A. 3 3a . B. 3 6a . C. 3 2a . D. 3 a . x  2  t Câu 27. Trong không gian 
Oxyz, cho đường thẳng d : y 1 2t . Vectơ nào dưới đây là một véctơ chỉ z  1   3t  phương của d ?   A. u  2;1;1 . B. u  2;1; 1 . 1   4     C. u  1;  2; 3 . D. u  1; 2; 3 . 3   3   5 1  Câu 28. Nếu f  xdx  3 thì f  xdx bằng 1 5 A. 3 . B. 4 . C. 6 . D. 5.
Câu 29. Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có AB  a , BC  2a và AA'  3a (tham khảo hình
bên). Khoảng cách giữa hai đường thẳng BD và A'C ' bằng
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 3 NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT A. 2a . B. 2a . C. 3a . D. a .
Câu 30. Hàm số nào dưới đây đồng biến trên  ? x 1 A. 4 2 y  x  x . B. 3 y  x  x . C. y  . D. 3 y  x  x . x  2
Câu 31. Giá trị trị lớn nhất của hàm số f x 3 2
 x  3x  9x 10 trên đoạn  2  ;  2 bằng A. 15 . B. 10 . C. 1. D. 12 .
Câu 32. Trong không gian Oxyz , cho ba điểm A1;2;  1 , B3;0;  1 và C 2;2; 2
  . Đường thẳng đi qua
A và vuông góc với mặt phẳng  ABC có phương trình là x 1 y  2 z 1 x 1 y  2 z 1 A.   . B.   . 1 2 1 1 2  3 x 1 y  2 z 1 x 1 y  2 z 1 C.   . D.   . 1 2 1 1 2 1
Câu 33. Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn 40;6 
0 . Xác suất để chọn được
số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng 2 4 3 3 A. . B. . C. . D. . 5 7 7 5
Câu 34. Trong không gian Oxyz , cho ba điểm A1;2;  1 , B3;0;  1 , C 2;2; 2
  . Đường thẳng đi qua
A và vuông góc với mặt phẳng  ABC có phương trình là: x 1 y  2 z 1 x 1 y  2 z 1 A.   . B.   . 1 2 1 1 2 3 x 1 y  2 z  1 x 1 y  2 z 1 C.   . D.   . 1 2 1 1 2 1
Câu 35. Gọi z , z là hai nghiệm phức của phương trình 2
z  z  6  0 . Khi đó z  z  z .z bằng 1 2 1 2 1 2 A. 5 . B. 7 . C. 7 . D. 5 . 1
Câu 36. Cho hàm số f  x 1
. Khẳng định nào dưới đay đúng? 2 cos 2x A. f  x 1 dx  x  cos 2x  C . B. f
 xdx  x  tan 2x  C . 2 C. f  x 1 dx  x  tan 2x  C . D. f  x 1 dx  x  tan 2x  C . 2 2
Câu 37. Có bao nhiêu số nguyên thuộc tập xác định của hàm số y  log 6  x x  2   ? A. 7 . B. 8 . C. Vô số. D. 9 .
Câu 38. Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông tại B , AC  2, AB  3
và AA 1 (tham khảo hình bên dưới). Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
Góc giữa hai mặt phẳng ABC và ABC bằng A. 90 . B. 60 . C. 30 . D. 45 . Câu 39. Cho hàm số 4 2
f (x)  mx  2(m 1)x với m là tham số thực. Nếu min f (x)  f (1) thì max f (x) [0;2] [0;2] bằng A. 2 . B. 1. C. 4 . D. 0 .
Câu 40. Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn 5b  1 .2b a 5  0 ? A. 20 . B. 21. C. 22 . D. 19 .
Câu 41. Biết F  x và G  x là hai nguyên hàm của hàm số f  x trên  và 5 f
 xdx  F 5G0 a, a  0. Gọi S là diện tích hình phẳng giới hạn bỡi các đường 0
y  F  x , y  G x , x  0 và x  5. Khi S  20 thì a bằng? A. 4 . B. 15. C. 25 . D. 20 .
Câu 42. Cho khối lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông cân tại A , AB  a . Góc
giữa đường thẳng BC và mặt phẳng  ACC A
  bằng 30 . Thể tích của khối lăng trụ đã cho bằng 1 3 3 2 2 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 8 8 2 2
Câu 43. Cho hình nón có góc ở đỉnh bằng 120 và chiều cao bằng 1. Gọi S  là mặt cầu đi qua đỉnh và
chứa đường tròn đáy của hình nón đã cho. Diện tích của S  bằng A. 16 . B. 12 . C. 4 . D. 48
Câu 44. Xét các số thực , x y sao cho 2 2 9 y 4 log7 49 x a  a 
với mọi số thực dương a . Giá trị lớn nhất của biểu thức 2 2
P  x  y  4x  3y bằng: 121 39 A. . B. . C. 24 . D. 39 . 4 4
Câu 45. Cho các số phức z , z , z thỏa mãn z  z  2 z  2 và 3z z  4z z  z . Gọi , A B,C 1 2 3  1 2  1 2 3 1 2 3
lần lượt là các điểm biểu diễn của z , z , z trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng 1 2 3 7 3 7 7 3 7 A. . B. . C. . D. . 4 4 2 2
Câu 46. Có bao nhiêu số phức z thỏa mãn 2
z  z  z và  z  z  i 2 2 2  z  2i ? A. 4 . B. 2 . C. 3 . D. 1.
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 5 NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT
Câu 47. Trong không gian Oxyz , cho điểm A2;1; 
1 . Gọi P là mặt phẳng chứa trục Oy sao cho
khoảng cách từ A đến P là lớn nhất. Phương trình của P là: A. 2x  z  0 . B. 2x  z  0. C. x  z  0 . D. x  z  0 .
Câu 48. Cho hàm số bậc bốn y  f  x . Biết rằng hàm số g  x  ln f  x có bảng biến thiên như sau:
Diện tích hình phẳng giới hạn bởi các đường y  f  x và y  g x thuộc khoảng nào dưới đây? A. 38;39 . B. 25;26 . C. 28;29 . D. 35;36 .
Câu 49. Trong không gian Oxyz , cho mặt cầu S  tâm I 4;1;2 bán kính bằng 2 . Gọi M ; N là hai
điểm lần lượt thuộc hai trục Ox ; Oy sao cho đường thẳng MN tiếp xúc với S  , đồng thời mặt 7
cầu ngoại tiếp tứ diện OIMN có bán kính bằng . Gọi A là tiếp điểm của MN và S  , giá trị 2 AM.AN bằng A. 6 2 . B. 14 . C. 8 . D. 9 2 .
Câu 50. Có bao nhiêu giá trị nguyên âm của tham số a để hàm số 4 2
y  x  2ax  8x có đúng ba điểm cực trị? A. 2 . B. 6 . C. 5 . D. 3 . Trang 6
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D B B A D D B B B D C C B B B A C A B B D B C C C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B C A C B A C B C D D A D C B A D A C A A A D A D Câu 1. Cho hàm số   x
f x  e  2x . Khẳng định nào dưới đây đúng? A. f  x x 2 dx  e  2x  C . B. f  x x 2 dx  e  x  C . C.    x f x dx  e  C . D. f  x x 2 dx  e  x  C . Lời giải
GVSB: Trần Thành Thống/ ; GVPB1: Bùi Hà; GVPB2: Chọn D Ta có f  x x 2 dx  e  x  C .
Câu 2. Đạo hàm của hàm số 3 y x  là 1 1 A. 4 y x    . B. 4 y 3x    . C. 4 y x    . D. 2 y x    . 3 2 Lời giải
GVSB: Trần Thành Thống; GVPB1: Bùi Hà; GVPB2: Chọn B Ta có 4 y 3x    .
Câu 3. Hàm số nào dưới đây có bảng biến thiên như sau? A. 3 y  x  3x . B. 3 y  x  3x . C. 4 2 y  x  2x . D. 4 2 y  x  2x . Lời giải
GVSB: Trần Quang Nam; GVPB1: Bùi Hà; GVPB2: Chọn B
Từ đồ thị ta có đây là đồ thị hàm số bậc 3 với hệ số a  0 .
Câu 4. Trong không gian Oxyz , phương trình mặt phẳng Oyz là A. x  0 . B. x  y  z  0 . C. z  0 . D. y  0 . Lời giải
GVSB: Trần Quang Nam; GVPB1: Bùi Hà; GVPB2: Chọn A 
Ta có một véc tơ pháp tuyến của mặt phẳng Oyz là: n 1; 0 ; 0.
Mặt phẳng đi qua gốc tọa độ O 0 ; 0 ; 0.
Phương trình mặt phẳng Oyz là: 1 x  0  0 y  0  0 z  0  0 hay x  0 .
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 7 NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT Ta chọn đáp án#A. 2x 1
Câu 5. Tiệm cận ngang của đồ thị hàm số y 
là đường thẳng có phương trình 2x  4 A. y  2 . B. x  2  . C. x  1. D. y  1. Lời giải
GVSB: Vũ Dự; GVPB1: Bùi Hà; GVPB2: Kim Dung Chọn D 2x 1 2x 1 Ta có lim y  lim  1 và lim y  lim  1 . x x 2x  4 x x 2x  4
Vậy đồ thị hàm số có tiệm cận ngang là đường thẳng có phương trình y  1.
Câu 6. Cho hàm số y  f (x) có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 0; . B. 1; . C.  1  ;0 . D. 0;  1 . Lời giải
GVSB: Vũ Dự; GVPB1: Bùi Hà; GVPB2: Kim Dung Chọn D
Câu 7. Cho hàm số y  f  x có bảng biến thiên như sau
Điểm cực tiểu của hàm số đã cho là A. x  2  . B. x  1. C. x  1  . D. x  2 . Lời giải
GVSB: Nguyễn Thị Nhung; GVPB1:...; GVPB2:… Chọn B
Từ bảng biến thiên suy ra điểm cực tiểu của hàm số đã cho là x  1.
Câu 8. Trên mặt phẳng tọa độ, điểm biểu diễn số phức z  2  7i có tọa độ là A. 2;7 . B. 2; 7 . C.  2  ;7 . D.  7  ;2 . Lời giải
GVSB: Nguyễn Thị Nhung; GVPB1:...; GVPB2:… Chọn B
Điểm biểu diễn số phức z  2  7i có tọa độ là 2; 7
Câu 9. Cho cấp số nhân u với u  1 và u  2. Công bội của cấp số nhân đã cho là n  1 2 1 1 A. . B. 2 . C. 2 . D. . 2 2 Trang 8
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022 Lời giải
GVSB: Lê Mẫn ; GVPB1: Tuyet Trinh; GVPB2: Thuy Nguyen Chọn B u 2
Công bội của cấp số nhân là 2 q    2. u 1 1
Câu 10. Cho 2 số phức z  2  3i và z  1 .i Số phức z  z 1 2 1 2 bằng A. 3 4 .i B. 1 4 .i C. z  5 .i D. 3 2 .i Lời giải
GVSB: Lê Mẫn ; GVPB1: Tuyet Trinh; GVPB2: Thuy Nguyen Chọn D
Ta có: z  z  2  3i 1 i  3 2 .i 1 2
Câu 11. Với a là số thực dương tùy ý, 4 log a bằng A. 4 log a . B. 8log a . C. 2 log a . D. 2 log a . Lời giải
GVSB: Thảo Nguyễn; GVPB1: Tuyet Trinh; GVPB2: Kim Dung Chọn C 1 Ta có: 2
4log a  4log a  2log a . Câu 12. Cho f
 xdx  cos x C . Khẳng định nào dưới đây đúng? A. f  x  sin x . B. f  x  cos x . C. f  x  sin x . D. f  x  cos x . Lời giải
GVSB: Dương Quá; GVPB1: Tuyet Trinh; GVPB2: Kim Dung Chọn C
Ta có: f  x  cos x C      sin x .
Câu 13. Cho hình trụ có chiều cao h  1 và bán kính đáy r  2 . Diện tích xung quanh của hình trụ đã cho bằng A. 3 . B. 4 . C. 2 . D. 6 . Lời giải
GVSB:Nguyễn Thị Thu ; GVPB1:Thuy Nguyen ; GVPB2: Chọn B
Diện tích xung quanh S  2 rl  4 . xq
Câu 14. Cho khối chóp S.ABC có chiều cao bằng 3 , đáy ABC có diện tích bằng 10. Thể tích khối chóp S.ABC bằng A. 15 . B. 10 . C. 2 . D. 30 . Lời giải
GVSB:Nguyễn Thị Thu ; GVPB1:Thuy Nguyen ; GVPB2: Chọn B 1 1 V  hB  3.10  10 . S.ABC 3 3
Câu 15. Mô đun của số phức z  3  4i bằng A. 7 B. 5 . C. 7 . D. 25 . Lời giải
GVSB: Chau Nguyen Minh; GVPB1:Thuy Nguyen ; GVPB2: Chọn B
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 9 NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT Ta có 2 2 z  3  4  5.
Câu 16. Nghiệm của phương trình 2x 1  2 3 3   x là 1 A. x  . B. x  0 . C. x  1  . D. x  1. 3 Lời giải
GVSB: Chau Nguyen Minh; GVPB1:Thuy Nguyen ; GVPB2: Chọn A Ta có 2 x 1  2 3 3   x  2x 1  2  x  3x  1 1  x   3 Câu 17. Cho hàm số   4 2
f x  ax  bx  c có đồ thị là đường cong trong hình vẽ sau
Số nghiệm thực của phương trình f  x 1 là A. 4 . B. 3 . C. 2 . D. 1. Lời giải
GVSB: Lưu Anh Bảo; GVPB1:Thuy Nguyen ; GVPB2: Chọn C
Số nghiệm thực của phương trình f  x 1 bằng với số giao điểm của đường thẳng d  : y 1
và đồ thị C của hàm số y  f  x . Dựa vào hình vẽ, ta thấy d  và C cắt nhau tại hai điểm
phân biệt nên phương trình đã cho có hai nghiệm thực phân biệt.
Câu 18. Tập nghiệm của bất phương trình log x 1  2 là 5   A. 24;   . B. 9;  . C. 25;  . D. 31;   . Lời giải
GVSB: Lưu Anh Bảo; GVPB1:Thuy Nguyen ; GVPB2: Chọn A Ta có log x 1  2 2
 x 1  5  x  24. 5  
Vậy tập hợp nghiệm của bất phương trình là S  24;   . Trang 10
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022 2 2 1  Câu 19. Nếu f  xdx  4 thì f  x 2 dx  bằng 2    0 0 A. 2 . B. 6 . C. 4 . D. 8 . Lời giải
GVSB: Hồng Hà Nguyễn ; GVPB1: Vu Khien; GVPB2: Chọn B 2 2 2 1  f  x 1  2 dx  f
 xdx  2dx  2 4  6   . 2    2 0 0 0
Câu 20. Tập xác định của hàm số y  log x  4 là. 3   A. ; 4 . B. 4; . C. 5;  . D.  ;   . Lời giải
GVSB: Hồng Hà Nguyễn ; GVPB1: Vu Khien; GVPB2: Chọn B
ĐKXĐ x  4  0  x  4 .
Vậy tập xác định của hàm số y  log x  4 là 4; . 3   Câu 21. Cho hàm số 4 2
y  ax  bx  c có đồ thị như đường cong trong hình bên.
Số điểm cực trị của hàm số đã cho là A. 1. B. 0 . C. 2 . D. 3 . Lời giải
GVSB: Tuoi Nguyenthihong; GVPB1:Vũ Khiên; GVPB2: Chọn D
Dựa vào đố thị hàm số suy ra hàm số có 3 điểm cực trị.
Câu 22. Số các tổ hợp chập 3 của 12 phần tử là A. 1728 . B. 220 . C. 1320 . D. 36. Lời giải
GVSB: Tuoi Nguyenthihong; GVPB1:Vũ Khiên; GVPB2: Chọn B
Số các tổ hợp chập 3 của 12 phần tử là 3 C  220 . 12
Câu 23. Trong không gian Oxyz , cho điểm A1;2;3 . Hình chiếu vuông góc của A lên mặt phẳng Oxy có tọa độ là A. 1;0; 3 . B. 1;0;0 . C. 1;2;0 . D. 0;2; 3 . Lời giải
GVSB: Đức Huy; GVPB1: Vũ Khiên; GVPB2: Kim Dung Chọn C
Hình chiếu vuông góc của A1;2;3 lên mặt phẳng Oxy có tọa độ là 1;2;0 .
Câu 24. Trong không gian Oxyz , cho mặt cầu S  x   y  2   z  2 2 : 2
1  6 . Đường kính của S  bằng A. 3 . B. 6 . C. 2 6 . D. 12 .
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 11 NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT Lời giải
GVSB: Đức Huy; GVPB1: Vũ Khiên; GVPB2: Kim Dung Chọn C
Đường kính của S  bằng 2R  2 6 .
Câu 25. Cho tam giác OIM vuông tại I có OI  3 và IM  4 . Khi quay tam giác OIM quanh cạnh góc
vuông OI thì đường gấp khúc OMI tạo thành hình nón có độ dài đường sinh bằng A. 4 . B. 3 . C. 5 . D. 7 . Lời giải
GVSB: Nguyễn Anh Tuấn; GVPB1: Linh Nguyen; GVPB2: Chọn C O l h I r M
Ta có chiều cao hình nón h  OI  3 , bán kính đáy r  IM  4 thì độ dài đường sinh 2 2 2 2
l  OM  IM  OI  3  4  5.
Câu 26. Cho khối lăng trụ có diện tích đáy 2
3a và chiều cao 2a . Thể tích khối lăng trụ đã cho bằng A. 3 3a . B. 3 6a . C. 3 2a . D. 3 a . Lời giải
GVSB: Nguyễn Anh Tuấn; GVPB1: Linh Nguyen; GVPB2: Chọn B
Ta có thể tích khối lăng trụ bằng 2 3 V  . B h  3a .2a  6a . x  2  t 
Câu 27. Trong không gian Oxyz, cho đường thẳng d : y 1 2t . Vectơ nào dưới đây là một véctơ chỉ z  1   3t  phương của d ?     A. u  2;1;1 . B. u  2; 1; 1 . C. u  1;  2; 3 . D. u  1; 2; 3 . 3   3   1   4   Lời giải
GVSB: Dương Chiến; GVPB1: Linh Nguyen; GVPB2: Chọn C 
Một véctơ chỉ phương của đường thẳng d là u  1;  2; 3 . 3   5 1  Câu 28. Nếu f  xdx  3 thì f  xdx bằng 1 5 A. 3 . B. 4 . C. 6 . D. 5. Lời giải
GVSB: Dương Chiến; GVPB1: Linh Nguyen; GVPB2: Chọn A 1  5 f  xdx   f  xdx 3. 5 1 
Câu 29. Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có AB  a , BC  2a và AA'  3a (tham khảo hình
bên). Khoảng cách giữa hai đường thẳng BD và A'C ' bằng Trang 12
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022 A. 2a . B. 2a . C. 3a . D. a . Lời giải
GVSB: Tai Pham Anh; GVPB:Hồ Đức Bân; GVPB2: Nguyễn Thị Nhung Chọn C d BD, A'C '  d B ,
D  A'B'C ' D'  d B, A'B 'C 'D'  BB'  3a .
Câu 30. Hàm số nào dưới đây đồng biến trên  ? x 1 A. 4 2 y  x  x . B. 3 y  x  x . C. y  . D. 3 y  x  x . x  2 Lời giải
GVSB: Tai Pham Anh; GVPB: Hồ Đức Bân; GVPB2: Nguyễn Thị Nhung Chọn B Hàm số 3 y  x  x 2  y '  3x 1  0, x
   . Do đó hàm số đồng biến trên  .
Câu 31. Giá trị trị lớn nhất của hàm số f x 3 2
 x  3x  9x 10 trên đoạn  2  ;  2 bằng A. 15 . B. 10 . C. 1. D. 12 . Lời giải
GVSB: Nguyễn Đức Tài; GVPB1: Hồ Đức Bân; GVPB2: Kim Dung Chọn A Ta có f  x 2  3x  6x 9 . x  1 f  x  0   x  3  lo¹i Do đó f  2    8 , f   1 15 , f 2  1  2.
Vậy max f x  f   1  15 . 2;2
Câu 32. Trong không gian Oxyz , cho ba điểm A1;2;  1 , B3;0;  1 và C 2;2; 2
  . Đường thẳng đi qua
A và vuông góc với mặt phẳng  ABC có phương trình là x 1 y  2 z 1 x 1 y  2 z 1 A.   . B.   . 1 2 1 1 2  3 x 1 y  2 z 1 x 1 y  2 z 1 C.   . D.   . 1 2 1 1 2 1 Lời giải
GVSB: Nguyễn Đức Tài; GVPB1: Hồ Đức Bân; GVPB2: Kim Dung Chọn C
Gọi  là đường thẳng cần tìm.  
Ta có  AB; AC   2;4;2  
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 13 NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT  
Đường thẳng  đi qua A1;2; 
1 và có VTCP u  n  1;2;  1 có phương trình x 1 y  2 z 1   . 1 2 1
Câu 33. Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn 40;60 . Xác suất để chọn được
số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng 2 4 3 3 A. . B. . C. . D. . 5 7 7 5 Lời giải
GVSB: Hoàng Văn Quảng; GVPB1: Cham Tran ; GVPB2: Chọn B
Số cách chọn 1 số thuộc đoạn 40;60 có 21 cách chọn.
Số có chữ số hàng đơn vị lớn hơn chữ số hàng chục:
 Đoạn 40;49 gồm 45;46;...4  9  có 5 số.
 Đoạn 50;59 gồm 56;57;...5  9  có 4 số.
 Đoạn 60;69 gồm 67;68;6  9  có 3 số.
Vậy có 3  4  5 12 số. 12 4
Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục là P   . 21 7
Câu 34. Trong không gian Oxyz , cho ba điểm A1;2;  1 , B3;0;  1 , C 2;2; 2
  . Đường thẳng đi qua
A và vuông góc với mặt phẳng  ABC có phương trình là: x 1 y  2 z 1 x 1 y  2 z 1 A.   . B.   . 1 2 1 1 2  3 x 1 y  2 z 1 x 1 y  2 z 1 C.   . D.   . 1 2 1 1 2 1 Lời giải
GVSB: Hoàng Văn Quảng; GVPB1: Cham Tran; GVPB2: Chọn C  
AB  2;2;2 , AC  1;0;  1 .  
AB, AC  2;4;2  21;2;  1  
Vì đường thẳng cần tìm vuông góc với mặt phẳng  ABC nên đường thẳng cần tìm có véctơ chỉ  phương là u  1;2;  1 và đi qua A1;2; 
1 . Suy ra phương trình đường thẳng cần tìm là: x 1 y  2 z  1   . 1 2 1
Câu 35. Gọi z , z là hai nghiệm phức của phương trình 2
z  z  6  0 . Khi đó z  z  z .z bằng 1 2 1 2 1 2 A. 5 . B. 7 . C. 7 . D. 5. Lời giải
GVSB: Trần Thị Vân; GVPB1: Cham Tran; GVPB2: Chọn D 1 6
z  z  z .z  z  z  z .z 
  5 (áp dụng định lý Vi-et). 1 2 1 2  1 2  1 2  1 1 1
Câu 36. Cho hàm số f  x 1
. Khẳng định nào dưới đay đúng? 2 cos 2x Trang 14
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022 A. f  x 1 dx  x  cos 2x  C . B. f
 xdx  x  tan 2x  C . 2 C. f  x 1 dx  x  tan 2x  C . D. f  x 1 dx  x  tan 2x  C . 2 2 Lời giải
GVSB: Trần Thị Vân; GVPB1: Bích Vân Bùi Thị; GVPB2: Minh Bùi Chọn D   f  x 1 1 dx  1  dx x  tan 2x  C  . 2   cos 2x  2
Câu 37. Có bao nhiêu số nguyên thuộc tập xác định của hàm số y  log 6  x x  2   ? A. 7 . B. 8 . C. Vô số. D. 9 . Lời giải
GVSB:Phương Lan; GVPB1:Bích Vân Bùi Thị; GVPB2: Chọn A
ĐKXĐ: 6  x x  2  0  2   x  6. Mà x   x 1  ;0;1;2;3;4;  5
Vậy có 7 số nguyên thuộc tập xác định của hàm số y  log 6  x x  2   .
Câu 38. Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông tại B , AC  2, AB  3
và AA 1 (tham khảo hình bên dưới).
Góc giữa hai mặt phẳng ABC và ABC bằng A. 90 . B. 60 . C. 30 . D. 45 . Lời giải
GVSB: Lê Huỳnh Cùng; GVPB1: Minh Bùi; GVPB2: Chọn D
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 15 NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT AB  CCCC   ABC Ta có      AB C CB AB C B. AB   BC  C AB  ABC AB C  B    AB  C AB ; ABC   C ;BBC          C BC . C  B  AB  A
 BC vuông tại B nên BC  AC  AB   2 2 2 2 2 3 1. C C  Trong tam giác vuông C B  C ,  1 tan C B  C   1. BC 1 Do đó  C B
 C  45. Vậy C AB ABC  ;  45 . Câu 39. Cho hàm số 4 2
f (x)  mx  2(m 1)x với m là tham số thực. Nếu min f (x)  f (1) thì max f (x) [0;2] [0;2] bằng A. 2 . B. 1. C. 4 . D. 0 .
GVSB: Đào Văn Tiến/ Văn Thắng Đình; GVPB1:…; GVPB2:… Lời giải Chọn C 3 f (
 x)  4mx  4(m 1)x . 1
Do f  x là hàm đa thức và min f (x)  f (1)  f  
1  0  4m  4m   1  0  m  . [0;2] 2 1
Thay m  vào hàm số ban đầu ta được 2 1  1  1 4 2 4 2 3 y  x  2
1 x  x  x  y  2x  2x  2x x   1  x     1 . 2  2  2 Ta có BBT: 1
Vậy với m  , thì min f (x)  f (1)TM  . 2 [0;2]
Dựa vào BBT ta có max f (x)  f (2)  4 . [0;2]
Câu 40. Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn 5b  1 .2b a 5  0 ? A. 20 . B. 21. C. 22 . D. 19 . Lời giải
GVSB: Tô Lê Diễm Hằng/ Đinh Văn Thư ; GVPB1:…; GVPB2:Doãn Hoàng Anh Trang 16
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022 Chọn B   b b 0     b  b a  5 1 0 5 1 .2 5 0        5 .  . a 2b  5  0 b  log2  a  5 log  0 TH1: 2  a  a  5 . a  0 b b 5 Vì hàm số x y  a a  
1 là hàm đồng biến nên 5   1  . a 2  5  0  log  b  0 . 2 a 5 1 5 1 a  40
Yêu cầu của bài toán suy ra * 3  log  2 a        a  21, 22,....40 2   a 8 a 4 a  20 .  5 log  0 TH1: 2  a  0  a  5 a  0 b b 5 Vì hàm số x y  a a  
1 là hàm đồng biến nên 5   1  .
a 2  5  0  0  b  log . 2 a  5 a  5 5 
Yêu cầu của bài toán suy ra * 4 2  log  3  4   8 a     a 1. 2 a a 5 a   8
Vậy có 21 số nguyên a thỏa mãn yêu cầu của bài toán.
Câu 41. Biết F  x và G  x là hai nguyên hàm của hàm số f  x trên  và 5 f
 xdx  F 5G0 a, a  0. Gọi S là diện tích hình phẳng giới hạn bỡi các đường 0
y  F  x , y  G x , x  0 và x  5. Khi S  20 thì a bằng? A. 4 . B. 15. C. 25 . D. 20 . Lời giải
GVSB: Nguyễn Anh Tuấn/ Nguyễn Thị Nhung; GVPB1:…; GVPB2:Doãn Hoàng Anh Chọn A
Đặt G x  F x  C (C là hằng số). 5 f
 xdx  F 5 F0  F5G0C  F 5G0C 0 Suy ra C  a . 5 5 5 S  F
 xGx dx  a dx  adx  5a   . 0 0 0
Theo giả thiết 5a  20  a  4
Câu 42. Cho khối lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông cân tại A , AB  a . Góc
giữa đường thẳng BC và mặt phẳng  ACC A
  bằng 30 . Thể tích của khối lăng trụ đã cho bằng 1 3 3 2 2 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 8 8 2 2
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 17 NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT Lời giải
GVSB: Lại Thị Quỳnh/ Dương Thùy; GVPB1: Doãn Hoàng Anh; GVPB2:... Chọn D 2 1 a Diện tích đáy: S  A . B AC  . ABC 2 2 AB  AC Ta có:   AB   ACC A
   BC , ACC A      BC A   30. AB  AA Khi đó AC  AB   a
 AA  AC  AC  a 2 2 2 2 .cot 30 3 3  a  a 2 . 2 a 2
Vậy, thể tích khối lăng trụ đã cho là: 3 V  S .AA  .a 2  .a . ABC 2 2
Câu 43. Cho hình nón có góc ở đỉnh bằng 120 và chiều cao bằng 1. Gọi S  là mặt cầu đi qua đỉnh và
chứa đường tròn đáy của hình nón đã cho. Diện tích của S  bằng A. 16 . B. 12 . C. 4 . D. 48 Lời giải
GVSB: Đỗ Ngọc Nam/ Phạm Quốc Toàn; GVPB1: Doãn Hoàng Anh; GVPB2: Minhhai Bui Chọn A OM OM
Xét tam giác vuông SMO có tan  MSO   tan 60   OM  3 OS 1
Kẻ đường kính SS của mặt cầu ngoại tiếp hình nón.
Tam giác SMS vuông tại M có MO  SS Trang 18
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
 MO  OS OS   2 2 . 3  1.OS  OS  3 OS  OS 1 3
Vậy bán kính mặt cầu ngoại tiếp hình nón là R    2 2 2 Diện tích S  là 2 2
S  4 R  4.2 16 .
Câu 44. Xét các số thực , x y sao cho 2 2 9 y 4 log7 49 x a  a 
với mọi số thực dương a . Giá trị lớn nhất của biểu thức 2 2
P  x  y  4x  3y bằng: 121 39 A. . B. . C. 24 . D. 39 . 4 4
GVSB: Nguyễn Thị Kim Cúc/ Quy Tín; GVPB: Nguyễn Duy Nam Lời giải Chọn C  Ta có 2 2 9 y 4 log 2 2  7 49 x a  a   log  9 49 y  log x a a  . 7  7 4 log7    2
9  y log 49   2 4x  log a log a  2 2
9  y   22x  log a log a .  1 7  7 7  7   7
Đặt t  log a , khi a  0 thì t   ,   1 trở thành 2 2 t  2 .
x t  9  y  0 . 2 7  
1 đúng với mọi a  0  2 đúng với mọi t   2 2
   x  9  y  0 2 2  x  y  9 .
 Xét  x  y2    x  y    x  y2 2 2 4 3 16 9 4 3  225  4x  3y 15  Suy ra 2 2
P  x  y  4x  3y  9 15  24 , đẳng thức xảy ra khi  12 9  x y x  ; y      5 5 4 3    . 12 9  2 2 x  y  9 x   ; y   5 5
Vậy GTLN của P bằng 24 .
Câu 45. Cho các số phức z , z , z thỏa mãn z  z  2 z  2 và 3z z  4z z  z . Gọi , A B,C 1 2 3  1 2  1 2 3 1 2 3
lần lượt là các điểm biểu diễn của z , z , z trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng 1 2 3 7 3 7 7 3 7 A. . B. . C. . D. . 4 4 2 2
GVSB: Trần Nhung/ Lê Trần Bảo An; GVPB1: Tô Lan ; GVPB2: Thanh bui Lời giải Chọn A
Ta có 3z z  4z z  z  3z z  4z z  z  3z z  4z z  z 1 2 3  1 2  1 2 3  1 2  1 2 3  1  2   z  z  3 . 1  2 
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 19 NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT
Lấy D đối xứng với B qua O , suy ra D biểu diễn z . 2  Ta có z  z  3  AD  3 . 1  2   1 ABD có trung tuyến AO 
BD nên  ABD vuông tại A 2 2  AB  BD  AD  7 . 2
+ 3z z  4z z  z  z 3z  4z  4z z 1  2 3  1 2 3  1 2  2 3  z 3z  4z  4z z 1 2 3 2 3  
 3z  4z  4  3OB  4OC  4 2 2  9OB 16OC  24O . B OC.cos  BOC  16 2 3   3 cos BOC  . 4 Áp dụng định lí cosin cho B  OC ta có: 3 2 2 BC  OB  OC  2O . B OC.cos  BOC  4 1 4.  2 . 4
Tương tự ta tính được AC  2 . 7 Vậy S  . A  BC 4
Câu 46. Có bao nhiêu số phức z thỏa mãn 2
z  z  z và  z  z  i 2 2 2  z  2i ? A. 4 . B. 2 . C. 3 . D. 1 . Lời giải
GVSB: Phạm Văn Bình; GVPB1: Tô Lan ; GVPB2: Thanh bui Chọn A Gọi z  a  bi với ; a b Ta có: 2 2 2
z  z  z  a  b  2 b *
Mặt khác  z   z  i 2 2 2  z  2i **
Vì z  2i  z  2i nên z  2i  z  2i .
 z  2i  0  z  2i Nên từ (**)   . z  2  z  2i 
Với z  2i  0  z  2i ( thoả mãn * Trang 20
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
Với z   z  i  a  2  b  a  b  2 2 2 2 2 2 2  a  b
 thay vào (*) ta được:  b  0  a  0 z  0 2 2 2 b b 2 b b b b 1        a  1    z  1   i    . b  1 a 1 z 1 i 
Vậy có tất cả 4 số phức thỏa mãn yêu cầu bài toán.
Câu 47. Trong không gian Oxyz , cho điểm A2;1; 
1 . Gọi P là mặt phẳng chứa trục Oy sao cho
khoảng cách từ A đến P là lớn nhất. Phương trình của P là: A. 2x  z  0 . B. 2x  z  0. C. x  z  0 . D. x  z  0 . Lời giải
GVSB: Hải Quan/ Hoàng Diệp Phạm; GVPB1: Thanh bui ; GVPB2: Chọn A
Gọi H là hình chiếu vuông góc của điểm A lên mặt phẳng P , A là hình chiếu vuông góc
của điểm A lên trục Oy suy ra A0;1;0 . Khi đó khoảng cách từ A đến P là đoạn thẳng
AH  AA ' . Độ dài đoạn thẳng AH dài nhất khi H và A trùng nhau. Khi đó mặt phẳng P  nhận A A   2;0; 
1 làm véc tơ pháp tuyến. Suy ra phương trình mặt phẳng P đi qua 
A0;1;0 có VTPT: AA  2;0; 
1 là: 2 x  0  0 y   1   
1  z  0  0  2x  z  0 .
Câu 48. Cho hàm số bậc bốn y  f  x . Biết rằng hàm số g  x  ln f  x có bảng biến thiên như sau:
Diện tích hình phẳng giới hạn bởi các đường y  f  x và y  g x thuộc khoảng nào dưới đây? A. 38;39 . B. 25;26 . C. 28;29 . D. 35;36 .
GVSB: Phí Mạnh Tiến; GVPB1:… ; GVPB2:… Lời giải Chọn D f  x + Ta có: g x    . f  x
+ Từ bảng biến thiên ta thấy g  x  0 , x   suy ra f  x gx  e 1, x   .
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 21 NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT
+ Phương trình f  x  g x  g x. f  x  g x  g x. f   x 1  0   gx  0 x  x1   x  x . 2  x  x  3
+ Diện tích hình phẳng giới hạn bởi các đường y  f  x và y  g x là 3 x x x        2  f  x   f  x  S f x
g x dx    f x   3   x    f  x   x f x f x x x    d      x    d  1 1 2 t f x 42 37  1  1  1 dt  1 d     
 t  35, 438 35;36 .  t   t  10 42
Câu 49. Trong không gian Oxyz , cho mặt cầu S  tâm I 4;1;2 bán kính bằng 2 . Gọi M ; N là hai
điểm lần lượt thuộc hai trục Ox ; Oy sao cho đường thẳng MN tiếp xúc với S  , đồng thời mặt 7
cầu ngoại tiếp tứ diện OIMN có bán kính bằng . Gọi A là tiếp điểm của MN và S  , giá trị 2 AM.AN bằng A. 6 2 . B. 14 . C. 8 . D. 9 2 . Lời giải
GVSB: Minh Phạm/ Bùi Thanh Sơn; GVPB1: ; GVPB2: Chọn A Cách 1:
Ta có : d I,(Oxy)  2 nên mặt cầu S  tiếp xúc với mặt phẳng Oxy tại điểm A4;1;0 , đồng
thời đường thẳng MN tiếp xúc với S  cũng tại điểm A4;1;0 do MN  Oxy
Gọi M m;0;0; N 0;n;0, m, n  0   m  4  4k  n
Do A MN nên AM  k AN    m  n   4 4 1  4  m  , n 1  0 . 1  k  n   1 n 1 21
Phương trình mặt phẳng trung trực đoạn OI :4x  y  2z   0 2 m
Phương trình mặt phẳng trung trực đoạn OM : x  2 n
Phương trình mặt phẳng trung trực đoạn ON : y  2 2  m n n  6n  21
Do đó tâm mặt cầu ngoại tiếp tứ diện OIMN là J ; ;    2 2 4n  4  7 7
Theo giả thuyết cầu ngoại tiếp tứ diện OIMN có bán kính bằng nên OJ  2 2 49 2  OJ  4 4n n n 6n 2 2 2 2 2 1 49     n  2 1 4 16n  2 1 4 4 3 2
 n  4n 10n  28n  49  0  n 1 2 2 Trang 22
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD & BIÊN SOẠN TOÁN NĂM HỌC: 2021-2022
Vì n  0 nên chọn n 1 2 2 , suy ra m  4  2 Khi đó AM .AN  6 2 . Cách 2:
Dễ thấy mặt cầu S  tiếp xúc với mặt phẳng Oxy tại điểm A4;1;0, đồng thời đường thẳng
MN tiếp xúc với S  cũng tại điểm A1;4;0 do MN  Oxy
Gọi M a;0;0 ; N 0;b;0 .   a  4  4k 
Do A MN nên AM  k AN    1 4   1. 1  k  b   1 b a  a b 
Gọi J là trung điểm MN  J ; ;0 
 và I 4;1;2 thuộc đường thẳng  vuông góc với  2 2   a x   2    b
Oxy tại điểm J . Phương trình  là y  2  z  t    a b 
Tâm của mặt cầu ngoại tiếp tứ diện OIMN là điểm K ; ;t   .  2 2  1 4 1 4   1     1 b a b a    7 2 2 a b 49
Theo giả thiết ta có hệ: OK   2    t  2  4 4 4   7 2 2  IK   a   b  49    4  1      t  22   2   2   2  4  4b  4b a  a   b 1 b 1   2   b  6b  21
4a  b  4t  21  0  t    4b    1 2 2 a b 49 2    t   2 2  4 4 4 a b 49 2    t   4 4 4 b 4b b 6b2 2 2 2 2 1 2 2  49      1   16 2  4b  64 1  b  5   196 4      b  2 1 16b  2 1 4  b 1  b 1  128 64 4b  64    b  52 1 256 2  32 b  5 .   196 2   b 1 b   1 b 1 b  2 1  320 1 64 2 5b 10b  25   32 b  5  4 . 132  b  2 1   16 2   b   1 b 1 b  2 1 b 1 2 2  b   2 2 1  8  0    b  2 1  8   b 1 2 2
Với b  1 2 2 ta được a  4  2  AM .AN  6 2 .
Với b  1 2 2 ta được a  4  2  AM .AN  6 2 .
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 23 NĂM HỌC: 2021-2022
NHÓM WORD & BIÊN SOẠN TOÁN THPT
Câu 50. Có bao nhiêu giá trị nguyên âm của tham số a để hàm số 4 2
y  x  2ax  8x có đúng ba điểm cực trị? A. 2 . B. 6 . C. 5 . D. 3 . Lời giải
GVSB: Bùi Thanh Sơn/ Kieu Hung ; GVPB1: Lê Văn Tùng ; GVPB2: Chọn D Xét hàm số f  x 4 2
 x  2ax  8x trên  . f x 3  4x  4ax  8. 2 f  x  0  3 4x  4ax  8  0  2
a  x  (Do x  0 không thỏa mãn nên x  0 ). x 2 Xét hàm số g x 2
 x  trên  \  0 . x g x 2  2x  . 2 x 2
f  x  0  2x   0  x  1. 2 x
Bảng biến thiên của hàm số g  x :
Dễ thấy phương trình f  x  0 có ít nhất hai nghiệm phân biệt, trong đó có ít nhất một nghiệm
đơn x  0 nên yêu cầu bài toán  Hàm số f  x có đúng một điểm cực trị  Phương trình
a  g  x có một nghiệm đơn duy nhất  a  3  .
Do a nguyên âm nên a  3  ; 2;  1 .
Vậy có 3 giá trị nguyên âm của tham số a thỏa mãn yêu cầu bài toán. Trang 24
TÀI LIỆU ÔN THI THPT QUỐC GIA
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
BỘ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TỐT NGHIỆP TRUNG HOC PHỔ THÔNG NĂM 2022 Bài thi: TOÁN Ngày thi: 07/7/2022
Thời gian làm bài: 90 phút (Đề thi gồm 07 trang)
(không kể thời gian chép đề) Mã đề thi 103 ĐỀ BÀI
Câu 1. Hàm số nào dưới đây có bảng biến thiên như sau A. 3 y  x  3x . B. 3 y   x  3x . C. 2 y  x  2x . D. 2 y  x  2x . 3 3 Câu 2. Nếu  1  f  xdx  6 thì  f  x  2 d  x bằng? 3    0 0 A. 8 . B. 5 . C. 9 . D. 6 .
Câu 3. Phần ảo của số phức z  2  i1 i bằng A. 3 . B. 1. C.  1 . D.  3 .
Câu 4. Khẳng định nào dưới đây đúng? A. xd x e x  xe C  . B. x x 1 e dx e   C  . C. x x 1 e dx e     C  . D. xd x e x  e C  . Câu 5. Cho hàm số 4 2
y  ax  bx  c có đồ thị là đường cong trong hình dưới. Giá trị cực tiểu của hàm số đã cho bằng y 4 3 x -1 O 1 A. 1. B. 4 . C.  1 . D. 3 . Câu 6. Cho 5 2 a  3 , b  3 và 6
c  3 mệnh đề nào dưới đây đúng A. a  c  b . B. a  b  c . C. b  a  c . D. c  a  b .
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 1.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 2 5 5
Câu 7. Nếu  f xdx  2 và  f xdx  5 thì  f xdx bằng 1 2 1 A  7 . B.  3 . C. 4 . D. 7 .
Câu 8. Cho hàm số y  f x có bảng biến thiên như sau
Số giao điểm của đồ thị hàm số đã cho và đường thẳng y 1 là A. 1. B. 0 . C. 2 . D. 3 .
Câu 9. Từ các chữ số 1,2,3,4,5 lập được bao nhiêu số tự nhiên gồm năm chữ số đôi một khác nhau? A. 120 . B. 5 . C. 3 1 2 5 . D. 1.
Câu 10. Cho khối nón có diện tích đáy bằng 2
3a và chiều cao 2 a . Thể tích của khối nón đã cho bằng? 2 A. 3 3a . B. 3 6a . C. 3 2a . D. 3 a . 3 2
Câu 11. Số nghiệm thực của phương trình x 1 2   4 là A. 1. B. 2 . C. 3 . D. 0 .
Câu 12. Với a là số thực dương tùy ý, log 100a  bằng A. 1loga . B. 2loga . C. 2loga. D. 1 log a.
Câu 13. Cho khối chóp S.ABC có chiều cao bằng 5 , đáy A B C có diện tích bằng 6 . Thể tích khối chóp S .ABC bằng A. 11. B. 10. C. 15. D. 3 0 .   
Câu 14. Hàm số F  x  cot x là một nguyên hàm của hàm số nào dưới đây trên khoảng 0;    2  1 1 A. f x  . B. f x   . 1   2   2 sin x 2 cos x 1 1 C. f x  . D. f x   . 3   4   2 cos x 2 sin x
Câu 15. Cho hàm số bậc ba y  f  x có đồ thị là đường cong hình bên.
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 2.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ A. 1; 1 . B. 3;  1 . C. 1;3 . D. 1; 1.
Câu 16. Số phức nào dưới đây có phần ảo bằng phần ảo của số phức w  1  4i A. z  3  4i . B. z  5 4i . C. z  1 5i . D. z 1 4i . 2 1 3 4
Câu 17. Cho cấp số nhân u u  3 q u n n với và công bội
2. Số hạng tổng quát n 2 bằng 1 A. n 1 3.2  . B. 2 3.2  n . C. 3.2n . D. n 1 3.2  . 2 2 2
Câu 18. Trong không gian Oxyz , cho mặt cầu  
S :x  2  y  
1  z 3  4 . Tâm của   S có tọa độ là A. 4; 2; 6 . B. 4; 2; 6 . C. 2;1;3. D. 2;1;3 .
Câu 19. Cho khối chóp và khối lăng trụ có diện tích đáy, chiều cao tương ứng bằng nhau và có thể tích lần V
lượt là V ,V . Tỉ số 1 bằng 1 2 V2 2 3 1 A. . B. 3 . C. . D. . 3 2 3 x  2 y 1 z 1
Câu 20. Trong không gian Oxyz , cho đường thẳng d :  
. Điểm nào dưới đây thuộc 1 2 3 d? A. Q 2;1;1 . B. M 1; 2;3 . C. P 2;1; 1 . D. N 1; 2;3.
Câu 21. Trong không gian Oxyz , phương trình của mặt phẳng Oxy là: A. z  0 . B. x  0 . C. y  0. D. x  y  0.
Câu 22. Cho điểm M nằm ngoài mặt cầu S O; R  . Khẳng định nào dưới đây đúng? A. OM  R . B. OM  R . C. OM  R . D. OM  R .
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 3.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
Câu 23. Trên mặt phẳng tọa độ, điểm biểu diễn số phức z  2  7i có tọa độ là A. 2; 7 . B. 2; 7  . C. 7; 2 . D. 2; 7.
Câu 24. Nghiệm của phương trình log 2x 1  0 1   là 2 3 1 2 A. x  . B. x  1 . C. x  . D. x  . 4 2 3
Câu 25. Tập xác định của hàm số y  log x 1 là 2   A. 2;   . B. ;   . C. 1;   . D. ;1 .
Câu 26. Cho hàm số y  f x có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình: A. x   1 . B. y  1  . C. y  2  . D. x  2 .    
Câu 27. Trong không gian Oxyz . Cho hai vectơ u 1; 4  ;  0 và v  1  ; 2  ; 
1 . Vectơ u3v có tọa độ là A. 2; 6;3 . B. 4; 8; 4  . C. 2; 10; 3 . D. 2; 10;3 .
Câu 28. Cho hàm số y  f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. 0; 3 . B. 0;. C. 1; 0 . D. ;1 . Câu 29. Cho hàm số 4 2
f (x)  ax  bx  c có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị
nguyên thuộc đoạn 2; 5 của tham số m để phương trình f ( )
x  m có đúng 2 nghiệm thực phân biệt?
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 4.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 A.1. B 6 . C. 7 . D. 5 . Câu 30. Cho hàm số 2 ( )  1 x f x
 e . Khẳng định nào dưới đây là đúng? 1 2x A. ( ) x f x dx  x  e  C.  B f ( ) x dx  x  2e  . C  2 1 2x C. 2 ( ) x f x dx  x  e  C.  D. f ( ) x dx  xe  . C  2
Câu 31. Gọi z và z là hai nghiệm phức của phương trình 2 z 2z 5  0. Khi đó 2 2 z  z bằng 1 2 1 2 A. 6 . B. 8i . C. 8i . D.  6 .
Câu 32. Cho hình lập phương ABCD.A ' B 'C ' D ' (tham khảo hình bên). Giá trị D C
sin của góc giữa đường thẳng AC ' và mặt phẳng  ABCD  bằng A 3 6 B A. . B. . 3 3 D' 3 2 C' C. . D. . 2 2 A' B'
Câu 33. Trong không gian Oxyz , cho điểm A 1; 2; 3 . Phương trình của mặt cầu
tâm A và tiếp xúc với mặt phẳng x 2y  2x 3  0 là 2 2 2 2 2 2 A.  x  
1  y 2 z   3  2. B.  x  
1  y 2 z   3  2. 2 2 2 2 2 2 C.  x  
1  y 2 z   3  4. D.  x  
1  y 2 z   3  4. 1 Câu 34. Với ,
a b là các số thực dương tùy ý và a  1, log1 bằng 3 b a
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 5.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 1 A. 3log b. B. log b . C. 3 log b . D. log b . a a a 3 a
Câu 35. Cho hình lập phương ABCD.A ' B 'C ' D ' có cạnh bằng 3 (tham A D
khảo hình bên). Khoảng cách từ B đến mặt phẳng  ACC ' A ' H bằng B C 3 2 3 A. . B. . 2 2 A' D' C. 3 2 . D. 3 . B' C'
Câu 36. Cho hàm số y  f  x có đạo hàm f  x   x  1 với mọi x   . Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 1; . B. 1; . C. ;  1 . D.  ;1 .
Câu 37. Trong không gian Oxyz , cho điểm M 2; 2;1 và mặt phẳng P  : 2x  3 y  z  1  0 . Đường thẳng
đi qua M và vuông với  P  có phương trình là: x  2 2t x  2 2t x  2 2t x  22t     A. y  23t . B. y  2  3t . C. y  2  3t . D. y  3  2t . z 1t     z 1t  z 1t  z  1  t 
Câu 38. Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn 30 ;50. Xác suất để chọn được số
có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng 11 8 13 10 A. . B. . C. . D. . 21 21 21 21
Câu 39. Biết F  x; G  x là hai nguyên hàm của hàm số f  x trên  và 4 f
 xdx  F4G0a a 0. Gọi S là diện tích hình phẳng giới hạn bởi các đường 0
y  F  x; y  G x;x  0; x  4. Khi S  8 thì a bằng A. 8 B. 4 C. 12 D. 2
Câu 40. Cho hàm số f  x 4  ax  a   2 2
4 x 1 với a là tham số thực. Nếu max f  x  f   1 0;2 thì min f  xbằng 0;2 A. 1  7 B. 1  6 C. 1  D. 3
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 6.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
Câu 41. Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn 4b 1 .3b a 10  0? A.182. B. 179. C. 180. D. 181.
Câu 42. Cho hình nón có góc ở đỉnh bằng 0
120 và chiều cao bằng 3. Gọi  
S là mặt cầu đi qua đỉnh và chứa
đường tròn đáy của hình nón đã cho. Diện tích của   S bằng A.144 . B. 108 . C. 48 . D. 96 .
Câu 43. Cho hàm số bậc bốn y  f  x . Biết rằng hàm số g  x   ln f  x  có bảng biến thiên
Diện tích hình phẳng giới hạn bởi các đường y  f   x  và y  gx thuộc khoảng nào dưới đây? A. 33;35 . B. 37;40 . C. 29;32 . D. 24;26.
Câu 44. Xét tất cả số thực 2 x , y sao cho 3 5 y 6 log3 27 x a  a 
với mọi số thực dương a . Giá trị nhỏ nhất của biểu thức 2 2
P  x  y  4x  8y bằng A. 15  . B. 25. C. 5  . D. 2  0 . Lời giải
Câu 45. Cho các số phức z , z , z thỏa mãn  
 và  z  z z  3z z . Gọi , A , B C lần 1 2  1 2 3 2 z 2 z z 2 1 2 3 3 1 2
lượt là các điểm biểu diễn của z , z , z trên mặt phẳng tọa độ. Diện tích tam giác 1 2 3 A B C bằng 5 7 5 7 5 7 5 7 A. . B. . C. . D. . 8 16 24 32
Câu 46. Trong không gian Oxyz , cho điểm A 1; 2; 2 . Gọi P  là mặt phẳng chứa trục Ox sao cho khoảng
cách từ A đến P  lớn nhất. Phương trình của  P  là: A. 2 y  z  0 . B. 2 y  z  0 . C. y  z  0 . D. y  z  0 .
Câu 47. Có bao nhiêu số phức z thỏa mãn 2
z  z  z và z   z  i 2 2 2  z  2i ? A. 2 . B. 3 . C. 1. D. 4 .
Câu 48. Cho khối lăng trụ đứng ABC.A ' B 'C ' có đáy A B C là tam giác vuông cân tại A , cạnh bên A A  2 a
, góc giữa hai mặt phẳng  ABC  và  ABC  bằng 30 . Thể tích của khối lăng trụ đã cho bằng
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 7.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 8 8 A. 3 24a . B. 3 a . C. 3 8a . D. 3 a . 3 9
Câu 49. Có bao nhiêu giá trị nguyên âm của tham số a để hàm số 4 2
y  x  ax 8x có đúng 3 điểm cực trị? A. 5 . B. 6 . C. 11. D. 10 .
Câu 50. Trong không gian Oxyz cho mặt cầu S  tâm I 9;3;1 bán kính bằng 3. Gọi M, N là hai điểm lần lượt thuộc 2 trục O ,
x Oz sao cho đường thẳng M N tiếp xúc với S, đồng thời mặt cầu ngoại tiếp 13
tứ diện O IM N có bán kính bằng
. Gọi A là tiếp điểm của M N và S , giá trị AM .AN bằng 2 A. 12 3 . B. 18 . C. 28 3 . D. 39.
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 8.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 BẢNG ĐÁP ÁN 1.B 2.A 3.B 4.D 5.D 6.C 7.B 8.D 9.A 10.C 11.B 12.B 13.B 14.D 15.D
16.B 17.A 18.C 19.D 20.C 21.A 22.B 23.B 24.B 25.C 26.D 27.D 28.C 29.C 30.C
31.D 32.A 33.D 34.A 35.A 36.C 37.B 38.A 39.A 40.B 41.D 42.A 43.A 44.A 45.B 46.D 47.D 48.A 49.B 50.A LỜI GIẢI CHI TIẾT
Câu 1. Hàm số nào dưới đây có bảng biến thiên như sau A 3 y  x  3x . B. 3 y   x  3x . C. 2 y  x  2x . D. 2 y  x  2x . Lời giải Chọn B
Dựa vào bảng biến thiên ta nhận thấy:  Đây là hàm 3 2
y  ax  bx  cx  d a  0 .  lim y    a  0 . x
Do đó hàm số thỏa mãn là 3 y   x  3x . 3 3 Câu 2. Nếu  1  f  xdx  6 thì  f  x  2 d  x bằng? 3    0 0 A. 8 . B. 5 . C. 9 . D. 6 . Lời giải Chọn A 3 3 3 1  1 1 Ta có f  x 2 dx  f
 xdx  2dx  6 6  8   . 3    3 3 0 0 0
Câu 3. Phần ảo của số phức z  2  i1 i bằng A 3 . B. 1. C.  1 . D.  3 . Lời giải Chọn B
Ta có z  2  i1 i  3  i . Vậy phần ảo là 1.
Câu 4. Khẳng định nào dưới đây đúng? A xd x e x  xe C  . B. x x 1 e dx e   C  . C. x x 1 e dx e     C  . D. xd x e x  e C  .
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 9.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 Lời giải Chọn D Ta có xd x e x  e C  . Câu 5. Cho hàm số 4 2
y  ax  bx  c có đồ thị là đường cong trong hình dưới. Giá trị cực tiểu của hàm số đã cho bằng y 4 3 -1 x O 1 A 1. B. 4 . C.  1 . D. 3 . Lời giải Chọn D
Dựa vào đồ thị hàm số ta thấy giá trị cực tiểu bằng 3 . Câu 6. Cho 5 2 a  3 , b  3 và 6
c  3 mệnh đề nào dưới đây đúng A a  c  b . B. a  b  c . C. b  a  c . D. c  a  b . Lời giải Chọn C  4  5  6 Ta có 5 2 4 6
a  3 , b  3  3 , c  3 và   b  a  c . 3  1 2 5 5
Câu 7. Nếu  f xdx  2 và  f xdx  5 thì  f xdx bằng 1 2 1 A  7 . B.  3 . C. 4 . D. 7 . Lời giải Chọn B 5 2 5 Ta có f  xdx  f  xdx  f
 xdx  25  3. 1 1 2
Câu 8. Cho hàm số y  f x có bảng biến thiên như sau
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 10.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
Số giao điểm của đồ thị hàm số đã cho và đường thẳng y 1 là A 1. B. 0 . C. 2 . D. 3 . Lời giải Chọn D
Dựa vào bảng biến thiên ta thấy đường thẳng y 1 cắt đồ thị hàm số tại 3 điểm.
Câu 9. Từ các chữ số 1,2,3,4,5 lập được bao nhiêu số tự nhiên gồm năm chữ số đôi một khác nhau? A. 120 . B. 5 . C. 3 1 2 5 . D. 1. Lời giải Chọn A
Số các số tự nhiên gồm năm chữ số khác nhau lập từ các số 1,2,3,4,5 là 5!  120 .
Câu 10. Cho khối nón có diện tích đáy bằng 2
3a và chiều cao 2 a . Thể tích của khối nón đã cho bằng? 2 A. 3 3a . B. 3 6a . C. 3 2a . D. 3 a . 3 Lời giải Chọn C 1
Thể tích của khối nón đã cho bằng 2 3 V  .3a .2a  2a . 3 2
Câu 11. Số nghiệm thực của phương trình x 1 2   4 là A. 1. B. 2 . C. 3 . D. 0 . Lời giải Chọn B   2 x 1 x 1  2 2 2 2
 2  x 1  2  x  1  x  1
Câu 12. Với a là số thực dương tùy ý, log 100a  bằng A. 1loga . B. 2loga . C. 2loga. D. 1 log a.
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 11.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 Lời giải Chọn B
log 100a   log 100  log a  2  log a
Câu 13. Cho khối chóp S.ABC có chiều cao bằng 5 , đáy A B C có diện tích bằng 6 . Thể tích khối chóp S .ABC bằng A. 11. B. 10. C. 15. D. 3 0 . Lời giải Chọn B 1 1 V  .S.h  .6.5  10 S .ABC 3 3   
Câu 14. Hàm số F  x  cot x là một nguyên hàm của hàm số nào dưới đây trên khoảng 0;    2  1 1 A. f x  . B. f x   . 1   2   2 sin x 2 cos x 1 1 C. f x  . D. f x   . 3   4   2 cos x 2 sin x Lời giải Chọn D 1    Có   cot   dx
x C suy ra F  x   cot x trên khoảng 0; 
 là một nguyên hàm của hàm 2 sin x  2  1 số f x   . 3   2 sin x
Câu 15. Cho hàm số bậc ba y  f  x có đồ thị là đường cong hình bên.
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 12.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ A. 1; 1 . B. 3;  1 . C. 1;3 . D. 1; 1. Lời giải Chọn D
Dựa vào đồ thị, điểm cực tiểu của đồ thị hàm số đã cho là 1; 1
Câu 16. Số phức nào dưới đây có phần ảo bằng phần ảo của số phức w  1  4i A. z  3  4i . B. z  5 4i . C. z  1 5i . D. z 1 4i . 2 1 3 4 Lời giải Chọn B
Cả hai số phức w  1  4i và z  5  4i đều có phần ảo bằng  4 nên ta chọn B. 1
Câu 17. Cho cấp số nhân u u  q u n n với 3 và công bội
2. Số hạng tổng quát n 2 bằng 1 A. n 1 3.2  . B. 2 3.2  n . C. 3.2n . D. n 1 3.2  . Lời giải Chọn A Cấp số nhân u u  3 q n với và công bội
2 có số hạng tổng quát 1 u 3.2   n . 1 n 2 2 2
Câu 18. Trong không gian Oxyz , cho mặt cầu  
S :x  2  y  
1  z 3  4 . Tâm của   S có tọa độ là A. 4; 2; 6 . B. 4; 2; 6 . C. 2;1;3. D. 2;1;3 . Lời giải Chọn C 2 2 2 Mặt cầu  
S : x  2  y  
1  z 3  4 có tâm là 2; 1  ;  3 .
Câu 19. Cho khối chóp và khối lăng trụ có diện tích đáy, chiều cao tương ứng bằng nhau và có thể tích lần V
lượt là V ,V . Tỉ số 1 bằng 1 2 V2 2 3 1 A. . B. 3 . C. . D. . 3 2 3 Lời giải Chọn D
Gọi diện tích đáy và chiều cao tương ứng của khối chóp và khối lăng trụ là B và h.  1 V   Bh V 1 Ta có 1 1  3   . V 3  2 V  Bh  2
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 13.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 x  2 y 1 z 1
Câu 20. Trong không gian Oxyz , cho đường thẳng d :  
. Điểm nào dưới đây thuộc 1 2 3 d? A. Q 2;1;1 . B. M 1; 2;3 . C. P 2;1; 1 . D. N 1; 2;3. Lời giải Chọn C x  2  0 x  2  
Cho y 1 0  y 1 vậy P 2;1; 1 d . z 1 0    z 1   
Câu 21. Trong không gian Oxyz , phương trình của mặt phẳng Oxy là: A. z  0 . B. x  0 . C. y  0. D. x  y  0. Lời giải Chọn A
Câu 22. Cho điểm M nằm ngoài mặt cầu S O; R  . Khẳng định nào dưới đây đúng? A. OM  R . B. OM  R . C. OM  R . D. OM  R . Lời giải Chọn B
Câu 23. Trên mặt phẳng tọa độ, điểm biểu diễn số phức z  2  7i có tọa độ là A. 2; 7 . B. 2; 7  . C. 7; 2 . D. 2; 7. Lời giải Chọn B
Câu 24. Nghiệm của phương trình log 2x 1  0 1   là 2 3 1 2 A. x  . B. x  1 . C. x  . D. x  . 4 2 3 Lời giải Chọn B
log 2x 1  0  2x 1  1  x  1. 1   2
Vậy nghiệm của phương trình là x  1.
Câu 25. Tập xác định của hàm số y  log x 1 là 2   A. 2;   . B. ;   . C. 1;   . D. ;1 . Lời giải Chọn C
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 14.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
Hàm số xác định khi x  1  0  x  1 .
Tập xác định của hàm số là D  1;  .
Câu 26. Cho hàm số y  f x có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình: A. x   1 . B. y  1  . C. y  2  . D. x  2 . Lời giải Chọn D
Ta thấy: lim f  x   và lim f  x  . x 2  x 2 
Vậy tiệm cận đứng của hàm số đã cho là x   2 .    
Câu 27. Trong không gian Oxyz . Cho hai vectơ u 1; 4  ;  0 và v  1  ; 2  ; 
1 . Vectơ u3v có tọa độ là A. 2; 6;3 . B. 4; 8; 4  . C. 2; 10; 3 . D. 2; 10;3 . Lời giải Chọn D  Ta có: u 1; 4  ;  0  3v  3  ; 6  ;  3   Vậy: u 3v   2  ; 1  0;  3
Câu 28. Cho hàm số y  f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. 0;3 . B. 0;. C. 1; 0 . D. ;1 .
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 15.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 Lời giải Chọn C Câu 29. Cho hàm số 4 2
f (x)  ax  bx  c có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị
nguyên thuộc đoạn 2; 5 của tham số m để phương trình f ( )
x  m có đúng 2 nghiệm thực phân biệt? A.1. B 6 . C. 7 . D. 5 . Lời giải Chọn C
Dựa vào đồ thị ta thấy phương trình f ( )
x  mcó đúng hai nghiệm thực phân biệt khi m  2
Hoặc m  1 . Vậy m  2;0;1; 2;3; 4; 
5 . Vậy có 7 giá trị m thĩa mãn. Câu 30. Cho hàm số 2 ( )  1 x f x
 e . Khẳng định nào dưới đây là đúng? 1 2x A. ( ) x f x dx  x  e  C.  B f ( ) x dx  x  2e  . C  2 1 2x C. 2 ( ) x f x dx  x  e  C.  D. f ( ) x dx  xe  . C  2 Lời giải Chọn C x 1 Ta có 2 2 (1 ) x e dx  x  e  . C  2
Câu 31. Gọi z và z là hai nghiệm phức của phương trình 2 z 2z 5  0. Khi đó 2 2 z  z bằng 1 2 1 2 A. 6 . B. 8i . C. 8i . D.  6 . Lời giải Chọn D
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 16.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 Phương trình 2
z 2z 5  0 có nghiệm là z 1 2i và z 1 2i nên ta có: 1 2
z  z  12i2 12i2 2 2  6  1 2 .
Câu 32. Cho hình lập phương ABCD.A ' B 'C ' D ' (tham khảo hình bên). Giá trị D C
sin của góc giữa đường thẳng AC ' và mặt phẳng  ABCD  bằng A B 3 6 A. . B. . 3 3 D' C' 3 2 C. . D. . 2 2 B' A' Lời giải Chọn A Ta có AC  CC ' 2 2 2
 AC '  AC  CC '  CC ' 3 Ta có  AC '; ABCD   AC';AC    CAC '  CC ' CC ' 3 sin CAC '    . AC ' CC ' 3 3
Câu 33. Trong không gian Oxyz , cho điểm A 1; 2; 3 . Phương trình của mặt cầu tâm A và tiếp xúc với mặt
phẳng x 2y  2x 3  0 là 2 2 2 2 2 2 A.  x  
1  y 2 z   3  2. B.  x  
1  y 2 z   3  2. 2 2 2 2 2 2 C.  x  
1  y 2 z   3  4. D.  x  
1  y 2 z   3  4. Lời giải Chọn D 1 2.2  2.3  3 6 Bán kính mặt cầu R    2   2 2 3 1 2  2
Do đó phương trình của mặt cầu
x 2  y 2 z 2 2 1 2 3  2  4 1 Câu 34. Với ,
a b là các số thực dương tùy ý và a  1, log1 bằng 3 b a 1 A. 3log b. B. log b . C. 3 log b . D. log b . a a a 3 a Lời giải
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 17.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 Chọn A 1 3 log log    b  3log b 1 3 a a b a
Câu 35. Cho hình lập phương ABCD.A ' B 'C ' D ' có cạnh bằng 3 (tham A D
khảo hình bên). Khoảng cách từ B đến mặt phẳng  ACC ' A ' H bằng B C 3 2 3 A. . B. . 2 2 A' D' C. 3 2 . D. 3 . B' C' Lời giải Chọn A
Gọi H là trung điểm của A C .
Vì ABCD.A ' B 'C ' D ' là hình lập phương nên BH   ACC ' A '  B  ACC A  1 ; ' '  BH  AC 2
Mà ABCD là hình vuông cạnh 3 nên AC  3 2  B  ACC A  3 2 ; ' '  2
Câu 36. Cho hàm số y  f  x có đạo hàm f  x  x  1 với mọi x   . Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 1; . B. 1; . C. ;  1 . D. ;1 . Lời giải Chọn C
Ta có: f   x  0  x  1  0  x  1 . Bảng xét dấu:
Vậy hàm số đã cho nghịch biến trên khoảng ;  1 .
Câu 37. Trong không gian Oxyz , cho điểm M 2; 2;1 và mặt phẳng P  : 2x  3 y  z  1  0 . Đường thẳng
đi qua M và vuông góc với  P  có phương trình là:
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 18.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 x  2 2t x  2 2t x  2 2t x  22t     A. y  23t . B. y  2  3t . C. y  2  3t . D. y  3  2t . z 1t     z 1t  z 1t  z  1  t  Lời giải Chọn B
Gọi d là đường thẳng đi qua M và vuông góc với  P  . Do 
d vuông góc với  P  nên d có một vectơ chỉ phương là u  2 ; 3; 1 . x  2  2t
Vậy phương trình của đường thẳng 
d là:  y  2  3t . z 1t 
Câu 38. Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn 30 ;50. Xác suất để chọn được số
có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng 11 8 13 10 A. . B. . C. . D. . 21 21 21 21 Lời giải Chọn A
Số phần tử của không gian mẫu là n    21 .
Gọi A là biến cố: "chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục".
Khi đó A  34;35;36;37 ;38;39; 45; 46 ; 47 ; 48; 49  n  A  11 . n A 11 Vậy P  A     . n  21
Câu 39. Biết F  x; G  x là hai nguyên hàm của hàm số f  x trên  và 4 f
 xdx  F4G0a a 0. Gọi S là diện tích hình phẳng giới hạn bởi các đường 0
y  F  x; y  Gx;x  0; x  4. Khi S  8 thì a bằng A. 8 B. 4 C. 12 D. 2 Lời giải Chọn D
Đặt F  x  G x  c
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 19.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 4 S  F
 xGx dx  FxGx  2 hay c  2 0 4 f
 xdx  F4G0 a 0
 F 4  F 0  F 4  G0  a  G  0  c  G  0  a  a  c  a  2  Mà a  0  a  2
Câu 40. Cho hàm số f  x 4  ax  a   2 2
4 x 1 với a là tham số thực. Nếu max f  x  f   1 0;2 thì min f  xbằng 0;2 A. 1  7 B. 1  6 C. 1  D. 3 Lời giải Chọn A
Từ giả thiết ta có f  1  0
 4a  4 a  4  0  a  2 và f  x 4 2  2 x  4 x  1
Ta có f 0   1, f 1  1, f 2  17
Vậy min f  x  f (2)  1  7 0;2
Câu 41. Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn 4b  1 .3b a 10  0? A.182. B. 179. C. 180. D. 181. Lời giải Chọn D
Theo đề bài a;a1 và b  . Trường hợp 1:   b b 0 4 1 0     10  3b a 10  0 b  log  3  a
Vì có đúng hai số nguyên b thỏa mãn nên b  2;   1 .
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 20.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 10 Do đó 2  log
 3  270  a  90 nên a91;92;...;27 
0 . Có 180 giá trị của a thoả mãn 3 a trường hợp 1. Trường hợp 2:   b b 0 4 1 0     10  3b a 10  0 b  log  3  a
Vì có đúng hai số nguyên b thỏa mãn nên b  1; 2 . 10 10 10 Do đó 3  log  2   a 
nên a  1 . Có 1 giá trị của a thoả mãn trường hợp 2. 3 a 9 27
Vậy có 180  1  181 giá trị của a thoả mãn yêu cầu bài toán.
Câu 42. Cho hình nón có góc ở đỉnh bằng 0
120 và chiều cao bằng 3. Gọi  
S là mặt cầu đi qua đỉnh và chứa
đường tròn đáy của hình nón đã cho. Diện tích của   S bằng A.144 . B. 108 . C. 48 . D. 96 . Lời giải Chọn A
Gọi H là tâm đáy, AB là đường kính của đáy hình nón và SC là đường kính của mặt cầu   S . Khi đó SH  3 và  0 ASC  60 . SH SA   6 (đvdd) 0 cos 60 2 2 SA  S .
H SC 6  3.SC  SC 12
Bán kính của mặt cầu  
S là R  6 nên diện tích của   S là 2 S 4.6 144 (đvdt).
Câu 43. Cho hàm số bậc bốn y  f  x . Biết rằng hàm số g  x   ln f  x  có bảng biến thiên
Diện tích hình phẳng giới hạn bởi các đường y  f   x  và y  g x thuộc khoảng nào dưới đây?
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 21.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 A. 33;35 . B. 37;40 . C. 29;32 . D. 24;26. Lời giải Chọn A
Từ bảng biến thiên hàm số g  x   ln f  x  ta có ln f  x  ln 3, x    f  x  3, x   . f  x Ta có g x    . f  x
Từ bảng biến thiên ta có đồ thị hàm số y  g  x  có 3 điểm cực trị là
A  x ; ln 30 , B x ; ln 35 , C x ; ln 3 nên
f  x  f  x  f  x  0 và 1   2   3  1   2   3 
f  x  30, f x  35, f x  3 . 1   2   3 
Do y  f   x  là hàm số bậc 3 nên phương trình f  x  0 chỉ có 3 nghiệm x , x , x . 1 2 3 Xét phương trình hoành độ giao điểm của f  x và g x ta có   f  x  f    x x x1 
f  x  g  x  f  x   0          .     x  x f x f x 1 VN 2   x  x  3
Diện tích hình phẳng giới hạn bởi các đường y  f   x  và y  gx là: 3 x x x    S  g  x f x 3 f  x 3 1 dx   f  x x  f  x      x f x  f x  x x     d  . x    1 d  1 1 1 x2 x      f   x 3 1 1 .   x  f  x     x  f x   f x  x    1 d  .  x    1 d  1 2 2 x 2  1 x   1  + Tính I  f  x .   1 dx  f  x .  1
dx (do f  x  0, x   x ; x ) 1 2  1    f x   f x  x       x     1 1
Đặt t  f  x   dt  f  x dx . Đổi cận:
x  x  t  f x  30 . 1  1 x  x  t  f x  35 . 2  2  35  1 35  6 Suy ra I  1 dt  t  ln t
 35  ln 35  30  ln 30  5  ln . 1     30  t  7 30 3 x 3  1 x   1  + Tính I  f  x .   1 dx   f  x .  1
dx (do f  x  0, x   x ; x ). 2 3  2    f x   f x  x       x     2 2
Đặt t  f  x   dt  f  x dx . Đổi cận:
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 22.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 x  x  t  f x  35 . 2  2  x  x  t  f x  3 . 3  3  3  1 35 Suy ra I   1 dt     
t ln t 3   3ln335 ln35  32ln . 2   35  t  3 35 6  35  18
Vậy S  5 ln  32  ln  37  ln  34,39   33;3 5. 7  3  245
Câu 44. Xét tất cả số thực 2 x , y sao cho 3 5 y 6 log3 27 x a  a 
với mọi số thực dương a . Giá trị nhỏ nhất của biểu thức 2 2
P  x  y  4x  8y bằng A. 15  . B. 25. C. 5  . D. 2  0 . Lời giải Chọn A Giả sử 2 x , y thỏa 3 5 y 6 log3 27 x a  a 
với mọi số thực dương a . Ta có 2 2 2 2
P  x  y  4x  8y  x  y  4x  8y  P  0
Suy ra điểm M x; y thuộc đường tròn tâm I 2;4 và bán kính R  2  42 2  P  20  P . 1 2 3 5 y 6xlog3 27 a  a   2 5 y .3   3 6x  log a  log a  2
5 y .3  6x  3log a log a 3 3   3  3
Đặt t  log a, t   . 3 Suy ra  2  y   x t 2 2 5 .3 6 3 t  3  t 6xt 153y  0 Theo đề bài ta có 2 3 5 y 6 log3 27 x a  a 
đúng với mọi số thực dương a nên 2 2
3t  6xt 15  3y  0 đúng với mọi t   . 3  0  Do đó   x  y    x  y  . 3x   3  153y  2 2 2 2 9 9 45 0 5 2 2  0
Suy ra tập hợp các điểm M x; y là hình tròn tâm O 0; 0  và bán kính R  5 . 2
Vậy để tồn tại cặp  x; y  thì đường tròn I ; R và hình tròn O; 5 phải có điểm chung 1 
Do đó IO  R  5  2  42 2
 20  P  5  5  20  P  P  15 . 1
Vậy giá trị nhỏ nhất của P là  1 5
Câu 45. Cho các số phức z , z , z thỏa mãn  
 và  z  z z  3z z . Gọi , A , B C lần 1 2  1 2 3 2 z 2 z z 2 1 2 3 3 1 2
lượt là các điểm biểu diễn của z , z , z trên mặt phẳng tọa độ. Diện tích tam giác 1 2 3 A B C bằng 5 7 5 7 5 7 5 7 A. . B. . C. . D. . 8 16 24 32
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 23.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 Lời giải Chọn B
Không mất tính tổng quát, giả sử z  2 . 3 1 1 3
Khi đó  z  z z  3z z trở thành 2  z  z  3z z    . 1 2  1 2  3 1 2 1 2 z z 2 1 2 1 1  3  Đặt
 x  yi  ,x y    x  yi . z   z  2 1  2 Ta có z  2 và    nên   1 1    . 3 2 z 2 z z 2 z z 1 1 1 2 3 1 2 z z 1 2  3  3 3 x    x   2 2 x  y 1 4  2 4     Suy ra 2  7 7  3    y    y   2   x  y 1   4 4     2     7  7  y    y    4  4 3 7 3 7 Do đó z   ;i z   i . 1 1 4 4 4 4  3 7   3 7 
Nên tọa độ các điểm là A ; ; B ; ;C 2;0  . 4 4   4 4      1 1 7  3  5 7
Diện tích tam giác A B C là S  A . B d C AB    . ABC  ;  .2. . 2   2 2 4  4  16
Câu 46. Trong không gian Oxyz , cho điểm A 1; 2; 2 . Gọi P  là mặt phẳng chứa trục Ox sao cho khoảng
cách từ A đến P  lớn nhất. Phương trình của  P  là: A. 2 y  z  0 . B. 2 y  z  0 . C. y  z  0 . D. y  z  0 . Lời giải Chọn D
Gọi hình chiếu vuông góc của điểm A 1; 2; 2 lên trục Ox là M 1; 0; 0  . 
Khoảng cách từ A đến  P  lớn nhất nên mặt phẳng  P  có vecto pháp tuyến là MA  0;2;  2 . 
Phương trình mặt phẳng  P  đi qua điểm M 1; 0; 0  và có vecto pháp tuyến là MA  0;2;  2 nên
0. x  1  2  y  0  2  z  0  0  y  z  0 .
Câu 47. Có bao nhiêu số phức z thỏa mãn 2
z  z  z và z   z  i 2 2 2  z  2i ? A. 2 . B. 3 . C. 1. D. 4 .
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 24.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 Lời giải Chọn D z  z  i 2 2
2  z  2i  z  2 z  2i  z  2i z  2i
 z 2i  z 2  z2i  Trường hợp 1.
z  2i  0  z  2i  z  2i Trường hợp 2.
z  2  z  2i  0  z  2  z  2i  0
Đặt z  x yi ta có z  2  x  2 yi và z  2i  x   y  2i . Khi đó
z   z  i   x  2  y  x  y  2 2 2 2 2 2 2 2 2 2 2
 x  4x  4  y  x  y  4y  4  4  x  4y  x  y Lại có 2 2 2 2
z  z  z  x  y  2 y  2y  2 y  2 y  y   1  0  y 0 hoặc y  1  .
Do đó ta có các số z  0;1 i; 1 i; 2i thỏa mãn.
Vậy có 4 số phức thỏa mãn yêu cầu bài toán.
Câu 48. Cho khối lăng trụ đứng ABC.A ' B 'C ' có đáy A B C là tam giác vuông cân tại A , cạnh bên A A  2 a
, góc giữa hai mặt phẳng  ABC  và  ABC  bằng 30 . Thể tích của khối lăng trụ đã cho bằng 8 8 A. 3 24a . B. 3 a . C. 3 8a . D. 3 a . 3 9 Lời giải Chọn A
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 25.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 A' C' B' A C H B
Kẻ A H  BC , ta có AA   ABC  nên AA '  BC .
A H  B C và A A '  B C suy ra BC   AAH   AH  BC .
Suy ra góc giữa  ABC  và  ABC  là  A H  A   AHA  30 . ΔA ' AH vuông tại A có  AA 2a 2a tan AHA   tan 30   AH   2a 3. AH AH tan 30
Δ A B C vuông cân tại A nên BC  2 AH  4a 3 . 1 1 2  S
 AH  BC  2a 3  4a 3  12a . ABC 2 2
Vậy thể tích của khối lăng trụ đứng ABC .A ' B 'C ' là
Câu 49. Có bao nhiêu giá trị nguyên âm của tham số a để hàm số 4 2
y  x  ax 8x có đúng 3 điểm cực trị? A. 5 . B. 6 . C. 11. D. 10 . Lời giải Chọn B Xét g  x 4 2  x  ax  8x g  x 3  4x  2ax  8 3 2x 4 4 Xét g x 3 2
 0  4x  2ax8  0  a  
 2x   hx (do x  0 không là nghiệm) x x x  0 g  x  3  0  x 8 8 3 2
x  ax 8  0  a   x   k  x  x x
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 26.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 h x 4  4x   0  x  1. 2 x k x 8 3  2x   0  x  4 . 2 x
Để hàm số y  g  x có đúng 3 cực trị   a  6  a  6 .
Mà a là số nguyên âm nên a  6; 5; 4; 3; 2;   1 .
Câu 50. Trong không gian Oxyz cho mặt cầu S  tâm I 9;3;1 bán kính bằng 3. Gọi M, N là hai điểm lần lượt thuộc 2 trục O ,
x Oz sao cho đường thẳng M N tiếp xúc với S, đồng thời mặt cầu ngoại tiếp 13
tứ diện O IM N có bán kính bằng
. Gọi A là tiếp điểm của M N và S  , giá trị AM .AN bằng 2 A. 12 3 . B. 18 . C. 28 3 . D. 39. Lời giải Chọn A
I 9; 3;1  d I Oxz   3  R  S  tiếp xúc với Oxz . Gọi M a;0; 0 Ox N 0; 0; b  Oz
M N tiếp xúc với S  tại A nên A là hình chiếu của I lên Oxz . Suy ra A 9; 0;1 .  a b 
Gọi K là trung điểm MN  K ;0;   .  2 2  13
Gọi H là tâm mặt cầu ngoại tiếp tứ diện OIMN  OH   HK  MN . 2 OM  KT 
Gọi T là trung điểm OM 
  OM   KHT   OM  HK  HK  OMN  OM  HT 
Mà IA  OMN   HK // IA .
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 27.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022  Ta có AI  0;3;0   a b  KH  x  ; y  0; z   . H   2 H H 2   a x    H  2 
AI cùng phương KH nên y  c c  H  0  b z  H  2  a b   H ; ; c    2 2  2 2 13 a 2 b 169 OH   c    1 2 4 4 4 2 2 13  a    HI  OH     c  2 b 169 9 3  1      2 2  2   2  4 2 2 2 2 a b  a   b Từ   1 và 2 suy ra  c       c  2 2 9 3  1   4 4  2   2 
 9a  b  6c  91 3  AM  a  9;0;  1  AN  9;0;b   1 , A M,N a  9 1 thẳng hàng   9 b 1  a  2b   1  9  ab  a 9b  9  9  ab  a 9b  0  ab   1  ab 9b  a  b1 b Từ   9 3  9.  b  6c  91 b 1 81b b  6c  91 b 1 2 2 2 b  80b b  80b b  11b  91   6c  91  6c  91  b 1 b 1 b 1 2 b 11b  91  c  6b   1 Ta có 2 2 2 a  4c b 169
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 28.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022 2 2 2  9b   b  11b  91 2   4        b    b  b 169 1 6 1    
 9.81b  b 121b 8281 22b 182b  2002b  9b b  2 1  169.  9. b  2 2 4 2 3 2 2 1 2 4 2 3 2 4 3 2 2
 729b  b 121b 8281 22b 182b  2002b  9b 18b  9b 1521b  3042b 1521 4 3 2
 10b  40b  480b 1040b  6760  0  913 3 b 13 3  a   9  3  3 3   913 3 b 13 3  a   9  3  3  3 
+ Trường hợp 1: a  9  3; b  1 3 3  AM   3;0;  1  AM  2 .   AN   9
 ;0;3 3  AN  108 . AM .AN  2. 108  12 3 . 
+ Trường hợp 2: a  9  3; b 1 3 3  AM   3;0;  1  AM  2 .   AN   9  ;0; 3  3  AN  108. AM .AN  2. 108  12 3 .  HẾT 
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 29.
BGD-KỲ THI TỐT NGHIỆP THPT-Môn TOÁN-Chính thức-Ngày 07-7-2022
LỜI GIẢI ĐƯỢC THỰC HIỆN BỞI
Tập Thể Giáo Viên Nhóm Toán “Tiểu Học – THCS – THPT VIỆT NAM” Tạ Thị Huyền Trang Nguyễn Trí Chính Phạm Thụ Trần Hùng Quân Le Hoop Việt Dũng Lê Hường Nguyễn Đông Ngonnguyen Quocman Phạm Thái Ly Trần Lệnh Ánh Võ Tự Lực Tran Tran Do Lan Anh Nguyen Lê Cảnh Hoài Người Dạy Toán Phạm Thu Hà Kien Cao Vũ Đình Thắng Duy Dang Đường Ngọc Lan Lê Minh Đức Ngọc Diệp Nguyễn Huy Hoàng Phạm Hoài Phạm Hồng Nhung Thế Long Thống Trần Hoàng Điệp Phạm Xu Ka Trần Tuấn Tú
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM Trang: 30.
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022 KỲ THI TN THPT QUỐC GIA NĂM HỌC 2021 – 2022
Môn: TOÁN – Mã đề: 104
HỌC HỎI - CHIA SẺ KIẾN THỨC
Thời gian: 90 phút (không kể thời gian phát đề)
LINK NHÓM: https://www.facebook.com/groups/1916660125164699
Câu 1. Số phức nào dưới đây có phần ảo bằng phần ảo của số phức w  1 4i ? A. z  5  4i . B. z  1 4i . C. z  1 5i . D. z  3  4i . 1 4 3 2
Câu 2. Cho hàm số bậc ba y  f x có đồ thị là đường cong trong hình bên dưới.
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là A. 1;3 . B. 3;  1 . C.  1  ;  1 . D. 1;  1 .
Câu 3. Phần ảo của số phức z  2  i1 i bằng A. 3  . B. 1. C. 3 . D. 1. 2 5 5 Câu 4. Nếu f
 xdx  2 và f xdx  5   thì f  xdx bằng 1 2 1 A. 7 . B. 3  . C. 7  . D. 4 .
Câu 5. Cho khối chóp S.ABC có chiều cao bằng 5, đáy ABC có diện tích bằng 6.Thể tích khối chóp S.ABC bằng A. 30 . B. 10 . C. 15 . D. 11.
Câu 6. Cho khối chóp và khối lăng trụ có diện tích đáy, chiều cao tương ứng bằng nhau và có thể tích V
lần lượt là V ,V . Tỉ số 1 bằng 1 2 V2 2 3 1 A. . B. . C. 3 . D. . 3 2 3
Câu 7. Với a là số thực dương tuỳ ý, log 100a bằng A. 2  log a . B. 2  log a . C. 1 log a . D. 1 log a .
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 1
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Câu 8. Hàm số nào dưới đây có bảng biến thiên như sau? A. 3 y  x  3x . B. 2 y  x  2x . C. 3 y  x  3x . D. 2 y  x  2x .
Câu 9. Số nghiệm thực của phương trình 2x 1 2   4 là A. 1. B. 2 . C. 0 . D. 3 .
Câu 10. Trong không gian 0xyz , phương trình của mặt phẳng Oxy là A. y  0 . B. x  0 . C. x  y  0 . D. z  0 .   
Câu 11. Hàm số F  x  cot x là một nguyên hàm của hàm số nào dưới đây trên khoảng 0;   ?  2  1 1 1 1 A. f x  . B. f x   . C. f x   . D. f x  . 4   3   1   2   2 sin x 2 cos x 2 sin x 2 cos x
Câu 12. Cho hàm số y  f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ;  1 . B. 0;3 . C. 0;  . D.  1;  0 . x  2 y 1 z 1
Câu 13. Trong không gian Oxyz , cho đường thẳng d :  
. Điểm nào dưới đây thuộc d ? 1 2 3 A. P 2;1;  1 . B. M 1;2;3 . C. Q 2;1;  1 . D. N 1; 2;3 .
Câu 14. Trên mặt phẳng tọa độ, điểm biểu diễn số phức z  2  7i có tọa độ là A. 2; 7 . B. 2; 7 . C. 7;2 . D. 2;7 .
Câu 15: Cho điểm M nằm ngoài mặt cầu S O; R. Khẳng định nào dưới đây đúng? A. OM  . R B. OM  . R C. OM  . R D. OM  . R
Câu 16: Khẳng định nào sau đây đúng? A. exd  ex x  C  . B. exd  ex x x  C  . C. x x 1 e dx e     C  . D. x x 1 e dx e    C  .    
Câu 17. Trong không gian Oxyz , cho hai vectơ u  1; 4  ;0 và v   1  ; 2  ; 
1 . Vectơ u  3v có tọa độ là Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022 A. 2;10;3 . B. 2;6;3 . C.  4  ; 8  ;4. D. 2;10; 3   .
Câu 18. Cho cấp số nhân u
u  3 và công bội q  2 . Số hạng tổng quát u n  2 bằng n  n  1 A. 3.2n . B. 2 3.2n . C. 1 3.2n . D. 1 3.2n . Câu 19. Cho 5 a  3 , 2 b  3 và 6
c  3 . Mệnh đề nào dưới đây đúng? A. a  b  c . B. a  c  b . C. c  a  b . D. b  a  c .
Câu 20. Cho khối nón có diện tích đáy 2
3a và chiều cao 2a . Thể tích của khối nón đã cho là 2 A. 3 3a . B. 3 6a . C. 3 2a . D. 3 a . 3 3 3 1  Câu 21. Nếu f  xdx  6 thì f  x 2 dx  bằng 3    0 0 A. 6 . B. 5 . C. 9 . D. 8 .
Câu 22. Tập xác định của hàm số y  log x 1 là 2   A. 2;  . B.  ;    . C.  ;   1 . D. 1;  . Câu 23. Cho hàm số 4 2
y  ax  bx  c có đồ thị là đường cong trong hình bên. Giá trị cực tiểu của hàm số đã cho bằng y 4 3 1O 1 x A. 3 . B. 4 . C. 1  . D. 1.
Câu 24. Nghiệm của phương trình log 2x 1  0 là 1   2 3 2 1 A. x  1. B. x  . C. x  . D. x  . 4 3 2
Câu 25. Cho hàm số y  f x có bảng biến thiên như sau: x - 2 - ∞ + ∞ - - f ' x ( ) - 1 + ∞ f x ( ) - ∞ - 1
Tiệm cận đứng của đồ thị đã cho là đường thẳng có phương trình: A. y  1. B. y  2  . C. x  2  . D. x  1 .
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 3
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Câu 26. Trong không gian Oxyz , cho mặt cầu S   x  2   y  2   z  2 : 2 1
3  4 . Tâm của S  có tọa độ là A. 2;1; 3   . B. 4;2; 6   . C. 4;2;6 . D. 2; 1  ;3.
Câu 27. Từ các chữ số 1, 2, 3, 4, 5 lập được bao nhiêu số tự nhiên có năm chữ số đôi một khác nhau? A. 3125 . B. 1. C. 120 . D. 5 .
Câu 28. Cho hàm số y  f x có bảng biến thiên như sau:
Số giao điểm của đồ thị hàm số đã cho và đường thẳng y  1 là A. 2 . B. 1. C. 3 . D. 0 .
Câu 29. Cho hình lập phương ABC . D A B  C  D
  (tham khảo hình vẽ bên dưới).
Giá trị sin của góc giữa đường thẳng AC và mặt phẳng (ABCD) bằng 3 2 3 6 A. . B. . C. . D. . 3 2 2 3
Câu 30. Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn 30;50 . Xác suất để chọn được
số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng 11 13 10 8 A. . B. . C. . D. . 21 21 21 21 1
Câu 31. Với a,b là các số thực dương tùy ý và a  1, log bằng 1 3 b a 1 A. log b . B. 3log b . C. log b . D. 3log b . a a 3 a a Câu 32. Cho hàm số   2 1 e x f x  
. Khẳng định nào dưới đây đúng? A.    1 d   ex f x x x  C . B.    2 d   2e x f x x x  C . 2 1 C.    2 d   e x f x x x  C . D.    2 d   e x f x x x  C . 2 Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Câu 33. Gọi z , z là hai nghiệm phức của phương trình 2
z  2z  5  0 . Khi đó 2 2 z  z bằng 1 2 1 2 A. 6 . B. 8i . C. 8i . D. 6  .
Câu 34. Cho hàm số y  f x có đạo hàm f  x  x 1 với mọi x   . Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A.  ;    1 . B.  ;   1 . C.  1  ; . D. 1; .
Câu 35. Trong không gian Oxyz , cho điểm A1;2;3 . Phương trình của mặt cầu tâm A và tiếp xúc với
mặt phẳng x  2 y  2z  3  0 là
A.  x  2   y  2   z  2 1 2 3  2 .
B.  x  2   y  2   z  2 1 2 3  2 .
C.  x  2   y  2   z  2 1 2 3  4 .
D.  x  2   y  2   z  2 1 2 3  4 . Câu 36. Cho hàm số 4 2
f (x)  ax  bx  c có đồ thị là đường cong trong hình bên dưới.
Có bao nhiêu giá trị nguyên thuộc đoạn  2
 ;5 của tham số m để phương trình f (x)  m có
đúng 2 nghiệm thực phân biệt? A. 7. B. 6. C. 5. D. 1.
Câu 37. Trong không gian Oxyz , cho điểm M 2; 2; 
1 và mặt phẳng . Đường thẳng đi qua M và vuông
góc với mặt phẳng P có phương trình là x  2  2t x  2  2t x  2  2t x  2  2t     A. y  2  3t . B. y  2  3t . C. y  2   3t . D. y  3   2t . z 1t     z  1 t  z  1 t  z  1   t 
Câu 38. Cho hình lập phươn P : 2x  3y  z 1  0 g ABC . D AB C  D
  có cạnh bằng 3 (tham khảo hình bên dưới).
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 5
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Khoảng cách từ B đến mặt phẳng  ACC A   bằng 3 2 3 A. 3 . B. 3 2 . C. . D. . 2 2
Câu 39. Có bao nhiêu số nguyên dương a sao cho với mỗi a có đúng hai số nguyên b thỏa mãn 3b 3 .2b a 16  0 A. 34 . B. 32. C. 31. D. 33.
Câu 40. Cho hàm số f  x  a   4 2
3 x  2ax 1 với a là tham số thực. Nếu max f  x  f 2 thì 0; 3 min f  x bằng 0; 3 A. 9  . B. 4 . C. 1. D. 8  .
Câu 41. Biết F  x và G  x là hai nguyên hàm của hàm số f  x trên  và 2 f
 xdx F 2G0 a a  0 . Gọi S là diện tích hình phẳng giới hạn bởi các đường 0
y  F  x , y  G  x , x  0 và x  2 , Khi S  6 thì a bằng A. 4 . B. 6 . C. 3 . D. 8 .
Câu 42. Cho các số phức z , z , z thỏa mãn 2 z  2 z  z  2 và  z  z z  2z z . Gọi , A B,C lần 1 2  1 2 3 1 2 3 3 1 2
lượt là các điểm biểu diễn của z , z , z trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng 1 2 3 3 3 3 3 3 3 A. . B. . C. . D. . 4 8 8 4
Câu 43. Cho khối lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông cân tại A , cạnh bên
AA  2a , góc giữa hai mặt phẳng  A B
 C và  ABC bằng 60. Thể tích của khối lăng trụ đã cho bằng 8 8 A. 3 a . B. 3 8a . C. 3 a . D. 3 24a . 9 3
Câu 44. Cho hình nón có góc ở đỉnh bằng 120 và chiều cao bằng 2 . Gọi S  là mặt cầu đi qua đỉnh và
chứa đường tròn đáy của hình nón đã cho. Diện tích của S  bằng 16 64 A. . B. . C. 64 . D. 48 . 3 3
Câu 45: Xét tất cả các số thực x , y sao cho 2 3 9 y 6 log2 8 x a  a 
với mọi số thực dương a . Giá trị nhỏ nhất của biểu thức 2 2
P  x  y  6x  8y bằng A. 21. B. 6  . C. 25 . D. 39 .
Câu 46. Cho hàm số bậc bốn y  f  x . Biết rằng hàm số g  x  ln f  x có bảng biến thiên như sau Trang 6
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Diện tích hình phẳng giới hạn bởi các đường y  f  x và y  g x thuộc khoảng nào dưới đây? A. 7;8. B. 6;7 . C. 8;9 . D. 10;  11 .
Câu 47. Trong không gian Oxyz , cho điểm A2;1; 
1 . Gọi P là mặt phẳng chứa trục Oy sao cho
khoảng cách từ A đến P lớn nhất. Phương trình của P là A. x  z  0 . B. x  z  0 . C. 2x  z  0 . D. 2x  z  0 .
Câu 48. Có bao nhiêu số phức z thỏa 2
z  2 z  z và  z  z  i 2 4 4  z  4i . A. 4 . B. 2 . C.1 D. 3 .
Câu 49. Có bao nhiêu số nguyên dương của tham số m để hàm số 4 2
y  x  mx  64x có đúng 3 điểm cực trị ? A. 23. B. 12 . C. 24 . D. 11.
Câu 50. Trong không gian Oxyz , cho mặt cầu S  tâm I 1;4;2 , bán kính bằng 2. Gọi M , N là hai điểm
lần lượt thuộc hai trục Ox,Oy sao cho đường thẳng MN tiếp xúc với S  , đồng thời mặt cầu 7
ngoại tiếp tứ diện OIMN có bán kính bằng . Gọi A S , giá trị 2
là tiếp điểm của MN và   AM .AN bằng A. 9 2 . B. 14 . C. 6 2 . D. 8 .
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 7
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT BẢNG ĐÁP ÁN 1.A 2.C 3.B 4.B 5.B 6.D 7.B 8.C 9.B 10.D 11.C 12.D 13.A 14.D 15.C 16.A 17.A 18.D 19.D 20.C 21.D 22.D 23.A 24.A 25.C 26.D 27.C 28.C 29.A 30.A 31.D 32.D 33.D 34.A 35.D 36.A 37.C 38.C 39.D 40.D 41.C 42.A 43.C 44.C 45.A 46.A 47.C 48.A 49.C 50.C LỜI GIẢI CHI TIẾT
Câu 1. Số phức nào dưới đây có phần ảo bằng phần ảo của số phức w  1 4i ? A. z  5  4i . B. z  1 4i . C. z  1 5i . D. z  3  4i . 1 4 3 2 Lời giải
GVSB: Vân Anh Đào Nguyễn; GVPB1: Nguyen Ly; GVPB2: Bùi Kim Thoa Chọn A
Số phức w  1 4i có phần ảo bằng 4 .
Trong các số phức đã cho, số phức z  5  4i cũng có phần ảo bằng 4  . 1
Câu 2. Cho hàm số bậc ba y  f x có đồ thị là đường cong trong hình bên dưới.
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là A. 1;3 . B. 3;  1 . C.  1  ;  1 . D. 1;  1 . Lời giải
GVSB: Vân Anh Đào Nguyễn; GVPB1: Nguyen Ly; GVPB2: Bùi Kim Thoa Chọn C
Từ đồ thị hàm số bậc ba y  f x , ta có điểm cực tiểu của đồ thị hàm số có tọa độ là 1;  1 .
Câu 3. Phần ảo của số phức z  2  i1 i bằng A. 3  . B. 1. C. 3 . D. 1. Lời giải
GVSB: Nguyễn Bình; GVPB1: Bông Thối; GVPB2: Bùi Kim Thoa Chọn B
Ta có: z  2  i1 i  3  i .
Vậy phần ảo của số phức z bằng 1. Trang 8
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022 2 5 5 Câu 4. Nếu f
 xdx  2 và f xdx  5   thì f  xdx bằng 1  2 1  A. 7 . B. 3  . C. 7  . D. 4 . Lời giải
GVSB: Nguyễn Bình; GVPB1: Bông Thối; GVPB2: Bùi Kim Thoa Chọn B 5 2 5 Ta có: f  xdx  f  xdx  f
 xdx  25  3. 1 1 2
Câu 5. Cho khối chóp S.ABC có chiều cao bằng 5, đáy ABC có diện tích bằng 6.Thể tích khối chóp S.ABC bằng A. 30 . B. 10 . C. 15 . D. 11. Lời giải
GVSB: Vũ Ngọc Thành; GVPB1: Suol Nguyen; GVPB2: Thuỳ Dung Chọn B 1
Thể tích khối chóp S.ABC là V  .5.6  10 . S.ABC 3
Câu 6. Cho khối chóp và khối lăng trụ có diện tích đáy, chiều cao tương ứng bằng nhau và có thể tích V
lần lượt là V ,V . Tỉ số 1 bằng 1 2 V2 2 3 1 A. . B. . C. 3 . D. . 3 2 3 Lời giải
GVSB: Vũ Ngọc Thành; GVPB1: Suol Nguyen; GVPB2: Thuỳ Dung Chọn D
Gọi đường cao, diện tích đáy lần lượt là h, B . 1
Khi đó áp dụng công thức thể tích khối chóp, khối lăng trụ ta được V  . B h và V  . B h . 1 3 2 1 .Bh V 1 Suy ra: 1 3   . V . B h 3 2
Câu 7. Với a là số thực dương tuỳ ý, log 100a bằng A. 2  log a . B. 2  log a . C. 1 log a . D. 1 log a . Lời giải
GVSB: Võ Thành Tài; GVPB1: Phạm Trung Khuê; GVPB2: Thuỳ Dung Chọn B Với a  0 , ta có  a 2 log 100
 log100  log a  log10  log a  2  log a .
Câu 8. Hàm số nào dưới đây có bảng biến thiên như sau?
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 9
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022 A. 3 y  x  3x . B. 2 y  x  2x . C. 3 y  x  3x . D. 2 y  x  2x . Lời giải
GVSB: Võ Thành Tài; GVPB1: Phạm Trung Khuê; GVPB2: Thuỳ Dung Chọn C
Dựa vào bảng biến thiên trên, ta nhận thấy đây là hàm số bậc ba có dạng 3 2 y  ax  bx  cx  d với a  0 . Mà  3 2
lim ax  bx  cx  d     a  0 . x
Do đó có duy nhất hàm số 3
y  x  3x thoả mãn.
Câu 9. Số nghiệm thực của phương trình 2x 1 2   4 là A. 1. B. 2 . C. 0 . D. 3 . Lời giải
GVSB: Trần Hương Trà; GVPB1: Trần Hương Trà; GVPB2: Đỗ Ngọc Đức Chọn B Ta có 2x 1  2 2 2
 4  x 1  2  x  1  x  1. 
Câu 10. Trong không gian Oxyz , phương trình của mặt phẳng Oxy là A. y  0 . B. x  0 . C. x  y  0 . D. z  0 . Lời giải
GVSB: Trần Hương Trà; GVPB1: Trần Hương Trà; GVPB2:Đỗ Ngọc Đức Chọn D
Phương trình của mặt phẳng Oxy là z  0 .   
Câu 11. Hàm số F  x  cot x là một nguyên hàm của hàm số nào dưới đây trên khoảng 0;   ?  2  1 1 1 1 A. f x  . B. f x   . C. f x   . D. f x  . 4   3   1   2   2 sin x 2 cos x 2 sin x 2 cos x Lời giải
GVSB: Vu Ngoc Anh; GVPB1: ThienMinh Nguyễn; GVPB2: Đỗ Ngọc Đức Chọn C 1 Ta có:  dx  cot x  C  . 2 sin x
Câu 12. Cho hàm số y  f x có bảng biến thiên như sau: Trang 10
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ;  1 . B. 0;3 . C. 0;  . D.  1;  0 . Lời giải
GVSB: Vu Ngoc Anh; GVPB1: ThienMinh Nguyễn; GVPB2: Đỗ Ngọc Đức Chọn D
Ta có đồ thị tăng trên khoảng  1
 ;0 , nên đó là đáp án đúng. x  2 y 1 z 1
Câu 13. Trong không gian Oxyz , cho đường thẳng d :  
. Điểm nào dưới đây thuộc d ? 1 2 3 A. P 2;1;  1 . B. M 1;2;3 . C. Q 2;1;  1 . D. N 1; 2;3 . Lời giải
GVSB: Phạm Quang Linh; GVPB1:Phan Huy; GVPB2: Tuan Pham; Chọn A
Thay tọa độ điểm P 2;1; 
1 vào phương trình đường thẳng d  ta có : 2  2 11 1  1 0 0 0       0 (thỏa mãn). 1 2 3 1 2  3
Thay tọa độ điểm M 1;2;3 vào phương trình đường thẳng d  ta có : 1 2 2 1 3 1 1  1 4      (vô lí). 1 2 3 1 2  3
Thay tọa độ điểm Q 2;1; 
1 vào phương trình đường thẳng d  ta có : 2  2 11 11 0 0 2      (vô lí). 1 2 3 1 2  3
Thay tọa độ điểm N 1; 2;3 vào phương trình đường thẳng d  ta có : 1 2 2 1 3 1 1 3 4      (vô lí). 1 2  3 1 2  3 Vậy điểm P 2;1; 
1 thuộc đường thẳng d  .
Câu 14. Trên mặt phẳng tọa độ, điểm biểu diễn số phức z  2  7i có tọa độ là A. 2; 7 . B. 2; 7 . C. 7;2 . D. 2;7 . Lời giải
GVSB: Phạm Quang Linh; GVPB1:Phan Huy; GVPB2: Tuan Pham; Chọn D
Trên mặt phẳng tọa độ, điểm biểu diễn số phức z  2  7i có tọa độ là 2;7 .
Câu 15: Cho điểm M nằm ngoài mặt cầu S O; R. Khẳng định nào dưới đây đúng? A. OM  . R B. OM  . R C. OM  . R D. OM  . R
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 11
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022 Lời giải
GVSB: Minh Hiếu; GVPB2: Tuan Pham; Chọn C
M nằm ngoài mặt cầu S O; R  OM  R .
Câu 16: Khẳng định nào sau đây đúng? A. exd  ex x  C  . B. exd  ex x x  C  . C. x x 1 e dx e     C  . D. x x 1 e dx e    C  . Lời giải
GVSB: Minh Hiếu; GVPB2: Tuan Pham; Chọn A exd  ex x  C  .    
Câu 17. Trong không gian Oxyz , cho hai vectơ u  1; 4  ;0 và v  1; 2  ; 
1 . Vectơ u  3v có tọa độ là A. 2;10;3 . B. 2;6;3 . C. 4;8;4. D. 2;10;3 . Lời giải
GVSB: Nguyễn Đức Tài; GVPB1: Nguyễn Minh Luận; GVPB2: Chọn A  Ta có 3v   3  ; 6  ;3.   Do đó u  3v   2  ; 10  ;3 .
Câu 18. Cho cấp số nhân u u  3 và công bội q  2 . Số hạng tổng quát u n  2 bằng n  n  1 A. 3.2n . B. 2 3.2n . C. 1 3.2n . D. 1 3.2n . Lời giải
GVSB: Nguyễn Đức Tài; GVPB1: Nguyễn Minh Luận; GVPB2: Chọn D Ta có n 1 n 1 u u .q  3.2    . n 1 Câu 19. Cho 5 a  3 , 2 b  3 và 6
c  3 . Mệnh đề nào dưới đây đúng? A. a  b  c . B. a  c  b . C. c  a  b . D. b  a  c . Lời giải
GVSB: Nguyễn Minh Luận; GVPB1: Nguyễn Thắng; GVPB2: Chọn D
Ta có 2  5  6 mà cơ số 3 1 nên 2 5 6
3  3  3 hay b  a  c .
Câu 20. Cho khối nón có diện tích đáy 2
3a và chiều cao 2a . Thể tích của khối nón đã cho là 2 A. 3 3a . B. 3 6a . C. 3 2a . D. 3 a . 3 Lời giải
GVSB: nguyễn Minh Luận ; GVPB1: Ngguyễn Thắng; GVPB2: Chọn C 1 1
Thể tích của khối nón đã cho là 2 3 V  . . B h  .3a .2a  2a . 3 3 Trang 12
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022 3 3 1  Câu 21. Nếu f  xdx  6 thì f  x 2 dx  bằng 3    0 0 A. 6 . B. 5 . C. 9 . D. 8 . Lời giải
GVSB: Hoàng Dương; GVPB1: Hoàng Dương; GVPB2: Hoàng Dương Chọn D 3 3 3 1  1 Ta có f  x  2 dx  f
 xdx 2dx  26  8   . 3    3 0 0 0
Câu 22. Tập xác định của hàm số y  log x 1 là 2   A. 2;  . B.  ;    . C.  ;   1 . D. 1;  . Lời giải
GVSB: Hoàng Dương; GVPB1: Hoàng Dương; GVPB2: Hoàng Dương Chọn D
Điều kiện: x 1  0  x  1.
Vậy tập xác định của hàm số đã cho là D  1;  . Câu 23. Cho hàm số 4 2
y  ax  bx  c có đồ thị là đường cong trong hình bên. Giá trị cực tiểu của hàm số đã cho bằng y 4 3 1  O 1 x A. 3 . B. 4 . C. 1  . D. 1. Lời giải
GVSB: Nguyễn Loan; GVPB1: Nguyễn Loan; GVPB2: Hoàng Dương Chọn A
Dựa vào đồ thị hàm số đã cho ta dễ dàng thấy giá trị cực tiểu của hàm số đã cho bằng 3 .
Câu 24. Nghiệm của phương trình log 2x 1  0 là 1   2 3 2 1 A. x  1. B. x  . C. x  . D. x  . 4 3 2 Lời giải
GVSB: Nguyễn Loan; GVPB1: Nguyễn Loan; GVPB2: Hoàng Dương Chọn A x  1 2x 1  1  Có log 2x 1  0     1  x  1. 1   2x 1  0 x  2  2
Vậy nghiệm phương trình đã cho là x  1 .
Câu 25. Cho hàm số y  f x có bảng biến thiên như sau:
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 13
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022 x - 2 - ∞ + ∞ - - f ' x ( ) - 1 + ∞ f x ( ) - ∞ - 1
Tiệm cận đứng của đồ thị đã cho là đường thẳng có phương trình: A. y  1. B. y  2  . C. x  2  . D. x  1 . Lời giải
GVSB: Kim Anh; GVPB1: Kim Anh; GVPB2: Nguyễn Ngọc Minh Châu Chọn C
Từ bảng biến thiên ta có lim f  x   và lim f  x   , suy ra đồ thị hàm số đã cho có x  2   x  2  
tiệm cận đứng là đường thẳng x  2  .
Câu 26. Trong không gian Oxyz , cho mặt cầu S   x  2   y  2   z  2 : 2 1
3  4 . Tâm của S  có tọa độ là A. 2;1; 3   . B. 4;2; 6   . C. 4;2;6 . D. 2; 1  ;3. Lời giải
GVSB: Kim Anh; GVPB1: Kim Anh; GVPB2: Nguyễn Ngọc Minh Châu Chọn D
Mặt cầu S   x  2   y  2   z  2 : 2 1 3  4 có tâm I 2; 1  ;3 .
Câu 27. Từ các chữ số 1, 2, 3, 4, 5 lập được bao nhiêu số tự nhiên có năm chữ số đôi một khác nhau? A. 3125 . B. 1. C. 120 . D. 5 . Lời giải
GVSB: Nguyễn Thị Kiên; GVPB1: Trần Đại Nghĩa; GVPB2: Nguyễn Ngọc Minh Châu Chọn C
Số các số tự nhiên có năm chữ số đôi một khác nhau được lập từ các chữ số 1, 2, 3, 4, 5 là hoán
vị của 5 phẩn tử nên có 5!  120 (số).
Câu 28. Cho hàm số y  f x có bảng biến thiên như sau:
Số giao điểm của đồ thị hàm số đã cho và đường thẳng y  1 là A. 2 . B. 1. C. 3 . D. 0 . Lời giải
GVSB: Nguyễn Thị Kiên; GVPB1: Trần Đại Nghĩa; GVPB2: Nguyễn Ngọc Minh Châu Chọn C Trang 14
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Ta vẽ đường thẳng y  1
Đường thẳng y  1 cắt đồ thị hàm số tại 3 giao điểm.
Câu 29. Cho hình lập phương ABC . D A B  C  D
  ( tham khảo hình vẽ bên dưới).
Giá trị sin của góc giữa đường thẳng AC và mặt phẳng (ABCD) bằng 3 2 3 6 A. . B. . C. . D. . 3 2 2 3 Lời giải
GVSB: Thành đặng; GVPB1: Hoang Ha Chọn A
Hình chiếu của đường thẳng AC ' lên mặt phẳng (ABCD) là đường thẳng AC suy ra góc giữa
đường thẳng AC và mặt phẳng (ABCD) , suy ra CA , ACBCD   C ,ACA    CAC .
Gọi cạnh hình lập phương bằng 1, suy ra AC  2 .
Xét tam giác vuông CAC vuông tại C ta có: AC  CC  AC   2 2 2 2 1  3 . CC Suy ra: CA ABCD     3 sin ,( ) sin CAC   . AC 3
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 15
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Câu 30. Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn 30;50 . Xác suất để chọn được
số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng 11 13 10 8 A. . B. . C. . D. . 21 21 21 21 Lời giải
GVSB: Thành Đặng; GVPB1: Hoang Ha Chọn A
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn 30;50, nên ta có số phần tử của
không gian mẫu: n  50  30 1  21.
Gọi A “Biến cố để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục”.
TH1: Chữ số hàng chục là 3, có 6 cách chọn số tự nhiên có chữ số hàng đơn vị lớn hơn chữ số
hàng chục { 34, 35, 36, 37, 38, 39}.
TH2: Chữ số hàng chục là 4, có 5 cách chọn số tự nhiên có chữ số hàng đơn vị lớn hơn chữ số
hàng chục { 45, 46, 47, 48, 49}.
Suy ra n  A  6  5 11.
Xác suất của biến cố A : P  A 11  . 21 1
Câu 31. Với a,b là các số thực dương tùy ý và a  1, log bằng 1 3 b a 1 A. log b . B. 3log b . C. log b . D. 3log b . a a 3 a a Lời giải
GVSB: Nguyễn Linh Trang; GVPB1: Nguyễn Thị Hường; GVPB2: Minh Văn Nguyễn Chọn D 1 Ta có: 3 log log b   3log b . 1 1 3 a a b  a Câu 32. Cho hàm số   2 1 e x f x  
. Khẳng định nào dưới đây đúng? A.    1 d   ex f x x x  C . B.    2 d   2e x f x x x  C . 2 1 C.    2 d   e x f x x x  C . D.    2 d   e x f x x x  C . 2 Lời giải
GVSB: Nguyễn Linh Trang; GVPB1: Nguyễn Thị Hường; GVPB2: Minh Văn Nguyễn Chọn D x 1
Ta có:   d   2 1 e  2 d   e x f x x x x  C . 2
Câu 33. Gọi z , z là hai nghiệm phức của phương trình 2
z  2z  5  0 . Khi đó 2 2 z  z bằng 1 2 1 2 A. 6 . B. 8i . C. 8i . D. 6  . Lời giải
GVSB: Vân Vũ; GVPB2: Bùi Văn Huấn Chọn D Trang 16
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022  b z  z    2  1 2 
Vì z , z là hai nghiệm của phương trình 2
z  2z  5  0 nên ta có: a . 1 2  c z .z   5 1 2  a
Ta có: z  z   z  z 2 2 2 2
 2.z .z  2  2.5  6 . 1 2 1 2 1 2
Câu 34. Cho hàm số y  f x có đạo hàm f  x  x 1 với mọi x   . Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A.  ;    1 . B.  ;   1 . C.  1  ; . D. 1; . Lời giải
GVSB:Vân Vũ; GVPB2: Bùi Văn Huấn Chọn A
Ta có : f  x  0  x 1 0  x  1  .
Vậy hàm số y  f x nghịch biến trên khoảng  ;    1 .
Câu 35. Trong không gian Oxyz , cho điểm A1;2;3 . Phương trình của mặt cầu tâm A và tiếp xúc với
mặt phẳng x  2 y  2z  3  0 là
A.  x  2   y  2   z  2 1 2 3  2 .
B.  x  2   y  2   z  2 1 2 3  2 .
C.  x  2   y  2   z  2 1 2 3  4 .
D.  x  2   y  2   z  2 1 2 3  4 . Lời giải
GVSB: Lê Minh; GVPB1:Dương Ju-i; GVPB2: Bùi Văn Huấn Chọn D 1 2.2  2.3  3
Mặt cầu tâm A tiếp xúc với mặt phẳng đã cho có bán kính R   2 1 4  4
Vậy phương trình mặt cầu cần tìm là:  x  2   y  2   z  2 1 2 3  4 . Câu 36. Cho hàm số 4 2
f (x)  ax  bx  c có đồ thị là đường cong trong hình bên dưới.
Có bao nhiêu giá trị nguyên thuộc đoạn  2
 ;5 của tham số m để phương trình f (x)  m có
đúng 2 nghiệm thực phân biệt? A. 7. B. 6. C. 5. D. 1. Lời giải
GVSB: Trần Ba; GVPB1: Dương Ju-i; GVPB2: Bùi Văn Huấn Chọn A
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 17
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022 m  2
Ta có yêu cầu bài toán tương đương với  . m  1
Do m 2;5 và m nguyên nên có 7 giá trị m cần tìm là 2  ,0,1,2,3,4,5.
Câu 37. Trong không gian Oxyz , cho điểm M 2; 2; 
1 và mặt phẳng P : 2x  3y  z 1  0 . Đường
thẳng đi qua M và vuông góc với mặt phẳng P có phương trình là x  2  2t x  2  2t x  2  2t x  2  2t     A. y  2  3t . B. y  2  3t . C. y  2   3t . D. y  3   2t . z 1t     z  1 t  z  1 t  z  1   t  Lời giải
GVSB: Trần Thông; GVPB1: Thanh Huyền; GVPB2: Bùi Thanh Sơn Chọn C  
Đường thẳng vuông góc với mặt phẳng P có véc tơ chỉ phương là u  n  2; 3;1 . (P)   x  2  2t 
Đường thẳng đi qua M và vuông góc với mặt phẳng P có phương trình là y  2   3t . z 1t 
Câu 38. Cho hình lập phương ABC . D A B  C  D
  có cạnh bằng 3 (tham khảo hình bên dưới).
Khoảng cách từ B đến mặt phẳng  ACC A   bằng 3 2 3 A. 3 . B. 3 2 . C. . D. . 2 2 Lời giải
GVSB: Trần Bảo Nghĩa; GVPB1: Thanh Huyền; GVPB2: Bùi Thanh Sơn Chọn C Trang 18
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Gọi O là tâm hình vuông ABCD .
Do ABCD là hình vuông nên BD  AC tại O . Do ABC . D AB C  D
  là hình lập phương nên AA   ABCD  AA  BD .  1 3 BO   ACC A
  tại O  d B; ACC A   2  BO  BD  . 2 2
Câu 39. Có bao nhiêu số nguyên dương a sao cho với mỗi a có đúng hai số nguyên b thỏa mãn 3b 3 .2b a 16  0 A. 34 . B. 32. C. 31. D. 33. Lời giải
GVSB: Đoàn Văn Định; GVPB1: Trịnh Đềm; GVPB2: … Chọn D TH1: 1 3b 32b a    16  0.
Nếu b  1 hoặc b  4 không thỏa mãn bpt và b 2;  3 thỏa mãn. Vậy a  1 thỏa mãn. TH2: a  b  b   b  b 1 2 3 3 2.2 16 0 3 3 2         16  0.
Nếu b  1 hoặc b  3 không thỏa mãn bpt và b  2 thỏa mãn.
Vậy a  2 không thỏa mãn. TH3: 3 3b 33.2b a    16  0 .
Nếu b  1 hoặc b  3 không thỏa mãn bpt và b  2 thỏa mãn.
Vậy a  3 không thỏa mãn. TH4: a  3.
Ta cần tìm a để bpt 3b 3 .2b a
16  0 có 2 nghiệm b .
 Nếu  3  3b 3 .2b b a
16  24.3.816  0 không thỏa mãn bpt.
 Nếu  2  3b 3 .2b b a
16  64.4 16  0 không thỏa mãn bpt.
 Nếu b  1 không thỏa mãn.  Nếu 1 3b b  
 3  0 . BPT tương đương .2b a 16  0 . 16 Hay a 
có hai nghiệm b suy ra 33  a  64 . 2b
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 19
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Kết hợp lại suy ra có tất cả 33 số nguyên dương a thỏa mãn. Cách 2: b  1 Xét 3b  3 .2b a 16  0. Do * a   nên  16 . b  log2  a 16 TH1: log 1  a  8 . 2 a 16
BPT có đúng 2 nghiệm nguyên b  3  log
 4  1  a  2  a  1 (thỏa mãn). 2 a 16 TH2: log  1  a  8 . 2 a 16
BPT có đúng 2 nghiệm nguyên b  2  log  14
  32  a  64  có 32 giá trị a . 2 a
Vậy có 33 giá trị của a thỏa mãn.
Câu 40. Cho hàm số f  x  a   4 2
3 x  2ax 1 với a là tham số thực. Nếu max f  x  f 2 thì 0; 3 min f  x bằng 0; 3 A. 9  . B. 4 . C. 1. D. 8  . Lời giải
GVSB: Đoàn Văn Định; GVPB1: Trịnh Đềm…; GVPB2: … Chọn D
Xét hàm f  x  a   4 2
x  ax   f  x  a   3 3 2 1 4 3 x  4ax .
Hàm số đạt GTLN tại x  2 và liên tục trên đoạn 0;  3 .
 f 2  0  32a  3 8a  0  a  4 . Với a  4  ta có f x 4 2
 x  8x 1 với x 0;  3 . f  x 3  4x 16x . x  0 TM  
Cho f  x  0  x  2 TM . x  2   L
Khi đó f 0  1, f 2  17 , f 3  8  .
Suy ra max f  x  f 2 17 (thỏa mãn giả thiết). 0; 3
Vậy min f  x  f 3  8. 0; 3
Câu 41. Biết F  x và G  x là hai nguyên hàm của hàm số f  x trên  và 2 f
 xdx F 2G0 a a  0 . Gọi S là diện tích hình phẳng giới hạn bởi các đường 0
y  F  x , y  G  x , x  0 và x  2 , Khi S  6 thì a bằng A. 4 . B. 6 . C. 3 . D. 8 . Lời giải Trang 20
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
GVSB: Công Phan Đình; GVPB1: …; GVPB2: … Chọn C
F  x và G  x là hai nguyên hàm của hàm số f  x trên  nên ta có x
   : F  x  Gx  C (với C là hằng số).
Do đó F 0  G 0  C (1). 2 Lại có f
 xdx F 2 F 0 0
 F 2  G0  a  F 2  F 0  F 0  G0  a (2).
Từ (1) và (2) suy ra C  a .
Khi đó F  x  G  x  a , x
    F x  G x  a , x    .
Diện tích hình phẳng giới hạn bởi các đường y  F  x , y  G x , x  0 và x  2 là 2 2 S  F
 xGx .dx  .adx  2a  6  a  3  . 0 0
Câu 42. Cho các số phức z , z , z thỏa mãn 2 z  2 z  z  2 và  z  z z  2z z . Gọi , A B,C lần 1 2  1 2 3 1 2 3 3 1 2
lượt là các điểm biểu diễn của z , z , z trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng 1 2 3 3 3 3 3 3 3 A. . B. . C. . D. . 4 8 8 4 Lời giải
GVSB: Hoàng Đức Hùng; GVPB1: Vũ Thơm; GVPB2: Nguyễn Thị Thùy Nương. Chọn A
- Từ giả thiết ta được z  z  1 và z  2 . 1 2 3
- Theo giả thiết  z  z z  2z z  z  z z  2 z z  z  z  1. 1 2  3 1 2 1 2 3 1 2 1 2 - Từ đẳng thức 2 2 z  z  z  z  2 2 2 z  z
 z  z  3  AB  3. 1 2 1 2 1 2  1 2
- Theo giả thiết  z  z z  2z z  z  z z  2 z  z z 1 2  3 1 2  1 2 3  1 3 2  z  z z  2 z  z z 1 2 3 1 3 2
 z  z  3  AC  3. 1 3
- Theo giả thiết  z  z z  2z z  z  z z  z  z z 1 2  3 1 2  3 2  1  1 3 2  z  z z  z  z z 3 2 1 1 3 2
 z  z  3  BC  3. 3 2 3 3
Suy ra tam giác ABC đều cạnh 3 . Suy ra S  . A  BC 4
Câu 43. Cho khối lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông cân tại A , cạnh bên
AA  2a , góc giữa hai mặt phẳng  A B
 C và  ABC bằng 60. Thể tích của khối lăng trụ đã cho bằng 8 8 A. 3 a . B. 3 8a . C. 3 a . D. 3 24a . 9 3 Lời giải
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 21
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
GVSB: Phan Thị Thúy Hà; GVPB1: Tuyet Trinh; GVPB2: Nguyễn Thị Hồng Gấm Chọn C A' C' B' A C I B
Gọi I là trung điểm của BC .
Ta có: + ABC là tam giác vuông cân tại A nên AI  BC + ABC.AB C
  là khối lăng trụ đứng nên AA  BC
suy ra BC   AAI   BC  A I .
Do đó, góc giữa hai mặt phẳng  ABC và  ABC  bằng góc giữa A I và AI , mà tam giác AAI vuông tại A nên ta có 
AIA là góc nhọn. Suy ra góc giữa hai mặt phẳng  ABC và  ABC  bằng  AIA  60 . AA 2a Trong tam giác vuông AA I  , ta có AI   . tan 60 3 4a BC 2a 6
ABC là tam giác vuông cân tại A nên BC  2AI  , AB  AC   . 3 2 3 2 3 1 1  2a 6  8a
Vậy thể tích khối lăng trụ đã cho là V  AA .S  AA . . AB AC  .2 a.   . A  BC 2 2  3  3  
Câu 44. Cho hình nón có góc ở đỉnh bằng 120 và chiều cao bằng 2 . Gọi S  là mặt cầu đi qua đỉnh và
chứa đường tròn đáy của hình nón đã cho. Diện tích của S  bằng 16 64 A. . B. . C. 64 . D. 48 . 3 3 Lời giải
GVSB: …; GVPB1: …; GVPB2: Lê Duy Chọn C
Gọi hình nón đỉnh A , đường kính đáy hình nón là BC .
Gọi I là tâm mặt cầu S  . Trang 22
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022 A B C O I Ta có AB  C cân tại A có 
BAC  120 và AI  BC tại O nên 
BAI  60 suy ra IAB đều.
Tam giác IAB đều và OB  IA tại O suy ra OB là đường trung tuyến của I  AB .
Mà OA  2 suy ra AI  2OA  4 .
Vậy diện tích mặt cầu S  là: 2 S  4 A  I  64 .
Câu 45: Xét tất cả các số thực x , y sao cho 2 3 9 y 6 log2 8 x a  a 
với mọi số thực dương a . Giá trị nhỏ nhất của biểu thức 2 2
P  x  y  6x  8y bằng A. 21. B. 6 . C. 25  . D. 39 . Lời giải GVSB: Tu Duy; GVPB: Thien Pro Chọn A Ta có: 2 3 9 y 6 log2 8 x a  a  , a   0  3 2
9  y   6x  3log a log a , a   0 2  2 2 2
 log a  2x log a  9  y  0 , a   0 2 2 2 2
   x  y  9  0 .
Gọi M  x; y thuộc hình tròn C tâm O , bán kính R  3 .
Gọi A3;4 , ta có: OA  5  R . Do đó A nằm ngoài hình tròn C .
Khi đó: P   x  2   y  2   MA   OA R2 2 3 4 25 25  25  21.
Vậy min P  21 khi O, M , A theo thứ tự thẳng hàng.
Câu 46. Cho hàm số bậc bốn y  f  x . Biết rằng hàm số g  x  ln f  x có bảng biến thiên như sau
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 23
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Diện tích hình phẳng giới hạn bởi các đường y  f  x và y  g x thuộc khoảng nào dưới đây? A. 7;8. B. 6;7 . C. 8;9 . D. 10;  11 . Lời giải
GVSB:; GVPB1: Hoàng Ngọc Hùng; GVPB2: Nam Bui Chọn A
Từ BBT của g  x ta có ln f  x  ln 4  f  x  4; x   R . f  x Ta có g x    . f  x  f x  0 (*)
Xét phương trình f  x  g x   f x1 (**)
Do f  x  4;x R suy ra phương trình (**) vô nghiệm. x  x1
Từ đó suy ra f  x  0  g  x  0     x  x . 2  x  x  3  1 
Mặt khác f  x  g x  f  x. 1    . f  x Ta có bảng xét dấu 3 x x2 x3 Vậy S  f 
 x gx dx   f 
  x gxdx   f  
  x gxdx  1 x 1 x x2
  f  x  g  x 2x
   f  x  g  x 3x      1 x 2 x
 2 f x  f x  f x  2ln f x  ln f x  ln f x 2   1  3  2  1  3 199 199  2 12  4  2ln
 ln12  ln 4  7,7047;8 . 16 16
Câu 47. Trong không gian Oxyz , cho điểm A2;1; 
1 . Gọi P là mặt phẳng chứa trục Oy sao cho
khoảng cách từ A đến P lớn nhất. Phương trình của P là A. x  z  0 . B. x  z  0 . C. 2x  z  0 . D. 2x  z  0 . Trang 24
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022 Lời giải
GVSB: …; GVPB1: …; GVPB2: Vũ Hồng Toàn Chọn C
Gọi H và K lần lượt là hình chiếu của A trên P và trục Oy . Ta có d  ,
A P  AH  AK . Do đó khoảng cách từ A đến P lớn nhất khi H  K 0;1;0 . 
Khi đó P đi qua K 0;1;0 và có một vectơ pháp tuyến là AK   2  ;0;  1  2;0;  1 nên có
phương trình là 2x  z  0 .
Câu 48. Có bao nhiêu số phức z thỏa 2
z  2 z  z và  z  z  i 2 4 4  z  4i . A. 4 . B. 2 . C.1 D. 3 . Lời giải
GVSB: Tran Phuc; GVPB1: Tran Phuc; GVPB2: Ngô Trí Thụ Chọn A
Gọi z  a  bi , a,b   . Ta có : 2 2 2
z  2 z  z  a  b  4 b (1). z  z  i 2 2 4
4  z  4i  z  4 . z  4i  z  4i
 a  2  b a  b  2  a  b  2 2 2 2 4 . 4 4
 a  b  2  a  2 b  a b 2 2 2 2 4 . 4 4   0. a  0 + TH-1: a  b  42 2  0   thỏa (1) . b   4 Vậy z  4i .
+ TH-2: a  2  b  a  b  2 2 2 4 4  0  a  b . Thay vào ta được (1) : 2
2b  4 b  0  b  0  b  2 . b   0
Với b  0  b  0    z  0 . a  0 b   2 b   2 
Với b  2  b  2    
 z  2  2i  z  2  2i . a  2 a  2
Kết luận: có 4 số phức z .
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 25
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022
Câu 49. Có bao nhiêu số nguyên dương của tham số m để hàm số 4 2
y  x  mx  64x có đúng 3 điểm cực trị ? A. 23. B. 12 . C. 24 . D. 11. Lời giải
GVSB: Lê Năng; GVPB1: …; GVPB2: Nguyễn Ninh Chọn C Xét hàm số g  x 4 2
 x  mx  64x ; gx 3
 4x  2mx  64 ; có lim f x   . x   g  x x 0  0  
 g  x  0 có ít nhất 2 nghiệm phân biệt. 3 x  mx  64  0
Do đó hàm số y  g  x có đúng 3 điểm cực trị  hàm số y  g  x có đúng 1 cực trị 
g x đổi dấu đúng 1 lần (*).
Nhận xét nếu x  0  g0  64  0  g  x không có cực trị (hay x  0 không thỏa mãn). Nên g x 2 32  0  m  2x  . Đặt h x 2 32  2x  . x x 32 4 3 x  8 Có hx  4x  
; h x  0  x  2  . 2 2 x x Bảng biến thiên
Từ bảng biến thiên suy ra   *  m  24 .
Kết hợp với điều kiện m nguyên dương suy ra m 1;2;3;...;  24 .
Câu 50. Trong không gian Oxyz , cho mặt cầu S  tâm I 1;4;2 , bán kính bằng 2. Gọi M , N là hai điểm
lần lượt thuộc hai trục Ox,Oy sao cho đường thẳng MN tiếp xúc với S  , đồng thời mặt cầu 7
ngoại tiếp tứ diện OIMN có bán kính bằng . Gọi A S , giá trị 2
là tiếp điểm của MN và   AM .AN bằng A. 9 2 . B. 14 . C. 6 2 . D. 8 . Lời giải
GVSB: Tuấn Anh; GVPB1: Anh Tuấn; GVPB2: Anh Tuấn Chọn C Trang 26
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 104 – NĂM HỌC 2021 - 2022 Gọi M  ; a 0;0Ox, N 0; ; b 0Oy .
Ta có d I;Oxy  2  R nên S  tiếp xúc với mặt phẳng Oxy tại điểm A1;4;0 và MN cũng đi qua A .   Lại có AM  a 1; 4
 ;0, AN  1;b  4;0 và 3 điểm ,
A M , N thẳng hàng nên ta được: a 1 4   a   1 b  4  4   1 . 1 b  4
Tứ diện OIMN có IA  OMN  và O
 MN vuông tại O nên nếu gọi J là tâm mặt cầu ngoại
tiếp tứ diện OIMN thì J IMN .
Suy ra bán kính mặt cầu ngoại tiếp tứ diện OIMN bằng bán kính đường tròn ngoại tiếp I  MN . IM .IN.MN 7 Ta có S  (với r   ). I  MN 4r
2 bán kính đường tròn ngoại tiếp IMN 1 IM .IN.MN  I . A MN 
 IM.IN  7IA  IM.IN 14 2 7 4. 2
 a  2   b  2 1 20 4  5  196 2     . m  a 1 Đặt  . n  b  4  4 n  3 mn  4    m
Từ (1|) và (2) ta có hệ  .    2 m  20 2 n  5 196   16 2    m  20  5  196 4  2      m  Từ (4) ta được:  2 m   2  m  2 20 16 5  196m m  2 2 n  2 4 2 2
 5m  80m  320  0  m  8     . m  2 2 n   2
a 1 2 2, b  4  2 Suy ra  . Vậy AM .AN  6 2 .
a 1 2 2, b  4  2
ĐỀ THI TN THPT - MÃ ĐỀ 104 Trang 27
Document Outline

  • DĐGVT-Mã 101.Thi TN THPT Bộ GD_ĐT 2022
  • Mã 102. Thi TN THPT Bộ GD_ĐT 2022
  • Mã 103. Thi TN THPT Bộ GD_ĐT 2022
  • Mã 104. Thi TN THPT Bộ GD_ĐT 2022

Tài liệu liên quan: