


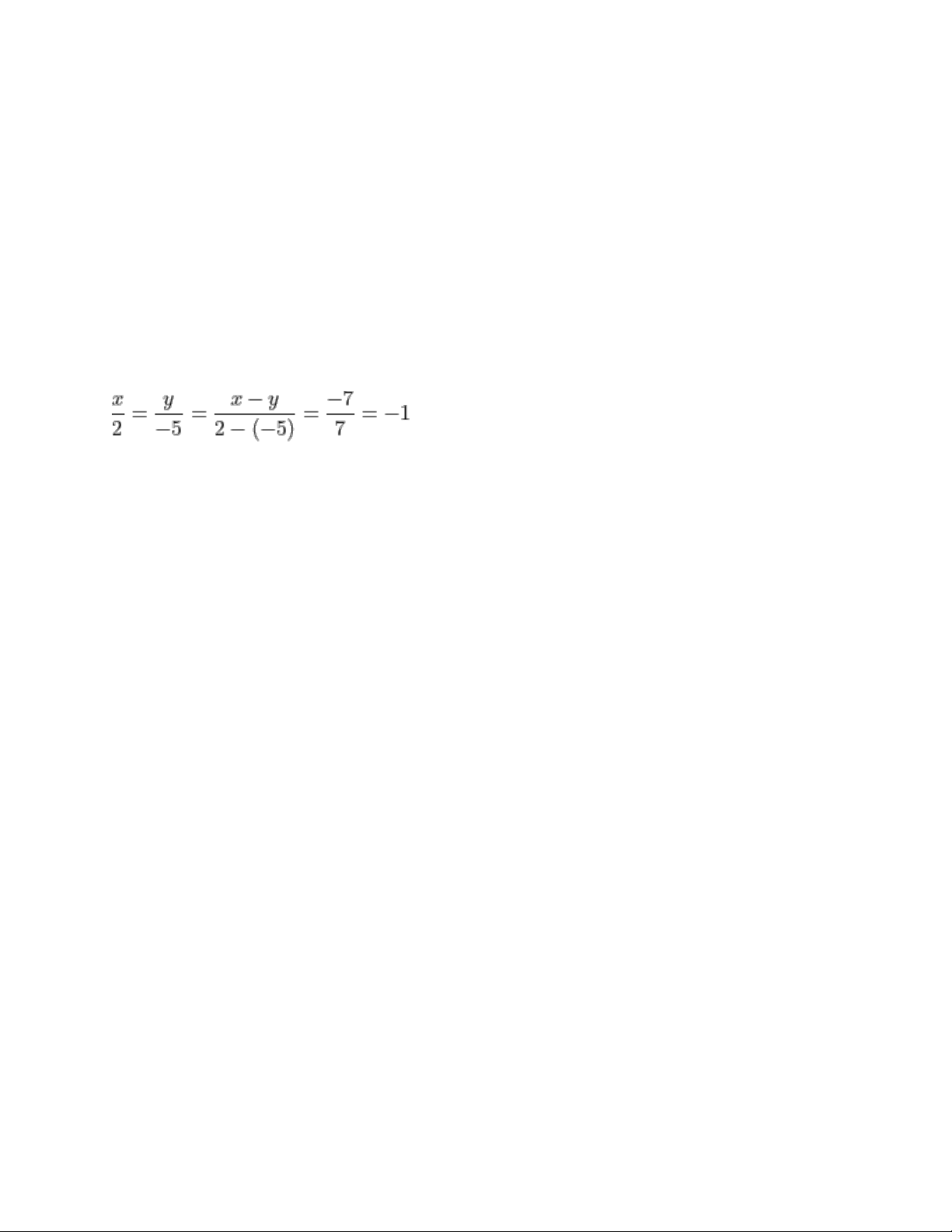


Preview text:
Dãy tỉ số bằng nhau là gì? Công thức về tính chất của dãy tỉ số bằng nhau
Chuyên đề tính chất của dãy tỉ số bằng nhau là một bài học quan trọng nằm trong chương trình toán
lớp 7. Học sinh cần nắm vững tỉ lệ thức tính chất dãy tỉ số bằng nhau cũng như lý thuyết và các bài
toán tính chất dãy tỉ số bằng nhau… Hãy cùng tìm hiểu thêm về chủ đề này thông qua bài viết dưới
đây của Luật Minh Khuê nhé!
Mục lục bài viết
1. Dãy tỉ số bằng nhau là gì?
Khi nói các số a, b, c tỉ lệ với các số 2, 3, 5 tức là ta có:
Đây được gọi là dãy tỉ số bằng nhau.
2. Tính chất của dãy tỉ số bằng nhau
2.1 Định nghĩa tỉ lệ thức là gì?
Định nghĩa về Tỉ lệ thức tính chất dãy tỉ số bằng nhau:
Tỉ lệ thức là đẳng thức của hai tỉ số: Dạng tổng quát : hoặc a : b = c : d
Các số hạng a và d gọi là ngoại tỉ; b và c gọi là trung tỉ.
2.2 Một số tính chất của tỉ lệ thức • Nếu
thì ad = bc. (Tính chất cơ bản)
• Nếu ad = bc và a, b, c, d 0 thì ; ; ;
2.3 Tính chất dãy tỉ số bằng nhau Xét tỉ lệ thức
. Gọi giá trị chung của các tỉ số đó là k, ta có: (1) Ta có:
Từ (1), (2), (3), suy ra:
Tính chất trên còn được mở rộng cho dãy tỉ số bằng nhau: Chẳng hạn:
Từ dãy tỉ số bằng nhau:
(với điều kiện các tỉ số đều có nghĩa) Mở rộng: Lưu ý:
Khi nói các số x, y, z tỉ lệ với các số a, b, c nghĩa là ta có: .
Cũng có thể viết: x : y : z = a : b : c
3. Các bài toán tính chất dãy tỉ số bằng nhau
3.1 Dạng 1: Tìm hai số x, y biết tổng (hoặc hiệu) và tỉ số Phương pháp giải:
- Để tìm hai số x, y khi biết tổng x + y = s và tỉ số x : y = a : b, ta làm như sau:
Ta có: x : y = a : b => x : a = y : b
Áp dụng dãy tỉ số bằng nhau ta có:
x : a = y : b = (x + y) : (a + b) = s : (a + b) Từ đó: x = y =
- Để tìm hai số x, y khi biết hiệu x - y = p và tỉ số x : y = a : b, ta làm như sau:
Ta có: x : y = a : b => x : a = y : b
Áp dụng dãy tỉ số bằng nhau ta có:
x : a = y : b = (x - y) : (a - b) = p : (a - b) Từ đó: x = y =
3.2 Dạng 2: Chia một số thành các phần tỉ lệ với các số
Giả sử chia số P thành 3 phần x, y, z tỉ lệ với các số a, b, c Ta làm như sau:
Ta có: x : a = y : b = z : c = ( x + y + z) : (a + b + c) = p : (a + b + c) Từ đó suy ra: x = ; y = ; z =
3.3 Dạng 3: Tìm hai số khi biết tổng và tỉ số của chúng Phương pháp giải:
Ta có: x : y = a : b => hay => x2 = aP : b
Từ đó ta tìm được ra x và y
3.4 Dạng 4: Chứng minh đẳng thức từ một tỉ lệ thức cho trước Phương pháp giải:
Áp dụng tính chất tỉ lệ thức và tính chất dãy tỉ số bằng nhau.
3.5 Dạng 5: Bài toán cụ thể về tỉ lệ thức Phương pháp giải:
• Bước 1: Xác định mối quan hệ giữa các yếu tố của đề bài.
• Bước 2: Lập tỉ lệ thức.
• Bước 3: Áp dụng tính chất của dãy tỉ số bằng nhau để giải bài toán.
4. Bài tập áp dụng tính chất dãy tỉ số bằng nhau
Câu 1: Tìm hai số x, y biết x : 2 = y : (-5) và x - y = -7 Hướng dẫn giải:
x : 2 = -1 => x = (-1).2 = -2
y : (-5) = -1 => y = (-1). (-5) = 5
Câu 2: Số viên bi của ba bạn Minh, Hùng, Dũng tỉ lệ với các số 2; 4; 5. Tính số viên bi của mỗi bạn biết
rằng ba bạn có 44 viên bi. Hướng dẫn giải:
Gọi x, y, z lần lượt là số viên bi của ba bạn Minh, Hùng, Dũng
Theo đề bài ta có:
x : 2 = y : 4 = z : 5 và x + y + z = 44
Theo tính chất của dãy tỉ số bằng nhau ta có:
x : 2 = y : 4 = z : 5 = (x + y + z) : ( 2 + 4 + 5) = 44/11 = 4
=> x = 2.4 = 8; y = 4.4 = 16; z = 5.4 = 20
Vậy số viên bi của Minh, Hùng, Dũng lần lượt là 8, 16, 20.
Câu 3: Số học sinh bốn khối 6; 7; 8; 9 tỉ lệ với các số 9; 8; 7; 6. Biết rằng số học sinh khối 9 ít hơn số học
sinh khối 7 là 70 học sinh. Tìm số học sinh mỗi khối. Hướng dân giải:
Gọi x, y, z, t lần lượt là số học sinh của các khối 6, 7, 8, 9
Theo đề bài ta có: x : 9 = y : 8 = z : 7 = t : 6 và y - t = 70;
Ta có: y : 8 = t : 6 = (y - t) : (8 - 6) = 70 : 2 = 35 => y = 35.8 = 280 => t = 6.35 = 210
x : 9 = y : 8 => x : 9 = 210 : 8 = 35 => x = 9.35 = 315
z : 7 = t : 6 = 210 : 6 => z = 35.7 = 245
Câu 4: Cho tỉ lệ thức a : b = c : d. Chứng minh rằng (a + b) : (a - b) = (c + d) : (c - d) Hướng dẫn giải:
Phương pháp: Chứng tỏ rằng a.d = b.c Ta có:
( a + b).(c - d) = ac - ad + bc - bd
(a - b).(c + d) = ac + ad - bc - bd
Vì a : b = c : d => ad = bc
=> ( a + b).(c - d) = (a - b).(c + d)
=> (a + b) : (a - b) = (c + d) : ( c - d )
Câu 5: Tìm diện tích của một hình chữ nhật biết rằng tỉ số giữa hai cạnh của nó bằng và chu vi bằng 28 m. Hướng dẫn giải:
Gọi x (m) là chiều rộng, y (m) là chiều dài (x, y > 0)
Tỉ số giữa hai cạnh là nên suy ra x : y = 2 : 5 hay x : 2 = y : 5
Chu vi của hình chữ nhật bằng 28m nên:
Theo tính chất của dãy tỉ số bằng nhau ta có:
x : 2 = y : 5 = (x + y) : ( 2 + 5) = (x + y): 7 = 14 : 7 = 2
=> x : 2 = 2 => x = 2.2 = 4 (m)
y : 5 = 2 => y = 2.5 = 10 (m)
Vậy diện tích hình chữ nhật là: S = 4.10 = 40 (m2)
Câu 6: Số học sinh bốn khối 6, 7, 8, 9 tỉ lệ với các số 9, 8, 7, 6. Biết rằng số học sinh khối 9 ít hơn số học
sinh khối 7 là 70 học sinh. Tính số học sinh mỗi khối? Hướng dẫn giải:
Gọi x, y, z, t lần lượt là số học sinh các khối 6, 7, 8, 9 tỉ lệ với các số 9, 8, 7, 6 nên ta có: x : 9 = y : 8 = z : 7 = t : 6
Số học sinh khối 9 ít hơn số học sinh khối 7 là 70 học sinh nên ta có: y - t = 70
Theo tính chất của dãy tỉ số bằng nhau ta có:
x : 9 = y : 8 = z : 7 = t : 6 = ( y - t ) : ( 8 - 6) = 70 : 2 = 35 Do đó: x = 9.35 = 315 y = 8.35 = 280 z = 7.35 = 245 t = 6.35 = 210
Câu 7: Có 3 đội A, B, C có tất cả là 130 người đi trồng cây. Biết rằng số cây mỗi người đội A, B, C trồng
được theo thứ tự là 2; 3; 4 cây. Biết số cây mỗi đội trồng được như nhau. Hỏi mỗi đội có bao nhêu
người đi trồng cây? Hướng dẫn giải:
Gọi số người đi trồng cây của đội A; B; C lần lượt là x; y; z (người), điều kiện: x, y, z N* Theo bài ra ta có:
x.2 = y.3 = 4.z (1) và x + y + z = 130
Bội chung nhỏ nhất (2;3;4) = 12
=> x = 60 ; y = 10; z = 30
Đội A; B; C có số người đi trồng cây theo thứ tự là 60; 40; 30.
Như vậy, bài viết trên đây của Luật Minh Khuê đã giúp bạn tổng hợp lý thuyết, bài tập cũng như các
bài toán tính chất dãy tỉ số bằng nhau. Hy vọng với những kiến thức trong bài viết sẽ hữu ích với bạn
trong quá tình tìm hiểu và nghiên cứu của bản thân về chủ đề tính chất của dãy tỉ số bằng nhau. Chúc bạn luôn học tốt!




