DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier môn Xử lý tín hiệu số| Đại học Bách khoa Hà Nội

14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu 2011 Chương 6
Giải thuật cho biến đổi Fourier (FFT) BK TP.HCM
©2011, TS. Đinh Đức Anh Vũ CuuDuongThanCong.com
https://fb.com/tailieudientucntt 14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 Nội dung Tính DFT & IDFT Tính ực ếp Biến đổi Chia-Trị Lọc tuyến tính
Cơ số2Cơ số4 Tách cơ số Goertzel Chirp-z
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 DFT & IDFT
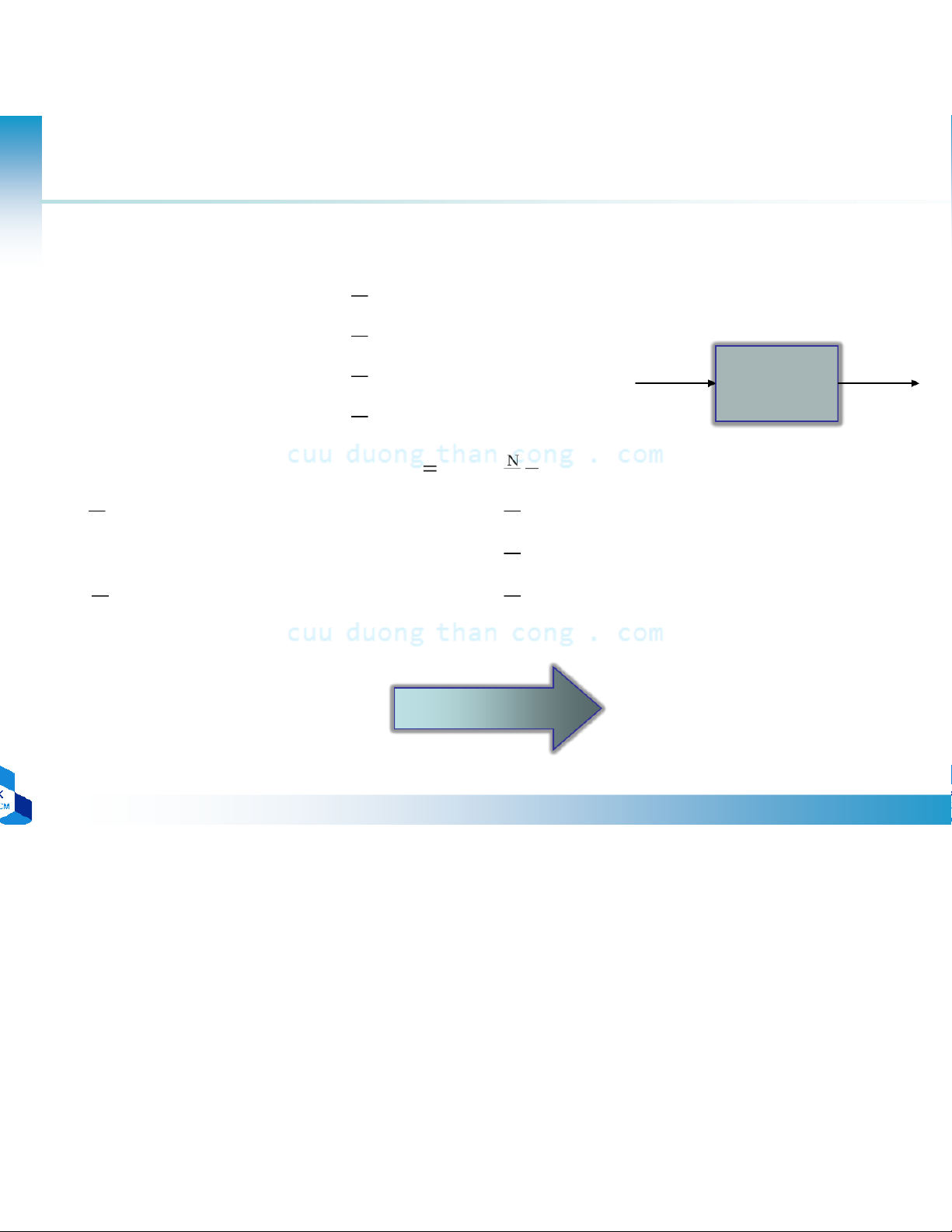
•Tính DFT: xác định chuỗi N giá trị phức {X(k)} khi biết trước chuỗi {x(n)} chiều dài N N 1 − DFT X (k) = ∑ x(n)W knN 0 ≤ k ≤ N −1 n=0 x(nN) − 1 1 IDFTX k W = ∑ ( )n kn − N N 0 ≤ ≤ −1 N k=0 – Giải thuật tín ính IDFT  N −1 •Tính tr 2π kn 2 k π n ực tiếp X (k) = x n x n R ∑[ ( )cos( )+ ( )sin( )] nN R N I – N  =0 2phép nhân phức  – N(N-1) phép c N −1 ộng phức X (k) = − x n π x n π I ∑ 2 [ ( )sin( kn) − 2 ( )cos( kn)] → Độ phức tạp : O(N nN R N I 2)  =0 • Biến đổi WN – 2N
Giải thuật tính DFT tối ưu mỗi phép toán 2phép tính lượng giác – 4N2phép nhân số thực theo những cách khác nhau
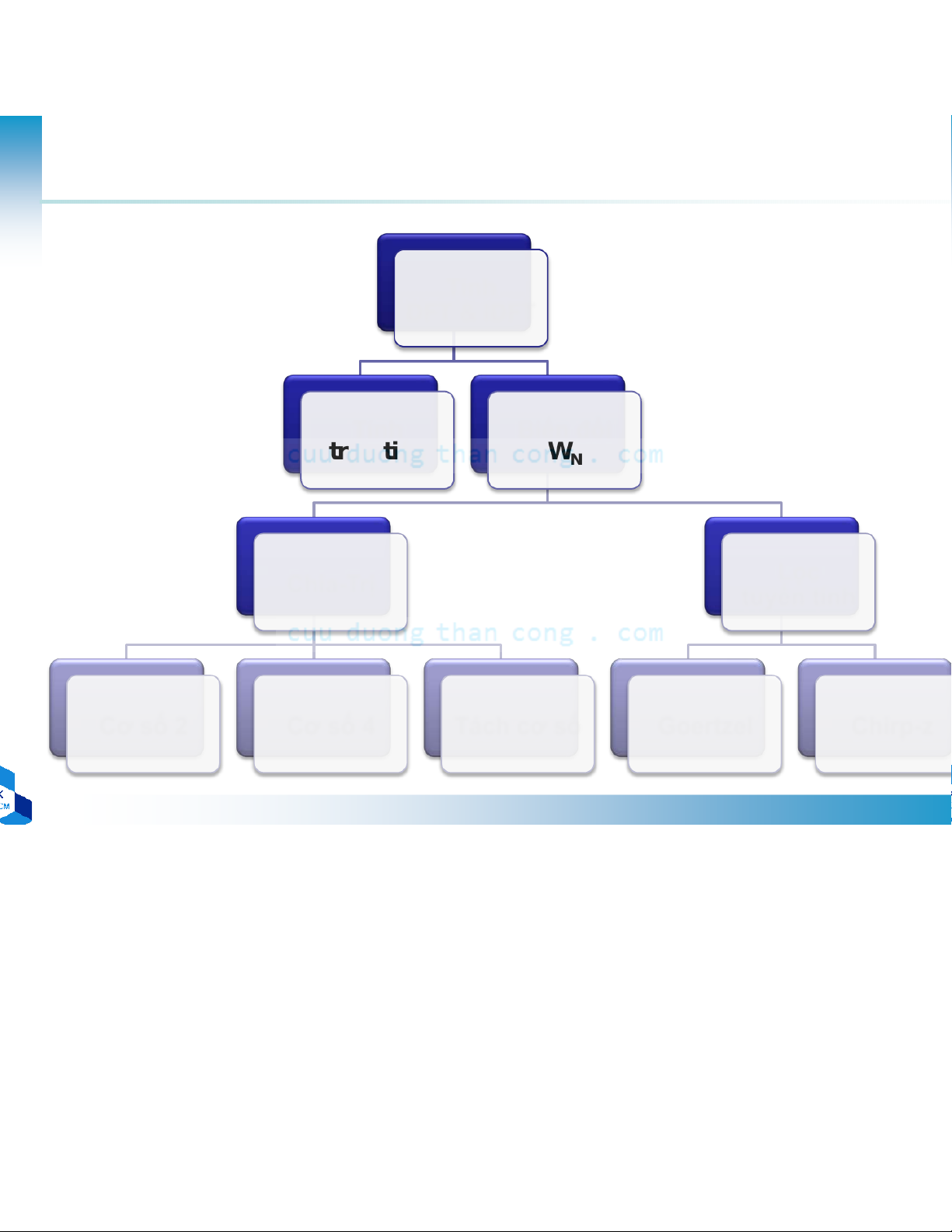
– 4N(N-1) phép cộng số thực k N + /2 k Doi xung W W = − – M N N
ột số phép toán chỉ số
và địa chỉ để nạp x(n) k N + k Tuan hoan = N W NW
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 Phương pháp chia-trị (1)
• Nguyên tắc: phân rã nhỏviệc tính DFT N điểm thành việc tính các DFT kích thước
nhỏhơn → các giải thuật FFT •Phương pháp – GiảsửN=L.M
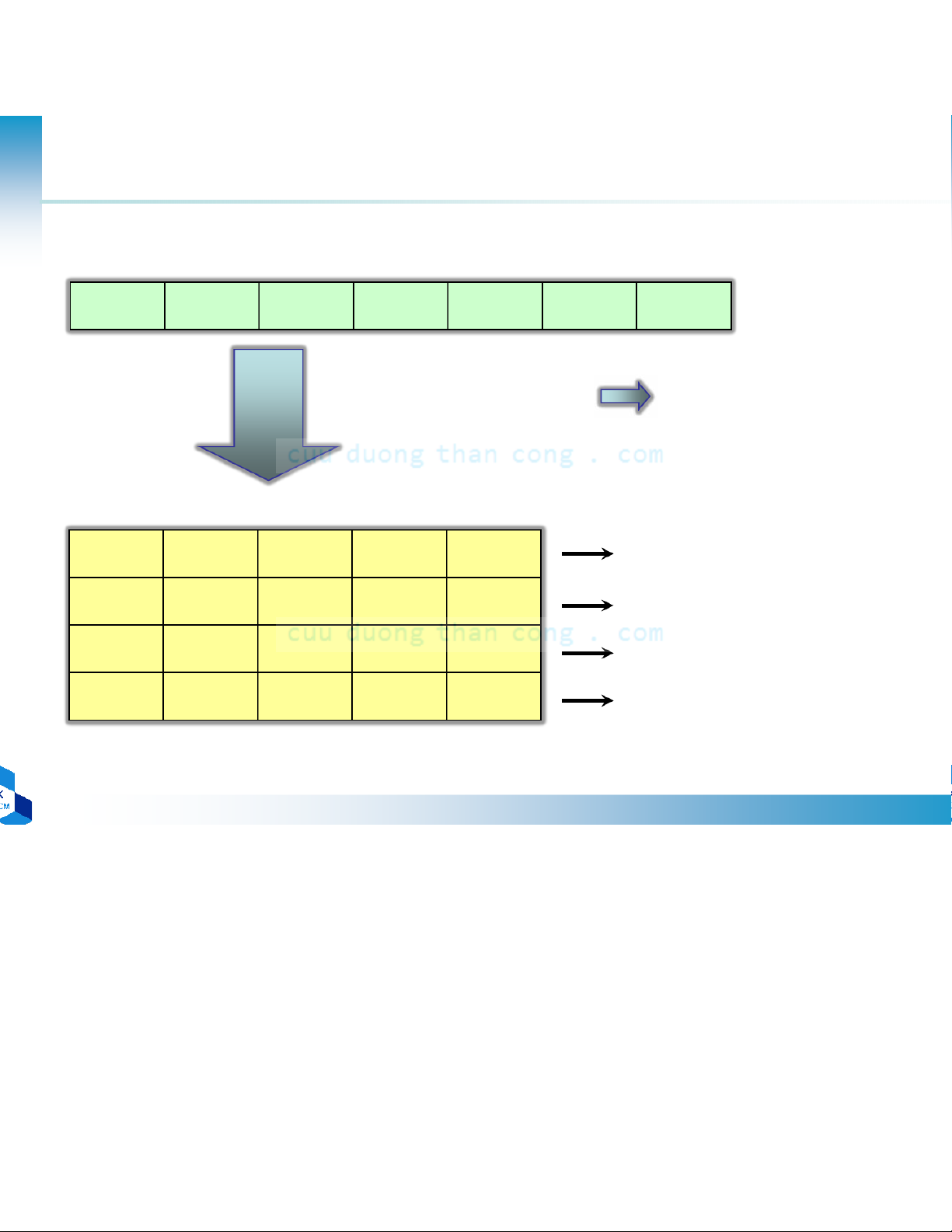
–Lưu trữx(n) vào mảng 2 chiều L ×M (l: chỉsốhàng, m: chỉsốcột) n → 0 1 2 … N-1 x(0) x(1) x(2) … x(N-1) m0 1 … M-1 0 x(0,0) x(0,1) … x(0,M-1) 1 x(1,0) x(1,1) … x(1,M-1) – Cách lưu trữ 2 x(2,0) x(2,1) … x(2,M-1)
•Theo dòng n= Ml+ m •Theo cột n= … … … … L-1 x(L-1,0) x(L-1,1) … x(L-1,M-1)
–Tương tự, các giá trịDFT X(k) tính được cũng sẽđược lưu trữtrong ma trận L×M
(p: chỉsốhàng, q: chỉsốcột)
•Theo dòng k= Mp+ q
•Theo cột k= p+ qL
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
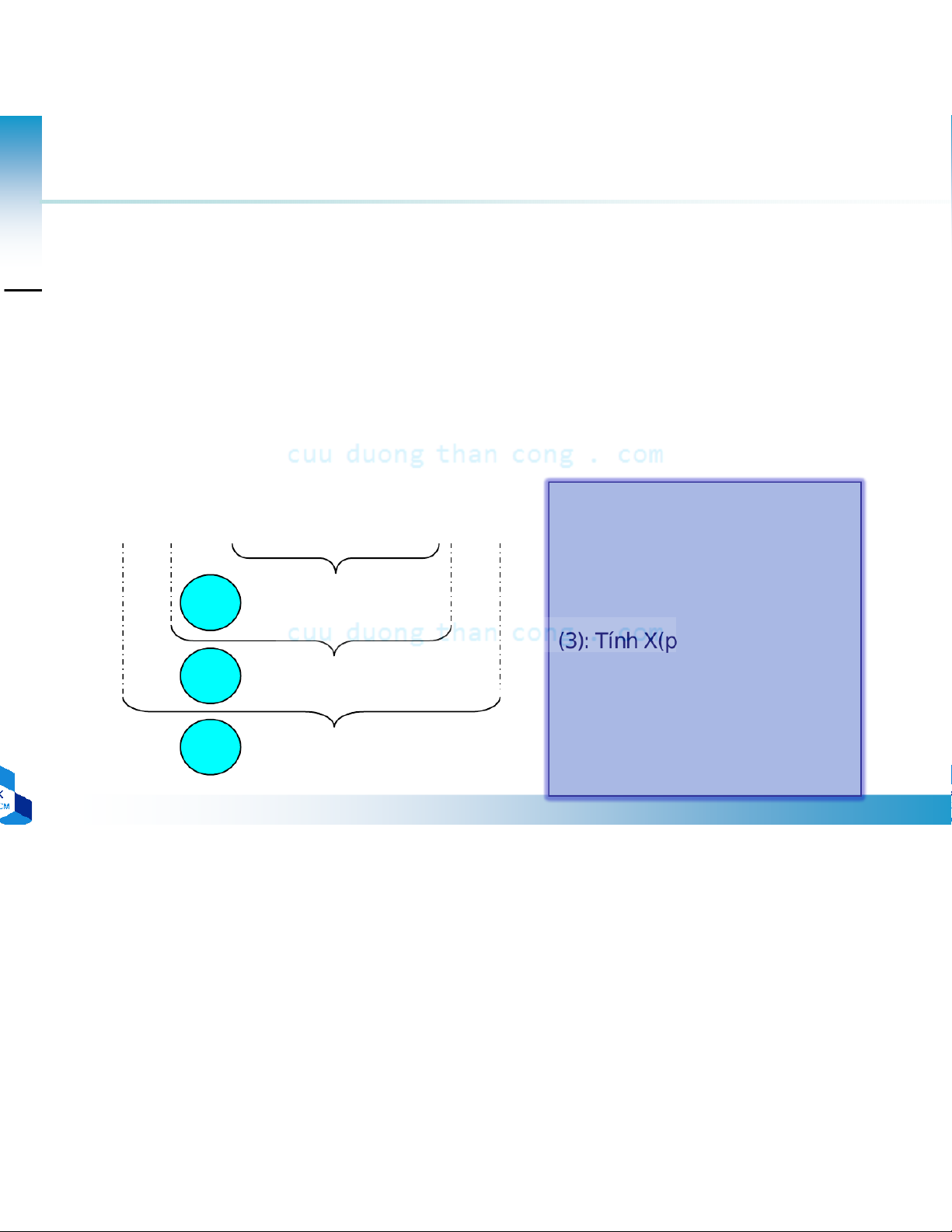
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 Phương pháp chia-trị (2) X ( − N 1 k) x(n)Wkn 0 k N 1 = ∑ N ≤ ≤ − V n=0 ới: M −1 − L 1 x(n) : theo cột X (p,q) = ∑∑ (Mp+q)(mL+l) x(l,m)WN X(k) : theo hàng m=0 l=0 Nmp W = 1 N ) M ( p+q) mL l MLmp mLq Mpl lq NW + mqL mq mq N N N N N W = N W /L = WM Mpl p N lM pl L−1 M −1 W = W = / W N L  lq  mq  lp X( p ∑, q∑ =)  N W  x( l, m) M W W  L (1): Tính L DFT M điểm l =0  m=0  Nhân phức :LM2 Cộng phức: LM(M-1) DFT M điểm (2): Tính G(l,q) 1 F(l,q) Nhân phức : LM ,q) 2 G(l,q) Nhân phức : ML2 Cộng phức: ML(L-1) Độ phức tạp DFT L điểm 3 Nhân phức : N(M+L+1) X(p,q) Cộng phức: N(M+L-2)
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
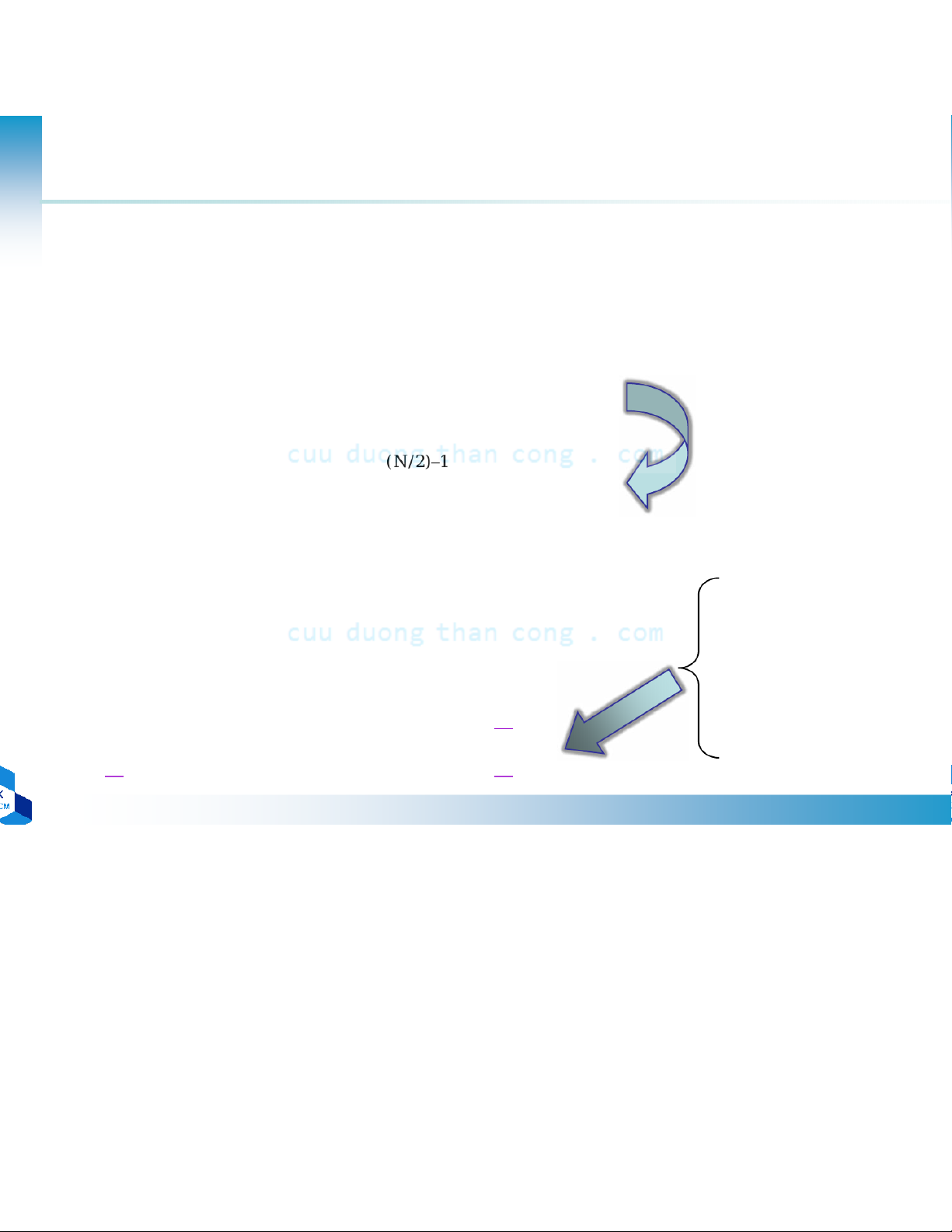
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 Phương pháp chia-trị (3) • Hiệu quả PP tính trực tiếp PP chia-trị •Nhân phức : N2 •Nhân phức : N(M+L+1) • Cộng phức : N(N-1) • Cộng phức : N(M+L-2) N=1000 →L=2, M=500
106nhân phức →503,000 (~ N/2) •PP chia-trị rất hiệu
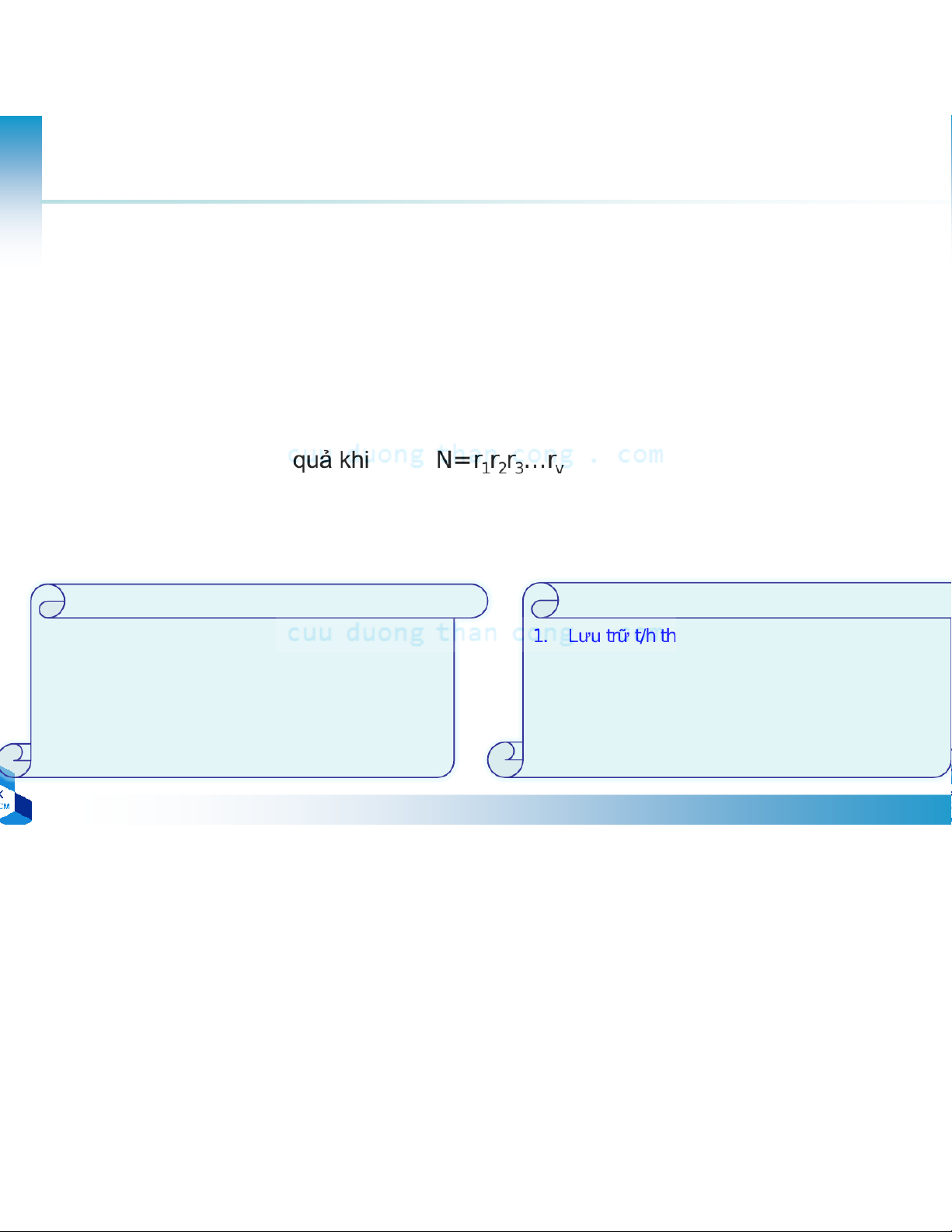
–Phân rã nhỏ hơn đến (v-1) lần • Giải thuật n = l + mL n = Ml + m k = Mp + q k = qL + p Giải thuật 1 Giải thuật 2 1. Lưu trữt/h theo cột eo hàng
2. Tính DFT M điểm của mỗi hàng
2. Tính DFT L điểm của mỗi cột
3. Nhân ma trận kết quảvới hệsốpha WNlq
3. Nhân ma trận kết quảvới hệsốpha WNpm
4. Tính DFT L điểm của mỗi cột
4. Tính DFT M điểm của mỗi hàng
5. Đọc ma trận kết quảtheo hàng
5. Đọc ma trận kết quảtheo cột
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 Phương pháp chia-trị (4)
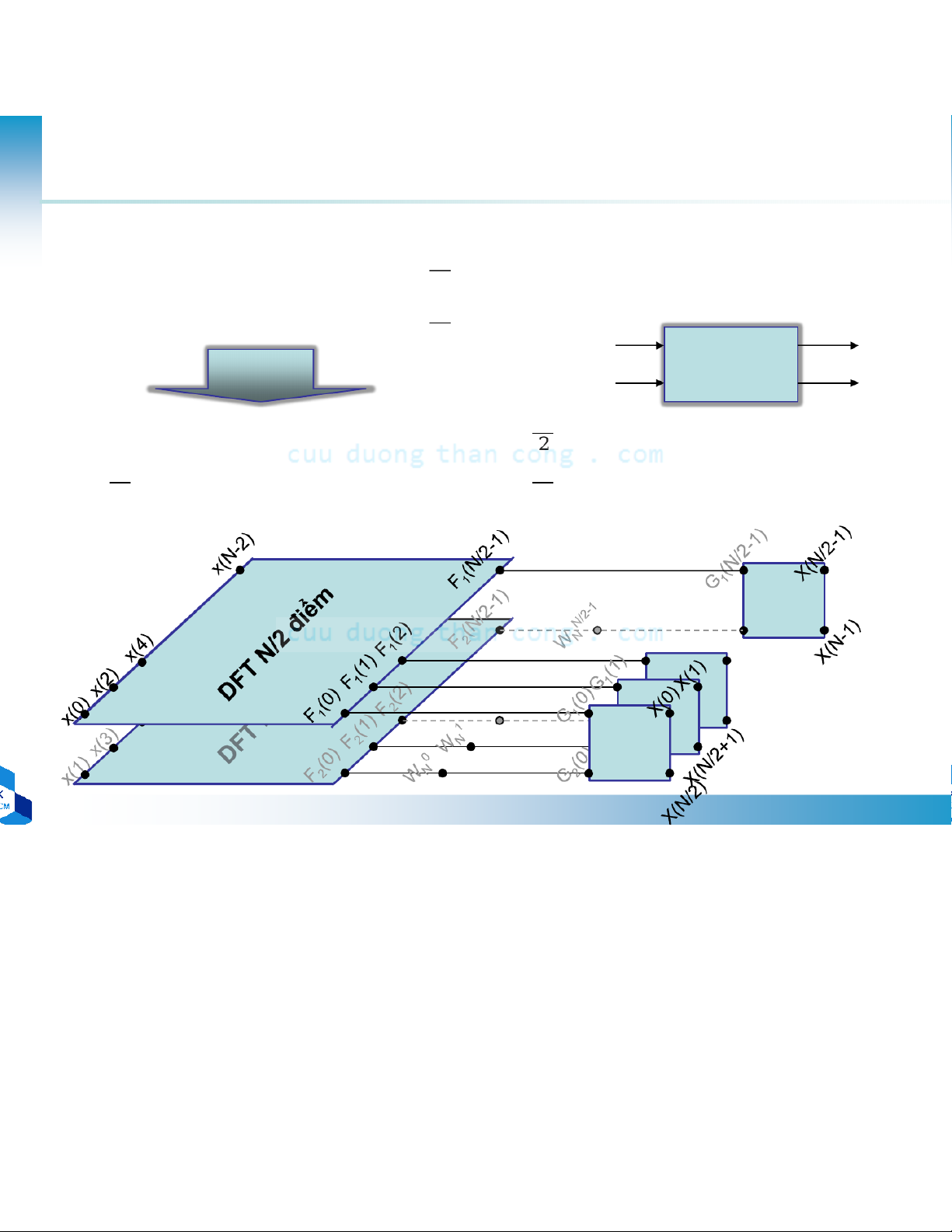
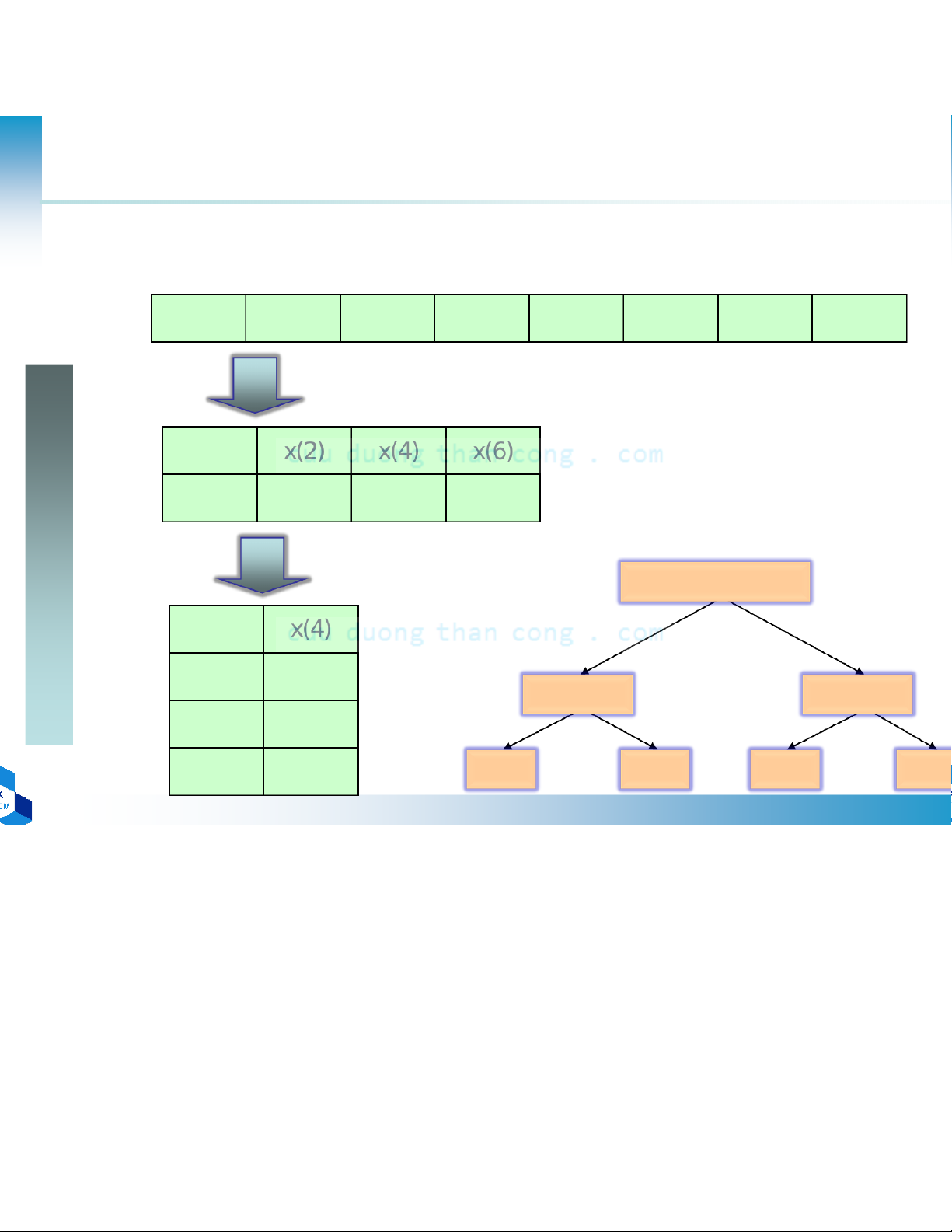
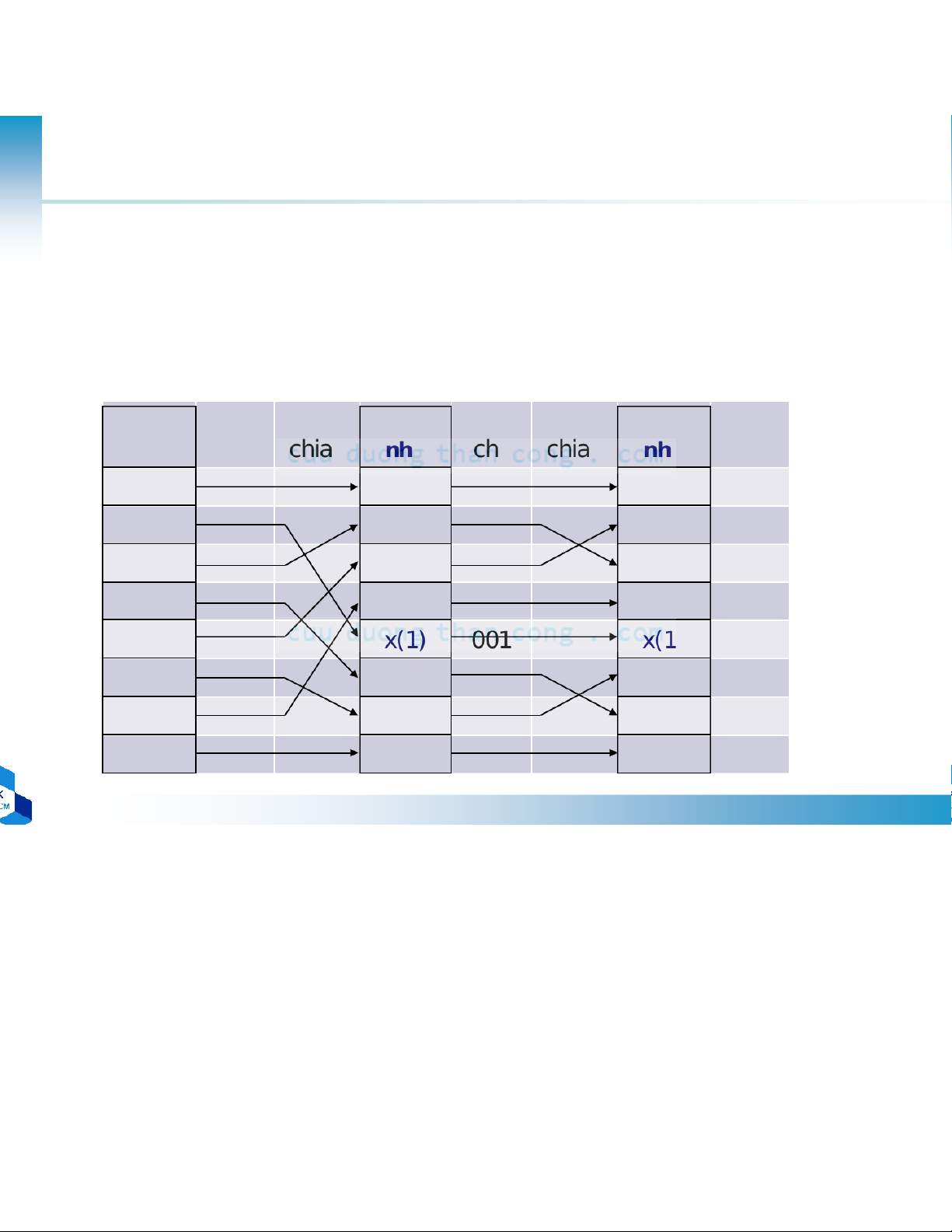
•Mô hình tính toán DFT 6 điểm thông qua việc tính DFT 3 điểm và DFT 2 điểm W6lq x(4) X(2) x(5) X(5) x(2) X(1) x(3) X(4) x(0) X(0) x(1) D 2 điểm
• Giải thuật tính FFT cơ số 2
– Nếu N = r1r2r3…rv= rv→ mô hình tính DFT có cấu trúc đều (chỉdùng 1 DFT r điểm) –r = 2 → FFT cơ số 2 –Chọn M = N/2 vàL = 2 … … x(N-1) Giải thuật m=0 m=1 m=M-1 f1(2n) chia theo thời gian l=0 x(0) x(2) … x(N-2) f2(2n+1) n= 0,1, …, N/2-1 l=1 x(1) x(3) … x(N-1)
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 FFT cơ số 2 (1) N−1 X (k) = ∑x(n) kn W k = N N ,1 , 0 . ., −1 n=0 = ∑ x(n) kn W + x n W N ∑ ( ) knN n even n old (N / 2)−1 (N / 2)−1 = ∑ 2 x(2m) mk W + N ∑ k (2m+ x(2m + ) 1 ) 1 WN m=0 m=0 N 2N W = W /2 (N / 2) 1 − X (k) = ∑ km + k km 01f (m) / W2N WN 02f (m)WN / 2 m= m= = F k +W kN F k k = N − 1 ( ) 2 ( ) ,1 , 0 . ., 1 ←   → = F1(k), F2(k) tuần hoàn 1 f (m )DFT 1F (k ) k ,1 , 0 . .,N / 2 N / 2 chu kỳ N/2 ←   → = 2f (m )DFT 2F (k ) k ,1 , 0 . .,N / 2 F1(k+ N/2) = F1(k) N / 2 F2(k+ N/2) = F2(k)  X (k ) = k N 1 F (k )+ N W 2F (k ) k = ,1 , 0 . , − 2 1 k +/N 2 k  W= − NW N   X (k +N k N F k W F k k 2 ) = 1 ( )− N 2 ( ) = ,1 , 0 . , − 2 1
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 FFT cơ số 2 (2)  N 1 G (k) = 1F(k) k = ,1 , 0 . , − 2 1   k  N 2 G (k) = N W 2 F (k) k = ,1 , 0 . , − 2 1 G1(k) G2(k) DFT2X(k) X(k+ N/2)  X (k ) = N k=0,1,…,(N/2-1 1 G (k ) + 2 G (k ) k = ,1 , 0 . ., −1   X (k + N N G k G k k 2 ) = 1 ( ) − 2 ( ) = ,1 , 0 . ., − 2 1 DFT 2 điểm DFT DFT m DFT m 2 điểm
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 FFT cơ số 2 (3)
• Tiếp tục phân f1(n) và f2(n) thành các chuỗi N/4 điểm  N 1 v 1( ) n = 1f(2 ) n n = ,1 , 0 . ., −1  4  N 1 v 2( ) n = 1f(2n + ) 1 n = ,1 , 0 . ., − 4 1   N DFT 2 v 1( ) n = f2(2 ) n n = ,1 , 0 . ., −1 4 vij(n) Vij(k)  N/4 điểm  N 2 v 2( ) n = f2(2n + ) 1 n = ,1 , 0 . ., − 4 1  k F k V k W V k k 1 ( ) = 11 ( ) + N / 2 12 ( ) ,1 , 0 . ., 1  4  N k N F k V k W V k k 1 ( + ) = 4 11 ( ) − N / 2 12 ( ) = ,1 , 0 . ., −1  4  k N F k V k W V k k 2 ( ) = 21 ( ) + N / 2 22 ( ) = ,1 , 0 . ., −1 4  N k  N F k V k W V k k 2 ( + ) = 4 21 ( ) − N / 2 22 ( ) = ,1 , 0 . ., −1 4 • Hiệu quả
DFT trực tiếp N=2vđiểm FFT cơ số 2 Các DFT 2 điểm Nhân C ph ộng ứ phức: N2– N Nhân phức: (N/2)log2N Cộng phức: Nlog2N
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 FFT cơ số 2 (4)
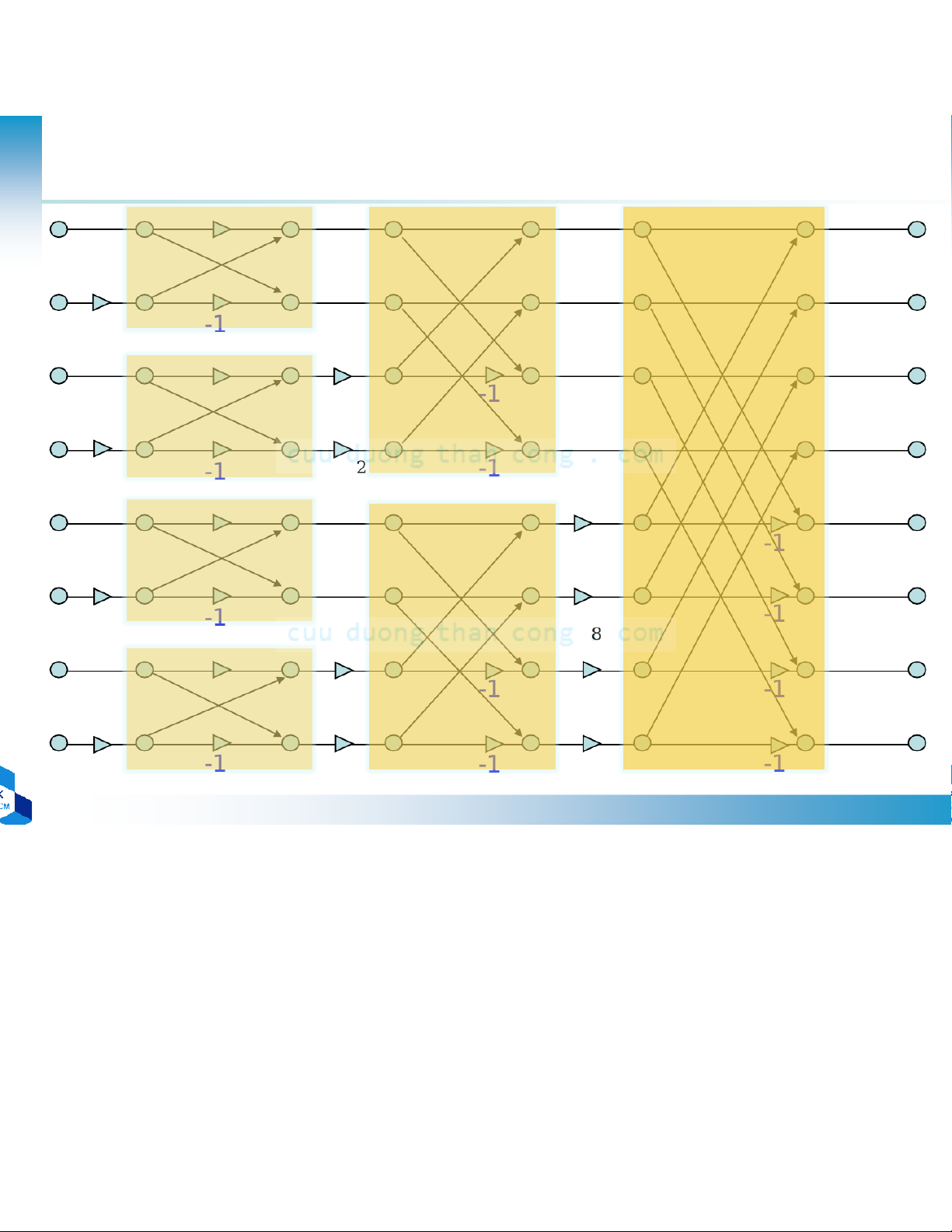
•Ví dụ: tính DFT 8 điểm
x(0) x(1) x(2) x(3) x(4) x(5) x(6) x(7) Phân theo th x(0) ời gian x(1) x(3) x(5) x(7) [0,1,2,3,4,5,6,7] x(0) x(2) x(6) [0,2,4,6] [1,3,5,7] x(1) x(5) x(3) x(7) [0,4] [2,6] [1,5] [3,7]
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 FFT cơ số 2 (5)
• Khối tính toán cơ bản cho DFT 2 điểm (hình con bướm) a A = a+WN’b Độ phức tạp •1 nhân phức b B = a–WN’b •2 cộng phức W N’ –1
N= 2 :v+ Log2N : tầng tính toán + N/2
: khối tính toán cơ bản cho mỗi lớp Bộ nhớ: + Vào : + Ra : (A,B) – số phức
+ Có thể lưu (A,B) đè lên (a,b)
Chỉ cần N ô nhớ phức (2N ô nhớ thực) Tính toán tại chỗ
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 FFT cơ số 2 (6) x(0) X(0 x(4) X(1 0 W8 x(2) X(2 0 W8 x(6) X(3 0 W8 W8 x(1) X(4 0 W8 x(5) X(5 0 W 1 8 W x(3) X(6 0 W 2 W 8 8 x(7) X(7 0 W 2 W 3 8 8 W8
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
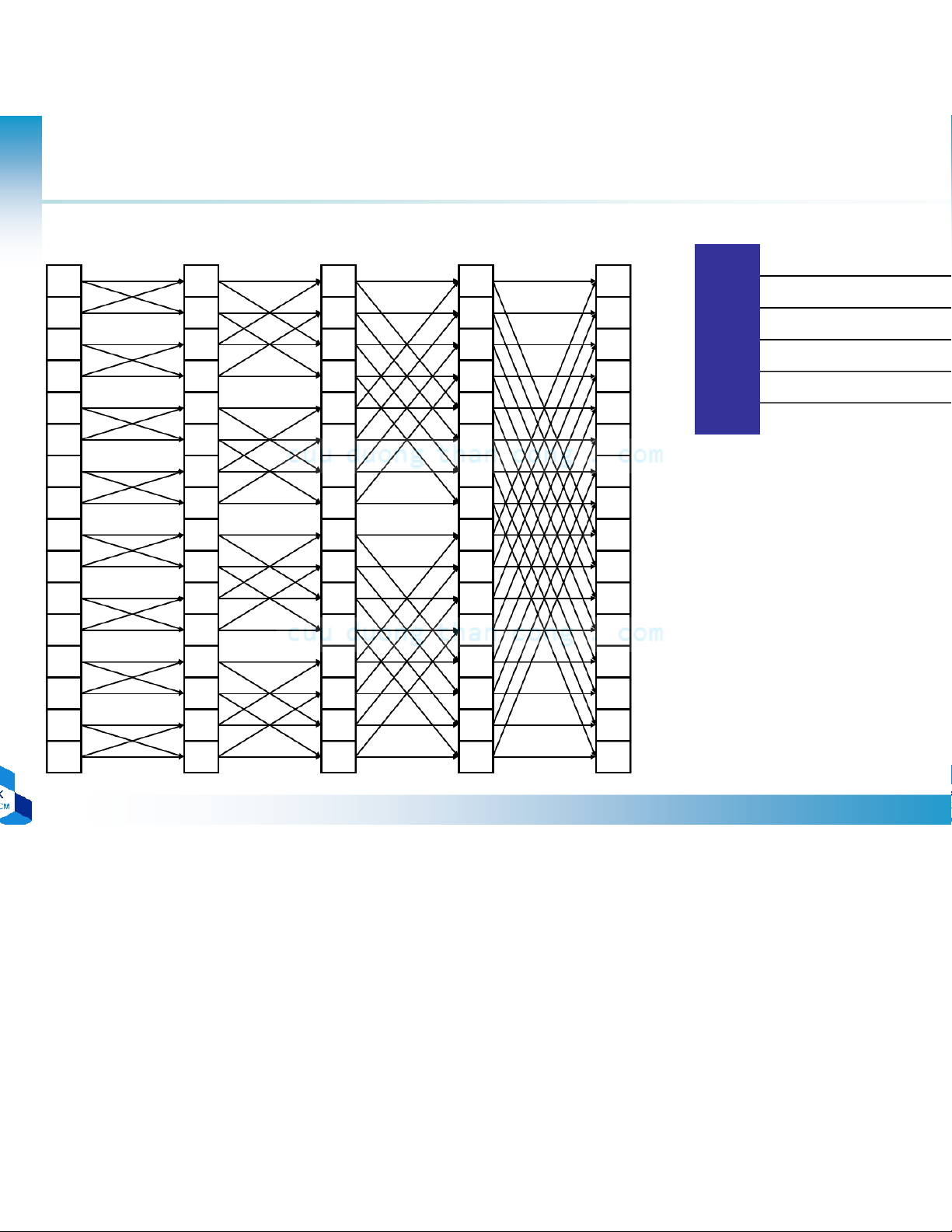
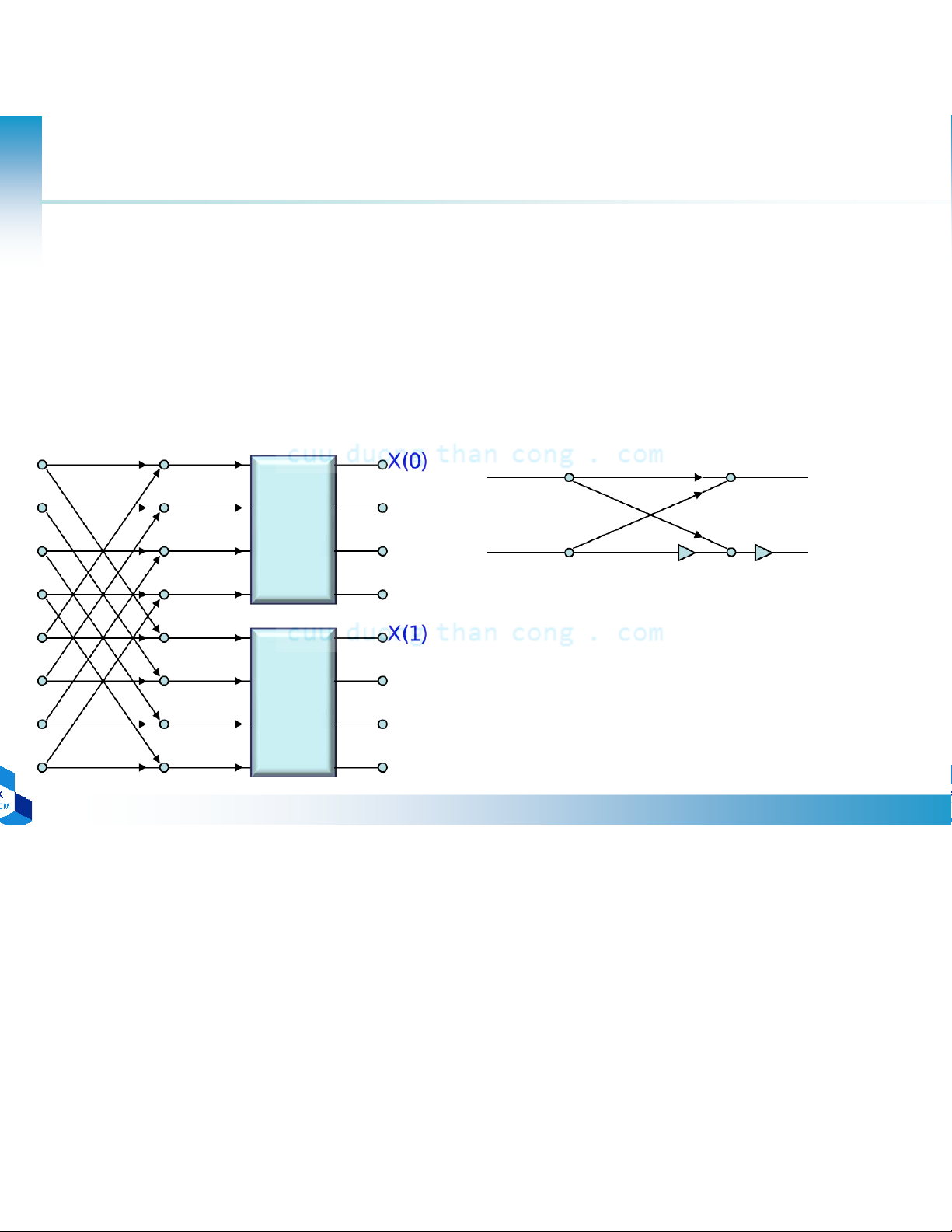
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 Baseline Parallel Architecture Size 16 8192 ∆ 1 1 1 1 Pins 448 229K 2 2 2 2 Fly 32 53K 3 3 3 3 Mult 4 4 4 4 Add 5 5 5 5 Shift 0 0 6 6 6 6 7 7 7 7 8 8 8 8 Parallel FFT 9 9 9 9 Butterfly structure 10 10 10 10 Removes redundant 11 11 11 11 calculation 12 13 13 13 13 14 14 14 14 15 15 15 15 16 16 16 16
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011
Parallel-Pipelined Architecture Size 16 8192 ∆ Pins 448 229K Fly 32 53K Mult 96 159K Add 288 480K Shift 0 0 A pipelined version IO Bound 100% Ef icient
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 FFT cơ số 2 (7)
• Thứ tự chuỗi dữ liệu vào sau khi phân (v-1) lần
– Biểu diễn các chỉ số ở dạng nhị phân
– Chuỗi sau khi phân chia sẽ là lấy theo thứ tự đảo các bit Địa
BnộhớBộ chỉPhân Địa ớBộ ỉPhân Địa ớ chỉ x(0) x(0 000 ) 000 x(0) 000 x(1) x(2 001 ) 010 x(4) 100 x(2) x(4 010 ) 100 x(2) 010 x(3) x(6 01 ) 1 110 x(6) 110 x(4) 100 ) 001 x(5) x(3 101 ) 011 x(5) 101 x(6) x(5 1 ) 10 101 x(3) 011 x(7) x(7 1 ) 11 111 x(7) 111
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 FFT cơ số 2 (8) •Phân chia theo tần số
–Phương pháp chia và trị – M = 2, L = N/2
– Chuỗi dữ liệu nhập được sắp xếp theo cột
–Phân chia X(k) thành X(2k) và X(2k+1)
–Sau đó có thể phân chia tiếp tục mỗi X(k chẵn) và X(k lẻ) (0) a A = (a+b) WN (1) X(2) DFT 4 điểm (2) X(4) b B = (a–b)WN’ –1 W N’ (3) X(6) (4) 0 -1 W8 (5) X(3) 1 -1 W DFT 8 4 điểm (6) X(5) 2 -1 8 W (7) X(7) 3 -1 W8
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 FFT cơ số 4 (1) x(0) x(2) x(4) … … … x(N-1) N = 4v L = 4, M = N/4 l,p = 0,1,2,3 n = 4m + l m,q = 0,1,…,N/4 – 1 k = (N/4)p + q m=0 m=1 m=(N/4)-1 l=0 x(0) x(4) … … x(N-4) x(4n) l=1 x(1) x(5) … … x(N-3) x(4n+1) n = 0,1,…,N/4-1 l=2 x(2) x(6) … … x(N-2) x(4n+2) l=3 x(3) x(7) … … x(N-1) x(4n+3)
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 FFT cơ số 4 (2) L−1 M −  1 lq  mq  lp W ( x, l) m= W ∑ NW ∑  ( , ) M  L l=0  m  =0  3 X (p,q) = ∑[W l ]q N F l q W lp p 04 ( , ) = ,1 , 0 3 , 2 l = N / 4 l = ,1 , 0 3 , 2 DFT N/4 điểm F(l,q) = ∑ mq 0 ( x l, ) m W  m=  4 x(l,m) = x(4m +l)   X ( , p q) = X ( N p + q 4 )  X ( , 0 q)  1 1 1 1  0 W F ( , 0 q)       q   X , 1
( q)   1 − j −1 j  WN F ,1 ( q)  =  X ( ,
2 q)  1 − 1 1 − 1 2q  WN F ( ,2q)        X , 3 ( q)  1 j −1 − j  3 W q N F , 3 ( q) 
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ 14:26, 10/01/2026
DCE 2011 Chương 6 Giải Thuật Biến Đổi Fourier (FFT) - Đinh Đức Anh Vũ - Studocu c e 2011 FFT cơ số 4 (3) 0 WN -j q W -1 N j 1 q WN2 -1 j -1 -j 0 q N W 3 q 2q Dạng rút gọn 3q
DSP – Giải thuật cho Biến đổi CuuDuongThanCong.com Fourier
https://fb.com/tailieudientucntt
© 2 0 1 1, Đinh Đức An h Vũ