DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số môn Xử lý tín hiệu số| Đại học Bách khoa Hà Nội

14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu 2011 Chương 8
Thiết kếBộlọc Số BK TP.HCM
©2011, TS. Đinh Đức Anh Vũ CuuDuongThanCong.com
https://fb.com/tailieudientucntt 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu c e 2011 Nội dung • Bộ lọc lý tưởng • Bộ lọc thực tế
– Bộ lọc với đáp ứng xung hữu hạn (FIR)
• Bộ lọc tuyến tính pha –Phương pháp cửa sổ
–Phương pháp mẫu tần số
• Bộ lọc tuyến tính pha tối ưu • Bộ biến đổi Hilbert
•So sánh các phương pháp thiết kế
– Bộ lọc với đáp ứng xung vô hạn (IIR)
•Phương pháp xấp xỉ đạo hàm
•Phương pháp bất biến xung
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu c e 2011 Giới thiệu
•Phương pháp thiết kế bộ lọc tần số
–Đặc tính bộ lọc được mô tả bởi đáp ứng biên độ và pha
–Tùy theo đáp ứng mong muốn, bộ lọc nhân quả FIR hoặc IIR sẽ được chọn • FIR
–Được dùng khi có yêu cầu đáp ứng pha tuyến tính trong passband
– Nhiều thông số hơn IIR → Độ phức tạp tính toán cao • I R
–Có các thuỳ biên ở dải stopband thấp hơn bộ lọc FIR có cùng số tham
số → được dùng nhiều hơn so với FIR (khi độméo pha trong passb
–Độ phức tạp tính toán không cao và tiêu tốn ít bộnhớ
–Xác định các hệ số bộ lọc
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu c e 2011 Tính nhân quả
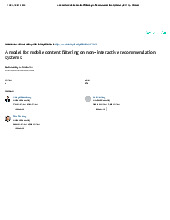
•Xét bộ lọc lý tưởng 1 ω ≤ ω  c ω π n = 0 ω ( )  =  c H0 sin(h( n )n) =  0 cω n ωcn  ω <ω ≤ π c  ≠ π ωc H(ω) 1 ω π c= /4 ω -ωc ωc Bộ lọc không nhân quả
→ không hiện thực được
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu c e 2011
Đ/k để bộ lọc nhân quả •Định lý Paley-Wiener π
h(n) có năng lượng hữu hạn ln H ( ω ) ω d < ∞ ∫ h(n) = 0 ∀n<0 −π π ∫ ln H ω ( ) ω d < ∞ Voi ( Θ=), ωω ( H ) H −π π ( h )n : nhân qua ∫ H ω 2 ( ) ω d < ∞ −π
– H(ω) chỉ được phép = 0 tại một tập hữu hạn các tần số
– |H(ω)| không được là hằng số cho một khoảng tần
• Việc chuyển từ passband sang stopband không được thẳng góc
– HR(ω) và HI(ω) phụ thuộc nhau →Phổ biên độ và phổ pha không thể chọn độc lập được
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu c e 2011
Đ/k để bộ lọc nhân quả he(n) 1 = [h n + h −n 2 (]) ( ) n h ( )n ( ) ( ) ho(n) 1 = [h n − h −n 2 (]) ( ) h(n) nhân quả h( ) n = 2h δ e (n)u(n) − he ( ) 0 (n) n ≥ 0 n o ( ) ≥ e ( ) 1 ( h ) n = 2h ( ) n u(n) + h( ) 0 δ (n) n ≥1
h(n) được mô tả bởi he(n) h n h ( )n ( ) ( ) h(n) thực F F
H(ω) được mô tả bởi HR(ω) H + (ωH )
H(ω) được mô tả bởi H R (ω jH) I (ω) I(ω) và h(0) π BĐ Hilbert rời rạc H ω( ) = 21 2 I H λ( )cot( ) λ R d π ∫ ω − − λ −π
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu c e 2011
Đ/k để bộ lọc nhân quả
•Ví dụ: xác định đáp ứng tần số của h/t ổn định với đáp ứng xung là hàm
thực và chẵn, nếu biết 1 1 2 cos−a cos ω ω R ( ) a H =a a < 1 2 − ω + e = −21 cos [ ω ω j ] ω e + j 1) a− − 2z + )(za z/−z 2 a() 1 (2 + a 1 z (z ) ) =− = − ( + z 1) + a2 − − ROC : a < z <1/ a a = + δ n u n = ( ) e ( ) 2 1 21n ( ) H =11 − ω ( ) ω j − ae
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu c e 2011
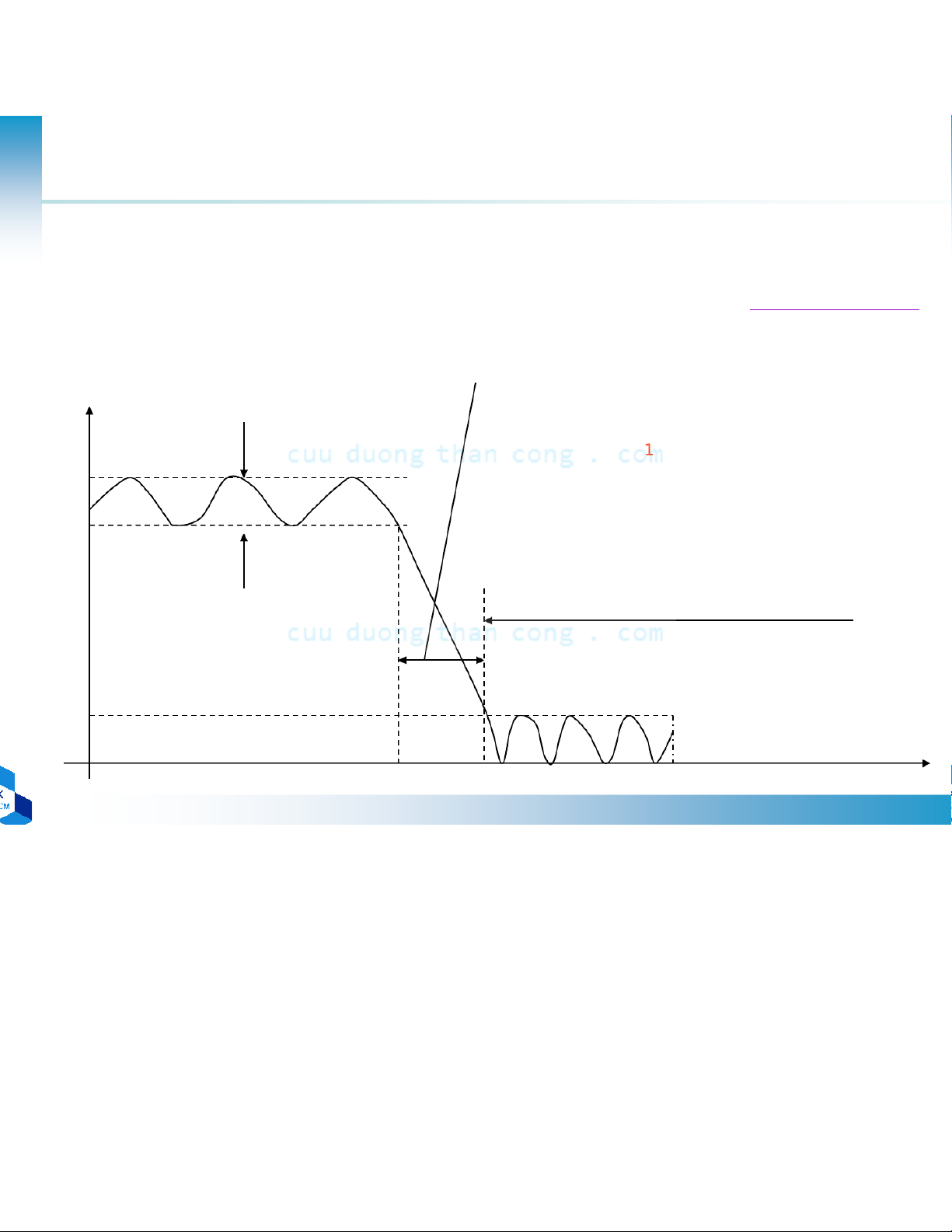
Bộ lọc tần số trong thực tế • LTI M −j k ω = − ∑b e M N − + − k b x n k =0 = ∑ kkk = ∑ kk H(ω) = N − 1+ j k a e ω • ∑ Đặc trưng k Transition Band |H( k=1 ω)| δ : Passband ripple 1+δ1 δ2: Stopband ripple 1- ωp: Passband edge ripple δ1 ωs: Stopand edge ripple Passband ripple StopBand δ2 ω 0ωpωsπ
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu c e 2011
Bộ lọc FIR – Tính đối xứng & phản đối xứng ộ lọc FIR
• Bộ lọc FIR tuyến tính pha − = 1 )M ( 0 − )
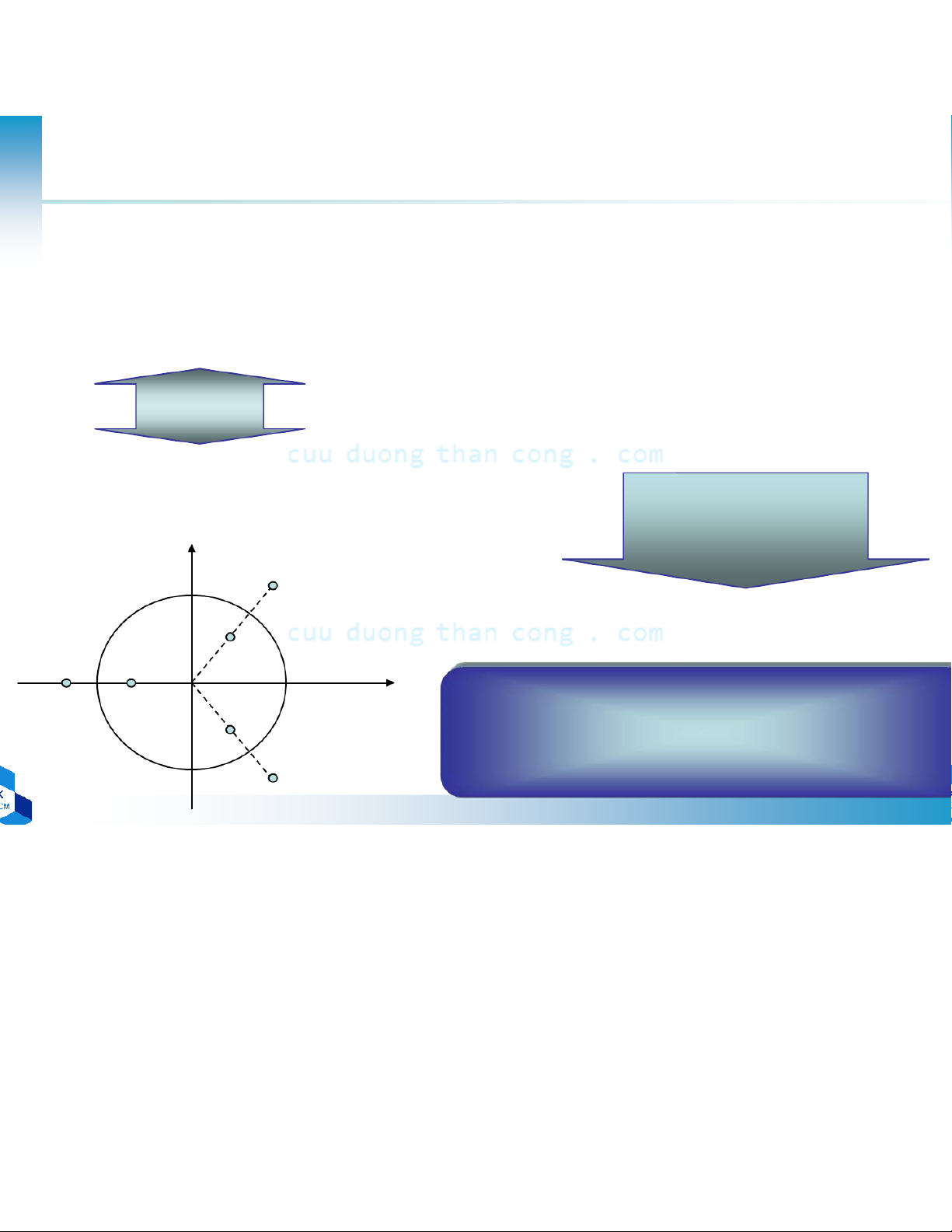
– H(ω) có pha Ө(ω) là hàm tuyến tính n b x n ∑ kkk –Đ/k: h(n) = ±h(M–1–n) = n = 0, 1, …, M-1 − h(k) = b M =1 ( ) ( k H z ∑0) −k h k z k = − = ( ) ( h k x n ∑10 − ) kk •Thay z bởi z-1 = •Nhân 2 vế với z-(M-1) •h(n) = ± h(M–1–n) 1/z1* z − − − M = ± H z H ( z )1 ( 1 ) ( ) z1
1/z2z2•Nếu z1là nghiệm ( 1 hoặc zero) của H(z) z1*
thì 1/z1cũng là nghiệm
•Để h(n) thực thì z1*cũng là nghiệm 1/z
và 1/ z1*cũng là nghiệm 1
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu c e 2011
Bộ lọc FIR –Tính đối xứng & phản đối xứng •Hàm h/t 1 − −− ( 1) H ( )z = (h0 + ) (h1+)+z −. . (hM 1) M z M 3 − (1)M− 2 ( 1 2M)n −− −− ( 1 2 M n) −−  2 M −1  22 z h( ) +±∑h( )n z z M le 20    n= = M −  − 2 1 ( 1) M ( 1 2M)n −− −− ( 1 2 M n) −− 2 2 2 z ∑h( )n z ±  z M chan 
•Đáp ứng xung đơn vị đối xứng h(n) = h(M – 1 – n) ( 21) H ( − =M jω − ω ) H r ( eω ) M 3 − + 2 M 1 − M 1 n−− 2 h( ) 2∑h( )ncos (ω ) M le 2 2  n=0 Biên độ thực H ω = 2 1 − 1 2 2∑ (h )ncos ( Mn ω −− ) M chan  2  n=0  − M − ω (21 ) H r (ω ) > 0 Đặc tính pha Θ( − ω) =  Tuyến tính  −ω (2 M 1 )+π H r (ω ) < 0
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu c e 2011
Bộ lọc FIR –Tính đối xứng & phản đối xứng
•Đáp ứng xung đơn vị phản đối xứng h(n) = –h(M–1–n) –Khi M lẻh[(M–1)/2] = 0 − j[ ( 2 M1) − 2π ω − ] H (ω )H= r (ω e ) M 3 −  2 M −1 n− 2 2∑ h( )nsin ( ω ) M le 2  n=0 Biên độ thực H ( )ω = 1 2 2∑h( )nsin ( Mn ω −− ) M chan  2  n=0  π − M − ω ( 21 H ω 2 ) r ( ) > 0 Đặc tính pha Θ(ω)π =  Tuyến tính 3 − M − ω ( 21 H ω 2 ) r ( ) < 0
•Đối xứng hay phản đối xứng ? – Tùy Không thích hợp h(n) = –h(M–1–n) Hr(0) = 0
cho các bộ lọc thông thấp M lẻ Hr(π) = 0 và thông cao
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu c e 2011
Bộ lọc FIR tuyến tính pha – PP cửa sổ • Giả sử ∞ – H − jωn
d(ω): hàm đáp ứng tần số mong muốn H (h n ) d n eω = ∑ ( 0) d =π
– hd(n): hàm đáp ứng xung đơn vị mong muốn ( 2)1 hj n n( =) H ω ωe ω d d ∫ π d
• hd(n) có chiều dài vô hạn π −
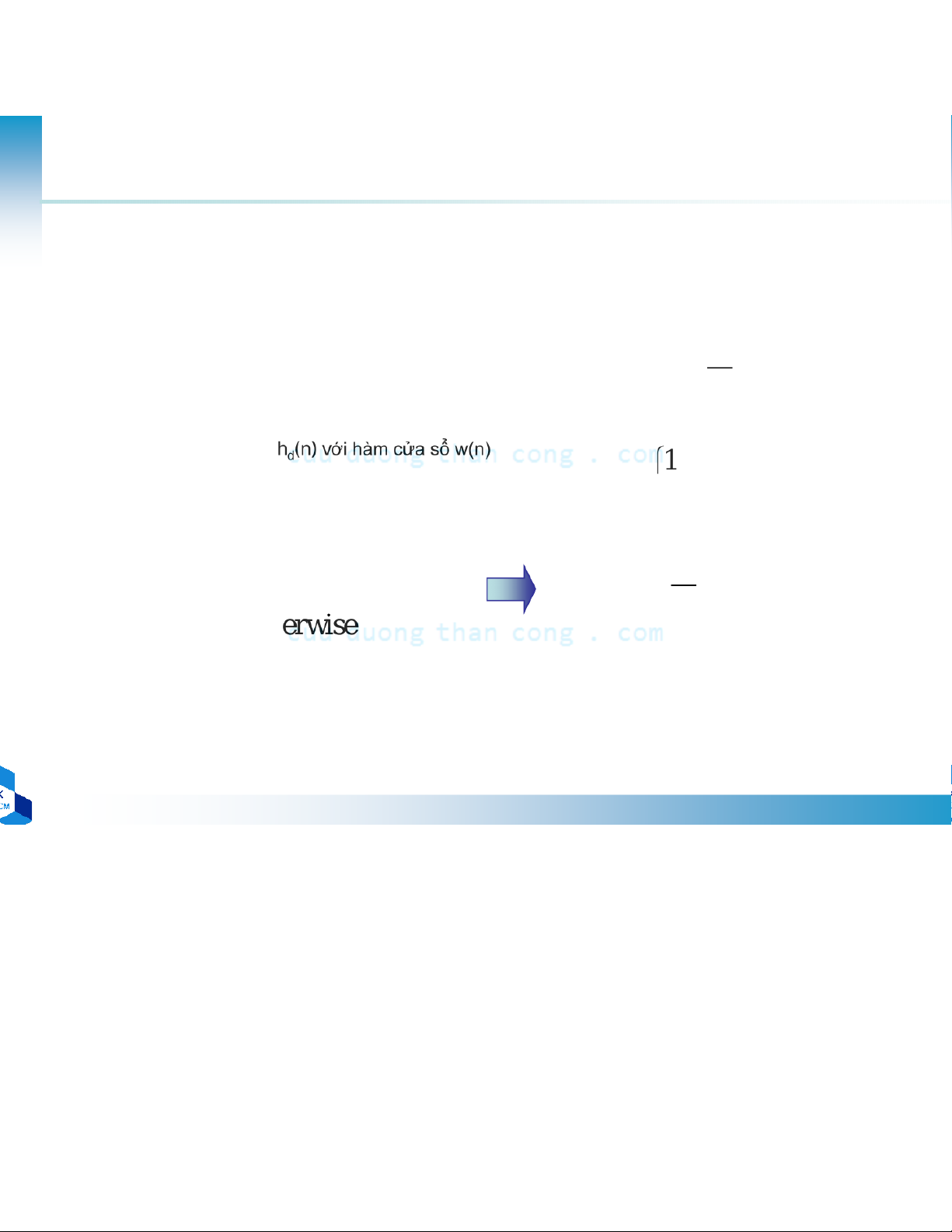
•Để chiều dài hd(n) hữu hạn, cắt hd(n) tại điểm n = M-1 –Nhân = − – C n ,1 , 0 . .,M 1 ửa sổ hình chữ nhật w(n0) • =  otherwise
Đáp ứng xung mẫu của bộ lọc  h(n) = hd (n)w(n) π −h ( 2 )1 ω d n ( ) n = ,1 , 0 . ,M 1
( ) ( H d) = πω H v W − v dv = ∫  0 oth −π
– Với Hd(ω) cho trước, thì W(ω) có tác dụng làm trơn Hd(ω) – Một W(ω) tốt khi
•Có thuỳ chính phải rộng, cao hơn nhiều so với thuỳ phụ
•w(n) không nên giảm xuống 0 tại hai bên cạnh
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu c e 2011
Bộ lọc FIR tuyến tính pha – PP cửa sổ M ω M 1 − − j M sin( 2 ) − ω j n 1 ω W( −e ω) W (ω ) = −π ≤ω ≤ π = e ∑ = − jω sin(ω2 ) n=0 1− e − M − ω ( 2 1 ) sin( 2M ω ) ≥ − jω( s M i−n) 1 (/2 sin/(2 ω) / M 2) = e Θ(ω) = ω  π − M − ω( 2 1) sin( 2M ω ) <
ộ rộng của thùy chính: 4π/M
ược đo bởi điểm zero đầu tiên của W(ω)] hận xét:
- Thuỳ chính hẹp hơn khi M tăng
-Các thuỳ phụ tương đối lớn so với thuỳ
hính và không thay đổi khi M t
- Chiều cao thuỳ phụ tăng khi M tăng
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu
c e Bộ lọc FIR tuyến tính pha –PP lấy 2011 mẫu tần số
• Hd(ω) được định nghĩa tại M điểm tần sốcách đều 21π + ωα = (k ) k 0,1, , M− = kM M le 2 k = 0,1 − , , M 1 M chan 2 1 α = 0 | 2 M −1 H h n e ω ω d ( ) ∑ − = d ( ) j n n=0 H π α α d ( k + ) ≡ H d[ 2M (k + )] M 1 − α=0, 2 công thức H π α α  d (k + ) = ∑hd (n) −j2 (k+ )n/ e M k = ,1 , 0 ,M −1 n=0 này chính là công thức M−1 DFT và IDFT n /  M ∑ M n = ,1 , 0 , M −1 k=0 Chuỗi h(n) thực d H d k H ( *M α + )k = ( − −α)
Chỉ cần định nghĩa Hd(ω) tại (M+1)/2 điểm khi M lẻ
hoặc tại M/2 điểm khi M chẵn
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu
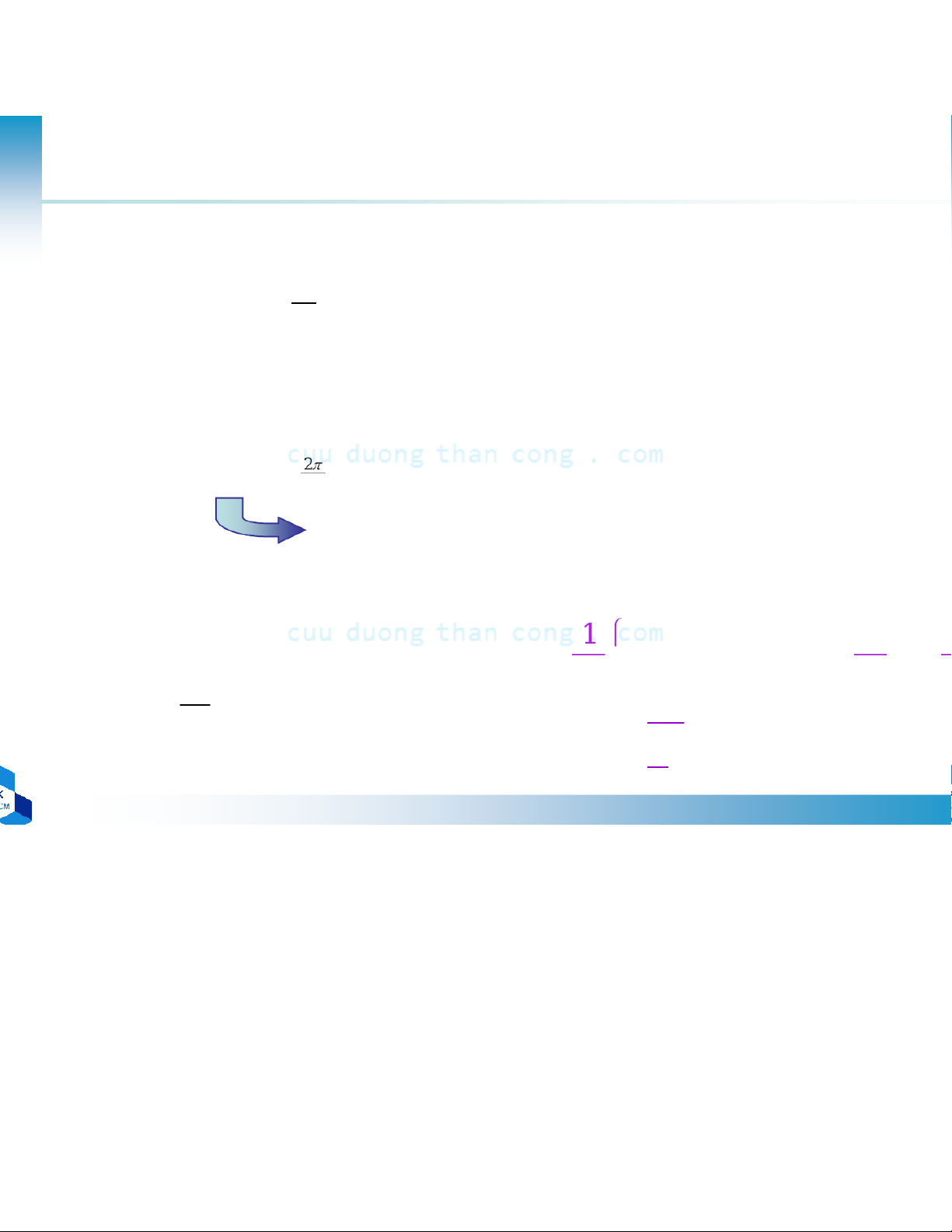
c e Bộ lọc FIR tuyến tính pha –PP lấy 2011 mẫu tần số • Mẫu tần số H ( α k + ) = H (2π ) j[β ] π / 2−2π (k +α )(M − ) 1 / 2M (k α + ) e d r M β = 0 { (h )n} doi xung Với β=  1 { (h )n} phan doi xung
•Định nghĩa các mẫu tần số thực G(k+m) ( H α + )k = (− ) 1 k r ( )( +α) / 2 2 ( )( H ) 1 / k 2 G k e d jk e π [jβ ] π π k α M M − + ( −+α ) = ( +α)
•Tùy theo giá trị α(0|½) vàβ(0|1), H(k) vàh(n) sẽcó công thức đơn giản – Ví dụkhi α= 0 vàβ= 0 Uk  π 21π
H (k) = G(k ) j k/ e M k = ,1 , 0 ,M −1 ++h( )n =  ( G 0) 2 ∑ ( G ) k cos n M ( )2 M  k 1 = G(k ) = (− ) 1 k H (2 kπ r M ) M 1 −  khi M le 2
G (k ) = G − (M − k) voi U =− khi M chan M  1 2
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu
c e Bộ lọc FIR tuyến tính pha –Phương 2011 pháp tối ưu
•Bài toán xấp xỉ Chebyshev
– Tối ưu: sai số xấp xỉ giữa đáp ứng t/s mong muốn
và thực tế phân bố đều trên passband và
stopband ⇒tối thiểu hóa các sai số cực đại – Bộ lọc có sband và stopband
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu c e 2011
Bộ lọc FIR tuyến tính pha –PP tối ưu
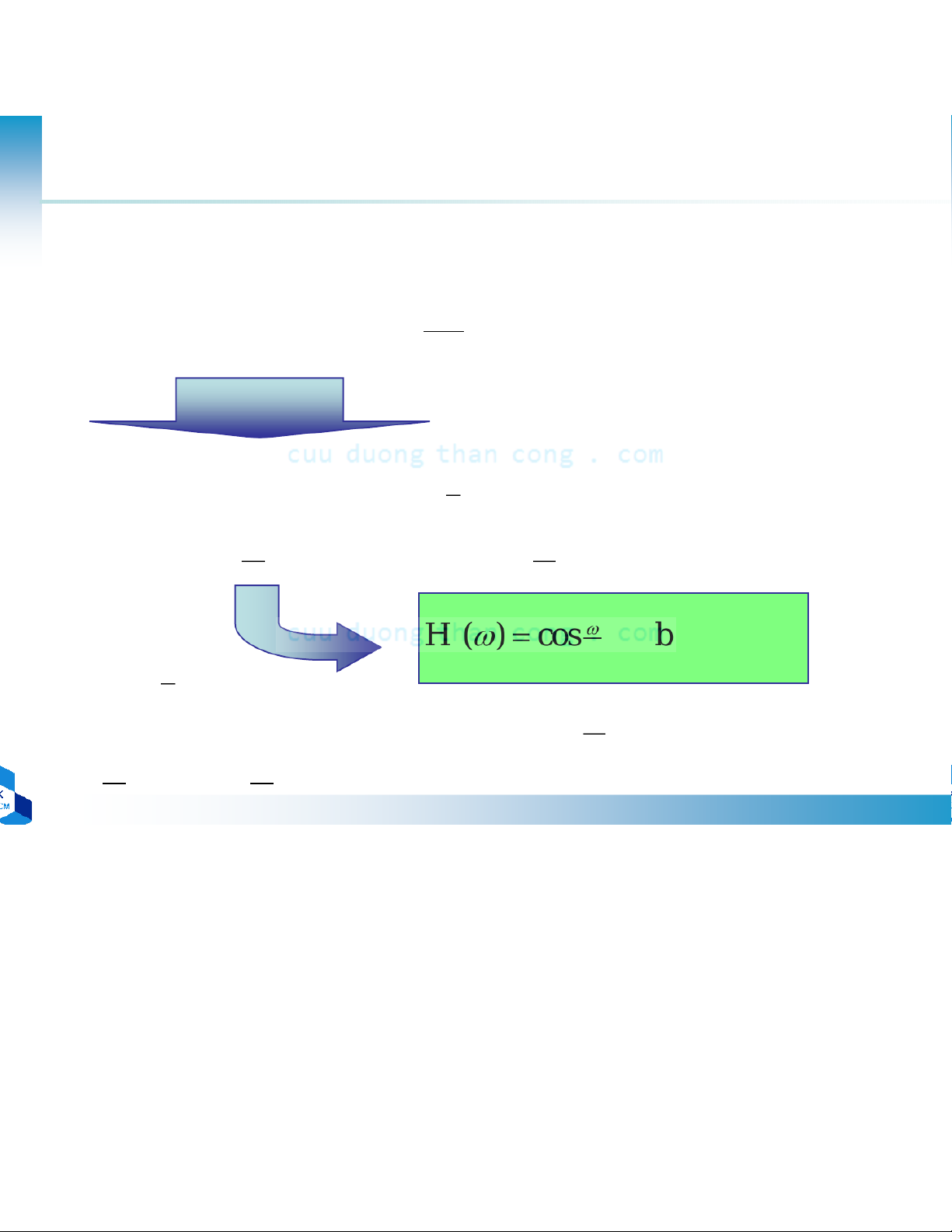
•Trường hợp 1: đáp ứng xung đơn vị đối xứng và M lẻ − + − − ( )cos ω ( 2 M 1) rn ∑ − 021 M ω = n k = (M-1)/2 – n − ( M =) 1 / 2 ( ) a k rkω ∑ ( 0)cos ω k=  M−21 h( ) k = 0 − α(k)M =   −  21 2h( − k) k = 21 ,1 , 2 ,
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu c e 2011
Bộ lọc FIR tuyến tính pha – PP tối ưu
•Trường hợp 2: đáp ứng xung đơn vị đối xứng và M chẵn M / 2 −1 H ω h n ω n r ( ) = 2 ∑021 M − ( )cos ( − ) = n k = M/2 – n = ( M ω ) b k rk ∑ / 2 − ( )cos ( 1 ω ) 12 k = ) ,1 , 2 2 , 2 / 2 1 M '( 2) k rk ∑ cos− ω k=0 b'( ) 0 1 = 2 b ) 1 (
b'(k) + b'(k − ) 1 = 2b(k) k = , 1 , 2 , M − 2 2 b'( M M 2 − ) 1 = 2b( 2 )
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu c e 2011
Bộ lọc FIR tuyến tính pha –PP tối ưu
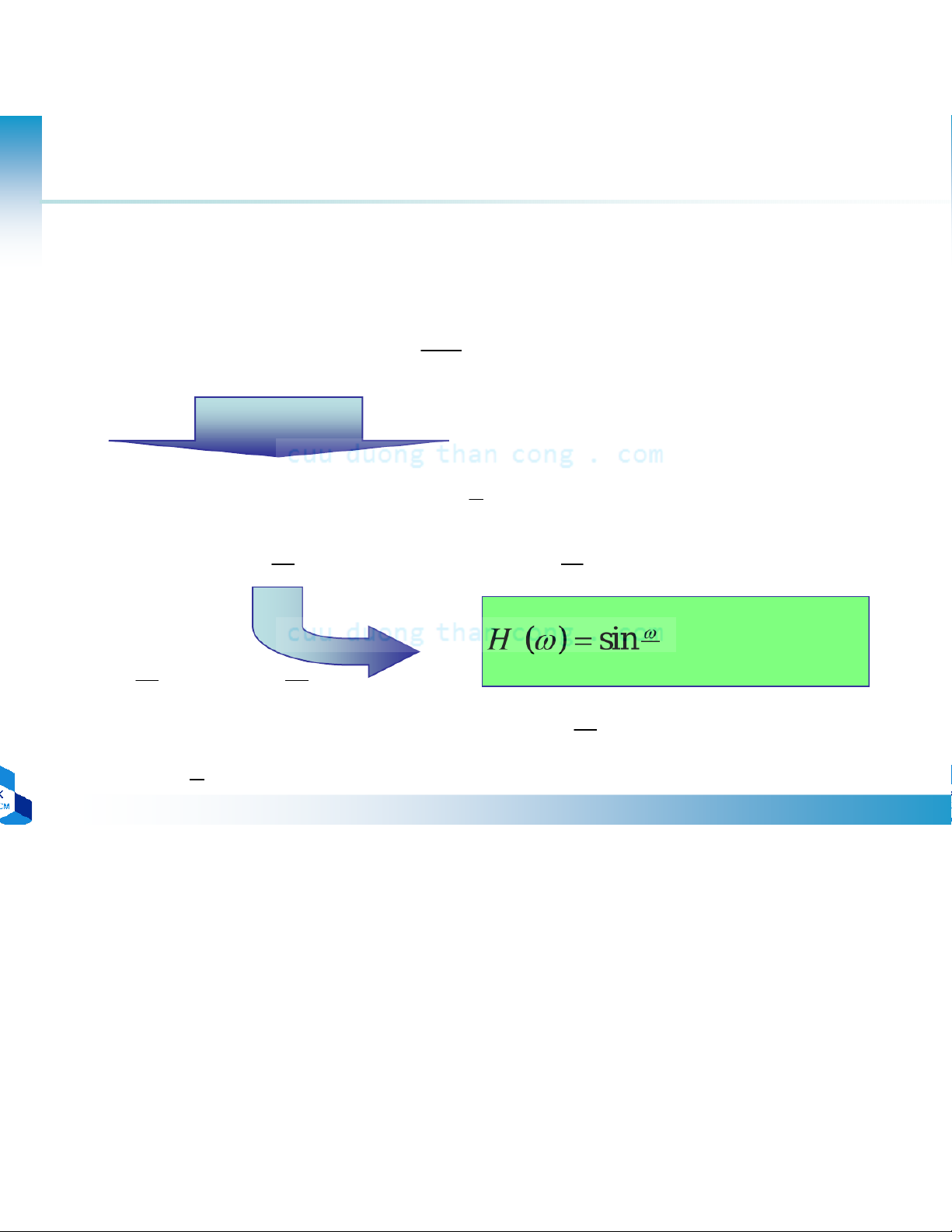
•Trường hợp 3: đáp ứng xung đơn vị phản đối xứng và M lẻ − ( =3)/ 2 ( )sin ( ω ∑ −− 021) M rn ω n = k = (M-1)/2 – n − ( =) 1 / 2 ( ) M ( k rk ω ∑1)sin ω k= 21 ) ,1 , 2 21, c'( 2 M 3 − ) = c( 2 M 1 − )
c'( 2 ) = 2c( 2 ) − ( = 3)/ 2 ) M sin ' rkω ω ∑ ( 0)cos ω    k = c'(k − ) 1 − 'c(k + ) 1 = 2c(k) 2 2 ≤ k M ≤ −
CuuDuongThanCong.com https://fb.com/tailieudientucntt c'(0) 1 + = 2 c' (2) c ) 1 (
DSP – Th iết kếBộlọc Số© 2 0 1 1 , Đinh Đức An h Vũ 14:28, 10/01/2026
DCE 2011 Chương 8: Thiết Kế Bộ Lọc Số - Đinh Đức Anh Vũ - Studocu c e 2011
Bộ lọc FIR tuyến tính pha –PP tối ưu
•Trường hợp 4: đáp ứng xung đơn vị phản đối xứng và M chẵn =/2 1 2 ( )sin ω ( ∑ −− − 021) M rn ω = n k = M/2 – n = ( M ω ) d k rk ∑ / 2 − ( )sin ( 1 ω ) 12 k = ( ) ,1 , 2 2 , 2 / 2 1 M d k rk '( 2) ∑ cos − ω M M k =0 d '( − = 2 ) 1 2d( 2 ) d'(k − )
1 − d'(k) = 2d(k) 2 ≤ k M ≤ 2 −1 d '( ) 0 1 − = 2 d ' ) 1 ( d ) 1 (
DSP – Th i CuuDuongThanCong.com https://fb.com/tailieudientucntt
ết kếBộlọc Số© 2 0 1 1 , Đinh Đức A n h Vũ