Đề 7 - Ôn tập full lớp 12 môn Toán ứng dụng | Trường Đại học Sư phạm Thành phố Hồ Chí Minh

lOMoAR cPSD| 22014077 ĐỀ SỐ 7
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12+
Câu 1. Trong không gian với hệ tọa ộ Oxyz , cho mặt cầu ( )S : x2 + − + =(y 1)2 z2 2. Trong các iểm cho dưới
ây, iểm nào nằm ngoài mặt cầu ( )S ? A. M (1;1;1). B. N (0;1;0). C. P(1;0;1). D. Q(1;1;0).
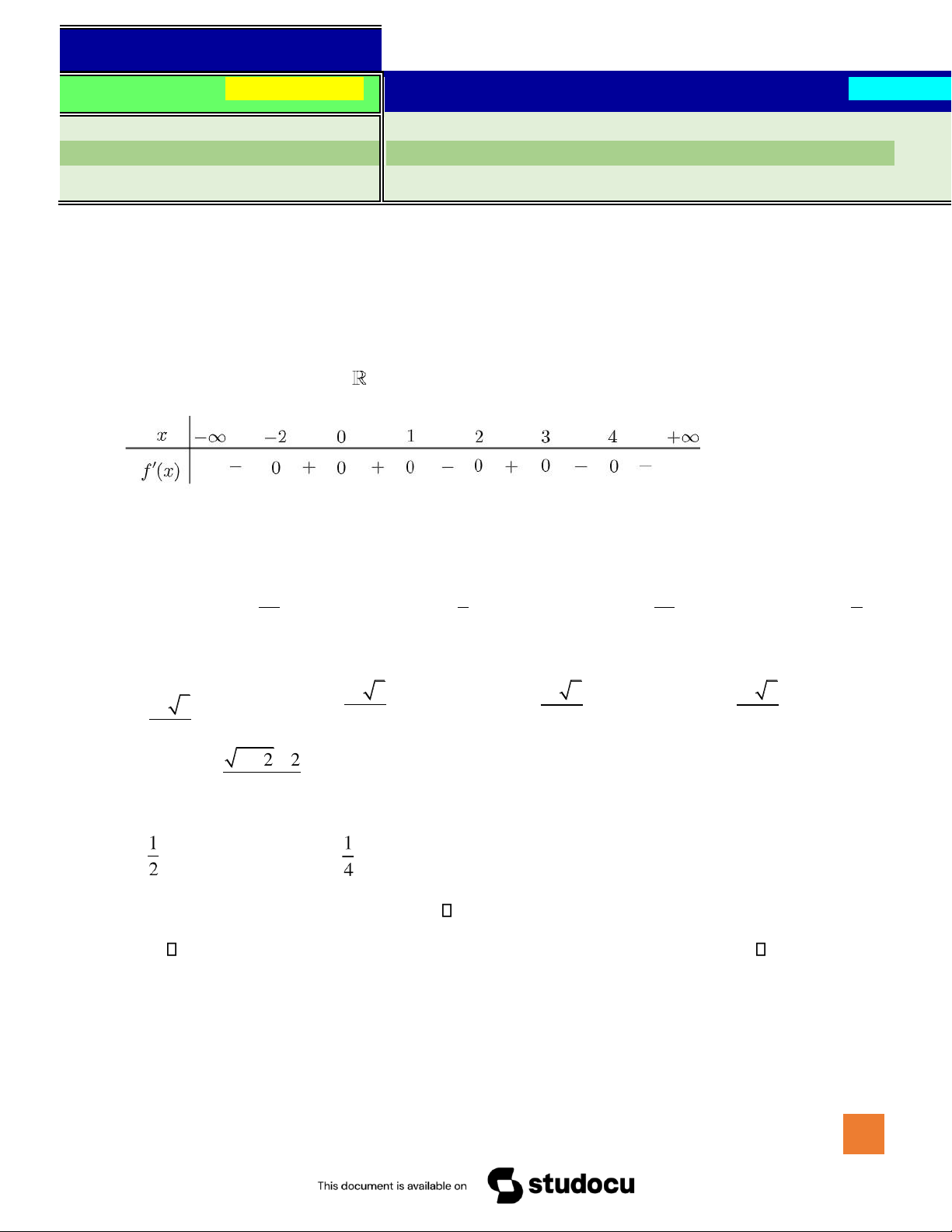
Câu 2. Cho hàm số f x( ) xác ịnh trên và có bảng xét dấu ạo hàm như sau. Hỏi hàm số có bao nhiêu iểm cực trị dương? A. 2. B. 3. C. 1. D. 4.
Câu 3. Đặt a=log 35 . Tính theo a giá trị của biểu thức log 11259 . 3 3 A. log 1125 = + = = = + 9 1 . B. log 11259 2+ 3 . C. log 11259 2+ 2 . D. log 11259 1 . 2a a 3a a
Câu 4. Thể tích khối tứ diện ều cạnh a bằng 3 A. B. a3 3 .
C. a3 2 . D. a3 3 a 2 . . 4 2 12 6 2 +− 2 x −2 Câu 5. x Giới hạn limx bằng →2 A. . B. . C. 0 . D. 1.
Câu 6. Tập nghiệm của bất phương trình log ( 2 x−1) 3 là: A. (− ;10) . B. (1;9). C. (1;10). D. (− ;9) . HO NG XU´N NH N 589 Downloaded by mai hoa lý (lymaihoa28@gmail.com) lOMoAR cPSD| 22014077
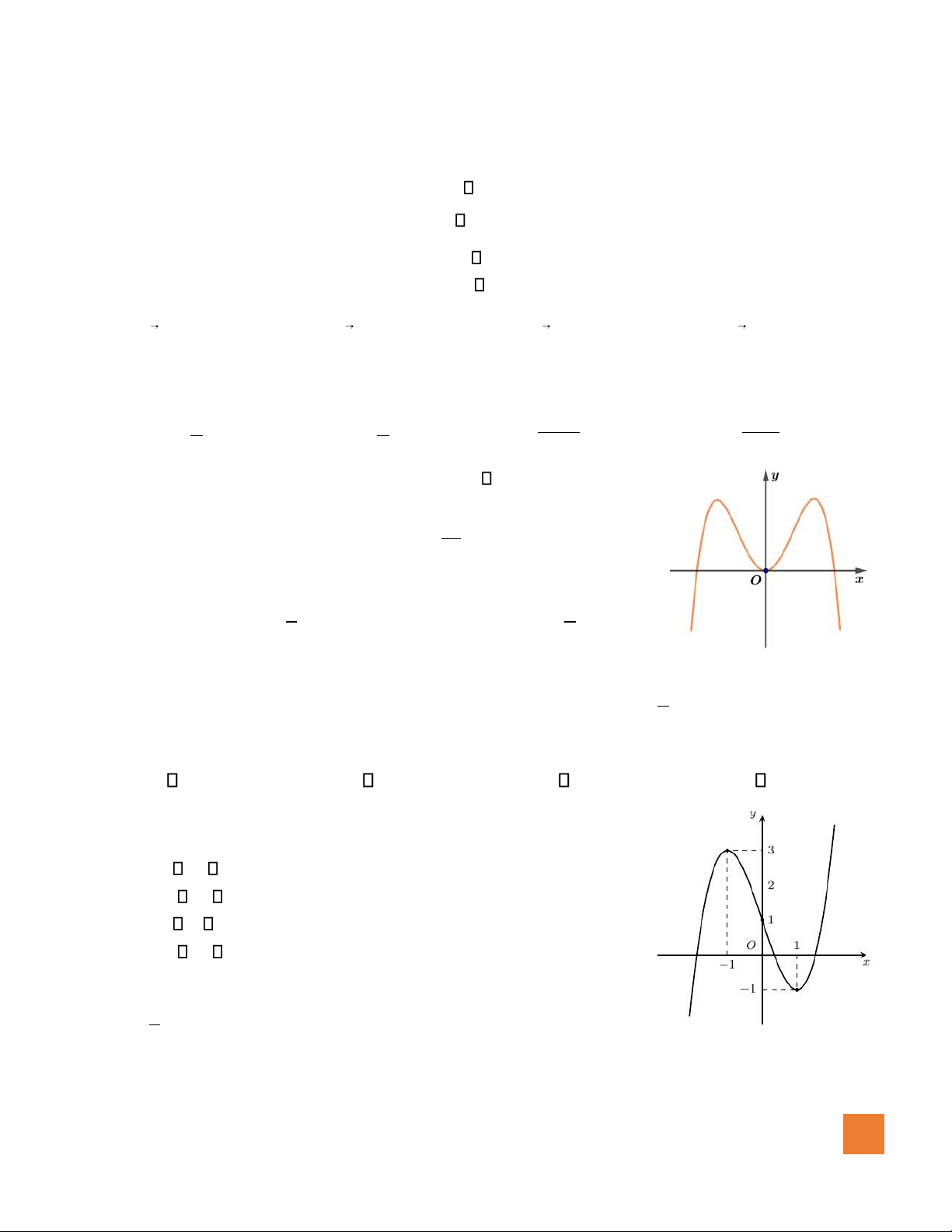
Câu 7. Đồ thị hàm bậc bốn trùng phương nào dưới ây có dạng ồ thị hình vẽ bên
A. f x( ) = −x4 2x2 .
B. f x( ) =− +x4 2x2 .
C. f x( ) = +x4 2x2.
D. f x( ) =− +x4 2x2 −1. x = −1 t
Câu 8. Trong không gian Oxyz , cho ường thẳng d : y 2 2t . Vectơ nào z = +1 t
dưới ây là vectơ chỉ phương của d ?
A. n = −(1;2;1). B. n =(1;2;1) .
C. n = − −( 1;2;1).
D. n = −( 1;2;1) .
Câu 9. Đồ thị hàm số nào trong các hàm số ược cho dưới ây không có tiệm cận ngang?
A. y = x ++ +− 2 21.
B. y = xx++12 . C. y = xx2 21. D. y = x+1 2 . x =− + + 1
Câu 10. Nguyên hàm của hàm số f x( ) = 5cos x 2 là hàm số nào sau ây: x
A. F x( ) = −5sin x− 1 +C .
B. F x( ) = 5sin x + 1 +C . x x
C. F x( ) =5sin x+ln x C+ .
D. F x( ) = 5sin x − 1 +C . x
Câu 11. Thể tích của khối nón có chiều cao bằng 4 và ường sinh bằng 5 bằng A. 16 . B. 48 . C. 12 . D. 36 .
Câu 12. Đồ thị hàm số y = − +x3 3x 1 cho ở hình bên. Phương trình x3 − −
=3x m 0 (mlà tham số) có ba nghiệm phân biệt khi A. −1 m 3. B. −2 m 2. C. −2 m 3. D. −2 m 2.
Câu 13. Cho khối chóp S ABCD.
có SA vuông góc với mặt phẳng áy,
SA=3a , ABCD là hình chữ nhật và AB = 2a, AD = a. Thể tích của
khối chóp S ABCD. bằng 3 3 B. 3a3. A. a . HO NG XU´N NH N 590
Downloaded by mai hoa lý (lymaihoa28@gmail.com) lOMoAR cPSD| 22014077 2 C. 2a3. D. 9a3.
Câu 14. Với a và b là các số thực dương. Biểu thức log (
a a b2 ) bằng A. 2−log D. 2log ab. B. 2+logab. C. 1 2+ loga b. ab.
Câu 15. Tính diện tích hình phẳng giới hạn bởi ồ thị y x= −2 4x và trục hoành. A. S = . B. S = . C. S = . D. S = .
Câu 16. Trong không gian với hệ tọa ộ Oxyz, phương trình nào ược cho dưới ây là phương trình mặt phẳng ( ) Oyz ? A. y=0. B. z=0.
C. y+ =z 0. D. x = 0.
Câu 17. Cho số phức z = +1 i2020. Số phức liên hợp của z là A. z= 2.
B. z =− +2 2i . C. z =0. D. z =−2.
Câu 18. Cho khối lăng trụ có diện tích áy bằng a2 và khoảng cách giữa hai áy bằng 3a . Tính thể tích V của khối lăng trụ ã cho. = 3
D. V =9a3. A. V a3 .
B. V =3a3.
C. V =a3 . 2
Câu 19. Cho x, y là các số thực tùy ý. Mệnh ề nào sau ây là úng? A. e + = + − = − = e x y e ex y . B. ex y e ex y.
C. exy eex y . x D. = e 2 y x y− . e Câu 20. Tích phân 2 dx bằng. 2x+1 0 A. 2ln5. B. ln5 . C. ln5. D. 4ln5. 5
Câu 21. Hàm số nào dưới ây nghịch biến trên khoảng (1; )?
A. y = x +1 . B. x−3 . C. y = 3x −1. D. 2x+1. 3x + 2 x− 4 x +1 x−2
Câu 22. Nghiệm của phương trình 23 2 1x− = 278 là A. x = 2. B. x =3. HO NG XU´N NH N 591 Downloaded by mai hoa lý (lymaihoa28@gmail.com) lOMoAR cPSD| 22014077 C. x = −1. D. x = 4.
Câu 23. Thể tích V của khối lăng trụ tam giác ều có cạnh áy bằng 2a và cạnh bên bằng a là 3 3 3
A. V = a3 .
B. V =a3 3.
C. V = a3 .
D. V = a3 . 24 3
Câu 24. Cho số phức z thỏa mãn: (3+ 2i z) + − = +(2 i)2 4
i . Hiệu phần thực và
phần ảo của số phức z là A. 3. B. 2 . C. 1. D. 0 .
Câu 25. Trong các hàm số ược cho dưới ây, hàm số nào có tập xác ịnh là D= ?
A. y = ln(x2 −1).
B. y = ln 1( − x2).
C. y = ln(x+1)2 .
D. y = ln(x2 +1) .
Câu 26. Cho khối lăng trụ ABCDABCD. có thể tích bằng 12, áy ABCD là hình vuông tâm O. Thể tích
của khối chóp A BCO . bằng A. 1. B. 4 . C. 3. D. 2 . 0
Câu 27. Ta xác ịnh ược các số a, b , c ể ồ thị hàm số y = +x3 ax2 + +bx
c i qua iểm (1; ) và có iểm
cực trị (−2;0) . Tính giá trị biểu thức T = + +a2 b2 c2. A. 25. B. −1. C. 7 . D. 14.
Câu 28. Hình chóp ều S ABCD. tất cả các cạnh bằng a. Diện tích mặt cầu ngoại tiếp hình chóp là: A.
4 a2. B. a2 . C. 2 a2 . D. 2 a2. 4
Câu 29. Cho A = 1,2,3,
. Từ A lập ược bao nhiêu số tự nhiên có 4 chữ số ôi một khác nhau? A. 32. B. 24. C. 256. D. 1. = mx +16
Câu 30. Tìm tất cả các giá trị của m ể hàm số y ồng biến trên (0;10). x + m
A. m − − + ( ;
10 (4; ). B. m − − + ( ; 4)(4; ).
C. m − − + ( ;
10 4;) . D. m − − + ( ; 4 4; ) x−4
Câu 31. Trong không gian Oxyz , cho
iểm M (2;−2;3) và hai ường thẳng :
= y +3 = z −2 , 3 −1 2 x+1 = y −2 = z :
. Phương trình nào dưới ây là phương trình tham số của ường thẳng i qua M 2 3 1 HO NG XU´N NH N 592
Downloaded by mai hoa lý (lymaihoa28@gmail.com) = lOMoAR cPSD| 22014077 a Câu 32. Cho x 0 dx
+bln2+cln3 với a, b , c là các số nguyên. Giá trị của a b c++ bằng 4+2 x+1 3 A. 1. B. 2 . C. 7 . D. 9. và vuông x = −2 7t x =− −2 7t x = −27t x =− −2 7t góc với hai ường B. y = +2 3t . A. y =− +2 C. y =− −2 t thẳng D. y = −2 z =− +3 11t . t . và ? t . z = +38t z = +38t 3 z = +3 11t Câu 33. Cho hình chóp S ABCD. có áy ABCD là hình
vuông cạnh a . Cạnh
bên SA vuông góc với áy. Biết a 3
khoảng cách từ A ến ( ) SCD bằng
. Tính thể tích khối chóp S ABCD. theo a. 2 a 3 a 3 B. . C.a3 3 . D. 3 A. 3 . 34
Câu 34. Cho hàm số y = + + +ax3 bx2
cx d . Hỏi hàm số luôn ồng biến trên khi nào?
a = =b 0,c 0
a = =b 0,c 0 A. a 0 ; b − − 2 3ac 0. B.
a 0 ; b2 3ac 0.
a = =b 0,c 0 a = = =b c 0 C. a 0 ; b − − 2 3ac 0. D.
a 0 ; b2 3ac 0. x −3 = y = z +1
Câu 35. Trong không gian Oxyz , cho ường thẳng :
và iểm M (2; 1;− 5). Phương trình 2 −3 1
mặt phẳng ( )P qua M và vuông góc với là
A. 2x− + − =3y z 12 0.
B. 2x− + + =3y z 12 0.
C. 2x− + − =y 5 12 0z .
D. 2x− + + =y 5 12 0z .
Câu 36. Cho số phức z , biết rằng các iểm biểu diễn hình học của các số phức z ;iz và z+iz tạo thành một tam
giác có diện tích bằng 18. Mô un của số phức z bằng A. 2 3. B. 3 2 . C. 6 . D. 9. HO NG XU´N NH N 593 Downloaded by mai hoa lý (lymaihoa28@gmail.com) lOMoAR cPSD| 22014077
Câu 37. Số nghiệm của phương trình log ( (
x x2− +2 x+ =3) logx+5 x+3) là: A. 3. B. 1. C. 2 . D. 0 .
Câu 38. Trong không gian Oxyz , cho hai mặt phẳng ( )P : x+ − − =2y 2z 6 0 và ( )Q : x+ − + =2y 2z 3 0 .
Khoảng cách giữa hai mặt phẳng ( )P và ( )Q bằng A. 1. B. 3. C. 9. D. 6 .
Câu 39. Tính thể tích V của vật thể nằm giữa hai mặt phẳng x = 0 và x= , biết rằng thiết diện của vật thể bị cắt
bởi mặt phẳng vuông góc với trục Ox tại iểm có hoành ộ x (0 x ) là một tam giác ều cạnh 2 sinx .
A. V = 3.
B. V =3 .
C. V = 2 3.
D. V = 2 3. z −1 z −3i
Câu 40. Cho số phức z = +a bi , (a b, )thỏa mãn =1 và
=1. Tính P = a+b. z −i z +i A. P = 7 . B. P=−1. C. P=1. D. P=2.
Câu 41. Cho tam giác ABC vuông tại A có AC =1cm, AB = 2cm, M là trung iểm của AB. Quay tam giác BMC
quanh trục AB, gọi V là thể tích khối tròn xoay thu ược, khi ó V bằng: 3 3. B. cm3. C. cm3. D. cm3. A. cm 4 3 2
Câu 42. Tập hợp tất cả các iểm biểu diễn các số phức z thỏa mãn: z + − =2i4 là ường tròn có tâm I và bán kính
R lần lượt là:
A. I (− −2; 1) ; R=4.
B. I (− −2; 1) ;R=2.
C. I (2;−1); R=4.
D. I (2;−1); I (2;−1).
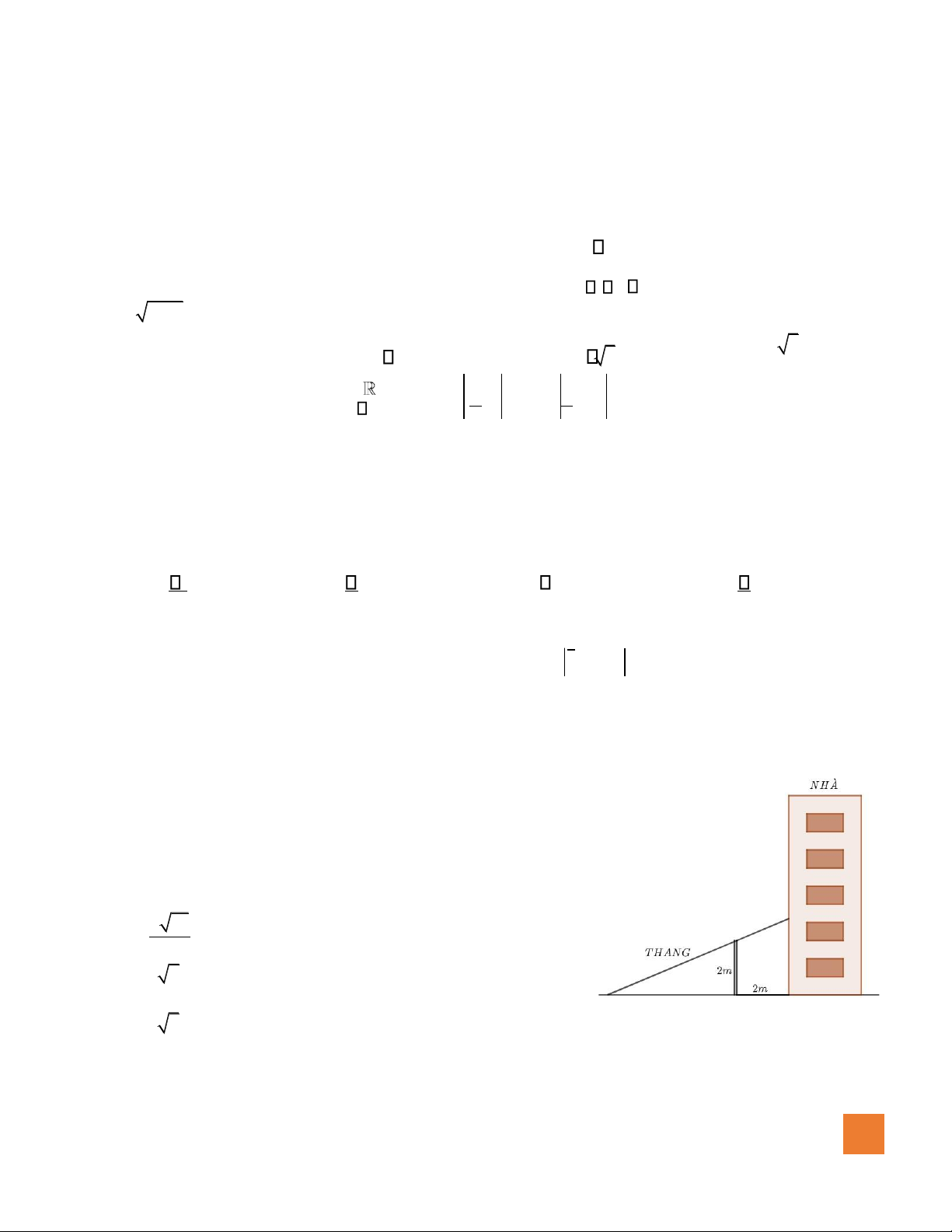
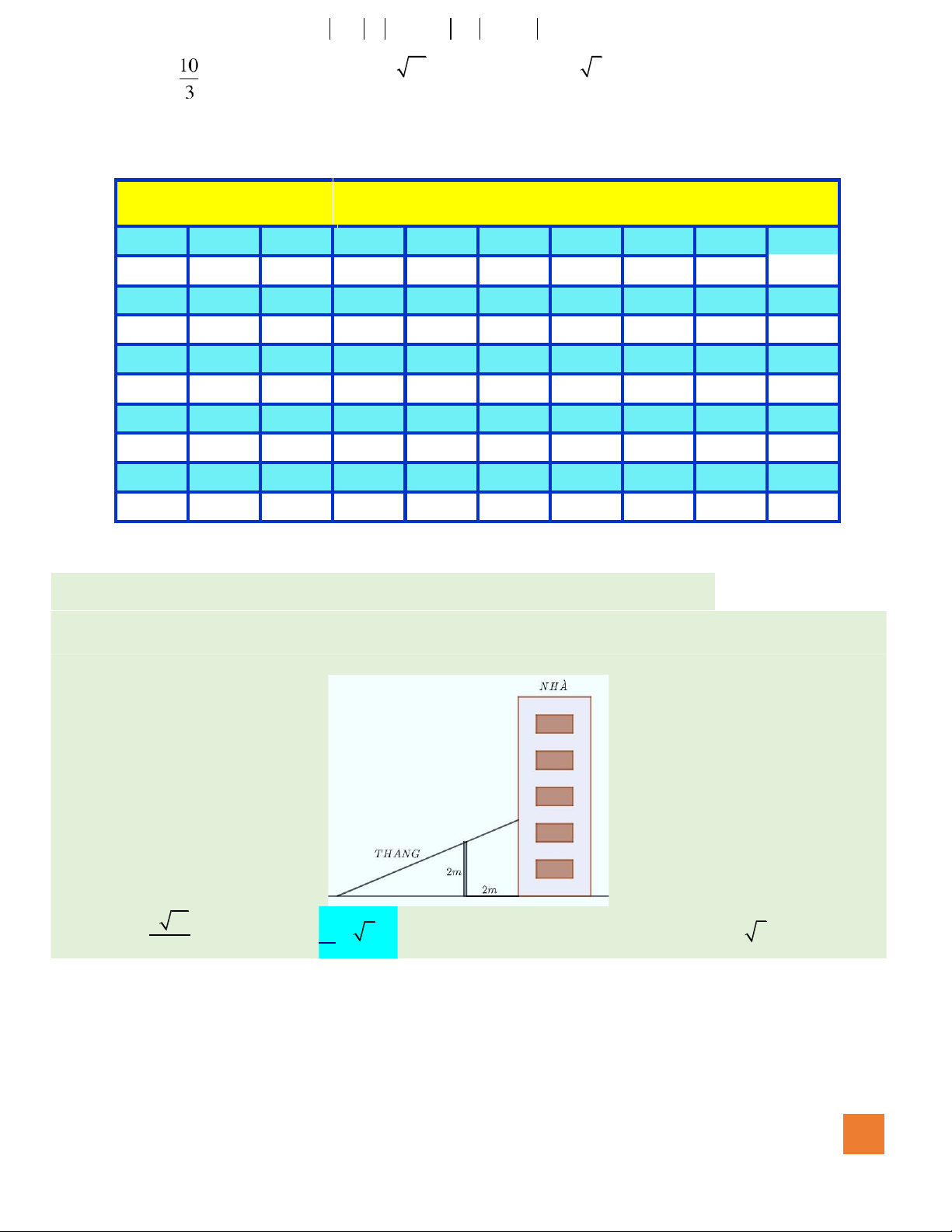
Câu 43. Một bức tường cao 2m nằm song song với tòa nhà và cách tòa
nhà 2m. Người ta muốn chế tạo một chiếc thang bắc từ mặt ất
bên ngoài bức tường, gác qua bức tường và chạm vào tòa nhà
(xem hình vẽ). Hỏi chiều dài tối thiểu của thang bằng bao nhiêu mét ? 5 13 A. m . 3 B. 4 2m . C. 6m. D. 3 5m. HO NG XU´N NH N 594
Downloaded by mai hoa lý (lymaihoa28@gmail.com) lOMoAR cPSD| 22014077 ( ) )
Câu 44. Tập các giá trị của m ể phương trình 4.
5 + 2 x +( 5 − − + =2 x m 3
0 có úng hai nghiệm âm phân biệt là: A. (− − + ; 1) (7; ) . B. (7; 8) . C. (− ; 3). D. (7; 9).
Câu 45. Tìm tất cả các giá trị của tham số m ể ồ thị hàm số y= x−1 có úng bốn ường
2x2 − − − −2x m x 1 tiệm cận.
A. m − 5;4 \ −4 . B. m − 5;4 .
C. m −( 5;4 \) −4 . D. m −( 5;4 \ −4 . 10
Câu 46. Cho tập hợp A = 1;2;3;...;
. Chọn ngẫu nhiên ba số từ A. Tìm xác suất ể trong ba số chọn ra không
có hai số nào là hai số nguyên liên tiếp. A. P = . B. P = . C. P = . D. P = .
Câu 47. Cho tứ diện ABCD có AB = 2, AC = 3, AD = BC = 4, BD = 2 5, CD = 5. Khoảng cách giữa hai ường
thẳng AC và BD bằng. 3 15 240 A. . B. 2. C. . D. 3. 4 79
Câu 48. Cho hai hàm số y = + − −x3 x2
3x 1, y = 2x3 +2x2 − +mx
2 có ồ thị lần lượt là (C ) ( 1 , C ) ) )
2 và m là tham số thực. Biết rằng tồn tại m ể (C1 cắt (C2 tại ba iểm phân biệt có tung ộ là y1, y2, y + + +
3 thỏa mãn 1 + 1 + 1 = 2 , khi ó: y1 4 y2 4 y3 4 3 A. m (4;7). B. m (9;12). C. m (6;9) . D. m (8;11). log
Câu 49. Cho x, y 0 thỏa mãn
(x+ 2y) = log( )x +log( )y . Khi ó, giá trị nhỏ nhất của biểu thức x2 4y2 P= + là: 1+2y 1+x A. 6 . B. . C. . D. .
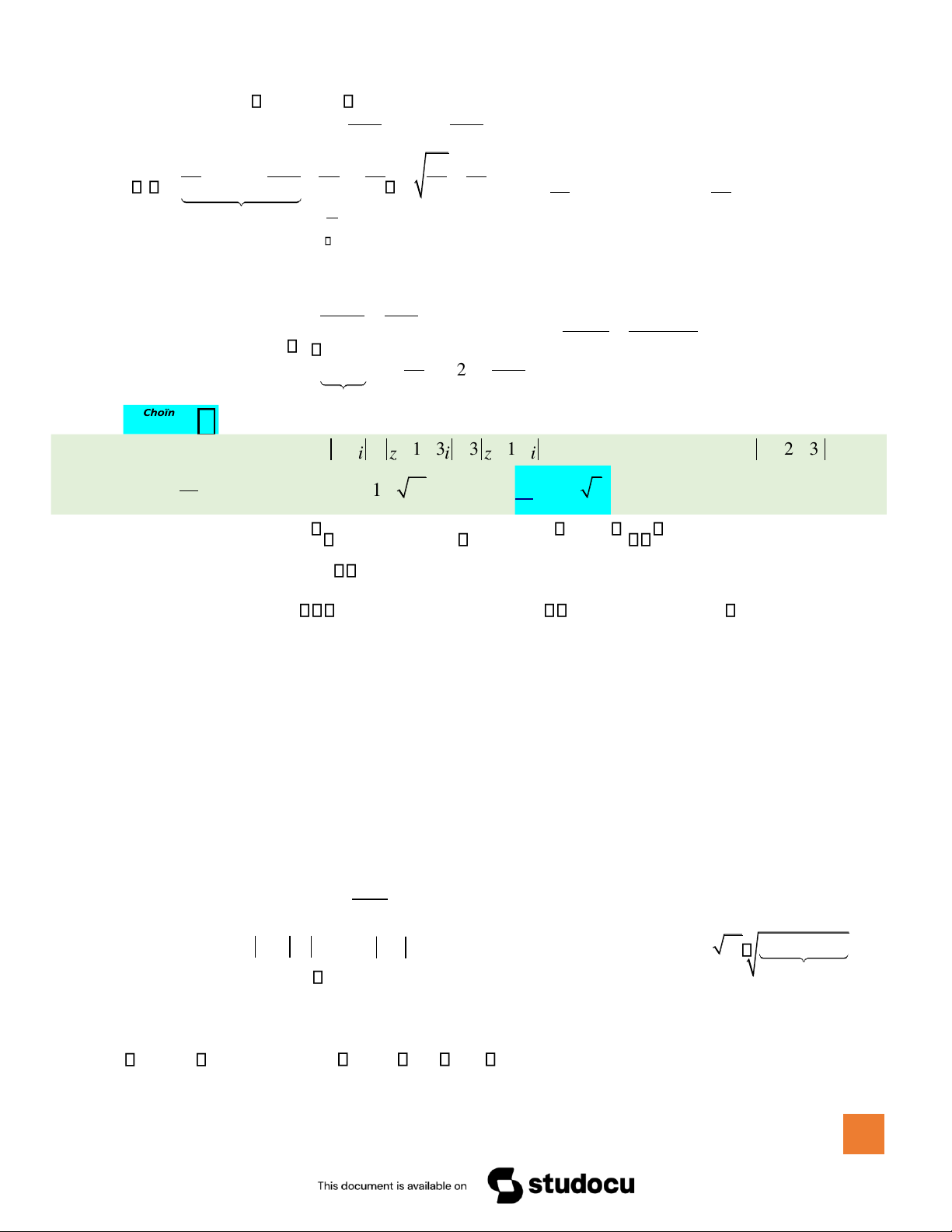
Câu 50. Cho số phức z thỏa mãn 5 z − = + − + − +i z 1 3i
3 z 1 i . Tìm giá trị lớn nhất T của z − +2 3i ? HO NG XU´N NH N 595 Downloaded by mai hoa lý (lymaihoa28@gmail.com) lOMoAR cPSD| 22014077 A. T = . B. T = +1 13. C. T = 4 5 . D. T = 9.
________________HẾT________________ AP AN E SO` 56 1 2 3 4 5 6 7 8 9 10 C B A C B B B D C D 11 12 13 14 15 16 17 18 19 20 C B C B B D A B D C 21 22 23 24 25 26 27 28 29 30 A C B D D A A D B A 31 32 33 34 35 36 37 38 39 40 A A A A A C A B D D 41 42 43 44 45 46 47 48 49 50 B A B B D D C D B C
Lłi giaßi cau hoßi van dung cao æe soÆ 56
Câu 43. M ộ t b ức tườ ng cao 2 m n ằ m song song v ớ i tòa nhà và cách tòa nhà 2 m . Ngườ i ta mu ố n ch ế t ạ o m ộ t
chi ế c thang b ắ c t ừ m ặt ấ t bên ngoài b ức tườ ng, gác qua b ức tườ ng và ch ạ m vào tòa nhà (xem hình v ẽ ). H
ỏ i chi ề u dài t ố i thi ể u c ủ a thang b ằ ng bao nhiêu mét ? 5 13 A. m . B. 4 2 m . C. 6 m . D. 3 5 m . 3
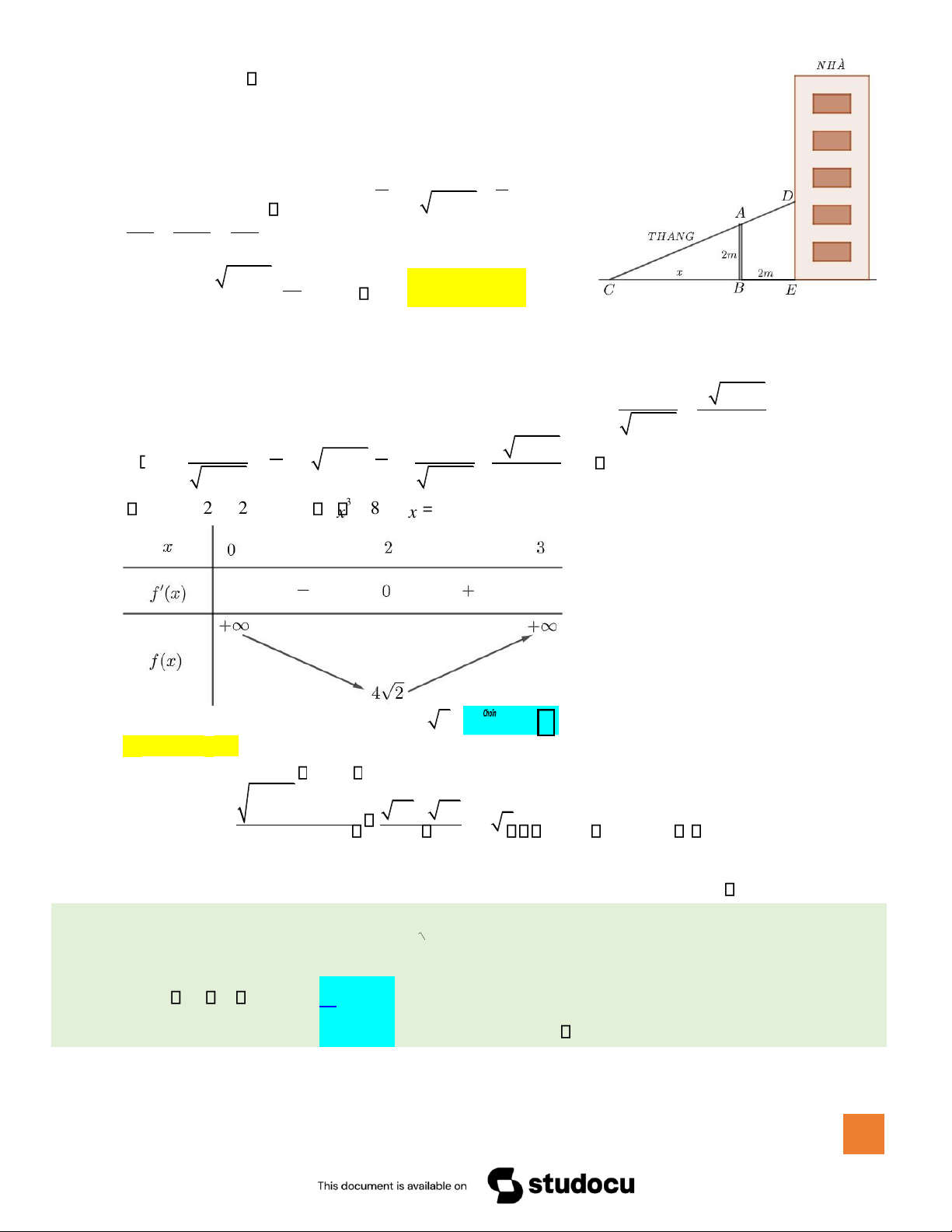
Hướng dẫn giải: Xét hệ iểm A B C D E, , , , như hình vẽ. HO NG XU´N NH N 596
Downloaded by mai hoa lý (lymaihoa28@gmail.com) lOMoAR cPSD| 22014077
Gọi BC = x x( 0). Ta cần tìm x ể ộ dài CD ạt giá trị nhỏ nhất.
Dễ thấy hai tam giác CAB CDE, ồng dạng, suy ra: BC x AC x+2 2 x+2 = = CD = AC. = x + 4. . CE x+2 CD xx Đặ x+ 2
t f x( ) = x2 + 4.
với x 0. x ☺ Cách giải 1: + − + + + + f () 2 2 2 2 2 2 4 2 2 4 x x 2 x x x x = . + +4. = − =0 x x = 2 2 2 2 2 2 +4 x x +4 x +4 x x x x 2 ( 2 3 2 x ) += 2( +4 x ) = 8 =2 x x x
. B ả ng bi ế n thiên c ủ a () fx :
V ậ y chi ề u dài t ố i thi ể u c ủ a thang b ằ ng 42 . ⎯ ⎯ ⎯ → B
☺ Cách gi ả i 2: Ta có: f x( )= + = AM GM AM GMx2 4 x+ 2 4 .2 2x x x2
4 =x 2. − − = 4 2 . Dấu ẳng thức xảy tra x x x= 2 ( ) ( )
Câu 44. Tập các giá trị của m ể phương trình 4. 5 + +2 x
5 − − + =2 x m 3 0 có úng hai nghiệm âm phân biệt là: A. (− − + ; 1) (7; B. (7; 8) . ) . C. (− ; 3). D. (7; 9). HO NG XU´N NH N 597 Downloaded by mai hoa lý (lymaihoa28@gmail.com) lOMoAR cPSD| 22014077 = Hướng dẫn giải: ( ) Đặt t 5 + 2 x 0 =x +1 log +
5 2+ t . Phương trình ã cho trở thành: 4t 3 = m ( )* . t Nhận xét: 1
Với mỗi t (0; ) thì ta tìm ược úng một nghiệm x 0. 1
Bài toán trở thành: Tìm m ể phương trình ( )* có úng hai nghiệm phân biệt t ( ) 1,2 0; .
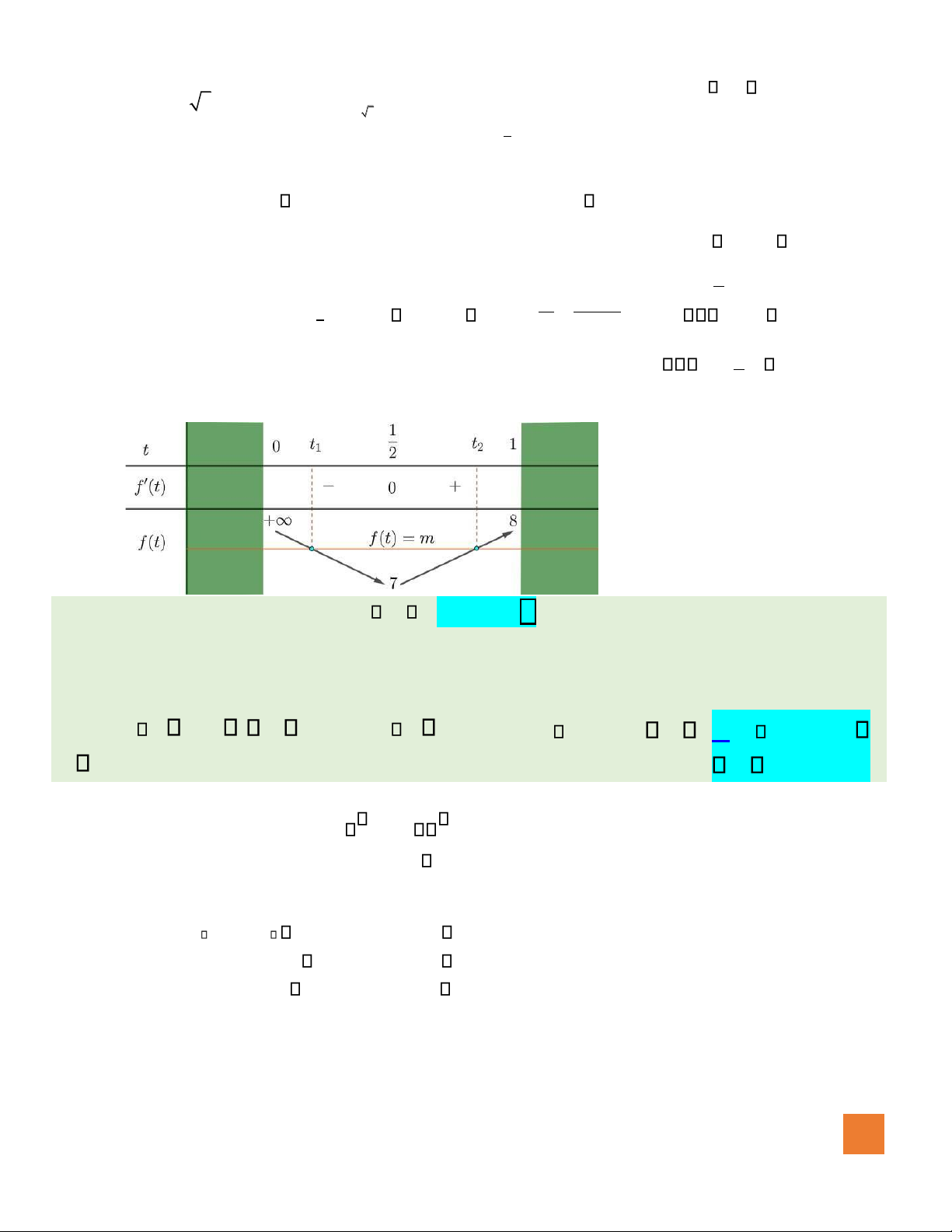
Xét hàm số f t( ) = 4t +1 +3 với t (0; 1); f ( )t = 4− 1 4 1 = − = 2 t22 0 t = 12 (0;1) . t t t t =− 12 (0;1) Bảng biến thiên:
Dựa vào bảng biến thiên ta có: 7 m 8. ⎯Choïn⎯⎯→B ồ
Câu 45. Tìm tất cả các giá trị của tham số m ể thị hàm số C. y = x−1 có úng bốn ường tiệm cận.
2x2 − − − −2xm x 1
A. m − 5;4 \ −4 . B. m −
m −( 5;4 \) −4 . D. m −( 5;4 \ 5;4 . −4 . Hướng dẫn giải: x 1− 1 = 1 = +1 2 ; x Ta có: lim y= lim x→+ x→+ 2 m 1 2 −1 x 2− − − − 2 1 x x x HO NG XU´N NH N 598
Downloaded by mai hoa lý (lymaihoa28@gmail.com) lOMoAR cPSD| 22014077 x x 1− 1
= 1 = −1 2 . Do ó ồ thị hàm số có hai ường tiệm lim y= lim x→− x→− 2 m 1 − 2 −1 x − 2− − − − 2 1 x x x
cận ngang là y = +1 2 và y = −1
2 . Vì vậy ta cần tìm m ể ồ thị hàm số ã cho có hai ường
tiệm cận ứng.
Khi tìm tiệm cận ứng, ta xét:
2x2 − − − − =2x m
x 10 2x2 − − = +2x m x 1 x −1 2x − + 2
2x m x− = 2 2x+1
xx2 −−g x4( )1x− =1 m (*) .
Yêu cầu bài toán ( )* có hai nghiệm phân biệt x − 1,2
1 và khác 1 (không trùng nghiệm của tử số).
Xét hàm số g x( ) = x2 −4x −1 với x −1 và x 1. Ta có: g x ( ) = 2x −4 = 0 x = 2 . Bảng biến thiên:
⎯Choïn⎯⎯→
Dựa vào bảng biến thiên, ta có m −( 5;4 \ −4 . D 10
Câu 46. Cho tập hợp A = 1;2;3;...;
. Chọn ngẫu nhiên ba số từ A. Tìm xác suất ể trong ba số chọn ra không
có hai số nào là hai số nguyên liên tiếp. . A. P = . B. P = . C. P = . D. P =
Hướng dẫn giải: Số
phần tử không gian mẫu là n( ) = C 3 = 10 120.
Gọi B là biến cố “Ba số chọn ra không có hai số nào là hai số nguyên liên tiếp”.
B là biến cố “Ba số ược chọn có ít nhất hai số là các số tự nhiên liên tiếp”.
Tìm các kết quả thuận lợi cho B : HO NG XU´N NH N 599 Downloaded by mai hoa lý (lymaihoa28@gmail.com) lOMoAR cPSD| 22014077 \ 1;2
Xét bộ ba số có dạng (1;2;a ) 1 , với a1 A : có 8 bộ thỏa mãn. \ 1;2;3
Xét bộ ba số có dạng (2;3;a ) 2 , với a2 A : có 7 bộ thỏa mãn. \ 2;3;4
Xét bộ ba số có dạng (3,4,a ) 3 với a3 A : có 7 bộ thỏa mãn.
Thực hiện tương tự mỗi bộ ba số dạng: (4,5,a ) ) ) ) ) ) 4 , (5,6,a5
, (6,7,a6 , (7,8,a7 , (8,9,a8 , (9,10,a9 : ều có 7 bộ thỏa mãn. 64 7 Suy ra: () nB 8 =+ 8.7 =64 . Do v ậ y: () 1 PB =− () PB 1 =−
= . ⎯ ⎯ ⎯ → D 120 15
Câu 47. Cho t ứ di ệ n ABCD có =2 , =3 , = =4 , = 25 , =5. AB AC ADBC BD CD
Kho ả ng cách gi ữa hai ườ ng
th ẳ ng AC và BD b ằ ng. 315 240 A. . B. 2. C. . D. 3. 4 79 Hướng dẫn giải: Ta có: D
AD2 + AC2 =CD2 nên tam giác ACD vuông
tại A hay AD ⊥ AC . Mặt khác: AD2 +AB2 =BD2 nên
tam giác ABD vuông tại A hay AD⊥ AB. 5 2 4 5 AD ⊥ AC G AD A 3 Ta có: ⊥ AB ⊥ (ABC). 4 2 AD
C Dựng hình bình hành ACBE.Khi ó AC//(BDE). Suy ra khoảng cách cần tìm: E F B d AC BD( ,) = d AC BDE( ,()) = d A BDE( ,() (1)) .
Trong mặt phẳng (ABCD), kẻ AF BE⊥ tại F , trong
tam giác ADF, dựng ường cao AG. Ta sẽ chứng minh AG ⊥ (BDE). BE ⊥ AF
Thật vậy: ⊥ AD BE ⊥ (ADF) mà AG (ADF) AG ⊥ BE. BE AG ⊥ BE ( , )= . d AC BD AG
Vì ⊥ DF AG ⊥ (BDE) (2). Từ (1)&(2) AG HO NG XU´N NH N 600
Downloaded by mai hoa lý (lymaihoa28@gmail.com) lOMoAR cPSD| 22014077 + Đặt: + 9 315 ABBEAE = = = ( − )( − )( − ) p S ppABpBEpAE = . 2 2 ABE 4 1 15 Ta l ại có: = . S AF = . ABE AFBE 2 3 = 2
⎯Choïn⎯⎯→
Xét tam giác ADF vuông tại A có ường cao AG= ADAF. = 240 . C AD2 +AF2 79
Câu 48. Cho hai hàm số y = + − −x3 x2
3x 1, y = 2x3 +2x2 − +mx
2 có ồ thị lần lượt là (C ) ( 1 , C ) ) )
2 và m là tham số thực. Biết rằng tồn tại m ể (C1 cắt (C2 tại ba iểm phân biệt có tung ộ là y1, y2,
y3 thỏa mãn + 1 + 1 =2 , khi ó: 1 y + + + 1 4 y2 4 y3 4 3 A. m (4;7). B. m (9;12). C. m (6;9) . D. m (8;11). Hướng dẫn giải:
 Cần nhớ: Định lí Vi-ét dành cho phương trình bậc ba. + + =− 1 2 3b x x x a
Nếu phương trình ax + + + + = 3
bx2 cx d+ = 0 có ba nghiệm x x x1, 2, 3 thì xx x x xx1 2 2 3 1 3 c . a =−d xx x1 2 3 a
Phương trình hoành ộ giao iểm của (C ) ( ) 1
, C2 : x3 + x2 +(3−m x) +3= 0 (*). Giả sử
A B C, , là giao iểm của hai ồ thị hàm số ã cho thì tọa ộ A B C, , thỏa hệ y x x= + − − + − − 3 2 3x 1
2y= 2x3 2x2 6x 2. Suy ra
y= −(m 6)x−4 . y= 2x + − + + − + 3 2x mx2 2
y= 2x3 2x mx2 2 HO NG XU´N NH N 601 Downloaded by mai hoa lý (lymaihoa28@gmail.com) lOMoAR cPSD| 22014077
Khi ó, ta có: y + = − + = − + = − 1 4 (m 6)x y1; 2
4 (m 6)x2; y3
4 (m 6)x3 với x x x1, 2, 3 là nghiệm của phương trình (*). m
xx x x x x1 2 + 2 3 + 3 1 = −3
Theo ịnh lí Vi-ét bậc ba, ta có xx x =− 1 2 3 3 .
Theo giả thiết: 2 = 1 + 1 + 1 = 1 . x x + + = 1 2 x x2 3 x x3 1
m−3 . Suy ra m =9. 3 y + + + 1 4 y2 4 y3 4 m−6 x x x1 2 3 3(m−6)
Thử lại: với m =9 thì (*) trở thành x3
+x2 −6x+ =30. Phương trình này có 3 nghiệm phân biệt.
Vậy m =9 là giá trị cần tìm. ⎯Choïn⎯⎯→ D log
Câu 49. Cho x , y 0 thỏa mãn
(x+ 2y) = log( )x +log( )y . Khi ó, giá trị nhỏ nhất của biểu thức x2 4y2 P= + là: 1+2y 1+x A. 6 . B. . C. . D. . Hướng dẫn giải:
 Cần nhớ: c Cauchy-Schwarz dạng Engel (còn gọi là bất ẳng thức công Bất ẳng thứ mẫu): x ( 2 y2 + x y)2 x = y . + a
. Dấu ẳng thức xảy ra khi và chỉ khi b a +b a b
Điều kiện: x 0, y 0.
Ta có: log(x+ 2y)= log( )x +log( )y log(x+2y)= log(x y. ) x+ =2y xy (*).
Áp dụng bất ẳng thức Cauchy-Schwarz dạng Engel , ta có: P = x + ( ( 2 2y)2 x + 2y)2 . 1+ 2y 1+ x 2+ x+ 2y
Theo AM-GM, ta có: x+ 2y 2 x.2y (1)= 2 2(x+ 2y) +(x 2y)2 8(x+ 2y) x 2 y
0 (loaïi) (do iều kiện x 0, y 0). Suy ra x 2y 8 . HO NG XU´N NH N 602
Downloaded by mai hoa lý (lymaihoa28@gmail.com) lOMoAR cPSD| 22014077 x 2 y 8 (nhaän) 4
Đặt t = +x 2y 8, ta có: P t2 = − +t2 t +2 t +2
P 1 (t + +2) 4 + 24t − 52 2 4 + 24.8− =52 32 . Do vậy Pmin = 32 . 24 25 t + 2 25 25 25 25 25 5 5 25 AM GM− .8
D ấu ẳ ng th ứ c x ả y ra ( 2 t ) += 2 25 +2 y t t ⎯ ⎯ ⎯ → B
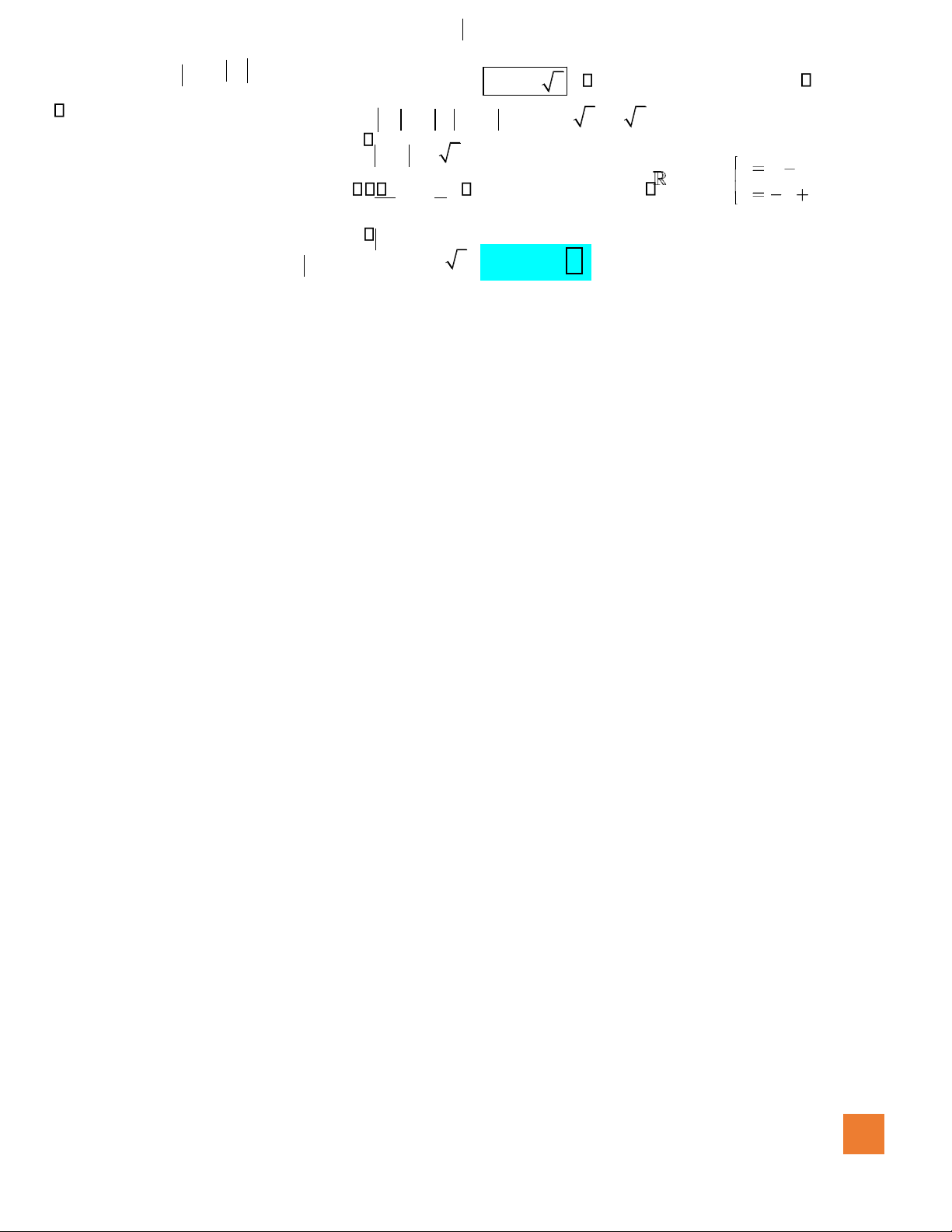
Câu 50. Cho s ố ph ứ c z th ỏ a mãn 5 −=+−+ 1 − +3 3 1 z i z i z
i . Tìm giá tr ị l ớ n nh ấ t T c ủ a 2 3 z −+ i ? 10 A. T = . B. 1 13 T =+ . C. 45 T = . D. 9 T = . 3 x = 4
1+x2y = 12+yx 8−2y = 2y 1+ 2y 1+ −8 2y = 2. x+ 2y = 8; 1 4 x = −8 y Hướng dẫn giải: 1 ;3 ,
Gọi M là iểm biểu diễn của z; gọi A(0; ), B(−1 ) (
C 1;−1). Ta thấy A là trung iểm của BC .
Ta có : MB2 + MC2 = 2MA2 + BC2 = 2MA2 +10. 2 Cauchy Schwarz−
Theo giả thiết : 5 z − = + − + − +i z 1
3i 3 z 1 i 5MA MB MC= +3 10. MB MC2 + 2 =2MA2+10
25MA2 10 2( MA2 +10) 5MA2 100 MA 2 5 (1). HO NG XU´N NH N 603 Downloaded by mai hoa lý (lymaihoa28@gmail.com) lOMoAR cPSD| 22014077
Xét z − + = − + − +2 3i(z i) ( 2
4i) − + −z i 2 4i MA+2 5 4 5 (do (1)). z − =i 2 5
Dấu " "= xảy ra khi và chỉ khi:
a = b−1 0, với z = a bi+ ; a b, . Suy ra zz
22 53i (loaïii ). −2 4
⎯Choïn⎯⎯→C
Vậy giá trị lớn nhất của z − +2 3i là T = 4 5 . HO NG XU´N NH N 604
Downloaded by mai hoa lý (lymaihoa28@gmail.com)