




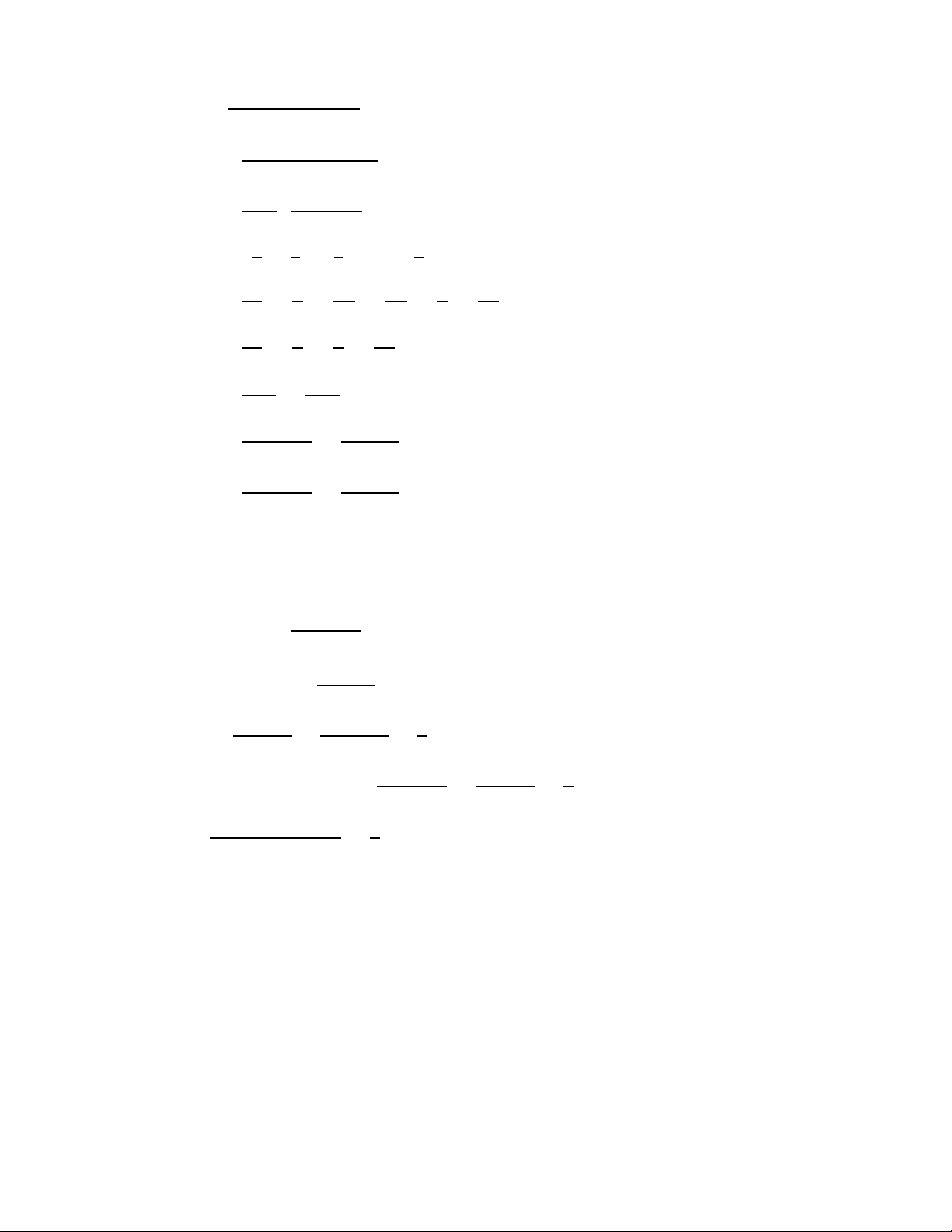
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI
TỈNH PHÚ YÊN
TRUNG HỌC CƠ SỞ CẤP TỈNH
Ngày thi: 05/03/2025
NĂM HỌC 2024 – 2025
Câu 1: (4.00 điểm) Cho biểu thức: 𝐴𝐴 = � 𝑥𝑥−1 + 1 � × √𝑥𝑥+1+1 𝑥𝑥+2√𝑥𝑥+1+1 √𝑥𝑥+1+2 √𝑥𝑥+1−1
a) Tìm điều kiện xác định của 𝐴𝐴
b) Chứng minh rằng: 𝐴𝐴 = √𝑥𝑥+1+1 √𝑥𝑥+1
c) Với giá trị nguyên nào của 𝑥𝑥 thì 𝐴𝐴 có giá trị nguyên. ⎧ 𝑎𝑎 = 𝑥𝑥 + 1 ⎪ 𝑥𝑥
Câu 2: (3.00 điểm) Cho 𝑏𝑏 = 𝑦𝑦 + 1 và biểu thức 𝐵𝐵 = 𝑎𝑎2 + 𝑏𝑏2 + 𝑐𝑐2 − 𝑎𝑎𝑏𝑏𝑐𝑐 ⎨ 𝑦𝑦 ⎪
⎩𝑐𝑐 = 𝑥𝑥𝑦𝑦 + 1 𝑥𝑥𝑦𝑦
Chứng minh rằng với mọi giá trị của 𝑥𝑥, 𝑦𝑦 thì biểu thức 𝐵𝐵 không phụ thuộc vào biến 𝑥𝑥, 𝑦𝑦. 2
Câu 3: (4.00 điểm) Giải phương trình sau: 𝑥𝑥2 + � 𝑥𝑥 � = 5 𝑥𝑥−1 4
Câu 4: (4.00 điểm)
1. Cho đường tròn tâm (O) và hai dây cung MN, PQ cắt nhau tại I với cung QN không chứa
điểm P và cung MP không chứa điểm Q. Chứng minh rằng: 𝑁𝑁𝑁𝑁𝑁𝑁
� = 1 𝑠𝑠𝑠𝑠(𝑁𝑁𝑁𝑁 � + 𝑀𝑀𝑀𝑀 � ). 2
2. Chứng minh rằng một tứ giác có tổng hai góc đối bằng 180 độ là tứ giác nội tiếp.
3. Trên đường tròn tâm (O) lấy ba điểm A, B, C sao cho 𝐴𝐴𝐵𝐵 � = 𝐵𝐵𝐵𝐵
� . Dựng hai dây cung BD
và BE, chúng cắt dây AC lần lượt tại hai điểm M và N. Chứng minh rằng.
a) Tứ giác EDMN là tứ giác nội tiếp
b) Nếu AN = CM thì tứ giác EDMN là hình gì? Vì sao?
Câu 5: (3.00 điểm) Cho hai đường tròn (O1; R) và (O2; r) tiếp xúc ngoài tại I (R > r). Một
đường thẳng d không đi qua I đồng thời tiếp xúc với (O1; R) và (O2; r) lần lượt tại hai điểm A,
B. Gọi H là chân đường cao kẻ từ O2 đến cạnh O1A. Gọi M là trung điểm của AH, đường thẳng
qua M vuông góc với AH cắt đường tròn (O1; R) tại điểm K (K khác phía I so với AH). Chứng minh rằng:
a) AK = √𝑅𝑅𝑅𝑅.
b) Đường thẳng KH tiếp xúc với (O2; r).
Câu 6: (2.00 điểm) Cho hai số 𝑥𝑥 ≥ 0, 𝑦𝑦 ≥ 0. Chứng minh rằng: (𝑥𝑥−2𝑦𝑦)(1−2𝑥𝑥𝑦𝑦) ≤ 1 (𝑥𝑥+1)2(1+2𝑦𝑦)2 4
LỜI GIẢI ĐỀ THI HỌC SINH GIỎI TỈNH PHÚ YÊN
NĂM HỌC 2024 – 2025
(ĐÁP ÁN THAM KHẢO)
Câu 1: (4.00 điểm) Cho biểu thức: 𝐴𝐴 = � 𝑥𝑥−1 + 1 � × √𝑥𝑥+1+1 𝑥𝑥+2√𝑥𝑥+1+1 √𝑥𝑥+1+2 √𝑥𝑥+1−1
a) Tìm điều kiện xác định của 𝐴𝐴
b) Chứng minh rằng: 𝐴𝐴 = √𝑥𝑥+1+1 √𝑥𝑥+1
c) Với giá trị nguyên nào của 𝑥𝑥 thì 𝐴𝐴 có giá trị nguyên. Bài giải:
𝑥𝑥 + 2√𝑥𝑥 + 1 + 1 ≠ 0
a) Để biểu thức 𝐴𝐴 xác định thì: � √𝑥𝑥 + 1 − 1 ≠ 0 𝑥𝑥 + 1 ≥ 0
Với 𝑥𝑥 + 2√𝑥𝑥 + 1 + 1 ≠ 0 thì ta có:
𝑥𝑥 + 2√𝑥𝑥 + 1 + 1 = √𝑥𝑥 + 1�√𝑥𝑥 + 1 + 2� ≠ 0
Suy ra: √𝑥𝑥 + 1 ≠ 0 hoặc √𝑥𝑥 + 1 + 2 ≠ 0 (luôn đúng)
Do đó: √𝑥𝑥 + 1 ≠ 0, suy ra 𝑥𝑥 ≠ −1
Với √𝑥𝑥 + 1 − 1 ≠ 0 thì ta có: √𝑥𝑥 + 1 ≠ 1 𝑥𝑥 + 1 ≠ 1 𝑥𝑥 ≠ 0
Với 𝑥𝑥 + 1 ≥ 0 thì ta có: 𝑥𝑥 ≥ −1
Vậy để biểu thức 𝐴𝐴 xác định thì: 𝑥𝑥 > −1 và 𝑥𝑥 ≠ 0 b) 𝐴𝐴 = � 𝑥𝑥−1 + 1 � × √𝑥𝑥+1+1 𝑥𝑥+2√𝑥𝑥+1+1 √𝑥𝑥+1+2 √𝑥𝑥+1−1 𝐴𝐴 = � 𝑥𝑥−1 + 1 � × √𝑥𝑥+1+1
√𝑥𝑥+1�√𝑥𝑥+1+2� √𝑥𝑥+1+2 √𝑥𝑥+1−1
𝐴𝐴 = 𝑥𝑥−1+√𝑥𝑥+1 × √𝑥𝑥+1+1
√𝑥𝑥+1�√𝑥𝑥+1+2� √𝑥𝑥+1−1
Đặt 𝑎𝑎 = √𝑥𝑥 + 1, khi đó biểu thức trở thành:
𝐴𝐴 = 𝑎𝑎2−2+𝑎𝑎 × 𝑎𝑎+1 = (𝑎𝑎2+𝑎𝑎−2)(𝑎𝑎+1) 𝑎𝑎(𝑎𝑎+2) 𝑎𝑎−1
𝑎𝑎(𝑎𝑎−1)(𝑎𝑎+2)
Ta có: 𝑎𝑎2 + 𝑎𝑎 − 2 = 𝑎𝑎2 − 𝑎𝑎 + 2𝑎𝑎 − 2 = 𝑎𝑎(𝑎𝑎 − 1) + 2(𝑎𝑎 − 1) = (𝑎𝑎 − 1)(𝑎𝑎 + 2)
Khi đó biểu thức trở thành:
𝐴𝐴 = (𝑎𝑎−1)(𝑎𝑎+1)(𝑎𝑎+2) = 𝑎𝑎+1 = √𝑥𝑥+1+1 (đpcm)
𝑎𝑎(𝑎𝑎−1)(𝑎𝑎+2) 𝑎𝑎 √𝑥𝑥+1
c) Ta có 𝐴𝐴 = √𝑥𝑥+1+1 = 1 + 1 √𝑥𝑥+1 √𝑥𝑥+1
Để 𝐴𝐴 có giá trị nguyên thì 1 + 1 sẽ có giá trị nguyên, mà 1 đã là số nguyên nên do đó √𝑥𝑥+1
1 cũng sẽ là số nguyên hay 1 chia hết cho √𝑥𝑥 + 1. √𝑥𝑥+1
Điều này tương đương với √𝑥𝑥 + 1 thược ước của 1.
Hay √𝑥𝑥 + 1 ∈ {±1} mà √𝑥𝑥 + 1 > 0 nên √𝑥𝑥 + 1 = 1, suy ra: 𝑥𝑥 + 1 = 1 hay 𝑥𝑥 = 0.
Nhưng để 𝐴𝐴 xác định thì 𝑥𝑥 phải thỏa mãn 𝑥𝑥 > −1 và 𝑥𝑥 ≠ 0.
Do đó không có giá trị nguyên nào xủa 𝑥𝑥 thỏa mãn để 𝐴𝐴 là số nguyên. ⎧ 𝑎𝑎 = 𝑥𝑥 + 1 ⎪ 𝑥𝑥
Câu 2: (3.00 điểm) Cho 𝑏𝑏 = 𝑦𝑦 + 1 và biểu thức 𝐵𝐵 = 𝑎𝑎2 + 𝑏𝑏2 + 𝑐𝑐2 − 𝑎𝑎𝑏𝑏𝑐𝑐 ⎨ 𝑦𝑦 ⎪
⎩𝑐𝑐 = 𝑥𝑥𝑦𝑦 + 1 𝑥𝑥𝑦𝑦
Chứng minh rằng với mọi giá trị của 𝑥𝑥, 𝑦𝑦 thì biểu thức 𝐵𝐵 không phụ thuộc vào biến 𝑥𝑥, 𝑦𝑦. Bài giải:
Ta có: 𝑎𝑎 = 𝑥𝑥 + 1 , suy ra 𝑥𝑥
𝑎𝑎2 = 𝑥𝑥2 + 1 + 2𝑥𝑥 1 = 𝑥𝑥2 + 1 + 2 𝑥𝑥2 𝑥𝑥 𝑥𝑥2
𝑏𝑏 = 𝑦𝑦 + 1 , suy ra 𝑦𝑦
𝑏𝑏2 = 𝑦𝑦2 + 1 + 2𝑦𝑦 1 = 𝑦𝑦2 + 1 + 2 𝑦𝑦2 𝑦𝑦 𝑦𝑦2
𝑐𝑐 = 𝑥𝑥𝑦𝑦 + 1 , suy ra 𝑥𝑥𝑦𝑦
𝑐𝑐2 = 𝑥𝑥𝑦𝑦2 + 1 + 2𝑥𝑥𝑦𝑦 1 = (𝑥𝑥𝑦𝑦)2 + 1 + 2 (𝑥𝑥𝑦𝑦)2 (𝑥𝑥𝑦𝑦) (𝑥𝑥𝑦𝑦)2
𝑎𝑎𝑏𝑏𝑐𝑐 = �𝑥𝑥 + 1𝑥𝑥��𝑦𝑦 + 1𝑦𝑦��𝑥𝑥𝑦𝑦 + 1𝑥𝑥𝑦𝑦� = �𝑥𝑥𝑦𝑦 + 1𝑥𝑥𝑦𝑦 + 𝑥𝑥𝑦𝑦 + 𝑦𝑦𝑥𝑥��𝑥𝑥𝑦𝑦 + 1𝑥𝑥𝑦𝑦�
= (𝑥𝑥𝑦𝑦)2 + 1 + 𝑥𝑥2 + 1 + 𝑦𝑦2 + 1 + 2 (𝑥𝑥𝑦𝑦)2 𝑥𝑥2 𝑦𝑦2 Do đó:
𝐵𝐵 = 𝑎𝑎2 + 𝑏𝑏2 + 𝑐𝑐2 − 𝑎𝑎𝑏𝑏𝑐𝑐
𝐵𝐵 = 𝑥𝑥2 + 1 + 2 + 𝑦𝑦2 + 1 + 2 + (𝑥𝑥𝑦𝑦)2 + 1 + 2 – (𝑥𝑥𝑦𝑦)2 + 1 + 𝑥𝑥2 + 1 + 𝑦𝑦2 + 1 + 2 𝑥𝑥2 𝑦𝑦2 (𝑥𝑥𝑦𝑦)2 (𝑥𝑥𝑦𝑦)2 𝑥𝑥2 𝑦𝑦2
𝐵𝐵 = 4 Vậy với mọi giá trị của 𝑥𝑥,𝑦𝑦 thì biểu thức 𝐵𝐵 không phụ thuộc vào biến 𝑥𝑥,𝑦𝑦. 2
Câu 3: (4.00 điểm) Giải phương trình sau: 𝑥𝑥2 + � 𝑥𝑥 � = 5 𝑥𝑥−1 4 Bài giải:
Thực hiện quy đòng vế trái ta có: 2
𝑥𝑥2 + � 𝑥𝑥 � = 𝑥𝑥2(𝑥𝑥−1)2 = 𝑥𝑥2�𝑥𝑥2−2𝑥𝑥+1�+𝑥𝑥2 = 𝑥𝑥4−2𝑥𝑥3+2𝑥𝑥2 𝑥𝑥−1 (𝑥𝑥−1)2 (𝑥𝑥2−2𝑥𝑥+1) 𝑥𝑥2−2𝑥𝑥+1
Khi đó phương trình trở thành: 𝑥𝑥4−2𝑥𝑥3+𝑥𝑥2 = 5 𝑥𝑥2−2𝑥𝑥+1 4
Điều đó tương đương:
4(𝑥𝑥4 − 2𝑥𝑥3 + 2𝑥𝑥2) = 5 (𝑥𝑥2 − 2𝑥𝑥 + 1)
4𝑥𝑥4 − 8𝑥𝑥3 + 8𝑥𝑥2 = 5𝑥𝑥2 − 10𝑥𝑥 + 5
4𝑥𝑥4 − 8𝑥𝑥3 + 3𝑥𝑥2 + 10𝑥𝑥 − 5 = 0
4𝑥𝑥4 + 4𝑥𝑥3 − 12𝑥𝑥3 − 12𝑥𝑥2 + 15𝑥𝑥2 + 15𝑥𝑥 − 5𝑥𝑥 − 5 = 0
4𝑥𝑥3(𝑥𝑥 + 1) − 12𝑥𝑥2(𝑥𝑥 + 1) + 15𝑥𝑥(𝑥𝑥 + 1) − 5(𝑥𝑥 + 1) = 0
(𝑥𝑥 + 1)(4𝑥𝑥3 − 12𝑥𝑥2 + 15𝑥𝑥 − 5) = 0
(𝑥𝑥 + 1)(4𝑥𝑥3 − 2𝑥𝑥2 − 10𝑥𝑥2 + 5𝑥𝑥 + 10𝑥𝑥 − 5) = 0
(𝑥𝑥 + 1)[2𝑥𝑥2(2𝑥𝑥 − 1) − 5𝑥𝑥(2𝑥𝑥 − 1) + 5(2𝑥𝑥 − 1] = 0
(𝑥𝑥 + 1)(2𝑥𝑥 − 1)(2𝑥𝑥2 − 5𝑥𝑥 + 5) = 0
Suy ra: 𝑥𝑥 + 1 = 0 hoặc 2𝑥𝑥 − 1 = 0 hoặc 2𝑥𝑥2 − 5𝑥𝑥 + 5 = 0
Với 𝑥𝑥 + 1 = 0 thì 𝑥𝑥 = −1 (𝑇𝑇𝑀𝑀)
Với 2𝑥𝑥 − 1 = 0 thì 𝑥𝑥 = 1 (𝑇𝑇𝑀𝑀) 2
Với 2𝑥𝑥2 − 5𝑥𝑥 + 5 = 0
Xét ∆ = 𝑏𝑏2 − 4𝑎𝑎𝑐𝑐 = 25 − 4.2.5 = 25 − 40 = −15 < 0
Do đó phương trình vô nghiệm.
Vậy phương trình có hai nghiệm là 𝑥𝑥 = −1, 𝑥𝑥 = 1. 2
Câu 4: (4.00 điểm)
1. Cho đường tròn tâm (O) và hai dây cung MN, PQ cắt nhau tại I với cung QN không chứa
điểm P và cung MP không chứa điểm Q. Chứng minh rằng: 𝑁𝑁𝑁𝑁𝑁𝑁
� = 1 𝑠𝑠𝑠𝑠(𝑁𝑁𝑁𝑁 � + 𝑀𝑀𝑀𝑀 � ). 2
2. Chứng minh rằng một tứ giác có tổng hai góc đối bằng 180 độ là tứ giác nội tiếp.
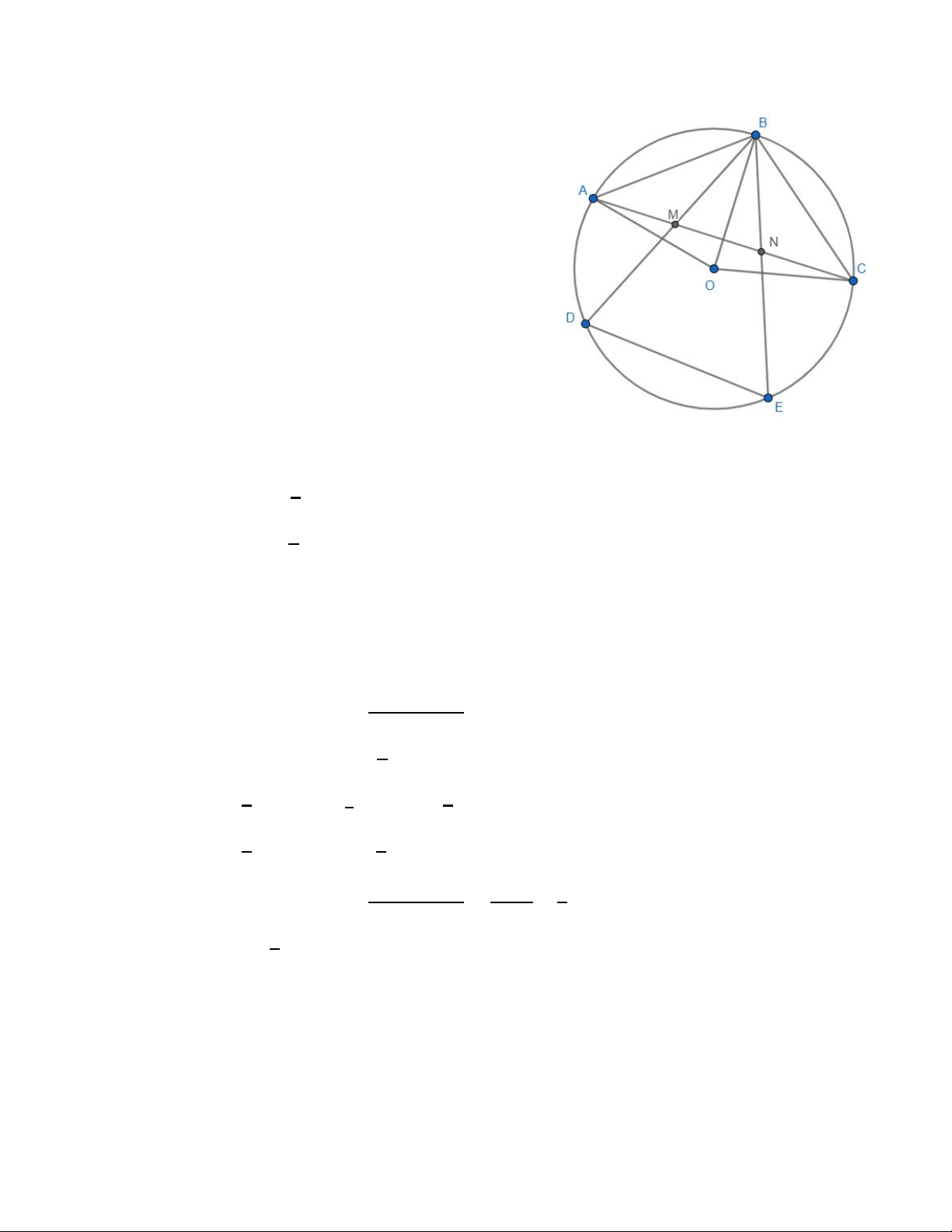
3. Trên đường tròn tâm (O) lấy ba điểm A, B, C sao cho 𝐴𝐴𝐵𝐵 � = 𝐵𝐵𝐵𝐵
� . Dựng hai dây cung BD
và BE, chúng cắt dây AC lần lượt tại hai điểm M và N. Chứng minh rằng:
a) Tứ giác EDMN là tứ giác nội tiếp
b) Nếu AN = CM thì tứ giác EDMN là hình gì? Vì sao? Bài giải:
1. Ta có 𝑁𝑁𝑁𝑁𝑁𝑁
� là góc ngoài của tam giác 𝑁𝑁𝑁𝑁𝑀𝑀, do đó: 𝑁𝑁𝑁𝑁𝑁𝑁 � = 𝑁𝑁𝑀𝑀𝑁𝑁 � + 𝑁𝑁𝑁𝑁𝑀𝑀 � Mà: 𝑁𝑁𝑀𝑀𝑁𝑁 � = 1 sđ 𝑁𝑁𝑁𝑁 � (chắn cung QN), 2 𝑁𝑁𝑀𝑀𝑁𝑁 � = 1 sđ 𝑀𝑀𝑀𝑀 � (chắn cung MP), 2
Do đó: 𝑁𝑁𝑁𝑁𝑁𝑁
� = 1 𝑠𝑠𝑠𝑠(𝑁𝑁𝑁𝑁 � + 𝑀𝑀𝑀𝑀 � ). 2 2.
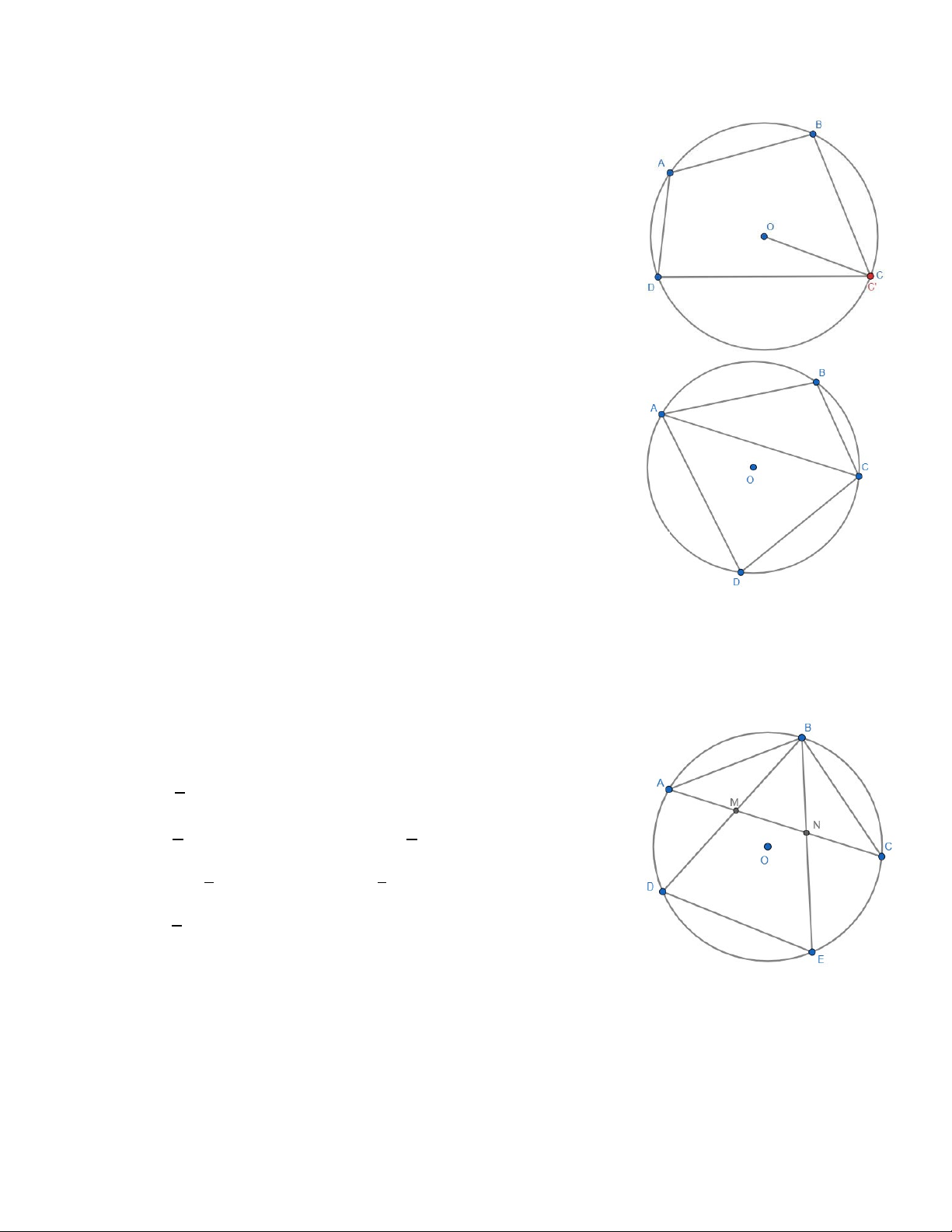
Cách 1: Dựng đường tròn (O) ngoại tiếp tam giác ABD.
Giả sử đường tròn (O) cắt OC tại C’.
Ta có tứ giác ABC’D nội tiếp đường tròn tâm O
Suy ra: 𝐵𝐵𝐴𝐴𝐵𝐵
� + 𝐵𝐵𝐵𝐵′𝐵𝐵 � = 1800 Mà 𝐵𝐵𝐴𝐴𝐵𝐵 � + 𝐵𝐵𝐵𝐵𝐵𝐵 � = 1800(𝑔𝑔𝑔𝑔)
Suy ra: 𝐵𝐵𝐵𝐵𝐵𝐵
� = 𝐵𝐵𝐵𝐵′𝐵𝐵 �
Mà 𝐵𝐵, 𝐵𝐵 cố định, nên 𝐵𝐵′ thuộc 𝑂𝑂𝐵𝐵
Từ đó suy ra 𝐵𝐵 ≡ 𝐵𝐵′
Suy ra 𝐵𝐵 thuộc đường tròn tâm O.
Vậy ABCD nội tiếp.
Cách 2: Giả sử tứ giác ABCD có 𝐵𝐵� + 𝐵𝐵� = 1800.
Ta vẽ đường tròn tâm O qua A, B, C (bao giờ cũng vẽ được
đường tròn như thế này vì A, B, C không thẳng hàng). Hai điểm
A và C chia đường tròn (O) thành hai cung ABC và AmC, trung đó 𝐴𝐴𝐴𝐴𝐵𝐵
� là cung chứa góc (1800 − 𝐵𝐵�) dựng trên đoạn thẳng AC.
Mặt khác, từ giả thiết suy ra 𝐵𝐵� = 1800 − 𝐵𝐵�. m
Vậy điểm D nằm trên 𝐴𝐴𝐴𝐴𝐵𝐵
� nói trên. Tức là tứ giác ABCD có
bốn đỉnh nằm trên đường tròn (O).
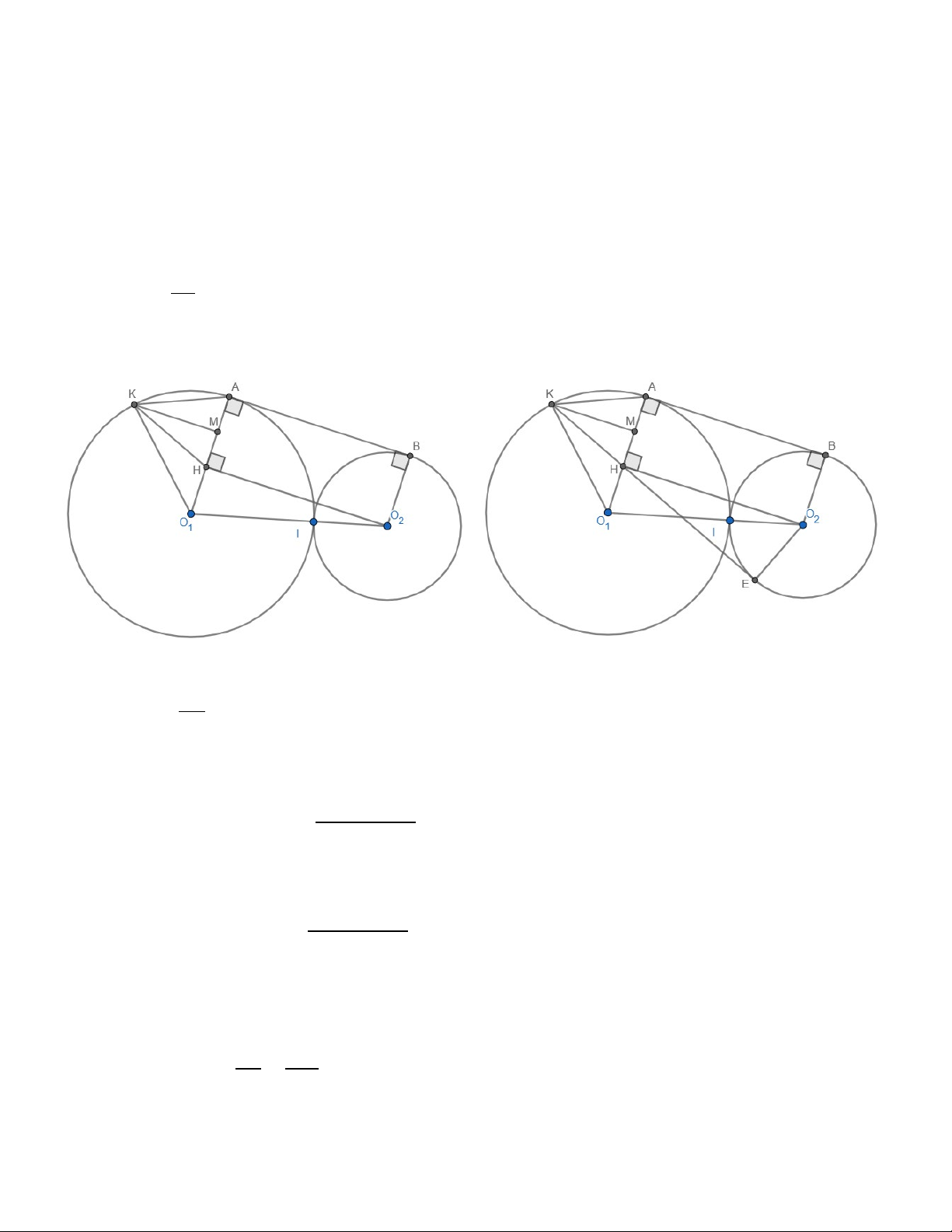
3. a) Tứ giác EDMN là tứ giác nội tiếp
Ta có 𝐵𝐵𝑀𝑀𝐵𝐵
� là góc ngoài của tam giác 𝐴𝐴𝑀𝑀𝐵𝐵, do đó: 𝐵𝐵𝑀𝑀𝐵𝐵 � = 𝑀𝑀𝐵𝐵𝐴𝐴 � + 𝑀𝑀𝐴𝐴𝐵𝐵 � Mà: 𝑀𝑀𝐵𝐵𝐴𝐴 � = 1 sđ 𝐴𝐴𝐵𝐵 � (chắn cung AD), 2 𝐵𝐵𝐴𝐴𝑀𝑀 � = 1 sđ 𝐵𝐵𝐵𝐵
� (chắn cung BC) = 1 sđ 𝐴𝐴𝐵𝐵
� (𝑠𝑠đ𝐴𝐴𝐵𝐵
� = 𝑠𝑠đ𝐵𝐵𝐵𝐵 � ), 2 2
Do đó: 𝐵𝐵𝑀𝑀𝐵𝐵
� = 1 𝑠𝑠𝑠𝑠�𝐴𝐴𝐵𝐵 � + 𝐴𝐴𝐵𝐵
� � = 1 𝑠𝑠𝑠𝑠𝐵𝐵𝐵𝐵 � . 2 2 Mà: 𝐵𝐵𝐵𝐵𝐵𝐵 � = 1 sđ 𝐵𝐵𝐵𝐵 � (chắn cung BD) 2
Suy ra: 𝐵𝐵𝐵𝐵𝐵𝐵 � = 𝐵𝐵𝑀𝑀𝐵𝐵
� , mà 𝐵𝐵𝑀𝑀𝐵𝐵 � + 𝐵𝐵𝑀𝑀𝑁𝑁 � = 1800
Suy ra: 𝐵𝐵𝐵𝐵𝐵𝐵 � + 𝐵𝐵𝑀𝑀𝑁𝑁 � = 1800
Mà tứ giác có tổng hai góc đối bằng 180 độ là tứ giác nội tiếp.
Do đó Tứ giác EDMN là nội tiếp.
b) Nếu AN = CM thì tứ giác EDMN là hình gì? Vì sao?
Ta có: 𝐴𝐴𝑂𝑂𝐵𝐵 � = sđ 𝐴𝐴𝐵𝐵
� (góc ở tâm chắn cung AB), 𝐵𝐵𝑂𝑂𝐵𝐵 � = sđ 𝐵𝐵𝐵𝐵
� (góc ở tâm chắn cung CB)
Mà: 𝑠𝑠đ𝐴𝐴𝐵𝐵
� = 𝑠𝑠đ𝐵𝐵𝐵𝐵 �
Suy ra: 𝐴𝐴𝑂𝑂𝐵𝐵 � = 𝐵𝐵𝑂𝑂𝐵𝐵 � Kết hợp: OA = OC, OB là cạnh chung
Suy ra: ∆𝐴𝐴𝑂𝑂𝐵𝐵 = ∆𝐵𝐵𝑂𝑂𝐵𝐵(𝑐𝑐. 𝑔𝑔. 𝑐𝑐), Suy ra: AB = BC (1)
Suy ra: ∆𝐴𝐴𝐵𝐵𝐵𝐵 cân tại A.
Suy ra: 𝐵𝐵𝐴𝐴𝐵𝐵 � = 𝐵𝐵𝐵𝐵𝐴𝐴 � (2)
Từ (1) và (2) kết hợp AN = CM
Suy ra: ∆𝐴𝐴𝑁𝑁𝐵𝐵 = ∆𝐵𝐵𝑀𝑀𝐵𝐵(𝑐𝑐. 𝑔𝑔. 𝑐𝑐)
Suy ra: 𝐴𝐴𝐵𝐵𝑁𝑁 � = 𝐵𝐵𝐵𝐵𝑀𝑀 � Mà: 𝐴𝐴𝐵𝐵𝑁𝑁 � = 𝐴𝐴𝐵𝐵𝑀𝑀 � + 𝑁𝑁𝐵𝐵𝑀𝑀 � 𝐵𝐵𝐵𝐵𝑀𝑀 � = 𝐵𝐵𝐵𝐵𝐵𝐵 � + 𝑁𝑁𝐵𝐵𝑀𝑀 �
Suy ra: 𝐴𝐴𝐵𝐵𝑀𝑀 � = 𝐵𝐵𝐵𝐵𝐵𝐵 � Mà: 𝐵𝐵𝐵𝐵𝐴𝐴 � = 1 sđ 𝐴𝐴𝐵𝐵 � (chắn cung AD), 2 𝐵𝐵𝐵𝐵𝐵𝐵 � = 1 sđ 𝐵𝐵𝐵𝐵 � (chắn cung EC) 2 Suy ra: sđ 𝐴𝐴𝐵𝐵 � = sđ 𝐵𝐵𝐵𝐵 � .
Ta có: ∆𝐴𝐴𝑁𝑁𝐵𝐵 = ∆𝐵𝐵𝑀𝑀𝐵𝐵(𝑐𝑐. 𝑔𝑔. 𝑐𝑐), Suy ra: MB = BN
Suy ra: ∆𝑀𝑀𝐵𝐵𝑁𝑁 cân tại N.
Suy ra: 𝐵𝐵𝑀𝑀𝑁𝑁
� = 1800−𝑀𝑀𝑀𝑀𝑀𝑀 � . 2
Ta có: 1800 − 𝑀𝑀𝐵𝐵𝑁𝑁
� = 1 (3600 − 2𝑀𝑀𝐵𝐵𝑁𝑁 � ) 2
= 1 (3600 − 2. 1 .𝑠𝑠đ𝐵𝐵𝐵𝐵
� ) = 1 (3600 − 𝑠𝑠đ𝐵𝐵𝐵𝐵 � ) 2 2 2
= 1 (𝑠𝑠đ𝐵𝐵𝐵𝐵
� 𝑙𝑙ớ𝑛𝑛) = 1 (2𝑠𝑠đ𝐵𝐵𝐵𝐵
�) = 𝑠𝑠đ𝐵𝐵𝐵𝐵 � 2 2
Suy ra: 𝐵𝐵𝑀𝑀𝑁𝑁
� = 1800−𝑀𝑀𝑀𝑀𝑀𝑀
� = 𝑠𝑠đ𝑀𝑀𝐵𝐵� = 1 sđ 𝐵𝐵𝐵𝐵 � 2 2 2 Mà 𝐵𝐵𝐵𝐵𝐵𝐵 � = 1 sđ 𝐵𝐵𝐵𝐵 � (chắn cung BE). 2
Suy ra: 𝐵𝐵𝑀𝑀𝑁𝑁 � = 𝐵𝐵𝐵𝐵𝐵𝐵 �
Mà hai góc ở vị trí đồng vị. Do đó: MN // DE.
Suy ra: EDMN là hình thang.
Ta có: 𝑀𝑀𝐵𝐵𝐵𝐵 � + 𝐵𝐵𝑀𝑀𝑁𝑁
� = 1800 (2 góc trong cũng phía thì bù nhau) Mà: 𝐵𝐵𝐵𝐵𝐵𝐵 � + 𝐵𝐵𝑀𝑀𝑁𝑁 � = 1800 (cmt)
Suy ra: 𝑀𝑀𝐵𝐵𝐵𝐵 � = 𝐵𝐵𝐵𝐵𝐵𝐵 �.
Suy ra: EDMN là hình thang cân.
Câu 5: (3.00 điểm) Cho hai đường tròn (O1; R) và (O2; r) tiếp xúc ngoài tại I (R > r). Một
đường thẳng d không đi qua I đồng thời tiếp xúc với (O1; R) và (O2; r) lần lượt tại hai điểm A,
B. Gọi H là chân đường cao kẻ từ O2 đến cạnh O1A. Gọi M là trung điểm của AH, đường thẳng
qua M vuông góc với AH cắt đường tròn (O1; R) tại điểm K (K khác phía I so với AH). Chứng minh rằng:
a) AK = √𝑅𝑅𝑅𝑅.
b) Đường thẳng KH tiếp xúc với (O2; r). Bài giải: Hình 1 Hình 2
a) AK = √𝑹𝑹𝑹𝑹.
Ta có: O1A = O1K (= R)
Suy ra: Tam giác O1AK cân tại O1.
Suy ra: 𝐾𝐾𝑂𝑂1𝐴𝐴
� = 1800−𝑂𝑂1𝐴𝐴𝐴𝐴 � (1). 2
Xét tam giác AKH có KM vừa là đường cao, đường trung tuyến.
Do đó: tam giác AKH cân tại K.
Suy ra: 𝐴𝐴𝐾𝐾𝐴𝐴
� = 1800−𝑂𝑂1𝐴𝐴𝐴𝐴 � (2). 2
Từ (1) và (2), ta suy ra: 𝐾𝐾𝑂𝑂1𝐴𝐴 � = 𝐴𝐴𝐾𝐾𝐴𝐴 � .
Kết hợp: 𝑂𝑂1𝐴𝐴𝐾𝐾 � là góc chung.
Do đó: ∆𝐴𝐴𝐾𝐾𝐴𝐴~∆𝐴𝐴𝑂𝑂1𝐾𝐾 (𝑔𝑔. 𝑔𝑔).
Suy ra: 𝐴𝐴𝐴𝐴 = 𝐴𝐴𝑂𝑂1. 𝐴𝐴𝐴𝐴 𝐴𝐴𝐴𝐴
Suy ra: 𝐴𝐴𝐾𝐾2 = 𝐴𝐴𝐴𝐴. 𝐴𝐴𝑂𝑂1.
Ta có: AB tiếp xúc với (O1; R) và (O2; r)
Do đó: 𝐴𝐴𝐴𝐴𝐵𝐵
� = 𝐴𝐴𝐴𝐴𝑂𝑂2
� = 𝐴𝐴𝐵𝐵𝑂𝑂2 � = 900.
Suy ra: tứ giác AHO2B là hình chữ nhật. Suy ra: AH = BO2 = r.
Do đó: 𝐴𝐴𝐾𝐾2 = 𝐴𝐴𝐴𝐴. 𝐴𝐴𝑂𝑂1= Rr.
Suy ra: 𝐴𝐴𝐾𝐾 = √𝑅𝑅𝑅𝑅.
b) Đường thẳng KH tiếp xúc với (O2; r).
Kẻ OE vuông góc KH, khi đó ta chỉ cần chứng minh E thuộc (O2; r) hay OE = r.
Ta có: MK // O2H (cũng vuông góc với O1A).
Khi đó: 𝑀𝑀𝐾𝐾𝐴𝐴
� = 𝑂𝑂2𝐴𝐴𝐵𝐵
� (2 góc ở vị trí đồng vị).
Kết hợp 𝐾𝐾𝑀𝑀𝐴𝐴
� = 𝐴𝐴𝐵𝐵𝑂𝑂2 � = 900.
Suy ra: ∆𝑀𝑀𝐾𝐾𝐴𝐴~∆𝐵𝐵𝐴𝐴𝑂𝑂2 (𝑔𝑔. 𝑔𝑔)
Suy ra: 𝑀𝑀𝐴𝐴 = 𝐴𝐴𝐴𝐴 . (*)
𝐵𝐵𝑂𝑂2 𝑂𝑂2𝐴𝐴
Ta có: AK = HK (tam giác KHA cân tại K).
Mà 𝐴𝐴𝐾𝐾 = √𝑅𝑅𝑅𝑅, suy ra: HK = 𝐴𝐴𝐾𝐾 = √𝑅𝑅𝑅𝑅.
Ta có: O1H = O1A – AH = R – r.
O1O2 = O1I + O2I = R + r.
Ta có: tam giác O1HO2 vuông tại H, theo định lý Pythagore ta có: O 2 1O2 = O1H2 + O2H2 Suy ra: O 2
2H2 = O1O2 – O1H2 = (R + r)2 – (R – r)2
O2H2 = (R + r + R – r)( R + r – R + r) O2H2 = 4Rr
O2H = 2√𝑅𝑅𝑅𝑅, 𝑟𝑟
Từ (*), ta suy ra: EO 2.2.√𝑅𝑅𝑅𝑅
2 = 𝑀𝑀𝐴𝐴.𝑂𝑂2𝐴𝐴 = = r 𝐴𝐴𝐴𝐴 √𝑅𝑅𝑅𝑅
Từ đó, ta sẽ suy ra E thuộc (O2; r)
Mà KH lại vuông góc OE.
Do đó: KH tiếp xúc với (O2; r).
Câu 6: (2.00 điểm) Cho hai số 𝑥𝑥 ≥ 0, 𝑦𝑦 ≥ 0. Chứng minh rằng: (𝑥𝑥−2𝑦𝑦)(1−2𝑥𝑥𝑦𝑦) ≤ 1 (𝑥𝑥+1)2(1+2𝑦𝑦)2 4 Bài giải:
Ta có: 𝑥𝑥 − 2𝑦𝑦 = 𝑥𝑥 + 1 − 1 − 2𝑦𝑦 = (𝑥𝑥 + 1) − (1 + 2𝑦𝑦)
1 − 2𝑥𝑥𝑦𝑦 = 1 + 𝑥𝑥 − 𝑥𝑥 − 2𝑥𝑥𝑦𝑦 = (𝑥𝑥 + 1) − 𝑥𝑥(1 + 2𝑦𝑦)
Đặt 𝑎𝑎 = 𝑥𝑥 + 1, 𝑏𝑏 = 1 + 2𝑦𝑦, khi đó:
Ta có: 𝑥𝑥 − 2𝑦𝑦 = (𝑥𝑥 + 1) − (1 + 2𝑦𝑦) = 𝑎𝑎 − 𝑏𝑏
1 − 2𝑥𝑥𝑦𝑦 = (𝑥𝑥 + 1) − 𝑥𝑥(1 + 2𝑦𝑦) = 𝑎𝑎 − (𝑎𝑎 − 1)𝑏𝑏 = 𝑎𝑎 − 𝑎𝑎𝑏𝑏 + 𝑏𝑏
Ta có: (𝑥𝑥−2𝑦𝑦)(1−2𝑥𝑥𝑦𝑦) (𝑥𝑥+1)2(1+2𝑦𝑦)2
= (𝑎𝑎−𝑏𝑏)(𝑎𝑎−𝑎𝑎𝑏𝑏+𝑏𝑏) (𝑎𝑎𝑏𝑏)2
= 𝑎𝑎−𝑏𝑏 . 𝑎𝑎−𝑎𝑎𝑏𝑏+𝑏𝑏 𝑎𝑎𝑏𝑏 𝑎𝑎𝑏𝑏 = �1 − 1 𝑏𝑏
𝑎𝑎� . �1𝑏𝑏 – 1 + 1𝑎𝑎� = 1 + 1 − 1 + 1 − 1 𝑏𝑏2 − 1𝑏𝑏 𝑎𝑎𝑏𝑏 𝑎𝑎𝑏𝑏 𝑎𝑎 𝑎𝑎2 = 1 + 1 − 1 𝑏𝑏2 − 1𝑏𝑏 𝑎𝑎 𝑎𝑎2 = 1−𝑏𝑏 𝑏𝑏2 + 𝑎𝑎−1 𝑎𝑎2 = 1−1−2𝑦𝑦
(1+2𝑦𝑦)2 + 𝑥𝑥+1−1 (𝑥𝑥+1)2 = −2𝑦𝑦 (1+2𝑦𝑦)2 + 𝑥𝑥 (𝑥𝑥+1)2
Ta có: 𝑦𝑦 ≥ 0, suy ra: 2 𝑦𝑦 ≥ 0 Do đó: −2 𝑦𝑦 ≤ 0
Ta có: (1 + 2𝑦𝑦)2 ≥ 0, mà (1 + 2𝑦𝑦)2 ở dưới mẫu nên (1 + 2𝑦𝑦)2 > 0.
Suy ra: −2𝑦𝑦 ≤ 0 (1) (1+2𝑦𝑦)2
Lại có: = 𝑥𝑥. 1 ≤ (𝑥𝑥+1)2. 4
Do đó: 𝑥𝑥 ≤ (𝑥𝑥+1)2 ≤ 1 (2) (𝑥𝑥+1)2 4(𝑥𝑥+1)2 4
Từ (1) và (2), ta suy ra: −2𝑦𝑦 (1+2𝑦𝑦)2 + 𝑥𝑥 (𝑥𝑥+1)2 ≤ 14
Hay (𝑥𝑥−2𝑦𝑦)(1−2𝑥𝑥𝑦𝑦) .
(𝑥𝑥+1)2(1+2𝑦𝑦)2 ≤ 14
Dấu bằng xảy ra khi và chỉ khi: �𝑥𝑥 = 1 𝑦𝑦 = 0




