




Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THCS CẤP TỈNH S ÓC TRĂNG Năm học 2024-2025 ĐỀ CHÍNH THỨC Môn: TOÁN
(Thời gian làm bài 150 phút, không kể thời gian phát đề)
Đề thi này có 01 trang 2 x 2 − x
Bài 1: (4,0 điểm) Cho biểu thức P = +
+ 2 x − 5 với x ≥ 0 và x ≠ 1, x ≠ 9. x − 4 x + 3 x −1 x − 3
a) Rút gọn biểu thức P.
b) Tìm tất cả các số nguyên x sao cho P nhận giá trị là số chẵn.
Bài 2: (4,0 điểm)
a) Một con ếch đang ở giữa một bảng có 5× 5 ô vuông được tô hai màu
trắng và đen (như hình vẽ). Mỗi bước nhảy con ếch nhảy sang một ô khác có
chung cạnh hoặc chung đỉnh với ô trước đó. Tính xác suất sau hai bước nhảy con ếch ở ô màu đen.
b) Tìm tất cả các số nguyên x, y thoả mãn x ( x + 2)(2x +1)(2x + 5) = y2.
Bài 3: (4,0 điểm) . a) Giải hệ phương trình
��3𝑥𝑥 + 2𝑦𝑦 + 5 − �𝑥𝑥 + 𝑦𝑦 = 2 4𝑥𝑥 + 3𝑦𝑦 = 5
b) Trên một cánh đồng trống tiếp giáp với một bờ
sông, người nông dân dự định rào lại cánh đồng hình chữ
nhật để trồng cây với diện tích cần rào là 180 000 m2 và
không cần rào phía giáp bờ sông. Người nông dân cần chọn
các kích thước cần rào như thế nào để độ dài của hàng rào là nhỏ nhất?
Bài 4: (4,0 điểm) Cho hai đường tròn (O; R) và (O′; R′) cắt nhau tại A và B ( R > R′). Vẽ hai tiếp
tuyến chung của hai đường tròn đó, chúng cắt nhau ở S. Gọi C và M là hai tiếp điểm của hai tiếp tuyến
trên với (O; R), D là tiếp điểm của tiếp tuyến SC với (O′; R′) (ba điểm A, C và D thuộc cùng nửa
mặt phẳng bờ SO ). Gọi F là giao điểm của tia BA với CD.
a) Chứng minh FC 2 = FA.FB.
b) Tia SA cắt (O; R) tại E, SO cắt CM tại H. Chứng minh tứ giác AHOE nội tiếp.
c) Chứng minh ADC = CAE.
Bài 5: (4,0 điểm)
a) Cho tam giác ABC nội tiếp đường tròn tâm O, ngoại tiếp đường tròn tâm I. Tia AI cắt BC
tại A1 và cắt đường tròn (O) tại A2. Tương tự, lần lượt ta thu được các điểm B1, B2 và C1, C2. Chứng
minh rằng A2 B = A2C = A2 I và A2 B + A2C + B2 A + B2C + C2 A + C2 B ≥ 12. A1 A2 B1B2 C1C2
b) Trên bàn có 2026 tấm thẻ được đánh số từ 1 đến 2026. Hai bạn An và Bình tiến hành trò
chơi bằng cách thay phiên nhau lấy thẻ, đến lượt chơi mỗi bạn sẽ lấy một thẻ cho đến khi hết tấm thẻ
trên bàn. Sau đó mỗi người cộng số trên các thẻ mà mình có, ai ra số chẵn sẽ thắng. Nếu An chơi
trước thì bạn nào có chiến thuật để luôn thắng và chiến thuật đó như thế nào? ------ Hết ------
Họ tên thí sinh: .................................................................. Số báo danh: …………………….
Chữ ký của Giám thị 1: .....................................; Chữ ký của Giám thị 2: …...........................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THCS CẤP TỈNH SÓC TRĂNG Năm học 2024-2025 ĐỀ CHÍNH THỨC Môn: TOÁN
(Thời gian làm bài 150 phút, không kể thời gian phát đề) HƯỚNG DẪN CHẤM
(Hướng dẫn chấm này có 05 trang) Bài Đáp án Điểm Cho biểu thức P = 2 x
+ 2 − x + 2 x − 5 với x ≥ 0 và x ≠ 1, x ≠ 9. 4,0 x − 4 x + 3 x −1 x − 3
a) Rút gọn biểu thức P. 3,0 2 x
2 − x 2 x − 5 P = ( +
x −1)( x − 3) + x −1 x − 3
2 x + (2 − x )( x − 3) + (2 x − 5)( x −1) P =
( x −1)( x − 3)
P = 2 x − x + 5 x − 6 + 2x − 7 x + 5
( x −1)( x − 3) 3,0 x −1
P = ( x −1)( x − 3)
( x −1)( x + 1)
1 P = ( x −1)( x − 3) P = x +1 . x − 3
b) Tìm tất cả các số nguyên x sao cho P nhận giá trị là số chẵn. 1,0
P = x − 3 + 4 = 1+ 4 0,25 x − 3 x − 3
P nhận giá trị là số chẵn khi x − 3 là ước số của 4. Ta có các trường hợp sau:
+ x − 3 = 4 hay x = 49
+ x − 3 = −4 hay x = −1 (vô nghiệm)
+ x − 3 = 2 hay x = 25 0,5
+ x − 3 = −2 hay x =1 (loại)
+ x − 3 =1 hay x = 16
+ x − 3 = −1 hay x = 4
Thử lại ta thấy P nhận giá trị là số chẵn khi x = 49. 0,25 2
a) Một con ếch đang ở giữa một bảng có 5×5 ô vuông
được tô hai màu trắng và đen (như hình vẽ). Mỗi bước
nhảy con ếch nhảy sang một ô khác có chung cạnh hoặc
chung đỉnh với ô trước đó. Tính xác suất sau hai bước 2,0
nhảy con ếch ở ô màu đen.
Số các kết quả có thể xảy ra là n (Ω) = 8.8 = 64 0,5
Gọi A là biến cố sau hai bước nhảy con ếch ở ô được tô màu đen
Số các kết quả thuận lợi cho biến cố A là n ( A) = 8.4 = 32 1,0 n ( A)
2 Xác suất của biến cố A là P ( A) = = 32 = 0,5. 0,5 n (Ω) 64
b) Tìm tất cả các số nguyên x, y thoả mãn x(x + 2)(2x +1)(2x + 5) = y2 (1). 2,0
(2x2 + 5x)(2x2 + 5x + 2) = y2 0,25
Đặt t = 2x2 + 5x +1
Phương trình (1) trở thành (t −1)(t +1) = y2 0,5
(t − y)(t + y) = 1 0,25
t + y = t − y hay y = 0 0,25
Thay vào phương trình (1) ta được các nghiệm nguyên là x1 = 0, x2 = −2 0,5
Vậy phương trình đã cho có nghiệm nguyên là (0; 0), (−2; 0). 0,25
a) Giải hệ phương trình 2,0
��3𝑥𝑥 + 2𝑦𝑦 + 5 − �𝑥𝑥 + 𝑦𝑦 = 2 4𝑥𝑥 + 3𝑦𝑦 = 5 3 Điều kiện: 0,25
�3𝑥𝑥 + 2𝑦𝑦 + 5 ≥ 0 𝑥𝑥 + 𝑦𝑦 ≥ 0 Đặt:
𝑎𝑎 = �3𝑥𝑥 + 2𝑦𝑦 + 5 0,25 �
(𝑎𝑎 ≥ 0; 𝑏𝑏 ≥ 0)
𝑏𝑏 = �𝑥𝑥 + 𝑦𝑦
Hệ phương trình đã cho trở thành � 𝑎𝑎 − 𝑏𝑏 = 2 𝑎𝑎2 + 𝑏𝑏2 = 10 0,25 � 𝑎𝑎 = 𝑏𝑏 + 2
(𝑏𝑏 + 2)2 + 𝑏𝑏2 = 10 hay � 𝑎𝑎 = 𝑏𝑏 + 2
𝑏𝑏2 + 2𝑏𝑏 − 3 = 0 0,5 � 𝑎𝑎 = 𝑏𝑏 + 2
𝑏𝑏 = 1 ℎ𝑜𝑜ặ𝑐𝑐 𝑏𝑏 = −3(𝑙𝑙𝑜𝑜ạ𝑖𝑖) suy ra �𝑎𝑎 = 3 𝑏𝑏 = 1 0,5 3
Khi đó �3𝑥𝑥 + 2𝑦𝑦 + 5 = 3 �
hay �3𝑥𝑥 + 2𝑦𝑦 = 4 0,5 �𝑥𝑥 + 𝑦𝑦 = 1
𝑥𝑥 + 𝑦𝑦 = 1 suy ra � 𝑥𝑥 = 2
𝑦𝑦 = −1 ( 𝑛𝑛ℎậ𝑛𝑛)
Vậy hệ phương trình đã cho có nghiệm (2;-1)
b) Trên một cánh đồng trống
tiếp giáp với một bờ sông,
người nông dân dự định rào
lại cánh đồng hình chữ nhật
để trồng cây với diện tích 2,0 cần rào là 180 000 m2 và
không cần rào phía giáp bờ
sông. Người nông dân cần
chọn các kích thước cần rào như thế nào để độ dài của hàng rào là nhỏ nhất?
Gọi x, y (m) là hai kích thước của hàng rào ( x, y > 0) 0,25
Ta có diện tích cần rào là 180 000 m2 nên xy = 180 000 hay y = 180 000 0,25 x
Tổng độ dài của hàng rào là C = x + 2 y = x + 2.180 000 = x + 360 000 0,5 x x
Áp dụng bất đẳng thức Cauchy, ta có
C = x + 360 000 ≥ 2 x. 360 000 = 1200 0,5 x x
Dấu “=” xảy ra khi và chỉ khi x = 360 000 hay x = 600 0,25 x
Vậy hàng rào có độ dài nhỏ nhất là 1200 m, khi hai kích thước là 600 m và 300 m. 0,25
Cho hai đường tròn (O; R) và (O′; R′) cắt nhau tại A và B (R > R′). Vẽ hai tiếp
tuyến chung của hai đường tròn đó, chúng cắt nhau ở
S. Gọi C và M là hai tiếp
điểm của hai tiếp tuyến trên với (O; R), D là tiếp điểm của tiếp tuyến SC với 4,0
(O′; R′) (ba điểm A, C và D thuộc cùng nửa mặt phẳng bờ SO ). Gọi F là giao
điểm của tia BA với CD.
a) Chứng minh FC 2 = FA.FB. 1,5 C E F D A S 4 O H O' B M
Xét ∆BFC và ∆CFA, ta có AFC chung 0,25
CBA = ACF = 1 AC 0,5 2 4
∆BFC ∽∆CFA 0,25
FB = FC hay FC 2 = FA.FB. 0,5 FC FA
b) Tia SA cắt (O; R) tại E, SO cắt CM tại H. Chứng minh tứ giác AHOE nội 1,5 tiếp.
Ta có SC = SM (tính chất hai tiếp tuyến cắt nhau)
Và OC = OM (= R) 0,25
Nên SO là đường trung trực của đoạn CM nên SO ⊥ CM
SO và SO ' là hai tia phân giác của CSM nên ba điểm S, O, O′ thẳng hàng 0,5
∆SCO vuông tại C, CH đường cao nên SC 2 = SH .SO (1)
Ta có SCA = SEC = 1 AC và ASC chung 2
Nên ∆CSA∽∆ESC 0,5
SC = SA hay SC 2 = SE.SA (2) SE SC
Từ (1) và (2), ta được SE.SA = SH.SO
Do đó tứ giác AHOE nội tiếp (phương tích). 0,25
c) Chứng minh ADC = CAE. 1,0
Ta có OC //O′D (cùng ⊥ SC ) nên SO′ = O′D = R′ = O′A SO OC R OE 0,25
Do đó O′A//OE
DO′A = COE (cạnh tương ứng song song song) (3) 0,25
Mà ADC = 1 DO′A (cùng chắn AD ) và CAE = 1 COE (cùng chắn CE ) (4) 0,25 2 2
Từ (3) và (4), ta được ADC = CAE. 0,25
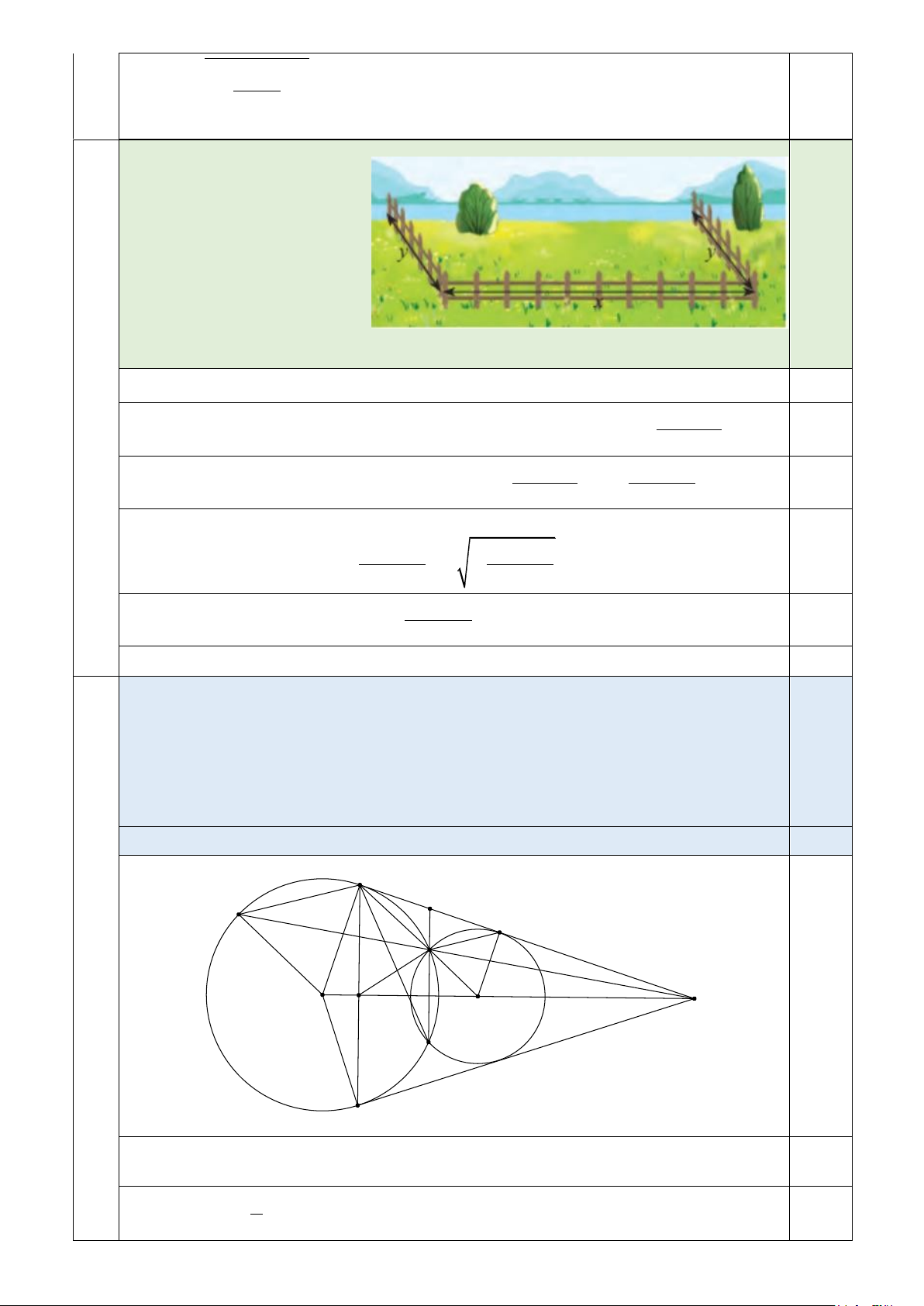
a) Cho tam giác ABC nội tiếp đường tròn tâm O, ngoại tiếp đường tròn tâm I.
Tia AI cắt BC tại A1 và cắt đường tròn (O) tại A2. Tương tự, lần lượt ta thu
được các điểm B1, B2 và C1, C2 . Chứng minh rằng A2 B = A2C = A2 I và 2,0
A2 B + A2C + B2 A + B2C + C2 A + C2 B ≥ 12. A1 A2 B1B2 C1C2 A
Ta có BAA = A AC nên A 2 2
2 B = A2C (1) 0,25
Mà A BI = A BC + CBI = A AC + ABI 2 2 2 5
= BAI + ABI = BIA2 I O Do đó ∆A
2 BI cân tại A2 nên A2 B = A2 I (2)
Từ (1) và (2), ta được A2 B = A2C = A2 I. 0,75 B A C 1 5 A2
Áp dụng định lý Ptôlêmê cho tứ giác nội tiếp CA2BA, ta được A
2C.AB + A2B.AC = BC.AA2 hay A2C ( AB + AC ) = BC.AA2
Do đó AA2 = AB + AC A 2C BC
Mà A2 B + A2C = 2.A2C 0,5 A1 A2 A1 A2
Mặt khác CA A ∽ ACA nên A C 2 = AA2 1 2 2 A A A C 1 2 2 2( AB + AC )
Từ đó, ta được A B + A C 2 2 = A1 A2 BC 2( AB + BC ) 2( AC + BC )
Tương tự, ta có B A + B C 2 2 =
và C2 A + C2 B = B1B2 AC C1C2 AB
Khi đó A2 B + A2C + B2 A + B2C + C2 A + C2 B = 2 AB + AC + AB + BC + AC + BC 0,25 A A B B C C BC AC AB 1 2 1 2 1 2 = 2 AB
+ AC + AB + BC + AC + BC (3) BC BC AC AC AB AB
Áp dụng bất đẳng thức Cauchy, ta có AB
+ BC ≥ 2; AC + BC ≥ 2; AB + AC ≥ 2 BC AB BC AC AC AB
Do đó AB + AC + AB + BC + AC + BC ≥ 6 (4) 0,25 BC BC AC AC AB AB
Từ (3) và (4), ta được A B + A C A + B C A + C B 2 2 + B2 2 + C2 2 ≥ 12. A1 A2 B1B2 C1C2
b) Trên bàn có 2026 tấm thẻ được đánh số từ 1 đến 2026. Hai bạn An và Bình tiến
hành trò chơi bằng cách thay phiên nhau lấy thẻ, đến lượt chơi mỗi bạn sẽ lấy một
thẻ cho đến khi hết tấm thẻ trên bàn. Sau đó mỗi người cộng số trên các thẻ mà 2,0
mình có, ai ra số chẵn sẽ thắng. Nếu An chơi trước thì bạn nào có chiến thuật để
luôn thắng và chiến thuật đó như thế nào?
An là người có chiến thuật để luôn thắng
An rút trước và rút một thẻ đánh số chẵn
Trên bàn còn lại 1013 thẻ đánh số lẻ và 1012 thẻ đánh số chẵn
Sau đó An sẽ rút các thẻ đánh số cùng tính chẵn cùng lẻ với Bình đã rút 2,0
Khi đó An sẽ luôn có 506 thẻ đánh số lẻ và 507 thẻ đánh số chẵn. Suy ra An luôn
có chiến thuật chiến thắng. --- HẾT --- 6
Xem thêm: ĐỀ THI HSG TOÁN 9
https://thcs.toanmath.com/de-thi-hsg-toan-9
Document Outline
- De thi HSG Toan 9 tỉnh Sóc Trăng 24-25
- Môn: TOÁN
- HƯỚNG DẪN CHẤM
- HSG 9





