Đề chọn học sinh giỏi tỉnh Toán THCS năm 2024 – 2025 sở GD&ĐT Thanh Hóa

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THANH HÓA NĂM HỌC 2024 - 2025 ĐỀ CHÍNH THỨC
MÔN THI: TOÁN - THCS.
Thời gian làm bài 150 phút, không kể thời gian phát đề.
(Đề thi có 02 trang, gồm 10 câu).
Câu 1 (2,0 điểm). Rút gọn biểu thức: 2 2  a − b a − b  a + b A =  +  ⋅ 
(với a > b > 0 ). 2 2  2 2
 a − b + a + b
a − b − a + b  a − b
Câu 2 (2,0 điểm). Cho a, b là các số thực dương phân biệt thỏa mãn: 8 4 2 8b 4b 2b b + + + = 4 và 2 2 a = 2025 + b . 8 8 4 4 2 2 a − b a + b a + b a + b
Tính giá trị biểu thức: 2
P = (a − b −10) + 2000 . 13 
x −1 + 9 y + 2 =  16x
Câu 3 (2,0 điểm). Giải hệ phương trình: ( . 2  x + x  ) 2
x − y + 3 = 2x + x + y +1
Câu 4 (2,0 điểm). Cho các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9 . Gọi X là tập hợp các số
tự nhiên có 5 chữ số khác nhau viết được từ các chữ số nói trên. Lấy ngẫu nhiên
một số từ tập hợp X . Tính xác suất của biến cố A : “Số lấy ra là số lớn hơn 59000” .
Câu 5 (2,0 điểm). Tìm tất cả các nghiệm nguyên của phương trình: ( − y − )2 = ( 2 2x 2
7 x − 2y − y − ) 1 .
Câu 6 ( 2,0 điểm). Cho số tự nhiên n ≥ 2 và số nguyên tố p . Chứng minh rằng nếu
p −1 chia hết cho n và 6
n −1 chia hết cho p thì ít nhất một trong hai số p − n và
p + n là số chính phương.
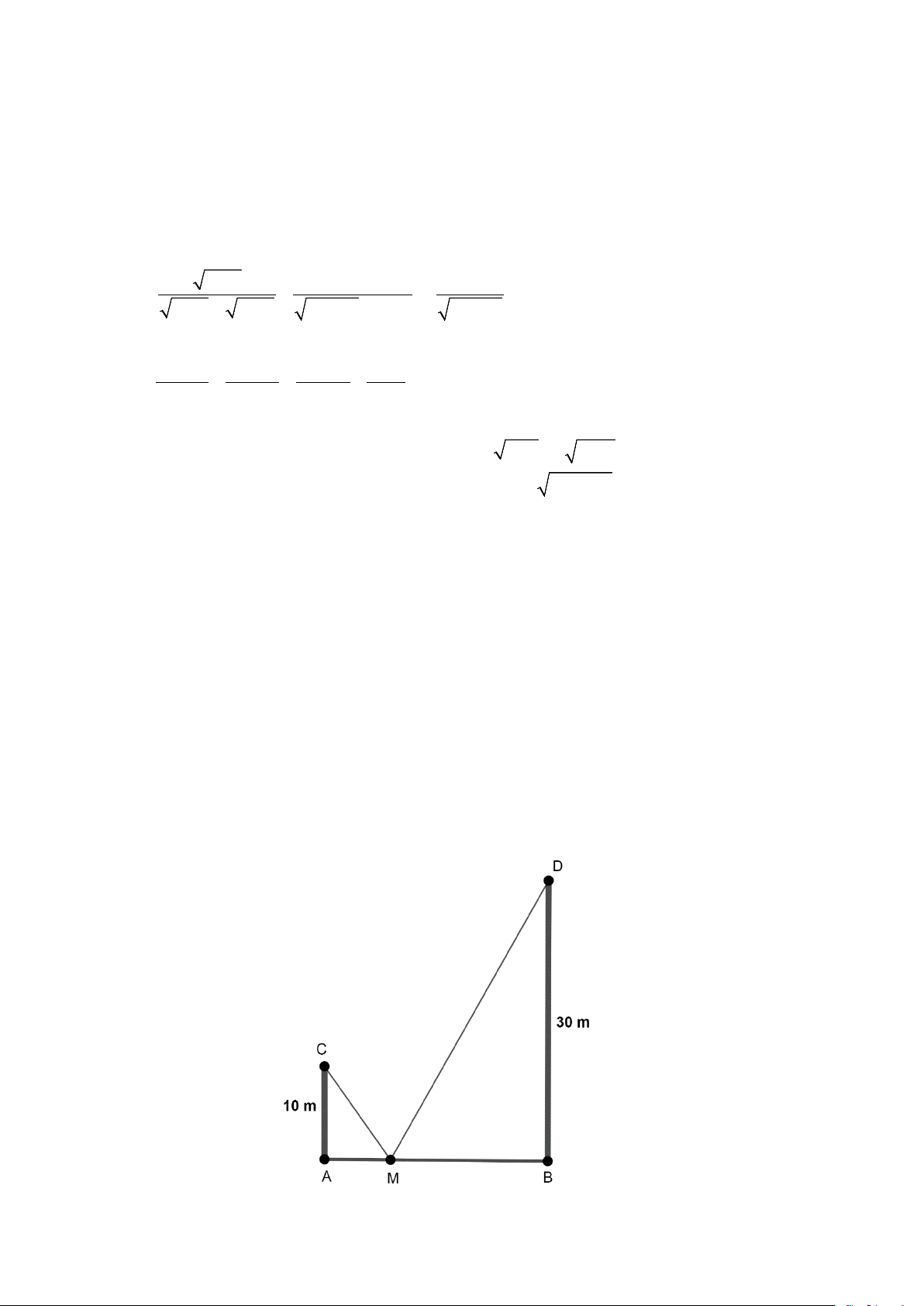
Câu 7 (1,5 điểm). Có hai chiếc cọc cao 10m và 30m đặt vuông góc với mặt đất tại
hai vị trí A và B . Biết khoảng cách giữa hai cọc bằng 24m . Người ta đặt một cái
chốt ở vị trí M trên mặt đất, nằm giữa hai chân cọc để giăng dây nối đến hai đỉnh
C và D của hai cọc (như hình vẽ). Hỏi người ta phải đặt chốt ở vị trí cách A một
khoảng bằng bao nhiêu trên mặt đất để tổng độ dài của hai sợi dây đó là ngắn nhất? Trang 1
Câu 8 (3,5 điểm). Cho tam giác nhọn ABC nội tiếp đường tròn (O) , ba đường cao
AD, BF,CE cắt nhau tại H , vẽ OK ⊥ BC (K ∈ BC) . Gọi I là trung điểm của AH , gọi
J là giao điểm của AH và EF , kẻ đường kính AP của đường tròn (O) . a. Chứng minh: 1
OK = AH và IK đi qua trung điểm của EF . 2
b. Đường thẳng qua B song song với AC cắt đường thẳng CE tại S . Chứng minh: 2
IF = IJ.ID và KS / /CJ .
Câu 9 (1,5 điểm). Cho tam giác ABC có ba cạnh tiếp xúc với đường tròn (I ) . Gọi
E, F lần lượt là tiếp điểm của đường tròn (I ) với AC và AB . Gọi M , N lần lượt là
trung điểm của BC và AC . Chứng minh ba đường thẳng BI,MN,EF đồng quy.
Câu 10 (1,5 điểm). Cho x, y, z là các số thực dương thỏa mãn: xyz(x + y + z) = 3. Chứng minh rằng: 1
x + y + z ≤
(x −2x+4)2 (y −2y+4)2 (z −2z +4)2 2 2 2 5 5 5 . 243
------------------------ HẾT ------------------------
Thí sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm
Họ và tên thí sinh:.............................................; Số báo danh:.................................................
Chữ ký của Giám thị 1:.....................................; Chữ ký của Giám thị 2:................................. Trang 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THANH HÓA NĂM HỌC 2024 - 2025
ĐÁP ÁN, THANG ĐIỂM CHẤM
ĐỀ THI MÔN: TOÁN - THCS.
(Hướng dẫn chấm gồm 10 trang). Câu Nội dung đáp án Điểm Rút gọn biểu thức: Câu 2 2  a − b a − b  a + b 2,0 1 A =  +  ⋅ 
(với a > b > 0 ). 2 2  2 2
 a − b + a + b
a − b − a + b  a − b
Với a > b > 0 , ta có: 2 2 0,25  a − b a − b  a + b A =  +  ⋅  2 2  2 2
 a − b + a + b
a − b − a + b  a − b   2 2 a − b a − b a + b A =  +  ⋅
 a − b + a + b
(a −b)(a +b) 2 2 − (a − b) a − b   2 2  a − b a − b  a + b 0,25 A =  +  ⋅   2 2
 a − b + a + b
a + b − a − b  a − b
 a −b ( a +b − a −b) a −b ( a +b + a −b) 2 2 0,25 a + b A   = ( + ⋅ 
a + b) − (a −b)
(a +b)−(a −b)  2 2 a − b   2 2 2 2 2 2
a − b − a + b + a − b + a − b a + b A = ⋅ 2 2 2b a − b 0,5 2 2 2 2 2 a − b a + b A = ⋅ 2 2 2b a − b 0,25 2 2 a + b A = 0,25 b 2 2 Vậy a + b A =
với a > b > 0 . b 0,25
Cho a, b là các số thực dương phân biệt thỏa mãn: Câu 8 4 2 8b 4b 2b b 2 + + + = 4 và 2 2 a = 2025 + b . 8 8 4 4 2 2 a − b a + b a + b a + b 2,0
Tính giá trị biểu thức: 2
P = (a − b −10) + 2000 . 8 4 2 8b 4b 2b b + + + = 4 8 8 4 4 2 2 a − b a + b a + b a + b Trang 3 4 8b 4b ( 4 4 8 a − b ) 2 2b b ⇔ + + + = 4 8 8 8 8 2 2 a − b a − b a + b a + b 0,25 8 4 4 8 2
8b + 4a b − 4b 2b b ⇔ + + = 4 8 8 2 2 a − b a + b a + b 4 4 8 2 4a b + 4b 2b b ⇔ + + = 4 8 8 2 2 a − b a + b a + b 4 4b ( 4 4 a + b ) 2 2b b 0,25 ⇔ ( + + = 4 4 4 a + b )( 4 4 a − b ) 2 2 a + b a + b 4 2 4b 2b b ⇔ + + = 4 4 4 2 2 a − b a + b a + b 2 4b 2b ( 2 2 4 a − b ) b ⇔ + + = 4 4 4 4 4 a − b a − b a + b 0,25 2 2 4 2a b + 2b b ⇔ + = 4 4 4 a − b a + b 2 2b ( 2 2 a + b ) b ⇔ ( + = 4 2 2 a + b )( 2 2
a − b ) a + b 2 2b b ⇔ + = 4 2 2 a − b a + b 2 2b b(a −b) 0,25 ⇔ + = 4 2 2 2 2 a − b a − b 2 ab + b ⇔ = 4 2 2 a − b b(a + b) ⇔ ( =
a + b)(a − b) 4 b ⇔ = 4 ⇔ 4a = 5b a − b 2 2 a b a b ⇔ = ⇒ = 0,25 2 2 5 4 5 4 Từ 2 2 2 2
a = 2025 + b ⇔ a − b = 2025
Áp dụng tính chất dãy tỉ số bằng nhau ta có: 2 2 2 2 a b a − b 2025 = = = = 225 2 2 5 4 25 −16 9 0,25 a b
⇒ = = 15 (vì a > 0, b > 0 ). 5 4
suy ra: a = 75, b = 60.
Thay a = 75, b = 60 vào biểu thức P ta có: 0,25 2 2
P = (75 − 60 −10) + 2000 = 5 + 2000 = 2025 Vậy P = 2025 . 0,25
Chú ý: nếu học sinh xét thừa trường hợp thì trừ 0,25 điểm. Trang 4 13 
x −1 + 9 y + 2 =  16x ( ) 1 2,0
Câu Giải hệ phương trình:  2 2 3 (x + x 
) x− y +3 = 2x + x+ y +1 (2) x ≥1
Điều kiện y ≥ 2 − 0,25
x − y +3 ≥  0
Từ phương trình (2) ta có ( 2x + x) x − y + = ( 2
3 2 x + x) − x + y +1 ⇔ ( 2
x + x)( x − y +3 − 2)+ x − y −1= 0 0,25
⇔ ( 2x +x) x− y−1 +x− y−1=0 x − y + 3 + 2 0,25 2 ⇔ ( − − ) +  1 x x x y  +1 = 0  x y 3 2  − + +   2 Vì x ≥1 nên x + x +1 > 0 0,25 x − y + 3 + 2
Suy ra: x − y −1= 0 ⇔ y = x −1thế vào phương trình (1) ta được:
13 x −1+9 x +1 =16x 0,25  1   9 13 x 1 x 1 3 x 1 3 x 1  ⇔ − − − + + + − + + =     0  4   4  2 2  1   3 0,25 13 x 1 3 x 1  ⇔ − − + + − =     0  2   2  2 2 Vì  1   3 x 1 0; x 1  − − ≥ + − ≥    
0 với mọi x ≥1 nên  2   2  2 2 0,25  1   3 13 x 1 3 x 1  − − + + − ≥     0  2   2   1 x −1 = 
Dấu " = " xảy ra khi và chỉ khi:  2  3  x +1 =  2 Suy ra: 5 1 x = ⇒ y = (thỏa mãn). 4 4
Vậy hệ phương trình đã cho có nghiệm ( ;x y) là  5 1 ;   . 0,25  4 4 
Cho các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9 . Gọi X là tập hợp các số tự
Câu nhiên có 5 chữ số khác nhau viết được từ các chữ số nói trên. Lấy ngẫu
4 nhiên một số từ tập hợp X . Tính xác suất của biến cố A: “Số lấy ra là số 2,0
lớn hơn 59000” .
Gọi số có 5 chữ số khác nhau là abcde (a ≠ 0).
Vì a ≠ 0 nên a có 9 cách chọn, b có 9 cách chọn, c có 8 cách chọn, d có 0,25
7 cách chọn, e có 6 cách chọn. Trang 5
Số các số tự nhiên có 5 chữ số khác nhau được viết từ các chữ số
0; 1; 2; 3; 4; 5; 6; 7; 8; 9 là: 9⋅9⋅8⋅7⋅6 = 27216 (số).
Suy ra có 27216 kết quả có thể. 0,25
Các kết quả là đồng khả năng xảy ra.
Để abcde lớn hơn 59000 nên ta xét các trường hợp:
Trường hợp 1: a = 5 ; b = 9 thì c có 8 cách chọn, d có 7 cách chọn, e có 0,25 6 cách chọn.
Suy ra có 8⋅7⋅6 = 336 (số). 0,25
Trường hợp 2: a > 5 thì a có 4 cách chọn, b có 9 cách chọn, c có 8 cách
chọn, d có 7 cách chọn, e có 6 cách chọn. 0,25
Suy ra có 4⋅9⋅8⋅7⋅6 =12096 (số). 0,25
Vậy có 336+12096 =12432 kết quả thuận lợi cho biến cố A. 0,25
Xác suất của biến cố A là P( A) 12432 37 = = . 27216 81 0,25
Tìm tất cả các nghiệm nguyên của phương trình: Câu 2,0
5 ( − y − )2 = ( 2 2x 2
7 x − 2y − y − ) 1 .
Phương trình đã cho tương đương với: ( − y − )2 = ( 2 2 2x 2
7 2x − y − 2 − 2y − 3y)
⇔ ( − y − )2 = ( − y − ) − ( 2 2 2x 2 7 2x 2 7 2y + 3y) 0,5
⇔ ( − y − )2 − ( − y − ) + ( 2 2 2x 2 7 2x
2 7 2y + 3y) = 0
Đặt t = 2x − y − 2 (t ∈), ta được: 2t − t + ( 2 2
7 7 2y + 3y) = 0 0,25 2 ⇔ t − t + + ( 2 16
56 49 7 16y + 24y + 9) =112 0,25
⇔ ( t − )2 + ( y + )2 4 7 7 4 3 =112 Vì ( t − )2
4 7 > 0 với mọi t ∈ nên ( y + )2 7 4 3 <112 0,25 suy ra ( y + )2 4 3 <16 ⇔ 4 − < 4y + 3 < 4 ⇔ 7 − < 4y <1 7 − 1 ⇔ < y < 0,25 4 4
Mà y∈ nên y∈{ 1; − } 0 Với y = 1 − thì ( t − )2 4 7 =105 (loại).
Với y = 0 thì ( t − )2 4 7 = 49 suy ra 7
t = hoặc t = 0 0,25 2
Mà t ∈ nên t = 0, khi đó: x =1 (thỏa mãn).
Vậy phương trình có nghiệm nguyên ( ;x y)là (1;0) . 0,25
Cho số tự nhiên n ≥ 2 và số nguyên tố p . Chứng minh rằng nếu p −1
Câu chia hết cho n và 6n −1 chia hết cho p thì ít nhất một trong hai số p −n và 2,0 6
p + n là số chính phương. Trang 6
Ta có: n − = (n )2 6 3 − = ( 3 n − )( 3 1 1 1 n + ) 1
= (n − )( 2n + n + )(n + )( 2 1 1 1 n − n + ) 1 . 0,25 Vì 6
n −1 p và p là số nguyên tố nên ta xét các trường hợp sau:
Trường hợp 1: n −1 p ⇒ n − = lp ( * 1
l ∈ ) ⇔ n = lp +1 0,25
Mà p −1n nên ta có:
( p − )1(lp + )1 ⇒ p −1≥ lp +1( vì p −1> 0 ) 0,25 ⇒ (l − ) 1 p ≤ 2
− ⇒ l −1< 0 ⇒ l <1 (loại vì * l ∈ )
Trường hợp 2: n +1 p ⇒ n + = ap( * 1
a ∈ ) ⇔ n = ap −1
Mà p −1n nên ta có:
( p − )1(ap − )1 ⇒ p −1≥ ap −1 ( vì p −1> 0 ) ⇒ (a − ) 1 p ≤ 0 0,25
⇒ a −1≤ 0 ⇔ a ≤1 Mà *
a ∈ ⇒ a =1; n = p −1
Khi đó p − n =1 là số chính phương. Trường hợp 3: 2
n + n +1 p
Vì p −1n nên p − = kn ( * 1
k ∈ ) ⇔ p = kn +1 Ta có: 2 2
n + n +1 = n − kn + n + kn +1 = n(n − k + )
1 + kn +1 là bội của kn +1 0,25
Suy ra n(n − k + ) 1 kn +1 Do ( ,nkn + )
1 =1 nên (n − k + ) 1 (kn + ) 1 Với *
k, n∈ , ta có: −(kn + )
1 ≤ −k −1< n − k +1≤ n ≤ kn < kn +1 Suy ra n 0,25
− k +1 = 0 hay k = n +1. Khi đó 2
p = n + n +1
Như vậy p + n = (n + )2 1 là số chính phương. Trường hợp 4: 2
n − n +1 p .
Vì p −1n nên p − = kn( * 1
k ∈ ) ⇔ p = kn +1 Ta có: 2 2
n − n +1 = n − kn − n + kn +1 = n(n − k − )
1 + kn +1 là bội của kn +1 0,25
Suy ra n(n − k − ) 1 kn +1 Do ( ,nkn + )
1 =1nên (n − k − ) 1 (kn + ) 1 Với *
k, n∈ , ta có: −(kn + )
1 ≤ −k −1< n − k −1< n ≤ kn < kn +1 Suy ra n 0,25
− k −1 = 0 hay k = n −1. Khi đó 2
p = n − n +1
Như vậy p − n = (n − )2 1 là số chính phương. Trang 7
Câu Có hai chiếc cọc cao 10 m và 30 m 7
đặt vuông góc với mặt đất tại hai vị
trí A và B . Biết khoảng cách giữa
hai cọc bằng 24m . Người ta đặt một
cái chốt ở vị trí M trên mặt đất, nằm
giữa hai chân cọc để giăng dây nối 1,5
đến hai đỉnh C và D của hai cọc
(như hình vẽ). Hỏi người ta phải đặt
chốt ở vị trí cách A một khoảng
bằng bao nhiêu trên mặt đất để tổng
độ dài của hai sợi dây đó là ngắn nhất?
Đặt AM = x (m) ,(0 < x < 24) . Khi đó MB = 24− x (m) . 0,25
Áp dụng định lý Pythagore vào các tam giác vuông CAM và DBM , ta có: 2 2 2 2
CM = CA + AM = 10 + x (m) 0,25 2 2 2 DM = D
B + BM = 30 + (24 − x)2 (m) 0,25 2 2 2
CM + DM = 10 + x + 30 + (24 − x)2 (m)
Ta chứng minh bất đẳng thức sau: Với mọi số thực a,b,c,d thì: 2 2 2 2 a
+ b + c + d ≥ (a + c)2 + (b + d )2 .
Thật vậy: Với mọi số thực a,b,c,d thì: 2 2 2 2
a + b + c + d ≥ (a + c)2 + (b + d )2 ( )1 0,25 2 2 2 2
⇔ a + b + c + d + ( 2 2 a + b )( 2 2 2
c + d ) ≥ (a + c)2 + (b + d )2 ⇔ ( 2 2 a + b )( 2 2
c + d ) ≥ ac + bd (2)
Nếu ac +bd < 0 thì (2) luôn đúng.
Nếu ac +bd ≥ 0 , bình phương hai vế của (2) ta được:
(ad −bc)2 ≥ 0 ( luôn đúng), suy ra: 2 2 2 2
a + b + c + d ≥ (a + c)2 + (b + d )2
Dấu " = " xảy ra khi và chỉ khi: ad = bc .
Áp dụng bất đẳng thức trên, ta có: 2 2 2
CM + DM = 10 + x + 30 + (24 − x)2 ≥ (10 + 30)2 + (x + 24 − x)2 0,25
CM + DM ≥ 2176 .
Dấu " = " xảy ra khi và chỉ khi: 10 (24− x) = 30 x suy ra x = 6 (thỏa mãn).
Vậy người ta phải đặt chốt ở vị trí M cách A một đoạn 6 m thì tổng độ dài hai dây ngắn nhất. 0,25
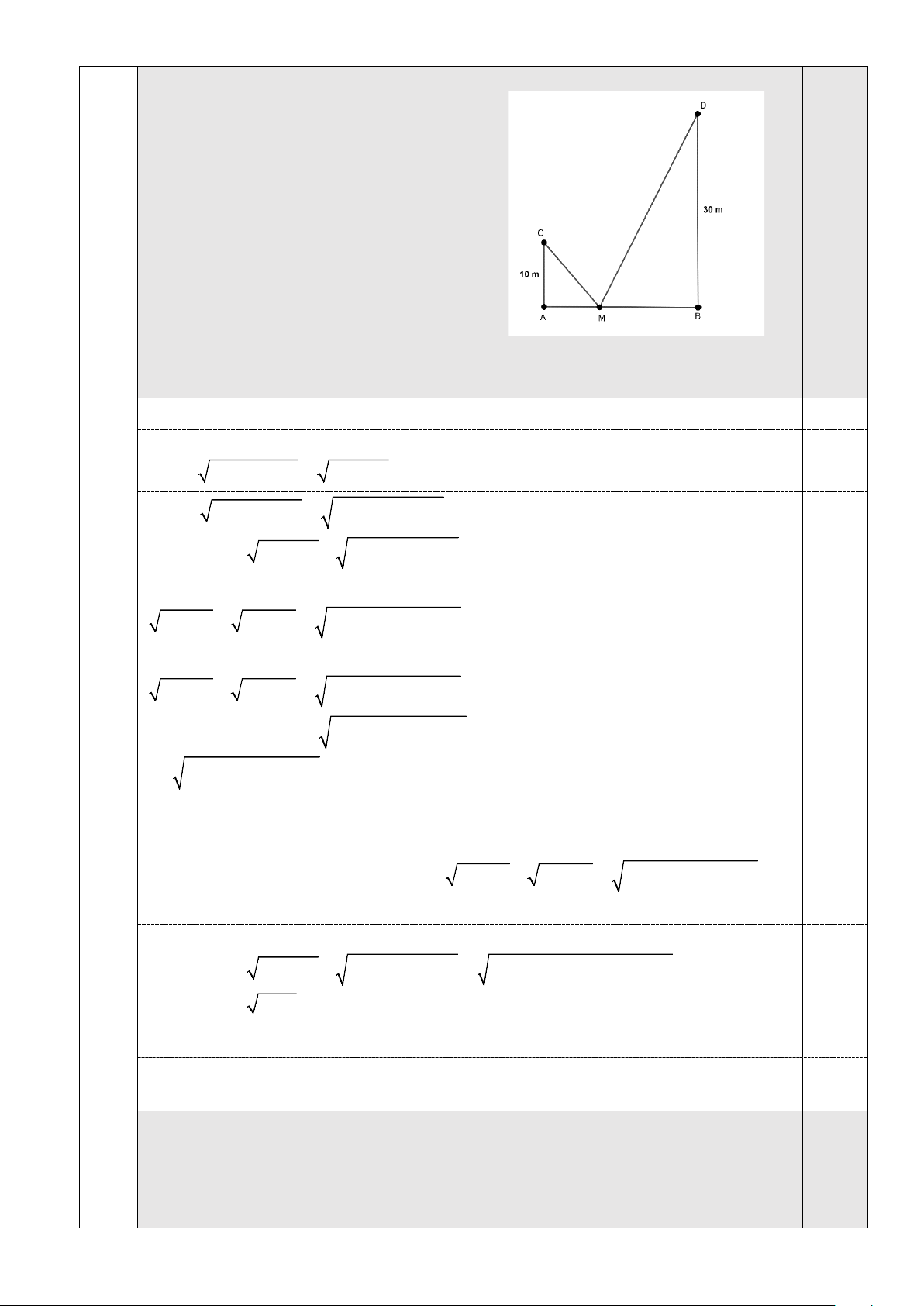
Cho tam giác nhọn ABC nội tiếp đường tròn (O) , ba đường cao Câu D,
A BF,CE cắt nhau tại H , vẽ OK ⊥ BC (K ∈ BC) . Gọi I là trung điểm của 8 3,5
AH , gọi J là giao điểm của AH và EF , kẻ đường kính AP của đường tròn (O) . Trang 8 a. Chứng minh: 1
OK = AH và IK đi qua trung điểm của EF . 2,0 2
Vì C thuộc đường tròn đường kính AP nên A
∆ CP vuông tại C
⇒ PC ⊥ AC mà BH ⊥ AC ⇒ PC / /BH .
Tương tự ta có: PB / /CH 0,25
Suy ra tứ giác BHCP là hình bình hành nên BC và HP cắt nhau tại trung điểm mỗi đường. Mà OB ∆
C cân tại O có OK ⊥ BC nên K là trung điểm của BC do đó K
cũng là trung điểm của PH . 0,25
Tam giác AHP có O và K lần lượt là trung điểm của AP và HP nên OK
là đường trung bình của 1 A
∆ PH ⇒ OK = AH . 0,5 2 A
∆ HF vuông tại F có FI là đường trung tuyến nên 1 FI = AH . 0,25 2 Tương tự: 1 EI = AH 2 Suy ra 0,25
EI = FI nên I thuộc đường trung trực của đoạn thẳng EF .
Chứng minh tương tự: K thuộc đường trung trực của đoạn thẳng EF .
Do đó IK là đường trung trực của đoạn thẳng EF 0,5
hay IK đi qua trung điểm của EF .
b. Đường thẳng qua B song song với AC cắt đường thẳng CE tại S . Chứng minh: 2
IF = IJ.ID và KS / /CJ . 1,5
Gọi L là giao điểm của KI và EF . Vì AH IF = IA = nên A
∆ IF cân tại I ⇒  =  FAI IFA 2 Tương tự:  =  KFC KCF 0,25 Mà  + 
KCF FAI = 90° nên  +  = ° ⇒  AFI CFK 90 IFK = 90° IF
∆ K vuông tại F có FL là đường cao suy ra: 2 IF = . IL IK (1) Trang 9 IL ∆ J ∆ ( . ) IL IJ IDK g g ⇒ = ⇒ .
IL IK = IJ.ID (2) ID IK 0,25 Từ (1) và (2) suy ra : 2
IF = IJ.ID . Ta có: DB ∆ H ∆ ( . ) DB DH DAC g g ⇒ = ⇒ .
DB DC = DH.DA (3) DA DC Lại có: 2 2
IF = IJ.ID ⇒ IA = ID(ID − JD) 0,25 2 2 ⇒ .
ID JD = ID − IA = (ID + IA)(ID − IA) = D .
A (ID − IH ) = D . A HD (4) Từ (3) và (4) suy ra: . = . DB ID DB DC ID JD ⇒ = JD DC DB ∆ I và D ∆ JC có  =  0
BDI JDC = 90 và DB ID = 0,25 JD DC suy ra DB ∆ I D
∆ JC (c.g.c)⇒  =  DIB DCJ (5) Do S
B //AC mà BF ⊥ AC ⇒ BF ⊥ BS suy ra  = 
BSC HBA (cùng phụ với  SBE ) Lại có  = 
BCS BAH ( cùng phụ với  ABC ) 0,25 Suy ra S ∆ BC SB BC 2 ∆ ( . ) BK BK BHA g g ⇒ = = = BH HA 2IH IH S ∆ BK và B ∆ HI có:  =  SBK BHI và SB BK = ⇒ S ∆ BK B ∆ HI( . c g.c) BH IH ⇒  =  BKS HIB hay  =  BKS DIB (6) 0,25
Từ (5) và (6) suy ra:  = 
BKS DCJ , mà 2 góc này ở vị trí đồng vị nên
KS / /CJ .
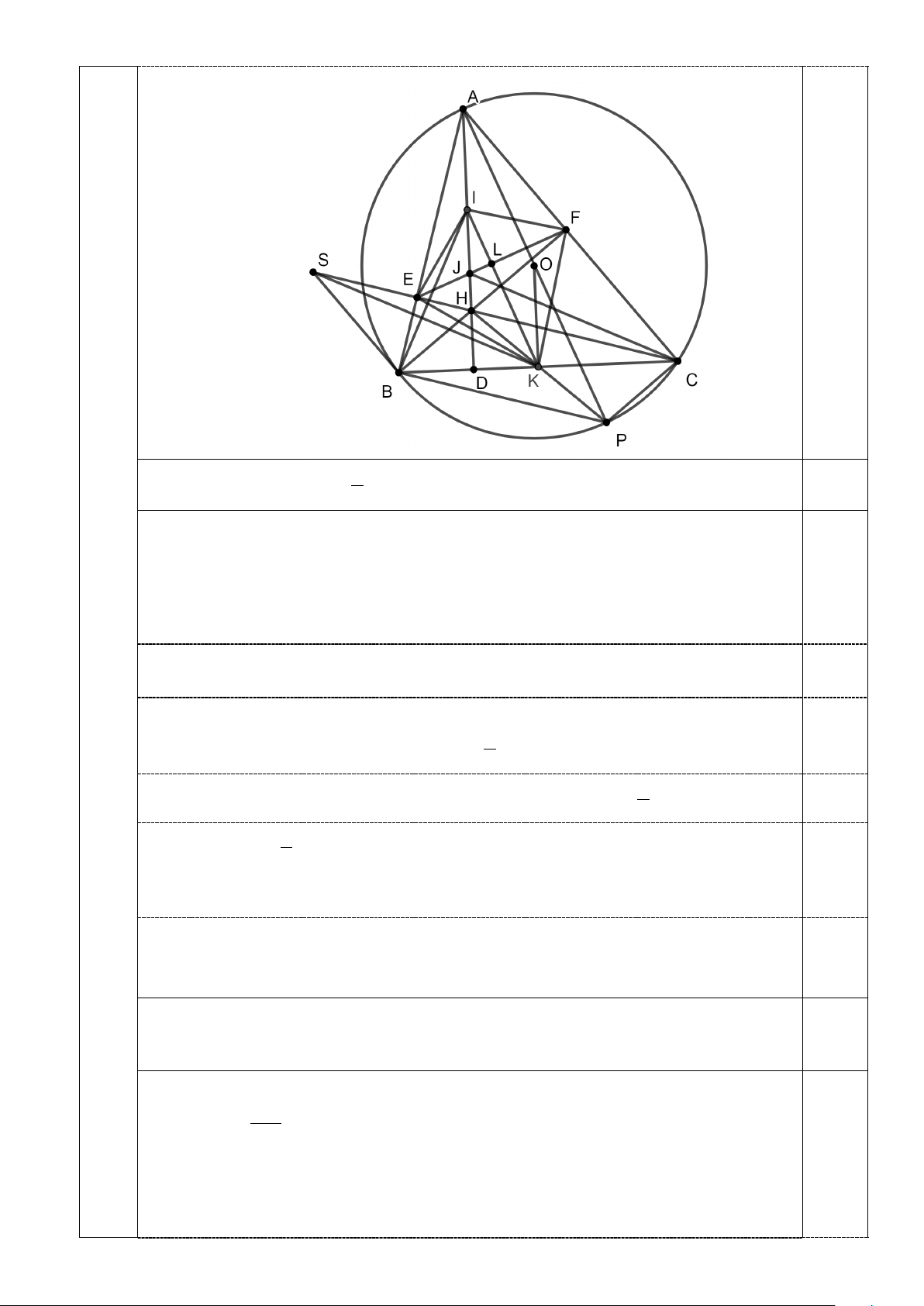
Cho tam giác ABC có ba cạnh tiếp xúc với đường tròn (I ) . Gọi E,F lần
Câu lượt là tiếp điểm của đường tròn (I) với AC và AB . Gọi M,N lần lượt là 9 1,5
trung điểm của BC và AC . Chứng minh ba đường thẳng BI,MN,EF đồng quy.
Gọi K là giao điểm của BI và EF . Ta có     180 B C 90 A BIC = ° − − = ° + 0,25 2 2 2 Suy ra   90 A KIC = ° − 0,25 2
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AE = AF ⇒ A
∆ EF cân tại A     180 A 0,25 90 A AEF AFE ° − ⇒ = = = ° − 2 2 Suy ra  =  KIC AEF mà  = 
KEC AEF (đối đỉnh). Trang 10 Suy ra  =  KIC KEC .
Gọi P là giao điểm của BK và AC . ⇒ IP ∆ C E ∆ PK (g.g) Suy ra PI PC = mà  = 
EPI KPC (đối đỉnh) PE PK 0,25 ⇒ IE ∆ P CKP ∆ (c.g.c)  = 
IEP CKP = 90° (hai góc tương ứng) Hay  BKC = 90° ( ) 1
Gọi K′là giao điểm của BI và MN .
Vì MN là đường trung bình của A
∆ BC nên MN / / AB . 0,25 Suy ra  ′ = 
BK M ABK′ (so le trong) Mà  ′ = 
K BM ABK′ (Tính chất hai tiếp tuyến cắt nhau) ⇒  ′ =  BK M K B ′ M ⇒ B ∆ K M ′ cân tại M .
⇒ MB = MK′ mà MB = MC ⇒ MB = MC = MK′ Suy ra B ∆ K C
′ vuông tại K′ hay  BK C ′ = 90° (2) 0,25 Từ ( )
1 và (2) suy ra K trùng K′.
Vậy ba đường thẳng BI,MN,EF đồng quy.
Cho x, y, z là các số thực dương thỏa mãn: xyz(x + y + z) = 3. Chứng Câu 1 2 2 2 10 minh rằng: 2 2 2
x + y + z ≤
( 5x −2x+4) ( 5y −2y+4) ( 5z −2z +4) . 1,5 243 Ta có: 5
x − x + − ( 3 x + ) 5 3 2 4
2 = x − x − 2x + 2 = (x − )2 ( 3 2
1 x + 2x + 2x + 2) ≥ 0 với mọi x > 0 5 3
⇒ x − 2x + 4 ≥ x + 2 với mọi x > 0 Tương tự 0,25 5 3
y − 2y + 4 ≥ y + 2 với mọi y > 0 5 3
z − 2z + 4 ≥ z + 2 với mọi z > 0.
Suy ra ( 5x − x + )( 5y − y + )( 5z − z + ) ≥ ( 3x + )( 3y + )( 3 2 4 2 4 2 4 2 2 z + 2) ( ) 1
Cần chứng minh bất đẳng thức phụ sau: Cho a,b,c, x, y, z, ,
m n, p là các số
thực dương, ta có: ( 3 3 3 + + )( 3 3 3 + + )( 3 3 3 a b c x y
z m + n + p ) ≥ (axm + byn + czp)3
Thật vậy, áp dụng bất đẳng thức AM-GM, ta có: 3 3 3 a x m 3axm + + ≥ 3 3 3 3 3 3 3 3 3 a + b + c x + y + z m + n + p ( 3 3 3 a + b + c )( 3 3 3
x + y + z )( 3 3 3 3
m + n + p ) Tương tự, ta có: 3 3 3 b y n 3byn + + ≥ 0,25 3 3 3 3 3 3 3 3 3 a + b + c x + y + z m + n + p ( 3 3 3 a + b + c )( 3 3 3
x + y + z )( 3 3 3 3
m + n + p ) 3 3 3 c z p 3czp + + ≥ 3 3 3 3 3 3 3 3 3 a + b + c x + y + z m + n + p ( 3 3 3 a + b + c )( 3 3 3
x + y + z )( 3 3 3 3
m + n + p )
Cộng theo vế ba bất đẳng thức trên ta được: ( 3 3 3 + + )( 3 3 3 + + )( 3 3 3 a b c x y
z m + n + p ) ≥ (axm + byn + czp)3
(với a,b,c, x, y, z, , m n, p ).
Áp dụng bất đẳng thức trên, ta có: Trang 11
( 3x +2)( 3y +2)( 3z +2) = ( 3 3 3 x +1 +1 )( 3 3 3 1 + y +1 )( 3 3 3 1 +1 + z ) 0,25
≥ (x⋅1⋅1+1⋅ y ⋅1+1⋅1⋅ z)3 = (x + y + z)3 (2) Từ ( )
1 , (2) suy ra: ( 5x − x + )( 5 y − y + )( 5 2 4 2
4 z − 2z + 4) ≥ (x + y + z)3
⇔ (x + y + z)6 ≤( 5 x − x + )2 ( 5 y − y + )2 ( 5 2 4 2 4
z − 2z + 4)2 (3)
Từ bất đẳng thức: 2 2 2
a + b + c ≥ ab + bc + ca ⇔ (a + b + c)2 ≥ 3(ab + bc + ca) , ta 0,25
được:(xy + yz + zx)2 ≥ 3xyz(x + y + z). Mặt khác: ( + + )6 = ( + + ) 3 2 2 2 2 x y z
x y z  = x + y + z + (xy + yz + zx) + (xy + yz + zx) 3       ( 2 2 2 x y
z )(xy yz zx)(xy yz zx) 3 ≥ + + + + + + = ( 2 2 2 3 3
27 x + y + z )(xy + yz + zx)2    0,25 ≥ ( 2 2 2
x + y + z )⋅ xyz ⋅(x + y + z) = ( 2 2 2
x + y + z )⋅ ⋅ = ( 2 2 2 27 3 27
3 3 243 x + y + z ) 2 2 2 1
⇒ x + y + z ≤
(x + y + z)6 (4) 243 Từ (3),(4) suy ra: 1
x + y + z ≤
(x −2x+4)2 (y −2y+4)2 (z −2z +4)2 2 2 2 5 5 5 243
 x −1 = y −1 = z −1 = 0
Dấu " = " khi và chỉ khi:  2 2 2
x + y + z = xy + yz + zx xyz 
(x + y + z) = 3 0,25
Suy ra: x = y = z =1. Vậy 1
x + y + z ≤
(x −2x+4)2 (y −2y+4)2 (z −2z +4)2 2 2 2 5 5 5
, với x, y, z là các 243
số thực dương thỏa mãn: xyz(x + y + z) = 3. Chú ý:
- Các cách làm khác nếu đúng vẫn cho điểm tối đa, điểm thành phần giám
khảo tự phân chia trên cơ sở tham khảo điểm thành phần của đáp án.
- Để giải các dạng bài tập Hình Học trong đề thi học sinh chỉ sử dụng
kiến thức đến tại thời điểm thi. Bài Hình nếu không vẽ hình hoặc vẽ hình sai thì
không cho điểm.
- Học sinh được dùng dấu ' ⇒ ', ' ⇔ '
- Các trường hợp khác tổ chấm thống nhất phương án chấm.
------------------------ HẾT ------------------------ Trang 12