Đề chọn học sinh giỏi Toán 8 năm 2024 – 2025 phòng GD&ĐT Vĩnh Châu – Sóc Trăng

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP THỊ XÃ THỊ XÃ VĨNH CHÂU Năm học 2024-2025 Môn: Toán 8 Đề chính thức
(Thời gian làm bài 150 phút, không kể thời gian phát đề)
(Học sinh không được sử dụng máy tính cầm tay)
(Đề thi này có 01 trang)
Bài 1 (4 điểm) a) Phân tích đa thức sau thành nhân tử: 4 2 x − 7x +1.
 2 − x 3− x 2 − x   x 
b) Cho biểu thức A = − + : 1−    . 2
 x+ 3 x + 2 x + 5x + 6   x −1
b1) Tìm điều kiện xác định của biểu thức A.
b2) Rút gọn biểu thức A.  1   1   1   1 
b3) Tính giá trị của biểu thức A khi x = 1− . 1− . 1− ... 1−         . 2 2 2 2  2   3   4   2024  2 x − 2x + 2025
Bài 2 (6 điểm) a) Tìm x để B có giá trị nhỏ nhất: B = với x > 0. 2 x b) Cho 2 2 x + y = 2
− (x − y +1) . Tính 2024 2025 C = 22x −12y + 2024xy . a b c
c) Chứng minh rằng nếu abc = 1 thì + + = 1 . ab + a +1 bc + b +1 ac + c +1
Bài 3 (4 điểm) a) Chứng minh rằng với mọi số nguyên a ta có: a(a + 1)(2a + 1) 6 .
b) Vào ngày 7 tháng 9 năm 2024, Siêu bão Yagi - cơn bão mạnh nhất tấn công
Việt Nam trong 70 năm qua - đã đổ bộ vào các tỉnh phía Bắc, ảnh hưởng đến hàng triệu trẻ em và
gia đình. Hướng ứng lễ phát động quyên góp ủng hộ nhân dân bị thiệt hại bởi cơn bão Yagi, khối 8
của một Trường THCS A trên địa bàn thị xã Vĩnh Châu đã quyên góp được một số tiền, trong đó
có 80 tờ giấy bạc gồm ba loại 10000 đồng, 20000 đồng và 100000 đồng. Biết rằng tổng giá trị của
mỗi loại giấy bạc trên đều bằng nhau. Hỏi mỗi loại giấy bạc có bao nhiêu tờ?
Bài 4 (4 điểm) Cho tam giác ABC cân ở A. Trên cạnh AB lấy điểm D, trên tia đối của tia CA lấy
điểm E sao cho AD + AE = 2AB.
a) Chứng minh rằng: BD = CE.
b) Gọi F là giao điểm của BC và DE. Chứng minh rằng: F là trung điểm của DE.
c) Đường trung trực của DE và tia phân giác của BAC cắt nhau tại G. Chứng minh rằng: GC ⊥ AC.
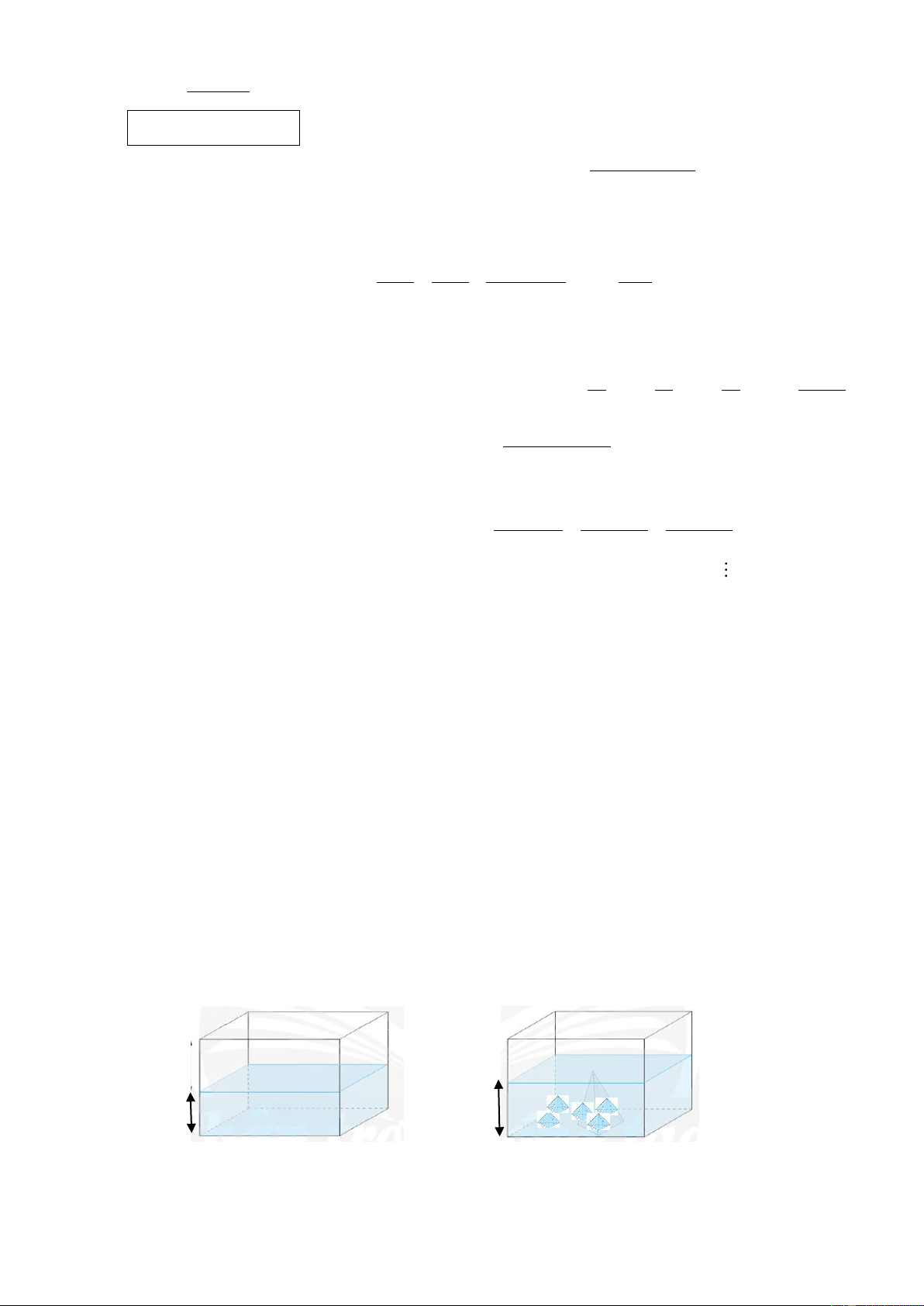
Bài 5 (2 điểm). Một bể cá hình hộp chữ nhật được làm bằng kính chứa nước có hai cạnh đáy là
80cm và 50cm, chiều cao mực nước 30cm. Người ta muốn trang trí bể cá nên đã đặt vào bể 5 khối
đá hình chóp tứ giác đều như nhau với cạnh 10cm và chiều cao 12cm. Khi đặt 5 khối đá hình chóp
tứ giác đều như trên vào bể thì chiều cao mực nước của bể là bao nhiêu? (Biết rằng bề dày của đáy
bể và thành bể không đáng kể). ? 30cm 50cm cm 50cm cm 80cm cm 80cm cm -------HẾT------- cm
(Cán bộ coi thi không giải thích gì thêm)
Họ tên thí sinh:…………………………………………… Số báo danh:……………………
Chữ ký giám thị 1:………………………… Chữ ký giám thị 2:………………………….….
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP THỊ XÃ THỊ XÃ VĨNH CHÂU Năm học 2024-2025 MÔN TOÁN 8 Đề chính thức HƯỚNG DẪN CHẤM
Dưới đây là biểu điểm chi tiết của đề thi Học sinh giỏi môn Toán 8. Các Giám khảo
thảo luận thống nhất thêm chi tiết lời giải cũng như thang điểm của biểu điểm đã trình bày (nếu có).
Nội dung thảo luận và đã thống nhất khi chấm được ghi vào biên bản cụ thể để việc
chấm phúc khảo sau này được thống nhất và chính xác.
Học sinh có lời giải khác đúng, chính xác thì bài làm đúng đến ý nào giám khảo cho điểm ý đó.
Việc làm tròn số điểm bài kiểm tra được thực hiện theo quy định của Bộ Giáo dục và Đào tạo. Bài Đáp án Điểm
a) Phân tích đa thức sau thành nhân tử: 4 2 x − 7x +1.
 2 − x 3− x 2 − x   x 
b) Cho biểu thức A = − + : 1−    . 2
 x+ 3 x + 2 x + 5x + 6   x −1
b1) Tìm điều kiện xác định của biểu thức A. 1 4
b2) Rút gọn biểu thức A.  1   1   1   1 
b3) Tính giá trị của biểu thức A khi x = 1− . 1− . 1− ... 1−         . 2 2 2 2  2   3   4   2024  Ta có: 4 2 4 2 2
x − 7x +1 = x + 2x +1− 9x 0,5 a 2 2 2
= (x +1) − (3x) . 0,25 2 2 = 0,25
(x + 3x +1)(x − 3x +1) b1 ĐKXĐ : x  2
− ; x  −3; x  1 0,5 2 2
4 − x − (9 − x ) + 2 − x x −1− x 0,5 A = : (x+ 2)(x+ 3) x −1 0,5 2 2
4 − x − 9 + x + 2 − x x −1 = . (x+ 2)(x+ 3) 1 − b2 −x − 3 x −1 = . 0,25 (x+ 2)(x+ 3) 1 − x −1 0,25 = (x  2 − ; x  3 − ; x  1) x + 2 Ta có :  1   1   1   1  x = 1− . 1− . 1− ... 1−         2 2 2 2  2   3   4   2024  2 2 2 2 2 −1 3 −1 4 −1 2024 −1 = . . ... 2 2 2 2 2 3 4 2024 b3
(2 +1)(2 −1) (3 −1)(3 +1) (4 −1)(4 +1) (2024 −1)(2024 +1) = . . ... 2 2 2 2 2 3 4 2024 2 Bài Đáp án Điểm 3.1 2.4 3.5 2023.2025 = . . ... 2.2 3.3 4.4 2024.2024 1.2.3...2023 3.4.5...2024.2025 = . 2.3.4...2023.2024 2.3.4...2024 1 2025 = . 2024 2 0,5 2025 = 4048 2025 Thay x = vào A, ta được: 4048 2025 2025 − 4048 −1 4048 4048 A = = 2025 2025 + 8096 + 2 4048 4048 2023 − 2023 4048 = = − 0,5 10121 10121 4048 2 x − 2x + 2025
a) Tìm x để B có giá trị nhỏ nhất: B = với x > 0. 2 x 2 b) Cho 2 2 x + y = 2
− (x − y +1) . Tính 2024 2025 C = 22x −12y + 2024xy . 6 a b c
c) Chứng minh rằng nếu abc = 1 thì + + = 1 . ab + a +1 bc + b +1 ac + c +1 2 x − 2x + 2025 B = 2 x 2
2025(x − 2x + 2025) 0,5 = 2 2025x 2 2 2025x − 2 .2 x 025 + 2025 = 0,25 2 2025x a 2 2 2
2024x + x − 2 .2 x 025 + 2025 = 2 2025x 0,25 2 2024 (x − 2025) 2024 = +  2 2025 2025x 2025 0,5
Dấu “=” xảy ra  x − 2025 = 0  x = 2025 0,25 2024
Vậy giá trị nhỏ nhất của B là  x = 2025 2025 0,25 Ta có: 2 2
x + y = −2(x − y +1) 2 2 0,25
x + y = −2x + 2 y − 2 2 2 b
(x + 2x +1) + ( y − 2 y +1) = 0 0,25 2 2
(x +1) + ( y −1) = 0 (*) 2 (x +1)  0 x  Vì 0,25 2 ( y −1)  0 y  3 Bài Đáp án Điểm Nên 2 2
(x +1) + ( y −1)  0  , x y 0,25
Từ (*) thì dấu “=” xảy ra khi: 2 2
(x +1) = 0; ( y −1) = 0 0,25
Nên x = −1; y = 1 thay vào C, ta được: 02,5 2024 2025 C = 22.( 1 − ) −12.1 + 2024.( 1
− ).1 = 22 −12 − 2024 = 2 − 014 0,5 1 0,5 Do abc = 1  a = bc Ta có : a b c + + ab + a +1 bc + b +1 ac + c +1 1 b c = + + 0,5 c  1 1  bc + b +1 c bc . b + +1 + c +1    bc bc  bc 1 b bc = + + 0,5 b +1+ bc
bc + b +1 1+ bc + b 1+ b + bc = 0,25 1+ b + bc = 1 0,25
a) Chứng minh rằng với mọi số nguyên a ta có: a(a + 1)(2a + 1) 6.
b) Vào ngày 7 tháng 9 năm 2024, Siêu bão Yagi - cơn bão mạnh nhất tấn công
Việt Nam trong 70 năm qua - đã đổ bộ vào các tỉnh phía Bắc, ảnh hưởng đến
hàng triệu trẻ em và gia đình. Hướng ứng lễ phát động quyên góp ủng hộ nhân 3
dân bị thiệt hại bởi cơn bão Yagi, khối 8 của một Trường THCS A trên địa 4
bàn thị xã Vĩnh Châu đã quyên góp được một số tiền, trong đó có 80 tờ giấy
bạc gồm ba loại 10000 đồng, 20000 đồng và 100000 đồng. Biết rằng tổng giá
trị của mỗi loại giấy bạc trên đều bằng nhau. Hỏi mỗi loại giấy bạc có bao nhiêu tờ?
Ta có 2a + 1 = (a − 1) + (a + 2) 0,25
 a(a + 1)(2a + 1) = a(a + 1)[ (a − 1) + (a + 2)]
= a(a + 1)(a − 1) + a(a + 1)(a + 2) 0,25
Ta có a, (a + 1), (a − 1) là 3 số nguyên liên tiếp
Trong 2 số a, (a + 1) phải có một số chia hết cho 2  a(a + 1) 2  a(a + 1)(a − 1) 2 0,25 a
Trong 3 số a, (a + 1), (a − 1) phải có một số chia hết cho 3  a(a + 1)(a − 1) 3 0,25 Mà (2; 3) = 1  a(a + 1)(a − 1) 6 0,25
Tương tự: a(a + 1)(a + 2) 6 0,25
 a(a + 1)(a − 1) + a(a + 1)(a + 2) 6 0,25 Vậy a(a + 1)(2a + 1) 6 0,25
Gọi số tờ của ba loại giấy bạc mệnh giá 10000 đồng, 20000 đồng và 100000
đồng lần lượt là x, y, z (tờ) (x, y, z N*). 0,25 Theo đề bài ta có:
x + y + z = 80 và 10000x = 20000 y = 100000z b 0,25 Từ x y
10000x = 20000 y = 100000z suy ra = = z 0,25 10 5 0,5 4 Bài Đáp án Điểm + +
Áp dụng tính chất dãy tỉ số bằn x y x y z 80 g nhau, ta có: = = z = = = 5 10 5 10 + 5 +1 16 x = 5  x = 5.10 = 50; 10 0,5
Do đó: y = 5  x = 5.5 = 25; (thỏa mãn) 5 0,25 z = 5
Vậy có 50 tờ loại 10000 đồng, 25 tờ loại 20000 đồng và 5 tờ loại 100000 đồng.
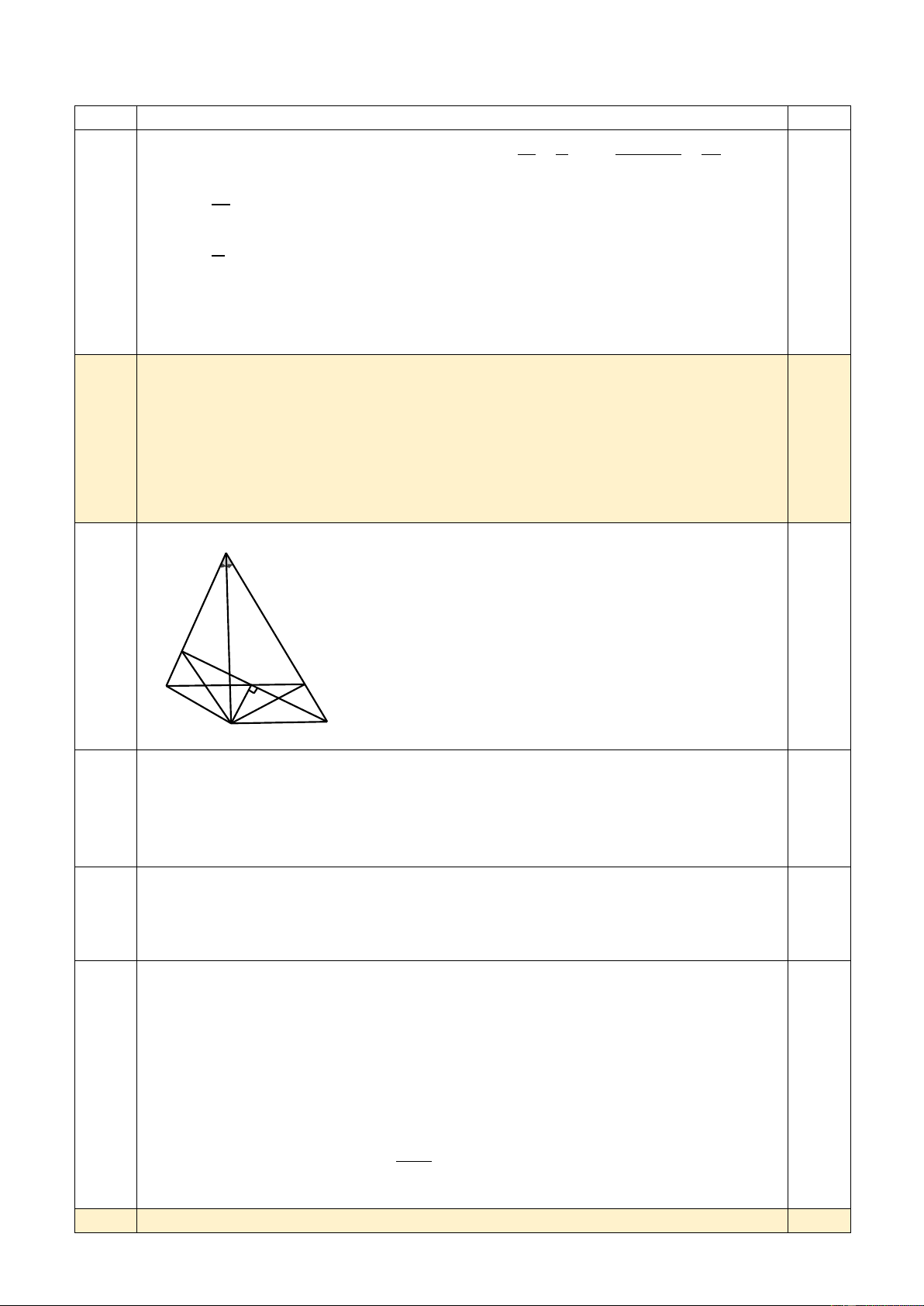
Cho tam giác ABC cân ở A. Trên cạnh AB lấy điểm D, trên tia đối của tia CA
lấy điểm E sao cho AD + AE = 2AB.
a) Chứng minh rằng: BD = CE. 4
b) Gọi F là giao điểm của BC và DE. Chứng minh rằng: F là trung 4 điểm của DE.
c) Đường trung trực của DE và tia phân giác của BAC cắt nhau tại G.
Chứng minh rằng: GC ⊥ AC. A 0,5 D F C B H E G
Ta có: 2AB = AB + AB = AB + AD + BD (1) 0,25
Theo giả thiết AD + AE = 2AB a Hay AD + AC + CE = 2AB (2) 0,25 Mà ABC  cân tại A  AB = AC (3) 0.25
Từ (1), (2) và (3)  BD = CE (đpcm) 0,25 Qua D kẻ DH//AC (HBC) 0,25 ABC  cân tại A  B
 DH cân D  HD = BD = CE 0,25 b  D  HF = E
 CF (g-c-g) FD = FE 0,25
Vậy F là trung điểm của DE (đpcm). 0,25
G thuộc đường trung trực của DE  GD = GE (3) 0,25 A  BG = A  CG (c-g-c) GB = GC (4)
và ABG = ACG (5) 0,25
Mặt khác BD = CE (c/m câu a) (6) c
Từ (3), (4) và (6)  B  DG = C  EG (c-c-c) 0,25  0,25 ABG = ECG (7) 0 180 Từ (5) và (7)  0 ACG = ECG = = 90 0,25 2 0,25 Vậy GC ⊥ AC (đpcm). 5
Một bể cá hình hộp chữ nhật được làm bằng kính chứa nước có hai cạnh đáy 2 5 Bài Đáp án Điểm
là 80cm và 50cm, chiều cao mực nước 30cm. Người ta muốn trang trí bể cá
nên đã đặt vào bể 5 khối đá hình chóp tứ giác đều như nhau với cạnh 10cm và
chiều cao 12cm. Khi đặt 5 khối đá hình chóp tứ giác đều như trên vào bể thì
chiều cao mực nước của bể là bao nhiêu? (Biết rằng bề dày của đáy bể và
thành bể không đáng kể).
Thể tích 5 khối đá hình chóp tứ giác đều là: 1 1 2 3 0,75 V = 5. .S
.h = 5. .10 .12 = 2000 (cm ) 3 Ð hc hc 3 V 2000 1 0,75
Chiều cao mực nước tăng thêm là: h = = = = 0,5(c ) m S 80.50 2 Ðb
Vậy chiều cao mực nước của bể khi đặt 5 khối đá hình chóp tứ giác đều vào 0,5
bể là: 30 + 0,5 = 30,5 (cm).
HS chứng minh cách khác đúng vẫn cho đủ điểm --- HẾT---
Document Outline

• 2. Toan 8 CT_de
• 2. Toan 8 CT_HDC